心中学(北师大版)七年级数学下册专项训练:证明题(无答案)
北师大七年级下几何证明入门专项练习

几何证明题专项训练13、如图,Z 1二Z 2,AC 平分Z DAB 试说明:DC72,如图,AZ\/\ E ( 1 ) V Z ABD 二Z BDC (已 知), ••• //E( );(2):DBC Z ADB(已知),••• // ,( );(3):CBE Z DCB(已知),•••//,()(4 ) v Z CBE= Z A ,(已知),•••//();(5 ) v Z A+ Z ADC=180o (已知), 二//();(6 ) v Z A+ Z ABC=180o (已知),二//();,((4) vZ ADC # C=180o(已知),二 //(已知), );// —,(2)vZ 3二/ 4 (已知),二—//—, );(3)vZ 2二/ 5(已知),二 //,);1、( 1 ) ••• / 1= / A (②•••/ 3=Z 4 (已知), ______ // _____ ( )③ T Z FAD=Z FBC (已知),• ___________ // ____7、如图 2-57,直线 AB CD EF 被直线 GH 所截,Z 1 = 70出,Z2=110",Z 3=70 .求证:AB//CD .证明:TZ 1=70,Z 3=70 (已知),4,如图,/ ABC 玄ADC BF 和 DE 分另U 平分/ ABCDE// FB.5.如图 2-67,已知Z 1 = Z 2, 求Z 3+Z 4的度数. (两直线平行,内错角相等)• Z BCD+=80° (和 Z ADC / 1=Z 2,试说明:// AB.6、如图2-56 •••ZABC=①••• AB//CD (已知),• Z 1 = Z 3 ( )二___ // _____ (•••/ 2=110,/ 3=70 ( ),AB//CD ()•8. 如图2-58,①直线DE AC被第三条直线BA所截,则/ 1和/2是__________ ,如果/ 仁/2,则___//__其理由是().②/ 3和/ 4是直线、 ________被直线截,因此____//___ ./ 3 /4,其理由是().9. 如图2-59,已知AB//CD,BE平分/ ABC CE平分/BCD求证/ 1+Z 2=90 .证明:••• BE平分/ ABC(已知),•••/ 2= _________ ( )同理/ 1= _______________ ,• / 1+ / 2= -2又••• AB//CD (已知),・・ZABC+ ZBCD=()・・Z1 +Z2=O90()10、如图 2-60,E 、F 、G 分别是 AB AC BC 上 点.①如 果 Z B= Z FGC ,则// ,其 理 由 是()②ZBEG= Z EGF ,则// ,其 理 由 是()③如 果 Z AEG+Z EAF=180 ,则//■ ? 其理 由 是( )11.如图 2-61,已知 AB//CD , AB//DE ,求证:/ B+Z D 二/ BCF+Z DCF证明:T AB//CF (已知),•••Z _____ =Z (两直线平行,内错角相等)•••• AB//CF , AB//DE (已知), 二 CF//DE(•••Z图 2-<il・Z B+Z D=Z BCF+Z DCF (等式6U)性质).几何证明题专项训练21、如图,/ B 二/ C , AB// EF ,试说明:/ BGF M C 。
新北师大版七年级下数学三角形全等证明典型习题

新北师大版七年级下数学三角形全等证明典型习题1.这个零件的形状如下图所示。
已知∠A=90º,∠C=25º,∠B=25º。
如果测量得到∠BCD=150º,那么可以判断这个零件是不合格的。
根据三角形的相关知识,我们可以解释这个不合格的原因。
2.已知如下图,在△ABC中,AD是高,AE是角平分线,∠B=30°,∠C=50°。
我们需要求出∠XXX的度数,并描述∠DAE与∠C-∠B之间的关系,不需要证明。
3.如下图所示,已知D是△ABC边BC延长线上的一点,DF⊥XXX于E,∠A=35°,∠D=42°。
我们需要求出∠ACD的度数。
4.如下图所示,在△ABC中,∠B=∠C,∠BAD=40°,且∠ADE=∠AED。
我们需要求出∠XXX的度数。
5.有一座小山,现在需要在小山A、B的两端开一条隧道。
施工队为了知道A、B两端的距离,在平地上选了一个可以直接到达A和B的点C,连接AC并延长到D使CD=CA,连接BC并延长到E,使CE=CB,连接DE。
那么量出DE的长度,就是A、B的距离。
这是因为DE是平面上的一条直线,而且△ABC和△CDE是相似的。
6.如下图所示,已知DC=BA,BE⊥AC于点E,DF⊥AC于点F,且BE=DF。
我们需要证明AB∥DC。
8.如下图所示,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
我们需要证明BC=AB+DC。
9.如下图所示,AE、BC交于点M,F点在AM上,BE∥CF,BE=CF。
我们需要证明AM是△ABC的中线。
10.已知AB=AC,DB=DC,F是AD的延长线上的一点。
我们需要证明BF=CF。
11.如下图所示,AB=AD,BC=DC,E、F分别是DC、BC的中点。
我们需要证明AE=AF。
12.如下图所示,AB=AC,BD⊥AC,CE⊥AB,垂足分别为D、E,BD、CE相交于点F。
北师大版七年级下册数学证明题练习

北师大版七年级下册数学证明题练习以下15题15分,第8题10分,其余的每小题5分。
1.如图,已知AB∥CD,EF交AB,CD于G, H, GM, HN分别平分EHDAGF∠∠,,试说明GM ∥HN.2.已知:如图,AD∥BC,∠BAD = ∠BCD,求证:AB∥CD。
3.如图,AB∥CD,P为AB,CD之间的一点,已知︒2,求BPC∠25∠∠32=1,︒=的度数。
4.已知AB∥CD,BC∥DE.试说明D∠.B∠=5.已知:,21,,,∠=∠⊥⊥⊥G AB FG AC BC E AC DE 于于求证:AB CD ⊥.6.在ABC ∆中,,D AB CD 于⊥AB FG ⊥于G ,ED ∥BC,试说明21∠=∠.7.已知:在△ABC 中,∠BAC=80°,∠B=60°,AD ⊥BC 于D ,AE 平分∠DAC ,求∠AEC8.如图,已知∠A=∠F ,AB ∥EF ,BC=DE ,请说明AD ∥CF.BA CDE CBEAD解:∵ BC=DE (已知) ∴ 在△ABD 与△FEC 中, ∴ BC+CD=DE+CD ( ) ∠A=∠F (已知) 即:_________=_________ _______=______(已证) 又∵AB ∥EF (已知)_______=______(已证) ∴ ________=_________ ∴△ABD ≌△FEC (________)∴∠ADB =∠FCE (_____________________) ∴ AD ∥CF (_________________________) 9.如图,AB=AD ,AC=AE ,∠BAE=∠DAC ,试说明∠C=∠E10.如图,已知OC=OE ,OD=OB ,试说明△ADE ≌△ABC.11.已知AO 是△ABC 中BC 边上的高,点D 、点E 是三角形外的两个点,且满足AD=AE ,DB =EC ,∠D =∠E ,试说明AO 平分∠BAC12.如图,在△ABC 中,BC=10,边BC 的垂直平分线分别交AB ,BC 于点E 和D ,BE=6, 求△BCE 的周长.ODEACBECBODA1.如图,已知在AB=AC ,DB=DC ,则AD ⊥BC ,为什么?14、在Rt △ABC 中,BD 是∠B 的平分线,DE ⊥AB 于E, 则DE = DC 吗?说明你的理由.15、如图,△ABC 中∠C = 900,沿过B 点的直线BE 折叠△ABC ,使点C 恰好落在AB 的中点D 处. (1)求∠A 的度数;(2)若CE = 2cm ,则求出ED 的长度; (3)若CB = 4cm ,则求出AB 的长度.16、如图,在△ABC 中,AB = AC ,D 是BC 的中点,E 在AD 上,BE = CE 吗?说明你的理由.(8分)17、如图,△ABC 中,AB=AC ,D 是AB 边上的一点, DE 垂直平分AC ,∠A BCDE ABC DE┌A=040,求∠BDC的度数。
完整word版北师大版七年级下册全等三角形证明经典题.docx

让优秀成为一种习惯七年级下册《全等三角形》证明专题练习1、已知: AB=4 ,AC=2 , D 是 BC 中点, AD 是整数,求ADAB CD2、已知: D 是 AB 中点,∠ ACB=90 °,求证:CD 1 AB2ADC B3、已知:BC=DE ,∠ B=∠ E,∠ C=∠D ,F 是 CD 中点,证12A21B EC F D4、已知:∠ 1=∠ 2,CD=DE , EF//AB ,求证: EF=ACA12FCDEB5、已知: AD 平分∠ BAC , AC=AB+BD ,求证:∠ B=2 ∠ CACB D6、已知: AC 平分∠ BAD , CE⊥AB ,∠ B+∠ D=180 °,求证: AE=AD+BE7、已知: AB=6 , AC=2 ,D 是 BC 中线,求AD 的取值范围。
AB CD8. 如图,四边形ABCD 中, AB ∥ DC, BE 、 CE 分别平分∠ ABC 、∠ BCD ,且点 E 在 AD 上。
求证: BC=AB+DC 。
9、已知: AB//ED ,∠ EAB= ∠ BDE , AF=CD , EF=BC ,求证:∠ F=∠ CE DCFA B10、已知: AB=CD ,∠ A= ∠ D,求证:∠ B= ∠ CA DB C11、已知∠ ABC=3 ∠ C,∠ 1=∠2, BE⊥ AE ,求证: AC-AB=2BE12.如图,在△ABC 中, BD =DC ,∠ 1=∠ 2,求证: AD⊥BC .13.如图, OM 平分∠ POQ ,MA ⊥ OP,MB⊥ OQ , A、 B 为垂足, AB 交 OM 于点 N.求证:∠ OAB=∠OBA14.如图,已知 AD∥ BC,∠ PAB 的平分线与∠ CBA 的平分线相交于E, CE 的连线交 AP 于 D.求证: AD +BC=AB.PCEDA B 15.如图,△ ABC 中, AD 是∠ CAB 的平分线,且∠C=2 ∠ B,求证 :AB=AC+CDAC16.如图①, E、F 分别为线段AC 上的两个动点,且 DE⊥AC 于 E,BF⊥ AC 于 F,若 AB=CD ,AF=CE ,BD 交 AC 于点 M.(1)求证: MB=MD , ME =MF(2)当 E、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.17.已知:如图, DC∥ AB,且 DC =AE, E 为 AB 的中点,( 1)求证:△ AED≌△ EBC.( 2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):AE O DB C18.如图,△ ABC 中,∠ BAC=90 度, AB=AC, BD 是∠ ABC 的平分线, BD 的延长线垂直于过 C 点的直线于E,直线 CE 交 BA 的延长线于F.F 求证: BD =2CE.AEDB C19、如图: DF=CE, AD=BC,∠ D=∠ C。
北师大版七年级下证明
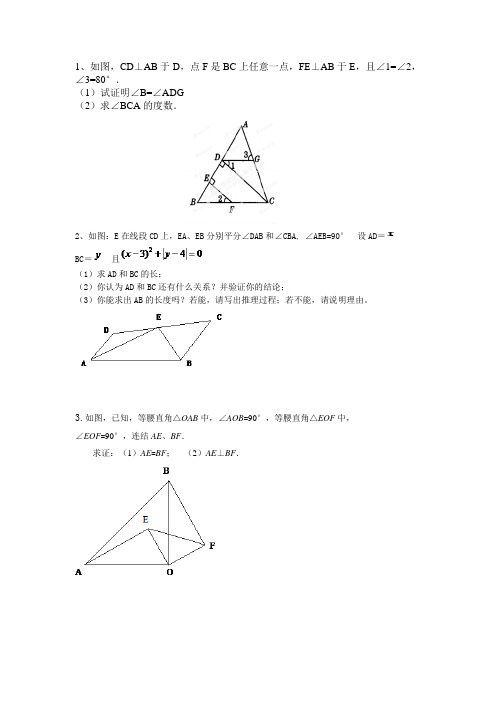
1、如图,CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2,∠3=80°.(1)试证明∠B=∠ADG(2)求∠BCA的度数.2、如图:E在线段CD上,EA、EB分别平分∠DAB和∠CBA, ∠AEB=90°设AD=BC=且(1)求AD和BC的长;(2)你认为AD和BC还有什么关系?并验证你的结论;(3)你能求出AB的长度吗?若能,请写出推理过程;若不能,请说明理由。
3.如图,已知,等腰直角△OAB中,∠AOB=90°,等腰直角△EOF中,∠EOF=90°,连结AE、BF.求证:(1)AE=BF;(2)AE⊥BF.4.等边⊿ABC边AB上有一点G,过G做GE∥BC,交AB于G,交AC于D,延长GD至E,使得∠E=∠ABD,(1)求证:⊿AGD是等边三角形(2)探索线段BG,AD,GE三者之间的关系,并证明。
5.如图,在中,,点在线段上运动(D不与B、C 重合),连接AD,作,交线段于.(1)当时,°,°;点D从B向C 运动时,逐渐变(填“大”或“小”);(本小题3分)(2)当等于多少时,≌,请说明理由;(本小题4分)(3)在点D的运动过程中,的形状可以是等腰三角形吗?若可以,请直接写出的度数.若不可以,请说明理由。
(本小题3分)6.已知:如图,△ABC 中,∠ABC=45°,CD ⊥AB 于D ,BE 平分∠ABC ,且BE ⊥AC 于E ,与CD 相交于点F ,H 是BC 边的中点,连接DH 与BE 相交于点G .(1)求证:BF=AC ;(2)求证:CE=BF ;(3)CE 与BG 的大小关系如何?试证明你的结论.7.如图,等腰直角三角形ABC 中,∠ACB =90°,AD 为腰CB 上的中线,CE ⊥AD 交AB 于E .求证∠CDA =∠EDB .12A B CD E8. 在Rt △ABC 中,∠A =90°,CE 是角平分线,和高AD 相交于F ,作FG ∥BC 交AB 于G ,求证:AE =BG .C D。
北师大版七年级下册__全等三角形证明经典题
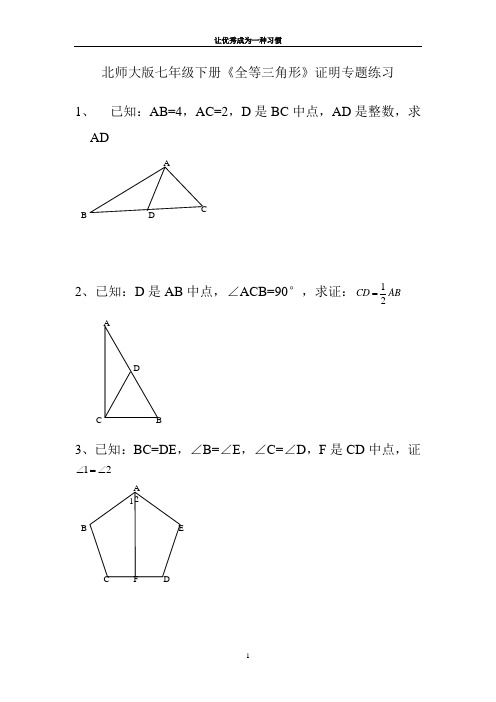
北师大版七年级下册《全等三角形》证明专题练习1、 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2、已知:D 是AB 中点,∠ACB=90°,求证:12CD AB =3、已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,证21∠=∠ADBC4、已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC5、已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C6、已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE7、已知:AB=6,AC=2,D 是BC 中线,求AD 的取值范围。
BA CDF2 1 ECDB A8. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
9、已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠CADB CDCBAFE10、已知:AB=CD ,∠A=∠D ,求证:∠B=∠C11、已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE12.如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .13.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBA14.如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .15.如图,△ABC 中,AD 是∠CAB 的平分线,且∠C =2∠B,求证:AB=AC+CD16.如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M .(1)求证:MB =MD ,ME =MF(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.PEDCBA D CBA17.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点,(1)求证:△AED ≌△EBC .(2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):18.如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F . 求证:BD =2CE .19、如图:DF=CE ,AD=BC ,∠D=∠C 。
北师大版七年级下册《全等三角形证明题练习》

北北北北北北北北北北北北北北10北北北北北北北北北北北3一、解答题1.如图,AD,BC分别平分∠CAB,∠DBA,且∠1=∠2,试探究AC与BD的数量关系,并说明理由.2.如图,点C,F在线段BE上,BF=EC,∠1=∠2,AC=DF,试说明:△ABC≌△DEF.3.如图,已知∠1=∠2,∠B=∠D,试说明:CB=CD.4.已知在如图所示的“风筝”图案中,AB=AD,AC=AE,∠BAE=∠DAC.试说明:∠E=∠C.5.如图,已知AB,CD交于点O,E,F为AB上的两点,OA=OB,OE=OF,∠A=∠B,∠ACE=∠BDF,试说明:△ACE≌△BDF.6.如图,D是AC上一点,AB=DA,DE // AB,∠B=∠DAE,试说明:△ABC≌△DAE.7.如图,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE.试说明:BD=CE.8.如图,点B,F,C,E在同一直线上,AB=DE,BF=CE,AB∥DE,求证,AC=DF.9.如图,点A,B,C,D在同一条直线上,且AB=CD,若∠1=∠2,EC=FB,求证:∠E=∠F.10.如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C,求证:BD=CE.11.如图,在△ABC中,AB=AC,AD⊥BC于点D,BE⊥AC于点E,AD、BE相交于点H,AE=BE.试说明:(1)△AEH≌△BEC.(2)AH=2BD.12.如图,在中△ABC,AB=CB,∠ABC=90°,D为AB的延长线上一点,点E在BC边上,且BE=BD,连接AE,DC.(1)求证△ABE≌△CBD;(2)若∠CAE=33°,∠ACB=45°,求∠BDC的度数.13.如图,已知∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.(1)求证:△AEC≌△BED;(2)若∠1=44°,求∠BDE的度数.14.已知:如图,AB∥CD,AB=CD,BF=CE.(1)求证:△ABF≌DCE.(2)已知∠AFC=80°,求∠DEC的度数.15.如图,在△ABC中,AB=AC,点D,E在BC上(BD<BE),BD=CE.(1)求证:△ABD≌△ACE.(2)若∠ADE=2∠B,BD=2,求AE的长.16.如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD=BE.(1)求证:AD+DE=BC;(2)若∠BDC=70°,求∠ADB的度数.17.已知:如图,已知线段AB、CD相交于点O,AD、CB的延长线交于点E,OA=OC,EA=EC,求证:∠A=∠C.18.已知,如图,AB⊥AC,AD⊥AE,AB=AC,AD=AE.求证:(1)BE=DC;(2)BE⊥DC.19.如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC,AE与BD交于点F.试判断AE、BD之间的关系,并说明理由.20.如图,在△ABC中,AB=AC,AD平分∠BAC,点M、N分别在AB、AC边上,AM=2MB,AN=2NC.求证:△AMD≌△AND.21.已知△ABC和△CEF是两个等腰直角三角形,∠ABC=∠CEF=90°.连接AF,M是AF的中点,连接MB、ME.(1)如图1,当CB与CE在同一直线上时,求证:BM⊥ME;(2)如图2,当∠BCE=45°时,求证:BM=ME.22.在△ABC和△ACD中,AB=AC=AD,AE平分∠BAD,交BC于点E,交DC边的延长线于点F.(1)如图①,求证;∠F=∠B(2)如图②,当∠BAC=60°时,请探究线段FA、FC、CD的数量关系,并证明你的结论.23.CD是经过∠BCA定点C的一条直线,CA=CB,E、F分别是直线CD上两点,且∠BEC=∠CFA=∠β.(1)若直线CD经过∠BCA内部,且E、F在射线CD上,①若∠BCA=90°,∠β=90°,例如图1,则BE ______ CF,EF ______ |BE-AF|.(填“>”,“<”,“=”);②若0°<∠BCA<180°,且∠β+∠BCA=180°,例如图2,①中的两个结论还成立吗?并说明理由;(2)如图3,若直线CD经过∠BCA外部,且∠β=∠BCA,请直接写出线段EF、BE、AF的数量关系(不需要证明).24.已知,在▵ABC中,BD、CE分别是AC、AB边上的高,BQ=AC,点F在CE的延长线上,CF=AB.试说明AF与AQ之间的关系.25.(1)如图1,△ABC与△ADE均是顶角为40°的等腰三角形,BC、DE分别是底边,求证:BD=CE.(2)拓展探究如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.①求∠AEB的度数;②证明:AE=BE+2CM.26.在△ABC中,AB=AC,点D是BC上一点(不与B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.(1)如图1,若∠BAC=90°,①试说明:△ABD≌△ACE;②求∠BCE的度数;(2)设∠BAC=α,∠BCE=β.如图2,则α,β之间有怎样的数量关系?请直接写出你的结论.27.把两个全等的直角三角板的斜边重合,组成一个四边形ACBD以D为顶点作∠MDN,交边AC、BC于M、N.(1)若∠ACD=30°,∠MDN=60°,当∠MDN绕点D旋转时,AM、MN、BN三条线段之间有何种数量关系?证明你的结论;(2)当∠ACD+∠MDN=90°时,AM、MN、BN三条线段之间有何数量关系?证明你的结论;(3)如图③,在(2)的结论下,若将M、N改在CA、BC的延长线上,完成图3,其余条件不变,则AM、MN、BN之间有何数量关系(直接写出结论,不必证明)28.如图1,△ABE是等腰三角形,AB=AE,∠BAE=45°,过点B作BC⊥AE于点C,在BC上截取CD=CE,连接AD、DE并延长AD交BE于点P;(1)求证:AD=BE;(2)试说明AD平分∠BAE;(3)如图2,将△CDE绕着点C旋转一定的角度,那么AD与BE的位置关系是否发生变化,说明理由.。
北师大版七年级下册_全等三角形证明经典题
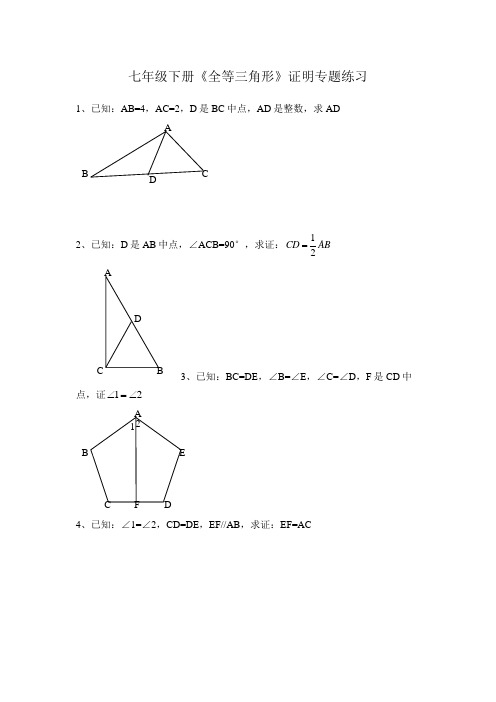
七年级下册《全等三角形》证明专题练习1、已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2、已知:D 是AB 中点,∠ACB=90°,求证:12CD AB =3、已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,证21∠=∠4、已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=ACADB C5、已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C6、已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE7、已知:AB=6,AC=2,D 是BC 中线,求AD 的取值范围。
8. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
9、已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠CADBCCDB BA CD F2 1 EA10、已知:AB=CD ,∠A=∠D ,求证:∠B=∠C11、已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE12.如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .13.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBA14.如图,已知AD ∥BC ,∠PAB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .ABC DD CBAF EPE DCBA15.如图,△ABC 中,AD 是∠CAB 的平分线,且∠C =2∠B,求证:AB=AC+CD16.如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M . (1)求证:MB =MD ,ME =MF(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.17.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点, (1)求证:△AED ≌△EBC .(2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):OEDCBADC BA18.如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F . 求证:BD =2CE .19、如图:DF=CE ,AD=BC ,∠D=∠C 。
(完整版)北师大七年级下几何证明入门专项练习

几何证明题专项训练11、( 1)∵∠ 1=∠ A(已知),∴∥,();( 2)∵∠ 3=∠4(已知),∴∥,();( 3)∵∠ 2=∠5(已知),∴∥,();( 4)∵∠ ADC+∠ C=180o(已知),∴∥,();2,如图,( 1)∵∠ ABD=∠ BDC(已知),∴∥,();( 2)∵∠ DBC=∠ ADB(已知),∴∥,();( 3)∵∠ CBE=∠ DCB(已知),∴∥,();( 4)∵∠ CBE=∠ A,(已知),∴∥,();( 5)∵∠ A+∠ ADC=180o(已知),∴∥,();( 6)∵∠ A+∠ ABC=180o(已知),∴∥,();3、如图,∠ 1=∠ 2, AC均分∠ DAB,试说明: DC∥ AB.4,如图,∠ ABC=∠ ADC, BF 和 DE分别均分∠ ABC和∠ ADC,∠1=∠ 2,试说明: DE∥ FB.5.如图 2-67,已知∠ 1= ∠2,求∠ 3+∠ 4 的度数.6、如图 2-56①∵ AB//CD (已知),∴∠ ABC=_______ ()______=______ (两直线平行,内错角相等),∴∠ BCD+______= 180()②∵∠ 3=∠ 4(已知),∴ ______∥ _____()③∵∠ FAD= ∠ FBC(已知),∴ _____∥()7、如图 2-57,直线 AB ,CD,EF 被直线 GH 所截,∠ 1= 70,∠ 2=110,∠3= 70.求证: AB//CD .证明:∵∠ 1= 70,∠ 3= 70(已知),∴∠ 1=∠ 3()∴ ____∥ _____()∵∠ 2=110,∠ 3= 70(),∴______+_____=____,∴_____//______,∴ AB//CD ().8.如图 2-58,①直线 DE ,AC 被第三条直线BA 所截,则∠ 1 和∠ 2 是 ________,假如∠ 1= ∠ 2,则 ___//___,其原因是().②∠ 3 和∠ 4 是直线 __________ 、 __________ ,被直线 ____________所截,所以 ____//____ .∠ 3____∠ 4,其原因是().9.如图 2-59,已知 AB//CD ,BE 均分∠ ABC , CE 均分∠ BCD ,求证∠ 1+∠ 2= 90 .证明:∵BE 均分∠ ABC (已知),∴∠ 2=_________()同理∠ 1=_______________,∴∠1)1+∠2= ____________ (2又∵ AB//CD (已知),∴∠ ABC+ ∠ BCD=_____ ()∴∠ 1+ ∠2= 90()10、如图 2-60,E、 F、 G 分别是 AB 、 AC 、BC 上一点.①假如∠ B= ∠ FGC,则 ____//____, 其原因是()②∠ BEG= ∠EGF,则 _____//____ ,其原因是()③假如∠ AEG+ ∠ EAF= 180,则 ____//____ ,其原因是()11.如图2-61,已知AB//CD , AB//DE ,求证:∠ B+ ∠D= ∠BCF+∠DCF.证明:∵ AB//CF(已知),∴∠ ______=∠ ________(两直线平行,内错角相等).∵ AB//CF ,AB//DE (已知),∴ CF//DE ()∴∠ _________=∠ _________()∴∠ B+ ∠ D=∠ BCF+ ∠ DCF(等式性质).EA CGBD 图 7 F几何证明题专项训练 21、如图,∠ B=∠ C, AB ∥ EF,试说明:∠BGF= ∠ C。
北师大版七年级下册-全等三角形证明经典题

七年级下册《全等三角形》证明专题练习1、 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2、已知:D 是AB 中点,∠ACB=90°,求证:12CD AB =3、已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,证21∠=∠4、已知:∠1=∠2,CD=DE ,EF//AB,求证:EF=ACADBCBA CDF2 1 E5、已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C6、已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE7、已知:AB=6,AC=2,D 是BC 中线,求AD 的取值范围。
8. 如图,四边形ABCD 中,AB ∥DC,BE 、CE 分别平分∠ABC 、∠BCD,且点E 在AD 上。
求证:BC=AB+DC.9、已知:AB//ED,∠EAB=∠BDE ,AF=CD,EF=BC,求证:∠F=∠CADBCCDB DCBA FEA10、已知:AB=CD ,∠A=∠D ,求证:∠B=∠C11、已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE12.如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .13.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBA14.如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP于D .求证:AD +BC =AB .15.如图,△ABC 中,AD 是∠CAB 的平分线,且∠C =2∠B,求证:AB=AC+CDAB C DPEDCB A D CBA16.如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M . (1)求证:MB =MD ,ME =MF(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.17.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点, (1)求证:△AED ≌△EBC .(2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):18.如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .19、如图:DF=CE ,AD=BC ,∠D=∠C 。
北师大版七年级下册数学证明题练习

北师大版七年级下册数学证明题练习以下15题15分,第8题10分,其余的每小题5分。
2. 已知:如图,AD //BC,/BAD = /BCD,求证:AB //CD。
3.如图,AB //CD,P为AB,CD 之间的一点,已知1 32的度数。
7A,2 25,求:BPC]_______4.已知AB //CD,BC//DE.试说明B D.B5. 已知:DE AC于E,BC AC,FG AB于G, 16. 在ABC 中,CD AB于D, FG AB于G , ED //BC,试说明12.7. 已知:在/△ABC 中,/BAC=80 ° ,B=60求/AEC8.如图,已知/A= ZF, AB //EF,BC=DE,请说明AD //CF.2,求证:CD AB.解:••• BC=DE (已知)•••在△ABD 与 AFEC 中,••• BC+CD=DE+CD ( )ZA= ZF (已知)I「即: _________ = __________ :, ________ = _______ (已证)I气又 VAB //EF (已知) [[ ________ = _______ (已证)II••• _______ = _________ ; /-ZABD 也/EEC ( ___________ )I:/.zADB = ZFCE (________________________________________ )*;••• AD //CF (________________________________________ )10. 如图,已知 OC=OE , OD=OB ,试说明厶ADE 也E BC.9.女口图,AB=AD ,AC=AE , ZBAE= ZDAC ,试说明/C= ZE且满足AD=AE ,解:••• BC=DE (已知)•••在△ABD 与AFEC 中,11. 已知AO是AKBC中BC边上的高,点D、点E是三角形外的两个点, DB = EC,ZD = Z E,试说明AO 平分Z BAC12 .如图,在△ ABC中,BC=10,边BC的垂直平分线分别交AB,BC于点E和D,BE=6,求E BCE的周长.1 .如图,已知在 AB=AC , DB=DC ,贝U AD 丄BC ,为什么?15、如图,A ABC 中/C = 90 °,沿过B 点的直线BE 折叠△ABC ,使点C 恰好 落在AB 的中点D 处.吗?说明你的理由.(8分)14、在Rt △KBC 中,BD 是/B 的平分线, 则DE = DC 吗?说明你的理由D(1 [求/A 的度数;(2) 若CE = 2cm ,则求出 (3) 若CB = 4cm ,则求出16、如图,在△ ABC 中,AB17、如图,A ABC中,AB=AC , D是AB边上的一点,DE垂直平分AC ,Z A= 40°,求Z BDC的度数。
北师大版七年级下册-全等三角形证明经典题
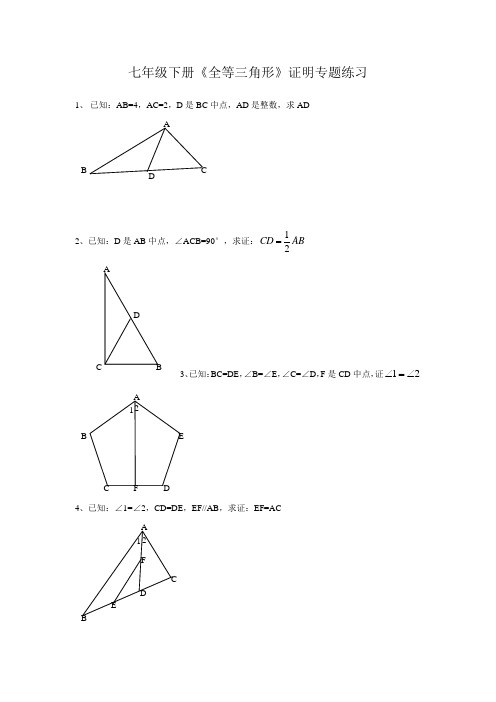
七年级下册《全等三角形》证明专题练习1、 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2、已知:D 是AB 中点,∠ACB=90°,求证:12CD AB =3、已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,证21∠=∠4、已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=ACADBCBA CDF2 1 E5、已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C6、已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE7、已知:AB=6,AC=2,D 是BC 中线,求AD 的取值范围。
8. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
9、已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠CADBCCDB DCBA FEA10、已知:AB=CD ,∠A=∠D ,求证:∠B=∠C11、已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE12.如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .13.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBA14.如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP于D .求证:AD +BC =AB .15.如图,△ABC 中,AD 是∠CAB 的平分线,且∠C =2∠B,求证:AB=AC+CDAB C DPEDCB A DCBA16.如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M . (1)求证:MB =MD ,ME =MF(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.17.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点, (1)求证:△AED ≌△EBC .(2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):18.如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .19、如图:DF=CE ,AD=BC ,∠D=∠C 。
北师大版七年级下册-全等三角形证明经典题
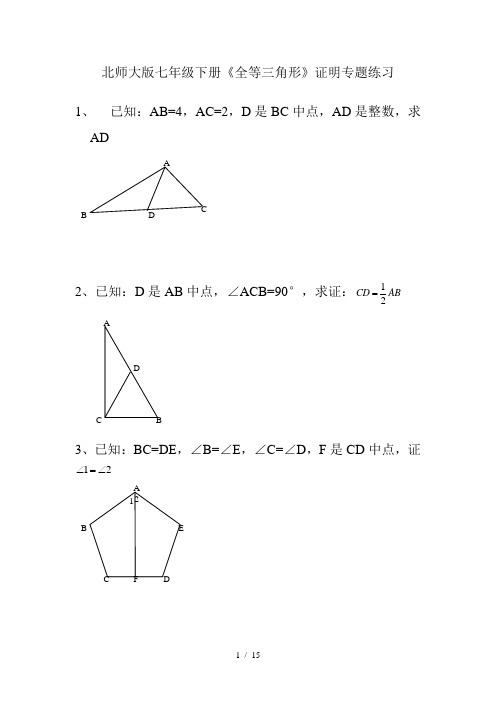
北师大版七年级下册《全等三角形》证明专题练习1、 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2、已知:D 是AB 中点,∠ACB=90°,求证:12CD AB =3、已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,证21∠=∠ADBC4、已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC5、已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C6、已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE7、已知:AB=6,AC=2,D 是BC 中线,求AD 的取值范围。
BA CDF2 1 ECDB A8. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
9、已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠CADB CDCBAFE10、已知:AB=CD ,∠A=∠D ,求证:∠B=∠C11、已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE12.如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .13.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBAAB C D14.如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .15.如图,△ABC 中,AD 是∠CAB 的平分线,且∠C =2∠B,求证:AB=AC+CD16.如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M .(1)求证:MB =MD ,ME =MF(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.PEDCBA D CBA17.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点,(1)求证:△AED ≌△EBC .(2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):18.如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F . 求证:BD =2CE .19、如图:DF=CE ,AD=BC ,∠D=∠C 。
北师大版七年级下册数学证明题练习(2021年整理)

北师大版七年级下册数学证明题练习(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(北师大版七年级下册数学证明题练习(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为北师大版七年级下册数学证明题练习(word版可编辑修改)的全部内容。
北师大版七年级下册数学证明题练习以下15题15分,第8题10分,其余的每小题5分。
1.如图,已知AB∥CD,EF交AB,CD于G, H, GM, HN分别平分EHD∠,,试说明AGF∠GM ∥HN。
2. 已知:如图,AD∥BC,∠BAD = ∠BCD,求证:AB∥CD。
3。
如图,AB∥CD,P为AB,CD之间的一点,已知︒2,求BPC∠25∠的度数。
∠32=1,︒=4。
已知AB∥CD,BC∥DE.试说明D∠。
=B∠5.已知:,21,,,∠=∠⊥⊥⊥GABFGACBCEACDE于于求证:ABCD⊥.6.在ABC∆中,,DABCD于⊥ABFG⊥于G,ED∥BC,试说明21∠=∠。
7。
已知:在△ABC中,∠BAC=80°,∠B=60°,AD⊥BC于D,AE平分∠DAC,求∠AEC8。
如图,已知∠A=∠F,AB∥EF,BC=DE,请说明AD∥CF。
解:∵ BC=DE(已知)∴在△ABD与△FEC中BACD EA∴ BC+CD=DE+CD ( ) ∠A=∠F (已知) 即:_________=_________ _______=______(已证) 又∵AB ∥EF (已知) _______=______(已证) ∴ ________=_________ ∴△ABD ≌△FEC (________)∴∠ADB =∠FCE (_____________________) ∴ AD ∥CF (_________________________) 9.如图,AB=AD ,AC=AE ,∠BAE=∠DAC ,试说明∠C=∠E10.如图,已知OC=OE,OD=OB ,试说明△ADE ≌△ABC.11。
