山东大学数值计算实验报告7

合集下载

数值计算实践报告_实习总结_总结汇报_实用文档

---数值计算实践上机报告学院:理学院指导老师：范晓娜老师姓名：***学号：B********日期：2015年10月11日—24日一、方程求根(一)实验目的熟悉掌握Newton法,割线法,抛物线法三种方法求方程近似根的算法思想，在matlab软件上分别使用这三种方法编程解决给定的三次方程的求根问题。

（二）问题描述一. 方程求根(1).给定一个三次方程,分别用Newton法,割线法,抛物线法求解.方程的构造方法:(a)根:方程的根为学号的后三位乘以倒数第二位加1再除以1000.假设你的学号为B06060141,则根为141*(4+1)/1000=0.564(b)方程:以你的学号的后三位数分别作为方程的三次项,二次项,一次项的系数,根据所给的根以及三个系数确定常数项.例如:你的学号是B06060141,则你的方程是x3+4x2+x+a0=0的形式.方程的根为0.564,因此有0.5643+4*0.5642+0.564+a0=0,于是a0=-2.015790144你的方程为x3+4x2+x-2.015790144=0.(2)假设方程是sinx+4x2+x+a0=0的形式（三个系数分别是学号中的数字），重新解决类似的问题(3)构造一个五次方程完成上面的工作.四次方程的构造:将三次多项式再乘以(x-p*)2得到对应的五次多项式(p*为已经确定的方程的根,显然,得到的五次方程有重根).(4)将（2）中的方程同样乘以(x-p*)得到一个新的方程来求解注:(1)Newton法取0.5为初值,割线法以0,1为初值,抛物线法以0,0.5,1为初值, (2)计算精度尽量地取高.终止准则：根据|p n-p n-1|<ε来终止|(3)可供研究的问题：（一）ε的取值不同对收敛速度有多大的影响（二）将注（1）中的初值该为其它的初值，对收敛性以及收敛速度有无影响 (三)能否求出方程的所有的根（三）算法介绍（包括基本原理）牛顿法牛顿法是一种能在许多不同情况下应用的通用过程。

数值计算实验报告

数值计算实验报告数值计算实验报告引言：数值计算是一门研究利用计算机进行数值计算的学科，它在科学研究和工程实践中具有重要的应用价值。

本实验报告旨在通过对数值计算实验的探索和分析，展示数值计算在解决实际问题中的应用和效果。

一、实验目的本次实验的主要目的是研究数值计算在求解非线性方程和数值积分中的应用。

通过实验，我们将探索不同数值计算方法的优劣，并分析其适用范围和精度。

二、实验原理1. 非线性方程求解非线性方程是指未知数与其系数之间存在非线性关系的方程。

常见的求解方法有二分法、牛顿法和割线法等。

本实验将比较不同方法在求解非线性方程时的收敛速度和计算精度。

2. 数值积分数值积分是通过将一个函数在一定区间上进行离散化，然后进行求和来近似计算定积分的方法。

本实验将使用复合梯形公式和复合辛普森公式来计算定积分，并比较两种方法的精度和计算效率。

三、实验步骤1. 非线性方程求解实验首先，我们选择一个非线性方程作为实验对象，例如：f(x) = x^3 - 2x - 5。

然后，我们使用二分法、牛顿法和割线法分别求解该方程，并记录每种方法的迭代次数和解的精度。

2. 数值积分实验我们选取一个函数作为被积函数，例如：f(x) = sin(x)。

然后，我们使用复合梯形公式和复合辛普森公式对该函数在一定区间上进行积分，并记录每种方法的计算结果和误差。

四、实验结果与分析1. 非线性方程求解结果通过实验，我们得到了使用二分法、牛顿法和割线法求解非线性方程的结果。

比较三种方法的迭代次数和解的精度，我们可以发现牛顿法收敛速度较快，但对初始值的选取较为敏感；割线法在收敛速度和精度上相对稳定；而二分法则收敛速度较慢，但对初始值的选取要求较低。

2. 数值积分结果通过实验，我们得到了使用复合梯形公式和复合辛普森公式进行数值积分的结果。

比较两种方法的计算结果和误差，我们可以发现复合辛普森公式具有更高的精度，但计算效率相对较低；而复合梯形公式计算速度较快，但精度相对较低。

数值计算方法实验报告

数值计算方法实验报告一、实验介绍本次实验是关于数值计算方法的实验，旨在通过计算机模拟的方法，实现对于数值计算方法的掌握。

本次实验主要涉及到的内容包括数值微积分、线性方程组的求解、插值与拟合、常微分方程的数值解等。

二、实验内容1. 数值微积分数值微积分是通过计算机模拟的方法，实现对于微积分中的积分运算的近似求解。

本次实验中，我们将会使用梯形公式和辛普森公式对于一定区间上的函数进行积分求解，并比较不同公式的计算误差。

2. 线性方程组的求解线性方程组求解是数值计算领域中的重要内容。

本次实验中，我们将会使用高斯消元法、LU分解法等方法对于给定的线性方程组进行求解，并通过比较不同方法的计算效率和精度，进一步了解不同方法的优缺点。

3. 插值与拟合插值与拟合是数值计算中的另一个重要内容。

本次实验中，我们将会使用拉格朗日插值法和牛顿插值法对于给定的数据进行插值求解，并使用最小二乘法对于给定的函数进行拟合求解。

4. 常微分方程的数值解常微分方程的数值解是数值计算中的难点之一。

本次实验中，我们将会使用欧拉法和龙格-库塔法等方法对于给定的常微分方程进行数值解的求解，并比较不同方法的计算精度和效率。

三、实验结果通过本次实验，我们进一步加深了对于数值计算方法的理解和掌握。

在数值微积分方面，我们发现梯形公式和辛普森公式都能够有效地求解积分，但是辛普森公式的计算精度更高。

在线性方程组求解方面，我们发现LU分解法相对于高斯消元法具有更高的计算效率和更好的数值精度。

在插值与拟合方面，我们发现拉格朗日插值法和牛顿插值法都能够有效地进行插值求解，而最小二乘法则可以更好地进行函数拟合求解。

在常微分方程的数值解方面，我们发现欧拉法和龙格-库塔法都能够有效地进行数值解的求解，但是龙格-库塔法的数值精度更高。

四、实验总结本次实验通过对于数值计算方法的模拟实现，进一步加深了我们对于数值计算方法的理解和掌握。

在实验过程中，我们了解了数值微积分、线性方程组的求解、插值与拟合、常微分方程的数值解等多个方面的内容，在实践中进一步明确了不同方法的特点和优缺点，并可以通过比较不同方法的计算效率和数值精度来选择合适的数值计算方法。

数值计算实验报告

一、实验目的1. 熟悉数值计算的基本原理和方法。

2. 掌握常用数值计算方法在数学建模和科学计算中的应用。

3. 培养运用计算机进行数值计算的能力。

二、实验内容1. 矩阵运算2. 解线性方程组3. 求函数的零点4. 解微分方程三、实验环境1. 操作系统：Windows 102. 编程语言：Python3. 库：NumPy、SciPy、Matplotlib四、实验步骤及结果1. 矩阵运算（1）实验步骤：1）导入NumPy库；2）创建一个3x3的矩阵A；3）创建一个3x1的矩阵B；4）进行矩阵乘法运算：C = A B；5）打印结果。

（2）实验结果：A = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]B = [[1], [2], [3]]C = A Bprint(C) # 输出：[[14], [32], [50]]2. 解线性方程组（1）实验步骤：1）导入NumPy库；2）创建一个3x3的系数矩阵A和一个3x1的常数向量b；3）使用NumPy的线性代数模块求解线性方程组：x = np.linalg.solve(A, b)；4）打印结果。

（2）实验结果：A = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]b = [2, 5, 6]x = np.linalg.solve(A, b)print(x) # 输出：[0.5, 0.5, 0.5]3. 求函数的零点（1）实验步骤：1）导入NumPy库；2）定义一个待求零点的函数f(x)；3）使用NumPy的根求解器求f(x)的零点：x = np.roots(f(x))；4）打印结果。

（2）实验结果：def f(x):return x2 - 4x = np.roots(f(x))print(x) # 输出：[2.0, -2.0]4. 解微分方程（1）实验步骤：1）导入SciPy库；2）定义一个微分方程函数ode_f，其中包含微分方程的系数；3）创建一个OdeSolver对象，并设置微分方程的初始条件；4）使用OdeSolver对象的solve方法求解微分方程；5）打印结果。

《数值计算》实验报告

《数值计算》实验报告第一部分：简答题（请简要回答以下问题，每小题字数不少于200字）1、Matlab变量命名有什么要求？以下变量名是否合法？对不合法的变量名说明理由。

abcd-2xyz_33chan NaN ABCDefgh2、插值、拟合、回归这三种方法是用来解决什么问题的？面对一组数据，如何选择用什么方法？3、数值积分的主要思想是什么？常用的数值积分公式有哪几个？4、请结合自己的学习，举例说明《数值计算》课程中所学方法在解决实际问题中是如何应用的。

第二部分：基础题（请完成以下问题，要求给出程序语句及计算结果，用截图方式附在各题目下方）1、已知点(1,3.0),(2,3.7),(5,3.9),(6,4.2),(7,5.7),(8,6.6),(10,7.1),(13,6.7), (17,4.5)，绘出经过这些点的函数曲线图形，并给出曲线方程。

答：采取三次样条插值法，九个输入数据分成八段，每一段就是一个三次函数。

这八段的函数形式为y = a0 + a1*x + a2*x^2 + a3*x^3，每个分段函数的参数构成下图所示的coefs 矩阵。

2、在我国某海域测得海洋不同深度处的水温如表1所示，求水深为800m和1500m处的温度。

答：采取线性插值法求得800m和1500m处的温度3、求解方程组⎪⎪⎩⎪⎪⎨⎧=-++=--=-++=++56533332821w z y x w y x w z y x z y x ，请至少使用两种方法求解，并对这两种方法的计算结果进行说明。

高斯消元法LU 分解QR分解Jacobi迭代法使用 Jacobi 迭代法无法求出结果，表示迭代的过程中不收敛4、计算积分dx eI x ⎰-=1022，精度为10-6。

被积函数总共调用 13 次，求得积分值为 0.85565、求方程t et t f t5.0)(sin )(1.02-⋅=-在[0.5,1]内的根。

6、求解微分方程0)1(22=+'--''y y y y ，0)0(,1)0(,300='=≤≤y y x ，绘出解函数的图形。

数值计算基础实验报告(3篇)

第1篇一、实验目的1. 理解数值计算的基本概念和常用算法；2. 掌握Python编程语言进行数值计算的基本操作；3. 熟悉科学计算库NumPy和SciPy的使用；4. 分析算法的数值稳定性和误差分析。

二、实验内容1. 实验环境操作系统：Windows 10编程语言：Python 3.8科学计算库：NumPy 1.19.2，SciPy 1.5.02. 实验步骤（1）Python编程基础1）变量与数据类型2）运算符与表达式3）控制流4）函数与模块（2）NumPy库1）数组的创建与操作2）数组运算3）矩阵运算（3）SciPy库1）求解线性方程组2）插值与拟合3）数值积分（4）误差分析1）舍入误差2）截断误差3）数值稳定性三、实验结果与分析1. 实验一：Python编程基础（1）变量与数据类型通过实验，掌握了Python中变量与数据类型的定义方法，包括整数、浮点数、字符串、列表、元组、字典和集合等。

（2）运算符与表达式实验验证了Python中的算术运算、关系运算、逻辑运算等运算符，并学习了如何使用表达式进行计算。

（3）控制流实验学习了if-else、for、while等控制流语句，掌握了条件判断、循环控制等编程技巧。

（4）函数与模块实验介绍了Python中函数的定义、调用、参数传递和返回值，并学习了如何使用模块进行代码复用。

2. 实验二：NumPy库（1）数组的创建与操作通过实验，掌握了NumPy数组的基本操作，包括创建数组、索引、切片、排序等。

（2）数组运算实验验证了NumPy数组在数学运算方面的优势，包括加、减、乘、除、幂运算等。

（3）矩阵运算实验学习了NumPy中矩阵的创建、操作和运算，包括矩阵乘法、求逆、行列式等。

3. 实验三：SciPy库（1）求解线性方程组实验使用了SciPy库中的线性代数模块，通过高斯消元法、LU分解等方法求解线性方程组。

（2）插值与拟合实验使用了SciPy库中的插值和拟合模块，实现了对数据的插值和拟合，并分析了拟合效果。

山东大学数值计算实验报告13-14

得到结果如下：步长 1 中点求积 3.2000 梯形公式 3.0000 辛普森公 3.1333 式 1.2 用自适应求积的库函数 0.5 3.1624 3.1000 3.1416 0.2 3.1449 3.1349 3.1416 0.1 3.1424 3.1399 3.1416 0.01 3.1416 3.1416 3.1416 0.001 3.1416 3.1416 3.1416
y = @(x)4./(1+x.^2); integral(y,0,1)
运行结果如下：
1.3 蒙特卡洛积分：
s=0; m=0; f=0; r=0; n=50; h(1:10)=0; for j=1:10 for i=1:n a=unifrnd(0,pi/2,n,1); x=sort(a); y=pi/2*mean(x.*sin(x)); s=s+y; end b=s./n; fprintf('b=%.4f\n',b); h(j)=b; s=0; m=m+b; end p=m./10 z=1 for j=1:10 r=(h(j)-z).^2; f=f+r; end f=f./10;
山东大学
软件
学院
数值计算课程实验报告
学号：实验题目：数值积分 P378 8.1 一、二、三、 Computer Problems P378 8.1(a)(c)(d) 上一题目的积分，用 2 点 gauss 积分计算上一题目的积分，用 n(n=3,4,5)点 gauss 积分计算(选做) 实验日期：2017 年 12 月 26 日姓名：班级：5 班
实验学时：4 实验目的：数值积分硬件环境： PC 机软件环境： MATLAB 实验步骤与内容：

山东大学数值计算实验报告6

运行结果：
5.0 因为 A 不是不是方阵，所以 A 的所有条件数都是无穷大 5.1 一次多项式拟合下 AA 的条件数代码：
B = A'*A; fprintf('%s\n','1 范数下矩阵 AA 的条件数') c1=cond(B,1) fprintf('%s\n','2 范数下矩阵 AA 的条件数') c2=cond(B) fprintf('%s\n','无穷范数下矩阵 AA 的条件数') c3=cond(B,inf)
实验学时：2 实验目的：最小二乘法数据拟合硬件环境： PC 机软件环境： MATLAB 实验步骤与内容： 1. 利用 plot 函数画出散点图代码：实验日期：2017 年 11 月 14 日
t=[0.0 1.0 2.0 3.0 4.0 5.0]; y=[1.0 2.7 5.8 6.6 7.5 9.9]; plot(t,y,'*')
山东大学
软件
学院
数值计算课程实验报告
学号：实验题目：姓名：班级：5 班
1、Computer Problems 3.1(P152) 1.1 画出散点图（plot 函数） 1.2 用一次多项式拟合。给出拟合函数，确定矛盾方程组的系数矩阵、右端项。正规方程的方法得到结果，并画图显示该拟合函数 1.3 用二次多项式拟合，画图 1.4 用三次多项式拟合，画图 1.5 前面几个曲线拟合，假设对应的矛盾方程组为 Ax≌b，分别计算 A 和 ATA 的条件数，并比较
运行结果：
5.2 二次多项式下 AA 的条件数代码：和上面相同运行结果：
5.3 三次多项式下 AA 的条件数

山东大学数值计算实验报告2

山东大学计算机科学与技术学院数值计算课程实验报告2.（1）用MATLAB写出楚列斯基分解函数代码如下所示Cholesky.mfunction [ B ] = Cholesky(A )%UNTITLED2 此处显示有关此函数的摘要% 楚列斯基分解B = A;n = length(A);for k = 1:nB(k,k) = sqrt(B(k,k));for i = k+1:nB(i,k) = B(i,k)/B(k,k);endfor j = k+1:nfor i = k+1:nB(i,j) = B(i,j)-B(i,k)*B(j,k);（3）计算范数和条件数代码如下f222.mfunction [ ] = f222(n )conda1 = fanshua1*max(a)fprintf('%s\n','2范数下矩阵A的2条件数') B = A_'*A_;[v d] = eig(B);conda2 = sqrt(max(max(d)))*fanshua2fprintf('%s\n','无穷范数下矩阵A的条件数') for i = 1:nfor j = 1:nsum = sum + abs(A_(i,j));enda(i) = sum;sum = 0;endconda3 = max(a)*fanshua3endtest222.mclc,clearfprintf('%s\n','n = 2时')f222(2)fprintf('%s\n','n = 5时')f222(5)fprintf('%s\n','n = 10时')f222(10)运行结果截图如下所示3.（1）Jacobi迭代法MATLAB实现代码如下D(i,i)=A(i,i);end;L=-tril(A,-1);U=-triu(A,1);while error>=errorBound & step<maxSp x0=inv(D)*(L+U)*x0+inv(D)*b;vChain(k,:)=x0';k=k+1;error=norm(x0-fx0);fx0=x0;step=step+1;endv=x0;sN=step;可见Jacobi迭代了3次得到的解为x=[111],收敛。

数值计算方法实验报告

数值计算方法实验报告一、实验目的本实验旨在通过Python语言编写数值计算方法程序，掌握常见数值计算方法的实现原理及应用。

具体包括：插值法、最小二乘法、数值微积分、数值解方程、数值解微分方程等。

二、实验环境Python编程语言、Jupyter Notebook环境三、实验内容1.插值法（1）代码实现：在Python中使用Scipy库中的Interpolate模块实现拉格朗日插值法和牛顿插值法，并通过数据可视化展示其效果。

（2）实验步骤：- 导入所需库，准备所需数据；- 定义拉格朗日插值法函数；- 定义牛顿插值法函数；- 测试函数并可视化结果。

（3）实验结果：2.最小二乘法（1）代码实现：在Python中使用Numpy库实现最小二乘法，并通过数据可视化展示其效果。

（2）实验步骤：- 导入所需库，准备所需数据；- 定义最小二乘法函数；- 测试函数并可视化结果。

（3）实验结果：3.数值微积分（1）代码实现：在Python中实现梯形法和辛普森法，并通过数据可视化展示其效果。

（2）实验步骤：- 导入所需库，准备所需数据；- 定义梯形法函数和辛普森法函数；- 测试函数并可视化结果。

（3）实验结果：4.数值解方程（1）代码实现：在Python中实现二分法、牛顿法和割线法，并通过数据可视化展示其效果。

（2）实验步骤：- 导入所需库，准备所需数据；- 定义二分法函数、牛顿法函数和割线法函数；- 测试函数并可视化结果。

（3）实验结果：5.数值解微分方程（1）代码实现：在Python中实现欧拉法和龙格-库塔法，并通过数据可视化展示其效果。

（2）实验步骤：- 导入所需库，准备所需数据；- 定义欧拉法函数和龙格-库塔法函数；- 测试函数并可视化结果。

（3）实验结果：四、实验总结通过本次实验，我学习了数值计算方法的常用算法和实现原理，掌握了Python 语言实现数值计算方法的方法，加深了对数值计算方法的理解和应用。

实验中遇到的问题，我通过查找资料和与同学的讨论得到了解决，也更加熟练地掌握了Python语言的使用。

山东大学数值计算实验报告1

山东大学计算机科学与技术学院数值计算课程实验报告for i = 1:ny1(i) = abs(errorj(x(i)));y2(i) = abs(errorx(x(i)));end% scatter(x,y1)% hold onscatter(x,y2,'p')hold on当n取1到15时，绘制出绝对误差的图像如下所示：当n取1到100时，绘制出绝对误差的图像如下所示：当n取1到15时，绘制出相对误差的图像如下所示：当n取1到100时，绘制出相对误差的图像如下所示：观察以上四个图我们可以发现，随着n的增加绝对误差不但增大，并且增大地越来越快。

而相对误差越来越小，并接近于0 。

2.Write a program to compute the mathematical constant e, the base of naturallogarithms, from the de f i nition e=limn→∞(1+1n)n. Speciﬁcally, compute (1 +1/n)n for n =10k, k = 1,2,...,20. If the programming language youusedoesnothaveanoperatorforexponentiation, you may use the equivalent formula (1+1/n)n = exp(nlog(1+1/n)), where exp and log are built-in functions. Determine the error in your successive approximations by comparing them with the value of exp(1). Does the error always decrease as n increases? Explain your results.根据题意编写代码如下：ejinsi.mfunction [y] = ejinsi(x )y = exp(1)-(1+1/10^x)^(10^x);test1_4.mn = 10;x = 1:1:n;y = zeros(1,n);for i = 1:ny(i) = ejinsi(x(i));endscatter(x,y)n取101到1010时，绘制出绝对误差变化趋势图如下图所示：我们可以看到随着n的增大，误差越来越小并接近于0 。

山东大学数值计算实验报告6

山东大学计算机科学与技术学院
数值计算课程实验报告
软件环境： MATLAB、JAVA、C++
实验步骤与内容：
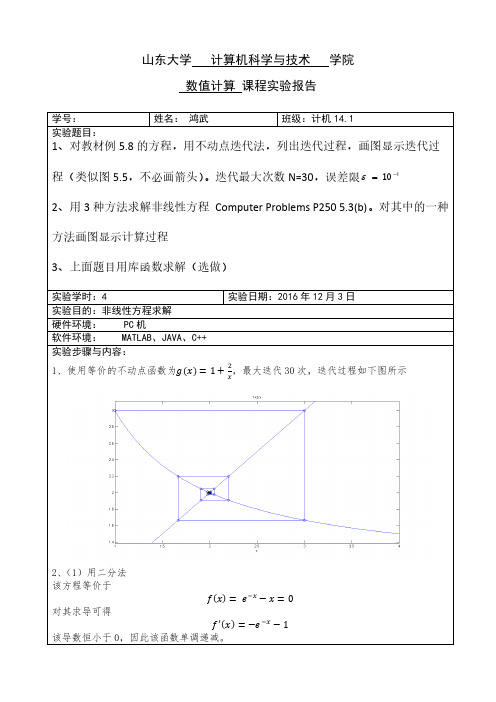
，最大迭代30次，迭代过程如下图所示1、使用等价的不动点函数为g(x)=1+2
x
2、（1）用二分法
该方程等价于
f(x)=e−x−x=0
对其求导可得
f′(x)=−e−x−1
该导数恒小于0，因此该函数单调递减。

因为
f(0)=1−0>0而
f(1)=1
e
−1<0
因而该方程有且仅有一个解，且在0与1之间。

用二分法进行迭代，可以求得
x=0.5671
（2）用不动点法
此方程本身就是一个可以直接用作不动点迭代的表达式。

迭代过程如下图所示，最终求得的解为x=0.5671。

（3）割线法
该方程等价于
f(x)=x−e−x=0
因为该函数的导数为
f′(x)=1+e−x>0
所以该函数单调递增
又因为
f(0)=−1<0，f(1)=1−1
e
>0
所以该方程有且仅有一个解，且在0和1之间。

运用割线法求解迭代过程如下图
最终求得解为
x=0.5671 3、调用库函数fsolve('x-exp(-x)',0)，解得
x=0.5671
结论分析与体会：。

大学计算实验实验报告

实验名称：数值计算方法实验日期：2021年10月15日实验地点：计算机实验室实验目的：1. 理解数值计算的基本原理和方法。

2. 掌握常用数值计算算法的编程实现。

3. 培养分析和解决实际问题的能力。

实验内容：本次实验主要涉及以下内容：1. 线性方程组的求解2. 函数求值与数值微分3. 函数求根4. 数据插值实验原理：数值计算是计算机科学和工程领域中非常重要的一个分支，它涉及到将数学问题转化为计算机可以处理的数值问题。

本实验主要探讨了以下数值计算方法：1. 高斯消元法：用于求解线性方程组。

2. 牛顿法：用于求解函数的根。

3. 二分法：用于求解函数的根。

4. 拉格朗日插值法：用于数据插值。

实验步骤：1. 线性方程组的求解：- 编写程序实现高斯消元法，用于求解线性方程组。

- 输入方程组的系数和常数项。

- 输出方程组的解。

2. 函数求值与数值微分：- 编写程序实现中点法和辛普森法，用于求函数的近似值。

- 编写程序实现中心差分法，用于求函数的导数近似值。

- 输入函数表达式、求值点和微分点。

- 输出函数的近似值和导数的近似值。

3. 函数求根：- 编写程序实现牛顿法和二分法，用于求解函数的根。

- 输入函数表达式、初始猜测值和误差容忍度。

- 输出函数的根。

4. 数据插值：- 编写程序实现拉格朗日插值法，用于数据插值。

- 输入数据点和待插值点。

- 输出插值结果。

实验结果：1. 线性方程组的求解：- 输入方程组系数和常数项：`2x + 3y = 6`，`x - y = 1`。

- 输出解：`x = 2`，`y = 1`。

2. 函数求值与数值微分：- 输入函数表达式：`f(x) = x^2`，求值点：`x = 2`。

- 输出函数的近似值：`f(2) ≈ 4.000000`。

- 输入微分点：`x = 2`。

- 输出导数的近似值：`f'(2) ≈ 4.000000`。

3. 函数求根：- 输入函数表达式：`f(x) = x^2 - 2`，初始猜测值：`x = 1`，误差容忍度：`10^-6`。

山东大学操作系统实验七实验报告

计算机科学与技术学院实验报告
8 }
在文件../test/第5行上的语句Exec是一条Nachos的系统功能调用，它的功能为装入并执行以其参数为名的可执行文件，即创建一个新的用户进程。

假设我们先执行../test/ 程序，则../test/ 会在它还没有执行结束时又装入并执行另外一个程序，并与它同时驻留内存.
pageTable[i].physicalPage=usermap-->Find();避免从头开始物理存储覆盖了前一个用户程序的内存内容
利用Nachos在../userprog/ 中文件定义的Bitmap类。

利用bitmap记录和申请内存物理帧，使不同的程序装入到不同的物理空间中去，下面是对新的内存分配存储算法，改进了对多个用户程序的同时进驻内存的支持
这是对BitMap的代码修改，每次分配的时候要找到bitmap中的空闲页进行分配，而不能从0页开始分配在AddressSpace类中声明bitmap对象
static BitMap *mbitmap=new BitMap(NumPhysPages);
运行./nachos –x ../test/
结论分析与体会：
nachos无法运行多个用户程序的原因在于物理页的分配，那么改变物理页的分配，使多个程序的物理页不会相互覆盖，每个程序都能分配到对应的独立的物理页，那么不就可以同时执行多个用户程序了吗。

物理页的分配算法在BitMap类中有实现，使用一个数组作为物理页的数据结构。

在给用户程序分配物理页时，不再使用与逻辑页相同的数值，而是使用Find()方法查找下一个可用的物理页。

山东大学第七次数字信号处理实验报告

數字信號處理實驗報告實驗七、綜合練習題已知信號。

現對該信號進行頻譜分析，請用Matlab編程實現：1、選擇合適の抽樣頻率和記錄時間，對進行抽樣，要求抽樣得到の信號是周期の，且能分辨上述三個信號。

2、畫出上述信號の頻譜。

3、設計兩個巴特沃斯濾波器，將分離為,其中由獲得, 由獲得。

4、用升餘弦窗設計兩個濾波器，完成3の任務。

注：所有結果畫圖表示。

實驗內容及實驗結果：1、選擇合適の抽樣頻率和記錄時間，對進行抽樣，要求抽樣得到の信號是周期の，且能分辨上述三個信號。

2、畫出上述信號の頻譜。

以上兩問の實驗程序：clc;clear all;close all;t=0:0.00001:0.4;x=cos(2*pi*100*t)+0.5*cos(2*pi*105*t)+0.75*cos(2*pi*280*t); %原信號subplot(2,2,1);plot(t,x);grid on;title('原信號x(t)');t3=1/1000;L=50;n1=L/t3;D=2*pi/(n1*t3);n2=0:n1-1;x2=cos(2*pi*100*t3*n2)+0.5*cos(2*pi*105*t3*n2)+0.75*cos(2*pi*280*t3*n2);k1=floor(-(n1-1)/2:(n1-1)/2);Xw1=t3*fftshift(fft(x2));subplot(2,2,2);stem(k1*D/(2*pi),abs(Xw1));grid on;title('原信號頻譜X(f)');t10=1/1000;t2=0:t10:0.4;x3=cos(2*pi*100*t2)+0.5*cos(2*pi*105*t2)+0.75*cos(2*pi*280*t2); %抽樣後の信號subplot(2,2,3);stem(t2,x3,'b');grid on;title('抽樣信號');hold on;plot(t,x)L10=50;n10=L10/t10;D10=2*pi/(n10*t10);n11=0:n10-1;x10=cos(2*pi*100*n11*t10)+0.5*cos(2*pi*105*n11*t10)+0.75*cos(2*pi*280*n11*t10);k2=floor(-(n10-1)/2:(n10-1)/2);Xw11=t10*fftshift(fft(x10));subplot(2,2,4);stem(k2*D10,abs(Xw11));grid on;title('抽樣信號頻譜')以上兩問の實驗結果：3、設計兩個巴特沃斯濾波器，將分離為,其中由獲得, 由獲得。

数值计算方法实验报告

数值计算方法实验报告一、实验目的本实验旨在通过数值计算方法的实验操作，深入理解数值计算方法的原理与应用，掌握数值计算方法的相关技能，提高数值计算方法的实际应用能力。

二、实验内容1.数值微积分2.数值代数3.数值微分方程4.数值线性代数5.数值优化6.数值统计分析7.数值随机模拟8.数值傅立叶分析9.数值偏微分方程三、实验步骤1.数值微积分：通过不同的数值积分方法，计算给定函数的定积分值，并对不同数值积分方法的误差进行分析。

2.数值代数：通过使用线性代数方法，求解给定的线性方程组，并分析不同线性方程组求解方法的优劣。

3.数值微分方程：通过使用常微分方程数值解法，求解给定的微分方程，并比较不同求解方法的精度和稳定性。

4.数值线性代数：通过使用特征值分解方法，对给定的矩阵进行特征值分解，并分析不同特征值分解方法的优缺点。

5.数值优化：通过使用不同的优化方法，求解给定的优化问题，并比较不同的优化方法的效率和精度。

6.数值统计分析：通过使用不同的统计分析方法，对给定的数据进行统计分析，并分析不同的统计方法的优缺点。

7.数值随机模拟：通过使用随机模拟方法，模拟给定的概率分布，并分析不同随机模拟方法的效率和精度。

8.数值傅立叶分析：通过使用傅立叶分析方法，对给定的信号进行频谱分析，并分析不同的傅立叶分析方法的优缺点。

9.数值偏微分方程：通过使用偏微分方程数值解法，求解给定的偏微分方程，并比较不同求解方法的精度和稳定性。

四、实验结果与分析本实验中，通过对不同的数值计算方法的实验操作，我们可以更深入地理解数值计算方法的原理与应用，并掌握数值计算方法的相关技能，提高数值计算方法的实际应用能力。

同时，通过实验结果的分析，我们可以更好地比较不同数值计算方法的优缺点，为实际应用提供参考依据。

五、实验总结本实验旨在通过数值计算方法的实验操作，深入理解数值计算方法的原理与应用，掌握数值计算方法的相关技能，提高数值计算方法的实际应用能力。

山东大学数值计算实验报告3

运行结果如下：
2.1.2 直接解方程组
fprintf('%s\n','n=2 时，解法 2');
x12 = H1\b1
运行结果如下：
2.2 当 n=5 时
%生成 n=5 时希尔伯特矩阵 H2=zeros(5,5); n2=5; for i = 1:5 for j = 1:5 H2(i,j) = 1/(i+j-1); end end fprintf('%s\n','n=5 时，解法 1：'); L2=c_1(H2,n2)%楚列斯基函数得到 L %得到 b t2=ones(5,1); b2=H2*t2; %利用之前实验 2 所写的前代，后代函数得到答案 front2 = a_3_a( L2,b2 ); x21 = a_3_b(L2',front2)
%当 n=10 时 fprintf('%s\n','当 n=10 时，该矩阵的 1 范数及 1 范数下的条件数为：'); fan31 = norm(H3,1) cond31 = cond(H3,1) fprintf('%s\n','当 n=10 时，该矩阵的 2 范数及 2 范数下的条件数为：'); fan32 = norm(H3,2) cond32 = cond(H3) fprintf('%s\n','当 n=10 时，该矩阵的无穷范数及无穷范数下的条件数为： '); fan33 = norm(H3,inf) cond33 = cond(H3,inf)
运行结果如下：
fprintf('%s\n','n=10 时，解法 2'); x32 = H3\b3

数值计算的实验报告

一、实验目的1. 熟悉数值计算的基本原理和方法。

2. 掌握常用的数值计算算法及其应用。

3. 提高数值计算软件的使用能力。

4. 培养分析问题和解决问题的能力。

二、实验环境1. 操作系统：Windows 102. 编程语言：Python3. 数值计算软件：NumPy、SciPy、Matplotlib三、实验内容1. 实验一：数值积分（1）实验目的：学习数值积分方法，计算定积分的近似值。

（2）实验内容：a. 使用辛普森法则计算函数f(x) = x^2在区间[0, 1]上的定积分。

b. 使用梯形法则计算函数f(x) = e^x在区间[0, 1]上的定积分。

（3）实验步骤：a. 编写Python代码，实现辛普森法则和梯形法则。

b. 分别使用两种方法计算定积分的近似值。

c. 对比两种方法的计算结果，分析误差来源。

2. 实验二：数值微分（1）实验目的：学习数值微分方法，计算函数在某点的导数近似值。

（2）实验内容：a. 使用中心差分法计算函数f(x) = sin(x)在x = π/2处的导数近似值。

b. 使用前向差分法和后向差分法计算函数f(x) = cos(x)在x = 0处的导数近似值。

（3）实验步骤：a. 编写Python代码，实现中心差分法、前向差分法和后向差分法。

b. 分别使用三种方法计算导数的近似值。

c. 对比三种方法的计算结果，分析误差来源。

3. 实验三：线性方程组求解（1）实验目的：学习线性方程组求解方法，掌握高斯消元法和迭代法。

（2）实验内容：a. 使用高斯消元法求解线性方程组：3x + 2y - z = 72x - y + 3z = -1-x + 2y + 2z = 4b. 使用雅可比迭代法求解线性方程组：3x + 2y - z = 72x - y + 3z = -1-x + 2y + 2z = 4（3）实验步骤：a. 编写Python代码，实现高斯消元法和雅可比迭代法。

b. 分别使用两种方法求解线性方程组。

山东大学数值计算实验6报告

figure;
plot(x',fx1,'g');
title('zhenggui');
figure;
plot(x',fx2,'b');
title('qr');
QR.m:
function[r,x] = QR(A,b)
m = size(A,1);
n = size(A,2);
Q = zeros(m,n);
fori = 1:n
end
e = zeros(m,1);
e(i) = 1;
v = a - (-sign)*calL2(a)*e;
H = eye(m)-2*v*v'/(v'*v);
A = H*A;
b = H*b;
end
c = b;
c1 = c(1:n,1);
c2 = c(n+1:m,1);
r = calL2(c2);
R = A(1:n,:);
A = H*A;
b = H*b;
end
c = b;
c1 = c(1:n,1);
c2 = c(n+1:m,1);
r = calL2(c2);
R = A(1:n,:);
x = Back_substitution(R,c1);
end
ZhengGui.m:
function[twoFanshu,xx] = ZhengGui(A,b)
x = Back_substitution(R,c1);
end
调用下面的命令：
[fanshu2,c2] = QR(A,y)
求得结果如下：
C1
1.00000005136773