山东大学数值计算实验四
疫情下基于手机的IPv6网络安全实验技术与教学应用

0 引 言疫情防控期间,政府为主导下政校企以及社会力量各方协同联动、多措并举,合力保障高校“停课不停教、停课不停学”。
在此基础上,针对计算机类专业课程实践性要求高的特点,为保证在线学习与线下课堂教学质量实质等效,中国高校计算机教育MOOC 联盟联合高校和企业单位推出了Trustie 、Educoder 、ModelArts 等一批在线实践教学平台,力促“停课不停练”。
在此支持下,各高校因校制宜,“一课一策”,灵活多样地开展实验教学,例如:西安邮电大学计算机学院采用程序设计类实验辅助教学平台PTA (Programming Teaching Assistant )实施全校C 语言课程线上实验教学[1],湘潭大学信息工程学院和西藏大学信息科学技术学院采用Educoder 开展计算机语言和程序设计类课程实验教学[2-3]。
随着疫情期间在线实验教学的展开,一部分学生因没有电脑无法参与实验教学的问题逐步显现。
例如:山东大学管理学院本科生的调查数据显示,8.25%的学生没有电脑[4];南京邮电大学通达学院调研发现,58.9% 的学生使用手机而非电脑进行在线学习,如此高比例的原因之一正是其中部分学生家中没有电脑[5]。
如何充分发掘“互联网+教育”的巨大潜力和作用,有效克服因为学生居家条件的差异而导致的教学资源鸿沟,发展公平而有质量的教育成为疫情期间线上实验教学实践过程中凸显出来的现实问题。
面对疫情防控期间实验教学面临教学资源鸿沟的现状,紧密结合国内互联网产业和技术体系从IPv4向IPv6过渡升级的必然性和紧迫性要求,高校网络空间安全专业实验教学改革如何以新工科建设为引领,探索IPv6网络环境下以手机为接入终端的网络安全实验新技术,通过基于手机基金项目:国家自然科学基金项目“基于移动社会网络的校园协作学习交互与微视频扩散关键技术研究”(61877037);陕西省科技计划重点研发项目“基于移动社会网络的智慧校园共性关键技术研究与应用示范”(2020GY-221);陕西师范大学2020年教师教学模式创新与实践研究专项基金项目“金课导向下计算机网络协议课程体验式教学改革与实践”(JSJX2020Z28)。
硕士培养方案-山东大学数学学院

应用数学专业攻读硕士学位研究生(学术型)培养方案(专业代码:070104)一、培养目标在本门学科上掌握坚实的理论基础和系统的专门知识;具有从事科学研究工作或独立担负专门技术工作的能力。
培养面向世界,面向未来,面向现代化,德智体全面发展的,为社会主义现代化建设服务的高层次专门人才。
具体要求是:1、较好地掌握马列主义、毛泽东思想和邓小平建设有中国特色的社会主义理论,坚持四项基本原则, 树立正确的世界观、人生观、价值观,遵纪守法,热爱祖国,热爱社会主义,具有勇于追求真理和献身于科学教育事业的敬业精神,富有历史责任感。
具有良好的道德品质和学术修养。
2、掌握本专业坚实的基础理论和系统的专业知识,了解本学科目前的进展与动向,具有从事科学研究工作或独立担负专门技术工作的能力。
3、掌握一门外国语,并能运用该门外国语比较熟练的阅读本专业的外文资料。
4、具有健康的体魄和心理素质。
二、研究方向1.数学物理逆问题2.数值代数3.非牛顿流体力学4.资源与环境模拟5. 近代数学史6. 数学建模方法及其应用7. 生物统计三、学习年限全日制硕士研究生的学制为3年,在校学习期限为2-3年。
原则上不提前毕业,对于特别优秀者,最多可提前一年。
提前毕业的硕士研究生除完成培养方案规定的课程外,必须有一篇以上SCI论文发表,并须经学位委员会审核通过。
所取得的科研成果均要求研究生为第一作者,作者单位需为山东大学。
四、培养方式根据宽口径、厚基础的原则,提倡按一级学科培养硕士研究生;充分利用校内外优质教育资源,鼓励研究生进行“三种经历”,实行双导师合作培养。
五、应修满的总学分数应修总学分:30 ,其中必修24学分(含前沿讲座与社会实践),选修6学分。
六、课程的类别及设置硕士研究生课程分为必修课与选修课两大类。
1.必修课是为达到培养目标要求,保证研究生培养质量而必须学习的课程。
必修课分学位公共课、学位基础课和学位专业课。
学位基础课一般按一级学科进行设置,学位专业课一般按二级学科设置。
山东大学网络教育计算机应用基础课后答案

2019年4月第一章绪论1【多选题】关于信息社会,下列说法不正确的是()A、计算机的发明和广泛使用是人类社会进入信息社会的唯一标志。
B、信息社会中所有的工业生产都是自动化的。
C、在信息社会,信息技术催生大批新兴产业,同时,传统产业也普遍实行技术改造。
D、信息社会中信息产业高度发展,在产业结构优势的地位日益突出。
E、在信息社会,信息、知识成为重要的生产力要素。
F、计算机的发明是第三次科技革命的重要标志,是人类文明史上继蒸汽技术革命和电力技术革命之后科技领域里的又一次重大飞跃。
正确答案: AB2【多选题】关于信息技术(Information Technology,IT)下列说法正确的是()A、广义而言,能充分利用与扩展人类信息器官功能的各种方法、工具与技术都可称为信息技术。
B、现代信息技术是指以微电子技术、计算机技术和通信技术为特征的技术。
C、信息技术就是计算机技术和计算机网络技术。
D、在信息社会,所有的信息处理中都用到了信息技术。
E、在信息处理的每一个环节,都必须使用信息技术。
F、信息技术无法对工业社会形成的传统设备进行技术改造,成为智能设备。
正确答案: AB3【多选题】在人体器官中,下列说法不正确的是()A、大脑的思维是对外部事物的直接反应。
B、大脑是一种直接感觉器官。
C、人体器官可分为直接感觉器官和间接感觉器官。
D、大脑具有记忆和思维功能。
E、大脑是一种间接感觉器官。
F、大脑是人体的思维器官。
正确答案: AB4【多选题】二进制是由下列哪位科学家首先提出来的()A、莱布尼兹B、布尔C、巴贝奇D、图灵E、冯•诺依曼正确答案: A5【多选题】对于计算思维,下列说法错误的是()A、计算思维是计算机科学家独有的思维方式。
B、计算思维是一种借助于计算能力进行问题求解的思维和意识。
C、计算思维的产生与信息社会发展的时代背景有关,工具影响我们的思维方式。
D、计算思维的本质是抽象和自动化。
E、计算思维并不是继逻辑思维和形象思维以后的人类思维的第三种形态。
大学物理实验 数据处理和实验基本要求

有一个反映准确程度的极限误差指标,习惯上称之为仪器
误差,用来 仪表示。这个指标在仪器说明书中都有明确的
说明。
第五节 测量结果的不确定度
对一个量进行测量后,应给出测量结果,并要对测 量结果的可靠性作出评价。
近年来,引入了不确定度这一概念来评价测量结果的 可靠程度。
系统误差按产生原因的不同可分为: 原因可知,有规律
(1)仪器误差
(2) 方法误差
(4)环境 条件误差
注意:
依靠多次重复测量一般不能发现系统误差的存在。
(3)个人误差
2、随机误差
15
相同的实验条件下
系统误差产生的因素
每次测量结果可能都不一样, 测量误差或大或小、或正或负, 完全是随机的
次数足够多
/94
所以
lim
n
A
A0
结论
可以用有限次数重复测量的算术平均值 A作为真值 A0
的最佳估计值。
由于平均值只是最接近真值但不是真值,因此, 误差也是无法得到的。在实际测量的数据处理中,用偏 差来估算每次测量对真值的偏差。偏差的定义为
i Ai A
4.有限次测量的标准偏差
(i 1,2, , n)
可以证明,当测量次数为有限时,可以用标准偏
1.不确定度的基本概念 测量结果的不确定度也称实验不确定度,简称为不确
定度,是对被测量的真值所处量值范围的评定。 不确定度给出了在被测量的平均值附近的一个范围,
真值以一定的概率落在此范围中。 不确定度越小,标志着测量结果与真值的误差可能值
越小;不确定度越大,标志着测量结果与真值的误差可能值越
2.不确定度分量的分类及其性质 按照“国际计量局实验不确定度的规定建议书”
山东大学气体定压比热容的测定实验

实验一 气体定压比热容的测定一、 实验目的1. 掌握气体定压比热测定装置的基本原理。
2. 熟悉本实验中的温度、压力、热量(加热功率)、湿空气流量的测量方法。
3. 掌握由基本数据计算出定压比热值和求得定压比热公式的方法。
4. 分析本实验产生误差的原因及减小误差的可能途径。
二、实验原理根据定压比热的定义:c p =δqdT (1) δq =c p ·dT (2) Q =q m ∫c p ·dt t2t 1(3)气体定压比热容的积分平均值:c p |t 1t2=Qqm (t 2−t 1)=Qq m △t(4)式中,Q ——气体在定压流动过程中由温度t 1被加热到t 2时所吸收的热量,W ; q m ——气体的质量流量, kg/s ;△t ——气体定压流动受热的温升,℃。
因此,准确的测出气体的定压温升△t ,质量流量q m 和加热量Q ,就可以求得气体由温度t 1被加热到t 2时的平均定压比热容c p |t 1t2(J /(kg ·℃)。
在温度变化范围不太大的条件下,气体的定压比热容可以表示为温度的线性函数,即c p =a +bt (5)温度t 1至t 2之间的平均比热容,在数值上等于平均温度t m =t 1+t 22下气体的真实比热容,即c p |t 1t2=a +bt m (6) 改变t 1和t 2,就可以测出不同平均温度下的比热容,从而求得比热容与温度的关系。
三、实验装置实验装置由风机、湿式气体流量计、比热仪主体、电功率调节器和温度测量系统等组成(如图1所示)。
图1 实验装置示意图1.电箱2.离心式鼓风机3.湿式气体流量计4.比热仪主体5.干球温度6.进口温度7.出口温度8.外热式电烙铁芯9.铜闸阀10.湿球温度11.U型压力计图2 比热仪主体实验时,被测空气(也可以是其它气体)由风机经流量计送入比热仪主体,经加热、均流、旋流、混流后流出。
在此过程中,分别测定:空气在流量计出口处的湿球温度t w(℃)和干球温度t0(℃);气体经比热仪主体的进出口温度t1、t2(℃、℃);电加热器的输入电压U(V)和输入电流I(A);气体的体积流量q v(m3/s)以及实验时相应的大气压p b(Pa)和流量计出口处的表压p e(Pa)。
山东大学通讯原理第一次实验报告

通讯原理第一次实验报告1 DDS信号源使用实验人员:同组人员:一、实验目的1.了解DDS信号源的工作原理;2.掌握RZ9681实验平台DDS信号源使用方法;3.理解DDS信号源各种输出信号的特性;4.配合示波器完成系统测试。
二、实验仪器1.RZ9681实验平台2.实验模块:主控模块3.100M双通道示波器三、实验原理1.DDS信号产生原理直接数字频率合成(DDS—Digital Direct Frequency Synthesis),是一种全数字化的频率合成器,由相位累加器、波形ROM、D/A转换器和低通滤波器构成。
时钟频率给定后,输出信号的频率取决于频率控制字,频率分辨率取决于累加器位数,相位分辨率取决于ROM 的地址线位数,幅度量化噪声取决于ROM的数据位字长和D/A转换器位数。
图2.1.1.1 DDS信号源产生原理信号源由主控模块上的M4芯片内置的DA产生,M4产生的函数信号经直流交流电路转换和驱动电路驱动从DDS1锚孔输出。
幅度调节旋钮控制输出信号幅度,频率调节旋钮控制输出信号频率,旋钮左右旋转时产生脉冲信号,M4检测到后调整DA的速率(改变信号频率)和数字电位器阻值(改变输出幅度);信号种类:正弦、方波、三角、半波、全波、复合信号等;频率:0-200KHZ,幅度:10V(峰峰值)。
抽样脉冲采用M4的PWM功能实现,脉冲的频率和占空比可调(鼠标),脉冲频率:0-99KHZ,占空比12.5%-87.5%;经直流交流转换电路从P01输出。
2.DDS信号操作设置主控模块可以提供两路DDS信号源,分别是低频信号源DDS1和高频信号源DDS2,其中DDS2信号源除了作为调幅和调频的载波输出外,其他功能暂时保留。
实验中主要用到的是DDS1信号源,DDS1信号源可以生成各种类型的信号,提供可调的频率、幅度。
四、实验内容及步骤1.加电打开系统电源开关,底板的电源指示灯正常显示。
若电源指示灯显示不正常,请立即关闭电源,查找异常原因。
山东大学本科毕业论文(设计)开题报告模板

山东大学
本科毕业论文(设计)开题报告
山东大学本科生院制
毕业论文(设计)写作计划
(2022年1月7日至2022年5月8日)
各阶段工作
时间
论文(设计)各阶段工作内容及要求检查方式检查情况
2021年1月-2月
2021年2月-3月
2021年3月-4月
2021年4月-5月
资料查阅阶段:查阅论文撰写和数值计
算相关的资料论文,重点在于不同围岩支护
参数数值计算模型构建方法和隧道开挖后围
岩变形和应力分布规律,为毕业论文提供理
论基础。
软件学习阶段:学习使用3DEC进行不
同围岩支护参数的数值计算模型构建和网格
划分,学习3DEC软件进行该模型下隧道开
挖的数值计算。
数值计算阶段:通过实验设计方法,研
究含断层隧道施工过程围岩变形和应力分布
规律,揭示衬砌厚度和弹性模量,锚杆间距
和长度对隧道围岩变形及应力分布的影响规
律。
论文撰写阶段:论文内容、结构、引用
等符合学术规范。
论文旨在分析含断层隧道
施工过程围岩变形和应力分布规律,揭示衬
砌厚度和弹性模量,锚杆间距和长度对隧道
围岩变形及应力分布的影响规律。
论文笔记
模型建立
模拟结果
PPT汇报
通过
通过
通过
通过。
现代数值分析详解

工程数值分析题解
学习方法
1.注意掌握各种方法的基本原理
2.注意各种方法的构造手法
3.重视各种方法的误差分析
4.做一定量的习题 5.注意与实什么? 研究使用计算机求解各种数学问题的 数值方法(近似方法),对求得的解的 精度进行评估,以及如何在计算机上实 现求解等
In 1 I n 1 5 5n
( n 8, 7, ,1)
算法的优劣:
评价标准:(1) 计算量的大小
n n1 P ( x ) a x a x a n1x an 例:计算 n 0 1
直接计算:需 n ( n +1)/2 次乘法和 n 次加法。 迭代计算:P n ( x) {[(a 0 x a1 ) x a2 ]x a n1}x an 按下列迭代公式计算
u0 a0 uk x uk 1 ak P ( x) u n n , k 1, 2, , n
只需 n 次乘法和 n 次加法。
(2) 存储量的多少 (3) 逻辑结构是否简单
二、数值分析的特点
1. 近似:由此产生“误差” 在计算数学和应用数学中一个有趣的问题: 什么是零? 1 原点附近
2. 与计算机不能分离:上机实习(掌握一 门语言:C语言,会用Matlab)
1.2 误差
( Error )
§1 误差的背景介绍 ( Introduction ) 1. 来源与分类 ( Source & Classification )
模型误差 ( Modeling Error ): 从实际问题中抽象出数学模型 观测误差 ( Measurement Error ): 通过测量得到模型中参数 的值 方法误差 (截断误差 Truncation Error): 求近似解。求解数 学模型时,用简单代替复杂,或者用有限过程代替无限过程所引 起的误差 舍入误差 ( Roundoff Error ): 机器字长有限,通常用四舍五 入的办法取近似值,由此引起的误差.
电力系统数值仿真计算与分析

教育部重点实验室
27
山东大学电气工程学院
(1)6阶模型——次暂态模型
ud
(Ed"XΒιβλιοθήκη " qiq
)
ra id
uq
(
E
'' q
X
'' d
id
)
ra iq
Td' 0
dEq' dt
Ef
Xd
X
' d
Xl Xl
Eq'
Xd
X
' d
X
' d
Xl
E
'' q
(Xd
X
' d
)(X
" d
X
' d
Xl
X l ) id
Tq'0
dEd' dt
Xq Xl
X
' q
Xl
Ed'
Xq
X
' q
X
' q
Xl
E d''
(Xq
X
' q
)(X
" q
X
' q
Xl
Xl
)
iq
T '' d0
dEq'' dt
X
" d
X
' d
X X
L L
T '' d0
dEq' dt
Eq''
f (xn ) h2 2!
xn
数值计算方法

1979 9.李岳生,黄友谦.数值逼近.北京:人民教育出版社,1978 10.张宜华.精通 MATIAB 5.北京:清华大学出版社,1999 11.王沐然.MATLAB 5.X 与科学计算.北京:清华大学出版社,2000 12.徐士良.C 常用算法程序集(第二版).北京:清华大学出版社,1996
Ax b
i 2,3, , n
参考书目:
1. 武汉大学、山东大学计算数学教研室.计算方法.北京:人民教育出版社,
1979 2.李庆扬,关治,白峰杉.数值计算原理.北京:清华大学出版社,2000 3.易大义,沈云宝,李有法.计算方法.杭州:浙江大学出版社,1989 4.杨大地,谈骏渝.实用数值分析.重庆:重庆大学出版社,2000 5.蔡大用,白峰杉.现代科学计算.北京:科学出版社,2001 6.关治,陆金甫.数值分析基础.北京:高等教育出版社,1998 7.Richard L.Burden,J.Douglas Faires.NUMERICAL ANALYSIS(Seventh
*4.计算矩阵特征值问题的幂法 5.迭代法的加速
4
ቤተ መጻሕፍቲ ባይዱ
3
第四章 数值积分和数值微分
1.Newton-Cotes公式 2.复合求积法 3.Romberg算法 *4.Gauss求积法 5.数值微分
第五章 常微分方程的数值解法
1.引言
2.Runge-Kutta法
*3.线性多步法
4.常微分方程组和高阶微分方程简介
第六章 逐次逼近法
1.基本概念 2.线性方程组的迭代法 3.非线性方程组的迭代法
山东大学数值计算实验报告2
山东大学计算机科学与技术学院数值计算课程实验报告2.(1)用MATLAB写出楚列斯基分解函数代码如下所示Cholesky.mfunction [ B ] = Cholesky(A )%UNTITLED2 此处显示有关此函数的摘要% 楚列斯基分解B = A;n = length(A);for k = 1:nB(k,k) = sqrt(B(k,k));for i = k+1:nB(i,k) = B(i,k)/B(k,k);endfor j = k+1:nfor i = k+1:nB(i,j) = B(i,j)-B(i,k)*B(j,k);(3)计算范数和条件数代码如下f222.mfunction [ ] = f222(n )conda1 = fanshua1*max(a)fprintf('%s\n','2范数下矩阵A的2条件数') B = A_'*A_;[v d] = eig(B);conda2 = sqrt(max(max(d)))*fanshua2fprintf('%s\n','无穷范数下矩阵A的条件数') for i = 1:nfor j = 1:nsum = sum + abs(A_(i,j));enda(i) = sum;sum = 0;endconda3 = max(a)*fanshua3endtest222.mclc,clearfprintf('%s\n','n = 2时')f222(2)fprintf('%s\n','n = 5时')f222(5)fprintf('%s\n','n = 10时')f222(10)运行结果截图如下所示3.(1)Jacobi迭代法MATLAB实现代码如下D(i,i)=A(i,i);end;L=-tril(A,-1);U=-triu(A,1);while error>=errorBound & step<maxSp x0=inv(D)*(L+U)*x0+inv(D)*b;vChain(k,:)=x0';k=k+1;error=norm(x0-fx0);fx0=x0;step=step+1;endv=x0;sN=step;可见Jacobi迭代了3次得到的解为x=[111],收敛。
山东大学 液液传热实验 数据处理
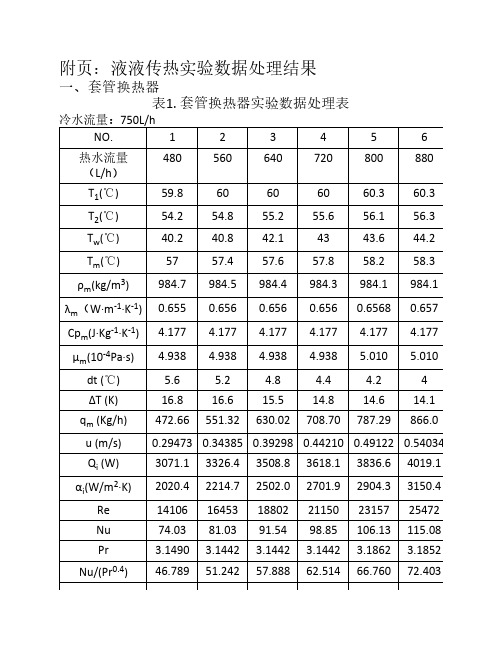
附页:液液传热实验数据处理结果一、套管换热器表1. 套管换热器实验数据处理表冷水流量:750L/hNO.123456480560640720800880热水流量(L/h)T1(℃)59.860606060.360.3T2(℃)54.254.855.255.656.156.3 T w(℃)40.240.842.14343.644.2 T m(℃)5757.457.657.858.258.3ρm(kg/m3)984.7984.5984.4984.3984.1984.1λm(W·m-1·K-1)0.6550.6560.6560.6560.65680.657 Cp m(J·Kg-1·K-1) 4.177 4.177 4.177 4.177 4.177 4.177μm(10-4Pa·s) 4.938 4.938 4.938 4.938 5.010 5.010 dt (℃) 5.6 5.2 4.8 4.4 4.24ΔT (K)16.816.615.514.814.614.1 q m (Kg/h)472.66551.32630.02708.70787.29866.0 u (m/s)0.294730.343850.392980.442100.491220.54034 Q i (W)3071.13326.43508.83618.13836.64019.1αi(W/m2·K)2020.42214.72502.02701.92904.33150.4 Re141061645318802211502315725472Nu74.0381.0391.5498.85106.13115.08Pr 3.1490 3.1442 3.1442 3.1442 3.1862 3.1852 Nu/(Pr0.4)46.78951.24257.88862.51466.76072.403ln(Re)9.5549.7089.8429.95910.05010.145 ln[Nu/(Pr0.4)] 3.8457 3.9366 4.0585 4.1354 4.2011 4.2822注:1.ρm、λm、Cp m、μm均根据近似Tm值查表得到2. 相关计算过程详见实验报告“数据处理”部分①根据表1的对流传热系数αi和雷诺准数Re的数值,绘制出它们之间的关系曲线②求算出关联式Nu=C·Re m·Pr0.4中常数C、m的值对ln(Nu/Pr0.3)~ln(Re)作图,该直线的斜率即为m,截距即为lnC。
HJB偏微分方程的数值计算

山东大学硕士学位论文HJB偏微分方程的数值计算姓名:曹海峰申请学位级别:硕士专业:概率论与数理统计指导教师:赵卫东20090507HJB偏微分方程的数值计算作者:曹海峰学位授予单位:山东大学1.学位论文吕峰推广的Lipschitz条件下的倒向随机微分方程及g—期望2004该文主要讨论了在一类推广的Lipschitz条件下的倒向随机微分方程和g期望及其相关性质.这个限制使得我们无法将倒向随机微分方程的相关理论应用于一个更广的范围.该文中,我们假设g满足如下形式的一类推广的Lipschitz条件:|g(t,y<,1>,z<,1>)-g(t,y<,2>,z<,2>)|≤r<,t>|y<,1>-y<,2>|+μ<,t>|z<,1>-z<,2>|在此假设之下,得到了倒向随机微分方程解的存在唯一性定理,相对于经典情况而言,在这种情形中,该文的结果对于解的可积性有一个更严格的要求;进一步的,该文还得到了在此条件之下的比较定理.以此为基础,类似于经典情形,定义了相应的g-期望,并以此为工具,得到了在此假设之下的倒向随机微分方程的逆比较定理.2.学位论文杨维强倒向随机微分方程和非线性期望在金融中的应用:风险度量,定价机制的估计以及期权定价2006倒向随机微分方程(BSDE)的线性形式首先由Bismut(1973)在引入,1990年Pardoux&Peng(1990)研究了Lipschitz条件下非线性倒向随机微分方程解的存在唯一性定理。
Duffie&Epstein(1992b)在研究随机微分效用过程中也独立地引进了一类倒向随机微分方程。
倒向随机微分方程在随机控制、偏微分方程、数理金融、经济等领域都有着广泛的应用。
经典的期望是一个线性泛函,在线性期望和可加测度之间存在一一对应的关系。
但是这种一一对应的关系在非线性情形下并不成立,一般地,给定一个非线性期望,我们仍然可以导出一个非可加概率测度,但是却存在无穷多的非线性期望满足这一关系。
山东大学数学系教科书目录

山东大学数学系教科书目录一、初等数学1、初等数学(一)2、初等数学(二)3、高等数学(一)4、高等数学(二)5、数学分析(一)6、数学分析(二)7、数学分析(三)8、概率论与数理统计9、线性代数(一)10、线性代数(二)11、微积分12、微分方程13、椭圆型微分方程14、复变函数15、定积分与欧拉积分16、无穷积17、常微分方程与泛函微分方程18、常微分方程上的特殊解19、插值与拟合、数值分析20、向量论21、实变函数论22、函数论二、高等数学1、常微分方程2、泛函微分方程3、实变函数4、积分变换与积分系统5、泛函分析6、重积分与调和级数7、几何与向量论8、定性理论9、线性系统10、傅里叶级数11、矩阵分析12、动力系统13、幾何学三、理论数学1、组合论2、抽象代数3、群论4、余环论5、环论6、整数论7、拓扑学8、复变函数论9、函数空间论10、数理逻辑11、数论12、模论四、工程数学1、统计学2、微分方程与数值分析3、概率论及其应用4、随机数学5、矩阵加速法6、特征值问题及其应用7、Lyapunov不稳定性定理及其应用8、大数定律及其应用9、最优控制10、故障诊断理论及其应用11、算法分析及其应用12、统计识别13、多模式计算14、特殊函数干扰理论五、信息论1、数字信号处理2、数字通信3、信息论4、数据通讯5、隐私保护与数据科学6、机器学习7、安全技术8、数据挖掘六、数值分析1、数值算法2、无穷矩阵分析3、多元数值积分4、随机数值分析5、标量、矢量与矩阵数值算法6、并行计算、移动计算和存储7、最优化算法8、实际运算技术参考文献1、微积分手册2、数学分析手册3、数理统计与编程语言手册4、线性代数手册5、概率论与统计机器学习6、数值分析基础7、数值计算技术。
山东大学《matlab程序设计》期末作业

《Matlab 程序设计》 期末作业学院: 专业: 班级:学号: 姓名: 成绩:一 、 简答题(每题10分,共50分)1、假设有两个矩阵A 和B ,请用这两个矩阵说明Matlab 数值计算中的“左除”与“右除”有什么区别?2、脚本M 文件与函数M 文件的主要区别是什么?3、设矩阵A=[1 4 3 9;5 30 12 42;2 18 32 15],试编程找出A 中所有大于或等于5的元素,并把这些元素组成一个列向量,并计算出这些元素的总和(注意附上标注说明)4、利用Matlab 编写程序求取335lim 21x x x →∞++和120()t t dt -⎰,并对求取结果进行分子和分母的提取(注意附上标注说明)。
5、利用Matlab 编写程序求微分方程x e y y y x 2cos 52=+'-''的通解。
二、 综合题(每题20分,共40分)1、在同一张图上分别画出两组坐标)10,,2,1(),4,(),,(3222 =+i i i i i i 的散点图和折线图。
要求只能利用plot 命令进行绘制,X 坐标范围[0,105] ,Y 坐标范围[0,1450]。
2、已知学生的名字和百分制分数。
编写相应的程序要求输入所有学生的百分制分数后,一次性判断每个学生的成绩分别是“满分”、“优秀”、“良好”、“及格”还是“不及格”,并要求最后用单元数组按行分别输出每个学生的名字、分数和成绩判断结果。
学生姓名 Jack Marry Peter Rose Tom成 绩 72 83 56 94 100判断标准:满分(100),优秀(90-99),良好(80-89),及格(60-79),不及格(<60)三、 论述题(共10分)浅谈一下Fortran 、matlab 、maple 和mathematic 这四种计算语言的特点和区别。
山东大学空气绝热指数测定实验

实验二 空气绝热指数测定一、实验目的1. 通过测量空气绝热膨胀和定容加热过程中压力变化,计算空气绝热指数;2. 理解绝热膨胀过程和定容加热过程以及实验装置的使用方法。
二、实验原理1. 气体的绝热指数定义:气体的比定压热容与比定容热容之比,即k =c p c v。
2. 本实验利用定量空气在绝热膨胀过程和定容加热过程中的变化规律来测定空气的绝热指数k 。
实验过程的p-v 图如图1所示。
图中A-B (Ⅰ-Ⅱ)为绝热膨胀过程;B-C (Ⅱ-Ⅲ)为定容加热过程。
图1 实验过程p-v 图AB 为绝热过程,1122k kp v p v = (1)BC 为定容过程,23v v = (2)假设状态A 和C 温度相同,则T 1=T 3。
根据理想气体的状态方程,对于状态A 、C 可得:1133p v p v = (3)将(3)式两边k 次方得:()()1133kkp v p v = (4)由(1)、(4)两式得,1132kp p p p ⎛⎫= ⎪⎝⎭,再两边取对数,得:1213ln ln p p k p p ⎛⎫ ⎪⎝⎭=⎛⎫ ⎪⎝⎭(5)因此,只要测出A 、B 、C 三状态下的压力p 1、p 2、p 3且将其代入(5)式,即可求得空气的绝热指数k 。
三、实验装置空气绝热指数测定仪由刚性密闭容器、数显压力表、气泵,排气阀和温度传感器组成,实验装置简图如下图2所示:图2 实验装置简图1.可调式静音气泵2.进气电磁阀3.数显电压力表4.气源温度5.喷塑安装桌6.刚性密闭容器7.弹簧式安全阀8.排气阀四、实验步骤1. 气密性检查。
通过进气开关和气泵开关对刚性容器充气,使数显压力表数值达到2000 Pa 左右,5分钟后再观察数显压力表数值是否发生变化。
若不变化,说明气密性满足要求。
若变化,说明装置漏气。
若漏气,检查管路连接处,排除漏气故障。
此步骤需严格执行,否则将给实验结果带来较大的误差。
2. 向大容器内充气达到状态A点。
山东大学数值计算实验报告3

2.1.2 直接解方程组
fprintf('%s\n','n=2 时,解法 2');
x12 = H1\b1
运行结果如下:
2.2 当 n=5 时
%生成 n=5 时希尔伯特矩阵 H2=zeros(5,5); n2=5; for i = 1:5 for j = 1:5 H2(i,j) = 1/(i+j-1); end end fprintf('%s\n','n=5 时,解法 1:'); L2=c_1(H2,n2)%楚列斯基函数得到 L %得到 b t2=ones(5,1); b2=H2*t2; %利用之前实验 2 所写的前代,后代函数得到答案 front2 = a_3_a( L2,b2 ); x21 = a_3_b(L2',front2)
%当 n=10 时 fprintf('%s\n','当 n=10 时,该矩阵的 1 范数及 1 范数下的条件数为:'); fan31 = norm(H3,1) cond31 = cond(H3,1) fprintf('%s\n','当 n=10 时,该矩阵的 2 范数及 2 范数下的条件数为:'); fan32 = norm(H3,2) cond32 = cond(H3) fprintf('%s\n','当 n=10 时, 该矩阵的无穷范数及无穷范数下的条件数为: '); fan33 = norm(H3,inf) cond33 = cond(H3,inf)
运行结果如下:
fprintf('%s\n','n=10 时,解法 2'); x32 = H3\b3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
K^
AOSNO e
5
i
+'
,/ * h
L g i
f
,' l g0
,/ *
f 3 *3 +h w
h
p
i ~ KLh hl :KMYLS h h 5 wt A l h h o e d K^
h AOSNO h
A h h d K^
e u AOSNO g h
h
:KMYLS w f e
K] KL wi ^XM]SYX G %U 3 K^ JAOSNO % )w X 3 SbO 5%* 1 3 )1 U3) _RS O
XY[ 5 L %+ 4[ Y[ S3*0X ^ )3)1 Y[ T3*0X S S33T MYX]SX^O1 OXN ^ ) 3 ^ ) 5 S%T T%* 1 OXN S%* 3 L S%* ^ ) (5 S%S 1 OXN U 3 U *1 i f.g p k
OXN Ø e f-g Ø iA _ h Ø _ A A i mp K^ AOSNO K^ AOSNO h K^ AOSNO mh ~ e h
e K] KL wi ^XM]SYX G %U 3A 5%L%[% )%_ % )w X 3 SbO 5%* 1
[ w
Ø f.g A Ø
J ^K 3 )1 3 )1 *3 )1 U3) _RS O XY[ 5 L %+ 4[ Y[ S3*0X ^ )3)1 Y[ T3*0X S S33T MYX]SX^O1 OXN ^ ) 3 ^ ) 5 S%T T%* 1 OXN J ^K S%* 3 L S%* ^ ) (5 S%S 1 S%* 3 * _ * S%* _ J ^K S%* 1 OXN *3 1 U 3 U *1 OXN i f.g p k e m :KMYLS d K^ AOSNO h e :KMYLS i k :KMYLS h w) h ~ h o h w hn [f g *) . h U h n i
w U*3.. e A w) h [ f U i
h g w U+
m
w
i
e
m
w
[f
g
A
[ i Ø hU3*). l [f
:KMYLS *). 10CJ
w ;+3*/
% h
_ _
h g i*)I .
K^ AOSNO .. 10CJ
w *'-). w *'-).e ni
A */ 10CJ
h:KMYLS A ld *' ,/ ,/ h
Ø f/g e su h i 5 h
m h 5 3L 5 wt i o h
h su e h 5o e h h t h ku
o
~
5 t k k o i
h h
u +' +i p f*g f+g f,g f-g f.g h f*g Ø
* K^ A AOSNO h h f*gcf.g ~X u
:KMYLS h h u i e i R3*( X * % e
i
^ ) 5 S%T * T%* 1 OXN S%* 3 L S%* ^ ) (5 S%S 1 OXN U 3 U *1 *3 1 OXN f-g Ø n + fw w10 h g i
CJ
OXN ^ ) 3
h h h h o m
Ø
m o n x ~ [)e h U hku h w
i i
f.g
Ø
i [) w *) . e ku“ ” h wku e o h Uw ku“ ” o f X >K>g h h ~ h ku p lu h w i −2" + $ + 5& = 15 (1) 4" − 8$ + & = −21 (2) 4" − $ + & = 7 (3) m h n fw h m CJ w10 g i
f,g
f+g h m h =5B<56 h n i ^XM]SYX G %U 3 :KMYLS 5%L%[% ) [ w % )w h U ww [ X 3 SbO 5%* 1 * 3 )1 z 3 )1 U3) _RS O XY[ 5 L %+ 4[ Y[ S3*0X ^ )3)1 Y[ T3*0X S S33T MYX]SX^O1
e
h
i 17?@,H − 217,H + 17C@,H 17,H?@ − 217,H + 17,HC@ + = 0 8, : = 1,2, … , < ℎK ℎK ku X X u h ni 417,H − 17C@,H − 17?@,H − 17,HC@ − 17,H?@ = 0 8, : = 1, … , < Ø h 17,HC@ w n h ~ um h h 17C@,H =5B<56
e AOSNO e
mp :KMYLS
h h K^ AOSNO h h K^ AOSNO h n S h XfX2Sg h ~ ~S e ~ u "7>?@ Ø = D7 −
>?@ HM7 G7H "H
uk u :KMYLS i h h h −
> HL7 G7H "H
k k
mk wi
G77 5%L%[% ) [ w
Ø >% h i
i:KMYLS h h h ~ 5 3Lh =w h x p5 h< 5 t nl t i=3 %>3 < ' " >?@ = BC@ (D − (E + F)" > ) m wi " (>?@) = D7 −
(>) 7IH G7H "H
i53= ml
G77
8 = 1,2, … , <
i ^XM]SYX G5%L 3M[OK]OJ<KZ KMO X% O ]% Y_%[S R]%^Z X wk u 1 O ]% Y_%[S R]%^Z w d nd dm 1 5w %L w 6 G*0X %G*0X 3)1 y 3X X1 5 G*0 %G*0 3)1 L *0 3)1 Y[ U3*0 5 U%U 3-1 wG %a 3 O]D La U%X 1 S *4) b3 O] LaD *%a%X 5 U%b 3 *1 O O L U 3L U O ]1 OXN S a *4) b3 O] LaD %a *%X 5 U%b 3 *1 O O L U 3L U Y_1 OXN S *2X * b3 O] LaD *%a%X 5 U%b 3 *1 O O L U 3L U [S R]1 OXN S a2X b3 O] LaD %a *%X
U 1
w %a
1
1
1
5 U%b 3 *1 O OXN OXN L3L X3/ h o h O L U 3L U ^Z1
Ø
,/ * e
L
,/ ,/ n i ~ h
h
m
w
pL
m w f+g h pA f,g Ø
5 k :KMYLS p K^ K^ i:KMYLS AOSNO AOSNO ku f.g k e p K^
m
w
i
e
m
w
[f
g
:KMYLS
i Ø
[ hU3*). K^ AOSNO w) [f U h
i ~ w * g *) h
w *). e k h h .
K^ o h n h n
AOSNO h
w U*
i
m
w
i
e
m
w
[f
g
K^
AOSNO
i Ø A
[ hU3.. i h h .
k o h n h n
~ w + *) h
r
i+)*.)),)**-i ii :KMYLSd K^ AOSNO dA i
i i
i
+)*.
*
i =5B<56+)*-K p i kd i *' :KMYLS 4" − $ + & = 7 (1) 4" − 8$ + & = −21 (2) −2" + $ + 5& = 15 (3) j d *g,g s h h f*g f,g h
f*g f+g f,g f-g f.g +'
i m 122 + 133 = 0, 0 ≤ " ≤ 1 , 0 ≤ $ ≤ 1 n K h y m yk h L e wi("7 , $7 ) = 8ℎ, :ℎ , 8, : = 1,2, … , <.
h
X3/% f*g f+g
h :KMYLS K^ AOSNO
)
h e e
w
e
f,g f-g d *' p *i f*g
A h e
ni 7 − &> + $> 4 21 + 4 ∗ ">?@ + &> $>?@ = 8 15 + 2 ∗ "> − $> &>?@ = 5 i ">?@ =
f+g Ø ki
h h h h h i:KMYLS
