福建省2013届福州八中高三毕业班模拟考数学文科试卷

合集下载

福建省福州八中2013届高三高考模拟考试数学文试题含答案

福州八中2012-2013学年高三毕业班模拟考数学（文）试题考试时间:120分钟试卷满分：150分参考公式:回归直线方程：y bx a =+，其中1221,ni ii nii x y nx yb a y bx x nx==-==--∑∑ 锥体体积公式：13V Sh =, 其中S 为底面面积，h 为高;球的表面积公式：24S R π=；球的体积公式：343V R π=，其中R 为球的半径。

第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题,每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．设复数i z 21+=（i 是虚数单位），则复数z 的虚部为A ．2- B. 2C 。

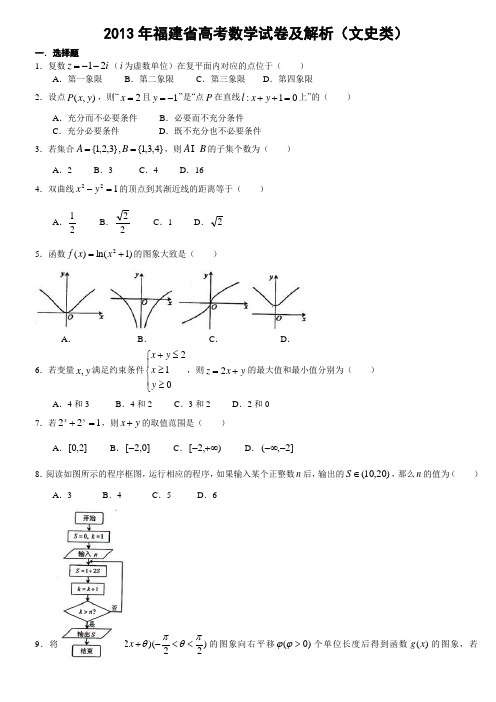
i 2- D.i 22．命题||||,:y x y x p <<则若，命题:q 若22abc c >，则a b >．则A ．“p 或q ”为真B ．“p 且q ”为真C ．p 真q 假D ．,p q 均为假 3．在递增等比数列{na }中，,2342=-=a a aA ．—1B ．1 C4．某程序框图如图所示，则该程序运行后输出的值是 A ．2B ．3C ．4D ．55。

下列说法中，正确的是A ．与定点F 和定直线的距离相等的点的轨迹是抛物线B ．抛物线x 2＝2my 的焦点坐标为错误!，准线方程为y ＝－错误!ks5uC ．准线方程为x ＝－4的抛物线的标准方程为y 2＝8xD ．焦准距（焦点到准线的距离)为p (p 〉0)的抛物线的标准方程为y 2＝±2px6。

若角α的终边与单位圆交于第三象限的一点P ，其横坐标为1010-,则=αtan A 。

31-B.31 C. 3- D 。

37. 如图正四棱锥(底面是正方形,顶点在底面的射影是底面的中心）P-ABCD 的底面边长为6cm ，侧棱长为5cm ，则它的侧视图的周长等于A 。

17cmB.cm 5119+C.16cmD.14cm8．设M 是平行四边形ABCD 的对角线的交点，O 为任意一点，则=+++OD OC OB OAA ．OMB ．OM 2C ．OM 3D ．OM 49．在长为10cm 的线段AB 上任取一点C ，现作一个矩形,邻边长分别等于线段AC 、CB 的长，则该矩形的面积大于224cm 的概率是A ．16B ．15C ．14D ．1310．在半径为a 的圆桌中心上方安装一吊灯,桌面上灯光的强度22sin r ky θ=，其中k 是常数，r 是灯与桌面上被照点的距离，是光线与桌面的夹角（如图），现为使桌边最亮，则θsin = A.23B.33C.32 D 。

2013届福州八中最后一卷(语文)

福州八中2012—2013高三毕业班模拟考语文试题考试时间：150分钟试卷满分：150分一、古代诗文阅读(27分)(一)默写常见的名句名篇(6分)1．补写出下列名句名篇中的空缺部分。

（6分）（1）民生各有所乐兮，。

（屈原《离骚》）（2）母孙二人，更相为命，。

（李密《陈情表》）（3）嗟夫！_________________，则足以拒秦。

（杜牧《阿房宫赋》）（4），只是朱颜改。

（李煜《虞美人》）（5），衣冠简朴古风存。

（陆游《游山西村》）（6）既加冠，。

（宋濂《送东阳马生序》）(二)文言文阅读(15分)阅读下面的文言文，完成2一5题。

阮裕，字思旷，以德业知名。

弱冠辟太宰掾。

大将军王敦命为主簿，甚被知遇。

裕以敦有不臣之心，乃终日酣觞，以酒废职。

敦谓裕非当世实才，徒．有虚誉而已，出为溧阳令，复以公事免官。

由是得违敦难，论者以此贵之。

咸和初，除尚书郎。

时事故之后，公私弛废，裕遂去职还家，居会稽剡县。

司徒王导引为从事中郎，固辞不就。

朝廷将欲征之，裕知不得已，乃求为王舒抚军长史。

舒薨，除吏部郎，不就。

即家拜临海太守，少．时去职。

司空郗鉴请为长史，诏征秘书监，皆以疾辞。

复除东阳太守。

寻征侍中，不就。

还剡山，有肥遁之志。

有以问王羲之，羲之曰：‚此公近不惊宠辱，虽古之沈冥①，何以过此！‛成帝崩，裕赴山陵，事毕便还。

诸人相与追之，裕亦审．时流必当逐己，而疾去，至方山不相及。

刘惔叹曰：‚我入东，正当泊安石渚下耳，不敢复近思旷傍。

‛裕虽不博学，论难甚精。

尝问谢万云：‚未见《四本论》，君试为言之。

‛万叙说既毕，裕以傅嘏为长，于是构辞数百言，精义入微，闻者皆嗟味之。

裕尝以人不须广学，正应以礼让为先故终日静默，无所修综，而物自宗焉。

在剡曾有好车，借无不给。

有人葬母，意欲借而不敢言。

后裕闻之，乃叹曰：‚吾有车而使人不敢借，何以车为？‛遂命焚之。

在东山久之，复征散骑常侍，领国子祭酒。

经年敦逼，并无所就。

御史中丞周闵奏裕及谢安违诏累载，并应有罪，禁锢终身，诏书贳②之。

福建省福州八中2013届高三高考模拟考试数学文试题

福州八中2012—2013学年高三毕业班模拟考数学(文)试题考试时间：120分钟试卷满分：150分参考公式：回归直线方程：y bx a =+，其中1221,ni ii nii x y nx yb a y bx xnx==-==--∑∑锥体体积公式：13V Sh =，其中S 为底面面积，h 为高；球的表面积公式：24S R π=；球的体积公式：343V R π=，其中R 为球的半径。

第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．设复数i z 21+=（i 是虚数单位），则复数z 的虚部为A ．2-B. 2C. i 2-D. i 22．命题||||,:y x y x p <<则若，命题:q 若22a bc c >，则a b >．则 A ．“p 或q ”为真 B ．“p 且q ”为真 C ．p 真q 假D ．,p q 均为假 3．在递增等比数列{n a }中，4,2342=-=a a a ，则公比q ＝ A ．-1 B ．1 C ．2D4．某程序框图如图所示，则该程序运行后输出的值是 A ．2 B ．3C ．4D ．55.下列说法中，正确的是A ．与定点F 和定直线的距离相等的点的轨迹是抛物线B ．抛物线x 2＝2my 的焦点坐标为⎝⎛⎭⎫0，m2，准线方程为y ＝－m2ks5u C ．准线方程为x ＝－4的抛物线的标准方程为y 2＝8xD ．焦准距(焦点到准线的距离)为p (p >0)的抛物线的标准方程为y 2＝±2px6.若角α的终边与单位圆交于第三象限的一点P ，其横坐标为1010-，则=αtanA. 31-B.31 C. 3- D. 37. 如图正四棱锥（底面是正方形，顶点在底面的射影是底面的中心）P-ABCD 的底面边长为6cm ，侧棱长为5cm ，则它的侧视图的周长等于A.17cmB.cm 5119+C.16cmD.14cm8．设M 是平行四边形ABCD 的对角线的交点，O 为任意一点，则=+++A ．B ．2C ．3D ．49．在长为10cm 的线段AB 上任取一点C ，现作一个矩形，邻边长分别等于线段AC 、CB 的长，则该矩形的面积大于224cm 的概率是 A ．16B ．15C ．14D ．1310．在半径为a 的圆桌中心上方安装一吊灯,桌面上灯光的强度22sin rk y θ=，其中k 是常数，r 是灯与桌面上被照点的距离，是光线与桌面的夹角（如图），现为使桌边最亮，则θsin =A.23B.33raӨC.32 D.22 11. 已知定义在R 上的函数)(x f 是偶函数，且满足)1()1(x f x f -=+，当[]1,1-∈x 时，21)(x x f -=，若函数x x g 5log )(=，则)()()(x g x f x h -=在区间（0,5]内的零点的个数是A ．2B ．3C ．4D ．512．若双曲线116922=-y x 渐近线上的一个动点P 总在平面区域16)(22≥+-y m x 内，则实数m 的取值范围是A. [3,3]-B. (,3][3,)-∞-⋃+∞C. [5,5]-D. (,5][5,)-∞-⋃+∞第Ⅱ卷（非选择题共90分）二、填空题：本大题共4小题，每小题4分，共16分，把答案填在相应横线上．13．函数y ＝sin (2x ＋π4)的图象可由函数y ＝sin 2x 的图象向左平移个单位长度而得到．14．设函数⎪⎩⎪⎨⎧<≥+-=3,23,)(2x x b x x x f x ，若函数)(x f 在R 上为增函数，则实数b 的取值范围是．15．若关于x 的不等式()21m x x x ->-的解集为{}12x x <<，则实数m 的值为．16．已知椭圆15922=+y x 上任意一点P ，21,A A 是椭圆的左、右顶点，设直线21,PA PA 斜率分别为21,PA PA k k ，则=⋅21PA PA k k ，现类比上述求解方法，可以得出以下命题：已知双曲线12222=-by a x 上任意一点P ，21,A A 是双曲线的左、右顶点，设直线21,PA PA 斜率分别为21,PA PA k k ，则=⋅21PA PA k k .三、解答题：（本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤.） 17．（本题满分12分）某校从参加高三模拟考试的学生中随机抽取60名学生，将其数学成绩(均为整数)分成六组[90,100)，[100,110)，…， [140,150]后得到如下部分频率分布直方图，观察图形的信息，回答下列问题：(1)求分数在[120,130)内的频率；(2)若在同一组数据中，将该组区间的中点值(如：组区间[100,110)的中点值为100＋1102＝105)作为这组数据的平均分，据此，估计本次考试的平均分；(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本，将该样本看成一个总体，从中任取2人，求至多有1人在分数段[120,130)内的概率． 18．（本题满分12分）已知()x x ωωcos ,sin 3-=，)cos ,(cos x x ωω=，0>ω，函数x f ∙=)(，且)(x f 的图像相邻两条对称轴间的距离为2π．（Ⅰ）求函数)(x f 的最小正周期和单调增区间；（Ⅱ）若∆ABC 的三条边a ，b ，c 所对的角分别为A,B,C 满足22cos a A bc =，求角A 的取值范围．ks5u19．（本题满分12分）如图，在三棱柱111C B A ABC -中，侧面⊥C C AA 11底面ABC ，211===AC C A AA ，O BC AB BC AB ,,⊥=为AC 的中点.⑴ 证明:⊥O A 1平面ABC ；⑵若E 是线段B A 1上一点，且满足1111121C B A ABC BCC E V V --=，求E A 1的长度.20．（本题满分12分）数列{}n a 的前n 项和2n n S an b =+，已知112a =，256a =．（1）求数列{}n a 的前n 项和n S ；（2）求数列{}n a 的通项公式；（3）设21nn a b n n =+-，求数列{}n b 的前n 项和n T ．21．（本题满分12分）已知椭圆2222:1x y C a b +=(0)a b >>的离心率为2，且过点(0,1)-．（Ⅰ）求椭圆C 的方程；O CBAC 1B 1A 1（Ⅱ）若过点(2,0)M 的直线与椭圆C 相交于两点A B 、，设P 为椭圆上一点，且满足OA OB tOP +=（其中O 为坐标原点），求整数t 的最大值．22．（本题满分14分）若斜率为k 的两条平行直线l ，m 与曲线C 相切并至少有两个切点，且曲线C 上的所有点都在l ，m 之间（也可在直线l ，m 上），则把l ，m 称为曲线C 的“夹线”，把l ，m 间的距离称为曲线C 在“k 方向上的宽度”，记为).(k d 已知函数()+3cos f x x x =.（Ⅰ）若点P 横坐标为0，求()f x 图象在点P 处的切线方程；（Ⅱ）试判断3y x =+和3y x =-是否是()f x 的“夹线”，若是，求(1)d ；若不是，请说明理由；（Ⅲ）求证：函数31()3F x x x =-+的图象不存在“夹线”.稿纸福州八中2012—2013学年高三毕业班模拟考数学（文）试题参考答案1-12、BACCB DDDBD CD13、π8 14、),2[+∞ 15、2 16、59-； 22b a17、解：(1)分数在[120,130)内的频率为1－(0.1＋0.15＋0.15＋0.25＋0.05)＝1－0.7＝0.3 …………3分 (2)估计平均分为x ＝95×0.1＋105×0.15＋115×0.15＋125×0.3＋135×0.25＋145×0.05＝121………………………6分(3)依题意，[110,120)分数段的人数为60×0.15＝9(人)．ks5u [120,130)分数段的人数为60×0.3＝18(人)．∵用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本， ∴需在[110,120)分数段内抽取2人，并分别记为m ，n ；在[120,130)分数段内抽取4人，并分别记为a ，b ，c ，d ；设“从样本中任取2人，至多有1人在分数段[120,130)内”为事件A ，则基本事件共有(m ，n )，(m ，a )，…，(m ，d )，(n ，a )，…，(n ，d )，(a ，b )，…，(c ，d )共15种．则事件A 包含的基本事件有(m ，n )，(m ，a )，(m ，b )，(m ，c )，(m ，d )，(n ，a )，(n ，b )，(n ，c )，(n ，d )共9种．∴P (A )＝915＝35. …………12分18、解：（I ）x x x x x f ωωωωcos cos cos sin 3)(-=∙= 2162sin 212cos 212sin 23-⎪⎭⎫ ⎝⎛-=--=πωωωx x x ……….2分 ∵)(x f 相邻两条对称轴的距离为2π，∴)(x f 最小正周期为π 由πωπ=22得1=ω. 函数2162sin )(-⎪⎭⎫ ⎝⎛-=πx x f ……………… 4分由Z k k x k ∈+≤-≤-　226222πππππ 得 36ππππ+≤≤-k x k∴函数)(x f 的单调增区间[3,6ππππ+-k k ] Z k ∈……………….6分（II ）∵22cos a A bc = 又由余弦定理A bc c b a cos 2222-+=．∴22cos 4c b A bc += , ∴21424cos 22=≥+=bc bc bc c b A 又∵A 为三角形内角，所以30π≤<A . …………………….12分19、解：(1) 211===AC C A AA ，且O 为AC 的中点，AC O A ⊥∴1，又侧面⊥C C AA 11底面ABC ，交线为AC ，O A 1AC 1A 面⊂，∴⊥O A 1平面ABC ………… 6分(2) 11111141121BCC A C B A ABC BCC E V V V ---==，因此141BA BE =，即B A E A 1143=，又在OB R 1A t ∆中，1,3,11==⊥BO O A OB O A ，可得E A B A 11,2则=的长度为23………… 12分 20、解：（1）由1112S a ==，得112a b =+；由21243S a a =+=，得4423a b =+． ∴223a b a b +=⎧⎨+=⎩，解得11a b =⎧⎨=⎩，故21n n S n =+ ………… 4分（2）当2n ≥时，2232212(1)(1)(1)11(1)n n n n n n n n n n a S S n n n n n n----++-=-=-==+++．由于112a =也适合221n n n a n n +-=+． ∴通项221n n n a n n +-=+ ………8分（3）21111(1)1n n a b n n n n n n ===-+-++．∴数列{}n b 的前n 项和1211111111122311n n n T b b b b n n n n -=++++=-+-++-+--+ 1111nn n =-=++……… 12分 21、解：（Ⅰ）由题知2c e a ==，所以22222212c a b e a a -===．即222a b =． OC BA C 1B 1A 1又因为过点(0,1)-，所以21b =，22a =．故C 的方程为1222=+y x ……3分（Ⅱ）由题意知直线AB 的斜率存在.设AB ：(2)y k x =-，11(,)A x y ，22(,)B x y ，(,)P x y ，由22(2),1.2y k x x y =-⎧⎪⎨+=⎪⎩得2222(12)8820k x k x k +-+-=. 422644(21)(82)0k k k ∆=-+->，212k < ………………5分2122812k x x k +=+，21228212k x x k -=+∵OA OB tOP +=，∴1212(,)(,)x x y y t x y ++=，21228(12)x x k x t t k +==+， 1212214[()4](12)y y k y k x x k t t t k +-==+-=+. ………………8分∵点P 在椭圆上，∴222222222(8)(4)22(12)(12)k k t k t k -+=++， ∴22216(12)k t k =+2222161616422112222k t t k k==<=<<+++，则-， ………………11分∴t 的最大整数值为1. ……………………12分 22、解：（Ⅰ）由'()13sin f x x =-，'(0)13sin 01k f ==-=， (0)0+3cos03f ==，所以P 坐标为(0,3)P ，∴()f x 图象在点P 处的切线方程是30y x -=-即3y x =+ …………3分（Ⅱ）3y x =+和3y x =-是()f x 的“夹线”. …………4分由（Ⅰ）知3y x =+是()f x 图象在点P 处的切线，切点为（0,3）. '()13sin 1f x x =-=，∴ sin 0x =.当2x π=时，2+3y π=，(2)2+3cos 22+3f ππππ==， ∴+ππ（2，23）是函数3y x =+和()+3cos f x x x =图象的另一个切点. 3y x =+和()+3cos f x x x =的图象相切且至少有两个切点. 同理，（π，π-3），（π3，π3-3）是3y x =-和()+3cos f x x x =图象的两个切点因此，两条平行直线与曲线相切并至少有两个切点。

福州八中届高三高考模拟考试数学试题及答案(文)

福州八中2012—2013学年高三毕业班模拟考数学(文)试题考试时间：120分钟试卷满分：150分参考公式：回归直线方程：y b x a =+，其中1221,ni i i ni i x y n x yb a y b xx n x==-==--∑∑锥体体积公式：13V S h=，其中S 为底面面积，h 为高；球的表面积公式：24S Rπ=；球的体积公式：343V R π=，其中R 为球的半径。

第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．设复数i z 21+=（i 是虚数单位），则复数z 的虚部为A ．2-B. 2C. i 2-D. i 22．命题||||,:y x y x p <<则若，命题:q 若22a b cc>，则ab>．则A ．“p 或q ”为真B ．“p 且q ”为真C ．p 真q 假D ．,p q 均为假 3．在递增等比数列{n a }中，4,2342=-=a a a ，则公比q ＝A ．-1B ．1C ．2D ．214．某程序框图如图所示，则该程序运行后输出的值是 A ．2 B ．3C ．4D ．55.下列说法中，正确的是A ．与定点F 和定直线的距离相等的点的轨迹是抛物线B ．抛物线x 2＝2my 的焦点坐标为⎝⎛⎭⎫0，m 2，准线方程为y ＝－m2C ．准线方程为x ＝－4的抛物线的标准方程为y 2＝8xD ．焦准距(焦点到准线的距离)为p (p >0)的抛物线的标准方程为y 2＝±2px6.若角α的终边与单位圆交于第三象限的一点P ，其横坐标为1010-，则=αtanA. 31-B.31 C. 3- D. 37. 如图正四棱锥（底面是正方形，顶点在底面的射影是底面的中心）P-ABCD 的底面边长为6cm ，侧棱长为5cm ，则它的侧视图的周长等于A.17cmB.cm 5119+C.16cmD.14cm8．设M 是平行四边形ABCD的对角线的交点，O 为任意一点，则=+++OD OC OB OAA ．OMB ．OM 2C ．OM 3D ．OM 49．在长为10c m 的线段AB 上任取一点C ，现作一个矩形，邻边长分别等于线段AC 、CB 的长，则该矩形的面积大于224c m 的概率是 A ．16B ．15C ．14D ．1310．在半径为a 的圆桌中心上方安装一吊灯,桌面上灯光的强度22sin rky θ=，其中k 是常数，r 是灯与桌面上被照点的距离，是光线与桌面的夹角（如图），现为使桌边最亮，则θsin =A.23 B.33C.32D.2211. 已知定义在R 上的函数)(x f 是偶函数，且满足)1()1(x f x f -=+，当[]1,1-∈x 时，21)(xx f -=，若函数xx g 5log)(=，则)()()(x g x f x h -=在区间（0,5]内的零点的个数是A ．2B ．3C ．4D ．512．若双曲线116922=-yx渐近线上的一个动点P 总在平面区域16)(22≥+-y m x 内，则实数m 的取值范围是A. [3,3]-B. (,3][3,)-∞-⋃+∞C. [5,5]-D. (,5][5,)-∞-⋃+∞raӨ第Ⅱ卷（非选择题共90分）二、填空题：本大题共4小题，每小题4分，共16分，把答案填在相应横线上． 13．函数y ＝sin (2x ＋π4)的图象可由函数y ＝sin 2x 的图象向左平移个单位长度而得到．14．设函数⎪⎩⎪⎨⎧<≥+-=3,23,)(2x x b x x x f x ，若函数)(x f 在R 上为增函数，则实数b 的取值范围是．15．若关于x 的不等式()21m x x x ->-的解集为{}12x x <<，则实数m 的值为．16．已知椭圆15922=+yx上任意一点P ，21,A A 是椭圆的左、右顶点，设直线21,PAPA 斜率分别为21,PA PA k k ，则=⋅21PA PA k k ，现类比上述求解方法，可以得出以下命题：已知双曲线12222=-by ax 上任意一点P ，21,A A 是双曲线的左、右顶点，设直线21,PA PA 斜率分别为21,PA PA k k ，则=⋅21PA PA k k .三、解答题：（本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤.）17．（本题满分12分）某校从参加高三模拟考试的学生中随机抽取60名学生，将其数学成绩(均为整数)分成六组[90,100)，[100,110)，…， [140,150]后得到如下部分频率分布直方图，观察图形的信息，回答下列问题：(1)求分数在[120,130)内的频率；(2)若在同一组数据中，将该组区间的中点值(如：组区间[100,110)的中点值为100＋1102＝105)作为这组数据的平均分，据此，估计本次考试的平均分；(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本，将该样本看成一个总体，从中任取2人，求至多有1人在分数段[120,130)内的概率． 18．（本题满分12分）已知()xx a ωωcos ,sin 3-=，)cos ,(cosx x b ωω=，0>ω，函数b a x f ∙=)(，且)(x f 的图像相邻两条对称轴间的距离为2π．（Ⅰ）求函数)(x f 的最小正周期和单调增区间；（Ⅱ）若∆ABC 的三条边a ，b ，c 所对的角分别为A,B,C 满足22cos a A bc =，求角A 的取值范围．19．（本题满分12分）如图，在三棱柱111C B A ABC -中，侧面⊥C C AA 11底面A B C ，211===AC C A AA ，O BC AB BC AB ,,⊥=为AC 的中点.⑴ 证明:⊥O A 1平面ABC ； ⑵若E 是线段BA 1上一点，且满足1111121C B A ABCBCCE V V --=，求E A 1的长度.20．（本题满分12分）数列{}n a 的前n 项和2n nS a n b=+，已知112a =，256a =．（1）求数列{}n a 的前n 项和n S ；（2）求数列{}n a 的通项公式；（3）设21nn a b n n =+-，求数列{}n b 的前n 项和n T ．21．（本题满分12分）已知椭圆2222:1x y C ab+=(0)a b >>的离心率为2，且过点(0,1)-．（Ⅰ）求椭圆C 的方程；（Ⅱ）若过点(2,0)M 的直线与椭圆C 相交于两点A B 、，设P 为椭圆上一点，且满足O A O B t O P +=（其中O 为坐标原点），求整数t 的最大值．22．（本题满分14分）若斜率为k 的两条平行直线l ，m 与曲线C 相切并至少有两个切点，且曲线C 上的所有点都在l ，m 之间（也可在直线l ，m 上），则把l ，m 称为曲线C 的“夹线”，把l，m 间的距离称为曲线C 在“k 方向上的宽度”，记为).(k d 已知函数()+3c o s f x x x =. （Ⅰ）若点P 横坐标为0，求()f x 图象在点P 处的切线方程；（Ⅱ）试判断3y x =+和3y x =-是否是()f x 的“夹线”，若是，求(1)d ；若不是，请说明理由；（Ⅲ）求证：函数31()3F x x x=-+的图象不存在“夹线”.O CBAC 1B 1A 1数学（文）试题参考答案1-12、BACCB DDDBD CD 13、π814、),2[+∞ 15、2 16、59-；22b a17、解：(1)分数在[120,130)内的频率为1－(0.1＋0.15＋0.15＋0.25＋0.05)＝1－0.7＝0.3 …………3分 (2)估计平均分为x ＝95×0.1＋105×0.15＋115×0.15＋125×0.3＋135×0.25＋145×0.05＝121………………………6分(3)依题意，[110,120)分数段的人数为60×0.15＝9(人)． [120,130)分数段的人数为60×0.3＝18(人)．∵用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本， ∴需在[110,120)分数段内抽取2人，并分别记为m ，n ；在[120,130)分数段内抽取4人，并分别记为a ，b ，c ，d ；设“从样本中任取2人，至多有1人在分数段[120,130)内”为事件A ，则基本事件共有(m ，n )，(m ，a )，…，(m ，d )，(n ，a )，…，(n ，d )，(a ，b )，…，(c ，d )共15种．则事件A 包含的基本事件有(m ，n )，(m ，a )，(m ，b )，(m ，c )，(m ，d )，(n ，a )，(n ，b )，(n ，c )，(n ，d )共9种．∴P (A )＝915＝35. …………12分18、解：（I ）x x x x b a x f ωωωωcos cos cos sin 3)(-=∙= 2162sin 212cos 212sin 23-⎪⎭⎫ ⎝⎛-=--=πωωωx x x ……….2分 ∵)(x f 相邻两条对称轴的距离为2π，∴)(x f 最小正周期为π由πωπ=22得1=ω. 函数2162sin )(-⎪⎭⎫ ⎝⎛-=πx x f ……………… 4分由Z k k x k ∈+≤-≤-　226222πππππ 得 36ππππ+≤≤-k x k∴函数)(x f 的单调增区间[3,6ππππ+-k k ] Z k ∈……………….6分（II ）∵22cos a A bc = 又由余弦定理A bc c b a cos 2222-+=．∴22cos 4c b A bc += , ∴21424cos 22=≥+=bcbc bccbA又∵A 为三角形内角，所以30π≤<A . …………………….12分19、解：(1) 211===AC C A AA ，且O 为AC 的中点，AC O A ⊥∴1，又侧面⊥C C AA 11底面ABC ，交线为AC ，O A 1AC 1A 面⊂，∴⊥O A 1平面ABC ………… 6分 (2) 11111141121BCCAC B A ABCBCC E V V V ---==，因此141BA BE =，即B A E A 1143=，又在OB R 1A t ∆中，1,3,11==⊥BO O A OB O A ，可得E A B A 11,2则=的长度为23 ………… 12分20、解：（1）由1112S a ==，得112a b=+；由21243S a a =+=，得4423a b=+．∴223a b a b +=⎧⎨+=⎩，解得11a b =⎧⎨=⎩，故21n nS n =+ ………… 4分（2）当2n ≥时，2232212(1)(1)(1)11(1)n n n nn n n n n n a S S n nn n n n----++-=-=-==+++．由于112a =也适合221n n n a n n +-=+． ∴通项221n n n a n n+-=+ ………8分（3）21111(1)1nn a b n n n n nn ===-+-++．∴数列{}n b 的前n 项和1211111111122311n n n T b b b b n nnn -=++++=-+-++-+--+1111n n n =-=++……… 12分21、解：（Ⅰ）由题知2c e a==，所以22222212c a b e aa-===．即222a b =．又因为过点(0,1)-，所以21b =，22a =．故C 的方程为1222=+yx……3分（Ⅱ）由题意知直线A B 的斜率存在.设A B ：(2)y k x =-，11(,)A x y ，22(,)B x y ，(,)P x y ，由22(2),1.2y k x x y =-⎧⎪⎨+=⎪⎩得2222(12)8820k x k x k +-+-=. O CBAC 1B 1A 1422644(21)(82)0k k k ∆=-+->，212k<………………5分2122812kx x k+=+，21228212kx x k-=+∵O A O B t O P +=，∴1212(,)(,)x x y y t x y ++=，21228(12)x x kx tt k +==+，1212214[()4](12)y y k y k x x k ttt k +-==+-=+. ………………8分∵点P 在椭圆上，∴222222222(8)(4)22(12)(12)k k t k t k -+=++，∴22216(12)k t k =+2222161616422112222ktt kk==<=<<+++，则-， ………………11分∴t 的最大整数值为1. ……………………12分 22、解：（Ⅰ）由'()13s in f x x =-，'(0)13s in 01k f ==-=，(0)0+3c o s 03f ==，所以P 坐标为(0,3)P ，∴()f x 图象在点P 处的切线方程是30y x -=-即3y x =+ …………3分（Ⅱ）3y x =+和3y x =-是()f x 的“夹线”. …………4分由（Ⅰ）知3y x =+是()f x 图象在点P 处的切线，切点为（0,3）.'()13s in 1f x x =-=，∴ s in 0x =.当2x π=时，2+3y π=，(2)2+3c o s 22+3f ππππ==，∴+ππ（2，23）是函数3y x =+和()+3c o s f x x x =图象的另一个切点. 3y x =+和()+3c o s f x x x =的图象相切且至少有两个切点.同理，（π，π-3），（π3，π3-3）是3y x =-和()+3c o s f x x x =图象的两个切点因此，两条平行直线与曲线相切并至少有两个切点。

2013年福建省普通高中毕业班质量检查数学(文)试卷及答案.

2013年福建省普通高中毕业班质量检查文科数学本试卷分第1卷(选择题)和第Ⅱ卷(非选择题)．本试卷共5页．满分150分．考试时间120分钟．注意事项：1．答题前，考生先将自己的姓名、准考证号填写在答题卡上．2．考生作答时，将答案答在答题卡上．请按照题号在各题的答题区域(黑色线框)内作答，超出答题区域书写的答案无效．在草稿纸、试题卷上答题无效．3．选择题答案使用2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其他答案标号；非选择题答案使用0．5毫米的黑色中性(签字)笔或碳素笔书写，字体工整、笔迹清楚．4．保持答题卡卡面清洁，不折叠、不破损．考试结束后，将本试卷和答题卡一并交回．参考公式：样本数据x 1，x 2， …，x n 的标准差锥体体积公式V =31Sh 其中x 为样本平均数其中S 为底面面积，h 为高柱体体积公式球的表面积、体积公式 V =Sh24S R =π，343V R =π其中S 为底面面积，h 为高其中R 为球的半径第Ⅰ卷（选择题共60分）一．选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知复数1i z =-，z 为z 的共轭复数，则下列结论正确的是A ．1i z =--B ．1+i z =-C ．2z =D ．z =2．已知,0a b c >≠，则下列不等式一定成立的是 A ．22a b >B ．ac bc >C ．a c b c +>+D ．a b c c> 3．执行如图所示的程序框图，若输入的x 值为2，则输出的x 值为A ．3B ．8C ．9D ．63 4．“1x =”是“210x -=”的Ａ．充分而不必要条件Ｂ．必要而充分不条件Ｃ．充要条件Ｄ．既不充分也不必要条件5．函数2cos 22y x x x ππ⎛⎫=-≤≤ ⎪⎝⎭的图象是6．已知集合{}|28M x x =-≤≤，{}2|320N x x x =-+≤，在集合M 中任取一个元素x ，则 “x MN ∈”的概率是A ．110B ．16C ．310D ．127．已知1F ，2F 是椭圆C 的两个焦点，焦距为4.若P 为椭圆C 上一点，且12PF F ∆的周长为14，则椭圆C 的离心率e 为 A ．15 B ．25 C ．45D ．5A BCD8．若变量,x y 满足约束条件310,3110,2,x y x y y --≥⎧⎪+-≤⎨⎪≥⎩则2z x y =-的最小值为A ．4B ．1C ．0D ．1- 9．设,m n 为两条不同的直线，βα,是两个不同的平面，下列命题正确的是 A ．若β//,//m n m ，则β//n B ．若αα//,//n m ，则n m // C ．若β⊥m n m ,//，则β⊥n D ．若n m n m //,,βα⊂⊂，则βα// 10．已知点()0,0O ，()1,2A ,()3,2B ，以线段AB 为直径作圆C ，则直线:30l x y +-=与圆C 的位置关系是A ．相交且过圆心B ．相交但不过圆心C ．相切D ．相离 11．已知点()()()0000167n O ,,A ,,A ,,点()1212n A ,A ,,A n ,n -∈≥N 是线段0n A A 的n 等分点，则011+n n OA OA OA OA -+++等于A ．5nB ．10nC ．()51n +D ．()101n + 12．定义两个实数间的一种新运算“*”：()l g1010,x yx y *=+,x y ∈R .对任意实数,,a b c ，给出如下结论：①()()c b a c b a ****=； ②a b b a **=； ③()()()**a b c a c b c +=++；其中正确的个数是A ． 0B ．1C ．2D ．3第Ⅱ卷（非选择题共90分）二、填空题:本大题共4小题，每小题4分，共16分．把答案填在答题卡相应位置． 13．一支田径队有男运动员28人，女运动员21人，现按性别用分层抽样的方法，从中抽取14位运动员进行健康检查，则男运动员应抽取________人． 14．在ABC ∆中，角,,A B C 所对的边分别为,,a b c ．已知3a =，8b =，C=3π，则c = ．15．若函数2,0,()ln ,0x a x f x x x ⎧-≤=⎨>⎩有两个不同的零点，则实数a 的取值范围是． 16．观察下列等式：12133+=； 781011123333+++=； 16171920222339333333+++++=； …则当m n <且,m n ∈N 表示最后结果.313232313333n n m m ++--++++= （最后结果用,m n 表示最后结果）．三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤． 17．(本小题满分12分)某工厂生产,A B 两种元件，其质量按测试指标划分为：大于或等于7．5为正品，小于7．5为次品．现从一批产品中随机抽取这两种元件各5件进行检测，检测结果记录如下：由于表格被污损，数据y x ,看不清，统计员只记得x y <，且,A B 两种元件的检测数据的平均值相等，方差也相等．（Ⅰ）求表格中x 与y 的值；（Ⅱ）若从被检测的5件B 种元件中任取2件，求2件都为正品的概率． 18．(本小题满分12分)已知函数()sin cos f x x x =+，x ∈R ．（Ⅰ）求12f π⎛⎫⎪⎝⎭的值；（Ⅱ）试写出一个函数()g x ，使得()()cos2g x f x x =，并求()g x 的单调区间． 19．(本小题满分12分)某几何体111C B A ABC -的三视图和直观图如图所示．（Ⅰ）求证：平面11AB C ⊥平面11AAC C ；（Ⅱ）若E 是线段1AB 上的一点，且满足1111191C B A ABC C AA E V V --=，求AE 的长．20．(本小题满分12分)某工业城市按照“十二五”（2011年至2015年）期间本地区主要污染物排放总量控制要求，进行减排治污．现以降低SO 2的年排放量为例，原计划“十二五”期间每年的排放量都比上一年减少0.3万吨，已知该城市2011年SO 2的年排放量约为9.3万吨，（Ⅰ）按原计划，“十二五”期间该城市共排放SO 2约多少万吨？（Ⅱ）该城市为响应“十八大”提出的建设“美丽中国”的号召，决定加大减排力度．在2012年刚好按原计划完成减排任务的条件下，自2013年起，SO 2的年排放量每年比上一年减少的百分率为p ，为使2020年这一年的SO 2年排放量控制在6万吨以内，求p 的取值范围.（参考数据9505.0328≈，9559.0329≈）． 21．(本小题满分12分)已知函数()2e xf x ax bx =++．（Ⅰ）当0,1a b ==-时，求()f x 的单调区间；（Ⅱ）设函数()f x 在点()(),P t f t ()01t <<处的切线为l ，直线l 与y 轴相交于点Q .若点Q 的纵坐标恒小于1，求实数a 的取值范围． 22．(本小题满分14分)某同学用《几何画板》研究抛物线的性质：打开《几何画板》软件，绘制某抛物线2:2E y px =，在抛物线上任意画一个点S ，度量点S的坐标俯视图侧(左)视图正(主)视图1A(),S S x y ，如图．（Ⅰ）拖动点S ，发现当4S x =时，4S y =，试求抛物线E 的方程；（Ⅱ）设抛物线E 的顶点为A ，焦点为F ，构造直线SF 交抛物线E 于不同两点S 、T ，构造直线AS 、AT 分别交准线于M 、N 两点，构造直线MT 、NS ．经观察得：沿着抛物线E ，无论怎样拖动点S ，恒有MT //NS .请你证明这一结论．（Ⅲ）为进一步研究该抛物线E 的性质，某同学进行了下面的尝试：在（Ⅱ）中，把“焦点F ”改变为其它“定点(),0G g ()0g ≠”，其余条件不变，发现“MT 与NS 不再平行”．是否可以适当更改（Ⅱ）中的其它条件，使得仍有“MT //NS ”成立？如果可以，请写出相应的正确命题；否则，说明理由．2013年福建省普通高中毕业班质量检查文科数学试题参考解答及评分标准说明：一、本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制定相应的评分细则．二、对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数的一半；如果后继部分的解答有较严重的错误，就不再给分．三、解答右端所注分数，表示考生正确做到这一步应得的累加分数．四、只给整数分数．选择题和填空题不给中间分．一、选择题：本大题考查基础知识和基本运算．每小题5分，满分60分． 1．D 2．C 3．B 4．A 5．B 6．A 7．B 8．A 9．C 10．B 11．C 12．D二、填空题：本大题考查基础知识和基本运算．每小题4分，满分16分．13．8； 14．7； 15．01a <≤； 16．22n m -．三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．17．本小题主要考查古典概型、统计等基础知识，考查数据处理能力、运算求解能力以及应用意识，考查必然与或然思想等．满分12分．解：(Ⅰ)因为11=+7+75+9+95=8=858555x x x y ⋅⋅+⋅+⋅+A B （7），（6+），由=x x A B，得17x y +=． ① ………………………………………2分因为222211=1+1+0.25+1+2.25=1.1=4+8+0.25+0.25+855x y ⎡⎤--⎣⎦A B ，s （）s （）（），由22=A Bs s ，得228+8=1x y --（）（）． ② …………………………………………4分由①②解得89x y =⎧⎨=⎩，，或98.x y =⎧⎨=⎩，因为x y <，所以8x y ==． ………………………………………6分(Ⅱ) 记被检测的5件B 种元件分别为12345,,,,B B B B B ，其中2345,,,B B B B 为正品，从中任取2件,共有10个基本事件，列举如下:()12,B B ，()13,B B ，()14,B B ，()15,B B ，()23,B B ， ()24,B B ，()25,B B ，()34,B B ，()35,B B ，()45,B B ， ………………………………………8分记“2件都为正品”为事件C ，则事件C 包含以下6个基本事件：()23,B B ，()24,B B ，()25,B B ，()34,B B ，()35,B B ，()45,B B .……………………………10分所以63()105P C ==，即2件都为正品的概率为35. ………………………………………12分 18．本小题主要考查三角函数的图象与性质、两角和与差三角公式、二倍角公式、三角函数的恒等变换等基础知识，考查运算求解能力，考查化归与转化思想等．满分12分．解法一：(Ⅰ)因为())4f x x π=+，………………………………………3分所以121243f ππππ⎛⎫⎛⎫=+==⎪ ⎪⎝⎭⎝⎭……………………………6分 (Ⅱ)()cos sin g x x x =-. …………………………………………………………7分下面给出证明：因为()()22(cos sin )(sin cos )cos sin cos2,g x f x x x x x x x x =-+=-=所以()cos sin g x x x =-符合要求．……………………………………………………9分又因为()cos sin 4g x x x x π⎛⎫=-=+ ⎪⎝⎭，…………………………………………10分由222,4k x k πππππ+<+<+得3722,44k x k ππππ+<<+ 所以()g x 的单调递增区间为372244k k ππππ⎛⎫++ ⎪⎝⎭，k ∈Z .………………………………11分又由224k x k ππππ<+<+,得32244k x k ππππ-<<+, 所以()g x 的单调递减区间为32244k k ππππ⎛⎫-+⎪⎝⎭，，k ∈Z .………………………………12分解法二：(Ⅰ)因为()21s i n 2,fx x =+⎡⎤⎣⎦所以231s i n 1262f ππ⎡⎤⎛⎫=+= ⎪⎢⎥⎝⎭⎣⎦，………………………………3分又因为0,12f π⎛⎫>⎪⎝⎭所以12f π⎛⎫=⎪⎝⎭6分 (Ⅱ)同解法一．解法三：(Ⅰ)sin cos sin cos 1212123434f πππππππ⎛⎫⎛⎫⎛⎫=+=-+-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭sincoscossincoscossinsin34343434ππππππππ=-++…………………3分112222=-++=………………………………6分 (Ⅱ)同解法一．注：若通过()()cos 2xg x f x =得到()g x 或由()()(cos sin )(cos sin )g x f x x x x x =+-两边同时约去()f x 得到()g x 不扣分．19．本小题主要考查三视图、直线与直线、直线与平面、平面与平面的位置关系，几何体的体积等基础知识；考查空间想象能力、推理论证能力、运算求解能力；考查函数与方程思想、数形结合思想、化归与转化思想．满分12分．解法一：（Ⅰ）由三视图可知，几何体111C B A ABC -为三棱柱，侧棱1111C B A AA 底面⊥，1111C A C B ⊥,且41==AC AA ，2=BC ．………………………………………2分 1111C B A AA 平面⊥ ，11111111,C B AA C B A C B ⊥∴⊂平面， …………………3分 11111111,A C A AA C A C B =⊥ ，1111ACC A C B 平面⊥∴．……………………5分又1111C AB C B 平面⊂ ， C C AA C AB 1111平面平面⊥∴．………………………6分（Ⅱ）过点E 作11//C B EF 交1AC 于F ，由（Ⅰ）知，11ACC A EF 平面⊥，即EF 为C AA E 1-三棱锥的高. ………7分1111191C B A ABC C AA E V V --= ，,9131111AA S EF S ABC C AA ⋅=⋅∴∆∆ ……………………8分1111442443292EF ⎛⎫⎛⎫∴⨯⨯⨯⨯=⨯⨯⨯⨯ ⎪ ⎪⎝⎭⎝⎭，解得32=EF .……………………9分在Rt ABC ∆中，AB ===，在1Rt ABB ∆中，16AB ===，……………………10分由111C B EF AB AE =， ……………………11分得22326C B EFAB AE 111=⨯=⋅=. ……………………12分解法二：（Ⅰ）同解法一.（Ⅱ）过点E 作11//C B EF 交1AC 于F ，由（Ⅰ）知，11ACC A EF 平面⊥，即EF 为C AA E 1-三棱锥的高. ………7分11111111133C AA B C B A A C B A ABC V V V ---== ，111111113191C AA B C B A ABC C AA E V V V ---==∴ ………8分,313131111111C B S EF S C AA C AA ⋅⨯=⋅∴∆∆,3111C B EF =∴ ………9分在AB C Rt ∆中，5224AB 2222=+=+=BC AC ，在1ABB Rt ∆中，()6452AB 222121=+=+=BB AB ，……………………10分由111C B EFAB AE =， ……………………11分得2AB 31AE 1==. ……………………12分 20．本小题主要考查等差数列、等比数列等基础知识，考查运算求解能力和应用意识，考查函数与方程思想.满分12分.解：（Ⅰ）设“十二五”期间，该城市共排放SO 2约y 万吨，依题意，2011年至2015年SO 2的年排放量构成首项为9.3，公差为0.3-的等差数列，……………3分所以()55159.3(0.3)=43.52y ⨯-=⨯+⨯-（万吨）．所以按计划“十二五”期间该城市共排放SO 2约43．5万吨．……………………6分（2）由已知得， 2012年的SO 2年排放量9.60.32=9-⨯（万吨），……………………7分所以2012年至2020年SO 2的年排放量构成首项为9，公比为1p -的等比数列，…………………9分由题意得891p ⨯-（）＜6，即1p -＜832，所以10.9505p -<，解得 4.95%p >.所以SO 2的年排放量每年减少的百分率p 的取值范围4.95%1p <<<……………………12分21．本小题主要考查函数、导数等基础知识，考查推理论证能力、运算求解能力，考查分类与整合思想、数形结合思想、化归与转化思想．满分12分．解：（Ⅰ）当0,1a b ==-时，()e x f x x =-，()e 1xf x '=-，……………………1分所以，当(,0x ∈-∞时，()0f x '<；当(0,x ∈+∞时，()0f x '>；……………………3分所以函数()f x 的单调递减区间为(),0-∞，单调递增区间为(0,)+∞．……………………4分（Ⅱ）因为()2xf x e ax b '=++，所以()(),P t f t 处切线的斜率()2tk f t e at b '==++，所以切线l 的方程为()()()22t t y e at bt e at b x t -++=++-，令0x =，得()21ty t e a t=-- ()01t << (5)分当01t <<时，要使得点Q 的纵坐标恒小于1，只需()211tt e at --<，即()2110tt e at -++>()01t <<.……………… 6分令()()211tg t t e at =-++，则()()2t g t t e a '=+，………………………………………………………… 7分因为01t <<，所以1t e e <<， ①若21a ≥-即12a ≥-时，20te a +>，所以，当()0,1t ∈时，()0g t '>，即()g t 在()0,1上单调递增，所以()(0)0g t g >=恒成立，所以12a ≥-满足题意.………………………………8分 ②若2a e ≤-即2e a ≤-时，20te a +<，所以，当()0,1t ∈时，()0g t '<，即()g t 在()0,1上单调递减，所以()(0)0g t g <=，所以2ea ≤-不满足题意.………………………………………9分 ③若21e a -<<-即122e a -<<-时，0ln(2)1a <-<.则t 、()g t '、()g t 的关系如下表：所以()()l n (2)00g a g -<=，所以22a -<<-不满足题意.………………………………11分综合①②③，可得，当12a ≥-时，()0g t >()01t <<时，此时点Q 的纵坐标恒小于1.…………12分22．本小题主要考查抛物线的标准方程、直线与圆锥曲线的位置关系等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、分类与整合思想、数形结合思想等．满分14分．解法一：（Ⅰ）把4S x =，4S y =代入22y px =，得248p =，……………………2分所以2p =，………………………………………………………………………3分因此，抛物线E 的方程24y x =．…………………………………………………4分（Ⅱ）因为抛物线E 的焦点为()1,0F ，设()()1122,,,S x y T x y ，依题意可设直线:1l my x =-，由241y x my x ⎧=⎨=-⎩，得2440y my --=，则121244.y y m y y +=⎧⎨⋅=-⎩， ①……………………6分又因为11:AS y l y x x =，22:AT yl y x x =，所以111,y M x ⎛⎫-- ⎪⎝⎭，221,y N x ⎛⎫-- ⎪⎝⎭，所以12211,y MT x y x ⎛⎫=++⎪⎝⎭，21121,y NS x y x ⎛⎫=++ ⎪⎝⎭， ……………………7分又因为()()1221121211y y y x y x x x ⎛⎫⎛⎫++-++ ⎪ ⎪⎝⎭⎝⎭……………………………………8分 2221121241411144y y y y y y ⎛⎫⎛⎫⎛⎫⎛⎫=++-++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭22122112*********4y y y y y y y y y y ⎛⎫⎛⎫=+++-+++ ⎪ ⎪⎝⎭⎝⎭()21121212144y y y y y y y y -=-+()22121212164y y y y y y ⎛⎫-=- ⎪⎝⎭， ②把①代入②，得()221212121604y y y y y y ⎛⎫--= ⎪⎝⎭， (10)分即()()12211212110y y y x y x x x ⎛⎫⎛⎫++-++= ⎪ ⎪⎝⎭⎝⎭，所以//MT NS ，又因为M 、T 、N 、S 四点不共线，所以MT //NS ．……………………………………………11分（Ⅲ）设抛物线2:4E y x =的顶点为A ，定点()(),00G g g ≠，过点G 的直线l 与抛物线E 相交于S 、T 两点，直线AS 、AT 分别交直线x g =-于M 、N 两点，则MT //NS ．……………………14分解法二：（Ⅰ）同解法一.（Ⅱ）因为抛物线E 的焦点为()1,0F ，设()()221122,2,,2S t t T t t ，……………………5分依题意,可设直线:1ST l my x =-，由241y x my x ⎧=⎨=-⎩得2440y my --=，则1212224,224,t t m t t +=⎧⎨⋅=-⎩所以12124,1.t t m t t +=⎧⎨⋅=-⎩ (7)分又因为2:2AS l y t x =-，1:2AT l y t x =-，所以()21,2M t -，()11,2N t -，………………………………………………………………………10分所以MT k =，0NS k =，………………………………………………………………………………10分又因为M 、T 、N、S四点不共线，所以MT //NS .…………………………………………………11分（Ⅲ）同解法一. 解法三：（Ⅰ）同解法一.（Ⅱ）因为抛物线E 的焦点为()1,0F ，设()()1122,,,S x y T x y ，依题意，设直线:1l my x =-，由241y xmy x ⎧=⎨=-⎩得2440y my --=，则121244y y my y +=⎧⎨⋅=-⎩，…………………………………………6分又因为11:AS y l y x x =，22:AT yl y x x =，所以111,y M x ⎛⎫-- ⎪⎝⎭，221,y N x ⎛⎫-- ⎪⎝⎭，又因为212y y x ⎛⎫-- ⎪⎝⎭221122224404y y y y y x y +=+=，……………………………………9分所以212y y x =-，所以NS 平行于x 轴；同理可证MT 平行于x 轴；又因为M、T、N、S四点不共线，所以MT//NS.…………………………………………………11分（Ⅲ）同解法一.…………………………………………………14分。

《精编》福建省福州八中高三数学第一次质检文新人教A版.doc

福州八中—高三毕业班第一次质量检查数学(文)试题考试时间：120分钟试卷总分值：150分第I 卷一、选择题(本大题共12小题，每题5分，共60分. 在每题给出的四个选项中，只有一项为哪一项符合题目要求的，请将答案填入答题纸的相应位置，否那么不给分．．．．．．．．．．．．．．．．．．．．．) 1.i 是虚数单位，复数21i i -等于A. 1+iB. 1－iC. －1+iD. 1－i2.设集合U 是全集，假设已给的Venn 图表示了集合A, B, U 之间的关系，那么阴影局部表示的集合是3．假设集合}"4{""2"},4,2{},,3{2====B A a B a A 是则的 A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件4．向量b a m m b a //),1,1(),2,1(若-+=-=，那么实数m 的值为 A ．3 B ．－3 C ．2 D ．－2 5．运行右图程序，输出的结果为A ．15B ．21C ．28D ．366．命题"042,"2>+-∈∃x x R x 的否认是 A ．2,240x R x x ∃∈-+< B ．2,240x R x x ∀∈-+>C ．2,240x R x x ∀∈-+≥D ．2,240x R x x ∀∈-+≤7．函数⎪⎩⎪⎨⎧≥-<=)0(12)0(2x x x y x 的图象大致是8．在如以以下图的正方形中随机掷一粒豆子，豆子落在正方形内切圆的上半圆〔图第8题中阴影局部〕中的概率是A ．14B ．18C ．4πD ．8π9．一个空间几何体的三视图及局部数据如以以下图，那么这个几何体的外表积是A ．30B ．40C ．60D ．8010．在某种新型材料的研制中，实验人员获得了以下一组实验数据：x3 4 y12现准备用以下四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是A ．22-=x yB ．21(1)2y x =-C ．2log y x =D ．22x y =-11．将奇数1，3，5，7…排成五列〔如右表〕，按此表的排列规律，99所在的位置是 A ．第一列B ．第二列C ．第三列D ．第四列12．设曲线1(*)n y x n N +=∈在点〔1，1〕处的切线与x 轴的交点的横坐标为n x ，那么201012010220102009log log ......log x x x +++的值为A ．2010log 2009-B ．1-C ．()2010log 20091-(D ．1第二卷二、填空题:(本大题共4小题，每题4分，共16分. 请将答案填入答题纸的相应位．．．．．．．．．．．．．置，否那么不给分．．．．．．．．) 13．F 1，F 2是椭圆221169y x +=的两焦点，过点F 2的直线交椭圆于A ，B 两点，在B AF 1∆中，假设有两边之和是10，那么第三边的长度为 .14．函数)(x f 是),(+∞-∞上的偶函数，假设对于0≥x ，都有)()2(x f x f -=+，且当[)2,0∈x 时， 2()log (1)f x x =+，(2010)(2009)f f --的值为 .15．如以以下图是甲、乙两个班同学数学测试成绩数据的茎叶图，那么甲班成绩的中位数是___ _．乙班成绩的最高分为________；16．抛物线)0(22>=p px y 与双曲线22221(0,0)y x a b a b->>=有相同的焦点F ，点A 是两曲线的交点，且x AF ⊥轴，那么双曲线的离心率为三、解答题〔本大题共6小题，共74分，解容许写出文字说明、演算步骤或证明过程。

福州三中2013届高三高考模拟考(文科数学)试题(最后一卷)

福州三中2013届高三高考模拟考数学（文科）试卷本试卷共150分，考试时间120分钟注意事项： (1) 答卷前，考生务必用0.5mm 黑色签字笔将自己的班级、姓名、座号填写在试卷和答卷的密封线外。

(2) 请考生认真审题，将试题的答案正确书写在答卷上的指定位置，并认真检查以防止漏答、错答。

(3) 考试中不得使用计算器。

参考公式：球的表面积公式24S R π= 棱柱的体积公式 V Sh =球的体积公式343V R π=棱锥的体积公式13V Sh =棱台的体积公式121()3V h S S =+其中12,S S 分别表示棱台的上、下底面积，h 表示棱台的高其中R 表示球的半径，其中S 表示棱柱（锥）的底面积，h 表示棱柱（锥）的高如果事件,A B 互斥，那么()()()P A B P A P B +=+一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．已知集合(1,2),A =- 集合2{|230}B x x x =--+>，则A B = （） A ．(1,1)- B ．(3,2)- C ．(1,3)- D ． (1,2)- 2．设i 是虚数单位，则复数20131()1i z i+=-=（） A ．-1 B ．1 C ．i -D ． i3. 命题“x ∀∈R ，都有ln(x 2+1)>0”的否定为（）(A) x ∀∈R ，都有ln(x 2+1)≤0(B) 0x ∃∈R ，使得ln(x 02+1)>0 (C) x ∀∈R ，都有ln(x 2+l)<0(D) 0x ∃∈R ，使得ln(x 02+1)≤04．已知,l m 是直线，α是平面，且m a ⊂，则“l m ⊥”是“l α⊥”的（） A ．必要不充分条件 B ．充分不必要条件C ．充要条件D ．既不充分也不必要条件 5．阅读程序框图(如右图），如果输出的函数值在区间[14，1]上，则输入的实数x 的取值范围是（）A.(,2]-∞-B.［－2,0］C.［0,2］D.[2,)+∞ 6．在等差数列{}n a 中，+=4722a a ，则数列{}n a 的前9项和等于（）A ．3B ．9C ．6D ．12 7．设1122(,),(,),...,(,)n n x y x y x y ，是变量x 和y 的n 个样本点，直线l 是由这些样本点通过最小二乘法得到的线性回归方程(如图），以下结论中正确的是（） A ．x 和y 正相关B ．x 和y 的相关系数为直线l 的斜率C ．x 和y 的相关系数在－1到0之间D ．当n 为偶数时，分布在l 两侧的样本点的个数一定相同 8. 已知函数y=2sin 2（,2cos )4x x -+π则函数的最小正周期T 和它的图象的一条对称轴方程是（）A ．T=2π，一条对称轴方程为8π=x B ．T=2π，一条对称轴方程为83π=x C ．T=π，一条对称轴方程为8π=x D ．T=π，一条对称轴方程为83π=x9．函数l o g 1(0,m y x m m =+>≠的图像恒过定点M ，若点M 在直线1(0,0a xb y a b +=>>上，则14a b+的最小值为( ) A ．8 B ．9 C ．10 D ．1210．若某几何体的三视图如图所示，则这个几何体的体积是( ) A ．5 B ．6 C ．7 D ．8 11．函数sin x x y e -=的图象大致为（）12. 已知i 是虚数单位，记cos sin ie i θθθ=+，其中 2.718...,e θ=∈R ，给出以下结论：①10ieπ+= ②1ii eeθθ-= ③1212()ii i ee e θθθθ+⋅=，则其中正确结论的个数是（） A ．0 B ．1 C ．2 D ．3 二、填空题：本大题共4小题，每小题4分，共16分，把答案填在相应横线上．13．已知向量(,1),xa e =- 向量(1,1)b x =+ ，设函数(),f x a b =⋅ 则函数()f x 的零点个数为．14．若圆22240(3)x y x y m m ++-+=<的一条弦AB 的中点为P （O ，1），则垂直于AB的直径所在直线的方程为．15．若x,y 满足y ax z y x y x y x 2,22,1,1+=⎪⎩⎪⎨⎧≤--≥-≥+且仅在点（1，0）处取得最小值，则实数a 的取值范围是．16．已知命题：在平面直角坐标系xoy 中，ABC ∆的顶点)0,(p A -和)0,(p C ，顶点B 在椭圆),0(1222222n m p n m ny m x -=>>=+上，则B C A sin sin sin +e 1=（其中e 为椭圆的离心率）．试将该命题类比到双曲线中，给出一个真命题是．三、解答题：（本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤.） 17．（本题12分）已知函数211()22f x x x =+，数列{}n a 的前n 项和为n S ，点*(,)()n n S n N ∈均在函数()y f x =的图象上. (I) 求数列{}n a 的通项公式n a ；(II)若2n n nab =，求数列{}n b 的前n 项和n T . 18．（本题12分）某市为了配合宣传新《道路交通法》举办有奖征答活动,随机对该市15~65岁的人群抽样了n 人,回答问题统计结果如图表所示.（左图是样本频率分布直方图，右表是对样本中回答正确人数的分析统计表）.(Ⅰ)分别求出,,,,n a b x y 的值；(Ⅱ)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,有奖征答活动组委会决定在所抽取的6人中随机抽取2人颁发幸运奖,求获得幸运奖的2人来自不同年龄组的概率.19．（本题12分）如图三棱柱111ABC A B C -中, 侧棱与底面垂直，ABC ∆是等边三角形, 点D 是BC 的中点.(Ⅰ)证明：1//A B 平面1C AD ；(Ⅱ)若在三棱柱111ABC A B C -内部（含表面）随机投放一个点P ，求点P 落在三棱锥11C A AD -内部（含表面）的概率.20. （本题12分）如图所示扇形AOB ,半径为2，3AOB π∠=,过半径OA 上一点C 作OB 的平行线，交圆弧AB 于点P . (Ⅰ)若C 是OA 的中点,求PC 的长；(Ⅱ)设θ=∠COP ,求△POC 面积的最大值及此时θ的值.21. （本题12分）已知椭圆E 的中心在坐标原点O ,焦点在x 轴上,离心率e =(2,1)M .(Ⅰ)求椭圆E 的方程；(Ⅱ) 设平行于OM 的直线l 交椭圆E 于两个不同点A B 、,直线MA 与MB 的斜率分别为12k k 、；① 若直线l 过椭圆的左顶点，求12k k 、的值；② 试猜测12k k 、的关系；并给出你的证明.22. （本题14分）已知函数2()ln 23f x x x x =-+．（I ）求函数()f x 的极值；（Ⅱ）证明：存在(1,)m ∈+∞，使得1()()2f m f =；（Ⅲ）记函数y=()f x 的图象为曲线Γ．设点11(,)A x y ，22(,)B x y 是曲线Γ上的不同两点．如果在曲线Γ上存在点00(,)M x y ，使得：①1202x x x +=；②曲线Γ在点M 处的切线平行于直线AB ，则称函数()f x 存在“中值伴随切线”，试问：函数()f x 是否存在“中值伴随切线”，请说明理由．福州三中2013届高三高考模拟考数学（文史类）参考答案一．选择题：,,BDDAB CCDBC BD二．填空题：13．1 14．10x y +-= 15．(4,2)a ∈-16．在平面直角坐标系xoy 中，ABC ∆的顶点)0,(p A -和)0,(p C ，顶点B 在双曲线),0(1222222n m p n m n y m x +=>>=-上，则e B C A 1sin sin sin =-（其中e 为双曲线的离心率）．三．解答题：17．(I) 点*(,)()n n S n N ∈在函数()y f x =的图象上，211,22n S n n ∴=+即22n S n n =+，1n =时11;a = 2n ≥时212(1)(1)n S n n -=-+-，故12()2,n n S S n --=即n a n =.(II) 1()2nn b n =，2123111112()...(1)()()222211111()2()......(1)()()22222n n n n n n T n n T n n -+∴=+++-+∴=++++-+211111[1()]1111111122()...()()()1()()1222222221212(2)()2n n n n n n n nn T n n n T n +++-∴=+++-=-=---∴=-+ 18．(Ⅰ)由第1组数据知该组人数为5100.5=，因为第1组的频率是0.01100.1⨯=，故101000.1n ==；因为第2组人数为0.021010020⨯⨯=，故200.918a =⨯=；因为第3组人数为0.031010030⨯⨯=，故270.930x ==；因为第4组人数为0.025*******⨯⨯=，故250.36b =⨯=；因为第5组人数为0.0151010015⨯⨯=，故30.215y ==. (Ⅱ)第2,3,4组回答正确的人的比为18:27:92:3:1=，故这3组分别抽取2人，3人，1人.设第2组为12,A A ，第3组为123,,B B B ，第4组为1C ；则随机抽取2人可能是12111213(,),(,),(,),(,),A A A B A B A B 1121(,),(,),A C A B 222321(,),(,),(,),A B A B A C12(,),B B 1311232131(,),(,),(,),(,),(,)B B B C B B B C B C ，共15种.其中来自不同年龄组的有111213(,),(,),(,),A B A B A B 1121(,),(,),A C A B 222321(,),(,),(,),A B A B A C11(,),B C 2131(,),(,)B C B C 共11种，故获得幸运奖的2人来自不同年龄组的概率是1115. 19．(Ⅰ)连接1AC ，交1AC 于点E ，连接DE ，在1A BC 中DE 是中位线，故 1//DE A B ，111,DE C AD A B C AD ⊆⊄∴ 面面1//A B 平面1C AD .(Ⅱ)设底面边长为a ，侧棱长为h，则11124ABC A B C V a h -=，因为点D 是BC 的中点，过D 作AC 的垂线交AC 于F ，有DF=4a ，故111111342C A AD D A A C V V a a h --==⋅⋅，所以点P 落在三棱锥11C A AD -内部（含表面）的概率16.20．(Ⅰ)//,CP OB 3AOB π∠=，23OCP π∴∠=，若C 是OA 的中点，则在OPC ∆中，2222cos ,OP OC CP OC CP OCP =+-⋅⋅∠即241CP CP =++，解得1CP =. (Ⅱ) 由正弦定理2sin()sin33OC OPππθ=-，sin(),3OC πθ=-所以 1sin 2OCP S OP OC θ∆=⋅⋅112sin()sin sin )sin 232πθθθθθ=⋅-⋅=-⋅212cos sin sin 2cos 2)(2cos 2)333223θθθθθθθ=-=--=+-)(0,)63ππθθ=+∈，52(,)666OPC S πππθ∆+∈∴∈Q .max 63OPC S πθ∆==时. 21. (Ⅰ)设椭圆方程为22221x y a b +=，依题意有：22222222211a b e a a b ⎧-==⎪⎪⎨⎪+=⎪⎩，解得228,2a b ==，所以椭圆E 的方程为22182x y +=. (Ⅱ) ①若直线l 过椭圆的左顶点且直线l 平行于OM，则直线的方程是1:2l y x =，联立方程组2212182y x x y ⎧=⎪⎪⎨⎪+=⎪⎩，解得121200x x y y =⎧⎧=-⎪⎪⎨⎨==⎪⎪⎩⎩故1211,22k k =-=. ②因为直线l 平行于OM ,设在y 轴上的截距为b ,又12OM k =,所以直线l 的方程为12y x b =+. 由2212182y x b x y ⎧=+⎪⎪⎨⎪+=⎪⎩ 得222240x bx b ++-= .设11(,)A x y 、22(,)B x y ,则212122,24x x b x x b +=-=-. 又1111,2y k x -=-2221,2y k x -=- 故1212121122y y k k x x --+=+--122112(1)(2)(1)(2)(2)(2)y x y x x x --+--=--. 又112211,22y x b y x b =+=+, 所以上式分子122111(1)(2)(1)(2)22x b x x b x =+--++--21212(2)()4(1)24(2)(2)4(1)0x x b x x b b b b b =+-+--=-+----= ，故120k k +=.所以直线MA 与直线MB 的倾斜角互补.22．（I ）21431(1)(41)'()43(0)x x x x f x x x x x x -++--+=-+==>，'()01f x x =⇒=，(0,1)x ∈时'()0,f x >(1,)x ∈+∞时'()0,f x <故1x =时()f x 有极大值1，无极小值．(Ⅱ)构造函数：22113()()()ln 23(ln 2)ln 23ln 21222F x f x f x x x x x x =-=-+---+=-++-，由（I ）知1(1)()2f f >，故(1)0F >，又2()23ln2(32)ln20F e e e e e =-++=-+<，所以函数()F x 在区间(1,)e 上存在零点．即存在(1,)m ∈+∞，使得1()()2f m f =．（Ⅲ）22121212121212121212()()ln ln 2()3()ln ln 2()3AB f x f x x x x x x x x x k x x x x x x x x ----+--===-++--- 120001212'()43432x x f x x x x x +=-+=-++ ，假设存在“中值伴随切线”，则有0'()AB k f x =，可得1121121211212212221ln ln 2ln 2ln 21x x x x x x x x x x x x x x x x x x ---=⇒=⋅⇒=⋅-+++，令12xt x =，则1ln 21t t t -=⋅+，构造1()ln 2,1t g t t t -=-⋅+ 有22214(1)'()0(1)(1)t g t t t t t -=-=≥++恒成立，故函数()g t 单调递增，无零点，所以函数()f x 不存在“中值伴随切线” ．。

2013年福建省福州市高中毕业班数学质量检查试卷参考答案及评分标准(文科)网页版_高三试卷

2013年福建省福州市高中毕业班数学质量检查试卷参考答案及评分标准（文科）网页版_高
三试卷
2013年福州市高中毕业班质量检查
数学（文科）试卷参考答案及评分标准
说明：
一、本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制定相应的评分细则．二、对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数的一半；如果后继部分的解答有较严重的错误，就不再给分．
三、解答右端所注分数，表示考生正确做到这一步应得的累加分数．
四、只给整数分数．选择题和填空题不给中间分．
一、选择题：本大题考查基础知识和基本运算．每小题5分，共60分．
1.B
2.B
3.C
4.C
5.A
6.C
7.B
8.B
9.A 10.D 11.A 12.C
二、填空题：本大题考查基础知识和基本运算．每小题4分，共16分．
13.1 14. 7 15. ②、③、④ 16.
三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．
17. 本小题主要考查等差数列、等比数列等基础知识，考查运算求解能力和应用意识，考查函数与方程思想,满分12分.
点击此处下载：2013年福建省福州市高中毕业班数学质量检查试卷参考答案及评分标准（文科）全部内容word版.doc。

福建省福州八中2013届高三毕业班第三次质检(数学文)

福建省福州八中2013届高三毕业班第三次质检数学（文科）试题考试时间：120分钟试卷满分：150分注意事项：准考证号码填写说明：准考证号码共九位，每位都体现不同的分类，具体如下：答题卡上科目栏内必须填涂考试科目一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．若集合{}{},,1,,32R x x y y T R x y y S x ∈-==∈==则T S ⋂是A ．ΦB. SC. TD. 有限集2．i 为虚数单位，则复数)1(i i z -=在复平面内对应的点在A ．第一象限B ．第二象限C ．第三象限D ．第四象限3 要得到)42sin(3π+=x y 的图象只需将y=3sin2x 的图象A ．向左平移π个单位B ．向右平移4π个单位CD ．向右平移8π个单位4b a ,和不重合平面,αβ，则a ∥b 的一个充分条件是 A ．a ∥α, b ∥α B ．a ∥α，b ∥β，α∥βC ．a ⊥α，b ⊥β，α∥βD ．α⊥β，a ⊥α，b ∥β5．若数据123,,,,n x x x x 的平均数x =5，方差22σ=，则数据12331,31,31,,31n x x x x ++++ 的平均数和方差分别为A ．5，2B ．16，2C ．16，18D ．16，96．以曲线241xy =的焦点为圆心，和直线1-=x y 相切的圆的方程为A ．2)1(22=-+y x B ．2)1(22=+-y xC ．128225)161(22=+-yxD ．128225)161(22=-+y x7．已知等比数列的公比为2，且前四项之和等于1，那么前八项之和等于A ．15B ．21C ．19D ．178．在5张奖券中有1张是有奖的，甲、乙两人从中各抽一张，甲先抽，然后乙抽．设甲中奖的概率为1P ，乙中奖的概率为2P ，那么A ．1P >2PB ．1P =2PC ．1P <2PD ．1P 、2P 大小不能确定9．已知点O 、A 、B 不共线，点P 为该平面上一点，且32O A O BO P -=，则A ．点P 在线段AB 上 B ．点P 在线段AB 的反向延长线上C ．点P 在线段AB 的延长线上D ．点P 不在直线AB 上10．不等式组220,0,01,x y x y -+≥⎧⎪≤⎨⎪≤≤⎩表示的平面区域的面积是AB ．1C ．32D ．211．函数(),132++=ax ax x f 若)(x f >'()f x 对一切x 恒成立，则实数a 的取值范围是A ．134<a B ．0≥a C ．1340<<a D12．设函数()[)N n n n x n x f ∈+∈-=,1,,1，则满足方程()x x f 2log =根的个数是 A ．1 个 B ．2 个 C ．3 个 D ．无数个二、填空题：本大题共4小题，每小题4分，共16分 13．()f x 是奇函数，当[0,)x ∈+∞时，2()f x x =，则当(,0)x ∈-∞时()f x = .14．设正数x y 、满足220x y +=，则lg lg x y +的最大值为．15．按如图所示的程序框图运算．(1) 若输入8x =，则输出k = ；(2) 若输出2k =，则输入x 的取值范围是． 16．定义在*N 上的函数()f x 表示x 的个位数，例如(5)5,(28)8.f f ==数列{}n a 中122,3,a a ==当1n ≥时，21()n n n a f a a ++=⋅，则2009__________.a =三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤． 17．（本小题满分12分）已知向量：),sin 2,sin (cos ),cos 3,cos (sin x x x n x x x m -=+=，函数n m x f ⋅=)(，（I ）求()x f 的周期，并求)(x f 的最大值及相应x 的集合；（II ）在ABC ∆中，c b a ,,分别是C B A ,,所对的边，1)(,4,4===A f b B π，求边a 的长.18．（本小题满分12分）如图在棱长都相等的正三棱柱（底面是正三角形，侧棱垂直于底面）ABC-A 1B 1C 1中，D 、E 分别为AA 1、B 1C 的中点.DCBAB 11⑴ 求证：DE∥平面ABC ； ⑵ 求证：B 1C⊥平面BDE.19．（本小题满分12分）甲、乙二人用4张扑克牌（分别是红桃2，红桃3，红桃4，方片4）玩游戏，他们将扑克牌洗匀后，背面朝上放在桌面上，甲先抽，乙后抽，抽出的牌不放回，各抽一张。

福建省福州八中高三毕业班第六次质量检查文科数学试题参考答案

福建省福州八中高三毕业班第六次质量检查文科数学试题&参考答案考试时间：120分钟试卷满分：150分参考公式：样本数据x 1，x 2， …，x n 的标准差锥体体积公式V =Sh 其中为样本平均数其中S 为底面面积，h 为高柱体体积公式球的表面积、体积公式V =Sh ，其中S 为底面面积，h 为高其中R 为球的半径第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}0)3)(1(|<--=x x x A ，{}33|≤≤-=x x B ，则A B = A. (]2,1- B.(]2,1 C.[)1,2--D. [)1,3-2.复数21ii-=-A.322i- B.322i+ C.322i-+D.322i --3.已知,a b R ∈，则"01a ≤≤且01"b ≤≤是"01"ab ≤≤的31x 24S R =π343V R =πA.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.已知向量(,1),(2,1)a b λλ==+，若a b a b +=-，则实数λ的值为 A ．﹣1 B ．2 C ．1 D ．﹣25.等比数列中，，则数列的前9项和等于A ．6B ．9C ．12D ．166.已知命题p ：1ln ,000-≥∈∃x x R x .命题q ：R ∈∀θ,1cos sin <+θθ.则下列命题中为真命题的是A. q p ∧B.q p ∨⌝)（C.)()q p ⌝∧⌝（ D. )(q p ⌝∧8.执行如右图所示的程序框图，则输出=A ．26B ．57C ．120D ．2479.已知函数（为2.71828……），则的大致图象是S 2()(1)x f x e x =-+e ()f xABCD10．一圆锥底面半径为2，母线长为6，有一球在该圆锥内部且与它的侧面和底面都相切，则这个球的半径为AB ．1 C．2D．11．已知抛物线22y x =上一点A 到焦点F 的距离与其到对称轴的距离之比为9：4，且2AF >，则A 点到原点的距离为AB． C ．4 D ．812.已知定义在R 上的偶函数()f x 满足()()4f x f x +=，且当02x ≤≤时，(){}2min 2,2f x x x x =-+-，若方程()0f x mx -=恰有两个根，则m 的取值范围是 A. 11(,)(,+)33-∞-∞B .11(,][,+)33-∞-∞C.11(2,)(,2)33--D.11[2,][,2]33--第Ⅱ卷本卷包括必考题和选考题两部分。

福建省福州市第八中学高三数学上学期第一次质量检测考试试题文

福州八中2015—2016学年高三毕业班第一次质量检查数学(文)试题考试时间：120分钟试卷满分：150分2015.8.28一、选择题：本大题共12小题，每小题5分，共60分．在每个小题给出的四个选项中，只有一项是符合题目要求的．1、设全集U R =，集合{}(){}222,log 3A y y x B x y x ==-==-，则()U C A B =IA. {}23x x -≤<B. {}2x x ≤-C. {}3x x <D. {}2x x <-2、已知命题p: 已知实数,a b ，则0>⋅b a 是0a >且0b >的必要不充分条件，命题q :在曲线cos y x = A ．p 是假命题 B ．q 是真命题 C ．()p q ∧⌝是真命题 D ．()p q ⌝∧是真命题3、从正方形四个顶点及其中心这5个点中，任取2个点，则这2个点的距离小于该正方形边长的概率为A.15B.25C.35D.454、已知向量m =(λ+1,1),n =(λ+2,2),若(m+n )⊥(m-n ),则λ= A.-4 B.-3 C.-2 D.-15、函数()20.4–34y log x x =++的值域是A ．(0，–2]B ．[–2，+∞)C ．(–∞，–2]D ．[2，+∞) 6、若将函数f (x )＝sin 2x ＋cos 2x 的图像向右平移φ个单位，所得图像关于y 轴对称，则φ的最小正值是A.π8B.π4C.3π8D.3π47、若,,l m n 是不相同的空间直线，,αβ是不重合的平面，则下列命题正确的是 A.//,,//l n l n αβαβ⊂⊂⇒ B. ,//l n m n l m ⊥⊥⇒ C. ,//l l αβαβ⊥⇒⊥ D. ,l l αβαβ⊥⊂⇒⊥ 8、已知数列{a n }满足3a n+1+a n =0,a 2=34-,则{a n }的前10项和等于A.-6(1-3-10) B.(1-310)C.3(1-3-10)D.3(1+3-10)9、已知双曲线22–100ax by a b =（＞，＞）的一条渐近线方程是0x =，它的一个焦点在抛物线2–4y x =的准线上，则双曲线的方程为A. 4x 2–12y 2=1 B. 4x 2–34y 2=1 C. 12x 2–4y 2=1 D. 3422–41x y = 10、已知()2243,023,0x x x f x x x x ⎧-+≤⎪=⎨--+>⎪⎩，不等式()()2f x a f a x +>-在[],1a a +上恒成立，则实数a 的取值范围是A.(),2-∞-B.(),0-∞C.()0,2D.()2,0-11、如图是函数f （x ）=x 2+ax+b 的部分图象，则函数g （x ）=lnx+f′（x ）的零点所在的区间是A ．（）B ．（1，2）C ．（，1）D ．（2，3）12、已知函数⎩⎨⎧>+≤+-=0),1ln(0,2)(2x x x x x x f ，若|f (x )|≥ax ,则a 的取值范围是A .(-∞,0]B .(-∞,1]C .[-2,1]D .[-2,0]二、填空题：本大题共4小题，每小题4分，共16分。

2013届福州八中高三毕业班模拟考(数学)文

第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．设复数i z 21+=（i 是虚数单位），则复数z 的虚部为A ．2-B. 2C. i 2-D. i 22．命题||||,:y x y x p <<则若，命题:q 若22a bc c>，则a b >．则 A ．“p 或q ”为真 B ．“p 且q ”为真 C ．p 真q 假D ．,p q 均为假 3．在递增等比数列{n a }中，4,2342=-=a a a ，则公比q ＝ A ．-1 B ．1 C ．2D4．某程序框图如图所示，则该程序运行后输出的值是 A ．2 B ．3C ．4D ．55.下列说法中，正确的是A ．与定点F 和定直线的距离相等的点的轨迹是抛物线B ．抛物线x 2＝2my 的焦点坐标为⎝⎛⎭⎫0，m2，准线方程为y ＝－m2 C ．准线方程为x ＝－4的抛物线的标准方程为y 2＝8xD ．焦准距(焦点到准线的距离)为p (p >0)的抛物线的标准方程为y 2＝±2px6.若角α的终边与单位圆交于第三象限的一点P ，其横坐标为1010-，则=αtanA. 31-B.31 C. 3- D. 37. 如图正四棱锥（底面是正方形，顶点在底面的射影是底面的中心）P-ABCD 的底面边长为6cm ，侧棱长为5cm ，则它的侧视图的周长等于A.17cmB.cm 5119+C.16cmD.14cm8．设M 是平行四边形ABCD 的对角线的交点，O 为任意一点，则=+++A ．OMB ．2C ．3D ．49．在长为10cm 的线段AB 上任取一点C ，现作一个矩形，邻边长分别等于线段AC 、CB 的长，则该矩形的面积大于224cm 的概率是 A ．16B ．15C ．14D ．1310．在半径为a 的圆桌中心上方安装一吊灯,桌面上灯光的强度22sin rk y θ=，其中k 是常数，r 是灯与桌面上被照点的距离，是光线与桌面的夹角（如图），现为使桌边最亮，则θsin =A.23B.33raӨC.32 D.22 11. 已知定义在R 上的函数)(x f 是偶函数，且满足)1()1(x f x f -=+，当[]1,1-∈x 时，21)(x x f -=，若函数x x g 5log )(=，则)()()(x g x f x h -=在区间（0,5]内的零点的个数是A ．2B ．3C ．4D ．512．若双曲线116922=-y x 渐近线上的一个动点P 总在平面区域16)(22≥+-y m x 内，则实数m 的取值范围是A. [3,3]-B. (,3][3,)-∞-⋃+∞C. [5,5]-D. (,5][5,)-∞-⋃+∞第Ⅱ卷（非选择题共90分）二、填空题：本大题共4小题，每小题4分，共16分，把答案填在相应横线上．13．函数y ＝sin (2x ＋π4)的图象可由函数y ＝sin 2x 的图象向左平移个单位长度而得到．14．设函数⎪⎩⎪⎨⎧<≥+-=3,23,)(2x x b x x x f x ，若函数)(x f 在R 上为增函数，则实数b 的取值范围是．15．若关于x 的不等式()21m x x x ->-的解集为{}12x x <<，则实数m 的值为．16．已知椭圆15922=+y x 上任意一点P ，21,A A 是椭圆的左、右顶点，设直线21,PA PA 斜率分别为21,PA PA k k ，则=⋅21PA PA k k ，现类比上述求解方法，可以得出以下命题：已知双曲线12222=-by a x 上任意一点P ，21,A A 是双曲线的左、右顶点，设直线21,PA PA 斜率分别为21,PA PA k k ，则=⋅21PA PA k k .三、解答题：（本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤.） 17．（本题满分12分）某校从参加高三模拟考试的学生中随机抽取60名学生，将其数学成绩(均为整数)分成六组[90,100)，[100,110)，…， [140,150]后得到如下部分频率分布直方图，观察图形的信息，回答下列问题：(1)求分数在[120,130)内的频率；(2)若在同一组数据中，将该组区间的中点值(如：组区间[100,110)的中点值为100＋1102＝105)作为这组数据的平均分，据此，估计本次考试的平均分；(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本，将该样本看成一个总体，从中任取2人，求至多有1人在分数段[120,130)内的概率． 18．（本题满分12分）已知()x x ωωcos ,sin 3-=，)cos ,(cos x x ωω=，0>ω，函数x f ∙=)(，且)(x f 的图像相邻两条对称轴间的距离为2π．（Ⅰ）求函数)(x f 的最小正周期和单调增区间；（Ⅱ）若∆ABC 的三条边a ，b ，c 所对的角分别为A,B,C 满足22cos a A bc =，求角A 的取值范围．19．（本题满分12分）如图，在三棱柱111C B A ABC -中，侧面⊥C C AA 11底面ABC ，211===AC C A AA ，O BC AB BC AB ,,⊥=为AC 的中点.⑴ 证明:⊥O A 1平面ABC ；⑵若E 是线段B A 1上一点，且满足1111121C B A ABC BCC E V V --=，求E A 1的长度.20．（本题满分12分）数列{}n a 的前n 项和2n n S an b=+，已知112a =，256a =．（1）求数列{}n a 的前n 项和n S ；（2）求数列{}n a 的通项公式；（3）设21nn a b n n =+-，求数列{}n b 的前n 项和n T ．21．（本题满分12分）已知椭圆2222:1x y C a b +=(0)a b >>，且过点(0,1)-．（Ⅰ）求椭圆C 的方程；（Ⅱ）若过点(2,0)M 的直线与椭圆C 相交于两点A B 、，设P 为椭圆上一点，且满足O CBAC 1B 1A 1OA OB tOP +=（其中O 为坐标原点），求整数t 的最大值．22．（本题满分14分）若斜率为k 的两条平行直线l ，m 与曲线C 相切并至少有两个切点，且曲线C 上的所有点都在l ，m 之间（也可在直线l ，m 上），则把l ，m 称为曲线C 的“夹线”，把l ，m 间的距离称为曲线C 在“k 方向上的宽度”，记为).(k d 已知函数()+3cos f x x x =.（Ⅰ）若点P 横坐标为0，求()f x 图象在点P 处的切线方程；（Ⅱ）试判断3y x =+和3y x =-是否是()f x 的“夹线”，若是，求(1)d ；若不是，请说明理由；（Ⅲ）求证：函数31()3F x x x =-+的图象不存在“夹线”.稿纸福州八中2012—2013学年高三毕业班模拟考数学（文）试题参考答案1-12、BACCB DDDBD CD13、π8 14、),2[+∞ 15、2 16、59-； 22b a17、解：(1)分数在[120,130)内的频率为1－(0.1＋0.15＋0.15＋0.25＋0.05)＝1－0.7＝0.3 …………3分 (2)估计平均分为x ＝95×0.1＋105×0.15＋115×0.15＋125×0.3＋135×0.25＋145×0.05＝121………………………6分(3)依题意，[110,120)分数段的人数为60×0.15＝9(人)． [120,130)分数段的人数为60×0.3＝18(人)．∵用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本， ∴需在[110,120)分数段内抽取2人，并分别记为m ，n ；在[120,130)分数段内抽取4人，并分别记为a ，b ，c ，d ；设“从样本中任取2人，至多有1人在分数段[120,130)内”为事件A ，则基本事件共有(m ，n )，(m ，a )，…，(m ，d )，(n ，a )，…，(n ，d )，(a ，b )，…，(c ，d )共15种．则事件A 包含的基本事件有(m ，n )，(m ，a )，(m ，b )，(m ，c )，(m ，d )，(n ，a )，(n ，b )，(n ，c )，(n ，d )共9种．∴P (A )＝915＝35. …………12分18、解：（I ）x x x x x f ωωωωcos cos cos sin 3)(-=∙= 2162sin 212cos 212sin 23-⎪⎭⎫ ⎝⎛-=--=πωωωx x x ……….2分 ∵)(x f 相邻两条对称轴的距离为2π，∴)(x f 最小正周期为π 由πωπ=22得1=ω. 函数2162sin )(-⎪⎭⎫ ⎝⎛-=πx x f ……………… 4分由Z k k x k ∈+≤-≤-　226222πππππ 得 36ππππ+≤≤-k x k∴函数)(x f 的单调增区间[3,6ππππ+-k k ] Z k ∈……………….6分（II ）∵22cos a A bc = 又由余弦定理A bc c b a cos 2222-+=．∴22cos 4c b A bc += , ∴21424cos 22=≥+=bc bc bc c b A 又∵A 为三角形内角，所以30π≤<A . …………………….12分19、解：(1) 211===AC C A AA ，且O 为AC 的中点，AC O A ⊥∴1，又侧面⊥C C AA 11底面ABC ，交线为AC ，O A 1AC 1A 面⊂，∴⊥O A 1平面ABC ………… 6分(2) 11111141121BCC A C B A ABC BCC E V V V ---==，因此141BA BE =，即B A E A 1143=，又在OB R 1A t ∆中，1,3,11==⊥BO O A OB O A ，可得E A B A 11,2则=的长度为23………… 12分 20、解：（1）由1112S a ==，得112a b =+；由21243S a a =+=，得4423a b =+． ∴223a b a b +=⎧⎨+=⎩，解得11a b =⎧⎨=⎩，故21n n S n =+ ………… 4分（2）当2n ≥时，2232212(1)(1)(1)11(1)n n n n n n n n n n a S S n n n n n n ----++-=-=-==+++．由于112a =也适合221n n n a n n +-=+． ∴通项221n n n a n n +-=+ ………8分（3）21111(1)1n n a b n n n n n n ===-+-++． ∴数列{}n b 的前n 项和1211111111122311n n n T b b b b n n n n -=++++=-+-++-+--+1111n n n =-=++……… 12分 21、解：（Ⅰ）由题知2c e a ==，所以22222212c a b e a a -===．即222a b =．又因为过点(0,1)-，所以21b =，22a =．故C 的方程为1222=+y x ……3分（Ⅱ）由题意知直线AB 的斜率存在.设AB ：(2)y k x =-，11(,)A x y ，22(,)B x y ，(,)P x y ，OC BA C 1B 1A 1由22(2),1.2y k x x y =-⎧⎪⎨+=⎪⎩得2222(12)8820k x k x k +-+-=. 422644(21)(82)0k k k ∆=-+->，212k < ………………5分2122812k x x k +=+，21228212k x x k-=+ ∵OA OB tOP +=，∴1212(,)(,)x x y y t x y ++=，21228(12)x x k x t t k +==+， 1212214[()4](12)y y ky k x x k t t t k +-==+-=+. ………………8分 ∵点P 在椭圆上，∴222222222(8)(4)22(12)(12)k k t k t k -+=++， ∴22216(12)k t k =+2222161616422112222k t t k k==<=<<+++，则-， ………………11分 ∴t 的最大整数值为1. ……………………12分 22、解：（Ⅰ）由'()13sin f x x =-，'(0)13sin 01k f ==-=， (0)0+3cos03f ==，所以P 坐标为(0,3)P ，∴()f x 图象在点P 处的切线方程是30y x -=-即3y x =+ …………3分（Ⅱ）3y x =+和3y x =-是()f x 的“夹线”. …………4分由（Ⅰ）知3y x =+是()f x 图象在点P 处的切线，切点为（0,3）.'()13sin 1f x x =-=，∴ sin 0x =.当2x π=时，2+3y π=，(2)2+3cos 22+3f ππππ==，∴+ππ（2，23）是函数3y x =+和()+3cos f x x x =图象的另一个切点. 3y x =+和()+3cos f x x x =的图象相切且至少有两个切点. 同理，（π，π-3），（π3，π3-3）是3y x =-和()+3cos f x x x =图象的两个切点因此，两条平行直线与曲线相切并至少有两个切点。

2013年福建省高考数学试卷(文科)学生版

2013 年福建省高考数学试卷（文科）一、选择题：本大题共12 小题，每题 5 分，共 60 分.在每题给出的四个选项中，只有一项为哪一项切合题目要求的.1．（5 分）（2013?福建）复数的 Z=﹣1﹣2i（i 为虚数单位）在复平面内对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限2．（5 分）（2013?福建）设点 P（x，y），则“ x=2且 y=﹣1”是“点 P 在直线 l ：x+y ﹣1=0 上”的（）A．充足而不用要条件B．必需而不充足条件C．充足必需条件D．既不充足也不用要条件3．（5 分）（2013?福建）若会合 A={ 1，2， 3} ，B={ 1，3，4} ，则 A∩B 的子集个数为（）A．2B．3C．4D．164．（5 分）（2013?福建）双曲线x2﹣y2=1 的极点到其渐近线的距离等于（）A．B．C．1D．5．（5 分）（2013?福建）函数 f （x）=ln（x2+1）的图象大概是（）A．B．C．D．6．（ 5 分）（2013?福建）若变量 x ，知足拘束条件，则 z=2x+y 的最大y值和最小值分别为（）A．4和 3B．4和 2C．3和2D．2和0．（分）（ 2013? 福建）若 2 x +2y ，则 x+y 的取值范围是（）7 5 =1A ．[ 0，2]B ．[ ﹣2，0]C ．[ ﹣2，+∞）D ．（﹣∞，﹣ 2]8．（5 分）（2013?福建）阅读如下图的程序框图，运转相应的程序，假如输入某个正整数 n 后，输出的 S ∈（ 10， 20），那么 n 的值为（）A ．3B ．4C ．5D ．69．（5 分）（2013?福建）将函数 f （x ）=sin （ 2x+θ）（＜＜）的图象向右平移 φ（ φ＞1）个单位长度后获得函数 g （x ）的图象，若 f （x ），g （x ）的图象都经过点 P （，），则 φ的值能够是（）A ．B ．C ．D ．10．（ 5 分）（2013?福建）在四边形 ABCD 中， =（1，2），=（﹣ 4， 2），则该四边形的面积为（）A ．B ．C ．5D ．1011．（ 5 分）（2013?福建）已知 x 与 y 之间的几组数据如表：x 1 2 3 4 5 6 y21334假定依据上表数据所得线性回归直线方程为= x+ ，若某同学依据上表中的前两组数据（ 1，0）和（ 2， 2）求得的直线方程为 y=b′x+a′，则以下结论正确的选项是（）．＞b′，＞a′ B．＞b′，＜a′ C．＜b′，＞ a′ D．＜b′，＜ a′A．（分）（福建）设函数f （）的定义域为0（x0≠0）是f（x）的12 52013?x R，x极大值点，以下结论必定正确的选项是（）A．? x∈R，f（x）≤ f （x0）B．﹣ x0是 f （﹣ x）的极小值点C．﹣ x0是﹣ f （x）的极小值点D．﹣ x0是﹣ f （﹣ x）的极小值点二、填空题：本大题共 4 小题，每题 4 分.，＜13（．4 分）（ 2013?福建）已知函数（f x）=，则（f（f））=．，14．（4 分）（ 2013?福建）利用计算机产生0～1 之间的均匀随机数a，则事件“ 3a﹣1＞0”发生的概率为．15．（4 分）（ 2013?福建）椭圆Γ：F2，焦距为 2c，若直线 y=MF2F1，则该椭圆的离心率等于=1（ a＞ b＞ 0）的左右焦点分别为F1，与椭圆Γ的一个交点 M 知足∠ MF1F2=2∠．16．（ 4 分）（2013?福建）设 S， T 是R 的两个非空子集，假如存在一个从S 到 T 的函数 y=f（x）知足：（ i）T={ f（x）| x∈ S} ；（ ii）对随意 x1，x2∈S，当 x1＜ x2时，恒有 f（x1）＜f （ x2），那么称这两个会合“保序同构”，现给出以下 3 对会合：①A=N，B=N*；②A={ x| ﹣1≤x≤3} ， B={ x| ﹣8≤x≤10} ；③ A={ x| 0＜x＜ 1} ，B=R．此中，“保序同构”的会合对的序是．（写出“保序同构”的会合对的序）．三、解答题：本大题共 6 小题，共 74 分．解答应写出文字说明、证明过程或演算步骤．17．（ 12 分）（ 2013?福建）已知等差数列 { a n} 的公差 d=1，前 n 项和为S n．（Ⅰ）若 1，a1，a3成等比数列，求 a1；（Ⅱ）若 S5＞a1a9，求 a1的取值范围．18．（ 12 分）（2013?福建）如图，在四棱锥P﹣ABCD中， PD⊥平面 ABCD，AB∥DC，AB⊥ AD，BC=5， DC=3， AD=4，∠ PAD=60°．（Ⅰ）当正视方向与向量的方向同样时，画出四棱锥P﹣ABCD的正视图（要求标出尺寸，并写出演算过程）；（Ⅱ）若 M 为 PA的中点，求证： DM∥平面 PBC；（Ⅲ）求三棱锥D﹣PBC的体积．19．（ 12 分）（2013?福建）某工厂有 25 周岁以上（含 25 周岁）工人 300 名， 25 周岁以下工人 200 名．为研究工人的日均匀生产量能否与年纪相关，现采纳分层抽样的方法，从中抽取了 100 名工人，先统计了他们某月的日均匀生产件数，而后按工人年纪在“25周岁以上（含 25 周岁）”和“25周岁以下”分为两组，再将两组工人的日均匀生产件数分为 5 组： [ 50，60），[ 60， 70），[ 70，80），[ 80，90），[ 90，100）分别加以统计，获得如下图的频次散布直方图．P（x2≥ k）0.1000.0500.0100.001 k 2.706 3.841 6.63510.828（Ⅰ）从样本中日均匀生产件数不足60 件的工人中随机抽取 2 人，求起码抽到一名“25周岁以下组”工人的概率；（Ⅱ）规定日均匀生产件数许多于80 件者为“生产好手”，请你依据已知条件完成列联表，并判断能否有 90%的掌握以为“生产好手与工人所在的年纪组相关”？附：（注：此公式也可以写成k2=）20．（ 12 分）（ 2013?福建）如图，抛物线 E：y2=4x 的焦点为 F，准线 l 与 x 轴的交点为 A．点 C 在抛物线 E 上，以 C 为圆心， | CO| 为半径作圆，设圆 C 与准线 l 交于不一样的两点 M，N．（Ⅰ）若点 C 的纵坐标为 2，求 | MN| ；（Ⅱ）若 | AF| 2=| AM| ?| AN| ，求圆 C 的半径．21．（ 12 分）（ 2013?福建）如图，在等腰直角△OPQ 中，∠ POQ=90°， OP=2，点 M 在线段 PQ上，（Ⅰ）若 OM= ，求 PM 的长；（Ⅱ）若点 N 在线段 MQ 上，且∠ MON=30°，问：当∠ POM 取何值时，△ OMN的面积最小？并求出头积的最小值．22．（ 14 分）（ 2013?福建）已知函数 f （x）=x﹣1+（a∈ R，e为自然对数的底数）．（Ⅰ）若曲线 y=f（x）在点（ 1，f（1））处的切线平行于x 轴，求 a 的值；（Ⅱ）求函数 f （x）的极值；（Ⅲ）当 a=1 的值时，若直线l：y=kx﹣ 1 与曲线 y=f（x）没有公共点，求 k 的最大值．。

福建省2013届高三毕业班质量检测数学文试题含解析

2013年福建省普通高中毕业班质量检查文科数学本试卷分第1卷(选择题）和第Ⅱ卷(非选择题）．本试卷共5页．满分150分．考试时间120分钟．注意事项:1．答题前，考生先将自己的姓名、准考证号填写在答题卡上． 2．考生作答时，将答案答在答题卡上．请按照题号在各题的答题区域(黑色线框)内作答，超出答题区域书写的答案无效．在草稿纸、试题卷上答题无效．3．选择题答案使用2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其他答案标号；非选择题答案使用0．5毫米的黑色中性(签字）笔或碳素笔书写，字体工整、笔迹清楚．4．保持答题卡卡面清洁，不折叠、不破损．考试结束后,将本试卷和答题卡一并交回．参考公式：样本数据x 1,x 2， …，x n 的标准差锥体体积公式V =31Sh其中x 为样本平均数其中S 为底面面积,h 为高柱体体积公式球的表面积、体积公式V =Sh24S R =π，343V R =π其中S 为底面面积，h 为高其中R 为球的半径第Ⅰ卷（选择题共60分）一．选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中,只有一项是符合题目要求的．1．已知复数1i z =-,z 为z 的共轭复数,则下列结论正确的是A ．1i z =--B ．1+i z =-C ．2z =D ．2z =【答案】D【KS5U 解析】1z i =+，因此,A ，B 不正确；而2z =D 正确.2．已知,0a b c >≠，则下列不等式一定成立的是A ．22ab > B ．ac bc >C ．a c b c +>+D ．a b cc >【答案】C【KS5U 解析】当1a =-,2b =-时显然A 项不对;当0c <时B 和D 项不对;不等式两边加上同一个数不等式方向不改变，因此C 项对。

3．执行如图所示的程序框图，若输入的x 值为2，则输出的x 值为 A ．3 B ．8 C ．9 D ．63 【答案】B【KS5U 解析】由输入x 的值是2,循环一次x 的值是3，循环两次x 的值是8，恰好可以满足条件8x ≥,结束程序，输出的值是8。

2013年福州市质检数学文科试卷(0509)

2013年福州市高中毕业班质量检查数学(文科)试卷（完卷时间120分钟；满分150分）注意事项：1．本科考试分试题卷和答题卷，考生须在答题卷上作答，答题前，请在答题卷内填写学校、班级、准考证号、姓名；2．本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，全卷满分150分，考试时间120分钟．参考公式：第Ⅰ卷（选择题共60分）一、选择题（本大题共12小题，每小题5分，共60分．在每小题所给的四个答案中有且只有一个答案是正确的．把正确选项涂在答题卡的相应位置上．） 1. i 是虚数单位，复数(2)z x i i =+()x R ∈，若z 的虚部为2，则x =A ．-2B ． 2C ．-1D ．12. 已知集合A ={}01x x <<，{}c x x B <<=0，若=A B B ，则实数c 的取值范围是A. (0,1]B. [1,+)∞C. )1,0(D. ),1(+∞3. 命题“存在x R ∈，3210x x -+>”的否定是A ．不存在x R ∈，3210x x -+≤B ．存在x R ∈，3210x x -+≤ C ．对任意的x R ∈，3210x x -+≤ D ．对任意的x R ∈，3210x x -+> 4.已知圆C ：x 2＋y 2＝2与直线l ：x ＋y ＋2＝0，则圆C 被直线l 所截得的弦长为 A ．1B ． 3C ．2D ．235. 已知命题“直线l 与平面α有公共点”是真命题，那么下列命题：锥体体积公式13V Sh =其中S 为底面面积，h 为高球的表面积、体积公式24S R =π，343V R =π其中R 为球的半径样本数据1x ，2x ，，n x 的标准差()()()222121n s x x x x x x n ⎡⎤=-+-++-⎣⎦ 其中x 为样本平均数柱体体积公式 V Sh =其中S 为底面面积，h 为高①直线l 上的点都在平面α内； ②直线l 上有些点不在平面α内；③平面α内任意一条直线都不与直线l 平行．其中真命题的个数是 A.0 B.1 C.2 D.3 6. 在正项等比数列{}n a 中，已知6453=⋅a a ，则71a a +的最小值为 A.64 B. 32 C. 16 D.87. 如图面积为4的矩形ABCD 中有一个阴影部分，若往矩形ABCD 投掷1000个点，落在矩形ABCD 的非阴影部分中的点数为400个，试估计阴影部分的面积为A.2.2B.2.4C.2.6D.2.88. 设动点),(y x P 满足⎪⎩⎪⎨⎧≥≥+≤+02242x y x y x ，则y x z -=的最小值是A. 2B. -4C. -1D. 49. 如图所示为函数≤≤>+=ϕωϕω0,0)(sin(2)(x x f )π的部分图象，其中A ，B 两点之间的距离为5，那么=-)1(f .A ．2B ．1C ．-1D ．2-10. 已知OA =1，OB =3，OA ·OB =0，点C 在∠AOB 内，且∠AOC=60°，设OC =m OA +n OB （m ，n ∈Ｒ），则nm= A ．41 B ．31 C ．21D ．111. 已知抛物线24x y =-的准线与双曲线22221(0,0)y x a b a b-=>>的两条渐近线围成一个等腰直角三角形，则该双曲线的离心率是 A.2B.2C.5D.512.对于函数()f x 与()g x 和区间D ，如果存在0x D ∈，使00()()1f x g x -≤，则称0x 是函数()f x 与()g x 在区间D 上的“友好点”．现给出两个函数 ①2()f x x =，()23g x x =- ②()f x x =，()2g x x =+③()x f x e -=，1()g x x=-④()ln f x x = ，1()2g x x =-第7题图第9题图其中在区间()0,+∞上存在“友好点”的有A ．①②B ．②③C ．③④D ．①④第Ⅱ卷（非选择题共90分）二、填空题（本大题共4小题，每小题4分，共16分，把答案填在答题卡的相应位置上．）13.已知函数1,()0,Z x N f x x N∈⎧=⎨∈⎩ð，则((2))f f -= . 14．．已知在ABC ∆中，0120,A ∠=且三边长构成公差为2的等差数列，则A ∠所对的边a = .15．已知程序框图如右图所示，执行该程序，如果输入10=x ，输出4=y ，则在图中“？”处可填入的算法语句是（写出以下所有满足条件的序号） ①1-=x x ②2-=x x ③3-=x x ④4-=x x16.设数列｛a n ｝是集合｛3s＋3t| 0≤s ＜t ，且s ，t ∈Z ｝中所有的数从小到大排列成的数列，即a 1＝4，a 2＝10，a 3＝12，a 4＝28，a 5＝30，a 6＝36，…，将数列｛a n ｝中各项按照上小下大，左小右大的原则排成如下等腰直角三角形数表：410 1228 30 36 …200a = （用3s ＋3t 形式表示）．三、解答题：本大题共6小题，共74分．解答应写出文字说明、证明过程或演算步骤．17．（本小题满分12分）数列{}n a 的前n 项和为122n n S +=-，数列{}n b 是首项为a ，公差为(0)d d ≠的等差数列，且139,,b b b 成等比数列．（Ⅰ）求数列{}n a 与{}n b 的通项公式；（Ⅱ）若*)()1(2N n b n c nn ∈+=，求数列}{n c 的前n 项和T ．第15题图开始 _？0?x ³结束输出y是否输入x1()2x y =18．(本小题满分12分)已知平面向量(2,2),(sin ,cos)44x x ππ==a b 错误！未找到引用源。

福建省2013届高三文科数学试题

福建省2013届高三文科数学试题一、选择题（本题共12个小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的）。

1、设复数z 满足2z i i ⋅=-，i 为虚数单位，则=z （）A 、2i -B 、12i +C 、12i -+D 、12i --2、设f (x )＝3x －x 2，则在下列区间中，使函数f (x )有零点的区间是( )A ．（0,1）B ．（1,2）C ．(－2，－1)D ．(－1,0) 3、集合2{|20}A x x x =-≤，{|lg(1)}B x y x ==-，则A B 等于（）A 、{|01}x x <≤B 、{|12}x x ≤<C 、{|12}x x <≤D 、{|01}x x ≤<4、已知向量,a b满足||1,||1a b a b ==⋅= ,则a 与b的夹角为 ( )A 、3π B 、34π C 、4π D 、6π5．已知等差数列{}n a 满足32=a ，)2(,171≥=-n a n ，100=n S ，则n 的值为A ．8B ．9C ．10D ．116.已知A 是三角形A B C 的内角，则“1cos 2A =”是“23sin =A ”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件7. 已知0<a <1，b >1，且ab >1，则M ＝log a 1b ，N ＝log a b ，P ＝log b 1b ，则这三个数的大小关系为( )A ．P <N <MB ．N <P <MC ．N <M <PD ．P <M <N8.已知m ,n ，l 为三条不同的直线，α,β为两个不同的平面，则下列命题中正确的是( )A ．//,,//m n m n αβαβ⊂⊂⇒B ．l l ⇒⊥⊥βαβ,∥αC ．,//m m n n αα⊥⊥⇒D ．α∥,l l βαβ⊥⇒⊥9．某同学设计右面的程序框图用以计算和式222212320++++ 的值，则在判断框中应填写A ．19i ≤B ．19i ≥C ．20i ≤D ．21i ≤10．若变量x y ，满足约束条件30101x y x y y +-≤⎧⎪-+≥⎨⎪≥⎩，则2z x y =-的最大值为A ．1-B ．0C ．3D ．411．则使方程()x f x m +=有解的实数m 的取值范围是（）A ．（1，2）B ．(,2]-∞-C ．(,1)(2,)-∞⋃+∞D ．(,1][2,)-∞⋃+∞12．椭圆)0(12222>>=+b a by ax 的离心率为21=e ，右焦点为)0,(c F ，方程02=-+c bx ax 的两个实根分别为21,x x 则点),(21x x P 位置（）A ．必在圆222=+y x 内B ．必在圆222=+y x 上C ．必在圆222=+y x 外D ．以上三种情况都有可能ks5u二、填空题（本大题共4小题，每小题4分，共16分）13．已知函数1)(23++=ax x x f 的导函数为偶函数，则=a .14.圆x 2＋y 2－2x －2y ＋1＝0上的动点Q 到直线3x ＋4y ＋8＝0距离的最小值为______． 15．一个空间几何体的三视图(单位：cm )如图所示，则该几何体的体积为_______3cm ．16.记123k k k k k S n =+++⋅⋅⋅+, 当123k =⋅⋅⋅,, , 时，观察下列等式：211122S n n =+，322111326S n n n =++，4323111424S n n n =++， 5434111152330S n n n n=++-， 6542515212S An n n Bn =+++，⋅⋅⋅可以推测，A B -= .三、解答题（本题共6小题，共74分。

福建省2013届高三毕业班质量检测数学文试题 Word版含答案

2013年福建省普通高中毕业班质量检查文科数学本试卷分第1卷(选择题)和第Ⅱ卷(非选择题)．本试卷共5页．满分150分．考试时间120分钟．注意事项：1．答题前，考生先将自己的姓名、准考证号填写在答题卡上．2．考生作答时，将答案答在答题卡上．请按照题号在各题的答题区域(黑色线框)内作答，超出答题区域书写的答案无效．在草稿纸、试题卷上答题无效．3．选择题答案使用2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其他答案标号；非选择题答案使用0．5毫米的黑色中性(签字)笔或碳素笔书写，字体工整、笔迹清楚．4．保持答题卡卡面清洁，不折叠、不破损．考试结束后，将本试卷和答题卡一并交回．参考公式：样本数据x 1，x 2， …，x n 的标准差锥体体积公式V =31Sh 其中x 为样本平均数其中S 为底面面积，h 为高柱体体积公式球的表面积、体积公式 V =Sh24S R =π，343V R =π其中S 为底面面积，h 为高其中R 为球的半径第Ⅰ卷（选择题共60分）一．选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知复数1i z =-，z 为z 的共轭复数，则下列结论正确的是A ．1i z =--B ．1+i z =-C ．2z =D ．z =2．已知,0a b c >≠，则下列不等式一定成立的是 A ．22a b >B ．ac bc >C ．a c b c +>+D ．a b c c> 3．执行如图所示的程序框图，若输入的x 值为2，则输出的x 值为 A ．3 B ．8 C ．9 D ．63 4．“1x =”是“210x -=”的Ａ．充分而不必要条件Ｂ．必要而充分不条件Ｃ．充要条件Ｄ．既不充分也不必要条件5．函数2cos 22y x x x ππ⎛⎫=-≤≤ ⎪⎝⎭的图象是6．已知集合{}|28M x x =-≤≤，{}2|320N x x x =-+≤，在集合M 中任取一个元素x ，则 “x M N ∈ ”的概率是A ．110B ．16C ．310D ．127．已知1F ，2F 是椭圆C 的两个焦点，焦距为4.若P 为椭圆C 上一点，且12PF F ∆的周长为14，则椭圆C 的离心率e 为 A ．15 B ．25 C ．45D ．5A CD8．若变量,x y 满足约束条件310,3110,2,x y x y y --≥⎧⎪+-≤⎨⎪≥⎩则2z x y =-的最小值为A ．4B ．1C ．0D ．1- 9．设,m n 为两条不同的直线，βα,是两个不同的平面，下列命题正确的是 A ．若β//,//m n m ，则β//n B ．若αα//,//n m ，则n m // C ．若β⊥m n m ,//，则β⊥n D ．若n m n m //,,βα⊂⊂，则βα// 10．已知点()0,0O ，()1,2A ,()3,2B ，以线段AB 为直径作圆C ，则直线:30l x y +-=与圆C 的位置关系是A ．相交且过圆心B ．相交但不过圆心C ．相切D ．相离11．已知点()()()0000167n O ,,A ,,A ,,点()1212n A ,A ,,A n ,n -∈≥N 是线段0n A A 的n 等分点，则011+n n OA OA OA OA -+++等于A ．5nB ．10nC ．()51n +D ．()101n +12．定义两个实数间的一种新运算“*”：()lg 1010,x yx y *=+,x y ∈R .对任意实数,,a b c ，给出如下结论：①()()c b a c b a ****=； ②a b b a **=； ③()()()**a b c a c b c +=++；其中正确的个数是A ． 0B ．1C ．2D ．3第Ⅱ卷（非选择题共90分）二、填空题:本大题共4小题，每小题4分，共16分．把答案填在答题卡相应位置． 13．一支田径队有男运动员28人，女运动员21人，现按性别用分层抽样的方法，从中抽取14位运动员进行健康检查，则男运动员应抽取________人． 14．在ABC ∆中，角,,A B C 所对的边分别为,,a b c ．已知3a =，8b =，C=3π，则c = ．15．若函数2,0,()ln ,0x a x f x x x ⎧-≤=⎨>⎩有两个不同的零点，则实数a 的取值范围是．16．观察下列等式：12133+=； 781011123333+++=； 16171920222339333333+++++=； …则当m n <且,m n ∈N 表示最后结果.313232313333n n m m ++--++++= （最后结果用,m n 表示最后结果）．三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤． 17．(本小题满分12分)某工厂生产,A B 两种元件，其质量按测试指标划分为：大于或等于7．5为正品，小于7．5为次品．现从一批产品中随机抽取这两种元件各5件进行检测，检测结果记录如下：由于表格被污损，数据y x ,看不清，统计员只记得x y <，且,A B 两种元件的检测数据的平均值相等，方差也相等．（Ⅰ）求表格中x 与y 的值；（Ⅱ）若从被检测的5件B 种元件中任取2件，求2件都为正品的概率． 18．(本小题满分12分)已知函数()sin cos f x x x =+，x ∈R ．（Ⅰ）求12f π⎛⎫⎪⎝⎭的值；（Ⅱ）试写出一个函数()g x ，使得()()cos 2g x f x x =，并求()g x 的单调区间． 19．(本小题满分12分)某几何体111C B A ABC -的三视图和直观图如图所示．（Ⅰ）求证：平面11AB C ⊥平面11AA C C ；（Ⅱ）若E 是线段1AB 上的一点，且满足1111191C B A ABC C AA E V V --=，求AE 的长．20．(本小题满分12分)某工业城市按照“十二五”（2011年至2015年）期间本地区主要污染物排放总量控制要求，进行减排治污．现以降低SO 2的年排放量为例，原计划“十二五”期间每年的排放量都比上一年减少0.3万吨，已知该城市2011年SO 2的年排放量约为9.3万吨，（Ⅰ）按原计划，“十二五”期间该城市共排放SO 2约多少万吨？（Ⅱ）该城市为响应“十八大”提出的建设“美丽中国”的号召，决定加大减排力度．在2012年刚好按原计划完成减排任务的条件下，自2013年起，SO 2的年排放量每年比上一年减少的百分率为p ，为使2020年这一年的SO 2年排放量控制在6万吨以内，求p 的取值范围. （参考数据9505.0328≈，9559.0329≈）． 21．(本小题满分12分)已知函数()2e xf x ax bx =++．（Ⅰ）当0,1a b ==-时，求()f x 的单调区间；（Ⅱ）设函数()f x 在点()(),P t f t ()01t <<处的切线为l ，直线l 与y 轴相交于点Q .若点Q 的纵坐标恒小于1，求实数a 的取值范围． 22．(本小题满分14分)某同学用《几何画板》研究抛物线的性质：打开《几何画板》软件，绘俯视图侧(左)视图正(主)视图1A制某抛物线2:2E y px =，在抛物线上任意画一个点S ，度量点S 的坐标(),S S x y ，如图．（Ⅰ）拖动点S ，发现当4S x =时，4S y =，试求抛物线E 的方程；（Ⅱ）设抛物线E 的顶点为A ，焦点为F ，构造直线SF 交抛物线E 于不同两点S 、T ，构造直线AS 、AT 分别交准线于M 、N 两点，构造直线MT 、NS ．经观察得：沿着抛物线E ，无论怎样拖动点S ，恒有MT //NS .请你证明这一结论．（Ⅲ）为进一步研究该抛物线E 的性质，某同学进行了下面的尝试：在（Ⅱ）中，把“焦点F ”改变为其它“定点(),0G g ()0g ≠”，其余条件不变，发现“MT 与NS 不再平行”．是否可以适当更改（Ⅱ）中的其它条件，使得仍有“MT //NS ”成立？如果可以，请写出相应的正确命题；否则，说明理由．2013年福建省普通高中毕业班质量检查文科数学试题参考解答及评分标准说明：一、本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制定相应的评分细则．二、对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数的一半；如果后继部分的解答有较严重的错误，就不再给分．三、解答右端所注分数，表示考生正确做到这一步应得的累加分数．四、只给整数分数．选择题和填空题不给中间分．一、选择题：本大题考查基础知识和基本运算．每小题5分，满分60分． 1．D 2．C 3．B 4．A 5．B 6．A 7．B 8．A 9．C 10．B 11．C 12．D二、填空题：本大题考查基础知识和基本运算．每小题4分，满分16分． 13．8； 14．7； 15．01a <≤； 16．22n m -．三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．17．本小题主要考查古典概型、统计等基础知识，考查数据处理能力、运算求解能力以及应用意识，考查必然与或然思想等．满分12分．解：(Ⅰ)因为11=+7+75+9+95=8=858555x x x y ⋅⋅+⋅+⋅+A B （7），（6+），由=x x A B，得17x y +=． ① ………………………………………2分因为222211=1+1+0.25+1+2.25=1.1=4+8+0.25+0.25+855x y ⎡⎤--⎣⎦A B ，s （）s （）（），由22=A Bs s ，得228+8=1x y --（）（）． ② …………………………………………4分由①②解得89x y =⎧⎨=⎩，，或98.x y =⎧⎨=⎩，因为x y <，所以8x y ==． ………………………………………6分(Ⅱ) 记被检测的5件B 种元件分别为12345,,,,B B B B B ，其中2345,,,B B B B 为正品，从中任取2件,共有10个基本事件，列举如下:()12,B B ，()13,B B ，()14,B B ，()15,B B ，()23,B B ， ()24,B B ，()25,B B ，()34,B B ，()35,B B ，()45,B B ， ………………………………………8分记“2件都为正品”为事件C ，则事件C 包含以下6个基本事件：()23,B B ，()24,B B ，()25,B B ，()34,B B ，()35,B B ，()45,B B .……………………………10分所以63()105P C ==，即2件都为正品的概率为35. ………………………………………12分 18．本小题主要考查三角函数的图象与性质、两角和与差三角公式、二倍角公式、三角函数的恒等变换等基础知识，考查运算求解能力，考查化归与转化思想等．满分12分．解法一：(Ⅰ)因为())4f x x π=+，………………………………………3分所以1212432f ππππ⎛⎫⎛⎫=+==⎪ ⎪⎝⎭⎝⎭……………………………6分 (Ⅱ)()cos sin g x x x =-. …………………………………………………………7分下面给出证明：因为()()22(cos sin )(sin cos )cos sin cos 2,g x f x x x x x x x x =-+=-=所以()cos sin g x x x =-符合要求．……………………………………………………9分又因为()cos sin 4g x x x x π⎛⎫=-=+ ⎪⎝⎭，…………………………………………10分由222,4k x k πππππ+<+<+得3722,44k x k ππππ+<<+ 所以()g x 的单调递增区间为372244k k ππππ⎛⎫++ ⎪⎝⎭，k ∈Z .………………………………11分又由224k x k ππππ<+<+,得32244k x k ππππ-<<+,所以()g x 的单调递减区间为32244k k ππππ⎛⎫-+⎪⎝⎭，，k ∈Z .………………………………12分解法二：(Ⅰ)因为()21s i n 2,fxx =+⎡⎤⎣⎦所以231s i n 1262f ππ⎡⎤⎛⎫=+=⎪⎢⎥⎝⎭⎣⎦，………………………………3分又因为0,12f π⎛⎫>⎪⎝⎭所以12f π⎛⎫= ⎪⎝⎭．………………………………6分 (Ⅱ)同解法一．解法三：(Ⅰ)sin cos sin cos 1212123434f πππππππ⎛⎫⎛⎫⎛⎫=+=-+-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭sincoscossincoscossinsin34343434ππππππππ=-++…………………3分1122222222=-++2=………………………………6分 (Ⅱ)同解法一．注：若通过()()cos 2xg x f x =得到()g x 或由()()(cos sin )(cos sin )g x f x x x x x =+-两边同时约去()f x 得到()g x 不扣分．19．本小题主要考查三视图、直线与直线、直线与平面、平面与平面的位置关系，几何体的体积等基础知识；考查空间想象能力、推理论证能力、运算求解能力；考查函数与方程思想、数形结合思想、化归与转化思想．满分12分．解法一：（Ⅰ）由三视图可知，几何体111C B A ABC -为三棱柱，侧棱1111C B A AA 底面⊥，1111C A C B ⊥,且41==AC AA ，2=BC ．………………………………………2分 1111C B A AA 平面⊥ ，11111111,C B AA C B A C B ⊥∴⊂平面， …………………3分 11111111,A C A AA C A C B =⊥ ，1111ACC A C B 平面⊥∴．……………………5分又1111C AB C B 平面⊂ ， C C AA C AB 1111平面平面⊥∴．………………………6分（Ⅱ）过点E 作11//C B EF 交1AC 于F ，由（Ⅰ）知，11ACC A EF 平面⊥，即EF 为C AA E 1-三棱锥的高. ………7分1111191C B A ABC C AA E V V --= ，,9131111AA S EF S ABC C AA ⋅=⋅∴∆∆ ……………………8分1111442443292EF ⎛⎫⎛⎫∴⨯⨯⨯⨯=⨯⨯⨯⨯ ⎪ ⎪⎝⎭⎝⎭，解得32=EF .……………………9分在Rt ABC ∆中，AB ===，在1Rt ABB ∆中，16AB ===，……………………10分由111C B EFAB AE =， ……………………11分得22326C B EFAB AE 111=⨯=⋅=. ……………………12分解法二：（Ⅰ）同解法一.（Ⅱ）过点E 作11//C B EF 交1AC 于F ，由（Ⅰ）知，11ACC A EF 平面⊥，即EF 为C AA E 1-三棱锥的高. ………7分11111111133C AA B C B A A C B A ABC V V V ---== ，111111113191C AA B C B A ABC C AA E V V V ---==∴ ………8分,313131111111C B S EF S C AA C AA ⋅⨯=⋅∴∆∆,3111C B EF =∴ ………9分在ABC Rt ∆中，5224AB 2222=+=+=BC AC ，在1ABB Rt ∆中，()6452AB 222121=+=+=BB AB ，……………………10分由111C B EFAB AE =， ……………………11分得2AB 31AE 1==. ……………………12分 20．本小题主要考查等差数列、等比数列等基础知识，考查运算求解能力和应用意识，考查函数与方程思想.满分12分.解：（Ⅰ）设“十二五”期间，该城市共排放SO 2约y 万吨，依题意，2011年至2015年SO 2的年排放量构成首项为9.3，公差为0.3-的等差数列，……………3分所以()55159.3(0.3)=43.52y ⨯-=⨯+⨯-（万吨）．所以按计划“十二五”期间该城市共排放SO 2约43．5万吨．……………………6分（2）由已知得， 2012年的SO 2年排放量9.60.32=9-⨯（万吨），…………………7分所以2012年至2020年SO 2的年排放量构成首项为9，公比为1p -的等比数列，…………………9分由题意得891p ⨯-（）＜6，即1p -＜832，所以10.9505p -<，解得 4.95%p >.所以SO 2的年排放量每年减少的百分率p 的取值范围4.95%1p <<<……………………12分21．本小题主要考查函数、导数等基础知识，考查推理论证能力、运算求解能力，考查分类与整合思想、数形结合思想、化归与转化思想．满分12分．解：（Ⅰ）当0,1a b ==-时，()e xf x x =-，()e 1xf x '=-，……………………1分所以，当(,0x ∈-∞时，()0f x '<；当(0,x ∈+∞时，()0f x '>；……………………3分所以函数()f x 的单调递减区间为(),0-∞，单调递增区间为(0,)+∞．……………………4分（Ⅱ）因为()2xf x e ax b '=++，所以()(),P t f t 处切线的斜率()2tk f t e at b '==++，所以切线l 的方程为()()()22t ty e at bt e at bx t -++=++-，令0x =，得()21ty t e at =-- ()01t <<.…………………………………………5分当01t <<时，要使得点Q 的纵坐标恒小于1，只需()211tt e at --<，即()2110tt e at -++>()01t <<.……………… 6分令()()211tg t t e at =-++，则()()2tg t t e a '=+，………………………………………………………… 7分因为01t <<，所以1t e e <<， ①若21a ≥-即12a ≥-时，20t e a +>，所以，当()0,1t ∈时，()0g t '>，即()g t 在()0,1上单调递增，所以()(0)0g t g >=恒成立，所以12a ≥-满足题意.………………………………8分 ②若2a e ≤-即2ea ≤-时，20t e a +<，所以，当()0,1t ∈时，()0g t '<，即()g t 在()0,1上单调递减，所以()(0)0g t g <=，所以2ea ≤-不满足题意.………………………………………9分 ③若21e a -<<-即122e a -<<-时，0ln(2)1a <-<.则t 、()g t '、()g t 的关系如下表：所以()()ln(2)00g a g -<=，所以22a -<<-不满足题意.……………………11分综合①②③，可得，当12a ≥-时，()0g t >()01t <<时，此时点Q 的纵坐标恒小于1.…………12分22．本小题主要考查抛物线的标准方程、直线与圆锥曲线的位置关系等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、分类与整合思想、数形结合思想等．满分14分．解法一：（Ⅰ）把4S x =，4S y =代入22y px =，得248p =，……………………2分所以2p =，………………………………………………………………………3分因此，抛物线E 的方程24y x =．…………………………………………………4分（Ⅱ）因为抛物线E 的焦点为()1,0F ，设()()1122,,,S x y T x y ，依题意可设直线:1l my x =-，由241y x my x ⎧=⎨=-⎩，得2440y my --=，则121244.y y m y y +=⎧⎨⋅=-⎩， ①……………………6分又因为11:AS y l y x x =，22:AT yl y x x =，所以111,y M x ⎛⎫-- ⎪⎝⎭，221,y N x ⎛⎫-- ⎪⎝⎭，所以12211,y MT x y x ⎛⎫=++ ⎪⎝⎭ ，21121,y NS x y x ⎛⎫=++ ⎪⎝⎭ ， ……………………7分又因为()()1221121211y y y x y x x x ⎛⎫⎛⎫++-++ ⎪ ⎪⎝⎭⎝⎭……………………………………8分 2221121241411144y y y y y y ⎛⎫⎛⎫⎛⎫⎛⎫=++-++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭22122112*********4y y y y y y y y y y ⎛⎫⎛⎫=+++-+++ ⎪ ⎪⎝⎭⎝⎭()21121212144y y y y y y y y -=-+()22121212164y y y y y y ⎛⎫-=- ⎪⎝⎭， ②把①代入②，得()221212121604y y y y y y ⎛⎫--= ⎪⎝⎭，………………………………………………10分即()()12211212110y y y x y x x x ⎛⎫⎛⎫++-++= ⎪ ⎪⎝⎭⎝⎭，所以//MT NS，又因为M 、T 、N 、S 四点不共线，所以MT //NS ．………………………………11分（Ⅲ）设抛物线2:4E y x =的顶点为A ，定点()(),00G g g ≠，过点G 的直线l 与抛物线E 相交于S 、T 两点，直线AS 、AT 分别交直线x g =-于M 、N 两点，则MT //NS ．……………………14分解法二：（Ⅰ）同解法一.（Ⅱ）因为抛物线E 的焦点为()1,0F ，设()()221122,2,,2S t t T t t ，……………………5分依题意,可设直线:1ST l my x =-，由241y x my x ⎧=⎨=-⎩得2440y my --=，则1212224,224,t t m t t +=⎧⎨⋅=-⎩所以12124,1.t t m t t +=⎧⎨⋅=-⎩…………………………………………………………………………7分又因为2:2AS l y t x =-，1:2AT l y t x =-，所以()21,2M t -，()11,2N t -，………………………………………………………10分所以0MT k =，0NS k =，…………………………………………………………………10分又因为M 、T 、N 、S 四点不共线，所以MT //NS .…………………………………11分（Ⅲ）同解法一. 解法三：（Ⅰ）同解法一.（Ⅱ）因为抛物线E 的焦点为()1,0F ，设()()1122,,,S x y T x y ，依题意，设直线:1l my x =-，由241y x my x ⎧=⎨=-⎩得2440y my --=，则121244y y m y y +=⎧⎨⋅=-⎩，……………………………6分又因为11:AS y l y x x =，22:AT yl y x x =，所以111,y M x ⎛⎫-- ⎪⎝⎭，221,y N x ⎛⎫-- ⎪⎝⎭，又因为212y y x ⎛⎫--⎪⎝⎭2212111222224404y y y y y y y y x y y +=+=+=+==，……………………9分所以212y y x =-，所以NS 平行于x 轴；同理可证MT 平行于x 轴；又因为M 、T 、N 、S 四点不共线，所以MT //NS .………………………………11分（Ⅲ）同解法一. …………………………………………………14分。

福建省福州八中高三数学毕业班第三次质检考试试题文新人教A版

考试时间：120分钟试卷满分：150分2013.11.4第Ⅰ卷（选择题共60分）一、选择题：（每小题5分，共60分. 在给出的A 、B 、C 、D 四个选项中，只有一项符合题目要求，在答题纸的相应区域内作答） 1. 函数)13lg(13)(2++-=x xx x f 的定义域是A ．),31(+∞-B ． )1,31(- C ． )31,31(-D ． )31,(--∞2.“4πθ=”是“sin 21θ=”的 A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件3．若a ，b 是任意实数，且b a >，则A ．22b a > B ．1<ab C ．()0>-b a lgD ．ba ⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛21214. 设向量=→a(1,0)a =,=→b 11(,)22b =,则下列结论中正确的是 A ．→→=b a B ．22=⋅→→b aC ．→→-b a 与→b 垂直D ．→→b a //5.“m=21”是“直线(m+2)x+3my+1=0与直线(m －2)x+(m+2)y －3=0相互垂直”的 A ．充分必要条件 B ．充分而不必要条件C ．.必要而不充分条件D ．既不充分也不必要条件6．若方程()02=-x f 在()0,∞-内有解，则()x f y =的图象是7．设f ：A →B 是集合A 到B 的映射，下列命题中是真命题的是 A. A 中不同元素必有不同的象 B. B 中每个元素在A 中必有原象C. A 中每一个元素在B 中必有象D. B 中每一个元素在A 中的原象唯一8. 设曲线2y ax =在点(1,)a 处的切线与直线260x y --=平行，则a = A ．-1B ．12C ．12-D ．19. 函数)1ln()(2+=x x f 的图象大致是A ．B ．C ．D ．10. 1sin()63πα+=，则2cos(2)3πα-的值等于A. 59-B. 79-C.D.11. 已知函数()|lg |f x x =,若a b ≠且()()f a f b =，则a b +的取值范围是A.(1,)+∞B. [1,)+∞C. (2,)+∞D.[)+∞,212. 已知椭圆)0(1:2222>>=+b a b y a x C 的离心率为23,双曲线12222=-y x 的渐近线与椭圆有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆的方程为A ．12822=+y xB ．161222=+y xC ．141622=+y xD ．152022=+y x第Ⅱ卷（非选择题共90分）二、填空题：本大题共4小题，每小题4分，共16分．将答案填在答题卡的相应位置．13．计算：=+-ii21____________. 14．等比数列}{n a 的前n 项和为n S ，若4,184==S S ，则=+++16151413a a a a __________．15.已知a ∈[－1,1]，不等式x 2＋(a －4)x ＋4－2a ＞0恒成立，则x 的取值范围为16. 对于函数 ①f(x)=lg(|x -2|+1), ②f(x)=(x -2)2, ③f(x)=cos(x+2), 判断如下三个命题的真假：命题甲：f(x+2)是偶函数；命题乙：f(x)在（-∞，2）上是减函数，在（2，+∞）上是增函数；命题丙：f(x+2)-f(x)在（-∞，+∞）上是增函数.能使命题甲、乙、丙均为真的所有函数的序号是 _________ 三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤． 17．（本小题满分12分）如图，测量河对岸的塔高AB 时，可以选与塔底B 在同一水平面内的两个测点C 与D ．测得 03030BDC CD ∠==，米，并在点C 测得塔顶A 的仰角为060,（1）若测得015BCD ∠=，求塔高AB ；（2）若BCD ∠=，θ且15105︒<θ<︒，求AB 的范围.18．（本小题满分12）已知各项不为零数列{a n }满足a 1＝23，且对任意的正整数m ，n 都有a m ＋n ＝a m ·a n ，求：（1）a n a 1n 的值；（2）201420122010422014201220104220132011200931a a a a a ...a a a a a ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++++ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭的值.19．（本小题满分12分）已知函数 ()22sin 2sin cos 3cos f x x x x x =++．（1）求函数()f x 图象的对称中心的坐标；（2）求函数()f x 的最大值，并求函数()f x 取得最大值时x 的值；（3）求函数()f x 的单调递增区间．20. （本小题满分12分）过点Q(-2作圆O:x 2+y 2=r 2(r>0)的切线，切点为D ，且|QD|=4.(1)求r 的值.(2)设P 是圆O 上位于第一象限内的任意一点，过点P 作圆O 的切线l ，且l 交x 轴于点A ，交y 轴于点B ，设OM OA OB =+，求OM 的最小值(O 为坐标原点).21．（本小题满分12分）设直线:54l y x =+是曲线:C 321()23f x x x x m =-++的一条切线，2()223g x ax x =+-．（Ⅰ）求切点坐标及m 的值；（Ⅱ）当m Z ∈时，存在[0,)x ∈+∞()()f x g x ≤使成立，求实数a 的取值范围．22．（本小题满分14分）设()()1122,,,A x y B x y 是椭圆()222210y x a b a b +=>>的两点，11,x y m b a ⎛⎫= ⎪⎝⎭，22,x y n b a ⎛⎫= ⎪⎝⎭，且0m n ⋅=，椭圆离心率2e =，短轴长为2，O 为坐标原点。

2013年福建省高考数学试卷及解析(文史类)高清整理版

2013年福建省高考数学试卷及解析（文史类）一．选择题1．复数i z 21--=（i 为虚数单位）在复平面内对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．设点),(y x P ，则“2=x 且1-=y ”是“点P 在直线01:=++y x l 上”的（）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件 3．若集合}4,3,1{},3,2,1{==B A ，则B A 的子集个数为（）A ．2B ．3C ．4D ．164．双曲线122=-y x 的顶点到其渐近线的距离等于（）A ．21 B ．22 C ．1 D ．2 5．函数)1ln()(2+=x x f 的图象大致是（）A ．B ．C ．D ．6．若变量y x ,满足约束条件⎪⎩⎪⎨⎧≥≥≤+012y x y x ，则y x z +=2的最大值和最小值分别为（）A ．4和3B ．4和2C ．3和2D ．2和07．若122=+yx ，则y x +的取值范围是（）A ．]2,0[B ．]0,2[-C ．),2[+∞-D ．]2,(--∞8．阅读如图所示的程序框图，运行相应的程序，如果输入某个正整数n 后，输出的)20,10(∈S ，那么n 的值为（）A ．3B ．4C ．5D ．69．将函数)22)(2sin()(πθπθ<<-+=x x f 的图象向右平移)0(>ϕϕ个单位长度后得到函数)(x g 的图象，若)(),(x g x f 的图象都经过点)23,0(P ，则ϕ的值可以是（） A ．35π B ．65π C ．2π D ．6π 10．在四边形ABCD 中，)2,4(),2,1(-==BD AC ，则该四边形的面积为（）A ．5B ．52C ．5D ．10 11．已知x 与y 之间的几组数据如下表：假设根据上表数据所得线性回归直线方程为a x b yˆˆˆ+=．若某同学根据上表中前两组数据)0,1(和)2,2(求得的直线方程为a x b y '+'=，则以下结论正确的是（）A ．a a b b'>'>ˆ,ˆ B ．a a b b '<'>ˆ,ˆ C ．a a b b '>'<ˆ,ˆ D ．a a b b '<'<ˆ,ˆ 12．设函数)(x f 的定义域为R ，)0(00≠x x 是)(x f 的极大值点，以下结论一定正确的是（）A ．)()(,0x f x f R x ≤∈∀B ．0x -是)(x f -的极小值点C ．0x -是)(x f -的极小值点D ．0x -是)(x f --的极小值点二．填空题13．已知函数⎪⎩⎪⎨⎧<≤-<=20,tan 0,2)(3πx x x x x f ，则=))4((πf f ．14．利用计算机产生1~0之间的均匀随机数a ，则事件“013<-a ”发生的概率为15．椭圆)0(1:2222>>=+Γb a by a x 的左、右焦点分别为21,F F ，焦距为c 2．若直线与椭圆Γ的一个交点M 满足12212F MF F MF ∠=∠，则该椭圆的离心率等于 16．设T S ,是R 的两个非空子集，如果存在一个从S 到T 的函数)(x f y =满足；（i ）}|)({S x x f T ∈=；（ii ）对任意S x x ∈21,，当21x x <时，恒有)()(21x f x f <．那么称这两个集合“保序同构”．现给出以下3对集合： ①*,N B N A ==；②}108|{},31|{≤≤-=≤≤-=x x B x x A ； ③R B x x A =<<=},10|{．其中，“保序同构”的集合对的序号是（写出所有“保序同构”的集合对的序号）x 1 2 3 4 5 6 y213343三．解答题17．（本小题满分12分）已知等差数列{}n a 的公差1d =，前n 项和为n S ．（1）若131,,a a 成等比数列，求1a ；（2）若519S a a >，求1a 的取值范围．18．（本小题满分12分）如图，在四棱锥P ABCD -中，PD ABCD ⊥面，//AB DC ，AB AD ⊥，5BC =，3DC =，4AD =，60PAD ∠=．（1）当正视图方向与向量AD 的方向相同时，画出四棱锥P ABCD -的正视图.（要求标出尺寸，并画出演算过程）；（2）若M 为PA 的中点，求证：//DM PBC 面；（3）求三棱锥D PBC -的体积．19．（本小题满分12分）某工厂有25周岁以上（含25周岁）工人300名，25周岁以下工人200名．为研究工人的5日平均生产量是否与年龄有关．现采用分层抽样的方法，从中抽取了100名工人，先统计了他们某月的日平均生产件数，然后按工人年龄在“25周岁以上（含25周岁）”和“25周岁以下”分为两组，在将两组工人的日平均生产件数分成5组：[50,60)，[60,70)，[70,80)，[80,90)，[90,100)分别加以统计，得到如图所示的频率分布直方图．（1）从样本中日平均生产件数不足60件的工人中随机抽取2人，求至少抽到一名“25周岁以下组”工人的频率．（2）规定日平均生产件数不少于80件者为“生产能手”，请你根据已知条件完成22⨯的列联表，并判断是否有90% 的把握认为“生产能手与工人所在的年龄组有关”？附表：20．（本小题满分12分）如图，在抛物线2:4E y x =的焦点为F ，准线l 与x 轴的交点为A ．点C 在抛物线E 上，以C 为圆心OC 为半径作圆，设圆C 与准线l 的交于不同的两点,M N ．（1）若点C 的纵坐标为2，求MN ；（2）若2AFAM AN =⋅，求圆C 的半径．21（本小题满分12分）如图，在等腰直角三角形OPQ ∆中，90OPQ ∠=，22OP =，点M 在线段PQ 上．（1）若3OM =，求PM 的长；7（2）若点N 在线段MQ 上，且30MON ∠=，问：当POM ∠取何值时，OMN ∆的面积最小？并求出面积的最小值．22（本小题满分14分）已知函数()1x af x x e=-+（a R ∈，e 为自然对数的底数）．（1）若曲线()y f x =在点(1,(1))f 处的切线平行于x 轴，求a 的值；（2）求函数()f x 的极值；（3）当1a =的值时，若直线:1l y kx =-与曲线()y f x =没有公共点，求k 的最大值．9【解析】本题考查的知识点是复数的几何意义．由几何意义可知复数在第三象限． 2. 【答案】A【解析】本题考查的知识点是逻辑中充要条件的判定．因为)1,2(点代入直线方程，符合方程，即“2=x 且1-=y ”可推出“点P 在直线01:=++y x l 上”；而点P 在直线上，不一定就是)1,2(点，即“点P 在直线01:=++y x l 上”推不出“2=x 且1-=y ”．故“2=x 且1-=y ”是“点P 在直线01:=++y x l 上”的充分而不必要条件． 3. 【答案】C【解析】本题考查的是集合的交集和子集．因为}3,1{=B A ，有2个元素，所以子集个数为422=个．4. 【答案】B【解析】本题考查的是双曲线的性质．因为双曲线的两个顶点到两条渐近线的距离都相等，故可取双曲线的一个顶点为)0,1(，取一条渐近线为x y =，所以点)0,1(到直线x y =的距离为22． 5. 【答案】A【解析】本题考查的是对数函数的图象．由函数解析式可知)()(x f x f -=，即函数为偶函数，排除C ；由函数过)0,0(点，排除B,D ． 6. 【答案】B【解析】本题考查的简单线性规划．如图，可知目标函数最大值和最小值分别为4和2．122O xy7. 【答案】D【解析】本题考查的是均值不等式．因为y x y x 222221⋅≥+=，即222-+≤yx ，所以2-≤+y x ，当且仅当yx 22=，即y x =时取等号． 8. 【答案】B【解析】本题考查的是程序框图．循环前：2,1==k S ；第1次判断后循环：3,3==k S ；第2次判断后循环：4,7==k S ；第3次判断后循环：5,15==k S ．故4=n ．9. 【答案】B【解析】本题考查的三角函数的图像的平移．把)23,0(P 代入)22)(2sin()(πθπθ<<-+=x x f ，解得3πθ=，所以)232sin()(ϕπ-+=x x g ，把)23,0(P 代入得，πϕk =或6ππϕ-=k ，观察选项，故选B【解析】本题考查的是向量垂直的判断以及向量的模长．因为022)4(1=⨯+-⨯=⋅BD AC ，所以BC AC ⊥，所以四边形的面积为522)4(212||||2222=+-⋅+=⋅BD AC ，故选C11. 【答案】C【解析】本题考查的是线性回归方程．画出散点图，可大致的画出两条直线（如下图），由两条直线的相对位置关系可判断a a b b'>'<ˆ,ˆ．故选 C 1234123456Oxy12. 【答案】D【解析】本题考查的是函数的极值．函数的极值不是最值，A 错误；因为)(x f --和)(x f 关于原点对称，故0x -是)(x f --的极小值点，D 正确．13. 【答案】2-【解析】本题考查的是分段函数求值．2)1(2)1()4tan ())4((3-=-=-=-=f f f f ππ 14.【答案】31 【解析】本题考查的是几何概型求概率．013<-a ，即31<a ，所以31131==P ．15. 【答案】13-【解析】本题考查的是圆锥曲线的离心率．由题意可知，21F MF ∆中，︒=∠︒=∠︒=∠90,30,60211221MF F F MF F MF ，所以有⎪⎩⎪⎨⎧==+==+12212221222132)2(MF MF a MF MF c F F MF MF ，整理得13-==a c e ，故答案为13-．16. 【答案】①②③【解析】本题考查的函数的性质．由题意可知S 为函数的一个定义域，T 为其所对应的值域，且函数)(x f y =为单调递增函数．对于集合对①，可取函数)(2)(N x x f x∈=，是“保序同构”；对于集合对②，可取函数)31(2729≤≤--=x x y ，是“保序同构”；对于集合对③，可取函数)10)(2tan(<<-=x x y ππ，是“保序同构”．故答案为①②③．1117. 本小题主要考查等比等差数列、等比数列和不等式等基础知识，考查运算求解能力，考查函数与方程思想、化归与转化思想．满分12分．解：（1）因为数列{}n a 的公差1d =，且131,,a a 成等比数列，所以2111(2)a a =⨯+，即21120a a --=，解得11a =-或12a =．（2）因为数列{}n a 的公差1d =，且519S a a >，所以21115108a a a +>+；即2113100a a +-<，解得152a -<<18. 本小题主要考查直线与直线、直线与平面的位置关系及几何体的三视图和体积等基础知识，考查空间想象能力，推理论证能力．运算求解能力，考查数形结合能力、化归与转化思想，满分12分．解法一：（Ⅰ）在梯形ABCD 中，过点C 作CE AB ⊥，垂足为E ，由已知得，四边形ADCE 为矩形，3AE CD ==在Rt BEC ∆中，由5BC =，4CE =,依勾股定理得：3BE =，从而6AB =又由PD ⊥平面ABCD 得，PD AD ⊥从而在Rt PDA ∆中，由4AD =，60PAD ∠=︒,得43PD =正视图如右图所示：（Ⅱ）取PB 中点N ，连结MN ，CN在PAB ∆中，M 是PA 中点，∴MN AB ，132MN AB ==，又CD AB ,3CD = ∴MN CD ，MN CD =∴四边形MNCD 为平行四边形，∴DM CN又DM ⊄平面PBC ，CN ⊂平面PBC∴DM 平面PBC （Ⅲ）13D PBC P DBC DBC V V S PD --∆==⋅又6PBC s ∆=，43PD =，所以83D PBC V -=解法二：（Ⅰ）同解法一（Ⅱ）取AB 的中点E ，连结ME ,DE在梯形ABCD 中，BE CD ，且BE CD =∴四边形BCDE 为平行四边形∴DE BC ，又DE ⊄平面PBC ，BC ⊂平面PBC∴DE 平面PBC ，又在PAB ∆中，ME PBME ⊄平面PBC ,PB ⊂平面PBC∴ME 平面PBC .又DE ME E =,∴平面DME 平面PBC ，又DM ⊂平面DME∴DM 平面PBC（Ⅲ）同解法一19. 本小题主要考查古典概型、抽样方法、独立性检验等基础知识，考查运算求解能力、应用意识，考查必然和或然思想、化归与转化思想等，满分12分．解：（Ⅰ）由已知得，样本中有25周岁以上组工人60名，25周岁以下组工人40名所以，样本中日平均生产件数不足60件的工人中，25周岁以上组工人有600.053⨯=（人），记为1A ，2A ，3A ；25周岁以下组工人有400.052⨯=（人），记为1B ，2B从中随机抽取2名工人，所有可能的结果共有10种，他们是：12(,)A A ，13(,)A A ，23(,)A A ，11(,)A B ，12(,)A B ，21(,)A B ，22(,)A B ，31(,)A B ，32(,)A B ，12(,)B B其中，至少有名“25周岁以下组”工人的可能结果共有7种，它们是：11(,)A B ，12(,)A B ，21(,)A B ，22(,)A B ，31(,)A B ，32(,)A B ，12(,)B B .故所求的概率：710P =（Ⅱ）由频率分布直方图可知，在抽取的100名工人中，“25周岁以上组”中的生产能手600.2515⨯=（人），“25周岁以下组”中的生产能手400.37515⨯=（人），据此可得22⨯列联表如下：生产能手非生产能手合计 25周岁以上组15 45 60 25周岁以下组15 25 40 合计30 70 100 所以得：222()100(15251545)25 1.79()()()()6040307014n ad bc K a b c d a c b d -⨯⨯-⨯===≈++++⨯⨯⨯ 因为1.79 2.706<，所以没有90%的把握认为“生产能手与工人所在的年龄组有关”20. 本小题主要考查抛物线的方程、圆的方程与性质、直线与圆的位置关系等基础知识，考查运算求解能力、推理论证能力，考查函数与方程思想、数形结合思想、化归与转化思想．满分12分．解：（Ⅰ）抛物线24y x =的准线l 的方程为1x =-，由点C 的纵坐标为2，得点C 的坐标为(1,2)所以点C 到准线l 的距离2d =，又||5CO =．所以22||2||2542MN CO d =-=-=.（Ⅱ）设200(,)4y C y ，则圆C 的方程为242220000()()416y y x y y y -+-=+，即22200202y x x y y y -+-=. 由1x =-，得22002102y y y y -++= 设1(1,)M y -，2(1,)N y -，则：222000201244(1)240212y y y y y y ⎧∆=-+=->⎪⎪⎨⎪=+⎪⎩由2||||||AF AM AN =⋅，得12||4y y =13 所以20142y +=，解得06y =±，此时0∆> 所以圆心C 的坐标为3(,6)2或3(,6)2- 从而233||4CO =，33||2CO =，即圆C 的半径为332 21. 本小题主要考查解三角形、同角三角函数的基本关系、两角和与差的三角函数等基础知识，考查推理论证能力、抽象概括能力、运算求解能力，考查函数与方程思想、数形结合思想、化归与转化思想．满分12分．解：（Ⅰ）在OMP ∆中，45OPM ∠=︒，5OM =，22OP =，由余弦定理得，2222cos 45OM OP MP OP MP =+-⨯⨯⨯︒，得2430MP MP -+=，解得1MP =或3MP =．（Ⅱ）设POM α∠=，060α︒≤≤︒，在OMP ∆中，由正弦定理，得sin sin OM OP OPM OMP =∠∠，所以()sin 45sin 45OP OM α︒=︒+，同理()sin 45sin 75OP ON α︒=︒+ 故1sin 2OMN S OM ON MON ∆=⨯⨯⨯∠ ()()221sin 454sin 45sin 75OP αα︒=⨯︒+︒+ ()()1sin 45sin 4530αα=︒+︒++︒ ()()()131sin 45sin 45cos 4522ααα=⎡⎤︒+︒++︒+⎢⎥⎣⎦ ()()()2131sin 45sin 45cos 4522ααα=︒++︒+︒+ ()()1311cos 902sin 90244αα=-︒++︒+⎡⎤⎣⎦ 1331sin 2cos 2444αα=++()131sin 23042α=++︒因为060α︒≤≤︒，30230150α︒≤+︒≤︒，所以当30α=︒时，()sin 230α+︒的最大值为1，此时OMN ∆的面积取到最小值．即230POM ∠=︒时，OMN ∆的面积的最小值为843-．22. 本小题主要考查函数与导数，函数的单调性、极值、零点等基础知识，考查推理论证能力、运算求解能力，考查函数与方程思想、数形结合思想、分类与整合思想、化归与转化思想．满分14分．解：（Ⅰ）由()1x a f x x e =-+，得()1x a f x e'=-．又曲线()y f x =在点()()1,1f 处的切线平行于x 轴，得()10f '=，即10a e-=，解得a e =．（Ⅱ）()1x a f x e '=-， ①当0a ≤时，()0f x '>，()f x 为(),-∞+∞上的增函数，所以函数()f x 无极值．②当0a >时，令()0f x '=，得x e a =，ln x a =．(),ln x a ∈-∞，()0f x '<；()ln ,x a ∈+∞，()0f x '>．所以()f x 在(),ln a -∞上单调递减，在()ln ,a +∞上单调递增，故()f x 在ln x a =处取得极小值，且极小值为()ln ln f a a =，无极大值．综上，当0a ≤时，函数()f x 无极小值；当0a >，()f x 在ln x a =处取得极小值ln a ，无极大值．（Ⅲ）当1a =时，()11xf x x e =-+ 令()()()()111xg x f x kx k x e =--=-+，则直线l ：1y kx =-与曲线()y f x =没有公共点，等价于方程()0g x =在R 上没有实数解．假设1k >，此时()010g =>，1111101k g k e -⎛⎫=-+< ⎪-⎝⎭，又函数()g x 的图象连续不断，由零点存在定理，可知()0g x =在R 上至少有一解，与“方程()0g x =在R 上没有实数解”矛盾，故1k ≤．又1k =时，()10xg x e =>，知方程()0g x =在R 上没有实数解．所以k 的最大值为1．15 解法二：（Ⅰ）（Ⅱ）同解法一．（Ⅲ）当1a =时，()11x f x x e=-+．直线l ：1y kx =-与曲线()y f x =没有公共点，等价于关于x 的方程111xkx x e -=-+在R 上没有实数解，即关于x 的方程： ()11x k x e-= （*）在R 上没有实数解．①当1k =时，方程（*）可化为10xe =，在R 上没有实数解． ②当1k ≠时，方程（*）化为11x xe k =-．令()x g x xe =，则有()()1xg x x e '=+．令()0g x '=，得1x =-，当x 变化时，()g x '的变化情况如下表： x(),1-∞- 1- ()1,-+∞ ()g x ' -0 + ()g x1e - 当1x =-时，()min 1g x e=-，同时当x 趋于+∞时，()g x 趋于+∞，从而()g x 的取值范围为1,e ⎡⎫-+∞⎪⎢⎣⎭．所以当11,1k e ⎛⎫∈-∞- ⎪-⎝⎭时，方程（*）无实数解，解得k 的取值范围是()1,1e -．综上，得k 的最大值为1．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

A．2 B．3 C．4 D．5
2
12 ．若双曲线
x2 y2 − = 1 渐近线上的一个动点 P 总在平面区域 ( x − m) 2 + y 2 ≥ 16 内，则 9 16
B. (−∞, −3] ∪[3, +∞) D. ( −∞, −5] ∪ [5, +∞ ) 第Ⅱ卷（非选择题共 90 分）
实数 m 的取值范围是 A. [−3, 3] C. [ −5, 5]
9．在长为 10cm 的线段 AB 上任取一点 C，现作一个矩形，邻边长分别等于线段 AC、CB 的长，则该矩形的面积大于 24 cm2 的概率是 A．
1 6
B．
1 5
C．
1 4
D．
1 3 sin 2 θ ，其中 k 是常 r2
10．在半径为 a 的圆桌中心上方安装一吊灯,桌面上灯光的强度 y = k 数， r 是灯与桌面上被照点的距离，是光线与桌面的夹角（如图），现为使桌边最亮，则 sin θ = A.
福州八中 2012—2013 学年高三毕业班模拟考
数学(文)试题
考试时间：120 分钟参考公式：回归直线方程： ̂ y = bx + a ，其中 b = 试卷满分：150 分
n
∑ x y − nx y
i i i =1 n
, a = y − bx
2
∑ xi2 − nx
i =1
1 锥体体积公式： V = Sh ，其中 S 为底面面积， h 为高； 3
n 是奇数 n＝3n-5 i＝i ＋1 n＝2
是输出 i 结束否否 n n＝ 2
1
为 y＝－
m 2 C．准线方程为 x＝－4 的抛物线的标准方程为 y2＝8x
D．焦准距(焦点到准线的距离)为 p (p >0)的抛物线的标准方程为 y2 ＝±2px
6.若角α 的终边与单位圆交于第三象限的一点 P，其横坐标为 − A. −
x ＝95×0.1＋105×0.15＋115×0.15＋125×0.3＋135×0.25＋145×0.05＝121
………………………6 分 (3)依题意，[110,120)分数段的人数为 60×0.15＝9(人)． [120,130)分数段的人数为 60×0.3＝18(人)． ∵用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为 6 的样本， ∴需在[110,120)分数段内抽取 2 人，并分别记为 m，n；在[120,130)分数段内抽取 4 人，并分别记为 a，b，c，d；设“从样本中任取 2 人，至多有 1 人在分数段[120,130)内”为事件 A，则基本事件共有(m， n)， (m，a)，…，(m，d)，(n，a)，…，(n，d)，(a，b)，…，(c，d)共 15 种．则事件 A 包含的基本事件有(m，n)，(m，a)，(m，b)，(m，c)，(m，d)，(n，a)，(n，b)，(n， 9 3 c)，(n，d)共 9 种．∴P(A)＝＝ . 15 5 …………12 分
A1 B1 C1
VE − BCC1 =
1 V ABC − A1B1C1 ，求 A1 E 的长度. 12
A
O B
C
20 ．（本题满分 12 分）数列 { an }的前 n 项和 Sn =
n2 1 5 ，已知 a1 = ， a2 = ． an + b 2 6
（1）求数列 { an }的前 n 项和 Sn ；（2）求数列 { an }的通项公式；（3）设 bn =
an ，求数列 {bn } 的前 n 项和 Tn ． n + n −1
2
21．（本题满分 12 分）
x2 y2 2 ，且过点 (0, −1) ． + 2 = 1 (a > b > 0) 的离心率为 2 a b 2 （Ⅰ）求椭圆 C 的方程；
已知椭圆 C : （Ⅱ）若过点 M (2, 0) 的直线与椭圆 C 相交于两点 A、 B ，设 P 为椭圆上一点，且满足
3 2 2 3
B.
3 3 2 2
r
Ө
C.
D.
a
11. 已知定义在 R 上的函数 f (x ) 是偶函数，且满足 f (1 + x ) = f (1 − x ) ，当 x ∈ [− 1,1]时，
f ( x ) = 1 − x 2 ，若函数 g ( x) = log 5 x ，则 h ( x ) = f ( x ) − g ( x ) 在区间（0,5]内的零点的个数是
由 2 kπ − （II）∵2 bc cos A = a 2
2 2
又由余弦定理 a 2 = b 2 + c 2 − 2bc cos A ．
∴ 4bc cos A = b + c
,
∴ cos A =
b 2 + c 2 2bc 1 ≥ = 4bc 4bc 2
…………………….12 分
又∵ A 为三角形内角，所以 0 < A ≤
19 ．（本题满分 12 分）如图，在三棱柱 ABC − A1 B1 C1 中，侧面 AA1C1 C ⊥ 底面 ABC ， AA1 = A1 C = AC = 2 ，
AB = BC , AB ⊥ BC , O 为 AC 的中点.
⑴ 证明: A1 O ⊥ 平面 ABC ； ⑵ 若 E 是线段 A1 B 上一点，且满足
二、填空题：本大题共 4 小题，每小题 4 分，共 16 分，把答案填在相应横线上． π 13．函数 y＝sin (2x ＋ )的图象可由函数 y＝sin 2 x 的图象向左平移个单位长度 4 而得到． 14．设函数 f ( x ) = ⎨ 围是． 15．若关于 x 的不等式 m ( x − 1) > x 2 − x 的解集为 { x 1 < x < 2} ，则实数 m 的值为
开始
A． − 2
B. 2
C. − 2i
3．在递增等比数列{ a n }中， a 2 = 2, a 4 − a3 = 4 ，则公比 q ＝ A．-1 B．1 C．2 D．
1 2
是
n＝6, i＝1
4．某程序框图如图所示，则该程序运行后输出的值是 A．2 B．3 C．4 D．5 5.下列说法中，正确的是 A．与定点 F 和定直线的距离相等的点的轨迹是抛物线 m (0 ， ) B．抛物线 x2 ＝2my 的焦点坐标为 2 ，准线方程
2π π⎞ 1 = π 得 ω = 1 . 函数 f ( x ) = sin ⎛ ⎜ 2x − ⎟ − 2ω 6⎠ 2 ⎝
……………π π π ≤ 2 x − ≤ 2kπ + k ∈ Z 得 kπ − ≤ x ≤ kπ + 2 6 2 6 3 π π ∴函数 f ( x ) 的单调增区间[ kπ − , kπ + ] k ∈ Z ……………….6 分 6 3
1 3
福州八中 2012—2013 学年高三毕业班模拟考
数学（文）试题参考答案
1-12、BACCB DDDBD 13、 CD 15、2 16、 −
π 8
14、 [ 2,+∞)
5 b2 ； 2 9 a
…………3 分
17、解：(1)分数在[120,130)内的频率为 1－(0.1＋0.15＋0.15＋0.25＋0.05)＝1－0.7＝0.3 (2)估计平均分为
16．已知椭圆
x2 y 2 − = 1上任意一点 P ， A1 , A2 是双曲线的左、右顶点，设直线 PA1 , PA2 斜率分别 a2 b2 为 k PA1 , k PA2 ，则 k PA1 ⋅ k PA2 = .
双曲线三、解答题：（本大题共 6 小题，共 74 分，解答应写出文字说明、证明过程或演算步骤.） 17．（本题满分 12 分）某校从参加高三模拟考试的学生中随机抽取 60 名学生，将其数学成绩(均为整数)分成六组[90,100) ， [100,110)， …， [140,150]后得到如下部分频率分布直方图，观察图形的信息，回答下列问题： (1)求分数在[120,130)内的频率； (2)若在同一组数据中，将该组区间的中点值(如：组区 100＋110 间[100,110) 的中点值为＝105) 作为这组数据的平 2 均分，据此，估计本次考试的平均分； (3)用分层抽样的方法在分数段为[110,130) 的学生中抽取一个容量为 6 的样本，将该样本看成一个总体，从中任取 2 人，求至多有 1 人在分数段[120,130)内的概率．
�� ，求整数 t 的最大值． OA + OB = tOP （其中 O 为坐标原点）
4
22 ．（本题满分 14 分）若斜率为 k 的两条平行直线 l ， m 与曲线 C 相切并至少有两个切点，且曲线 C 上的所有点都在 l ， m 之间（也可在直线 l ， m 上），则把 l ， m 称为曲线 C 的“夹线” ，把 l ， m 间的距离称为曲线 C 在“ k 方向上的宽度” ，记为 d ( k ). 已知函数 f ( x ) = x +3cos x . （Ⅰ）若点 P 横坐标为 0，求 f ( x ) 图象在点 P 处的切线方程；（Ⅱ）试判断 y = x + 3 和 y = x − 3 是否是 f ( x ) 的“夹线” ，若是，求 d (1) ；若不是，请说明理由；（Ⅲ）求证：函数 F ( x) = − x 3 + x 的图象不存在“夹线”.
球的表面积公式： S = 4π R2 ；球的体积公式： V =
4 π R3 ，其中 R 为球的半径。 3
第Ⅰ卷（选择题共 60 分）
一、选择题：本大题共 12 小题，每小题 5 分，共 60 分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．设复数 z = 1 + 2i （ i 是虚数单位），则复数 z 的虚部为 D. 2i a b 2．命题 p : 若x < y, 则 | x |<| y | ，命题 q : 若 2 > 2 ，则 a > b ．则 c c A． “ p 或 q ”为真 C． p 真 q 假 B． “ p 且 q ”为真 D． p , q 均为假