4章专项拓展与训练4
人教版数学上册三年级第4单元教案:拓展练习教案

本文主要介绍人教版数学上册三年级第4单元的拓展练习教案。
本教案主要包括四个部分,分别为导入、新课讲解、拓展练习和课堂总结。
介绍导入环节。
为了提高学生的学习积极性,我们可以在导入环节中加入一些趣味性的内容,比如玩一些数学游戏。
比如,可以让学生拿出手中的小计算器,让他们利用计算器计算出一些有趣的数字。
或者我们可以通过数谜来进行导入,比如给学生数一个谜语:我有四个数字,这四个数字一起可以组成一个三位数,而这个三位数又刚好是4的倍数,你们知道这四个数字是什么吗?等学生想出了正确答案,就可以顺带着跟学生介绍4的倍数的概念。
是新课讲解环节。
本单元主要讲解的是3位数的概念和数的大小关系,我们可以通过举一些实际的例子来帮助学生更好地理解这些概念。
比如我们可以说:“小明家有一栋楼房,这栋楼房的门牌号是235,那你们觉得这个数字是不是一个三位数呢?”当学生回答答案后,我们可以再问他们:“那你们知道235和355哪一个比较大吗?”通过这样的方式,我们可以帮助学生理解概念,掌握大小关系。
是拓展练习。
我们可以为学生设计一些有趣的练习题目,让他们能够在实践中更好地掌握学习内容。
比如,可以出一道作业题:小明有一些玻璃球,他想把这些玻璃球分成三份,每份都有237个,你能帮他算算他应该准备多少个玻璃球吗?当学生们做完这道题目后,老师可以让他们相互交流、互相探讨,从而达到共同进步的目的。
是课堂总结。
在课堂总结中,我们可以让学生将本节课所学到的内容进行回顾和总结,在这个过程中让学生思考,思考自己哪些方面需要更加努力,哪些方面已经掌握得较好,从而提高学生的自我认知。
本教案通过趣味性的导入、生动实际的新课讲解、有趣的拓展练习、全面的课堂总结,帮助学生更好地掌握了学习内容,同时也激发了学生的学习兴趣,希望本教案能够对广大三年级学生有所帮助。
部编版四年级语文下册拓展阅读训练-鹿和狼的故事课件(共23张PPT)

引导学生思考在狼被除掉之后, 为什么鹿会迅速地繁育,泛滥成 灾?鹿为什么会生病并导致数量 骤减?
森林生态为什么失衡?
狼被除掉了,为什么鹿的数量经 历了有迅速增长,并发展到植被 遭受严重破坏,进而整个生态失 衡?
引导学生掌握学习方法
科学公道的学习方法是自我发展的前提
方法指点
六年级阶段的学生由于其生理发育和心理发育尚未成 熟,掌握语文课的科学学习方法难度较大,因此,教师 应当适时进行指点,交给学生会学习,会思考
森林生态平遭到严重破坏
两年之后,鹿群的总量由十万只锐减到四 万只。到1942年,整个凯巴伯森林中只 剩下不到八千只病鹿在苟延残喘
启示学生进行思考
政府为什么要除狼?
启示学生思考为什么美国 政府在西部选择了除狼行 动以保护鹿的生存?
交给学生正确的学习方法很重要。新课程 标准明确规定提倡学生自主学习,在此过 程中,交给学生独立思考是非常关键的
道理的表达方法
第4 章 延伸拓展
自主探究合作的教学方式
突破传统模式
教学过程中,我重视培养学生自主 合作探究学习方法的培养由学生提
出问题,再让学生自己去找答案
自主探究
讨论合作学习
合作学习中提高了学生自学能 力,培养了学生与他人交往的合 作精神,体现了人文性
简要讲述产生在凯巴伯森林中关于 鹿和狼的故事,并说说你从中懂得 一个什么道理?让学生根据自己的 喜好,用自己喜欢的方式自读课文 并自己去找答案,使学生最大限度 地发挥其主观能动性
文章前两部分
第一部分第1一6自然段,讲凯
巴伯森林中产生的狼与鹿的故
事。第二部分第7自然段,讲鹿 和狼与森林的关系
文章后两部分
第三部分第8自然段,讲人们对
2024年足球教案丨1v1进攻专项训练

2024年足球教案丨1v1进攻专项训练一、教学内容本节课选自《足球训练教程》第四章,详细内容主要围绕1v1进攻专项训练展开。
包括1v1进攻基本技巧、实战应用以及相关战术配合等内容。
二、教学目标1. 让学生掌握1v1进攻的基本技巧,提高个人进攻能力。
2. 培养学生在1v1对抗中观察、分析、判断和应变的能力。
3. 提高学生团队配合意识,为后续战术训练打下基础。
三、教学难点与重点1. 教学难点:1v1进攻时的观察、判断和应变能力。
2. 教学重点:1v1进攻基本技巧的掌握和实战应用。
四、教具与学具准备1. 足球若干个;2. 训练场地一块;3. 训练标志盘若干个;4. 训练用背心若干件。
五、教学过程1. 实践情景引入(5分钟)教师组织学生进行简单的1v1对抗练习,让学生体会1v1进攻的重要性。
2. 技能讲解与示范(15分钟)教师讲解1v1进攻的基本技巧,包括:带球、突破、射门等。
教师示范1v1进攻技巧,并让学生跟随示范进行练习。
3. 例题讲解(10分钟)教师设置1v1进攻场景,讲解如何运用基本技巧进行进攻。
教师引导学生分析场景,找出最佳进攻路线和时机。
4. 随堂练习(10分钟)学生分组进行1v1对抗练习,教师巡回指导,纠正错误动作。
5. 教学比赛(10分钟)教师组织学生进行1v1教学比赛,检验训练效果。
教师针对比赛情况进行点评,指导学生改进不足。
学生分享学习心得,教师给予鼓励和指导。
六、板书设计1. 1v1进攻基本技巧带球突破射门2. 1v1进攻实战应用观察对方弱点判断进攻时机选择最佳进攻路线七、作业设计1. 作业题目:结合本节课所学内容,设计一场1v1教学比赛,并记录比赛过程。
答案:(1)比赛双方:甲队 vs 乙队(2)比赛时间:10分钟(3)比赛过程:记录双方球员在比赛中的进攻、防守表现,以及1v1对抗情况。
答案:(1)优点:带球稳定,突破能力强。
(2)不足:射门准确性有待提高,观察对方弱点不够敏锐。
04第4章(柳)

§4.1 生活中的立体图形【学习目的】能辨别生活中所遇到的立体图形的区别;能正确识别和判断具体的图形,从而体验数学概念的抽象和形成过程。
【典型例题】【例】将图中的几何体分类,并说明理由。
【解】按柱、锥、球划分,(1)(2)(4)(6)(7)是一类,即柱体,(5)是锥体,(3)是球体; 按组成它们的面中至少有一个是曲面或平的划分,(3)(4)(5)是一类的,组成它们的面中至少有一个是曲的,(1)(2)(6)(7)是一类,组成它们的面都是平的。
【点拨】柱体有上、下两个相同的底面,锥体只有一个底面;柱体和锥体由底面和侧面围成,球体只有一个面。
【基础训练】 一、判断题1、柱体的上、下两个面不一样大。
( ) 【答案】×2、圆柱、圆锥的底面都是圆。
( ) 【答案】√3、棱柱的底面不一定是四边形。
( ) 【答案】√4、圆柱的侧面是长方形。
( ) 【答案】×5、棱锥的侧面不一定是三角形。
( ) 【答案】×6、柱体都是多面体。
( ) 【答案】√ 二、选择题7、下面图形是棱柱的是( )(1)(2)(4) (6)(7)(A )(B )(C )(D )(3)(5)【答案】A三、填表你得到的结论:。
【答案】填表略,(F+V)-E=2【拓展训练】9、三棱柱有9条棱,6个顶点,5个面;三棱锥有6条棱,4个顶点,4个面;四棱柱有12条棱,8个顶点,6个面;四棱锥有8条棱,5个顶点,5个面等等。
问能否组成一个有24条棱,10个面,15个顶点的多面体?为什么?【答案】不能,因为这个多面体的棱数、面数、顶点数不满足(F+V)-E=2。
【探究实践】10、一个四棱柱被一刀切去一个角,请你画图说明剩下的部分的形状。
【答案】略§4.2 画立体图形(1)【学习目标】1、经历“从不同的方向观察物体”活动过程,发展空间观念;2、在观察物体的过程中,初步体会从不同的方向观察同一个物体可能看到不一样的结果;3、能描述简单的立体图形的视图,能画出图形,并能识别所见到的视图形状和类别。
06-专项拓展训练1 二次函数的最值问题高中数学必修一人教A版

类型2 动轴定区间
4.已知函数 = 2 − 2 + 1在[2,5]上单调,且 的最大值为8,则实
9
数的值为__.
5
【解析】 = 2 − 2 + 1 = − 2 + 1 − 2 ,函数 的图象开口
向上,对称轴为直线 = .因为 在[2,5]上单调,所以 ≤ 2或 ≥ 5.当
与 ≥
9
5矛盾,故舍去.综上,实数的值为 .
5
3
,
4
【归纳总结】解决动轴定区间的二次函数最值问题时,可以让轴沿轴正方
向移动,分析移动到不同位置时对函数最值有什么影响.
5.[2024重庆八中期中]已知函数 = − 2 + 2 + .当 ∈ [−1,1]时,
设 的最大值为,求的最小值.
所给区间内.
1
即
4
+2
2
−
1
2
+
+2 +
1
4
= −5,
化简得2 + 2 − 7 = 0,解得 = −1 + 2 2或 = −1 − 2 2(舍去).
综上,存在实数,使得函数 = − 在区间[, + 2]上有最小
值−5,此时 = −3或 = −1 + 2 2.
9.已知函数 = 2 − 2 + 5 > 1 .
3.(多选)已知函数 = 2 − 2 + 4,则( BCD
A. 在区间[−1,0]上的最小值为1
B. 在区间[−1,2]上的最小值为3,最大值为7
C. 在区间[2,3]上的最小值为4,最大值为7
D. 在区间 2, +∞ 上无最值
第4章 一元一次方程(压轴必刷30题3种题型专项训练)(原卷版)-2024-2025学年七年级数学上

第4章一元一次方程(压轴必刷30题3种题型专项训练)一.一元一次方程的解(共2小题)1.(2022秋•启东市校级月考)我们规定,若关于x的一元一次方程ax=b的解为x=b﹣a,则称该方程为“差解方程”,例如:2x=4的解为2,且2=4﹣2,则方程2x=4是差解方程.请根据上述规定解答下列问题:(1)判断3x=4.5是否是差解方程;(2)若关于x的一元一次方程5x=m+1是差解方程,求m的值.2.(2022秋•宿城区期中)我们规定,若关于x的一元一次方程ax=b的解为b﹣a,则称该方程为“差解方程”,例如:2x=4的解为2,且2=4﹣2,则方程2x=4是差解方程.请根据上边规定解答下列问题:(1)判断3x=4.5是否是差解方程;(2)若关于x的一元一次方程6x=m+2是差解方程,求m的值.二.解一元一次方程(共3小题)3.(2021秋•高新区期末)用“*”定义一种新运算:对于任意有理数a和b,规定a*b=ab2+2ab+a.如:1*3=1×32+2×1×3+1=16(1)求2*(﹣2)的值;(2)若(其中x为有理数),试比较m,n的大小;(3)若=a+4,求a的值.4.(2022秋•工业园区校级月考)如图,小明在一张纸面上画了一条数轴,折叠纸面,使表示数﹣1的点与表示数5的点重合,请你回答以下问题:(1)表示数﹣2的点与表示数的点重合;表示数7的点与表示数的点重合.(2)若数轴上点A在点B的左侧,A,B两点之间的距离为12,且A,B两点按小明的方法折叠后重合,则点A表示的数是;点B表示的数是;(3)已知数轴上的点M分别到(2)中A,B两点的距离之和为2022,求点M表示的数是多少?5.(2021秋•溧阳市期末)阅读理解学:我们都应该知道,任何无限循环小数都应该属于有理数,那是因为所有无限循环小数都可以化成分数形式,而分数属于有理数.那么无限循环小数怎么化成分数呢?下面的学习材料会告诉我们原因和方法:问题:利用一元一次方程将0.化成分数.设0.=x.由0.=0.7777…,可知10×0.=7777…=7+0.7777…=7+0.,即10x=7+x.可解得,即0.=.(1)将0.直接写成分数形式为.(2)请仿照上述方法把下列小数化成分数,要求写出利用一元一次方程进行解答的过程.①0.;②0.1.三.一元一次方程的应用(共25小题)6.(2022秋•高新区期末)甲、乙两个旅行团同时去苏州旅游,已知乙团人数比甲团人数多4人,两团人数之和恰等于两团人数之差的18倍.(1)问甲、乙两个旅行团的人数各是多少?(2)若乙团中儿童人数恰为甲团中儿童人数的3倍少2人,某景点成人票价为每张100元,儿童票价是成人票价的六折,两旅行团在此景点所花费的门票费用相同,求甲、乙两团儿童人数各是多少?7.(2022秋•兴化市校级期末)甲、乙两班学生到集市上购买苹果,苹果的价格如表:50千克以上购买苹果数不超过30千克30千克以上但不超过50千克每千克价格3元 2.5元2元甲班分两次共购买苹果80千克(第二次多于第一次),共付出185元,乙班则一次购买苹果80千克.(1)乙班比甲班少付出多少元?(2)甲班第一次、第二次分别购买苹果多少千克?8.(2023秋•海门市校级月考)已知A、B、C三点在同一条数轴上,点A、B表示的数分别为﹣2,18,点C在原点右侧,且AC=AB.(1)A、B两点相距个单位;(2)求点C表示的数;(3)点P、Q是该数轴上的两个动点,点P从点A出发,沿数轴以每秒1个单位的速度向右运动,点Q 从点B出发,沿数轴以每秒2个单位的速度向左运动,它们同时出发,运动时间为t秒,求当t为何值时,P、Q两点到C点的距离相等?9.(2022秋•建邺区校级期末)扬子江药业集团生产的某种药品的长方体包装盒的侧面展开图如图所示.根据图中数据,如果长方体盒子的长比宽多4cm,求这种药品包装盒的体积.10.(2023秋•滨海县月考)生活与数学日一二三四五六12345678910111213141516171819202122232425262728293031(1)山姆同学在某月的日历上圈出2×2个数,如图1,正方形的方框内的四个数的和是48,那么这四个数是.(2)小丽也在上面的日历上圈出2×2个数,如图2,斜框内的四个数的和是46,则它们分别是.(3)刘莉也在日历上圈出5个数,呈十字框形,如图3,它们的和是55,则中间的数是.(4)某月有5个星期日的和是75,则这个月中最后一个星期日是号?11.(2022秋•兴化市校级月考)结合数轴与绝对值的知识回答下列问题:(1)探究:①数轴上表示5和2的两点之间的距离是.②数轴上表示﹣1和﹣5的两点之间的距离是.③数轴上表示﹣3和4的两点之间的距离是.(2)归纳:一般的,数轴上表示数a和数b的两点之间的距离等于.(3)应用:①若数轴上表示数a的点位于﹣4与3之间,则|a+4|+|a﹣3|的值=.②若a表示数轴上的一个有理数,且|a﹣1|=|a+3|,则a=.③若a表示数轴上的一个有理数,|a﹣1|+|a+2|的最小值是.④若a表示数轴上的一个有理数,且|a+3|+|a﹣5|>8,则有理数a的取值范围是.(4)拓展:已知,如图2,A、B分别为数轴上的两点,A点对应的数为﹣20,B点对应的数为100.若当电子蚂蚁P 从A点出发,以4个单位/秒的速度向右运动,同时另一只电子蚂蚁Q恰好从B点出发,以3单位/秒的速度向左运动,求经过多长时间两只电子蚂蚁在数轴上相距20个单位长度,并写出此时点P所表示的数.12.(2022秋•海安市月考)已知:在一条东西向的双轨铁路上迎面驶来一快一慢两列火车,快车长AB=2(单位长度),慢车长CD=4(单位长度),设正在行驶途中的某一时刻,如图,以两车之间的某点O为原点,取向右方向为正方向画数轴,此时快车头A在数轴上表示的数是a,慢车头C在数轴上表示的数是b.若快车AB以6个单位长度/秒的速度向右匀速继续行驶,同时慢车CD以2个单位长度/秒的速度向左匀速继续行驶,且|a+8|+(b﹣16)2=0.(1)求此时刻快车头A与慢车头C之间相距单位长度;(2)从此时刻开始算起,问再行驶多少秒钟两列火车行驶到车头AC相距8个单位长度?(3)此时在快车AB上有一位爱动脑筋的七年级学生乘客P,他发现行驶中有一段时间t秒钟,他的位置P到两列火车头A、C的距离和加上到两列火车尾B、D的距离和是一个不变的值(即P A+PC+PB+PD 为定值).你认为学生P发现的这一结论是否正确?若正确,求出这个时间及定值;若不正确,请说明理由.13.(2022秋•淮阴区期中)据电力部门统计,每天8:00至21:00是用电高峰期,简称“峰时”,21:00至次日8:00是用电低谷期,简称“谷时”.为了缓解供电需求紧张的矛盾,我市电力部门拟逐步统一换装“峰谷分时”电表,对用电实行“峰谷分时电价”新政策,具体见下表: 时间换表前换表后峰时(8:00﹣21:00)谷时(21:00﹣8:00)电价每度0.52元每度0.55元每度0.30元小明家对换表后最初使用的95度电进行测算,经测算比换表前使用95度电节约了5.9元,问小明家使用“峰时”电和“谷时”电分别是多少度?14.(2022秋•姜堰区期中)阅读理解:M 、N 、P 为数轴上三点,若点P 到M 的距离是点P 到N 的距离的k (k >0)倍,即满足PM =k .PN 时,则称点P 关于M 、N 的“相对关系值”为k .例如,当点M 、N 、P 表示的数分别为0、2、3时,PM =3PN ,则称点P 关于M 、N 的“相对关系值”为3;PN =MN ,则称点N 关于P 、M 的“相对关系值”为.如图,点A 、B 、C 、D 在数轴上,它们所表示的数分别为﹣1、2、6、﹣6.(1)原点O 关于A 、B 的“相对关系值“为a ,原点O 关于B 、A 的“相对关系值”为b ,则a = ,b = .(2)点E 为数轴上一动点,点E 所表示的数为x ,若x 满足|x +3|+|x ﹣2|=5,且点E 关于C 、D 的“相对关系值”为k ,则k 的取值范围是 .(3)点F 从点B 出发,以每秒1个单位的速度向左运动,设运动时间为t (t >0)秒,当经过t 秒时,C 、D 、F 三点中恰有一个点关于另外两点的“相对关系值”为2,求t 的值.15.(2022秋•苏州期中)【问题背景】落实“双减”政策后,某校开展了丰富多彩的科技活动.如图1,电子蚂蚁P 、Q 在长18分米的赛道AB 上同时相向匀速运动,电子蚂蚁P 从A 出发,速度为4分米/分钟,电子蚂蚁Q从B出发,速度为2分米/分钟,当电子蚂蚁P到达B时,电子蚂蚁P,Q停止运动.经过几分钟P,Q之间相距6分米?【问题解决】小辰同学在学习《有理数》之后,发现运用数形结合的方法建立数轴可以较快地解决上述问题:如图2,将点A与数轴的原点O重合,点B落在正半轴上.设运动的时间为t(0≤t≤4.5).(1)t分钟后点P在数轴上对应的数是;点Q对应的数是;(用含t的代数式表示)(2)我们知道,如果数轴上M,N两点分别对应数m,n,则MN=|m﹣n|.试运用该方法求经过几分钟P,Q之间相距6分米?(3)在赛道AB上有一个标记位置C,AC=6.若电子蚂蚁P与标记位置C之间的距离为a,电子蚂蚁Q与B之间的距离为b.在运动过程中,是否存在某一时刻t,使得a+b=4?若存在,请求出运动的时间;若不存在,请说明理由.16.(2022秋•海陵区校级月考)阅读理解,完成下列各题:定义:已知A、B、C为数轴上任意三点,若点C到点A的距离是它到点B的距离的3倍,则称点C是[A,B]的3倍点,例如:如图1,点C是[A,B]的3倍点,点D不是[A,B]的3倍点,但点D是[B,A]的3倍点,根据这个定义解决下面问题:(1)在图1中,点A[C,D]的3倍点(填写“是”或“不是”);[D,C]的3倍点是点(填写A或B或C或D);(2)如图2,M、N为数轴上两点,点M表示的数是﹣3,点N表示的数是5,若点E是[M,N]的3倍点,则点E表示的数是;(3)若P、Q为数轴上两点,点P在点Q的左侧,PQ=a,一动点H从点P出发,以每秒3个单位长度的速度沿数轴向右运动,设运动时间为t秒,求当t为何值时,点H恰好是P和Q两点的3倍点?(用含a的代数式表示)17.(2022秋•昆山市校级月考)如图所示,将连续的奇数1,3,5,7…排列成如下的数表,用十字形框框出5个数.探究规律一:设十字框中间的奇数为x,则框中五个奇数的和用含x的整式表示为,这说明被十字框框中的五个奇数的和一定是正整数p(p>1)的倍数,这个正整数p是.探究规律二:落在十字框中间且位于第二列的一组奇数是15,27,39…,则这一组数可以用整式表示为12m+3 (m为正整数),同样,落在十字框中间且位于第三列的一组奇数可以表示为;(用含m的式子表示)运用规律(1)被十字框框中的五个奇数的和可能是625吗?若能,请求出这五个数,若不能,请说明理由.(2)请问(1)中的十字框中间的奇数落在第几行第几列?18.(2022秋•广陵区校级月考)从泰州乘“K”字头列车A、“T”字头列车B都可直达南京,已知A车的平均速度为80km/h,B车的平均速度为A车的1.5倍,且行完全程B车所需时间比A车少40分钟.(1)求泰州至南京的铁路里程;(2)若两车以各自的平均速度分别从泰州、南京同时相向而行,问经过多少时间两车相距40km?19.(2022秋•江都区月考)某地的一种绿色蔬菜,在市场上若直接销售,每吨利润为1000元,经粗加工后销售,每吨利润4000元,经精加工后销售,每吨利润7000元.当地一家公司现有这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨,如果对蔬菜进行精加工,每天可加工6吨,但每天两种方式不能同时进行.受季节等条件的限制,必须用15天时间将这批蔬菜全部销售或加工完毕.为此,公司研制了三种方案:方案一:将蔬菜全部进行粗加工;方案二:尽可能地对蔬菜进行精加工,没来得及加工的蔬菜,在市场上直接出售;方案三:将一部分蔬菜进行精加工,其余蔬菜进行粗加工,并刚好15天完成.如果你是公司经理,你会选择哪一种方案,说说理由.20.(2023秋•锡山区期中)如图,数轴上有A、B、C、D四点,点D对应的数为x,已知OA=5,OB=3,CD=2,P、Q两点同时从原点O出发,沿着数轴正方向分别以每秒钟a和b个单位长度的速度运动,且a<b.点Q到点D后立即朝数轴的负方向运动,速度不变,在点C处与点P相遇,相遇后点P也立即朝着数轴的负方向运动,且P点的速度变为2a,Q点的速度不变.(1)P、Q两点相遇时,点P前进的路程为;Q、P两点相遇前的速度比=;(用含有x的式子表示)(2)若点B为线段AD的中点,①此时,点D表示的数x=;②相遇后,当点P到达点A处时,点Q在原点O的(填“左”或“右”)侧,并求出此时点Q在数轴上所表示的数字;(3)在(2)的条件下,当点P到达点A处时,立即掉头朝数轴的正方向运动,速度变为3a,点Q的速度始终不变,这两点在点M处第二次相遇,则点M在数轴上所表示的数字为.21.(2023秋•沭阳县校级月考)探索规律:将连续的偶2,4,6,8,…,排成如图:(1)十字框中的五个数的和与中间的数16有什么关系?(2)设中间的数为x,用代数式表示十字框中的五个数的和;(3)若将十字框上下左右移动,可框住另外的五位数,其它五位数的和能等于2010吗?如能,写出这五位数,如不能,说明理由.22.(2021秋•姑苏区校级期末)为增强公民节水意识,合理利用水资源,某市采用“阶梯收费”,标准如下表:用水量单价不超过6m3的部分2元/m3超过6m3不超过10m3的部分4元/m3超出10m3的部分8元/m3譬如:某用户2月份用水9m3,则应缴水费:2×6+4×(9﹣6)=24(元)(1)某用户3月用水15m3应缴水费多少元?(2)已知某用户4月份缴水费20元,求该用户4月份的用水量;(3)如果该用户5、6月份共用水20m3(6月份用水量超过5月份用水量),共交水费64元,则该户居民5、6月份各用水多少立方米?23.(2021秋•惠山区期末)【探索新知】如图1,点C将线段AB分成AC和BC两部分,若BC=πAC,则称点C是线段AB的圆周率点,线段AC、BC称作互为圆周率伴侣线段.(1)若AC=3,则AB=;(2)若点D也是图1中线段AB的圆周率点(不同于C点),则AC DB;(填“=”或“≠”)【深入研究】如图2,现有一个直径为1个单位长度的圆片,将圆片上的某点与数轴上表示1的点重合,并把圆片沿数轴向右无滑动地滚动1周,该点到达点C的位置.(3)若点M、N均为线段OC的圆周率点,求线段MN的长度.(4)在图2中,若点D在射线OC上,且线段CD与图中以O、C、D中某两点为端点的线段互为圆周率伴侣线段,直接写出D点所表示的数.24.(2022秋•江都区校级月考)元旦期间,某商场打出促销广告(如下表)优惠条件一次性购物不超过200元一次性购物超过200元但不超过一次性购物超过500元500元优惠办法无优惠全部按9折优惠其中500元仍按9折优惠,超过500元部分按8折优惠小明妈妈第一次购物用了134元,第二次购物用了490元.(1)小明妈妈第一次所购物品的原价是元;(2)小明妈妈第二次所购物品的原价是多少元?(写出解答过程)(3)若小明妈妈将两次购买的物品一次性买清,可比两次购买节省多少元?25.(2022秋•梁溪区校级月考)在数轴上A点表示数a,B点表示数b,且a、b满足|a+2|+|b﹣4|=0;(1)点A表示的数为;点B表示的数为;(2)如果M、N为数轴上两个动点,点M从点A出发,速度为每秒1个单位长度;点N从点B出发,速度为点A的3倍,它们同时向左运动,点O为原点.当运动2秒时,点M、N对应的数分别是、.当运动t秒时,点M、N对应的数分别是、.(用含t的式子表示)运动多少秒时,点M、N、O中恰有一个点为另外两个点所连线段的中点?(可以直接写出答案)26.(2022秋•兴化市校级月考)如图,已知A、B分别为数轴上的两点,A点对应的数为﹣20,B点对应的数为80.(1)请直接写出AB的中点M对应的数;(2)现在有一只电子蚂蚁P从A点出发,以2个单位/秒的速度向右运动,同时另一只电子蚂蚁Q恰好从B点出发,以3个单位/秒的速度向左运动,设两只电子蚂蚁在数轴上的C点相遇,请求出C点对应的数是多少;(3)若当电子蚂蚁P从A点出发时,以2个单位/秒的速度向右运动,同时另一只电子蚂蚁Q恰好从B 点出发,以3个单位/秒的速度向左运动,经过多长时间两只电子蚂蚁在数轴上相距25个单位长度?27.(2022秋•昆山市校级月考)在购买足球赛门票时,设购买门票张数为x(张),现有两种购买方案:方案一:若单位赞助广告费10000元,则该单位购买门票的价格为60元(总费用=广告赞助费+门票费).方案二:若购买的门票数不超过100张,每张100元,若所购门票超过100张,则超出部分按八折计算.解答下列问题:(1)方案一中,用含x的代数式来表示总费用为.方案二中,当购买的门票数x不超过100张时,用含x的代数式来表示总费用为.当所购门票数x超过100张时,用含x 的代数式来表示总费用为.(2)甲、乙两单位分别采用方案一、方案二购买本次足球赛门票,合计700张,花去的总费用计58000元,求甲、乙两单位各购买门票多少张?28.(2021秋•江都区期中)把2100个连续的正整数1、2、3、…、2100,按如图方式排成一个数表,如图用一个正方形框在表中任意框住4个数,设左上角的数为x.(1)另外三个数用含x的式子表示出来,从小到大排列是;(2)被框住4个数的和为416时,x值为多少?(3)能否框住四个数和为324?若能,求出x值,若不能,说明理由;(4)从左到右,第1至第7列各数之和分别为a1、a2、a3、a4、a5、a6、a7,求7个数中最大的数与最小的数之差.29.(2021秋•秦淮区期中)生活与数学:(1)吉姆同学在某月的日历上圈出2×2个数,正方形的方框内的四个数的和是32,那么第一个数是;(2)玛丽也在日历上圈出2×2个数,斜框内的四个数的和是42,则它们分别是;(3)莉莉也在日历上圈出5个数,呈十字框形,它们的和是50,则中间的数是;(4)某月有5个星期日的和是75,则这个月中最后一个星期日是号;(5)若干个偶数按每行8个数排成图4:①图中方框内的9个数的和与中间的数有什么关系:;②汤姆所画的斜框内9个数的和为360,则斜框的中间一个数是;③托马斯也画了一个斜框,斜框内9个数的和为252,则斜框的中间一个数是.30.(2021秋•洪泽区校级月考)请根据图中提供的信息,回答下列问题:(1)一个暖瓶与一个水杯分别是多少元?(2)甲、乙两家商场同时出售同样的暖瓶和水杯.为了迎接新年,两家商场都在搞促销活动.甲商场规定:这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯.若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.。
《经典常谈》第四章《诗经》专项训练

八年级语文下册《经典常谈》第4章《诗经》专项训练内容要点梳理由来:诗的源头是歌谣。
上古时候,没有文字,只有唱的歌谣,没有写的诗。
乐工收集天下歌谣以供贵族祭祖、宴饮等,战国时,贵族没落,乐工流离,乐谱也渐渐亡失,流传下来的便是《诗经》。
发展历程:①春秋时宴饮通行赋诗,都从诗篇里断章取义,表示这国对那国或这人对那人的愿望、感谢、责难等等。
②孔子时代,诗篇的本义渐渐模糊,于是孔子用《诗》来讨论做学问做人的道理,孔子以后,《诗》三頁”成为儒家的《六经》之一,《庄子》和《荀子》都说到“诗言志,“志”便指教化而言。
③解释《诗经》最有权威的是毛氏《诗传》和郑玄《诗笺》,差不多全是断章取义,甚至断句取义。
诗序:《诗序》有《大序》和《小序》。
《大序》是总论说明诗的教化作用,这种作用似乎建立在所谓“六义”上。
《大序》只解释了风雅颂。
赋是“直铺陈今之政教善恶”;比兴是“主文而谲谏”,不直陈而用譬喻叫“主文”,委婉讽刺叫“谲谏”《小序》是毛氏两人所作。
及至郑玄,按着《诗经》中的国别和篇次,系统的附合史料,编成了《诗谱》,差不多给每篇诗确定了时代。
同步练习一、填空1.诗的源头是_____。
歌谣可分为______和乐歌。
徒歌是随口唱,乐歌是随着乐器唱。
其中______的节奏更规律化些。
2.歌谣的节奏最主要的靠_____,也叫______。
3.有了文字以后,大概是_____将那些歌谣纪录下来,便是最初的写的诗了。
4.春秋时的太师们保存下带着乐谱的唱本;唱词共有三百多篇,当时通称做________。
5.“诗言志”是一句古话,“志”关联着______或______。
6.春秋时宴饮通行赋诗,当时都从诗篇里______,即不管上下文的意义,只将一章中一两句拉出来,就当前的环境,作________,表示这国对那国或这人对那人的愿望、感谢、责难等等。
7.到了_____时代,诗篇的本义渐渐模糊,孔子就按着_____的办法,用《诗》来讨论______的道理。
第四章 植物组织培养拓展技术

4.6.3 人工种子的结构
4.6.3.1
体细胞胚 4.6.3.2 人工胚乳 4.6.3.3 人工种皮
人工种子结构示意图
4.6.4 人工种子包埋方法
4.6.4.1 干燥包理法
23℃,相对湿度为70%土5%,黑暗条件下逐 渐干燥。
4.6.4.2 液胶包理法
将胚状体悬浮在一种黏滞的流体胶中,直接插 入土壤。
机械分离法和酶解分离法的比较
机械法 1. 细胞不受到酶的伤害; 2. 机械法不用质壁分离; 3. 细胞产量低; 4. 细胞易破。 1. 细胞受到酶的伤害; 2. 要质壁分离; 3. 细胞产量高; 4. 细胞不易破。
酶解法
4.1.2 单细胞的培养 4.1.2.1 看护培养法
含义:用一块活跃生长的愈伤组织块来看 护单个细胞,并使其生长和增殖的方法。 用途:诱导形成单细胞系。 要求:看护愈伤组织处于活跃生长状态; 愈伤组织和所要培养的细胞可以是同一个 物种也可以不同。
先将植物叶片取下经过无菌处理后,在研钵 中轻轻研碎,经过一定孔径的纱布或不绣钢 滤网过滤,取出过滤后的研磨介质经过低速 离心等其他处理使细胞得到纯化。
4.1.1.2 酶解分离
用纤维素酶和果胶酶等酶液处理适合植物外 植体即可得到所需要的单细胞。
4.1.1.3 由组织培养物分离
离体培养的愈伤组织分离单细胞。
4.3 花药和花粉培养
4.3.1 花药培养
4.3.1.1 花药材料的选择
选择大致处于所需要时期的花蕾。由于 花粉发育时期和植株的某些外部形态特征 之间的大致相关性,因此利用这些外部标 志,选择符合条件的花蕾,经镜检确定花 粉发育的准确时期。
4.3.1.2 培养基的选择
《老子》四章-高二语文选修-同步拓展训练

《老子》四章-高二语文选修-同步拓展训练阅读下面的文言文,回答后面的问题。
天下皆知美之为.美,斯恶矣;皆知善之为善,斯不善矣。
故有无相生,难易相成,长短相形,高下相倾.,音声相和,前后相随,恒也.。
(《老子》第二章)三十辐,共一毂,当.其无,有车之用。
埏.埴以为器,当其无,有器之用。
凿户牖以为室,当其无,有室之用。
故有之以为利,无之以为用。
(《老子》第十一章)企者不立,跨者.不行,自见者不明,自是者不彰,自伐者无功,自矜.者不长。
其在道也,曰余食赘行,物或恶之,故有道者不处。
(《老子》第二十四章)知人者智,自知者明。
胜人者有力,自胜者强。
知足者富,强行者有志。
不失其.所者久,死而不亡者寿。
(《老子》第三十三章))1.对下列句中加点词的解释,不正确的一项是A.长短相形,高下相倾.倾:依靠B.当.其无,有车之用当:当作C.埏.埴以为器埏:揉和D.自矜.者不长矜:夸耀2.对下列句中加点词意义和用法的解释,不正确的一项是A.天下皆知美之为.美为:动词,是B.前后相随,恒也.也:语气词,表判断C.跨者.不行者:代词,……的人D.不失其.所者久其:指示代词,那些3.下列对原文有关内容的概括和分析,不正确的一项是A.《老子》把很多现象提炼为一系列的对立项,如美与丑、善与恶、有与无、难与易、长与短等,认为所有这些对立因素都是相反相成的。
B.《老子》运用三个例子来说明“有”和“无”的关系,并认为“无用”才是最大的用,正是因为有了“无”,“有”才能发挥作用。
C.《老子》认为自以为是的人不能明辨是非,自我夸耀的人不能成就大功。
D.《老子》认为“自知”比“知人”更加重要,“胜人”比“自胜”更加难得,这是极富哲理的判断。
4.把文中画横线的句子翻译成现代汉语。
(1)其在道也,曰余食赘行,物或恶之,故有道者不处。
(2)知人者智,自知者明。
胜人者有力,自胜者强。
知足者富,强行者有志。
阅读下面的材料,完成小题。
①子适卫,冉有仆。
4.4 能力提升练和拓展练

略
2019/4/24
7
单击此处编辑母版标题样式
• 单11.击下此面处的图编形辑是母平行版四文边本形吗样?式如果不是,怎样改才
– 二能级成为平行四边形?请你画出来。
• 三级
– 四级 » 五级
2019/4/24
2
单击此处编辑母版标题样式
作业提升练
• 单击此处编辑母版文本样式6–.二画级出下面平行四边形底 Nhomakorabea上的一条高。
• 三级
– 四级 » 五级
略
2019/4/24
3
单击此处编辑母版标题样式
• 单7.击在下此面处的编格辑子图母里版先文画一本个样平式行四边形,再画出它的
– 二一级条高。
• 三级
2019/4/24
9
单击此处编辑母版标题样式
作业拓展练
• 单击此处编辑母版文本样式
1–3.二数级一数,下面图形中各有多少个平行四边形?
• 三级
– 四级
18
» 五级
2019/4/24
3
10
单击此处编辑母版标题样式
• 单击此处编辑母版文本样式
– 二级
• 三级
– 四级 » 五级
2019/4/24
11
2019/4/24
5
单击此处编辑母版标题样式
• 单9.击以A此B为处底编,辑CD母为高版,文画本一个样平式行四边形。
– 二级
• 三级
– 四级 » 五级
略
2019/4/24
6
单击此处编辑母版标题样式
10.根据要求在下面的方格纸上画图。(每个小方格的边
第四单元拓展提高练习(课件)部编版语文五年级下册

一班的肖文明,我为大家讲的故事是《小红帽》……”
( )故事讲完了,全场响起了热烈的掌声。
( )所有老师和同学都在聚精会神地听着。
请给这些句
子排排队。
手术台上,一向从容镇定的沃克医生,这次双手却有些 颤抖,他额上汗珠滚滚,护士帮他擦了一次又一次。最后他 忍不住对病人说:“你挺不住可以哼叫。” 病人一声不吭,他的双手紧紧抓住身下的白垫单,手背青筋暴起, 汗如雨下。他越来越使劲,崭新的白垫单居然被抓破了。
第一自然段的第一句写沃克医生的神态变化:过去“一向从容镇 定”,这次双手“有些颤抖”,“额上汗珠滚滚”。第二句写沃 克医生“忍不住”的神态和对刘伯承说的话。这就从侧面烘托出 刘伯承的意志坚强。第二自然段的第一句写了刘伯承“一声不吭” 的神态和“手背青筋暴起,汗如雨下”的外貌以及“紧紧抓住” 的动作。第二句写刘伯承“使劲”“抓”等动作。这就从正面表 现出刘伯承的意志坚强。请学习运用正面描写和侧面描写相结合 的方法,写一段话,表现一个人的特点。
⑶看到有人冻死,军长气得两眼发红。
(改为夸张句)
请按要求完 成句子练习。
⑷毛主席一支接着一支地吸着烟。
(照样子写人物动作)
⑸他头也不抬,冷冷地问:“你叫什么名字?” (照样子写人物神态、语言)
⑹沃克医生的眉毛扬了起来,他走进手术室,生气地说:“年轻人,在这
儿要听医生的指挥!”
(照样子写人物动作、神态、语言)
董晓艺同学迈着轻盈的步伐走到舞台中央, 深深鞠了一躬。她来到电子琴后面,弹奏 起了《洗衣歌》。她面带微笑,手指在键 盘上跳跃,身体随着音乐的节奏轻轻摇晃。 (描写董晓艺的神情动作,正面表现她弹 琴技艺高超。)台下鸦雀无声,大家都陶 醉在美妙的音乐之中。演奏结束了,全场 立刻响起了雷鸣般的掌声。(描写大家的动 作神情,侧面烘托董晓艺弹琴技艺高超。)
4.6-4.7第四章拓展提高题
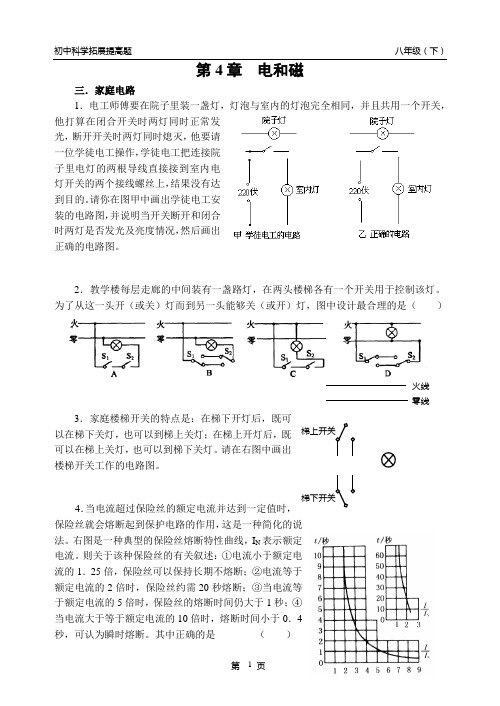
第4章 电和磁三.家庭电路1.电工师傅要在院子里装一盏灯,灯泡与室内的灯泡完全相同,并且共用一个开关,他打算在闭合开关时两灯同时正常发光,断开开关时两灯同时熄灭,他要请一位学徒电工操作,学徒电工把连接院子里电灯的两根导线直接接到室内电灯开关的两个接线螺丝上,结果没有达到目的。
请你在图甲中画出学徒电工安装的电路图,并说明当开关断开和闭合时两灯是否发光及亮度情况,然后画出正确的电路图。
2.教学楼每层走廊的中间装有一盏路灯,在两头楼梯各有一个开关用于控制该灯。
为了从这一头开(或关)灯而到另一头能够关(或开)灯,图中设计最合理的是( )3.家庭楼梯开关的特点是:在梯下开灯后,既可以在梯下关灯,也可以到梯上关灯;在梯上开灯后,既可以在梯上关灯,也可以到梯下关灯。
请在右图中画出楼梯开关工作的电路图。
4.当电流超过保险丝的额定电流并达到一定值时,保险丝就会熔断起到保护电路的作用,这是一种简化的说法。
右图是一种典型的保险丝熔断特性曲线,I N 表示额定电流。
则关于该种保险丝的有关叙述:①电流小于额定电流的1.25倍,保险丝可以保持长期不熔断;②电流等于额定电流的2倍时,保险丝约需20秒熔断;③当电流等于额定电流的5倍时,保险丝的熔断时间仍大于1秒;④当电流大于等于额定电流的10倍时,熔断时间小于0.4秒,可认为瞬时熔断。
其中正确的是 ( )(A )只有①正确 (B )只有①②正确(C )①②③正确 (D )①②③④都正确5.已知导线的电阻跟其长度成正比,跟其横截面积成反比。
如果直径为0.3毫米的细铅丝通过1.8安的电流将被熔断,直径为0.6毫米的粗铅丝通过5安的电流被熔断,现在用上述规格的长度相同的20根细铅丝和1根粗铅丝并联接在电路中,则当通过的电流超过 时,将会使电路断开。
6.测电笔内部有一个大电阻,这样当测电笔的笔尖接触家庭电路的火线时,使得加在人体上的电压在安全电压(36伏以下)范围内。
若测电笔氖管发光放电时的电流为0.32毫安,则此大电阻的阻值至少应大于____________欧(不计氖管发光放电时的电阻)。
高考物理总复习 4章专项拓展与训练4 新人教版
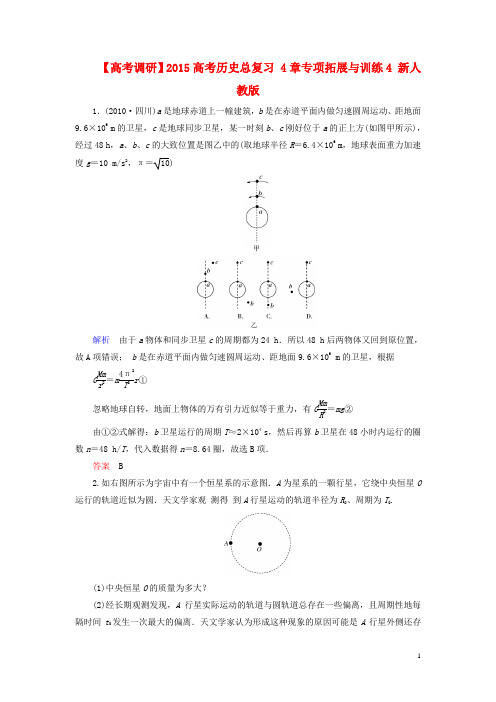
【高考调研】2015高考历史总复习 4章专项拓展与训练4 新人教版1.(2010·四川)a 是地球赤道上一幢建筑,b 是在赤道平面内做匀速圆周运动、距地面9.6×106m 的卫星,c 是地球同步卫星,某一时刻b 、c 刚好位于a 的正上方(如图甲所示),经过48 h ,a 、b 、c 的大致位置是图乙中的(取地球半径R =6.4×106m ,地球表面重力加速度g =10 m/s 2,π=10)解析 由于a 物体和同步卫星c 的周期都为24 h .所以48 h 后两物体又回到原位置,故A 项错误; b 是在赤道平面内做匀速圆周运动、距地面9.6×106m 的卫星,根据G Mm r 2=m 4π2T2r ① 忽略地球自转,地面上物体的万有引力近似等于重力,有G MmR2=mg ②由①②式解得:b 卫星运行的周期T ≈2×104s ,然后再算b 卫星在48小时内运行的圈数n =48 h/T ,代入数据得n =8.64圈,故选B 项.答案 B2.如右图所示为宇宙中有一个恒星系的示意图.A 为星系的一颗行星,它绕中央恒星O 运行的轨道近似为圆.天文学家观 测得 到A 行星运动的轨道半径为R 0、周期为T 0.(1)中央恒星O 的质量为多大?(2)经长期观测发现,A 行星实际运动的轨道与圆轨道总存在一些偏离,且周期性地每隔时间t 0发生一次最大的偏离.天文学家认为形成这种现象的原因可能是A 行星外侧还存在着一颗未知的行星B (假设其运行轨道与A 在同一水平面内,且与A 的绕行方向相同),它对A 行星的万有引力引起A 轨道的偏离.(由于B 对A 的吸引而使A 的周期引起的变化可以忽略)根据上述现象及假设,试求未知行星B 的运动周期T 及轨道半径R .解析 (1)设中央恒星质量为M ,A 行星质量为m ,则有G Mm R 20=m 4π2T 20R 0,得M =4π2R 3GT 20(2)A 、B 相距最近时,A 偏离最大,根据题意,有 2πT 0t 0-2πT t 0=2π,得T =T 0t 0-T 0t 0 根据开普勒第三定律R 3T 2=R 30T 20,得R =(t 0t 0-T 0)23R 0答案 (1)4π2R 3GT 20(2)T 0t 0t 0-T 0 (t 0t 0-T 0)23R 0 3.科学家在地球轨道外侧发现了一颗绕太阳运行的小行星,经过观测该小行星每隔t 时间与地球相遇一次,已知地球绕太阳公转半径是R ,周期是T ,设地球和小行星都是圆轨道,求小行星距太阳的距离.解析 设小行星绕太阳周期为T ′,T ′>T ,地球和小行星每隔t 时间相遇一次,则有(t T -tT ′)2π=2π 设小行星绕太阳轨道半径为R ′,万有引力提供向心力有GMm ′R ′2=m ′(2πT ′)2R ′ 同理对于地球绕太阳运动,也有G Mm R2=m (2πT)2R由上面两式有R ′3R 3=T ′2T 2,R ′=(t t -T )23R答案 (tt -T )23R 4.计划发射一颗距离地面的高度为地球半径R 0的圆形轨道上运行的地球卫星,卫星轨道平面与赤道平面重合,已知地球表面重力加速度为g .(1)求出卫星绕地心运动周期T .(2)设地球自转周期T 0,该卫星绕地旋转方向与地球自转方向相同,则在赤道上一点的人能连续看到该卫星的时间是多少?解析 (1)卫星绕地球做圆周运动的向心力由万有引力提供,有GMm 2R 02=m4π2T 2·(2R 0)忽略地球自转,地面上物体的万有引力近似等于重力,有G Mm R2=mg 联立以上两式,解得T =4π2R 0g(2)所谓恰能看到要根据光学原理,比如某时刻(日出)地面上的人在B 1点恰能看到卫星在轨道上的A 1,经一段时间t ,人随地球自转到了B 2点,这时卫星转到A 2点,恰不能看到(若卫星再沿轨道向后,不是被地球挡住了吗?).由几何关系,可知∠A 1OB 1=∠A 2OB 2=α=π3,∠B 1OB 2=θ卫星的运动角度、周期和时间的关系为23π+θ2π=tT观察者随地球运动的角度、周期和时间的关系为θ2π=tT 0联立以上两式,并代入T =4π2R 0g,得t =4π·T 02R 0g3T 0-4π2R 0g答案 (1)4π(2R 0g) (2)4π·T 02R 0g3T 0-4π2R 0g5.如右图所示,A 、B 两行星在同一平面内绕同一颗恒星运动,运动的方向相同,A 、B 两行星的轨道半径分别为r 1、r 2 ,已知恒星的质量为M ,且恒星对两行星的引力远远大于两行星间的引力,两行星的轨道半径r 1<r 2,若在某一时刻两行星相距最近,试求:(1)经多长时间两行星相距最近?(2)经多长时间两行星相距最远?解析(1)设经过时间t,A、B两行星转过的角度分别是ωA t和ωB t,则两行星相距最近的条件是ωA t-ωB t=n·2π(n=1,2,3,…)又因为恒星对行星万有引力提供向心力,则G Mmr2=mω2r,即ω=GMr3对A、B两行星,则有ωA=GMr31,ωB=GMr32由此可得t=2πnGM/r31-GM/r32,(n=1,2,3,…)(2)如果经过时间t′,A、B两行星处于同心圆的同一条直线上,则A、B两星必然相距最远,A、B二星各自转过的角度之差必为π的奇数倍,即ωA t-ωB t=(2k-1)π(k=1,2,3,…)代入ωA、ωB的值,可得t=2k-1πGM/r31-GM/r32,(k=1,2,3,…)答案t=2πnGM/r31-GM/r32,(n=1,2,3,…)t=2k-1πGM/r31-GM/r31,(k=1,2,3,…)6.(2010·上海)如右图所示,三个质点a、b、c质量分别为m1、m2、M(M≫m1,M≫m2),在c的万有引力作用下,a、b在同一平面内绕c沿逆时针方向做匀速圆周运动,轨道半径之比为r a∶r b=1∶4,则它们的周期之比T a∶T b=________;从图示位置开始,在b运动一周的过程中,a、b、c共线了________次.解析 根据G Mm r 2=m 4π2T2r ,得T =4π2r3GM ,所以T a T b =18方法一 物理情境分析法如右图所示,(注:原图中,a 在b 前55°左右.)在算出T a ∶T b =1∶8后,我们知道:在a 运动第1周的时间内,b 运动了1/8周,如图,从b 到b 1位置,圆心角为45°,a 与b 共线2次,1次是a 在bc 的延长线上,另1次是a 在bc 之间.(注:如前所述,原图中a 在b 前55°左右)在a 运动第2周的时间内,从b 1到b 2位置,a 与b 共线1次,这1次是a 在bc 的延长线上;在a 运动第2周到第5周的时间内,b 运动了4/8周,到b 5位置,a 每周与b 共线2次;在a 运动第6周的时间内,b 运动了1/8周,如图所示,也是共线1次,这1次是a 在bc 之间;在a 运动第6周到第8周的时间内,b 运动了3/8周,到b 8位置即初始位置,a 每周与b 共线2次.所以从题图位置开始,在b 运动一周的过程中,a 、b 、c 共线了14次.方法二 设每隔时间t ,a 、b 共线一次,(ωa -ωb )t =π,t =πωa -ωb,所以b 运动一周的过程中,a 、b 、c 共线的次数为n =T b t =T b ωa -ωb π=T b (2T a -2T b )=2T bT a-2=14答案 1∶8,147.如右图所示,质量相同的三颗卫星a 、b 、c 绕地球做匀速圆周运动,其中b 、c 在地球的同步轨道上,a 距离地球表面的高度为R ,此时a 、b 恰好相距最近,已知地球质量为M 、半径为R 、地球自转的角速度为ω.万有引力常量为G ,则( )A .发射卫星b 时速度要大于11.2 km/sB .卫星a 的机械能小于卫星b 的机械能C .卫星a 和b 下一次相距最近还需经过t =2πGM8R3-ωD .若要卫星c 与b 实现对接,可让卫星c 加速【解析】 发射卫星需要的速度为7.9 km/s≤v ≤11.2 km/s,卫星位置越高机械能越大,因为发射上去的能量越高,(ωa -ωb )t =2π,利用万有引力提供物体做圆周运动的向心力,解出ωa ,则可得到卫星a 和b 下一次相距最近还需经过t =2πGM8R3-ω.【答案】 BC8.侦察卫星在通过两极上空的圆形轨道上运动,它的运动轨道距离地面的高度为h ,要使卫星在一天时间内将地面上赤道各处在日照条件下的情况全部拍摄下来,卫星在通过赤道上空时卫星的摄像机至少能拍摄地面上赤道的弧长是多少?(设地球的半径为R ,地面处的重力加速度为g ,地球自转周期为T )【解析】 卫星的周期T ′=2πR +h3GM,由mg =G Mm R2,知gR 2=GM ,所以T ′=2πR +h 3gR 2,地球自转周期为T ,则在一天时间内卫星绕地球的圈数n =TT ′,地球周长l =2πR ,所以卫星每次拍摄的弧长l ′=l n =4π2TR +h3g【答案】4π2TR +h 3g【学法指导】 本题的题眼为“要使卫星在一天时间内将地面上赤道各处在日照条件下的情况全部拍摄下来”,如果用几何关系,无法突破.。
高考物理总复习 4章专项拓展与训练2 新人教版

专项拓展与训练1.2008年9月25日至28日我国成功实施了“神舟”七号载人航天飞行并实现了航天员首次出舱.飞船先沿椭圆轨道飞行,后在远地点343千米处点火加速,由椭圆轨道变成高度为343千米的圆轨道,在此圆轨道上飞船运行周期约为90分钟.下列判断正确的是( )A .飞船变轨前后的机械能相等B .飞船在圆轨道上时航天员出舱前后都处于失重状态C .飞船在此圆轨道上运动的角速度大于同步卫星运动的角速度D .飞船变轨前通过椭圆轨道远地点时的加速度大于变轨后沿圆轨道运动的加速度 解析 飞船点火变轨,前后的机械能不守恒,所以A 项不正确.飞船在圆轨道上时万有引力来提供向心力,航天员出舱前后都处于失重状态,B 项正确.飞船在此圆轨道上运动的周期90分钟小于同步卫星运动的周期24小时,根据T =2πω可知,飞船在此圆轨道上运动的角速度大于同步卫星运动的角速度,C 项正确.飞船变轨前通过椭圆轨道远地点时只有万有引力来提供加速度,变轨后沿圆轨道运动也是只有万有引力来提供加速度,所以相等,D 项不正确.答案 BC【考点分析】 机械能守恒定律,完全失重,万有引力定律.【学法指导】 若物体除了重力、弹力做功以外,还有其他力(非重力、弹力)做功,且其他力做功之和不为零,则机械能不守恒.根据万有引力等于卫星做圆周运动的向心力可求卫星的速度、周期、动能、动量等状态量.由G Mm r 2=m v 2r ,得v =GM r ,由G Mm r 2=m 4π2T 2r ,得T =2πr 3GM ,由G Mm r2=mω2r ,得ω=GM r 3,G Mm r 2=ma 向可求向心加速度.由G Mm r 2=ma 向,得a 向=GMr2. 2.(2010·天津)探测器绕月球做匀速圆周运动,变轨后在周期较小的轨道上仍做匀速圆周运动,则变轨后与变轨前相比( )A .轨道半径变小B .向心加速度变小C .线速度变小D .角速度变小 答案 A3.宇宙飞船在半径为R 1的轨道上运行,变轨后的半径为R 2,R 1>R 2.宇宙飞船绕地球做匀速圆周运动,则变轨后宇宙飞船的( )A .线速度变小B .角速度变小C .周期变大D .向心加速度变大解析 根据G Mm r 2=m v 2r =mω2r =m 4π2T 2r =ma 向,得v =GM r,可知变轨后飞船的线速度变大,A 项错;ω=GM r 3,角速度变大,B 项错,周期变小,C 项错;a =GM r2,向心加速度在增大,D 项正确.答案 D 4.2010年10月1日18时59分57秒,搭载着嫦娥二号卫星的长征三号丙运载火箭在西昌卫星发射中心点火发射,卫星由地面发射后,进入地月转移轨道,经多次变轨最终进入距离月球表面100公里,周期为118分钟的工作轨道,开始对月球进行探测( )A .卫星在轨道Ⅲ上的运动速度比月球的第一宇宙速度小B .卫星在轨道Ⅲ上经过P 点的速度比在轨道Ⅰ上经过P 点时大C .卫星在轨道Ⅲ上运动周期比在轨道Ⅰ上短D .卫星在轨道Ⅰ上经过P 点的加速度大于在轨道Ⅱ上经过P 点的加速度解析 A 项,根据G Mm r 2=m v 2r ,解得v =GM r,第一宇宙速度的轨道半径等于月球的半径,小于轨道Ⅲ的半径大小,所以卫星在轨道Ⅲ上的运动速度比月球的第一宇宙速度小,故A 项正确;B 项,卫星在轨道Ⅲ上的P 点需加速做离心运动可以进入轨道Ⅰ,所以卫星在轨道Ⅲ上经过P 点的速度比在轨道Ⅰ上经过P 点时小,故B 项错误;C 项,根据开普勒第三定律R 3T2=k 知,轨道Ⅲ的半径小于轨道Ⅰ的半长轴,所以卫星在轨道Ⅲ上的运动周期比在轨道Ⅰ上短,故C 项正确;D 项,根据牛顿第二定律得,卫星在轨道Ⅰ上经过P 点与在轨道Ⅱ上经过P 点所受的万有引力相等,则加速度相等,故D 项错误.答案 AC5.2007年10月24日18时05分,我国成功发射了“嫦娥一号”探月卫星.卫星经过八次点火变轨后,绕月球做匀速圆周运动.图中所示为探月卫星运行轨迹的示意图(图中1、2、3、…、8为卫星运行中的八次点火位置):①卫星第2、3、4次点火选择在绕地球运行轨道的近地点,是为了有效地利用能源,提高远地点高度;②卫星沿椭圆轨道由近地点向远地点运动的过程中,加速度逐渐增大,速度逐渐减小;③卫星沿椭圆轨道由近地点向远地点运动的过程中,机械能守恒;④卫星沿椭圆轨道由远地点向近地点运动的过程中,卫星中的科考仪器处于超重状态;⑤卫星在靠近月球时需要紧急制动被月球所捕获,为此实施第6次点火,则此次发动机喷气方向与卫星运动方向相反.上述说法正确的是( )A.①④ B.②③C.①⑤D.①③解析在近地点点火加速后,卫星做离心运动,离地面的高度逐渐增加,①对.卫星沿椭圆轨道由近地点向远地点运动的过程中,只有万有引力做功,机械能守恒.③对.但万有引力逐渐减小,所以加速度减小,速度也减小,②错.卫星由远地点向近地点运动过程中是加速向地球运动,科考仪器处于失重状态,④错.靠近月球时要减速,故喷气方向与卫星运动方向相同,获得反方向的作用力,⑤错.答案 D名师点拨①的说法是否正确,从各种材料上看,应该是便于观测和控制.6.(2013·山东济宁)2007年10月24日,“嫦娥一号”卫星星箭分离,卫星进入绕地球轨道.在绕地运行时,要经过三次近地变轨:12小时椭圆轨道①→24小时椭圆轨道②→48小时椭圆轨道③→地月转移轨道④.11月5日11时,当卫星经过距月球表面高度为h的A点时,再一次实施变轨,进入12小时椭圆轨道⑤,后又经过两次变轨,最后进入周期为T的月球极月圆轨道⑦.如图所示,已知月球半径为R.(1)请回答:“嫦娥一号”在完成第三次近地变轨时需要加速还是减速?(2)写出月球表面重力加速度的表达式.解析 (1)加速(2)设月球表面的重力加速度为g 月,在月球表面有 G Mm R 2=mg 月 卫星在极月圆轨道,有G Mm R +h2=m 4π2T 2(R +h ) 解得g 月=4π2R +h3T 2R 2答案 (1)加速 (2)4π2R +h3T 2R 2名师点拨 本题跟变轨关系不大.7.我国发射的“嫦娥一号”探月卫星的简化路线示意图如下图所示.卫星由地面发射后,先经发射轨道进入停泊轨道,在停泊轨道经多次调速后进入地月转移轨道,接近月球后再经过多次调速进入工作轨道,对月球进行探测.已知地球与月球的质量之比为a ,卫星的停泊轨道与工作轨道的半径之比为b ,卫星在停泊轨道和工作轨道上均可视为做匀速圆周运动,则下列说法中正确的是( )A .在停泊轨道和工作轨道运行的速度之比为ab B .在停泊轨道和工作轨道运行的周期之比为b aC .在停泊轨道运行时的速度大于地球的第一宇宙速度D .在地月转移轨道上卫星只受万有引力作用,速率是逐渐减小的解析 根据G Mm r 2=m v 2r =mω2r =m 4π2T 2r ,得v =GM r,可知A 项正确,C 项错误;由以上方程得T =2πr 3GM,知在停泊轨道和工作轨道运行的周期之比为b 3a ,B 选项错误;卫星受到地球和月球的万有引力,在接近月球的过程中,两个万有引力的合力先减小后增大,因此卫星先减速后加速,D 项错误.答案 A8.美国重启登月计划,打算在绕月轨道上建造空间站.如右图所示,关闭动力的航天飞机在月球引力作用下沿椭圆轨道向月球靠近,并将在P 处进入空间站轨道,与空间站实现对接.已知空间站绕月轨道半径为r ,周期为T ,引力常量为G ,下列说法中正确的是( )A .航天飞机向P 处运动过程中速度逐渐变小B .根据题中条件可以算出月球质量C .根据题中条件可以算出空间站受到月球引力的大小D .航天飞机在与空间站对接过程中速度将变小解析 设航天飞机的质量为m ,月球的质量为M ,空间站的质量为m 0,对空间站的圆周运动有G Mm r 2=m 4π2T 2r ,得M =4π2r 3GT 2,故B 选项正确;由于不知空间站的质量,故C 选项错误;由机械能守恒或由万有引力做正功可知,A 选项错误;由高轨道到低轨道,应减速,由此可以判断出航天飞机在与空间站对接过程中速度将变小,D 选项正确.答案 BD。
2021年高考物理总复习 4章专项拓展与训练1 新人教版

2021年高考物理总复习 4章专项拓展与训练1 新人教版1.(广东高考变式题)如下图PNQ 是一个固定的光滑轨道.其中PN 是直线部分,NQ 是半径为R 的半圆弧,PN 与NQ 在N 点相切.P 、Q 两点处于同一水平高度.现有一小球自P 点由静止开始沿轨道下滑,那么( )A .小球不能到达Q 点,P 比Q 至少高R2才能经Q 点沿切线方向飞出B .小球到达Q 点后.又沿轨道返回C .小球到达Q 点后.将自由下落D .小球到达Q 点后.恰能沿圆弧的切线方向飞出解析 由机械能守恒,知小球如到达Q 点,速度必为0.而小球在圆弧上做的是圆周运动,若到达Q 点最小速度v =gR .设小球在Q 点上高度h 处才恰能完成圆周运动.由机械能守恒可列方程mgh =12mv 2,解得h =R2,故A 项正确,选项B 、C 、D 错误.答案 A2.(创新题)在竖直平面内有一由内径为r 1的光滑圆管弯曲而成的环形轨道,环形轨道半径R 远远大于r 1,如下图所示.有一质量为m 的小球,直径r 2略小于r 1,可在圆管中运动.在最低点应给小球一个多大的初速度才能使小球在竖直环轨道内恰能完成圆周运动?解析 小球恰能完成圆周运动有两种可能:①到达最高点时只与管下壁接触,此时最小速度可以为零.由惯性可完成下半周运动.设在最低点速度为v 1,由机械能守恒,知12mv 21=mg (2R ),所以v 1=2gR ,故在最低点速度v 1=2gR②到达最高点时只与管上壁接触,此时恰能完成圆周运动的条件为只有重力提供物体做圆周运动的向心力.最高点速度为v 3,则有mg =m v 23R,再由机械能守恒,可得最低点速度v 2与v 3的关系为12mv 22=mg (2R )+12mv 23,联立以上两式,可得v 2=5gR ,故在最低点速度v 2=5gR答案 两种可能:其一为2gR ,其二为5gR名师点拨 本题实质考查了两种模型.即绳模型与杆模型.球与管下壁接触的临界条件对应杆模型,球与管上壁接触的临界条件对应绳模型.3.(xx·安徽)如图所示,ABD 为竖直平面内的光滑绝缘轨道,其中AB 段是水平的,BD 段为半径R =0.2 m 的半圆,两段轨道相切于B 点,整个轨道处在竖直向下的匀强电场中,场强大小E =5.0×103V/m.一不带电的绝缘小球甲,以速度v 0沿水平轨道向右运动,与静止在B 点带正电的小球乙发生弹性碰撞.已知甲、乙两球的质量均为m =1.0×10-2kg ,乙所带电荷量q =2.0×10-5C ,g 取10 m/s 2.(水平轨道足够长,甲、乙两球可视为质点,整个运动过程无电荷转移)(1)甲、乙两球碰撞后,乙恰能通过轨道的最高点D ,求乙在轨道上的首次落点到B 点的距离;(2)在满足(1)的条件下,求甲的速度v 0;(3)若甲仍以速度v 0向右运动,增大甲的质量,保持乙的质量不变,求乙在轨道上的首次落点到B 点的距离范围.解析 (1)在乙球恰能通过轨道最高点的情况下,设乙到达最高点速度为v D ,乙离开D 点到达水平轨道的时间为t .乙的落点到B 点的距离为x .一般情况下乙球在最高点受重力、轨道给球的向下的压力、电场力,其中重力和电场力的大小和方向是不变的,只有压力可以变化,因此乙球恰能通过轨道最高点的条件为只有重力和电场力提供物体在D 点做圆周运动的向心力.mg +qE =m v 2DR①小球脱离D 点做类平抛运动,竖直方向是初速度为零的匀加速运动,加速度为a y =mg +qEm,则有 2R =12(mg +qE m)t 2②水平方向为匀速运动,有x =v D t ③ 联立①②③,得x =0.4 m ④(2)设碰撞后甲、乙的速度分别为v 甲、v 乙,根据动量守恒定律和机械能守恒定律,有mv 0=mv 甲+mv 乙⑤12mv 20=12mv 2甲+12mv 2乙⑥ 联立⑤⑥,得v 乙=v 0⑦ 由动能定理,得-mg ·2R -qE ·2R =12mv 2D -12mv 2乙⑧联立①⑦⑧,得v 0=5mg +qE Rm=2 5 m/s ⑨(3)设甲的质量为M ,碰撞后甲、乙的速度分别为v M 、v m . 根据动量守恒定律和机械能守恒定律,有Mv 0=Mv M +mv m ⑩12Mv 20=12Mv 2M +12mv 2m ⑪ 联立⑩⑪,得v m =2Mv 0M +m⑫ 由⑫和M ≥m ,可得v 0≤v m <2v 0⑬设乙球过D 点时速度为v ′D ,由动能定理,得 -mg ·2R -qE ·2R =12mv ′2D -12mv 2m ⑭联立⑨⑬⑭,得2 m/s≤v D <8 m/s ⑮设乙在水平轨道上的落点距B 点的距离为x ′,有x ′=v ′D t ⑯联立②⑮⑯,得0.4 m≤x <1.6 m答案 (1)0.4 m (2)2 5 m/s (3)0.4 m≤x <1.6 m4.如图所示,直线形挡板p 1p 2p 3与半径为r 的圆弧形挡板p 3p 4p 5平滑连接并安装在水平台面b 1b 2b 3b 4上,挡板与台面均固定不动.线圈C 1C 2C 3的匝数为n ,其端点C 1、C 3通过导线分别与电阻R 1和平行板电容器相连,电容器两极板间的距离为d ,电阻R 1的阻值是线圈C 1C 2C 3阻值的2倍,其余电阻不计,线圈C 1C 2C 3内有一面积为S 、方向垂直于线圈平面向上的匀强磁场,磁场的磁感应强度B 随时间均匀增大.质量为m 的小滑块带正电,电荷量始终保持为q ,在水平台面上以初速度v 0从p 1位置出发,沿挡板运动并通过p 5位置.若电容器两板间的电场为匀强电场,p 1、p 2在电场外,间距为L ,其间小滑块与台面的动摩擦因数为μ,其余部分的摩擦不计,重力加速度为g .求:(1)小滑块通过p 2位置时的速度大小. (2)电容器两极板间电场强度的取值范围. (3)经过时间t ,磁感应强度变化量的取值范围.解析 (1)小滑块运动到位置p 2时速度为v 1,由动能定理,有-μmgL =12mv 21-12mv 20①v 1=v 20-2μgL ②(2)由题意可知,电场方向如右图,若小滑块能通过位置p ,则小滑块可沿挡板运动且通过位置p 5,设小滑块在位置p 的速度为v ,受到的挡板的弹力为N ,匀强电场的电场强度为E ,由动能定理,有-μmgL -qE ×2r =12mv 2-12mv 20③当滑块在位置p 时,由牛顿第二定律,有N +qE =m v 2r④由题意,有N ≥0⑤由以上三式,可得E ≤m v 20-2μgL5qr ⑥E 的取值范围:0<E ≤m v 20-2μgL5qr⑦(3)设线圈产生的电动势为ε1,其电阻为R ,平行板电容器两端的电压为U ,t 时间内磁感应强度的变化量为ΔB ,得U =Ed ⑧由法拉第电磁感应定律,得ε1=n ΔBtS ⑨由全电路的欧姆定律,得ε1=I (R +2R )⑩U =2RI经过时间t ,磁感应强度变化量的取值范围:0<ΔB ≤3mdv 20-2μgL10nqrSt答案 (1)v 20-2μgL (2)0<E ≤m v 20-2μgL5qr(3)0<ΔB ≤3mdv 20-2μgL10nqrSt5.过山车是游乐场中常见的设施.下图是一种过山车的简易模型,它由水平轨道和在竖直平面内的三个圆形轨道组成,B 、C 、D 分别是三个圆形轨道的最低点,B 、C 间距与C 、D 间距相等,半径R 1=2.0 m 、R 2=1.4 m .一个质量为m =1.0 kg 的小球(视为质点),从轨道的左侧A 点以v 0=12.0 m/s 的初速度沿轨道向右运动,A 、B 间距L 1=6.0 m .小球与水平轨道间的动摩擦因数μ=0.2,圆形轨道是光滑的.假设水平轨道足够长,圆形轨道间不相互重叠.重力加速度取g =10 m/s 2,计算结果保留小数点后一位数字.求:(1)小球在经过第一个圆形轨道的最高点时,轨道对小球作用力的大小; (2)如果小球恰能通过第二圆形轨道,B 、C 间距L 应是多少;(3)在满足(2)的条件下,如果要使小球不能脱离轨道,在第三个圆形轨道的设计中,半径R 3应满足的条件;小球最终停留点与起点A 的距离.解析 (1)设小球经过第一个圆轨道的最高点时的速度为v 1,根据动能定理,得 -μmgL 1-2mgR 1=12mv 21-12mv 20①小球在最高点受到重力mg 和轨道对它的作用力F ,根据牛顿第二定律,得F +mg =m v 21R 1②由①②,得F =10.0 N ③(2)设小球在第二个圆轨道最高点的速度为v 2,由题意mg =m v 22R④-μmg (L 1+L )-2mgR 2=12mv 22-12mv 20⑤由④⑤,得L =12.5 m(3)要保证小球不脱离轨道,可分两种临界情况进行讨论:①轨道半径较小时,小球恰能通过第三个圆轨道,设在最高点的速度为v 3,应满足mg=m v 23R 3⑦ -μmg (L 1+2L )-2mgR 3=12mv 23-12mv 20⑧由⑥⑦⑧,得R 3=0.4 m②轨道半径较大时,小球上升的最大高度为R 3,根据动能定理,得-μmg (L 1+2L )-mgR 3=0-12mv 2解得R 3=1.0 m为了保证圆轨道不重叠,R 3最大值应满足 (R 2+R 3)2=L 2+(R 3-R 2)2解得R 3=27.9 m综合①、②,要使小球不脱离轨道,则第三个圆轨道的半径须满足下面的条件0<R 3≤0.4 m 或1.0 m≤R 3≤27.9 m(或写成“1.0 m≤R 3<27.9 m”也可)当0<R 3≤0.4 m 时,小球最终停留点与起点A 的距离为L ′,则-μmgL ′=0-12mv 20L ′=36.0 m当1.0 m≤R 3≤27.9 m 时,小球最终停留点与起点A 的距离为L ″,则L ″=L ′-2(L ′-L 1-2L )=26.0 m答案 (1)10.0 N (2)12.5 m(3)当0<R 3≤0.4 m 时,36.0 m ;当1.0 m≤R 3≤27.9 m 时,26.0 m 见解析名师点拨 当1.0 m≤R 3≤27.9 m 时,也可通过分过程求解,先求出通过D 点的速度v D ,上升到最高点后,再回到D 点的速度大小还是v D ,然后向C 减速运动,设减速运动的位移大小为x ,则有-μmg (L 1+2L )-2mgR 3=12mv 2D -12mv 20-μmgx =0-12mv 2D以上两式联立可得,x =5 m ,故小球最终停留点与起点A 的距离为L ″,则L ″=L 1+2L -x =26.0 m本题题眼:“圆形轨道间不相互重叠”“恰能通过第二圆形轨道”“使小球不能脱离轨道”注意易失分点:“计算结果保留小数点后一位数字”.28114 6DD2 淒p20077 4E6D 乭38746 975A 靚^839192 9918 餘8lz37406 921E 鈞P-34281 85E9 藩35620 8B24 謤。
(精选)北师大版八年级数学上册第四章 拓展资源:分层练习2

-2-13204211xy 拓展资源:分层练习题根据本班学生及教学情况可在教学过程中选择拓展资源中内容进行补充或拓展,也可留作课后作业.基础训练:1.一次函数y=kx+b 的图象如图所示,看图填空:(1)当x=0时,y=____________,当x=____________时,y=0;(2)k=__________,b=____________;(3)当x=5时,y=__________,当y=30时,x=___________.2.油箱中存油20升,油从油箱中均匀流出,流速为0.2升/分钟,则油箱中剩余油量 Q (升)与流出时间t(分钟)的函数关系是( ).A .t Q 2.0=B .t Q 2.020-=C .Q t2.0= D .Q t 2.020-= 提高训练:3.某地长途汽车客运公司规定旅客可随身携带一定质量的行李,如果超过规定,则需要购买行李票,行李票费用y 元是行李质量x (千克)的一次函数,其图象如下图所示.(1)写出y 与x 之间的函数关系式;(2)旅客最多可免费携带多少千克行李?知识拓展:4.已知直线b kx y +=经过点(0,25)且与坐标轴围成的三角形的面积为425,求该直线的表达式.5.如图,某气象中心观测一场沙尘暴从开始到结束的全过程.开始时风速平均每小时增加2km/h,4h后,沙尘暴经过开阔的荒漠地,风速变为平均每小时增加4km/h.一段时间,风速保持不变.当沙尘暴遇到绿色植被区时,其风速平均每小时减少1km/h,最终停止.结合图象,回答下列问题:(1)在y轴括号内填入相应的数值;(2)沙尘暴从发生到结束,共经过多少小时?(3)求出当h≥,风速y(km/h)与时间x(小时)之间的函数关系式.x25意图:教学设计都是针对特定的学生群体,有一定的针对性.例如从整节课的设计来看,可能对学习能力较强的学生关注不够.因此这里提供一些分层训练,以供针对各种情况调整教学加以选择.既可课内完成也可课外作业.效果:利用分层能更加全面的照顾到各种层次的学生,也更能调动学生的学习热情,另外题目见得多方法的积累也更全面和完善,不同的题目还有着不同的教学效果,教师应根据学生出现的情况适时地进行教学调整.我教学时选择了知识拓展的第4题,结果学生在做此题时出现以下情况:1、不知画图分析;2、不明确与坐标轴围成的三角形是哪一个;3、在把线段长转化为点的坐标时出错;4、出现最多的问题是漏解,只考虑一种情况.根据教学情况来看此题可让学生先独立思考,故意让学生出现以上错误,再进行纠错教学效果更好.在学生已掌握一次函数表达式的求法之后设置这个题目,目的是为了进一步培养学生数形结合的能力,综合解决问题的能力,以及通过此题的分析有两种情况教育学生考虑分析问题要严谨.答案:1.(1)2y;=x,4=(2)4,2=-=b k ;(3)13,6-=-=x y .2.B .3.(1)651-=x y ;(2)千克30. 4.5252-=+-=x y x y 或.5.(1)8,32;(2)57小时;(3)57+-=x y .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专项拓展与训练1.(2010·四川)a 是地球赤道上一幢建筑,b 是在赤道平面内做匀速圆周运动、距地面9.6×106 m 的卫星,c 是地球同步卫星,某一时刻b 、c 刚好位于a 的正上方(如图甲所示),经过48 h ,a 、b 、c 的大致位置是图乙中的(取地球半径R =6.4×106 m ,地球表面重力加速度g =10 m/s 2,π=10)解析 由于a 物体和同步卫星c 的周期都为24 h .所以48 h 后两物体又回到原位置,故A 项错误; b 是在赤道平面内做匀速圆周运动、距地面9.6×106 m 的卫星,根据G Mm r 2=m 4π2T2r ① 忽略地球自转,地面上物体的万有引力近似等于重力,有G MmR2=mg ②由①②式解得:b 卫星运行的周期T ≈2×104 s ,然后再算b 卫星在48小时内运行的圈数n =48 h/T ,代入数据得n =8.64圈,故选B 项.答案 B2.如右图所示为宇宙中有一个恒星系的示意图.A 为星系的一颗行星,它绕中央恒星O 运行的轨道近似为圆.天文学家观 测得 到A 行星运动的轨道半径为R 0、周期为T 0.(1)中央恒星O 的质量为多大?(2)经长期观测发现,A 行星实际运动的轨道与圆轨道总存在一些偏离,且周期性地每隔时间t 0发生一次最大的偏离.天文学家认为形成这种现象的原因可能是A 行星外侧还存在着一颗未知的行星B (假设其运行轨道与A 在同一水平面内,且与A 的绕行方向相同),它对A 行星的万有引力引起A 轨道的偏离.(由于B 对A 的吸引而使A 的周期引起的变化可以忽略)根据上述现象及假设,试求未知行星B 的运动周期T 及轨道半径R .解析 (1)设中央恒星质量为M ,A 行星质量为m ,则有G Mm R 20=m 4π2T 20R 0,得M =4π2R 30GT 20 (2)A 、B 相距最近时,A 偏离最大,根据题意,有 2πT 0t 0-2πT t 0=2π,得T =T 0t 0-T 0t 0根据开普勒第三定律R 3T 2=R 30T 20,得R =(t 0t 0-T 0)23R 0答案 (1)4π2R 30GT 20(2)T 0t 0t 0-T 0 (t 0t 0-T 0)23R 03.科学家在地球轨道外侧发现了一颗绕太阳运行的小行星,经过观测该小行星每隔t 时间与地球相遇一次,已知地球绕太阳公转半径是R ,周期是T ,设地球和小行星都是圆轨道,求小行星距太阳的距离.解析 设小行星绕太阳周期为T ′,T ′>T ,地球和小行星每隔t 时间相遇一次,则有(t T -t T ′)2π=2π 设小行星绕太阳轨道半径为R ′,万有引力提供向心力有G Mm ′R ′2=m ′(2πT ′)2R ′ 同理对于地球绕太阳运动,也有G Mm R 2=m (2πT )2R由上面两式有R ′3R 3=T ′2T 2,R ′=(t t -T )23R答案 (t t -T )23R4.计划发射一颗距离地面的高度为地球半径R 0的圆形轨道上运行的地球卫星,卫星轨道平面与赤道平面重合,已知地球表面重力加速度为g .(1)求出卫星绕地心运动周期T .(2)设地球自转周期T 0,该卫星绕地旋转方向与地球自转方向相同,则在赤道上一点的人能连续看到该卫星的时间是多少?解析 (1)卫星绕地球做圆周运动的向心力由万有引力提供,有G Mm (2R 0)2=m 4π2T 2·(2R 0)忽略地球自转,地面上物体的万有引力近似等于重力,有G MmR 2=mg联立以上两式,解得 T =4π2R 0g(2)所谓恰能看到要根据光学原理,比如某时刻(日出)地面上的人在B 1点恰能看到卫星在轨道上的A 1,经一段时间t ,人随地球自转到了B 2点,这时卫星转到A 2点,恰不能看到(若卫星再沿轨道向后,不是被地球挡住了吗?).由几何关系,可知∠A 1OB 1=∠A 2OB 2=α=π3,∠B 1OB 2=θ卫星的运动角度、周期和时间的关系为23π+θ2π=tT观察者随地球运动的角度、周期和时间的关系为 θ2π=tT 0联立以上两式,并代入T =4π2R 0g,得 t =4π·T 02R 0g3(T 0-4π2R 0g)答案 (1)4π(2R 0g ) (2)4π·T 02R 0g 3(T 0-4π2R 0g)5.如右图所示,A 、B 两行星在同一平面内绕同一颗恒星运动,运动的方向相同,A 、B 两行星的轨道半径分别为r 1、r 2 ,已知恒星的质量为M ,且恒星对两行星的引力远远大于两行星间的引力,两行星的轨道半径r 1<r 2,若在某一时刻两行星相距最近,试求:(1)经多长时间两行星相距最近? (2)经多长时间两行星相距最远?解析 (1)设经过时间t ,A 、B 两行星转过的角度分别是ωA t 和ωB t ,则两行星相距最近的条件是ωA t -ωB t =n ·2π(n =1,2,3,…)又因为恒星对行星万有引力提供向心力,则 G Mmr 2=m ω2r ,即ω=GMr 3对A 、B 两行星,则有 ωA =GMr 31,ωB =GMr 32由此可得 t =2πnGM /r 31-GM /r 32,(n =1,2,3,…) (2)如果经过时间t ′,A 、B 两行星处于同心圆的同一条直线上,则A 、B 两星必然相距最远,A 、B 二星各自转过的角度之差必为π的奇数倍,即ωA t -ωB t =(2k -1)π(k =1,2,3,…)代入ωA 、ωB 的值,可得 t =(2k -1)πGM /r 31-GM /r 32,(k =1,2,3,…) 答案 t =2πn GM /r 31-GM /r 32,(n =1,2,3,…)t =(2k -1)πGM /r 31-GM /r 31,(k =1,2,3,…) 6.(2010·上海)如右图所示,三个质点a 、b 、c 质量分别为m 1、m 2、M (M ≫m 1,M ≫m 2),在c 的万有引力作用下,a 、b 在同一平面内绕c 沿逆时针方向做匀速圆周运动,轨道半径之比为r a ∶r b =1∶4,则它们的周期之比T a ∶T b =________;从图示位置开始,在b 运动一周的过程中,a 、b 、c 共线了________次.解析 根据G Mm r 2=m 4π2T 2r ,得T =4π2r 3GM ,所以T a T b =18方法一 物理情境分析法如右图所示,(注:原图中,a 在b 前55°左右.)在算出T a ∶T b =1∶8后,我们知道:在a 运动第1周的时间内,b 运动了1/8周,如图,从b 到b 1位置,圆心角为45°,a 与b 共线2次,1次是a 在bc 的延长线上,另1次是a 在bc 之间.(注:如前所述,原图中a 在b 前55°左右)在a 运动第2周的时间内,从b 1到b 2位置,a 与b 共线1次,这1次是a 在bc 的延长线上;在a 运动第2周到第5周的时间内,b 运动了4/8周,到b 5位置,a 每周与b 共线2次;在a 运动第6周的时间内,b 运动了1/8周,如图所示,也是共线1次,这1次是a 在bc 之间;在a 运动第6周到第8周的时间内,b 运动了3/8周,到b 8位置即初始位置,a 每周与b 共线2次.所以从题图位置开始,在b 运动一周的过程中,a 、b 、c 共线了14次.方法二 设每隔时间t ,a 、b 共线一次,(ωa -ωb )t =π,t =πωa -ωb,所以b 运动一周的过程中,a 、b 、c 共线的次数为n =T b t =T b (ωa -ωb )π=T b (2T a -2T b )=2T bT a-2=14答案 1∶8,147.如右图所示,质量相同的三颗卫星a 、b 、c 绕地球做匀速圆周运动,其中b 、c 在地球的同步轨道上,a 距离地球表面的高度为R ,此时a 、b 恰好相距最近,已知地球质量为M 、半径为R 、地球自转的角速度为ω.万有引力常量为G ,则( )A .发射卫星b 时速度要大于11.2 km/sB .卫星a 的机械能小于卫星b 的机械能C .卫星a 和b 下一次相距最近还需经过t =2πGM8R 3-ωD .若要卫星c 与b 实现对接,可让卫星c 加速【解析】 发射卫星需要的速度为7.9 km/s ≤v ≤11.2 km/s ,卫星位置越高机械能越大,因为发射上去的能量越高,(ωa -ωb )t =2π,利用万有引力提供物体做圆周运动的向心力,解出ωa ,则可得到卫星a 和b 下一次相距最近还需经过t =2πGM8R 3-ω.【答案】 BC8.侦察卫星在通过两极上空的圆形轨道上运动,它的运动轨道距离地面的高度为h ,要使卫星在一天时间内将地面上赤道各处在日照条件下的情况全部拍摄下来,卫星在通过赤道上空时卫星的摄像机至少能拍摄地面上赤道的弧长是多少?(设地球的半径为R ,地面处的重力加速度为g ,地球自转周期为T )【解析】 卫星的周期T ′=2π(R +h )3GM ,由mg =G MmR2,知gR 2=GM ,所以T ′=2π(R +h )3gR 2,地球自转周期为T ,则在一天时间内卫星绕地球的圈数n =TT ′,地球周长l =2πR ,所以卫星每次拍摄的弧长l ′=l n =4π2T(R +h )3g【答案】4π2T(R +h )3g【学法指导】 本题的题眼为“要使卫星在一天时间内将地面上赤道各处在日照条件下的情况全部拍摄下来”,如果用几何关系,无法突破.。
