2020-2021学年河北省唐山市路北区九年级上学期期末考试数学试卷及答案解析

合集下载

人教版2020-2021学年度上学期期末考试数学试卷(Word版含解析)

人教版2020-2021学年度上学期期末考试数学试卷（全册）一、选择题（本大题共10小题，共30.0分）1.下列关于事件发生可能性的表述，正确的是（）A. 事件：“在地面，向上抛石子后落在地上”，该事件是随机事件B. 体育彩票的中奖率为10%，则买100张彩票必有10张中奖C. 在同批次10000件产品中抽取100件发现有5件次品，则这批产品中大约有500件左右的次品D. 掷两枚硬币，朝上的一面是一正面一反面的概率为 132.下列四个银行标志中，既是轴对称图形又是中心对称图形的是( )． A. B. C. D.3.关于 x 的一元二次方程 x 2−5x +2p =0 的一个根为 1 ，则另一根为（）.A. -6B. 2C. 4D. 14.下列关于二次函数 y =2x 2+3 ，下列说法正确的是（）.A. 它的开口方向向下B. 它的顶点坐标是 (2,3)C. 当 x <−1 时， y 随 x 的增大而增大D. 当 x =0 时， y 有最小值是35.如图，AB 为⊙O 的直径，点D 是弧AC 的中点，过点D 作DE ⊥AB 于点E ，延长DE 交⊙OO 于点F ，若AC = 12，AE = 3，则⊙O 的直径长为（）A. 10B. 13C. 15D. 166.某校食堂每天中午为学生提供A 、 B 两种套餐，甲乙两人同去该食堂打饭，那么甲乙两人选择同款套餐的概率为（）A. 12B. 13C. 14D. 237.如图，某幢建筑物从2.25米高的窗口A 用水管向外喷水，喷的水流呈抛物线型(抛物线所在平面与墙面垂直)，如果抛物线的最高点M 离墙1米，离地面3米，则水流下落点B 离墙的距离OB 是( )A. 2.5米B. 3米C. 3.5米D. 4米8.小明同学是一位古诗文的爱好者，在学习了一元二次方程这一章后，改编了苏轼诗词《念奴娇·哧壁怀古》：“大江东去浪淘尽，千古风流人物。

而立之年督东吴，早逝英年两位数。

2020-2021学年河北省唐山市路北区七年级(上)期中数学试卷(含解析)

2020-2021学年河北省唐山市路北区七年级第一学期期中数学试卷一、选择题（共14小题）.1．（2分）如果向北走5步记作﹣5步，那么向南走7步记作（）A．+7步B．﹣7步C．+12步D．2步2．（2分）在10.1、﹣（﹣5）、﹣|﹣|、10%、0、2、（﹣1）3、﹣22、﹣（﹣2）2这九个数中，非负数有（）A．4个B．5个C．6个D．7个3．（2分）下列各对数中，相等的一对数是（）A．（﹣2）3与﹣23B．﹣22与（﹣2）2C．﹣（﹣3）与﹣|﹣3|D．与（）24．（2分）下列各式运算正确的是（）A．2a+3b＝5ab B．5x6+8x6＝13x12C．8y﹣3y＝5D．3ab2﹣5ab2＝﹣2ab25．（2分）对乘积（﹣3）×（﹣3）×（﹣3）×（﹣3）记法正确的是（）A．﹣34B．（﹣3）4C．﹣（+3）4D．﹣（﹣3）4 6．（2分）已知x，y都是有理数，且|x+1|+（y﹣4）2＝0，则xy＝（）A．1B．4C．﹣1D．﹣47．（2分）|﹣4|＝4表示的意义是（）A．﹣4的相反数是4B．表示4的点到原点的距离是4C．4的相反数是﹣4D．表示﹣4的点到原点的距离是48．（2分）下列各组式子中，是同类项的是（）A．3x2y与﹣3xy2B．3xy与﹣2xyC．2x与2x3D．5xy与5yz9．（2分）下列关于单项式﹣2x2y的说法中，正确的是（）A．系数为2，次数为2B．系数为2，次数为3C．系数为﹣2，次数为2D．系数为﹣2，次数为310．（2分）下列各式中去括号正确的是（）A．﹣（﹣a﹣b）＝a﹣bB．a2+2（a﹣2b）＝a2+2a﹣2bC．5x﹣（x﹣1）＝5x﹣x+1D．3x2﹣（x2﹣y2）＝3x2﹣x2﹣y211．（2分）一根1m长的绳子，第一次剪去绳子的，第二次剪去剩下绳子的，如此剪下去，第100次剪完后剩下绳子的长度是（）A．B．C．D．12．（2分）用代数式表示“m的2倍与n平方的差”，正确的是（）A．（2m﹣n）2B．2（m﹣n）2C．2m﹣n2D．（m﹣2n）2 13．（2分）下列式子可读作：“负1，负3，正6，负8的和”的是（）A．﹣1+（﹣3）+（+6）﹣（﹣8）B．﹣1﹣3+6﹣8C．﹣1﹣（﹣3）﹣（﹣6）﹣（﹣8）D．﹣1﹣（﹣3）﹣6﹣（﹣8）14．（2分）点A，B在数轴上的位置如图所示，其对应的数分别是a和b，对于以下结论：甲：b﹣a＜0；乙：a+b＞0；丙：|a|＜|b|；丁：ab＞0，其中正确的是（）A．甲、乙B．丙、丁C．甲、丙D．乙、丁二、填空题（本大题共4个小题；每小题3分，共12分，把正确答案填在横线上）15．比较大小：．16．若a、b互为相反数，c、d互为倒数，则2﹣（a+b）+（﹣3cd）＝．17．若关于x的多项式x4﹣ax3+x3﹣5x2﹣bx﹣3x﹣1不存在含x的一次项和三次项，则a+b ＝．18．如图，数轴上的点A向左移动4个单位长度得到点B，则点B表示的数是．三、解答题（本题共8道题，满分60分）19．（8分）计算：（1）10﹣（﹣9）+（﹣4）﹣5；（2）﹣32﹣35÷（﹣7）+18×．20．（8分）计算：（1）3x2﹣6x﹣x2﹣3+4x﹣2x2﹣1；（2）（5a2+2a﹣1）﹣4（3﹣8a+2a2）21．（5分）先化简，后求值：3（a2﹣ab+7）﹣2（3ab﹣a2+1）+3，其中a＝2，b＝．22．（6分）计算：一个整式A与多项式x2﹣x﹣1的和是多项式﹣2x2﹣3x+4．（1）请你求出整式A；（2）当x＝2时求整式A的值．23．（8分）如图1，点A，B，C是数轴上从左到右排列的三点，分别对应的数为﹣5，b，4．某同学将刻度尺如图2放置，使刻度尺上的数字0对齐数轴上的点A，发现点B对齐刻度尺1.8cm处，点C对齐刻度尺5.4cm处．（1）在图1的数轴上，AC＝个单位长，数轴上的1个单位长对应刻度尺上的实际长度是cm；（2）求数轴上点B所对应的数b；（3）在图1的数轴上，点Q是数轴上的一点，且满足AQ＝2BQ，直接写出点Q表示的数和AQ的实际长度．24．（7分）对于有理数a，b，c，规定一种新运算：a★b★c＝ab﹣c．（1）计算：（﹣3）★4★2＝；（2）计算：（﹣2）★（1﹣x）★3＝；（3）将﹣2，﹣7，4三数代入该新运算，使得计算结果最小，请直接写出此时a，b，c 对应的值．25．（10分）旭东中学附近某水果超市最近新进了一批百香果，每斤8元，为了合理定价，在第一周试行机动价格，卖出时每斤以10元为标准，超出10元的部分记为正，不足10元的部分记为负，超市记录第一周百香果的售价情况和售出情况：星期一二三四五六日每斤价格相对于标准价格（元）+1﹣2+3﹣1+2+5﹣4售出斤数2035103015550（1）这一周超市售出的百香果单价最高的是星期，最高单价是元．（2）这一周超市出售此种百香果的收益如何？（盈利或亏损的钱数）（3）超市为了促销这种百香果，决定从下周一起推出两种促销方式：方式一：购买不超过5斤百香果，每斤12元，超出5斤的部分，每斤打8折；方式二：每斤售价10元．于老师决定买35斤百香果，通过计算说明用哪种方式购买更省钱．26．（8分）如图，在一条不完整的数轴上，从左到右的点A，B，C把数轴分成①②③④四部分，点A，B，C对应的数分别是a，b，c，已知bc＜0．（1）请说明原点在第几部分；（2）若AC＝5，BC＝3，b＝﹣1，求a；（3）若点B到表示1的点的距离与点C到表示1的点的距离相等，且a﹣b﹣c＝﹣3，求﹣a+3b﹣（b﹣2c）的值．参考答案一、选择题（本大题共14个小题，每题2分，共28分。

2020-2021学年第一学期期末教学质量检测人教版九年级数学试卷(含答案)

2020--2021学年度第一学期期末教学质量检测九年级数学试卷（考试时间：90分钟满分：120分）一.选择题（本大题共10个小题，每小题3分，共30分）1.下列图形既是轴对称图形，又是中心对称图形的是（）A．B．C．D．2.将抛物线y＝﹣2x2向上平移3个单位长度，再向右平移2个单位长度，所得到的抛物线为（）A．y＝B．y＝C．y＝D．y＝3．已知m，n是方程x2+2x﹣5=0的两个实数根，则下列选项错误的是（）A．B．C．D．4．某商品经过连续两次降价，售价由原来的每件25元降到每件16元，则平均每次降价的百分率为（）A．18%B．20%C．36%D．40%5.如图，AB是⊙O的直径，AC是⊙O的切线，A为切点，BC与⊙O交于点D，连结OD．若∠C＝50°，则∠AOD的度数为（）A．40°B．50°C．80°D．100°6.如图，△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F，且AB＝5，BC＝13，CA＝12，则阴影部分（即四边形AEOF）的面积是（）A．4B．6.25C．7.5D．97．从甲、乙、丙三人中任选两人参加“青年志愿者”活动，甲被选中的概率为（）A．B．C．D．8.若点A（﹣1，y1），B（2，y2），C（3，y3）在反比例函数的图象上，则y1，y2，y3的大小关系是（）A．y3＜y2＜y1B．y2＜y1＜y3C．y1＜y3＜y2D．y1＜y2＜y39.若二次函数的与的部分对应值如下表：x-2-10123y1472-1-2-1则当x=5时，y的值为（）A．-1B．2C．7D．1410.已知，则函数和的图象大致是（）A．B．C．D．二.填空题（本大题共7个小题，每小题4分，共28分）11.方程x2＝3x根为．12.关于x的一元二次方程（x+3）2＝m有实数根，则m的值可以为（写出一个即可）．13.教练对小明推铅球的录像进行技术分析，发现铅球行进高度y(m)与水平距离x(m)之间的关系为，由此可知铅球推出的距离是m．14.如图，将△ABC绕点C逆时针旋转得到△A′B′C，其中点A′与A是对应点，点B′与B是对应点，点A′落在直线BC上，连接AB′，若∠ACB＝45°，AC＝3，BC＝2，则AB′的长为．15.一圆锥的底面半径为2，母线长3，则这个圆锥的侧面积为．16.如图，在平面直角坐标系中，点O为坐标原点，平行四边形OABC的顶点A在反比例函数上，顶点B在反比例函数上，点C在x轴的正半轴上，则平行四边形OABC的面积是．17.二次函数y＝ax2+bx+c（a≠0）的图象如图所示，下列结论：①b＞0；②a﹣b+c＝0；③当x＜﹣1或x＞3时，y＞0．④一元二次方程ax2+bx+c+1＝0（a≠0）有两个不相等的实数根；上述结论中正确的是．（填上所有正确结论的序号）第14题第16题第17题三.解答题（一）（本大题共3个小题，每小题6分，共18分）18.解方程：19.如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，△OAB的三个顶点O（0，0）、A（4，1）、B（4，4）均在格点上．⑴画出△OAB绕原点O顺时针旋转90°后得到的OA1B1，并写出点A1的坐标；⑵在⑴的条件下，求线段OA在旋转过程中扫过的面积（结果保留π）．19.如图，在⊙O中，半径OC垂直弦AB于D，点E在⊙O上，∠E＝22.5°，AB＝2．求半径OB的长．三.解答题（二）（本大题共3个小题，每小题8分，共24分）21.如图，反比例函数和一次函数y＝kx﹣1的图象相交于A（m，2m），B两点．⑴求一次函数的表达式；⑵求出点B的坐标，并根据图象直接写出满足不等式＜kx﹣1的x的取值范围．22.甲、乙两名同学玩一个游戏：在一个不透明的口袋中装有标号分别为1，2，3，4的四个小球（除标号外无其它差异）．从口袋中随机摸出一个小球，记下标号后放回口袋中，充分摇匀后，再从口袋中随机摸出一个小球，记下该小球的标号，两次记下的标号分别用x、y表示．若x+y为奇数，则甲获胜；若x+y为偶数，则乙获胜．⑴用列表法或树状图法（树状图也称树形图）中的一种方法，求（x，y）所有可能出现的结果总数；⑵你认为这个游戏对双方公平吗？请说明理由．23.新冠疫情期间，某网店以100元/件的价格购进一批消毒用紫外线灯，该网店店主结合店铺数据发现，日销量（件）是售价（元/件）的一次函数，其售价和日销售量的四组对应值如表：售价（元/件）150160170180日销售量（件）200180160140另外，该网店每日的固定成本折算下来为2000元．注：日销售纯利润=日销售量×（售价-进价）-每日固定成本.（1）求关于的函数解析式（不要求写出自变量的取值范围）；（2）日销售纯利润为（元），求出与的函数表达式；（3）当售价定为多少元时，日销售纯利润最大，最大纯利润是多少．三.解答题（三）（本大题共2个小题，每小题10分，共20分）24.如图，AB是⊙O的弦，过点O作OC⊥OA，OC交AB于P，CP＝BC，点Q是上的一点．⑴求证：BC是⊙O的切线；⑵已知∠BAO＝25°，求∠AQB的度数；⑶在⑵的条件下，若OA＝18，求的长．25．已知：如图，抛物线y＝ax2+bx+3与坐标轴分别交于点A，B（﹣3，0），C（1，0），点P是线段AB 上方抛物线上的一个动点，过点P作x轴的垂线，交线段AB于点D，再过点P作PE∥x轴交抛物线于点E．⑴求抛物线解析式；⑵当点P运动到什么位置时，DP的长最大？⑶是否存在点P使△PDE为等腰直角三角形？若存在，求点P的坐标；若不存在，说明理由．惠城区2020--2021学年度第一学期期末教学质量检测九年级数学试卷答案一.选择题（本大题共10个小题，每小题3分，共30分）1.D2.B3.D4.B5.C6.A7.B8.C9.C10.A二.填空题（本大题共7个小题，每小题4分，共28分）11.0，312.略（m即可）13.1014.15.6π16.417.②③④三.解答题（一）（本大题共3个小题，每小题6分，共18分）18.解：19.解：⑴如图所示，点A1的坐标是（1，﹣4）；……2分⑵∵点A（4，1），∴OA＝，∴线段OA在旋转过程中扫过的面积是：．……6分20.解：∵半径OC⊥弦AB于点D，∴＝，……2分∴∠E＝∠BOC＝22.5°，∴∠BOD＝45°，∴△ODB是等腰直角三角形，……4分∵AB＝2，∴DB＝OD＝1，∴OB＝……6分三.解答题（二）（本大题共3个小题，每小题8分，共24分）21.解：⑴∵A（m，2m）在反比例函数图象上，∴2m＝，∴m＝1，∴A（1，2）．……2分又∵A（1，2）在一次函数y＝kx﹣1的图象上，∴2＝k﹣1，即k＝3，∴一次函数的表达式为：y＝3x﹣1．……4分⑵由解得或，∴B（﹣，﹣3）……6分∴由图象知满足不等式＜kx﹣1的x的取值范围为﹣＜x＜0或x＞1．……8分22.解：树状图如图所示，……3分⑴共有16种等可能的结果数；……5分⑵x+y为奇数的结果数为8，x+y为偶数的结果数为8，∴P（甲胜）＝，P（乙胜）＝，∴P（甲胜）＝P（乙胜），∴这个游戏对双方公平．……8分23.解：(1)(3分)设一次函数的表达式为y=kx+b，将点(150,250)，(160,180)代入上式得解得故y关于x的函数解析式为y=-2x+500.(2)（2分）由题意得：=y(x-100)-2000=(-2x+500)(x-100)-2000=-2x2+700x-52000(3)（3分），∵-2＜0，∴有最大值，∴当175(元/件)时，的最大值为9250（元）．三.解答题（三）（本大题共2个小题，每小题10分，共20分）24.⑴证明：连接OB，∵OA＝OB，∴∠OAB＝∠OBA，∵PC＝CB，∴∠CPB＝∠PBC，∵∠APO＝∠CPB，∴∠APO＝∠CBP，∵OC⊥OA，∴∠AOP＝90°，∴∠OAP+∠APO＝90°，∴∠CBP+∠ABO＝90°，∴∠CBO＝90°，∴BC是⊙O的切线；……4分⑵解：∵∠BAO＝25°，∴∠ABO＝25°，∠APO＝65°，∴∠POB＝∠APO﹣∠ABO＝40°，∴∠AQB＝（∠AOP+∠POB）＝130°＝65°……7分⑶解：由⑵得，∠AQB＝65°，∴∠AOB＝130°，∴的长＝的长＝＝．……10分25.解：⑴∵抛物线y＝ax2+bx+3过点B（﹣3，0），C（1，0）∴解得：∴抛物线解析式为y＝﹣x2﹣2x+3……2分⑵过点P作PH⊥x轴于点H，交AB于点F∵x＝0时，y＝﹣x2﹣2x+3＝3∴A（0，3）∴直线AB解析式为y＝x+3∵点P在线段AB上方抛物线上∴设P（t，﹣t2﹣2t+3）（﹣3＜t＜0）∴D（t，t+3）∴PD＝﹣t2﹣2t+3﹣（t+3）＝﹣t2﹣3t＝∵∴当时，DP的长最大此时，点P运动到坐标为（﹣，）.……6分⑶存在点P使△PDE为等腰直角三角形设P（t，﹣t2﹣2t+3）（﹣3＜t＜0），则D（t，t+3）∴PD＝﹣t2﹣2t+3﹣（t+3）＝﹣t2﹣3t∵抛物线y＝﹣x2﹣2x+3＝﹣（x+1）2+4∴对称轴为直线x＝﹣1∵PE∥x轴交抛物线于点E∴E、P关于对称轴对称∴﹣（﹣1）＝（﹣1）﹣t∴＝﹣2﹣t∴PE＝|﹣|＝|﹣2﹣2t|……8分∵△PDE为等腰直角三角形，∠DPE＝90°∴PD＝PE①当﹣3＜t≤﹣1时，PE＝﹣2﹣2t，如图(1)∴﹣t2﹣3t＝﹣2﹣2t解得：t1＝1（舍去），t2＝﹣2∴P（﹣2，3）②当﹣1＜t＜0时，PE＝2+2t，如图(2)∴﹣t2﹣3t＝2+2t解得：t1＝，t2＝（舍去）∴P（，）综上所述，点P坐标为（﹣2，3）或（，）时，使△PDE为等腰直角三角形．……10分图(1)图(2)备用图。

2021-2022学年河北省唐山市路北区九年级(上)期末数学试卷(含答案解析)

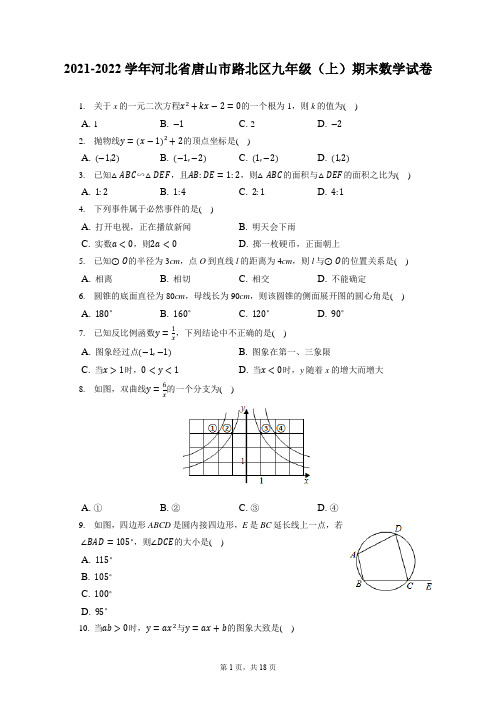
2021-2022学年河北省唐山市路北区九年级（上）期末数学试卷1.关于x的一元二次方程x2+kx−2=0的一个根为1，则k的值为( )A. 1B. −1C. 2D. −22.抛物线y=(x−1)2+2的顶点坐标是( )A. (−1,2)B. (−1,−2)C. (1,−2)D. (1,2)3.已知△ABC∽△DEF，且AB:DE=1:2，则△ABC的面积与△DEF的面积之比为( )A. 1:2B. 1:4C. 2:1D. 4:14.下列事件属于必然事件的是( )A. 打开电视，正在播放新闻B. 明天会下雨C. 实数a<0，则2a<0D. 掷一枚硬币，正面朝上5.已知⊙O的半径为3cm，点O到直线l的距离为4cm，则l与⊙O的位置关系是( )A. 相离B. 相切C. 相交D. 不能确定6.圆锥的底面直径为80cm，母线长为90cm，则该圆锥的侧面展开图的圆心角是( )A. 180∘B. 160∘C. 120∘D. 90∘，下列结论中不正确的是( )7.已知反比例函数y=1xA. 图象经过点(−1,−1)B. 图象在第一、三象限C. 当x>1时，0<y<1D. 当x<0时，y随着x的增大而增大8.如图，双曲线y=6的一个分支为( )xA. ①B. ②C. ③D. ④9.如图，四边形ABCD是圆内接四边形，E是BC延长线上一点，若∠BAD=105∘，则∠DCE的大小是( )A. 115∘B. 105∘C. 100∘D. 95∘10.当ab>0时，y=ax2与y=ax+b的图象大致是( )A. B. C. D.11.如图，在平面直角坐标系中，半径为2的圆P的圆心P的坐标为(−3,0)，将圆P沿x轴的正方向平移，使得圆P与y轴相切，则平移的距离为( )A. 1B. 3C. 5D. 1或512.如图，在一块斜边长30cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF，点D 在边BC上，点E在斜边AB上，点F在边AC上，若AF：AC=1：3，则这块木板截取正方形CDEF后，剩余部分的面积为( )A. 100cm2B. 150cm2C. 170cm2D. 200cm213.图中四个阴影的三角形中与△ABC相似的是( )A.B.C.D.(x>0)14.如图，直线l⊥x轴于点P，且与反比例函数y1=k1x(x>0)的图象分别交于点A，B，连接OA，OB，已及y2=k2x知k1=k2+2，则△OAB的面积是( )A. 1B. 2C. 4D. 0.5图象上的一个点，则k的值为______.15.已知A(−1,2)是反比例函数y=kx16.如图，在△ABC中，点D，E分别在AB，AC上，且DE//BC.若AD=2，AB=3，DE=4，则BC的长为______.17.已知二次函数y=x2+1，当x<0时，y随x的增大而______(填“增大”或“减小”)⋅18.如图，在半径为2的⊙O中，弦AB⊥直径CD，垂足为E，∠ACD=30∘，点P为⊙O上一动点，CF⊥AP于点F.①弦AB的长度为______；②点P在⊙O上运动的过程中，线段OF长度的最小值为______.19.解方程：x2−2x−5=0.20.如图所示，扇形OAB的面积为4πcm2，∠AOB=90∘，用这个扇形围成一个圆锥的侧面．求这个圆锥的底面圆的半径．21.如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B.(1)求证：△ADF∽△DEC；(2)若AB=4，AD=3√3，AE=3，求AF的长．22.如图，已知A(−4,2)、B(n,−4)是一次函数y=kx+b的图象与反比例函数y=m的图象的x两个交点.(1)求此反比例函数和一次函数的解析式；(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围；(3)求ΔAOB的面积.23.4件同型号的产品中，有1件不合格品和3件合格品．(1)从这4件产品中随机抽取1件进行检测，求抽到的是不合格品的概率；(2)从这4件产品中随机抽取2件进行检测，求抽到的都是合格品的概率；(3)在这4件产品中加入x件合格品后，进行如下试验：随机抽取1件进行检测，然后放回，多次重复这个试验，通过大量重复试验后发现，抽到合格品的频率稳定在0.95，则可以推算出x的值大约是多少？24.如图，矩形ABCD的两边AD，AB的长分别为3，8，且B，C在x轴的负半轴上，E是(x<0)的图象经过点E，与AB交于点F.DC的中点，反比例函数y=mx(1)若点B坐标为(−6,0)，求m的值；(2)若AF−AE=2，且点E的横坐标为a.①用含a的代数式表示出点F的坐标；②求出反比例函数的表达式．25.如图，二次函数y=1x2+bx+c的图象与x轴交于B、C两点(点B在点C的左侧)，一次2函数y=kx+1的图象经过点B和二次函数图象上另一点A.其中点A的坐标为(4,3).(1)求二次函数和一次函数的解析式；(2)若抛物线上的点P在第四象限内，过点P作x轴的垂线PQ，交直线AB于点Q，求线段PQ的最大值．26.如图，正方形ABCD的边长为8，M是AB的中点，P是BC边上的动点，连结PM，以点P为圆心，PM长为半径作⊙P.(1)当BP=______时，△MBP∼△DCP；(2)当⊙P与正方形ABCD的边相切时，求BP的长；(3)设⊙P的半径为x，请直接写出正方形ABCD中恰好有两个顶点在圆内的x的取值范围．答案和解析1.【答案】A【解析】解：把x=1代入方程x2+kx−2=0，可得12+k−2=0，即k=1，故选：A.把x=1代入已知方程，列出关于k的新方程，通过解新方程可以求得k的值．本题主要考查了方程的解的定义，把求未知系数的问题转化为方程求解的问题．2.【答案】D【解析】解：∵顶点式y=a(x−ℎ)2+k，顶点坐标是(ℎ,k)，∴抛物线y=(x−1)2+2的顶点坐标是(1,2).故选：D.直接利用顶点式的特点可写出顶点坐标．主要考查了求抛物线的顶点坐标的方法．熟记二次函数的顶点式的形式是解题的关键．3.【答案】B【解析】解：∵△ABC∽△DEF，且相似比为1:2，∴其面积之比为相似比的平方为1:4.故选：B.利用相似三角形的面积比等于相似比的平方即可求．本题考查相似三角形的性质：相似三角形的面积比等于相似比的平方．4.【答案】C【解析】【分析】本题考查的是必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下，一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件，不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．根据事件发生的可能性大小判断相应事件的类型即可．【解答】解：A.是随机事件；B.是随机事件；C.是必然事件；D.是随机事件；故选：C.5.【答案】A【解析】解：∵⊙O的半径r为3cm，点O到直线l的距离d为4cm，∴d>r∴l与⊙O的位置关系相离．故选：A.根据直线与圆的位置关系判定方法，假设圆心到直线的距离为d，当d>r，直线与圆相离，当d=r，直线与圆相切，当d<r，直线与圆相交，由⊙O的半径为3cm，点O到直线l的距离为4cm，得出d>r，进而可得l与⊙O的位置关系．此题主要考查了直线与圆的位置关系，解决问题的关键是判断出圆的半径与圆心到直线的距离，再根据判定方法得出位置关系．6.【答案】B【解析】解：设圆锥的侧面展开图的圆心角的度数为n，=80π，由题意得：nπ×90180解得：n=160，故选：B.根据弧长公式、圆的周长公式计算即可．本题考查的是圆锥的计算，正确理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长是解题的关键．7.【答案】D【解析】【分析】本题主要考查反比例函数的性质，当k>0时，函数图象在第一、三象限，在每个象限内，y的值随x的值的增大而减小．根据反比例函数的性质，利用排除法求解．【解答】=−1，∴图象经过点(−1,−1)，正确；解：A、x=−1，y=1−1B、∵k=1>0，∴图象在第一、三象限，正确；C、∵k=1>0，∴图象在第一象限内y随x的增大而减小，∴当x>1时，0<y<1，正确；D、应为当x<0时，y随着x的增大而减小，错误．故选：D.8.【答案】D中，k=6>0，【解析】解：∵在y=6x∴它的两个分支分别位于第一、三象限，排除①②；又当x=2时，y=3，排除③；所以应该是④．故选：D.此题可直接根据反比例函数的图象性质作答．的图象是双主要考查了反比例函数的图象性质，要掌握它的性质才能灵活解题．反比例函数y=kx曲线，当k>0时，它的两个分支分别位于第一、三象限；当k<0时，它的两个分支分别位于第二、四象限．9.【答案】B【解析】解：∵四边形ABCD是圆内接四边形，∴∠BAD+∠BCD=180∘，而∠BCD+∠DCE=180∘，∴∠DCE=∠BAD，而∠BAD=105∘，∴∠DCE=105∘.故选：B.根据圆内接四边形的对角互补得到∠BAD+∠BCD=180∘，而∠BCD与∠DEC为邻补角，得到∠DCE=∠BAD=105∘.本题考查了圆内接四边形的性质：圆内接四边形的对角互补．也考查了邻补角的定义以及等角的补角相等．10.【答案】D【解析】解：根据题意，ab>0，则a、b同号，当a>0时，b>0，y=ax2开口向上，过原点，y=ax+b过一、二、三象限；此时，没有选项符合，当a<0时，b<0，y=ax2开口向下，过原点，y=ax+b过二、三、四象限；此时，D选项符合，故选：D.根据题意，ab>0，则a、b同号，分a>0与a<0两种情况讨论，分析选项可得答案．本题考查二次函数与一次函数的图象的性质，要求学生理解系数与图象的关系．11.【答案】D【解析】解：当圆P在y轴的左侧与y轴相切时，平移的距离为3−2=1，当圆P在y轴的右侧与y轴相切时，平移的距离为3+2=5，故选：D.分圆P在y轴的左侧与y轴相切、圆P在y轴的右侧与y轴相切两种情况，根据切线的判定定理解答．本题考查的是切线的判定、坐标与图形的变化-平移问题，掌握切线的判定定理是解题的关键，解答时，注意分情况讨论思想的应用．12.【答案】A【解析】解：设AF=xcm，则AC=3xcm，∵四边形CDEF为正方形，∴EF=CF=2xcm，EF//BC，∴△AEF∽△ABC，∴EF BC =AFAC=13，∴BC=6xcm，在Rt△ABC中，AB2=AC2+BC2，即302=(3x)2+(6x)2，解得，x=2√5，∴AC=6√5cm，BC=12√5cm，EF=CF=4√5cm，∴剩余部分的面积=12×12√5×6√5−4√5×4√5=100(cm2)，故选A.13.【答案】B【解析】【分析】根据网格中的数据求出AB，AC，BC的长，求出三边之比，利用三边对应成比例的两三角形相似判断即可．此题考查了相似三角形的判定，熟练掌握相似三角形的判定方法是解本题的关键．【解答】解：由勾股定理得：AC=√2，BC=2，AB=√10，∴AC：BC：AB=1：√2：√5，A、三边之比为1：√5：2√2，图中的三角形(阴影部分)与△ABC不相似；B、三边之比：1：√2：√5，图中的三角形(阴影部分)与△ABC相似；C、三边之比为√2：√5：3，图中的三角形(阴影部分)与△ABC不相似；D、三边之比为2：√5：√13，图中的三角形(阴影部分)与△ABC不相似．故选：B.14.【答案】A【解析】解：根据反比例函数k的几何意义可知：△AOP的面积为k12，△BOP的面积为k22，∴△AOB的面积为(k12−k22)=12(k1−k2)，∵k1=k2+2，∴k1−k2=2，∴△AOB的面积为12×2=1，故选：A.根据反比例函数k的几何意义得出△AOB的面积为(k12−k22)=12(k1−k2)，再根据k1=k2+2，得k1−k2=2，即可得出．本题主要考查反比例函数k的几何意义，熟练利用反比例函数k的几何意义计算三角形面积是解题的关键．15.【答案】−2【解析】解：∵A(−1,2)是反比例函数y=kx图象上的一个点，∴k=−1×2=−2故答案为：−2将点A坐标代入解析式可求k的值．本题考查了反比例函数图象上点的坐标特征，熟练掌握图象上的点满足函数图象解析式是本题的关键．16.【答案】6【解析】解：∵DE//BC，∴∠ABC=∠ADE，∠ACB=∠AED，∴△ABC∽△ADE，∴BC DE =ABAD，即BC4=32，∴BC=6.故答案为：6.由DE//BC可得出∠ABC=∠ADE，∠ACB=∠AED，根据相似三角形的判定定理可得出△ABC∽△ADE，再利用相似三角形的性质可得出BCDE =ABAD，代入AD=2，AB=3，DE=4即可求出BC的长．本题考查了相似三角形的判定与性质，牢记相似三角形对应边的比相等是解题的关键．17.【答案】减小【解析】解：二次函数y=x2+1的图象开口向上，对称轴为y轴，当x<0时，y随x的增大而减小，故答案为：减小．根据二次函数的性质即可得出结论．本题主要考查了二次函数的性质，解答本题的关键是求出二次函数的对称轴为y轴，开口向上，此题难度不大．18.【答案】2√3；√3−1【解析】解：①如图，连接OA.∵OA=OC=2，∴∠OCA=∠OAC=30∘，∴∠AOE=∠OAC+∠ACO=60∘，∴AE=OA⋅sin60∘=√3，∵OE⊥AB，∴AE=EB=√3，∴AB=2AE=2√3，故答案为2√3.②取AC的中点H，连接OH，OF，HF，∵OA=OC，AH=HC，∴OH ⊥AC ， ∴∠AHO =90∘， ∵∠COH =30∘，∴OH =12OC =1，HC =√3，AC =2√3， ∵CF ⊥AP ， ∴∠AFC =90∘， ∴HF =12AC =√3，∴OF ≥FH −OH ，即OF ≤√3−1， ∴OF 的最小值为√3−1. 故答案为√3−1.①在Rt △AOE 中，解直角三角形求出AE 即可解决问题．②取AC 的中点H ，连接OH ，OF ，HF ，求出OH ，FH ，根据OF ≥FH −OH ，即OF ≤√3−1，由此即可解决问题．本题考查轨迹，圆周角定理，解直角三角形等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．19.【答案】解：∵x 2−2x =5，∴x 2−2x +1=6，则(x −1)2=6，解得x −1=±√6， ∴x 1=1+√6，x 2=1−√6.【解析】本题考查了解一元二次方程-配方法．先利用配方法得到(x −1)2=6，然后利用直接开平方法解方程．20.【答案】解：设扇形的半径为R cm ，根据题意得90×π×R 2360=4π，解得R =4(负值舍去)，设这个圆锥的底面圆的半径为r cm ，则12×2πr ×4=4π，解得r =1，所以这个圆锥的底面圆的半径为1cm.【解析】设扇形的半径为Rcm ，利用扇形的面积公式得到90×π×R 2360=4π，解得R =4，再设这个圆锥的底面圆的半径为rcm ，利用扇形面积公式得到12×2πr ×4=4π，然后解关于r 的方程即可．本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．21.【答案】解：(1)∵四边形ABCD 是平行四边形，∴AB//CD ，AD//BC ，∴∠B +∠C =180∘，∠ADF =∠DEC ， ∵∠AFD +∠AFE =180∘，∠AFE =∠B ， ∴∠AFD =∠C ， ∴△ADF ∽△DEC ；(2)∵AE ⊥BC ，AD =3√3，AE =3，∴在Rt △DAE 中，DE =√AD 2+AE 2=√(3√3)2+32=6，由(1)知△ADF ∽△DEC ，得AF DC=AD DE， ∴AF =DC×AD DE=4×3√36=2√3.【解析】(1)根据四边形ABCD 是平行四边形，得出AB//CD ，AD//BC ，再根据平行线的性质得出∠B +∠C =180∘，∠ADF =∠DEC ，然后根据∠AFD +∠AFE =180∘，∠AFE =∠B ，得出∠AFD =∠C ，从而得出△ADF ∽△DEC ；(2)根据已知和勾股定理得出DE =√AD 2+AE 2，再根据△ADF ∽△DEC ，得出AFDC =ADDE ，即可求出AF 的长．此题考查了相似三角形的判定与性质、平行四边形的性质以及勾股定理．此题难度不大，注意掌握数形结合思想的应用．22.【答案】解：(1)由于点A 在反比例函数y =mx 的图象上，所以2=m−4，所以m =−8，即反比例函数解析式为y =−8x； ∵点B 在反比例函数图象上，所以n ×(−4)=−8，∴n =2.因为点A 、B 在一次函数y =kx +b 的图象上，∴{−4k +b =22k +b =−4∴k=−1，b=−2，∴一次函数解析式为：y=−x−2.(2)由图象知，当−4<x<0或x>2时，一次函数的值小于反比例函数的值．(3)设一次函数图象与y轴交于点C，点A、B的横坐标分别用x A，x B表示．则C(0,−2)，所以OC=2，∵S△AOB=S△OBC+S△AOC=12OC×|x B|+12OC×|x A|=12×2×2+12×2×4=6.答：△AOB的面积是6.【解析】(1)根据点A的坐标求出反比例函数解析式，根据反比例函数解析式，求出点B的横坐标n，再根据点A、B求出一次函数解析式；(2)通过观察图象，直接得到结果．(3)设一次函数与y轴交点是C，可把△AOB分成两个三角形△AOC、△BOC，分别求出它们的面积．本题考查了待定系数法确定一次函数、反比例函数解析式，直线与轴的交点及三角形的面积．解决三角形的面积可采用分割的办法．若一次函数的解析式与x轴的交点为D，亦可把△AOB分成△AOD、△DOB求面积．23.【答案】解：(1)∵4件同型号的产品中，有1件不合格品，∴抽到的是不合格品的概率P=14；(2)令不合格产品为甲，合格产品为乙、丙、丁，画树状图如下：共有12种情况，其中抽到的都是合格品的有6种情况，则抽到的都是合格品的概率P=612=12；(3)∵大量重复试验后发现，抽到合格品的频率稳定在0.95，∴抽到合格品的概率等于0.95，=0.95，∴x+3x+4解得：x=16，经检验，x=16是分式方程的解.答：x的值大约是16.【解析】本题考查了概率的公式、用频率估计概率的知识，解题的关键是了解大量重复试验中事件发生的频率可以估计概率．(1)用不合格品的数量除以总量即可求得抽到不合格品的概率；(2)令不合格产品为甲，合格产品为乙、丙、丁，画出树状图，得出所有的情况以及抽到的都是合格品的情况，再根据概率公式计算即可；(3)根据频率估计出概率，利用概率公式列式计算即可求得x的值.24.【答案】解：(1)∵AD，AB的长分别为3，8，E是DC的中点，∴BC=3，CD=8，又∵E是DC的中点，点B坐标为(−6,0)，∴CE=4，CO=6−3=3，∴E(−3,4)，(x<0)的图象经过点E，又∵反比例函数y=mx∴m=−3×4=−12；(2)①如图，连接AE，∵点E的横坐标为a，BC=3，∴点F的横坐标为a−3，又∵Rt△ADE中，AE=√AD2+DE2=5，∴AF=AE+2=7，BF=8−7=1，∴点F的纵坐标为1，∴F(a−3,1)；②∵反比例函数经过点E(a,4)，F(a−3,1)，∴4a=1(a−3)，解得a=−1，∴E(−1,4)，∴k =−1×4=−4，∴反比例函数的表达式为y =−4x .【解析】(1)依据矩形的性质即可得出E(−3,4)，再根据反比例函数y =mx (x <0)的图象经过点E ，即可得到m =−3×4=−12；(2)①依据勾股定理可得AE =√AD 2+DE 2=5，进而得出点F 的纵坐标为1，于是得到结论； ②根据反比例函数经过点E ，F ，可得a =−1，进而得到E(−1,4)，代入反比例函数可得反比例函数的表达式为y =−4x.本题考查了反比例函数的综合题，反比例函数图象上点的坐标特征以及矩形的性质，解题时注意：反比例函数图象上的点(x,y)的横纵坐标的积是定值k ，即xy =k.25.【答案】解：(1)把A(4,3)代入y =kx +1得：4k +1=3，解得：k =12，∴一次函数解析式为y =12x +1，当y =0时，12x +1=0，解得x =−2，则B(−2,0)，把B(−2,0)，A(4,3)代入y =12x 2+bx +c 得： 2−{2−2b +c =08+4b +c =3，解得：{b =−12c =−3∴抛物线解析式为y =12x 2−12x −3； (2)设P(x,12x 2−12x −3)，则Q(x,12x +1)，∴PQ =12x +1−(12x 2−12x −3) =−12x 2+x +4=−12(x −1)2+92，∴当x =1时，PQ 最大，最大值为92.【解析】(1)先把A 点坐标代入y =kx +1可求出k ，从而得到一次函数解析式为y =12x +1，则易得B(−2,0)，然后利用待定系数法求抛物线解析式；(2)利用二次函数图象上点的坐标特征和一次函数图象上点的坐标特征，设P(x,12x 2−12x −3)，Q(x,12x+1)，则PQ=12x+1−(12x2−12x−3)，把解析式配成顶点式得到PQ=−12(x−1)2+92，然后根据二次函数的性质求PQ的最大值．本题考查了二次函数综合题：熟练掌握二次函数图象上点的坐标特征、二次函数的性质和一次函数图象上点的坐标特征；会运用待定系数法求二次函数解析式．26.【答案】解：(1)83；(2)如图1，当⊙P与边CD相切时，设PC=PM=x，在Rt△PBM中，∵PM2=BM2+PB2，∴x2=42+(8−x)2，∴x=5，∴PC=5，BP=BC−PC=8−5=3.如图2，当⊙P与边AD相切时，设切点为K，连接PK，则PK⊥AD，四边形PKDC是矩形，∴PM=PK=CD=2BM，∴BM=4，PM=8，在Rt△PBM中，PB=√82−42=4√3，综上所述，BP的长为3或4√3；(3)如图1，当PM=5时，⊙P经过点M，点C；如图3，当⊙P经过点M、点D时，∵PC2+DC2=BM2+PB2，∴42+BP2=(8−BP)2+82，∴BP=7，∴PM=√72+42=√65.综上，5<x≤√65.【解析】【分析】本题是圆的综合问题，主要考查切线的性质、正方形的性质、勾股定理等知识，解题的关键是学会用分类讨论的思想思考问题，学会利用参数构建方程解决问题．(1)设BP=a，则PC=8−a，由△MBP∼△DCP知MBDC =BPCP，代入计算可得；(2)分别求出⊙P与边CD相切时和⊙P与边AD相切时BP的长即可得；(3)①当PM=5时，⊙P经过点M，点C；②当⊙P经过点M、点D时，由PC2+DC2=BM2+PB2，可求得BP=7，继而知PM=√72+42=√65，据此可得答案．【解答】解：(1)设BP=a，则PC=8−a，∵AB=8，M是AB中点，∴AM=BM=4，∵△MBP∼△DCP，∴MB DC =BPCP，即48=a8−a，解得a=83，故答案为：83.(2)见答案；(3)见答案.。

【化学】河北省唐山市路北区2023-2024学年九年级上学期1月期末试题(解析版)

A.条形码黏在答题卡上主要发生化学变化
B.丙烯酸中含有氧气
C.丙烯酸燃烧可能生成水和二氧化碳
D.丙烯酸由3个碳元素、4个氢元素和2个元素组成
【答案】C
【解析】A、条形码利用胶黏剂黏在答题卡上，无新物质生成，属于物理变化，不符合题意；
B、丙烯酸由丙烯酸分子构成，属于纯净物，丙烯酸中不含氧气，不符合题意；
C、该实验中，铜片上的白磷与氧气接触，温度没有达到着火点，不燃烧，红磷与氧气接触，温度没有达到着火点，不燃烧，水中白磷温度没有达到着火点，隔绝氧气，不燃烧，无法探究燃烧的条件，不符合题意；
D、二氧化碳能溶于水，也能导致塑料瓶内气体减少，压强减小，软塑料瓶变瘪，无法探究二氧化碳能与水反应，不符合题意。
A、溶液①中溶质与溶剂的质量比为10g：100g=1：10，不符合题意；
B、溶液②中溶质与溶剂的质量比为20g：100g=1：5，符合题意；
C、溶液③中溶质与溶剂的质量比为30g：100g=3：10，不符合题意；
D、溶液④中100g水中最多溶解36.0g氯化钠，则溶质与溶剂的质量比为36.0g：100g=9：25，不符合题意；
4.考生必须保持答题卡的整洁，不要折叠答题卡。
可能用到的相对原子质量：H-1 O-16 C-12 N-14 Cu-64 Ag-108 Fe-56 Zn-65
一、选择题(本题共20小题，每题2分，共40分。在每小题只有一项符合题目要求)
1.下列成语的含义中涉及化学变化的是
A.火上浇油B.木已成舟C.聚沙成塔D.滴水成冰
【答案】A
【解析】A、火上浇油是指油的燃烧，有新物质生成，是化学变化；
B、木已成舟没有新物质生成，是物理变化；
C、聚沙成塔没有新物质生成，是物理变化；

河北省唐山市路北区2020-2021学年九年级英语上册期中测试卷(冀教版)(无听力,有答案)

2020-2021 学年度第一学期学生素质中期评价九年级英语试卷 2020.11听力（略）笔试部分(75分)L词汇(共10小题，每小题1分，计10分)根据短文内容及所给提示，在中的空白处填写一个正确的单词。

Xiao Gong felt so sad because his grandma was 26._____________ (die). He grew 27.____________ with her in the countryside. At 28. _____________ (one), he couldn't 29.a____________ the fact that his grandma had passed away. He refused to play soccer or go to the movies with his friends. Instead, he just 30. ________ (lie) in bed and didn't talk to anyone even his parents. After 31.___________ few months, Xiao Gong began to understand that it was 32.____________ (meaning) to be sad. Now he still 33. __________(miss) his grandma, but he is beginning to talk with his parents and this makes 34._____________（they) very happy. "We are 35. __________ (true) happy with you",said his parents, “You’re brave enough to deal with the problem in life!"I.单项选择(共10小题，每小题1分，计10分)36. Chen Wei, together with her team ____________ researching and developing the vaccine (疫苗) to fight against the disease.A. wereB.isC.areD.be37. Let’s put the bookshelf over there, ________ the wall.A.aboveB. aroundC.againstD.across38. What a _______________ classroom it is!A. soundB.voiceC.noiseD.noisy39, The teacher made us _______________ these old Chinese poems by heart.A.learnB.to learnC.learningD.learned40. -- Need we eat foods from each food group?-- Yes, we ___________.A.mustB. needC.shouldD.can41. --- I don't know how to use the APP Dubbing.— Ask Jimmy for help. He has lots of __________ in doing it.A. successB. courageC.experienceD.effort42. He stayed up late last night. ______________ he woke up in the morning, the sun was already high up in the sky.A.UntilB.AfterC.WhileD.As43. The students ____________ the school when an electric motorcycle came around the corner.A.leftB. will leaveC. have leftD. were leaving44. Some statues on the squares ____________ by angry people in the cities.A. pulled overB.will bring downC.were knocked downD. have taken out45. --- I wonder __________________.--- Yes, we all enjoyed it.A. that your school held a special sports meet this new termB. how the special sports meet was in your school this new termC.whether there was a special sports meet in your school this new termD.why you all enjoyed the special sports meet this new termI 完型填空(共10小题，每小题1分，计10分)The Magic of WavingIt began a year ago, around Christmas.While driving around the corner of our townhouse sports center, I always noticed an old man sitting by his frontyard. He was usually smoking or drinking and looked grumpy (脾气不好).One day, while I was driving past him with my daughter, I decided to 46 at him with a lot of excitement. At the beginning, when he noticed me waving at him, he looked a bit shocked (震惊). Then, I saw his 47 go up and he waved back.“Why did you wave at him?" my daughter askedI told her that it was just an act of kindness that didn't 48 anything, and it gave both him and me a sense of joy. She answered by saying that she was a bit embarrassed (局促不安)to wave to a 49, but next time she would try it as well.Lucky for us, we lived close to the old man, so we _50 him rather often. Whenever we drove by, both of us would wave at him and, pretty soon, the old man _51 waving at everyone who passed by his house.One day, my daughter's friend came to visit and she told my daughter that she saw this strange old man near our home who waved at her very52_. She mentioned that she waved back at him, even though she didn't know him, and that it felt really good.Upon hearing this, my daughter told her friend the story of how all the waving began.Her friend answered, “Tell your mom that's really_53 ！”Other friends made similar comments (评论), and this experience taught my daughter just how much an act of kindness can be very natural and effort less, if you really want to do it. It showed us how giving happiness _54_ both the giver and the receiver.Inspired(激励) by all these positive effects, we're planning to give our elder waving neighbor a thank-you card, to express our thanks for the warmth that he communicated through his enthusiastic (热情的) waves. And to thankhim for 55 this simple joy with all who pass by his house.46.A.look B. laugh C.shout D. wave47.A.leg B.hand C.foot D.head48.A.cost B.bring C.break D.hide49. A.smoker B.stranger C.manager D.driver50. A.saw B.asked C.thanked D.visited51. A.started B.succeeded C.guided D. lasted52.A.slowly B.finally C.excitedly D.safely53.A.different B.easy C.cool D. humorous54. A.attracted B.controlled C.remembered D.benefited55.A.getting B.sharing C. following D.keepingIV.阅读理解(共15小题，每小题2分，计30分)CloudsOn a beautiful spring afternoon,I relax ---- and lie down.On the soft green grass,Breathing in the fresh smell that I can feel all around.My attention is taken up to the clouds.For up there in the bright blue skyIs a fluffy white world of cotton candy animalsAnd castles built with marshmallow bricks.But I must be creative and take the timeTo bring this world into focus,So I take a breath,And close my eyes just a little bit.As a tiny, cotton ball mouseJumps out from a lion's house.What a treat to spend my afternoonWith these newly found friends moving by!56. The poet is watching clouds ____________.A. in the morningB.at noonC. in the afternoonD. at night57. Which word can best describe the poet in the poem?A. BusyB.TiredC.PeacefulD. Bored58. The poet wrote this poem to _____________.A. show us where to watch cloudsB. teach us about cloud shapesC. explain to us how clouds can changeD.tell us about his cloud watchingBOn December 10 each year the Alfred Nobel Foundation presents six prizes. These prizes are named after Alfred Nobel who invented dynamite (炸药) in the I9è century. During his life, Mr. Nobel made a lot of money from his invention. It was his idea to create the prizes. He put the money in a bank, and money made more money through interest from the bank.Mr. Nobel wanted to use his money to help scientists, artists and people helping others around the world. The prizes include physics, medicine, chemistry, literature and peace.These five Nobel Prizes were first given out in 1901. Later, Nobel Prize in Economic (经济) Sciences was set up to celebrate the 300* year business of the Central Bank of Sweden (瑞典) in 1968.Each winner is given a cash prize, a medal and a special paper which explains the prize the person won. Theamount of money each person gets is calculated (计算) from the interest made from all of Mr. Nobel's money still in the bank. This interest is divided equally between the five prize winners in physics, medicine, chemistry, literature and peace. The Central Bank of Sweden then pays the same amount to the winner of the prize in economics.Affected by the COVID-19, this year's Nobel Prize Award Ceremony (仪式) will be held online instead of the traditional one.59. The Nobel Prizes are presented _____________.A.every four yearsB.in DecemberC. at different timesD.at UN headquarters60. The word “interest" in the first paragraph means _____________ in Chinese.A.利息B.兴趣C.名胜D.储蓄61. Which is TRUE according to the passage?A.A silver medal, an invention and money are given to each Nobel Prize winner.B.All the Nobel Prize winners are given money from the Central Bank of Sweden.C. The Nobel Prize in Economics was not set up by Alfred Nobel.D.The Central Bank of Sweden won the Nobel Prize in Economics in 1968.CMore than two thirds of the world's polar bears will be wiped out ( 消灭) by 2050, according to a shocking new study. By then, scientists say, global warming will have melted 42percent of the Arctic sea ice. By 2100, only a very few of these important creatures will be left. The report has been produced by the US Geological (地质学的) Survey. The scientists have publicized their findings in the hope of influencing US Interior Secretary (内政部长)，Dirk Kempthorne, who has been asked to put polar bears on the US endangered species list. Polar bearsdepend on floating sea ice as a platform for hunting seals, which are their main food. Without enough ice, polar bears would be forced to go onto the land, where they are poorly skilled hunters, and would be unlikely to adapt (适应) to the life on the land in time. Experts say few little bears would survive and the stress could make many females unable to get pregnant.The team of American and Canadian scientists spent six months studying bears, on the ground, from spotter planes (侦察机) and in the lab, using computer models. Some team members fear the result is even worse for the bears than what their report says..They say the Arctic is warming faster than anywhere in the world and muchfaster than their computers had been forecasting(预测). Satellite observations have showed that the ice has decreased to an all-time(空前的)low.However, not everyone in the scientific community believes that global warming is happening on such an alarming scale (报警规模). Another investigation has found that polar bears are still being hunted by wealthy “sportsmen” who want their skins and heads. At least ten international companies offer bear-hunting trips.62. What do we know about Dirk Kempthorne according to the passage?A.He is an animal scientist.B. He is a protector of animals working for the US government.C.He was asked to put polar bears on the US endangered species list.D.He offered to put polar bears on the endangered species list.63. Why will polar bears die out if there is not enough sea ice?A. Because polar bears can't catch enough food without ice.B.Because polar bears eat ice when they feel thirsty.C. Because polar bears will be easily found by hunters without ice.D.Because most female bears are used to giving birth under ice.64. What does the writer want to tell us in the last paragraph?A.The forecast about the future of polar bears is not correct.B.Global warming won't have any effect on hunting trips in the Arctic.C.Polar bears are an endangered species as a result of bear-hunting.D.People don't pay enough attention to the protection of endangered bears.65. What is this passage mainly about?A. Global warming makes the whole world different.B. Human beings are responsible for the endangered species.C. Most of the polar bears will be wiped out by the end of this century.D. Scientists have found that most animals in the Arctic will die out by the end of this century.D阅读短文，并按要求完成下列试题。

九年级数学上册2020-2021学年度第一学期九年级期末学业水平质量检测含答案

2020—2021学年第一学期九年级期末学业水平质量检测数学试卷一、选择题（本题共8个小题，每小题2分，共16分.每小题只有一个正确选项）1．如图，点D、E分别在△ABC的AB、AC边上，下列条件中：①∠ADE=∠C；②AE DEAB BC=；③AD AEAC AB=. 使△ADE与△ACB一定相似的是A．①②B．②③C．①③D．①②③2. 如图，A、B、C是半径为4的⊙O上的三点. 如果∠ACB=45°，那么AB的长为A．πB．2πC．3πD．4π3. 小王抛一枚质地均匀的硬币，连续抛4次，硬币均正面朝上落地. 如果他再抛第5次，那么硬币正面朝上的概率为A．1 B．12C．14D．154．如图，数轴上有A、B、C三点，点A、C关于点B对称，以原点O为圆心作圆，如果点A、B、C分别在⊙O外、⊙O内、⊙O上，那么原点O的位置应该在A．点A与点B之间靠近A点B．点A与点B之间靠近B点C．点B与点C之间靠近B点D．点B与点C之间靠近C点5. 如图，P A和PB是⊙O的切线，点A和点B为切点，AC是⊙O的直径. 已知∠P=50°，那么∠ACB的大小是A．65°B．60°C．55°D．50°6. 如图，为了测量某条河的宽度，现在河边的一岸边任意取一点A，又在河的另一岸边取两点B、C，测得∠α=30°，∠β=45°，量得BC长为80米．如果设河的宽度为x米，那么下列关系式中正确的是A．1802xx=+B．180xx=+C．802xx=+D．803xx=+cCBA7. 体育节中，某学校组织九年级学生举行定点投篮比赛，要求每班选派10名队员参加．下面是一班和二班参赛队员定点投篮比赛成绩的折线统计图（每人投篮10次，每投中1次记1分），请根据图中信息判断：①二班学生比一班学生的成绩稳定；②两班学生成绩的中位数相同；③两班学生成绩的众数相同. 上述说法中，正确的序号是 A ．①② B ．①③C ．②③D ．①②③8. 运动员将足球沿与地面成一定角度的方向踢出，足球飞行的路线可以看作是一条抛物线，不考虑空气阻力，足球距离地面的高度y （单位：m ）与足球被踢出后经过的时间x （单位：s ）近似满足函数关系()20y ax bx c a =++≠．如图记录了3个时刻的数据，根据函数模型和所给数据，可推断出足球飞行到最高点时，最接近的时刻x 是 A ．4 B ．4.5C ．5D ．6二、填空题（本题共8个小题，每小题2分，共16分）9. 如图，线段BD 、CE 相交于点A ，DE ∥BC ．如果AB =4，AD =2，DE =1.5，那么BC 的长为_________．10.在平面直角坐标系xOy 中，二次函数()214y x =--+的图象如图，将二次函数()214y x =--+的图象平移，使二次函数()214y x =--+的图象的最高点与坐标原点重合，请写出一种平移方法：__________________________________________.11.如图，将一把两边都带有刻度的直尺放在半圆形纸片上，使其一边经过圆心O ，另一边所在直线与半圆相交于点D 、E ，量出半径OC =5cm ，弦DE =8cm ，则直尺的宽度为____cm.12. “阅读让自己内心强大，勇敢面对抉择与挑战.”某校倡导学生读书，下面的表格是该校九年级学生本学期内阅读课外书籍情况统计表. 请你根据统计表中提供的信息，求出表中a 、b 的值：a = ，b = ．13．中国“一带一路”倡议给沿线国家和地区带来很大的经济效益，沿线某地区居民2017年年人均收入300美元，预计2019年年人均收入将达到y 美元. 设2017年到2019年该地区居民年人均收入平均增长率为x ，那么y 与x 的函数关系式是________________________. 图书种类频数频率科普常识 210 b 名人传记 204 0.34 中外名著 a 0.25 其他360.06x s ()y m ()182014O yx4O 1EDBCA二班一班成绩/分109876109876543201514. 如图，直角三角形纸片ABC ，90ACB ∠=︒，AC 边长为10 cm. 现从下往上依次裁剪宽为4 cm 的矩形纸条，如果剪得第二张矩形纸条恰好是正方形，那么BC 的长度是____cm ．15. 已知二次函数()210y ax bx a =++≠的图象与x 轴只有一个交点．请写出一组满足条件的a ，b 的值：a =______，b =________.16. 下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程．已知：直线a 和直线外一点P ．求作：直线a 的垂线，使它经过P ．作法：如图2.（1）在直线a 上取一点A ，连接P A ；（2）分别以点A 和点P 为圆心，大于12AP 的长为半径作弧，两弧相交于B ，C 两点，连接BC 交P A 于点D ；（3）以点D 为圆心，DP 为半径作圆，交直线a 于点E （异于点A ），作直线PE ．所以直线PE 就是所求作的垂线．请回答：该尺规作图的依据是_____________________________________________．三、解答题（本题共68分，第17—25题，每小题6分，第26—27题，每小题7分） 17．计算：(4cos30π1︒+--.18. 已知:如图，AB 为⊙O 的直径，OD ∥AC . 求证：点D 平分BC .19．如图，在□ABCD 中，连接DB ，F 是边BC 上一点，连接DF 并延长，交AB=∠A ．（1）求证：△BDF ∽△BCD ；（2）如果BD =9BC =，求ABBE的值．图1aaP20. 如图，菱形ABCD 的对角线交于点O ，点E 是菱形外一点，DE ∥AC ，CE ∥BD ．（1）求证：四边形DECO 是矩形；（2）连接AE 交BD 于点F ，当∠ADB =30°，DE=2时，求AF 的长度．21．如图，直线2y x =+与反比例函数()00ky k x x=>>，的图象交于点A （2，m ），与y 轴交于点B .（1）求m 、k 的值；（2）连接OA ，将△AOB 沿射线BA 方向平移，平移后A 、O 、B 的对应点分别为A'、O'、B'，当点O'恰好落在反比例函数()0ky k x=>的图象上时，求点O' 的坐标；（3）设点P 的坐标为（0，n ）且04n <<，过点P 作平行于x 轴的直线与直线2y x =+和反比例函数()0ky k x=>的图象分别交于点C ，D ，当C 、D 间距离小于或等于4时，直接写出n 的取值范围．22．如图，AB 为⊙O 的直径，C 、D 为⊙O 上不同于A 、B 的两点，∠ABD =2∠BAC ，连接CD ，过点C 作CE ⊥DB ，垂足为E ，直径AB 与CE 的延长线相交于F 点．（1）求证：CF 是⊙O 的切线；（2）当185BD=，3sin 5F=时，求OF 的长．23. 为提升学生的艺术素养，学校计划开设四门艺术选修课：A ．书法；B ．绘画；C ．乐器；D ．舞蹈．为了解学生对四门功课的喜欢情况，在全校范围内随机抽取若干名学生进行问卷调查（每名被调查的学生必须选择而且只能选择其中一门）．将数据进行整理，并绘制成如下两幅不完整的统计图，请结合图中所给信息解答下列问题：（1）本次调查的学生共有_______人，扇形统计图中α的度数是_______；（2）请把条形统计图补充完整；（3）学校为举办2018年度校园文化艺术节，决定从A ．书法；B ．绘画；C ．乐器；D ．舞蹈四项艺术形式中选择其中两项组成一个新的节目形式，请用列表法或画树状图法求出选中书法与乐器组合在一起的概率．24．如图，AB 是⊙O 的直径，点C 是⊙O 上一点，30CAB ∠=︒，D 是直径AB 上一动点，连接CD 并过点D 作CD 的垂线，与⊙O 的其中一个交点记为点E （点E 位于直线CD 上方或左侧），连接EC ．已知AB =6 cm ，设A 、D 两点间的距离为x cm ，C 、D 两点间的距离为1y cm ，E 、C 两点间的距离为2y cm ．小雪根据学习函数的经验，分别对函数1y ，2y 随自变量x 的变化而变化的规律进行了探究．下面是小雪的探究过程：（1）按照下表中自变量x 的值进行取点、画图、测量，分别得到了1y ，2y 与x 的几组对应值，请将表格补充完整； x /cm 0 1 2 3 4 5 61y /cm5.20 4.36 3.60 2.65 2.65 2y /cm5.204.564.224.244.775.606.00 （2）在同一平面直角坐标系xOy 中，描出补全后的表中各组数值所对应的点（x ，y ），（x ，y ），并画出函数y 的图象；y 2cm6543学生选修课程条形统计图学生选修课程扇形统计图25. 在平面直角坐标系xOy 中，抛物线()240y ax ax m a =-+≠与x 轴的交点为A 、B ，（点A 在点B 的左侧），且AB =2. （1）求抛物线的对称轴及m 的值(用含字母a 的代数式表示)；（2）若抛物线()240y ax ax m a =-+≠与y 轴的交点在（0，-1）和（0，0）之间，求a 的取值范围；（3）横、纵坐标都是整数的点叫做整点．若抛物线在点A ，B 之间的部分与线段AB 所围成的区域内（包括边界）恰有5个整点，结合函数的图象，直接写出a 的取值范围．26. 如图1，在正方形ABCD 中，点F 在边BC 上，过点F 作EF ⊥BC ，且FE =FC （CE <CB ），连接CE 、AE ，点G 是AE 的中点，连接FG .（1）用等式表示线段BF 与FG 的数量关系是___________________；（2）将图1中的△CEF 绕点C 按逆时针旋转，使△CEF 的顶点F 恰好在正方形ABCD 的对角线AC 上，点G 仍是AE 的中点，连接FG 、DF .①在图2中，依据题意补全图形； ②求证:DF =.图2图127. 在平面直角坐标系xOy中，⊙C的半径为r，点P与圆心C不重合，给出如下定义：若在⊙C上存在一点M，使30MPC∠=︒，则称点P为⊙C的特征点．（1）当⊙O的半径为1时，如图1.①在点P1（-1，0），P2（1，P3（3，0）中，⊙O的特征点是______________．②点P在直线y b=+上，若点P为⊙O的特征点，求b的取值范围．（2）如图2，⊙C的圆心在x轴上，半径为2，点A（-2，0），B（0，．若线段AB上的所有点都是⊙C的特征点，直接写出圆心C的横坐标m的取值范围．2020—202021学年第一学期九年级期末学业水平质量检测数学试卷参考答案及评分标准一、选择题（本题共8个小题，每小题2分，共16分）二、填空题（本题共8个小题，每小题2分，共16分）9. 3 10. 向左平移1个单位，再向下平移4个单位（答案不唯一） 11. 312. 150，0.3513. ()23001y x =+ 14. 20 15. 1，2（答案不唯一） 16. 到线段两个端点距离相等的点在这条线段的垂直平分线上，直径所对的圆周角是直角，两点确定一条直线三、解答题（本题共68分，第17—25题，每小题6分，第26—27题，每小题7分） 17. 解：原式=411+-， ………………… 4分 =11+-，=0. ………………… 6分18．证明：连接CB . ………………… 1分∵AB 为⊙O 的直径，∴90ACB ∠=︒. ………………… 3分 ∵OD ∥AC ，∴OD ⊥CB ，. …………………5分 ∴点D 平分BC . ………………… 6分另证：可以连接OC 或AD .19. （1）证明：∵四边形ABCD 是平行四边形，∴DC ∥AE ，A C ∠=∠，AB =DC . ………………… 1分 ∵EDB A ∠=∠，∴EDB C ∠=∠. ………………… 2分 ∵DBF CBD ∠=∠，∴△BDF ∽△BCD . ………………… 3分（2）解：∵△BDF ∽△BCD ，∴BF BDBD BC =. ………………… 4分9=.∴5BF=. …………………5分∵DC∥AE，∴△DFC∽△EFB.∴CF DCBF BE=.∴45ABBE=. …………………6分20. （1）证明：∵四边形ABCD是菱形，∴AC⊥BD. ………………1分∵DE∥AC，CE∥BD，∴四边形DECO是平行四边形.∴四边形DECO是矩形. ………………2分（2）解：∵四边形ABCD是菱形，∴AO OC=.∵四边形DECO是矩形，∴DE OC=.∴2DE AO==. ………………3分∵DE∥AC，∴OAF DEF∠=∠.∵AFO EFD∠=∠，∴△AFO≌△EFD.∴OF DF=. ………………4分在Rt△ADO中，tanOAADBDO∠=.∴2DO=.∴DO=………………5分∴FO=∴AF===. ………………6分方法二：∴△AFO≌△EFD.在Rt △ACE 中，AC =4，CE =OD=∴AE=∴AF =12AE. 21. 解：（1）∵直线2y x =+过点A （2，m ），∴224m =+=. ……………… 1分 ∴点A （2，4）. 把A （2，4）代入函数ky x=中， ∴42k =. ∴8k =. ……………… 2分（2）∵△AOB 沿射线BA 方向平移，∴直线OO' 的表达式为y x =. ……………… 3分∴,8y x y x =⎧⎪⎨=⎪⎩.解得x =. ……………… 4分 ∴点O'的坐标为（. ……………… 5分（3）24n <≤. ……………… 6分22．（1）证明：连接OC .∵CB CB =，∴2BOC BAC ∠=∠. ……………… 1分 ∵∠ABD =2∠BAC ， ∴BOC ABD ∠=∠.∴BD ∥OC . ……………… 2分 ∵CE ⊥DB ，∴CE ⊥OC . ……………… 3分 ∴CF 是⊙O 的切线.（2）解：连接AD .∵AB 为⊙O 的直径，∴BD ⊥AD . ∵CE ⊥DB ， ∴AD ∥CF .在Rt △ABD 中， ∴3sin sin 5BD F=BAD AB ∠==. ∴18355AB =. ∴6AB =. ……………… 5分 ∴3OC =. 在Rt △COF 中， ∴3sin 5OC F OF ==. ∴335OF =. ∴5OF =. ……………… 6分另解：过点O 作OG ⊥DB 于点G .23. 解：（1）40，108︒； ……………… 2分（2）条形统计图补充正确； ……………… 4分（3）列表法或画树状图正确： ……………… 5分∴P （AC ）=126=. ……………… 6分 24. 解：（1）3，3 ……………… 2分（2） ……………… 4分（3）4.5 或6 ……………… 6分25.解：（1）对称轴为直线422ax a-=-=. ……………… 1分 ∵AB =2，点A 在点B 的左侧，∴A ()10,，B ()30, 把A （1，0）代入()240y ax ax m a =-+≠中，y 2cm 65432∴3m a =. ……………… 2分（2）∵抛物线()2430y ax ax a a =-+≠与y 轴的交点在（0，-1）和（0，0）之间，∴0a <. ……………… 3分当抛物线()2430y ax ax a a =-+≠经过点（0，-1）时，可得13a =-. ∴a 的取值范围是103a -<<. ……………… 4分（3）32a -<-≤或2<3a ≤. ……………… 6分26. （1）BF =． ……………… 1分（2）①依据题意补全图形； ……………… 3分②证明：如图，连接BF 、GB .∵四边形ABCD 是正方形，∴AD =AB ，90ABC BAD ∠=∠=︒，AC 平分BAD ∠. ∴45BAC DAC ∠=∠=︒. 在△ADF 和△ABF 中，AD AB DAC BAC AF AF =⎧⎪∠=∠⎨⎪=⎩，，， ∴△ADF ≌△ABF . ……………… 4分∴DF BF =.∵EF ⊥AC ，90ABC ∠=︒，点G 是AE 的中点，∴AG EG BG FG ===. ……………… 5分 ∴点A 、F 、E 、B 在以点G 为圆心，AG 长为半径的圆上. ∵BF BF =，45BAC ∠=︒，∴290BGF BAC ∠=∠=︒. ……………… 6分 ∴△BGF 是等腰直角三角形.∴BF =.∴DF =. ……………… 7分27. 解：（1） P 1，P 2．……………… 2分②当0b >时，设直线y b =+与以2为半径的⊙O 相切于点C ，与y 轴交于点E ，与x 轴交于点F . ∴E （0，b ），F，0），OC ⊥EF .∴3tan OF FEO OE b ∠===. ∴30FEO ∠=︒. (3)∵1sin 2OC FEO OE ∠==，∴212b =. ∴4b =. ……………… 4分当0b <时，由对称性可知：4b =-. ……………… 5分 ∴b 的取值范围是44b -≤≤． ……………… 6分（2）∴m 的取值范围为22m -<≤. ……………… 7分。

2020-2021学年河北省唐山市滦州市九年级(上)期中数学试卷

2020-2021学年河北省唐山市滦州市九年级（上）期中数学试卷一、选择题[本大题有16个小题，共42分.1～10小题各3分，1-16小题各2分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1．（3分）如图，直线AB∥CD∥EF，若AC＝4，AE＝10，BF＝，则DF的长为（）A．B．10C．3D．2．（3分）已知如图（1）、（2）中各有两个三角形，其边长和角的度数如图上标注，则对图（1）、（2）中的两个三角形，下列说法正确的是（）A．都相似B．都不相似C．只有（1）相似D．只有（2）相似3．（3分）从一组数据1，2，2，3中任意取走一个数，剩下三个数不变的是（）A．平均数B．众数C．中位数D．方差4．（3分）利用配方法解方程x2﹣12x+13＝0，经过配方得到（）A．（x+6）2＝49B．（x+6）2＝23C．（x﹣6）2＝23D．（x﹣6）2＝49 5．（3分）如图是小颖前三次购买苹果单价的统计图，第四次又买的苹果单价是a元/千克，发现这四个单价的中位数恰好也是众数，则a＝（）A．9B．8C．7D．66．（3分）如图，A，B两地被池塘隔开，小明通过下列方法测出了A、B间的距离：先在AB外选一点C，然后测出AC，BC的中点M，N，并测量出MN的长为12m，由此他就知道了A、B间的距离．有关他这次探究活动的描述错误的是（）A．AB＝24m B．MN∥AB C．△CMN∽△CAB D．CM：MA＝1：2 7．（3分）在Rt△ABC中，∠C＝90°，cos A＝，则sin A＝（）A．B．C．D．8．（3分）一元二次方程kx2﹣2x﹣2＝0有实数根，则k的取值范围是（）A．k≥﹣且k≠0B．k≥﹣1C．k≤﹣1且k≠0D．k≥﹣1或k≠0 9．（3分）如图，快艇从P处向正北航行到A处时，向左转50°航行到B处，再向右转80°继续航行，此时的航行方向为（）A．北偏东30°B．北偏东80°C．北偏西30°D．北偏西50°10．（3分）如图，将△ABC沿BC边上的中线AD平移到△A'B'C'的位置，已知△ABC的面积为9，阴影部分三角形的面积为4．若AA'＝1，则A'D等于（）A．2B．3C．D．11．（2分）疫情期间，若有1人染上“新冠”，不及时治疗，经过两轮传染后有361人染上“新冠”，平均一个人传染（）个人．A．14B．16C．18D．2012．（2分）在如图所示的网格中，以点O为位似中心，四边形ABCD的位似图形是（）A．四边形NPMQ B．四边形NPMR C．四边形NHMQ D．四边形NHMR 13．（2分）如图，在Rt△ABC中，∠C＝90°，CD⊥AB于点D且AD：BD＝9：4，则tan B 的值为（）A．9：4B．9：2C．3：4D．3：214．（2分）小刚在解关于x的方程ax2+bx+c＝0（a≠0）时，只抄对了a＝1，b＝4，解出其中一个根是x＝﹣1．他核对时发现所抄的c比原方程的c值小2．则原方程的根的情况是（）A．不存在实数根B．有两个不相等的实数根C．有一个根是x＝﹣1D．有两个相等的实数根15．（2分）如图，在长为32m，宽为20m的长方形地面上修筑同样宽的道路（图中阴影部分），余下的部分种上草坪，要使草坪的面积为540m2，则道路的宽（）m．A．1B．1.5C．2D．2.516．（2分）如图，D、E分别是△ABC的边AB、BC上的点，且DE∥AC，AE、CD相交于点O，若S△BDE：S△DEC＝1：4，则S△DOE与S△AOC的比是（）A．1：2B．1：4C．1：5D．1：25二、填空题（本大题有3个小题，共12分）17．（3分）若关于x的一元二次方程x2+mx+2n＝0有一个根是﹣2，则m﹣n＝．18．（3分）河堤横断面如图所示，堤高BC＝6米，迎水坡AB的坡比为1：，则AB的长为．19．（3分）已知一组数据x1、x2、x3、x4、x5的平均数是5，则另一组新数组x1+1、x2+2、x3+3、x4+4、x5+5的平均数是．20．（3分）如图，在四边形ABCD中，AB∥CD，∠B＝∠C＝90°，AB＝2，BC＝7，CD ＝6，若图中两个阴影部分的两个三角形相似，则点P到点B的距离为．三、解答题（本大题共6小题，共69分.解答应写出文字说明、证明过程或演算步骤）21．（12分）（1）解方程：①x2﹣24x﹣16＝0；②（x﹣5）（x+4）＝10．（2）计算：．22．（10分）嘉淇同学利用业余时间进行射击，一共射击7次，经过统计，制成如图所示折线统计图．（1）这组成绩的众数是．（2）求这组成绩的方差．（3）若嘉淇同学再射击一次（成绩为整数环），得到这8次成绩的中位数恰好是原来7次成绩的中位数，求第8成绩的最大环数．23．（10分）已知，如图，在四边形ABCD中，∠ADB＝∠ACB，延长AD、BC相交于点E．求证：（1）△ACE∽△BDE；（2）BE•DC＝AB•DE．24．（10分）如图所示，A，B两地之间有条河，原来从A地到B地需要经过桥DC，沿折线A⇒D⇒C⇒B到达．现在新建了桥EF，可直接沿直线AB从A地到达B地．已知BC＝11km，∠A＝45°，∠B＝37°，桥DC和AB平行，则现在从A地到B地可比原来少走多少路程（结果精确到0.1km．参考数据：≈1.41，sin37°≈0.60，cos37°≈0.80）25．（11分）某商场购进一批每盒40元的月饼销售，根据销售经验，应季销售每盒月饼的售价为60元时，每天可售出400盒．当售价每提高1元时，销量就相应减少10盒．（1）若商场要每天获得9000元的利润，每盒月饼的售价应定为多少元？（2）过季处理时，经过两次打折商品每盒售价为29.4元，商场平均每次打几折？26．（13分）如图1和图2，在△ABC中，AB＝AC，BC＝8，tan C＝，点M在AB上，且AM＝2．点P从点M出发沿折线MB﹣BC匀速移动，不与点C重合，点Q在边AC 上，点P运动的过程中始终保持∠APQ＝∠B．（1）当点P在BC上时，求点P与点A的最短距离；（2）若点P在MB上，且PQ将△ABC的面积分成上下4：5两部分时，求MP的长．（3）设点P移动的路程为x，当0≤x≤3及3＜x≤9时，直接写出点P到直线AC的距离（用含x的式子表示）．2020-2021学年河北省唐山市滦州市九年级（上）期中数学试卷参考答案与试题解析一、选择题[本大题有16个小题，共42分.1～10小题各3分，1-16小题各2分。

2023-2024学年河北省唐山市路北区二十一中八年级(上)月考数学试卷(10月份)(含解析)

2023-2024学年河北省唐山市路北区二十一中八年级（上）月考数学试卷（10月份）一、选择题：本题共18小题，每小题3分，共54分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.在Rt△ABC中，∠C=90°，若∠A=50°，则∠B等于( )A. 55°B. 50°C. 45°D. 40°2.一个多边形的每一个内角都是135°，则这个多边形是( )A. 七边形B. 八边形C. 九边形D. 十边形3.在△ABC中，∠A=12∠B=13∠C，则△ABC是( )A. 锐角三角形B. 直角三角形C. 钝角三角形D. 无法确定4.如图，以正方形ABCD的边CD向外作正五边形CDEFG，则∠ADE的度数为( )A. 172°B. 162°C. 152°D. 150°5.已知三角形三边长分别为3，a，8，且a为奇数，则这样的三角形有( )A. 2个B. 3个C. 4个D. 5个6.下列生活实例中，利用了“三角形稳定性”的是( )A. B. C. D.7.如图，四边形ABCD为一矩形纸带，点E、F分别在边AB、CD上，将纸带沿EF折叠，点A、D的对应点分别为A′、D′，若∠2=35°，则∠1的度数为( )A. 62.5°B. 72.5°C. 55°D. 45°8.如图所示，两个三角形全等，则∠1的度数为( )A. 41°B. 51°C. 62°D. 77°9.如图，△ABC≌△DEC，B、C、D在同一直线上，且CE=5，AC=7，则BD长( )A. 12B. 7C. 2D. 1410.如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B到C的方向平移到△DEF的位置，AB=6，DO=2，平移距离为4，则阴影部分面积为( )A. 20B. 24C. 28D. 3011.如图，∠1=∠2，下列条件中不能使△ABD≌△ACD的是( )A. AB=ACB. ∠B=∠CC. ∠ADB=∠ADCD. DB=DC12.如图，点A，E，F，C在同一直线上，AB//CD，BF//DE，BF=DE，且AE=2，AC=8，则EF的长为( )A. 4B. 3.5C. 2D. 2.513.如图，EF=CF，BF=DF，则下列结论错误的是( )A. △BEF≌△DCFB. △ABC≌△ADEC. AB=ADD. DC=AC14.2022年10月12日某中学八年级(4)班的同学在听了“天宫课堂”第三课，即我国航天员在中国空间站进行的太空授课后，组成数学兴趣小组进行了设计伞的实践活动.康康所在的小组依据全等三角形的判定设计了截面如图所示的伞骨结构，当伞完全打开后，测得AB=AC，E，F分别是AB，AC的中点，ED=DF，那么△AED≌△AFD的依据是( )A. SASB. ASAC. HLD. SSS15.如图，BD=BC，BE=CA，∠DBE=∠C=62°，∠BDE=75°，则∠AFD的度数等于( )A. 30°B. 32°C. 33°D. 35°16.如图，已知△ABC中，AD平分∠BAC，过点A作MN⊥AD.若点E是直线MN上异于点A的一点，连结BE、CE，设△ABC的周长为L1，△EBC的周长为L2，则L1与L2的大小关系为( )A. L1>L2B. L1=L2C. L1<L2D. 无法判断17.如图所示，△ABC≌△AEF，∠B=∠E，有以下结论：①AC=AE；②EF=BC；③∠EAB=∠FAC；④∠EFA=∠AFC.其中正确的个数是( )A. 4B. 3C. 2D. 118.如图，△ABC是锐角三角形，E是BC的中点，分别以AB，AC为边向外侧作等腰三角形ABM和等腰三角形ACN.点D，F分别是底边BM，CN的中点，连接DE，EF，若∠BAM=∠CAN=θ(θ是锐角)，则∠DEF的度数是( )A. 180−2θB. 180−θC. 90+2θD.90+θ二、填空题：本题共5小题，每小题3分，共15分。

2021-2022学年河北省唐山市路北区八年级(上)期末数学试卷(解析版)

2021-2022学年河北省唐山市路北区八年级第一学期期末数学试卷一、选择题（本大题共14个小题，每题2分，共28分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知，正多边形的一个外角是30°，则这个正多边形是（）A．六边形B．九边形C．十边形D．十二边形2．在，，，，，中，分式有（）A．2B．3C．4D．53．若分式有意义，则x的取值范围是（）A．x≠﹣2B．x≠2C．x≥﹣2D．x≥24．已知△ABC的三边长分别为a，b，c，则a，b，c的值可能分别是（）A．1，2，3B．3，4，7C．1，π，4D．4，5，105．下列图形中，是轴对称图形的是（）A．B．C．D．6．下列各式从左到右的变形中，是因式分解的为（）A．ax+bx+c＝x（a+b）+cB．x2﹣1＝（x+1）（x﹣1）C．x（a﹣b）＝ax+bxD．x2﹣1+y2＝（x+1）（x﹣1）+y27．点M（﹣3，﹣5）关于x轴的对称点的坐标为（）A．（﹣3，5）B．（﹣3，﹣5）C．（3，5）D．（3，﹣5）8．如图，△ABC中，EF是AB的垂直平分线，与AB交于点D，BF＝6，CF＝2，则AC的长度为（）A．6B．7C．8D．99．要使x2+kx+是完全平方式，那么k的值是（）A．k＝±1B．k＝1C．k＝﹣1D．k＝±10．若（2a+3b）（）＝9b2﹣4a2，则括号内应填的代数式是（）A．﹣2a﹣3b B．2a+3b C．2a﹣3b D．3b﹣2a11．如图，把一张长方形的纸，按图中虚线对折，并剪去阴影部分，再把它展开，得到的△ABC是（）A．直角三角形B．等边三角形C．等腰三角形D．等腰直角三角形12．某工程队要铺建一条长2000米的管道，采用新的施工方式，工作效率提高了25%，结果比原计划提前2天完成了任务，设这个工程队原计划每天要铺建x米管道，则依题意所列方程正确的是（）A．+2＝B．﹣2C．＝2D．＝213．如图，四边形ABCD中，∠A＝90°，AD＝3，连接BD，BD⊥CD，垂足是D且∠ADB ＝∠C，点P是边BC上的一动点，则DP的最小值是（）A．1B．2C．3D．414．已知在一个凸多边形中，和一个内角相邻的外角与其余内角度数总和为600°，则这个多边形的边数是（）A．5B．6C．7D．5或6二、填空题（本大题共4个小题；每小题3分，共12分。

河北省唐山市路北区2020-2021学年度九年级上学期期末英语试卷(文字版含答案)

2020—2021学年度第一学期学生素质终期评价本试卷分听力和笔试两部分, 共II大踱75小题, 满分100分. 考试用时90分钟注意事项：1. 答卷前, 考生务必在答题卡上用黑色字迹的签字笔填写自己的学校, 班级、姓名及考生号, 并用2B铅笔把对应考生号的标号涂黑.2. 选择题每小题选出答案后, 用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动, 用橡皮擦干净后, 再选涂其他答案标号；不能答在试卷上.3.非选择題必须用0.5mm黑色字迹签字笔作答, 渉及作图的题目, 用2B铅笔画图. 答案必须写在答题卡各題指定区域内的相应位實上；如需改动, 先划掉原来的答案, 然后再写上新的答案；改动的答梁也不能超出指定的区域. 不准使用铅笔、圆珠笔和涂改液. 不按以上要求作答的答案无效.4. 考生必须保持答题卡的整洁, 不要折叠答题卡.听力部分（25分）I听句子, 选出句子中所包含的信息. （共5小题, 每小題1分, 计5分）1. A. tennis B. test C. text2. A. look out B. come out C. take out3. A. in 1970 B. in 1917 C. in 19604. A. Let's have fish tonight B. Let's have meat tonightC. Let's have fish and meat tonight5. A. She's too old to move. B. She wants to move. C. She's too tired to move.II. 听句子, 选出该句的最佳答语。

（共5小题,6. A. Of course, you can't. B. I'm afraid so. C. You'd better not.7 A. Wow, good job. B. Bad luck. C. That's all right.8. A. Take it easy! B. What a pity! C. Sounds great!9. A. Nice to meet you again. B. Nice to meet you. C. How do you do?10. A. Yes. I will. B. I agree with you. C. It's kind of you.III. 听对话和问題, 选择正确答案。

2021年河北省唐山市路北区九年级一模数学试题

（2）在扇形统计图中，选择“爱国”主题所对应的圆心角是_____度；
（3）如果该校七年级共有1200名考生，请估计选择以“友善”为主题的七年级学生有______名；
（4）学生会宣传部有七年级的2名男生和2名女生，现从中随机挑选2名同学参加“主题征文”宣传活动，请用树状图法或列表法求出恰好选中“1男1女”的概率．
2021年河北省唐山市路北区九年级一模数学试题
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．sin45°的值等于（）
A． B． C． D．1
2．将630万用科学记数法表示为，则的值为（）
A．5B．6C．7D．8
3．下列手机手势解锁图案中,是轴对称图形的是( )
C．实际每天的工作效率比原计划降低了，结果延误30天完成了这一任务
D．实际每天的工作效率比原计划降低了，结果提前30天完成了这一任务
14．如图，矩形中，，，以为圆心，为半径画弧，交于点，以为圆心，为半径画弧，交于点，则的长为（）
A．3B．4C． D．5
15．如图，将函数的图象沿y轴向上平移得到一条新函数的图象，其中点A（-4，m），B（-1，n）,平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9（图中的阴影部分），则新图象的函数表达式是（）
18．已知正方形和正六边形边长均为1，如图所示，把正方形放置在正六边形外，使边与边重合，按下列步骤操作：将正方形在正六边形外绕点逆时针旋转，使边与边重合，完成第一次旋转；再绕点逆时针旋转，使边与边重合，完成第二次旋转；此时点经过路径的长为___________．若按此方式旋转，共完成六次，在这个过程中点，之间距离的最大值是______．

2021-2022学年河北省唐山市路北区九年级上学期期末道法试题及答案

2021-2022学年度第一学期学生素质期末评价九年级道德与法治（人教版）2022.01提示：本卷共6页，30题。

注意事项：1.本科评价，满分100分，时间为60分钟。

2.答卷前，考生在答题卡上用0.5m黑色签字笔填写学校、班级、姓名及考生号，并用2B铅笔把对应考生号的标号涂黑。

3.选择题选出答案后，用2B铅笔在答题卡上对应题目的答案标号涂黑；非选择题用0.5m黑色签字笔作答；答案写在答题卡各题指定区域内的相应位置上；不准使用涂改液。

涉及作图的题目，用2B铅笔画图。

答在试卷上无效。

4.保持答题卡的整洁，不要折叠答题卡。

一、选择题。

（在每题列出的四个选项中，只有一项最符合题意。

请选出正确答案并填在答题卡，共26题，每题2分，共52分。

相信你一定能有最准确的判断！）1.中国共产党_________于2021年11月8日至11日在北京召开，审议通过了_________。

（）①十九届五中全会②十九届六中全会③《中共中央关于制定国民经济和社会发展第十四个五年规划和二零三五年远景目标的建议》④《中共中央关于党的百年奋斗重大成就和历史经验的决议》A.①③B.①④C.②④D.③④2.“因改革开放而生，因改革开放而兴”，30年来浦东在一片农田上建起了一座功能集聚、要素齐全、设施先进的现代化新城，形成了高水平的对外开放体系、充满活力的区域创新体系、现代化的产业体系、健全的民生保障体系。

这印证了改革开放（）①以增进民生福祉为根本目的②影响着世界③极大解放和发展了社会生产力④是强国之路A.①②B.①③C.②④D.③④3.2021年2月25日，习近平总书记在全国脱贫攻坚总结表彰大会上庄严宣告，我国脱贫攻坚战取得了全面胜利，现行标准下9899万农村贫困人口全部脱贫，832个贫困县全部摘帽……这说明我国（）①实现了共同富裕②已经消除了绝对贫困③尊重和保障人权④解决了发展不平衡不充分问题A.①②③④B.①④C.②③D.②③④4.又到一年樱花季，武汉大学与多家媒体展开合作，推出为期10天左右的网络“云赏樱”通道。

2023-2024学年河北省唐山市路北区九年级(上)月考化学试卷(10月份)(含解析)

2023-2024学年河北省唐山市路北区九年级（上）月考化学试卷（10月份）一、选择题（本大题共25小题，共50分）1.在空气的成分中，体积分数约占21%的是( )A. 氮气B. 二氧化碳C. 氧气D. 稀有气体2.下列叙述涉及化学变化的是( )A. 天然气燃烧B. 固体研磨C. 玻璃破碎D. 冰雪融化3.2023年9月21日景海鹏、朱杨柱、桂海潮面向全国青少年进行太空科普授课。

下列能供给航天员呼吸的气体是( )A. 氧气B. 氮气C. 二氧化硫D. 氦气4.空气质量日报的主要内容不包括( )A. 空气污染指数B. 首要污染物C. 空气质量级别D. 空气湿度5.物质的下列性质，属于化学性质的是( )A. 溶解性B. 可燃性C. 颜色D. 沸点6.下列物质不属于空气污染物的是( )A. 二氧化硫B. 一氧化碳C. 氮气D. 可吸入颗粒物7.下列关于氧气的说法正确的是( )A. 氧气具有可燃性，可以支持燃烧B. 水生动物能在水中生存是因为氧气易溶于水C. 工业上利用分离液态空气的方法制取氧气D. 氧气的化学性质很活泼，常温下能与所有物质发生化学反应8.下列化学仪器需垫加石棉网才能用酒精灯加热的是( )A. 试管B. 烧杯C. 燃烧匙D. 蒸发皿9.下列物质属于纯净物的是( )A. 食盐水B. 雪碧C. 二氧化硫D. 洁净的空气10.近年来唐山蓝天白云的天气明显多了，唐山更宜居了。

下列做法与这改变不和谐的是( )A. 使用新能源公交车B. 集中烧落叶C. 积极参与植树造林D. 循环用教材11.下列反应既不属于分解反应，也不属于化合反应的是( )A. 镁+氧气点燃→氧化镁 B. 过氧化氢二氧化锰→水+氧气C. 水通电→氢气+氧气 D. 石蜡+氧气点燃→二氧化碳+水12.铁生锈和蜡烛燃烧的共同点是( )A. 都是化合反应B. 都放出大量的热C. 都发光D. 都是氧化反应13.化学实验既要操作规范，更要保障安全。

2021-2022学年河北省唐山市路北区九年级(上)期中数学试卷

2021-2022学年河北省唐山市路北区九年级（上）期中数学试卷姓名___________班级__________学号__________分数___________一、选择题1．（28378）若(a －2)x 2－3x ＋a ＝0是关于x 的一元二次方程，则( )A ．a ≠2；B ．a ＞0；C ．a ≠0；D ．a ＜0； 2．（16623）方程02=+x x 的解是( ) A ．x ＝±1；B ．x ＝0； C ．x 1＝0，x 2＝－1；D ．x ＝1；3．（1153）抛物线y ＝－(x ＋2)2－3的顶点坐标是( ) A ．(2，－3)；B ．(－2，3)；C ．(2，3)；D ．(－2，－3)； 4．（29079）一元二次方程(x ＋3)(x －1)＝2x －4化为一般形式是( )A ．x 2－1＝0；B ．x 2－7＝0；C ．x 2＋4x ＋1＝0；D ．x 2＋1＝0；5．（22272）一元二次方程2x 2－5x ＋1＝0的根的情况是( )A ．有两个不相等的实数根；B ．有两个相等的实数根；C ．没有实数根；D ．无法确定；6．（29080）抛物线y ＝－x 2＋2x －7与y 轴的交点坐标为( )A ．(7，0)；B ．(－7，0)；C ．(0，7)；D ．(0，－7)； 7．（7607）把抛物线2y x =-向左平移1个单位，然后向上平移3个单位，则平移后抛物线的解析式为( )A ．2(1)3y x =---；B ．2(1)3y x =-+-；C ．2(1)3y x =--+；D ．2(1)3y x =-++；15．（2001）若关于x 的方程x 2－2x －m ＝0有两个相等的实数根，则m 的值是____________． 16．（9085）如图，△ABC 为⊙O的内接三角形，AB 为⊙O 的直径，点D 在⊙O 上，∠ADC ＝68°，则∠BAC ＝____________°．三、计算题19．（27379）解方程：x 2－3x ＋1＝0；20．（28534）解方程：3x (x －1)＝2－2x ；四、解答题21．（28278）已知抛物线y ＝ax 2－bx ＋3经过点A (1，2)，B (2，3)． (1)求此抛物线的函数解析式．(2)判断点C (－1，－4)是否在此抛物线上．22．（29090）已知关于x 的一元二次方程x 2－(m ＋3)x ＋m ＋2＝0．(1)求证：方程总有两个实数根；(2)若方程两个根的绝对值相等，求此时m 的值．23．（29091）张师傅今年初开了一家药店，二月份开始盈利，二月份的盈利是6000元，四月份的盈利达到8640元，且从今年二月到四月，每月盈利的平均增长率都相同． (1)求每月盈利的平均增长率；(2)按照这个平均增长率，预计今年五月份的盈利能达到多少元？＝a (x －2)2－4经过原点O ，与x 轴的另一个交点为A ，则a ＝____________，点A 的坐标为____________．【操作】将图①中的抛物线在x 轴下方的部分沿x 轴翻折到x 轴上方，如图②．直接写出翻折后的这部分抛物线对应的函数解析式：____________．【探究】在图②中，翻折后的这部分图象与原抛物线剩余部分的图象组成了一个“W ”形状的新图象，则新图象对应的函数y 随x 的增大而增大时，x 的取值范围是____________．【应用】结合上面的操作与探究，继续思考：如图③，若抛物线y ＝(x －h )2－4与x 轴交于A ，B 两点(A 在B 左)，将抛物线在x 轴下方的部分沿x 轴翻折，同样，也得到了一个“W ”形状的新图象． (1)求A 、B 两点的坐标；(用含h 的式子表示) (2)当1＜x ＜2时，若新图象的函数值y 随x 的增大而增大，求h 的取值范围．试卷答案一、选择题1．A ；2．C ；解析：运用因式分解法得(1)0x x +=，故.1,021-==x x 故C ．；正确．3．D ；4．D ；5．A ；解：∵△＝(－5)2－4×2×1＝25－8＝17＞0，∴方程有有两个不相等的实数根． 6．D ；7．D ；8．C ；9．D ；10．C ； 11．B ；12．D ；13．B ；14．D ；二、填空题15．解：∵关于x 的方程x 2－2x －m ＝0有两个相等的实数根，∴△＝0，∴(－2)2－4×1×(－m )＝0，解得m ＝－1．16．解：∵∠ABC 与∠ADC 是AC 对的圆周角， ∴∠ABC ＝∠ADC ＝68°，∵AB 为⊙O 的直径， ∴∠ACB ＝90°，∴∠BAC ＝90°－∠ABC ＝90°－68°＝22°． 17．x 1＝－3，x 2＝1； 18．y ＝x ＋2，92；三、计算题19．解：a ＝1，b ＝－3，c ＝1， △＝b 2－4ac ＝9－4＝5＞0， ∴方程有两个不相等的实数根，x =1x =1x =20．∵3x (x －1)＋2(x －1)＝0， ∴(x －1)(3x ＋2)＝0，则x －1＝0或3x ＋2＝0，解得：x 1＝1，x 2＝－23．四、解答题21．解：(1)将点A (1，2)，B (2，3)代入y ＝ax 2－bx ＋3，得324233a b a b -+=⎧⎨-+=⎩，解得12a b =⎧⎨=⎩，∴抛物线的函数解析式为y ＝x 2－2x ＋3，……………………………………4分 (2)当x ＝－1时，y ＝1＋2＋3＝6≠－4， ∴点C (－1，－4)不在此抛物线上．………………………………6分 22．解：(1)△＝(m ＋3)2－4(m ＋2)，＝(m ＋1)2≥0，2分 ∴方程总有两个实数根．3分 (2)∵x 2－(m ＋3)x ＋m ＋2＝0， ∴(x －m －2)(x －1)＝0， ∴x 1＝m ＋2，x 2＝1， ∵方程两个根的绝对值相等， ∴m ＋2＝±1， ∴m ＝－3或－1；第二问还可以分两种情况讨论，即①两根相等时，令△＝0，或两根互为相反数时，两根和为0去求；23．解：(1)设每月盈利平均增长率为x ，根据题意得：6000(1＋x )2＝8640．解得：x 1＝20%，x 2＝－220%(不符合题意，舍去)，答：每月盈利的平均增长率为20%； (2)8640(1＋20%)＝10368(元)，答：按照这个平均增长率，预计今年五月份的盈利将达到10368元．∴⊙O的半径为3．【应用】(1)令y＝0得(x－h)2－4＝0，解得：x1＝h＋2、x2＝h－2，∴点A(h－2，0)B(h＋2，0)；(2)∵当1＜x＜2时，新图象的函数值y随x的增大而增大，∴h－2≤1且2≤h或h＋2≤1，解得：2≤h≤3或h≤－1．。