第二章原子结构

合集下载

结构化学第二章

8h2224Z e20rE
精选可编辑ppt
17
球极坐标与笛卡儿坐标的关系
精选可编辑ppt
18
Schrödinger方程在球极坐标中的形式
精选可编辑ppt
19
2. 变数分离法
令 (r,)R( r())(),代入上式 r2si并 2n 乘以
R
s R 2 i r n r 2 R r s i n si n 1 2 2 8 h 2 2( E V ) r 2 s2 i 0 n
这样的原子称为Rydberg原子。在实验室里已造出n 约为105的H原子, n 约为104的Ba原子; 在宇宙中也观察到了n 从301到300之间的跃迁。
毋庸置疑, Rydberg原子是个大胖子。事实上, 它的半径大约相当于基态原子的十万倍! 这样一个胖原子, 即使受到微弱的电场或磁场作用, 也会显著变形。
第二章原子的结构和性质
精选可编辑ppt
1
精选可编辑ppt
2
在本章中，将用Schrödinger方程处理真实的化学物种，这自然要从最简单的H原子入手。为了更具一般性，也包括类氢离子，如He+、Li2+等，它们的区别仅在于原子序数Z的不同。
氢是化学中最简单的物种，也是宇宙中最丰富的元素。无论在矿石、海洋或生物体内，氢无所不在。
精选可编辑ppt
20
2. 变量分离
设ψ(r,θ,φ)=R(r)Θ(θ)Φ(φ)= R(r) Y (θ,φ). 方程两边同乘以r2/(RΘΦ)
R方程：
Y方程：
Y=ΘΦ.方程两边同乘以 sin2θ/(ΘΦ)并移项
精选可编辑ppt
21
经变数分离得到的三个分别只含，和r变量的方程依次称为方程、方程和R方程，将方程和方程合并，Y(，) =()()，代表波函数的角度部分。

普通化学：第二章-原子结构、分子结构与化学键4

作业：P71：2，3，4，5，6；P83：2；3；P81：9；更正：P71: 3. 给出电子在l = 4的5g 轨道的所有可能的量子数。

说明为什么不存在3f 轨道或4g 轨道。

为什么说只有原子序数从122 (121)开始的元素，5g 轨道才被电子所占有。

五、多电子原子的核外电子排布i) 处理多电子原子的结构，必须采用近似方法中心场近似只考察其中一个电子的运动，而把原子核对它的库仑吸引以及其他N -1个电子对它的库仑排斥笼统地看成是一个处在原子中心的正电荷Z* 对它的库仑吸引：V = -*2Z e 4r πε通过这个势函数，多电子原子就可以简单地当作单电子原子来处理。

这样，上一节处理单电子原子的全部结果，只要略作修正，都适用于多电子原子。

在多电子原子中，电子的运动状态也是由n , l , m l 和m s 四个量子数决定的，电子在由这四个量子数所决定的各运动状态上的空间分布特征完全和在单电子原子中一样。

在电荷为Z*的中心场作用下运动的电子的能量为：E = -Z m e h e *2422028n ε＝-Z Eh *222nZ*称为作用在电子上的有效核电荷：Z* = Z -σσ称为屏蔽常数，其意义是：一个核电荷为Z (>1) 的多电子原子，作用在电子上的电荷不再是核电荷Z，而是扣除了其它电子的屏蔽作用以后的有效核电荷Z*。

要了解多电子原子的电子结构，关键在于确定其它电子对被考察的电子的屏蔽常数。

电子的“屏蔽作用”是广义的，它包括了内层电子的真实的屏蔽作用，也包括了同层电子及外层电子的排斥作用。

这是氢原子的1s, 2s, 3s轨道的边界图，每个球包含约90％的电子密度。

简单地讲，轨道尺寸正比于n2。

内层电子对外层电子的屏蔽效应大，外层电子对内层电子的屏蔽效应小。

ii) 斯莱特规则在量子力学中，这个屏蔽作用是通过光谱实验数据得到的。

1930年，美国的斯莱特(J. C. Slater) 提出了一套估算屏蔽常数的半经验规则，按量子数n和l的递增，把多电子原子的原子轨道按如下的顺序分组：(1s) (2s, 2p) (3s, 3p) (3d) (4s, 4p) (4d) (4f) (5s, 5p)……可以按下面的简单规则估算一个电子对另一个电子的屏蔽系数：1. 处在右面的各轨道组内的电子对左面轨道组内的电子没有屏蔽作用，屏蔽系数为0；2. 在同一轨道组内的电子，除(1s)组的二个电子间的屏蔽系数为0.30外，其它各轨道组内电子间的屏蔽系数都是0.35；3. 主量子数为n-1的各轨道组内的电子对(ns, np)组各电子的屏蔽系数为0.85；4. 主量子数等于和小于n-2的各轨道组内的电子对(ns, np)组各电子的屏蔽系数均为1.00；5. 处在(nd)或(nf)组左面的各轨道组内的电子对(nd)或(nf)组内电子的屏蔽系数均为1.00。

无机化学2原子结构与元素周期律

第二章原子结构与元素周期律
表2-4
n、l、m的关系
第二章原子结构与元素周期律
六、多电子原子轨道的能级
用图形把原子轨道能级高低顺序表示出来，就是原子轨道能级图。
第二章原子结构与元素周期律
第二节核外电子的排布
多电子原子中，电子不仅受核的吸引，而且还存在电子间的相互排斥，这些都影响到原子核外电子的排布，而核外电子的排布又直接决定着元素的性质。因此，核外电子排布是多电子原子结构中的一个重要问题。人们根据光谱实验结果，并结合对元素周期律的分析，归纳、总结出基态原子核外电子排布的三个基本原理。
第二章原子结构与元素周期律
五、薛定谔方程和四个量子数
为了描述电子的运动状态，1926年薛定谔把电子运动和光的波动理论联系起来，提出了一种波动方程，该方程称为薛定谔方程。
为了得到电子运动状态合理的解，必须引用三个参数，主量子数n、角量子数l和磁量子数m，它们的取值是相互制约的。此外，还有用来描述电子自旋运动的自旋量子数ms。
第二章原子结构与元素周期律
迄今为止，人类已发现了一百多种元素，而这些元
素形成了数以百万计的物质，组成了丰富多彩的物质世界。要了解这些物质的性质和变化规律，就必须要认识其结构，从原子、分子水平上研究物质结构、性质及其变化规律之间的关系。
第二章原子结构与元素周期律
第一节核外电子运动状态一、氢原子光谱和玻尔理论
第二章原子结构与元素周期律
（一）主量子数n
主量子数表示电子离核的平均距离，n越大，电子离核平均距离越远，n相同的电子离核平均距离比较接近，即所谓电子处于同一电子层。
电子层能量高低顺序： K<L<M<N<O<P。

原子的结构完整版PPT课件

工业领域应用
放射性同位素可用于材料检测、无损探伤、辐射加工等。
其他领域应用
放射性同位素还可用于科学研究、环境保护、农业生产等领域。
放射性同位素对环境影响及安全防护措施
对环境影响
放射性同位素衰变产生的射线会对环境和生物体造成危害，如污染空气、水源和土壤等。
安全防护措施
为了保障人类和环境安全，需要采取一系列安全防护措施，如合理选址、屏蔽防护、废物处理等。
放射性同位素概念及来源
放射性同位素定义
01
具有相同原子序数但质量数不同的同位素，能自发地放出射线
并转变为另一种元素。
放射性同位素来源
02
天然放射性元素和人工合成放射性元素。
放射性同位素衰变类型
03
α衰变、β衰变和γ衰变。
放射性同位素在医学、工业等领域应用
医学领域应用
放射性同位素可用于诊断和治疗疾病，如放射性碘治疗甲状腺疾病、PET扫描等。
过渡元素位于周期表中间部分，包括3~12列的元素。它们具有多种氧化态和丰富的化学性质，是构成众多合金和催化剂的重要
成分。
稀有气体元素
稀有气体元素位于周期表的最右侧，它们具有稳定的8电子构型（氦为2电子构型），化学性质极不活泼，一般不易与其他物质
发生化学反应。
04
化学键与分子间作用力
化学键类型及特点
分子间作用力影响物质的物理性质
分子间作用力主要影响物质的熔点、沸点、密度、硬度等物理性质。一般来说，分子间作用力越强，物质的熔点、沸点越高，密度越大，硬度也越大。例如，氢键的存在使得水的熔沸点异常高，范德华力则主要影响由分子构成的物质的物理性质。
05
原子光谱与能级跃迁

选修3-5 第二章第1讲原子结构氢原子光谱

3.光谱分析
特征谱线可以用来鉴别物质和确定利用每种原子都有自己的_________
物质的组成成分，且灵敏度很高。在发现和鉴别化学元素上有
着重大的意义。
知识点 2
氢原子的能级结构、能级公式
Ⅰ
1.玻尔理论
不连续的能量状态中，在这（1）定态：原子只能处于一系列_______
稳定的，电子虽然绕核运动，但并不向些能量状态中原子是_____
表示电子由较高能级向较低能级跃迁，电子跃迁的条件为hν =Em-En
带箭头的竖线
2.对电子跃迁条件hν =Em-En的说明
（1）电子跃迁条件hν =Em-En只适用于光子和原子作用而使原子
在各定态之间跃迁的情况。
（2）当光子能量大于或等于13.6 eV时，也可以被处于基态的氢原子吸收，使氢原子电离；当处于基态的氢原子吸收的光子能量大于13.6 eV时，氢原子电离后，电子具有一定的初动能。（3）原子还可吸收外来实物粒子（例如自由电子）的能量而被激发。由于实物粒子的动能可全部或部分被原子吸收，所以只要入射粒子的能量大于或等于两能级的能量差值（E=Em-En），均
②利用原子能量公式En=Ekn+Epn判断，当轨道半径增大时，原
子能量增大，电子动能减小，故原子的电势能增大。反之，当
轨道半径减小时，原子能量减小，电子动能增大，故原子的电势能减小。
【典例透析2】氢原子辐射出一个光子后，根据玻尔理论，下述说法正确的是( )
A．电子绕核旋转的半径增大
B．电子的动能增大
【典例透析1】如图所示为氢原子能级
图，下列说法正确的是(
的光谱
)
A.玻尔理论也能很好地解释复杂原子 B.玻尔理论认为原子的能量是连续的，电子的轨道半径是不连续的

原子结构讲解

原子结构讲解
原子结构是指原子的组成以及各组成部分之间的相对位置。

原子是由原子核和核外电子组成的，原子核位于原子的中心，核外电子围绕原子核高速旋转。

原子结构示意图是一种表示原子结构的图示，它用圆圈和小圈分别表示原子核和核内质子数，弧线表示电子层，弧线上的数字表示该层的电子数。

原子的核外电子是分层排列的，从里到外分别称为第一层、第二层、第三层等。

每层最多可以排2×(n)^2个电子，其中n表示层数。

最外层电子数不
超过8个，次外层电子数不超过18个，倒数第三层不超过32个。

原子的性质由其核外电子的排布决定。

根据电子排布的不同，原子可以分为金属原子、非金属原子和稀有气体原子。

金属原子的最外层电子数一般小于4，容易失去电子，表现出金属的特性；非金属原子的最外层电子数一般大
于或等于4，容易得到电子，表现出非金属的特性；稀有气体原子的最外层电子数为8个（氦为2个），是一种稳定结构，表现出稀有气体的特性。

以上就是原子结构的简要介绍，如需获取更多信息，建议查阅化学书籍或咨询化学专家。

第二章原子的结构和性质2.3-2.4

作图方法主要包括：
函数-变量对画图等值面（线）图界面图网格图黑点图
有些图形只能用某一种方式来画, 有些图形则可能用几种不同方式来画。作图对象与作图方法结合起来, 产生了错综复杂的许多种图形。
采用列表的形式, 可使这种关系变得一目了然。
2.3 原子轨道和电子云的图形表示
波函数 ( ，原子轨道) 电子云 ( ||2 ，概率密度)
当n相同，l不同时， l越大，主峰离核越近； l越小峰越多，而且第一个峰离核越近，俗称钻得越深。钻穿效应
2.3.2 原子轨道和电子云 ||2 的角度分布
角度分布是以角度波函数 Y ,m ( , ) 在球坐标系中对 θ、角作图，其做法是在坐标系中，选原子核作为坐标原点，在每一个(θ, )方向上引一条直线，取长度为|Y|的线段，将这些线段的端点连接起来，在空间形成一个曲面，根据 Y值的大小标明正负号。若取直线的长度为|Y|2，所以直线端点构成的曲面称为电子云的角2 度分布。
毋庸置疑, Rydberg原子一定是个大胖子. 事实上, 它的半径大约相当于基态原子的十万倍! 这样一个胖原子, 即使受到微弱的电场或磁场作用, 也会显著变形.
由于 Yl,m (q ,f )只与角量子数 l 和磁量子数m有关，而与主量子数n无关，因此 l,m 相同的状态，其原子轨道的角度分布图都相同。如2pz, 3pz, 4pz角度部分图形都完全相同。
原子轨道ψ的角度分布
s 00
1
4
对s-型轨道而言，只
与r有关，没有角度依赖
+
性，所以从原点到曲线
数的形式。
5. 磁量子数及角动量在磁场方向的分量
角动量在Z方向(磁场方向)的分量Lz的算符作用于单电子原子波函数ψ，得：

结构化学讲义教案2原子结构和性质

第二章原子结构和性质教学目的：通过H 原子薛定谔方程的求解，了解原子结构中量子数的来源，类氢离子波函数的图形及其物理意义。

掌握多电子原子的原子轨道能级等，推导原子基态光谱项。

教学重点：1.类氢离子波函数量子数的物理意义。

2.掌握多电子原子的原子轨道能级、电离能的求解。

3.推导等价、非等价电子的原子光谱项，掌握基态原子谱项的快速推算法。

第一节单电子原子的薛定谔方程及其解引言：前面介绍了量子力学的概念，建立了量子力学的基础，下面我们要讨论原子结构的核心问题，即原子中电子的运动状态，其中最简单的体系就是原子核外只有一个电子的体系，也叫单电子原子结构，如氢原子和类氢离子（H ，Li 2+，He +，Be 3+……）。

一．建立单电子原子的Schrodinger 方程r Ze mh M h H e N 022********ˆπεππ-∇-∇-= 假设在研究电子运动时核固定不动，r Ze mh H 0222248ˆπεπ-∇-= 为了解题方便通常将x,y ,z 变量变换成极坐标变量r ，θ，φ由图可得如下关系：⎪⎭⎪⎬⎫⋅=⋅⋅=⋅⋅=θφθφθcos sin sin cos sin r z r y r x得极坐标形式的Schrodinger 方程：048sin 1sin sin 110222222222=⎪⎪⎭⎫⎝⎛++∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂ψπεπφψθθψθθθψr Ze E h m r r r r r r二、单电子Schrodinger 方程的一般解。

1. 变数分离法把含三个变量的微分方程化为三个各含一个变量的常微分方程来求解。

令()()r R r =φθψ,,Θ（θ）Φ（φ）()()φθ,,Y r R =代入薛定鄂方程，经过数学变换得三个方程：R(r)方程 ()()k E r hm r h mZe r r R r r r R =++⎪⎭⎫ ⎝⎛∂∂∂∂⋅2222022821πεπ Θ方程22sin )(sin )(sin m k =+⎪⎭⎫ ⎝⎛∂Θ∂⋅∂∂⋅Θθθθθθθθ Φ方程222)()(1m =∂Φ∂⋅Φ-φφφ 2. Φ方程的解Φ方程整理得：0222=Φ+Φm a a φ这是一个常系数2阶齐次线性方程，它的特征方程为022=+m p i m p ±=微分方程的两个特解为φim Ae m =Φ m m ±= A 由归一化求得： π21=A ∴φπim e m 21=Φ 这是解的复数形式，由于Φ是循环坐标所以()()πφφ2+Φ=Φm m 于是πφπφφ2)2(im im im im e e e e ⋅==+ 即12=πim e由欧拉公式12sin 2cos 2=+=m i m e im πππ故m 的取值必须为： 2,1,0±±=m 即取值是量子化的称为磁量子数。

大学无机化学第二章(原子结构)试题及答案

第五章原子结构和元素周期表本章总目标：1：了解核外电子运动的特殊性，会看波函数和电子云的图形2：能够运用轨道填充顺序图，按照核外电子排布原理，写出若干元素的电子构型。

3：掌握各类元素电子构型的特征4：了解电离势，电负性等概念的意义和它们与原子结构的关系。

各小节目标：第一节：近代原子结构理论的确立学会讨论氢原子的玻尔行星模型213.6E eV n =。

第二节：微观粒子运动的特殊性1：掌握微观粒子具有波粒二象性（h h P mv λ==）。

2：学习运用不确定原理（2h x P mπ∆∙∆≥）。

第三节：核外电子运动状态的描述1：初步理解量子力学对核外电子运动状态的描述方法——处于定态的核外电子在核外空间的概率密度分布（即电子云）。

2：掌握描述核外电子的运动状态——能层、能级、轨道和自旋以及4个量子数。

3：掌握核外电子可能状态数的推算。

第四节：核外电子的排布1：了解影响轨道能量的因素及多电子原子的能级图。

2;掌握核外电子排布的三个原则：○1能量最低原则——多电子原子在基态时，核外电子尽可能分布到能量最低的院子轨道。

○2Pauli 原则——在同一原子中没有四个量子数完全相同的电子，或者说是在同一个原子中没有运动状态完全相同的电子。

○3Hund 原则——电子分布到能量简并的原子轨道时，优先以自旋相同的方式分别占据不同的轨道。

3:学会利用电子排布的三原则进行第五节：元素周期表认识元素的周期、元素的族和元素的分区，会看元素周期表。

第六节：元素基本性质的周期性掌握元素基本性质的四个概念及周期性变化1：原子半径——○1从左向右，随着核电荷的增加，原子核对外层电子的吸引力也增加，使原子半径逐渐减小；○2随着核外电子数的增加，电子间的相互斥力也增强，使得原子半径增加。

但是，由于增加的电子不足以完全屏蔽增加的核电荷，因此从左向右有效核电荷逐渐增加，原子半径逐渐减小。

2：电离能——从左向右随着核电荷数的增多和原子半径的减小，原子核对外层电子的引力增大，电离能呈递增趋势。

print 第2章.原子的结构和性质

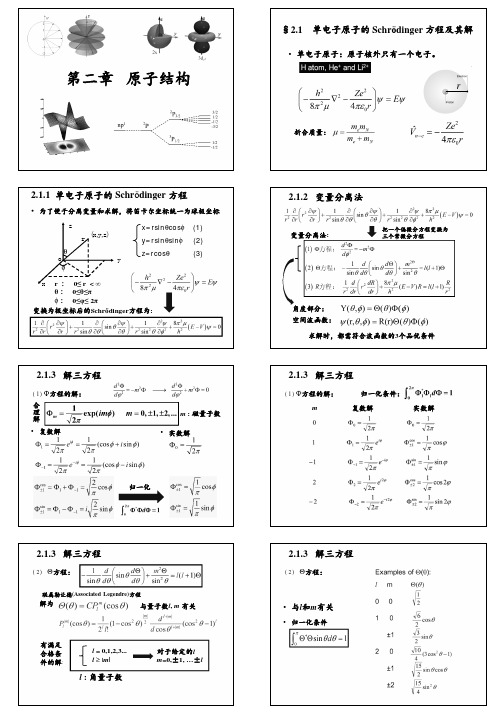
三个量子数n, l和m具有如下的关系
• 主量子数
n = 1, 2, 3, …, n;
• 角量子数
l = 0, 1, 2, …, n-1;
• 磁量子数
m= 0, ±1, ±2,…, ±l
每套量子数n, l和m决定一个波函数ψnlm的形式，即决定了单电子原子体系的一种状态，因此简称为原子轨
道(AO, Atomic Orbital)。
• 两个径向节面，
3s
即n-l-1=2，所以n=3
§2.4 多电子原子的结构
2.4.1 多电子原子的Schrödinger方程
• 原子单位 atomic unit， a.u.
定核近似
r
2.4.1 多电子原子的Schrödinger方程
两个电子的电子与原子核相互两电子之间相互作动能算符作用的势能算符用的势能算符
能级交错
2.4.1 多电子原子的Schrödinger方程
• 单电子波函数求解结果与类氢粒子波函数一样
n例：He原子基态
零级近似的计算结果：
实验值：
结论：零级近似的计算结果与实验值相差很大，说明电子间的相互作用不可忽略。
2.4.2 单电子原子轨道能
和单电子波函数 Ψi 相应的能量 Ei
2. 由屏蔽常数近似计算原子轨道能
l 单电子原子的能级公式：
单电子原子的能量E只与主量子数n有关
1. 主量子数
• 能量量子化 • 能量为负，电子离
核无穷远时作为位能的零点 • 简并度：在相同n 下，而l, m不同的 AO有n2个例如，n=2时，空间波函数有
2. 角量子数 l：决定电子的原子轨道角动量的大小。
• 原子只要有角动量也就有磁距

原子结构和结构示意

化学键合
相同或不同元素的原子通过电子交换和共享形成化学键合，形成分子或晶体结构。
02 原子结构
原子核
原子核位于原子的中心，由质子和中子组成，具有正电荷。
原子核通过核力与核外电子相互作用，维持着原子的整体结构。
原子核的质量约占整个原子的99.9%，但体积仅占整个原子的极小部分。
等于两能级间的能量差。
辐射与吸收
电子跃迁过程中可能伴随光子的发射或吸收，光子的能量与能级
差相等。
光的发射和吸收
发射光谱
原子受激发后释放出特定波长的光，形成发射光谱。
吸收光谱
原子吸收特定波长的光，产生能级跃迁，形成吸收光谱。
特征光谱
每种原子都有独特的发射和吸收光谱，可用于元素鉴定和分析。
05 原子光谱
当电子从低能级向高能级跃迁时，需要吸收能量。
电子云模型
电子在原子核周围的空间内随机分布，而不是沿轨道运动。电子云密度高的区域表示电子在该处出现的概率较大。
电子云模型能够更好地解释原子的化学性质和电子行为。
04 原子能级和跃迁
能级和能量
能级
原子中的电子在不同的能级上运动，能级由低到高，能量逐渐增
加。
能量
电子在各能级上具有确定的能量值，能量单位为电子伏特（eV）。
基态与激发态
原子处于最低能级的状态称为基态，受外界能量激发跃迁至较高能级的状态称为激发态。
电子跃迁
跃迁类型
电子在不同能级间跃迁有自发跃迁、受激跃迁和诱导跃迁等类型。
跃迁条件
电子跃迁需满足能量守恒和动量守恒，即吸收或释放的能量必须
THANKS FOR WATCHING
感谢您的观看

简述原子的结构

简述原子的结构
原子是最基本的物质构成单位，它们是由一系列原子核以及原子核周围的电子构成的。

原子结构是由原子核和电子组成的，这两部分都有一定的结构和特性。

原子核是一个稳定的复杂物质，它由质子和中子组成，中子相对稳定，质子是质量最小的质子，它有正负电荷；原子核的外围有若干电子，它们是负电荷的微粒，它们围绕原子核的轨道运动，形成电子云。

这些电子的运动形式不同，形成不同的结构。

原子核是一个非常小的球形物质，它的直径大约是由原子内部质子和中子数目决定的，约为10-15厘米；原子核外围电子分布在轨道上，我们称之为电子能级，电子能级由电子能量决定，电子能量大的在轨道外，电子能量小的在轨道内。

原子的结构受到电子的分布规律所限制，电子的轨道可分为能级，每个能级有不同的电子数，每一个能等级的轨道中的电子有一定的动量、角动量和能量，这就是原子的结构。

原子的能级由电子能量决定，分为能量级和发射级，能量级由电子能量决定，电子越高，能量级越高，能量级越低，发射越高，当电子能量超出原子核能量时，电子便会从原子核中脱离，从而发出光。

原子结构还受到外力的影响，如磁场、电场和重力场，会导致原子能级发生变化，改变原子结构。

总之，原子是由原子核、电子和外力构成的，它的结构的特征是由质子、中子、电子的数量以及电子的能量级来决定的，外力也会影响原子的结构。

九年级化学原子结构

在一定范围内，质子数和中子数的比例可以影响原子核的稳定性，过多的质子或中子可能导致原子核不稳定。
电子云与电子排布
03
电子云的概念
电子云是用来描述电子在原子核外空间运动所形成的概率分布的
图示。
电子云表示电子在原子核外某一区域出现的概率，而非电子的实
际运动轨迹。
电子云图可以显示电子在原子核外空间的分布情况，有助于理解
分子的极性与溶解性
分子的极性
根据分子中正负电荷中心是否重合，可以将分子分为极性和非极性。极性分子具有偏向的电负性差异，而非极性分子则没有。
溶解性
分子的溶解性受到分子极性的影响，极性分子通常更容易在极性溶剂中溶解，而非极性分子则更容易在非极性溶剂中溶解。
原子结构的应用
06
元素周期表的发现与应用
原子序数等于质子数，决定了元素的种类。
原子的内部结构
原子核由质子和中子组成，质子带正电荷，中子不带电。
电子围绕原子核旋转，带负电荷，与质子电荷数相等但电性相反。
原子核和电子之间的相互作用力是电磁力，由于电子带负电荷，它们被原子核的强大正电荷所吸引。
原子的电子排布
01
02
03
04
电子在原子中的排布遵循泡利不相容原理、能量最低原理和
能量值。
泡利不相容原理
奥地利物理学家泡利提出，在任何一个原子中，不可能存在两个或更多的电子处于完全相同的量子态。
洪特规则
德国物理学家洪特提出，在激发态原子中，电子优先以单电子形式占据各能级，且自旋方向相同。
化学键与分子结构
05
共价键的形成与类型
共价键的形成
原子间通过共享电子来形成共价键，电子云重叠使得两原子相互吸引。

2第二章原子的结构和性质

2.1 单电子原子的Schrödinger 方程及其解
• -1-单电子原子的 Schrödinger 方程的建立
写出势能和动能算符，得出氢原子和类氢离子的Schrödinger 方程：
2 Ze ˆ V 4 0 r
2 2 2 2 2 ˆ H , 2 2 2 2 8 x y z
或者说角动量的绝对值有确定值
h M l l 1 2
角量子数 l 决定电子的原子轨道角动量的大小。 l 的取值 0，1，2，3……n－1 对应着 s, p, d, f…... (亚层)
l 决定了ψ 的角度函数的形状。
角量子数 l
e 原子的角动量和原子的磁矩有关. 磁矩与角动量的关系 2m M e
2.2 量子数的物理意义
对于Schrö dinger方程
ˆ E H
n
ˆ 作用后都等于一个常数 En乘解此方程得出的每一个 n 正好被 H 以n , 即n代表的状态具有能量 E .
单电子原子的能级公式为
e4 Z 2 E n 8 2h 2 n 2 0
主量子数 n, n 为1，2，3，4 等正整数。
r : 径向坐标, 决定了球面的大小 θ: 角坐标, 由z轴沿球面延伸至r 的弧线所表示的角度. φ: 角坐标, 由r沿球面平行xy面延伸至 xz面的弧线所表示的角度.
x r sin cosφ r x2 y2 z2 y r sin sinφ tan y / x z r cos 2 2 2 1/ 2 cos z /( x y z )
氢原子能级：
4
E1 , E1 4 , E1 9 ,
氢原子能级图
En(eV) 0
-0.54 -0.85 -1.51

第二章原子结构与性质

③ 电子填入顺序基态原子: ns →(n–2)f→ (n–1)d→ np 价电子电离: np →ns→(n1)d → (n–2)f 徐光宪：原子 (n+0.7l)，离子(n+0.4l) 越大能级越高
28
ⅠA-ⅡA ⅠB-ⅡB
ⅢA-ⅧA ⅢB-Ⅷ
La系 Ac系
例:氩(Z=18)的电子组态 1s2 2s22p6 3s23p6 Fe (Z=26) Cu (Z=29)
轨道角动量与z轴的夹角
e m mμB 2. 磁矩在磁场方向的分量量子化: μz 2me
3. m决定磁场中轨道的空间方向，磁矩与外磁场的作用能
18
2.4 电子的自旋运动与泡利原理
一. 电子的自旋运动
19
●自旋角动量量子化
Ls s(s 1)
电子的自旋量子数 s ≡1/2
26
四. 原子核外电子的排布规则 1. Pauli不相容原理 2. 能量最低原理 3. Hund规则：简并轨道上全充满、半充满或全空较稳定 4. 原子的构造: ① 电子组态：确定每个电子的n,l ② 电子层：ns2到ns2np6构成一个能级组 4(N) 3(M) 2(L) 1 2 0 1 2 3 0 1 0 2s 2p 3s 3p 3d 4s 4p 4d 4f 0 0 0 0 0 0 0 0 0 ±1 ±1 ±1 ±1 ±1 ±1 ±2 ±2 ±2 ±3 亚层轨道数 1 1 3 5 7 3 5 1 3 1 42 12 22 32 电子层轨道数 27 第n能层有n2个“轨道”，可以容纳2n2个电子电子层 1(K) 角量子数l 0 电子亚层符号 1s 0 磁量子数m 可能取值
7
氢原子或类氢离子的轨道波函数举例轨道 n
1s 2s

基础化学-第二章物质结构

流；
③γ-射线：不带电的光子流，穿透能力很强。
• 2.放射性同位素的应用：
①示踪原子，例如125I、32P、60Co等。
②微量物质的含量测定。
1.某离子X3-质量数是75，中子数是42，那么它的核外电子数是（ C ）
A. 30
B. 33 C. 36
D. 39
2.同位素间不相等的是（ B ） A. 质子数 B.中子数 C. 电子数 D. 核电荷数
还原剂具有失去电子的性质，即还原性。物质失去电子能力越强，其还原性就越强。
• 卤素单质都是氧化剂，均具有氧化性，其氧化性的强弱顺序见下： F→Cl→Br→I（强→弱），得电子的能力逐渐减弱。
• 碱金属都是还原剂，具有还原性，其还原性强弱顺序是： Cs→Rb→K→Na→Li（强→弱），失电子的能力逐渐减弱。
的电子层结构，从而成为正价离子。 3.非金属元素
①其原子最外层电子数目一般多于4个。 ②化学反应中，易得到电子而达到稳定的电子层结构，从而成为负价离子。
e
Na
Na +
+11 2 8 1
+11 2 8
e Cl
+17 2 8 7
Cl -
+17 2 8 8
1. 某原子最外层电子排布是3S23P4，这种原子的核外电子数是（ C ）
Cu + H2O
得到 2 e ,被还原,化合价降低
当物质跟氧化合时，总是失去电子被氧化，其化合价升高；当含氧物质失去氧时，总是得到电子被还原，化合价降低。
• 结论：物质失去电子，化合价升高的反应，是
氧化反应；物质得到电子，化合价下降的反应，是还原反应。
凡是有电子得失，化合价变化的反应，叫做氧化还原反应。

第二章原子结构与性质

第二章原子结构与性质1. 填空题(1) He+离子的薛定谔方程为。

(2) 用分离变量法解类氢原子薛定谔方程采用的主要近似是。

(3) 已知Cu 的原子序数为29，写出核外电子排布。

(4) He+的2s电子能量比He(1s12s1)中2s电子能量。

(填高或低)(5) 钠的电子组态为1s22s22p63s1，其光谱项为，光谱支项为。

(6) 写出d2可能的总轨道角量子数。

(7) 离核越近径向函数R1s(r)其值，离核越近径向分布函数D=r2R1s2(r) 。

(8) 氢原子态函数Ψ(r,θ,φ) 可以写作R(r),Θ(θ), (φ) 三个函数的乘积，它们由量子数; ; 来规定。

(9) 如一原子的轨道磁量子数m=0, 主量子数n≤2,则可能的轨道为。

(10) 在一定电子组态下，描写多电子原子状态的量子数是。

(11) 两个氢原子，第一个的电子处于主量子数n=1的轨道，第二个处于n=4的轨道，原子势能较低的是,原子电离能较低的是。

(12) 多电子原子中的一个光谱项支项3D2，据此给出原子的总轨道角动量量子数，原子的总自旋角动量量子数，原子总角动量量子数，在磁场中分裂出个塞曼能级。

(13) 氢原子的态函数Ψ3,2,1，其轨道能量为，轨道角动量，轨道角动量在磁场方向的分量为。

(14) 氢原子3d电子轨道角动量沿磁场方向分量的可能值为。

(15) 对于氢原子及类氢离子的1s电子来说，出现在半径为r，厚度为d r的球壳内，各个方向的概率密度（填相等或不相等），对于2p x电子（填相等或不相等）。

(16) 同电子组态光谱项稳定性比较：3P1D; 3P21P02. 选择题(1) 关于四个量子数n, l, m, m s,下列叙述正确的是: ·············································· ( )A、由实验测定；B、解类氢原子薛定谔方程得到的；C、解类氢原子薛定谔方程得到的n, l, m, 由电子自旋假设引入m sD、由自旋假设引入的(2) 决定多电子原子轨道的能量是: ···································································( )A、nB、n, l, ZC、n+0.4lD、n, m(3) 用来表示核外某电子运动状态的下列各组量子数(n,l,m,m s)合理的是: ··················· ( )A、2, 1, 0, 0B、0, 0, 0, 12C、3, 1, 2,12D、2, 1, -1, -12(4) 氢原子3d状态轨道角动量沿磁场方向的分量最大值是:····································( )A、5B、4C、3D、2(5) 如下表达式为径向分布函数的是: ·······························································( )A、R2B、R2drC、r2R2D、r2R2d r(6) R n,l(r)-r图中，节点数为·············································································· ( )A、n-1个B、n-l-1个C、n-l+1个D、n-l-2个(7) 原子的电子云角度分布图应该用如下哪一个函数对参数作图······························ ( )A、|Y l,m(θ,φ)|2B、R n,l(r)C、Y l,m(θ,φ)D、|R n,l(r)Y l,m(θ,φ)|2(8) 对于单电子原子，在无外场时，能量相同的轨道数是: ······································· ( )A、n2B、2(l+1)C、n-1D、n-l-1(9) 已知Ca的第一激发态的电子组态为[Ar]3d14s1, 其光谱支项有如下四种，指出能量最低的光谱项：A、1D2B、3D3C、3D2D、3D1(10) 求解氢原子薛定谔方程，我们常采用下列哪些近似？······································( )①核固定②变数分离③以电子质量代替折合质量④球极坐标A、①③B、①②C、①④D、①②③④(11) 基态铬原子(原子序数是24)的核外电子排布为: ············································( )A、[Ar]3d44s2B、[Ar]3d54s1C、[Ar]3d64s0D、4s24p4(12) 某多电子原子中电子具有下列量子数(n,l,m,m s)，其中轨道角动量最大的是: ·······( )A、2,1,-1,12B、2,0,0,-12C、3,1,1,-12D、3,2,-1,12(13)描述原子轨道3d z2的一组量子数是: ····························································· ( )A、2,1,0B、3,2,0C、3,1,0D、3,2,1(14)3d z2轨道的角动量大小为: ·········································································( )A、B、 C、0 D(15) He+中一个电子处于径向分布图中总节面为3的d态，则该电子的能量应为：·······( )A、1E1B、19E1C、14E1D、116E1(16) 氢原子中处于Ψ2pz状态，其角动量在下列哪一个轴上的投影有确定值?···············( )A、x轴B、y轴C、z轴D、x轴和y轴(17) 对于类氢原子的基态, 下列结论不正确的是: ·················································( )A、E相同B、M z相同C、简并度相同D、l相同(18) Be3+ 的一个电子所处的轨道，能量等于氢原子1s轨道能，该轨道可能是: ······( )A、1sB、2sC、4dD、3p(19) 4d 的径向分布函数图的极大值数与节面数分别是: ··········································( )A、2,1B、2, 3C、4,2D、1,3(20) 下列是关于s轨道波函数ψ的认识，正确的是：················································( )A、ψ的值随着r的增大而减小B、ψ的节面数为nC、当r趋于无穷大时，ψ趋于0D、ψ2s-r曲线在r=2a0处达到最低点(21) 对氢原子和类氢离子的量子数l，下列叙述不正确的是:·····································( )A、l的取值规定了m的取值范围B、它的取值与体系能量大小有关C、它的最大可能取值由解R方程决定D、它的取值决定了M=(22) 对于氢原子和类氢离子的径向分布D(r)-r图，下列叙述错误的是:························( )A、径向峰数与节面数都与n,l有关B、l相同，n愈大，则最高峰离核愈远C、核周围电子出现的概率为0D、最高峰所对应的r处，电子出现的概率密度最大(23) 电子在核附近有非零概率密度的原子轨道是：··············································( )A、ψ3pB、ψ4dC、ψ2pD、ψ2s(24) 电子云图是下列哪一种函数的图形？··························································( )A、D(r)B、ψ2(r,θ,φ)C、R2(r)D、ψ(r,θ,φ)(25) 已知类氢波函数ψ2px的各种图形，推测ψ3px图形，下列说法错误的是:····················( )A、角度部分的图形相同B、电子云图相同C、径向分布函数图不同D、界面图不同(26) He+离子的3d和4s的能级次序为：······························································( )A、3d >4sB、3d < 4sC、3d = 4sD、存在交叉(27) 电子组态d9s1的光谱项是: ········································································ ( )A、3F，1DB、1D，3DC、2P，3PD、1S，2P(28) Fe的电子组态为[Ar]3d64s2，其能量最低的光谱支项是：····································( )A、5D4B、3P2C、5D0D、1S0(29) Cu的基谱项为，与其基谱项不同的原子是：····································( )A、AgB、AuC、ZnD、K(30) 已知Rh的基谱项为4F9/2，则它的价电子组态是：··········································( )A、s1d8B、s0d9C、s2d8D、s0d103. 简答题(1) 请用光谱项语言叙述洪特规则。

《原子的结构》

原子核内质子所带电荷与核外电子的电荷数相等，电性相反，所以，原子不显电性。
新知学习经典例题知能训练
原子中核电荷数 = 质子数 = 核外电子数=原子序数
原子核所带正电荷数叫做核电荷数。
新知学习
二、原子核外电子的排布
核外电子分层排布规律
电子层：
离原子核：电子能量：
1 2 3 4 5 6 7
03
点击添加标题
02
点击添加标题
在此录入上述图表的综合描述说明，在此录入上述图表的综合描述说明。
在此录入上述图表的综合描述说明，在此录入上述图表的综合描述说明，在此录入上述图表的综合描述说明。
01
9
中子原子核原子核外电子质子
不带电
每个质子带一个单位正电荷
电荷
每个电子带一个单位负
了解离子定义和氯化钠形成过程
4
第二章新知传授
一、原子的构成
同学们看，这是什么图片？
原子弹爆炸图片
6
7
一、原子的构成
原子由原子核和核外电子组成，原子核由质子和中子组成
新知学习
原子结构
点击添加标题
在此录入上述图表的综合描述说明，在此录入上述图表的综合描述说明，在此录入上述图表的综合描述说明。
近低远高
新知学习
表示原子核以及核内的质子数
+8
2
6
表示电子层以及电子层上的电子数
氧原子的结构示意图
原子的核外电子最少的只有一层，最多的有七层，最外层电子数不超过8 个（只有一层的，电子不超过2个）。
新知学习
1-18号原子的结构示意图
思考：通过这些原子结构示意图，你能总结出哪些规律？

第二章 原子结构

结构化学第二章

普通化学：第二章-原子结构、分子结构与化学键4

无机化学2原子结构与元素周期律

原子的结构完整版PPT课件

选修3-5 第二章 第1讲 原子结构 氢原子光谱

原子结构讲解

第二章 原子的结构和性质2.3-2.4

结构化学讲义教案2原子结构和性质

大学无机化学第二章(原子结构)试题及答案

print 第2章.原子的结构和性质

原子结构和结构示意

简述原子的结构

九年级化学原子结构

2第二章 原子的结构和性质

第二章 原子结构与性质

基础化学-第二章物质结构

第二章 原子结构与性质

《原子的结构》

第二章原子结构

选修3-5 第二章第1讲原子结构氢原子光谱

第二章原子的结构和性质2.3-2.4

2第二章原子的结构和性质

第二章原子结构与性质

第二章原子结构与性质