ECC算法入门
ECC算法介绍

ECC (Elliptic Curves Cryptography )加密算法是一种公钥加密算法,与主流的RSA 算法相比,ECC 算法可以使用较短的密钥达到相同的安全程度。
近年来,人们对ECC 的认识已经不再处于研究阶段,开始逐步进入实际应用,如国家密码管理局颁布的SM2算法就是基于ECC 算法的。
下面我们来认识一下ECC 的工作原理。
椭圆曲线定义在引入椭圆曲线之前,不得不提到一种新的坐标系-------射影平面坐标系,它是对笛卡尔直角坐标系的扩展,增加了无穷远点的概念。
在此坐标系下,两条平行的直线是有交点的,而交点就是无穷远点。
两者的变换关系为:笛卡尔坐标系中的点a (x,y ),令x=X/Z ,y=Y/Z ,则射影平面坐标系下的点a 的坐标为(X,Y,Z),如点(2,3)就转换为(2Z,3Z,Z )。
椭圆曲线定义:一条椭圆曲线在射影平面上满足方程:Y 2Z+a 1XYZ+a 3YZ 2=X 3+a 2X 2Z+a 4XZ 2+a 6Z 3的所有点的集合,且曲线上每个点都是非奇异的。
该方程有名维尔维斯特拉斯方程,椭圆曲线的形状不是椭圆,只是因为其描述的方程类似于计算一个椭圆周长的方程。
转换到笛卡尔坐标系下的方程为:y 2+a 1xy+a 3y = x 3+a 2x 2+a 4x+a 6 加法法则运算法则:任意取椭圆曲线上两点P 、Q (若P 、Q 两点重合,则做P 点的切线)做直线交于椭圆曲线的另一点R’,过R’做y 轴的平行线交于R 。
我们规定P+Q=R 。
(如图)●此处+不是简单的实数相加,是抽象出来的 ●O∞+P=P ,O∞为零元 ● 曲线上三个点A,B,C 处于一条直线上,则A+B+C=O∞下面,我们利用P 、Q 点的坐标(x 1,y 1),(x 2,y 2),求出R=P+Q 的坐标(x 4,y 4)。
P,Q,R'共线,设为y=kx+b ,若P≠Q ,k=(y 1-y 2)/(x 1-x 2)若P=Q ,k=(3x 2+2a 2x+a 4 -a 1y) /(2y+a 1x+a 3)解方程组得到:x 4=k 2+ka 1-a 2-x 1-x 2;y 4=k(x 1-x 4)-y 1-a 1x 4-a 3;密码学中的椭圆曲线定义在有限域Fp 中定义一个椭圆曲线,常用y 2=x 3+ax+b1.Fp 中只有p 个元素,p 为素数 2.Fp 中,a+b≡c (mod p),a×b≡c (mod p),a/b≡c (mod p) 3.4a 3+27b 2≠0 (mod p) a ,b 是小于p 的非负整数 4. x ,y 属于0到p-1间的证书,曲线标记为Ep (a ,b ) 阶:椭圆曲线上一点P ,存在正整数n ,使得nP=O∞,则n 为P 的阶,若n 不存在,则P 是无限阶的,有限域上定义的椭圆曲线上所有点的阶都存在。
ecc算法c语言实现

ecc算法c语言实现一、介绍ECC(Elliptic Curve Cryptography)椭圆曲线加密算法是一种公钥密码学,它利用椭圆曲线上的数学原理,实现了比传统RSA算法更高的安全性和更小的密钥长度。
ECC算法已经被广泛应用于移动设备、物联网等领域。
二、椭圆曲线基础知识1. 椭圆曲线方程椭圆曲线可以用如下的方程表示:y² = x³ + ax + b其中a和b是常数,x和y是变量。
这个方程描述了一个平面上的点集合,这个点集合形成了一个封闭的曲线。
2. 椭圆曲线上的运算在椭圆曲线上有两种运算:加法和乘法。
加法:两个不同点P(x1, y1)和Q(x2, y2)相加得到R(x3, y3),其中x3 = λ² - x1 - x2,y3 = λ(x1 - x3) - y1,λ = (y2 - y1) / (x2 - x1)乘法:将点P与一个整数k相乘得到另一个点Q,即Q = kP。
三、ECC算法实现步骤1. 寻找合适的椭圆曲线选择一个合适的椭圆曲线是ECC算法的第一步。
通常情况下,我们会选择一条已经被广泛使用并且被认为是安全的椭圆曲线。
2. 生成公私钥对在ECC算法中,公钥由椭圆曲线上的一个点P和一个整数n组成,私钥由一个整数d组成。
其中n是P点的阶(即nP = O),d是一个随机数。
3. 加密和解密加密:将明文M转换为椭圆曲线上的点P,然后选择一个随机数k,并计算C1 = kP和C2 = kQ + M,其中Q是接收者的公钥。
最终加密结果为(C1, C2)。
解密:接收到加密数据(C1, C2)后,用私钥d计算出Q = dP,并将C1乘以d得到C1' = dC1。
然后用C1'减去C2得到明文M。
四、ECC算法C语言实现以下是ECC算法在C语言中的实现代码:#include <stdio.h>#include <stdlib.h>#include <string.h>#include <openssl/ec.h>#include <openssl/ecdsa.h>#include <openssl/obj_mac.h>int main(){// 生成公私钥对EC_KEY *key;key = EC_KEY_new_by_curve_name(NID_secp256k1);EC_KEY_generate_key(key);const EC_GROUP *group = EC_KEY_get0_group(key);const BIGNUM *priv_key = EC_KEY_get0_private_key(key); const EC_POINT *pub_key = EC_KEY_get0_public_key(key);// 显示公私钥char *priv_hex = BN_bn2hex(priv_key);printf("Private key: %s\n", priv_hex);char *pub_hex = EC_POINT_point2hex(group, pub_key, POINT_CONVERSION_UNCOMPRESSED, NULL);printf("Public key: %s\n", pub_hex);// 加密和解密unsigned char plaintext[] = "Hello world";size_t plaintext_len = strlen(plaintext);// 加密unsigned char ciphertext[128];size_t ciphertext_len;ECDSA_SIG *sig;do {sig = ECDSA_do_sign(plaintext, plaintext_len, key); if (sig == NULL) {printf("Error signing message\n");break;}int r_len = BN_num_bytes(sig->r);int s_len = BN_num_bytes(sig->s);if (r_len + s_len > 127) {printf("Error: signature too long\n");break;}memset(ciphertext, 0, sizeof(ciphertext));memcpy(ciphertext, sig->r, r_len);memcpy(ciphertext + r_len, sig->s, s_len);ciphertext_len = r_len + s_len;printf("Encrypted data: ");for (int i=0; i<ciphertext_len; i++) {printf("%02x", ciphertext[i]);}printf("\n");// 解密sig->r = BN_bin2bn(ciphertext, r_len, sig->r);sig->s = BN_bin2bn(ciphertext + r_len, s_len, sig->s);int verify_result = ECDSA_do_verify(plaintext, plaintext_len, sig, key);if (verify_result == 1) {printf("Decrypted data: %s\n", plaintext);} else {printf("Error decrypting data\n");}} while(0);// 释放资源EC_KEY_free(key);free(priv_hex);free(pub_hex);return 0;}以上代码使用了OpenSSL库中的ECDSA函数来实现ECC算法。
ecc校验计算说明

ecc校验计算说明
好的,下面为你提供ECC校验计算的详细说明:
ECC(Error Correcting Code)校验是在传统奇偶检验的基础上发展而来的,主要是利用数据块的行、列奇偶校验信息生成ECC码,可以检测出给定数据块是否失真,但具有对该数据块辑位数出错、校验码冗长、不能纠错的局限性。
ECC算法思想为:ECC校验每256B(Byte)数据为一组进行操作,把256B数据看成256×8的矩阵,矩阵的每个元素表示一个比特(1bit)位。
矩阵进行编码后分别生成6bit的列校验信息和16bit的行校验信息。
ECC纠错算法检测和纠正错误的原理为:每向闪存写入256B数据时,生成22bit校验码,成为读校验码。
然后将写校验码与读校验码按位异或操作。
结果会出现以下3种情况:- 全为“0”,则数据不存在错误;
- 存在11bit为“1”,则存在一个比特错误,且可以纠正,因为在22bit数据中P和P'都是相互对立的,假如发生翻转,对写入产生的ECC和读出产生的ECC相异或,必然其中一个为1另一个为0,所以22bit中有11bit为1表示有1bit错误;
- 只存在1bit为1,则生成的校验码出错,数据本身无错。
当出现第二种情况时,改错误比特在数据组中的字节偏移量为P1024、P521、P256、P128、P64、P32、P16、P8。
错误比特所处的字节中的位偏移量为P4、P2、P1。
因此,根据字节的偏移量和字节中的位偏移量就可以确定数据中发生的翻转位,然后对其进行纠正。
ecc加密输入参数

ecc加密输入参数
ECC(椭圆曲线加密)是一种公钥加密算法,它使用椭圆曲线上的点来进行加密和解密操作。
在ECC加密中,输入参数通常包括以下几个方面:
1. 椭圆曲线参数,椭圆曲线加密算法的安全性和效率取决于所选择的椭圆曲线的参数。
这些参数包括椭圆曲线的方程、基点、模数等。
基点的选择对于密钥的生成和加密过程至关重要。
2. 公钥和私钥,在ECC加密中,公钥和私钥是必不可少的输入参数。
公钥用于加密数据,私钥用于解密数据。
它们是由椭圆曲线上的点和一些其他参数计算而来的。
3. 待加密的数据,作为输入参数的一部分,待加密的数据是需要进行加密的原始信息。
这可以是文本、数字、文件等各种形式的数据。
4. 加密算法的参数,除了椭圆曲线参数和密钥之外,还可能涉及到加密算法的一些其他参数,例如填充方式、哈希函数等。
这些参数会影响到加密过程的安全性和性能。
总的来说,ECC加密的输入参数包括了椭圆曲线参数、公钥和私钥、待加密的数据以及加密算法的相关参数。
这些参数共同作用于ECC加密算法,确保了加密过程的安全性和有效性。
ECC算法和加密应用大全

ECC算法和加密应用大全
一、ECC算法原理
ECC算法是基于椭圆曲线上的加法运算和数乘运算的。
其核心思想是利用椭圆曲线上的离散对数难题,即对于给定的椭圆曲线上的点P和整数k,求解kP的问题非常困难。
因此,ECC算法能够实现安全的公钥加密和密钥交换。
1.选择合适的椭圆曲线参数(椭圆曲线方程、基点、阶),通常使用的是特定标准的曲线参数。
2.选择一个私钥d,计算公钥Q=dG,其中G是椭圆曲线上的基点。
3.将公钥Q作为加密密钥或者签名验证密钥的一部分。
4.对于加密过程,选择一个随机数r,计算椭圆曲线上的点R=rG,再将明文消息与R进行一次异或运算,并进行加密操作。
5.对于解密过程,利用私钥d和加密的椭圆曲线上的点R,计算出明文消息。
1.电子邮件加密
2.虚拟私人网络(VPN)
3.数字签名
4.移动通信安全
5.物联网安全
6.金融安全
7.SSL/TLS安全通信
8.数字版权保护
9.云计算安全
10.区块链安全
总结:
ECC算法作为一种新兴的公钥加密算法,具有许多优势,包括较短的
密钥长度、高效的计算性能和较好的安全性。
它在各个领域的应用也日益
增多,包括电子邮件加密、VPN、数字签名、移动通信安全、物联网安全、金融安全、SSL/TLS安全通信、数字版权保护、云计算安全和区块链安全等。
随着对安全性要求的不断提高,ECC算法将在未来得到更广泛的应用。
ECC算法的详细说明

ECC算法的详细说明ECC(椭圆曲线密码学)是一种基于椭圆曲线数学的非对称加密算法。
它是公钥密码学的一部分,可以用于加密、数字签名、密钥交换等过程。
相比于其他非对称加密算法如RSA,ECC具有相同的安全强度下更小的密钥长度,对于资源受限的设备和网络通信而言具有更好的效率。
在ECC算法中,一个关键的概念是基点(base point),它是椭圆曲线上的一个点,用于生成其他点。
基点的选取是公开的,通常是一个事先确定好的固定点。
假设基点为G,可以通过连续重复点加法运算来获得其他点。
1.点加法:给定两个点P和Q,可以通过特定的算法将它们相加得到另一个点R。
点加法的规则是通过直线相交于曲线上的点求得R。
如果直线与曲线相交于两个点P和Q,那么R就是通过将P、Q关于x轴对称后的结果。
2.点倍乘:给定一个点P和一个整数n,可以通过连续重复的点加法运算将P倍乘n次得到另一个点Q。
点倍乘的规则是将点加法运算连续进行n次。
这个操作的结果是将点P相加n次得到Q。
3.密钥生成:ECC算法中的公钥由基点G和私钥d生成,公钥为Q=d*G。
私钥是一个随机生成的整数,范围在1到曲线上的一个恰当值之间。
通过点倍乘运算,可以将基点倍乘私钥得到公钥。
4.加密和解密:ECC算法可以用于加密和解密消息。
在加密过程中,公钥被用于将消息消息转换为曲线上的一个点,然后再将x轴坐标作为加密后的消息。
在解密过程中,私钥被用于找到加密点的y轴坐标,从而确定解密后的消息。
5.数字签名:ECC算法可以用于生成和验证数字签名。
在签名过程中,私钥被用于对消息进行加密,生成签名。
在验证过程中,公钥被用于验证签名的有效性。
ECC的数字签名具有不可伪造性和消息的完整性。
ECC算法的安全性基于离散对数问题,即在有限域上找到离散对数的困难性。
离散对数问题是指已知一个数的多次幂求解指数的问题,即已知y=g^x,求解x。
这个问题在大整数域上是计算上的NP问题,通常很难通过暴力破解或数学方法进行求解。
ecc椭圆曲线算法

ecc椭圆曲线算法【实用版】目录1.椭圆曲线算法的概念与背景2.椭圆曲线算法的原理与过程3.椭圆曲线算法的优势与应用4.椭圆曲线算法的局限性与发展前景正文一、椭圆曲线算法的概念与背景椭圆曲线算法(Elliptic Curve Cryptography,简称 ECC)是一种基于椭圆曲线数学理论的公钥加密算法。
椭圆曲线研究可以追溯至十九世纪中叶,那时代数学家、几何代数学家以及数论专家都在研究这一领域。
椭圆曲线加密算法因其独特的数学特性,具备较高的安全性和效率,被广泛应用于网络通信、数据存储等领域。
二、椭圆曲线算法的原理与过程椭圆曲线加密算法的主要原理是基于椭圆曲线上的离散对数问题。
离散对数问题指的是在给定椭圆曲线上找到一个整数 k,使得 k*G=H,其中G 和 H 是椭圆曲线上的点。
由于椭圆曲线的特殊性质,这个问题比大数分解和离散对数问题更难解决,因此可以用来实现加密。
椭圆曲线加密的过程如下:1.选择一条椭圆曲线。
椭圆曲线的方程形式为:y^2 = x^3 + ax + b (其中 a、b 为常数),曲线的形状类似于一个椭圆。
2.选择一个基点 G。
基点是椭圆曲线上的一个已知的点,用于生成其他点。
3.生成密钥对。
每个用户生成一个私钥和公钥。
私钥是一个大整数 k (小于等于椭圆曲线的阶 n),公钥是基点 G 和私钥的乘积,表示为 K = k*G。
4.加密和解密。
在通信过程中,发送方将信息加密后发送给接收方。
接收方使用发送方的公钥 K 进行解密。
三、椭圆曲线算法的优势与应用1.安全性高。
椭圆曲线加密算法基于数学难题,其安全性较高,难以被攻破。
2.计算效率高。
相较于其他公钥加密算法如 RSA、离散对数算法等,椭圆曲线加密算法的计算量较小,可以更快地完成加密和解密任务。
3.应用广泛。
椭圆曲线加密算法广泛应用于网络通信、电子商务、数据存储等领域,如比特币等加密货币就是采用椭圆曲线加密算法进行加密。
四、椭圆曲线算法的局限性与发展前景虽然椭圆曲线加密算法具有较高的安全性和效率,但也存在一定的局限性。
ECC加密算法入门介绍

ECC加密算法入门介绍前言同RSA(Ron Rivest,Adi Shamir,Len Adleman三位天才的名字)一样,ECC(Elliptic Curves Cryptography,椭圆曲线密码编码学)也属于公开密钥算法。
目前,国内详细介绍ECC的公开文献并不多。
本文主要侧重理论,代码实现暂不涉及。
这就要求你要有一点数学功底。
最好你能理解RSA算法,对公开密钥算法有一个了解。
一、从平行线谈起。
平行线,永不相交。
没有人怀疑把:)不过到了近代这个结论遭到了质疑。
平行线会不会在很远很远的地方相交了?事实上没有人见到过。
所以“平行线,永不相交”只是假设(大家想想初中学习的平行公理,是没有证明的)。
既然可以假设平行线永不相交,也可以假设平行线在很远很远的地方相交了。
即平行线相交于无穷远点P∞(请大家闭上眼睛,想象一下那个无穷远点P∞,P∞是不是很虚幻,其实与其说数学锻炼人的抽象能力,还不如说是锻炼人的想象力)。
给个图帮助理解一下:直线上出现P∞点,所带来的好处是所有的直线都相交了,且只有一个交点。
这就把直线的平行与相交统一了。
为与无穷远点相区别把原来平面上的点叫做平常点。
以下是无穷远点的几个性质。
▲直线L上的无穷远点只能有一个。
(从定义可直接得出)▲平面上一组相互平行的直线有公共的无穷远点。
(从定义可直接得出)(否则L1和L2有公共的无穷远点P,▲平面上任何相交的两直线L1,L2有不同的无穷远点。
则L1和L2有两个交点A、P,故假设错误。
)▲平面上全体无穷远点构成一条无穷远直线。
(自己想象一下这条直线吧)▲平面上全体无穷远点与全体平常点构成射影平面。
二、射影平面坐标系射影平面坐标系是对普通平面直角坐标系(就是我们初中学到的那个笛卡儿平面直角坐标系)的扩展。
我们知道普通平面直角坐标系没有为无穷远点设计坐标,不能表示无穷远点。
为了表示无穷远点,产生了射影平面坐标系,当然射影平面坐标系同样能很好的表示旧有的平常点(数学也是“向下兼容”的)。
ecc校验计算

ecc校验计算ECC,即椭圆曲线密码学(Elliptic Curve Cryptography),是一种基于椭圆曲线数学的公钥密码学体系。
在现代密码学中,ECC被广泛应用于数字签名、密钥交换和加密算法等领域。
其中,ECC校验计算是一种用于确认信息的完整性和真实性的校验方法。
ECC校验计算的原理是基于椭圆曲线上的点运算和离散对数难题。
首先,发送方需要选择一个椭圆曲线作为密码学基础,然后确定一个基点G,并选择一个私钥d。
私钥是一个随机数,用于生成发送方的公钥Q。
公钥Q是基点G乘以私钥d的结果,即Q = d * G。
在信息传输过程中,发送方会将原始数据使用哈希函数进行处理,生成一个摘要值。
然后,发送方使用自己的私钥对摘要值进行签名,生成一个签名值。
签名值是由摘要值和私钥计算得出的,可以用来验证信息的完整性和真实性。
接收方在收到信息后,会使用发送方的公钥对签名值进行验证。
验证的过程是将签名值与原始数据一起使用公钥进行计算,得到一个新的摘要值。
如果新的摘要值与接收方使用哈希函数处理原始数据得到的摘要值相同,那么说明信息的完整性和真实性得到了确认。
ECC校验计算具有以下几个优点:1. 安全性高:ECC校验计算基于椭圆曲线数学,其安全性与传统的RSA算法相当,但使用的密钥长度更短。
相比较而言,ECC算法在保证安全性的同时,减少了计算和存储资源的消耗。
2. 效率高:相比传统的RSA算法,ECC校验计算所需要的计算量更小。
这对于资源有限的移动设备和物联网设备来说,是一个重要的优势。
3. 存储空间小:ECC校验计算所需要的密钥长度较短,可以大幅减少密钥的存储空间。
这对于一些存储容量有限的设备来说,是非常有利的。
4. 多种应用:ECC校验计算不仅可以用于数字签名,还可以用于密钥交换、加密算法等多种场景。
它的灵活性使得它成为了现代密码学中不可或缺的一部分。
总结一下,ECC校验计算是一种基于椭圆曲线数学的公钥密码学方法,用于确认信息的完整性和真实性。
ecc签名算法数学计算举例

ecc签名算法数学计算举例
ECC(椭圆曲线密码学)签名算法是一种基于椭圆曲线离散对数
问题的加密算法。
它使用椭圆曲线上的点来进行数字签名。
下面我
将从数学角度给出一个简单的例子来说明ECC签名算法的数学计算
过程。
首先,我们需要选择一个椭圆曲线以及一个基点。
假设我们选
择的椭圆曲线方程为 y^2 = x^3 + ax + b (这里的a和b是椭圆
曲线的参数),基点为G。
接下来,选择一个私钥d作为签名者的
私钥,然后计算公钥Q = dG。
这个公钥Q将用于验证签名的有效性。
假设我们要对消息m进行签名。
首先,选择一个随机数k,然
后计算椭圆曲线上的点(kG)的x坐标的模n的值,其中n是椭圆曲
线上点的数量。
这个x坐标的模n的值将作为签名中的一部分。
接下来,计算消息m的哈希值h。
然后使用私钥d和哈希值h
计算签名s,s = (k^-1 (h + dr)) mod n,其中r是(kG)点的x
坐标的模n的值。
最后,签名(s, r)将作为消息m的签名。
在验证阶段,接收者
可以使用公钥Q、消息m、签名(s, r)以及椭圆曲线的参数来验证签
名的有效性。
这个例子涉及到了椭圆曲线上的点的加法、乘法运算,模运算,哈希函数等数学计算。
这些计算是ECC签名算法的核心。
通过这些
数学计算,ECC签名算法能够提供高效且安全的数字签名机制。
ecc签名验签原理

ecc签名验签原理
ECC(椭圆曲线密码学,Elliptic Curve Cryptography)是一种非对称加密算法,其签名和验签的原理如下:
1. 随机生成一个私钥(private key),该私钥是一个随机数,通常是一个大整数。
私钥用于生成公钥和签名。
2. 使用椭圆曲线参数和私钥来计算公钥(public key)。
公钥是一个点,其坐标用于加密和验签。
3. 对于要签名的数据,首先对数据进行哈希运算,得到消息摘要(message digest)。
4. 使用私钥和消息摘要来计算签名(signature)。
签名的计算过程是将消息摘要与私钥进行数学运算,得到一个签名值。
5. 将签名值与消息一起传递给接收者。
6. 接收者使用发件人的公钥、消息和签名来进行验签。
验签的过程是将消息和签名值与公钥进行数学运算,如果运算结果与签名值一致,则验签成功;否则,验签失败。
在以上的签名和验签过程中,椭圆曲线算法提供了安全性和效率的优势。
由于椭圆曲线上的运算是基于数学运算的,因此通过给定的参数和随机数,可以在合理的时间内求得签名,并且可以在合理的时间内验证签名的有效性。
ecc算法标准

ecc算法标准
ECC(Elliptic Curve Cryptography)算法是一种基于椭圆曲线数学的公钥加密算法。
其标准可以参考以下内容:
1. 标准制定机构:目前椭圆曲线密码学的主要标准制定机构是IEEE P1363标准委员会。
该委员会已经制定了多个关于椭圆曲线密码学的标准,其中最著名的标准是,也被称为ANSI 标准。
2. 标准内容:ANSI 标准定义了椭圆曲线密码学的数学基础和椭圆曲线的选择方法,同时还包括了一些常见的椭圆曲线密码学操作,如密钥交换、数字签名、加密和解密等。
该标准还规定了一些椭圆曲线的参数,以确保不同实现之间的兼容性和安全性。
3. 应用范围:由于椭圆曲线密码学具有高效和安全的特性,其广泛应用于金融、政府、军事等领域。
例如,很多国家的电子签名标准都采用了椭圆曲线密码学算法。
总的来说,椭圆曲线密码学的标准是由多个机构共同制定的,包括国际标准化组织、国家标准化组织以及行业协会等。
这些标准旨在规范算法的使用,提高安全性,并促进不同实现之间的兼容性。
ECC加密算法入门介绍

ECC加密算法入门介绍ECC(Elliptic Curve Cryptography)椭圆曲线密码学是一种公钥密码体系,是基于椭圆曲线数学问题的一种加密算法。
相较于传统的RSA算法,ECC在相同的安全强度下使用更短的密钥长度,因此具有更高的效率和更低的资源消耗。
本文将介绍ECC加密算法的基本原理、优势与应用场景。
1.ECC加密算法原理:ECC加密算法利用椭圆曲线在群上的离散对数难题,来实现安全的加密和解密过程。
该算法的基本原理是选取一个椭圆曲线和点作为公开参数,然后选择一个合适的私钥生成公钥,通过私钥和公钥进行加密和解密。
具体流程如下:-选择一个合适的椭圆曲线E和点G作为公开参数。
-私钥选择一个随机数k。
-通过椭圆曲线计算公钥Q=kG。
-要加密的明文经过哈希函数得到一个点P。
-选择一个随机数r,计算点S=rG。
-计算点P+rQ,得到加密后的密文C=P+rQ。
-解密时使用私钥k计算点P'=C-kS,然后通过哈希函数应用反过程得到明文。
2.ECC加密算法的优势:-安全性强:ECC利用椭圆曲线的离散对数难题,在相同的安全强度下所需要的密钥长度要短于传统的RSA算法。
这使得ECC在保证安全性的同时,降低了资源的消耗。
-效率高:相较于RSA算法,ECC在相同的安全强度下使用更短的密钥长度,从而提高了加密和解密的效率。
这对于处理大量数据的场景,尤其是在移动设备上使用时非常有用。
-存储空间小:ECC生成的密钥长度较短,这意味着所需的存储空间更小。
这对于物联网设备等资源受限的环境非常重要。
3.ECC加密算法的应用场景:-加密通信:ECC可用于保护网络通信中的数据安全。
通过使用ECC算法生成的公钥对数据进行加密,保证数据的机密性。
-数字签名:ECC可用于生成数字签名以验证消息的完整性和身份认证。
通过私钥对消息进行签名,然后使用相应的公钥进行验证。
-移动设备安全:由于ECC在资源受限的移动设备上具有更高的效率和更小的存储需求,因此适用于移动设备的安全通信和数据保护。
ECC椭圆曲线加密算法—加解密(SageMath实现)

ECC椭圆曲线加密算法—加解密(SageMath实现)简介ECC椭圆曲线加密,它的安全性基于椭圆曲线上的离散对数问题。
⽐特币和⽬前的⼆代居民⾝份证都采⽤了ECC作为加密算法。
ECC椭圆曲线函数为:y2=x3+ax+b (mod p)ECC算法如下:椭圆曲线Ep(a,b)(p为模数),基点(⽣成元)G(x,y),G点的阶数n,私钥k,公钥K(x,y),随机整数r,明⽂为⼀点m(x,y),密⽂为两点c1(x,y)和c2(x,y)(其中基点G,明⽂m,公钥K,密⽂c1、c2都是椭圆曲线E上的点)选择私钥k(k<n)得到公钥K = k*G选择随机整数r(r<n)加密:c1 = m+r*Kc2 = r*G解密:m = c1-k*c2(= c1-r*K)SageMath可以直接计算椭圆曲线加法和椭圆曲线乘法。
椭圆曲线运算(SageMath):点u(x,y),整数a,点v(x,y),点w(x,y)a_inv = inverse_mod(a,p) #a_inv是a关于模p的乘法逆元a_invv = a*uu = v*a_invw = u+v加解密脚本SageMath加密脚本:'''加密椭圆曲线选取时,模数p应是⼀个⼤质数常⽤的有⼏个公开的椭圆曲线,如Secp256k1、Secp256r1等'''p = 115792089210356248762697446949407573530086143415290314195533631308867097853951a = 115792089210356248762697446949407573530086143415290314195533631308867097853948b = 41058363725152142129326129780047268409114441015993725554835256314039467401291E = EllipticCurve(GF(p),[a,b]) #建⽴椭圆曲线EG = E(101981543389703054444906888236965100227902100585263327233246492901054535785571,105947302391877180514060433855403037184838385483621546199124860815209826713886) #选择⼀点作为⽣成元n = G.order() #G的阶数k = 78772200542717449282831156601030024198219944170436309154595818823706214492400K = k*Gr = 3546765m = E(80764032034929976879602863302323059647882062252124869895215418422992624743795,4964654783828069942602279691168356721024126126864424301508238062949726916347) #取E上⼀点m作为明⽂c1 = m+r*Kc2 = r*Gprint(c1)print(c2)SageMath解密脚本:'''解密'''p = 115792089210356248762697446949407573530086143415290314195533631308867097853951a = 115792089210356248762697446949407573530086143415290314195533631308867097853948b = 41058363725152142129326129780047268409114441015993725554835256314039467401291k = 78772200542717449282831156601030024198219944170436309154595818823706214492400E = EllipticCurve(GF(p),[a,b]) #建⽴椭圆曲线Ec1 = E(55527726590533087179712343802771216661752045890626636388680526348340802301667,99976146729305231192119179111453136971828647307627310904093286590128902629941)c2 = E(85460365972589567444123006081329559170090723413178386022601904195400422637884,58249081362527056631776731740177334121295518073095154119886890634279528757192)m = c1-k*c2print(m)其他使⽤Crypto.PublicKey.ECC⽣成ECC密钥:from Crypto.PublicKey import ECC#⽣成ECC密钥key = ECC.generate(curve='NIST P-256') #使⽤椭圆曲线NIST P-256#输出密钥(包括私钥k,基点G)print(key)#公钥(point_x,point_y是基点G的坐标)print(key.public_key())#椭圆曲线print(key.curve)#私钥kprint(key.d)#导出为pem密钥⽂件print(key.export_key(format='PEM'))#导⼊密钥⽂件key = ECC.import_key(f.read())通过fastecdsa.Curve可以查到公开椭圆曲线的参数import fastecdsa.curve as curve#P-384的acurve.P384.a#P-384的bcurve.P384.bProcessing math: 100%#P-384的pcurve.P384.p⼏种公开椭圆曲线参数:#NIST P-256(Secp256r1)#p = 2^224(2^32 − 1) + 2^192 + 2^96 − 1p = 115792089210356248762697446949407573530086143415290314195533631308867097853951a = 115792089210356248762697446949407573530086143415290314195533631308867097853948b = 41058363725152142129326129780047268409114441015993725554835256314039467401291#Secp256k1(⽐特币使⽤)#p = 2^256 − 2^32 − 2^9 − 2^8 − 2^7 − 2^6 − 2^4 − 1 = 2^256 – 2^32 – 977p = 115792089237316195423570985008687907853269984665640564039457584007908834671663a = 0b = 7#NIST P-384#p = 2^384 – 2^128 – 2^96 + 2^32 – 1p = 39402006196394479212279040100143613805079739270465446667948293404245721771496870329047266088258938001861606973112319a = -3b = 27580193559959705877849011840389048093056905856361568521428707301988689241309860865136260764883745107765439761230575#NIST P-521p = 6864797660130609714981900799081393217269435300143305409394463459185543183397656052122559640661454554977296311391480858037121987999716643812574028291115057151a = -3b = 1093849038073734274511112390766805569936207598951683748994586394495953116150735016013708737573759623248592132296706313309438452531591012912142327488478985984 SageMath取椭圆曲线上随机⼀点:E = EllipticCurve(GF(p),[a,b])E.random_point() #取椭圆曲线E上随机⼀点sagemath计算椭圆曲线上的离散对数问题(数据量不能太⼤)a = 1234577b = 3213242p = 7654319E = EllipticCurve(GF(p),[a,b])G = E(5234568, 2287747) #⽣成元#k = 1584718K = E(2366653, 1424308) #公钥#求解私钥,⾃动选择bsgs或Pohlig Hellman算法discrete_log(K,G,operation='+')#求解私钥,Pollard rho算法discrete_log_rho(K,G,operation='+')#求解私钥,Pollard Lambda算法,能够确定所求值在某⼀⼩范围时效率较⾼discrete_log_lambda(K,G,(1500000,2000000),operation='+')使⽤openssl查看ECC的pem密钥⽂件信息#查看ECC私钥信息openssl ec -in p384-key.pem -text -noout#查看ECC公钥信息openssl ec -pubin -in public.pem -text -noout。
ECC校验算法
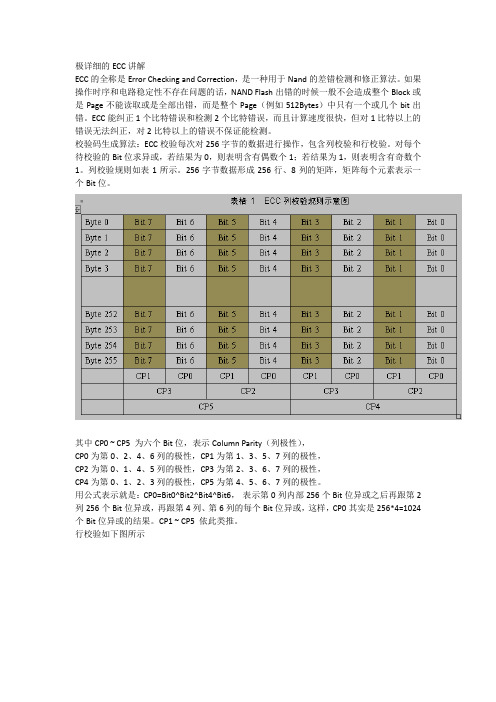
极详细的ECC讲解ECC的全称是Error Checking and Correction,是一种用于Nand的差错检测和修正算法。
如果操作时序和电路稳定性不存在问题的话,NAND Flash出错的时候一般不会造成整个Block或是Page不能读取或是全部出错,而是整个Page(例如512Bytes)中只有一个或几个bit出错。
ECC能纠正1个比特错误和检测2个比特错误,而且计算速度很快,但对1比特以上的错误无法纠正,对2比特以上的错误不保证能检测。
校验码生成算法:ECC校验每次对256字节的数据进行操作,包含列校验和行校验。
对每个待校验的Bit位求异或,若结果为0,则表明含有偶数个1;若结果为1,则表明含有奇数个1。
列校验规则如表1所示。
256字节数据形成256行、8列的矩阵,矩阵每个元素表示一个Bit位。
其中CP0 ~ CP5 为六个Bit位,表示Column Parity(列极性),CP0为第0、2、4、6列的极性,CP1为第1、3、5、7列的极性,CP2为第0、1、4、5列的极性,CP3为第2、3、6、7列的极性,CP4为第0、1、2、3列的极性,CP5为第4、5、6、7列的极性。
用公式表示就是:CP0=Bit0^Bit2^Bit4^Bit6,表示第0列内部256个Bit位异或之后再跟第2列256个Bit位异或,再跟第4列、第6列的每个Bit位异或,这样,CP0其实是256*4=1024个Bit位异或的结果。
CP1 ~ CP5 依此类推。
行校验如下图所示其中RP0 ~ RP15 为十六个Bit位,表示Row Parity(行极性),RP0为第0、2、4、6、….252、254个字节的极性RP1-----1、3、5、7……253、255RP2----0、1、4、5、8、9…..252、253(处理2个Byte,跳过2个Byte)RP3---- 2、3、6、7、10、11…..254、255(跳过2个Byte,处理2个Byte)RP4----处理4个Byte,跳过4个Byte;RP5----跳过4个Byte,处理4个Byte;RP6----处理8个Byte,跳过8个ByteRP7----跳过8个Byte,处理8个Byte;RP8----处理16个Byte,跳过16个ByteRP9----跳过16个Byte,处理16个Byte;RP10----处理32个Byte,跳过32个ByteRP11----跳过32个Byte,处理32个Byte;RP12----处理64个Byte,跳过64个ByteRP13----跳过64个Byte,处理64个Byte;RP14----处理128个Byte,跳过128个ByteRP15----跳过128个Byte,处理128个Byte;可见,RP0 ~ RP15 每个Bit位都是128个字节(也就是128行)即128*8=1024个Bit位求异或的结果。
ECC加密算法入门介绍

ECC加密算法入门介绍ECC(Elliptic Curve Cryptography)是一种基于椭圆曲线的公钥密码算法,与RSA和DSA等传统的公钥密码算法相比,具有更小的密钥尺寸和更高的安全性。
本文将介绍ECC加密算法的基本原理、优势以及应用领域。
一、ECC加密算法的基本原理ECC是基于椭圆曲线数学理论设计的加密算法。
其基本原理是利用离散对数问题的难解性来保护数据的安全性。
在ECC中,将椭圆曲线上的点作为密钥,利用椭圆曲线的加法等运算规则来实现加密和解密的过程。
1.椭圆曲线的定义椭圆曲线是一个由满足特定方程的点构成的集合,具有非常特殊的性质。
在ECC中,使用的椭圆曲线的方程一般为y^2 = x^3 + ax + b,其中a和b为曲线参数。
2.点的加法和乘法运算在椭圆曲线上,定义了点的加法和乘法运算。
点的加法运算可以简单理解为将两个点在曲线上进行连线,与曲线的其他点交点即为相加的结果。
点的乘法运算是将一个点通过多次相加的方式得到另一个点。
3.离散对数问题椭圆曲线加密算法的安全性基于离散对数问题的难解性。
在ECC中,给定椭圆曲线上的两个点P和Q,求解使得nP=Q成立的整数n所具有很高的复杂度,即离散对数问题。
二、ECC加密算法的优势相比传统的公钥密码算法,ECC具有以下优势:1.更小的密钥尺寸ECC相较于RSA和DSA等算法,使用更小的密钥尺寸即可达到相同的安全性。
例如,128位的ECC密钥与3072位的RSA密钥具有相当的安全强度,但ECC密钥的尺寸仅为RSA密钥的1/32.更高的加密效率由于使用更小的密钥尺寸,ECC在加密和解密的速度上比传统算法更快,尤其适合于移动设备等资源受限的环境。
3.更好的安全性ECC的安全性基于离散对数问题的难解性,且具有较高的抗量子计算攻击能力。
即使量子计算机出现,ECC仍然可以提供更好的保护。
三、ECC加密算法的应用领域ECC广泛应用于各种领域,特别适用于对计算资源要求高、带宽受限的环境:1.移动通信领域由于ECC具有更小的密钥尺寸和更高的加密效率,因此在移动通信领域广泛应用。
ecc签名验签算法计算举例

ecc签名验签算法计算举例ECC签名验签算法计算举例如下:1. 生成密钥对椭圆曲线密码(ECC)算法中的密钥对生成是第一步。
这个过程通常包括选择一条安全的椭圆曲线,并在其上生成一对私钥和公钥。
私钥是保密的,而公钥则是公开的。
在我们的示例中,我们选择一个名为"secp256r1"的常用椭圆曲线。
然后,我们使用随机数生成器生成一个随机的私钥。
私钥通常是一个整数,范围在[0, n-1],其中n是椭圆曲线上的点数量。
公钥可以通过椭圆曲线的数学性质从私钥中计算得出。
```pythonimport randomfrom ecc import EccKey# 选择椭圆曲线curve = 'secp256r1'# 生成私钥private_key = random.randint(0, 2**256)# 生成公钥public_key = EccKey.from_private_key_and_curve(private_key, curve)```2. 生成随机数在签名过程中,我们需要生成一个随机的随机数k,这个数将在签名过程中使用。
k的选择也是安全的,即它不应该与椭圆曲线上的其他点冲突。
```python# 生成随机数kk = random.randint(0, 2**256)```3. 计算签名值使用私钥、随机数k和要签名的数据来计算签名值。
这个过程涉及到椭圆曲线上的点运算和哈希函数。
```pythonfrom ecc import EccKey, Signatureimport hashlib# 要签名的数据,通常是一个哈希值或一段文本的哈希值data = b'example data'data_hash = hashlib.sha256(data).digest()# 使用私钥、随机数k和数据哈希来计算签名值signature = private_key.sign(data_hash, k)```4. 验证签名值验证签名值的过程是使用公钥、相同的随机数k(如果可获取)和要验证的数据来验证签名是否有效。
sram ecc算法原理

sramecc算法原理一、概述ECC(ErrorCorrectingCode)算法是一种广泛应用于计算机存储系统的错误检测技术。
在SRAM(StaticRandomAccessMemory)存储器中,ECC被广泛用于提高数据存储和读取的可靠性。
本章节将详细介绍SRAMECC算法的原理。
二、基本原理1.错误类型:SRAM在读写过程中,由于各种因素(如电学、机械等)的影响,数据可能会出现错误。
常见的错误类型包括数据丢失、数据插入、数据颠倒等。
2.ECC算法:ECC算法通过在原始数据周围添加冗余信息(也称为校验位),实现对数据错误的检测和纠正。
冗余信息的生成和校验通常基于特定的数学算法,如哈达玛矩阵、奇偶校验等。
3.冗余信息的生成:在SRAM中,当数据写入存储器时,会同时生成相应的冗余信息。
这些冗余信息可以是数据的多余位,也可以是特定的算法计算结果。
4.错误检测:在读取数据时,首先需要从原始数据中恢复出冗余信息,并将其与实际读取的数据进行比较。
如果发现冗余信息与预期不符,就意味着数据可能存在错误。
5.错误纠正:根据ECC算法,可以通过一定的计算过程,从错误的数据中恢复出正确的数据。
这个过程通常包括查找错误位置、进行纠正操作等步骤。
三、主要步骤1.数据写入:在写入数据时,生成相应的冗余信息并一同写入。
2.数据读取:首先恢复出冗余信息,并将其与实际读取的数据进行比较。
3.错误检测和纠正:根据ECC算法,查找并纠正可能的错误。
4.数据更新:如果错误得到纠正,则更新存储在SRAM中的数据;如果错误无法纠正,则可能需要采取其他措施(如重新写入)。
四、应用场景SRAMECC算法广泛应用于各种需要高可靠性的存储设备,如固态硬盘(SSD)、缓存内存等。
此外,由于其低功耗、高速度等优点,SRAMECC算法也在嵌入式系统、移动设备等领域得到广泛应用。
五、总结SRAMECC算法通过在原始数据周围添加冗余信息,实现对数据错误的检测和纠正,从而提高数据存储的可靠性。
ecc 密钥协商算法

ecc 密钥协商算法ECC密钥协商算法ECC(Elliptic Curve Cryptography)是一种基于椭圆曲线数学原理的公钥密码算法,广泛应用于安全通信中的密钥协商过程。
本文将介绍ECC密钥协商算法的原理、优势和应用场景。
一、ECC密钥协商算法的原理ECC密钥协商算法基于椭圆曲线离散对数问题,通过利用椭圆曲线上的一些特殊性质,实现了与其他公钥密码算法相比更高的安全性和更小的计算量。
其基本原理如下:1. 椭圆曲线的选择:在密钥协商过程中,首先需要选择一个合适的椭圆曲线。
常用的椭圆曲线有NIST推荐的P-256、P-384和P-521等。
选择合适的椭圆曲线对于安全性和性能都非常重要。
2. 密钥生成:Alice和Bob分别选择自己的私钥和公钥。
私钥是一个随机数,公钥是私钥通过椭圆曲线上的点乘运算得到的。
3. 密钥协商:Alice和Bob交换各自的公钥,并利用对方的公钥和自己的私钥计算出共享密钥。
这个计算过程是基于椭圆曲线上的点乘和点加运算实现的。
二、ECC密钥协商算法的优势相比传统的RSA和Diffie-Hellman等公钥密码算法,ECC密钥协商算法具有以下优势:1. 安全性高:ECC密钥协商算法基于椭圆曲线离散对数问题,该问题的求解难度与传统的大整数分解问题相比更高。
因此,ECC密钥协商算法具有更高的安全性。
2. 计算量小:椭圆曲线上的点乘运算比大整数的乘法运算更快速,因此ECC密钥协商算法在相同的安全性要求下,需要更小的计算量。
这使得ECC在资源受限的环境下具有更好的性能。
3. 存储空间小:由于椭圆曲线上的点可以用更小的数据表示,ECC 密钥协商算法所需的存储空间也更小。
这对于存储密钥信息的设备来说是非常有利的。
三、ECC密钥协商算法的应用场景ECC密钥协商算法在各种安全通信场景中得到了广泛的应用,特别是在移动设备和物联网领域。
以下是几个常见的应用场景:1. 移动通信安全:ECC密钥协商算法可以用于手机通信中的加密和解密过程,保护用户的隐私和数据安全。
ecc值计算方法

ecc值计算方法ECC(Error Correcting Code)是一种用于检测和纠正数据传输中错误的编码技术。
在计算机科学和通信领域,ECC被广泛应用于存储介质、网络传输和数据传输等方面,以提高数据的可靠性和完整性。
本文将介绍ECC值的计算方法。
ECC值是用于度量数据传输中错误检测和纠正能力的指标。
ECC值越高,表示数据传输过程中的错误检测和纠正能力越强。
计算ECC 值的方法通常基于校验位的生成和校验位的校验。
一种常见的ECC计算方法是基于海明码(Hamming Code)的。
海明码是一种常见的纠错码,通过添加冗余位(校验位)来实现对数据传输中的错误检测和纠正。
计算ECC值的方法如下:1. 将要传输的数据划分为若干个数据块,每个数据块的大小是根据具体情况确定的。
2. 对每个数据块进行编码,添加冗余位。
冗余位的数量取决于数据块的大小和纠错能力的要求。
3. 对编码后的数据块进行校验位的生成。
校验位是通过对数据块中的每个位进行异或运算得到的。
校验位的位置通常在数据块的末尾。
4. 将编码后的数据块和校验位传输给接收端。
5. 在接收端,对接收到的数据块进行校验位的校验。
校验位的校验方法同样是对数据块中的每个位进行异或运算,如果校验位与计算得到的校验位相同,则数据传输没有错误;如果不同,则表示数据传输发生了错误。
6. 如果数据传输发生了错误,根据校验位的位置和校验位的值,可以确定错误的位置,并进行纠正。
除了海明码,还有其他的ECC计算方法,如RS码(Reed Solomon Code)、BCH码(Bose-Chaudhuri-Hocquenghem Code)等。
这些方法的原理和步骤有所不同,但都是基于添加冗余位和校验位来实现错误检测和纠正。
ECC值的计算方法对于数据传输的可靠性和完整性至关重要。
通过使用ECC技术,可以有效地检测和纠正数据传输过程中的错误,提高数据的可靠性和完整性。
在存储介质、网络传输和数据传输等领域,ECC被广泛应用,以确保数据的安全和可靠。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ECC加密算法入门介绍作者:ZMWorm[CCG]E-Mail:zmworm@主页:/前言同RSA(Ron Rivest,Adi Shamir,Len Adleman三位天才的名字)一样,ECC(Elliptic Curves Cryptography,椭圆曲线密码编码学)也属于公开密钥算法。
目前,国内详细介绍ECC的公开文献并不多(反正我没有找到)。
有一些简介,也是泛泛而谈,看完后依然理解不了ECC的实质(可能我理解力太差)。
前些天我从国外网站找到些材料,看完后对ECC似乎懵懂了。
于是我想把我对ECC的认识整理一下,与大家分享。
当然ECC博大精深,我的认识还很肤浅,文章中错误一定不少,欢迎各路高手批评指正,小弟我洗耳恭听,并及时改正。
文章将采用连载的方式,我写好一点就贴出来一点。
本文主要侧重理论,代码实现暂不涉及。
这就要求你要有一点数学功底。
最好你能理解RSA算法,对公开密钥算法有一个了解。
《近世代数基础》《初等数论》之类的书,最好您先翻一下,这对您理解本文是有帮助的。
别怕,我尽量会把语言通俗些,希望本文能成为学习ECC的敲门砖。
一、从平行线谈起。
平行线,永不相交。
没有人怀疑把:)不过到了近代这个结论遭到了质疑。
平行线会不会在很远很远的地方相交了?事实上没有人见到过。
所以“平行线,永不相交”只是假设(大家想想初中学习的平行公理,是没有证明的)。
既然可以假设平行线永不相交,也可以假设平行线在很远很远的地方相交了。
即平行线相交于无穷远点P∞(请大家闭上眼睛,想象一下那个无穷远点P∞,P∞是不是很虚幻,其实与其说数学锻炼人的抽象能力,还不如说是锻炼人的想象力)。
给个图帮助理解一下:直线上出现P∞点,所带来的好处是所有的直线都相交了,且只有一个交点。
这就把直线的平行与相交统一了。
为与无穷远点相区别把原来平面上的点叫做平常点。
以下是无穷远点的几个性质。
▲直线L上的无穷远点只能有一个。
(从定义可直接得出)▲平面上一组相互平行的直线有公共的无穷远点。
(从定义可直接得出)▲ 平面上任何相交的两直线L1,L2有不同的无穷远点。
(否则L1和L2有公共的无穷远点P ,则L1和L2有两个交点A、P,故假设错误。
)▲平面上全体无穷远点构成一条无穷远直线。
(自己想象一下这条直线吧)▲平面上全体无穷远点与全体平常点构成射影平面。
二、射影平面坐标系射影平面坐标系是对普通平面直角坐标系(就是我们初中学到的那个笛卡儿平面直角坐标系)的扩展。
我们知道普通平面直角坐标系没有为无穷远点设计坐标,不能表示无穷远点。
为了表示无穷远点,产生了射影平面坐标系,当然射影平面坐标系同样能很好的表示旧有的平常点(数学也是“向下兼容”的)。
我们对普通平面直角坐标系上的点A的坐标(x,y)做如下改造:令x=X/Z ,y=Y/Z(Z≠0);则A点可以表示为(X:Y:Z)。
变成了有三个参量的坐标点,这就对平面上的点建立了一个新的坐标体系。
例2.1:求点(1,2)在新的坐标体系下的坐标。
解:∵X/Z=1 ,Y/Z=2(Z≠0)∴X=Z,Y=2Z ∴坐标为(Z:2Z:Z),Z≠0。
即(1:2:1)(2:4:2)(1.2:2.4:1.2)等形如(Z:2Z:Z),Z≠0的坐标,都是(1,2)在新的坐标体系下的坐标。
我们也可以得到直线的方程aX+bY+cZ=0(想想为什么?提示:普通平面直角坐标系下直线一般方程是ax+by+c=0)。
新的坐标体系能够表示无穷远点么?那要让我们先想想无穷远点在哪里。
根据上一节的知识,我们知道无穷远点是两条平行直线的交点。
那么,如何求两条直线的交点坐标?这是初中的知识,就是将两条直线对应的方程联立求解。
平行直线的方程是:aX+bY+c1Z =0;aX+bY+c2Z =0 (c1≠c2);(为什么?提示:可以从斜率考虑,因为平行线斜率相同);将二方程联立,求解。
有c2Z= c1Z= -(aX+bY),∵c1≠c2∴Z=0 ∴aX+bY=0;所以无穷远点就是这种形式(X:Y:0)表示。
注意,平常点Z≠0,无穷远点Z=0,因此无穷远直线对应的方程是Z=0。
例2.2:求平行线L1:X+2Y+3Z=0 与L2:X+2Y+Z=0 相交的无穷远点。
解:因为L1∥L2 所以有Z=0,X+2Y=0;所以坐标为(-2Y:Y:0),Y≠0。
即(-2:1:0)(-4:2:0)(-2.4:1.2:0)等形如(-2Y:Y:0),Y≠0的坐标,都表示这个无穷远点。
看来这个新的坐标体系能够表示射影平面上所有的点,我们就把这个能够表示射影平面上所有点的坐标体系叫做射影平面坐标系。
练习:1、求点A(2,4) 在射影平面坐标系下的坐标。
2、求射影平面坐标系下点(4.5:3:0.5),在普通平面直角坐标系下的坐标。
3、求直线X+Y+Z=0上无穷远点的坐标。
4、判断:直线aX+bY+cZ=0上的无穷远点和无穷远直线与直线aX+bY=0的交点,是否是同一个点?三、椭圆曲线上一节,我们建立了射影平面坐标系,这一节我们将在这个坐标系下建立椭圆曲线方程。
因为我们知道,坐标中的曲线是可以用方程来表示的(比如:单位圆方程是x2+y2=1)。
椭圆曲线是曲线,自然椭圆曲线也有方程。
椭圆曲线的定义:一条椭圆曲线是在射影平面上满足方程Y2Z+a1XYZ+a3YZ2=X3+a2X2Z+a4XZ2+a6Z3----------------[3-1]的所有点的集合,且曲线上的每个点都是非奇异(或光滑)的。
定义详解:▲ Y2Z+a1XYZ+a3YZ2 = X3+a2X2Z+a4XZ2+a6Z3是Weierstrass方程(维尔斯特拉斯,Karl Theodor Wilhelm Weierstrass,1815-1897),是一个齐次方程。
▲ 椭圆曲线的形状,并不是椭圆的。
只是因为椭圆曲线的描述方程,类似于计算一个椭圆周长的方程(计算椭圆周长的方程,我没有见过,而对椭圆线积分(设密度为1)是求不出来的。
谁知道这个方程,请告诉我呀^_^),故得名。
我们来看看椭圆曲线是什么样的。
▲ 所谓“非奇异”或“光滑”的,在数学中是指曲线上任意一点的偏导数F x(x,y,z),F y(x,y,z),F z(x,y,z)不能同时为0。
如果你没有学过高等数学,可以这样理解这个词,即满足方程的任意一点都存在切线。
下面两个方程都不是椭圆曲线,尽管他们是方程[3-1]的形式。
因为他们在(0:0:1)点处(即原点)没有切线。
▲椭圆曲线上有一个无穷远点O∞(0:1:0),因为这个点满足方程[3-1]。
知道了椭圆曲线上的无穷远点。
我们就可以把椭圆曲线放到普通平面直角坐标系上了。
因为普通平面直角坐标系只比射影平面坐标系少无穷远点。
我们在普通平面直角坐标系上,求出椭圆曲线上所有平常点组成的曲线方程,再加上无穷远点O∞(0:1:0),不就构成椭圆曲线了么?我们设x=X/Z ,y=Y/Z代入方程[3-1]得到:y2+a1xy+a3y = x3+a2x2+a4x+a6 -------------------------[3-2]也就是说满足方程[3-2]的光滑曲线加上一个无穷远点O∞,组成了椭圆曲线。
为了方便运算,表述,以及理解,今后论述椭圆曲线将主要使用[3-2]的形式。
本节的最后,我们谈一下求椭圆曲线一点的切线斜率问题。
由椭圆曲线的定义可以知道,椭圆曲线是光滑的,所以椭圆曲线上的平常点都有切线。
而切线最重要的一个参数就是斜率k。
例3.1:求椭圆曲线方程y2+a1xy+a3y=x3+a2x2+a4x+a6上,平常点A(x,y)的切线的斜率k。
解:令F(x,y)= y2+a1xy+a3y-x3-a2x2-a4x-a6求偏导数F x(x,y)= a1y-3x2-2a2x-a4F y(x,y)= 2y+a1x +a3则导数为:f'(x)=- F x(x,y)/ F y(x,y)=-( a1y-3x2-2a2x-a4)/(2y+a1x +a3)= (3x2+2a2x+a4-a1y) /(2y+a1x +a3)所以k=(3x2+2a2x+a4-a1y) /(2y+a1x +a3) ------------------------[3-3]看不懂解题过程没有关系,记住结论[3-3]就可以了。
练习:1、将给出图例的椭圆曲线方程Y2Z=X3-XZ2和Y2Z=X3+XZ2+Z3转换成普通平面直角坐标系上的方程。
四、椭圆曲线上的加法上一节,我们已经看到了椭圆曲线的图象,但点与点之间好象没有什么联系。
我们能不能建立一个类似于在实数轴上加法的运算法则呢?天才的数学家找到了这一运算法则☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆自从近世纪代数学引入了群、环、域的概念,使得代数运算达到了高度的统一。
比如数学家总结了普通加法的主要特征,提出了加群(也叫交换群,或Abel(阿贝尔)群),在加群的眼中。
实数的加法和椭圆曲线的上的加法没有什么区别。
这也许就是数学抽象把:)。
关于群以及加群的具体概念请参考近世代数方面的数学书。
☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆运算法则:任意取椭圆曲线上两点P、Q (若P、Q两点重合,则做P点的切线)做直线交于椭圆曲线的另一点R’,过R’做y轴的平行线交于R。
我们规定P+Q=R。
(如图)法则详解:▲这里的+不是实数中普通的加法,而是从普通加法中抽象出来的加法,他具备普通加法的一些性质,但具体的运算法则显然与普通加法不同。
▲根据这个法则,可以知道椭圆曲线无穷远点O∞与椭圆曲线上一点P的连线交于P’,过P’作y轴的平行线交于P,所以有无穷远点O∞+ P = P 。
这样,无穷远点O∞的作用与普通加法中零的作用相当(0+2=2),我们把无穷远点O∞ 称为零元。
同时我们把P’称为P的负元(简称,负P;记作,-P)。
(参见下图)▲根据这个法则,可以得到如下结论:如果椭圆曲线上的三个点A、B、C,处于同一条直线上,那么他们的和等于零元,即A+B+C= O∞▲k个相同的点P相加,我们记作kP。
如下图:P+P+P = 2P+P = 3P。
下面,我们利用P、Q点的坐标(x1,y1),(x2,y2),求出R=P+Q的坐标(x4,y4)。
例4.1:求椭圆曲线方程y2+a1xy+a3y=x3+a2x2+a4x+a6上,平常点P(x1,y1),Q(x2,y2)的和R(x4,y4)的坐标。
解:(1)先求点-R(x3,y3)因为P,Q,-R三点共线,故设共线方程为y=kx+b,其中若P≠Q(P,Q两点不重合) 则直线斜率k=(y1-y2)/(x1-x2)若P=Q(P,Q两点重合) 则直线为椭圆曲线的切线,故由例3.1可知:k=(3x2+2a2x+a4 -a1y) /(2y+a1x+a3)因此P,Q,-R三点的坐标值就是方程组:y2+a1xy+a3y=x3+a2x2+a4x+a6 -----------------[1]y=(kx+b) -----------------[2]的解。
