概率论与数理统计B09-10年真题(A卷)
《概率论与数理统计》考试题(含答案)

《概率论与数理统计》考试题一、填空题(每小题2分,共计60分)1、A 、B 是两个随机事件,已知0.3)B (p ,5.0)A (p ==,则a )、若B A ,互斥,则=)B -A (p 0.5 ;b )若B A ,独立,则=)B A (p 0.65 ;c )、若2.0)(=⋅B A p ,则=)B A (p 3/7 . 2、袋子中有大小相同的红球7只,黑球3只,(1)从中不放回地任取2只,则第一、二次取到球颜色不同的概率为: 7/15 。
(2)若有放回地任取2只,则第一、二次取到球颜色不同的概率为: 21/50 。
(3)若第一次取一只球后再追加一只与其颜色相同的球一并放入袋中再取第二只球,则第一、二次取到球颜色不同的概率为: 21/55 . 3、设随机变量X 服从泊松分布}8{}7{),(===X P X p λπ,则{}=X E 8 .4、设随机变量X 服从B (2,0. 8)的二项分布,则{}==2X p 0.64 , Y 服从B (8,0. 8)的二项分布, 且X 与Y 相互独立,则}1{≥+Y X P =1- 0.210,=+)(Y X E 8 。
5 设某学校外语统考学生成绩X 服从正态分布N (75,25),则该学校学生的及格率为 0.9987 ,成绩超过85分的学生占比}85{≥X P 为 0.0228 。
其中标准正态分布函数值9987.0)3(,9772.0)2(,8413.0)1(=Φ=Φ=Φ. 6、设二维随机向量),(Y X 的分布律是有 则=a _0.1_,X的数学期望=)(X E ___0.4___,Y X 与的相关系数=xy ρ___-0.25______。
7、设161,...,X X 及81,...,Y Y 分别是总体)16,8(N 的容量为16,8的两个独立样本,Y X ,分别为样本均值,2221,S S 分别为样本方差。
则:~X N(8,1) ,~Y X - N(0,1.5) ,{}5.12>-Y X p = 0.0456 ,~161521S )15(2χ,~2221S S F(15,7) 。
概率论与数理统计历年真题-2009.10

全国2009年10月高等教育自学考试概率论与数理统计(经管类)试题课程代码:04183一、单项选择题(本大题共10小题,每小题2分,共20分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.某射手向一目标射击两次,A i 表示事件“第i 次射击命中目标”,i =1,2,B 表示事件“仅第一次射击命中目标”,则B =( ) A .A 1A 2 B .21A A C .21A AD .21A A2.某人每次射击命中目标的概率为p (0<p <1),他向目标连续射击,则第一次未中第二次命中的概率为( ) A .p 2 B .(1-p )2 C .1-2pD .p (1-p )3.已知P (A )=0.4,P (B )=0.5,且A ⊂B ,则P (A |B )=( ) A .0 B .0.4 C .0.8D .14.一批产品中有5%不合格品,而合格品中一等品占60%,从这批产品中任取一件,则该件产品是一等品的概率为( )A .0.20B .0.30C .0.38D .0.57 5.设随机变量X 的分布律为 X0 1 2 ,则P {X <1}=( )P0.3 0.2 0.5A .0B .0.2C .0.3D .0.56.下列函数中可作为某随机变量的概率密度的是( ) A .⎪⎩⎪⎨⎧≤>100,0,100,1002x x xB .⎪⎩⎪⎨⎧≤>0,0,0,10x x xC .⎩⎨⎧≤≤-其他,0,20,1x D .⎪⎩⎪⎨⎧≤≤其他,0,232121x ,7.设随机变量X 与Y 相互独立,X 服从参数为2的指数分布,Y ~B (6,21),则E(X-Y)=( ) A .25- B .21 C .2D .58.设二维随机变量(X ,Y )的协方差Cov(X ,Y )=61,且D (X )=4,D (Y )=9,则X 与Y 的相关系数XY ρ为( ) A .2161 B .361 C .61 D .19.设总体X ~N (2,σμ),X 1,X 2,…,X 10为来自总体X 的样本,X 为样本均值,则X ~( ) A .)10(2σμ,NB .)(2σμ,NC .)10(2σμ,ND .)10(2σμ,N10.设X 1,X 2,…,X n 为来自总体X 的样本,X 为样本均值,则样本方差S 2=( ) A .∑=-ni iX Xn12)(1B .∑=--ni iX Xn 12)(11C .∑=-ni iX Xn12)(1D .∑=--ni iX Xn 12)(11二、填空题(本大题共15小题,每小题2分,共30分)请在每小题的空格中填上正确答案。
(完整版)自考本概率论与数理统计真题10套

2.设F(x)为随机变量X的分布函数,则有
A.F(-∞)=0,F(+∞)=0B.F(-∞)=1,F(+∞)=0
C.F(-∞)=0,F(+∞)=1D.F(-∞)=1,F(+∞)=1
3.设二维随机变量(X,Y)服从区域D:x2+y2≤1上的均匀分布,则(X,Y)的概率密度为
19. 设随机变量X与Y相互独立,且X~N(0,5),Y~X2(5),则随机变量 服从
自由度为5的_______________分布。
20. 设随机变量X与Y相互独立,且D(X)=2,D(Y)=1,则D(X-2Y+3)=___________.
21. 已知二维随机向量(X,Y)服从区域G:0≤x≤1, 0≤y≤2上的均匀分布,则 _______________.
Y
X
-1
0
1
0
0.3
0.2
0.1
1
0.1
0.3
0
求:(1)X和Y的分布律;(2)Cov(X,Y).
四、综合题(本大题共2小题,每小题12分,共24分)
28.某次抽样结果表明,考生的数学成绩(百分制)近似地服从正态分布N(75,σ2),已知85分以上的考生数占考生总数的5%,试求考生成绩在65分至85分之间的概率.
22. 设总体X~N( …,Xn为来自总体X的样本, 为样本均值,则D( )=.
23. 设二维随机向量(X,Y)的概率密度为f(x,y)= 则当
0≤y≤1时,(X,Y)关于Y的边缘概率密度fY(y)=.
24. 设总体X的分布列为
X
0
1
P
1-p
P
其中p为未知参数,且X1,X2,…,Xn为其样本,则p的矩估计 =___________.
随米-武汉理工大学2009~2010学年第一学期《概率论与数理统计》期末试卷(A卷)及参考答案

武汉理工大学考试试题纸(A 卷)课程名称概率论与数理统计专业班级全校本科2008级备注:学生不得在试题纸上答题(含填空题、选择题等客观题)一、填空题、)4283('=⨯'1. 已知()0.3P A =,()0.4P B =,()0.25P AB =,则=)(B A P . 2. 设二维随机变量),(Y X 满足{}30,07P X Y ≥≥=,且{}{}3007P X P Y <=<=,则{}max(,)0P X Y ≥=.3. 设二维随机变量),(Y X 的概率密度(2)2,0,0,(,)0,.x y e x y f x y -+⎧>>=⎨⎩其它则{}P Y X ≤=.4. 已知随机变量X 服从参数为1的泊松分布,则{}2()P X E X ==.5. 已知~(0,36)X N ,~(Y U ,相关系数0.5XY ρ=-,则ov(,)C X Y =.6. 1234,,,X X X X 是来自总体),(~2σμN X 的样本,2343X X X Y ++=,()422*212i i S X Y ==-∑,则1*X S μ-服从的分布是. 7. 设12,,,n X X X 为总体X 的一个随机样本,2(),()E X D X μσ==,要使()12211ˆn i i i a X X σ-+==-∑是2σ的无偏估计,则常数=a .8. 设921,,,X X X 为正态总体),(~2σμN X 的样本,其中29σ=,样本均值8.52x =,则总体均值μ的置信度为%95的置信区间为.(小数点后保留两位)二、)01('已知甲乙两箱中装有同种产品,其中甲箱中装有3件合格品和3件次品,乙箱中装有2件合格品和1件次品,现从甲箱中任取2件放入乙箱,然后再从乙箱中任取一件产品,求该产品为次品的概率及该次品是在从甲箱中没取到次品的情况下取得的概率(结果用分数形式表示).三、)01('一箱子装有6个球,其中红,白,黑球的个数分别为1,2,3个;现从箱中随机的取出2个球,设X 为取出的红球个数,Y 为取出的白球个数.试求随机变量),(Y X 的联合分布律及Y X ,的边缘分布律(要求画出分布律表格且结果用分数形式表示),并判断,X Y 是否相互独立.四、)01('设连续型随机变量X 的分布函数为:0,1,()ln ,1,1,.x F x A x x e x e <⎧⎪=≤<⎨⎪≥⎩试求:①常数A;②概率{0P X <≤;③X 的概率密度函数()f x .五、)01('设随机变量X 的概率密度为()14,1112,120,X x f x x -<<⎧⎪=≤<⎨⎪⎩其他,令2Y X =,求Y 的分布函数()Y F y .六、)01('某高校图书馆阅览室共有940个座位,该校共10000名学生,已知每天晚上每个学生到阅览室去自习的概率为10%.试估算阅览室晚上座位不够用的概率(小数点后保留三位).七、)01('设总体X 的概率密度函数为11()0,1x x f x x θθ--⎧>=⎨≤⎩,,其中1θ>是未知参数,12n,...,X X X 为来自该总体的一个样本,该样本取值为12,...,n x x x .求θ的矩估计量和极大似然估计量.八、)01('假定某车间生产的电子元件的寿命(小时h )服从正态分布2(,)N μσ,已知技术改变前的平均寿命为1000h ,现在随机测试9个革新以后的电子元件的寿命,计算得样本均值1124x =h ,样本标准差152S h =. 请问在显著性水平05.0=α下, 是否有理由认为技术革新改变了产品质量?九、)6('设连续型随机变量(0,1)X N ,Y 表示对X 的5次观测中事件{}||1X >发生的次数,试判断Y 的分布,并求Y 的方差(小数点后保留三位).查表数据:(1.00)0.8413Φ=975.0)96.1(=Φ95.0)645.1(=Φ9332.0)50.1(=Φ8595.1)8(05.0=t 3060.2)8(025.0=t 8331.1)9(05.0=t 2622.2)9(025.0=t2009~2010学年第一学期《概率论与数理统计》期末试卷(A 卷)参考答案一、填空题:(每空5分,共25分)(1)、0.4 (2)、57 (3)、1/3 (4)、1e- (5)、-3(6)、(2)t (7)、12(1)n - (8)、(6.56, 10.48)二、(共10分)解:设i A 表示“从甲箱中取了i 件次品放入乙箱”,0,1,2i =; B 表示“从乙箱中取到的是次品”。
2020-2021大学《概率论与数理统计》期末课程考试试卷A(含答案)

2020-2021大学《概率论与数理统计》期末课程考试试卷A适用专业: 考试日期:试卷类型:闭卷 考试时间:120分钟 试卷总分:100分一.填空题(每题2分,共10分)1设事件A,B 互不相容,若P (A )=0.3,P (B )=0.7,则P (AB )为_________。
设事件A,B 相互独立,若P (A )=0.3,P (B )=0.7,则P (AB )为______.3.设母体X 服从正态分布N (μ,σ2),X 1,X 2⋯,X n 为取自母体的子样,X̄为子样均值,则X ̄服从的分布为__________.4.设X 1,X 2⋯,X n 相互独立,且都服从正态分布N (0,1),则∑X i 2n i=1服从的分布为_____________.5. 将一枚硬币重复掷N 次,以X 和Y 分别表示正面向上和反面向上的次数,则X 和Y 的相关系数等于__________.二、选择题(每小题2分共10分)1.设A,B 为互不相容事件,且P (A )>0,P (B )>0,则结论正确的有( )(A )P (A |B )>0 (B )P (A |B )>P(A) (C) P (A |B )=0 (D) P (A |B )=P (A )P (B ) 2、设随机变量ξ,η相互独立,且有Dξ=6,Dη=3.则D (2ξ+η)为( ) (A )9 (B )15 (C)21 (D)27 3、设随机变量X 服从正态分布N (μ,σ2),则随着σ的增大,P (|X −μ|<σ)( )(A )单调增大 (B )单调减少 (C )保持不变 (D )增减不定4、任一连续型随机变量的概率密度函数ϕ(x )一定满足( )(A )0≤ϕ(x )≤1;(B )定义域内单调不减;(C )∫ϕ(x )+∞−∞dx =1;(D )lim x→+∞ϕ(x )=1。
5、设随机变量ξ,η满足条件D (ξ+η)=D (ξ−η),则有( )事实上 (A ) Dη=0 (B )ξ,η不相关 (C )ξ,η相互独立 (D )Dξ⋅Dη=0三、综合题(每小题5分共30分)1.某射击小组共有20名射手,其中一级射手4名,二级射手8名,三级射手7名,四级射手1名,一、二、三、四级射手能通过选拔进入决赛的概率分别是0.9,0.7,0.5,0.2,求在小组内任选一名射手,该射手能通过选拔进入决赛的概率。
大学《概率论与数理统计》期末考试试卷含答案

大学《概率论与数理统计》期末考试试卷含答案一、填空题(每空 3 分,共 30分)在显著性检验中,若要使犯两类错误的概率同时变小,则只有增加 样本容量 .设随机变量具有数学期望与方差,则有切比雪夫不等式 .设为连续型随机变量,为实常数,则概率= 0 . 设的分布律为,,若绝对收敛(为正整数),则=.某学生的书桌上放着7本书,其中有3本概率书,现随机取2本书,则取到的全是概率书的概率为. 设服从参数为的分布,则=. 设,则数学期望= 7 .为二维随机变量, 概率密度为, 与的协方差的积分表达式为 .设为总体中抽取的样本的均值,则= . (计算结果用标准正态分布的分布函数表X ()E X μ=2()D X σ={}2P X μσ-≥≤14X a {}P X a =X ,{}1,2,k k P X x p k ===2Y X =1n k k k x p ∞=∑n()E Y 21k k k x p ∞=∑17X λpoisson (2)E X 2λ(2,3)YN 2()E Y (,)X Y (,)f x y X Y (,)Cov X Y (())(())(,)d d x E x y E y f x y x y +∞+∞-∞-∞--⎰⎰X N (3,4)14,,X X {}15P X ≤≤2(2)1Φ-()x Φ示)10. 随机变量,为总体的一个样本,,则常数=.A 卷第1页共4页 概率论试题(45分) 1、(8分)题略解:用,分别表示三人译出该份密码,所求概率为 (2分)由概率公式 (4分)(2分) 2、(8分) 设随机变量,求数学期望与方差.解:(1) = (3分) (2) (3分) (2分)(8分) 某种电器元件的寿命服从均值为的指数分布,现随机地取16只,它们的寿命相互独立,记,用中心极限定理计算的近似值(计算结果用标准正态分布的分布函数表示).2(0,)XN σn X X X ,,,21 X221()(1)ni i Y k X χ==∑k 21n σA B C 、、P A B C ()P A B C P ABC P A P B P C ()=1-()=1-()()()1-1-1-p q r =1-()()()()1,()2,()3,()4,0.5XY E X D X E Y D Y ρ=====()E X Y +(23)D X Y -()E X Y +E X E Y ()+()=1+3=4(23)4()9()12ov(,)D X Y D X D Y C X Y -=+-8361244XYρ=+-=-100h i T 161ii T T ==∑{1920}P T ≥()x Φ解: (3分) (5分)(4分)(10分)设随机变量具有概率密度,.(1)求的概率密度; (2) 求概率.解: (1) (1分)A 卷第2页共4页(2分)(2分)概率密度函数 (2分)(2) . (3分) (11分) 设随机变量具有概率分布如下,且.i i ET D T E T D T 2()=100,()=100,()=1600,()=160000{1920}0.8}1P T P ≥=≥≈-Φ(0.8)X 11()0x x f x ⎧-≤≤=⎨⎩,,其它21Y X =+Y ()Y f y 312P Y ⎧⎫-<<⎨⎬⎩⎭12Y Y y F y y F y≤>时()=0,时()=1212,{}{1}()d Y y F yP Y y P X y f x x <≤≤=+≤=()=02d 1x y ==-2()=Y Y y f y F y≤⎧'⎨⎩1,1<()=0,其它3102Y YP Y F F ⎧⎫-<<=-=⎨⎬⎩⎭311()-(-1)=222(,)X Y {}110P X Y X +===(1)求常数; (2)求与的协方差,并问与是否独立?解: (1) (2分)由(2分) 可得 (1分)(2), , (3分) (2分) 由可知与不独立 (1分) 三、数理统计试题(25分)1、(8分) 题略. A 卷第3页共4页 证明:,相互独立(4分) ,(4分),p q X Y (,)Cov X Y X Y 1111134123p q p q ++++=+=,即{}{}{}{}{}101011010033P X Y X P Y X p P X Y X P X P X p +====+========+,,1p q ==EX 1()=2E Y 1()=-3E XY 1()=-6,-CovX Y E XY E X E Y ()=()()()=0..ij i j P P P ≠X Y 222(1)(0,1),(1)X n S N n χσ--22(1)X n S σ-2(1)X t n -(1)X t n -(10分) 题略解:似然函数 (4分)由 可得为的最大似然估计 (2分)由可知为的无偏估计量,为的有偏估计量 (4分) 、(7分) 题略 解: (2分)检验统计量,拒绝域 (2分)而 (1分)因而拒绝域,即不认为总体的均值仍为4.55 (2分)A 卷第4页共4页2221()(,)2n i i x L μμσσ=⎧⎫-=-⎨⎬⎩⎭∑2221()ln ln(2)ln() 222ni i x n n L μπσσ=-=---∑2222411()ln ln 0,022n ni i i i x x L L nμμμσσσσ==--∂∂===-+=∂∂∑∑221111ˆˆ,()n n i i i i x x n n μσμ====-∑∑2,μσ221ˆˆ(),()n nE E μμσσ-==11ˆn i i x n μ==∑μ2211ˆ()ni i x n σμ==-∑2σ01: 4.55: 4.55H H μμ=≠x z =0.025 1.96z z ≥=0.185 1.960.036z ==>0H。
【清华】2009-2010秋季学期概率统计参考答案
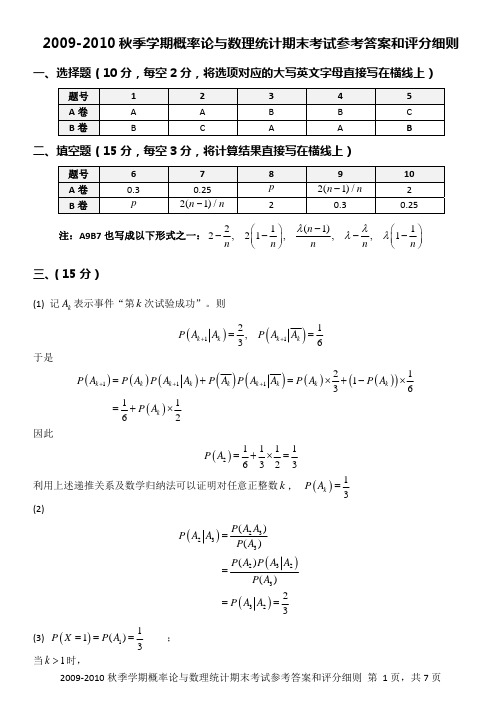
0 μ1μ2 eμ2u dv −∞ μ1 + μ2
= μ1 μ1 + μ2
pW
,V
(w,
v)
=
μ μ e 1 −μ1wv−μ2v
12
w>0,v>0
pW
(w)
=
μ1μ2
( μ1w + μ2
)2
1w>0
∫ P ( X1 < X 2 ) = P(W < 1) =
1 μ1μ2
0 ( μ1w + μ2
)2
dw
X
≤
t)
=
P( X
≥
e−t )
=
⎧1 − e−t , ⎨ ⎩ 0,
t ≥ 0; t < 0.
故 Z ∼ Exp(1)
(2) 解法 1:卷积公式
+∞
∫ f X +Y (t) = −∞ f X (x) fY (t − x)dx
∫=
1 0
e−
(t
−
x
)1t
−
x
>0
dx
∫ = 1t>0 e−t
min(1,t ) ex dx
∫ ∫ ⎪ t t−x
=⎨ ⎪0 0
f X (x) fY ( y)dydx,
⎪
0
⎩
t ≥ 1; 0 ≤ t < 1;
t < 0.
∫⎧
⎪
1
1
−
e
x−t
dx
0
= 1 − e−t (e −1)
∫ ⎪
=⎨
t
1−
ex−t dx
=
t
+
e−t
(完整版)自考本概率论与数理统计真题10套

全国2013年10月高等教育自学考试04183LSA .B 是枉》两个f®机班件,则FCAU S )为&设随机变fi X »从参数为4的泊松分布/!1下列姑论中正《的是 A T FCX> = O.S.£>(X) =0. 5 B.蓟X) =0.5.D<X)=0. 2& CE<X)=2<DCX) = 1D.£(X)^1*DCX)=4人设a 机变* X 与 Y 相互趣立>R X-B<36,y 5.则 OCX — Y+12C.9D,10、单项选择题(本大题共 10小题,每小题2分,共20分)d 玖A) +rtB>-F<AB)PCA>+PCBJ-PUa)G, PGA)十- HMB)D. FCA)+ P<B)乱已気随机?^件仏B 満足PtA) -C.3t P(B) =0.5T HA/m. 15*则B. PUMQ M HJOn. P 3|A S> = FWK. P(3|AB>=P(J3>3.做下函®中能成为挟髓机变■分布函数的是(Z T X O I 扎F (云)=■{5 X < 0-0, J < 0.C. F (工)fl - if"",D» FCr) =40,工vm氐设^ELS«tX~NWJhXW#ft 函数为况£ .则PCI X\>2y 的值対B. sets —1C. 2—血(打D. 1 一 2e(2)£ •设二维®机变的分布律与边绦分布律为E 设隧机变盘X 的Ed) = 80001 Pi7&00 < X<fi3OO}的值为 A. 0. 04 a. 0, £0 UA )=1OT,利用切KS 夫不零式tt 计 C. 0. S6 D. 1. 00则扎 ^=0.1SC. <:™ 0.叽 M=a 14久设CX|.Xj,-^.XJ是来自总休X~N33》的一亍样本.X足样木均値•那么C.10. S信度(1 一C表达了暨信邕冏的A.播册性圧箭确度 C.显善性 D.可黨®二、填空题(本大题共15小题,每小题2分,共30分)It «肘手射击的命中舉为a 6■在4次射击扌有且仪有3狀命审的柢率広设人与5是闊个郴互观立随机車件・P<A) =0.2 . PCB)-Q. 7S'J尸(A — B)=口・设A T H是网个剧机爭件’若卩〔人)=0•趴卩(A-B) -a氣则p(a|4)三M.SffiW变ffiX W分布律抑尸CX=k)二畀口4 = 1*2・3) *則a卩严心0,15.谊X的概華密度几为IE参® 0 *vo .^P{X < 11=^0. SPljPtX < 2}=lb设Wft变*X的分布律为IX-2 -1 0 10U 0.2 0.4 0. 1忆设/<Xry>为二维陆机变* CCY)的««函数.则匸匸和jCtyldzdy le.二堆随机变》(x,y》的分布律为则P{-Z<X< 1}=则rfxY =2}=19已知®机證*兀的分布律为X—21CP1 2 1 -4 4 4已a E (;O = l 侧常載C=巴知 E(X)=-l,t)(X)-3,KiJ EQW —2)= 2L —亍二项分布的re 机变ft ”其載学期龟与方蟹之比为W 阳刑该分布的参®22,设总体XJK 从iE 态分布N 〔宀屮〉・X, 刿圧样本・则參数^1^的笔估计值23■设制造某种炉件产品所需工时(璋位訂卜时》服从正蕊分布,为了估计M 造这沖产品所需的单件平均工时.现制造4件,记录每件所帚工时如下* L0.54ML,2若确定置蓿度为0+曹5•则平均工时的淹信国间为C fi,«C5) =2* 3534* (1011(3)工 3. 1624) 24.设总从正毎分布"3, m …“皿 为K 样本.卞輕%已知,丘倉样乘均1S-SW 于服设检腔冋膻H 才尸二丹,Hp 严护H.应薜用的统计®悬 麵已知一元性回归方程为yi +恳上・耳亍=氛y=9・WR L三、计算题(本大题共2小题,每小题8分,共16分)2札对同一目标进行三ft 独立射击,第一欢、第二》:•第三次射击的命中畢分别为0"、 ①5.0.7,衆在这三RBt 击中•恰好有一次击中目标的ft 耶.2匚设髓亂变竄X 在】.2▼氛4四个誥ft 中第可能的取ffi,另一随机变■ Y 在 g X 中 爭可ft 的耽值,试求x-y 的分布律,四、综合题(本大题共2小题,每小题12分,共24分)K<0* 0< j< 1,J m*起、2.试求dD 系数片I(2>X 的《率《度(⑶ p{xXMy .2缶设连aSK 机变* X 的分布函»为尸5)-彳0, AxS A J C羽•设甲・乙两射手.他们的射击技术分别如ffi 貂佔)表.題2900表所示•其中% , Y 分别 «示甲”乙肘手射击耳数的分茹悄况1X8 9 10 Y89 】0 P0.40.20*4P :0. 10.S5 1题295〉表fiS 29(b)表现耍从中选拔一名射手去奮加比奏,试讨邈选派哪位肘手鑫赛比敦合理?五、应用题(10分)30.某《居民日tt 入®从正®幷布,现ffi 机鞠査该K 姑位居民'得知他们的平均收人 i«66. 4元*标准差$ = 15元卜试问I<1: a = 0. 05下*是否可W 认为该镇居毘日平均收人为70 3c? (23ff a = 0,OSTi 是否耶氏认为该镇居民日收入的方签为16’?^fl.MsC24) = Z, 064 ,&耐(24)* 1, 7109*%咄* = 1* 96 * 划,=】* 65 述剛住4〉=39. 4,£M24〉=36. 4述刖二24〉= 12.4,x5.ii<24)=13, 84S金国201:?年・1月高竽教存口学莆试 概率论与数理统计(经管类)试题一、《念选摄题C 本尢H 其山小騒.毎小題2分,冀加分) 在毎小《列出的四个备a 项中只有一个堆符合Hl 目豪求的r 谓将其选出并郸“菩a 壤*的相应代码涤«・»途・茅涤或未滾均无分.L 耶,乙两人向剧一a 标射击* /董示-甲脂中a 極".fl 我示“乙饰中0标”,C* 示-ft 中a 标二wc-A. JB. BC. AB2*设为fifi 机■fb 尺舟・射,2)・0乳则尺4R)-A. 0JB. 02C. OJD ・0.43. ttffi 机$*rfn 分布瞒数为尺Q. W?i(i<rcfr)=A* 恥一0) — 卜'(—0)B, F9-0)-F(G C,尸O)-FGa-O)D.柯)-尸何血设二罐融杭变》CV ■门的分布律为X0 1 2 0 00J *2 10L 403B, 0-1G 0.2W^(v-o>A. 0绝空★考试结東前全国2013年4月高等教育口学考试概率论与数理统计(经管类)试题课程代码:»41«3a 考生按规定用«将所冇试a 的答«涂■写在笞a 維上。
《概率论与数理统计》期末考试(B)卷答案与评分标准

海南师范大学物理、电子、自动化、地理、城规、计算机专业《概率论与数理统计》 2009—2010学年度第一学期期末考试(B )卷答案与评分标准注意事项:1. 考前请将密封线内填写清楚 2. 所有答案请直接答在试卷上3.考试形式:闭卷4. 本试卷共五大题,满分100分, 考试时间100分钟一、单项选择题(本题共六小题,每小题3分,共18分。
在每小题列出的四个选项中只有一个是符合题目要求的,请将其代码填在题后的括号内。
错选或未选均无分)1、将3个不同的球随机地放入4个不同的杯中, 有一个杯子放入2个球的概率是( B ).. A :324234C C ⋅; B :324234P C ⋅ ; C :424233P C ⋅; D :424233C C ⋅.2、下列函数中,可看作某一随机变量X 的概率分布密度函数的是( C ) A :;,1)(2+∞<<-∞+=x x x f B :;,11)(2+∞<<-∞+=x xx fC :;,)1(1)(2+∞<<-∞+=x x x f π; D :.,)1(2)(2+∞<<-∞+=x x x f π3、己知随机变量Y X ,相互独立且都服从正态分布)4 ,2(N , 则( B ) . A :)4 ,4(~N Y X +; B :)8 ,4(~N Y X + ; C :)4 ,0(~N Y X -; D :Y X -不服从正态分布.4、己知随机变量X 服从二项分布)2.0 ,10(B , 则方差=)(X D ( D ). A :1; B :0.5; C :0.8; D :1.6.5、己知随机变量X 的期望5)(=X E , 方差4)(=X D , 则( A ). A :98}65-X {≥<P ; B :98}65-X {≤<P ; C :98}65-X {≥≥P ; D :98}65-X {≤≥P .6、设4321,,,X X X X 是来自正态总体) ,(2σμN 的简单随机样本,下列四个μ的无偏估计量中,最有效的是( D ). A :)(313211X X X ++=μ; B :)2(413214X X X ++=μ; C :)32(613213X X X ++=μ; D :)(4143212X X X X +++=μ.二、填空题(将答案直接填入栝号内,本题共六小题,每小题3分,共18分)1、设B A 与为随机事件,3.0)(,5.0)(==AB P A P ,则条件概率=)(A B P ( 0.6 )2、已知随机变量X 服从区间,10]2[内的均匀分布,X 的概率分布函数为),(x F 则=)4(F ( 0.25 )。
2013-2014学年《概率论与数理统计》期末考试试卷-(A)答案

1. 0.5 ;0.58 2. 2/5 3.4. 0.3 ;0.5 5. 10 ;8 6. 21 7. 8/9 8. )41.05,41.05(025.0025.0z z +-《概率论与数理统计》期末考试试卷 (A)一、填空题(每小题4分,共32分).1.设 A 、B 为随机事件, P (A ) = 0.3, P (B ) = 0.4, 若 P (A |B ) =0.5, 则 P (A ⋃B ) = __0.5_____; 若 A 与 B 相互独立, 则 P (A ⋃B ) = ____0.58____.2.设随机变量 X 在区间 [1, 6] 上服从均匀分布, 则 P { 1 < X < 3} = _____2/5_________.3.设随机变量 X 的分布函数为,2,1 21 ,6.011 ,3.01,0 )(⎪⎪⎩⎪⎪⎨⎧≥<≤<≤--<=x x x x x F 则 X 的分布律为___________________________ .4.若离散型随机变量 X 的分布律为则常数 a = _0.3________; 又 Y = 2X + 3, 则 P {Y > 5} = _0.5________ .5.设随机变量 X 服从二项分布 b (50, 0.2), 则 E (X ) = ___10_____, D (X ) = _8__________.6.设随机变量 X ~ N (0, 1), Y ~ N (1, 3), 且X 和 Y 相互独立, 则D (3X - 2Y ) =___21______.7.设随机变量 X 的数学期望 E (X ) = μ, 方差 D (X ) = σ 2, 则由切比雪夫不等式有 P {|X - μ | < 3σ } ≥ _________________.8.从正态总体 N (μ, 0.1 2) 随机抽取的容量为 16 的简单随机样本, 测得样本均值5=x ,则未知参数 μ 的置信度为0.95的置信区间是 ____________________________. (用抽样分布的上侧分位点表示). 1. D 2. A 3. C 4. B 5. D 6. C详解:2.因为⎰∞-=xt t f x F d )()( 故⎰-∞-=-at t f a F d )()( 令u =-t ⎰∞+--=-a u u f a F d )()(⎰+∞=au u f d )(⎰+∞=at t f d )(⎰-=a t t f 0d )(21 (21d )(0=⎰+∞t t f )详解:4.因为X ~)1,0(N ,Y ~)1,1(N 所以 1)(=+Y X E ,2)(=+Y X D 故)()(Y X D Y X E Y X ++-+21-+=Y X ~)1,0(N 所以21}021{=≤-+Y X P 即 21}01{=≤-+Y X P 21}01{=≤-+Y X P二、选择题(只有一个正确答案,每小题3分,共18分)1.设A , B , C 是三个随机变量,则事件“A , B , C 不多于一个发生” 的逆事件为( D ).(A) A , B , C 都发生 (B) A , B , C 至少有一个发生 (C) A , B , C 都不发生 (D) A , B , C 至少有两个发生2.设随机变量 X 的概率密度为 f (x ), 且满足 f (x ) = f (-x ), F (x ) 为 X 的分布函数, 则对任意实数 a , 下列式子中成立的是 ( A ). (A) 错误!未找到引用源。
概率论与数理统计考试试卷(附答案)

概率论与数理统计考试试卷(附答案)一、选择题(共6小题,每小题5分,满分30分) 1. 事件表达式B A -的意思是 ( ) (A) 事件A 与事件B 同时发生 (B) 事件A 发生但事件B 不发生 (C) 事件B 发生但事件A 不发生(D) 事件A 与事件B 至少有一件发生2. 假设事件A 与事件B 互为对立,则事件A B ( ) (A) 是不可能事件 (B) 是可能事件 (C) 发生的概率为1(D) 是必然事件3. 已知随机变量X ,Y 相互独立,且都服从标准正态分布,则X 2+Y 2服从 ( ) (A) 自由度为1的χ2分布 (B) 自由度为2的χ2分布 (C) 自由度为1的F 分布(D) 自由度为2的F 分布4. 已知随机变量X ,Y 相互独立,X ~N (2,4),Y ~N (-2,1), 则( )(A) X +Y ~P (4) (B) X +Y ~U (2,4) (C) X +Y ~N (0,5) (D) X +Y ~N (0,3)5. 样本(X 1,X 2,X 3)取自总体X ,E (X )=μ, D (X )=σ2, 则有( ) (A) X 1+X 2+X 3是μ的无偏估计(B)1233X X X ++是μ的无偏估计(C) 22X 是σ2的无偏估计(D) 21233X X X ++⎛⎫ ⎪⎝⎭是σ2的无偏估计6. 随机变量X 服从在区间(2,5)上的均匀分布,则X 的方差D (X )的值为( ) (A) 0.25(B) 3.5(C) 0.75(D) 0.5二、填空题(共6小题,每小题5分,满分30分。
把答案填在题中横线上) 1. 已知P (A )=0.6, P (B |A )=0.3, 则P (AB )= __________2. 三个人独立地向一架飞机射击,每个人击中飞机的概率都是0.4,则飞机被击中的概率为__________3. 一个袋内有5个红球,3个白球,2个黑球,任取3个球恰为一红、一白、一黑的概率为_____4. 已知连续型随机变量,01,~()2,12,0,.x x X f x x x ≤≤⎧⎪=-<≤⎨⎪⎩其它 则P {X ≤1.5}=_______.5. 假设X ~B (5, 0.5)(二项分布), Y ~N (2, 36), 则E (2X +Y )=__________6. 一种动物的体重X 是一随机变量,设E (X )=33, D (X )=4,10个这种动物的平均体重记作Y ,则D (Y )=_____________________ _______三、有两个口袋,甲袋中盛有两个白球,一个黑球,乙袋中盛有一个白球,两个黑球。
10-11Ⅰ概率论与数理统计试卷(A)参考答案

10-11Ⅰ概率论与数理统计试卷(A)参考答案| | | | | | | |装|| | | |订|| | | | |线| | | | | | | | |防灾科技学院2010~2011学年第⼀学期期末考试概率论与数理统计试卷(A )使⽤班级本科各班适⽤答题时间120分钟⼀、填空题(每题3分,共21分)1、设A 、B 、C 是三个事件,4/1)(=A P ,3/1)(=A B P ,2/1)(=B A P ,则=)(B A P1/3 ;2、已知10件产品中有2件次品,在其中任取2次,每次任取⼀件,作不放回抽样,则其中⼀件是正品,⼀件是次品的概率为16/45 ;3、随机变量X 的分布函数是??≥<≤<=.1,110,,0,0)(2x x x x x F ,=)}({2X E X P e21;5、从1,2,3中任取⼀个数,记为X ,再从X ,,1 任取⼀个数,记为Y ,则==}2{Y P 5/18 ;6、设随机变量X 和Y 相互独⽴,且均服从区间[]1,0的均匀分布,则3/4 ;7、设样本4321,,,X X X X 为来⾃总体)1,0(N 的样本,243221)(X X X C X Y +++=,若Y 服从⾃由度为2的2χ分布,则=C 1/3 。
⼆、单项选择题(本⼤题共7⼩题,每题3分,共21分)1、某⼈向同⼀⽬标独⽴重复射击,每次射击命中⽬标的概率为p ,则在第4次射击时恰好第2次命中⽬标的概率为( B )(A) 22)1(4p p -; (B) 22)1(3p p -; (C) 22)1(2p p -; (D) 3)1(p p -; 2、设随机变量X 的概率分布律为,2,1,0,!}{===k k A k X P ,则参数=A ( D )(A) 0 ; (B) 1; (C) e ; (D) 1-e ;3、设随机变量X 的分布函数为()F x ,则31Y X =+的分布函数为( A )(A )11()33F y -;(B ) (31)F y +;(C ) 3()1F y +;(D 11()33F y -;4、设连续型随机变量X 的概率密度为?<≥=-.0,0,0,)(x x e x f x λλ,则=≥})({X D X P ( C )(A) 0 ; (B) 1; (C) 1-e ; (D) e ;5、设随机变量X 与Y 相互独⽴,其概率分布分别为10.40.6XP 01(A )1}{==Y X P ;(B )0}{==Y X P ;(C )52.0}{==Y X P ;(D )5.0}{==Y X P ;6、若)2(,,,21≥n X X X n 为来⾃总体)1,0(N 的简单随机样本,X 为样本均值,2S为样本⽅差,则(C )(A ))1,0(~N X n ;(B ))(~22n nSχ;(C ))1(~/-n t nS X ;(D ))1,0(~N X ;7、总体X 的分布律 ()1/,0,1,2,,1P X k N k N ===- .已知取⾃总体的⼀个样本为(6,1,3,5,3,4,0,6,5,2),则参数N 的矩估计值是 ( A ))(A 8; )(B 7; )(C 6; )(D 5.(本⼤题共2⼩题,每题7分,共14分。
(完整版)自考本概率论与数理统计真题10套

X
-1
0
1
0
0.3
0.2
0.1
1
0.1
0.3
0
求:(1)X和Y的分布律;(2)Cov(X,Y).
四、综合题(本大题共2小题,每小题12分,共24分)
28.某次抽样结果表明,考生的数学成绩(百分制)近似地服从正态分布N(75,σ2),已知85分以上的考生数占考生总数的5%,试求考生成绩在65分至85分之间的概率.
11.设甲、乙两人独立地向同一目标射击,甲、乙击中目标的概率分别为0.8,0.5,则甲、乙两人同时击中目标的概率为_____________.
12.设A,B为两事件,且P(A)=P(B)= ,P(A|B)= ,则P( | )=_____________.
13.已知事件A,B满足P(AB)=P( ),若P(A)=0.2,则P(B)=_____________.
23.设x1,x2,…,xn是来自总体B(20,p)的样本,则p的矩估计 =__________.
24.设总体服从正态分布N(μ,1),从中抽取容量为16的样本, 是标准正态分布的上侧α分位数,则μ的置信度为0.96的置信区间长度是_________.
25.设总体X~N(μ,σ2),且σ2未知,x1,x2,…,xn为来自总体的样本, 和S2分别是样本均值和样本方差,则检验假设H0:μ=μ0;H1:μ≠μ0采用的统计量表达式为_________.
三、计算题(本大题共2小题,每小题8分,共16分)
26.一批零件由两台车床同时加工,第一台车床加工的零件数比第二台多一倍.第一台车床出现不合格品的概率是0.03,第二台出现不合格品的概率是0.06.
(1)求任取一个零件是合格品的概率;
(2)如果取出的零件是不合格品,求它是由第二台车床加工的概率.
第2学期《概率论与数理统计》B卷及答案

ni i 1
n 1 i1 i
证明
:
Y
X X n1
n ~ t(n 1) 。
S n1
N(, 2)
的一个样
第 3 页(共 3 页)
------------------------------------------------- 密 ---------------------------------- 封 ----------------------------- 线 ---------------------------------------------------------
一定相互独立。
第 1 页(共 3 页)
------------------------------------------------- 密 ---------------------------------- 封 ----------------------------- 线 ---------------------------------------------------------
7.设 X1, X 2 , X n , n 2 为正态总体 N (, 2 ) 的一个样本,当常数 C=-------------时,
n1
Q C ( Xi1 Xi )2 为 2 的无偏估计 i 1 8.设总体 X ~ N (,32 ) 如果希望 的 0.95 的置信区间长度不超过 2,那需要抽取的样本
3.设 X 1 n X , a 为任意常数,,则当 a X 时
n
( X a)2 到达计算题(共 55 分) 1.(11 分)三门高射炮对一架敌机独立地一齐各发射一炮,它们的命中率分别为 10%,
20%,30%,求:(1)敌机至少中一弹的概率;(2)敌机恰好中一弹的概率。
试卷09-10(2)概率论与数理统计A答案

四、(12分)已知连续型随机变量 的概率密度函数 ,
(1)确定常数 ;(2)求 的分布函数 ;(3)求 .
解:(1)因 ,故 .…………3’
则随机变量 的概率密度函数 …………1’
(2) 的分布函数 ……5’
(3) …………3’
五.(7分)已知 的概率密度 , ,求 的概率密度函数 .
统计量 的观察值 ,…………2’
故接受 ,即认为总体均值没有显著变化.…………1’
(1)一个新客户在购买保险后一年内需要理赔的概率为多少?
(2)如果该客户在购买保险后一年内出一次事故,他是第一类人的概率有多大?
解:设事件 :新客户是第一类人,事件 :新客户是第二类人;
事件B:新客户出事故,即需要理赔,
(1) …………3’
(2) …………3’
故一个新客户在购买保险后一年内需要理赔的概率为0.26
8.衡量估计量优良性的三个标准为一致性,无偏性,有效性_____.
9.已知随机变量 ,则 28/5.
10.设离散型随机变量 只能取0,1,2三个值,且取相应值的概率分别为 ,则 的分布律为 .
三、(6分)保险公司认为人可以分为两类:第一类是易出事故的人,第二类是比较谨慎,不易出事故的人。统计数字表明,第一类人一年内某时刻出一次事故的概率为0.4,第二类人在一年内某时刻出一次事故的概率为0.2,若第一类人占30%,问
令 ,…………1’
解得 的最大似然估计值为 …………1’
八、(7分)已知某炼铁厂的铁水含碳量在正常情况下服从正态分布 ,现测了5炉铁水,得其平均含碳量为4.364。若方差未变,问总体均值是否有显著变化?( )
解:假设 …………1’
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上海海洋大学试卷
姓名: 学号: 专业班名:
一、填空题(本大题共6小题,每小题3分,总计18分)
1. 设,A B 为随机事件,()0.8P A B = ,()0.4P B =,则()
|P A B = 3
2
2.10个球队平均分成两组进行比赛,则最强的两个队分到同一组的概率为
9
2
3.设随机变量X 在区间[0,1]上服从均匀分布,则X
Y e =的数学期望为 1-e
4.设X ~(,)b n p 为二项分布,且() 1.6E X =,() 1.28D X =,则n =_8___p = 2.0
5.设),(~2σμN X ,则
~n
X σμ
-( )1,0(N )
6. 设AB φ=,()0.3,()0.4,P A P B ==则=⋃)(B A P (
7.0 )。
二、选择题(在各小题四个备选答案中选出一个正确答案,填在题末的括号中,本大题共6个小题,
每小题3分,总计18分)
1.设事件,A B 相互独立,且()0P A >,()0P B >,则有 B
(A) ()|0P B A =; (B) ()()|P A B P A =; (C) ()|0P A B =; (D) ()()P AB P A =
2.设,A B 为事件,且A B ⊂,则下列式子一定正确的是( B )
(A) ()()P A B P A = ; (B); ()()P BA P A =
(C) ()()P AB P B =; (D) ()()()P A B P A P B -=-
3. 设随机变量X 的分布率为{}1!
k
P X k a k λ==⋅, ()1,2,k = ,则a = ( B )
(A) e
λ
-; (B) e λ; (C) 1e
λ
--; (D) 1e λ-
4. 设X ~)1,1(N ,概率密度为()f x ,分布函数为()F x ,则有( A )
(A) {1}{1}P X P X ≤=≥; (B) {0}{0}P X P X ≤=≥;
(C) ()()f x f x =-, x R ∈; (D) ()()1F x F x =--, x R ∈
5.掷一枚质地均匀的骰子,则在出现奇数点的条件下出现3点的概率为( D )。
(A) 1/3 (B)2/3 (C)1/6 (D) 3/6
6.12,,n X X X 是来自正态总体X ~()
2
,N μσ的样本,其中μ已知,σ未知,则下列不是统计量的是
( C )
(A) 1max k k n
X ≤≤; (B) X μ-; (C)
1
n
k
k X σ
=∑; (D) 1min k k n
X ≤≤
三、计算题(本大题共6小题,每小题9分,共计54分)
1. 有三个盒子,第一个盒子中有2个黑球,4个白球,第二个盒子中有4个黑球,2个白球,第三个盒子中
有3个黑球,3个白球,今从3个盒子中任取一个盒子,再从中任取1球. (1) 求此球是白球的概率;
(2) 若已知取得的为白球,求此球是从第一个盒子中取出的概率. 解: 设=i A “取中第i 个盒子” )3,2,1(=i ,=B “取中白球”,则
31)(=
i A P ,32)|(1=A B P ,31)|(2=A B P ,2
1
)|(3=A B P (1) 由全概率公式,得 21
)213132(31)|()()(3
1
=++==
∑=i
i i
A B P A P B P ;
(2) 由贝叶斯公式,得
94
2
132
31)()()|(11=⨯
==B P B A P B A P .
2.已知连续型随机变量X 的分布函数为0,
()arcsin ,1,
x a x F x A B a x a a x a ≤-⎧⎪⎪
=+-<≤⎨⎪
>⎪⎩,其中0a >为常数。
求: (1) 常数,A B 的值; (2) 随机变量X 的密度函数()f x ;(3) 2a P X a ⎛⎫
<<
⎪⎝⎭
解: (1)由
)()(lim
a F x F a x =+
→,有2arcsin
1π
B A a a B A +=+= 由
)()(lim
a F x F a x -=+
-→,有2
arcsin
0π
B A a a B A -=-+= 解得21=
A ,π
1
=B ;
(2) ⎪⎩
⎪
⎨⎧
≤≤--==,01)()(22'a x a x a x F x f π
(3) 3
1
)21arcsin 121(1)2()()2(=+-=-=<<πa F a F a X a P .
3.设连续型随即变量X 的概率密度1
,()0,
c x
d f x d c ⎧<<⎪
=-⎨⎪⎩其它,
求E(X ),D(X )
解: ;2
)()(d c dx c d x dx x xf X E d
c
+=-==⎰⎰
+∞∞
- 3
)()(2
222
2
d cd c dx c d x dx x f x X E d c
++=-==⎰⎰
∞
+∞
- 12
)()()()(2
2
2
c d X E X E X D -=-=.
4.某厂有三条流水线生产同一产品,每条流水线的产品分别占总量的40%,35%,25%,
又这三条流水线的次品率分别为0.02, 0.04,0.05。
现从出厂的产品中任取一件,问恰好取到次品的概率是多少?
解:设=i A “取到第i 条生产线的产品” )3,2,1(=i ,=B “取到次品”,则
4.0)(1=A P ,3
5.0)(2=A P ,25.0)(3=A P
02.0)|(1=A B P ,04.0)|(2=A B P ,05.0)|(3=A B P
由全概率公式,得 0345.005.025.004.035.002.04.0)|()()(3
1
=⨯+⨯+⨯==
∑=i
i i
A B P A P B P
5.有一大批糖果,现从中随机地抽取16袋,称得重量的平均值503.75x =克,样本方差6.2022S =。
求总体均值μ的置信度为0.95的置信区间。
(0.05α=,查表
()0.02515
2.1315t =) 解:建立统计量 )1(~2
--=
n t n
S
X T μ
则μ的置信度为α-1的置信区间为
,)1([2
--
n t n S
X α,)]1(2
-+
n t n S
X α
将1315
.2)15(,05.0,16,2022.6,75.503025.0=====t n S X α代入,计算得
]06.507,44.500[
6.某厂生产的固体燃料推进器的燃烧率服正态分布()2,N μσ,μ=40cm/s,2/cm s σ=。
现在用新
方法生产了一批推进器,从中随机取25n =只,测得燃烧率的样本均值为41.25/x cm s =。
设在新方法下总体均方差仍为2cm/s ,问这批推进器的燃烧率是否较以往生产的推进器的燃烧率有显著的提高?取显著性水平0.05α=。
(查表0.05 1.645Z =) 解:建立假设;40:00=≥μμH .:01μμ<H 选择检验统计量n
X Z σ
μ0
-=
,进行单侧Z 检验,拒绝0H 的条件为:645.105.0-=-<z Z 。
将25,2,25.41===n X σ代入,计算得125.325
2
40
25.41=-=
Z 。
因为645.1125.3->=Z ,故接受0H ,即可认为这批推进器的燃烧率较以往生产的推进器的燃烧率有显著的提高。
四.证明题(本题10分)
设总体为X , 期望()E X μ=,方差()2D X σ=,12,,,n X X X ⋅⋅⋅是取自总体X 的一个样本, 样本
均值11n i i X X n ==∑,样本方差()22
1
11n i
i S X X n ==--∑,证明:2S 是参数2σ的无偏估计量 证明:因为
2
1)(X X n i i ∑=-∑=-=n
i i X n X 1
2
2
,且)()()(22X E X D X E +=
得=
-∑=))((
2
1
X X E n
i i ∑=-n
i i X nE X E 12
2
)()(
-+=
∑=])()([1
2n
i i i
X E X
D )]()([2X
E X D n +
)(
)(22
1
2
2
μσμσ
+-+=
∑=n
n n
i
2
)1(σ-=n 故2
2)(σ=S E
即2
S 是参数2
σ的无偏估计量。
