粒子群算法及其优化方案
第6章粒子群优化算法

第6章粒子群优化算法PSO算法的基本原理是通过模拟粒子在空间中的移动,从而找到最优解。
每个粒子代表一个可能的解,并根据自身的经验和群体的经验进行。
粒子的速度和位置的更新使用以下公式:v(t+1) = w * v(t) + c1 * rand( * (pbest - x(t)) + c2 *rand( * (gbest - x(t))x(t+1)=x(t)+v(t+1)其中,v(t)代表粒子的当前速度,x(t)代表粒子的当前位置,w是惯性权重,c1和c2是学习因子,rand(是一个0到1之间的随机数,pbest 是粒子自身的最佳位置,gbest是整个群体的最佳位置。
PSO算法的过程如下:1.初始化粒子的位置和速度。
2.计算每个粒子的适应度值。
3. 更新每个粒子的pbest和gbest。
4.根据公式更新每个粒子的速度和位置。
5.重复步骤2到4,直到达到终止条件。
PSO算法有几个重要的参数需要设置:-群体大小:确定PSO算法中粒子的数量。
较大的群体大小可以增加整个空间的探索能力,但也增加了计算复杂度。
-惯性权重:控制粒子速度变化的因素。
较大的惯性权重可以增加粒子的飞行距离,但可能导致过程陷入局部最优解。
-学习因子:用于调节个体经验和群体经验的权重。
c1用于调节个体经验的权重,c2用于调节群体经验的权重。
较大的学习因子可以增加粒子的探索能力,但也可能增加时间。
PSO算法的优点是简单、易实现,收敛速度较快,对于多维、非线性、离散等问题具有良好的适应性。
然而,PSO算法也存在一些缺点,如易陷入局部最优解、对参数的敏感性等。
总之,粒子群优化算法是一种基于群体智能的优化算法,在求解复杂问题方面具有出色的性能。
它的基本原理是通过模拟粒子的移动来最优解,利用个体经验和群体经验进行自适应。
PSO算法在多个领域都有成功的应用,可以帮助解决实际问题。
高斯量子行为粒子群优化(gqpso)算法

高斯量子行为粒子裙优化(GQPSO)算法是一种基于量子行为的进化优化算法,它结合了粒子裙优化(PSO)算法和量子计算的特点,能够有效地解决复杂优化问题。
本文将从以下几个方面介绍GQPSO算法的原理、特点和应用,希望能够为读者提供深入的了解。
一、GQPSO算法的原理GQPSO算法是基于粒子裙优化算法和量子计算的原理而提出的,它采用了一种全新的粒子编码和演化方式,通过模拟粒子在量子力学中的行为进行搜索和优化。
GQPSO算法的原理如下:1. 量子位表示在GQPSO算法中,每个粒子被表示为一个量子位,根据其在搜索空间中的位置,每个粒子的量子位可以被编码为一个二进制字符串。
这种量子位表示方式能够更好地描述粒子的位置和速度,从而更好地指导搜索过程。
2. 高斯量子演化GQPSO算法通过高斯量子演化来更新粒子的量子位和速度,其中包括量子位的变换和速度的更新。
在高斯量子演化过程中,粒子会受到适应性函数的约束,从而导致不断演化、搜索和优化。
3. 适应性函数GQPSO算法中使用的适应性函数通常是目标函数或者问题的评价函数,它能够帮助粒子判断当前位置的优劣,并指导其向更优的位置演化。
适应性函数的选择对于算法的性能至关重要。
二、GQPSO算法的特点GQPSO算法相比于传统的优化算法有着独特的特点和优势,主要表现在以下几个方面:1. 全局搜索能力强GQPSO算法通过量子位表示和高斯量子演化,能够有效地克服传统算法在全局搜索能力上的不足,更好地发挥粒子裙优化算法的优势,从而在复杂优化问题中取得更好的效果。
2. 收敛速度快GQPSO算法利用了量子行为的特性,能够更快地收敛到全局最优解,从而大大提高了算法的搜索效率和优化能力。
在实际应用中,GQPSO 算法往往能够在较短的时间内找到较优的解。
3. 对高维问题有较好的适应性GQPSO算法对于高维优化问题的适应性较强,能够有效地应对复杂的实际问题,从而满足实际应用的需求。
这一特点使得GQPSO算法在实际工程和科研中有着广泛的应用前景。
粒子群优化算法 程序

粒子群优化算法程序粒子群优化算法(Particle Swarm Optimization, PSO)是一种基于群体智能的优化算法,它模拟了鸟群或鱼群等生物群体的行为,用于解决各种优化问题。
下面我将从程序实现的角度来介绍粒子群优化算法。
首先,粒子群优化算法的程序实现需要考虑以下几个关键步骤:1. 初始化粒子群,定义粒子的数量、搜索空间的范围、每个粒子的初始位置和速度等参数。
2. 计算适应度,根据问题的特定适应度函数,计算每个粒子的适应度值,以确定其在搜索空间中的位置。
3. 更新粒子的速度和位置,根据粒子的当前位置和速度,以及粒子群的最优位置,更新每个粒子的速度和位置。
4. 更新全局最优位置,根据所有粒子的适应度值,更新全局最优位置。
5. 终止条件,设置终止条件,如最大迭代次数或达到特定的适应度阈值。
基于以上步骤,可以编写粒子群优化算法的程序。
下面是一个简单的伪代码示例:python.# 初始化粒子群。
def initialize_particles(num_particles, search_space):particles = []for _ in range(num_particles):particle = {。
'position':generate_random_position(search_space),。
'velocity':generate_random_velocity(search_space),。
'best_position': None,。
'fitness': None.}。
particles.append(particle)。
return particles.# 计算适应度。
def calculate_fitness(particle):# 根据特定问题的适应度函数计算适应度值。
particle['fitness'] =evaluate_fitness(particle['position'])。
粒子群优化算法原理

粒子群优化算法原理
粒子群优化算法是一种群体智能算法,在仿真自然界粒子寻找食物的行为基础上,模拟多个个体在解空间中搜索全局最优解。
算法采用群体协同行为,通过不断迭代更新每个粒子的位置和速度,直至找到最优解。
算法流程:
1.初始化种群:随机生成一定数量的粒子,并随机初始化粒子的位置和速度。
2.评价粒子适应度:根据某个评价准则,评估每个粒子的适应度,并更新最优位置和全局最优位置。
3.更新每个粒子的速度和位置:根据一定的规则,更新每个粒子的速度和位置,使其朝向全局最优位置的方向移动,并在一定程度上考虑个体的最优位置。
4.重复迭代:不断循环进行步骤2和3,直到满足结束条件为止。
算法特点:
1.全局搜索能力较强,易于收敛到全局最优解。
2.算法复杂度较低,易于实现和应用。
3.算法具有较强的鲁棒性,对初始参数的选择和变异操作的变化相对不敏感。
4.算法应用范围广泛,可以用于目标函数的优化、机器学习参数的优化、图像处理等领域。
粒子群优化算法综述

粒子群优化算法综述粒子群优化算法的核心思想是模拟粒子通过信息交流来寻找最优解的过程。
每个粒子在空间中通过位置和速度进行与移动。
它们通过个体极值和全局极值的引导来调整自己的速度和位置。
具体而言,每个粒子根据自身经验和信息共享来更新速度和位置,并不断跟随历史经验和全局经验向最优解逼近。
在原始的粒子群优化算法中,粒子的速度和位置更新公式如下:\begin{{align*}}V_{ij}(t+1) &= wV_{ij}(t) + c_1r_1(p_{ij}(t) - x_{ij}(t)) + c_2r_2(g_{ij}(t) - x_{ij}(t)) \\x_{ij}(t+1) &= x_{ij}(t) + V_{ij}(t+1)\end{{align*}}\]其中,$V_{ij}(t)$为粒子$i$在维度$j$上的速度,$x_{ij}(t)$为粒子$i$在维度$j$上的位置,$p_{ij}(t)$为粒子$i$当前的个体最优位置,$g_{ij}(t)$为全局最优位置,$r_1$和$r_2$为[0, 1]的随机数,$c_1$和$c_2$为学习因子。
尽管原始的粒子群优化算法在一些简单问题上表现出良好的性能,但对于复杂问题,其效率和精度有待提升。
因此,研究者进行了一系列的改进与发展。
首先是关于学习因子的改进。
学习因子的选择会影响算法的性能。
经典的学习因子取值策略是将$c_1$和$c_2$设置为常数,但这种策略缺乏自适应性。
改进的学习因子选择方法包括线性递减学习因子、非线性学习因子和自适应学习因子等。
其次是关于收敛性和多样性的改进。
经典的粒子群优化算法容易陷入局部最优解,从而导致的收敛性不佳。
研究者通过引入惯性权重、控制种群多样性、引入随机性等方式改善了算法的收敛性和多样性。
此外,还有一些改进的算法思想在粒子群优化算法中得到了应用。
例如,粒子竞争机制、学习机制和混合策略等。
这些改进方法可以提高粒子群优化算法的效率和精度。
粒子群优化算法及其在多目标优化中的应用

粒子群优化算法及其在多目标优化中的应用一、什么是粒子群优化算法粒子群优化算法(Particle Swarm Optimization,PSO)是一种智能优化算法,源自对鸟群迁徙和鱼群捕食行为的研究。
通过模拟粒子受到群体协作和个体经验的影响,不断调整自身的位置和速度,最终找到最优解。
PSO算法具有简单、易于实现、收敛速度快等优点,因此在许多领域中得到了广泛应用,比如函数优化、神经网络训练、图像处理和机器学习等。
二、PSO在多目标优化中的应用1.多目标优化问题在现实中,多个优化目标相互制约,无法同时达到最优解,这就是多目标优化问题。
例如,企业在做决策时需要考虑成本、效益、风险等多个因素,决策的结果是一个多维变量向量。
多目标优化问题的解决方法有很多,其中之一就是使用PSO算法。
2.多目标PSO算法在传统的PSO算法中,只考虑单一目标函数,但是在多目标优化问题中,需要考虑多个目标函数,因此需要改进PSO算法。
多目标PSO算法(Multi-Objective Particle Swarm Optimization,MOPSO)是一种改进后的PSO算法。
其基本思想就是将多个目标函数同时考虑,同时维护多个粒子的状态,不断优化粒子在多个目标函数上的表现,从而找到一个可以在多个目标函数上达到较优的解。
3.多目标PSO算法的特点与传统的PSO算法相比,多目标PSO算法具有以下特点:(1)多目标PSO算法考虑了多个目标函数,解决了多目标优化问题。
(2)通过维护多个粒子状态,可以更好地维护搜索空间的多样性,保证算法的全局搜索能力。
(3)通过优化粒子在多个目标函数上的表现,可以寻找出在多目标情况下较优的解。
三、总结PSO算法作为一种智能优化算法,具备搜索速度快、易于实现等优点,因此在多个领域有广泛的应用。
在多目标优化问题中,多目标PSO算法可以通过同时考虑多个目标函数,更好地寻找在多目标情况下的最优解,具有很好的应用前景。
优化算法-粒子群优化算法

步骤四:对于粒子的每一维,根据式(1)计算得到一个随机点 的位置。
步骤五:根据式(2)计算粒子的新的位置。
步骤六:判断是否满足终止条件。
粒子群优化算法
PSO算法在组合优化问题中的应用
典型的组合优化问题:TSP
粒子群优化算法
量子行为粒子群优化算法的基本模型
群智能中个体的差异是有限的,不是趋向于无穷大的。群体的聚 集性是由相互学习的特点决定的。
个体的学习有以下特点: 追随性:学习群体中最优的知识
记忆性:受自身经验知识的束缚
创造性:使个体远离现有知识
粒子群优化算法
聚集性在力学中,用粒子的束缚态来描述。产生束缚态的原因是 在粒子运动的中心存在某种吸引势场,为此可以建立一个量子化 的吸引势场来束缚粒子(个体)以使群体具有聚集态。
描述为: 给定n 个城市和两两城市之间的距离, 求一条访问各城市
一次且仅一次的最短路线. TSP 是著名的组合优化问题, 是NP难题, 常被用来验证智能启发式算法的有效性。
vid (t 1) wvid (t) c1r1 pid (t) xid (t) c2r2( pgd (t) xid (t))
xid (t 1) xid (t) vid (t 1)
粒子群优化算法
w 惯性权重 可以是正常数,也可以是以时间为变量的线性或非线性
正数。
粒子群优化算法
通常动态权重可以获得比固定值更好的寻优结果,动态权重可以在 pso搜索过程中呈线性变化,也可以根据pso性能的某个测度函数 而动态改变,目前采用的是shi建议的随时间线性递减权值策略。
粒子群优化算法
粒子群优化方法范文

粒子群优化方法范文
具体而言,粒子群优化算法包括以下几个步骤:
1.初始化粒子群:设定种群中粒子的初始位置和初始速度,并为每个粒子随机分配初始解。
2.评估个体适应度:通过适应度函数评估每个粒子的适应度,确定其解的质量。
3.更新粒子速度和位置:根据自身历史最优解和全局历史最优解,调整粒子的速度和位置,并更新粒子自身的最优解。
4.更新全局最优解:根据所有粒子的最优解,更新全局最优解,记录当前到的最佳解。
5.判断终止条件:设定终止条件,例如达到最大迭代次数、适应度值的收敛等,判断是否结束优化。
6.迭代更新:不断重复步骤2至5,直到满足终止条件。
相对于其他优化算法,粒子群优化算法具有以下优点:
1.简单而直观:算法的核心思想易于理解,模拟了生物群体的行为规律。
2.全局能力:粒子群优化算法可以问题的全局最优解,避免陷入局部最优解。
3.并行化和分布式计算:粒子群优化算法的并行化和分布式计算非常容易实现,能够加速求解过程。
然而,粒子群优化算法也存在一些不足之处:
1.对参数的敏感性:算法的性能受到参数设置的影响,不同问题需要不同的参数组合。
2.适应度函数的选取:适应度函数的选择对算法的结果有着重要的影响,需要根据问题的特点进行合理的设计。
3.收敛速度较慢:在寻找复杂问题的最优解时,粒子群优化算法可能需要较长的时间来收敛。
总之,粒子群优化算法是一种有效的全局优化算法,能够在多种问题中找到较优解。
通过合理选择参数和适应度函数,并结合其他优化方法,可以进一步提高算法的性能和收敛速度。
粒子群算法的多目标优化

粒子群算法的多目标优化粒子群算法(Particle Swarm Optimization,PSO)是一种启发式优化算法,最初由Eberhart和Kennedy在1995年提出,灵感来自鸟群觅食行为。
它通过模拟鸟群中鸟的飞行行为,实现对多个目标的优化求解。
在传统的PSO算法中,只针对单个目标进行优化。
但在实际问题中,经常存在多个目标需要同时优化。
多目标优化问题具有复杂性、多样性和冲突性等特点,往往不能简单地通过将多个目标融合为一个综合目标进行求解,因此需要专门的多目标优化算法。
多目标粒子群算法(Multi-objective Particle Swarm Optimization,MOPSO)是一种扩展的PSO算法,可以解决多目标优化问题。
它通过改进传统PSO的算法机制,使得粒子在过程中能够维持一组非劣解集合(Pareto解集合),从而得到一系列最优解,满足不同领域的需求。
MOPSO算法的具体步骤如下:1.初始化粒子的位置和速度,并随机分布在空间内。
2.根据多个目标函数值计算每个粒子的适应度,用以评估其优劣程度。
3.更新粒子的速度和位置。
速度的更新包括惯性权重、自我认知因子和社会认知因子等参数。
位置的更新采用基本PSO的方式进行。
4.根据更新后的位置,重新计算粒子的适应度。
5.更新全局最优解集合,将非劣解加入其中。
采用非劣解排序方法来实现。
6.判断终止条件是否满足,若满足则输出所有非劣解;否则返回第3步。
MOPSO算法相对于传统的PSO算法,主要的改进在于更新全局最优解集合的方法上。
非劣解排序方法可以帮助保持解的多样性,避免陷入局部最优解。
多目标粒子群算法在多目标优化问题中具有一定的优势和应用价值。
它能够同时考虑多个目标的优化需求,并提供一系列的最优解供决策者选择。
在实际应用中,MOPSO算法已经成功应用于控制系统设计、图像处理、机器学习等多个领域。
总结起来,多目标粒子群算法是一种有效的多目标优化算法。
粒子群算法优化问题例子

粒子群算法优化问题例子1.简介粒子群算法(Pa rt ic l eS wa rm Op ti mi zat i on,P SO)是一种基于群体智能的搜索优化算法,模拟了鸟群或鱼群等生物群体在搜索食物或逃避危险时的行为。
粒子群算法通过不断更新粒子的速度和位置来找到问题的最优解。
本文将为你介绍粒子群算法以及其在解决优化问题中的应用。
2.粒子群算法原理粒子群算法借鉴了鸟群或鱼群等生物群体的行为模式,将优化问题转化为寻找适应度函数的最小值或最大值的问题。
每个粒子代表一个潜在解,通过不断迭代更新速度和位置,使粒子朝着全局最优解或局部最优解靠近。
2.1粒子的表示在粒子群算法中,每个粒子都有自己的速度和位置。
在优化问题中,通常将每个粒子的位置表示为一个n维向量,其中n为问题的维度。
2.2粒子的更新粒子的更新包括两个部分:速度的更新和位置的更新。
速度的更新通过考虑粒子当前的速度、个体最优解和群体最优解来计算,以确定粒子下一时刻的速度。
位置的更新则根据粒子当前的位置和速度,计算出粒子下一时刻的位置。
2.3群体最优解的更新群体最优解是指当前所有粒子的最优解。
通过比较粒子的适应度值,找出适应度函数最小值或最大值所对应的粒子位置作为群体最优解。
群体最优解的更新会影响粒子速度的计算。
3.粒子群算法的应用粒子群算法在优化问题中有着广泛的应用,下面将介绍两个粒子群算法应用的例子。
3.1函数优化问题函数优化问题是粒子群算法常见的应用场景之一。
例如,我们可以将一个多元函数的最大化或最小化问题转化为粒子群算法的求解过程。
通过不断更新粒子的位置和速度,迭代搜索最优解。
3.2旅行商问题旅行商问题是在给定限制条件下,求解访问一系列城市并回到起点的最短路径问题。
粒子群算法可以通过将每个粒子的位置表示为某一路径,通过不断迭代更新粒子的位置,找到最优的旅行路径。
4.总结粒子群算法是一种利用群体智能进行搜索和优化的算法,模拟了生物群体的行为。
本文简要介绍了粒子群算法的原理以及在优化问题中的应用。
粒子群优化算法综述

粒子群优化算法综述粒子群优化(Particle swarm optimization, PSO)是一种以群体行为模型为基础的进化算法,它是模拟群体中每个体的行动及各种影响机制来找到最优解。
1995年,Eberhart和Kennedy提出了粒子群优化(PSO)算法。
这个算法被用于多维、非线性优化问题,并认为其结果要好于其他搜索算法。
一、粒子群优化算法介绍:1、算法框架:粒子群优化算法是一种迭代搜索算法,它模拟生物世界中群体行为的进化机制来寻找最优解,它的基本框架如下:(1)初始化参数:决定搜索空间的边界条件,确定粒子群的初始状态;(2)计算适应度函数:按照不同的情况确定适应度函数,计算粒子群种群体的适应度;(3)更新种群体:根据当前种群体的适应度情况,更新个体的位置和速度;(4)迭代搜索:重复以上步骤,等待算法收敛到最优解;(5)结果输出:输出算法收敛的最优解。
2、算法特点:粒子群优化算法具有以下优势:(1)算法易于实现;(2)参数少;(3)计算局部搜索和全局搜索并重;(4)利用简单的几何形式,可以用于多目标优化问题。
二、应用情况:粒子群优化算法在多种复杂场景中应用十分灵活,它可以用于以下几个应用场景:(1)最优控制问题:用于解决轨道优化、多种自控问题。
(2)另一个应用领域是多元函数的优化求解,例如多元函数拟合、计算仿真等。
(3)另一个重要应用领域是信息处理,包括图像处理、模式识别等。
三、发展趋势:粒子群优化算法具有很好的搜索能力、实现简单以及参数少等优点,由于其交叉搜索能力和准确度,越来越受到关注,并被采用到各个领域。
然而,近些年,粒子群优化算法也因其原始算法难以改进收敛精度方面存在一定限制,受到两方面限制:一是获得最优解的能力较弱;二是收敛速度较慢。
四、结论:粒子群优化算法是一种利用生物行为模型进行优化的新算法,它在最优控制技术、多元函数优化求解以及信息处理等多个方面具有很好的应用价值。
虽然存在一定的缺点,但是随着计算机能力和计算机科学的发展,粒子群优化算法仍然具有良好的发展前景。
基本粒子群优化算法

基本粒子群优化算法基本粒子群优化算法(Particle Swarm Optimization, PSO)是一种基于群体智能的优化算法,灵感来自于鸟群捕食行为中的信息共享和合作。
该算法能够在空间内找到不错的解决方案,并且具有较强的全局收敛性和鲁棒性。
本文将详细介绍基本粒子群优化算法的原理、流程、变种以及应用领域。
一、基本粒子群优化算法的原理基本粒子群优化算法的原理是模拟社会性行为中物种群体的行为方式。
每个空间中的解被视为一个粒子,这些粒子之间通过其中一种形式的信息交流来寻找全局最优解。
在算法的每一代中,每个粒子记录着自身的位置、速度和当前最优解。
粒子迭代更新自己的速度和位置,通过与邻居粒子和全局最优解比较来引导方向。
通过不断迭代,粒子逐渐收敛于全局最优解。
二、基本粒子群优化算法的流程1.初始化粒子群:随机生成粒子群,设置每个粒子的初始位置和速度。
2.计算目标函数值:根据粒子的当前位置计算目标函数值,并更新该粒子的当前最优解。
3.更新全局最优解:比较粒子群中所有粒子的当前最优解,选取最优解作为全局最优解。
4.更新速度和位置:根据当前速度和位置,更新粒子的下一步速度和位置。
新位置在空间内随机选择,并根据速度进行调整。
5.收敛判断:判断是否满足停止条件,如果满足则结束;否则返回第2步。
三、基本粒子群优化算法的变种1.改进的基本粒子群优化算法:对基本粒子群优化算法进行改进,比如引入加速因子、惯性权重等参数来提升算法的收敛速度和精度。
2.多种群粒子群优化算法:将粒子群分为多个子群,在子群间进行信息共享和合作,以提高效率。
3.自适应权重的粒子群优化算法:根据过程中的适应度变化情况,自适应地调整粒子的权重,以提高算法的鲁棒性和全局收敛性。
四、基本粒子群优化算法的应用领域1.组合优化问题:如旅行商问题、背包问题等。
2.函数优化问题:如非线性优化、函数拟合等。
3.机器学习:如神经网络训练、特征选择等。
4.工程设计:如电力系统优化、通信网络设计等。
粒子群优化算法粒子群优化算法简介
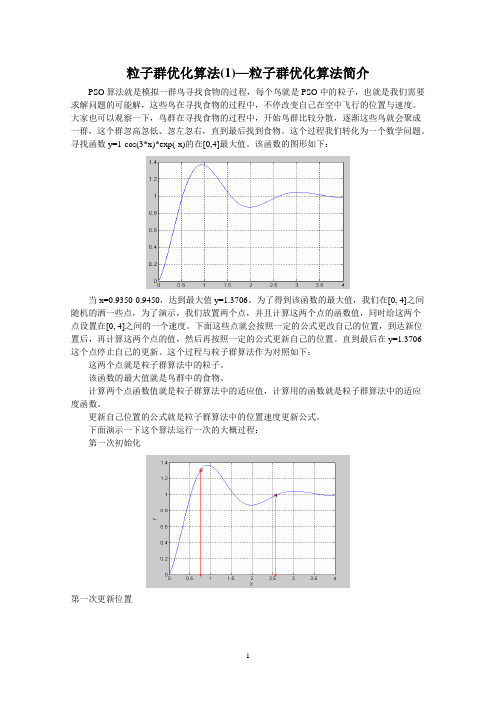
粒子群优化算法(1)—粒子群优化算法简介PSO算法就是模拟一群鸟寻找食物的过程,每个鸟就是PSO中的粒子,也就是我们需要求解问题的可能解,这些鸟在寻找食物的过程中,不停改变自己在空中飞行的位置与速度。
大家也可以观察一下,鸟群在寻找食物的过程中,开始鸟群比较分散,逐渐这些鸟就会聚成一群,这个群忽高忽低、忽左忽右,直到最后找到食物。
这个过程我们转化为一个数学问题。
寻找函数y=1-cos(3*x)*exp(-x)的在[0,4]最大值。
该函数的图形如下:当x=0.9350-0.9450,达到最大值y=1.3706。
为了得到该函数的最大值,我们在[0, 4]之间随机的洒一些点,为了演示,我们放置两个点,并且计算这两个点的函数值,同时给这两个点设置在[0, 4]之间的一个速度。
下面这些点就会按照一定的公式更改自己的位置,到达新位置后,再计算这两个点的值,然后再按照一定的公式更新自己的位置。
直到最后在y=1.3706这个点停止自己的更新。
这个过程与粒子群算法作为对照如下:这两个点就是粒子群算法中的粒子。
该函数的最大值就是鸟群中的食物。
计算两个点函数值就是粒子群算法中的适应值,计算用的函数就是粒子群算法中的适应度函数。
更新自己位置的公式就是粒子群算法中的位置速度更新公式。
下面演示一下这个算法运行一次的大概过程:第一次初始化第一次更新位置第二次更新位置第21次更新最后的结果(30次迭代)最后所有的点都集中在最大值的地方。
粒子群优化算法(2)—标准粒子群优化算法在上一节的叙述中,唯一没有给大家介绍的就是函数的这些随机的点(粒子)是如何运动的,只是说按照一定的公式更新。
这个公式就是粒子群算法中的位置速度更新公式。
下面就介绍这个公式是什么。
在上一节中我们求取函数y=1-cos(3*x)*exp(-x)的在[0, 4]最大值。
并在[0,4]之间放置了两个随机的点,这些点的坐标假设为x1=1.5,x2=2.5;这里的点是一个标量,但是我们经常遇到的问题可能是更一般的情况—x 为一个矢量的情况,比如二维z=2*x1+3*x22的情况。
粒子群优化算法

粒子群优化算法
在PSO算法中,问题解被表示为一个多维空间中的一个粒子。
每个粒
子都有一个位置和速度,位置表示当前解,速度表示解的更新方向。
粒子
的行为受到个体最优和群体最优的影响。
个体最优是指粒子自身经历过的
最佳位置,群体最优是指整个粒子群中所有粒子最佳位置的集合。
在每一次迭代中,粒子根据当前位置和速度进行更新。
更新的过程中,粒子会考虑个体最优和群体最优的信息,以及一个随机因子。
通过不断迭代,粒子的位置和速度会逐渐靠近最优解,最终收敛到全局最优解或者局
部最优解。
PSO算法的主要步骤如下:
1.初始化粒子群,包括粒子位置和速度。
2.计算粒子的适应度值,并更新个体最优解。
3.更新群体最优解。
4.更新粒子的速度和位置。
5.判断终止条件,如果满足条件则结束迭代,否则返回第2步。
PSO算法的优点是简单易实现,收敛速度快,鲁棒性强。
它能够处理
连续空间和非线性问题,并且不需要求导。
PSO算法也能够通过参数设置
和自适应机制来克服其缺点。
然而,PSO算法也存在一些不足之处。
首先,它对初始解的敏感度较高,不同的初始解可能导致不同的结果。
其次,PSO算法对于高维问题的
效果较差,易陷入局部最优解。
此外,PSO算法的收敛性和收敛速度与问
题的复杂性和特性有关。
综上所述,粒子群优化算法是一种有效的全局优化算法,适用于各种优化问题。
虽然PSO算法存在一些不足,但通过合理的参数设置和改进算法,可以扩大其适用范围和提高效果。
粒子群优化算法实例

粒子群优化算法(PSO)是一种基于群体智能的优化算法,通过模拟鸟群觅食行为中的社会心理学原理来求解优化问题。
下面是一个简单的粒子群优化算法实例:
假设我们要解决一个最小化问题,即找到一个函数f(x)的最小值。
我们可以使用粒子群优化算法来求解这个问题。
初始化粒子群:随机生成一组粒子,每个粒子代表问题的一个解。
粒子的位置表示解的取值,速度表示解的变化方向。
评估粒子适应度:计算每个粒子的适应度值,即函数f(x)的取值。
更新粒子速度和位置:根据粒子当前的位置、速度和全局最优解的信息,更新粒子的速度和位置。
具体更新公式如下:
速度更新公式:v[i] = w * v[i] + c1 * rand() * (pbest[i] - x[i]) + c2 * rand() * (gbest - x[i])
位置更新公式:x[i] = x[i] + v[i]
其中,w是惯性权重,c1和c2是学习因子,rand()是随机数生成函数,pbest[i]是粒子i的历史最优解,gbest是全局最优解。
更新全局最优解:比较每个粒子的适应度值和全局最优解的适应度值,如果某个粒子的适应度值更小,则更新全局最优解。
迭代执行步骤2-4,直到达到预设的迭代次数或满足停止条件。
返回全局最优解作为问题的近似解。
通过上述步骤,我们可以使用粒子群优化算法来求解最小化问题。
需要注意的是,粒子群优化算法是一种启发式算法,不能保证找到全局最优解,但在许多实际问题中,它能够找到较好的近似解。
粒子群优化算法介绍

粒子群优化算法介绍
粒子群优化算法是一种基于群体智能的优化算法,它模拟了鸟群或鱼群等生物群体的行为,通过不断地迭代寻找最优解。
该算法最初由美国加州大学的Eberhart和Kennedy于1995年提出,目前已经被广泛应用于各种优化问题中。
粒子群优化算法的基本思想是将待优化问题转化为一个多维空间中的搜索问题,将每个解看作空间中的一个粒子,每个粒子的位置表示该解的参数值,速度表示该解的变化方向和速度。
在算法的每一次迭代中,每个粒子都会根据自身的历史最优解和群体最优解来更新自己的速度和位置,以期望找到更优的解。
具体来说,粒子群优化算法的实现过程如下:
1. 初始化粒子群,包括粒子的位置和速度等信息。
2. 计算每个粒子的适应度值,即待优化问题的目标函数值。
3. 更新每个粒子的速度和位置,包括考虑自身历史最优解和群体最优解的影响。
4. 判断是否满足停止条件,如果满足则输出最优解,否则返回第2步。
粒子群优化算法的优点在于其简单易懂、易于实现和收敛速度较快等特点。
同时,该算法还具有较好的全局搜索能力和鲁棒性,能够
应对复杂的非线性优化问题。
然而,粒子群优化算法也存在一些缺点,如易陷入局部最优解、对参数的选择较为敏感等问题。
因此,在实际应用中需要根据具体问题进行调整和优化。
粒子群优化算法是一种有效的优化算法,已经被广泛应用于各种领域,如机器学习、图像处理、控制系统等。
随着人工智能和大数据技术的不断发展,相信粒子群优化算法将会有更广泛的应用前景。
粒子群算法组合优化

粒子群算法组合优化引言:组合优化问题是指在给定一组元素的情况下,通过选择其中的若干个元素,使得满足一定条件的目标函数取得最优值的问题。
在实际应用中,组合优化问题非常普遍,例如旅行商问题、背包问题等。
粒子群算法(Particle Swarm Optimization,简称PSO)是一种用于求解组合优化问题的优化算法,它模拟了鸟群觅食的过程,并通过群体合作来寻找全局最优解。
本文将详细介绍粒子群算法的原理、优缺点以及应用实例等内容。
一、粒子群算法的原理1.初始化粒子群:随机生成一组粒子,并为每个粒子分配一个随机的位置和速度。
2.计算适应度:根据问题的目标函数,计算每个粒子的适应度值。
3.更新粒子速度和位置:根据粒子自身的历史最优位置和全局最优位置,通过以下公式更新粒子的速度和位置:v(t+1) = ω * v(t) + c1 * rand( * (pbest - x(t)) + c2 *rand( * (gbest - x(t))x(t+1)=x(t)+v(t+1)其中,v(t)表示粒子在时刻t的速度,x(t)表示粒子在时刻t的位置,pbest表示粒子的历史最优位置,gbest表示全局最优位置,ω、c1、c2为控制速度更新的参数,rand(为随机函数。
4.更新粒子的历史最优位置和全局最优位置:如果当前位置的适应度值优于粒子的历史最优位置,则更新历史最优位置;如果当前位置的适应度值优于全局最优位置,则更新全局最优位置。
5.判断停止条件:如果满足停止条件(例如达到最大迭代次数或达到目标适应度值),则结束算法,否则返回步骤3二、粒子群算法的优缺点1.基于群体智能:粒子群算法模拟了鸟群觅食的过程,通过粒子之间的合作和信息交流来最优解,具有较强的全局能力。
2.全局收敛性:粒子群算法通过不断更新全局最优位置,可以快速收敛到全局最优解。
3.直观简单:粒子群算法的原理简单,易于理解和实现。
4.并行计算:粒子群算法中的每个粒子都可以进行并行计算,可加速求解过程。
Matlab中的粒子群优化算法详解

Matlab中的粒子群优化算法详解引言:粒子群优化算法(Particle Swarm Optimization, PSO)是一种模拟鸟群觅食行为的优化算法,具有简单易实现、无需求导和全局搜索能力强等特点。
该算法在解决多种问题中得到广泛应用,特别是在机器学习、智能优化等领域。
本文将详细介绍Matlab中粒子群优化算法的实现过程及应用。
一、粒子群优化算法原理粒子群优化算法源自于对鸟群觅食行为的模拟。
假设一个鸟群中的每个个体被称为粒子,所有粒子共同组成了一个搜索空间,每个粒子会根据自身的当前位置和历史最佳位置进行搜索,并且受到其邻近粒子的信息影响。
通过不断的迭代运算,粒子们逐渐收敛到全局最优解或局部最优解。
具体算法流程如下:1. 初始化粒子群的位置和速度。
2. 计算每个粒子的适应度值,并更新个体最优位置。
3. 根据全局最优位置调整粒子的速度和位置。
4. 重复执行第2步和第3步,直到满足终止条件。
二、Matlab中粒子群优化算法实现步骤在Matlab中,可以通过以下步骤来实现粒子群优化算法:1. 初始化粒子群的位置和速度。
首先需要确定粒子群的大小,即粒子的个数。
对于每个粒子,需要随机生成一个初始位置和速度。
可以使用Matlab中的rand函数来生成指定范围内的随机数。
问题优劣的指标,因此需要根据具体问题来确定。
对于更新个体最优位置,可以通过比较当前适应度值和历史最佳适应度值的大小,选择适应度更优的位置进行更新。
3. 根据全局最优位置调整粒子的速度和位置。
粒子的速度和位置的更新是通过以下公式实现的:V(i,j) = w * V(i,j) + c1 * rand() * (P(i,j) - X(i,j)) + c2 * rand() * (G(j) - X(i,j))X(i,j) = X(i,j) + V(i,j)其中,V(i,j)表示第i个粒子在第j个维度上的速度,X(i,j)表示第i个粒子在第j个维度上的位置,P(i,j)表示第i个粒子的历史最佳位置,G(j)表示全局最佳位置,w、c1和c2分别表示惯性权重、个体学习因子和社会学习因子。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
粒子群算法及其优化方案
【摘要】粒子群算法作为一种智能优化算法,由于其实现简单,易于与其他方法结合,在现实应用中逐渐显示出强大的优势。
本文首先介绍了基本的粒子群算法,分析了粒子群算法的优化方面,并且对不同的优化方面进行详细分析。
【关键词】粒子群算法;收敛性;优化
1 引言
粒子群算法(particle swarm optimization,PSO)也称粒子群优化算法,是由Kennedy与Eberhart在鸟类和鱼类等生物群体觅食行为的启发下提出的一种智能优化算法[1]。
PSO初始化为一群随机粒子,然后通过迭代找到最优解。
在每一次迭代中,粒子通过跟踪两个“极值”来进行自我更新。
第一个就是粒子本身的最优解,该解为个体极值(pBest)。
另一极值是整个种群的最优解,该极值为全局极值(gBest)。
PSO以其实现简单、精度高、收敛快等优点在科学计算中得到了广泛关注。
关于PSO算法的理论研究主要集中在算法的结构和性能改善方面,如参数分析,拓扑结构,粒子多样性保持,算法融合和性能比较等[2]。
在PSO算法的应用研究方面,最初应用于神经元网络的训练,之后被用于解决函数优化问题和约束优化问题,如将PSO应用于自动控制系统设计[3]、控制核电机组输出稳定电压[4]、大气中臭氧层的预测[5]等。
目前,PSO 算法已经广泛应用于非线性规划,车辆路径,多目标优化等问题[6]。
2 基本粒子群算法
对于基本的粒子群算法[1],在找到最优值时,粒子根据如下的公式来更新自己的速度和新的位置,具体如下:
算法流程:
1)随机初始化各粒子的速度和位置。
2)根据等式(1)和等式(2)更新粒子的速度和位置。
3)对每个粒子,将其当前位置与历史最优的位置比较,若更优,则将其作为历史最优位置,否则沿用历史最优位置。
4)将每个粒子的个体最优位置与群体所最优位置进行比较,若更优,则将其作为群体最优,否则群体最优位置保持不变。
5)若达到结束条件(即足够好的解或最大迭代次数),则结束,否则转步骤
2)。
3 关于粒子群算法的改进研究
(1)惯性权重
Yuhui Shi等人[7]提出了带有惯性权重的改进粒子群算法。
其进化过程为:
在等式(3)中,第一部分表示粒子的先前速度,用于保证算法的全局收敛性能;第二、第三部分使算法具有局部收敛能力。
可见,式(3)中惯性权重w 表示在多大程度上保留原来的速度。
若w较大,全局收敛能力强,局部收敛能力弱;若w较小,局部收敛能力强,全局收敛能力弱。
(2)限制因子
Clerc等[8]提出了带限制因子的PSO算法,通过正确的的选择w、c1、c2的值来保证算法的收敛性。
其速度更新公式为:
(3)多种群粒子群算法
基于种群优化算法可以通过将种群划分为多个子群来实现对优化目标的搜索,这样的多种群优化措施可以有效地保持种群多样性,提高算法的全局收敛性能。
4 总结
本文介绍了标准的PSO算法及其研究现状,分析了现有的PSO优化方案。
当然,作为一种新兴的群智能算法,粒子群算法的研究与应用还存在许多问题。
比如,算法的收敛性、收敛速度、鲁棒性、参数选择等,同时还应加强对PSO 算法的应用。
参考文献:
[1] Kennedy J,Eberhart R C.Particle swarm optimization [A].Proc IEEE Int Conf on Neural Networks [C].Perth,Australia:IEEE Press,1995.1942-l948.
[2] van der Bergh F,Engelbrecht A P.A study of particle swarm optimization trajectories. Information Sciences,2006,17(6):937-971.
[3] 刘益剑,张建明。
微粒群算法在自动控制系统设计中的应用。
高技术通讯,2005,15(7):24-28.
[4] Jiang C W,Etorre B.A hybrid method of chaotic paticle swarm optimization and linear interior for reactive power optimization. Mathematics and Computers in
Simulation,2005,68:57-65.
[5] Wang D,Lu W Z.Forecasting os ozone level in time series using MLP model with a novel hybrid training algorithm.Atmospheric Environment,2006,40:913-924.
[6] 陈严,刘利民.改进的PSO算法在VRP中的应用[J].计算机工程.2011,37(1):170-172.
[7] Shi Y,Eberhart R C.A modified particle swarm optimizer[C]//Pro-ceedings of the IEEE Congress on Evolutionary Computation.Piscat-away,NJ:IEEE Press,1998:69-73.
[8] Clerc M,Kennedy J.The particle swarm-exposion,stability,and convergence in a multidimen- sional complex space. IEEE Transactions on Ecolutionary Computation,2002,(1):58-73.
致谢:
曹倩通信作者。
本文得到北京市教委科研计划面上项目(No. KM201410011005)、北京市大学生科学研究与创业行动计划(No. SJ201402024)、北京工商大学本科生科技立项资助。
