2017-2018前山中学初三第一学期数学期中考试卷

合集下载

2017-2018上学期九年级期中数学试题及答案

线的解析式为
16.如图 ,△ ABC是等边二角形 ,D是 BC上一点 ,△ ABD经过旋转后到达 △农名的位置
则旋转中心是 `茕
,
,逆
时针旋转了
(第【 6题图
)
(第 17题图 )
17.如图所示 ,AB是 ⊙@的一条弦 ,∠ ⒕ GB=30° ,犭 B=6,则 ⊙@的直径为
茄 1=-1冖
△ }阿|
图1
・ ……・・・・・ …・・・・・・・ … …・ … ・ … ・・・・ …・・ … ……・・・ 3分
(2)如图 2,C2(丬
… ・ … 4分 ………。 ,1);… …………………………………∴,… …。
九年级数学试题参考答案第 1页 (共 3页 )
A.50(1+窝 )2=182
C.50(1 +2“ ) =182
B.50+50(1+x) +50(1+“ )2=182 D.50+50(1 +J) +50(1 +2x) =182
,若
7.二次函数 y=t2+fr x+b中
A。
σ+乙 =0,则它的图象必经过点
(-1,-1)
B(1,-1)
D。
C.(1,l)
(“ -1)=0的解是 2.一元二次方程夂
A,x=O
Ct=0或 t=1
D.× B・ D(凭
B.订 D.舟
BI=2x2
茁 =0再戈 =-1
(吖
3.用配方法解方程 ′ -2x-5=o时 ,原方程应变形为
-1)2=6 C(“ +1)2=6

2017-2018第一学期九年级数学期中试卷

2017-2018学年度第一学期期中检测九年级数学试题（全卷共120分，考试时间90分钟）一、选择题(本题共8题，每题3分，共24分. 在每题给出的四个选项中，有且只有一项是正确的，请将正确选项前的字母代号填涂在答题卡相应位置上) 1. 如图，点A ，B ，C 在⊙O 上，∠AOB =72°，则∠ACB =A ．28ºB ．54ºC ．18ºD ．36º2. 一元二次方程041242=+-x x 的根的情况是A ．有两个不相等的实数根B ．有两个相等的实数根C ．没有实数根D ．无法判断3．用配方法解方程x 2－6x －6=0时，配方后得到的方程是A ．(x +3)2=15 B ．( x +3)2 = 3 C ．(x －3)2 = 15 D ．( x －3)2 = 3 4．若x 1，x 2是一元二次方程x 2﹣2x ﹣3=0的两个根，则x 1•x 2的值是A ．2B ．﹣2C ．4D ．﹣35．将抛物线y ＝2x 2向右平移3个单位，再向下平移5个单位，得到的抛物线的表达式为 A ．y ＝2(x －3)2＋5 B ．y ＝2(x ＋3)2＋5 C ．y ＝2(x －3)2－5 D ．y ＝2(x ＋3)2－56．下列命题：①三角形的外心是三边垂直平分线的交点；②经过三个点一定可以作圆； ③三角形的内心到三角形各顶点的距离都相等；④长度相等的弧是等弧；其中正确结论的个数有A ．1个B ．2个C ．3．4个7．关于二次函数y =x 2－2x －3的图象，下列说法中错误的是A ．函数图像的开口方向向上B ．函数图像的顶点坐标是(1，－2)C ．当x ＜0时，y 随x 的增大而减小D ．函数图象与y 轴的交点坐标是(0，－3) 8．运用图形变化的方法研究下列问题：如图，AB 是⊙O 的直径，CD 、EF 是⊙O 的弦，且AB ∥CD ∥EF ，AB ＝10，CD ＝6，EF ＝8，则图中阴影部分的面积是A ．252π B ．10π C ．24＋4π D ．24＋5π( 第1题 ) （第10题）B( 第8题 )二、填空题(每小题3分，共30分．不需写出解答过程，请把答案直接填写在答题卡相应位置上) 9. 方程x 2－2x ＝0的解是_______▲________.10．四边形ABCD 内接于圆，若∠A ＝110°，则∠C ＝ ▲ 度．11．已知圆弧所在圆的半径为24，所对的圆心角为60°，这条弧的长是 ▲ ． 12．如图，P 是⊙O 外的一点，P A 、PB 分别与⊙O 相切于点A 、B ，C 是劣弧AB 上的任意一点，过点C 的切线分别交P A 、PB 于点D 、E ．若P A =4，则△PED 的周长为 ▲ ． 13．如图，AB 是⊙O 的直径，弦CD ⊥AB 于点E ，若AB ＝8，AE ＝1，则弦CD 的长是 ▲ ．14．若点M （-2，1y ），N （8，2y ）在抛物线x x y 2212+-=的图象上,则1y ▲ 2y （填“>”或“<”）．15．关于x 的一元二次方程02=-+k x x 有两个不相等的实数根，则k 的取值范围是▲ ． 16．中国“一带一路”战略给沿线国家和地区带来很大的经济效益，沿线某地区居民2015年年收入200美元，预计2017年年收入将达到1000美元，设2015年到2017年该地区居民年人均收入平均增长率为x ，可列方程为 ▲ ．17.如图，圆锥的侧面展开图是一个圆心角为120°的扇形，若圆锥的底面圆半径是2，则圆锥的母线l ＝ ▲ . 18. 如图，直线y =mx +n 与抛物线c bx ax y ++=2交于A (-1，p )， B (4，q )两点，则关于x 的不等式c bx ax n mx ++>+2的解集是 ▲ .三、解答题(本大题共有7小题，共66分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤) 19. 解方程 (每题5分，共10分)(1) 2x 2 + 3x －1 = 0； (2) (x －3)(x －1)＝3.( 第12题 )( 第13题 )( 第18题 )( 第17题 )20. (8分)已知⊙O 的直径AB 的长为4 cm ，C 是⊙O 上一点，∠BAC ＝30°，过点C 作 ⊙O 的切线交AB 的延长线于点P ，求BP 的长．21. (8分) 二次函数c bx x y ++=2的图象经过点（2,－3）、（0，5）.(1) 求b 、c 的值；(2) 在所给坐标系中画c bx x y ++=2的图象； (3) 指出当x 满足什么条件时，函数值小于0?22. (8分) 如图，在宽为20m 、长为30m 的矩形地面上，修建两条同样宽且互相垂直的道路，余下部分作为耕地．要使耕地面积达到551m 2，道路的宽应为多少?23. (10分)实践操作：如图，△ABC 是直角三角形，90∠=︒ABC ，利用直尺和圆规按下列要求作图，并在图中标明相应的字母（保留痕迹，不写作法）．(1)作∠BCA 的平分线，交AB 于点O ； (2)以O 为圆心，OB 为半径作圆．综合运用：在你所作的图中，(1)AC 与⊙O 的位置关系是 ▲ （直接写出答案）； (2)若BC ＝6，AB ＝8，求⊙O 的半径．（第23题）( 第20题 )( 第21题 ) ( 第22题 )24. (12分) 某商店经销《超能陆战队》超萌“小白”玩具，“小白”玩具每个进价60元，每个玩具不得低于80元出售．销售“小白”玩具的单价m（元/个）与销售数量n （个）之间的函数关系如图所示．(1)线段AB所表示的实际优惠销售政策是▲；(2)写出该店当一次销售n（10<n<30）个时，所获利润w（元）与n（个）之间的函数关系式；(3)经过一段时间的销售，店长发现：当一次销售数量小于30个时，一次销售数量越多，所获利润不一定越多，你能用数学知识解释这一现象吗?并求出一次销售多少个时，所获利润最大，最大利润是多少元?25. (10分) 在一次数学兴趣小组活动中，小明利用同弧所对的圆周角及圆心角的性质探索了一些问题，下面请你和小明一起进入探索之旅．问题情境：（1）如图1，在△ABC中，∠A＝30°，BC＝2，则△操作实践：（2）如图2，在矩形ABCD中，请利用以上操作所获得的经验，在矩形ABCD内部用直尺与圆规作出一点P．点P满足：∠BPC＝∠BEC，且PB＝PC．（要求：用直尺与圆规作出点P，保留作图痕迹.）迁移应用：（3）如图3，在平面直角坐标系的第一象限内有一点B，坐标为（2，m)．过点B作AB⊥y轴，BC⊥x轴，垂足分别为A、C，若点P在线段AB上滑动(点P可以与点A、B重合)，发现使得∠OPC＝45°的位置有两个，则m的取值范围为▲．( 第24题)( 第25题)。

2017-2018学年第一学期九年级数学(人教版)期中测试题及答案

五、解答题三（本大题 3 小题，每小题 9 分，共 27 分）
23、已知关于 x 的一元二次方程（a+c）x2+2bx+（a－c）=0，其中其中 a,b,c 分别为 △ABC 三边的长。（1）如果 x=－1 是方程的解，试判断△ABC 的形状，,并说明理由。（2）如果方程有两个相等的实数根，试判断△ABC 的形状，并说明理由。（3）如果△ABC 是等边三角形，试求这个一元二次方程的根。
19、如图，已知：BC 与 CD 重合，∠ABC=∠CDE=90°，△ABC≌△CDE，并且△CDE 可由△ ABC 逆时针旋转而得到．（1）请你利用尺规作出旋转中心 O（保留作图痕迹，不写作法，注意最后用墨水笔加黑）。（2）直接写出旋转角度度。
A
B
D
E
C
第 19 题图
第 2 页共 8 页
四、解答题二（本大题 3 小题，每小题 7 分，共 21 分）
。 E D
O
F 第 14 题图
C
y
三、解答题一（本大题 3 小题，每小题 6 分，共 18 分）
17、解方程：3x2－5x+2=0
A D P C
B
O
第 16 题图
18、已知 x=1 是关于 x 的一元二次方程 x2－4mx+m2=0 的根，求代数式 2m（m－2）－（m+ ��）（m－ ��）的值。
2017-2018 学年第一学期期中质量检测九年级数学试卷
说明：1、考试时间：100 分钟。2、满分：120 分。
一、单项选择题（本大题 10 小题，每小题 3 分，共 30 分）
1、下列方程是一元二次方程的是（ A、（x－3）x=x2+2 ） �� C、3x2－ +2=0 �� ） D、（3，4） �� D、2x2=1 B、ax2+bx+c=0

(答案)2017-2018学年度第一学期九年级期中联考数学科试卷

2017-2018学年度第一学期九年级期中联考数学科试卷(答案)13、-3 14、2400 15、6 16、三、解答题：17、解：（1）x2+4x+2=0移项，得：x2+4x=﹣2，配方，得：x2+4x+4=﹣2+4，……………………1分即（x+2）2=2，………………………………………..2分解这个方程，得：x+2=±；即x1=-2+，x2=-2﹣．………….……………3分（2）3x2+2x﹣1=0；这里a=3，b=2，c=﹣1，∵△=4+12=16，……………………1分∴x=，……………………2分∴x1=，x2=﹣1．……………………3分（3）（2x+1）2=﹣3（2x+1）（2x+1）2+3（2x+1）=0，（2x+1）[（2x+1）+3]=0，……………………1分（2x+1）（2x+4）=0，……………………2分解得：x1=﹣，x2=﹣2．……………………3分(其它方法参考给分)18、（1）10 ，80 ……………………2分（2）列表得：∵两次摸球可能出现的结果共有12种，每种结果出现的可能性相同，而所获购物券的金额不低于50元的结果共有6种．……………………5分∴该顾客所获购物券的金额不低于50元的概率是：．……………………6分19、解：(1) 如图，AC,BD即为所求。

…………………2分(2)如图，∵AE∥PO∥BF，∴△AEC∽△POC，△BFD∽△OPD，…………………3分∴，，PA BOC DE F即，，解得：PO=3.3m．…………………5分答：路灯的高为3.3m．…………………6分20、证明：∵四边形ABCD是平行四边形，∴AB∥CD，AD∥BC，∴∠B+∠C=180°，∠ADF=∠DEC．…………………1分∵∠AFD+∠AFE=180°，∠AFE=∠B∴∠AFD=∠C…………………2分∴△ADF∽△DEC；…………………3分（2）解：∵四边形ABCD是平行四边形，∴CD=AB=4，由（1）知△ADF∽△DEC，∴，…………………4分∴DE=12…………………6分在Rt△ADE中，由勾股定理得：==6．…………7分21、解：（1）200+400x…………………1分（2）设应将每千克小型西瓜的售价降低x元，根据题意，得[（3-2）-x]（200+-24=200可化为：50x2-25x+3=0，…………………4分解这个方程，得x1=0.2，x2=0.3．…………………6分为使每天的销量较大，应降价0.3元，即定价3-0.3=2.7元/千克．答：应将每千克小型西瓜的售价定为2.7元/千克．…………………7分22、解：（1）2t，10﹣4t…………………2分（2）设运动的时间为t秒，由勾股定理得，OC==10，1）当CQ=CP时，2t=10﹣4t，解得，t=，此时CP=2×=，∴AP=8﹣=，P 点坐标为（，6）…………………3分2）当PC=PQ 时，如图①，过点p 作OC 的垂线交OC 于点E ，CQ=10﹣4t ，CP=2t ． CE==5-2t 易证△CEP ∽△CAO ， ∴，即：解得 t=∴P 点坐标为（，6），…………………4分3）当QC=PQ 时，如图②，过点Q 作AC 的垂线交AC 于点F ， CQ=10﹣4t ，CP=2t ，CF=t ∵△CFQ ∽△CAO ， ∴，即：∴t=则P 点坐标为（，6），综上所述，P 点坐标为（，6），（，6），（，6）；…………………5分（3）如图③，连接EG ，由题意得：△AOE ≌△AFE ， ∴∠EFG=∠OBC=90°，∵E 是OB 的中点，∴EG=EG ，EF=EB=4，在Rt △EFG 和Rt △EBG 中，，∴Rt △EFG ≌Rt △EBG （HL ）……………6分 ∴∠3=∠4∵∠1+∠2+∠3+∠4=180°，∠1=∠2 ∴∠2+∠3=90°，可证△AOE ∽△EBG 。

2017-18-1九年级数学期中试卷(已排)定.pdf

2017～2018学年度素质教育评估试卷第一学期期中九年级数学试卷温馨提示：本卷共八大题，计23小题，满分150分，考试时间120分钟。

一．选择题：每小题给出的四个选项中，其中只有一个是正确的。

请把正确选项的代号写在下面的答题表内，（本大题共10小题，每题4分，共40分）答题表12345 6789101. 下列标志图中，既是轴对称图形，又是中心对称图形的是（）.A.B. C. D.2．方程(x ＋1)2=4的解是（）. A ．x 1=2，x 2=－2B ．x 1=3，x 2=－3C ．x 1=1，x 2=－3D ．x 1=1，x 2=－23．抛物线y=x 2－2x －3与y 轴的交点的纵坐标为（）.A ．－3B ．－1C ．1D ．34. 如图所示，将Rt △ABC 绕点A 按顺时针旋转一定角度得到Rt △ADE ，点B 的对应点D恰好落在BC 边上．若AB=1，∠B=60°，则CD 的长为（）.A ．0.5 B ．1.5C ．2D ．15．已知关于x 的一元二次方程mx 2＋2x －1=0有两个不相等的实数根，则m 的取值范围是（）.A ．m ＞－1且m ≠０B ．m ＜1且m ≠０C ．m ＜－1D ．m ＞1题号一二三四五六七八总分（1～10）（11～14）1516171819 20212223得分得分评卷人60°EDBAC第4题图九年级数学学校班级姓名学号……………………………………装……………………………………订……………………………………线……………………………………6．将函数y=x 2的图象向左、右平移后，得到的新图象的解析式不可能．．．是（）.A ．y=(x ＋1)2B ．y=x 2＋4x ＋4C ．y=x 2＋4x ＋3D ．y=x 2－4x ＋47．下列说法中正确的个数有（）.①垂直平分弦的直线经过圆心；②平分弦的直径一定垂直于弦；③一条直线平分弦，那么这条直线垂直这条弦；④平分弦的直线，必定过圆心；⑤平分弦的直径，平分这条弦所对的弧．A ．1个B ．2个C ．3个D ．4个8．两年前生产1吨甲种药品的成本是5000元．随着生产技术的进步，成本逐年下降，第二年的年下降率是第1年的年下降率的2倍，现在生产1吨甲种药品成本是2400元．为求第一年的年下降率，假设第一年的年下降率为x ，则可列方程（）.A ．5000(1－x －2x)=2400B ．5000(1－x)2=2400 C ．5000－x －2x=2400D ．5000(1－x) (1－2x)=24009．如图所示，在平面直角坐标系中，以O 为圆心，适当长为半径画弧，交x 轴于点M ，交y 轴于点N ，再分别以点M 、N 为圆心，大于12MN 的长为半径画弧，两弧在第二象限交于点P ．若点P 的坐标为(2a ，b ＋1)，则a 与b 的数量关系为（）.A ．a=bB ．2a －b=1C ．2a ＋b=－1D ．2a ＋b=110．如图所示是抛物线y=ax 2＋bx ＋c(a ≠0)的部分图象，其顶点坐标为(1，n)，且与x 轴的一个交点在点(3，0)和(4，0)之间，则下列结论：①a －b+c ＞0；②3a ＋b=0；③b 2=4a(c－n)；④一元二次方程ax 2＋bx ＋c =n －1有两个不相等的实根．其中正确结论的个数是（）.A ．1个B ．2个C ．3个D ．4个二、填空题（本大题共4小题，每小题5分，满分20分）11．已知抛物线y =(m ＋1) x 2开口向上，则m 的取值范围是___________.得分评卷人第10题图MN第9题图12．若抛物线y=x 2－2x －3与x 轴分别交于A 、B 两点，则线段AB 的长为____________.13．如图所示，⊙O 的半径OA=4，∠AOB=120°，则弦AB 长为____________. 14．如图所示，在四边形ABCD 中，∠ABC =30°，将△DCB 绕点C 顺时针旋转60°后，点D 的对应点恰好与点A 重合，得到△ACE ，若AB=6，BC=8，则BD =_____________.三、（本大题共2小题，每小题8分，满分16分）15．如图所示，在正方形网格中，每个小正方形的边长均为1个单位．将△ABC 向下平移4个单位，得到△A ′B ′C ′，再把△A ′B ′C ′绕点C ′顺时针旋转90°，得到△A ″B ″C ″，请你作出△A ′B ′C ′和△A ″B ″C ″（不要求写作法）．16. 已知关于x 的一元二次方程(a －1)x 2－x+a 2－1=0的一个根是0，求a 的值.得分评卷人ECADB第14题图第13题图AOB四、（本大题共2小题，每小题8分，满分16分）17．如图所示，在⊙O中，半径OC⊥弦AB，垂足为D，AB＝12，CD＝2．求⊙O半径的长．18.已知二次函数y=ax2＋bx的图象经过点(2，0)和(－1，6).（1）求二次函数的解析式；（2）求它的对称轴和顶点坐标.B AOCD五、（本大题共2小题，每小题10分，满分20分）19．为丰富职工业余生活，某单位要组织一次篮球赛，赛制为单循环形式（每两队之间都赛一场），计划安排28场比赛，应邀请多少支球队参加比赛？20．如图所示，二次函数y=－mx2＋4m的顶点坐标为(0，2)，矩形ABCD的顶点B，C在x 轴上，A、D在抛物线上，矩形ABCD在抛物线与x轴所围成的图形内，且点A在点D 的左侧．（1）求二次函数的解析式；（2）设点A的坐标为(x，y)，试求矩形ABCD的周长p关于自变量x的函数解析式，并求出自变量x的取值范围；（3）是否存在这样的矩形ABCD，使它的周长为9？试证明你的结论．六、（本题满分12分）21. 我市高新区某企业接到一批产品的生产任务，按要求必须在14天内完成．已知每件产品的出厂价．．．为60元．工人甲第x 天生产的产品数量为y 件，y 与x 满足如下关系：7.5(04)510(414)x x yx x ＜.（1）工人甲第几天生产的产品数量为70件？（2）设第x 天生产的产品成本．．．．为p 元/件，p 与x 的函数图象如图．工人甲第x 天创造的利润为W 元，求W 与x 的函数关系式，并求出第几天时，利润最大，最大利润是多少？七、（本题满分12分）22．如果关于x的一元二次方程ax2＋bx＋c=0 (a≠０)有两个不相等的实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”.例如,方程x2－6x＋8=0的两个根是2和4,则方程x2－6x＋8=0就是“倍根方程”．（1）若一元二次方程x2－3x＋c=0是“倍根方程”,则c= ；（2）若(x－2) (mx－n)=0(m≠０)是“倍根方程”,求代数式4m2－5mn＋n2的值；（3）若方程ax2＋bx＋c=0(a≠０)是倍根方程，且相异两点M(1＋t，s)，N(4－t，s)，都在抛物线y=ax2＋bx＋c上，求一元二次方程ax2＋bx＋c=0 (a≠０)的根.八、（本题满分14分）23．已知，点O 是等边△ABC 内的任一点，连接OA ，OB ，OC.（1）如图1所示，已知∠AOB=150°，∠BOC=120°，将△BOC 绕点C 按顺时针方向旋转60°得△ADC. ①求∠DAO 的度数；②用等式表示线段OA ，OB ，OC 之间的数量关系，并证明；（2）设∠AOB =α，∠BOC=β.①当α，β满足什么关系时，OA+OB+OC 有最小值？请在图2中画出符合条件的图形，并说明理由；②若等边△ABC 的边长为1，请你直接写出OA+OB+OC 的最小值.ABCDABCO图1图2得分评卷人…………………答…………………题…………………不…………………过…………………此……………………线……………………………。

初中数学2017-18-1九年级数学期中试卷答案

2017～2018学年度第一学期期中考试九年级数学参考答案一、选择题（本大题共10小题，每小题4分，共40分）二、填空题（本大题共4小题，每小题5分，共20分）11．m＞－1； 12．4； 13． 14．10三、（本大题共2小题，每小题8分，满分16分）15．解：如图，△A′B′C′和△A″B″C″为所作． ....................................................... .........8分16．解：∵一元二次方程（a+1）x2﹣ax+a2﹣1=0的一个根为0，∴a+1≠0且a2﹣1=0， ............................................................ ..........................4分∴a=1． ................................................. ......................................8分四、（本大题共2小题，每小题8分，满分16分）17．解：连接AO. ................................................................2分∵半径OC⊥弦AB，∴AD＝BD.∵AB＝12，∴AD＝BD＝6.设⊙O的半径为R，∵CD＝2，∴OD＝R－2，在Rt△AOD中，OA2＝OD2＋AD2，即：R2＝(R－2)2＋62. ................................................................6分∴R＝10.答：⊙O的半径长为10． ................................................................8分18．解：（1）依题意，得：⎩⎨⎧=-=+6024b a b a ，解得：⎩⎨⎧-==42b a ∴二次函数的解析式为：x x y 422-=． ................................................................4分（2）对称轴为x ＝1，顶点坐标为（1，－2）. ................................................................8分五、（本大题共2小题，每小题10分，满分20分）19．解：设应邀请x 支球队参加比赛． ................................................................1分由题意，得28)1(21=-x ， ................................................................6分解得：x 1＝8，x 2＝－7(舍去)，答：应邀请8支球队参加比赛． ................................................................10分20．解：（1）∵二次函数y =－mx 2+4m 的顶点坐标为（0，2），∴4m =2，即m =12，∴抛物线的解析式为：2212+=x y . ..............................................................2分（2）∵A 点在x 轴的负方向上坐标为（x ，y ），四边形ABCD 为矩形，BC 在x 轴上，∴AD ∥x 轴，又∵抛物线关于y 轴对称，∴D、C 点关于y 轴分别与A 、B 对称． ∴AD 的长为-2x ，AB 长为y ，∴周长p =2y -4x =2（－12x 2+2）－4x =－x 2－4x +4． ..................................6分∵A 在抛物线上，且ABCD 为矩形，又∵抛物线y =﹣12x 2+2与x 轴交于（-2,0）与（2,0），∴由图象可知﹣2＜x ＜2.综上所述，p =－x 2－4x +4，其中－2＜x ＜2． ..................................8分（3）不存在.假设存在这样的p ，即：－x 2－4x +4=9，解此方程，无实数解. ∴不存在这样的p ．来 .....................................................................................10分六、（本题满分12分）21．解：（1）根据题意，得：若7.5x=70，得：x=283＞4，不符合题意；若5x+10=70. 解得：x =12答：工人甲第12天生产的产品数量为70件. (2)分（2）由函数图象知，当0≤x≤4时，p=40，当4＜x≤14时，设p=kx+b，将（4，40）、（14，50）代入，联立方程组，解得：k=1,b=36.∴P=x+36. ............................................. ........................................5分①当0≤x≤4时，W=（60－40）×7.5x=150x.∵W随x的增大而增大，∴当x=4时，W最大=600元；②当4＜x≤14时，W=（60－x－36）（5x+10）=－5x2+110x+240=－5（x－11）2+845，∴当x=11时，W最大=845.∵845＞600，∴当x=11时，W取得最大值，845元.答：第11天时，利润最大，最大利润是845元． .....................................12分七、（本题满分12分）22．解：（1）c =2； ....................................................................................2分∴4n m n m ==或.∵()()22454m mn n m n m n -+=--，∴4m 2－5mn ＋n 2=0. .....................................6分（3）∵方程()200ax bx c a ++=≠是倍根方程，不妨设12=2,x x∵相异两点()()1,,4,M t s N t s +-都在抛物线2y ax bx c =++上，八、（本题满分14分）23．解：（1）①∵∠AOB =150°，∠BOC =120°，∴∠AOC =360°-150°-120°=90°又∵将△BOC 绕点C 按顺时针方向旋转60°得△ADC .∴∠OCD =60°，∠D =∠BOC =120°∴∠DAO =180°+180°-∠AOC -∠OCD -∠D =90°. ......................................2分②连接OD .∵将△BOC绕点C按顺时针方向旋转60°得△ADC.∴△ADC≌△BOC，∠OCD=60°∴CD=OC，∠ADC=∠BOC=120°，AD=OB∴△OCD是等边三角形∴OC=OD=CD.又∵∠DAO=90°∴OA2+AD2=OD2即OA2+OB2=OC2 ............................................. .......................................6分（2）①当α=β=120°时，OA+OB+OC有最小值. ...........................................................8分将△AOC绕点C按顺时针旋转60°得△A′O′C，连接OO′则OC=O′C，OA=O′A′，且△OCO′是等边三角形，∴∠C O O′ =∠CO′O=60°，OC=OO′又∵∠A′O′C=∠AOC=∠BOC =120°∴B，O，O′，A′四点共线∴OA+OB+OC= O′A′+OB+OO′=BA′时，值最小. ...............................................12分②......................................14分【注：以上各题解法不唯一，只要合理，均应酌情赋分】。

2017-18(九上期中数学试题)

2017—2018学年度上学期期中教学质量调研检测九年级数学试题注意事项：1.本卷共有4页，共有25小题，满分120分，考试时限120分钟．2.答题前，考生先将自己的姓名，准考证号填写在试卷和答题卡指定的位置，并认真核对条形码上的准考证号和姓名，在答题卡规定的位置贴好条形码．3.考生必须保持答题卡的整洁，考试结束后，请将本试卷和答题卡一并上交．一、选择题：（本大题共10小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的，请把正确选项的字母填涂在答题卡中相应的格子内．1. 平面直角坐标系中，点M （1，5）关于原点对称的点N 在A ．第一象限B ．第二象限C ．第三象限D ．第四象限2. 如图，将一个含30角的直角三角板ABC 绕点A 旋转，使得点B 、A 、C '在同一条直线上，则三角板ABC 旋转的角度是 A ．150° B ．120° C ．90° D ．60°3. 下列函数中，是x 的二次函数的是A ．13-=x yB ．x y 2-=C ．xxy 12+= D ．)1(x x y -= 4. 方程x x 22=的根是A ．0B ．2-C ．2D ．0或2 5. 下列抛物线中，经过原点的抛物线是A ．2)1(-=x y B ．x x y -=22 C ．12+=x yD ．12+-=x x y6. 若c a b +=，则关于x 的一元二次方程02=++c bx ax 必有一根为 A ．1-=xB ．0=xC ．1=xD ．2=x7. 如图，AB 是半圆的直径，C ，D 是半圆上的两点，且弧AD 等于弧CD ，∠BAC=20°，则∠DAC 的度数是A ．20 B ．30 C ．35 D ．45 8. 如图，⊙C 过原点O ，且与两坐标轴分别交于点A 、B.点B 的坐标为（-8， 0），点M是第三象限内弧OB 上一点，∠BMO=120°，则⊙O 的半径为第2题C 'B 'C B A 第7题A BA ．316B ．3316 C ．38 D ．3389. 如图，AB=AC=AD ，且∠BDC=30°，则∠BAC 的大小为A. 70°B. 60°C. 50°D. 45°10. 已知二次函数c bx ax y ++=2的部分图象如图所示，若0<y ，则x 的取值范围为 A ．31<<-x B ．21<<-xC ．1-<x 或 2>xD ．1-<x 或 3>x 二、填空题：(本大题共6小题,每小题3分,共18分) 11. 抛物线3)1(212--=x y 的顶点坐标是 . 12. 如图,将△ABC 绕点A 按逆时针旋转62°后得到△AD C '.则∠ABD 的是 .13．已知抛物线c ax ax y +-=22与x 轴的一个交点的坐标为（-2， 0）则方程022=+-c ax ax 的根为 .14. 据统计，东风公司某种品牌汽车2015年的产量为8.1万辆，2017年该汽车的年产量可达到14.4万辆，若该汽车的产量平均每年按相同的百分数增长，则预计到2018年该品牌汽车的产量为万辆. 15. 已知0≠ab ，且06522=-+b ab a .则abb a +的值为 . 16. 已知关于x 二次函数c bx ax y ++=2（0≠a ）的图象经过点（-2，1y ），（-1，2y ），（1， 0），且210y y <<.现有以下结论：①0>abc ；②023≤++c b a ；③对于自变量x 的任意一个取值，都有abx x b a 42-≥+；④在12-<<-x 中存在一个实数0x ，使得aba x +-=0.其中正确的结论是 .（只填写正确结论的序号）第9题AB C D 第12题CABDC '三、解答题：(本大题共9小题,共72分) 17．(8分)用你认为适当的方法解方程：（1）)3(3)3(5x x x -=- （2）0342=-+x x18．(6分)已知抛物线的顶点是（3， 1），且在x 轴上截得的线段长为6.求此抛物线的解析式.19．(7分) 定义：如果一元二次方程02=++c bx ax (0≠a )满足0=++c b a ，那么我们称这个方程为“凤凰”方程.已知方程022=++n mx x 是一个“凤凰”方程，且有两个相等的实数根，求22n m +的值.20．（7分）如图，在△ABC 中，∠ACB ＝90°，AC ＝2，将△ABC 绕点C 顺时针旋转60°得到△A /B /C ，点A 的对应点A /恰好落在AB 上，求BB /的长．21．（7分）如图，△ABC 的各顶点均在⊙O 上，连接OB 、OC ，若∠BAC+∠BOC=180°，BC=32. （1）求⊙O 的半径；（2）若点D 是弧BC 的中点，求证：四边形OBDC 是菱形.22．（7分）已知关于x 的方程02)32(22=+++-m x m x ．(1)若方程有实数根，求实数m 的取值范围；(2)设方程的两个实数根分别是1x ，2x ，当21222131x x x x =-+时，求实数m 的值． 23．（8分）如图，AB 是⊙O 的直径，弦CD ⊥AB 于点E ，点M 在⊙O 上，且MD 经过圆心O ，连接MB.（1）若CD=12，AB=20，求BE 的长；（2）若∠M=∠D ，求∠D 的度数.B /A /AC第20题第21题D24．（10分）某商品的进价为每件40元，售价为每件50元，每个月可卖出210件；如果每件商品的售价每上涨1元，则每个月少卖10件（每件售价不能高于65元）．设每件商品的售价上涨x 元（x 为正整数），每个月的销售利润为y 元．（1）求y 与x 的函数关系式并直接写出自变量x 的取值范围；（2）每件商品的售价定为多少元时，每个月的利润恰为2200元？（3）每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？25．（12分）如图，已知直线12--=x y 与y 轴交于点A ，与直线x y -=交于点B ，点B 关于原点O 的对称点为点C ，抛物线形c bx ax y ++=2经过点A ，B ，C. （1）求抛物线的解析式；（2）p 为抛物线上一点，它关于原点的对称点为Q ，①当四边形PBQC 为菱形时，求点P 的坐标；②若点P 的横坐标为t （11<<-t ），当t 为何值时，四边形PBQC 的面积最大？并说明理由.第23题A。

2017-2018学年度九年级上学期数学期中考试卷及答案

2017-2018学年第一学期期中考试九年级数学试题1. 计算()23-的结果是（）A.3B.3- C.3± D.92. 若P（x，－3）与点Q（4，y）关于原点对称，则x＋y＝（）A、7B、－7C、1D、－13. 下列二次根式是最简二次根式的是（）4. 一元二次方程22350xx++=的根的情况是( )A. 有两个不相等的实数根B. 有两个相等的实数根C. 没有实数根D. 无法判断5. 用配方法解方程0142=++xx，则配方正确的是（）A、3)2(2=+x B、5)2(2-=+x C、3)2(2-=+x D、3)4(2=+x6. 如图，AB、AC都是圆O的弦，OM⊥AB，ON⊥AC，垂足分别为M、N，如果MN＝3，那么BC＝（）. A． 4 B.5 C． 6 D.7二、填空题（共8小题，每小题3分，满分24分）7. 2-x在实数范围内有意义，则x的取值范围是．8. 221x-=的二次项系数是，一次项系数是，常数项是 .9. 一只蚂蚁沿图中所示的折线由A点爬到了C点，则蚂蚁一共爬行了______cm．(图中小方格边长代表1cm)NMOCBA10. 关于x 的一元二次方程04)2(22=-+-+m mx x m 有一根为0，则m= . 11. 对于任意不相等的两个数a,b ，定义一种运算*如下：ba b a b a -+=*，如523232*3=-+=，那么)5(*3-= .12. 有4个命题：①直径相等的两个圆是等圆；②长度相等的两条弧是等弧；③圆中最大的弦是通过圆心的弦；④在同圆或等圆中，相等的两条弦所对的弧是等弧，其中真命题是_________。

13. 有两个完全重合的矩形，将其中一个始终保持不动，另一个矩形绕其对称中心O 按逆时针方向进行旋转，每次均旋转22.5︒，第．2．次．旋转后得到图①，第．4．次．旋转后得到图②…，则第20次旋转后得到的图形与图①～图④中相同的是____. （填写序号）14. 等腰三角形两边的长分别为方程02092=+-x x 的两根，则三角形的周长是．三、解答题（共4小题，每小题6分,共24分） 15. 解方程：x(x-2)＋x-2＝016. 计算：0)15(282218-+--17. 下面两个网格图均是4×4正方形网格，请分别在两个网格图中选取两个白色的单位正方形并涂黑，使整个网格图满足下列要求．图① 图② 图③ 图④18. 如图，大正方形的边长为515+，小正方形的边长为515-，求图中的阴影部分的面积．四、（本大题共2小题，每小题8分，共16分）19. 数学课上，小军把一个菱形通过旋转且每次旋转120°后得到甲的图案。

2017-2018年广东省珠海市香洲区前山中学九年级上学期数学期中试卷带答案

2017-2018学年广东省珠海市香洲区前山中学九年级（上）期中数学试卷一、选择题（每小题3分，共30分）1．（3分）将方程3x2﹣8x=10化为一元二次方程的一般形式，其中二次项系数，一次项系数，常数项分别是（）A．3，﹣8，﹣10 B．3，﹣8，10 C．3，8，﹣10 D．﹣3，﹣8，﹣10 2．（3分）用配方法解方程x2﹣2x﹣5=0时，原方程应变形为（）A．（x+1）2=6 B．（x+2）2=9 C．（x﹣1）2=6 D．（x﹣2）2=93．（3分）在下列四个图案中，不是中心对称图形的是（）A．B．C．D．4．（3分）将二次函数y=（x﹣1）2﹣2的图象先向右平移1个单位，再向上平移1个单位后顶点为（）A．（1，3） B．（2，﹣1）C．（0，﹣1）D．（0，1）5．（3分）如图，在△ABC中，∠CAB=65°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为（）A．35°B．40°C．50°D．65°6．（3分）图（1）是一个横断面为抛物线形状的拱桥，当水面在l时，拱顶（拱桥洞的最高点）离水面2m，水面宽4m．如图（2）建立平面直角坐标系，则抛物线的关系式是（）A ．y=﹣2x 2B ．y=2x 2C ．y=﹣x 2D ．y=x 27．（3分）已知三角形两边长分别为2和9，第三边的长为二次方程x 2﹣14x +48=0的根，则这个三角形的周长为（）A ．11B ．17C ．17或19D ．198．（3分）已知二次函数y=kx 2﹣7x ﹣7的图象与x 轴有两个交点，则k 的取值范围为（）A ．k ＞﹣B ．k ＞﹣且k ≠0C ．k ≥﹣D ．k ≥﹣且k ≠09．（3分）已知点A 的坐标为（a ，b ），O 为坐标原点，连接OA ，将线段OA 绕点O 按逆时针方向旋转90°得OA 1，则点A 1的坐标为（）A ．（﹣a ，b ）B ．（a ，﹣b ）C ．（﹣b ，a ）D ．（b ，﹣a ）10．（3分）在平面直角坐标系中，二次函数y=a （x ﹣h ）2（a ≠0）的图象可能是（）A ．B ．C ．D ．二、填空题（每小题4分，共24分）11．（4分）若点A （2，1）与点B 是关于原点O 的对称点，则点B 的坐标为．12．（4分）二次函数y=x 2+2x 的顶点坐标为．13．（4分）如果关于x 的一元二次方程k 2x 2﹣（2k +1）x +1=0有两个不相等的实数根，那么k 的取值范围是．14．（4分）已知抛物线y=ax 2+bx +c 与x 轴的公共点是（﹣4，0），（2，0），则这条抛物线的对称轴是直线．15．（4分）如图，将矩形ABCD 绕点A 顺时针旋转90°后，得到矩形AB′C′D′，如果CD=2DA=2，那么CC′=．16．（4分）如图，二次函数y=ax2+bx+c的图象与y轴正半轴相交，其顶点坐标为，下列结论：①ac＜0；②b＜0；③4ac﹣b2＜0；④a+b+c＜0．其中正确的有．（填序号）三、解答题：（共3题，每题6分，共18分）17．（6分）解方程：x2+3x﹣1=0．18．（6分）解方程（x+1）（x+2）=2x+4．19．（6分）某种品牌的手机经过四、五月份连续两次降价，每部售价由2500元降到了1600元．求平均每月降价的百分率．四、解答题：（共3题，每题7分，共21分）20．（7分）如图，（1）分别写出A，B两点的坐标；（2）将△ABC绕点A顺时针旋转90°，画出旋转后的△AB1C1．21．（7分）在一块长16m、宽12m的矩形荒地上，小明要建造一个花园，并使花园所占的面积为荒地面积的一半，其中花园四周小路的宽度都相等，求小路的宽．22．（7分）已知二次函数中x和y的部分对应值如下表：（1）求二次函数的解析式；（2）如图，A、B、C为抛物线与坐标轴的交点，点D为抛物线的顶点，抛物线的对称轴DE上存在一点P，使得PB+PC的值最小，求出点P坐标．五、解答题：（共3题，每题9分，共27分）23．（9分）P n表示n边形的对角线的交点个数（指落在其内部的交点），如果这些交点都不重合，那么P n与n的关系式是：P n=•（n2﹣an+b）（其中a，b是常数，n≥4）（1）通过画图，可得：四边形时，P4=；五边形时，P5=（2）请根据四边形和五边形对角线交点的个数，结合关系式，求a，b的值．24．（9分）如图，点E是正方形ABCD的边DC上一点，把△ADE顺时针旋转△ABF的位置．（1）旋转中心是点，旋转角度是度；（2）若连结EF，则△AEF是三角形；并证明；（3）若四边形AECF的面积为25，DE=2，求AE的长．25．（9分）已知：如图，抛物线y=ax2+3ax+c（a＞0）与y轴交于C点，与x轴交于A、B两点，A点在B点左侧．点B的坐标为（1，0），OC=3BO．（1）求抛物线的解析式；（2）若点D是线段AC下方抛物线上的动点，求四边形ABCD面积的最大值．2017-2018学年广东省珠海市香洲区前山中学九年级（上）期中数学试卷参考答案与试题解析一、选择题（每小题3分，共30分）1．（3分）将方程3x2﹣8x=10化为一元二次方程的一般形式，其中二次项系数，一次项系数，常数项分别是（）A．3，﹣8，﹣10 B．3，﹣8，10 C．3，8，﹣10 D．﹣3，﹣8，﹣10【解答】解：由已知方程得到：3x2﹣8x﹣10=0，则它的二次项系数，一次项系数，常数项分别是3，﹣8，﹣10．故选：A．2．（3分）用配方法解方程x2﹣2x﹣5=0时，原方程应变形为（）A．（x+1）2=6 B．（x+2）2=9 C．（x﹣1）2=6 D．（x﹣2）2=9【解答】解：由原方程移项，得x2﹣2x=5，方程的两边同时加上一次项系数﹣2的一半的平方1，得x2﹣2x+1=6∴（x﹣1）2=6．故选：C．3．（3分）在下列四个图案中，不是中心对称图形的是（）A．B．C．D．【解答】解：根据中心对称图形的概念可得：图形B不是中心对称图形．故选：B．4．（3分）将二次函数y=（x﹣1）2﹣2的图象先向右平移1个单位，再向上平移1个单位后顶点为（）A．（1，3） B．（2，﹣1）C．（0，﹣1）D．（0，1）【解答】解：二次函数y=（x﹣1）2﹣2的图象先向右平移1个单位，再向上平移1个单位后，得出：y=（x﹣1﹣1）2﹣2+1，即y=（x﹣2）2﹣1；得到顶点坐标为（2，﹣1）．故选：B．5．（3分）如图，在△ABC中，∠CAB=65°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为（）A．35°B．40°C．50°D．65°【解答】解：∵CC′∥AB，∴∠ACC′=∠CAB=65°，∵△ABC绕点A旋转得到△AB′C′，∴AC=AC′，∴∠CAC′=180°﹣2∠ACC′=180°﹣2×65°=50°，∴∠CAC′=∠BAB′=50°．故选：C．6．（3分）图（1）是一个横断面为抛物线形状的拱桥，当水面在l时，拱顶（拱桥洞的最高点）离水面2m，水面宽4m．如图（2）建立平面直角坐标系，则抛物线的关系式是（）A．y=﹣2x2B．y=2x2C．y=﹣x2 D．y=x2【解答】解：设此函数解析式为：y=ax2，a≠0；那么（2，﹣2）应在此函数解析式上．则﹣2=4a即得a=﹣，那么y=﹣x2．故选：C．7．（3分）已知三角形两边长分别为2和9，第三边的长为二次方程x2﹣14x+48=0的根，则这个三角形的周长为（）A．11 B．17 C．17或19 D．19【解答】解：解方程x2﹣14x+48=0得第三边的边长为6或8，依据三角形三边关系，不难判定边长2，6，9不能构成三角形，2，8，9能构成三角形，∴三角形的周长=2+8+9=19．故选D．8．（3分）已知二次函数y=kx2﹣7x﹣7的图象与x轴有两个交点，则k的取值范围为（）A．k＞﹣B．k＞﹣且k≠0 C．k≥﹣D．k≥﹣且k≠0【解答】解：根据题意得，解得k＞﹣且k≠0．故选：B．9．（3分）已知点A的坐标为（a，b），O为坐标原点，连接OA，将线段OA绕点O按逆时针方向旋转90°得OA1，则点A1的坐标为（）A．（﹣a，b）B．（a，﹣b）C．（﹣b，a）D．（b，﹣a）【解答】解：设点A（a，b）坐标平面内一点，逆时针方向旋转90°后A1应与A 分别位于y轴的两侧，在x轴的同侧，横坐标符号相反，纵坐标符号相同．作AM⊥x轴于M，A′N⊥x轴于N点，在直角△OAM和直角△A1ON中，OA=OA1，∠AOM=∠OA1N，∠AMO=∠ONA1=90°，∴△OAM≌△A1ON∴A1N=OM，ON=AM∴A1的坐标为（﹣b，a）故选：C．10．（3分）在平面直角坐标系中，二次函数y=a（x﹣h）2（a≠0）的图象可能是（）A．B． C．D．【解答】解：二次函数y=a（x﹣h）2（a≠0）的顶点坐标为（h，0），它的顶点坐标在x轴上，故选：D．二、填空题（每小题4分，共24分）11．（4分）若点A（2，1）与点B是关于原点O的对称点，则点B的坐标为（﹣2，﹣1）．【解答】解：点A（2，1）与点B是关于原点O的对称点，则点B的坐标为（﹣2，﹣1），故答案为（﹣2，﹣1）．12．（4分）二次函数y=x2+2x的顶点坐标为（﹣1，﹣1）．【解答】解：∵a=1，b=2，c=0，∴﹣=﹣=﹣1，==﹣1，∴顶点坐标为（﹣1，﹣1），故答案为：（﹣1，﹣1）．13．（4分）如果关于x的一元二次方程k2x2﹣（2k+1）x+1=0有两个不相等的实数根，那么k的取值范围是k且k≠0．【解答】解：根据题意得k2≠0且△=（2k+1）2﹣4k2＞0，解得k＞﹣且k≠0．故答案为k＞﹣且k≠0．14．（4分）已知抛物线y=ax2+bx+c与x轴的公共点是（﹣4，0），（2，0），则这条抛物线的对称轴是直线x=﹣1．【解答】解：∵抛物线与x轴的交点为（﹣4，0），（2，0），∴两交点关于抛物线的对称轴对称，则此抛物线的对称轴是直线x==﹣1，即x=﹣1．故答案是：x=﹣1．15．（4分）如图，将矩形ABCD绕点A顺时针旋转90°后，得到矩形AB′C′D′，如果CD=2DA=2，那么CC′=．【解答】解：由旋转的性质可知，∠CAC′=90°，AC=AC′，Rt△ACD中，由勾股定理得，AC===，在Rt△CAC′中，由勾股定理得，CC′==．16．（4分）如图，二次函数y=ax2+bx+c的图象与y轴正半轴相交，其顶点坐标为，下列结论：①ac＜0；②b＜0；③4ac﹣b2＜0；④a+b+c＜0．其中正确的有①③．（填序号）【解答】解：由图象可得，a＜0，b＞0，c＞0，∴ac＜0，b＞0，故①正确，②错误，∵二次函数图象与x轴有两个交点，∴b2﹣4ac＞0，∴4ac﹣b2＜0，故③正确，∵该抛物线对称轴为x=，∴x=0和x=1时的函数值相等，∴当x=1时，y=a+b+c＞0，故④错误，故答案为：①③．三、解答题：（共3题，每题6分，共18分）17．（6分）解方程：x2+3x﹣1=0．【解答】解：这里a=1，b=3，c=﹣1，∵△=9+4=13，∴x=，则x1=，x2=．18．（6分）解方程（x+1）（x+2）=2x+4．【解答】解：（x+1）（x+2）﹣2（x+2）=0，（x+2）（x+1﹣2）=0，x+2=0或x+1﹣2=0，所以x1=﹣2，x2=1．19．（6分）某种品牌的手机经过四、五月份连续两次降价，每部售价由2500元降到了1600元．求平均每月降价的百分率．【解答】解：设平均降价x元，依题意得：2500（1﹣x）2=2050，化简得：（1﹣x）2=1.21，解得：x=0.1=10%或x=﹣2.1（舍去），答：平均每月降价的百分率为10%．四、解答题：（共3题，每题7分，共21分）20．（7分）如图，（1）分别写出A，B两点的坐标；（2）将△ABC绕点A顺时针旋转90°，画出旋转后的△AB1C1．【解答】解：（1）点A坐标为（2，0）、B（﹣1，﹣4）；（2）如图，△AB1C1即为所求．21．（7分）在一块长16m、宽12m的矩形荒地上，小明要建造一个花园，并使花园所占的面积为荒地面积的一半，其中花园四周小路的宽度都相等，求小路的宽．【解答】解：设小路宽问xm，由于花园四周小路的宽度相等，则根据题意，可得（16﹣2x）（12﹣2x）=×16×12，即x2﹣14x+24=0，解之得x=2或x=12．由于矩形荒地的宽是12m，故舍去x=12．答：花园四周小路宽为2m．22．（7分）已知二次函数中x和y的部分对应值如下表：（1）求二次函数的解析式；（2）如图，A、B、C为抛物线与坐标轴的交点，点D为抛物线的顶点，抛物线的对称轴DE上存在一点P，使得PB+PC的值最小，求出点P坐标．【解答】解：（1）设y=a（x+1）（x﹣3）把（0，﹣3）代入可得：﹣3=a（0+1）（0﹣3），解得：a=1，则y=（x+1）（x﹣3）=x2﹣2x﹣3，∴二次函数的解析式为：y=x2﹣2x﹣3；（2）如图，∵点B与A关于对称轴对称，∴连接AC交对称轴于P，此时PB+PC的值最小，设直线AC的解析式是y=kx+b，则，解得：，则直线AC的解析式是：y=x﹣3．当x=1时，y=1﹣3=﹣2，∴P（1，﹣2）．五、解答题：（共3题，每题9分，共27分）23．（9分）P n表示n边形的对角线的交点个数（指落在其内部的交点），如果这些交点都不重合，那么P n与n的关系式是：P n=•（n2﹣an+b）（其中a，b是常数，n≥4）（1）通过画图，可得：四边形时，P4=1；五边形时，P5=5（2）请根据四边形和五边形对角线交点的个数，结合关系式，求a，b的值．【解答】解：（1）画出图形如下．由画图，可得：当n=4时，P4=1；当n=5时，P5=5．故答案为：1；5．（2）将（1）中的数值代入公式，得：，解得：．24．（9分）如图，点E是正方形ABCD的边DC上一点，把△ADE顺时针旋转△ABF的位置．（1）旋转中心是点A，旋转角度是90度；（2）若连结EF，则△AEF是等腰直角三角形；并证明；（3）若四边形AECF的面积为25，DE=2，求AE的长．【解答】解：（1）如图，由题意得：旋转中心是点A，旋转角度是90度．故答案为A、90．（2）由题意得：AF=AE，∠EAF=90°，∴△AEF为等腰直角三角形．故答案为等腰直角．（3）由题意得：△ADE≌△ABF，=S正方形ABCD=25，∴S四边形AECF∴AD=5，而∠D=90°，DE=2，∴．25．（9分）已知：如图，抛物线y=ax2+3ax+c（a＞0）与y轴交于C点，与x轴交于A、B两点，A点在B点左侧．点B的坐标为（1，0），OC=3BO．（1）求抛物线的解析式；（2）若点D是线段AC下方抛物线上的动点，求四边形ABCD面积的最大值．【解答】解：（1）∵B（1，0），∴OB=1；∵OC=3BO，∴C（0，﹣3）；∵y=ax2+3ax+c过B（1，0）、C（0，﹣3），∴；解这个方程组，得，∴抛物线的解析式为：y=﹣3；（2）过点D作DM∥y轴分别交线段AC和x轴于点M、N，当y=0时，y=﹣3=0；（x+4）（x﹣1）=0，解这个方程，得x1=﹣4，x2=1，∴A（﹣4，0），设直线AC的解析式为y=kx+b，∴，解这个方程组，得，∴AC的解析式为：y=﹣x﹣3，设D （x ，﹣3），则M （x ，﹣x ﹣3），∴DM=﹣x ﹣3﹣（﹣3）=﹣﹣3x ，∵S 四边形ABCD =S △ABC +S △ADC ，=×5×3+×4（﹣﹣3x ），=+2（﹣﹣3x ）， =﹣﹣6x +，=﹣（x 2+4x +4﹣4）+，=﹣（x +2）2+，当x=﹣2时，四边形ABCD 面积有最大值．赠送初中数学几何模型【模型二】半角型：图形特征：AB正方形ABCD 中，∠EAF =45° ∠1=12∠BAD 推导说明：1.1在正方形ABCD 中，点E 、F 分别在BC 、CD 上，且∠FAE ＝45°，求证：EF ＝BE +DFE-a1.2在正方形ABCD中，点E、F分别在BC、CD上，且EF＝BE+DF，求证：∠FAE＝45°DEa+b-aa45°A BE挖掘图形特征：a+bx-aa 45°DBa+b-a45°A运用举例：1．正方形ABCD 的边长为3，E 、F 分别是AB 、BC 边上的点,且∠EDF =45°.将△DAE 绕点D 逆时针旋转90°，得到△DCM . （1）求证：EF =FM（2）当AE =1时，求EF 的长．E3．如图，梯形ABCD中，AD∥BC，∠C＝90°，BC＝CD＝2AD＝4，E为线段CD上一点，∠ABE＝45°.（1）求线段AB的长；（2）动点P从B出发，沿射线．．BE运动，速度为1单位/秒，设运动时间为t，则t为何值时，△ABP为等腰三角形；（3）求AE－CE的值.变式及结论：4.在正方形ABCD中，点E，F分别在边BC，CD上，且∠EAF=∠CEF=45°．（1）将△ADF绕着点A顺时针旋转90°，得到△ABG（如图1），求证：△AEG≌△AEF；（2）若直线EF与AB，AD的延长线分别交于点M，N（如图2），求证：EF2=ME2+NF2；（3）将正方形改为长与宽不相等的矩形，若其余条件不变（如图3），请你直接写出线段EF，BE，DF之间的数量关系．F。

2018-2017学年度第一学期初三期中数学试题

2018-2018学年度第一学期初三期中数学试题班姓名学号得分考查内容：判别式、旋转、相似、三角函数、二次函数一、选择题<本题共32分，每小题4分）1、如果两个相似三角形地相似比是，那么这两个相似三角形地周长比是< ）A．B．C．D．2．如果是一元二次方程地解，那么地值是< ）A. 0B.2 C.6D. -23．将二次函数地图像先向右平移1个单位，再向上平移3个单位后所得到地图像地解读式为< ）A．B．C．D．4．函数和<是常数，且）在同一直角坐标系中地图象可能是< ）5．某汽车销售公司2007年盈利1500万元，2009年盈利2160万元，且从2007年到2009年，每年盈利地年增长率相同．设每年盈利地年增长率为，根据题意，下面所列方程正确地是< ）．A． B.C． D.6．如图，在平面直角坐标系中，以P(4，6>为位似中心，把△ABC缩小得到△DEF，若变换后，点A、B地对应点分别为点D、E，则点C地对应点F地坐标应为< ）．A.(4，2>B.(4，4>C. (4，5>D. (5，4>7．如图，将△ABC绕着点C按顺时针方向旋转20°，B点落在位置，A点落在位置，若，则地度数是< ）EDACBA ．50°B ．60°C ． 70°D ．40° 8．汽车匀加速行驶路程为，匀减速行驶路程为，其中、为常数.一汽车经过启动、匀加速行驶、匀速行驶、匀减速行驶之后停车，若把这一过程中汽车地行驶路程看作时间地函数，其图象可能是 < ）<考查实际问题中二次函数及一次函数地应用）二、填空题<本题共16分，每小题4分） 9. 二次函数y=x 2+4x+6地最小值为. 10．二次函数地图像与x 轴有两个交点，则m 取值范围是<考查二次函数图像与判别式关系及二次项系数不为0） 11．函数地图象上有两点,，则<填“<”或“=”或“>”）.12．如图，∠DAB ＝∠CAE ，要使△ABC ∽△ADE ，则补充地一个条件可以是<只需写出一个正确答案即可）．三、解答题<本题共72分） 13.<本小题5分）计算：．14．<本题5分）以直线为对称轴地抛物线过点<3，0）,(0，3>，求此抛物线地解读式.15．<本题5分）如图，B 是AC 上一点，AD ⊥AB,EC ⊥BC,∠DBE=90°.求证：△ABD ∽△CEB. 16．<本题6分）如图，在中，，在边上取一点，使A CDB，过作交于，．求地长．17．<本小题满分6分）如图，某人在点A处测量树高，点A到树地距离AD为21M，将一长为2M地标杆BE在与点A相距3M地点B处垂直立于地面，此时，观察视线恰好经过标杆顶点E及树地顶点C，求此树CD地高．18．<本小题满分6分）如图，在8×11地方格纸中，每个小正方形地边长均为1，△ABC地顶点均在小正方形地顶点处．<1）画出△ABC绕点Ａ顺时针方向旋转90°得到地△；<2）求点B运动到点B′所经过地路径地长．<考查旋转与格点问题）19．<本题6分）已知关于地方程.<1）如果此方程有两个不相等地实数根，求m地取值范围；<2）在<1）中，若m为符合条件地最大整数，求此时方程地根.20．<本题6分）列方程解应用题某商店销售一种食用油，已知进价为每桶40元，市场调查发现，若以每桶50元地价格销售，平均每天可以销售90桶油，若价格每升高1元，平均每天少销售3桶油，设每桶食用油地售价为x元<），商店每天销售这种食用油所获得地利润为y元.<1）用含有x地代数式分别表示出每桶油地利润与每天卖出食用油地桶数；<2）求y与x之间地函数关系式；<3）当每桶食用油地价格为55元时，可获得多少利润？<4）当每桶食用油地价格定为多少时,该商店一天销售这种食用油获得地利润最大?最大利润为多少?<考查学生阅读能力及列二次函数关系式及最值）21．<本题6分）已知：如图，△ABC是等边三角形，D是AB边上地点，将DB绕点D顺时针旋转60°得到线段DE，延长ED交AC于点F，连结DC、AE．<1）求证：△ADE≌△DFC；<2）过点E作EH∥DC交DB于点G，交BC于点H，连结AH．求∠AHE地度数；<3）若BG=，CH=2，求BC地长．<考查全等、相似、旋转、等边三角形及其基本图形地应用）22、<本题7分）对于二次函数，如果当取任意整数时，函数值都是整数，此时称该点<，）为整点，该函数地图象为整点抛物线<例如：）．<1）请你写出一个整点抛物线地解式．<不必证明）； <2）请直接写出整点抛物线与直线围成地阴影图形中<不包括边界）所含地整点个数．23．<本小题满分7分）如图，已知抛物线y 1=-x 2+bx+c 经过A(1,0>，B(0,-2>两点，顶点为D ． <1）求抛物线y 1 地解读式；<2）将△AOB 绕点A 逆时针旋转90°后，得到△AO ′B ′ ，将抛物线y 1沿对称轴平移后经过点B′，写出平移后所得地抛物线y 2 地解读式；<3）设<2）地抛物线y 2与轴地交点为B 1，顶点为D 1，若点M 在抛物线y 2上，且满足△MBB 1地面积是△MDD 1面积地2倍，求点M 地坐标．<考查数形结合地思想、分类讨论地思想、学生解决代数几何综合题能地能力） 24．<本题满分7分）和是绕点旋转地两个相似三角形，其中与、与为对应角．<1）如图1，若和分别是以与为顶角地等腰直角三角形，且两三角形旋转到使点、、在同一条直线上地位置时，请直接写出线段与线段地关系；<2）若和为含有角地直角三角形，且两个三角形旋转到如图2地位置时，试确定线段与线段地关系，并说明理由；<3）若和为如图3地两个三角形，且=，，在绕点旋转地过程中，直线与夹角地度数是否改变？若不改变，直接用含、地式子表示夹角地度数；若改变，请说明理由．<考查学生综合运用几何知识解题能力）2010-2018学年度第一学期初三期中数学试题答案二、选择题<本题共32分，每小题4分）1C 2D 3 B 4A 5 D 6B 7C8A 二、填空题<本题共16分，每小题4分）9． 2 10.11. m<n 12. 答案不唯一三、解答题<本题共30分，每小题5分） 13．解：=-------------------------------------------------------------------- 3分= ----------------------------------------------------------------------- 4分=<或）．------------------------------------------------------------ 5分14．解：设抛物线地解读式为， ………………………………………1分抛物线过点<3，0）,(0，3>.∴ 解得………………4分∴抛物线地解读式为.……………………………………………5分15．证明：∵AD ⊥AB,EC ⊥BC ∴∠A=∠BCE=90°……………………1分又∵∠DBE=90°∴∠ABD+∠EBC=90° 又∵∠E+∠EBC =90°∴∠ABD=∠E ……………………3分 ∴△ABD ∽△CEB ……………………5分30︒30︒BCDE图3AB CDE图2图1D CB A16．解：在中，，．………………………………………1分又，．………………………………………2分，．又，………………………………………3分．………………………………………4分．………………………………………5分．………………………………………6分17．解：∵CD⊥AD，EB⊥AD，∴EB∥CD.∴△ABE∽△ADC．…………………………………………………2′∴．…………………………………………………3′∵EB=2，AB=3，AD=21，∴．…………………………………………………4′∴CD=14．…………………………………………………5′答：此树高为14M．………………………………………………………6′18．<1）略 <2）19<1）解：.. ············································1分∵该方程有两个不相等地实数根，∴. ···············································································2分解得.∴m地取值范围是.································································· 3分<2）解：∵，∴符合条件地最大整数是.····················································· 4分此时方程为，解得.∴方程地根为，. ···································· 6分20(本小题8分><1），或；…………………2分<2）设月销售利润为y元，由题意，…………………3分整理，得…………………4分<3）当每桶食用油地价格为55元时，答：当每桶食用油地价格为55元时，可获得利润1125元.…………………6分<4）…………………7分则：当时，y地最大值为，…………………8分答：当每桶食用油地价格定为60元时,该商店每天销售这种食用油获得地利润最大.最大利润为1200元21．<1）证明：如图9，∵线段DB顺时针旋转60°得线段DE，∴∠EDB =60°，DE=DB.∵△ABC是等边三角形，∴∠B=∠ACB =60°.∴∠EDB =∠B.∴EF∥BC. ········································· 1分∴DB=FC，∠ADF=∠AFD =60°.∴DE=DB=FC，∠ADE=∠DFC =120°，△ADF是等边三角形.∴AD=DF.∴△ADE≌△DFC. ·······································································2分<2）由△ADE≌△DFC，得AE=DC，∠1=∠2.∵ED∥BC， EH∥DC，∴四边形EHCD是平行四边形.∴EH=DC，∠3=∠4.∴AE=EH. ·························································································· 3分∴∠AEH=∠1+∠3=∠2+∠4=∠ACB=60°.∴△AEH是等边三角形.∴∠AHE=60°.····················································································· 4分<3）设BH=x，则AC= BC =BH＋HC= x＋2，由<2）四边形EHCD是平行四边形，∴ED=HC.∴DE=DB=HC=FC=2.∵EH∥DC，∴△BGH∽△BDC.··············································································· 5分∴.即.解得.∴BC=3. ·····························································································6分22．解：<1）或或等. ……3分<2）4．………………………………………………………………………………5分23．<本小题满分7分）解：(1>已知抛物线y1=-x2+bx+c经过点A(1,0>， B(0,-2>，∴解得∴所求抛物线地解读式为y1=-x2 +3x-2．……………………………2′<2）解法1：∵A(1,0>，B(0,-2>，∴OA=1,OB=2．由旋转性质可得O′A=OA=1，O′B′=OB=2．∴ B′点地坐标为(3，-1>．∵抛物线y1地顶点D(,>，且抛物线y2 是由y1沿对称轴平移后得到地，∴可设y2 地解读式为y2= -(x->2 +k ．∵y2经过点B′，∴-(3 ->2 +k= -1．解得k=．∴y2= -(x->2 +．……………………………………………………………4′解法2：同解法1 得B′ 点地坐标为 (3，-1> ．∵当x=3时，由y1=-x2 +3x-2得y=-2，可知抛物线y1过点(3，-2> ．∴将抛物线y1沿y轴向上平移1个单位后过点B′．∴平移后地抛物线y2地解读式为：y2=-x2 +3x-1 ．……………………………4′<3）∵y1=-x2+3x-2 = -(x->2 +，y2=-x2 +3x-1= -(x->2 +，∴顶点D(,>，D1(,>．∴ DD1=1．又B1(0，-2>，B1(0，-1>，∴BB1=1．设M点坐标为(m，n>，∵ BB1=DD1，由，可知当m≤0时，符合条件地M点不存在；……………………………………5′而当0<m<时，有m=2(-m>，解得m=1；当m>时，有m=2(m ->，解得m=3．当m=1时，n=1；当m=3时，n=-1．∴M1(1,1>，M2(3,-1>．……………………………………………………………7′24．解：<1）线段与线段地关系是. ………… 2分<2）如图2，连接、并延长，设交点为点．∵∽，∴，∴．∵，，．．∴∽．…………………… 4分．在中，，，∴．…………………… 5分又∴，∴.7654321F30︒30︒A BCDE图2∵∽，∴，∴，∴，∴.即. ………………………………………… 6分<3）在绕点旋转地过程中，直线与夹角地度数不改变，且度. ………………………………… 7分申明：所有资料为本人收集整理，仅限个人学习使用，勿做商业用途.。

2018届九年级上学期期中考试__数学试题

2017-2018学年第一学期期中试卷九年级数学考试时间：120分钟题号一二三总分得分一、选择题：（每小题3分，共3０分，每小题只有一个答案）1. 一元二次方程x2﹣9=0的解是（）A ． x=﹣3B ． x=3C ． x1=3，x2=﹣3D ．x=82. 若一个几何体的主视图、左视图、俯视图都是正方形，则这个几何体是（）A ．正方体B ．圆锥C ．圆柱D ．球3．点（2，﹣2）是反比例函数y=的图象上的一点，则k= （）A ． ﹣1B ．C ． ﹣4D ． ﹣4．下列关于x 的一元二次方程有实数根的是（）A ． x2+1=0B ． x2+x+1=0C ． x2﹣x+1=0D ． x2﹣x ﹣1=05．一个口袋中有2个红球，3个白球，这些球除色外都相同，从口袋中随机摸出一个球，这个球是红球的概率是（）A ．B ．C ．D ．6．顺次连结对角线相等的四边形的四边中点所得图形是（）A ．正方形B ．矩形C ．菱形D ．以上都不对7．下列命题中正确的是（）A.有一组邻边相等的四边形是菱形B.有一个角是直角的平行四边形是矩形C.对角线垂直的平行四边形是正方形D.一组对边平行的四边形是平行四边形8. 如果两个相似三角形的周长比是4:1，那么它们的面积比是 ( )A. 4:1B. 错误!未找到引用源。

C. 16:1D. 错误!未找到引用源。

9.如图，平行四边形ABCD 中，点E 是边AD 的中点，EC 交对角线 BD于点F ，则EF ∶FC 等于（）A.3∶2B.3∶1C.1∶1D.1∶210.如果矩形的面积为6cm2，那么它的长y cm 与宽x cm 之间的函数关系用图象表示大致为（）A B C D 评卷人得分评卷人 y xO o y x y x o y x o二、填空题：（每小题3分，共3０分）11.已知关于x 的方程x2+mx-6=0的一个根为2,则m= ,另一根是 . 12. 若43=x y ，则x y x +的值为___ __．13. 写出一个经过一、三象限的反比例函数y k x =(k ≠0)的解析式．14.在直角三角形中，若两条直角边长分别为6cm 和8cm ，则斜边上的中线长为 cm ．15.已知函数22(1)m y m x -=-是反比例函数，则m 的值为．16. 某钢铁厂去年1月份钢产量为4万吨,三月份钢产量为4.84万吨,求2、3月份平均每月的增长率。

2017年九年级上学期期中试题(定稿版)

2017—2018学年度上学期期中考试九年级数学试卷（考试时间∶120分钟试卷总分∶120分）第Ⅰ卷（选择题）一、选择题（共10小题，每小题3分，共30分）下列各题中均有四个备选答案，其中有且只有一个正确，请在答题卡上将正确答案的代号涂黑．1．方程x2－1＝0的根为A．1 B．﹣1 C．±1 D．0．2．抛物线y＝x2－4x＋6的对称轴为A．x＝4 B．x＝2 C．x＝﹣4 D．x＝﹣2．3．方程x2＋8x＋c＝0有相等的两个实数根，则c等于A．0 B．4 C．16 D．8．4．正六边形绕其中心旋转一定角度后，与自身重合，旋转角至少为A．30°B．60°C．120°D．180°．5．抛物线y＝－(x＋1)2＋2的顶点坐标为A．（﹣1，2）B．（﹣1，﹣2）C．（1，2）D．（1，﹣2）．6．用配方法解方程x2＝6x＋1，下列变形正确的是A ．(x＋3)2＝﹣8 B．(x－3)2＝﹣8C．(x＋3)2＝10 D．(x－3)2＝10．7．如图，△ABE绕点B顺时针旋转一定角度得到△CBD，点D刚好在AE的延长线上，若∠AEB ＝130°，则旋转角的度数为A．50°B．65°C．80°D．95°．8．如图，B为在⊙O的半径OC上一点（不与点O，C重合），点E在圆上，以OB，BE为边作矩形OBED，延长DO到点A，使OA＝OB，连接AC，则A．AC＞DB B．AC＜DBC．AC＝DB D．AC与BD的大小关系不能确定．C第7题图第8题图第9题图9．如图，两个等圆⊙O1和⊙O2相交于A，B两点，O1B的延长线交⊙O2于点C，若∠O1＝35°，则∠O1O2C的度数为A．65°B．70°C．75°D．80°．10．抛物线y ＝ax 2＋bx ＋c （a ≠0）交x 轴于A 、B 两点，交y 轴负半轴于C 点，其中21h -<<-，10B x -<<，下列结论①0abc <；②(4)(2)0a b a b --<；③40a c -<；④若OC =OB ，则(1)(1)0a c ++>．正确的为A ．①②③④B ．①②④C ．③④D ．①②③．第Ⅱ卷（非选择题，共90分)二、填空题（共6小题，每小题3分，共18分)下列各题不需要写出解答过程，请将结果直接填在答卷指定的位置．11．在平面直角坐标系中，点A （3，﹣4）关于原点对称点的坐标为．12．将抛物线y ＝﹣(x －2)2－3先向上平移2个单位，再向左平移3个单位得到的抛物线的解析式为． 13．制药厂连续两个月加大投入，提高生产量，其中九月份生产35万箱，十一月份生产51万箱．设九月份到十一月份平均每月增长的百分率为x ，根据以上信息可列方程为． 14．已知方程kx 2＋(2k ＋3)x ＋k ＝6有实数根，则k 的取值范围是．15．在直径为50的⊙O 中，弦AB ∥CD ，若AB =30，CD =48，则两弦的距离为． 16．在四边形ABCD 中，∠BAD ＝∠BCD ＝90°，AB ＝AD ，将△ABC 沿AB 翻折得到△ABE ．若AC ＝5，BC ＝2．则DE ＝．第16题图三、解答题(共8小题，共72分)下列各题需要在答题卷指定位置写出文字说明、证明过程、计算步骤或作出图形．17．（本题8分）求抛物线y＝x2－4x与直线y＝4交点的坐标．18．（本题8分）学校准备在校园里利用围墙的一段，再砌三面墙，围成一个矩形花园ABCD．围墙EF最长可利用25 米．与围墙平行的一边BC上要预留3米宽的入口MN (不用砌墙)．现已备足可以砌46 米长的墙的材料，问当矩形的长BC为多少米时，矩形花园的面积为299 平方米．19．（本题8分）如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，4）．请解答下列问题：（1）画出△ABC关于x轴对称的△A1B1C1，并写出点A1的坐标；（2）画出△ABC绕原点O逆时针旋转90°后得到的△A2B2C2，并写出点A2的坐标；（3）在x轴上有一点P，若PB+PC的和最小，请直接写出P点坐标．如图，△ABC的顶点在⊙O上，点E，F分别为边AB，AC的中点．（1）求证点A，E，O，F在同一个圆上，并在图中画出该圆的圆心；（2）⊙O的直径MN＝4，点A固定，点B在半圆弧上运动，当点B从点M运动到点N的过程中，请直接写出点E运动路径的长．21．（本题8分）如图，曲线Q1是抛物线y＝x2－2x－3的一部分，其中x≤3，曲线Q2与曲线Q1关于直线x ＝3对称，曲线Q1与x轴相交于A，B两点，C，D分别为曲线Q1和曲线Q2的顶点．（1）求曲线Q2的解析式，并直接写出自变量的取值范围；（2）如图，连接CD，求曲线Q1上的BC部分、线段CD、曲线Q2的AD部分、AB围成的图形的面积．xyyx公司成立之初投资1500万元购买新生产线生产新产品，此外，生产每件产品还需成本60元．按规定，产品售价不得低于100元/件且不得超过180元/件，产品年销售量y （万件）与产品售价x （元）之间的函数关系为13010y x =-+．（1）第一年公司是盈利还是亏损？求出当盈利最大或亏损最小时的产品售价；（2）在（1）的前提下，第二年公司重新确定产品售价，能否使两年共盈利达1340万元，若能，求出第二年的产品售价；若不能，请说明理由． 23．（本题10分）在△ABC 中，边AB 分别绕点A 逆时针旋转90°得到AM ，绕点B 顺时针旋转90°得到BN ，边AC 绕点A 顺时针旋转90°得到AP ，边BC 绕点B 逆时针旋转90°得到BQ ；四边形AMFP ，BQGN 为平行四边形．（1）如图1，当AC ＝BC 时，直接写出线段CF ，CG 的位置关系和数量关系；（2）如图2，当AC ≠BC 时，（1）中的结论是否仍然成立，若成立，请给出证明；若不成立，请说明理由．第23题图2GFP第23题图1GFP如图，抛物线y ＝﹣14x 2＋3x 与x 轴相交于点D ，直线y ＝(3﹣m ) x ＋m 2与y 轴相交于点B ，与抛物线有公共点A ．（1）求证：直线AB 与抛物线只有唯一的公共点；（2）过点A 作AF ⊥x 轴于点F ，当∠ADF ＝60°时，求AF 的长；（3）如图2，E 为抛物线的顶点，BE 交抛物线于点H ，当H 为BE 的中点时，求m 的值．。

2017—2018学年度九年级第一学期期中测试数学试卷1

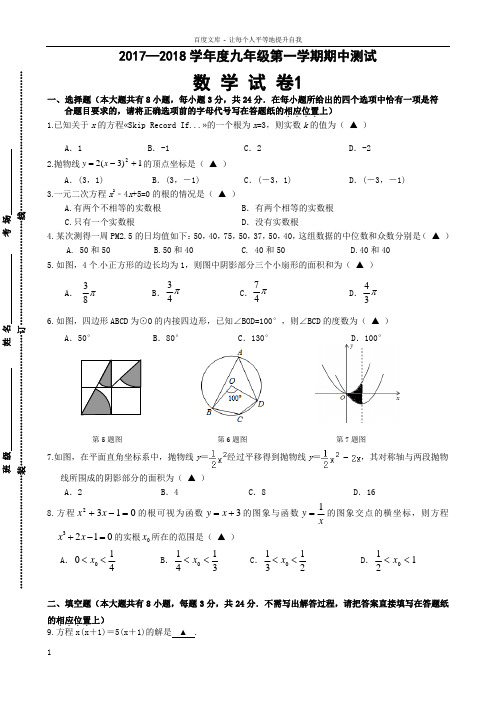
2017—2018学年度九年级第一学期期中测试数学试卷1 一、选择题（本大题共有8小题，每小题3分，共24分．在每小题所给出的四个选项中恰有一项是符合题目要求的，请将正确选项前的字母代号写在答题纸的相应位置．．．．上） 1.已知关于x 的方程«Skip Record If...»的一个根为x =3，则实数k 的值为（ ▲ ） A ．1 B ．-1 C ．2 D ．-2 2.抛物线1)3(22+-=x y 的顶点坐标是（ ▲ ） A ．(3，1) B ．(3，－1) C ．(－3，1) D ．(－3，－1) 3.一元二次方程x 2﹣4x +5=0的根的情况是（ ▲ ） A A.有两个不相等的实数根 B ．有两个相等的实数根 C C.只有一个实数根 D ．没有实数根 4.某次测得一周PM2.5的日均值如下：50，40，75，50，37，50，40，这组数据的中位数和众数分别是（ ▲ ） A. 50和50 B.50和40 C. 40和50 D.40和40 5.如图，4个小正方形的边长均为1，则图中阴影部分三个小扇形的面积和为（ ▲ ） A ． B ． C ． D ． 6.如图，四边形ABCD 为⊙O 的内接四边形，已知∠BOD=100°，则∠BCD 的度数为（ ▲ ） A ．50° B ．80° C ．130° D ．100° 第5题图第6题图第7题图 7.如图，在平面直角坐标系中，抛物线y ＝经过平移得到抛物线y ＝，其对称轴与两段抛物线所围成的阴影部分的面积为（ ▲ ） A ．2 B ．4 C ．8 D ．16 8.方程0132=-+x x 的根可视为函数3+=x y 的图象与函数x y 1=的图象交点的横坐标，则方程3210x x +-=的实根0x 所在的范围是（ ▲ ） A ．4100<<x B ．31410<<x C ．21310<<x D ．1210<<x二、填空题（本大题共有8小题，每题3分，共24分．不需写出解答过程，请把答案直接填写在答题纸的相应位置．．．．上） 9.方程x(x ＋1)＝5(x ＋1)的解是 ▲ .班级姓名考场 …………………………………装………………………………………订………………………………线………………………………………… π83π43π47π3410.某招聘考试分笔试和面试两种，其中笔试按60%、面试按40%计算加权平均数，作为总成绩。

【精品】2017年广东省珠海市香洲区前山中学九年级上学期数学期中试卷及解析

2017学年广东省珠海市香洲区前山中学九年级（上）期中数学试卷
一、选择题（每题3分，共30分）
1．（3分）下列图形中，中心对称图形有（）
A．1个 B．2个 C．3个 D．4个
2．（3分）平面直角坐标系内与点P（﹣2，3）关于原点对称的点的坐标是（）
A．（3，﹣2）B．（2，3） C．（2，﹣3）D．（﹣3，﹣3）
3．（3分）抛物线y=（x+1）2+2的对称轴为（）
A．直线x=1 B．直线y=1 C．直线y=﹣1 D．直线x=﹣1
4．（3分）如图，在等腰直角△ABC中，∠B=90°，将△ABC绕顶点A逆时针方向旋转60°后得到△AB′C′，则∠BAC′=（）
A．60°B．105°C．120° D．135
5．（3分）用配方法解一元二次方程x2+4x﹣5=0，此方程可变形为（）
A．（x+2）2=9 B．（x﹣2）2=9 C．（x+2）2=1 D．（x﹣2）2=1
6．（3分）若关于x的一元二次方程x2﹣2x+k=0有两个不相等的实数根，则k的取值范围是（）A．k≥2 B．k＞﹣2 C．k＜2 D．k≤﹣2
7．（3分）抛物线y=x2﹣4x﹣2的顶点坐标是（）
A．（2，6） B．（﹣2，﹣6）C．（2，﹣6）D．（﹣2，6）
8．（3分）已知1是关于x的一元二次方程（m﹣1）x2+x+1=0的一个根，则m的值是（）A．1 B．﹣1 C．0 D．无法确定
9．（3分）已知一元二次方程x2﹣4x﹣3=0的两根为m，n，则错误的结论是（）
A．m+n=4 B．m•n=﹣3 C．m2﹣4m﹣3=0 D．+=
10．（3分）如图，二次函数y=ax2+bx+c的图象开口向上，图象经过点（﹣1，2）和（1，0），。

2017～2018学年上学期九年级数学期中考试卷

2017～2018学年上学期期中考试卷九年级数学（考试时间：120分钟，试卷满分：120 ）一、选择题（每小题4分，共32分）.1、下列方程中，是一元二次方程的是〖〗.A 、222(1)x x x +=+B 、20ax bx c ++=C 、(1)(3)4x x +-=-D 、22352x y -= 2、下列图形中，既是中心对称又是轴对称的图形是〖〗. 3、下列一元二次方程中，没有实数根的是〖〗. A.02542=+-x x B. 0962=+-x x C.01452=--x x D.01432=+-x x 4、如图，AB 是⊙O 直径，CD ⊥AB 于点E ，则下列结论不正确的是〖〗. A 、CE=DE B 、»»AC AD = C 、OE=BE D 、∠CAB=∠DAB 5、二次函数223y x x =--+的图象是〖〗 A B C D 6、某果园2015年水果产量为100吨，2017年水果产量为144吨，求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为x ，则根据题意可列方程为〖〗. A 、100)1(1442=-x B 、144)1(1002=-x C 、100)1(1442=+x D 、144)1(1002=+x 7、如图，已知C 、D 在以AB 为直径的⊙O 上，若∠CAB=30°，则∠D 的度数是〖〗 A 、30° B 、40° C 、60° D 、70° 8、二次函数2(0)y ax bx c a =++?的图象过点（1，0），对称轴为直线2x =，下列结论：①40a b +=；②0a b c -+<； ③93a c b +=-；④当1x <时，y 的值随x 值的增大而减小. 其中正确的结论有〖〗. A 、4个 B 、3个 C 、2个 D 、1个二、填空题（每题3分，共计18分）. 9、在平面直角坐标系中，点A (4,2)-关于原点中心对称的点A ′的坐标为 . 10、已知12,x x 是一元二次方程2410x x -+=的两个根，则12x x += .11、二次函数2243y x x =-+的顶点坐标是 .12、如图，点A 、B 、C 是⊙O 上的点，OA=AB ，则∠C =___ 度.13、将抛物线22y x =-先向右平移3个单位，再向下平移2个单位，则所得的抛物线的表达式是 _.14、如图，在Rt △ABC 中，∠BCA=900，∠BAC = 300，AB=8cm ，把△ABC 以点B 为中心，逆时针旋转使点C 旋转到AB 边的延长线上点C`处，则AC 边扫过的图形（图中阴影部分）学校：班级：姓名：密封线密封线的面积为 _ __ _cm （结果保留π）.三、解答题（共计70分）.15、解方程（每小题5分，共计10分）（1）2230x x +-= （2）23100x x --=16、(7分)如图，在长为40米，宽为22米的矩形地面上，修筑两条同样宽的互相垂直的道路，余下的铺上草坪，要使草坪的面积为760平方米，道路的宽应为多少？17、（10分）在如图所示的平面直角坐标系中，已知△ABC .（1）将△ABC 沿x 轴负半轴方向平移4个单位，再沿y 轴的正半轴方向平移1个单位，得到△A 1B 1C 1，画出图形,并写出点A 1的坐标；（2）以原点O 为旋转中心，将△ABC 顺时针旋转90°得到△A 2B 2C 2，画出图形,并写出点A 2的坐标；（3）写出△A 2B 2C 2的面积.解：（1）点A 1的坐标是；（2）点A 2的坐标是；（3）△A 2B 2C 2的面积等于 .18、（6分）如图，水平放置的圆柱形排水管道的截面是一个半径为100cm 的圆，其中水面的宽AB 为160cm ，求排水管内水的最大深度？19、（10分）百货商店服装柜在销售中发现：某品牌童装平均每天可售出20件，每件盈利40元。