第六章 证明(一) 测试题 2
第六章:证明(一)经典试题

第一部分:基础复习八年级数学(下)第六章:证明(一)一、中考要求:l.理解证明的必要性和设置公理的必要性.2.关注现实,并通过具体例子了解定义、命题、定理的含义,会区分命题的条件和结论,知道反倒的意义和作用.3.初步掌握用综合法证明的格式,会证明两直线平行的有关判定定理,两直线平行的有关性质定理,三角形内角和定理及其椎论.4.体会推理的严谨性和结论的确定性,初步树立步步有据的推理意识,发展推理论证能力,同时,要善于表达自己的想法,并能与同伴交流.新课标对本章的要求不高,但比较简单的几何证明题仍是2006年中考的热点.二、中考卷研究(一)中考对知识点的考查:2004、2005年部分省市课标中考涉及的知识点如下表:(二)中考热点:新课标对本章的要求不高,但比较简单的几何证明题仍是2006年中考的热点.三、中考命题趋势及复习对策本章主要考查对命题,定理等概念的理解以及运用定义、定理证明问题的过程,在中考题中以证明题的形式出现,一般占5~7分,因此同学们在复习时应注意认真理解概念,分清题目的条件和结论,正确的写出证明过程.★★★(I)考点突破★★★考点1:一、考点讲解:定义:对名称和术语的含义加以描述,作出明确的规定,就叫做定义·命题:判断一件事情的句子叫命题,每个命题都由条件和结论两部分一组成,条件是已知的事项,结论是由已知事项推断出的事项,一般地,命题都可以写成“如果……,那么……”的形式,其中“如果”引出的部分是条件,“那么”引出的部分是结论.命题分为真命题和假命题.真命题:正确的命题是真命题;假命题:不正确的命题是假命题;要说明一个命题是假命题,通常可以举出一个例子,使之具备命题的条件,而不具有命题的结论,这种例子称为反例.公理:公认的真命题称为公理.证明:除了公理外,其他真命题的正确性都通过推理的方法证实,推理的过程称为证明.定理:经过证明的真命题称为定理.逆命题:把原命题的结论作为命题的条件,原命题的条件作为命题的结论,所组成的命题叫原命题的逆命题.逆定理:如果一个定理的逆命题是真命题,那么这个逆命题就叫原定理的逆定理.二、经典考题剖析:【考题1-1】(2004、宁安,9分)如图l-6-1,四边形ABCD中,点E在边CD上,连结AE、BE。
北师大八年级数学下第六章证明(一)期末复习题

学校 班级 考号 姓名__________________________◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆装◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆订◆◆◆◆◆◆◆◆◆◆◆◆◆线◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆第六章 证明(一)复习题一. 知识点回顾1、 一个命题可以写成“如果。
那么。
”的形式。
“如果”后面部分叫 ,“那么”后面部分叫 。
2、平行线的性质:两直线平行, 角相等, 角相等, 角互补。
3、平行线的判别: 角相等, 角相等, 角互补,两直线平行 4.、三角形内角和定理:三角形的三个内角的和等于 度。
推论1:三角形的一个外角等于和它不相邻的 . 推论 2:三角形的一个外角大于任何一个和它 . 二. 课堂练习 ( A 组)1、下列命题中为假命题的是( )A .内错角不相等,两直线不平行 B.一个角的余角一定大于这个角 C .一个钝角的补角必是锐角 D.过两点有且只有一条直线 2、如图,直线a 、b 都于直线c 相交,下列条件中,能判断a ∥b 的条件是( )① ∠1 = ∠2 ② ∠3 = ∠6③∠2 = ∠8 ④∠5 + ∠8 = 1800A .①③ B.①②④ C.①③④ D.②③④3、如图,已知a ∥b ,∠1 = 120°,则∠2 = 。
4、在三角形中,最多有 个直角,最多有 个钝角,至少有 个锐角5、在△ABC中,∠A ∶∠B∶∠C = 1∶2∶3,则这个三角形是 三角形。
6、已知,如图,直线a ,b 被直线c 所截,a ∥b 。
求证:∠1+∠2=180°证明:∵a ∥b ( ) ∴∠1+∠ =180°(两直线平行,同旁内角互补)∵∠3=∠2( ) ∴∠1+∠2=180°( )7、已知,如图,∠1+∠2=180°,求证:∠3=∠4.三. 课堂练习(B 组)8、把“等角的余角相等”改写成 “如果……,那么……”的形式是 。
它的条件是 ,结论是 ,, 9、图△ABC 中,BP 平分∠B ,CP 平分∠C ,若∠A=60°,则∠BPC= 度。
(完整版)第六章线性空间练习题参考答案

第六章 线性空间练习题参考答案一、填空题1.已知0000,,00V a bc a b c R c b ⎧⎫⎛⎫⎪⎪ ⎪=+∈⎨⎬ ⎪⎪⎪ ⎪+⎝⎭⎩⎭是33R ⨯的一个子空间,则维(V ) = 3 , V 的一组基是000000000100,100,010*********⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.2.在P 4中,若1234(1,2,0,1),(1,1,1,1),(1,,1,1),(0,1,,1)k k αααα===-=线性无关,则k 的取值范围是3k ≠(以1234,,,αααα为行或者列构成的行列式不为零). 3.已知a 是数域P 中的一个固定的数,而1{(,,,),1,2,,}n i W a x x x P i n =∈=是P n+1的一个子空间,则a = 0 ,而维(W)=n 4.维数公式为12dim dim V V +=1212dim()dim()V V V V ++.5.设123,,εεε是线性空间V 的一组基,112233x x x αεεε=++,则由基123,,εεε到基231,,εεε的过渡矩阵T =001100010⎛⎫⎪⎪ ⎪⎝⎭,而α在基321,,εεε下的坐标是321(,,)x x x 由基123,,εεε到基233112,,εεεεεε+++的过渡矩阵为T =011101110⎛⎫⎪⎪ ⎪⎝⎭.6.数域P 上n 级对称矩阵全体构成数域P 上(1)2n n +维线性空间,数域P 上n 级反对称矩阵全体构成数域P 上(1)2n n -维线性空间,数域P 上n 级上三角矩阵全体构成数域P 上(1)2n n +维线性空间,数域P 上n 级对交矩阵全体构成数域P 上n 维线性空间,数域P 上n 级数量矩阵全体构成数域P 上 1 维线性空间.二、判断题1.设n n V P ⨯=,则{,0}n n W A A P A ⨯=∈=是V 的子空间.错.行列式为零的两个方阵的和的行列式未必为零,因此W 中矩阵关于矩阵的加法运算不封闭,不能成为子空间.)2.已知{(,),,,}V a bi c di a b c d R =++∈为R 上的线性空间,且维(V )=2. 错.是子空间,但是是4维的,其基为(1,0),(,0),(0,1),(0,)i i .3.设,n n A B P ⨯∈,V 是0A X B ⎛⎫= ⎪⎝⎭的解空间,V 1是AX =0的解空间,V 2是(A +B)X =0的解空间,则12V V V =.正确. 12V V 中的向量既满足AX =0,又满足(A +B)X =0,因此也满足BX =0,即满足0A X B ⎛⎫= ⎪⎝⎭,即为V 中的向量.反之,V 中的向量既在1V 中,又在2V 中,即为12V V 中的向量.因此12V V V =.4.设线性空间V 的子空间W 中每个向量可由W 中的线性无关的向量组12,,,s ααα线性表出,则维(W)=s.正确.根据定理1.5.设W 是线性空间V 的子空间,如果,,V αβ∈但,W W αβ∉∉且则必有.W αβ+∉错误.可能.W αβ+∈如取,αβ为一对互为负向量,则0.W αβ=+∈ 6. }0|),,{(33321=∈=x R x x x W 是3R 的子空间.正确. 基为(1,0,0),(0,1,0),维数为2. 7.}1|),,{(23321=∈=x R x x x W 是3R 的子空间. 错误.不包含零向量.8.}|),,{(3213321x x x R x x x W ==∈= 是3R 的子空间. 正确.基为(1,1,1),维数为1.9.}|),,{(3213321x x x R x x x W -=∈= 是3R 的子空间. 正确. 基为(1,1,0),(1,0,-1),维数为2. 三、计算题1.求所有与A 可交换的矩阵组成的nn P ⨯的子空间()C A 的维数与一组基,其中100020003A ⎛⎫⎪= ⎪ ⎪⎝⎭.解:设矩阵33()ij B b ⨯=与A 可交换,即有AB BA =.即111213111213212223212223313233313233100100020020003003b b b b b b b b b b b b b b b b b b ⎛⎫⎛⎫⎛⎫⎛⎫⎪⎪⎪⎪= ⎪⎪ ⎪⎪ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭.111213111213212223212223313233313233232222333323b b b b b b b b b b b b b b b b b b ⎛⎫⎛⎫⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭. 所以有,()0,,1,2,3.ij ij ij ib b j i j b i j =-==当i j ≠时,0ij b =,因此11223300()0000b C A b b ⎧⎫⎛⎫⎪⎪⎪=⎨⎬ ⎪⎪⎪ ⎪⎝⎭⎩⎭ 维数为3,基为112233,,E E E .2.在线性空间P 4中,求由基1234,,,αααα到基1234,,,ββββ的过渡矩阵,并求(1,4,2,3)α=在基1234,,,αααα下的坐标,其中1234(1,0,0,0),(4,1,0,0),(3,2,1,0),(2,3,2,1)αααα===-=- 1234(1,1,8,3),(0,3,7,2),(1,1,6,2),(1,4,1,1).ββββ====--- 解:令过渡矩阵为T ,则有10111432131401238761001232210001T --⎛⎫⎛⎫⎪⎪- ⎪ ⎪=⎪ ⎪- ⎪⎪-⎝⎭⎝⎭因此1143210112379801231314633100128761232100132213221T ------⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪--⎪ ⎪ ⎪==⎪ ⎪ ⎪- ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭. 令1234114324012320012301x x x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪- ⎪⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭112341432114113611010123401274210012200122400013000133x x x x -----⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪⎪ ⎪-- ⎪ ⎪ ⎪ ⎪⎪ ⎪===⎪ ⎪ ⎪ ⎪⎪ ⎪-- ⎪ ⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ (1,4,2,3)α=在基1234,,,αααα下的坐标为(-101,21,-4,3) 四、证明题1.V 为定义在实数域上的函数构成的线性空间,令12{()(),()()},{()(),()()}W f x f x V f x f x W f x f x V f x f x =∈=-=∈=--证明:W 1、W 2皆为V 的子空间,且12.V W W =⊕证明:W 1、W 2 分别为偶函数全体及奇函数全体构成的集合,显然W 1、W 2均为非空的.由奇偶函数的性质可得W 1、W 2皆为V 的子空间.()()()()(),()22f x f x f x f x f x V f x +---∀∈=+. 而12()()()(),22f x f x f x f x W W +---∈∈,因此12.V W W =+又12{0}.W W =所以12.V W W =⊕2.设W 是P n 的一个非零子空间,若对于W 的每一个向量12(,,,)n a a a 来说,或者120n a a a ====,或者每一个i α都不等于零,证明:维(W)=1.证明:由W 是P n 的一个非零子空间,可得W 中含有非零向量设1212(,,,),(,,,)n n a a a b b b αβ==是W 中的任二个非零向量,由题意可得每一个,i i a b 都不等于零.考虑向量11112112121211(,,,)(,,,)(0,,,)n n n n b a b a a a a b b b b a a b b a a b W αβ-=-=--∈.由题设条件有1212110n n b a a b b a a b -==-=,即有1212n na a ab b b ===.即W 中的任二个非零向量均成比例,因此维(W)=1.。
2020—2021学年北师大版八年级下册第六章《平行四边形》常考综合题专练(一)

北师大版八年级下册第六章《平行四边形》常考综合题专练(一)1.如图1,在平行四边形ABCD中,过点A作AE⊥BC交BC于点E,连接ED,且ED平分∠AEC.(1)求证:AE=BC;(2)如图2,过点C作CF⊥DE交DE于点F,连接AF,BF,猜想△ABF的形状并证明.2.如图,△ABC中,D是AB边上任意一点,F是AC中点,过点C作CE∥AB交DF的延长线于点E,连接AE,CD.(1)求证:四边形ADCE是平行四边形;(2)若∠B=30°,∠CAB=45°,AC=,CD=BD,求AD的长.3.如图,在▱ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F.(1)求证:CD=BE;(2)若点F为DC的中点,DG⊥AE于G,且DG=1,AB=4,求AE的长.4.【教材呈现】如图是华师版九年级上册数学教材第80页的第3题,请完成这道题的证明.【结论应用】(1)如图②,在上边题目的条件下,延长图①中的线段AD交NM的延长线于点E,延长线段BC交NM的延长线于点F.求证:∠AEN=∠F.(2)若(1)中的∠A+∠ABC=122°,则∠F的大小为.5.如图,▱ABCD的对角线AC、BD交于点O,M,N分别是AB、AD的中点.(1)求证:四边形AMON是平行四边形;(2)若AC=6,BD=4,∠AOB=90°,求四边形AMON的周长.6.已知:如图所示,在平行四边形ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.(1)求证:BD、EF互相平分;(2)若∠A=60°,AE=2EB,AD=4,求线段BD的长.7.如图,在平行四边形ABCD中,M、N分别是AD,BC的中点,连接AN、CM.(1)求证:△ABN≌△CDM;(2)连接MN,过点C作CE⊥MN于点E,连接DN,交OM于点O交CE于点P,若∠AND=90°,PE=1,∠1=∠2,求AN的长.8.已知:在▱ABCD中,点E是边AD上一点,点F是线段AE的中点,连接BF并延长BF至点G,使FG=BF,连接DG、EG.(1)如图1,求证:四边形CDGE是平行四边形;(2)如图2,当DA平分∠CDG时,在不添加任何辅助线的情况下,请直接写出图2中与AB相等的线段(AB除外).9.如图,在▱ABCD中,点E、F分别在BC、AD上,AC与EF相交于点O,且AO=CO.(1)求证:△AOF≌△COE;(2)连接AE、CF,则四边形AECF(填“是”或“不是”)平行四边形.10.如图,已知平行四边形ABCD,过A作AM⊥BC于M,交BD于E,过C作CN⊥AD于N,交BD于F,连接AF、CE.(1)求证:BM=DN;(2)求证:四边形AECF为平行四边形.参考答案1.(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,又∵AE⊥BC,∴∠AEC=90°,又∵ED平分∠AEC,∴∠ADE=∠CED=45°,∴∠AED=∠ADE,∴AE=AD,∴AE=BC;(2)△ABF是等腰直角三角形,证明:∵CF⊥DE,∴∠CFE=90°,又∵∠CEF=45°,∴∠ECF=45°,∴∠FEC=∠FCE=∠AEF,∴EF=CF,在△AEF和△BCF中,,∴△AEF≌△BCF(SAS),∴AF=BF,∠AFE=∠BFC,∴∠AFE﹣∠BFE=∠BFC﹣∠BFE,即∠AFB=∠EFC=90°,∴△ABF是等腰直角三角形.2.(1)证明:∵AB∥CE,∴∠CAD=∠ACE,∠ADE=∠CED.∵F是AC中点,∴AF=CF.在△AFD与△CFE中,.∴△AFD≌△CFE(AAS),∴AD=CE,∴四边形ADCE是平行四边形;(2)解:过点C作CG⊥AB于点G.∵CD=BD,∠B=30°,∴∠DCB=∠B=30°,∴∠CDA=60°.在△ACG中,∠AGC=90°,,∠CAG=45°,∴.在△CGD中,∠DGC=90°,∠CDG=60°,,∴GD=1,∴.3.(1)证明:∵AE为∠BAD的平分线,∴∠DAE=∠BAE.∵四边形ABCD是平行四边形,∴AD∥BC,CD=AB.∴∠DAE=∠E.∴∠BAE=∠E.∴AB=BE.∴CD=BE.(2)解:∵四边形ABCD是平行四边形,∴CD∥AB,∴∠BAF=∠DFA.∴∠DAF=∠DFA.∴DA=DF.∵F为DC的中点,AB=4,∴DF=CF=DA=2.∵DG⊥AE,DG=1,∴AG=GF.∴AG=.∴AF=2AG=2.在△ADF和△ECF中,,∴△ADF≌△ECF(AAS).∴AF=EF,∴AE=2AF=4.4.【教材呈现】证明:∵P是BD的中点,M是DC的中点,∴PM=BC,同理,PN=AD,∵AD=BC,∴PM=PN,∴∠PMN=∠PNM,【结论应用】(1)证明:∵P是BD的中点,M是DC的中点,∴PM∥BC,∴∠PMN=∠F,同理,∠PNM=∠AEN,∵∠PMN=∠PNM,∴∠AEN=∠F;(2)解:∵PN∥AD,∴∠PNB=∠A,∵∠DPN是△PNB的一个外角,∴∠DPN=∠PNB+∠ABD=∠A+∠ABD,∵PM∥BC,∴∠MPD=∠DBC,∴∠MPN=∠DPN+∠MPD=∠A+∠ABD+∠DBC=∠A+∠ABC=122°,∵PM=PN,∴∠PMN=×(180°﹣122°)=29°,∴∠F=∠PMN=29°,故答案为:29°.5.(1)根据平行四边形的性质得到AO=OC,BO=OD,AB∥CD,AD∥BC,由三角形的中位线的性质得到MO∥BC,NO∥CD,∴MO∥AN,NO∥AM,∴四边形AMON是平行四边形;(2)解:∵AC=6,BD=4,∴AO=3,BO=2,∵∠AOB=90°,∴AB===,∴OM=AM=MB=,∴NO=AN=,四边形AMON的周长=AM+OM+AN+NO=2.6.(1)证明:∵四边形ABCD是平行四边形,∴CD∥AB,CD=AB,AD=BC,∵DE、BF分别是∠ADC和∠ABC的角平分线,∴∠ADE=∠CDE,∠CBF=∠ABF,∵CD∥AB,∴∠AED=∠CDE,∠CFB=∠ABF,∴∠AED=∠ADE,∠CFB=∠CBF,∴AE=AD,CF=CB,∴AE=CF,∴AB﹣AE=CD﹣CF即BE=DF,∵DF∥BE,∴四边形DEBF是平行四边形.∴BD、EF互相平分;(2)∵∠A=60°,AE=AD,∴△ADE是等边三角形,∵AD=4,∴DE=AE=4,∵AE=2EB,∴BE=GE=2,∴BG=4,过D点作DG⊥AB于点G,在Rt△ADG中,AD=4,∠A=60°,∴AG=AD=2,∴DG==2,∴BD===2.7.(1)证明:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,∠B=∠CDM,∵M、N分别是AD,BC的中点,∴BN=DM,在△ABN和△CDM中,,∴△ABN≌△CDM(SAS);(2)解:∵M是AD的中点,∠AND=90°,∴MN=MD=AD,∴∠1=∠MND,∵AD∥BC,∴∠1=∠CND,∵∠1=∠2,∴∠MND=∠CND=∠2,∴PN=PC,∵CE⊥MN,∴∠CEN=90°,∴∠2=∠PNE=30°,∵PE=1,∴PN=2PE=2,∴CE=PC+PE=3,∴CN==,∵N是BC的中点,∴AD=BC=CN=,∴AN=AD×sin∠1=4=.8.解:(1)∵点F是线段AE的中点,∴AF=EF,在△ABF和△EGF中,,∴△ABF≌△EGF(SAS),∴AB=GE,∠ABF=∠FGE,∴AB∥GE,又∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴GE=CD,GE∥DC,∴四边形CDGE是平行四边形;(2)图2中与AB相等的线段为:GE,GD,DC,CE.理由:∵DA平分∠CDG,∴∠CDE=∠GDE,由(1)可得,GE∥CD,∴∠CDE=∠GED,∴∠GDE=∠GED,∴GE=GD,又∵四边形CDGE是平行四边形,∴四边形CDGE是菱形,∴CD=DG=GE=CE,又∵AB=CD,∴图2中与AB相等的线段为:GE,GD,DC,CE.9.(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠OAF=∠OCE,在△AOF和△COE中,,∴△AOF≌△COE(ASA)(2)解:四边形AECF是平行四边形,理由如下:由(1)得:△AOF≌△COE,∴FO=EO,又∵AO=CO,∴四边形AECF是平行四边形;故答案为:是.10.证明:(1)∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∵AM⊥BC,CN⊥AD,∴AM∥CN,∴四边形AMCN为平行四边形,∴CM=AN,∴BC﹣CM=AD﹣AN,即BM=DN;(2)∵AD∥BC,∴∠ADB=∠CBD,∵AM⊥BC,CN⊥AD,∴∠EMB=∠FND=90°,在△BME和△DNF中,,∴△BME≌△DBF(ASA),∴EM=DF,∵四边形AMCN为平行四边形,∴AM=CN,AM∥CN,∴AE=CF,又∵AE∥CF,∴四边形AECF为平行四边形.。
北师大版八年级下册数学第六章平行四边形含辅助线证明题—截长补短类 训练
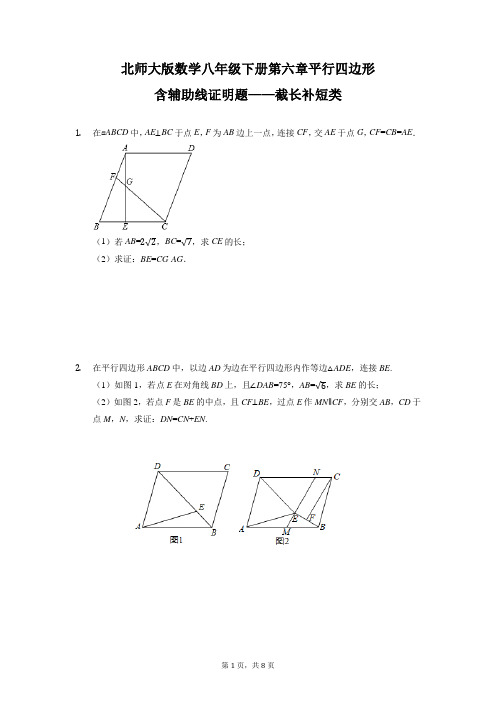
北师大版数学八年级下册第六章平行四边形含辅助线证明题——截长补短类1.在▱ABCD中,AE⊥BC于点E,F为AB边上一点,连接CF,交AE于点G,CF=CB=AE.(1)若AB=2√2,BC=√7,求CE的长;(2)求证:BE=CG-AG.2.在平行四边形ABCD中,以边AD为边在平行四边形内作等边△ADE,连接BE.(1)如图1,若点E在对角线BD上,且∠DAB=75°,AB=√6,求BE的长;(2)如图2,若点F是BE的中点,且CF⊥BE,过点E作MN∥CF,分别交AB,CD于点M,N,求证:DN=CN+EN.3.如图,在▱ABCD中,AE⊥BC,垂足为E,AE=CE.BF⊥AC,垂足为F,分别与AE,AD交于点G,H.(1)若AG=GE=BE=1,求▱ABCD的面积;(2)若CH平分∠BCD,求证:BC=AG+CH.4.已知在▱ABCD中,AE⊥CD,且AB=AE,F为AE上一点,且BF平分∠ABC,(1)若∠ABC=60°,AB=√3,求EF的长;(2)求证:AF+DE=BC.5.在平行四边形ABCD中,E为对角线AC上任意一点,连接BE(1)如图①所示,若AB=BE,AC=BC,∠BAC=75°,AB=2√2,求平行四边形ABCD的面积;(2)如图②所示,延长BE至F,使得EF=EB,连接CF,FD,求证:CE=AE+FD.6.在平行四边形ABCD中,连接BD,过点B作BE⊥BD于点B交DA的延长线于点E,过点B作BG⊥CD于点G.(1)如图1,若∠C=60°,∠BDC=75°,BD=6√2,求AE的长度;(2)如图2,点F为AB边上一点,连接EF,过点F作FH⊥FE于点F交GB的延长线于点H,在△ABE的异侧,以BE为斜边作Rt△BEQ,其中∠Q=90°,若∠QEB=∠BDC,EF=FH,求证:BF+BH=BQ.7.在平行四边形ABCD中,以AB为边作等边△ABE,点E在CD上,以BC为边作等边△BCF,点F在AE上,点G在BA延长线上且FG=FB.(1)若CD=6,AF=3,求△ABF的面积;(2)求证:BE=AG+CE.8.如图,在▱ABCD中,点F是对角线BD上一点,且满足AB=AF,过点F作EG交AD于E,交BC于G,作AH⊥BC于点H,交BD于M.(1)若F为MD中点,AF=2,AM=√3,求BC的长度;(2)若∠ABH=∠AFE,求证:BH+FG=HG.9.如图,平行四边形ABCD中,AB∥CD,AD∥BC,点G是线段BC的中点,点E是线段AD上的一点,点F是线段AB延长线上一点,连接DF,且∠ABE=∠CDG=∠FDG.(1)∠A=45°,∠ADF=75°,CD=3+√3,求线段BC的长;(2)求证:AB=BF+DF.10.如图,△ABC的高AD与中线BE相交于点F,过点C作BE的平行线,过点F作AB的平行线,两平行线相交于点G,连接BG,FG.(1)若AE=2.5,CD=3,BD=2,求AB的长;(2)若∠CBE=30°,求证:CG=AD+EF.11.如图,在□ABCD中,E为BC边的中点,连接AE,F为CD边上一点,且满足∠DFA=2∠BAE.(1)若∠D=100°,∠DAF=30°,求∠FAE的大小;(2)求证:AF=CD+CF.12.已知在平行四边形ABCD中,过点D作DE⊥BC于点E,且AD=DE.连接AC交DE于点F,作DG⊥AC于点G.(1)如图1,若EFDF =12,AF=√13,求DG的长;(2)如图2,作EM⊥AC于点M,连接DM,求证:AM-EM=2DG.13.如图,在平行四边形ABCD中,AE⊥BC于点E,AE=AD,EG⊥AB于点G,延长GE、DC交于点F,连接AF.(1)若BE=2EC,AB=√13,求AD的长;(2)请猜想线段EG、BG、FC之间的等量关系并证明.14.如图,已知平行四边形ABCD中,DE⊥BC于点E,DH⊥AB于点H,AF平分∠BAD,分别交DC、DE、DH于点F、G、M,且DE=AD,CE=3,AB=5.(1)求线段CF的长度;(2)求证:AB=DG+CE.15.如图所示,在平行四边形ABCD中,∠DAC=60°,点E是BC边上一点,连接AE,AE=AB,点F是对角线AC边上一动点,连接EF.(1)如图1,若点F与对角线交点O重合,已知BE=4,OC:EC=5:3,求AC的长度;(2)如图2,若EC=FC,点G是AC边上一点,连接BG、EG,已知∠AEG=60°,∠AGB+∠BCD=180°,求证:BG+EG=DC.16.如图所示,平行四边形ABCD和平行四边形CDEF有公共边CD,边AB和EF在同一条直线上,AC⊥CD且AC=AF,过点A作AH⊥BC交CF于点G,交BC于点H,连接EG.(1)若AE=2,CD=5,求△BCF的周长;(2)求证:BC=AG+EG.。
统计学第六章测试题

第六章 测试题A.参数估计B.统计推断C.区间估计D.假设检验 2.假设检验的概率依据是( )。
A.小概率原理B.最大似然原理C.大数定理D.中心极限定理3.下面有关小概率原则说法中正确的是( ) A 小概率原则事件就是不可能事件B 它是指当一个事件的概率不大于充分小的界限α(0<α<1)时,可认为该事件为不可能事件C 基于”小概率原则”完全可以对某一事件发生与否作出正确判断D 总体推断中可以不予考虑的事件4.通常研究者想收集证据予以支持的假设称为( ) A.原假设 B.备择假设 C.合理假设 D.正常假设5.当原假设为0μμ≥时,此时的假设检验称为( )A.双侧检验B.右侧检验C. 左侧检验D.显著性检验 6.研究表明,司机驾车时因接打手机而发生事故的比例超过20%,用来检验这一结论的原假设和备择假设应是( ) A.%20:0≥μH %20:1<μH B.%20:0≤μH %20:1>μH C.%20:0≤P H %20:1>P H D.%20:0≥P H %20:1<P H7.如果是总体方差已知,正态分布、小样本数据的均值检验,应该采用( )A. t 检验B. z 检验C. P 检验D. 以上都不对 8.在假设检验中,原假设和备选假设( )A 都有可能成立B 都有可能不成立C 只有一个成立而且必有一个成立D 原假设一定成立,备选假设不一定成立9.一种零件的标准长度5Cm ,要检验某天生产的零件是否符合标准要求,建立的原假设和备选假设就为( ) A .0:5H μ=,1:5H μ≠ B .0:5H μ≠,1:5H μ>C .0:5H μ≤,1:5H μ> D .0:5H μ≥,1:5H μ<10.若检验的假设为00H μμ≥:,10H μμ<:,则拒绝域为( )A .z z α<- B .z z α>C ./2z z α<-或/2z z α<- D .z z α>或z z α<-二、简答题1.假设检验的理论依据及推理的思想方法判断的理论依据:假设检验的理论依据是小概率事件原理。
八年级数学下册第六章证明(一)定义与命题

小结 拓展
1、定义:对名称和术语的含义加以描述, 作出明确的规定,也就是给出它们的定 义.
2、命题的定义:判断一件事情的句子,叫 做命题.
3、命题的结构:每个命题都由条件和结论 两部分组成.条件是已知事项,结论是由 已事项推断出的事项.
1、原名: 某些数学名词称为原名. 2、公理: 公认的真命题称为公理.
3、证明: 除了公理外,其它真命题的正确性都通过
推理的方法证实.推理的过程称为证明.
4、定理: 经过证明的真命题称为定理.
经过证明的真
一些条件
推理的过程 叫证明
命题叫定理
+
推理
证实其它命 题的正确性
原名、公理 温馨提示:证明所需的定义、公理和其它定理都
语句.像这样判断一件事情的句子,叫做命题.
寻找命题的“共同的结构特征”
观察下列命题,试找出命题的共同的结构特征 (1)如果两个三角形的三条边对应相等,那么这两个三角形全等 (2)如果一个四边形的一组对边平行且相等,那么这个四边形是
平行四边形; (3)如果一个三角形是等腰三角形,那么这个三角形的两个底角
第六章 证明(一)
定义与命题
眼见未必为实!
a
线段a与线段b哪个 比较长?
b
a bc
谁与线段d在 一条直线上?
d
a
a bc
b
线段a与线段b哪个 比较长?
d
谁与线段d在 一条直线上?
a
b
a=b
a bc d
假如用一根比地球赤道长1 米的铁丝将 地球赤道围起来,那么铁丝与赤道之间的间 隙能有多大(把地球看成球形)?
人教版初中高中化学必修二第六章《化学反应与能量》经典测试(含答案解析)(2)

一、选择题1.Mg-AgCl电池是一种能被海水激活的一次性贮备电池,电池反应方程式为:2AgCl+ Mg =Mg2++ 2Ag+2Cl-。
有关该电池的说法正确的是A.Mg为电池的正极B.负极反应为AgCl+e-=Ag+Cl-C.Cl-移向负极D.电流由镁电极经外电路流向正极2.下列有关实验操作、现象、解释或结论都正确的是选项实验操作现象解释或结论A 用坩埚钳夹持一片未打磨的薄铝片,在酒精灯火焰上加热,铝不能滴落下来,好像有一层膜兜着铝熔点高,没能熔化B将H2在充满Cl2的集气瓶中燃烧集气瓶口上方有白烟生成H2、Cl2化合生成HClC 取两支试管,分别放入一小片打磨过的铝片,再分别加入3mL20%的盐酸和氢氧化钠溶液都有气体产生前者生成氢气,后者生成氧气D 相同温度条件下,向两支试管中分别加入2mL质量分数为3%和6%的H2O2溶液,再分别加入等量二氧化锰粉末,比较H2O2的分解速率6%的H2O2溶液试管中产生气泡的速率较快相同条件浓度大H2O2分解速率快A.A B.B C.C D.D3.某同学用下图所示装置探究原电池的工作原理,并推出下列结论,正确的是A.Cu质量减少B.Zn用作负极C.电子由Cu并经导线流向Zn D.该装置将电能转换为化学能4.可以将反应Zn+Br2=ZnBr2设计成原电池,下列4个电极反应中,分别表示正极反应和负极反应的是①Br2+2e-=2Br-②2Br--2e-=Br2 ③Zn-2e-=Zn2+④Zn2++2e-=ZnA.②和③B.①和④C.②和④D.①和③5.在密闭容器中进行下列反应:X2(g) +Y2(g)⇌2Z (g)。
已知X2、Y2和Z的起始浓度分别为0.1mol·L-1、0.3mol·L-1、0.2mol·L-1,当反应在一定条件下达到平衡时,各物质的浓度有可能是A.Y2为0.2mol·L-1B.Z为0.3mol·L-1C.X2为0.2mol·L-1D.Z为0.4mol·L-1 6.一定温度下,在密闭容器中进行反应:4A(s )+3B(g)2C(g)+D(g),经2min,B的浓度减少0.6mol•L﹣1.对此反应的反应速率的表示,正确的是()①在2min内,用C表示的反应速率是0.1mol•L﹣1•min﹣1②反应的过程中,只增加A的量,反应速率不变③2分钟内,D的物质的量增加0.2 mol④分别用B、C、D表示的反应速率其比值为3:2:1A.①②B.③C.①D.②④7.一定温度下,将纯净的氨基甲酸铵(NH2COONH4)置于真空密闭恒容容器中(固体试样体积忽略不计)达到分解平衡:NH2COONH4(s)2NH3(g)+CO2(g)。
北师大八年级下册 第六章 平行四边形证明题专项练习(包含答案)

1.如图,四边形ABCD是平行四边形,DE平分∠ADC,交AB于点E,BF平分∠ABC,交CD于点F.求证:DE=BF2.如图,在平行四边形ABCD中,将△BCD沿BD翻折,使点C落在点E处,BE和AD相交于点O.求证:OA=OE.3.如图所示,把平行四边形ABCD折叠,使点C与点A重合,这时点D落在点D1处,折痕为EF,若∠BAE=55°,求∠D1AD 的度数4.如图(1),▱ABCD的对角线AC,BD相交于点O,EF过点O且与AD、BC分别相交于点E、F,则OE=OF.若将EF向两方延长与平行四边形的两对边的延长线分别相交(如图(2)和图(3)),OE与OF还相等吗?若相等,请你说明理由.5.如图,点E为▱ABCD的边AB上一点,将△BCE沿CE翻折得到△FCE,点F落在对角线AC上,且AE=AF,若∠BAC=28°,求∠BCD的度数。
6.如图,在▱ABCD中,点E是BC边的中点,连接AE并延长与DC的延长线交于F.(1)求证:CF=CD;(2)若AF平分∠BAD,连接DE,试判断DE与AF的位置关系,并说明理由.7.如图,在▱ABCD中,连接BD,在BD的延长线上取一点E,在DB的延长线上取一点F,使BF=DE,连接AF、CE.求证:AF∥CE.8.如图,在▱ABCD中,O是对角线AC的中点,EF经过点O交AD,BC于E,F.四边形AFCE是平行四边形吗?请说明理由.9.如图,四边形ABCD是平行四边形,直线EF∥BD,与CD、CB的延长线分别交于点E、F,与AB、AD交于点G、H.(1)求证:四边形FBDH为平行四边形;(2)求证:FG=EH.10.如图,已知△ABC是等边三角形,点D、F分别在线段BC、AB上,∠EFB=60°,EF=DC.(1)求证:四边形EFCD是平行四边形;(2)若BF=EF,求证:AE=AD.11.如图①,已知在△ABC中,AB=AC,点P为底边BC上(端点B、C除外)的任意一点,且PE∥AC,PF∥AB.(1)线段PE、PF、AB之间有什么数量关系?并说明理由;(2)如图②,将“点P为底边BC上任意一点”改为“点P为底边BC延长线上任意一点”,其他条件不变,上述结论还成立吗?如果不成立,你能得出什么结论?请说明你的理由.12.如图,已知△ABC是等边三角形,点D、F分别在线段BC、AB上,∠EFB=60°,EF=DC.(1)求证:四边形EFCD是平行四边形;(2)若BF=EF,求证:AE=AD.13.如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD.(1)求证:四边形MNCD是平行四边形;(2)求证:BD=3MN.14.如图,已知△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.求证:四边形DEFG是平行四边形.15.如图,在△ABC中,D、E分别是边AB、AC的中点,∠B=50°.将△ADE沿DE折叠,使点A落在点A1处,求∠BDA1的度数.16.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3.(1)求证:BN=DN;(2)求△ABC的周长.17.如图,在△ABC中,BC=AC,E、F分别是AB、AC的中点,延长EF交∠ACD的平分线于点G.(1)AG与CG有怎样的位置关系?说明你的理由;(2)求证:四边形AECG是平行四边形.18.我们知道“连接三角形两边中点的线段叫三角形的中位线”“三角形的中位线平行于三角形的第三边,且等于第三边的一半”.类似地,我们把连接梯形两腰中点的线段叫做梯形的中位线.如图所示,在梯形ABCD中,AD∥BC,点E,F分别是AB,CD的中点,那么EF就是梯形ABCD的中位线,通过观察、测量,猜想EF和AD,BC有怎样的位置和数量关系,并证明你的结论.19.如图,四边形纸片ABCD中,∠A=70°,∠B=80°,将纸片折叠,使C,D落在AB边上的C',D'处,折痕为MN,求∠AMD'+∠BNC' 的度数20.如图所示,E,F分别为平行四边形ABCD中AD,BC的中点,G,H在BD上,且BG=DH,求证四边形EGFH是平行四边形.21.如图所示,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24 ㎝,BC=26㎝,动点P从点A开始沿AD边以每秒1㎝的速度向D点运动,动点Q从点C开始沿CB边以每秒3㎝的速度向B运动,P,Q分别从A,C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t s.(1)t为何值时,四边形PQCD为平行四边形?(2)t为何值时,四边形PQCD为等腰梯形?(3)t为何值时,四边形ABQP为矩形?22.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3 (1)求证:BN=DN;(2)求△ABC的周长.23.(1)如图①,口ABCD的对角线AC,BD交于点O,直线EF过点O,分别交AD,BC于点E,F.求证:AE=CF.(2)如图②,将口ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.答案1.证法一:∵四边形ABCD是平行四边形,∴AD=CB,∠A=∠C,∠ADC=∠CBA.∵DE平分∠ADC,BF平分∠ABC,∴∠ADE= ∠ADC,∠CBF= ∠CBA,∴∠ADE=∠CBF,∴△ADE≌△CBF(ASA).∴DE=BF.证法二:∵四边形ABCD是平行四边形,∴DC∥AB,∴∠CDE=∠AED,∵DE平分∠ADC,∴∠ADE=∠CDE,∴∠ADE=∠AED, ∴AE=AD.同理,CF=CB,又AD=CB,∴AE=CF,∵AB=CD,∴DF=BE,∴四边形DEBF是平行四边形,∴DE=BF.2.证法一:∵四边形ABCD为平行四边形,∴AD∥BC,且AD=BC,∴∠ADB=∠CBD,由折叠可知∠EBD=∠CBD,BE=BC,∴∠EBD=∠ADB,AD=BE,∴BO=DO,∴AD-DO=BE-BO,即OA=OE.证法二:∵四边形ABCD为平行四边形,∴∠A=∠C,且AB=DC.由折叠可知∠E=∠C,DE=DC,∴∠A=∠E,AB=DE.在△AOB和△EOD中,∴△AOB≌△EOD,∴OA=OE.3.∵四边形ABCD是平行四边形,∴∠BAD=∠C,由折叠性质知,∠D1AE=∠C,∴∠D1AE=∠BAD,∴∠D1AD=∠BAE=55°.4.题图(2)中OE=OF.理由:在▱ABCD中,AB∥CD,OA=OC,∴∠E=∠F,又∵∠AOE=∠COF,∴△AOE≌△COF(AAS),∴OE=OF题图(3)中OE=OF.理由:在▱ABCD中,AD∥BC,OA=OC,∴∠E=∠F,又∵∠AOE=∠COF,∴△AOE≌△COF(AAS),∴OE=OF5.∵∠BAC=28°,AE=AF,∴∠AFE=∠AEF= =76°,∴∠EFC=180°-76°=104°,由折叠的性质知,∠B=∠EFC=104°,∵四边形ABCD是平行四边形,∴AB∥CD,∴∠B+∠BCD=180°,∴∠BCD=180°-104°=76°.6. (1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∵点F为DC的延长线上一点,∴AB∥DF,∴∠BAE=∠CFE,∠ECF=∠EBA,∵E为BC的中点,∴BE=CE,则在△BAE和△CFE中,∴△BAE≌△CFE(AAS),∴AB=CF,∴CF=CD.(2)DE⊥AF.理由:∵AF平分∠BAD,∴∠BAF=∠DAF,∵∠BAF=∠F,∴∠DAF=∠F,∴DA=DF,又由(1)知△BAE≌△CFE,∴AE=EF,∴DE⊥AF.7.∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.∴∠ADF=∠CBE.又∵BF=DE,∴BF+BD=DE+BD,∴DF=BE.∴△ADF≌△CBE.∴∠AFD=∠CEB.∴AF∥CE.8.四边形AFCE是平行四边形.理由如下:∵四边形ABCD是平行四边形,∴AD∥BC.∴∠DAC=∠BCA.又∵O是AC的中点,∴OA=OC.又∵∠AOE=∠COF,∴△AOE≌△COF.∴OE=OF.∵OE=OF,OA=OC,∴四边形AFCE是平行四边形.9. (1)∵四边形ABCD是平行四边形,∴AD∥BC,又∵EF∥BD,∴四边形FBDH为平行四边形.(2)由(1)知四边形FBDH为平行四边形,∴FH=BD,∵EF∥BD,AB∥DC,∴四边形BDEG是平行四边形,∴BD=EG,∴FH=EG,∴FH-GH=EG-GH,∴FG=EH.10. (1)∵△ABC是等边三角形,∴∠ABC=60°.∵∠EFB=60°,∴∠ABC=∠EFB.∴EF∥BC.又∵EF=DC,∴四边形EFCD是平行四边形.(2)连接BE.∵BF=EF,∠EFB=60°∴△BEF是等边三角形∴EB=EF∠ABE=60°又∵EF=DC∴BE=DC∵△ABC是等边三角形, ∴∠ACB=60°,AB=AC.∴∠ABE=∠ACD,又∵BE=DC,AB=AC,∴△ABE≌△ACD,∴AE=AD.11. (1)PE+PF=AB.理由:∵PE∥AC,PF∥AB,∴∠EPB=∠C,四边形PEAF是平行四边形,∴PF=AE,∵AC=AB,∴∠B=∠C,∴∠EPB=∠B,∴PE=BE.∵BE+AE=AB,∴PE+PF=AB.(2)(1)中结论不成立.此时结论为PE-PF=AB.理由:∵PE∥AC,PF∥AB,∴∠FPC=∠ABC,四边形PEAF是平行四边形,∴PE=AF,又AB=AC,∴∠ABC=∠ACB,∴∠FPC=∠ACB=∠FCP,∴PF=FC,∴PE-PF=AF-FC=AC=AB.12. (1)∵△ABC是等边三角形,∴∠ABC=60°.∵∠EFB=60°,∴∠ABC=∠EFB.∴EF∥BC.又∵EF=DC,∴四边形EFCD是平行四边形.(2)连接BE.∵BF=EF,∠EFB=60°,∴△BEF是等边三角形.∴EB=EF,∠ABE=60°.又∵EF=DC,∴BE=DC.∵△ABC是等边三角形,∴∠ACB=60°,AB=AC.∴∠ABE=∠ACD,又∵BE=DC,AB=AC,∴△ABE≌△ACD,∴AE=AD.13. (1)∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.∵M、N分别是AD、BC的中点,∴MD=NC,又MD∥NC,∴四边形MNCD是平行四边形.(3)如图,连接DN.∵N是BC的中点,BC=2CD,∴CD=NC.∵∠C=60°,∴△DCN是等边三角形.∴ND=NC,∠DNC=∠NDC=60°.∴ND=NB=CN.∴∠DBC=∠BDN=30°.∴∠BDC=∠BDN+∠NDC=90°.∴∵四边形MNCD是平行四边形,∴MN=CD.∴BD= MN.14.∵D,E 分别为AC 、AB 的中点,∴DE 是△ABC 的中位线,∴DE ∥BC,且DE=21BC,又∵F 、G 分别是OB 、OC 的中点, ∴FG 是△BCO 的中位线,∴FG ∥BC,且FG= 21BC,∴DE ∥FG,DE=FG,∴四边形DEFG 是平行四边形. 15.∵D 、E 分别是边AB 、AC 的中点,∴DE ∥BC,∴∠ADE=∠B=50°(两直线平行,同位角相等),又∵∠ADE=∠A1DE,∴∠A1DA=2∠B,∴∠BDA1=180°-2∠B=80°.16. (1)证明:∵AN 平分∠BAC,∴∠1=∠2,∵BN ⊥AN,∴∠ANB=∠AND=90°,又AN=AN,∴△ABN ≌△ADN,∴BN=DN.(2)由△ABN ≌△ADN 知,AD=AB=10,点N 为BD 的中点,又M 是BC 的中点,∴MN 为△BCD 的中位线,∴CD=2MN=6,∴AC=AD+CD=16,∴△ABC 的周长=AB+BC+AC=10+15+16=41.17. (1)AG ⊥CG.理由:∵E 、F 分别是AB 、AC 的中点,∴EF 是△ABC 的中位线,AF=CF,∴EF ∥BC,∴∠FGC=∠GCD, ∵CG 平分∠ACD,∴∠FCG=∠GCD,∴∠FCG=∠FGC,∴FG=FC,又∵AF=CF,∴AF=FG,∴∠FAG=∠AGF,∵∠FAG+∠AGC+∠ACG=180°,∴∠AGC=90°,∴AG ⊥CG.(2)证明:由(1)知,FG= 21AC,∵EF 是△ABC 的中位线,∴EF= 21BC,∴FG=EF,又∵AF=CF,∴四边形AECG 是平行四边形. 18. 结论:EF ∥AD ∥BC,EF= 21(AD+BC).证明如下:如图所示,连接AF 并延长交BC 的延长线于点G,∵AD ∥BC,∴∠DAF=∠G,在△ADF 和△GCF 中,∠DAF=∠G,∠DFA=∠CFG,DF=FC,∴△ADF ≌△GCF(AAS),∴AF=FG,AD=CG,又∵AE=EB,∴EF ∥BG,EF= 21BG,即EF ∥AD ∥BC,EF= 21(AD+BC).19.四边形纸片ABCD 中,∠A=70°,∠B=80°,∴∠D+∠C=360°-∠A-∠B=210°.∵将纸片折叠,使C,D 落在AB 边上的C',D'处,∴∠MD'B=∠D,∠NC'A=∠C,∴∠MD'B+∠NC'A=210°,∴∠AD'M+∠BC'N=150°,∴∠AMD'+∠BNC'=360°-∠A-∠B-∠AD'M-∠BC'N=60°20. 证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD =BC (平行四边形对边平行且相等).∴∠EDH =∠FBG . 又∵E ,F 分别为AD ,BC 的中点,∴DE =BF .又∵BG =DH ,∴.△DEH ≌△BFG (SAS ),∴EH =FG ,∠DHE =∠BGF . ∴∠EHG =∠FGH (等角的补角相等).∴EH ∥FG .∴四边形EGFH 是平行四边形21.由已知得AP =t ,CQ =3t ,PD =24-t ,BQ =26-3t .(1)∵PD ∥CQ ,∴当PD =CQ 时,即3t =24-t 时,四边形PQCD 为平行四边形,解得t =6.故当t =6时,四边形PQCD 为平行四边形. (2)如图3—38所示,作DE ⊥BC ,PF ⊥BC ,垂足分别为E ,F ,则CE =2.当QF =CE 时,即QF+CE =2CE =4时,四边形PQCD 是等腰梯形.此时有CQ -EF =4,即3t —(24一t )=4,解得t =7.故当t =7时,四边形PQCD 为等腰梯形.(3)若四边形ABQP 为矩形,则AP =BQ ,即t =26—3t ,解得t =213.故当t =213时,四边形ABQP 为矩形.22.(1)证明:在△ABN 和△ADN 中, ∵12AN ANANB AND ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABN ≌△ADN , ∴BN =DN .(2)解:∵△ABN ≌△ADN ,∴AD =AB =10,DN =NB , 又∵点M 是BC 中点,∴MN 是△BDC 的中位线, ∴CD =2MN =6, 故△ABC 的周长=AB +BC +CD +AD =10+15+6+10=41.23.证明:(1)∵四边形ABCD 是平行四边形,∴AD ∥BC ,OA =OC ,∴∠1=∠2,∵在△AOE 和△COF 中,1234OA OC∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AOE ≌△COF (ASA ),∴AE =CF ; (2)∵四边形ABCD 是平行四边形,∴∠A =∠C ,∠B =∠D ,由(1)得AE =CF ,由折叠的性质可得:AE =A 1E ,∠A 1=∠A ,∠B 1=∠B ,∴A 1E =CF ,∠A 1=∠A =∠C ,∠B 1=∠B =∠D ,又∵∠1=∠2,∴∠3=∠4,∵∠5=∠3,∠4=∠6,∴∠5=∠6,∵在△A 1IE 与△CGF 中,1156A C A E CF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△A1IE≌△CGF(AAS),∴EI=FG.。
第六章证明(一)测试题

3 在 AA C中 , : 0 , 曰、 C的平分线交 于 0点 , LB C等 于( . B 厶4 5 。 则 O
( 6。 A)5 ( 15 B) 1。 ( )0 C 8。
4 举 反例说明“ . 一个角 的余角大 于这个 角” 假命题 , 是 错误的是 ( () A 设这 个角是 4 。 它的余 角是 4 。但 4 。 4 。 5, 5 , 5 = 5
( ) 0 D 5。
Ⅱ
1下列语 句中 , . 是命 题 的是 ( ( 两点确定一 条直线 吗? A) ( 作 4的平分线 A C) M
2 两条平行线被第三条 直线 所截 , . 那么一组 同旁 内角 的平分线 ( ( 相互重合 A) ( 互 相平 行 B) () C 相互垂直
二、 填空题 ( 每小题 3分 , 2 ) 共 4分
1. n= 3当 时 , n+1n+ , +3 以 , 2 n 为线段长 的三角形是直角三角形. , 结论是 , 它是一个 . . 1. 所有 的质数都是 奇数” 4“ 的题设 是 命题 . 填 “ ” “ ” ( 真 或 假 ) l. 5 把命题 “ 对顶角相等 ” 改成 “ 如果 …… , 那么 ……” 的形式应 为 1. 6 若一个三角形 的三个 内角之 比为 4 3 2 则这个 三角形的最大 内角为 :: ,
=
.
. +LA B< 8 。④ LH C C 10 ; E
2. O 如图 5 下列结论 : , ① A>LA D; LB+LA B=10 一 A; C ② C 8 。 ③
— —
( 填上你认 为正确 的所 有序号 ) .
A
E
B C C
D
圈4
图5
《 新课程导 学》适 八 级 生 读・ 学北 大 下 ) . 合 年 学 阅 数 (师 版・册
2020-2021学年八年级数学北师大版下册第六章 6.1.1平行四边形的性质(一) 同步练习题
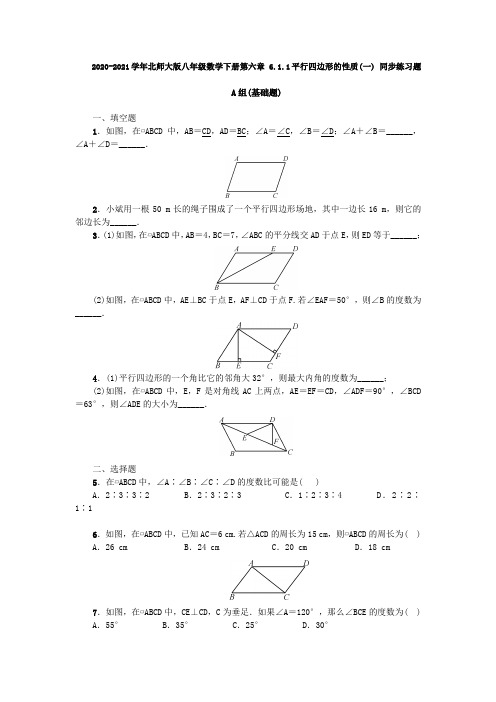
2020-2021学年北师大版八年级数学下册第六章 6.1.1平行四边形的性质(一) 同步练习题A组(基础题)一、填空题1.如图,在▱ABCD中,AB=CD,AD=BC;∠A=∠C,∠B=∠D;∠A+∠B=______,∠A+∠D=______.2.小斌用一根50 m长的绳子围成了一个平行四边形场地,其中一边长16 m,则它的邻边长为______.3.(1)如图,在▱ABCD中,AB=4,BC=7,∠ABC的平分线交AD于点E,则ED等于______;(2)如图,在▱ABCD中,AE⊥BC于点E,AF⊥CD于点F.若∠EAF=50°,则∠B的度数为______.4.(1)平行四边形的一个角比它的邻角大32°,则最大内角的度数为______;(2)如图,在▱ABCD中,E,F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD =63°,则∠ADE的大小为______.二、选择题5.在▱ABCD中,∠A∶∠B∶∠C∶∠D的度数比可能是( )A.2∶3∶3∶2 B.2∶3∶2∶3 C.1∶2∶3∶4 D.2∶2∶1∶16.如图,在▱ABCD中,已知AC=6 cm.若△ACD的周长为15 cm,则▱ABCD的周长为( ) A.26 cm B.24 cm C.20 cm D.18 cm7.如图,在▱ABCD中,CE⊥CD,C为垂足.如果∠A=120°,那么∠BCE的度数为( ) A.55°B.35°C.25°D.30°8.如图,在▱ABCD中,∠ADO=30°,AB=6,点A的坐标为(-2,0),则点C的坐标为( )A.(6,3) B.(3,23) C.(6,23) D.(6,3)三、解答题9.(1)如图,在▱ABCD中,将△ADC沿AC折叠后,点D恰好落在DC的延长线上的点E 处.若∠B=60°,AB=3,求△ADE的周长.10.(1)如图,四边形ABCD是平行四边形,点E在BA的延长线上,且BE=AD,点F在AD上,AF=AB.求证:△AEF≌△DFC.(2)如图,在▱ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且DN=32,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,求AP的长.B组(中档题)一、填空题11.如图,在▱ABCD中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4,则CE的长是______.12.如图,以▱ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE,BE,则∠AEB的度数是______.13.如图,在▱ABCD中,∠ABC=135°,AD=42,AB=8,作对角线AC的垂直平分线EF,分别交对边AB,CD于点E和点F,则AE的长为______.二、解答题14.如图,已知▱ABCD中,AB=5,BC=3,AC=213.(1)求▱ABCD的面积;(2)求证:BD⊥BC.C组(综合题)15.如图,在▱ABCD中,过点C作CH⊥AB,过点B作AC的垂线,分别交CH,AC,AD于点E,F,G,且∠ABC=∠BEH,BG=BC.(1)若BE=10,BC=25,求DG的值;(2)连接HF,求证:HA=2HF-HE.参考答案2020-2021学年北师大版八年级数学下册第六章 6.1.1平行四边形的性质(一) 同步练习题A组(基础题)一、填空题1.如图,在▱ABCD中,AB=CD,AD=BC;∠A=∠C,∠B=∠D;∠A+∠B=180°,∠A+∠D=180°.2.小斌用一根50 m长的绳子围成了一个平行四边形场地,其中一边长16 m,则它的邻边长为9_m.3.(1)如图,在▱ABCD中,AB=4,BC=7,∠ABC的平分线交AD于点E,则ED等于3;(2)如图,在▱ABCD中,AE⊥BC于点E,AF⊥CD于点F.若∠EAF=50°,则∠B的度数为50°.4.(1)平行四边形的一个角比它的邻角大32°,则最大内角的度数为106°;(2)如图,在▱ABCD中,E,F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD =63°,则∠ADE的大小为21°.二、选择题5.在▱ABCD中,∠A∶∠B∶∠C∶∠D的度数比可能是(B)A.2∶3∶3∶2 B.2∶3∶2∶3 C.1∶2∶3∶4 D.2∶2∶1∶16.如图,在▱ABCD中,已知AC=6 cm.若△ACD的周长为15 cm,则▱ABCD的周长为(D) A.26 cm B.24 cm C.20 cm D.18 cm7.如图,在▱ABCD中,CE⊥CD,C为垂足.如果∠A=120°,那么∠BCE的度数为(D) A.55°B.35°C.25°D.30°8.如图,在▱ABCD中,∠ADO=30°,AB=6,点A的坐标为(-2,0),则点C的坐标为(C)A.(6,3) B.(3,23) C.(6,23) D.(6,3)三、解答题9.(1)如图,在▱ABCD中,将△ADC沿AC折叠后,点D恰好落在DC的延长线上的点E 处.若∠B=60°,AB=3,求△ADE的周长.解:由折叠可得,∠ACD =∠ACE =90°. ∴∠BAC =90°.又∵∠B =60°,∴∠ACB =30°. ∴BC =2AB =6.∴AD =6.由折叠可得,∠E =∠D =∠B =60°, ∴∠DAE =60°.∴△ADE 是等边三角形. ∴△ADE 的周长为6×3=18.(2)如图,在▱ABCD 中,BE ,DF 分别平分∠ABC ,∠ADC.求证:BE =DF.证明:∵四边形ABCD 为平行四边形,∴∠A =∠C ,∠ABC =∠ADC ,AB =CD. 又∵BE ,DF 分别平分∠ABC ,∠ADC ,∴∠CBE =∠ADF. 又∵AD ∥BC ,∴∠ADF =∠DFC. ∴∠CBE =∠DFC.∴BE ∥DF.又∵DE ∥BF ,∴四边形DFBE 为平行四边形. ∴BE =DF.10.(1)如图,四边形ABCD 是平行四边形,点E 在BA 的延长线上,且BE =AD ,点F 在AD 上,AF =AB.求证:△AEF ≌△DFC.证明:∵四边形ABCD 是平行四边形,∴AB =CD ,AB ∥CD. ∴∠EAF =∠ADC.又∵AF =AB ,BE =AD , ∴AF =CD ,AE =DF.在△AEF 和△DFC 中,⎩⎪⎨⎪⎧AF =DC ,∠EAF =∠FDC ,AE =DF ,∴△AEF ≌△DFC.(2)如图,在▱ABCD 中,连接BD ,且BD =CD ,过点A 作AM ⊥BD 于点M ,过点D 作DN ⊥AB 于点N ,且DN =32,在DB 的延长线上取一点P ,满足∠ABD =∠MAP +∠PAB ,求AP 的长.解:∵BD =CD ,BA =CD , ∴BD =BA.又∵AM ⊥BD ,DN ⊥AB ,∴DN =AM =3 2.又∵∠ABD =∠MAP +∠PAB ,∠ABD =∠P +∠PAB , ∴∠P =∠PAM.∴△APM 是等腰直角三角形. ∴AP =2AM =6.B 组(中档题)一、填空题11.如图,在▱ABCD 中,CE 平分∠BCD ,交AB 于点E ,EA =3,EB =5,ED =4,则CE 的长是45.12.如图,以▱ABCD 的边CD 为斜边向内作等腰直角△CDE ,使AD =DE =CE ,∠DEC =90°,且点E 在平行四边形内部,连接AE ,BE ,则∠AEB 的度数是135°.13.如图,在▱ABCD 中,∠ABC =135°,AD =42,AB =8,作对角线AC 的垂直平分线EF ,分别交对边AB ,CD 于点E 和点F ,则AE 的长为203.二、解答题14.如图,已知▱ABCD 中,AB =5,BC =3,AC =213. (1)求▱ABCD 的面积; (2)求证:BD ⊥BC.解:(1)过点C 作CE ⊥AB 交AB 的延长线于点E , 设BE =x ,CE =h.在Rt △CEB 中,由勾股定理,得x 2+h 2=9.①在Rt △CEA 中,由勾股定理,得(5+x)2+h 2=52.② 联立①②,解得x =95,h =125.∴S ▱ABCD =AB ·h =12.(2)证明:过点D 作DF ⊥AB ,垂足为F. ∴∠DFA =∠CEB =90°.在▱ABCD 中,AD =BC ,AD ∥BC , ∴∠DAF =∠CBE.又∵∠DFA =∠CEB =90°,AD =BC , ∴△ADF ≌△BCE(AAS).∴AF =BE =95,BF =5-95=165,DF =CE =125.在Rt △DFB 中,由勾股定理,得 BD 2=DF 2+BF 2=(125)2+(165)2=16,∴BD =4.∵BC =3,DC =5,∴CD 2=DB 2+BC 2. ∴BD ⊥BC.C 组(综合题)15.如图,在▱ABCD 中,过点C 作CH ⊥AB ,过点B 作AC 的垂线,分别交CH ,AC ,AD 于点E ,F ,G ,且∠ABC =∠BEH ,BG =BC.(1)若BE =10,BC =25,求DG 的值;(2)连接HF ,求证:HA =2HF -HE.解:(1)∵四边形ABCD 是平行四边形, ∴AD =BC =25,∠ABC +∠BAG =180°. ∵∠ABC =∠BEH ,∴∠CEB +∠ABC =180°. ∴∠BAG =∠CEB.∵∠ABG +∠BEH =90°,∠ECB +∠ABC =90°, ∴∠ABG =∠ECB.在△BAG 和△CEB 中,⎩⎪⎨⎪⎧∠BAG =∠CEB ,∠ABG =∠ECB ,BG =CB ,∴△BAG ≌△CEB(AAS).∴AG =BE =10.∴DG =AD -AG =25-10=15.(2)证明:过点F 作FN ⊥HF ,交BA 的延长线于点N , ∵△BAG ≌△CEB ,∴CE =AB.∵∠ABG +∠BAC =∠ECB +∠ABC =90°,∠ABG =∠ECB , ∴∠BAC =∠ABC. ∴AC =BC.∵CH ⊥AB ,∴∠ACH =∠ECB =∠ABG. 在△ABF 和△ECF 中,⎩⎪⎨⎪⎧∠CFE =∠BFA ,∠ABF =∠ECF ,AB =EC ,∴△ABF ≌△ECF(AAS).∴AF =EF.∵∠HFN =∠EFA =90°,∴∠AFN =∠EFH. ∵∠BAC =∠ABC ,∠ABC =∠BEH , ∴∠NAF =∠HEF.在△ANF 和△EHF 中,⎩⎪⎨⎪⎧∠NAF =∠HEF ,AF =EF ,∠AFN =∠EFH ,∴△ANF ≌△EHF(ASA).∴HE =AN ,HF =NF.∴△HFN 是等腰直角三角形. ∴HN =2HF.∴HA +AN =HA +HE =2HF. ∴HA =2HF -HE.。
2018届数学复习第六章不等式、推理与证明课时作业36不等关系与不等式(含解析)文

课时作业36 不等关系与不等式一、选择题1.若a〈0,ay〉0且x+y〉0,则x与y之间的不等关系是()A.x=y B.x>yC.x〈y D.x≥y解析:由a〈0,ay>0知y〈0,又由x+y〉0知x>0,所以x〉y。
答案:B2.若1a〈错误!〈0,则下列结论不正确的是()A.a2<b2B.ab〈b2C.a+b〈0 D.|a|+|b|>|a+b|解析:∵错误!<错误!<0,∴b〈a〈0.∴a2<b2,ab<b2,a+b<0,|a|+|b|=|a+b|.答案:D3.设a,b是非零实数,若a<b,则下列不等式成立的是( )A .a 2〈b 2B .ab 2〈a 2b C.1ab 2〈错误! D.错误!<错误!解析:当a <0时,a 2〈b 2不一定成立,故A 错. 因为ab 2-a 2b =ab (b -a ).b -a 〉0,ab 符号不确定.所以ab 2与a 2b 的大小不能确定,故B 错.因为错误!-错误!=错误!<0.所以错误!〈错误!,故C 正确.D 项中b a 与错误!的大小不能确定.答案:C4.设α∈(0,π2),β∈[0,错误!],那么2α-错误!的取值范围是( )A .(0,5π6)B .(-错误!,错误!)C .(0,π)D .(-错误!,π)解析:由题设得0<2α<π,0≤错误!≤错误!.∴-π6≤-错误!≤0,∴-错误!<2α-错误!〈π.答案:D5.已知a=log23+log2错误!,b=log29-log2错误!,c =log32,则a,b,c的大小关系是()A.a=b<c B.a=b>cC.a<b<c D.a〉b>c解析:a=log23+log23=log23错误!。
b=log29-log2错误!=log2错误!=log23错误!。
∴a=b=log23错误!〉log22=1。
北师大版八年级下册数学第六章 证明(一)练习题(带解析)

北师大版八年级下册数学第六章 证明(一)练习题(带解析) 考试范围:xxx ;考试时间:100分钟;命题人:xxx 1. 答题前填写好自己的姓名、班级、考号等信息 2. 请将答案正确填写在答题卡上 分卷I 分卷I 注释 一、单选题(注释) 1、如图,∠x 的两条边被一直线所截,用含α和β的式子表示∠x 为( ) A .α-β B .β-α C .180°-α+β D .180°-α-β 2、如果一个三角形的一个内角大于相邻的外角,这个三角形是( ) A .锐角三角形 B .钝角三角形 C .直角三角形 D .等边三角形 3、三角形的三个外角之比为2∶2∶3,则此三角形为( ) A .锐角三角形 B .钝角三角形 C .直角三角形 D .等边三角形 4、下列说法正确的有( ) ①三角形的外角大于它的内角; ②三角形的一个外角等于和它不相邻的两个内角之和; ③三角形的外角中至少有两个钝角; ④三角形的外角都是钝角. A .1个 B .2个 C .3个 D .4个 5、如果一个三角形的一个外角等于与它相邻的内角,这个三角形是( ) A .直角三角形 B .锐角三角形 C .钝角三角形 D .等边三角形 6、以下命题中正确的是( )C .三角形的外角都比锐角大D .三角形中的内角中没有小于60°的 7、三角形中最大的内角一定是( ) - A .钝角--- B .直角; C .大于60°的角- D .大于等于60°的角 8、在△ABC 中,∠A-∠B=35°,∠C=55°,则∠B 等于( ) - A .50°- B .55°- C .45°- D .40° 9、△ABC 中,∠A+∠B=120°,∠C=∠A ,则△ABC 是( ) - A .钝角三角形- B .等腰直角三角形 C .直角三角形- D .等边三角形 10、下列叙述正确的是 ( ) A .-钝角三角形的内角和大于锐角三角形的内角和; B .三角形两个内角的和一定大于第三个内角; C .三角形中至少有两个锐角; D .三角形中至少有一个锐角. 11、关于三角形内角的叙述错误的是( ) A .-三角形三个内角的和是180° B .三角形两个内角的和一定大于60° C .三角形中至少有一个角不小于60° D .一个三角形中最大的角所对的边最长 12、如图所示,BC ⊥AD ,垂足是C ,∠B=∠D ,则∠AED 与∠BED 的关系是( ) - A .∠AED>∠BED- B .∠AED<∠BED C .∠AED=∠BED- D .无法确定 更多功能介绍/zt/ 13、如图,OP ∥QR ∥ST ,则下列等式中正确的是( )C .∠1-∠2+∠3=180°D .∠1+∠2+∠3=180° 14、如图,AB ∥CD ,AD 、BC 相交于O ,∠BAD =35°,∠BOD =76°,则∠C 的度数是( ) A 、31° B 、35° C 、41° D 、76° 15、已知∠A =50°,∠A 的两边分别平行于∠B 的两边,则∠B =( ) A .50° B .130° C .100° D .50°或130° 16、如图,AB ∥CD ,∠α=( ) A .50° B .80° C .85° D .95° 17、如图,直线AB ∥CD ,EF ⊥AB 于E ,交CD 于F ,直线MN 交AB 于M ,CD 于N ,EF 于O ,则直线AB 和CD 之间的距离是哪个线段的长( ) A .MN B .EF C .OE D .OF 18、若两条平行线被第三条直线所截,则下列说法错误的是( ) A .一对同位角的平分线互相平行 B .一对内错角的平分线互相平行 C .一对同旁内角的平分线互相平行 D .一对同旁内角的平分线互相垂直 19、下列命题中,真命题有 ( ) -①如果△A 1B 1C 1∽△A 2B 2C 2,△A 2B 2C 2∽△A 3B 3C 3,那么△A 1B 1C 1∽△A 3B 3C 3 ②直线外一点到这条直线的垂线段,叫做这个点到这条直线的距离 ③如果=0,那么x="±2" ④如果a=b ,那么a 3=b 3 - A .1个- B .2个- C .3个- D .4个- A .所有的命题都有条件和结论 B .所有的命题都是定理 - C .所有的定理都是命题 D .所有的公理都是真命题分卷II分卷II 注释二、填空题(注释)21、如图,把△ABC的纸片沿DE折叠,当点A落在四边形BCED内部时,则∠A与∠1.∠2之间有一种数量关系始终保持不变,请试着找出这个规律为___________________.22、如图,比较∠A、∠BEC、∠BDC的大小关系为_______________________.23、如图,∠1,∠2,∠3是△ABC的不同的三个外角,则∠1+∠2+∠3=________.24、在△ABC中,∠A等于和它相邻的外角的四分之一,这个外角等于等于∠B的两倍,那么∠A=______,∠B=_______,∠C=_______.25、如图△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=158°,则∠EDF=________.26、直接根据图示填空:(1)∠α=_________ (2)∠α=_________ (3)∠α=_________(4)∠α=_________ (5)∠α=_________ (6)∠α=_________(1) (2) (3) (4) (5) (6) 27、在一个三角形中,最多有______个钝角,至少有______个锐角. 28、如图,在△ABC 中,∠BAC=90°,AD ⊥BC 于D ,则∠B=∠___,∠C=∠____. 29、在△ABC 中,∠A+∠B=120°,∠A-∠B+∠C=120•°,则∠A=___,∠B=____. 30、在△ABC 中,∠A=∠B=∠C ,则∠C=_______. 三、计算题(注释) 四、解答题(注释) 31、如图,P 是△ABC 内一点,请用量角器量出∠ABP .∠ACP .∠A 和∠BPC 的大小,再计算一下,∠ABP +∠ACP +∠A 是多少度?这三个角的和与∠BPC 有什么关系?你能用学到的知识来解释其中的道理吗?你能判断∠BPC 和∠A 的大小吗?把你的想法与同伴交流,看谁说得更有道理. 32、如图,D 为AC 上一点,E 是BC 延长线上一点,连BD ,DE.求证:∠ADB >∠CDE. 33、如图,D 在BC 延长线上一点,∠ABC 、∠ACD 平分线交于E.求证:∠E =∠A 34、D 为△ABC 的边AB 上一点,且∠ADC =∠ACD.求证:∠ACB >∠B35、如图,求证:∠A +∠B +∠C +∠D +∠E =180° 36、我们已经证明了“三角形的内角等于180°”,易证“四边形的内角和等于360°=2×180°,五边形的内角和等于540°=3×180•°……”,试猜想一下十边形的内角等于多少度?n 边形的内角和等于多少度? 37、请你利用“三角形内角和定理”证明“四边形的内角和等于360°”.四边形ABCD 如图所示. 38、小明在证明“三角形内角和等于180°”时用了如图所示的辅助线的方法,即延长BC 到D ,延长AC 到E ,过点C 作CF ∥AB ,你能接着他的辅助线的做法证明出来吗? 39、如图,一块梯形玻璃的下底及两腰的一部分被摔碎,量得∠A=120•°,∠D=105°,你能否求出两腰的夹角∠P 的度数. 40、如图,在正方形ABCD 中,已知∠AEF=30°,∠BCF=28°,求∠EFC 的度数. 41、如图,在△ABC 中,∠B=30°,∠C=65°,AE ⊥BC 于E ,AD 平分∠BAC ,求∠DAE 的度数. 42、如图,已知:∠A=∠C.求证:∠ADB=∠CEB. 43、如图,AB ∥CD ,EF ⊥AB 于O ,∠2=135°,求∠1的度数. 下面提供三个思路: (1)过F 作FH ∥AB , (2)延长EF 交CD 于I ; (3)延长GF 交AB 于K . 请你利用三个思路中的两个思路,求∠1的度数. 44、如图,已知AB ∥CD ,分别探究下面四个图形中∠APC 和∠PAB 、∠PCD 的关系,并从所得的四个关系中任选一个加以说明,证明所探究的结论的正确性. 结论(1)____________________________;(2)____________________________; (3)____________________________;(4)____________________________; 选择结论________,说明理由是什么. 45、如图,直线AD 与AB 、CD 相交于A 、D 两点,EC 、BF 与AB 、CD 相交于E 、C 、B 、F ,如果∠1=∠2,∠B =∠C.说明∠A =∠D46、如图,已知∠B=∠C,AE∥BC,说明AE平分∠CAD.47、我们知道任何一个命题都由条件和结论两部分组成,•如果我们把一个命题的条件变结论,结论变条件,那么所得的是不是一个命题?试举例说明.48、把下列命题改写成“如果……,那么……”的形式:-同角或等角的余角相等.49、在讨论“对顶角不相等”是不是命题的问题时,甲认为:这不是命题,因为这句话是错误的.乙认为:这是命题,因为它作出了判断,只不过这一判断是错误的,所以它是假命题,你认为谁的说法是正确的?50、指出下列命题的条件和结论,并判断命题的真假,如果是假命题,请举出反例.-如果等腰三角形的两条边长为5和7,那么这个等腰三角形的周长为17.试卷答案1.【解析】试题分析:根据对顶角相等及三角形的一个外角等于和它不相邻的两个内角之和即可判断.由图可得用含α和β的式子表示∠x为β-α,故选B.考点:三角形的内角和外角的关系点评:熟练掌握与三角形有关的知识是同学们应该具备的基本能力,因而此类问题在中考中比较常见,常以填空题、选择题形式出现,难度一般.2.【解析】试题分析:根据内角与相邻的外角是互补的关系即可判断.∵内角大于相邻的外角∴这个内角是钝角∴这个三角形是钝角三角形故选B.考点:三角形的内角和外角的关系点评:熟练掌握三角形的性质及与三角形有关的知识是初中平面图形的基本要求,因而此类问题在中考中比较常见,常以填空题、选择题形式出现,难度不大.3.【解析】试题分析:根据三角形的三个外角的和为360°即可求得三个外角,再求得相邻的内角,从而可以得到结果.由题意得,这三个外角的度数分别为,,则对应的内角的度数分别为,,,均小于直角则此三角形为锐角三角形故选A.考点:三角形的外角和点评:利用三角形的性质进行角度的计算是学生初中数学学习中的最基本的能力,因而此类问题在中考中比较常见,常以填空题、选择题形式出现,难度不大.4.【解析】试题分析:根据三角形的内角和定理及内角与外角的关系依次分析即可.当内角为钝角时,内角为锐角,①④错误,②③正确,故选B.考点:三角形的内角和定理,三角形的外角点评:此类问题对学生逻辑推理能力及对三角形的性质的理解要求较高,因而在中考中比较常见,常以填空题、选择题形式出现,难度不大.5.【解析】试题分析:根据外角等于与它相邻的内角即可求得这个内角的度数,从而得到结果.∵外角等于与它相邻的内角∴这个内角为90°∴这个三角形是直角三角形故选A.考点:三角形的内角和定理,三角形的外角6.【解析】试题分析:根据三角形的内角和定理及内角与外角的关系依次分析即可.A、三角形的三个内角与三个外角的和为540°,本选项正确;B、当内角为钝角时,外角为锐角,C、当内角为锐角时,外角为钝角,D、三角形中的内角中有小于60°,故错误.考点:三角形的内角和定理,三角形的外角点评:三角形的内角和定理的应用贯穿于整个初中学习,是平面图形中极为重要的知识点,与各个知识点结合极为容易,是中考中的热点,在各种题型中均有出现,需多加关注.7.【解析】试题分析:因为三角形的内角和是180度,可以进行假设验证,如果最大角小于60度,则三角形的内角和小于180度,据此选择即可.假设三角形的最大角小于60°,则不能满足三角形的内角和是180度,这与三角形的内角和是180度相矛盾,所以三角形中最大的一个角一定不小于60°,即大于等于60°的角故选D.考点:三角形的内角和定理点评:此类问题对学生逻辑推理能力及对三角形的性质的理解要求较高,因而在中考中比较常见,常以填空题、选择题形式出现,难度较大.8.【解析】试题分析:由∠C=55°根据三角形的内角和定理∠A+∠B的度数,再结合∠A-∠B=35°即可组成方程组求得结果.∵∠C=55°∴∠A+∠B=180°-∠C=125°∵∠A-∠B=35°∴∠B=45°故选C.考点:三角形的内角和定理点评:方程思想在初中数学的学习中极为重要,也是中考中的热点,在各种题型中均有出现,需多加关注.9.【解析】试题分析:由∠A+∠B=120°根据三角形的内角和定理可得∠C的度数,即可得到∠A的度数,从而可以得到结果.∵∠A+∠B=120°∴∠C=180°-∠A-∠B=60°∴∠C=∠A∴△ABC是等边三角形故选D.考点:三角形的内角和定理点评:此类问题知识点综合性较强,在中考中比较常见,常以填空题、选择题形式出现,属于基础题,难度一般.10.【解析】试题分析:根据三角形的内角和定理依次分析各项即可判断.C、三角形中至少有两个锐角,本选项正确.考点:三角形的内角和定理点评:三角形的内角和定理的应用贯穿于整个初中学习,是平面图形中极为重要的知识点,与各个知识点结合极为容易,是中考中的热点,在各种题型中均有出现,需多加关注.11.【解析】试题分析:根据三角形的内角和定理结合三角形的边和角的关系依次分析各项即可判断.A.三角形三个内角的和是180°,C.三角形中至少有一个角不小于60°,D.一个三角形中最大的角所对的边最长,均正确,不符合题意;B.三角形两个内角的和可能小于60°,故错误,本选项符合题意.考点:三角形的内角和定理点评:三角形的内角和定理的应用贯穿于整个初中学习,是平面图形中极为重要的知识点,与各个知识点结合极为容易,是中考中的热点,在各种题型中均有出现,需多加关注.12.【解析】试题分析:根据∠B=∠D,公共角∠A,结合三角形的内角和定理及BC⊥AD即可得到结果.∵∠B=∠D,∠A=∠A,∠AED=180°-∠A-∠D,∠ABC=180°-∠A-∠B∴∠AED=∠ABC∵BC⊥AD∴∠ABC=90°∴∠AED=90°∴∠AED=∠BED故选C.考点:三角形的内角和定理点评:通过题目中的条件找到不相关的两个量的关系是学生学习过程中需要具备的基本能力,因而这类问题在中考中比较常见,在各种题型中均有出现,需多加关注.13.【解析】试题分析:由ST∥QR,可得∠QRS=∠3,由OP∥QR,可得∠QRP=180°-∠2,即得结论. ∵ST∥QR,∴∠QRS=∠3,即∠QRP+∠1=∠3;∵OP∥QR,∴∠QRP=180°-∠2,∴180°-∠2+∠1=∠3,即∠2+∠3-∠1=180°.故选B.考点:平行线的性质点评:平行线的判定与性质的应用贯穿于整个初中学习,是平面图形中极为重要的知识点,与各个知识点结合极为容易,是中考中的热点,在各种题型中均有出现,需多加关注.14.【解析】试题分析:由AB∥CD可得∠BAD=∠D=35°,再根据三角形的一个外角等于不相邻的两个内角的和即可求得结果. ∵AB ∥CD ∴∠BAD =∠D =35° ∵∠BOD =76° ∴∠C =∠BOD-∠D =41° 故选C. 考点:平行线的性质,三角形的外角的性质 点评:平行线的判定与性质的应用贯穿于整个初中学习,是平面图形中极为重要的知识点,与各个知识点结合极为容易,是中考中的热点,在各种题型中均有出现,需多加关注. 15.【解析】 试题分析:根据平行线的性质,若两个角的两边互相平行,则这两个角相等或互补. 如图:∠B=50°或130°;故选D . 考点:平行线的性质 点评:分类思想是学生学习过程中的一个薄弱环节,能否根据具体情况正确分类往往能够体现一个学生思考问题的全面性,因而这类问题在中考中比较常见,在各种题型中均有出现,一般难度较大,需多加关注. 16.【解析】 试题分析:如图,过α的顶点作AB 的平行线,运用两次平行线的性质可以得到∠α=180°-∠B+∠C ,然后利用已知条件即可求出∠α. 如图,过F 作EF ∥AB , ∵AB ∥CD , ∴AB ∥CD ∥EF , ∴∠ABF+∠BFE=180°,∠EFC=∠C , ∴∠α=180°-∠ABF+∠C=180°-120°+25°=85°. 故选C . 考点:平行线的性质 点评:辅助线问题是初中数学学习中的难点,能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力,因而这类问题在中考中比较常见,在各种题型中均有出现,一般难度较大,需多加关注. 17.【解析】 试题分析:根据夹在两条平行线间的垂线段的长度即为两平行线的距离,即可判断. 因为直线AB ∥CD ,EF ⊥AB 于E ,交CD 于F ,所以直线EF 也垂直于直线CD ,则直线AB 和CD 之间的距离是线段EF 的长. 故选B . 考点:平行线的距离点评:概念问题是数学学习的基础,很重要,但此类问题往往知识点比较独立,故在中考中不太常见,常以填空题、选择题形式出现,属于基础题,难度一般. 18.【解析】 试题分析:结合角平分线的性质,根据平行线的性质与判定进行分析. 如图所示: 若两条平行线被第三条直线所截,一对同位角和内错角的平分线互相平行,一对同旁内角的平分线互相垂直,所以C 错误.故选C . 考点:角平分线性质,平行线的性质与判定 点评:平行线的判定与性质的应用贯穿于整个初中学习,是平面图形中极为重要的知识点,与各个知识点结合极为容易,是中考中的热点,在各种题型中均有出现,需多加关注. 19.【解析】 试题分析:依次分析各选项即可得到结论. ①如果△A 1B 1C 1∽△A 2B 2C 2,△A 2B 2C 2∽△A 3B 3C 3,那么△A 1B 1C 1∽△A 3B 3C 3,本小题正确; ②直线外一点到这条直线的垂线段的长度,叫做这个点到这条直线的距离,本小题错误;③如果=0,那么x=-2,本小题错误; ④如果a=b ,那么a 3=b 3,本小题正确; 故选B. 考点:真命题 点评:此类问题知识点综合性较强,主要考查学生对所学知识的熟练掌握程度,在中考中比较常见,常以填空题、选择题形式出现,属于基础题,难度一般. 20.【解析】 试题分析:依次分析各选项即可得到结论. A.所有的命题都有条件和结论,C.所有的定理都是命题,D.所有的公理都是真命题,均正确,不符合题意; B.只有真命题才是定理,故错误,本选项符合题意. 考点:定义与命题 点评:概念问题是数学学习的基础,很重要,但此类问题往往知识点比较独立,故在中考中不太常见,常以填空题、选择题形式出现,属于基础题,难度一般. 21.【解析】 试题分析:根据折叠的性质结合三角形的内角和定理即可得到结果. ∠1+∠2=360°-(180°-∠A )-(180°-∠A )=360°-180°+∠A-180°+∠A =2∠A. 考点:三角形的内角和定理,折叠的性质 点评:图形的折叠变换是平面图形中极为重要的知识点,主要考查学生分析图形、发现规律的能力,是中考中的热点,在各种题型中均有出现,需多加关注.试题分析:根据三角形的一个外角大于任何一个与它不相邻的内角即可判断.∵∠A<∠BEC,∠BEC<∠BDC∴∠A<∠BEC<∠BDC.考点:三角形的内角和外角的关系点评:概念问题是数学学习的基础,很重要,但此类问题往往知识点比较独立,故在中考中不太常见,常以填空题、选择题形式出现,属于基础题,难度一般.23.【解析】试题分析:根据任意多边形的外角和均为360°即可得到结果.由图可得∠1+∠2+∠3=360°.考点:三角形的外角和点评:概念问题是数学学习的基础,很重要,但此类问题往往知识点比较独立,故在中考中不太常见,常以填空题、选择题形式出现,属于基础题,难度一般.24.【解析】试题分析:根据∠A等于和它相邻的外角的四分之一即可求得∠A及其相邻的外角的度数,从而得到∠B的度数,即可求得∠C度数.∵∠A等于和它相邻的外角的四分之一∴∠A=36°,其相邻的外角的度数为144°∵这个外角等于等于∠B的两倍∴∠B=72°∴∠C=72°.考点:三角形的内角和定理,三角形的外角点评:利用三角形的性质进行角度的计算是学生初中数学学习中的最基本的能力,因而此类问题在中考中比较常见,常以填空题、选择题形式出现,难度不大.25.【解析】试题分析:根据∠AFD=158°,FD⊥BC可得∠B=∠C的度数,再根据DE⊥AB可得∠BDE 的度数,即可求得结果.∵∠AFD=158°,FD⊥BC∴∠B=∠C=68°∵DE⊥AB∴∠BDE=32°∴∠EDF=180°-32°-90°=68°.考点:三角形的内角和定理,三角形的外角点评:此类问题知识点综合性较强,在中考中比较常见,常以填空题、选择题形式出现,属于基础题,难度一般.26.【解析】试题分析:根据三角形的内角和定理及三角形的内角和外角的关系依次分析即可. (1)∠α=38°+62°=100°;(2)∠α=30°+25°-20°=35°;(3)∠α=150°-90°=60°;(4)∠α=180°-(180°-70°)=70°;(5)∠α=180°-60°-20°-70°=30°;(6)∠α=135°-20°-45°=70°.考点:三角形的内角和定理,三角形的外角点评:利用三角形的性质进行角度的计算是学生初中数学学习中的最基本的能力,因而此类问题在中考中比较常见,常以填空题、选择题形式出现,难度不大. 27.【解析】 试题分析:根据三角形的内角和定理即可得到结果. 在一个三角形中,最多有1个钝角,至少有2个锐角. 考点:三角形的内角和定理 点评:此类问题对学生逻辑推理能力及对三角形的性质的理解要求较高,因而在中考中比较常见,常以填空题、选择题形式出现,难度较大. 28.【解析】 试题分析:由∠BAC=90°,可得∠B+∠C=90°,∠BAD+∠DAC=90°,由AD ⊥BC 可得∠B+∠BAD =90°,∠DAC+∠C=90°,根据同角的余角相等即可得到结果. ∵∠BAC=90° ∴∠B+∠C=90°,∠BAD+∠DAC=90° ∵AD ⊥BC ∴∠B+∠BAD =90°,∠DAC+∠C=90° ∴∠B=∠DAC ,∠C=∠BAD. 考点:三角形的内角和定理,同角的余角相等 点评:通过题目中的条件找到不相关的两个量的关系是学生学习过程中需要具备的基本能力,因而这类问题在中考中比较常见,在各种题型中均有出现,需多加关注. 29.【解析】 试题分析:由∠A+∠B=120°可得∠C 的度数,再根据∠A-∠B+∠C=•120•°可得∠A-∠B 的值,再结合∠A+∠B=120°即可求得结果. ∵∠A+∠B=120° ∴∠C=180°-∠A-∠B=60° ∵∠A-∠B+∠C=120•° ∴∠A-∠B=60° ∵∠A+∠B=120° ∴∠A=90°,∠B=30°. 考点:三角形的内角和定理 点评:三角形的内角和定理的应用贯穿于整个初中学习,是平面图形中极为重要的知识点,与各个知识点结合极为容易,是中考中的热点,在各种题型中均有出现,需多加关注. 30.【解析】 试题分析:由题意可设∠A=∠B=x°,则∠C=10x°,根据三角形的内角和定理即可列方程求出x 的值,从而得到结果. 设∠A=∠B=x°,则∠C=10x°,由题意得 解得 则∠C=10x°=150°. 考点:三角形的内角和定理 点评:方程思想在初中数学的学习中极为重要,也是中考中的热点,在各种题型中均有出现,需多加关注. 31.【解析】 试题分析:根据三角形的一个外角等于和它不相邻的两个内角之和即可得到结果. ∵∠PDC =∠ABP +∠A , ∴∠BPC =∠PDC+∠ACP =∠ABP +∠ACP +∠A.考点:三角形的内角和外角的关系,角平分线的性质 点评:熟练掌握与三角形有关的知识是同学们应该具备的基本能力,因而此类问题在中考中比较常见,常以填空题、选择题形式出现,难度一般. 32.【解析】 试题分析:根据三角形的一个外角大于任何一个与它不相邻的内角即可判断. ∵∠ADB >∠ACB ,∠ACB >∠CDE ∴∠ADB >∠CDE. 考点:三角形的内角和外角的关系 点评:概念问题是数学学习的基础,很重要,但此类问题往往知识点比较独立,故在中考中不太常见,常以填空题、选择题形式出现,属于基础题,难度一般. 33.【解析】 试题分析:根据三角形的一个外角等于和它不相邻的两个内角之和,再结合角平分线的性质即可得到结果. ∠E =∠ECD -∠EBC =(∠ACD -∠ABC )=∠A. 考点:三角形的内角和外角的关系,角平分线的性质 点评:熟练掌握与三角形有关的知识是同学们应该具备的基本能力,因而此类问题在中考中比较常见,常以填空题、选择题形式出现,难度一般. 34.【解析】 试题分析:根据三角形的一个外角大于任何一个与它不相邻的内角即可判断. ∵∠ADC =∠ACD ,∠ACD >∠B ∴∠ACB >∠B. 考点:三角形的内角和外角的关系 点评:概念问题是数学学习的基础,很重要,但此类问题往往知识点比较独立,故在中考中不太常见,常以填空题、选择题形式出现,属于基础题,难度一般. 35.【解析】 试题分析:连接BC ,根据三角形的内角和定理结合对顶角相等即可证得∠FBC +∠FCB =∠D +∠E ,结论. 连接BC , ∵∠FBC +∠FCB =180°-∠BFC ,∠D +∠E =180°-∠DFE ∴∠FBC +∠FCB =∠D +∠E ∴∠A +∠ABE +∠ACD +∠D +∠E =∠A +∠ABE +∠ACD +∠FBC +∠FCB =180°. 考点:三角形的内角和定理 点评:辅助线问题是初中数学学习中的难点,能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力,因而这类问题在中考中比较常见,在各种题型中均有出现,一般难度较大,需多加关注. 36.【解析】 试题分析:仔细分析题目中的条件即可得到规律,求得结果. 由题意得十边形的内角和:(10-2)×180°=1440°,n 边形的内角和:(n-2)×180°. 考点:多边形的内角和点评:培养学生独立分析问题、发现规律的能力是数学学科的指导思想,因而找规律问题在中考中极为常见,常见的不仅有式子的变化规律,往往更多的是图形的变化规律,一般难度较大. 37.【解析】 试题分析:连接AC ,根据三角形的内角和定理即可证得结论. 连接AC ∵∠B+∠BAC+∠ACB=180°,∠D+∠DAC+∠ACD=180° -∴ (∠B+∠BAC+∠ACB)+(∠D+∠DAC+∠ACD)=180°+180° -∴∠B+∠D+(∠BAC+∠DAC)+(∠ACB+∠ACD)=360° -∴∠B+∠C+∠BAD+∠BCD=360° -即四边形ABCD 的内角和等于360°. 考点:三角形的内角和定理 点评:辅助线问题是初中数学学习中的难点,能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力,因而这类问题在中考中比较常见,在各种题型中均有出现,一般难度较大,需多加关注. 38.【解析】 试题分析:由AB ∥CF 可得∠A=∠ACF ,∠B=∠FCD ,再结合对顶角相等、平角的定义即可得到结果. ∵AB ∥CF -∴∠A=∠ACF ,∠B=∠FCD -又∵∠ACB=∠DCE -∴∠A+∠B+∠C=∠ACF+∠FCD+∠DCE=180°. 考点:平行线的性质 点评:辅助线问题是初中数学学习中的难点,能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力,因而这类问题在中考中比较常见,在各种题型中均有出现,一般难度较大,需多加关注. 39.【解析】 试题分析:由∠BAD=120•°,∠ADC=105°可得∠PAD 与∠PDA 的度数,再根据三角形的内角和定理即可求得结果. ∴∠PAD+∠BAD=180°,∠PDA+∠ADC=180° -∴∠PAD=180°-∠BAD=180°-120°=60°,∠PDA=180°-∠ADC=180°-105°=75° -又∵∠P+∠PAD+∠PDA=180° -∴∠P=180°-∠PAD-∠PDA=180°-60°-75°=45°. 考点:三角形的内角和定理 点评:三角形的内角和定理的应用贯穿于整个初中学习,是平面图形中极为重要的知识点,与各个知识点结合极为容易,是中考中的热点,在各种题型中均有出现,需多加关注. 40.【解析】试题分析:根据正方形的性质可得∠A=∠B=90°,再根据三角形的内角和定理即可求得∠AFE 、∠BFC 的度数,即可求得结果. ∵四边形ABCD 是正方形 -∴∠A=∠B=90° -∴∠AFE=90°-∠AEF=90°-30°=60°,-∠BFC=90°-∠BCF=90°-28°=62° -∴∠EFC=180°-∠AFE-∠BFC=180°-60°-62°=58°. 考点:正方形的性质,三角形的内角和定理 点评:特殊四边形的性质的应用是初中数学平面图形中极为重要的知识点,与各个知识点结合极为容易,是中考中的热点,在各种题型中均有出现,需多加关注. 41.【解析】 试题分析:由∠B=30°,∠C=65°可得∠BAC 的度数,再根据AD 平分∠BAC 可得∠DAC 的度数,再结合AE ⊥BC 根据三角形的内角和定理即可求得结果. ∵∠B=30°,∠C=65° -∴∠BAC=180°-∠B-∠C=180°-30°-66°=84° -又∵AD 平分∠BAC -∴∠DAC=∠BAC=×84°=42° -∵AE ⊥BC -∴∠EAC=90°-∠C=90°-66°=24° -∴∠DAE=∠DAC-∠EAC=42°-24°=18°. 考点:三角形的内角和定理,角平分线的性质 点评:此类问题知识点综合性较强,在中考中比较常见,常以填空题、选择题形式出现,属于基础题,难度一般. 42.【解析】 试题分析:根据∠A=∠C ,公共角∠B ,结合三角形的内角和定理即可得到结果. ∵∠A=∠C ,∠B=∠B ,∠ADB=180°-∠A-∠B ,∠CEB=180°-∠C-∠B ∴∠ADB=∠CEB. 考点:三角形的内角和定理 点评:通过题目中的条件找到不相关的两个量的关系是学生学习过程中需要具备的基本能力,因而这类问题在中考中比较常见,在各种题型中均有出现,需多加关注. 43.【解析】 试题分析:(2)先根据平行线的性质求得∠FIG 的度数,由∠2的度数可得∠FGI 的度数,再根据三角形的外角的性质即可求得结果; (3)根据平行线的性质可得∠FKO 的度数,再根据三角形的外角的性质即可求得结果. (2)如图 ∵AB ∥CD ,EF ⊥AB ∴∠FIG =90° ∵∠2=135°。
数据结构课后习题及解析第六章

第六章习题1.试分别画出具有3个结点的树和3个结点的二叉树的所有不同形态。
2.对题1所得各种形态的二叉树,分别写出前序、中序和后序遍历的序列。
3.已知一棵度为k的树中有n1个度为1的结点,n2个度为2的结点,……,n k个度为k的结点,则该树中有多少个叶子结点并证明之。
4.假设一棵二叉树的先序序列为EBADCFHGIKJ,中序序列为ABCDEFGHIJK,请画出该二叉树。
5.已知二叉树有50个叶子结点,则该二叉树的总结点数至少应有多少个6.给出满足下列条件的所有二叉树:①前序和后序相同②中序和后序相同③前序和后序相同$7.n个结点的K叉树,若用具有k个child域的等长链结点存储树的一个结点,则空的Child域有多少个8.画出与下列已知序列对应的树T:树的先根次序访问序列为GFKDAIEBCHJ;树的后根次序访问序列为DIAEKFCJHBG。
9.假设用于通讯的电文仅由8个字母组成,字母在电文中出现的频率分别为:,,,,,,,请为这8个字母设计哈夫曼编码。
10.已知二叉树采用二叉链表存放,要求返回二叉树T的后序序列中的第一个结点指针,是否可不用递归且不用栈来完成请简述原因.11. 画出和下列树对应的二叉树:!12.已知二叉树按照二叉链表方式存储,编写算法,计算二叉树中叶子结点的数目。
13.编写递归算法:对于二叉树中每一个元素值为x的结点,删去以它为根的子树,并释放相应的空间。
14.分别写函数完成:在先序线索二叉树T中,查找给定结点*p在先序序列中的后继。
在后序线索二叉树T中,查找给定结点*p在后序序列中的前驱。
15.分别写出算法,实现在中序线索二叉树中查找给定结点*p在中序序列中的前驱与后继。
16.编写算法,对一棵以孩子-兄弟链表表示的树统计其叶子的个数。
17.对以孩子-兄弟链表表示的树编写计算树的深度的算法。
18.已知二叉树按照二叉链表方式存储,利用栈的基本操作写出后序遍历非递归的算法。
19.设二叉树按二叉链表存放,写算法判别一棵二叉树是否是一棵正则二叉树。
审计学练习题答案及解析(第六章)

《第六章、审计目标和管理层认定》一、单选题共10道【题目1】一般认为,注册会计师审计的目标的层次为( D )。
总体目标具体目标一般目标+项目目标(A)3个(B)1个(C)2个(D)4个【题目2】“发生”认定指记录的交易和事项已发生且与被审计单位有关,其目标主要针对( C )。
如:没有发生销售交易,却记录了一笔销售(A)数量(B)低估(C)高估(D)金额【题目3】“完整性”认定指所有应当记录的交易和事项均已记录,其目标主要针对( D )。
如:发生了销售交易,却没有记录销售(A)数量(B)金额(C)高估(D)低估【题目4】涉及总体合理性、真实性、所有权及披露等的审计目标是( D )。
(A)审计具体目标(B)审计一般目标(C)审计项目目标(D)审计总目标【题目5】既属于被审计单位管理层的认定,又属于注册会计师的审计目标的是( C )。
(A)真实性(B)估价(C)完整性(D)披露【题目6】其组成要素与“权利和义务”认定有关的是( A )。
(A)资产负债表(B)利润表(C)审计项目目标(D)审计总目标【题目7】下列有关“完整性”的认定中,表达不正确的是( D )。
(A)该认定是指应在财务报表中列示的所有交易和项目是否都列入了(B)该认定主要与财务报表组成要素的低估有关(C)该认定所要解决的问题是被审计单位管理层是否把应包括的项目给遗漏或省略了(D)该认定还涉及所报告的交易和项目的金额是否正确【题目8】下列认定中与利润表组成要素无关的是( C )。
(A)发生(B)完整性(C)权利和义务(D)准确性【题目9】注册会计师计划测试M公司20×7年度主营业务收入的完整性。
下述各项审计程序中,通常难以实现上述目标的是( D )。
(A)抽取20×7年12月31日开具的销售发票,检查相应的发运单和账簿记录(B)抽取20×7年12月31日的发运单,检查相应的销售发票和账簿记录(C)从主营业务收入明细账中抽取20×7年12月31日的明细记录,检查相应的记账凭证、发运单和销售发票(D)从主营业务收入明细账中抽取20×7年次年1月1日的明细记录,检查相应的记账凭证、发运单和销售发票【题目10】在对资产存在性认定获取审计证据时,正确的测试方向是( C )。
会计基础_第六章_会计凭证_练习题 (1)

会计基础 【零基础学员必练】第 1题:多选题(本题2分)下列会计凭证中,属于原始凭证的有( )。
A.发货票B.购货合同C.领料单D.火车票【正确答案】:ACD【答案解析】:原始凭证,又称单据,是指在经济业务发生或完成时取得或填制的,用以记录或证明经济业务的发生或完成情况的原始凭据。
第 2题:多选题(本题2分)关于会计凭证,以下说法正确的是( )。
A.会计凭证按填制程序和用途不同可分为原始凭证和记账凭证B.原始凭证是登记账簿的直接依据C.会计凭证是编制会计报表的依据D.记账凭证是根据审核无误的原始凭证编制的【正确答案】:AD【答案解析】:记账凭证是登记账簿的直接依据,会计账簿是编制会计报表的依据。
第 3题:多选题(本题2分)下列关于会计凭证的说法中,正确的有( )。
A.会计凭证是记录经济业务发生和完成情况的书面证明B.会计凭证是登记账簿的依据C.任何单位,每发生一项经济业务,经办人员必须按照规定的程序和要求,认真填制会计凭证D.任何会计凭证均可作为登记账簿的依据【正确答案】:ABC【答案解析】:会计凭证是记录经济业务事项发生或完成情况的书面证明,也是登记账簿的依据。
任何单位在处理任何经济业务时,都必须由执行和完成该项经济业务的有关人员从外单位取得或自行填制有关凭证。
一切会计凭证都必须经过有关人员的审核,只有经过审核无误的会计凭证才能作为登记账簿的依据。
第 4题:判断题(本题1分)原始凭证记载的信息是整个企业会计信息系统运行的起点,原始凭证的质量将影响会计信息的质量。
【正确答案】:对【答案解析】:原始凭证记载的信息是整个企业会计信息系统运行的起点,原始凭证的质量将影响会计信息的质量。
第 5题:判断题(本题1分)会计凭证按照填制程序和用途可分为原始凭证和记账凭证。
【正确答案】:对【答案解析】:会计凭证按照填制程序和用途可分为原始凭证和记账凭证。
第 6题:判断题(本题1分)会计凭证是指记录经济业务发生或完成情况的书面证明,也是登记账簿的依据。
北师大版八年级数学下册第六章达标测试卷附答案

北师大版八年级数学下册第六章达标测试卷一、选择题(每题3分,共30分)1.十边形的内角和为()A.180°B.360°C.1 080°D.1 440°2.在▱ABCD中,∠A+∠C=200°,则∠B的度数是()A.100°B.160°C.80°D.60°3.如图,▱ABCD的对角线AC,BD相交于点O,下列结论正确的是() A.S▱ABCD=4S△AOB B.AC=BDC.AC⊥BD D.▱ABCD是轴对称图形(第3题)(第4题)(第5题)4.如图,在平面直角坐标系中,点A,B,C的坐标分别是A(1,0),B(-1,3),C(-2,-1),再找一点D,使它与点A,B,C构成的四边形是平行四边形,则点D的坐标不可能是()A.(-3,2) B.(-4,2) C.(0,-4) D.(2,4)5.如图,D,E,F分别为△ABC三边的中点,则与△DEF全等的三角形有() A.1个B.2个C.3个D.0个6.如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF =6,AB=5,则AE等于()A.4 B.6 C.8 D.10(第6题)(第7题)(第8题)(第9题)7.如图,过正五边形ABCDE的顶点A作直线l∥BE,则∠1的度数为() A.30°B.36°C.38°D.45°8.如图,在▱ABCD中,AC⊥AB,∠ABD=30°,AC与BD交于点O,AO=1,则BC的长是()A.7B. 5 C.3 D.2 29.如图,在四边形ABCD中,E,F,P,Q分别为AB,AD,BC,CD的中点.若∠ABC=90°,∠AEF=60°,则∠CPQ的度数为()A.15°B.30°C.45°D.60°10.如图,六边形ABCDEF的六个内角都相等,若AB=1,BC=CD=3,DE=2,则这个六边形的周长是()A.12 B.13 C.14 D.15(第10题)(第11题)(第15题)(第16题)二、填空题(每题3分,共30分)11.如图,在△ABC中,D,E分别是AB,AC的中点,已知DE=5,则BC=________.12.正六边形的每个外角是________.13.在四边形ABCD中,对角线AC,BD交于点O,AD∥BC,请添加一个条件:____________,使四边形ABCD为平行四边形(不添加任何辅助线).14.若一个多边形的内角和为900°,则这个多边形的边数为________.15.如图,在▱ABCD中,对角线AC,BD相交于点O,如果AC=14,BD=8,AB =x,那么x的取值范围是____________.16.如图,在▱ABCD中,BE平分∠ABC,BC=6,DE=2,则▱ABCD的周长为________.17.如图,在平面直角坐标系中,▱OBCD的顶点O,B,D的坐标分别为(0,0),(5,0),(2,3),则顶点C的坐标是__________.(第17题)(第18题)(第19题)(第20题)18.如图,在四边形ABCD中,AB=DC,AD=BC,E,F是DB上的两点,且AE ∥CF.若∠AEB=115°,∠ADB=35°,则∠BCF=________.19.如图,点A,E,F,C在一条直线上,若将△DEC的边EC沿AC方向平移,平移过程中始终满足下列条件:AE=CF,DE⊥AC于点E,BF⊥AC于点F,且AB=CD,则当点E,F不重合时,BD与EF的关系是____________.20.如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边三角形ABD和等边三角形ACE,F为AB的中点,DE,AB相交于点G.若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为平行四边形;③AD=4AG;④△DBF≌△EF A.其中正确结论的序号是__________.三、解答题(21~23题每题8分,其余每题12分,共60分)21.如图,在▱ABCD中,AE⊥BC,AE交边BC于点E,点F为边CD上一点,且BE=DF,过点F作FG⊥CD,FG交边AD于点G.求证:GD=CD.22.如图,▱ABCD的对角线AC,BD相交于点O,EF经过点O并且分别和AB,CD相交于点E,F,点G,H分别为OA,OC的中点.求证:四边形EHFG 是平行四边形.23.如图,AD是△ABC的中线,E为AD的中点,连接BE并延长,交AC于点F,AF=13AC.求证:EF=14BF.24.如图,将▱ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB 于点E.(1)求证:∠EDB=∠EBD;(2)判断AF与DB是否平行,并说明理由.25.如图,在▱ABCD中,∠ADC,∠DAB的平分线DF,AE分别与线段BC相交于点F,E,DF与AE相交于点G.(1)求证:AE⊥DF;(2)若AD=10,AB=6,AE=4,求DF的长.26.在平面直角坐标系中,已知点A(3,0),点B(3,2),点C与点A关于y轴对称,点D与点B关于原点O对称,依次连接AB,BC,CD,DA.(1)请画出示意图,并写出点C与点D的坐标.(2)四边形ABCD是否为平行四边形?请说明理由.(3)在x轴上是否存在一点P,使得△BDP的面积等于四边形ABCD面积的一半?若存在,请直接写出点P的坐标;若不存在,请说明理由.答案一、1.D 2.C 3.A 4.A 5.C 6.C7.B8.A9.B10.D提示:如图,分别作AB,CD,EF的延长线和反向延长线使它们交于点G,P,H.∵六边形ABCDEF的六个内角都相等,故六个内角都是120°,∴六边形ABCDEF的每一个外角的度数都是60°.∴△AHF,△BGC,△DPE,△GHP都是等边三角形.∴GC=BC=BG=3,DP=DE=EP=2,AH=HF=AF.∴GH=HP=GP=GC+CD+DP=3+3+2=8,HF=F A=HA=GH-AB-BG =8-1-3=4,EF=PH-HF-EP=8-4-2=2.∴六边形的周长为1+3+3+2+4+2=15.二、11.1012.60°13.AD=BC(答案不唯一)14.715.3<x<1116.2017.(7,3)18. 80°19.互相平分20.①②③④提示:根据已知先证得△ABC≌△EF A,则∠AEF=∠BAC=30°,EF=AB,得出EF⊥AC.易得∠BDF=∠FEA=30°,∠BFD=∠F AE=90°,BD =FE,所以△DBF≌△EF A,则AE=DF.再由FE=AB=AD,得出四边形ADFE 为平行四边形,根据平行四边形的性质得出AG=GF,从而得出AB=AD=4AG.三、21.证明:∵四边形ABCD是平行四边形,∴AB=CD,∠B=∠D.∵AE⊥BC,FG⊥CD,∴∠AEB=∠GFD=90°.又∵BE=DF,∴△ABE ≌△GDF (ASA). ∴AB =GD . 又∵AB =CD , ∴GD =CD . 22.证明:如图所示.∵点O 为▱ABCD 对角线AC ,BD 的交点, ∴OA =OC ,OB =OD .∵G ,H 分别为OA ,OC 的中点, ∴OG =12OA ,OH =12OC . ∴OG =OH .又∵AB ∥CD ,∴∠1=∠2. 在△OEB 和△OFD 中,⎩⎨⎧∠1=∠2,OB =OD ,∠3=∠4,∴△OEB ≌△OFD (ASA). ∴OE =OF . 又∵OG =OH ,∴四边形EHFG 为平行四边形.23.证明:取CF 的中点G ,连接DG ,则CG =FG .∵D 为BC 的中点, ∴DG 为△BCF 的中位线. ∴DG =12BF .∵CG =FG ,AF =13AC , ∴AF =GF .又∵E 为AD 的中点, ∴EF 为△ADG 的中位线.∴EF=12DG.∴EF=14BF.24.(1)证明:由折叠可知∠CDB=∠EDB.∵四边形ABCD是平行四边形,∴DC∥AB.∴∠CDB=∠EBD.∴∠EDB=∠EBD.(2)解:AF∥DB.理由如下:∵∠EDB=∠EBD,∴DE=BE.由折叠可知DC=DF.∵四边形ABCD是平行四边形,∴DC=AB.∴DF=AB.∴AE=EF.∴∠EAF=∠EF A.在△BED中,∠EDB+∠EBD+∠DEB=180°,即2∠EDB+∠DEB=180°.同理,在△AEF中,2∠EF A+∠AEF=180°.∵∠DEB=∠AEF,∴∠EDB=∠EF A.∴AF∥DB.25.(1)证明:在▱ABCD中,AB∥CD,∴∠ADC+∠DAB=180°.∵DF,AE分别是∠ADC,∠DAB的平分线,∴∠ADF=∠CDF=12∠ADC,∠DAE=∠BAE=12∠DAB.∴∠ADF+∠DAE=12(∠ADC+∠DAB)=90°,∴∠AGD=90°.∴AE⊥DF.(2)解:如图,过点D作DH∥AE,DH交BC的延长线于点H.则四边形AEHD是平行四边形,且FD⊥DH.∴DH=AE=4,EH=AD=10.在▱ABCD中,AD∥BC,∴∠ADF=∠CFD,∠DAE=∠BEA.由(1)知∠CDF=∠ADF,∠BAE=∠DAE.∴∠CDF=∠CFD,∠BAE=∠BEA.∴DC=FC,AB=EB.在▱ABCD中,AD=BC=10,AB=DC=6,∴CF=BE=6,BF=BC-CF=10-6=4.∴FE=BE-BF=6-4=2.∴FH=FE+EH=2+10=12.在Rt△FDH中,DF=FH2-DH2=122-42=82,即DF的长是8 2. 26.解:(1)如图所示.∵点A(3,0),点C与点A关于y轴对称,∴C(-3,0).∵点B(3,2),点D与点B关于原点O对称,∴D(-3,-2).(2)四边形ABCD是平行四边形.理由如下:如图,连接BD.∵点C与点A关于y轴对称,∴OA=OC.∵点D与点B关于原点O对称,∴OB=OD.∴四边形ABCD是平行四边形.(3)存在.点P的坐标为(3,0)或(-3,0).。
应用多元统计分析课后习题答案高惠璇(第六章习题解答)

0,
第六章 聚类分析
6-5 试从定义直接证明最长和最短距离法的单调性. 证明:先考虑最短距离法: ( L1) ( L1) D D 设第L步从类间距离矩阵 ij
D
( L1) pq
min D
( L1) pq
( L1) ij
故合并Gp和Gq为一新类Gr,这时第L步的并类距离:
0, p (1 )
0, q (1 ) np nr (1 ) nq nr
nq nr
0, ( 1)
p q (1 )
11
18
故可变类平均法具有单调性。
第六章 聚类分析
对于可变法,因
1 1 0, p 0, q 0, ( 1) 2 2 1 1 p q 11 2 2
证明 : (1)设d 和d 为距离, 令d d
(1) ( 2)
(1)
d .
( 2)
2
以下来验证d满足作为距离所要求的3个条件.
第六章 聚类分析
① ② ③
(2) 设d是距离,a >0为正常数.令d*=ad,显然有
① ②
d cd ij 0, 且仅当X (i ) X ( j )时d 0;
应用多元统计分析
第六章部分习题解答
第六章 聚类分析
6-1 证明下列结论: (1) 两个距离的和所组成的函数仍是距离; (2) 一个正常数乘上一个距离所组成的函数 仍是距离; (3)设d为一个距离,c>0为常数,则 d * d d c 仍是一个距离; (4) 两个距离的乘积所组成的函数不一定是 距离;
(6.2.2)
9
第六章 聚类分析
《微分几何》陈维桓第六章习题及答案

§ 6.1测地曲率1. 证明:旋转面上纬线的测地曲率是常数。
证明:设旋转面方程为,二{ f(v)cosu, f (v)sin u, g(v)},2 2 2 2 2> f (v)(du) (f (v) g (v))(dv),E二 f (v),G = f (v) g (v)纬线即u—曲线: v= v(常数),」'(v 。
) f(v o ).f '2(v o )g '2 (v o )2、证明:在球面Sr 二(acosucosv,acosusinv,asinu),31Hu ,0 v 2 2 2上,曲线C 的测地曲率可表示成其测地曲率为k g1 ;:l n EIn f2, f '2 g '2::v为常数。
k gd^(s)ds-sin(u(s))dv(s )其中(u(s),v(s))是球面S上曲线C的参数方程,C的弧长参数,s是曲线(s)是曲线C与球面上经线(即u -曲线)之间的夹角。
证明易求出 E=a 2, F =0 , G=a 2cos 2u , 因此1 Jn E1 ::ln Gcos2 , G 2、E ;:u2 2d v 1ln(a cos u)sin ds 2a ;:ud r sin u si n,ds a cosu ?而屯=—Isin —sinr ds VG a cosu ?故 k g呼-sinu^ ods ds3、证明:在曲面S 的一般参数系(u,v)下,曲线C : u = u(s), v = v(s)的测地曲率是k g 二、g (Bu (s) - Av(s) u(s)v (s) -v (s)u (s)),其中s是曲线C 的弧长参数,g =EG -F 2,并且A 7 [(u (s))2 • 2丨,u (s)v(s) —(Ms))2,B -:(u (s))2 2^u(s)v(s) 】22(v(s))2特别是,参数曲线的测地曲率分别为k gdr dsk g.=討:(□ (s))3,ks =「J沁-;2(V (S))3。
2022年鲁教版(五四制)八年级数学下册第六章特殊平行四边形定向练习试题(含答案解析)

鲁教版(五四制)八年级数学下册第六章特殊平行四边形定向练习考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、如图,四边形ABCD 是平行四边形,过点A 作AM ⊥BC 于点M ,交BD 于点E ,过点C 作CN ⊥AD 于点N ,交BD 于点F ,连接CE ,当EA =EC ,且点M 为BC 的中点时,AB :AE 的值为( )A .2BC .32D 2、能够判断一个四边形是矩形的条件是( )A .对角线相等B .对角线垂直C .对角线互相平分且相等D .对角线垂直且相等3、如图,已知正方形ABCD 的边长为6,点E ,F 分别在边AB ,BC 上,BE =CF =2,CE 与DF 交于点H ,点G 为DE 的中点,连接GH ,则GH 的长为( )A B C .4.5 D .4.34、如图,在正方形ABCD 中,点E 、点F 分别在AD 、CD 上,且AE =DF ,若四边形OEDF 的面积是1,OA 的长为1,则正方形的边长AB 为( )A .1B .2CD .5、已知四边形ABCD 是平行四边形,下列结论:①当AB =BC 时,它是菱形;②当AC ⊥BD 时,它是菱形;③当∠ABC =90°时,它是矩形;④当AC =BD 时,它是正方形,其中错误的有( )A .1个B .2个C .3个D .4个6、矩形ABCD 的对角线交于点O ,∠AOD =120°,AO =3,则BC 的长度是( )A .3B .C .D .67、在矩形ABCD 中,对角线AC ,BD 交于点O ,且∠AOD =120°.若AB =3,则BC 的长为( )A B .3 C .D .68、如图,在MON ∠的两边上分别截取OA ,OB ,使OA OB =;再分别以点A ,B 为圆心,OA 长为半径作弧,两弧交于点C ;再连接AC ,BC ,AB ,OC .若2AB =,4OC =,则四边形AOBC 的面积是( )A.B.8 C.4 D.5 29、如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是()A.1 B.4 C.2 D.610、下列命题中是真命题的选项是()A.一组对边平行,另一组对边相等的四边形是平行四边形B.对角线互相垂直且相等的四边形是正方形C.对角线相等的平行四边形是矩形D.三条边都相等的四边形是菱形第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图,在边长为6的正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,将ADF绕点A顺时针旋转90°得到ABG,若BE=2,则EF的长为___.2、如图,在矩形ABCD 中,AB =6,BC =8.如果E、F 分别是AD 、BC 上的点,且EF 经过AC 中点O ,G ,H 是对角线AC 上的点.下列判断正确的有______.①在AC 上存在无数组G 、H ,使得四边形EGFH 是平行四边形;②在AC 上存在无数组G 、H ,使得四边形EGFH 是矩形;③在AC 上存在无数组G 、H ,使得四边形EGFH 是菱形;④当AG =54时,存在E 、F 、G ,H ,使得四边形EGFH 是正方形.3、在Rt ABC 中,90ACB ∠=︒,CD 是斜边AB 上的中线,已知AC =2BC =,则ACD △的周长等于______.4、如图,90MON ∠=︒,矩形ABCD 的顶点A 、B 分别在边OM 、ON 上,当B 在边ON 上运动时,A 随之在OM 上运动,矩形ABCD 的形状保持不变,其中6AB =,2BC =.在运动过程中:(1)Rt AOB ∆斜边中线的长度是否发生变化___(填“是”或“否”);(2)点D 到点O 的最大距离是___.5、如图,正方形ABCD 中,E 为CD 上一动点(不含C 、)D ,连接AE 交BD 于F ,过F 作FH AE ⊥交BC 于H ,过H 作HG BD ⊥于G ,连接AH ,EH .下列结论:①AF FH =;②45HAE ∠=︒;③FH 平分GHC ∠;④2BD FG =,正确的是__(填序号).三、解答题(5小题,每小题10分,共计50分)1、(1)【发现证明】如图1,在正方形ABCD 中,点E ,F 分别是BC ,CD 边上的动点,且45EAF ∠=︒,求证:EF DF BE =+.小明发现,当把ABE △绕点A 顺时针旋转90°至ADG ,使AB 与AD 重合时能够证明,请你给出证明过程.(2)【类比引申】①如图2,在正方形ABCD 中,如果点E ,F 分别是CB ,DC 延长线上的动点,且45EAF ∠=︒,则(1)中的结论还成立吗?若不成立,请写出EF ,BE ,DF 之间的数量关系______(不要求证明) ②如图3,如果点E ,F 分别是BC ,CD 延长线上的动点,且45EAF ∠=︒,则EF ,BE ,DF 之间的数量关系是______(不要求证明)(3)【联想拓展】如图1,若正方形ABCD 的边长为6,AE =AF 的长.2、如图,在平行四边形ABCD 中,点M 是AD 边的中点,连接BM ,CM ,且BM =CM .(1)求证:四边形ABCD 是矩形;(2)若△BCM 是直角三角形,直接写出AD 与AB 之间的数量关系.3、如图,在矩形ABCD 中,AB =6,BC =8.(1)用尺规作图法作菱形AECF ,使点E 、F 分别在BC 和AD 边上;(2)求EF 的长度.4、如图,把矩形ABCD 绕点A 按逆时针方向旋转得到矩形AEFG ,使点E 落在对角线BD 上,连接DG ,DF .(1)若∠BAE =50°,求∠DGF 的度数;(2)求证:DF =DC .5、如图,Rt ABC 中,90ACB ∠=︒,点D 在AB 上,8AD =,6BD =,DE BC ⊥于点E ,把DBE 绕点D 旋转得DGF △,且点G ,F 在AC 上.(1)求证:四边形CEDF是正方形;(2)求四边形CEDF的面积,-参考答案-一、单选题1、B【解析】【分析】根据平行四边形的性质、垂直的定义、平行线的判定定理可以推知AE∥CF;然后由全等三角形的判定定理ASA推知△ADE≌△CBF;最后根据全等三角形的对应边相等知AE=CF,所以对边平行且相等的四边形是平行四边形;连接AC交BF于点O,根据EA=EC推知▱ABCD是菱形,根据菱形的邻边相等知AB=BC;然后结合已知条件“M是BC的中点,AM⊥BC”证得△ADE≌△CBF(ASA),所以AE=CF,从而证得△ABC是正三角形;最后在Rt△BCF中,求得CF:BC AE=CF,AB=BC)AB:AE【详解】解:连接AC,∵四边形ABCD是平行四边形,∴BC ∥AD ;∴∠ADE =∠CBD ,∵AD =BC ,在△ADE 和△CBF 中,90DAE BCF AD CB ADE FBC ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩, ∴△ADE ≌△CBF (ASA ),∴AE =CF ,又∵AM ⊥BC ,∴AM ⊥AD ;∵CN ⊥AD ,∴AM ∥CN ,∴AE ∥CF ;∴四边形AECF 为平行四边形,∵EA =EC ,∴▱AECF 是菱形,∴AC ⊥BD ,∴平行四边形ABCD 是菱形,∴AB =BC ,∵M 是BC 的中点,AM ⊥BC ,∴AB =AC ,∴△ABC 为等边三角形,∴∠ABC=60°,∠CBD=30°;在Rt△BCF中,CF:BC又∵AE=CF,AB=BC,∴AB:AE故选:B.【点睛】本题综合考查了全等三角形的判定与性质、菱形的判定与性质以及等边三角形的判定与性质等知识点,证得▱ABCD是菱形是解题的难点.2、C【解析】略3、A【解析】【分析】根据正方形的四条边都相等可得BC=DC,每一个角都是直角可得∠B=∠DCF=90°,然后利用“边DE,利角边”证明△CBE≌△DCF,得∠BCE=∠CDF,进一步得∠DHC=∠DHE=90°,从而知GH=12用勾股定理求出DE的长即可得出答案.【详解】解:∵四边形ABCD为正方形,∴∠B=∠DCF=90°,BC=DC,在△CBE和△DCF中,BC CC B DCF BE CF =⎧⎪∠=∠⎨⎪=⎩, ∴△CBE ≌△DCF (SAS ),∴∠BCE =∠CDF ,∵∠BCE +∠DCH =90°,∴∠CDF +∠DCH =90°,∴∠DHC =∠DHE =90°,∵点G 为DE 的中点,∴GH =12DE ,∵AD =AB =6,AE =AB ﹣BE =6﹣2=4,∴DE === ∴GH故选A .【点睛】本题主要考查了正方形的性质,全等三角形的性质与判定,勾股定理,直角三角形斜边上的中线,解题的关键在于能够熟练掌握相关知识进行求解.4、C【解析】【分析】根据正方形的性质得到AB =AD ,∠BAE =∠ADF =90°,根据全等三角形的性质得到∠ABE =∠DAF ,求得∠AOB =90°,根据三角形的面积公式得到OA =1,由勾股定理即可得到答案.解:∵四边形ABCD 是正方形,∴AB =AD ,∠BAE =∠ADF =90°,在△ABE 与△DAF 中,AB AD BAE ADF AE DF =⎧⎪∠=∠⎨⎪=⎩, ∴△ABE ≌△DAF (SAS ),∴∠ABE =∠DAF ,∴∠ABE +∠BAO =∠DAF +∠BAO =90°,∴∠AOB =90°,∵△ABE ≌△DAF ,∴S △ABE =S △DAF ,∴S △ABE -S △AOE =S △DAF -S △AOE ,即S △ABO =S 四边形OEDF =1,∵OA =1,∴BO =2,∴AB故选:C .【点睛】本题考查了正方形的性质,全等三角形的判定和性质,勾股定理,证得△ABE ≌△DAF 是解题的关键.5、A【分析】根据矩形、菱形、正方形的判定可以判断题目中的各个小题的结论是否正确,从而可以解答本题.【详解】 解:四边形ABCD 是平行四边形,A 、当AB BC =时,它是菱形,选项不符合题意,B 、当AC BD ⊥时,它是菱形,选项不符合题意,C 、当90ABC ∠=︒时,它是矩形,选项不符合题意,D 、当AC BD =时,它是矩形,不一定是正方形,选项符合题意,故选:A .【点睛】本题考查正方形、菱形、矩形的判定,解答本题的关键是熟练掌握矩形、菱形、正方形的判定定理.6、C【解析】【分析】画出图形,由条件可求得△AOB 为等边三角形,则可求得AC 的长,在Rt △ABC 中,由勾股定理可求得BC 的长.【详解】解:如下图所示:∵四边形ABCD 是矩形,∴∠ABC=90°,OA=12AC,OB=12BD,AC=BD,∴OA=OB,∵∠AOD=120°,∴∠AOB=60°,∴△AOB是等边三角形,∴OA=AB=2,∴AC=2OA=4,∴BC2=AC2-AB2=36-9=27,∴BC=故选:D.【点睛】本题考查了矩形的性质、等边三角形的判定与性质以及勾股定理;熟练掌握矩形的性质,证明三角形是等边三角形是解决问题的关键.7、C【解析】【分析】根据矩形的性质和等边三角形的判定和性质,可以得到AC的长,再根据勾股定理,即可得到BC的长,本题得以解决.【详解】解:∵∠AOD=120°,∠AOD+∠AOB=180°,∴∠AOB=60°,∵四边形ABCD是矩形,∴OA=OB=OC,∠ABC=90°,∴△AOB是等边三角形,∴AB=OA=OC,∵AB=3,∴AC=6,∴BC=故选:C.【点睛】本题考查矩形的性质、等边三角形的判定与性质,以及勾股定理,解答本题的关键是明确题意,利用数形结合的思想解答.8、C【解析】【分析】根据作法判定出四边形OACB是菱形,再根据菱形的面积等于对角线乘积的一半计算即可得解.【详解】==,根据作图,AC BC OA=,∵OA OB===,∴OA OB BC AC∴四边形OACB是菱形,∵2AB=,4OC=,∴12442OACBS=⨯⨯=菱形.故选:C.【点睛】本题主要考查菱形的性质与判定,熟练掌握菱形的性质与判定是解题的关键.9、C【解析】略10、∴OM=12CD=故选:C.【点睛】此题考查了矩形的性质、直角三角形的性质以及三角形中位线的性质.注意利用直角三角形斜边上的中线等于斜边的一半,求得AC的长是关键.3.C【解析】【分析】利用平行四边形、矩形、菱形及正方形的判定方法分别判断后,即可确定正确的选项.【详解】解:A.一组对边平行且相等的四边形是平行四边形,原命题是假命题,不符合题意;B.对角线互相平分、垂直且相等的四边形是正方形,原命题是假命题,不符合题意;C.对角线相等的平行四边形是矩形,是真命题,符合题意;D.四条边都相等的四边形是菱形,原命题是假命题,不符合题意;故答案选:C .【点睛】考查了命题与定理的知识,解题的关键是了解平行四边形、矩形、菱形及正方形的判定方法,难度不大.二、填空题1、5【解析】【分析】由旋转的性质可得AF AG =,DAF BAG ∠=∠,90D ABG ∠=∠=︒,由“SAS ”可证GAE FAE ∆≅∆,可得EF GE ,由勾股定理可求解.【详解】解:由旋转的性质可知:AF AG =,DAF BAG ∠=∠,90D ABG ∠=∠=︒,180ABG ABE ∠+∠=︒,∴点G 在CB 的延长线上,四边形ABCD 为正方形,90BAD ∴∠=︒.又45EAF ∠=︒,45BAE DAF ∴∠+∠=︒.45BAG BAE ∴∠+∠=︒.GAE FAE ∴∠=∠.在GAE ∆和FAE ∆中,AG AF GAE FAE AE AE =⎧⎪∠=∠⎨⎪=⎩,()GAE FAE SAS ∴∆≅∆,EF GE ∴=,2EF GE GB BE DF ∴==+=+,222EF CF EC =+,222(2)(6)(62)DF DF ∴+=-+-,3DF ∴=,5EF ∴=,故答案为:5.【点睛】本题考查了旋转的性质、全等三角形的性质和判定、勾股定理的应用,正方形的性质,解题的关键是掌握利用勾股定理求线段的长.2、①②④【解析】【分析】如图,矩形ABCD ,O 为对角线的交点,由中心对称性证明:,OE OF = 所以当OG OH =时,四边形EGFH 是平行四边形,当OE OG OF OH 时,四边形EGFH 是矩形,当,,OG OH EF AC 四边形EGFH 是菱形,再利用正方形的性质求解,AG 从而可得答案.【详解】解:如图,矩形ABCD ,O 为对角线的交点,由中心对称性可得:,OE OF =所以当OG OH =时,四边形EGFH 是平行四边形,所以AC 上存在无数组G 、H ,使得四边形EGFH 是平行四边形;故①符合题意;当OE OG OF OH 时,四边形EGFH 是矩形,而OE 不是定值,所以在AC 上存在无数组G 、H ,使得四边形EGFH 是矩形;故②符合题意;当,,OG OH EF AC四边形EGFH 是菱形,而AC 位置确定,所以EF 唯一,所以在AC 上不存在无数组G 、H ,使得四边形EGFH 是菱形,故③不符合题意;如图,当四边形EGFH 是正方形时,,,,EG GF FH EH OE OF OG OH EF GH,FA FC由矩形ABCD 可得:90,6,8,,ABC AB DC AD BC OA OC 226810,,5,ACAG CH OA OC 2226+8,AF AF25,4AF 2225155,44OF OG 1555,44AG 所以当AG =54时,存在E 、F 、G ,H ,使得四边形EGFH 是正方形,故④符合题意; 故答案为:①②④【点睛】本题考查的是平行四边形的判定与性质,矩形的判定与性质,菱形的判定,正方形的性质,掌握“特殊四边形的判定与性质”是解本题的关键.3、4+4【解析】【分析】过点D 作DE AC ⊥,根据直角三角形斜边上的中线等于斜边的一半,可得DC AD =,根据等腰三角形的三线合一可得AE EC =,中位线的性质求得DE ,根据勾股定理求得AD ,继而求得ACD △的周长.【详解】解:如图,过点D 作DE AC ⊥在Rt ABC 中,90ACB ∠=︒,CD 是斜边AB 上的中线,12CD AB AD DB ∴=== DE AC ⊥12AE EC AC ∴===E ∴为AC 的中点,又D 为AB 的中点,则112ED BC ==在Rt AED △中,2AD == 2DC AD ∴==∴ACD △的周长等于4AD DC AC ++=+故答案为:4+【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半,三线合一,中位线的性质与判定,勾股定理,掌握以上知识是解题的关键.4、 否3【解析】【分析】(1)设斜边中点为Q ,根据直角三角形斜边中线132OQ AB ==即可; (2)取AB 的中点Q ,连接OQ 、DQ 、OD ,根据三角形的任意两边之和大于第三边可知当O 、D 、Q 三点共线时,点D 到点O 的距离最大,再根据勾股定理列式求出DQ 的长,根据直角三角形斜边上的中线等于斜边的一半求出OQ 的长,两者相加即可得解.【详解】解:(1)如图,设斜边中点为Q ,在运动过程中,斜边中线1 3.2OQ AB == AB 长度不变,故OQ 不变, 故答案为:否;(2)连接OQ 、DQ 、OD ,在矩形的运动过程当中,根据三角形的任意两边之和大于第三边有DQ OQ OD +,当D 、Q 、O 三点共线时,则有DQ OQ OD +=,此时,OD 取得最大值,如图所示, Q 为AB 中点,132AQ AB ∴==, 又2AD BC ==,DQ ∴=3OD DQ OQ ∴=+=.3+.【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半得到性质,三角形的三边关系,矩形的性质,勾股定理,根据三角形的三边关系判断出点O 、Q 、D 三点共线时,点D 到点O 的距离最大是解题的关键.5、①②④【解析】连接FC ,延长HF 交AD 于点L .可证ADF CDF ∆∆≌,进而可得FHC FCH ∠=∠,由此可得出FH AF =;再由FH AF =,即可得出45HAE ∠=︒;连接AC 交BD 于点O ,则2BD OA =,证明AOF FGH ≌,即可得出OA GF =,进而可得2BD FG =;过点F 作MN BC ⊥于点N ,交AD 于点M ,由于F 是动点,FN 的长度不确定,而FG OA =是定值,即可得出FH 不一定平分GHC ∠.【详解】解:如图,连接FC ,延长HF 交AD 于点L .∵BD 为正方形ABCD 的对角线∴45ADB CDF ∠=∠=︒,AD CD =在ADF 和CDF 中45AD CD ADB CDF DF DF =⎧⎪∠=∠=︒⎨⎪=⎩∴()ADF CDF SAS ∆∆≌∴AF FC =,DCF DAF ∠=∠∵90AFL ∠=︒,90ALH LAF ∠+∠=︒ ,ALH FHC ∠=∠∴90LHC DAF ∠+∠=︒∵DCF DAF ∠=∠,90FCD FCH ∠+∠=︒∴FHC FCH ∠=∠∴FH FC =故①正确;∵90AFH ∠=︒,AF FH =∴AFH 是等腰直角三角形∴45HAE ∠=︒故②正确;连接AC 交BD 于点O ,则2BD OA =∵90AFO GFH GHF GFH ∠+∠=∠+∠=︒∴AFO GHF ∠=∠在AOF 和FGH 中90AFO GHF AOF FGH AF FH ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴()AOF FGH AAS ∆∆≌∴OA GF =∴22BD OA GF ==故④正确.过点F 作MN BC ⊥于点N ,交AD 于点M ,F 是动点∵FN 的长度不确定,而FG OA =是定值∴FN 不一定等于FGFH ∴不一定平分GHC ∠故③错误;故答案为:①②④.【点睛】本题考查了正方形性质,全等三角形判定和性质,角平分线性质和判定,等腰三角形的性质与判定等,熟练掌握全等三角形判定和性质,合理添加辅助线构造全等三角形是解题关键.三、解答题1、(1)见解析;(2)①不成立,结论:EF DF BE =-;②BE EF DF =+,见解析;(3)【解析】【分析】(1)证明EAF GAF ∆≅∆,可得出EF FG =,则结论得证;(2)①将ABE ∆绕点A 顺时针旋转90︒至ADM ∆根据SAS 可证明EAF MAF ∆≅∆,可得EF FM =,则结论得证;②将ADF ∆绕点A 逆时针旋转90︒至ABN ∆,证明AFE ANE ∆≅∆,可得出EF EN =,则结论得证;(3)求出2DG =,设DF x =,则3EF FG x ==+,6CF x =-,在Rt EFC ∆中,得出关于x 的方程,解出x 则可得解.【详解】(1)证明:把ABE ∆绕点A 顺时针旋转90︒至ADG ∆,如图1,BAE DAG ∴∠=∠,AE AG =,90B ADG ∠=∠=︒,180ADF ADG ∴∠+∠=︒,F ∴,D ,G 三点共线,45EAF ∠=︒,45BAE FAD ∴∠+∠=︒,45DAG FAD ∴∠+∠=︒,EAF FAG ∴∠=∠,AF AF =,()EAF GAF SAS ∴∆≅∆,EF FG DF DG ∴==+,EF DF BE ∴=+;(2)①不成立,结论:EF DF BE =-;证明:如图2,将ABE ∆绕点A 顺时针旋转90︒至ADM ∆,EAB MAD ∴∠=∠,AE AM =,90EAM =︒∠,BE DM =,45FAM EAF ∴∠=︒=∠,AF AF =,()EAF MAF SAS ∴∆≅∆,EF FM DF DM DF BE ∴==-=-;②如图3,将ADF ∆绕点A 逆时针旋转90︒至ABN ∆,∴=,90AN AF∠=︒,NAFEAF∠=︒,45∴∠=︒,NAE45∴∠=∠,NAE FAEAE AE=,∴∆≅∆,()AFE ANE SAS∴=,EF EN∴=+=+.BE BN NE DF EF即BE EF DF=+.故答案为:BE EF DF=+.(3)解:由(1)可知AE AG==正方形ABCD的边长为6,6DC BC AD ∴===,∴3==DG .3BE DG ∴==,633CE BC BE ∴=-=-=,设DF x =,则3EF FG x ==+,6CF x =-,在Rt EFC 中,222CF CE EF +=,222(6)3(3)x x ∴-+=+,解得:2x =.2DF ∴=,AF ∴=【点睛】本题属于四边形综合题,主要考查了正方形的性质、旋转的性质、全等三角形的判定与性质以及勾股定理的综合应用,解题的关键是作辅助线构造全等三角形,根据全等三角形的对应边相等进行推导.2、 (1)见解析(2)AD =2AB ,理由见解析【解析】【分析】(1)由SSS 证明△ABM ≌△DCM ,得出∠A =∠D ,由平行线的性质得出∠A +∠D =180°,证出∠A =90°,即可得出结论;(2)先证明△BCM 是等腰直角三角形,得出∠MBC =45°,再证明△ABM 是等腰直角三角形,得出AB =AM ,即可得出结果.(1)证明:∵点M 是AD 边的中点,∴AM =DM ,∵四边形ABCD 是平行四边形,∴AB =DC ,AB ∥CD ,在△ABM 和△DCM 中,AM DM AB DC BM CM =⎧⎪=⎨⎪=⎩, ∴△ABM ≌△DCM (SSS ),∴∠A =∠D ,∵AB ∥CD ,∴∠A +∠D =180°,∴∠A =90°,∵四边形ABCD 是平行四边形,∴四边形ABCD 是矩形;(2)解:AD 与AB 之间的数量关系:AD =2AB ,理由如下:∵△BCM 是直角三角形,BM =CM ,∴△BCM 是等腰直角三角形,∴∠MBC =45°,由(1)得:四边形ABCD 是矩形,∴AD ∥BC ,∠A =90°,∴∠AMB =∠MBC =45°,∴△ABM 是等腰直角三角形,∴AB =AM ,∵点M 是AD 边的中点,∴AD =2AM ,∴AD =2AB .【点睛】本题考查了矩形的判定与性质、平行四边形的性质、平行线的性质、全等三角形的判定与性质、等腰直角三角形的的判定与性质等知识;熟练掌握平行四边形的性质,证明△ABM ≌△DCM 是解题的关键.3、 (1)作图见解析 (2)152【解析】【分析】(1)连接AC ,作线段AC 的垂直平分线MN ,交BC 于E ,交AD 于F ,连接AE ,CF ,四边形AECF 即为所作.(2)利用勾股定理,求出AC ,CF ,再利用勾股定理求出OF 即可.(1)解:如图,连接AC ,分别以A C 、为圆心,大于12AC 的长为半径画弧,连接两弧交点,即为线段AC 的垂直平分线MN ,MN 与线段BC AD 、分别交于点E F 、,连接AE ,CF ,菱形AECF 即为所求作.(2)解:AC 交EF 于点O∵四边形ABCD 是矩形∴6890AB CD BC AD D ====∠=︒,,由勾股定理得10AC =∴5OA OC ==设AF FC x ==,由勾股定理得222(8)6x x =-+ 解得254x = ∵90FOC∴154OF === ∴1522EF OF == ∴EF 的长为152. 【点睛】 本题考查垂直平分线的性质与作图,菱形的判定和性质,矩形的性质等知识.解题的关键在于灵活运用所学知识解决问题,属于中考常考题型.4、 (1)∠DGF =25°;(2)见解析【解析】【分析】(1)由旋转的性质得出AB =AE ,AD =AG ,∠BAD =∠EAG =∠AGF =90°,由等腰三角形的性质及三角形内角和定理可得出答案;(2)证出四边形ABDF是平行四边形,由平行四边形的性质可得出结论.(1)解:由旋转得AB=AE,AD=AG,∠BAD=∠EAG=∠AGF=90°,∴∠BAE=∠DAG=50°,∴∠AGD=∠ADG=180502︒-︒=65°,∴∠DGF=90°-65°=25°;(2)证明:连接AF,由旋转得矩形AEFG≌矩形△ABCD,∴AF=BD,∠FAE=∠ABE=∠AEB,∴AF∥BD,∴四边形ABDF是平行四边形,∴DF=AB=DC.【点睛】本题考查了矩形的性质,全等三角形的判定和性质,旋转的性质,平行四边形的判定与性质,等腰三角形的性质,熟记矩形的性质并准确识图是解题的关键.5、 (1)见解析 (2)57625【解析】【分析】(1)根据旋转的性质可得DBE ≌DGF △,进而可得90DEB DFG ∠=∠=︒,根据三个角是直角的四边形证明四边形CEDF 是矩形,根据邻边相等的矩形是正方形即可得证;(2)在Rt ADG 中,根据勾股定理得AG 根据等面积法即可求得DF ,进而求得正方形的面积.(1)∵DE BC ⊥,∴90DEC DEB ∠=∠=︒.由旋转得:DE DF =,DBE ≌DGF △.∴90DEB DFG ∠=∠=︒.∵90ACB ∠=︒,∴四边形CEDF 是矩形.∵DE DF =,∴四边形CEDF 是正方形.(2)由(1)得:四边形CEDF 是正方形,∴90EDF ∠=︒.由旋转得:DBE ≌DGF △,90EDF BDG ∠=∠=︒.∴6BD GD ==,90GDA ∠=︒.在Rt ADG 中,根据勾股定理得:10AG . ∵22ADG AD DG AG DF S ⋅⋅==△, ∴861022DF ⨯⋅=. ∴245DF =. ∴257625CEDF S DF ==正方形. 【点睛】本题考查了正方形的性质与判定,勾股定理,旋转的性质,全等的性质,掌握以上性质定理是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
福州十六中八年级下学期数学第六章证明(一)单元测试卷
命题人:段振富
班级座号姓名成绩
一、填空题(每空3分,共42分)
1、“两直线平行,同位角互补”是命题(填真、假)
2、把命题“对顶角相等”改写成“如果…那么…”的形式
3、如图所示,∠1+ ∠2=180°,若∠3=50°,则∠4=
4、如图所示,△ABC中,∠ACD=115°,∠B=55°,则∠A= , ∠ACB=
5、在△ABC中,∠C=90°,若∠A=30°,则∠B=
6、在△ABC中,∠B—∠C=40°,则∠C= ,∠B=
7、在三角形中,最多有个锐角,至少有个锐角,最多有个钝角(或直角)
8、△ABC的三个外角度数比为3∶4∶5,则它的三个外角度数分别为
9、在△ABC中,∠ABC和∠ACB的平分线交于点I, 若∠A=60°,则∠BIC=
10、已知如图,平行四边形ABCD中,E为AB上一点,DE与AC交于点F,AF∶FC=3∶7,则AE∶EB=
二、选择题(每小题3分,共18分)
11、下列命题是真命题的是()
A、同旁内角互补
B、直角三角形的两锐角互余
C、三角形的一个外角等于它的两个内角之和
D、三角形的一个外角大于内角
12、下列语句为命题的是()
A 、你吃过午饭了吗?B、过点A作直线MN
C 、同角的余角相等
D 、红扑扑的脸蛋
13、命题“垂直与同一条直线的两条直线互相平行”的题设是( )
A 、垂直
B 、两条直线
C 、同一条直线
D 、两条直线垂直于同一条直线
14、已知△ABC 的三个内角度数比为2∶3∶4,则个三角形是( )
A 、锐角三角形
B 、直角三角形
C 、钝角三角形
D 、等腰三角形
15、如图,一个任意的五角星,它的五个内角的度数和为( )
A 、90°
B 、180°
C 、360°
D 、120°
16、如图,AB ∥EF , ∠C=90°,则α、β、γ的关系为( )
A 、β=α+γ
B 、α+β+γ=180°
C 、β+γ-α=90°
D 、α+β-γ=90°
三、完型填空(每空2分,共8分)
17、已知如图,在△ABC 中,CH 是外角∠ACD 的平分
线,BH 是∠ABC 的平分线。
求证:∠A= 2∠H
证明: ∵∠ACD 是△ABC 的一个外角,
∴∠ACD=∠ABC+∠A ( )
∠2是△BCD 的一个外角,
∠2=∠1+∠H ( )
∵CH 是外角∠ACD 的平分线,BH 是∠ABC 的平分线
∴∠1= 21∠ABC ,∠2= 2
1∠ACD ( ) ∴∠A =∠ACD-∠ABC= 2 (∠2 - ∠1) (等式的性质)
而 ∠H=∠2 - ∠1 (等式的性质)
∴∠A= 2∠H ( )
四、解答题(每题8分,共32分)新课标第一网
18、已知如图,在△ABC中,∠1是它的一个外角,E为边AC上一点,延长BC到D,连接DE。
求证:∠1 > ∠2
19、求证:两条直线平行,同旁内角的角平分线互相垂直。
(提示:先画图,写出已知,求证,然后进行证明)
19、已知如图,O是四边形ABCD的两条对角线的交点,过点O作OE∥CD,交AD于
E,作OF∥BC,交AB于F,连接EF。
求证:EF∥BD
20、已知如图,AB∥DE。
(1)、猜测∠A、∠ACD、∠D有什么关系,并证明你的结论。
(2)、若点C向右移动到线段AD的右侧,此时∠A、∠ACD、∠D之间的关系,仍然满足(1)中的结论吗?若符合请你证明,若不符,请你写出正确的结论并证明。
要求画出相应的图形。
新课标第一网。
