苏科版八年级数学上册第三章《勾股定理》专题练习 (2)
苏科版八年级上册数学第三章 勾股定理 含答案

苏科版八年级上册数学第三章勾股定理含答案一、单选题(共15题,共计45分)1、如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB,垂足为D,CD=1,则AB 的长为()A.2B.C.D.2、下列四组数中,其中有一组与其他三组规律不同,这一组是()A.3,4,5B.6,8,10C.5,12,13D.4,5,73、如图,在4×4的正方形方格网中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中∠ABC的余弦值是()A. B. C. D.24、如图,E是正方形ABCD内一点,BA=BE,P是对角线AC上的一点,若AC=,则PE+PD的最小值为()A. B.1 C. D.25、如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为()A. B. C.5 D.46、如图,∠AOB=30°,内有一点P且OP=,若M、N为边OA、OB上两动点,那么△PMN的周长最小为().A. B.6 C. D.7、如图,在平面直角坐标系中,菱形在第一象限内,边与轴平行,,两点的纵坐标分别为4,1,反比例函数的图象经过,两点,菱形的面积为,则的值为()A.4B.5C.6D.98、在Rt△ABC中,若斜边AB=3,则AC2+BC2等于( )A.6B.9C.12D.189、如图,在等边△ABC中,AB=6,点D是BC的中点,将△ABC绕点A逆时针旋转后得到△ACE,那么线段DE的长为()A. B.6 C. D.10、如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE 折叠,使点B落在矩形内点F处,连接CF,则CF的长为()A. B. C. D.11、在下列各组数据中,不能作为直角三角形的三边长的是()A.4,5,6B.6,8,10C.7,24,25D.9,12,1512、以下列长度的线段为边,能构成直角三角形的是()A.1,,2B.C.5,6,7D.7,8,913、下列各组数中的三个数作为三角形的边长,其中能构成直角三角形的是( )A.1,,B.2, 3, 4C.5,6,7D.7,8,914、如图所示,梯子AB靠在墙上,梯子的底端A到墙根O的距离为2m,梯子的顶端B到地面距离为7m,现将梯子的底端A向外移到A',使梯子的底端A'到墙根O距离为3m,同时梯子顶端B下降至B',那么BB' ( )A.等于1mB.小于1mC.大于1mD.以上都不对15、要用一条长24 cm的铁丝围成一个斜边长是10 cm的直角三角形,则两直角边的长分别为( )A.4 cm,8 cmB.6 cm,8 cmC.4 cm,10 cmD.7 cm,7 cm二、填空题(共10题,共计30分)16、如图,已知抛物线y=ax2+bx+4与x轴、 y轴正半轴分别交于点A、B、D,且点B的坐标为(4,0),点C在抛物线上,且与点D的纵坐标相等,点E在x轴上,且BE=AB,连接CE,取CE的中点F,则BF的长为________.17、在中,若,,,则边上的高线长是________.18、将长为3cm的线段OA绕O点旋转90°得到OA′,则点A到点A′的距离为________cm;19、如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC、BC为直径作半圆,面积分别记为S1、S2,则S1+S2等于________.20、如图所示,折叠长方形的一边AD,使点D落在边BC的点F处,已知AB=8cm,BC=10cm,则EC的长为________ cm.21、如图,PA切⊙O于点A,该圆的半径为3,PO=5,则PA的长等于________ .22、在△ABC中,若∠C=90°,∠B=30°,BC=5,则AB的长为________.(结果保留根号)23、如图,正方形OABC的边长为6,点A、C分别在x轴,y轴的正半轴上,点D(2,0)在OA上,P是OB上一动点,则PA+PD的最小值为________.24、如图,在△ABC中,CA=CB,AD⊥BC,BE⊥AC,AB=5,AD=4,则AE=________.25、有一块田地的形状和尺寸如图,则它的面积为________.三、解答题(共5题,共计25分)26、如图,中,于D.求及的长.27、如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行多少米?28、求知中学有一块四边形的空地ABCD,如下图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要250元,问学校需要投入多少资金买草皮?29、在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图,AB为⊙O的直径,弦CD⊥AB于点E,AE = 1寸,CD = 10寸,求直径AB的长.请你解答这个问题.30、如图,在中,是上的一点,若,,,,求的面积.参考答案一、单选题(共15题,共计45分)2、D3、A4、B5、D6、D7、A8、B9、C10、D11、A12、A13、A14、B15、B二、填空题(共10题,共计30分)16、18、19、20、22、23、24、25、三、解答题(共5题,共计25分)26、29、。
苏教版初二数学第三章《勾股定理》单元基础练习(含答案)

第三章《勾股定理》单元基础练习一.选择题(共10小题)1.已知在ABC∠的度数是()∠=︒,则BAACB∆中,90∠=︒,60A.30︒B.35︒C.40︒D.502.若直角三角形两直角边长分别为5和12,则斜边的长为()A.17 B.7 C.14 D.133.如图,正方形ABCD的面积是()A.5 B.25 C.7 D.1第3题第4题4.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若2+=,大正方形的面积为13,则小正a b()21方形的边长为()A.3B.2 C.5D.65.如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若BC=,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2 6AC=,5所示的“数学风车”,则这个风车的外围周长是()A.72 B.52 C.80 D.766.如图所示,将一个含有45︒角的三角板的直角顶点放在直线b上,已知//∠=︒,a b,若135那么2∠的度数是()A.35︒B.45︒C.55︒D.65︒第6题第9题7.以下列各组数为边长,不能构成直角三角形的是()A.1,3,2 B.4,5,6 C.5,12,13 D.1,2,5 8.下列各组数据中,不是勾股数的是()A.3,4,5 B.7,24,25 C.8,15,17 D.5,6,99.已知直线//m n,将一块含45︒角的直角三角板ABC按如图方式放置,其中斜边BC与直线n交于点D.若125∠=︒,则2∠的度数为()A.60︒B.65︒C.70︒D.75︒10.勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,已知90AB=,8AC=,∠=︒,6BAC点D、E、F、G、H、I都在矩形KLMJ的边上,则矩形KLMJ的周长为()A.40 B.44 C.84 D.88二.填空题(共10小题)11.如图,在Rt ABC∠=︒,点D是AB延长线上的一点,则CBD∠A∠=︒,50ACB∆中,90的度数是︒.第11题第12题12.图中阴影部分是一个正方形,则此正方形的面积为.13.如图,是2002年8月北京第24届国际数学家大会会标,由4个全等的直角三角形拼合而成.如果图中大、小正方形的面积分别为52和4,那么一个直角三角形的两直角边的和等于.第13题第14题14.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.图中是由弦图变化得到,它是由八个全等的直角三角形拼凑而成的.记图中正方形ABCD 、正方形EFGH 、正方形MNKT 的面积分别为1S ,2S ,3S ,若12310S S S ++=,则2S 的值是 .15.如图所示的图形由4个等腰直角形组成,其中直角三角形(1)的腰长为1cm ,则直角三角形(4)的斜边长为 .第15题第16题16.如图所示的网格是正方形网格,则PAB PBA ∠+∠= ︒(点A ,B ,P 是网格线交点).17.已知三角形三边长分别是6,8,10,则此三角形的面积为 .18.如图,每个小正方形边长为1,A 、B 、C 是小正方形的顶点,则2AB = ,ABC ∠=︒.第18题第19题第20题19.如图所示,一架梯子AB 长2.5米,顶端A 靠墙AC 上,这时梯子下端B 与墙角C 距离为0.7米,梯子滑动后停在DE 的位置上,测得AE 长为0.9米,则梯子底端点B 移动的距离为了 米.20.你听说过亡羊补牢的故事吗如图,为了防止羊的再次丢次,小明爸爸要在高0.9m ,宽1.2m 的栅栏门的相对角顶点间加一个加固木板,这条木板需 m 长.三.解答题(共6小题)21.如图,90B ACD ∠=∠=︒,3BC =,13AD =,12CD =,求AB 的长.22.如图所示,已知ABC ∆中,90B ∠=︒,16AB cm =,20AC cm =,P 、Q 是ABC ∆的边上的两个动点,其中点P 从点A 开始沿A B →方向运动,且速度为每秒1cm ,点Q 从点B 开始沿B C A →→方向运动,且速度为每秒2cm ,它们同时出发,设出发的时间为ts .(1)则BC = cm ;(2)当t 为何值时,点P 在边AC 的垂直平分线上?此时CQ = ;(3)当点Q 在边CA 上运动时,直接写出使BCQ ∆成为等腰三角形的运动时间.23.如图,已知30MAN ∠=︒,点B 在射线AM 上,且6AB =,点C 在射线AN 上. (1)若ABC ∆是直角三角形,求AC 的长;(2)若ABC ∆是等腰三角形,则满足条件的C 点有 个; (3)设BC x =,当ABC ∆唯一确定时,直接写出x 的取值范围.24.细心观察图形,认真分析各式,然后解答问题.2221(1)2OA =+=,11S =22231(2)3OA =+=,22S =22241(3)4OA =+=,13S =⋯(1)(直接写出答案)210OA = ,并用含有(n n 是正整数)的等式表示上述变规律:2n OA = ;n S = .(2)若一个三角形的面积是5,计算说明它是第几个三角形?25.如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.(1)在图1中,画一个三角形,使它的三边长都是有理数;(2)在图2中,画一个直角三角形,使它们的三边长都是无理数;(3)在图3中,画一个正方形,使它的面积是10.26.如图所示,已知ABCBC cm∆边上=,12=,P、Q是ABCAB cmB∆中,90∠=︒,16的两个动点,其中点P从点A开始沿A B→方向运动,且速度为每秒1cm,点Q从点B开始沿B C A→→方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为ts.(1)出发3s后,求PQ的长;(2)当点Q在边BC上运动时,出发多久后,PQB∆能形成等腰三角形?(3)当点Q在边CA上运动时,求能使BCQ∆成为等腰三角形的运动时间.参考答案一.选择题(共10小题)1.已知在ABC ∆中,90ACB ∠=︒,60A ∠=︒,则B ∠的度数是( ) A .30︒ B .35︒ C .40︒ D .50【解答】在ABC ∆中,90ACB ∠=︒,60A ∠=︒, 30B ∴∠=︒,故选:A .2.若直角三角形两直角边长分别为5和12,则斜边的长为( ) A .17 B .7 C .14 D .13【解答】由勾股定理可得:斜边2251213=+=,故选:D .3.如图,正方形ABCD 的面积是( ) A .5B .25C .7D .1【解答】设正方形的边长为c , 由勾股定理可知:22234c =+, 225c ∴=,故选:B .4.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a ,较短直角边长为b ,若2()21a b +=,大正方形的面积为13,则小正方形的边长为( ) A .3B .2C .5D .6【解答】如图所示:2()21a b +=, 22221a ab b ∴++=,大正方形的面积为13, 221138ab =-=,∴小正方形的面积为1385-=.故小正方形的边长为5, 故选:C .5.如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若6AC =,5BC =,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )A .72B .52C .80D .76【解答】依题意,设“数学风车”中的四个直角三角形的斜边长为x ,则 222125169x =+=所以13x =所以“数学风车”的周长是:(136)476+⨯=. 故选:D .6.如图所示,将一个含有45︒角的三角板的直角顶点放在直线b 上,已知//a b ,若135∠=︒,那么2∠的度数是( ) A .35︒B .45︒C .55︒D .65︒【解答】490∠=︒,134180∠+∠+∠=︒, 3180359055∴∠=︒-︒-︒=︒,直线//a b , 2355∴∠=∠=︒故选:C .7.以下列各组数为边长,不能构成直角三角形的是( ) A .1,3,2B .4,5,6C .5,12,13D .1,2,5【解答】A 、2221(3)2+=,符合勾股定理的逆定理,故此选项不合题意;B 、222456+≠,不符合勾股定理的逆定理,故此选项符合题意;C 、22251213+=,符合勾股定理的逆定理,故此选项不合题意;D 、22212(5)+=,符合勾股定理的逆定理,故此选项不合题意.故选:B .8.下列各组数据中,不是勾股数的是( ) A .3,4,5B .7,24,25C .8,15,17D .5,6,9【解答】A 、222345+=,是勾股数;B 、22272425+=,是勾股数;C 、22281517+=,是勾股数;D 、222569+≠,不是勾股数.故选:D .9.已知直线//m n ,将一块含45︒角的直角三角板ABC 按如图方式放置,其中斜边BC 与直线n 交于点D .若125∠=︒,则2∠的度数为( )A .60︒B .65︒C .70︒D .75︒【解答】设AB 与直线n 交于点E , 则1254570AED B ∠=∠+∠=︒+︒=︒. 又直线//m n ,270AED ∴∠=∠=︒.故选:C .10.勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,已知90BAC ∠=︒,6AB =,8AC =,点D 、E 、F 、G 、H 、I 都在矩形KLMJ 的边上,则矩形KLMJ 的周长为( )A .40B .44C .84D .88【解答】如图,延长AB 交KF 于点O ,延长AC 交GM 于点P ,∴四边形AOLP 是正方形,边长6814AO AB AC =+=+=,61420KL ∴=+=,81422LM =+=,∴矩形KLMJ 的周长为2(2022)84⨯+=.故选:C .二.填空题(共10小题)11.如图,在Rt ABC ∆中,90ACB ∠=︒,50A ∠=︒,点D 是AB 延长线上的一点,则CBD ∠的度数是 140 ︒.【解答】90ACB ∠=︒,50A ∠=︒, 9050140CBD ∴∠=︒+︒=︒,故答案为:140.12.图中阴影部分是一个正方形,则此正方形的面积为 36 .【解答】正方形的边长为221086-,∴此正方形的面积为2636=,故答案为:36.13.如图,是2002年8月北京第24届国际数学家大会会标,由4个全等的直角三角形拼合而成.如果图中大、小正方形的面积分别为52和4,那么一个直角三角形的两直角边的和等于 10 .【解答】设设三角形的两直角边分别为x ,y , 则22252()4x y x y ⎧+=⋯⎨-=⋯⎩①②, 由②得2224x y xy +-=⋯③, ①-③得248xy =则()22225248100x y x y xy +=++=+=, 10010x y +==.故答案是:10.14.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.图中是由弦图变化得到,它是由八个全等的直角三角形拼凑而成的.记图中正方形ABCD 、正方形EFGH 、正方形MNKT 的面积分别为1S ,2S ,3S ,若12310S S S ++=,则2S 的值是 103.【解答】将四边形MTKN 的面积设为x ,将其余八个全等的三角形面积一个设为y , 正方形ABCD ,正方形EFGH ,正方形MNKT 的面积分别为1S ,2S ,3S ,12310S S S ++=,∴得出18S y x =+,24S y x =+,3S x =,12331210S S S x y ∴++=+=,故31210x y +=,1043x y +=,所以21043S x y =+=,故答案为:103.15.如图所示的图形由4个等腰直角形组成,其中直角三角形(1)的腰长为1cm ,则直角三角形(4)的斜边长为 4 .【解答】4个三角形均为等腰直角三角形,∴直角三角形④的斜边长122224=⨯⨯⨯⨯=.故答案为:4.16.如图所示的网格是正方形网格,则PAB PBA ∠+∠= 45 ︒(点A ,B ,P 是网格线交点).【解答】45CPA ∠=︒,CPA PAB PBA ∠=∠+∠, 45PAB PBA ∴∠+∠=︒,故答案为:45.17.已知三角形三边长分别是6,8,10,则此三角形的面积为 24 . 【解答】2226810+=,∴此三角形为直角三角形, ∴此三角形的面积为:168242⨯⨯=. 故答案为:24.18.如图,每个小正方形边长为1,A 、B 、C 是小正方形的顶点,则2AB = 10 ,ABC ∠=︒.【解答】连接AC . 根据勾股定理可以得到:2221310AB =+=,2222125AC BC ==+=,5510+=,即222AC BC AB +=, ABC ∴∆是等腰直角三角形, 45ABC ∴∠=︒.故答案为:10,45.19.如图所示,一架梯子AB 长2.5米,顶端A 靠墙AC 上,这时梯子下端B 与墙角C 距离为0.7米,梯子滑动后停在DE 的位置上,测得AE 长为0.9米,则梯子底端点B 移动的距离为了 1.3 米.【解答】在直角ABC ∆中,已知 2.5AB =米,0.7BC =米,22222507 2.4AC AB BC ∴--=米,在直角CDE ∆中,已知 2.4CE CE EA =+=米, 2.5DE AB ==米,0.9AE =米,1.5CE AC AE ∴=-=米,222225152CD ED CE ∴=-=-=米,2BD ∴=米0.7-米 1.3=米故答案为:1.3.20.你听说过亡羊补牢的故事吗如图,为了防止羊的再次丢次,小明爸爸要在高0.9m ,宽1.2m 的栅栏门的相对角顶点间加一个加固木板,这条木板需 1.5 m 长.【解答】由图可知这条木板的长为220.9 1.2 2.25 1.5m +==.三.解答题(共6小题)21.如图,90B ACD ∠=∠=︒,3BC =,13AD =,12CD =,求AB 的长.【解答】在Rt ACD ∆中,90ACD ∠=︒,13AD =,12CD =,由勾股定理得:2213125AC =-=,在Rt ABC ∆中,90B ∠=︒,5AC =,3BC =,由勾股定理得:22534AB =-=.故AB 的长是4. 22.如图所示,已知ABC ∆中,90B ∠=︒,16AB cm =,20AC cm =,P 、Q 是ABC ∆的边上的两个动点,其中点P 从点A 开始沿A B →方向运动,且速度为每秒1cm ,点Q 从点B 开始沿B C A →→方向运动,且速度为每秒2cm ,它们同时出发,设出发的时间为ts .(1)则BC = 12 cm ;(2)当t 为何值时,点P 在边AC 的垂直平分线上?此时CQ = ;(3)当点Q 在边CA 上运动时,直接写出使BCQ ∆成为等腰三角形的运动时间.【解答】(1)90B ∠=︒,16AB cm =,20AC cm =2222201612()BC AC AB cm ∴=--=.故答案为:12; (2)点P 在边AC 的垂直平分线上,PC PA t ∴==,16PB t =-,在Rt BPC ∆中,222BC BP CP +=,即22212(16)t t +-=解得:252t =. 此时,点Q 在边AC 上,2521213()2CQ cm =⨯-=; 故答案为:13cm .(3)①当CQ BQ =时,如图1所示,则C CBQ ∠=∠,90ABC ∠=︒,90CBQ ABQ ∴∠+∠=︒.90A C ∠+∠=︒,A ABQ ∴∠=∠,BQ AQ ∴=,10CQ AQ ∴==,22BC CQ ∴+=,22211t ∴=÷=秒.②当CQ BC =时,如图2所示,则24BC CQ +=,24212t ∴=÷=秒.③当BC BQ =时,如图3所示,过B 点作BE AC ⊥于点E ,∴121648205AB BC BE AC ⨯===, ∴22365CE BC BE =-=. 214.4CQ CE ∴==,26.4BC CQ ∴+=,26.4213.2t ∴=÷=秒.综上所述:当t 为11秒或12秒或13.2秒时,BCQ ∆为等腰三角形.23.如图,已知30MAN ∠=︒,点B 在射线AM 上,且6AB =,点C 在射线AN 上.(1)若ABC ∆是直角三角形,求AC 的长;(2)若ABC ∆是等腰三角形,则满足条件的C 点有 3 个;(3)设BC x =,当ABC ∆唯一确定时,直接写出x 的取值范围.【解答】(1)当90ABC ∠=︒时,30A ∠=︒,12BC AC ∴=, ∴设BC x =,则2AC x =, 在Rt ABC ∆中,由勾股定理得22364x x +=,解得23x =,23x =-(舍去).43AC ∴=,当90ACB ∠=︒时,30A ∠=︒132BC AB ∴==, 33AC ∴=.(2)如图3,当AC BC =时,满足题意.如图4,当AC AB =时,满足题意.如图3,当AB BC =时,满足题意.故答案为:3.(3)当6BC 或3BC =时,ABC ∆唯一确定. 即3x =或6x . 24.细心观察图形,认真分析各式,然后解答问题.2221(1)2OA =+=,11S =22231(2)3OA =+=,22S = 22241(3)4OA =+=,13S =⋯ (1)(直接写出答案)210OA = 10 ,并用含有(n n 是正整数)的等式表示上述变规律:2n OA = ;n S = .(2)若一个三角形的面积是5,计算说明它是第几个三角形?【解答】(1)2221(1)2OA =+=,22231(2)3OA =+=,22241(3)4OA =+=, 21010OA ∴=,1010OA ∴=,2221(1)2OA =+=,112S =22231(2)3OA =+=,222S = 22241(3)4OA =+=,13S =⋯ 2n OA n ∴=,n n S =; 故答案为:10,n ,n ; (2)设它是第m 个三角形,由题意得,5m =, 解得,20m =答:一个三角形的面积是5,它是第20个三角形.25.如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.(1)在图1中,画一个三角形,使它的三边长都是有理数;(2)在图2中,画一个直角三角形,使它们的三边长都是无理数;(3)在图3中,画一个正方形,使它的面积是10.【解答】(1)三边分别为:3、4、5 (如图1);(2)三边分别为:2、22、10(如图2);(3)画一个边长为10的正方形(如图3).26.如图所示,已知ABC ∆中,90B ∠=︒,16AB cm =,12BC cm =,P 、Q 是ABC ∆边上的两个动点,其中点P 从点A 开始沿A B →方向运动,且速度为每秒1cm ,点Q 从点B 开始沿B C A →→方向运动,且速度为每秒2cm ,它们同时出发,设出发的时间为ts .(1)出发3s 后,求PQ 的长; (2)当点Q 在边BC 上运动时,出发多久后,PQB ∆能形成等腰三角形?(3)当点Q 在边CA 上运动时,求能使BCQ ∆成为等腰三角形的运动时间.【解答】(1)当3t =时,则3AP =,26BQ t ==,16AB cm =,16313()BP AB AP cm ∴=-=-=,在Rt BPQ ∆中,2222613205()PQ BQ BP cm =++.(2)由题意可知AP t =,2BQ t =,16AB =,16BP AB AP t ∴=-=-,当PQB ∆为等腰三角形时,则有BP BQ =,即162t t -=,解得163t =, ∴出发163秒后PQB ∆能形成等腰三角形;(3)①当CQ BQ =时,如图1所示, 则C CBQ ∠=∠,90ABC ∠=︒,90CBQ ABQ ∴∠+∠=︒.90A C ∠+∠=︒,A ABQ ∴∠=∠,BQ AQ ∴=,10CQ AQ ∴==,22BC CQ ∴+=,22211t ∴=÷=秒.②当CQ BC =时,如图2所示,则24BC CQ +=,24212t ∴=÷=秒.③当BC BQ =时,如图3所示,过B 点作BE AC ⊥于点E ,则121648205AB BC BE AC ⨯===, 2222483612()55CE BC BE ∴=-=-=, 214.4CQ CE ∴==,26.4BC CQ ∴+=,26.4213.2t ∴=÷=秒.综上所述:当t 为11秒或12秒或13.2秒时,BCQ ∆为等腰三角形.。
苏科版八年级上册第三章《勾股定理》单元专题培优训练卷【含答案】

苏科版八年级上册第三章《勾股定理》单元专题培优训练卷一.选择题1.下列各组数中,不是勾股数的一组是()A.3,4,5B.4,5,6C.6,8,10D.5,12,132.三个正方形的面积如图所示,则S的值为()A.3B.12C.9D.43.在△ABC中,∠A、∠B、∠C的对边分别记为a、b、c.下列条件中;不能说明△ABC 是直角三角形的是()A.∠A=∠B=∠C B.a2=b2+c2C.∠A+∠B=∠C D.a:b:c=3:4:54.如图,∠C=90o,AB=12,BC=3,CD=4,若∠ABD=90°,则AD的长为()A.8B.10C.13D.155.如图,一棵大树在暴风雨中被台风刮倒,在离地面3米处折断,测得树顶端距离树根4米,已知大树垂直地面,则大树高约多少米?()A.5米B.8米C.9米D.256.若a、b、c是△ABC三条边的长,且满足a2﹣2ab+b2+|a2+b2﹣c2|=0,则△ABC是()A.等腰三角形B.等腰直角三角形C.直角三角形D.锐角三角形7.将一根长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露出在杯子外面长为hcm,则h的取值范围是()A.0≤h≤12B.12≤h≤13C.11≤h≤12D.12≤h≤24 8.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列结论:①x2+y2=49;②x﹣y=2;③2xy+4=49;④x+y=7.其中正确的结论是()A.①②B.②④C.①②③D.①③二.填空题9.在没有直角工具之前,聪明的古埃及人用如图的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中5这条边所对的角便是直角.依据是.10.在△ABC中,若∠C=90°,∠A=46°,则∠B=°.11.在△ABC中,∠C=90°,若a=5,b=12,则c=.12.如图,是一个直角三角形以三边为边长向外作三个正方形,则字母A所代表的正方形的面积为.13.如图在Rt△ABC中,∠C=90°,CD⊥AB于D,若AC=12,BC=5,则CD =.14.如图,在高为5m,坡面长为13m的楼梯表面铺地毯,地毯的长度至少需要m.15.我国古代数学著作《九章算术》中有这样一个问题:“今有池方一丈,葭(jiā)生其中央,出水一尺,引葭赴岸,适与岸齐,问水深几何?”(注:丈,尺是长度单位,1丈=10尺)这段话翻译成现代汉语,即为:如图,有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.设这个水池深x尺,则根据题意,可列方程为.16.“赵爽弦图”巧妙的利用面积关系证明了勾股定理.如图所示的“赵爽弦图”,△ABH,△BCG,△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,若AB=10,EF=2,则AH=.三.解答题17.某中学校园有一块四边形草坪ABCD(加图所示),测得∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m,求这块四边形草坪的面积.18.如图,在四边形ABCD中,已知∠B=90°,AB=3,BC=4,CD=12,AD=13,求证AC⊥CD.19.八(3)班小明和小亮同学学习了“勾股定理”之后,为了测得下图风筝CE的高度,他们进行了如下操作:(1)测得BD的长度为25米;(2)根据手中剩余线的长度计算出风筝线BC的长为65米;(3)牵线放风筝的小明身高1.68米.求风筝的高度CE.20.三水九道谷漂流项目深受欢迎,在景区游船放置区,工作人员把偏离的游船从点A拉回点B的位置(如图).在离水面高度为8m的岸上点C,工作人员用绳子拉船移动,开始时绳子AC的长为17m,经过10秒后游船移动到点D的位置,此时BD=6m,问工作人员拉绳子的速度是多少?21.在甲村至乙村的公路旁有一块山地需要开发,现有一C处需要爆破,已知点C与公路上的停靠点A的距离为800米,与公路上另一停靠点B的距离为600米,且CA⊥CB,如图,为了安全起见,爆破点C周围半径450米范围内不得进入,问在进行爆破时,公路AB段是否有危险需要暂时封锁?请通过计算进行说明.22.我们根据图形的移、拼、补可以简单直观地推理验证数学规律和公式,这种方法称之为“无字证明”,它比严谨的数学证明更为优雅与有条理.下面是用三块全等的直角三角形移、拼、补所形成的“无字证明”图形.(1)此图可以用来证明你学过的什么定理?请写出定理的内容;(2)已知直角三角形直角边长分别为a、b,斜边长为c,图1、图2的面积相等,请你根据此图证明(1)中的定理.参考答案一.选择题1.解:A、32+42=52,能构成直角三角形,是整数,故是勾股数,此选项错误;B、42+52≠62,不是勾股数,此选项正确;C、62+82=102,三边是整数,同时能构成直角三角形,故是勾股数,此选项错误;D、52+122=132,是正整数,故是勾股数,此选项错误.故选:B.2.解:如图,由题意可得:AB=4,AC=5,∵AC2=AB2+BC2,∴BC2=25﹣16=9,∴S=9,故选:C.3.解:A、∵∠A=∠B=∠C,∠A+∠B+∠C=180°,∴∠A=∠B=∠C=60°,∴△ABC不为直角三角形,故此选项符合题意;B、∵a2=b2+c2,∴△ABC为直角三角形,故此选项不合题意;C、∵∠A+∠B=∠C,∠A+∠B+∠C=180°,∴∠C=90°,∴△ABC为直角三角形,故此选项不合题意;D、∵a:b:c=3:4:5,设a=3x,b=4x,c=5x,∵(3x)2+(4x)2=(5x)2,∴能构成直角三角形,故此选项不合题意;故选:A.4.解:在Rt△BCD中,∠C=90o,由勾股定理得:BD=,在Rt△ABD中,∠ABD=90°,由勾股定理得:AD=,故选:C.5.解:设大树高约有x米,由勾股定理得:(x﹣3)2=32+42,解得:x=8,答:大树高约8米.故选:B.6.解:∵a2﹣2ab+b2+|a2+b2﹣c2|=0,即(a﹣b)2+|a2+b2﹣c2|=0,∴(a﹣b)2=0,且|a2+b2﹣c2|=0,∴(a﹣b)2=0,且a2+b2=c2,∴a=b,且△ABC是直角三角形,∴△ABC是等腰直角三角形,故选:B.7.解:当筷子与杯底垂直时h最大,h最大=24﹣12=12(cm).当筷子与杯底及杯高构成直角三角形时h最小,如图所示:此时,AB===13(cm),故h=24﹣13=11(cm).故h的取值范围是:11cm≤h≤12cm.故选:C.8.解:由题意知,由①﹣②得2xy=45 ③,∴2xy+4=49,①+③得x2+2xy+y2=94,∴(x+y)2=94,∴x+y=.∴结论①②③正确,④错误.故选:C.二.填空题9.解:设相邻两个结点的距离为m,则此三角形三边的长分别为3m、4m、5m,∵(3m)2+(4m)2=(5m)2,∴以3m、4m、5m为边长的三角形是直角三角形.(如果三角形的两条边的平方和等于第三边的平方,那么这个三角形是直角三角形)故答案为:如果三角形的两条边的平方和等于第三边的平方,那么这个三角形是直角三角形.10.解:∵∠C=90°,∠A=46°,∴∠B=90°﹣46°=44°,故答案为:44.11.解:在△ABC中,∠C=90°,a=5,b=12,∴,故答案为:13.12.解:∵正方形PQED的面积等于225,∴即PQ2=225,∵正方形PRGF的面积为289,∴PR2=289,又△PQR为直角三角形,根据勾股定理得:PR2=PQ2+QR2,∴QR2=PR2﹣PQ2=289﹣225=64,则正方形QMNR的面积为64.故答案是:64.13.解:Rt△ABC中,∠C=90°,由勾股定理得:AB=,由S△ABC=得:∴5×12=13×CD,∴CD=.故答案为:.14.解:由勾股定理得:楼梯的水平宽度==12,∵地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,∴地毯的长度至少是12+5=17(米).故答案为:17.15.解:设水池里水的深度是x尺,由题意得,(x+1)2=x2+25,故答案为:(x+1)2=x2+25.16.解:∵AB=10,EF=2,∴大正方形的面积是100,小正方形的面积是4,∴四个直角三角形面积和为100﹣4=96,设AE为a,DE为b,即4×ab=96,∴2ab=96,a2+b2=100,∴(a+b)2=a2+b2+2ab=100+96=196,∴a+b=14,∵a﹣b=2,解得:a=8,b=6,∴AE=8,AH=DE=6,∴AH=8﹣2=6.故答案为:6.三.解答题17.解:连接AC,如图:∵∠B=90°,AB=24m,BC=7m,∴AC2=AB2+BC2=242+72=625,∴AC=25(m).又∵CD=15m,AD=20m,152+202=252,即AD2+DC2=AC2,∴△ACD是直角三角形,∴S四边形ABCD=S△ABC+S△ADC=•AB•BC+•AD•DC=×24×7+×20×15=234(m2).答:这块四边形草坪的面积是234m2.18.证明:∵∠B=90°,∴△ABC为直角三角形,又∵AB=3,BC=4,∴根据勾股定理得:AC==5,又∵CD=12,AD=13,∴AD2=132=169,CD2+AC2=122+52=144+25=169,∴CD2+AC2=AD2,∴△ACD为直角三角形,∠ACD=90°,即AC⊥CD.19.解:在Rt△CDB中,由勾股定理得,CD2=BC2﹣BD2=652﹣252=3600,所以,CD=±60(负值舍去),所以,CE=CD+DE=60+1.68=61.68(米),答:风筝的高度CE为61.68米.20.解:由题意得:∠B=90°,∵BC=8m,BD=6m,∴CD===10m,∵AC=17m,∴绳子移动了AC﹣DC=17﹣10=7(m),用时10秒,∴工作人员拉绳子的速度是7÷10=0.7米/秒.21.解:公路AB不需要暂时封锁.理由如下:如图,过C作CD⊥AB于D.∵CA⊥CB,∴∠ACB=90°,因为BC=800米,AC=600米,所以,根据勾股定理有AB==1000(米).因为S△ABC=AB•CD=BC•AC所以CD===480(米).由于400米<480米,故没有危险,因此AB段公路不需要暂时封锁.22.解:(1)勾股定理:直角三角形的两条直角边长分别为a、b,斜边长为c,那么a2+b2=c2;(2)图1的面积为:S1=,图2的面积为S2=,∵图1、图2的面积相等,∴=,∴a2+b2=c2.。
第三章 勾股定理数学八年级上册-单元测试卷-苏科版(含答案)

第三章勾股定理数学八年级上册-单元测试卷-苏科版(含答案)一、单选题(共15题,共计45分)1、由线段a,b,c组成的三角形是直角三角形的是()A.a = 3, b = 4, c = 6B.a = 6, b = 9, c = 10C.a = 8,b = 15, c = 17D.a = 13, b = 14, c = 152、如图是一株美丽的勾股树,所有的四边形都是正方形,所有的三角形都是直角三角形.其中最大的直角三角形两直角边长分别为2,3,则正方形A,B,C,D的面积之和为()A.13B.26C.47D.943、如图,在以O为圆心的两个同心圆中,A为大圆上任意一点,过A作小圆的割线AXY,若AX•AY=4,则图中圆环的面积为()A.16πB.8πC.4πD.2π4、如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于()A. B. C.4 D.35、如图,在矩形ABCD中,DE⊥AC+于E,∠EDC:∠EDO=1:2,且AC=10,则DE的长度是A.3B.5C.D.6、如图,为等腰直角三角形,OA1=1,以斜边OA2为直角边作等腰直角三角形OA2A3,再以OA3为直角边作等腰直角三角形OA3A4,…,按此规律作下去,则OA n的长度为()A.()nB.()n﹣1C.()nD.()n﹣17、直角三角形的两条边长分别是5和12,则斜边上的中线长是()A.6B.6.5C.6或6.5D.6或2.58、如图1,在正方形铁皮上剪下一个扇形和一个半径为1cm的圆形,使之恰好围成图2所示的一个圆锥,则圆锥的高为()A. cmB.4cmC. cmD. cm9、在下列长度的各组线段中,能组成直角三角形的是()A.5,6,7B.5,12,13C.1,4,9D.5,11,1210、下列各数中,是勾股数的是()A.0.3,0.4,0.5B.6,8,10C. ,,D.10,15,1811、如图,已知△ABC 中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3 上,且 l1,l2 之间的距离为 1,l2,l3 之间的距离为 3,则 AC 的长是()A. B. C. D.512、如图,在△中,,将△绕点顺时针旋转,得到△,连接,若,,则线段的长为()A. B. C. D.13、如图,已知在中,是边上的高线,平分,交于点是上一动点,,则的最小值是()A.10B.7C.5D.414、如图,周长为16的菱形ABCD中,点E,F分别在AB,AD边上,AE=1,AF=3,P为BD 上一动点,则线段EP+FP的长最短为()A.3B.4C.5D.615、若△ABC三边长口,b,c满足+l| b-a-1|+(c-5)2=0,则△ABC是( )A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形二、填空题(共10题,共计30分)16、如图中,由一个直角三角形和两个正方形组成,如果大正方形的面积为41,AB=5,则小正方形的面积为________.17、在等腰直角中,,,如果以的中点为旋转中心,将这个三角形旋转180°,点落在点处,则的长度为________.18、如图,在锐角△ABC中,AB=,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD,AB上的动点,则BM+MN的最小值是________.19、如图,在平面直角坐标系中,边长为1的正方形OA1B1C的对角线A1C和OB1交于点M1;以M1A1为对角线作第二个正方形A2A1B2 M1,对角线A1 M1和A2B2交于点M2;以M2A1为对角线作第三个正方形A3A1B3 M2,对角线A1 M2和A3B3交于点M3;……,依次类推,这样作的第n个正方形对角线交点的坐标为M n________.20、如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是边AC的中点,点E,F在边AB上,当△DEF是等腰三角形,且底角的正切值是时,△DEF腰长的值是________.21、如图,AB是⊙O的直径,AB=2,点C在⊙O上,∠CAB=30°,D为的中点,P是直径AB上一动点,则PC+PD的最小值为________.22、若直角三角形的两直角边长分别为,,则斜边的长为________cm.23、如图,在中,,,,垂足为,点,分别是线段,上的动点,且,则线段的最小值为________.24、如图,在菱形ABCD中,∠BAD=45°,DE是AB边上的高,BE=2,则AB的长是________.25、如图,在△ABC中,AB=BC=4,S△ABC=4 ,点P、Q、K分别为线段AB、BC、AC上任意一点,则PK+QK的最小值为________.三、解答题(共5题,共计25分)26、如图,在每个小正方形的边长为1的方格纸中有线段AB和CD,点A、B、C、D均在小正方形的顶点上。
苏科版八年级上册数学第三章 勾股定理 含答案

苏科版八年级上册数学第三章勾股定理含答案一、单选题(共15题,共计45分)1、如图,点是中斜边(不与,重合)上一动点,分别作于点,作于点,连接、,若,,当点在斜边上运动时,则的最小值是()A.1.5B.2C.4.8D.2.42、如图,AB是⊙O的直径,点D,C在⊙O上,∠DOC=90°,AD=,BC=1,则⊙O的半径为()A. B. C. D.3、如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,连结CE交AD于点F,连结BD交CE于点G,连结BE.下列结论中,正确的结论有()①CE=BD;②△ADC是等腰直角三角形;③∠ADB=∠AEB;④S= BD•四边形BCDECE;⑤BC2+DE2=BE2+CD2.A.1个B.2个C.3个D.4个4、如图,在矩形ABCD中,AB=5,BC=8,E是边BC的中点,M是AE的中点,连接CM,则CM的长为()A.6B.6.5C.7D.7.55、如图,在中,,,D是AB的中点,点E在AC上,点F在BC上,且,给出以下四个结论:(1);(2)是等腰直角三角形;(3)四边形CEDF面积;(4)的最小值为2.其中正确的有().A.4个B.3个C.2个D.1个6、如图,AB是半圆O的直径,点C、D、E是半圆弧上的点,且弦AC=CD=2,弦DE=EB=,则直径AB的长是()A. B. C. D.7、下列各组数中是勾股数的是()A.4,5, 6B.1.5,2, 2.5C.11,60, 61D.1,,28、下列说法错误的是()A.若△ABC中,a 2=(b+c)(b−c),则△ABC是直角三角形B.若△ABC中,a 2+b 2≠c 2,则△ABC不是直角三角形C.若△ABC中,a:b:c=13:5:12,则∠A=90° D.若△ABC中,a、b、b三边长分别为n 2−1、2n、n 2+1(n>1),则△ABC是直角三角形9、如图,在▱ABCD中,对角线AC与BD相交于点O,且AB⊥AC.若AD=5,AB =3,则对角线BD的长为()A. B.2 C.9 D.810、如图,在中,,分别以、为直径作半圆,则图中阴影部分的面积是()A. B. C. D.11、如图,在△ABC 中,∠ACB =90°,AD 平分∠BAC 交 BC 于D,DE 垂直平分AB交AB 于E。
八年级数学苏科版上册课时练第3单元《3.3 勾股定理的简单应用》(2) 练习试题试卷 含答案
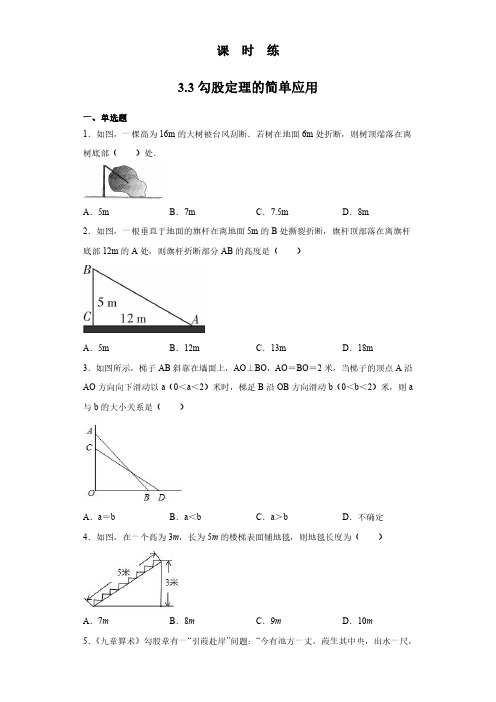
课时练3.3勾股定理的简单应用一、单选题1.如图,一棵高为16m的大树被台风刮断.若树在地面6m处折断,则树顶端落在离树底部()处.A.5m B.7m C.7.5m D.8m2.如图,一根垂直于地面的旗杆在离地面5m的B处撕裂折断,旗杆顶部落在离旗杆底部12m的A处,则旗杆折断部分AB的高度是()A.5m B.12m C.13m D.18m3.如图所示,梯子AB斜靠在墙面上,AO⊥BO,AO=BO=2米,当梯子的顶点A沿AO方向向下滑动以a(0<a<2)米时,梯足B沿OB方向滑动b(0<b<2)米,则a 与b的大小关系是()A.a=b B.a<b C.a>b D.不确定4.如图,在一个高为3m,长为5m的楼梯表面铺地毯,则地毯长度为()A.7m B.8m C.9m D.10m5.《九章算术》勾股章有一“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问:水深,葭长各几何.”意思是:如示意图,有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度和芦苇的长度分别是多少?备注:1丈=10尺.设芦苇长x 尺,则可列方程为()A .22210(1)x x +=+B .222(1)5x x -+=C .2225(1)x x +=-D .2221(1)x x +=-6.小明同学先向北行进4千米,然后向东进4千米,再向北行进2千米,最后又向东行进一定距离,此时小明离出发点的距离是10千米,小明最后向东行进了()A .3千米B .4千米C .5千米D .6千米7.如图是一圆柱玻璃杯,从内部测得底面半径为6cm ,高为16cm ,现有一根长为25cm 的吸管任意放入杯中,则吸管露在杯口外的长度最少是()A .6cmB .5cmC .9cm Dcm8.如图,一艘轮船位于灯塔P 的北偏东60°方向,与灯塔P 的距离为30海里的A 处,轮船沿正南方向航行一段时间后,到达位于灯塔P 的南偏东30°方向上的B 处,则此时轮船所在位置B 处与灯塔P 之间的距离为()A .60海里B .45海里C .20海里D .9.如图,长方体的底面边长为1cm 和3cm ,高为6cm.如果用一根细线从点A 开始经过4个侧面缠绕一圈到达B ,那么所用细线最短需要()A .12cmB .11cmC .10cmD .9cm10.中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由“弦图”变化得到,它是由八个全等的直角三角形拼接而成.将图中正方形MNKT ,正方形EFGH ,正方形ABCD 的面积分别记为S 1,S 2,S 3,若S 1+S 2+S 3=18,则正方形EFGH 的面积为()A .92B .5C .6D .9二、填空题11.长是4米的梯子搭在墙上,与地面成45°角,作业时调整为60°角,则梯子的顶端沿墙面升高了______米12.如图,90AOB Ð=°,9OA m =,3OB m =,一机器人在点B 处看见一个小球从点A 出发沿着AO 方向匀速滚向点O ,机器人立即从点B 出发,沿直线匀速前进拦截小球,恰好在点C 处截住了小球,如果小球滚动的速度与机器人行走的速度相等,则机器人行走的路程BC 为__________.13.一艘轮船在小岛A的北偏东60°方向距小岛60海里的B处,沿正西方向航行3小时后到达小岛的北偏西45°的C处,则该船行驶的速度为_____海里/小时.14.如图,有一个三级台阶,它的每一级的长,宽和高分别是16,3,1,点A和点B 是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶表面爬到B点的最短路程是____.15.如图,在一次测绘活动中,在港口A的位置观测停放于B、C两处的小船,测得船B在港口A北偏东75°方向12海里处,船C在港口A南偏东15°方向9海里处,则船B 与船C之间的距离为__________海里.三、解答题16.如图,某人为了测量小山顶上的塔顶离地面的高度CD,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60m到达山脚点B,测得塔尖点D的仰角为60°,求CD的高度(结果保留根号)17.如图,星期天小明去钓鱼,鱼钩A在离水面的BD的1.3米处,在距离鱼线1.2米处D点的水下0.8米处有一条鱼发现了鱼饵,于是以0.2米/秒的速度向鱼饵游去,那么这条鱼至少几秒后才能到达鱼饵处?18.台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点C 为一海港,且点C与直线AB上两点A,B的距离分别为300km和400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域.(1)海港C受台风影响吗?为什么?(2)若台风的速度为20km/h,台风影响该海港持续的时间有小时.参考答案1.D2.C3.C4.A5.B6.B7.B8.D9.C10.C11.12.5m13.(10+14.2015.1516.(90m+17.6.518.(1)海港C受台风影响.理由:如图,过点C作CD⊥AB于D,∵AC=300km,BC=400km,AB=500km,∴AC2+BC2=AB2.∴△ABC是直角三角形.∴AC•BC=CD•AB∴CD=240(km)∵以台风中心为圆心周围250km以内为受影响区域,∴海港C受到台风影响.(2)当EC=250km,FC=250km时,正好影响C港口,∵ED70(km)∴EF=140km∵台风的速度为20km/h,∴140÷20=7(小时)即台风影响该海港持续的时间为7小时.故答案为:7.。
八年级数学苏科版上册课时练第3单元《3.1勾股定理》(2) 练习试题试卷 含答案

课时练3.1勾股定理一.选择题1.在Rt △ABC 中,∠C =90°,AB =2AC ,若AC =6,则BC 的长为()A .8B .12C .D .2.在Rt △ABC 中,90ACB Ð=°,3AB =,则222AB BC AC ++=()A .9B .18C .20D .243.如图,在ABC 中,90C °Ð=,2AC =,点D 在BC 上,ADC 2B Ð=Ð,AD =则BC 的长为()A1-B .1+C 1D 14.如图,等边ABC 中,AD BC ^,DE AC ^,8AB =,则DE =()A.2B .4C .D .5.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A ,B ,C ,D 的面积分别为6,10,4,6,则最大正方形E 的面积是()A .94B .26C .22D .166.如图,数轴上点A 对应的数是0,点B 对应的数是1,BC⊥AB,垂足为B,且BC=2,以A 为圆心,AC 为半径画弧,交数轴于点D,则点D 表示的数为()A.2.2B.C.D.7.若直角三角形的三边长分别为2,4,x,则x 的值可能有().A.1个B.2个C.3个D.4个8.以面积为9cm 2的正方形对角线为边作正方形,其面积为()A.9cm2B.13cm2C.18cm2D.24cm29.我国是最早了解勾股定理的国家之一.下面四幅图中,不能证明勾股定理的是()A .B .C .D .10.等腰直角三角形的斜边长为5cm ,则它的面积是()A .25cm 2B .12.5cm 2C .10cm 2D .6.25cm 2二.填空题11.若一个直角三角形的两边长分别是4cm ,3cm ,则第三条边长是cm .12.如图所示,图1中x 的值为_______,图2中的y 的值为_______.13.如图,在ABC 中,90ABC Ð=°,分别以BC 、AB 、AC 为边向外作正方形,面积分别记为1S 、2S 、3S ,若24S =,36S =,则1S =______.14.如图,AB ⊥CD 于B ,△ABD 和△BCE 都是等腰直角三角形,如果CD =17,BE =5,那么AC 的长为_______15.图示是一种“羊头”形图案,其作法是,从正方形1开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2,和2′,…,依次类推,若正方形7的边长为1cm,则正方形1的边长为__________cm.三.解答题16.如图,∠BAC=90°,BC=28,AC=14,BD=13,AD=15.(1)求AB的长度;(2)作DH⊥AB,并求△ADB的面积.17.如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.(1)求证:BF=2AE;(2)若CD=2,求AD的长.18.在学习勾股定理时,我们学会运用图(Ⅰ)验证它的正确性.图中大正方形的面积可表示为(a+b)2,也可表示为c2+4×ab,即(a+b)2=c2+4×ab.由此推出勾股定理a2+b2=c2这种方法可以极简单地直观推论或验证出数学规律和公式.(1)请你用图(Ⅱ)的面积表达式验证勾股定理(其中四个全等的直角三角形围成一个大正方形ABCD,中间的部分是一个小正方形EFGH,AE=a,BE=b,AB=c);(2)请你用图(Ⅲ)提供的图形进行组合,用组合图形的面积表达式验证:(x+y)2=x2+2xy+y2.参考答案一.选择题1.C2.B3.D4.C6.D.7.B.8.C.9.D.10.D二.填空题11.5或.12.41313.214.1315.8三.解答题16.AB=25,CD=12=,连结BG、FG,17.延长ED至G,使DG DEÐ=Ð,=AD BD,ADE BDG\D@D,ADE BDGÐ=Ð,AE BG\=,A DBG\,AC BG\Ð+Ð=°,90\Ð=°,FBGC FBG180222\+=,BG BF GF=,又ED FD,ED GD^\=,EF GF222AE BF EF\+=.55 4.18.(1);(2)20;(3)Sn(4)。
2022-2023学年苏科版八年级数学上册《第3章勾股定理》期末综合复习题(附答案)

2022-2023学年苏科版八年级数学上册《第3章勾股定理》期末综合复习题(附答案)一.选择题1.下列各组数,可以作为直角三角形的三边长的是()A.2,3,4B.7,24,25C.8,12,20D.5,13,15 2.在平面直角坐标系中,点P(3,4)到原点的距离是()A.3B.4C.5D.±53.一直角三角形的两边长分别为3和4.则第三边的长为()A.5B.C.D.5或4.如图,在平面直角坐标系中,点A,B的坐标分别为(﹣6,0),(0,8),以点A为圆心,以AB长为半径画弧,交x轴正半轴于点C,则点C的坐标为()A.(10,0)B.(0,4)C.(4,0)D.(2,0)5.已知,如图,一轮船以20海里/时的速度从港口A出发向东北方向航行,另一轮船以15海里/时的速度同时从港口A出发向东南方向航行,则2小时后,两船相距()A.35海里B.40海里C.45海里D.50海里6.如图,将一个边长分别为4,8的长方形纸片ABCD折叠,使C点与A点重合,则BE 的长是()A.3B.4C.5D.67.如图,数轴上的点A表示的数是﹣2,点B表示的数是1,CB⊥AB于点B,且BC=2,以点A为圆心,AC为半径画弧交数轴于点D,则点D表示的数为()A.B.+2C.﹣2D.28.如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是()A.12≤a≤13B.12≤a≤15C.5≤a≤12D.5≤a≤139.如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行()A.8米B.10米C.12米D.14米10.如图,在矩形纸片ABCD中,已知AD=8,折叠纸片,使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为()A.3B.4C.5D.6二.填空题11.在“寻找滨河最美,拒绝不文明行为”系列活动中,细心的董明同学发现:学校六号楼前有一块长方形花圃(如图所示),有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,请你计算,他们仅仅少走了步路(假设2步为1米),却踩伤了花草.12.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为cm2.13.如图,已知在Rt△ABC中,∠ACB=90°,AB=8,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于.14.如图,矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为.15.如图所示,圆柱的高AB=15cm,底面周长为40cm,现在有一只蚂蚁想要从A处沿圆柱表面爬到对角C处捕食,则它爬行的最短距离是.16.某小区楼梯如图所示,欲在楼梯上铺设红色地毯,已知这种地毯每平方米售价为20元,楼梯宽为2m,则购买这种地毯至少需要元.17.在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S1,S2,S3,S4,则S1+S2+S3+S4=.三.解答题18.如图,铁路上A,B两点相距25km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=16km,CB=11km,现在要在铁路AB上建一个土特产品收购站E,使得C,D 两村到E站的距离相等,则E站应建在离A站多少km处?19.在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形.在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各为多少?20.“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?(参考数据转换:1m/s=3.6km/h)21.在甲村至乙村的公路旁有一块山地正在开发,现有一C处需要爆破.已知点C与公路上的停靠站A的距离为500米,与公路上另一停靠站B的距离为1200米,且CA⊥CB,如图,为了安全起见,爆破点C周围半径400米范围内不得进入,问在进行爆破时,公路AB段是否有危险,是否需要暂时封锁?请通过计算进行说明.22.如图,在Rt△ABC中,∠BCA=90°,AC=12,AB=13,点D是Rt△ABC外一点,连接DC,DB,且CD=4,BD=3.(1)求BC的长;(2)求证:△BCD是直角三角形.23.如图(1)所示,一个梯子AB长2.5米,顶端A靠在墙AC上(墙与地面垂直),这时梯子下端B与墙角C距离为1.5米.(1)求梯子顶端A与地面的距离AC的长;(2)若梯子滑动后停在DE位置上,如图(2)所示,测得BD=0.5米,求梯子顶端A 下滑了多少米?24.如图,正方形网格中有△ABC.若每个小方格边长均为1,请你根据所学的知识解答下列问题:(1)判断△ABC的形状,并说明理由;(2)求△ABC中BC边上的高.25.我国大部分东部地区属于亚热带季风气候,夏季炎热多雨.如图,A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内是受台风影响的区域.(1)A城是否受到这次台风的影响?为什么?(2)若A城受到这次台风影响,那么A城遭受这次台风影响有多长时间?参考答案一.选择题1.解:A、∵22+32≠42,∴不能构成直角三角形;B、∵72+242=252,∴能构成直角三角形;C、∵82+122≠202,∴不能构成直角三角形;D、∵52+132≠152,∴不能构成直角三角形.故选:B.2.解:∵点P(3,4),∴点P到原点的距离是=5.故选:C.3.解:(1)当两边均为直角边时,由勾股定理得,第三边为5,(2)当4为斜边时,由勾股定理得,第三边为,故选:D.4.解:∵点A,B的坐标分别为(﹣6,0),(0,8),∴OA=6,OB=8,在Rt△AOB中,由勾股定理得:AB==10,∴AC=AB=10,∴OC=10﹣6=4,∴点C的坐标为(4,0),故选:C.5.解:∵两船行驶的方向是东北方向和东南方向,∴∠BAC=90°,两小时后,两艘船分别行驶了20×2=40海里,15×2=30海里,根据勾股定理得:=50(海里).故选:D.6.解:根据翻折的性质得,AE=CE,设BE=x,∵长方形ABCD的长为8,∴AE=CE=8﹣x,在Rt△ABE中,根据勾股定理,AE2=AB2+BE2,即(8﹣x)2=42+x2,解得x=3,所以,BE的长为3.故选:A.7.解:由题意可得,AB=3,BC=2,AB⊥BC,∴AC===,∴AD=.∴点D表示数为﹣2.故选:C.8.解:a的最小长度显然是圆柱的高12,最大长度根据勾股定理,得:=13.即a的取值范围是12≤a≤13.故选:A.9.解:如图,设大树高为AB=10m,小树高为CD=4m,过C点作CE⊥AB于E,则EBDC是矩形,连接AC,∴EB=4m,EC=8m,AE=AB﹣EB=10﹣4=6m,在Rt△AEC中,AC==10m,故选:B.10.解:∵四边形ABCD是矩形,AD=8,∴BC=8,∵△AEF是△AEB翻折而成,∴BE=EF=3,AB=AF,△CEF是直角三角形,∴CE=8﹣3=5,在Rt△CEF中,CF===4,设AB=x,在Rt△ABC中,AC2=AB2+BC2,即(x+4)2=x2+82,解得x=6,故选:D.二.填空题11.解:根据勾股定理可得斜边长是=5m.则少走的距离是3+4﹣5=2m,∵2步为1米,∴少走了4步,故答案为:4.12.解:由图形可知四个小正方形的面积和等于最大正方形的面积,故正方形A,B,C,D的面积之和=49cm2.故答案为:49cm2.13.解:S1=π()2=πAC2,S2=πBC2,所以S1+S2=π(AC2+BC2)=πAB2=8π.故答案为:8π.14.解:易证△AFD′≌△CFB,∴D′F=BF,设D′F=x,则AF=8﹣x,在Rt△AFD′中,(8﹣x)2=x2+42,解之得:x=3,∴AF=AB﹣FB=8﹣3=5,∴S△AFC=•AF•BC=10.故答案为:10.15.解:把圆柱侧面展开,展开图如右图所示,点A、C的最短距离为线段AC的长.在Rt△ADC中,∠ADC=90°,CD=AB=15,AD为底面半圆弧长,AD=40=20,所以AC===25,故答案为:25cm.16.解:已知直角三角形的一条直角边是3m,斜边是5m,根据勾股定理得到:水平的直角边是4m,地毯水平的部分的和是水平边的长,竖直的部分的和是竖直边的长,则购买这种地毯的长是3m+4m=7m,则面积是14m2,价格是14×20=280(元).17.解:观察发现,∵AB=BE,∠ACB=∠BDE=90°,∴∠ABC+∠BAC=90°,∠ABC+∠EBD=90°,∴∠BAC=∠EBD,∴△ABC≌△BDE(AAS),∴BC=ED,∵AB2=AC2+BC2,∴AB2=AC2+ED2=S1+S2,即S1+S2=1,同理S3+S4=3.则S1+S2+S3+S4=1+3=4.故答案为:4.三.解答题18.解:设AE=xkm,∵C、D两村到E站的距离相等,∴DE=CE,即DE2=CE2,由勾股定理,得x2+162=112+(25﹣x)2,解得x=9.8,∴E站应建在离A站9.8 km处.19.解:设水池的深度为x尺,由题意得:x2+52=(x+1)2,解得:x=12,则x+1=13,答:水深12尺,芦苇长13尺.20.解:在Rt△ABC中,AC=30m,AB=50m;根据勾股定理可得:(m)∴小汽车的速度为v==20(m/s)=20×3.6(km/h)=72(km/h);∵72(km/h)>70(km/h);∴这辆小汽车超速行驶.答:这辆小汽车超速了.21.解:公路AB不需要暂时封锁.理由如下:如图,过C作CD⊥AB于D.∵CA⊥CB,∴∠ACB=90°,因为BC=1200米,AC=500米,所以,根据勾股定理有AB==1300(米).因为S△ABC=AB•CD=BC•AC所以CD===(米).由于400米<米,故没有危险,因此AB段公路不需要暂时封锁.22.(1)解:∵Rt△ABC中,∠BCA=90°,AC=12,AB=13,∴BC===5;(2)证明:∵在△BCD中,CD=4,BD=3,BC=5,∴CD2+BD2=42+32=52=BC2,∴△BCD是直角三角形.23.解:(1)在Rt△ABC中,∠C=90°根据勾股定理,得:AC===2(米)∴梯子顶端A与地面的距离AC为2米;(2)依题意,得:CD=BC+BD=1.5+0.5=2(米)在Rt△CDE中,∠C=90°,根据勾股定理,得:∴AE=AC﹣CE=2﹣1.5=0.5(米)∴梯子顶端A下滑了0.5米.24.解:(1)∵由勾股定理得:AB2=12+22=5,AC2=22+42=20,BC2=32+42=25,∴AB2+AC2=BC2,∴△ABC是直角三角形;(2)∵AB2=12+22=5,AC2=22+42=20,BC2=32+42=25,∴AB=,AC=2,BC=5,设△ABC的边BC上的高为h,则AB×AC=×h,∴×2=5h,h=2,即△ABC中BC边上的高是2.25.解:(1)由A点向BF作垂线,垂足为C,在Rt△ABC中,∠ABC=30°,AB=320km,则AC=160km,因为160<200,所以A城要受台风影响;(2)设BF上点D,G,使AD=AG=200千米,∴△ADG是等腰三角形,∵AC⊥BF,∴AC是DG的垂直平分线,∴CD=GC,在Rt△ADC中,DA=200千米,AC=160千米,由勾股定理得,CD===120(千米),则DG=2DC=240千米,遭受台风影响的时间是:t=240÷40=6(小时).。
八年级数学苏科版上册随堂测试第3单元《 3.2 勾股定理的逆定理》 练习试题试卷 含答案

随堂测试3.2勾股定理的逆定理一、选择题1.满足下列条件的△ABC,不是直角三角形的是()A.a:b:c=3:4:5B.∠A:∠B:∠C=9:12:15C.∠C=∠A﹣∠B D.b2﹣a2=c22.适合下列条件的△ABC中,∠A,∠B,∠C是三个内角,a,b,c分别是∠A,∠B,∠C的对边,直角三角形的个数是()①a=7,b=24,C=25;②a=1.5,b=2,c=7.5;③∠A:∠B:∠C=1:2:3;④a=1,b=,c=.A.1个B.2个C.3个D.4个3.在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,下列结论中不正确的是()A.如果∠A﹣∠B=∠C,那么△ABC是直角三角形B.如果a2=b﹣2c2,那么△ABC是直角三角形且∠C=90°C.如果∠A:∠B:∠C=1:3:2,那么△ABC是直角三角形D.如果a2:b2:c2=9:16:25,那么△ABC是直角三角形4.适合下列条件的△ABC中,直角三角形的个数为()①a=3,b=4,c=5;②a=6,∠A=45°;③a=2,b=2,c=2;④∠A=38°,∠B=52°.A.1个B.2个C.3个D.4个5.在下列以线段a、b、c的长为边,能构成直角三角形的是()A.a=3,b=4,c=6B.a=5,b=6,c=7C.a=6,b=8,c=9D.a=7,b=24,c=256.三角形的三边长a,b,c满足2ab=(a+b)2-c2,则此三角形是()A.钝角三角形B.锐角三角形C.直角三角形D.等边三角形7.△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,由下列条件不能判定△ABC为直角三角形的是()A.∠A:∠B:∠C=l:2:3B.三边长为a,b,c的值为1,2,C.三边长为a,b,c的值为,2,4D.a2=(c+b)(c﹣b)8.在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,下列判断错误的是()A.如果∠C-∠B=∠A,则△ABC是直角三角形B.如果a2+c2=b2,则△ABC不是直角三角形C.如果(c-a)(c+a)=b2,则△ABC是直角三角形D.如果∠A∶∠B∶∠C=5∶2∶3,则△ABC是直角三角形9.如图,在4×4的方格中,△ABC的形状是()A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形10.五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,如图,其中正确的是()二、填空题11.在△ABC中,三边长分别为8、15、17,那么△ABC的面积为.12.一个三角形的三边的比为5∶12∶13,它的周长为60cm,则它的面积是.13.在△ABC中,如果(a+b)(a﹣b)=c2,那么∠=90°.14.如果△ABC的三边长a,b,c满足关系式(a-24)2+∣b-18∣+∣c-30∣=0,则△ABC的形状是。
2020年苏科版初二数学上册第三章《勾股定理》单元测试题及答案

苏科版八年级数学上册第三章《勾股定理》单元测试卷一、选择题:1、将直角三角形的三边扩大相同的倍数后,得到的三角形是( )A. 直角三角形B. 锐角三角形C. 钝角三角形D. 不能判断2、一个直角三角形的两直角边长分别为7和24,下列说法正确的是( )A .斜边长为625B .三角形的周长为84C .斜边长为25D .三角形的面积为1683、如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a 的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )A. 12≤a≤13B. 12≤a≤15C. 5≤a≤12D. 5≤a≤134、若直角三角形的两边长分别为a ,b ﹣4|=0,则该直角三角形的第三边长为( )A. 5B. √7C. 4D. 5或√75、在Rt△ABC 中,∠C=90°,AC =9,BC =12,则点C 到AB 的距离是( )A .536B .2512C .49 D .以上均不正确 6、如图,在由边长均为1个单位长度的小正方形组成的网格中,A 、B 都是格点,则线段AB的长为 ( )A .5B .6C .7D .257、如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为 ( )A.0.7米 B.1.5米 C.2.2米 D.2.4米8、如图是一张直角三角形纸片,两直角边AC=3cm,BC=4cm.现将△ABC折叠,使点B 与点A重合,折痕为DE,则BE的长为()A.2cm B.2. 5cm C.3cm D.5cm9、如图,点A的正方体左侧面的中心,点B是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A沿其表面爬到点B的最短路程是()A. 3 +2 D. 410、如图,一艘轮船以16海里/时的速度从港口A出发向东北方向航行,同时另一艘轮船以12海里/时的速度从港口A出发向东南方向航行,离开港口3小时后,两船相距()A.36海里 B.48海里 C.60海里 D.84海里11、如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B、C).若线段AD的长为正整数,则点D共有()A .5个B .4个C .3个D .2个12、已知直角三角形纸片的两条直角边长分别为m 和n (n m <),过锐角顶点把该纸片剪成两个三角形.若这两个三角形都为等腰三角形,则 ( )A .0222=++n mn mB .0222=+-n mn mC .0222=-+n mn mD .0222=--n mn m二、填空题:13、已知在三角形ABC 中,∠C=90°,AC=15,BC=20,则AB 的长等于________.14、两只小鼹鼠在地下从同一处开始打洞,一只朝北面挖,每分钟挖8cm ,另一只朝东面挖,每分钟挖6cm ,10分钟之后两只小鼹鼠相距 .15、在△ABC 中,AB =5,BC =12,AC =13,则边AC 上的高是______________.16、已知三角形的三边长分别为a 、b 、c .如果(a-9)2+|b-15|+(12+c)2=0,那么△ABC (填是或不是)直角三角形17、如图,一架2.5米长的梯子AB ,斜靠在一竖直的墙AC 上,这时梯足B 到墙底端C 的距离为0.7米,如果梯子的顶端下滑0.4米,则梯足将向外移 .18、在平静的湖面上,有一枝红莲,高出水面1m ,一阵风吹来,红莲被吹到一边,花朵齐及水面,已知红莲移动的水平距离为2m ,这里水深是 米。
苏科版数学八年级上册数学期末几何专题复习——三角形综合(全等与勾股定理)(二)

八年级上册数学期末几何专题复习——三角形综合(全等与勾股定理)(二)1.如图,已知△ABC中,AB=6cm,∠B=∠C,BC=4cm,点D为AB的中点.若点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?2.(1)在等边三角形ABC中,①如图①,D,E分别是边AC,AB上的点且AE=CD,BD与EC交于点F,则∠BFE的度数是度;②如图②,D,E分别是边AC,BA延长线上的点且AE=CD,BD与EC的延长线交于点F,此时∠BFE的度数是度;(2)如图③,在△ABC中,AC=BC,∠ACB是锐角,点O是AC边的垂直平分线与BC的交点,点D,E分别在AC,OA的延长线上,AE=CD,BD与EC的延长线交于点F,若∠ACB =α,求∠BFE的大小.(用含α的代数式表示).3.如图,在等边△ABC中,点D是边AB上一点,E是BC延长线上一点,CE=DA,连接DE 交AC于点F,过点D作DG⊥AC于点G,过点D作DH∥BC交AC于点H.(1)求证:AG=AD;(2)求证:DF=EF;=2,求△DGF的面积.(3)若CF=CE,S△ADG4.如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A,B重合),BE⊥CD于E,交直线AC于F.(1)点D在边AB上时,试探究线段BD,AB和AF的数量关系,并证明你的结论;(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请直接写出正确结论.5.已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.(1)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.6.如图,在△ABC中,AB=AC=2,∠B=36°,点D在线段BC上运动(点D不与点B、C 重合),连接AD,作∠ADE=36°,DE交线段AC于点E.(1)当∠BDA=128°时,∠EDC=,∠AED=;(2)线段DC的长度为何值时,△ABD≌△DCE?请说明理由;(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.7.如图,在△AEC和△DFB中,∠E=∠F,点A、B、C、D在同一直线上,有如下三个关系式:①AE∥DF,②AB=CD,③CE=BF.(1)请用其中两个关系式作为条件,另一个作为结论,写出你认为正确的所有命题(用序号写出命题书写形式:“如果⊗、⊗,那么⊗”)(2)选择(1)中你写出的一个命题,说明它正确的理由.8.(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD.求证:EF=BE+FD;(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?(3)如图3,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.9.已知四边形ABCD中,∠A=∠C=90°,AB=BC,∠ABC=120°,∠MBN=60°,∠MBN 绕B点旋转,它的两边分别交AD,DC(或它们的延长线)于E,F.当∠MBN绕B点旋转到AE=CF时(如图1),易证AE+CF=EF;当∠MBN绕B点旋转到AE≠CF时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段AE,CF,EF又有怎样的数量关系?请写出你的猜想,不需证明.10.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,(1)求证:AD平分∠BAC;(2)已知AC=20,BE=4,求AB的长.参考答案1.解:(1)全等,理由如下:∵t=1秒,∴BP=CQ=1×1=1厘米,∵AB=6cm,点D为AB的中点,∴BD=3cm.又∵PC=BC﹣BP,BC=4cm,∴PC=4﹣1=3cm,∴PC=BD.∵∠B=∠C,∴△BPD≌△CPQ;(2)∵v P≠v Q,∴BP≠CQ,又∵△BPD≌△CPQ,∠B=∠C,则BP=CP=2,BD=CQ=3,∴点P,点Q运动的时间为:t=2秒,∴v Q=1.5cm/s;2.解:(1)如图①中,∵△ABC是等边三角形,∴AC=CB,∠A=∠BCD=60°,∵AE=CD,∴△ACE≌△CBD,∴∠ACE=∠CBD,∴∠BFE=∠CBD+∠BCF=∠ACE+∠BCF=∠BCA=60°.故答案为60.(2)如图②中,∵△ABC是等边三角形,∴AC=CB,∠A=∠BCD=60°,∴∠CAE=∠BCD=′120°∵AE=CD,∴△ACE≌△CBD,∴∠ACE=∠CBD=∠DCF,∴∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA=60°.故答案为60.(3)如图③中,∵点O是AC边的垂直平分线与BC的交点,∴OC=OA,∴∠EAC=∠DCB=180°﹣α,∵AC=BC,AE=CD,∴△AEC≌△CDB,∴∠E=∠D,∴∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α.3.(1)证明:∵△ABC是等边三角形,∴∠A=60°,∵DG⊥AC,∴∠AGD=90°,∠ADG=30°,∴AG=AD;(2)解:∵DH∥BC,∴∠ADH=∠B,∠AHD=∠ACB,∠FDH=∠E,∵△ABC是等边三角形,∴∠B=∠ACB=∠A=60°,∴∠A=∠ADH=∠AHD=60°,∴△ADH是等边三角形,∴DH=AD,∵AD=CE,∴DH=CE,在△DHF和△ECF中,,∴△DHF≌△ECF(AAS),∴DF=EF;(3)∵△ABC是等边三角形,DG⊥AC,AD=DH,∴AG=GH,∵△DHF≌△ECF,∴HF=CF,∵CF=CE,DH=CE,∴HF=AH,∴GF=3AG,∵△DGF和△ADG等高,∴S△DGF =3S△ADG=6.4.解:(1)AB=FA+BD.证明:如图1,∵BE⊥CD即∠BEC=90°,∠BAC=90°,∴∠F+∠FBA=90°,∠F+∠FCE=90°.∴∠FBA=∠FCE.∵∠FAB=180°﹣∠DAC=90°,∴∠FAB=∠DAC.在△FAB和△DAC中,.∴△FAB≌△DAC(ASA).∴FA=DA.∴AB=AD+BD=FA+BD.(2)(1)中的结论不成立.点D在AB的延长线上时,AB=AF﹣BD;点D在AB的反向延长线上时,AB=BD﹣AF.理由如下:①当点D在AB的延长线上时,如图2.同理可得:FA=DA.则AB=AD﹣BD=AF﹣BD.②点D在AB的反向延长线上时,如图3.同理可得:FA=DA.则AB=BD﹣AD=BD﹣AF.5.(1)证明:∵点D是AB中点,AC=BC,∠ACB=90°,∴CD⊥AB,∠ACD=∠BCD=45°,∴∠CAD=∠CBD=45°,∴∠CAE=∠BCG,又∵BF⊥CE,∴∠CBG+∠BCF=90°,又∵∠ACE+∠BCF=90°,∴∠ACE=∠CBG,在△AEC和△CGB中,∴△AEC≌△CGB(ASA),∴AE=CG,(2)解:BE=CM.证明:∵CH⊥HM,CD⊥ED,∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,∴∠CMA=∠BEC,又∵∠ACM=∠CBE=45°,在△BCE和△CAM中,,∴△BCE≌△CAM(AAS),∴BE=CM.6.解:(1)∵AB=AC,∴∠C=∠B=36°,∵∠ADE=36°,∠BDA=128°,∵∠EDC=180°﹣∠ADB﹣∠ADE=16°,∴∠AED=∠EDC+∠C=16°+36°=52°,故答案为:16°;52°;(2)当DC=2时,△ABD≌△DCE,理由:∵AB=2,DC=2,∴AB=DC,∵∠C=36°,∴∠DEC+∠EDC=144°,∵∠ADE=36°,∴∠ADB+∠EDC=144°,∴∠ADB=∠DEC,在△ABD和△DCE中,,∴△ABD≌△DCE(AAS);(3)当∠BDA的度数为108°或72°时,△ADE的形状是等腰三角形,①当DA=DE时,∠DAE=∠DEA=72°,∴∠BDA=∠DAE+∠C=72°+36°=108°;②当AD=AE时,∠AED=∠ADE=36°,∴∠DAE=108°,此时,点D与点B重合,不合题意;③当EA=ED时,∠EAD=∠ADE=36°,∴∠BDA=∠EAD+∠C=36°+36°=72°;综上所述,当∠BDA的度数为108°或72°时,△ADE的形状是等腰三角形.7.解:(1)如果①②,那么③;如果①③,那么②;(2)若选择如果①②,那么③,证明:∵AE∥DF,∴∠A=∠D,∵AB=CD,∴AB+BC=BC+CD,即AC=DB,在△ACE和△DBF中,,∴△ACE≌△DBF(AAS),∴CE=BF;若选择如果①③,那么②,证明:∵AE∥DF,∴∠A=∠D,在△ACE和△DBF中,,∴△ACE≌△DBF(AAS),∴AC=DB,∴AC﹣BC=DB﹣BC,即AB=CD.8.证明:(1)延长EB到G,使BG=DF,连接AG.∵∠ABG=∠ABC=∠D=90°,AB=AD,∴△ABG≌△ADF.∴AG=AF,∠1=∠2.∴∠1+∠3=∠2+∠3=∠EAF=∠BAD.∴∠GAE=∠EAF.又∵AE=AE,∴△AEG≌△AEF.∴EG=EF.∵EG=BE+BG.∴EF=BE+FD(2)(1)中的结论EF=BE+FD仍然成立.(3)结论EF=BE+FD不成立,应当是EF=BE﹣FD.证明:在BE上截取BG,使BG=DF,连接AG.∵∠B+∠ADC=180°,∠ADF+∠ADC=180°,∴∠B=∠ADF.∵AB=AD,∴△ABG≌△ADF.∴∠BAG=∠DAF,AG=AF.∴∠BAG+∠EAD=∠DAF+∠EAD=∠EAF=∠BAD.∴∠GAE=∠EAF.∵AE=AE,∴△AEG≌△AEF.∴EG=EF∵EG=BE﹣BG∴EF=BE﹣FD.9.解:∵AB⊥AD,BC⊥CD,AB=BC,AE=CF,在△ABE和△CBF中,,∴△ABE≌△CBF(SAS);∴∠ABE=∠CBF,BE=BF;∵∠ABC=120°,∠MBN=60°,∴∠ABE=∠CBF=30°,∴AE=BE,CF=BF;∵∠MBN=60°,BE=BF,∴△BEF为等边三角形;∴AE+CF=BE+BF=BE=EF;图2成立,图3不成立.证明图2.延长DC至点K,使CK=AE,连接BK,在△BAE和△BCK中,则△BAE≌△BCK,∴BE=BK,∠ABE=∠KBC,∵∠FBE=60°,∠ABC=120°,∴∠FBC+∠ABE=60°,∴∠FBC+∠KBC=60°,∴∠KBF=∠FBE=60°,在△KBF和△EBF中,∴△KBF≌△EBF,∴KF=EF,∴KC+CF=EF,即AE+CF=EF.图3不成立,AE、CF、EF的关系是AE﹣CF=EF.10.(1)证明:∵DE⊥AB,DF⊥AC,∴∠E=∠DFC=90°,∴在Rt△BED和Rt△CFD中,,∴Rt△BED≌Rt△CFD(HL),∴DE=DF,∵DE⊥AB,DF⊥AC,∴AD平分∠BAC;(2)解:∵∠AED=∠AFD=90°,AD=AD,DE=DF,∴Rt△ADE≌Rt△ADF(HL)∴AE=AF,∵AC=20,CF=BE=4,∴AE=AF=20﹣4=16,∴AB=AE﹣BE=16﹣4=12.。
2019--2020学年江苏省八年级上册数学(苏科版)期末考试《勾股定理》试题分类——解答题(2)

2019--2020学年江苏省八年级上册数学(苏科版)期末考试《勾股定理》试题分类——解答题(2)1.如图,在四边形ABCD中,AB=BC=3,CD,DA=5,∠B=90°,求∠BCD的度数.2.如图,已知某开发区有一块四边形空地ABCD,现计划在该空地上种植草皮,经测量∠ADC=90°,CD =6m,AD=8m,BC=24m,AB=26m,若每平方米草皮需200元,则在该空地上种植草皮共需多少钱?3.如图1,一架云梯斜靠在一竖直的墙上,云梯的顶端距地面15米,梯子的长度比梯子底端离墙的距离大5米.(1)这个云梯的底端离墙多远?(2)如图2,如果梯子的顶端下滑了8m,那么梯子的底部在水平方向滑动了多少米?4.如图,在等腰△ABC中,AB=AC,BC=5.点D为AC上一点,且BD=4,CD=3.(1)求证:BD⊥AC;(2)求AB的长.5.《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”翻译成数学问题是:如图所示,△ABC中,∠ACB =90°,AC+AB=10,BC=3,求AC的长.6.一个零件的形状如图所示,工人师傅按规定做得∠B=90°,AB=3,BC=4,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗?7.已知:如图,在△ABC中,CD⊥AB,垂足为点D,AC=20,BC=15,DB=9.(1)求CD的长.(2)求AB的长.8.如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积.9.两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);(2)证明:DC⊥BE.10.已知△ABC中,∠A=90°,AB=AC,D为BC的中点.(1)如图,若E、F分别是AB、AC上的点,且BE=AF.求证:△DEF为等腰直角三角形;(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么△DEF是否仍为等腰直角三角形?证明你的结论.11.已知某校有一块四边形空地ABCD如图,现计划在该空地上种草皮,经测量∠A=90°,AB=3m,BC =12m,CD=13m,DA=4m.若种每平方米草皮需100元,问需投入多少元?12.如图,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13米,此人以0.5米每秒的速度收绳,10秒后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号)13.如图,正方形网格中的每个小正方形的边长都是1,每个顶点叫做格点.(1)在图(1)中以格点为顶点画一个面积为10的正方形;(2)在图(2)中以格点为顶点画一个三角形,使三角形三边长分别为2,,;这个三角形的面积为.14.如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.(1)当t=2秒时,求PQ的长;(2)求出发时间为几秒时,△PQB是等腰三角形?(3)若Q沿B→C→A方向运动,则当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.15.如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.(1)出发2秒后,求PQ的长;(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.16.如图,∠ABC=90°,AB=6cm,AD=24cm,BC+CD=34cm,C是直线l上一动点,请你探索当C离B多远时,△ACD是一个以CD为斜边的直角三角形?17.如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?18.如图,笔直的公路上A、B两点相距25km,C、D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15km,CB=10km,现在要在公路的AB段上建一个土特产品收购站E,使得C、D两村到收购站E 的距离相等,则收购站E应建在离A点多远处?19.如图,四边形ABCD中,AB=4cm,BC=3cm,CD=12cm,DA=13cm,且∠ABC=90°,求四边形ABCD的面积.20.正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点,(1)在图①中,画一个面积为10的正方形;(2)在图②、图③中,分别画两个不全等的直角三角形,使它们的三边长都是无理数.21.如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.(1)在图1中,画一个三角形,使它的三边长都是有理数;(2)在图2中,画一个直角三角形,使它们的三边长都是无理数;(3)在图3中,画一个正方形,使它的面积是10.22.“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上的行驶速度不得超过70千米/时.一辆“小汽车”在一条城市街路上直道行驶,某一时刻刚好行驶到路对面“车速检测仪A”正前方50米C 处,过了6秒后,测得“小汽车”位置B与“车速检测仪A”之间的距离为130米,这辆“小汽车”超速了吗?请说明理由.23.“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?(参考数据转换:1m/s=3.6km/h)2019--2020学年江苏省八年级上册数学(苏科版)期末考试《勾股定理》试题分类——解答题(2)参考答案与试题解析一.解答题(共23小题)1.【答案】见试题解答内容【解答】解:∵在Rt△ABC中,AB=BC=3,∠B=90°,∴由勾股定理得:AC2=AB2+BC2=32+32=18,∵CD,DA=5,∴CD2+AC2=DA2,∴∠ACD=90°,∵在Rt△ABC中,AB=BC,∴∠BAC=∠ACB=45°,∴∠BCD=∠ACB+∠ACD=45°+90°=135°.2.【答案】见试题解答内容【解答】解:连接AC,在Rt△ACD中,AC2=CD2+AD2=62+82=102,在△ABC中,AB2=262,BC2=242,而102+242=262,即AC2+BC2=AB2,∴∠ACB=90°,S四边形ABCD=S△ACB﹣S△ACD•AC•BCAD•CD,10×248×6=96.所以需费用96×200=19200(元).3.【答案】见试题解答内容【解答】解:(1)根据题意可得OA=15米,AB﹣OB=5米,由勾股定理OA2+OB2=AB2,可得:152+OB2=(5+OB)2解得:OB=20,答:这个云梯的底端离墙20米远;(2)由(1)可得:AB=20+5=25米,根据题意可得:CO=7米,CD=AB=25米,由勾股定理OC2+OD2=CD2,可得:,∴BD=24﹣20=4米,答:梯子的底部在水平方向滑动了4米.4.【答案】见试题解答内容【解答】(1)证明:∵CD=3,BC=5,BD=4,∴CD2+BD2=9+16=25=BC2,∴△BCD是直角三角形,∴BD⊥AC;(2)解:设AD=x,则AC=x+3.∵AB=AC,∴AB=x+3.∵∠BDC=90°,∴∠ADB=90°,∴AB2=AD2+BD2,即(x+3)2=x2+42,解得:x,∴AB3.5.【答案】见试题解答内容【解答】解:设AC=x,∵AC+AB=10,∴AB=10﹣x.∵在Rt△ABC中,∠ACB=90°,∴AC2+BC2=AB2,即x2+32=(10﹣x)2.解得:x=4.55,即AC=4.55.6.【答案】见试题解答内容【解答】解:∵42+32=52,52+122=132,即AB2+BC2=AC2,故∠B=90°,同理,∠ACD=90°,∴S四边形ABCD=S△ABC+S△ACD3×45×12=6+30=36.答:这块钢板的面积等于36.7.【答案】见试题解答内容【解答】解:(1)∵CD⊥AB,∴∠CDB=∠CDA=90°,在Rt△BCD中,∵BC=15,DB=9,∴CD12;(2)在Rt△ACD中,∵AC=20,CD=12,∴AD16,则AB=AD+DB=16+9=25.8.【答案】见试题解答内容【解答】解:连接AC,过点C作CE⊥AB于点E.∵AD⊥CD,∴∠D=90°.在Rt△ACD中,AD=5,CD=12,AC13.∵BC=13,∴AC=BC.∵CE⊥AB,AB=10,∴AE=BEAB10=5.在Rt△CAE中,CE12.∴S四边形ABCD=S△DAC+S△ABC5×1210×12=30+60=90.9.【答案】见试题解答内容【解答】(1)△ABE≌△ACD.证明:∵△ABC与△AED均为等腰直角三角形,∴AB=AC,AE=AD,∠BAC=∠EAD=90°.∴∠BAC+∠CAE=∠EAD+∠CAE.即∠BAE=∠CAD,在△ABE与△ACD中,,∴△ABE≌△ACD;(2)证明∵△ABE≌△ACD,∴∠ACD=∠ABE=45°,又∵∠ACB=45°,∴∠BCD=∠ACB+∠ACD=90°,∴DC⊥BE.10.【答案】见试题解答内容【解答】解:(1)证明:连接AD∵AB=AC,∠A=90°,D为BC中点∴ADBD=CD且AD平分∠BAC∴∠BAD=∠CAD=45°在△BDE和△ADF中,,∴△BDE≌△ADF(SAS)∴DE=DF,∠BDE=∠ADF∵∠BDE+∠ADE=90°∴∠ADF+∠ADE=90°即:∠EDF=90°∴△EDF为等腰直角三角形.(2)解:仍为等腰直角三角形.理由:∵△AFD≌△BED∴DF=DE,∠ADF=∠BDE∵∠ADF+∠FDB=90°∴∠BDE+∠FDB=90°即:∠EDF=90°∴△EDF为等腰直角三角形.11.【答案】见试题解答内容【解答】解:∵∠A=90°,AB=3m,DA=4m,∴DB5(m),∵BC=12m,CD=13m,∴BD2+BC2=DC2,∴△DBC是直角三角形,∴S△ABD+S△DBC3×45×12=36(m2),∴需投入总资金为:100×36=3600(元).12.【答案】见试题解答内容【解答】解:在Rt△ABC中:∵∠CAB=90°,BC=13米,AC=5米,∴AB12(米),∵此人以0.5米每秒的速度收绳,10秒后船移动到点D的位置,∴CD=13﹣0.5×10=8(米),∴AD(米),∴BD=AB﹣AD=12(米),答:船向岸边移动了(12)米.13.【答案】见试题解答内容【解答】解:(1)面积为10的正方形的边长为,∵,∴如图1所示的四边形即为所求;(2)∵,,∴如图2所示的三角形即为所求这个三角形的面积2×2=2;故答案为:2.14.【答案】见试题解答内容【解答】(1)解:(1)BQ=2×2=4cm,BP=AB﹣AP=8﹣2×1=6cm,∵∠B=90°,PQ2(cm);(2)解:根据题意得:BQ=BP,即2t=8﹣t,解得:t;即出发时间为秒时,△PQB是等腰三角形;(3)解:分三种情况:①当CQ=BQ时,如图1所示:则∠C=∠CBQ,∵∠ABC=90°,∴∠CBQ+∠ABQ=90°,∠A+∠C=90°,∴∠A=∠ABQ∴BQ=AQ,∴CQ=AQ=5,∴BC+CQ=11,∴t=11÷2=5.5秒.②当CQ=BC时,如图2所示:则BC+CQ=12∴t=12÷2=6秒.③当BC=BQ时,如图3所示:过B点作BE⊥AC于点E,则BE4.8(cm)∴CE3.6cm,∴CQ=2CE=7.2cm,∴BC+CQ=13.2cm,∴t=13.2÷2=6.6秒.由上可知,当t为5.5秒或6秒或6.6秒时,△BCQ为等腰三角形.15.【答案】见试题解答内容【解答】解:(1)∵BQ=2×2=4(cm),BP=AB﹣AP=16﹣2×1=14(cm),∠B=90°,∴PQ(cm);(2)BQ=2t,BP=16﹣t,根据题意得:2t=16﹣t,解得:t,即出发秒钟后,△PQB能形成等腰三角形;(3)①当CQ=BQ时,如图1所示,则∠C=∠CBQ,∵∠ABC=90°,∴∠CBQ+∠ABQ=90°.∠A+∠C=90°,∴∠A=∠ABQ,∴BQ=AQ,∴CQ=AQ=10,∴BC+CQ=22,∴t=22÷2=11秒.②当CQ=BC时,如图2所示,则BC+CQ=24,∴t=24÷2=12秒.③当BC=BQ时,如图3所示,过B点作BE⊥AC于点E,则BE,∴CE,∴CQ=2CE=14.4,∴BC+CQ=26.4,∴t=26.4÷2=13.2秒.综上所述:当t为11秒或12秒或13.2秒时,△BCQ为等腰三角形.16.【答案】见试题解答内容【解答】解:设BC=xcm时,三角形ACD是以DC为斜边的直角三角形,∵BC+CD=34,∴CD=34﹣x,在Rt△ABC中,AC2=AB2+BC2=36+x2,在Rt△ACD中,AC2=CD2﹣AD2=(34﹣x)2﹣576,∴36+x2=(34﹣x)2﹣576,∴当C离点B8cm时,△ACD是以DC为斜边的直角三角形.17.【答案】见试题解答内容【解答】解:连结AC,在Rt△ACD中,∠ADC=90°,AD=4米,CD=3米,由勾股定理得:AC5(米),∵AC2+BC2=52+122=169,AB2=132=169,∴AC2+BC2=AB2,∴∠ACB=90°,该区域面积S=S△ACB﹣S△ADC5×123×4=24(平方米),即铺满这块空地共需花费=24×100=2400元.18.【答案】见试题解答内容【解答】解:∵使得C,D两村到E站的距离相等.∴DE=CE,∵DA⊥AB于A,CB⊥AB于B,∴∠A=∠B=90°,∴AE2+AD2=DE2,BE2+BC2=EC2,∴AE2+AD2=BE2+BC2,设AE=x,则BE=AB﹣AE=(25﹣x),∵DA=15km,CB=10km,∴x2+152=(25﹣x)2+102,解得:x=10,∴AE=10km,∴收购站E应建在离A点10km处.19.【答案】见试题解答内容【解答】解:连接AC,∵∠ABC=90°,AB=4cm,BC=3cm,∵CD=12cm,DA=13cm,AC2+CD2=52+122=169=132=DA2,∴△ADC为直角三角形,∴S四边形ABCD=S△ACD﹣S△ABCAC×CDAB×BC5×124×3=30﹣6=24.故四边形ABCD的面积为24cm2.20.【答案】见试题解答内容【解答】解:(1)如图①所示:(2)如图②③所示.21.【答案】见试题解答内容【解答】解:(1)三边分别为:3、4、5 (如图1);(2)三边分别为:、2、(如图2);(3)画一个边长为的正方形(如图3).22.【答案】见试题解答内容【解答】解:由题意知,AB=130米,AC=50米,且在Rt△ABC中,AB是斜边,根据勾股定理AB2=BC2+AC2,可以求得:BC=120米=0.12千米,且6秒时,所以速度为72千米/时,故该小汽车超速.答:该小汽车超速了,平均速度大于70千米/时.23.【答案】见试题解答内容【解答】解:在Rt△ABC中,AC=30m,AB=50m;据勾股定理可得:(m)∴小汽车的速度为v20(m/s)=20×3.6(km/h)=72(km/h);∵72(km/h)>70(km/h);∴这辆小汽车超速行驶.答:这辆小汽车超速了.。
第三章《勾股定理》实际应用综合训练(二)2021-2022学年八年级数学苏科版上册

第三章《勾股定理》实际应用综合训练(二)1.某校机器人兴趣小组在如图所示的三角形场地上开展训练.已知:AB=10,BC=6,AC=8;机器人从点C出发,沿着△ABC边按C→B→A→C的方向匀速移动到点C停止;机器人移动速度为每秒2个单位,移动至拐角处调整方向需要1秒(即在B、A处拐弯时分别用时1秒).设机器人所用时间为t秒时,其所在位置用点P表示(机器人大小不计).(1)点C到AB边的距离是;(2)是否存在这样的时刻,使△PBC为等腰三角形?若存在,求出t的值;若不存在,请说明理由.2.如图,学校操场边有一块四边形空地ABCD,其中AB⊥AC,AB=CD=4m,BC=9m,AD=7m.为了美化校园环境,创建绿色校园,学校计划将这块四边形空地进行绿化整理.(1)求需要绿化的空地ABCD的面积;(2)为方便师生出入,设计了过点A的小路AE,且AE⊥BC于点E,试求小路AE的长.3.如图,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中AB =AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H,(A、H、B在同一条直线上),并新修一条路CH,已知CB=千米,CH=2千米,HB=1千米.(1)CH是否为从村庄C到河边的最近路?请通过计算加以说明;(2)求新路CH比原路CA少多少千米?4.某中学A,B两栋教学楼之间有一块如图所示的四边形空地ABCD,学校为了绿化环境,计划在空地上种植花草,经测量∠ABC=90°,AB=20米,BC=15米,CD=7米,AD=24米.(1)求出四边形空地ABCD的面积;(2)若每种植1平方米的花草需要投入120元,求学校共需投入多少元.5.今有竹高一丈,末折抵地,去根三尺,问折者高几何?意思是:有一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?6.我国明朝数学著作《直指算法统宗》中有一道关于勾股定理的问题:“平地秋千为起,踏板一尺高地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.二公高士好争,算出索长有几?(注:二步=10尺).”大意是:“当秋千静止时,它的踏板离地的距离为1尺,将秋千的踏板往前推2步(这里的每1步合5尺),它的踏板与人一样高,这个人的身高为5尺,秋千的绳索始终是呈直线状态的,现在问:这个秋千的绳索有多长?”请解答上述问题.7.如图,公路MN和公路PQ在点P处交会,公路PQ上点A处有学校,点A到公路MN 的距离为80m,现有一卡车在公路MN上以5m/s的速度沿PN方向行驶,卡车行驶时周围100m以内都会受到噪音的影响,请你算出该学校受影响的时间多长?8.如图(1)是超市的儿童玩具购物车,图(2)为其侧面简化示意图,测得支架AC=24cm,CB=18cm,两轮中心的距离AB=30cm,求点C到AB的距离.(结果保留整数)9.我市某中学有一块四边形的空地ABCD(如图所示),为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,CD=13m,BC=12m.(1)求出空地ABCD的面积.(2)若每种植1平方米草皮需要200元,问总共需投入多少元?10.为了绿化环境,我县某中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量,∠ADC=90°,CD=6m,AD=8m,AB=26m,BC=24m,(1)求出空地ABCD的面积.(2)若每种植1平方米草皮需要200元,问总共需投入多少元?11.如图,在一次夏令营活动中,小明从营地A出发,沿北偏东60°方向走了80m到达点B,然后再沿北偏西30°方向走了60m到达目的地C.(1)求A、C两点之间的距离;(2)确定目的地C在营地A的北偏东多少度方向.12.数学综合实验课上,同学们在测量学校旗杆的高度时发现:将旗杆顶端升旗用的绳子垂到地面还多2米;当把绳子的下端拉开8米后,下端刚好接触地面,如图,根据以上数据,同学们准确求出了旗杆的高度,你知道他们是如何计算出来的吗?13.如图1,一架云梯斜靠在一竖直的墙上,云梯的顶端距地面15米,梯子的长度比梯子底端离墙的距离大5米.(1)这个云梯的底端离墙多远?(2)如图2,如果梯子的顶端下滑了8m,那么梯子的底部在水平方向滑动了多少米?14.如图,有一个透明的直圆柱状的玻璃杯,现测得内径为5cm,高为12cm,今有一支14cm的吸管任意斜放于杯中,若不考虑吸管的粗细,则吸管露出杯口外的长度最少为多少?15.台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力,如图,2017年第21号台风“兰恩”的中心从A点以速度为20千米/小时,沿AB方向移动,以台风中心为圆心周围250km以内为受影响区域.已知点C 为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,请问海港C受台风影响吗?若受到影响,台风影响该海港的时间有多长?若不会受到影响,请说明理由.16.一架梯子AB长25米,如图所示,斜靠在一面上,此时梯子底端B离墙7米;如果梯子的顶端A下滑了4米至点A',那么梯子的底端水平滑动的距离BB'是多少米?17.如图,已知某山的高度AC为800米,从山上A处与上下B处各建一个索道口,且BC=1500米,欢欢从山下索道口坐缆车到山顶,已知缆车每分钟走50米,那么大约多少分钟后,欢欢才能达到山顶?18.如图,市政部门计划在一块三角形空地ABC内部种植草坪,并紧靠AB边外侧修建宽3m,长17m的硬化甬路(阴影图形为长方形).已知AC=8cm,BC=15cm,经过市政部门市场调研,种植草坪的费用为每平米600元,硬化甬路的费用为每平米800元,求此项工程的预计总费用.19.如图,MN是一条东西朝向的笔直的公路,C是位于该公路上的一个检测点,一辆长为9m的小货车BD行驶在该公路上.小王位于检测点C正西北方向的点A处观察小货车,某时刻他发现车头D与车尾B分别距离他10m与17m.(1)过点A向MN引垂线,垂足为E,请利用勾股定理找出线段AE、DE与AE、BE 之间所满足的数量关系;(2)在上一问的提示下,继续完成下列问题:①求线段DE的长度;②该小货车的车头D距离检测点C还有多少米?20.甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源.为了避免走散,他们用两部对话机联系,已知对话机的有效距离为15千米,早晨8:00甲先出发,他以6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?。
苏科版八年级上册数学第三章 勾股定理 含答案

苏科版八年级上册数学第三章勾股定理含答案一、单选题(共15题,共计45分)1、下列四组线段中,不能构成直角三角形的是()A.5,12,13B.8,15,17C.3,4,5D.2,3,42、如图,正方形ABCD的边长为4,点E,点F分别是边BC,边CD上的动点,且BE=CF,AE与BF相交于点P.若点M为边BC的中点,点N为边CD上任意一点,则MN+PN的最小值等于()A. B.5 C. D.3、下列各组数中,能成为直角三角形的三条边长的是( )A.3,5,7B.5,7,8C.1,,2D.4,6,74、如图,在半径为5cm的⊙O中,直线l交⊙O于A、B两点,且弦AB=8cm,要使直线l与⊙O相切,则需要将直线l向下平移( )A.1 cmB.2 cmC.3 cmD.4 cm5、如图,在中,弦AB垂直平分半径OC,OC=2,则弦AB的长为()A. B. C. D.6、如图,在中,是的内切圆,连结,,则图中阴影部分的面积之和为()A. B. C.12 D.147、已知:如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,则菱形ABCD的周长是()A.20B.16C.12D.108、满足下列条件的中,不是直角三角形的是A. B. C. D.9、在△ABC中,已知AB=AC=5cm,BC=8cm,D是BC的中点,以D为圆心作一个半径为3cm的圆,则下列说法正确的是()A.点A在⊙D外B.点A在⊙D 上C.点A在⊙D内D.无法确定10、若一个直角三角形两边的长分别为6和8,则第三边的长为()A.10B.C.10或D.10或11、如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为()A.140°B.100°C.50°D.40°12、如图,在矩形ABCD中,AB=3,BC=4,P是对角线AC上的动点,连接DP,将直线DP绕点P顺时针旋转使∠DPG=∠DAC,且过D作DG⊥PG,连接CG,则CG最小值为( )A. B. C. D.13、以下列各组数据为三角形三边,能构成直角三角形的是()A.4 cm, 8 cm, 7 cmB.2 cm, 2 cm, 2 cmC.2 cm, 2 cm, 4 cmD.13 cm, 12 cm, 5 cm14、如图,圆锥的底面半径OA=2cm,高为PO=4cm,现有一个蚂蚁从A出发引圆锥侧面爬到母线PB的中点,则它爬行的最短路程为()A.3 cmB.6cmC.4 cmD.6 cm15、如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD的长为()A. cmB. cmC. cmD.4cm二、填空题(共10题,共计30分)16、如图,OP=1,过P作PP1⊥OP,得OP1= ;再过P1作P1P2⊥OP1且P1P2=1,得OP2= ;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依此法继续作下去,若△OPn Pn+1的面积大于6时,n至少是________.17、如图,在直角坐标系中,点A、B的坐标分别为(2,4)和(3、0)点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,在运动的过程中,当△ABC是以AB为底的等腰三角形时,此时点C的坐标为________.18、在Rt△ABC中,已知∠ACB=90°,AC=BC=4,若点E在△ABC内部运动,且满足AE2=BE2+2CE2,则点E的运动路径长是________.19、如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,则以AB为边长的正方形面积为________.20、已知点A(1,5),B(4,2),点P在x轴上,当PA﹣PB最大时,点P 的坐标为________.21、如图,正方体的棱长为5,一只蚂蚁如果要沿着正方体的表面从点A爬到点B,需要爬行的最短距离是________.22、已知a、b、c是△ABC三边的长,且满足关系式||=0,则△ABC的形状是________.23、如图,P是等边△ACB中的一个点,PA=2,,PC=4,则△ACB 的边长是________.24、如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为5,则正方形A,B,C,D的面积的和为________25、如图,和都是等腰直角三角形,,的顶点在的斜边上,若,则________.三、解答题(共5题,共计25分)26、如图,在每个小正方形的边长为1的方格纸中有线段AB和CD,点A、B、C、D均在小正方形的顶点上。
苏科版八年级上册数学第三章 勾股定理 含答案

苏科版八年级上册数学第三章勾股定理含答案一、单选题(共15题,共计45分)1、下列能够成直角三角形的是()A.1,2,3B.3,4,5C.5,6,7D.12,13,182、如图,在△ABC中,∠ACB=90°,边AB的垂直平分线交AB于点D,交AC 于点E,连接BE,CD,若BC=5,CD=6.5,则△BCE的周长为()A.16.5B.17C.18D.203、如果下列各组数是三角形的三边,那么不能组成直角三角形的一组数是()A.2,3,4B.3,4,5C.6,8,10D. ,,14、在下列各组数据中,不能作为直角三角形的三边长的是()A.4,5,6B.6,8,10C.7,24,25D.9,12,155、如图,在▱ABCD中,对角线AC与BD相交于点O,且AB⊥AC.若AD=5,AB =3,则对角线BD的长为()A. B.2 C.9 D.86、三角形三边长分别为8,15,17,则最短边上的高为()A.8B.15C.16D.177、在下列由线段a,b,c的长为三边的三角形中,不能构成直角三角形的是()A.a=4,b=5,c=6B.a=12,b=5,c=13C.a=6,b=8,c=10D.a=7,b=24,c=258、如图,⊙O过点B、C,圆心O在等腰直角三角形ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为()A.6B.13C.D.29、我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知正方形的边长是,,则的长为()A. B. C. D.10、在△ABC中,AC2﹣AB2=BC2,那么()A.∠A=90°B.∠B=90°C.∠C=90°D.不能确定11、如图,正方形的边长为6,点是的中点,连接与对角线交于点,连接并延长,交于点,连接交于点,连接.以下结论:①;②;③;④,其中正确结论的个数是()A.1B.2C.3D.412、如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤当△PMN∽△AMP时,点P是AB的中点.其中正确的结论有A.5个B.4个C.3个D.2个13、如图,为直径,弦,垂足为,连接、,若,则的值为()A. B. C. D.14、如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N使△AMN周长最小,则∠AMN+∠ANM的度数为()A.60°B.120°C.90°D.45°15、如图所示,二次函数的图象与x轴负半轴相交与A、B两点,是二次函数图象上的一点,且,则的值为()A. B. C. D.二、填空题(共10题,共计30分)16、如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=________.17、在平面直角坐标系中,为原点,点在第一象限,,,,把绕点顺时针旋转60°得到,点,的对应点分别为,,则的值为________.18、如图所示,已知四边形ABCD是等边长为2的正方形,AP=AC,则数轴上点P所表示的数是________.19、如图,已知△ABC中,AB=5cm,BC=12cm,AC=13cm,那么AC边上的中线BD 的长为________cm.20、若直角三角形两直角边长为6和8,则此直角三角形斜边上的中线长是________.21、边长为整数,且周长等于12的三角形的面积为________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章《勾股定理》专题练习
(时间:90分钟满分:100分)
一、选择题(每小题3分,共30分)
1.直角三角形两锐角的平分线所成钝角的度数是( )
A.115°B.125°C.135°D.无法确定
2.有四个三角形,分别满足下列条件:①一个内角等于另外两个内角之和;②三个内角之比为3:4:5;③三边之比为5:12:13;④三边长分别为7,24,25.其中直角三角形有( )
A.1个B.2个C.3个D.4个
3.在Rt△ABC中,∠C=90°,周长为60,斜边与一条直角边之比为13:5,则这个三角形三边长分别为( )
A.5,4,3 B.13,12,5 C.10,8,6 D.26,24,10
4.一等腰三角形底边长为10 cm,腰长为13 cm,则腰上的高为( )
A.12 cm B.60
13
cm C.
120
13
cm D.
13
5
cm
5.如图,在把易拉罐中的水倒入一个圆水杯的过程中,若水杯中的水在点P与易拉罐刚好接触,则此时水杯中的水深为( )
A.2 cm B.4 cm C.6 cm D.8 cm
6.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为( )
A.42 B.32 C.37或33 D.42或32
7.如图,一架长2.5 m的梯子,斜靠在竖直的墙上,这时梯子顶端离地面2.4 m,为了安装壁灯.梯子顶端离地面降至2m,请你计算一下,此时梯子底端应再向远离墙的方向移动( )
A.0.4 m B.0.8 m C.1.2 m D.不能确定
8.如图,在一个高为3m,长为5m的楼梯表面铺地毯,则地毯长度为( )
A.7 m B.8 m C.9 m D.10 m
9.如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( ) A.600 m B.500 m C.400 m D.300 m
10.在一次课外社会实践中,王强想知道学校旗杆的高,但不能爬上旗杆也不能把绳子解下来,可是他发现旗杆上的绳子垂到地面上还多1 m,当他拿着绳子的下端沿水平方向走5m后,发现绳子下端刚好接触地面,则旗杆的高为( )
A.13 m B.12 m C.4m D.10 m
二、填空题(每小题3分,共24分)
11.在△ABC中,若AC2+BC2=AB2,则∠C=_______;若∠A=90°,则AC2+_______=_______.
12.直角三角形两条直角边的长分别为6,8,则斜边上的高长为_______.
13.在Rt△ABC中,∠B=90°,BC=3 cm,AC=4 cm,则AB=_______cm.
14.如图,在四边形ABCD中,∠BAD=90°,AD=3 cm,AB=4 cm,BC=12 cm,CD =13 cm,则∠DBC=_______.
15.如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1,1.21,1.44,正放置的四个正方形的面积分别为S1,S2,S3,S4,则S1+2S2+2S3+S4=_______.16.如图,在长、宽都是3,高是8的长方体纸箱的外部,一只蚂蚁从顶点A沿纸箱表面爬到顶点B,那么它所爬行的最短路线的长是_______.
17.如图,在△ABC中,CE平分∠ACB,CF平分外角∠ACD,且EF∥BC交AC于点M,若CM=5,则CE2+CF2=_______.
18.如图,在△ABC中,AB=BC=2,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D',则(BD')2=_______.
三、解答题(共46分)
19.(6分)假期中,小明和同学们到某海岛上去探宝旅游,按照探宝图,他们登陆后先往东走8 km,又往北走2 km,遇到障碍后又往西走了3 km,再折向北走到6 km处往东一拐,仅走了1 km就找到宝藏,问登陆点A到宝藏埋藏点B的距离是多少千米?
20.(8分)如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3 m,BC=4 m,CD=12 m,DA=13 m,∠B=90°.小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地共需花费多少元?
21.(8分)在等腰直角三角形ABC中,∠ABC=90°,D为AC边上的中点,过点D作DE⊥DF,交AB于点E,交BC于点F,若AE=4.FC=3,求EF的长.
22.(8分)周老师在一次“探究性学习”课中,设计了如下数表:
(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:
a=_______;b=_______;c=_______;
(2)猜想:以a,b,c为边长的三角形是否是直角三角形?证明你的猜想.
23.(8分)实践与探究
问题情境:勾股定理是一条古老的数学定理,它有多种证明方法,我国汉代数学家赵爽根据弦图,利用面积法进行了证明,著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.问题1 请你根据图①中的直角三角形叙述勾股定理(用文字及符号语言叙述);
探究2 以图①中的直角三角形为基础,可以构造出以a,b为底,以a+b为高的直角梯形(如图②),请你利用图②,尝试验证证明勾股定理;
拓展3 利用图②中的直角梯形,我们可以证明a b
c
+
<2,其证明步骤如下:
∵BC=a+b,AD=_______,
又在直角梯形ABCD中,BC_______AD(填“>”“<”或“=”),即_______.
∴a b
c
+
<2.
24.(8分)我们给出如下新定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.(1)如图①,请你在图中画出以格点为顶点,OA,OB为勾股边且对角线相等的勾股四边形OAMB:
(2)如图②,将△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,连接AD,DC.若∠DCB=30°,则四边形ABCD是勾股四边形,为什么?
参考答案
1.C
2.C
3.D
4.C
5.C
6.D
7.B
8.A
9.B 10.B 11.90° AB 2 BC 2 12.
245
13.7 14.90° 15.3.65 16.10 17.100 18.5
19.AB =10 km .
20.3600(元).
21.5.
22.(1)a =n 2-1,b =2n ,c =n 2+1.(2)是直角三角形
23.(1)直角三角形中两直角边的平方和等于斜边的平方,用式子表示为在△ABC 中,如果∠C =90°,那么a 2+b 2=c 2.(2)c < a +b<c
24.(1)如图①,勾股四边形OAMB(或OAM'B).(2)是勾股四边形.
初中数学试卷。
