平方图的汉米尔顿性
有关汉密尔顿回路的定理

定理4 定理4 当且仅当一 个简单图的闭包 闭包是汉 个简单图的闭包是汉 密尔顿图时, 密尔顿图时,这个简 单图是汉密尔顿图 汉密尔顿图。 单图是汉密尔顿图。
汉密尔顿图
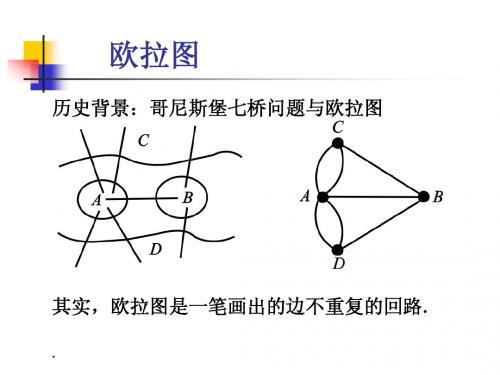
与欧拉回路非常类 似的问题是汉密尔 似的问题是汉密尔 顿回路的问题。 顿回路的问题。 的问题
1859年 威廉汉密 1859年,威廉 汉密 尔顿爵士在给他朋友 的一封信中, 的一封信中,首先谈 到关于十二面体 十二面体的一 到关于十二面体的一 数学游戏: 个数学游戏:
能不能在图中找到一 条回路, 条回路,使它含有这 个图的所有结点? 所有结点 个图的所有结点?
定理1 若图G=<V,E> 定理1 若图G=<V,E>具 G=<V,E>具 有汉密尔顿回路 回路, 有汉密尔顿回路,则对 于结点集V 于结点集V的每个非空子 W(G-S)≤|S| ≤|S|成 集S均有 W(G-S)≤|S|成 其中W(G S)是 W(G立。其中W(G-S)是G-S中 连通分支数G,若存在 一条路经过图中的每个结 点恰好一次, 点恰好一次,这条路称作 汉密尔顿路。 汉密尔顿路。若存在一条 回路, 回路,经过图中的每个结 点恰好一次, 点恰好一次,这条回路称 作汉密尔顿回路。 作汉密尔顿回路。
具有汉密尔顿 回路的图称作汉密 回路的图称作汉密 尔顿图。 尔顿图。
彼得森图(Petersen) 彼得森图(Petersen)
定理2 定理2 设G具有n个 具有n 结点的简单图, 结点的简单图,如果 G中每一对结点度数 之和大于等于 大于等于n 之和大于等于n-1, 则在G 则在G中存在一条汉 密尔顿路 密尔顿路。
定理3 定理3 设G是具有n 是具有n 个结点的简单图。 个结点的简单图。如 果G中每一对结点度 数之和大于等于 大于等于n 数之和大于等于n,则 在G中存在一条汉密 尔顿回路 回路。 尔顿回路。
两类图的哈密尔顿性

两类图的哈密尔顿性
Hamilton问题是图论中主要研究的问题之一.一个连通图是Hamilton图的充要条件至今尚未找到.许多学者都致力于研究某一类图的Hamilton性问题.关于无爪图的Hamilton性问题曾在一段时间内受到广大图论研究者的关注.1998年, Ainouche中首次提出半无爪图的概念,使许多无爪图的结果可以推广到半无爪图. H.J.Boersma和E.Vumar于2009年又引进P3-支配图的概念,再次把半无爪图推广到更大图类.本文得出P3-支配图哈密顿性的一个充分条件:若G是3-连通的P3-支配图,其阶为n,则当n 5δ- 4时, G是Hamiltonian图.2006年,李明楚等人在《Quadrangularly connected claw-free graphs》中证明了连通, N2-局部连通图是四边形连通图这一性质,且证明了定理:没有1度点的四边形连通无爪图,如不包含同构于两个图的导出子图H,使得H中每个4度点x的N1(x,G)是不连通的,那么它是Hamilton图.我们修改了此文中存在的问题,我们指出连通, N2-局部连通图是四边形连通图这个性质的叙述是不完整的,并给出了新的证明.与此性质的不完整性相反,定理中“没有1度顶点”的条件是多余的,事实上,四边形连通图没有1度点.我们还注意到定理的证明存在一些问题,尽管它的证明基本正确的.事实上,我们认为断言2 ? 4是有错误的.本文以稍微不同的形式重述了这个定理,并且给出了证明的一个修正.。
图论05-哈密尔顿图

A F
B
A
C
F
B C
E
D
E
D
竞赛图
底图为K4的竞赛图: A
B
C
以上每个图可以看作4个选手参加的循环赛的一种结果
竞赛图与有向哈密尔顿通路
底图是完全图的有向图称为竞赛图。 利用归纳法可以证明竞赛图含有向哈密尔顿通路。
循环赛该如何排名次
A F
E
B
按照在一条有向Hamilton通路 (一定存在)上的顺序排名:
Ore定理的证明
Ore定理(1960) 设G是无向简单图,|G|=n3,若
对G中任意不相邻的顶点u和v, d(u)+d(v)n (*)
则G有哈密尔顿回图。
证明.反证法, 若存在满足(*)的图G,但是G没有Hamilton回 路. 不妨假设G是边极大的非Hamilton图,且满足(*)。若G不是 边极大的非Hamilton图,则可以不断地向G增加若干条边,把G 变成边极大的非Hamilton图G’,G’依然满足(*),因为对 vV(G), dG(v)dG’(v)。
设G是无向简单图, |G|=n2, 若G中任意不相邻的顶点对
u,v均满足:d(u)+d(v)n-1,则G是连通图。
假设G不连通,则至少含2个连通分支,设为G1, G2。取xVG1, yVG2, 则:d(x)+d(y)(n1-1)+(n2-1)n-2 (其中ni是Gi的顶பைடு நூலகம்个数), 矛盾。
有限图G是Hamilton图充分必要其闭合图C(G)是 Hamilton图.
闭合图(举例)
a
b
f
c e
d
判定定理的盲区
从“常识”出发个案处理
离散数学中汉密尔顿回路求解思路

离散数学中汉密尔顿回路求解思路离散数学是研究离散结构及其关系的一门学科,其中汉密尔顿回路问题是研究图论中的重要问题之一。
本文将探讨汉密尔顿回路的求解思路,并介绍常用的算法。
一、汉密尔顿回路概述汉密尔顿回路是指图中经过每个顶点一次且只一次的回路,也称为哈密顿回路。
对于给定的图,求解是否存在汉密尔顿回路的问题被称为汉密尔顿回路问题。
该问题的解决对于理论研究和实际应用具有重要意义。
二、暴力搜索算法暴力搜索算法是最直观、最简单的求解汉密尔顿回路的方法。
其基本思路是对图中的每一条路径进行遍历,判断是否满足汉密尔顿回路的条件。
该算法的时间复杂度为O(n!),因为需要对所有可能的路径进行枚举。
然而,由于其时间复杂度过高,在大型图中求解问题时效率低下。
三、回溯算法回溯算法是一种通过试错的方式来搜索解空间的方法。
对于汉密尔顿回路问题,回溯算法的基本思路是从图中的某个顶点开始遍历,按照某种策略选择下一个未被访问的顶点,直到回到起始顶点形成回路。
如果当前路径无法满足汉密尔顿回路的条件,则回溯到上一个顶点,换一个未被访问的顶点进行尝试。
通过不断地回溯和尝试,最终找到汉密尔顿回路。
四、分支限界算法分支限界算法是一种通过剪枝和优先队列等手段来减少搜索空间的方法。
在求解汉密尔顿回路问题时,分支限界算法主要通过定义优先级函数和界函数来判断当前路径是否有可能成为汉密尔顿回路。
如果当前路径无法满足界函数的条件,那么该路径可以被剪枝。
通过不断地剪枝和选择有希望成为汉密尔顿回路的路径,最终找到问题的解。
五、动态规划算法动态规划算法是一种以递推的方式来求解问题的方法。
在求解汉密尔顿回路问题时,动态规划算法将问题划分为多个子问题,并通过求解子问题的最优解来推导出整体的最优解。
具体而言,该算法通过定义状态转移方程和初始化条件来求解汉密尔顿回路问题。
动态规划算法的优势在于可以通过存储已解决子问题的结果来减少重复计算,提高求解效率。
六、启发式算法启发式算法是一种通过启发式规则和策略来搜索解空间的方法。
6汉密尔顿图
例15.3
设图为G2,则G2=<V1,V2,E>,其中 V1={a,g,h,i,c},V2={b,e,f,j,k,d}, 易知,p(G2-V1)=|V2|=6>|V1|=5, 由定理15.6可知,G2不是哈密顿图, 但G2是半哈密顿图。 baegjckhfid为G2中一条哈密顿通路。 设图为G3,G3=<V1,V2,E>,其中 V1={a,c,g,h,e},V2={b,d,i,j,f}, G3中存在哈密顿回路。 如 abcdgihjefa, 所以G3是哈密顿图。33Fra bibliotek极大路径
是一条路径,如果的始点和终点都不 与外的顶点相邻,则称是一条极大路 径。 极大:不能再向外延伸
34
无向半汉密尔顿图的充分条件
定理15.7 设G是n阶无向简单图,若对于G中任意不相邻的顶点
vi,vj,均有 d(vi)+d(vj)≥n-1
则G中存在哈密顿通路。
(15.1)
证明 首先证明G是连通图.否则G至少有两个连通分支, 设G1,G2是阶数为n1,n2的两个连通分支,设v1∈V(G1), v2∈V(G2),因为G是简单图,所以 dG(v1)+dG(v2)=dG1(v1)+dG2(v2)≤n1-1+n2-1≤n-2 这与(15.1)矛盾,所以G必为连通图.
35
定理15.7
下面证G中存在哈密顿通路。 设Г=v1v2„vl为G中用“扩大路径法”得到的“极大路 径”,即Г的始点v1与终点vl不与Г外的顶点相邻.显然有 l≤n. (1)若l=n,则Г为G中哈密顿通路。
(2)若l<n,这说明Г不是哈密顿通路,即G中还存在着Г外的 顶点.但可以证明G中存在经过Г上所有顶点的圈.
哈密尔顿图的判定及应用

中国计量学院本科毕业设计(论文)哈密尔顿图的判定及应用Judgement and application of Hamiltongraph学生姓名徐杰一村学号0900801110学生专业信息与计算科学班级 09信算1班二级学院理学院指导教师陈琴中国计量学院2013年5月郑重声明本人呈交的毕业设计论文,是在导师的指导下,独立进行研究工作所取得的成果,所有数据、图片资料真实可靠。
尽我所知,除文中已经注明引用的内容外,本学位论文的研究成果不包含他人享有著作权的内容。
对本论文所涉及的研究工作做出贡献的其他个人和集体,均已在文中以明确的方式标明。
本学位论文的知识产权归属于培养单位。
学生签名:日期:分类号:O157 密级:公开UDC:62 学校代码:10356中国计量学院本科毕业设计(论文)哈密尔顿图的判定及应用Judgement and application of Hamiltongraph作者徐杰一村学号0900801110申请学位理学学士指导教师陈琴学科专业信息与计算科学培养单位中国计量学院答辩委员会主席评阅人2013年5月致谢论文的撰写工作已经基本上完成,这段时间也经历了很多的波折。
从论文开始到结束,一直是在陈琴老师的指导下完成的,可以说没有老师的悉心指导,就没有这篇论文的诞生,在此,衷心感谢陈琴老师对我的指导。
感谢老师不厌其烦的帮我修正论文中的错误,也感谢老师在我失去信心时的谆谆教诲。
陈琴老师的严谨教学,用于创新,善于发现的精神不但在学习上为我树立了榜样,也给我未来的生活带来了帮助。
再次感谢陈琴老师对我的指导!同时,也感谢理学院老师的辛勤教育,感谢所有给我帮助的同学和朋友们。
哈密尔顿图的判定及应用摘要:哈密尔顿图的研究是图论中不可或缺的一部分,这个问题的研究已经应用到了各个领域。
合理的利用哈密尔顿图的结论,不仅可以节约大量的时间,更可以降低发展的成本。
因此很多学者致力于哈密尔顿图的问题研究,也得到了很多了不起的突破。
哈密尔顿图-精选
K3
K4
Kn(n3)有Hamilton回路
b
b
b
a
c
a
ca
c
e
d
e
d
e
d
一个基本的必要条件
如果图G=(V, E)是Hamilton图,则对V的任一非空子 集S,都有 P(G-S) |S|
其中, P(G-S)表示图G-S的连通分支数.
理由:设C是G中的Hamilton回路, P(G-S) P(C-S) |S| 向一个图中顶点之间加边不会增加连通分支。
必要条件的应用
举例
c
a
b
将图中点a, b, c的集合记为S, G-S有4个 连通分支,而|S|=3. G不是Hamilton图.
举例
Kh
Kh
Kn-2h
下图给出的是 C2,7的具体图 (h=2,n=7)
必要条件的局限性
必要条件只能判定一个图不是哈密尔顿图
Petersen图满足上述必要条件,但不是哈密尔顿图。
u,v均满足:d(u)+d(v)n-1,则G是连通图。
假设G不连通,则至少含2个连通分支,设为G1, G2。取xVG1, yVG2, 则:d(x)+d(y)(n1-1)+(n2-1)n-2 (其中ni是Gi的顶点个数), 矛盾。
充分条件的讨论
“ (G) n/2”不能减弱为: (G) 举例,n=5, (G)=2 . G不是Hamilton图.
有限图G是Hamilton图充分必要其闭合图C(G)是 Hamilton图.
闭合图(举例)
a
b
f
c e
d
判定定理的盲区
从“常识”出发个案处理
一顶点关联的边中恰有两 条边在哈密尔顿回路中。
图的Hamilton性和连通性的谱刻画的开题报告

图的Hamilton性和连通性的谱刻画的开题报告概述:该开题报告主要讨论了图的Hamilton性和连通性的谱刻画。
具体来说,报告分为三部分:第一部分介绍了图论基础,包括图的定义、图的表示方法、路径和环的定义等。
第二部分讨论了图的Hamilton性和连通性的谱刻画。
首先,我们介绍了谱图理论和图Laplacian矩阵的定义。
然后,我们通过定义图的特征值和特征向量,提出了一些基本结果,例如图的度数和图的谱半径等。
接着,我们详细讨论了图的Hamilton性和连通性的谱刻画,并介绍了基于谱方法的算法,以及它们的优劣势。
第三部分总结了我们的研究成果,并提出了一些研究方向,例如将图谱方法应用于大规模的复杂网络,提高算法的精度和效率,以及探索图的其他性质的谱刻画等。
正文:一、图论基础图是由节点和边组成的抽象数学对象。
一个无向图G可以用顶点集V和边集E表示,其中V={v1,v2,v3, …, vn}表示节点集合,E={(vi,vj)}代表边集合。
路径是通过一系列节点和边连接的节点序列,环是一个路径从起点到终点的一条边。
在无向图中,简单路径是没有重复节点的路径。
简单环是没有重复节点或边的环。
二、图的Hamilton性和连通性的谱刻画1. 谱图理论和图Laplacian矩阵谱图理论是一种用特征值和特征向量描述图的方法。
我们可以通过谱图理论来研究图的结构和性质,例如连通性、Hamilton性、与自然图模型的比较等。
图Laplacian矩阵也是谱图理论中的一个重要概念。
它是由图的节点和边定义的矩阵,可以用于研究图的能量和其他性质。
对于无向图G=(V,E),Laplacian矩阵$L_G$被定义为:$$L_G=D_G-A_G$$其中$A_G$是邻接矩阵,$D_G$是对角矩阵,$D_{ii}$是节点i的度数。
对于一个无环图,Laplacian矩阵具有下列性质:(1)它是一个实对称矩阵。
(2)它至少有一个非零特征值,当前这个特征值就是0。
汉密顿圈的必要条件

汉密尔顿圈是指在一个无向图中找到一条闭合路径,这条路径经过图中的每一个顶点恰好一次,并最终回到起点。
虽然寻找一个图是否存在哈密尔顿圈的问题至今仍没有找到一个简单易行的充分必要条件,但是我们可以列出一些有助于判断一个图可能包含哈密尔顿圈的必要条件或启发性条件:
1.连通性:一个图要包含哈密尔顿圈,首先必须是连通的,这意味着图中的
任意两个顶点都通过一系列边相连。
2.顶点度数条件:一般情况下,顶点的度数较大有利于形成哈密尔顿圈。
例
如,Dirac定理指出,如果一个简单的无向图中每个顶点的度数至少为n/2
(其中n是图中顶点的数量),那么这个图一定包含哈密尔顿圈。
3.结构特性:例如,对于完全图、完全二部图(当每部分的顶点数至少为2
时)、以及一些特定构造的图(如强连通的有向图中每个顶点的入度和出度均大于1的情形),存在哈密尔顿圈。
尽管这些条件可以帮助我们识别某些情况下图中可能存在的哈密尔顿圈,但它们都不是绝对的充分必要条件。
对于一般的图,确定其是否包含哈密尔顿圈仍然是一个NP完全问题,意味着没有已知的有效多项式时间算法可以解决这个问题。
因此,研究者们通常依赖于各种启发式方法或者特定类别的图的特殊性质来进行分析。
欧拉图与汉密尔顿图

构造欧拉回路
思想:在画欧拉回路时,已经经过的边不能再用。因此, 在构造欧拉回路过程中的任何时刻,假设将已经经过的边 删除,剩下的边必须仍在同一连通分支当中。
构造欧拉回路-Fleury算法
算法:
输入:欧拉图G
输出:简单通路P = v0e1v1e2,…,eiviei+1,…,emvm, 其中包含了 EG中所有的元素。
若图中有n个顶点, 则Hamilton回路恰有n条边.
注:Hamilton回路问题主要针对简单图。
Hamilton回路的存在性问题
21
K3
K4
Kn(n3)有Hamilton回路 b a c a b c a b c
e
d
e
d
e
d
哈密尔顿图的必要条件
22
如果图G=(V, E)是Hamilton图,则对V的任一非空子 集S,都有
Fleury算法的证明
(2) (证明含所有边)假设Pm没有包括G中所有的边,令Gm中所有 非零度顶点集合为S(非空), 令S' =VG-S, 则vmS'。
考察序列e1,e2,…ej,ej+1,…,em 。假设 j 是满足 vjS, 而vj+1S’的最大下标。 如果没有这样的 j,G就不连通,矛盾。因为Pm的终点在S’中,因此ej+1 一定是Gj中的割边。 令 e 是在 Gj 中与 vj 相关联的异于 ej+1 的边 ( 非零度点一定有 ), 根据算法选择 ej+1( 割边)的原则,e也一定是割边。但是, Gm中任意顶点的度数必是偶 数,e在Gm中的连通分支是欧拉图,e在Gm的某个
G中的欧拉回路构造如下:从Ck+1上任一点(设为v0)出发遍历 Ck+1上的边,每当遇到一个尚未遍历的Ci'与Ck+1的交点(设为 vi'), 则转而遍历Ci'上的边,回到vi'继续沿Ck+1进行。
汉密尔顿定理

汉密尔顿定理
汉密尔顿定理是一个重要的数学定理,它指出,在任何一个有向图中,如果每一个顶点都有一条边指向另一个顶点,那么这个图中必定存在一条环路。
汉密尔顿定理的发现者是英国数学家爱德华·汉密尔顿,他在1859年发表了这个定理。
汉密尔顿定理的发现是一个重大的突破,它为数学家们提供了一种新的思路,用来解决复杂的数学问题。
汉密尔顿定理的应用非常广泛,它可以用来解决许多复杂的数学问题,比如求解最短路径问题、求解最大流问题等等。
此外,汉密尔顿定理也被广泛应用于计算机科学、经济学、物理学等领域。
汉密尔顿定理是一个重要的数学定理,它为解决复杂的数学问题提供了一种新的思路,并且在计算机科学、经济学、物理学等领域都有着广泛的应用。
汉密尔顿定理的发现是一个重大的突破,它为数学家们提供了一种新的思路,用来解决复杂的数学问题。
itif 汉密尔顿指数

itif 汉密尔顿指数什么是汉密尔顿指数?汉密尔顿指数是图论中的一个概念,用来衡量一个有向图中存在的哈密顿回路的难度程度。
一个哈密顿回路是指一个简单回路,它经过图中的每个顶点恰好一次。
在该指数中,汉密尔顿回路的难度可以通过该图中的节点数量和各个节点的出度和入度来计算得出。
当每个节点的出度和入度越接近图中总节点数的一半时,汉密尔顿回路的存在性越难确定,难度程度也就越大。
汉密尔顿指数的计算方法如下:1. 首先,从给定有向图中计算每个节点的出度和入度。
2. 接下来,对于每个节点的出度和入度,计算与总节点数的一半的差值。
如果这个差值是负数,则取绝对值。
这个差值代表了该节点对哈密顿回路存在性的贡献。
3. 将每个节点的贡献值相加,得到汉密尔顿指数。
指数越大表示存在哈密顿回路的难度越大。
为了更好地理解汉密尔顿指数,举个例子来说明:考虑一个有向图,其中有5个节点,分别记作A、B、C、D和E。
它们之间的连接关系如下:A -> BB -> CC -> DD -> EE -> A我们可以看到,每个节点的出度和入度都为1,所以该图中的汉密尔顿回路是存在的,且存在性也相对简单。
这是因为出度和入度都等于1,与总节点数的一半相等。
但是,如果我们修改这个图的连接关系:A -> BB -> CC -> DD -> EE -> AB -> D此时,节点A和节点E的出度和入度仍然是1,但节点B和节点D的出度和入度变为2。
根据计算方法,我们可以得知节点B和节点D对于汉密尔顿回路的存在性有贡献,因为它们的差值为1(节点的出度和入度减去总节点数的一半)。
节点A和节点E的差值为0,因为它们的出度和入度都等于总节点数的一半。
将这些差值相加,我们可以得到汉密尔顿指数为2。
这说明,即使在这个有向图中节点数量较少,但由于节点B和节点D的存在,汉密尔顿回路的存在性变得更加困难。
综上所述,汉密尔顿指数是用来衡量有向图中汉密尔顿回路的难度程度的一个指标。
关于hamilton3-正则2-连通平面图的一个注记

关于hamilton3-正则2-连通平面图的一个注记关于Hamilton3-正则2-连通平面图的一个注记:
Hamilton3-正则2-连通平面图是指一种由三条连续的折线段组成的平面图。
它有一个重要的特征,即三条连续的折线段必须相交,而且必须由图中的所有点连接,使得该图是连通的。
Hamilton3-正则2-连通平面图最初是由Joseph Hamilton于1840年提出的,他是基于发现这样一个平面图可以用于表示一定数量的点之间的关系来提出这一定理的。
它是一种经典的图论问题,同时也是一种数学问题,其研究得出的解决方案可以帮助人们更好地了解和掌握数学概念,增强数学思维能力。
Hamilton3-正则2-连通平面图对于寻找更优化的路径和结构也有用处。
例如,当需要确定数据中两个点之间最短的路径时,这样的图有助于帮助进行路径搜索,并根据需求快速确定最佳解。
另外,Hamilton3-正则2-连通平面图也可以用来分析和解决一些比较复杂的运筹学问题,比如交通网络的优化规划,地区行政区划,物流系统的优化设计等等。
总之,Hamilton3-正则2-连通平面图是一种非常强大的工具,可以帮助人们解决许多复杂的数学和运筹学问题,为我们的生活带来了许多便利。
图的可迹性与哈米尔顿—连通性的谱刻画

图的可迹性与哈米尔顿—连通性的谱刻画谱图理论是代数图论的一个重要研究方向,也是国内外组合矩阵理论与代数组合研究的一个重要课题,它在其他非数学学科,如:化学、统计力学、通信网络、计算机及信息科学等领域均有着广泛的应用.谱图理论是利用矩阵理论,将图的基本结构方面的性质与图的相关矩阵的参数关联起来,并找出它们之间的内在联系.为了研究图的性质是怎样通过与这些图相关矩阵的代数性质所反映出来,人们引入了各种不同的矩阵,如:图G的邻接矩阵A(G)、关联矩阵M(G)、距离矩阵D(G)、拉普拉斯矩阵L(G)以及无符号拉普拉斯矩阵Q(G)等.著名的哈密尔顿问题旨在确定一个给定的简单图是否含有哈密尔顿圈,是图论研究的经典问题.迄今为止,虽然有许多相关的研究成果不断涌现,但最理想的解决方案仍尚未找到。
近年来,人们试图将谱图理论应用到这个问题的研究中.自Fiedler和Nikiforov
于2010年用邻接谱半径刻画图的哈密尔顿性以来,许多图论工作者都致力于图的哈密尔顿谱刻画的研究,并得到很多很好的结论.本文主要内容安排如下:第一章,首先介绍谱图理论的研究背景与意义以及本文涉及到的学术术语和基本概念,接下来阐述研究的问题与相关的进展,并对本文主要结论进行展示;第二章,可迹图的谱半径条件;第三章,哈密尔顿-连通图与可迹图的拉普拉斯谱充分条件.。
5汉密尔顿图
vi+1
vn
21
无向汉密尔顿图的充分条件
推论2: 设G是n(3)阶无向简单图,若对G 中任意顶点u有 d(u)n/2 则G是汉密尔顿图. 推论3:Kn(n>2)为汉密尔顿图
22
图的闭包C(G)
定义:给定简单图G=<V,E>,|V|=n, 将图G中度数之和至少为n的非邻接顶点 连接起来得到图G ',对G '重复上述步骤, 直到不再有这样的顶点对为止,所得到 的图称为G 的闭包,记作C(G) 。
2
马的周游路线(knight’s tour)
棋盘上马的周游路线(knight’s tour on a chessboard)
3
汉密尔顿图
1. 周游世界,汉密尔顿通(回)路,汉密尔顿 图 2. 判定汉密尔顿图的必要条件 3. 判定汉密尔顿图的充分条件 4. 旅行商问题
4
马的周游路线(knight’s tour)
每个顶点对应一门考试课程两个顶点之间有边当且仅当对应两课程由不同教师担任每个顶点的度数至少是3任两个顶点度数之和至少为6因此一定存在一条汉密尔顿通路
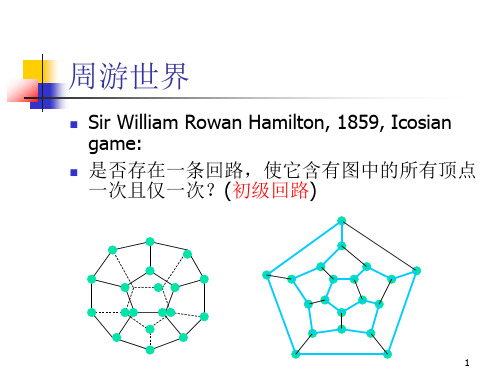
周游世界
Sir William Rowan Hamilton, 1859, Icosian game: 是否存在一条回路,使它含有图中的所有顶点 一次且仅一次?(初级回路)
v0
v0
vi vi+1
vk
vk
20
无向汉密尔顿图的充分条件
推论1: 设G是n(3)阶无向简单图,若对G 中任意不相邻顶点u与v有 d(u)+d(v)n 则G是汉密尔顿图. 证明: 由定理4知G连通且有汉密尔顿通 路=v0v1…vn. (1) 若(v0,vn)E,则得汉密 尔顿回路C=v0v1…vnv0. (2) 若(v0,vk)E, 则与定理4证明(2b)类似,也存在汉密尔顿 回路. # v0 vn
图的哈密尔顿性

那么G是H图。 证明: 若不然,设G是一个满足定理条件的 。显然G ,否则,G是H图。
于是,可以在G中任意取两个不相邻顶点u与v。考虑 图G + u v,由G的极大性,G+u v是H图。且G+u v的每一 个H圈必然包含边uv。
12
所以,在G中存在起点为u而终点为v的H路P。
不失一般性,设起点为u而终点为v的H路P为:
迷茫的旅行商 ——
图的哈密尔顿性
1
(一)、哈密尔顿图的概念
1、背景
1857年, 哈密尔顿发明了一个游戏(Icosian Game). 它是由一个木制的正十二面体构成,在它的每个棱角 处标有当时很有名的城市。游戏目的是“ ”。 为了容易记住被旅游过的城市 ,在每个棱角上放上一 个钉子,再用一根线绕在那些旅游过的城市上(钉子), 由此可以获得旅程的直观表示。
15
1960年,美国耶鲁大学数学家Ore院士考察不相邻两 点度和情况,弱化了Dirac条件 ,得到一个著名的结果。 Ore发表关于H问题论文59篇。 定理3 (充分条件)
对于n≧3的单图G,如果G中的任意两个不相邻顶点u与 v,有:
d (u) d (v) n
16
注: (1) 该定理证明和定理2完全一致! (2) 该定理的条件是紧的。例如:设G是由Kk+1的一个顶 点和另一个Kk+1的一个顶点重合得到的图,那么对于G的任 意两个不相邻顶点u与v,有:
定义2 如果图G的一条路P含有G的所有顶点,则称P 为图G的哈密尔顿路, 简称哈路或者H-路。
u
v
定义3 如果图G含有哈密尔顿圈,则称G为哈密尔顿 图 例1、正十二面体是H图。
例2 下图G是非H图。
u
关于几乎正则2-连通图的Hamilton性的注记

关于几乎正则2-连通图的Hamilton性的注记
谢德政
【期刊名称】《西南师范大学学报(自然科学版)》
【年(卷),期】2004(029)004
【摘要】研究几乎正则图的Hamilton性,得到了定理1设G是2-连通的(k,k+1)-图,并且k≥|V(G)/3|+1/3,如果G是偶数阶的图,则G是Hamilton图.定理2设G 是(k,k+2)-图,并且k≥n/3+10/3,如果存在G的一个非空独立集B1,使得|
B1|≥n/3-13/3,而且对于G的所有独立集B,都有| B |≤n/2-1,则G是Hamilton图.【总页数】3页(P570-572)
【作者】谢德政
【作者单位】重庆工商大学,理学院,重庆,400067
【正文语种】中文
【中图分类】O157.5
【相关文献】
1.几乎Hamilton连通图和部分平方图 [J], 吴正声;周兴和
2.几乎正则多部竞赛图的Hamilton性 [J], 张杰明;景冰清
3.关于Hamilton3-正则2-连通平面图的一个注记 [J], 杨爱民;高太平
4.3—正则3—连通无爪平面图的Hamilton圈问题和Hamilton路问题的NP—完全性 [J], 原晋江
5.关于Hamilton-Jacobi方程解的正则性和全局结构的注记 [J], 王靖华; 赵引川; 温海瑞
因版权原因,仅展示原文概要,查看原文内容请购买。
