5.2 二次函数的图像和性质(3)
苏科版 九年级数学 下第5章二次函数 5.2二次函数的图像和性质课件(15张PPT)-经典教学教辅文

反馈检测 拓展延伸
1.抛物线y=(x-1)2+1的顶点坐标是( ) A.(1,1) B.(-1,1) C.(1,-1) D.(-1,-1)
2.将抛物线y=3x2向左平移3个单位,再向下平移2个单位后,所得图像的函数表达式是_____.
3.函数y=2x2-4x-1写成y=a(x+h)2+k的形式是______,
向上移 2个单位
y 10
9 y= (x+3)2+2 8
7
6
5 变式:
4 二次函数y= (x-1)2 - 6的图像和y=x2的图像
3 的位置有什么关系?
2 y= (x+3)2 1
y= (x+3)2 +2 y=x2
-6 -5 -4 -3 -2 -1 o 1 2 3 4 5 x
5.2 二次函数的图像和性质(4)
活动二:转化迁移 问题(3)函数y=x2+2x+3 的图像也是抛物线吗?如何说明
问题(4) 你能将函数y=ax2+bx+c 转化为 y=a(x+h)2+k 的形式吗?
5.2 二次函数的图像和性质(4) 合作探究 集思广益
函数y=x2+2x+3 的图像也是抛物线吗?
y =x2+2x+3 =x2+2x+1+2 = (x+1)2+2.
y=x2+2可以看成是y=x2向 上平移两个单位长度.
y= (x+3)2可以看成是y=x2向 左平移三个单位长度.
5.2 二次函数的图像和性质(4)
有什么关系?
y= (x+3)2+2的图像与y=x2的图像
y = x2
向左移 3个单位
y= (x+3)2
(2)观察图像: 函数y= (x+3)2 +2有哪些性质?
初中数学
九年级(下册)
二次函数的图象和性质3(含答案)
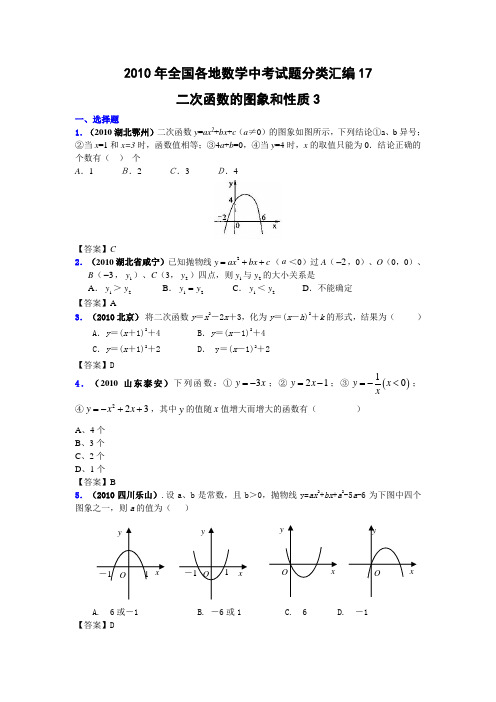
2010年全国各地数学中考试题分类汇编17二次函数的图象和性质3一、选择题 1.(2010湖北鄂州)二次函数y =ax 2+bx +c (a ≠0)的图象如图所示,下列结论①a 、b 异号;②当x =1和x=3时,函数值相等;③4a +b =0,④当y =4时,x 的取值只能为0.结论正确的个数有( ) 个A .1 B.2 C.3 D.4【答案】C2.(2010湖北省咸宁)已知抛物线2y ax bx c =++(a <0)过A (2-,0)、O (0,0)、 B (3-,1y )、C (3,2y )四点,则1y 与2y 的大小关系是 A .1y >2y B .1y 2y = C .1y <2y D .不能确定【答案】A3.(2010北京) 将二次函数y =x 2-2x +3,化为y =(x -h )2+k 的形式,结果为( )A .y =(x +1)2+4 B .y =(x -1)2+4 C .y =(x +1)2+2D . y =(x -1)2+2【答案】D4.(2010山东泰安)下列函数:①3y x =-;②21y x =-;③()10y x x=-<;④223y x x =-++,其中y 的值随x 值增大而增大的函数有( )A 、4个B 、3个C 、2个D 、1个 【答案】B5.(2010四川乐山).设a 、b 是常数,且b >0,抛物线y=ax 2+bx +a 2-5a -6为下图中四个图象之一,则a 的值为( )A. 6或-1B. -6或1C. 6D. -1【答案】DyxO yx Oyx O1 -1 yxO1 -16.(2010黑龙江哈尔滨)在抛物线42-=x y 上的一个点是( )(A )(4,4) (B )(1,-4) (C )(2,0) (D ).(0,4) 【答案】C7.(2010江苏徐州)平面直角坐标系中,若平移二次函数y=(x-2009)(x-2010)+4的图象,使其与x 轴交于两点,且此两点的距离为1个单位,则平移方式为 A .向上平移4个单位 B .向下平移4个单位 C .向左平移4个单位 D .向右平移4个单位 【答案】B8.(2010陕西西安)已知抛物线103:2-==x x y C ,将抛物线C 平移得到抛物线C '若两条抛物线C 、C ' 关于直线1=x 对称,则下列平移方法中,正确的是A .将抛物线C 向右平移25个单位 B .将抛物线C 向右平移3个单位 C .将抛物线C 向右平移5个单位 D .将抛物线C 向右平移6个单位【答案】C9.(2010 福建三明)抛物线772--=x kx y 的图象和x 轴有交点,则k 的取值范围是( )A .47-≥k B .47-≥k 且0≠k C .47->k D .47->k 且0≠k 【答案】B10.(2010 山东东营) 二次函数2y ax bx c =++的图象如图所示,则一次函数ac bx y -=与反比例函数xcb a y +-=在同一坐标系内的图象大致为( )【答案】B二、填空题1.(2010江苏扬州)y =2x 2-bx +3的对称轴是直线x =1,则b 的值为__________.x(B)x(A)x(C)(D)【答案】42.(2010山东泰安)将y=2x 2-12x-12变为y=a (x-m )2+n 的形式,则m·n=. 【答案】-903.(2010湖北襄樊)将抛物线212y x =-向上平移2个单位,再向右平移1个单位后,得到的抛物线的解析式为____________..【答案】21(1)22x --+或21322x x -++ 4.(2010江苏 镇江)已知实数y x y x x y x +=-++则满足,033,2的最大值为 .【答案】45.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20 三、解答题1.(2010湖北鄂州)如图,在直角坐标系中,A (-1,0),B (0,2),一动点P 沿过B 点且垂直于AB 的射线BM 运动,P 点的运动速度为每秒1个单位长度,射线BM 与x 轴交与点C .(1)求点C 的坐标.(2)求过点A 、B 、C 三点的抛物线的解析式.(3)若P 点开始运动时,Q 点也同时从C 出发,以P 点相同的速度沿x 轴负方向向点A 运动,t 秒后,以P 、Q 、C 为顶点的三角形为等腰三角形.(点P 到点C 时停止运动,点Q 也同时停止运动)求t 的值.(4)在(2)(3)的条件下,当CQ =CP 时,求直线OP 与抛物线的交点坐标.【答案】(1)点C 的坐标是(4,0);(2)设过点A 、B 、C 三点的抛物线的解析式为y =ax 2+bx +c (a ≠0),将点A 、B 、C 三点的坐标代入得:020164a b c c a b c =-+⎧⎪=⎨⎪=++⎩解得12322a b c ⎧=-⎪⎪⎪=⎨⎪=⎪⎪⎩,∴抛物线的解析式是:y = 12-x 2+32x +2. (3)设P 、Q 的运动时间为t 秒,则BP =t ,CQ =t .以P 、Q 、C 为顶点的三角形为等腰三角形,可分三种情况讨论.①若CQ =PC ,如图所示,则PC = CQ =BP =t .∴有2t =BC =5t 5②若PQ =QC ,如图所示,过点Q 作DQ ⊥BC 交CB 于点D ,则有CD =PD .由△ABC ∽△QDC ,可得出PD =CD =255t ,∴555t =,解得t =40511-. ③若PQ =PC ,如图所示,过点P 作PE ⊥AC 交AC 于点E ,则EC =QE =255PC ,∴12t =255(5t ),解得t 32540-(4)当CQ =PC 时,由(3)知t 5P 的坐标是(2,1),∴直线OP 的解析式是:y =12x ,因而有12x =12-x 2+32x +2,即x 2-2x -4=0,解得x =15OP 与抛物线的交点坐标为(5152)和(5,152). 2.(2010湖北省咸宁)已知二次函数2y x bx c =+-的图象与x 轴两交点的坐标分别为(m ,0),(3m -,0)(0m ≠).(1)证明243c b =;(2)若该函数图象的对称轴为直线1x =,试求二次函数的最小值.【答案】(1)证明:依题意,m ,3m -是一元二次方程20x bx c +-=的两根.根据一元二次方程根与系数的关系,得(3)m m b +-=-,(3)m m c ⨯-=-. ∴2b m =,23c m =. ∴224312c b m ==.(2)解:依题意,12b-=,∴2b =-.由(1)得2233(2)344c b ==⨯-=.∴2223(1)4y x x x =--=--. ∴二次函数的最小值为4-.3.(2010湖北恩施自治州) 如图,在平面直角坐标系中,二次函数c bx x y ++=2的图象与x 轴交于A 、B 两点, A 点在原点的左侧,B 点的坐标为(3,0),与y 轴交于C (0,-3)点,点P 是直线BC 下方的抛物线上一动点. (1)求这个二次函数的表达式.(2)连结PO 、PC ,并把△POC 沿CO 翻折,得到四边形POP /C , 那么是否存在点P ,使四边形POP /C 为菱形?若存在,请求出此时点P 的坐标;若不存在,请说明理由. (3)当点P 运动到什么位置时,四边形 ABPC 的面积最大并求出此时P 点的坐标和四边形ABPC 的最大面积.【答案】解:(1)将B 、C 两点的坐标代入得⎩⎨⎧-==+33c c b解得:⎩⎨⎧-=-=32c b所以二次函数的表达式为:322--=x x y(2)存在点P ,使四边形POP /C 为菱形.设P 点坐标为(x ,322--x x ), PP /交CO 于E若四边形POP /C 是菱形,则有PC =PO .连结PP / 则PE ⊥CO 于E ,∴OE=EC =23∴y =23-.∴322--x x =23-解得1x =2102+,2x =2102-(不合题意,舍去) ∴P 点的坐标为(2102+,23-)…………………………8分 (3)过点P 作y 轴的平行线与BC 交于点Q ,与OB 交于点F ,设P (x ,322--x x ),易得,直线BC 的解析式为3-=x y 则Q 点的坐标为(x ,x -3).EB QP OE QP OC AB S S S S CPQ BPQ ABC ABPC ⋅+⋅+⋅=++=∆∆∆212121四边形 3)3(2134212⨯+-+⨯⨯=x x =87523232+⎪⎭⎫ ⎝⎛--x当23=x 时,四边形ABPC 的面积最大 此时P 点的坐标为⎪⎭⎫⎝⎛-415,23,四边形ABPC 的 面积875的最大值为. 4.(2010北京)在平面直角坐标系xOy 中,抛物线23454122+-++--=m x x mx m y 与x 轴的交点分别为原点O 和点A ,点B (2,n )在这条抛物线上.(1)求B 点的坐标;(2)点P 在线段OA 上,从O 点出发向A 点运动,过P 点作x 轴的垂线,与直线OB 交与点E ,延长PE 到点D ,使得ED =PE ,以PD 为斜边,在PD 右侧做等等腰直角三角形PCD (当P 点运动时,C 点、D 点也随之运动).① 当等腰直角三角形PCD 的顶点C 落在此抛物线上时,求OP 的长;② 若P 点从O 点出发向A 点作匀速运动,速度为每秒1个单位,同时线段OA 上另一个点Q 从A 点出发向O 点作匀速运动,速度为每秒2个单位(当Q 点到达O 点时停止运动,P 点也同时停止运动).过Q 点做x 轴的垂线,与直线AB 交与点F ,延长QF 到点M ,使得FM =QF ,以QM 为斜边,在QM 的左侧作等腰直角三角形QMN (当Q点运动时,M 点、N 点也随之运动).若P 点运动到t分别有一条边恰好落在同一条直线上,求此刻t 的值.【答案】解:(1)∵抛物线23454122+-++--=m m x mx m y 经过原点, ∴m 2—3m +2=0. 解的m 1=1,m 2=2. 由题意知m ≠1. ∴m =2,∴抛物线的解析式为x x y 25412+-= ∵点B (2,n )在抛物线x x y 25412+-=,n=4.∴B 点的坐标为(2,4)(2)①设直线OB 的解析式为y =k 1x 求得直线OB 的解析式y =2x ∵A 点是抛物线与x 轴的一个交点, 可求得A 点的坐标为(10,0),设P 点的坐标为(a ,0),则E 点的坐标为(a ,2a ). 根据题意做等腰直角三角形PCD ,如图1.(第24题)可求得点C 的坐标为(3a ,2a ), 有C 点在抛物线上,得2a =-41x (3a )2+25x 3a . 即49a 2— 211a =0解得 a 1=922,a 2=0(舍去)∴OP =922②依题意作等腰直角三角形QMN . 设直线AB 的解析式y =k 2x +b由点A (10 ,0),点B (2,4),求得直线AB 的解析式为y =-21x +5 当P 点运动到t 秒时,两个等腰直角三角形分别有一条边恰好落在同一条直线上,有以下三种情况:第一种情况:CD 与NQ 在同一条直线上,如图2所示,可证△DPQ 为等腰直角三角形.此时QP 、OP 、AQ 的长可依次表示为t 、4t 、 2t 个单位. ∴PQ = DP = 4t ∴t +4t +2t =10 ∴t=710第二种情况:PC 与MN 在同一条直线上,如图3所示.可证△PQM 为等腰直角三角形.此时OP 、AQ 的长依次表示为t 、2t 个单位, ∴OQ = 10 - 2t ∵F 点在直线AB 上 ∴FQ =t ∵MQ =2t ∴PQ =MQ =CQ =2t ∴t +2t +2t =10 ∴t =2.第三种情况:点P 、Q 重合时,PD 、QM 在同一条直线上,如图4所示,此时OP 、AQ 的长依次表示为t 、2t 个单位.∴t +2t=10 ∴t =310 综上,符合题意的值分别为710,2,310. 5.(2010云南红河哈尼族彝族自治州)二次函数2x y =的图像如图8所示,请将此图像向右平移1个单位,再向下平移2个单位.(1)画出经过两次平移后所得到的图像,并写出函数的解析式.(2)求经过两次平移后的图像与x 轴的交点坐标,指出当x 满足什么条件时,函数值大于0?【答案】解:画图如图所示: 依题意得:2)1(2--=x y=2122-+-x x =122--x x∴平移后图像的解析式为:122--x x (2)当y=0时,122--x x =0 2)1(2=-x 21±=-x 212121+=-=x x ,∴平移后的图像与x 轴交与两点,坐标分别为(21-,0)和(21+,0) 由图可知,当x<21-或x>21+时,二次函数2)1(2--=x y 的函数值大于0. 6.(2010云南楚雄)已知:如图,抛物线2y ax bx c =++与x 轴相交于两点A (1,0),B (3,0).与y 轴相较于点C (0,3). (1)求抛物线的函数关系式; (2)若点D (7,2m )是抛物线2y ax bx c =++上一点,请求出m 的值,并求处此时△ABD 的面积.【答案】解:(1)由题意可知09303a b c a b c c ++=⎧⎪++=⎨⎪=⎩ 解得143a b c =⎧⎪=-⎨⎪=⎩所以抛物线的函数关系式为243y x x =-+. (2)把D (7,2m )代人函数解析式243y x x =-+中,得2775()43224m =-⨯+=.所以155(31)244ABD S ∆=⨯-⨯=. 7.(2010湖北随州)已知抛物线2(0)y ax bx c a =++≠顶点为C (1,1)且过原点O.过抛物线上一点P (x ,y )向直线54y =作垂线,垂足为M ,连FM (如图). (1)求字母a ,b ,c 的值;(2)在直线x =1上有一点3(1,)4F ,求以PM 为底边的等腰三角形PFM 的P 点的坐标,并证明此时△PFM 为正三角形;(3)对抛物线上任意一点P ,是否总存在一点N (1,t ),使PM =PN 恒成立,若存在请求出t 值,若不存在请说明理由.【答案】(1)a =-1,b =2,c =0(2)过P 作直线x=1的垂线,可求P 的纵坐标为14,横坐标为1132.此时,MP =MF =PF =1,故△MPF 为正三角形. (3)不存在.因为当t <54,x <1时,PM 与PN 不可能相等,同理,当t >54,x >1时,PM 与PN 不可能相等.8.(2010河南)在平面直角坐标系中,已知抛物线经过A(4,0),B(0,一4),C(2,0)三点.(1)求抛物线的解析式;(2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S.求S 关于m 的函数关系式,并求出S 的最大值;(3)若点P 是抛物线上的动点,点Q 是直线y=-x 上的动点,判断有几个位置能使以点P 、Q 、B 、0为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.【答案】(1)设抛物线的解析式为y =ax 2+bx +c (a ≠0),则有1640,4,420.a b c c a b c -+=⎧⎪=-⎨⎪++=⎩解得1,21,4.a b c ⎧=⎪⎪=⎨⎪=-⎪⎩∴抛物线的解析式y =12x 2+x ﹣4(2)过点M 作MD ⊥x 轴于点D .设M 点的坐标为(m ,n ). 则AD =m +4,MD =﹣n ,n =12m 2+m -4 . ∴S = S △AMD +S 梯形DMBO -S △ABO =12( m +4) (﹣n )+12(﹣n +4) (﹣m ) -12×4×4 = ﹣2n -2m -8 = ﹣2(12m 2+m -4) -2m -8 = ﹣m 2-4m (-4< m < 0)∴S 最大值 = 4(3)满足题意的Q 点的坐标有四个,分别是:(-4 ,4 ),(4 ,-4), (-2+52-25-2-52+59.(2010四川乐山)如图(13.1),抛物线y =x2+bx+c 与x 轴交于A ,B 两点,与y 轴交于点C(0,2),连接AC ,若tan ∠OAC =2. (1)求抛物线对应的二次函数的解析式;(2)在抛物线的对称轴l 上是否存在点P ,使∠APC =90°,若存在,求出点P 的坐标;若不存在,请说明理由;(3)如图(13.2)所示,连接BC ,M 是线段BC 上(不与B 、C 重合)的一个动点,过点M 作直线l ′∥l ,交抛物线于点N ,连接CN 、BN ,设点M 的横坐标为t .当t 为何值时,△BCN 的面积最大?最大面积为多少?【答案】解:(1)∵抛物线y=x2+bx+c过点C(0,2). ∴x=2又∵tan∠OAC=OCOA=2, ∴OA=1,即A(1,0).又∵点A在抛物线y=x2+bx+2上. ∴0=12+b×1+2,b=-3 ∴抛物线对应的二次函数的解析式为y=x2-3x+2(2)存在过点C作对称轴l的垂线,垂足为D,如图所示,∴x=-332212ba-=-=⨯.∴AE=OE-OA=32-1=12,∵∠APC=90°,∴tan∠PAE= tan∠CPD∴PE CDEA DP=,即12PE322PE=-,解得PE=12或PE=32,∴点P的坐标为(32,12)或(32,32)。
5.2 二次函数的图像和性质(3) 导学案

5.2.1二次函数的图像与性质⑷班级 姓名 【学习目标】1.会用描点法画二次函数()k h x a y ++=2的图像,掌握它的性质.2.渗透数形结合思想.【课前自习】22.抛物线22+=x y 的开口向 ,对称轴是 ;顶点坐标是 ,说明当x = 时,y 有最 值是 ;无论x 取任何实数,y 的取值范围是 . 3.抛物线()232--=x y 的开口向 ,对称轴是 ;顶点坐标是 ,说明当x = 时,y 有最 值是 ;无论x 取任何实数,y 的取值范围是 . 4.抛物线()2121+-=x y 与抛物线 关于x 轴成轴对称; 抛物线()2121+-=x y 与抛物线 关于y 轴成轴对称【课堂助学】一、 自主探索: 1.画出二次函数()2121-=x y 和()21212+-=x y 的图像:⑵在下列平面直角坐标系中描出表中各点,并把这些点连成平滑的曲线:2.观察上图:⑴函数 的图像与的图像的 相同, 相同, 不同, 不同;⑵函数可以看成 的图像先向 平移 个单位长度得到 函数 的图像,再向 平移 个单位长度得到.⑶函数 的对称轴是 ,在对称轴的左侧,即x 时,y 随x 的增大而 ;在对称轴的右侧,即x 时,y 随x 的增大而 .⑷函数 顶点坐标是 ,说明当x = 时,y 有最 值是 .二、探究归纳:1.二次函数()k h x a y ++=2的图像是一条 ,它对称轴是 ;顶点坐标是 ,说明当x = 时,y 有最值是 .2.当0>k 时,()k h x a y ++=2的图像可以看成是()2h x a y +=的图像向 平移个单位得到;当0<k 时,()k h x a y ++=2的图像可以看成是()2h x a y +=的图像向 平移 个单位得到.3.当0>a 时,抛物线开口向 ,顶点是抛物线的最 点.在对称轴的左侧,即x 时,y 随x 的增大而 ;在对称轴的右侧,即x 时,y 随x 的增大而 ;当0<a 时,抛物线开口向 ,顶点是抛物线的最 点.在对称轴的左侧,即x 时,y 随x 的增大而 ;在对称轴的右侧,即x 时,y 随x 的增大而 .4. 由于根据()k h x a y ++=2的解析式可直接得到函数图像的顶点坐标,故称之为. 三、典型例题:例1、⑴已知抛物线开口大小与221x y =的开口大小一样,但方向相反,且当x =-2时, y 有最值4,该抛物线的解析式是 ;()21212+-=x y ()21212+-=x y 221x y =221x y =()21212+-=x y ()21212+-=x y⑵抛物线()5122+--=x y 是由一抛物线先向左平移2个单位,再向下平移3个单位得到,则原抛物线的解析式是 ;⑶抛物线()212-+-=x y 与抛物线 关于x 轴成轴对称;抛物线()212-+-=x y 与抛物线 关于y 轴成轴对称.【课堂检测】1.二次函数()3522-+=x y 的图像是 ,开口 ,对称轴是 ;顶点坐标是 ,说明当x= 时,y 有最 值是 . 2.二次函数()2432+--=x y 的图像是由抛物线23x y -=先向 平移 个单位,再向 平移 个单位得到的;开口 ,对称轴是 ,顶点坐 标是 ,说明当x= 时,y 有最 值是 .3.将二次函数y=2x 2的图像向左平移3个单位后得到函数 的图像,再向上平移2个单位得到函数 的图像;新函数的顶点坐标是 ,其对称轴是 ,说明当x 时,y 随x 的增大而增大,当x 时,y 随x 的增大而减小.4.在同一坐标系中画出下列函数的图像:①()23+-=x y ②()23--=x y观察左图:⑴函数()122++-=x y 图像与()22+-=x y 的图像的 相同, 相同,相同, 不同.⑵函数()122++-=x y 可以看成2x y -=的图像先向 平移 个单位长度得到函数 的图像,再向 平移 个单位长度得到.⑶函数()122++-=x y 的对称轴是 ,在对称轴的左侧,即x 时,y 随x 的增大而 ;在对称轴的右侧,即x 时,y 随x 的增大而 .⑷函数()122++-=x y 顶点坐标是 ,说明当x = 时,y 有最 值是 .【课外作业】1.将抛物线y= -3x 2的图像先向左平移3个单位,再向下平移2个单位得到 的图像,新图像的对称轴是 ,顶点坐标是 ,当x= 时,y 有最 值是 . 2.函数y=3(x+6)2+2的图象是由函数y=3x 2的图象先向 平移 个单位,再向 平 移 个单位得到的;其图象开口向 ,对称轴是 ,顶点坐标 是 ;当x= 时,y 有最 值是 ;当x 时,y 随x 的增大而增大. 3.抛物线y=a (x+h )2+k 是由函数y=231x 的图象先向左平移1个单位长度,再向下平移2 个单位长度得到的,则a= ,h= ,k= .4.将函数y=3(x -4)2+3的图象沿x 轴对折后得到的函数解析式是 ;将函数y=3(x -4)2+3的图象沿y 轴对折后得到的函数解析式是 .5.将抛物线y= -2(x-3)2-1先向上平移3单位,就得到函数 的 图象,再向 平移 个单位得到函数y= 2(x+1)2+2的图象.6.抛物线()k h x a y ++=2经过点(-1,-4),且当x=1时,y 有最值是-2,求该抛物线的解析式.。
苏科版九年级下册:5.2《二次函数的图像和性质》同步练习 含答案

5.2《二次函数的图像和性质》同步练习一.选择题1.二次函数y=x2+2x﹣5有()A.最大值﹣5B.最小值﹣5C.最大值﹣6D.最小值﹣62.在同一坐标系中,一次函数y=﹣mx+n2与二次函数y=x2+m的图象可能是()A.B.C.D.3.已知点A(1,y1),B(2,y2)在抛物线y=﹣(x+1)2+2上,则下列结论正确的是()A.2>y1>y2B.2>y2>y1C.y1>y2>2D.y2>y1>24.将抛物线y=x2﹣6x+21向左平移2个单位后,得到新抛物线的解析式为()A.y=(x﹣8)2+5B.y=(x﹣4)2+5C.y=(x﹣8)2+3D.y=(x﹣4)2+35.已知二次函数y=x2+(m﹣1)x+1,当x>1时,y随x的增大而增大,而m的取值范围是()A.m=﹣1B.m=3C.m≤﹣1D.m≥﹣16.如图是二次函数y=ax2+bx+c的图象,下列结论:①二次三项式ax2+bx+c的最大值为4;②4a+2b+c<0;③一元二次方程ax2+bx+c=1的两根之和为﹣1;④使y≤3成立的x的取值范围是x≥0.其中正确的个数有()A.1个B.2个C.3个D.4个7.对于二次函数y=﹣x2+x﹣4,下列说法正确的是()A.当x>0时,y随x的增大而增大B.当x=2时,y有最大值﹣3C.图象的顶点坐标为(﹣2,﹣7)D.图象与x轴有两个交点8.点P1(﹣1,y1),P2(3,y2),P3(5,y3)均在二次函数y=﹣x2+2x+c的图象上,则y1,y2,y3的大小关系是()A.y3>y2>y1B.y3>y1=y2C.y1>y2>y3D.y1=y2>y39.已知抛物线y=﹣x2+bx+4经过(﹣2,n)和(4,n)两点,则n的值为()A.﹣2B.﹣4C.2D.410.在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点旋转180°得到抛物线y=x2+5x+6,则原抛物线的解析式是()A.y=﹣(x﹣)2﹣B.y=﹣(x+)2﹣C.y=﹣(x﹣)2﹣D.y=﹣(x+)2+11.把函数y=﹣x2的图象,经过怎样的平移变换以后,可以得到函数y=﹣(x﹣1)2+1的图象()A.向左平移1个单位,再向下平移1个单位B.向左平移1个单位,再向上平移1个单位C.向右平移1个单位,再向上平移1个单位D.向右平移1个单位,再向下平移1个单位12.将抛物线y=x2向左平移2个单位,再向下平移5个单位,平移后所得新抛物线的表达式为()A.y=(x+2)2﹣5B.y=(x+2)2+5C.y=(x﹣2)2﹣5D.y=(x﹣2)2+5 13.如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0 ②2a+b=0③a+b+c>0 ④当﹣1<x<3时,y>0其中正确的个数为()A.1B.2C.3D.414.函数y=与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是()A.B.C.D.15.如图,一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b﹣1)x+c的图象可能是()A.B.C.D.16.已知二次函数y=(x﹣h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为()A.1或﹣5B.﹣1或5C.1或﹣3D.1或317.如图,抛物线y=ax2+bx+c(a≠0)过点(﹣1,0)和点(0,﹣3),且顶点在第四象限,设P=a+b+c,则P的取值范围是()A.﹣3<P<﹣1B.﹣6<P<0C.﹣3<P<0D.﹣6<P<﹣3二.填空题18.抛物线y=ax2+bx+2经过点(﹣2,3),则3b﹣6a=.19.已知二次函数y=x2+2mx+2,当x>2时,y的值随x值的增大而增大,则实数m的取值范围是.20.已知点A(4,y1),B(,y2),C(﹣2,y3)都在二次函数y=(x﹣2)2﹣1的图象上,则y1、y2、y3的大小关系是.21.已知二次函数的图象经过点P(2,2),顶点为O(0,0)将该图象向右平移,当它再次经过点P时,所得抛物线的函数表达式为.22.矩形的周长等于40,则此矩形面积的最大值是.23.二次函数y=x2﹣4x+a在﹣2≤x≤3的范围内有最小值﹣3,则a=.24.已知四个二次函数的图象如图所示,那么a1,a2,a3,a4的大小关系是.(请用“>”连接排序)25.如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(,0),有下列结论:①abc >0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是.(填写正确结论的序号)三.解答题26.画出函数y=(x﹣2)2﹣1的图象.27.如图,抛物线y=﹣x2+x+c经过点(﹣2,2),求c的值及函数的最大值.28.已知抛物线y=﹣2x2﹣4x+1.(1)求这个抛物线的对称轴和顶点坐标;(2)将这个抛物线平移,使顶点移到点P(2,0)的位置,写出所得新抛物线的表达式和平移的过程.29.已知点(2,8)在函数y=ax2+b的图象上,当x=﹣1时,y=5.(1)求a,b的值.(2)如果点(12,m),(n,17)也在这个函数的图象上,求m与n的值.30.在平面直角坐标系xOy中,抛物线y=ax2+bx﹣与y轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.(1)求点B的坐标(用含a的式子表示);(2)求抛物线的对称轴;(3)已知点P(,﹣),Q(2,2).若抛物线与线段PQ恰有一个公共点,结合函数图象,求a的取值范围.31.下表给出一个二次函数的一些取值情况:x…01234…y…30﹣103…(1)请在直角坐标系中画出这个二次函数的图象;(2)根据图象说明:当x取何值时,y的值大于0?32.如图,已知点A(0,2),B(2,2),C(﹣1,﹣2),抛物线F:y=x2﹣2mx+m2﹣2与直线x=﹣2交于点P.(1)当抛物线F经过点C时,求它的表达式;(2)设点P的纵坐标为y P,求y P的最小值,此时抛物线F上有两点(x1,y1),(x2,y2),且x1<x2≤﹣2,比较y1与y2的大小;(3)当抛物线F与线段AB有公共点时,直接写出m的取值范围.参考答案一.选择题1.解:y=x2+2x﹣5=(x+1)2﹣6,∵a=1>0,∴当x=﹣1时,二次函数由最小值﹣6.故选:D.2.解:A、由直线与y轴的交点在y轴的负半轴上可知,n2<0,错误;B、由抛物线与y轴的交点在y轴的正半轴上可知,m>0,由直线可知,﹣m>0,错误;C、由抛物线y轴的交点在y轴的负半轴上可知,m<0,由直线可知,﹣m<0,错误;D、由抛物线y轴的交点在y轴的负半轴上可知,m<0,由直线可知,﹣m>0,正确,故选:D.3.解:当x=1时,y1=﹣(x+1)2+2=﹣(1+1)2+2=﹣2;当x=2时,y1=﹣(x+1)2+2=﹣(2+1)2+2=﹣7;所以2>y1>y2.故选:A.4.解:y=x2﹣6x+21=(x2﹣12x)+21=[(x﹣6)2﹣36]+21=(x﹣6)2+3,故y=(x﹣6)2+3,向左平移2个单位后,得到新抛物线的解析式为:y=(x﹣4)2+3.故选:D.5.解:抛物线的对称轴为直线x=﹣,∵当x>1时,y的值随x值的增大而增大,由图象可知:﹣≤1,解得m≥﹣1.故选:D.6.解:∵抛物线的顶点坐标为(﹣1,4),∴二次三项式ax2+bx+c的最大值为4,①正确;∵x=2时,y<0,∴4a+2b+c<0,②正确;根据抛物线的对称性可知,一元二次方程ax2+bx+c=1的两根之和为﹣2,③错误;使y≤3成立的x的取值范围是x≥0或x≤﹣2,④错误,故选:B.7.解:∵二次函数y=﹣+x﹣4可化为y=﹣(x﹣2)2﹣3,又∵a=﹣<0∴当x=2时,二次函数y=﹣x2+x﹣4的最大值为﹣3.故选:B.8.解:∵y=﹣x2+2x+c,∴对称轴为x=1,开口向下,P2(3,y2),P3(5,y3)在对称轴的右侧,y随x的增大而减小,∵3<5,∴y2>y3,根据二次函数图象的对称性可知,P1(﹣1,y1)与(3,y1)关于对称轴对称,故y1=y2>y3,故选:D.9.解:抛物线y=﹣x2+bx+4经过(﹣2,n)和(4,n)两点,可知函数的对称轴x=1,∴=1,∴b=2;∴y=﹣x2+2x+4,将点(﹣2,n)代入函数解析式,可得n=﹣4;故选:B.10.解:∵抛物线的解析式为:y=x2+5x+6,设原抛物线上有点(x0,y0),绕原点旋转180°后,变为(﹣x0,﹣y0),点(﹣x0,﹣y0)在抛物线y=x2+5x+6上,将(﹣x0,﹣y0)代入y=x2+5x+6得到新抛物线﹣y0=x02﹣5x0+6,所以原抛物线的方程为y0=﹣x02+5x0﹣6=﹣(x0﹣)2+,∴向下平移3个单位长度的解析式为y0=﹣(x0﹣)2+﹣3=﹣(x0﹣)2﹣.故选:A.11.解:抛物线y=﹣x2的顶点坐标是(0,0),抛物线线y=﹣(x﹣1)2+1的顶点坐标是(1,1),所以将顶点(0,0)向右平移1个单位,再向上平移1个单位得到顶点(1,1),即将函数y=﹣x2的图象向右平移1个单位,再向上平移1个单位得到函数y=﹣(x ﹣1)2+1的图象.故选:C.12.解:抛物线y=x2的顶点坐标为(0,0),先向左平移2个单位再向下平移5个单位后的抛物线的顶点坐标为(﹣2,﹣5),所以,平移后的抛物线的解析式为y=(x+2)2﹣5.故选:A.13.解:①图象开口向下,能得到a<0;②对称轴在y轴右侧,x==1,则有﹣=1,即2a+b=0;③当x=1时,y>0,则a+b+c>0;④由图可知,当﹣1<x<3时,y>0.故选:C.14.解:解法一:由解析式y=﹣kx2+k可得:抛物线对称轴x=0;A、由双曲线的两支分别位于二、四象限,可得k<0,则﹣k>0,抛物线开口方向向上、抛物线与y轴的交点为y轴的负半轴上;本图象与k的取值相矛盾,故A错误;B、由双曲线的两支分别位于一、三象限,可得k>0,则﹣k<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象符合题意,故B正确;C、由双曲线的两支分别位于一、三象限,可得k>0,则﹣k<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象与k的取值相矛盾,故C错误;D、由双曲线的两支分别位于一、三象限,可得k>0,则﹣k<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象与k的取值相矛盾,故D错误.解法二:①k>0,双曲线在一、三象限,﹣k<0,抛物线开口向下,顶点在y轴正半轴上,选项B符合题意;②K<0时,双曲线在二、四象限,﹣k>0,抛物线开口向上,顶点在y轴负半轴上,选项B符合题意;故选:B.15.解:点P在抛物线上,设点P(x,ax2+bx+c),又因点P在直线y=x上,∴x=ax2+bx+c,∴ax2+(b﹣1)x+c=0;由图象可知一次函数y=x与二次函数y=ax2+bx+c交于第一象限的P、Q两点,∴方程ax2+(b﹣1)x+c=0有两个正实数根.∴函数y=ax2+(b﹣1)x+c与x轴有两个交点,又∵﹣>0,a>0∴﹣=﹣+>0∴函数y=ax2+(b﹣1)x+c的对称轴x=﹣>0,∴A符合条件,故选:A.16.解:∵当x>h时,y随x的增大而增大,当x<h时,y随x的增大而减小,∴①若h<1≤x≤3,x=1时,y取得最小值5,可得:(1﹣h)2+1=5,解得:h=﹣1或h=3(舍);②若1≤x≤3<h,当x=3时,y取得最小值5,可得:(3﹣h)2+1=5,解得:h=5或h=1(舍);③若1≤h≤3时,当x=h时,y取得最小值为1,不是5,∴此种情况不符合题意,舍去.综上,h的值为﹣1或5,故选:B.17.解:∵抛物线y=ax2+bx+c(c≠0)过点(﹣1,0)和点(0,﹣3),∴0=a﹣b+c,﹣3=c,∴b=a﹣3,∵当x=1时,y=ax2+bx+c=a+b+c,∴P=a+b+c=a+a﹣3﹣3=2a﹣6,∵顶点在第四象限,a>0,∴b=a﹣3<0,∴a<3,∴0<a<3,∴﹣6<2a﹣6<0,即﹣6<P<0.故选:B.二.填空题18.解:把点(﹣2,3)代入y=ax2+bx+2得:4a﹣2b+2=3,2b﹣4a=﹣1,3b﹣6a=﹣,故答案为:﹣.19.解:抛物线的对称轴为直线x=﹣=﹣m,∵当x>2时,y的值随x值的增大而增大,∴﹣m≤2,解得m≥﹣2.故答案为:m≥﹣2.20.解:把A(4,y1),B(,y2),C(﹣2,y3)分别代入y=(x﹣2)2﹣1得:y1=(x﹣2)2﹣1=3,y2=(x﹣2)2﹣1=5﹣4,y3=(x﹣2)2﹣1=15,∵5﹣4<3<15,所以y3>y1>y2.故答案为y3>y1>y2.21.解:设原来的抛物线解析式为:y=ax2(a≠0).把P(2,2)代入,得2=4a,解得a=.故原来的抛物线解析式是:y=x2.设平移后的抛物线解析式为:y=(x﹣b)2.把P(2,2)代入,得2=(2﹣b)2.解得b=0(舍去)或b=4.所以平移后抛物线的解析式是:y=(x﹣4)2.故答案是:y=(x﹣4)2.22.解:设矩形的宽为x,则长为(20﹣x),S=x(20﹣x)=﹣x2+20x=﹣(x﹣10)2+100,当x=10时,S最大值为100.故答案为100.23.解:y=x2﹣4x+a=(x﹣2)2+a﹣4,当x=2时,函数有最小值a﹣4,∵二次函数y=x2﹣4x+a在﹣2≤x≤3的范围内有最小值﹣3,﹣2≤x≤3,y随x的增大而增大,∴a﹣4=﹣3,∴a=1,故答案为1.24.解:如图所示:①y=a1x2的开口小于②y=a2x2的开口,则a1>a2>0,③y=a3x2的开口大于④y=a4x2的开口,开口向下,则a4<a3<0,故a1>a2>a3>a4.故答案为;a1>a2>a3>a425.解:由抛物线的开口向下可得:a<0,根据抛物线的对称轴在y轴左边可得:a,b同号,所以b<0,根据抛物线与y轴的交点在正半轴可得:c>0,∴abc>0,故①正确;直线x=﹣1是抛物线y=ax2+bx+c(a≠0)的对称轴,所以﹣=﹣1,可得b=2a,a﹣2b+4c=a﹣4a+4c=﹣3a+4c,∵a<0,∴﹣3a>0,∴﹣3a+4c>0,即a﹣2b+4c>0,故②错误;∵抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(,0),∴抛物线与x轴的另一个交点坐标为(,0),当x=﹣时,y=0,即,整理得:25a﹣10b+4c=0,故③正确;∵b=2a,a+b+c<0,∴,即3b+2c<0,故④错误;假设结论正确可得:a﹣b+c≥m2a﹣mb+c∴am2﹣mb+b﹣a≤0,∵△=(b)2﹣4ab;b=2a∴△=4a2﹣4a(b﹣a)=0,∴关于y=am2﹣mb+b的图象与x轴有一个交点,又∵a<0,∴y=am2﹣mb+b﹣a有最大值ymax=0,所以⑤正确;故答案为:①③⑤.三.解答题26.解:列表得:x…01234…y…30﹣103…如图:27.解:把点(﹣2,2)代入y=﹣x2+x+c中得:﹣﹣+c=2解得c=,所以这个二次函数的关系式为y=﹣x2+x+.(2)∵y=﹣x2+x+=﹣(x﹣1)2+5,∴抛物线的开口向下,当x=1时,函数有最大值5.28.解:(1)y=﹣2x2﹣4x+1,=﹣2(x2+2x+1)+2+1,=﹣2(x+1)2+3,所以,对称轴是直线x=﹣1,顶点坐标为(﹣1,3);(2)∵新顶点P(2,0),∴y=﹣2(x﹣2)2,∵2﹣(﹣1)=2+1=3,0﹣3=﹣3,∴平移过程为:向右平移3个单位,向下平移3个单位.29.解(1)由题意可知:,解得.(2)将(12,m),(n,17)代入y=x2+4,得:m=144+4,17=n2+4,解得m=148,n=±.30.解:(1)A(0,﹣)点A向右平移2个单位长度,得到点B(2,﹣);(2)A与B关于对称轴x=1对称,∴抛物线对称轴x=1;(3)∵对称轴x=1,∴b=﹣2a,∴y=ax2﹣2ax﹣,①a>0时,当x=2时,y=﹣<2,当y=﹣时,x=0或x=2,∴函数与PQ无交点;②a<0时,当y=2时,ax2﹣2ax﹣=2,x=或x=当≤2时,a≤﹣;∴当a≤﹣时,抛物线与线段PQ恰有一个公共点;31.解:(1)描点、连线得:(2)由函数图象可知:当x<1或x>3时,y>0.32.解:(1)∵抛物线F经过点C(﹣1,﹣2),∴﹣2=(﹣1)2﹣2×m×(﹣1)+m2﹣2,解得,m=﹣1,∴抛物线F的表达式是:y=x2+2x﹣1;(2)当x=﹣2时,y p=4+4m+m2﹣2=(m+2)2﹣2,∴当m=﹣2时,y p取得最小值,最小值是﹣2,此时抛物线F的表达式是:y=x2+4x+2=(x+2)2﹣2,∴当x≤﹣2时,y随x的增大而减小,∵x1<x2≤﹣2,∴y1>y2;(3)m的取值范围是﹣2≤m≤0或2≤m≤4,理由:∵抛物线F与线段AB有公共点,点A(0,2),B(2,2),∴或或,解得,﹣2≤m≤0或2≤m≤4.。
新苏科版九年级数学下册《5章 二次函数 5.2 二次函数的图像和性质 y=ax^2+k、y=a(x+m)^2的图像》教案_27

学习目标:1.经历探索二次函数y=ax2+k(a≠0),y=a(x-h)2(a≠0)的图象作法和性质的过程;2.能够理解函数y=ax2+k(a≠0)、y=a(x-h)2与y=ax2的图象的关系,知道a、h对二次函数的图象的影响;3.能正确说出函数y=ax2+k(a≠0)、y=a(x-h)2的图象的性质.教学过程:一、探索二次函数y=ax2+k(a≠0)的图象和性质。
(2)在下图的直角坐标系中,描点并画出函数2y x=和21y x=+的图象;2.思考:函数y=x2+1的图象与y=x2的图象有什么关系?(1)形状相同吗?(2)相同自变量的值所对应的两个函数值有何关系?(3)从点的位置看,函数y=x2+1的图象与函数y=x2的图象的位置有什么关系?3.归纳:图象向上移还是向下移,移多少个单位长度,有什么规律吗?函数y=ax2 (a≠0)和函数y=ax2+ k (a≠0)的图象形状,只是位置不同;当k >0时,函数y=ax2+ k的图象可由y=ax2的图象向平移个单位得到;当k〈0时,函数y=ax2+c的图象可由y=ax2的图象向平移个单位得到。
二、探索二次函数y=a(x-h)2(a≠0)的图象作法和性质:1.操作:在上图右边直角坐标系中,描点并画出函数y=(x+3)2的图象;2.思考:函数y=(x+3)2的图象与y=x2的图象有什么关系?(1)形状相同吗?(2)从表格中的数值看,函数y=(x+3)2的函数值与函数y=x2的函数值相等时,它们所对应的自变量的值有什么关系?(3)从点的位置看,函数y=(x+3)2的图象与函数y=x 2的图象的位置有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么?3.结论:函数y=(x+3)2的图象可以由函数y=x 2的图像沿x 轴向 平移 个单位长度得到,所以它是 ,这条抛物线的对称轴是 ,顶点坐标是 ,当x 时,y 随x 的增大而增大,当x 时,y 随x 的增大而减小.4.①抛物线y=-3(x-1)2可以看作是抛物线y=-3x 2沿x 轴 平移了 个单位;抛物线y=-3(x+1)2可以看作是抛物线y=-3x 2沿x 轴 平移了 个单位. ②图象向左平移还是向右平移,移多少个单位长度,有什么规律吗?三、例题:1.函数y=4x 2+5的图象可由y=4x 2的图象向 平移 个单位得到;y=4x 2-11的图象可由 y=4x 2的图象向 平移 个单位得到。
5.2 二次函数的图像和性质(第3课时)(课件)九年级数学下册课件(苏科版)

的两点,那么y1________y
2.(填“>”“<”或“=”)
当堂检测
9.已知二次函数y=(a-2)x2+a2-2的最高点为(0,2)则a=____.
-2
10.若y=x2+(k-2)的顶点是原点,则k____;若顶点位于x轴上方,
=2
>2
则k____;若顶点位于x轴下方,则k
<2 .
当堂检测
C )
A.开口向上
B.顶点坐标都是(0,0)
C.对称轴是y轴
D.在对称轴的右侧,y随x的增大而增大
5.已知函数y=x2-2,当函数值y随x的增大而减小时,x的取值范围是( D )
A.x<2
B.x>0
C.x>-2
D.x<0
当堂检测
6.在同一直角坐标系中,一次函数y=ax+k和二次函数y=ax2+k的
平移︱k︱单位.
第二种方法:描点法,三步即列表、描点和连线.
2.抛物线y=ax2+k 中的a决定什么?怎样决定的?k决定什么?它的对称
轴是什么?顶点坐标怎样表示?
a决定开口方向和大小,k决定顶点的纵坐标.
课堂小结
与y=ax2的关系 上加下减
开口方向由a的符号决定
二次函数y=ax2+k
的图像和性质
图像
又∵y轴是该抛物线的对称轴,
∴点A与点B关于y轴对称,
∴MA=MB=2,即点A的横坐标是2,
则其纵坐标y= ×22+1=2,即点A的坐标为(2,2),
故点M的坐标为(0,2).
大而______,当x=___时,取得最____值,这个值等于___.
0
5
减小
大
y轴
5.2二次函数的图像和性质 第3课时 二次函数y=ax^2 bx c的图像和性质(教学课件)-初中数

新知导入 课程讲授 随堂练习 课堂小结
y=ax2+bx+c(a≠0)的性质
二次函数y=-x2-4x-5 的图像如图所示.
由图像可知, 当x=-2时, y的值最大, 最大值是-1.
新知导入 课程讲授 随堂练习 课堂小结
y=ax2+bx+c(a≠0)的图像
y=
1 2
x2-6x+21
y=
1 2
(x2-12x)+21
你知道是怎样配方的吗? 1. “提”:提出二次项系数;
1 y= 2 (x2-12x+36-36)+21
y= 1 (x-6) 2+21-18 2
2.“配”:括号内配成完全平方式;
a<0时,抛物线开口向下,函数有最大值;
4ac - b2
函数在顶点处取得有最大(小)值 4a
.
新知导入 课程讲授 随堂练习 课堂小结
y=ax2+bx+c(a≠0)的图像
练一练:用配方法将二次函数y=x2-8x-9化为y=a(x-h)2+k的形式 为( B ) A.y=(x-4)2+7 B.y=(x-4)2-25 C.y=(x+4)2+7 D.y=(x+4)2-25
新知导入 课程讲授 随堂练习 课堂小结
y=ax2+bx+c(a≠0)的性质
例1 画出二次函数y=-x2-4x-5的图像,并指出它的开口方向、顶点坐 标、对称轴、最大值或最小值. 【分析】要画出二次函数y=-x2-4x-5的图像,可先将函数表达式变
【精】 《二次函数的图象和性质(第3课时)》精品教案

《二次函数(第3课时)》精品教案
(1)抛物线顶点坐标___________;
(2)对称轴为________;
(3)当x=____时,y有最大值是_____;
(4)当________时,y随着x得增大而增大.(5)当____________时,y>0.
4.将函数y=3x+1的图象向______平行移动_____个单位,可使它经过点(1,-1).
5.若将函数y=2x2的图象向右平行移动1个单位,再向上平移5个单位,可得到________________。
课堂小结通过本节课的内容,你有哪些收获?
(2)对称轴是x=h.
(3)顶点是(h,k).
(4)平移规律:h值正右移,负左移;k值正上移,负下移. 学会总结学
习收获,巩
固知识点,
理清知识间
的联系。
让学生
来谈本
节课的
收获,培
养学生
自我检
查、自我
小结的
良好习
惯,将知
识进行
整理并
系统化。
5.2二次函数的图像与性质(3)

课题:5.2二次函数的图像与性质(3)主备人:张亚元 学生姓名学习内容:2)(h x a y -=与2ax y =2)(h x a y -=与k h x a y +-=2)(函数图像之间的关系。
预习指导:阅读教材p14——15的内容。
教学过程:1、用描点法在同一直角坐标系中,画出下列函数的图象.221x y =,2)2(21+=x y ,2)2(21-=x y ,并指出它们的开口方向、对称轴和顶点坐标. (1)列表:(2)描点,连线(3)从表中的数值看,函数221x y =,2)2(21+=x y ,2)2(21-=x y (42、研究2)(h x a y -=与2ax y =的图像有什么关系?由2ax y =如何变化可以得到2)(h x a y -=的图像?3、 2)(h x a y -=(a 、h 是常数,a ≠0)的图象的开口方向、对称轴、顶点坐标归纳如下:(1).抛物线2)1(-=x y 的开口 ,对称轴是 ,顶点坐标是 ,它可以看作是由抛物线2x y =向 平移 个单位得到的.(2).在同一直角坐标系中,画出下列函数的图象. 22x y -=,2)3(2--=x y ,2)3(2+-=x y ,并指出它们的开口方向4、函数3)2(212+-=x y 的图像时抛物线吗?试用描点法画出它的图像,它的图像与2)2(21-=x y 的图像有什么关系?探索 你能说出函数2)(h x a y -=+k (a 、h 、k 是常数,a ≠0)的图象的开口方向、对称轴和顶点坐标吗?试填写下表.小结:二次函数的图象的上下平移,只影响二次函数2)(h x a y -=+k 中k 的值;左右平移,只影响h 的值,抛物线的形状不变,所以平移时,可根据顶点坐标的改变,确定平移前、后的函数关系式及平移的路径.此外,图象的平移与平移的顺序无关.课堂练习:1.将抛物线1)4(22--=x y 如何平移可得到抛物线22x y = ( )A .向左平移4个单位,再向上平移1个单位B .向左平移4个单位,再向下平移1个单位C .向右平移4个单位,再向上平移1个单位D .向右平移4个单位,再向下平移1个单位2.把抛物线223x y -=向左平移3个单位,再向下平移4个单位,所得的抛物线的函数关系式为 .3.抛物线4)2(212-+-=x y 可由抛物线221x y -=向 平移 个单位,再向 平移 个单位而得到. *4、把抛物线c bx x y ++=2向上平移2个单位,再向左平移4个单位,得到抛物线2x y =,求b 、c 的值.【课后作业】一、感受·理解1.抛物线y=12(x-3)2,则此抛物线的顶点坐标是_______.2.抛物线y=2x2向左平移1个单位,再向下平移3•个单位,得到的抛物线表达式为__________.3.抛物线y=2x2沿x轴向_____平移________个单位,再沿y轴向_____平移____个单位,可以得到抛物线y=2(x+2)2-3.4.将抛物线y=ax2向右平移2个单位,再向上平移3个单位,移动后的抛物线经过点(3,-1),那么移动后的抛物线的关系式为________.5.抛物线y=2(x-3)2+7•的开口方向是________,•顶点坐标为_______,•对称轴是________.6.根据图中的抛物线,当x______时,y随x的增大而增大;当x______时,y随x的增大而减小.7.有3个二次函数,甲:y=x2-1;乙:y=-x2+1;丙:y=x2+2x-1,则下列叙述中正确的是()A.甲的图形经过适当的平行移动后,可以与乙的图形重合;B.甲的图形经过适当的平行移动后,可以与丙的图形重合;C.乙的图形经过适当的平行移动后,可以与丙的图形重合;D.甲、乙、丙3个图形经过适当的平行移动后,都可以重合二、思考·运用8.用配方法将函数y=12x2-2x+1化为y=a(x-h)2+R的形式是()A.y=12(x-2)2-1 B.y=12(x-1)2-1C.y=12(x-2)2-3 D.y=12(x-1)2-39.二次函数y=-3(x-2)2+9的图像的开口方向,对称轴和顶点坐标分别为()A.开口向下,对称轴为x=-2,顶点为(2,9);B.开口向下,对称轴为x=2,顶点为(2,9);C.开口向上,对称轴为x=-2,顶点为(-2,9);D.开口向上,对称轴为x=2,顶点为(-2,-9)10.图中有相同对称轴的两条抛物线,下列关系不正确的是()A.h=m B.k=n C.k>n D.h>0,k>011.在同一坐标系中,画出函数y=12(x-1)2+1和函数y=12(x+2)2-1的图象,•并回答下列问题:(1)分别指出这两条抛物线的对称轴和顶点坐标;(2)抛物线y=12(x+2)2-1经过怎样的平移可得到抛物线y=12(x-1)2+1?三、探究·拓展12.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a+b+c<0;②a-b+c<0;③b+2a<0;④abc>0,其中所有正确结论的序号是()A.③④B.②③C.①④D.①②③13.函数y=ax2+bx+c的图象如图所示,x=13为该函数图象的对称轴,根据这个函数图象,你能得到关于该函数的哪些性质和结论?(写出四个即可)。
《二次函数的图象与性质(第3课时)》优秀课件

小结:
本节课主要运用了数形结合的思想方法,通过对
函数图象的讨论,分析归纳出 y a(x h)2 k
的性质:(1)a的符号决定抛物线的开口方向 (2)对称轴是直线x=h
(3)顶点坐标是(h,k)
抛物线
开口方向 对称轴 顶点坐标
y ax2 (a 0)
y ax 2 k(a 0) y a(x h)2 (a 0)
开口向上 开口向上 开口向上
直线X=0 直线X=0 直线X=h
(0,0) (0,k)
(h,0)
y a(x h)2 k(a 0) 开口向上 直线X=h (h,k)
2
直线x=-1
(- 1, 0)4,y2)(
1 4
,y3)为二次函数
y=(x-2)2图象上的三点,则y1 ,y2 ,y3的大小关系为
___y_3_<__y_2_<__y1____.
典例精析
例1 抛物线y=ax2向右平移3个单位后经过点(-1,4), 求a的值和平移后的函数关系式.
解:设平移后的函数关系式为y=a(x-3)2,
把x=-1,y=4代入,得4=a(-1-3)2, ,
∴
1 a=
4
∴平移后二次函数关系式为y= 1 (x-3)2.
4
小结
比较y=ax2 , y=ax²+k , y=a(x-h)²的图像的不同
y=ax2 y=ax²+k
对称轴 Y轴
Y轴
(直线x=0) (直线x=0)
2) 如何将抛物线y=2(x-1) 2+3经过平移得到 抛物线y=2x2
3) 将抛 物线y=2(x -1)2+3经过怎样的平移得 到抛物线y=2(x+2)2-1
4) 若抛物线y=2(x-1)2+3沿x轴方向平移后,经 过(3,5),求平移后的抛物线的解析式_______
5.2 第3课时 二次函数y=a(x+h)2的图像和性质

5.2 二次函数的图像和性质(3)一、学习目标:1、能解释..二次函数222)(ax y m x a y k ax y =+=+=和二次函数、的图像的位置关系;2、体会本节中图形的变化与图形上的点的坐标变化之间的关系(转化),感受形数结合的数学思想等。
二、学习重点与难点:对二次函数222)(ax y m x a y k ax y =+=+=和二次函数、的图像的位置关系解释和研究问题的数学方法的感受是学习重点;难点是对数学问题研究问题方法的感受和领悟。
三、自学质疑:【要点梳理】(活动一)复习二次函数2y ax k =+的图象和性质:当0a >时,开口向 ,对称轴是 ,顶点坐标为 ,当x =0时,y 最小= ;当x >0时,y 随x 的增大而 ;当x <0时,y 随x 的增大而 .当0a <时,开口向 ,对称轴是 ,顶点坐标为 ,当x =0时,y 最大= ;当x >0时,y 随x 的增大而 ;当x <0时,y 随x 的增大而 .二次函数2()y a x h =-的图象(活动二)在同一平面直角坐标系中,画出221x y -=、()2121--=x y 、()2121+-=x y 的图象,并比较它们的开口方向,对称轴和顶点坐标以及增减性.由图象可知1:抛物线()2121--=x y 的开口向 ,对称轴是直线 ,顶点坐标是 ,在对称轴的左侧,即当x 时,y 随x 的增加而 ,在对称轴的右侧,即当x 时,y 随x 的增加而 ; 抛物线()2121+-=x y 的开口向 ,对称轴是直线 ,顶点坐标是 ,在对称轴的左侧,即当x 时,y 随x 的增加而 ,在对称轴的右侧,即当x 时,y 随x 的增加而 ;2.把抛物线221x y -=向 平移 个单位就可得到抛物线()2121--=x y ,将抛物线221x y -=向 平移 个单位就可得到抛物线()2121+-=x y .(活动三)小结:1.二次函数2()y a x h =-的图象与抛物线2y ax =形状相同,只是位置不同,可由抛物线2y ax =左右平移得到:①当0h >时,抛物线2y ax =向左平移h 个单位,得到2()y a x h =-的图象; ②当0h <时,抛物线2y ax =向右平移h 个单位,得到2()y a x h =-的图象. 2.抛物线2()y a x h =-的性质:①当0a >时,开口向上,对称轴是直线x h =,顶点坐标为(h ,0),当x =h 时,y 最小=0;当x >h 时,y 随x 的增大而增大;当x <h 时,y 随x 的增大而减少.②当0a <时,开口向下,对称轴是直线x h =,顶点坐标为(h ,0),当x =h 时,y 最大=0;当x >例 抛物线y ax =向右平移3个单位后经过点(-1,4),求a 的值和平移后的抛物线解析式.【课堂操练】2.抛物线()253-=x y 可由抛物线()233+=x y 向 平移 个单位而得到.3.抛物线()2121+-=x y 向右平移3个单位得 . 4.将抛物线2y ax =向左平移2个单位后,经过点(-4,-4),求原抛物线的解析式.【课后盘点】1.抛物线21(5)2y x =-+的图象开口向________,对称轴为___________,当x =__________时,y 有最_____值,为_______,当x ________时, y 随x 的增大而增大.2.把函数()2121--=x y 的图象沿x 轴对折,得到的图象解析式是____ ____; 把函数()2121--=x y 的图象沿y 轴对折,得到的图象解析式是_____ ___.3.函数()212-=x y 的图象是由()212+=x y 的图象经过________得到的.4.将抛物线y =3x 2向左平移2个单位,再向下平移1个单位,所得抛物线为( ) A . y =3(x ﹣2)2﹣1 B . y =3(x ﹣2)2+1C . y =3(x +2)2﹣1D . y =3(x +2)2+15.顶点坐标为(-3,0)开口方向、形状与函数231x y =的图象相同的抛物线是 ( ) A .()2331-=x y B .()2331+=x y C .()2331--=x y D .()2331+-=x y6.已知抛物线2()y a x h =-的对称轴为1x =-,与y 轴交于(0,2),求a 和h 的值.7. y=-3(x -1)2的图象(1)向左平移2个单位,(2)向右平移3个单位.写出平移后的解析式.8.抛物线()2h x a y +=的对称轴是直线2-=x ,过点(1,-3),(1)求解析式,(2)求抛物线的顶点坐标,(3)当x 为何值时,y 随x 的增大而增大?9.一条抛物线的形状、开口方向与221x y =相同,对称轴与抛物线()223-=x y 相同,求其解析式.10.将抛物线()2123-=x y 向右平移3个单位后得抛物线与y 轴交于点A ,求点A 的坐标.11.将抛物线221x y -=向左平移4个单位后,其顶点为C ,并与直线y x =分别交于A 、B 两点(点A 在点B 的左边),求三角形ABC 的面积.12.二次函数()2h x a y -=的图象如图:已知21=a ,OA =OC ,试求该抛物线的解析式.13.如图所示,已知直线122y x =-+与抛物线2(2)y a x =+ 相交于A 、B 两点,点A 在y 轴上,M 为抛物线的顶点.(1)请直接写出点A 的坐标及该抛物线的解析式; (2)若P 为线段AB 上一个动点(A 、B 两端点除外),连接PM ,设线段PM 的长为l ,点P 的横坐标为x ,请求出2l 与x 之间的函数关系式,并直接写出自变量x 的取值范围;(3)在(2)的条件下,线段AB 上是否存在点P ,使以A 、M 、P 为顶点的三角形是等腰三角形?若存在,求出点P 的坐标;若不存在,请说明理由.参考答案二次函数y =a (x-h )2的图象(第3课时)【要点梳理】上,y 轴,(0,k ), k ,增大,减小,下,y 轴,(0,k ), k , 减小,增大.二次函数2()y a x h =-的图象 (活动二)图象略,下, x =1,(1,0),>1,减小,<,增大. 下,x =-1,(-1,0),>-1时,减小,<-1时,增大. 2.右,1,左,1.例 a =14,()2134y x =-.【课堂操练】2.右,8. 3. ()2122y x =--4. 2y x =-.【课后盘点】1.下,直线x =-5,-5,大,0,<-5.2. ()2112y x =-,()2112y x =-+.3.向右平移2个单位.4. B5. B6. h =-1,a =2.7. y=-3(x +1)2 ,y=-3(x -4)2.8.⑴y=-13(x +2)2 ,⑵(-2,0),⑶x <-2.9. y=21(x -2)2 10.(0,24)11.由题意,得平移后抛物线的解析式为()2142y x =-+,与y x =联立可得A (-8,-8)、B (-2,-2),∴三角形ABC 的面积为21×4×8-21×4×2=12.12.⑴由题意,得C (h ,0),A (0,h ),∴212h h =,∴h =2,0(不合题意,舍去),∴()2122y x =-.13.(1)A 的坐标是(0,2)抛物线线的解析式是21(2)2y x =+(2)如图,P 为线段AB 上任意一点,连接PM ,过点P 作PD ⊥x 轴于点D设P 的坐标是(x ,122x -+),则在Rt △PDM 中,PM 2=DM 2+PD 2即 222215(2)(2)2824l x x x x =--+-+=++x 的取值范围是:-5<x <0(3)存在满足条件的点P连接AM,则题意得,AM === ①当PM =PA 时,2225128(22)42x x x x ++=+-+- 解得:x =-4,此时y =4∴点P 1(-4,4)②当PM =AM 时,225284x x ++= 解得:128,05x x =-=(舍去),此时1814()2255y =-⨯-+= ∴点P 2(85-,145)③当PA =AM 时,2221(22)2x x +-+-=解得:1255x x =-=(舍去)此时110(2255y =-⨯-+=∴点P 3()综上所述,满足条件的点为P 1(-4,4)、P 2(85-,145)、P 3().。
苏科版九年级下册数学 5.2 y=ax^2+k、y=a^2的图像(共19张PPT)

二次函数y=a(x + m)2( m<0)的图像是由二次函数 y=ax2的图像沿 x 轴向_右_平移|_m_|个单位长度得到的.
二次函数y=a(x+m)2 顶点坐标是_(-m,0)_ ,对称轴
是_过(_-m,0)与y轴平行的直线
.
1.将函数y=2x2-2的图像先向 上 平移 2 个单 位,就得到函数y = 2x2的图像,再向 右 平移 3 个
幻灯片 7
(2)描点、连线.
从对应点的位置看:函数y=x2+1的图像和y=
x2的图像的位置有什么关系?
y
10
(3)函数y=x2-2的图像和
9 8
y=x2的图像的位置有何关系?
7 6
5
4
3
2
1
-5 -4 -3 -2 -1 o 1 2 3 4 5 x
幻灯片 8
y
y=x2+1
8
6
4
2
y=x2
-10
-5
O
5
x 10
-2
y
8
6
4
y=x2
2
-10
-5
O
5
x 10
y=x2-2
-2
y 10
9 8 7 6 5 4 3 2 1
-5 -4 -3 -2 -1 o 1 2 3 4 5 x
2. y=-x2+3, y=-x2-2 与 y=-x2
又有什么关系呢? 画出草图,进行比较
函数y=-x2+3的图
象可由y=-x2的图
a>0
向上
(0 ,c)
y轴
当x<0时, y随着x的增大而减小。
当x>0时, y随着x的增大而增大。
新版苏科版九年级下5.2二次函数的图像和性质(3)导学案

6.2 二次函数的图像和性质(3)学生姓名:______ 班级:目标导航:1、能解释..二次函数222)(ax y m x a y k ax y =+=+=和二次函数、的图像的位置关系; 2、体会本节中图形的变化与图形上的点的坐标变化之间的关系(转化),感受形数结合的数学思想等。
学习重点与难点:对二次函数222)(ax y m x a y k ax y =+=+=和二次函数、的图像的位置关系解释和研究问题的数学方法的感受是学习重点;难点是对数学问题研究问题方法的感受和领悟。
学习过程: 一、知识准备本节课的学习的内容是课本P 12-P 14的内容,内容较长,课本上问题较多,需要你操作、观察、思考和概括,请你注意:学习时要圈、点、勾.....、画..,随时记录甚至批注课本,想想“那个人”是如何研究出来的。
你有何新的发现呢?二、问题导学:1.思考:二次函数12+=x y 的图象是个什么图形?是抛物线吗?为什么?(请你仔细看课本P12-P13,作出合理的解释)类似的:二次函数k ax y +=2的图象与函数2ax y =的图象有什么关系?它的对称轴、顶点、最值、增减性如何?()23+=x 的图象是抛物线吗?如果结合下表和看课本P13-P14你的解释是什么?x24类似的:二次函数()2m x a y +=的图象与二次函数2ax y =的图象有什么关系?它的对称轴、顶点呢?它的对称轴、顶点、最值、增减性如何呢 三、知识梳理1、二次函数222)(ax y m x a y k ax y =+=+=和二次函数、图像的形状,位置的关系是:2、它们的性质是:四、例题点评:例1: 函数y=4x 2+5的图象可由y=4x 2的图象向 平移 个单位得到; y=4x 2-11的图象可由 y=4x 2的图象向 平移 个单位得到。
五、当堂检测⒈将抛物线y=4x 2向上平移3个单位,所得的抛物线的函数式是 。
将抛物线y=-5x 2+1向下平移5个单位,所得的抛物线的函数式是 。
九年级数学下第五章二次函数5.2二次函数的图象与性质5.2.3二次函数y=ax2+bx+c(a≠0)

知2-讲
例2 [期末·南通] 关于抛物线y=-x2-2x-3,下列说法 中错误的是( C ) A. 开口向下 B. 对称轴是直线x=-1 C. 当x>-1 时,y随x的增大而增大 D. 顶点坐标为(-1,-2)
知2-讲
解题秘方:紧扣函数表达式中的系数和二次函数的性 质逐一判断各个选项中的说法是否正确
当x= -2ba 时,
4ac-b2
y最小值= 4a
当x= -2ba 时, y最大值= 4ac-b2
4a
活学巧记:
知2-讲
曲线名叫抛物线,线轴交点是顶点,顶点纵标是最值.
如果要画抛物线,描点平移两条路.
提取配方定顶点,平移描点皆成图.
列表描点后连线,五点大致定全图.
若要平移也不难,先画基础抛物线,
顶点移到新位置,开口大小都不变
a>0
a<0
开后方向
对称轴
向上
向下
对称轴 顶点坐标
增减性
最值
知2-讲
直线 x=-2ba
(-2ba,4ac4-a b2)
当x< -2ba 时,y 当x< -2ba 时,y 随 随x的增大而减小;x 的增大而增大; 当x> -2ba 时,y随 当x> -2ba 时,y 随 x的增大而增大 x的增大而减小
又∵
4ac-b2 4×(-1)×(-3)-(-2)2
4a =
4×(-1)
=-2,∴顶点坐
标是(-1,-2),故选项D 正确.
方法总结:
知2-讲
若不画图像直接得出函数图像的特征,则必须根据
函数图像的特征与二次函数表达式中系数之间的
关系来确定.对于抛物线y=ax2+bx+c,其中a决定
苏科版九年级下5.2二次函数的图象和性质(3)课件

平移规律:左加右减.
二次函数y=a(x+h)2(a≠0) 的性质
根据图形填表: 抛物线 顶点坐标 对称轴 位置 y=a(x+h)2 (a>0) (-h,0) 直线x=-h 在x轴的上方(除顶点外) 向上 y=a(x+h)2 (a<0) (-h,0) 直线x=-h 在x轴的下方( 除顶点外) 向下
y=ax2+c
a<0
在同一直角坐标系内画出下列函数的图象.
y=-x2
y=-(x+1)2 x=-1
y
1
y=-(x-1)2
x=1
1 2 3 4ቤተ መጻሕፍቲ ባይዱ5x
-4
-3
-2
-1
o
-1 -2
y=-(x-1)2
y=-(x+1)2
-3
-4
y=-x2
-5
抛物线
2 y=-(x+1) 是由抛物线
2 怎样移动得到 y=-x
的?抛物线 y=-(x-1)2 呢? y
(4)将二次函数y= -3(x-2)2的图像向左平移3个单位后得 到函数 的图像,其顶点坐标是 ,对称轴是 , 当x= 时,y有最 值,是 .
(5)将函数y=3(x-4)2的图象沿x轴翻折180°后得到的函数解 析式是 ;将函数y=3(x-4)2的图象沿y轴翻折180° 后得到的函数解析式是 . (6)把抛物线y=a(x-4)2向左平移6个单位长度后得到抛物线 y=- 3(x+h)2的图象,则a= ,h= .
开口方向
增减性 最值 开口大小
在对称轴的左侧,y随着x的增大而减小. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
《二次函数的图象与性质》二次函数PPT课件(第3课时)

13.抛物线y=a(x+2)2过点(1,-3). (1)求抛物线对应的函数表达式; (2)指出抛物线的对称轴、顶点坐标; (3)当x取何值时,y的值随x值的增大而减小?
解:(1)∵抛物线经过点(1,-3),∴-3=9a,a=-13. ∴抛物线的函数表达式为 y=-13(x+2)2. (2)对称轴为直线 x=-2,顶点坐标为(-2,0). (3)∵a=-13<0,∴当 x>-2 时,y 的值随 x 值的增大而减小.
15.如图,抛物线y=a(x-h)2+k与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为 C,对称轴为直线x=1.
(1)求抛物线对应的函数表达式; (2)M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标. 解:(1)抛物线对应的函数表达式为y=-(x-1)2+4. (2)①当MA=MB时,点M(0,0); ②当AB=AM时,点M(0,-3);
关系是 ( B )
A.y1>y2>y3 B.y2>y1>y3
C.y3>y1>y2 D.y3>y2>y1
【变式拓展】对于二次函数y=-
1 3
x2+2,当x为x1和x2时,对应的函数值分别为y1和y2.
假设x1>x2>0,那么y1和y2的大小关系是 ( B )
A.y1>y2 B.y1<y2
C.y1=y2 D.无法比较
《二次函数的图象与性 质》二次函数PPT课件(
第3课时)
第二章 二次函数
二次函数的图象与性质
第3课时
知识点1 二次函数y=a(x-h)2的图象与性质
1.对于函数y=-2(x-3)2,以下说法不正确的 ( D )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.2 二次函数的图像和性质(3)
教学目标1.会用描点法画函数y=ax2+k和函数y=a(x+m)2(a≠0)的图像;
2.能用平移变换解释二次函数y=ax2+k、y=a(x+m)2和二次函数y=ax2(a≠0)的位置关系;
3.能根据图像认识和理解二次函数y=ax2+k、y=a(x+m)2(a≠0)的性质;
4.体会数学研究问题由具体到抽象
.....、特殊到一般
.....的思想方法.
教学重点从“坐标的数值变化”与“图形的位置变化”的关系着手,探索二次函数y=ax2+k、y=a(x +m)2的图像和二次函数y=ax2的(a≠0)位置关系.
教学难点从二次函数y=ax2+k、y=a(x+m)2的图像和二次函数y=ax2(a≠0)的图像的异同从中体会它们之间的关系.
教学过程(教师)学生活动设计思路
回顾与猜想
你还记得二次函数y=x2的图像是怎样的吗?
那么y=x2+1的图像与y=x2的图像有什么关系?
回顾二次函数y=x2图像的性
质,为本节课学习打下基础.
新旧知识比
较,猜想激发学
生学习新知识的
欲望.
活动一:画图与观察
1.填表:画函数y=x2和y=x2+1的图像.
x …-3 -2 -1 0 1 2 y=x2…
y=x2+
1
…
2.画图:在平面直角坐标系中,描点并画出函数y=x2+1的图像和y=x2的图像;
3.观察:(1)从表格的数值看:相同的自变量所对应的两个函数的函数值有什么关系?
(2)从对应点的位置看:函数y=x2+1的图像和y=x2的图像的位置有什么关系?
(3)根据图像,你能得出函数y=x2+1的图像的性质吗?
4.猜想:函数y=x2-2的图像和y=x2的图像的位置有何关系?函数y=x2-2的图像有哪些性质?
按照列表、描点、连线的过程画
函数图像.
画图,观察、思考并交流提出的
问题.
学生经历列
表、描点、作图、
观察、比较、思
考的过程,引导
学生观察表中数
据的变化与点在
平面内位置的变
化的关系,进而
得到函数图像位
置的变化规律,
初步感受点坐标
的变化带来图形
位置的变化;新
问题y=ax2+k将
k的取值由1变为
-2,丰富了学生
对上下平移的认
识.
总结与归纳
思考:(1)由上面的例子,你发现函数y =ax2+k的图像与函数y=ax2(a≠0)的图像有什么关系?
(2)二次函数y=ax2+k(a≠0)有什么性质?
学生先交流、尝试概括,师生共
同总结出结论:
(1)函数y=ax2+k的图像可
以看成函数
y=ax2(a≠0)的图像上下平移得到,
当k>0时,向上平移k个单位,当k
<0时,向下平移-k个单位.
(2)函数y=ax2+k顶点坐标是
(0,k),对称轴是y轴.
通过学生相
互交流、补充,
逐步完善函数y
=ax2+k的性质,
函数的增减性、
开口方向和最大
(小)值要分
a>0和a<0来讨
论.
1 2 3 4 5 x
1
2
3
4
5
6
7
8
9
1
y
o
-
---
-
活动二:观察与思考 1.填表:画函数y =x 2和y =(x +3)2的图像.
x … -3 -2 -1 0 1 2 y =x 2
…
x … -6 -5 -4 -3 -2 -1 y =(x +3)2
…
2.画图:在平面直角坐标系中,描点并画出函数y =x 2
与函数y =(x +3)2
的图像;
3.观察:(1)从表格的数值看:函数y =(x +3)2
与函数
y =x 2的函数值相等时,它们所对应的自变量的值有什么关系?
(2)从对应点的位置看:函数y =(x +3)2
的图像与y =x 2
的图像的位置有什么关系? (3)根据图像,你能得出函数y =(x +3)2
图像的性质吗?
4.猜想:函数y =(x -1)2
的图像和y =x
2的图像的位置有何关系?函数y =(x -1)2
的图像有哪些性质?
按照列表、描点、连线的过程画
函数图像.
学生画图,观察、思考并交流提
出的问题. 与活动一类似:也按照四个层次组织活动二,将两个表格设计成“错位”的方式,引导学
生展开观察和思考活动,引导学生发现函数值相等的两个函数的自变量之间的关系,从中感受函数图像的“平移”关系;进一步感受在平面直角坐标系中,点坐标的变化与图形运动变化之间的关系.
x
y
O
总结与归纳
思考:(1)由上面的例子,函数y=a(x+m)2的图像与函数y=ax2(a≠0)的图像有什么关系?
(2)函数y=a(x+m)2有什么性质?
学生先交流、尝试概括,师生共
同总结出结论:
(1)函数y=a(x+m)2的图像
可以看成函数
y=ax2(a≠0)的图像左右平移得到,
当m>0时,向左平移m个单位,当
m<0时,向右平移-m个单位.
(2)函数y=a(x+m)2顶点坐标
是(-m,0),对称轴是过(-m,0)
且平行于y轴的直线.
通过学生相
互交流、补充,
逐步完善函数y
=a(x+m)2的性
质,函数的增减
性、开口方向和
最大(小)值要
分
a>0和a<0来讨
论,提倡利用图
像总结性质,突
出“数形结合”
的思想.
检验与反馈
课本练习:课本15页练习,20页习题5.2第4、5题;
补充练习:
1.将函数y=2x2-2的图像先向___平移
___个单位,
就得到函数y=2x2的图像,再向___平移___个单位得到函数
y=2(x-3)2的图像.
2.二次函数y=-3(x+4)2的图像开口_____,是由抛物线
y=-3x2向___平移___个单位得到的;对称轴是_________,当x=_____时,y有最______值,是______.
3.将二次函数y=6x2的图像向右平移1个单位后得到函数___________的图像,顶点坐标是_____,当x_______时,y随x的增大而增大;当x_______时,y随x的增大而减小.
学生在画图和练习中,进一步感
受二次函数
y=ax2+k、y=a(x+m)2和二次函数y
=ax2(a≠0)的位置关系.并学会用
图像来解决函数开口方向、最大(小)
值、对称轴、顶点坐标等问题,体会
数学结合思考问题的好处.
通过学生练
习,培养学生运
用知识的能力,
加深对知识的理
解,体会对“变
化与对应”和“数
形结合”等数学
思想的理解.
小结与反思
本节课我学会了哪些知识和方法?
我对所学知识还有什么疑惑之处?你认为还有继续探究的问题吗?
学生讨论,互相补充,师生共同
归纳.
促进学生学
会反思,总结知
识和方法,将新
知识纳入到自己
原有的知识体
系,学会自我建
构.
课后反思:。
