安徽省亳州市高二下学期数学3月月考试卷
安徽省亳州市涡阳县高二数学3月月考试题理

安徽省亳州市涡阳县2016-2017学年高二数学3月月考试题 理注意事项:1.本试题第I 卷(选择题)和第II 卷两部分,全卷共150分,时间120分钟.2.第I 卷必须使用2B 铅笔填涂答题卡相应题目的答案标号,修改时,要用橡皮擦干净. 3.第II 卷必须使用0.5毫米的黑色墨水签字笔书写在答题纸的指定位置,在草稿纸和本卷上答题无效.第I 卷(选择题)一.选择题(本大题共12小题,每小题5分,共60分.每小题只有1个答案正确)1.有一段“三段论”推理是这样的:对于可导函数()f x ,如果0()0f x '=,那么0x x =是函数()f x 的极值点,因为函数3()f x x =在0x =处的导数值(0)0f '=,所以,0x =是函数3()f x x =的极值点.以上推理中:( )A .大前提错误B .小前提错误C .推理形式错误D .结论正确2.用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,反设正确的是( ) A .假设三内角都不大于60度 B .假设三内角都大于60度C .假设三内角至多有一个大于60度D .假设三内角至多有两个大于60度3.某个命题与正整数有关,若当()*n k k N =∈时该命题成立,那么可推得当1n k =+时该命题也成立,现已知当5n =时该命题不成立,那么可推得( ) A.当6n =时,该命题不成立 B.当6n =时,该命题成立 C.当4n =时,该命题成立D.当4n =时,该命题不成立4.若()f x 在R 上可导,2()2()sin 22f x x f x x π'=++,则1()f x dx =⎰( )A.7cos 23π-- B. 111cos 262π-+ C.171cos 262π-- D. 111cos 262π-- 5.在平面几何中有如下结论:正三角形ABC 的内切圆面积为1S ,外接圆面积为2S ,则1214S S =,推广到空间中可以得到类似结论:已知正四面体P ABC -的内切球体积为1V ,外接球体积为2V ,则12V V =( )A.18B.19C.164D.1276.函数1sin y x x=-的图象大致是( )A.B.C.D.7.2222π=--⎰-dx x x m,则m 等于( )A .-1B .0C .1D .28.如右图是函数32()f x x bx cx d =+++的大致图象,则2212x x +等于( )A .23B .43C .83D .1239.正整数按右表的规律排列,则上起第2015行, 左起第2016列的数应为( ) A .22015 B .22016 C .20152016+D .20152016⨯10.设()f x 是定义在R 上的偶函数,当0x >时,()()0f x xf x '+>,且(1)0f =,则不等式()0xf x >的解集为( )A .(-1,0)∪(1,+∞)B .(-1,0)∪(0,1)C .(-∞,-1)∪(1,+∞)D .(-∞,-1)∪(0,1)11.若点P 是曲线2ln y x x =-上任意一点,则点P 到直线2y x =-的最小值为( )A .1BC.2D12.关于函数2()ln f x x x=+,下列说法错误的是( ) A.2x =是()f x 的极小值点B.函数()y f x x =-有且只有1个零点C.存在正实数k ,使得()f x kx >恒成立D.对任意两个正实数12,x x ,且21x x >,若12()()f x f x =,则124x x +>第II 卷(非选择题)二、填空题(本大题共4题,每题5分,共20分)13.设2()24ln f x x x x =--,则函数()f x 的单调递增区间是 . 14.如图,函数()()215g x f x x =+的图象在点P 处的切线方程是8y x =-+,则()()5'5f f += .15.已知函数()(]212,0,1f x ax x x=-∈.若函数()f x 在(]0,1上是增函数,则a 的取值范围是 .16.已知函数()f x 的定义域为[]5,1-,部分对应值如表,()f x 的导函数()y f x '=的图象如右图所示,下列关于()f x 的命题:①函数()y f x =是周期函数;②函数()y f x =在[]0,2上减函数; ③如果当[]1,x t ∈-时,()f x 的最大值是2,那么t 的最大值是4; ④当12a <<时,函数()y f x a =-有4个零点; ⑤函数()y f x a =-的零点个数可能为0,1,2,3,4. 其中正确命题的序号是 (写出所有正确命题的序号).三、解答题(本大题共6题,第17题10分,其余每题12分,共70分.解答题应写出文字说明、证明过程或演算步骤.)17.已知a b c >>,且0a b c ++=<.18.已知函数3()3f x x x =- (1)求函数()f x 的极值;(2)过点(2,6)P -作曲线()y f x =的切线,求此切线的方程.19.设函数21()2x x f x x e xe =+-. (1)求()f x 的单调区间;(2)若当[2,2]x ∈-时,不等式()f x m >恒成立,求实数m 的取值范围.20.已知数列{}n a 满足11n n a a +-=,11a =,试比较12321111na a a a ++++与*2()2n n N +∈的大小并证明.21.已知函数()ln a f x x x=-. (Ⅰ)若0a >,试判断()f x 在定义域内的单调性; (Ⅱ)若()f x 在[]1,e 上的最小值为32,求a 的值; (Ⅲ)若()2f x x <在()1,+∞上恒成立,求a 的取值范围.22.设函数()()1011ln <<--+-=a xaax x x f . (1)求函数()x f 的单调区间; (2)当31=a 时,设函数()9522--=bx x x g ,若对于[][],1,0,2,121∈∃∈∀x x 使()()21x g x f ≥成立,求实数b 的取值范围.。
安徽省高二下学期月考(3月)数学试题(解析版)

一、单选题1.已知函数在处可导,若,则=( ) ()f x 0x x =()()00Δ02Δ2Δlim 2Δx f x x f x x x→+--=0()f x 'A .1 B .C .2D .812【答案】B【分析】利用导数的定义求解. 【详解】. 0()f x '=()()()()0000Δ0Δ02Δ2Δ2Δ2Δ111lim lim 24Δ4Δ42x x f x x f x x f x x f x x xx →→+--+--==⨯=故选:B2.下列结论中正确的是( ) A .若,则πcos3y =1πsin 33y '=-B .若,则 sin(2)y x =()2cos 2y x ='C .若,则 ()ln 5y x =15y x'=D .若,则 2e x y =2e x y '=【答案】B【分析】运用求导法则求函数的导数.【详解】A :是常数,所以,不正确; π1cos 32=0y '=B :,正确; cos(2)(2)2cos 2y x x x =⋅=''C :,不正确; 11(5)5y x x x'='⋅=D :,不正确. 22e (2)2e x x y x '⋅='=故选:B3.在等比数列中,,则( ) {}n a 151,3a a ==3a =A .BC .D .3【答案】B【解析】由结合等比数列的通项公式求出,最后得出.151,3a a ==2q =3a【详解】设的公比为q ,则,所以,所以(如果利用等比{}n a 44513a a q q ===2q =231a a q ==中项性质求的话,要注意等比数列奇数项的保号性特点). 故选:B .4.若曲线在点(0,)处的切线方程为,则( ) 2y x ax b =++b 20x y ++=A ., B ., 1a =2b =1a =2b =-C ., D .,1a =-2b =1a =-2b =-【答案】D【分析】由可知切线的斜率为,所以切线方程为,又切线方程为2y x a '=+k a =()0y b a x -=-,比较系数可得a ,b 的值.20x y ++=【详解】因为,切点为(0,),2y x a '=+b 所以切线的斜率为,则切线方程为,即, 0|x k y a ='==y b ax -=y ax b =+又切线方程为,即, 20x y ++=2y x =--所以,. 1a =-2b =-故选:D5.要排一份有5个独唱节目和3个舞蹈节目的节目单,若任意两个舞蹈节目不排在一起,则不同的排法种数是( ) A . B . 3588A A 5355A A C . D .5356A A 5456A A 【答案】C【分析】运用插空法,先排5个独唱节目,再插入3个舞蹈节目,即可得结果. 【详解】三个舞蹈节目不排在一起,可先排独唱节目,有种排法,55A 将三舞蹈节目排在5个独唱节目间,即从6个空位中选3个空位插入舞蹈节目,有种排法, 36A 根据乘法原理,共有种不同的排法. 5356A A 故选:C 6.若函数在区间(,)内存在最小值,则实数的取值范围是( ) 3212()33f x x x =+-1a -5a +a A .[-5,1) B .(-5,1) C .[-2,1) D .(-2,1)【答案】C【分析】先求出函数的极值点,要使函数在区(,)内存在最小值,只需极小值点在该区间1a -5a +内,且在端点处的函数值不能超过极小值.【详解】由,令,可得或,2()2f x x x =+'()0f x '=2x =-0x =由得:或,由得:,()0f x '><2x -0x >()0f x '<20x -<<所以函数在上单调递增,在上单调递减,在上单调递增,()f x (,2)-∞-(2,0)-(0,)+∞所以函数在处取得极小值,0x =2(0)3f =-令,解得或, ()32122333f x x x =+-=-0x =3x =-若函数在(,)内存在最小值,则,得. ()f x 1a -5a +3105a a -≤-<<+21a -≤<故选:C7.一矩形地图被分割成了4块,小刚打算对该地图的4个区域涂色,每个区域涂一种颜色,相邻区域(有公共边)涂不同颜色.现有5种颜色可供选择(5种颜色不一定用完),则不同的涂色方法种数有( )A .180B .240C .80D .260【答案】D【分析】将图中的地图涂色,最少需要2种颜色,最多可用4种颜色,可对所用颜色的种数分类计数.【详解】四部分分别记为ABCD ,如图所示,由题意知给四部分涂色,至少要用两种颜色,故可分成三类涂色:第一类,用4种颜色涂色,有种方法.45A 120=第二类,用3种颜色涂色,选3种颜色的方法有种.在涂的过程中,选对顶的两部分(A 、C 或35C B 、D )涂同色,另两部分涂异色有种选法;3种颜色涂上去有种涂法,根据分步计数原理求12C 33A 得共种涂法.313523C C A 120⋅⋅=第三类,用两种颜色涂色.选颜色有种选法,A 、C 用一种颜色,B 、D 涂一种颜色,有种涂25C 22A 法,故共种涂法.2252C A 20⋅=∴共有涂色方法120+120+20=260种. 故选:D .8.如图,方格蜘蛛网是由一簇正方形环绕而成的图形.除最外边的正方形外,每个正方形的四个顶点都在其外接正方形的四边上,且将边长分为3:4两部分.现用13米长的铁丝材料制作一个方格蜘蛛网,若最外边正方形的边长为1米,并按由外到内的顺序制作,记由外到内第个正方形的n 边长为,则( )(参考数据:) n a 7lg0.155≈A .由外到内第二个正方形的周长为 57B .57nn a ⎛⎫= ⎪⎝⎭C .完整的正方形最多有7个D .完整的正方形最多有8个 【答案】C【分析】根据条件可得由外到内的正方形的边长依次构成等比数列,再根据等比数列求和公式得这些正方形的周长,列不等式,解得结果.【详解】记由外到内的第个正方形的边长为,则,,,…,n n a 11a =257a =2357a ⎛⎫= ⎪⎝⎭157n n a -⎛⎫= ⎪⎝⎭.这个正方形所用铁丝的总长为,n 2151555574141415777717nn n -⎛⎫- ⎪⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎝⎭++++=⨯=-⎢⎥⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦- 令≤,则≥,即≤14,51417n ⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦1357n ⎛⎫ ⎪⎝⎭11475n ⎛⎫ ⎪⎝⎭两边取对数,得≤,则≤,解得≤, 7lg5n 7lg141lg 5=+0.15n 1.15n 273即可制作完整的正方形的个数最多为7,所以C 正确,D 不正确. 而第二正方形的周长应为,,所以A ,B 均不正确.22047a =157n n a -⎛⎫= ⎪⎝⎭故选:C二、多选题9.在数列中,,,则( ){}n a 11a =11(1)n n a a n n +-=+A . B .374a =353=a C . D .121n a n =-+12n a n=-【答案】BD【分析】由递推公式、运用累加法可求出数列的通项公式. 【详解】由得:,,…,1111(1)1n n a a n n n n +-==-++1111n n a a n n--=--121121n n a a n n ---=---,,321123a a -=-21112a a -=-将各式相加得:,则,当时,. 111n a a n -=-12n a n =-3n =315233a =-=故选:BD10.已知定义在R 上的函数,其导函数的大致图象如图所示,则下列叙述错误的是()f x ()f x '( )A .()()()f c f b f a >>B .函数在处取得极小值,在处取得极大值 ()f x x c =x e =C .函数在处取得极大值,在处取得极小值 ()f x x c =x e =D .函数的最小值为 ()f x ()f d 【答案】BD【分析】观察导函数的图象,可得的零点,使中的区间,从而确定函()f x '()f x '()0f x '>()0f x '<数的极值点和单调区间,根据函数的单调性比较函数值的大小,通过分析可得函数极大值、极()f x 小值以及最值情况.【详解】由的图象可知,当时,,当时,,()f x '(,)(,)x c e ∈-∞⋃+∞()0f x '>(,)x c e ∈()0f x '<所以函数在上单调递增,在上单调递减,在上单调递增. ()f x (),c -∞(,)c e (,)e +∞对于A ,因为,所以,所以A 正确;a b c <<()()()f c f b f a >>对于B ,C ,由单调性可知:为极大值点,为极小值点,所以B 不正确,C 正确; c e 对于D ,由于,则,不是最小值,所以D 不正确. d (,)c e ∈()()()f c f d f e >>()f d 故选:BD .11.下列等式正确的有( )A .B .C C m n mn n -=111C C C m m m n n n -+-=-C . D .11C C m m n n m n --=122C C 2C C m m m m n n n n --+=++【答案】ACD【分析】利用组合数公式,进行逐项计算判断,也可以通过取特殊值排除错误答!C !()!mn n m n m =-案.【详解】,故A 正确;()()()!!C C !!!!n mmn n n n n m n n m n m m -===--+-令,,则,而,故B 不正确;5n =2m =25C 10=2212125151645C C C C 15411C -+--=-=-=≠,,所以()()()!!C !!1!!m n m n n m m n m m n m ⨯==---()()()()()111!!C 1!11!1!!m n n n n n m n m m n m --⨯-==---+--,C 正确.11C C m m n n m n --=12C 2C C m m m n n n--++=()()()()()!2!!!!1!1!2!2!n n n m n m m n m m n m ++---+--+()()()()()()()!122!2!1!2!!2!!2!n n m n m n n m m n m m m n m m n m m n m -+-+-+-=++-+-+-+()()()()()!12221!2!n n m n m n m m m m m n m ⎡⎤-+-++-++-⎣⎦=-+,故D 正确. ()()()()()()()22!32!122!C !2!!2!!2!m n n n n n n n n m n m m n m m n m ++++++====-+-+⎡⎤+-⎣⎦故选:ACD12.已知函数,函数,下列选项正确的是( )3e ,1()e ,1x x x x f x x x ⎧<⎪=⎨≥⎪⎩()()g x xf x =A .点是函数的零点;()0,0()f xB .,,使()10,1x ∃∈2(1,3)x ∃∈12()()f x f x >C .若关于的方程有一个根,则实数的取值范围是x ()20-=g x a a 222e e ,,e 82⎛⎫⎛⎫⋃+∞ ⎪ ⎪⎝⎭⎝⎭D .函数的值域为 ()f x )1e ,--+∞⎡⎣【答案】BD【分析】由函数零点的定义可判断A 不正确,根据函数的单调性,结合图像可判断B 与D 是()f x 否正确,根据函数的单调性与极值情况,结合图像可确定a 的取值范围,可判断选项C . ()g x 【详解】令,可得,是函数的零点,零点是实数0,不是点,A 错()0f x =0x =0x =()f x ()0,0误;因为,当时,,当时,,当时,24(1)e ,1()(3)e ,1x x x f x x x x ⎧+<⎪=≥'⎨-⎪⎩1x <-()0f x '<11x -<<()0f x '>13x <<,当时,,()0f x '<3x >()0f x '>所以在上单调递减,在上单调递增,在上单调递减,在上单调递()f x (),1-∞-()-11,13(,)()3,+∞增,且的极小值为和,且, ()f x 1(1)e f --=-3e (3)27f =(1)e f =当时,,当时,,如图,作出函数的图像,0x <()0f x <0x >()0f x >()f x观察图像可知,,,使,所以B 正确;()10,1x ∃∈2(1,3)x ∃∈12()()f x f x >函数的值域为,D 正确;()f x )1e ,--+∞⎡⎣对于C ,由,得,因为,则()20-=g x a ()2g x a =22e ,1()()e ,1x x x x g x xf x x x ⎧<⎪==⎨≥⎪⎩23(2)e ,1()(2)e ,1x xx x x g x x x x ⎧+<⎪=⎨-≥'⎪⎩,令,得或或,当变化时,,的变化情况,如下表()0g x '=2x =-0x =2x =x ()g x '()g xx(,2)-∞- 2- (2,0)-0 (0,1) 1(1,2) 2 (2,)+∞()g x '+ 0-+-+()g x 递增24e 递减 0 递增e 递减2e 4递增如图,当或或时,关于的方程有一个根,所以a 的取值范围是224e 2e 4a <<2a e >20a =x ()20-=g x a ,C 不正确.{}222e e ,,0e 82∞⎛⎫⎛⎫⋃+⋃ ⎪ ⎪⎝⎭⎝⎭故选:BD .三、填空题13.在等差数列中,若,,则数列的通项公式为____________. {}n a 513a =6818a a +={}n a 【答案】223n a n =-+【分析】利用等差数列基本量间的关系和性质,求得公差即可. 【详解】设的公差为,由,得, {}n a d 687218a a a +==79a =所以, 759132752a a d --===--所以,即. ()()551325n a a n d n =+-=--223n a n =-+故答案为:223n a n =-+14.从四棱锥的5个顶点中任选4个,以这4个点为顶点,可以组成________个四面体. 【答案】4【分析】从四棱锥的5个顶点中选出的4个点不共面时,可以组成四面体,用间接法.【详解】从四棱锥的5个顶点中选出的4个不同的点,有=5种取法, 45C 其中从底面四边形的四个顶点不能组成四面体, 故取出的四点能组成四面体的个数为5-1=4. 故答案为:415.若函数在上只有一个零点,则的取值范围是__________.()(1)e x f x x a =--(2,)-+∞a 【答案】{}23,1e ∞⎡⎫-+⋃-⎪⎢⎣⎭【分析】问题化为方程只有一个解,等价于的图象与直线只有一个(1)e x x a -=()(1)e x g x x =-y a =交点,结合函数图象可得的取值范围.a 【详解】由题意,方程在上只有一个解, (1)e x x a -=(2,)-+∞令,则,()(1)e x g x x =-()e x g x x '=当时,,当时,, (2,0)x ∈-()0g x '<,()0x ∈+∞()0g x '>即在上单调递减,在上单调递增, ()g x (2,0)-(0,)+∞所以,又,当趋向于时,趋向, min ()(0)1g x g ==-()232e g -=-x +∞()g x +∞当或时,与的图象只有一个交点,即在上只有一个零点, 23ea ≥-1a =-y a =()g x ()f x (2,)-+∞故的取值范围是.a {}23,1e ∞⎡⎫-+⋃-⎪⎢⎣⎭故答案为:{}23,1e ∞⎡⎫-+⋃-⎪⎢⎣⎭16.已知函数,若存在,使得成立,则ln (),()e x xf xg x x x-==12(0,),∈+∞∈R x x ()()12==f x g x k 下列命题正确的有___________. ①当时,0k >121x x +>②当时,0k >212e 2e xx <+<③当时,0k <121+<x x ④当时,的最小值为0k <21e k x x ⋅1e -【答案】①③④【分析】根据可求得在上单调递增,在上单调递减,则可画出的图像;()f x '()f x (0,e)(e,)+∞()f x 利用同构可知等价于,结合图像则可判断① ②③;当时,12()()f x g x k ==2211ln ln e e x x x k x ==0k <可得,,构造函数可判断④. 21e x x =1(0,1)x ∈【详解】解:①, 21ln ()(0)xf x x x -'=>令得,在上递增,且值域;()0f x '>0e x <<()f x (0,e)1(,)e-∞令得,在上递减,且值域;()0f x '<e x >()f x (e,)+∞1(0,e作图如下:当时,由知:若,使得,则, 0k >(1)=0f 1(0,)x ∃∈+∞1()f x k =11x >当时,若,使得,则, 0k <1(0,)x ∃∈+∞1()f x k =101x <<由得:, ()e x g x x -=1()e xxg x -'=令得,在上递增,且值域;()0g x '>1x <()g x (,1)-∞1(,e-∞令得,在上递减,且值域;()0g x '<1x >()g x (1,)+∞1(0,e作出图象如下:()g x当时,由知:若使得,则, 0k >(0)0g =2x ∃∈R 2()g x k =20x >当时, 若使得,则, 0k <2x ∃∈R 2()g x k =20x <∴当时,.故①正确.0k >121x x +>②当时,由得:,即, 0k >()()12==f x g x k 2121ln e x x x x -=2211ln ln e e x x x x =∴可看成的两零点, 21,e x x ln xk x=作出的图象如下: ln xy x=由图象易知:或均可趋向于,故②错误; 1x 2e x +∞③当时,由①的讨论知:,,0k <20x <101x <<.故③正确;121x x ∴+<④当时,此时,由②知:,0k <1(0,1)x ∈21e x x =,则, 21ln x x ∴=2111ln x x k x x ==∴要求的最小值即求的最小值即可, 21e kx x ⋅e k k 令,则,()e (0)k h k k k =<()e e (1)e k k k h k k k '=+=+令,解得:,易知为极小值点,故的最小值为.故④正确. e e 0k k k +=1k =-1k =-()h k 1(1)eh -=-故答案为:①③④.【点睛】关键点点睛:同构找到,通过与的图象及性质判断求解,在处理④时,21e x x =()f x ()g x 要注意消元思想的运用.四、解答题17.某传统文化学习小组有10名同学,其中男生5名,女生5名,现要从中选取4人参加学校举行的汇报展示活动.(1)如果4人中男生、女生各2人,有多少种选法? (2)如果男生甲与女生乙至少有一人参加,有多少种选法? 【答案】(1)100 (2)140【分析】(1)分两步完成,第一步先选2名男生;第二步再选2名女生,根据乘法原理求得结果;(2)先求出从10人中任选4人的方法数,再减去男生甲与女生乙都不参加的方法数,即得男生甲与女生乙至少有一个参加的选法种数.【详解】(1)第一步,从5名男生中选2人,有种选法;第二步,从5名女生中选2人,有25C 25C 种选法.根据分步乘法计数原理,共有种选法.2255C C 100=(2)从10人中选取4人,有种选法;男生甲与女生乙都不参加,有种选法.410C 48C 所以男生甲与女生乙至少有1人参加,共有种选法.44108C C 140-=18.某商场销售某种商品的经验表明,该商品每日的销售量y (单位:千克)与销售价格x (单位:元/千克)满足关系式其中3<x <6,a 为常数,已知销售价格为5元/千克时,()21063,ay x x =+--每日可售出该商品11千克. (1)求a 的值;(2)若该商品的成本为3元/千克,试确定销售价格x 的值,使商场每日销售该商品所获得的利润最大.【答案】(1)2a =(2)当销售价格时,商场每日销售该商品所获得的利润最大. 4x =【分析】(1)设,由题有,据此可得答案; ()f x =()21063ax x +--()511f =(2)设商场每日销售该商品所获得的利润为,则由题可得()g x ,后利用导数可得答案. ()32101507201078g x x x x =-+-【详解】(1)设, ()f x =()21063ax x +--则由题有:. ()5101122af a =+=⇒=(2)设商场每日销售该商品所获得的利润为,则由题可得:()g x ,()()()()()232321063101507201078g x f x x x x x x x =-=+--=-+-其中.则,36x <<()()()2303007203046g x x x x x '=-+=--得在上单调递增,在上单调递减, ()g x ()34,()4,6故当销售价格时,商场每日销售该商品所获得的利润最大. 4x =19.已知函数().2()ln f x ax x x =+-R a ∈(1)当时,求函数在区间上的最值;1a =()f x 1,13⎡⎤⎢⎥⎣⎦(2)若在定义域内仅有一个零点,求的取值范围. ()()g x f x x =-a 【答案】(1),; max ()2f x =()min 3ln24f x =+(2).(]1,02e ∞⎧⎫-⋃⎨⎬⎩⎭【分析】(1)求出函数的极值点,并求极值和端点处的函数值,可得函数最大值与最小值; (2)分离参数,构造函数,将问题转化为直线与函数的图象仅有一个交a 2ln ()x h x x=y a =()h x 点,求的取值范围.a 【详解】(1)当时,,则,1a =2()ln f x x x x =+-()()()211x x f x x-+'=当时,当时,11,32x ⎡⎫∈⎪⎢⎣⎭()0f x '<1,12x ⎛⎤∈ ⎥⎝⎦()0f x '>所以,在上单调递减,在上单调递增,则.()f x 11,32⎡⎫⎪⎢⎣⎭1,12⎛⎤⎥⎝⎦()min 13ln224f x f ⎛⎫==+ ⎪⎝⎭又,>,所以. 14ln 339f ⎛⎫=+ ⎪⎝⎭(1)2f =13f ⎛⎫⎪⎝⎭max ()(1)2f x f ==(2)由,得,令,则,()()0g x f x x =-=2ln x a x =2ln ()xh x x =212ln ()x h x x -'=令得,令得 ()0h x '>0x <<()0h x '<x >∴在上单调递增,在)上单调递减, ()h x +∞∴,当趋向于时,趋向,当趋向于时,趋向. max 1()e2h x h ==x 0()h x -∞x +∞()h x 0作出函数的图象和直线, 2ln ()x h x x=y a =如图示,在定义域内有且仅有一个零点,即和有且只有一个交点, ()g x 2ln ()x h x x =y a=由图象知,的取值范围是.a (]1,02e ∞⎧⎫-⋃⎨⎬⎩⎭20.已知数列的前项和为,若对任意,都有.{}n a n n S *N n ∈23()n n S a n =-(1)求证:数列为等比数列;32n a ⎧⎫+⎨⎬⎩⎭(2)记,数列的前项和为,求证:<1.213n n n n b a a ++={}n b n n T n T 【答案】(1)证明见解析 (2)证明见解析【分析】(1)利用得,得,依据等比1n n n a S S -=-123()3(1)n n n a a n a n -=---+133322n n a a -⎛⎫+=+ ⎪⎝⎭数列的定义进行证明;(2)运用裂项相消法求,即可证明. n T 1n T <【详解】(1)证明:由, 23()n n S a n =-当时,,解得, 1n =1123(1)a a =-13a =当时,,2n ≥1123(1)n n S a n --=-+则, 11122()3()3(1)333n n n n n n n a S S a n a n a a ---=-=---+=--即,所以,, 133n n a a -=+133322n n a a -⎛⎫+=+ ⎪⎝⎭又因为,所以数列是首项为,公比为3的等比数列.133930222a +=+=≠32n a ⎧⎫+⎨⎬⎩⎭92(2)证明:由(1)可知,,所以,139322n n a -+=⨯3(31)2n n a =-则22111133431129(31)(31)3131(31)(31)4n n n n n n n n n n n n b a a ++++++⨯⎛⎫====- ⎪----⎝⎭--所以 22311111112313131313131n n n T +⎡⎤⎛⎫⎛⎫⎛⎫=-+-++-⎪ ⎪ ⎪⎢⎥------⎝⎭⎝⎭⎝⎭⎣⎦ .111122123131n n ++⎛⎫=-=- ⎪--⎝⎭由,有,则,即.*n ∈N 1310n +->121131n +-<-1n T <21.已知函数(为自然对数的底数).21()e xax x f x +-=e (1)若是函数的极值点,求的值; 3x =()f x a (2)若,讨论的单调性.0a ≥()f x 【答案】(1);13a =-(2)答案见解析.【分析】(1)可导函数在极值点处的导数为0,求得a 的值后,再进行检验; (2)分和两种情况进行讨论,根据符号,研究的单调性.0a =0a >()f x '()f x 【详解】(1), 2(21)2(1)(2)()e e x x ax a x ax x f x -+-++-=-'=因为是函数的极值点,所以,3x =()f x (3)0f '=即,解得,()()31320a -+-=13a =-经检验,符合题意,故.13a =-13a =-(2)由(1),,若,则,(1)(2)()e xax x f x +-'=-0a =2()e x xf x -=-'当时,当时,2x <()0f x '>2x >()0f x '<所以在上单调递增,在上单调递减; ()f x (,2)-∞(2,)+∞若,令,解得或,且,0a >()0f x '=1x a=-2x =12a -<当时,当或时,12x a-<<()0f x '>1x a <-2x >()0f x '<所以在上单调递减,在上单调递增,在上单调递减.()f x 1,a ⎛⎫-∞- ⎪⎝⎭1,2a ⎛⎫- ⎪⎝⎭()2,+∞22.设函数,为的导函数.()e kx f x x a =+()f x '()f x (1)当时,若存在实数,使得不等式成立,求实数的取值范围; 1k =-0x >()ln f x x x ≥-a (2)当时,设,若,其中,证明:. 1k =()()g x f x '=12()()g x g x =12x x ≠124x x >【答案】(1)11,e ⎡⎫-+∞⎪⎢⎣⎭(2)证明见解析【分析】(1)当时,存在实数,使得不等式成立,等价于:存在实数1k =-0x >()ln f x x x ≥-,使得不等式成立,构造函数,则等价于,利用0x >ln e x x a x x ≥--()ln e xxx x x φ=--min ()a x φ≥导数求出即可;min ()x φ(2)当时,,则,由此可得函数有极小值点,由函1k =()(1)e x g x x =+()(2)e x g x x '=+()g x 2x =-数单调性可判断在极值点的两侧,不妨假设,则,利用分析法得,()g x 12,x x 12x x <1221x x <-<<-要证明,只需证明,于是构造函数(),利用124x x >224()g x g x ⎛⎫> ⎪⎝⎭4()()h x g x g x ⎛⎫=- ⎪⎝⎭2<<1x --导数证明在上恒成立即可得证.()0h x >()2,1--【详解】(1)当时,存在实数,使得不等式成立, 1k =-0x >()ln f x x x ≥-等价于:存在实数,使得不等式成立, 0x >ln e xxa x x ≥--设, ()()ln 0e xxx x x x φ=-->,当时,,1111()1(1)e ex xx x x x x φ-⎛⎫'=--=-+ ⎪⎝⎭0x >110e x x +>所以当时,,当时,, 01x <<()0x φ'<1x >()0x φ'>所以在上单调递减,在上单调递增,()x φ()0,1()1,+∞所以,所以,()()min 111e x φφ==-11e a ≥-即实数的取值范围为;a 11,e ⎡⎫-+∞⎪⎢⎣⎭(2)当时,,所以,, 1k =()e x f x x a =+()()(1)e x g x f x x '==+()(2)e x g x x '=+当时,,当时,,<2x -()0g x '<2x >-()0g x '>所以在上单调递减,在上单调递增, ()g x (),2-∞-()2,-+∞所以, ()()2min 120e g x g =-=-<且当时,,当时,, 1x <-()0g x <1x >-()0g x >不妨设,则, 12x x <1221x x <-<<-于是要证明,只需证, 124x x >1242x x <<-因为在上单调递减,故只需证,()g x (),2-∞-124()g x g x ⎛⎫> ⎪⎝⎭又,所以只需证,, 12()()g x g x =224()g x g x ⎛⎫> ⎪⎝⎭221x -<<-设,,4()()h x g x g x ⎛⎫=- ⎪⎝⎭2<<1x --则, 4443233448(2)2()()(2)e e e (e 8)x x x xx x x h x g x g x x x x x x -++⎛⎫'''=+=++=+ ⎪⎝⎭设,,则,43()e8x xF x x -=+2<<1x --2437()e24x xF x x x -⎡⎤⎛⎫'=++⎢⎥ ⎪⎝⎭⎢⎥⎣⎦当时,,, 2<<1x --4e0x x->237024x ⎛⎫++> ⎪⎝⎭所以,在单调递减,所以,()0F x '<()F x ()2,1--()()20F x F <-=又,所以, 43(2)e 0x x x +<()0h x '>所以在单调递增, ()h x ()2,1--所以,()(2)(2)(2)0h x h g g >-=---=即在上恒成立,4()g x g x ⎛⎫> ⎪⎝⎭()2,1--又,所以成立,2(2,1)x ∈--224()g x g x ⎛⎫> ⎪⎝⎭所以.124x x >【点睛】方法点睛:利用导数证明不等式常见类型及解题策略:(1)构造差函数,根据差函数导函数符号,确定差函数单调性,利用单调性得()()()h x f x g x =-不等量关系,进而证明不等式;(2)根据条件,寻找目标函数,一般思路为利用条件将求和问题转化为对应项之间大小关系,或利用放缩、等量代换将多元函数转化为一元函数.。
2023-2024学年安徽省亳州市高二下学期第一次月考数学质量检测模拟试题(含解析)

2023-2024学年安徽省亳州市高二下册第一次月考数学试题一、单选题1.函数443y x x =-+在区间[2,3]-上的最小值为A .72B .36C .12D .0【正确答案】D【分析】先根据给出的函数求出导函数;再令0'>y ,求出单调递增区间,再令0'<y ,求出单调递减区间,确定出函数[2,3]-上的单调性,从而求出最小值.【详解】解:344y x '=-,令0y '=,即3440x -=解得1x =当1x <时,0'<y 当1x >时,0'>y ∴1|0x y y ===极小值,而端点的函数值2|27x y =-=,3|72x y ==,得min 0y =.故选D.本题主要考查了利用导数求函数的最值,关键是确定函数在区间上的单调区间,进而确定最值.2.已知函数()f x 定义域为R ,其导函数为()f x ¢,且()()30f x f x '->在R 上恒成立,则下列不等式定成立的是()A .()()310f e f <B .()()210f e f <C .()()310f e f >D .()()210f e f >【正确答案】A 构造函数()()3xf xg x e=,由()()30f x f x '->得()0g x ¢>,进而判断函数()g x 的单调性,判断各选项不等式.【详解】()()3x f x g x e =,则()()()()()()3323333x x xx f x e f x e f x f x g x e e ⋅--==''',因为()()30f x f x '->在R 上恒成立,所以()0g x ¢<在R 上恒成立,故()g x 在R 上单调递减,所以()()10g g <,即()()3010f f e e<,即()()310f e f <,故选:A.函数的单调性是函数的重要性质之一,它的应用贯穿于整个高中数学的教学之中.某些数学问题从表面上看似乎与函数的单调性无关,但如果我们能挖掘其内在联系,抓住其本质,那么运用函数的单调性解题,能起到化难为易、化繁为简的作用.因此对函数的单调性进行全面、准确的认识,并掌握好使用的技巧和方法,这是非常必要的.根据题目的特点,构造一个适当的函数,利用它的单调性进行解题,是一种常用技巧.许多问题,如果运用这种思想去解决,往往能获得简洁明快的思路,有着非凡的功效.3.已知函数f (x ),g (x )均为[a ,b ]上的可导函数,在[a ,b ]上连续且f ′(x )<g ′(x ),则f (x )-g (x )的最大值为()A .f (a )-g (a )B .f (b )-g (b )C .f (a )-g (b )D .f (b )-g (a )【正确答案】A【分析】求导,借助单调性研究最大值即可【详解】令F (x )=f (x )-g (x ),∵f ′(x )<g ′(x ),∴F ′(x )=f ′(x )-g ′(x )<0,∴F (x )在[a ,b ]上单调递减,∴F (x )max =F (a )=f (a )-g (a ).故选:A4.若函数1111πsin20,22y x x ⎛⎫⎡⎤=+∈ ⎪⎢⎥⎣⎦⎝⎭,函数223y x =+,则()()221212x x y y -+-的最小值为()A BC .2⎝⎭D .2(π15)72-【正确答案】Dy 1上与直线y 2平行的切线的切点到直线y 2的距离.【详解】由题可得112cos 2y x '=,令11y '=,则11cos22x =,得1π6x =或5π6(舍去),所以1y =223y x =+平行切线对应切点为π1,62⎛⎫ ⎪ ⎪⎝⎭.则切点到直线2y=又()()221212x x y y -+-最小值为切点π6⎛ ⎝⎭到直线2y 的距离的平方,所以()()221212x x y y -+-故选:D.5.若函数()y f x =满足()()xf x f x '>-在R 上恒成立,且a b >,则()A .()()af b bf a >B .()()af a bf b >C .()()af a bf b <D .()()af b bf a <【正确答案】B【分析】构造函数()()g x xf x =,根据导数确定函数单调性,进而判断各选项.【详解】由()()xf x f x '>-,设()()g x xf x =,则()()()0g x xf x f x ''=+>,所以()g x 在R 上是增函数,又a b >,所以()()g a g b >,即()()af a bf b >,故选:B.6.已知函数()sin(2)12f x x π=+,()f x '是()f x 的导函数,则函数2()()y f x f x '=+的一个单调递减区间是()A .7[,1212ππB .5[,]1212ππ-C .2[,]33ππ-D .5[,]66ππ-【正确答案】A【分析】由题意,根据三角函数的求导公式以及辅助角公式,整理单角三角函数,根据正弦型函数的单调性,可得答案.【详解】()()22sin 22cos 2212123y f x f x x x x πππ⎛⎫⎛⎫⎛⎫=+=+++=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭',令()3222,Z 232k x k k πππππ+≤+≤+∈,得:()7,Z 1212k x k k ππππ+≤≤+∈,∴单调递减区间为7,1212ππ⎡⎤⎢⎥⎣⎦故选:A.7.若函数()312f x x x =-在区间()1,1k k -+上不单调,则实数k 的取值范围是()A .(][][),31,13,-∞-⋃-⋃+∞B .()()3,11,3--⋃C .()2,2-D .不存在这样的实数k【正确答案】B【分析】利用导数与函数单调性的关系以及一元二次方程的根进行求解.【详解】由题意得,()23120x x f '=-=在区间()1,1k k -+上至少有一个实数根,又()23120x x f '=-=的根为2±,且()f x '在2x =或2x =-两侧异号,而区间()1,1k k -+的区间长度为2,故只有2或-2在区间()1,1k k -+内,∴121k k -<<+或121k k -<-<+,∴13k <<或31k -<<-,故A ,C ,D 错误.故选:B.8.已知函数()f x 的导函数()f x '满足22()()()f x xf x x x R >'+∈,则对x ∀∈R 都有A .2()0x f x ≥B .2()0x f x ≤C .2[()1]0x f x -≥D .2[()1]0x f x -≤【正确答案】A【详解】构造函数F (x )=x 2f (x ),则F ′(x )=2xf (x )+x 2f ′(x )=x (2f (x )+xf ′(x ),当x >0时,F ′(x )>x 3>0,F (x )递增;当x <0时,F ′(x )<x 3<0,F (x )递减,所以F (x )=x 2f (x )在x =0时取最小值,从而F (x )=x 2f (x )⩾F (0)=0,故选A.二、多选题9.给出定义:若函数()f x 在D 上可导,即()f x '存在,且导函数()f x '在D 上也可导,则称()f x 在D 上存在二阶导函数,记()()()f x f x ''''=,若()0f x ''<在D 上恒成立,则称()f x 在D 上为凸函数,以下四个函数在0,2π⎛⎫⎪⎝⎭上是凸函数的是()A .()sin cos f x x x=+B .()ln 2f x x x=-C .()321f x x x =-+-D .()xf x xe-=-【正确答案】ABC【分析】利用凸函数的定义逐个分析判断即可【详解】解:对于A ,由()sin cos f x x x =+,得()'cos sin f x x x =-,则()f x ''sin cos (sin cos )x x x x =--=-+,因为0,2x π⎛⎫∈ ⎪⎝⎭,所以()f x ''sin cos (sin cos )0x x x x =--=-+<,所以此函数是凸函数,所以A 正确;对于B ,由()ln 2f x x x =-,得()'12f x x =-,则()f x ''21x =-,因为0,2x π⎛⎫∈ ⎪⎝⎭,所以()f x ''210x =-<,所以此函数是凸函数,所以B 正确;对于C ,由()321f x x x =-+-,得()2'32f x x =-+,则()f x ''6x =-,因为0,2x π⎛⎫∈ ⎪⎝⎭,所以()f x ''60x =-<,所以此函数是凸函数,所以C 正确;对于D ,由()x f x xe -=-,得()'x xf x e xe --+=-,则()f x ''(2)x x x x e e e x x e ----=-=+-,因为0,2x π⎛⎫∈ ⎪⎝⎭,所以()f x ''(2)0x x e -=->,所以此函数不是凸函数,所以D 不合题意,故选:ABC10.如图是函数()y f x =的导函数()f x '的图像,则下列判断正确的是()A .在区间()2,1-上,()f x 单调递增B .在区间()1,2上,()f x 单调递增C .在区间()4,5上,()f x 单调递增D .在区间()3,2--上,()f x 单调递增【正确答案】BC【分析】当()0f x ¢>,则()f x 单调递增,当()0f x '<,则()f x 单调递减,据此可得答案.【详解】由题图知当()()1245,,,x x ∈∈时,()0f x ¢>,所以在区间()()1245,,,上,()f x 单调递增,BC 正确;当()2,1x ∈--时,()0f x '<,当()1,1x ∈-时,()0f x ¢>,所以在区间()2,1--上,()f x 单调递减.在()1,1-上递增,A 错误;当()3,2x ∈--时,()0f x '<,所以在区间()3,2--上,()f x 单调递减,D 错误;故选:BC11.设函数()f x 的定义域为R ,则下列命题中正确的有()A .若存在常数M ,使得对任意x ∈R ,有()f x M ≤,则M 是函数()f x 的最大值B .若存在0x ∈R ,使得对任意x ∈R ,且0x x ≠,有()()0f x f x ≤,则()0f x 是函数()f x 最大值C .若存在0x ∈R ,使得对任意x ∈R ,有()()0f x f x ≤,则()0f x 是函数()f x 的最大值D .若()21f x +的最大值为2,则()41f x -的最大值也为2【正确答案】BCD【分析】由最大值的定义可判断A 、B 、C ;由()21f x +的最大值为2,可知对任意的实数x 恒有01(41)2412x f x f +⎛⎫-≤=⨯- ⎪⎝⎭,可判断D.【详解】由最大值的定义可知,仅满足对任意的意x ∈R ,有()f x M ≤,还不能确定M 是()f x 的最大值,这是因为还必须在定义域中存在0x 使()0f x M =,才能说明M 是()f x 的最大值,故A 错误.由函数最大值的定义可知B ,C 正确.在D 中,由于()21f x +的最大值为2,所以存在0x 使得()0212f x +=,且对任意的x ∈R 有()212f x +≤.故对任意的实数x 恒有01(41)2412x f x f +⎛⎫-≤=⨯- ⎪⎝⎭,所以()41f x -的最大值也为2,D 正确.故选:BCD.12.若存在过点()0,0O 的直线l 与曲线()3232f x x x x =-+和2y x a =+都相切,则a 的值可以是()A .1B .164C .132D .164-【正确答案】AB【分析】根据题意,分点O 是切点与点O 不是切点,两种情况讨论,然后结合切线方程的求解方法,得到相应的切线方程,从而得到a 的值.【详解】由题意可得,()2362f x x x '=-+,因为()0,0在直线l 上,当()0,0O 为()f x 的切点时,则()02f '=,所以直线l 的方程为2y x =,又直线l 与2y x a =+相切,所以220x a x +-=满足440a ∆=-=,得1a =;当()0,0O 不是()f x 的切点时,设切点为()()3200000,320x x x x x-+≠,则()2000362f x x x =-+',所以32200000032362x x x x x x -+=-+,得032x =,所以3124f ⎛⎫=- ⎪⎝⎭,所以直线l 的方程为14y x =-.由214y x y x a⎧=-⎪⎨⎪=+⎩,得2104x x a ++=,由题意得1Δ4016a =-=,所以164a =.综上得1a =或164a =.故选:AB三、填空题13.函数221f x x ax =++()在[0]1,上的最小值为1f (),则a 的取值范围为__________.【正确答案】,1]∞--(【分析】求导,根据函数在[0]1,上的最小值为1f ()即可判断函数的单调性,将恒成立转化为函数最值问题求解.【详解】22f x x a '=+(),f x ()在[0]1,上的最小值为1f (),说明f x ()在[0]1,上单调递减,所以当]1[0x ∈,时,0f x '≤()恒成立,即220.x a +≤所以.a x ≤-所以 1.a ≤-故,1]∞--(14.已知函数241e ln(25)2x y x +=-+,则该函数的图象在2x =-处的切线的倾斜角为__________.【正确答案】3π4【分析】对函数求导数,计算2x =-时的斜率,得倾斜角.【详解】因为()241e ln 252x y x +=-+,所以2424112e e 2222525x x y x x ++=⨯-⨯=-++',所以2121x y =-=-'=-∣,即切线的斜率为-1,倾斜角为3π4.故答案为.3π415.已知f (x )=2x 3﹣6x 2+m (m 为常数),在[﹣2,2]上有最大值3,那么此函数在[﹣2,2]上的最小值为.【正确答案】﹣37【详解】试题分析:本题是典型的利用函数的导数求最值的问题,只需要利用已知函数的最大值为3,进而求出常数m 的值,即可求出函数的最小值.解:由已知,f′(x )=6x 2﹣12x ,有6x 2﹣12x≥0得x≥2或x≤0,因此当x ∈[2,+∞),(﹣∞,0]时f (x )为增函数,在x ∈[0,2]时f (x )为减函数,又因为x ∈[﹣2,2],所以得当x ∈[﹣2,0]时f (x )为增函数,在x ∈[0,2]时f (x )为减函数,所以f (x )max =f (0)=m=3,故有f (x )=2x 3﹣6x 2+3所以f (﹣2)=﹣37,f (2)=﹣5因为f (﹣2)=﹣37<f (2)=﹣5,所以函数f (x )的最小值为f (﹣2)=﹣37.﹣37利用导数求闭区间上函数的最值.16.已知函数3213221(0)()3236(0)x x x m x f x x m x ⎧+++-≤⎪=⎨⎪+->⎩,若函数()f x 有四个不同的零点,则m 的取值范围为______【正确答案】511(,612【分析】先利用导数求出0x 时,函数()f x 的单调性及极值,再结合题意,建立关于m 的不等式组,解不等式组即可得出答案.【详解】当0x 时,2()32(1)(2)f x x x x x '=++=++,故函数()f x 在(,2)-∞-,(1,0)-单调递增,在(2,1)--单调递减,∴当0x 时,()5()223f x f m =-=-极大值,()11()126f x f m =-=-极小值,(0)21f m =-,由于3213()22132f x x x x m =+++-最多有3个零点,()36f x x m =+-最多只有一个零点,故要使函数()f x 有四个不同的零点,则需520311206210360m m m m ⎧->⎪⎪⎪-<⎨⎪->⎪⎪-<⎩,解得511612m <<.故511(,612.本题考查函数零点与方程根的关系,考查利用导数研究函数的极值及最值,考查推理能力及计算能力,属于中档题.四、解答题17.已知函数21()ln(1)2f x x x x =+-+,求证:当0x >时,()0f x >.【正确答案】证明见解析【分析】利用导数,求函数单调性,证明不等式.【详解】证明:21()ln(1)2f x x x x =+-+,函数定义域为()1,-+∞,21()111x f x x x x'=-+=++,当()1,x ∈-+∞时,()0f x '>,∴()f x 在()1,-+∞上是增函数.于是当0x >时,()()00f x f >=.18.如图是函数()y f x =在区间[,]a b 上的图象,写出函数的极大值、极小值、最大值和最小值.【正确答案】极小值为()()13,f x f x ,极大值为()2f x ;最小值是()3f x ,最大值为()f b .利用函数的极值和最值的定义,结合题中图象即得结果.【详解】由题图可知,()y f x =在13,x x 处取极小值,在2x 处取极大值,所以极小值为()()13,f x f x ,极大值为()2f x ;比较极值和端点值可知函数的最小值是()3f x ,最大值在b 处取得,最大值为()f b .19.设函数()()32143x f x a x ax b =-+++,其中a ,b ∈R .(1)若函数()f x 在3x =处取得极小值12,求a ,b 的值;(2)求函数()f x 的单调递增区间;(3)若函数()f x 在(1,1)-上只有一个极值点,求实数a 的取值范围.【正确答案】(1)32a =;4b =-(2)见解析;(3)11,22⎛⎫- ⎪⎝⎭.【分析】(1)首先对函数求导,根据题意,得到()30f '=,()132f =,得到,a b 所满足的等量关系,求得结果;(2)对函数求导,并进行因式分解得到()()()()221422f x x a x a x a x '=-++=--,比较2a 和2的大小,从而进行分类讨论,进而确定函数的单调区间;(3)函数()f x 在(1,1)-上只有一个极值点,等价于'()0f x =在(1,1)-上只有一个解,结合(2)及零点存在性定理可得()()1,110a f f <⎧⎨-⋅<''⎩,从而求得a 的范围.【详解】(1)因为()()2214f x x a x a '=-++,所以()()396140f a a '=-++=,得32a =.由()15313279433222f b =⨯-⨯+⨯⨯+=,解得4b =-.(2)因为()()()()221422f x x a x a x a x '=-++=--,令()0f x '=,得2x a =或2x =.当1a >时,()f x 的单调递增区间为()(),2,2,a ∞-+∞;当1a =时,()f x 的单调递增区间为(),-∞+∞;当1a <时,()f x 的单调递增区间为()(),2,2,a -∞+∞.(3)由题意可得()()1,110a f f <⎧⎨-⋅<''⎩,即13(12)(1)(12)0a a a <⎧⎨---⋅--<⎩,化简得1(21)(21)0a a a <⎧⎨+-<⎩,解得1122a -<<,所以a 的取值范围是11,22⎛⎫- ⎪⎝⎭.该题考查的是有关函数与导数的问题,涉及到的知识点有利用导数求函数的极值,利用导数确定函数的单调区间,理解函数的极值的定义是解题的关键,属于中档题目.20.已知函数31()3()3f x x xf a =+'(其中R a ∈),且7()6f a =,求:(1)f (x )的表达式;(2)曲线y =f (x )在x =a 处的切线方程.【正确答案】(1)()31332f x x x=-(2)3640x y +-=【分析】(1)运用导数运算公式解得()22a f a '=-,再根据已知条件解得a 的值即可.(2)由(1)可解得切点及切线斜率,再运用点斜式方程写出切线方程即可.【详解】(1)()()23f x x f a =+'',于是有()()()2232a f a a f a f a =+⇒=-''',所以()231332a f x x x =-,又()76f a =,即331371326a a a -=⇒=-,()31332f x x x =-.(2)由(1)知,1a =-,所以137(1)326f -=-+=,所以切点为71,6⎛⎫- ⎪⎝⎭,切线的斜率()12f a '=-,所以切线方程为()71162y x -=-+,即3640x y +-=.21.已知函数2()(2)ln ()f x x a x a x a R =---∈.(1)求函数()y f x =的单调区间;(2)当1a =时,证明:对任意的0x >,2()2x f x x x +>++e .【正确答案】(1)见解析(2)见解析【分析】(1)利用导数求单调区间;(2)将不等式等价转化为e ln 20x x -->,利用导数讨论最值即可求解.【详解】(1)由题可知函数()f x 的定义域为(0,)+∞,22(2)()2(2)a x a x af x x a x x---'=---=,即(1)(2)()x x a f x x+-'=,(i)若0a ≤,则()0f x '>在定义域(0,)+∞上恒成立,此时函数()f x 在(0,)+∞上单调递增;(ii)若0a >,令()0f x '>,即20x a ->,解得2a x >,令()0f x '<,即20x a -<,解得02a x <<,所以()f x 在(0,)2a上单调递减,(,)2a +∞上单调递增.综上,0a ≤时,()f x 在(0,)+∞上单调递增;0a >时,()f x 在(0,)2a上单调递减,(,)2a +∞上单调递增.(2)当1a =时,2()ln f x x x x =+-,要证明2()2x f x x x +>++e ,只用证明e ln 20x x -->,令g()=e ln 2x x x --,1()=e xg x x'-,令1()=e xg x x '-,即1e xx=,可得方程有唯一解设为0x ,且01x ≠,所以001e xx =,当x 变化时,()g x '与g()x 的变化情况如下,x0(0,)x 0x 0(,+)x ∞()g x '-+g()x 单调递减单调递增所以0min 00001()()e ln 22xg x g x x x x ==--=+-,因为001220x x +-≥-=,因为01x ≠,所以不取等号,即00120x x +->,即min ()0g x >恒成立,所以,e ln 20x x -->恒成立,得证.22.已知函数()ln xf x x=,()(1)g x k x =-.(1)证明:R k ∀∈,直线()y g x =都不是曲线()y f x =的切线;(2)若2e,e x ⎡⎤∃∈⎣⎦,使1()()+2f xg x ≤成立,求实数k 的取值范围.【正确答案】(1)证明见解析;(2)实数k 的取值范围为1,2⎡⎫+∞⎪⎢⎣⎭.【分析】(1)若直线()y g x =与曲线()y f x =相切,设切点000,ln x x x ⎛⎫⎪⎝⎭则可得00ln 10x x +-=化简可得01x =,与已知矛盾,完成证明.(2)()()12f x g x ≤+可转化为()11ln 2x k x x --≤,令()()1ln x x k x x ϕ=--,2e,e x ⎡⎤∈⎣⎦,()min12x ϕ≤,分类讨论求()x ϕ的最小值即可.【详解】(1)()f x 的定义域为()()0,11,+∞ ,()()2ln 1ln x f x x -'=,直线()y g x =过定点()1,0,若直线()y g x =与曲线()y f x =相切于点000,ln xx x ⎛⎫⎪⎝⎭(00x >且01x ≠),则()000200ln 1ln 1ln x x x k x x -==-,即00ln 10x x +-=①,设()ln 1h x x x =+-,()0,x ∈+∞,则()110h x x+'=>,所以()h x 在()0,∞+上单调递增,又()10h =,从而当且仅当01x =时,①成立,这与01x ≠矛盾.所以,R k ∀∈,直线()y g x =都不是曲线()y f x =的切线;(2)()()12f x g x ≤+即()11ln 2x k x x --≤,令()()1ln x x k x x ϕ=--,2e,e x ⎡⎤∈⎣⎦,则2e,e x ⎡⎤∃∈⎣⎦,使()()12f xg x ≤+成立()min 12x ϕ⇔≤,()()222ln 111111ln ln ln 24ln x x k k k x x x x ϕ-⎛⎫⎛⎫=-=-+-=--+- ⎪ ⎪⎝⎭⎝⎭'.(i )当14k ≥时,()0'ϕ≤x ,()x ϕ在2e,e ⎡⎤⎣⎦上为减函数,于是()()()222min e e 12e x k ϕϕ==--,由()22e 1e 122k --≤得12k ≥,满足14k ≥,所以12k ≥符合题意;(ii )当14k <时,因为1ln t x =在2e,e ⎡⎤⎣⎦上为减函数,所以1,12t ⎡⎤∈⎢⎥⎣⎦由21124y t k ⎛⎫=--+- ⎪⎝⎭在1,12⎡⎤⎢⎥⎣⎦上为减函数,所以()2111ln 24x k x ϕ⎛'⎫=--+- ⎪⎝⎭在2e,e ⎡⎤⎣⎦上为增函数,所以()()()2e e x ϕϕϕ'≤≤'',即()14k x k ϕ-≤'≤-.①若0k -≥,即0k ≤,则()0x ϕ'≥,所以()x ϕ在2e,e ⎡⎤⎣⎦为增函数,于是()()()min 1e e e 1e 2x k ϕϕ==--≥>,不合题意;②若0k -<,即104k <<,因为()e 0k ϕ'=-<,()21e 04k ϕ=->',()x ϕ'在2e,e ⎡⎤⎣⎦上为增函数,所以存在唯一()20e,e x ∈,使()00x ϕ'=,且当()0e,x x ∈时,()0x ϕ'<,()x ϕ为减函数;当()20,ex x ∈时,()0x ϕ'>,()x ϕ为增函数;所以()()()000min 01ln x x x k x x ϕϕ==--,由()00011ln 2x k x x --≤得000001111111ln 212224x x k x x x ⎛⎫⎛⎫≥->-=> ⎪ ⎪--⎝⎭⎝⎭,这与104k <<矛盾,不合题意.综上可知,k 的取值范围是1,2⎡⎫+∞⎪⎢⎣⎭.对于恒成立问题,常用到以下两个结论:(1)()a f x ≥恒成立⇔()max a f x ≥;(2)()a f x ≤恒成立⇔()min .a f x ≤。
安徽省亳州市数学高二下学期理数3月月考试卷

安徽省亳州市数学高二下学期理数 3 月月考试卷姓名:________班级:________成绩:________一、 单选题 (共 12 题;共 24 分)1. (2 分) 设 是虚数单位,复数为纯虚数,则实数 的值为( )A.B.C.D.2. (2 分) (2020 高二下·浙江月考) 若曲线 ()在点A.1B.2C.3D.43. (2 分) 已知 R 上可导函数的图像如图所示,则不等式处的切线方程为,则的解集为( )A. B. C.第1页共8页D.4. (2 分) 在平面几何中有如下结论:正三角形推广到空间中可以得到类似结论:已知正四面体 ()的内切圆面积为 ,外接圆面积为 ,则,的内切球体积为 ,外接球体积为 ,则为A.B.C.D.5. (2 分) 若函数的图象上存在不同的两点,使得函数的图象在这两点处的切线的斜率之和等于常数 t,则称函数为“t 函数”.下列函数中为“2 函数”的是( )①②③④A.①②B . ③④C . ①③D . ②④6. (2 分) (2019 高三上·西湖期中) 已知函数A.,是的一个周期B.,是的一个周期C.,是的一个周期第2页共8页,则( )D.,最小正周期不存在7. (2 分) 若复数 A.7 B . -7( a 为实数, i 为虚数单位)是纯虚数,则 a= ( )C.D. 8. (2 分) (2019 高二下·九台期中) 用反证法证明命题:“若实数 , 满足 为 0”,其反设正确的是 ( ) A . , 至少有一个为 0 B . , 至少有一个不为 0 C . , 全不为 0 D . , 全为 09. (2 分) 函数 A.0在上取最大值时,x 的值为( )B.,则 , 全C.D.10. (2 分) 设函数在上的导函数为,在上的导函数为上,恒成立,则称函数上是“凸函数”,则在在 上(上为“凸函数”.已知当 )时,A . 既没有最大值,也没有最小值第3页共8页, 若在 在B . 既有最大值,也有最小值 C . 有最大值,没有最小值 D . 没有最大值,有最小值 11. (2 分) 已知函数 取值范围是( ) A. B. C. D.,若,使得成立,则实数 的12. (2 分) 已知偶函数 f(x)满足:f(x)=f(x+2),且当 x∈[0,1]时,f(x)=sinx,其图象与直线 y=在 y 轴右侧的交点按横坐标从小到大依次记为 P1 , P2…,则等于( )A.2B.4C.8D . 16二、 填空题 (共 4 题;共 4 分)13. (1 分) (2019 高二下·葫芦岛月考) 函数的图像在处的切线方程为________.14. (1 分) (2020·奉贤模拟) 设( 为虚数单位),若,则实数________15. (1 分) 据某报《自然健康状况》的调查报道,所测血压结果与相应年龄的统计数据如下表,观察表中数 据规律,并将最适当的数据填入表中括号内.年龄(岁)3035404550556065…第4页共8页收缩压110115120125130135 ________ 145…(水银柱/毫米)舒张压70737578807385 ________ …(水银柱/毫米)16. (1 分) 函数,则使得三、 解答题 (共 2 题;共 15 分)成立的 的取值范围是________.17. (5 分) 当实数 m 为何值时,,(1) 为实数;(2) 为虚数;(3) 为纯虚数;(4) 复数 z 对应的点在复平面内的第二象限.18. (10 分) (2019 高三上·淮南月考) 已知函数.(1) 若在上单调递增,求实数 的取值范围;(2) 当时,若实数满足,求证:.第5页共8页一、 单选题 (共 12 题;共 24 分)1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、 9-1、 10-1、 11-1、 12-1、二、 填空题 (共 4 题;共 4 分)13-1、 14-1、参考答案15-1、第6页共8页16-1、三、 解答题 (共 2 题;共 15 分)17-1、 17-2、 17-3、 17-4、18-1、第7页共8页18-2、第8页共8页。
安徽省高二下学期第三次月考数学(理)试题 Word版含答案
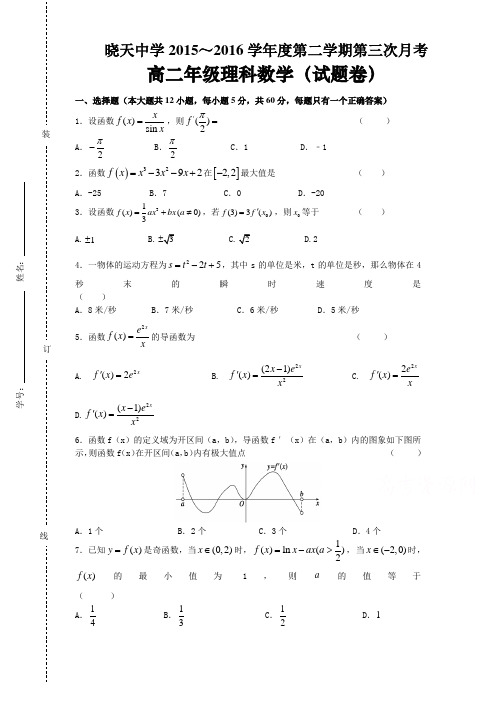
一、选择题(本大题共12小题,每小题5分,共60分,每题只有一个正确答案)1.设函数()sin x f x x=,则'()2f π= ( )A .2π- B .2πC .1D .﹣12.函数()32392f x x x x =--+在[]2,2-最大值是 ( )A .-25B .7C .0D .-203.设函数31()(0)3f x ax bx a =+≠,若0(3)3()f f x '=,则0x 等于 ( )A.1±B.4.一物体的运动方程为225s t t =-+,其中s 的单位是米,t 的单位是秒,那么物体在4秒末的瞬时速度是( )A .8米/秒B .7米/秒C .6米/秒D .5米/秒5.函数2()xe f x x=的导函数为 ( )A.2()2xf x e'= B.22(21)()xx e f x x -'=C.22()xe f x x'=D.22(1)()xx e f x x -'=6.函数f (x )的定义域为开区间(a ,b ),导函数f ′(x )在(a ,b )内的图象如下图所示,则函数f (x )在开区间(a ,b )内有极大值点 ( )A .1个B .2个C .3个D .4个 7.已知()y f x =是奇函数,当(0,2)x ∈时,1()ln ()2f x x ax a =->,当(2,0)x ∈-时,()f x 的最小值为1,则a的值等于( ) A .41 B .31 C .21D .1晓天中学2015~2016学年度第二学期第三次月考高二年级理科数学(试题卷)学号: 姓名:8.若函数f(x)=2x 2-lnx 在其定义域内的一个子区间(k -1,k +1)内不.是单调函数,则实数k的取值范围是( )A .[1,+∞) B.31,2⎡⎫⎪⎢⎣⎭ C .[1,2) D.3,22⎡⎫⎪⎢⎣⎭9.若点P 是曲线2ln y x x =-上任意一点,则点P 到直线2y x =-的最小距离为 ( )A .1B .2D 10.已知函数f (x )对定义域R 内的任意x 都有f (x )=f (4﹣x ),且当x≠2时其导函数f′(x )满足(x ﹣2)f′(x )>0,若2<a <4则 ( )A .f (2a )<f (3)<f (log 2a )B .f (log 2a )<f (3)<f (2a)C .f (3)<f (log 2a )<f (2a )D .f (log 2a )<f (2a)<f (3) 11.设函()f x 在定数义域内可导,()y f x =的图象如图所示,则导函数()y f x '=可能为( )12.已知函数()y f x =对任意的(,)22x ππ∈-满足()cos ()sin 0f x x f x x '+> (其中()f x '是函数()f x 的导函数),则下列不等式成立的是( )A ()()34f ππ-<- B ()()34f ππ<C .(0)2()3f f π> D .(0)()4f π>二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中的横线上) 13.函数x x x f ln )(-=的单调增区间是________.14.使sin y x ax =+在R 上是增函数的a 的取值范围为 .15.若函数[]1)2(33)(23++++=x a ax x x f 有极大值又有极小值,则a 的取值范围是______.16.已知函数()f x (R x ∈)满足()11f =,且()f x 的导数()12f x '<,则不等式()22122x f x <+的解集为 .三、解答题(本大题共70分). 17.(10分)已知函数R x x x x f ∈-=,sin 21)(. (1)试求函数)(x f 的递减区间;(2)试求函数)(x f 在区间[]ππ,-上的最值.18.(12分)已知()xg x e x =-.(Ⅰ)求()g x 的最小值; (Ⅱ)若存在(0,)x ∈+∞,使不等式2()x mx g x ->成立,求m 的取值范围.19.(12分)已知f (x )=e x-ax -1. (1)求f (x )的单调增区间;(2)若f (x )在定义域R 内单调递增,求a 的取值范围.20.(12分)已知函数()ln f x ax x =+,其中a 为常数,e 为自然对数的底数. (1)求()f x 的单调区间;(2)若0a <,且()f x 在区间(0,]e 上的最大值为2-,求a 的值; (3)当1a =-时,试证明:1|()|ln 2x f x x x >+.21.(12分)已知函数()ln ,()ax f x xe x e a R =+-∈.(Ⅰ)当1a =时,求函数()y f x =的点(1,(1))f 处的切线方程; (Ⅱ)设1()ln g x x e x=+-,若函数()()()h x f x g x =-在定义域内存在两个零点,求实数a 的取值范围.22.(12分)已知函数)(1ln )(R a x x a x f ∈+-=. (1)求)(x f 的单调区间;(2)若0)(≤x f 在),0(+∞上恒成立,求所有实数a 的值; (3)证明:)1,(4)1(1ln 53ln 43ln 32ln >∈-<++⋅⋅⋅+++n N n n n n n .2. 填空题13 . 14 .15 . 16 .3. 解答题 17.18.晓天中学2015~2016学年度第二学期第三次月考高二年级理科数学(答题卷)学号: 姓名:19.20.21.22.参考答案1.C试题分析:∵'2sin cos ()sin x x x f x x -=,则'1()121f π==,故选:C . 2.B试题分析:()()322392'369f x x x x f x x x =--+∴=--Q ,[]2,2x ∈-,令()0'f x >,得[)2,1--单调递增,(]1,2-单调递减,所以()()max 113927f x f =---++==.3.C试题分析:将3代入函数解析式求出f (3);求出函数的导函数,将x 0代入求出函数值 f ′(x 0),列出方程求出0x ;2393,f a b f x ax b =+'=+(),()2000,33'f x ax b f f x ∴'=+=()()(),2009333a b ax b x ∴+=+∴=,故选C4.C试题分析:22dsv t dt==-,∴物体在4秒末的瞬时速度为6米/秒. 5.B试题分析:=-=-=2222'2'2'2)()()(x e x e x x e x e x f x x x x 22(21)xx e x -,故选B.6.B试题分析:函数()x f y =在点0x 处连续且()00='x f ,若在点0x 附近左侧()00>'x f ,右侧()00<'x f ,则点0x 为函数的极大值点,满足定义的点有2个. 7.D试题分析:根据奇函数关于原点对称,()y f x =在(0,2)x ∈内有最大值-1,又'11()()2f x a a x =->,可知当1x a =时取最大值,代入111()ln 1,f a a a a=-⋅=-可得1a =.8.B试题分析:因为f(x)定义域为(0,+∞),f′(x)=4x -1x ,由f′(x)=0,得x =12.据题意,111210k k k ⎧-<<+⎪⎨⎪-≥⎩,解得1≤k<32. 9.B试题分析:可设点),(00y x P ,由题意可知,过点P 且与直线2y x =-平行的直线为曲线2ln y x x =-在点P 的切线.由此)1,1(,1,1,012,00000'0P y x x x y x x ∴=∴=∴=-∴==,则点P 到直线2y x =-B. 10.B试题分析:因为函数()f x 对定义域R 内的任意x 都有()()4f x f x =-,()f x ∴ 关于直线2x =对称;又当2x ≠时其导函数()f x '满足()()20f x x '->,所以当2x >时,()()0,f x f x '>在()2,+∞上的单调递增;同理可得,当2x <时,()f x 在(),2-∞单调递减;24a <<,21log 2a ∴<<,224log 3a ∴<-<,又()()()224216,log 4log ,a f a f a f x <<=-在()2,+∞上的单调递增;()()()2log 32a f a f f ∴<<,故选B.11.D试题分析:由函数图象可知()f x 在y 轴左侧为增函数,右侧从左至右依次为增、减、增,利用导函数的性质,可知选D. 12.A试题分析:令()()()()()()()()xx x f x x f x x x f x x f x g x x f x g 2'2'''cos sin cos cos cos cos ,cos -=-==则,由对任意的(,)22x ππ∈-满足()cos ()sin 0f x x f x x '+>可得()0'>x g ,即函数()x g 在⎪⎭⎫ ⎝⎛-2,2ππ上为增函数,则⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛-43ππg g 即⎪⎭⎫ ⎝⎛-⎪⎭⎫⎝⎛-<⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-4cos 43cos 3ππππf f 即⎪⎭⎫ ⎝⎛-<⎪⎭⎫ ⎝⎛-432ππf f ;故选A . 13.(1,)+∞试题分析:函数()f x 的定义域是(0,)+∞,1'()1f x x=-,当01x <<时'()0f x <,当1x >时,'()0f x >,所以()f x 在(1,)+∞上递增. 14.[)1,+∞试题分析:sin y x ax =+在R 上是增函数等价于'cos 0y x a =+≥在R 上恒成立, 即cos a x ≥-恒成立,[]cos 1,1x -∈-,1a ≥.15.21>-<a a 或试题分析:)2(363)(2'+++=a ax x x f ,因为[]1)2(33)(23++++=x a ax x x f 有极大值又有极小值,所以0)('=x f 有两个不相等的实根,所以21,0)2(36362>-<∴>+-=∆a a a a 或.16.11-∞-+∞(,)(,)试题分析:设()()12F x f x x =-根据题意可得函数F x ()在R 上单调递减,然后根据()22122x f x <+可得221122x f x f -<-()(),最后根据单调性可求出x 的取值范围.设()()12F x f x x =-,()111,0222Fx f x f x F x f x '='-'<∴'='-<∴()()()(), 即函数F (x )在R 上单调递减,()()()2222211,112222x x f x f x f F x F <+∴-<-∴<()(),而函数F (x )在R 上单调递减, 21x ∴>,即11x ∴∈-∞-+∞(,)(,),故答案为:11-∞-+∞(,)(,)17.(I )Z k k k ∈++-),23,23(ππππ;(2)最大值为2)(ππ=f ,最小值为2)(ππ-=-f .试题分析:(I )求导数得:,cos 21)(x x f -=' 令,0)(<'x f 即,0cos 21<-x 得:Z k k x k ∈+<<+-,2323ππππ, ∴函数)(x f 在每个区间Z k k k ∈++-),23,23(ππππ上为减函数.(2)由(I )知,函数)(x f 在区间),3(),3,(ππππ--上为增函数,在区间)3,3(ππ-上为减函数,∴函数)(x f 在3π-=x 处取极大值623)3(ππ-=-f ,在3π=x 处取极小值236)3(-=ππf ,∵2)(ππ-=-f ,2)(ππ=f ∴函数()f x 在区间[]ππ,-上的最大值为2)(ππ=f ,最小值为2)(ππ-=-f .18.(Ⅰ)最小值1)1(=f ;(Ⅱ)2ln 2<m ;试题解析:(Ⅰ)∵1)(-='x e x g ,由0)(='x g ,得0=x∴当0<x 时,0)(<'x g ,)(x g 在)0,(-∞上为减函数, 当0>x 时,0)(>'x g ,)(x g 在),0(∞+上为增函数,∴)(g x 在0=x 时有最小值1)0(g =.(Ⅱ))0)()((2)(2>-=>-⇔>-x e x g x xg m x x x g mx x x x xe x x m x xe m x -+<⇔->-⇔2222令x xe x x x h -+=2)(2)0(>x则)2)(1()2()2(22)(-+-=-+-=--+='x x x x x e x e e x xe e x x h ∴当2ln >x 时0)(<'x h ,当2ln 0<<x 时0)(>'x h∴2ln )2(ln )(2max ==h x h ,要想存在正数x ,使)(x h m <,则有2ln )(2max =<x h m ∴所求的m 的取值范围是2ln 2<m .19.(1)当a ≤0时,f (x )的单调增区间为(-∞,+∞);当a >0时,f (x )的单调增区间为(ln a ,+∞).(2)(-∞,0].(1)∵f (x )=e x -ax -1(x ∈R),∴f ′(x )=e x -a .令f ′(x )≥0,得e x≥a .当a ≤0时,f ′(x )>0在R 上恒成立;当a >0时,有x ≥ln a .综上,当a ≤0时,f (x )的单调增区间为(-∞,+∞);当a >0时,f (x )的单调增区间为(ln a ,+∞).(2)由(1)知f ′(x )=e x-a .∵f (x )在R 上单调递增,∴f ′(x )=e x -a ≥0恒成立,即a ≤e x在R 上恒成立.∵x ∈R 时,e x>0,∴a ≤0, 即a 的取值范围是(-∞,0].20.(1)单调增区间为1(0,)a -,单调减区间为1(,)a-+∞;(2)a e =-;(3)证明过程详见解析.试题解析:(1)11()ax f x a x x+'=+=当0a ≥时,'()0f x >恒成立,故()f x 的单调增区间为(0,)+∞当0a <时,令'()0f x >解得10x a <<-,令'()0f x <解得1x a>-,故()f x 的单调增区间为1(0,)a -,()f x 的单调减区间为1(,)a-+∞(2)由(I )知,①当1e a -≥,即1a e ≥-时,()f x 在(]0,e 上单调递增,∴max ()()10f x f e ae ==+≥舍;②当10e a <-<,即1a e<-时,()f x 在1(0,)a -上递增,在1(,)a e -上递减,11max ()()1ln()a a f x f =-=-+-,令11ln()2a -+-=-,得a e =-(Ⅲ)即要证明ln 1|()|2x f x x >+,由(Ⅰ)知当1a =-时,max ()(1)1f x f ==-,∴|()|1f x ≥,又令ln 1()2x x x ϕ=+,21ln ()xx xϕ-'=,故()x ϕ在(0,)e 上单调递增,在(,)e +∞上单调递减,故11()()12x e e ϕϕ≤=+<即证明ln 1|()|2x f x x >+.21.(Ⅰ)(21)(1)y e x =+-;(Ⅱ)20a e-<<.试题解析:(Ⅰ)()y f x =的定义域为(0,)+∞,∵1a =,∴()ln ,(1)0x f x xe x e f =+-=,∴1()(1)x f x x e x'=++,∴(1)21f e '=+, 所以函数()y f x =在点(1,(1))f 处的切线方程为(21)(1)y e x =+-(Ⅱ)2111()()()ln (ln )ax axaxx e h x f x g x xe x e x e xe x x x-=-=+--+-=-=在定义域内存在两个零点,即210axx e -=在(0,)+∞有两个零点.令22()1,()2(2)ax ax axax x x e x ax e xe xe ax ϕϕ'=-=+=+ⅰ.当0a ≥时,()(2)0ax x xe ax ϕ'=+>,∴()y x ϕ=在(0,)+∞上单调递增由零点存在定理,()y x ϕ=在(0,)+∞至多一个零点,与题设发生矛盾.ⅱ.当0a <时,(2)0axxe ax +=则2x =-因为(0)1ϕ=-,当x →+∞,()1x ϕ→-,所以要使2()1axx x e ϕ=-在(0,)+∞内有两个零点,则2()0a ϕ->即可,得224a e <,又因为0a <,所以20a e-<<22.(1)当0≤a 时,)(x f 减区间为),0(+∞,当0>a 时,)(x f 递增区间为),0(a ,递减区间为),(+∞a ;(2)1=a ;(3)见解析. 试题解析:(1))0(1)(>-=-='x xxa x a x f . 当0≤a 时,0)(<'x f ,∴)(x f 减区间为),0(+∞,当0>a 时,由0)(>'x f 得a x <<0,由0)(<'x f 得a x >, ∴)(x f 递增区间为),0(a ,递减区间为),(+∞a .(2)由(1)知:当0≤a 时,)(x f 在),0(+∞上为减函数,而0)1(=f , ∴0)(≤x f 在区间),0(+∞∈x 上不可能恒成立; 当0>a 时,)(x f 在),0(a 上递增,在),(+∞a 上递减,1ln )()(max +-==a a a a f x f ,令1ln )(+-=a a a a g ,依题意有0)(≤a g ,而a a g ln )(=',且0>a ,∴)(a g 在)1,0(上递减,在),1(+∞上递增,∴0)1()(min ==g a g ,故1=a .(3)由(2)知,当1=a 时,0)(≤x f 在),0(+∞上恒成立,即1ln -≤x x 在),0(+∞上恒成立,当且仅当1=x 时等号成立.令)1,(2>∈=k N k k x ,则有1ln 22-<k k ,即)1)(1(ln 2+-<k k k ,整理得211ln -<+k k k ,当n k ,...,4,3,2=时, 分别有211ln ,,2353ln ,2243ln ,2132ln -<+⋅⋅⋅<<<n n n , 叠加得4)1(2)1(3211ln 53ln 43ln 32ln -=-+⋅⋅⋅+++<++⋅⋅⋅+++n n n n n , 即4)1(1ln 53ln 43ln 32ln -<++⋅⋅⋅+++n n n n 得证.。
安徽省亳州市涡阳一中2016-2017学年高二(下)3月月考数学试卷(理科)

2016-2017学年安徽省亳州市涡阳一中高二(下)3月月考数学试卷(理科)一.选择题(本大题共12小题,每小题5分,共60分.每小题只有1个答案正确)1.有一段“三段论”推理是这样的:对于可导函数f(x),如果f′(x0)=0,那么x=x0是函数f(x)的极值点,因为函数f(x)=x3在x=0处的导数值f′(0)=0,所以,x=0是函数f(x)=x3的极值点.以上推理中()A.大前提错误B.小前提错误C.推理形式错误D.结论正确2.用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,假设正确的是()A.假设三内角都不大于60度B.假设三内角都大于60度C.假设三内角至多有一个大于60度D.假设三内角至多有两个大于60度3.某个命题与自然数n有关,若n=k(k∈N*)时命题成立,那么可推得当n=k+1时该命题也成立.现已知当n=5时,该命题不成立,那么可推得()A.当n=6时,该命题不成立B.当n=6时,该命题成立C.当n=4时,该命题不成立D.当n=4时,该命题成立4.若f(x)在R上可导,,则=()A.B.C.D.5.在平面几何中有如下结论:正三角形ABC的内切圆面积为S1,外接圆面积为S2,则=,推广到空间可以得到类似结论,已知正四面体P﹣ABC的内切球体积为V1,外接球体积为V2,则=()A.B.C.D.6.函数y=sinx﹣的图象大致是()A.B.C.D.7.,则m等于()A.﹣1 B.0 C.1 D.28.如图所示的是函数f(x)=x3+bx2+cx+d的大致图象,则x12+x22等于()A.B.C.D.9.正整数按下表的规律排列(下表给出的是上起前4行和左起前4列)则上起第2015行,左起第2016列的数应为()A.20152B.20162C.2015+2016 D.2015×201610.设f(x)是定义在R上的偶函数,当x>0时,f(x)+xf′(x)>0,且f(1)=0,则不等式xf(x)>0的解集为()A.(﹣1,0)∪(1,+∞) B.(﹣1,0)∪(0,1)C.(﹣∞,﹣1)∪(1,+∞)D.(﹣∞,﹣1)∪(0,1)11.若点P是曲线y=x2﹣lnx上任意一点,则点P到直线y=x﹣2的最小距离为()A.1 B.C.D.12.关于函数f(x)=+lnx,下列说法错误的是()A.x=2是f(x)的极小值点B.函数y=f(x)﹣x有且只有1个零点C.存在正实数k,使得f(x)>kx恒成立D.对任意两个正实数x1,x2,且x2>x1,若f(x1)=f(x2),则x1+x2>4二、填空题(本大题共4题,每题5分,共20分)13.设f(x)=x2﹣2x﹣4lnx,则函数f(x)单调递增区间是.14.如图,函数F(x)=f(x)+x2的图象在点P处的切线方程是y=﹣x+8,则f (5)+f′(5)=.15.已知函数f(x)=2ax﹣,x∈(0,1上是增函数,则实数a的取值范围是.16.已知函数f(x)的定义域为,部分对应值如下表.x﹣1045f(x)1221f(x)的导函数y=f′(x)的图象如图所示:下列关于f(x)的命题:①函数f(x)是周期函数;②函数f(x)在是减函数;③如果当x∈时,f(x)的最大值是2,那么t的最大值为4;④当1<a<2时,函数y=f(x)﹣a有4个零点;⑤函数y=f(x)﹣a的零点个数可能为0、1、2、3、4个.其中正确命题的序号是.三、解答题(本大题共6题,第17题10分,其余每题12分,共70分.解答题应写出文字说明、证明过程或演算步骤.)17.已知a>b>c,且a+b+c=0,求证:<.18.已知函数f(x)=x3﹣3x(1)求函数f(x)的极值;(2)过点P(2,﹣6)作曲线y=f(x)的切线,求此切线的方程.19.设函数f(x)=x2+e x﹣xe x(1)求f(x)的单调区间;(2)若当x∈时,不等式f(x)>m恒成立,求实数m的取值范围.20.已知数列{a n}满足a n﹣a n=1,a1=1,试比较与+1的大小并证明.21.已知函数f(x)=lnx﹣.(Ⅰ)若a>0,试判断f(x)在定义域内的单调性;(Ⅱ)若f(x)在上的最小值为,求实数a的值;(Ⅲ)若f(x)<x2在(1,+∞)上恒成立,求实数a的取值范围.22.设函数f(x)=lnx﹣ax+﹣1(0<a<1)(1)求函数f(x)的单调区间;(2)当a=时,设函数g(x)=x2﹣2bx﹣,若对于∀x1∈,∃x2∈,使f(x1)≥g(x2)成立,求实数b的取值范围.2016-2017学年安徽省亳州市涡阳一中高二(下)3月月考数学试卷(理科)参考答案与试题解析一.选择题(本大题共12小题,每小题5分,共60分.每小题只有1个答案正确)1.有一段“三段论”推理是这样的:对于可导函数f(x),如果f′(x0)=0,那么x=x0是函数f(x)的极值点,因为函数f(x)=x3在x=0处的导数值f′(0)=0,所以,x=0是函数f(x)=x3的极值点.以上推理中()A.大前提错误B.小前提错误C.推理形式错误D.结论正确【考点】F6:演绎推理的基本方法.【分析】在使用三段论推理证明中,如果命题是错误的,则可能是“大前提”错误,也可能是“小前提”错误,也可能是推理形式错误,我们分析的其大前提的形式:“对于可导函数f(x),如果f'(x0)=0,那么x=x0是函数f(x)的极值点”,不难得到结论.【解答】解:∵大前提是:“对于可导函数f(x),如果f'(x0)=0,那么x=x0是函数f(x)的极值点”,不是真命题,因为对于可导函数f(x),如果f'(x0)=0,且满足当x=x0附近的导函数值异号时,那么x=x0是函数f(x)的极值点,∴大前提错误,故选A.2.用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,假设正确的是()A.假设三内角都不大于60度B.假设三内角都大于60度C.假设三内角至多有一个大于60度D.假设三内角至多有两个大于60度【考点】R9:反证法与放缩法.【分析】一些正面词语的否定:“是”的否定:“不是”;“能”的否定:“不能”;“都是”的否定:“不都是”;“至多有一个”的否定:“至少有两个”;“至少有一个”的否定:“一个也没有”;“是至多有n个”的否定:“至少有n+1个”;“任意的”的否定:“某个”;“任意两个”的否定:“某两个”;“所有的”的否定:“某些”.【解答】解:根据反证法的步骤,假设是对原命题结论的否定,“至少有一个”的否定:“一个也没有”;即“三内角都大于60度”.故选B3.某个命题与自然数n有关,若n=k(k∈N*)时命题成立,那么可推得当n=k+1时该命题也成立.现已知当n=5时,该命题不成立,那么可推得()A.当n=6时,该命题不成立B.当n=6时,该命题成立C.当n=4时,该命题不成立D.当n=4时,该命题成立【考点】RG:数学归纳法.【分析】本题考查的知识点是数学归纳法,由归纳法的性质,我们由P(n)对n=k成立,则它对n=k+1也成立,由此类推,对n>k的任意整数均成立,结合逆否命题同真同假的原理,当P(n)对n=k不成立时,则它对n=k﹣1也不成立,由此类推,对n<k的任意正整数均不成立,由此不难得到答案.【解答】解:由题意可知,P(n)对n=4不成立(否则n=5也成立).同理可推得P(n)对n=3,n=2,n=1也不成立.故选C4.若f(x)在R上可导,,则=()A.B.C.D.【考点】67:定积分.【分析】先求导,再求导,求出函数的表达式,再根据定积分的计算法则计算即可.【解答】解:f′(x)=2x+2f′()+2cos2x,∴f′()=2×+2f′()+2cosπ,∴f′()=2﹣π,∴f(x)=x2+2(2﹣π)x+sin2x,∴f(x)dx=(x2+2(2﹣π)x+sin2x)dx=(x3+(2﹣π)x2﹣cos2x)| =(+2﹣π﹣cos2)﹣(0+0﹣)=﹣π﹣cos2,故选:C5.在平面几何中有如下结论:正三角形ABC的内切圆面积为S1,外接圆面积为S2,则=,推广到空间可以得到类似结论,已知正四面体P﹣ABC的内切球体积为V1,外接球体积为V2,则=()A.B.C.D.【考点】F3:类比推理.【分析】平面图形类比空间图形,二维类比三维得到,类比平面几何的结论,确定正四面体的外接球和内切球的半径之比,即可求得结论.【解答】解:从平面图形类比空间图形,从二维类比三维,如图,设正四面体的棱长为a,则AE=,DE=设OA=R,OE=r,则∴R=,r=∴正四面体的外接球和内切球的半径之比是3:1故正四面体P﹣ABC的内切球体积为V1,外接球体积为V2之比等于故选C6.函数y=sinx﹣的图象大致是()A.B.C.D.【考点】6B:利用导数研究函数的单调性;3O:函数的图象.【分析】判断函数的奇偶性,通过函数的导数,判断函数的单调性,利用特殊函数值判断图象即可.【解答】解:函数y=sinx﹣是奇函数,排除D,函数y′=cosx+,x∈(0,)时,y′>0,函数是增函数,排除A,并且x=时,y=1﹣>0,排除C,故选:B.7.,则m等于()A.﹣1 B.0 C.1 D.2【考点】67:定积分.【分析】利用定积分的几何意义计算定积分.【解答】解:y=,即(x+1)2+y2=1,表示以(﹣1,0)为圆心,以1为半径的圆,圆的面积为π,∵,∴表示为圆的面积的二分之一,∴m=0,故选:B8.如图所示的是函数f(x)=x3+bx2+cx+d的大致图象,则x12+x22等于()A.B.C.D.【考点】63:导数的运算;36:函数解析式的求解及常用方法;7H:一元二次方程的根的分布与系数的关系.【分析】由图象知f(x)=0的根为0,1,2,求出函数解析式,x1,x2为导函数的两根,可结合根与系数求解.【解答】解:由图象知f(x)=0的根为0,1,2,∴d=0.∴f(x)=x3+bx2+cx=x(x2+bx+c)=0.∴x2+bx+c=0的两个根为1和2.∴b=﹣3,c=2.∴f(x)=x3﹣3x2+2x.∴f′(x)=3x2﹣6x+2.∵x1,x2为3x2﹣6x+2=0的两根,∴.∴.9.正整数按下表的规律排列(下表给出的是上起前4行和左起前4列)则上起第2015行,左起第2016列的数应为()A.20152B.20162C.2015+2016 D.2015×2016【考点】F1:归纳推理.【分析】观察图形可知这些数字排成的是一个正方形,上起第2015行,左起第2016列的数是一个2016乘以2016的正方形的倒数第二行的最后一个数字,进而可得答案【解答】解:这些数字排成的是一个正方形上起第2015行,左起第2016列的数是一个2016乘以2016的正方形的倒数第二行的最后一个数字,所以这个数是2016×=2015×2016.故选:D10.设f(x)是定义在R上的偶函数,当x>0时,f(x)+xf′(x)>0,且f(1)=0,则不等式xf(x)>0的解集为()A.(﹣1,0)∪(1,+∞) B.(﹣1,0)∪(0,1)C.(﹣∞,﹣1)∪(1,+∞)D.(﹣∞,﹣1)∪(0,1)【考点】3L:函数奇偶性的性质;6B:利用导数研究函数的单调性.【分析】由题意构造函数g(x)=xf (x),再由导函数的符号判断出函数g(x)的单调性,由函数f(x)的奇偶性得到函数g(x)的奇偶性,由f(1)=0得g (1)=0、还有g(﹣1)=0,再通过奇偶性进行转化,利用单调性求出不等式得解集.【解答】解:设g(x)=xf(x),则g'(x)='=x'f(x)+xf'(x)=xf′(x)+f(x)>0,∴函数g(x)在区间(0,+∞)上是增函数,∵f(x)是定义在R上的偶函数,∴g(x)=xf(x)是R上的奇函数,∴函数g(x)在区间(﹣∞,0)上是增函数,∵f(1)=0,∴f(﹣1)=0;即g(﹣1)=0,g(1)=0∴xf(x)>0化为g(x)>0,设x>0,故不等式为g(x)>g(1),即1<x;设x<0,故不等式为g(x)>g(﹣1),即﹣1<x<0.故所求的解集为(﹣1,0)∪(1,+∞)故选A.11.若点P是曲线y=x2﹣lnx上任意一点,则点P到直线y=x﹣2的最小距离为()A.1 B.C.D.【考点】IT:点到直线的距离公式.【分析】设出切点坐标,利用导数在切点处的函数值,就是切线的斜率,求出切点,然后再求点P到直线y=x﹣2的最小距离.【解答】解:过点P作y=x﹣2的平行直线,且与曲线y=x2﹣lnx相切,设P(x0,x02﹣lnx0)则有k=y′|x=x0=2x0﹣.∴2x0﹣=1,∴x0=1或x0=﹣(舍去).∴P(1,1),∴d==.故选B.12.关于函数f(x)=+lnx,下列说法错误的是()A.x=2是f(x)的极小值点B.函数y=f(x)﹣x有且只有1个零点C.存在正实数k,使得f(x)>kx恒成立D.对任意两个正实数x1,x2,且x2>x1,若f(x1)=f(x2),则x1+x2>4【考点】6B:利用导数研究函数的单调性.【分析】对选项分别进行判断,即可得出结论.【解答】解:f′(x)=,∴(0,2)上,函数单调递减,(2,+∞)上函数单调递增,∴x=2是f(x)的极小值点,即A正确;y=f(x)﹣x=+lnx﹣x,∴y′=<0,函数在(0,+∞)上单调递减,x→0,y→+∞,∴函数y=f(x)﹣x有且只有1个零点,即B正确;f(x)>kx,可得k<,令g(x)=,则g′(x)=,令h(x)=﹣4+x﹣xlnx,则h′(x)=﹣lnx,∴(0,1)上,函数单调递增,(1,+∞)上函数单调递减,∴h(x)≤h(1)<0,∴g′(x)<0,∴g(x)=在(0,+∞)上函数单调递减,函数无最小值,∴不存在正实数k,使得f(x)>kx恒成立,即C不正确;对任意两个正实数x1,x2,且x2>x1,(0,2)上,函数单调递减,(2,+∞)上函数单调递增,若f(x1)=f(x2),则x1+x2>4,正确.故选:C.二、填空题(本大题共4题,每题5分,共20分)13.设f(x)=x2﹣2x﹣4lnx,则函数f(x)单调递增区间是2,+∞),故答案为:.若函数f(x)在(0,1上是增函数,f′(x)=2a+≥0在(0,1上是增函数,∴f′(x)=2a+≥0在(0,1上恒成立,∴2a≥﹣2,∴a≥﹣1.故答案为:a≥﹣1.16.已知函数f(x)的定义域为,部分对应值如下表.x﹣1045f(x)1221f(x)的导函数y=f′(x)的图象如图所示:下列关于f(x)的命题:①函数f(x)是周期函数;②函数f(x)在是减函数;③如果当x∈时,f(x)的最大值是2,那么t的最大值为4;④当1<a<2时,函数y=f(x)﹣a有4个零点;⑤函数y=f(x)﹣a的零点个数可能为0、1、2、3、4个.其中正确命题的序号是②⑤.【考点】6E:利用导数求闭区间上函数的最值;3Q:函数的周期性;51:函数的零点;6B:利用导数研究函数的单调性.【分析】先由导函数的图象和原函数的关系画出原函数的大致图象,再借助与图象和导函数的图象,对五个命题,一一进行验证,对于假命题采用举反例的方法进行排除即可得到答案.【解答】解:由导函数的图象和原函数的关系得,原函数的大致图象可由以下两种代表形式,如图:由图得:①为假命题.函数f(x)不能断定为是周期函数.②为真命题,因为在上导函数为负,故原函数递减;③为假命题,当t=5时,也满足x∈时,f(x)的最大值是2;④为假命题,当a离1非常接近时,对于第二个图,y=f(x)﹣a有2个零点,也可以是3个零点.⑤为真命题,动直线y=a与y=f(x)图象交点个数可以为0、1、2、3、4个,故函数y=f(x)﹣a的零点个数可能为0、1、2、3、4个.综上得:真命题只有②⑤.故答案为:②⑤三、解答题(本大题共6题,第17题10分,其余每题12分,共70分.解答题应写出文字说明、证明过程或演算步骤.)17.已知a>b>c,且a+b+c=0,求证:<.【考点】R6:不等式的证明.【分析】本题宜用分析法证.欲证要证<a,平方后寻求使之成立的充分条件即可.【解答】证明:因为a>b>c,且a+b+c=0,所以a>0,c<0,要证明原不等式成立,只需证明<a,即证b2﹣ac<3a2,即证b2+a(a+b)<3a2,即证(a﹣b)(2a+b)>0,即证(a﹣b)(a﹣c)>0.∵a>b>c,∴(a﹣b)•(a﹣c)>0成立.∴原不等式成立.18.已知函数f(x)=x3﹣3x(1)求函数f(x)的极值;(2)过点P(2,﹣6)作曲线y=f(x)的切线,求此切线的方程.【考点】6D:利用导数研究函数的极值;6H:利用导数研究曲线上某点切线方程.【分析】(1)求出函数的导数,通过导数为0,判断函数的单调性,然后求解函数的极值.(2)设出切点,求出斜率,然后求解切线方程.【解答】解:(1)∵f(x)=x3﹣3x,∴f'(x)=3x2﹣3=3(x﹣1)(x+1)…令f'(x)=0,解得x=﹣1或x=1…列表如下x(﹣∞,﹣﹣1(﹣1,1)1(1,+∞)1)f'(x)+0﹣0+f(x)↗极大值↘极小值↗…当x=﹣1时,有极大值f(﹣1)=2;当x=1时,有极小值f(1)=﹣2…(2)设切点,∴…∴切线方程…∵切线过点P(2,﹣6)∴,∴x°=0或x°=3…所以切线方程为y=﹣3x或y=24x﹣54…19.设函数f(x)=x2+e x﹣xe x(1)求f(x)的单调区间;(2)若当x∈时,不等式f(x)>m恒成立,求实数m的取值范围.【考点】6B:利用导数研究函数的单调性;6K:导数在最大值、最小值问题中的应用.【分析】(1)求出导数,讨论x>0,x<0,导数的符号,注意运用指数函数的单调性,求出单调区间;(2)当x∈时,不等式f(x)>m恒成立,即为当x∈时,f(x)min>m,由(1)即可求出最小值.【解答】解:(1)∵函数f(x)=x2+e x﹣xe x.∴f(x)的定义域为R,f'(x)=x+e x﹣(e x+xe x)=x(1﹣e x),当x<0时,1﹣e x>0,f'(x)<0;当x>0时,1﹣e x<0,f'(x)<0∴f(x)在R上为减函数,即f(x)的单调递减区间为(﹣∞,+∞).(2)当x∈时,不等式f(x)>m恒成立,即为当x∈时,f(x)min>m.由(1)可知,f(x)在上单调递减,∴f(x)min=f(2)=2﹣e2,∴m<2﹣e2时,不等式f(x)>m恒成立.20.已知数列{a n}满足a n﹣a n=1,a1=1,试比较与+1的大小并证明.【考点】RG:数学归纳法.【分析】先求出数列的通项公式,再利用数学归纳法证明即可﹣a n=1,a1=1,【解答】解:a n+1∴数列的通项公式为a n=n,要证≥只要证1+++…+≥,下面用数学归纳法证明:(1)当n=1时,1+=,结论成立,(2)假设n=k时成立,即1++…+≥,则当n=k+1时,1++…+++…+>++…+,>+++…+,>+=,即当n=k+1时,结论成立,综上(1)(2)可知,对一切正整数,都有1+++…+≥21.已知函数f(x)=lnx﹣.(Ⅰ)若a>0,试判断f(x)在定义域内的单调性;(Ⅱ)若f(x)在上的最小值为,求实数a的值;(Ⅲ)若f(x)<x2在(1,+∞)上恒成立,求实数a的取值范围.【考点】6B:利用导数研究函数的单调性;6E:利用导数求闭区间上函数的最值;6K:导数在最大值、最小值问题中的应用.【分析】(Ⅰ)先求出f(x)的定义域,再求出f′(x)=,从而得出函数的单调区间;(Ⅱ)分别讨论①若a≥﹣1,②若a≤﹣e,③若﹣e<a<﹣1的情况,结合函数的单调性,得出函数的单调区间,从而求出a的值;(Ⅲ)由题意得a>xlnx﹣x3,令g(x)=xlnx﹣x3,得到h(x)=g′(x)=1+lnx﹣3x2,h′(x)=,得出h(x)在(1,+∞)递减,从而g(x)在(1,+∞)递减,问题解决.【解答】解:(Ⅰ)由题意得f(x)的定义域是(0,+∞),且f′(x)=,∵a>0,∴f′(x)>0,故f(x)在(0,+∞)单调递增;(Ⅱ)由(Ⅰ)可得f′(x)=,①若a≥﹣1,则x+a≥0,即f′(x)≥0在上恒成立,此时f(x)在上递增,∴f(x)min=f(1)=﹣a=,∴a=﹣(舍),②若a≤﹣e,则x+a≤0,即f′(x)≤0在上恒成立,此时f(x)在上递减,∴f(x)min=f(e)=1﹣=,∴a=﹣(舍),③若﹣e<a<﹣1,令f′(x)=0,得x=﹣a,当1<x<﹣a时,f′(x)<0,∴f(x)在(1,﹣a)递减,当﹣a<x<e时,f′(x)>0,∴f(x)在(﹣a,e)递增,∴f(x)min=f(﹣a)=ln(﹣a)+1=,∴a=﹣,综上a=﹣;(Ⅲ)∵f(x)<x2,∴lnx﹣<x2,又x>0,∴a>xlnx﹣x3,令g(x)=xlnx﹣x3,h(x)=g′(x)=1+lnx﹣3x2,h′(x)=,∵x∈(1,+∞)时,h′(x)<0,∴h(x)在(1,+∞)递减,∴h(x)<h(1)=﹣2<0,即g′(x)<0,∴g(x)在(1,+∞)递减,∴g(x)<g(1)=﹣1,∴a≥﹣1时,f(x)<x2在(1,+∞)恒成立.22.设函数f(x)=lnx﹣ax+﹣1(0<a<1)(1)求函数f(x)的单调区间;(2)当a=时,设函数g(x)=x2﹣2bx﹣,若对于∀x1∈,∃x2∈,使f(x1)≥g(x2)成立,求实数b的取值范围.【考点】6B:利用导数研究函数的单调性.【分析】(1)直接利用函数与导数的关系,求出函数的导数,再讨论函数的单调性;(2)利用导数求出f(x)的最小值、利用二次函数知识或分离常数法求出g(x)在闭区间上的最大值,然后解不等式求参数.【解答】解:(1)∵函数f(x)=lnx﹣ax+﹣1(0<a<1),所以f′(x)=(x>0),令h(x)=ax2﹣x+1﹣a(x>0)当a≠0时,由f′(x)=0,即ax2﹣x+1﹣a=0,解得x1=1,x2=﹣1.当a=时x1=x2,h(x)≥0恒成立,此时f′(x)≤0,函数f(x)单调递减;当0<a<时,﹣1>1>0,x∈(0,1)时h(x)>0,f′(x)<0,函数f(x)单调递减;x∈(1,﹣1)时,h(x)<0,f′(x)>0,函数f(x)单调递增;x∈(﹣1,+∞)时,h(x)>0,f′(x)<0,函数f(x)单调递减.当<a<1时,0<﹣1<1,x∈(0,﹣1)时h(x)>0,f′(x)<0,函数f(x)单调递减;x∈(﹣1,1)时,h(x)<0,f′(x)>0,函数f(x)单调递增;x∈(1,+∞)时,h(x)>0,f′(x)<0,函数f(x)单调递减综上所述:当0<a<时,函数f(x)在(0,1)、(﹣1,+∞)单调递减,(1,﹣1)单调递增;当a=时x1=x2,h(x)≥0恒成立,此时f′(x)≤0,函数f(x)在(0,+∞)单调递减;当<a<1时,函数f(x)在(0,﹣1)单调递减,(﹣1,1)单调递增,(1,+∞)单调递减.(2)a=时,由(1)得函数f(x)在区间(1,2)递增,故函数f(x)在区间上的最小值是f(1)=﹣,原题等价于g(x)在上的最小值小于或等于f(x)在区间的最小值,又∵g(x)=(x﹣b)2﹣b2﹣,x∈,则①b<0时,g(x)在递增,g(x)min=g(0)=﹣>﹣,不合题意;②0≤b≤1时,g(x)min=g(b)=﹣b2﹣≤﹣,解得:≤b≤1;③b>1时,g(x)在递减,g(x)min=g(1)=﹣2b≤﹣,解得:b≥,此时,b>1,综上,b的范围是b≥.2017年5月27日。
安徽省亳州市涡阳县高二数学3月月考试题理

安徽省亳州市涡阳县2016-2017学年高二数学3月月考试题 理注意事项:1.本试题第I 卷(选择题)和第II 卷两部分,全卷共150分,时间120分钟.2.第I 卷必须使用2B 铅笔填涂答题卡相应题目的答案标号,修改时,要用橡皮擦干净. 3.第II 卷必须使用0。
5毫米的黑色墨水签字笔书写在答题纸的指定位置,在草稿纸和本卷上答题无效.第I 卷(选择题)一.选择题(本大题共12小题,每小题5分,共60分.每小题只有1个答案正确)1.有一段“三段论”推理是这样的:对于可导函数()f x ,如果0()0f x '=,那么0x x =是函数()f x 的极值点,因为函数3()f x x =在0x =处的导数值(0)0f '=,所以,0x =是函数3()f x x =的极值点。
以上推理中:( ) A .大前提错误B .小前提错误C .推理形式错误D .结论正确2.用反证法证明命题:“三角形的内角中至少有一个不大于60度"时,反设正确的是( )A .假设三内角都不大于60度B .假设三内角都大于60度C .假设三内角至多有一个大于60度D .假设三内角至多有两个大于60度3.某个命题与正整数有关,若当()*n k k N =∈时该命题成立,那么可推得当1n k =+时该命题也成立,现已知当5n =时该命题不成立,那么可推得( ) A 。
当6n =时,该命题不成立 B 。
当6n =时,该命题成立 C 。
当4n =时,该命题成立D.当4n =时,该命题不成立4.若()f x 在R 上可导,2()2()sin 22f x x f x x π'=++,则10()f x dx =⎰( )A.7cos23π-- B.111cos262π-+ C.171cos262π--D。
111cos262π--5.在平面几何中有如下结论:正三角形ABC的内切圆面积为1S,外接圆面积为2S,则1214SS=,推广到空间中可以得到类似结论:已知正四面体P ABC-的内切球体积为1V,外接球体积为2V,则12VV=()A.18B.19C.164D.1276.函数1siny xx=-的图象大致是()A. B.C. D.7.2222π=--⎰-dx xxm,则m等于( )A.—1 B.0C.1 D.28.如右图是函数32()f x x bx cx d=+++的大致图象,则2212x x+等于( )A.23B.43C.83D.1239.正整数按右表的规律排列,则上起第2015行,左起第2016列的数应为( ) A .22015 B .22016C .20152016+D .20152016⨯10.设()f x 是定义在R 上的偶函数,当0x >时,()()0f x xf x '+>,且(1)0f =,则不等式()0xf x >的解集为( )A .(-1,0)∪(1,+∞)B .(-1,0)∪(0,1)C .(-∞,-1)∪(1,+∞)D .(-∞,-1)∪(0,1)11.若点P 是曲线2ln y x x =-上任意一点,则点P 到直线2y x =-的最小值为( ) A .1B .2C .22D .3 12.关于函数2()ln f x x x=+,下列说法错误的是( ) A 。
安徽省高二数学下学期第三次月考试题 理(含解析)

安徽省2016-2017学年高二下学期第三次月考数学(理)试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 复数的共轭复数()A. B. C. D.【答案】B【解析】 ,选B.2. 函数的最大值为()A. B. C. D.【答案】D【解析】 ,所以当时, ; 当时,,因此当时,取最大值,选D.3. 观察下列各式:,,,,,则的末位数字为()A. B. C. D.【答案】A【解析】末位数字变化周期为4,而,所以的末位数字为的末位数字1,选A.4. 设离散型随机变量的分布列为:则()A. B. C. D. b【答案】B【解析】由题意得,选B. 5. 设函数,曲线在点处的切线方程为,则()A. B. C. D.【答案】C【解析】,从而,选C.点睛:(1)求曲线的切线要注意“过点P的切线”与“在点P处的切线”的差异,过点P的切线中,点P不一定是切点,点P也不一定在已知曲线上,而在点P处的切线,必以点P为切点.(2)利用导数的几何意义解题,主要是利用导数、切点坐标、切线斜率之间的关系来进行转化.以平行、垂直直线斜率间的关系为载体求参数的值,则要求掌握平行、垂直与斜率之间的关系,进而和导数联系起来求解.6. 西北某地根据历年的气象资料显示,春季中一天发生沙尘暴的概率为,连续两天发生沙尘暴的概率为,已知某天发生了沙尘暴,则随后一天发生沙尘暴的概率为()A. B. C. D.【答案】C【解析】由条件概率得随后一天发生沙尘暴的概率为,选C.7. 某大学的外文系有一个翻译小组,该小组中会法语不会英语的有1人,英语法语都会的有2人,从该小组任取2人,设为选出的人中英语法语都会的人数,若,则该小组的人数为()A. B. C. D.【答案】B【解析】由题意得,选B.8. 若,,则()A. B. C. D.【答案】A【解析】令得;令得,选A.点睛:赋值法研究二项式的系数和问题“赋值法”普遍适用于恒等式,是一种重要的方法,对形如的式子求其展开式的各项系数之和,常用赋值法,只需令即可;对形如的式子求其展开式各项系数之和,只需令即可.9. 已知数列中,,,则()A. B. C. D.【答案】A【解析】,选A.10. 的展开式中,的系数为()A. B. C. D.【答案】D【解析】因为,所以,即,从而的系数为,选D.点睛:求二项展开式有关问题的常见类型及解题策略(1)求展开式中的特定项.可依据条件写出第项,再由特定项的特点求出值即可.(2)已知展开式的某项,求特定项的系数.可由某项得出参数项,再由通项写出第项,由特定项得出值,最后求出其参数.11. 用五种不同的颜色给图中六个小长方形区域涂色,要求颜色齐全且有公共边的区域颜色不同,则共有涂色方法()A. 种B. 种C. 种D. 种【答案】D【解析】其中可能共色的区域有AC,AD,AE,AF,BE,BF,CD,CF,DF共9种,故共有涂色方法为 ,选D.点睛:求解排列、组合问题常用的解题方法:(1)元素相邻的排列问题——“捆邦法”;(2)元素相间的排列问题——“插空法”;(3)元素有顺序限制的排列问题——“除序法”;(4)带有“含”与“不含”“至多”“至少”的排列组合问题——间接法.12. 某竞猜活动有54人参加.设计者给每位参与者1道填空题和3道选择题,答对一道填空题得2分,答对一道选择题得1分,答错得0分,若得分总数大于或等于4分可获得纪念品.假定每位参与者答对每道填空题的概率为,答对每道选择题的概率为,且每位参与者答题互不影响.设参与者中可获得纪念品的人数为,则均值(数学期望)()A. B. C. D.【答案】B【解析】由题意得某位参与者得4分的概率为 ,得5分的概率为,所以参与者获得纪念品的概率为 ,因为 ,所以选B.点睛:求解离散型随机变量的数学期望的一般步骤为:第一步是“判断取值”,即判断随机变量的所有可能取值,以及取每个值所表示的意义;第二步是“探求概率”,即利用排列组合、枚举法、概率公式(常见的有古典概型公式、几何概型公式、互斥事件的概率和公式、独立事件的概率积公式,以及对立事件的概率公式等),求出随机变量取每个值时的概率;第三步是“写分布列”,即按规范形式写出分布列,并注意用分布列的性质检验所求的分布列或某事件的概率是否正确;第四步是“求期望值”,一般利用离散型随机变量的数学期望的定义求期望的值,对于有些实际问题中的随机变量,如果能够断定它服从某常见的典型分布(如二项分布),则此随机变量的期望可直接利用这种典型分布的期望公式()求得.因此,应熟记常见的典型分布的期望公式,可加快解题速度.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 设是虚数单位,复数的实部与虚部相等,则__________.【答案】【解析】点睛:本题重点考查复数的基本运算和复数的概念,属于基本题.首先对于复数的四则运算,要切实掌握其运算技巧和常规思路,如. 其次要熟悉复数相关基本概念,如复数的实部为、虚部为、模为、对应点为、共轭为14. 的展开式中常数项为__________.【答案】【解析】常数项为15. 对于任意实数,定义,若,则__________.【答案】【解析】16. 某高三理科班组织摸底考试,六门学科在两天内考完,其中上午考一门,下午考两门,语文安排在第一天的上午,数学和英语必有一门安排在上午,若安排在下午必须安排在第一场,数学和物理不能安排在同一天,则不同的考试安排方案有__________.【答案】【解析】三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 在中,用综合法证明:是的充分不必要条件.【答案】见解析【解析】试题分析:先由正弦定理将角的关系转化为边的关系:,去分母整理得.再由余弦定理得,根据基本不等式可得,即得,因此充分性成立,而必要性不成立,只需举一个反例,如3,4,5构成的三角形,3对应的角B满足,但不满足.试题解析:.,而不可逆,故是的充分不必要条件.18. 已知的展开式中第6项为常数项.(Ⅰ)求展开式中的系数;(Ⅱ)求展开式中所有的有理项.【答案】(1)(2),,.【解析】试题分析:首先写出通项公式并化简得,令,解得.(1)令,求得,由此得到项的系数.(2)依题意有,通过列举的值得出所有的有理项.试题解析:(Ⅰ)由通项公式得,因为第6项为常数项,所以时,有,解得,令,得,故所求系数为 .(Ⅱ)根据通项公式,由题意得 ,令,则,即,因为,所以应为偶数,所以可以取,即可以取2,5,8,所以第3项,第6项,第9项为有理数,它们分别为, , .19. 新一届班委会的7名成员有、、三人是上一届的成员,现对7名成员进行如下分工. (Ⅰ)若正、副班长两职只能由、、三人选两人担任,则有多少种分工方案?(Ⅱ)若、、三人不能再担任上一届各自的职务,则有多少种分工方案?【答案】(1)720(2)【解析】试题分析:(1)先安排正、副班长,再安排其他位置,最后根据分布计算原理求;(2)讨论、、三人不能再担任上一届各自的职务情形:任意一人都不担任原来三个职务;一人担任担任原来三个职务某个职务;两人担任担任原来三个职务某两个职务;三人担任担任原来三个职务;最后根据分类计算原理求.试题解析:(Ⅰ)先确定正、副班长,有种选法,其余全排列有种,共有种分工方案.(Ⅱ)方法一:设、、三人的原职务是、、,当任意一人都不担任职务时有种;当中一人担任中的职务时,有种;当中两人担任中的职务时,有种;当中三人担任中的职务时,有种;故共有种分工方案.方法二:担任职务总数为种,当担任原职务时有种,同理各自担任原职务时也各自有种,而当、、同时担任原职务时各有种;当同时担任原职务时有种,故共有种分工方案.20. 把1、2、3、4、5这五个数字组成无重复数字的五位数,并把它们由小大到的顺序排成一个数列.(Ⅰ)求是这个数列的第几项;(Ⅱ)求这个数列的第96项;(Ⅲ)求这个数列的所有项和.【答案】(1)第项.(2).(3).【解析】试题分析:(1)可从反面出发:大于的数可分为以下三类:以5开头,以45(2)比第项所表示的五位数大的五位数有开头,以435开头,最后用减即得,个,而以5开头的有(个),所以第项为(3)每位数字之和为,共有(个),所以所有项和为试题解析:(Ⅰ)大于的数可分为以下三类:第一类:以5开头的有(个),第二类:以45开头的有(个),第三类:以435开头的有(个),故不大于的五位数有(个),即是第项.(Ⅱ)数列共有项,项之后还有项。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
安徽省亳州市高二下学期数学3月月考试卷
姓名:________ 班级:________ 成绩:________
一、单选题 (共12题;共24分)
1. (2分) (2016高二下·卢龙期末) 记者要为5名志愿者和他们帮助的2位老人拍照,要求排成一排,2位老人相邻但不排在两端,不同的排法共有()
A . 1440种
B . 960种
C . 720种
D . 480种
2. (2分)(2017·海淀模拟) 二项式的展开式的第二项是()
A . 6x4
B . ﹣6x4
C . 12x4
D . ﹣12x4
3. (2分)(2020·河南模拟) 已知正方形,其内切圆与各边分别切于点E,F,G、H,连接,
,,.现向正方形内随机抛掷一枚豆子,记事件A:豆子落在圆I内,事件B:豆子落在四边形外,则()
A .
B .
C .
D .
4. (2分) (2019高二下·中山期末) 的值等于()
A . 7351
B . 7355
C . 7513
D . 7315
5. (2分)从5位同学中选派4位同学在星期五、星期六、星期日参加公益活动,每人一天,要求星期五有2人参加,星期六、星期日各有1人参加,则不同的选派方法共有()
A . 40种
B . 60种
C . 100种
D . 120种
6. (2分)在二项式的展开式中,各项系数之和为A,各项二项式系数之和为B,且A+B=72,则展开式中常数项的值为()
A . 6
B . 9
C . 12
D . 18
7. (2分) (2017高二下·蚌埠期末) 若对于任意实数x,有x4=a0+a1(x﹣2)+a2(x﹣2)2+a3(x﹣2)3+a4(x﹣2)4 ,则a2的值为()
A . 4
B . 12
C . 24
D . 48
8. (2分) (2019高三上·赤峰月考) 连续投掷2粒大小相同,质地均匀的骰子3次,则恰有2次点数之和不小于10的概率为()
A .
B .
C .
D .
9. (2分)(2017·昆明模拟) (x2+xy+2y)5的展开式中x6y2的系数为()
A . 20
B . 40
C . 60
D . 80
10. (2分)(2020·芜湖模拟) 我国古代典籍《周易》用“卦”描述万物的变化,每一卦由六爻组成.其中有一种起卦方法称为“金钱起卦法”,其做法为:取三枚相同的钱币合于双手中,上下摇动数下使钱币翻滚摩擦,再随意抛撒钱币到桌面或平盘等硬物上,如此重复六次,得到六爻.若三枚钱币全部正面向上或全部反面向上,就称为变爻.若每一枚钱币正面向上的概率为,则一卦中恰有三个变爻的概率为()
A .
B .
C .
D .
11. (2分) (2017高三·三元月考) 若的展开式中所有项系数的绝对值之和为1024,则该展开式中的常数项是()
A . ﹣270
B . 270
C . ﹣90
D . 90
12. (2分) (2019高二下·大庆期末) 在个排球中有个正品,个次品.从中抽取个,则正品数比次品数少的概率为()
A .
B .
C .
D .
二、填空题 (共4题;共4分)
13. (1分) (2019高二下·荆门期末) 在的二项展开式中,只有第5项的二项式系数最大,则该二项展开式中的常数项等于________.
14. (1分) (2019高二下·上海月考) 将6名男生,4名女生分成两组,每组5人,参加两项不同的活动,每组3名男生和2名女生,则不同的分配方法有________种.
15. (1分) (2020高二下·河西期中) 已知离散型随机变量X的分布列为:
X012
P0.5
则常数 ________.
16. (1分) (2018高二上·南通月考) 叙利亚内战接近尾声,中国红十字会相应国际号召,支持叙利亚人民战后重建,为解决现阶段叙利亚人民急需的医疗保障,现拟从北京某知名医院的专职教授的医生6人(其中男医生3人,女医生3人),护士8人(其中男护士2人,女护士6人)中选派医生、护士各三人组成卫生医疗对,要求男医生至少两人,男护士至少一人,则这样的选派方案共有________种.(请用数字作答)
三、解答题 (共6题;共70分)
17. (10分) (2020高二下·武汉期中) 设 .
(1)求;
(2)求及关于的表达式 .
18. (25分)解不等式:>6.
19. (5分) (2017高二下·桂林期末) 计算:
(1)已知A =6C ,求n的值;
(2)求二项式(1﹣2x)4的展开式中第4项的系数.
20. (10分) (2018高三上·丰台期末) 某校为了鼓励学生热心公益,服务社会,成立了“慈善义工社”.2017年12月,该校“慈善义工社”为学生提供了4次参加公益活动的机会,学生可通过网路平台报名参加活动.为了解学生实际参加这4次活动的情况,该校随机抽取100名学生进行调查,数据统计如下表,其中“√”表示参加,“×”表示未参加.
根据表中数据估计,该校4000名学生中约有120名这4次活动均未参加.
(Ⅰ)求的值;
(Ⅱ)从该校4000名学生中任取一人,试估计其2017年12月恰参加了2次学校组织的公益活动的概率;
(Ⅲ)已知学生每次参加公益活动可获得10个公益积分,任取该校一名学生,记该生2017年12月获得的公益积分为,求随机变量的分布列和数学期望 .
21. (10分) (2019高三上·玉林月考) 某学校为了选拔学生参加“XX市中学生知识竞赛”,先在本校进行选拔测试,若该校有100名学生参加选拔测试,并根据选拔测试成绩作出如图所示的频率分布直方图.
(1)根据频率分布直方图,估算这100名学生参加选拔测试的平均成绩;
(2)该校推荐选拔测试成绩在110以上的学生代表学校参加市知识竞赛,为了了解情况,在该校推荐参加市知识竞赛的学生中随机抽取2人,求选取的两人的选拔成绩在频率分布直方图中处于不同组的概率.
22. (10分)(2019·全国Ⅰ卷理) 为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验。
试验方案如下:每一轮选取两只白鼠对药效进行对比试验。
对于两只白鼠,随机选一只施以甲药,另一只施以乙药。
一轮的治疗结果得出后,再安排下一轮试验。
当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效。
为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得-1分:若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得-1分:若都治愈或都未治愈则两种药均得0分。
甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X。
(1)求X的分布列;
(2)若甲药、乙药在试验开始时都赋予4分,pi(i=0,1,…,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效“的概率,则P0=0,P8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=P(X=-1),b=P(X=0),c=P(X=1)。
假设α=0.5,β=0.8。
(i)证明:(i=0,1,2,…,7)为等比数列;
(ii)求P4 ,并根据P4的值解释这种试验方案的合理性。
参考答案一、单选题 (共12题;共24分)
1-1、
2-1、
3-1、
4-1、
5-1、
6-1、
7-1、
8-1、
9-1、
10-1、
11-1、
12-1、
二、填空题 (共4题;共4分)
13-1、
14-1、
15-1、
16-1、
三、解答题 (共6题;共70分)
17-1、
17-2、
18-1、
19-1、
19-2、
20-1、
21-1、
21-2、
22-1、
22-2、
第11 页共11 页。
