自动控制原理(中英文对照李道根)习题3.题解

自动控制原理习题及其解答第三章

第三章例3-1 系统的结构图如图3-1所示。

已知传递函数 )12.0/(10)(+=s s G 。

今欲采用加负反馈的办法，将过渡过程时间t s减小为原来的0.1倍，并保证总放大系数不变。

试确定参数K h 和K 0的数值。

解首先求出系统的传递函数φ（s ），并整理为标准式，然后与指标、参数的条件对照。

一阶系统的过渡过程时间t s 与其时间常数成正比。

根据要求，总传递函数应为)110/2.0(10)(+=s s φ即HH K s K s G K s G K s R s C 1012.010)(1)()()(00++=+= )()11012.0(101100s s K K K HHφ=+++=比较系数得⎪⎩⎪⎨⎧=+=+1010110101100H HK K K 解之得9.0=H K 、100=K解毕。

例3-10 某系统在输入信号r (t )=(1+t )1(t )作用下，测得输出响应为：t e t t c 109.0)9.0()(--+= （t ≥0）已知初始条件为零，试求系统的传递函数)(s φ。

解因为22111)(ss s s s R +=+=)10()1(10109.09.01)]([)(22++=+-+==s s s s s s t c L s C 故系统传递函数为11.01)()()(+==s s R s C s φ 解毕。

例3-3 设控制系统如图3-2所示。

试分析参数b 的取值对系统阶跃响应动态性能的影响。

解由图得闭环传递函数为1)()(++=s bK T Ks φ系统是一阶的。

动态性能指标为)(3)(2.2)(69.0bK T t bK T t bK T t s r d +=+=+= 因此，b 的取值大将会使阶跃响应的延迟时间、上升时间和调节时间都加长。

解毕。

例 3-12 设二阶控制系统的单位阶跃响应曲线如图3-34所示。

试确定系统的传递函数。

解首先明显看出，在单位阶跃作用下响应的稳态值为3，故此系统的增益不是1，而是3。

自动控制原理英文版课后全部_答案

Module3Problem 3.1(a) When the input variable is the force F. The input variable F and the output variable y are related by the equation obtained by equating the moment on the stick:2.233y dylF lk c l dt=+Taking Laplace transforms, assuming initial conditions to be zero,433k F Y csY =+leading to the transfer function31(4)Y k F c k s=+ where the time constant τ is given by4c kτ=(b) When F = 0The input variable is x, the displacement of the top point of the upper spring. The input variable x and the output variable y are related by the equation obtained by the moment on the stick:2().2333y y dy k x l kl c l dt-=+Taking Laplace transforms, assuming initial conditions to be zero,3(24)kX k cs Y =+leading to the transfer function321(2)Y X c k s=+ where the time constant τ is given by2c kτ=Problem 3.2 P 54Determine the output of the open-loop systemG(s) = 1asT+to the inputr(t) = tSketch both input and output as functions of time, and determine the steady-state error between the input and output. Compare the result with that given by Fig3.7 . Solution ：While the input r(t) = t , use Laplace transforms, Input r(s)=21sOutput c(s) = r(s) G(s) = 2(1)aTs s ⋅+ = 211T T a s s Ts ⎛⎫ ⎪-+ ⎪ ⎪+⎝⎭the time-domain response becomes c(t) = ()1t Tat aT e ---Problem 3.33.3 The massless bar shown in Fig.P3.3 has been displaced a distance 0x and is subjected to a unit impulse δ in the direction shown. Find the response of the system for t>0 and sketch the result as a function of time. Confirm the steady-state response using the final-value theorem. Solution ：The equation obtained by equating the force:00()kx cxt δ+=Taking Laplace transforms, assuming initial condition to be zero,K 0X +Cs 0X =1leading to the transfer function()XF s =1K Cs +=1C1K s C+The time-domain response becomesx(t)=1CC tK e -The steady-state response using the final-value theorem:lim ()t x t →∞=0lim s →s 1K Cs +1s =1K00000()()()1;11111()K t CK x x Cx t Kx X K Cs Kx Kx X C Cs K K s KKx x t eCδ-++=⇒++=--∴==⋅++-=⋅According to the final-value theorem:0001lim ()lim lim 01t s s Kx sx t s X C K s K→∞→→-=⋅=⋅=+ Problem 3.4 Solution:1.If the input is a unit step, then1()R s s=()()11R s C s sτ−−−→−−−→+ leading to,1()(1)C s s sτ=+taking the inverse Laplace transform gives,()1tc t e τ-=-as the steady-state output is said to have been achieved once it is within 1% of the final value, we can solute ―t‖ like this,()199%1tc t e τ-=-=⨯ (the final value is 1) hence,0.014.60546.05te t sττ-==⨯=(the time constant τ=10s)2.the numerical value of the numerator of the transfer function doesn’t affect the answer. See this equation, If ()()()1C s AG s R s sτ==+ then()(1)A C s s sτ=+giving the time-domain response()(1)tc t A e τ-=-as the final value is A, the steady-state output is achieved when,()(1)99%tc t A e A τ-=-=⨯solute the equation, t=4.605τ=46.05sthe result make no different from that above, so we said that the numerical value of the numerator of the transfer function doesn’t affect the answer.If a<1, as the time increase, the two lines won`t cross. In the steady state the output lags the input by a time by more than the time constant T. The steady error will be negative infinite.R(t)C(t)Fig 3.7 tR(t)C(t)tIf a=1, as the time increase, the two lines will be parallel. It is as same as Fig 3.7.R(t)C(t)tIf a>1, as the time increase, the two lines will cross. In the steady state the output lags the input by a time by less than the time constant T.The steady error will be positive infinite.Problem 3.5 Solution: R(s)=261s s+, Y(s)=26(51)s s s +⋅+=229614551s s s -+++ /5()62929t y t t e -∴=-+so the steady-state error is 29(-30). To conform the result:5lim ()lim(62929);tt t y t t -→∞→∞=-+=∞6lim ()lim ()lim ()lim(51)t s s s s y t y s Y s s s →∞→→→+====∞+.20lim ()lim ()lim [()()]161lim [()1]()lim (1)()5130ss t s s s s e e t S E S S Y S R S S G S R S S S S S→∞→→→→==⋅=⋅-=⋅-=⋅-⋅++=- Therefore, the solution is basically correct.Problem 3.623yy x += since input is of constant amplitude and variable frequency , it can be represented as:j tX eA ω=as we know ,the output should be a sinusoidal signal with the same frequency of the input ,it can also be represented as:R(t)C(t)t0j t y y e ω=hence23j tj tj tj yyeeeA ωωωω+=00132j y Aω=+ 0294Ayω=+ 2tan3w ϕ=- Its DC(w→0) value is 003Ay ω==Requirement 01122w yy==21123294AA ω=⨯+ →32w = while phase lag of the input:1tan 14πϕ-=-=-Problem 3.7One definition of the bandwidth of a system is the frequency range over which the amplitude of the output signal is greater than 70% of the input signal amplitude when a system is subjected to a harmonic input. Find a relationship between the bandwidth and the time constant of a first-order system. What is the phase angle at the bandwidth frequency ？ Solution ：From the equation 3.41000.71r A r ωτ22=≥+ (1)and ω≥0 (2) so 1.020ωτ≤≤so the bandwidth 1.02B ωτ=from the equation 3.43the phase angle 110tan tan 1.024c πωτ--∠=-=-=Problem 3.8 3.8 SolutionAccording to generalized transfer function of First-Order Feedback Systems11C KG K RKGHK sτ==+++the steady state of the output of this system is 2.5V .∴if s →0, 2.51104C R→=. From this ,we can get the value of K, that is 13K =.Since we know that the step input is 10V , taking Laplace transforms,the input is 10S.Then the output is followed1103()113C s S s τ=⨯++Taking reverse Laplace transforms,4/4332.5 2.5 2.5(1)t t C e eττ--=-=-From the figure, we can see that when the time reached 3s,the value of output is 86% of the steady state. So we can know34823(2)*4393τττ-=-⇒-=-⇒=, 4/3310.8642t t e ττ-=-=⇒=The transfer function is3128s +146s+Let 12+8s=0, we can get the pole, that is 1.5s =-2/3- Problem 3.9 Page 55 Solution:The transfer function can be represented,()()()()()()()o o m i m i v s v s v s G s v s v s v s ==⋅While,()1()111//()()11//o m m i v s v s sRCR v s sC sC v s R R sC sC =+⎛⎫+ ⎪⎝⎭=⎡⎤⎛⎫++ ⎪⎢⎥⎝⎭⎣⎦Leading to the final transfer function,21()13()G s sRC sRC =++ And the reason:the second simple lag compensation network can be regarded as the load of the first one, and according to Load Effect , the load affects the primary relationship; so the transfer function of the comb ination doesn’t equal the product of the two individual lag transfer functio nModule4Problem4.14.1The closed-loop transfer function is10(6)102(6)101610S S S S C RS s +++++==Comparing with the generalized second-order system,we getProblem4.34.3Considering the spring rise x and the mass rise y. Using Newton ’s second law of motion..()()d x y m y K x y c dt-=-+Taking Laplace transforms, assuming zero initial conditions2mYs KX KY csX csY =-+-resulting in the transfer funcition where2Y cs K X ms cs K +=++ And521.26*10cmkc ζ== Problem4.4 Solution:The closed-loop transfer function is210263101011n n d n W EW E W W E ====-=2121212K C K S S K R S S K S S ∙+==+++∙+Comparing the closed-loop transfer function with the generalized form,2222n n nCR s s ωξωω=++ it is seen that2n K ω= And that22n ξω= ; 1Kξ=The percentage overshoot is therefore21100PO eξπξ--=11100k keπ-∙-=Where 10%PO ≤When solved, gives 1.2K ≤（2.86）When K takes the value 1.2, the poles of the system are given by22 1.20s s ++=Which gives10.45s j =-±±s=-1 1.36jProblem4.5ReIm0.45-0.45-14.5 A unity-feedback control system has the forward-path transfer functionG (s) =10)S(s K+Find the closed-loop transfer function, and develop expressions for the damping ratio And damped natural frequency in term of K Plot the closed-loop poles on the complex Plane for K = 0,10,25,50,100.For each value of K calculate the corresponding damping ratio and damped natural frequency. What conclusions can you draw from the plot?Solution: Substitute G(s)=(10)K s s + into the feedback formula : Φ(s)=()1()G S HG S +.And in unitfeedback system H=1. Result in: Φ(s)=210Ks s K++ So the damped natural frequencyn ω=K ,damping ratio ζ=102k =5k.The characteristic equation is 2s +10S+K=0. When K ≤25,s=525K -±-; While K>25,s=525i K -±-; The value ofn ω and ζ corresponding to K are listed as follows.K 0 10 25 50 100 Pole 1 1S 0 515-+ -5 -5+5i 553i -+Pole 2 2S -10 515-- -5 -5-5i553i --n ω 010 5 52 10 ζ ∞2.51 0.5 0.5Plot the complex plane for each value of K:We can conclude from the plot.When k ≤25,poles distribute on the real axis. The smaller value of K is, the farther poles is away from point –5. The larger value of K is, the nearer poles is away from point –5.When k>25,poles distribute away from the real axis. The smaller value of K is, the further (nearer) poles is away from point –5. The larger value of K is, the nearer (farther) poles is away from point –5.And all the poles distribute on a line parallels imaginary axis, intersect real axis on the pole –5.Problem4.61tb b R L C b o v dv i i i i v dt C R L dt=++=++⎰Taking Laplace transforms, assuming zero initial conditions, reduces this equation to011b I Cs V R Ls ⎛⎫=++ ⎪⎝⎭20b V RLs I Ls R RLCs =++ Since the input is a constant current i 0, so01I s=then,()2b RLC s V Ls R RLCs==++ Applying the final-value theorem yields ()()0lim lim 0t s c t sC s →∞→==indicating that the steady-state voltage across the capacitor C eventually reaches the zero ,resulting in full error.Problem4.74.7 Prove that for an underdamped second-order system subject to a step input, thepercentage overshoot above the steady-state output is a function only of the damping ratio .Fig .4.7SolutionThe output can be given by222222()(2)21()(1)n n n n n n C s s s s s s s ωζωωζωζωωζ=+++=-++- (1)the damped natural frequencyd ω can be defined asd ω=21n ωζ- (2)substituting above results in22221()()()n n n d n d s C s s s s ζωζωζωωζωω+=--++++ (3) taking the inverse transform yields22()1sin()11tan n t d e c t t where ζωωφζζφζ-=-+--=(4)the maximum output is22()1sin()11n t p d p p d n e c t t t ζωωφζππωωζ-=-+-==-(5)so the maximum is2/1()1p c t eπζζ--=+the percentage overshoot is therefore2/1100PO eπζζ--=Problem4.8 Solution to 4.8:Considering the mass m displaced a distance x from its equilibrium position, the free-body diagram of the mass will be as shown as follows.aP cdx kxkxmUsing Newton ’s second law of motion,22p k x c x mx m x c x k x p--=++=Taking Laplace transforms, assuming zero initial conditions,2(2)X ms cs k P ++= results in the transfer function2/(1/)/((/)2/)X P m s c m s k m =++ 2(2/)(2/)((/)2/)k k m s c m s k m =++As we see2(2)X m s c s k P++= As P is constantSo X ∝212ms cs k ++ . When 56.25102cs m-=-=-⨯ ()25min210mscs k ++=4max5100.110X == This is a second-order transfer function where 22/n k m ω= and/2/22n c w m c k m ζ== The damped natural frequency is given by 2212/1/8d n k m c km ωωζ=-=-22/(/2)k m c m =- Using the given data,462510/2100.050.2236n ω=⨯⨯⨯== 462502.79501022100.05ζ-==⨯⨯⨯⨯ ()240.22361 2.7950100.2236d ω-=⨯-⨯= With these data we can draw a picture14.0501160004.673600p de s e T T πωτζωτ======222222112/1222()22,,,428sin (sin cos )0tan 7.030.02n n pp dd n dd n ntd d t t t n d p d d p ddd p p p nX k m c k P ms cs k k m s s s m m k c k c cm m m m km p x e tm p xe t t m t t x m ζωζωωωζωωωωζζωωωζωωωωωωωζω--===⋅=⋅++++++=-===∴==-+=∴=⇒=⇒= 其中Problem4.10 4.10 solution:The system is similar to the one in the book on PAGE 58 to PAGE 63. The difference is the connection of the spring. So the transfer function is2222l n d n n w s w s w θθζ=++222(),;p a m ld a m p m l m l l m mm l lk k k N RJs RCs R k k N k J N J J C N c c N N N θθωθωθ=+++=+=+===p a mn K K K w NJ R='damping ratio 2p a m c NRK K K J ζ='But the value of J is different, because there is a spring connected.122s m J J J J N N '=++Because of final-value theorem,2l nd w θθζ=Module5Problem5.45．4 The closed-loop transfer function of the system may be written as2221010(1)610101*********CR K K K S S K K S S K S S +++==+++++++ The closed-loop poles are the solutions of the characteristic equation6364(1010)3110210(1)n K S K JW K -±-+==-±+=+ 210(1)6310(1)E K E K +==+In order to study the stability of the system, the behavior of the closed-loop poles when the gain K increases from zero to infinte will be observed. So when12K = 3010E =321S J =-± 210K = 3110110E =3101S J =-± 320K = 21070E =3201S J =-±双击下面可以看到原图ReProblem5.5SolutionThe closed-loop transfer function is2222(1)1(1)KC K KsKR s K as s aKs Kass===+++++∙+Comparing the closed-loop transfer function with the generalized form, 2222nn nCR s sωξωω=++Leading to2nKa Kωξ==The percentage overshoot is therefore2110040%PO eξπξ--==Producing the result0.869ξ=（0.28）And the peak time241PnT sπωξ==-Leading to1.586nω=（0.82）Problem5.75.7 Prove that the rise time T r of a second-order system with a unit step input is given byT r = d ω1 tan -1n dζωω = d ω1 tan -1d ωζ21--Plot the rise against the damping ratio.Solution:According to (4.33):c(t)=1-2(cos sin )1n t d d e t t ζωζωωζ-+-. 4.33When t=r T ,c(t)=1.substitue c(t)= 1 into (4.33) Producing the resultr T =d ω1 tan -1n dζωω = d ω1 tan -112ζζ--Plot the rise time against the damping ratio:Problem5.9Solution to 5.9:As we know that the system is the open-loop transfer function of a unity-feedback control system.So ()()GH S G S = Given as()()()425KGH s s s =-+The close-loop transfer function of the system may be written as()()()()()41254G s C Ks R GH s s s K ==+-++ The characteristic equation is()()2254034100s s K s s K -++=⇒++-=According to the Routh ’s method, the Routh ’s array must be formed as follow20141030410s K s s K -- For there is no closed-loop poles to the right of the imaginary axis4100 2.5K K -≥⇒≥ Given that 0.5ζ=4103 4.752410n K K K ωζ=-=⇒=- When K=0, the root are s=+2,-5According to the characteristic equation, the solutions are349424s K =-±-while 3.0625K ≤, we have one or two solutions, all are integral number.Or we will have solutions with imaginary number. So we can drawK=102 -5 K=0K=3.0625K=2.5 K=10Open-loop polesClosed-loop polesProblem5.10 5.10 solution:0.62/n w rad sζ==according to()211sin()21n w t d e c w t ζφζ-=-+=- 1.2sin(1.6)0.4t e t φ-⋅+= 4t a n3φ= finally, t is delay time:1.23t s ≈(0.67)Module6Problem 6.3First we assume the disturbance D to be zero:e R C =-1011C K e s s =⋅⋅⋅+Hence:(1)10(1)e s s R K s s +=++ Then we set the input R to be zero:10()(1)C K e D e s s =⋅+⋅=-+ ⇒ 1010(1)e D K s s =-++Adding these two results together:(1)1010(1)10(1)s s e R D K s s K s s +=⋅-⋅++++21()R s s =; 1()D s s= ∴222110910(1)10(1)100(1)s s e Ks s s Ks s s s s s +-=-=++++++ the steady-state error:232200099lim lim lim 0.09100100ss s s s s s s e s e s s s s s →→→--=⋅===-++++Problem 6.4Determine the disturbance rejection ratio(DRR) for the system shown in Fig P.6.4+fig.P.6.4 solution ：from the diagram we can know :0.210.05mv K RK c === so we can get that()0.21115()0.05v m m OL n CL K K DRR cR ωω∆⨯==+=+=∆210.10.050.050.025s s =++, so c=0.025, DRR=9Problem 6.5 6.5 SolutionFor the purposes of determining the steady-state error of the system, we should get to know the effect of the input and the disturbance along when the other will be assumed to be zero.First to simplify the block diagram to the following patter:110s +2021Js Tddθoθ0.220.10.05s ++__+d T—Allowing the transfer function from the input to the output position to be written as01220220d Js s θθ=++ 012222020240*220220(220)dJs s Js s s Js s sθθ===++++++ According to the equation E=R-C:022*******(2)()lim[()()]lim[(1)]lim 0.2220220ssr d s s s Js e s s s s Js s Js s δδδθθ→→→+=-=-==++++问题;1. 系统型为2，对于阶跃输入，稳态误差为0.2. 终值定理写的不对。

自动控制原理(中英文对照李道根)习题2题解

)c(
2C ov
� � R� R � ) s( iVs 1C � )s ( oV� s 1C � � � )s ( A V �� 1� 1 � )c( � R R R �� )s ( oV � )s ( A V� s 2 C � �� 1 1 2 �� ) s ( iV
.5.2P erugiF
) s ( 2 X 2 s 2 M � ]) s ( 2 X � ) s ( 1 X [ K
snቤተ መጻሕፍቲ ባይዱituloS■
�
)s ( F )s( 2 X
3
3 Z 1Z � 3 Z 2 Z � 2 Z 1Z
3Z0 Z
��
)s ( iV )s ( oV
�
�3 2Z 2 1 �� Z � Z � Z �� ) s ( oV � ) s( A V� � 1 1 1 �� 1 � )d( 1 0Z� Z � � ) s ( iV � 1 1 � )s ( A V
2 3
�
) s( R )s ( C
evah ew ,yaw emas a nI )b( si noitcnuf refsnart eht ,ecneH
� ) s( R )s ( C
evah ew ,snoitidnoc laitini orez gnimussa ,mrofsnart ecalpaL gnikaT )a( :noituloS
C
)1 � s (s 0K
5X 2K 2N
4X
sT 1
3X
2X
1G
1X
1N
R
.nwohs sa margaid kcolb eht evah ew , redro ni thgir ot tfel morf )s ( C dna )s ( 5 X , ) s ( 4 X , ) s( 3 X , ) s ( 2 X , )s ( 1 X , )s (R selbairav eht gnignarraeR

完整word版,《自动控制原理》试卷及答案(英文10套),推荐文档

AUTOMATIC CONTROL THEOREM (1)⒈ Derive the transfer function and the differential equation of the electric network⒉ Consider the system shown in Fig.2. Obtain the closed-loop transfer function)()(S R S C , )()(S R S E . （12%） ⒊ The characteristic equation is given 010)6(5)(123=++++=+K S K S S S GH . Discuss the distribution of the closed-loop poles. (16%)① There are 3 roots on the LHP ② There are 2 roots on the LHP② There are 1 roots on the LHP ④ There are no roots on the LHP . K=?⒋ Consider a unity-feedback control system whose open-loop transfer function is )6.0(14.0)(++=S S S S G . Obtain the response to a unit-step input. What is the rise time for this system? What is the maximum overshoot? （10%）Fig.15. Sketch the root-locus plot for the system )1()(+=S S K S GH . ( The gain K is assumed to be positive.)① Determine the breakaway point and K value.② Determine the value of K at which root loci cross the imaginary axis.③ Discuss the stability. (12%)6. The system block diagram is shown Fig.3. Suppose )2(t r +=, 1=n . Determine the value of K to ensure 1≤e . (12%)Fig.37. Consider the system with the following open-loop transfer function:)1)(1()(21++=S T S T S K S GH . ① Draw Nyquist diagrams. ② Determine the stability of the system for two cases, ⑴ the gain K is small, ⑵ K is large. (12%)8. Sketch the Bode diagram of the system shown in Fig.4. (14%)⒈212121121212)()()(C C S C C R R C S C C R S V S V ++++=⒉ 2423241321121413211)()(H G H G G G G G G G H G G G G G G G S R S C ++++++=⒊ ① 0<K<6 ② K ≤0 ③ K ≥6 ④ no answer⒋⒌①the breakaway point is –1 and –1/3; k=4/27 ② The imaginary axis S=±j; K=2③⒍5.75.3≤≤K⒎ )154.82)(181.34)(1481.3)(1316.0()11.0(62.31)(+++++=S S S S S S GHAUTOMATIC CONTROL THEOREM (2)⒈Derive the transfer function and the differential equation of the electric network⒉ Consider the equation group shown in Equation.1. Draw block diagram and obtain the closed-loop transfer function )()(S R S C . （16% ） Equation.1 ⎪⎪⎩⎪⎪⎨⎧=-=-=--=)()()()()]()()([)()]()()()[()()()]()()[()()()(3435233612287111S X S G S C S G S G S C S X S X S X S G S X S G S X S C S G S G S G S R S G S X⒊ Use Routh ’s criterion to determine the number of roots in the right-half S plane for the equation 0400600226283)(12345=+++++=+S S S S S S GH . Analyze stability.（12% ）⒋ Determine the range of K value ,when )1(2t t r ++=, 5.0≤SS e . （12% ）Fig.1⒌Fig.3 shows a unity-feedback control system. By sketching the Nyquist diagram of the system, determine the maximum value of K consistent with stability, and check the result using Routh ’s criterion. Sketch the root-locus for the system （20%）（18% ）⒎ Determine the transfer function. Assume a minimum-phase transfer function.（10% ）⒈1)(1)()(2122112221112++++=S C R C R C R S C R C R S V S V⒉ )(1)()(8743215436324321G G G G G G G G G G G G G G G G S R S C -+++=⒊ There are 4 roots in the left-half S plane, 2 roots on the imaginary axes, 0 root in the RSP. The system is unstable.⒋ 208<≤K⒌ K=20⒍⒎ )154.82)(181.34)(1481.3)(1316.0()11.0(62.31)(+++++=S S S S S S GHAUTOMATIC CONTROL THEOREM (3)⒈List the major advantages and disadvantages of open-loop control systems. (12% )⒉Derive the transfer function and the differential equation of the electric network⒊ Consider the system shown in Fig.2. Obtain the closed-loop transfer function)()(S R S C , )()(S R S E , )()(S P S C . （12%）⒋ The characteristic equation is given 02023)(123=+++=+S S S S GH . Discuss the distribution of the closed-loop poles. (16%)5. Sketch the root-locus plot for the system )1()(+=S S K S GH . (The gain K is assumed to be positive.)④ Determine the breakaway point and K value.⑤ Determine the value of K at which root loci cross the imaginary axis. ⑥ Discuss the stability. (14%)6. The system block diagram is shown Fig.3. 21+=S K G , )3(42+=S S G . Suppose )2(t r +=, 1=n . Determine the value of K to ensure 1≤SS e . (15%)7. Consider the system with the following open-loop transfer function:)1)(1()(21++=S T S T S K S GH . ① Draw Nyquist diagrams. ② Determine the stability of the system for two cases, ⑴ the gain K is small, ⑵ K is large. (15%)⒈ Solution: The advantages of open-loop control systems are as follows: ① Simple construction and ease of maintenance② Less expensive than a corresponding closed-loop system③ There is no stability problem④ Convenient when output is hard to measure or economically not feasible. (For example, it would be quite expensive to provide a device to measure the quality of the output of a toaster.)The disadvantages of open-loop control systems are as follows:① Disturbances and changes in calibration cause errors, and the output may be different from what is desired.② To maintain the required quality in the output, recalibration is necessary from time to time.⒉ 1)(1)()()(2122112221122112221112+++++++=S C R C R C R S C R C R S C R C R S C R C R S U S U ⒊351343212321215143211)()(H G G H G G G G H G G H G G G G G G G G S R S C +++++= 35134321232121253121431)1()()(H G G H G G G G H G G H G G H G G H G G G G S P S C ++++-+=⒋ R=2, L=1⒌ S:①the breakaway point is –1 and –1/3; k=4/27 ② The imaginary axis S=±j; K=2⒍5.75.3≤≤KAUTOMATIC CONTROL THEOREM (4)⒈ Find the poles of the following )(s F :se s F --=11)( (12%)⒉Consider the system shown in Fig.1,where 6.0=ξ and 5=n ωrad/sec. Obtain the rise time r t , peak time p t , maximum overshoot P M , and settling time s t when the system is subjected to a unit-step input. （10%）⒊ Consider the system shown in Fig.2. Obtain the closed-loop transfer function)()(S R S C , )()(S R S E , )()(S P S C . （12%）⒋ The characteristic equation is given 02023)(123=+++=+S S S S GH . Discuss the distribution of the closed-loop poles. (16%)5. Sketch the root-locus plot for the system )1()(+=S S K S GH . (The gain K is assumed to be positive.)⑦ Determine the breakaway point and K value.⑧ Determine the value of K at which root loci cross the imaginary axis.⑨ Discuss the stability. (12%)6. The system block diagram is shown Fig.3. 21+=S K G , )3(42+=S S G . Suppose )2(t r +=, 1=n . Determine the value of K to ensure 1≤SS e . (12%)7. Consider the system with the following open-loop transfer function:)1)(1()(21++=S T S T S K S GH . ① Draw Nyquist diagrams. ② Determine the stability of the system for two cases, ⑴ the gain K is small, ⑵ K is large. (12%)8. Sketch the Bode diagram of the system shown in Fig.4. (14%)⒈ Solution: The poles are found from 1=-s e or 1)sin (cos )(=-=-+-ωωσωσj e e j From this it follows that πωσn 2,0±== ),2,1,0(K =n . Thus, the poles are located at πn j s 2±=⒉Solution: rise time sec 55.0=r t , peak time sec 785.0=p t ,maximum overshoot 095.0=P M ,and settling time sec 33.1=s t for the %2 criterion, settling time sec 1=s t for the %5 criterion.⒊ 351343212321215143211)()(H G G H G G G G H G G H G G G G G G G G S R S C +++++= 35134321232121253121431)1()()(H G G H G G G G H G G H G G H G G H G G G G S P S C ++++-+=⒋R=2, L=15. S:①the breakaway point is –1 and –1/3; k=4/27 ② The imaginary axis S=±j; K=2⒍5.75.3≤≤KAUTOMATIC CONTROL THEOREM (5)⒈ Consider the system shown in Fig.1. Obtain the closed-loop transfer function )()(S R S C , )()(S R S E . （18%）⒉ The characteristic equation is given 0483224123)(12345=+++++=+S S S S S S GH . Discuss the distribution of the closed-loop poles. (16%)⒊ Sketch the root-locus plot for the system )15.0)(1()(++=S S S K S GH . (The gain K is assumed to be positive.)① Determine the breakaway point and K value.② Determine the value of K at which root loci cross the imaginary axis. ③ Discuss the stability. (18%)⒋ The system block diagram is shown Fig.2. 1111+=S T K G , 1222+=S T K G . ①Suppose 0=r , 1=n . Determine the value of SS e . ②Suppose 1=r , 1=n . Determine the value of SS e . (14%)⒌ Sketch the Bode diagram for the following transfer function. )1()(Ts s K s GH +=, 7=K , 087.0=T . (10%)⒍ A system with the open-loop transfer function )1()(2+=TS s K S GH is inherently unstable. This system can be stabilized by adding derivative control. Sketch the polar plots for the open-loop transfer function with and without derivative control. (14%)⒎ Draw the block diagram and determine the transfer function. (10%)⒈∆=321)()(G G G S R S C ⒉R=0, L=3,I=2⒋①2121K K K e ss +-=②21211K K K e ss +-= ⒎11)()(12+=RCs s U s UAUTOMATIC CONTROL THEOREM (6)⒈ Consider the system shown in Fig.1. Obtain the closed-loop transfer function )()(S R S C , )()(S R S E . （18%）⒉The characteristic equation is given 012012212010525)(12345=+++++=+S S S S S S GH . Discuss thedistribution of the closed-loop poles. (12%)⒊ Sketch the root-locus plot for the system )3()1()(-+=S S S K S GH . (The gain K is assumed to be positive.)① Determine the breakaway point and K value.② Determine the value of K at which root loci cross the imaginary axis. ③ Discuss the stability. (15%)⒋ The system block diagram is shown Fig.2. SG 11=, )125.0(102+=S S G . Suppose t r +=1, 1.0=n . Determine the value of SS e . (12%)⒌ Calculate the transfer function for the following Bode diagram of the minimum phase. (15%)⒍ For the system show as follows, )5(4)(+=s s s G ,1)(=s H , (16%) ① Determine the system output )(t c to a unit step, ramp input.② Determine the coefficient P K , V K and the steady state error to t t r 2)(=.⒎ Plot the Bode diagram of the system described by the open-loop transfer function elements )5.01()1(10)(s s s s G ++=, 1)(=s H . (12%)w⒈32221212321221122211)1()()(H H G H H G G H H G G H G H G H G G G S R S C +-++-+-+= ⒉R=0, L=5 ⒌)1611()14)(1)(110(05.0)(2s s s s s s G ++++= ⒍t t e e t c 431341)(--+-= t t e e t t c 41213445)(---+-= ∞=P K , 8.0=V K , 5.2=ss eAUTOMATIC CONTROL THEOREM (7)⒈ Consider the system shown in Fig.1. Obtain the closed-loop transfer function)()(S R S C , )()(S R S E . （16%）⒉ The characteristic equation is given 01087444)(123456=+--+-+=+S S S S S S S GH . Discuss the distribution of the closed-loop poles. (10%)⒊ Sketch the root-locus plot for the system 3)1()(S S K S GH +=. (The gain K is assumed to be positive.)① Determine the breakaway point and K value.② Determine the value of K at which root loci cross the imaginary axis. ③ Discuss the stability. (15%)⒋ Show that the steady-state error in the response to ramp inputs can be made zero, if the closed-loop transfer function is given by:nn n n n n a s a s a s a s a s R s C +++++=---1111)()(Λ ;1)(=s H （12%）⒌ Calculate the transfer function for the following Bode diagram of the minimum phase.（15%）w⒍ Sketch the Nyquist diagram (Polar plot) for the system described by the open-loop transfer function )12.0(11.0)(++=s s s S GH , and find the frequency and phase such that magnitude is unity. （16%）⒎ The stability of a closed-loop system with the following open-loop transfer function )1()1()(122++=s T s s T K S GH depends on the relative magnitudes of 1T and 2T . Draw Nyquist diagram and determine the stability of the system.（16%） ( 00021>>>T T K )⒈3213221132112)()(G G G G G G G G G G G G S R S C ++-++=⒉R=2, I=2,L=2 ⒌)1()1()(32122++=ωωωs s s s G⒍o s rad 5.95/986.0-=Φ=ωAUTOMATIC CONTROL THEOREM (8)⒈ Consider the system shown in Fig.1. Obtain the closed-loop transfer function)()(S R S C , )()(S R S E . （16%）⒉ The characteristic equation is given 04)2(3)(123=++++=+S K KS S S GH . Discuss the condition of stability. (12%)⒊ Draw the root-locus plot for the system 22)4()1()(++=S S KS GH ;1)(=s H .Observe that values of K the system is overdamped and values of K it is underdamped. (16%)⒋ The system transfer function is )1)(21()5.01()(s s s s K s G +++=,1)(=s H . Determine thesteady-state error SS e when input is unit impulse )(t δ、unit step )(1t 、unit ramp t and unit parabolic function221t . (16%)⒌ ① Calculate the transfer function (minimum phase);② Draw the phase-angle versus ω (12%) w⒍ Draw the root locus for the system with open-loop transfer function.)3)(2()1()(+++=s s s s K s GH (14%)⒎ )1()(3+=Ts s Ks GH Draw the polar plot and determine the stability of system. (14%)⒈43214321432143211)()(G G G G G G G G G G G G G G G G S R S C -+--+= ⒉∞ππK 528.0⒊S:0<K<0.0718 or K>14 overdamped ;0.0718<K<14 underdamped⒋S: )(t δ 0=ss e ; )(1t 0=ss e ; t K e ss 1=; 221t ∞=ss e⒌S:21ωω=K ; )1()1()(32121++=ωωωωs s ss GAUTOMATIC CONTROL THEOREM (9)⒈ Consider the system shown in Fig.1. Obtain the closed-loop transfer function)(S C , )(S E . （12%）⒉ The characteristic equation is given0750075005.34)(123=+++=+K S S S S GH . Discuss the condition of stability. (16%)⒊ Sketch the root-locus plot for the system )1(4)()(2++=s s a s S GH . (The gain a isassumed to be positive.)① Determine the breakaway point and a value.② Determine the value of a at which root loci cross the imaginary axis. ③ Discuss the stability. (12%)⒋ Consider the system shown in Fig.2. 1)(1+=s K s G i , )1()(2+=Ts s Ks G . Assumethat the input is a ramp input, or at t r =)( where a is an arbitrary constant. Show that by properly adjusting the value of i K , the steady-state error SS e in the response to ramp inputs can be made zero. (15%)⒌ Consider the closed-loop system having the following open-loop transfer function:)1()(-=TS S KS GH . ① Sketch the polar plot ( Nyquist diagram). ② Determine thestability of the closed-loop system. (12%)⒍Sketch the root-locus plot. (18%)⒎Obtain the closed-loop transfer function )()(S R S C . （15%）⒈354211335421243212321313542143211)1()()(H G G G G H G H G G G G H G G G G H G G H G H G G G G G G G G G S R S C --++++-= 354211335421243212321335422341)()(H G G G G H G H G G G G H G G G G H G G H G H G G G H H G S N S E --+++--= ⒉45.30ππK⒌S: N=1 P=1 Z=0; the closed-loop system is stable ⒎2423241321121413211)()(H G H G G G G G G G H G G G G G G G S R S C ++++++=AUTOMATIC CONTROL THEOREM (10)⒈ Consider the system shown in Fig.1. Obtain the closed-loop transfer function)()(S R S C ,⒉ The characteristic equation is given01510520)(1234=++++=+S S KS S S GH . Discuss the condition of stability. (14%)⒊ Consider a unity-feedback control system whose open-loop transfer function is)6.0(14.0)(++=S S S S G . Obtain the response to a unit-step input. What is the rise time forthis system? What is the maximum overshoot? （10%）⒋ Sketch the root-locus plot for the system )25.01()5.01()(s S s K S GH +-=. (The gain K isassumed to be positive.)③ Determine the breakaway point and K value.④ Determine the value of K at which root loci cross the imaginary axis. Discuss the stability. (15%)⒌ The system transfer function is )5(4)(+=s s s G ,1)(=s H . ①Determine thesteady-state output )(t c when input is unit step )(1t 、unit ramp t . ②Determine theP K 、V K and a K , obtain the steady-state error SS e when input is t t r 2)(=. （12%）⒍ Consider the closed-loop system whose open-loop transfer function is given by:①TS K S GH +=1)(; ②TS K S GH -=1)(; ③1)(-=TS KS GH . Examine the stabilityof the system. （15%）⒎ Sketch the root-locus plot 。

自动控制原理精品课程第三章习题解(1)精品文档6页

3-1 设系统特征方程式：试按稳定要求确定T 的取值范围。

解：利用劳斯稳定判据来判断系统的稳定性，列出劳斯列表如下：欲使系统稳定，须有故当T>25时,系统是稳定的。

3-2 已知单位负反馈控制系统的开环传递函数如下，试分别求出当输入信号为,21(),t t t 和时，系统的稳态误差(),()().ssp ssv ssa e e e ∞∞∞和解：（1）根据系统的开环传递函数可知系统的特征方程为：由赫尔维茨判据可知，n=2且各项系数为正，因此系统是稳定的。

由G(s)可知，系统是0型系统，且K=10，故系统在21(),t t t 和输入信号作用下的稳态误差分别为：(2)根据系统的开环传递函数可知系统的特征方程为：由赫尔维茨判据可知，n=2且各项系数为正，且2212032143450,/16.8a a a a a a a ∆=-=>∆>=以及，因此系统是稳定的。

由G(s)可知，系统式I 型系统，且K=7/8,故系统在21(),t t t 和信号作用下的稳态误差分别为：(3)根据系统的开环传递函数可知系统的特征方程为：由赫尔维茨判据可知，n=2且各项系数为正，且21203 3.20a a a a ∆=-=>因此系统是稳定的。

由G(s)可知，系统是Ⅱ型系统，且K=8,故系统在21(),t t t 和信号作用下的稳态误差分别为：3-3 设单位反馈系统的开环传递函数为试求当输入信号2()12r t t t =++时，系统的稳态误差.解：由于系统为单位负反馈系统，根据开环传递函数可以求得闭环系统的特征方程为：由赫尔维茨判据可知，n=2且各项系数为正，因此系统是稳定的。

由G(s)可知，系统是Ⅱ型系统，且K=8,故系统在21(),t t t 和信号作用下的稳态误差分别为10,,K∞，故根据线性叠加原理有：系统的稳态误差为： 3-4 设舰船消摆系统如图3-1所示，其中n(t)为海涛力矩产生，且所有参数中除1K 外均为已知正值。

完整word版,《自动控制原理》试卷及答案(英文10套),推荐文档

AUTOMATIC CONTROL THEOREM (1)⒈ Derive the transfer function and the differential equation of the electric network⒉ Consider the system shown in Fig.2. Obtain the closed-loop transfer function)()(S R S C , )()(S R S E . （12%） ⒊ The characteristic equation is given 010)6(5)(123=++++=+K S K S S S GH . Discuss the distribution of the closed-loop poles. (16%)① There are 3 roots on the LHP ② There are 2 roots on the LHP② There are 1 roots on the LHP ④ There are no roots on the LHP . K=?⒋ Consider a unity-feedback control system whose open-loop transfer function is )6.0(14.0)(++=S S S S G . Obtain the response to a unit-step input. What is the rise time for this system? What is the maximum overshoot? （10%）Fig.15. Sketch the root-locus plot for the system )1()(+=S S K S GH . ( The gain K is assumed to be positive.)① Determine the breakaway point and K value.② Determine the value of K at which root loci cross the imaginary axis.③ Discuss the stability. (12%)6. The system block diagram is shown Fig.3. Suppose )2(t r +=, 1=n . Determine the value of K to ensure 1≤e . (12%)Fig.37. Consider the system with the following open-loop transfer function:)1)(1()(21++=S T S T S K S GH . ① Draw Nyquist diagrams. ② Determine the stability of the system for two cases, ⑴ the gain K is small, ⑵ K is large. (12%)8. Sketch the Bode diagram of the system shown in Fig.4. (14%)⒈212121121212)()()(C C S C C R R C S C C R S V S V ++++=⒉ 2423241321121413211)()(H G H G G G G G G G H G G G G G G G S R S C ++++++=⒊ ① 0<K<6 ② K ≤0 ③ K ≥6 ④ no answer⒋⒌①the breakaway point is –1 and –1/3; k=4/27 ② The imaginary axis S=±j; K=2③⒍5.75.3≤≤K⒎ )154.82)(181.34)(1481.3)(1316.0()11.0(62.31)(+++++=S S S S S S GHAUTOMATIC CONTROL THEOREM (2)⒈Derive the transfer function and the differential equation of the electric network⒉ Consider the equation group shown in Equation.1. Draw block diagram and obtain the closed-loop transfer function )()(S R S C . （16% ） Equation.1 ⎪⎪⎩⎪⎪⎨⎧=-=-=--=)()()()()]()()([)()]()()()[()()()]()()[()()()(3435233612287111S X S G S C S G S G S C S X S X S X S G S X S G S X S C S G S G S G S R S G S X⒊ Use Routh ’s criterion to determine the number of roots in the right-half S plane for the equation 0400600226283)(12345=+++++=+S S S S S S GH . Analyze stability.（12% ）⒋ Determine the range of K value ,when )1(2t t r ++=, 5.0≤SS e . （12% ）Fig.1⒌Fig.3 shows a unity-feedback control system. By sketching the Nyquist diagram of the system, determine the maximum value of K consistent with stability, and check the result using Routh ’s criterion. Sketch the root-locus for the system （20%）（18% ）⒎ Determine the transfer function. Assume a minimum-phase transfer function.（10% ）⒈1)(1)()(2122112221112++++=S C R C R C R S C R C R S V S V⒉ )(1)()(8743215436324321G G G G G G G G G G G G G G G G S R S C -+++=⒊ There are 4 roots in the left-half S plane, 2 roots on the imaginary axes, 0 root in the RSP. The system is unstable.⒋ 208<≤K⒌ K=20⒍⒎ )154.82)(181.34)(1481.3)(1316.0()11.0(62.31)(+++++=S S S S S S GHAUTOMATIC CONTROL THEOREM (3)⒈List the major advantages and disadvantages of open-loop control systems. (12% )⒉Derive the transfer function and the differential equation of the electric network⒊ Consider the system shown in Fig.2. Obtain the closed-loop transfer function)()(S R S C , )()(S R S E , )()(S P S C . （12%）⒋ The characteristic equation is given 02023)(123=+++=+S S S S GH . Discuss the distribution of the closed-loop poles. (16%)5. Sketch the root-locus plot for the system )1()(+=S S K S GH . (The gain K is assumed to be positive.)④ Determine the breakaway point and K value.⑤ Determine the value of K at which root loci cross the imaginary axis. ⑥ Discuss the stability. (14%)6. The system block diagram is shown Fig.3. 21+=S K G , )3(42+=S S G . Suppose )2(t r +=, 1=n . Determine the value of K to ensure 1≤SS e . (15%)7. Consider the system with the following open-loop transfer function:)1)(1()(21++=S T S T S K S GH . ① Draw Nyquist diagrams. ② Determine the stability of the system for two cases, ⑴ the gain K is small, ⑵ K is large. (15%)⒈ Solution: The advantages of open-loop control systems are as follows: ① Simple construction and ease of maintenance② Less expensive than a corresponding closed-loop system③ There is no stability problem④ Convenient when output is hard to measure or economically not feasible. (For example, it would be quite expensive to provide a device to measure the quality of the output of a toaster.)The disadvantages of open-loop control systems are as follows:① Disturbances and changes in calibration cause errors, and the output may be different from what is desired.② To maintain the required quality in the output, recalibration is necessary from time to time.⒉ 1)(1)()()(2122112221122112221112+++++++=S C R C R C R S C R C R S C R C R S C R C R S U S U ⒊351343212321215143211)()(H G G H G G G G H G G H G G G G G G G G S R S C +++++= 35134321232121253121431)1()()(H G G H G G G G H G G H G G H G G H G G G G S P S C ++++-+=⒋ R=2, L=1⒌ S:①the breakaway point is –1 and –1/3; k=4/27 ② The imaginary axis S=±j; K=2⒍5.75.3≤≤KAUTOMATIC CONTROL THEOREM (4)⒈ Find the poles of the following )(s F :se s F --=11)( (12%)⒉Consider the system shown in Fig.1,where 6.0=ξ and 5=n ωrad/sec. Obtain the rise time r t , peak time p t , maximum overshoot P M , and settling time s t when the system is subjected to a unit-step input. （10%）⒊ Consider the system shown in Fig.2. Obtain the closed-loop transfer function)()(S R S C , )()(S R S E , )()(S P S C . （12%）⒋ The characteristic equation is given 02023)(123=+++=+S S S S GH . Discuss the distribution of the closed-loop poles. (16%)5. Sketch the root-locus plot for the system )1()(+=S S K S GH . (The gain K is assumed to be positive.)⑦ Determine the breakaway point and K value.⑧ Determine the value of K at which root loci cross the imaginary axis.⑨ Discuss the stability. (12%)6. The system block diagram is shown Fig.3. 21+=S K G , )3(42+=S S G . Suppose )2(t r +=, 1=n . Determine the value of K to ensure 1≤SS e . (12%)7. Consider the system with the following open-loop transfer function:)1)(1()(21++=S T S T S K S GH . ① Draw Nyquist diagrams. ② Determine the stability of the system for two cases, ⑴ the gain K is small, ⑵ K is large. (12%)8. Sketch the Bode diagram of the system shown in Fig.4. (14%)⒈ Solution: The poles are found from 1=-s e or 1)sin (cos )(=-=-+-ωωσωσj e e j From this it follows that πωσn 2,0±== ),2,1,0(K =n . Thus, the poles are located at πn j s 2±=⒉Solution: rise time sec 55.0=r t , peak time sec 785.0=p t ,maximum overshoot 095.0=P M ,and settling time sec 33.1=s t for the %2 criterion, settling time sec 1=s t for the %5 criterion.⒊ 351343212321215143211)()(H G G H G G G G H G G H G G G G G G G G S R S C +++++= 35134321232121253121431)1()()(H G G H G G G G H G G H G G H G G H G G G G S P S C ++++-+=⒋R=2, L=15. S:①the breakaway point is –1 and –1/3; k=4/27 ② The imaginary axis S=±j; K=2⒍5.75.3≤≤KAUTOMATIC CONTROL THEOREM (5)⒈ Consider the system shown in Fig.1. Obtain the closed-loop transfer function )()(S R S C , )()(S R S E . （18%）⒉ The characteristic equation is given 0483224123)(12345=+++++=+S S S S S S GH . Discuss the distribution of the closed-loop poles. (16%)⒊ Sketch the root-locus plot for the system )15.0)(1()(++=S S S K S GH . (The gain K is assumed to be positive.)① Determine the breakaway point and K value.② Determine the value of K at which root loci cross the imaginary axis. ③ Discuss the stability. (18%)⒋ The system block diagram is shown Fig.2. 1111+=S T K G , 1222+=S T K G . ①Suppose 0=r , 1=n . Determine the value of SS e . ②Suppose 1=r , 1=n . Determine the value of SS e . (14%)⒌ Sketch the Bode diagram for the following transfer function. )1()(Ts s K s GH +=, 7=K , 087.0=T . (10%)⒍ A system with the open-loop transfer function )1()(2+=TS s K S GH is inherently unstable. This system can be stabilized by adding derivative control. Sketch the polar plots for the open-loop transfer function with and without derivative control. (14%)⒎ Draw the block diagram and determine the transfer function. (10%)⒈∆=321)()(G G G S R S C ⒉R=0, L=3,I=2⒋①2121K K K e ss +-=②21211K K K e ss +-= ⒎11)()(12+=RCs s U s UAUTOMATIC CONTROL THEOREM (6)⒈ Consider the system shown in Fig.1. Obtain the closed-loop transfer function )()(S R S C , )()(S R S E . （18%）⒉The characteristic equation is given 012012212010525)(12345=+++++=+S S S S S S GH . Discuss thedistribution of the closed-loop poles. (12%)⒊ Sketch the root-locus plot for the system )3()1()(-+=S S S K S GH . (The gain K is assumed to be positive.)① Determine the breakaway point and K value.② Determine the value of K at which root loci cross the imaginary axis. ③ Discuss the stability. (15%)⒋ The system block diagram is shown Fig.2. SG 11=, )125.0(102+=S S G . Suppose t r +=1, 1.0=n . Determine the value of SS e . (12%)⒌ Calculate the transfer function for the following Bode diagram of the minimum phase. (15%)⒍ For the system show as follows, )5(4)(+=s s s G ,1)(=s H , (16%) ① Determine the system output )(t c to a unit step, ramp input.② Determine the coefficient P K , V K and the steady state error to t t r 2)(=.⒎ Plot the Bode diagram of the system described by the open-loop transfer function elements )5.01()1(10)(s s s s G ++=, 1)(=s H . (12%)w⒈32221212321221122211)1()()(H H G H H G G H H G G H G H G H G G G S R S C +-++-+-+= ⒉R=0, L=5 ⒌)1611()14)(1)(110(05.0)(2s s s s s s G ++++= ⒍t t e e t c 431341)(--+-= t t e e t t c 41213445)(---+-= ∞=P K , 8.0=V K , 5.2=ss eAUTOMATIC CONTROL THEOREM (7)⒈ Consider the system shown in Fig.1. Obtain the closed-loop transfer function)()(S R S C , )()(S R S E . （16%）⒉ The characteristic equation is given 01087444)(123456=+--+-+=+S S S S S S S GH . Discuss the distribution of the closed-loop poles. (10%)⒊ Sketch the root-locus plot for the system 3)1()(S S K S GH +=. (The gain K is assumed to be positive.)① Determine the breakaway point and K value.② Determine the value of K at which root loci cross the imaginary axis. ③ Discuss the stability. (15%)⒋ Show that the steady-state error in the response to ramp inputs can be made zero, if the closed-loop transfer function is given by:nn n n n n a s a s a s a s a s R s C +++++=---1111)()(Λ ;1)(=s H （12%）⒌ Calculate the transfer function for the following Bode diagram of the minimum phase.（15%）w⒍ Sketch the Nyquist diagram (Polar plot) for the system described by the open-loop transfer function )12.0(11.0)(++=s s s S GH , and find the frequency and phase such that magnitude is unity. （16%）⒎ The stability of a closed-loop system with the following open-loop transfer function )1()1()(122++=s T s s T K S GH depends on the relative magnitudes of 1T and 2T . Draw Nyquist diagram and determine the stability of the system.（16%） ( 00021>>>T T K )⒈3213221132112)()(G G G G G G G G G G G G S R S C ++-++=⒉R=2, I=2,L=2 ⒌)1()1()(32122++=ωωωs s s s G⒍o s rad 5.95/986.0-=Φ=ωAUTOMATIC CONTROL THEOREM (8)⒈ Consider the system shown in Fig.1. Obtain the closed-loop transfer function)()(S R S C , )()(S R S E . （16%）⒉ The characteristic equation is given 04)2(3)(123=++++=+S K KS S S GH . Discuss the condition of stability. (12%)⒊ Draw the root-locus plot for the system 22)4()1()(++=S S KS GH ;1)(=s H .Observe that values of K the system is overdamped and values of K it is underdamped. (16%)⒋ The system transfer function is )1)(21()5.01()(s s s s K s G +++=,1)(=s H . Determine thesteady-state error SS e when input is unit impulse )(t δ、unit step )(1t 、unit ramp t and unit parabolic function221t . (16%)⒌ ① Calculate the transfer function (minimum phase);② Draw the phase-angle versus ω (12%) w⒍ Draw the root locus for the system with open-loop transfer function.)3)(2()1()(+++=s s s s K s GH (14%)⒎ )1()(3+=Ts s Ks GH Draw the polar plot and determine the stability of system. (14%)⒈43214321432143211)()(G G G G G G G G G G G G G G G G S R S C -+--+= ⒉∞ππK 528.0⒊S:0<K<0.0718 or K>14 overdamped ;0.0718<K<14 underdamped⒋S: )(t δ 0=ss e ; )(1t 0=ss e ; t K e ss 1=; 221t ∞=ss e⒌S:21ωω=K ; )1()1()(32121++=ωωωωs s ss GAUTOMATIC CONTROL THEOREM (9)⒈ Consider the system shown in Fig.1. Obtain the closed-loop transfer function)(S C , )(S E . （12%）⒉ The characteristic equation is given0750075005.34)(123=+++=+K S S S S GH . Discuss the condition of stability. (16%)⒊ Sketch the root-locus plot for the system )1(4)()(2++=s s a s S GH . (The gain a isassumed to be positive.)① Determine the breakaway point and a value.② Determine the value of a at which root loci cross the imaginary axis. ③ Discuss the stability. (12%)⒋ Consider the system shown in Fig.2. 1)(1+=s K s G i , )1()(2+=Ts s Ks G . Assumethat the input is a ramp input, or at t r =)( where a is an arbitrary constant. Show that by properly adjusting the value of i K , the steady-state error SS e in the response to ramp inputs can be made zero. (15%)⒌ Consider the closed-loop system having the following open-loop transfer function:)1()(-=TS S KS GH . ① Sketch the polar plot ( Nyquist diagram). ② Determine thestability of the closed-loop system. (12%)⒍Sketch the root-locus plot. (18%)⒎Obtain the closed-loop transfer function )()(S R S C . （15%）⒈354211335421243212321313542143211)1()()(H G G G G H G H G G G G H G G G G H G G H G H G G G G G G G G G S R S C --++++-= 354211335421243212321335422341)()(H G G G G H G H G G G G H G G G G H G G H G H G G G H H G S N S E --+++--= ⒉45.30ππK⒌S: N=1 P=1 Z=0; the closed-loop system is stable ⒎2423241321121413211)()(H G H G G G G G G G H G G G G G G G S R S C ++++++=AUTOMATIC CONTROL THEOREM (10)⒈ Consider the system shown in Fig.1. Obtain the closed-loop transfer function)()(S R S C ,⒉ The characteristic equation is given01510520)(1234=++++=+S S KS S S GH . Discuss the condition of stability. (14%)⒊ Consider a unity-feedback control system whose open-loop transfer function is)6.0(14.0)(++=S S S S G . Obtain the response to a unit-step input. What is the rise time forthis system? What is the maximum overshoot? （10%）⒋ Sketch the root-locus plot for the system )25.01()5.01()(s S s K S GH +-=. (The gain K isassumed to be positive.)③ Determine the breakaway point and K value.④ Determine the value of K at which root loci cross the imaginary axis. Discuss the stability. (15%)⒌ The system transfer function is )5(4)(+=s s s G ,1)(=s H . ①Determine thesteady-state output )(t c when input is unit step )(1t 、unit ramp t . ②Determine theP K 、V K and a K , obtain the steady-state error SS e when input is t t r 2)(=. （12%）⒍ Consider the closed-loop system whose open-loop transfer function is given by:①TS K S GH +=1)(; ②TS K S GH -=1)(; ③1)(-=TS KS GH . Examine the stabilityof the system. （15%）⒎ Sketch the root-locus plot 。

自控原理习题解答

②R(s)和N(s)同时作用时系统的输出
∴ C(s) = CR (s) + CN (s)
=
G1G2 + G1G3 + G1G2G3H1
R(s) +
1+ G1G3 + G2H1 + G1G2 + G1G2G3H1
+ 1+ G2H1 + G1G2G4 + G1G3G4 + G1G2G3G4H1 N (s) 1+ G1G3 + G2H1 + G1G2 + G1G2G3H1
s(s + 1)
Kts
1.试分析速度反馈系数Kt对系统稳定性的影响。 2.试求KP、Kv、Ka并说明内反馈对稳态误差的影响。解: 1.如果没有内反馈，系统的开环和闭环传递函数为
解：将系统开环传递函数与二阶系统典型开环传递函
数比较：所以：
G(s) =
ωn2
s(s + 2ζωn )
ωn = 10K
2ζωn = 10 ζωn = 5
ζ= 5
10K
−πζ
σ = e 1−ζ 2 ×100%
tp
=π ωd
=
ωn
π 1−ζ 2
tS
(5%)
≈
3
ζωn
分别将K＝10 ，K＝20代入计算，结果如下：
10K1 = 10 1 + 10 K 2
解之得：K2＝0.9 K1＝10
Ø 3-4 单位反馈系统的开环传递函数为
G(s) = K = 10K s(0.1s + 1) s(s +10)
试分别求出K=10s–1和K=20s–1时，系统的阻尼比ζ 和

自动控制原理课后习题答案

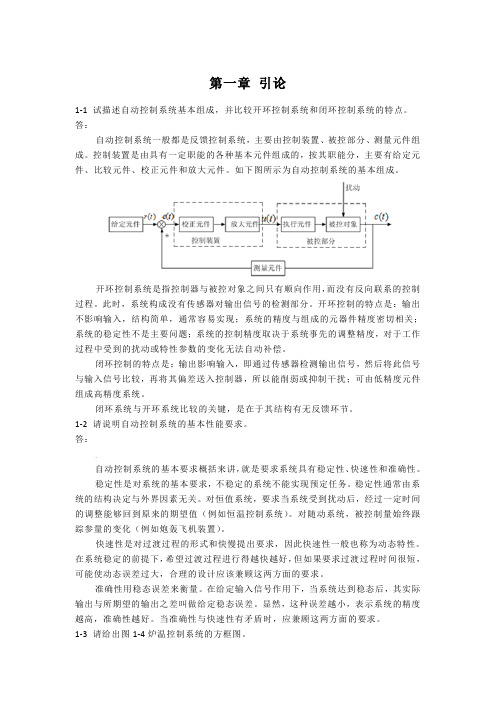
第一章引论1-1 试描述自动控制系统基本组成，并比较开环控制系统和闭环控制系统的特点。

答：自动控制系统一般都是反馈控制系统，主要由控制装置、被控部分、测量元件组成。

控制装置是由具有一定职能的各种基本元件组成的，按其职能分，主要有给定元件、比较元件、校正元件和放大元件。

如下图所示为自动控制系统的基本组成。

开环控制系统是指控制器与被控对象之间只有顺向作用，而没有反向联系的控制过程。

此时，系统构成没有传感器对输出信号的检测部分。

开环控制的特点是：输出不影响输入，结构简单，通常容易实现；系统的精度与组成的元器件精度密切相关；系统的稳定性不是主要问题；系统的控制精度取决于系统事先的调整精度，对于工作过程中受到的扰动或特性参数的变化无法自动补偿。

闭环控制的特点是：输出影响输入，即通过传感器检测输出信号，然后将此信号与输入信号比较，再将其偏差送入控制器，所以能削弱或抑制干扰；可由低精度元件组成高精度系统。

闭环系统与开环系统比较的关键，是在于其结构有无反馈环节。

1-2 请说明自动控制系统的基本性能要求。

答：、自动控制系统的基本要求概括来讲，就是要求系统具有稳定性、快速性和准确性。

稳定性是对系统的基本要求，不稳定的系统不能实现预定任务。

稳定性通常由系统的结构决定与外界因素无关。

对恒值系统，要求当系统受到扰动后，经过一定时间的调整能够回到原来的期望值（例如恒温控制系统）。

对随动系统，被控制量始终跟踪参量的变化（例如炮轰飞机装置）。

快速性是对过渡过程的形式和快慢提出要求，因此快速性一般也称为动态特性。

在系统稳定的前提下，希望过渡过程进行得越快越好，但如果要求过渡过程时间很短，可能使动态误差过大，合理的设计应该兼顾这两方面的要求。

准确性用稳态误差来衡量。

在给定输入信号作用下，当系统达到稳态后，其实际输出与所期望的输出之差叫做给定稳态误差。

显然，这种误差越小，表示系统的精度越高，准确性越好。

当准确性与快速性有矛盾时，应兼顾这两方面的要求。

自动控制原理课后习题及答案

第一章绪论1-1 试比较开环控制系统和闭环控制系统的优缺点.解答：1开环系统(1) 优点:结构简单,成本低,工作稳定;用于系统输入信号及扰动作用能预先知道时,可得到满意的效果;(2) 缺点：不能自动调节被控量的偏差;因此系统元器件参数变化,外来未知扰动存在时,控制精度差;2 闭环系统⑴优点：不管由于干扰或由于系统本身结构参数变化所引起的被控量偏离给定值,都会产生控制作用去清除此偏差,所以控制精度较高;它是一种按偏差调节的控制系统;在实际中应用广泛;⑵缺点：主要缺点是被控量可能出现波动,严重时系统无法工作;1-2 什么叫反馈为什么闭环控制系统常采用负反馈试举例说明之;解答：将系统输出信号引回输入端并对系统产生控制作用的控制方式叫反馈;闭环控制系统常采用负反馈;由1-1中的描述的闭环系统的优点所证明;例如,一个温度控制系统通过热电阻或热电偶检测出当前炉子的温度,再与温度值相比较,去控制加热系统,以达到设定值;1-3 试判断下列微分方程所描述的系统属于何种类型线性,非线性,定常,时变122()()()234()56()d y t dy t du t y t u t dt dt dt ++=+ 2()2()y t u t =+3()()2()4()dy t du t ty t u t dt dt +=+ 4()2()()sin dy t y t u t t dt ω+= 522()()()2()3()d y t dy t y t y t u t dt dt ++=62()()2()dy t y t u t dt +=7()()2()35()du t y t u t u t dtdt =++⎰解答： 1线性定常 2非线性定常 3线性时变 4线性时变 5非线性定常 6非线性定常7线性定常1-4 如图1-4是水位自动控制系统的示意图,图中Q1,Q2分别为进水流量和出水流量;控制的目的是保持水位为一定的高度;试说明该系统的工作原理并画出其方框图;题1-4图水位自动控制系统解答：1 方框图如下：⑵工作原理：系统的控制是保持水箱水位高度不变;水箱是被控对象,水箱的水位是被控量,出水流量Q2的大小对应的水位高度是给定量;当水箱水位高于给定水位,通过浮子连杆机构使阀门关小,进入流量减小,水位降低,当水箱水位低于给定水位时,通过浮子连杆机构使流入管道中的阀门开大,进入流量增加,水位升高到给定水位;1-5 图1-5是液位系统的控制任务是保持液位高度不变;水箱是被控对象,水箱液位是被控量,电位器设定电压时表征液位的希望值Cr 是给定量;题1-5图液位自动控制系统解答:1 液位自动控制系统方框图：2当电位器电刷位于中点位置对应Ur 时,电动机不动,控制阀门有一定的开度,使水箱中流入水量与流出水量相等;从而液面保持在希望高度上;一旦流入水量或流出水量发生变化,例如当液面升高时,浮子位置也相应升高,通过杠杆作用使电位器电刷从中点位置下移,从而给电动机提供一事实上的控制电压,驱动电动机通过减速器减小阀门开度,使进入水箱的液位流量减少;此时,水箱液面下降,浮子位置相应下降,直到电位器电刷回到中点位置,系统重新处于平衡状态,液面恢复给定高度;反之,若水箱液位下降,则系统会自动增大阀门开度,加大流入量,使液位升到给定的高度;1-6题图1-6是仓库大门自动控制系统的示意图,试说明该系统的工作原理,并画出其方框图;题1-6图仓库大门自动控制系统示意图解答：（1）仓库大门自动控制系统方框图：2工作原理：控制系统的控制任务是通过开门开关控制仓库大门的开启与关闭;开门开关或关门开关合上时,对应电位器上的电压,为给定电压,即给定量;仓库大门处于开启或关闭位置与检测电位器上的电压相对应,门的位置是被控量;当大门所处的位置对应电位器上的电压与开门或关门开关合上时对应电位器上的电压相同时,电动机不动,控制绞盘处于一定的位置,大门保持在希望的位置上,如果仓库大门原来处于关门位置,当开门开关合上时,关门开关对应打开,两个电位器的电位差通过放大器放大后控制电动机转动,电动机带动绞盘转动将仓库大门提升,直到仓库大门处于希望的开门位置,此时放大器的输入为0,放大器的输出也可能为0;电动机绞盘不动,大门保持在希望的开门位置不变;反之,则关闭仓库大门;1-7题图1-7是温湿度控制系统示意图;试说明该系统的工作原理,并画出其方框图;题1-7图温湿度控制系统示意图解答：1方框图：2被控对象为温度和湿度设定,控制任务是控制喷淋量的大小来控制湿度,通过控制蒸汽量的大小来控制温度;被控量为温度和湿度,设定温度和设定湿度为给定量;第二章控制系统的数学模型2-2 试求图示两极RC 网络的传递函数U c S ／U r S;该网络是否等效于两个RC 网络的串联解答：故所给网络与两个RC 网络的串联不等效;2-4 某可控硅整流器的输出电压U d =KU 2Φcos α式中K 为常数,U 2Φ为整流变压器副边相电压有效值,α为可控硅的控制角,设在α在α0附近作微小变化,试将U d 与α的线性化;解答：.202002020cos (sin )()...sin sin )d u ku ku ku ku φφφφαααααααα=--+∆=-⋅∆=-d d 线性化方程：u 即u （2-9系统的微分方程组为式中1T 、2T 、1K 、2K 、3K 均为正的常数,系统地输入量为()r t ,输出量为()c t ,试画出动态结构图,并求出传递函数()()C s R s ; 解答：2-12 简化图示的动态结构图,并求传递函数()()C s R s ; 解答：ab c d e2-13 简化图示动态结构图,并求传递函数()()C s R s ;解答： a bcde(d)f第三章时域分析法3-1 已知一阶系统的传递函数今欲采用负方馈的方法将过渡过程时间s t 减小为原来的倍,并保证总的放大倍数不变,试选择H K 和0K 的值;题3-1图解答：闭环传递函数：10()0.2110s s θ=+由结构图知：00010()10110()0.21()0.21101110HHh HK k G S k K s K G S s k S K θ+===+++++由00101011011010100.910H H H k k k k k ⎧⎪⎪⎨⎪⎪⎩⎧⎪⎨⎪⎩=++===3-2已知系统如题3-2图所示,试分析参数b 对输出阶跃过渡过程的影响;题3-2 图解答：系统的闭环传递函数为：由此可以得出：b 的大小影响一阶系统的时间常数,它越大,系统的时间常数越大,系统的调节时间,上升时间都会增大;3-3 设温度计可用1(1)Ts +描述其特性;现用温度计测量盛在容器内的水温,发现1分钟可指示98％的实际水温值;如果容器水温依10℃/min 的速度线性变化,问温度计的稳态指示误差是多少解答：本系统是个开环传递函数系统的闭环传递函数为：系统的传递函数：1()1G s Ts =+则题目的误差传递函数为：3-4 设一单位反馈系统的开环传递函数试分别求110K s -=和120K s -=时系统的阻尼比ζ、无阻尼自振频率n w 、单位阶跃响应的超调量p σ％和峰值时间p t ,并讨论K 的大小对动态性能的影响;解答：开环传递函数为3-8 设控制系统闭环传递函数试在s 平面上给出满足下列各要求的闭环特征根可能位于的区域： 1. 10.707,2n ζω>≥≥ 2. 0.50,42n ζω≥>≥≥ 3. 0.7070.5,2n ζω≥≥≤解答：欠阻尼二阶系统的特征根：1. 由0.7071,arccos ζβζ<<=,得045β︒︒<≤,由于对称关系,在实轴的下半部还有;2. 由00.5,arccos ζβζ<≤=,得6090β︒︒≤<,由于对称关系,在实轴的下半部还有;3. 由0.50.707,arccos ζβζ≤≤=,得出4560β︒︒≤≤,由于对称关系,在实轴的下半部还有;则闭环特征根可能位于的区域表示如下：1． 2． 3．3-10 设单位反馈系统开环传递函数分别为： 1.[]()(1)(0.21)G s K s s s =-+2. ()(1)[(1)(0.21)]G s K s s s s =+-+ 试确定使系统稳定的K 值;解答：1.系统的特征多项式为：()D s 中存在特征多项式中存在负项,所以K 无论取什么值,系统都不会稳定;2.系统的特征多项式为：32()0.20.8(1)D s s s k s k =++-+ 劳斯阵列为：3s k-12s k 0s k系统要稳定则有 0.60.800.80k k ⎧⎪⎨⎪⎩->>所以系统稳定的K 的范围为43k >3-14 已知单位反馈系统开环传递函数如下： 1.]()10(0.11)(0.51)G s s s =++2.2()7(1)(4)(22)G s s s s s s ⎡⎤=++++⎣⎦ 3.2()8(0.51)(0.11)G s s s s ⎡⎤=++⎣⎦ 解答:1.系统的闭环特征多项式为: 可以判定系统是稳定的.则对于零型系统来说,其静态误差系数为:那么当()1()r t t =时, 11111ss p e k ==+当()1()r t t t =⋅时, 1ss ve k ==∞当2()1()r t t t =⋅时, 2ss ae k ==∞2.系统的闭环特征多项式为: 可以用劳斯判据判定系统是稳定的. 则对于一型系统来说,其静态误差系数为:那么当()1()r t t =时, 11ss p e k ==∞+ 当()1()r t t t =⋅时,187ss v e k ==当2()1()r t t t =⋅时, 20ss ae k ==3.系统的闭环特征多项式为: 可以用劳斯判据判定系统是稳定的. 则对于零型系统来说,其静态误差系数为:那么当()1()r t t =时, 11ss p e k ==+ 当()1()r t t t =⋅时, 10ss v e k ==当2()1()r t t t =⋅时, 214ss a e k ==第四章根轨迹法4-2 已知单位反馈系统的开环传递函数,绘出当开环增益1K 变化时系统的根轨迹图,并加以简要说明;1.1()(1)(3)K G s s s s =++2.12()(4)(420)K G s s s s s =+++解答:1 开环极点： p1=0,p2=－1,p3=－3实轴上的根轨迹区间：－∞,－3,－1,0 渐进线：分离点：111013d d d ++=++解得d1、2=－,;d2=－不在根轨迹上,舍去; 与虚轴交点：特征方程321()430D s s s s K =+++= 将s =j ω代入后得解之得 ω= 112K =当 ∞<≤10K 时,按180相角条件绘制根轨迹如图4-21所示;2 开环极点：p1=0,p2=－4,p3、4=－2±j4实轴上的根轨迹区间：－4,0 渐进线：分离点：)8018368(2341++++-=s s s s K 由01=ds dK解得 s1、2=－2,624,3j s ±-= 分离点可由a 、b 、c 条件之一进行判定：a ．∠Gs 3=－129o+51o －90o+90o=－180o,满足相角条件；b ．100)80368()(62234313>=+++-=+-=j s s s s s s KK 1在变化范围 )0[∞→ 内；c ．由于开环极点对于σ=－2直线左右对称,就有闭环根轨迹必定也是对于σ=－2直线左右对称,故s3在根轨迹上;与虚轴交点：特征方程Routh 表s 4 1 36 K 1 s 3 8 80 s 2 26 K 1 s 80－8K1/26 s 0 K 1由 80－8k1/26=0和26s2+ k1=0,解得k1=260,102,1j s ±= ;当 ∞<≤10K 时,按180相角条件绘制根轨迹如图4－22所示;4-3 设单位反馈系统的开环传递函数为（1）试绘制系统根轨迹的大致图形,并对系统的稳定性进行分析;、（2）若增加一个零点1z =-,试问根轨迹有何变化,对系统的稳定性有何影响解答1 K 1>0时,根轨迹中的两个分支始终位于s 右半平面,系统不稳定；2 增加一个零点z=－1之后,根轨迹左移,根轨迹中的三个分支始终位于s 左半平面,系统稳定;4-4 设系统的开环传递函数为12(2)()()(2)K s G s H s s s s a +=++,绘制下列条件下的常规根轨迹;11a =； 2 1.185a = 33a =解答： 11=a实轴上的根轨迹区间：－∞,－1,－1,0 渐进线：分离点：22231+++-=s as s s K解得01=ds dK只取253+-=d ;与虚轴交点：特征方程022)(1123=++++=K s K as s s s D 令jw s =代入上式：得出与虚轴的交点系统的根轨迹如下图： 2185.1=a 零点为2-=z极点为0,43.01j p ±-=实轴上的根轨迹区间：－∞,－1,－1,0 渐进线：分离点：22231+++-=s as s s K解得01=ds dK特征方程022)(1123=++++=K s K as s s s D 令jw s =代入上式：得出与虚轴的交点系统的根轨迹如下图： 33=a 零点为2-=z极点为0,41.11j p ±-=实轴上的根轨迹区间：－∞,－1,－1,0 渐进线：分离点：22231+++-=s as s s K解得01=ds dK特征方程022)(1123=++++=K s K as s s s D 令jw s =代入上式：得出与虚轴的交点系统的根轨迹如下图：4-8 根据下列正反馈回路的开环传递函数,绘出其根轨迹的大致形状;1()()1()()12K G s H s s s =++ 2()()1()()12K G s H s s s s =++3()()()12()()13(4)K s G s H s s s s s +=+++解答：1 2 34-15 设单位反馈系统的开环传递函数为确定a 值,使根轨迹图分别具有：0、1、2个分离点,画出这三种情况的根轨迹;解答：首先求出分离点：分离点：321s s K s a +=-+ 解得2122(31)20()dK s a s as ds s a +++=-=+得出分离点1,2d =当119a <<时,上面的方程有一对共轭的复根当911<>a a 或时,上面的方程有两个不等的负实根当119a a ==或时,上面的方程有两个相等的实根1当1=a 时系统的根轨迹为：可以看出无分离点 ,故排除2当91=a 时系统的根轨迹为：可以看出系统由一个分离点 3当1>a 时比如3=a 时系统的根轨迹为：可以看出系统由无分离点 4当91<a 时比如201=a 时系统的根轨迹为：可以看出系统由两个分离点 5当191<<a 时比如21=a 时系统的根轨迹为：可以看出系统由无分离点第五章频域分析法5-1设单位反馈控制系统开环传递函4()1G s s =+,当将()sin(260)2cos(45)r t t t =+--作用于闭环系统时,求其稳态输出;解答：开环传递函数14)(+=s s G 闭环传递函数54)(+=Φs s闭环频率特性54)()()(+==Φωωωωαj e M j j当ω=2时,M2=,α2=；当ω=1时,M1=,α1=；则闭环系统的稳态输出：5-2 试求110()4G s s =+24()(21)G s s s =+3(1)()(1,)1K s G s K T Ts ττ+=>>+的实频特性()X ω、虚频特性()Y ω、幅频特性()A ω、相频特性()ϕω;解答：⑴4arctan 222216101610164016)4(10410)(wj e w w w j w w jw jw jw G -+=+-+=+-=+=则21640)(w w X +=,21610)(w ww Y +-=⑵)21arctan 180(2331444448)12(4)(wj ew w w w j w w w jw jw jw G ++=+-+-=+=则 w w w w X +-=348)( , w w w Y +-=344)(⑶)]arctan()[arctan(222222222111)(1)1(1)1()(wT w j e w T w k w T w T k j w T Tw k jTw w j k jw G -++=+-+++=++=τττττ则2221)1()(w T Tw k w X ++=τ,221)()(w T wT k w Y +-=τ 5-4 绘制下列传递函数的对数幅频渐近线和相频特性曲线;14()(21)(81)G s s s =++ 2()242()(0.4)(40)s G s s s +=++ 3228(0.1)()(1)(425)s G s s s s s s +=++++ 4210(0.4)()(0.1)s G s s s +=+解答：1转折频率为21,8121==w w2 3 45-10 设单位负反馈系统开环传递函数; 110()(0.51)(0.021)G s s s s =++,21()as G s s +=试确定使相角裕量等于45的α值; 2 3()(0.011)KG s s =+,试确定使相角裕量等于45的K 值;32()(100)KG s s s s =++,,试确定使幅值裕量为20dB 的开环增益K 值;解答：1由题意可得：解得： ⎩⎨⎧==84.019.1αc w2由题意可得：解得： ⎩⎨⎧==83.2100k w c3由题意可得：解得： ⎩⎨⎧==1010k w g5-13 设单位反馈系统开环传递函数试计算系统的相角裕量和幅值裕量;解答：由18002.0arctan 5.0arctan 90)(-=---=g g g w w w γ所以幅值裕量)(14dB h =故16102.0arctan 5.0arctan 90)(-=---=c c c w w w ϕ所以相角裕量19161180)(=-=c w γ系统的幅频特性曲线的渐近线：系统的幅相特性曲线：第六章控制系统的综合与校正6-1 试回答下列问题：1 进行校正的目的是什么为什么不能用改变系统开环增益的办法来实现答：进行校正的目的是达到性能指标;增大系统的开环增益在某些情况下可以改善系统的稳态性能,但是系统的动态性能将变坏,甚至有可能不稳定;2 什么情况下采用串联超前校正它为什么能改善系统的性能答：串联超前校正主要用于系统的稳态性能已符合要求,而动态性能有待改善的场合;串联超前校正是利用校正装置的相位超前特性来增加系统的橡胶稳定裕量,利用校正装置幅频特性曲线的正斜率段来增加系统的穿越频率,从而改善系统的平稳性和快速性;（3）什么情况下采用串联滞后校正它主要能改善系统哪方面的性能答：串联滞后校正主要是用于改善系统的稳态精度的场合,也可以用来提高系统的稳定性,但要以牺牲快速性为代价;滞后校正是利用其在高频段造成的幅值衰减,使系统的相位裕量增加,由于相位裕量的增加,使系统有裕量允许增加开环增益,从而改善稳态精度,同时高频幅值的衰减,使得系统的抗干扰能力得到提高;思考题：1. 串联校正装置为什么一般都安装在误差信号的后面,而不是系统股有部分的后面2. 如果1型系统在校正后希望成为2型系统,但又不影响其稳定性,应采用哪种校正规律6-3 设系统结构如图6-3图所示,其开环传递函数0()(1)KG s s s =+;若要求系统开环截至频率 4.4c ω≥rad/s,相角裕量045γ≥,在单位斜坡函数输入信号作用下,稳态误差0.1ss e ≤,试求无源超前网络参数;解答：1由10.1ss e K =≤可得：10K ≥,取10K =2原系统 3.16c ω= rad/s,017.6γ=,不能满足动态性能指标;3选' 4.4c ω=rad/s,由'0()10lg c L ωα=-即'21020lg10lg cαω=-可得:3.75α=那么0.12T == 无源超前校正网络：10.531()10.121c Ts s G s Ts s α++==++（4）可以得校正后系统的'51.8γ=,满足性能指标的要求;6-4 设单位反馈系统开环传递函数()()()010.51KG s s s s =++;要求采用串联滞后校正网络,使校正后系统的速度误差系数5(1)v K s =,相角裕量40γ≥;解答： ⑴由00lim ()v s K sG s K→==可得：5K =2 原系统 2.15c ω=,22.2γ=-不满足动态要求3 确定新的'c ω由''1804012(90arctan arctan 0.5)c c ωω-++=---可解得：'0.46c ω=⑷由020lg 20lg (')c b G j ω=-得：0.092b =取'111510cbT ω⎛⎫= ⎪⎝⎭='15c ω得：118T =校正网络为：1111()11181c Tbs s G s Ts s ++=≈++校正后系统的相角裕量'42γ=,故校正后的系统满足性能指标的要求;第七章非线性控制系统7-1 三个非线性系统的非线性环节一样,线性部分分别为1.2()(0.11)G s s s =+ 2.2()(1)G s s s =+ 3. 2(1.51)()(1)(0.11)s G s s s s +=++ 解答：用描述函数法分析非线性系统时,要求线性部分具有较好的低通滤波性能即是说低频信号容易通过,高频信号不容易通过; 从上图可以看出：系统2的分析准确度高;7-2 一个非线性系统,非线性环节是一个斜率1N -的饱和特性;当不考虑饱和因素时,闭环系统是稳定的;问该系统有没有可能产生自振荡解答：饱和特性的负倒描述函数如下：当1k =时,1()N A -曲线的起点为复平面上的(1,0)j -点; 对于最小相位系统有：闭环系统稳定说明系统的奈氏曲线在实轴(,1)-∞-段没有交点,因此,当存在1k =的饱和特性时,该系统不可能产生自激振荡7-4 判断图中各系统是否稳定,1()N A -与()G j ω的交点是否为自振点;图中P为()G s的右极点个数;解答：首先标出各图的稳定区用阴影部分表示abc da1N-曲线由稳定区穿入不稳定区,交点a是自激振荡点;b1N-曲线由稳定区穿入不稳定区,交点a是自激振荡点;c 交点,a c为自激振荡点,交点b不时自激振荡点;d 闭环系统不稳定;e 交点a不是自激振荡点;f 交点a是自激振荡点7-5 非线性系统如图所示,试确定其自振振幅和频率;题7-5图解答：由题可得下图：由1()()G j N A ω-=得1()()N A G j ω-=即：()()10*412j j j A ωωωπ++=- 320ωω-=得：ω=2403A ωπ-=-得：24020 2.1233A ππω===振幅为203π7-6非线性系统如图所示,试用描述函数法分析当10K =时,系统地稳定性,并求K 的临界稳定值;题7-6图解答：由题可得下图：K 的临界稳定值为：010653K == 所以,当06K <<时,()G j ω曲线不包围1()N A -曲线,系统闭环稳定;第八章线性离散系统8-1 求函数()x t 的Z 变换;1.()1at x t e -=- 2. ()sin x t t t ω=3. ()sin x t t t ω=4. 2()atx t t e -=解答：1. (1)()1(1)()aT aT aT z e z z X z z z e z z e ----=-=----2.2222(1)sin sin ()()2cos 1(2cos 1)Tz z T d z T X z Tz dz z z T z z T ωωωω-=-=-+-+Z 域微分定理3.22222(cos )cos ()2cos 12cos aT aT aT aT aT aT aTze ze T z ze T X z z e ze T z ze T e ωωωω-----==-+-+复数位移定理4.23(1)()4(1)aT aT aT Tze ze X z ze +=-复数位移定理8-2 已知()X s ,试求对应的()X z ;1.3()(1)(2)s X z s s +=++ 2.2()(1)s X z s s =+3.21()s X z s += 4. 21()(1)s e X z s s --=+解答：1. ()321()12(1)2s X s s s s s +==-++++ 2. 2111()1(1)(1)s X s s s s s s s ===-+++ 3. 22111()s X s s s s +==+4. ()()221111()111s s e X s e s s s s s --⎡⎤⎢⎥⎢⎥⎣⎦-==--+++()1211(1)T T Tzz z X z z z z e z --⎛⎫⎡⎤⎪⎢⎥⎪⎢⎥⎣⎦⎝⎭=--+---()121(1)1(1)1()T T T T z z z e T T e z z e ----⎛⎫⎡⎤⎪⎢⎥ ⎪⎣⎦⎝⎭-+++-+=--负偏移定理8-3 已知()X z ,试求()X nT ;1. ()()()1012zX z z z =--2. ()()()20.80.1z X z z z =--3. ()2(1)1.250.25z z X z z z -=-+解答：1. ()()()1012zX z z z =--=10()21zz z z ---2. ()()()20.80.1z X z z z =--81770.80.1z zz z =---3.()2(1)1.250.25z zX zz z-=-+(1)(0.25)(1)z zz z-=--(0.25)zz=-8-6 已知系统的结构如图所示,1T s=,试求系统的闭环脉冲传递函数()zφ;解答：211111 ()*(1)1(1)TsTseG s es s ss s s--⎛⎫⎪⎪⎝⎭-==--+++思考题：1. 在单位阶跃输入作用下,试求上题所给系统的输出()c t;2. 系统结构如上题,试求当输入为()1()r t t=、t、2t时的稳态误差;。

自动控制原理习题及答案

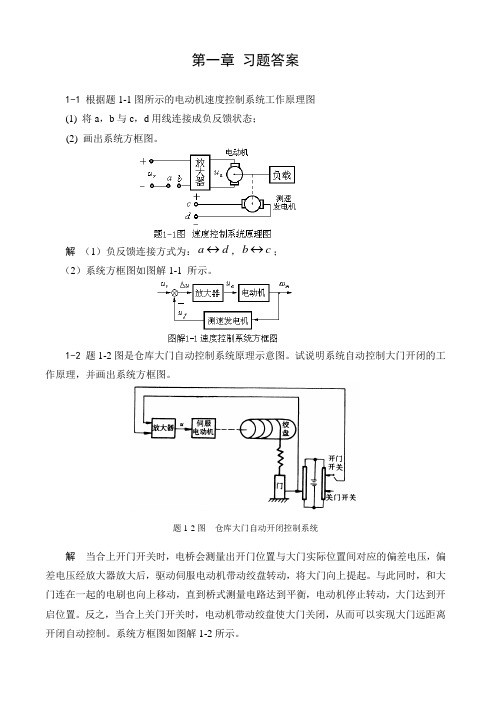
第一章习题答案1-1 根据题1-1图所示的电动机速度控制系统工作原理图(1) 将a ，b 与c ，d 用线连接成负反馈状态；(2) 画出系统方框图。

解（1）负反馈连接方式为：d a ↔，c b ↔；（2）系统方框图如图解1-1 所示。

1-2 题1-2图是仓库大门自动控制系统原理示意图。

试说明系统自动控制大门开闭的工作原理，并画出系统方框图。

题1-2图仓库大门自动开闭控制系统解当合上开门开关时，电桥会测量出开门位置与大门实际位置间对应的偏差电压，偏差电压经放大器放大后，驱动伺服电动机带动绞盘转动，将大门向上提起。

与此同时，和大门连在一起的电刷也向上移动，直到桥式测量电路达到平衡，电动机停止转动，大门达到开启位置。

反之，当合上关门开关时，电动机带动绞盘使大门关闭，从而可以实现大门远距离开闭自动控制。

系统方框图如图解1-2所示。

1-3 题1-3图为工业炉温自动控制系统的工作原理图。

分析系统的工作原理，指出被控对象、被控量和给定量，画出系统方框图。

题1-3图炉温自动控制系统原理图解加热炉采用电加热方式运行，加热器所产生的热量与调压器电压c u 的平方成正比，c u 增高，炉温就上升，c u 的高低由调压器滑动触点的位置所控制，该触点由可逆转的直流电动机驱动。

炉子的实际温度用热电偶测量，输出电压f u 。

f u 作为系统的反馈电压与给定电压r u 进行比较，得出偏差电压e u ，经电压放大器、功率放大器放大成a u 后，作为控制电动机的电枢电压。

在正常情况下，炉温等于某个期望值T °C ，热电偶的输出电压f u 正好等于给定电压r u 。

此时，0=-=f r e u u u ，故01==a u u ，可逆电动机不转动，调压器的滑动触点停留在某个合适的位置上，使c u 保持一定的数值。

这时，炉子散失的热量正好等于从加热器吸取的热量，形成稳定的热平衡状态，温度保持恒定。

当炉膛温度T °C 由于某种原因突然下降(例如炉门打开造成的热量流失)，则出现以下的控制过程：控制的结果是使炉膛温度回升，直至T °C 的实际值等于期望值为止。

自动控制原理课后习题与答案

目录1自动控制系统的基本概念1.1内容提要1.2习题与解答2自动控制系统的数学模型2.1内容提要2.2习题与解答3自动控制系统的时域分析3.1内容提要3.2习颗与他答4根轨迹法4.1内容提要4.2习题与解答5频率法5.1内容提要5.2习题与解答6控制系统的校正及综合6.1内容提要6.2习题与解答7非线性系统分析7.1内容提要7.2习题与解答8线性离散系统的理论基础8.1内容提要8.2习题与解答9状态空间法9.1内容提要9.2习题与解答附录拉普拉斯变换参考文献1自动控制系统的基本概念1. 1内容提要基本术语：反馈量，扰动量，输人量，输出量，被控对象；基本结构：开环，闭环，复合；基本类型：线性和非线性，连续和离散，程序控制与随动；基本要求：暂态，稳态，稳定性。

本章要解决的问题，是在自动控制系统的基本概念基础上，能够针对一个实际的控制系统，找出其被控对象、输人量、输出量，并分析其结构、类型和工作原理。

1.2习题与解答题1-1图P1-1所示，为一直流发电机电压白动控制系统示意图。

图中，1为发电机；2为减速器；3为执行电机；4为比例放大器；5为可调电位器。

(1)该系统有哪些环节组成，各起什么作用” (2)绘出系统的框图，说明当负载电流变化时，系统如何保持发电机的电压恒定 (3)该系统是有差系统还是无差系统。

(4)系统中有哪些可能的扰动，答(1)该系统由给定环节、比较环节、中间环节、执行结构、检测环节、发电机等环节组成。

给定环节:电压源0U 。

用来设定直流发电机电压的给定值。

比较环节:本系统所实现的被控量与给定量进行比较，是通过给定电压与反馈电压反极性相接加到比例放大器上实现的中间环节:比例放大器。

它的作用是将偏差信号放大，使其足以带动执行机构工作。

该环节又称为放大环节执行机构:该环节由执行电机、减速器和可调电位器构成。

该环节的作用是通过改变发电机励磁回路的电阻值，改变发电机的磁场，调节发电机的输出电压被控对象:发电机。

自动控制原理(中英文对照李道根)习题4.题解

G ( s) k (s 1) s 4s 5
2
,
(a) Find the angles of departure of the root locus from the complex poles. (b) Find the entry point for the root locus as it enters the real axis. Solution: G ( s)
Solving the breakaway-point equation
2s 4 s 4s 8
2

1 s3

s 2 6s 4 0
we have s b 5.24 . Or, z1 p1 5 , s b 3 5 5.24 . The angles of departure of the root locus from the complex poles are
k ( s 3) s 4s 8
2

k ( s 3) (s 2) 2 2 2
. By inspection, we have p1， 2 2 j 2 and
z1 5 . The root locus in the complex plane is a part of a circle with the center at the zero and a radius of the length from the zero to one pole. There is a breakaway point on the real-axis segment, ( ， 3) . The root locus is plotted as shown.
z1 1 . k (s 1) s 4s 5

自动控制原理+课后答案.

解：（a）由图得
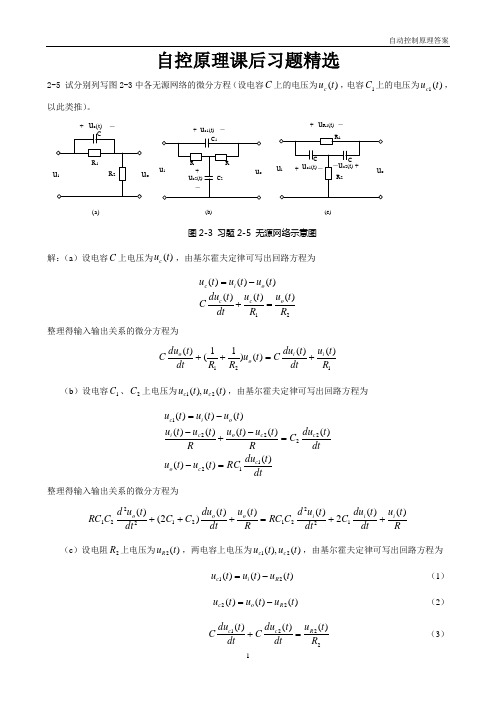
（1）
（2）
（2）代入（1），整理得传递函数为
（b）由图得
（1）
（2）
整理得传递函数为
（c）由图得
（1）
（2）
（3）
（4）
整理得传递函数为
2-8 试简化图2-6中所示系统结构图，并求传递函数和。
解：（a）
⑴求传递函数，按下列步骤简化结构图：
1 令，利用反馈运算简化如图2-8a所示
求系统传递函数
由信号流图2-10b可见，从源节点到阱节点之间，有一条前向通路，其增益为
有三个相互接触的单独回路，其回路增益分别为
，，
与互不接触
流图特征式为
由于前向通路与所有单独回路都接触，所以余因子式
根据梅森增益公式，得系统闭环传递函数为
3-3已知二阶系统的单位阶跃响应为，试求系统的超调量，峰值时间和调节时间。
②实轴上根轨迹区间为
③根轨迹的渐近线条数为，，
④分离点方程为
解得分离点
根轨迹如下图4-2d所示：
4-6已知单位反馈系统的开环传递函数为：范围。
解：由题得
开环极点：和
开环零点：
分离、会合点：从平面的零点、极点分布可知在区间内可能有分离、会合点。
解：
(1)对于题5-4的系统，分和的两种情况来讨论系统的闭环稳定性。
当时，系统的开环幅相曲线如图5-4a所示，由图可知，系统的开环幅相曲线不包围，根据奈奎斯特判据可得
又由系统得开环传递函数可知
即，闭环系统在右半平面无极点，时闭环系统稳定。
当时，系统的开环幅相曲线如图5-4b所示，由图可知，
解：
由题目可知，系统的频率特性如下

《自动控制原理》试卷及答案(英文10套)

AUTOMATIC CONTROL THEOREM (1)⒈ Derive the transfer function and the differential equation of the electric network⒉ Consider the system shown in Fig.2. Obtain the closed-loop transfer function)()(S R S C , )()(S R S E . （12%） ⒊ The characteristic equation is given 010)6(5)(123=++++=+K S K S S S GH . Discuss the distribution of the closed-loop poles. (16%)① There are 3 roots on the LHP ② There are 2 roots on the LHP② There are 1 roots on the LHP ④ There are no roots on the LHP . K=?⒋ Consider a unity-feedback control system whose open-loop transfer function is )6.0(14.0)(++=S S S S G . Obtain the response to a unit-step input. What is the rise time for this system? What is the maximum overshoot? （10%）5. Sketch the root-locus plot for the system )1()(+=S S K S GH . ( The gain K is assumed to be positive.)① Determine the breakaway point and K value.② Determine the value of K at which root loci cross the imaginary axis. ③ Discuss the stability. (12%)Fig.16. The system block diagram is shown Fig.3. Suppose )2(t r +=, 1=n . DetermineFig.37. Consider the system with the following open-loop transfer function:)1)(1()(21++=S T S T S K S GH . ① Draw Nyquist diagrams. ② Determine the stability of the system for two cases, ⑴ the gain K is small, ⑵ K is large. (12%)8. Sketch the Bode diagram of the system shown in Fig.4. (14%)⒈212121121212)()()(C C S C C R R C S C C R S V S V ++++=⒉ 2423241321121413211)()(H G H G G G G G G G H G G G G G G G S R S C ++++++=⒊ ① 0<K<6 ② K ≤0 ③ K ≥6 ④ no answer⒋⒌①the breakaway point is –1 and –1/3; k=4/27 ② The imaginary axis S=±j; K=2③⒍5.75.3≤≤K⒎ )154.82)(181.34)(1481.3)(1316.0()11.0(62.31)(+++++=S S S S S S GH AUTOMATIC CONTROL THEOREM (2)⒈Derive the transfer function and the differential equation of the electric network⒉ Consider the equation group shown in Equation.1. Draw block diagram and obtain the closed-loop transfer function )()(S R S C . （16% ） Equation.1 ⎪⎪⎩⎪⎪⎨⎧=-=-=--=)()()()()]()()([)()]()()()[()()()]()()[()()()(3435233612287111S X S G S C S G S G S C S X S X S X S G S X S G S X S C S G S G S G S R S G S X⒊ Use Routh ’s criterion to determine the number of roots in the right-half S plane for the equation 0400600226283)(12345=+++++=+S S S S S S GH . Analyze stability.（12% ）⒋ Determine the range of K value ,when )1(2t t r ++=, 5.0≤SS e . （12% ）Fig.1⒌Fig.3 shows a unity-feedback control system. By sketching the Nyquist diagram of the system, determine the maximum value of K consistent with stability, and check the result using Routh ’s criterion. Sketch the root-locus for the system （20%）（18% ）⒎ Determine the transfer function. Assume a minimum-phase transfer function.（10% ）⒈ 1)()(2122112221112++++=S C R C R C R S C R C R S V ⒉ )(1)()(8743215436324321G G G G G G G G G G G G G G G G S R S C -+++= ⒊ There are 4 roots in the left-half S plane, 2 roots on the imaginary axes, 0 root in the RSP. The system is unstable.⒋ 208<≤K⒌ K=20⒎ )154.82)(181.34)(1481.3)(1316.0()11.0(62.31)(+++++=S S S S S S GHAUTOMATIC CONTROL THEOREM (3)⒈List the major advantages and disadvantages of open-loop control systems. (12% )⒉Derive the transfer function and the differential equation of the electric network⒊ Consider the system shown in Fig.2. Obtain the closed-loop transfer function)()(S R S C , )()(S R S E , )()(S P S C . （12%）⒋ The characteristic equation is given 02023)(123=+++=+S S S S GH . Discuss the distribution of the closed-loop poles. (16%)5. Sketch the root-locus plot for the system )1()(+=S S K S GH . (The gain K is assumed to be positive.)④ Determine the breakaway point and K value.⑤ Determine the value of K at which root loci cross the imaginary axis.⑥ Discuss the stability. (14%)6. The system block diagram is shown Fig.3. 21+=S K G , )3(42+=S S G . Suppose )2(t r +=, 1=n . Determine the value of K to ensure 1≤SS e . (15%)7. Consider the system with the following open-loop transfer function:)1)(1()(21++=S T S T S K S GH . ① Draw Nyquist diagrams. ② Determine the stability of the system for two cases, ⑴ the gain K is small, ⑵ K is large. (15%) ⒈ Solution: The advantages of open-loop control systems are as follows: ① Simple construction and ease of maintenance② Less expensive than a corresponding closed-loop system③ There is no stability problem④ Convenient when output is hard to measure or economically not feasible. (For example, it would be quite expensive to provide a device to measure the quality of the output of a toaster.)The disadvantages of open-loop control systems are as follows:① Disturbances and changes in calibration cause errors, and the output may be different from what is desired.② To maintain the required quality in the output, recalibration is necessary from time to time.⒉ 1)(1)()()(2122112221122112221112+++++++=S C R C R C R S C R C R S C R C R S C R C R S U S U ⒊351343212321215143211)()(H G G H G G G G H G G H G G G G G G G G S R S C +++++= 35134321232121253121431)1()()(H G G H G G G G H G G H G G H G G H G G G G S P S C ++++-+= ⒋ R=2, L=1⒌ S:①the breakaway point is –1 and –1/3; k=4/27 ② The imaginary axis S=±j; K=2⒍5.75.3≤≤KAUTOMATIC CONTROL THEOREM (4)⒈ Find the poles of the following )(s F :s es F --=11)( (12%) ⒉Consider the system shown in Fig.1,where 6.0=ξ and 5=n ωrad/sec. Obtain the rise time r t , peak time p t , maximum overshoot P M , and settling time s t when the system is subjected to a unit-step input. （10%）⒊ Consider the system shown in Fig.2. Obtain the closed-loop transfer function)()(S R S C , )()(S R S E , )()(S P S C . （12%）⒋ The characteristic equation is given 02023)(123=+++=+S S S S GH . Discuss the distribution of the closed-loop poles. (16%)5. Sketch the root-locus plot for the system )1()(+=S S K S GH . (The gain K is assumed to be positive.)⑦ Determine the breakaway point and K value.⑧ Determine the value of K at which root loci cross the imaginary axis.⑨ Discuss the stability. (12%)6. The system block diagram is shown Fig.3. 21+=S K G , )3(42+=S S G . Suppose )2(t r +=, 1=n . Determine the value of K to ensure 1≤SS e . (12%))1)(1()(21++=S T S T S K S GH . ① Draw Nyquist diagrams. ② Determine the stability of the system for two cases, ⑴ the gain K is small, ⑵ K is large. (12%8. Sketch the Bode diagram of the system shown in Fig.4. (14%)⒈ Solution: The poles are found from 1=-s e or 1)sin (cos )(=-=-+-ωωσωσj e e j From this it follows that πωσn 2,0±== ),2,1,0( =n . Thus, the poles are located at πn j s 2±=⒉Solution: rise time sec 55.0=r t , peak time sec 785.0=p t ,maximum overshoot 095.0=P M ,and settling time sec 33.1=s t for the %2 criterion, settling time sec 1=s t for the %5 criterion.⒊ 351343212321215143211)()(H G G H G G G G H G G H G G G G G G G G S R S C +++++= 35134321232121253121431)1()()(H G G H G G G G H G G H G G H G G H G G G G S P S C ++++-+=⒋R=2, L=15. S:①the breakaway point is –1 and –1/3; k=4/27 ② The imaginary axis S=±j; K=2⒍5.75.3≤≤KAUTOMATIC CONTROL THEOREM (5)⒈ Consider the system shown in Fig.1. Obtain the closed-loop transfer function )()(S R S C , )()(S R S E . （18%）⒉ The characteristic equation is given 0483224123)(12345=+++++=+S S S S S S GH . Discuss the distribution of the closed-loop poles. (16%)⒊ Sketch the root-locus plot for the system )15.0)(1()(++=S S S K S GH . (The gain K is assumed to be positive.)① Determine the breakaway point and K value.② Determine the value of K at which root loci cross the imaginary axis.③ Discuss the stability. (18%)⒋ The system block diagram is shown Fig.2. 1111+=S T K G , 1222+=S T K G . ①Suppose 0=r , 1=n . Determine the value of SS e . ②Suppose 1=r , 1=n . Determine the value of SS e . (14%)⒌ Sketch the Bode diagram for the following transfer function. )1()(Ts s K s GH +=, 7=K , 087.0=T . (10%)⒍ A system with the open-loop transfer function )1()(2+=TS s K S GH is inherently unstable. This system can be stabilized by adding derivative control. Sketch the polar plots for the open-loop transfer function with and without derivative control. (14%) ⒎ Draw the block diagram and determine the transfer function. (10%)⒈∆=321)()(G G G S R S C ⒉R=0, L=3,I=2⒋①2121K K K e ss +-=②21211K K K e ss +-= ⒎11)()(12+=RCs s U s U AUTOMATIC CONTROL THEOREM (6)⒈ Consider the system shown in Fig.1. Obtain the closed-loop transfer function )()(S R S C , )()(S R S E . （18%）⒉The characteristic equation is given 012012212010525)(12345=+++++=+S S S S S S GH . Discuss the distribution of the closed-loop poles. (12%)⒊ Sketch the root-locus plot for the system )3()1()(-+=S S S K S GH . (The gain K is assumed to be positive.)① Determine the breakaway point and K value.② Determine the value of K at which root loci cross the imaginary axis.③ Discuss the stability. (15%)⒋ The system block diagram is shown Fig.2. SG 11=, )125.0(102+=S S G . Suppose t r +=1, 1.0=n . Determine the value of SS e . (12%)⒌ Calculate the transfer function for the following Bode diagram of the minimum phase. (15%)⒍ For the system show as follows, )5(4)(+=s s s G ,1)(=s H , (16%) ① Determine the system output )(t c to a unit step, ramp input.② Determine the coefficient P K , V K and the steady state error to t t r 2)(=.⒎ Plot the Bode diagram of the system described by the open-loop transfer function elements )5.01()1(10)(s s s s G ++=, 1)(=s H . (12%) ⒈32221212321221122211)1()()(H H G H H G G H H G G H G H G H G G G S R S C +-++-+-+= ⒉R=0, L=5w⒌)1611()14)(1)(110(05.0)(2s s s s s s G ++++= ⒍t t e e t c 431341)(--+-= t t e e t t c 41213445)(---+-= ∞=P K , 8.0=V K , 5.2=ss eAUTOMATIC CONTROL THEOREM (7)⒈ Consider the system shown in Fig.1. Obtain the closed-loop transfer function)()(S R S C , )()(S R S E . （16%）⒉ The characteristic equation is given 01087444)(123456=+--+-+=+S S S S S S S GH . Discuss the distribution of the closed-loop poles. (10%)⒊ Sketch the root-locus plot for the system 3)1()(S S K S GH +=. (The gain K is assumed to be positive.)① Determine the breakaway point and K value.② Determine the value of K at which root loci cross the imaginary axis.③ Discuss the stability. (15%)⒋ Show that the steady-state error in the response to ramp inputs can be made zero, if the closed-loop transfer function is given by:nn n n n n a s a s a s a s a s R s C +++++=---1111)()( ;1)(=s H （12%）⒌ Calculate the transfer function for the following Bode diagram of the minimum phase.w（15%⒍ Sketch the Nyquist diagram (Polar plot) for the system described by the open-loop transfer function )12.0(11.0)(++=s s s S GH , and find the frequency and phase such that magnitude is unity. （16%）⒎ The stability of a closed-loop system with the following open-loop transfer function )1()1()(122++=s T s s T K S GH depends on the relative magnitudes of 1T and 2T . Draw Nyquist diagram and determine the stability of the system. （16%） ( 00021>>>T T K ) ⒈3213221132112)()(G G G G G G G G G G G G S R S C ++-++= ⒉R=2, I=2,L=2 ⒌)1()1()(32122++=ωωωs s ss G ⒍o srad 5.95/986.0-=Φ=ω。

(完整word版)《自动控制原理》部分中英文词汇对照表(英文解释)

(完整word版)《自动控制原理》部分中英文词汇对照表(英文解释)《自动控制原理》部分中英文词汇对照表AAcceleration 加速度Angle of departure分离角Asymptotic stability渐近稳定性Automation自动化Auxiliary equation辅助方程BBacklash间隙Bandwidth带宽Block diagram方框图Bode diagram波特图CCauchy’s theorem高斯定理Characteristic equation特征方程Closed—loop control system闭环控制系统Constant常数Control system控制系统Controllability可控性Critical damping临界阻尼DDamping constant阻尼常数Damping ratio阻尼比DC control system直流控制系统Dead zone死区Delay time延迟时间Derivative control 微分控制Differential equations微分方程Digital computer compensator数字补偿器Dominant poles主导极点Dynamic equations动态方程EError coefficients误差系数Error transfer function误差传递函数FFeedback反馈Feedback compensation反馈补偿Feedback control systems反馈控制系统Feedback signal反馈信号Final—value theorem终值定理Frequency—domain analysis频域分析Frequency-domain design频域设计Friction摩擦GGain增益Generalized error coefficients广义误差系数IImpulse response脉冲响应Initial state初始状态Initial-value theorem初值定理Input vector输入向量Integral control积分控制Inverse z-transformation反Z变换JJordan block约当块Jordan canonical form约当标准形LLag-lead controller滞后-超前控制器Lag-lead network 滞后—超前网络Laplace transform拉氏变换Lead-lag controller超前—滞后控制器Linearization线性化Linear systems线性系统MMass质量Mathematical models数学模型Matrix矩阵Mechanical systems机械系统NNatural undamped frequency自然无阻尼频率Negative feedback负反馈Nichols chart尼科尔斯图Nonlinear control systems非线性控制系统Nyquist criterion柰奎斯特判据OObservability可观性Observer观测器Open-loop control system开环控制系统(完整word版)《自动控制原理》部分中英文词汇对照表(英文解释)Output equations输出方程Output vector输出向量PParabolic input抛物线输入Partial fraction expansion部分分式展开PD controller比例微分控制器Peak time峰值时间Phase-lag controller相位滞后控制器Phase—lead controller相位超前控制器Phase margin相角裕度PID controller比例、积分微分控制器Polar plot极坐标图Poles definition极点定义Positive feedback正反馈Prefilter 前置滤波器Principle of the argument幅角原理RRamp error constant斜坡误差常数Ramp input斜坡输入Relative stability相对稳定性Resonant frequency共振频率Rise time上升时间调节时间accommodation timeRobust system鲁棒系统Root loci根轨迹Routh tabulation（array）劳斯表SSampling frequency采样频率Sampling period采样周期Second—order system二阶系统Sensitivity灵敏度Series compensation串联补偿Settling time调节时间Signal flow graphs信号流图Similarity transformation相似变换Singularity奇点Spring弹簧Stability稳定性State diagram状态图State equations状态方程State feedback状态反馈State space状态空间State transition equation状态转移方程State transition matrix状态转移矩阵State variables状态变量State vector状态向量Steady-state error稳态误差Steady-state response稳态响应Step error constant阶跃误差常数Step input阶跃输入TTime delay时间延迟Time-domain analysis时域分析Time—domain design时域设计Time—invariant systems时不变系统Time—varying systems时变系统Type number型数Torque constant扭矩常数Transfer function转换方程Transient response暂态响应Transition matrix转移矩阵UUnit step response单位阶跃响应VVandermonde matrix范德蒙矩阵Velocity control system速度控制系统Velocity error constant速度误差常数ZZero-order hold零阶保持z-transfer function Z变换函数z-transform Z变换。

自动控制原理(中英文对照 李道根)习题3.题解

自动控制原理习题及其解答第三章

自动控制原理英文版课后全部_答案

自动控制原理(中英文对照李道根)习题2题解

完整word版,《自动控制原理》试卷及答案(英文10套),推荐文档

自动控制原理精品课程第三章习题解(1)精品文档6页

完整word版,《自动控制原理》试卷及答案(英文10套),推荐文档

自控原理习题解答

自动控制原理课后习题答案

自动控制原理课后习题及答案

自动控制原理习题及答案

自动控制原理课后习题与答案

自动控制原理(中英文对照 李道根)习题4.题解

自动控制原理+课后答案.

《自动控制原理》试卷及答案(英文10套)

(完整word版)《自动控制原理》部分中英文词汇对照表(英文解释)

自动控制原理(中英文对照李道根)习题3.题解

自动控制原理(中英文对照李道根)习题4.题解