2018年天津市高考数学试卷理科-精品下载
2018年高考理数真题试卷(天津卷)

2018年高考理数真题试卷(天津卷)一、选择题1. ( 2分) (2018•天津)设全集为R,集合A={x|0<x<2},B={x|x≥1},则A∩(∁R B)=()A. {x|0<x≤1}B. {x|0<x<1}C. {x|1≤x<2}D. {x|0<x<2}2. ( 2分) (2018•天津)设变量x,y满足约束条件{x+y≤5,2x−y≤4,−x+y≤1,y≥0, 则目标函数z=3x+5y的最大值为()A. 6B. 19C. 21D. 453. ( 2分) (2018•天津)阅读如图的程序框图,运行相应的程序,若输入N的值为20,则输出T的值为()A. 1B. 2C. 3D. 44. ( 2分) (2018•天津)设x∈R,则“ |x−12|<12”是“ x3<1”的()A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件5. ( 2分 ) (2018•天津)已知 a =log 2e , b =ln2 , c =log 1213 ,则a , b , c 的大小关系为( )A. a >b >cB. b >a >cC. c >b >aD. c >a >b6. ( 2分 ) (2018•天津)将函数 y =sin(2x +π5) 的图象向右平移 π10 个单位长度,所得图象对应的函数( ) A. 在区间 [3π4,5π4] 上单调递增 B. 在区间 [3π4,π] 上单调递减 C. 在区间 [5π4,3π2] 上单调递增 D. 在区间 [3π2,2π] 上单调递减7. ( 2分 ) (2018•天津)已知双曲线 x 2a 2−y 2b 2=1 (a >0 , b >0) 的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于A , B 两点. 设A , B 到双曲线同一条渐近线的距离分别为 d 1 和 d 2 ,且 d 1+d 2=6 ,则双曲线的方程为( ) A.x 24−y 212=1 B.x 212−y 24=1 C.x 23−y 29=1 D.x 29−y 23=1 8. ( 2分 ) 如图,在平面四边形ABCD 中, AB ⊥BC , AD ⊥CD , ∠BAD =120° , AB =AD =1 . 若点E 为边CD 上的动点,则 AE⃗⃗⃗⃗⃗ ⋅BE ⃗⃗⃗⃗⃗ 的最小值为( )A. 2116B. 32C. 2516D. 3二、填空题:9. ( 1分 ) (2018•天津)i 是虚数单位,复数 6+7i 1+2i = ________10. ( 1分 ) (2018•天津)在 (x 2√x )5 的展开式中, x 2 的系数为________11. ( 1分 ) (2018•天津)已知正方体 ABCD −A 1B 1C 1D 1 的棱长为1,除面 ABCD 外,该正方体其余各面的中心分别为点E , F , G , H , M (如图),则四棱锥 M −EFGH 的体积为________12. ( 1分 ) (2018•天津)已知圆 x 2+y 2−2x =0 的圆心为C , 直线 {x =−1+√22t,y =3−√22t( t 为参数)与该圆相交于A , B 两点,则 ΔABC 的面积为________.13. ( 1分 ) (2018•天津)已知 a , b ∈R ,且 a −3b +6=0 ,则 2a +18b 的最小值为________. 14. ( 1分 ) (2018•天津)已知 a >0 ,函数 f(x)={x 2+2ax +a, x ≤0,−x 2+2ax −2a,x >0.若关于 x 的方程 f(x)=ax 恰有2个互异的实数解,则 a 的取值范围是________.三、解答题:15. ( 5分 ) (2018•天津)在 ΔABC 中,内角A ,B,C 所对的边分别为a,b ,c. 已知 bsinA =acos(B −π6) . (Ⅰ)求角B 的大小;(Ⅱ)设a =2,c =3,求b 和 sin(2A −B) 的值.16. ( 5分 ) (2018•天津)已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.(Ⅰ)应从甲、乙、丙三个部门的员工中分别抽取多少人? (Ⅱ)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查. (i )用X 表示抽取的3人中睡眠不足的员工人数,求随机变量X 的分布列与数学期望;(ii )设A 为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A 发生的概率. 17. ( 5分 ) (2018•天津)如图, AD//BC 且AD =2BC , AD ⊥CD , EG//AD 且EG =AD , CD//FG 且CD =2FG , DG ⊥平面ABCD ,DA =DC =DG =2.(Ⅰ)若M 为CF 的中点,N 为EG 的中点,求证: MN//平面CDE ; (Ⅱ)求二面角 E −BC −F 的正弦值;(Ⅲ)若点P 在线段DG 上,且直线BP 与平面ADGE 所成的角为60°,求线段DP 的长.18. ( 5分 ) (2018•天津)设 {a n } 是等比数列,公比大于0,其前n 项和为 S n (n ∈N ∗) , {b n } 是等差数列.已知 a 1=1 , a 3=a 2+2 , a 4=b 3+b 5 , a 5=b 4+2b 6 . (Ⅰ)求 {a n } 和 {b n } 的通项公式;(Ⅱ)设数列 {S n } 的前n 项和为 T n (n ∈N ∗) , (i )求 T n ; (ii )证明 ∑(T k +b k+2)b k (k+1)(k+2)nk=1=2n+2n+2−2(n ∈N ∗) .19. ( 5分 ) (2018•天津)设椭圆x 2a 2+x 2b 2=1 (a >b >0)的左焦点为F , 上顶点为B .已知椭圆的离心率为 √53,点A 的坐标为 (b,0) ,且 |FB|⋅|AB|=6√2 .(Ⅰ)求椭圆的方程;(Ⅱ)设直线l : y =kx(k >0) 与椭圆在第一象限的交点为P , 且l 与直线AB 交于点Q .若 |AQ||PQ|=5√24sin ∠AOQ (O 为原点),求k 的值.20. ( 5分 ) (2018•天津)已知函数 f(x)=a x , g(x)=log a x ,其中a >1. (Ⅰ)求函数 ℎ(x)=f(x)−xlna 的单调区间;(Ⅱ)若曲线 y =f(x) 在点 (x 1,f(x 1)) 处的切线与曲线 y =g(x) 在点 (x 2,g(x 2)) 处的切线平行,证明 x 1+g(x 2)=−2lnlna lna;(Ⅲ)证明当 a ≥e 1e 时,存在直线l , 使l 是曲线 y =f(x) 的切线,也是曲线 y =g(x) 的切线.答案解析部分一、<b >选择题</b>1.【答案】B【考点】交、并、补集的混合运算【解析】【解答】解:∵A={x|0<x<2}, B={x|x≥1}∴C RB={x|x<1}则A∩C RB={x|0<x<1}故答案为:B【分析】先求B的补集,再与A取交集.2.【答案】C【考点】简单线性规划【解析】【解答】解:将z=3x+5y平移至-x+y=1与x+y=5的交点(2,3)时,z max=3×2+5×3=21故答案为:C【分析】先画出可行域,再将目标函数平移至点(2,3)时z有最大值.3.【答案】B【考点】程序框图【解析】【解答】解:N=20,i=2,T=0.N =20=10∈z∴T=1,i=3,i<5∴Ni =203∉z∴i=4,i<5∴Ni =204=5∈z∴T=2,i=5≥5即T=2故答案为:B【分析】按照程序方框图,一步计算,直到i≥5为止. 4.【答案】A【考点】必要条件、充分条件与充要条件的判断 【解析】【解答】解:∵ |x −12|<12⇒0<x <1x 3<1⇒x <1故|x−12|<12 ”是“ x 3<1 ”的充分不必要条件, 故答案为:A【分析】先解绝对值不等式,再解高次不等式,找到集合之间关系. 5.【答案】D【考点】对数值大小的比较【解析】【解答】解: a =log 2e >1,b =ln2<1,c =log 1213=log 23>log 2e =a则a , b , c 的大小关系为:c>a>b 故答案为:D【分析】先判断出b 比1小,再将比1都大的a,c 化为同底,由对函数的单调性,可比较a,c 的大小. 6.【答案】A【考点】函数y=Asin (ωx+φ)的图象变换 【解析】【解答】解: y =sin(2x +π5)→右平移π10y =sin2x ,∵3π4≤x ≤5π4⇒3π2≤2x ≤5π2故答案为:A【分析】先求出平移后的解析式,再对A 、B 、C 、D 进行检验. 7.【答案】C【考点】双曲线的简单性质 【解析】【解答】解: ca =2⇒c =2a ∴b =√3a∴双曲线渐近线方程为 y =±√3x 又 A(c,b 2a ),B(c,−b 2a) 即 A(2a,3a),B(2a,−3a)则 d 1=|2√3a−3a|2=(2√3−3)a2d 2=2√3a +3a2⇒d 1+d 2=2√3a =6⇒a =√3 则b=3∴双曲线方程为 x 23−y 29=1故答案为:C【分析】先由离心率,将双曲线方程用一个参数a 表示,再利用通径两端点到渐近线距离之和为6,求出a ,即可得到双曲线方程. 8.【答案】A【考点】平面向量数量积的性质及其运算律【解析】【解答】解:以A 为原点,AB 为x 轴建立直角坐标系,则 A(0,0),B(1,0),D(−12,√32)设 C(1,y 0) ∴ DC⃗⃗⃗⃗⃗ =(32,y 0−√32) 又 DC ⃗⃗⃗⃗⃗ ⋅AD ⃗⃗⃗⃗⃗ =0⇒−34+√32y 0−34=0∴ y 0=√3 ∴ DC⃗⃗⃗⃗⃗ =(−12,√32) 又E 在CD 上设 DE ⃗⃗⃗⃗⃗ =λDC ⃗⃗⃗⃗⃗ ⇒AE ⃗⃗⃗⃗⃗ =λ(32,√32)+(−12,√32)⇒AE ⃗⃗⃗⃗⃗ =(3λ2−12,√32λ+√32) 又 BE ⃗⃗⃗⃗⃗ =AE⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ =(3λ2−32,√32λ+√32) AE ⃗⃗⃗⃗⃗ ⋅BE⃗⃗⃗⃗⃗ =3λ2−3λ2+32=3(λ−14)2+2116又 0≤λ≤1 ,当 λ=14 时, AE ⃗⃗⃗⃗⃗ ⋅BE ⃗⃗⃗⃗⃗ 有最大值 2116 故答案为:A【分析】先建系,利用垂直,求出C ,再利用数量积,得到二次函数,求出最值. 二、<b >填空题:</b> 9.【答案】4−i【考点】复数代数形式的乘除运算 【解析】【解答】解: 6+7i 1+2i =(6+7i)(1−2i)(1+2i)(1−2i)=6+14−5i5=4−i 【分析】将分子,分母乘以分母的共轭复数.10.【答案】52 【考点】二项式定理【解析】【解答】解:∵ (x −2x )5 的通式为 T r+1=C 5r ⋅x 5−r (−12)r ⋅x −r2∴ 5−3r 2=2⇒r =2则 C 5r⋅(−12)2=52【分析】先写出二项式的通式,令x 的指数为2,求出是通式中第3项,则可得到系数. 11.【答案】112【考点】棱柱、棱锥、棱台的体积【解析】【解答】解:∵四凌锥M-EFGH 为所有棱长均为 √22 的正四棱锥.∴ V M−EFGH =13×(√22)2×12=112【分析】判断四棱锥为正四棱锥,高为棱长的一半.12.【答案】12【考点】直线与圆的位置关系,参数方程化成普通方程【解析】【解答】解:∵ x 2+y 2−2x =0⇒(x −1)2+y 2=1又直线 {x =−1+√22ty =3−√22t (t 为参数) ⇒x +1=3−y ⇒y =2−x∴圆心到直线距离 d =2,又 |AB|=2√1−12=√2即 S △ABC =12|AB|⋅d =12【分析】先将参数方程化为普通方程,再用勾股定理算弦长. 13.【答案】14【考点】函数的最值及其几何意义【解析】【解答】解:∵a-3b+6=0 ⇒ a-3b=-6又 2a +18b≥2√2a +18b=2√2a−3b =14【分析】对 2a +18b 用均值不等式. 14.【答案】(4,8)【考点】根的存在性及根的个数判断【解析】【解答】解:∵ f(x)={x 2+2ax +a,x ≤0−x 2+2ax −2a,x >0∴ f(x)−ax =0⇒f(x)−ax ={x 2+ax +a,x ≤0−x 2+ax −2a,x >0x 2+ax +a =0与 −x 2+ax −2a =0要么无根,要么有同号根,同号根时在范围内. 则 {△1=a 2−4a >0△2=a 2−8a <0或{△1=a 2−4a <0△2=a 2−8a >0或{△1=a 2−4a =0△2=a 2−8a =0 ⇒4<a <8【分析】两方程若有根,正好是合题意的同号根,则分类讨论. 三、<b >解答题:</b>15.【答案】解:.解:(Ⅰ) △ABC 中,由正弦定理 asinA =bsinB ⇒bsinA =asinB =acos(B −π6)⇒asinB =acos(B −π6)⇒sinB =cos(B −π6) ∴ tanB =√3 又 0<B <π∴B =π3(Ⅱ) △ABC 中,∵a=2,c=3, B =π3 则 b 2=a 2+c 2−2accosB =7⇒b =√7由 bsinA =acos(B −π6)⇒sinA =√37=√217∵ a <c ∴ cosA =√7∴sin2A=2sinAcosA=4√37cos2A=2cos2A−1=1 7∴sin(2A−B)=sin2A⋅cosB−cos2AsinB=3√314【考点】正弦定理【解析】【分析】(Ⅰ)由正弦定理,得到A.B关系,代入等式,解出∠B.(Ⅱ)由余弦定理,得到b,再由正弦定理得到sinA,从而cosA,sin2A,cos2A由二倍角公式算出.16.【答案】解:解:(Ⅰ)由已知甲乙丙三个部门员工人数之比为3:2:2,∴从甲乙丙三个部门中分别抽到3人,2人,2人(Ⅱ)(i)随机变量ξ取值可能为0.1.2.3p(x=k)=C4k⋅C33−kC73(k=0,1,2,3)∴随机变量x的分布列为X 0 1 2 3P 13512351835435∴x的数学期望为E(x)=0×135+1×1235+2×1835+3×435=127(ii)解:设事件B为:“抽取3人中,睡眠充足的员工有1人,睡眠不足的员工有2人”,事件C为:“抽取3人中,睡眠充足的员工有2人,睡眠不足的员工有1人”,则A=B∪C,且BC互斥由①知P(B)=P(x=2),P(C)=P(x=1)则:P(A)=P(B∪C)=P(x=2)+P(x=1)=67则事件A发生的概率为67.【考点】离散型随机变量的期望与方差【解析】【分析】(Ⅰ)分层抽样对应成比例;(Ⅱ)概率分布列通式写出来,再算期望。
2018年天津高考理科数学试题及答案(精美Word版,精校版)
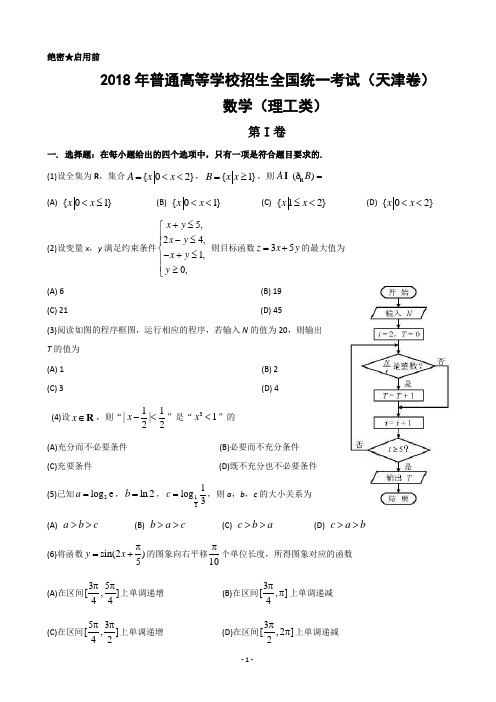
绝密★启用前2018年普通高等学校招生全国统一考试(天津卷)数学(理工类)第I 卷一. 选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设全集为R ,集合{02}A x x =<<,{1}B x x =≥,则()=R I A B ð (A) {01}x x <≤(B) {01}x x <<(C) {12}x x ≤<(D) {02}x x <<(2)设变量x ,y 满足约束条件5,24,1,0,x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩ 则目标函数35z x y =+的最大值为(A) 6 (B) 19 (C) 21 (D) 45(3)阅读如图的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为 (A) 1 (B) 2(C) 3(D) 4(4)设x ∈R ,则“11||22x -<”是“31x <”的 (A)充分而不必要条件 (B)必要而不充分条件 (C)充要条件 (D)既不充分也不必要条件 (5)已知2log e =a ,ln 2b =,121log 3c =,则a ,b ,c 的大小关系为 (A) a b c >> (B) b a c >>(C) c b a >>(D) c a b >>(6)将函数sin(2)5y x π=+的图象向右平移10π个单位长度,所得图象对应的函数 (A)在区间35[,]44ππ上单调递增(B)在区间3[,]4ππ上单调递减 (C)在区间53[,]42ππ上单调递增(D)在区间3[,2]2ππ上单调递减(7)已知双曲线22221(0,0)x y a b a b-=>>的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于A ,B两点. 设A ,B 到双曲线同一条渐近线的距离分别为1d 和2d ,且126d d +=,则双曲线的方程为(A)221412x y -=(B)221124x y -= (C)22139x y -=(D) 22193x y -= (8)如图,在平面四边形ABCD 中,AB BC ⊥,AD CD ⊥,120BAD ∠=︒,1AB AD ==. 若点E 为边CD 上的动点,则⋅uu u r uu rAE BE 的最小值为(A)2116(B)32(C)2516(D) 3第Ⅱ卷二. 填空题:本大题共6小题,每小题5分,共30分。
2018年天津市高考数学试卷(理科)(解析版)

2018年天津市高考数学试卷(理科)一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设全集为R ,集合A ={x|0<x <2},B ={x|x ≥1},则A ∩(∁R B)=( ) A.{x|0<x ≤1} B.{x|0<x <1}C.{x|1≤x <2}D.{x|0<x <2}2. 设变量x ,y 满足约束条件{x +y ≤52x −y ≤4−x +y ≤1y ≥0 ,则目标函数z =3x +5y 的最大值为( )A.6B.19C.21D.453. 阅读如图所示的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为( )A.1B.2C.3D.44. 设x ∈R ,则“|x −12|<12”是“x 3<1”的( ) A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件5. 已知a =log 2 e ,b =ln 2,c =log 1213,则a ,b ,c 的大小关系为( )A.a >b >cB.b >a >cC.c >b >aD.c >a >b6. 将函数y =sin (2x +π5)的图象向右平移π10个单位长度,所得图象对应的函数( ) A.在区间[3π4, 5π4]上单调递增 B.在区间[3π4, π]上单调递减 C.在区间[5π4, 3π2]上单调递增 D.在区间[3π2, 2π]上单调递减7. 已知双曲线x 2a 2−y 2b 2=1(a >0, b >0)的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于A ,B 两点.设A ,B 到双曲线同一条渐近线的距离分别为d 1和d 2,且d 1+d 2=6,则双曲线的方程为( ) A.x 24−y 212=1 B.x 212−y 24=1 C.x 23−y 29=1 D.x 29−y 23=18. 如图,在平面四边形ABCD 中,AB ⊥BC ,AD ⊥CD ,∠BAD =120∘,AB =AD =1.若点E 为边CD 上的动点,则AE →⋅BE →的最小值为( )A.2116B.32C.2516D.3二.填空题:本大题共6小题,每小题5分,共30分.9. i 是虚数单位,复数6+7i1+2i =________.10. 在(x −2√x )5的展开式中,x 2的系数为________.11. 已知正方体ABCD −A 1B 1C 1D 1的棱长为1,除面ABCD 外,该正方体其余各面的中心分别为点E ,F ,G ,H ,M (如图),则四棱锥M−EFGH 的体积为________.12. 已知圆x 2+y 2−2x =0的圆心为C ,直线{x =−1+√22ty =3−√22t,(t 为参数)与该圆相交于A ,B 两点,则△ABC 的面积为________.13. 已知a ,b ∈R ,且a −3b +6=0,则2a+18b 的最小值为________.14. 已知a >0,函数f(x)={x 2+2ax +a,x ≤0−x 2+2ax −2a,x >0 .若关于x 的方程f(x)=ax 恰有2个互异的实数解,则a的取值范围是________.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.15. 在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知b sin A =a cos (B −π6).(1)求角B 的大小;(2)设a =2,c =3,求b 和sin (2A −B)的值.16. 已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.(1)应从甲、乙、丙三个部门的员工中分别抽取多少人?(2)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查. (i)用X 表示抽取的3人中睡眠不足的员工人数,求随机变量X 的分布列与数学期望;(ii)设A 为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A 发生的概率.17. 如图,AD // BC 且AD =2BC ,AD ⊥CD ,EG // AD 且EG =AD ,CD // FG 且CD =2FG ,DG ⊥平面ABCD ,DA =DC =DG =2.(1)若M 为CF 的中点,N 为EG 的中点,求证:MN // 平面CDE ;(2)求二面角E −BC −F 的正弦值;(3)若点P 在线段DG 上,且直线BP 与平面ADGE 所成的角为60∘,求线段DP 的长.18. 设{a n }是等比数列,公比大于0,其前n 项和为S n (n ∈N ∗),{b n }是等差数列.已知a 1=1,a 3=a 2+2,a 4=b 3+b 5,a 5=b 4+2b 6. (1)求{a n }和{b n }的通项公式;(2)设数列{S n }的前n 项和为T n (n ∈N ∗), ①求T n ; ②证明∑(T k +b k+2)b k (k+1)(k+2)n k=1=2n+2n+2−2(n ∈N ∗).19. 设椭圆x 2a 2+y 2b 2=1(a >b >0)的左焦点为F ,上顶点为B .已知椭圆的离心率为√53,点A 的坐标为(b,0),且|FB|⋅|AB|=6√2. (1)求椭圆的方程;(2)设直线l:y =kx (k >0)与椭圆在第一象限的交点为P ,且l 与直线AB 交于点Q .若|AQ||PQ|=5√24sin ∠AOQ (O 为原点),求k 的值.20. 已知函数f(x)=a x ,g(x)=log a x ,其中a >1. (1)求函数ℎ(x)=f(x)−x ln a 的单调区间;(2)若曲线y =f(x)在点(x 1, f(x 1))处的切线与曲线y =g(x)在点(x 2, g(x 2))处的切线平行,证明x 1+g(x2)=−2lnln a;ln a(3)证明当a≥e1e时,存在直线l,使l是曲线y=f(x)的切线,也是曲线y=g(x)的切线.参考答案与试题解析2018年天津市高考数学试卷(理科)一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.【答案】B【考点】交、并、补集的混合运算【解析】根据补集、交集的定义即可求出.【解答】∵A={x|0<x<2},B={x|x≥1},∴∁R B={x|x<1},∴A∩(∁R B)={x|0<x<1}.2.【答案】C【考点】简单线性规划【解析】先画出约束条件的可行域,利用目标函数的几何意义,分析后易得目标函数z=3x+5y的最大值.【解答】由变量x,y满足约束条件{x+y≤5 2x−y≤4−x+y≤1y≥0,得如图所示的可行域,由{x+y=5−x+y=1解得A(2, 3).当目标函数z=3x+5y经过A时,直线的截距最大,z取得最大值.将其代入得z的值为21,3.【答案】B【考点】程序框图【解析】本题主要考查循环结构的程序框图.【解答】解:运行程序,Ni=10是整数,T=1,i=3;N i =203不是整数,i=4;Ni=5是整数,T=2,i=5,退出循环.输出T的值为2.故选B.4.【答案】A【考点】必要条件、充分条件与充要条件的判断其他不等式的解法【解析】此题暂无解析【解答】解:由|x−12|<12可得−12<x−12<12,解得0<x<1;由x3<1,解得x<1;故“|x−12|<12”是“x3<1”的充分不必要条件,故选A.5.【答案】D【考点】对数值大小的比较【解析】此题暂无解析【解答】解:因为1=log22<log2e<log24=2,所以1<a<2;因为0<ln2<ln e=1,所以0<b<1;因为log1213=log23>log2e,所以c>a.所以c>a>b.故选D.6.【答案】A【考点】函数y=Asin(ωx+φ)的图象变换【解析】本题考查三角函数的单调区间的确定,考查三角函数的图象与性质、平移等基础知识,考查运算求解能力,考查函数与方程思想.【解答】解:将函数y =sin (2x +π5)的图象向右平移π10个单位长度, 得到的函数为:y =sin 2x ,增区间满足:−π2+2kπ≤2x ≤π2+2kπ,k ∈Z , 减区间满足:π2+2kπ≤2x ≤3π2+2kπ,k ∈Z ,∴ 增区间为[−π4+kπ, π4+kπ],k ∈Z , 减区间为[π4+kπ, 3π4+kπ],k ∈Z ,∴ 将函数y =sin (2x +π5)的图象向右平移π10个单位长度, 所得图象对应的函数在区间[3π4, 5π4]上单调递增.故选A . 7.【答案】 C【考点】双曲线的渐近线 双曲线的离心率 双曲线的标准方程【解析】画出图形,利用已知条件,列出方程组转化求解即可. 【解答】解:由题意可得图象如图,可得CD 是双曲线的一条渐近线, y =ba x ,即bx −ay =0,F(c, 0),因为AC ⊥CD ,BD ⊥CD , FE ⊥CD ,ACDB 是梯形, F 是AB 的中点,EF =d 1+d 22=3,EF =bc √a 2+b2=b , 所以b =3,双曲线x 2a 2−y 2b 2=1(a >0, b >0)的离心率为2, 可得c a =2, 可得:a 2+b 2a 2=4,解得a =√3.则双曲线的方程为:x 23−y 29=1.故选C . 8.【答案】 A【考点】二次函数在闭区间上的最值 平面向量数量积的运算 平面向量的坐标运算【解析】 此题暂无解析 【解答】解:如图所示,以D 为原点,以DA 所在的直线为x 轴,以DC 所在的直线为y 轴, 过点B 做BN ⊥x 轴,过点B 做BM ⊥y 轴,∵ AB ⊥BC ,AD ⊥CD ,∠BAD =120∘,AB =AD =1, ∴ AN =AB cos 60∘=12,BN =AB sin 60∘=√32, ∴ DN =1+12=32, ∴ BM =32,∴ CM =MB tan 30∘=√32, ∴ DC =DM +MC =√3,∴ A(1, 0),B(32, √32),C(0, √3), 设E(0, m),∴ AE →=(−1, m),BE →=(−32, m −√32),0≤m ≤√3,∴ AE →⋅BE →=32+m 2−√32m =(m −√34)2+32−316=(m −√34)2+2116,当m =√34时,取得最小值为2116. 故选A .二.填空题:本大题共6小题,每小题5分,共30分. 9.【答案】 4−i 【考点】 复数的运算 【解析】根据复数的运算法则计算即可. 【解答】解:6+7i1+2i =(6+7i)(1−2i)(1+2i)(1−2i)=6+14+7i−12i5=20−5i 5=4−i ,故答案为:4−i 10. 【答案】5 【考点】二项展开式的特定项与特定系数 【解析】写出二项展开式的通项,由x 的指数为2求得r 值,则答案可求. 【解答】解:(x −2√x )5的二项展开式的通项为:T r+1=C 5r⋅x 5−r ⋅2x)r =(−12)r⋅C 5r ⋅x10−3r 2.由10−3r 2=2,得r =2.∴ x 2的系数为(−12)2⋅C 52=52.故答案为:52. 11. 【答案】112【考点】柱体、锥体、台体的体积计算 【解析】此题暂无解析【解答】解:依题意知,四棱锥M −EFGH 为正四棱锥,正方形EFGH 的边长为√(12)2+(12)2=√22,四棱锥M −EFGH 的高为12,所以四棱锥M −EFGH 的体积为13×(√22)2×12=112.故答案为:112. 12. 【答案】12【考点】直线与圆的位置关系参数方程与普通方程的互化【解析】把圆的方程化为标准方程,写出圆心与半径;直线的参数方程化为普通方程,求出圆心到直线的距离, 计算弦长|AB|,利用三角形面积公式求出△ABC 的面积. 【解答】解:圆x 2+y 2−2x =0化为标准方程是(x −1)2+y 2=1,圆心为C(1, 0),半径r =1; 直线{x =−1+√22t y =3−√22t 化为普通方程是x +y −2=0,则圆心C 到该直线的距离为d =2=√22, 弦长|AB|=2√r 2−d 2=2√1−12=2×√22=√2,∴ △ABC 的面积为S =12⋅|AB|⋅d =12×√2×√22=12.故答案为:12. 13.【答案】14【考点】函数的最值及其几何意义 【解析】本题主要考查利用基本不等式求最值. 【解答】解:由题知a −3b =−6,因为2a >0,8b >0,所以2a +18≥2×√2a +18=2×√2a−3b =14.当且仅当2a =18b ,即a =−3b ,a =−3,b =1时取等号.故答案为:14. 14.【答案】 (4, 8) 【考点】分段函数的应用 【解析】分别讨论当x ≤0和x >0时,利用参数分离法进行求解即可. 【解答】当x ≤0时,由f(x)=ax 得x 2+2ax +a =ax , 得x 2+ax +a =0, 得a(x +1)=−x 2, 得a =−x 2x+1,设g(x)=−x 2x+1,则g′(x)=−2x(x+1)−x 2(x+1)2=−x 2+2x(x+1)2,由g′(x)>0得−2<x <−1或−1<x <0,此时递增,由g′(x)<0得x <−2,此时递减,即当x =−2时,g(x)取得极小值为g(−2)=4, 当x >0时,由f(x)=ax 得−x 2+2ax −2a =ax , 得x 2−ax +2a =0,得a(x −2)=x 2,当x =2时,方程不成立, 当x ≠2时,a =x 2x−2 设ℎ(x)=x 2x−2,则ℎ′(x)=2x(x−2)−x 2(x−2)2=x 2−4x (x−2)2,由ℎ′(x)>0得x >4,此时递增,由ℎ′(x)<0得0<x <2或2<x <4,此时递减,即当x =4时,ℎ(x)取得极小值为ℎ(4)=8, 要使f(x)=ax 恰有2个互异的实数解, 则由图象知4<a <8,三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15. 【答案】解:(1)在△ABC 中,由正弦定理得asin A =bsin B , 得b sin A =a sin B , 又b sin A =a cos (B −π6). ∴ a sin B =a cos (B −π6),即sin B =cos (B −π6) =cos B cos π6+sin B sin π6=√32cos B +12sin B ,∴ tan B =√3,又B ∈(0, π),∴ B =π3.(2)在△ABC 中,a =2,c =3,B =π3, 由余弦定理得b =√a 2+c 2−2ac cos B =√7, 由b sin A =a cos (B −π6), 得sin A =√3√7, ∵ a <c , ∴ cos A =√7,∴ sin 2A =2sin A cos A =4√37, cos 2A =2cos 2A −1=17,∴ sin (2A −B)=sin 2A cos B −cos 2A sin B =4√37×12−17×√32=3√314. 【考点】两角和与差的余弦公式 余弦定理 正弦定理三角函数中的恒等变换应用 【解析】(1)由正弦定理得b sin A =a sin B ,与b sin A =a cos (B −π6).由此能求出B .(2)由余弦定理得b =√7,由b sin A =a cos (B −π6),得sin A =√3√7,cos A =√7,由此能求出sin (2A −B).【解答】解:(1)在△ABC 中,由正弦定理得asin A =bsin B , 得b sin A =a sin B , 又b sin A =a cos (B −π6). ∴ a sin B =a cos (B −π6),即sin B=cos(B−π6)=cos B cos π6+sin B sinπ6=√32cos B+12sin B,∴tan B=√3,又B∈(0, π),∴B=π3.(2)在△ABC中,a=2,c=3,B=π3,由余弦定理得b=√a2+c2−2ac cos B=√7,由b sin A=a cos(B−π6),得sin A=√3√7,∵a<c,∴cos A=√7,∴sin2A=2sin A cos A=4√37,cos2A=2cos2A−1=17,∴sin(2A−B)=sin2A cos B−cos2A sin B=4√37×12−17×√32=3√314.16.【答案】解:(1)单位甲、乙、丙三个部门的员工人数分别为24,16,16.人数比为:3:2:2,从中抽取7人,应从甲、乙、丙三个部门的员工中分别抽取3,2,2人.(2)(i)随机变量X的取值为:0,1,2,3,P(X=0)=C33C73=135,P(X=1)=C41C32C73=1235,P(X=2)=C42C31C73=1835,P(X=3)=C43C73=435,所以随机变量的分布列为:E(X)=0×135+1×1235+2×1835+3×435=127;(ii)设事件B为:抽取的3人中,睡眠充足的员工有1人,睡眠不足的员工有2人,事件C为抽取的3人中,睡眠充足的员工有2人,睡眠不足的员工有1人,则:A=B∪C,且P(B)=P(X=2),P(C)=P(X=1),故P(A)=P(B∪C)=P(X=2)+P(X=1)=67.所以事件A发生的概率为67.【考点】互斥事件的概率加法公式离散型随机变量的期望与方差离散型随机变量及其分布列分层抽样方法【解析】(1)利用分层抽样,通过抽样比求解应从甲、乙、丙三个部门的员工中分别抽取人数;(2)若(I)用X表示抽取的3人中睡眠不足的员工人数,的可能值,求出概率,得到随机变量X的分布列,然后求解数学期望;(II)利用互斥事件的概率求解即可.【解答】解:(1)单位甲、乙、丙三个部门的员工人数分别为24,16,16.人数比为:3:2:2,从中抽取7人,应从甲、乙、丙三个部门的员工中分别抽取3,2,2人.(2)(i)随机变量X的取值为:0,1,2,3,P(X=0)=C33C73=135,P(X=1)=C41C32C73=1235,P(X=2)=C42C31C73=1835,P(X=3)=C43C73=435,所以随机变量的分布列为:E(X)=0×135+1×1235+2×1835+3×435=127;(ii)设事件B为:抽取的3人中,睡眠充足的员工有1人,睡眠不足的员工有2人,事件C为抽取的3人中,睡眠充足的员工有2人,睡眠不足的员工有1人,则:A=B∪C,且P(B)=P(X=2),P(C)=P(X=1),故P(A)=P(B∪C)=P(X=2)+P(X=1)=67.所以事件A 发生的概率为67.17. 【答案】依题意,可以建立以D 为原点,分别以DA →,DC →,DG →的方向为x 轴,y 轴,z 轴的正方向的空间直角坐标系(如图),可得D(0, 0, 0),A(2, 0, 0),B(1, 2, 0),C(0, 2, 0),E(2, 0, 2),F(0, 1, 2),G(0, 0, 2),M (0,32,1),N(1, 0, 2).(1)证明:依题意DC →=(0,2,0),DE →=(2,0,2). 设n 0→=(x,y,z)为平面CDE 的法向量,则{n 0→⋅DE →=0,n 0→⋅DC →=0,即{2y =0,2x +2z =0,不妨令z =−1,可得n 0→=(1,0,−1), 又MN →=(1,−32,1),可得MN →⋅n 0→=0,又因为直线MN ⊄平面CDE , 所以MN // 平面CDE .(2)解:依题意,可得BC →=(−1,0,0),BE →=(1,−2,2),CF →=(0,−1,2). 设n →=(x,y,z)为平面BCE 的法向量, 则{n →⋅BC →=0,n →⋅BE →=0,即{−x =0,x −2y +2z =0,不妨令z =1,可得n →=(0,1,1). 设m →=(x,y,z)为平面BCF 的法向量,则{m →⋅BC →=0,m →⋅CF →=0,即{−x =0,−y +2z =0,不妨令z =1,可得m →=(0,2,1). 因此有cos ⟨m →,n →⟩=m →⋅n→|m →||n →|=3√1010,于是sin ⟨m →,n →⟩=√1010. 所以,二面角E −BC −F 的正弦值为√1010.(3)解:设线段DP 的长为ℎ(ℎ∈[0, 2]),则点P 的坐标为(0, 0, ℎ), 可得BP →=(−1,−2,ℎ).易知,DC →=(0,2,0)为平面ADGE 的一个法向量, 故|cos ⟨BP →,DC →⟩|=|BP →⋅DC →||BP →||DC →|=√ℎ2+5.由题意,可得√ℎ2+5=sin 60∘=√32,解得ℎ=√33∈[0, 2].所以,线段DP 的长为√33. 【考点】直线与平面所成的角 直线与平面平行 【解析】 此题暂无解析 【解答】依题意,可以建立以D 为原点,分别以DA →,DC →,DG →的方向为x 轴,y 轴,z 轴的正方向的空间直角坐标系(如图),可得D(0, 0, 0),A(2, 0, 0),B(1, 2, 0),C(0, 2, 0),E(2, 0, 2),F(0, 1, 2),G(0, 0, 2),M (0,32,1),N(1, 0, 2).(1)证明:依题意DC →=(0,2,0),DE →=(2,0,2).设n 0→=(x,y,z)为平面CDE 的法向量,则{n 0→⋅DE →=0,n 0→⋅DC →=0,即{2y =0,2x +2z =0,不妨令z =−1,可得n 0→=(1,0,−1), 又MN →=(1,−32,1),可得MN →⋅n 0→=0, 又因为直线MN ⊄平面CDE ,所以MN // 平面CDE .(2)解:依题意,可得BC →=(−1,0,0),BE →=(1,−2,2),CF →=(0,−1,2). 设n →=(x,y,z)为平面BCE 的法向量, 则{n →⋅BC →=0,n →⋅BE →=0,即{−x =0,x −2y +2z =0,不妨令z =1,可得n →=(0,1,1). 设m →=(x,y,z)为平面BCF 的法向量, 则{m →⋅BC →=0,m →⋅CF →=0,即{−x =0,−y +2z =0,不妨令z =1,可得m →=(0,2,1). 因此有cos ⟨m →,n →⟩=m →⋅n→|m →||n →|=3√1010,于是sin ⟨m →,n →⟩=√1010. 所以,二面角E −BC −F 的正弦值为√1010.(3)解:设线段DP 的长为ℎ(ℎ∈[0, 2]),则点P 的坐标为(0, 0, ℎ), 可得BP →=(−1,−2,ℎ).易知,DC →=(0,2,0)为平面ADGE 的一个法向量, 故|cos ⟨BP →,DC →⟩|=|BP →⋅DC →||BP →||DC →|=√ℎ2+5.由题意,可得2=sin 60∘=√32,解得ℎ=√33∈[0, 2].所以,线段DP 的长为√33. 18. 【答案】(1)解:设等比数列{a n }的公比为q ,由a 1=1,a 3=a 2+2,可得q 2−q −2=0.∵ q >0,可得q =2. 故a n =2n−1.设等差数列{b n }的公差为d ,由a 4=b 3+b 5,得b 1+3d =4, 由a 5=b 4+2b 6,得3b 1+13d =16, ∴ b 1=d =1. 故b n =n .所以数列{a n }的通项公式为a n =2n−1,数列{b n }的通项公式为b n =n . (2)①解:由(1),有S n =1−2n 1−2=2n −1,故T n =∑(n k=12k −1)=∑2kn k=1−n =2×(1−2n )1−2−n =2n+1−n −2.②证明:因为(T k +b k+2)b k (k+1)(k+2)=(2k+1−k−2+k+2)k(k+1)(k+2)=k⋅2k+1(k+1)(k+2)=2k+2k+2−2k+1k+1, 所以∑(T k +b k+2)b k (k+1)(k+2)n k=1=(233−222)+(244−233)+⋯+(2n+2n+2−2n+1n+1)=2n+2n+2−2.【考点】等差数列与等比数列的综合 数列的求和【解析】 此题暂无解析 【解答】(1)解:设等比数列{a n }的公比为q ,由a 1=1,a 3=a 2+2,可得q 2−q −2=0. ∵ q >0,可得q =2. 故a n =2n−1.设等差数列{b n }的公差为d ,由a 4=b 3+b 5,得b 1+3d =4, 由a 5=b 4+2b 6,得3b 1+13d =16, ∴ b 1=d =1. 故b n =n .所以数列{a n }的通项公式为a n =2n−1,数列{b n }的通项公式为b n =n . (2)①解:由(1),有S n =1−2n 1−2=2n −1,故T n =∑(n k=12k −1)=∑2kn k=1−n =2×(1−2n )1−2−n =2n+1−n −2.②证明:因为(T k +b k+2)b k(k+1)(k+2)=(2k+1−k−2+k+2)k(k+1)(k+2)=k⋅2k+1(k+1)(k+2)=2k+2k+2−2k+1k+1, 所以∑(T k +b k+2)b k (k+1)(k+2)n k=1=(233−222)+(244−233)+⋯+(2n+2n+2−2n+1n+1)=2n+2n+2−2.19. 【答案】解:(1)设椭圆的焦距为2c ,由已知有c 2a 2=59,又由a 2=b 2+c 2,可得2a =3b . 由已知可得,|FB|=a ,|AB|=√2b .由|FB|⋅|AB|=6√2,可得ab =6,从而a =3,b =2.所以椭圆的方程为x 29+y 24=1.(2)设点P 的坐标为(x 1, y 1),点Q 的坐标为(x 2, y 2). 由已知有y 1>y 2>0,故|PQ|sin ∠AOQ =y 1−y 2. 又因为|AQ|=y 2sin ∠OAB,且∠OAB =π4,故|AQ|=√2y 2.由|AQ||PQ|=5√24sin ∠AOQ ,可得5y 1=9y 2.由方程组{y =kx,x 29+y 24=1,消去x ,可得y 1=√9k 2+4,易知直线AB 的方程为x +y −2=0,由方程组{y =kx,x +y −2=0,消去x ,可得y 2=2k k+1.由5y 1=9y 2,可得5(k +1)=3√9k 2+4,两边平方,整理得56k 2−50k +11=0,解得k =12或k =1128. 所以k 的值为12或1128. 【考点】直线与椭圆结合的最值问题 椭圆的标准方程 【解析】 此题暂无解析 【解答】解:(1)设椭圆的焦距为2c ,由已知有c 2a 2=59,又由a 2=b 2+c 2,可得2a =3b . 由已知可得,|FB|=a ,|AB|=√2b .由|FB|⋅|AB|=6√2,可得ab =6,从而a =3,b =2. 所以椭圆的方程为x 29+y 24=1.(2)设点P 的坐标为(x 1, y 1),点Q 的坐标为(x 2, y 2). 由已知有y 1>y 2>0,故|PQ|sin ∠AOQ =y 1−y 2.又因为|AQ|=y 2sin ∠OAB ,且∠OAB =π4,故|AQ|=√2y 2.由|AQ||PQ|=5√24sin ∠AOQ ,可得5y 1=9y 2.由方程组{y =kx,x 29+y 24=1,消去x ,可得y 1=√9k 2+4,易知直线AB 的方程为x +y −2=0,由方程组{y =kx,x +y −2=0,消去x ,可得y 2=2k k+1.由5y 1=9y 2,可得5(k +1)=3√9k 2+4,两边平方,整理得56k 2−50k +11=0,解得k =12或k =1128. 所以k 的值为12或1128.20.【答案】(1)解:由已知,ℎ(x)=a x −x ln a ,有ℎ′(x)=a x ln a −ln a , 令ℎ′(x)=0,解得x =0.由a >1,可知当x 变化时,ℎ′(x),ℎ(x)的变化情况如下表:(0, +∞);(2)证明:由f ′(x)=a x ln a ,可得曲线y =f(x)在点(x 1, f(x 1))处的切线的斜率为a x 1ln a . 由g ′(x)=1x ln a,可得曲线y =g(x)在点(x 2, g(x 2))处的切线的斜率为1x 2ln a.∵ 这两条切线平行,故有a x 1ln a =1x 2ln a,即x 2a x 1(ln a)2=1,两边取以a 为底数的对数,得log a x 2+x 1+2log a ln a =0, ∴ x 1+g(x 2)=−2lnln a ln a;(3)证明:曲线y =f(x)在点(x 1,a x 1)处的切线l 1:y −a x 1=a x 1ln a(x −x 1), 曲线y =g(x)在点(x 2, log a x 2)处的切线l 2:y −log a x 2=1x2ln a(x −x 2).要证明当a ≥e 1e时,存在直线l ,使l 是曲线y =f(x)的切线,也是曲线y =g(x)的切线, 只需证明当a ≥e 1e 时,存在x 1∈(−∞, +∞),x 2∈(0, +∞)使得l 1与l 2重合, 即只需证明当a ≥e 1e 时,方程组{a x 1ln a =1x2ln a①,a x 1−x 1a x 1ln a =log a x 2−1ln a②.由①得x 2=1a x 1(ln a)2,代入②得: a x 1−x 1a x 1ln a +x 1+1ln a+2lnln a ln a=0③.因此,只需证明当a ≥e 1e时,关于x 1 的方程③存在实数解.设函数u(x)=a x −xa x ln a +x +1ln a+2lnln a ln a,即要证明当a ≥e 1e 时,函数y =u(x)存在零点.u′(x)=1−(ln a)2xa x ,可知x ∈(−∞, 0)时,u′(x)>0;x ∈(0, +∞)时,u′(x)单调递减. 又u′(0)=1>0,u′(1(ln a)2)=1−a1(ln a)2<0,故存在唯一的x 0,且x 0>0,使得u′(x 0)=0,即1−(ln a)2x 0a x 0=0. 由此可得,u(x)在(−∞, x 0)上单调递增,在(x 0, +∞)上单调递减,u(x)在x=x0处取得极大值u(x0).∵a≥e1e,故lnln a≥−1,∴u(x0)=a x0−x0a x0ln a+x0+1ln a +2lnln aln a=1x0(ln a)2+x0+2lnln aln a≥2+2lnln aln a≥0.下面证明存在实数t,使得u(t)<0,由(1)可得a x≥1+x ln a,当x>1ln a时,有u(x)≤(1+x ln a)(1−x ln a)+x+1ln a +2lnln aln a=−(ln a)2x2+x+1+1ln a+2lnln aln a.∴存在实数t,使得u(t)<0.因此,当a≥e 1e时,存在x1∈(−∞, +∞),使得u(x1)=0.∴当a≥e1e时,存在直线l,使l是曲线y=f(x)的切线,也是曲线y=g(x)的切线.【考点】利用导数研究不等式恒成立问题利用导数研究曲线上某点切线方程利用导数研究函数的单调性对数的运算性质【解析】(1)把f(x)的解析式代入函数ℎ(x)=f(x)−x ln a,求其导函数,由导函数的零点对定义域分段,由导函数在各区间段内的符号可得原函数的单调区间;(2)分别求出函数y=f(x)在点(x1, f(x1))处与y=g(x)在点(x2, g(x2))处的切线的斜率,由斜率相等,两边取对数可得结论;(3)分别求出曲线y=f(x)在点(x1,a x1)处的切线与曲线y=g(x)在点(x2, log a x2)处的切线方程,把问题转化为证明当a≥e 1e时,存在x1∈(−∞, +∞),x2∈(0, +∞)使得l1与l2重合,进一步转化为证明当a≥e1e时,方程a x1−x1a x1ln a+x1+1ln a +2lnln aln a=0存在实数解.然后利用导数证明即可.【解答】(1)解:由已知,ℎ(x)=a x−x ln a,有ℎ′(x)=a x ln a−ln a,令ℎ′(x)=0,解得x=0.由a>1,可知当x变化时,ℎ′(x),ℎ(x)的变化情况如下表:(0, +∞);(2)证明:由f′(x)=a x ln a,可得曲线y=f(x)在点(x1, f(x1))处的切线的斜率为a x1ln a.由g′(x)=1x ln a ,可得曲线y=g(x)在点(x2, g(x2))处的切线的斜率为1x2ln a.∵这两条切线平行,故有a x1ln a=1x2ln a,即x2a x1(ln a)2=1,两边取以a为底数的对数,得logax2+x1+2logaln a=0,∴x1+g(x2)=−2lnln aln a;(3)证明:曲线y=f(x)在点(x1,a x1)处的切线l1:y−a x1=a x1ln a(x−x1),曲线y=g(x)在点(x2, log a x2)处的切线l2:y−log a x2=1x2ln a(x−x2).要证明当a≥e1e时,存在直线l,使l是曲线y=f(x)的切线,也是曲线y=g(x)的切线,只需证明当a≥e1e时,存在x1∈(−∞, +∞),x2∈(0, +∞)使得l1与l2重合,即只需证明当a≥e1e时,方程组{a x1ln a=1x2ln a①,a x1−x1a x1ln a=logax2−1ln a②.由①得x2=1a x1(ln a)2,代入②得:a x1−x1a x1ln a+x1+1ln a+2lnln aln a=0③.因此,只需证明当a≥e1e时,关于x1的方程③存在实数解.设函数u(x)=a x−xa x ln a+x+1ln a+2lnln aln a,即要证明当a≥e1e时,函数y=u(x)存在零点.u′(x)=1−(ln a)2xa x,可知x∈(−∞, 0)时,u′(x)>0;x∈(0, +∞)时,u′(x)单调递减.又u′(0)=1>0,u′(1(ln a)2)=1−a1(ln a)2<0,故存在唯一的x0,且x0>0,使得u′(x0)=0,即1−(ln a)2x0a x0=0.由此可得,u(x)在(−∞, x0)上单调递增,在(x0, +∞)上单调递减,u(x)在x=x0处取得极大值u(x0).∵a≥e1e,故lnln a≥−1,∴u(x0)=a x0−x0a x0ln a+x0+1ln a+2lnln aln a=1x0(ln a)2+x0+2lnln aln a≥2+2lnln aln a≥0.下面证明存在实数t,使得u(t)<0,由(1)可得a x≥1+x ln a,当x>1ln a时,有u(x)≤(1+x ln a)(1−x ln a)+x+1ln a+2lnln aln a=−(ln a)2x2+x+1+1ln a+2lnln aln a.∴存在实数t,使得u(t)<0.因此,当a≥e1e时,存在x1∈(−∞, +∞),使得u(x1)=0.∴当a≥e1e时,存在直线l,使l是曲线y=f(x)的切线,也是曲线y=g(x)的切线.。
2018年普通高等学校招生全国统一考试数学试题 理(天津卷,含解析)

2018年普通高等学校招生全国统一考试数学试题理(天津卷)本试卷分为第I卷(选择题)和第II卷(非选择题)两部分,共150分,考试用时120分钟。
第I卷1至2页,第II卷3至5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第I卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:如果事件A,B互斥,那么 .如果事件A,B相互独立,那么 .棱柱的体积公式,其中表示棱柱的底面面积,表示棱柱的高.棱锥的体积公式,其中表示棱锥的底面面积,表示棱锥的高.一. 选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设全集为R,集合,,则A. B. C. D.【答案】B【解析】分析:由题意首先求得,然后进行交集运算即可求得最终结果.详解:由题意可得:,结合交集的定义可得:.本题选择B选项.点睛:本题主要考查交集的运算法则,补集的运算法则等知识,意在考查学生的转化能力和计算求解能力.2. 设变量x,y满足约束条件则目标函数的最大值为A. 6B. 19C. 21D. 45【答案】C【解析】分析:首先画出可行域,然后结合目标目标函数的几何意义确定函数取得最大值的点,最后求解最大值即可.详解:绘制不等式组表示的平面区域如图所示,结合目标函数的几何意义可知目标函数在点A处取得最大值,联立直线方程:,可得点A的坐标为:,据此可知目标函数的最大值为:.本题选择C选项.点睛:求线性目标函数z=ax+by(ab≠0)的最值,当b>0时,直线过可行域且在y轴上截距最大时,z值最大,在y轴截距最小时,z值最小;当b<0时,直线过可行域且在y轴上截距最大时,z值最小,在y 轴上截距最小时,z值最大.3. 阅读右边的程序框图,运行相应的程序,若输入N的值为20,则输出T的值为A. 1B. 2C. 3D. 4【答案】B【解析】分析:由题意结合流程图运行程序即可求得输出的数值.详解:结合流程图运行程序如下:首先初始化数据:,,结果为整数,执行,,此时不满足;,结果不为整数,执行,此时不满足;,结果为整数,执行,,此时满足;跳出循环,输出.本题选择B选项.点睛:识别、运行程序框图和完善程序框图的思路:(1)要明确程序框图的顺序结构、条件结构和循环结构.(2)要识别、运行程序框图,理解框图所解决的实际问题.(3)按照题目的要求完成解答并验证.4. 设,则“”是“”的A. 充分而不必要条件B. 必要而不重复条件C. 充要条件D. 既不充分也不必要条件【答案】A【解析】分析:首先求解绝对值不等式,然后求解三次不等式即可确定两者之间的关系.详解:绝对值不等式,由.据此可知是的充分而不必要条件.本题选择A选项.点睛:本题主要考查绝对值不等式的解法,充分不必要条件的判断等知识,意在考查学生的转化能力和计算求解能力.5. 已知,,,则a,b,c的大小关系为A. B. C. D.【答案】D【解析】分析:由题意结合对数函数的性质整理计算即可求得最终结果.详解:由题意结合对数函数的性质可知:,,,据此可得:.本题选择D选项.点睛:对于指数幂的大小的比较,我们通常都是运用指数函数的单调性,但很多时候,因幂的底数或指数不相同,不能直接利用函数的单调性进行比较.这就必须掌握一些特殊方法.在进行指数幂的大小比较时,若底数不同,则首先考虑将其转化成同底数,然后再根据指数函数的单调性进行判断.对于不同底而同指数的指数幂的大小的比较,利用图象法求解,既快捷,又准确.6. 将函数的图象向右平移个单位长度,所得图象对应的函数A. 在区间上单调递增B. 在区间上单调递减C. 在区间上单调递增D. 在区间上单调递减【答案】A【解析】分析:由题意首先求得平移之后的函数解析式,然后确定函数的单调区间即可.详解:由函数图象平移变换的性质可知:将的图象向右平移个单位长度之后的解析式为:.则函数的单调递增区间满足:,即,令可得一个单调递增区间为:.函数的单调递减区间满足:,即,令可得一个单调递减区间为:.本题选择A选项.点睛:本题主要考查三角函数的平移变换,三角函数的单调区间的判断等知识,意在考查学生的转化能力和计算求解能力.7. 已知双曲线的离心率为2,过右焦点且垂直于x轴的直线与双曲线交于A,B两点. 设A,B到双曲线同一条渐近线的距离分别为和,且,则双曲线的方程为A. B. C. D.【答案】C【解析】分析:由题意首先求得A,B的坐标,然后利用点到直线距离公式求得b的值,之后求解a的值即可确定双曲线方程.详解:设双曲线的右焦点坐标为(c>0),则,由可得:,不妨设:,双曲线的一条渐近线方程为:,据此可得:,,则,则,双曲线的离心率:,据此可得:,则双曲线的方程为.本题选择C选项.点睛:求双曲线的标准方程的基本方法是待定系数法.具体过程是先定形,再定量,即先确定双曲线标准方程的形式,然后再根据a,b,c,e及渐近线之间的关系,求出a,b的值.如果已知双曲线的渐近线方程,求双曲线的标准方程,可利用有公共渐近线的双曲线方程为,再由条件求出λ的值即可.8. 如图,在平面四边形ABCD中,,,,. 若点E为边CD上的动点,则的最小值为A. B. C. D.【答案】A【解析】分析:由题意建立平面直角坐标系,然后结合点的坐标得到数量积的坐标表示,最后结合二次函数的性质整理计算即可求得最终结果.详解:建立如图所示的平面直角坐标系,则,,,,点在上,则,设,则:,即,据此可得:,且:,,由数量积的坐标运算法则可得:,整理可得:,结合二次函数的性质可知,当时,取得最小值.本题选择A选项.点睛:求两个向量的数量积有三种方法:利用定义;利用向量的坐标运算;利用数量积的几何意义.具体应用时可根据已知条件的特征来选择,同时要注意数量积运算律的应用.第Ⅱ卷注意事项:1. 用黑色墨水的钢笔或签字笔将答案写在答题卡上。
(精校版)2018年天津理数高考试题文档版(含答案)

绝密★启用前2018年普通高等学校招生全国统一考试(天津卷)数学(理工类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考证号填写在答题考上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第I 卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:如果事件A ,B 互斥,那么()()()P A B P A P B =+ . 如果事件A ,B 相互独立,那么()()()P AB P A P B = .棱柱的体积公式V Sh =,其中S 表示棱柱的底面面积,h 表示棱柱的高. 棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高. 一. 选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设全集为R ,集合{02}A x x =<<,{1}B x x =≥,则()=R I A B ð (A) {01}x x <≤(B) {01}x x << (C) {12}x x ≤<(D) {02}x x <<(2)设变量x ,y 满足约束条件5,24,1,0,x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩ 则目标函数35z x y =+的最大值为(A) 6 (B) 19 (C) 21 (D) 45(3)阅读如图的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为 (A) 1(B) 2(C) 3(D) 4(4)设x ∈R ,则“11||22x -<”是“31x <”的 (A)充分而不必要条件 (B)必要而不充分条件 (C)充要条件(D)既不充分也不必要条件(5)已知2log e =a ,ln 2b =,121log 3c =,则a ,b ,c 的大小关系为 (A) a b c >> (B) b a c >>(C) c b a >>(D) c a b >>(6)将函数sin(2)5y x π=+的图象向右平移10π个单位长度,所得图象对应的函数 (A)在区间35[,]44ππ上单调递增(B)在区间3[,]4ππ上单调递减(C)在区间53[,]42ππ上单调递增(D)在区间3[,2]2ππ上单调递减 (7)已知双曲线22221(0,0)x y a b a b-=>>的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于A ,B两点. 设A ,B 到双曲线同一条渐近线的距离分别为1d 和2d ,且126d d +=,则双曲线的方程为(A)221412x y -=(B)221124x y -= (C)22139x y -=(D) 22193x y -= (8)如图,在平面四边形ABCD 中,AB BC ⊥,AD CD ⊥,120BAD ∠=︒,1AB AD ==. 若点E 为边CD 上的动点,则⋅uu u r uurAE BE 的最小值为(A)2116(B)32(C)2516(D) 3第Ⅱ卷注意事项:1. 用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2018年普通高等学校招生统一考试理科数学真题及参考答案(天津卷)

2018年普通高等学校招生全国统一考试(天津卷、)数学试卷(理工类)注意事项:1.答卷前,考生务必将自己姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
第I 卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A ,B 互斥,那么()()()P AB P A P B =+、·如果事件A ,B 相互独立,那么()()()P AB P A P B =、·棱柱体积公式V Sh =,其中S 表示棱柱底面面积,h 表示棱柱高、 ·棱锥体积公式13V Sh =,其中S 表示棱锥底面面积,h 表示棱锥高、 一、 选择题:在每小题给出四个选项中,只有一项是符合题目要求、 (1)设全集为R ,集合{02}A x x =<<,{1}B x x =≥,则()=R I A B ð (A){01}x x <≤ (B){01}x x << (C){12}x x ≤<(D){02}x x <<(2)设变量x ,y 满足约束条件5,24,1,0,x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩ 则目标函数35z x y =+最大值为(A) 6 (B) 19 (C) 21 (D)45 (3)阅读如图程序框图,运行相应程序,若输入N 值为20,则输出T 值为 (A) 1(B) 2(C) 3(D)4(4)设x ∈R ,则“11||22x -<”是“31x <” (A)充分而不必要条件 (B)必要而不充分条件 (C)充要条件(D)既不充分也不必要条件(5)已知2log e =a ,ln 2b =,121log 3c =,则a ,b ,c 大小关系为 (A) a b c >> (B) b a c >>(C)c b a >>(D)c a b >>(6)将函数sin(2)5y x π=+图象向右平移10π个单位长度,所得图象对应函数 (A)在区间35[,]44ππ上单调递增(B)在区间3[,]4ππ上单调递减 (C)在区间53[,]42ππ上单调递增(D)在区间3[,2]2ππ上单调递减 (7)已知双曲线22221(0,0)x y a b a b-=>>离心率为2,过右焦点且垂直于x 轴直线与双曲线交于A ,B 两点、 设A ,B 到双曲线同一条渐近线距离分别为1d 和2d ,且126d d +=,则双曲线方程为(A)221412x y -=(B)221124x y -= (C)22139x y -=(D)22193x y -= (8)如图,在平面四边形ABCD 中,AB BC ⊥,AD CD ⊥,120BAD ∠=︒,1AB AD ==、若点E 为边CD 上动点,则⋅uu u r uurAE BE 最小值为(A)2116(B)32(C)2516(D) 3第Ⅱ卷注意事项:1、 用黑色墨水钢笔或签字笔将答案写在答题卡上。
精品解析:2018年全国普通高等学校招生统一考试理科数学(天津卷)(原卷版)

绝密★启用前2018年普通高等学校招生全国统一考试(天津卷)数学(理工类)本试卷分为第I卷(选择题)和第II卷(非选择题)两部分,共150分,考试用时120分钟。
第I卷1至2页,第II卷3至5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第I卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:如果事件A,B互斥,那么 .如果事件A,B相互独立,那么 .棱柱的体积公式,其中表示棱柱的底面面积,表示棱柱的高.棱锥的体积公式,其中表示棱锥的底面面积,表示棱锥的高.一. 选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设全集为R,集合,,则A. B. C. D.2. 设变量x,y满足约束条件则目标函数的最大值为A. 6B. 19C. 21D. 453. 阅读右边的程序框图,运行相应的程序,若输入N的值为20,则输出T的值为学§科§网...学§科§网...A. 1B. 2C. 3D. 44. 设,则“”是“”的A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件5. 已知,,,则a,b,c的大小关系为A. B. C. D.6. 将函数的图象向右平移个单位长度,所得图象对应的函数A. 在区间上单调递增B. 在区间上单调递减C. 在区间上单调递增D. 在区间上单调递减7. 已知双曲线的离心率为2,过右焦点且垂直于x轴的直线与双曲线交于A,B两点. 设A,B到双曲线的同一条渐近线的距离分别为和,且,则双曲线的方程为A. B. C. D.8. 如图,在平面四边形ABCD中,,,,. 若点E为边CD上的动点,则的最小值为A. B. C. D.2018年普通高等学校招生全国统一考试(天津卷)数学(理工类)第Ⅱ卷注意事项:1. 用黑色墨水的钢笔或签字笔将答案写在答题卡上。
(word完整版)2018年高考天津卷理科数学真题及答案,推荐文档

2018年普通高等学校招生全国统一考试(天津卷)数学(理工类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考证号填写在答题考上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第I 卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:如果事件A ,B 互斥,那么()()()P A B P A P B =+U . 如果事件A ,B 相互独立,那么()()()P AB P A P B = .棱柱的体积公式V Sh =,其中S 表示棱柱的底面面积,h 表示棱柱的高.棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高.一. 选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设全集为R ,集合{02}A x x =<<,{1}B x x =≥,则()=R I A B ð (A) {01}x x <≤ (B) {01}x x << (C) {12}x x ≤< (D) {02}x x <<(2)设变量x ,y 满足约束条件5,24,1,0,x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩ 则目标函数35z x y =+的最大值为(A) 6 (B) 19 (C) 21 (D) 45(3)阅读如图的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为(A) 1 (B) 2 (C) 3 (D) 4(4)设x ∈R ,则“11||22x -<”是“31x <”的 (A)充分而不必要条件 (B)必要而不充分条件 (C)充要条件(D)既不充分也不必要条件(5)已知2log e =a ,ln 2b =,121log 3c =,则a ,b ,c 的大小关系为(A) a b c >> (B) b a c >> (C) c b a >> (D) c a b >>(6)将函数sin(2)5y x π=+的图象向右平移10π个单位长度,所得图象对应的函数(A)在区间35[,]44ππ上单调递增 (B)在区间3[,]4ππ上单调递减 (C)在区间53[,]42ππ上单调递增 (D)在区间3[,2]2ππ上单调递减(7)已知双曲线22221(0,0)x y a b a b-=>>的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于A ,B 两点. 设A ,B 到双曲线同一条渐近线的距离分别为1d 和2d ,且126d d +=,则双曲线的方程为(A) 221412x y -=(B) 221124x y -=(C) 22139x y -=(D) 22193x y -=(8)如图,在平面四边形ABCD 中,AB BC ⊥,AD CD ⊥,120BAD ∠=︒,1AB AD ==. 若点E 为边CD 上的动点,则⋅uu u r uurAE BE 的最小值为(A)2116(B) 32 (C)2516(D) 3第Ⅱ卷注意事项:1. 用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2018年天津市高考数学试卷(理科)(解析版)

2018年天津市高考数学试卷(理科)一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设全集为R,集合A={x|0<x<2},B={x|x≥1},则A∩(∁R B)=()A.{x|0<x≤1}B.{x|0<x<1}C.{x|1≤x<2}D.{x|0<x<2}2.(5分)设变量x,y满足约束条件,则目标函数z=3x+5y的最大值为()A.6B.19C.21D.453.(5分)阅读如图的程序框图,运行相应的程序,若输入N的值为20,则输出T的值为()A.1B.2C.3D.44.(5分)设x∈R,则“|x﹣|<”是“x3<1”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件5.(5分)已知a=log2e,b=ln2,c=,则a,b,c的大小关系为()A.a>b>c B.b>a>c C.c>b>a D.c>a>b6.(5分)将函数y=sin(2x+)的图象向右平移个单位长度,所得图象对应的函数()A.在区间[,]上单调递增B.在区间[,π]上单调递减C.在区间[,]上单调递增D.在区间[,2π]上单调递减7.(5分)已知双曲线=1(a>0,b>0)的离心率为2,过右焦点且垂直于x轴的直线与双曲线交于A,B两点.设A,B到双曲线的同一条渐近线的距离分别为d1和d2,且d1+d2=6,则双曲线的方程为()A.﹣=1B.﹣=1C.﹣=1D.﹣=18.(5分)如图,在平面四边形ABCD中,AB⊥BC,AD⊥CD,∠BAD=120°,AB=AD=1.若点E为边CD上的动点,则的最小值为()A.B.C.D.3二.填空题:本大题共6小题,每小题5分,共30分.9.(5分)i是虚数单位,复数=.10.(5分)在(x﹣)5的展开式中,x2的系数为.11.(5分)已知正方体ABCD﹣A1B1C1D1的棱长为1,除面ABCD外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥M﹣EFGH的体积为.12.(5分)已知圆x2+y2﹣2x=0的圆心为C,直线,(t为参数)与该圆相交于A,B两点,则△ABC的面积为.13.(5分)已知a,b∈R,且a﹣3b+6=0,则2a+的最小值为.14.(5分)已知a>0,函数f(x)=.若关于x的方程f(x)=ax 恰有2个互异的实数解,则a的取值范围是.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.(13分)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b sin A=a cos(B ﹣).(Ⅰ)求角B的大小;(Ⅱ)设a=2,c=3,求b和sin(2A﹣B)的值.16.(13分)已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.(Ⅰ)应从甲、乙、丙三个部门的员工中分别抽取多少人?(Ⅱ)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.(i)用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;(ii)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.17.(13分)如图,AD∥BC且AD=2BC,AD⊥CD,EG∥AD且EG=AD,CD∥FG且CD =2FG,DG⊥平面ABCD,DA=DC=DG=2.(Ⅰ)若M为CF的中点,N为EG的中点,求证:MN∥平面CDE;(Ⅱ)求二面角E﹣BC﹣F的正弦值;(Ⅲ)若点P在线段DG上,且直线BP与平面ADGE所成的角为60°,求线段DP的长.18.(13分)设{a n}是等比数列,公比大于0,其前n项和为S n(n∈N*),{b n}是等差数列.已知a1=1,a3=a2+2,a4=b3+b5,a5=b4+2b6.(Ⅰ)求{a n}和{b n}的通项公式;(Ⅱ)设数列{S n}的前n项和为T n(n∈N*),(i)求T n;(ii)证明=﹣2(n∈N*).19.(14分)设椭圆+=1(a>b>0)的左焦点为F,上顶点为B.已知椭圆的离心率为,点A的坐标为(b,0),且|FB|•|AB|=6.(Ⅰ)求椭圆的方程;(Ⅱ)设直线l:y=kx(k>0)与椭圆在第一象限的交点为P,且l与直线AB交于点Q.若=sin∠AOQ(O为原点),求k的值.20.(14分)已知函数f(x)=a x,g(x)=log a x,其中a>1.(Ⅰ)求函数h(x)=f(x)﹣xlna的单调区间;(Ⅱ)若曲线y=f(x)在点(x1,f(x1))处的切线与曲线y=g(x)在点(x2,g(x2))处的切线平行,证明x1+g(x2)=﹣;(Ⅲ)证明当a≥时,存在直线l,使l是曲线y=f(x)的切线,也是曲线y=g(x)的切线.2018年天津市高考数学试卷(理科)参考答案与试题解析一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.【解答】解:∵A={x|0<x<2},B={x|x≥1},∴∁R B={x|x<1},∴A∩(∁R B)={x|0<x<1}.故选:B.2.【解答】解:由变量x,y满足约束条件,得如图所示的可行域,由解得A(2,3).当目标函数z=3x+5y经过A时,直线的截距最大,z取得最大值.将其代入得z的值为21,故选:C.3.【解答】解:若输入N=20,则i=2,T=0,==10是整数,满足条件.T=0+1=1,i=2+1=3,i≥5不成立,循环,=不是整数,不满足条件.,i=3+1=4,i≥5不成立,循环,==5是整数,满足条件,T=1+1=2,i=4+1=5,i≥5成立,输出T=2,故选:B.4.【解答】解:由|x﹣|<可得﹣<x﹣<,解得0<x<1,由x3<1,解得x<1,故“|x﹣|<”是“x3<1”的充分不必要条件,故选:A.5.【解答】解:a=log2e>1,0<b=ln2<1,c==log23>log2e=a,则a,b,c的大小关系c>a>b,故选:D.6.【解答】解:将函数y=sin(2x+)的图象向右平移个单位长度,得到的函数为:y=sin2x,增区间满足:﹣+2kπ≤2x≤,k∈Z,减区间满足:≤2x≤,k∈Z,∴增区间为[﹣+kπ,+kπ],k∈Z,减区间为[+kπ,+kπ],k∈Z,∴将函数y=sin(2x+)的图象向右平移个单位长度,所得图象对应的函数在区间[,]上单调递增.故选:A.7.【解答】解:由题意可得图象如图,CD是双曲线的一条渐近线y=,即bx﹣ay=0,F(c,0),AC⊥CD,BD⊥CD,FE⊥CD,ACDB是梯形,F是AB的中点,EF==3,EF==b,所以b=3,双曲线=1(a>0,b>0)的离心率为2,可得,可得:,解得a=.则双曲线的方程为:﹣=1.故选:C.8.【解答】解:如图所示,以D为原点,以DA所在的直线为x轴,以DC所在的直线为y轴,过点B做BN⊥x轴,过点B做BM⊥y轴,∵AB⊥BC,AD⊥CD,∠BAD=120°,AB=AD=1,∴AN=AB cos60°=,BN=AB sin60°=,∴DN=1+=,∴BM=,∴CM=MB tan30°=,∴DC=DM+MC=,∴A(1,0),B(,),C(0,),设E(0,m),∴=(﹣1,m),=(﹣,m﹣),0≤m≤,∴=+m2﹣m=(m﹣)2+﹣=(m﹣)2+,当m=时,取得最小值为.故选:A.二.填空题:本大题共6小题,每小题5分,共30分.9.【解答】解:====4﹣i,故答案为:4﹣i10.【解答】解:(x﹣)5的二项展开式的通项为=.由,得r=2.∴x2的系数为.故答案为:.11.【解答】解:正方体的棱长为1,M﹣EFGH的底面是正方形的边长为:,四棱锥是正四棱锥,棱锥的高为,四棱锥M﹣EFGH的体积:=.故答案为:.12.【解答】解:圆x2+y2﹣2x=0化为标准方程是(x﹣1)2+y2=1,圆心为C(1,0),半径r=1;直线化为普通方程是x+y﹣2=0,则圆心C到该直线的距离为d==,弦长|AB|=2=2=2×=,∴△ABC的面积为S=•|AB|•d=××=.故答案为:.13.【解答】解:a,b∈R,且a﹣3b+6=0,可得:3b=a+6,则2a+==≥2=,当且仅当2a=.即a=﹣3时取等号.函数的最小值为:.故答案为:.14.【解答】解:当x≤0时,由f(x)=ax得x2+2ax+a=ax,得x2+ax+a=0,得a(x+1)=﹣x2,得a=﹣,设g(x)=﹣,则g′(x)=﹣=﹣,由g′(x)>0得﹣2<x<﹣1或﹣1<x<0,此时递增,由g′(x)<0得x<﹣2,此时递减,即当x=﹣2时,g(x)取得极小值为g(﹣2)=4,当x>0时,由f(x)=ax得﹣x2+2ax﹣2a=ax,得x2﹣ax+2a=0,得a(x﹣2)=x2,当x=2时,方程不成立,当x≠2时,a=设h(x)=,则h′(x)==,由h′(x)>0得x>4,此时递增,由h′(x)<0得0<x<2或2<x<4,此时递减,即当x=4时,h(x)取得极小值为h (4)=8,要使f(x)=ax恰有2个互异的实数解,则由图象知4<a<8,故答案为:(4,8)三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.【解答】解:(Ⅰ)在△ABC中,由正弦定理得,得b sin A=a sin B,又b sin A=a cos(B﹣).∴a sin B=a cos(B﹣),即sin B=cos(B﹣)=cos B cos+sin B sin=cos B+,∴tan B=,又B∈(0,π),∴B=.(Ⅱ)在△ABC中,a=2,c=3,B=,由余弦定理得b==,由b sin A=a cos(B﹣),得sin A=,∵a<c,∴cos A=,∴sin2A=2sin A cos A=,cos2A=2cos2A﹣1=,∴sin(2A﹣B)=sin2A cos B﹣cos2A sin B==.16.【解答】解:(Ⅰ)单位甲、乙、丙三个部门的员工人数分别为24,16,16.人数比为:3:2:2,从中抽取7人现,应从甲、乙、丙三个部门的员工中分别抽取3,2,2人.(Ⅱ)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.(i)用X表示抽取的3人中睡眠不足的员工人数,随机变量X的取值为:0,1,2,3,,k=0,1,2,3.所以随机变量的分布列为:随机变量X的数学期望E(X)==;(ii)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,设事件B为:抽取的3人中,睡眠充足的员工有1人,睡眠不足的员工有2人,事件C 为抽取的3人中,睡眠充足的员工有2人,睡眠不足的员工有1人,则:A=B∪C,且P(B)=P(X=2),P(C)=P(X=1),故P(A)=P(B∪C)=P(X=2)+P(X=1)=.所以事件A发生的概率:.17.【解答】(Ⅰ)证明:依题意,以D为坐标原点,分别以、、的方向为x轴,y轴,z轴的正方向建立空间直角坐标系.可得D(0,0,0),A(2,0,0),B(1,2,0),C(0,2,0),E(2,0,2),F(0,1,2),G(0,0,2),M(0,,1),N(1,0,2).设为平面CDE的法向量,则,不妨令z=﹣1,可得;又,可得.又∵直线MN⊄平面CDE,∴MN∥平面CDE;(Ⅱ)解:依题意,可得,,.设为平面BCE的法向量,则,不妨令z=1,可得.设为平面BCF的法向量,则,不妨令z=1,可得.因此有cos<>=,于是sin<>=.∴二面角E﹣BC﹣F的正弦值为;(Ⅲ)解:设线段DP的长为h,(h∈[0,2]),则点P的坐标为(0,0,h),可得,而为平面ADGE的一个法向量,故|cos<>|=.由题意,可得,解得h=∈[0,2].∴线段DP的长为.18.【解答】(Ⅰ)解:设等比数列{a n}的公比为q,由a1=1,a3=a2+2,可得q2﹣q﹣2=0.∵q>0,可得q=2.故.设等差数列{b n}的公差为d,由a4=b3+b5,得b1+3d=4,由a5=b4+2b6,得3b1+13d=16,∴b1=d=1.故b n=n;(Ⅱ)(i)解:由(Ⅰ),可得,故=;(ii)证明:∵==.∴==﹣2.19.【解答】解:(Ⅰ)设椭圆+=1(a>b>0)的焦距为2c,由椭圆的离心率为e=,∴=;又a2=b2+c2,∴2a=3b,由|FB|=a,|AB|=b,且|FB|•|AB|=6;可得ab=6,从而解得a=3,b=2,∴椭圆的方程为+=1;(Ⅱ)设点P的坐标为(x1,y1),点Q的坐标为(x2,y2),由已知y1>y2>0;∴|PQ|sin∠AOQ=y1﹣y2;又|AQ|=,且∠OAB=,∴|AQ|=y2,由=sin∠AOQ,可得5y1=9y2;由方程组,消去x,可得y1=,由(Ⅰ)知直线AB的方程为x+y﹣2=0;由方程组,消去x,可得y2=;由5y1=9y2,可得5(k+1)=3,两边平方,整理得56k2﹣50k+11=0,解得k=或k=;∴k的值为或.20.【解答】(Ⅰ)解:由已知,h(x)=a x﹣xlna,有h′(x)=a x lna﹣lna,令h′(x)=0,解得x=0.由a>1,可知当x变化时,h′(x),h(x)的变化情况如下表:∴函数h(x)的单调减区间为(﹣∞,0),单调递增区间为(0,+∞);(Ⅱ)证明:由f′(x)=a x lna,可得曲线y=f(x)在点(x1,f(x1))处的切线的斜率为lna.由g′(x)=,可得曲线y=g(x)在点(x2,g(x2))处的切线的斜率为.∵这两条切线平行,故有,即,两边取以a为底数的对数,得log a x2+x1+2log a lna=0,∴x1+g(x2)=﹣;(Ⅲ)证明:曲线y=f(x)在点()处的切线l1:,曲线y=g(x)在点(x2,log a x2)处的切线l2:.要证明当a≥时,存在直线l,使l是曲线y=f(x)的切线,也是曲线y=g(x)的切线,只需证明当a≥时,存在x1∈(﹣∞,+∞),x2∈(0,+∞)使得l1与l2重合,即只需证明当a≥时,方程组由①得,代入②得:,③因此,只需证明当a≥时,关于x1的方程③存在实数解.设函数u(x)=,既要证明当a≥时,函数y=u(x)存在零点.u′(x)=1﹣(lna)2xa x,可知x∈(﹣∞,0)时,u′(x)>0;x∈(0,+∞)时,u′(x)单调递减,又u′(0)=1>0,u′=<0,故存在唯一的x0,且x0>0,使得u′(x0)=0,即.由此可得,u(x)在(﹣∞,x0)上单调递增,在(x0,+∞)上单调递减,u(x)在x=x0处取得极大值u(x0).∵,故lnlna≥﹣1.∴=.下面证明存在实数t,使得u(t)<0,由(Ⅰ)可得a x≥1+xlna,当时,有u(x)≤=.∴存在实数t,使得u(t)<0.因此,当a≥时,存在x1∈(﹣∞,+∞),使得u(x1)=0.∴当a≥时,存在直线l,使l是曲线y=f(x)的切线,也是曲线y=g(x)的切线.。
2018年高考天津卷理数真题(含答案)

绝密★启用前2018年普通高等学校招生全国统一考试(天津卷)数学(理工类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考证号填写在答题考上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第I 卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:如果事件A ,B 互斥,那么()()()P AB P A P B =+ .如果事件A ,B 相互独立,那么()()()P AB P A P B = .棱柱的体积公式V Sh =,其中S 表示棱柱的底面面积,h 表示棱柱的高. 棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高. 一. 选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设全集为R ,集合{02}A x x =<<,{1}B x x =≥,则()=R I A B ð(A) {01}x x <≤(B) {01}x x << (C) {12}x x ≤<(D) {02}x x <<(2)设变量x ,y 满足约束条件5,24,1,0,x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩ 则目标函数35z x y =+的最大值为(A) 6 (B) 19 (C) 21 (D) 45(3)阅读如图的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为 (A) 1(B) 2(C) 3(D) 4(4)设x ∈R ,则“11||22x -<”是“31x <”的 (A)充分而不必要条件 (B)必要而不充分条件 (C)充要条件(D)既不充分也不必要条件(5)已知2log e =a ,ln 2b =,121log 3c =,则a ,b ,c 的大小关系为 (A) a b c >> (B) b a c >>(C) c b a >>(D) c a b >>(6)将函数sin(2)5y x π=+的图象向右平移10π个单位长度,所得图象对应的函数 (A)在区间35[,]44ππ上单调递增(B)在区间3[,]4ππ上单调递减 (C)在区间53[,]42ππ上单调递增 (D)在区间3[,2]2ππ上单调递减 (7)已知双曲线22221(0,0)x y a b a b-=>>的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于A ,B 两点. 设A ,B 到双曲线同一条渐近线的距离分别为1d 和2d ,且126d d +=,则双曲线的方程为(A)221412x y -=(B)221124x y -= (C)22139x y -=(D) 22193x y -= (8)如图,在平面四边形ABCD 中,AB BC ⊥,AD CD ⊥,120BAD ∠=︒,1AB AD ==.若点E 为边CD 上的动点,则⋅uu u r uurAE BE 的最小值为(A)2116(B)32(C)2516(D) 3第Ⅱ卷注意事项:1. 用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2018年高考真题——理科数学(天津卷)

绝密★启用前2018年普通高等学校招生全国统一考试(天津卷)数学(理工类)本试卷分为第I卷(选择题)和第II卷(非选择题)两部分,共150分,考试用时120分钟。
第I卷1至2页,第II卷3至5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第I卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:如果事件A,B互斥,那么.如果事件A,B相互独立,那么.棱柱的体积公式,其中表示棱柱的底面面积,表示棱柱的高.棱锥的体积公式,其中表示棱锥的底面面积,表示棱锥的高.一. 选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设全集为R,集合,,则A. B. C. D.2. 设变量x,y满足约束条件则目标函数的最大值为A. 6B. 19C. 21D. 453. 阅读右边的程序框图,运行相应的程序,若输入N的值为20,则输出T的值为A. 1B. 2C. 3D. 44. 设,则“”是“”的A. 充分而不必要条件B. 必要而不重复条件C. 充要条件D. 既不充分也不必要条件5. 已知,,,则a,b,c的大小关系为A. B. C. D.6. 将函数的图象向右平移个单位长度,所得图象对应的函数A. 在区间上单调递增B. 在区间上单调递减C. 在区间上单调递增D. 在区间上单调递减7. 已知双曲线的离心率为2,过右焦点且垂直于x轴的直线与双曲线交于A,B两点. 设A,B到双曲线同一条渐近线的距离分别为和,且,则双曲线的方程为A. B. C. D.8. 如图,在平面四边形ABCD中,,,,. 若点E为边CD上的动点,则的最小值为A. B. C. D.2018年普通高等学校招生全国统一考试(天津卷)数学(理工类)第Ⅱ卷注意事项:1. 用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2018年天津高考数学试卷(理科)

2018年普通高等学校招生全国统一考试(天津卷)数 学(理工类)一. 选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1. (2018年天津理)设全集为R ,集合{}20<<=x x A ,{}1≥=x x B ,则=⋂)(B C A RA .{}10≤<x x B .{}10<<x xC .{}21<≤x xD .{}20<<x x【答案】B【解析】由题意可得:{}1<=x x B C R ,结合交集的定义可得:.{}10)(<<=⋂x x B C A R 【考点】交集的运算法则+补集的运算法则 【难度】★★★2.(2018年天津理)设变量,x y 满足约束条件52410x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩,,,,则目标函数35z x y =+的最大值为( )A .6B .19C .21D .45【答案】C【解析】绘制不等式组表示的平面区域如图所示,结合目标函数的几何意义可知目标函数在点A 处取得最大值,联立直线方程:51x y x y +=⎧⎨-+=⎩,可得点(2,3)A ,所以max 35325321z x y =+=⨯+⨯=. 本题选择C 选项.【考点】求线性目标函数()0z ax by ab =+≠的最值, 【难度】★★★3.(2018年天津理)阅读如图所示的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为( )A .1B .2C .3D .4【答案】B【解析】结合流程图运行程序如下: 首先初始化数据:20,2,0N i T ===,10Ni=,结果为整数, 执行11,13T T i i =+==+=,此时不满足5i ≥;203N i =,结果不为整数,执行14i i =+=,此时不满足5i ≥; 2054N i ==,结果为整数,执行12,15T T i i =+==+=,此时满足5i ≥; 跳出循环,输出2T =.故选择B 选项. 【考点】程序框图 【难度】★★★4. (2018年天津理)设R x ∈,则“2121<-x ”是“13<x ”的( ) A. 充分而不必要条件 B. 必要而不重复条件 C. 充要条件 D. 既不充分也不必要条件【答案】A【解析】绝对值不等式 102121212121<<⇔<-<-⇔<-x x x ,由113<⇔<x x .据此可知2121<-x 是13<x 的充分而不必要条件.本题选择A 选项.【考点】绝对值不等式的解法+充分不必要条件 【难度】★★★5.(2018年天津理)已知e a 2log =,2ln =b ,31log 21=c ,则a ,b ,c 的大小关系为( )A .a b c >>B .b a c >>C .c b a >>D .c a b >>【答案】D【解析】由题意结合对数函数的性质可知:1log 2>=e a ,)1,0(log 12ln 2∈==eb ,ec 2221log 3log 31log >==,据此可得:c a b >>.本题选择D 选项. 【考点】对于指数幂的大小的比较. 【难度】★★★6.(2018年天津理)将函数sin(2)5y x π=+的图象向右平移10π个单位长度,所得图象对应的函数( )A .在区间]45,43[ππ上单调递增 B .在区间],43[ππ上单调递减 C .在区间]2,4[ππ上单调递增D .在区间],2[ππ上单调递减【答案】A【解析】由函数sin(2)5y x π=+的图象平移变换的性质可知: 将sin(2)5y x π=+的图象向右平移10π个单位长度之后的解析式为:sin[2())]sin 2105y x x ππ=-+=则函数的单调递增区间满足:222()22k x k k z ππππ-≤≤+∈,即()44k x k k z ππππ-≤≤+∈,令1=k 可得函数的一个单调递增区间为]45,43[ππ,选项A 正确. 函数的单调递减区间满足:3222()22k x k k z ππππ+≤≤+∈, 即3()44k x k k z ππππ+≤≤+∈, 令1=k 可得函数的一个单调递减区间为]47,45[ππ,选项C ,D 错误;故选择A 选项. 【考点】本题主要考查三角函数的平移变换,三角函数的单调性 【难度】★★★7.(2018年天津理)已知双曲线22221(0,0)x y a b a b-=>> 的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于,A B 两点.设,A B 到双曲线的同一条渐近线的距离分别为1d 和2d ,且126,d d +=则双曲线的方程为( )A .221412x y -= B .221124x y -= C .22139x y -= D .22193x y -= 【答案】C【解析】设双曲线的右焦点坐标为(,0)(0)F c c >,则A B x x c ==,由22221c y a b -=可得:2b y a=±,不妨设: 22(,),(,)b b A c B c a a-,双曲线的一条渐近线方程为0bx ay -=,据此可得:221bc b d c -==,222bc b d c +==, 则12226,bcd d b c+===则23,9b b ==,双曲线的离心率:2c e a ====, 据此可得:23a =,则双曲线的方程为22139x y -=,故选择C 选项.【考点】待定系数法求双曲线的标准方程;渐近线方程 【难度】★★★★8.(2018年天津理)如图,在平面四边形ABCD 中,BC AB ⊥,CD AD ⊥,︒=∠120BAD ,1==AD AB . 若点E 为边CD 上的动点,则⋅的最小值为( )A .1621 B .23 C..1625D . 3【答案】A【解析】建立如图所示的平面直角坐标系,则)210(,A ,)023(,B ,)230(,C ,)023(,-D ,点E 在CD 上,则)10(≤≤=λλ,设),(y x E ,则:)23,23(),23(λ=+y x ,即⎪⎪⎩⎪⎪⎨⎧==+λλ232323y x , 据此可得:)23,23,23(λλ-E ,且:31)22AE λ=+u u u r,3)2BE λ=-u u u r ,由数量积的坐标运算法则可得:331()(()222222AB BE λλλλ⋅=-+⨯+u u u r u u u r ,整理可得:23(422)(01)4AB BE λλλ⋅=-+≤≤u u u r u u u r ,结合二次函数的性质可知,当41=λ时,BE AB ⋅取得最小值1621. 本题选择A 选项.【考点】向量的数量积+向量的坐标运算+数量积的几何意义 【难度】★★★★第Ⅱ卷二、填空题:本大题共6小题,每小题5分,共30分. 9.(2018年天津理)i 是虚数单位,复数67i___________12i+=+. 【答案】4i -【解析】由复数的运算法则得:67i (67i)(12i)205412i (12i)(12i)5ii ++--==-++-. 【考点】复数的运算法则及其应用,意在考查学生的转化能力和计算求解能力. 【难度】★★★10.(2018年天津理)在5)21(xx -的展开式中,2x 的系数为____________.【答案】25【解析】结合二项式定理的通项公式有:r r r rrr r x C xx C T 2355551)21()21(--+-=-=,令2235=-r 可得:2=r ,则2x 的系数为:251041)21(252=⨯=-C . 【考点】二项式定理 【难度】★★★11.(2018年天津理)已知正方体1111ABCD A B C D -的棱长为1,除面ABCD 外,该正方体其余各面的中心分别为点E ,F ,G ,H ,M (如图),则四棱锥EFGH M -的体积为__________.【答案】121 【解析】分析:由题意首先求解底面积,然后结合四棱锥的高即可求得四棱锥的体积. 详解:由题意可得,底面四边形EFGH 为边长为22的正方形,其面积21222=⎪⎪⎭⎫ ⎝⎛=EFGH S , 顶点M 到底面四边形EFGH 的距离为21=d , 由四棱锥的体积公式可得:.121212131=⨯⨯=-EFGH M V 【考点】四棱锥的体积 【难度】★★★12.(2018年天津理)已知圆0222=-+x y x 的圆心为C ,直线⎪⎪⎩⎪⎪⎨⎧-=+-=t y t x 223221(为参数)与该圆相交于A ,B 两点,则ABC ∆的面积为___________. 【答案】21【解析】分析:由题意首先求得圆心到直线的距离,然后结合弦长公式求得弦长,最后求解三角形的面积即可.详解:由题意可得圆的标准方程为:1)1(22=+-y x , 直线的直角坐标方程为:)1(3+-=-x y ,即02=-+y x , 则圆心到直线的距离:222201=-+=d , 由弦长公式可得:2)22(122=-⨯=AB , 则2122221=⨯⨯=∆ABC S . 【考点】直线与圆的位置关系+点到直线的距离.【难度】★★★13.(2018年天津理)已知,a b R ∈,且360a b -+=,则128ab+的最小值为__________. 【答案】14【解析】由360a b -+=可知36a b -=-,且:312228aa b b -+=+, 因为对于任意x , 20x >恒成立,结合均值不等式的结论可得:31122284aa b b-+=+≥==. 当且仅当32236a b a b -⎧=⎨-=-⎩,即31a b =-⎧⎨=⎩时等号成立.综上可得128ab +的最小值为14. 【考点】在应用基本不等式求最值时,要把握不等式成立的三个条件,就是“一正——各项均为正;二定——积或和为定值;三相等——等号能否取得”,若忽略了某个条件,就会出现错误. 【难度】★★★★14.(2018年天津理)已知0>a ,函数⎪⎩⎪⎨⎧>-+-≤++=0,220,2)(22x a ax x x a ax x x f ,若关于x 的方程ax x f =)(恰有2个互异的实数解,则a 的取值范围是______________. 【答案】)8,4( 【解析】:分类讨论:当0≤x 时,方程ax x f =)(即ax a ax x =++22,整理可得:)1(2+-=x a x ,很明显1-=x 不是方程的实数解,则12+-=x x a ,当0>x 时,方程ax x f =)(即ax a ax x =-+-222, 整理可得:)2(2-=x a x ,很明显2=x 不是方程的实数解,则22-=x x a ,令⎪⎪⎩⎪⎪⎨⎧>-≤+-=0,20,1)(22x x x x x x x g ,其中)2-111(12+++-=+-x x x x ,424222+-+-=-x x x x原问题等价于函数)(x g 与函数a y =有两个不同的交点,求a 的取值范围.结合对勾函数和函数图象平移的规律绘制函数)(x g 的图象, 同时绘制函数a y =的图象如图所示,考查临界条件, 结合0>a 观察可得,实数a 的取值范围是)8,4(.【考点】函数零点的求解与判断 【难度】★★★★15.(2018年天津理)在ABC ∆中,内角,,A B C 所对的边分别为,,a b c .已知sin cos()6b A a B π=-.(Ⅰ)求角B 的大小;(Ⅱ)设2a =,3c =,求b 和sin(2)A B -的值.【答案】(Ⅰ)3B π=;(Ⅱ)b =;sin(2)A B -=【解析】(Ⅰ)在ABC ∆中,由正弦定理sin sin a bA B=,可得sin sin b A a B =,又由πsin cos()6b A a B =-,得πsin cos()6a B a B =-,即πsin cos()6B B =-,可得tan B =.又因为(0,π)B ∈,可得3B π=.(Ⅱ)在ABC ∆中,由余弦定理及2,3,3a c B π===,有2222cos 7b a c ac B =+-=,故b =.由πsin cos()6b A a B =-,可得sin A =.因为a c <,故cos A =.因此sin 22sin cos A A A ==21cos22cos 17A A =-=. 所以,sin(2)sin 2cos cos2sin AB A B A B -=-=1127-= 【考点】1.同角三角函数的基本关系;2.两角差的正弦与余弦公式;3.二倍角的正弦与余弦公式;4.正弦定理、余弦定理 【难度】★★★16.(2018年天津理)已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查. (I )应从甲、乙、丙三个部门的员工中分别抽取多少人?(II )若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.(i )用X 表示抽取的3人中睡眠不足的员工人数,求随机变量X 的分布列与数学期望; (ii )设A 为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A 发生的概率. 【答案】(Ⅰ)从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人.(Ⅱ)(i )答案见解析;(ii )76. 【解析】(Ⅰ)由已知,甲、乙、丙三个部门的员工人数之比为2:2:3, 由于采用分层抽样的方法从中抽取7人,因此应从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人. (Ⅱ)(i )随机变量X 的所有可能取值为0,1,2,3.)3,2,1,0()(37334=⋅==-k C C C k x P kk 所以,随机变量X 的分布列为随机变量X 的数学期望712354335182351213510)(=⨯+⨯+⨯+⨯=X E . (ii )设事件B 为“抽取的3人中,睡眠充足的员工有1人,睡眠不足的员工有2人”; 事件C 为“抽取的3人中,睡眠充足的员工有2人,睡眠不足的员工有1人”, 则C B A ⋃=,且B 与C 互斥,由(i )知,)2()(==X P B P ,)1()(==X P C P ,故76)1()2()()(==+==⋃=X P X P C B P A P .所以,事件A 发生的概率为76.【考点】超几何分布+分层抽样. 【难度】★★★ 17.(2018年天津理)如图,//AB BC 且BC AD 2=,CD AD ⊥,//EG AD 且AD EG =,//CD FG 且FG CD 2=, DG ⊥平面ABCD ,2===DG DC DA . (I )若M 为CF 的中点,N 为EG 的中点,求证:MN//平面CDE ; (II )求二面角F BC E --的正弦值;(III )若点P 在线段DG 上,且直线BP 与平面ADGE 所成的角为︒60,求线段DP 的长.【答案】(Ⅰ)证明见解析;(Ⅱ)1010;(Ⅲ)33. 【解析】依题意,可以建立以D 为原点,分别以,DC ,DG 的方向为x 轴,y 轴,z 轴的正方向的空间直角坐标系(如图), 可得)0,0,0(D ,)0,0,2(A ,)0,2,1(B ,)0,2,0(C ,)2,0,2(E ,)2,1,0(F ,)2,0,0(G ,)1,23,0(M ,)2,0,1(N .(Ⅰ)依题意)0,2,0(=,)2,0,2(=. 设),,(0z y x n =为平面CDE 的法向量,则 0000n DC n DE ⎧⋅=⎪⎨⋅=⎪⎩u u r u u u r u u r u u u r 即 ⎩⎨⎧=+=02202z x y 不妨令1-=z ,可得)1,0,1(0-=n .又3(1,,1)2MN =-u u u u r ,可得00=⋅n ,又因为直线MN ⊄平面CDE ,所以MN//平面CDE .(Ⅱ)依题意,可得(1,0,0)BC =-u u u r ,(1,2,2)BE =-u u u r ,(0,1,2)CF =-u u u r.设),,(z y x n =为平面BCE 的法向量,则 0n BC n BE ⎧⋅=⎪⎨⋅=⎪⎩r u u u r r u u u r 即 ⎩⎨⎧=+-=-0220z y x x 不妨令1=z ,可得)1,1,0(=n . 设),,(z y x m =为平面BCF 的法向量,则0m BC m CF ⎧⋅=⎪⎨⋅=⎪⎩u r u u u rur u u u r 即 ⎩⎨⎧=+-=-020z y x 不妨令1=z ,可得)1,2,0(=m .因此有10103,cos =<,于是sin ,10m n <>=u r r . 所以,二面角F BC E --的正弦值为1010.(Ⅲ)设线段DP 的长为])2,0[(∈h h ,则点P 的坐标为),0,0(h , 可得),2,1(h BP --=.易知,)0,2,0(=为平面ADGE 的一个法向量,故cos ,BP DC BP DC BP DC ⋅<==u u u r u u u r u u u r u u u r u u u r u u u r ,由题意,可得2360sin 522==+︒h ,解得]2,0[33∈=h . 所以线段DP 的长为33. 【考点】空间向量的应用+线面平行的证明+二面角 【难度】★★★★18.(2018年天津理)设{}n a 是等比数列,公比大于0,其前n 项和为)(*N n S n ∈,{}n b 是等差数列,已知11=a ,223+=a a ,534b b a +=,6452b b a +=. (I )求{}n a 和{}n b 的通项公式;(II )设数列{}n S 的前n 项和为)(*N n T n ∈,(i )求n T ;(ii )证明)(222)2)(1()(*212N n n k k b b T n nk k k k ∈-+=++++=+∑ 【答案】(Ⅰ)12-=n n a ,n b n =;(Ⅱ)(i )221--=+n T n n .(ii )证明见解析.【解析】(I )设等比数列{}n a 的公比为q .由11=a ,223+=a a可得022=--q q .因为0>q ,可得2=q ,故12-=n n a .设等差数列{}n b 的公差为d ,由534b b a +=,可得431=+d b 由6452b b a +=,可得 161331=+d b 从而 1,11==d b 故n b n = 所以数列{}n a 的通项公式为12-=n n a ,数列{}n b 的通项公式为n b n =(II )(i )由(I ),有122121-=--=n nn S ,故.2221)21(2)2()12(111--=--⨯=-=-=+==∑∑n n T n nk nk n kkn (ii )因为1222)2)(1(2)2)(1()222()2)(1()12112+-+=++⋅=++++--=++++++++k k k k k k k k k k k k b b T k k k k k k k (,所以222)1222()3242()2232()2)(1()(212342312-+=+-+++-+-=++++++=+∑n n n k k b b T n n n nk k k k Λ 【考点】数列通项公式+数列求和【难度】★★★★19.(2018年天津理)设椭圆)0(12222>>=+b a by a x 的左焦点为F ,上顶点为B . 已知椭圆的离心率为35,点A 的坐标为)0,(b ,且26=⋅AB FB . (I )求椭圆的方程;(II )设直线)0(:>=k kx y l 与椭圆在第一象限的交点为P ,且l 与直线AB 交于点Q . 若AOQ PQAQ ∠=sin 425(O 为原点) ,求k 的值. 【答案】(Ⅰ)14922=+y x ;(Ⅱ)21或2811 【解析】(Ⅰ)设椭圆的焦距为2c ,由已知有9522=a c ,又由222c b a +=,可得b a 32=.由已知可得,a FB =,b AB 2=, 由26=⋅AB FB ,可得6=ab ,从而3=a ,2=b .所以,椭圆的方程为14922=+y x .(Ⅱ)设点P 的坐标为),(11y x ,点Q 的坐标为),(22y x . 由已知有021>>y y ,故21sin y y AOQ PQ -=∠. 又因为OAB y AQ ∠=sin 2,而4π=∠OAB ,故22y AQ =.由AOQ PQAQ ∠=sin 425,可得2195y y =. 由方程组⎪⎩⎪⎨⎧=+=14922y x kxy 消去x ,可得49621+=k k y . 易知直线AB 的方程为02=-+y x ,由方程组⎩⎨⎧=-+=02y x kx y 消去x ,可得122+=k ky .由2195y y =,可得493)1(52+=+k k , 两边平方,整理得01150562=+-k k ,解得21=k ,或2811=k . 所以,k 的值为21或2811【考点】直线与椭圆的综合问题 【难度】★★★★20.(2018年天津理)已知函数xa x f =)(,x x g a log )(=,其中1>a .(I )求函数a x x f x h ln )()(-=的单调区间;(II )若曲线)(x f y =在点))(,(11x f x 处的切线与曲线)(x g y =在点))(,(22x g x 处的切线平行,证明aax g x ln ln ln 2)(21-=+; (III )证明当e e a 1≥时,存在直线l ,使l 是曲线)(x f y =的切线,也是曲线)(x g y =的切线.【答案】(Ⅰ)单调递减区间)0,(-∞,单调递增区间为)0(∞+,;(Ⅱ)证明见解析;(Ⅲ)证明见解析.【解析】(I )由已知,a x a x h xln )(-=,有a a a x h xln ln )(-='. 令0)(='x h ,解得0=x由,可知当x 变化时,)(x h ',)(x h 的变化情况如下表:所以函数)(x h 的单调递减区间为)0,(-∞,单调递增区间为)0(∞+,. (II )由a a x f xln )(=',可得曲线)(x f y =在点))(,(11x f x 处的切线斜率为a a x ln 1.由a x x g ln 1)(=',可得曲线)(x g y =在点))(,(22x g x 处的切线斜率为a x ln 12. 因为这两条切线平行,故有ax a a x ln 1ln 21=,即1)(ln 222=a a x x .两边取以a 为底的对数,得0ln log 2log 212=++a x x a ,所以aax g x ln ln ln 2)(21-=+. (III )曲线)(x f y =在点),(11x a x 处的切线.)(ln :1111x x a a a y l xx -⋅=-曲线)(x g y =在点)log ,(22x x a 处的切线)(ln 1log :2222x x ax x y l a -⋅=- 要证明当e e a 1≥时,存在直线l ,使l 是曲线)(x f y =的切线,也是曲线)(x g y =的切线, 只需证明当e e a 1≥时,存在),(1+∞-∞∈x ,),0(2+∞∈x ,使得1l 和2l 重合.即只需证明当e e a 1≥时,方程组1112121ln ln 1ln log ln x x x a a a x a a x a a x a ⎧=⎪⎪⎨⎪-=-⎪⎩有解,由①得22)(ln 11a a x x =,代入②,得.0ln ln ln 2ln 1ln 1111=+++-aa a x a a x a x x ③ 因此,只需证明当e e a 1≥时,关于1x 的方程③存在实数解. 设函数aaa x a xa a x u xx ln ln ln 2ln 1ln )(+++-=, 即要证明当e e a 1≥时,函数)(x u y =存在零点.x xa a x u 2)(ln 1)(-=',可知)0,(-∞∈x 时,0)(>'x u ; ),0(+∞∈x 时,)(x u '单调递减,又01)0(>='u ,01])(ln 1[2)(ln 12<-='a a a u ,故存在唯一的0x ,且00>x ,使得0)(0='x u ,即0)(ln 1002=-x a x a .由此可得)(x u 在),(0x -∞上单调递增,在)(0∞+,x 上单调递减.)(x u 在0x x =处取得极大值)(0x u .因为e e a 1≥,故1)ln(ln -≥a , 所以.0ln ln ln 22ln ln ln 2)(ln 1ln ln ln 2ln 1ln )(02000000≥+≥++=+++-=aa a a x a x a a a x a a x a x u x x 下面证明存在实数t ,使得0)(<t u .由(I )可得a x a x ln 1+≥, 当ax ln 1>时, 有aaa x a x a x x u ln ln ln 2ln 1)ln 1)(ln 1()(+++-+≤ aaa x x a ln ln ln 2ln 11)(ln 22++++-=,所以存在实数t ,使得0)(<t u因此,当e e a 1≥时,存在),(1+∞-∞∈x ,使得0)(1=x u .所以,当e e a 1≥时,存在直线l ,使l 是曲线)(x f y =的切线,也是曲线)(x g y =的切线. 【考点】用导数求函数的单调性、极值(最值) 【难度】★★★★★。
2018年普通高等学校招生全国统一考试理科数学(天津卷)

绝密★启用前2018年普通高等学校招生全国统一考试数学(天津卷,理)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟.第Ⅰ卷1至2页,第Ⅱ卷2至4页.答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码.答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效.考试结束后,将本试卷和答题卡一并交回.祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.2.本卷共8小题,每小题5分,共40分.参考公式:·如果事件A,B互斥,那么P(A∪B)=P(A)+P(B).·如果事件A,B相互独立,那么P(AB)=P(A)P(B).·棱柱的体积公式V=Sh,其中S表示棱柱的底面面积,h表示棱柱的高.·棱锥的体积公式V=13Sh,其中S表示棱锥的底面面积,h表示棱锥的高.一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集为R,集合A={x|0<x<2},B={x|x≥1},则A∩(∁R B)=A.{x|0<x≤1}B.{x|0<x<1}C.{x|1≤x<2}D.{x|0<x<2}2.设变量x,y满足约束条件{x+y≤5,2x-y≤4,-x+y≤1,y≥0,则目标函数z=3x+5y的最大值为A.6B.19C.21D.45 3.阅读右边的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为 A .1 B .2 C .3D .44.设x ∈R ,则“|x -12|<12”是“x 3<1”的 A .充分而不必要条件 B .必要而不充分条件 C .充要条件D .既不充分也不必要条件5.已知a=log 2e,b=ln 2,c=lo g 121,则a ,b ,c 的大小关系为 A .a>b>c B .b>a>c C .c>b>aD .c>a>b6.将函数y=sin (2x +π5)的图象向右平移π10个单位长度,所得图象对应的函数A .在区间[3π4,5π4]上单调递增 B .在区间[3π4,π]上单调递减 C .在区间[5π4,3π2]上单调递增 D .在区间[3π2,2π]上单调递减7.已知双曲线x 2a2−y 2b 2=1(a>0,b>0)的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于A ,B 两点.设A ,B 到双曲线的同一条渐近线的距离分别为d 1和d 2,且d 1+d 2=6,则双曲线的方程为A .x 24−y 212=1B .x 212−y 24=1C .x 23−y 29=1D .x 29−y 23=18.如图,在平面四边形ABCD 中,AB ⊥BC ,AD ⊥CD ,∠BAD=120°,AB=AD=1.若点E 为边CD 上的动点,则AE ⃗⃗⃗⃗⃗ ·BE ⃗⃗⃗⃗⃗ 的最小值为 A .2116 B .32 C .2516D .3第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上.2.本卷共12小题,共110分.二、填空题:本大题共6小题,每小题5分,共30分. 9.i 是虚数单位,复数6+7i1+2i = . 10.在(x 2√x)5的展开式中,x 2的系数为 . 11.已知正方体ABCD-A 1B 1C 1D 1的棱长为1,除面ABCD 外,该正方体其余各面的中心分别为点E ,F ,G ,H ,M (如图),则四棱锥M-EFGH 的体积为 .12.已知圆x 2+y 2-2x=0的圆心为C ,直线{x =-1+√22t ,y =3-√22t(t 为参数)与该圆相交于A ,B 两点,则△ABC 的面积为 .13.已知a ,b ∈R ,且a-3b+6=0,则2a +18b 的最小值为 .14.已知a>0,函数f (x )={x 2+2ax +a ,x ≤0,-x 2+2ax -2a ,x >0.若关于x 的方程f (x )=ax 恰有2个互异的实数解,则a 的取值范围是 .三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.(本小题满分13分)).在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b sin A=a cos(B-π6(1)求角B的大小;(2)设a=2,c=3,求b和sin(2A-B)的值.16.(本小题满分13分)已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.(1)应从甲、乙、丙三个部门的员工中分别抽取多少人?(2)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.①用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;②设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.17.(本小题满分13分)如图,AD∥BC且AD=2BC,AD⊥CD,EG∥AD且EG=AD,CD∥FG且CD=2FG,DG⊥平面ABCD,DA=DC=DG=2.(1)若M 为CF 的中点,N 为EG 的中点,求证:MN ∥平面CDE ; (2)求二面角E-BC-F 的正弦值;(3)若点P 在线段DG 上,且直线BP 与平面ADGE 所成的角为60°,求线段DP 的长.18.(本小题满分13分)设{a n }是等比数列,公比大于0,其前n 项和为S n (n ∈N *),{b n }是等差数列.已知a 1=1,a 3=a 2+2,a 4=b 3+b 5,a 5=b 4+2b 6. (1)求{a n }和{b n }的通项公式;(2)设数列{S n }的前n 项和为T n (n ∈N *),①求T n ; ②证明∑k=1n (T k +bk+2)b k(k+1)(k+2)=2n+2-2(n ∈N *).19.(本小题满分14分) 设椭圆x 2a 2+y 2b2=1(a>b>0)的左焦点为F ,上顶点为B.已知椭圆的离心率为√53,点A 的坐标为(b ,0),且|FB|·|AB|=6√2. (1)求椭圆的方程;(2)设直线l :y=kx (k>0)与椭圆在第一象限的交点为P ,且l 与直线AB 交于点Q.若|AQ ||PQ |=5√24sin ∠AOQ (O 为原点),求k 的值.20.(本小题满分14分)已知函数f (x )=a x ,g (x )=log a x ,其中a>1.(1)求函数h (x )=f (x )-x ln a 的单调区间;(2)若曲线y=f (x )在点(x 1,f (x 1))处的切线与曲线y=g (x )在点(x 2,g (x 2))处的切线平行,证明x 1+g (x 2)=-2ln lnalna; (3)证明当a ≥e 1e时,存在直线l ,使l 是曲线y=f (x )的切线,也是曲线y=g (x )的切线.数学(天津卷,理)1.B ∵B={x|x ≥1},∴∁R B={x|x<1}.∵A={x|0<x<2},∴A ∩(∁R B )={x|0<x<1}.故选B .2.C 作出不等式组{x +y ≤5,2x -y ≤4,-x +y ≤1,y ≥0表示的平面区域如图阴影部分所示.由{x +y =5,-x +y =1,解得点A 的坐标为(2,3). 由z=3x+5y ,得y=-35x+z 5.由图可知,当直线y=-35x+z 5过点A 时,z 5最大,即z 最大. 所以z 的最大值z max =3×2+5×3=21.3.B 输入N=20,i=2,T=0,此时202=10是整数,T=1,i=3,不满足i ≥5;此时203不是整数,i=4,不满足i ≥5;此时204=5是整数,T=2,i=5,满足i ≥5,输出T=2.4.A 由|x -12|<12,可得0<x<1.由x 3<1,可得x<1. 所以“|x -12|<12”是“x 3<1”的充分而不必要条件.故选A .5.D 因为c=lo g 1213=log 23,a=log 2e,且y=log 2x 在(0,+∞)上单调递增,所以log 23>log 2e >log 22=1,即c>a>1.因为y=ln x 在(0,+∞)上单调递增,且b=ln 2, 所以ln 2<ln e =1,即b<1. 综上可知,c>a>b.故选D .6.A 将函数y=sin (2x +π5)的图象向右平移π10个单位长度,所得图象对应的函数解析式为y=sin [2(x -π10)+π5]=sin 2x.当-π2+2k π≤2x ≤π2+2k π,k ∈Z ,即-π4+k π≤x ≤π4+k π,k ∈Z 时,y=sin 2x 单调递增. 当π2+2k π≤2x ≤3π2+2k π,k ∈Z ,即π4+k π≤x ≤3π4+k π,k ∈Z 时,y=sin 2x 单调递减, 结合选项,可知y=sin 2x 在[3π4,5π4]上单调递增.故选A . 7.C由双曲线的对称性,不妨取渐近线y=ba x.如图所示,|AD|=d 1,|BC|=d 2,过点F 作EF ⊥CD 于点E. 由题易知EF 为梯形ABCD 的中位线, 所以|EF|=12(d 1+d 2)=3.又因为点F (c ,0)到y=b ax 的距离为|bc -0|√a 2+b =b ,所以b=3,b 2=9.因为e=c =2,c 2=a 2+b 2,所以a 2=3,所以双曲线的方程为x 2−y 2=1.故选C .8.A 如图,取AB 的中点F ,连接EF.AE⃗⃗⃗⃗⃗ ·BE ⃗⃗⃗⃗⃗ =(AE ⃗⃗⃗⃗⃗⃗ +BE ⃗⃗⃗⃗⃗⃗ )2-(AE ⃗⃗⃗⃗⃗⃗ -BE ⃗⃗⃗⃗⃗⃗ )24=(2FE ⃗⃗⃗⃗⃗⃗ )2-AB ⃗⃗⃗⃗⃗⃗ 24=|FE⃗⃗⃗⃗⃗ |2-14. 当EF ⊥CD 时,|EF ⃗⃗⃗⃗⃗ |最小,即AE ⃗⃗⃗⃗⃗ ·BE⃗⃗⃗⃗⃗ 取最小值. 过点A 作AH ⊥EF 于点H ,由AD ⊥CD ,EF ⊥CD ,可得EH=AD=1,∠DAH=90°.因为∠DAB=120°,所以∠HAF=30°. 在Rt △AFH 中,易知AF=12,HF=14, 所以EF=EH+HF=1+14=54. 所以(AE ⃗⃗⃗⃗⃗ ·BE⃗⃗⃗⃗⃗ )min =(54)2−14=2116. 9.4-i 6+7i 1+2i =(6+7i )(1-2i )(1+2i )(1-2i )=6-12i+7i+145=20-5i5=4-i .10.52(x 2√x )5的展开式的通项为T r+1=C 5r x 5-r(2√x )r =C 5r x 5-r (-12)rx -r 2=(-12)r C 5r x 5-3r 2.令5-3r 2=2,可得r=2.所以(x 2√x )5的展开式中的x 2的系数为(-12)2C 52=52.11.112 由题意可知,四棱锥M-EFGH 的底面EFGH 为正方形且边长为√22,其高为12,所以V 四棱锥M-EFGH =13×(√22)2×12=112.12.12 由圆C 的方程为x 2+y 2-2x=0,可得圆心为C (1,0),半径为1. 由{x =-1+√22t ,y =3-√22t(t 为参数),可得直线的普通方程为x+y-2=0.所以圆心C (1,0)到直线x+y-2=0的距离d=√1+1=√22.所以|AB|=2√1-(√22)2=√2.所以S △ABC =1·|AB|·d=1×√2×√2=1. 13.14 因为2a >0,18b >0,所以2a +18b =2a +2-3b ≥2√2a ·2-3b =2√2a -3b ,当且仅当a=-3,b=1时,等号成立. 因为a-3b+6=0,所以a-3b=-6.所以2a +18b ≥2-6=14,即2a +18b 的最小值为14.14.(4,8) 由f (x )=ax ,可得当x ≤0时,x 2+2ax+a=ax ,即x 2+ax+a=0,可得a=-x 2x+1. 由a>0,可得x<-1. 可设函数g (x )=-x 2x+1,其中x ∈(-∞,-1). 当x>0时,-x 2+2ax-2a=ax ,即x 2-ax+2a=0,可得a=x 2x -2.由a>0,可得x>2. 可设函数h (x )=x 2x -2,其中x ∈(2,+∞).对g (x )求导,可得g'(x )=-x 2+2x(x+1)2.令g'(x )<0,可得x<-2;令g'(x )>0,可得-2<x<-1,则g (x )在(-∞,-2)上单调递减,在(-2,-1)上单调递增. 同理可得h (x )在(2,4)上单调递减,在(4,+∞)上单调递增. 画出g (x )和h (x )的大致图象如图所示.由图可知,满足题意的a 的取值范围是(4,8). 15.解 (1)在△ABC 中,由正弦定理a sinA=bsinB,可得b sin A=a sin B.又由b sin A=a cos (B -π6),得a sinB=a cos (B -π6),即sin B=cos (B -π6),可得tan B=√3.又因为B ∈(0,π),所以B=π3.(2)在△ABC 中,由余弦定理及a=2,c=3,B=π3,有b 2=a 2+c 2-2ac cos B=7,故b=√7.由b sin A=a cos (B -π6),可得sin A=√3√7.因为a<c ,故cos A=√7.因此sin 2A=2sin A cos A=4√37,cos2A=2cos 2A-1=1.所以,sin(2A-B )=sin 2A cos B-cos 2A sin B=4√3×1−1×√3=3√3.16.解 (1)由已知,甲、乙、丙三个部门的员工人数之比为3∶2∶2,由于采用分层抽样的方法从中抽取7人,因此应从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人.(2)①随机变量X 的所有可能取值为0,1,2,3. P (X=k )=C 4k ·C 33-kC 73(k=0,1,2,3).所以,随机变量X 的分布列为X 0 1 2 3P 135 **** **** 435随机变量X 的数学期望E (X )=0×135+1×1235+2×1835+3×435=127.②设事件B 为“抽取的3人中,睡眠充足的员工有1人,睡眠不足的员工有2人”;事件C 为“抽取的3人中,睡眠充足的员工有2人,睡眠不足的员工有1人”,则A=B ∪C ,且B 与C 互斥.由①知,P (B )=P (X=2),P (C )=P (X=1),故P (A )=P (B ∪C )=P (X=2)+P (X=1)=67.所以,事件A 发生的概率为67. 17.解 依题意,可以建立以D 为原点,分别以DA ⃗⃗⃗⃗⃗ ,DC ⃗⃗⃗⃗⃗ ,DG ⃗⃗⃗⃗⃗ 的方向为x 轴、y 轴、z 轴的正方向的空间直角坐标系(如图),可得D (0,0,0),A (2,0,0),B (1,2,0),C (0,2,0),E (2,0,2),F (0,1,2),G (0,0,2),M (0,32,1),N (1,0,2).(1)证明:依题意DC⃗⃗⃗⃗⃗ =(0,2,0),DE ⃗⃗⃗⃗⃗ =(2,0,2). 设n 0=(x ,y ,z )为平面CDE 的法向量, 则{n 0·DC⃗⃗⃗⃗⃗ =0,n 0·DE⃗⃗⃗⃗⃗ =0,即{2y =0,2x +2z =0,不妨令z=-1,可得n 0=(1,0,-1).又MN ⃗⃗⃗⃗⃗⃗⃗ =(1,-32,1),可得MN ⃗⃗⃗⃗⃗⃗⃗ ·n 0=0.又因为直线MN ⊄平面CDE ,所以MN ∥平面CDE.(2)依题意,可得BC⃗⃗⃗⃗⃗ =(-1,0,0),BE ⃗⃗⃗⃗⃗ =(1,-2,2),CF ⃗⃗⃗⃗⃗ =(0,-1,2). 设n =(x ,y ,z )为平面BCE 的法向量,则{n ·BC⃗⃗⃗⃗⃗ =0,n ·BE ⃗⃗⃗⃗⃗ =0,即{-x =0,x -2y +2z =0,不妨令z=1,可得n =(0,1,1).设m =(x ,y ,z )为平面BCF 的法向量,则{m ·BC⃗⃗⃗⃗⃗ =0,m ·CF ⃗⃗⃗⃗⃗ =0,即{-x =0,-y +2z =0,不妨令z=1,可得m =(0,2,1).因此有cos <m ,n >=m ·n |m ||n |=3√10,于是sin <m ,n >=√10. 所以,二面角E-BC-F 的正弦值为√1010.(3)设线段DP 的长为h (h ∈[0,2]),则点P 的坐标为(0,0,h ),可得BP⃗⃗⃗⃗⃗ =(-1,-2,h ).易知,DC ⃗⃗⃗⃗⃗ =(0,2,0)为平面ADGE 的一个法向量,故|cos <BP ⃗⃗⃗⃗⃗ ,DC ⃗⃗⃗⃗⃗ >|=|BP ⃗⃗⃗⃗⃗⃗ ·DC ⃗⃗⃗⃗⃗⃗ ||BP ⃗⃗⃗⃗⃗⃗ ||DC ⃗⃗⃗⃗⃗⃗ |=√ℎ+5. 由题意,可得√ℎ+5=sin 60°=√32,解得h=√33∈[0,2]. 所以,线段DP 的长为√33.18.(1)解 设等比数列{a n }的公比为q.由a 1=1,a 3=a 2+2,可得q 2-q-2=0.因为q>0,可得q=2,故a n =2n-1.设等差数列{b n }的公差为d.由a 4=b 3+b 5,可得b 1+3d=4.由a 5=b 4+2b 6,可得3b 1+13d=16,从而b 1=1,d=1,故b n =n.所以,数列{a n }的通项公式为a n =2n-1,数列{b n }的通项公式为b n =n.(2)①解 由(1),有S n =1-2n 1-2=2n -1, 故T n =∑k=1n (2k -1)=∑k=1n 2k -n=2×(1-2n )1-2-n=2n+1-n-2. ②证明 因为(T k +b k+2)b k (k+1)(k+2)=(2k+1-k -2+k+2)k(k+1)(k+2)=k ·2k+1(k+1)(k+2)=2k+2k+2−2k+1k+1, 所以,∑k=1n (T k +b k+2)b k(k+1)(k+2)=(233-222)+(244-233)+…+(2n+2n+2-2n+1n+1)=2n+2n+2-2. 19.解 (1)设椭圆的焦距为2c ,由已知有c 22=5,又由a 2=b 2+c 2,可得2a=3b.由已知可得,|FB|=a ,|AB|=√2b.由|FB|·|AB|=6√2,可得ab=6,从而a=3,b=2.所以,椭圆的方程为x 2+y 2=1.(2)设点P 的坐标为(x 1,y 1),点Q 的坐标为(x 2,y 2).由已知有y 1>y 2>0,故|PQ|sin ∠AOQ=y 1-y 2.又因为|AQ|=y 2sin∠OAB ,而∠OAB=π4,故|AQ|=√2y 2.由|AQ ||PQ |=5√24sin ∠AOQ ,可得5y 1=9y 2.由方程组{y =kx ,x 29+y 24=1,消去x ,可得y 1=√9k +4.易知直线AB 的方程为x+y-2=0,由方程组{y =kx ,x +y -2=0,消去x ,可得y 2=2k k+1.由5y 1=9y 2,可得5(k+1)=3√9k 2+4,两边平方,整理得56k 2-50k+11=0,解得k=12,或k=1128.所以,k 的值为12或1128.20.(1)解 由已知,h (x )=a x -x ln a ,有h'(x )=a x ln a-ln a.令h'(x )=0,解得x=0.由a>1,可知当x 变化时,h'(x ),h (x )的变化情况如下表:所以函数h (x )的单调递减区间为(-∞,0),单调递增区间为(0,+∞).(2)证明 由f'(x )=a x ln a ,可得曲线y=f (x )在点(x 1,f (x 1))处的切线斜率为a x 1ln a.由g'(x )=1xlna ,可得曲线y=g (x )在点(x 2,g (x 2))处的切线斜率为1x 2lna .因为这两条切线平行,故有a x 1ln a=1x 2lna,即x 2a x 1(ln a )2=1.两边取以a 为底的对数,得log a x 2+x 1+2log a ln a=0,所以x 1+g (x 2)=-2ln lna lna .(3)证明 曲线y=f (x )在点(x 1,a x 1)处的切线l 1:y-a x 1=a x 1ln a ·(x-x 1).曲线y=g (x )在点(x 2,log a x 2)处的切线l 2:y-log a x 2=1x 2lna (x-x 2). 要证明当a ≥e 1e 时,存在直线l ,使l 是曲线y=f (x )的切线,也是曲线y=g (x )的切线,只需证明当a ≥e 1e 时,存在x 1∈(-∞,+∞),x 2∈(0,+∞),使得l 1与l 2重合.即只需证明当a ≥e 1e 时,方程组{a x 1lna =1x 2lna ,①a x 1-x 1a x 1lna =log a x 2-1lna ②有解. 由①得x 2=1a x 1(lna )2,代入②,得a x 1-x 1a x 1ln a+x 1+1lna +2ln lnalna =0.③ 因此,只需证明当a ≥e 1e 时,关于x 1的方程③存在实数解.设函数u (x )=a x -xa x ln a+x+1lna +2ln lna lna ,即要证明当a ≥e 1e 时,函数y=u (x )存在零点. u'(x )=1-(ln a )2xa x ,可知当x ∈(-∞,0)时,u'(x )>0;当x ∈(0,+∞)时,u'(x )单调递减,又u'(0)=1>0,u'(1(lna )2)=1-a 1(lna )2<0,故存在唯一的x 0,且x 0>0,使得u'(x 0)=0,即1-(ln a )2x 0a x 0=0.由此可得u (x )在(-∞,x 0)上单调递增,在(x 0+∞)上单调递减,u (x )在x=x 0处取得极大值u (x 0).因为a ≥e 1e ,故ln ln a ≥-1,所以u (x 0)=a x 0-x 0a x 0ln a+x 0+1lna +2ln lna lna =1x 0(lna )2+x 0+2ln lnalna ≥2+2ln lna lna ≥0.下面证明存在实数t ,使得u (t )<0. 由(1)可得a x ≥1+x ln a ,当x>1lna 时,有u (x )≤(1+x ln a )(1-x ln a )+x+1lna +2ln lna lna=-(ln a )2x 2+x+1+1lna +2ln lna lna , 所以存在实数t ,使得u (t )<0. 因此,当a ≥e 1e 时,存在x 1∈(-∞,+∞),使得u (x 1)=0. 所以,当a ≥e 1e 时,存在直线l ,使l 是曲线y=f (x )的切线,也是曲线y=g (x )的切线.。
2018年普通高等学校招生统一考试理科数学真题及参考答案(天津卷)

2018年普通高等学校招生全国统一考试(天津卷、)数学试卷(理工类)注意事项:1.答卷前,考生务必将自己姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
第I 卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A ,B 互斥,那么()()()P AB P A P B =+ .·如果事件A ,B 相互独立,那么()()()P AB P A P B = .·棱柱体积公式V Sh =,其中S 表示棱柱底面面积,h 表示棱柱高. ·棱锥体积公式13V Sh =,其中S 表示棱锥底面面积,h 表示棱锥高. 一. 选择题:在每小题给出四个选项中,只有一项是符合题目要求. (1)设全集为R ,集合{02}A x x =<<,{1}B x x =≥,则()=R I A B ð (A) {01}x x <≤(B) {01}x x << (C) {12}x x ≤<(D) {02}x x <<(2)设变量x ,y 满足约束条件5,24,1,0,x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩ 则目标函数35z x y =+最大值为(A) 6 (B) 19 (C) 21 (D) 45 (3)阅读如图程序框图,运行相应程序,若输入N 值为20,则输出T 值为 (A) 1(B) 2(C) 3(D) 4(4)设x ∈R ,则“11||22x -<”是“31x <” (A)充分而不必要条件 (B)必要而不充分条件 (C)充要条件(D)既不充分也不必要条件(5)已知2log e =a ,ln 2b =,121log 3c =,则a ,b ,c 大小关系为 (A) a b c >> (B) b a c >>(C) c b a >>(D) c a b >>(6)将函数sin(2)5y x π=+图象向右平移10π个单位长度,所得图象对应函数 (A)在区间35[,]44ππ上单调递增(B)在区间3[,]4ππ上单调递减 (C)在区间53[,]42ππ上单调递增(D)在区间3[,2]2ππ上单调递减 (7)已知双曲线22221(0,0)x y a b a b-=>>离心率为2,过右焦点且垂直于x 轴直线与双曲线交于A ,B 两点. 设A ,B 到双曲线同一条渐近线距离分别为1d 和2d ,且126d d +=,则双曲线方程为(A)221412x y -=(B)221124x y -= (C)22139x y -=(D) 22193x y -= (8)如图,在平面四边形ABCD 中,AB BC ⊥,AD CD ⊥,120BAD ∠=︒,1AB AD ==.若点E 为边CD 上动点,则⋅uu u r uurAE BE 最小值为(A)2116(B)32(C)2516(D) 3第Ⅱ卷注意事项:1. 用黑色墨水钢笔或签字笔将答案写在答题卡上。
18年高考真题理科数学(天津卷)

2018年普通高等学校招生全国统一考试数 学(理)(天津卷)一.选择题(共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项)1.设全集为R ,集合{}|02A x x =<<,{}|1B x x =≥,则()R A B =I ð( ) (A ){}|01x x <≤ (B ){}|01x x << (C ){}|12x x ≤< (D ){}|02x x <<2.变量,x y 满足约束条件52410x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩,则目标函数35z x y =+的最大值是( ) (A )6 (B )19 (C )21 (D )453.阅读如图的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为( ) (A )1 (B )2 (C )3 (D )44.设x R ∈,则“11||22x -<”是“31x <”的( ) (A )充分不必要条件 (B )必要不充分条件(C )充分必要条件 (D )既不充分也不必要条件5.已知2log a e =,ln 2b =,121log 3a =,则,,abc 的大小关系为( ) (A )a b c >> (B )b a c >> (C )c b a >> (D )c a b >>6.将函数()sin 25f x x π⎛⎫=+⎪⎝⎭的图象向右平移10π个单位长度,所得图象对应的函数( ) (A )在区间35,44ππ⎡⎤⎢⎥⎣⎦上单调递增 (B )在区间3,4ππ⎡⎤⎢⎥⎣⎦上单调递减 (C )在区间53,42ππ⎡⎤⎢⎥⎣⎦上单调递增 (D )在区间3,22ππ⎡⎤⎢⎥⎣⎦上单调递减7.已知双曲线()222210,0x y a b a b-=>>的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于,A B 两点。
2018年天津市高考理科数学试题Word版含答案

绝密★启用前2018年普通高等学校招生全国统一考试(天津卷)数学(理工类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2本卷共8小题,每小题5分,共40分。
参考公式:•如果事件A,B互斥,那么•如果事件A,B相互独立,那么()()()P A B P A P B=+()()()P AB P A P B=.•圆柱的体积公式V Sh=.•圆锥的体积公式13V Sh =.其中S表示圆柱的底面面积,其中S表示圆锥的底面面积,h表示圆柱的高.h表示圆锥的高.一、选择题:在每小题给出的四个选项中只有一项是符合题目要ED CBA 求的.(1)i 是虚数单位,复数734ii+=+( ) (A )1i - (B )1i -+ (C )17312525i + (D )172577i -+ (2)设变量x ,y 满足约束条件0,20,12,y x y y x +-⎧≥--≤≥⎪⎨⎪⎩则目标函数2z x y =+的最小值为( )(A )2 (B )3 (C )4 (D )5(3)阅读右边的程序框图,运行相应的程序,输出的S 的值为( )(A )15 (B )105 (C )245 (D )945(4)函数()()212log 4f x x =-的单调递增区间是( )(A )()0,+¥ (B )(),0-¥ (C )()2,+¥ (D )(),2-?(5)已知双曲线22221x y a b -=()0,0a b >>的一条渐近线平行于直线l :210y x =+,双曲线的一个焦点在直线l 上,则双曲线的方程为( )(A )221520x y -= (B )221205x y -= (C )2233125100x y -= (D )2233110025x y -= (6)如图,ABC D 是圆的内接三角形,BAC Ð的平分线交圆于点D ,交BC 于点E ,过点B 的圆的切线与AD 的延长线交于点F .在上述条件下,给出下列四个结论:①BD 平分CBFÐ;②2FB FD FA =?;③AE CE BE DE ??;④AF BD AB BF ??.则所有正确结论的序号是( )(A )①② (B )③④ (C )①②③ (D )①②④ (7)设,a b R Î,则|“a b >”是“a a b b >”的( ) (A )充要不必要条件 (B )必要不充分条件 (C )充要条件 (D )既不充要也不必要条件(8)已知菱形ABCD 的边长为2,120BAD ?,点,E F 分别在边,BC DC 上,BE BC l =,DF DC m =.若1AE AF ?,23CE CF ?-,则l m +=( ) (A )12 (B )23 (C )56 (D )712第Ⅱ卷注意事项:1.用黑色墨水钢笔或签字笔将答案写在答题卡上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年天津市高考数学试卷(理科)一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. 1.(5.00分)设全集为R,集合A={x|0<x<2},B={x|x≥1},则A∩(∁R B)=()A.{x|0<x≤1}B.{x|0<x<1}C.{x|1≤x<2}D.{x|0<x<2}2.(5.00分)设变量x,y满足约束条件,则目标函数z=3x+5y的最大值为()A.6 B.19 C.21 D.453.(5.00分)阅读如图的程序框图,运行相应的程序,若输入N的值为20,则输出T的值为()A.1 B.2 C.3 D.44.(5.00分)设x∈R,则“|x﹣|<”是“x3<1”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件5.(5.00分)已知a=log2e,b=ln2,c=log,则a,b,c的大小关系为()A.a>b>c B.b>a>c C.c>b>a D.c>a>b6.(5.00分)将函数y=sin(2x+)的图象向右平移个单位长度,所得图象对应的函数()A.在区间[,]上单调递增B.在区间[,π]上单调递减C.在区间[,]上单调递增D.在区间[,2π]上单调递减7.(5.00分)已知双曲线=1(a>0,b>0)的离心率为2,过右焦点且垂直于x轴的直线与双曲线交于A,B两点.设A,B到双曲线的同一条渐近线的距离分别为d1和d2,且d1+d2=6,则双曲线的方程为()A.﹣=1 B.﹣=1 C.﹣=1 D.﹣=18.(5.00分)如图,在平面四边形ABCD中,AB⊥BC,AD⊥CD,∠BAD=120°,AB=AD=1.若点E为边CD上的动点,则的最小值为()A.B.C.D.3二.填空题:本大题共6小题,每小题5分,共30分.9.(5.00分)i是虚数单位,复数=.10.(5.00分)在(x﹣)5的展开式中,x2的系数为.11.(5.00分)已知正方体ABCD﹣A1B1C1D1的棱长为1,除面ABCD外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥M﹣EFGH的体积为.12.(5.00分)已知圆x2+y2﹣2x=0的圆心为C,直线,(t为参数)与该圆相交于A,B两点,则△ABC的面积为.13.(5.00分)已知a,b∈R,且a﹣3b+6=0,则2a+的最小值为.14.(5.00分)已知a>0,函数f(x)=.若关于x的方程f (x)=ax恰有2个互异的实数解,则a的取值范围是.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.15.(13.00分)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知bsinA=acos (B﹣).(Ⅰ)求角B的大小;(Ⅱ)设a=2,c=3,求b和sin(2A﹣B)的值.16.(13.00分)已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.(Ⅰ)应从甲、乙、丙三个部门的员工中分别抽取多少人?(Ⅱ)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.(i)用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;(ii)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.17.(13.00分)如图,AD∥BC且AD=2BC,AD⊥CD,EG∥AD且EG=AD,CD∥FG且CD=2FG,DG⊥平面ABCD,DA=DC=DG=2.(Ⅰ)若M为CF的中点,N为EG的中点,求证:MN∥平面CDE;(Ⅱ)求二面角E﹣BC﹣F的正弦值;(Ⅲ)若点P在线段DG上,且直线BP与平面ADGE所成的角为60°,求线段DP 的长.18.(13.00分)设{a n}是等比数列,公比大于0,其前n项和为S n(n∈N*),{b n}是等差数列.已知a1=1,a3=a2+2,a4=b3+b5,a5=b4+2b6.(Ⅰ)求{a n}和{b n}的通项公式;(Ⅱ)设数列{S n}的前n项和为T n(n∈N*),(i)求T n;(ii)证明=﹣2(n∈N*).19.(14.00分)设椭圆+=1(a>b>0)的左焦点为F,上顶点为B.已知椭圆的离心率为,点A的坐标为(b,0),且|FB|•|AB|=6.(Ⅰ)求椭圆的方程;(Ⅱ)设直线l:y=kx(k>0)与椭圆在第一象限的交点为P,且l与直线AB交于点Q.若=sin∠AOQ(O为原点),求k的值.20.(14.00分)已知函数f(x)=a x,g(x)=log a x,其中a>1.(Ⅰ)求函数h(x)=f(x)﹣xlna的单调区间;(Ⅱ)若曲线y=f(x)在点(x1,f(x1))处的切线与曲线y=g(x)在点(x2,g (x2))处的切线平行,证明x1+g(x2)=﹣;(Ⅲ)证明当a≥e时,存在直线l,使l是曲线y=f(x)的切线,也是曲线y=g (x)的切线.2018年天津市高考数学试卷(理科)参考答案与试题解析一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. 1.(5.00分)设全集为R,集合A={x|0<x<2},B={x|x≥1},则A∩(∁R B)=()A.{x|0<x≤1}B.{x|0<x<1}C.{x|1≤x<2}D.{x|0<x<2}【分析】根据补集、交集的定义即可求出.【解答】解:∵A={x|0<x<2},B={x|x≥1},∴∁R B={x|x<1},∴A∩(∁R B)={x|0<x<1}.故选:B.【点评】本题考查了集合的化简与运算问题,是基础题目.2.(5.00分)设变量x,y满足约束条件,则目标函数z=3x+5y的最大值为()A.6 B.19 C.21 D.45【分析】先画出约束条件的可行域,利用目标函数的几何意义,分析后易得目标函数z=3x+5y的最大值.【解答】解:由变量x,y满足约束条件,得如图所示的可行域,由解得A(2,3).当目标函数z=3x+5y经过A时,直线的截距最大,z取得最大值.将其代入得z的值为21,故选:C.【点评】在解决线性规划的小题时,常用“角点法”,其步骤为:①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证,求出最优解.也可以利用目标函数的几何意义求解最优解,求解最值.3.(5.00分)阅读如图的程序框图,运行相应的程序,若输入N的值为20,则输出T的值为()A.1 B.2 C.3 D.4【分析】根据程序框图进行模拟计算即可.【解答】解:若输入N=20,则i=2,T=0,==10是整数,满足条件.T=0+1=1,i=2+1=3,i≥5不成立,循环,=不是整数,不满足条件.,i=3+1=4,i≥5不成立,循环,==5是整数,满足条件,T=1+1=2,i=4+1=5,i≥5成立,输出T=2,故选:B.【点评】本题主要考查程序框图的识别和判断,根据条件进行模拟计算是解决本题的关键.4.(5.00分)设x∈R,则“|x﹣|<”是“x3<1”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件【分析】先解不等式,再根据充分条件和必要条件的定义即可求出.【解答】解:由|x﹣|<可得﹣<x﹣<,解得0<x<1,由x3<1,解得x<1,故“|x﹣|<”是“x3<1”的充分不必要条件,故选:A.【点评】本题考查了不等式的解法和充分必要条件,属于基础题.5.(5.00分)已知a=log2e,b=ln2,c=log,则a,b,c的大小关系为()A.a>b>c B.b>a>c C.c>b>a D.c>a>b【分析】根据对数函数的单调性即可比较.【解答】解:a=log 2e>1,0<b=ln2<1,c=log=log23>log2e=a,则a,b,c的大小关系c>a>b,故选:D.【点评】本题考查了对数函数的图象和性质,属于基础题,6.(5.00分)将函数y=sin(2x+)的图象向右平移个单位长度,所得图象对应的函数()A.在区间[,]上单调递增B.在区间[,π]上单调递减C.在区间[,]上单调递增D.在区间[,2π]上单调递减【分析】将函数y=sin(2x+)的图象向右平移个单位长度,得到的函数为:y=sin2x,增区间为[﹣+kπ,+kπ],k∈Z,减区间为[+kπ,+kπ],k ∈Z,由此能求出结果.【解答】解:将函数y=sin(2x+)的图象向右平移个单位长度,得到的函数为:y=sin2x,增区间满足:﹣+2kπ≤2x≤,k∈Z,减区间满足:≤2x≤,k∈Z,∴增区间为[﹣+kπ,+kπ],k∈Z,减区间为[+kπ,+kπ],k∈Z,∴将函数y=sin(2x+)的图象向右平移个单位长度,所得图象对应的函数在区间[,]上单调递增.故选:A.【点评】本题考查三角函数的单调区间的确定,考查三角函数的图象与性质、平移等基础知识,考查运算求解能力,考查函数与方程思想,是中档题.7.(5.00分)已知双曲线=1(a>0,b>0)的离心率为2,过右焦点且垂直于x轴的直线与双曲线交于A,B两点.设A,B到双曲线的同一条渐近线的距离分别为d1和d2,且d1+d2=6,则双曲线的方程为()A.﹣=1 B.﹣=1 C.﹣=1 D.﹣=1【分析】画出图形,利用已知条件,列出方程组转化求解即可.【解答】解:由题意可得图象如图,CD是双曲线的一条渐近线y=,即bx﹣ay=0,F(c,0),AC⊥CD,BD⊥CD,FE⊥CD,ACDB是梯形,F是AB的中点,EF==3,EF==b,所以b=3,双曲线=1(a>0,b>0)的离心率为2,可得,可得:,解得a=.则双曲线的方程为:﹣=1.故选:C.【点评】本题考查双曲线的简单性质的应用,双曲线方程的求法,考查计算能力.8.(5.00分)如图,在平面四边形ABCD中,AB⊥BC,AD⊥CD,∠BAD=120°,AB=AD=1.若点E为边CD上的动点,则的最小值为()A.B.C.D.3【分析】如图所示,以D为原点,以DA所在的直线为x轴,以DC所在的直线为y轴,求出A,B,C的坐标,根据向量的数量积和二次函数的性质即可求出.【解答】解:如图所示,以D为原点,以DA所在的直线为x轴,以DC所在的直线为y轴,过点B做BN⊥x轴,过点B做BM⊥y轴,∵AB⊥BC,AD⊥CD,∠BAD=120°,AB=AD=1,∴AN=ABcos60°=,BN=ABsin60°=,∴DN=1+=,∴BM=,∴CM=MBtan30°=,∴DC=DM+MC=,∴A(1,0),B(,),C(0,),设E(0,m),∴=(﹣1,m),=(﹣,m﹣),0≤m≤,∴=+m2﹣m=(m﹣)2+﹣=(m﹣)2+,当m=时,取得最小值为.故选:A.【点评】本题考查了向量在几何中的应用,考查了运算能力和数形结合的能力,属于中档题.二.填空题:本大题共6小题,每小题5分,共30分.9.(5.00分)i是虚数单位,复数=4﹣i.【分析】根据复数的运算法则计算即可.【解答】解:====4﹣i,故答案为:4﹣i【点评】本题考查了复数的运算法则,属于基础题.10.(5.00分)在(x﹣)5的展开式中,x2的系数为.【分析】写出二项展开式的通项,由x的指数为2求得r值,则答案可求.【解答】解:(x﹣)5的二项展开式的通项为=.由,得r=2.∴x2的系数为.故答案为:.【点评】本题考查二项式定理的应用,考查二项式系数的性质,关键是熟记二项展开式的通项,是基础题.11.(5.00分)已知正方体ABCD﹣A1B1C1D1的棱长为1,除面ABCD外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥M﹣EFGH的体积为.【分析】求出四棱锥中的底面的面积,求出棱锥的高,然后利用体积公式求解即可.【解答】解:正方体的棱长为1,M﹣EFGH的底面是正方形的边长为:,四棱锥是正四棱锥,棱锥的高为,四棱锥M﹣EFGH的体积:=.故答案为:.【点评】本题考查几何体的体积的求法,考查空间想象能力以及计算能力.12.(5.00分)已知圆x2+y2﹣2x=0的圆心为C,直线,(t为参数)与该圆相交于A,B两点,则△ABC的面积为.【分析】把圆的方程化为标准方程,写出圆心与半径;直线的参数方程化为普通方程,求出圆心到直线的距离,计算弦长|AB|,利用三角形面积公式求出△ABC的面积.【解答】解:圆x2+y2﹣2x=0化为标准方程是(x﹣1)2+y2=1,圆心为C(1,0),半径r=1;直线化为普通方程是x+y﹣2=0,则圆心C到该直线的距离为d==,弦长|AB|=2=2=2×=,∴△ABC的面积为S=•|AB|•d=××=.故答案为:.【点评】本题考查了直线与圆的位置关系应用问题,也考查了参数方程应用问题,是基础题.13.(5.00分)已知a,b∈R,且a﹣3b+6=0,则2a+的最小值为.【分析】化简所求表达式,利用基本不等式转化求解即可.【解答】解:a,b∈R,且a﹣3b+6=0,可得:3b=a+6,则2a+==≥2=,当且仅当2a=.即a=﹣3时取等号.函数的最小值为:.故答案为:.【点评】本题考查函数的最值的求法,基本不等式的应用,也可以利用换元法,求解函数的最值.考查计算能力.14.(5.00分)已知a>0,函数f(x)=.若关于x的方程f(x)=ax恰有2个互异的实数解,则a的取值范围是(4,8).【分析】分别讨论当x≤0和x>0时,利用参数分离法进行求解即可.【解答】解:当x≤0时,由f(x)=ax得x2+2ax+a=ax,得x2+ax+a=0,得a(x+1)=﹣x2,得a=﹣,设g(x)=﹣,则g′(x)=﹣=﹣,由g′(x)>0得﹣2<x<﹣1或﹣1<x<0,此时递增,由g′(x)<0得x<﹣2,此时递减,即当x=﹣2时,g(x)取得极小值为g(﹣2)=4,当x>0时,由f(x)=ax得﹣x2+2ax﹣2a=ax,得x2﹣ax+2a=0,得a(x﹣2)=x2,当x=2时,方程不成立,当x≠2时,a=设h(x)=,则h′(x)==,由h′(x)>0得x>4,此时递增,由h′(x)<0得0<x<2或2<x<4,此时递减,即当x=4时,h(x)取得极小值为h(4)=8,要使f(x)=ax恰有2个互异的实数解,则由图象知4<a<8,故答案为:(4,8)【点评】本题主要考查函数与方程的应用,利用参数分离法结合函数的极值和导数之间的关系以及数形结合是解决本题的关键.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.15.(13.00分)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知bsinA=acos (B﹣).(Ⅰ)求角B的大小;(Ⅱ)设a=2,c=3,求b和sin(2A﹣B)的值.【分析】(Ⅰ)由正弦定理得bsinA=asinB,与bsinA=acos(B﹣).由此能求出B.(Ⅱ)由余弦定理得b=,由bsinA=acos(B﹣),得sinA=,cosA=,由此能求出sin(2A﹣B).【解答】解:(Ⅰ)在△ABC中,由正弦定理得,得bsinA=asinB,又bsinA=acos(B﹣).∴asinB=acos(B﹣),即sinB=cos(B﹣)=cosBcos+sinBsin=cosB+,∴tanB=,又B∈(0,π),∴B=.(Ⅱ)在△ABC中,a=2,c=3,B=,由余弦定理得b==,由bsinA=acos(B﹣),得sinA=,∵a<c,∴cosA=,∴sin2A=2sinAcosA=,cos2A=2cos2A﹣1=,∴sin(2A﹣B)=sin2AcosB﹣cos2AsinB==.【点评】本题考查角的求法,考查两角差的余弦值的求法,考查运算求解能力,考查函数与方程思想,是中档题.16.(13.00分)已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.(Ⅰ)应从甲、乙、丙三个部门的员工中分别抽取多少人?(Ⅱ)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.(i)用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;(ii)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.【分析】(Ⅰ)利用分层抽样,通过抽样比求解应从甲、乙、丙三个部门的员工中分别抽取人数;(Ⅱ)若(i)用X表示抽取的3人中睡眠不足的员工人数,的可能值,求出概率,得到随机变量X的分布列,然后求解数学期望;(ii)利用互斥事件的概率求解即可.【解答】解:(Ⅰ)单位甲、乙、丙三个部门的员工人数分别为24,16,16.人数比为:3:2:2,从中抽取7人现,应从甲、乙、丙三个部门的员工中分别抽取3,2,2人.(Ⅱ)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.(i)用X表示抽取的3人中睡眠不足的员工人数,随机变量X的取值为:0,1,2,3,,k=0,1,2,3.所以随机变量的分布列为:X0123P随机变量X的数学期望E(X)==;(ii)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,设事件B为:抽取的3人中,睡眠充足的员工有1人,睡眠不足的员工有2人,事件C为抽取的3人中,睡眠充足的员工有2人,睡眠不足的员工有1人,则:A=B∪C,且P(B)=P(X=2),P(C)=P(X=1),故P(A)=P(B∪C)=P(X=2)+P(X=1)=.所以事件A发生的概率:.【点评】本题考查分层抽样,考查对立事件的概率,考查离散型随机变量的分布列与期望,确定X的可能取值,求出相应的概率是关键.17.(13.00分)如图,AD∥BC且AD=2BC,AD⊥CD,EG∥AD且EG=AD,CD∥FG且CD=2FG,DG⊥平面ABCD,DA=DC=DG=2.(Ⅰ)若M为CF的中点,N为EG的中点,求证:MN∥平面CDE;(Ⅱ)求二面角E﹣BC﹣F的正弦值;(Ⅲ)若点P在线段DG上,且直线BP与平面ADGE所成的角为60°,求线段DP 的长.【分析】(Ⅰ)依题意,以D为坐标原点,分别以、、的方向为x轴,y 轴,z轴的正方向建立空间直角坐标系.求出对应点的坐标,求出平面CDE的法向量及,由,结合直线MN⊄平面CDE,可得MN∥平面CDE;(Ⅱ)分别求出平面BCE与平面平面BCF的一个法向量,由两法向量所成角的余弦值可得二面角E﹣BC﹣F的正弦值;(Ⅲ)设线段DP的长为h,(h∈[0,2]),则点P的坐标为(0,0,h),求出,而为平面ADGE的一个法向量,由直线BP与平面ADGE所成的角为60°,可得线段DP的长.【解答】(Ⅰ)证明:依题意,以D为坐标原点,分别以、、的方向为x 轴,y轴,z轴的正方向建立空间直角坐标系.可得D(0,0,0),A(2,0,0),B(1,2,0),C(0,2,0),E(2,0,2),F(0,1,2),G(0,0,2),M(0,,1),N(1,0,2).设为平面CDE的法向量,则,不妨令z=﹣1,可得;又,可得.又∵直线MN⊄平面CDE,∴MN∥平面CDE;(Ⅱ)解:依题意,可得,,.设为平面BCE的法向量,则,不妨令z=1,可得.设为平面BCF的法向量,则,不妨令z=1,可得.因此有cos<>=,于是sin<>=.∴二面角E﹣BC﹣F的正弦值为;(Ⅲ)解:设线段DP的长为h,(h∈[0,2]),则点P的坐标为(0,0,h),可得,而为平面ADGE的一个法向量,故|cos<>|=.由题意,可得,解得h=∈[0,2].∴线段DP的长为.【点评】本题考查直线与平面平行的判定,考查空间角的求法,训练了利用空间向量求解空间角,是中档题.18.(13.00分)设{a n}是等比数列,公比大于0,其前n项和为S n(n∈N*),{b n}是等差数列.已知a1=1,a3=a2+2,a4=b3+b5,a5=b4+2b6.(Ⅰ)求{a n}和{b n}的通项公式;(Ⅱ)设数列{S n}的前n项和为T n(n∈N*),(i)求T n;(ii)证明=﹣2(n∈N*).【分析】(Ⅰ)设等比数列{a n}的公比为q,由已知列式求得q,则数列{a n}的通项公式可求;等差数列{b n}的公差为d,再由已知列关于首项与公差的方程组,求得首项与公差,可得等差数列的通项公式;(Ⅱ)(i)由等比数列的前n项和公式求得S n,再由分组求和及等比数列的前n 项和求得数列{S n}的前n项和为T n;(ii)化简整理,再由裂项相消法证明结论.【解答】(Ⅰ)解:设等比数列{a n}的公比为q,由a1=1,a3=a2+2,可得q2﹣q ﹣2=0.∵q>0,可得q=2.故.设等差数列{b n}的公差为d,由a4=b3+b5,得b1+3d=4,由a5=b4+2b6,得3b1+13d=16,∴b1=d=1.故b n=n;(Ⅱ)(i)解:由(Ⅰ),可得,故=;(ii)证明:∵==.∴==﹣2.【点评】本题主要考查等差数列、等比数列的通项公式及前n项和等基础知识,考查数列求和的基本方法及运算能力,是中档题.19.(14.00分)设椭圆+=1(a>b>0)的左焦点为F,上顶点为B.已知椭圆的离心率为,点A的坐标为(b,0),且|FB|•|AB|=6.(Ⅰ)求椭圆的方程;(Ⅱ)设直线l:y=kx(k>0)与椭圆在第一象限的交点为P,且l与直线AB交于点Q.若=sin∠AOQ(O为原点),求k的值.【分析】(Ⅰ)设椭圆的焦距为2c,根据椭圆的几何性质与已知条件,求出a、b的值,再写出椭圆的方程;(Ⅱ)设出点P、Q的坐标,由题意利用方程思想,求得直线AB的方程以及k的值.【解答】解:(Ⅰ)设椭圆+=1(a>b>0)的焦距为2c,由椭圆的离心率为e=,∴=;又a2=b2+c2,∴2a=3b,由|FB|=a,|AB|=b,且|FB|•|AB|=6;可得ab=6,从而解得a=3,b=2,∴椭圆的方程为+=1;(Ⅱ)设点P的坐标为(x1,y1),点Q的坐标为(x2,y2),由已知y1>y2>0;∴|PQ|sin∠AOQ=y1﹣y2;又|AQ|=,且∠OAB=,∴|AQ|=y2,由=sin∠AOQ,可得5y1=9y2;由方程组,消去x,可得y1=,∴直线AB的方程为x+y﹣2=0;由方程组,消去x,可得y2=;由5y1=9y2,可得5(k+1)=3,两边平方,整理得56k2﹣50k+11=0,解得k=或k=;∴k的值为或.【点评】本题主要考查了椭圆的标准方程与几何性质、直线方程等知识的应用问题,也考查了利用代数方法求研究圆锥曲线的性质应用问题,考查了运算求解能力与运用方程思想解决问题的能力.20.(14.00分)已知函数f(x)=a x,g(x)=log a x,其中a>1.(Ⅰ)求函数h(x)=f(x)﹣xlna的单调区间;(Ⅱ)若曲线y=f(x)在点(x1,f(x1))处的切线与曲线y=g(x)在点(x2,g(x2))处的切线平行,证明x1+g(x2)=﹣;(Ⅲ)证明当a≥e时,存在直线l,使l是曲线y=f(x)的切线,也是曲线y=g (x)的切线.【分析】(Ⅰ)把f(x)的解析式代入函数h(x)=f(x)﹣xlna,求其导函数,由导函数的零点对定义域分段,由导函数在各区间段内的符号可得原函数的单调区间;(Ⅱ)分别求出函数y=f(x)在点(x1,f(x1))处与y=g(x)在点(x2,g(x2))处的切线的斜率,由斜率相等,两边取对数可得结论;(Ⅲ)分别求出曲线y=f(x)在点()处的切线与曲线y=g(x)在点(x2,log a x2)处的切线方程,把问题转化为证明当a≥时,存在x1∈(﹣∞,+∞),x2∈(0,+∞)使得l1与l2重合,进一步转化为证明当a≥时,方程存在实数解.然后利用导数证明即可.【解答】(Ⅰ)解:由已知,h(x)=a x﹣xlna,有h′(x)=a x lna﹣lna,令h′(x)=0,解得x=0.由a>1,可知当x变化时,h′(x),h(x)的变化情况如下表:x(﹣∞,0)0(0,+∞)h′(x)﹣0+h(x)↓极小值↑∴函数h(x)的单调减区间为(﹣∞,0),单调递增区间为(0,+∞);(Ⅱ)证明:由f′(x)=a x lna,可得曲线y=f(x)在点(x1,f(x1))处的切线的斜率为lna.由g′(x)=,可得曲线y=g(x)在点(x2,g(x2))处的切线的斜率为.∵这两条切线平行,故有,即,两边取以a为底数的对数,得log a x2+x1+2log a lna=0,∴x1+g(x2)=﹣;(Ⅲ)证明:曲线y=f(x)在点()处的切线l1:,曲线y=g(x)在点(x2,log a x2)处的切线l2:.要证明当a≥时,存在直线l,使l是曲线y=f(x)的切线,也是曲线y=g(x)的切线,只需证明当a≥时,存在x1∈(﹣∞,+∞),x2∈(0,+∞)使得l1与l2重合,即只需证明当a≥时,方程组由①得,代入②得:,③因此,只需证明当a≥时,关于x1的方程③存在实数解.设函数u(x)=,既要证明当a≥时,函数y=u(x)存在零点.u′(x)=1﹣(lna)2xa x,可知x∈(﹣∞,0)时,u′(x)>0;x∈(0,+∞)时,u′(x)单调递减,又u′(0)=1>0,u′=<0,故存在唯一的x0,且x0>0,使得u′(x0)=0,即.由此可得,u(x)在(﹣∞,x0)上单调递增,在(x0,+∞)上单调递减,u(x)在x=x0处取得极大值u(x0).∵,故lnlna≥﹣1.∴=.下面证明存在实数t,使得u(t)<0,由(Ⅰ)可得a x≥1+xlna,当时,有u(x)≤=.∴存在实数t,使得u(t)<0.因此,当a≥时,存在x1∈(﹣∞,+∞),使得u(x1)=0.∴当a≥时,存在直线l,使l是曲线y=f(x)的切线,也是曲线y=g(x)的切线.【点评】本题考查导数的运算,导数的几何意义,运用导数研究指数函数与对数公式的性质等基础知识和方法,考查函数与方程思想,化归思想,考查抽象概括能力,综合分析问题和解决问题的能力,是难题.。
