转动惯量公式表
转动惯量公式表
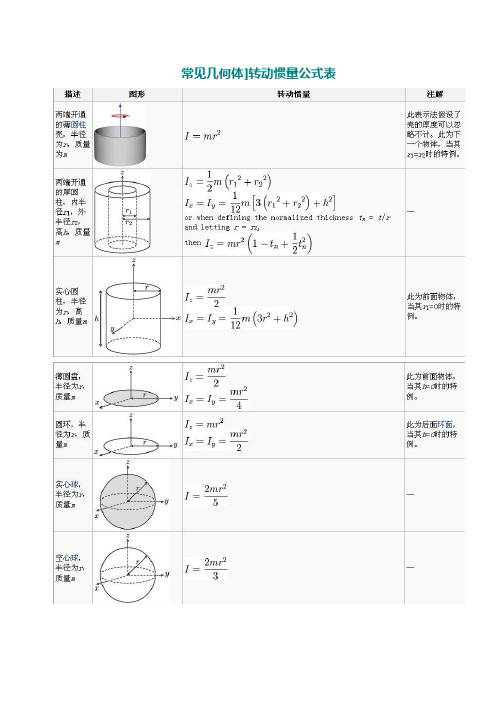
常见几何体]转动惯量公式表对于细杆当回转轴过杆得中点并垂直于杆时;J=m(L^2)/12 其中m就是杆得质量,L就是杆得长度。
当回转轴过杆得端点并垂直于杆时:J=m(L^2)/3 其中m就是杆得质量,L就是杆得长度。
对于圆柱体当回转轴就是圆柱体轴线时;J=m(r^2)/2其中m就是圆柱体得质量,r就是圆柱体得半径。
对于细圆环当回转轴通过中心与环面垂直时,J=mR^2;当回转轴通过边缘与环面垂直时,J=2mR^2;R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时,J=﹙1/2﹚mR^2;当回转轴通过边缘与盘面垂直时,J=﹙3/2﹚mR^2;R为其半径对于空心圆柱当回转轴为对称轴时,J=﹙1/2﹚m[(R1)^2+(R2)^2];R1与R2分别为其内外半径。
对于球壳当回转轴为中心轴时,J=﹙2/3﹚mR^2;当回转轴为球壳得切线时,J=﹙5/3﹚mR^2;R为球壳半径。
对于实心球体当回转轴为球体得中心轴时,J=﹙2/5﹚mR^2;当回转轴为球体得切线时,J=﹙7/5﹚mR^2;R为球体半径对于立方体当回转轴为其中心轴时,J=﹙1/6﹚mL^2;当回转轴为其棱边时,J=﹙2/3﹚mL^2;当回转轴为其体对角线时,J=(3/16)mL^2;L为立方体边长。
只知道转动惯量得计算方式而不能使用就是没有意义得。
下面给出一些(绕定轴转动时)得刚体动力学公式。
角加速度与合外力矩得关系:角加速度与合外力矩式中M为合外力矩,β为角加速度。
可以瞧出这个式子与牛顿第二定律就是对应得。
角动量:角动量刚体得定轴转动动能:转动动能注意这只就是刚体绕定轴得转动动能,其总动能应该再加上质心动能。
只用E=(1/2)mv^2不好分析转动刚体得问题,就是因为其中不包含刚体得任何转动信息,里面得速度v只代表刚体得质心运动情况。
由这一公式,可以从能量得角度分析刚体动力学得问题。
转动惯量(Moment of Inertia)就是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止得特性)得量度,用字母I或J表示。
转动惯量计算公式高数

转动惯量计算公式高数
在高等数学中,转动惯量是描述刚体旋转惯性特性的物理量。
以下是常见的刚体转动惯量计算公式:
1. 点质量绕轴旋转:
转动惯量公式:I = m * r^2
其中,I 表示转动惯量,m 表示点质量,r 表示质点到旋转轴的距离。
2. 细长杆绕轴旋转:
转动惯量公式:I = (1/12) * m * L^2
其中,I 表示转动惯量,m 表示杆的质量,L 表示杆的长度。
3. 薄环绕轴旋转:
转动惯量公式:I = m * r^2
其中,I 表示转动惯量,m 表示环的质量,r 表示环的半径。
4. 薄球壳绕轴旋转:
转动惯量公式:I = (2/3) * m * r^2
其中,I 表示转动惯量,m 表示球壳的质量,r 表示球壳的半径。
5. 均匀圆盘绕轴旋转:
转动惯量公式:I = (1/4) * m * r^2
其中,I 表示转动惯量,m 表示圆盘的质量,r 表示圆盘的半径。
这些公式仅适用于特定形状的刚体,并假设刚体质量分布均匀。
在实际计算中,根据刚体的形状和质量分布,可能需要使用更复杂的积分计算或使用转动惯量表进行查询。
最新转动惯量计算公式

1. 圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)82MD J =对于钢材:341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量(kg);D-圆柱体直径(cm); L-圆柱体长度或厚度(cm); r-材料比重(gf /cm 3)。
2. 丝杠折算到马达轴上的转动惯量:2i Js J = (kgf·cm·s 2)J s –丝杠转动惯量(kgf·cm·s 2); i-降速比,12z z i =3. 工作台折算到丝杠上的转动惯量g w22⎪⎭⎫ ⎝⎛⋅=n v J π g w2s 2⎪⎭⎫⎝⎛=π (kgf·cm·s 2) v -工作台移动速度(cm/min); n-丝杠转速(r/min); w-工作台重量(kgf);g-重力加速度,g = 980cm/s 2; s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J iJ J S tJ 1-齿轮z 1及其轴的转动惯量; J 2-齿轮z 2的转动惯量(kgf·cm·s 2); J s -丝杠转动惯量(kgf·cm·s 2); s-丝杠螺距,(cm); w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf·cm·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1,J 2-分别为Ⅰ轴,Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2);R-齿轮z 分度圆半径(cm); w-工件及工作台重量(kgf)。
转动惯量公式表

两端开通 的厚圆 柱,商半 径巧;外 咼打展量
[常见几何体]转动惯量公式表
R =严 H + r ?2) h = Iy =
[3 (ti 2 + r 22) + h 2
or when defining the normalized thickness ; fn = t/-r and letting r = 12,
then
h = mr 2 (1 —
打 + 折)
描述 转动惯量 注解
两端开通 的薄圆柱 壳,半径 为口质量 为烟
此表示法假设了
壳的厚度可味忍 略不计。
此为下 一节物体,当其 辺=22时的特例。
霽高禺
此为前面物体, 当其巧=0时的特
薄圆盘, 半径为确 质量帀
■mr 2
2
此为前面物体,
当其H 朋寸的特 例耘
半成
环为衆 圆径量
此为后面环面费 当其H 邙寸的特 例。
实心球, 半径为邛 质量丹 空心球, 半径为邛 质量帀
2?nr 2 3。
转动惯量公式表
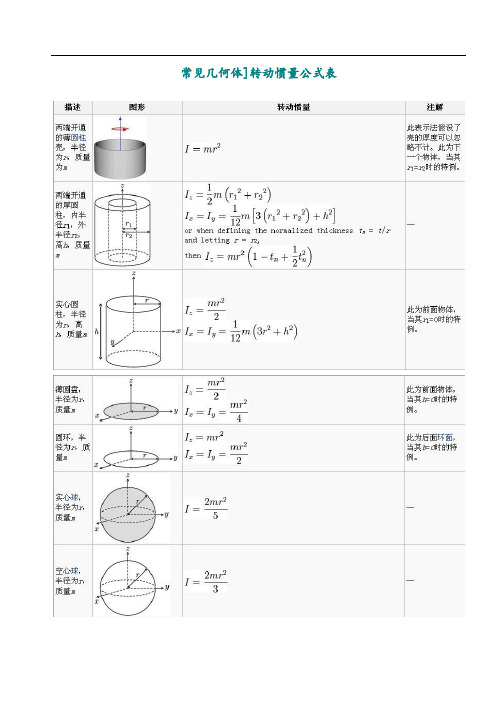
常见几何体]转动惯量公式表对于细杆当回转轴过杆的中点并垂直于杆时;J=m(L^2)/12 其中m是杆的质量,L是杆的长度。
当回转轴过杆的端点并垂直于杆时:J=m(L^2)/3 其中m是杆的质量,L是杆的长度。
对于圆柱体当回转轴是圆柱体轴线时;J=m(r^2)/2其中m是圆柱体的质量,r是圆柱体的半径。
对于细圆环当回转轴通过中心与环面垂直时,J=mR^2;当回转轴通过边缘与环面垂直时,J=2mR^2;R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时,J=﹙1/2﹚mR^2;当回转轴通过边缘与盘面垂直时,J=﹙3/2﹚mR^2;R为其半径对于空心圆柱当回转轴为对称轴时,J=﹙1/2﹚m[(R1)^2+(R2)^2];R1和R2分别为其内外半径。
对于球壳当回转轴为中心轴时,J=﹙2/3﹚mR^2;当回转轴为球壳的切线时,J=﹙5/3﹚mR^2;R为球壳半径。
对于实心球体当回转轴为球体的中心轴时,J=﹙2/5﹚mR^2;当回转轴为球体的切线时,J=﹙7/5﹚mR^2;R为球体半径对于立方体当回转轴为其中心轴时,J=﹙1/6﹚mL^2;当回转轴为其棱边时,J=﹙2/3﹚mL^2;当回转轴为其体对角线时,J=(3/16)mL^2;L为立方体边长。
只知道转动惯量的计算方式而不能使用是没有意义的。
下面给出一些(绕定轴转动时)的刚体动力学公式。
角加速度与合外力矩的关系:角加速度与合外力矩式中M为合外力矩,β为角加速度。
可以看出这个式子与牛顿第二定律是对应的。
角动量:角动量刚体的定轴转动动能:转动动能注意这只是刚体绕定轴的转动动能,其总动能应该再加上质心动能。
只用E=(1/2)mv^2不好分析转动刚体的问题,是因为其中不包含刚体的任何转动信息,里面的速度v 只代表刚体的质心运动情况。
由这一公式,可以从能量的角度分析刚体动力学的问题。
转动惯量(Moment of Inertia)是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度,用字母I或J表示。
转动惯量公式表
常见几何体]转动惯量公式表R =严 H + Γ22)I x = Iy =[3 (T l 2 + τ√) + /Or WhEn defining the normalized thiCkness ; f∏ = t∕-r and Ietting r = 22jthenΛ = mr 2(1 —打 + 折)描述 转动惯量 注解两端开通 的薄圆柱 壳,半径 为口质量 为烟此表示法假设了壳的厚度可扩忽 略不计。
此为下 一∙⅛物体,当其 辺=22时的特例。
‰⅛ ⅛ ■ r a p - ∙⅛⅛j 妝⅛此为前面物体, 当其巧=O 时的特薄圆盘, 半径为硏 质量帀 m τ22777T Z此为前面物体, 当其扫朋寸的特 例耘半成环为衆 圆径量此为后面环面费 当其H 邙寸的特 例。
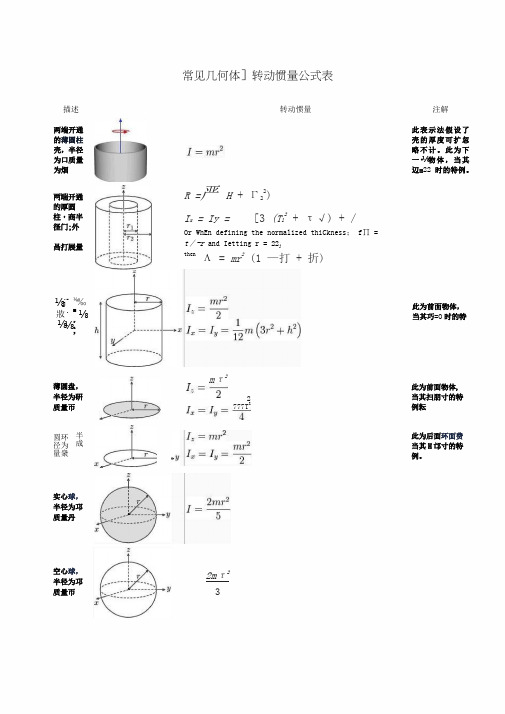
实心球, 半径为邛 质量丹 空心球, 半径为邛 质量帀 2mτ23两端开通的厚圆 柱,商半 径门;外 咼打展量对于细杆当回转轴过杆的中点并垂直于杆时;J=m(L^2)∕12其中m是杆的质量,L是杆的长度。
当回转轴过杆的端点并垂直于杆时:J=m(L^2)∕3其中m是杆的质量,L是杆的长度。
对于圆柱体当回转轴是圆柱体轴线时;J=m(r^2)∕2其中m 是圆柱体的质量,r 是圆柱体的半径。
对于细圆环当回转轴通过中心与环面垂直时, 当回转轴通过边缘与环面垂直时,R 为其半径对于薄圆盘R 为其半径对于空心圆柱R1和R2分别为其内外半径。
对于球壳R 为球壳半径。
对于实心球体当回转轴为球体的中心轴时, 当回转轴为球体的切线时,R 为球体半径对于立方体当回转轴为其中心轴时, J= ( 1/6 ) mL^2 ; 当回转轴为其棱边时,J= ( 2/3 ) mL^2 ;当回转轴为其体对角线时,J= ( 3/16 ) mL^2 ;L 为立方体边长。
只知道转动惯量的计算方式而不能使用是没有意义的。
下面给出一些(绕定轴转动时)的刚体动力学公 式。
角加速度与合外力矩的关系:J=mR^2 ; J=2mR^2 ;当回转轴通过中心与盘面垂直时, 当回转轴通过边缘与盘面垂直时,J= ( 1/2 J= ( 3/2 )mR^2 ; )mR^2 ;当回转轴为对称轴时,J= ( 1/2 m[ (R1 ) ^2+ ( R2) ^2];当回转轴为中心轴时,J= 当回转轴为球壳的切线时,(2/3 mR^2 ;J= ( 5/3 ) mR^2 ;J= ( 2/5 ) mR^2 ; J= ( 7/5 ) mR^2 ;角加速度与合外力矩式中M 为合外力矩,β为角加速度。
[常见几何体]转动惯量公式表
![[常见几何体]转动惯量公式表](https://img.taocdn.com/s3/m/0a601c4f910ef12d2bf9e791.png)
[常见几何体]转动惯量公式表
R =严 H + r ?2) h = Iy =
[3 (ti 2 + r 22) + h 2
or when defining the normalized thickness ; fn = t/-r and letting r = 12,
then
h = mr 2 (1 —
打 + 折)
描述 转动惯量 注解
两端开通 的薄圆柱 壳,半径 为口质量 为烟
此表示法假设了
壳的厚度可味忍 略不计。
此为下 一节物体,当其 辺=22时的特例。
霽高
禺
此为前面物体, 当其巧=0时的特
薄圆盘, 半径为确 质量帀
■mr 2
2
此为前面物体,
当其H 朋寸的特 例耘
半成
环为衆 圆径量
此为后面环面费 当其H 邙寸的特 例。
实心球, 半径为邛 质量丹 空心球, 半径为邛 质量帀 2?nr 2
3
两端开通 的厚圆 柱,商半 径巧;外 咼打展量。
转动惯量的计算

转动惯量的计算转动惯量(也称为惯性矩)是描述物体对绕轴转动的惯性特性的物理量,通常用字母 "I" 表示。
它是旋转运动的类似于质量的性质,表示了物体绕轴旋转时抵抗改变转速的能力。
计算转动惯量的公式取决于物体的形状和轴线的位置。
本文将介绍几种常见物体的转动惯量计算方法。
1. 点质量的转动惯量点质量的转动惯量是最简单的情况,它表示物体质点绕某一轴旋转时的惯性。
点质量的转动惯量的计算公式如下:I = m * r^2其中,I 表示转动惯量,m 表示质量,r 表示质点到旋转轴的距离。
2. 杆状物体的转动惯量杆状物体是另一种常见情况,它是指质量均匀分布在长度为 L 的细长杆上的物体。
杆状物体绕与之垂直的一个端点旋转时的转动惯量计算公式如下:I = (1/3) * m * L^2其中,I 表示转动惯量,m 表示质量,L 表示杆的长度。
3. 薄圆环的转动惯量薄圆环是一个质量均匀分布的圆环,它绕圆心垂直于环面的轴旋转时的转动惯量计算公式如下:I = m * R^2其中,I 表示转动惯量,m 表示质量,R 表示圆环的半径。
4. 薄圆盘的转动惯量薄圆盘是一个质量均匀分布的圆盘,它绕与之垂直的轴旋转时的转动惯量计算公式如下:I = (1/2) * m * R^2其中,I 表示转动惯量,m 表示质量,R 表示圆盘的半径。
5. 球体的转动惯量球体是一个质量均匀分布的球形物体,它绕通过球心的轴旋转时的转动惯量计算公式如下:I = (2/5) * m * R^2其中,I 表示转动惯量,m 表示质量,R 表示球体的半径。
6. 转动惯量的叠加原理对于复杂形状的物体,可以将其分解为若干简单形状,并利用转动惯量的叠加原理求解总的转动惯量。
叠加原理表明,当一个物体由多个组成部分组成时,其总的转动惯量等于每个部分转动惯量的代数和。
I_total = I_1 + I_2 + I_3 + ...其中,I_total 表示总的转动惯量,I_1、I_2、I_3 等表示各个组成部分的转动惯量。
转动惯量公式表
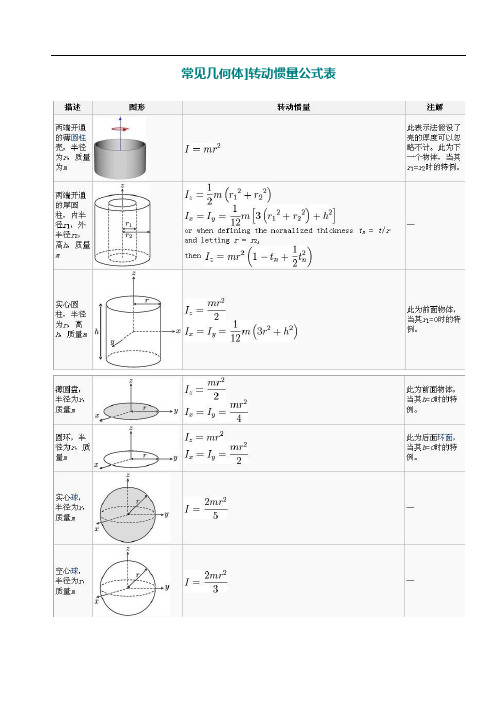
常见几何体]转动惯量公式表对于细杆当回转轴过杆的中点并垂直于杆时;J=m(L^2)/12 其中m是杆的质量,L是杆的长度。
当回转轴过杆的端点并垂直于杆时:J=m(L^2)/3 其中m是杆的质量,L是杆的长度。
对于圆柱体当回转轴是圆柱体轴线时;J=m(r^2)/2其中m是圆柱体的质量,r是圆柱体的半径。
对于细圆环当回转轴通过中心与环面垂直时,J=mR^2;当回转轴通过边缘与环面垂直时,J=2mR^2;R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时,J=﹙1/2﹚mR^2;当回转轴通过边缘与盘面垂直时,J=﹙3/2﹚mR^2;R为其半径对于空心圆柱当回转轴为对称轴时,J=﹙1/2﹚m[(R1)^2+(R2)^2];R1和R2分别为其内外半径。
对于球壳当回转轴为中心轴时,J=﹙2/3﹚mR^2;当回转轴为球壳的切线时,J=﹙5/3﹚mR^2;R为球壳半径。
对于实心球体当回转轴为球体的中心轴时,J=﹙2/5﹚mR^2;当回转轴为球体的切线时,J=﹙7/5﹚mR^2;R为球体半径对于立方体当回转轴为其中心轴时,J=﹙1/6﹚mL^2;当回转轴为其棱边时,J=﹙2/3﹚mL^2;当回转轴为其体对角线时,J=(3/16)mL^2;L为立方体边长。
只知道转动惯量的计算方式而不能使用是没有意义的。
下面给出一些(绕定轴转动时)的刚体动力学公式。
角加速度与合外力矩的关系:角加速度与合外力矩式中M为合外力矩,β为角加速度。
可以看出这个式子与牛顿第二定律是对应的。
角动量:角动量刚体的定轴转动动能:转动动能注意这只是刚体绕定轴的转动动能,其总动能应该再加上质心动能。
只用E=(1/2)mv^2不好分析转动刚体的问题,是因为其中不包含刚体的任何转动信息,里面的速度v 只代表刚体的质心运动情况。
由这一公式,可以从能量的角度分析刚体动力学的问题。
转动惯量(Moment of Inertia)是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度,用字母I或J表示。
转动惯量公式表

转动惯量公式表 Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】常见几何体]转动惯量公式表对于细杆当回转轴过杆的中点并垂直于杆时;J=m(L^2)/12其中m是杆的质量,L是杆的长度。
当回转轴过杆的端点并垂直于杆时:J=m(L^2)/3其中m是杆的质量,L是杆的长度。
对于圆柱体当回转轴是圆柱体轴线时;J=m(r^2)/2其中m是圆柱体的质量,r是圆柱体的半径。
对于细圆环当回转轴通过中心与环面垂直时,J=mR^2;当回转轴通过边缘与环面垂直时,J=2mR^2;R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时,J=﹙1/2﹚mR^2;当回转轴通过边缘与盘面垂直时,J=﹙3/2﹚mR^2;R为其半径对于空心圆柱当回转轴为对称轴时,J=﹙1/2﹚m[(R1)^2+(R2)^2];R1和R2分别为其内外半径。
对于球壳当回转轴为中心轴时,J=﹙2/3﹚mR^2;当回转轴为球壳的切线时,J=﹙5/3﹚mR^2;R为球壳半径。
对于实心球体当回转轴为球体的中心轴时,J=﹙2/5﹚mR^2;当回转轴为球体的切线时,J=﹙7/5﹚mR^2;R为球体半径对于立方体当回为其中心轴时,J=﹙1/6﹚mL^2;当回转轴为其棱边时,J=﹙2/3﹚mL^2;当回转轴为其体对角线时,J=(3/16)mL^2;L为立方体边长。
只知道转动惯量的计算方式而不能使用是没有意义的。
下面给出一些(绕定轴转动时)的刚体动力学公式。
角加速度与合外力矩的关系:角加速度与合外力矩式中M为合外,β为。
可以看出这个式子与牛顿第二定律是对应的。
角动量:角动量刚体的定轴转动动能:转动动能注意这只是刚体绕定轴的转动动能,其总动能应该再加上质心动能。
只用E=(1/2)mv^2不好分析转动刚体的问题,是因为其中不包含刚体的任何转动信息,里面的速度v只代表刚体的质心运动情况。
由这一公式,可以从能量的角度分析刚体动力学的问题。
各类刚体转动惯量公式

各类刚体转动惯量公式在物理学中,刚体是指具有固定形状和大小的物体,其各个部分相对位置不会发生改变。
刚体的转动惯量是描述了刚体对绕某一轴旋转的运动抵抗能力的物理量。
在本文中,我们将介绍各类刚体的转动惯量公式,并深入探讨其应用。
一、点质量的转动惯量公式对于一个质量为m,距离轴距离为r的点质量,其转动惯量可以用以下公式表示:I = m * r^2其中,I表示转动惯量,m表示质量,r表示距离轴的距离。
这个公式表明,质量越大或者距离轴越远,转动惯量就越大。
二、细长杆的转动惯量公式对于一个质量为m,长度为L的细长杆绕通过其质心的轴旋转,其转动惯量可以用以下公式表示:I = (1/12) * m * L^2这个公式表明,细长杆的转动惯量与其质量和长度的平方成正比。
如果杆的质量或长度增加,转动惯量也会增加。
三、圆盘的转动惯量公式对于一个质量为m,半径为R的圆盘绕通过其质心的轴旋转,其转动惯量可以用以下公式表示:I = (1/2) * m * R^2与细长杆类似,圆盘的转动惯量与其质量和半径的平方成正比。
圆盘的质量或半径增加,转动惯量也会增加。
四、刚体的复合体的转动惯量公式对于一个由多个质点组成的刚体,其转动惯量可以通过对各个组成部分的转动惯量进行求和来计算。
I = Σmᵢrᵢ^2其中,Σ表示对所有组成部分进行求和,mᵢ表示第i个组成部分的质量,rᵢ表示该部分到转轴的距离。
总结:以上是各类刚体转动惯量的公式,这些公式在物理学中被广泛应用于解决与刚体相关的问题。
通过了解转动惯量的计算方法,我们可以更好地理解刚体的旋转运动特性,并在实际问题中应用这些公式进行计算。
掌握这些公式的应用,可以帮助我们更好地理解刚体的运动规律,提高物理学的学习和应用能力。
通过本文的介绍,我们了解了各类刚体转动惯量的公式及其应用。
这些公式在解决刚体旋转问题时非常有用,同时也为进一步研究和理解刚体运动提供了基础。
希望本文能为读者对于刚体转动惯量的理解提供帮助,同时也能促进对物理学的学习兴趣与探索精神的培养。
转动惯量计算公式

1. 圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)82MD J =对于钢材:341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量(kg); D-圆柱体直径(cm); L-圆柱体长度或厚度(cm); r-材料比重(gf /cm 3)。
2. 丝杠折算到马达轴上的转动惯量:2i Js J = (kgf·cm·s 2)J s –丝杠转动惯量(kgf·cm·s 2); i-降速比,12z z i =3. 工作台折算到丝杠上的转动惯量g w22⎪⎭⎫ ⎝⎛⋅=n v J π g w2s 2⎪⎭⎫⎝⎛=π (kgf·cm·s 2) v -工作台移动速度(cm/min); n-丝杠转速(r/min); w-工作台重量(kgf);g-重力加速度,g = 980cm/s 2; s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J iJ J S tJ 1-齿轮z 1及其轴的转动惯量; J 2-齿轮z 2的转动惯量(kgf·cm·s 2); J s -丝杠转动惯量(kgf·cm·s 2); s-丝杠螺距,(cm); w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf·cm·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1,J 2-分别为Ⅰ轴,Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2);R-齿轮z 分度圆半径(cm); w-工件及工作台重量(kgf)。
转动惯量计算公式

1. 圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)82MD J =对于钢材:341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量(kg); D-圆柱体直径(cm); L-圆柱体长度或厚度(cm); r-材料比重(gf /cm 3)。
2. 丝杠折算到马达轴上的转动惯量:2i Js J = (kgf·cm·s 2)J s –丝杠转动惯量(kgf·cm·s 2); i-降速比,12z z i =3. 工作台折算到丝杠上的转动惯量g w22⎪⎭⎫ ⎝⎛⋅=n v J π g w2s 2⎪⎭⎫⎝⎛=π (kgf·cm·s 2) v -工作台移动速度(cm/min); n-丝杠转速(r/min); w-工作台重量(kgf);g-重力加速度,g = 980cm/s 2; s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J iJ J S tJ 1-齿轮z 1及其轴的转动惯量; J 2-齿轮z 2的转动惯量(kgf·cm·s 2); J s -丝杠转动惯量(kgf·cm·s 2); s-丝杠螺距,(cm); w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf·cm·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1,J 2-分别为Ⅰ轴,Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2);R-齿轮z 分度圆半径(cm); w-工件及工作台重量(kgf)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常见几何体]转动惯量公式表
对于细杆
当回转轴过杆的中点并垂直于杆时;J=m(L^2)/12 其中m是杆的质量,L是杆的长度。
当回转轴过杆的端点并垂直于杆时:J=m(L^2)/3 其中m是杆的质量,L是杆的长度。
对于圆柱体
当回转轴是圆柱体轴线时;J=m(r^2)/2
其中m是圆柱体的质量,r是圆柱体的半径。
对于细圆环
当回转轴通过中心与环面垂直时,J=mR^2;
当回转轴通过边缘与环面垂直时,J=2mR^2;
R为其半径
对于薄圆盘
当回转轴通过中心与盘面垂直时,J=﹙1/2﹚mR^2;
当回转轴通过边缘与盘面垂直时,J=﹙3/2﹚mR^2;
R为其半径
对于空心圆柱
当回转轴为对称轴时,J=﹙1/2﹚m[(R1)^2+(R2)^2];
R1和R2分别为其内外半径。
对于球壳
当回转轴为中心轴时,J=﹙2/3﹚mR^2;
当回转轴为球壳的切线时,J=﹙5/3﹚mR^2;
R为球壳半径。
对于实心球体
当回转轴为球体的中心轴时,J=﹙2/5﹚mR^2;
当回转轴为球体的切线时,J=﹙7/5﹚mR^2;
R为球体半径
对于立方体
当回转轴为其中心轴时,J=﹙1/6﹚mL^2;
当回转轴为其棱边时,J=﹙2/3﹚mL^2;
当回转轴为其体对角线时,J=(3/16)mL^2;
L为立方体边长。
只知道转动惯量的计算方式而不能使用是没有意义的。
下面给出一些(绕定轴转动时)的刚体动力学公式。
角加速度与合外力矩的关系:
角加速度与合外力矩
式中M为合外力矩,β为角加速度。
可以看出这个式子与牛顿第二定律是对应的。
角动量:
角动量
刚体的定轴转动动能:
转动动能
注意这只是刚体绕定轴的转动动能,其总动能应该再加上质心动能。
只用E=(1/2)mv^2不好分析转动刚体的问题,是因为其中不包含刚体的任何转动信息,里面的速度v 只代表刚体的质心运动情况。
由这一公式,可以从能量的角度分析刚体动力学的问题。
转动惯量(Moment of Inertia)是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度,用字母I或J表示。
其量值取决于物体的形状、质量分布及转轴的位置。
转动惯量只决定于刚体的形状、质量分布和转轴的位置,而同刚体绕轴的转动状态(如角速度的大小)无关。
形状规则的匀质刚体,其转动惯量可直接用公式计算得到。
而对于不规则刚体或非均质刚体的转动惯量,一般通过实验的方法来进行测定,因而实验方法就显得十分重要。
转动惯量的表达式为I=∑ mi*ri^2,若刚体的质量是连续分布的,则转动惯量的计算公式可写成I=∫r^2dm=∫r^2ρdV(式中mi表示刚体的某个质元的质量,ri表示该质元到转轴的垂直距离,ρ表示该处的密度,求和号(或积分号)遍及整个刚体。
)转动惯量的量纲为L^2M,在SI单位制中,它的单位是kg·m^2。
平行轴定理
平行轴定理:设刚体质量为m,绕通过质心转轴的转动惯量为Ic,将此轴朝任何方向平行移动一个距离d,则绕新轴的转动惯量I为:
I=Ic+md^2
这个定理称为平行轴定理。
一个物体以角速度ω绕固定轴z轴的转动同样可以视为以同样的角速度绕平行于z轴且通过质心的固定轴的转动。
也就是说,绕z轴的转动等同于绕过质心的平行轴的转动与质心的转动的叠加
垂直轴定理
垂直轴定理:一个平面刚体薄板对于垂直它的平面的轴的转动惯量,等于绕平面内与垂直轴相交的任意两正交轴的转动惯量之和。
垂直轴定理
表达式: Iz=Ix+Iy
式中Ix,Iy,Iz分别代表刚体对x,y,z三轴的转动惯量.
对于非平面薄板状的刚体,亦有如下垂直轴定理成立[2]:
垂直轴定理
利用垂直轴定理可对一些刚体对一特定轴的转动惯量进行较简便的计算.
刚体对一轴的转动惯量,可折算成质量等于刚体质量的单个质点对该轴所形成的转动惯量。
由此折算所得的质点到转轴的距离,称为刚体绕该轴的回转半径κ,其公式为I=Mκ^2,式中M为刚体质量;I为转动惯量。
