嘉兴学院概率论与数理统计(II)2015年毕业重考复习资料
概率论与数理统计总复习

pi
1 1 1 5 5
5 1 5 1 5
1
1 65 EXY xi y j Pij COV ( X , Y ) EXY EX EY 8 8 i j
COV ( X , Y ) 3 20 320 DX DY
6. 设随机变量X ~N (1,3 ), Y ~ N (0, 4 ),已知
X z M z Y z
由于 X 和 Y 相互独立,于是得到 M = max(X,Y) 的分布 函数为: FM(z) =P(X≤z)P(Y≤z)
即有 FM(z)= FX(z)FY(z)
2. N = min(X,Y) 的分布函数 FN(z)=P(N≤z) =1-P(N>z)
=1-P(X>z,Y>z)
例1 设 X 具有概率密度f X ( x ), 求 Y=X2 的概率密度.
解 设Y 和 X 的分布函数分别为 FY ( y)和 FX ( x),
2
注意到Y X 0, 故当y 0时有,FY ( y) P(Y y) 0
当 y>0 时,
2 P ( X y) FY ( y ) P(Y y )
P ( y X y ) FX ( y ) FX ( y )
FY y P Y y
求导可得
1 f X ( y ) f X ( y ) , dFY ( y ) fY ( y ) 2 y dy 0,
y0 y0
若
1 fX ( x) 2
2、解:设 X 表示电子管寿命,
Y 表示5个电子管使用1000小时后损坏的个数。则
Y ~ b(5, p),其中p P( X 1000 ) x 1 e 1000 , x 0 f ( x) 1000 0, 其他
概率论与数理统计复习资料要点总结

《概率论与数理统计》复习资料一、复习提纲注:以下是考试的参考内容,不作为实际考试范围,仅作为复习参考之用。
考试内容以教学大纲和实施计划为准;注明“了解”的内容一般不考。
1、能很好地掌握写样本空间与事件方法,会事件关系的运算,了解概率的古典定义2、能较熟练地求解古典概率;了解概率的公理化定义3、掌握概率的基本性质和应用这些性质进行概率计算;理解条件概率的概念;掌握加法公式与乘法公式4、能准确地选择和运用全概率公式与贝叶斯公式解题;掌握事件独立性的概念及性质。
5、理解随机变量的概念,了解(0—1)分布、二项分布、泊松分布的分布律。
6、理解分布函数的概念及性质,理解连续型随机变量的概率密度及性质。
7、掌握指数分布(参数 )、均匀分布、正态分布,特别是正态分布概率计算8、会求一维随机变量函数分布的一般方法,求一维随机变量的分布律或概率密度。
9、会求分布中的待定参数。
10、会求边缘分布函数、边缘分布律、条件分布律、边缘密度函数、条件密度函数,会判别随机变量的独立性。
11、掌握连续型随机变量的条件概率密度的概念及计算。
12、理解二维随机变量的概念,理解二维随机变量的联合分布函数及其性质,理解二维离散型随机变量的联合分布律及其性质,理解二维连续型随机变量的联合概率密度及其性质,并会用它们计算有关事件的概率。
13、了解求二维随机变量函数的分布的一般方法。
14、会熟练地求随机变量及其函数的数学期望和方差。
会熟练地默写出几种重要随机变量的数学期望及方差。
15、较熟练地求协方差与相关系数.16、了解矩与协方差矩阵概念。
会用独立正态随机变量线性组合性质解题。
17、了解大数定理结论,会用中心极限定理解题。
18、掌握总体、样本、简单随机样本、统计量及抽样分布概念,掌握样本均值与样本方差及样本矩概念,掌握2分布(及性质)、t分布、F分布及其分位点概念。
19、理解正态总体样本均值与样本方差的抽样分布定理;会用矩估计方法来估计未知参数。
概率论与数理统计期末考试复习资料
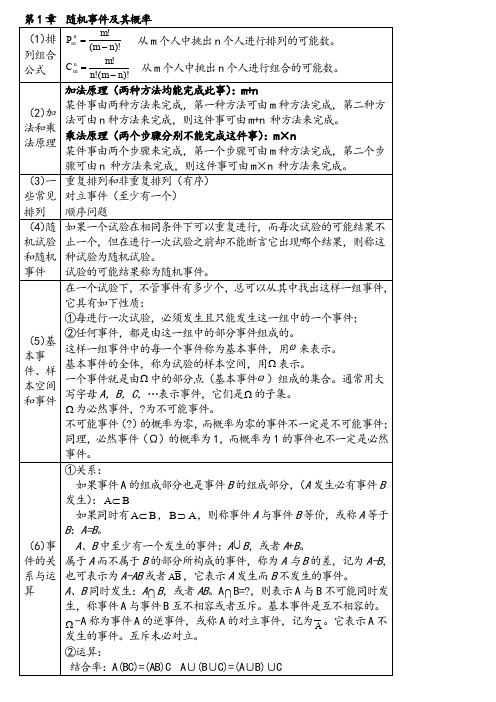
(1)排 列组合 公式
Pmn
m! (m n)!
C
n m
m! n!(m n)!
从 m 个人中挑出 n 个人进行排列的可能数。 从 m 个人中挑出 n 个人进行组合的可能数。
加法原理(两种方法均能完成此事):m+n
(2)加 法和乘 法原理
某件事由两种方法来完成,第一种方法可由 m 种方法完成,第二种方 法可由 n 种方法来完成,则这件事可由 m+n 种方法来完成。 乘法原理(两个步骤分别不能完成这件事):m×n 某件事由两个步骤来完成,第一个步骤可由 m 种方法完成,第二个步
率。分布函数F(x) 表示随机变量落入区间(– ∞,x]内的概率。
分布函数具有如下性质:
1° 0 F(x) 1, x ;
2° F(x) 是单调不减的函数,即x1 x2 时,有 F(x1) F(x2) ;
3° F() lim F(x) 0, F() lim F(x) 1;
设F(x) 是随机变量 X 的分布函数,若存在非负函数 f (x) ,对任意 实数x ,有
F (x) x f (x)dx ,
则称 X 为连续型随机变量。f (x) 称为 X 的概率密度函数或密度函 数,简称概率密度。 密度函数具有下面 4 个性质: 1° f (x) 0 。
2° f (x)dx 1。
X
| x1, x2,, xk, 。
P( X xk) p1, p2,, pk,
显然分布律应满足下列条件:
(1) pk 0 ,k 1,2,, (2) pk 1。 k 1
(2)连 续型随 机变量 的分布 密度
数理统计复习资料

数理统计复习资料数理统计复习资料数理统计是一门应用数学的学科,主要研究数据的收集、整理、分析和解释。
它在各个领域都有广泛的应用,包括经济学、医学、社会科学等。
在学习数理统计时,我们需要掌握一些基本的概念和方法,以及一些常用的统计分布和假设检验。
下面是一些数理统计复习资料的内容。
1. 概率论基础概率论是数理统计的基础,它研究随机事件的发生概率。
在学习概率论时,我们需要了解一些基本的概念,如样本空间、事件、概率等。
同时,还需要掌握概率的计算方法,包括加法法则、乘法法则、条件概率等。
此外,还需要了解一些常用的概率分布,如二项分布、泊松分布、正态分布等。
2. 统计推断统计推断是数理统计的核心内容,它研究如何通过样本对总体进行推断。
在学习统计推断时,我们需要了解抽样分布和估计量的性质。
同时,还需要学习点估计和区间估计的方法,包括最大似然估计、矩估计、置信区间等。
此外,还需要掌握假设检验的基本原理和方法,包括单样本均值检验、两样本均值检验、方差分析等。
3. 回归分析回归分析是数理统计的重要应用,它研究自变量与因变量之间的关系。
在学习回归分析时,我们需要了解线性回归模型和非线性回归模型的基本原理。
同时,还需要学习回归系数的估计方法,包括最小二乘估计、岭回归、lasso回归等。
此外,还需要掌握回归模型的诊断方法,包括残差分析、模型选择等。
4. 方差分析方差分析是数理统计的一种重要方法,它研究不同因素对观测值的影响。
在学习方差分析时,我们需要了解单因素方差分析和多因素方差分析的基本原理。
同时,还需要学习方差分析的假设检验方法,包括F检验、多重比较等。
此外,还需要掌握方差分析的扩展方法,如混合设计、重复测量设计等。
5. 非参数统计非参数统计是数理统计的一种重要分支,它不依赖于总体分布的假设。
在学习非参数统计时,我们需要了解秩和检验、符号检验、Wilcoxon秩和检验等基本方法。
同时,还需要学习非参数回归、非参数方差分析等扩展方法。
2015年10月自考概率论与数理统计(二)试题及答案解析

2015年10月高等教育自学考试全国统一命题考试概率论与数理统计(二) 试卷本试卷共4页。
满分l00分,考试时间l50分钟。
考生答题注意事项:1.本卷所有试题必须在答题卡上作答。
答在试卷上无效,试卷空白处和背面均可作草稿纸. 2.第一部分为选择题。
必须对应试卷上的题号使用2B铅笔将“答题卡”的相应代码涂黑. 3.第二部分为非选择题必须注明大、小题号,使用0.5毫米黑色字迹签字笔作答。
4.合理安排答题空间。
超出答题区域无效。
第一部分选择题一、单项选择题(本大题共l0小题,每小题2分,共20分)在每小题列出的四个备选项中只有一个是符合题目要求的。
请将其选出并将“答题卡”的相应代码涂黑。
未涂、错涂或多涂均无分。
1.设事件4与B互不相容,且P(A)=0.4,P(B)=0.2,则P(A∪B)=A.0 B.O.2 C.O.4 D.O.62.设随机变量X~B(3,0.3),则P{X=2}=A.0.1 89 B.0.2l C.0.441 D.0.7A.0.2 B.0.4 C.0.6 D.0.85.设二维随机变量(X,Y)的分布律为6.设随机变量X~N(3,22),则E(2X+3)=A.3 B.6 C.9 D.157.设随机变量X,Y,相互独立,且,Y在区间上服从均匀分布,则第二部分非选择题二、填空题(本大题共l5小题。
每小题2分,共30分)请在答题卡上作答。
11.袋中有编号为0,l,2,3,4的5个球.今从袋中任取一球,取后放回;再从袋中任取一球,则取到两个0号球的概率为_______.12.设A,B为随机事件,则事件“A,B至少有一个发生”可由A,B表示为_______.13.设事件A,B相互独立,且P(A)=0.3,P(B)=0.4.则= _______.14.设X表示某射手在一次射击中命中目标的次数,该射手的命中率为0.9,则P{X=0}= _______.15.设随机变量X服从参数为单科自考包过:qq:18606240单科自考包过:qq:186062401的指数分布,则= _______.16.设二维随机变量(X,Y)的分布律为则c= _______.17.设二维随机变量(X,Y)服从正态分布N(0,0;1,l;0),则(X,Y)的概率密度F(x,y)= _______.18.设二维随机变量(X,Y)服从区域D:-l≤x≤2,0≤y≤2上的均匀分布,则(X,Y) 的概率密度f(x,y)在D上的表达式为_______.19.设X在区间上服从均匀分布,则E(X)= _______.20.设的= _______.21.设随机变量x与y的协方差= _______.22.在贝努利试验中,若事件A发生的概率为P(0<p<1),今独立重复观察n次,记三、计算题(本大题共2小题,每小题8分,共l6分)请在答题卡上作答。
《概率论与数理统计》复习资料

《概率论与数理统计》复习资料《概率论与数理统计》复习资料李裕奇一、作业习题解答参见《概率论与数理统计习题详解》(李裕奇赵联文刘海燕编西南交通大学出版社2005年第2版)第一章(1) §1.1, §1.2, §1.3, §1.4, §1.5 基本练习前8题;(2)第一章自测题(3)综合练习一1,2,3,4,5,6,8,13第二章(1) §2.1, §2.2, §2.3, §2.4基本练习前8题;(2) 第二章自测题(3) 综合练习二1,2,3,4,5,7,17,18第三章(1) §3.1,§3.3,基本练习前8题;(2) 第三章自测题(3) 综合练习三1, 2, 7第四章(1) §4.1,§4.2,基本练习前8题;(2) 第四章自测题(3) 综合练习四1, 2, 3,4,5,6第六章(1) §6.1,§6.2,§6.3基本练习前6题;(2) 第六章自测题(3) 综合练习六1, 2, 3,4,5,7,8第七章(1) §7.1,§7.2,§7.3基本练习前6题;(2) 综合练习六1, 2, 3,10,15,16,17,18二、考试重点1、古典概型公式运用,注意抽球问题;2、全概率公式与贝叶斯公式运用;3、离散型随机变量的概率分布求法,分布函数,数学期望,方差的求法;4、连续性随机变量的分布, 分布函数,数学期望,方差的求法;常见分布,特别是正态分布的有关计算;5、已知X 的概率密度函数,X 的函数的概率密度求法;6、离散型随机变量(X,Y)的数字特征求法,特别注意相关系数的求法;7、极差,经验分布函数,总体概率的近似计算;8、单个正态总体均值与方差的置信区间的求法。
三、模拟试题概率论与数理统计模拟试题1一、(12分)某商店有4桶油漆,分别为红漆,白漆、蓝漆与黑漆,在搬运过程中所有的标签脱落,售货员随意将这些油漆卖给需要红漆,白漆,蓝漆与黑漆的4位顾客,试求:(1)至少有一位顾客买到所需颜色的油漆的概率;(2)恰有一位顾客买到所需颜色的油漆的概率。
概率论与数理统计(II)总复习资料

概率论与数理统计期末总复习一、填空题1. 设来自总体X 的一个样本观察值为:2.1,5.4,3.2,9.8,3.5,则样本均值 = 4.8 ,样本方差 = 9.23 。
2.设随机变量12100,,,X X X 独立同分布,且0,10,i i EX DX == 1,2,,100i =,令10011100i i X X ==∑,则10021{()}i i E X X =-=∑__________. 解: 设1100,,X X 为总体X 的样本,则1002211()99i i S X X ==-∑为样本方差,于是210ES DX ==,即10021()1099990.i i E X X =-=⨯=∑3.设12,,,n X X X 是总体(,4)N μ的样本,X 是样本均值,则当n ≥__________时,有2E X 4. 设12,,,n X X X 是来自0–1分布:(1),(0)1P X p P X p ====-的样本,则EX =__________,DX =__________,2ES =__________.解:11,(1)ni i i i X X EX p DX pq p p n =====-∑2111(1)i i EX nEX pDX nDX p p n n n=⋅==⋅=- 22222111()[]11n i i i ES E X nX nEX nEX n n ==-=⋅---∑ 2211[((1))((1))]1n p p p n p p p n n =-+--+-21[(1)](1).1np p n p p p n =---=--5.设总体12~(),,,,n X P X X X λ为来自X 的一个样本,则EX =_________,DX =__________.解:~()i i X P EX DX EX DX nλλλλ====6.设总体12~[,],,,n X U a b X X X 为X 的一个样本,则EX =________,DX =__________.解:2()~[,]212a b b a X U a b EX DX +-==2a bEX += 2()12b a DX n -=7.设总体2126~(0,),,,,X N X X X σ为来自X 的一个样本,设22123456()()Y X X X X X X =+++++,则当C =_________时,2~(2).CY χ解:123456()()0E X X X E X X X ++=++=2123456()()33i D X X X D X X X DX σ++=++==12312321)]()13D X X X D X X X σ++=++=123)~(0,1)X X X N ∴++,456)~(0,1)X X X N ++且独立 213C σ∴= 8.设1216,,,X X X 是总体2(,)N μσ的样本,X 是样本均值,2S 是样本方差,若()0.95P X aS μ>+=,则a =__________.解:0.95()((15))0.95X P X aS P P t t μ>+=≥=≥-=,查t 分布表0.954(15) 1.750.4383.a t a =-=-⇒=-9. 在总体~(5,16)X N 中随机地抽取一个容量为36的样本,则均值X 落在4与6之间的概率 = ()2 1.51Φ- 。
嘉兴学院概率论与数理统计(II)2015年毕业重考复习资料

概率论与数理统计(II)复习资料一、填空题1. 设总体12~(),,,,n X P X X X λ 为来自X 的一个样本,则EX =_ λ_,DX =_nλ_. 2. 设总体12~[,],,,n X U a b X X X 为X 的一个样本,则EX =________,DX =_______. 解:2()~[,]212a bb a X U a b EX DX +-==2a b EX += 2()12b a DX n-=3. 设随机变量12100,,,X X X 独立同分布,且0,10,i i EX DX == 1,2,,100i = ,令10011100i i X X ==∑,则10021{()}ii E X X =-=∑__________. 解: 设1100,,X X 为总体X 的样本,则1002211()99i i S X X ==-∑为样本方差,于是210ES DX ==,即10021()1099990.i i E X X =-=⨯=∑4. 设12,,,n X X X 是总体(,4)N μ的样本,X 是样本均值,则当n ≥__________时,有2()0.1E X μ-≤.解:24,EX DX nn σμ===, 40.1n≤, 40n ≥ 5.设总体2126~(0,),,,,X N X X X σ 为来自X 的一个样本,设22123456()()Y X X X X X X =+++++,则当C =____213σ_____时,2~(2).CY χ6. 设随机变量()~X t n ,则21~Y X =(,1)F n . 7. 在总体~(5,16)X N 中随机地抽取一个容量为36的样本,则均值X 落在4与6之间的概率 = ()2 1.51Φ- 。
8. 设1,n X X 是取自总体2~(,)X N μσ的样本,2211()1n ni i S X X n ==-+∑,则 2()n Var S = ()422(1)1n n σ-+ 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
概率论与数理统计(II)复习资料一、填空题1. 设总体12~(),,,,n X P X X X λ 为来自X 的一个样本,则EX =_ λ_,DX =_nλ_. 2. 设总体12~[,],,,n X U a b X X X 为X 的一个样本,则EX =________,DX =_______. 解:2()~[,]212a bb a X U a b EX DX +-==2a b EX += 2()12b a DX n-=3. 设随机变量12100,,,X X X 独立同分布,且0,10,i i EX DX == 1,2,,100i = ,令10011100i i X X ==∑,则10021{()}ii E X X =-=∑__________. 解: 设1100,,X X 为总体X 的样本,则1002211()99i i S X X ==-∑为样本方差,于是210ES DX ==,即10021()1099990.i i E X X =-=⨯=∑4. 设12,,,n X X X 是总体(,4)N μ的样本,X 是样本均值,则当n ≥__________时,有2()0.1E X μ-≤.解:24,EX DX nn σμ===, 40.1n≤, 40n ≥ 5.设总体2126~(0,),,,,X N X X X σ 为来自X 的一个样本,设22123456()()Y X X X X X X =+++++,则当C =____213σ_____时,2~(2).CY χ6. 设随机变量()~X t n ,则21~Y X =(,1)F n . 7. 在总体~(5,16)X N 中随机地抽取一个容量为36的样本,则均值X 落在4与6之间的概率 = ()2 1.51Φ- 。
8. 设1,n X X 是取自总体2~(,)X N μσ的样本,2211()1n ni i S X X n ==-+∑,则 2()n Var S = ()422(1)1n n σ-+ 。
9.设18,,X X 是从正态总体(10,9)N 中抽取的样本,则样本均值x 的标准差为1.06= 10.设随机变量,X Y 相互独立,均服从2~(0,3)X N 分布且129,,,X X X 与129,,,Y Y Y 分别是来自总体,X Y的简单随机样本,则统计量U =服从参数 为的 分布。
[答案:参数为(9)的(t )分布]解:由Y X ,相互独立,均服从)3,0(2N 分布,又91,,X X 与91,,Y Y 分别来自总体Y X ,,可知91,,X X 与91,,Y Y 之间均相互独立,均服从分布)3,0(2N因而)39,0(~291⨯∑=N X i i ,)1,0(~9191N X X i i ∑==,)1,0(~3N Y i ,)9(~32912χ∑=⎪⎭⎫⎝⎛i i Y ,且∑==9191i i X X 与∑=⎪⎭⎫⎝⎛9123i i Y 相互独立,因而()292191912919123919191Y Y X X YXXi ii ii Y i ii ++++==∑∑∑∑==== 服从参数为9的t 分布。
11.设1234,,,X X X X 是取自正态总体2~(0,2)X N 的简单随机样本且()()221234234Y a X X b X X =-+-,则a = ,b = 时,统计量Y 服从2χ分布,其自由度为 。
[答案:=a (201),=b (1001)时,统计量Y 服从2χ分布,其自由度为(2)] 12.设12,X X 是2~(0,)X N σ的样本,则21212X X Y X X ⎛⎫+= ⎪-⎝⎭的分布 ()1,1F13.设随机变量~()(1)X t n n >,21Y X =,则~Y (),1F n 。
14. 设随机变量~(,)X F n n 且()0.2P X A >=,这里A 为常数,则1P X A ⎛⎫>= ⎪⎝⎭0.8 。
15. 设总体~(0,)X U θ,现从该总体抽取容量为10的样本,样本值为0.5 1.3 0.6 1.7 2.2 1.2 0.8 1.5 2.0 1.6则参数θ的矩估计为 2.68 。
16. 由来自正态总体2~(,0.9),X N μ容量为9的简单随机样本,若得到样本均值0.5X =,则未知参数μ的置信度为0.95的置信区间为[-0.088,1.088] 。
17. 已知某种材料的抗压强度2~(,),X N μσ现随机地抽取10个试件进行抗压试验,测得样本均值457.5,x =标准差35.217,s =则μ的95%的置信区间为 [432.31,482.69] .18. 从一批电子元件中抽取8个进行寿命测试,测得如下数据(单位:小时):1050 1100 1130 1040 1250 1300 1200 1080设电子元件的寿命服从指数分布,试对这批元件的平均寿命的矩估计为 1143.75 。
19. 由来自正态总体)9.0,(~2μN X ,容量为9的简单随机样本,若得到样本均值5=X ,则未知参数μ的置信度为95.0的置信区间为()。
答案:[4.412,5.588]20. 设X 是来自正态总体2(,)N μσ的样本均值,样本容量为n ,2σ已知,则假设00:H μμ=的检验统计量是X .21. 设1,,n X X 为来自2(,)N μσ的一个样本,2211()1ni i S X X n ==--∑,其中参数2,μσ未知,要检验假设2200:H σσ=应用 2χ 检验法,检验的统计量是221n S σ-() 。
22. 设总体22~(,),,X N μσμσ都是未知参数,把从X 中抽取的容量为n 的样本均值记为X ,样本标准差记为S , 当2σ未知时,在显著性水平α下,检验假设0010::H H μμμμ≤↔>的统计量为)0x t sμ-=,拒绝域为 {}1t t α-≥ 。
23.设12,,n X X X 是来自正态总体的样本,其中参数μ未知,2σ已知。
要检验假设00:H μμ=应用 u 检验法,检验的统计量是 )0x u μσ-= ;当0H成立时该统计量服从 (0,1)N 。
24.要使犯两类错误的概率同时减小,只有 增加样本量 。
二、单项选择题1. 样本1234,,X X X X ,为取自正态总体X 的样本,EX μ=为已知,且2VarX σ=未知,则下列随机变量中不是统计量的是 ( C ) (A ) 4141ii X X==∑ (B )14M X X μ=+-(C )42211()i i R XX σ==-∑ (D )422131()ii S XX ==-∑ 2. 设1,,n X X 为来自2(,)N μσ的一个样本,其中μ已知而2σ未知,则下列各选项中的量不是统计量的是( C )。
()(){}22211111.;.;.;.min nnni i ii i ni i i X A X B X X C D X n μσ≤≤===⎛⎫-- ⎪⎝⎭∑∑∑ 3.设123,,X X X 为来自2(,)N μσ的一个样本,其中μ已知而2σ未知,则下列各选项中的量不是统计量的是( D )。
32123311.;.3;.;.i i A X X X B X C X D X μσ=+++∑ 4.设18,,X X 和110,,Y Y 分别来自两个正态总体()21,2N -和(2,5)N 的样本,且相互独立,2212,S S 分别为两个样本的样本方差,则服从(7,9)F 的统计量是(B )。
2222111122222222545.;.;.;..452S S S S A B C D S S S S 5. 设1,,n X X 为来自2(0,)N σ的一个样本,X 和2S 分别为样本均值和样本方差,则服从自由度为1n -的t -分布的随机变量是( A )。
2...;..nX nXA B C D S S6. 设1,,n X X 为来自2(,)N μσ的一个样本,X 和2S 分别为样本均值和样本方差,则下面结论不成立的有( D )。
A . X 和2S 相互独立; B . X 和2(1)n S -相互独立;C .X 和()2211ni i XX σ=-∑相互独立; D .X 和()2211ni i X μσ=-∑相互独立。
7.设1,,n X X 为来自2(,)N μσ的一个样本,()22111n ii S X X n ==--∑,则2DS =( D )。
444422.;.;.;..11A B C D n n n n σσσσ-- 8.设n X X X ,,,21 是总体X 的样本,2,σμ==DX EX ,X 是样本均值,2S 是样本方差,则( D ).(A )2~,X N n σμ⎛⎫ ⎪⎝⎭; (B )2S 与X 独立;(C ))1(~)1(222--n S n χσ; (D )2S 是2σ的无偏估计量.解:已知总体X 不是正态总体 ∴(A )(B )(C )都不对. ∴ 选D. 9.设n X X X ,,,21 是总体),0(2σN 的样本,则( A )可以作为2σ的无偏估计量.(A )∑=n i i X n 121; (B )∑=-n i i X n 1211; (C )∑=n i i X n 11; (D )∑=-n i i X n 111. 解:2222)(,0σ==-==i i i i i EX EX EX DX EX ,22121)1(σσ=⋅=∑n nX n E n i 。
∴ 选A.10. 设总体X 服从正态分布),(2σμN ,其中μ为未知参数,2σ已知,12,n X (X ,X ,)为取自总体的样本,记11nini X X==∑,则0.950.95u X u + (X - 作为 μ的置信区间,其置信度为 ( B ) (A )0.95 (B )0.90 (C )0.975 (D )0.05 11. 设总体X 服从区间],[θθ-上均匀分布)0(>θ,n x x ,,1 为样本,则θ的极大似然估计为( C )(A )},,max{1n x x ; (B )},,min{1n x x (C )|}|,|,max{|1n x x (D )|}|,|,min{|1n x x解:1[,]()20x f x θθθ⎧∈-⎪=⎨⎪⎩其它似然函数∏==ni i n x f x x L 11),();,,(θθ 1,||1,2,,(2)0,i nx i n θθ⎧≤=⎪=⎨⎪⎩其它∴ )(θL 在)(n X =θ处取得极大值 |}|,|,max{|ˆ1nn X X X ==θ ∴ 选C.12. 设总体X 的密度函数为:,0,),(11≥=-x e x P xλλ其他为0,其中0>λ为未知参数,12(,,,)n X X X 是从总体X 中抽取的样本,记11nini X X==∑,则λ的最大似然估计为 :( A )(A ) X (B )1X (C )2211()nn ini S XX ==-∑ (D )22111()nnin i SXX *==-∑-13.设ˆθ是θ的无偏估计,且ˆ0Var θ>,则2ˆθ是2θ的 ( C )(A) 无偏估计量 (B) 有效估计量 (C) 有偏估计 (D) A 和B 同时成立 14.在一个确定的假设检验问题中,与判断结果有关的因素有( D )。
