MATLAB编辑一维热传导方程的模拟程序
一维非稳态导热方程求解 附Matlab程序
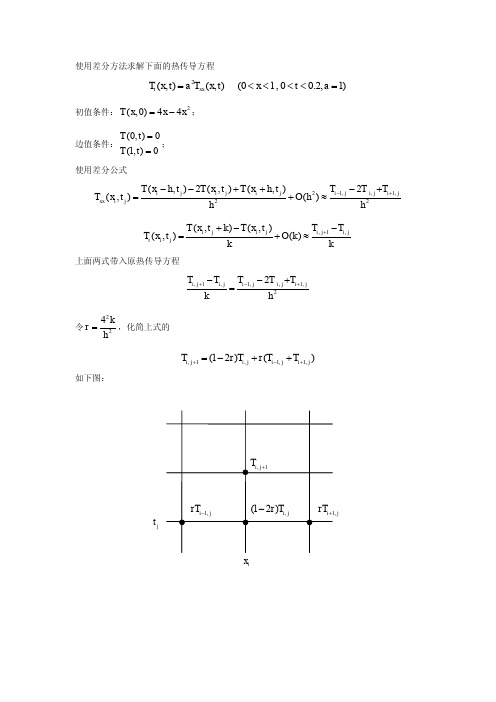
使用差分方法求解下面的热传导方程2(,)(,)(01,00.2,1)t xx T x t a T x t x t a =<<<<=初值条件:2(,0)44T x x x =-;边值条件:(0,)0(1,)0T t T t ==;使用差分公式1,,1,222(,)2(,)(,)2(,)()i j i j i j i j i j i jxx i j T x h t T x t T x h t T T T T x t O h h h -+--++-+=+≈,1,(,)(,)(,)()i j i j i j i jt i j T x t k T x t T T T x t O k kk++--=+≈上面两式带入原热传导方程,1,1,,1,22i j i ji j i j i jT T T T T kh +-+--+=令224kr h=,化简上式的,1,1,1,(12)()i j i j i j i j T r T r T T +-+=-++如下图:ix jt j编程MA TLAB 程序,运行结果如下1xtTfunction mypdesolution c=1;xspan=[0 1]; tspan=[0 0.2]; ngrid=[100 10]; f=@(x)4*x-4*x.^2; g1=@(t)0; g2=@(t)0;[T,x,t]=rechuandao(c,f,g1,g2,xspan,tspan,ngrid); [x,t]=meshgrid(x,t); mesh(x,t,T); xlabel('x') ylabel('t') zlabel('T')function [U,x,t]=rechuandao(c,f,g1,g2,xspan,tspan,ngrid) % 热传导方程:% Ut(x,t)=c^2*Uxx(x,t) a<x<b ts<t<tf % 初值条件: % u(x,0)=f(x)% 边值条件:% u(a,t)=g1(t)% u(b,t)=g2(t)%% 参数说明% c:方程中的系数% f:初值条件% g1,g2:边值条件% xspan=[a,b]:x的取值范围% tspan=[ts,tf]:t的取值范围% ngrid=[n,m]:网格数量,m为x网格点数量,n为t的网格点数量% U:方程的数值解% x,t:x和t的网格点n=ngrid(1);m=ngrid(2);h=range(xspan)/(m-1);x=linspace(xspan(1),xspan(2),m);k=range(tspan)/(n-1);t=linspace(tspan(1),tspan(2),n);r=c^2*k/h^2;if r>0.5error('为了保证算法的收敛,请增大步长h或减小步长k!')ends=1-2*r;U=zeros(ngrid);% 边界条件U(:,1)=g1(t);U(:,m)=g2(t);% 初值条件U(1,:)=f(x);% 差分计算for j=2:nfor i=2:m-1U(j,i)=s*U(j-1,i)+r*(U(j-1,i-1)+U(j-1,i+1));endend%%%%%%本文来自互联网%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%。
一维热传导MATLAB模拟

昆明学院2015届毕业设计(论文)设计(论文)题目一维热传导问题的数值解法及其MATLAB模拟子课题题目无姓名伍有超学号************所属系物理科学与技术系专业年级2011级物理学2班指导教师王荣丽2015 年 5 月摘要本文介绍了利用分离变量法和有限差分法来求解一维传导问题的基本解,并对其物理意义进行了讨论。
从基本解可以看出,在温度平衡过程中,杠上各点均受初始状态的影响,而且基本解也满足归一化条件,表示在热传导过程中杆的总热量保持不变。
通过对一维杆热传导的分析,利用分离变量法和有限差分法对一维热传导进行求解,并用MATLAB 数学软件来对两种方法下的热传导过程进行模拟,通过对模拟所得三维图像进行取值分析,得出由分离变量法和有限差分法绘制的三维图基本相同,且均符合热传导过程中温度随时间、空间的变化规律,所以两种方法均可用来解决一维热传导过程中的温度变化问题。
关键词:一维热传导;分离变量法;有限差分法;数值计算;MATLAB 模拟AbstractIn this paper, the method of variable separation and finite difference method are introduced to solve the problem of one-dimensional heat conduction problems, and the physical significance of numerical methods for heat conduction problems are discussed. From the basic solution, we can see the temperature on the bar are affected by the initial state during the process of temperature balance, and basic solution also satisfy the normalization condition which implied the invariance of the total heat in the bar during the heat conduction process. Through the analysis of the one-dimensional heat conduction, by taking use of variable separation method and finite difference method, we simulated the one-dimensional heat conduction problem by MATLAB. The three-dimensional images of the simulation results obtained by the method of separation of variables and finite difference method are similar to each other, and the temperature curve is in accordance with the law of temperature variation during heat conduction. Thus, we can go to the conclusion that both methods can be used to deal with the one-dimensional heat conduction problems.Keywords: One-dimensional heat conduction; method of variable separation;finite difference method; numerical method; MATLAB simulation目录第一章绪论 (1)1.1热传导的概念 (1)1.2热质的运动和传递 (1)第二章一维热传导问题的两种数值解法 (3)2.1一维热传导问题的初值问题 (3)2.2一维热传导问题的分离变量法 (4)2.3一维热传导问题的有限差分法 (6)第三章一维有界杆热传导问题的MATLAB模拟 (9)3.1一维有界杆热传导问题 (9)3.2分离变量法的MATLAB模拟 (9)3.3有限差分法的MATLAB模拟 (12)第四章总结与展望 (18)参考文献 (19)谢辞 (20)第一章绪论1.1热传导的概念由于温度分布不均匀,热量从介质中温度高的地方流向温度低的地方称为热传导。
一维热传导MATLAB模拟

一维热传导MATLAB模拟昆明学院2015届毕业设计(论文)设计(论文)题目一维热传导问题的数值解法及其MATLAB模拟子课题题目无姓名伍有超学号 2所属系物理科学与技术系专业年级 2011级物理学2班指导教师王荣丽2015 年 5 月摘要本文介绍了利用分离变量法和有限差分法来求解一维传导问题的基本解,并对其物理意义进行了讨论。
从基本解可以看出,在温度平衡过程中,杠上各点均受初始状态的影响,而且基本解也满足归一化条件,表示在热传导过程中杆的总热量保持不变。
通过对一维杆热传导的分析,利用分离变量法和有限差分法对一维热传导进行求解,并用MATLAB 数学软件来对两种方法下的热传导过程进行模拟,通过对模拟所得三维图像进行取值分析,得出由分离变量法和有限差分法绘制的三维图基本相同,且均符合热传导过程中温度随时间、空间的变化规律,所以两种方法均可用来解决一维热传导过程中的温度变化问题。
关键词:一维热传导;分离变量法;有限差分法;数值计算;MATLAB 模拟AbstractIn this paper, the method of variable separation andfinite difference method are introduced to solve the problem of one-dimensional heat conduction problems, and the physical significance of numerical methods for heat conduction problems are discussed. From the basic solution, we can see the temperature on the bar are affected by the initial state during the process of temperature balance, and basic solution also satisfy the normalization condition which implied the invariance of the total heat in the bar during the heat conduction process. Through the analysis of the one-dimensional heat conduction, by taking use of variable separation method and finite difference method, we simulated the one-dimensional heat conduction problem by MATLAB. The three-dimensional images of the simulation results obtained by the method of separation of variables and finite difference method are similar to each other, and the temperature curve is in accordance with the law of temperature variation during heat conduction. Thus, we can go to the conclusion that both methods can be used to deal with the one-dimensional heat conduction problems.Keywords: One-dimensional heat conduction; method of variableseparation; finite difference method; numerical2method; MATLAB simulation目录第一章绪论11.1热传导的概念......................................................... .. (1)1.2热质的运动和传递......................................................... (1)第二章一维热传导问题的两种数值解法32.1一维热传导问题的初值问题32.2一维热传导问题的分离变量法42.3一维热传导问题的有限差分法63第三章一维有界杆热传导问题的MATLAB模拟9 3.1一维有界杆热传导问题93.2分离变量法的MATLAB模拟93.3有限差分法的MATLAB模拟12第四章总结与展望18参考文献19谢辞204第一章绪论1.1热传导的概念由于温度分布不均匀,热量从介质中温度高的地方流向温度低的地方称为热传导。
一维热传导方程数值解法及matlab实现

问题描述实验原理分离变量法实验原理有限差分法实验目的利用分离变量法和有限差分法解热传导方程问题利用matlab进行建模构建图形研究不同的情况下采用何种方法从更深层次上理解热量分布与时间、空间分布关系。
模拟与仿真作业(1)分离变量法(代码):x=0:0.1*pi:pi;y=0:0.04:1;[x,t]=meshgrid(x,y);s=0;m=length(j);%matlab可计算的最大数相当于无穷for i=1:ms=s+(200*(1-(-1)^i))/(i*pi)*(sin(i*x).*exp(-i^2*t)); end;surf(x,t,s);xlabel('x'),ylabel('t'),zlabel('T');title(' 分离变量法(无穷)');axis([0 pi 0 1 0 100]);所得到的三维热传导图形为:有限差分法:u=zeros(10,25); %t=1 x=pi 构造一个1025列的矩阵(初始化为0)用于存放时间t和变量x 横坐标为x 纵坐标为ts=(1/25)/(pi/10)^2;fprintf('稳定性系数S为:\n');disp(s);for i=2:9u(i,1)=100;end;for j=1:25u(1,j)=0;u(10,j)=0;end;for j=1:24for i=2:9u(i,j+1)=s*u(i+1,j)+(1-2*s)*u(i,j)+s*u(i-1,j); endenddisp(u);[x,t]=meshgrid(1:25,1:10);surf(x,t,u);xlabel('t'),ylabel('x'),zlabel('T');title(' 有限差分法解');所得到的热传导图形为:(2)i分离变量法(取前100项和)x=0:0.1*pi:pi;y=0:0.04:1;[x,t]=meshgrid(x,y);s=0;for i=1:100s=s+(200*(1-(-1)^i))/(i*pi)*(sin(i*x).*exp(-i^2*t)); end;surf(x,t,u);xlabel('x'),ylabel('t'),zlabel('T');title(' 分离变量法');axis([0 pi 0 1 0 100]);所得到的热传导图形为:Ii有限差分法根据(1)我们有如下图结论:比较可得这两幅图基本相同,有限差分法和分离变量法对本题都适应(3)第一种情况(取无穷项):在原来程序代码的基础上加上disp(s(:,6)); 可得出第六列(即x=pi/2)处温度随时间的变化情况x=0:0.1*pi:pi;y=0:0.04:1;[x,t]=meshgrid(x,y);s=0;m=length(j);%matlab可计算的最大数,相当于无穷for i=1:ms=s+(200*(1-(-1)^i))/(i*pi)*(sin(i*x).*exp(-i^2*t));end;surf(x,t,s);xlabel('x'),ylabel('t'),zlabel('T');title(' 分离变量法(无穷)');axis([0 pi 0 1 0 100]);disp(s(:,6));我们得到如下一组数据:当温度低于50度是时间为t=23.5*0.04=0.94第二种情况(取前100项和)在原来程序代码的基础上加上disp(s(:,6)); 可得出第六列(即x=pi/2)处温度随时间的变化情况x=0:0.1*pi:pi;y=0:0.04:1;[x,t]=meshgrid(x,y);r=0.04/(0.1*pi)^2;fprintf('稳定性系数S为:')disp(r);s=0;for i=1:100s=s+(200*(1-(-1)^i))/(i*pi)*(sin(i*x).*exp(-i^2*t));end;surf(x,t,s);xlabel('x'),ylabel('t'),zlabel('T');title(' 分离变量法');axis([0 pi 0 1 0 100]);disp(s(:,6));当温度低于50度是时间为t=23.5*0.04=0.94第三种情况(有限差分法)在原来程序代码的基础上加上disp(u(5,:));可得出第五行(即x=pi/2)处温度随时间的变化情况u=zeros(10,25); %t=1 x=pi 10行25列横坐标为x 纵坐标为ts=(1/25)/(pi/10)^2;fprintf('稳定性系数S为:\n');disp(s);for i=2:9u(i,1)=100;end;for j=1:25u(1,j)=0;u(10,j)=0;end;for j=1:24for i=2:9u(i,j+1)=s*u(i+1,j)+(1-2*s)*u(i,j)+s*u(i-1,j);endenddisp(u);[x,t]=meshgrid(1:25,1:10);surf(x,t,u);xlabel('t'),ylabel('x'),zlabel('T');title(' 有限差分法解');disp(u(5,:));得到如下结果我们知19列为50.3505 20列是数据为47.8902 所以时间t为20*0.04=0.78结论:比较一二三种情况,我们得到不同的时间,这是由于:1、加和不同一种为100,一种为无穷;2、采用的方法不同:一种为分离变量法,一种为有限差分法造成的。
一维介质中的热传导问题 卡尔曼滤波 matlab

一维介质中的热传导问题一、概述热传导是物理学中的一个重要问题,特别是对于介质的热传导问题更是如此。
一维介质中的热传导问题是指介质在一维空间内热量的传导过程。
这一问题不仅在物理学中具有重要性,而且在工程领域中也有着广泛的应用。
在实际工程中,我们常常需要对介质中的热传导问题进行分析和研究,以便更好地设计和优化热传导设备,提高能源利用效率。
二、热传导方程介质中的热传导过程可以用热传导方程来描述。
一维情况下,热传导方程可以写为:其中,u(x, t)为介质中的温度分布,k为介质的热导率,c为介质的比热容,ρ为介质的密度,t为时间,x为空间坐标。
三、数值模拟对于介质中的热传导问题,我们常常需要进行数值模拟来解决热传导方程。
数值模拟可以采用有限差分法、有限元法等数值方法来进行。
在进行数值模拟时,我们通常需要借助计算机软件来进行计算,其中Matlab是一种非常实用的数学建模和仿真软件,特别适用于解决热传导问题。
四、卡尔曼滤波卡尔曼滤波是一种最优状态估计算法,可以用于对系统的状态进行预测和估计。
在介质中的热传导问题中,我们可以利用卡尔曼滤波算法来对系统的温度状态进行估计,从而更好地理解和分析热传导过程。
五、Matlab仿真在研究介质中的热传导问题时,我们可以利用Matlab软件进行仿真计算。
通过编写Matlab程序,我们可以对介质中的热传导过程进行模拟,并得到系统的温度分布。
我们也可以借助Matlab提供的工具,如ODE求解器等,对热传导方程进行数值求解,得到系统的温度变化规律。
六、结论介质中的热传导问题是一个具有重要意义的物理问题,对其进行深入的研究不仅有助于提高工程设备的效率,而且可以推动物理学领域的发展。
卡尔曼滤波和Matlab仿真技术的应用为介质中的热传导问题研究提供了新的方法和手段,可以更好地帮助我们理解和解决这一重要问题。
希望未来能够有更多的研究者投入到介质中的热传导问题的研究中,共同推动科学技术的进步。
一维热传导方程matlab程序

一维热传导方程matlab程序一维热传导方程是研究物体在一维情况下的温度分布变化的方程,其数学表达式为:∂u/∂t = α∂²u/∂x²其中,u表示温度,t表示时间,x表示空间位置,α表示热扩散系数。
为了求解一维热传导方程,我们可以采用有限差分法来进行数值计算。
具体来说,我们可以将时间和空间进行离散化,然后利用差分公式来逼近偏微分方程。
下面是一维热传导方程的matlab程序:% 定义参数L = 1; % 空间长度T = 1; % 时间长度N = 100; % 空间网格数M = 1000; % 时间网格数dx = L/N; % 空间步长dt = T/M; % 时间步长alpha = 0.1; % 热扩散系数% 初始化温度分布u = zeros(N+1,1);u(1) = 100; % 左端点温度为100度% 迭代求解for k = 1:Mfor i = 2:Nu(i) = u(i) + alpha*dt/dx^2*(u(i+1)-2*u(i)+u(i-1)); endend% 绘制温度分布图像x = linspace(0,L,N+1);plot(x,u,'LineWidth',2);xlabel('位置');ylabel('温度');title('一维热传导方程的数值解');在上述程序中,我们首先定义了一些参数,包括空间长度L、时间长度T、空间网格数N、时间网格数M、空间步长dx、时间步长dt 以及热扩散系数alpha。
然后,我们初始化了温度分布,将左端点的温度设为100度。
接下来,我们使用双重循环来迭代求解温度分布,最后绘制出了温度分布的图像。
通过这个程序,我们可以方便地求解一维热传导方程,并得到其数值解。
当然,如果需要更精确的结果,我们可以增加空间网格数和时间网格数,来提高计算精度。
利用Matlab进行数值模拟的方法

利用Matlab进行数值模拟的方法引言数值模拟是现代科学领域中不可或缺的一种工具,它通过数学模型和计算机算法,模拟和预测实际系统的行为。
随着科学技术的不断发展,数值模拟方法逐渐成为各个学科的重要组成部分。
Matlab作为一种强大的科学计算工具,为数值模拟提供了丰富的函数库和易于使用的编程环境。
本文将介绍一些利用Matlab进行数值模拟的方法,以及其在不同领域的应用。
一、常微分方程的数值解法常微分方程在物理、工程、生物等领域中广泛存在。
利用Matlab进行常微分方程的数值解法,可以有效地求得方程的近似解。
Matlab中的ode45函数是常用的数值解法之一,它基于龙格-库塔算法,可以处理非刚性和刚性问题。
通过设定初始条件和方程形式,利用ode45函数可以得到系统的数值解,并绘制出相应的曲线图。
例如,考虑一个一阶常微分方程dy/dx = -2xy,初始条件为y(0) = 1。
可以通过以下代码进行数值模拟:```Matlabfun = @(x, y) -2*x*y;[x, y] = ode45(fun, [0, 10], 1);plot(x, y)xlabel('x')ylabel('y')title('Solution of dy/dx = -2xy')```运行以上代码后,可以得到方程解的图像,从而对其行为有更直观的理解。
二、偏微分方程的数值解法偏微分方程在物理、流体力学、电磁学等领域中具有重要应用。
常用的偏微分方程的数值解法有有限差分法(Finite Difference Method)和有限元法(Finite Element Method)等。
在Matlab中,可以利用pdepe函数进行偏微分方程的数值模拟,其中包含了一维和二维问题的求解算法。
以热传导方程为例,假设一个长为L的均匀杆子,其温度分布满足偏微分方程∂u/∂t = α*∂²u/∂x²,其中u(x, t)表示温度分布。
matlab 一维非稳态导热

matlab 一维非稳态导热一维非稳态导热问题是研究物体在时间和空间上温度分布变化的问题。
在导热过程中,物体内部的温度会随着时间的变化和空间位置的不同而发生变化。
为了研究这个问题,我们可以使用MATLAB进行数值模拟和分析。
我们需要定义问题的边界条件和初始条件。
边界条件包括物体的两端温度,初始条件是物体的初始温度分布。
通过设定合适的边界条件和初始条件,我们可以模拟不同情况下的一维非稳态导热问题。
然后,我们可以使用MATLAB的偏微分方程求解工具箱来求解一维非稳态导热方程。
该工具箱提供了一系列函数,可以用于求解偏微分方程问题。
我们可以将一维非稳态导热方程转化为偏微分方程的数值解,并使用MATLAB进行求解。
在MATLAB中,我们可以使用有限差分方法来近似求解偏微分方程。
有限差分方法是将连续的偏微分方程转化为离散的差分方程,通过迭代求解差分方程来逼近偏微分方程的解。
通过调整空间步长和时间步长,我们可以获得更精确的数值解。
在求解过程中,我们可以使用MATLAB的循环结构来迭代求解差分方程。
通过迭代过程,我们可以得到物体在不同时间点上的温度分布。
可以将每个时间点的温度分布绘制成图形,以直观地展示温度随时间变化的情况。
除了求解一维非稳态导热方程,MATLAB还提供了其他功能来分析和处理导热问题。
例如,可以使用MATLAB的插值函数来对温度分布进行插值,以获得更精确的温度数值。
还可以使用MATLAB的统计分析工具箱来对温度数据进行统计分析和可视化。
MATLAB是一个强大的工具,可以用于求解一维非稳态导热问题。
通过合适的边界条件和初始条件,以及适当的数值方法和工具箱函数,我们可以在MATLAB中模拟和分析物体的温度分布变化。
这对于研究导热问题和设计热传导器件等具有重要的意义。
matlab 偏微分方程

MATLAB是一个强大的数值计算环境,可以用来解决各种各样的数学问题,包括偏微分方程。
下面是一个简单的例子,展示如何在MATLAB中解决一维的偏微分方程。
假设我们要解决以下一维的热传导方程:
∂u∂t=∂2u∂x2
在给定的初始条件和边界条件下:
u(x,0)=sin(πx)u(0,t)=0, u(1,t)=0
我们可以使用MATLAB中的pdepe函数来求解这个问题。
以下是一个简单的MATLAB代码示例:
```matlab
定义参数
T = 1; 最终时间
h = 0.01; 空间步长
t = 0:T/h:T; 时间向量
x = 0:h:1; 空间向量
n = length(x); 空间点的数量
m = length(t); 时间点的数量
初始化矩阵存储解
U = zeros(m, n);
U(:,1) = sin(pi*x); 初始条件
定义偏微分方程
pdepe('u_tt', U, t, x, 'heat', 'periodic');
使用pdepe求解偏微分方程
[U, ~] = pdepe(U, t, x);
绘制结果
surf(x, t, U);
```
这个代码示例使用了MATLAB的pdepe函数,这是一个用于求解偏微分方程的函数。
在上面的代码中,我们首先定义了参数,然后初始化了存储解的矩阵。
然后,我们定义了偏微分方程,并使用pdepe 函数求解它。
最后,我们使用surf函数绘制了结果。
利用matlab程序解决热传导问题

哈佛大学能源与环境学院课程作业报告作业名称:传热学大作业——利用matlab程序解决热传导问题院系:能源与环境学院专业:建筑环境与设备工程学号:姓名:盖茨比2015年6月8日一、题目及要求1.原始题目及要求2.各节点的离散化的代数方程3.源程序4.不同初值时的收敛快慢5.上下边界的热流量(λ=1W/(m℃))6.计算结果的等温线图7.计算小结题目:已知条件如下图所示:二、各节点的离散化的代数方程各温度节点的代数方程ta=(300+b+e)/4 ; tb=(200+a+c+f)/4; tc=(200+b+d+g)/4; td=(2*c+200+h)/4 te=(100+a+f+i)/4; tf=(b+e+g+j)/4; tg=(c+f+h+k)/4 ; th=(2*g+d+l)/4ti=(100+e+m+j)/4; tj=(f+i+k+n)/4; tk=(g+j+l+o)/4; tl=(2*k+h+q)/4tm=(2*i+300+n)/24; tn=(2*j+m+p+200)/24; to=(2*k+p+n+200)/24; tp=(l+o+100)/12 三、源程序【G-S迭代程序】【方法一】函数文件为:function [y,n]=gauseidel(A,b,x0,eps)D=diag(diag(A));L=-tril(A,-1);U=-triu(A,1);G=(D-L)\U;f=(D-L)\b;y=G*x0+f;n=1;while norm(y-x0)>=epsx0=y;y=G*x0+f;n=n+1;end命令文件为:A=[4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0,0;-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0;0,-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0;0,0,-2,4,0,0,0,-1,0,0,0,0,0,0,0,0;-1,0,0,0,4,-1,0,0,-1,0,0,0,0,0,0,0;0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0,0;0,0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0;0,0,0,-1,0,0,-2,4,0,0,0,-1,0,0,0,0;0,0,0,0,-1,0,-1,0,4,0,0,0,-1,0,0,0;0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0,0;0,0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0;0,0,0,0,0,0,0,-1,0,0,-2,4,0,0,0,-1;0,0,0,0,0,0,0,0,-2,0,0,0,24,-1,0,0;0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1,0;0,0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1;0,0,0,0,0,0,0,0,0,0,0,-1,0,0,-1,12];b=[300,200,200,200,100,0,0,0,100,0,0,0,300,200,200,100]';[x,n]=gauseidel(A,b,[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]',1.0e-6) xx=1:1:4;yy=xx;[X,Y]=meshgrid(xx,yy);Z=reshape(x,4,4);Z=Z'contour(X,Y,Z,30)Z =139.6088 150.3312 153.0517 153.5639108.1040 108.6641 108.3119 108.1523 84.1429 67.9096 63.3793 62.4214 20.1557 15.4521 14.8744 14.7746 【方法2】>> t=zeros(5,5);t(1,1)=100;t(1,2)=100;t(1,3)=100;t(1,4)=100;t(1,5)=100;t(2,1)=200;t(3,1)=200;t(4,1)=200;t(5,1)=200;for i=1:10t(2,2)=(300+t(3,2)+t(2,3))/4 ;t(3,2)=(200+t(2,2)+t(4,2)+t(3,3))/4;t(4,2)=(200+t(3,2)+t(5,2)+t(4,3))/4;t(5,2)=(2*t(4,2)+200+t(5,3))/4;t(2,3)=(100+t(2,2)+t(3,3)+t(2,4))/4;t(3,3)=(t(3,2)+t(2,3)+t(4,3)+t(3,4))/4; t(4,3)=(t(4,2)+t(3,3)+t(5,3)+t(4,4))/4; t(5,3)=(2*t(4,3)+t(5,2)+t(5,4))/4;t(2,4)=(100+t(2,3)+t(2,5)+t(3,4))/4;t(3,4)=(t(3,3)+t(2,4)+t(4,4)+t(3,5))/4;t(4,4)=(t(4,3)+t(4,5)+t(3,4)+t(5,4))/4;t(5,4)=(2*t(4,4)+t(5,3)+t(5,5))/4;t(2,5)=(2*t(2,4)+300+t(3,5))/24;t(3,5)=(2*t(3,4)+t(2,5)+t(4,5)+200)/24;t(4,5)=(2*t(4,4)+t(3,5)+t(5,5)+200)/24;t(5,5)=(t(5,4)+t(4,5)+100)/12;t'endcontour(t',50);ans =100.0000 200.0000 200.0000 200.0000 200.0000 100.0000 136.8905 146.9674 149.8587 150.7444 100.0000 102.3012 103.2880 103.8632 104.3496 100.0000 70.6264 61.9465 59.8018 59.6008 100.0000 19.0033 14.8903 14.5393 14.5117【Jacobi迭代程序】函数文件为:function [y,n]=jacobi(A,b,x0,eps)D=diag(diag(A));L=-tril(A,-1);U=-triu(A,1);B=D\(L+U);f=D\b;y=B*x0+f;n=1;while norm(y-x0)>=epsx0=y;y=B*x0+f;n=n+1;end命令文件为:A=[4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0,0;-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0; 0,-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0; 0,0,-2,4,0,0,0,-1,0,0,0,0,0,0,0,0;-1,0,0,0,4,-1,0,0,-1,0,0,0,0,0,0,0; 0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0,0; 0,0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0;0,0,0,-1,0,0,-2,4,0,0,0,-1,0,0,0,0;0,0,0,0,-1,0,-1,0,4,0,0,0,-1,0,0,0;0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0,0;0,0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0;0,0,0,0,0,0,0,-1,0,0,-2,4,0,0,0,-1;0,0,0,0,0,0,0,0,-2,0,0,0,24,-1,0,0;0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1,0;0,0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1;0,0,0,0,0,0,0,0,0,0,0,-1,0,0,-1,12];b=[300,200,200,200,100,0,0,0,100,0,0,0,300,200,200,100]'; [x,n]=jacobi(A,b,[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]',1.0e-6); xx=1:1:4;yy=xx;[X,Y]=meshgrid(xx,yy);Z=reshape(x,4,4);Z=Z'contour(X,Y,Z,30)n =97Z =139.6088 150.3312 153.0517 153.5639108.1040 108.6641 108.3119 108.152384.1429 67.9096 63.3793 62.421420.1557 15.4521 14.8744 14.7746四、不同初值时的收敛快慢1、[方法1]在Gauss 迭代和Jacobi 迭代中,本程序应用的收敛条件均为norm(y-x0)>=eps ,即使前后所求误差达到e 的-6次方时,跳出循环得出结果。
有限体积法 matlab代码

有限体积法(Finite Volume Method)是一种常用的数值计算方法,用于求解偏微分方程。
下面是一个简单的示例,展示如何使用MATLAB实现一维热传导方程的有限体积法。
```matlab% 参数设置nx = 50; % 空间离散点数L = 1; % 空间长度dx = L/nx; % 空间步长nt = 100; % 时间步数dt = 0.01; % 时间步长alpha = 0.1; % 热扩散率% 初始化温度场T = zeros(nx, 1);T(1) = 100; % 左边界温度T(nx) = 0; % 右边界温度% 时间迭代计算for t = 1:nt% 临时温度场变量T_tmp = T;% 空间迭代计算for i = 2:nx-1% 更新温度T(i) = T_tmp(i) + alpha * dt * (T_tmp(i+1) - 2*T_tmp(i) + T_tmp(i-1)) / dx^2;end% 边界条件T(1) = 100; % 左边界温度T(nx) = 0; % 右边界温度% 绘制温度分布图plot(linspace(0, L, nx), T, 'r-');xlabel('位置');ylabel('温度');title(['时间步: ', num2str(t)]);drawnow;end```上述代码实现了一维热传导方程的有限体积法求解过程。
其中,空间离散点数`nx`和时间步数`nt`可以根据需要进行调整。
`alpha`是热扩散率,依赖于材料的性质。
初始温度场通过设置边界条件和初始条件进行定义。
在每个时间步中,通过计算更新温度场的中心差分格式,同时保持边界条件不变。
绘制温度分布图可以实时观察温度的变化。
请注意,这只是一个简单的示例,实际问题可能涉及到更复杂的边界条件、非均匀网格、时间步长控制等。
具体实现需要根据具体问题进行调整和扩展。
一维导热方程有限差分法matlab实现

第五次作业(前三题写在作业纸上)一、用有限差分方法求解一维非定常热传导方程,初始条件和边界条件见说明.pdf 文件,热扩散系数α=const ,22T T t xα∂∂=∂∂ 1. 用Tylaor 展开法推导出FTCS 格式的差分方程2. 讨论该方程的相容性和稳定性,并说明稳定性要求对求解差分方程的影响。
3. 说明该方程的类型和定解条件,如何在程序中实现这些定解条件。
4. 编写M 文件求解上述方程,并用适当的文字对程序做出说明。
(部分由网络搜索得到,添加,修改后得到。
)function rechuandaopde%以下所用数据,除了t 的范围我根据题目要求取到了20000,其余均从pdf 中得来 a=0.00001;%a 的取值xspan=[0 1];%x 的取值范围tspan=[0 20000];%t 的取值范围ngrid=[100 10];%分割的份数,前面的是t 轴的,后面的是x 轴的f=@(x)0;%初值g1=@(t)100;%边界条件一g2=@(t)100;%边界条件二[T,x,t]=pdesolution(a,f,g1,g2,xspan,tspan,ngrid);%计算所调用的函数[x,t]=meshgrid(x,t);mesh(x,t,T);%画图,并且把坐标轴名称改为x ,t ,Txlabel('x')ylabel('t')zlabel('T')T%输出温度矩阵dt=tspan(2)/ngrid(1);%t 步长h3000=3000/dt;h9000=9000/dt;h15000=15000/dt;%3000,9000,15000下,温度分别在T矩阵的哪些行T3000=T(h3000,:)T9000=T(h9000,:)T15000=T(h15000,:)%输出三个时间下的温度分布%不再对三个时间下的温度-长度曲线画图,其图像就是三维图的截面%稳定性讨论,傅里叶级数法dx=xspan(2)/ngrid(2);%x步长sta=4*a*dt/(dx^2)*(sin(pi/2))^2;if sta>0,sta<2fprintf('\n%s\n','有稳定性')elsefprintf('\n%s\n','没有稳定性')errorend%真实值计算[xe,te,Te]=truesolution(a,f,g1,g2,xspan,tspan,ngrid);[xe,te]=meshgrid(xe,te);mesh(xe,te,Te);%画图,并且把坐标轴名称改为xe,te,Texlabel('xe')ylabel('te')zlabel('Te')Te%输出温度矩阵%误差计算jmax=1/dx+1;%网格点数[rms]=wuchajisuan(T,Te,jmax)rms%输出误差function [rms]=wuchajisuan(T,Te,jmax)for j=1:jmaxrms=((T(j)-Te(j))^2/jmax)^(1/2)endfunction[Ue,xe,te]=truesolution(a,f,g1,g2,xspan,tspan,ngrid)n=ngrid(1);%t份数m=ngrid(2);%x份数Ue=zeros(ngrid);xe=linspace(xspan(1),xspan(2),m);%画网格te=linspace(tspan(1),tspan(2),n);%画网格for j=2:nfor i=2:m-1for g=1:m-1Ue(j,i)=100-(400/(2*g-1)/pi)*sin((2*g-1)*pi*xe(j))*exp(-a*(2*g-1)^2*pi^2*te(i)) endendendfunction [U,x,t]=pdesolution(a,f,g1,g2,xspan,tspan,ngrid)n=ngrid(1);%t份数m=ngrid(2);%x份数h=range(xspan)/(m-1);%x网格长度x=linspace(xspan(1),xspan(2),m);%画网格k=range(tspan)/(n-1); %t网格长度t=linspace(tspan(1),tspan(2),n);%画网格U=zeros(ngrid);U(:,1)=g1(t);%边界条件U(:,m)=g2(t);U(1,:)=f(x);%初值条件%差分计算for j=2:nfor i=2:m -1U(j,i)=(1-2*a*k/h^2)*U(j -1,i)+a*k/h^2*U(j -1,i -1)+a*k/h^2*U(j -1,i+1);endend5. 将温度随时间变化情况用曲线表示x t T6. 给出3000、9000、15000三个时刻的温度分布情况,对温度随时间变化规律做说明。
MATLAB编辑一维热传导方程的模拟程序

求解下列热传导问题: 【1 】()()()()⎪⎪⎪⎩⎪⎪⎪⎨⎧====-=≤≤=∂∂-∂∂1,10,,1,010,001222ααL t L T t T zz T L z t T z T程序:function heat_conduction() %一维齐次热传导方程options={'空间杆长L','空间点数N' ,'时光点数M','集中系数alfa','稳固前提的值lambda(取值必须小于0.5)',};topic='seting';lines=1;def={'1','100','1000','1','0.5'};h=inputdlg(options,topic,lines,def);L=eval(h{1});N=eval(h{2});M=eval(h{3});alfa=eval(h{4});lambda=eval(h{5});%lambda 的值必须小于%***************************************************h=L/N;%空间步长z=0:h:L;z=z';tao=lambda*h^2/alfa;%时光步长tm=M*tao;%热传导的总时光tmt=0:tao:tm;t=t';%盘算初值和边值T=zeros(N+1,M+1);Ti=init_fun(z);To=border_funo(t);Te=border_fune(t);T(:,1)=Ti;T(1,:)=To;T(N+1,:)=Te;%用差分法求出温度T与杆长L.时光t的关系for k=1:Mm=2;while m<=NT(m,k+1)=lambda*(T(m+1,k)+T(m-1,k))+(-2*lambda+1)*T(m,k); m=m+1;end;end;%设置立体网格for i=1:M+1X(:,i)=z;end;for j=1:N+1Y(j,:)=t;endmesh(X,Y,T);view([1 -1 1]);xlabel('Z');ylabel('t');zlabel('T');function y=init_fun(z)%初值前提y=1-z.^2;returnfunction y=border_funo(t)%z=0的鸿沟前提y=1+t.*0;returnfunction y=border_fune(t)%z=L的鸿沟前提y=t*.0;return运行情形:按“run”运行时,弹出窗口将图中相干数据更改为:点击图框中的“OK”,在“command window”中输出成果为:。
一维非稳态无内热源导热 matlab

以下是一维非稳态无内热源导热的MATLAB 代码示例:```matlab设置初始条件和边界条件T = zeros(1,100); 初始温度场T(50) = 20; 室内初始温度T(1:10) = -25.4; 室外初始温度alpha = 0.05; 导热系数rho = 1.2; 密度Cp = 1.0; 比热容dx = 0.1; 空间步长dt = dx^2 / (4 * alpha); 时间步长t_end = 100 * dt; 结束时间t = 0:dt:t_end; 时间数组x = -10:dx:10; x坐标数组计算初始温度场for i = 1:length(t)T_old = T; 保存上一步的温度场for j = 2:length(x)if x(j-1) < x(j)T(j) = T_old(j-1) + alpha * dt / (dx^2) * (x(j)^2 - x(j-1)^2);elseT(j) = T_old(j) - alpha * dt / (dx^2) * (x(j)^2 - x(j+1)^2);endendend绘制温度场随时间变化的图像figure;hold on;for i = 1:length(t)plot(x, T(:, i));xlim([-15, 15]);ylim([-1, 40]);title(['Time = ', num2str(t(i)/dt), ' s']);xlabel('Position (m)');ylabel('Temperature (K)');drawnow;pause(0.1);end```以上代码使用显式离散格式求解一维非稳态无内热源导热问题,计算了不同时刻的瞬态温度场,并绘制了温度场随时间变化的图像。
注意,以上代码仅供参考,实际应用中需要根据具体问题进行修改和优化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MATLAB编辑一维热传
导方程的模拟程序
-CAL-FENGHAI-(2020YEAR-YICAI)」INGBIAN
求解下列热传导问题:
^-1^=0 (。
"5厶)
a dt
r(z,o)=i-z2 r(07)=i, T(LJ)=O
L = l, a = 1
程序:
function heat_conduction() %一维齐次热传导方程
options彳空间杆长L:空间点数NJ时间点数扩散系数alfa^稳定条件的值lambdaf 取值必须小于
topic=,seting,;
lin es=l;
def={'l,;100,z,1000,z,l,/"};
h=in putdlg(opti on s,topic,li nes’def);
L=eval(h{l});
N=eval(h{2});
M=eval(h{3});
alfa=eval(h{4});
lambda=eval(h{5});%lambda 的值必须小于
h=L/N;%空间步长
z=O:h:L;
z=z';
tao=lambda*h A2/alfa;% 时间步长
tm=M*tao;%热传导的总时间tm
t=0:tao:tm;
t=f;
%计算初值和边值
T=zeros(N+l,M+l);
Ti=init_fu n(z);
To=border_funo(t);
Te=border_fu ne(t);
T(:,l)=Ti;
T(l,:)=To;
T(N+l,:)=Te;
%用差分法求出温度T与杆长L、时间t的关系
for k=l:M
m=2;
while m<=N
T(m,k+l)=lambda* (T(m+l/k)+T(m-l/k))+(-2*lambda+l)*T(m,k); m=m+l;
end;
end;
%设置立体网格
for i=l:M+l
X(:,i)=z;
end;
for j=l:N+l
Y(j,:)=t;
end
mesh(X'Y’T); view([l -1 1]); xlabel('Z'); ylabelCf); zlabel(T); function y=init_fun(z)%初值条件y=l-z.A2;
return
function y=border_funo(t)%z=0的边界条件y=l+t.*O;
return
function y=border_fune(t)%z=L的边界条件y=t*.O; return
运行情况:
按"run"运行时,弹出窗口
将图中相关数据更改为:
点击图框中的“OK",在"command window^中输出结果为:
1 0
Z。
