广东中考数学三角形和四边形专题复习

合集下载

中考数学三角形与四边形复习题及答案

第二部分空间与图形第四章三角形与四边形第1讲线、角、相交线和平行线一级训练1．(2011年安徽芜湖)一个角的补角是36°35′，这个角是________．2．如图4－1－12，已知线段AB＝10 cm，AD＝2 cm，D为线段AC的中点，那么线段CB＝________cm.图4－1－123．(2012年湖南株洲)如图4－1－13，已知直线a∥b，直线c与a，b分别交于点A，B，且∠1＝120°，则∠2＝()图4－1－13A．60°B．120°C．30°D．150°4．(2011年四川南充)如图4－1－14，直线DE经过点A，DE∥BC，∠B＝60°，下列结论成立的是()图4－1－14A．∠C＝60°B．∠DAB＝60°C．∠EAC＝60°D．∠BAC＝60°5．下列命题中，正确的是()A．若a·b＞0，则a＞0，b＞0 B．若a·b＜0，则a＜0，b＜0C．若a·b＝0，则a＝0且b＝0 D．若a·b＝0，则a＝0或b＝06．(2012年湖北孝感)已知∠α是锐角，∠α与∠β互补，∠α与∠r互余，则∠β－∠r的值等于()A．45°B．60°C．90°D．180°7．(2011年浙江丽水)如图4－1－15，有一块含有45°角的直角三角板的两个顶点放在直尺的对边上．如果∠1＝20°，那么∠2的度数是()A．30°B．25°C．20°D．15°图4－1－158．如图4－1－16，下列条件中，不能判断l1∥l2的是()图4－1－16A．∠1＝∠3 B．∠2＝∠3 C．∠4＝∠5 D．∠2＋∠4＝180°9．(2011年湖北孝感)如图4－1－17，直线AB，CD相交于点O，OT⊥AB于点O，CE∥AB交CD于点C.若∠ECO＝30°，则∠DOT＝()图4－1－17A．30°B．45° C. 60° D. 120°10．(2012年湖南怀化)如图4－1－18，已知AB∥CD，AE平分∠CAB，且交CD于点D，若∠C＝110°，则∠EAB＝()A．30°B．35°C．40°D．45°图4－1－1811．下列四个生活、生产现象：①用两个钉子就可以把木条固定在墙上；②植树时，只要定出两棵树的位置，就能确定同一行所在的直线；③从A地到B地架设电线，总是尽可能沿着线段AB架设；④把弯曲的公路变直，就能缩短路程．其中可用公理“两点之间，线段最短”来解决的现象有()A．①②B．①③C．②④D．③④12．如图4－1－19，一束光线垂直照射在水平地面，在地面上放一个平面镜，欲使这束光线经过平面镜反射后成水平光线，则平面镜与地面所成锐角的度数为()图4－1－19A．45°B．60°C．75°D．80°二级训练13．(2012年四川广元)一辆汽车在公路上行驶，两次拐弯后，仍在原来的方向上平行行驶，那么两个拐弯的角度()A．先向左转130°，再向左转50°B．先向左转50°，再向右转50°C．先向左转50°，再向右转40°D．先向左转50°，再向左转40°14．如图4－1－20，在△ABC中，∠C＝90°.若BD∥AE，∠DBC＝20°，则∠CAE的度数是()A．40°B．60°C．70°D．80°图4－1－2015．如图4－1－21，把一张长方形纸片沿EF折叠后，点D，C分别落在点D′，C′的位置．若∠EFB＝65°，则∠AED′＝()图4－1－21A．70°B．65°C．50°D．25°w16．观察下图4－1－22，寻找对顶角(不含平角)：(1)(2)(3)图4－1－22(1)如图4－1－22(1)，图中共有______对对顶角；(2)如图4－1－22(2)，图中共有______对对顶角；(3)如图4－1－22(3)，图中共有______对对顶角；(4)研究(1)～(3)小题中直线条数与对顶角的对数之间的关系，若有n条直线相交于一点，则可形成______对对顶角；(5)若有2 008条直线相交于一点，则可形成______对对顶角．三级训练17．如图4－1－23，∠AOB＝90°，∠BOC＝30°，射线OM平分∠AOC，ON平分∠BOC.图4－1－23(1)求∠MON的度数；(2)如果(1)中，∠AOB＝α，其他条件不变，求∠MON的度数；(3)如果(1)中，∠BOC＝β(β为锐角)，其他条件不变，求∠MON的度数；(4)从(1)、(2)、(3)的结果中，你能看出什么规律？第2讲三角形第1课时三角形一级训练1．已知在△ABC中，若∠A＝70°－∠B，则∠C＝()A．35°B．70°C．110°D．140°2．如图4－2－14，在△ABC中，∠A＝70°，∠B＝60°，点D在BC的延长线上，则∠ACD＝()A．100°B．120°C．130°D．150°图4－2－143．已知如图4－2－15的两个三角形全等，则α的度数是()图4－2－15A．72°B．60°C．58°D．50°4．(2011年湖南怀化)如图4－2－16，∠A，∠1，∠2的大小关系是()图4－2－16A. ∠A>∠1>∠2B. ∠2>∠1>∠AC. ∠A>∠2>∠1D. ∠2>∠A>∠15．(2011年江西)如图4－2－17，下列条件中，不能证明△ABD≌△ACD的是()图4－2－17A．BD＝DC，AB＝AC B．∠ADB＝∠ADC，∠BAD＝∠CADC．∠B＝∠C，∠BAD＝∠CAD D．∠B＝∠C，BD＝DC6．(2011年上海)下列命题中，是真命题的是()A．周长相等的锐角三角形都全等B．周长相等的直角三角形都全等C．周长相等的钝角三角形都全等D．周长相等的等腰直角三角形都全等7．(2012年山东德州)不一定在三角形内部的线段是()A．三角形的角平分线B．三角形的中线C．三角形的高D．三角形的中位线8．(2012年山东济宁)用直尺和圆规作一个角的平分线的示意图如图4－2－18，则能说明∠AOC＝∠BOC的依据是()A．SSS B．ASAC．AAS D．角平分线上的点到角两边距离相等图4－2－189．(2011年安徽芜湖)如图4－2－19，已知在△ABC中，∠ABC＝45°，F是高AD和BE 的交点，CD＝4，则线段DF的长度为()图4－2－19A．2 2B．4C．3 2D．4 210．以三条线段3,4，x－5为边组成三角形，则x的取值范围为________．11．若△ABC的周长为a，点D，E，F分别是△ABC三边的中点，则△DEF的周长为__________．12．(2011年江西)如图4－2－20，两块完全相同的含30°的直角三角形叠放在一起，且∠DAB＝30°.有以下四个结论：①AF⊥BC；②△ADG≌△ACF; ③O为BC的中点；④AG∶DE ＝3∶4.其中正确结论的序号是__________．图4－2－20二级训练13．(2011年山东威海)在△ABC中，AB＞AC，点D，E分别是边AB，AC的中点，点F 在边BC上，连接DE，DF，EF，则添加下列哪一个条件后，仍无法判定△BFD与△EDF全等？()A．EF∥AB B．BF＝CF C．∠A＝∠DFE D．∠B＝∠DEF14．(2011年浙江)如图4－2－21，点D，E分别在AC，AB上．(1)已知BD＝CE，CD＝BE，求证：AB＝AC；(2)分别将“BD＝CE”记为①，“CD＝BE”记为②，“AB＝AC”记为③.添加条件①、③，以②为结论构成命题1，添加条件②、③，以①为结论构成命题2.命题1是________命题，命题2是_________命题(选择“真”或“假”填入空格)．图4－2－2115．(2012年湖北随州)如图4－2－22，在△ABC中，AB＝AC，点D是BC的中点，点E 在AD上．求证：(1)△ABD≌△ACD；(2)BE＝CE.图4－2－22三级训练16．(2011年湖南衡阳)如图4－2－23，在△ABC 中，∠B ＝90°，AB ＝3，AC ＝5，将△ABC 折叠，使点C 与点A 重合，折痕为DE ，则△ABE 的周长为________．图4－2－2317．如图4－2－24，两根旗杆间相距12 m ，某人从点B 沿BA 走向点A ，一定时间后他到达点M ，此时他仰望旗杆的顶点C 和D ，两次视线的夹角为90°，且CM ＝DM ，已知旗杆AC 的高为3 m ，该人的运动速度为1 m/s ，求这个人运动了多长时间？图4－2－24第二部分空间与图形第四章三角形与四边形第1讲线、角、相交线和平行线【分层训练】 1．143°25′ 2.B 3.B 4.B 5.D 6.C 7.B 8.B 9．C 10.B 11.D 12．A 解析：如图D9，过点O 作OD ⊥OC ，根据平面镜反射定律，可得∠AOD ＝∠BOD .又∵AO 垂直于水平面，OB 平行于水平面，∴∠AOB ＝90°.∴∠AOD ＝∠BOD ＝45°.又∵OD ⊥OC ，∴∠BOC ＝90°－∠BOD ＝45°.由于OB 平行于水平面，可得∠1＝∠BOC ＝45°.图D911．D 13.B14．C 解析：由题意，可得∠EAB ＋∠DBA ＝180°，又由∠C ＝90°，可得∠CAB ＋∠CBA ＝90°，于是∠CAE ＋∠DBC ＝90°.故∠CAE ＝90°－∠DBC ＝70°.15．C 解析：∠D ′EF ＝∠DEF ＝∠EFB ＝65°，于是∠AED ′＝180°－∠D ′ED ＝50°. 16．(1)2 (2)6 (3)12 (4)n (n －1) (5)4 030 056解析：(1)如图4－1－22(1)，图中共有1×2＝2对对顶角； (2)如图4－1－22(2)，图中共有2×3＝6对对顶角； (3)如图4－1－22(3)，图中共有3×4＝12对对顶角；(4)研究(1)～(3)小题中直线条数与对顶角的对数之间的关系，若有n 条直线相交于一点，则可形成(n －1)n 对对顶角；(5)若有2 008条直线相交于一点，则可形成(2 008－1)×2 008＝4 030 056对对顶角．17．解：(1)∠MON ＝∠COM －∠CON ＝12∠AOC －12∠BOC ＝12×120°－12×30°＝45°.(2)∠MON ＝∠COM －∠CON ＝12∠AOC －12∠BOC ＝12(α＋30°)－12×30°＝12α.(3)∠MON ＝∠COM －∠CON ＝12∠AOC －12∠BOC ＝12(90°＋β)－12β＝45°.(4)∠MON 的大小等于∠AOB 的一半，与∠BOC 的大小无关．第2讲三角形第1课时三角形【分层训练】1．C 2.C 3.D 4.B 5.D 6.D 7.C 8.A 9.B10．6<x <12 解析：由题意，可得1<x －5<7，解得6<x <12. 11.a 2 解析：由题意，可得△DEF 的三边为△ABC 的中位线，故其周长为a 2. 12．①②③④ 13.C 14．(1)证明：连接BC ，∵ BD ＝CE ，CD ＝BE ，BC ＝CB ， ∴ △DBC ≌△ECB (SSS)． ∴ ∠DBC ＝∠ECB . ∴ AB ＝AC . (2)真假15．证明：(1)∵D 是BC 的中点， ∴BD ＝CD .在△ABD 和△ACD 中， ⎩⎪⎨⎪⎧BD ＝CD ，AB ＝AC ，AD ＝AD (公共边)，∴△ABD ≌△ACD (SSS)．(2)由(1)，可知：△ABD ≌△ACD ， ∴∠BAD ＝∠CAD ，即∠BAE ＝∠CAE . 在△ABE 和△ACE 中， ⎩⎪⎨⎪⎧AB ＝AC ，∠BAE ＝∠CAE ， AE ＝AE ，∴△ABE ≌△ACE (SAS)．∴BE ＝CE (全等三角形的对应边相等).16．7 解析：因为将△ABC 折叠，使点C 与点A 重合，折痕为DE ，所以EC ＝AE ，故△ABE 的周长为AB ＋BE ＋AE ＝AB ＋BE ＋EC ＝AB ＋BC ＝3＋4＝7.17．解：∵∠CMD ＝90°， ∴∠CMA ＋∠DMB ＝90°. 又∵∠CAM ＝90°，∴∠CMA ＋∠ACM ＝90°. ∴∠ACM ＝∠DMB . 又∵CM ＝MD ，∴Rt △ACM ≌Rt △BMD . ∴AC ＝BM ＝3.∴他到达点M 时，运动时间为3÷1＝3(s)．答：这人运动了3 s.。

中考数学冲刺专题训练(附答案)：三角形与四边形

精品基础教育教学资料，仅供参考，需要可下载使用！中考数学冲刺专题训练（附答案）：三角形与四边形一、选择题（本大题共8个小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的）1．一个等腰三角形的底边长是6，腰长是一元二次方程28150x x -+=的一根，则此三角形的周长是（） A ．16 B ．12C ．14D ．12或16【答案】A 【解析】解方程28150x x -+=，得：3x =或5x =，若腰长为3，则三角形的三边为3、3、6，显然不能构成三角形；若腰长为5，则三角形三边长为5、5、6，此时三角形的周长为16，故选：A ．2．如图，在△ABC 中，BE 是∠ABC 的平分线，CE 是外角∠ACM 的平分线，BE 与CE 相交于点E ，若∠A =60°，则∠BEC 是（）A ．15°B ．30°C ．45°D ．60°【答案】B 【解析】∵BE 是∠ABC 的平分线， ∴∠EBM=12∠ABC ， ∵CE 是外角∠ACM 的平分线， ∴∠ECM=12∠ACM ，则∠BEC=∠ECM-∠EBM=12×（∠ACM-∠ABC ）=12∠A=30°，故选：B ．3．如图，在△ABC 中，∠C ＝90°，AC ＝12，AB 的垂直平分线EF 交AC 于点D ，连接BD ，若cos ∠BDC ＝57，则BC 的长是（）A ．10B ．8C ．3D ．6【答案】D 【解析】∵∠C ＝90°，cos ∠BDC ＝57，设CD ＝5x ，BD ＝7x ， ∴BC ＝6x ，∵AB 的垂直平分线EF 交AC 于点D ， ∴AD ＝BD ＝7x ， ∴AC ＝12x ， ∵AC ＝12， ∴x ＝1， ∴BC ＝6；故选D.4．一个菱形的边长为6，面积为28，则该菱形的两条对角线的长度之和为( ) A ．8 B ．12C ．16D ．32【答案】C 【解析】如图所示：四边形ABCD 是菱形，12AO CO AC ∴==， 12DC BO BD ==，AC BD ⊥，面积为28，∴12282AC BD OD AO ⋅=⋅=① 菱形的边长为6，2236OD OA ∴+=②，由①②两式可得：222()2362864OD AO OD OA OD AO +=++⋅=+=，8OD AO ∴+=，2()16OD AO ∴+=，即该菱形的两条对角线的长度之和为16，故选C ．5．如图，点B 、F 、C 、E 在一条直线上，AB ∥ED ，AC ∥FD ，那么添加下列一个条件后，仍无法判定△ABC ≌△DEF 的是（）A ．AB =DE B ．AC =DF C ．∠A =∠D D ．BF =EC【答案】C 【解析】解：选项A 、添加AB=DE 可用AAS 进行判定，故本选项错误；选项B 、添加AC=DF 可用AAS 进行判定，故本选项错误；选项C 、添加∠A=∠D 不能判定△ABC ≌△DEF ，故本选项正确；选项D 、添加BF=EC 可得出BC=EF ，然后可用ASA 进行判定，故本选项错误．故选C ．6．如图，ABCD 中，对角线AC 、BD 相交于点O ，OE BD ⊥交AD 于点E ，连接BE ，若ABCD 的周长为28，则ABE ∆的周长为（）A ．28B ．24C ．21D ．14【答案】D 【解析】∵四边形ABCD 是平行四边形， ∴OB OD =，AB CD =，AD BC =， ∵平行四边形的周长为28， ∴14AB AD += ∵OE BD ⊥，∴OE 是线段BD 的中垂线， ∴BE ED =，∴ABE ∆的周长14AB BE AE AB AD =++=+=，故选：D ．7．如图，在ABCD 中，将ADC ∆沿AC 折叠后，点D 恰好落在DC 的延长线上的点E 处．若=60B ︒∠，=3AB ，则ADE ∆的周长为（）A ．12B ．15C ．18D ．21【答案】C 【解析】由折叠可得，90ACD ACE ︒∠=∠=，90BAC ︒∴∠=，又60B ︒∠=，30ACB ︒∴∠=，26BC AB ∴==，6AD ∴=，由折叠可得，60E D B ︒∠=∠=∠=，60DAE ︒∴∠=，ADE ∴∆是等边三角形， ADE ∴∆的周长为6318⨯=，故选：C ．8．如图，在正方形ABCD 中，E 、F 分别是BC 、CD 上的点，且∠EAF ＝45°，AE 、AF 分别交BD 于M 、N ，连按EN 、EF 、有以下结论：①AN ＝EN ，②当AE ＝AF 时，BEEC＝2﹣2，③BE+DF ＝EF ，④存在点E 、F ，使得NF ＞DF ，其中正确的个数是（）A ．1B ．2C ．3D ．4【答案】B 【解析】 ①如图1，∵四边形ABCD 是正方形，∴∠EBM ＝∠ADM ＝∠FDN ＝∠ABD ＝45°，∵∠MAN＝∠EBM＝45°，∠AMN＝∠BME，∴△AMN∽△BME，∴AM MN BM EM=，∵∠AMB＝∠EMN，∴△AMB∽△NME，∴∠AEN＝∠ABD＝45°∴∠NAE＝∠AEN＝45°，∴△AEN是等腰直角三角形，∴AN＝EN，故①正确；②在△ABE和△ADF中，∵AB ADABE ADF90 AE AF︒=⎧⎪∠=∠=⎨⎪=⎩，∴Rt△ABE≌Rt△ADF（HL），∴BE＝DF，∵BC＝CD，∴CE＝CF，假设正方形边长为1，设CE＝x，则BE＝1﹣x，如图2，连接AC，交EF于H，∵AE＝AF，CE＝CF，∴AC是EF的垂直平分线，∴AC⊥EF，OE＝OF，Rt △CEF 中，OC ＝12EF ＝22x ， △EAF 中，∠EAO ＝∠FAO ＝22.5°＝∠BAE ＝22.5°， ∴OE ＝BE ， ∵AE ＝AE ，∴Rt △ABE ≌Rt △AOE （HL ）， ∴AO ＝AB ＝1， ∴AC ＝2＝AO+OC ，∴1+22x ＝2， x ＝2﹣2，∴BE EC ＝1(22)22---＝(21)(22)2-+＝22；故②不正确； ③如图3，∴将△ADF 绕点A 顺时针旋转90°得到△ABH ，则AF ＝AH ，∠DAF ＝∠BAH ， ∵∠EAF ＝45°＝∠DAF+∠BAE ＝∠HAE ， ∵∠ABE ＝∠ABH ＝90°， ∴H 、B 、E 三点共线，在△AEF 和△AEH 中，AE AE FAE HAE AF AH =⎧⎪∠=∠⎨⎪=⎩，∴△AEF ≌△AEH （SAS ）， ∴EF ＝EH ＝BE+BH ＝BE+DF ，故③正确；④△ADN 中，∠FND ＝∠ADN+∠NAD ＞45°， ∠FDN ＝45°， ∴DF ＞FN ，故存在点E 、F ，使得NF ＞DF ，故④不正确；故选B ．二、填空题（本大题共4个小题，每小题6分，共24分）9．如图，在△ABC 中，以点B 为圆心，以BA 长为半径画弧交边BC 与点D ，连结AD ，若∠B =40°，∠C =36°，则∠DAC 的度数是____________．【答案】34° 【解析】由作图过程可知BD=BA ， ∵∠B=40°， ∴∠BDA=∠BAD=12(180°-∠B)=70°， ∴∠DAC=∠BDA-∠C=70°-36°=34°. 故答案为34°. 10．如图，在矩形ABCD 中，1AB =，BC a =，点E 在边BC 上，且35BE α=．连接AE ，将ABE ∆沿AE 折叠，若点B 的对应点B '落在矩形ABCD 的边上，则 a 的值为________．【答案】53或53【解析】分两种情况：①当点B '落在AD 边上时，如图1．四边形ABCD 是矩形，90BAD B ︒∴∠=∠=，将ABE ∆沿AE 折叠，点B 的对应点B '落在AD 边上，1452BAE B AE BAD '︒∴∠=∠=∠=，AB BE ∴=，315a ∴=， 53a ∴=；②当点B '落在CD 边上时，如图2． ∵四边形ABCD 是矩形，90BAD B C D ︒∴∠=∠=∠=∠=，AD BC a ==．将ABE ∆沿AE 折叠，点B 的对应点B '落在CD 边上，90B AB E '︒∴∠=∠=，1AB AB '==，35EB EB a '==，2221DB B A AD a ''∴=-=-，3255EC BC BE a a =-=-=．在ADB '∆与B CE '∆中，90A 90B AD EBC B DD C ︒︒⎧∠=∠=-∠'''⎨∠=∠=⎩， ADB B CE ''∴∆⋃∆，DB AB CE B E'''∴=，即2112355a a a -=，解得153a =，20a =（舍去）．综上，所求a 的值为53或53．故答案为53或53． 11．如图，正方形ABCD 的边长为4，点E 是CD 的中点，AF 平分BAE ∠交BC 于点F ，将ADE ∆绕点A 顺时针旋转90°得ABG ∆，则CF 的长为_____．【答案】6-25 【解析】作FM AD M FN AG N ⊥⊥于，于，如图，易得四边形CFMD 为矩形，则4FM ＝∵正方形ABCD的边长为4，点是的中点，2DE ∴＝，∴224225AE =+=∵△ADE 绕点A 顺时针旋转90°得△ABG ，∴252349090AG AE BG DE GAE ABG D ∠∠∠︒∠∠︒＝＝，＝＝，＝，＝，＝＝而90ABC ∠︒＝， ∴点G 在CB 的延长线上，∵AF 平分∠BAE 交BC 于点F ，∴∠1＝∠2，∴∠2+∠4＝∠1+∠3，即F A 平分∠GAD ， ∴FN ＝FM ＝4， ∵11••22AB GF FN AG ＝, ∴425254GF ⨯==, ∴4225625CF CG GF +=-＝﹣＝﹣ ．故答案为6-25．12．如图，在平面直角坐标系中，OA ＝1，以OA 为一边，在第一象限作菱形OAA 1B ，并使∠AOB ＝60°，再以对角线OA 1为一边，在如图所示的一侧作相同形状的菱形OA 1A 2B 1，再依次作菱形OA 2A 3B 2，OA 3A 4B 3，……，则过点B 2018，B 2019，A 2019的圆的圆心坐标为_____．【答案】（-32018，3）2019）【解析】过A 1作A 1C ⊥x 轴于C ，∵四边形OAA1B是菱形，∴OA＝AA1＝1，∠A1AC＝∠AOB＝60°，∴A1C＝32，AC＝12，∴OC＝OA+AC＝32，在Rt△OA1C中，OA1＝2213OC AC+=，∵∠OA2C＝∠B1A2O＝30°，∠A3A2O＝120°，∴∠A3A2B1＝90°，∴∠A2B1A3＝60°，∴B1A3＝23，A2A3＝3，∴OA3＝OB1+B1A3＝33＝（3）3∴菱形OA2A3B2的边长＝3＝（3）2，设B1A3的中点为O1，连接O1A2，O1B2，于是求得，O1A2＝O1B2＝O1B133）1，∴过点B1，B2，A2的圆的圆心坐标为O1（0，23，∵菱形OA3A4B3的边长为333，∴OA4＝934，设B2A4的中点为O2，连接O2A3，O2B3，同理可得，O2A3＝O2B3＝O2B2＝3＝（3）2，∴过点B2，B3，A3的圆的圆心坐标为O2（﹣3，33），…以此类推，菱形OA2019A2020B2019的边长为（3）2019，OA2020＝（3）2020，设B2018A2020的中点为O2018，连接O2018A2019，O2018B2019，求得，O2018A2019＝O2018B2019＝O2018B2018＝（3）2018，∴点O2018是过点B2018，B2019，A2019的圆的圆心，∵2018÷12＝168…2，∴点O2018在射线OB2上，则点O2018的坐标为（﹣（3）2018，（3）2019），即过点B2018，B2019，A2019的圆的圆心坐标为：（﹣（3）2018，（3）2019），故答案为：（﹣（3）2018，（3）2019）．三、解答题（本大题共3个小题，每小题12分，共36分．解答应写出文字说明、证明过程或演算步骤）13．如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F、H在菱形ABCD的对角线BD上.=；（1）求证：BG DEFH=，求菱形ABCD的周长。

2021年广东省广州市九年级中考数学三轮冲刺复习：三角形(含答案)

2021广州中考三轮冲刺复习：三角形一、选择题1. 下面是小强用三根火柴组成的图形，其中符合三角形概念的是()2. 在一个三角形中，有一个角是55°，则另外的两个角可能是()A．95°，20°B．45°，80°C．55°，60°D．90°，20°3. 如图，在△ABC中，表示AB边上的高的图形是()4. 已知等腰三角形的腰和底的长分别是一元二次方程x2－6x＋8＝0的根，则该三角形的周长为()A. 8B. 10C. 8或10D. 125. 如图，在△ABC中，AB＝AC，BD平分∠ABC交AC于点D，AE∥BD交CB的延长线于点E，若∠E＝35°，则∠BAC的度数为()A. 40°B. 45°C. 60°D. 70°6. 在△ABC中，若∠B＝3∠A，∠C＝2∠B，则∠B的度数为()A．18°B．36°C．54°D．90°7. (2019•荆门)将一副直角三角板按如图所示的位置摆放，使得它们的直角边互相垂直，则1的度数是A．95︒B．100︒C．105︒D．110︒8. 如图，在△ABC中，∠B＝46°，∠C＝54°，AD平分∠BAC交BC于点D，DE∥AB交AC 于点E，则∠ADE的度数是()A．54°B．50°C．45°D．40°二、填空题9. 如图，已知AB，CD相交于点O，且∠A＝38°，∠B＝58°，∠C＝44°，则∠D＝________°.10. 若正多边形的一个外角是60°，则这个正多边形的内角和是________．11. 如图，已知∠A＝54°，∠B＝31°，∠C＝21°，则∠1＝________°.12. 如图，在△ABC中，∠ABC，∠ACB的平分线相交于点O，OD⊥OC交BC于点D.若∠A ＝80°，则∠BOD＝________°.13. 在△ABC中，AB＝4，AC＝3，AD是△ABC的角平分线，则△ABD与△ACD的面积之比是________．14. 模拟某人为机器人编制了一段程序(如图)，如果机器人以2 cm/s的速度在平地上按照程序中的步骤行走，那么该机器人从开始到停止所需的时间为________s.15. 如图，在△ABC中，BO平分∠ABC，CO平分∠ACB.若∠A＝70°，则∠BOC＝________°.16. 如图，若该图案是由8个形状和大小相同的梯形拼成的，则∠1＝________°.三、解答题17. 如图，佳佳和音音住在同一小区(A点)，每天一块去学校(B点)上学.一天，佳佳要先去文具店(C点)买练习本再去学校，音音要先去书店(D点)买书再去学校(B，D，C三点在同一条直线上).这天两人从家到学校谁走的路程远?为什么?18. 如图，已知BE 、CF 分别为ABC ∆中B ∠、C ∠的平分线，AM BE ⊥于M ，AN CF ⊥于N ，求证：MN BC ∥．19. 某单位修建正多边形花台，已知正多边形花台的一个外角的度数比一个内角度数的15多12°.(1)求出这个正多边形的一个内角的度数; (2)求这个正多边形的边数.20. 如图，CE是△ABC 的外角∠ACD 的平分线，且CE 交BA 的延长线于点E ，∠B ＝25°，∠E＝30°，求∠BAC 的度数．21. 如图，在△ABC中，BD 是角平分线，CE 是AB 边上的高，且∠ACB=60°，∠ADB=97°，求∠A 和∠ACE 的度数.NMEFCBA22. 观察与转化思想如图是五角星形，求∠A＋∠B＋∠C＋∠D＋∠E的度数．23. 已知:如图1-Z-20，在四边形ABCD中，∠D=90°，∠ABC=∠BCD，点E在直线BC上，点F在直线CD上，且∠AEB=∠CEF.(1)如图①，若AE平分∠BAD，求证:EF⊥AE;(2)如图②，若AE平分四边形ABCD的外角，其余条件不变，则(1)中的结论是否仍然成立?说明理由.24. 如图①所示，在△ABC中，∠1＝∠2，∠C>∠B，E为AD上一点，且EF⊥BC于点F.(1)试探索∠DEF与∠B，∠C之间的数量关系；(2)如图②所示，当点E在AD的延长线上时，其余条件都不变，你在(1)中探索得到的结论是否还成立？2021广州中考三轮冲刺复习：三角形-答案一、选择题1. 【答案】C2. 【答案】B[解析] ∵在一个三角形中，有一个角是55°，∴另外的两个角的和为125°，各选项中只有B选项中的两个角的和为125°.故选B.3. 【答案】D4. 【答案】B【解析】解一元二次方程x2－6x＋8＝0，得x1＝2，x2＝4.当三角形三边为2，2，4时，∵2＋2＝4，∴不符合三边关系，应舍去；当三角形三边为2，4，4时，∵2＋4>4，符合三边关系，∴三角形的周长为10，故选B.5. 【答案】A【解析】由AE∥BD，可得∠DBC＝∠E＝35°，由BD平分∠ABC可得∠ABC＝2∠DBC＝70°，由AB＝AC可得∠ABC＝∠C＝70°，由三角形内角和定理可得∠BAC＝180°－70°－70°＝40°.6. 【答案】C[解析] ∵在△ABC中，∠B＝3∠A，∠C＝2∠B，∴∠C＝6∠A.设∠A＝x，则∠B＝3x，∠C＝6x.由三角形内角和定理可得x＋3x＋6x＝180°，解得x＝18°，∴∠B＝3x＝54°.7. 【答案】C【解析】如图，由题意得，2454903060∠=︒∠=︒︒=︒，-，∴3245∠=∠=︒，由三角形的外角性质可知，134105∠=∠+∠=︒，故选C ．8. 【答案】D[解析] 由三角形内角和定理可知∠BAC ＝180°－∠B －∠C ＝180°－46°－54°＝80°.因为AD 平分∠BAC ，所以∠BAD ＝12∠BAC ＝40°. 因为DE ∥AB ，所以∠ADE ＝∠BAD ＝40°.二、填空题9. 【答案】64[解析] 由三角形内角和定理可知∠A ＋∠D ＋∠AOD ＝180°，∠B ＋∠C ＋∠BOC＝180°.∵∠AOD ＝∠BOC ， ∴∠A ＋∠D ＝∠B ＋∠C. ∴∠D ＝64°.10. 【答案】720°[解析] 该正多边形的边数为360°÷60°＝6.该正多边形的内角和为(6－2)×180°＝720°.11. 【答案】106[解析] 由三角形的外角性质可知，∠CDB ＝∠A ＋∠C ＝75°，∴∠1＝∠CDB ＋∠B ＝106°.12. 【答案】4013. 【答案】4∶3【解析】如解图，过D 作DE ⊥AB ，DF ⊥AC ，垂足分别为E 、F ，∵AD 是∠BAC 的平分线，∴DE ＝DF(角平分线上的点到角两边的距离相等)，设DE ＝DF ＝h ，则S △ABD S △ACD＝12AB·h 12AC·h ＝43.14. 【答案】16[解析] 由题意得，该机器人所经过的路径是一个正多边形，多边形的边数为36045＝8，则所走的路程是4×8＝32(cm)，故所用的时间是32÷2＝16(s)．15. 【答案】125[解析] ∵BO 平分∠ABC ，CO 平分∠ACB ，∴∠ABO ＝∠CBO ，∠BCO ＝∠ACO.∴∠CBO ＋∠BCO ＝12(∠ABC ＋∠ACB)＝12(180°－∠A)＝12(180°－70°)＝55°. ∴在△BOC 中，∠BOC ＝180°－55°＝125°.16. 【答案】67.5三、解答题17. 【答案】解:佳佳从家到学校走的路程远.理由:佳佳从家到学校走的路程是AC+CD+BD ，音音从家到学校走的路程是AD+BD.∵在△ACD 中，AC+CD>AD ，∴AC+CD+BD>AD+BD ，即佳佳从家到学校走的路程远.18. 【答案】延长AM 、AN 交BC 于点Q 、R ．由等腰三角形三线合一可得AM QM =、AN RN =再由三角形中位线可得MN BC ∥．19. 【答案】解:(1)设这个多边形的一个内角的度数是x °，则与其相邻的外角度数是15x °+12°.由题意，得x+1x+12=180，解得x=140.5即这个正多边形的一个内角的度数是140°.=9.(2)这个正多边形的每一个外角的度数为180°-140°=40°，所以这个正多边形的边数是36040 20. 【答案】解：∵∠B＝25°，∠E＝30°，∴∠ECD＝∠B＋∠E＝55°.∵CE是∠ACD的平分线，∴∠ACE＝∠ECD＝55°.∴∠BAC＝∠ACE＋∠E＝85°.21. 【答案】解:∵∠ADB=∠DBC+∠ACB，∴∠DBC=∠ADB-∠ACB=97°-60°=37°.∵BD是△ABC的角平分线，∴∠ABC=74°.∴∠A=180°-∠ABC-∠ACB=46°.∵CE是AB边上的高，∴∠AEC=90°.∴∠ACE=90°-∠A=44°.22. 【答案】解：如图，∵∠1是△CEG的外角，∴∠1＝∠C＋∠E.同理可得∠AFB＝∠B＋∠D.∵在△AFG中，∠A＋∠1＋∠AFG＝180°，∴∠A＋∠B＋∠C＋∠D＋∠E＝180°.23. 【答案】解:(1)证明:∵∠BAE=180°-∠ABC-∠AEB，∠EFC=180°-∠BCD-∠CEF，且∠ABC=∠BCD，∠AEB=∠CEF，∴∠BAE=∠EFC.∵AE平分∠BAD，∴∠BAE=∠DAE.∴∠EFC=∠DAE.∵∠EFC+∠EFD=180°，∴∠DAE+∠EFD=180°.∴∠AEF+∠D=360°-(∠DAE+∠EFD)=180°.又∵∠D=90°，∴∠AEF=90°.∴EF⊥AE.(2)EF⊥AE仍成立.理由如下:如图.∵∠1=∠ABC-∠AEB，∠F=∠BCD-∠CEF，且∠ABC=∠BCD，∠AEB=∠CEF，∴∠1=∠F.∵AE平分四边形ABCD的外角，∴∠1=∠2.∴∠F=∠2.∵∠2+∠EAD=180°，∴∠F+∠EAD=180°.∴∠AEF+∠D=360°-(∠F+∠EAD)=180°.又∵∠D=90°，∴∠AEF=90°.∴EF⊥AE.24. 【答案】解：(1)∵∠1＝∠2，∴∠1＝12∠BAC.又∵∠BAC ＝180°－(∠B ＋∠C)，∴∠1＝12[180°－(∠B ＋∠C)]＝90°－12(∠B ＋∠C)．∴∠EDF ＝∠B ＋∠1＝∠B ＋90°－12(∠B ＋∠C)＝90°＋12(∠B －∠C)．∵EF ⊥BC ，∴∠EFD ＝90°.∴∠DEF ＝90°－∠EDF ＝90°－[90°＋12(∠B －∠C)]＝12(∠C －∠B)．(2)当点E 在AD 的延长线上时，其余条件都不变，在(1)中探索得到的结论仍成立．。

2023中考数学复习：三角形、四边形图形变换

此时∠BA'C=90°.
当A'在BC的上方时,如图4,
又∵AB=A'B,AE⊥AA'于E,
∴∠ABF=∠A'BF.
又∵BF=BF,∴△ABF≌△A'BF(SAS),
∴∠BA'F=∠BAF=90°.
例题 1
1
2
返回类型清单
∴C,A',F在一条直线上.
1
1
∵S△BCF= BC·AB= A'B·CF,∴CF=BC=8.
∠BAC=30°+90°=120°,
∴∠D=180°-(∠ABD+∠BAD)=60°.
例题 1
1
2
返回类型清单
(3)当△A1B1C绕点C逆时针旋转过程中,
①请直接写出S△ABA 的最大值;

(3)解:①由题意,AC=2,AB=2 3,CA1=1,当点A1落在AC的延长线时,△ABA1
1
的面积最大,最大值为 ×2 3×(2+1)=3 3.
2
2
当A'在BC的下方时,如图5,
连接AF,A'F,则AF=A'F,
∵A'B=6,BC=8,∴A'C=2 .
过A'作A'P⊥CD,垂足落在DC的延长线上,
∵∠BCA'+∠A'CP=90°,∠A'CP+∠CA'P=90°,
例题 1
1
2
返回类型清单
∴∠BCA'=∠CA'P.
∵∠BA'C=∠A'PC,∴△A'BC∽△PCA',
形;
(2)把握运动中的特殊位置,临界位置,分段、分情况进行讨论;

广东中考数学第15讲三角形与多边形

导航
考点2三角形的中位线定理(5年1考) 中考典例
5.(2021·衢州)如图,在△ABC中,AB＝4, AC＝5,BC＝6,点D,E,F分别是AB,BC, CA的中点,连结DE,EF,则四边形ADEF的周长为( B )
A.6
B.9
C.12 D.15
解析:∵点D,E,F分别是AB,BC,CA的中点,
∴DE＝1AC＝2.5,AF＝1AC＝2.5,EF＝1AB＝2,AD＝1AB＝2,
2
2
2
2
∴四边形ADEF的周长＝AD+DE+EF+AF＝9,故选:B.
导航
6.(2020·株洲)如图所示,点D、E分别是
△ABC的边AB、AC的中点,连接BE,过
点C作CF∥BE,交DE的延长线于点F,
3
若EF＝3,则DE的长为 2 .
A.50 cm
B.45 cm
C.30 cm
D.15cm
2
6.如图,在△ABC中,点D,E分别是边AB,
BC的中点,若DE的长是3,则AC的长为
6.
导航
考点解读本考点是广东中考的高频考点,难度较低,命题形式一般为选择题或填空题.解答本考点的有关题目,关键在于掌握三角形的中位线定理,并加以灵活运用.注意以下要点:三角形的中位线平行于第三边并且等于第三边的一半.
115° .
导航
考点解读本考点是广东中考的高频考点,难度简单,命题形式一般为选择题或填空题.解答本考点的有关题目,关键在于掌握三角形的有关概念,注意以下要点: 1.三角形的三边关系,即任意两边之和大于第三边,任意两边之差小于第三边,解题时其实可以选定三边后,给三边大小排序,只要较短的两边之和大于最长的边即可. 2.应用三角形的外角性质解题时,要特别注意“不相邻”的理解. 三角形的外角和其相邻的内角是邻补角的关系;其性质都是针对与其不相邻的内角的.

中考数学中的三角形与四边形性质总结

中考数学中的三角形与四边形性质总结在中考数学中，三角形和四边形是重要的几何概念。

它们具有不同的性质和特点，理解和掌握它们的性质对于解题和应用几何知识都非常重要。

下面将对中考数学中的三角形和四边形的性质进行总结。

一、三角形的性质总结1. 三角的角度性质：- 三角形的内角和等于180度，即三个内角的和为180度。

- 直角三角形的两个锐角之和为90度。

2. 三角形的边长性质：- 三角形的任意两边之和大于第三边。

- 等边三角形的三条边相等，等腰三角形的两边相等。

- 在一般三角形中，较长边对应较大的角，较短边对应较小的角。

3. 三角形的相似性质：- 两个三角形的对应角相等，则这两个三角形相似。

- 两个三角形的对应边成比例，则这两个三角形相似。

二、四边形的性质总结1. 平行四边形的性质：- 对角线互相平分，即对角线的交点是对角线的中点。

- 对边相等，即平行四边形的对边长度相等。

- 对角线等分平行四边形的内角。

2. 矩形的性质：- 二对相对边平行。

- 二对相对边相等。

- 二对相对角相等，且为直角。

3. 菱形的性质：- 对角线互相垂直且互相平分。

- 对边相等。

4. 正方形的性质：- 矩形的所有性质都满足。

- 对角线相等且垂直。

总结：通过以上对三角形和四边形的性质总结，我们可以发现几何知识中的基本规律和特点。

掌握三角形和四边形的性质对于应用和解题非常重要。

在解决各种与三角形和四边形相关的问题时，我们可以利用这些性质来推导和证明，帮助我们更好地理解和解决问题。

在数学中，几何是一个重要的分支，而三角形和四边形是其中重要的基本图形。

了解和掌握三角形和四边形的性质，对于中考数学的学习和考试都是至关重要的。

通过不断练习和巩固，我们可以更加熟练地应用这些性质，解决各种与三角形和四边形相关的问题。

总之，通过对中考数学中的三角形和四边形性质的总结，我们可以更好地理解和应用这些知识，提高数学解题的能力。

在学习中，我们要善于总结和归纳，将所学的知识应用到实际问题中，不断提高自己的数学水平。

广东中考数学复习各地区2022年模拟试题分类(深圳专版)(5)——三角形(含解析)

广东中考数学复习各地区2018-2022年模拟试题分类（深圳专版）（5）——三角形一．选择题（共23小题） 1．（2022•福田区校级模拟）如图，在正方形ABCD 中，对角线AC 、BD 相交于点O ，以AD 为边向外作等边△ADE ，AE =√6，连接CE ，交BD 于F ，若点M 为AB 的延长线上一点，连接CM ，连接FM 且FM 平分∠AMC ，下列选项正确的有（） ①DF =√3−1；②S △AEC =3(1+√3)2；③∠AMC ＝60°；④CM +AM =√2MF ．A ．1个B ．2个C ．3个D ．4个2．（2022•龙华区二模）如图，直线a ∥b ∥c ，等边三角形△ABC 的顶点A 、B 、C 分别在直线a 、b 、c 上，边BC 与直线c 所夹的角∠1＝25°，则∠2的度数为（）A ．25°B ．30°C ．35°D ．45°3．（2022•宝安区二模）如图，在△ABC 中，分别以点A 和点B 为圆心，大于12AB 的长为半径作弧，两弧相交于M 、N 两点，连接MN ，交AB 于点H ，以点H 为圆心，HA 的长为半径作的弧恰好经过点C ，以点B 为圆心，BC 的长为半径作弧交AB 于点D ，连接CD ，若∠A ＝22°，则∠BDC ＝（）A ．52°B ．55°C ．56°D ．60° 4．（2022•福田区一模）如图，正方形ABCD 中，E 是BC 延长线上一点，在AB 上取一点F ，使点B 关于直线EF 的对称点G 落在AD 上，连接EG 交CD 于点H ，连接BH 交EF 于点M ，连接CM ．则下列结论，其中正确的是（） ①∠1＝∠2； ②∠3＝∠4； ③GD =√2CM ；④若AG ＝1，GD ＝2，则BM =√5．A ．①②③④B ．①②C ．③④D ．①②④ 5．（2022•光明区一模）如图，AB ∥CE ，∠A ＝40°，CE ＝DE ，则∠C ＝（）A ．40°B ．30°C ．20°D ．15° 6．（2022•南山区模拟）如图，△ABC 中，AB ＝5，AC ＝4，以点A 为圆心，任意长为半径作弧，分别交AB 、AC 于D 和E ，再分别以点D 、E 为圆心，大于二分之一DE 为半径作弧，两弧交于点F ，连接AF 并延长交BC 于点G ，GH ⊥AC 于H ，GH ＝2，则△ABG 的面积为（）A ．4B ．5C ．9D ．10 7．（2022•龙岗区模拟）平面直角坐标系中，已知A （1，2）、B （3，0）．若在坐标轴上取点C ，使△ABC 为等腰三角形，则满足条件的点C 的个数是（） A ．5 B ．6 C ．7 D ．8 8．（2022•宝安区三模）如图，在三角形ABC 中，AB ＝AC ，BC ＝6，三角形DEF 的周长是7，AF ⊥BC 于F ，BE ⊥AC 于E ，且点D 是AB 的中点，则AF ＝（）A ．√5B ．√7C ．√3D ．79．（2022•龙岗区校级模拟）如图，△ABC 中，D 是AB 的中点，E 在AC 上，且∠AED ＝90°+12∠C ，则BC +2AE 等于（）A ．ABB ．ACC ．32ABD ．32AC10．（2022•南山区校级一模）等腰三角形的一边为4，另一边为9，则这个三角形的周长为（）A ．17B ．22C ．13D ．17或22 11．（2022•罗湖区一模）由三角函数定义，对于任意锐角A ，有sin A ＝cos （90°﹣A ）及sin 2A +cos 2A ＝1成立．如图，在△ABC 中，∠A ，∠B 是锐角，BC ＝a ，AC ＝b ，AB ＝c ．CD ⊥AB 于D ，DE ∥AC 交BC 于E ，设CD ＝h ，BE ＝a '，DE ＝b '，BD ＝c '，则下列条件中能判定△ABC 是直角三角形的个数是（） ①a 2+b 2＝c 2；②aa '+bb '＝cc '；③sin 2A +sin 2B ＝1；④1a 2+1a 2=1a 2．A ．1个B ．2个C ．3个D ．4个 12．（2022•龙华区二模）如图，已知a ∥b ，将一块等腰直角三角板的两个顶点分别放在直线a 、b 上．若∠1＝23°，则∠2的度数为（）A ．68°B ．112°C ．127°D ．132° 13．（2022•福田区校级模拟）如图，在△ABC 中，∠B ＝45°，∠ACB ＝60°，AB ＝16，AD ⊥BC ，垂足为D ，∠ACB 的平分线交AD 于点E ，则AE 的长为（）A ．83√2 B ．4√2C ．163√2D ．6√214．（2022•罗湖区一模）在联欢会上，甲、乙、丙3人分别站在不在同一直线上的三点A 、B 、C 上，他们在玩抢凳子的游戏，要在他们中间放一个木凳，谁先抢到凳子谁获胜，为使游戏公平，凳子应放的最恰当的位置是△ABC 的（） A ．三条高的交点 B ．重心 C ．内心 D ．外心 15．（2022•福田区校级模拟）下列性质中，直角三角形具有而等腰三角形不一定具有的是（） A ．两边之和大于第三边 B ．内角和等于180°C ．有两个锐角的和等于90°D ．有一个角的平分线垂直于这个角的对边 16．（2022•南山区校级二模）如图，等腰△ABC 中，AB ＝AC ＝10，BC ＝6，直线EF 垂直平分AB 交AC 于D ，连接BD ，则△BCD 的周长等于（）A ．13B ．14C ．15D ．16 17．（2022•龙岗区校级二模）等腰三角形的两边分别为1和2，则其周长为（） A ．4 B ．5 C ．4或5 D ．无法确定 18．（2022•盐田区二模）如图，直线AB ∥CD ，直线EF 分别交AB ，CD 于E ，F 两点，EG 平分∠AEF ．若∠1＝29°，则∠2＝（）A．29°B．58°C．61°D．60°19．（2022•福田区一模）如图，已知a∥b，点A在直线a上，点B，C在直线b上，若∠1＝125°，∠2＝50°，则∠3为（）A．55°B．65°C．70°D．75°20．（2022•坪山区一模）如图，AB∥CD，∠1＝58°，FG平分∠EFD，则∠FGB的度数等于（）A．97°B．116°C．122°D．151°21．（2022•福田区校级模拟）如图，直线AB∥CD，直线EF分别交AB、CD于E、F两点，EG平分∠AEF，如果∠1＝32°，那么∠2的度数是（）A．64°B．68°C．58°D．60°22．（2022•福田区一模）如图，已知a∥b，点A在直线a上，点B、C在直线b上，∠1＝120°，∠2＝50°，则∠3为（）A．70°B．60°C．45°D．30°23．（2022•宝安区二模）如图，将一副直角三角板按图中所示的位置摆放，两条斜边互相平行，则∠1＝（）A．75°B．70°C．65°D．60°二．填空题（共8小题）24．（2022•龙岗区校级模拟）如图，在△ABC中，AD⊥BC于D，BE⊥AC于E，M为AB边的中点，连结ME、MD、ED，设AB＝10，∠DBE＝30°，则△EDM的面积为．25．（2022•龙岗区一模）如图，在△ABC中，∠BAC的平分线AD和边BC的垂直平分线ED相交于点D，过点D作DF垂直于AC交AC的延长线于点F，若AB＝8，AC＝4，则CF的长为．26．（2022•宝安区校级一模）如图，在等腰Rt△OAA1中，∠OAA1＝90°，OA＝1，以OA1为直角边作等腰Rt△OA1A2，以OA2为直角边作等腰Rt△OA2A3，…则OA8的长度为．27．（2022•龙岗区模拟）如图△ABC中，AB＝AC，∠BAC＝120°，∠DAE＝60°，BD＝5，CE＝8，则DE的长为．28．（2022•深圳三模）如图，在△ABC中，AB＝AC．M、N分别是AB、AC的中点，D、E为BC上的点，连接DN、EM．若AB＝5cm，BC＝6cm，DE＝3cm，则图中阴影部分的面积为cm2．29．（2022•福田区校级模拟）如图，△ABC中，AB＝AC＝8，D为BC上一点，BD＝3，∠ADE＝∠B＝30°，则AE的长为．30．（2022•龙岗区校级模拟）如图，D、E分别是△ABC边AB、BC上的点，AD＝2BD，BE＝CE．设△ADF 的面积为S1，△CEF的面积为S2，若S△ABC＝6，则S1﹣S2＝．31．（2022•深圳模拟）如图，△ABC的顶点均在坐标轴上AE⊥BC于点E，交y轴于点D，已知点B，C的坐标分别为B（0，6），C（2，0）．若AD＝BC，则△AOD的面积为．三．解答题（共5小题）32．（2022•宝安区二模）如图1，在平面直角坐标系中，等边△ABC的边BC在x轴上，A（0，3），B（−√3，0），点M（m，0）为x轴上的一个动点，连接AM，将AM绕点A逆时针旋转60°得到AN．（1）当M点在B点的左方时，连接CN，求证：△BAM≌△CAN；（2）如图2，当M点在边BC上时，过点N作ND∥AC交x轴于点D，连接MN，若S四边形ACDN=43S△MND，试求D点的坐标；（3）如图3，是否存在点M，使得点N恰好在抛物线y＝﹣2x2+4√3x+3上，如果存在，请求出m的值，如果不存在，请说明理由．33．（2022•龙岗区模拟）四边形ABCD中，AD＝BC，BE＝DF，AE⊥BD，CF⊥BD，垂足分别为E、F．（1）求证：△ADE≌△CBF；（2）若AC与BD相交于点O，求证：AO＝CO．34．（2022•龙岗区模拟）如图，在△ABC中，∠ABC＝60°，AD、CE分别平分∠BAC、∠ACB，求证：AC ＝AE+CD．35．（2022•宁波一模）如图，在△ABC中，∠C＝90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E．（1）求证：△ACD≌△AED；（2）若∠B＝30°，CD＝1，求BD的长．36．（2022•南山区一模）如图，在Rt△ABC中，∠C＝90°，∠A＝30°．点D是AB中点，点E为边AC 上一点，连接CD，DE，以DE为边在DE的左侧作等边三角形DEF，连接BF．（1）△BCD的形状为；（2）随着点E位置的变化，∠DBF的度数是否变化？并结合图说明你的理由；（3）当点F落在边AC上时，若AC＝6，请直接写出DE的长．广东中考数学复习各地区2022-2022年模拟试题分类（深圳专版）（5）——三角形参考答案与试题解析一．选择题（共23小题）1．【答案】C【解答】解：如图，过点F作FG⊥CD于G，作∠HFC＝∠DCE，交CD于H，连接OE交AD于P，连接AF，在AM上截取MQ＝MC，连接FQ，∵四边形ABCD是正方形，△ADE是等边三角形，∴AD＝CD，AE＝AD=√6，∠ADE＝60°，∠ADC＝90°，∠ADB＝∠CDB＝45°，∴∠EDC＝150°，DE＝DC=√6，∴∠DEC＝∠DCE＝15°，∴∠HFC＝∠DCE＝15°，∴HC＝HF，∠FHG＝30°，∵FG⊥CD，∠BDC＝45°，∠FHG＝30°，∴DG＝GF，GH=√3GF，HF＝2GF＝HC，∴DF=√2GF，∵CD＝DG+HG+HC＝（3+√3）GF=√6，∴GF=√6−√22，∴DF=√2GF=√3−1，故①正确；∵DE＝AE，DO＝AO，∴EO垂直平分AD，∴EP⊥AD，又∵△AED是等边三角形，AD＝DE=√6，∴AP=√62，EP=√3AP=3√22，∵DO＝AO，∠AOD＝90°，OP⊥AD，AD=√6，∴OP=√6 2，∴EO＝OP+EP=3√2+√62，∵S△AEC＝S△AEO+S△EOC=12×3√2+√62×√6=3(√3+1)2，故②正确；∵FM平分∠AMC，∴∠CMF＝∠AMF，又∵CM＝QM，FM＝FM，∴△CMF≌△QMF（SAS），∴∠MCF＝∠FQM，FC＝FQ，∵AD＝CD，∠ADB＝∠CDB，DF＝DF，∴△ADF≌△CDF（SAS），∴AF＝CF，∠DCF＝∠DAF＝15°，∴∠F AQ＝75°，F A＝FQ＝FC，∴∠FQA＝F AQ＝75°，∴∠FQM＝∠FCM＝105°，∴∠DCM＝120°，∵DC∥AB，∴∠AMC+∠DCM＝180°，∴∠AMC＝60°，故③正确；如图，过点C作CN⊥MF于N，设BM＝a，∵∠CBM＝90°，∠CMB＝60°，∴CM＝2BM＝2a，CB=√3a＝AB，∴AM=√3a+a，∴AM+CM＝（√3+3）a，∵∠CMF=12∠CMA＝30°，∴∠CFM＝180°﹣105°﹣30°＝45°，∵CN⊥FM，∠CMN＝30°，∠CFM＝45°，∴CN=12CM＝a，MN=√3a，FN＝CN＝a，∴MF=√3a+a，∴AM+CM=√3MF，故④错误，故选：C．2．【答案】C【解答】解：∵b∥c，∴∠3＝∠1＝25°，∵△ABC是等边三角形，∴∠ABC＝60°，∴∠4＝∠ABC﹣∠3＝60°﹣25°＝35°，∵a∥b，∴∠2＝∠4＝35°，故选：C．3．【答案】C【解答】解：连接CH，由题意得，直线MN是线段AB的垂直平分线，∴AH＝BH，∵CH＝AH，∴CH=12AB，∴∠ACB＝90°，∵∠A＝22°，∴∠ACH＝∠A＝22°，∴∠BCH＝∠B＝68°，∵BC＝BD，∴∠BDC＝∠BCD=12（180°﹣68°）＝56°，故选：C．4．【答案】A【解答】解：如图1中，过点B作BK⊥GH于K．∵B，G关于EF对称，∴EB＝EG，∴∠EBG＝∠EGB，∵四边形ABCD是正方形，∴AB＝BC，∠A＝∠ABC＝∠BCD＝90°，AD∥BC，∴∠AGB＝∠EBG，∴∠AGB＝∠BGK，∵∠A＝∠BKG＝90°，BG＝BG，∴△BAG≌△BKG（AAS），∴BK＝BA＝BC，∠ABG＝∠KBG，∵∠BKH＝∠BCH＝90°，BH＝BH，∴Rt△BHK≌Rt△BHC（HL），∴∠1＝∠2，∠HBK＝∠HBC，故①正确，∴∠GBH＝∠GBK+∠HBK=12∠ABC＝45°，过点M作MQ⊥GH于Q，MP⊥CD于P，MR⊥BC于R．∵∠1＝∠2，∴MQ＝MP，∵∠MEQ＝∠MER，∴MQ＝MR，∴MP＝MR，∴∠4＝∠MCP=12∠BCD＝45°，∴∠GBH＝∠4，故②正确，如图2中，过点M作MW⊥AD于W，交BC于T．∵B，G关于EF对称，∴BM＝MG，∵CB＝CD，∠4＝∠MCD，CM＝CM，∴△MCB≌△MCD（SAS），∴BM＝DM，∴MG＝MD，∵MW⊥DG，∴WG＝WD，∵∠BTM＝∠MWG＝∠BMG＝90°，∴∠BMT+∠GMW＝90°，∵∠GMW+∠MGW＝90°，∴∠BMT＝∠MGW，∵MB＝MG，∴△BTM≌△MWG（AAS），∴MT＝WG，∵MC=√2TM，DG＝2WG，∴DG=√2CM，故③正确，∵AG＝1，DG＝2，∴AD＝AB＝TM＝3，EM＝WD＝TM＝1，BT＝AW＝2，∴BM=√aa2+aa2=√22+12=√5，故④正确，故选：A．5．【答案】C【解答】解：∵AB∥CE，∴∠AEC＝∠A＝40°，∵CE＝DE，∴∠C＝∠D，∴∠AEC＝∠C+∠D＝2∠C，∴∠C=12∠AEC=12×40°＝20°．故选：C．6．【答案】B【解答】解：作GM⊥AB于M，如图，由作法得AG平分∠BAC，而GH⊥AC，GM⊥AB，∴GM＝GH＝2，∴S△ABG=12×5×2＝5．故选：B．7．【答案】C【解答】解：∵点A、B的坐标分别为（1，2）、B（3，0）．∴AB＝2√2，①若AC＝AB，以A为圆心，AB为半径画弧与坐标轴有3个交点（B点除外），即（﹣1，0）、（0，2+√7）、（0，2−√7），即满足△ABC是等腰三角形的C点有3个；②若BC＝AB，以B为圆心，BA为半径画弧与坐标轴有2个交点，即满足△ABC是等腰三角形的C点有2个；③若CA＝CB，作AB的垂直平分线与坐标轴有2个交点，即满足△ABC是等腰三角形的C点有2个．综上所述：点C在坐标轴上，△ABC是等腰三角形，符合条件的点C共有7个．故选：C．8．【答案】B【解答】解：∵AF⊥BC，BE⊥AC，D是AB的中点，∴DE＝DF=12AB，∵AB＝AC，AF⊥BC，∴点F是BC的中点，∴BF＝FC＝3，∵BE⊥AC，∴EF=12BC＝3，∴△DEF的周长＝DE+DF+EF＝AB+3＝7，∴AB＝4，由勾股定理知AF=√aa2−aa2=√7，故选：B．9．【答案】B【解答】解：如图，过点B作BF∥DE交AC于点F．则∠BFC＝∠DEF．又∵点D是AB的中点，∴EF＝AE．∵∠DEF＝∠BFC＝180°﹣∠AED＝180°﹣（90°+12∠C）＝90°−12∠C，∴∠FBC＝∠BFC，∴BC＝FC，∴BC+2AE＝AC．故选：B．10．【答案】B【解答】解：当腰长为4时，则三角形的三边长为：4、4、9；∵4+4＜9，∴不能构成三角形；因此这个等腰三角形的腰长为9，则其周长＝9+9+4＝22．故选：B．11．【答案】D【解答】解：∵a2+b2＝c2，∴∠ACB＝90°，∴△ABC 是直角三角形，故①正确，∵DE ∥AC ，∴△DEB ∽△ACB ， ∴aa aa =aa aa =aa aa ， ∴a′a =a′a =a′a ，不妨设a′a =a′a =a′a =k ，则a ′＝ak ，b ′＝bk ，c ′＝ck ，∵aa '+bb '＝cc '，∴a 2k +b 2k ＝c 2k ，∴a 2+b 2＝c 2，∴△ABC 是直角三角形，故②正确， ∵sin 2A +sin 2B ＝1，sin 2A +cos 2A ＝1，∴sin 2B ＝cos 2A ，∴sin B ＝cos A ，∵sin A ＝cos （90°﹣A ），∴90°﹣∠B ＝∠A ，∴∠A +∠B ＝90°，∴△ABC 是直角三角形，故③正确，∵1a 2+1a 2=1a 2， ∴a 2a 2+a 2a 2=1，∴sin 2B +sin 2A ＝1，∴△ABC 是直角三角形，故④正确．故选：D ．12．【答案】B【解答】解：如图，∵a ∥b ，∴∠1＝∠3＝23°，∵∠4＝45°，∠2＝∠5，∴∠2＝180°﹣∠3﹣∠5＝112°，故选：B ．13．【答案】C【解答】解：在Rt △ABD 中，∵∠ADB ＝90°，AB ＝16，∠B ＝45°，∴BA ＝DA ＝8√2，在Rt △ADC 中，∵∠ADC ＝90°，∠ACD ＝60°，AD ＝8√2，∴CD =8√63，∵CE 平分∠ACD ，∴∠ECD ＝30°，∴DE ＝CD •tan30°=8√23， ∴AE ＝AD ﹣DE ＝8√2−8√23=16√23，故选：C ．14．【答案】D【解答】解：∵三角形的三条垂直平分线的交点到中间的凳子的距离相等，∴凳子应放在△ABC 的三条垂直平分线的交点最适当．15．【答案】C【解答】解：A、两边之和大于第三边，不符合题意；B、对于任意一个三角形都有内角和等于180°，不符合题意；C、只有直角三角形才有两个锐角的和等于90°，符合题意；D、等腰三角形顶角的平分线垂直于顶角的对边，而直角三角形（等腰直角三角形除外）没有任何一个角的平分线垂直于这个角的对边，不符合题意．故选：C．16．【答案】D【解答】解：∵MN是线段AB的垂直平分线，∴AD＝BD，∵AB＝AC＝10，∴BD+CD＝AD+CD＝AC＝10，∴△BCD的周长＝AC+BC＝10+6＝16．故选：D．17．【答案】B【解答】解：由题意可知，三角形为等腰三角形，又由三边关系得出三角形第三边只能是2，所以周长是5．若另一边是1的话，则1+1＝2不成立．故选：B．18．【答案】B【解答】解：∵AB∥CD，∴∠1＝∠AEG．∵EG平分∠AEF，∴∠AEF＝2∠AEG，∴∠AEF＝2∠1＝58°．∵AB∥CD，∴∠2＝58°．故选：B．19．【答案】D【解答】解：∵a∥b，∠1＝125°，∴∠ACD＝125°，∵∠2＝50°，∴∠3＝125°﹣50°＝75°．故选：D．20．【答案】D【解答】解：∵AB∥CD，∠1＝58°，∴∠EFD＝∠1＝58°，∵FG平分∠EFD，∴∠GFD=12∠EFD=12×58°＝29°，∵AB∥CD，∴∠FGB＝180°﹣∠GFD＝151°．故选：D．21．【答案】A【解答】解：∵AB∥CD，∴∠1＝∠AEG．∵EG平分∠AEF，∴∠AEF＝2∠AEG，∴∠AEF＝2∠1＝64°．∴∠2＝64°．22．【答案】A【解答】解：∵a ∥b ，∠1＝120°，∴∠ACD ＝120°，∵∠2＝50°，∴∠3＝120°﹣50°＝70°，故选：A ．23．【答案】A【解答】解：如图，∵AB ∥DE ，∴∠ABC ＝∠D ＝45°，又∵∠A ＝30°，∴∠1＝∠A +∠ABC ＝75°，故选：A ．二．填空题（共8小题）24．【答案】见试题解答内容【解答】解：∵在△ABC 中，AD ⊥BC ，垂足为点D ，BE ⊥AC ，垂足为点E ，∴△ABE ，△ADB 是直角三角形，∴EM ，DM 分别是它们斜边上的中线，∴EM ＝DM =12AB ＝5，∵ME =12AB ＝MA ，∴∠MAE ＝∠MEA ， ∴∠BME ＝2∠MAE ，同理，MD =12AB ＝MA ，∴∠MAD ＝∠MDA ，∴∠BMD ＝2∠MAD ，∴∠EMD ＝∠BME ﹣∠BMD ＝2∠MAE ﹣2∠MAD ＝2∠DAC ＝60°，∴△EDM 是边长为5的等边三角形，∴S △EDM =√34×52=25√34．故答案为：25√34．25．【答案】见试题解答内容【解答】解：连接CD ，DB ，过点D 作DM ⊥AB 于点M ，∵AD 平分∠F AB ，∴∠F AD ＝∠DAM ，在△AFD 和△AMD 中，{∠aaa =∠aaaaaaa =aaaa aa =aa ，∴△AFD ≌△AMD （AAS ）∴AF ＝AM ，FD ＝DM ，∵DE 垂直平分BC∴CD ＝BD ，在Rt △CDF 和Rt △BDM 中，{aa =aa aa =aa ， ∴Rt △CDF ≌Rt △BDM （HL ）∴BM ＝CF ，∵AB ＝AM +BM ＝AF +MB ＝AC +CF +MB ＝AC +2CF ，∴8＝4+2CF ，解得，CF ＝2，故答案为：2．26．【答案】见试题解答内容【解答】解：∵△OAA 1为等腰直角三角形，OA ＝1，∴AA 1＝OA ＝1，OA 1=√2OA =√2；∵△OA 1A 2为等腰直角三角形，∴A 1A 2＝OA 1=√2，OA 2=√2OA 1＝2；∵△OA 2A 3为等腰直角三角形，∴A 2A 3＝OA 2＝2，OA 3=√2OA 2＝2√2；∵△OA 3A 4为等腰直角三角形，∴A 3A 4＝OA 3＝2√2，OA 4=√2OA 3＝4．∵△OA 4A 5为等腰直角三角形，∴A 4A 5＝OA 4＝4，OA 5=√2OA 4＝4√2．∵△OA 5A 6为等腰直角三角形，∴A 5A 6＝OA 5＝4√2，OA 6=√2OA 5＝8．∴OA 8的长度为√28=16．故答案为：16．27．【答案】见试题解答内容【解答】解：∵AB ＝AC ，∴可把△AEC 绕点A 顺时针旋转120°得到△AE ′B ，∴BE ′＝EC ＝8，AE ′＝AE ，∠E ′AB ＝∠EAC ，∵∠BAC ＝120°，∠DAE ＝60°，∴∠BAD +∠EAC ＝60°，∴∠E ′AD ＝∠E ′AB +∠BAD ＝60°，在△E ′AD 和△EAD 中{aa ′=aa aa′aa =aaaa aa =aa，∴△E ′AD ≌△EAD （SAS ），∴E ′D ＝ED ，过E ′作EF ⊥BD 于点F ，∵AB ＝AC ，∠BAC ＝120°，∴∠ABC ＝∠C ＝∠E ′BA ＝30°，∴∠E′BF＝60°，∴∠BE′F＝30°，∴BF=12BE′＝4，E′F＝4√3，∵BD＝5，∴FD＝BD﹣BF＝1，在Rt△E′FD中，由勾股定理可得E′D=√(4√3)2+12=7，∴DE＝7．故答案为7．28．【答案】见试题解答内容【解答】解：连接MN，作AF⊥BC于F，∵M、N分别是AB、AC的中点，∴MN=12BC＝3，MN∥BC，∴AF⊥MN，∵AB＝AC，AF⊥BC，∴FC=12BC＝3，在Rt△AFC中，AF=√aa2−aa2=4，图中阴影部分的三个三角形的底长都是3cm，高的和为4cm，∴图中阴影部分的面积=12×3×4＝6（cm2），故答案为：6．29．【答案】见试题解答内容【解答】解：如下图所示∵AB＝AC∠B＝∠C＝30°＝∠ADE而∠ADB＝∠DAE+∠C∠DEC＝∠DAE+∠ADE∴∠ADB＝∠DEC又由∠B＝∠C∴△ABD∽△DCE∴aa aa =aa aa又∵AB ＝8，∠B ＝30°∴AM ＝4，BM ＝CM ＝4√3∴CD ＝8√3−3于是有3aa =8√3−3 ∴CE ＝3√3−98于是AE ＝AC ﹣CE ＝8﹣3√3+98=738−3√3 故答案为738−3√3．30．【答案】见试题解答内容【解答】解：∵BE ＝CE ，∴BE =12BC ，∵S △ABC ＝6， ∴S △ABE =12S △ABC =12×6＝3．∵AD ＝2BD ，S △ABC ＝6， ∴S △BCD =13S △ABC =13×6＝2，∵S △ABE ﹣S △BCD ＝（S △ADF +S 四边形BEFD ）﹣（S △CEF +S 四边形BEFD ）＝S △ADF ﹣S △CEF ，即S △ADF ﹣S △CEF ＝S △ABE ﹣S △BCD ＝3﹣2＝1．故答案为：131．【答案】见试题解答内容【解答】解：∵AE ⊥BC ，∴∠AEC ＝90°，∵∠EAC +∠ACE ＝90°，∠DAO +∠ADO ＝90°，∴∠ADO ＝∠ACE ，在△ADO 和△BCO 中{∠aaa =∠aaaaaaa =aaaa aa =aa，∴△ADO ≌△BCO （AAS ），∴OD ＝OC ＝2，OA ＝OB ＝6，∴△AOD 的面积=12×2×6＝6．故答案为6．三．解答题（共5小题）32．【答案】见试题解答内容【解答】解：（1）证明：∵△ABC 是等边三角形，∴∠BAC ＝60°，AB ＝AC ，∵将AM 绕点A 逆时针旋转60°得到AN ，∴AM ＝AN ，∠MAN ＝60°＝∠BAC ，即∠CAN +∠BAN ＝∠MAB +∠BAN ，∴∠CAN ＝∠MAB ，∴△BAM ≌△CAN （SAS ）；（2）如图1，连接CN ，由（1）可知△BAM ≌△CAN ，∴∠B ＝∠ACN ＝60°，∵DN ∥AC ，∴∠NDC ＝∠ACB ＝60°，∴∠NCD ＝60°，∴△CDN 是等边三角形，∴CN ＝DN ，∠CND ＝60°，∵AM ＝AN ，∠MAN ＝60°，∴△AMN 是等边三角形，∴AN ＝MN ，∠ANM ＝60°，∴∠ANC ＝∠MND ，∴△ANC ≌△MND （SAS ），∴S △ACN ＝S △MND ，∵S 四边形ACDN =43S △MND ＝S △ACN +S △CDN ， ∴13a △aaa =a △aaa ，∴CD =13aa =13AB ，∵A （0，3），B （−√3，0），∴OA ＝3，OB =√3，∴AB =√aa 2+aa 2=2√3，∴CD =2√33，∴OD ＝OC +CD =√3+2√33=5√33， ∴D （5√33，0）；（3）如图2，过点C 作CE ∥AB 交y 轴于点E ，由（1），（2）可知点N 在直线CE 上，CE 与抛物线交于点N 1，N 2，∴∠ABC ＝∠OCE ＝60°，OC ＝OB =√3， ∴OE ＝3，∴E （0，﹣3），设直线CE 的解析式为y ＝kx +b ， ∴{√3a +a =0a =−3，解得：{a =√3a =−3， ∴直线CE 的解析式为y =√3x ﹣3， ∴{a =−2a 2+4√3a +3a =√3a −3，解得：{a 1=2√3a 1=3，{a 2=−√32a 2−92， ∴N 1（2√3，3），N 2（−√32，−92），若AM 绕点A 逆时针旋转60°得到AN 1时，M （m ，0）， ∴AM ＝AN 1＝2√3，∵AB ＝2√3，AN 1∥x 轴，∴点M 与点C 重合，即m =√3，若AM 绕点A 逆时针旋转60°得到AN 2时，M （m ，0）， ∵C （0，√3），∴CN 2=(√3+|√32)2+(0+92)2=3√3，由（1）可知BM 2＝CN 2＝3√3， ∴OM 2＝OB +BM 2=√3+3√3=4√3， ∴m ＝﹣4√3．综合以上可得，m =√3或﹣4√3．33．【答案】见试题解答内容【解答】证明：（1）∵BE ＝DF ， ∴BE ﹣EF ＝DF ﹣EF ，即BF ＝DE ，∵AE ⊥BD ，CF ⊥BD ，∴∠AED ＝∠CFB ＝90°，在Rt △ADE 与Rt △CBF 中，{aa =aa aa =aa ， ∴Rt △ADE ≌Rt △CBF ；（2）如图，连接AC 交BD 于O ，∵Rt △ADE ≌Rt △CBF ，∴∠ADE ＝∠CBF ，∴AD ∥BC ，∴四边形ABCD 是平行四边形，∴AO ＝CO ．34．【答案】见试题解答内容【解答】证明：在AC 上取AF ＝AE ，连接OF ，∵AD 平分∠BAC 、∴∠EAO ＝∠F AO ，在△AEO 与△AFO 中，{aa =aa aaaa =aaaa aa =aa∴△AEO ≌△AFO （SAS ），∴∠AOE ＝∠AOF ；∵AD 、CE 分别平分∠BAC 、∠ACB ，∴∠ECA +∠DAC =12∠ACB +12∠BAC =12（∠ACB +∠BAC ）=12（180°﹣∠B ）＝60°则∠AOC ＝180°﹣∠ECA ﹣∠DAC ＝120°；∴∠AOC ＝∠DOE ＝120°，∠AOE ＝∠COD ＝∠AOF ＝60°，则∠COF ＝60°，∴∠COD ＝∠COF ，∴在△FOC 与△DOC 中，{∠aaa =∠aaa aa =aa aaaa =aaaa，∴△FOC ≌△DOC （ASA ），∴DC ＝FC ，∵AC ＝AF +FC ，∴AC ＝AE +CD ．35．【答案】见试题解答内容【解答】（1）证明：∵AD 平分∠CAB ，DE ⊥AB ，∠C ＝90°， ∴CD ＝ED ，∠DEA ＝∠C ＝90°，∵在Rt △ACD 和Rt △AED 中{aa =aaaa =aa ， ∴Rt △ACD ≌Rt △AED （HL ）；（2）∵DC ＝DE ＝1，DE ⊥AB ，∴∠DEB ＝90°，∵∠B ＝30°，∴BD ＝2DE ＝236．【答案】见试题解答内容【解答】解：（1）∵在Rt △ABC 中，∠C ＝90°，∠A ＝30°， ∴AB ＝2BC ，∠CBD ＝60°．∵点D 是AB 中点，∴BD ＝BC ，∴△BCD 为等边三角形．故答案为：等边三角形．（2）∠DBF 的度数不变，理由如下：∵∠ACB ＝90°，点D 是AB 中点，∴CD =12AB ＝AD ， ∴∠ECD ＝30°．∵△BDC 为等边三角形，∴BD ＝DC ，∠BDC ＝60°．又∵△DEF 为等边三角形，∴DF ＝DE ，∠FDE ＝60°，∴∠BDF +∠FDC ＝∠EDC +∠FDC ＝60°，∴∠BDF ＝∠CDE ．在△BDF 和△CDE 中，{aa =aaaaaa =aaaa aa =aa ，∴△BDF ≌△CDE （SAS ），∴∠DBF ＝∠DCE ＝30°，即∠DBF 的度数不变．（3）∵△DEF 为等边三角形，∴∠DEF ＝∠DFE ＝60°．∵∠A ＝∠ECD ＝30°，∴∠ADE ＝∠CDF ＝30°，∴△CDF 、△ADE 为等腰三角形，∴CF ＝DF ＝EF ＝DE ＝AE ，∴DE ＝AE =13AC ＝2．。

2024年中考数学压轴题型(广东专用)专题04特殊平行四边形中全等相似与最值问题(学生版)

专题04特殊平行四边形中全等相似与最值问题通用的解题思路:一、四边形与全等相似1.三角形与全等之六大全等模型:(1)一线三等角模型锐角一线三等角(2)手拉手模型(3)半角模型(4)倍长中线模型模型(6)雨伞等模型(5)平行线中等模型2.三角形与相似之四大相似模型:(1)A字模型(3)手拉手模型(2)8字模型(4)一线三等角模型B 二、四边形线段最值问题囹 1 C B D 02B （1）将军饮马模型两定一动模型一定两动模型两线段相减的最大值模型（三点共线）• B（2）费马点模型：将边以A 为顶点逆时针旋转60。

，得到AQE,连接P0则^APQ 为等边三角形,PA=PQ O1. （2023-r 东深圳•中考真题）（1）如图，在矩形ABCD 中，E 为AD 边上一点，连接BE,①若= 过C 作CFLBE 交BE 于点、F ,求证：AABE^AFCB ；②若S 矩形倔8 = 2。

时，则BECF=(2)如图，在菱形ABCD 中，cosA = |,过。

作CE1AB 交A8的延长线于点E,过E 作EF _LAD 交AD 于点、F ,若S 菱形*d =24时，求EF BC 的值.(3)如图，在平行四边形ABCD 中，匕4 = 60。

，AB = 6, AD=5,点E 在CD 上，且CE = 2,点F 为BC 上一点，连接时，过E 作EGLEF 交平行四边形ABCD 的边于点G,若EF ・EG = 70时，请直接写出AG 的长.D,E E a C C A B AB备用图2.（2022广东广州•中考真题）如图，在菱形ABCQ中，0BAD=120°,AB=6,连接8Q.⑴求BQ的长；⑵点E为线段BQ上一动点（不与点B,。

重合），点E在边AQ上，且BE二也DF,①当CE±AB时，求四边形的面积；②当四边形的面积取得最小值时，CE+右CT的值是否也最小？如果是，求CE+也CF的最小值；如果不是，请说明理由.题型一特殊平行四边形中全等相似计算1.（2024-P东汕头•一模）（1）如图1,在矩形ABCD中，E为AD边上一点，连接8E,①若BE=BC,过。

中考数学几何压轴题(有关三角形、四边形)的综合专题(含答案解析)

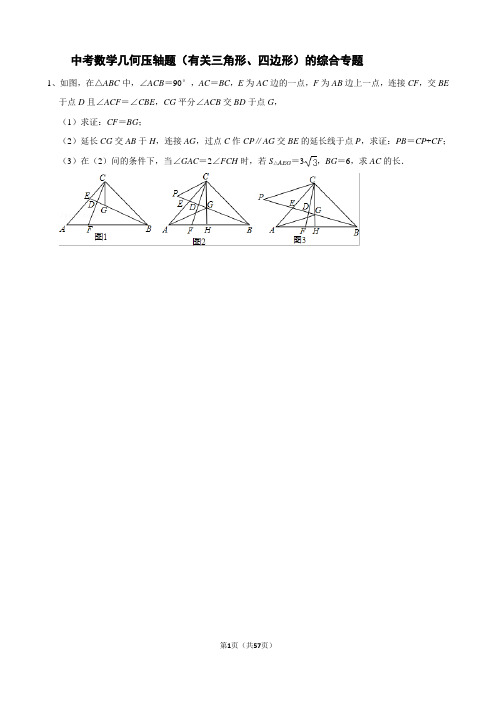
中考数学几何压轴题（有关三角形、四边形）的综合专题1、如图，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的一点，F为AB边上一点，连接CF，交BE于点D且∠ACF＝∠CBE，CG平分∠ACB交BD于点G，（1）求证：CF＝BG；（2）延长CG交AB于H，连接AG，过点C作CP∥AG交BE的延长线于点P，求证：PB＝CP+CF；（3）在（2）问的条件下，当∠GAC＝2∠FCH时，若S△AEG＝3，BG＝6，求AC的长．2、[问题背景]如图1所示，在△ABC中，AB＝BC，∠ABC＝90°，点D为直线BC上的一个动点（不与B、C重合），连结AD，将线段AD绕点D按顺时针方向旋转90°，使点A旋转到点E，连结EC．[问题初探]如果点D在线段BC上运动，通过观察、交流，小明形成了以下的解题思路：过点E作EF⊥BC 交直线BC于F，如图2所示，通过证明△DEF≌△，可推证△CEF是三角形，从而求得∠DCE＝．[继续探究]如果点D在线段CB的延长线上运动，如图3所示，求出∠DCE的度数．[拓展延伸]连接BE，当点D在直线BC上运动时，若AB＝，请直接写出BE的最小值．3、（2019秋•锦江区校级期末）在Rt△ABC中，∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线．（1）如图1，求证：AD＝2DC．（2）如图2，作∠CBD的角平分线交线段CD于点M，若CM＝1，求△DBM的面积；（3）如图3，过点D作DE⊥AB于点E，点N是线段AC上一点（不与C、D重合），以BN为一边，在BN的下方作∠BNG＝60°，NG交DE延长线于点G，试探究线段ND，DG与AD之间的数量关系，并说明理由．4、（2019•镇平县三模）如图1，已知直角三角形ABC，∠ACB＝90°，∠BAC＝30°，点D是AC边上一点，过D作DE⊥AB于点E，连接BD，点F是BD中点，连接EF，CF．（1）发现问题：线段EF，CF之间的数量关系为；∠EFC的度数为；（2）拓展与探究：若将△AED绕点A按顺时针方向旋转α角（0°＜α＜30°），如图2所示，（1）中的结论还成立吗？请说明理由；（3）拓展与运用：如图3所示，若△AED绕点A旋转的过程中，当点D落到AB边上时，AB边上另有一点G，AD＝DG＝GB，BC＝3，连接EG，请直接写出EG的长度．5、（2017春•西城区校级期末）如图1，在等腰△ABC中，AB＝AC，∠BAC＝a，点P是线段AB的中点，点E是线段CB延长线上一点，且PE＝PC，将线段PC绕点P顺时针旋转α得到PD，连接BD．（1）如图2，若α＝60°，其他条件不变，先补全图形，然后探究线段BD和BC之间的数量关系，并说明理由．（2）如图3，若α＝90°，其他条件不变，探究线段BP、BD和BC之间的等量关系，并说明理由．6、【发现问题】如图1，已知△ABC，以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE．请你以A为直角顶点、AC为腰，向△ABC外作等腰直角△ACD（不写作法，保留作图痕迹）．连接BD、CE．那么BD与CE的数量关系是BD＝CE．【拓展探究】如图2，已知△ABC，以AB、AC为边向外作正方形AEFB和正方形ACGD，连接BD、CE，试判断BD与CE之间的数量关系，并说明理由．【解决问题】如图3，有一个四边形场地ABCD，∠ADC＝60°，BC＝15，AB＝8，AD＝CD，求BD的最大值．7、（1）如图1，点C为线段AB外一个动点，已知AB＝a，AC＝b．当点C位于BA的延长线上时，线段BC取得最大值，则最大值为（用含a，b的式子表示）；（2）如图2，点C为线段AB外一个动点，若AB＝10，AC＝3，分别以AC，BC为边，作等边三角形ACD和等边三角形BCE，连接AE，DB．①求证：AE＝DB；②请直接写出线段AE的最大值；（3）如图3，AB＝6，点M为线段AB外一个动点，且AM＝2，MB＝MN，∠BMN＝90°，请直接写出线段AN的最大值．8、【初步探索】（1）如图1：在四边形ABC中，AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF ＝BE+FD，探究图中∠BAE、∠F AD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G，使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是；【灵活运用】（2）如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；【拓展延伸】（3）如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF＝BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．9、（2018•大东区一模）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点O为AB中点，点P为直线BC上的动点（不与点B、点C重合），连接OC、OP，将线段OP绕点P逆时针旋转60°，得到线段PQ，连接BQ．（1）如图1，当点P在线段BC上时，请直接写出线段BQ与CP的数量关系．（2）如图2，当点P在CB延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由；（3）如图3，当点P在BC延长线上时，若∠BPO＝45°，AC＝，请直接写出BQ的长．10、模型发现：同学们知道，三角形的两边之和大于第三边，即如图1，在△ABC中，AB+AC＞BC．对于图1，若把点C看作是线段AB外一动点，且AB＝c，AC＝b，则线段BC的长会因为点C的位置的不同而发生变化．因为AB、AC的长度固定，所以当∠BAC越大时，BC边越长．特别的，当点C位于时，线段BC的长取得最大值，且最大值为（用含b，c的式子表示）（直接填空）.模型应用：点C为线段AB外一动点，且AB＝3，AC＝2，如图2所示，分别以AC，BC为边，作等边三角形ACD 和等边三角形BCE，连接BD，AE．（1）求证：BD＝AE．（2）线段AE长的最大值为．模型拓展：如图3，在平面直角坐标系中，点A是y轴正半轴上的一动点，点B是x轴正半轴上的一动点，且AB ＝8．若AC⊥AB，AC＝3，试求OC长的最大值．11、已知：△ABC中，∠ACB＝90°，AC＝BC．（1）如图1，点D在BC的延长线上，连AD，过B作BE⊥AD于E，交AC于点F．求证：AD＝BF；（2）如图2，点D在线段BC上，连AD，过A作AE⊥AD，且AE＝AD，连BE交AC于F，连DE，问BD与CF有何数量关系，并加以证明；（3）如图3，点D在CB延长线上，AE＝AD且AE⊥AD，连接BE、AC的延长线交BE于点M，若AC ＝3MC，请直接写出的值．12、已知在△ABC中，AB＝AC，射线BM、BN在∠ABC内部，分别交线段AC于点G、H．（1）如图1，若∠ABC＝60°，∠MBN＝30°，作AE⊥BN于点D，分别交BC、BM于点E、F．①求证：∠1＝∠2；②如图2，若BF＝2AF，连接CF，求证：BF⊥CF；（2）如图3，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE＝∠BAC＝2∠CFE，求的值．13、已知，△ABC中，AB＝AC，∠BAC＝90°，E为边AC任意一点，连接BE．（1）如图1，若∠ABE＝15°，O为BE中点，连接AO，且AO＝1，求BC的长；（2）如图2，F也为AC上一点，且满足AE＝CF，过A作AD⊥BE交BE于点H，交BC于点D，连接DF交BE于点G，连接AG；①若AG平分∠CAD，求证：AH＝AC；②如图3，当G落在△ABC外时，若将△EFG沿EF边翻折，点G刚好落在AB边上点P，直接写出AG与EF的数量关系．14、如图所示，Rt△ABC中，∠ACB＝90°，E为AC中点，作ED⊥AC交AB于D，连接CD；（1）如图1，求证：AB＝2CD；（2）如图2，作CF⊥AB交AB于F，点G为CF上一点，点H为DE延长线上一点，分别连接AH、GH，若∠AHG＝2∠B，求证：AH＝GH；（3）如图3，在（2）的条件下，连接DG，且有DE＝BF，∠EDG＝90°，若AC＝6，求AH的长度．15、【问题情境】一节数学课后，老师布置了一道课后练习题：如图：已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，点E、F分别在A和BC上，∠1＝∠2，FG⊥AB于点G，求证：△CDE≌△EGF．（1）阅读理解，完成解答本题证明的思路可用下列框图表示：根据上述思路，请你完整地书写这道练习题的证明过程；（2）特殊位置，证明结论若CE平分∠ACD，其余条件不变，求证：AE＝BF；（3）知识迁移，探究发现如图，已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，若点E是DB的中点，点F在直线CB上且满足EC＝EF，请直接写出AE与BF的数量关系．（不必写解答过程）16、在正方形ABCD和等腰直角△BGF中，∠BGF＝90°，P是DF的中点，连接PG、PC．（1）如图1，当点G在BC边上时，延长GP交DC于点E．求证：PG＝PC；（2）如图2，当点F在AB的延长线上时，（1）中的结论是否成立？请证明你的结论；（3）如图3，若四边形ABCD为菱形，且∠ABC＝60°，△BGF为等边三角形，点F在CB的延长线上时，线段PC、PG又有怎样的数量关系，请直接写出你的结论，并画出论证过程中需要添加的辅助线．17、在△ABC中，∠BAC＝60°，点D、E分别在边AC、AB上，AD＝AE，连接CE、BD相交于点F，且∠BEC＝∠ADF，连接AF．（1）如图1，连接ED，求证：∠ABD＝∠CED；（2）如图2，求证：EF+FD＝AF；（3）如图3，取BC的中点G，连接AG交BD于点H，若∠GAC＝3∠ABD，BH＝7，求△ABH的面积．18、点D，E分别在△ABC的边AC，BD上，BD，CE交于点F，连接AF，∠F AE＝∠F AD，FE＝FD．（1）如图1，若∠AEF＝∠ADF，求证：AE＝AD；（2）如图2，若∠AEF≠∠ADF，FB平分∠ABC，求∠BAC的度数；（3）在（2）的条件下，如图3，点G在BE上，∠CFG＝∠AFB若AG＝6，△ABC的周长为20，求BC长．中考数学几何压轴题（有关三角形、四边形）的综合专题参考答案1、如图，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的一点，F为AB边上一点，连接CF，交BE于点D且∠ACF＝∠CBE，CG平分∠ACB交BD于点G，（1）求证：CF＝BG；（2）延长CG交AB于H，连接AG，过点C作CP∥AG交BE的延长线于点P，求证：PB＝CP+CF；（3）在（2）问的条件下，当∠GAC＝2∠FCH时，若S△AEG＝3，BG＝6，求AC的长．证明：（1）如图1，∵∠ACB＝90°，AC＝BC，∴∠A＝45°，∵CG平分∠ACB，∴∠ACG＝∠BCG＝45°，∴∠A＝∠BCG，在△BCG和△CAF中，∵，∴△BCG≌△CAF（ASA），∴CF＝BG；（2）如图2，∵PC∥AG，∴∠PCA＝∠CAG，∵AC＝BC，∠ACG＝∠BCG，CG＝CG，∴△ACG≌△BCG，∴∠CAG＝∠CBE，∵∠PCG＝∠PCA+∠ACG＝∠CAG+45°＝∠CBE+45°，∠PGC＝∠GCB+∠CBE＝∠CBE+45°，∴∠PCG＝∠PGC，∴PC＝PG，∵PB＝BG+PG，BG＝CF，∴PB＝CF+CP；（3）解法一：如图3，过E作EM⊥AG，交AG于M，∵S△AEG＝AG•EM＝3，由（2）得：△ACG≌△BCG，∴BG＝AG＝6，∴×6×EM＝3，EM＝，设∠FCH＝x°，则∠GAC＝2x°，∴∠ACF＝∠EBC＝∠GAC＝2x°，∵∠ACH＝45°，∴2x+x＝45，x＝15，∴∠ACF＝∠GAC＝30°，在Rt△AEM中，AE＝2EM＝2，AM＝＝3，∴M是AG的中点，∴AE＝EG＝2，∴BE＝BG+EG＝6+2，在Rt△ECB中，∠EBC＝30°，∴CE＝BE＝3+，∴AC＝AE+EC＝2+3+＝3+3．解法二：同理得：∠CAG＝30°，AG＝BG＝6，如图4，过G作GM⊥AC于M，在Rt△AGM中，GM＝3，AM＝＝＝3，∵∠ACG＝45°，∠MGC＝90°，∴GM＝CM＝3，∴AC＝AM+CM＝3+3．2、[问题背景]如图1所示，在△ABC中，AB＝BC，∠ABC＝90°，点D为直线BC上的一个动点（不与B、C重合），连结AD，将线段AD绕点D按顺时针方向旋转90°，使点A旋转到点E，连结EC．[问题初探]如果点D在线段BC上运动，通过观察、交流，小明形成了以下的解题思路：过点E作EF⊥BC 交直线BC于F，如图2所示，通过证明△DEF≌△ADB，可推证△CEF是等腰直角三角形，从而求得∠DCE＝135°．[继续探究]如果点D在线段CB的延长线上运动，如图3所示，求出∠DCE的度数．[拓展延伸]连接BE，当点D在直线BC上运动时，若AB＝，请直接写出BE的最小值．解：[问题初探]如图2，过点E作EF⊥BC交直线BC于F，∴∠DFE＝90°＝∠ABD，∴∠EDF+∠DEF＝90°，由旋转知，AD＝DE，∠ADE＝90°，∴∠ADB+∠EDF＝90°，∴∠ADB＝∠DEF，∴△ABD≌△DFE（AAS），∴BD＝EF，DF＝AB，∵AB＝BC，∴BC＝DF，∴BD＝CF，∴EF＝CF，∴△CEG是等腰直角三角形，∴∠ECF＝45°，∴∠DCE＝135°，故答案为：ADB，等腰直角，135；[继续探究]如图3，过点E作EF⊥BC于F，∴∠DFE＝90°＝∠ABD，∴∠EDF+∠DEF＝90°，由旋转知，AD＝DE，∠ADE＝90°，∴∠ADB+∠EDF＝90°，∴∠ADB＝∠DEF，∴△ABD≌△DFE（AAS），∴BD＝EF，DF＝AB，∵AB＝BC，∴BC＝DF，∴BD＝CF，∴EF＝CF，∴△CEG是等腰直角三角形，∴∠ECF＝45°，∴∠DCE＝45°；[拓展延伸]如图4，在△ABC中，∠ABC＝90°，AB＝BC＝，∴∠ACB＝45°当点D在射线BC上时，由[问题初探]知，∠BCM＝135°，∴∠ACM＝∠BCM﹣∠ACB＝90°，当点D在线段CB的延长线上时，由[继续探究]知，∠BCE＝45°，∴∠ACN＝∠ACB+∠BCM＝90°，∴点E是过点C垂直于AC的直线上的点，∴当BE⊥MN时，BE最小，∵∠BCE＝45°，∴∠CBE＝45°＝∠BCE，∴BE＝CE，∴BE最小＝BC＝，即：BE的最小值为．3、在Rt△ABC中，∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线．（1）如图1，求证：AD＝2DC．（2）如图2，作∠CBD的角平分线交线段CD于点M，若CM＝1，求△DBM的面积；（3）如图3，过点D作DE⊥AB于点E，点N是线段AC上一点（不与C、D重合），以BN为一边，在BN的下方作∠BNG＝60°，NG交DE延长线于点G，试探究线段ND，DG与AD之间的数量关系，并说明理由．证明：（1）如图1，过点D作DE⊥AB，∵BD是△ABC的角平分线，DE⊥AB，∠ACB＝90°，∴DC＝DE，∵∠A＝30°，DE⊥AB，∴AD＝2DE，∴AD＝2DC；（2）如图2，过点M作ME∥BD，∵∠ACB＝90°，∠A＝30°，∴∠ABC＝60°，∵BD是△ABC的角平分线，∴∠ABD＝∠DBC＝30°，∵BM平分∠CBD，∴∠CBM＝15°＝∠DBM，∵ME∥BD，∴∠MEC＝∠CBD＝30°，∠EMB＝∠DBM＝∠MBE，∴ME＝BE，∵∠MEC＝30°，∠C＝90°∴CE＝MC＝，ME＝2MC＝2＝BE，∴BC＝+2，∵∠CBD＝30°，∠C＝90°，∴BC＝CD，∴CD＝1+，∴DM＝，∴△DBM的面积＝××（+2）＝1+；（3）若点N在CD上时，AD＝DG+DN，理由如下：如图3所示：延长ED使得DW＝DN，连接NW，∵∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线，DE⊥AB于点E，∴∠ADE＝∠BDE＝60°，AD＝BD，∵DN＝DW，且∠WDN＝60°∴△WDN是等边三角形，∴NW＝DN，∠W＝∠WND＝∠BNG＝∠BDN＝60°，∴∠WNG＝∠BND，在△WGN和△DBN中，∴△WGN≌△DBN（SAS），∴BD＝WG＝DG+DN，∴AD＝DG+DN．（3）若点N在AD上时，AD＝DG﹣DN，理由如下：如图4，延长BD至H，使得DH＝DN，连接HN，由（1）得DA＝DB，∠A＝30°．∵DE⊥AB于点E．∴∠2＝∠3＝60°．∴∠4＝∠5＝60°．∴△NDH是等边三角形．∴NH＝ND，∠H＝∠6＝60°．∴∠H＝∠2．∵∠BNG＝60°，∴∠BNG+∠7＝∠6+∠7．即∠DNG＝∠HNB．在△DNG和△HNB中，∴△DNG≌△HNB（ASA）．∴DG＝HB．∵HB＝HD+DB＝ND+AD，∴DG＝ND+AD．∴AD＝DG﹣ND．4、如图1，已知直角三角形ABC，∠ACB＝90°，∠BAC＝30°，点D是AC边上一点，过D作DE⊥AB于点E，连接BD，点F是BD中点，连接EF，CF．（1）发现问题：线段EF，CF之间的数量关系为EF＝CF；∠EFC的度数为120°；（2）拓展与探究：若将△AED绕点A按顺时针方向旋转α角（0°＜α＜30°），如图2所示，（1）中的结论还成立吗？请说明理由；（3）拓展与运用：如图3所示，若△AED绕点A旋转的过程中，当点D落到AB边上时，AB边上另有一点G，AD＝DG＝GB，BC＝3，连接EG，请直接写出EG的长度．解：（1）如图1中，∵DE⊥AB，∴∠BED＝90°，∵∠BCD＝90°，BF＝DF，∴FE＝FB＝FD＝CF，∴∠FBE＝∠FEB，∠FBC＝∠FCB，∴∠EFC＝∠EFD+∠CFD＝∠FBE+∠FEB+∠FBC+∠FCB＝2（∠FBE+∠FBC）＝2∠ABC＝120°，故答案为：EF＝CF，120°．（2）结论成立．理由：如图2中，取AB的中点M，AD的中点N，连接MC，MF，ED，EN，FN．∵BM＝MA，BF＝FD，∴MF∥AD，MF＝AD，∵AN＝ND，∴MF＝AN，MF∥AN，∴四边形MFNA是平行四边形，∴NF＝AM，∠FMA＝∠ANF，在Rt△ADE中，∵AN＝ND，∠AED＝90°，∴EN＝AD＝AN＝ND，同理CM＝AB＝AM＝MB，在△AEN和△ACM中，∠AEN＝∠EAN，∠MCA＝∠MAC，∵∠MAC＝∠EAN，∴∠AMC＝∠ANE，又∵∠FMA＝∠ANF，∴∠ENF＝∠FMC，在△MFC和△NEF中，，∴△MFC≌△NEF（SAS），∴FE＝FC，∠NFE＝∠MCF，∵NF∥AB，∴∠NFD＝∠ABD，∵∠ACB＝90°，∠BAC＝30°，∴∠ABC＝60°，△BMC是等边三角形，∠MCB＝60°∴∠EFC＝∠EFN+∠NFD+∠DFC＝∠MCF+∠ABD+∠FBC+∠FCB＝∠ABC+∠MCB＝60°+60°＝120°．（3）如图3中，作EH⊥AB于H．在Rt△ABC中，∵∠BAC＝30°，BC＝3，∴AB＝2BC＝6，在Rt△AED中，∠DAE＝30°，AD＝2，∴DE＝AD＝1，在Rt△DEH中，∵∠EDH＝60°，DE＝1，∴EH＝ED•sin60°＝，DH＝ED•cos60°＝，在Rt△EHG中，EG＝＝．5、如图1，在等腰△ABC中，AB＝AC，∠BAC＝a，点P是线段AB的中点，点E是线段CB延长线上一点，且PE＝PC，将线段PC绕点P顺时针旋转α得到PD，连接BD．（1）如图2，若α＝60°，其他条件不变，先补全图形，然后探究线段BD和BC之间的数量关系，并说明理由．（2）如图3，若α＝90°，其他条件不变，探究线段BP、BD和BC之间的等量关系，并说明理由．解：（1）BC＝2BD，理由：如图2，连接CD，由旋转可得，CP＝DP，∠CPD＝60°，∴△CDP是等边三角形，∴∠CDP＝60°＝∠PCD，又∵P是AB的中点，AB＝AC，∠A＝60°，∴等边三角形ABC中，∠PCB＝30°，CP⊥AB，∴∠BCD＝30°，即BC平分∠PCD，∴BC垂直平分PD，∴∠BDC＝∠BPC＝90°，∴Rt△BCD中，BC＝2BD．（2）如图3，取BC中点F，连接PF，∵∠A＝90°，AB＝AC，∴△ABC是等腰直角三角形，∵P是AB的中点，F是BC的中点，∴PF是△ABC的中位线，∴PF∥AC，∴∠PFB＝∠ACB＝45°，∠BPF＝∠A＝90°，∴△BPF是等腰直角三角形，∴BF＝BP，BP＝PF，∵∠DPC＝∠BPF＝90°，∴∠BPD＝∠FPC，又∵PD＝PC，∴△BDP≌△FCP，∴BD＝CF，∵BC＝BF+FC，∴BC＝BD+BP．6、【发现问题】如图1，已知△ABC，以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE．请你以A为直角顶点、AC为腰，向△ABC外作等腰直角△ACD（不写作法，保留作图痕迹）．连接BD、CE．那么BD与CE的数量关系是BD＝CE．【拓展探究】如图2，已知△ABC，以AB、AC为边向外作正方形AEFB和正方形ACGD，连接BD、CE，试判断BD与CE之间的数量关系，并说明理由．【解决问题】如图3，有一个四边形场地ABCD，∠ADC＝60°，BC＝15，AB＝8，AD＝CD，求BD的最大值．【发现问题】解：延长CA到M，作∠MAC的平分线AN，在AN上截取AD＝AC，连接CD，即可得到等腰直角△ACD；连接BD、CE，如图1所示：∵△ABE与△ACD都是等腰直角三角形，∴AB＝AE，AD＝AC，∠BAE＝∠CAD＝90°，∴∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE，【拓展探究】解：BD＝CE；理由如下：∵四边形AEFB与四边形ACGD都是正方形，∴AB＝AE，AD＝AC，∠BAE＝∠CAD＝90°，∴∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE；【解决问题】解：以AB为边向外作等边三角形ABE，连接CE，如图3所示：则∠BAE＝60°，BE＝AB＝AE＝8，∵AD＝CD，∠ADC＝60°，∴△ACD是等边三角形，∴∠CAD＝60°，AC＝AD，∴∠CAD+∠BAC＝∠BAE+∠BAC，即∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE；当C、B、E三点共线时，CE最大＝BC+BE＝15+8＝23，∴BD的最大值为23．7、如图1，点C为线段AB外一个动点，已知AB＝a，AC＝b．当点C位于BA的延长线上时，线段BC取得最大值，则最大值为a+b（用含a，b的式子表示）；（2）如图2，点C为线段AB外一个动点，若AB＝10，AC＝3，分别以AC，BC为边，作等边三角形ACD和等边三角形BCE，连接AE，DB．①求证：AE＝DB；②请直接写出线段AE的最大值；（3）如图3，AB＝6，点M为线段AB外一个动点，且AM＝2，MB＝MN，∠BMN＝90°，请直接写出线段AN的最大值．（1）解：∵点C为线段AB外一动点，且AC＝b，AB＝a，∴当点C位于BA的延长线上时，线段BC的长取得最大值，且最大值为AC+AB＝a+b，（2）①证明：如图2中，∵△ACD与△BCE是等边三角形，∴CD＝AC，CB＝CE，∠ACD＝∠BCE＝60°，∴∠DCB＝∠ACE，在△CAD与△EAB中，，∴△CAD≌△EAB（SAS），∴AE＝BD．②∵线段AE长的最大值＝线段BD的最大值，由（1）知，当线段BD的长取得最大值时，点D在BA的延长线上，∴最大值为AD+AB＝3+10＝13；（3）如图3中，连接BN，∵将△AMN绕着点M顺时针旋转90°得到△PBM，连接AP，则△APM是等腰直角三角形，∴MA＝MP＝2，BP＝AN，∴P A＝2，∵AB＝6，∴线段AN长的最大值＝线段BP长的最大值，∴当P在线段BA的延长线时，线段BP取得最大值最大值＝AB+AP＝6+2．8、【初步探索】（1）如图1：在四边形ABC中，AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF ＝BE+FD，探究图中∠BAE、∠F AD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G，使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是∠BAE+∠F AD＝∠EAF；【灵活运用】（2）如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；【拓展延伸】（3）如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF＝BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．解：（1）∠BAE+∠F AD＝∠EAF．理由：如图1，延长FD到点G，使DG＝BE，连接AG，根据SAS可判定△ABE≌△ADG，进而得出∠BAE＝∠DAG，AE＝AG，再根据SSS可判定△AEF≌△AGF，可得出∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF．故答案为：∠BAE+∠F AD＝∠EAF；（2）仍成立，理由：如图2，延长FD到点G，使DG＝BE，连接AG，∵∠B+∠ADF＝180°，∠ADG+∠ADF＝180°，∴∠B＝∠ADG，又∵AB＝AD，∴△ABE≌△ADG（SAS），∴∠BAE＝∠DAG，AE＝AG，∵EF＝BE+FD＝DG+FD＝GF，AF＝AF，∴△AEF≌△AGF（SSS），∴∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF；（3）∠EAF＝180°﹣∠DAB．证明：如图3，在DC延长线上取一点G，使得DG＝BE，连接AG，∵∠ABC+∠ADC＝180°，∠ABC+∠ABE＝180°，∴∠ADC＝∠ABE，又∵AB＝AD，∴△ADG≌△ABE（SAS），∴AG＝AE，∠DAG＝∠BAE，∵EF＝BE+FD＝DG+FD＝GF，AF＝AF，∴△AEF≌△AGF（SSS），∴∠F AE＝∠F AG，∵∠F AE+∠F AG+∠GAE＝360°，∴2∠F AE+（∠GAB+∠BAE）＝360°，∴2∠F AE+（∠GAB+∠DAG）＝360°，即2∠F AE+∠DAB＝360°，∴∠EAF＝180°﹣∠DAB．9、如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点O为AB中点，点P为直线BC上的动点（不与点B、点C重合），连接OC、OP，将线段OP绕点P逆时针旋转60°，得到线段PQ，连接BQ．（1）如图1，当点P在线段BC上时，请直接写出线段BQ与CP的数量关系．（2）如图2，当点P在CB延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由；（3）如图3，当点P在BC延长线上时，若∠BPO＝45°，AC＝，请直接写出BQ的长．解：（1）CP＝BQ，理由：如图1，连接OQ，由旋转知，PQ＝OP，∠OPQ＝60°⊅∴△POQ是等边三角形，∴OP＝OQ，∠POQ＝60°，在Rt△ABC中，O是AB中点，∴OC＝OA＝OB，∴∠BOC＝2∠A＝60°＝∠POQ，∴∠COP＝∠BOQ，在△COP和△BOQ中，，∴△COP≌△BOQ（SAS），∴CP＝BQ，（2）CP＝BQ，理由：如图2，连接OQ，由旋转知，PQ＝OP，∠OPQ＝60°∴△POQ是等边三角形，∴OP＝OQ，∠POQ＝60°，在Rt△ABC中，O是AB中点，∴OC＝OA＝OB，∴∠BOC＝2∠A＝60°＝∠POQ，∴∠COP＝∠BOQ，在△COP和△BOQ中，，∴△COP≌△BOQ（SAS），∴CP＝BQ，（3）如图3，在Rt△ABC中，∠A＝30°，AC＝，∴BC＝AC•tan∠A＝，过点O作OH⊥BC，∴∠OHB＝90°＝∠BCA，∴OH∥AB，∵O是AB中点，∴CH＝BC＝，OH＝AC＝，∵∠BPQ＝45°，∠OHP＝90°，∴∠BPQ＝∠PQH，∴PH＝OH＝，∴CP＝PH﹣CH＝﹣＝，连接BQ，同（1）的方法得，BQ＝CP＝．10、模型发现：同学们知道，三角形的两边之和大于第三边，即如图1，在△ABC中，AB+AC＞BC．对于图1，若把点C看作是线段AB外一动点，且AB＝c，AC＝b，则线段BC的长会因为点C的位置的不同而发生变化．因为AB、AC的长度固定，所以当∠BAC越大时，BC边越长．特别的，当点C位于线段BA的延长线上时，线段BC的长取得最大值，且最大值为b+c（用含b，c的式子表示）（直接填空）模型应用：点C为线段AB外一动点，且AB＝3，AC＝2，如图2所示，分别以AC，BC为边，作等边三角形ACD 和等边三角形BCE，连接BD，AE．（1）求证：BD＝AE．（2）线段AE长的最大值为5．模型拓展：如图3，在平面直角坐标系中，点A是y轴正半轴上的一动点，点B是x轴正半轴上的一动点，且AB ＝8．若AC⊥AB，AC＝3，试求OC长的最大值．解：当点C位于线段BA的延长线上时，线段BC的长取得最大值，最大值为b+c，故答案为：线段BA的延长线上；b+c；模型应用：（1）证明：∵△ACD、△BCE都是等边三角形，∴CD＝CA＝AD，CB＝CE，∠ACD＝60°，∠BCE＝60°，∴∠DCB＝∠ACE，在△DCB和△ACE中，，∴△DCB≌△ACE（SAS）∴BD＝AE；（2）当点D位于线段BA的延长线上时，线段BD的长取得最大值，最大值为AB+AD＝AB+AC＝3+2＝5，∵AE＝BD，∴线段AE长的最大值为5，模型拓展：取AB的中点G，连接OG、CG，在Rt△AOB中，G为AB的中点，∴OG＝AB＝4，在Rt△CAG中，CG＝＝＝5，当点O、G、C在同一条直线上时，OC最大，最大值为4+5＝9．11、已知：△ABC中，∠ACB＝90°，AC＝BC．（1）如图1，点D在BC的延长线上，连AD，过B作BE⊥AD于E，交AC于点F．求证：AD＝BF；（2）如图2，点D在线段BC上，连AD，过A作AE⊥AD，且AE＝AD，连BE交AC于F，连DE，问BD与CF有何数量关系，并加以证明；（3）如图3，点D在CB延长线上，AE＝AD且AE⊥AD，连接BE、AC的延长线交BE于点M，若AC ＝3MC，请直接写出的值．（1）证明：如图1中，∵BE⊥AD于E，∴∠AEF＝∠BCF＝90°，∵∠AFE＝∠CFB，∴∠DAC＝∠CBF，∵BC＝CA，∴△BCF≌△ACD，∴BF＝AD．（2）结论：BD＝2CF．理由：如图2中，作EH⊥AC于H．∵∠AHE＝∠ACD＝∠DAE＝90°，∴∠DAC+∠ADC＝90°，∠DAC+∠EAH＝90°，∴∠DAC＝∠AEH，∵AD＝AE，∴△ACD≌△EHA，∴CD＝AH，EH＝AC＝BC，∵CB＝CA，∴BD＝CH，∵∠EHF＝∠BCF＝90°，∠EFH＝∠BFC，EH＝BC，∴△EHF≌△BCF，∴FH＝CF，∴BD＝CH＝2CF．（3）如图3中，同法可证BD＝2CM．∵AC＝3CM，设CM＝a，则AC＝CB＝3a，BD＝2a，∴＝＝．12、已知在△ABC中，AB＝AC，射线BM、BN在∠ABC内部，分别交线段AC于点G、H．（1）如图1，若∠ABC＝60°，∠MBN＝30°，作AE⊥BN于点D，分别交BC、BM于点E、F．①求证：∠1＝∠2；②如图2，若BF＝2AF，连接CF，求证：BF⊥CF；（2）如图3，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE＝∠BAC＝2∠CFE，求的值．（1）①证明：如图1中，∵AB＝AC，∠ABC＝60°∴△ABC是等边三角形，∴∠BAC＝60°，∵AD⊥BN，∴∠ADB＝90°，∵∠MBN＝30°，∠BFD＝60°＝∠1+∠BAF＝∠2+∠BAF，∴∠1＝∠2②证明：如图2中，在Rt△BFD中，∵∠FBD＝30°，∴BF＝2DF，∵BF＝2AF，∴BF＝AD，∵∠BAE＝∠FBC，AB＝BC，∴△BFC≌△ADB，∴∠BFC＝∠ADB＝90°，∴BF⊥CF（2）在BF上截取BK＝AF，连接AK．∵∠BFE＝∠2+∠BAF，∠CFE＝∠4+∠1，∴∠CFB＝∠2+∠4+∠BAC，∵∠BFE＝∠BAC＝2∠EFC，∴∠1+∠4＝∠2+∠4∴∠1＝∠2，∵AB＝AC，∴△ABK≌CAF，∴∠3＝∠4，S△ABK＝S△AFC，∵∠1+∠3＝∠2+∠3＝∠CFE＝∠AKB，∠BAC＝2∠CEF，∴∠KAF＝∠1+∠3＝∠AKF，∴AF＝FK＝BK，∴S△ABK＝S△AFK，∴＝2．13、已知，△ABC中，AB＝AC，∠BAC＝90°，E为边AC任意一点，连接BE．（1）如图1，若∠ABE＝15°，O为BE中点，连接AO，且AO＝1，求BC的长；（2）如图2，F也为AC上一点，且满足AE＝CF，过A作AD⊥BE交BE于点H，交BC于点D，连接DF交BE于点G，连接AG；①若AG平分∠CAD，求证：AH＝AC；②如图3，当G落在△ABC外时，若将△EFG沿EF边翻折，点G刚好落在AB边上点P，直接写出AG与EF的数量关系．（1）解：如图1中，在AB上取一点M，使得BM＝ME，连接ME．在Rt△ABE中，∵OB＝OE，∴BE＝2OA＝2，∵MB＝ME，∴∠MBE＝∠MEB＝15°，∴∠AME＝∠MBE+∠MEB＝30°，设AE＝x，则ME＝BM＝2x，AM＝x，∵AB2+AE2＝BE2，∴（2x+x）2+x2＝22，∴x＝（负根已经舍弃），∴AB＝AC＝（2+）•，∴BC＝AB＝+1．方法二：作EH⊥BC于H，求出BH，CH即可解决问题．（2）证明：如图2中，作CP⊥AC，交AD的延长线于P，GM⊥AC于M．∵BE⊥AP，∴∠AHB＝90°，∴∠ABH+∠BAH＝90°，∵∠BAH+∠P AC＝90°，∴∠ABE＝∠P AC，在△ABE和△CAP中，，∴△ABE≌△CAP，∴AE＝CP＝CF，∠AEB＝∠P，在△DCF和△DCP中，，∴△DCF≌△DCP，∴∠DFC＝∠P，∴∠GFE＝∠GEF，∴GE＝GF，∵GM⊥EF，∴FM＝ME，∵AE＝CF，∴AF＝CE，∴AM＝CM，在△GAH和△GAM中，，∴△AGH≌△AGM，∴AH＝AM＝CM＝AC（3）解：结论：AG＝EF．理由：如图3中，作CM⊥AC交AD的延长线于M，连接PG交AC于点O．由（2）可知△ACM≌△BAE，△CDF≌△CDM，∴∠AEB＝∠M＝∠GEF，∠M＝∠CFD＝∠GFE，AE＝CM＝CF，∴∠GEF＝∠GFE，∴GE＝GF，∵△EFP是由△EFG翻折得到，∴EG＝EP＝GF＝PF，∴四边形EGFP是菱形，∴PG⊥AC，OE＝OF，∵AE＝CF，∴AO＝OC，∵AB∥OP，∴BP＝PC，∵PF∥BE，∴EF＝CF＝AE，∵PB＝PC，AO＝OC，∴PO＝OG＝AB，∴AB＝PG，AB∥PG，∴四边形ABPG是平行四边形，∴AG∥BC，∴∠GAO＝∠ACB＝45°，设EO＝OF＝a，则OA＝OG＝3a，AG＝3a，∴＝＝，∴AG＝EF14、如图所示，Rt△ABC中，∠ACB＝90°，E为AC中点，作ED⊥AC交AB于D，连接CD；（1）如图1，求证：AB＝2CD；（2）如图2，作CF⊥AB交AB于F，点G为CF上一点，点H为DE延长线上一点，分别连接AH、GH，若∠AHG＝2∠B，求证：AH＝GH；（3）如图3，在（2）的条件下，连接DG，且有DE＝BF，∠EDG＝90°，若AC＝6，求AH的长度．解：（1）∵E为AC中点，作ED⊥AC交AB于D，∴AD＝CD，∵∠ACB＝90°，∴BC∥DE，∴AD＝BD，∴CD＝BD，∴AB＝2CD；（2）如图2，连接CH，∵点E是AC的中点，∴AE＝CE，∵DE⊥AC，∴CH＝AH，∴∠ACH＝∠CAH，∵∠ACB＝90°，∴∠B+∠BAC＝90°，∵CF⊥AB，∴∠BAC+∠ACF＝90°，∴∠ACF＝∠B，∴∠HCG＝∠ACH+∠ACF＝∠CAH+∠B，∠AHG＝2∠B∴在四边形AHGF中，∠AFG+∠FGH+∠AHG+∠F AH＝360°，∴∠FGH＝360°﹣（∠AFG+∠AHG+∠F AH）＝360°﹣（90°+2∠B+∠CAH+∠BAC）＝360°﹣（90°+2∠B+∠CAH+90°﹣∠B）＝360°﹣（180°+∠B+∠CAH）＝180°﹣（∠B+∠CAH），∵∠CGH＝180°﹣∠FGH＝∠B+∠CAH＝∠HCG，∴CH＝GH，∵CH＝AH，∴AH＝GH；（3）如图3，由（1）知，DE∥BC，∴∠B＝∠ADE，在△BFC和△DEA中，，∴△BFC≌△DEA，∴BC＝AD，∵AD＝BD＝CD，∴BC＝BD＝CD，∴△BCD是等边三角形，∴∠B＝60°，在Rt△ABC中，AC＝6，∴BC＝2，AB＝4，∵CF⊥BD，∴DF＝，CF＝3，∵∠BAC＝30°，∴∠ADE＝60°，∵∠EDG＝90°，∠FDG＝30°，在Rt△DFG中，DF＝，∴FG＝1，DG＝2，∴CG＝CF﹣FG＝2过点H作HN⊥CF，由（2）知，CH＝GH，∴NG＝CG＝1，∴FN＝NG+FG＝2，过点H作HM⊥AB，∴∠FMH＝∠NFM＝∠HNF＝90°，∴四边形NFMH是矩形，∴HM＝FN＝2，在Rt△DMH中，∠ADE＝60°，HM＝2，∴DH＝，在Rt△HDG中，根据勾股定理得，HG＝＝．15、【问题情境】一节数学课后，老师布置了一道课后练习题：如图：已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，点E、F分别在A和BC上，∠1＝∠2，FG⊥AB于点G，求证：△CDE≌△EGF．（1）阅读理解，完成解答本题证明的思路可用下列框图表示：根据上述思路，请你完整地书写这道练习题的证明过程；（2）特殊位置，证明结论若CE平分∠ACD，其余条件不变，求证：AE＝BF；（3）知识迁移，探究发现如图，已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，若点E是DB的中点，点F在直线CB上且满足EC＝EF，请直接写出AE与BF的数量关系．（不必写解答过程）（1）证明：∵AC＝BC，∠ACB＝90°，∴∠A＝∠B＝45°，∵CD⊥AB，∴∠CDB＝90°，∴∠DCB＝45°，∵∠ECF＝∠DCB+∠1＝45°+∠1，∠EFC＝∠B+∠2＝45°+∠2，∠1＝∠2，∴∠ECF＝∠EFC，∴CE＝EF，∵CD⊥AB，FG⊥AB，∴∠CDE＝∠EGF＝90°，在△CDE和△EGF中，，∴△CDE≌△EGF（AAS）；（2）证明：由（1）得：CE＝EF，∠A＝∠B，∵CE平分∠ACD，∴∠ACE＝∠1，∵∠1＝∠2，∴∠ACE＝∠2，在△ACE和△BEF中，，∴△ACE≌△BEF（AAS），∴AE＝BF；（3）AE＝BF，作EH⊥BC与H，如图3所示：设DE＝x，根据题意得：BE＝DE＝x，AD＝BD＝2x，CD＝AD＝2x，AE＝3x，根据勾股定理得：BC＝AC＝2x，∵∠ABC＝45°，EH⊥BC，∴BH＝x，∴CH＝BC﹣BH＝x，∵EC＝EF，∴FH＝CH＝x，∴BF＝x﹣x＝x，∴＝，∴AE＝．16、在正方形ABCD和等腰直角△BGF中，∠BGF＝90°，P是DF的中点，连接PG、PC．（1）如图1，当点G在BC边上时，延长GP交DC于点E．求证：PG＝PC；（2）如图2，当点F在AB的延长线上时，（1）中的结论是否成立？请证明你的结论；（3）如图3，若四边形ABCD为菱形，且∠ABC＝60°，△BGF为等边三角形，点F在CB的延长线。

中考数学中的三角形与四边形面积计算技巧总结

中考数学中的三角形与四边形面积计算技巧总结在中考数学考试中，求解三角形与四边形的面积是一个常见的题型。

正确运用计算技巧可以快速准确地得出结果。

本文将总结中考数学中常用的三角形与四边形面积计算技巧，帮助同学们提高解题效率。

一、三角形面积计算技巧1. 直角三角形面积计算直角三角形是最简单的三角形，其面积计算公式为：面积 = 底边长度 ×高其中，底边是直角边，高是与底边垂直的边。

在解题时，可以利用勾股定理求得直角三角形的底边与高，从而计算出面积。

2. 一般三角形面积计算对于一般的三角形，我们可以利用海伦公式计算面积。

海伦公式的表达式为：面积= √[s × (s - a) × (s - b) × (s - c)]其中，s是三角形的半周长，等于三边长之和的一半；a、b、c分别是三角形的边长。

二、四边形面积计算技巧1. 矩形面积计算矩形是一种特殊的四边形，其面积计算公式为：面积 = 长 ×宽矩形的特点是四个角都是直角，且相对的两边长度相等。

在考试中遇到矩形的面积计算问题时，只需知道其长和宽即可直接计算出结果。

2. 平行四边形面积计算平行四边形也是一种常见的四边形，其面积计算公式为：面积 = 底边长度 ×高平行四边形的特点是两对边平行且相等，且相对的两个角也相等。

在计算平行四边形面积时，只需知道底边的长度以及与底边平行的高的长度即可。

3. 梯形面积计算梯形是一种具有两对平行边的四边形，其面积计算公式为：面积 = (上底 + 下底) ×高的一半梯形的关键是知道上底、下底和高的长度，通过将梯形划分为两个三角形和一个矩形，可以利用三角形和矩形的面积计算公式得出最终结果。

4. 菱形面积计算菱形是一种具有四个边相等的四边形，其面积计算公式为：面积 = 对角线1长度 ×对角线2长度的一半在计算菱形面积时，只需知道两条对角线的长度即可。

总结：在中考数学中，掌握三角形与四边形的面积计算技巧对解题非常重要。

2024年广东省中考数学总复习专题14：三角形及其全等

2024年广东省中考数学总复习专题14三角形及其全等一、三角形的基础知识1．三角形的概念:由三条线段首尾顺次相接组成的图形，叫做三角形．2．三角形的三边关系1）三角形三边关系定理：三角形的两边之和大于第三边．推论：三角形的两边之差小于第三边．2）三角形三边关系定理及推论的作用：①判断三条已知线段能否组成三角形；②当已知两边时，可确定第三边的范围；③证明线段不等关系．3．三角形的内角和定理及推论三角形的内角和定理：三角形三个内角和等于180°．推论：①直角三角形的两个锐角互余；②三角形的一个外角等于和它不相邻的两个内角的和；③三角形的一个外角大于任何一个和它不相邻的内角．4．三角形中的重要线段1）三角形的一个角的平分线与这个角的对边相交，这个角的顶点和交点间的线段叫做三角形的角平分线．2）在三角形中，连接一个顶点和它对边的中点的线段叫做三角形的中线．3）从三角形一个顶点向它的对边做垂线，顶点和垂足之间的线段叫做三角形的高线（简称三角形的高）．4）连接三角形两边中点的线段叫做三角形的中位线，三角形的中位线平行于第三边，且等于第三边的一半．二、全等三角形1．三角形全等的判定定理：1）边边边定理：有三边对应相等的两个三角形全等（可简写成“边边边”或“SSS”）；2）边角边定理：有两边和它们的夹角对应相等的两个三角形全等（可简写成“边角边”或“SAS”）；3）角边角定理：有两角和它们的夹边对应相等的两个三角形全等（可简写成“角边角”或“ASA”）；4）角角边定理：有两角和它们所对的任意一边对应相等的两个三角形全等（可简写成“角角边”或“AAS”）；5）对于特殊的直角三角形，判定它们全等时，还有HL定理（斜边、直角边定理）：有斜边和一条直角边对应相等的两个直角三角形全等（可简写成“斜边、直角边”或“HL”）．2．全等三角形的性质：第1页（共9页）。

2024年中考数学三角形与四边形专题

2024年中考数学三角形与四边形专题在中考数学中，三角形与四边形是非常重要的知识点，也是考试中经常出现的题型。

今天，咱们就来好好梳理一下这部分内容。

三角形，是最基础也是最常见的几何图形之一。

它具有稳定性，这一特性在生活中有着广泛的应用，比如自行车的车架、塔吊的支架等等。

三角形的内角和为 180 度，这是一个非常关键的性质。

我们可以通过这个性质来求解三角形中未知角的度数。

比如，已知一个三角形的两个内角分别为 50 度和 70 度，那么第三个角就是 180 50 70 ＝ 60 度。

三角形的三边关系也很重要。

任意两边之和大于第三边，任意两边之差小于第三边。

这一关系可以用来判断三条线段能否组成一个三角形。

比如，有三条线段，长度分别为 3、4、8，因为 3 ＋ 4 ＜ 8，所以这三条线段不能组成三角形。

等腰三角形和等边三角形也是常见的类型。

等腰三角形的两腰相等，两个底角也相等。

等边三角形则更为特殊，它的三条边都相等，三个角都是 60 度。

直角三角形在三角形中也有着特殊的地位。

它满足勾股定理，即两条直角边的平方和等于斜边的平方。

比如，一个直角三角形的两条直角边分别为 3 和 4，那么斜边的长度就是√（3²＋ 4²) ＝ 5。

三角形的全等和相似也是中考的重点。

全等三角形的对应边和对应角都相等，判定全等三角形有“SSS”（边边边）、“SAS”（边角边）、“ASA”（角边角）、“AAS”（角角边）和“HL”（斜边、直角边）等方法。

相似三角形的对应边成比例，对应角相等，判定相似三角形的方法有“两角对应相等”“两边对应成比例且夹角相等”“三边对应成比例”。

说完三角形，咱们再来说说四边形。

四边形包括平行四边形、矩形、菱形、正方形等。

平行四边形的两组对边分别平行且相等，对角线互相平分。

矩形是特殊的平行四边形，它的四个角都是直角，对角线相等。

菱形也是特殊的平行四边形，它的四条边都相等，对角线互相垂直且平分每组对角。

中考数学专题复习：几何综合题

【考点总结】四、全等三角形的性质与判定
1．概念：能够完全重合的两个三角形叫做全等三角形． 2．性质：全等三角形的对应边、对应角分别相等． 3．判定：(1)有三边对应相等的两个三角形全等，简记为(SSS)； (2)有两边和它们的夹角对应相等的两个三角形全等，简记为(SAS)； (3)有两角和它们的夹边对应相等的两个三角形全等，简记为(ASA)； (4)有两角和其中一角的对边对应相等的两个三角形全等，简记为(AAS)； (5)有斜边和一条直角边对应相等的两个直角三角形全等，简记为(HL)．
三角形专题
1，掌握三角形相关基础知识（2课时）
目标
2，掌握三角形有关模型的全等或相似证明（3课时） 3，完成三角形有关模型的全等或相似证明（3课时）
三角形
模型
手拉手模型
三垂直模型
相似模型
三角形有关的知识
【考点总结】一、三角形中的重要线段 1．三角形的高线：从三角形的一个顶点向它的对边所在的直线作垂线，顶点和垂足之间的线段叫做三角形的高线，简称高．特性：三角形的三条高线相交于一点． 2．三角形的中线：在三角形中，连接一个顶点和它对边中点的线段叫做三角形的中线．特性：三角形的三条中线交于一点． 3．三角形的中位线：连接三角形两边中点的线段叫做三角形的中位线．定理：三角形的中位线平行于第三边，且等于它的一半 4．三角形的角平分线：三角形一个角的平分线和这个角的对边相交，这个角的顶点和交点之间的线段叫做三角形的角平分线．特性：三角形的三条角平分线交于一点，这点叫做三角形的内心．性质：角平分线上的点到角的两边的距离相等．
小组合作
1.在△ABC中，∠BAC＝90°，AB＝AC，AD⊥BC于点D．
（1）如图1，点M，N分别在AD，AB上，且∠BMN＝90°，当∠AMN＝30°，AB＝2时，求线段

广东省2022年中考数学总复习指导课件：第2部分专题4 第2讲三角形或四边形的计算与证明

∴△BED≌△CFD(AAS)，∴DE＝DF． (2)解：∵∠BDE＝40°，∴∠B＝50°，∵∠B＝∠C，∴∠C＝50°． ∴∠BAC＝180°－∠B－∠C＝80°．
30
第一部分专题四中档解答题——提分练
返回导航
3．(2020 海珠区一模)如图，已知△ABC 中， AB＝BC＝10，tan∠ABC＝34．
【思路点拨】(1)根据SAS可证明△AHB≌△AGC； (2)①证明△AEH≌△AFG(SAS)，可得∠AFG＝∠AEH＝45°，从而根据两角的和可得结论；②分两种情况：(i)AQ＝QG时，(ii)当AG＝QG 时，分别根据等腰三角形的性质可得结论． (1)证明：由旋转得AH＝AG，∠HAG＝90°． ∵∠BAC＝90°，∴∠BAH＝∠CAG． ∵AB＝AC，∴△ABH≌△ACG(SAS)．
第一部分专题四中档解答题——提分练
返回导航
26
返回导航
1．(2020孝感)如图，在□ABCD中，点E在AB的延长线上，点F在
CD的延长线上，满足BE＝DF．连接EF，分别与BC，AD交于点G， H．求证：EG＝FH．
27
第一部分专题四中档解答题——提分练
返回导航
证明：∵四边形 ABCD 是平行四边形，∴AB∥CD，∠ABC＝∠CDA． ∴∠EBG＝∠FDH，∠E＝∠F．
25
第一部分专题四中档解答题——提分练
解：(1)∵四边形 ABCD 是平行四边形， ∴AB∥CD，AO＝CO，∴∠FCO＝∠EAO． ∵∠AOE＝∠COF，∴△AOE≌△COF(ASA)， ∴OE＝OF＝32，∴EF＝2OE＝3． (2)四边形 AECF 是菱形，理由如下： ∵△AOE≌△COF，∴AE＝CF． ∵AE∥CF，∴四边形 AECF 是平行四边形． ∵EF⊥AC，∴四边形 AECF 是菱形．

广东省各市中考数学分类解析专题10：四边形

广东中考数学试题分类解析汇编专题10：四边形一、选择题1. （广东佛山3分）依次连接任意四边形各边的中点，得到一个特殊图形（可认为是一般四边形的性质），则这个图形一定是【】A．平行四边形B．矩形C．菱形D．梯形【答案】 A。

【考点】三角形中位线定理，平行四边形的判定。

【分析】根据题意画出图形，如右图所示：连接AC，∵四边形ABCD各边中点是E、F、G、H，∴HG∥AC，HG=12AC，EF∥AC，EF=12AC。

∴EF=GH，EF∥GH。

∴四边形EFGH是平行四边形。

由于四边形EFGH是平行四边形，它就不可能是梯形；同时由于是任意四边形，所以AC=BD或AC⊥BD不一定成立，从而得不到矩形或菱形的判断。

故选A。

2．（广东广州3分）如图，在等腰梯形ABCD中，BC∥AD，AD=5，DC=4，DE∥AB交BC于点E，且EC=3，则梯形ABCD的周长是【】A．26B．25C．21D．20【答案】C。

【考点】等腰梯形的性质，平行四边形的判定和性质。

【分析】∵BC∥AD，DE∥AB，∴四边形ABED是平行四边形。

∴BE=AD=5。

∵EC=3，∴BC=BE+EC=8。

∵四边形ABCD是等腰梯形，∴AB=DC=4。

∴梯形ABCD的周长为：AB+BC+CD+AD=4+8+4+5=21。

故选C。

3. （广东广州3分）在平面中，下列命题为真命题的是【】A．四边相等的四边形是正方形B．对角线相等的四边形是菱形C．四个角相等的四边形是矩形D．对角线互相垂直的四边形是平行四边形【答案】C。

【考点】命题与定理，正方形的判定，菱形的判定，矩形的判定，平行四边形的判定。

【分析】分析是否为真命题，需要分别分析各题设是否能推出结论，从而利用排除法得出答案，不是真命题的可以举出反例排除：A、四边相等的四边形不一定是正方形，例如菱形，故此选项错误；B、对角线相等的四边形不是菱形，例如矩形，等腰梯形，故此选项错误；C、四个角相等的四边形是矩形，故此选项正确；D、对角线互相垂直的四边形不一定是平行四边形，如铮形（如图），故此选项错误。

中考数学专题复习《三角形和四边形中的中点问题》课件

A
解：如图，延长BM交AC于点E，
∵AM为∠BAC的平分线,BM⊥AM, ∴∠BAM=∠EAM，∠AMB=∠AME=90°.
E
M
又∵AM=AM，
B
D
C
∴△ABM≌△AEM(ASA).
∵D为△ABC中BC边的中点，
∴BM=ME，AB=AE=12. ∴CE=AC-AE=18-12=6.
∴DM是△BCE的中位线.
练一练
4.如图，∠ACB=90°，D为AB的中点，连接DC,并延长DC交AF于点E,
过点B作BF//DE，与AE的延长线交于点F，若BF长为 x ,AB长为 y ，
EC=2.求 y关于 x 的函数表达式.并说明理由.
F
解：y关于x的函数表达式为y=x-4.
理由如下：
∵D为AB的中点，BF//DE,
1.如图，在等腰三角形ABC中，点D 是底边BC的中点，若连接AD.
2.已知Rt△ABC中，∠C＝90°， D为AB的中点．
结论：AD⊥BC；∠BAD＝∠CAD.
结论：CD＝AD ＝BD ＝ 1 AB. 2
练一练
5. 如图，已知D为△ABC中BC边的中点，AB=12，AC=18，BM⊥AM
于点M.连接DM，若AM为∠BAC的平分线，求MD的长.
三角形和四边形中的中点问题
练一练
1.如图，在矩形ABCD中，BD＝12，E，F分别是AB，BC的中点，则 EF的长为 6 ．
【变式】如图，在Rt△ABC中，∠C=90°，AC=3，BC=4，N是BC边上一
点，M为AB边上的动点，点D，E分别为CN，MN的中点，则DE的最小值
是（ D ）
A.2.5
C D
N
B.12

2020年广东省中考数学基础过关：三角形和多边形课件(共35张PPT)

180°n－2 n
3当n为奇数时，正n边形是轴对称图形；当n为偶数时，既是轴对称图形，又是
中心对称图形
知识过关
知识点 1 三角形的三边关系(7年未考)
1．已知三角形的三边长为5，x, 8，那么x的取值范围是__3_＜_x_＜__1_3__.
2．(2019毕节)在下列长度的三条线段中，不能组成三角形的是( C )
1内角和定理：nn≥3边形的内角和等于⑥_(n_－__2_)_×__1_8_0_°
2外角和定理：nn≥3边形的外角和等于⑦___3_6_0_°____
3经过nn≥3边形的一个顶点可以作n－3条对角线，它们将n边形分成n－2个
三角形，n边形的所有对角线条数为nn2－3条
2．正多边形的性质
1正n边形的各边相等，各角相等，每一个内角的度数为 2正n边形有n条对称轴
考情分析 2018年第8题，2017年第9题均涉及三角形内角和；2015年第4题涉及三角形内、外角关系．
4．在△ABC中，若∠A＝30°，∠B＝50°，则∠C＝____1_00_°____.
5．(2019孝感)如图1，直线l1∥l2，直线l3与l1， l2分别交于点A，C，BC⊥l3交l1于点B，若∠1 ＝70°，则∠2的度数为( B )
6．(2019广东)一个多边形的内角和是1 080°，这个多边形的边数是_____8_____.
7．(2014广东)一个等腰三角形的两边长分别是 3和7，则它的周长是( A )
A．17 B．15
C．13 D．13或17
8．下列语句错误的是( C ) A．三角形的垂心是三角形三条高的交点 B．三角形的重心是三角形三条中线的交点 C．三角形的垂心是三角形三条垂直平分线的

广东省数学中考一轮复习第四章三角形第15讲三角形的基本概念和性质课件

分
题19,4分
题
三角形的中位线题6,3分
题7,3分
19(2),
3分
三角形的内心
题24(3), 2分
◇链接教材◇人教版:八上第十一章P2－P17,八下第十八章P47－
P49
北师版:七下第四章P81－P91,八上第七章P178－P183,八下第六章
P150－P152
课前预习
1.(202X柳州)若长度分别为3,4,a的三条线段能组成一个三角形,则整数a的值可以是 5(答案不唯一) (写出一个即可). 2.(202X梧州)在△ABC中,∠A＝20°,∠B＝4∠C,则∠C等于 (A) A.32° B.36° C.40° D.128°
3.(202X湖北)如图,在△ABC中,∠C＝90°,点D在AC上,
DE∥AB,若∠CDE＝160°,则∠B的度数为( D )
A.40°
B.50°
C.60°
D.70°
第3题图
4.(202X宿迁)如图,在△ABC中,∠A＝70°,∠C＝30°,BD平
分∠ABC交AC于点D,DE∥AB,交BC于点E,则∠BDE的度数
A.①②③④ B.①②④
C.①②③
④
第6题图
7.(202X梧州)如图,在Rt△ABC中,点D,E,F分别是边AB,AC,
BC的中点,AC＝8,BC＝6,则四边形CEDF的面积是( B )
A.6
B.12
C.24
D.48
第7题图
8.(202X济宁)如图,在△ABC中,点D为△ABC的内心, ∠A＝60°,CD＝2,BD＝4,则△DBC的面积是( B )
|a－6|+ b－8＝0,则这个三角形的最大边 c 的取值范围是