2015～2016学年度盐城市第一学期高二学业水平必修科目期终考试

合集下载

高二年级上学期期中考试完形与阅读题（部分原创）

高二年级上学期期中考试完形与阅读题（部分原创）完形填空：请认真阅读下面短文，从短文后各题所给的A、B、C、D四个选项中，选出最佳选项。

“Fire! Fire!” The cry crept out on the still night air, and the fire bel ls began to ring. Fred was ___36___ by the alarm and the red light streaming into his room. He ___37___ himself in a moment, almost, and tapped at the door of his mother?s bedroom.“It is Mr. Barton?s house, mother. Do let me go,” he said in eager, excited tones. Mrs. Liscom thought a moment. He was ___38___, but she could trust him, and she knew how much his heart was in the ___39___.“Yes, you may go,” she answered, “but be careful, my boy. If you can help, do so;b ut do nothing rashly.” Fred ___40___ to follow her advice, and hurried to the fire.Mr. and Mrs. Barton were not at home. The house had been left in the charge of the servants. The fire ___41___ with fearful speed, for there was a high wind, and it was found impossible to save the __42___. The servants ran about, screaming, but doing ___43___ to any purpose.Fred found T om outside, in safety. “Where is Katy?” he aske d. Tom, shaking with ___44___, seemed to have had no thought but of his own escape. He said, “Katy is in the house!” “In what room?” asked Fred. “In that one,” pointing to a window in the upper story.It was no time for ___45___, but for instant action. The staircase was already on fire; there was but one way to ___46___ Katy, and that full of danger. The second floor might fall at anymoment, and Fred ___47___ it. But he trusted in an arm stronger than his own, and silently sought help and guidance.A ladder was quickly brought, and placed ___48___ the house. Fred climbed it, ___49___ by the hired man, dashed in the sash(窗框) of the window, and pushed his way into the room ___50___ the poor child lay nearly suffocated(窒息) with smoke.He roused(叫醒) her with some difficulty, ___51___ her to the window, and placed her upon the sill(窗台). She was instantly grasped by strong arms, and carried down the ladder, Fred following as ___52___ as possible. They had scarcely reached the ground ___53___a crash of falling timbers(木头) told them that they had barely escaped with their lives.Tom Barton never forgot the ___54___ of that night; and he came to believe, and to ___55___ the belief, in after years, that true manliness is in harmony with gentleness, kindness, and self-denial.36. A. wakened B. frightened C. interrupted D. cheated37. A. concerned B. devoted C. dressed D. adjusted38. A. smart B. cool C. academic D. young39. A. request B. air C. way D. charge40. A. longed B. promised C. decided D. desired41. A. started B. spread C. developed D. increased42. A. child B. furniture C. host D. house43. A. everything B. something C. nothing D. anything44. A. cold B. terror C. surprise D. excitement南京师大附中高二第一学期英语期中试卷45. A. correspondence B. description C. words D. worries46. A. reach B. call C. locate D. search47. A. knew B. ignored C. doubted D. imagined48. A. below B. against C. inside D. near49. A. followed B. led C. supported D. pushed50. A. when B. so that C. where D. as if51. A. invited B. attached C. linked D. carried52. A carefully B. quickly C. willingly D. freely53. A. before B. until C. after D. since54. A. wonder B. story C. lesson D. accident55. A. act upon B. refer to C. rely on D. attend to阅读理解：请认真阅读下列短文，从短文后各题所给的A、B、C、D四个选项中，选出最佳选项。

2015年江苏省普通高中学业水平测试(必修科目)试题及答案

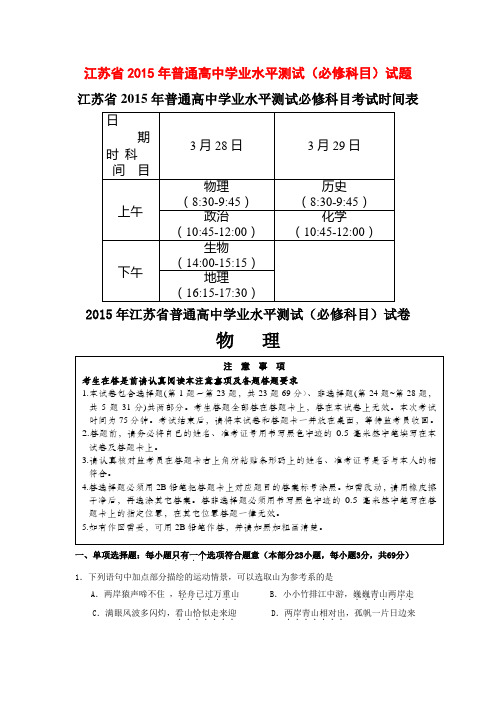
江苏省2015年普通高中学业水平测试（必修科目）试题江苏省2015年普通高中学业水平测试必修科目考试时间表2015年江苏省普通高中学业水平测试（必修科目）试卷物理一、单项选择题：每小题只有一个．．．．选项符合题意（本部分23小题，每小题3分，共69分） 1．下列语句中加点部分描绘的运动情景，可以选取山为参考系的是A ．两岸猿声啼不住，轻舟已过万重山．．．．．．．B ．小小竹排江中游，巍巍青山两岸走．．．．．．．C ．满眼风波多闪灼，看山恰似走来迎．．．．．．．D ．两岸青山相对出．．．．．．．，孤帆一片日边来注意事项考生在答是前请认真阅读本注意事项及各题答题要求1.本试卷包含选择题(第1题～第23题，共23题69分〉、非选择题(第24题~第28题，共5题31分)共两部分。

考生答题全部答在答题卡上，答在本试卷上无效。

本次考试时间为75分钟。

考试结束后，请将本试卷和答题卡一并放在桌面，等待监考员收回。

2.答题前，请务必将自己的姓名、准考证号用书写黑色字迹的0.5毫米签字笔填写在本试卷及答题卡上。

3.请认真核对监考员在答题卡右上角所粘贴条形码上的姓名、准考证号是否与本人的相符合。

4.答选择题必须用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，请用橡皮擦干净后，再选涂其它答案。

答非选择题必须用书写黑色字迹的0.5毫米签字笔写在答题卡上的指定位置，在其它位置答题一律无效。

5.如有作图需妥，可用2B 铅笔作答，并请加黑加粗画清楚。

2．某物体的x--t图象如图所示，则该物体A.处于静止状态B.做匀速直线运动C.做变速直线运动D.做匀加速直线运动3.如图所示为“探究求合力的方法”的实验装置，则A.实验中所用的两根细线越短越好B.弹簧测力计的拉力方向必须与木板平行C.实验中只需记录弹簧测力计拉力的大小D.每次实验中两个分力间的夹角必须大于9004.某汽车发动机铭牌上标有“200kW”的字样，其表示A.实际功率B.瞬时功率C.平均功率D.额定功率5.如图所示，质量不同的两个小球从同一高度同时做自由落体运动，则A.质量大的下落得快B.质量小的下落得快C.两球下落的时间相同D.两球下落的加速度不同6.如图所示，小强用与水平方向成θ角的轻绳拉木箱，未拉动，此时绳中拉力为F，则木箱所受摩擦力的大小为A.FcosθB.FsinθC.0D.F7.均匀小球A、B的质量分别为m、5m，球心相距为R，引力常量为G，则A球受到B球的万有引力大小是A.225mGRB.25mGRC.22mGRD.2mGR8.按照“江苏省校园足球振兴行动计划”要求，我省将建立1000所足球特色学校，如图所示，某校一学生踢球时A.脚对球的作用力大于球对脚的作用力B.脚对球的作用力与球对脚的作用力大小相等C.脚对球的作用力与球的重力是一对平衡力D.脚对球的作用力与球对脚的作用力是一对平衡力9.如图所示，小朋友在玩蹦蹦杆游戏的过程中，关于杆上弹簧，下列说法中不正．．确．的是A.弹簧恢复到原长时，弹性势能为零B.弹簧恢复原长过程中，弹性势能转化为其他形式的能C.弹簧形变量最大时，弹性势能不一定最大D.弹簧压缩过程中，其他形式的能转化为弹性势能10.如图所示，在地面上发射一个飞行器，进入近地圆轨道Ⅰ并绕地球运行，其发射速度v应满足A.v＜7.9km/sB.v=7.9km/sC.v=11.2km/sD.v＞11.2km/s11.伽利略的理想斜面实验示意图如图所示，不计摩擦和空气阻力，下列说法中正确的是A.该实验没有以可靠事实为依据，只是逻辑推理B.小球在水平面上不受外力作用C.小球沿右侧斜面上升的高度与其倾角有关D.该实验否定了“力是维持物体运动的原因”的观点12.一端固定的轻质弹簧处于原长，现用互成角度的两个力F1、F2拉弹簧的另一端至O点，如图所示，在此过程F1、F2分别做了6J、8J的功；换用另一个力F仍使弹簧重复上述过程，该过程F所做的功是A.2JB.8JC.10JD.14J13．在“探究加速度与力、质量的关系”实验中，为了消除打点计时器和木板对小车阻力的影响，关于该操作环节，下列四种装置图中正确的是14．如图所示，一光滑球用细线悬挂在升降机竖直壁上，设细线对小球的拉力为F1,竖直壁对球的弹力为F2.升降机竖直向上加速运动，当加速度增大时A．F1变小，F2变小B．F1变小，F2变大C．F1变大，F2变大D．F1变大，F2变小15．某电场的电场线如图所示，A、B是一电场线上的两点，则A、B两点的电场强度A．大小相等，方向不同B．大小不等，方向不同C．大小相等，方向相同D．大小不等，方向相同16．如图所示，当闭合开关S后，螺旋管通以恒定电流，不计其他磁场的影响，螺旋管上方A点的磁感应强度方向为A．向右B．向左C．垂直纸面向里 D．垂直纸面向外17．如图所示，线框平面与磁场方向垂直，现将线框沿垂直磁场方向拉出磁场的过程中，穿过线框磁通量的变化情况是A．变小B．变大C．不变D．先变小后变大18.探究影响安培力大小因素的实验装置如图所示，直导线垂直磁场方向置于磁场中某处。

2015年江苏省普通高中历史学业水平测试(必修科目)说明小高考

2015年江苏省普通高中学业水平测试（必修科目）说明历史一、命题指导思想历史（必修科目）学业水平测试的命题以教育部制订的《普通高中历史课程标准（实验）》和《江苏省普通高中历史课程标准教学要求（修订稿）》为依据，坚持从江苏高中历史教育的实际情况出发，充分体现学业水平测试的功能价值和历史课程的学科特点，力图体现基础性、公平性、时代性、创新性和情境性，密切联系学生生活和社会实际，以科学评价引导高中历史课程标准的有效实施。

二、测试内容和要求（一）测试范围测试的内容包括《普通高中历史课程标准（实验）》规定的3个必修模块的25个专题的有关内容。

历史（必修科目）学业水平测试除了规定必要的测试内容，还提出了相应的测试能级，旨在测试学生对主要史实的了解状况、历史思维能力和必备的人文素养。

（二）测试能力要求测试能级主要分为调动和运用历史知识、获取和解读材料信息、叙述和阐释历史事物以及论证和探讨历史问题四大类，主要侧重于前三类，在本考试说明的测试要求中主要用“了解”、“理解”、“认识”和“探讨”四个行为动词来体现这些要求，新课程的情感态度与价值观目标也包含其中。

（三）测试的具体内容和要求历史（I）1．古代中国的政治制度三、试卷结构（一）题型比例试题分为客观题和主观题两大类，客观题包括单项选择题和判断题，主观题包括材料解析题和问答题，客观题和主观题的比例为7：3。

（二）试题难度比例试卷由容易题、中等难度题、较难题组成，其占分比例约为7：2：1。

（三）内容比例历史（I）约占40%，历史（Ⅱ）约占35%，历史（Ⅲ）约占25%。

四、测试方法与时间（一）测试方式闭卷笔试。

（二）测试时间75分钟。

（三）试卷满分值满分为100分。

江苏省盐城市五校联考2024-2025学年高二上学期10月月考试题英语

听下面一段较长对话，回答以下小题。【此处可播放相关音频，请去附件查看】
6.What’s the man?
A.A hotel receptionist.B.A salesman.C.A painter.
7.Which colour will the woman try on?
A.Red.B.Black.C.Purple.
A.It’s in a hurry.
B.It’s unimportant.
C.It’s timeconsuming.
15.What’s the man’s last task?
A.Writing a report.
B.Starting a new project.
C.Sending an email.
16.When will the woman give a presentation?
A.Today.B.Next week.C.Next month.
听下面一段独白，回答以下小题。【此处可播放相关音频，请去附件查看】
17.What is Belfast famous for?
A.Making ropes.B.Building ships.C.Selling tea.
A.She failed to behave herself in public.
B.She got lost with her brother.
C.She served the wrong dish.
第二节（共15小题；每小题1.5分，满分22.5分）
听下面5段对话或独白。每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项。听每段对话或独白前，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。每段对话或独白读两遍。

2022-2023学年江苏省盐城中学高二年级上册学期期中数学试题

2022-2023学年度江苏省盐城中学高二年级第一学期期中考试一、单选题（本大题共8小题，共40.0分。

在每小题列出的选项中，选出符合题目的一项） 1．过()2,1A ，()3,2B 两点的直线的倾斜角为（） A ．60︒B ．45-︒C ．135︒D ．45︒2．已知双曲线2221y x m-=的渐近线方程为y =，则2m =（）A ．5BC ．15D ．253．直线1:20l x ay a ++=和直线()2:230l a x y -+=互相垂直，则实数a 的值为（） A ．3a =- B ．12a =C ．1a =或3a =D ．1a =-或3a =4．已知椭圆221259x y +=上一点P 的横坐标为2，F 是椭圆的右焦点，则点P 到点F 的距离为（） A ．5B ．85C ．335D ．1755．已知平面内两定点()1,0A -，()1,0B ，动点C 满足3AC BC ⋅=，则BC 的最小值为（） A ．B ．3C ．2D ．06．若直线:20l x my m +--=与曲线2214x y -=有且只有一个交点，则满足条件的直线有（） A ．4条B ．3条C ．2条D ．条7．若直线():40l x m y +-=与曲线x =有两个交点，则实数m 的取值范围是（）A ．0m <<B ．0m ≤<C ．0m <≤D ．0m ≤≤8．已知P 是圆()221:316F x y ++=上的一动点，点()23,0F ，线段2PF 的垂直平分线交直线1PF 于点Q ，则Q 点的轨迹方程为（）A ．22154x y -= B ．22149x y -= C ．22145x y -=D ．()221045x y x -=> 二、多选题（本大题共4小题，共20.0分。

在每小题有多项符合题目要求）9．已知直线过原点，且()1,4A ，()3,2B 两点到直线的距离相等，则直线方程可以为（） A ．0x y +=B ．50x y +-=C ．320x y -=D ．320x y +=10．已知曲线22:1C ax y +=，则下列说法正确的是（） A ．若01a <<，则C 是椭圆，其焦点在y 轴上B ．若0a <，则C 是双曲线，其渐近线方程为y = C ．若曲线C 为椭圆，其焦点为()1,0，则2a =D ．若0a =，则C 是两条直线11．设m ，n 为实数，已知椭圆2214x y m+=与双曲线221y x n -=有相同的焦点1F ，2F ，且椭圆与双曲线在第一象限的交点为3P y ⎛⎫⎪ ⎪⎝⎭，则下列说法正确的是（）A ．y =B ．2n =C ．1m =D ．左焦点为()12．已知直线:40l x y +-=和曲线22:4O x y +=，点A 是直线上的一个动点，点D 是曲线O 上的一个动点，过点A 作曲线O 的两条切线，切点分别为B 、C ，则下列说法正确的是（）A ．AB 的最小值为2B ．曲线O 上存在2个点到直线的距离等于2C ．若曲线O 上总存在点D ，使得30OAD ∠=︒，则A 的横坐标的取值范围是[]0,4 D ．直线BC 过定点()1,1三、填空题（本大题共4小题，共20.0分）13．法国数学家蒙日(),17461818Monge -发现：双曲线()2222:10x y a b a bΓ-=>>的两条互相垂直切线的交点P 的轨迹方程为：2222x y a b +=-，这个圆被称为蒙日圆．若某双曲线()22210x y a a-=>对应的蒙日圆方程为223x y +=，则a =______．14．写出与圆224x y +=和圆22120x y +--+=都相切的一条直线的方程：______．15．数学中有很多形状优美，寓意美好的曲线，曲线22:220C x y x y +--=就是其中之一，则曲线C 所围成的封闭图形的面积是______．16．已知P 、Q 分别在直线1:10l x y -+=与直线2:10l x y --=上，且1PQ l ⊥，点()4,4A -，()4,0B ，则AP PQ QB ++的最小值为______．四、解答题（本大题共6小题，共70.0分。

高二上学期期中考试数学试卷含答案(共5套)

高二上学期期中考试数学试题本卷分Ⅰ（选择题）、Ⅱ卷（非选择题）两部分，其中Ⅰ卷1至2页，第二卷2至4页，共150分，考试时间120分钟。

第Ⅰ卷（选择题，共60分）一、单选题：本题共12个小题，每小题5分1．“”是“”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件2．有下列四个命题：（1）“若，则，互为倒数”的逆命题；（2）“面积相等的三角形全等”的否命题；（3）“若（4）“若，则，则有实数解”的逆否命题；”的逆否命题.其中真命题为（）A．（1）（2）B．（2）（3）C．（4）D．（1）（2）（3）3．若则为（）A．等边三角形B．等腰直角三角形C．有一个内角为30°的直角三角形D．有一个内角为30°的等腰三角形4．已知.若“”是真命题，则实数a的取值范围是A．(1，+∞)B．(－∞，3)C．(1，3)D．5．为的内角，，的对边分别为，，，若，，，则的面积A．B．C．D．6．已知中，，则等于（）A．B．或C．D．或7．等差数列的前项和为，若，则等于（）A．58B．54C．56D．528．已知等比数列中，，，则（）A．2B．C．D．49．已知，则z=22x+y的最小值是A．1B．16C．8D．4）10．若关于的不等式的解集为，则的取值范围是（A．B．C．D．11．当ａ＞０，关于代数式，下列说法正确的是（）A．有最小值无最大值B．有最大值无最小值C．有最小值也有最大值D．无最小值也无最大值12．在△ABC中，AB＝2，C＝，则AC＋BC的最大值为A．B．3C．4D．2第Ⅱ卷（非选择题，共90分）二、填空题：共4个小题，每小题5分，共20分13．命题的否定是______________．114．已知的三边长构成公差为 2 的等差数列，且最大角的正弦值为，则这个三角形的周长为________.15．已知数列{a n }的前 n 项和为 S n ，a 1＝1，当 n≥2时，a n ＋2S n －＝n ，则 S 2017的值____ ___16．已知变量满足约束条件若目标函数的最小值为2，则的最小值为__________．三、解答题：共 6 题，共 70 分，解答应写出必要的文字说明、证明过程或演算步骤。

江苏省盐城市五校联考2023-2024学年高二下学期期中英语答案

2023/2024学年度第二学期联盟校期中考试高二年级英语试题答案第一部分听力（共两节，满分30 分）1-5 ABCBA6-10 BCACA 11-15 ACBCA 16-20 CBCAB第二部分阅读(共两节, 每小题2.5分,满分50分)21．C 22．C 23．B24．D 25．A 26．A 27．D28. A 29．D 30．B 31．D32．B 33．B34．C 35．C36．D 37．G38．C 39．E 40．F第三部分语言运用(共两节，满分30分)第一节(共15小题；每小题1分，满分15分)41．A 42．D 43．A 44．C 45．B 46．B 47．C 48．D 49．C 50．B 51．A 52．D 53．C 54．B 55．D第二节(共10小题；每小题1. 5分, 满分15分)56.athletic57.However58. was recognized59.which60.Typically 61.the62.popularity63.started 64.featuring65. to第四部分写作(共两节, 满分40分)第一节(满分15分)Dear Peter,I hope this letter finds you well. It’s my pleasure to contribute to the 3rd anniversary edition of the Students’ Space by sharing a few thoughts on how we can improve the newspaper.Firstly, I believe the content of the paper could be more diverse. Secondly, I suggest improving the readability of the paper. Lastly, I propose that we increase the frequency of the paper to twice a month.Thank you for considering my suggestions. I look forward to reading a more diverse, readable, and informative Students’ Space in the future.Yours,Li Hua第二节(满分25分)Hearing Momma’s words, Niesha stared at the precious blue ribbon, lost in thought. She pictured the scene where her mom tried her best to overcome her fears and gathered all her courage to deliver a fantastic speech to the audience. And Momma, aware of Neisha’s inner confusion and anxiety, reached out her hand to tie the blue ribbon onto Niesha’s wrist with a sweetsmile, saying she would be with her all the time. Greatly touched and determined to find her courage, Neisha stood in front of the mirror, constantly practicing from pronunciation to tone and even each gesture. “Try harder, and I can make it!” she kept cheering herself up.The next day Niesha again walked to the front of the classroom to give her presentation. Still shy and nervous, she customarily lowered her head to avoid making eye contact with others, numb there for seconds. But shortly afterwards, courage found its way back the moment she caught sight of the blue ribbon. Comforted and inspired, she took a deep breath, straightened her shoulders and then got started, “Dear fellow students, ...” While presenting herself, Niesha glanced at Mr. Roberts smiling at her and listening attentively. A spark of joy flashing across her eyes, she knew for sure that she had found her courage, in the mill and in the adversity.书面表达评分标准第四部分写作（共两节，满分40分）第一节：应用文（满分15分）本题总分为 15 分，按五个档次进行评分。

2015年江苏省高中地理学业水平测试(必修科目)考试说明小高考

2015年江苏省高中地理学业水平测试(必修科目)考试说明地理1宇宙中的地球测试内容测试要求地球所处的宇宙环境了解不同级别的天体系统，说明地球在太阳系中的位置知道地球是太阳系中一颗既普通又特殊的行星，理解地球存在生命的条件太阳对地球的影响了解太阳辐射对地球的影响了解太阳活动对地球的影响地球运动的地理意义知道地球自转和公转的方向、周期和速度理解黄赤交角的地理意义理解昼夜更替和地方时产生的原因，能够进行简单的区时计算了解四季更替的现象，解释四季形成的原因地球的圈层结构知道地球的圈层结构，了解各圈层的主要特点自然环境中的物质运动和能量测试内容测试要求地壳内部物质循环了解岩石圈三大类岩石的主要特点，了解地壳内部物质循环过程地表形态的变化了解褶皱，断层的主要特点、成因及对地表形态的影响结合实例，说明流水，风力，冰川等外力作用对地表形态的影响大气受热过程了解大气的受热过程理解大气保温作用的基本原则结合实例，说明大气热力环流的形成过程气压带与风带结合实际，说明气压带、风带的分布、移动规律及其对气候的影响理解季风环流的形成原因及影响天气系统结合实例，说明锋面系统（冷锋、暖锋及准静止锋）的特点及对天气的影响结合实际，说明低压（气旋）、高压（反气旋）系统的特点及对天气的影响水循环了解水循环的过程和主要环节结合实际，说明水循环的地理意义洋流了解洋流的概念及类型（寒流和暖流）了解世界洋流的分布规律，结合实例说明洋流对地理环境的影响自然环境的整体性和差异性测试内容测试要求自然地理要素与地理环境知道自然地理环境的组成要素知道自然地理要素（生物）在地理环境形成和演变中的作用地理环境的整体性结合实例，说明地理环境各要素间的相互作用理解地理环境的整体性对人类活动的影响地理环境的差异性结合实例，说明地理环境从赤道到两极、从沿海向内陆及垂直地带的地域分异规律理解地理环境的差异性对人类活动的影响自然环境对人类活动的影响测试内容测试要求地表形态与聚落及交通线路结合实例，说明地表形态对聚落和交通线路分布的影响气候变化与人类活动了解气候变化对人类活动的影响自然资源与人类活动结合实例，说明在不同生产力条件下，自然资源的数量与质量对人类生存与发展的意义自然灾害结合实例，说明旱涝、台风、寒潮和地震发生的主要原因、危害及防治措施地理2人口与城市测试内容测试要求人口增长模式知道不同人口增长模式的主要特点及地区分布人口迁移结合实例，分析人口迁移的主要原因人口数量与环境区别环境承载力与人口合理容量的含义城市的空间结构结合实例，分析城市空间结构，解释其形成原因城市服务功能比较不同规模城市的服务范围和服务功能的差异城市化结合实例，说明城市化的过程和特点，分析城市化对地理环境的影响地域文化结合实例，说明地域文化对城市的影响生产活动与地域联系测试内容测试要求农业区位与农业地域类型结合实例，分析影响农业区位的主要因素结合实例，说明主要农业地域类型的特点及其形成条件工业区位与工业地域结合实例，分析影响工业区位的主要因素结合实例，说明工业地域的形成条件与发展特点生产活动对地理环境的影响结合实例，说明工、农业生产活动对地理环境的影响生产活动中的地域联系结合实例，说明生产活动中地域联系的重要性和主要方式交通与聚落、商业网点结合实例，分析影响交通运输方式和布局的变化对聚落空间形态和商业网点布局的影响人类与地理环境的协调发展测试内容测试要求人地关系思想的历史演变了解人地关系思想在不同历史阶段的特点环境问题了解人类所面临的主要环境问题结合实例，分析环境问题产生的主要原因可持续发展理解可持续发展的基本内涵了解协调人际关系的主要途径理解人类走可持续发展道路的必然性地理3区域地理环境与人类活动测试内容测试要求区域的含义了解区域的含义区域差异比较不同区域自然环境及人类活动的差异不同发展阶段区域地理环境对人类生产和生活方式的影响结合实例，比较不同发展阶段区域地理环境对人类生产和生活方式的影响产业转移和资源跨区域调配与区域地理环境结合实际，分析产业转移和资源跨区域调配对区域地理环境的影响区域可持续发展测试内容测试要求区域环境与发展结合实例，分析区域的环境与发展问题，说明其危害和综合治理保护措施流域开发结合实际，分析某流域开发的地理条件，说明该流域开发建设的基本内容和综合治理的对策措施区域农业生产与农业持续发展结合实例，分析某区域农业生产的条件、布局特点和面临的主要问题，说明该区域农业持续发展的方法和途径区域能源和矿产资源的开发与区域可持续发展结合实例，分析某区域能源和矿产资源的合理开发与区域可持续发展的关系区域工业化和城市化结合实例，分析某区域工业化和城市化的推进过程，产生的主要问题，说明解决这些问题的对策措施地理信息技术的应用测试内容测试要求遥感（RS）了解遥感在资源普查、环境和灾害监测中的应用全球定位系统（GPS）了解全球定位系统在定位导航中的应用地理信息系统（GIS）了解地理信息系统在城乡管理中的应用数字地球知道数字地球的含义。

2015-2016年江苏省盐城市响水中学高一上学期数学期中试卷带答案

第 7 页（共 17 页）
（ 2）因为 A? B， a＜ 0 时，
，所以
所以 a 的取值范围是（﹣ a≤﹣ 1，
16．（ 14 分）已知扇形的周长为 16cm，圆心角为 2rad，求该扇形的面积．
【解答】解设扇形的半径为 r，弧长为 l，则有
，得， …（10 分）
∴ g（ x）的自变量 x 需满足
，解得 x∈ [ 1， ] ，
又 g（x）在 x∈[ 1， ] 上单调递增，所以 g（x）min=g（1）=4， g（ x）max=g（）= ，因此，函数 g（x）的值域为 [ 4， ] ，故填： [ 4， ] ．
10．（ 5 分）已知 f（x）=3kx3+ ﹣2（k∈ R），f（lg7）=1（ k∈ R），则 f（ lg ）= ﹣5 ．【解答】解： f（x） =3kx3+ ﹣ 2（ k∈ R），f（lg7）=1（k∈R），可得 3klg37+ ﹣2=1，可得 3klg37+ =3． f（lg ）=f（﹣ lg7）=﹣（3klg37+ ）﹣ 2=﹣ 5．故答案为：﹣ 5．
第 2 页（共 17 页）
2015-2016 学年江苏省盐城市响水中学高一（上）期中数学试卷
参考答案与试题解析
一、填空题：本大题共 14 小题，每小题 5 分，计 70 分.请把答案填写在答题卡相应位置上 . 1．（5 分）设集合 A={ 1，2，3} ，B={ 2，4} ，则 A∩B= { 2} ．【解答】解：∵ A={ 1， 2，3} ，B={ 2，4} ， ∴ A∩ B={ 2} ，故答案为： { 2} ．
9．（5 分）已知定义域为 [ 1，2] 的函数 f （x） =2+logax（ a＞ 0， a≠1）的图象过

江苏省盐城市2017-2018学年高二上学期学业水平必修科目期终考试+化学

2017/2018学年度第一学期高二学业水平必修科目期终考试化学试题本试卷可能用到的相对原子质量：H-1 C-12 N-14 O-16 Fe-56 Cu-64一、单项选择题：在每题的4个选项中，只有1个选项是符合要求的(本部分23题，每题3分，共69分)。

1．三位欧洲科学家因发展冷冻电镜技术而分享了2017年诺贝尔化学奖，利用该技术可以解析生物大（高）分子原子结构模型。

下列不属于．．．生物大分子的是A．油脂B．淀粉C．纤维素D．蛋白质2．我国科学家预言的T－碳（四个碳原子构成的正四面体分别取代金刚石结构中所有碳原子，如右图）最近在实验室成功合成。

T－碳属于A．混合物B．化合物C．氧化物D．单质3．136C在新药开发等领域用途十分广泛。

这里的“13”是指该原子的A．质子数B．中子数C．质量数D．电子数4．下列诗句描述的过程中包含化学变化的是A．宝剑锋从磨砺出B．蜡烛对烧红泪乾C．风吹柳花满店香D．玉碗冰寒滴露华5．下列物质中含有离子键的是A．CO2B．NaF C．HCl D．NH36．下列常见物质的俗名与化学式对应正确的是A．纯碱——NaOH B．生石灰——CaCO3C．可燃冰——CO2D．石英——SiO27．下列化学用语表示正确的是A．苯的结构式：C6H6 B．H2O的电子式：C．Mg2+的结构示意图：D．硝酸的电离方程式：HNO3 = H+ + NO－38．下列气体可用右图所示方法收集的是A．H2B．CO 2C．NOD．NH39．反应2SO2＋O22SO3在密闭容器中进行。

下列关于该反应的说法正确的是A．增大压强能减慢反应速率B．升高温度能减慢反应速率C．使用恰当的催化剂能加快反应速率D．0.2molSO2与0.1mol O2充分反应生成0.2molSO310．在含有大量Ba2+、OH－、Cl－的溶液中，还可能大量共存的离子是A．NH4B．SO－24C．Mg2+D．NO－311．下列反应属于置换反应的是A．2C +SiO2高温Si + 2CO↑B ．Na 2CO 3+CO 2+H 2O ＝2NaHCO 3C ．2H 2O 2MnO 22H 2O + O 2↑D ．Fe(OH)3 + 3HCl = FeCl 3 +3H 2O 12．下列过程吸收热量的是A ．液氨气化B ．生石灰加入水中C ．天然气燃烧D ．盐酸与氢氧化钾溶液反应13．下列有关苯和乙烯的说法正确的是A ．均易溶于水B ．均含有碳碳双键C ．均能发生加成反应D ．均能使酸性KMnO 4溶液褪色14．用右图所示装置萃取溴水中的溴，下列说法正确的是A ．使用前不需要检查分液漏斗是否漏液B ．萃取剂可用酒精或CCl 4C ．“振荡”后立刻进行分液D ．分液时，先从分液漏斗下口放出下层液体，关闭旋塞，再从上口倒出上层液体 15．我国已经成功研制出性能先进的铼镍合金单晶涡轮叶片。

盐城市2015-2016学年高二暑假作业英语试题(七)含答案

高二英语作业（7）M5U2 The environment编写：尹红梅审阅：唐为龙一、语法专区(一) 单项选择1. ________ his learning method, his cousin was sure that he would achieve a good mark in theexamination .A．Being improved B．Improved C．To be improved D．Having improved2. _________ from his looks, he is a kind man.A. JudgingB. Being judgedC. To judgeD. Judge3. When I got back home, I saw a message pinned to the door _______ “Sorry to miss you; I’llcall later.”A. readB. readsC. to readD. reading4. He sent me an e-mail, _______ to get further information.A. hopedB. hopingC. to hopeD. hope5. He was busy writing a story, only ________ once in a while to smoke a cigarette.A to stopB stoppingC to have stoppedD having stopped6. It is one of the funniest things ______ on the Internet so far this year.A findingB being foundC to findD found7. The flowers his friend gave him will die unless __________ every day.A wateredB wateri ngC waterD to water8. ________ in the mountains for a week, the two students were finally saved by the local police.A Having lostB LostC Being lostD Losing9. More and more people are signing up for Yoga classes nowadays, _________ advantages of thehealth and relaxation benefits.A takingB takenC having takenD having been taken10. Reading is an experience quite different from watching TV; there are pictures _____ in yourmind instead of before your eyes.A to formB formC formingD having formed11. ________ the project as planned, we’ll have to work two more hours a day.A CompletingB CompleteC CompletedD To complete12. We had an anxious couple of weeks ______ for the results of the experiment.A waitB to be waitingC waitedD waiting13. _______ to reach them on the phone, we sent an email instead.A FailB FailedC To failD Having failed14.The meeting _______ next week is sure to be a great success.A. to take placeB. to be taken placeC. to have taken placeD. being taken place15._______ by the Comrade Lei Feng, we try our best to do good deeds.A. InspiredB. Being inspiredC. To be inspiredD. Inspiring16.It's no good _______ here. Let's go home.A. to waitB. waitedC. waitingD. being waited17.I li stened to the wind, ______that he would not come tonight.A. thinkingB. to thinkC. thoughtD. being thinking18.As a result of my laziness, I failed ________ my work in time.A. and finishedB. to finishC. and finishingD. to finished19.I am sorry ______ written you a letter at the ti me.A. to have notB. to not haveC. not to haveD. not having20.The article _________on this subject was written by Mr. Black.A. referringB. referredC. referring toD. referred to21.Living near the sea, ___________________.A. we enjoy healthy air and beautiful sightB. healthy air and beautiful sight is what we enjoyC. it is healthy air and beautiful sight we enjoyD. so we enjoy healthy air and beautiful sight22.__________ since the night before, I felt very hungry.A. Having not eaten anythingB. Not eating anythingC. I hadn't eaten anythingD. Not having eaten anything23.We then listened to the child ________ the article ______ on the blackboard.A. read, writingB. reading, writingC. to read, writtenD. read, written24.________ it with me and I'll see what I can do.A. When leftB. LeavingC. If you leaveD. Leave25._________ such a chance, why don't you have a try?A. To giveB. Having givenC. GivenD. Giving26.We discussed the plan that we would like to see ________ the next week.A. carry onB. carrying outC. carried outD. to carry out27.Five people were reported ________ in the accident.A. to be killedB. to killC. killedD. to have been killed28.____________ , I went to the park with my uncle.A. As holidayB. Being no classesC. Since have no classesD. It being a holiday29. "Do you mind _________?" "Go ahead."A. opening the doorB. your opening the doorC. my opening the doorD. I opening the door30. I have one or two things ____________.A. to lookB. to seeC. to see toD. to look to31._________ is bad for his health.A. Mike smokingB. Mike's smokingC. Mike's being smokingD. Mike smokes32.I came into the classroom, ______ my seat and sat down to read.A. findingB. to findC. foundD. founded33.I am tired and I don't feel like _____ any further.A. to walkB. to be walkingC. walkingD. walk34.She did nothing but ________walk in the street.A. takingB. takeC. to takeD. took35.It is a problem that doesn't need ________ right now.A. to solveB. solvingC. being solvedD. to be solving36.I ________ my handbag stolen last week.A. hadB. letC. lostD. left37.________ by a crowd of people, I felt nervous, ______ what to say.A. Watching, didn't knowB. Having watched, and not knewC. Having been watch, not knownD. Being watched, not knowing（二）对比练习1. ________many times , but he still couldn't understand it .2. ________many times , he still couldn't understand it .A. Having been told .B. ToldC. He was toldD. Though he had been told3. ________to the left , you'll find the post office .4. If you ________to the left , you'll find the post office .5. ________to the left , and you'll find the post office .A. TurningB. To turnC. TurnD. Turned6. ______from space , the earth looks blue .7.______from space , we can see the earth is blue .A. SeenB. SeeingC. To seeD. See8. The dirty clothes ______ , the girl hung them up outside .9. ______ the dirty clothes ,the girl hung them up outside .A. was washedB. washedC. were washedD. having washed10 The building ______now will be a restaurant .11. The building ______next year will be a restaurant .12. The building ______last year is a restaurant.A. having been builtB. to be builtC. being builtD. built13. He stood there ______for his mother .14. ______for two hours , he went away .A. waitingB. to waitC. waitedD. Having waited二知识点回顾1. ---“Would you like to go with us for a picnic tomorrow?”---“Yes, __________.”A. I would likeB. I’d like to goC. I’d loveD. I’d like to2. If you compare food costs today ______ of a year ago, you will find the difference.A. to thatB. to themC. with thatD. with those3. The grass has grown so tall that it needs _________.A. to cutB. to be cut itC. cuttingD. being cut4. Jerry is such a person that he ca n’t _______ being laughed at by others, especially by hisclassmates.A. hesitateB. sufferC. standD. admit5. ---“What’s made you so upset?”--- “_________ three tickets to the pop music concert.”A. Lo stB. LosingC. Because of losingD. Since I lost6. He advised that I ____to hospital for a medical exam, so I consider____ tosee a doctor.A. should go; to goB. go; goingC. went; goingD. to go; go7.---Have you seen the headmaster today?---No, he is said _____ Yuhan on business.A. to goB. to have gone toC. t o have been toD. to has gone to8．It is required that the students _______ mobile phones in their school, so seldom ______ them using one.A．shouldn’t use; you w ill see B．not use; will you seeC．don’t use; will you see D．shan’t use; you will see9．The Tower of Lo ndon is _______ the Church tower.A．twice high than B．two times high asC．twice higher as D．three times the height of10. —Is this stick long enough?—No, I need one _____.A. twice so longB. so long twiceC. twice as longD. as long twice11. He stood for a moment with one of his hands still ______.A. risenB. raisingC. raisedD. having raised12. Please keep on trying. I’m sure the efforts you are _______ will pay off.A. doingB. givingC. makingD. sparing13. The bus rolled into the valley, _______ ten deaths and more wounded.A. to causeB. causingC. causedD. having caused14. The discovery of new evidence resulted in _____.A. the thief having caughtB. catch the thiefC. the thief being caughtD. the thief to be caught15. The project ,______by the end of 2009, will expand the city’s telephone network to cover1,000,000 users.A. accomplishedB. being accomplishedC. to be accomplishedD. having been accomplished答案：（作业7）一DADBB DABAC DDDAA CABCD ADDDC CDDCC BCCBB ADCA(D) ACC AB BD CBD AD 二DDCCB BBBDC CCBCC。

高二年级学业水平测试(必修科目)适应性练习

高二年级学业水平测试（必修科目）适应性练习物理考试时间：75分钟试卷满分：100分一、单项选择题：每小题只有一个．．．．选项符合题意（本大题23小题，每小题3分，共69分）。

1、第一个发现电磁感应现象的科学家是（）A.牛顿B.焦耳C.奥斯特D.法拉第 2、关于合力与其两个分力的关系，下列说法中不正确．．．的是（） A ．合力的作用效果与两个分力共同作用的效果相同 B ．合力的大小总是大于每一个分力 C ．合力可能小于也可能大于它的任一个分力D ．两个分力夹角在0°到180°之间时，夹角越大，合力越小3、物体在两个相互垂直的力作用下运动，力F 1对物体做功6J ，物体克服力F 2做功8J ，则F 1、F 2的合力对物体做功为（） A.14JB.10JC.2JD.－2J4、以下说法正确的是（）A.力、路程、速度都是矢量B.力、位移、质量、速度、加速度都是矢量C.路程和质量都是矢量D.力、位移、速度、加速度都是矢量5、如下图所示，物体做平抛运动时，描述物体在竖直方向上的速度v y （取向下为正）随时间变化的图像是（）6、一石块从地面上方高H 处自由落下，不计空气阻力，当它的速度大小等于着地时速度的一半时，石块下落的高度是（）A.4H B. 83HC. 2H D. 43H7、如图所示，质量为10kg 的物体，在水平地面上向左运动，物体与地面间的动摩擦因数为0.2，与此同时，物体受到一个水平向右的推力F =20N 的作用，则物体的加速度是（g 取10m /s 2）（）A ．0B ．4 m /s 2，水平向右 C ．2m /s 2，水平向右 D ．2m /s 2，水平向左AOBCD8、下列关于摩擦力的说法中正确的是（）A．相互压紧的粗糙物体间必有摩擦力B．静摩擦力不一定随正压力增大而增大C．静止的物体一定不会受到滑动摩擦力作用D．摩擦力方向一定不会与物体运动方向相同9、物体做匀加速直线运动,加速度为2m/s2，在任意1秒内下列说法正确的是（）A．物体的初速度一定比前1秒内的末速度大2 m/sB．物体的末速度一定比前1秒内的初速度大2 m/sC．物体的末速度一定比初速度大2米／秒D．物体的加速度一定等于物体速度的2倍10、在机场和海港，常用传送带运送旅客的行李和货物，如图所示，a为水平传送带，b为倾斜传送带，当行李箱m随传送带一起匀速运动时（不计空气阻力），下列几种判断中正确的是（）A．a、b两种情形中的行李箱都受到两个力作用B．a、b两种情形中的行李箱都受到三个力作用C．情形a中的行李箱受到两个力作用，情形b中的行李箱受到三个力作用D．情形a中的行李箱受到两个力作用，情形b中的行李箱受到四个力作用11、关于物体的惯性，下列说法中正确的是（）A．汽车运动的速度越大越不容易停下来，是因为汽车运动的速度越大惯性越大B．小球由于重力的作用而自由下落时，它的惯性就不存在了C．小球被竖直向上抛出后继续上升，是因为小球受到一个向上的惯性D．物体惯性的大小仅与物体的质量有关，质量大的惯性大12、在以加速度a=13g加速上升的电梯里，有一质量为m的人，下列说法中正确的是（）A. 人的重力为13mg B．人的重力为23mgC．人对电梯的压力为23mg D．人对电梯的压力为43mg13、 A、B两个物体在同一直线上做匀变速直线运动，它们的速度时间图象如图所示，则下列说法正确的是（）A. A、B两物体运动方向相反B. 前4s内A、B两物体的位移相同C. t=4s时，A、B两物体的速度相同D. A物体的加速度比B物体的加速度大14、水平横梁一端插在墙壁里，另一端装小滑轮B ，一轻绳的一端C 固定于墙壁上，另一端跨过滑轮后悬挂一质量m =20kg 的物体，∠CBA =30º，如图所示．则滑轮受到绳子的作用力为（）（绳与滑轮间的摩擦不计，g =102m/s ）A ．100NB ．5NC ．200ND ．1015．如图所示，某人由A 点划船渡河，船头指向始终与河岸垂直，则（）A ．小船能到达对岸的位置是正对岸的B 点 B ．小船过河时间比船头指向其他方向要短C ．水流加快，过河的时间将变短D ．小船过不了河16．物体在地面附近绕地球做匀速圆周运动的速度叫“第一宇宙速度”，关于这个速度，下列说法正确的是（） A ．它的大小是11.2 km /s B ．它的大小是16.7 km /sC ．它是物体环绕地球作圆周运动的最大速度D ．物体发射时的最大速度17．用电梯将货物沿竖直方向匀速提升一段距离。

2023-2024学年江苏省苏州市高二(上)期中数学试卷【答案版】

2023-2024学年江苏省苏州市高二（上）期中数学试卷一、单项选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确的选项填涂在答题卡相应的位置上． 1．直线3x +y ﹣2＝0的方向向量为（） A ．（﹣1，3）B ．（1，3）C ．（﹣3，1）D ．（3，1）2．等差数列{a n }中，若2a 3+a 9＝18，则a 2+3a 6的值为（） A ．36B ．24C ．18D ．93．与直线3x ﹣4y +5＝0关于y 轴对称的直线方程是（） A ．3x +4y ﹣5＝0B ．3x +4y +5＝0C ．3x ﹣4y +5＝0D ．3x ﹣4y ﹣5＝04．经过原点和点（3，﹣1）且圆心在直线3x +y ﹣5＝0上的圆的方程为（） A ．（x ﹣5）2+（y +10）2＝125 B ．（x +1）2+（y ﹣2）2＝5C ．（x ﹣1）2+（y ﹣2）2＝5D ．(x −53)2+y 2=2595．设{a n }是公差不为0的无穷等差数列，则“{a n }为递减数列”是“存在正整数N 0，当n ＞N 0时，a n ＜0”的（）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件6．已知点P （4，3），点Q 在x 2+y 2＝4的圆周上运动，点M 满足PM →=MQ →，则点M 的运动轨迹围成图形的面积为（） A ．πB ．2πC ．3πD ．4π7．等比数列{a n }，满足a 1+a 2+a 3+a 4+a 5＝3，a 12+a 22+a 32+a 42+a 52=15，则a 1﹣a 2+a 3﹣a 4+a 5的值是（）A ．3B ．√5C ．−√5D ．58．过点P （2，0）作圆x 2+y 2﹣4y ＝1的两条切线，设切点分别为A ，B ，则△P AB 的面积为（） A ．3√158B ．√152C ．5√158D ．√15二、多项选择题：本题共4小题，每小题5分，共20分，在每小题给出的选项中，有多项符合题目要求、全部选对得5分，选对但不全得2分，选错或不答得0分，请把正确的选项填涂在答题卡相应的位置上． 9．已知直线l ：x +my +m ＝0，若直线l 与连接A （﹣3，2），B （2，1）两点的线段总有公共点，则直线l 的倾斜角可以是（） A ．2π3B ．π2C ．π4D ．π610．设S n ，T n 分别是等差数列{a n }和等比数列{b n }的前n （n ∈N *）项和，下列说法正确的是（）A ．若a 15+a 16＞0，a 15+a 17＜0，则使S n ＞0的最大正整数n 的值为15B ．若T n =5n +c （c 为常数），则必有c ＝﹣1C ．S 5，S 10﹣S 5，S 15﹣S 10必为等差数列D ．T 5，T 10﹣T 5，T 15﹣T 10必为等比数列11．已知等比数列{a n }的公比为q ，前n （n ∈N *）项和为S n ，前n （n ∈N *）项积为T n ，若a 1=132，T 5＝T 6，则（） A ．q ＝2B ．当且仅当n ＝6时，T n 取得最小值C ．T n ＝T 11﹣n （n ∈N *，n ＜11）D ．S n ＞T n 的正整数n 的最大值为1112．已知圆C ：x 2+y 2＝4，圆M ：x 2+y 2﹣8x ﹣6y +m ＝0（） A ．若m ＝8，则圆C 与圆M 相交且交线长为165B ．若m ＝9，则圆C 与圆M 有两条公切线且它们的交点为（﹣3，﹣4） C ．若圆C 与圆M 恰有4条公切线，则m ＞16D ．若圆M 恰好平分圆C 的周长，则m ＝﹣4三、填空题：本题共4小题，每小题5分，共20分，请把答案写在答题卡相应的位置上．13．若{a n }是公差不为0的等差数列，a 2，a 4，a 8成等比数列，a 1＝1，S n 为{a n }的前n （n ∈N *）项和，则1S 1+1S 2+⋯+1S 10的值为．14．平面直角坐标系xOy 中，过直线l 1：7x ﹣3y +1＝0与l 2：x +4y ﹣3＝0的交点，且在y 轴上截距为1的直线l 的方程为．（写成一般式）15．如图，第一个正六边形A 1B 1C 1D 1E 1F 1的面积是1，取正六边形A 1B 1C 1D 1E 1F 1各边的中点A 2，B 2，C 2，D 2，E 2，F 2，作第二个正六边形A 2B 2C 2D 2E 2F 2，然后取正六边形A 2B 2C 2D 2E 2F 2各边的中点A 3，B 3，C 3，D 3，E 3，F 3，作第三个正六边形，依此方法一直继续下去，则前n 个正六边形的面积之和为．16．已知实数a ，b ，c 成等差数列，在平面直角坐标系xOy 中，点A （4，1），O 是坐标原点，直线l ：ax +2by +3c ＝0．若直线OM 垂直于直线l ，垂足为M ，则线段|AM |的最小值为．四、解答题：本题共6小题，共70分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．17．（10分）已知直线l 1：2x ﹣（a ﹣1）y ﹣2＝0，l 2：（a +2）x +（2a +1）y +3＝0（a ∈R ）．（1）若l 1⊥l 2，求实数a 的值；（2）若l 1∥l 2，求l 1，l 2之间的距离．18．（12分）已知等差数列{a n }，前n （n ∈N *）项和为S n ，又a 2＝4，S 9＝90．（1）求数列{a n }的通项公式a n ；（2）设b n ＝|9﹣a n |，求数列{b n }的前n 项和T n ． 19．（12分）已知数列{a n }的首项a 1=23，且满足a n−1=2a na n +1．（1）求证：数列{1a n−1}为等比数列；（2）设b n =(−1)n−1a n，求数列{b n }的前2n 项和S 2n ．20．（12分）如图，等腰梯形ABCD 中，AB ∥CD ，AB ＝2CD ＝8，AB ，CD 间的距离为4，以线段AB 的中点为坐标原点O ，建立如图所示的平面直角坐标系xOy ，记经过A ，B ，C ，D 四点的圆为圆M ．（1）求圆M 的标准方程；（2）若点E 是线段AO 的中点，P 是圆M 上一动点，满足PO →•PE →≥24，求动点P 横坐标的取值范围．21．（12分）平面直角坐标系xOy 中，直线l ：3x +2y ﹣13＝0，圆M ：x 2+y 2﹣12x ﹣8y +48＝0，圆C 与圆M 关于直线l 对称，P 是直线l 上的动点．（1）求圆C 的标准方程；（2）过点P 引圆C 的两条切线，切点分别为A ，B ，设线段AB 的中点是Q ，是否存在定点H ，使得|QH |为定值，若存在，求出该定点H 的坐标；若不存在，请说明理由． 22．（12分）记首项为1的递增数列为“W ﹣数列”．（1）已知正项等比数列{a n }，前n （n ∈N *）项和为S n ，且满足：a n +2＝2S n +2．求证：数列{a n }为“W ﹣数列”；（2）设数列{b n }(n ∈N ∗)为“W ﹣数列”，前n （n ∈N *）项和为S n ，且满足∑b i 3=S n 2(n ∈N ∗)ni=1．（注：∑b i 3=b 13+b 23+⋯+b n 3ni=1） ①求数列{b n }的通项公式b n ； ②数列{c n }(n ∈N ∗)满足c n =b n33bn，数列{c n }是否存在最大项？若存在，请求出最大项的值，若不存在，请说明理由．（参考数据：√2≈1.41，√33≈1.44）2023-2024学年江苏省苏州市高二（上）期中数学试卷参考答案与试题解析一、单项选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确的选项填涂在答题卡相应的位置上．1．直线3x+y﹣2＝0的方向向量为（）A．（﹣1，3）B．（1，3）C．（﹣3，1）D．（3，1）解：根据直线方程3x+y﹣2＝0，可得直线的斜率为﹣3，所以直线的一个方向向量为（1，﹣3），又（1，﹣3）＝﹣（﹣1，3），所以（﹣1，3）也是直线的一个方向向量．故选：A．2．等差数列{a n}中，若2a3+a9＝18，则a2+3a6的值为（）A．36B．24C．18D．9解：设等差数列{a n}的公差为d，2a3+a9＝18，则2（a1+2d）+a1+8d＝3a1+12d＝18，即a1+4d＝6，a2+3a6＝a1+d+3（a1+5d）＝4a1+16d＝4（a1+4d）＝4×6＝24．故选：B．3．与直线3x﹣4y+5＝0关于y轴对称的直线方程是（）A．3x+4y﹣5＝0B．3x+4y+5＝0C．3x﹣4y+5＝0D．3x﹣4y﹣5＝0解：令x＝0，则y=54，可得直线3x﹣4y+5＝0与y轴的交点(0，54)．令y＝0，可得x=−53，可得直线3x﹣4y+5＝0与x轴的交点(−53，0)，此点关于y轴的对称点为(53，0)．∴与直线3x﹣4y+5＝0关于y轴对称的直线经过两点：(0，54)，(53，0)．其方程为：x53+y54=1，化为：3x+4y﹣5＝0．故选：A．4．经过原点和点（3，﹣1）且圆心在直线3x+y﹣5＝0上的圆的方程为（）A．（x﹣5）2+（y+10）2＝125B．（x+1）2+（y﹣2）2＝5C．（x﹣1）2+（y﹣2）2＝5D．(x−53)2+y2=259解：设圆心C（a，5﹣3a），则由所求的圆经过原点和点（3，﹣1），即√a 2+(5−3a)2=√(a −3)2+(5−3a +1)2，求得a =53，可得圆心为（53，0），半径为√a 2+(5−3a)2=53，故圆的方程为（x −53）2+y 2=259．故选：D ．5．设{a n }是公差不为0的无穷等差数列，则“{a n }为递减数列”是“存在正整数N 0，当n ＞N 0时，a n ＜0”的（）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件解：因为{a n }是公差不为0的无穷等差数列，若“{a n }为递减数列”，可得{a n }的通项公式为一次函数且一次项系数小于0，一定有a n ＜0，即“{a n }为递减数列”是“存在正整数N 0，当n ＞N 0时，a n ＜0”的充分条件；若“存在正整数N 0，当n ＞N 0时，a n ＜0”，设通项公式为a n ＝pn +q ，则p ＜0，n ∈N +，即{a n }为递减数列，所以“{a n }为递减数列”是“存在正整数N 0，当n ＞N 0时，a n ＜0”的必要条件，综上所述：“{a n }为递减数列”是“存在正整数N 0，当n ＞N 0时，a n ＜0”的充要条件．故选：C ．6．已知点P （4，3），点Q 在x 2+y 2＝4的圆周上运动，点M 满足PM →=MQ →，则点M 的运动轨迹围成图形的面积为（） A ．πB ．2πC ．3πD ．4π解：设M （x ，y ），点P （4，3），点M 满足PM →=MQ →，可得Q （2x ﹣4，2y ﹣3），点Q 在x 2+y 2＝4的圆周上运动，可得（2x ﹣4）2+（2y ﹣3）2＝4，即（x ﹣2）2+（y −32）2＝1，点M 的运动轨迹是以（2，32）为圆心，1为半径的圆，点M 的运动轨迹围成图形的面积为π．故选：A ．7．等比数列{a n }，满足a 1+a 2+a 3+a 4+a 5＝3，a 12+a 22+a 32+a 42+a 52=15，则a 1﹣a 2+a 3﹣a 4+a 5的值是（）A ．3B ．√5C ．−√5D ．5解：设数列{a n }的公比为q ，且q ≠1，则a 1+a 2+a 3+a 4+a 5=a 1(1−q 5)1−q=3①，a 12+a 22+a 32+a 42+a 52=a 12(1−q 10)1−q 2=15②∴②÷①得a 12(1−q 10)1−q 2÷a 1(1−q 5)1−q=a 1(1+q 5)1+q=5，∴a 1﹣a 2+a 3﹣a 4+a 5=a 1(1+q 5)1+q=5．故选：D ．8．过点P （2，0）作圆x 2+y 2﹣4y ＝1的两条切线，设切点分别为A ，B ，则△P AB 的面积为（） A ．3√158B ．√152C ．5√158D ．√15解：由题设，圆的标准方程为x 2+（y ﹣2）2＝5，圆心为C （0，2），半径r =√5，所以|CP|=2√2，如图所示，切点分别为A ，B ，则|BP|=|AP|=√8−5=√3，所以sin ∠BPC =|BC||CP|=√52√2，cos ∠BPC =|BP||CP|=32√2，又∠BP A ＝2∠BPC ，所以sin ∠BP A ＝sin2∠BPC ＝2sin ∠BPC cos ∠BPC =2√52√2×32√2=√154，所以S △PAB =12|BP||AP|sin∠BPA =12×√3×√3×√154=3√158．故选：A ．二、多项选择题：本题共4小题，每小题5分，共20分，在每小题给出的选项中，有多项符合题目要求、全部选对得5分，选对但不全得2分，选错或不答得0分，请把正确的选项填涂在答题卡相应的位置上． 9．已知直线l ：x +my +m ＝0，若直线l 与连接A （﹣3，2），B （2，1）两点的线段总有公共点，则直线l 的倾斜角可以是（） A ．2π3B ．π2C ．π4D ．π6解：直线l ：x +my +m ＝0，即x +（y +1）m ＝0，故直线l 过定点C （0，﹣1）， A （﹣3，2），B （2，1），则k AC =2−(−1)−3−0=−1，k BC =1−(−1)2−0=1，直线AC 的倾斜角为3π4，直线BC 的倾斜角为π4，直线l 与连接A （﹣3，2），B （2，1）两点的线段总有公共点，则直线l 的倾斜角范围为[π4，3π4]．故选：ABC ．10．设S n ，T n 分别是等差数列{a n }和等比数列{b n }的前n （n ∈N *）项和，下列说法正确的是（） A ．若a 15+a 16＞0，a 15+a 17＜0，则使S n ＞0的最大正整数n 的值为15 B ．若T n =5n +c （c 为常数），则必有c ＝﹣1 C ．S 5，S 10﹣S 5，S 15﹣S 10必为等差数列D ．T 5，T 10﹣T 5，T 15﹣T 10必为等比数列解：令{a n }的公差为d ，则a n ＝a 1+（n ﹣1）d ＝dn +（a 1﹣d ），所以{a 15+a 16=2a 1+29d ＞0a 15+a 17=2a 1+30d ＜0，故−292d ＜a 1＜−15d ，且d ＜0，使S n =na 1+n(n−1)2d =d 2n 2+(a 1−d2)n ＞0，则0＜n ＜1−2a1d ，而29＜−2a 1d＜30，即1−2a 1d∈(30，31)，故0＜n ≤30，所以使S n ＞0的最大正整数n 的值为30，故A 错；令{b n }的公比为q 且q ≠0，则T n =b 1(1−q n )1−q =b 11−q −b 1⋅q n1−q =5n +c （公比不能为1），所以{q =5b 11−q=−1，即c ＝﹣1，故B 对；根据等差、等比数列片段和的性质知：S 5 S 10﹣S 5，S 15﹣S 10必为等差数列，T 5，T 10﹣T 5，T 15﹣T 10必为等比数列，C 、D 对．故选：BCD ．11．已知等比数列{a n }的公比为q ，前n （n ∈N *）项和为S n ，前n （n ∈N *）项积为T n ，若a 1=132，T 5＝T 6，则（）A ．q ＝2B ．当且仅当n ＝6时，T n 取得最小值C ．T n ＝T 11﹣n （n ∈N *，n ＜11）D ．S n ＞T n 的正整数n 的最大值为11 解：根据题意，依次分析选项：对于A ，若T 5＝T 6，则a 6=T6T 5=1，又由a 1=132，则q 5=a6a 1=32，则q ＝2，A 正确；对于B ，由A 的结论，当1≤n ≤5时，a n ＜1，a 6＝1，当n ＞6时，a n ＞1，故当n ＝5或6时，T n 取得最小值，B 错误；对于C ，由A 的结论，a 6＝1，则有a n a 12﹣n ＝（a 6）2＝1，当n ＜6时，11﹣n ＞n ，则有T 11−n T n =a n +1a n +2……a 10﹣n a 11﹣n ＝1，即T n ＝T 11﹣n ，同理：当6≤n ＜11时，也有T n ＝T 11﹣n ，故T n ＝T 11﹣n （n ∈N *，n ＜11）成立，C 正确；对于D ，若S n ＞T n ，即a 1(1−q n )1−q＞a 1a 2a 3……a n ，即2n −125＞2n 2−11n 2，当n ＝12时，S 12=212−125=27−132，T 12＝26，此时S n ＞T n ，D 错误．故选：AC ．12．已知圆C ：x 2+y 2＝4，圆M ：x 2+y 2﹣8x ﹣6y +m ＝0（） A ．若m ＝8，则圆C 与圆M 相交且交线长为165B ．若m ＝9，则圆C 与圆M 有两条公切线且它们的交点为（﹣3，﹣4） C ．若圆C 与圆M 恰有4条公切线，则m ＞16D ．若圆M 恰好平分圆C 的周长，则m ＝﹣4解：对于A ，m ＝8时，圆M ：（x ﹣4）2+（y ﹣3）2＝17，则M （4，3），半径r =√17．而圆C ：x 2+y 2＝4中C （0，0），半径r ＝2，所以|CM |=√42+32=5，故√17−2＜|CM|＜√17+2，即两圆相交，此时相交弦方程为4x +3y ﹣6＝0，所以C （0，0）到4x +3y ﹣6＝0的距离d =65，故相交弦长为2×√22−(65)2=165，故A 正确；对于B ，当m ＝9时，圆M ：（x ﹣4）2+（y ﹣3）2＝16，则M （4，3），半径r ＝4，类似于A 的分析，可得4﹣2＜|CM |＜4+2，故两圆相交，故B 错误；对于C ，若圆C 与圆M 恰有4条公切线，则两圆相离，可得|CM |＞r +r ′＝2+r ，而圆M ：（x ﹣4）2+（y ﹣3）2＝25﹣m ，即r =√25−m ，所以{25−m ＞02+√25−m ＜5，解得16＜m ＜25，故C 错误；对于D ，若圆M 恰好平分圆C 的周长，则相交弦所在直线必过C （0，0），两圆方程相减，可得相交弦方程为8x +6y ﹣m ﹣4＝0，将点代入可得m ＝﹣4，故D 正确．故选：AD ．三、填空题：本题共4小题，每小题5分，共20分，请把答案写在答题卡相应的位置上．13．若{a n }是公差不为0的等差数列，a 2，a 4，a 8成等比数列，a 1＝1，S n 为{a n }的前n （n ∈N *）项和，则1S 1+1S 2+⋯+1S 10的值为2011．解：设数列{a n }是公差d 不为0的等差数列，a 2，a 4，a 8成等比数列，a 1＝1，故(a 1+3d)2=(a 1+d)(a 1+7d)，整理得（1+3d ）2＝（1+d ）（1+7d ），解得d ＝1；故a n ＝1+（n ﹣1）＝n ，所以S n =1+2+3+...+n =n(n+1)2，故1S n=2n(n+1)=2(1n −1n+1)；所以1S 1+1S 2+⋯+1S 10=2(1−12+12−13+...+110−111)=2×1011=2011．故答案为：2011．14．平面直角坐标系xOy 中，过直线l 1：7x ﹣3y +1＝0与l 2：x +4y ﹣3＝0的交点，且在y 轴上截距为1的直线l 的方程为 9x +5y ﹣5＝0 ．（写成一般式）解：联立{7x −3y +1=0x +4y −3=0，解得x =531，y =2231，即直线l 1，l 2的交点（531，2231），由题意设l 的方程为：y ＝kx +1，即2231=531k +1，即k =−95，所以直线l 的方程为y =−95x +1，即9x +5y ﹣5＝0．故答案为：9x +5y ﹣5＝0．15．如图，第一个正六边形A 1B 1C 1D 1E 1F 1的面积是1，取正六边形A 1B 1C 1D 1E 1F 1各边的中点A 2，B 2，C 2，D 2，E 2，F 2，作第二个正六边形A 2B 2C 2D 2E 2F 2，然后取正六边形A 2B 2C 2D 2E 2F 2各边的中点A 3，B 3，C 3，D 3，E 3，F 3，作第三个正六边形，依此方法一直继续下去，则前n 个正六边形的面积之和为 4[1−(34)n ] ．解：由题设知：后一个正六边形与前一个正六边形的边长比值为√32，故它们面积比为34，所以前n 个正六边形的面积是首项为1，公比为34的等比数列，所以前n 个正六边形的面积之和S =1−(34)n 1−34=4[1﹣（34）n ]．故答案为：4[1﹣（34）n ]． 16．已知实数a ，b ，c 成等差数列，在平面直角坐标系xOy 中，点A （4，1），O 是坐标原点，直线l ：ax +2by +3c ＝0．若直线OM 垂直于直线l ，垂足为M ，则线段|AM |的最小值为 √2 ．解：因为实数a ，b ，c 成等差数列，所以2b ＝a +c ，所以直线l ：ax +2by +3c ＝0为ax +（a +c ）y +3c ＝0，整理得a （x +y ）+c （y +3）＝0，令{x +y =0y +3=0，解得x ＝3，y ＝﹣3，即直线l 过定点（3，﹣3），设该点为点P ，如图所示，因为OM ⊥l ，所以点M 在以OP 为直径的圆上，该圆的圆心为Q （32，−32），半径为r =12|OP |=3√22，所以|AM |≥|AQ |﹣r =√(4−32)2+(1+32)2−3√22=√2，当且仅当A ，M ，Q 三点共线时，等号成立，所以线段|AM |的最小值为√2．故答案为：√2．四、解答题：本题共6小题，共70分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．17．（10分）已知直线l1：2x﹣（a﹣1）y﹣2＝0，l2：（a+2）x+（2a+1）y+3＝0（a∈R）．（1）若l1⊥l2，求实数a的值；（2）若l1∥l2，求l1，l2之间的距离．解：（1）因为l1⊥l2，可得2（a+2）﹣（a﹣1）（2a+1）＝0，即2a2﹣3a﹣5＝0，解得a＝﹣1或a=−5 2；（2）因为l1∥l2，则2（2a+1）＝（a+2）[﹣（a﹣1）]，且﹣2（2a+1）＝﹣（a﹣1）×3＝0，解得：a＝0或a＝﹣5（舍），所以直线l1的方程为：2x+y﹣2＝0，直线l2的方程：2x+y+3＝0．所以l1，l2之间的距离d=|−2−3|√2+1=√5．18．（12分）已知等差数列{a n}，前n（n∈N*）项和为S n，又a2＝4，S9＝90．（1）求数列{a n}的通项公式a n；（2）设b n＝|9﹣a n|，求数列{b n}的前n项和T n．解：（1）等差数列{a n}，前n（n∈N*）项和为S n，又a2＝4，S9＝90．设首项为a1，公差为d，所以{a1+d=49a1+9×82d=90，解得{a1=2d=2．故a n＝2n；（2）由（1）得：b n＝|9﹣a n|＝|9﹣2n|；当n≤4时，T n=7+9−2n2⋅n=8n−n2，当n≥5时，T n＝（b1+b2+b3+b4）﹣（b5+b6+...+b n）＝32﹣（8n﹣n2）＝n2﹣8n+32．故T n={8n−n2(n≤4的正整数)n2−8n+32(n≥5的正整数)．19．（12分）已知数列{a n}的首项a1=23，且满足a n−1=2a na n+1．（1）求证：数列{1a n−1}为等比数列；（2）设b n=(−1)n−1a n，求数列{b n}的前2n项和S2n．证明：（1）因为a n+1=2a n a n +1，a 1=23，所以a n ≠0，所以1a n+1=a n +12a n =12a n +12，所以1a n+1−1=12a n −12，因为a 1=23，1a 1−1=12≠0，1a n+1−11a n −1=12，所以{1a n −1}是以12为首项，12为公比的等比数列；（2）S 2n =1a 1−1a 2+1a 3−1a 4+⋯+1a 2n−1−1a 2n=(1a 1−1)−(1a 2−1)+(1a 3−1)−(1a 4−1)+⋯+(1a 2n−1−1)−(1a 2n−1)．又{1a n −1}是以12为首项，−12为公比的等比数列，所以S 2n =12[1−(−12)2n ]1−(−12)=1−(12)2n 3=4n−13×4n ． 20．（12分）如图，等腰梯形ABCD 中，AB ∥CD ，AB ＝2CD ＝8，AB ，CD 间的距离为4，以线段AB 的中点为坐标原点O ，建立如图所示的平面直角坐标系xOy ，记经过A ，B ，C ，D 四点的圆为圆M ．（1）求圆M 的标准方程；（2）若点E 是线段AO 的中点，P 是圆M 上一动点，满足PO →•PE →≥24，求动点P 横坐标的取值范围．解：（1）如图，因为AB ＝2CD ＝8，AB ，CD 间的距离为4，所以A （﹣4，0），B （4，0），C （2，4），D （﹣2，4），则经过A ，B ，C ，D 四点的圆即经过A ，B ，C 三点的圆，又AB 中垂线方程为x ＝0，BC 中点为（3，2），k BC =0−44−2=−2，所以BC 的中垂线方程为y −2=12(x −3)，即y =12x +12，联立{x =0y =12x +12，得圆心坐标M(0，12)，则MB =√(4−0)2+(0−12)2=√652，所以圆M 的标准方程为x 2+(y −12)2=654；（2）由已知可得E （﹣2，0），设圆M 上一点P （x ，y ），则PO →=(−x ，−y)，PE →=(−2−x ，−y)，因为PO →⋅PE →≥24，所以﹣x （﹣2﹣x ）+（﹣y ）（﹣y ）≥24，即x 2+y 2+2x ﹣24≥0，所以P 点在圆（x +1）2+y 2＝25上及其外部，联立{x 2+y 2−y −16=0x 2+y 2+2x −24=0，解得x 1＝2，x 2＝4，所以两圆交点恰为B （4，0），C （2，4），结合图形，当圆M 上一点纵坐标为12时，横坐标为x 3=√652＞4，所以点P 横坐标的取值范围是[2，√652]．21．（12分）平面直角坐标系xOy 中，直线l ：3x +2y ﹣13＝0，圆M ：x 2+y 2﹣12x ﹣8y +48＝0，圆C 与圆M 关于直线l 对称，P 是直线l 上的动点．（1）求圆C 的标准方程；（2）过点P 引圆C 的两条切线，切点分别为A ，B ，设线段AB 的中点是Q ，是否存在定点H ，使得|QH |为定值，若存在，求出该定点H 的坐标；若不存在，请说明理由．解：（1）圆M ：（x ﹣6）2+（y ﹣4）2＝4，圆心M （6，4），设圆心C （x 0，y 0），由圆C 与圆M 关于直线l ：3x +2y ﹣13＝0对称，所以{y 0−4x 0−6=233×x 0+62+2×y 0+42−13=0，即{3y 0=2x 03x 02+y 0=0，解得{x 0=0y 0=0，所以C （0，0），又r ＝2，故圆C 的方程为x 2+y 2＝4；（2）因为P 是直线l 上的动点，设P(2t ，132−3t)， P A ，PB 分别与圆C 切于A ，B 两点，所以CA ⊥P A ，CB ⊥PB ，所以A ，B 在以PC 为直径的圆N 上，圆N 的方程x(x −2t)+y[y −(132−3t)]=0，即x 2+y 2−2tx +(3t −132)y =0，又AB 为圆C 与圆N 的公共弦，由{x 2+y 2−4=0x 2+y 2−2tx +(3t −132)y =0，作差可得AB 的方程为2tx −(3t −132)y −4=0，即t(2x −3y)+132y −4=0，令{2x −3y =0132y −4=0，得{x =1213y =813，设T(1213，813)，则直线AB 过定点T(1213，813)，又Q 是AB 中点，所以CQ ⊥AB ，所以Q 点是在以CT 为直径的圆上，所以存在点H （613，413）是CT 的中点，使得QH 为定值．22．（12分）记首项为1的递增数列为“W ﹣数列”．（1）已知正项等比数列{a n }，前n （n ∈N *）项和为S n ，且满足：a n +2＝2S n +2．求证：数列{a n }为“W ﹣数列”；（2）设数列{b n }(n ∈N ∗)为“W ﹣数列”，前n （n ∈N *）项和为S n ，且满足∑b i 3=S n 2(n ∈N ∗)ni=1．（注：∑b i 3=b 13+b 23+⋯+b n 3n i=1） ①求数列{b n }的通项公式b n ；②数列{c n }(n ∈N ∗)满足c n =b n 33b n ，数列{c n }是否存在最大项？若存在，请求出最大项的值，若不存在，请说明理由．（参考数据：√2≈1.41，√33≈1.44）证明：（1）设正项等比数列{a n }的公比为q （q ＞0），因为a n +2＝2S n +2，则a n +3＝2S n +1+2，两式相减得a n +3﹣a n +2＝2a n +1，即a n+1(q 2−q −2)=a n+1(q −2)(q +1)=0因为a n ＞0，q ＞0，所以q ＝2，a n +2＝2S n +2中，当n ＝1时，有a 3＝2a 1+2，即4a 1＝2a 1+2，解得a 1＝1，因此数列{a n }为“W ﹣数列”；解：（2）①因为∑b i 3=S n 2(n ∈N ∗)ni=1所以b 13=b 12，得又{b n }为“W ﹣数列”，所以b 1＝1，且b n +1＞b n ，所以{b n }各项为正数，当n ≥2，∑b i 3=S n 2n i=1①，∑b i 3=S n−12n−1i=1②，①一②得：b n 3=S n 2−S n−12，即b n 3=(S n −S n−1)(S n +S n−1)，所以b n 2=S n +S n−1③，从而b n+12=S n+1+S n ④，④﹣③得：b n+12−b n 2=b n+1+b n ，由于{b n }为“W ﹣数列”，必有b n +1+b n ＞0，所以b n +1﹣b n ＝1，（n ≥2），又由③知b 22=S 2+S 1，即b 22=2b 1+b 2，解得b 2＝2或b 2＝﹣1（舍）；所以b 2﹣b 1＝1，故b n+1−b n =1(n ∈N ∗)，所以{b n }是以1为首项，公差是1的等差数列，所以b n ＝n ；②c n =n 33n ＞0，所以c n+1c n =13(n+1n)3＜1，整理得n √33−1≈2.27，所以当n ≥3时，c n +1＜c n ，即c 3＞c 4＞c 5＞⋯，又c 1=13，c 2=89，c 3=1，所以{c n }中存在最大项，为c 3＝1．。

2023-2024学年江苏省苏州中学高二(上)期中数学试卷【答案版】

2023-2024学年江苏省苏州中学高二（上）期中数学试卷一、单选题（每题5分，共8题。

选对得5分，选错或不选得0分） 1．已知直线l 的方程为x +√3y −1=0，则直线的倾斜角为（） A ．30°B ．60°C ．120°D ．150°2．已知等差数列{a n }满足4a 3＝3a 2，则{a n }中一定为零的项是（） A ．a 6B ．a 4C ．a 10D ．a 12 3．在等比数列{a n }中，a 2，a 10是方程x 2﹣6x +4＝0的两根，则a 3a 9a 6=（） A ．2B ．﹣2C ．﹣2或2D ．3±√54．直线l ：y ＝kx +1与圆O ：x 2+y 2＝1相交于A ，B 两点，则“k ＝1”是“|AB |=√2”的（） A ．充分而不必要条件 B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件5．已知圆x 2+y 2＝4上有四个点到直线y ＝x +b 的距离等于1，则实数b 的取值范围为（） A ．(−√2，√2)B ．[−√2，√2]C ．（﹣2，2）D ．（﹣1，1）6．某家庭打算为子女储备“教育基金”，计划从2021年开始，每年年初存入一笔专用存款，使这笔款到2027年底连本带息共有40万元收益．如果每年的存款数额相同，依年利息2%并按复利计算（复利是一种计算利息的方法，即把前一期的利息和本金加在一起算作本金，再计算下一期的利息），则每年应该存入约（）万元．（参考数据：1.027≈1.149，1.028≈1.172） A ．5.3B ．4.6C ．7.8D ．67．已知数列{a n }满足a 1=2，a n+1={a n +1，n 为奇数a n +3，n 为偶数，记b n ＝a 2n ﹣1，则（）A ．b 1＝3B ．b 2＝8C ．b n +1﹣b n ＝4D ．b n ＝4n +28．已知圆O ：x 2+y 2＝1，点P （x 0，y 0）是直线l ：3x +2y ﹣4＝0上的动点，若圆O 上总存在不同的两点A ，B ，使得直线AB 垂直平分OP ，则x 0的取值范围为（） A ．(0，2413)B ．(0，2413]C ．[−1013，2)D ．(−1013，2)二、多选题（每题5分，共4题。

2023-2024学年江苏省盐城市阜宁中学高二(上)期中数学试卷【答案版】

2023-2024学年江苏省盐城市阜宁中学高二（上）期中数学试卷一、单项选择题（本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知点A （﹣2，4），B （4，﹣1），则直线AB 在y 轴上的截距为（） A ．83B ．73C ．145D ．1352．圆C 1：x 2+y 2−2x =0与圆C 2：x 2+y 2+2x −8y =0的位置关系为（） A ．外切B ．内切C ．相交D ．外离3．设函数f(x)=x 2−1x ，则lim Δx→0f(1+2Δx)−f(1)Δx =（） A ．6 B ．4C ．3D ．24．已知椭圆x 25+y 2m=1的一个焦点坐标为（0，﹣2），则实数m 的值为（） A ．1B ．4C ．7D ．95．已知函数f （x ）＝2x 3﹣me x （m ∈R ），则曲线y ＝f （x ）在点（0，f （0））处的切线经过定点（） A ．（﹣1，0）B ．（0，0）C ．（1，0）D ．（2，0）6．已知等比数列{a n }的前n 项和为S n ，2S 3＝a 4﹣a 1，且a 2+a 4＝15，则a 3+a 5＝（） A ．3B ．5C ．30D ．457．已知双曲线E ：x 2a 2−y 2b 2=1(a ＞0，b ＞0)的左、右顶点分别为A 、B ，M 是E 上一点，△ABM 为等腰三角形，且△ABM 的外接圆面积为3πa 2，则双曲线E 的离心率为（） A ．2B ．√2C ．√3D ．√58．设数列{a n }的前n 项和为S n ，a 2＝3，且（n +1）S n +1＝（n +1）S n +（n +2）a n ，若存在n ∈N *，使得2S n +22≤ka n 成立，则实数k 的最小值为（） A ．4√5+1B ．8C ．323D ．10二、多项选择题（本题共4小题，每小题5分，共20分，在每小题给出的四个选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分） 9．下列函数的图象可能与直线2x ﹣y +m ＝0（m ∈R ）相切的是（） A ．f （x ）＝x 2+x B ．f （x ）＝2x +e xC ．f(x)=12x 2+lnxD ．f(x)=2x +√x10．在平面直角坐标系xOy 中，已知点A （a ，﹣1），B （2a +1，2），直线l ：x ﹣y +4＝0，其中a ∈R ，则下列结论正确的是（）A ．直线AB 恒过定点，且定点坐标为（﹣1，﹣4） B ．若直线AB 在两坐标轴上的截距相等，则a ＝﹣4C ．若直线AB 过第一、三象限，则a ＞﹣1D ．若直线AB 和直线l 与两坐标轴围成的四边形有外接圆，则a ＝﹣411．已知数列{a n }满足a 1+3a 2+⋯+3n−1a n =n ⋅3n+1（n ∈N *），设数列{a n }的前n 项和为S n ，则下列结论正确的是（） A ．数列{a n }为等差数列B ．S n =3n 2+6nC ．数列{（﹣1）n a n }的前100项和为300D ．数列{|a n ﹣20|}的前20项和为28412．已知O 为坐标原点，点A （﹣2，﹣1）在抛物线C ：x 2＝﹣2py （p ＞0）上，过点B （0，1）的直线交抛物线C 于P ，Q 两点，则下列结论正确的是（） A ．抛物线C 的准线方程为y ＝1 B ．直线AB 与抛物线C 相切 C ．OP →⋅OQ →为定值3D ．|BP |•|BQ |＞|BA |2三、填空题（本题共4小题，每小题5分，共20分）13．设f ′（x ）为函数f （x ）的导函数，若f （x ）＝2（x +1）e x ﹣f ′（0）•x ，则f （0）+f ′（0）＝．14．设各项均为正数的等差数列{a n }的前n 项和为S n ，若a 92−a 7+12a 5=3，则S 17＝．15．已知直线l ：x +y ﹣2＝0关于直线y ＝a 的对称直线与圆（x ﹣1）2+y 2＝2有公共点，则实数a 的取值范围为．16．希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名，他发现：“平面内到两个定点A ，B 的距离之比为定值λ（λ≠1）的点的轨迹是圆”．后来，人们将这个圆以他的名字命名，称为阿波罗尼斯圆，简称阿氏圆．已知在平面直角坐标系xOy 中，点A （﹣2，1），B （﹣2，4），点P 是满足λ=12的阿氏圆上的任一点，则该阿氏圆的方程为；若点M 为抛物线y 2＝8x 上的动点，点M 在y 轴上的射影为N ，则12|PB|+|PM|+|MN|的最小值为．四、解答题（本题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤） 17．（10分）已知数列{a n }的前n 项和为S n ，且S n ＝2a n +n ﹣3（n ∈N *）．（1）求证：数列{a n ﹣1}是等比数列，并求数列{a n }的通项公式；（2）设c n =1a n−1，数列{c n }的前n 项和为T n ，求证：T n ＜2．18．（12分）已知直线l 过直线l 1：x ﹣y +5＝0和直线l 2：2x +y +1＝0的交点P ．（1）若坐标原点O 到直线l 的距离为2，求直线l 的方程；（2）若直线l 的倾斜角为α，且sinα=45，求直线l 的方程．19．（12分）已知直线l ：y ＝kx 与圆C ：x 2+y 2﹣2x ﹣3＝0相交于A ，B 两点．（1）若|AB|=√13，求直线l 的倾斜角；（2）问在x 轴上是否存在点P ，使得当实数k （k ≠0）变化时，总有k P A +k PB ＝0？若存在，求出点P 的坐标；若不存在，请说明理由．20．（12分）设数列{a n }的前n 项和为S n ，且S n =n 2（n ∈N *）．（1）求数列{a n }的通项公式；（2）若数列{b n }满足b 2＝3b 1＝9，b n ≠0，且b n+12=b n b n+2，设c n =1a n a n+1+(−1)n b n ，求数列{c n }的前n 项和T n ．21．（12分）在平面直角坐标系xOy 中，已知点F(0，−√3)，直线l ：y =−4√33，设动点G 到直线l 的距离为d ，且|GF|=√32d ．（1）求动点G 的轨迹C 的方程，并指出它表示什么曲线；（2）已知过点A （1，2）的直线与曲线C 交于P ，Q 两点，点B （1，0），直线BP ，BQ 与y 轴分别交于点M ，N ，试问：线段MN 的中点是否为定点，若是定点，求出该定点坐标；若不是，请说明理由． 22．（12分）如图，椭圆x 2a 2+y 2b 2=1(a ＞b ＞0)的下顶点为C ，右顶点为D ，且|CD|=2√3，左焦点为F（﹣2，0），过F 且斜率为k （k ＞0）的直线l 与椭圆相交于A ，B 两点，交y 轴于点P ，M 为线段AB 的中点，直线OM 交CD 于点N ，过点P 作PE ⊥MN 交x 轴于点E ．（1）求椭圆的方程和直线CD 的斜率；（2）当△MAE 的面积为√64时，求|OM||ON|的值．2023-2024学年江苏省盐城市阜宁中学高二（上）期中数学试卷参考答案与试题解析一、单项选择题（本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知点A （﹣2，4），B （4，﹣1），则直线AB 在y 轴上的截距为（） A ．83B ．73C ．145D ．135解：因为直线经过两点A （﹣2，4）、B （4，﹣1），所以直线方程为y+14+1=x−4−2−4，化简得5x +6y ﹣14＝0，令x ＝0，得6y ﹣14＝0，解得y =73，即直线AB 在y 轴上的截距为73．故选：B ．2．圆C 1：x 2+y 2−2x =0与圆C 2：x 2+y 2+2x −8y =0的位置关系为（） A ．外切B ．内切C ．相交D ．外离解：由题意知，C 1：x 2+y 2−2x =0⇒(x −1)2+y 2=1，则C 1（1，0），r 1＝1， C 2：x 2+y 2+2x −8y =0⇒(x +1)2+(y −4)2=17，则C 2(−1，4)，r 2=√17，又d =|C 1C 2|=√(−1−1)2+(4−0)2=2√5，则r 2﹣r 1＜d ＜r 2+r 1，所以圆C 1与圆C 2相交．故选：C ．3．设函数f(x)=x 2−1x，则lim Δx→0f(1+2Δx)−f(1)Δx =（）A ．6B ．4C ．3D ．2解：函数f(x)=x 2−1x ，则lim Δx→0f(1+2Δx)−f(1)Δx =2lim 2Δx→0f(1+2Δx)−f(1)2Δx =2f ′（1），又f ′(x)=2x +1x 2，则f ′（1）＝3，则lim Δx→0f(1+2Δx)−f(1)Δx =2×3＝6．故选：A ． 4．已知椭圆x 25+y 2m=1的一个焦点坐标为（0，﹣2），则实数m 的值为（） A ．1B ．4C ．7D ．9解：由已知可得椭圆x 25+y 2m=1的焦点在y 轴上，故a 2＝m ，b 2＝5，c ＝2，则c 2＝a 2﹣b 2＝m ﹣5＝4，得m ＝9．故选：D ．5．已知函数f （x ）＝2x 3﹣me x （m ∈R ），则曲线y ＝f （x ）在点（0，f （0））处的切线经过定点（）A ．（﹣1，0）B ．（0，0）C ．（1，0）D ．（2，0）解：因为f （x ）＝2x 3﹣me x ，所以f ′（x ）＝6x 2﹣me x ，则f ′（0）＝﹣m ，又f （0）＝﹣m ，直线过（0，﹣m ），则直线方程为y +m ＝﹣mx ，即y ＝﹣m （x +1），令x +1＝0，得y ＝0，即直线不受参数m 的影响，恒过定点（﹣1，0）．故选：A ．6．已知等比数列{a n }的前n 项和为S n ，2S 3＝a 4﹣a 1，且a 2+a 4＝15，则a 3+a 5＝（） A ．3B ．5C ．30D ．45解：等比数列{a n }中，2S 3＝a 4﹣a 1，且a 2+a 4＝15，所以2（a 1+a 1q +a 1q 2）=a 1q 3−a 1，a 1q +a 1q 3=15，解得a 1=12，q ＝3，则a 3+a 5=12×32+12×34=45．故选：D ． 7．已知双曲线E ：x 2a 2−y 2b 2=1(a ＞0，b ＞0)的左、右顶点分别为A 、B ，M 是E 上一点，△ABM 为等腰三角形，且△ABM 的外接圆面积为3πa 2，则双曲线E 的离心率为（） A ．2B ．√2C ．√3D ．√5解：不妨设点M 在第一象限，如下图所示：由图可知，|AM |＞|BM |，且|AM |＞|AB |，因为△ABM 为等腰三角形，则|BM |＝|AB |＝2a ，设△ABM 的外接圆半径为r ，则πr 2＝3πa 2，可得r =√3a ，由正弦定理可得|AB|sin∠AMB =2r ，则sin ∠AMB =|AB|2r =2a 2√3a=√33，即sin ∠BAM =√33，易知，∠BAM 为锐角，则cos ∠BAM =√1−sin 2∠BAM =√1−(33)2=√63，所以，tan ∠BAM =sin∠BAM cos∠BAM =√3336=√22，tan ∠xBM =tan(2∠BAM)=2tan∠BAM1−tan 2∠BAM =2×√221−(√22)2=2√2，所以，直线AM 的方程为y =√22(x +a)，直线BM 的方程为y =2√2(x −a)，联立{y =√22(x +a)y =2√2(x −a)，解得{x =5a3y =4√23a，即点M(53a ，4√23a)，将点M 的坐标代入双曲线E 的方程可得(5a 3)2a 2−(4√23a)2b 2=1，可得b 2a 2=2，因此，双曲线E 的离心率为e =c a =√c 2a 2=√1+b2a2=√1+2=√3．故选：C ．8．设数列{a n }的前n 项和为S n ，a 2＝3，且（n +1）S n +1＝（n +1）S n +（n +2）a n ，若存在n ∈N *，使得2S n +22≤ka n 成立，则实数k 的最小值为（） A ．4√5+1B ．8C ．323D ．10解：由（n +1）S n +1＝（n +1）S n +（n +2）a n得（n +1）a n +1＝（n +1）S n +1﹣（n +1）S n ＝（n +2）a n ，则有a n+1n+2=a n n+1对任意n ∈N *成立，又a 2＝3，则a nn+1=a 23=1，故a n ＝n +1，且a n +1﹣a n ＝（n +1）﹣n ＝1，则数列{a n }是以2为首项，1为公差的等差数列，则S n =n(2+n+1)2=n(n+3)2，由2S n +22≤ka n 得，n （n +3）+22≤k （n +1），分离参数得，k ≥n(n+3)+22n+1，令n +1＝t （t ≥2，t ∈N *）则g(t)=t 2+t+20t =t +20t+1，令g(x)=x +20x +1(x ＞0)，则g ′(x)=1−20x2=x 2−20x ，当x ∈(0，2√5)时，g ′（x ）＜0，g （x ）单调递减；当x ∈(2√5，+∞)时，g ′（x ）＞0，g （x ）单调递增；由t ≥2，t ∈N *，则当t ≤4时，g （2）≥g （3）≥g （4），当t ≥5时，恒有g （t ）≤g （t +1），又g （4）＝g （5）＝10，故g （t ）的最小值为10．若存在n ∈N *，使得2S n +22≤ka n 成立，则k ≥g （t ）min ，则有k ≥10，即实数k 的最小值为10．故选：D ．二、多项选择题（本题共4小题，每小题5分，共20分，在每小题给出的四个选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分） 9．下列函数的图象可能与直线2x ﹣y +m ＝0（m ∈R ）相切的是（） A ．f （x ）＝x 2+x B ．f （x ）＝2x +e xC ．f(x)=12x 2+lnxD ．f(x)=2x +√x解：因为直线2x ﹣y +m ＝0的斜率为2，所以f ′（x ）＝2有解，则直线2x ﹣y +m ＝0就可以为该函数图象的切线．对于A ，令f ′（x ）＝2x +1＝2，解得x =12，满足条件；对于B ，因为f ′（x ）＝2+e x ＞2恒成立，不满足条件；对于C ，令f ′(x)=x +1x=2，解得x ＝1，满足条件；对于D ，f ′(x)=212√x 2恒成立，不满足条件．故选：AC ．10．在平面直角坐标系xOy 中，已知点A （a ，﹣1），B （2a +1，2），直线l ：x ﹣y +4＝0，其中a ∈R ，则下列结论正确的是（）A ．直线AB 恒过定点，且定点坐标为（﹣1，﹣4） B ．若直线AB 在两坐标轴上的截距相等，则a ＝﹣4C ．若直线AB 过第一、三象限，则a ＞﹣1D ．若直线AB 和直线l 与两坐标轴围成的四边形有外接圆，则a ＝﹣4 解：对A ，当a ≠﹣1时，k AB =3a+1，直线AB 的方程为y +1=3a+1(x −a)，即3x ﹣（a +1）y ﹣4a ﹣1＝0，所以3x ﹣y ﹣1﹣a （y +4）＝0，令{3x −y −1=0y +4=0，解得{x =−1y =−4，直线AB 恒过定点（﹣1，﹣4），当a ＝﹣1时，A （﹣1，﹣1），B （﹣1，2），直线AB 的方程为x ＝﹣1也过点（﹣1，﹣4），所以直线AB 恒过定点，且定点坐标为（﹣1，﹣4），故A 正确；对B ，直线AB 在两坐标轴上的截距相等，当a ＝﹣1时，直线AB 的方程为x ＝﹣1不合题意；故a ≠﹣1，此时直线AB 的方程3x ﹣（a +1）y ﹣4a ﹣1＝0，令y ＝0，则x =4a+13，令x ＝0，则y =−4a+1a+1，令4a+13=−4a+1a+1，即（4a +1）（a +4）＝0，即4a 2+17a +4＝0，即（4a +1）（a +4）＝0，解得a =−14或a ＝﹣4，故B 错误；对C ，若直线AB 过第一、三象限，则直线AB 的斜率一定存在且为正数，即3a+1＞0，即a +1＞0，所以a ＞﹣1，故C 正确；对于D ，若直线AB 和直线l ：x ﹣y +4＝0与两坐标轴围成的四边形有外接圆，即该四边形对角互补，而直线AB 恒过定点（﹣1，﹣4），故需满足直线AB ⊥l ，则3a+1×1=−1，即a +1＝﹣3，所以a ＝﹣4，故D 正确．故选：ACD ．11．已知数列{a n }满足a 1+3a 2+⋯+3n−1a n =n ⋅3n+1（n ∈N *），设数列{a n }的前n 项和为S n ，则下列结论正确的是（） A ．数列{a n }为等差数列B ．S n =3n 2+6nC ．数列{（﹣1）n a n }的前100项和为300D ．数列{|a n ﹣20|}的前20项和为284 解：由a 1+3a 2+⋯+3n−1a n =n ⋅3n+1（n ∈N *），设b n =3n−1a n ，则b 1+b 2+⋯+b n =n ⋅3n+1，所以当n ≥2时，b 1+b 2+⋯+b n−1=(n −1)⋅3n ，两式相减得，b n =(2n +1)⋅3n ，当n ＝1时，b 1＝a 1＝9也适合上式．则b n =(2n +1)⋅3n =3n−1a n ，解得，a n ＝3（2n +1），所以a n +1﹣a n ＝6，故数列{a n }是以9为首项，6为公差的等差数列，则S n =n(9+6n+3)2=3n(n +2)=3n 2+6n ，故选项AB 正确；选项C ，数列{（﹣1）n a n }的前100项和M ＝3[（﹣3+5）+（﹣7+9）+⋯+（﹣199+201）] ＝3×2×50＝300，故C 项正确；选项D ，|a n −20|=|6n −17|={17−6n ，n ≤26n −17，n ≥3，n ∈N ∗，则{|a n ﹣20|}前20项和为N =11+5+1+7+13+⋯+103=16+18(1+103)2=952，故D 项错误．故选：ABC ．12．已知O 为坐标原点，点A （﹣2，﹣1）在抛物线C ：x 2＝﹣2py （p ＞0）上，过点B （0，1）的直线交抛物线C 于P ，Q 两点，则下列结论正确的是（） A ．抛物线C 的准线方程为y ＝1 B ．直线AB 与抛物线C 相切 C ．OP →⋅OQ →为定值3D ．|BP |•|BQ |＞|BA |2解：对于A ：∵点A （﹣2，﹣1）在抛物线C ：x 2＝﹣2py （p ＞0）上，则4＝2p ，解得p ＝2， ∴抛物线C ：x 2＝﹣4y ，其准线为y ＝1，故A 正确；对于B ：过A 、B 的直线方程为y ＝x +1，代入抛物线方程得x 2﹣4x +4＝0，Δ＝16﹣16＝0，故直线AB 与抛物线只有一个公共点，且k AB =1−(−1)2=1，即AB 不垂直于x 轴， ∴直线AB 与抛物线C 相切，故B 正确；对于C ：由题意可知，直线PQ 斜率存在，设直线PQ 的方程为y ＝kx +1，P （x 1，y 1），Q （x 2，y 2），联立方程{y =kx +1x 2=−4y ，消去y 得：x 2+4kx +4＝0，可得Δ＝16k 2﹣16＞0，得k 2＞1，且{x 1+x 2=−4kx 1x 2=4，∵OP →⋅OQ →=x 1x 2+y 1y 2=x 1x 2+(−x 124)(−x 224)=x 1x 2+x 12x 2216=4+1=5，故C 错误；对于D ：由题意可知|BA |2＝（﹣2﹣0）2+（﹣1﹣1）2＝8，∵|BP|⋅|BQ|=√1+k 2|x 1−0|⋅√1+k 2|x 2−0|=(1+k 2)|x 1x 2|=4(1+k 2)，则|BP |•|BQ |＝4（1+k 2）＞8， ∴|BP |•|BQ |＞|BA |2，故D 正确．故选：ABD ．三、填空题（本题共4小题，每小题5分，共20分）13．设f′（x）为函数f（x）的导函数，若f（x）＝2（x+1）e x﹣f′（0）•x，则f（0）+f′（0）＝．解：由题意知，令x＝0，则f（0）＝2e0＝2，f′（x）＝2（x+2）e x﹣f′（0），令x＝0，则f′（0）＝2（0+2）e0﹣f′（0），解得f′（0）＝2，∴f（0）+f′（0）＝4．故答案为：4．14．设各项均为正数的等差数列{a n}的前n项和为S n，若a92−a7+12a5=3，则S17＝．解：由题意，设等差数列{a n}的公差为d（d＞0），因为a92−a7+12a5=3，可得a92−(a1+6d)+12(a1+4d)=a92−12(a1+8d)=3，即a92−12a9=3，可得2a92−a9−6=0，且a n＞0，解得a9＝2，又由S17=17(a1+a17)2=17×2a92=17a9=34．故答案为：34．15．已知直线l：x+y﹣2＝0关于直线y＝a的对称直线与圆（x﹣1）2+y2＝2有公共点，则实数a的取值范围为．解：圆（x﹣1）2+y2＝2，圆心C（1，0），半径为√2，设圆（x﹣1）2+y2＝2关于直线y＝a的对称圆圆心C′（x，y），且圆的半径仍为√2，则圆心C（1，0）与C′关于直线y＝a对称，有{x=1y+02=a，解得{x=1y=2a，即对称圆圆心C′（1，2a）．由对称性可知，直线l：x+y﹣2＝0与圆C′有公共点，则有圆心C′（1，2a）到直线l：x+y﹣2＝0的距离d=|1+2a−2|√1+1≤√2，化简得|2a ﹣1|≤2，解得−12≤a ≤32，则实数a 的取值范围为[−12，32]．故答案为：[−12，32]．16．希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名，他发现：“平面内到两个定点A ，B 的距离之比为定值λ（λ≠1）的点的轨迹是圆”．后来，人们将这个圆以他的名字命名，称为阿波罗尼斯圆，简称阿氏圆．已知在平面直角坐标系xOy 中，点A （﹣2，1），B （﹣2，4），点P 是满足λ=12的阿氏圆上的任一点，则该阿氏圆的方程为；若点M 为抛物线y 2＝8x 上的动点，点M 在y 轴上的射影为N ，则12|PB|+|PM|+|MN|的最小值为．解：设P （x ，y ），已知A （﹣2，1），B （﹣2，4），因为|PA||PB|=12，所以|PA||PB|=2222=12，两边平方化简整理得（x +2）2+y 2＝4，所以点P 的轨迹为以（﹣2，0）为圆心，2为半径的圆．抛物线C ：y 2＝8x 的焦点F （2，0），准线方程为x ＝﹣2，则12|PB|+|PM|+|MN|=|PA|+|PM|+|MN|=|AP|+|PM|+|MF|−2≥|AF|−2=√(−2−2)2+12−2=√17−2，当且仅当A ，P ，M ，F （P ，M 两点在A ，F 两点中间）四点共线时取等号，所以12|PB|+|PM|+|MN|的最小值为√17−2．故答案为：（x +2）2+y 2＝4；√17−2．四、解答题（本题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤） 17．（10分）已知数列{a n }的前n 项和为S n ，且S n ＝2a n +n ﹣3（n ∈N *）．（1）求证：数列{a n ﹣1}是等比数列，并求数列{a n }的通项公式；（2）设c n =1a n −1，数列{c n }的前n 项和为T n ，求证：T n ＜2．证明：（1）∵S n ＝2a n +n ﹣3，∴S n ﹣1＝2a n ﹣1+n ﹣4（n ≥2），两式相减得：S n ﹣S n ﹣1＝2a n ﹣2a n ﹣1+1＝a n ，∴a n ＝2a n ﹣1﹣1（n ≥2）， ∴a n ﹣1＝2（a n ﹣1﹣1）（n ≥2），令n ＝1得：S 1＝a 1＝2a 1﹣2，∴a 1＝2，a 1﹣1＝1≠0， ∴{a n ﹣1}是以1为首项，2为公比的等比数列， ∴a n −1=2n−1，即a n =2n−1+1．（2）由（1）得：c n =1a n −1=(12)n−1，{c n }是以1为首项，12为公比的等比数列， ∴T n =1−(12)n1−12=2−(12)n−1＜2．18．（12分）已知直线l 过直线l 1：x ﹣y +5＝0和直线l 2：2x +y +1＝0的交点P ．（1）若坐标原点O 到直线l 的距离为2，求直线l 的方程；（2）若直线l 的倾斜角为α，且sinα=45，求直线l 的方程．解：（1）联立{x −y +5=02x +y +1=0得：{x =−2y =3，所以点P 的坐标为（﹣2，3），当直线l 的斜率不存在时，则方程为x ＝﹣2，适合题意；当直线l 的斜率存在时，设其方程为y ﹣3＝k （x +2），即kx ﹣y +2k +3＝0，因为坐标原点O 到直线l 的距离为2，所以√k 2=2，解得k =−512，此时直线l 的方程为5x +12y ﹣26＝0，所以直线l 的方程为x ＝﹣2或5x +12y ﹣26＝0；（2）以为直线l 的倾斜角为α，α∈[0，π），且sinα=45，所以tan α＝±√52−42=±43；当k =−43时，直线l 的方程为4x +3y ﹣1＝0；当k =43时，直线l 的方程为4x ﹣3y +17＝0．所以直线l 的方程为4x +3y ﹣1＝0或4x ﹣3y +17＝0．19．（12分）已知直线l ：y ＝kx 与圆C ：x 2+y 2﹣2x ﹣3＝0相交于A ，B 两点．（1）若|AB|=√13，求直线l 的倾斜角；（2）问在x 轴上是否存在点P ，使得当实数k （k ≠0）变化时，总有k P A +k PB ＝0？若存在，求出点P 的坐标；若不存在，请说明理由．解：（1）∵圆C 的方程为（x ﹣1）2+y 2＝4，∴圆C 的圆心为C （1，0），半径r ＝2，∵|AB|=√13，∴圆心C 到直线l 的距离d =|k|√k +1=√22−(√132)2=√32，解得k 2＝3，即k =±√3，当k =tanα=√3时，倾斜角α＝60°，当k =tanα=−√3时，倾斜角α＝120°， ∴直线l 的倾斜角为60°或120°；（2）设点A （x 1，y 1），B （x 2，y 2），假设存在满足题意的点P （x 0，0），即k P A +k PB ＝0，由{y =kx x 2+y 2−2x −3=0得：（1+k 2）x 2﹣2x ﹣3＝0，Δ＝4+12（1+k 2）＞0， ∴x 1+x 2=21+k2，x 1x 2=−31+k2，∴k PA +k PB =y 1x 1−x 0+y 2x 2−x 0=kx 1x 1−x 0+kx 2x 2−x 0=0，由k ≠0得：x 1（x 2﹣x 0）+x 2（x 1﹣x 0）＝2x 1x 2﹣x 0（x 1+x 2）＝0， ∴−61+k2−2x 01+k2=0，解得：x 0＝﹣3，∴在x 轴上存在满足题意的点P ，且点P 的坐标为（﹣3，0）． 20．（12分）设数列{a n }的前n 项和为S n ，且S n =n 2（n ∈N *）．（1）求数列{a n }的通项公式；（2）若数列{b n }满足b 2＝3b 1＝9，b n ≠0，且b n+12=b n b n+2，设c n =1a n a n+1+(−1)n b n ，求数列{c n }的前n 项和T n ．解：（1）由题意，当n ＝1时，a 1＝S 1＝1，当n ≥2时，a n ＝S n ﹣S n ﹣1＝n 2﹣（n ﹣1）2＝2n ﹣1， ∵当n ＝1时，a 1＝1也适合上式， ∴a n ＝2n ﹣1，n ∈N *．（2）依题意，由b n ≠0，且b n+12=b n b n+2，可得b n+2b n+1=b n+1b n，故数列{b n }是等比数列，设等比数列{b n }的公比为q ， ∵b 2＝3b 1＝9， ∴公比q =a 2a 1=3，首项b 1＝3， ∴b n ＝3×3n ﹣1＝3n ，n ∈N *，∴c n =1a n a n+1+(−1)nb n =1(2n−1)(2n+1)+(−1)n ×3n =12(12n−1−12n+1)+(−3)n ，∴T n ＝c 1+c 2+⋯+c n=12(1−13+13−15+⋯+12n−1−12n+1)+(−3)+(−3)2+⋯+(−3)n=12(1−12n+1)+(−3)[1−(−3)n]1−(−3)=n2n+1−34[1−(−3)n]．21．（12分）在平面直角坐标系xOy中，已知点F(0，−√3)，直线l：y=−4√33，设动点G到直线l的距离为d，且|GF|=√32d．（1）求动点G的轨迹C的方程，并指出它表示什么曲线；（2）已知过点A（1，2）的直线与曲线C交于P，Q两点，点B（1，0），直线BP，BQ与y轴分别交于点M，N，试问：线段MN的中点是否为定点，若是定点，求出该定点坐标；若不是，请说明理由．解：（1）设点G（x，y），由|GF|=√32d得：√x2+(y+√3)2=√32|y+4√33|，整理得：x2+y24=1，即y24+x2=1，它表示中心在坐标原点，焦点在y轴上的椭圆，且长轴长为4，短轴长为2；（2）设直线PQ的方程为y﹣2＝k（x﹣1）（k＞0），即y＝kx﹣k+2（k＞0），由{4x2+y2=4y=kx−k+2得：（4+k2）x2+（4k﹣2k2）x+k2﹣4k＝0，由Δ＝（4k﹣2k2）2﹣4（4+k2）（k2﹣4k）＝64k＞0得：k＞0，设点P（x1，y1），Q（x2，y2），则x1+x2=2k 2−4k4+k2，x1x2=k2−4k4+k2，直线BP的方程为y=y1x1−1(x−1)，令x＝0得：y=y11−x1，所以点M(0，y11−x1)，直线BQ的方程为y=y2x2−1(x−1)，令x＝0得：y=y21−x2，所以点N(0，y21−x2)，∴y M +y N =y 11−x 1+y 21−x 2=kx 1−k+21−x 1+kx 2−k+21−x 2=21−x 1+21−x x−2k =4−2(x 1+x 2)1−(x 1+x 2)+x 1x 2−2k =4−2⋅2k 2−4k 4+k21−2k 2−4k 4+k 2+k 2−4k 4+k2−2k =4−2k +2k =4，∴y M +y N2=2，即线段MN 的中点坐标为（0，2），∴线段MN 的中点为定点，其坐标为（0，2）． 22．（12分）如图，椭圆x 2a 2+y 2b 2=1(a ＞b ＞0)的下顶点为C ，右顶点为D ，且|CD|=2√3，左焦点为F（﹣2，0），过F 且斜率为k （k ＞0）的直线l 与椭圆相交于A ，B 两点，交y 轴于点P ，M 为线段AB 的中点，直线OM 交CD 于点N ，过点P 作PE ⊥MN 交x 轴于点E ．（1）求椭圆的方程和直线CD 的斜率；（2）当△MAE 的面积为√64时，求|OM||ON|的值．解：（1）由|CD|=2√3，左焦点为F （﹣2，0），可得c ＝2，a 2+b 2＝12，又a 2﹣b 2＝4，解得a ＝2√2，b ＝2，则椭圆方程为x 28+y 24=1；由C （0，﹣2），D （2√2，0），可得直线CD 的斜率为√22；（2）过F 且斜率为k （k ＞0）的直线l 的方程为y ＝k （x +2），可得P （0，2k ），设A （x 1，y 1），B （x 2，y 2），M （x 0，y 0），则x 12+2y 12=8，x 22+2y 22=8，两式相减可得（x 1﹣x 2）（x 1+x 2）+2（y 1﹣y 2）（y 1+y 2）＝0，则2x 0+4ky 0＝0，即k OM =−12k ，由PE ⊥MN ，可得k PE ＝2k ，直线PE 的方程为y ＝2kx +2k ，则E （﹣1，0）， △MAE 的面积为√64，可得△ABE 的面积为√62．由{y =k(x +2)x 2+2y 2=8可得（1+2k 2）x 2+8k 2x +8k 2﹣8＝0，可得x 1+x 2=−8k22k 2+1，x 1x 2=8k 2−81+2k 2，又E 到直线AB 的距离为d =k√1+k，所以12|AB |d =12√1+k 2•√64k 4(1+2k 2)2−32k 2−321+2k 2•√1+k 2=√62，化为4k 4+4k 2﹣3＝0，解得k 2=12，则k =√22，中点M 的横坐标为x M =−4k21+2k 2=−1，纵坐标为y M =√22（2﹣1）=√22，M （﹣1，√22），直线OM 的方程为y =−√22x ，又直线CD 的方程为y =√22x ﹣2，联立两直线的方程可得N （√2，﹣1），所以|OM||ON|=√1+1√2+1=√22．。

2022-2023学年江苏省盐城市阜宁中学高二(上)期中物理试卷【答案版】

2022-2023学年江苏省盐城市阜宁中学高二（上）期中物理试卷一、单选题（包括11小题，每题4分，共44分。

每小题只有一个选项符合题意）1．随着科技信息电子产品的快速发展，人们对手机的依赖性越来越强，据有关方面不完全统计，人们一天平均看手机的次数在150次以上。

许多人喜欢躺着看手机，经常出现手机砸伤眼睛的情况。

如图所示，若手机质量为120g，从离人眼睛约20cm的高度无初速度跌落，砸到眼睛后手机未反弹，眼睛受到的手机的冲击时间约为0.2s，重力加速度g＝10m/s2，下列分析正确的是（）A．手机接触眼睛之前的速度约为1m/sB．手机对眼睛的冲量大小约为0.56N•sC．手机对眼睛的作用力大小约为1.2ND．手机与眼睛作用过程中手机的动量变化量约为0.24kg•m/s2．如图甲所示，一轻弹簧的两端与质量分别为m1、m2的两物块A、B相连接，并静止在光滑水平面上。

现使A获得水平向右、大小为3m/s的瞬时速度，从此刻开始计时，两物块的速度随时间变化的规律如图乙所示，从图像提供的信息可得（）A．在t1和t3时刻两物块达到共同速度1m/s，且弹簧分别处于压缩和拉伸状态B．在t1～t2时间内A、B的距离逐渐增大，t2时刻弹簧的弹性势能最大C．两物块的质量之比为m1：m2＝2：1D．在t2时刻A、B两物块的动能之比为E k1：E k2＝1：63．如图所示，木块在水中沿竖直方向做简谐运动．运动过程木块受到的合力F和动能E k随相对平衡位置的位移x、运动的速度v和相对平衡位置的位移x随时间t变化的关系图像可能正确的是（）A．B．C．D．4．如图甲所示，水平弹簧振子的平衡位置为O点，在B、C两点之间做简谐运动，规定水平向右为正方向。

图乙是弹簧振子做简谐运动的x﹣t图像，则（）A．弹簧振子从B点经过O点再运动到C点为一次全振动B．弹簧振子的振动方程为x＝0.1sin（2πt+3π2）mC．图乙中的P点时刻振子的速度方向与加速度方向都沿正方向D．弹簧振子在前2.5s内的路程为1m5．如图所示是一列沿x轴正方向传播的简谐横波在t＝0时刻的波形图，已知波的传播速度v＝2m/s。

江苏省盐城市盐城中学2022高二数学上学期期中试题(含解析)

【点睛】本题考查基本不等式求最值，解题的关键是“1”的代换，属于中档题.
15.已知数列{an}满足a1＝21，an+1﹣an＝2n，则的最小值为__．
【答案】
【解析】
【分析】
根据已知条件用累加法求出的通项，再构造函数，利用函数单调性，求出数列的单调性，即可求的最小值.
【详解】时，
时，
，也满足上式，
∴根据二次函数的性质可知，x2+2x的最小值﹣1，
故P：a≤﹣1，
由x2﹣4x+3≤0可得1≤x≤3，
由（x﹣m）[x﹣（m+1）]≤0，可得m≤x≤m+1，
故q：A＝[1，3]，r：B＝[m，m+1]，
（1）若命题p的否定是假命题，即p为真命题，
故a的范围（﹣∞，﹣1]，
（2）若q是r的必要条件，则r⇒q，从而有B⊆A，
(2)已知（即）求，作差法：；
(3)已知求，作商法：；
(4)若求累加法：；
(5)已知求，累乘法：；
(6)形如或，倒数成等差；
(7)形如用待定系数法转化为等比数列.
16.已知椭圆 1（a＞b＞0）的左、右焦点分别为F1、F2，半焦距为c，且在该椭圆上存在异于左、右顶点的一点P，满足2a•sin∠PF1F2＝3c•sin∠PF2F1，则椭圆离心率的取值范围为_____．
②判断直线AB与EQ是否平行？并说明理由．
【答案】(1) 1．(2) ① ．②平行．理由见解析
【解析】
【分析】
（1）离心率值转化为关系，再把点坐标代入方程，即可求出椭圆标准方程；
（2）①求出方程，设出点坐标，可求出直线PA与PB的斜率之积；

2023-2024学年江苏省徐州一中高二(上)期中数学试卷【答案版】

2023-2024学年江苏省徐州一中高二（上）期中数学试卷一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项符合题目条件要求．1．直线x +√3y +1＝0的倾斜角是（） A ．30° B ．60°C ．120°D ．150°2．通过椭圆x 24+y 23=1的焦点且垂直于x 轴的直线l 被椭圆截得的弦长等于（） A ．2√3 B ．3C ．√3D ．63．双曲线x 24−y 2=1的焦点到渐近线的距离为（）A ．1B ．√2C ．2D ．34．设F 为抛物线C ：y 2＝3x 的焦点，过F 且倾斜角为30°的直线交于C 于A ，B 两点，则|AB |＝（） A ．√303B ．6C ．12D ．7√35．许多建筑融入了数学元素，更具神韵，数学赋予了建筑活力，数学的美也被建筑表现得淋漓尽致．已知图1是单叶双曲面（由双曲线绕虚轴旋转形成立体图形）型建筑，图2是其中截面最细附近处的部分图象．上、下底面与地面平行．现测得下底面直径AB ＝20√10米，上底面直径CD ＝20√2米，AB 与CD 间的距离为80米，与上下底面等距离的G 处的直径等于CD ，则最细部分处的直径为（）A ．20米B ．10√5米C ．10√3米D ．10米6．若圆x 2+y 2﹣2x ﹣6y +1＝0上恰有三点到直线y ＝kx 的距离为2，则k 的值为（） A ．12或2B ．34或43C ．2D ．437．已知⊙M ：x 2+y 2﹣2x ﹣2y ﹣2＝0，直线l ：2x +y +2＝0，P 为l 上的动点，过点P 作⊙M 的切线P A ，PB ，切点为A ，B ，当|PM |•|AB |最小时，直线AB 的方程为（） A ．2x ﹣y ﹣1＝0B ．2x +y ﹣1＝0C ．2x ﹣y +1＝0D ．2x +y +1＝08．已知F （﹣c ，0）是椭圆x 2a 2+y 2b 2=1（a ＞b ＞0）的左焦点，直线y ＝x +c 与该椭圆相交于M ，N 两点，O 是坐标原点，P 是线段OF 的中点，线段MN 的中垂线与x 轴的交点在线段PF 上．该椭圆离心率的取值范围是（） A ．[√63，1) B ．[√22，1) C ．(0，√63] D ．[√22，√63] 二、多项选择题：本题共4小题，每小题5分，共20分在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，有选错的得0分部分选对的得2分．9．已知a 为实数，若三条直线ax +2y +8＝0，4x +3y ﹣10＝0和2x ﹣y ﹣10＝0不能围成三角形，则a 的值为（） A ．83B ．1C ．﹣1D ．﹣410．若方程x 22−t−y 21−t=1所表示的曲线为C ，则下列命题正确的是（）A ．若曲线C 为双曲线，则t ＜1或t ＞2B ．若曲线C 为椭圆，则1＜t ＜2C ．曲线C 可能是圆D ．若曲线C 为焦点在x 轴上的椭圆，则1＜t ＜3211．如图，已知椭圆x 24+y 22=1的左、右顶点分别是A 1，A 2，上顶点为B 1，在椭圆上任取一点C ，连结A 1C 交直线x ＝2于点P ，连结A 2C 交PO 于点M （O 是坐标原点），则下列结论正确的是（）A ．k CA 1•k CA 2为定值B ．k A 1P =12k OP C ．OP ⊥A 2CD ．MB 1的最大值为√612．已知抛物线C ：y 2＝4x ，过点P （2，0）的直线l 交C 于A ，B 两点，O 为坐标原点，则下列说法正确的有（）A ．若直线l 的斜率为2，则△OAB 的面积为12 B ．|AB |的最小值为4√2C ．1|PA|+1|PB|=√24D ．若M （﹣2，0），则|MA||MB|=|PA||PB|三、填空题本题共4小题，每小题5分，共20分．13．已知S n 为等差数列{a n }的前n 项和，且满足a 2＝4，S 4＝22，则S 8＝．14．已知直线y ＝k （x +1）截圆（x ﹣1）2+（y ﹣1）2＝4所得两段圆弧的弧长之比为1：2，则k ＝．15．双曲线x 2a 2−y 2b 2=1（a ＞0，b ＞0）的右焦点为F ，左、右顶点为A 1、A 2，过F 作A 1A 2的垂线与双曲线交于B 、C 两点，若A 1B ⊥A 2C ，则该双曲线的渐近线斜率为．16．若正方形ABCD 的一条边在直线y ＝2x ﹣17上，另外两个顶点在抛物线y ＝x 2上．则该正方形面积的最小值为．四、解答题：本题共6小题，共70分．解答题应写出文字说明、证明过程或演算步骤． 17．（10分）等差数列{a n }的前n 项和为S n ，a 3+a 5＝a 4+7且a 1+a 10＝20．（1）求{a n }的通项公式；（2）求满足不等式S n ＜3a n ﹣2的n 的值．18．（12分）已知圆C ：x 2+y 2+2x ﹣4y +m ＝0与y 轴相切，O 为坐标原点，动点P 在圆外，过P 作圆C 的切线，切点为M ．（1）求圆C 的圆心坐标及半径；（2）求满足|PM |＝2|PO |的点P 的轨迹方程． 19．（12分）若椭圆E ：x 2a 2+y 2b 2=1（a ＞b ＞0）过抛物线x 2＝4y 的焦点，且与双曲线x 2﹣y 2＝1有相同的焦点．（1）求椭圆E 的方程；（2）不过原点O 的直线l ：y ＝x +m 与椭圆E 交于A ，B 两点，当△OAB 的面积为√32时，求直线l 的方程．20．（12分）已知抛物线C ：y 2＝2px （p ＞0），过抛物线的焦点F 且垂直于x 轴的直线交抛物线于不同的两点A ，B ，且|AB |＝4．（1）求抛物线C 的方程；（2）若不经过坐标原点O 的直线l 与抛物线C 相交于不同的两点M ，N ，且满足OM →⊥ON →证明直线l 过x 轴上一定点Q ，并求出点Q 的坐标． 21．（12分）已知双曲线C ：x 2a 2−y 2b 2=1（a ＞0，b ＞0）的虚轴长为4，直线2x ﹣y ＝0为双曲线C 的一条渐近线．（1）求双曲线C 的标准方程；（2）记双曲线C 的左、右顶点分别为A ，B ，过点T （2，0）的直线l 交双曲线C 于点M ，N （点M 在第一象限），记直线MA 斜率为k 1，直线NB 斜率为k 2，求证：k 1k 2为定值．22．（12分）已知椭圆C 1：x 24+y 2＝1的左右顶点分别为A 1、A 2，上下顶点分别为B 1、B 2，记四边形A 1B 1A 2B 2的内切圆为C 2．（1）求圆C 2的标准方程；（2）已知P 为椭圆C 1上任意一点，过点P 作圆C 2的切线分别交椭圆C 1于M 、N 两点，试求三角形PMN 面积的最小值．2023-2024学年江苏省徐州一中高二（上）期中数学试卷参考答案与试题解析一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项符合题目条件要求．1．直线x +√3y +1＝0的倾斜角是（） A ．30°B ．60°C ．120°D ．150°解：直线x +√3y +1＝0的斜率k =1√3=−√33，设其倾斜角为θ（0°≤θ＜180°），则tan θ=−√33，∴θ＝150°．故选：D ． 2．通过椭圆x 24+y 23=1的焦点且垂直于x 轴的直线l 被椭圆截得的弦长等于（） A ．2√3B ．3C ．√3D ．6解：由题设，不妨设过焦点（1，0）且垂直于x 轴的直线l ：x ＝1，代入椭圆方程得14+y 23=1可得y =±32，故被椭圆截得的弦长等于3．故选：B ． 3．双曲线x 24−y 2=1的焦点到渐近线的距离为（）A ．1B ．√2C ．2D ．3解：双曲线中，焦点坐标为（±√5，0），渐近线方程为：y =±12x ， ∴双曲线x 24−y 2=1的焦点到渐近线的距离：d =|±√5|√1+4=1．故选：A ．4．设F 为抛物线C ：y 2＝3x 的焦点，过F 且倾斜角为30°的直线交于C 于A ，B 两点，则|AB |＝（） A ．√303B ．6C ．12D ．7√3解：由y 2＝3x 得其焦点F （34，0），准线方程为x =−34．则过抛物线y 2＝3x 的焦点F 且倾斜角为30°的直线方程为y ＝tan30°（x −34）=√33（x −34）．代入抛物线方程，消去y ，得16x 2﹣168x +9＝0．设A （x 1，y 1），B （x 2，y 2）则x 1+x 2=16816=212，所以|AB |＝x 1+34+x 2+34=34+34+212=12 故选：C ．5．许多建筑融入了数学元素，更具神韵，数学赋予了建筑活力，数学的美也被建筑表现得淋漓尽致．已知图1是单叶双曲面（由双曲线绕虚轴旋转形成立体图形）型建筑，图2是其中截面最细附近处的部分图象．上、下底面与地面平行．现测得下底面直径AB ＝20√10米，上底面直径CD ＝20√2米，AB 与CD 间的距离为80米，与上下底面等距离的G 处的直径等于CD ，则最细部分处的直径为（）A ．20米B ．10√5米C ．10√3米D ．10米解：建立如图的坐标系，由题意可知D （10√2，20），B （10√10，﹣60），设双曲线方程为：x 2a 2−y 2b 2=1，∴{200a 2−400b 2=11000a 2−3600b2=1，解得a 2＝100，b 2＝400，|EF |＝2a ＝20，故选：A ．6．若圆x 2+y 2﹣2x ﹣6y +1＝0上恰有三点到直线y ＝kx 的距离为2，则k 的值为（） A ．12或2B ．34或43C ．2D ．43解：圆x 2+y 2﹣2x ﹣6y +1＝0的圆心C （1，3），半径r =12√4+36−4=3，∵圆上恰有三点到直线y ＝kx 的距离为2， ∴圆心C （1，3）到直线y ＝kx 的距离为1，即d =|k−3|√k +1=1，解得k =43．故选：D ．7．已知⊙M ：x 2+y 2﹣2x ﹣2y ﹣2＝0，直线l ：2x +y +2＝0，P 为l 上的动点，过点P 作⊙M 的切线P A ，PB ，切点为A ，B ，当|PM |•|AB |最小时，直线AB 的方程为（） A ．2x ﹣y ﹣1＝0B ．2x +y ﹣1＝0C ．2x ﹣y +1＝0D ．2x +y +1＝0解：化圆M 为（x ﹣1）2+（y ﹣1）2＝4，圆心M （1，1），半径r ＝2．∵S 四边形PAMB =12|PM|⋅|AB|=2S △P AM ＝|P A |•|AM |＝2|P A |=2√|PM|2−4． ∴要使|PM |•|AB |最小，则需|PM |最小，此时PM 与直线l 垂直．由直线l ：2x +y +2＝0，可得直线PM 的斜率为12，直线PM 的方程为y ﹣1=12（x ﹣1），即y =12x +12，联立{y =12x +122x +y +2=0，解得P （﹣1，0）．则以PM 为直径的圆的方程为x 2+(y −12)2=54．联立{x 2+y 2−2x −2y −2=0x 2+y 2−y −1=0，相减可得直线AB 的方程为2x +y +1＝0．故选：D ．8．已知F （﹣c ，0）是椭圆x 2a 2+y 2b 2=1（a ＞b ＞0）的左焦点，直线y ＝x +c 与该椭圆相交于M ，N 两点，O 是坐标原点，P 是线段OF 的中点，线段MN 的中垂线与x 轴的交点在线段PF 上．该椭圆离心率的取值范围是（） A ．[√63，1) B ．[√22，1) C ．(0，√63] D ．[√22，√63] 解：设M （x 1，y 1），N （x 2，y 2），设MN 的中点为B ，与OF 的交点为A ，联立{y =x +c x 2a2+y 2b2=1，整理可得：（a 2+b 2）x 2+2a 2cx +a 2（c 2﹣b 2）＝0，所以x 1+x 2=−2a 2c a 2+b2，x 1x 2=a 2(c 2−b 2)a 2+b2，y 1+y 2＝x 1+x 2+2c =2b 2c a 2+b2，因为直线MN 的斜率为1，所以线段MN 的中点B （−a 2ca 2+b2，b 2ca 2+b 2）所以由题意可得直线AB 的斜率为﹣1，所以直线AB 的方程为：y −b 2c a 2+b2=−（x +a 2c a 2+b2），将A （x A ，0）的坐标代入可得−b 2ca 2+b2=−（x A +a 2c a 2+b2），所以可得x A =b 2c−a 2ca 2+b 2，由﹣c ≤x A ≤−c 2，可得﹣1≤b 2−a 2a 2+b2≤−12，又b 2＝a 2﹣c 2，所以可得﹣1≤−c 22a 2−c 2≤−12，e =ca ，所以可得23≤e 2≤1，又因为e ∈（0，1），解得：√63≤e ＜1，故选：A ．二、多项选择题：本题共4小题，每小题5分，共20分在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，有选错的得0分部分选对的得2分．9．已知a 为实数，若三条直线ax +2y +8＝0，4x +3y ﹣10＝0和2x ﹣y ﹣10＝0不能围成三角形，则a 的值为（） A ．83B ．1C ．﹣1D ．﹣4解：联立{2x −y −10=04x +3y −10=0，得x ＝4，y ＝﹣2，即交点（4，﹣2），三条直线ax +2y +8＝0，4x +3y ﹣10＝0和2x ﹣y ﹣10＝0不能围成三角形，所以直线ax +2y +8＝0过点（4，﹣2）或与已知一条直线平行，当直线ax +2y +8＝0过点（4，﹣2）是，a ＝﹣1，当ax +2y +8＝0与4x +3y ﹣10＝0平行时，a =83，当ax +2y +8＝0与2x ﹣y ﹣10＝0平行时，a ＝﹣4，综上，a ＝﹣1或a ＝﹣4或a =83．故选：ACD ． 10．若方程x 22−t−y 21−t=1所表示的曲线为C ，则下列命题正确的是（）A ．若曲线C 为双曲线，则t ＜1或t ＞2B ．若曲线C 为椭圆，则1＜t ＜2C ．曲线C 可能是圆D ．若曲线C 为焦点在x 轴上的椭圆，则1＜t ＜32解：对于A ，方程表示双曲线，则（2﹣t ）（1﹣t ）＞0，解得t ＜1或t ＞2，故A 正确；对于B ，方程表示椭圆，则{2−t ＞0t −1＞02−t ≠t −1，解得1＜t ＜2且t ≠32，故B 错误；对于C ，当t =32时，方程表示圆，故C 正确；对于D ，方程表示焦点在x 轴上的椭圆，则2﹣t ＞t ﹣1＞0，解得1＜t ＜32，故D 正确；故选：ACD ． 11．如图，已知椭圆x 24+y 22=1的左、右顶点分别是A 1，A 2，上顶点为B 1，在椭圆上任取一点C ，连结A 1C 交直线x ＝2于点P ，连结A 2C 交PO 于点M （O 是坐标原点），则下列结论正确的是（）A ．k CA 1•k CA 2为定值B ．k A 1P =12k OP C ．OP ⊥A 2CD ．MB 1的最大值为√6解：椭圆的左右顶点分别A 1（﹣2，0），A 2（2，0），因为点C 在椭圆上，所以设点C 的坐标为(2cosθ，√2sinθ)，θ∈[0，2π]，对于A ，k CA 1k CA 2=√2sinθ2cosθ+2+√2sinθ2cosθ−2=2sin 2θ4cos 2θ−4=sin 2θ−2sin 2θ=−12，所以A 正确；对于B ，因为k A 1P =k C A 1=√2sinθ2cosθ+2，所以直线AP 为y =√2sinθ2cosθ+2x +2√2sinθ2cosθ+2，令x ＝2，得y =2√2sinθcosθ+1，所以点P 的坐标为(2，2√2sinθcosθ+1)，所以k OP =√2sinθcosθ+1，所以k A 1P =12k OP ，所以B 正确；对于C ，因为k k A 2=√2sinθ2cosθ−2，所以k CA 2⋅k OP =√2sinθ2cosθ−2⋅√2sinθcosθ+1=2sin 2θ2(cos 2θ−1)=−1，所以OP ⊥A 2C ，所以C 正确；对于D ，直线OP 为y =√2sinθcosθ+1x ，直线A 2C 为y =√2sinθ2cosθ−2x −2√2sinθ2cosθ−2，由两直线的方程联立方程组，解得x =2(cosθ+1)3−cosθ，y =2√2sinθ3−cosθ，所以点M 的坐标为(2(cosθ+1)3−cosθ，2√2sinθ3−cosθ)，因为B 1(0，√2)，所以|MB 1|2=4(cosθ+1)2(3−cosθ)2+(2√2sinθ3−cosθ−√2)2，当cosθ=45，sinθ=−35时，|MB 1|2=4(45+1)2(3−45)2+(−2√2×353−45−√2)2=902121＞7，所以D 错误．故选：ABC ．12．已知抛物线C ：y 2＝4x ，过点P （2，0）的直线l 交C 于A ，B 两点，O 为坐标原点，则下列说法正确的有（）A ．若直线l 的斜率为2，则△OAB 的面积为12 B ．|AB |的最小值为4√2C ．1|PA|+1|PB|=√24D ．若M （﹣2，0），则|MA||MB|=|PA||PB|解：A ．抛物线C ：y 2＝4x ，过点P （2，0）的直线l 交C 于A ，B 两点，若直线l 的斜率为2，则直线l 的方程为y ＝2（x ﹣2），即x =y2+2，设A （x 1，y 1），B （x 2，y 2），由{x =y2+2y 2=4x，得y 2﹣2y ﹣8＝0，∴y 1+y 2＝2，y 1y 2＝﹣8，∴△OAB 的面积S =12|PO||y 1−y 2|=|y 1−y 2|=√(y 1+y 2)2−4y 1y 2=6，故A 错误； B 和C ．由题意知，直线l 的斜率不为0，设直线l 的方程为x ＝my +2，A （x 1，y 1），B （x 2，y 2），由{x =my +2y 2=4x ，得y 2﹣4my ﹣8＝0，∴y 1+y 2＝4m ，y 1y 2＝﹣8， ∴|AB|=√(1+m 2)[(y 1+y 2)2−4y 1y 2]=√(1+m 2)(16m 2+32)=4√m 4+3m 2+2=4√(m 2+32)2−14≥4√2，当且仅当m ＝0时等号成立，故B 正确；|AP|=√(x 1−2)2+y 12=√[(my 1+2)−2]2+y 12=√1+m 2|y 1|，同理，可得|BP|=√1+m 2|y 2|，则1|AP|+1|BP|=√m 21+√m 22=21√m 2+1|y1y 2|=128√m 2+1=√28√m 2+1=√22√m 2+1≠√24，故C 错误；D .k AM +k BM =y 1x 1+2+y 2x 2+2=y 1(x 2+2)+y 2(x 1+2)(x 1+2)(x 2+2)=2my 1y 2+4(y 1+y 2)(x 1+2)(x 2+2)=2m×(−8)+4×4m(x 1+2)(x 2+2)=0，即∠AMP ＝∠BMP ，∴|MA||MB|=|PA||PB|，故D 正确．故选：BD ．三、填空题本题共4小题，每小题5分，共20分．13．已知S n 为等差数列{a n }的前n 项和，且满足a 2＝4，S 4＝22，则S 8＝．解：S n 为等差数列{a n }的前n 项和，且满足a 2＝4，S 4＝22， ∴{a 1+d =44a 1+4×32d =22，解得a 1＝1，d ＝3，则S 8＝8×1+8×72×3=92．故答案为：92．14．已知直线y ＝k （x +1）截圆（x ﹣1）2+（y ﹣1）2＝4所得两段圆弧的弧长之比为1：2，则k ＝．解：由（x ﹣1）2+（y ﹣1）2＝4可知圆心为C （1，1），半径为2，设直线与圆交于A 、B 两点，又直线y ＝k （x +1）截圆（x ﹣1）2+（y ﹣1）2＝4所得两段圆弧的弧长之比为1：2，∴∠ACB ＝120°，∴圆心到直线的距离为半径的一半， ∴√1+k 2=1，解得k ＝0或k =43．故答案为：0或43．15．双曲线x 2a 2−y 2b 2=1（a ＞0，b ＞0）的右焦点为F ，左、右顶点为A 1、A 2，过F 作A 1A 2的垂线与双曲线交于B 、C 两点，若A 1B ⊥A 2C ，则该双曲线的渐近线斜率为．解：由题意，A 1（﹣a ，0），A 2（a ，0），B （c ，b 2a ），C （c ，−b 2a ）， ∵A 1B ⊥A 2C ，∴b 2a c+a ⋅−b 2a c−a =−1，∴a ＝b ，∴双曲线的渐近线的斜率为±1．故答案为：±1．16．若正方形ABCD 的一条边在直线y ＝2x ﹣17上，另外两个顶点在抛物线y ＝x 2上．则该正方形面积的最小值为．解：不妨设C ，D 在抛物线上，C （x 1，x 12），D （x 2，x 22）．不妨设x 1＜x 2，∵CD ∥AB ，∴k CD ＝k AB ，∴化为x 1+x 2＝2．①由正方形ABCD 可得|BC |＝|CD |， ∴112√5=√(x 1−x 2)2+(x 12−x 22)2，②①②联立解得x 1＝3或9或﹣1或﹣7．取3或9时，|BC |＝4√5，∴正方形ABCD 的面积S 取得最小值80．故答案为80．四、解答题：本题共6小题，共70分．解答题应写出文字说明、证明过程或演算步骤．17．（10分）等差数列{a n }的前n 项和为S n ，a 3+a 5＝a 4+7且a 1+a 10＝20．（1）求{a n }的通项公式；（2）求满足不等式S n ＜3a n ﹣2的n 的值．解：（1）设数列{a n }的公差为d ，由a 3+a 5＝a 4+7，得2a 1+5d ＝a 1+3d +7①．由a 1+a 10＝20，得10a 1+45d ＝100②，解得a 1＝1，d ＝2，所以a n ＝a 1+（n ﹣1）d ＝2n ﹣1；（2）因为a 1＝1，a n ＝2n ﹣1，所以S n =a 1+a n 2n ＝n 2，由不等式S n ＜3a n ﹣2，得n 2＜3（2n ﹣1）﹣2，所以n 2﹣6n +5＜0，解得1＜n ＜5，因为n ∈N *，所以n 的值为2，3，4．18．（12分）已知圆C ：x 2+y 2+2x ﹣4y +m ＝0与y 轴相切，O 为坐标原点，动点P 在圆外，过P 作圆C 的切线，切点为M ．（1）求圆C 的圆心坐标及半径；（2）求满足|PM |＝2|PO |的点P 的轨迹方程．解：（1）圆C 的方程可化为（x +1）2+（y ﹣2）2＝5﹣m ，因为圆C 与y 轴相切，所以5﹣m ＝1，所以m ＝4，即圆心C （﹣1，2），半径为1；（2）设P （x ，y ），则|PM |2＝|PC |2﹣|MC |2＝（x +1）2+（y ﹣2）2﹣1，|PO |2＝x 2+y 2，因为|PM |＝2|PO |，所以|PM |2＝4|PO |2，即（x +1）2+（y ﹣2）2﹣1＝4（x 2+y 2），化简得3x 2+3y 2﹣2x +4y ﹣4＝0，所以点P 的轨迹方程为3x 2+3y 2﹣2x +4y ﹣4＝0．19．（12分）若椭圆E ：x 2a 2+y 2b 2=1（a ＞b ＞0）过抛物线x 2＝4y 的焦点，且与双曲线x 2﹣y 2＝1有相同的焦点．（1）求椭圆E 的方程；（2）不过原点O 的直线l ：y ＝x +m 与椭圆E 交于A ，B 两点，当△OAB 的面积为√32时，求直线l 的方程．解：（1）抛物线x 2＝4y 的焦点为（0，1），双曲线x 2﹣y 2＝1的焦点为(±√2，0)，依题意可得，{b =1c =√2，则a 2＝b 2+c 2＝3，所以椭圆C 的方程为x 23+y 2=1；（2）根据题意，设A （x 1，y 1），B （x 2，y 2），联立直线与椭圆方程，可得{x 2+3y 2=3y =x +m，消去y 并整理可得，4x 2+6mx +3m 2﹣3＝0，则x 1+x 2=−3m 2，x 1x 2=3m 2−34，由弦长公式可得，|AB|=√2×√(−3m 2)2−4×3m 2−34=√22⋅√2−3m 2，又点O 到直线AB 的距离为d =|m|1+1=√22|m|，依题意，令S △AOB =12d|AB|=12×√22×|m|×√22×√2−3m 2=14√−3(m 2−2)2+12=√32，当且仅当m 2＝2，即m =±√2（符合题意）时，△AOB 的面积取得最大值为√32，此时直线l 的方程为y =x ±√2．20．（12分）已知抛物线C ：y 2＝2px （p ＞0），过抛物线的焦点F 且垂直于x 轴的直线交抛物线于不同的两点A ，B ，且|AB |＝4．（1）求抛物线C 的方程；（2）若不经过坐标原点O 的直线l 与抛物线C 相交于不同的两点M ，N ，且满足OM →⊥ON →证明直线l 过x 轴上一定点Q ，并求出点Q 的坐标．解：（1）抛物线C 的焦点为F(p 2，0)，由于线段AB ⊥x 轴，且|AB |＝4，所以，点(p 2，±2)在抛物线C 上，将点的坐标代入抛物线C 的方程得2p ⋅p 2=4，即p 2＝4，由于p ＞0，得p ＝2，因此，抛物线C 的方程为y 2＝4x ；（2）设直线l 的方程为x ＝my +t ，则直线l 与x 轴的交点为Q （t ，0），设点M （x 1，y 1）、N （x 2，y 2），则x 1=y 124，x 2=y 224，将直线l 的方程与抛物线C 的方程联立{x =my +t y 2=4x，得y 2﹣4my ﹣4t ＝0，由韦达定理得y 1+y 2＝4m ，y 1y 2＝﹣4t ，∵OM →⊥ON →，∴OM →⋅ON →=x 1x 2+y 1y 2=y 12y 2216+y 1y 2=(−4t)216−4t =t 2−4t =0，解得t ＝0或t ＝4．当t ＝0时，直线l 过原点O ，不合乎题意，舍去！所以，t ＝4，因此，直线l 过x 轴上的定点Q ，且点Q 的坐标为（4，0）．21．（12分）已知双曲线C ：x 2a 2−y 2b 2=1（a ＞0，b ＞0）的虚轴长为4，直线2x ﹣y ＝0为双曲线C 的一条渐近线．（1）求双曲线C 的标准方程；（2）记双曲线C 的左、右顶点分别为A ，B ，过点T （2，0）的直线l 交双曲线C 于点M ，N （点M 在第一象限），记直线MA 斜率为k 1，直线NB 斜率为k 2，求证：k 1k 2为定值．解：（1）∵虚轴长为4，∴2b ＝4，即b ＝2，∵直线2x ﹣y ＝0为双曲线C 的一条渐近线，∴b a=2，∴a ＝1，故双曲线C 的标准方程为x 2−y 24=1．（2）由题意知，A （﹣1，0），B （1，0），设直线l 的方程为x ＝ny +2，M （x 1，y 1）N （x 2，y 2），联立{x 2−y 24=1x =ny +2，得（4n 2﹣1）y 2+16ny +12＝0，∴y 1+y 2=−16n 4n 2−1，y 1y 2=124n 2−1， ∴ny 1y 2=−34（y 1+y 2），∵直线MA 的斜率k 1=y 1x 1+1，直线NB 的斜率k 2=y2x 2−1， ∴k 1k 2=y 1x 1+1y 2x 2−1=y 1(ny 2+1)y 2(ny 1+3)=ny 1y 2+y 1ny 1y 2+3y 2=−34(y 1+y 2)+y 1−34(y 1+y 2)+3y 2=−13，为定值． 22．（12分）已知椭圆C 1：x 24+y 2＝1的左右顶点分别为A 1、A 2，上下顶点分别为B 1、B 2，记四边形A 1B 1A 2B 2的内切圆为C 2．（1）求圆C 2的标准方程；（2）已知P 为椭圆C 1上任意一点，过点P 作圆C 2的切线分别交椭圆C 1于M 、N 两点，试求三角形PMN 面积的最小值．解：（1）因为椭圆C 1的左右顶点分别为A 1、A 2，上下顶点分别为B 1、B 2，所以A 2（2，0），B 1（0，1），此时直线A 2B 1的方程为x +2y ＝2，而原点O 到直线A 2B 1的距离d =2√5，可得圆C 2的半径r ＝d =2√5，则圆C 2的标准方程为x 2+y 2=45；（2）不妨设直线PM 方程为y ＝mx +n ，P （x 1，y 1），M （x 2，y 2），因为直线PM 与圆C 2相切，所以原点O 到直线PM 距离d =1√m 2+n 2=2√5，整理得5n 2＝4m 2+4，联立{y =mx +n x 24+y 2=1，消去y 并整理得（1+4m 2）x 2+8mnx +4n 2﹣4＝0，此时x 1x 2+y 1y 2=(1+m 2)x 1x 2+mn(x 1+x 2)+n 2=(1+m 2)4n 2−41+4m 2+mn −8mn 1+4m2+n 2=0，即k OP •k OM ＝﹣1，所以OP ⊥OM ，同理得OP ⊥ON ，则M ，O ，N 三点共线，所以S △PMN ＝2S △OPM ＝|OP |•|OM |，不妨设直线OP 的方程为y ＝k ，将y ＝k 代入椭圆方程中，解得x 2=41+4k 2，所以OP 2=x 2+y 2=(1+k 2)x 2=4(1+k 2)1+4k 2，同理得OM 2=4[1+(−1k )2]1+4(−1k )2=4(k 2+1)k 2+4，则1OP 2+1OM 2=1+4k 24(1+k 2)+k 2+44(1+k 2)=54，此时54=1OP 2+1OM 2≥2|OP||OM|，解得|OP |•|OM |≥85，则S △PMN ＝|OP |•|OM |≥85，当且仅当|OP|=|OM|=2√105时，等号成立．故△PMN 面积的最小值为85．。