第四章光 的 衍 射
第四章光的衍射-PPT课件

0
1
七、干涉和衍射的联系与区别
干涉和衍射都是波的相干叠加, 但干涉是 有限多个分立光束的相干叠加, 衍射是波阵面
上无限多个子波的相干叠加。 二者又常出现在 同一现象中。 双缝干涉是干涉和衍射的共同效果。
§3 光栅衍射
一、光栅
大量等宽等间距的平行狭缝(或反射面) 构成的光学元件。 从工作原理分
衍射光栅 (透射光栅)
1 I / I0
相对光强曲线
0.017 0.047
2 a
0.047 0.017 0
a
a
2 a
sin
•波长对衍射条纹的影响
•缝宽对衍射条纹的影响
•单缝位置对衍射条纹的影响
•光源位置对衍射条纹的影响
条纹在屏幕上的位置与波长成正比,如果用白 光做光源,中央为白色明条纹,其两侧各级都 为彩色条纹。该衍射图样称为衍射光谱。 3 -2 -1 2 3
A C a
f
o
x
P
B
L
分割成偶数个半波带, P 点为暗纹。
分割成奇数个半波带, P 点为明纹。
二、加强减弱条件
A C a
f
o
x
P
B
L
( k 1 , 2 )减弱 2k 2 a sin k 1 , 2 )加强 ( 2k 1 ) ( 2
B
1 2 3
I
2. 明纹位置
A C a
f
o
3 2 1
2 1
x
P
B
L
x ( 2 k 1 ) k 1 , 2 ) 2 a ( 3f x1 两条,对称分布屏幕中央两侧。 2a 其它各级明纹也两条,对称分布。
第四章光的衍射

d
0
Q
R
S
n
dU (P) U0 (Q) 瞳函数
dU (P) d
次波中心面
r
dU (P) dU (P) eikr
r
元面积 球面波
P dU (P) F(0, ) 倾斜因子
dU (P)
KF(0, )U0 (Q)
eikr r
d
dU(P)
KF (0 ,
基尔霍夫(G. Kirchhoff,1882)边界条件
取一个封闭曲面, Σ=Σ0+Σ1+Σ2
1
基尔霍夫边界条件:
i) Σ0全透
S
2
ii) Σ1全遮蔽
0 P
dU (P) 0 1
1
iii) Σ2积分为0
dU (P) 0 2
仅需要对区域Σ0,求积分即可 仅屏上对透光区域求积分即可
定性而不能定量不能准确回 答振幅、位相的传播问题
6
惠更斯-费涅耳原理:空间某点的振动可看作波前上所有面元所发 次波在该点的相干迭加,数学上表述为:
U ( p) dU ( p)
d
Q
S
r
dU (P) P
7
次波的复振幅
• 选取波前Σ上任一个次波中心Q,及Q点周围一面积元dΣ
• 可以先求出该面积元发出的球面次波在场点P处引起的复 振幅dŨ(P)
光孔和接收范围都满足傍轴条件:
U (x, y) ei /2
r0
U0 (x, y)eikrdxdy
0
13
3. 巴俾涅(A. Babinet,1837)原理
互补屏衍射场的复振幅之和等于自由传播波场,表述为:
光学 第四章光的衍射

解:(1)
(2) 出现缺极情况, 用缺极条件
d k k a 此题:k 3 k 1
(3)在选定了上述 射角
和
之后,求在衍
范围内可能观察到的
全部主级大的级次?
k max
d sin
2 4
实际可能观察到 k=0 +1 -1 +2 –2 (k=+3 -3缺级; k=+4 -4 实际无法 看到 )
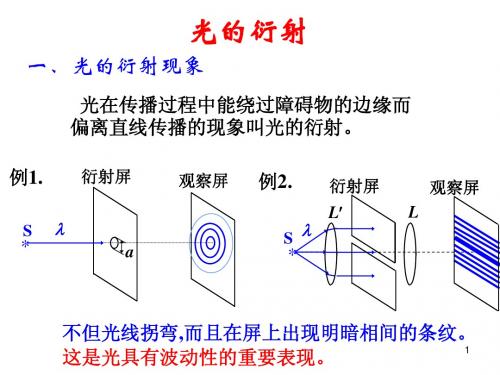
一、光的衍射( diffraction of light )
★ 定义 光在传播过程中能够 绕过障碍物的边缘而 偏离直线传播的现象。 ★ 现象示意图 屏幕
缝很小时,衍射现象明显
1. 惠更斯—菲涅尔原理 (Huygens-Fresnel Principle)
① 波前S上各点都可以看作新的发射球面子光 的新光源,在其后任一时刻,这些子波的包 迹形成新的波振面(确定波的传播方向) ② 空间任一点的光振动是所有子光在该点的相 干叠加。(确定衍射图样中的光强分布) 惠更斯:子波的概念 菲涅尔:子波干涉(子波相干叠加)的思想
6 光栅光谱 ① 在垂直入射时,中央是零级明纹。 无光谱。 ② 完整光谱: 没有重叠的清晰光谱
条件:
③ 光栅的分辨本领R R kN
5、光栅光谱 如果复色光投射在光栅上, 在屏上将出现光栅光谱。 复色光 屏 φ f 0 x
三级光谱 二级光谱
一级光谱
汞光的光栅光谱
汞光的光栅光谱
汞光的光栅光谱
2. 衍
射 的 分 类
(近场衍射)
(远场衍射)
P
S
(近场衍射)
有限远
P
S
f
(远场衍射)
f
无限远
《大学物理教程》郭振平主编第四章 光的衍射

第四章 光的衍射一、基本知识点光的衍射:当光遇到小孔、狭缝或其他的很小障碍物时,传播方向将发生偏转,而绕过障碍物继续前行,并在光屏上形成明暗相间的圆环或条纹。
光波的这种现象称为光的衍射。
菲涅耳衍射:光源、观察屏(或者是两者之一)到衍射屏的距离是有限的,这类衍射又称为近场衍射。
夫琅禾费衍射:光源、观察屏到衍射屏的距离均为无限远,这类衍射也称为远场衍射。
惠更斯-菲涅耳原理:光波在空间传播到的各点,都可以看作一个子波源,发出新的子波,在传播到空间某一点时,各个子波之间可以相互叠加。
这称为惠更斯-菲涅耳原理。
菲涅耳半波带法:将宽度为a 的缝AB 沿着与狭缝平行方向分成一系列宽度相等的窄条,1AA ,12A A ,…,k A B ,对于衍射角为θ的各条光线,相邻窄条对应点发出的光线到达观察屏的光程差为半个波长,这样等宽的窄条称为半波带。
这种分析方法称为菲涅耳半波带法。
单缝夫琅禾费衍射明纹条件:sin (21)(1,2,...)2a k k λθ=±+=单缝夫琅禾费衍射暗纹条件:sin (1,2,...)a k k θλ=±=在近轴条件下,θ很小,sin θθ≈, 则第一级暗纹的衍射角为 1aλθ±=±第一级暗纹离开中心轴的距离为 11x f faλθ±±==±, 式中f 为透镜的焦距。
中央明纹的角宽度为 112aλθθθ-∆=-=中央明纹的线宽度为 002tan 2l f f faλθθ=≈∆=衍射图样的特征:① 中央明纹的宽度是各级明纹的宽度的两倍,且绝大部分光能都落在中央明纹上。
② 暗条纹是等间隔的。
③ 当入射光为白光时,除中央明区为白色条纹外,两侧为由紫到红排列的彩色的衍射光谱。
④ 当波长一定时,狭缝的宽度愈小,衍射愈显著。
光栅: 具有周期性空间结构或光学性能(透射率,反射率和折射率等)的衍射屏,统称为光栅。
光栅常数: 每两条狭缝间距离d a b =+称为光栅常数。
光的衍射

12
(3) 次极大位置: 满足 d I 0 tg d
y y1 = tg
·
· y2 =
-2 - ·0
2
·
·
-2.46 -1.43
0
+1.43 +2.46
解得 : 1.43, 2.46, 3.47,…
相应 : a sin 1.43, 2.46, 3.47,… 13
(4)光强: 将 1.43, 2.46, 3.47,…
第四章光的衍射(Diffraction of light)
§4.1 衍射现象、惠更斯——菲涅耳原理 §4.2 单缝的夫琅禾费衍射 §4.3 光学仪器的分辨本领 §4.4 光栅衍射 §4.5 光栅光谱
§4.6 X射线的衍射
1
§4.1 衍射现象、惠更斯——菲涅耳原理
一. 光的衍射 1.现象
衍射屏
S
*
a
E0
……
E0
对于其他点 p: ≠ 0,
Ep
Ep < E0 。 E0 当N 时, N个相接的折线将变为一个圆弧10 。
Φ N a sin 2
Ep
Φ 2R sin
2
,
E0 RΦ
R
EP
Ep
2
E0 sin Φ
Φ 2
E0 Φ 2
sin
Φ 2
E0
令
Φ a sin
2
,有
Ep
E0
sin ,
又
I
E
2 p
爱里斑
圆孔孔径为D f
D sin1 1.22
D 爱里斑变小 集 中 了 约
84% 的 衍
2.透镜的分辩本领
( 经透镜 )
光学第4章光的衍射

短片
特征: 光不仅能绕过障碍物传播, 而且还能产生明暗相间的条纹
根据惠更斯原理能很自然地解释波在障碍物附近
发生的衍射现象,
但却不能说明光在衍射的同时,
为什么会出现明暗相间的条纹。
光学第4章光的衍射
3
惠更斯原理
• 在波的传播过程中,波阵面(波前)上的 每一点都可看作是发射子波的波源 (点波源)。
• 在以后的任一时刻, 这些子波面的包络面 就成为新的波阵面(即实际的波在该时刻的波前)
因此单缝面为单色平行光波阵面的一部分——单缝波阵面
将单缝波阵面沿缝长方向划分为N个窄条面元,
每一个窄条面元可视为线光源,发出柱面光波
光学第4章光的衍射
14
3. 定性解释
E
L2
L1
a
a●
S
其波线——衍射线 衍射线与单缝面法线的夹角——衍射角
根据惠——菲原理,单缝后面空间任一点的光振动 是单缝波阵面上窄条子波源发出柱面光波 传到该点的振动的相干叠加
相邻平面的点的光程差为λ/2
光学第4章光的衍射
17
E
B
aC
A
2
●P
● ●
a
●
●
●
●
●
●
●
半波带 半波带 半波带
这样单缝波阵面AB 被这些平行平面分成许多等宽的条带,
相邻条带上对应点发出的光在P点的光程差为λ/2 (半个波长)
相邻两波带对应点发出的子波位相差π,
在P点相干叠加时将相互抵消
这样的条带称为半波带,
菲涅耳还指出,对于t 时刻波阵面上给定面元dS,
它在P点的振幅由下式决定
a(Q)K()
dA (p) r
第四章 光的衍射

d = 120 cm
眼睛的最小分辨角为
D = 5.0 mm λ 取 δθ = 1.22
D
λ = 550 nm
d ≈ S δθ
Dd 5.0 × 10 3 × 1.20 S≈ = = = 8.94 × 103 m δθ 1.22λ 1.22 × 550 × 109 d
δθ
观察者 S
d =120 cm
§4.4光栅衍射 光栅衍射
(2) N 缝干涉 ) 对N 缝干涉两主极大间 有N - 1个极小, N - 2 个极小, 个次极大. 个次极大. 衍射屏上总能量
k = 1
4I 0
I
k =1
k =0
N =2
缝干涉强度分布
25I 0
I
E∝N
k = 1 k =0 k =1
主极大的强度 I ∝ N 2 由能量守恒, 由能量守恒,主极大的 宽度 ∝ 1 N 随着N 的增大, 随着 的增大,主极大 变得更为尖锐, 变得更为尖锐,且主极 大间为暗背景
λ = 16 cm x0 = 2 ftg θ 1 = 2 f
a
一级明纹宽度是中央明纹宽度的一半即8cm. 一级明纹宽度是中央明纹宽度的一半即8cm 是中央明纹宽度的一半即8cm. 另解: 另解: 一级暗纹在屏上的位置坐标为
x1 = ftg θ 1 ≈ f sin θ 1 = f
二级暗纹满足 a sin θ 2
式中 f 是透镜焦距
3,光学仪器的分辨本领
瑞利判据
0.8I 0
当一个爱里斑中心刚好落在另一个爱里斑的边缘上时,就认为这 一个爱里斑中心刚好落在另一个爱里斑的边缘上时 刚好落在另一个爱里斑的边缘上 两个爱里斑刚好能分辨. 两个爱里斑刚好能分辨.
光学仪器的通光孔径 D
04光的衍射
解:)由单缝衍射明纹公式可知: (1
a sin θ 1 = (2k + 1)
λ 1 = 3λ 1
2 2
tgθ 1 = x1 , f
a sin θ 2
λ = (2k + 1) 2 = 3λ 2
2 2
tgθ 2 =
x2 , f
3 f λ1 所以 x1 = , 2a 两第一级明纹之间的距离为
由于 sin θ1 ≈ tgθ1 ,
5
f
当 光程差
δ = a sinθ = 2×λ/2 时, θ ×
衍射角. θ -----衍射角 衍射角
如图所示,可将缝分成了两个“半波带” 如图所示,可将缝分成了两个“半波带”:
θ
a B 半波带 半波带 A
1 2 1′ ′ 2′ ′
C
λ/2
1 2 1′ ′ 2′ ′
半波带 半波带
两个“半波带”上相应的光线 与 在 点的相位差为 点的相位差为π 两个“半波带”上相应的光线1与1’在P点的相位差为π, 两个“半波带”上相应的光线2与 在 点的相位差为 点的相位差为π 两个“半波带”上相应的光线 与2’在P点的相位差为π, 所以两个“半波带”上发的光, 处干涉相消, 所以两个“半波带”上发的光,在 P 点处干涉相消, 6 就形成第一条暗纹。 就形成第一条暗纹。
7
一般情况: 一般情况: 分割成偶数个半波带, 点为暗纹。 分割成偶数个半波带, P 点为暗纹。 波面AB 波面 分割成奇数个半波带, 点为明纹。 分割成奇数个半波带, P 点为明纹。
二、衍射图样分析
1、 1、明暗纹条件
♦ a sin θ = 0
中央明纹(中心) ……中央明纹(中心)
λ
2
光的衍射

A λ/2
• 明纹(中心):a sin (2k 1) , k 1,2,3…
2
• 暗纹:
a sin 2k ,k 1,2,3…
2
• 介于明纹中心与暗纹之间时,条纹逐渐变暗。
边缘模糊
k大,级次高,
• 衍射角θ愈大,条纹亮度愈小。 明条纹亮度降低
2. 条纹光强分布
1 相对光强曲线
0.01 0.04
第四章 光的衍射
§1 光的衍射 惠更斯—菲涅耳原理
一. 光的衍射
1.现象:
衍射屏
S
*
a
观察屏
衍射屏
L S *
观察屏
L
a ≤1000λ
2.定义: 光在传播过程中能绕过障碍物的 边缘而偏离直线传播规律的现象
3. 分类: (1) 菲涅耳衍射 近场衍射
S 光源与狭缝之间、狭缝与屏幕之间 *
至少有一个是有限远
K ( )
, K0 2
§2 单缝的夫琅禾费衍射
一.装置
缝平面 透镜L
观察屏
透镜L
S
*
a
B
·p
0
Aδ f
f
二.半波带法
S: 单色光源
: 衍射角
AB a(缝宽)
A→P和B→P的光程差 a sin
中央明纹(中心) 0, 0
当a sin 带”
B
半波带
a 半波带
A
时,可将缝分为两个“半波
(C)不动;
(B) 向下平移; (D)条纹间距变大。
L S
C
只与缝宽有关
例2. 若有一波长为 600nm 的单色平行光,垂
直入射到缝宽 a =0.6mm 的单缝上,缝后有一焦
第四章 光的衍射

一维矩形波振幅光栅 按d,a,N分为四种类型
S
光栅透射系数即及其频谱:
g
1 d
rect
a
comb
d
rect
Nd
G
f
aNsinc af
m
f
m d
sinc
Ndf
令
C
K f
exp
jk(
f
x2 2f
按照惠更斯——菲涅耳原理: E( p) 应等于各栅缝发射子波对 p(x)
点贡献量叠加,E( p) 的值与相邻栅缝的子波传到 p(x)点的位相差 或光程差 有关。利用 与 f 的关系,即可求出 E( p) 的与 的
关系。
位相差 或光程差 与空频 f 的关系
由图看出:
BC d sin
• 第四章 光的衍射
§4.4 衍射光栅
-2级光谱 -1级光谱
中央亮纹
1级光谱
2级光谱
【引言】
1、 定义:在一定的空间范围内,具有空间周期性结构,能够按一 定规律对光波(电磁波)进行调制(振幅和位相)的物体或者装置。 2、 研究方法:多光束干涉和衍射;傅里叶变换。 3、 分类:衍射光栅和计量光栅;1D,2D,3D 光栅;透射和反射光栅
a d
3 7
时, m缺
=7,14,21,28……
小结:a,d,N对衍射图形分布的影响
a :单缝因子 sin c2 ( a ) ,影响主亮纹相对强度分布。 d 2
当 a->0 时, sin c2 ( a ) 1,各级主亮纹强度相等。 d 2
d : 决定主亮纹位置: sin m
d
N:决定主亮纹宽度: b 2 ,当 N 时,各主亮纹成为脉冲序列。振幅为:
第四章 光的衍射 物理光学课件

AS U 0(Q )ei(trk)r(0,)ds
E(P)eit
---Fresnel-Kirchhofer衍射积分
其中 E(P)AS U 0(Q )erik r(0,)ds
从严格的波动理论可证明:
(0,)co0s2 cos
A i
Fa-Qiang Wang
16
倾斜因子 (0,)co0s2 cos
S 为球面波时, 00
下一个时刻的波前为所有子波的共同包络面;
波的传播方向在子波源与子波面和包络面的 切点的连线方向上
子波在空间中带权重线性迭加。
Fa-Qiang Wang
13
4-3 Fresnel衍射 4-4-1 Huygens-Fresnel 原理的数学表示
图示:Q处面元ds对P点的子波贡献
Fa-Qiang Wang
r0n2
U0
r0(n-1)2
QK
eikrds r
E P E 1 E 2 E 3 E m
Fa-Qiang Wang
19
( ) ( ) ( ) En
i r0n2
P
U0
r0(n-1)2
QK
eikrds r
=?
球坐标系中:
取面元 ds为阴影处的环带 r0
d 2 s p(s i) n d
()1cos
2
p 时,()0 无后退波
E(P)iS U 0(Q)1c2oe srikdrs
Fa-Qiang Wang
17
4-4-2 半周期带(Half-period zone)和振幅矢量图 (Phasor diagram)
在实际应用中,通常不易直接计算Fresnel-Kirchhofer衍 射积分,需要概念清晰,计算简单的方法。
物理光学第四章 光的衍射

因为E1 和E2 分别来自S1和S2的透明区的贡献,所以 两个透明区的总贡献等于无衍射物时光在自由空间
传
播到E P1点 的E 光2场 振E 幅0E0编。辑--pp-t-------
Fa-Qiang Wang
Babinet 原理
20
掌握了一个屏的衍射分布,其互补屏的衍射也就知道了。
特别是当 E0 = 0 时,E1 = -E2
编辑ppt
Fa-Qiang Wang
8
左 : m = 奇数个半周期带; 右 :m = 偶数个半周期带
EP
E1 2
Em 2
EP
E1 2
-
Em 2
编辑ppt
Fa-Qiang Wang
9
图示:m 时,
EP
E1 2
编辑ppt
Fa-Qiang Wang
10
例:球面波的自由传播。
因为 1cos
2
最后一个半周期带的mp
m 时,E编P辑ppt
E1 2
,与无衍射物时相同;
13
b. 轴外一点的振幅和光强
图示:圆孔对轴外点露出的半周期带
P1点相对于P点距离变化时,露出的半周期 带的面积改变。P1点的光场发生亮暗变化。
以PO为对称轴形编辑成ppt 圆对称衍射花样
Fa-Qiang Wang
14
图示:圆孔的Fresnel衍射花样
En Em 22
m-n = 奇数时,取正号; m-n = 偶数时,取负号。
实际上,圆屏外没有遮挡,所以m
EP
En 2
IP
In 4
即轴上点P处的振幅为未被圆屏挡 住的第一个半周期带的贡献的一半。
编辑ppt
Fa-Qiang Wang
第4章 光的衍射

4.设θ的取值满足
a sin
3
2
P 点为一级亮纹
B
B
a sin
A
a sin
A
5. 设θ的取值满足
以此类推:
a sin 4 P 点为二级暗纹
2
2k ( / 2) 暗纹
a sin
( 0)
(2k
1)(
/ 2)
明纹
k 1, 2,
讨论
a sin
( 0)
2k (2k
2
1)
2
暗纹 明纹
k 1, 2,
(1) 缝可分为几个半波带? 由衍射角定 (由P点位置定)
设半波带数为N,则 N a sin 2 2
(2) 同一确定的θ,分成的各半波带的面积一样大; 不同的θ ,分成的各半波带的面积不一样大;
而半波带的面积与衍射条纹中明纹的亮度成正比。 (3) 明纹亮度由一个半波带的子波源发出的光波在P点x来自x1x12
f
a
➢任一明纹宽度:相邻两 暗纹的间距
x xk1 xk
f
a
∴ 中央明纹宽度是其他明纹宽度的2倍。
3. 条纹的角宽度(条纹位置的另一种表示)
角宽度——相邻两条纹中心对应的衍射角之差。
透镜
观测屏
1
x2 x1
1 o
明
(2k
1)
2a
暗
k
a
衍射屏
0
x1
f
0
2
a
a sin
干涉叠加的结果决定。
明纹的亮度随θ的增大而减小。
条纹分析
AC asin a tan a x
f
B
AC
· P x
0 f
光学 第四章光的衍射

杨氏双缝
2
3 4
薄膜
劈尖 牛顿环
5 迈克尔逊干涉仪
1 杨氏双缝 θ δ = d sin + kλ ={ λ + ( 2 k + 1) 2
( k =0,1,2,... ) 明纹 ( k =0,1,2,... ) 暗纹
明条纹的位置: + k λ x = D d
相邻两明纹或暗纹的间距:
λ Δx = D d
三、光栅(Grating) 1 基本概念 (1)光栅 (2)光栅常数(Grating Constant)
2 光栅衍射的本质 透射光栅的实验装置图
光栅衍射图样是单缝衍射和多缝干涉的 综合结果。
屏
b a
f
0
x
a d= a + b
b 缝宽 不透光部分宽度 4 6 ~ 10 ~ 10 m 光栅常数
3 光栅衍射图样的描述 ① 产生主极大的条件
例 在通常亮度下,人眼睛瞳孔直径约 为3mm,问人眼的最小分辨角是多大? 远处两根细丝之间的距离为2.0mm,问 离开多远时恰能分辨?
五、X射线(X-ray) 布拉格条件(Bragg Condition):
当 时, 原子散射线相干加强。波动性的体现。
布喇格父子(W.H.Bragg, W.L.Bragg)
一、基本概念 1 衍射现象 光在传播过程中遇到障碍物时,能够绕 过障碍物的边缘前进,光的这种偏离直线 传播的现象称为光的衍射现象。
屏幕 阴 影
屏幕
缝较大时, 光是直线传播的
缝很小时, 衍射现象明显
2 衍射的本质(惠更斯—菲涅尔原理) (Huygens-Fresnel Principle)
波阵面S 上每个面元 ds 都可以看成是发 出球面子波的新波源,空间任一点 P 的振 动是所有这些子波在该点的相干叠加。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3. 分类: 分类:
光源 S
障碍物
观察屏
*
L B
D P
(1)菲涅耳(Fresnel)衍射 — 近场衍射 菲涅耳( ) L 和 D中至少有一个是有限值。 中至少有一个是有限值。 中至少有一个是有限值 (2)夫琅禾费(Fraunhofer)衍射 — 远场衍射 夫琅禾费( ) L 和 D皆为无限大(也可用透镜实现)。 皆为无限大( 皆为无限大 也可用透镜实现)。
4
圆孔的衍射图样: 圆孔的衍射图样:
L S P1
B
P2
P3
P4
屏上 图形: 图形:
孔的投影 菲涅耳衍射 夫琅禾费衍射 5
刀片边缘的衍射
圆屏衍射 泊松点) (泊松点)
6
二. 惠更斯—菲涅耳原理 惠更斯— (Huygens — Fresnel principle) ) 波传到的任何一点都是子波的波源, 波传到的任何一点都是子波的波源, 各子波在空间某点的相干叠加, 各子波在空间某点的相干叠加,就决定 了该点波的强度。 了该点波的强度。
2 0
p 处波的强度I p ∝ E ( p )
1882年以后,基尔霍夫(Kirchhoff)解电 年以后,基尔霍夫( 年以后 ) 磁波动方程,也得到了 的表示式, 磁波动方程,也得到了E(p)的表示式, 这使得 的表示式 菲涅耳原理有了波动理论的根据。 惠更斯 — 菲涅耳原理有了波动理论的根据。
8
§4.2 单缝的夫琅禾费衍射、半波带法 单缝的夫琅禾费衍射、
一 . 装置和光路
缝平面 透镜 透镜L 透镜L′ 透镜 ′ B 观察屏 p
S
*
f′
a
θ
·
S:单色线光源
缝宽) AB = a(缝宽)
θ
0
Aδ f
θ : 衍射角
二 . 半波带法 ▲ A→p和B→p 的光程差为 δ = a sinθ θ = 0 ,δ = 0 —— 中央明纹(中心) 中央明纹(中心)
9
此后 θ ↑→ δ ↑ → I p ↓(p点明亮程度变差) 点明亮程度变差) 点明亮程度变差
从中央( 从中央(光强 I0)往外各次极大的光强依 次为0.0472 次为0.0472I0 , 0.0165I0, 0.0083I0 …
1 I / I0 相对光强曲线 0.017 0.047
−2
∴
极大
I 次极大 <<
sinθ
I主
0.047 0.017 0
λ
a 2
λ
a
−
λ
a
λ
a
16
sin θ
单缝衍射图样 演示 单缝衍射(KG008,KG010) , )
13
极小(暗纹) 2. 极小(暗纹)位置
当
α = ± k π(k = 1,2,3 L)时,
sin α = 0 → I = 0
由
α=
π a sin θ
λ
= ±kπ
此时应有
a sin θ = ± kλ
这正是缝宽可以分成偶数个半波带的情形。 这正是缝宽可以分成偶数个半波带的情形。
14
dI = 0 → tgα = α 次极大位置: 3. 次极大位置:满足 dα y y1 = tgα y2 = α
·
-2π -π
·
·0
π
·
-2.46π
·
0
+1.43π
2π
α
-1.43π
+2.46π
± ± … α 解得 : = ±1.43π , 2.46π , 3.47π , 相应 :a sin θ = ±1.43λ , ± 2.46λ , ± 3.47λ , …
15
± ± … 将 光强: 4. 光强: α = ±1.43π , 2.46π, 3.47π , 2 sin α 依次带入光强公式 I = I 0 , 得到 α
n dS
· Q
θ
r
S(波前 波前) 波前 设初相为零
a (Q ) K (θ ) d E ( p) ∝ dS r dE(p) a(Q)取决于波前上Q处的 ( ) p 强度, ( 方向因子。 强度 , K(θ ) 称 方向因子 。 θ = 0, K=Kmax ,
·
↑→K( ↓ K(θ ): θ ↑→ θ )↓ (
∆Φ E p = 2 R sin , 0 = R∆ Φ R E 2 E0 ∆Φ ∴ Ep = sin 2 ∆Φ 2
λ
∆Φ
EP E0 ∆Φ
20
∆Φ π a sin θ = , α= 令 2 λ sin α E0 ∆Φ = E0 , sin 有 Ep = α 2 ∆Φ 2
又 I∝
2 Ep
,I 0 ∝
2 E0
第四章 第四章
光 的 衍 射
light) (Diffraction of light)
1
本章目录
衍射现象、惠更斯— §4.1 衍射现象、惠更斯— 菲涅耳原理 单缝的夫琅禾费衍射、 §4.2 单缝的夫琅禾费衍射 、 半波带 法 光栅衍射( §4.3 光栅衍射(书2.4 节) 光学仪器的分辨本领( 2.3、 §4.4 光学仪器的分辨本领(书2.3、2.5 节) X射线的衍射 §4.5 衍射小结
2
衍射现象、惠更斯— §4.1 衍射现象、惠更斯—菲涅耳原理
光的衍射( 一. 光的衍射( diffraction of light ) 1.现象 1.现象
衍射屏 观察屏 衍射屏 观察屏 L
S
*
λ
a
S λ
L′ ′
一般a ≯ 10-3 λ
2.定义: 2.定义: 定义 光在传播过程中能绕过障碍物的边缘 而偏离直线传播的现象叫光的衍射。 而偏离直线传播的现象叫光的衍射。
a a
22
2. 其他明纹(次极大)宽度 其他明纹(次极大) 在 t g θ ≈ sin θ ≈ θ 时, 有
kλ x k ≈ f sin θ k = f , a λ 1 ∴ ∆x ≈ f = ∆x0 a 2 —— 单缝衍射明纹宽度的特征
3. 波长对条纹间隔的影响 波长越长,条纹间隔越宽。 ∆x ∝ λ — 波长越长,条纹间隔越宽。
27
光栅的种类: 2. 光栅的种类: 透射光栅
d
反射光栅 d
3. 光栅常数 光栅常数是光栅空间周期性的表示。 光栅常数是光栅空间周期性的表示。 设:a是透光(或反光)部分的宽度, 是透光(或反光)部分的宽度, (或不反光)部分的宽度, b 是不透光 或不反光)部分的宽度, d = a+b 光栅常 则: 数 普通光栅刻线为数十条/mm — 数千条 普通光栅刻线为数十条 数千条/mm, , 用电子束刻制可达数万条/mm(d ∼10-1µm)。 用电子束刻制可达数万条 ( ) 28
, ∴ 得到
2
光强公式
sin α I = I0 α
21
五. 条纹宽度 1.中央明纹宽度 1.中央明纹宽度
a >> λ 时,sin θ 1 ≈ θ 1
衍射屏透镜
λ
λ
a
∆θ
观测屏 x2 ∆x x1
θ1
∆θ 0
0
∆x0
I
角宽度 ∆θ 0 = 2θ 1 ≈ 2
f
线宽度 ∆ x 0 = 2 f ⋅ tg θ 1 = 2 f θ 1 λ λ =2f ∝ —— 衍射反比定律
17
∆ 四. 用振幅矢量法推导光强公式 将缝等分成 N 缝平面 透镜 观测屏 x 缝宽a p 个窄带, 每个 个窄带, B ∆x 窄带宽为: 窄带宽为: θ λ 0 C a ∆x = A N f ∆xsinθ 点振幅近似相等,设为∆ 各窄带发的子波在 p点振幅近似相等,设为∆E0, 点的相位差为: 相邻窄带发的子波到 p点的相位差为: ∆x sin θ a ⋅ sin θ 2π ∆ϕ = ⋅ 2π = ⋅ 很大) ( N 很大) λ λ N 18
λ/ 2
11
一般情况: 一般情况:
a sin θ = 0
λ
中央明纹(中心) —— 中央明纹(中心)
a sin θ = ± kλ,k = 1,2,3 … —— 暗纹
明纹(中心) a sinθ = ±(2k′ +1) , ′ = 1,2,3… —— 明纹(中心) k 2 上述暗纹和中央明纹(中心) 上述暗纹和中央明纹(中心)位置是准确的 其余明纹中心的位置较上稍有偏离。 其余明纹中心的位置较上稍有偏离。
p点处是多个同方向、同频率、同振幅、 处是多个同方向、同频率、同振幅、
初相依次差一个恒量∆ 的简谐振动的合成, 初相依次差一个恒量∆ϕ 的简谐振动的合成, 合成的结果仍为简谐振动。 合成的结果仍为简谐振动。
p点合振幅Ep 就是各子波的振幅矢量和的模。 就是各子波的振幅矢量和的模。
对于中心点: 对于中心点:
12
三. 光强公式 用振幅矢量法(见后)可导出单缝衍射的 振幅矢量法(见后)
sin α 光强公式: 光强公式: I = I 0 α
2
其中 α =
π a sin θ
λ
,
主极大(中央明纹中心) 1. 主极大(中央明纹中心)位置 sin α =1 θ = 0 处, α = 0 → α → I = I 0 = I max
24
∆x = f
λ
缝宽越小,条纹间隔越宽。 — 缝宽越小,条纹间隔越宽。
六. 干涉和衍射的联系与区别 干涉和衍射都是波的相干叠加, 但干涉是 干涉和衍射都是波的相干叠加, 有限多个分立光束的相干叠加, 有限多个分立光束的相干叠加, 衍射是波阵面 上无限多个子波的相干叠加。 上无限多个子波的相干叠加。 二者又常出现在 公路 同一现象中。 同一现象中。 L [例]如图示: 如图示:
= 15(ctg 6.37 − ctg 23.63 ) ≈ 100 m
