BP网络的统计意义及实例分析
bp神经网络实例分析

数据集划分
01
02
03
训练集
用于训练神经网络,占总 数据的70%-90%。
验证集
用于调整超参数和选择最 佳模型,占估模型的性能,占 总数据的10%-30%。
03
BP神经网络模型构建
神经元模型
神经元模型
神经元是神经网络的基本单元, 它模拟了生物神经元的基本功能,
误差计算
根据实际输出与期望输出计算误差。
权值调整
根据误差反向传播算法调整各层的权值和阈值。
迭代训练
重复前向传播和权值调整过程,直到达到预设的迭代次 数或误差要求。
02
BP神经网络实例选择与数据准备
实例选择
选择一个具有代表性的问题
为了展示BP神经网络的应用,选择一个具有代表性的问题,例如 分类、回归或聚类等。
成。
节点数量
02
每一层的节点数量需要根据具体问题来确定,过多的节点可能
导致过拟合,而节点过少则可能无法充分提取数据特征。
连接权重
03
连接权重是神经网络中非常重要的参数,它决定了神经元之间
的连接强度和信息传递方式。
激活函数选择
激活函数的作用
激活函数用于引入非线性特性,使得神经网络能够更好地处理复 杂的非线性问题。
误差反向传播
当实际输出与期望输出不符时,进入 误差反向传播阶段,误差信号从输出 层开始逐层向输入层传播,并根据误 差调整各层的权值和阈值。
训练过程
数据准备
准备训练数据和测试数据,并对数据进行预 处理,如归一化等。
网络初始化
为各层神经元设置初始权值和阈值。
前向传播
输入样本数据,通过正向传播计算每一层的输出 值。
3
关于BP网络的总结

关于BP网络的总结1.辨识模型的建立目前,在人工神经网络的实际应用中,绝大部分的神经网络模型是采用BP网络和它的变化形式。
BP网络就是按照误差逆传播(error back propagation)学习算法(BP算法)进行训练的多层前向神经网络,亦称为误差逆传播神经网络。
它的优点有:23第三章基于肌电信号的人手肘关节运动轨迹的预测播,得到输出响应。
如果网络输出与需要输出的误差大于标定值,将进行第二步,即输出误差反向传播过程,输出的误差值由输出层开始反向传播到输入层,传播到每一层的误差大小决定该层权值的改变。
网络的训练实质上是一个最优化的过程,即找到使输出误差最小的网络权值。
训练结束后的网络权值,代表了神经网络输入输出的映射关系。
在该网络中,输入层和隐层采用非线性的Sigmoid 函数(图3-7 所示)作为神经元激励函数,输出层采用线性函数。
图3-7 Sigmiod函数下面介绍此算法的具体过程:首先,我们定义误差函数为:(3-5)上式中,为期望输出值,即手臂实际运动角度,为网络输出值,即神经网络预测的手臂运动角度。
本文所定误差需小于0.001,在大于这个限定值以前,需要由输出层开始反向推导网络权系数的修正值。
(1).输出层神经元输出值及权值修正:25第三章基于肌电信号的人手肘关节运动轨迹的预测式中f (• )为线性函数,为隐层2 中第j 个神经元与输出层的权系数,为隐层2 的神经元输出值,=(3),=-1,即把神经元偏置的调整归入权系数的学习中,下面各隐层的情况也与之相同。
(2).隐层2 神经元输出值及权值修正:式中f (• )为sigmoid 函数,为隐层1 中第i 个神经元与隐层2 中第j 个神经元的权系数,为隐层1 中第i 个神经元输出值。
(2)(3).隐层1 神经元输出值及权值修正:为sigmoid 函数,为输入层中第m 个神经元与隐层 1 中第i 个神经元的权系数,为输入层中第m 个神经元输入值。
BP人工神经网络的基本原理模型与实例

BP人工神经网络的基本原理模型与实例BP(Back Propagation)人工神经网络是一种常见的人工神经网络模型,其基本原理是模拟人脑神经元之间的连接和信息传递过程,通过学习和调整权重,来实现输入和输出之间的映射关系。
BP神经网络模型基本上由三层神经元组成:输入层、隐藏层和输出层。
每个神经元都与下一层的所有神经元连接,并通过带有权重的连接传递信息。
BP神经网络的训练基于误差的反向传播,即首先通过前向传播计算输出值,然后通过计算输出误差来更新连接权重,最后通过反向传播调整隐藏层和输入层的权重。
具体来说,BP神经网络的训练过程包括以下步骤:1.初始化连接权重:随机初始化输入层与隐藏层、隐藏层与输出层之间的连接权重。
2.前向传播:将输入向量喂给输入层,通过带有权重的连接传递到隐藏层和输出层,计算得到输出值。
3.计算输出误差:将期望输出值与实际输出值进行比较,计算得到输出误差。
4.反向传播:从输出层开始,将输出误差逆向传播到隐藏层和输入层,根据误差的贡献程度,调整连接权重。
5.更新权重:根据反向传播得到的误差梯度,使用梯度下降法或其他优化算法更新连接权重。
6.重复步骤2-5直到达到停止条件,如达到最大迭代次数或误差小于一些阈值。
BP神经网络的训练过程是一个迭代的过程,通过不断调整连接权重,逐渐减小输出误差,使网络能够更好地拟合输入与输出之间的映射关系。
下面以一个简单的实例来说明BP神经网络的应用:假设我们要建立一个三层BP神经网络来预测房价,输入为房屋面积和房间数,输出为价格。
我们训练集中包含一些房屋信息和对应的价格。
1.初始化连接权重:随机初始化输入层与隐藏层、隐藏层与输出层之间的连接权重。
2.前向传播:将输入的房屋面积和房间数喂给输入层,通过带有权重的连接传递到隐藏层和输出层,计算得到价格的预测值。
3.计算输出误差:将预测的价格与实际价格进行比较,计算得到输出误差。
4.反向传播:从输出层开始,将输出误差逆向传播到隐藏层和输入层,根据误差的贡献程度,调整连接权重。
BP人工神经网络的基本原理、模型与实例

wm
f (·)
y= f
σ
i=1 wi xi −θ
θ
xm
-1
其中x1~ xm这m个变量是与此神经元连接的上一层神经元
的输出,或者为网络的原始输入变量。在实际操作中,
可以将-1看作此神经元的第m+1个输入,把激发阈值变
量θ作为相应的权值变量。
8.1人工神经网络的基本概念
当多个神经元组合起来时,人工神经网络的总体结构如下:
为抑制态,输出为负。
σ
i=1 wi xi −θ 为正,否则
8.1人工神经网络的基本概念
单极sigmoid函数
1
f(x)=
1+e−x
8.1人工神经网络的基本概念
双曲函数
1−e−x
f(x)=
1+e−x
8.1人工神经网络的基本概念
增加激活阈值后的神经元模型
激活阈值:θ
输入变量:x1
净输入:w1x1-θ
θ5
θ6
0.408
-0.194
-0.218
小练习:若将各权值与阈值换成以上各值,各节点的净输入和净输出分别是多
少?
8.1人工神经网络的基本概念
x1
x2
1
2
w14
w15
w24
w25
x3
3
w34
w35
与0.474相比
更接近“1”了
-0.522 0.6276
4
θ4
w46 -0.1842
6
0.082 0.4795
Errj为节点j从输出端误差(Tj-Oj)反向传播而来的的输入端误差,其中Oj为神经元
j的净输出,Oj(1-Oj)为f(x)=1/(1+e^(-x))的导函数,Tj为单元j的期望输出。
BP神经网络详解与实例

模型,它是一个互联的非线性动力学网络.他解决问题
的方法是一种反复运算的动态过程,这是符号逻辑处理 方法所不具备的性质. 1987年首届国际ANN大会在圣地 亚哥召开,国际ANN联合会成立,创办了多种ANN国际
人工神经网络研究的局限性
(1)ANN研究受到脑科学研究成果的限制。 (2)ANN缺少一个完整、成熟的理论体系。
图6 简单网络
假设有P个训练样本,即有P个输入输出对 (Ip, Tp),p=1,…,P, 其中
输入向量为 :
I p (i p1 ,...,i pm )
pn
T
目标输出向量为(实际上的):
Tp
(t p1 ,...,t
)
T
网络输出向量为 (理论上的)
Op (o p1 ,...,o pn )T
y f ( wi xi )
i 1
• θ 为阈值,f(X)是激发函数;它可以是线性 函数,也可以是非线性函数.
m
例如,若记
z
w x
i 1 i
m
i
取激发函数为符号函数
1, sgn( x) 0,
则
1, y f ( z) 0,
x 0, x 0.
ANN研究的目的和意义
(1)通过揭示物理平面与认知平面之间的映射,了 解它们相互联系和相互作用的机理,从而揭示思 维的本质,探索智能的本源。 (2)争取构造出尽可能与人脑具有相似功能的计算
机,即ANN计算机。
(3)研究仿照脑神经系统的人工神经网络,将在模
式识别、组合优化和决策判断等方面取得传统计
算机所难以达到的效果。
人工神经网络 (Artificial Neural Netwroks -----ANN) -----HZAU 数模基地
BP神经网络模型应用实例

BP神经网络模型第1节基本原理简介近年来全球性的神经网络研究热潮的再度兴起,不仅仅是因为神经科学本身取得了巨大的进展.更主要的原因在于发展新型计算机和人工智能新途径的迫切需要.迄今为止在需要人工智能解决的许多问题中,人脑远比计算机聪明的多,要开创具有智能的新一代计算机,就必须了解人脑,研究人脑神经网络系统信息处理的机制.另一方面,基于神经科学研究成果基础上发展出来的人工神经网络模型,反映了人脑功能的若干基本特性,开拓了神经网络用于计算机的新途径.它对传统的计算机结构和人工智能是一个有力的挑战,引起了各方面专家的极大关注.目前,已发展了几十种神经网络,例如Hopficld模型,Feldmann等的连接型网络模型,Hinton等的玻尔茨曼机模型,以及Rumelhart等的多层感知机模型和Kohonen的自组织网络模型等等。
在这众多神经网络模型中,应用最广泛的是多层感知机神经网络。
多层感知机神经网络的研究始于50年代,但一直进展不大。
直到1985年,Rumelhart等人提出了误差反向传递学习算法(即BP算),实现了Minsky的多层网络设想,如图34-1所示。
BP 算法不仅有输入层节点、输出层节点,还可有1个或多个隐含层节点。
对于输入信号,要先向前传播到隐含层节点,经作用函数后,再把隐节点的输出信号传播到输出节点,最后给出输出结果。
节点的作用的激励函数通常选取S 型函数,如Qx e x f /11)(-+=式中Q 为调整激励函数形式的Sigmoid 参数。
该算法的学习过程由正向传播和反向传播组成。
在正向传播过程中,输入信息从输入层经隐含层逐层处理,并传向输出层。
每一层神经元的状态只影响下一层神经输入层 中间层 输出层 图34-1 BP 神经网络模型元的状态。
如果输出层得不到期望的输出,则转入反向传播,将误差信号沿原来的连接通道返回,通过修改各层神经元的权值,使得误差信号最小。
社含有n 个节点的任意网络,各节点之特性为Sigmoid 型。
BP神经网络详解与实例_2样

kjkjkhjk
29
记wij为从输入向量的第j (j=1,…,m) 个分量到输出向量
的第i (i=1,…,n)个分量的权重。通常理论值与实际值有一误
差,网络学习那么是指不断地把与比较,并根据极小原那
么修改参数wij,使误差平方和达最小:
n
min (t piopi)2 (p=1,…,P) i1
(2)
W.Pitts在提出了一个简单的神经元模型,即MP模型。 1958年,F.Rosenblatt等研制出了感知机 (Perceptron〕。 (2)低潮(70-80年代初): (3)第二次热潮
1982年,美国物理学家J.J.Hopfield提出 Hopfield模型,它是一个互联的非线性动力学网络.他 解决问题的方法是一种反复运算的动态过程,这是符号 kjkjkhjk逻辑处理方法所不具备的性质. 1987年首届国际ANN大 6 会在圣地亚哥召开,国际ANN联合会成立,创办了多种
• Delta学习规那么: 记 wij 表示递推一次的修改量,那么有
w ijw ij w ij
(3)
P
P
w ij (tpiop) iipj
piipj (4)
p 1
p 1
pi
t pi opi
称为学习的速率
kjkjkhjk
30
注:由〔1〕 式,第i个神经元的输出可表示为
m
opi f ( wijipj) j1
❖ 注:假设将阈值看作是一个权系数,-1是一个固定 的输入,另有m-1个正常的输入,那么〔1〕式也可 表示为:
m
y f ( wixi ) i1
(1)
• 参数识别:假设函数形式,那么可以从已有的输 入输出数据确定出权系数及阈值。
BP神经网络应用实例1

人口数量 20.55 22.44 25.37 27.13 29.45 30.1 30.96 34.06 36.42 38.09 39.13 39.99 41.93 44.59
某地区20年公路运量数据
机动车数量 公路面积 公路客运量
0.6
0.09
5126
0.75
0.11
6217
0.85
0.11
7730
年份 2004 2005 2006 2007 2008 2009
人口数量 47.30 52.89 55.73 56.76 59.17 60.63
机动车数量 2.50 2.60 2.70 2.85 2.95 3.10
公路面积 0.56 0.59 0.59 0.67 0.69 0.79
公路客运量 25107 33442 36836 40548 42927 43462
0.90
0.14
9145
1.05
0.20
10460
1.35
0.23
11387
1.45
0.23
12353
1.60
0.32
15750
1.70
0.Hale Waihona Puke 2183041.85
0.34
19836
2.15
0.36
21024
2.20
0.36
19490
2.25
0.38
20433
2.35
0.49
22598
公路货运量 1237 1379 1385 1399 1663 1714 1834 4322 8132 8936 11099 11203 10524 11115
公路货运量 13320 16762 18673 20724 20803 21804
BP神经网络实验报告

BP神经网络实验报告BP神经网络实验报告一、实验目的本实验的目的是熟悉MATLAB中神经网络工具箱的使用方法,同时通过编程实现BP网络逼近标准正弦函数,来加深对BP网络的了解和认识,理解信号的正向传播和误差的反向传递过程。
二、实验原理传统的感知器和线性神经网络无法解决线性不可分问题,因此在实际应用过程中受到了限制。
而BP网络却拥有良好的繁泛化能力、容错能力以及非线性映射能力,因此成为应用最为广泛的一种神经网络。
BP算法将研究过程分为两个阶段:第一阶段是信号的正向传播过程,输入信息通过输入层、隐层逐层处理并计算每个单元的实际输出值;第二阶段是误差的反向传递过程,若在输入层未能得到期望的输出值,则逐层递归的计算实际输出和期望输出的差值(即误差),以便根据此差值调节权值。
这种过程不断迭代,最后使得信号误差达到允许或规定的范围之内。
基于BP算法的多层前馈型网络模型的拓扑结构如下图所示:BP算法的数学描述:三层BP前馈网络的数学模型如下图所示。
三层前馈网中,输入向量为X=(x1,x2.xi。
xn)T;隐层输入向量为Y=(y1,y2.___。
y_m)T;输出层输出向量为O=(o1,o2.ok。
ol)T;期望输出向量为d=(d1,d2.dk。
dl)T。
输入层到隐层之间的权值矩阵用V表示,V=(v1,v2.其中列向量vj 为隐层第j个神经元对应的权向量;v_j。
v_m)Y,隐层到输出层之间的权值矩阵用W表示,W=(w1,w2.wk。
wl),其中列向量wk为输出层第k个神经元对应的权向量。
下面分析各层信号之间的数学关系。
对于输出层,有:yj=f(netj)。
j=1,2.mnetj=∑vijxi。
j=1,2.m对于隐层,有:Ok=f(netk)。
k=1,2.l___∑wjk*yi。
k=1,2.lj=1其中转移函数f(x)均为单极性Sigmoid函数:f(x)=1/(1+e^-x),具有连续、可导的特点,且f'(x)=f(x)[1-f(x)]。
BP神经网络的一个解析算例

。 由f(x)在 x0点的一 阶 Taylor展开 式:
我们可 以假设 神经网络的 期望输出为 0.4,那么在初始 状 态下,全 局误 差 为:
其 中, 为 一 阶 展 开 式 的 误 差 。我 们 可 知 ,当 x = x 1时,
( x 1- x 0 ) 即 为 初 始 点 到 下 一 个 点 的 调 整 量 ,并 且 为了 得 到
图1 神经网络的拓扑结构图
3 梯度下降算法的实现
结合梯度下 降 算 法 [4]的实 现 过 程,我们以 BP 神 经网络为
例,详 细 介绍 神经网络 的原 理和实 现 过 程。
对于 一个 n 维值函数
而 言 ,若 采 用
梯 度 下 降 算 法 计 算 其 极 小 值 ,需 要 选 择 一 个 初 始 点
的偏导数 ; (8)利用 和 来 修正两 种 连 接 权T k i和 ; (9)计 算全 局 误 差 E,并 判 断 网络 误 差 是 否满 足 精度 要 求 。当 误 差 达 到 预 设 精度 或 学 习次 数 大 于 设 定 的 最 大 迭 代 次 数,则 结 束 程 序;否则,返回第(3)步,选 择下一 个 学习样 本及 对应的 期望输出,进 入下一 轮 学习。
90
科技创新导报 Science and Technology Innovation Herald
信息科学
科技创新导报 2016 NO.25
Science and Technology Innovation Herald
,如 果 该 点 对 应 的
非
极 小 值,则 必 须 对
进 行 修 正,并 得 到
摘 要:BP神经网络是误差反向传播神经网络的简称,是一种常用的人工智能算法。它具有非常高的求解精度,同时也具有很强
bp神经网络的应用综述

bp神经网络的应用综述近年来,随着人工智能(AI)发展的飞速发展,神经网络技术也在迅速发展。
BP神经网络是一种能够将输入大量信息并有效学习并做出正确决策的广泛应用的深度学习算法。
它的强大的学习能力令人印象深刻,从很多方面来看都是一种具有潜在潜力的技术。
在科学和工程方面,BP神经网络的应用非常广泛。
它可以用于模式识别,数据挖掘,图像处理,语音识别,机器翻译,自然语言处理和知识发现等等。
当可用的数据量很大时,BP神经网络可以有效地自动分析和提取有用的信息,从而有效地解决问题。
例如,在图像处理领域,BP神经网络可以用于图像分类、目标检测和图像语义分析。
它能够以准确的速度检测目标图像,包括人脸、行人、汽车等等,这在过去难以实现。
在机器翻译等技术中,BP神经网络可以用于语义分析,以确定机器翻译的正确语义。
此外,BP神经网络还可以用于人工智能的自动控制,例如机器人与机器人感知、模式识别、语音识别和控制系统。
除此之外,BP神经网络还可以用作在计算机游戏和科学研究中的决策支持系统,以便帮助决策者做出正确的决策。
总而言之,BP神经网络是一种具有广泛应用的深度学习算法,它能够自动处理大量复杂的信息,并能够做出正确的决策。
它可以用于各种科学和工程任务,如模式识别、机器翻译、图像处理、语音识别、机器人感知及自动控制等领域。
此外,它还可以用于决策支持系统,以便帮助决策者做出正确的决策。
BP神经网络在许多领域都具有巨大的潜力,希望以后能得到更多的研究和应用。
因为随着计算机技术的发展,BP神经网络在未来有望发挥更大的作用,帮助人们实现和科学研究的突破。
BP神经网络的潜力巨大,尽管它的应用前景十分广阔,但许多研究仍然存在挑战。
因此,有必要开展更多的研究,并利用其强大的特性,尽可能多地发掘它的潜力,以便最大限度地利用它的优势。
我们期待着BP神经网络会给人类的发展带来更多的惊喜。
用BP神经网络预测股票市场涨跌

用BP神经网络预测股票市场涨跌用BP神经网络预测股票市场涨跌引言:股票市场的涨跌一直是投资者和金融从业者关注的焦点之一。
预测股票市场的涨跌对于投资决策和风险控制有着重要的意义。
在过去的几十年里,人们尝试了各种方法来预测股票市场的涨跌,包括传统的统计模型、技术指标分析、基本面分析等。
然而,由于股票市场的复杂性和不确定性,这些方法的预测效果往往不尽如人意。
近年来,人工智能技术的迅猛发展为预测股票市场带来了新的希望。
其中,BP神经网络作为一种重要的人工神经网络模型,被广泛运用于股票市场的预测中。
一、BP神经网络的原理和特点BP神经网络是一种前向反馈的人工神经网络,由输入层、隐含层和输出层组成。
其基本原理是通过将输入信号进行加权求和并通过激活函数传递到下一层,从而逐层进行信息传递和处理,最终获得输出结果。
BP神经网络具有以下几个特点:1. 自适应学习能力:BP神经网络可以通过学习算法自适应地调整权值和阈值,从而提高预测的准确性。
2. 非线性映射能力:BP神经网络可以通过引入非线性激活函数,模拟复杂的非线性映射关系,更好地适应股票市场的涨跌特性。
3. 并行处理能力:BP神经网络的计算过程可以并行进行,充分利用计算资源提高计算效率。
4. 适应噪声和非线性问题:BP神经网络通过多层网络结构,具有一定的容错性和适应噪声的能力。
同样,其非线性映射特性使其在处理非线性问题方面更具优势。
二、BP神经网络在股票市场预测中的应用BP神经网络作为一种强大的模式识别和非线性映射工具,在股票市场的预测中已被广泛应用。
1. 数据准备与处理:股票市场的预测需要大量的历史数据作为样本进行训练。
首先,需要收集相关的股票市场数据,包括股价、成交量、涨跌幅等指标。
然后,对数据进行预处理,包括去除异常值、缺失值处理、特征标准化、数据平滑等步骤。
2. 网络模型设计:根据股票市场的特点和预测目标,设计BP神经网络的网络结构。
通常情况下,网络包括一个输入层、一个或多个隐含层和一个输出层。
BP人工神经网络的基本原理、模型与实例
BP人工神经网络的实例
BP人工神经网络可以应用于多个领域,如图像识别、语音处理、预测分析等,为解决复杂问题提供了有效的神经网络的输入是具体问题的相关数据,比如图像数据、声音数据等。 输出是经过神经网络计算后得出的结果。
神经元和连接权重
神经元是BP人工神经网络的基本单元,通过调整连接权重来不断优化神经网 络的表现和学习能力。
前向传播和反向传播
前向传播是指输入数据从输入层经过隐藏层到达输出层的过程。反向传播是指根据误差计算,通过调整连接权 重来优化神经网络的过程。
训练和优化算法
BP人工神经网络的训练过程是通过不断调整连接权重使得神经网络的输出结 果接近于期望结果的过程。优化算法如梯度下降算法等可以加速训练的过程。
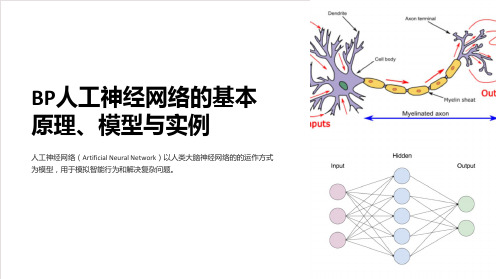
BP人工神经网络的基本 原理、模型与实例
人工神经网络(Artificial Neural Network)以人类大脑神经网络的的运作方式 为模型,用于模拟智能行为和解决复杂问题。
BP人工神经网络的基本原理
BP人工神经网络通过多层神经元和连接权重的组合,实现输入数据到输出结 果的计算和转换过程。
BP人工神经网络的模型
BP神经网络与实例

– 样本数据个数:
bo
– 激活函数:
k 1,2, m
– 误差函数: f()
e
1 2
q o1
(do (k )
yoo
(k ))2
BP网络的标准学习算法
• 第一步,网络初始化
– 给各连接权值分别赋一个区间(-1,1)内的
随机数,设定误差函数e,给定计算精度值
和最大学习 次数M。
•
第二步,随机选取第 望输出
who
e <0,
who
此时Δwho>0
BP神经网络的特点
• 非线性映射能力
– 能学习和存贮大量输入-输出模式映射关系,而无需事 先了解描述这种映射关系的数学方程。只要能提供足够 多的样本模式对供网络进行学习训练,它便能完成由n 维输入空间到m维输出空间的非线性映射。
• 泛化能力
– 当向网络输入训练时未曾见过的非样本数据时,网络也 能完成由输入空间向输出空间的正确映射。这种能力称 为泛化能力。
hik)
p
f(
h1
whohoh (k)
bo )2 ))
hoh (k)
hoh (k)
hih (k)
q o1
(do
(k)
yoo (k
))
f
(
yio
(k ))who
hoh (k ) hih (k)
q
( o (k)who ) f (hih (k)) h (k)
(do(k) yoo (k))f ( yio(k)) o(k)
BP网络的标准学习算法
第五步,利用隐含层到输出层的连接权 值、输出层的 o (k )和隐含层的输出计算误 差函数对隐含层各神经元的偏导数 h (k)。
BP神经网络实例分析

目标值 0.9 0.9 0.9 0.1 0.9 0.9 0.9 0.1
❖ 翼长 ❖ 1.64 ❖ 1.82 ❖ 1.90 ❖ 1.70 ❖ 1.82 ❖ 1.82 ❖ 2.08
触角长 类别 1.38 Af 1.38 Af 1.38 Af 1.40 Af 1.48 Af 1.54 Af 1.56 Af
W2( p1) (1,
j)
W2( p) (1,
j)
( 2
p1)
(1)a1(
p1)
(
j)
j=1,2,3
(4) 训练隐藏单元的权值
PS:利用隐含层各神经元的误差项1( p1) (i) 和输入层 各神经元的输入来修正权值。
1( p1) (i)
f
'[u1
(i)]
( 2
p1)
(1)W2(
其中wi ( j,3) i ( j) 表示第i层第j个神经元的阈值
(2) 根据输入数据计算网络输出
取 a0 (3) 1, a1(3) 1 将各神经元的阈值作为固定输入
3
u1 (1) w1 (1,1)a0 (1) w1 (1,2)a0 (2) w1 (1,3)a0 (3) w1 (1, j)a0 ( j) j 1
——蚊子分类问题
一、BP网络的标准学习算法-学习过程
正向传播:
◦ 输入样本---输入层---各隐层---输出层
判断是否转入反向传播阶段:
◦ 若输出层的实际输出与期望的输出(教师信号)不 符
误差反传
◦ 误差以某种形式在各层表示----修正各层单元 的权值
网络输出的误差减少到可接受的程度或达到 预先设定的学习次数为止
BP人工神经网络的基本原理模型与实例

8.1人工神经网络的基本概念
x1 1 w14
w15
4
x2
2 w24
θ4
w46 6
w25
w34
x3
3
w35
5 θ5
w56
θ6
初始输入、权重和偏倚值
x1 x2 x3 w14 w15 w24 w25 w34 w35 w46 w56 θ4 θ5 θ6
1
0
1
0.192 -0.306 0.4
2.反向传播 反向传播时,把误差信号按原来正向传播的通路反向
传回,并对每个隐层的各个神经元的权系数进行修改,以 望误差信号趋向最小。
8.2 误差反向传播(BP)神经网 络
8.2 误差反向传播(BP)神经网 络
x1 x2
x3
单元 j 6
1 w14
Err4=
0.332
w15 2 w24
-0.0087
w34
x3
3
w35
4 θ4
0.082 0.4795
5 θ5
w46 -0.1842
0.5459
6
w56
θ6
净输入和输出的计算
单元 j
净输入 Ij
净输出 Oj
4
0.192+0-0.306-0.408=-0.522
1/(1+e-0.522)=0.6276
5
-0.306+0+0.194+0.194=0.082
第8章 人工神经网络 方法
2016年4月27日
本讲大纲:
人工神经网络的基本概念 误差反向传播(BP)神经网络
8.1人工神经网络的基本概念
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
导了 BP 网络是传统回归模型 的 推 广 具 有 广 阔 的 应 用 前 景 并 给 出 了 应 用 实 例 进 一 步 揭 示 了 BP 网 络 具 有 传 统
统计方法不可替代的作用O
关键词: BP 网络; 回归模型; 第三产业; 预测
中图分类号: TP18
文献标识码: A
1 BP 网络
目前已有大量的预测算法 但经常选用神经网络来进行预测 这是因为: ( 1D 神经网络不需要建立数学 模型 只是把已有的数据交给网络 网络将选择自己的模型 而且一般都能很好地解决问题O ( 2D 神经网络 比其它方法更能容忍噪声 而时间序列的量往往伴随有大量的噪声O
反向传播网络模型是一种前馈型网 简记为 BP 网络 是目前应用最多也是最成功的网络之一O 它是 由输入层~ 输出层以及若干隐层节点互连而成的一种多层网( 如图 1 所 示 D O 它的输入以及输出是在[0 1]或[-1 1]区间上连续取值的 每个处 理单元对其输入的加权和加以非线性处理得到其活性输出O
E( E( Y| X) - f ( X W) ) 2 = Dg( X) + Df ( X W) - 2COv( g( X) f ( X W) ) + ( Ef ( X W) - Eg( X) ) 2 其中第一~ 二项分别为 g( X) ~ f ( X W) 的方差 第三项是 g( X) 和 f ( X W) 的协方差 第四项称为 g( X) = E ( Y| X) 与 f( X W) 间的偏置G 当偏置不为零时 称 f( X W) 是 g( X) 的有偏估计; 否则 称为无偏估计G
Xz = ( :z1 :z2
:zn ) z = 1 2
N
相应的 y 记为 y1 y2 ynG 一般说来 y 与 X 之间的关系记为;
y = g( X) + E
( 1)
其中 g 为确定性函数 G 为随机误差G
相 对于 X 的 N 次观测值 G 的值记为; Ez ( z= 1 2 N) { Ez I z = 1 2 N} 是均值为 O 方差为 1 的
Y = g( X) +
( 5)
其 中 S 为一随机变量或向量 回归函数 g( X) 可定义为, g( X) = E( Y| X) 即给定 X 后 Y 的期望 此模型
满足两个条件,
( 1) 给定 X 后 的均值为 0 即 E( | X) = 0;
( 2) 与 g( X) 不相关 即 E( - g( X) ) = 0G
m) = G( X)
( 4)
为( 3) 式的广义回归方程( 模型) 这时
最小( ' 是某种范数)G
N
/
Z
-2
z
z
z= 1
3 BP 网络的统计意义
3. 1 统计方法的缺陷 目 前的统计方法能够解决如( 2) 式的 n( n2 1) 对 1 的回归问题 而不能很好地解决如同( 4) 式的 n 对
第1期
-
/
Y) 2Βιβλιοθήκη =1 2E( Y
-
f(
X
W) )2
取得最小值G 上式可改写为,
J( Z) =
1 2
E( Y
-
g(
X)
+
g( X)
- f(X
W) )2
=
1 2
E(
Y
-
g(
X)
)
2
+
E( Y - g( X) ) ( g( X)
- f(X
W) )
+
1 2
E(
g(
X)
- f(X
W) )2
=
1 2
E(
Y
-
g(
X)
度G 虽然如此 但却无法确切估计用 f( X W) 近似 g( X) 的误差 只能探讨在寻求 f( X W) 的过程中 f( X
/
W) 与由( 5) 式给出的期望输出的误差向量 e= Y-Y的范数 G G 要使 f 高度逼近 g 就是使下述目标函数
e
2 = J( Z) =
1 2
Ee2
=
1 2
E( Y
这种前馈网络的训练所采用的算法[1]是反向传播法 这是一种有导师 学习方法O 其基本思想是首先对权值随机设置小的初值 然后选择一个训 练样本并计算相对于该样本的误差梯度O 这涉及到两个过程: 前向过程 以便计算各神经元的活性直到求出网络的输出; 反向过程 以便逐层计算 梯度O 一旦梯度已知 便可采取小步幅来更新连接权 直至算法收敛O
/
对于 BP 网络 网络的实际输入输出关系可设为, Y= f ( X W) 其中 W 是权向量G
对于自然界众多关系来说 真正精确的 g( I) 是找不到的 只能通过统计学的方法 从大量的样本( X
Y) 中去抽象出一个 g( X) G 现在是要用 f( X W) 去近似代替 g( X) G 由定理 此种近似可以达到很高的精确
白 噪声序列G E 是无法预先估计的 因而由 X 估计 y 的取值范围G 称函数 g( :) 为由 X 估计 y 的回归函数
记
/
y= g( :)
( 2)
根据最小二乘原理 使误差平方和
/
Z ( yz - y) 2
最 小 的 g 即 为 所 求 的 回 归 函 数G 当 { :z I z = 1 2 N} 是 时 间 序 列 时 称 ( 2) 式 为 时 间 序 列 回 归 方 程 ( 模
)
2
+
1 2
E(
g(
X)
- f(X
W) )2
第二个等号的中间项为 0 因为 = Y-g( X) 与 g( X) 和 f( X W) 都不相关G 最后一个式子的第一项与 W 无
关 因此使 J( Z) 最小等价于使
E( g( X) - f( X W) ) 2
( 6)
最小G 从理论上 ( 6) 式是可以达到任意小的 这取决于 W 的最终值G 这时 这样求出的 Z 是使 f( X W) 成
型) G
2. 2 广义回归模型
设向量 X 的意义同前 Z= ( 1 2
m) 为相应的依存向量 对 X 的 N 次观察记为;
相应的 Z 记为;
Xz = ( :z1 :z2
:zn ) z = 1 2
N
Zz = ( z1 z2 类似( 1) 式 把 Z 与 X 之间的关系记为;
zm) z = 1 2 N
Z = G( X) + E 其 中 G 为一确定性函数 反映了自变量对因变量的决定性影响; E= ( E1 E2 N 次观察
多层前向网络可实现从输入到输出的非线性映像 这是由以下定理所 保 证 的 [1] O
定 理 令 g( :D 为 非 常 量 有 界 单 调 递 增 连 续 函 数 有 界 闭 集 K;Rn 固定参数 K2 3 则任意连续映射
f : K - Rm X = ( :1 :2 - :n D - ( f 1( XD f 2( XD - fm( XD D 存在着一个 k 层网络( k2 3D 可以任意精度一致逼近此映像 f 此网络隐 单元之输出关系为 <( XD 而输入及输出单元之输出则是线性的O
D 收稿日期: 2000-08-20. 第 1 作者简介: 严玉清( 1963~ D 女 河南人 湛江师范学院副教授.
2
河南师范大学学报( 自然科学版)
2OO1 年
2 广义回归模型
2. 1 传统回归模型 设 :1 :2 :n 为描述某物理现象的独立变量 记为 X= ( :1 :2
观测值记为;
:n ) y 为依存变量 对 X 的 N 次
第 29 卷 第 1 期
河南师范大学学报( 自然科学版D
2001 年 2 月
Jou7ncZ of Hencn No7mcZ UnlUe7sl }( Nc u7cZ SclenceD
文章编号: 1000-2367( 2001D 01-0031-06
VoZ. 29 No. 1 Feb. 2001
BP 网络的统计意义及实例分析D
根据( 2) 式~ ( 4) 式的定义及上述定理 BP 网络不但可以实现传统的回归模型 也可以实现广义回归模 型G 就是说 存在 BP 网络 使其可以任意精度逼近( 1) 式或( 3) 式所表达的映像 从而代替( 2) 式~ ( 4) 式所 表示的回归模型G
下面探讨用 BP 网络进行统计回归( 数据拟合) 时的误差问题G 把( 1) 式和( 3) 式统一为,
严玉清等, BP 网络的统计意义及实例分析
3
m( n 1 m 2) 的回归问题 特别是非线性回归G 并且( 2) 式的回归预测精度随着 g 的不同而有较大差异G 除了数据来源质量这种客观因素外 还包含着人为主观因素的影响G 另外 数理统计常识[2]告诉我们 当使 用 回归方程作预测预报时 用于 预 测 的 自 变 量 只 有 在 方 程 建 立 时 所 使 用 的 因 子 值 ( II) 的 范 围 之 内 预 测 的 结果才是合适的 并能达到一定的精度G 因子值作为范围的外延有一定的参考价值; 外延幅度大 则预测精 度显着下降 以至与实际相差甚远 甚至于根本没有实际意义G 因此 有必要建立预测精度更高~ 稳定性更 好的预测模型G 3. 2 BP 网络的统计学意义
X( ) = ( 11( ) 12( ) 13( ) 14( ) 15( ) ) = 1 2 3 ~
预测
y(t) = (y1(t) y2(t) ) t= 1 2 3 ~
的广义回归模型( 4) 这是一个时间序列回归模型 是从 R5 到 R2 的一个非线性映像G
由以上的讨论知 第三产业的广义时间序列回归模型可用一个三层 BP 网络以任意精度逼近 使得均
4
河南师范大学学报( 自然科学版)
2001 年
