Clones and Genoids in Lambda Calculus and First Order Logic
The Fundamental Theorem of Calculus

P (x)dx
= (165x − 0.05x2 )|1600 1500 = 1000 . Thus, increasing monthly production from 1,500 units to 1,600 units will increase the monthly profit by $1,000. (See College Mathematics for Business, §12-5, Example 5.)
tkzg@ 5 / 9
§6-2 The Fundamental Theorem of Calculus
Applications of Definite Integrals
Example (Useful life)
An amusement company maintains records for each video game it installs in an arcade. Suppose that C(t) and R(t) represent the total accumulated costs and revenues (in thousands of dollars), respectively, t years after a particular game has been installed and that C (t) = 2 , R (t) = 9e−0.5t .
Example (Useful life)
An amusement company maintains records for each video game it installs in an arcade. Suppose that C(t) and R(t) represent the total accumulated costs and revenues (in thousands of dollars), respectively, t years after a particular game has been installed and that C (t) = 2 , R (t) = 9e−0.5t .
Calculus I

Calculus ICalculus, also known as mathematical analysis, is a branch of mathematics that deals with the study of rates of change and how things change over time. It is a fundamental mathematical tool that has become essential in many fields such as physics, engineering, economics, and biology. In this essay, we will explore Calculus I, which is the introductory course for Calculus.The study of Calculus is divided into two main branches: differential calculus and integral calculus. Differential calculus is concerned with the study of rates of change, while integral calculus is concerned with the study of accumulation. Calculus I focuses on the fundamental concepts of differential calculus.One of the key ideas in Calculus I is the concept of limit. A limit is the value that a function approaches as the independent variable approaches a certain value. Limits are an essential tool for studying the behavior of functions, especially at points where the function may not be defined.Another important concept in Calculus I is the derivative. The derivative of a function is the rate of change of the function at a particular point. It is defined as the limit of the difference quotient as the change in the independent variable approaches zero. The derivative is a fundamental concept in Calculus and is used extensively in many fields, including physics, engineering, and economics.The derivative has many important properties, including the power rule, product rule, quotient rule, and chain rule. These rules allowus to find the derivative of complicated functions quickly and efficiently.The derivative also has many applications, including optimization problems and finding the location of maximum and minimum values of a function. For example, in economics, the derivative is used to find the marginal cost and marginal revenue of a company. In physics, the derivative is used to find the instantaneous velocity and acceleration of an object.Another important concept in Calculus I is the notion of differentiation. Differentiation is the process of finding the derivative of a function. It is an integral part of Calculus and is used extensively in many fields.One of the most important applications of differentiation is in the study of optimization problems. Optimization problems involve finding the maximum or minimum value of a function subject to certain constraints. For example, in economics, firms try to maximize their profits subject to certain constraints, such as the cost of production.Integration is the second branch of Calculus, and it deals with finding the area under a curve. Integration is the inverse of differentiation, and it is used extensively in many fields, including physics and engineering.One of the most important applications of integration is in the study of volumes and areas. For example, in physics, the volume of a solid can be found by integrating the area under the curve of itscross-section. In engineering, the area of an irregular shape can be found by integrating the area under the curve of its boundary.Calculus I also covers important topics such as limits, continuity, and trigonometric functions. Limits are used extensively in Calculus to study the behavior of functions. Continuity is a fundamental concept in Calculus that ensures that a function is well-behaved and has no abrupt changes.Trigonometric functions are essential in Calculus because they are used extensively in the study of differential equations, which are equations that involve derivatives. Differential equations are used to model many real-world phenomena, such as the growth of a population and the spread of diseases.In conclusion, Calculus I is an essential course for any student studying mathematics, physics, engineering, or economics. It provides a solid foundation for more advanced courses in Calculus and other fields. The concepts of differential calculus, such as limits, derivatives, and differentiation, are fundamental in the study of many real-world problems. The concepts covered in Calculus I, such as optimization and integration, have many applications in numerous fields and are essential for solving problems in many areas of science and engineering.In addition to the topics mentioned above, Calculus I also covers related rates, which are useful in real-world scenarios where things are changing at different rates. For example, if you are filling a pool with water and you want to know how fast the water level is rising, you would use related rates. This involves finding the relationship between the rates of change of different variables and using this relationship todetermine one rate when the other rate is known.Another important concept in Calculus I is the Mean Value Theorem. This theorem states that if a function is continuous on a closed interval and differentiable on the open interval, then there exists a point in the interval where the derivative is equal to the average rate of change of the function over the interval. This theorem has applications in many areas, including economics, where it is used to prove the existence of equilibrium prices.Calculus I also covers curve sketching, which involves studying the behavior of a function as it approaches zero and infinity, finding its intercepts, and determining where it is increasing or decreasing. This is important in many fields as it allows us to understand the behavior of functions and predict their future values.One of the most important applications of Calculus I is in physics, where it is used extensively in studying motion. The concepts of calculus are used to determine the velocity, acceleration, and position of an object at any given point in time. Understanding these concepts is essential in fields such as aerospace engineering, where the motion of objects in space is critical to the success of missions.Calculus I is also used extensively in engineering, especially in the design and analysis of systems. For example, in electrical engineering, calculus is used to determine the power consumed by a circuit, while in civil engineering, it is used to calculate the stress on structures such as bridges and buildings. Calculus is also essential in chemical engineering, where it is used to determine therate of chemical reactions.In economics, calculus is used to model and analyze various economic phenomena, such as supply and demand, consumer behavior, and production optimization. The concepts of calculus are essential in understanding the dynamics of markets and the behavior of firms in different situations.Calculus I has numerous real-life applications, from modeling the growth of populations to understanding the spread of diseases. It is used in biostatistics to determine the probability of an individual developing a certain disease and in epidemiology to model the spread of infectious diseases. In ecology, calculus is used to study predator-prey relationships and competition between species.In the field of finance, calculus is used to determine the value of financial securities such as stocks and bonds. Understanding the concepts of calculus is essential in the field of quantitative finance, which involves using mathematical models to predict the behavior of financial markets.Overall, Calculus I is a fundamental course in mathematics that teaches students the basic concepts of differential calculus, including limits and derivatives, and their applications in various fields. It provides a solid foundation for more advanced courses in Calculus and other related fields. The concepts covered in Calculus I have numerous applications in many fields, including physics, engineering, economics, and biology, making it an essential tool for solving real-world problems.。
Quantum mechanics and umbral calculus

This introductory exposition of the modern theory of the Umbral Calculus, developed mainly by Rota and Roman, follows mainly Ref. [23]. The umbral algebra, L, is the algebra of linear operators acting on the algebra, F , of formal power series in a variable or acting on the algebra of real or complex polynomials in a variable, P . The elements of F are of the form
1
Introduction
In the last years the interest in physics for discrete space-time theories has increased mainly in relation with quantum gravity [1]. In a scenario where the physical space-time may be discrete (i.e. there is a fundamental length in the space-time –let σ be the fundamental space length and τ the fundamental time length – that could be related with Planck’s constant), continuous theories would only be approximations to the reality. Hence, it seems interesting the study of discrete physical theories such that in the limit of σ going to zero we recover the well known and established continuous physical theories. One way to do that is to discretize continuous physical theories, in particular quantum theories. It is obvious, that after discretization some properties will be conserved and other ones will disappear. A detailed study about when, how and why this happens would be pertinent and very interesting. This is the aim of this work: to study how to discretize a physical theory in such a way that properties related with symmetries in the continuous case can be preserved in the process, and so, to analyse the behaviour of quantum mechanics after discretization. The Umbral Calculus is the mathematical tool that we will use to discretize Quantum Mechanics. It has been used recently to provide discrete representations of canonical commutation relations (i.e. [∂x , x] = 1) in order to discretize linear differential equations [2]–[9], in such a way that the continuous point symmetries are preserved the most cases. In this paper we will consider a fixed lattice and use the umbral correspondence to obtain discrete solutions maintaining certain commutation relations [9]. 1
Matrix Derivative_wiki

Matrix calculusIn mathematics, matrix calculus is a specialized notation for doing multivariable calculus, especially over spaces of matrices, where it defines the matrix derivative. This notation was to describe systems of differential equations, and taking derivatives of matrix-valued functions with respect to matrix variables. This notation is commonly used in statistics and engineering, while the tensor index notation is preferred in physics.NoticeThis article uses another definition for vector and matrix calculus than the form often encountered within the field of estimation theory and pattern recognition. The resulting equations will therefore appear to be transposed when compared to the equations used in textbooks within these fields.NotationLet M(n,m) denote the space of real n×m matrices with n rows and m columns, such matrices will be denoted using bold capital letters: A, X, Y, etc. An element of M(n,1), that is, a column vector, is denoted with a boldface lowercase letter: a, x, y, etc. An element of M(1,1) is a scalar, denoted with lowercase italic typeface: a, t, x, etc. X T denotes matrix transpose, tr(X) is trace, and det(X) is the determinant. All functions are assumed to be of differentiability class C1 unless otherwise noted. Generally letters from first half of the alphabet (a, b, c, …) will be used to denote constants, and from the second half (t, x, y, …) to denote variables.Vector calculusBecause the space M(n,1) is identified with the Euclidean space R n and M(1,1) is identified with R, the notations developed here can accommodate the usual operations of vector calculus.•The tangent vector to a curve x : R→ R n is•The gradient of a scalar function f : R n→ RThe directional derivative of f in the direction of v is then•The pushforward or differential of a function f : R m→ R n is described by the Jacobian matrix The pushforward along f of a vector v in R m isMatrix calculusFor the purposes of defining derivatives of simple functions, not much changes with matrix spaces; the space of n×m matrices is isomorphic to the vector space R nm. The three derivatives familiar from vector calculus have close analogues here, though beware the complications that arise in the identities below.•The tangent vector of a curve F : R→ M(n,m)•The gradient of a scalar function f : M(n,m) → RNotice that the indexing of the gradient with respect to X is transposed as compared with the indexing of X. The directional derivative of f in the direction of matrix Y is given by•The differential or the matrix derivative of a function F : M(n,m) → M(p,q) is an element of M(p,q) ⊗ M(m,n), a fourth-rank tensor (the reversal of m and n here indicates the dual space of M(n,m)). In short it is an m×n matrix each of whose entries is a p×q matrix.is a p×q matrix defined as above. Note also that this matrix has its indexing and note that each ∂F/∂Xi,jtransposed; m rows and n columns. The pushforward along F of an n×m matrix Y in M(n,m) is thenas formal block matrices.Note that this definition encompasses all of the preceding definitions as special cases.According to Jan R. Magnus and Heinz Neudecker, the following notations are both unsuitable, as the determinants of the resulting matrices would have "no interpretation" and "a useful chain rule does not exist" if these notations are being used:[1]1.2.The Jacobian matrix, according to Magnus and Neudecker,[1] isIdentitiesNote that matrix multiplication is not commutative, so in these identities, the order must not be changed.•Chain rule: If Z is a function of Y which in turn is a function of X, and these are all column vectors, then•Product rule:In all cases where the derivatives do not involve tensor products (for example, Y has more than one row and X has more than one column),ExamplesDerivative of linear functionsThis section lists some commonly used vector derivative formulas for linear equations evaluating to a vector.Derivative of quadratic functionsThis section lists some commonly used vector derivative formulas for quadratic matrix equations evaluating to a scalar.Related to this is the derivative of the Euclidean norm:Derivative of matrix tracesThis section shows examples of matrix differentiation of common trace equations.Derivative of matrix determinantRelation to other derivativesThe matrix derivative is a convenient notation for keeping track of partial derivatives for doing calculations. The Fréchet derivative is the standard way in the setting of functional analysis to take derivatives with respect to vectors. In the case that a matrix function of a matrix is Fréchet differentiable, the two derivatives will agree up to translation of notations. As is the case in general for partial derivatives, some formulae may extend under weaker analytic conditions than the existence of the derivative as approximating linear mapping.UsagesMatrix calculus is used for deriving optimal stochastic estimators, often involving the use of Lagrange multipliers. This includes the derivation of:•Kalman filter•Wiener filter•Expectation-maximization algorithm for Gaussian mixtureAlternativesThe tensor index notation with its Einstein summation convention is very similar to the matrix calculus, except one writes only a single component at a time. It has the advantage that one can easily manipulate arbitrarily high rank tensors, whereas tensors of rank higher than two are quite unwieldy with matrix notation. Note that a matrix can be considered simply a tensor of rank two.Notes[1]Magnus, Jan R.; Neudecker, Heinz (1999 (1988)). Matrix Differential Calculus. Wiley Series in Probability and Statistics (revised ed.).Wiley. pp. 171–173.External links•Matrix Calculus (/engineering/cas/courses.d/IFEM.d/IFEM.AppD.d/IFEM.AppD.pdf) appendix from Introduction to Finite Element Methods book on University of Colorado at Boulder.Uses the Hessian (transpose to Jacobian) definition of vector and matrix derivatives.•Matrix calculus (/hp/staff/dmb/matrix/calculus.html) Matrix Reference Manual , Imperial College London.•The Matrix Cookbook (), with a derivatives chapter. Uses the Hessian definition.Article Sources and Contributors5Article Sources and ContributorsMatrix calculus Source: /w/index.php?oldid=408981406 Contributors: Ahmadabdolkader, Albmont, Altenmann, Arthur Rubin, Ashigabou, AugPi, Blaisorblade,Bloodshedder, CBM, Charles Matthews, Cooli46, Cs32en, Ctacmo, DJ Clayworth, DRHagen, Dattorro, Dimarudoy, Dlohcierekim, Enisbayramoglu, Eroblar, Esoth, Excirial, Fred Bauder,Freddy2222, Gauge, Geometry guy, Giftlite, Giro720, Guohonghao, Hu12, Immunize, Jan mei118, Jitse Niesen, Lethe, Michael Hardy, MrOllie, NawlinWiki, Oli Filth, Orderud, Oussjarrouse, Ozob, Pearle, RJFJR, Rich Farmbrough, SDC, Sanchan89, Stpasha, TStein, The Thing That Should Not Be, Vgmddg, Willking1979, Xiaodi.Hou, Yuzisee, 170 anonymous editsLicenseCreative Commons Attribution-Share Alike 3.0 Unported/licenses/by-sa/3.0/。
SITH 商品说明书

Package‘SITH’October12,2022Type PackageTitle A Spatial Model of Intra-Tumor HeterogeneityVersion1.1.0Date2021-01-03Author Phillip B.NicolMaintainer Phillip B.Nicol<**********************>Description Implements a three-dimensional stochastic model of cancer growth and mutation simi-lar to the one described in Waclaw et al.(2015)<doi:10.1038/nature14971>.Allows for interac-tive3D visualizations of the simulated tumor.Provides a comprehensive summary of the spa-tial distribution of mutants within the tumor.Contains functions which create synthetic sequenc-ing datasets from the generated tumor.License GPL(>=2)Depends R(>=3.6.0)Imports Rcpp(>=1.0.4),scatterplot3d,stats,graphics,grDevicesSuggests rgl,igraph,knitr,rmarkdown,testthatLinkingTo RcppRoxygenNote7.1.1VignetteBuilder knitrEncoding UTF-8URL https:///phillipnicol/SITHBugReports https:///phillipnicol/SITH/issuesNeedsCompilation yesRepository CRANDate/Publication2021-01-0515:10:02UTC12SITH-package R topics documented:SITH-package (2)bulkSample (3)plotSlice (5)progressionChain (5)progressionDAG_from_igraph (6)randomBulkSamples (7)randomNeedles (8)randomSingleCells (9)simulateTumor (10)singleCell (12)spatialDistribution (13)visualizeTumor (14)Index15 SITH-package Visualize and analyze intratumor heterogeneity using a spatial modelof tumor growthDescriptionThe SITH(spatial model of intratumor heterogeneity)package implements a lattice based spatial model of tumor growth and mutation.Interactive3D visualization of the tumor are possible using rgl.Additional functions for visualization and investigating the spatial distribution of mutants are provided.SITH also provides functions to simulate single cell sequencing and bulk sampling data sets from the simulated tumor.BackgroundOn-lattice models of tumor growth and mutation are computationally efficient and provide a simple setting to study how spatially constrained growth impacts intratumor heterogeneity.While this model has been studied extensively in literature(see Waclaw(2015),Chkhaidze(2019),Opasic (2019)),existing software is either not publicly available or inconvenient to use with R.The motivation for creating the SITH package was to provide a spatial simulator that is both easy to use and can be used entirely with R.The core function in the package is simulateTumor(),which wraps a C++implementation of the model into R using the Rcpp package.Once the results of the simulation are saved as an R object,SITH provides several other useful functions for studying this model.See the package vignette for more information on the model and the algorithm used.Author(s)Phillip B.NicolReferencesB.Waclaw,I.Bozic,M.Pittman,R.Hruban,B.V ogelstein and M.Nowak.A spatial model pre-dicts that dispersal and cell turnover limit intratumor heterogeneity.Nature,pages261-264,2015.https:///10.1038/nature14971.K.Chkhaidze,T.Heide,B.Werner,M.Williams,W.Huang,G.Caravagna,T.Graham,and A.Sot-toriva.Spatially constrained tumour growth affects the patterns of clonal selection and neutral driftin cancer genomic data.PLOS Computational Biology,2019.https:///10.1371/journal.pcbi.1007243.L.Opasic,D.Zhou,B.Wener,D.Dingli and A.Traulsen.How many samples are needed to infertruly clonal mutations from heterogeneous tumours?BMC Cancer,https:///10.1186/s12885-019-5597-1.Examples#Simulate tumor growthout<-simulateTumor()#3d interactive visualization using rglvisualizeTumor(out)#or see regions with lots of mutantsvisualizeTumor(out,plot.type="heat")#get a summary on the spatial dist.of mutantssp<-spatialDistribution(out)#simulate single cell sequencingScs<-randomSingleCells(tumor=out,ncells=5,fnr=0.1)#simulate bulk samplingBulks<-randomBulkSamples(tumor=out,nsamples=5)bulkSample Simulate bulk samplingDescriptionSimulate bulk sequencing data by taking a local sample from the tumor and computing the variantallele frequencies of the various mutations.UsagebulkSample(tumor,pos,cube.length=5,threshold=0.05,coverage=0)Argumentstumor A list which is the output of simulateTumor().pos The center point of the sample.cube.length The side length of the cube of cells to be sampled.threshold Only mutations with an allele frequency greater than the threshold will be in-cluded in the sample.coverage If nonzero then deep sequencing with specified coverage is performed.DetailsA local region of the tumor is sampled by constructing a cube with side length cube.length aroundthe center point pos.Each cell within the cube is sampled,and the reported quantity is variant(ormutation)allele ttice sites without cells are assumed to be normal tissue,and thus thereported MAF may be less than1.0even if the mutation is present in all cancerous cells.If coverage is non-zero then deep sequencing can be simulated.For a chosen coverage C,it isknown that the number of times the base is read follows a P ois(C)distribution(see Illumina’swebsite).Let d be the true coverage sampled from this distribution.Then the estimated V AF isdrawn from a Bin(d,p)/d distribution.Note that cube.length is required to be an odd integer(in order to have a well-defined centerpoint).ValueA data frame with1row and columns corresponding to the mutations.The entries are the mutationallele frequency.Author(s)Phillip B.NicolReferencesK.Chkhaidze,T.Heide,B.Werner,M.Williams,W.Huang,G.Caravagna,T.Graham,and A.Sot-toriva.Spatially con-strained tumour growth affects the patterns of clonal selection and neutral driftin cancer genomic data.PLOS Computational Biology,2019.https:///10.1371/journal.pcbi.1007243.Lander ES,Waterman MS.(1988)Genomic mapping byfingerprinting random clones:a mathemat-ical analysis,Genomics2(3):231-239.Examplesset.seed(116776544,kind="Mersenne-Twister",normal.kind="Inversion")out<-simulateTumor(max_pop=1000)df<-bulkSample(tumor=out,pos=c(0,0,0))plotSlice5 plotSlice2D cross section of the simulated tumorDescription2D cross section of the simulated tumor.UsageplotSlice(tumor,slice.dim="x",level=0,plot.type="normal")Argumentstumor A list which is the output of simulateTumor().slice.dim One of"x","y"or"z",which denotes the dimension which will befixed to obtain a2D cross section.level Which value will the dimension given in slice.dim befixed at?plot.type Which type of plot to draw."Normal"assigns a random rgb value to each geno-type while"heat"colors cells with more mutations red and cells with fewermutations blue.This is exactly the same as plot.type in visualizeTumor.ValueNone.Author(s)Phillip B.NicolprogressionChain Create a linear chain graph to describe the order of mutationsDescriptionA helper function for simulateTumor()which returns to the user the edge list for a linear chain.UsageprogressionChain(n)Argumentsn Number of vertices in the chain6progressionDAG_from_igraph ValueA matrix with4columns and n-1rows which will be accepted as input to simulateTumor().Author(s)Phillip B.Nicol<**********************>ExamplesG<-progressionChain(3)progressionDAG_from_igraphDefine the progression of mutations from an igraph objectDescriptionA helper function for simulateTumor()which returns to the user the edge list for a DAG which isdefined as an igraph object.UsageprogressionDAG_from_igraph(iG)ArgumentsiG An igraph object for a directed acyclic graph.ValueA matrix with4columns which contains the edges of the graph as well as the rate of crossing eachedge and the selective advantage/disadvantage obtained by crossing each edge.Author(s)Phillip B.Nicol<**********************>randomBulkSamples7 randomBulkSamples Simulate multi-region bulk samplingDescriptionSimulate bulk sequencing data by taking a local sample from the tumor and computing the variant allele frequencies of the various mutations.UsagerandomBulkSamples(tumor,nsamples,cube.length=5,threshold=0.05,coverage=0)Argumentstumor A list which is the output of simulateTumor().nsamples The number of bulk samples to take.cube.length The side length of the cube of cells to be sampled.threshold Only mutations with an allele frequency greater than the threshold will be in-cluded in the sample.coverage If nonzero then deep sequencing with specified coverage is performed.DetailsThis is the same as bulkSample(),except multiple samples are taken with random center points. ValueA data frame with nsamples rows and columns corresponding to the mutations.The entries are themutation allele frequency.Author(s)Phillip B.NicolExamplesout<-simulateTumor(max_pop=1000)df<-randomBulkSamples(tumor=out,nsamples=5,cube.length=5,threshold=0.05)8randomNeedles randomNeedles Simulatefine needle aspirationDescriptionSimulate a sampling procedure which takes afine needle through the simulated tumor and reportsthe mutation allele frequency of the sampled cells.UsagerandomNeedles(tumor,nsamples,threshold=0.05,coverage=0)Argumentstumor A list which is the output of simulateTumor().nsamples The number of samples to take.threshold Only mutations with an allele frequency greater than the threshold will be in-cluded in the sample.coverage If nonzero then deep sequencing with specified coverage is performed.DetailsThis sampling procedure is inspired by Chkhaidze et.al.(2019)and simulatesfine needle aspira-tion.A random one-dimensional cross-section of the tumor is chosen,and the cells within this crosssection are sampled,reporting mutation allele frequency.Author(s)Phillip B.NicolReferencesK.Chkhaidze,T.Heide,B.Werner,M.Williams,W.Huang,G.Caravagna,T.Graham,and A.Sot-toriva.Spatially con-strained tumour growth affects the patterns of clonal selection and neutral driftin cancer genomic data.PLOS Computational Biology,2019.https:///10.1371/journal.pcbi.1007243.Examplesout<-simulateTumor(max_pop=1000)df<-randomNeedles(tumor=out,nsamples=5)randomSingleCells9 randomSingleCells Simulate single cell sequencing dataDescriptionSimulate single cell sequencing data by random selecting cells from the tumor.UsagerandomSingleCells(tumor,ncells,fpr=0,fnr=0)Argumentstumor A list which is the output of simulateTumor().ncells The number of cells to sample.fpr The false positive ratefnr The false negative rateDetailsThe procedure is exactly the same as singleCell()except that it allows multiple cells to be se-quenced at once(chosen randomly throughout the entire tumor).ValueA data frame with sample names on the row and mutation ID on the column.A1indicates that themutation is present in the cell and a0indicates the mutation is not present.Author(s)Phillip B.Nicol<**********************>Examplesout<-simulateTumor(max_pop=1000)df<-randomSingleCells(tumor=out,ncells=5,fnr=0.1)10simulateTumor simulateTumor Spatial simulation of tumor growthDescriptionSimulate the spatial growth of a tumor with a multi-type branching process on the three-dimensional integer lattice.UsagesimulateTumor(max_pop=250000,div_rate=0.25,death_rate=0.18,mut_rate=0.01,driver_prob=0.003,selective_adv=1.05,disease_model=NULL,verbose=TRUE)Argumentsmax_pop Number of cells in the tumor.div_rate Cell division rate.death_rate Cell death rate.mut_rate Mutation rate.When a cell divides,both daughter cell acquire P ois(u)genetic alterationsdriver_prob The probability that a genetic alteration is a driver mutation.selective_adv The selective advantage conferred to a driver mutation.A cell with k driver mutations is given birth rate bs k.disease_model Edge list for a directed acyclic graph describing possible transitions between states.See progressionChain()for an example of a valid input matrix.verbose Whether or not to print simulation details to the R console.DetailsThe model is based upon Waclaw et.al.(2015),although the simulation algorithm used is different.A growth of a cancerous tumor is modeled using an exponential birth-death process on the three-dimensional integer lattice.Each cell is given a birth rate b and a death rate d such that the time until cell division or cell death is exponentially distributed with parameters b and d,respectively.A cell can replicate if at least one of the six sites adjacent to it is unoccupied.Each time cell replication occurs,both daughter cells receive P ois(u)genetic alterations.Each alteration is a driver mutation with some probability du.A cell with k driver mutations is given birth rate bs k.The simulation begins with a single cell at the origin at time t=0.simulateTumor11 The model is simulated using a Gillespie algorithm.See the package vignette for details on how the algorithm is implemented.ValueA list with components•cell_ids-A data frame containing the information for the simulated cells.(x,y,z)posi-tion,allele ID number(note that0is the wild-type allele),number of genetic alterations,and Euclidean distance from origin are included.•muts-A data frame consisting of the mutation ID number,the count of the mutation within the population,and the mutation allele frequency(which is the count divided by N).•phylo_tree-A data frame giving all of the information necessary to determine the order of mutations.The parent of a mutation is defined to be the most recent mutation that precedes it.Since the ID0corresponds to the initial mutation,0does not have any parents and is thus the root of the tree.•genotypes-A data frame containing the information about the mutations that make up each allele.The i-th row of this data frame corresponds to the allele ID i−1.The positive numbers in each row correspond to the IDs of the mutations present in that allele,while a-1is simplya placeholder and indicates no mutation.The count column gives the number of cells whichhave the specific allele.•color_scheme-A vector containing an assignment of a color to each allele.•drivers-A vector containing the ID numbers for the driver mutations.•time-The simulated time(in days).•params-The parameters used for the simulation.Author(s)Phillip B.Nicol<**********************>ReferencesB.Waclaw,I.Bozic,M.Pittman,R.Hruban,B.V ogelstein and M.Nowak.A spatial model predictsthat dispersal and cell turnover limit intratumor heterogeneity.Nature,pages261-264,2015.D.Gillespie.Exact stochastic simulation of coupled chemical reactions.The Journal of PhysicalChemistry,volume81,pages2340-2361,1970.Examplesout<-simulateTumor(max_pop=1000)#Take a look at mutants in order of decreasing MAFsig_muts<-out$muts[order(out$muts$MAF,decreasing=TRUE),]#Specify the disease modelout<-simulateTumor(max_pop=1000,disease_model=progressionChain(3))12singleCell singleCell Simulate single cell sequencing dataDescriptionSimulate single cell sequencing data by selecting a cell at a specified positionUsagesingleCell(tumor,pos,noise=0)Argumentstumor A list which is the output of simulateTumor().pos A vector of length3giving the(x,y,z)coordinates of the cell to sample.noise The false negative rate.DetailsThis function selects the cell at pos(error if no cell at specified position exists)and returns the list of mutations present in the cell.Due to technological artifacts,the false negative rate can be quite higher(10-20percent).To account for this,the noise parameter introduces false negatives into the data set at the specified rate.ValueA data frame with1row and columns corresponding to the mutations present in the cell.A1indicates that the mutation is detected while a0indicates the mutation is not detected.Author(s)Phillip B.Nicol<**********************>ReferencesK.Jahn,J.Kupiers and N.Beerenwinkel.Tree inference for single-cell data.Genome Biology, volume17,2016.https:///10.1186/s13059-016-0936-x.Examplesset.seed(1126490984)out<-simulateTumor(max_pop=1000)df<-singleCell(tumor=out,pos=c(0,0,0),noise=0.1)spatialDistribution13 spatialDistribution Quantify the spatial distribution of mutantsDescriptionProvides a summary the spatial distribution of mutants within the simulated tumor.UsagespatialDistribution(tumor,N=500,cutoff=0.01,make.plot=TRUE) Argumentstumor A list which is the output of simulateTumor().N The number of pairs to sample.cutoff For a plot of clone sizes,all mutations with a MAF below cutoff are ignored.make.plot Whether or not to make plots.DetailsThe genotype of a cell can be interpreted as a binary vector where the i-th component is1if mutationi is present in the cell and is0otherwise.Then a natural comparison of the similarity between twocells is the Jaccard index J(A,B)=|I(A,B)|/|U(A,B)|,where I(A,B)is the intersection ofA andB and U(A,B)is the union.This function estimates the Jaccard index as a function ofEuclidean distance between the cells by randomly sampling N pairs of cells.ValueA list with the following components•mean_mutant-A data frame with2columns giving the mean number of mutants as a function of Euclidean distance from the lattice origin(Euclid.distance rounded to nearest integer).•mean_driver-The same as mean_mutant except for driver mutations only.Will be NULL if no drivers are present in the simulated tumor.•jaccard A data frame with two columns giving mean jaccard index as a function of Euclidean distance between pairs of cells(rounded to nearest integer).Author(s)Phillip B.NicolExamplesset.seed(1126490984)out<-simulateTumor(max_pop=1000,driver_prob=0.1)sp<-spatialDistribution(tumor=out,make.plot=FALSE)14visualizeTumor visualizeTumor Interactive visualization of the simulated tumorDescriptionInteractive visualization of the simulated tumor using the rgl package(if available).UsagevisualizeTumor(tumor,plot.type="normal",background="black",axes=FALSE)Argumentstumor A list which is the output of simulateTumor().plot.type Which type of plot to draw."Normal"assigns a random rgb value to each geno-type while"heat"colors cells with more mutations red and cells with fewermutations blue.background If rgl is installed,this will set the color of the backgroundaxes Will include axes(rgl only).DetailsIf rgl is installed,then the plots will be interactive.If rgl is unavailable,static plots will be cre-ated with scatterplot3d.Since plotting performance with scatterplot3d is reduced,it is strongly recommended that rgl is installed for optimal use of this function.ValueNone.Author(s)Phillip B.NicolIndexbulkSample,3,7plotSlice,5progressionChain,5,10progressionDAG_from_igraph,6 randomBulkSamples,7randomNeedles,8randomSingleCells,9simulateTumor,2,4–9,10,12–14singleCell,9,12SITH(SITH-package),2SITH-package,2spatialDistribution,13visualizeTumor,1415。
advances in mathematics介绍

advances in mathematics介绍Advances in mathematics refer to the progress made in the field of mathematics that has greatly impacted various areas of science, technology, engineering, and even everyday life. These advances include discoveries, theories, techniques, algorithms, and computational methods that have broadened the understanding and application of mathematical concepts.One significant advance in mathematics is the development of calculus by Sir Isaac Newton and Gottfried Wilhelm Leibniz in the 17th century. Calculus allows for the study of change and the analysis of various mathematical functions, making it essential in physics, engineering, economics, and other sciences.Another important advance is the creation of non-Euclidean geometries, such as hyperbolic and elliptic geometries. These non-Euclidean geometries challenge the traditional Euclidean geometry and have applications in fields like relativity, computer graphics, and cryptography.The introduction of number theory and abstract algebra has also been a significant advancement in mathematics. Number theory deals with the properties and relationships of numbers, while abstract algebra studiesalgebraic structures such as groups, rings, and fields. These areas of mathematics have paved the way for cryptography, coding theory, and other fields related to secure communication and data encryption.Advances in mathematical modeling and simulation have greatly impacted various scientific disciplines. Mathematical models help scientists and researchers understand complex phenomena and make predictions about real-world systems. Simulation techniques, such as Monte Carlo methods and numerical optimization, allow for the analysis of large datasets and the implementation of mathematical models into computer algorithms.Furthermore, the development of computational methods and algorithms has greatly expanded the capabilities of mathematical analysis. Techniques such as linear programming, network optimization, and numerical analysis have revolutionized fields such as operations research, data analysis, and computer science.Advances in mathematics have also led to breakthroughs in cryptography, data compression, image processing, machine learning, and artificial intelligence. These advancements have influenced various technological advancements, including the development of fastercomputers, improved data storage, and advanced algorithms.In summary, advances in mathematics have transformed various fields of science, technology, and everyday life by providing tools and concepts for understanding and solving complex problems. The continuous progress in mathematics continues to shape our understanding of the world and drive innovation in various disciplines.。
calculus我的calculus笔记,按照国际标准排版

1.2
Mathematical Models: A Catalog of Essential Functions
1. A mathematical model is a mathematical description (often by means of a function or an equation) of a real-world phenomenon. 2. If there is no physical law or principle to help us formulate a model, we construct an empirical model. 3. A function P is called a polynomial if P pxq an xn an¡1 xn¡1 ¤ ¤ ¤ a2 x2 a1 x a0 when n N and the numbers a0 , a1 , a2 , . . . , an are constants called coefficients of the polynomial. The domain of any polynomial is R. If the leading coefficient an $ 0, then the degree of the polynomial is n. A polynomial of degree 1 is of the form P pxq mx b and is a linear function. A polynomial of degree 2 is of the form P pxq ax2 bx c and is called a quadratic function.
1
CHAPTER 1
高等工程热力学2热力学第一定律

2. The Law of Universal Gravitation, The Newton Three Laws of Motion, and Geometric Calculus (Newton, 1687)
volume in space; 3. Boundary must be shared by both the system and the
environment, because, after all, the system and the environment are in contact at this point.
The Heat Transfer
1. The proportionality between cooling rate & body-surroundings temperature difference [ Newton, 1701]
2. Comparative measurement of thermal conductivity 3. Convection as a principal heat transfer mechanism through
column of mercury as indicator (1600s) 4. The mercury-in-glass thermometer [ Fahrenheit, 1714]
H.-C. Zhang (张昊春)
Advanced Engineering Thermodynamics
lambda-calculus

Lambda-演算在形式语义学的中应用1傅庆芳1.形式语义学与组合原则自Chomsky创立生成语法(generative grammar)以来,人们开始普遍承认语法是可以按组合原则逐步生成的。
生成语法的一个基本出发点是:自然语言中存在无穷多的句子,同时大脑的功能是有限的,所以我们的语言能力必须包含某种可以描述这些无穷多句子类型的有穷机制。
也就是说,通过这些有穷的机制,我们可以不断地对已有的元素进行组合,并生成无穷多的句子或语法类型。
因此,可以用形式化的方法分析句子的语法及其生成过程。
但是,在很长一段时间里,Chomsky反对把组合原则和形式化方法应用到语义学的研究中。
这是因为语义问题不像语法结构那样有比较清楚的结构,尤其是,很难有与语法相对应的组合生成的语义解释。
然而,组合原则对于形式语义学是至关重要的,如果不能在自然语言的语义研究中很好地贯彻组合原则,那么也就没有形式语义学这一研究领域。
这成为形式语义学发展的一个瓶颈。
Chomsky对形式语义学基本持怀疑态度。
在很长的时间里,MIT一直没有研究形式语义学的人,直到1989年Chomsky才聘请了Irene Heim2去MIT工作。
这时的形式语义学已经发展得比较成熟。
形式语义学的想法是,对应于语法中的组合原则,语义解释也应该是可以通过应用组合原则逐步生成的,即:一个语言的说话者可以知道无穷多句子的意义,也能够理解或表达他从未听说过意思。
因此,对于语义学来说,也一定存在某种有穷的机制可以让人们理解任何一种自然语言的无穷多的句子。
因此,形式语义学的一个主要原则是语法与语义之间的关系是组合的。
任何一个自然语言的语法和语义各自是按组合原则生成的,同时这两个组合原则又是相互对应的。
这类似于一阶逻辑这种形式语言,其句法和语义都要遵循组合原则,且相互之间存在一种组合的对应关系。
也就是说,语法与语义之间并非都是随意联系在一起的,而是可以遵循某些规则逐步组合而成的。
GammaFunction:伽玛函数
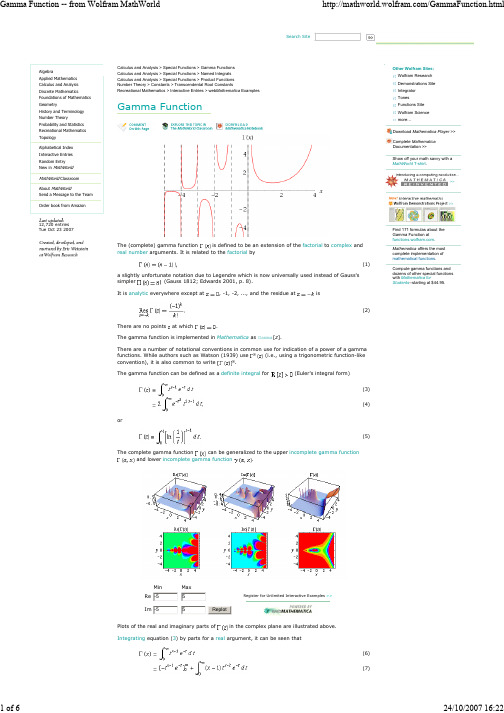
Search Site12,720 entries Calculus and Analysis > Special Functions > Gamma Functions Calculus and Analysis > Special Functions > Named Integrals Calculus and Analysis > Special Functions > Product Functions Gamma FunctionThe (complete) gamma function is defined to be an extension of the factorial to arguments. It is related to the factorial bya slightly unfortunate notation due to Legendre which is now universally used instead of Gauss's simpler (Gauss 1812; Edwards 2001, p. 8). everywhere except at, -1, -2, ..., and the residue atisThere are no points at which.There are a number of notational conventions in common use for indication of a power of a gamma functions. While authors such as Watson (1939) use (i.e., using a trigonometric function-like convention), it is also common to write . for(Euler's integral form)The complete gamma function can be generalized to the upper and lower incomplete gamma function .Min MaxRe Register for Unlimited Interactive Examples >>Im ReplotPlots of the real and imaginary parts of in the complex plane are illustrated above.Wolfram Research Demonstrations Site Integrator Tones Functions Site Wolfram Science more…Download Complete Documentation >>Find 171 formulas about the Gamma Function at -55-55(8)(9)If is an integer, 2, 3, ..., then(10)(11)so the gamma function reduces to the factorial for a positive integer argument.A beautiful relationship betweenand the Riemann zeta functionis given by(12)for(Havil 2003, p. 60).The gamma function can also be defined by an infinite product form (Weierstrass form )(13)where is the Euler-Mascheroni constant (Krantz 1999, p. 157; Havil 2003, p. 57). This can be written(14)where(15)(16)for, where is the Riemann zeta function (Finch 2003). Taking the logarithm of both sidesof (◇),(17)Differentiating,(18)(19)(20)(21)(22)(23)(24)(25)where is the digamma function and is the polygamma function . th derivatives are given in terms of the polygamma functions , , ..., .The minimum valueoffor real positiveis achieved when(26)(27)This can be solved numerically to give (Sloane's A030169; Wrench 1968), which has continued fraction [1, 2, 6, 63, 135, 1, 1, 1, 1, 4, 1, 38, ...] (Sloane's A030170). At ,achieves the value 0.8856031944... (Sloane's A030171), which has continued fraction [0, 1, 7, 1, 2, 1, 6, 1, 1, ...] (Sloane's A030172).The Euler limit form is(28)so(29)(30)(31)(32)(Krantz 1999, p. 156).One over the gamma functionis an entire function and can be expressed as(33)where is the Euler-Mascheroni constant and is the Riemann zeta function (Wrench 1968). An asymptotic series for is given by(34) Writing(35) the satisfy(36) (Bourguet 1883, Davis 1933, Isaacson and Salzer 1943, Wrench 1968). Wrench (1968) numerically computed the coefficients for the series expansion about 0 of(37) The Lanczos approximation gives a series expansion for for in terms of an arbitrary constant such that .The gamma function satisfies the functional equations(38)(39) Additional identities are(40)(41)(42)(43)Using (40), the gamma function of a rational number can be reduced to a constant times or . For example,(44)(45)(46)(47) For ,(48) Gamma functions of argument can be expressed using the Legendre duplication formula(49) Gamma functions of argument can be expressed using a triplication formula(50) The general result is the Gauss multiplication formula(51) The gamma function is also related to the Riemann zeta function by(52) For integer , 2, ..., the first few values of are 1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880, ... (Sloane's A000142). For half-integer arguments, has the special form(53)where is a double factorial. The first few values for , 3, 5, ... are therefore(54)(55)(56), , ... (Sloane's A001147 and A000079; Wells 1986, p. 40). In general, for a positive integer, 2, ...(57)(58)(59)(60) Simple closed-form expressions of this type do not appear to exist for for a positive integer . However, Borwein and Zucker (1992) give a variety of identities relating gamma functions to square roots and elliptic integral singular values, i.e., elliptic moduli such that(61)where is a complete elliptic integral of the first kind and is the complementary integral. M. Trott (pers. comm.) has developed an algorithm for automatically generating hundreds of such identities.(62)(63)(64)(65)(66)(67)(68)(69)(70)(71)(72)(73)(74)(75)(76)(77)(78)(79)(80)(81)(82)Several of these are also given in Campbell (1966, p. 31).A few curious identities include(83)(84)(85)(86)(87)(88)(89) of which Magnus and Oberhettinger 1949, p. 1 give only the last case,(90) and(91)(Magnus and Oberhettinger 1949, p. 1). Ramanujan also gave a number of fascinating identities:(92)(93) where(94)(95)(Berndt 1994).Ramanujan gave the infinite sums(96)(97) and(98)(99)(Hardy 1923; Hardy 1924; Whipple 1926; Watson 1931; Bailey 1935; Hardy 1999, p. 7).The following asymptotic series is occasionally useful in probability theory (e.g., theone-dimensional random walk):(100) (Graham et al. 1994). This series also gives a nice asymptotic generalization of Stirling numbers of the first kind to fractional values.It has long been known that is transcendental (Davis 1959), as is (Le Lionnais 1983; Borwein and Bailey 2003, p. 138), and Chudnovsky has apparently recently proved thatis itself transcendental (Borwein and Bailey 2003, p. 138).There exist efficient iterative algorithms for for all integers (Borwein and Bailey 2003, p. 137). For example, a quadratically converging iteration for (Sloane'sA068466) is given by defining(101)(102) setting and , and then(103)(Borwein and Bailey 2003, pp. 137-138).No such iteration is known for (Borwein and Borwein 1987; Borwein and Zucker 1992; Borwein and Bailey 2003, p. 138).SEE ALSO:Bailey's Theorem, Barnes G-Function, Binet's Fibonacci Number Formula, Bohr-Mollerup Theorem, Digamma Function, Double Gamma Function, Fransén-Robinson Constant Gauss Multiplication Formula, Incomplete Gamma Function, Knar's Formula, Lambda Function, LanczosApproximation, Legendre Duplication Formula, Log Gamma Function, Mellin's Formula, Mu Function, Nu Function, Pearson's Function, Polygamma Function, Regularized Gamma Function, Stirling's Series, Superfactorial. [Pages Linking Here]RELATED WOLFRAM SITES:/GammaBetaErf/Gamma/,/GammaBetaErf/LogGamma/REFERENCES:Abramowitz, M. and Stegun, I. A. (Eds.). "Gamma (Factorial) Function" and "Incomplete Gamma Function." §6.1 and 6.5 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 255-258 and 260-263, 1972.Arfken, G. "The Gamma Function (Factorial Function)." Ch. 10 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 339-341 and 539-572, 1985.Artin, E. The Gamma Function. New York: Holt, Rinehart, and Winston, 1964.Bailey, W. N. Generalised Hypergeometric Series. Cambridge, England: Cambridge University Press, 1935.Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 334-342, 1994.Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 218, 1987.Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.Borwein, J. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, p. 6, 1987.Borwein, J. M. and Zucker, I. J. "Fast Evaluation of the Gamma Function for Small Rational Fractions Using Complete Elliptic Integrals of the First Kind." IMA J. Numerical Analysis12, 519-526, 1992.Bourguet, L. "Sur les intégrales Eulériennes et quelques autres fonctions uniformes." Acta Math.2, 261-295, 1883. Campbell, R. Les intégrales eulériennes et leurs applications. Paris: Dunod, 1966.Davis, H. T. Tables of the Higher Mathematical Functions. Bloomington, IN: Principia Press, 1933.Davis, P. J. "Leonhard Euler's Integral: A Historical Profile of the Gamma Function." Amer. Math. Monthly66, 849-869, 1959.Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. "The Gamma Function." Ch. 1 in Higher Transcendental Functions, Vol. 1. New York: Krieger, pp. 1-55, 1981.Finch, S. R. "Euler-Mascheroni Constant." §1.5 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 28-40, 2003.Gauss, C. F. "Disquisitiones Generales Circa Seriem Infinitametc. Pars Prior." Commentationes Societiones Regiae Scientiarum Gottingensis Recentiores, Vol. II. 1812. Reprinted in Gesammelte Werke, Bd. 3, pp. 123-163 and 207-229, 1866.Graham, R. L.; Knuth, D. E.; and Patashnik, O. Answer to Problem 9.60 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994.Hardy, G. H. "A Chapter from Ramanujan's Note-Book." Proc. Cambridge Philos. Soc.21, 492-503, 1923.Hardy, G. H. "Some Formulae of Ramanujan." Proc. London Math. Soc. (Records of Proceedings at Meetings) 22,xii-xiii, 1924.Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.Havil, J. "The Gamma Function." Ch. 6 in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 53-60, 2003.Isaacson, E. and Salzer, H. E. "Mathematical Tables--Errata: 19. J. P. L. Bourget, 'Sur les intégrales Eulériennes et quelques autres fonctions uniformes,' Acta Mathematica, v. 2, 1883, pp. 261-295.' " Math. Tab. Aids Comput.1, 124, 1943.Koepf, W. "The Gamma Function." Ch. 1 in Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, pp. 4-10, 1998.Krantz, S. G. "The Gamma and Beta Functions." §13.1 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 155-158, 1999.Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 46, 1983.Magnus, W. and Oberhettinger, F. Formulas and Theorems for the Special Functions of Mathematical Physics. New York: Chelsea, 1949.Nielsen, N. "Handbuch der Theorie der Gammafunktion." Part I in Die Gammafunktion. New York: Chelsea, 1965. Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Gamma Function, Beta Function, Factorials, Binomial Coefficients" and "Incomplete Gamma Function, Error Function, Chi-Square Probability Function, Cumulative Poisson Function." §6.1 and 6.2 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 206-209 and 209-214, 1992.Sloane, N. J. A. Sequences A000079/M1129, A000142/M1675, A001147/M3002, A030169, A030170, A030171,A030172, and A068466 in "The On-Line Encyclopedia of Integer Sequences."Spanier, J. and Oldham, K. B. "The Gamma Function " and "The Incomplete Gamma and Related Functions." Chs. 43 and 45 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 411-421 and 435-443, 1987. Watson, G. N. "Theorems Stated by Ramanujan (XI)." J. London Math. Soc.6, 59-65, 1931.Watson, G. N. "Three Triple Integrals." Quart. J. Math., Oxford Ser. 210, 266-276, 1939.Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 40, 1986. Whipple, F. J. W. "A Fundamental Relation between Generalised Hypergeometric Series." J. London Math. Soc.1,138-145, 1926.Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.Wrench, J. W. Jr. "Concerning Two Series for the Gamma Function." Math. Comput.22, 617-626, 1968.LAST MODIFIED:December 26, 2005CITE THIS AS:Weisstein, Eric W. "Gamma Function." From MathWorld--A Wolfram Web Resource./GammaFunction.html© 1999 CRC Press LLC, © 1999-2007 Wolfram Research, Inc. | Terms of Use。
2019_2018学年高中英语Module5CloningSectionⅣOtherPartsoft

suspect ’ s ○63 saliva ○64 which ○63 suspect/'sʌspekt/ n.嫌疑人
they spit at a crime scene or the dirt under their fingernails○65 .
1973 年,生物化学家科恩和博耶发现了如下步骤:利用 人体内形成的化学物质酶解旋 DNA,截取一定顺序的基因 片断,最后把它们植入宿主细胞,使之与其 DNA 结合。
[原文呈现]
[读文清障]
Cloning takes the DNA from a single cell to create a whole new individual○21 . A clone is an organism ○22 which is genetically ○23 identical to ○24 another one. But it's now certain that○25 no clone is an exact copy because of differences in experiences and upbringing○26 .
be combined with 被与…… 结合/联合在一起
克隆与 DNA [第 1~2 段译文]
许多人认为基因学与克隆是最近出现的。确实如此,在 1953 年,英国剑桥大学的两名科学家沃森和克里克发现了酸 性 DNA 的结构——一种透明的由生命基本元素构成的双螺 旋结构。但是事实上,孟德尔在 1866 年第一个记录了种植 豌豆的结果。他了解到植物的父本和母本都会影响子代的基 因构成。
函子范畴和两种语言

Functor categories and two-level languagesE.MoggiDISI-Univ.di Genova,via Dodecaneso35,16146Genova,Italy phone:+3910353-6629,fax:+3910353-6699,email:moggi@disi.unige.itAbstract.We propose a denotational semantics for the two-level lan-guage of[GJ91,Gom92],and prove its correctness w.r.t.a standarddenotational semantics.Other researchers(see[Gom91,GJ91,Gom92,JGS93,HM94])have claimed correctness for lambda-mix(or extensionsof it)based on denotational models,but the proofs of such claims relyon imprecise definitions and are basicallyflawed.At a technical levelthere are two important differences between our model and more naivemodels in Cpo:the domain for interpreting dynamic expressions is moreabstract(we interpret code asλ-terms moduloα-conversion),the seman-tics of newname is handled differently(we exploit functor categories).The key idea is to interpret a two-level language in a suitable functorcategory Cpo D op rather than Cpo.The semantics of newname followsthe ideas pioneered by Oles and Reynolds for modeling the stack disci-pline of Algol-like languages.Indeed,we can think of the objects of D(i.e.the natural numbers)as the states of a name counter,which is in-cremented when entering the body of aλ-abstraction and decrementedwhen coming out.Correctness is proved using Kripke logical relations(see[MM91,NN92]).IntroductionTwo-level languages are an important tool for analyzing programs.In the context of partial evaluation they are used to identify those parts of the program that can be reduced statically,and those that have to be evaluated dynamically.We take as representative of these two-level languages that described in[GJ91],which we call P CF2,since it can be considered as the“P CF of two-level languages”. The main aims of this paper are:to point out theflaws in the semantics and correctness proof given in[Gom92],and to propose an alternative semantics for which one can prove correctness.The interpretation of dynamicλ-abstraction given in[GJ91,Gom92]uses a newname construct“informally”.Indeed,Gomard and Jones warn that“the generation of new variable names relies on a side-effect on a global state(a name counter).In principle this could have been avoided by adding an extra parameter to the semantic function,but for the sake of notational simplicity we use a less formal solution”.Because of this informality,[GJ91,Gom92]are able to use a simplified semantic domain for dynamic expressions,but have to hand wave when it comes to the clause for dynamicλ-abstraction.This informality is maintained also in the correctness proof of[Gom92].It is possible tofix the informal semantics using a name-counter(as suggested by Gomard and Jones),but then it is unclear how tofix the correctness proof.In fact,several experts were unable to propose a ck of precision in the definition of denota-tional semantics and consequentflaws in correctness proofs are not confined to [Gom92],indeed–Chapter4of[Gom91]and Chapter8of[JGS93]contain the same definitions, results and proofs–[GJ91]quotes the same definitions and results(but without proofs)–while[HM94]adapts Gomard’s technique to establish correctness for a poly-morphic binding-time analysis(and introduces furtherflaws in the denota-tional semantics).The specific model we propose is based on a functor category.In denotational semantics functor categories have been advocated by[Ole85]to model Algol-like languages,and more generally they have been used to model locality and dynamic creation(see[OT92,PS93,FMS96]).For this kind of modeling they outperform the more traditional category Cpo of cpos(i.e.posets with lubs of ω-chains andω-continuous maps).Therefore,they are a natural candidate for modeling the newname construct of[GJ91].In the proposed functor category model the domain of residual programs is a bit more abstract than expected,namelyα-convertible programs are identified.This identification is necessary for defining the category D of dynamic expressions, but it seems also a desirable abstraction.Functor categories are definitely more complex than Cpo,but one can avoid most of the complexities by working in a metalanguage(with computational types).Indeed,it is only in few critical places, where it is important to know which category(and which monad)is used.The graduate textbook[Ten91]gives the necessary background on functor categories for denotational semantics to understand our functor category model.In Cpo models the renaming of bound dynamic variables(used in the interpretation of dynamicλ-abstraction)is modeled via a side-effect monad with a name-counter as state,on the contrary in the functor category model renaming is handled by the functor category itself(while non-termination at specialization-time is modeled by the lifting monad).The paper is organized as follows:Section1recall the two-level language of [GJ91,Gom92]which we call P CF2;Section2describes a general way for in-terpreting P CF2via translation into a metalanguage with computational types, and explains what’s wrong with previously proposed semantics of P CF2;Sec-tion3describes our functor category model for P CF2and proves correctness; Section4make a comparison of the semantics.Acknowledgments.I wish to thank Olivier Danvy and Neil Jones for e-mail discussions,which were very valuable to clarify the intended semantics in[GJ91, Gom92],and to identify the critical problem in the correctness proof.Neil Jones has kindly provided useful bibliographic references and made available relevant internal reports.We have used Paul Taylor’s package for commutative diagrams.1The two-level language of Gomard and JonesIn this section we recall the main definitions in[GJ91,Gom92],namely:the untyped object languageλo and its semantics,the two-level language P CF2 and its semantics(including with the problematic clause forλn into a suitable metalanguage with computational types,s.t.aλo-term M is translated into a meta-term M n of type T V with V=const+(T V→T V),or more preciselyx:–x n=x–c n=[inl(c)]–(λx.M)n=[inr(λx:T V.M n)]–(M1@M2)n=let u⇐M1n in case u of inr(f)⇒f(M2n)⇒⊥–(fix M)n=let u⇐M n in case u of inr(f)⇒Y(f)1.2The two-level language P CF2The two-level language P CF2can be described as a simply typedλ-calculus over the base types base and code with additional operations.The raw syntax of P CF2is given by–typesτ::=base|code|τ1→τ2–terms e::=x|λx:τ.e|e1@e2|fixτe|ifτe1e2e3|c|ift e|λe2|fix e1e2e3|c:(code→code)→code,following Church we have takenλx.e of[GJ91]can be replaced byλcan be defined asλf:code→code.λ:code,code→code–fix:code,code,code→code–cs into a suitable met-alanguage with computational types,s.t.x1:τ1s,...,x n:τn s ML e s:τswhen x1:τ1,...,x n:τn P CF2e:τ.The translation highlights that staticcomputations take place only at ground types(just like in P CF and Algol).–base s=T(const),where const is theflat cpo of ground constants–code s=T(exp),where exp is theflat cpo of openλo-terms with(free and bound)variables included in var={x n|n∈N}.When translating terms of P CF2we make use of the following expression-building operations:•buildvar:var→exp is the inclusion of variables into terms.•buildfix and build•build⇒⊥where⊥is the least element ofτs–(fixτe)s=Y(e s),where Y is the leastfixed-point ofτs–( ift e)s=let x⇐e s in[builds=[buildM⇐ope)s=let x⇐newname in let M⇐e s([buildλ(x,M)]where newname:T(var)generates a fresh variable of the object language. The monad T for static computations should satisfy the same additional prop-erties stated in Note1.Remark.In the above interpretation/translation the meaning of newname(and λ–(λvar(x)])in[build2.1Correctness:attempts and failuresInformally speaking,correctness for P CF2should say that for any∅ P CF2e:code if the static evaluation of e terminates and produces aλo-term M:exp,then λo-terms M and eφare equivalent,wherex:code P CF2e:code with free dynamicvariables.In a denotational setting one could prove correctness by defining a logical relation (see[MW85,Mit96])between two interpretations of P CF2P CF2I oThe parameterized logical relation Rτρ⊆[[τs]]×D,whereρ:var→D,proposed by[Gom92]is defined as follows–⊥R baseρd and up(b)R baseρd∆⇐⇒d=up(in1b)–⊥R codeρd and up(M)R codeρd∆⇐⇒d=[[M]]oρ–f Rτ1→τ2ρd∆⇐⇒x Rτ1ρy⊃(f@x)Rτ2ρ(d@o y),this is the standard way ofdefining at higher types a logical relation between typed applicative struc-tures.Gomard interprets types according to the informal semantics,i.e.[[base s]]= const⊥and[[code s]]=exp⊥.According to the fundamental lemma of logical relations,if the two interpretations of each operation/constant of P CF2are logically related,then the two interpretations of each P CF2-term are logically related.It is easy to do this check for all operations/constants exceptλone can only hand wave,since the interpretation is informally given. Therefore,Gomard concludes that he has proved correctness.Remark.Gomard does not mention explicitly logical relations.However,his def-inition of R is given by induction on the structure of P CF2-types,while correct-ness is proved by induction of the structure P CF2-termsΓ P CF2e:τ.This istypical of logical relations.In order to patch the proof one would have to change the definition of R codeρ, since in the intended semantics[[code s]]=exp N⊥or(exp×N)N⊥,and check the case ofλ–The interpretation ofλy.x:code,which is a function f:exp N⊥→exp N⊥,and the element[M]=λn.up(M)of exp N⊥, then f([M])=λn.up(λx n.M)(here there is some overloading in the use of λ,sinceλn is a semantic lambda whileλx n is syntactic).Depending on the choice of n we may bind a variable free in M,therefore the semantics ofλRemark.We can provide an informal justification for the choice of D .The objects of D correspond to the states of a name-counter:state m means that m names,say x 0,...,x m −1,have been created so far.For the choice of morphisms the justification is more technical:it is almost forced when one wants D(exp m ,exp )to be isomorphic to the set of λo -terms whose free variables are included in {x 0,...,x m −1}.In fact,the natural way of interpreting exp in Dis with a functor s.t.exp (m )=the set of λo -terms with free names among those available at state m .If we require F =Y (1),i.e.the image of 1∈D via the Yoneda embedding,and m to be the product in D of m copies of 1,then we have D(exp m ,exp )= D (Y (1)m ,Y (1))= D (Y (m ),Y (1))=D (m,1)=exp (m ).Therefore,we can conclude that D (m,n )=exp (m )n .Moreover,to define composition in D we are forced to take λo -terms modulo α-conversion.3.2The static categoryWe define D as the functor category Cpo D op ,which is a variant of the more familiar topos of presheaves Set D op .Categories of the form W(where W is a small category)have been used in [Ole85]for modeling local variables in Algol-like languages. Wenjoys the following properties:–it has small limits and colimits (computed pointwise),and exponentials;–it is Cpo -enriched,thus one can interpret fix-point combinators and solve recursive domain equations by analogy with Cpo ;–there is a full and faithful embedding Y :W → W,which preserves limits and exponentials.This is basically the Yoneda embedding Y (w )=W ()=X has left and right adjoints.Since D has a terminal object,∆:Cpo → D is full and faithful,and its right adjoint is the global section functor Γ: D →Cpo s.t.ΓF = D (1,F )=F (0).A description of several constructions in Wrelevant for denotational semantics can be found in [Ten91].Here we recall only the definition of exponentials.Definition 2.The exponential object G F in Wis the functor s.t.–G F (w )is the cpo of families s ∈ f :w →w Cpo (F w ,Gw )ordered pointwiseand satisfying the compatibility conditionw 'g in W implies F w 1Gg in Cpo–(G F fs )g =s f ◦g for any w E w E w in W .We recall also the notion of ω-inductive relation in a Cpo -enriched functor category W,which is used in the correctness proof.Definition3.Given an object X∈ W,a(unary)ω-inductive relation R⊆X in W consists of a family R w⊆Xw|w∈W ofω-inductive relations in Cpo satisfying the monotonicity condition:–f:w →w in W and x∈R w⊆Xw implies Xfx∈R w ⊆Xw .3.3Interpretation of P CF2By analogy with Section1,we parameterize the interpretation of P CF2in D w.r.t.a strong monad T on Cpo satisfying the additional properties stated in Note1.Any such T induces a strong monad T D op on D satisfying the same additional properties.With some abuse of language we write T for its pointwise extension(T D op F)(m)=T(F(m)).In the proof of correctness we take T X=X⊥,since the monad has to account only for the possibility of non-termination at specialization-time,while the inter-pretation ofλs into a suitable metalanguage with computational types(which play only a minor role).The key differences w.r.t.the interpretation/translation of Section2are:the interpretation of exp(which is not the image of a cpo via the functor∆),and the expression-building operation buildconst:∆(const)→exp s.t.buildconst via the isomorphism D(∆(const),exp)∼=Cpo(const,Λ(0)) induced by the adjunction∆ Γ.•build@n:Λ(n),Λ(n)→Λ(n)is the function M1,M2→M1@M2which builds an application.Alternatively, one can define buildfix and buildλ:exp exp→exp is the trickiest part and is defined below.–the interpretation of static operations/constants is obvious,in particular wehave least fixed-points because D is Cpo -enriched.–( ift e )s =let x ⇐e s in [builds =[buildM ⇐op:code code →code is defined in terms of buildλ:exp exp →expwe use the following fact,which is an easy consequence of Yoneda’s lemma.Lemma 4.For any u ∈W and F ∈ Wthere is a natural isomorphism between the functors F Y (u )and F (λamounts to a natural transformation from D (,1).We describe buildλm E(λx m .M )∈Λ(m )in Cpo n σT◦(σ+1)c build ◦σObserve that D (),the substitution (σ+1):m +1→Λ(n +1)is like σon m and maps m to x n ,while the commutativity of the diagram follows from (λx n .M [σ+1])≡α(λx m .M )[σ].To define λ:T (exp )T (exp )→T (exp )in a metalanguage with computationaltypes asλλ(f )]Remark.The category D has two full sub-categories D and Cpo,which have a natural interpretation:D corresponds to dynamic types,while Cpo corre-sponds to pure static types,i.e.those producing no residual code at special-ization time(e.g.base).A key property of pure static expressions is that they cannot depend on dynamic expressions.Semantically this means that the canon-ical map(∆X)→(∆X)Y(u),i.e.x→λy:Y(u).x,is an isomorphism.In fact, by Lemma4(∆X)Y(u)is naturally isomorphic to(∆X)(φfrom P CF2toλo,i.e.τ P CF2 e:τimpliese)φ=op eφand( ift e)φ=eφ.By composing the translationφwith the interpretation I o we get an interpretation of I1of P CF2 in Cpo,where every type is interpreted by the cpo D=(const+(D→D))⊥. At this stage we can state two correctness criteria(thefirst being a special case of the second),which exploit in an essential way the functor category structure:–Given a closed P CF2-expression∅ e:code,its I2interpretation is a global element d of exp⊥∈ D,and therefore d0∈Λ(0)⊥.Correctness for e means: d0=up(M)implies[[M]]o=[[eφ]]o∈D,for any M∈Λ(0).–Given an open P CF2-expression x=x0,...,x n−1, its I2interpretation is a morphism f:exp n⊥→exp⊥,and therefore f n:Λ(n)n⊥→Λ(n)⊥.Correctness for e means:f n(up(x0),...,up(x n−1))=up(M) implies[[x eφ]]o:D n→D,for any M∈Λ(n).The proof of correctness requires a stronger result,which amounts to prove that the two interpretations of P CF2are logically related.However they live in different categories.Therefore,before one can relate them via a(Kripke)logical relation R between typed applicative structures(see[MM91]),they have to be moved(via limit preserving functors)to a common category E.P CF2ˆ!=∆–E is the category whose objects are pairs m∈D,ρ∈D m ,while morphisms from m,ρ → n,ρ are thoseσ:m→n in D s.t.ρ =[[σ]]ρ–π:E→D is the obvious projection functor m,ρ →m.the Kripke logical relation R is a family of ω-inductive relations (see Definition 3)R τin Edefined by induction on the structure of types τin P CF 2.base R base m,ρ ⊂const ⊥×D s.t.⊥R m,ρ d and up (c )R m,ρ d ∆⇐⇒d =up (inl c )code R code m,ρ ⊂Λ(m )⊥×D s.t.⊥R m,ρ d and up (M )R m,ρ d ∆⇐⇒d =[[M ]]ρWe must check that R code satisfies the monotonicity property of a Kripke re-lation,i.e.σ: m,ρ → n,ρ in E and up (M )R code n,ρ d implies up (M [σ])R code m,ρ d .This follows from ρ =[[σ]]ρ,i.e.from the definition of morphism in E ,and[[M [σ]]]ρ=[[M ]][[σ]]ρ,i.e.the substitution lemma for the interpretation of λo .More diagrammatically this means DE code R code D mm,ρ up (M [σ])R m,ρ [[M [σ]]]ρn σc up (M )code (σ)T Since @2up (M 2)∆=up (M 1@M 2)R m,ρ d 1@1d 2∆=d 1@λ:(code→code)→code is the most delicate one.Suppose that fR code→codem,ρg,we have to prove thatλm (f)∈Λ(m)⊥•λm (f)=up(λx m.M)when up(M)=fπ:m+1→m(up x m)∈Λ(m+1)⊥.We can ignore thefirst case,since whenλ:code,code→code andλGomard’s patched functor categorySet Set D opexp NΛ(n)at stage n(exp N)(exp N)Λ(n+1)at stage n ]]not definedR code Rρ:N→Dcorrectness proof not meaningful–The functor category interpretation is very similar to Gomard’s naive in-terpretation,when it comes to the definition of[[code]]and R code,though more care is taken in spelling out what object variables may occur free in an object expression.–The advantage of working in a functor category becomes apparent in the interpretation code→code,this explains also why the functor category can handle the interpretation ofλ[JGS93]Neil D.Jones,Carsten K.Gomard,and Peter Sestoft.Partial Evaluation and Automatic Program Generation.Prentice Hall International,1993. [Law63] wvere.Functorial semantics of algebraic theories.Proc.Nat.Acad.Sci.U.S.A.,50,1963.[Mit96]John C.Mitchell.Foundations of Programming Languages.The MIT Press, Cambridge,MA,1996.[MM91]J.Mitchell and E.Moggi.Kripke-style models for typed lambda calculus.Journal of Pure and Applied Algebra,51,1991.[Mog91] E.Moggi.Notions of computation and rmation and Computa-tion,93(1),1991.[Mog97a] E.Moggi.A categorical account of two-level languages.In MFPS XIII, ENTCS.Elsevier,1997.[Mog97b] E.Moggi.Metalanguages and applications.In Semantics and Logics of Computation,Publications of the Newton Institute.CUP,1997.[MW85] A.Meyer and M.Wand.Continuation semantics in typed lambda calculus.In R.Parikh,editor,Logics of Programs’85,volume193of LNCS.SpringerVerlag,1985.[NN92] F.Nielson and H.R.Nielson.Two-Level Functional Languages.Number34 in Cambridge Tracts in Theoretical Computer Science.CUP,1992.[Ole85] F.J.Oles.Type algebras,functor categories and block structure.In M.Nivat and J.C.Reynolds,editors,Algebraic Methods in Semantics,1985.[OT92]P.W.O’Hearn and R.D.Tennent.Semantics of local variables.In Appli-cations of Categories in Computer Science,number177in L.M.S.LectureNotes Series.CUP,1992.[PS93] A.M.Pitts and I.D.B.Stark.Observable properties of higher order functions that dynamically create local names,or:What’s new?In Math.Found.ofComp.Sci.’93,volume711of LNCS.Springer Verlag,1993.[Ten91]R.D.Tennent.Semantics of Programming Languages.Prentice Hall,1991. [Wan93]Mitchell Wand.Specifying the correctness of binding-time analysis.Journal of Functional Programming,3(3):365–387,July1993.。
Higher-order matching and tree automata

fcomon,jurskig@lsv.ens-cachan.fr
1 Introduction
A solution of an equation s = t where s; t are two terms of the simply typed lambda calculus is an assignment to the free variables of s; t such that (s) and (t) are equal modulo -reduction and equivalence. Finding a solution (if one exists) is known as higher-order uni cation and was shown undecidable some time ago 5]. The higher-order matching problem consists in deciding the existence of a solution when t does not contain any free variables. This problem is still open. In a classical way, we can associate to each type (and to each term of that type) an order: basic types o have order 1 and if = 1 ; : : : ; n ! o, then the order of is one plus the maximum of the orders of 1 ; : : : ; n . If the order of all the free variables of s is smaller or equal to n, we get a matching problem of order n. For instance, rst-order matching (as rst-order uni cation) is decidable and there are actually either 1 or 0 solution to each matching problem. At order two, matching is again decidable (see e.g. 7]) and the number of solutions is, roughly, nite (up to -conversion and if we discard the variables whose value is irrelevant and hence may be assigned to any term). Third-order matching is again decidable (see 2]), however the set of solutions might be in nite (modulo -conversion) as shown by the example: x( y:y) = a where a is a constant of basic type. Then the solutions are the terms x1 :xn (a) 1 where n is any natural number. This example also shows that there is not necessary any nite set of most general solutions (contrary to e.g. rst-order uni cation). 4th order matching has also been shown decidable by V. Padovani 8] and there are partial results for fth order matching 9]. Our purpose here is to relate tree automata and higher-order matching. More precisely, we show how to e ectively compute an automaton which accepts the solutions of any 4th order matching problem. This gives of course a new proof of the decidability of 4th order matching since emptiness of the language recognized by a nite tree automaton can be decided (in linear time). This also provides a representation of the set of all solutions for 3rd or 4th order matching (the known decision algorithms do not yield such representations). This means in particular
2主要程序设计语言的发展

Millennium: C# • Markup/Programming Hybrid Languages
1-4
Genealogy of Common Languages
powerful input/output (for business software)
1-13
Fortran I Overview
• First implemented version of Fortran
– Names could have up to six characters – Post-test counting loop (DO) – Formatted I/O – User-defined subprograms – Three-way selection statement (arithmetic IF) – No data typing statements
• ACM(计算机协会) and GAMM(应用数学和 力学社团) met for four days for design (May 27 to June 1, 1958)
• Goals of the language
– Close to mathematical notation – Good for describing algorithms – Must be translatable to machine code
1-17
Fortran 77
• Became the new standard in 1978
– Character string handling – Logical loop control statement – IF-THEN-ELSE statement
Chapter 1. An Introduction to Lambda-calculus 7

Chapter 3. §3.1. §3.2. §3.3. §3.4.
Lambda Calculus revisited Coalgebras The Category of Coalgebras Bi.5. §3.6.
The Flattening Lemma References A Coalgebraic Approach to Lambda-calculus
Chapter 5. Appendix A. Appendix B. §B.1. §B.2.
The Proof of Proposition 4.3.2 The Proof of Proposition 4.4.2 Bibliography
Appendix.
Introduction
Wiskunde is een zeer respectabele wetenschap, hoewel men bij de beoefening ervan kan stuiten op perversiteiten, radicale idealen, duistere motieven en smerige integralen (J. F. A. A. Nagel, RU Leiden) Lambda-calculus is a theory often used in computer science. Its applications are manifold, ranging from proof-checkers to functional programming languages. Precisely because of these applications, infinitary lambdacalculus has recently become of interest among others at the Free University of Amsterdam. In this thesis I will use a new approach to describing infinitary lambdacalculus; using coalgebraic techniques I hope to find a natural way to describe infinite terms and the operations on these. The objectives in writing this thesis were not restricted to describing my results. Above all, I have tried to write something that is understandable to a somewhat broader public than just myself. In order to accomplish this, a large part of thesis consists of introductory material on the theories used for my description. In the first chapter the concept of lambda-calculus will briefly be described. This chapter will merely explain the basics of the pure lambda calculus without so much as hinting at other lambda-calculi such as the typed lambda-calculus, the polymorphic lambda-calculus, and so on. Any trade-offs that had to be made between formal completeness and understandability were made in favor of the latter. The next chapter deals with category theory, which forms the basis of coalgebra. Again, only those elements necessary for the final chapter have 5
Anomalies in Instanton Calculus

ANOMALIES IN INSTANTON CALCULUS
arXiv:hep-th/9411049v3 11 Jan 1995
Damiano Anselmi Lyman Laboratory, Harvard University, Cambridge MA 02138, U.S.A. Abstract I develop a formalism for solving topological field theories explicitly, in the case when the explicit expression of the instantons is known. I solve topological Yang-Mills theory with the k = 1 Belavin et al. instanton and topological gravity with the Eguchi-Hanson instanton. It turns out that naively empty theories are indeed nontrivial. Many unexpected interesting hidden quantities (punctures, contact terms, nonperturbative anomalies with or without gravity) are revealed. Topological Yang-Mills theory with G = SU (2) is not just Donaldson theory, but contains a certain link theory. Indeed,
不定积分的符号定义问题

不定积分的符号定义问题
在很多教材⾥\int_{}^{}{f(x){dx}}都被定义成是f(x)的所有原函数的集合,如《数学分析教程》,第⼆版,常庚哲,史济怀,p228:
既然\int_{}^{}{f(x){dx}}是⼀个集合,那么根据定义来看应该有
\int_{}^{}{f(x)dx = \{ F(x) + c:c \in R\}}
⽽不是第⼆个红框⾥⾯的内容。
鉴于实际应⽤过程中\int_{}^{}{f(x){dx}}仍然被等同于F(x) + c,如:
那么“\int_{}^{}{f(x){dx}}被定义为f(x)的原函数的⼀般式”更为合理,正如The Fundamentals of Mathematical Analysis, Volume 1, 1st Edition, G. M. Fikhtengol'ts, p300(中译本:菲赫⾦哥尔茨《数学分析原理》)⾥所说的那样
Introduction to Calculus and Analysis Volume I, Reprint of the 1989 edition, Richard Courant, Fritz John, p189⾥也表达了同样的观点
上⾯说到的这个问题,国内的另外两本数学分析书上也同样存在:
数学分析,第⼆版,陈纪修,於崇华,⾦路,p242
数学分析(上册),第四版,华东师范⼤学数学系,p177
国外的有些书上也存在这种问题,如
Thomas’ calculus, 14th edition, Joel R. Hass, Christopher E. Heil, Maurice D. Weir , p232
Processing math: 0%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a r X i v :0712.3088v 2 [c s .L O ] 19 D e c 2007Clones and GenoidsinLambda Calculus and First Order LogicZhaohua Luo Content :0.Introduction.1.Genoids.2.Clones.3.Binding Algebras mbda Calculus.5.First Order Logic 6.Clones Over A Subcategory.7.Relate Work.IntroductionA genoid (A,G )consists of a monoid G with an element +,a right act A of G with an element x ,such that for any a ∈A and u ∈G there is a unique element [a,u ]∈G such that x [a,u ]=a and +[a,u ]=u .A genoid represents a category with two objects such that one is the dense product of itself with the other.Denote by Act G the category of right acts of G.The infinite sequence offinite powers of A in Act G determines a Lawvere theory T h(A,G):A0,A,A2,A3,...A genoid may be viewed as a Lawvere theory with extra capacity provided by G.For any right act P of G,we define a new right act P A=(P,◦),which has the same universe as P,but the action for any u∈G is defined by a◦u=a[x,u+]. Let ev:P A×A→P be the map defined by ev(p,a)=p[a,e]for any p∈P and a∈A.ThenΛ:hom(T×A,P)→hom(T,P A)defined by(Λf)t=f(t+,x) for any t∈T is bijective,with the inverseΛ′:hom(T,P A)→hom(T×A,P)defined by(Λ′g)(t,a)=ev(g(t),a).Thus(P A,ev)is the exponent in the cartesian closed category Act G.In particular if T=P=A we obtain a canonical bijectionΛ:hom(A×A,A)→hom(A,A A).This is the starting point of lambda calculus.We define an extensive lambda genoid to be a genoid(A,G)together with two homomorphismsλ:A A→A and•:A×A→A such that(Λ•)λ=id A (β-conversion)andλ(Λ•)=id A(η-conversion).This means that A and A A are isomorphic as right acts of G.Conversely,any genoid(A,G)such that A and A A are isomorphic determines an extensive lambda genoid.A quantifier algebra of a genoid(A,G)is a Boolean algebra P which is also a right act of G with Boolean algebra endomorphisms as actions,together with a homomorphism∃:P A→P such that∃(p∨q)=(∃p)∨(∃q)and p<(∃p)+ for any p,q∈P.The study of afirst order theory can also be reduced to the study of a quantifier algebra for a genoid(A,G).We say a genoid(A,G)is a clone if G is the countable power Aωof A.Alge-braically the class of clones forms a(non-finitary)variety.A general theory of clones over any full subcategory of a category is presented at the end of this paper.The theory of clones considered in this paper originated from the theory of monads.Two equivalent definitions of monads,namely monads in clone form and monads in extension form given by E.Mane[7],can be interpreted as only defined over a given subcategory of a category.These are clones in al-gebraic form and clones in extension form over a subcategory respectively.It turns out that these two forms of clones are no longer equivalent unless the subcategory is dense.But morphisms of clones,algebras of clones,and mor-phisms of algebras can all be defined for these two types of clones.Since manyfamiliar algebraic structures,such as monoids,unitary Menger algebras,Law-vere theories,countable Lawvere theories,classical and abstract clones are all special cases of clones over various dense subcategories of Set,the syntax and semantics of these algebraic structures can be developed in a unified way,so that it is much easier to extend these results to many-sorted sets.1GenoidsA genoid theory is a category(A,G)of two objects together with two mor-phisms x:G→A and+:G→A such that(G,x,+)is the product of A and G,i.e.G=A×G.We also assume that G is a dense object,although this is not essential.A left algebra of(A,G)is a functor from(A,G)to the category Set of sets preserving the product.A morphism of left algebras is a natural transformation.Recursively we haveG=A n×G=A×...×A×Gfor any positive integer n.If G is the countable power of A,i.e.G=Aω=A×A×...then we say that(A,G)is a clone theory.Let A=hom(G,A)and G=hom(G,G).Then G is a monoid and A is a right act of G.For any pair(a,u)∈A×G let[a,u]:G→G be the unique morphism such that x[a,u]=a and+[a,u]=u.Then u=[xu,+u]for any u∈G.Definition1A genoid(A,G,x,+,[])consisting of a monoid(G,e),a right act A of G,x∈A,+∈G,and a map[]:A×G→G such that for any a∈A and u∈G we have(G1)x[a,u]=a.(G2)+[a,u]=u.(G3)u=[xu,+u].A genoid is simply denoted by(A,G).Clearly any genoid theory(A,G)deter-mines a genoid(A,G).Since we assume G is a dense object,(A,G)is uniquely determines by(A,G).Conversely if(A,G)is a genoid then the subcategory of right acts of G generated by A and G is a genoid theory.Hence the notions of genoid theory and genoid are equivalent.Remark2Genoids form a variety of2-sorted heterogeneousfinitary algebras with universes A and G.A genoid(A,G)is called standard if it is generated by A as a2-sorted algebra.Suppose(A,G)is a genoid.We have e=[x,+]and[a,u]v=[au,vu]for any a∈A and u∈G.We shall write[a1,a2,..a n,u]for[a1,[a2,[...[a n,u]...]]].Let x1=x,x i+1=x i+for any i>0.Then axiom(G3)extends tou=[x1u,x2u,...,x n u,+n u]for any n>0.It is easy to define a many-sorted genoid for a nonempty set S of sorts:Definition3An S-genoid theory is a category({A s}s∈S,G)of objects{A s}s∈S and G,together with morphisms{x s:G→A s}s∈S and{+s:G→G}s∈S such that(G,x s,+s)is the product of A s and G for all s∈S,and x s+t=x s, +s+t=+t+s for any distinct s,t∈S.We also assume that G is a dense object.A left algebra of({A s}s∈S,G)is a functor from this category to Set preserving the products.Definition4An S-genoid is a pair(A,G)consisting of a monoid G and a set A={(A s,G,x s,+s,[]s)}s∈S of genoids such that x s+t=x s and+s+t=+t+s for any two distinct elements s,t∈S.Suppose(A,G)is an S-genoid.For any s∈S letκs n:G→(A s)n be the map sending each u∈G to[x s1u,x s2u,...,x n u]s∈(A s)n.Let(T,n)be a pair consisting of afinite subset T of S and an integer n>0.We say an element p of P has afinite support(T,n)(or p has afinite rank n)if pu=pv for anyu,v∈G withκsn (u)=κs n(v)for any s∈T.We say p has afinite rank0(orp is closed)if pu=pv for any u,v∈G.An element of P is calledfinitary if it has afinite support.We say P is locallyfinitary if any of its element is finitary.We say(A,G)is a locallyfinitary genoid if A is locallyfinitary as a right act of G.Example1.1An algebraic genoid is a monoid G together with two elements x,+∈G such that xx=+x=x,and(xG,G,x,+)is a genoid.Algebraic genoids form afinitary variety.Example1.2An algebraic S-genoid with a zero element0is a monoid G with a zero element0together with a set{x s,+s}s∈S of pairs of elements ofG such that1.x s x t=0for any distinct s,t∈S.2.+s x t=x t x t=x t for any s,t∈S.3.(A,G)is an S-genoid with A={(x s G,G,x s,+s)}s∈S.Algebraic S-genoids form afinitary variety.2ClonesLet N be the set of positive integers.Definition5A clone theory over N is a category(A,G)of two objects to-gether with an infinite sequence of morphisms x1,x2,..from G to A such that (G,{x1,x2,..})is a countable power of A.A left algebra of(A,G)is a functor from(A,G)to Set preserving the countable power.Let A=hom(G,A)and G=hom(G,G).Then G is a monoid and A is a right act of G.For any infinite sequence a1,a2,....of elements of A let[a1,a2...]∈G be the unique morphism such that x i[a1,a2...]=a i for any integer i>0.Then u=[x1u,x2u,...]for any u∈G.Any clone theory determines a genoid theory with x=x1,and+=[x2,x3,...].Definition6A clone in extension form over N is a nonempty set A such that(i)The set A∗of all the infinite sequences[a1,a2,...]of elements of A is a monoid with a unit[x1,x2,...].(ii)A is a right act of A∗.(iii)x i[a1,a2,...]=a i for any[a1,a2,...]and i>0.Any clone A in extension form determines a genoid(A,A∗,x1,+,[])with +=[x2,x3,...]and[a1,[b1,b2,..]]=[a1,b1,b2,..].Thus we may speak of locally finitary clones.Conversely,assume(A,G)is a any genoid.Denote by F(A) the set offinitary elements of A.For any a∈F(A)with afinite rank n>0 and[a1,a2,...]∈F(A)∗definea[a1,a2,...]=a[a1,a2,...,a n,e],which is independent of the choice of n.Let[a1,a2,...][b1,b2,...]=[a1[b1,b2,...],a2[b1,b2,...],...].Then F(A)∗is a monoid with the unit[x1,x2,...],F(A)is a right act of A∗,and x i[a1,a2,...]=a i.Thus F(A)is a locallyfinitary clone.If A=F(A)is locally finitary then we have a canonical homomorphism of genoids(A,G)→(A,A∗) sending each u∈G to[x1u,x2u,...x n u,...].Remark7Clones form a variety of infinitary algebras with universe A. Remark8The notion of a locallyfinitary clone is equivalent to that of a Lawvere theory(without the0-ary object).Definition9Let A be a clone.A left algebra of A(or a left A-algebra)is a set D together with a multiplication A×D N→D such that for any a∈A, [a1,a2,...]∈A N and[d1,d2,...]∈D N1.(a[a1,a2,...])[d1,d2,...]=a([a1[d1,d2,...],a2[d1,d2,...],...].2.x i[d1,d2,...]=d i.Remark10Left algebras of clones are main objects of study in universal algebra(cf.[8]).Definition11A clone in algebraic form over N is a nonempty set A such that the set A N of maps from N to A is a monoid and(ru)v=r(uv)for any maps r:N→N and u,v:N→A.Remark12Since N is dense in Set,one can show easily that the two forms of clones over N are equivalent.Therefore in the following we shall not distin-guish these two types of clones.3Binding AlgebrasLet(A,G)be a genoid.The mapδ:G→G sending u to[x,u+]is an endomorphism of monoid G.Let−=[x,e].One can show that(δ,+,−)is a monad on the one-object category determined by the monoid G,as we have +−=(δ+)−=e and−−=(δ−)−.The Kleisli category of this monad is the monoid(G,∗)with u∗v=u[x1,v].If P is any right act of G denote by P A the new right act(P,◦)of G defined by p◦u=p(δu)=p[x,u+]for any p∈P and u∈G.Let ev:P A×A→P be the map defined by ev(p,a)=p[a,e].DefineΛ:hom(T×A,P)→hom(T,P A) by(Λf)t=f(t+,x)for any t∈T,andΛ′:hom(T,P A)→hom(T×A,P)by (Λ′g)(t,a)=ev(g(t),a).Then bothΛ′ΛandΛΛ′are identities(which implies thatΛis bijective).Thus(P A,ev)is the exponent in the the cartesian closed category Act G of right acts of G.Let∆:Act G→Act G be the functor sending each act P to P A,and each morphism f:P→Q to f:P A→Q A.The actions of+and−induces two natural transformations+:Id→∆and−:∆2→∆.It is easy to see that (∆,+,−)is a monad on Act G.Definition13A binding operation is a homomorphism P A→P.A cobind-ing operation is a homomorphism P→P A.Remark14We assume y,z,w,...,y1,y2,...,z1,z2,...∈{x1,x2,x3...},which are called syntactical variables.Supposeσis a binding operation.The tradi-tional operationσx i:P→P(for each variable x i)is defined as the derived operation:σx i.p=σ(p[x2,x3,...,x i,x1,+i+1]).If y=x i thenσy.p meansσx i.p.Example3.1For any p∈P we have1.σx1.p=σ(p[x1,++])=(σp)+.2.σp=(σx1.p)−.3.If p has afinite rank n>0thenσp has afinite rank n−1.Thusσn p is closed.4.If p is closed thenσp is closed.Definition15Let S be any set of sorts.Let k be a non-negative integer.An S-arity of rank k is afinite sequenceα=<(s1,n1),...,(s k,n k),(s k+1,n k+1)> with s i∈S and n i≥0.Anα-binding operation on a right act P of an S-genoid(A,G)is a homomorphism of right acts(∆s1)n1P×...×(∆s k)n k P→(∆s k+1)n k+1P(assume(∆s i)0P=P),where∆s i is the functor sending each right act Q of G to Q A s i.Definition16An S-signature is a setΣof operation symbols such that for each symbol f∈Σan S-arity ar(f)is attached.AΣ-binding algebra for an S-genoid(G,A)is a right act P of G such that for each symbol f∈Σan ar(f)-binding operation f P on P is assigned.Remark17We shall drop all the references to the elements of S if S is a sin-gleton.Thus an arity of rank k is simply afinite sequenceα=<n1,...,n k,n k+1> of non-negative integers.Example3.21.A binding operation is a<1,0>-operation.2.A cobinding is a<0,1>-operation.3.A homomorphism P2→P is a<0,0,0>-operation.4.A homomorphism P0→P is a<0>-operation,which reduces to a closed element of P.Lambda genoids and predicate algebras defined below are examples of binding algebras.4Lambda CalculusA genoid(A,G)is reflexive if A A is a retract of A(as right acts of G).It is extensive if A A is isomorphic to A.A lambda genoid is a genoid(A,G)together with two homomorphismsλ: A A→A and A2→A of right acts of G.If((λa)+)x=a for any a∈A we say A is a reflexive lambda genoid(or aλβ-genoid).If furthermoreλ((a+)x)=a for any a∈A then we say A is an extensive lambda genoid(or aλβη-genoid). Thus a genoid is reflexive(resp.extensive)iffit is the underlying genoid of a reflexive(resp.extensive)lambda genoid.Remark18Lambda clones(resp.reflective lambda clones,resp.extensive lambda clones)form a variety of(infintary)algebras.The initial lambda clone is precisely the clone determined by terms inλσ-calculus(cf[2]).Remark19Lambda algebraic genoids(resp.reflective lambda algebraic genoids, resp.extensive lambda algebraic genoids)form a variety offinitary algebras.Remark20The classical operationλx i:A→A(for each variable x i)is defined as the derived operation:λx i.a=λ(a[x2,x3,...,x i,x1,+i+1]).If y=x i thenλy.a meansλx i.a.Suppose(A,G)is an extensive lambda genoid.Assume a,b,c∈A and u∈G. Here are some useful formulas:(1)(λa)b=a[b,e].(2)((λa)u)b=a[b,u].(3)(λa+)b=a.(4)(λn a)+n x n...x1=a for any integer n>0.(5)If a has afinite rank n>0thenλn a is closed and(λn a)x n...x1=a.Thus(λn a)a n...a1=(λn a)x n...x1[a1,...,a n,e]=a[a1,...,a n](6)An element a has afinite rank n>0if and only if there is a closed elementc such thata=cx n...x1.The following closed terms play important roles in lambda calculus(notation:λy1...y n.a=λy1.(λy2.(..(λy n.a)...)).)I=λy.y=λx1.K=λyz.y=λλx2.S=λyzw.yw(zw)=λλλx3x1(x2x1).It follows from(5)we haveI a=x1[a,e]=a.K ab=x2[b,a,e]=a.S abc=(x3x1(x2x1))[c,b,a,e]=ac(bc).Definition21Let S be a nonempty set carrying a binary operation→.An S-simply typed lambda genoid is an S-genoid(A,G)together with homomor-phisms{λs:(A t)A s→A s→t}and{A s→t×A s→A t}such that for any a∈A t and c∈A s→t we have(λs a)+s x s=a andλs(c+s x s)=c.5First Order LogicA predicate algebra of an S-genoid(A,G)is a right act P of G together with homomorphisms of right acts{∃s:P A s→P}s∈S,F:P0→P,and ⇒:P×P→P.Define the following derived operations on P:¬p=(p⇒F),T=¬F,p∨q=(¬p)⇒q,p∧q=¬(p⇒¬q).We say P is a reduced predicate algebra if for any p,q,∈P and s∈S(i)(∨,∧,¬,F,T)defines a Boolean algebra P.(ii)∃s(p∨q)=(∃s p)∨(∃s q).(iii)p<(∃s p)+sA reduced predicate algebra is also called a quantifier algebra.Remark22The class of predicate algebras(resp.quantifier algebras)of a genoid is a variety offinitary algebras.An interpretation of a predicate algebra P is a pair(Q,µ)consisting of a reduced predicate algebra Q and a homomorphismµ:P→Q of predicate algebras.We say p∈P is logical valid(written|=p)if for any interpretation (Q,µ)we haveµ(p)=T.If p,q∈P then we say that p and q are logically equivalent(written p≡q)if(p⇒q)∧(q⇒p)is logically valid.Then≡is a congruence on P.The set of congruence classes of P with respect to the congruence≡is a reduced predicate algebra called the Lindenbaum-Tarski algebra of P.(see[8]for a further development of the theory of predicate algebras).Theorem23Suppose A is a locallyfinitary clone.Any left algebra D of A determines a locallyfinitary reduced predicate algebra P(D N),where P(D N) is the power set of D N.A locallyfinitary predicate algebra of A is reduced iffit belongs to the variety generated by predicate algebras P(D N)for all left algebras D of A.6Clones Over A SubcategoryDefinition24Let N be a full subcategory of a category X.A clone(in ex-tension form,or Kleisli triple)over N is a system T=(T,η,∗−)consisting of functions(a)T:Ob N→Ob X.(b)ηassigns to each object A∈N a morphismηA:A→T A.(c)∗−maps each morphism f:B→T C with B,C∈N to a morphism ∗f:T B→T C,such that for any g:C→T D with D∈N(i)∗f∗g=∗(f∗g).(ii)ηB∗f=f.(iii)∗ηC=id T C.Remark25If N=X we obtain the original definition for a Kleisli triple over a category,which is an alternative description of a monad.Definition26Let N be a full subcategory of a category X.A clone theory in extension form(resp.in algebraic form)over N is a pair(K,T)where K is a category and T is a functor T:K→X(resp.T is a function T:Ob K→Ob X)such that for any A,B,C,D∈N(i)Ob N=Ob K.(ii)K(A,B)=X(A,T B).(iii)f(T g)=fg(resp.r(fg)=(rf)g)for any f∈K(A,B),g∈K(B,C) and r∈N(D,A).Remark27If N is dense then these two forms of clone theory are equivalent. In particular,a clone theory over N=X in both forms corresponds to a monad on X.Remark28Any clone over N determines a clone theory in extension form over N,called its Kleisli category.Conversely any clone theory in extension form over N induces a clone over N(see[8]for details).Example6.1Let X=Set be the category of sets.1.A clone over a singleton is equivalent to a monoid.2.A clone over afinite set is equivalent to a unitary Menger algebra.3.A clone over a countable set is equivalent to a clone over N defined above.4.A clone over the subcategory{0,1,2,...}offinite sets is equivalent to a clone in the classical sense(i.e.a Lawvere theory).Remark291.A clone theory over N=X is equivalent to a monad on X.2.A clone(or a monad)over a one-object category is called a Kleisli algebra.3.Any genoid(A,G)determines a Kleisli algebra since(δ,+,−)is a monad on the one-object category G.7Relate WorkIn classical universal algebra one studies left algebras of a clone over N.Such a clone can be defined in many different ways(see[3][9][10][15]).Our approach to binding algebras and untyped lambda calculus was greatly inspired by[1].For other algebraic approaches to untyped lambda calculus see[2][5][6][12][14][16].Our definition of a quantifier algebra of a genoid was based on Pinter[13](see also[4][11]).References[1]M.Fiore,G.Plotkin,D.Turi,Abstract syntax and variable binding Proceedingsof the14th Annual IEEE Symposium on Logic in Computer Science,LICS’99, (1999)193–202[2] C.Hankin,An Introduction to Lambda Calculus for computer Scientists CollegePublications(February2,2004)[3]P.M.Cohn,Universal Algebra,Kluwer Academic Publishers(1981)[4]J.Cirulis,An algebraization offirst order logic with terms Colloq.Math.Soc.J.Bolyai54,Algebraic logic,1991,125146[5] B.Jacobs,Simply typed and untyped lambda calculus revisited In:M.P.Fourman,P.T.Johnstone and A.M.Pitts(eds.)Applications of Category Theory in Computer Science(LMS177,Camb.Univ.Press,1992),119-142.[6]M.Maggesi,A.Hirschowitz,The algebraicity of the lambda-calculus preprint2007arXiv:0704.2900.[7] E.Manes,Algebraic Theories,Springer-Verlag,1976.[8]Z.Luo,Clone theory,its syntax and semantics,and applications to lambdacalculus and algebraic logic(2007).[9]W.D.Neumann,Representing varieties of algebras by algebras,J.Austral.Math.Soc.11(1970),1–8.[10]B.Pareigis and H.Rohrl,Left linear theories–A generalization of moduletheory,Applied Categorical Structures.Vol.11,No.2,(1994),145-171. [11]B.Plotkin,Algebraic logic,varieties of algebras and algebraic varietiesarXiv:math/0312420[12]A.Obtulowicz,A.Wiweger,Categorical,functorial,and algebraic aspects ofthe.type-free lambda calculus Banach Center Publications9,Warsaw(1982), 399-422[13]C,C.Pinter,A simple algebra offirst order logic,Notre Dame Journal of FormalLogic,Vol.XIV,No.3,(1973),361-366.[14]A.Salibra,R.Goldblatt Afinite equational axiomatization of the functionalalgebras for the lambda calculus Information and Computation,vol.148,n.1, pp.71-130(1999).[15]B.M.Schein,V.S.Trohimenko,Algebras of multiplace functions,Semi-groupForum17,(1979),1-64[16]P.Selinger,The lambda calculus is algebraic Journal of Functional Programming(2002),12:549-566。
