江苏扬州市2016届高三四模试题(5月)数学 Word版含答案
江苏省扬州中学高三5月第四次模拟考试数学含答案【精选】.doc

扬州中学高三数学试卷必做题部分一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置.......上.. 1、已知集合{1,0,2},{21,},A B x x n n Z =-==-∈则A B ⋂= ▲ .2、已知复数1212,2z i z a i =-=+(其中i 是虚数单位,a R ∈),若12z z ⋅是纯虚数,则a 的值为 ▲ .3、从集合{1,2,3}中随机取一个元素,记为a ,从集合{2,3,4}中随机取一个元素,记为b ,则a b ≤的概率为 ▲ .4、对一批产品的长度(单位毫米)进行抽样检测,样本容量为400, 右图为检测结果的频率分布直方图,根据产品标准,单件产品长度 在区间[25,30)的为一等品,在区间[20,25) 和[30,35)的为二等品, 其余均为三等品,则样本中三等品的件数为 ▲ .5、运行右面的算法伪代码,输出的结果为S= ▲ .6、若双曲线2222:1(0,0)x y C a b a b -=>>10则双曲线C 的渐近线方程为 ▲ .7、正三棱柱ABC -A 1B 1C 1的底面边长为2,3D 为BC 中点,则三棱锥A -B 1DC 1的体积为 ▲ .8、函数cos(2)()y x ϕπϕπ=+-≤≤的图象向右平移2π个单位后,与函数sin(2)3y x π=+的图象重合,则ϕ= ▲ .9、若函数2()ln()f x x x a x =+为偶函数,则a = ▲ .10、已知数列{}n a 与2n a n ⎧⎫⎨⎬⎩⎭均为等差数列(n N *∈),且12a =,则10=a ▲ . 11、若直线20kx y k --+=与直线230x ky k +--=交于点P ,则OP 长度的最大值为 ▲ .12、如图,已知4AC BC ==,90ACB ∠=o ,M 为BC 的中点,D 为以AC 为直径的圆上一动点,S 011011(1)Pr int For i FromTo Step S S i i End ForS ←←++则AM DC ⋅u u u r u u u r的最小值是 ▲ .13、已知函数()()22,22,2x x f x x x ⎧-≤⎪=⎨->⎪⎩ ,函数()()2g x b f x =-- ,其中b R ∈,若函数 ()()y f x g x =- 恰有4个零点,则实数b 的取值范围是 ▲ .14、已知,x y 均为非负实数,且1x y +≤,则22244(1)x y x y ++--的取值范围为 ▲ .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答.解答时应写出文字说明、证明过程或演算步骤.15、已知ABC ∆的三个内角,,A B C 所对的边分别为,,a b c ,向量(1,2)m =u r ,2(cos2,cos )2An A =r ,且1m n ⋅=u r r.(1)求角A 的大小;(2)若223b c a +==,求sin()π-4B 的值16、如图,四棱锥P —ABCD 中,四边形ABCD 为菱形,P A ⊥平面ABCD ,BD 交AC 于点E ,F 是线段PC 中点,G 为线段EC 中点. (1)求证:FG//平面PBD ; (2)求证:BD ⊥FG .17、已知椭圆)0(1:2222>>=+b a b y a x C 的左焦点为F ,上顶点为A ,直线AF 与直线023=-+y x 垂直,垂足为B ,且点A 是线段BF 的中点.(1)求椭圆C 的方程;(2)若M ,N 分别为椭圆C 的左,右顶点,P 是椭圆C 上位于第一象限的一点,直线MP 与直线4=x 交于点Q ,且9MP NQ =u u u r u u u rg ,求点P 的坐标.18、中国古建筑中的窗饰是艺术和技术的统一,给人以美的享受.如图为一花窗中的一部分,呈长方形,长30 cm ,宽26 cm ,其内部窗芯(不含长方形边框)用一种条形木料做成,由两个菱形和六根支条构成,整个窗芯关于长方形边框的两条对称轴成轴对称.设菱形的两条对角线长分别为 cm 和y cm ,窗芯所需条形木料的长度之和为L . (1)试用,y 表示L ;(2)如果要求六根支条的长度均不小于2 cm ,每个菱形的面积为130 cm 2,那么做这样一个窗芯至少需要多长的条形木料(不计榫卯及其它损耗)?19、已知函数2()=x x f x e,(1)求函数()f x 的单调区间;(2)当240m e <<时,判断函数2(),(0)x xg x m x e=-≥有几个零点,并证明你的结论;(3)设函数21111()+()()22⎡⎤=-----⎢⎥⎣⎦h x x f x x f x cx x x ,若函数()h x 在()0,+∞为增函数,求实数c 的取值范围.20、已知数列{}n a 中,11a =,前n 项和为n S ,若对任意的*n N ∈,均有n n k S a k +=-(k 是常数,且*k N ∈)成立,则称数列{}n a 为“()H k 数列”. (1)若数列{}n a 为“(1)H 数列”,求数列{}n a 的前n 项和n S ;(2)若数列{}n a 为“(2)H 数列”,且2a 为整数,试问:是否存在数列{}n a ,使得211||40n n n a a a -+-≤对任意2n ≥,*n N ∈成立?如果存在,求出这样数列{}n a 的2a 的所有可能值,如果不存在,请说明理由。
江苏省扬州中学2016届高三4月质量监测 数学 含答案

高三数学试卷一、填空题.(本大题共14小题,每小题5分,共70分.)1. 已知集合M ={0, 1, 2},N ={x |x =2a , a ∈M },则集合M ∩N =___________.2. {0,2}3.若复数z 1=3+4i ,z 2=a +i ,且z 1·错误!是实数(其中错误!为z 2的共轭复数),则实数a =___________.错误!4. 有3个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为_______.错误!5. “m =-1”是“直线mx +(2m -1)y +1=0和直线3x +my +3=0垂直"的___________条件.充分不必要6. 右边程序输出的结果是___________.107.8. 在三棱锥P -ABC 中,D ,E 分别为PB ,PC 的中点,记三棱锥DABE 的体积为V 1,PABC的体积为V 2,则错误!=____________.错误!9. 在平面直角坐标系xOy 中,已知A 、B 分别是双曲线x 2-错误!=1的左、右焦点,△ABC 的顶点C 在双曲线的右支上,则错误!的值是 .-错误!10. 在等差数列{a n }中,a 1+3a 8+a 15=120,则3a 9―a 11的值为_________.4811. 若sin α+2cos α=0,则错误!的值为________.-错误!。
12. 在平面内,若A (1,7)、B (5,1)、M (2,1),点P 是直线OM 上的一个动点,且错误!·错误!=-8,则cos ∠APB =__________.-错误!. 13. 设f (x )是R 上的奇函数,且f (-1)=0,当x >0时,(x 2+1)·f ¢(x )-2x ·f (x )<0,则不等式f (x )>0的解集为________ . (-S ←1 For I From 1 To 5 Step 2∞,-1)∪(0,1).14. 已知△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且BC 边上的高为a ,则错误!+错误!的最大值为______.错误! 15. 已知定义在R 上的函数f (x )存在零点,且对任意m ,n ∈R 都满足f [m ·f (m )+f (n )]=f 2(m )+n ,若关于x 的方程f [ f (x ]-3)=1-log a x (a >0,a ≠1)恰有三个不同的根,则实数a 的取值范围是.___________16. 【分析】:需要函数f [ f (x )]的解析式!∵f (x )存在零点,∴令f (x 0)=0 ∴令m =x 0 ∴f [x 0·f (x 0)+f (n )]=f 2(x 0)+n ∴f [ f (n )]=n ∴x -3=1-log a x 恰有三个不同的根,∴log a x =1-错误! (下略)a >3. 17. 若点P 在曲线C 1:y 2=8x 上,点Q 在曲线C 2:(x -2)2+y 2=1上,点O 为坐标原点,则错误!的最大值是 . 18. 【知识点:抛物线定义、多变量问题、函数求最值问题】 19. 解:注意到圆C 2的圆心恰好为抛物线的焦点F ,因为P 、Q 为两个独立的点,可先考虑一个点动,注意到只有分母有Q ,故先求出|PQ |的最小值为|PF |-1=x p +p2-1=x p +1,20. ∵|OP |2=错误!+错误!=错误!+8x p ∴错误!=错误! 21. 令t =x p +1≥1 ∴y =错误!=错误! (错误!∈(0,1]) 22. ∴错误!=错误!时,y max =错误!=错误!. 二、解答题.(本大题共6小题,共计90分.)23. 如图,斜三棱柱ABC -A 1B 1C 1中,侧面AA 1C 1C ⊥底面ABC ,侧面AA 1C 1C 是菱形,∠A 1AC =60º,E 、F 分别是A 1C 1、AB 的中点. 24. 求证:(1)EF ∥平面BB 1C 1C ;25. (2)平面CEF ⊥平面ABC .1A 1B 1CACE26. 如图,函数y =2cos (ωx +φ)(ω>0,0≤φ≤错误!)的图象与y 轴交于点(0,错误!),周期是π. 27. (1)求ω、φ的值; 28. (2)已知点A (错误!,0),点P 是该函数图象上一点,点Q (x 0,y 0)是PA 的中点,当y 0=错误!,x 0∈[错误!,π]时,求x 0的值. 解:(1)y =2cos(2x +错误!) (2)∵A (错误!,0),Q (x 0,y 0)是PA 中点,y 0=错误!,∴P (2x 0-错误!,错误!). 又因为点P 在y =2cos (2x +错误!)的图象上,∴2cos(4x 0-π+错误!)=错误!.∴cos (4x 0+错误!)=-错误! ∵x 0∈[错误!,π],∴4x 0+错误!∈[2π+错误!,4π+错误!]∴4x 0+错误!=2π+π-错误!或4x 0+错误!=2π+π+错误! ∴x 0=错误!或错误!.29. 如图,已知海岛A 到海岸公路BC 的距离AB 为50㎞,B ,C 间的距离为100㎞,从A 到C ,必须先坐船到BC 上的某一点D ,船速为25㎞/h ,再乘汽车到C ,车速为50㎞/h ,记∠BDA =θ. 30. (1)试将由A 到C 所用的时间t 表示为θ的函数t (θ); 31. (2)问θ为多少时,由A 到C 所用的时间t 最少? 解:(1)∵AD =错误!, ∴A 到D 所用时间t 1=错误!BD =错误!=错误!, CD =100-BD =100-错误!BACDθ∴D 到C 所用时间t 2=2-错误!∴t (θ)=t 1+t 2=错误!+2(θ0<θ<错误!,其中tan θ0=错误!)··························6分 (2)t(θ)=错误!=错误!····································8分 令t(θ)>0,得:cos θ<错误! ∴错误!<θ<错误!;∴当θ∈错误!,错误!时,t (θ)单调递增;同理θ0<θ<错误!,t(θ)<0,t (θ)单调递减·····················12分 ∴θ=错误!,t (θ)取到最小值错误!+2;·························································13分答:当θ=π3时,由A 到C 的时间最少为3+2小时.·····························14分32. 如图,已知点F 1,F 2是椭圆C l :22x +y 2 =1的两个焦点,椭圆C 2:22x +y 2 =经过点F 1,F 2,点P 是椭圆C 2上异于F 1,F 2的任意一点,直线PF 1和PF 2与椭圆C 1的交点分别是A ,B 和C ,D .设AB 、CD 的斜率分别为k 、k 。
2016年5月2016届高三第四次全国大联考(新课标Ⅲ卷)理数卷(解析版)

【学易大联考】2016年第四次全国大联考统考【新课标Ⅲ卷】理科数学试卷第I 卷(共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若复数12z =-,则21z z +在复平面内对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 【答案】D【命题意图】本题考查复数的基本运算及其几何意义,意在考查学生的基本运算能力和对基础知识的掌握程度.2.设全集U R =,集合{}2|760A x x x =--≥, {}|lg(2)(4)B x y x x ==+-,则()U B A = ð( ) A .[4,6) B .]9,4( C .[1,2] D .[2,1]- 【答案】D【命题意图】本题主要考查集合的基本运算,涉及一元二次不等式的求解、对数函数定义域的求法,意在考查学生的基本运算能力.【解析】由2760(1)(7)071x x x x x --≥⇒-+≤⇒-≤≤,即{}|71A x x =-≤≤,又由(2)(4)02x x x +->⇒<-或4x >,即{|2B x x =<-或4}x >, 从而U B ð{}|24x x =-≤≤,故()U B A = ð{}|21x x -≤≤,选D .3.在6与316中间插入n 个数,组成各项和为18916的等比数列,则此数列的项数为( ) A .8 B .7 C .6 D .5【答案】C【命题意图】本题考查等比数列的通项公式及前n 项和公式的应用,意在考查学生的计算能力和对基本公式的熟练应用能力.4.已知圆C :)0(4)2()(22<=-+-a y a x 及直线03:=+-y x l ,若直线l 被圆C 截得的弦长为32,则a 的值为( )A .12--B .2-C .13--D .3-【答案】A【命题意图】本题主要考查直线与圆的位置关系,可利用半径、半弦长及弦心距三者之间的关系进行求解,意在考查数形结合思想的应用.【解析】由于圆C 的半径为2,弦长为32,因此,弦心距为1)3(222=-=d ,即圆心到直线的距离为12|32|=+-a ,解得21±-=a ,又因为0<a ,所以=a 12--,选A5.执行如图所示的程序框图,若输入的2,2a n ==,则输出的q 的值为( ) A .24 B . 25 C .26 D . 27 【答案】A【命题意图】本题考查程序框图的阅读、理解与应用,意在考查学生的识图、读图能力.【解析】运行程序,依次可得:0,0,1,2,p q i i ===≤成立;2,2,20,2p q a i ====,2,i 成立≤;22,24,200,3p q a i ====,2,i 不成立≤,跳出循环体,此时输出24q =.选A .6.已知角ϕ的终边经过点P (-4,3),函数f (x )=sin(ωx +ϕ)(ω>0)的图象的相邻两条对称轴之间的距离等于π2,则f (π4)的值为( ) A .35 B .45 C .35- D .45-【答案】D【命题意图】本题主要考查三角函数的定义,三角函数的图象与性质,诱导公式等,意在考查学生的运算求解能力和对基础知识的综合运用能力.【解析】由题意得,53sin =ϕ,4cos 5φ=-,由函数)(x f 的图象的相邻两条对称轴之间的距离等于π2,可得函数)(x f 的周期π2π2T =?,又2πT ω=,所以2=ω,所以ππ4()sin()cos 425f φφ=+==-.选D .7.设12F F 、是椭圆22221x y a b+=的两个焦点,P 是椭圆上的点,1:2||:||21=PF PF ,且12PF F △为直角三角形,则椭圆的离心率为( )A 或B 或CD 或 【答案】C【命题意图】本题考查椭圆方程中基本量之间的关系,意在考查学生的转化变形能力和对分类讨论思想的熟练应用能力.8.△ABC 中,点D 在BC 上,∠A =60°,若1()4||||AB AC AD k AC AB AB AC λ=+=+,且4AB =,则AD 的长为( )A B . C . D . 【答案】C【命题意图】本题考查单位向量的应用,向量共线的性质,向量的加法等基础知识与基本技能的应用,意在考查学生的转化与化归能力及对一些常用结论的熟知程度. 【解析】由于点D 在BC 上,即D 、B 、C 三点共线,所以13144λλ+=⇒=. 由3344||||AB k k AB AB AB =⇒=,又4AB =,即4AB = ,所以3k =. 所以3()||||AB ACAD AB AC =+, 所以222||9[()2()()()]=||||||||AB AB AC ACAD AB AB AC AC =+⋅+2291+211cos 60+127()⨯⨯⨯⨯= ||AD ⇒=.9.已知一几何体的三视图如图所示,其中,正视图与侧视图完全一样,根据图中的数据,该几何体的表面积为( )A B . C .4 D .6【答案】B【命题意图】本题考查三视图与直观图的转化,几何体的表面积,意在考查学生将三视图转化为直观图的转化能力、计算能力及空间想象能力.10.若n xx )3(3+的展开式中存在常数项,则正整数n 的最小值及相应的常数项分别为( )A .6,280B .6,270C .5,280D .5,270 【答案】D【命题意图】本题考查二项式定理的应用,意在考查学生的计算能力及对公式的理解和掌握程度.【解析】由二项展开式的通项公式得3561C C 3n rr n rr r rr nn T x --+=⋅=⋅⋅,令0653=-r n ,即r n 53=,因为*n ÎN ,所以最小的正整数5=n ,此时3=r ,所以相应的常数项为335C 3270?.选D .11.已知数列{}n a 的前n 项和为n S ,若112a =且21()(1)n n n a n a a n n -=---,则下列四个结论:①1n n a a +>; ②(1)2n n n S ->; ③{}n n a -是增数列; ④{}(1)n n a +是等差数列,其中正确的个数为( )A .1B .2C .3D .4 【答案】C【命题意图】本题主要考查数列的基本运算,数列中的有关概念,意在考查学生综合分析问题、解决问题的能力.【解析】将21()(1)n n n a n a a n n -=---的两边同除以(1)n n -,得1(1)11n n n a na n n -+-=-,又1211a=,所以数列(1)n n a n +⎧⎫⎨⎬⎩⎭是以1为首项,1为公差的等差数列. 所以2(1)1n n n a n n a n n +=⇒=+, 因为2221(1)31021(2)(1)n n n n n n a a n n n n ++++-=-=>++++,所以1n n a a +>,①正确; 因为221111n n n a n n n -=>=-++,所以[0(1)](1)22n n n n n S +-->=,②正确;由22111n n n n na n a n n n n =⇒-=-=+++,所以易得数列{}n n a -为增数列,③正确; 由22(1)1n n n a n a n n =⇒+=+,显然{}(1)n n a +不是等差数列,故④不正确.综上可知,选C .12.设函数()f x =若曲线e 1e 1sin 22y x -+=+上存在点00(,)x y 使得00(())f f y y =成立,则实数a 的取值范围为( )A . 2[0,e e 1]-+ B . 2[0,e e 1]+- C . 2[0,e e 1]-- D . 2[0,e e 1]++ 【答案】C【命题意图】本题主要考查函数与导数的综合问题,意在考查学生的转化与化归能力、运算求解能力以及利用所学知识综合分析问题、解决问题的能力.第Ⅱ卷(非选择题 共90分)二、填空题(每小题5分,满分20分.将答案填在答题纸上)13. 定义在R 上的函数()f x 满足22,0()(1)(2),0x x x f x f x f x x ⎧-≤=⎨--->⎩,则(2016)f 的值为 .【答案】1-【命题意图】本题考查分段函数求值,函数的周期性等知识,意在考查学生对递推式子和函数周期性的应用能力,以及对抽象函数的理解程度.【解析】当0x >时,由)2()1()(---=x f x f x f ,得(+1)()(1)f x f x f x =--,两式相加得(+1)(2)f x f x =--,所以(+3)()f x f x =-,所以()(+6)f x f x =,故20(2016)(6336)(0)021f f f =⨯==-=-.14.已知乒乓球队的10名队员中有3名主力队员,现要派5名参加比赛,3名主力队员一定参加且安排在第一、三、五位置,其余7名队员中选2名安排在第二、四位置,则不同的出场安排有 种. 【答案】252【命题意图】本题主要考查排列、组合的应用,意在考查学生的阅读理解能力和分析问题、解决问题的能力.【解析】先安排3名主力队员在第一、三、五位置,有33A 种方法,再从7名队员中选2名放在第二、四位置上,有27A 种方法,所以不同的出场安排有3237A A 252=种.15.若,x y 满足不等式组⎪⎩⎪⎨⎧≤-≤+≤1222y x y x xy ,则32z x y =+的最大值为 .【答案】72【命题意图】本题考查线性规划的基本应用,意在考查学生的作图能力和数形结合思想.16. 已知双曲线()222210,0x y a b a b-=>>的半焦距为c ,过右焦点且斜率为1的直线与双曲线的右支交于两点,若抛物线24y cx =2(e 为双曲线的离心率),则e 的值为 .【解析】由题意,得抛物线的准线为x c =-,它正好经过双曲线的左焦点,所以准线被双曲线截得的弦长为22b a ,所以222b a =,即2b a =,所以e ==,整理,得422990e e -+=,解得e =或e =1的直线与双曲线的右支交于两点,所以2b a =<1,所以e =. 三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分12分)在ABC △中,角,,A B C 所对的边分别为c b a ,,,且ABC △的面积S 满足2()()S c a b c a b =-++-.(1)求cos C ;(2)若2c =,2cos b a C =,求边长b .【命题意图】本题考查余弦定理、三角形的面积公式等,意在考查学生的灵活变形能力和对基本公式的掌握程度.18.(本小题满分12分)如图,90BCD?o ,⊥==AB CD BC ,1平面BCD ,60ADB ?o ,F E ,分别是AD AC ,上的动点,且AE AFAC AD=. (1)若平面BEF 与平面BCD 的交线为l ,求证://EF l ;(2)当平面⊥BEF 平面ACD 时,求平面BEF 与平面BCD 所成的二面角的余弦值.【命题意图】本题考查线面平行、垂直的判定定理与性质定理,空间向量求解二面角等,意在考查学生的空间想象能力和对基本定理的掌握程度.【解析】(1)由CD EF ADAFAC AE //⇒=, ……………(2分) 又EF ⊄平面BCD ,CD ⊂平面BCD ,所以EF ∥平面BCD , 又EF ⊂平面BEF ,且平面BCD 平面BEF l =,故EF l ∥. ……………(4分)(2)因为AB ^平面BCD ,所以AB DC ^,又BC DC ⊥,所以⊥DC 平面ABC , 所以DC BE ^,又EF CD ∥,所以EF BE ⊥.若平面⊥BEF 平面ACD ,则⊥BE 平面ACD ,所以BE AC ^,由1==CD BC 且90BCD ?o 2=⇒BD ,又60ADB?o ,所以6=AB . ……………(6分)以B 为坐标原点,,BD BA 所在的直线分别为,y z 轴,以过点B 且垂直于BD 的直线为x 轴建立空间直角坐标系,则(0,0,0),A B C ,设(,,)E a a b ,则(,,),(,,BE a a b AC AE a a b ===-,由,aBE ACAC AEb可得∥⎧+-==⎪⎧⋅=⎪⎪⇒⎨⎨⎪⎪⎩==⎪⎩,即E所以可得F,所以BE BF,==……………(8分)设平面BEF的一个法向量为(,,)x y z=m,则0000x yBE zBF zy z+=⎧⋅=++=⎪⇒⇒⎨⋅=+=⎪⎪⎩⎩=mm,取z=,得1,1x y=-=-,所以(1,1,=--m,……………(10分)易知平面BCD的一个法向量为(0,0,1)=n,设平面BEF与平面BCD所成的二面角为θ,则cosθ==,结合图形可知平面BEF与平面BCD.……………(12分)19.(本小题满分12分)某班n名同学的数学小测验成绩的频率分布直方图如图所示,其中,,a b c成等差数列,且分数在[90,100]的有6人.(1)求n的值;(2)若分数在[40,50)的人数是分数在[50,60)的人数的13,现从不及格的人中任意选取3人进行谈话,记分数在50分以下的人数为X ,求X 的分布列和数学期望.【命题意图】本题考查频率分布直方图的应用,离散型随机变量的分布列和数学期望的求解,意在考查整体运算的基本思想,以及学生的阅读理解能力、运算求解能力.(2)由(1)及题意可得0.020.00510.0153a c a c a c +=⎧=⎧⎪⇒⎨⎨==⎩⎪⎩, ……………(6分) 所以分数在[40,50)的有0.0051060=3⨯⨯(人),分数在[50,60)的有0.0151060=9⨯⨯(人),即不及格的有12人.现从中任选3人,记分数在50分以下的人数为X ,则X 的所有可能取值分别为:0,1,2,3,30219393331212C C C C 2127(0),(1),C 55C 55P X P X ======12039393331212C C C C 271(2),(3)C 220C 220P X P X ======.所以,X 的分布列如下表:………………(10分)故X 的数学期为21272713012355552202204EX =⨯+⨯+⨯+⨯=. ……………(12分) 20.(本小题满分12分)已知椭圆22221(0)x y a b a b+=>>的左、右焦点分别为12F F 、,上、下顶点分别是12,B B C 、是12B F 的中点,且11122B F B F ⋅= ,112CF B F ⊥.(1)求椭圆的标准方程;(2)点,M N 是椭圆上的两个动点,过,M N 两点的切线交于点P ,当0PM PN ⋅=时,求点P 的轨迹方程.【命题意图】本题考查椭圆的标准方程及简单的几何性质,直线与椭圆的位置关系等,意在考查学生的基本运算能力及对常用技巧的灵活应用能力.(2)设点()00,y x P ,①当PM x ⊥轴或PM x ∥轴时,对应PN x ∥轴或PN x ⊥轴,可知点(P ±或点(2,P ±. ……………(6分)②当PM 与x 轴不垂直且不平行时,设直线PM 的斜率为k ,则0k ≠,且直线PN 的斜率为1k-,所以直线PM 的方程为00()y y k x x -=-,与22143x y +=联立,得00222220000()(34)8()4()120143y y k x x k x k y kx x y kx x y -=-⎧⎪⇒++-+--=⎨+=⎪⎩,因为直线与椭圆相切,所以=∆0,即222200004()(34)[()3]0k y kx k y kx --+--=,即2220000(4)230x k x y k y --+-=,所以k 是方程2220000(4)230x x x y x y --+-=的一个根, ……………(9分) 同理1k-是方程2220000(4)230x x x y x y --+-=的另一个根,2220002031()74y k x y k x -⋅-=⇒+=-,其中02x ≠±,所以点P 的轨迹方程为227x y +=(2x ≠±),因为点(P ±或点(2,P ±均满足上式.综上可知,点P 的轨迹方程为227x y +=. ……………(12分) 21.(本小题满分12分)已知函数22()(1)ln(1)f x m x n x =+-+.(1)若函数21()()2g x f x nx =-在区间[2,4]上单调递增,且,m n 均为正数,求mn 的取值范围;(2)若函数()f x 的图象在点(0,(0))f 处的切线方程为2(1)y n x n =-+,设2()h x x x b =++,若函数()()f x h x ≥在区间]2,0[上恒成立,求实数b 的取值范围.【命题意图】本题考查导数在函数中的应用,恒成立问题的转化与求解等,意在考查学生的转化与化归能力、运算求解能力以及利用所学知识综合分析问题、解决问题的能力.【解析】(1)由题意可知222211()()=(1)ln(1)22g x f x nx m x n x nx =-+-+-,则2()2(1)1ng x m x nx x'=+--+, 因为函数21()()2g x f x nx =-在区间[2,4]上单调递增,所以()0g x '≥恒成立, …………(2分) 即221112(1)01(1)2(1)2n m m x nx x n x x +--≥⇒≥-++++在区间[2,4]上恒成立,即max 2111[](1)2(1)2m n x x ≥-+++. 由11124513x x ≤≤⇒≤≤+,令1=1t x +, 则221111111=()(1)2(1)22253t t t x x -+-+≤≤++的最大值为49. 故m n 的取值范围为4[,)9+∞. ……………(5分)即实数b 的取值范围为(,22ln 2]-∞-. .……………(12分)请考生在第(22)、(23)、(24)三题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做第一个题目计分.22.(本小题满分10分)选修4-1:几何证明选讲如图,直线ΡQ 与O 相切于点A ,AB 是O 的弦,PAB ∠的平分线AC 交O 于点C ,连接CB 并延长与直线PQ 相交于点Q ,若6AQ =,5AC =.(1)求证:22QC QA BC QC -=⋅; (2)求弦AB 的长.【命题意图】本题主要考查切割线定理,弦切角定理,相似三角形的证明等,意在考查学生的识图能力、运算能力、逻辑推理能力以及对基本定理的掌握程度.【解析】(1)因为PQ 与O 相切于点A ,所以由切割线定理可得: 22()=QA QB QC QC BC QC QC BC QC =⋅=-⋅-⋅,所以22QC QA BC QC -=⋅. …………(5分) (2)因为PQ 与O 相切于点A ,所以PAC CBA ∠=∠.因为PAC BAC ∠=∠,所以BAC CBA ∠=∠,所以5AC BC ==,又6AQ =,22QC QA BC QC -=⋅,所以9QC =(负值不合题意,舍去).由QAB ACQ ∠=∠,AQB CQA ∠=∠易知QAB QCA △∽△,所以AB QAAC QC=,即659AB =,所以103AB =,即弦AB 的长为103. ………………(10分)23.(本小题满分10分)选修4-4:坐标系与参数方程在平面直角坐标系中,以坐标原点为极点,x 轴非负半轴为极轴建立极坐标系.已知直线l 与椭圆C 的极坐标方程分别为cos 2sin 0θθ+=,2224cos 4sin ρθθ=+.(1)求直线与椭圆的直角坐标方程;(2)若点Q 是椭圆C 上的动点,求点Q 到直线l 的距离的最大值.【命题意图】本题主要考查极坐标方程与直角坐标方程的互化,普通方程与参数方程的互化,点到直线的距离的最大值问题等,意在考查学生的转化与化归能力、运算求解能力. 【解析】(1)由cos 2sin 0cos 2sin 020x y θθρθρθ+=⇒+=⇒+=,即直线l 的直角坐标方程为20x y +=. .……………(2分) 又由2222222224cos 4sin 444cos 4sin x y ρρθρθθθ=⇒+=⇒+=+ 22+=14x y ⇒,即椭圆C 的直角坐标方程为22+=14x y . .……………(4分)24.(本小题满分10分)选修4-5:不等式选讲已知不等式|21||1|2x x --+<的解集为{|}x a x b <<.(1)求,a b 的值;(2)已知x y z >>,求证:存在实数k ,使32()4()a b kx y y z x z-+≥---恒成立,并求k 的最大值. 【命题意图】本题主要考查绝对值不等式的求解,不等式恒成立问题等,意在考查学生的化归与转化能力.【解析】(1)(i )当1x <-时,不等式可转化为(21)[(1)]2x x ----+<,得0x >,此时无解; (ii )当112x -≤≤时,不等式可转化为(21)(1)2x x ---+<,得23x >-,此时,不等式的解集为:2132x -<≤; (iii )当12x >时,不等式可转化为21(1)2x x --+<,得4x <,此时,不等式的解集为:142x <<. 由(i )、(ii )、(iii )得不等式的解集为2{|4}3x x -<<,比较即得2,43a b =-=. .……………(5分):。
江苏省扬州中学高三数学5月卷(四模卷)
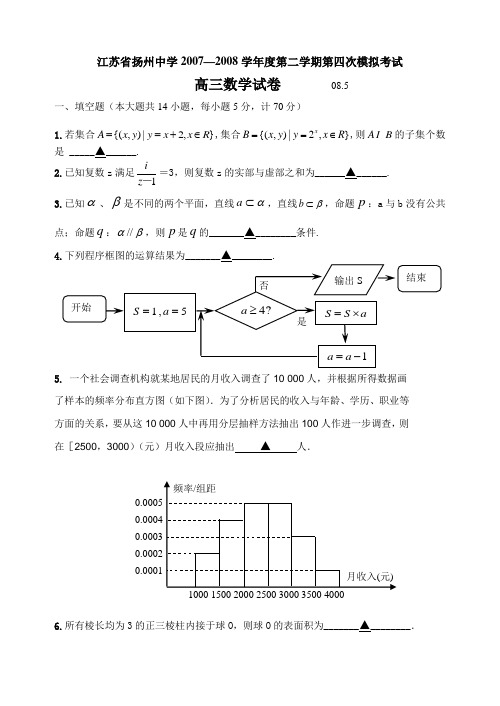
江苏省扬州中学2007—2008学年度第二学期第四次模拟考试高三数学试卷 08.5一、填空题(本大题共14小题,每小题5分,计70分)1.若集合{(,)|2,}A x y y x x R ==+∈,集合{(,)|2,}x B x y y x R ==∈,则A B 的子集个数是 _____▲______. 2.已知复数z 满足1iz -=3,则复数z 的实部与虚部之和为______▲______. 3.已知α、β是不同的两个平面,直线α⊂a ,直线β⊂b ,命题p :a 与b 没有公共点;命题q :βα//,则p 是q 的_______▲________条件.4.下列程序框图的运算结果为_______▲________.5. 一个社会调查机构就某地居民的月收入调查了10 000人,并根据所得数据画 了样本的频率分布直方图(如下图).为了分析居民的收入与年龄、学历、职业等 方面的关系,要从这10 000人中再用分层抽样方法抽出100人作进一步调查,则 在[2500,3000)(元)月收入段应抽出 ▲ 人.6.所有棱长均为3的正三棱柱内接于球O ,则球O 的表面积为_______▲________.7.函数y =f(x)定义域为(a ,b),y =f '(x)在(a ,b)上的图象如图,则y =f(x)在区间(a ,b)上极大值点的个数为_____▲____.8.在坐标平面内,由不等式组123y x y x ⎧≥--⎪⎨≤-+⎪⎩ 所确定的平面区域的面积为_____▲______.9. 已知等差数列{}n a 的前n 次和为n s ,且2510,55S S ==,则过点),(n a n P 和),2(2++n a n Q (*N n -∈)的直线方向向量的坐标可以是_______▲_______.10. 已知函数⎩⎨⎧≥+-<=)0(4)3(),0()(x a x a x a x f x 满足对任意121212()(),f x f x x x x x -≠-都有0<成立,则a 的取值范围是_______▲_______.11. 在数列{}n a 中,已知11a =, 2a =, 21n n n a a ++=-,则2008a 等于_______▲_______.12.已知ABC k Z k ∆≤==∈则若,4||),4,2(),1,(,是直角三角形的概率是 ▲ .13. ω是正实数,设{|()S f x ωθ==cos[()]x ωθ+是奇函数},若对每个实数a ,)1,(+⋂a a S ω的元素不超过2个,且有a 使)1,(+⋂a a S ω含2个元素,则ω的取值范围是 ▲ .14. 一只球放在桌面上,桌面上一点A 的正上方有一点光源O ,OA 与球相切,让A 在桌面上运动,OA 始终与球相切,OA 形成一个轴截面顶角为45O的圆锥,则点A 的轨迹椭圆的离心率为 ▲ .二、解答题(本大题共6小题,计90分)15. (本小题14分)已知向量a =(cos α,sin α),求b =(cos β,sin β), |a -b |=552(1)求cos(α-β)的值;(2)若202π<α<<β<π-,且sin β=-135,求sin α的值..16. (本小题14分)在正三角形ABC 中,E 、F 分别是AB 、 AC 边上的点,满足AE EB =12CF FA =(如图1). 将△AEF 沿EF 折起到EF A 1∆的位置,使二 面角A 1-EF -B 成直二面角,连结A 1B 、A 1C. (如图2) (1)求证:A 1E⊥平面BEC ;(2)求直线A 1E 与平面A 1BC 所成角的大小.17. (本小题15分)运货卡车以每小时x 千米的速度匀速行驶130千米(60≤100)x ≤.假设汽油的价格是每升2元,而汽车每小时耗油)3602(2x +升,司机的工资是每小时14元.(1)求这次行车总费用y 关于x 的表达式;(2)当x 为何值时,这次行车的总费用最低,并求出最低费用的值.18. (本小题15分)在平面直角坐标系xOy 中,过定点),0(p C 作直线与抛物线)0(22>=p py x 相交于A 、B 两点.(1)若点N 是点C 关于坐标原点O 的对称点,求△ANB 面积的最小值;(2)是否存在垂直于y 轴的直线l ,使得l 被以AC 为直径的圆截得的弦长恒为定值?若存在,求出l 的方程;若不存在,说明理由. 19.(本小题16分)已知数列{}n a 的前n 项和n S 满足2(1),1n n n S a n =+-≥.(1)写出数列{}n a 的前两项12,a a ; (2)求数列{}n a 的通项公式. (3)证明:对任意的整数4>m ,有4511178ma a a +++<.20. (本小题16分)已知函数()ln()x f x e a =+(a 为常数)是实数集R 上的奇函数,函数()()sin g x f x x λ=+是区间[1,1]-上的减函数. (1)求()g x 在[1,1]x ∈-上的最大值;(2)若2()1g x t t λ≤++对[1,1]x ∀∈-及(],1λ∈-∞-恒成立,求t 的取值范围; (3)讨论关于x 的方程2ln ()2x f x x ex m =-+的根的个数.命题:张福俭 校对:唐一良图2图1B A BFC理科附加题1.一个袋子里装有大小相同的3个红球和2个黄球,从中同时取出2个,求其中含红球个数的数学期望与标准差分别是多少?2.曲线C 的极坐标方程是1cos ρθ=+,点A 的极坐标是(2,0),求曲线C 在它所在的平面内绕点A 旋转一周而形成的图形的周长考场号_____ 考试号________________ 学号_____ 班级___________座位号__________ 姓名_____________………………密……………封……………线……………内……………不……………要……………答……………题………………3.(Ⅰ)过曲线2(0)y x x =≥上某一点A 作一切线l ,使之与曲线以及x 轴所围成的图形的面积为112,试求: ⑴切点A 的坐标;⑵过切点A 的切线l 的方程;⑶上述所围成的平面图形绕x 轴旋转一周所得旋转体的体积4.若兔子和狐狸的生态模型为111 1.1.10.3,0.20.4n n n n n n R R F F R F ----=-⎧⎨=+⎩(1)n ≥对初始群00010050R F α⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,讨论第n 年种群数量n α及当n 越来越大时,种群数量n α的变化趋势命题、校对:张春琦、侯绪兵高三数学第四次模拟试卷答题纸一、填空题:(本大题共14小题,每小题5分,计70分)1. 2. 3. 4.5. 6. 7. 8. 9.10. 11. 12. 13. 14.三、解答题(本大题共6小题,计90分) 15.解:16.解:17.解:考场号_____ 考试号________________ 学号_____ 班级___________座位号__________ 姓名_____________………………密……………封……………线……………内……………不……………要……………答……………题………………18.解:第19、20题做在反面高三数学第四次模拟试卷参考答案1. 42.433.必要不充分4. 205.256. 21π7. 28. 169. 2 10. ⎥⎦⎤ ⎝⎛41,0 11.0 12. 7313. 2πωπ<≤1-15. 解:(I )∵|a -b |=552,∴a 2-2a ·b +b 2=54,又a =(cos α,sin α), b =(cos β,sin β),∴a 2=b 2=1, a ·b =cos αcos β+sin αsin β=cos(α-β).∴cos(α-β)=532542=-. (II )∵-202π<α<<β<π,∴0<α-β<π,由(1)得cos(α-β)=53, ∴sin(α-β)=54. 又sin β=-135,∴cos β= 1312. ∴sin α=sin [(α-β)+β]=sin(α-β)cos β+cos(α-β)sin β=54×6533)135(531312=-⨯+16.解 不妨设正三角形ABC 的边长为3,则(1)在图1中,取BE 中点D ,连结DF ,则∵12AE CF EB FA ==, ∴1AE =,2AF =而060A ∠=,∴EF AE ⊥∴在图2中有1A E EF ⊥,BE EF ⊥, ∴1A EB ∠为二面角1A EF B --的平面角 ∵二面角1A EF B --为直二面角, ∴1A E BE ⊥ 又∵BEEF E =, ∴1A E ⊥平面BEC .(2)建立坐标系,则不妨设平面A 1BP 的法向量1(,,)n x y z =,则1110A B n BC n ⎧⋅=⎪⎨⋅=⎪⎩,得1n =∴111111cos ,||||14n EA n EA n EA ⋅<>===⋅⨯ 故直线A 1E 与平面A 1BP 所成角的大小为3π. 或:过E 作EH BC ⊥于H ,连A 1H ,作EO 1A H ⊥于O ,证明EO 1A BC ⊥平面,在直角三角形A 1EH 中求得直线A 1E 与平面A 1BP 所成角的大小为3π. 17. 解:(1)设行车所用时间为)(130h xt = ,2130141302(2),[60,100]360x y x x x⨯=⨯⨯++∈ 所以,这次行车总费用y 关于x 的表达式是234013([60,100])18y x x x=+∈(2),2234013018y x=-+>所以234013([60,100])18y x x x=+∈为增函数.所以,当60x =时,这次行车的总费用最低,最低费用为2473元18.(1)依题意,点N 的坐标为(0)N p -,,可设1122()()A x y B x y ,,,, 直线AB 的方程为y kx p =+,与22x py =联立得22x py y kx p ⎧=⎨=+⎩,.消去y 得22220x pkx p --=.由韦达定理得122x x pk +=,2122x x p =-.于是12122AMN BCN ACN S S S p x x =+=-△△△·12p x x =-=2p==,∴ 当0k =,2min ()ABN S =△.(2)假设满足条件的直线l 存在,其方程为y a =,设AC 的中点为O ',l 与AC 为直径的圆相交于点P ,Q PQ ,的中点为H ,则O H PQ '⊥,Q '点的坐标为1122x y p +⎛⎫⎪⎝⎭,.12O P AC '===∵ 111222y p O H a a y p +'=-=--, 222PH O P O H ''=-∴2221111()(2)44y p a y p =+--- 1()2p a y a p a ⎛⎫=-+- ⎪⎝⎭,22(2)PQ PH =∴14()2p a y a p a ⎡⎤⎛⎫=-+- ⎪⎢⎥⎝⎭⎣⎦.令02p a -=,得2pa =,此时PQ p =为定值,故满足条件的直线l 存在,其方程为2py =,即抛物线的通径所在的直线.19.解 (1)由111121,1;a S a a ==-=得由2122222(1),0;a a S a a +==+-=得 (2) 当2≥n 时,有,)1(2)(211n n n n n n a a S S a -⨯+-=-=--即有 ,)1(2211---⨯+=n n na a 从而,)1(22221----⨯+=n n n a a32322(1),n n n a a ---=+⨯- …….2212-=a a接下来,逐步迭代就有122111)1(2)1(2)1(22-----⨯++-⨯+-⨯+=n n n n n a a].)1(2[323])2(1[2)1(2)]2()2()2[()1(21211211--------+=----=-++-+--+=n n n nn n n n n经验证a 1也满足上式,故知 .1],)1(2[3212≥-+=--n a n n n或:对1122(1)n n n a a --=+⨯-的两边同除以(1)n-,便得122(1)(1)nn a a -=-⋅---.令,(1)nn n a b =-就有122nn b b -=--,于是1222()33n n b b -+=-+,这说明数列23n b ⎧⎫+⎨⎬⎩⎭是等比数列,公比2,q =- 首项11b =-,从而,得111221()(2)()(2)333n n n b b --+=+⋅-=-⋅-,即 121()(2)(1)33n n n a -+=-⋅--,故有.1],)1(2[3212≥-+=--n a n n n(3)由通项公式得.24=a当3≥n 且n 为奇数时, ]121121[2311121-++=+--+n n n na a).2121(232222312222223123221213221----------+=+⨯<--++⨯=n n n n n n n n n n当m m 且4>为偶数时,m a a a 11154+++ )212121(2321)11()11(14431654--++++<+++++=m m m a a a a a .878321)211(4123214=+<-⨯⨯+=-m 当m m 且4>为奇数时,1m +为偶数,可以转化为上面的情景 .87111111115454<++++<++++m m m a a a a a a a故任意整数m>4,有.8711154<+++m a a a20.(1))ln()(a e x f x+=是奇函数,则)ln()ln(a e a ex x+-=+-恒成立. .1))((=++∴-a e a e xx .0,0)(,112=∴=++∴=+++--a a e e a a ae ae x x x x又)(x g 在[-1,1]上单调递减,,1sin )1()(max --=-=∴λg x g(2)2sin11t t λλ--≤++只需在(],1λ∈-∞-上恒成立,(]2(1)sin1101.t t λλ∴++++≥∈∞在-,-恒成立令),1(11sin )1()(2-≤++++=λλλt t h 则⎩⎨⎧≥+++--≤+,011sin 1012t t t221sin10,sin10t t t t t ≤-⎧∴-+≥⎨-+≥⎩而恒成立1-≤∴t . (3)由(1)知,2ln ,)(2m ex x xxx x f +-=∴=方程为 令m ex x x f x xx f +-==2)(,ln )(221, 21ln 1)(x xx f -=' ,当],0()(,0)(,),0(11e x f x f e x 在时∴≥'∈上为增函数; ),0[)(,0)(,),[11e x f x f e x 在时∴≤'+∞∈上为减函数,当e x =时,.1)()(1max 1ee f x f ==而222)()(e m e x x f -+-=,)(1x f 函数∴、)(2x f 在同一坐标系的大致图象如图所示,∴①当e e m e e m 1,122+>>-即时,方程无解.②当e e m e e m 1,122+==-即时,方程有一个根.③当ee m e e m 1,122+<<-即时,方程有两个根.[附加题]1.解:设其中含红球个数为X ,则X=0,1或2,11223232222555133(0),(1),(2)10510C C C C P X P X P X C C C ⋅=========故含红球个数的数学期望为1336012105105⨯+⨯+⨯= 含红球个数的方差为2226163639(0)(1)(2)5105551025-⨯+-⨯+-⨯=35, 2.解:设(,)P ρθ是曲线C 上的任意一点,则||1cos OP ρθ==+,由余弦定理,得 22222||||||2||||cos (1cos )2AP OP OA OP OA θθ=+-⋅=++21614(1cos )cos 3(cos )33θθθ-+=-+,当1cos 3θ=-时,||APA (2,0)代入曲线C 的极坐标方程,是满足的,知点A 在曲线C 上,所以曲线C 在它所在的平面内绕点A 旋转一周而形成的图形是以点A为圆心、||AP =23.解:⑴设点A 的坐标为2(,)a a ,过点A 的切线的斜率为'|2x a k y a ===,故过点A 的切线l 的方程为22()y a a x a -=-,即22y ax a =-,令0y =,得2ax =, 则321224ABC a a S a ∆=⋅⋅=,33200|33a a ABO x a S x dx ∆===⎰,∴311212ABO ABC a S S S ∆∆====∴1a =或解:232220112[()222430a a y y S a dy ay y a a =+=+-⎰3111212a ==,∴1a = ∴切点A 的坐标为(1,1)⑵直线方程为21y x =-⑶l 与x 轴的交点为1(,0)2,故1142510211(21)05V x dx x dx x πππ=--=⎰⎰311(21)162x π--130=π 4.解:,n n n R M F α⎡⎤==⎢⎥⎣⎦ 1.10.30.20.4-⎡⎤⎢⎥⎣⎦,2n 1220M ()n n n n M M M M ααααα---=====M 的特征值11λ=对应的特征向量123,0.51αλ⎡⎤==⎢⎥⎣⎦对应的特征向量020*******,301025012R F αα⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤====+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦=12011223010,3010n n n n M ααααλαλα+==+319010(0.5)3010(0.5)123020(0.5)n n n ⎡⎤+⨯⎡⎤⎡⎤=+⨯=⎢⎥⎢⎥⎢⎥+⨯⎢⎥⎣⎦⎣⎦⎣⎦,当n 越来越大时,(0.5)n 趋向于0,n α趋向于9030⎡⎤⎢⎥⎣⎦,即兔子和狐狸的数量趋于稳定在90和30。
2016年江苏省扬州市高考数学四模试卷(解析版)

2016年江苏省扬州市高考数学四模试卷一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应位置)1.已知集合A={x|﹣1<x<2},Z是整数集,则A∩Z=______.2.若复数z满足iz=1+i(i为虚数单位),则z=______.3.命题“∃x∈R,x2+x+1=0”的否定是:______.4.已知△ABC中,a=1,b=2,C=,则边c的长度为______.5.如图是一个算法的伪代码.如果输出的y的值是20,则输入的x的值是______.6.在区间[﹣1,2]内随机选取一个实数,则该数为正数的概率是______.7.在三棱锥P﹣ABC中,PA、PB、PC两两垂直,且PA=3,PB=2,PC=1,则三棱锥P﹣ABC的体积为______.8.已知tanα=2且α为锐角,则cos2α=______.9.在平面直角坐标系xOy中,如果直线l将圆x2+y2﹣4x﹣2y=0平分,且不经过第四象限,那么l的斜率的取值范围是______.10.已知等边△ABC中,若=(+),=+t,且⊥,则实数t的值为______.11.设双曲线﹣=1(a>0,b>0)的右焦点为F,右准线l与两条渐近线交于P、Q 两点,如果△PQF是等边三角形,则双曲线的离心率是______.12.设函数f(x)=,若关于x的方程f2(x)﹣af(x)=0恰有三个不同的实数解,则实数a的取值范围为______.13.已知数列{a n}是各项均不为零的等差数列,S n为其前n项和,且a n=(n∈N*).若不等式λS n≥a n﹣2016对任意n∈N*恒成立,则实数λ的最小值为______.14.已知函数f(x)=ax3+bx2+cx+d在O、A两点处取得极值,其中O是坐标原点,A在曲线y=xsinx(x∈[,])上,则曲线y=f(x)的切线斜率的最大值为______.二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明、证明过程或演算步骤)15.已知向量=(sin(x+φ),1),=(1,cos(x+φ))(ω>0,0<φ<),记函数f(x)=(+)•(﹣).若函数y=f(x)的周期为4,且经过点M(1,).(1)求ω的值;(2)当﹣1≤x≤1时,求函数f(x)的最值.16.在三棱锥P﹣SBC中,A,D分别为边SB,SC的中点,且AB=3,BC=8,CD=5.PA ⊥BC.(1)求证:平面PSB⊥平面ABCD;(2)若平面PAD∩平面PBC=l,求证:l∥BC.17.某工厂生产某种黑色水笔,每百支水笔的成本为30元,并且每百支水笔的加工费为m 元(其中m为常数,且3≤m≤6).设该工厂黑色水笔的出厂价为x元/百支(35≤x≤40),根据市场调查,日销售量与e x成反比例,当每百支水笔的出厂价为40元时,日销售量为10万支.(1)当每百支水笔的日售价为多少元时,该工厂的利润y最大,并求y的最大值.(2)已知工厂日利润达到1000元才能保证工厂的盈利.若该工厂在出厂价规定的范围内,总能盈利,则每百支水笔的加工费m最多为多少元?(精确到0.1元)18.已知椭圆+=1(a>b>0)的长轴长为4,椭圆的离心率为.设点M是椭圆上不在坐标轴上的任意一点,过点M的直线分别交x轴、y轴于A、B两点上,且满足=.(1)求证:线段AB的长是一定值;(2)若点N是点M关于原点的对称点,一过原点O且与直线AB平行的直线与椭圆交于P、Q两点(如图),求四边形MPNQ面积的最大值,并求出此时直线MN的斜率.19.数列{a n}是公差为d(d≠0)的等差数列,它的前n项和记为A n,数列{b n}是公比为q (q≠1)的等比数列,它的前n项和记为B n.若a1=b1≠0,且存在不小于3的正整数k,m,使a k=b m.(1)若a1=1,d=2,q=3,m=4,求A k.(2)若a1=1,d=2,试比较A2k与B2m的大小,并说明理由;(3)若q=2,是否存在整数m,k,使A k=86B m,若存在,求出m,k的值;若不存在,说明理由.20.已知函数f(x)=+alnx,a∈R.(1)求函数f(x)的单调递减区间;(2)当x∈[1,2]时,f(x)的最小值是0,求实数a的值;(3)试问过点P(0,2)可作多少条直线与曲线y=f(x)相切?并说明理由.数学试题Ⅱ(全卷满分0分,考试时间30分钟)(B)(本小题满分0分)21.已知矩阵A=,若矩阵A属于特征值3的一个特征向量为=,求该矩阵的另一个特征值.22.在直角坐标系xOy中,直线l的参数方程为(t为参数)在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,极轴与x轴的非负半轴重合)中,圆C的方程为ρ=4cosθ.若直线l被圆C截得的弦长为,求实数a的值.23.长时间上网严重影响着学生的健康,某校为了解甲、乙两班学生上网的时长,分别从这6(1)从甲班的样本中有放回地抽取3个数据,求恰有1个数据为“过度上网”的概率;(2)从甲班、乙班的样本中各随机抽取2名学生的数据,记“过度上网”的学生人数为X,写出X的分布列和数学期望E(X).24.已知f n(x)=C x k(n∈N*).(1)若g(x)=f4(x)+2f5(x)+3f6(x),求g(x)中含x4项的系数;(2)证明:C+2C+3C+…+nC=[]C.2016年江苏省扬州市高考数学四模试卷参考答案与试题解析一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应位置)1.已知集合A={x|﹣1<x<2},Z是整数集,则A∩Z={0,1} .【考点】交集及其运算.【分析】由A与Z,求出两集合的交集即可.【解答】解:∵A={x|﹣1<x<2},Z是整数集,∴A∩Z={0,1},故答案为:{0,1}.2.若复数z满足iz=1+i(i为虚数单位),则z=1﹣i.【考点】复数代数形式的乘除运算.【分析】由iz=1+i,两边除以i,按照复数除法运算法则化简计算.【解答】解:由iz=1+i,得z==1﹣i故答案为:1﹣i.3.命题“∃x∈R,x2+x+1=0”的否定是:∀x∈R,x2+x+1≠0.【考点】命题的否定;特称命题.【分析】欲求存在性命题的否定,必须将:“∃”改写成:“∀”,同时对后面的内容进行否定即可.【解答】解:由于存在性命题的否定,将:“∃”改写成:“∀”,同时对后面的内容进行否定,∴命题“∃x∈R,x2+x+1=0”的否定是:∀x∈R,x2+x+1≠0,故答案为:∀x∈R,x2+x+1≠0.4.已知△ABC中,a=1,b=2,C=,则边c的长度为.【考点】余弦定理.【分析】直接利用余弦定理,列出方程求解即可.【解答】解:△ABC中,a=1,b=2,C=,则边c===.故答案为:.5.如图是一个算法的伪代码.如果输出的y的值是20,则输入的x的值是2或6.【考点】伪代码.【分析】分析流程图所示的顺序,可知:该程序的作用是计算并输出分段函数的函数值,若输出的y的值为20,可根据分段函数的解析式,逆推出自变量x的值.【解答】解:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是计算并输出分段函数的函数值,当x≤5时,y=10x=20,解得:x=2当x>5时,y=2.5x+5=20,解得:x=6,故答案为:2或6.6.在区间[﹣1,2]内随机选取一个实数,则该数为正数的概率是.【考点】几何概型.【分析】根据几何概型公式,将符合题意的区间长度除以总的区间长度,即得本题的概率.【解答】解:记事件A=“该数为正数”,∵区间[﹣1,2]长度是3,该数为正数的取值区间长度是2,∴由几何概型公式,得P(A)=故答案为:7.在三棱锥P﹣ABC中,PA、PB、PC两两垂直,且PA=3,PB=2,PC=1,则三棱锥P﹣ABC的体积为1.【考点】棱柱、棱锥、棱台的体积.【分析】利用侧棱PA、PB、PC两两互相垂直,证出PA⊥平面PBC,即可用锥体体积公式求三棱锥的体积.【解答】解:∵侧棱PA、PB、PC两两互相垂直,即PA⊥PB,PA⊥PC,而PB、PC是平面PBC内的相交直线,∴PA⊥平面PBC,∵PA=3,PB=2,PC=1,∴三棱锥P﹣ABC的体积V=•S△PBC•PA=××3×2×1=1.故答案为:1.8.已知tanα=2且α为锐角,则cos2α=﹣.【考点】二倍角的余弦;三角函数的化简求值.【分析】由条件利用同角三角函数的基本关系,二倍角的余弦公式,求得cos2α的值.【解答】解:∵tanα=2且α为锐角,则cos2α====﹣,故答案为:﹣.9.在平面直角坐标系xOy中,如果直线l将圆x2+y2﹣4x﹣2y=0平分,且不经过第四象限,那么l的斜率的取值范围是[0,].【考点】直线与圆的位置关系.【分析】由直线将圆平分得直线l过圆心(2,1),再由直线l不经过第四象限,能求出直线l的斜率的取值范围.【解答】解:∵在平面直角坐标系xOy中,直线l将圆x2+y2﹣4x﹣2y=0平分,∴直线l过圆心(2,1),∵直线l将圆x2+y2﹣4x﹣2y=0平分,且不经过第四象限,∴直线l的斜的最小值为k min=0,直线l的斜率的最大值为k max==,∴l的斜率的取值范围是[0,].故答案为:[0,].10.已知等边△ABC 中,若=(+),=+t ,且⊥,则实数t 的值为﹣ .【考点】平面向量数量积的运算.【分析】根据的加减运算法则和向量的数量积的运算法则和向量垂直的条件即可求出. 【解答】解:在等边△ABC 中, ∴AB=AC ,∠A=60°∵=(+),∴=+t =(+)+t=(+t )+,∵⊥,∴•=(+)•[(+t )+]=(+t )||2+||2+(+t ),=(+t )||2+||2+(+t )||||•=0,∴+t +++t=0,解得t=﹣,故答案为:﹣.11.设双曲线﹣=1(a >0,b >0)的右焦点为F ,右准线l 与两条渐近线交于P 、Q两点,如果△PQF 是等边三角形,则双曲线的离心率是 2 .【考点】双曲线的简单性质.【分析】求出右准线与渐近线的交点P ,Q ,△PQF 为等边三角形,可得直线PF 的斜率为tan30°=,求出a ,b 的关系,与c 2=a 2+b 2联立求e .【解答】解:双曲线的右准线l :x=,两条渐近线方程是y=±x ,二者联立得,y=±,可设P (,﹣),又△PQF 为等边三角形,且F (c ,0),可得直线PF 的斜率为tan30°=,=得b=a,即c2﹣a2=3a2,即有c=2a,则e==2.故答案为:2.12.设函数f(x)=,若关于x的方程f2(x)﹣af(x)=0恰有三个不同的实数解,则实数a的取值范围为[1,+∞).【考点】根的存在性及根的个数判断.【分析】由题意作函数f(x)=的图象,由f2(x)﹣af(x)=0得f (x)=0或f(x)=a;从而解得.【解答】解:由题意作函数f(x)=的图象如下,,∵f2(x)﹣af(x)=0,∴f(x)=0或f(x)=a;∵f(x)=0有且只有一个解,∴f(x)=a有且只有两个解,故a∈[1,+∞);故答案为:[1,+∞).13.已知数列{a n}是各项均不为零的等差数列,S n为其前n项和,且a n=(n∈N*).若不等式λS n≥a n﹣2016对任意n∈N*恒成立,则实数λ的最小值为.【考点】数列递推式.【分析】由已知数列递推式求得数列首项和公差,进一步求得数列通项和前n项和,代入λS n ≥a n﹣2016,分离参数λ,然后利用二次函数求得最值得答案.,【解答】解:由a n=,得a n2=S2n﹣1令n=1,n=2,得,即,∵a n≠0,解得a1=1,d=2,∴a n=a1+(n﹣1)d=1+2(n﹣1)=2n﹣1,.由不等式λS n≥a n﹣2016,得λn2≥2n﹣1﹣2016=2n﹣2017.∴.由二次函数的性质可知,当,即n=2017时,.∴实数λ的最小值为.故答案为:.14.已知函数f(x)=ax3+bx2+cx+d在O、A两点处取得极值,其中O是坐标原点,A在曲线y=xsinx(x∈[,])上,则曲线y=f(x)的切线斜率的最大值为.【考点】利用导数研究函数的极值.【分析】由函数f(x)=ax3+bx2+cx+d在O,A(p,q)点处取到极值,其中O是坐标原点,得到d=0,f′(0)=0,f′(p)=0,得到c=0,p=﹣,f′(x)=3ax2﹣3apx,再由A在曲线上,运用两角和的正弦,判断a<0,b>0.得到f′(x)≤f′()=sinp,根据p的范围即可判断.【解答】解:∵函数f(x)=ax3+bx2+cx+d在O,A(p,q)点处取到极值,其中O是坐标原点,∴f(0)=0,即d=0,f(x)=ax3+bx2+cx,f′(x)=3ax2+2bx+c,f′(0)=0,f′(p)=0,∴c=0,p=﹣,f′(x)=3ax2﹣3apx,∵p∈[,],∴q=psinp>0,f(p)>f(0),即f(x)分别在x=0和x=p处取极小值和极大值,则a<0,b>0.∴f′(x)≤f′(),∵q=f(p)=ap3+bp2=psinp,∴ap2+bp==sinp,即b=,a=﹣=﹣,∴f′()=﹣ap2=sinp,p∈[,],∴p=时,f′()最大,最大值是,故答案为:.二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明、证明过程或演算步骤)15.已知向量=(sin(x+φ),1),=(1,cos(x+φ))(ω>0,0<φ<),记函数f(x)=(+)•(﹣).若函数y=f(x)的周期为4,且经过点M(1,).(1)求ω的值;(2)当﹣1≤x≤1时,求函数f(x)的最值.【考点】平面向量数量积的运算;三角函数的周期性及其求法.【分析】(1)由数量积的坐标运算化简得到函数解析式,结合周期公式求得ω的值;(2)由(1)及函数图象经过点M(1,)求得函数具体解析式,在由x的范围求得相位的范围,则函数f(x)的最值可求.【解答】解:(1)f(x)=(+)•(﹣)===﹣cos(ωx+2φ).由题意得:周期,故;(2)∵图象过点M(1,),∴﹣cos(2φ)=,即sin2φ=,而0<φ<,故2φ=,则f(x)=﹣cos().当﹣1≤x≤1时,,∴.∴当x=﹣时,f(x)min=﹣1,当x=1时,.16.在三棱锥P﹣SBC中,A,D分别为边SB,SC的中点,且AB=3,BC=8,CD=5.PA ⊥BC.(1)求证:平面PSB⊥平面ABCD;(2)若平面PAD∩平面PBC=l,求证:l∥BC.【考点】平面与平面垂直的判定;直线与平面平行的判定.【分析】(1)由已知及勾股定理可证BC⊥SB,结合已知PA⊥BC,可证BC⊥平面PSB,从而可证平面PSB⊥平面ABCD;(2)可证BC∥平面PAD,又BC⊂平面PBC,平面PAD∩平面PBC=l,即可证明l∥BC.【解答】证明:(1)∵A,D分别为边SB,SC的中点,且BC=8,∴AD∥BC且AD=4,∵AB=SA=3,CD=SD=5,∴SA2+AD2=SD2,∴∠SAD=90°,即SA⊥AD,∴BC⊥SB,…∵PA⊥BC,PA∩SB=A,PA,SB⊂平面PSB∴BC⊥平面PSB,∵BC⊂平面ABCD,∴平面PSB⊥平面ABCD;…(2)在梯形ABCD中,AD∥BC,BC⊄平面PAD,AD⊂平面PAD,所以BC∥平面PAD,又BC⊂平面PBC,平面PAD∩平面PBC=l,所以l∥BC.…17.某工厂生产某种黑色水笔,每百支水笔的成本为30元,并且每百支水笔的加工费为m 元(其中m为常数,且3≤m≤6).设该工厂黑色水笔的出厂价为x元/百支(35≤x≤40),根据市场调查,日销售量与e x成反比例,当每百支水笔的出厂价为40元时,日销售量为10万支.(1)当每百支水笔的日售价为多少元时,该工厂的利润y最大,并求y的最大值.(2)已知工厂日利润达到1000元才能保证工厂的盈利.若该工厂在出厂价规定的范围内,总能盈利,则每百支水笔的加工费m最多为多少元?(精确到0.1元)【考点】函数模型的选择与应用.【分析】(1)由条件“日销售量与e x(e为自然对数的底数)成反比例”可设日销量,根据日利润y=每件的利润×件数,建立函数关系式,注意实际问题自变量的范围.对函数进行求导,求出极值点,利用3≤m≤6,可得函数在35≤x≤40范围内的单调性,从而求出函数的最值;(2)由题意35≤x≤40,(x﹣30﹣m)≥1000恒成立,x=35时,e5(5﹣m)≥1,m≤5﹣e﹣5,即可得出结论.【解答】解:(1)设日销量为s,则s=∵x=40,s=1000,∴1000=,∴k=1000e40,∴s=∴y=(x﹣30﹣m)(35≤x≤40);y′=(31+m﹣x),令y′=0,可得x=31+m3≤m≤6,34≤31+m≤37当35≤x≤m+31时,y′>0当m+31≤x≤40时,y′<0故x=31+m时,y max=1000e9﹣m.(2)由题意35≤x≤40,(x﹣30﹣m)≥1000恒成立,∴x=35时,e5(5﹣m)≥1,∴m≤5﹣e﹣5,∴每百支水笔的加工费m最多为5.0元18.已知椭圆+=1(a>b>0)的长轴长为4,椭圆的离心率为.设点M是椭圆上不在坐标轴上的任意一点,过点M的直线分别交x轴、y轴于A、B两点上,且满足=.(1)求证:线段AB的长是一定值;(2)若点N是点M关于原点的对称点,一过原点O且与直线AB平行的直线与椭圆交于P、Q两点(如图),求四边形MPNQ面积的最大值,并求出此时直线MN的斜率.【考点】直线与圆锥曲线的综合问题;椭圆的标准方程.【分析】(1)由椭圆长轴长为4,离心率为,求出椭圆方程,由此利用,且A、B分别在x轴、y轴上,能证明AB为定值.(2)设P(x0,y0),由AB∥PQ,得k PQ=k AB=﹣,=4,直线PQ的方程为:y=﹣,由此利用点到直线距离公式、弦长公式能求出结果.【解答】证明:(1)∵椭圆+=1(a>b>0)的长轴长为4,椭圆的离心率为.∴由题意得:,解得a=2,c=,∴b=,∴椭圆方程为:,…设M(x1,y1),则=1,∵,且A、B分别在x轴、y轴上,∴A(,0),B(0,3y1),∴,∴AB=3为定值.…解:(2)设P(x0,y0),∵AB∥PQ,∴k PQ=k AB=﹣,=4,则直线PQ的方程为:y=﹣,…∵,∴,∴PQ2=4OP2=4•=,点M到直线PQ:2y0x+x0y=0的距离:d==,…=2S△MPQ=2××PQ×d=•∴S四边形MPNQ=12=12=12=12,令t=3y02+1,t≥1,则==﹣,当且仅当t=2时,取等号,即3y02+1=2时,(S)max=4,四边形MPNQ此时,∴.…19.数列{a n}是公差为d(d≠0)的等差数列,它的前n项和记为A n,数列{b n}是公比为q (q≠1)的等比数列,它的前n项和记为B n.若a1=b1≠0,且存在不小于3的正整数k,m,使a k=b m.(1)若a1=1,d=2,q=3,m=4,求A k.(2)若a1=1,d=2,试比较A2k与B2m的大小,并说明理由;(3)若q=2,是否存在整数m,k,使A k=86B m,若存在,求出m,k的值;若不存在,说明理由.【考点】等差数列与等比数列的综合;数列递推式.【分析】(1)运用等差数列和等比数列的通项公式,可得a n=2n﹣1,b n=3n﹣1,由a k=b4,求得k=14,由等差数列求和公式可得所求和;(2)求得a n =2n ﹣1,A n =n 2,A 2k =4k 2,运用等比数列的求和公式可得B 2m ==[(2k ﹣1)2q 2﹣1],运用作差法,构造二次函数,运用单调性,即可得到大小关系;(3)由a k =b m =a 1•2m ﹣1,运用等差数列和等比数列的求和公式,A k =86B m 得:•k=86•,可得2m ==﹣2,通过分析,可得存在m=8且k=340.【解答】解:(1)由a 1=1,d=2,q=3,可得a n =2n ﹣1,b n =3n ﹣1,a k =b 4=33=27,即2k ﹣1=27,解得k=14,A 14=14+×2=196;(2)依题意,a 1=1,d=2,可得a n =2n ﹣1,A n =n 2,A 2k =4k 2,且q m ﹣1=2k ﹣1,显然q >1.又B 2m ==[(2k ﹣1)2q 2﹣1],所以B 2m ﹣A 2k =[(2k ﹣1)2q 2﹣1]﹣4k 2=[(2k ﹣1)2q 2﹣4qk 2+(4k 2﹣1)], 设f (x )=(2k ﹣1)2x 2﹣4xk 2+(4k 2﹣1),f (1)=(2k ﹣1)2x 2﹣1,它是关于x 的二次函数,它的图象的开口向上,它的对称轴方程x=<1,故f (x )是(1,+∞)上的增函数,所以当x >1时f (x )>f (1)>0,即B 2m ﹣A 2k >0,所以A 2k <B 2m . (3)依题意:a k =b m =a 1•2m ﹣1,由A k =86B m 得:•k=86•,即•k=86•,可得2m ==﹣2,所以344﹣k=,因为29=512,故m ﹣1≤9,且516=4×129=4×3×43,且2m ﹣1+1为奇数,则其中2m ﹣1+1=129时,是整数,故m ﹣1=7,可得存在m=8且k=340.20.已知函数f (x )=+alnx ,a ∈R . (1)求函数f (x )的单调递减区间;(2)当x∈[1,2]时,f(x)的最小值是0,求实数a的值;(3)试问过点P(0,2)可作多少条直线与曲线y=f(x)相切?并说明理由.【考点】利用导数研究曲线上某点切线方程.【分析】(1)求出f(x)的导数,讨论a≤0时,a>0时,令导数小于0,可得减区间;(2)讨论①a≤,②a≥1,③<a<1,结合单调性,可得最小值,解方程可得a;(3)a≤0时,有1条切线;a>0时,有2条切线.设切点坐标是(x0,f(x0)),运用两点的斜率公式和导数的几何意义,设F(x)=+alnx﹣2﹣a,x>0,故函数F(x)在(0,+∞)上零点个数,即是曲线切线的条数.求得F(x)的导数,对a讨论,运用函数的单调性和零点存在定理,即可得到结论.【解答】解:(1)f(x)=+alnx的导数为f′(x)=﹣+=,a≤0时,f′(x)<0在(0,+∞)上恒成立,则f(x)的单调递减区间(0,+∞),a>0时,令ax﹣1<0则x<,即0<x<时,f′(x)<0,则f(x)的单调递减区间(0,);(2)①a≤,f(x)在[1,2]上单调递减,即f(x)min=f(2)=+aln2=0解得a=﹣≤,适合题意;②a≥1,f(x)在[1,2]上单调递增,可得f(x)min=f(1)=1≠0,无解;③<a<1,f(x)在[1,]上单调递减,[,2]上单调递增,可得f(x)min=f()=a+aln=0,解得a=e,舍去;综上可得,a═﹣.(3)a≤0时,有1条切线;a>0时,有2条切线.设切点坐标是(x0,f(x0)),依题意:=,即+alnx0﹣2=a﹣,化简得: +alnx0﹣2﹣a=0,设F(x)=+alnx﹣2﹣a,x>0,故函数F(x)在(0,+∞)上零点个数,即是曲线切线的条数.F′(x)=﹣+=,①当a=0时,F(x)=﹣2,在(0,+∞)上恰有一个零点1;③当a<0时,F′(x)=<0在(0,+∞)上恒成立,F(x)在(0,+∞)上单调递减,且F(1)=﹣a>0,F(e)=﹣2<0,故F(x)在(1,e)上有且只有一个零点,当a<0时,F(x)在(0,+∞)上恰有一个零点;③a>0时,F(x)在(0,)上递减,在(,+∞)上递增,故F(x)在(0,+∞)上至多有两个零点,且F(1)=2﹣2﹣a=﹣a<0,又函数y=lnx在(1,+∞)单调递增,且值域是(0,+∞),故对任意实数a,必存在x0∈(1,+∞),使lnx0>,此时F(x0)=+alnx0﹣2﹣a=+a(lnx0﹣)>0,由于>1,即函数F(x)在(1,x0)上必有一零点;F(e)=2e﹣a(1+a+)﹣2﹣a=2e﹣(a2+2a+3),先证明当a>0时,e≥(a+2)2,即证1+a+≥2ln(a+2),若0<a<2,1+a+≥3,而2ln(a+2)≤2ln4,由于2ln4=ln16<3,若a≥2,构建函数φ(x)=1+x+﹣2ln(x+2),φ′(x)=1﹣﹣=>0,φ(x)在[2,+∞)为增函数,φ(a)≥φ(2)=3+﹣2ln4>0,综上a>0时,e≥(a+2)2,所以2e≥2(a+2)2=a2+2a+3+(a2+6a+5)>a2+2a+3,故F(e)>0,又F(1)<0,e<1,所以在(e,1)必有一零点.则当a>0时,F(x)在(0,+∞)上有两个零点综上:a≤0时,有1条切线;a>0时,有2条切线.数学试题Ⅱ(全卷满分0分,考试时间30分钟)(B)(本小题满分0分)21.已知矩阵A=,若矩阵A属于特征值3的一个特征向量为=,求该矩阵的另一个特征值.【考点】特征值与特征向量的计算.【分析】根据矩阵A属于特征值3的一个特征向量为=,可得a,b的值,再回代到方程f(λ)=0即可解出另一个特征值为λ=﹣1.【解答】解:因为•=3,则,解得,所以A=,由f(λ)==(λ﹣1)2﹣4=0,所以(λ+1)(λ﹣3)=0,解的λ=﹣1或λ=3,所以该矩阵的另一个特征值是﹣122.在直角坐标系xOy中,直线l的参数方程为(t为参数)在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,极轴与x轴的非负半轴重合)中,圆C的方程为ρ=4cosθ.若直线l被圆C截得的弦长为,求实数a的值.【考点】参数方程化成普通方程;简单曲线的极坐标方程.【分析】把参数方程与极坐标方程分别化为直角坐标方程,求出圆心到直线的距离,利用弦长公式即可得出.【解答】解:直线l的参数方程为(t为参数),消去参数t可得:直线的直角坐标系方程是:2x+y﹣a﹣2=0,圆C的方程为ρ=4cosθ,即ρ2=4ρcosθ,直角坐标系方程是:x2+y2=4x,配方为(x﹣2)2+y2=4,可得圆心(2,0),半径r=2.设圆心到直线l的距离为d,d==.又d===,∴a=2,∴a=,或.23.长时间上网严重影响着学生的健康,某校为了解甲、乙两班学生上网的时长,分别从这两个班中随机抽取6名同学进行调查,将他们平均每周上网时长作为样本,统计数据如表:(1)从甲班的样本中有放回地抽取3个数据,求恰有1个数据为“过度上网”的概率;(2)从甲班、乙班的样本中各随机抽取2名学生的数据,记“过度上网”的学生人数为X,写出X的分布列和数学期望E(X).【考点】离散型随机变量及其分布列;离散型随机变量的期望与方差.【分析】(1)确定为独立重复试验类型即可求解概率P(A)==;(2)确定随机变量ξ的可能取值为0,1,2,3,4.利用排列组合知识求解相应的概率类型,得出分布列,可求数学期望.【解答】解:(1)设“恰有一个数据为过度上网”为事件A,则P(A)==…(2)甲组六人中有两人过度上网,乙组六人中有四人过度上网,则P(X=0)==,P(X=1)==,P(X=2)==,P(X=3)==,P(X=4)==…∴E(X)=+2×+3×+4×=2.答:数学期望为2 …24.已知f n(x)=C x k(n∈N*).(1)若g(x)=f4(x)+2f5(x)+3f6(x),求g(x)中含x4项的系数;(2)证明:C+2C+3C+…+nC=[]C.【考点】二项式定理的应用;数列的应用.【分析】(1)利用f n(x)=(1+x)n,即可求出g(x)中含x4项的系数;(2)令h(x)=(1+x)m+1+2(1+x)m+2+3(1+x)m+3+…+n•(1+x)m+n,利用错位相减法,即可证明结论.【解答】(1)解:f n(x)=C x k(n∈N*)=•x0+•x+•x2+•x n=(1+x)n,g(x)=f4(x)+2f5(x)+3f6(x)=(1+x)4+2(1+x)5+3(1+x)6,故g(x)中含x4项的系数为+2+3=56.(2)证明:∵C+2C+3C+…+nC=+2+3+…+n,令h(x)=(1+x)m+1+2(1+x)m+2+3(1+x)m+3+…+n•(1+x)m+n.则函数h(x)中含x m+1项的系数为C+2C+3C+…+n,…同乘1+x,由错位相减法得:﹣xh(x)=(1+x)m+1+(1+x)m+2+(1+x)m+3+…+(1+x)m+n﹣n•(1+x)m+n+1=﹣n•(1+x)m+n+1,∴x2h(x)=(1+x)m+1﹣(1+x)m+n+1+n•(1+x)m+n+1,h(x)中含x m+1项的系数,即是等式左边含x m+3项的系数,等式右边含x m+3项的系数为﹣+n,…﹣+n=﹣+n=﹣+n=[]C,所以C+2C+3C+…+nC=[]C.…2016年9月19日。
江苏省扬州市高三数学第四次模拟考试试卷-人教版高三全册数学试题

扬州市2014—2015学年度第四次调研测试试题高 三 数 学 参 考 答 案第一部分1.已知集合{1,2,4},{2,3,4,5}A B ==,则AB =.{2,4}2.设复数z 满足()132i z i +=-+,则z =____________.13i -3.命题“2,10x R x ∀∈+>”的否定是 .2,10x R x ∃∈+≤ 4.已知α为第三象限角,且tan 2α=,则sin 2α= .455.从3名男同学,2名女同学中任选2人参加体能测试,则选到的2名同学中至少有一名男同学的 概率是 .9106.已知向量(1,3)=a ,(2,1)=-b ,(3,2)=c .若向量c 与向量k +a b 共线,则实数k = -17.锐角ABC △中角,,A B C 的对边分别是,,a b c ,4,5a b ==, ABC △的面积为53则c.218.用半径为6的半圆形铁皮卷成一个圆锥的侧面,则此圆锥的体积是 .93π 9.已知等比数列{}n a 的前n 项和为n S ,若2244a S a S =,则12015S S 等于 .110.若函数()cos f x k x =⋅的图象过点(,1)3P π,则该函数图象在P 点处的切线倾斜角等于 .23π析:∵函数()cos f x k x =⋅的图象经过点(,1)3P π,∴()cos 1233f k k ππ==⇒=,∴x x f cos 2)(=,()2sin f x x '=-,()2sin333k f ππ'==-=-11.若直线30x y m ++=截半圆225y x =-8,则m = .310-12.平面内四点,,,O A B C 满足4,25,5,0OA OB OC OB OC ===⋅=,则ABC ∆面积的最大值为 .1513.已知椭圆E :22221(0)x y a b a b +=>>的右焦点为F ,离心率为32,过原点O 且倾斜角为3π的直线l 与椭圆E 相交于A 、B 两点,若△AFB 的周长为13413+,则椭圆方程为 .2214x y += 析:由已知2a b =,椭圆方程可化为:2224x y a +=,将:3l y x =代入得13||A x =,DB由椭圆对称性,△AFB 的周长=2||24||A a AB a x +=+,可得2a =. 14.已知函数||()()xx f x x R e=∈,12()421()x x g x a a a a R +=-+⋅++-∈, 若{|(g())}R A x f x e =>=, 则a 的取值范围是 .[1,0]- 析:当0x ≥时,1'()xxf x e -=,得()f x 在[)0,1上是增函数,在()1,+∞上是减函数,当1x =时有极大值1e ; 当0x <时,1'()0x x f x e-=<恒成立,()f x 是减函数,且(1)f e -=.设()g x t =,由()f t e >得1t <-,即()1g x <-对x R ∈恒成立,22()(2)21x g x a a a =--++-,当0a >时,2()21g x a a ≤+-,而2211a a +->-,不合题意;当0a ≤时,2()(,1)g x a a ∈-∞+-,∴211a a +-≤-,得10a -≤≤. 15.如图,三棱锥A BCD -中,侧面ABC 是等边三角形,M 是ABC ∆的中心. ⑴若DM BC ⊥,求证AD BC ⊥;⑵若AD 上存在点N ,使//MN 平面BCD ,求AN ND的值.证⑴连AM 并延长交BC 于E ,连DE因为M 是等边ABC ∆的中心,所以E 是BC 的中点,AE BC ⊥ ……………2分又因为DM BC ⊥,AE DM M =,,AE DM ⊂平面ADE ,所以BC ⊥平面ADE , ……………5分 因为AD ⊂平面ADE ,所以AD BC ⊥; ……………7分 ⑵,M AE AE ∈⊂平面ADE ,所以M ∈平面ADE , 因为AD 上存在点N ,所以N ∈平面ADE ,所以MN ⊂平面ADE , ……………9分 又//MN 平面BCD ,平面ADE平面BCD DE =,所以//MN DE , ……………12分 在ADE ∆中,因为12AM ME =,所以12AN ND =. ……………14分16.ABC ∆的内角,A B 满足2cossin 22A B A Ba i j +-=+(单位向量,i j 互相垂直),且6||2a =. ⑴求tan tan A B 的值; ⑵若sin A =,边长2a =,求边长c . 解⑴因为2223||2cossin 222A B A B a +-=+=, 即1cos()31cos()22A B A B --+++=, ……………3分所以cos cos sin sin cos cos sin sin 02A B A BA B A B +--=,化简整理,得13tan tan 022A B-=,故tan tan A B =13. ……………7分(2)由(1)可知,A B 为锐角.因为sin A =,所以2tan 3A =,1tan 2B =,tan tan 7tan tan()1tan tan 4A B C A B AB +=-+=-=--,sin C =……………12分因为正弦定理sin sin a cA C=,所以227c =,所以边长c =. ……………14分 17.一件要在展览馆展出的文物近似于圆柱形,底面直径为0.8米,高1.2米,体积约为0.6立方米.为保护文物需要设计各面是玻璃平面的正四棱柱形无底保护罩,保护罩底面边长不少于1.2米,高是底面边长的2 倍.保护罩内充满保护文物的无色气体,气体每立方米500元.为防止文物发生意外,展览馆向保险公司 进行了投保,保险费用与保护罩的占地面积成反比例,当占地面积为1平方米时,保险费用为48000元. ⑴若保护罩的底面边长为2.5米,求气体费用与保险费用的和; ⑵为使气体费用与保险费用的和最低,保护罩应如何设计? 解⑴2248000500(2.550.6)230052.5⨯-+=; ……………4分 ⑵保护罩的底面边长为x 米,底面积为S 平方米,体积为V 立方米,总费用为y 元,则 48000500(0.6)y V S =-+=2248000500(20.6)x x x ⋅-+32480001000300x x=+-,( 1.2x ≥)……9分 52339600032'30003000x y x x x-=-=,令'0y =得2x =, 当1.22x ≤<时'0y <,y 递减;当2x >时'0y >,y 递增∴当2x =时,y 有极小值即最小值.答:为了使这两项总费用最低,保护罩的底面边长应设计为2米. ……………14分18.已知椭圆22221(0)x y a b a b+=>>的左顶点为A ,右焦点为F ,右准线为l ,l 与x 轴相交于点T ,且F 是AT 的中点.⑴求椭圆的离心率;⑵过点T 的直线与椭圆相交于,M N 两点,,M N 都在x 轴上方,并且M 在,N T 之间,且2NF MF =.①记,NFM NFA ∆∆的面积分别为12,S S ,求12S S ; ②若原点O 到直线TMN 的距离为4141,求椭圆方程. 解⑴因为F 是AT 的中点,所以22a a c c-+=,即(2)()0a c a c -+=, 又a 、0c >,所以2a c =,所以12c e a ==; ……………4分 ⑵①解法一:过,M N 作直线l 的垂线,垂足分别为11,M N ,依题意,11NF MFe NN MM ==, 又2NF MF =,故112NN MM =,故M 是NT 的中点,∴12MNF TNF S S ∆∆= 又F 是AT 中点,∴ANF TNF S S ∆∆=,∴1212S S =; ……………8分 解法二:∵2a c =,∴3b c =,椭圆方程为2222143x y c c+=,(,0)F c ,(4,0)T c设11(,)M x y ,22(,)N x y ,点M 在椭圆2222143x y c c +=上,即有22211334y c x =-,∴2222211113()()34MF x c y x c c x =-+=-+-22111111124|2|2422x cx c x c c x =-+=-=-同理2122NF c x =-, 又2NF MF =,故1224x x c -=得M 是,N T 的中点,∴12MNF TNF S S ∆∆=, 又F 是AT 中点,∴ANF TNF S S ∆∆=,∴1212S S =; ……………8分 ②解法一:设(,0)F c ,则椭圆方程为2222143x y c c+=,由①知M 是,N T 的中点,不妨设00(,)M x y ,则00(24,2)N x c y -,又,M N 都在椭圆上,即有⎧⎪⎨⎪⎩220022220022143(24)4143x y c c x c y c c +=-+=即⎧⎪⎨⎪⎩220022220022143(2)1434x y c c x c y c c +=-+=两式相减得:220022(2)3444x x c c c --=,解得074x c =, ……………10分可得0y =,故直线MN的斜率为8744k c c ==-, ……………13分直线MN的方程为4)y x c =-60y +-= 原点O 到直线TMN的距离为d ==,41=,解得c = 故椭圆方程为2212015x y +=. ……………16分解法二:设(,0)F c ,则椭圆方程为2222143x y c c+=,由①知M 是,N T 的中点,故1224x x c -=,直线MN 的斜率显然存在,不妨设为k ,故其方程为(4)y k x c =-,与椭圆联立,并消去y 得:22222(4)143x k x c c c-+=,整理得:222222(43)3264120k x ck x k c c +-+-=,(*) 设11(,)M x y ,22(,)N x y ,依题意:⎧⎪⎨⎪⎩21222221223243641243ck x x k k c c x x k +=+-=+ 由⎧⎨⎩212212324324ck x x k x x c +=+-=解得:⎧⎨⎩2122221644316443ck c x k ck c x k +=+-=+所以222222221641646412434343ck c ck c k c c k k k +--⨯=+++,解之得:2536k =,即k =. 直线MN的方程为(4)6y x c =--60y +-= 原点O 到直线TMN的距离为d ==,41=,解得c =, 故椭圆方程为2212015x y +=. ……………16分19.设m 个正数m a a a ,...,,21()*4,m m N ≥∈依次围成一个圆圈.其中1231,,,...,,k k a a a a a -*(,)k m k N <∈ 是公差为d 的等差数列,而111,,,...,,m m k k a a a a a -+是公比为2的等比数列. ⑴若12a d ==,8k =,求数列m a a a ,...,,21的所有项的和m S ; ⑵若12a d ==,2015m <,求m 的最大值; ⑶是否存在正整数k ,满足1211213()k k k k m m a a a a a a a a -++-++++=++++?若存在,求出k 值;若不存在,请说明理由.解⑴依题意16k a =,故数列m a a a ,...,,21即为2,4,6,8,10,12,14,16,8,4共10个数,此时10m =,84m S =, ……………4分 ⑵由数列1231,,,...,,k k a a a a a -是首项为2、公差为2的等差数列知,2k a k =,而111,,,...,,m m k k a a a a a -+是首项为2、公比为2的等比数列知,22m kk a +-=,故有222m kk +-=,12m kk +-=,即k 必是2的整数次幂,由122km k +⋅=知,要使m 最大,k 必须最大,又2015k m <<,故k 的最大值102,从而1010241222m +⋅=,m 的最大值是1033. ……………9分⑶由数列1231,,,...,,k k a a a a a -是公差为d 的等差数列知,1(1)k a a k d =+-,而111,,,...,,m m k k a a a a a -+是公比为2的等比数列112m k k a a +-=⋅, 故1(1)a k d +-112m k a +-=⋅,11(1)(21)m kk d a +--=- 又121113()k k k k m m a a a a a a a a -+-+++=++++,12m a a =则11112(1)32212m k ka k k d a --+-=⨯⨯-,即11111[(21)]32(21)2m km k ka k a a +--+-=⨯-,则11126(21)22m k m k k k +--⋅+=-,即1126212m k m k k k +-+-⋅+=⨯-, 显然6k ≠,则112182166m k k k k+-+==-+-- 所以6k <,将12345k =,,,,一一代入验证知,当4k =时,上式右端为8,等式成立,此时6m =,综上可得:当且仅当6m =时,存在4k =满足等式. ……………16分20.设函数1()1f x x =-,()1x g x ax =+(其中a R ∈,e 是自然对数的底数). ⑴若函数()()()F x f x g x =-没有零点,求实数a 的取值范围;⑵若函数(),()f x g x 的图象有公共点P ,且在点P 有相同的切线,求实数a 的值;⑶若()()xf eg x ≤在x ∈[0,)+∞恒成立,求实数a 的取值范围. 解⑴由()()()0F x f x g x =-=得2(1)(1)10a x a x ----=,显然0x =,1x a=-都不是此方程的根,当1a =时,没有实根,则1a ≠,由2(1)4(1)0a a -+-<得:31a -<<, 故当(3,1]a ∈-时,函数()()()F x f x g x =-没有零点; ……………3分⑵21'()f x x=,21'()(1)g x ax =+,设它们的公共点为(,)P P P x y ,则有⎧⎪⎨⎪⎩()()'()'()P P P P P P y f x y g x f x g x ===即⎧⎨⎩()()'()'()P P P P f x g x f x g x ==也就是⎧⎪⎨⎪⎩2211111()(1)P P P P Px x ax x ax -=+=+当1P P ax x +=时111P x -=,无解;当1P P ax x +=-时111P x -=-,12P x =,3a =-;…………8分 ⑶由题得111xx e ax -≤+在[0,)+∞上恒成立,因为0x ≥,故1[0,1)xe --∈, 所以110x e -≥在[0,)+∞上恒成立,故01xax ≥+在[0,)+∞上恒成立,所以,0a ≥. ……………10分解法一:不等式11x x e ax --≤+恒成立等价于(1)(1)0xax e x -+--≤在[0,)+∞上恒成立, 令1()(1)(1)1x x ax h x ax e x ax x e -+=+--=-+--,则1'()1x ax a h x a e -+=+-,再设()'()m x h x =,则21'()xax a m x e-+-=,同时,'(0)21m a =-,'(0)0h =,(0)0h =, ①当0a =时,1'()0,x m x e=-<,则()'()m x h x =在[0,)+∞上单调递减,∴ '()'(0)=0h x h ≤,∴()h x 在[0,)+∞上单减,∴ ()(0)=0h x h ≤,即()()xf eg x ≤在[0,)+∞上恒成立,②当102a <≤时,21()'()xa a x a m x e ---=,因为210a a-->,所以'()0m x <,则()'()m x h x =在[0,)+∞上单调递减,∴'()'(0)=0h x h ≤,∴ ()h x 在[0,)+∞上单减, ∴()(0)=0h x h ≤,即()()xf eg x ≤在[0,)+∞上恒成立,③当12a >时,21()'()xa a x a m x e ---=,210a a->若210a x a-<<,则'()0m x >,即()'()m x h x =在21(0,)a a -上单调递增,所以'()'(0)0h x h >=即()h x 在21(0,)a a-上也单调递增,∴()(0)=0h x h >,即()()xf eg x ≥,不满足条件.综上,()()xf eg x ≤在[0,)+∞上恒成立时,实数a 的取值范围是1[0,]2. (16)分解法二:不等式11x x e ax --≤+恒成立等价于(1)(1)0x xax e e x +--≤在[0,)+∞上恒成立, 设()(1)(1)=(1)(1)xxxh x ax e e x e ax x ax =+---+-+,则'()()xh x e ax x a a =-+-, 再设()'()()xm x h x e ax x a a ==-+-,则'()[(1)(21)]xm x e a x a =-+- 同时,'(0)21m a =-,(0)'(0)0m h ==,(0)0h =,①当1a ≥时,'(0)210m a =->,故函数'()h x 是(0,)+∞上的增函数所以'()'(0)0h x h >=, 所以函数()h x 是(0,)+∞上的增函数,所以当(0,)x ∈+∞时,()(0)0h x h >=, 即()()xf eg x ≤,与()()x f e g x ≤在[0,)+∞上恒成立不符,②当102a ≤≤时2101a a -≥-,21'()(1)()01x a m x a e x a -=-+<-,故函数'()h x 是(0,)+∞上的减函数 所以'()'(0)0h x h <=,函数()h x 是(0,)+∞上的减函数,所以当(0,)x ∈+∞时,()(0)0h x h ≤=, 即()()f x g x ≤在[0,)+∞上恒成立,③当112a <<时,2101a a -<-,21'()(1)()1x a m x a e x a -=-+-当21(0,)1a x a -∈--时,'()0m x >, 故函数'()h x 是21(0,)1a a ---上的增函数所以在21(0,)1a x a -∈--上,'()'(0)0h x h >=,所以函数()h x 是21(0,)1a a ---上的增函数,所以当21(0,)1a x a -∈--时,()(0)0h x h >=,即()()xf eg x ≥,与()()xf eg x ≤在[0,)+∞上恒成立不符,综上可得,使()()xf eg x ≤在[0,)+∞上恒成立实数a 的取值范围是1[0,]2.第二部分21B .已知矩阵213,125M β ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦,计算2M β. 解法一:矩阵M 的特征多项式为221()4312f λλλλλ- -==-+- -,令()0f λ=,解得1,3λλ==,对应的一个特征向量分别为1211,11αα⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦, ……………5分 令12m n βαα=+,得1,4m n =-=,22221212(4)()4()M M M M βαααα=-+=-+22113511431137⎡⎤⎡⎤⎡⎤=-⨯+⨯=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦. ……………10分解法二:因为221211212M 5 4⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥ 4 5⎣⎦⎣⎦⎣⎦, ……………5分所以2335537M β5 4⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥4 5⎣⎦⎣⎦⎣⎦. ……………10分 21C .已知圆C 的极坐标方程是4sin ρθ=,以极点为平面直角坐标系的原点,极轴为x 轴的正半轴,建立平面直角坐标系,直线l的参数方程是2(12x t t y t m ⎧=⎪⎪⎨⎪=+⎪⎩是参数).若直线l 与圆C 相切,求正数m 的值. 解:由4sin ρθ=,得24sin ρρθ=,所以2240x y y +-=,即圆C 方程为22(2)4x y +-= ……………4分又由212x t y t m ⎧=⎪⎪⎨⎪=+⎪⎩,消t得0x +=, ……………8分 因为直线l 与圆C相切,所以||22-=得23m =±,又0m >,所以323m =+. ……………10分 22.如图,平行四边形ABCD 所在平面与直角梯形ABEF 所在平面互相垂直, 且11,//2AB BE AF BE AF ===,,,2,3AB AF CBA BC P π⊥∠==为 DF 中点.⑴求异面直线DA 与PE 所成的角;⑵求平面DEF 与平面ABCD 所成的二面角(锐角)的余弦值.解:在ABC ∆中,1,,23AB CBA BC π=∠==, 所以2222cos 3AC BA BC BA BC CBA =+-⨯∠=所以222AC BA BC +=,所以AB AC ⊥又因为平面ABCD ⊥平面ABEF ,平面ABCD 平面ABEF AB =, AC ⊂平面ABCD ,所以AC ⊥平面ABEF如图,建立空间直角坐标系{,,}AB AF AC ,则13(0,0,0),(1,0,0),3),(3),(1,1,0),(0,2,0),(2A B C D E F P -- ⑴33(1,0,3),(,0,22DA PE =-=- 设异面直线DA 与PE 所成的角为α,则3cos |||2||||23DA PE DA PE α⋅===⨯⨯ 所以异面直线DA 与PE 所成的角为6π; ……………5分 ⑵(0,2,0)AF =是平面ABCD 的一个法向量,设平面DEF 的一个法向量(,,)n x y z =,(2,1,3),(1,2,3)DE DF =-=则(,,)(2,1,3)230(,,)(1,2,3)230n DE x y z x y z n DF x y z x y z ⎧⋅=⋅=+-=⎪⎨⋅=⋅=+=⎪⎩, 得33z x ==,取1x =,则1,3y z ==故(1,1,3)n =是平面DEF 的一个法向量,设平面DEF 与平面ABCD 所成的二面角(锐角)为β,则2cos |||||||2AF n AF n β⋅===⨯⨯. ……………10分 23.设集合{1,0,1}M =-,集合123{(,,)|,1,2,,}n n i A x x x x x M i n =∈=,,, 集合n A 中满足条件“121||||||n x x x m ≤+++≤”的元素个数记为n m S .⑴求22S 和42S 的值;⑵当m n <时,求证:n m S 111322n m n +++<+-. 解⑴228S =,4232S =; ……………3分 ⑵设集合{0}P =,{1,1}Q =-.若12||||||1n x x x +++=,即123,,n x x x x ,,中有1n -个取自集合P ,1个取自集合Q ,故共有112n n C -种可能,即为112n C ,同理,12||||||2n x x x +++=,即123,,n x x x x ,,中有2n -个取自集合P ,2个取自集合Q , 故共有222n nC -种可能,即为222n C , ……若12||||||n x x x m +++=,即123,,n x x x x ,,中有n m -个取自集合P ,m 个取自集合Q , 故共有2n m m n C -种可能,即为2m m n C ,所以1122222n m m m n n n S C C C =++⋅⋅⋅+,因为当0k n ≤≤时,1k n C ≥,故10k n C -≥所以1122222n m m m n n n S C C C =+++001122112(222)(1)2(1)2m m m m n n n n n n n n C C C C C C ++<+++++-++- 0011221112(222222)(222)m m m m n n m m n n n n n n n C C C C C C ++++=+++++++-++11(12)(22)n n m ++=+--11322n n m ++=-+. ……………10分。
江苏省扬州中学2016届高三4月质量监测考试数学试题 含解析

一、填空题:本大题共14个小题,每小题5分,共70分。
1.已知集合M ={0, 1, 2},N ={x |x =2a , a ∈M },则集合M ∩N =___________. 【答案】{0,2} 【解析】试题分析:因为}4,2,0{=N ,所以{02}M N =,考点:集合运算【方法点睛】集合的基本运算的关注点(1)看元素组成.集合是由元素组成的,从研究集合中元素的构成入手是解决集合运算问题的前提.(2)有些集合是可以化简的,先化简再研究其关系并进行运算,可使问题简单明了,易于解决.(3)注意数形结合思想的应用,常用的数形结合形式有数轴、坐标系和Venn 图.2.若复数z 1=3+4i,z 2=a +i,且z 1·错误!是实数(其中错误!为z 2的共轭复数),则实数a =___________.【答案】34【解析】试题分析:因为i a a i a i z z )34(43))(43(21-++=-+=⋅是实数,所以.43,034==-a a 考点:复数概念与运算3。
有3个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为_______.【答案】13考点:古典概型概率4。
“m=-1”是“直线mx+(2m-1)y+1=0和直线3x+my+3=0垂直"的___________条件.【答案】充分不必要考点:充要关系,两直线垂直【方法点睛】判断充分条件和必要条件的方法(1)命题判断法:设“若p,则q”为原命题,那么:①原命题为真,逆命题为假时,p是q的充分不必要条件;②原命题为假,逆命题为真时,p是q的必要不充分条件;③原命题与逆命题都为真时,p是q的充要条件;④原命题与逆命题都为假时,p是q的既不充分也不必要条件.(2)集合判断法:从集合的观点看,建立命题p,q相应的集合:p:A={x|p(x)成立},q :B ={x|q (x)成立},那么:①若A ⊆B ,则p 是q 的充分条件;若A ≠⊂B 时,则p 是q 的充分不必要条件;②若B ⊆A ,则p 是q 的必要条件;若B ≠⊂A 时,则p 是q 的必要不充分条件;③若A ⊆B 且B ⊆A ,即A =B 时,则p 是q 的充要条件. (3)等价转化法:p 是q 的什么条件等价于綈q 是綈p 的什么条件. 5.右边程序输出的结果是___________.【答案】10 【解析】试题分析:第一次循环:2=S ,第二次循环:532=+=S ,第三次循环:1055=+=S ,输出的结果是10.考点:循环结构流程图6。
江苏省扬州市2016届高三上学期期末调研考试数学试题word版(含答案)全解

扬州市2021—2021学年度第一学期期末检测试题高三数学2021.1第一局部一、填空题〔本大题共14小题,每题5分,共70分,请将答案填写在答题卡相应地点〕.会合Ax2x<B,1,2,那么AB▲.i(32i)〔i是虚数单位〕,那么z的虚部为▲.3.如图,假定输入的x值为,那么相应输出的值为▲.34.某学校从高三年级共800名男生中随机抽取50名丈量身高.据丈量被测学生身高所有介于155cm和195cm之间,将丈量结果按以下方式分红八组:第一组155,160、第二组160,165、、第八组190,195.按上述分组方式获取的频次散布直方图的一局部以下列图,预计这所学校高三年级全体男生身高180cm以上〔含180cm〕的人数为▲.x2y21的焦点到渐近线的距离为▲.1696.从1,2,3,4,5这5个数中,随机抽取2个不一样的数,那么这2个数的和为偶数的概率是▲.n知足a22a14,a32a5,那么该数列的前5项的和为▲. 42,体积为32,那么此四棱锥的侧棱长为▲.9.f(x)sin(2x)x<f()f()1.函数〕,且〔〕,那么▲3〔02(cos,sin),n(2,1),,,假定mn1,那么sin(23)▲.222-1-11.a >b >1且2log a b3log b a7,那么a1.的最小值为▲b 2112. 圆O :x 2y 24,假定可是原点O 的直线l 与圆O 交于P 、Q 两点,且知足直线OP 、PQ 、OQ 的斜率挨次成等比数列,那么直线l 的斜率为▲.13.a n中,a 1a 〔0<aa n 2 (a n >2)〔nN*数列 2〕,a n13 (a n2) 〕,记a nS na 1a 2a n,假定S n2021,那么n▲.14. 函数f(x)是定义在R 上的奇函数,当x1 ax 2a3a 〕.假定会合0时,f(x)〔x2x|f(x1) f(x)>0,xR ,那么实数a 的取值范围为▲.二、解答题〔本大题共 6小题,计90分.解允许写出必需的文字说明、证明过程或演算步骤〕15. 〔本小题总分值 14分〕如图,直三棱柱ABCA 1B 1C 1中,AB AC ,D 、E 分别为BC 、CC 1中点,BC 1 B 1D .1〕求证:DE//平面ABC 1;2〕求证:平面AB 1D 平面ABC 1.〔本小题总分值14分〕 函数 f(x) 3cos 2 xsin xcosx 〔 >0〕的周期为 .〔1〕当x0, 时,求函数 f(x)的值域;2〔2〕ABC 的内角 A , , 对应的边分别为 a ,,,假定A )3 ,且a 4,bc5,BCbcf(2求ABC 的面积.-2-〔本小题总分值15分〕如图,椭圆x2 y 21〔a>b>0〕的左、右焦点为F1、F2,P是椭圆上一点,M在a2 b2PF1 上,且知足FM MP〔R〕,PO F2M,O为坐标原点.1〔1〕假定椭圆方程为x2 y2 1 ,且P〔2,2 〕,求点M的横坐标;42〕假定2,求椭圆离心率e的取值范围.18.〔本小题总分值15分〕某地道设计为双向四车道,车道总宽20米,要求通行车辆限高米,地道口截面的拱线近似地当作抛物线形状的一局部,以下列图成立平面直角坐标系xoy.〔1〕假定最大拱高h为6米,那么地道设计的拱宽l是多少?〔2〕为了使施工的土方工程量最小,需地道口截面面积最小.现地道口的最大拱高h不小于6米,那么应怎样设计拱高h和拱宽l,使得地道口截面面积最小?〔地道口截面面积公式为S2lh〕3-3-〔本小题总分值16分〕函数 f(x) (ax2 x 2)e x〔a>0〕,此中e是自然对数的底数.〔1〕当a2时,求f(x)的极值;〔2〕假定f(x)在2,2上是单一增函数,求a的取值范围;〔3〕当a1时,求整数t的所有值,使方程f(x) x 4在t,t1上有解.〔本小题总分值16分〕假定数列a n 中不超出f(m)的项数恰为b m〔mN*〕,那么称数列b m 是数列a n的生成数列,称相应的函数f(m)是数列a n 生成b m 的控制函数.〔1〕a n n2,且f(m) m2,写出b1、b2、b3;〔2〕a n 2n,且f(m) m,求b m的前m项和S m;〔3〕a n 2n,且f(m) Am3〔A N*〕,假定数列b m 中,b1,b2 ,b3是公差为d〔d 0〕的等差数列,且b310,求d的值及A 的值.-4-第二局部〔加试局部〕21.〔本小题总分值10分〕mn直线l:x y1在矩阵A对应的变换作用下变成直线l:x y1,求矩阵A.0 122.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.〔本小题总分值10分〕在极坐标系中,求圆8sin上的点到直线〔R〕距离的最大值.3-5-〔本小题总分值10分〕某商场举办“迎新年摸球〞活动,主办方准备了甲、乙两个箱子,此中甲箱中有四个球,乙箱中有三个球〔每个球的大小、形状完整同样〕 ,每一个箱子中只有一个红球,其他都是黑球 .假定摸中 甲箱中的红球,那么可获奖金 m 元,假定摸中乙箱中的红球,那么可获奖金 n 元.活动规定:①参加者每 个箱子只好摸一次,一次摸一个球;②可选择先摸甲箱,也可先摸乙箱;③假如在第一个箱子中摸 到红球,那么可持续在第二个箱子中摸球,否那么活动停止 .〔1〕假如参加者先在乙箱中摸球,求其恰巧获取奖金 n 元的概率;〔2〕假定要使得该参加者获奖金额的希望值较大,请你帮他设计摸箱子的次序,并说明原因 .〔本小题总分值10分〕函数f(x)2x3x 2,设数列 a n 知足:a 11 ,a n1f(a n ).4〔1〕求证:nN *,都有0<a n <1;3〔2〕求证:31 3 1 3 4n14.1 3a 1 3a2 3a n-6-扬州市2021-2021学年度第一学期高三期末调研测试 数学试题Ⅰ参照答案2021.1 一、填空1.12.33.14.1445.46.27.318.5259.710.7 11. 312.113.134314.(,1 ]6256二、解答〔本大共 6小, 90分.解答写出必需的文字明、明程或演算步〕 15.明:〔1〕D 、E 分BC 、CC 1中点,DE//BC 1,⋯⋯⋯⋯2分DE平面ABC 1,BC 1平面ABC 1DE//平面ABC 1⋯⋯⋯⋯6分〔2〕直三棱柱ABC A 1B 1C 1中,CC 1平面ABC AD 平面ABCCC 1AD ⋯8分AB AC ,D BC 中点ADBC ,又 CC 1 BC C ,CC 1,BC平面BCC 1B 1,AD 面BCC 1B 1BC 1平面BCC 1B 1 ADBC 1⋯⋯⋯⋯11分又 BC 1B 1D ,B 1DADD ,B 1D ,AD平面AB 1DBC 1 平面AB 1DBC 1 平面ABC 1 平面AB 1D 平面ABC 1⋯⋯⋯⋯14分16.解:〔1〕f(x)3(1cos2x) 1sin2xsin(2 x) 3⋯⋯⋯⋯2分2232f(x)的周期,且0 ,2,解得1f(x)sin(2x) 32⋯⋯⋯⋯4分32又 0 x,得 2x4, 3) 1 ,3sin(2x2 3 3230 sin(2x) 33 即函数yf(x)在x[0,321 ]上的域[0,1].⋯⋯⋯7分3222〔2〕f(A)3 sin(A) 3由A(0, ),知A4 ,22333 3解得:A2⋯⋯⋯⋯9分3,因此A 33由余弦定理知:a 2b 2c 22bccosA ,即16 b 2 c 2bc16 (b23bc ,因bc 5,因此bc3⋯⋯⋯⋯12分 c) ∴S ABC1bcsinA3 3.⋯⋯⋯⋯14分2417.〔 1〕x 2y 2 1F 1( 2,0),F 2(2,0)k OP2 2,k F 1M2 84,k F 2M 42-7-直线F 2M 的方程为:y2(x2),直线F 1M 的方程为:y2 (x2)4分4y2(x 2) 6 点M 的横坐标为6由 2解得:x 6分y (x 2) 5 542〕设P(x 0,y 0),M(x M ,y M )F 1M 2MP F 1M 2 (x 0 c,y 0)(x M c,y M )2 1 2 y 0),F 2M 24 2 3M( x 0 c, ( x 0c, y 0) 3 3 333 3POF 2M ,OP(x 0,y 0) 2 4 2 2 0(x 0 c)x 0 3 y 02 23 3即x 0 y 0 2cx 09分x 0 2 y 0 22cx 0 得:c 2x 02 2a 2cx 0a 2(a 2c 2)联立方程得:x 02y 0 2 1,消去y 0 0a2b2解得:x 0a(a c)或x 0 a(a c)12分ccax 0 ax 0 a(a c)(0,a)0 a 2ac ac 解得: 1ce2综上,椭圆离心率 e 的取值范围为(1,1).15分218.解:〔1〕设抛物线的方程为:y ax 2(a0),那么抛物线过点 (10, 3 ),2代入抛物线方程解得: a3 ,3分200令y 6,解得:x20,那么地道设计的拱宽 l 是40米;5分〔2〕抛物线最大拱高为h 米,h6,抛物线过点(10,(h9hh ,解得:x2100h,那么(l )2令yh ,那么2 x 210092h29 9h2)),代入抛物线方程得:a10029100hl 2,h2 9分9l 2 400h29 l 2229 l 23l 3h626即20l40lh2(20 l40)l 2400Sll 2400l 2400339l 2(l 23l 33l 2(l 23l 2(l12分S'400) 2l1200)20 3)(l 20 3)(l 2 400)2 (l2 400)2(l 2 400)2当20 l 20 3时,S' 0;当20 3 l40时,S'0,即S 在(20,20 3)上单一减,在(203,40]上单一增,S 在l203时获得最小值,此时 l 20 3,h27427米,拱宽为答:当拱高为203米时,使得地道口截面面积最小.15分419.解:〔1〕f(x) (2x 2x2)e x ,那么f '(x)(2x 2 5x3)e x(x1)(2x 3)e x2分令f '(x)0,x1, 32x( 3 3( 31(1, ),)2,1)22-8-11f '(x)f(x)增极大值 减极小值增33f(x)极大值=f() 5 e 2 ,f(x)极小值=f(1) 3e1 4分2〔2〕问题转变成 f '(x)ax 2 (2a 1)x 3e x0在x [2,2] 上恒成立;x0即ax 2(2a1)x3 0在x [ 2,2] 上恒成立;6分又e 令g(x)2(2a 1)x3a0,对称轴x1 0ax12a①当112,即0a1 时,g(x)在[ 2,2]上单一增, 2a2g(x)ming( 2)10 a18分2②当21 1 0,即a1 时,g(x)在[ 2, 1 1 ]上单一减,在[1 1 ,2]上单一增, 2a2 2a2a212a 0 解得: 1 3 1 3 1 3(2a1) a 2a 12 2 23综上,a 的取值范围是 (0,1 ].10分2〔3〕 a1,设h(x)2x x 4 ' 2 3x x1(x x2)e ,h(x) (x3)e令(x) (x 2 3x 3)e x 1 ,'(x)(x 2 5x 6)e x令'(x)(x 2 5x 6)e x0,得x 2, 3x(,3)3(3, 2)2(2,)'(x)(x)增极大值 减 极小值增 (x)极大值=( 3)3 1 0 , (x)极小值=( 2)11 013分32ee(1)1 1 0,(0)2 0存在x 0 ( 1,0),x(- ,x 0)时(x)0,x(x 0,+)时(x)0eh(x)在( ,x 0)上单一减,在(x 0, )上单一增又h(4)140,h(3)81 0,h(0)20,h(1) 4e 5 043ee由零点的存在性定理可知: h(x) 0的根x 1 ( 4,3),x 2(0,1) 即t4,0 . 16分20.解:〔1〕m1,那么a 11 1b 1 1;m2,那么a 1 1 4,a 2 4 4 b 22m 3 ,那么a 1 1 9,a 24 9a 3 99b 333分-9-12〔2〕m 为偶数时,那么2nm ,那么mm ; m 为奇数时,那么2nm1 ,那么mm1 ;b2b 2m 1 为奇数 )2 (mb m5分m为偶数 )2(mm 为偶数时,那么S m b 1 b 2b m1(1 2 m)1 m m2 ;22 2 4m 为奇数时,那么S m b 1 b 2b m S m1b m1(m 1)2 m 1 m 2 1;4 2 4m 2 1为奇数 )4 (mS m8分m 2为偶数 )4(m〔3〕依题意:a n2n ,f(1)A ,f(2) 8A ,f(5) 125A ,设b 1 t ,即数列{a n }中,不超出A 的项恰有t 项,因此2tA2t1,t+d8Atd1 t+2d125A t2d1, 同理:22,222t A 2t 1,故max{2t ,2t+d3,2t+2d}d2,2t2d1即2t+d 3 A 2td 2,A min{2t1,2t }2t+2dA2t 2d 1 ,1251251251252t+d 32t1,由2t+2dtd 2, 得d4, d 为正整数d 1,2,,310分125 2当d1时,max{2t ,2t+d3,2t+2d }=max{2t ,2t,42t }2t ,1254125min{2t1,2td2,2t2d 1}=min{2t1,2t,82t } 8 2t 2t 不合题意,舍去;1252 125 125当d2时,max{2t,2t+d3,2t2d}=max{2t ,2t1,162t } 2t ,125125min{2t 1,2td2,2t2d 1}=min{2t 1,2t ,32 2t} 322t 2t 不合题意,舍去;125125 125当d3时,max{2t,2t+d3, 2t+2d}=max{2t ,2t ,642t}2t125125min{2t1,2td2,2t2d1}=min{2t1,2t+1,1282t }125125,1282t2t 合适题意,12分125t128 tt,b 2t 3,b 5t6,t3b 3t6 此时2A2 ,b 1125b104t7t 为整数 t4,t5,t6t73或-10-13f(3)27A ,b 3101027A112102112 2A⋯⋯⋯14分2727当t4,24 A211无解125当t5,25 A212无解125当t6,26 A21364A213125125当t7,27 A214无解12526A213AN*A64或A65125上:d3,A 64或65.⋯⋯⋯16分2021-2021学年度第一学期高三期末调研测试数学试题Ⅱ参照答案21.解:〔1〕设直线l:x y 1上随意一点M(x,y)在矩阵A 的变换作用下,变换为点M(x,y).x' m n xmx ny,得xmxny 由1yyy⋯⋯⋯⋯5分y'y又点 M(x,y), xy 1,(mxny)y1在l 上因此即依题意m 1m 11 2 11 ,解得2 , A⋯⋯⋯⋯10分n n122.解:的直角坐方程x 2 (y4)2 16,⋯⋯⋯⋯3分 直的直角坐方程y3x ,⋯⋯⋯⋯6分心(0,4到)直的距离d0 42,上点到直距离最大2( 3) 21Ddr 2 4 6.⋯⋯⋯⋯10分23.解:〔1〕设参加者先在乙箱中摸球,且恰巧获取奖金n 元为事件M .那么P(M) 13 1即参加者先在乙箱中摸球,且恰巧获取奖金n 元的概率为1.34 44⋯⋯⋯⋯4分〔2〕参加者摸球的次序有两种,分别议论以下:-11-精选文档14①先在甲箱中摸球,参加者获奖金 x 可取0,m,m+n那么P(x=0)=3,P(x=m)=1?2 1,P(x=m+n)=1?11443 64 3123 1 (m+n)? 1 m n ⋯⋯⋯⋯6分Ex=0?m?+124612 4②先在乙箱中摸球,参加者获奖金h 可取0,n,m+n那么P(0)2 13 1 ,P(1 1 1,P( n)44 mn)4 12333 Eh=0?2n?1(m+n)?1m +n ⋯⋯⋯⋯8分341212 32m-3nEx-Eh= 12当m3时,先在甲箱中摸球,再在乙箱中摸球,参加者获奖金希望值较大;n2当m =3时,两种次序参加者获奖金希望值相等;n2当m <3时,先在乙箱中摸球,再在甲箱中摸球,参加者获奖金希望值较大.n 2答:当m3时,先在甲箱中摸球,再在乙箱中摸球,参加者获奖金希望值较大;当n 2m =3时,n2两种次序参加者获奖金希望值相等;当m <3时,先在乙箱中摸球,再在甲箱中摸球,参加者n2获奖金希望值较大.⋯⋯⋯⋯10分24.〔1〕解:①当n1,a 11,有0a 1143n 1,不等式成立⋯⋯⋯⋯1分②假当nk(kN *),不等式成立,即a k13当n k1,a k1f(a k )2a k 22 2a k )3(a k213a k3(a k1)3 33于是1a k13(1a k )2330a k1,03( 1a k )21,即01 a k11,可得0a k11 3 33333因此当nk 1,不等式也成立由①②,可知,随意的正整数n ,都有 0 a n1 ⋯⋯⋯⋯4分3〔2〕由〔1〕可得1a n13( 1 a n )233-12-精选文档15两边同时取 3为底的对数,可得 log 3(112log 3(1a n1) a n )33化简为1log 3(1 a n 1)2[1 log 3(1 a n )]33因此数列{1log 3( 1a n )}是以log 31为首项,2 为公比的等比数列7分341log 3( 1a n ) n1 1 1 a n112n1 12n13 2log 3,化简求得:3 ( ),344341a n3n2时,2n1 C n 01 C n 1 1 C n 21 C n n 11 1n1n ,n1时,2n1 1nN *时,2n1n ,1342n134n1 a n31 1 11 1 3[42042142n1]3[41 424n ]4n141a 1a 2a n3331 3 1 33 4n 1 4.10分3a 1 3a 21 3a n-13-。
江苏扬州市2016届高三四模试题(5月)物理

扬州市2015-2016学年度高三第四次模拟测试物 理 试 题 2016.05本试卷共15题,满分为120分,考试时间100分钟一、单项选择题:本题共5小题,每小题3分,共15分.每小题只有一个....选项符合题意.选对的得 3 分,错选或不答的得 0 分.1.学习物理除了知识的学习外,还要领悟并掌握处理物理问题的思想与方法.下列关于物理学中的思想方法,叙述正确的是A .伽利略在研究自由落体运动时采用了微元法B .在探究求合力方法的实验中使用了理想实验法C .在探究决定导线电阻大小的因素实验中采用了控制变量法D .法拉第在研究电磁感应现象时运用了等效替代的思想2.2015年7月14日,“新视野”号太空探测器近距离飞掠冥王星.冥王星与其附近的另一星体卡戎可视为双星系统,同时绕它们连线上的O 点做匀速圆周运动.O 点到冥王星的距离为两者连线距离的八分之一,下列关于冥王星与卡戎的说法正确的是 A .质量之比为8∶1 B .向心力大小之比为1∶7 C .角速度大小之比为 1∶7 D .线速度大小之比为1∶7 3.将一质量为m 的小球靠近墙面竖直向上抛出,图甲是向上运动小球的频闪照片,图乙是下降时的频闪照片,O 是运动的最高点,甲、乙两次的闪光频率相同.重力加速度为g .假设小球所受阻力大小不变,则可估算小球受到的阻力大小约为 A .mg B .13mg C .12mg D .110mg4.如图所示, A 、B 、C 为直角三角形的三个顶点,∠A=30°,D 为AB 的中点,负点电荷Q 位于D 点.A 、B 、C 三点的电势分别用A ϕ、B ϕ、C ϕ表示,下列说法正确的是 A .C ϕ大于A ϕB .A 、B 两点电场强度相同C .负检验电荷在BC 连线上各点具有的电势能都相等二、多项选择题:本题共 4 小题,每小题 4 分,共16 分.每小题有多个选项符合题意.全部选对的得 4 分,选对但不全的得 2 分,错选或不答的得 0 分.6.如图所示,高为H 的塔吊臂上有一可以沿水平方向运动的小车A ,小车A 下的绳索吊着重物B .在小车A 与物体B 以相同的水平速度沿吊臂向右匀速运动的同时,绳索将重物B 向上吊起,A 、B 之间的距离以2d H t =-规律随时间t 变化,则在上述过程中A .绳索受到的拉力不断增大B .绳索对重物做功的功率不断增大C .重物做速度大小不断增大的曲线运动D .重物做加速度大小不断减小的曲线运动7.钳形电流表的外形和结构如图甲所示.图甲中电流表的读数为0.9 A ,图乙中用同一电缆线绕了3匝,则 A .这种电流表能测出交变电流的有效值 B .这种电流表既能测直流电流,又能测交变电流 C .这种电流表能测交变电流,图乙的读数为0.3A D .这种电流表能测交变电流,图乙的读数为2.7 A8.如图所示电路中,电源电动势为E (内阻不可忽略),线圈L 的电阻不计.以下判断正确的是A .闭合S 稳定后,电容器两端电压为EB .闭合S 稳定后,电容器的a 极板带负电C .断开S 的瞬间,通过R 1的电流方向向右D .断开S 的瞬间,通过R 2的电流方向向右9.如图所示,在竖直平面内固定有两个很靠近的同心圆轨道,外圆光滑,内圆粗糙.一质量为m 的小球从轨道的最低点以初速度v 0向右运动,球的直径略小于两圆间距,球运动的轨道半径为R ,不计空气阻力.设小球过最低点时重力势能为零, 下列说法正确的是A .若小球运动到最高点时速度为0,则小球机械能一定不守恒B .若经过足够长时间,小球最终的机械能可能为mgR 23C .若使小球始终做完整的圆周运动,则v 0一定不小于gR 5D .若小球第一次运动到最高点时速度大小为0,则v 0一定大于gR 4三、简答题:本题分必做题(第10、11题)和选做题(第12题)两部分,共计42分.请将解答填写在答题卡相应的位置. 10.(8分)某同学在用如图甲所示的装置做“探究加速度与物体受力的关系”实验.(1)该同学在实验室找到了一个小正方体木块,用实验桌上的一把游标卡尺测出正方体木块的边长,如图甲所示,则正方体木块的边长为 ▲ cm .(2)接着用这个小正方体木块把小车轨道的一端垫高,通过速度传感器发现小车刚好做匀速直线运动.设小车的质量为M ,正方体木块的边长为a ,并用刻度尺量出图中AB 的距离为L (a L ,已知θ很小时tan θ≈sin θ),则小车向下滑动时受到的摩擦力为 ▲(3)然后用细线通过定滑轮挂上重物让小车匀加速下滑,不断改变重物的质量m ,测出对应的加速度a ,则下列图像中能正确反映小车加速度a 与所挂重物质量m 的关系的是 ▲5 (cm) 图甲 3 4 5 01011.(10分)实验室有下列器材:灵敏电流计G (内阻约为50Ω);电压表V (0~3V ,内阻约为10kΩ); 电阻箱R 1(0~9999Ω);滑动变阻器R 2(0~100Ω,1.5A ); 旧干电池一节;导线开关若干.(1)某实验小组先测灵敏电流计的内阻,电路如图甲所示,测得电压表示数为2V ,灵敏电流计示数为4mA ,电阻箱旋钮位置如图乙所示,则灵敏电流计内阻为 ▲ Ω.(2)为将灵敏电流计的量程扩大为原来的10倍,该实验小组将电阻箱与灵敏电流计并联,则应将电阻箱R 1的阻值调为 ▲ Ω.调好后连接成如图丙所示的电路测干电池的电动势和内阻,调节滑动变阻器读出了几组电压表和电流计的示数如下表,请在图丁所(3)由作出的I G -U 图线求得干电池的电动势 E = ▲ V ,内阻r = ▲ Ω.12.【选做题】本题包括A 、B 、C 三小题,请选定两题作答,并在答题卡上把所选题目对应字母后的方框涂满涂黑.如都作答则按A 、B 两小题评分. A .(选修模块3-3)(12分)(1)关于饱和汽和相对湿度,下列说法中错误的是 ▲A .使未饱和汽变成饱和汽,可采用降低温度的方法B .空气的相对湿度越大,空气中水蒸气的压强越接近饱和汽压C .密闭容器中装有某种液体及其饱和蒸汽,若温度升高,同时增大容器的容积,饱和汽压可能会减小D .相对湿度过小时,人会感觉空气干燥(2)如图所示,一定质量的理想气体发生如图所示的状态变化,从状态A 到状态B ,在相同时间内撞在单位面积上的分子数 ▲ (选填“增大”、“不变”或“减小”),从状态A 经B 、C 再回到状态A ,气体吸收的热量 ▲ 放出的热量(选填“大于”、“小于”或“等于”) .甲乙丙 丁/LP(3)已知阿伏加德罗常数为6.0×1023mol -1,在标准状态(压强p 0=1atm 、温度t 0=0℃)下任何气体的摩尔体积都为22.4L ,已知第(2)问中理想气体在状态C 时的温度为27℃,求该气体的分子数.(计算结果取两位有效数字)B .(选修模块3-4)(12分)(1)下列说法中正确的是 ▲A .变化的电场一定能够在其周围空间产生变化的磁场从而形成电磁波B .当观察者向静止的声源运动时,接收到的声音的波长大于声源发出的波长C .相对论认为时间和空间与物质的运动状态有关D .泊松亮斑是光的干涉现象,全息照相的拍摄利用了光的衍射原理 (2)如图所示,在某一均匀介质中,A 、B 是振动情况完全相同的两个波源,其简谐运动表达式均为x =0.3sin(200πt ) m ,两波源形成的简谐横波分别沿AP 、BP 方向传播,波速都是500 m/s .某时刻在P 点两列波的波峰相遇,则简谐横波的波长为▲ m ,介质中P 点的振幅为 ▲ m .(3)如图所示,ABCD 为一棱镜的横截面,∠A =∠B =90°,∠C =60°,CD 面为镀银的反射面,BC 边长为L ,一束单色光垂直AB 面射入棱镜,从BC 面中点P 射出后垂直射到与水平方向成30°的光屏MN 上,光在真空中速度为c ,求: (1)棱镜材料的折射率;(2)光束在棱镜中传播的时间.C .(选修模块3-5)(12分)(1)下列说法中正确的是 ▲A .一定强度的入射光照射某金属发生光电效应时,入射光的频率越高,单位时间内逸出的光电子数就越多B .各种气体原子的能级不同,跃迁时发射光子的能量(频率)不同,因此利用不同的气体可以制成五颜六色的霓虹灯C .德布罗意在爱因斯坦光子说的基础上提出物质波的概念,认为只有高速运动的粒子才具有波粒二象性D .核力将核子束缚在核内,说明核力一定是吸引力(2)已知质子的质量为m 1,中子的质量为m 2,碳核(C 126)的质量为m 3,则碳核(C 126)的比结合能为 ▲ ,碳-14是碳的一种具有放射性的同位素,研究发现外来的宇宙射线与大气作用产生宇宙射线中子,宇宙射线中子和大气中氮核(147N )起核反应产生碳-14,请写出核反应方程 ▲ . (3)在列车编组站里,一辆m 1=3.6×104kg 的甲货车在平直轨道上以v 1=2m/s 的速度运动,碰上一辆m 2=2.4×104kg 的静止的乙货车,它们碰撞后结合在一起继续运动,求货车碰撞后运动的速度以及甲货车在碰撞过程中动量的变化量.30° P60°v 1 乙 甲四、计算或论述题:本题共3小题,共47分.解答时应写出必要的文字说明、方程式和重要演算步骤,只写出最后答案的不能得分,有数值计算的题,答案中必须明确写出数值和单位.13.(15分)小亮观赏跳雪比赛,看到运动员先后从坡顶水平跃出后落到斜坡上.斜坡长80m,如图所示,某运动员的落地点B与坡顶A的距离L=75m,斜面倾角为37°,忽略运动员所受空气阻力.重力加速度取g=10m/s2,sin37°=0.6,cos37°=0.8.(1)求运动员在空中的飞行时间;(2)小亮认为,无论运动员以多大速度从A点水平跃出,他们落到斜坡时的速度方向都相同.你是否同意这一观点?请通过计算说明理由;(3)假设运动员在落到倾斜雪道上时,靠改变姿势进行缓冲使自己只保留沿斜坡的分速度而不弹起.运动员与斜坡和水平地面的动摩擦因数均为μ=0.4,经过C处运动员速率不变,求运动员在水平面上滑行的最远距离.14.(16分)如图所示,光滑的金属导轨间距为L,导轨平面与水平面成α角,导轨下端接有阻值为R的电阻.质量为m的金属细杆ab与绝缘轻质弹簧相连静止在导轨上,弹簧劲度系数为k,上端固定,弹簧与导轨平面平行,整个装置处在垂直于导轨平面斜向上的匀强磁场中,磁感应强度为B.现给杆一沿导轨向下的初速度v0,杆向下运动至速度为零后,再沿导轨平面向上运动达最大速度v1,然后减速为零,再沿导轨平面向下运动,一直往复运动到静止(金属细杆的电阻为r,导轨电阻忽略不计).试求:(1)细杆获得初速度的瞬间,通过R的电流大小;(2)当杆速度为v1时,离最初静止位置的距离L1;(3)杆由v0开始运动直到最后静止,电阻R上产生的焦耳热Q.15.(16分)在竖直平面内建立一平面直角坐标系xoy,x轴沿水平方向,如图甲所示.第二象限内有一水平向右的匀强电场,场强为E1.坐标系的第一、四象限内有一正交的匀强电场和匀强交变磁场,电场方向竖直向上,场强E2=12E1,匀强磁场方向垂直纸面.处在第三象限的发射装置(图中未画出)竖直向上射出一个比荷qm=102C/kg的带正电的粒子(可视为质点),该粒子以v0=4m/s的速度从-x上的A点进入第二象限,并以v1=8m/s 速度从+y上的C点沿水平方向进入第一象限.取粒子刚进入第一象限的时刻为0时刻,磁感应强度按图乙所示规律变化(以垂直纸面向外的磁场方向为正方向),g=10 m/s2.试求:(1)带电粒子运动到C 点的纵坐标值h 及电场强度E 1; (2)+x 轴上有一点D ,OD=OC ,若带电粒子在通过C 点后的运动过程中不再越过y 轴,要使其恰能沿x 轴正方向通过D 点,求磁感应强度B 0及其磁场的变化周期T 0; (3)要使带电粒子通过C 点后的运动过程中不再越过y 轴,求交变磁场磁感应强度B 0和变化周期T 0的乘积00T B 应满足的关系.扬州市2015/2016学年度高三第四次模拟测试物理试卷参考答案与评分标准一、单项选择题:本题共5小题,每小题3分,共15分.每小题只有一个....选项符合题意.选对的得 3 分,错选或不答的得 0 分. 1.C 2.D 3.B 4.D 5.C 二、多项选择题:本题共 4 小题,每小题 4 分,共16 分.每小题有多个选项符合题意.全部选对的得 4 分,选对但不全的得 2 分,错选或不答的得 0 分. 6.BC 7.AD 8.BC 9.ACD三、简答题:本题分必做题(第10、11题)和选做题(第12题)两部分,共计42分.请将解答填写在答题卡相应的位置.10.(8分)(1)3.150 (3分) (2)MgaL (2分) (3)C (3分) 11.(10分)(1)45 (2分) (2)5 (2分);如右图所示(2分) (3)1.4 (2分); 15.5(2分)12.A .(选修模块3-3)(12分) (1)C (3分);(2)减小、大于(每空2分)(3)0101V V T T =,解得标准状态下气体的体积为0.91L (2分)A AV n N V ==2.4×1022 (3分)B .(选修模块3-4)(12分) (1)C (3分)(2)5,0.6(每空2分)丁(3)sin sin in r==2分),3c v n ==(1分), 1.254L t v c ==(2分)C .(选修模块3-5)(12分) (1)B (3分)(2)()21236612m m m c +-,114141761n N C H +→+(每空2分)(3)对整个系统,碰撞过程动量守恒,设结合在一起继续运动的速度为v则 1112=()m v m m v + (2分)货车碰撞后运动的速度1112 1.2()m v v m m ==+m/s , (1分)甲货车的动量的变化量4111 2.8810p m v m v ∆=-=-⨯kg ·m/s (2分)(或“动量变化量大小为42.8810⨯ kg ·m/s ,方向向左”,同样给2分)四、计算或论述题:本题共3小题,共47分.解答时应写出必要的文字说明、方程式和重要演算步骤,只写出最后答案的不能得分. 13.(15分)解析:(1)︒=37sin L h 221gt h =解得:s t 3= (4分) (2)设在斜坡上落地点到坡顶长为L ,斜坡与水平面夹角为α,则运动员运动过程中的竖直方向位移sin h L α=,水平方向位移cos x L α=,运动时间由212h gt =得t =由此得运动员落到斜坡时,速度的水平方向分量x xv t==,速度的竖直方向分量y v gt ==,实际速度与水平方向夹角为tan 2tan yxv v βα==,由此可说明,速度方向与初速度无关,只跟斜坡与水平面的夹角α有关。
江苏省扬州市2016届高三上学期期末调研考试数学试题word版(含答案)

扬州市2015— 2016学年度第一学期期末检测试题3.如图,若输入的x 值为一,则相应输出的值为3、填空题 (本大题共1.已知集合 A二(x| x 2 2•若复数z = i(3 _2i) 第一部分14小题,每小题5分,共70分,请将答案填写在答题卡相应位置)—2XV 。
}, ^'0,1,2?,贝U A B =(i 是虚数单位),则z 的虚部为2016.1频率4•某学校从高三年级共 800名男生中随机抽取 和195cm 之间,将测量结果按如下方式分成八组:第一组 50名测量身高.据测量被测学生身高全部介于 155cm 155,160、第二组 160,165、……、第 八组190,95 1.按上述分组方式得到的频率分布直方图的一部分如图所示,估计这所学校高三年级 全体男生身高180cm 以上(含180cm )的人数为 2 2 5.双曲线X y 1的焦点到渐近线的距离为 9 16 6. 从1,2,3, 4, 5这5个数中,随机抽取2个不同的数,则这2个数的和为偶数的概率是 7. 已知等比数列[满足a 2 ■ 2a^ 4 , a ?2二,则该数列的前 5项的和为 — 8.已知正四棱锥底面边长为 4*2,体积为32,则此四棱锥的侧棱长为 JT 9.已知函数 f (x) = sin(2x )( 0 一 x v 「1 ),且 f (〉)= f (:)-(二),则〉二一▲210.已知 m =(cos : ,si n :), n =(2,1),其三I 2'2〕,若,则 Sn (i/=—___3■:小1 11. 已知 a > b >1 且 2log a b - 3log b a =7,贝V a •二的最小值为 ________ ▲.b -112. 已知圆O : x 2 y^4,若不过原点0的直线I 与圆0交于P 、Q 两点,且满足直线OP 、PQ 、0Q 的斜率依次成等比数列,则直线 I 的斜率为 _______ ▲13.已知数列i a j 中,內=a ( 0<a 兰2 ) , a“ =丿也一2(弘>2)( n = N * ),记— a . +3 (a .兰 2)S n = a 1 亠 a 2 亠'亠 a n ,若 S n = 2015,贝y n = _______ ▲ ______114.已知函数f(x)是定义在R 上的奇函数,当x^0时,f(x)= -(x -a+|x-2a-3a ).若集合「x| f(x -1) - f(x)>0, x ・R?—:」,则实数a 的取值范围为▲.、解答题(本大题共 6小题,计90分.解答应写出必要的文字说明、证明过程或演算步骤) 15. (本小题满分14分)如图,已知直三棱柱 ABC -AB 1C 1中,AB 二AC , D 、E 分别为BC 、CC 1中点,BC 1 _ B1D .16. (本小题满分14分)已知函数 f (x^ .3 cos^ x sin 「xcos 「x (「>0 )的周期为 二.(2)已知.ABC 的内角A , B , C 对应的边分别为a , b , c ,若f (△) ,且a = 4 ,b ,c = 5 ,2求ABC 的面积. 17. (本小题满分15 分)(1) 求证:DE // 平面 ABC 1 ; (2) 求证:平面AB^ _平面ABC 1.B(第1爲题(1 )当 x0,—时,求函数f (x)的值域;IL 22 2X y如图,已知椭圆—不=1 ( a> b>0)的左、右焦点为F i、F2, P是椭圆上一点,M在a bPF1上,且满足RM =hMP (丸乏R),P0丄F2M,O为坐标原点2 2(1)若椭圆方程为—y 1,且P (2, 2 ),求点M的横坐标;8 4(2 )若■ =2,求椭圆离心率e的取值范围.18. (本小题满分15分)某隧道设计为双向四车道,车道总宽20米,要求通行车辆限高 4.5米,隧道口截面的拱线近似地看成抛物线形状的一部分,如图所示建立平面直角坐标系xoy.(1)若最大拱高h为6米,则隧道设计的拱宽I是多少?(2)为了使施工的土方工程量最小,需隧道口截面面积最小.现隧道口的最大拱高h不小于6米,2则应如何设计拱咼h和拱宽I,使得隧道口截面面积最小?(隧道口截面面积公式为S lh)3(第KBS)19. (本小题满分16分)已知函数f (x) = (ax2+x+2)e x( a>0),其中e是自然对数的底数.(1 )当a = 2时,求f (x)的极值;(2 )若f(x)在2,2 1上是单调增函数,求a的取值范围;(3)当a =1时,求整数t的所有值,使方程f (x) = x • 4在t,t - 11上有解.20. (本小题满分16分)若数列a 冲不超过f (m)的项数恰为b m ( m N*),则称数列是数列3n 的生成数列,称相应的函数f(m)是数列:a n'生成"b m』的控制函数.(1)已知a n二n2,且f (m)二m2,写出b1、b2、b3;(2)已知a. =2n,且f(m) =m,求'b^?的前m项和S m ;(3)已知a* =2n,且f (m) = Am3( A N* ),若数列叽中,d,b?,b3是公差为d ( d = 0 ) 的等差数列,且b3 =10,求d的值及A的值.第二部分(加试部分)21. (本小题满分10分)已知直线l: x + y = 1在矩阵A = n"对应的变换作用下变为直线丨:x - y = 1 ,求矩阵A . I。
2016年5月2016届高三第四次全国大联考(江苏卷)数学卷(原卷版)

【学易大联考】2016年第四次全国大联考【江苏卷】数学试卷一、填空题:(本大题共14个小题,每小题5分,共70分,将答案填在答题纸上)1.已知全集U {1,2,3,4},=集合{1,2},{2,4}A B ==,则集合()U A B U ð等于_______. 2. 已知复数z满足(1i)i z -=(i 是虚数单位),则z 的模为_______.3. 已知一组数据:8,10,,12,11a 的方差为2,那么相对应的另一组数据:17,21,21,25,23a +的方差为_______.4. 运行如图所示的伪代码,其运行后输出的结果为_______.5. 袋中有形状、大小都相同的五只球,其中2只红球,3只白球,从中一次随机摸出2只球,则至少有1只白球的概率为_______.6.已知sin 2cos αα+=,那么tan 2α的值为_______. 7. 已知正三棱柱的各条棱长均为1,圆锥侧面展开图为半径为2的半圆,那么这个正三棱柱与圆锥的体积比是_______.8. 在ABD ∆中,13112,,343AB AD AE AD BC BD BE AC ====⋅= ,,则BAD ∠的值为_______. 9. 已知等比数列{}n a 的前n 项和为n S ,满足243n n S S +=+,且30S <,则 2a 的值为_______.10. 已知正数,,a b c 满足42250a b c -+=,则lg lg 2lg a c b +-的最大值为_______.11.设F 为双曲线22221(0,0)x y a b a b-=>>的右焦点,过点F 作双曲线一条渐近线的垂线,垂足为A ,垂线交另一条渐近线于B 点,若向量BF 与FA 同向,且3AB OA OB =+,则双曲线的离心率为_______.12. 在平面直角坐标系xOy 中,圆221x y +=交x 轴于,A B 两点,且点A 在点B 左边,若直线0x m +=p ←1For k From 1 To 10 Step 3p ←2k p -End ForPrint p第4题图上存在点P ,使得2PA PB =,则m 的取值范围为_______.13.扇形AOB 中,弦1AB =,C 为劣弧 AB 上的动点,AB 与OC 交于点P ,则OP BP ⋅ 的最小值是_______.14.已知函数(),()()()(),()()f x f xg xh x g x f x g x ≤⎧=⎨>⎩, 31(),()ln 4f x x ax g x x =++=-,若()0h x =在(0,)+∞上有三个不同的实数根,则实数a 的取值范围为_______.二、解答题 (本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.)15. (本小题满分14分)在ABC ∆中,角C B A 、、分别是边c b a 、、的对角,且(cos ,sin ),(cos ,sin ),cos 2,sin sin 3sin sin A A B B C A B A B =-=⋅=+=m n m n ,(Ⅰ)求角C 的值;(Ⅱ)若3c =,求ABC ∆的面积.16. (本小题满分14分)如图,在四棱锥E -ABCD 中,底面ABCD 是正方形,AC 与BD 交于点O ,EC ⊥底面ABCD ,F 为BE 上一点,G 为EO 中点.(Ⅰ)若DE //平面ACF ,求证:F 为BE 的中点;(Ⅱ)若AB CE ,求证:CG ⊥平面BDE .17. (本小题满分14分)如图,等边三角形OAB 的边长为4km.现在线段OB 上取一点D (不含线段OB端点)建发电站向,A B 两点供电.如果线段DB 上每公里建设费用为a 万元(a 为正常数),线段AD 上每公里建设费用为3a 万元,设ADO θ∠=,建设总费用为S 万元.(Ⅰ) 写出S 关于θ的函数关系式,并指出θ的取值范围;(Ⅱ)AD 等于多少时,可使建设总费用S 最少?18. (本小题满分16分)已知椭圆2222:1(0)x y C a b a b +=>>直线2x =为椭圆的一条准线. 椭圆上两点1122(,)(,)A x y B x y 、.(Ⅰ)求椭圆C 的标准方程;(Ⅱ)若点M 满足2OM OA OB =+ ,且121222x x y y +=-,求证:点M 在椭圆C 上;(Ⅲ)若点(1,0)M -满足2,OM OA OB λ=+ 求实数λ的取值范围.19. (本小题满分16分)已知数列{}n a 中任意连续三项的和为零,且212 1.a a ==-(Ⅰ) 求数列{}n a 的通项公式;(Ⅱ)若数列{}n b 满足*1111(N ),n n n b b a n b a ++=∈=,求数列{}n b 的前n 项和n S 的取值范围.20. (本小题满分16分)已知函数()ln .a f x x ax x=-+(Ⅰ) 若函数()f x 在1x =处的切线过点(0,)a ,求a 的值; (Ⅱ)若01a <<,求证:2()02a f >; (Ⅲ)若()f x 恰有三个不同的零点,求a 的取值范围.附加题部分21.【选做题】(本题包括A 、B 、C 、D 四小题,请选定其中两题.......,并在相应的答题区域内作答.............若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.)A .【选修4—1几何证明选讲】(本小题满分10分)如图,在锐角三角形ABC 中,AB AC =,以AB 为直径的圆O 与边,BC AC 的交点分别为,D E ,且DF AC ⊥于点F .(Ⅰ)求证:DF 是O ⊙的切线;(Ⅱ)若3CD =,7=5EA ,求AB 的长.B .【选修4—2:矩阵与变换】(本小题满分10分)在平面直角坐标系xOy 中,设点P (x ,5)在矩阵M 1234⎡⎤=⎢⎥⎣⎦对应的变换下得到点Q (y -2,y ),求1x y -⎡⎤⎢⎥⎣⎦M . C.【选修4—4:坐标系与参数方程】(本小题满分10分)以直角坐标系的原点O 为极点,x 轴的正半轴为极轴建立极坐标系,已知点P 的直角坐标为(1,2),直线l 过点P ,且倾斜角为π6,圆C :θρsin 6=.(Ⅰ)求直线l 的参数方程和圆C 的直角坐标方程;(Ⅱ)设直线l 与圆C 相交于,A B 两点,求PA PB ⋅.D .【选修4—5:不等式选讲】(本小题满分10分)已知函数()f x 的定义域为R .(Ⅰ)求实数m 的取值范围;(Ⅱ)若m 的最大值为n ,当正数b a ,满足41532n a b a b +=++时,求47a b +的最小值. 【必做题】(第22题、第23题,每题10分,共20分.解答时应写出文字说明、证明过程或演算步骤)22. (本小题满分10分)过直线2y =-上的动点P 作抛物线214y x =的两条切线,PA PB ,其中A ,B 为切点. (Ⅰ)若切线,PA PB 的斜率分别为12,k k ,求证:12k k 为定值;(Ⅱ)求证:直线AB 过定点.23. (本小题满分10分)设f (n )=(a +b )n (n ∈N *,n ≥2),若f (n )的展开式中,存在某连续3项,其二项式系数依次成等差数列,则称f (n )具有性质P .(Ⅰ)求证:f (7)具有性质P ;(Ⅱ)若存在n ≤2016,使f (n )具有性质P ,求n 的最大值.:。
扬州中学2016届高三四模 数学试卷(word版有答案)

江苏省扬州中学高三模拟考试数学试题 2016.5一、填空题:(共14题,总分70分)1.已知集合{0}A x x =>,{1012}B =-,,,,则A B 等于 ▲ . 2.已知虚数z 满足216i z z -=+,则||z = ▲ .3.对一批产品的长度(单位:毫米)进行抽样检测,样本容量为400,右图为检测结果的频率分布直方图.根据产品标准,单件产品长度在区间[25,30)的为一等品,在区间[20,25)和[30,35)的为二等品,其余均为三等品.则样本中三等品的件数为 ▲ .4.在平面直角坐标系xOy 中,“双曲线C 的标准方程为221169y x -=”是“双曲线C 的渐近线方程为34y x =±”成立的 ▲ 条件.(填“充要”、“充分非必要”、“必要非充分”、“非充分非必要”中的一种)5. 下图是一个算法流程图,则输出的x 的值是 ▲ 。
6.如果实数,x y 满足线性约束条件20,3501,x y x y y -≤⎧⎪-+≥⎨⎪≥⎩,则2z x y =+-的最小值等于(第3题)0.0.0.0.0.▲ .7. 为强化安全意识,某校拟在周一至周五的五天中随机选择2天进行紧急疏散演练,则选择的2天恰好为连续2天的概率是 ▲ .8. 设a ,b ,c 为三条不同的直线,给出如下两个命题: ①若//a b ,b c ⊥,则a c ⊥;②若a b ⊥,b c ⊥,则//a c .试类比以上某个命题,写出一个正确的命题:设α,β,γ为三个不同的平面, ▲ . 9..若数列}{n a 满足211n n n na a k a a ++++=(k 为常数),则称数列}{n a 为等比和数列,k 称为公比和.已知数列}{n a 是以3为公比和的等比和数列,其中2,121==a a ,则=2015a ▲ .10.函数1()2sin(),[2,4]1f x x x xπ=-∈--的所有零点之和为 ▲ . 11.已知tan()1αβ+=,tan()2αβ-=,则sin 2αβ的值为 ▲ .12.如果将直线l :20x y c ++=向左平移1个单位,再向下平移2个单位,所得直线l '与圆C :22240x y x y ++-=相切,则实数c 的值构成的集合为 ▲ .13.已知点O 为△ABC 的重心,且OA OB ⊥,6AB =,则AC BC ⋅的值为 ▲ .14.若幂函数()a f x x =(a ∈R )及其导函数()f x '在区间(0,+∞)上的单调性一致(同为增函数或同为减函数),则实数a 的取值范围是 ▲ .二、 解答题:本大题共6小题,共90分. 解答时应写出必要的文字说明、证明过程或演算步骤.15. (本小题满分14分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c.已知b c =233,A +3C =π.(1) 求cosC 的值; (2) 求sinB 的值;(3) 若b =33,求△ABC 的面积.16. (本小题满分14分)如图,四边形AA 1C 1C 为矩形,四边形CC 1B 1B 为菱形,且平面CC 1B 1B ⊥平面AA 1C 1C ,D 、E 分别为A 1B 1、C 1C 的中点.求证: (1) BC 1⊥平面AB 1C ;(2) DE ∥平面AB 1C.17.(本小题满分14分)如图,某水域的两直线型岸边l 1,l 2 成定角120o,在该水域中位于该角角平分线上且与顶点A 相距1公里的D 处有一固定桩.现某渔民准备经过该固定桩安装一直线型隔离网BC (B ,C 分别在l 1和l 2上),围出三角形ABC 养殖区,且AB 和AC 都不超过5公里.设AB =x 公里,AC =y 公里.(1)将y 表示成x 的函数,并求其定义域; (2)该渔民至少可以围出多少平方公里的养殖区?18.(本题满分16分)定义:如果一个菱形的四个顶点均在一个椭圆上,那么该菱形叫做这个椭圆的内接菱形,且该菱形的对角线的交点为这个椭圆的中心.如图,在平面直角坐标系xOy 中,设椭圆2214x y +=的所有内接菱形构成的集合为F . (1)求F 中菱形的最小的面积;(2)是否存在定圆与F 中的菱形都相切?若存在,求出定圆的方程;若不存在,说明理由;19.(本题满分16分)设函数()f x ,()g x 的定义域均为R ,且()f x 是奇函数,()g x 是偶函数,()()f x g x + e x =,其中e 为自然对数的底数. (1)求()f x ,()g x 的表达式;(2)设0a ≤,1b ≥,0x >,证明:()()(1)()(1)f x ag x a bg x b x+-<<+-.20. 己知数列{}n a 是公差不为零的等差数列,数列{}n b 是等比数列. (1)若()1n n n n c a a b +=-(n ∈N*),求证:{}n c 为等比数列;(2)设n n n b a c =(n ∈N*),其中n a 是公差为2的整数项数列,nn b ⎪⎭⎫⎝⎛=1312,若1234516842c c c c c >>>>,且当17n ≥时,{}n c 是递减数列,求数列{}n a 的通项公式; (3)若数列{}n c 使得⎭⎬⎫⎩⎨⎧n n n c b a 是等比数列,数列{}nd 的前n 项和为n nn c c a -,且数列{}n d 满足:对任意2n ≥,n ∈N*,或者0n d =恒成立或者存在正常数M ,使M d Mn <<1恒成立,求证:数列{}n c 为等差数列.附加题1. (本小题满分10分)已知矩阵312221A ⎡⎤⎢⎥=⎢⎥⎣⎦(1)求1A -;(2)满足AX =1A -二阶矩阵X2. (本小题满分10分)在平面直角坐标系xOy 中,曲线C 的参数方程为cos(0,sin x a a b y b ϕϕϕ=⎧>>⎨=⎩为参数),且曲线C 上的点M 对应的参数π3ϕ=,以O 为极点,x 轴的正半轴为极轴建立极坐标系.(1)求曲线C 的普通方程;(2)若12π(,)(,)A B ρθρθ+,是曲线C 上的两点,求221211ρρ+的值.3、(本小题满分10分)某公司有10万元资金用于投资,如果投资甲项目,根据市场分析知道:一年后可能获利10%,可能损失10%,可能不赔不赚,这三种情况发生的概率分别为12,14,14;如果投资乙项目,一年后可能获利20%,也可能损失20%,这两种情况发生的概率分别为α和β(α+β=1).(1) 如果把10万元投资甲项目,用X 表示投资收益(收益=回收资金-投资资金),求X 的概率分布列及数学期望E(X);(2) 若10万元资金投资乙项目的平均收益不低于投资甲项目的平均收益,求α的取值范围.4.(本小题满分10分)设i 为虚数单位,n 为正整数.(1)证明:(cos isin )cos isin n x x nx nx +=+;(2)结合等式“[][]1(cos isin )(1cos )isin nnx x x x ++=++”证明:121C cos C cos2C cos n n n n x x nx +++⋅⋅⋅+2cos cos 22n n x nx =.江苏省扬州中学高三数学五月质量检测参考答案一、填空题:(共14题,总分70分)1.已知集合,,则等于▲ . 1.2.已知虚数满足,则▲ .2.3. 对一批产品的长度(单位:毫米)进行抽样检测,样本容量为400,右图为检测结果的频率分布直方图.根据产品标准,单件产品长度在区间[25,30)的为一等品,在区间[20,25)和[30,35)的为二等品,其余均为三等品.则样本中三等品的件数为 ▲ . 3. 【答案】1004.在平面直角坐标系xOy中,“双曲线的标准方程为”是“双曲线的渐近线方程为”成立的▲条件.(填“充要”、“充分非必要”、“必要非充分”、“非充分非必要”中的一种)4.【答案】充分非必要5.下图是一个算法流程图,则输出的的值是5.596.如果实数满足线性约束条件,则的最小值等于.6.7.为强化安全意识,某校拟在周一至周五的五天中随机选择2天进行紧急疏散演练,则选择的2天恰好为连续2天的概率是7.8.设,,为三条不同的直线,给出如下两个命题:①若,,则;②若,,则.试类比以上某个命题,写出一个正确的命题:设,,为三个不同的平面,▲.8.若,,则9..若数列满足(为常数),则称数列为等比和数列,k称为公比和.已知数列是以3为公比和的等比和数列,其中,则.9.10.函数的所有零点之和为.10.答案:8方程即,令,,这两个函数的图象都关于点对称,在区间内共有8个零点,从左往右记为,则,故所有零点和为8.11.已知,,则的值为▲.11.【解析】.12.如果将直线:向左平移1个单位,再向下平移2个单位,所得直线与圆:相切,则实数的值构成的集合为▲.12.易得直线:,即,圆:的圆心到直线:的距离,解得或.13.如图,点为△的重心,且,,则的值为▲.13.以AB 的中点M 为坐标原点,AB 为x 轴建立平面直角坐标系,则,, 设,则,因为OA OB ,所以,从而,化简得,,所以.14.若幂函数(a)及其导函数在区间(0,)上的单调性一致(同为增函数或同为减函数),则实数a 的取值范围是 ▲ . 14.【答案】【解析】易得,,当时,,;当时,,;当时,,;当时,,;当时,,,综上得,.二、 解答题:本大题共6小题,共90分. 解答时应写出必要的文字说明、证明过程或演算步骤.15. (本小题满分14分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c.已知c b =33,A +3C =π. (1) 求cosC 的值; (2) 求sinB 的值;(3) 若b =3,求△ABC 的面积.15. 解:(1) 因为A +B +C =π,A +3C =π,所以B =2C.(2分)又由正弦定理,得sinB b =sinC c ,c b =sinC sinB ,33=sinC 2sinCcosC ,化简,得cosC =33.(5分) (2) 因为C ∈(0,π),所以sinC ==31=36. 所以sinB =sin2C =2sinCcosC =2×36×33=32.(8分)(3) 因为B =2C ,所以cosB =cos2C =2cos 2C -1=2×31-1=-31.(10分)因为A +B +C =π,所以sinA =sin(B +C)=sinBcosC +cosBsinC =32×33+31×36=96.(12分)因为c b =33,b =3,所以c =29.所以△ABC 的面积S =21bcsinA =21×3×29×96=42.(14分)16. (本小题满分14分)如图,四边形AA 1C 1C 为矩形,四边形CC 1B 1B 为菱形,且平面CC 1B 1B ⊥平面AA 1C 1C ,D 、E 分别为A 1B 1、C 1C 的中点.求证: (1) BC 1⊥平面AB 1C ; (2) DE ∥平面AB 1C.16. 证明:(1) ∵ 四边形AA 1C 1C 为矩形,∴ AC ⊥C 1C.(1分)又平面CC 1B 1B ⊥平面AA 1C 1C ,平面CC 1B 1B ∩平面AA 1C 1C =CC 1, ∴ AC ⊥平面CC 1B 1B.(3分)∵ C 1B 平面CC 1B 1B, ∴ AC ⊥C 1B.(4分) 又四边形CC 1B 1B 为菱形,∴ B 1C ⊥BC 1.(5分)∵ B 1C ∩AC =C ,AC 平面AB 1C, B 1C 平面AB 1C ,∴ BC 1⊥平面AB 1C.(7分) (2) 取AA 1的中点F ,连结DF ,EF.∵ 四边形AA 1C 1C 为矩形,E ,F 分别为C 1C ,AA 1的中点,∴ EF ∥AC. 又EF 平面AB 1C ,AC平面AB 1C ,∴ EF ∥平面AB 1C.(9分)∵ D ,F 分别为边A 1B 1,AA 1的中点,∴ DF ∥AB 1. 又DF平面AB 1C ,AB 1平面AB 1C ,∴ DF ∥平面AB 1C.∵ EF ∩DF =F ,EF 平面DEF ,DF 平面DEF ,∴ 平面DEF ∥平面AB 1C.(12分) ∵ DE平面DEF, ∴ DE ∥平面AB 1C.(14分)17.(本小题满分14分)如图,某水域的两直线型岸边l 1,l 2 成定角120o ,在该水域中位于该角角平分线上且与顶点A 相距1公里的D 处有一固定桩.现某渔民准备经过该固定桩安装一直线型隔离网BC (B ,C 分别在l 1和l 2上),围出三角形ABC 养殖区,且AB 和AC 都不超过5公里.设AB =x 公里,AC =y 公里.(1)将y 表示成x 的函数,并求其定义域; (2)该渔民至少可以围出多少平方公里的养殖区?试题解析:解:(1)由SΔABD+SΔACD=SΔABC得x sin60º+y sin60º=xy sin120º ……………2分所以x+y=xy,所以y=……………4分又0<y≤5,0<x≤5,所以≤x≤5所以定义域为{x|≤x≤5} ………………6分18.(本题满分16分)定义:如果一个菱形的四个顶点均在一个椭圆上,那么该菱形叫做这个椭圆的内接菱形,且该菱形的对角线的交点为这个椭圆的中心.如图,在平面直角坐标系中,设椭圆的所有内接菱形构成的集合为.(1)求中菱形的最小的面积;(2)是否存在定圆与中的菱形都相切?若存在,求出定圆的方程;若不存在,说明理由;(3)当菱形的一边经过椭圆的右焦点时,求这条边所在的直线的方程.18.解:(1)如图,设,,当菱形的对角线在坐标轴上时,其面积为;当菱形的对角线不在坐标轴上时,设直线的方程为:,①则直线的方程为:,又椭圆,②由①②得,,,从而,同理可得,,(3分)所以菱形的面积为(当且仅当时等号成立),综上得,菱形的最小面积为;(6分)(2)存在定圆与中菱形的都相切,设原点到菱形任一边的距离为,下证:,证明:由(1)知,当菱形的对角线在坐标轴上时,,当菱形的对角线不在坐标轴上时,,即得,综上,存在定圆与中的菱形都相切;(12分)(3)设直线的方程为,即,则点到直线的距离为,解得,所以直线的方程为.(16分)19.(本题满分16分)设函数,的定义域均为,且是奇函数,是偶函数,其中为自然对数的底数.(1)求,的表达式;(2)设,,,证明:.解:(1)由得,,因为是奇函数,是偶函数,所以,从而,(4分)(2)当时,,所以,.(6分)由(1)得,,,(8分)当时,,,设函数,(10分)则,(12分)若,,则,故为上增函数,所以,若,,则,故为上减函数,所以,综上知,.(16分)20. 己知数列是公差不为零的等差数列,数列是等比数列.(1)若(n∈N*),求证:为等比数列;(2)设(n∈N*),其中是公差为2的整数项数列,,若,且当时,是递减数列,求数列的通项公式;(3)若数列使得是等比数列,数列的前项和为,且数列满足:对任意,N*,或者恒成立或者存在正常数,使恒成立,求证:数列为等差数列.(1)证明:,设公差为且,公比为,=常数,为等比数列………3分(2)由题意得:对恒成立且对恒成立,…5分对恒成立…… ……7分对恒成立………… ……9分而或或. ………… ……10分(3)证明:设不妨设,,即. ………… ……13分若,满足,若,则对任给正数M,则取内的正整数时,,与矛盾.若,则对任给正数T=,则取内的正整数时=,与矛盾.,而是等差数列,设公差为,为定值,为等差数列. ………… ……16分附加题答案1.已知矩阵(1)求;(2)满足AX=二阶矩阵X1.解:(1) ………4分(2)………10分2.在平面直角坐标系中,曲线的参数方程为为参数),且曲线上的点对应的参数,以O 为极点,x 轴的正半轴为极轴建立极坐标系.(1)求曲线的普通方程;(2)若是曲线上的两点,求的值.(1) (2)3、某公司有10万元资金用于投资,如果投资甲项目,根据市场分析知道:一年后可能获利10%,可能损失10%,可能不赔不赚,这三种情况发生的概率分别为21,41,41;如果投资乙项目,一年后可能获利20%,也可能损失20%,这两种情况发生的概率分别为α和β(α+β=1).(1) 如果把10万元投资甲项目,用X 表示投资收益(收益=回收资金-投资资金),求X 的概率分布列及数学期望E(X);(2) 若10万元资金投资乙项目的平均收益不低于投资甲项目的平均收益,求α的取值范围.3. 解:(1) 依题意,X 的可能取值为1,0,-1,(2分)(4分)E(X)=1×21-1×41=41.(5分)万元投资乙项目的收益,则Y 的分布列为(8分)E(Y)=2α-2β=4α-2,依题意要求4α-2≥41,∴ 169≤α≤1.(10分) 23.(本小题满分10分)设为虚数单位,为正整数.(1)证明:;(2)结合等式“”证明:.证明:(1)①当时,,即证;②假设当时,成立,则当时,,故命题对时也成立,由①②得,;(5分)(2)由(1)知,,其实部为;,其实部为,根据两个复数相等,其实部也相等可得:.(10分)。
【高考模拟】江苏扬州市2016届高三四模试题(5月)英语 Word版含答案

扬州市2015-2016学年度高三第四次模拟测试英语试卷本试卷分五部分。
满分120分。
考试时间120分钟。
第Ⅰ卷(共85 分)第一部分:听力(共两节,满分20分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1分,满分5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What does the man imply?A. He can’t go now.B. He can’t wait any longer.C. He wants to call someone.2. What does the woman mean?A. Furnished apartments will cost more.B. She can provide the man with the apartment he needs.C. The apartment is just what the man is looking for.3. What is the man going to do?A. Look for a hotel.B. Have his watch repaired.C. Meet someone at the hotel.4. What are the speakers mainly talking about?A. A book.B. A teacher.C. An exam.5. What do the speakers think of the music?A. Pleasant.B. Acceptable.C. Disturbing.第二节(共15小题;每小题1分,满分15分)听下面5段对话或独白。
2016年5月2016届高三第四次全国大联考(新课标Ⅲ卷)理数卷(原卷版)

绝密★启用前【学易大联考】2016年第四次全国大联考统考【新课标Ⅲ卷】理科数学试卷考试时间: 120分钟 满分:150分第I 卷(共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若复数12z =-,则21z z +在复平面内对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限2.设全集U R =,集合{}2|760A x x x =--≥, {}|lg(2)(4)B x y x x ==+-,则()U B A =ð( ) A .[4,6) B .]9,4( C .[1,2] D .[2,1]-3.在6与316中间插入n 个数,组成各项和为18916的等比数列,则此数列的项数为( ) A .8 B .7 C .6 D .54.已知圆C :)0(4)2()(22<=-+-a y a x 及直线03:=+-y x l ,若直线l 被圆C 截得的弦长为32,则a 的值为( )A .12--B .2-C .13--D .3- 5.执行如图所示的程序框图,若输入的2,2a n ==,则输出的q 的值为( )A .24B . 25C .26D . 276.已知角ϕ的终边经过点P (-4,3),函数f (x )=sin(ωx +ϕ)(ω>0)的图象的相邻两条对称轴之间的距离等于π2,则f (π4)的值为( ) A .35 B .45 C .35- D .45- 7.设12F F 、是椭圆22221x y a b+=的两个焦点,P 是椭圆上的点,1:2||:||21=PF PF ,且12PF F △为直角三角形,则椭圆的离心率为( )A 或B 或C 或D 或 8.△ABC 中,点D 在BC 上,∠A =60°,若1()4||||AB AC AD k AC AB AB AC λ=+=+,且4AB =,则AD 的长为( )A B . C . D .9.已知一几何体的三视图如图所示,其中,正视图与侧视图完全一样,根据图中的数据,该几何体的表面积为( )A B . C .4 D .610.若n x x )3(3+的展开式中存在常数项,则正整数n 的最小值及相应的常数项分别为( )A .6,280B .6,270C .5,280D .5,27011.已知数列{}n a 的前n 项和为n S ,若112a =且21()(1)n n n a n a a n n -=---,则下列四个结论:①1n n a a +>; ②(1)2n n n S ->; ③{}n n a -是增数列; ④{}(1)n n a +是等差数列,其中正确的个数为( ) A .1 B .2 C .3 D .412.设函数()f x =若曲线e 1e 1sin 22y x -+=+上存在点00(,)x y 使得00(())f f y y =成立,则实数a 的取值范围为( )A . 2[0,e e 1]-+B . 2[0,e e 1]+-C . 2[0,e e 1]--D . 2[0,e e 1]++第Ⅱ卷(非选择题 共90分)二、填空题(每小题5分,满分20分.将答案填在答题纸上)13. 定义在R 上的函数()f x 满足22,0()(1)(2),0x x x f x f x f x x ⎧-≤=⎨--->⎩,则(2016)f 的值为 .14.已知乒乓球队的10名队员中有3名主力队员,现要派5名参加比赛,3名主力队员一定参加且安排在第一、三、五位置,其余7名队员中选2名安排在第二、四位置,则不同的出场安排有 种.15.若,x y 满足不等式组⎪⎩⎪⎨⎧≤-≤+≤1222y x y x x y ,则32z x y =+的最大值为 .16. 已知双曲线()222210,0x y a b a b-=>>的半焦距为c ,过右焦点且斜率为1的直线与双曲线的右支交于两点,若抛物线24y cx =2(e 为双曲线的离心率),则e 的值为 .三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分12分)在ABC △中,角,,A B C 所对的边分别为c b a ,,,且ABC △的面积S 满足2()()S c a b c a b =-++-.(1)求cos C ;(2)若2c =,2cos b a C =,求边长b .18.(本小题满分12分)如图,90BCD?o ,⊥==AB CD BC ,1平面BCD ,60ADB ?o ,F E ,分别是AD AC ,上的动点,且AE AF AC AD=. (1)若平面BEF 与平面BCD 的交线为l ,求证://EF l ;(2)当平面⊥BEF 平面ACD 时,求平面BEF 与平面BCD 所成的二面角的余弦值.19.(本小题满分12分)某班n 名同学的数学小测验成绩的频率分布直方图如图所示,其中,,a b c 成等差数列,且分数在[90,100]的有6人.(1)求n 的值;(2)若分数在[40,50)的人数是分数在[50,60)的人数的13,现从不及格的人中任意选取3人进行谈话,记分数在50分以下的人数为X ,求X 的分布列和数学期望.20.(本小题满分12分) 已知椭圆22221(0)x y a b a b+=>>的左、右焦点分别为12F F 、,上、下顶点分别是12,B B C 、是12B F 的中点,且11122B F B F ⋅=,112CF B F ⊥.(1)求椭圆的标准方程;(2)点,M N 是椭圆上的两个动点,过,M N 两点的切线交于点P ,当0PM PN ⋅=时,求点P 的轨迹方程.21.(本小题满分12分)已知函数22()(1)ln(1)f x m x n x =+-+.(1)若函数21()()2g x f x nx =-在区间[2,4]上单调递增,且,m n 均为正数,求m n 的取值范围; (2)若函数()f x 的图象在点(0,(0))f 处的切线方程为2(1)y n x n =-+,设2()h x x x b =++,若函数()()f x h x ≥在区间]2,0[上恒成立,求实数b 的取值范围.请考生在第(22)、(23)、(24)三题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做第一个题目计分.22.(本小题满分10分)选修4-1:几何证明选讲如图,直线ΡQ 与O 相切于点A ,AB 是O 的弦,PAB ∠的平分线AC 交O 于点C ,连接CB并延长与直线PQ 相交于点Q ,若6AQ =,5AC =.(1)求证:22QC QA BC QC -=⋅;(2)求弦AB 的长.23.(本小题满分10分)选修4-4:坐标系与参数方程在平面直角坐标系中,以坐标原点为极点,x 轴非负半轴为极轴建立极坐标系.已知直线l 与椭圆C 的极坐标方程分别为cos 2sin 0θθ+=,2224cos 4sin ρθθ=+. (1)求直线与椭圆的直角坐标方程;(2)若点Q 是椭圆C 上的动点,求点Q 到直线l 的距离的最大值.24.(本小题满分10分)选修4-5:不等式选讲已知不等式|21||1|2x x --+<的解集为{|}x a x b <<.(1)求,a b 的值;(2)已知x y z >>,求证:存在实数k ,使32()4()a b k x y y z x z-+≥---恒成立,并求k 的最大值.:。
2016年5月2016届高三第四次全国大联考(新课标Ⅰ卷)理数卷(解析版)

第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合,π2π{|sin ,(,]}63B y y x x ==?,则()A B R I ð=A.1(2,](1,4)2--U B.1(2,]4)2--U C.{-1,2,3} D.{-1,1,2,3}【命题意图】本题主要考查函数的定义域、值域及集合运算,考查运算求解能力,是基础题. 【答案】C2. 已知复数z 的共轭复数z 在复平面内对应的点的坐标为(2,-1),则复数i1+z的虚部为 ( ) A.1- B.21-C.23-D.23 【命题意图】本题主要考查复数的概念及复数的运算,考查运算求解能力,是基础题. 【答案】B【解析】由题知z =i 2-,所以i 2+=z ,所以i 1+z =i 1i 2++= )i 1)(i 1()i 1)(i 2(-+-+=i 2123-,故其虚部为21-,选B.3 下列函数既是奇函数又在(-1,1)上是增函数的是 ( )A.πcos()2y x =+ B.x y 2-= C.xx y +-=22ln D.x x y --=22 【命题意图】本题主要考查函数的奇偶性与单调性,考查运用数学基础知识解决问题的能力,是基础题. 【答案】D【解析】πcos()2y x =+=x sin -是奇函数,但在(-1,1)上是减函数,故A 不符合题意; xy 2-=是奇函数,但在(-1,1)上不是单调函数,故B 不符合题意;xxy +-=22ln=)2ln()2ln(x x +--是奇函数,但在(-1,1)上是减函数,故C 不符合题意;x x y --=22是奇函数,且在(-1,1)上是增函数,故D 符合题意,选D.4. 《九章算术》有这样一个问题:今有男子善走,日增等里,九日走一千二百六十里,第一日、第四日、第七日所走之和为三百九十里,问第八日所走里数为 ( ) A .150 B .160 C .170 D .180 【命题意图】本题主要考查等差数列的通项公式与前n 项和公式,是基础题. 【答案】C5. 执行如图所示的程序框图,输入p =10,则输出的A 为 ( )A .-12B .10C .16D .32 【命题意图】本题主要考查程序框图,考查运算求解能力,是基础题. 【答案】C【解析】第1次执行循环体:102+-=n S S =0-2+10=8>A =0,是,A =S =8,n =1≥p =10,否,n n 2==2,第2次执行循环体:102+-=n S S =8-4+10=14>A =8,是,A =S =14,n=2≥p=10,否,n n 2==4, 第3次执行循环体:102+-=n S S =14-8+10=16>A =14,是,A =S =16,n =4≥p =10,否, n n 2==8, 第4次执行循环体:102+-=n S S =16-16+10=10>A =16,否,n =8≥p =10,否, n n 2==16, 第5次执行循环体:102+-=n S S =10-32+10=-12>A =16,否,n =16≥p =10,是,输出A =16,故选C.6. 某空间几何体的三视图如图所示,则该几何体的体积为 ( )A.128B.3128 C.364 D.332【命题意图】本题主要考查简单几何体的三视图及其体积的计算,考查空间想象能力、运算求解能力,是基础题. 【答案】C7. 已知函数)(x f =)sin(ϕω+x A )π||,0,0(<>>ϕωA 的图象向右平移6π个单位得到)(x g 的部分图象如图所示,则)cos(ϕω+=x A y 的单调增区间为( )A.]3ππ,π65π[--k k ,Z k ∈ B.]6π,π31π[π+-k k ,Z k ∈C. ]12ππ,π127π[--k k ,Z k ∈ D.]125ππ,π121π[+-k k ,Z k ∈ 【命题意图】本题主要考查三角函数的图象变换、三角函数的图象与性质,考查运算求解能力,是基础题. 【答案】A【解析】由题知)(x g =])6(sin[ϕπω+-x A =)6sin(ϕωπω+-x A ,由五点作图法知,⎪⎪⎩⎪⎪⎨⎧=+-⨯=+-⨯π6π3π2π6π12πϕωωϕωω,解得2=ω,3π2=ϕ,2=A ,所以)32π2cos(2+=x y ,令π23π22ππ2k x k ≤+≤-,Z k ∈,解得365ππππ-<≤-k x k ,Z k ∈,所以)cos(ϕω+=x A y 的单调增区间为]3,65[ππππ--k k ,Z k ∈,故选A. 8. 已知1A 、2A 与1F 、2F 分别为双曲线22221x y a b-=(00a b >>,)的左、右顶点与左、右焦点,P 是双曲线右支上任意一点,则以线段1PF 和12A A 为直径的两圆一定 ( ) A .相交B.相切C.相离D.以上都可能【命题意图】本题主要考查双曲线的定义及两圆的位置关系的判定,考查运算求解能力,是基础题. 【答案】B9.如图所示,在△DEF 中,M 在线段DF 上,DE =3,DM =EM =2,sin F =35,则边EF 的长为( ) A.4916C.154【命题意图】本题主要考查利用正、余弦定理解三角形,考查运算求解能力,是基础题. 【答案】D10. 已知函数()f x =ln 2b a x x x ++(,a b R ∈)的两个极值点分别在区间(12,1)和(1,2)内,则z a b =+的最大值为 ( ) A.-10 B.-7 C. -4 D.4【命题意图】本题主要考查函数的极值及简单线性规划的解法,考查转化与化归思想、运算求解能力,是中档题. 【答案】C【解析】易知函数()f x 的定义域为(0,+∞),()f x '=22a bx x -+=222x ax b x +-,由题知22x ax b +-=0的两解分别在区间(12,1)和(1,2)内,设()g x =22x ax b +-,则111()0222(1)20(2)820g a b g a b g a b ⎧=+->⎪⎪=+-<⎨⎪=+->⎪⎩,即21020280a b a b a b -+>⎧⎪-+<⎨⎪-+>⎩,作出可行域如图中阴影部分所示,作出直线0l : 0a b +=,平移直线0l ,当直线z a b =+过点A 时,z 取得最大值,由21020a b a b -+=⎧⎨-+=⎩解得A (-3,-1),z max =-3-1=-4,故选C.11.在三棱锥BCD A -中,△ABC 与△BCD 都是边长为6的正三角形,平面ABC ⊥平面BCD ,则该三棱锥的外接球的体积为 ( ) A.π155 B.π60 C.π1560 D.π1520 【命题意图】本题主要考查球的截面性质及球的体积计算,考查空间想象能力、运算求解能力、逻辑推理能力,是难题..【答案】D12. 已知函数)(x f =ax ax x +-2ln 恰有两个零点,则实数a 的取值范围为 ( )A.(-∞,0)B.(0,+∞)C.(0,1)∪(1,+∞)D.(-∞,0)∪{1}【命题意图】本题主要考查函数零点、利用导数研究函数的图象与性质等综合问题,考查转化与化归思想、数形结合思想和运算求解能力,是难题. 【答案】C【解析】函数)(x f 的定义域为(0,+∞),由题知方程 ax ax x +-2ln =0,即方程)1(ln -=x a xx恰有两解,设x x x g ln )(=,则)(x g '=2ln 1xx-,当e 0<<x 时,)(x g '>0,当e >x 时,)(x g '<0,所以)(x g 在(0,e )上是增函数,在(e ,+∞)上是减函数,且0)1(=g ,当e >x 时,)(x g >0,1)1(='g ,作出函数)(x g y =与函数)1(-=x a y 的图象如下图所示,由图可知,函数)(x g y =的图象与函数)1(-=x a y 的图象恰有2个交点的充要条件为10<<a 或1>a ,故选C.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 已知二项式n xx )3(2-的展开式的各项系数和为64,则展开式中含3x 的项的系数为 .【命题意图】本题主要考查二项式定理及其展开式的通项公式的应用,考查运算求解能力,是基础题. 【答案】540-14. 在△ABC 中,AB=3,AC=2,∠BAC=60°,M 是BC 的中点,N 在线段AM 上,且BN ⊥AM ,则向量在向量上的投影为 .【命题意图】本题主要考查向量的线性运算及向量数量积的应用,考查运算求解能力,是基础题. 【答案】3827【解析】以A 为原点、AB 所在直线为x 轴建立直角坐标系,则A (0,0),B (3,0),C (1,3),所以)23,2(M ,设λ==)23,2(λλ,∴-==)23,32(λλ-,因为BN AM ⊥,所以AM BN ×uuu r uuu r =0232332(2=⨯+-λλ),解得1924=λ,所以)19312,199(-=,所以BN AC ×uuu r uuu r =193123199⨯+-=1927,所以向量BN 在向量AC 上的投影为||BN AC AC ×uuu r uuu ruuu r =3827. 15. 已知P 是抛物线x y 42=上一点,F 是该抛物线的焦点,则以PF 为直径且过(0,2)的圆的标准方程为 .【命题意图】本题主要考查抛物线的定义、圆的标准方程,考查运算求解能力,是基础题.【答案】22223939()(()(2424x y x y -+=-+-=或 【解析】设),4(020y y P ,由题知)0,1(F ,由抛物线的定义知,圆的直径为||PF =4120y +,圆心为)2,821(020y y +,由题知20220)02()2821(-+-+y y = )41(2120y +,解得220±=y ,所以圆心为)2,23(±,半径为23,所以所求圆的标准方程为49)2()23(22=±+-y x . 16.已知函数)(x f =))(1(22b ax x x ++-的图象关于直线3=x 对称,则函数)(x f 的值域为 .【命题意图】本题主要考查函数的对称性、函数的值域,考查转化与化归思想、数形结合思想、运算求解能力,是难题.【答案】[-36,+∞)三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. (本小题满分12分)已知数列{n a }的前n 项和为n S ,且满足*2()n n S a n n =+?N .(Ⅰ)求数列{n a }的通项公式;(Ⅱ)若n b =n na ,求数列{n b }的前n 项和n T .【命题意图】本题主要考查等比数列的概念、构造法求数列通项公式、错位相减法求和等,考查转化与化归思想、运算求解能力,是基础题.【解析】(Ⅰ)当n =1时,12111+==a S a ,解得11-=a , 当2≥n 时,n a =1--n n S S =)12(21-+-+-n a n a n n , 即121-=-n n a a ,………………2分 即)1(211-=--n n a a ,∵0211≠-=-a ,∴01≠-n a ,∴{1-n a }是首项为-2,公比为2的等比数列,………………4分 ∴1-n a =n2-,∴12+-=n n a . ………………6分 (Ⅱ)由(Ⅰ)知n b =n n n +⨯-2, ∴231212223232nn T n n =-?-?-?--?L=n n n ++++⨯++⨯+⨯+⨯- 21223222132)(,………………8分 设n n n M 223222132⨯++⨯+⨯+⨯= ,则13222)1(22212+⨯+-++⨯+⨯=n n n n n M ,两式相减得13222222+⨯-++++=-n nn n M =1221)21(2+⨯---n n n =22)1(1--+n n , ∴n M =22)1(1+-+n n ,………………10分∵2)1(321+=++++n n n , ∴n T =22)1(2)1(1-++-+n n n n . .………………12分 18.(本小题满分12分)中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”,为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研,人社部从网上年龄在15~65的人群中随机调查50人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:(Ⅰ)由以上统计数据填下面2´2列联表,并问是否有90%的把握认为以45岁为分界点对“延迟退休年龄政策”的支持度有差异;(Ⅱ)若从年龄在[45,55),[55,65]的被调查人中各随机选取两人进行调查,记选中的4人中支持“延迟退休”人数为ξ,求随机变量ξ的分布列及数学期望. 参考数据:【命题意图】本题主要考查总体估计、独立性检验、离散型随机变量的分布列与期望,考查阅读理解能力、运算求解能力,是基础题.(Ⅱ)由频率分布直方图知,被调查的50人中年龄在[45,55)和年龄在[55,65]的人数都为0.01×10×50=5,其中年龄在[45,55)和年龄在[55,65]支持“延迟退休”的人数分别为2,1,故ξ的所有可能取值为0, 1,2,3, ………………………6分22342255C C 9(0),C C 50P ξ=== ()11221234342255C C C C C 1C C P ξ+===2512, ()22111242342255C C C C C 2C C P ξ+===103, 142255C (3)C C P ξ===251,……………………10分所以的分布列是所以的期望值是012350251025E ξ=⨯+⨯+⨯+⨯=56. ………………………12分 19.(本小题满分12分)如图,在直角三角形ABC 中,∠BAC =60°,点F 在斜边AB 上,且AB=4AF ,D ,E 是平面ABC 同一侧的两点,AD ⊥平面ABC ,BE ⊥平面ABC ,AD =3,AC =BE =4. (Ⅰ)求证:平面CDF ⊥平面CEF ;(Ⅱ)若点M 是线段CB 的中点,求EM 与平面CEF 所成角的正弦值.ξξ【命题意图】本题主要考查空间线线垂直、线面垂直、面面垂直的判定与性质及线面角的计算,考查空间想象能力、运算求解能力,是中档题.(Ⅱ)以C 为坐标原点,建立如图所示的空间直角坐标系xyz C -,则)0,0,0(C ,)0,34,0(B ,)4,34,0(E ,)0,3,3(F ,)0,32,0(M ,∴=)4,34,0(,=)0,3,3(,=(0,4)--, ┄┄┄7分设平面CEF 的法向量为m =),,(z y x ,则4030CEz CFx ìï?+=ïíï?+=ïïîuur uu u rm m ,取x =1,则3-=y ,z =3,∴平面CEF 的一个法向量为m =(1,3-,3), ┄┄┄9分 设直线ME 与平面CEF 所成的角为θ,则θsin =||||||EM EM ××uuu ruuu rm m91919, ┄┄┄11分 ∴直线ME 与平面12分20. (本小题满分12分)已知1F 、2F 分别是椭圆E :)0(12222>>=+b a by a x 的左、右焦点,M 是椭圆E上一点,线段M F 1的中点为N ,△O NF 1(O 为坐标原点)的周长为3,过右焦点2F 与x 轴垂直的直线与椭圆E 在第一象限交于点C,23||2=C F .(Ⅰ)求椭圆E 的标准方程;(Ⅱ)过1F 作直线l 交椭圆E 于B A ,两点,)0,5(-P ,以PB PA ,为邻边作平行四边形PAQB ,求四边形PAQB 面积的取值范围.【命题意图】本题主要考查椭圆的定义、几何性质及直线与椭圆的位置关系,考查运算求解能力、逻辑思维能力,是难题.21. (本小题满分12分)已知函数2()x xf x x x e=+-(其中e 2.71828=L ). (Ⅰ)求)(x f 在))1(,1(f 处的切线方程;(Ⅱ)若函数2()ln[()]g x f x x x b =-+-的两个零点为12,x x ,证明:1()g x '+2()g x '12()2x x g +'>. 【命题意图】本题主要考查常见函数的导数、导数的运算法则、导数的综合应用,考查运算求解能力、转化与化归思想,是难题. 【解析】(Ⅰ)由题意得1()+21e x x f x x -'=-,e1)1(=f , ∴)(x f 在))1(,1(f 处的切线斜率为1)1(='f , ∴)(x f 在))1(,1(f 处的切线方程为1e1-=-x y ,即01e e e =+--y x . ……………4分 (Ⅱ)由题意知函数()ln g x x x b =--,所以1()1g x x'=-, 因为12,x x 是函数()g x 的两个零点,所以1122ln ln x b x x b x +=⎧⎨+=⎩,相减得2211ln xx x x -=请考生在第22,23,24题中任选一题作答,如果多做,则按所做的第一题计分.22.(本小题满分10分)选修4—1:几何证明选讲如图,点P是△ABC的外接圆O在C点的切线与直线AB的交点.(Ⅰ)若∠ACB=∠APC,证明:BC⊥PC;2,PC=4,求CD的长.(Ⅱ)若D是圆O上一点,∠BPC=∠DAC,AC=2,AB=2【命题意图】本题主要考查三角形相似的判定与性质、弦切角定理、切割线定理等平面几何知识,考查推理论证能力,是容易题.【证明】(Ⅰ)由弦切角定理知,∠ABC=∠ACP,∵∠ACB=∠APC,∴△ACB∽△APC,∴∠BAC=∠CAP,∵∠BAC+∠CAP=180°,∴∠BAC=∠CAP =90°,∴BC 是圆O 的直径,又PC 是圆O 的的切线,∴BC ⊥PC . ┄┄┄5分 (Ⅱ)由切割线定理知,PB PA PC ⨯=2,即)22(42+=PA PA , 即016222=-+PA PA ,解得22=PA (负值舍去),由弦切角定理及同弧所对的圆周角相等知,∠ACP =∠ABC =∠CDA , ∵∠BPC =∠DAC ,∴△CAD ∽△APC ,∴CD AC AC AP =,∴22)2(22==AP AC CD =22. ┄┄┄10分23. (本小题满分10分)选修4—4 :坐标系与参数方程在直角坐标系xOy 中,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线C :2sin 4cos ρθθ-=0,直线l 过点M (0,4)且斜率为-2.(Ⅰ)将曲线C 的极坐标方程化为直角坐标方程,写出直线l 的标准参数方程; (Ⅱ)若直线l 与曲线C 交于A 、B 两点,求||AB 的值.【命题意图】本题主要考查参数方程与普通方程的互化、极坐标方程与直角坐标方程的互化、直线参数方程的应用,是基础题.(Ⅱ)由(Ⅰ)知直线l的标准参数方程为xy⎧=⎪⎪⎨⎪=⎪⎩(t为参数),代入24y x=整理得2200t++=,┄┄6分设BA,点对应的参数分别为1t,2t,则20,552121=-=+t ttt,┄┄8分则||AB=||21tt-.┄┄10分24. (本小题满分10分)选修4—1:不等式选讲(Ⅰ) 若a,b,均为正数,且1a b+=.证明:11(1)(1)9a b++≥;(Ⅱ)若不等式2|||3|≥--+axx的解集为}1|{≥xx,求实数a的值.【命题意图】本题主要考查简单不等式的证明、基本不等式的应用、含绝对值不等式的解法,考查运算求解能力,是基础题.:。
江苏扬州市2016届高三数学5月四模试卷有答案

江苏扬州市2016届高三数学5月四模试卷(有答案)扬州市2015-2016学年度高三第四次模拟测试数学试题Ⅰ(全卷满分160分,考试时间120分钟)2016.5注意事项:1.答卷前,请考生务必将自己的学校、姓名、考试号等信息填写在答卷规定的地方.2.试题答案均写在答题卷相应位置,答在其它地方无效.一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应位置)1.已知集合,是整数集,则▲.2.若复数满足(为虚数单位),则▲.3.命题“”的否定▲.4.已知中,,则边的长度为▲.5.下面是一个算法的伪代码.如果输出的y值是20,则输入的x值是▲.6.在区间内随机选取一个实数,则该数为正数的概率是▲.7.在三棱锥中,、、两两垂直,且,则三棱锥的体积为▲.8.已知且为锐角,则▲.9.在平面直角坐标系中,如果直线将圆平分,且不经过第四象限,那么的斜率的取值范围是▲.10.已知等边中,若,,且,则实数的值为▲.11.设双曲线的右焦点为F,右准线l与两条渐近线交于P、Q两点,如果是等边三角形,则双曲线的离心率是▲.12.设函数,若关于的方程恰有三个不同的实数解,则实数的取值范围为▲.13.已知数列是各项均不为零的等差数列,为其前项和,且().若不等式对任意恒成立,则实数的最小值为▲.14.已知函数在O、A两点处取得极值,其中O是坐标原点,A在曲线上,则曲线的切线斜率的最大值为▲.二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明、证明过程或演算步骤)15.(本小题满分14分)已知向量,,记函数.若函数的周期为4,且经过点.(1)求的值;(2)当时,求函数的最值.16.(本小题满分14分)在三棱锥P-SBC中,A,D分别为边SB,SC的中点,且PA⊥BC.(1)求证:平面PSB平面ABCD;(2)若平面PAD平面,求证:.17.(本小题满分14分)某工厂生产某种黑色水笔,每百支水笔的成本为30元,并且每百支水笔的加工费为元(其中为常数,且).设该工厂黑色水笔的出厂价为元/百支(),根据市场调查,日销售量与成反比例,当每百支水笔的出厂价为元时,日销售量为10万支.(1)当每百支水笔的日售价为多少元时,该工厂的利润最大,并求的最大值.(2)已知工厂日利润达到元才能保证工厂的盈利.若该工厂在出厂价规定的范围内,总能盈利,则每百支水笔的加工费最多为多少元?(精确到元)18.(本小题满分16分)已知椭圆的长轴长为4,椭圆的离心率为.设点M是椭圆上不在坐标轴上的任意一点,过点M的直线分别交轴、轴于A、B两点上,且满足.(1)求证:线段AB的长是一定值;(2)若点N是点M关于原点的对称点,一过原点O且与直线AB平行的直线与椭圆交于P、Q两点(如图),求四边形MPNQ面积的最大值,并求出此时直线MN的斜率.19.(本小题满分16分)数列是公差为的等差数列,它的前项和记为,数列是公比为的等比数列,它的前项和记为.若,且存在不小于的正整数,使.(1)若,,,,求.(2)若,,试比较与的大小,并说明理由;(3)若,是否存在整数,使,若存在,求出的值;若不存在,说明理由.20.(本小题满分16分)已知函数.(1)求函数的单调递减区间;(2)当时,的最小值是,求实数的值;(3)试问过点可作多少条直线与曲线相切?并说明理由.扬州市2015-2016学年度高三第四次模拟测试数学试题Ⅱ(全卷满分40分,考试时间30分钟)2016.521(B).(本小题满分10分)已知矩阵,若矩阵属于特征值3的一个特征向量为,求该矩阵的另一个特征值.21(C).(本小题满分10分)在直角坐标系中,直线的参数方程为(为参数)在极坐标系(与直角坐标系取相同的长度单位,且以原点为极点,极轴与轴的非负半轴重合)中,圆的方程为.若直线被圆截得的弦长为,求实数的值.22.(本小题满分10分)长时间上网严重影响着学生的健康,某校为了解甲、乙两班学生上网的时长,分别从这两个班中随机抽取6名同学进行调查,将他们平均每周上网时长作为样本,统计数据如下:甲班101215182436乙班121622262838如果学生平均每周上网的时长超过19小时,则称为“过度上网”.(1)从甲班的样本中有放回地抽取3个数据,求恰有1个数据为“过度上网”的概率;(2)从甲班、乙班的样本中各随机抽取2名学生的数据,记“过度上网”的学生人数为,写出的分布列和数学期望.23.(本小题满分10分)已知.(1)若,求中含项的系数;(2)证明:.2015-2016学年度高三第四次模拟测试数学试题Ⅰ参考答案2016.5一、填空题1.{0,1}2.3.“”4.5.2或66.7.18.9.10.11.212.13.14.二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明、证明过程或演算步骤)15.解:(1)………………………4分由题意得:周期,故……………………6分(2)∵图象过点,即,而,故,则.……………………10分当时,当时,,当时,.……………………14分16.证:(1)A,D分别为边SB,SC的中点,且且即……………………3分,,、平面平面平面∴平面PSB平面ABCD……………………7分(2),平面,平面平面……………………10分平面,平面PAD平面……………………14分17.解:(1)设日销量为,则.则日售量为日利润.即,其中.………………3分令得.①当时,当时,.当时,取最大值,最大值为.………………5分②当时,,函数在上单调递增,在上单调递减.当时,取最大值.………………7分当时,时,日利润最大值为元当时,时,日利润最大值为元.………………8分(2)由题意得:对恒成立………………10分则对恒成立设,则在上单调增,则,即∴每百支水笔的加工费最多约为元答:每百支水笔的加工费最多约为元. (14)分18.解:(1)由题意得:,则椭圆方程为:……………………3分设,则且A、B分别在轴、轴上为定值……………………7分(2)方法(一)设,则直线PQ的方程为:…………………9分∵点到直线的距离:………12分,令,则当且仅当时,取等号;即时,,此时………16分方法(二)设直线MN的斜率为,则,则直线MN方程为,直线PQ方程为,…………………9分解方程组,用代得,,由椭圆的对称性知,点P到直线MN的距离,………12分由椭圆的对称性知,四边形MPNQ的面积=当且仅当,即时取等号,所以,四边形MPNQ的面积的最大值为4,此时直线MN的斜率.………16分19.解:(1),即,,.………3分(2)依题意,,且,显然.又,所以,………6分设,它是关于的二次函数,它的图象的开口向上,它的对称轴方程,故是上的增函数,所以当时,即,所以.………9分(3)依题意:,由得:,即,,………12分所以,因为,故,且,且为奇数则其中时,是整数,故,且.………16分20.解:(1),时,在上恒成立,则的单调递减区间,时,令则,即时,,则的单调递减区间.………3分(2)①,在上单调递减,,解得:,适合题意;②,在上单调递增,,无解;③,在上单调递减,上单调递增,,解得:,舍去;综上可得:.………8分(3)时,有1条切线;时,有2条切线.设切点坐标是,依题意:即,化简得:设,故函数在上零点个数,即是曲线切线的条数. (10)分①当时,,在上恰有一个零点1;………11分③当时,在上恒成立,在上单调递减,且,故在上有且只有一个零点,当时,在上恰有一个零点;………12分③时,在上递减,在上递增,故在上至多有两个零点,且又函数在单调递增,且值域是,故对任意实数,必存在,使,此时由于,即函数在上必有一零点;………14分先证明当时,,即证若,,而,由于若,构建函数,在为增函数,综上时,,所以,故又,所以在必有一零点.∴当时,在上有两个零点∴综上:时,有1条切线;时,有2条切线. (16)分数学试题Ⅱ参考答案21(B).解:因为,则,解得所以…5分由,所以.………………………………10分21(C).解:直线的参数方程为(为参数)所以直线的直角坐标系方程是:………………………………2分圆的直角坐标系方程是:,圆心(2,0),半径……………………4分设圆心到直线的距离为d,,所以……………………………7分又所以………………………………10分22.解:(1)设“恰有一个数据为过度上网”为事件A,则……3分(2)甲组六人中有两人过度上网,乙组六人中有四人过度上网,则……………8分01234P答:数学期望为2…………………………10分23.解:(1)…………………………1分中项的系数为;…………………………3分(2)设①则函数中含项的系数为……5分由错位相减法得:②,中含项的系数,即是等式左边含项的系数,等式右边含项的系数为…………………………7分所以………………10分2015-2016学年度高三第四次模拟测试数学试题Ⅰ参考答案2016.5一、填空题1.{0,1}2.3.“”4.5.2或66.7.18.9.10.11.212.13.14.二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明、证明过程或演算步骤)15.解:(1)………………………4分由题意得:周期,故……………………6分(2)∵图象过点,即,而,故,则.……………………10分当时,当时,,当时,.……………………14分16.证:(1)A,D分别为边SB,SC的中点,且且即……………………3分,,、平面平面平面∴平面PSB平面ABCD……………………7分(2),平面,平面平面……………………10分平面,平面PAD平面……………………14分17.解:(1)设日销量为,则.则日售量为日利润.即,其中.………………3分令得.④当时,当时,.当时,取最大值,最大值为.………………5分⑤当时,,函数在上单调递增,在上单调递减.当时,取最大值.………………7分当时,时,日利润最大值为元当时,时,日利润最大值为元.………………8分(2)由题意得:对恒成立………………10分则对恒成立设,则在上单调增,则,即∴每百支水笔的加工费最多约为元答:每百支水笔的加工费最多约为元. (14)分18.解:(1)由题意得:,则椭圆方程为:……………………3分设,则且A、B分别在轴、轴上为定值……………………7分(2)方法(一)设,则直线PQ的方程为:…………………9分∵点到直线的距离:………12分,令,则当且仅当时,取等号;即时,,此时………16分方法(二)设直线MN的斜率为,则,则直线MN方程为,直线PQ方程为,…………………9分解方程组,用代得,,由椭圆的对称性知,点P到直线MN的距离,………12分由椭圆的对称性知,四边形MPNQ的面积=当且仅当,即时取等号,所以,四边形MPNQ的面积的最大值为4,此时直线MN的斜率.………16分19.解:(1),即,,.………3分(2)依题意,,且,显然.又,所以,………6分设,它是关于的二次函数,它的图象的开口向上,它的对称轴方程,故是上的增函数,所以当时,即,所以.………9分(3)依题意:,由得:,即,,………12分所以,因为,故,且,且为奇数则其中时,是整数,故,且.………16分20.解:(1),时,在上恒成立,则的单调递减区间,时,令则,即时,,则的单调递减区间.………3分(2)①,在上单调递减,,解得:,适合题意;②,在上单调递增,,无解;③,在上单调递减,上单调递增,,解得:,舍去;综上可得:.………8分(3)时,有1条切线;时,有2条切线.设切点坐标是,依题意:即,化简得:设,故函数在上零点个数,即是曲线切线的条数. (10)分①当时,,在上恰有一个零点1;………11分⑥当时,在上恒成立,在上单调递减,且,故在上有且只有一个零点,当时,在上恰有一个零点;………12分③时,在上递减,在上递增,故在上至多有两个零点,且又函数在单调递增,且值域是,故对任意实数,必存在,使,此时由于,即函数在上必有一零点;………14分先证明当时,,即证若,,而,由于若,构建函数,在为增函数,综上时,,所以,故又,所以在必有一零点.∴当时,在上有两个零点∴综上:时,有1条切线;时,有2条切线. (16)分数学试题Ⅱ参考答案21(B).解:因为,则,解得所以…5分由,所以.………………………………10分21(C).解:直线的参数方程为(为参数)所以直线的直角坐标系方程是:………………………………2分圆的直角坐标系方程是:,圆心(2,0),半径……………………4分设圆心到直线的距离为d,,所以……………………………7分又所以………………………………10分22.解:(1)设“恰有一个数据为过度上网”为事件A,则……3分(2)甲组六人中有两人过度上网,乙组六人中有四人过度上网,则……………8分01234P答:数学期望为2…………………………10分23.解:(1)…………………………1分中项的系数为;…………………………3分(2)设①则函数中含项的系数为……5分由错位相减法得:②,中含项的系数,即是等式左边含项的系数,等式右边含项的系数为…………………………7分所以………………10分。
【方案】江苏省省2016届高三第四次模拟5月考试数学试题Word版含答案

【关键字】方案省姜堰二中高三年级第四次模拟考试数学试题2016.5命题:高三数学组(考试时间:120分钟总分:160分)一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应的位置上.1、已知集合,集合,则=2、已知为虚数单位,复数,则复数的模为3、命题“∃x≥0,使x(x+3)≥0”的否定是4、下列程序:For I From 1 to 10 Step 3End ForPrint输出的结果是5、在圆x2+y2=4所围成的区域内随机取一个点P(x,y),则| x |+ y ≤ 0的概率为6、底面边长和高都为2的正四棱锥的表面积为.7、函数()在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与轴的交点,且△ABC为正三角形,则=8、已知O为坐标原点,A,B两点的坐标均满足不等式组,则tan∠AOB的最大值等于9、,,则最小值10、已知sin +sin α=,则sin的值是11、设点为双曲线(,)上一点,,分别是左右焦点,是△的内心,若△,△,△的面积,,满足,则双曲线的离心率为12、已知函数,,,恒有,则实数a的取值范围13、已知点O为△ABC的垂心,,则角A=14、设各项均为正整数的无穷等差数列{an},满足a54=4028,且存在正整数k,使a1,a54,ak成等比数列,则公差d的所有可能取值之和为二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明或演算步骤.15、(本小题满分14分)如图,三棱柱为正三棱柱,,是中点.(Ⅰ)求证:平面;(Ⅱ)求点到平面的距离. 16、(本小题满分14分)已知中,,记.(1)求解析式及定义域;(2)设 ,是否存在实数,使函数的值域为?若存在,请求出的值;若不存在,请说明理由. 17、(本小题满分14分)如图,某广场为一半径为的半圆形区域,现准备在其一扇形区域OAB 内建两个圆形花坛,该扇形的圆心角为变量2θ(),其中半径较大的花坛⊙P 内切于该扇形,半径较小的花坛⊙Q 与⊙P 外切,且与OA 、OB 相切.(1)求半径较大的花坛⊙P 的半径(用θ表示); (2)求半径较小的花坛⊙Q 的半径的最大值. 18、(本小题满分16分)已知椭圆+=1(a >b >0)上顶点A(0,2),右焦点F(1,0),设椭圆上任一点到点Q(0,6)的距离为d .(1)求d 的最大值;(2)过点F 的直线交椭圆于点S ,T 两点,P 为直线l 上一动点,l 为椭圆的右准线.①若PF ⊥ST ,求证:直线OP 平分线段ST ;②设直线PS ,PF ,PT 的斜率分别为k1,k2,k3,求证:k1,k2,k3成等差数列. 19、(本小题满分16分) 已知函数(1)当41,43=-=c a 时,求函数)(x f 的单调区间; (2)当12+=a c 时,若41)(≥x f 对任意),(+∞∈c x 恒成立,求实数 a 的取值范围;(3)设函数)(x f 的图像在两点P ))(,(11x f x ,Q ))(,(22x f x 处的切线分别为l 1,l 2,若21ax -=,c x =2,且l 1⊥l 2,求实数c 的最小值. 20、(本小题满分16分)已知有穷数列}{n a 各项均不相等,将}{n a 的项从大到小重新排序后相应的项数构成新数列}{n P ,称}{n P 为}{n a 的“序数列”,例如数列:1a ,2a ,3a 满足1a >3a >2a ,则其序数列}{n P 为1,3,2.(1)求证:有穷数列}{n a 的序数列}{n P 为等差数列的充要条件是有穷数列}{n a 为单调数列;(2)若项数不少于5项的有穷数列}{n b ,}{n c 的通项公式分别是)()53(*N n n b n n ∈⋅=,)(*2N n tn n c n ∈+-=,且}{n b 的序数列与}{n c 的序数列相同,求实数t 的取值范围;(3)若有穷数列}{n d 满足1d =1,)()21(||*1N n d d n n n ∈=-+,且}{12-n d 的序数列单调减,}{2n d 的序数列单调递增,求数列}{n d 的通项公式.省姜堰二中高三年级第四次模拟考试数学试题附加题 2016.5注意事项:1.附加题供选修物理的考生使用. 2.本试卷共40分,考试时间30分钟.3.答题前,考生务必将自己的姓名、学校、班级、学号写在答题纸的密封线内.试题的答案写在答题纸...上对应题目的答案空格内.考试结束后,交回答题纸. 21.【选做题】在A 、B 、C 、D 四小题中只能选做2题,每小题10分,共计20分.请在答.卷纸指定区域内.......作答.解答应写出文字说明、证明过程或演算步骤. 21、A .【选修4-1:几何证明选讲】(本小题满分10分) 如图,AB 为⊙O 的直径,直线CD 与⊙O 相切于点D ,AC ⊥CD ,D E ⊥AB ,C 、E 为垂足,连接,AD BD . 若4AC =,3DE =,求BD 的长.B .【选修4-2:矩阵与变换】(本小题满分10分)已知矩阵⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡=10021,2001N M ,试求曲线x y sin =在矩阵1()MN -变换下的函数解析式.C .【选修4-4:坐标系与参数方程】(本小题满分10分)已知直线l :cos sin x t m y t αα=+⎧⎨=⎩(t 为参数)恒经过椭圆C :⎩⎨⎧==ϕϕsin cos 2y x (ϕ为参数)的右焦点F .(1)求m 的值;(2)当4πα=时直线l 与椭圆C 相交于A ,B 两点,求FB FA ⋅的值.D .【选修4-5:不等式选讲】(本小题满分10分)已知正实数,,a b c 满足231a b c ++=,求证:24627111a b c ++≥. ABDEOC·22、 (本小题满分10分)自2016年1月1日起,我国全面二孩政策正式实施,这次人口与生育政策的历史性调整,使得“要不要再生一个”,“生二孩能休多久产假”等问题成为千千万万个家庭在生育决策上避不开的话题.为了解针对产假的不同安排方案形成的生育意愿,某调查机构随机抽取了200(1)估计某家庭有生育意愿的概率分别为多少?(2)假设从5种不同安排方案中,随机抽取2种不同安排分别作为备选方案,然后由单位根据单位情况自主选择.①求两种安排方案休假周数和不低于32周的概率;②如果用ξ表示两种方案休假周数之和.求随机变量ξ的分布列及数学期望. 23、(本小题满分10分)在数列{}n a 中,11a t =-,其中0t >且1t ≠,且满足关系式:11(1)(1),()n n n n n a a t a t n N ++++-=-∈.(1)猜出数列{}n a 的通项公式并用数学归纳法证明之;(2)求证:1n n a a +>,()n N +∈.省姜堰二中高三年级第四次模拟考试数学附加题 2016.5注意事项:1.附加题供选修物理的考生使用. 2.本试卷共40分,考试时间30分钟.3.答题前,考生务必将自己的姓名、学校、班级、学号写在答题纸的密封线内.试题的答案写在答题纸...上对应题目的答案空格内.考试结束后,交回答题纸. 21.【选做题】在A 、B 、C 、D 四小题中只能选做2题,每小题10分,共计20分.请在答.卷纸指定区域内.......作答.解答应写出文字说明、证明过程或演算步骤. A .【选修4-1:几何证明选讲】(本小题满分10分)如图,AB 为⊙O 的直径,直线CD 与⊙O 相切于点DAC ⊥CD ,D E ⊥AB ,C 、E 为垂足,连接,AD BD . 若4AC =,3DE =,求BD 的长. B .【选修4-2:矩阵与变换】(本小题满分10分)已知矩阵⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡=10021,2001N M ,试求曲线x y sin =在矩阵1()MN -变换下的函数解析式.C .【选修4-4:坐标系与参数方程】(本小题满分10分)已知直线l :cos sin x t my t αα=+⎧⎨=⎩(t 为参数)恒经过椭圆C :⎩⎨⎧==ϕϕsin cos 2y x (ϕ为参数)的右焦点F .ABDEOC·(1)求m 的值; (2)当4πα=时直线l 与椭圆C 相交于A ,B 两点,求FB FA ⋅的值.D .【选修4-5:不等式选讲】(本小题满分10分) 已知正实数,,a b c 满足231a b c ++=,求证:24627111a b c++≥. 22、 (本小题满分10分)自2016年1月1日起,我国全面二孩政策正式实施,这次人口与生育政策的历史性调整,使得“要不要再生一个”,“生二孩能休多久产假”等问题成为千千万万个家庭在生育决策上避不开的话题.为了解针对产假的不同安排方案形成的生育意愿,某调查机构随机抽取了200(1)估计某家庭有生育意愿的概率分别为多少?(2)假设从5种不同安排方案中,随机抽取2种不同安排分别作为备选方案,然后由单位根据单位情况自主选择.①求两种安排方案休假周数和不低于32周的概率;②如果用ξ表示两种方案休假周数之和.求随机变量ξ的分布列及数学期望. 23、(本小题满分10分)在数列{}n a 中,11a t =-,其中0t >且1t ≠,且满足关系式:11(1)(1),()n n n n n a a t a t n N ++++-=-∈.(1)猜出数列{}n a 的通项公式并用数学归纳法证明之;(2)求证:1n n a a +>,()n N +∈.高三数学四模参考答案1、[-1,3]2、23、∀x ≥0,使x (x +3)<04、8805、41 6、4+45 7、4π 8、0.75 9、1.5 10、54- 11、2 12、a 3≥ 13、4π14、33915(Ⅰ)连结1BC ,交1B C 于O ,连DO .在三棱柱111ABC A B C -中,四边形11BB C C 为平行四边形,则1BO OC =,又D 是11AC 中点,∴1DO A B ∥,而DO ⊂平面1B CD ,1A B ⊄平面1B CD ,∴1A B ∥平面1B CD . ……………6分(Ⅱ)设点C 到平面111A B C 的距离是h ,则11111=3C B C D B C D V S h -△,1=4h CC = 由(Ⅰ)知:1BO OC =,所以B 到平面1B CD 的距离与1C 到平面1B CD 的距离相等. ∵1CC ⊥平面111A B C ,1B D ⊂平面111A B C ,∴11CC B D ⊥, ∵ABC △是等边三角形,D 是11AC 中点,∴111A C B D ⊥,又1111=CC AC C ,1CC ⊂平面11AA C C ,11AC ⊂平面11AA C C ,∴1B D ⊥平面11AA C C ,∴1B D CD ⊥,由计算得:1B D CD =1B CD S ∆设1C 到平面1B CD 的距离为h ',由1111=C B C D C B CD V V --114=3B CD S h h ''⇒=△以B 到平面1B CD……………14分 15. 解:(1)由正弦定理有:12sin sin sin()33BC ABx x ππ==-;…………………………2分 ∴1sin 2sin3BC x π=,sin()32sin 3x AB ππ-=…………………………………………4分 ∴41()sin sin()332f x AB BC x x π=•=⋅-⋅21sin )sin 32x x x =-11sin(2)(0)3663x x ππ=+-<< ……………………………………… 6分 (2)()6()1g x mf x =+=2sin(2)1(0)63m x m x ππ+-+<<假设存在实数m 符合题意,(0,)3x π∈∴512sin(2)(,1]66662x x ππππ<+<+∈,则 ……………………9分 当0m >时, ()2sin(2)16g x m x m π=+-+的值域为(1,1]m +又()g x 的值域为3(1,]2,解得 12m = ………………11分当0m <时,()2sin(2)16g x m x m π=+-+ 的值域为[1,1)m +又∵()g x 的值域为3(1,]2 解得m 无解………………………13分∴存在实数12m =,使函数)(x f 的值域恰为3(1,]2……………14分17解:(1)设⊙P 切OA 于M ,连PM ,⊙Q 切OA 于N ,连QN ,记⊙P 、⊙Q 的半径分别为r P 、r Q . ∵⊙P 与⊙O 内切,∴|OP |=80-r P , ∴r Psin θ+r P =80,………4分∴r P =80·sin θ1+sin θ (0<θ<π2) ………6分(2)∵|PQ |=r P +r Q ∴|OP |-|OQ |=r P sin θ-r Qsin θ=r P +rQ∴r Q =80·sin θ(1-sin θ)1+sin θ (0<θ<π2) ………10分法一:令t =1+sin θ∈(1,2),∴r Q =80·(t -1)(2-t )t 2=80⎝⎛⎭⎫-1-2t 2+3t令m =1t ∈(12,1),r Q =80(-2m 2+3m -1) ∴m =34时,有最大值10.………13分 注意:换元不写范围扣1分 法二:∵2sin θ(1-sin θ)≤2sin θ+(1-sin θ)2=1+sin θ2 ∴sin θ(1-sin θ)≤(1+sin θ)28∴r Q≤10.此时sin θ=13………14分 注意:不指出取等号的条件扣1分法三:令t =sin θ∈(0,1),r Q =80(t -t 2)(1+t )2,∴r Q'=80(1-3t )(1+t )3令r Q '=0得:t =13,【列表略】故t =13时,⊙Q 的半径的最大值为10.………13分 注意:不列表扣1分答:⊙Q 的半径的最大值为10.………14分 注意:应用题不写答扣1分18(1)由题意知b =2,c =1,则a =5,所以椭圆方程为x 25+y 24=1.d=8 ………5分(2)①当ST 斜率不存在时,由PF ⊥ST ,得P 为直线l 与x 轴的交点,此时线段ST 被直线OP 平分;当ST 斜率为0时,不合题意;当ST 斜率存在时,设直线ST 方程为y =k (x —1),联立直线与椭圆方程⎩⎪⎨⎪⎧y =k (x —1) x 25+y 24=1,消去y ,得(4+5k 2)x 2—10k 2x +5k 2—20=0.设S (x 1,y 1),T (x 2,y 2),则x 1+x 2=10k 24+5k 2,x 1x 2=5k 2-20 4+5k 2,且△>0.设线段ST 中点为(x 0,y 0),则x 0=x 1+x 22=5k 24+5k 2,y 0= k (x 0—1)=-4k 4+5k 2,所以ST 中点为(5k 2 4+5k 2,-4k 4+5k 2).因为PF ⊥ST ,所以直线PF 方程为y =-1k (x —1),所以点P坐标为(5,—4k ),则直线OP 方程为y =- 45k x ,而y 0=- 45k x 0,即(x 0,y 0)在直线OP 上,即直线OP 平分线段ST .综上,直线OP 平分线段ST .………10分(2)当ST 斜率不存在时,易得S (1,455),T (1,-455).设P (5,t ),则k 1=t -4554,k 2=t 4,k 3=t +4554,则k 1+k 3=t —4554+t +4554=t2=2k 2,即k 1,k 2,k 3成等差数列. 当ST 斜率存在时,设直线ST 方程为y =k (x —1)(同第(1)问).设P (5,t ),则k 1=t —y 15—x 1=t —k (x 1—1)5—x 1=k +t —4k 5—x 1,k 2=t 4,k 3=t —y 25—x 2=t —k (x 2—1)5—x 2=k +t —4k 5—x 2,则k 1+k 3=k +t —4k5—x 1+k+t —4k 5—x 2=2k +(t —4k )(10—x 1—x 2)(5—x 1)( 5—x 2)=2k +(t —4k )[10—(x 1+x 2)]25—5(x 1+x 2)+x 1x 2.由(1)知x 1+x 2=10k 2 4+5k 2,x 1x 2=5k 2—204+5k 2,代入上式得k 1+k 3=2k +(t —4k )[10— 10k 24+5k 2]25—510k 2 4+5k 2+5k 2—20 4+5k 2=2k +(t —4k )(40+40k 2)80+80k 2=2k+t —4k 2=t 2,又k 2=t 4,所以k 1+k 3=2k 2,即k 1,k 2,k 3成等差数列.………6分综上:k 1,k 2,k 3成等差数列.【说明】考查直线与椭圆的位置关系,解析几何中的恒成立问题及分类讨论思想.19、函数⎪⎩⎪⎨⎧<<--≥-+=,0,)(ln ,,)(ln )(22c x c x x a c x c x x a x f 求导得 (1)当43-=a ,41=c 时,⎝⎛<<-+-≥--=410,4328,41,4328)('22x x x x x x x x x f 若0<x<14 ,则04328)('2<-+-=x x x x f 恒成立,所以f(x)在(0,14 )上单调递减若x ≥14 ,则xx x x f 4)34)(12()('-+=,令f'(x)=0,解得x=34 或x=- 12 (舍去)当14 ≤x<34 时,f'(x)<0,f(x)在[14 ,34 ]上单调递减; 当x>34 时,f'(x)>0,f(x)在(34,+∞)上单调递增综合,函数f(x)的单调减区间是(0,34 ),单调增区间是(34,+∞)(2)当x>c ,c=a 2 +1时, xa x x x f )2)(1()('--=,而c=a2 +1<1所以当c<x<1时,f'(x)<0,f(x)在(c ,1)上单调递减;当x>1时,f'(x)>0,f(x)在(1,+∞)上单调递增 所以函数f(x)在(c ,+∞)上的最小值为f(1)=a24 ,所以a 24≥14 恒成立,解得a ≤-1或a ≥1(舍去)又由c=a2+1>0,得a>-2,所以实数a 的取值范围是(-2,-1] (3)由l 1⊥l 2知, )(')2('c f a f -=-1,而f'(c)=ac ,则a c a f -=-)2(',若c a ≥-2,则c aa ac a a f 2222)2(2)2('-=-+---=-,所以-2c=-c a ,解得a=12 ,不合题意 故2a -<c ,则222)2(2)2('aa a c a a f -+-+--=-=--8a +2c=-c a ,整理理,128+-=a a a c ,由c>0,得a<- 12 ,令-8a =t ,则a=- t 28 ,t>2, 所以821482322-=+-⋅-=t t t tt c ,设g(t)=8223-t t ,则g'(t)=2222)82()12(2--t t t当2<t<2 3 时,g'(t)<0,g(t)在(2,2 3 )上单调递减; 当t>2 3 时,g'(t)>0,g(t)在(2 3 ,+∞)上单调递增所以函数g(t)的最小值为g(2 3 )=3 3 2 ,故实数c 的最小值为3 3220.(1)充分性:当数列{a n }为单调数列时,即a 1>a 2>…>a n-1>a n ,或a 1<a 2<…<a m-1<a m ,所以其序数列{p m }为1,2,…,n-1,n ,或n ,n-1,…,2,1,均为等差数列 必要性:当列{a m }的序数列为等差数列时,其序数列{p m }必为1,2,…,n-1,n ,或n ,n-1,…,2,1,所以有a 1>a 2>…>a n-1>a n ,或a 1<a 2<…<a n-1<a n ,所以数列{a n }为单调数列综上,有穷数列{a m }的序数列{p m }为等差数列的充要条件是有穷数列{a m }为单调数列 (2)由题意得,b n+1-b n =(35 )n ·3-2n5 ,当n=1时,易得b 2>b 1,当n ≥2时,b n+1<b n ,又b 1=35 ,b 3=3×(35 )3,b 4=4×(35 )4,b 4<b 1<b 3,即b 2>b 3>b 1>b 4>…>b n ,故数列{b n }的序数列为2,3,1,4,…,n ,则数列{c n }的序数列 所以对于数列{c n }有2<t 2 <52,解得4<t<5(3)因为{d 2n +1}的序数列单调递减,所以{d 2n-1}是递增数列,故d 2n+1-d 2n-1>0,于是(d 2n+1-d 2n )+(d 2n -d 2n-1)>0,又(12 )2n <(12 )2n-1,所以|d 2n+1-d 2n |<|d 2n -d 2n-1|,从而d 2n -d 2n-1>0,d 2n -d 2n-1=(12 )2n-1=1222)1(--n n,因为{d 2n }的序数列单调递增,所以{d 2n }是递减数列,同理可得d 2n+1-d 2n <0,故d 2n+1-d 2n =-(12 )2n =n n 2122)1(+-,由①②得d n+1-d n =nn 2)1(1+- 所以d n =d 1+(d 2-d 1)+(d 3-d 2)+…+(d n -d n-1)=1+122)1(2121--+++n n=1+211)21(1211+--⋅-n=12)1(3134--⋅+n n, 即数列{d n }的通项公式为d n =12)1(3134--⋅+n n (n *N ∈)21.B 解:MN =1002⎡⎤⎢⎥⎣⎦10201⎡⎤⎢⎥⎢⎥⎣⎦=10202⎡⎤⎢⎥⎢⎥⎣⎦, 由逆矩阵公式得, 1()MN -=20102⎡⎤⎢⎥⎢⎥⎣⎦……4分 即在矩阵MN 变换下11022022x x x x y y y y ⎡⎡⎤⎤'⎡⎡⎡⎤⎤⎤⎢⎢⎥⎥→==⎢⎢⎢⎥⎥⎥⎢⎢⎥⎥'⎦⎦⎦⎣⎣⎣⎢⎣⎦⎦⎣, ……6分 1,22x x y y ''==, ……8分代入得:1sin 22y x ''=, 即曲线sin y x =在矩阵MN 变换下的函数解析式为2sin 2y x =. ……10分 C (1)m=1 ……4分 (2)32……10分 解:(1)由表中信息可知,当产假为14周时某家庭有生育意愿的概率为14120050P ==; 当产假为16周时某家庭有生育意愿的概率为216220025P == (2)①设“两种安排方案休假周数和不低于32周”为事件A ,由已知从5种不同安排方案中,随机地抽取2种方案选 法共有2510C =(种), 其和不低于32周的选法有(14,18)、(15,17)、(15,18)、(16,17)、(16,18)、(17,18),共6种, 由古典概型概率计算公式得63()105P A ==. ②由题知随机变量ξ的可能取值为29,30,31,32,33,34,35.1(29)0.110P ξ===,12(30)0.1,(31)0.21010P P ξξ======, 2211(32)0.2,(33)0.2,(34)0.1,(35)0.110101010P P P P ξξξξ============, 因而ξ的分布列为所以()290.1300.1310.2320.2330.2340.1350.132E ξ=⨯+⨯+⨯+⨯+⨯+⨯+⨯=23.(1)解:由原递推式得到11(1)1n n n n n t a a a t ++-=+-22121(1)1(1)12t a a t a t -==-+- 3233232221(1)(1)(1)1231)3(1)2t t t a t a a t t -⋅---===+-- 猜想得到1n n t a n -=…………(2分) 下面用数学归纳法证明1n n t a n-= 10当n=1时 a 1=t —1 满足条件 20假设当n=k 时,1k k t a k -=则1111(1)(1)k k k k k t t a t t k k++--+-=- ∴1111k k k t a k k ++--⋅= ∴1111k k t a k ++-=+, 即当n=k+1时,原命题也成立。
江苏省扬州市高三考前调研测试(5月)数学Word版含答案

江苏省扬州市高三考前调研测试(5月)数学Word版含答案2017.05试题I(全卷满分160分,考试时间120分钟)注意事项:1 •答卷前,请考生务必将自己的学校、姓名、考试号等信息填写在答卷规定的地方.2 •试题答案均写在答题卷相应位置,答在其它地方无效.一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应位置)1 •已知A 0,1,2 ,B 2,4,则A B ▲•2•若复数z满足(2 i)z 1 i,则复数z在复平面上对应的点在第▲象限.3•随着社会的发展,食品安全问题渐渐成为社会关注的热点,为了提高学生的食品安全意识,某学校组织全校学生参加食品安全知识竞赛,成绩的频率分布直方图如下图所示,数据的分组依次为20,40 , 40,60 , 60,80 , 80,100,若该校的学生总人数为3000,则成绩不超过60分的学生人数大约为▲.5•如图是一个算法流程图,则输出S的值为▲第5题4•在区间0,5内任取一个实数m,则满足3m 4的概率为6•函数f(x)J(1)x 4的定义域为▲.2 2X y7•已知双曲线 —1(a 0)的一条渐近线方程为 y 2x ,则该双曲线的焦距为a 201&已知 sin 一,(0,—),则 tan2▲.329•已知圆锥的侧面展开图是半径为 4,圆心角等于—的扇形,则这个圆锥的体积是▲210•已知圆C: x 2 y 2 2ax 2y 20(a 为常数)与直线 y x 相交于 代B 两点,若ACB ,则实数a3值为 ____ ▲11、设等差数列 a n 的前n 项和为S ,若a 5 3, S 。
40 , 则nS n 的最小值为 ▲12.若动直线x t (tR )与函数 2f(x)cos ( x),g(x)、Vsin(x)cos( x)的44图象分别交于P,Q 两点,则线段 PQ 长度的最大值为13.在 ABC 中,D 、E 分别是AB 、AC 的中点, M 是直线DE 上的动点.若ABC 的面积为2,则MBMC ------ 2BC 的最小值为14.已知函数f (x )2x kx1,x1 x (0 1] 有两个不相等的零点(1,)二、解答题(本大题共 6小题,共 90分•解答应写出必要的文字说明、证明过程或演算步骤)15. (本小题满分14分)2在 ABC 中,角A,B,C 的对边分别为a,b,c ,若a C 2 &ac b 2 , sinA 第⑴求sinC 的值;⑵若a 2,求ABC 的面积.16. (本小题满分14分) 如图,在四棱锥 P-ABCD 中,底面 ABCD 为梯形, CD II AB , AB=2CD , AC 交 BD 于 O ,锐角 PAD 所在平面丄底面 ABCD , PA 丄BD ,点Q 在侧棱PC 上,且PQ=2QC. 求证:⑴PA I 平面QBD ;17. (本小题满分14分)如图是一座桥的截面图, 桥的路面由三段曲线构成,曲线AB 和曲线DE 分别是顶点在路面A 、E 的抛物线的一部分,曲线 BCD 是圆弧,已知它们在接点 B 、D 处的切线相同, 若桥的最高点C 到水平面的距离 H 6米,圆弧的弓高h 1米,圆弧所对的弦长 BD 10 米.(1) 求弧BCD 所在圆的半径; (2) 求桥底AE 的长.18. (本小题满分16分)3b 0)的左顶点A( 2,0),且点(1厂)在椭圆上,2F 1、F 2分别是椭圆的左、右焦点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
扬州市2015-2016学年度高三第四次模拟测试数 学 试 题Ⅰ(全卷满分160分,考试时间120分钟)2016.5注意事项:1. 答卷前,请考生务必将自己的学校、姓名、考试号等信息填写在答卷规定的地方.2.试题答案均写在答题卷相应位置,答在其它地方无效.一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应位置)1.已知集合{|12}A x x =-<<,Z 是整数集,则A Z = ▲ . 2.若复数z 满足1iz i =+(i 为虚数单位),则z = ▲ . 3.命题“2,10x R xx ∃∈++=”的否定 ▲ .4.已知ABC ∆中,21,2,3a b C π===,则边c 的长度为 ▲ . 5.下面是一个算法的伪代码.如果输出的y 值是20, 则输入的x 值是 ▲ .6.在区间]2,1[-内随机选取一个实数,则该数为正数的概率是 ▲ .7.在三棱锥P ABC -中,PA 、PB 、PC 两两垂直,且3,2,1PA PB PC ===,则三棱锥P ABC -的体积为 ▲ .8.已知tan 2α=且α为锐角,则cos 2α= ▲ .9.在平面直角坐标系xOy 中,如果直线l 将圆22420x y x y +--=平分,且不经过第四象限,那么l 的斜率的取值范围是 ▲ .10.已知等边ABC ∆中,若1()3AP AB AC =+,AQ AP t AB =+ ,且AP AQ ⊥,则实数t 的值为 ▲ .11.设双曲线)0,0(12222>>=-b a by a x 的右焦点为F ,右准线l 与两条渐近线交于P 、Q 两点,如果PQF ∆是等边三角形,则双曲线的离心率是 ▲ .12.设函数2log ()(0)()2(0)xx x f x x -<⎧=⎨≥⎩,若关于x 的方程2()()0f x af x -=恰有三个不同的实数解,则实数a 的取值范围为 ▲ .13.已知数列{}n a 是各项均不为零的等差数列,n S 为其前n项和,且na (n *∈Ν).若不等式2016n n S a λ≥-对任意n *∈Ν恒成立,则实数λ的最小值为 ▲ .14.已知函数32()f x ax bx cx d =+++在O 、A 两点处取得极值,其中O 是坐标原点,A 在曲线2sin ([,])33y x x x ππ=∈上,则曲线()y f x =的切线斜率的最大值为 ▲ .二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明、证明过程或演算步骤) 15.(本小题满分14分)已知向量(sin(),1)2a x ωϕ=+ ,(1,cos())2b x ωϕ=+ (0,0)4πωϕ><<,记函数()()()f x a b a b =+⋅- .若函数()y f x =的周期为4,且经过点1(1,)2M .(1)求ω的值;(2)当11x -≤≤时,求函数()f x 的最值.16.(本小题满分14分)在三棱锥P -S BC 中,A ,D 分别为边SB ,SC 的中点,且3,8, 5.AB BC CD ===PA ⊥BC . (1)求证:平面PSB ⊥平面ABCD ;(2)若平面PAD 平面PBC l =,求证://l BC .PSDCBA17.(本小题满分14分)(第16题图)某工厂生产某种黑色水笔,每百支水笔的成本为30元,并且每百支水笔的加工费为m 元(其中m 为常数,且36m ≤≤).设该工厂黑色水笔的出厂价为x 元/百支(3540x ≤≤),根据市场调查,日销售量与x e 成反比例,当每百支水笔的出厂价为40元时,日销售量为10万支. (1)当每百支水笔的日售价为多少元时,该工厂的利润y 最大,并求y 的最大值.(2)已知工厂日利润达到1000元才能保证工厂的盈利.若该工厂在出厂价规定的范围内,总能盈利,则每百支水笔的加工费m 最多为多少元?(精确到0.1元)18.(本小题满分16分)已知椭圆22221(0)x y a b a b +=>>的长轴长为4.设点M 是椭圆上不在坐标轴上的任意一点,过点M 的直线分别交x 轴、y 轴于A 、B 两点上,且满足13AM AB =.(1)求证:线段AB 的长是一定值;(2)若点N 是点M 关于原点的对称点,一过原点O 且与直线AB 平行的直线与椭圆交于P 、Q 两点(如图),求四边形MPNQ 面积的最大值,并求出此时直线MN 的斜率.19.(本小题满分16分)数列{}n a 是公差为d (0)d ≠的等差数列,它的前的等比数列,它的前n 项和记为n B .若110a b =≠(1)若11a =,2d =,3q =,4m =,求k A .(2)若11a =,2d =,试比较2k A 与2m B 的大小,并说明理由;(3)若2q =,是否存在整数,m k ,使86k m A B =,若存在,求出,m k 的值;若不存在,说明理由.20.(本小题满分16分)已知函数()f x =1ln ,a x a x+∈R . (1)求函数()f x 的单调递减区间; (2)当[]1,2x ∈时,()f x 的最小值是0,求实数a 的值;(3)试问过点(02)P ,可作多少条直线与曲线()y f x =相切?并说明理由.扬州市2015-2016学年度高三第四次模拟测试数 学 试 题Ⅱ(全卷满分40分,考试时间30分钟)2016.521(B ).(本小题满分10分)已知矩阵21a A b ⎡⎤=⎢⎥⎣⎦,若矩阵A 属于特征值3的一个特征向量为11α⎡⎤=⎢⎥⎣⎦ ,求该矩阵的另一个特征值.21(C ).(本小题满分10分)在直角坐标系xOy 中,直线l 的参数方程为12x ty a t =+⎧⎨=-⎩(t 为参数)在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,极轴与x 轴的非负半轴重合)中,圆C 的方程为4cos ρθ=.若直线l 被圆C 截得的弦长为a 的值.22.(本小题满分10分)长时间上网严重影响着学生的健康,某校为了解甲、乙两班学生上网的时长,分别从这两个班中随机抽取6名同学进行调查,将他们平均每周上网时长作为样本,统计数据如下:如果学生平均每周上网的时长超过19小时,则称为“过度上网”.(1)从甲班的样本中有放回地抽取3个数据,求恰有1个数据为“过度上网”的概率;(2)从甲班、乙班的样本中各随机抽取2名学生的数据,记“过度上网”的学生人数为X ,写出X 的分布列和数学期望()E X .23.(本小题满分10分)已知*0()()nk k n nk f x Cx n N ==∈∑.(1)若456()()2()3()g x f x f x f x =++,求)(x g 中含4x 项的系数;(2)证明:012121231(2)123[]3n m mm m m n m n m n C C C nC C m -+++++++++++++=+ .2015-2016学年度高三第四次模拟测试数 学 试 题Ⅰ参 考 答 案2016.5一、填空题1.{0,1} 2.1i - 3.“2,10x R x x ∀∈++≠” 4 5.2或66.23 7.1 8.35- 9.1[0,]2 10.23- 11.2 12.[1,)+∞ 13.12017 14.32二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明、证明过程或演算步骤) 15.解:(1)2222()()()sin ()cos ()cos(2)22f x a b a b a b x x x ωωϕϕωϕ=+⋅-=-=+-+=-+………………………4分由题意得:周期24T πω==,故2πω=……………………6分(2)∵图象过点1(1,)2M ,1cos(2)22πϕ∴-+=即1sin 22ϕ=,而04πϕ<<,故26πϕ=,则()cos()26f x x ππ=-+. ……………………10分 当11x -≤≤时,23263x ππππ-≤+≤1cos()1226x ππ∴-≤+≤ ∴当13x =-时,min ()1f x =-,当1x =时,max 1()2f x =. ……………………14分16.证:(1) A ,D 分别为边SB ,SC 的中点,且8BC = //AD BC ∴且4AD =3,AB SA == 5CD SD ==222SA AD SD ∴+=90SAD ∴∠=︒即SA AD ⊥BC SB ∴⊥ ……………………3分 PA BC ⊥ ,PA SB A = ,PA 、SB ⊂平面PSB BC ∴⊥平面PSBBC ⊂ 平面ABCD ∴平面PSB ⊥平面ABCD ……………………7分 (2)//AD BC ,AD ⊂平面PAD ,BC ⊄平面PAD//BC ∴平面PAD ……………………10分 BC ⊂ 平面PBC ,平面PAD 平面PBC l =//l BC ∴ ……………………14分17.解:(1)设日销量为x k e ,则401000k e=401000k e ∴=. 则日售量为401000x e e ∴日利润401000(30)xe y x m e =--⋅. 即 401000(30)xe x m y e--=,其中3540x ≤≤. ………………3分 令'0y =得31x m =+.① 当34m ≤<时,343135m ≤+< ∴当3540x ≤≤时,'0y ≤.∴当35x =时,y 取最大值,最大值为51000(5)m e -. ………………5分 ② 当46m ≤≤时,353137m ≤+≤,函数y 在[35,31]m +上单调递增,在[31,40]m +上单调递减. ∴ 当31x m =+时,y 取最大值91000m e -. ………………7分∴当34m ≤<时,35x =时,日利润最大值为51000(5)m e -元当46m ≤≤时,31x m =+时,日利润最大值为91000m e -元. ………………8分(2)由题意得:401000(30)1000xe x m e --≥对[35,40]x ∀∈恒成立 ………………10分 则4030x em x e ≤--对[35,40]x ∀∈恒成立设40()30x e h x x e =--,[35,40]x ∈ 404040'()1x xe e e h x e e-∴=-= 则()h x 在[35,40]上单调增,则min 51()(35)5h x h e ==-,即515m e≤- 5.0≈∴每百支水笔的加工费m 最多约为4.9元答:每百支水笔的加工费m 最多约为4.9元. ………………14分18.解:(1)由题意得:24a c e a =⎧⎪⎨==⎪⎩2a c =⎧⎪⎨=⎪⎩1b ∴= ∴椭圆方程为:2214x y += ……………………3分设00(,)M x y ,则220014xy +=13AM AB = 且A 、B 分别在x 轴、y 轴上 003(,0),(0,3)2A xB y ∴222220000999()944x AB x y y ∴=+=+= 3AB ∴=为定值 ……………………7分(2)方法(一)设11(,)P x y //AB PQ 02P Q A By k kx ∴==-,220044x y += 则直线PQ 的方程为:02y y x x =-…………………9分 ∵0022214y y x x x y ⎧=-⎪⎪⎨⎪+=⎪⎩ 22012200220122004161616x x x y y y x y ⎧=⎪+⎪∴⎨⎪=⎪+⎩2222002222000041664441616x y PQ OP x y x y +∴==⋅=++ 点M 到直线00:20PQ y x x y +=的距离:00|3|2x y d ==………12分003||12222四边形MPQMPNQ x y S S PQ d ∆∴==⨯⋅===2031,1t y t =+≥,则242002011()14133(5)3199t t y yt y t t ---+-+==-+-≤+ 当且仅当2t =时,取等号;即20312y +=时,max ()4四边形MPNQ S =,此时220018,33y x ==MN k ∴= ………16分 方法(二)设直线MN 的斜率为k ,则003232PQ AB y k k k x -===-,则直线MN 方程为y kx =, 直线PQ 方程为2y kx =-, …………………9分解方程组22,1,4y kx x y =⎧⎪⎨+=⎪⎩M x =,用2k -代k得,P x =,由椭圆的对称性知2|M MNOM x ===,点P 到直线MN的距离|||(2)|3||kx y kx kx kx d ---===, ………12分由椭圆的对称性知,四边形MPNQ 的面积1226||||2PMN M P S S MN d x kx ∆==⋅⋅=⋅=4,==≤=当且仅当22164k k =,即4k =±时取等号, 所以,四边形MPNQ 的面积的最大值为4,此时直线MN的斜率k =. ………16分 19.解:(1)34327k a b ===,即2127k -=,14k =,14196A =. ………3分(2)依题意,224k A k =,且121m q k -=-,显然1q >.又222211[(21)1]11m m q B k q q q -==----, 所以222221[(21)1]41m k B A k q k q -=---- 22221[(21)4(41)]1k q k q k q =--+--, ………6分 设2222()(21)4(41)f x k x k x k =--+-,2(1)(21)10f k =--> 它是关于x 的二次函数,它的图象的开口向上,它的对称轴方程22412(21)k x k =<-,故()f x 是(1,)+∞上的增函数, 所以当1x >时()(1)0f x f >>,即220m k B A ->,所以22k m A B <. ………9分 (3)依题意:112m k m a b a -==⋅,由86k m A B =得:118621k ma a a qa k q+-⨯=⨯-, 即111112286212m m a a a a k --+⋅⨯=⨯-, 4862128622486486m k k k⨯+⨯==-⨯-⨯-, ………12分所以151634421m k --=+,因为92512=,故19m -≤,且51641294343=⨯=⨯⨯,且121m -+为奇数则其中121129m -+=时,151621m -+是整数,故17m -=,8m =且340k =. ………16分20.解:(1)2211'()a ax f x x x x-=-+=, 0a ≤时,'()0f x <在(0,)+∞上恒成立,则()f x 的单调递减区间(0,)+∞, 0a >时,令10ax -<则1x a <,即10x a<<时,'()0f x <,则()f x 的单调递减区间1(0,)a. ………3分 (2)①12a ≤,()f x 在[1,2]上单调递减,min 1()(2)ln 202f x f a ∴==+=,解得:112ln 22a =-≤,适合题意;②1a ≥,()f x 在[1,2]上单调递增,min ()(1)10f x f ∴==≠,无解;③112a <<,()f x 在1[1,]a 上单调递减,1[,2]a 上单调递增,min 11()()ln 0f x f a a a a ∴==+=,解得:a e =,舍去;综上可得:12ln 2a =-. ………8分(3)0a ≤时,有1条切线;0a >时,有2条切线.设切点坐标是00(,())x f x ,依题意:00200()210f x ax x x --=- 即00011ln 2a x a x x +-=-,化简得:002ln 20a x a x +--= 设2()ln 2F x a x a x=+--,0x > 故函数()F x 在(0,)+∞上零点个数,即是曲线切线的条数. ………10分2222'()a ax F x x x x-=-+= ①当0a =时,2()2F x x=-,在(0,)+∞上恰有一个零点1; ………11分③ 当0a <时,22'()0ax F x x -=<在(0,)+∞上恒成立,()F x 在(0,)+∞上单调递减,且(1)0F a =->,2()20F e e=-<故()F x 在(1,)e 上有且只有一个零点,当0a <时,()F x 在(0,)+∞上恰有一个零点; ………12分③0a >时,()F x 在2(0,)a上递减,在2(,)a +∞上递增,故()F x 在(0,)+∞上至多有两个零点,且(1)220F a a =--=-<又函数ln y x =在(1,)+∞单调递增,且值域是(0,)+∞, 故对任意实数a ,必存在0(1,)x ∈+∞,使02ln a x a+>,此时 00000222()ln 2(ln )0a F x a x a a x x x a+=+--=+-> 由于21a a+>, 即函数()F x 在0(1,)x 上必有一零点; ………14分111(1)1121()2(1)22(23)a a a aaa F e e a a a e a a a-++++++=-++--=-++先证明当0a >时,112(2)a ae a ++≥+,即证112ln(2)a a a++≥+若(0,2)a ∈,113a a++≥,而2ln(2)2ln 4a +≤,由于2ln 4ln163=<若[2,)a ∈+∞,构建函数1()12ln(2)x x x x ϕ=++-+,32222122(1)2'()102(2)(2)x x x x x x x x x x x ϕ----=--==>+++()x ϕ在[2,)+∞为增函数,1()(2)32ln 402a ϕϕ≥=+->综上0a >时,112(2)a aea ++≥+,所以11222222(2)23(25)23a aea a a a a a a ++≥+=+++++>++,故1(1)()0a aF e-++>又1(1)(1)0,1a aF e-++<<,所以在1(1)(,1)a ae-++必有一零点.∴当0a >时,()F x 在(0,)+∞上有两个零点∴综上:0a ≤时,有1条切线;0a >时,有2条切线. ………16分数 学 试 题Ⅱ参考答案21(B ).解:因为2113111a b ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,则2313a b +=⎧⎨+=⎩ ,解得12a b =⎧⎨=⎩所以1221A ⎡⎤=⎢⎥⎣⎦ …5分由212()(1)4021f λλλλ--==--=--,所以(1)(3)0λλ+-= 211,3λλ=-= 1λ=-所以另一个特征值是. ………………………………10分21(C ).解:直线l 的参数方程为12x ty a t =+⎧⎨=-⎩(t 为参数)所以直线的直角坐标系方程是:220x y a +--= ………………………………2分圆的直角坐标系方程是:2224x y -+=(),圆心(2,0),半径2r =……………………4分 设圆心到直线的距离为d,224d +=⎝⎭,所以d = ……………………………7分又d ===所以9122a =-或 ………………………………10分22.解:(1)设“恰有一个数据为过度上网”为事件A ,则213124()()339P A C ⎛⎫== ⎪⎝⎭ ……3分(2)甲组六人中有两人过度上网,乙组六人中有四人过度上网,则224222666(0)225C C P X C C === 112112422244226656(1)225C C C C C C P X C C +=== 11112222424244222266101(2)225C C C C C C C C P X C C ++=== 2112112424422256(3)225C C C C C C P X C C +=== 22242266(4)225C C P X C C === ……………8分 ()2342225225225225E X ∴=+⨯+⨯+⨯= 答:数学期望为2 …………………………10分23.解:(1)00110()(1)nk k n nn n nn n n k f x C x C x C x C x x ===+++=+∑ …………………………1分456456()()2()3()(1)2(1)3(1)g x f x f x f x x x x =++=+++++()g x 中4x 项的系数为4444562356C C C ++=; …………………………3分(2) 012111111231232323n m m m m m m m m n m m m m nC C C nC C C C nC -++++++++++++++++=++++ 设12()(1)2(1)(1)m m m n h x x x n x +++=++++++ ①则函数()h x 中含1m x +项的系数为111112323m m m m m m m m n C C C nC ++++++++++++ ……5分由错位相减法得:1231()(1)(1)(1)(1)(1)m m m m n m n xh x x x x x n x ++++++-=++++++++-+ ②11(1)1(1)()(1)1(1)m nm n x x xh x n x x +++⎡⎤+-+⎣⎦-=-+-+2111()(1)(1)(1)m m n m n x h x x x n x +++++=+-+++,()h x 中含1m x +项的系数,即是等式左边含3m x +项的系数,等式右边含3m x +项的系数为3211m m m n m n C nC ++++++-+ …………………………7分3211m m m n m n C nC ++++++-+21(1)!(3)!(2)!m m n m n nC m n +++++=-++-221113m m m n m n n C nC m ++++++-=-++ 21(3)(1)3m m n m n n C m ++++--=+21(2)13m m n m n C m +++++=+所以012121231(2)123[]3n m m m m m nm n m n C C C nC C m -+++++++++++++=+………………10分2015-2016学年度高三第四次模拟测试数 学 试 题Ⅰ参 考 答 案2016.5一、填空题1.{0,1} 2.1i - 3.“2,10x R x x ∀∈++≠” 4 5.2或66.23 7.1 8.35- 9.1[0,]2 10.23- 11.2 12.[1,)+∞ 13.12017 14.32二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明、证明过程或演算步骤) 15.解:(1)2222()()()sin ()cos ()cos(2)22f x a b a b a b x x x ωωϕϕωϕ=+⋅-=-=+-+=-+………………………4分由题意得:周期24T πω==,故2πω=……………………6分(2)∵图象过点1(1,)2M ,1cos(2)22πϕ∴-+=即1sin 22ϕ=,而04πϕ<<,故26πϕ=,则()cos()26f x x ππ=-+. ……………………10分 当11x -≤≤时,23263x ππππ-≤+≤1cos()1226x ππ∴-≤+≤∴当13x =-时,min ()1f x =-,当1x =时,max 1()2f x =. ……………………14分16.证:(1) A ,D 分别为边SB ,SC 的中点,且8BC = //AD BC ∴且4AD =3,AB SA == 5CD SD ==222SA AD SD ∴+=90SAD ∴∠=︒即SA AD ⊥BC SB ∴⊥ ……………………3分 PA BC ⊥ ,PA SB A = ,PA 、SB ⊂平面PSB BC ∴⊥平面PSBBC ⊂ 平面ABCD ∴平面PSB ⊥平面ABCD ……………………7分 (2)//AD BC ,AD ⊂平面PAD ,BC ⊄平面PAD//BC ∴平面PAD ……………………10分 BC ⊂ 平面PBC ,平面PAD 平面PBC l =//l BC ∴ ……………………14分17.解:(1)设日销量为x k e ,则401000ke=401000k e ∴=.则日售量为401000x e e ∴日利润401000(30)xe y x m e =--⋅. 即 401000(30)xe x m y e --=,其中3540x ≤≤. ………………3分令'0y =得31x m =+.④ 当34m ≤<时,343135m ≤+< ∴当3540x ≤≤时,'0y ≤.∴当35x =时,y 取最大值,最大值为51000(5)m e -. ………………5分 ⑤ 当46m ≤≤时,353137m ≤+≤,函数y 在[35,31]m +上单调递增,在[31,40]m +上单调递减. ∴ 当31x m =+时,y 取最大值91000m e -. ………………7分∴当34m ≤<时,35x =时,日利润最大值为51000(5)m e -元当46m ≤≤时,31x m =+时,日利润最大值为91000m e -元. ………………8分(2)由题意得:401000(30)1000xe x m e --≥对[35,40]x ∀∈恒成立 ………………10分则4030xe m x e ≤--对[35,40]x ∀∈恒成立设40()30x e h x x e =--,[35,40]x ∈ 404040'()1x xe e e h x e e -∴=-=则()h x 在[35,40]上单调增,则min 51()(35)5h x h e ==-,即515m e≤- 5.0≈∴每百支水笔的加工费m 最多约为4.9元答:每百支水笔的加工费m 最多约为4.9元. ………………14分18.解:(1)由题意得:24a c e a =⎧⎪⎨==⎪⎩2a c =⎧⎪⎨=⎪⎩1b ∴=∴椭圆方程为:2214x y += ……………………3分设00(,)M x y ,则220014xy +=13AM AB = 且A 、B 分别在x 轴、y 轴上 003(,0),(0,3)2A xB y ∴222220000999()944x AB x y y ∴=+=+= 3AB ∴=为定值 ……………………7分(2)方法(一)设11(,)P x y //AB PQ 002P Q A B yk k x ∴==-,220044x y +=则直线PQ 的方程为:002yy x x =- …………………9分∵0022214y y x x x y ⎧=-⎪⎪⎨⎪+=⎪⎩ 22012200220122004161616x x x y y y x y ⎧=⎪+⎪∴⎨⎪=⎪+⎩2222002222000041664441616x y PQ OP x y x y +∴==⋅=++ 点M 到直线00:20PQ y x x y +=的距离:00|3|2x y d ==………12分003||12222四边形MPQMPNQ x y S S PQ d ∆∴==⨯⋅===231,1t y t =+≥,则242002011()14133(5)3199t t y y t y t t ---+-+==-+-≤+ 当且仅当2t =时,取等号;即20312y +=时,max ()4四边形MPNQ S =,此时220018,33y x ==MN k ∴= ………16分 方法(二)设直线MN 的斜率为k ,则003232PQ AB y k k k x -===-,则直线MN 方程为y kx =, 直线PQ 方程为2y kx =-, …………………9分解方程组22,1,4y kx x y =⎧⎪⎨+=⎪⎩M x =,用2k -代k得,P x =,由椭圆的对称性知2|M MNOM x ===,点P 到直线MN的距离|||(2)|3||kx y kx kx kx d ---===, ………12分由椭圆的对称性知,四边形MPNQ 的面积1226||||2PMN M P S S MN d x kx ∆==⋅⋅=⋅=4, ==≤=当且仅当22164kk=,即4k=±时取等号,所以,四边形MPNQ的面积的最大值为4,此时直线MN的斜率k=.………16分19.解:(1)34327ka b===,即2127k-=,14k=,14196A=.………3分(2)依题意,224kA k=,且121mq k-=-,显然1q>.又222211[(21)1]11mmqB k qq q-==----,所以222221[(21)1]41m kB A k q kq-=----22221[(21)4(41)]1k q k q kq=--+--,………6分设2222()(21)4(41)f x k x k x k=--+-,2(1)(21)10f k=-->它是关于x的二次函数,它的图象的开口向上,它的对称轴方程22412(21)kxk=<-,故()f x是(1,)+∞上的增函数,所以当1x>时()(1)0f x f>>,即22m kB A->,所以22k mA B<.………9分(3)依题意:112mk ma b a-==⋅,由86k mA B=得:118621k ma a a qakq+-⨯=⨯-,即111112286212mm a aa ak--+⋅⨯=⨯-,4862128622486486mkk k⨯+⨯==-⨯-⨯-,………12分所以151634421mk--=+,因为92512=,故19m-≤,且51641294343=⨯=⨯⨯,且121m-+为奇数则其中121129m-+=时,151621m-+是整数,故17m-=,8m=且340k=.………16分20.解:(1)2211'()a axf xx x x-=-+=,a≤时,'()0f x<在(0,)+∞上恒成立,则()f x的单调递减区间(0,)+∞,a>时,令10ax-<则1xa<,即10xa<<时,'()0f x<,则()f x的单调递减区间1(0,)a.………3分(2)①12a ≤,()f x 在[1,2]上单调递减,min 1()(2)ln 202f x f a ∴==+=,解得:112ln 22a =-≤,适合题意;②1a ≥,()f x 在[1,2]上单调递增,min ()(1)10f x f ∴==≠,无解;③112a <<,()f x 在1[1,]a 上单调递减,1[,2]a 上单调递增,min 11()()ln 0f x f a a a a ∴==+=,解得:a e =,舍去;综上可得:12ln 2a =-. ………8分(3)0a ≤时,有1条切线;0a >时,有2条切线.设切点坐标是00(,())x f x ,依题意:00200()210f x ax x x --=- 即00011ln 2a x a x x +-=-,化简得:002ln 20a x a x +--= 设2()ln 2F x a x a x=+--,0x > 故函数()F x 在(0,)+∞上零点个数,即是曲线切线的条数. ………10分2222'()a ax F x x x x -=-+=①当0a =时,2()2F x x=-,在(0,)+∞上恰有一个零点1; ………11分⑥ 当0a <时,22'()0ax F x x-=<在(0,)+∞上恒成立, ()F x 在(0,)+∞上单调递减,且(1)0F a =->,2()20F e e=-<故()F x 在(1,)e 上有且只有一个零点,当0a <时,()F x 在(0,)+∞上恰有一个零点; ………12分③0a >时,()F x 在2(0,)a上递减,在2(,)a +∞上递增, 故()F x 在(0,)+∞上至多有两个零点,且(1)220F a a =--=-<又函数ln y x =在(1,)+∞单调递增,且值域是(0,)+∞, 故对任意实数a ,必存在0(1,)x ∈+∞,使02ln a x a+>,此时 00000222()ln 2(ln )0a F x a x a a x x x a+=+--=+-> 由于21a a+>, 即函数()F x 在0(1,)x 上必有一零点; ………14分111(1)1121()2(1)22(23)a a a aaa F e e a a a e a a a-++++++=-++--=-++先证明当0a >时,112(2)a ae a ++≥+,即证112ln(2)a a a++≥+若(0,2)a ∈,113a a++≥,而2ln(2)2ln 4a +≤,由于2ln 4ln163=< 若[2,)a ∈+∞,构建函数1()12ln(2)x x x x ϕ=++-+,32222122(1)2'()102(2)(2)x x x x x x x x x x x ϕ----=--==>+++()x ϕ在[2,)+∞为增函数,1()(2)32ln 402a ϕϕ≥=+->综上0a >时,112(2)a aea ++≥+,所以11222222(2)23(25)23a aea a a a a a a ++≥+=+++++>++,故1(1)()0a aF e-++>又1(1)(1)0,1a aF e -++<<,所以在1(1)(,1)a ae-++必有一零点.∴当0a >时,()F x 在(0,)+∞上有两个零点∴综上:0a ≤时,有1条切线;0a >时,有2条切线. ………16分数 学 试 题Ⅱ参考答案21(B ).解:因为2113111a b ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,则2313a b +=⎧⎨+=⎩,解得12a b =⎧⎨=⎩所以1221A ⎡⎤=⎢⎥⎣⎦ …5分 由212()(1)4021f λλλλ--==--=--,所以(1)(3)0λλ+-= 211,3λλ=-=1λ=-所以另一个特征值是. ………………………………10分21(C ).解:直线l 的参数方程为12x ty a t=+⎧⎨=-⎩(t 为参数)所以直线的直角坐标系方程是:220x y a +--= ………………………………2分圆的直角坐标系方程是:2224x y -+=(),圆心(2,0),半径2r =……………………4分 设圆心到直线的距离为d,224d +=⎝⎭,所以d = ……………………………7分又d ===所以9122a =-或 ………………………………10分22.解:(1)设“恰有一个数据为过度上网”为事件A ,则213124()()339P A C ⎛⎫== ⎪⎝⎭ ……3分(2)甲组六人中有两人过度上网,乙组六人中有四人过度上网,则224222666(0)225C C P X C C === 112112422244226656(1)225C C C C C C P X C C +=== 11112222424244222266101(2)225C C C C C C C C P X C C ++=== 2112112424422256(3)225C C C C C C P X C C +=== 22242266(4)225C C P X C C === ……………8分()2342225225225225E X ∴=+⨯+⨯+⨯= 答:数学期望为2 …………………………10分23.解:(1)00110()(1)nk k n nn n nn n n k f x C x C x C x C x x ===+++=+∑ …………………………1分456456()()2()3()(1)2(1)3(1)g x f x f x f x x x x =++=+++++()g x 中4x 项的系数为4444562356C C C ++=; …………………………3分(2) 012111111231232323n m m m m m m m m n m m m m nC C C nC C C C nC -++++++++++++++++=++++ 设12()(1)2(1)(1)m m m n h x x x n x +++=++++++ ① 则函数()h x 中含1m x +项的系数为111112323m m m m m m m m n C C C nC ++++++++++++ ……5分由错位相减法得:1231()(1)(1)(1)(1)(1)m m m m n m n xh x x x x x n x ++++++-=++++++++-+ ②11(1)1(1)()(1)1(1)m nm n x x xh x n x x +++⎡⎤+-+⎣⎦-=-+-+2111()(1)(1)(1)m m n m n x h x x x n x +++++=+-+++,()h x 中含1m x +项的系数,即是等式左边含3m x +项的系数,等式右边含3m x +项的系数为3211m m m n m n C nC ++++++-+ …………………………7分3211m m m n m n C nC ++++++-+21(1)!(3)!(2)!m m n m n nC m n +++++=-++-221113m m m n m n n C nC m ++++++-=-++ 21(3)(1)3m m n m n n C m ++++--=+21(2)13m m n m n C m +++++=+所以012121231(2)123[]3n m m m m m nm n m n C C C nC C m -+++++++++++++=+………………10分。
