人教版八年级数学几何专题
人教版初二数学8年级下册 第18章(平行四边形)四边形几何专题回顾(含解析)

八年级数学四边形几何专题回顾一.三角形中位线定理(共4小题)1.如图,在Rt△ABC中,∠C=90°,D,E分别为CA,CB的中点,BF平分∠ABC,交DE于点F,若,则DF的长为( )A.B.1C.D.22.如图,AD是△ABC的中线,E是AD的中点,F是BE延长线与AC的交点,若AC=4,则AF=( )A.B.C.1D.3.如图,在△ABC中,AB=6,AC=4,AD,AE分别是角平分线和中线,过点C作CF⊥AD于点F,连接EF,则线段EF的长为( )A.1B.2C.4D.4.如图,四边形ABCD中,∠A=90°,AB=12,AD=5,点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF长度的可能为( )A.2B.5C.7D.9二.平行四边形的性质(共2小题)5.如图,在▱ABCD 中,BE 平分∠ABC 交AD 于点E ,CF 平分∠BCD 交AD 于点F ,若BE =4,CF =3,EF =1,求AB 为( )A .3B .2.5C .3.5D .46.如图,平行四边形ABCD 的对角线AC ,BD 交于点O ,AB =,∠AOB =60°,过点O 作OE ⊥AC ,交AD 于点E ,过点E 作EF ⊥BD ,垂足为F ,则OE +2EF 的值为( )A .+1B .C .D .三.菱形的性质(共2小题)7.如图,菱形ABCD 的对角线AC 和BD 相交于点O ,AC =8,BD =12,E 是OB 的中点,P 是CD 的中点,连接PE ,则线段PE 的长为( )A .B .C .D .8.在菱形ABCD 中,∠D =60°,CD =4,E 为菱形内部一点,且AE =2,连接CE ,点F 为CE 中点,连接BF ,取BF 中点G ,连接AG ,则AG 的最大值为 .四.矩形的性质(共6小题)9.如图,在矩形ABCD 中,对角线AC 、BD 相交于点O ,且AD =6,CD =8,P 是AB 上的动点,PM⊥AC于M,PN⊥BD于N,则PM+PN的值为( )A.4.8B.6.4C.9.6D.2.410.如图,矩形ABCD的对角线AC,BD相交于点O,点P是AD边上的一个动点,过点P分别作PE ⊥AC于点E,PF⊥BD于点F.若AB=6,BC=8,则PE+PF的值为( )A.10B.9.6C.4.8D.2.411.如图,在矩形ABCD中,对角线AC、BD相交于点O,DF垂直平分OC,交AC于点E,交BC 于点F,连接AF,若AD=3,则AF的长为( )A.B.C.2D.312.如图,在矩形ABCD中,AB=2,BC=4,对角线AC,BD相交于点O,OE⊥AC交BC于点F,EF⊥BD于点F,则OE+EF的值为( )A.B.2C.D.213.如图,四边形ABCD是矩形,点E是边AB上的一动点,连接DE,点A与点P关于DE对称,连接EP、DP、BP,若AB=3,AD=5,则BP的最小值为 .14.如图,在矩形ABCD中,AB=6,AD=5,点P在边AD上,点Q在边BC上,且AP=CQ,连接CP,QD,则PC+QD的最小值为 .五.矩形的判定与性质(共1小题)15.如图,矩形ABCD中,AB=,BC=3,AE⊥BD于E,则EC=( )A.B.C.D.六.正方形的性质(共4小题)16.如图,在正方形ABCD中,点E在对角线BD上,连接AE,EF⊥AE于点E,交DC于点F,连接AF,已知BC=4,DE=3,则△AEF的面积为( )A.4B.5C.10D.517.正方形ABCD的边长为4,点E、F分别是BC,CD上的一动点,且BE=CF,连结AE,BF,两线交于点P,连接CP,则CP的最小值是( )A.B.C.D.18.如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,则线段GH的长为( )A.B.C.D.19.如图所示,正方形ABCD中,AB=4,点E为BC中点,BF⊥AE于点G,交CD边于点F,连接DG,则DG长为( )A.B.4C.D.七.翻折变换(折叠问题)(共3小题)20.如图,在△ABC中,AC=BC=2,AB=1,将它沿AB翻折得到△ABD,则四边形ADBC的形状是 形,点P、E、F分别为线段AB、AD、DB的任意点,则PE+PF的最小值是 .21.如图,在等腰△ABC中,AB=BC=4,把△ABC沿AC翻折得到△ADC.则(1)四边形ABCD是 形;(2)若∠B=120°,点P、E、F分别为线段AC、AD、DC上的任意1点,则PE+PF的最小值为 .22.如图,在△ABC中,AC=BC=5,AB=6,将它沿AB翻折得到△ABD,点P、E、F分别为线段AB、AD、DB的任意点,则PE+PF的最小值是 .八.旋转的性质(共3小题)23.如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA 交GF于点K.若正方形ABCD的边长为,则HD的长为( )A.﹣1B.﹣1C.1﹣D.1﹣24.如图,点E在正方形ABCD的边CD上,将△ADE绕点A顺时针旋转90°到△ABF的位置,连接EF,过点A作EF的垂线,垂足为点H,与BC交于点G.若BG=4,CG=3,则CE的长为( )A.5B.5C.5D.25.如图,在边长为a正方形ABCD中,把边BC绕点B逆时针旋转60°,得到线段BM,连接AM 并延长交CD于N,连接MC,则△MNC的面积为( )A.B.C.D.九.旋转的性质(共1小题)26.如图,将边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AEFG的位置,则图中阴影部分的面积为( )A.B.C.D.参考答案与试题解析一.三角形中位线定理(共4小题)1.如图,在Rt△ABC中,∠C=90°,D,E分别为CA,CB的中点,BF平分∠ABC,交DE于点F,若,则DF的长为( )A.B.1C.D.2【解答】解:在Rt△ABC中,AC=2,BC=4,由勾股定理得:AB==6,∵BF平分∠ABC,∴∠ABF=∠EBF,∵D,E分别为CA,CB的中点,∴DE∥AB,DE=AB=3,BE=BC=2,∴∠ABF=∠EFB,∴∠EFB=∠EBF,∴EF=BE=2,∴DF=DE﹣EF=1,故选:B.2.如图,AD是△ABC的中线,E是AD的中点,F是BE延长线与AC的交点,若AC=4,则AF=( )A.B.C.1D.【解答】解:取BF的中点H,连接DH,∵BD=DC,BH=HF,∴DH=FC,DH∥AC,∴∠HDE=∠FAE,在△AEF和△DEH中,,∴△AEF≌△DEH(ASA),∴AF=DH,∴AF=FC,∵AC=4,∴AF=,故选:B.3.如图,在△ABC中,AB=6,AC=4,AD,AE分别是角平分线和中线,过点C作CF⊥AD于点F,连接EF,则线段EF的长为( )A.1B.2C.4D.【解答】解:延长CF交AB于G,∵AD为△ABC的角平分线,CG⊥AD,∴△ACG是等腰三角形,∴AG=AC=4,FG=CF,∴BG=AB﹣AG=6﹣4=2,∵AE为△ABC的中线,∴EF是△BCG的中位线,∴EF=BG=1,故选:A.4.如图,四边形ABCD中,∠A=90°,AB=12,AD=5,点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF长度的可能为( )A.2B.5C.7D.9【解答】解:连接DN,∵ED=EM,MF=FN,∴EF=DN,∴DN最大时,EF最大,DN最小时,EF最小,∵N与B重合时DN最大,此时DN=DB===13,∴EF的最大值为6.5.∵∠A=90°,AD=5,∴DN≥5,∴EF≥2.5,∴EF长度的可能为5;故选:B.二.平行四边形的性质(共2小题)5.如图,在▱ABCD中,BE平分∠ABC交AD于点E,CF平分∠BCD交AD于点F,若BE=4,CF =3,EF=1,求AB为( )A.3B.2.5C.3.5D.4【解答】解:如图,过点E作EG∥FC交BC延长线于点G,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠AEB=∠EBC,∵BE平分∠ABC,∴∠ABE=∠EBC,∴∠ABE=∠AEB,∴AE=AB,同理可证:DC=DF,∵AB∥DC,∴∠ABC+∠DCB=180°,∵BE平分∠ABC,CF平分∠BCD,∴∠EBC+∠FCB=×180°=90°,∴BE⊥CF,∵EG∥FC,∴BE⊥EG,∵EF∥CG,∴四边形EFCG是平行四边形,∴EG=FC,在△BEG中,BE=4,EG=CF=3,根据勾股定理,得BG=,∵AB=AE=CD=DF,EF=CG=1,AD=BC,∴BG=BC+CG=AE+DE+CG=AE+DF﹣EF+EF=2AB,∴5=2AB,∴AB=2.5.故选:B.6.如图,平行四边形ABCD的对角线AC,BD交于点O,AB=,∠AOB=60°,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+2EF的值为( )A.+1B.C.D.【解答】解:∵∠BAO=90°,∠AOB=60°,∴∠ABO=30°,∴BO=2AO,∵AB=,∴AO=1,BO=2,∴S△ABO=AO•AB=,∵四边形ABCD为平行四边形,∴DO=BO=2,S△ADO=S△ABO=,∵OF⊥AO,EF⊥OD,∴S△ADO=S△AEO+S△EDO===,即OE+2EF=.故选:B.三.菱形的性质(共2小题)7.如图,菱形ABCD的对角线AC和BD相交于点O,AC=8,BD=12,E是OB的中点,P是CD 的中点,连接PE,则线段PE的长为( )A.B.C.D.【解答】解:如图,取OD的中点H,连接HP,∵四边形ABCD是菱形,∴AC⊥BD,AO=CO=4,OB=OD=6,∵点H是OD中点,点E是OB的中点,点P是CD的中点,∴OH=3,OE=3,HP=OC=2,HP∥AC,∴EH=6,∠DOC=90°,∴EP===2,故选:A.8.在菱形ABCD中,∠D=60°,CD=4,E为菱形内部一点,且AE=2,连接CE,点F为CE中点,连接BF,取BF中点G,连接AG,则AG的最大值为 .【解答】解:如图所示:连接BD交AC于点O,连接FO,取OB的中点H,连接HG和AH,∵在菱形ABCD中,∴O为AC中点,∵F为CE中点,∴OF=AE=1,当C、F、E、A共线时,OF也为1,∵G为BF中点、H为OB中点,∴GH=OF=,∵在菱形ABCD中且∠D=60°,∴∠ABO=∠ABC=∠ADC=30°,∠BOA=90°,∴OA=AB=2,,∴OB==,∴OH=,∴AH==,∵AG≤AH+HG,∴AG≤,∴AG的最大值为.故答案为:.四.矩形的性质(共6小题)9.如图,在矩形ABCD中,对角线AC、BD相交于点O,且AD=6,CD=8,P是AB上的动点,PM ⊥AC于M,PN⊥BD于N,则PM+PN的值为( )A.4.8B.6.4C.9.6D.2.4【解答】解:连接PO,∵在矩形ABCD中,AB=8,BC=6,∴AD=BC=6,∠DAB=90°,BO=OD,由勾股定理得:BD===10,∴BO=DO=5,∴S△DAB=×AD×AB=×8×6=24,∴S△AOB=S△DAB=12,∴×AO×PM+×BO×PN=12,∴PM+PN=4.8.故选:A.10.如图,矩形ABCD的对角线AC,BD相交于点O,点P是AD边上的一个动点,过点P分别作PE ⊥AC于点E,PF⊥BD于点F.若AB=6,BC=8,则PE+PF的值为( )A.10B.9.6C.4.8D.2.4【解答】解:连接OP,∵矩形ABCD的两边AB=6,BC=8,∴S矩形ABCD=AB•BC=48,OA=OC,OB=OD,AC=BD,AC==10,∴S△AOD=S矩形ABCD=12,OA=OD=5,∴S△AOD=S△AOP+S△DOP=OA•PE+OD•PF=OA(PE+PF)=×5×(PE+PF)=12,∴PE+PF==4.8.故选:C.11.如图,在矩形ABCD中,对角线AC、BD相交于点O,DF垂直平分OC,交AC于点E,交BC 于点F,连接AF,若AD=3,则AF的长为( )A.B.C.2D.3【解答】解:∵四边形ABCD是矩形,∴BC=AD=3,OA=OB=OC=OD,∵DF垂直平分OC,∴OD=OC,∴△OCD是等边三角形,设CD=x,则AC=2x,在Rt△ACD中,由勾股定理得可知:AD2+CD2=AC2,即32+x2=(2x)2,解得x=,∴,∴,∵△OCD是等边三角形,DF⊥OC,∴,设CF=y,则DF=2y,在Rt△CDF中,由勾股定理可知:CF2+CD2=DF2,即,解得y=1,∴CF=1,BF=2,在Rt△ABF中,由勾股定理可知:AB2+BF2=AF2,即,∴,故选:B.12.如图,在矩形ABCD中,AB=2,BC=4,对角线AC,BD相交于点O,OE⊥AC交BC于点F,EF⊥BD于点F,则OE+EF的值为( )A.B.2C.D.2【解答】解:∵AB=2,BC=4,∴矩形ABCD的面积为8,AC===2,∴BO=CO=AC=,∵对角线AC,BD交于点O,∴△BOC的面积为2,∵EO⊥AO,EF⊥DO,∴S△BOC=S△BOE+S△COE,2=CO×EO+BO×EF,∴2=××EO+×EF,∴(EO+EF)=4,∴EO+EF=,故选:A.13.如图,四边形ABCD是矩形,点E是边AB上的一动点,连接DE,点A与点P关于DE对称,连接EP、DP、BP,若AB=3,AD=5,则BP的最小值为 ﹣5 .【解答】解:如图,连接BD,AP,∵四边形ABCD是矩形,∴∠A=90°,∵AB=3,AD=5,∴BD===,∵点A与点P关于DE对称,∴DE垂直平分AP,∴PD=AD=5,∵BP+PD≥BD,∴BP+5≥,∴BP≥﹣5,∴BP的最小值为﹣5,故答案为:﹣5.14.如图,在矩形ABCD中,AB=6,AD=5,点P在边AD上,点Q在边BC上,且AP=CQ,连接CP,QD,则PC+QD的最小值为 13 .【解答】解:如图,连接BP,在矩形ABCD中,AD∥BC,AD=BC,∵AP=CQ,∴AD﹣AP=BC﹣CQ,∴DP=QB,DP∥BQ,∴四边形DPBQ是平行四边形,∴PB∥DQ,PB=DQ,则PC+QD=PC+PB,则PC+QD的最小值转化为PC+PB的最小值,在BA的延长线上截取AE=AB=6,连接PE,∵PA⊥BE,∴PA是BE的垂直平分线,∴PB=PE,∴PC+PB=PC+PE,连接CE,则PC+QD=PC+PB=PC+PE≥CE,∵BE=2AB=12,BC=AD=5,∴CE==13.∴PC+PB的最小值为13.故答案为:13.五.矩形的判定与性质(共1小题)15.如图,矩形ABCD中,AB=,BC=3,AE⊥BD于E,则EC=( )A.B.C.D.【解答】解:作EF⊥BC于F,∵四边形ABCD是矩形,∴AD=BC=3,AB=CD=,∠BAD=90°.∴tan∠ADB==,∴∠ADB=30°,∴∠ABE=60°,∴在Rt△ABE中cos∠ABE===,∴BE=,∴在Rt△BEF中,cos∠FBE===,∴BF=,∴EF==,∴CF=3﹣=,在Rt△CFE中,CE==.故选:D.六.正方形的性质(共4小题)16.如图,在正方形ABCD中,点E在对角线BD上,连接AE,EF⊥AE于点E,交DC于点F,连接AF,已知BC=4,DE=3,则△AEF的面积为( )A.4B.5C.10D.5【解答】解:过E作GH∥AD交AB于G,交DC于H,如图:,∵四边形ABCD是正方形,∴∠ABD=∠BDC=45°,AB=CD=BC=4,∴△BGE、△DHE是等腰直角三角形,BD=BC=4,∴EH=DE=×3=3,BE=BD﹣DE=4﹣3=,∴BG=GE=BE=1,∴AG=AB﹣BG=3=EH,∴AE===,∵AE⊥EF,∴∠AEG=90°﹣∠FEH=∠EFH,又∠AGE=∠EHF=90°,∴△AGE≌△EHF(AAS),∴AE=EF=,∴△AEF的面积为AE•EF=××=5,故选:B.17.正方形ABCD的边长为4,点E、F分别是BC,CD上的一动点,且BE=CF,连结AE,BF,两线交于点P,连接CP,则CP的最小值是( )A.B.C.D.【解答】解:在正方形ABCD中,AB=BC,∠ABC=∠BCD,在△ABE和△BCF中,,∴△ABE≌△BCF(SAS),∴∠BAE=∠CBF,∵∠CBF+∠ABF=90°,∴∠BAE+∠ABF=90°,∴∠APB=90°,∴点P在以AB为直径的圆上,设AB的中点为G,当CPG在同一直线上时,CP有最小值,如图所示:∵正方形ABCD的边长为4,∴BC=4,BG=2,∴CG===2,∵PG=AG=BG=2,∴CP=2﹣2,故选:A.18.如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,则线段GH的长为( )A.B.C.D.【解答】解:如图,延长BG交CH于点E,∵AB=CD=10,BG=DH=6,AG=CH=8,∴AG2+BG2=AB2,∴△ABG和△DCH是直角三角形,在△ABG和△CDH中,,∴△ABG≌△CDH(SSS),∴∠1=∠5,∠2=∠6,∴∠1+∠2=90°,∠5+∠6=90°,又∵∠2+∠3=90°,∠4+∠5=90°,∴∠1=∠3=∠5,∠2=∠4=∠6,在△ABG和△BCE中,,∴△ABG≌△BCE(ASA),∴BE=AG=8,CE=BG=6,∠BEC=∠AGB=90°,∴GE=BE﹣BG=8﹣6=2,同理可得HE=2,在Rt△GHE中,GH===2,故选:A.19.如图所示,正方形ABCD中,AB=4,点E为BC中点,BF⊥AE于点G,交CD边于点F,连接DG,则DG长为( )A.B.4C.D.【解答】解:如图,作DL⊥AE于点H,交AB于点L,∵BF⊥AE,∴DL∥BF,∵四边形ABCD是正方形,∴AB∥CD,AB=BC=CD,∠ABE=∠C=90°,∴BL∥DF,∴四边形BFDL是平行四边形,∵∠AGB=90°,∠BAE=90°﹣∠ABG=∠CBF,在△ABE和△BCF中,,∴△ABE≌△BCF(ASA),∴BE=CF,∵E为BC中点,∴BE=CF=BC=CD,∴DF=CF=CD,∴BL=DF=CD=AB,∴AL=BL=AB,∴==1,∴AH=GH,∵DA=AB=4,∴DG=DA=4,故选:B.七.翻折变换(折叠问题)(共3小题)20.如图,在△ABC中,AC=BC=2,AB=1,将它沿AB翻折得到△ABD,则四边形ADBC的形状是 菱 形,点P、E、F分别为线段AB、AD、DB的任意点,则PE+PF的最小值是 .【解答】解:∵△ABC沿AB翻折得到△ABD,∴AC=AD,BC=BD,∵AC=BC,∴AC=AD=BC=BD,∴四边形ADBC是菱形,故答案为菱;如图作出F关于AB的对称点M,再过M作ME⊥AD,交AB于点P,此时PE+PF最小,此时PE+PF =ME,过点A作AN⊥BC,∵AD∥BC,∴ME=AN,作CH⊥AB,∵AC=BC,∴AH=,由勾股定理可得,CH=,∵,可得,AN=,∴ME=AN=,∴PE+PF最小为,故答案为.21.如图,在等腰△ABC中,AB=BC=4,把△ABC沿AC翻折得到△ADC.则(1)四边形ABCD是 菱 形;(2)若∠B=120°,点P、E、F分别为线段AC、AD、DC上的任意1点,则PE+PF的最小值为 .【解答】解:(1)∵AB=BC,△ABC沿AC翻折得到△ADC,∴AB=BC=AD=CD,∴四边形ABCD是菱形.故答案为菱.(2)作CM⊥AD交AD的延长线于M,连接PD.当PE⊥AD,PF⊥CD时,PE+PF最短,∵∠B=∠ADC=120°,∴∠CDM=60°,∵CD=AB=4,∠CMD=90°,∴sin60°=,∴CM=2,∵S△ADC=S△ADP+S△CDP=•AD•PE+•CD•PF=•AD•CM,∴PE+PF=CM=2,∴PE+PF的最小值为2.故答案为2.22.如图,在△ABC中,AC=BC=5,AB=6,将它沿AB翻折得到△ABD,点P、E、F分别为线段AB、AD、DB的任意点,则PE+PF的最小值是 .【解答】解:作出F关于AB的对称点M,再过M作ME′⊥AD,交AB于点P′,此时P′E′+P ′F最小,此时P′E′+P′F=ME′,过点A作AN⊥BC,CH⊥AB于H,∵△ABC沿AB翻折得到△ABD,∴AC=AD,BC=BD,∵AC=BC,∴AC=AD=BC=BD,∴四边形ADBC是菱形,∵AD∥BC,∴ME′=AN,∵AC=BC,∴AH=AB=3,由勾股定理可得,CH==4,∵×AB×CH=×BC×AN,可得,AN=,∴ME′=AN=,∴PE+PF最小为,故答案为.八.旋转的性质(共3小题)23.如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA 交GF于点K.若正方形ABCD的边长为,则HD的长为( )A.﹣1B.﹣1C.1﹣D.1﹣【解答】解:连接BH,如图所示:∵四边形ABCD和四边形BEFG是正方形,∴∠BAH=∠ABC=∠BEH=∠F=90°,由旋转的性质得:AB=EB,∠CBE=30°,∴∠ABE=60°,在Rt△ABH和Rt△EBH中,,∴Rt△ABH≌△Rt△EBH(HL),∴∠ABH=∠EBH=∠ABE=30°,AH=EH,∴AH=AB•tan∠ABH=×=1,∴HD=AD﹣AH=﹣1.故选:A.24.如图,点E在正方形ABCD的边CD上,将△ADE绕点A顺时针旋转90°到△ABF的位置,连接EF,过点A作EF的垂线,垂足为点H,与BC交于点G.若BG=4,CG=3,则CE的长为( )A.5B.5C.5D.【解答】解:如图所示,连接EG,由旋转可得,△ADE≌△ABF,∴AE=AF,DE=BF,又∵AG⊥EF,∴H为EF的中点,∴AG垂直平分EF,∴EG=FG,设CE=x,则DE=7﹣x=BF,FG=CF﹣CG=11﹣x,∴EG=11﹣x,∵∠C=90°,∴Rt△CEG中,CE2+CG2=EG2,即x2+32=(11﹣x)2,解得x=,∴CE的长为,故选:C.25.如图,在边长为a正方形ABCD中,把边BC绕点B逆时针旋转60°,得到线段BM,连接AM 并延长交CD于N,连接MC,则△MNC的面积为( )A.B.C.D.【解答】解:作MG⊥BC于G,MH⊥CD于H,则BG=GC,AB∥MG∥CD,∴AM=MN,∵MH⊥CD,∠D=90°,∴MH∥AD,∴NH=HD,由旋转变换的性质可知,△MBC是等边三角形,∴MC=BC=a,由题意得,∠MCD=30°,∴MH=MC=a,CH=a,∴DH=a﹣a,∴CN=CH﹣NH=a﹣(a﹣a)=(﹣1)a,∴△MNC的面积=××(﹣1)a=a2,故选:C.九.旋转的性质(共1小题)26.如图,将边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AEFG的位置,则图中阴影部分的面积为( )A.B.C.D.【解答】解:作MH⊥DE于H,如图,∵四边形ABCD为正方形,∴AB=AD=1,∠B=∠BAD=∠ADC=90°,∵正方形ABCD绕点A逆时针旋转30°到正方形AEFG的位置,∴AE=AB=1,∠1=30°,∠AEF=∠B=90°,∴∠2=60°,∴△AED为等边三角形,∴∠3=∠4=60°,DE=AD=1,∴∠5=∠6=30°,∴△MDE为等腰三角形,∴DH=EH=,在Rt△MDH中,MH=DH=×=,∴S△MDE=×1×=.故选:D.。
人教版八年级数学下册期末复习专题在直角坐标系中求几何图形的面积(含详解)

人教版八年级数学下册期末复习专题训练——在直角坐标系中求几何图形的面积1.如图,四边形OABC是矩形,点A,C在坐标轴上,△ODE是由△OCB绕点O顺时针旋转90∘得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H,线段BC =2,OC=4(1)求直线BD的解析式.(2)求△OFH的面积.2.直线a:y=x+2和直线b:y=﹣x+4相交于点A,分别与x轴相交于点B和点C,与y轴相交于点D和点E.(1)在同一坐标系中画出函数图象;(2)求△ABC的面积;(3)求四边形ADOC的面积;(4)观察图象直接写出不等式x+2≤﹣x+4的解集和不等式﹣x+4≤0的解集.3.如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2,b1≠b2,那么称这两个一次函数为“平行一次函数”.已知函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点,一次函数y=kx+b与y=﹣2x+4是“平行一次函数”(1)若函数y=kx+b的图象过点(3,1),求b的值;(2)若函数y=kx+b的图象与两坐标轴围成的面积是△AOB面积的,求y=kx+b的解析式.4.如图,10个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这10个正方形分成面积相等的两部分,求该直线l的解析式5.如图1,直线3y分别与y轴、x轴交于点A、点B,点C的坐标为(-3,0),D为直线AB -=x3+3上一动点,连接CD交y轴于点E(1) 点B的坐标为__________,不等式+3>-x的解集为___________33(2) 若S△COE=S△ADE,求点D的坐标(3) 如图2,以CD为边作菱形CDFG,且∠CDF=60°.当点D运动时,点G在一条定直线上运动,请求出这条定直线的解析式.6.在直角坐标系中,一条直线经过A(﹣1,5),P(﹣2,a),B(3,﹣3)三点.(1)求a的值;(2)设这条直线与y轴相交于点D,求△OPD的面积.7.如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0)、(8,0),将△ABC沿x轴向右平移,当点C落在直线y=x﹣5上时,求线段BC扫过的面积8.已知:如图,已知直线AB的函数解析式为y=﹣2x+8,与x轴交于点A,与y轴交于点B.(1)求A、B两点的坐标;(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x 轴于点E,PF⊥y轴于点F,连接EF,若△PAO 的面积为S ,求S 关于m 的函数关系式,并写出m 的取值范围;9. 如图,已知直线343+=x y 与坐标轴交于B,C 两点,点A 是x 轴正半轴上一点,并且15=∆ABC S .点F 是线段AB 上一动点(不与端点重合),过点F 作FE ∥x 轴,交BC 于E.(1) 求AB 所在直线的解析式;(2) 若FD ⊥x 轴于D,且点D 的坐标为)0,(m ,请用含m 的代数式,表示DF 与EF 的长;(3) 在x 轴上是否存在一点P,使得△PEF 为等腰直角三角形,若存在,请直接写出点P 的坐标,若不存在,请说明理由.10.如图,在平面直角坐标系xOy 中,直线y=﹣2x +a 与y 轴交于点C (0,6),与x 轴交于点B . (1)求这条直线的解析式;(2)直线AD 与(1)中所求的直线相交于点D (﹣1,n ),点A 的坐标为(﹣3,0).①求n 的值及直线AD 的解析式; ②求△ABD 的面积;③点M 是直线y=﹣2x+a 上的一点(不与点B 重合),且点M 的横坐标为m ,求△ABM 的面积S 与m 之间的关系式.11.已知一次函数的图象经过(1,1)和(﹣1,﹣5).(1)求这个一次函数的表达式;(2)求这个一次函数的图象与x 轴、y 轴的交点坐标,并求出该图象与两坐标轴围成的三角形的面积.12.如图,边长为5的正方形OABC的顶点0在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是0A边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AG交于点P.(1)求证:CE=EP;(2)若点E的坐标为(3,O),在y轴上是否存在点M,使得四边形BMEP是平行四边形?若存在,求出点M的坐标:若不存在,说明理由.13.已知一次函数的图象经过(1,1)和(﹣1,﹣5).(1)求这个一次函数的表达式;(2)求这个一次函数的图象与x轴、y轴的交点坐标,并求出该图象与两坐标轴围成的三角形的面积.14.直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).(1)求直线AB的解析式;(2)若直线AB上一点C在第一象限且点C的坐标为(2,2),求△BOC的面积.15.在平面直角坐标系xOy中,直线y=kx+4(k≠0)与y轴交于点A.(1)如图,直线y=-2x+1与直线y=kx+4(k≠0)交于点B,与y轴交于点C,点B的横坐标为-1.①求点B的坐标及k的值;②直线y=-2x+1、直线y=kx+4与y轴所围成的△ABC的面积等于____________;(2)直线y=kx+4(k≠0)与x轴交于点E(x0,0),若-2<x0<-1,求k的取值范围.16.如图,己知直线l:y=x+1(k≠0)的图象与x轴、y轴交于A、B两点.(1)直接写出A、B两点的坐标;(2)若P是x轴上的一个动点,求出当△PAB是等腰三角形时P的坐标;(3)在y轴上有点C(0,3),点D在直线l上.若△ACD面积等于4.请直接写出D的坐标.17.如图①所示,正方形ABCD的边长为6 cm,动点P从点A出发,在正方形的边上沿A→B→C→D运动,设运动的时间为t(s),三角形APD的面积为S(cm2),S与t的函数图象如图②所示,请回答下列问题:(1)点P在AB上运动的时间为________s,在CD上运动的速度为________cm/s,三角形APD的面积S的最大值为________cm2;(2)求出点P在CD上运动时S与t之间的函数解析式;(3)当t为何值时,三角形APD的面积为10 cm2?18.已知:如图,已知直线AB的函数解析式为y=﹣2x+8,与x轴交于点A,与y轴交于点B.(1)求A、B两点的坐标;(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接EF,若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围;答案:1. (1) OC=4,BC=2,B(-2,4)∵OD =OC =4,∴D (4,0).设 BD 解析式为 y =kx +b (k ≠0), ∴{−2k +b =4,4k +b =0 ∴{k =−23,b =83.∴y =−23x +83. (2) ∵DE =2, ∴E (4,2). ∴ 直线 OE:y =12x ,∴{y =−23x +83,y =12x, ∴{x =167,y =87, ∴H (167,87).当 x =0,y =83, ∴F (0,83), ∴S △OFH =12×83×167=6421. 2.(1)依照题意画出图形,如图所示.(2)令y=x +2中y=0,则x +2=0,解得:x=﹣2,∴点B (﹣2,0);令y=﹣x +4中y=0,则﹣x +4=0,解得:x=4,∴点C (4,0);联立两直线解析式得:,解得:,∴点A (1,3).S △ABC =BC•y A =×[4﹣(﹣2)]×3=9.(3)令y=x +2中x=0,则y=2,∴点D (0,2).S 四边形ADOC =S △ABC ﹣S △DBO =9﹣×2×2=7.(4)观察函数图形,发现:当x <1时,直线a 在直线b 的下方,∴不等式x +2≤﹣x +4的解集为x ≤1;当x >4时,直线b 在x 轴的下方,∴不等式﹣x +4≤0的解集为x ≥4.3.(1)∵一次函数y=kx +b 与y=﹣2x +4是“平行一次函数”,∴k=﹣2,即y=﹣2x +b . ∵函数y=kx +b 的图象过点(3,1),∴1=﹣2×3+b ,∴b=7.(2)在y=﹣2x +4中,令x=0,得y=4,令y=0,得x=2,∴A (2,0),B (0,4),∴S △AOB =OA•OB=4.由(1)知k=﹣2,则直线y=﹣2x +b 与两坐标轴交点的坐标为(,0),(0,b ),于是有|b |•||=4×=1,∴b=±2,即y=kx +b 的解析式为y=﹣2x +2或y=﹣2x ﹣2.4.设直线l 和10个正方形的最上面交点为A ,过A 作AB ⊥OB 于B ,过A 作AC ⊥OC 于C , ∵正方形的边长为1,∴OB=3,∵经过原点的一条直线l 将这10个正方形分成面积相等的两部分,∴两边分别是5,∴三角形ABO 面积是7,∴OB•AB=7,∴AB=,∴OC=AB=,由此可知直线l 经过(,3),设直线方程为y=kx (k ≠0),则3=k ,解得k=∴直线l 解析式为y=x .故答案为:y=x .5.(1) (3,0)、x <3(2) ∵S △COE =S △ADE ∴S △AOB =S △CBD 即33321621⨯⨯=⨯⨯D y ,y D =233 当y =233时,23233333==+-x x ,∴D (23323,) (3) 连接CF ∵∠CDF =60°∴△CDF 为等边三角形连接AC ∵AB =AC =BC =6∴△ABC 为等边三角形∴△CAF ≌△CBD (SAS )∴∠CAF =∠ACB =60°∴AF ∥x 轴设D (m ,333+-m )过点D 作DH ⊥x 轴于H ∴BH =3-m ,DB =6-2m =AF∴F (2m -6,33)由平移可知:G (m -9,m 3-)令⎪⎩⎪⎨⎧-=-=m y m x 39∴点G 在直线393--=x y 上6. (1)设直线的解析式为y=kx +b ,把A (﹣1,5),B (3,﹣3)代入,可得:{533=+--=+b k b k ,解得:,所以直线解析式为:y=﹣2x +3,把P (﹣2,a )代入y=﹣2x +3中,得:a=7;(2)由(1)得点P 的坐标为(﹣2,7),令x=0,则y=3,所以直线与y 轴的交点坐标为(0,3),所以△OPD 的面积=.7.∵点A 、B 的坐标分别为(2,0)、(8,0),∴AB=6,∵∠CAB=90°,BC=10, ∴CA==8,∴C 点纵坐标为:8,∵将△ABC 沿x 轴向右平移,当点C 落在直线y=x ﹣5上时,∴y=8时,8=x ﹣5,解得:x=13,即A 点向右平移13﹣2=11个单位, ∴线段BC 扫过的面积为:11×8=88.故选:B .8.(1)令x=0,则y=8,∴B (0,8),令y=0,则﹣2x +8=0,∴x=4,∴A (4,0), (2)∵点P (m ,n )为线段AB 上的一个动点,∴﹣2m +8=n ,∵A (4,0),∴OA=4,∴0<m <4∴S △PAO =OA ×PE=×4×n=2(﹣2m +8)=﹣4m +16,(0<m <4) )3,0(30343)1(,9B y x x y 即时,中,当在==+= ∴OB=3同理OC=4 ∵15)(21=⋅+OB OA OC ,153)4(21=⨯+⨯OA ∴OA=6 即点A 的坐标为(6,0) 设AB 所在直线的解析式为y=kx+b⎩⎨⎧⎩⎨⎧=+=-==213063k b b k b 解得则∴AB 所在直线的解析式为 (2)在中,当,即DF= 在中,当mx m y 32,321-=+-=时mm m EF 35)32(=--= (3)10.(1)∵直线y=﹣2x +a 与y 轴交于点C (0,6),∴a=6,∴该直线解析式为y=﹣2x +6 (2)①∵点D (﹣1,n )在直线BC 上,∴n=﹣2×(﹣1)+6=8,∴点D (﹣1,8) 设直线AD 的解析式为y=kx +b ,将点A (﹣3,0)、D (﹣1,8)代入y=kx +b 中, 得:,解得:,∴直线AD 的解析式为y=4x +12.②令y=﹣2x +6中y=0,则﹣2x +6=0,解得:x=3,∴点B (3,0).∵A(﹣3,0)、D (﹣1,8),∴AB=6.S △ABD =AB•y D =×6×8=24.③∵点M 在直线y=-2x+6上,∴M (m ,-2m+6),当m <3时,S=16(26)2m ⨯⨯-+即618S m =-+;当m >3时,即S=6m -18.11. (1)设函数解析式为y=kx +b ,由题意将两点代入得:{15=+-=+-b k b k ,解得:{32=-=k b .∴一次函数的解析式为:y=3x ﹣2;(2)令y=0,得x=32,令x=0,得y=﹣2, 3232221=⨯⨯=∴s 12.(1)在OC 上截取OK =OE .连接EK .∵OC =OA ,∠1=90°,∠OEK =∠OKE =45°,∵AP 为矩形外角平分线,∴∠BAP =45°∴∠EKC =∠PAE =135°.∴CK =EA .∵EC ⊥EP ,∴∠3=∠4.∴△EKC ≌△PAE . ∴EC =EP (2)y 轴上存在点M ,使得四边形BMEP 是平行四边形.如图,过点B 作BM ∥PE 交y 轴于点M ,∴∠5=∠CEP =90°,∴∠6=∠ 4.在△BCM 和△COE 中,⎪⎩⎪⎨⎧∠=∠=∠=∠,,,46COE BCM OC BC ∴△BCM ≌△COE ,∴BM =CE 而CE =EP ,∴BM =EP .由于BM ∥EP ,∴四边形BMEP 是平行四边形由△BCM ≌△COE可得CM =OE =3,∴OM =CO -CM =2.故点M 的坐标为(0,2).13.(1)设函数解析式为y=kx +b ,由题意将两点代入得:,解得:.∴一次函数的解析式为:y=3x ﹣2;(2)令y=0,得x=,令x=0,得y=﹣2,∴S=×2×=.14.(1)设直线AB 的解析式为y =kx +b(k ≠0).将A(1,0),B(0,-2)代入解析式,得⎩⎪⎨⎪⎧k +b =0,b =-2.解得⎩⎪⎨⎪⎧k =2,b =-2.∴直线AB 的解析式为y =2x -2.(2)S △BOC =12×2×2=2.15.(1)32 当x =-1时,y =-2×(-1)+1=3,∴B(-1,3).将B(-1,3)代入y =kx +4,得k =1.(2)y =kx +4与x 轴的交点为(-4k ,0),∵-2<x 0<-1,∴-2<-4k <-1,(1) 解得2<k <4.16.(1)当y=0时,x+1=0,解得x=﹣2,则A (﹣2,0),当x=0时,y=x+1=1,则B (0,1);(2)AB==,当AP=AB 时,P 点坐标为(﹣,0)或(,0);当BP=BA时,P点坐标为(2,0);当PA=PB时,作AB的垂直平分线交x轴于P,连结PB,如图1,则PA=PB,设P(t,0),则OA=t+2,OB=t+2,在Rt△OBP中,12+t2=(t+2)2,解得t=﹣,此时P 点坐标为(﹣,0);(3)如图2,设D(x,x+1),当x>0时,∵S△ABC+S△BCD=S△ACD,∴•2•2+•2•x=4,解得x=2,此时D点坐标为(2,2);当x<0时,∵S△BCD﹣S△ABC=S△ACD,∴•2•(﹣x)﹣•2•2=4,解得x=﹣6,此时D点坐标为(﹣6,﹣2),综上所述,D点坐标为(2,2)或(﹣6,﹣2).故答案为(﹣2,0),(0,1);(2,2)或(﹣6,﹣2).17.略18.(1)令x=0,则y=8,∴B(0,8),令y=0,则﹣2x+8=0,∴x=4,∴A(4,0),(2)∵点P(m,n)为线段AB上的一个动点,∴﹣2m+8=n,∵A(4,0),∴OA=4,∴0<m<4∴S△PAO=OA×PE=×4×n=2(﹣2m+8)=﹣4m+16,(0<m<4)。
人教版八年级数学上册专题复习证明三角形全等的常见题型

证明三角形全等的常见题型全等三角形是初中几何的重要内容之一,全等三角形的学习是几何入门最关键的一步,这部分内容学习的好坏直接影响着今后的学习。
而一些初学的同学,虽然学习了几种判定三角形全等的公理和推论,但往往仍不知如何根据已知条件证明两个三角形全等。
在辅导时可以抓住以下几种证明三角形全等的常见题型,进行分析。
一、已知一边与其一邻角对应相等1.证已知角的另一边对应相等,再用SAS证全等。
例1已知:如图1,点E、F在BC上,BE=CF,AB=DC,∠B=∠C .求证:AF=DE。
证明∵BE=CF(已知),∴BE+ EF=CF+EF,即 BF=CE。
在△ABF和△DCE中,∴△ABF≌△DCE(SAS)。
∴ AF=DE(全等三角形对应边相等)。
2.证已知边的另一邻角对应相等,再用ASA证全等。
例2已知:如图2,D是△ABC的边AB上一点,DF交AC于点E,DE=FE,FC∥AB。
求证:AE=CE。
证明∵ FC∥AB(已知),∴∠ADE=∠CFE(两直线平行,内错角相等)。
在△ADE和△CFE中,∴△ADE≌△CFE(ASA).∴ AE=CE(全等三角形对应边相等)3.证已知边的对角对应相等,再用AAS证全等。
例3(同例2).证明∵ FC∥AB(已知),∴∠A=∠ECF(两直线平行,内错角相等).在△ADE和△CFE中,∴△ADE≌△CFE(AAS).∴ AE=CE(全等三角形对应边相等)。
二、已知两边对应相等1.证两已知边的夹角对应相等,再用SAS证等。
例4已知:如图3,AD=AE,点D、E在BCBD=CE,∠1=∠2。
求证:△ABD≌△ACE.证明∵∠1=∠2(已知),∠ADB=180°-∠1,∠AEC=180°-∠2(邻补角定义),∴∠ADB = ∠AEC,在△ABD和△ACE中,∴△ABD≌△ACE(SAS).2.证第三边对应相等,再用SSS证全等。
例5已知:如图4,点A、C、B、D在同一直线AC=BD,AM=CN,BM=DN。
人教版八年级数学下《一次函数与几何综合》专题练习题
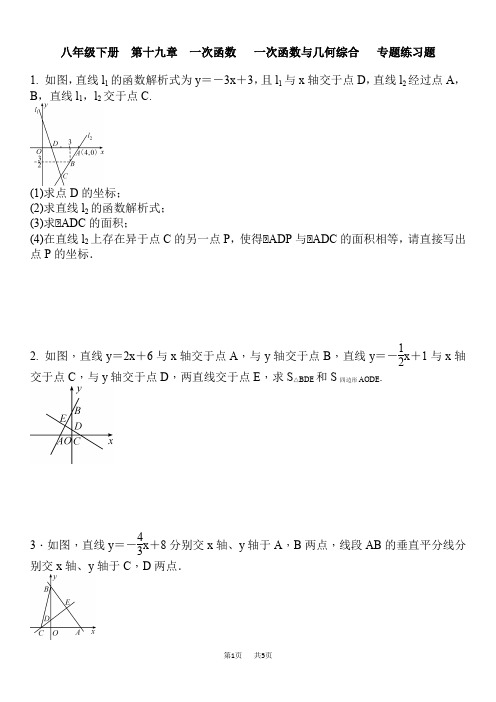
八年级下册第十九章一次函数一次函数与几何综合专题练习题1. 如图,直线l1的函数解析式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.(1)求点D的坐标;(2)求直线l2的函数解析式;(3)求△ADC的面积;(4)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.2. 如图,直线y=2x+6与x轴交于点A,与y轴交于点B,直线y=-12x+1与x轴交于点C,与y轴交于点D,两直线交于点E,求S△BDE和S四边形AODE.3.如图,直线y=-43x+8分别交x轴、y轴于A,B两点,线段AB的垂直平分线分别交x轴、y轴于C,D两点.(1)求点C的坐标;(2)求直线CE的解析式;(3)求△BCD的面积.4. 如图,在平面直角坐标系中,点A(-1,0),B(0,3),直线BC交坐标轴于B,C两点,且△CBA=45°.求直线BC的解析式.5. 如图,A(0,4),B(-4,0),D(-2,0),OE⊥AD于点F,交AB于点E,BM⊥OB 交OE的延长线于点M.(1)求直线AB和直线AD的解析式;(2)求点M的坐标;(3)求点E,F的坐标.6. 如图,正方形OBAC中,O(0,0),A(-2,2),B,C分别在x轴、y轴上,D(0,1),CE⊥BD交BD延长线于点E,求点E的坐标.7. 如图,在平面直角坐标系中,A(0,1),B(3,12),P 为x 轴上一动点,则PA +PB 最小时点P 的坐标为________.8. 如图,直线y =x +4与坐标轴交于点A ,B ,点C(-3,m)在直线AB 上,在y 轴上找一点P ,使PA +PC 的值最小,求这个最小值及点P 的坐标.答案:1. 分析:(1)令y =-3x +3=0,求出x 可得点D 的坐标;(2)设直线l 2的解析式为y =kx +b ,把A ,B 的坐标代入求出k ,b 可得;(3)先求出点C 的坐标,再求S △ADC ;(4)在l 2上且到x 轴的距离等于点C 纵坐标的相反数的点即为点P.解:(1)由y =-3x +3,令y =0,得-3x +3=0,∴x =1,∴D(1,0) (2)y =32x -6 (3)由⎩⎨⎧y =-3x +3,y =32x -6,解得⎩⎪⎨⎪⎧x =2,y =-3,△C(2,-3),△AD =3,△S △ADC =12×3×|-3|=92 (4)P(6,3)2. 解:易求A (-3,0),B(0,6),C(2,0),D(0,1),△BD =5,解⎩⎨⎧y =2x +6,y =-12x +1,得⎩⎪⎨⎪⎧x =-2,y =2, △E(-2,2),△S △BDE =5,S 四边形AODE =S △AOB -S △BDE =9-5=43. 解:(1)易得A(6,0),B(0,8),设C 点坐标为(x ,0),则BC =AC =6-x ,由勾股定理得x 2+82=(6-x)2,△x =-73,△C(-73,0) (2)△点E 是AB 的中点,△点E 的坐标为(3,4),易得直线CE 的解析式为y =34x +74 (3)由CE 解析式得,点D 坐标为(0,74),S △BCD =12×(8-74)×73=175244. 分析:过点A 作AD△AB ,AD 交BC 于点D ,可得△BAD 是等腰直角三角形,再过点D 作DE△x 轴于点E ,通过证△DEA△△AOB 求出点D 的坐标,最后由点B ,D 的坐标利用待定系数法可求出直线BC 的解析式.解:过点A 作AD△AB ,AD 交BC 于点D ,可得AD =AB ,过点D 作DE△x 轴于点E ,可证△DEA△△AOB ,△DE =OA =1,EA =OB =3,△D(-4,1),可求直线BC的解析式为y =12x +35. 解:(1)AB :y =x +4,AD :y =2x +4 (2)由△OBM△△AOD 得BM =OD ,△M(-4,2) (3)由(2)得OM :y =-12x ,联立⎩⎨⎧y =-12x ,y =x +4,得E(-83,43);联立⎩⎨⎧y =2x +4,y =-12x ,得F(-85,45)6. 解:延长CE 交x 轴于点F ,则有△BOD△△COF ,△OD =OF =1,△F(1,0),△C(0,2),△CF :y =-2x +2,△B(-2,0),D(0,1),△BD :y =12x +1,由⎩⎨⎧y =12x +1,y =-2x +2,得E(25,65)7. (2,0) 分析:先作出点A 关于x 轴对称的点A′,再连接A′B 交x 轴于点P ,则点P 即为所求.由题中条件易求出直线A′B 的解析式,再求出直线A′B 与x 轴的交点坐标即可.8. 解:作点A 关于y 轴的对称点A′,连接CA′交y 轴于P ,此时PA +PC 值最小,最小值为CA′,易求C(-3,1),△A′(4,0),△CA′:y =-17x +47,△P(0,47),作CE△x 轴于E ,△CA′=CE 2+A′E 2=52。
专题五几何证明人教版八年级数学(上册)-【完整版】

∴△DAB≌△CBA(AAS). ∴BD=AC. ∴AD=BC. 在△ADC和△BCD中,
∴△ADC≌△BCD(SSS). ∴∠CDA=∠DCB.
四、 证明线段垂直
15. 如图,点 C 在线段 AB 上,AD∥EB,AC=BE,
AD=BC,CF 平分∠DCE.求证:CF⊥DE.
∵F为CE的中点, ∴AF平分∠EAC. ∴AF⊥CE.即∠AFC=90°. 又∠FAC+∠ACE=180°-∠AFC=90°, ∠DAC=∠ACE, ∴∠DAC+∠FAC=90°. 即∠DAF=90°. ∴AF⊥AD.
五、 证明等边三角形
20. 如图,在△ABC 中,D 为 AC 边上一点,DE⊥AB
专题五 几何证明人教版八年级数学上册-精 品课件p pt(实 用版)
专题五 几何证明人教版八年级数学上册-精 品课件p pt(实 用版)
在△ACM和△DCN中,
∴△ACM≌△DCN(ASA). ∴CM=CN. 又∠DCN=60°, ∴△CMN为等边三角形.
专题五 几何证明人教版八年级数学上册-精 品课件p pt(实 用版)
证明:∵△ABC≌△EDC, ∴BC=DC,∠ACB=∠DCE.
在△BCF和△DCH中,
∴△BCF≌△DCH(SAS). ∴∠FBC=∠HDC. 在△FBC和△FDK中, ∵∠FBC=∠HDC,∠BFC=∠DFK, ∴∠DKF=∠ACB.
14. 如图,AC 与 BD 相交于点 O,∠DBA=∠CAB, ∠1=∠2. 求证:∠CDA=∠DCB.
点 F,连接 BE. 求证:BE⊥AF.
证明:∵AD∥BC, ∴∠DAE=∠F,∠ADE=∠FCE.
在△ADE和△FCE中,
人教版八年级数学几何专题

人教版八年级数学几何专题本页仅作为文档页封面,使用时可以删除This document is for reference only-rar21year.March2八年级数学下册期末专题复习和训练:几何计算题、证明题一、题型特点:四边形(五种常见的)、三角形的中位线、矩形的推论穿插其中,……二、常见新型题型:动点、折纸、开放(条件、结论开放)、探索性(数量关系、位置关系),……三、图形搭建:三角形中搭建四边形、四边形中搭建三角形、组合图形,…… 下面我根据图形搭建结构特征进行分类,列举一部分和本期几何部分(主要是平行四边形)的计算题、证明题,让我们共同来探究、解析. 一、以平行四边形搭建起来的图形 例1.ABCD 中,AB=4cm ,AD=7cm, ∠ABC 的平分线交AD 于E,交CO 的延长线于F,求DF 的长? 分析:本题要求的DF 长的途径有两条:其一.DF CF CD =-;其二. DF DE AD AE ==-.比较容易得出BCF 是等腰三角形,即CF CB =的对边相等可以得出:,CD AB 4cm CB AD 7cm ====.故DF 743cm =-= 例2.△ABC 、△ADE 都是正三角形,CD=BF. (1)、求证:△ACD ≌△CBF(边上的何处时,四边形CDEF 为平行四边形,且∠DEF=30°, 分析:⑴.证明△ACD ≌△CBF 已经有了CD=BF ,而△ABC 、△ADE都是正三角形又可以给我们提供,CA CB ACD CBF 60=∠=∠=条件,根据“SAS ”判定方法可以证得△ACD ≌△CBF.⑵.根据⑴问的△ACD ≌△CBF 得出AD CF =,又△ADE 是正三角形的DE CF =,所以CF DE =;要使四边形CDEF 为平行四边形可以证CF DE .若四边形CDEF 为平行四边形,则FCD DEF 30∠=∠=;当EDB 30∠=时,就有FCD EDB ∠=∠,此时就能证得CF DE .由正△ADE 可以得出ADE 60∠=,则ADB 603090∠=+=,AD BC ⊥;由于等腰三角形具有“三线合一”的特征,所以当D 运动至BC 边上中点时,四边形CDEF 为平行四边形.练习:1.如图,在□ABCD 中,AE ⊥BC,AF ⊥CD,∠EAF=60°,则∠B=(2.□ABCD 的周长为60cm,对角线AC 、BD 交于点O,△AOB 的周 长比△BOC 的周长多10cm,则AD=( ),DC=( );3.□ABCD 中,∠ABC 的平分线BE 交AD 于E 点,若∠ABE=25°CD=5cm,BC=7cm,那么∠ABE=( ),∠BED=( ),AE=( )4. 已知□ABCD ,BE=AB,BF =BD. 求证:5. △ABC 是正三角形,AE=BD,DF ∥CE,EF ∥CD. 求证: △AGF ≌△EAC6.以△ABC 的三边在BC 的同侧做等边△EBC 、等边△FBA3⑴.判断四边形FADE 的形状?⑵.当∠BAC 为多少度时,四边形FADE 为矩形?⑶.当∠BAC 为多少度时,四边形FADE 不存在?7. 有一块如图的玻璃,不小心把DEF 部分打碎,现在只测得AB=60cm,BC=80cm ,∠A=120°,∠B=60°,∠C=150°,你能根据测得的数据计算AD 的长?二、以矩形搭建起来的图形例1.D 为□ABCD 外一点,∠APC=∠BPD=90°.求证: □ABCD 为矩形 分析:判定矩形的方法主要有三种.但在已知了四边形ABCD 是平行 四边形的情况下,要判定ABCD 是矩形的途径有两条:其一、找一内角是直角;其二、找出对角线相等,即找出AC BD =.由于本题的另一主要条件是∠APC=∠BPD=90°,要根据题中条件和图形位置转换成四边形的内角为90°比较困难,所以本题我们先想办法找出对角线相等,即找出AC BD =.我们发现本题在APC Rt 和BPD Rt 的两斜边的交点O 恰好是平行四边形对角线的交点,根据平行四边形对角线互相平分可知:O 同时是AC BD 、的中点;所以自然联想到连结PO 这条两直角三角形公共的中线(见图).根据以上条件,在APC Rt 和BPD Rt 中就有:AC 2PO =BD 2PO =,故AC BD =,由对角线相等的平行四边形是矩形,可判定ABCD 是矩形.例2. 矩形ABCD 中,AB=3,AD=4,PE ⊥AC ,PF ⊥BD , ⑴.求PE+PF 的值?⑵.若点P 是AD 上的一动点(不与A D 、重合),还是作PE ⊥AC ,PF ⊥BD ,则PE+PF 的值是否会发生变化为什么分析:求线段的和或差我们会联想到证明中的“截长补短”法,但本题不具备这方面的条件.本题从面积入手可以破题:如图连结PO ,只要我们能求出APO 和DPO 的面积之和问题便可以获得解决.略解:⑴.∵四边形ABCD 是矩形∴BAD 90∠=,,11OA AC OD BD 22==, AC BD =∴1OA OD BD 2==在ABD Rt 中,AB=3,AD=4;并且根据勾股定理有:222BD AB AD =+,即222BD 34=+,又BD 0> ,所以.=BD 5∴.==11OA OD BD 52522==⨯∵,11AOP OA PE DOP OD PF 22S S=⋅=⋅,且ABCD 11AOD 34344SS ==⨯⨯=矩形(过程略)∴++=11AOP DOP OA PE OD PF AOD 22SSS=⋅⋅,即..1125PE 25PF 322⨯⨯+⨯⨯=A BCDP E FO4∴12PE PF 5+=. ⑵.不会发生变化.这是因为AOD AOP POD 、、的面积以及作为底边的OA OD、不会发生变化. 练习:1. 矩形ABCD 中,AF=DE.求证:2. 矩形ABCD 中,BE ⊥AC ,CF ⊥BD.求证:BE=CF3. 矩形ABCD 中,DF 平分∠ADC, ∠BDF=15°. 求∠DOC 与∠COF 的度数?4、矩形ABCD 中,CE ∥BD ,则△ACE 为等腰三角形吗为什么5.如图,在矩形ABCD 中,点E ,F 分别在BC ,CD 上,将△ABE 沿AE 折叠,使点B 落在AC 上的点B′处,又将△CEF 沿EF 折叠,使点C 落在EB′与AD 的交点C′处.则BC :AB 的值为多少?三、以菱形搭建起来的图形例1. △ABC 中,∠BAC=90°,BD 平分∠ABC ,AH ⊥BC 于H 交BD 于E,DF ⊥BC 于F,求证:四边形AEFD 是菱形分析:判定菱形方法主要有三种,三种方法都可以使本题获得解决. 下面我们选择“四边都相等的四边形是菱形”这一途径来分析. 可以先根据角平分线的性质得出AD FD =,进而容易证明ABD ≌AFD ,所以BA BF =;再证明ABE ≌AFE可以得到EA EF =(也可以利用等腰三角形的“三线合一”);利用等角的余角相等可以推出ADE AED ∠=∠,所以EA DA =,于是AE EF FD DA ===,故四边形AEFD 是菱形.例2.(2012中考·自贡) 如图所示,在菱形ABCD 中,,AB 4BAD 120=∠=,AEF 为正三角形,点E F 、分别在菱形的边BC CD 、上滑动,且E F 、不与B C D 、、重合.⑴.证明不论E F 、在BC CD 、D 上如何滑动,总有BE CF =⑵.当点E F 、在BC CD 、上滑动时,探讨四边形AECF 的面积是否发生变化?如果不变,求出这个定值.分析:⑴.先求证AB AC =,进而求证ABC ACD 、为等边三角形,得=BAC 60AC AB ∠=,进而求证ABE ≌ACF ,即可求得BE CF = ⑵.根据ABE ≌ACF 可得ABE ACF SS =;根据S四边形AECF=AEC S+ACFS=AEC S+BAE S =ABC S即可解得.⑴.证明:连接AC ,如下图所示. ∵四边形ABCD 为菱形,BAD 120∠= ∴,1EAC 602EAC 60∠+∠=∠+∠= ∴12∠=∠ ∵BAD 120∠=∴ABC 60∠=∴ABC 和ACD 都为等边三角形∴=460AC AB ∠=,∴在ABE 和ACF 中,12AB AC ABC 3∠=∠⎧⎪=⎨⎪∠=∠⎩∴ABE ≌ACF ()ASA ∴BE CF =⑵.解:四边形AECF 的面积不变.理由:由⑴得ABE ≌ACF ,则ABE ACF SS=.故S 四边形AECF =AEC S +ACF S =AEC S +BAE S =ABC S 是定值. 作AH BC ⊥于H 点,则BH 2=S四边形ABCD =S ABC =2211BC AH BC AB BH 4322⋅=-练习:EFODAEFDBCAODACA B DE321E HABF1.已知ABCD,添加下列一个条件:①.AC⊥BD;②.∠BAD=90°;③.AB=BC;④.AC=BD.其中能使ABCD是菱形的为() A .①③ B.②③ C.④D.①②③2.菱形ABCD中,E为AB上的一点,CE交BD于F.求证:⑴.△ABF≌△CBF;⑵.∠BEC=∠DAF.3. 菱形的对角线的比是2:3,周长为1304cm,求菱形的面积?4.如图,平行四边形ABCD的对角线AC的垂直平分线与AD AC BC、、分别交于点E O F、、求证:四边形AFCE是菱形 .5. 如图,菱形ABCD中,∠B=60°,AB=2,点E、F分别是AB、AD上的动点,且满足BE=AF,接连EF、EC、CF.求证:△EFC是等边三角形6. 9、Rt△ABC中,∠ACB=90°,∠BAC=60°,DE垂直平分BC,且AF=CE.求证:四边形ACEF为菱形四、以正方形搭建起来的图形例1.正方形ABCD中,△DCE是等边三角形.⑴.求∠AED的度数?⑵.若OF=1,求AB的长?分析:⑴.根据正方形和等边三角形的性质综合可以得出,DA DE ADE9060150=∠=+=,所以得出:DAE DEA∠=∠,所以()11AED DAE180150301522∠=∠=-=⨯=.⑵.根据正方形的性质综合可以得出AC BD⊥,在AOFRt中,,FAO451530OF1∠=-==所以AF2OF2==,根据勾股定理可以求出22OA213=-=,所以AC BD23==.根据勾股定理或者面积公式可以得出:211AB AC BD2323622=⋅=⨯⨯=.又.AB0AB6>∴=.例2、正方形ABCD的面积为64,DE=2,P为AC上的一动点;求PD+PE的最小值?分析:在一条直线同侧的两点,到直线某点的距离之和最小,按如图所示作E的对称点'E(根据正方形的对称性,对称点'E恰好落在边BC上)连结'DE交AC于点'P,根据轴对称的性质''''''DE DP E P DP EP=+=+,此时和是最小的.根据正方形ABCD的面积为64可求得边长DC8=,所以CE CD DE826=-=-=。
人教版八年级数学上册期末专题复习:几何压轴题强化训练试题(含答案)

人教版八年级数学上册期末专题复习:几何压轴题强化训练试题1、如图,AB>AC,∠BAC的平分线与BC边的中垂线GD相交于点D,过点D作DE⊥AB于点E,DF⊥AC于点F,求证:BE=CF.2、如图,△ABC中,∠ACB=90°,AC=BC,将△ABC绕点C逆时针旋转角α.(0°<α<90°)得到△A1B1C1,连接BB1.设CB1交AB于D,A1B1分别交AB、AC于E、F.(1)在图中不再添加其它任何线段的情况下,请你找出一对全等的三角形,并加以说明(△ABC与△A1B1C1全等除外);(2)当△BB1D是等腰三角形时,求α.3、如图,在△ABC中,∠BAC=120°,AD,BE分别为△ABC的角平分线,连结DE.(1)求证:点E到DA,DC的距离相等;(2)求∠DEB的度数.4、在△ABC中,∠ACB=90°,AC=BC,直线,MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.(1)当直线MN绕点C旋转到如图1的位置时,求证:DE=AD+BE;(2)当直线MN绕点C旋转到如图2的位置时,求证:DE=AD﹣BE;(3)当直线MN绕点C旋转到如图3的位置时,线段DE、AD、BE之间又有什么样的数量关系?请你直接写出这个数量关系,不要证明.5、概念学习:规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.理解概念(1)如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB,请写出图中两对“等角三角形”.概念应用(2)如图2,在△ABC中,CD为角平分线,∠A=40°,∠B=60°.求证:CD为△ABC的等角分割线.(3)在△ABC中,∠A=42°,CD是△ABC的等角分割线,直接写出∠ACB的度数.6、如图,∠ABC=∠BAD=90°,点E,F分别是AC,BC的中点。
八年级下册数学重难点题型(人教版)专题 几何中常见模型及辅助线题型大视野(解析版)

专题几何中常见模型及辅助线题型大视野【例题精讲】题型一、手拉手模型例题. 【2019·惠州市期末】如图,正方形ABCD的对角线AC、BD相交于点O,正方形A′B′C′D′的顶点A′与点O重合,A′B′交BC于点E,A′D′交CD于点F.(1)求证:OE=OF;(2)若正方形ABCD的边长为1,求两个正方形重叠部分的面积;(3)若正方形A′B′C′D′绕着O点旋转,EF的长度何时最小,并求出最小值.【答案】见解析.【解析】解:(1)∵四边形ABCD是正方形,四边形OB’C’D’是正方形,∵OB=OC,∵BOC=90°,∵B’OD’=90°,∵OBE=∵OCF=45°,∵∵BOE=∵FOC,∵∵BOE∵∵COF,∵OE=OF;(2)由(1)知,∵BOE∵∵COF,∵S∵BOE=S∵COF∵两正方形重叠部分面积=S四边形OECF=S∵COF+S∵OCE= S∵BOE +S∵OCE=S∵BOC=1 4(3)由(1)知OE=OF,则∵EOF是等腰直角三角形,∵EF= OE,由垂线段最短,知当OE∵BC时,OE长度最小,最小为12,此时EF长度最小,即EF题型二、一线三直角模型例题. 【2019·临沂市期中】如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.(1)如图∵,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;(2)如图∵,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.【答案】见解析.【解析】解:(1)结论:PB=PQ,理由:过P作PE∵BC于E,PF∵CD于F,∵P为正方形对角线AC上的点,∵PC平分∵DCB,∵DCB=90°,∵PF=PE,∵四边形PECF为正方形.∵∵BPE+∵QPE=90°,∵QPE+∵QPF=90°,∵∵BPE=∵QPF,∵Rt∵PQF∵Rt∵PBE,∵PB=PQ;(2)结论:PB=PQ.理由:过P作PE∵BC于E,PF∵CD于F,∵P为正方形对角线AC上的点,∵PC平分∵DCB,∵DCB=90°,∵PF=PE,∵四边形PECF为正方形,∵∵BPF+∵QPF=90°,∵BPF+∵BPE=90°,∵∵BPE=∵QPF,∵Rt∵PQF∵Rt∵PBE,∵PB=PQ.题型三、辅助线例1. 【2019·莆田市期末】如图1,在正方形ABCD中,E、F分别是BC、AB上一点,且AF=BE,AE与DF交于点G.(1)求证:AE=DF.(2)如图2,在DG上取一点M,使AG=MG,连接CM,取CM的中点P.写出线段PD与DG之间的数量关系,并说明理由.【答案】见解析.【解析】(1)证明:∵四边形ABCD是正方形,∵AD=AB,∵DAF=∵ABE=90°,∵AF=BE,∵∵DAF∵∵ABE(SAS),∵AE=DF.(2)解:结论:DG PD.理由:连接GP并延长至H,使GP=PH,连接DH、CH,∵PM=PC,∵MPG=∵CPH,PG=PH,∵∵MPG∵∵CPH(SAS),∵∵PMG=∵PCH,GM=CH=AG,∵DF∵CH,∵∵FDC=∵DCH,∵∵DAG+∵ADG=90°,∵ADG+∵CDF=90°,∵∵DAG=∵CDG=∵DCH,∵DA=DC,∵∵DAG∵∵DCH(SAS),∵DG=DH,∵ADG=∵CDH,∵∵GDH=∵ADC=90°,∵∵GDH是等腰直角三角形,∵GP=PH,∵PD=PG,PD∵GH,∵DG PD.例2. 【2019·武汉市期末】在平行四边形ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF 上取一点G,使得∠EGB=∠EAB,连接AG.(1)如图①,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;(2)如图②,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.【答案】见解析.【解析】(1)证明:在EG上截取EH=BG,∵∠EAB=∠EGB,∠APE=∠BPG,∴∠ABG=∠AEH.在△ABG和△AEH中,∵AE=AB,∠ABG=∠AEH,BG=EH,∴△ABG≌△AEH,∴AH=AG,∠EAH=∠GAB,∴∠GAH=∠EAB=60°,∴△AGH是等边三角形,∴GH=AG,∴EG=AG+BG;(2)EG=√2AG-BG.如图,过点A作AH∵AG,交GE的延长线于H,则∵GAH=∵EAB=90°,∵∵GAB=∵HAE.∵∵EGB=∵EAB=90°,∵∵AGH+∵AGB=∵AGH+∵H=90°.∵∵AGB=∵H,∵AB=AE,∵∵ABG∵∵AEH.∵BG=EH,AG=AH,∵∵GAH=∵EAB=90°,∵∵AGH是等腰直角三角形.∵√2AG=HG.∵EG=√2AG-BG.【刻意练习】1. 【2018·容县期末】如图,已知∵ABC中,AC=BC=5,AB=,三角形顶点在相互平行的三条直线L1,L2,L3上,且L2,L3之间的距离为3,则L1,L3之间的距离是.【答案】4.【解析】解:如图过点A作AM∵L3于M,过点B作BN∵L3于N.∵AC=BC=5,AB=,∵AC2+BC2=AB2,∵∵ACB=90°,∵∵AMC=∵BNC=90°,∵∵ACM+∵BCN=90°,∵∵BCN+∵CBN=90°,∵∵ACM=∵CBN,∵∵ACM∵∵CBN(AAS),∵AM=CN=3,在Rt∵NCB中,由勾股定理得:BN=4,故答案为:4.2. 【2019·长沙市雨花区期末】在正方形ABCD中,连接BD,P为射线CB上的一个动点(与点C不重合),连接AP,AP的垂直平分线交线段BD于点E,连接AE,PE.提出问题:当点P运动时,∵APE的度数,DE与CP的数量关系是否发生改变?探究问题:(1)首先考察点P的两个特殊位置:∵当点P与点B重合时,如图1-1所示,∵APE=______°,用等式表示线段DE与CP之间的数量关系:______;∵当BP=BC时,如图1-2所示,∵中的结论是否发生变化?直接写出你的结论:______;(填“变化”或“不变化”)(2)然后考察点P的一般位置:依题意补全图2-1,2-2,通过观察、测量,发现:(1)中∵的结论在一般情况下______(填“成立”或“不成立”)(3)证明猜想:若(1)中∵的结论在一般情况下成立,请从图2-1和图2-2中任选一个进行证明;若不成立,请说明理由.【答案】(1)45,PC=√2DE;不变化;(2)成立;(3)见解析.【解析】解:(1)∵当点P与点B重合时,∵四边形ABCD是正方形,∵∵APE=45°,EA=EB=ED,∵PC=√2DE.∵当BP=BC时,∵中的结论不发生变化;故答案为:45,PC=√2DE,不变化;(2)结论仍然成立;(3)如图,过点E作EF∵AD于F,延长FE交BC于G,连接AC、EC,∵点E在线段AP的垂直平分线上,∵EA=EP,∵四边形ABCD是正方形,∵BD是AC的垂直平分线,∵EA=EC,∵∵EAC=∵ECA,∵BA=BC,∵∵BAC=∵BCA,∵∵EAB=∵ECB,∵EA=EP,EA=EC,∵EP=EC,∵∵EPC=∵ECP,∵∵EPC+∵EPB=180°,∵∵BAE+∵EPB=180°,∵∵ABP+∵AEP=180°,∵∵ABP=90°,∵∵AEP=90°,∵∵APE=∵P AE=45°,∵EF∵AD,∵∵DFG=90°,∵∵BCD=∵ADC=90°,∵四边形FGCD是矩形,∵CG=FD,∵FGC=90°,∵∵BDA=45°,∵FD=DE,2∵EP=EC,∵CP=2CG=2DF DE.3. 【2019·阳江市期中】(1)如图(1),在平行四边形ABCD中,DE∵AB,BF∵CD,垂足分别为E、F,求证:AE=CF;(2)如图(2),在平行四边形ABCD中,AC、BD是两条对角线,求证AC2+BD2=2(AB2+BC2)(3)如图(3),PQ是∵PMN的中线,若PM=11,PN=13,MN=10,求出PQ的长度.【答案】见解析.【解析】解:(1)∵平行四边形ABCD中,DE∵AB,BF∵CD,∵AD=CB,DE=BF,∵AED=∵CFB=90°,∵Rt∵AED∵Rt∵CFB(HL),∵AE=CF;(2)如图,分别过A,D作AE∵BC交CB延长线于E,DF∵BC于F.根据勾股定理可得:AC2=AE2+(BE+BC)2 ∵,AE2=AB2-BE2 ∵,BD2=DF2+(BC-CF)2 ∵,DF2=DC2-CF2∵,∵四边形ABCD是平行四边形,∵AB=DC,又∵AE∵BC,DF∵BC,∵∵AEB=∵DFC=90°,AE=DF,∵Rt∵AEB∵Rt∵DFC(HL),∵BE=CF,而AB=DC,把∵代入∵,∵代入∵,可得:AC2=AB2-BE2+(BE+BC)2BD2=DC2-CF2+(BC-CF)2上面两式相加,可得:AC2+BD2=2(AB2+BC2);(3)如图,延长PQ至R,使得QR=PQ,连接RM,RN,∵PQ是∵PMN的中线,∵NQ=MQ,∵四边形NPMR是平行四边形,由(2)可得,MN2+PR2=2(NP2+MP2),又∵PM=11,PN=13,MN=10,∵102+(2PQ)2=2(132+112),解得:PQ=2√30.4. 【2019·十堰市外国语期末】如图,已如等腰Rt∵ABC和∵CDE,AC=BC,CD=CE,连接BE、AD,P为BD中点,M为AB中点、N为DE中点,连接PM、PN、MN.(1)试判断∵PMN的形状,并证明你的结论;(2)若CD=5,AC=12,求∵PMN的周长.【答案】见解析.【解析】解:(1)∵PMN是等腰直角三角形,理由如下:延长BE交AD于F,如图所示:∵P为BD中点,M为AB中点、N为DE中点,∵PM∵AD,PM=12AD,PN∵BE,PN=12BE,∵∵BCE∵∵ACD(SAS),∵BE=AD,∵CBE=∵CAD,∵PM=PN,∵∵CBE+∵BEC=90°,∵AEF=∵BEC,∵∵CAD+∵AEF=∵CBE+∵BEC=90°,∵∵AFE=90°,∵BE∵AD,∵PM∵AD,PN∵BE,∵PM∵PN,即∵PMN是等腰直角三角形;(2)∵∵ACD=90°,CD=5,AC=12,由勾股定理得:AD=√CD2+AD2=13,∵PN=PM=12AD=132,∵∵PMN是等腰直角三角形,∵MN PM=2,即∵PMN的周长=PM+PN+MN=13+2.5. 【2019·固始县期末】如图,在正方形ABCD中,E、F分别是边AB、BC的中点,连接AF、DE相交于点G,连接CG.(1)求证:AF∵DE;(2)求证:CG=CD.【答案】见解析.【解析】证明:(1)∵四边形ABCD为正方形∵AB=BC=CD=AD,∵ABF=∵DAE=90°,∵E,F分别是边AB.BC的中点∵AE=12AB,BF=12BC,∵AE=BF.在∵ABF与∵DAE中,∵AD=AB,∵DAF=∵ABF,AE=BF,∵∵DAE∵∵ABF(SAS).∵∵ADE=∵BAF,∵∵BAF+∵DAG=90°,∵∵ADG+∵DAG=90°,∵∵DGA=90°,即AF∵DE.(2)证明:延长AF交DC延长线于M,∵F为BC中点,∵CF=FB∵DM∵AB,∵∵M=∵F AB.在∵ABF与∵MCF中,∵∵M=∵F AB,∵CFM=∵BF A,CF=BF,∵∵ABF∵∵MCF(AAS),∵AB=CM.∵AB=CD=CM,∵∵DGM是直角三角形,∵CG=12DM=CD.6. 【2019·高阳县期中】如图,正方形ABCD的边长为2√2,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM∵BE于点M,交BD于点F.(1)求证:AF=BE;(2)求点E到BC边的距离.【答案】见解析.【解析】(1)证明:∵四边形ABCD为正方形,∵OA=OB,∵AOB=∵BOC=90°,∵AM∵BE于点M,∵∵AME=90°,∵∵MAE=∵OBE,∵∵AOF∵∵BOE,∵AF=BE;(2)解:作EN∵BC于N,如图,∵四边形ABCD为正方形,∵OC BC=2,∵OCB=45°,∵E是OC的中点,∵CE=1,在Rt∵ECN中,∵ECN=45°,∵CEN为等腰直角三角形,∵EN CE.即点E到BC边的距离为27. 【2019·汕头市期中】如图,四边形ABCD和四边形CEFG都是正方形,且BC=CD,CE=CG,∵BCD=∵GCE=90°.(1)求证:∵BCG∵∵DCE;(2)求证:BG∵DE.【答案】见解析.【解析】证明:(1)∵∵BCD=∵GCE=90°,∵∵BCG=∵DCE,在∵BCG与∵DCE中,∵BC=CD,∵BCG=∵DCE,CE=CG,∵∵BCG∵∵DCE(SAS);(2)∵∵BCG∵∵DCE,∵∵HBC=∵ODH,∵∵BHC=∵DHO,∵∵HBC+∵BHC=90°,∵∵ODH+∵DHO=90°,∵∵DOH=90°,∵BG∵DE.8. 【2019·北师大附属中学期末】如图,在∵ABCD中,BC=2AB,点E、F分别是BC、AD的中点,AE、BF交于点O,连接EF,OC.(1)求证:四边形ABEF是菱形;(2)若AB=4,∵ABC=60°,求OC的长.【答案】见解析.【解析】(1)证明:∵四边形ABCD是平行四边形,∵BC∵AD,BC=AD.∵E,F分别是BC,AD的中点,∵BE=12BC,AF=12AD,∵BE=AF.∵四边形ABEF是平行四边形.∵BC=2AB,∵AB=BE.∵平行四边形ABEF是菱形.(2)解:过点O作OG∵BC于点G,如图所示:∵E是BC的中点,BC=2AB,∵BE=CE=AB,∵四边形ABEF是菱形,∵ABC=60°,∵BE=CE=AB=4,∵OBE=30°,∵BOE=90°.∵OE=2,∵OEB=60°.∵GE=1,OG∵GC=GE+CE=5.在Rt∵OCG中,由勾股定理得:OC=9. 【2019·厦门六中月考】正方形ABCD中,点P是边CD上的任意一点,连接BP,O为BP的中点,作PE∵BD于E,连接EO,AE.(1)若∵PBC=α,求∵POE的大小(用含α的式子表示);(2)用等式表示线段AE与BP之间的数量关系,并证明.【答案】见解析.【解析】解:(1)在正方形ABCD中,BC=DC,∵C=90°∵∵DBC=∵CDB=45°∵∵PBC=α∵∵DBP=45°-α∵PE∵BD,且O为BP的中点∵EO=BO∵∵EBO=∵BEO∵∵EOP=∵EBO+∵BEO=90°-2α(2)连接OC,EC,在正方形ABCD中,AB=BC,∵ABD=∵CBD,BE=BE∵ΔABE∵ΔCBE∵AE=CE在RtΔBPC中,O为BP的中点∵CO=BO=12 BP∵∵OBC=∵OCB∵∵COP=2α由(1)知∵EOP=90°-2α∵∵EOC=∵COP+∵EOP=90°又由(1)知BO=EO∵EO=CO∵∵EOC是等腰直角三角形∵EO2+OC2=EC2∵EC OC BP即BP EC∵BP AE.10. 【2018·莆田市期中】(1)如图1的正方形ABCD中,点E,F分别在边BC,CD上,∵EAF=45°,延长CD到点G,使DG=BE,连接EF,AG.求证:EF=FG;(2)如图2,等腰Rt∵ABC中,∵BAC=90°,AB=AC,点M,N在边BC上,且∵MAN=45°.若BM=1,CN=3,求MN的长.【答案】见解析.【解析】解:(1)证明:在正方形ABCD中,∵ABE=∵ADG,AD=AB,DG=BE,∵∵ABE∵∵ADG(SAS),∵∵BAE=∵DAG,AE=AG,∵∵EAG=90°,∵∵F AE∵∵GAF(SAS),∵EF=FG;(2)解:如图,过点C作CE∵BC,垂足为点C,截取CE,使CE=BM.连接AE、EN.∵AB=AC,∵BAC=90°,∵∵B=∵ACB=45°.∵CE∵BC,∵∵ACE=∵B=45°.∵∵ABM∵∵ACE(SAS).∵AM=AE,∵BAM=∵CAE.∵∵BAC=90°,∵MAN=45°,∵∵BAM+∵CAN=45°.由∵BAM=∵CAE,得∵MAN=∵EAN=45°.∵∵MAN∵∵EAN(SAS).∵MN=EN.在Rt∵ENC中,由勾股定理,得EN2=EC2+NC2.∵MN2=BM2+NC2.∵BM=1,CN=3,∵MN2=12+32,∵MN=√10.11. 【2019·北师大附属中学期末】四边形ABCD是边长为4正方形,点E是边BC上一动点(含端点B,不含端点C),点F是正方形外角∵DCM的平分线上一点,且满足∵AEF=90°.(1)当点E与点B重合时,直接写出线段AE与线段EF的数量关系;(2)如图1,当点E是边BC的中点时,∵补全图形;∵请证明(1)中的结论仍然成立;(3)取线段CF的中点N,连接DE、NE、DN,∵求证:EN=DN;∵直接写出线段EN长度的取值范围.【答案】见解析.【解析】解:(1)当点E与点B重合时,AE=EF.(2)∵如图,∵如图,在AB上取AB中点H,连接HE,∵四边形ABCD是正方形∵AB=CB,且点H是AB中点,点E是BC中点,∵AH=BH=BE=CE,∵∵BEH=∵BHE=45°,∵∵AHE=135°,∵CF平分∵DCM,∵∵DCF=45°∵∵ECF=135°=∵AHE,∵∵AEF=90°∵∵AEB+∵FEC=90°,且∵AEB+∵BAE=90°,∵∵BAE=∵FEC,且AH=EC,∵AHE=∵ECF,∵∵AHE∵∵ECF(ASA)∵AE=EF.(3)∵如图,延长DN,使HN=DN,连接FH,EH,∵CN=FN,∵DNC=∵HNF,DN=NH,∵∵DCN∵∵HFN(SAS)∵DC=FH,∵DCF=∵FCM=45°,∵FH∵DC,且CD∵BC,∵FH∵BM,∵∵FEM+∵EFH=90°,且∵FEM=∵BAE,∵BAE+∵DAE=90°,∵∵DAE=∵EFH,∵AD=CD,CD=FH,∵AD=FH,且AE=EF,∵DAE=∵EFH,∵∵ADE∵∵FHE,∵DE=EH,且DN=NH,∵EN=DN.∵∵DE=EH,DN=NH,∵EN=DN,EN∵DN∵DE EN,∵点E是边BC上一动点(含端点B,不含端点C),∵4<DE,∵2<EN≤4.12. 【2019·宿迁市期末】(1)如图1,在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E 是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN∵DM,垂足为M,且MN=DM.设OM=a,请你利用基本活动经验直接写出点N的坐标______(用含a的代数式表示);(2)如果(1)的条件去掉“且MN=DM”,加上“交∵CBE的平分线与点N”,如图2,求证:MD=MN.将这个问题解决,请写出你的证明过程.(3)在(2)的条件下,如图3,请你继续探索:连接DN交BC于点F,连接FM,下列两个结论:∵FM 的长度不变;∵MN平分∵FMB,请你指出正确的结论,并给出证明.【答案】(1)N(2+a,a);(2)(3)见解析.【解析】(1)解:过点N作NE∵OB于E,∵∵DMN=90°,∵∵DMO+∵NME=90°,∵NME+∵MNE=90°,∵∵DMO=∵MNE,∵DM=MN,∵∵DMO∵∵MNE,∵ME=DO=2,NE=OM=a,∵OE=OM+ME=2+a,∵点N坐标(2+a,a),故答案为:(2+a,a).(2)证明:在OD上截取OH=OM,连接HM,∵OD=OB,OH=OM,∵HD=MB,∵OHM=∵OMH,∵∵DHM=180°-45°=135°,∵NB平分∵CBE,∵∵NBE=45°,∵∵NBM=180°-45°=135°,∵∵DHM=∵NBM,∵∵DMN=90°,∵∵DMO+∵NMB=90°,∵∵HDM+∵DMO=90°,∵∵HDM=∵NMB,∵∵DHM∵∵MBN,∵DM=MN.(3)结论:MN平分∵FMB成立.理由:在BO延长线上取OA=CF,易证:∵DOA∵∵DCF,∵AD=DF,∵ADO=∵CDF,∵∵MDN=45°,∵∵CDF+∵ODM=45°,∵∵ADO+∵ODM=45°,∵∵DMA∵∵DMF,∵∵DFM=∵DAM=∵DFC,过M作MP∵DN于P,则∵FMP=∵CDF,由(2)可知∵NMF+∵FMP=∵PMN=45°,∵∵NMB=∵MDH,∵MDO+∵CDF=45°,∵∵NMB=∵NMF,即MN平分∵FMB.13. 【2019·福州市期末】如图1,点E为正方形ABCD的边AB上一点,EF∵EC,且EF=EC,连接AF.求∵EAF 的度数;如图2,连接FC交BD于M,交AD于N.求证:BD=AF+2DM.【答案】见解析.【解析】(1)解:过点F 作FM∵AB 交AB 的延长线于点M,∵四边形ABCD 是正方形,∵∵B=∵M=∵CEF=90°,∵∵MEF+∵CEB=90°,∵CEB+∵BCE=90°,∵EC=EF,∵∵EBC∵∵FME,∵FM=BE,∵EM=BC∵BC=AB,∵EM=AB,∵EM﹣AE=AB﹣AE∵AM=BE,∵FM=AM,∵FM∵AB,∵∵MAF=45°,∵∵EAF=135°.(2)证明:过点F 作FG∵AB 交BD 于点G,由(1)可知∵EAF=135°,∵∵ABD=45°∵∵EAF+∵ABD=180°,∵AF∵BG,∵FG∵AB,∵四边形ABGF 为平行四边形,AF=BG,FG=AB,∵AB=CD,∵AB∵CD,∵FG∵CD,∵∵FGM=∵CDM,∵∵FMG=∵CMD∵∵FGM∵∵DMC(AAS),∵GM=DM,∵DG=2DM,∵BD=BG+DG=AF+2DM.14. 【2019·漯河市期中】如图1,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ∵AP交CD于点Q,将∵BQC沿BQ所在的直线对折得到∵BQC',延长QC′交BA的延长线于点M.(1)试探究AP与BQ的数量关系,并证明你的结论;(2)求证:MQ=MB;(3)若AB=3,BP=2PC,求QM的长.【答案】见解析.【解析】(1)解:结论:AP=BQ.理由:∵四边形ABCD是正方形,∵AB=BC,∵ABC=∵C=90°,∵∵ABQ+∵CBQ=90°.∵BQ∵AP,∵∵P AB+∵QBA=90°,∵∵P AB=∵CBQ.∵∵PBA∵∵QCB,(2)证明:∵四边形ABCD是正方形,∵DC∵AB,∵∵CQB=∵QBA.由折叠可得:∵C′QB=∵CQB,∵∵QBA=∵C′QB,∵MQ=MB.(3)解:过点Q作QH∵AB于H,∵四边形ABCD是正方形,∵QH=BC=AB=3.∵BP=2PC,∵BP=2,PC=1,由勾股定理得:BQ=AP BH=2.∵四边形ABCD是正方形,∵DC∵AB,∵∵CQB=∵QBA,由折叠可得:∵C′QB=∵CQB,∵∵QBA=∵C′QB,∵MQ=MB.设QM=x,则有MB=x,MH=x﹣2.在Rt∵MHQ中,由勾股定理,x2=(x﹣2)2+32,解得x=134.∵QM的长为13 4.15. 【2019·黑龙江秋实中学期中】如图,矩形ABCD的对角线AC、BD交于点O,以BD为斜边作直角三角形BED,∵BED=90°,连结AE、CE、OE.(1)如图∵,请直接写出线段OE与线段AC的数量关系;(2)如图∵,延长EO交AD于H,连AG与HC,若AE=CE,求证:四边形AGCH是菱形.图1 图2【答案】见解析.【解析】解:(1)AC=2OE;∵四边形ABCD是矩形,∵AC=BD,O是BD、AC的中点∵∵BED=90°,∵2OE=BD=AC;(2)由(1)知,O是AC中点,∵AE=CE,∵EH∵AC,∵四边形ABCD是矩形,∵AD∵BC,∵∵OAH=∵OCG,在∵AOH和∵COG中,∵AO=OC,∵OAH=∵OCG,∵AOH=∵COG,∵∵AOH∵∵COG,∵AH=CG,∵四边形AGCH为平行四边形,∵EH∵AC,∵四边形AGCH为菱形.16. 【2019·禹城市期末】如图所示,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A、B重合),另一直角边与∵CBM的平分线BF相交于点F.(1)如图1,当点E在AB边得中点位置时:∵通过测量DE、EF的长度,猜想DE与EF满足的数量关系是.∵连接点E与AD边的中点N,猜想NE与BF满足的数量关系是,请证明你的猜想.(2)如图2,当点E在AB边上的任意位置时,猜想此时DE与EF有怎样的数量关系,并证明你的猜想.【答案】见解析.【解析】解:(1)∵DE=EF;∵NE=BF;理由如下:∵四边形ABCD为正方形,∵AD=AB,∵DAB=∵ABC=90°,∵N,E分别为AD,AB中点,∵AN=DN=12AD,AE=EB=12AB,∵DN=BE,AN=AE,∵∵DEF=90°,∵∵AED+∵FEB=90°,∵∵ADE+∵AED=90°,∵∵FEB=∵ADE,∵AN=AE,∵∵ANE=∵AEN,∵∵A=90°,∵∵ANE=45°,∵∵DNE=180°﹣∵ANE=135°,∵∵CBM=90°,BF平分∵CBM,∵∵CBF=45°,∵EBF=135°,∵∵DNE∵∵EBF,∵DE=EF,NE=BF.(2)DE=EF,理由如下:连接NE,在DA边上截取DN=EB,∵四边形ABCD是正方形,DN=EB,∵AN=AE,∵∵AEN为等腰直角三角形,∵∵ANE=45°,∵∵DNE=180°﹣45°=135°,∵BF平分∵CBM,AN=AE,∵∵EBF=90°+45°=135°,∵∵DNE=∵EBF,∵∵NDE+∵DEA=90°,∵BEF+∵DEA=90°,∵∵NDE=∵BEF,∵∵DNE∵∵EBF,∵DE=EF.17. 【2019·费县期末】在平行四边形ABCD中,∵BAD的平分线交直线BC于点E,交直线DC于点F.(1)在图1中证明:CE=CF;(2)若∵ABC=90°,G是EF的中点(如图2),求出∵BDG的度数;(3)若∵ABC=120°,FG∵CE,FG=CE,分别连接DB、DG(如图3),求∵BDG的度数.【答案】见解析.【解析】解:证明:(1)∵AF平分∵BAD,∵∵BAF=∵DAF,∵四边形ABCD是平行四边形,∵AD∵BC,AB∵CD,∵∵DAF=∵CEF,∵BAF=∵F,∵∵CEF=∵F.∵CE=CF.(2)连接GC、BG,∵四边形ABCD为平行四边形,∵ABC=90°,∵四边形ABCD为矩形,∵AF平分∵BAD,∵∵DAF=∵BAF=45°,∵∵DCB=90°,DF∵AB,∵∵DF A=45°,∵ECF=90°∵∵ECF为等腰直角三角形,∵G为EF中点,∵EG=CG=FG,CG∵EF,∵∵ABE为等腰直角三角形,AB=DC,∵BE=DC,∵∵CEF=∵GCF=45°,∵∵BEG=∵DCG=135°∵∵BEG∵∵DCG,∵BG=DG,∵CG∵EF,∵∵DGC+∵DGA=90°,又∵∵DGC=∵BGA,∵∵BGA+∵DGA=90°,∵∵DGB为等腰直角三角形,∵∵BDG=45°.(3)延长AB、FG交于H,连接HD.∵AD∵GF,AB∵DF,∵四边形AHFD为平行四边形∵∵ABC=120°,AF平分∵BAD∵∵DAF=30°,∵ADC=120°,∵DF A=30°∵∵DAF为等腰三角形∵AD=DF,∵CE=CF,∵平行四边形AHFD为菱形∵∵ADH,∵DHF为全等的等边三角形∵DH=DF,∵BHD=∵GFD=60°∵FG=CE,CE=CF,CF=BH,∵BH=GF∵∵BHD∵∵GFD,∵∵BDH=∵GDF∵∵BDG=∵BDH+∵HDG=∵GDF+∵HDG=60°.18. 【2019·抚顺市期中】∵ABC中,∵BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.(1)观察猜想如图1,当点D在线段BC上时,∵BC与CF的位置关系为:.∵BC,CD,CF之间的数量关系为:;(将结论直接写在横线上)(2)数学思考如图2,当点D在线段CB的延长线上时,结论∵,∵是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.(3)拓展延伸如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=,CD=14 BC,请求出GE的长.【答案】见解析.【解析】解:(1)∵正方形ADEF中,AD=AF,∵∵BAC=∵DAF=90°,∵∵BAD=∵CAF,∵AB=AC,∵∵DAB∵∵F AC,∵∵B=∵ACF,∵∵ACB+∵ACF=90°,即BC∵CF;故答案为:垂直;∵∵DAB∵∵F AC,∵CF=BD,∵BC=BD+CD,∵BC=CF+CD;故答案为:BC=CF+CD;(2)CF∵BC成立;BC=CD+CF不成立,CD=CF+BC.理由如下:∵正方形ADEF中,AD=AF,∵∵BAC=∵DAF=90°,∵∵BAD=∵CAF,∵AB=AC,∵∵DAB∵∵F AC,∵∵ABD=∵ACF,∵∵BAC=90°,AB=AC,∵∵ACB=∵ABC=45°.∵∵ABD=180°﹣45°=135°,∵∵BCF=∵ACF﹣∵ACB=135°﹣45°=90°,∵CF∵BC.∵CD=DB+BC,DB=CF,∵CD=CF+BC.(3)解:过A作AH∵BC于H,过E作EM∵BD于M,EN∵CF于N,∵∵BAC=90°,AB=AC,∵BC=4,AH=12BC=2,∵CD=14BC=1,CH=12BC=2,∵DH=3,由(2)得BC∵CF,CF=BD=5,∵四边形ADEF是正方形,∵AD=DE,∵ADE=90°,∵BC∵CF,EM∵BD,EN∵CF,∵四边形CMEN是矩形,∵NE=CM,EM=CN,∵∵AHD=∵ADE=∵EMD=90°,∵∵ADH+∵EDM=∵EDM+∵DEM=90°,∵∵ADH=∵DEM,∵∵ADH∵∵DEM,∵EM=DH=3,DM=AH=2,∵CN=EM=3,EN=CM=3,∵∵ABC=45°,∵∵BGC=45°,∵∵BCG是等腰直角三角形,∵CG=BC=4,∵GN=1,由勾股定理得:EG。
(word完整版)人教版八年级上册数学几何练习题

人教版八年级上册数学几何练习题1、已知:在⊿ABC中,∠A=90,AB=AC,在BC上任取一点P,作PQ∥AB交AC于Q,作PR∥CA交BA于R,D是BC的中点,求证:⊿RDQ是等腰直角三角形。
2、已知:在⊿ABC中,∠A=90,AB=AC,D是AC的中点,AE⊥BD,AE延长线交BC于F,求证:∠ADB=∠FDC。
B3、已知:在⊿ABC中BD、CE是高,在BD、CE或其延长线上分别截取BM=AC、CN=AB,求证:MA⊥NA。
C4、已知:如图,在△ABC中,BP、CP分别平分∠ABC 和∠ACB,DE过点P交AB于D,交AC于E,且DE∥BC.求证:DE-DB=EC. APE DBC图⑴5、在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点。
写出点O到△ABC的三个顶点A、B、C的距离的大小关系;如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形状,并证明你的结论。
A M B6、如图,△ABC为等边三角形,延长BC到D,延长BA到E,AE=BD,连结EC、ED,求证:CE=DE7、如图,等腰三角形ABC中,AB=AC,∠A=90°,BD平分∠ABC,DE⊥BC且BC=10,求△DCE的周长。
几何证明习题答案1. 连接AD,由△ABC为等腰直角三角形可得AD垂直AC,且AD=BD,∠DAQ=∠DBR=45度, 又由平行关系得,四边形RPQA为矩形,所以AQ=RP, △BRP也是等腰直角三角行,即BR=PR,所以AQ=BR由边角边,△BRD全等于△AQD,所以∠BDR=∠ADQ,DR=DQ, ∠RDQ=∠RDA+∠ADQ=∠RDA+∠BDR=90度, 所以△RDQ是等腰RT△。
2. 作AG平分∠BAC交BD于G ∵∠BAC=90° ∴∠CAG= ∠BAG=45° ∵∠BAC=90° AC=AB ∴∠C=∠ABC=45°∴∠C=∠BAG ∵AE⊥BD ∴∠ABE+∠BAE=90°∵∠CAF+∠BAE=90° ∴∠CAF=∠ABE ∵ AC=AB ∴△ACF ≌△BAG ∴CF=AG ∵∠C=∠DAG =45°CD=AD ∴△CDF ≌△ADG ∴∠CDF=∠ADB3. 易证△ABM≌△NAC.∠NAM=∠NAE+∠BAM=∠NAE+ANE=90°4. 略5.因为直角三角形的斜边中点是三角形的外心,所以O到△ABC的三个顶点A、B、C距离相等;△OMN是等腰直角三角形。
初中数学八年级几何专题汇总

初中数学八年级几何专题汇总
以下为初中数学八年级几何专题的汇总:
1. 平面图形的认识
- 研究正方形、长方形、菱形、平行四边形等图形的定义、性质以及相互之间的关系。
- 了解图形的内角和为多少度以及如何计算。
2. 三角形的认识
- 掌握三角形的定义,研究三角形内角和的计算方法。
- 理解三角形分类的方式,包括按角度分类和按边长分类。
- 了解勾股定理及其应用,研究如何利用勾股定理解决实际问题。
3. 四边形的认识
- 研究梯形、矩形、菱形、正方形等四边形的定义以及它们之间的关系。
- 掌握四边形内角和的计算方法。
- 了解象限、平行四边形对角线互相平分、平行四边形的性质
以及平面内一点到直线的距离计算方法。
4. 圆的认识
- 理解圆的定义以及圆的相关术语。
- 掌握计算圆的周长和面积的方法。
- 研究如何利用圆的性质解决实际问题。
5. 空间几何图形的认识
- 研究三棱锥、四棱锥、棱台、圆锥、圆柱等空间几何图形的
定义、性质以及它们之间的关系。
- 掌握这些图形表面积和体积的计算方法。
- 了解正方体、长方体、正四面体、正六面体的定义、性质及
它们之间的关系。
通过研究以上几何知识,可以帮助同学们更好地理解和解决数
学中的几何问题。
同时,也为后续高中数学的研究打下坚实的基础。
最新人教版八年级数学上册几何解答题专项突破(超级经典)

最新人教版八年级数学上册几何解答题专项突破(超级经典)1.已知在等边三角形ABC中,AC的垂直平分线EF交AC于点E,交BC于点F,求证BF=2CF。
2.已知E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D,求证:(1)∠ECD=∠EDC;(2)OE是CD的垂直平分线。
3.(1)如图(1),点P是等腰三角形ABC底边BC上的一动点,过点P作BC的垂线,交AB于点Q,交CA的延长线于点R。
观察AR与AQ,猜想它们相等,证明这个猜想。
(2)如图(2),如果点P沿着底边BC所在的直线,按由C向B的方向运动到CB的延长线上时,(1)中所得的结论是否成立,给出证明。
4.已知△ABC中,AD平分∠BAC,AE为BC边上的高,∠B=40°,∠C=60°,求∠DAE的度数。
5.在△ABC中,AB=CB,AB⊥CB,E为CB延长线上一点,点F在AB上,且AE=CF,(1)求证:Rt△ABE≌Rt△CBF;(2)判断直线CF和直线AE的位置关系,并说明理由。
6.在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,已知AB=AC,CF⊥AE于点F,BD⊥AE于点D,点B、C在∠MAN的边AM、AN上,点E、F在∠MAN内部的射线AD 上,∠1、∠2分别是△ABE、△CAF的外角,求证:△ABD≌△CAF;在△ABC中,AB=AC,AB>BC,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC,若△ABC的面积为15,则△ACF与△BDE的面积之和为45/4.7.在直角坐标系xOy中,直线AB交x轴于A(1,0),交y轴负半轴于B(0,-5),C为x轴正半轴上一点,且OC=5OA。
求证:AE+CE=BC.B同学们开始思考,其中XXX认为可以用勾股定理证明,因为△ABC是等边三角形,所以AC=BC,而AE可以表示为AC-CE,代入勾股定理中即可得证.C但是,XXX认为可以用相似三角形证明,因为△ABC和△AEC相似,所以可以列出比例式,推导可得AE+CE=BC.D最后,XXX给出了自己的证明,他利用了三角形面积公式,将△ABC分成两个三角形,再利用△AEC的高等于△ABC的高减去CE,最终得到AE+CE=BC.E通过这道题目,同学们学会了不同的证明方法,也体会到了数学证明的多样性和美妙之处.点D在CB的延长线上,且ED=EC,如图。
专题四 几何计算人教版八年级数学上册教材

(1)证明:∵FG∥AE,∴∠2 =∠FGC. ∵∠1=∠2, ∴∠1=∠FGC. ∴AB∥CD.
专题四 几何计算人教版八年级数学上册教材
专题四 几何计算人教版八年级数学上册教材
(2)若FG⊥BC 于点H,BC 平分∠ABD,∠D=100°,
求∠1 的度数. (2)解:∵AB∥CD,∴∠ABD+∠D=180°. ∵∠D=100°,∴∠ABD=180°-∠D=80°. ∵BC 平分∠ABD,∴∠ABC= ∠ABD=40°. ∵FG⊥BC, ∴∠1+∠ABC=90°. ∴∠1=90°-40°=50°.
16. 如图,△ABC 为正三角形,点 B,C,D,E
在同一直线上,且 CG=CD=DF=DE,则
∠E= 15
°.
专题四 几何计算人教版八年级数学上册教材
专题四 几何计算人教版八年级数学上册教材
17. 如图,点 F 在线段 AB 上,点 E,G 在线段 CD 上,FG∥AE,∠1=∠2.
(1)求证:AB∥CD; (2)若FG⊥BC 于点H,BC 平分∠ABD,∠D=100°,
专题四 几何计算人教版八年级数学上册教材
专题四 几何计算人教版八年级数学上册教材
13. 如果等腰三角形的一个角是 80°,那么它 的底角是( A ) A. 80°或 50° B. 50°或 20° C. 80°或 20° D. 50°
专题四 几何计算人教版八年级数学上册教材
专题四 几何计算人教版八年级数学上册教材
专题四 几何计算人教版八年级数学上册教材
专题四 几何计算人教版八年级数学上册教材
(3)如图 3,若△ABC 中∠B 的平分线 BO 与△ABC 外角平分线 CO 交于点 O,过点 O 作 OE∥BC 交 AB 于点 E,交 AC 于点 F. 这时图中还有等腰 三角形吗?如果有,分别写出他们.EF 与 BE, CF 之间的数量关系又如何?请说明理由.
人教版八年级数学下册-考点综合专题:一次函数与几何图形的综合问题

考点综合专题:一次函数与几何图形的综合问题——代几综合,明确中考风向标◆类型一一次函数与面积问题1.如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=5,点A,B 的坐标分别为(1,0),(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为________.2.如图,直线y=-2x+3与x轴相交于点A,与y轴相交于点B.【易错7】(1)求A,B两点的坐标;(2)过B点作直线BP与x轴相交于点P,且使OP=2OA,求△ABP的面积.3.如图,直线y=-x+10与x轴、y轴分别交于点B,C,点A的坐标为(8,0),点P(x,y)是在第一象限内直线y=-x+10上的一个动点.(1)求△OPA的面积S与x的函数解析式,并写出自变量x的取值范围;(2)当△OPA的面积为10时,求点P的坐标.◆类型二一次函数与三角形、四边形的综合4.(2016·长春中考)如图,在平面直角坐标系中,正方形ABCD的对称中心与原点重合,顶点A的坐标为(-1,1),顶点B在第一象限,若点B在直线y=kx+3上,则k的值为________.第4题图第5题图5.(2016·温州中考)如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10,则该直线的函数解析式是()A.y=x+5 B.y=x+10C.y=-x+5 D.y=-x+10◆类型三一次函数与几何图形中的规律探究问题6.(2017·安顺中考)如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y 轴于点A1,点A2,A3,…在直线l上,点B1,B2,B3,…在x轴的正半轴上,若△A1OB1,△A2B1B2,△A3B2B3,…依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形A n B n-1B n顶点B n的横坐标为________.第6题图第7题图7.★(2016·潍坊中考)在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O,正方形A2B2C2C1,…,正方形A n B n C n C n-1,使得点A1,A2,A3,…在直线l上,点C1,C2,C3,…在y轴正半轴上,则点B n的坐标是________.参考答案与解析1.16解析:如图,∵点A,B的坐标分别为(1,0),(4,0),∴AB=3.∵∠CAB=90°,BC=5,∴在Rt△ABC中,由勾股定理得AC=BC2-AB2=4,∴A′C′=4.∵点C′在直线y=2x-6上,∴2x-6=4,解得x=5.即OA′=5,∴CC′=AA′=5-1=4.∴S▱BCC′B′=CC′·CA=4×4=16.即线段BC扫过的面积为16.2.解:(1)令y =0,则-2x +3=0,解得x =32;令x =0,则y =3,∴点A 的坐标为⎝⎛⎭⎫32,0,点B 的坐标为(0,3).(2)由(1)得点A ⎝⎛⎭⎫32,0,∴OA =32,∴OP =2OA =3,∴点P 的坐标为(3,0)或(-3,0),∴AP =OP -OA =32或AP =OP +OA =92,∴S △ABP =12AP ·OB =12×92×3=274或S △ABP =12AP ·OB=12×32×3=94.综上所述,△ABP 的面积为274或94. 3.解:(1)∵点P 在直线y =-x +10上,且点P 在第一象限内,∴x >0且y >0,即-x +10>0,解得0<x <10.∵点A (8,0),∴OA =8,∴S =12OA ·|y P |=12×8×(-x +10)=-4x +40(0<x <10).(2)当S =10时,即-4x +40=10,解得x =152.当x =152时,y =-152+10=52,∴当△OP A的面积为10时,点P 的坐标为⎝⎛⎭⎫152,52.4.-2 5.C6.2n +1-2 解析:由题意得OA =OA 1=2,∴OB 1=OA 1=2,B 1B 2=B 1A 2=4,B 2A 3=B 2B 3=8,∴B 1(2,0),B 2(6,0),B 3(14,0)….∵2=22-2,6=23-2,14=24-2,…∴B n 的横坐标为2n +1-2.故答案为2n +1-2.7.(2n -1,2n -1) 解析:∵y =x -1与x 轴交于点A 1,∴点A 1的坐标为(1,0).∵四边形A 1B 1C 1O 是正方形,∴A 1B 1=OA 1=1,∴点B 1的坐标为(1,1).∵C 1A 2∥x 轴,点A 2在直线y =x -1上,∴点A 2的坐标为(2,1).∵四边形A 2B 2C 2C 1是正方形,∴A 2B 2=A 2C 1=2,∴点B2的坐标为(2,3),同理可得点B3的坐标为(4,7).∵B1(20,21-1),B2(21,22-1),B3(22,23-1),…,∴点B n的坐标为(2n-1,2n-1).19.2.3 一次函数与方程、不等式一.选择题(共8小题)1.一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为()A.x=2B.y=2C.x=﹣1D.y=﹣12.一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x 的方程kx+b=0的解为()A.x=﹣1B.x=2C.x=0D.x=33.一元一次方程ax﹣b=0的解x=3,函数y=ax﹣b的图象与x轴的交点坐标为()A.(3,0)B.(﹣3,0)C.(a,0)D.(﹣b,0)4.已知方程kx+b=0的解是x=3,则函数y=kx+b的图象可能是()A.B.C.D.5.若方程x﹣3=0的解也是直线y=(4k+1)x﹣15与x轴的交点的横坐标,则k的值为()A.﹣1B.0C.1D.±16.如图,直线y1=x+b与y2=kx﹣1相交于点P,点P的横坐标为﹣1,则关于x的不等式x+b>kx﹣1的解集在数轴上表示正确的是()A.B.C.D.7.如图,直线y=﹣x+m与y=nx+4n(n≠0)的交点的横坐标为﹣2,则关于x的不等式﹣x+m >nx+4n>0的整数解为()A.﹣1B.﹣5 C.﹣4D.﹣38.如图,一次函数y=kx+b的图象经过A、B两点,则不等式kx+b<0的解集是()A.x<0B.0<x<1C.x<1 D.x>1二.填空题(共10小题)9.若直线y=2x+b与x轴交于点(﹣3,0),则方程2x+b=0的解是_________.10.如图是一次函数y=kx+b的图象,则方程kx+b=0的解为_________.11.一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=0的解为_________.12.如图,已知直线y=ax﹣b,则关于x的方程ax﹣1=b的解x=_________.13.如图,直线y=kx+b分别交x轴和y轴于点A、B,则关于x的方程kx+b=0的解为_________.14.如图,已知函数y=2x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),根据图象可得方程2x+b=ax﹣3的解是_________.15.如图,已知函数y=2x+b与函数y=kx﹣3的图象交于点P,则不等式kx﹣3>2x+b的解集是_________.16.如图,直线y=kx+b过A(﹣1,2)、B(﹣2,0)两点,则0≤kx+b≤﹣2x的解集为_________.17.一次函数y1=kx+b与y2=x+a的图象如图,则kx+b>x+a的解集是_________.18.如图,函数y=kx和的图象相交于A (a,2),则不等式的解集为_________.三.解答题(共4小题)19.如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:(1)方程kx+b=0的解;(2)式子k+b的值;(3)方程kx+b=﹣3的解.20.如图,直线l1:y=2x与直线l2:y=kx+3在同一平面直角坐标系内交于点P.(1)写出不等式2x>kx+3的解集:_________;(2)设直线l2与x轴交于点A,求△OAP的面积.21.在平面直角坐标系x0y中,直线y=kx+b(k≠0)过(1,3)和(3,1)两点,且与x轴、y轴分别交于A、B两点,求不等式kx+b≤0的解.22.在直角坐标系xOy中,直线y=kx+b(k≠0)经过(﹣2,1)和(2,3)两点,且与x 轴、y轴分别交于A、B两点,求不等式kx+b≥0的解集.19.2.3 一次函数与方程、不等式一.选择题(共8小题)1.一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为()A.x=2B.y=2C.x=﹣1D.y=﹣12.一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x 的方程kx+b=0的解为()A.x=﹣1B.x=2C.x=0D.x=33.一元一次方程ax﹣b=0的解x=3,函数y=ax﹣b的图象与x轴的交点坐标为()A.(3,0)B.(﹣3,0)C.(a,0)D.(﹣b,0)4.已知方程kx+b=0的解是x=3,则函数y=kx+b的图象可能是()A.B.C.D.5.若方程x﹣3=0的解也是直线y=(4k+1)x﹣15与x轴的交点的横坐标,则k的值为()A.﹣1B.0C.1D.±16.如图,直线y1=x+b与y2=kx﹣1相交于点P,点P的横坐标为﹣1,则关于x的不等式x+b>kx﹣1的解集在数轴上表示正确的是()A.B.C.D.7.如图,直线y=﹣x+m与y=nx+4n(n≠0)的交点的横坐标为﹣2,则关于x的不等式﹣x+m >nx+4n>0的整数解为()A.﹣1B.﹣5 C.﹣4D.﹣38.如图,一次函数y=kx+b的图象经过A、B两点,则不等式kx+b<0的解集是()A.x<0B.0<x<1C.x<1 D.x>1二.填空题(共10小题)9.若直线y=2x+b与x轴交于点(﹣3,0),则方程2x+b=0的解是_________.10.如图是一次函数y=kx+b的图象,则方程kx+b=0的解为_________.11.一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=0的解为_________.12.如图,已知直线y=ax﹣b,则关于x的方程ax﹣1=b的解x=_________.13.如图,直线y=kx+b分别交x轴和y轴于点A、B,则关于x的方程kx+b=0的解为_________.14.如图,已知函数y=2x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),根据图象可得方程2x+b=ax﹣3的解是_________.15.如图,已知函数y=2x+b与函数y=kx﹣3的图象交于点P,则不等式kx﹣3>2x+b的解集是_________.16.如图,直线y=kx+b过A(﹣1,2)、B(﹣2,0)两点,则0≤kx+b≤﹣2x的解集为_________.17.一次函数y1=kx+b与y2=x+a的图象如图,则kx+b>x+a的解集是_________.18.如图,函数y=kx和的图象相交于A (a,2),则不等式的解集为_________.三.解答题(共4小题)19.如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:(1)方程kx+b=0的解;(2)式子k+b的值;(3)方程kx+b=﹣3的解.20.如图,直线l1:y=2x与直线l2:y=kx+3在同一平面直角坐标系内交于点P.(1)写出不等式2x>kx+3的解集:_________;(2)设直线l2与x轴交于点A,求△OAP的面积.21.在平面直角坐标系x0y中,直线y=kx+b(k≠0)过(1,3)和(3,1)两点,且与x轴、y轴分别交于A、B两点,求不等式kx+b≤0的解.22.在直角坐标系xOy中,直线y=kx+b(k≠0)经过(﹣2,1)和(2,3)两点,且与x 轴、y轴分别交于A、B两点,求不等式kx+b≥0的解集.。
人教版数学八年级上册几何知识点

人教版数学八年级上册的几何知识点主要包括以下几个方面:
1.三角形的基本性质:三角形具有稳定性,即三角形三条边的长度确定后,它的形状
就固定了。
此外,三角形还有中线、角平分线和高线等基本性质。
2.全等三角形:如果两个三角形的三边分别相等,或者两边和夹角分别相等,则这两
个三角形全等。
全等三角形具有性质对应边相等、对应角相等。
3.轴对称和中心对称:轴对称是指一个图形关于一条直线对称,中心对称是指一个图
形关于一个点对称。
4.四边形:四边形是由四条边组成的封闭图形,其中有平行四边形、矩形、菱形和正
方形等特殊情况。
5.勾股定理:勾股定理是一个重要的几何定理,它描述了直角三角形中三边的关系。
具体来说,直角三角形的两直角边的平方和等于斜边的平方。
6.面积和周长:面积是指一个平面图形所占的区域大小,周长是指一个平面图形的边
的总长度。
7.相似三角形:如果两个三角形的对应角相等,则这两个三角形相似。
相似三角形对
应边之间的比例是一个常数,这个常数叫做相似比。
以上是八年级上册的主要几何知识点,通过掌握这些知识点,学生可以更好地理解几何学的基本概念和性质,提高自己的几何思维能力。
新人教版八年级数学上册高频考点微专题03 一线三等角模型证全等

专题03一线三等角模型证全等★模型感知1.【感知模型】“一线三等角”模型是平面几何图形中的重要模型之一,请根据以下问题,把你的感知填写出来:如图1,ABC 是等腰直角三角形,90C ∠=︒,AE =BD ,则AED ≌_______;如图2,ABC 为正三角形,,60BD CF EDF =∠=︒,则BDE ≌________;如图3,正方形ABCD 的顶点B 在直线l 上,分别过点A 、C 作AE l ⊥于E ,CF l ⊥于F .若1AE =,2CF =,则EF 的长为________.★类型一一线三直角证全等2.在△ABC 中,∠ACB =90°,AC =BC ,且AD ⊥MN 于D ,BE ⊥MN 于E .(1)直线MN 绕点C 旋转到图(1)的位置时,求证:DE =AD +BE ;(2)当直线MN 绕点C 旋转到图(2)的位置时,试问DE 、AD 、BE 具有怎样的等量关系?请直接写出这个等量关系(不写证明过程);(3)当直线MN 绕点C 旋转到图(3)的位置时,试问DE 、AD 、BE 具有怎样的等量关系?请直接写出这个等量关系(不写证明过程).3.通过对下面数学模型的研究学习,解决下列问题:(1)如图1,点A 在直线l 上,90,BAD AB AD ∠=︒=,过点B 作BC l ⊥于点C ,过点D 作DE l ⊥交于点E .由12290D ∠+∠=∠+∠=︒,得1D ∠=∠.又90BCA AED ∠=∠=︒,可以推理得到()ABC DAE AAS ≌.进而得到结论:AC =_____,BC =_____.我们把这个数学模型称为“K 字”模型或“一线三直角”模型;(2)如图2,90,,,BAD MAN AB AD AM AN BM l ∠=∠=︒==⊥于点C ,NG l ⊥于点G ,由(1)易知NG =_______,ND 与直线l 交于点P ,求证:NP DP =.★类型二一线非直角证全等4.(1)如图1,直线m 经过等边三角形ABC 的顶点A ,在直线m 上取两点D ,E ,使得∠ADB =60°,∠AEC =60°.求证:BD +CE =DE ;(2)将(1)中的直线m 绕着点A 逆时针方向旋转一个角度到如图2的位置,并使∠ADB =120°,∠AEC =120°.若BD =3,CE =7,求DE 的长.5.已知:CD 是经过BCA ∠的顶点C 的一条直线,CA CB =.E 、F 是直线CD 上两点,BEC CFA α∠=∠=∠.(1)若直线CD 经过BCA ∠的内部,BCD ACD ∠>∠.①如图1,90BCA ∠=︒,90α∠=︒,直接写出BE ,EF ,AF 间的等量关系:__________.②如图2,α∠与BCA ∠具有怎样的数量关系,能使①中的结论仍然成立?写出α∠与BCA ∠的数量关系,并对结论进行证明;(2)如图3,若直线CD 经过BCA ∠的外部,BCA α∠=∠,①中的结论是否成立?若成立,进行证明;若不成立,写出新结论并进行证明.★类型三综合运用6.(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在ABC 中,90BAC ∠=︒,AB AC =,直线l 经过点A ,BD ⊥直线l ,CE ⊥直线l ,垂足分别为点D ,E .求证:DE BD CE =+.(2)组员小明想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在ABC 中,AB AC =,D ,A ,E 三点都在直线l 上,并且有BDA AEC BAC α∠=∠=∠=,其中α为任意锐角或钝角.请问结论DE BD CE =+是否成立?若成立,请你给出证明;若不成立,请说明理由.(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过ABC 的边AB ,AC 向外作正方形ABDE 和正方形ACFG ,AH 是BC 边上的高.延长HA 交EG 于点I .若7AEG S =△,则AEI S =△______.7.(1)如图(1),已知:在△ABC 中,∠BAC =90°,AB =AC ,直线m 经过点A ,BD ⊥直线m ,CE ⊥直线m ,垂足分别为点D 、E .证明∶DE =BD +CE .(2)如图(2),将(1)中的条件改为:在△ABC 中,AB =AC ,D 、A 、E 三点都在直线m 上,并且有∠BDA =∠AEC =∠BAC =α,其中α为任意锐角或钝角.请问结论DE =BD +CE 是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D 、E 是D 、A 、E 三点所在直线m 上的两动点(D 、A 、E 三点互不重合),点F 为∠BAC 平分线上的一点,且△ABF 和△ACF 均为等边三角形,连接BD 、CE ,若∠BDA =∠AEC =∠BAC ,试判断△DEF 的形状.8.通过对下面数学模型的研究学习,解决下列问题:【模型呈现】(1)如图,90BAD ∠=︒,AB AD =,过点B 作BC AC ⊥于点C ,过点D 作DE AC ⊥于点E .由12290D ∠+∠=∠+∠=︒,得1D ∠=∠.又90ACB AED ∠=∠=︒,可以推理得到ABC DAE ∆∆≌.进而得到AC =__________,BC AE =.我们把这个数学模型称为“K 字”模型或“一线三等角”模型;【模型应用】(2)如图,90BAD CAE ∠=∠=︒,AB AD =,AC AE =,连接BC ,DE ,且BC AF ⊥于点F ,DE 与直线AF 交于点G .求证:点G 是DE 的中点;【深入探究】(3)如图,已知四边形ABCD 和为正方形,AFD ∆的面积为1S ,DCE ∆的面积为2S ,则有1S __________2S (填“>、=、<”)(4)如图,点A 、B 、C 、D 、E 都在同一条直线上,四边形ABAH 、KCMG 、DENM 都是正方形,若该图形总面积是16,正方形KCMG 的面积是4,则HKG D 的面积是__________.9.(1)【问题情境】八上《伴你学》第138页有这样一个问题:如图1,把一块三角板(,90AB BC ABC =∠=︒)放入一个“U ”形槽中,使三角形的三个顶点A 、B 、C 分别在槽的两壁及底边上滑动,已知90D E ∠=∠=︒,在滑动过程中,你发现线段AD 与BE 有什么关系?试说明你的结论;(2)【变式探究】小明在解决完这个问题后,将其命名为“一线三等角”模型;如图2,在ABC ∆中,点D 、E 、F 分别在边BC 、AC 、AB 上,若B FDE C ∠=∠=∠,则这三个相等的角之间的联系又会使图形中出现其他的一些等角.请你写出其中的一组,并加以说理;(3)【拓展应用】如图3,在ABC ∆中,BA BC =,45B ∠=︒,点D 、F 分别是边BC 、AB 上的动点,且2AF BD =.以DF 为腰向右作等腰DEF ∆,使得DE DF =,45EDF ∠=︒,连接CE .①试判断线段DC 、BD 、BF 之间的数量关系,并说明理由;②如图4,已知2AC =,点G 是AC 的中点,连接EA 、EG ,直接写出EA EG +的最小值.专题03一线三等角模型证全等模型感知1.【感知模型】“一线三等角”模型是平面几何图形中的重要模型之一,请根据以下问题,把你的感知填写出来:①如图1,ABC 是等腰直角三角形,90C ∠=︒,AE =BD ,则AED ≌_______;②如图2,ABC 为正三角形,,60BD CF EDF =∠=︒,则BDE ≌________;③如图3,正方形ABCD 的顶点B 在直线l 上,分别过点A 、C 作AE l ⊥于E ,CF l ⊥于F .若1AE =,2CF =,则EF 的长为________.【答案】①△BDF ;②△CFD ;③3;①根据等腰直角三角形的性质及和角关系,可得△AED ≌△BDF ;②根据等边三角形的性质及和角关系,可得△BDE ≌△CFD ;③根据正方形的性质及和角关系,可得△ABE ≌△BCF ,由全等三角形的性质即可求得EF 的长;类型一一线三直角证全等2.在△ABC 中,∠ACB =90°,AC =BC ,且AD ⊥MN 于D ,BE ⊥MN 于E .(1)直线MN绕点C旋转到图(1)的位置时,求证:DE=AD+BE;(2)当直线MN绕点C旋转到图(2)的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系(不写证明过程);(3)当直线MN绕点C旋转到图(3)的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系(不写证明过程).【答案】(1)证明见详解(2)DE+BE=AD.理由见详解(3)DE=BE-AD(或AD=BE-DE,BE=AD+DE等).理由见详解.【解析】【分析】(1)根据题意由垂直得∠ADC=∠BEC=90°,由同角的余角相等得:∠DAC=∠BCE,因此根据AAS可以证明△ADC≌△CEB,结合全等三角形的对应边相等证得结论;(2)由题意根据全等三角形的判定定理AAS推知△ACD≌△CBE,然后由全等三角形的对应边相等、图形中线段间的和差关系以及等量代换证得DE+BE=AD;(3)由题意可知DE、AD、BE具有的等量关系为:DE=BE-AD(或AD=BE-DE,BE=AD+DE等).证明的方法与(2)相同.(1)证明:如图1,∵AD⊥MN,BE⊥MN,∴∠ADC=∠BEC=90°,∴∠DAC+∠ACD=90°,∵∠ACB=90°,∴∠ACD+∠BCE=90°,∴∠DAC=∠BCE,在△ADC和△CEB中,∵ADC BEC DAC BCE AC BC∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADC≌△CEB;∴DC =BE ,AD =EC ,∵DE =DC +EC ,∴DE =BE +AD .(2)解:DE +BE =AD .理由如下:如图2,∵∠ACB =90°,∴∠ACD +∠BCE =90°.又∵AD ⊥MN 于点D ,∴∠ACD +∠CAD =90°,∴∠CAD =∠BCE .在△ACD 和△CBE 中,90ADC CEB CAD BCE AC BC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△CBE (AAS ),∴CD =BE ,AD =CE ,∴DE +BE =DE +CD =EC =AD ,即DE +BE =AD .(3)解:DE =BE -AD (或AD =BE -DE ,BE =AD +DE 等).理由如下:如图3,易证得△ADC ≌△CEB ,∴AD =CE ,DC =BE ,∴DE =CD -CE =BE -AD ,即DE =BE -AD .【点睛】本题属于几何变换综合题,考查等腰直角三角形和全等三角形的性质和判定,熟练掌握全等三角形的四种判定方法是关键:SSS 、SAS 、AAS 、ASA ;在证明线段的和与差时,利用全等三角形将线段转化到同一条直线上得出结论.3.通过对下面数学模型的研究学习,解决下列问题:(1)如图1,点A 在直线l 上,90,BAD AB AD ∠=︒=,过点B 作BC l ⊥于点C ,过点D 作DE l ⊥交于点E .由12290D ∠+∠=∠+∠=︒,得1D ∠=∠.又90BCA AED ∠=∠=︒,可以推理得到()ABC DAE AAS ≌.进而得到结论:AC =_____,BC =_____.我们把这个数学模型称为“K 字”模型或“一线三直角”模型;(2)如图2,90,,,BAD MAN AB AD AM AN BM l ∠=∠=︒==⊥于点C ,NG l ⊥于点G ,由(1)易知NG =_______,ND 与直线l 交于点P ,求证:NP DP =.【答案】(1)DE ,AE ;(2)AC .证明见详解.【解析】【分析】(1)根据(AAS)≌ABC DAE ,得出AC =DE ,BC =AE 即可;(2)过D 作DE ⊥直线l 于E ,先证△MCA ≌△AGN (AAS ),得出AC =NG ,由(1)知(AAS)≌ABC DAE ,得出AC =DE ,再证△NGP ≌△DEP (AAS )即可.(1)解:∵(AAS)≌ABC DAE ,∴AC =DE ,BC =AE ,故答案为DE ,AE ;(2)证明:过D 作DE ⊥直线l 于E ,∵90MAN ∠=︒,∴∠CAM +∠NAG =90°,∵BM ⊥l ,∴∠MCA =90°,∴∠M +∠CAM =90°,∴∠M =∠NAG ,∵NG l ⊥,∴∠AGN =90°,在△MCA 和△AGN 中,MCA AGN M GAN MA AN ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△MCA ≌△AGN (AAS ),∴AC =NG ,由(1)知(AAS)≌ABC DAE ,∴AC =DE ,∴NG =DE ,在△NGP 和△DEP 中,90NGP DEP GPN EPD NG DE ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴△NGP ≌△DEP (AAS )∴NP =DP ,故答案为AC.【点睛】本题考查一线三直角全等问题,掌握余角性质,三角形全等判定与性质是解题关键.类型二一线非直角证全等4.(1)如图1,直线m 经过等边三角形ABC 的顶点A ,在直线m 上取两点D ,E ,使得∠ADB =60°,∠AEC =60°.求证:BD +CE =DE ;(2)将(1)中的直线m 绕着点A 逆时针方向旋转一个角度到如图2的位置,并使∠ADB =120°,∠AEC =120°.若BD =3,CE =7,求DE【答案】(1)证明见解析;(2)DE =4【解析】【分析】(1)利用等边三角形的性质和已知角的度数,证明∠ABD =∠CAE ,利用AAS 证明△ABD ≌△CAE ,推出BD =AE ,AD =CE ,即可证明;(2)同(1)证明△ABD ≌△CAE ,推出BD =AE ,AD =CE ,则DE =AD -AE =CE -BD .【详解】(1)证明:∵△ABC 为等边三角形,∴AB =AC ,∠BAC =60°,∴∠DAB +∠CAE =120°又∠ADB =∠AEC =60°,∴∠ABD +∠DAB =120°,∴∠ABD =∠CAE ,∴△ABD ≌△CAE (AAS ),∴BD =AE ,AD =CE ,∴DE =AD +AE =BD +CE .(2)解:∵△ABC 为等边三角形,∴AB =AC ,∠BAC =60°,∴∠BAD +∠CAE =60°又∠ADB =∠AEC =120°,∴∠ABD +∠BAD =60°,∴∠ABD =∠CAE ,∴△ABD ≌△CAE (AAS ),∴BD =AE ,AD =CE ,∴DE =AD -AE =CE -BD =4.【点睛】本题考查等边三角形的性质,全等三角形的判定和性质,读懂题意,找出图形中的全等三角形是解题的关键.5.已知:CD 是经过BCA ∠的顶点C 的一条直线,CA CB =.E 、F 是直线CD 上两点,BEC CFA α∠=∠=∠.(1)若直线CD 经过BCA ∠的内部,BCD ACD ∠>∠.①如图1,90BCA ∠=︒,90α∠=︒,直接写出BE ,EF ,AF 间的等量关系:__________.②如图2,α∠与BCA ∠具有怎样的数量关系,能使①中的结论仍然成立?写出α∠与BCA ∠的数量关系,并对结论进行证明;(2)如图3,若直线CD 经过BCA ∠的外部,BCA α∠=∠,①中的结论是否成立?若成立,进行证明;若不成立,写出新结论并进行证明.【答案】(1)①EF BE AF =-;②180BCA α∠+∠=︒,证明见解析;(2)不成立,EF FA BE =+,理由见解析【解析】【分析】(1)①根据题意,推导得ACF CBE ∠=∠,通过证明ACF CBE ∠≌△,得BE CF =,CE AF =,结合EF CF CE =-,即可得到答案;②结合题意,根据三角形内角和性质,推导得CBE ACF ∠=∠,通过证明BCE CAF ≌△△,即可完成证明;(2)根据题意,结合三角形内角和的性质,推导得CBE ACF ∠=∠,通过证明BCE CAF ≌△△,得EC FA =,BE CF =;根据EF CE CF =+,即可得到答案.【详解】(1)①∵90BCA ∠=︒,90α∠=︒∴90ACF BCE ∠+∠=︒,90CBE BCE ∠+∠=︒∴ACF CBE∠=∠∴BEC CFA ACF CBE CA CB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ACF CBE∠≌△∴BE CF =,CE AF=∵EF CF CE=-∴EF BE AF =-;②满足180BCA α∠+∠=︒,理由如下:∵180CBE BCE BEC ∠+∠+∠=︒,180BCA α∠+∠=︒∴CBE BCE BEC BCAα∠+∠+∠=∠+∠∴CBE BCE BCE ACFαα∠+∠+∠=∠+∠+∠∴CBE ACF∠=∠∵BEC CFA ∠=∠,CA CB =,∴BCE CAF≌△△∴BE CF =,CE AF=∵EF CF CE =-,∴EF BE AF=-(2)不成立,EF BE AF =+,理由如下:∵180CBE BCE BEC ∠+∠+∠=︒,180BCE BCA ACF ∠+∠+∠=︒,BEC CFA BCA α∠=∠=∠=∠∴CBE BCE BCE ACFαα∠+∠+∠=∠+∠+∠∴CBE ACF∠=∠∵BEC CFA ∠=∠,CA CB =,∴BCE CAF≌△△∴BE CF =,CE AF=∵EF CF CE =+,∴EF BE AF=+【点睛】本题考查了三角形内角和、余角、全等三角形的知识;解题的关键是熟练掌握三角形内角和、全等三角形的性质,从而完成求解.类型三综合运用6.(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在ABC 中,90BAC ∠=︒,AB AC =,直线l 经过点A ,BD ⊥直线l ,CE ⊥直线l ,垂足分别为点D ,E .求证:DE BD CE =+.(2)组员小明想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在ABC 中,AB AC =,D ,A ,E 三点都在直线l 上,并且有BDA AEC BAC α∠=∠=∠=,其中α为任意锐角或钝角.请问结论DE BD CE =+是否成立?若成立,请你给出证明;若不成立,请说明理由.(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过ABC 的边AB ,AC 向外作正方形ABDE 和正方形ACFG ,AH 是BC 边上的高.延长HA 交EG 于点I .若7AEG S =△,则AEI S =△______.【答案】(1)见解析;(2)结论成立,理由见解析;(3)3.5【解析】【分析】(1)由条件可证明△ABD ≌△CAE ,可得DA =CE ,AE =BD ,可得DE =BD +CE ;(2)由条件可知∠BAD +∠CAE =180°-α,且∠DBA +∠BAD =180°-α,可得∠DBA =∠CAE ,结合条件可证明△ABD ≌△CAE ,同(1)可得出结论;(3)由条件可知EM =AH =GN ,可得EM =GN ,结合条件可证明△EMI ≌△GNI ,可得出结论I 是EG 的中点.【详解】解:(1)证明:如图1中,∵BD ⊥直线l ,CE ⊥直线l ,∴∠BDA =∠CEA =90°,∵∠BAC =90°,∴∠BAD +∠CAE =90°,∵∠BAD +∠ABD =90°,∴∠CAE =∠ABD ,在△ADB 和△CEA 中,ABD CAE BDA CEA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADB ≌△CEA (AAS ),∴AE =BD ,AD =CE ,∴DE =AE +AD =BD +CE .(2)解:成立.理由:如图2中,∵∠BDA =∠BAC =α,∴∠DBA +∠BAD =∠BAD +∠CAE =180°-α,∴∠DBA =∠CAE ,在△ADB 和△CEA 中,BDA AEC DBA CAE AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADB ≌△CEA (AAS ),∴AE =BD ,AD =CE ,∴DE =AE +AD =BD +CE .(3)如图3,过E 作EM ⊥HI 于M ,GN ⊥HI 的延长线于N .∴∠EMI =∠GNI =90°由(1)和(2)的结论可知EM =AH =GN∴EM =GN在△EMI 和△GNI 中,GIN EIM EM GN GNI EMI ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△EMI ≌△GNI (AAS ),∴EI =GI ,∴I 是EG 的中点.∴S △AEI =12S △AEG =3.5.故答案为:3.5.【点睛】等三角形的判定与性质是解题的关键.7.(1)如图(1),已知:在△ABC 中,∠BAC =90°,AB =AC ,直线m 经过点A ,BD ⊥直线m ,CE ⊥直线m ,垂足分别为点D 、E .证明∶DE =BD +CE .(2)如图(2),将(1)中的条件改为:在△ABC 中,AB =AC ,D 、A 、E 三点都在直线m 上,并且有∠BDA =∠AEC =∠BAC =α,其中α为任意锐角或钝角.请问结论DE =BD +CE 是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D 、E 是D 、A 、E 三点所在直线m 上的两动点(D 、A 、E 三点互不重合),点F 为∠BAC 平分线上的一点,且△ABF 和△ACF 均为等边三角形,连接BD 、CE ,若∠BDA =∠AEC =∠BAC ,试判断△DEF的形状.【答案】(1)见解析(2)成立,证明见解析(3)△DEF为等边三角形,证明见解析【解析】【分析】(1)因为DE=DA+AE,故由AAS证△ADB≌△CEA,得出DA=EC,AE=BD,从而证得DE=BD+CE.(2)成立,仍然通过证明△ADB≌△CEA,得出BD=AE,AD=CE,所以DE=DA+AE=EC+BD.(3)由△ADB≌△CEA得BD=AE,∠DBA=∠CAE,由△ABF和△ACF均等边三角形,得∠ABF=∠CAF=60°,FB=FA,所以∠DBA+∠ABF=∠CAE+∠CAF,即∠DBF=∠FAE,所以△DBF≌△EAF,所以FD=FE,∠BFD=∠AFE,再根据∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=600得到△DEF是等边三角形.【详解】解:(1)证明:∵BD⊥直线m,CE⊥直线m,∴∠BDA=∠CEA=90°.∵∠BAC=90°,∴∠BAD+∠CAE=90°.∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD.又AB=AC,∴△ADB≌△CEA(AAS).∴AE=BD,AD=CE.∴DE=AE+AD=BD+CE.(2)成立.证明如下:∵∠BDA=∠BAC=α,∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α.∴∠DBA=∠CAE.∵∠BDA=∠AEC=α,AB=AC,∴△ADB≌△CEA(AAS).∴AE=BD,AD=CE.∴DE=AE+AD=BD+CE.(3)△DEF为等边三角形.理由如下:由(2)知,△ADB≌△CEA,BD=AE,∠DBA=∠CAE,∵△ABF和△ACF均为等边三角形,∴∠ABF=∠CAF=60°.∴∠DBA+∠ABF=∠CAE+∠CAF.∴∠DBF=∠FAE.∵BF=AF,∴△DBF ≌△EAF (ASA ).∴DF =EF ,∠BFD =∠AFE .∴∠DFE =∠DFA +∠AFE =∠DFA +∠BFD =60°.∴△DEF 为等边三角形.【点睛】此题考查了全等三角形的性质和判定,等边三角形的性质和判定,解题的关键是熟练掌握全等三角形的性质和判定,等边三角形的性质和判定.8.通过对下面数学模型的研究学习,解决下列问题:【模型呈现】(1)如图,90BAD ∠=︒,AB AD =,过点B 作BC AC ⊥于点C ,过点D 作DE AC ⊥于点E .由12290D ∠+∠=∠+∠=︒,得1D ∠=∠.又90ACB AED ∠=∠=︒,可以推理得到ABC DAE ∆∆≌.进而得到AC =__________,BC AE =.我们把这个数学模型称为“K 字”模型或“一线三等角”模型;【模型应用】(2)如图,90BAD CAE ∠=∠=︒,AB AD =,AC AE =,连接BC ,DE ,且BC AF ⊥于点F ,DE 与直线AF 交于点G .求证:点G 是DE 的中点;【深入探究】(3)如图,已知四边形ABCD 和DEGF 为正方形,AFD ∆的面积为1S ,DCE ∆的面积为2S ,则有1S __________2S (填“>、=、<”)(4)如图,点A 、B 、C 、D 、E 都在同一条直线上,四边形ABAH 、KCMG 、DENM 都是正方形,若该图形总面积是16,正方形KCMG 的面积是4,则HKG D 的面积是__________.【答案】(1)DE ;(2)见解析;(3)=;(42【解析】【分析】(1)根据全等三角形的性质即可得到答案;(2)分别过点D 和点E 作DM FG ⊥于点M ,EN FG ⊥于点N ,由(1)中结论可得到AF =DM ,AF =EN ,然后只需要证明DMG ENG △≌△即可得到答案;(3)过点D 作DO ⊥AF 交AF 于O ,过点E 错EN ⊥OD 交OD 延长线于N ,过点C 作CM ⊥OD 交OD 延长线于M ,然后同(2)中证明AOD DMC △≌△,FOD DNE △≌△,ENP CMP △≌△即可得到答案;(4)同(3)中的方法可以证明GHK KBC CMD GMN S S S S =△△△△==,然后利用勾股定理得到ABKH MDEN KCMG S S S +=正方形正方形正方形即可得到答案.【详解】解:(1)∵ABC DAE△≌△∴AC DE=(2)分别过点D 和点E 作DM FG ⊥于点M ,EN FG ⊥于点N ,∴90DAM ADM ∠+∠=︒,∵90BAD ∠=︒,∴90BAF DAM ∠+∠=︒,∴BAF ADM∠=∠∵BC AF ⊥,∴90BFA AMD ∠=∠=︒,在ABF ∆和DAM ∆中,BAF ADN ∠=∠,BFA AMD ∠=∠,BA AD =,∴ABF DAM ∆∆≌,∴AF DM=同理AF EN=∴DM EN =,∵DM FG ⊥,EN FG ⊥,∴DMG ENG ∠=∠,在DMG △和ENG △中,DGM EGN ∠=∠,DMG ENG ∠=∠,DM EN =,∴DMG ENG△≌△∴DG EG =,即点G 是DE 的中点;(3)如图所示,过点D 作DO ⊥AF 交AF 于O ,过点E 作EN ⊥OD 交OD 延长线于N ,过点C 作CM ⊥OD 交OD 延长线于M∵四边形ABCD 与四边形DEGF 都是正方形∴∠ADC =∠90°,AD =DC ,DF =DE∵DO ⊥AF ,CM ⊥OD∴∠AOD =∠CMD =90°,∠OAD +∠ODA =90°,∠CDM +∠DCM =90°,又∵∠ODA +∠DCM =90°∴∠A DO =∠DCM∴AOD DMC△≌△∴AOD DMC S S =△△,OD =MC同理可以证明FOD DNE△≌△∴FOD DNE S S =△△,OD =NE∴MC =NE∵EN ⊥OD ,CM ⊥OD ,∠EPN =∠CMP∴ENP CMP△≌△∴ENP CMPS S △△=∵ADF AOD FOD S S S +△△△=,DCE DCM CMP DEN ENPS S S S S -++△△△△△=∴=DCE DCM DEN AOD FODS S S S S ++△△△△△=∴DCE ADF S S △△=即12S S =;(4)同(3)中的方法可以证明GHK KBC CMD GMN S S S S =△△△△==,且KBC CDM △≌△即BC DM=由勾股定理得:222KB BC KC +=∴222KB DM KC +=∴ABKH MDEN KCMGS S S +=正方形正方形正方形∵图形总面积是16,正方形KCMG 的面积是4∴=4ABKH MDEN KCMG S S S +=正方形正方形正方形∴=8GHK KBC CMD GMN S S S S +△△△△++∴2GHK S △=【点睛】本题主要考查了全等三角形的性质与判定,正方形的性质,解题的关键在于能够熟练掌握全等三角形的性质与判定.9.(1)【问题情境】八上《伴你学》第138页有这样一个问题:如图1,把一块三角板(,90AB BC ABC =∠=︒)放入一个“U ”形槽中,使三角形的三个顶点A 、B 、C 分别在槽的两壁及底边上滑动,已知90D E ∠=∠=︒,在滑动过程中,你发现线段AD 与BE 有什么关系?试说明你的结论;(2)【变式探究】小明在解决完这个问题后,将其命名为“一线三等角”模型;如图2,在ABC ∆中,点D 、E 、F 分别在边BC 、AC 、AB 上,若B FDE C ∠=∠=∠,则这三个相等的角之间的联系又会使图形中出现其他的一些等角.请你写出其中的一组,并加以说理;(3)【拓展应用】如图3,在ABC ∆中,BA BC =,45B ∠=︒,点D 、F 分别是边BC 、AB 上的动点,且2AF BD =.以DF 为腰向右作等腰DEF ∆,使得DE DF =,45EDF ∠=︒,连接CE .①试判断线段DC 、BD 、BF 之间的数量关系,并说明理由;②如图4,已知2AC =,点G 是AC 的中点,连接EA 、EG ,直接写出EA EG +的最小值.【答案】【小问1】AD BE =,说明见解析【小问2】BED FDC ∠=∠,EDB DFC ∠=∠;说理见解析【小问3】①BD BF CD +=,理由见解析;②AE EG +【解析】【分析】(1)【问题情境】证明()ABD BCE AAS ∆≅∆,即可求解.(2)【变式探究】利用等量代换即可求解.(3)【拓展应用】①等量代换即可求解;②在CD 上截取DM BF =,连接EM ,作点G 关于CE 的对称点N ,连接CN ,AN ,先证明()BDF MED SAS ∆≅∆,得到EM =CM ,在求出22.5ECM MEC ∠=∠=︒,即可确定E 点在射线CE 上运动,当A 、E 、N 三点共线时,EA +EG 的值最小,最小值为AN ,在Rt ANC 中求出AN 即可.【详解】(1)【问题情境】AD BE =,理由如下:90ABC ∠=︒ ,90ABD CBE ∴∠+∠=︒,90BAD ABD ∠+∠=︒ ,BAD CBE ∴∠=∠,AB BC = ,()ABD BCE AAS ∴∆≅∆,AD BE ∴=;(2)【变式探究】BED FDC ∠=∠,EDB DFC ∠=∠;理由如下:B FDEC ∠=∠=∠ ,180EDB BED EDB FDC FDC DFC EDF ∴∠+∠=∠+∠=∠+∠=︒-∠,BED FDC ∴∠=∠,EDB DFC ∠=∠;(3)【拓展应用】①AB BC = ,AF BF BD CD ∴+=+,2AF BD = ,2BD BF BD CD ∴+=+,BD BF CD ∴+=;②在CD 上截取DM BF =,连接EM ,作点G 关于CE 的对称点N ,连接CN ,AN ,45B ∠=︒ ,45EDF ∠=︒,BFD EDM ∴∠=∠,DF DE = ,()BDF MED SAS ∴∆≅∆,B D E M ∴=,EM BD =,45B DME ∠=∠=︒,CD BD BF =+ ,CM BD ∴=,EM CM ∴=,MCE MEC ∴∠=∠,45EMD ∠=︒ ,22.5ECM MEC ∴∠=∠=︒,E ∴点在射线CE 上运动,G 点与N 的关于CE 对称,EG EN ∴=,EA EG EA EN AN ∴+=+,∴当A 、E 、N 三点共线时,EA EG +的值最小,最小值为AN ,45B ∠=︒ ,AB BC =,67.5ACB ∴∠=︒,45ACE ∴∠=︒,由对称性可知,ACE ECN ∠=∠,90ACN ∴∠=︒,点G 是AC 的中点,2AC =,1CG ∴=,1CN ∴=,在Rt ANC 中,AN =AE EG ∴+【点睛】本题是三角形的综合题,熟练掌握三角形全等的判定及性质,轴对称求最短距离的方法是解题的关键.。
八年级数学几何最值问题(人教版)(专题)(含答案)

几何最值问题(人教版)(专题)一、单选题(共10道,每道10分)1.如图,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点,则PB+PE的最小值是( )A. B.C. D.答案:C解题思路:1.思路分析2.解题过程根据正方形的性质,点B和点D关于AC对称,此时连接DE,与AC的交点即为点P,线段DE的长即为所求.∵正方形ABCD的边长为2,E为AB的中点,∴AE=1,AD=2,∴,故选C试题难度:三颗星知识点:略2.如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )A.3B.C. D.答案:C解题思路:定点:D,E动点:P(在定线段AC上运动)要使PD+PE最小,需要通过对称把PD,PE转移到直线AC异侧.如图,由正方形的性质知,D,B关于AC所在直线对称,所以PD=PB,故所求可转化为“PB+PE的最小值”.根据“两点之间线段最短”,当B,P,E共线时,PB+PE最小,最小值为BE的长度.∵正方形ABCD的面积为12,∴,∴,故选C.试题难度:三颗星知识点:略3.如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为边BC,CD,BD上的动点,则PK+QK的最小值为( )A.1B.C.2D.答案:B解题思路:如图,作点Q关于BD的对称点,根据菱形的对称性,点落在AD边上,则题目转化为求的最小值,根据两点之间线段最短,的最小值为线段的长度,当⊥AD时,最小.如图,过点C作CE⊥AD,则.∵四边形ABCD为菱形,∴∠CDE=180°-∠A=60°,CD=AB=2,∴,故选B.试题难度:三颗星知识点:略4.在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A,B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.若E,F为边OA上的两个动点,且EF=2,则当四边形CDEF的周长最小时,点F的坐标为( )A. B.C. D.答案:B解题思路:1.思路分析2.解题过程通过题意可知,EF和CD的长固定,所以若要四边形CDEF的周长最小,则DE+CF最小即可.如图,CF向左平移两个单位到,此时就转化为要求即可.作出点D关于x轴的对称点,此时连接,与x轴的交点即为点E.根据题意可得,点的坐标为(1,4),点的坐标为(0,-2),∴的直线解析式为:,∴点E的坐标为,∴点F的坐标为.故选B试题难度:三颗星知识点:略5.如图,正方形ABCD的边长为2,顶点A,D分别在x轴、y轴上.当点A在x轴上运动时,点D随之在y轴上运动,则在运动过程中,点B到原点O的最大距离为( )A. B.C. D.答案:B解题思路:如图,取AD的中点M,连接OM,MB.∵OM为Rt△AOD斜边上的中线,∴,在Rt△AMB中,由勾股定理,得,在△OBM中,根据三角形的三边关系定理,得OM+BM OB,即,当O,M,B三点共线时,OM+BM=OB,此时OB最大,最大值为.故选B.试题难度:三颗星知识点:略6.如图,∠MON=90°,长方形ABCD的顶点B、C分别在边OM、ON上,当B在边OM上运动时,C随之在边ON上运动,若CD=5,BC=24,运动过程中,点D到点O的最大距离为( )A.24B.25C. D.26答案:B解题思路:取BC的中点M,连接OM,MD.∵OM为Rt△BOC斜边上的中线,∴,在Rt△DMC中,由勾股定理,得,在△ODM中,根据三角形的三边关系定理,得OM+DM OD,即,当O,M,B三点共线时,OM+DM=OD,此时OD最大,最大值为.故选B.试题难度:三颗星知识点:略7.动手操作:在矩形纸片ABCD中,AB=5,AD=13.如图所示,折叠纸片,使点A落在BC 边上的处,折痕为PQ,当点在BC边上移动时,折痕的端点P,Q也随之移动.若限定点P,Q分别在AB,AD边上移动,则点在BC边上可移动的最大距离为( )A.2B.3C.4D.5答案:C解题思路:试题难度:三颗星知识点:略8.如图,折叠矩形纸片ABCD,使点B落在AD上的点E处,折痕的两端点分别在AB,BC上(含端点),且AB=6,BC=10.设AE=x,则x的取值范围是( )A. B.C. D.答案:D解题思路:当点M与点A重合时,AE最大,如图,此时AE=6;当点N与点C重合时,AE最小,如图,此时AE=2.∴,故选D.试题难度:三颗星知识点:略9.如图,在矩形ABCD中,AB=5,BC=12,E是BC边上一动点,则以BD为对角线的所有平行四边形BEDF中,EF的最小值是( )A. B.5C.6D.12答案:B解题思路:在平行四边形BEDF中,EF=2OE,由“直线外一点到直线上所有点的连线中,垂线段最短”可知,当OE⊥BC时,OE最短,如图,此时,,∴EF的最小值为5.试题难度:三颗星知识点:略10.如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF 沿EF所在直线折叠得到△,连接,则的最小值是( )A. B.C. D.4答案:A解题思路:如图,连接ED,由题意,,在Rt△AED中,AE=2,AD=6,∴,由翻折得BE=B′E=2,由三角形三边关系得:B′D-B′E,∴当,B′,D三点共线时,B′D-B′E,B′D取最小值,当,B′,D三点共线时,如图,∴B′D=DE-B′E=,∴B′D 的最小值是.试题难度:三颗星知识点:略第11页共11页。
人教版八年级数学上册期末专题复习:以等腰三角形为桥梁的几何题例析(含解析、点评、跟踪训练)

新人教版八年数学上册期末专题复习资料以等腰三角形为桥梁的几何题例析新人教版八年级数学上册前面三个单元都是几何内容,其中以等腰三角形为桥梁的题所占比例较大,在期末统考试题中高频出现,也是中考的热点题型;等腰三角形含特殊等腰三角形等边三角形和等腰直角三角形的“等对等关系” 和“三线合一”是桥梁作用的支撑. 题目一. 平分角添加“垂直”,“平行”元素构成等腰三角形的举例.例1. 如图,⊿ABC 中,过点C 作出∠BAC 的平分线的垂线于点D ,交AB 于点E .=BC 7 ⑴.若∠=346,∠=B 39;求∠BCE 的度数; ⑵.若==AB 12,AC 10;求BE 的长. 分析:对于⑴问利用12∠=∠和∠+∠=1490,∠+∠=2390可以得到:∠=∠43 ;因为∠=∠+∠4B BCE ,结合∠=346,∠=B 39 可以求出∠=-=BCE 46397.⑵问结合⑴问∠=∠43可以得出=AE AC ,所以=-=-=-=BE AB AE AB AE 12102.例2.已知⊿ABC 中,∠=ACB 90,⊥CD AB 于点D ,AE 平分∠BAC ,交CD 于点F ,⊥EG AB 于点G .求证:=EG CF .分析:由AE 平分∠BAC ,∠=ACB 90,⊥EG AB 可以得出: =CE GE ;根据直角三角形的锐角互余和对顶角相等可以得到∠+∠=CEA CAE 90, ∠+∠=CFE DAF 90,而AE 平分∠BAC 可以得到:∠=∠CAE DAE ,所以∠=∠CFE CEF ,所以=CE CF ;综上可证:=EG CF . 点评:例1、例2都是在平分线的基础上添加“垂直”条件,利用互余关系和平分角来得到同一个三角形的两角相等,从而得到等腰三角形为桥梁解决问题.例3.如图,在⊿ABC 中,∠=∠ABC 2C ,BD 平分∠ABC 交AC 于点D ,⊥AE BC 于点E ;求证:=AC 2BE .解析: 过点A 作AF ∥BC 交BD 的延长线于点F .∴∠=∠1F ,∠=∠2C∵BD 平分∠ABC 交AC 于点D本题有3个等腰三角形,其中通过作平行线构建出的等腰⊿ABF 是关键的一环;当然本题方法不止一种.特别注意当有平行线和角平分线结合,往往要通过其中构建出的等腰三角形为桥梁解决问题.追踪练习: 1. 如图,在△ABC ,B C ∠∠、的平分线交于点P ,过点P 作DE ∥BC ,别交AB AC 、于点D E 、两点,已知,,AB a AC b BC 10===,则△ADE 的周长为 ( )A. 10B. 2a 2b +C.a b +D.a b 10++ 2. 如图,⊿ABC 中,过点C 作出∠BAC 的平分线的垂线于点D . 求证:∠>∠1C3.在四边形ABCD 中,AB ∥CD BD AD ⊥,BD 平分ABC ∠,,=∠=BC AD C 120,CD 2cm =;求AB 的长?M .138,则MAB ∠A5.如图,已知△ABC 是等腰直角三角形,∠=BAC 90 ,BE 平分∠ABC ,⊥DE BC ,垂足为点D .⑴.求证:⊥AD BE ; ⑵.如果=BC 10 ,求+AB AE 的长.题目二.遇“垂直+中点”型以及“T 字”型结构连起的等腰三角形举例.例1.如图,在四边形ABCD 中,点E 是边BC 的中点,点F 是边CD 的中点,且有AE BC,AF CD ⊥⊥ . ⑴.求证:AB AD =;⑵.若BCD 114∠= ,求BAD ∠的度数.解析:⑴.连结AC .∵点E 是边BC 的中点,AE BC ⊥ ∴AB AC = (垂直平分线的性质) 同理AD AC = ∴=AB AD⑵.∵AB AC,AD AC == ,且有AE BC,AF CD ⊥⊥。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级数学下册期末专题复习和训练:几何计算题、证明题一、题型特点:四边形(五种常见的)、三角形的中位线、矩形的推论穿插其中,…… 二、常见新型题型:动点、折纸、开放(条件、结论开放)、探索性(数量关系、位置关系),……三、图形搭建:三角形中搭建四边形、四边形中搭建三角形、组合图形,…… 下面我根据图形搭建结构特征进行分类,列举一部分和本期几何部分(主要是平行四边形)的计算题、证明题,让我们共同来探究、解析. 一、以平行四边形搭建起来的图形例1.ABCD 中,AB=4cm ,AD=7cm, ∠ABC 的平分线交AD 于E,交CO 的延长线于F,求DF 的长? 分析:本题要求的DF 长的途径有两条:其一.DF CF CD =-;其二. DF DE AD AE ==-. 采取第一途径可以少一些环节,根据平行四边形的性质和角的平分线的定义可以 比较容易得出BCF 是等腰三角形,即CF CB =;由于平行四边形的对边相等可以得出:,CD AB 4cm CB AD 7cm ====.故DF 743cm =-=例2.△ABC 、△ADE 都是正三角形,CD=BF. (1)、求证:△ACD ≌△CBF(2)、当D 运动至BC 边上的何处时,四边形CDEF 为平行四边形,且∠DEF=30°,并证明你的结论. 分析:⑴.证明△ACD ≌△CBF 已经有了CD=BF ,而△ABC 、△ADE都是正三角形又可以给我们提供,CA CB ACD CBF 60=∠=∠=条件,根据“SAS ”判定方法可以证得△ACD ≌△CBF.⑵.根据⑴问的△ACD ≌△CBF 得出AD CF =,又△ADE 是正三角形的DE CF =,所以CF DE =;要使四边形CDEF 为平行四边形可以证CF DE .若四边形CDEF 为平行四边形,则FCD DEF 30∠=∠=;当EDB 30∠=时,就有FCD EDB ∠=∠,此时就能证得CF DE .由正△ADE 可以得出ADE 60∠=,则ADB 603090∠=+=,AD BC ⊥;由于等腰三角形具有“三线合一”的特征,所以当D 运动至BC 边上中点时,四边形CDEF 为平行四边形.练习:1.如图,在□ABCD 中,AE ⊥BC,AF ⊥CD,∠EAF=60°,则∠B=( );2.□ABCD 的周长为60cm,对角线AC 、BD 交于点O,△AOB 的周 长比△BOC 的周长多10cm,则AD=( ),DC=( );3.□ABCD 中,∠ABC 的平分线BE 交AD 于E 点,若∠ABE=25°CD=5cm,BC=7cm,那么∠ABE=( ),∠BED=( ),AE=( ).4. 已知□ABCD ,BE=AB,BF =BD. 求证:CD=CM5. △ABC 是正三角形,AE=BD,DF ∥CE,EF ∥CD. 求证: △AGF ≌△EAC6.以△ABC 的三边在BC 的同侧做等边△EBC 、等边△FBA 、等边△DAC. ⑴.判断四边形FADE 的形状?⑵.当∠BAC 为多少度时,四边形FADE 为矩形? ⑶.当∠BAC 为多少度时,四边形FADE 不存在? 7. 有一块如图的玻璃,不小心把DEF 部分打碎,现在只测得AB=60cm,BC=80cm ,∠A=120°,∠B=60°,∠C=150°,你能根据测得的数据计算AD 的长? 二、以矩形搭建起来的图形例1.D 为□ABCD 外一点,∠APC=∠BPD=90°.求证: □ABCD 为矩形 分析:判定矩形的方法主要有三种.但在已知了四边形ABCD 是平行 四边形的情况下,要判定ABCD 是矩形的途径有两条:其一、找 一内角是直角;其二、找出对角线相等,即找出AC BD =. 由于本题的另一主要条件是∠APC=∠BPD=90°,要根据题中条件和图形位置转换成四边形的内角为90°比较困难,所以本题我们先想办法找出对角线相等,即找出AC BD =.我们发现本题在APC Rt 和BPD Rt 的两斜边的交点O 恰好是平行四边形对角线的交点,根据平行四边形对角线互相平分可知:O 同时是AC BD 、的中点;所以自然联想到连结PO 这条两直角三角形公共的中线(见图).根据以上条件,在APC Rt 和BPD Rt 中就有:AC 2PO =BD 2PO =,故AC BD =,由对角线相等的平行四边形是矩形,可判定ABCD 是矩形. 例2. 矩形ABCD 中,AB=3,AD=4,PE ⊥AC ,PF ⊥BD , ⑴.求PE+PF 的值?⑵.若点P 是AD 上的一动点(不与A D 、重合),还是作PE ⊥AC ,PF ⊥BD ,则PE+PF 的值是否会发生变化?为什么?分析:求线段的和或差我们会联想到证明中的“截长补短”法,但本题不具备这方面的条件.本题从面积入手可以破题:如图连结PO ,只要我们能求出APO 和DPO 的面积之和问题便可以获得解决.略解:⑴.∵四边形ABCD 是矩形M C DF B A E FED BCA DF EBC AA BC D P E FOF A B F EDAC∴BAD 90∠=,,11OA AC OD BD 22==, AC BD = ∴1OA OD BD 2==在ABD Rt 中,AB=3,AD=4;并且根据勾股定理有:222BD AB AD =+,即222BD 34=+,又BD 0> ,所以.=BD 5∴.==11OA OD BD 52522==⨯∵,11AOP OA PE DOP OD PF 22S S=⋅=⋅,且ABCD 11AOD 34344SS ==⨯⨯=矩形(过程略) ∴++=11AOP DOP OA PE OD PF AOD 22SSS=⋅⋅,即..1125PE 25PF 322⨯⨯+⨯⨯=∴12PE PF 5+=.⑵.不会发生变化.这是因为AOD AOP POD 、、的面积以及作为底边的OA OD、不会发生变化.练习: 1. 矩形ABCD 中,AF=DE.求证: 2. 矩形ABCD 中,BE ⊥AC ,CF ⊥BD.求证:BE=CF3. 矩形ABCD 中,DF 平分∠ADC, ∠求∠DOC 与∠COF 的度数?4、矩形ABCD 中,CE ∥BD ,则△ACE 为等腰三角形吗?为什么?5.如图,在矩形ABCD 中,点E ,F 分别在BC ,CD 上,将△ABE 沿AE 折叠,使点B落在AC 上的点B′处,又将△CEF 沿EF 折叠,使点C 落在EB′与AD 的交点C′处.则BC :AB 的值为多少? 三、以菱形搭建起来的图形例1. △ABC 中,∠BAC=90°,BD 平分∠ABC ,AH ⊥BC 于H 交BD 于E,DF ⊥BC 于F,求证:四边形AEFD 是菱形分析:判定菱形方法主要有三种,三种方法都可以使本题获得解决.下面我们选择“四边都相等的四边形是菱形”这一途径来分析.可以先根据角平分线的性质得出AD FD =,进而容易证明ABD ≌AFD ,所以BA BF =;再证明ABE ≌AFE可以得到EA EF =(也可以利用等腰三角形的“三线合一”);利用等角的余角相等可以推出ADE AED ∠=∠,所以EA DA =,于是AE EF FD DA ===,故四边形AEFD 是菱形. 例2.(2012中考·自贡) 如图所示,在菱形ABCD 中,,AB 4BAD 120=∠=,AEF 为正三角形,点E F 、分别在菱形的边BC CD 、上滑动,且E F 、不与B C D 、、重合. ⑴.证明不论E F 、在BC CD 、D 上如何滑动,总有BE CF =?⑵.当点E F 、在BC CD 、上滑动时,探讨四边形AECF 的面积是否发生变化?如果不变,求出这个定值.分析:⑴.先求证AB AC =,进而求证ABC ACD 、为等边三角形,得=BAC 60AC AB ∠=,进而求证ABE ≌ACF ,即可求得BE CF = ⑵.根据ABE ≌ACF 可得ABE ACF SS =;根据S四边形AECF=AEC S+ACFS=AEC S+BAE S =ABC S即可解得.⑴.证明:连接AC ,如下图所示. ∵四边形ABCD 为菱形,BAD 120∠= ∴,1EAC 602EAC 60∠+∠=∠+∠= ∴12∠=∠ ∵BAD 120∠=∴ABC 60∠=∴ABC 和ACD 都为等边三角形∴=460AC AB ∠=,∴在ABE 和ACF 中,12AB AC ABC 3∠=∠⎧⎪=⎨⎪∠=∠⎩∴ABE ≌ACF ()ASA∴BE CF =⑵.解:四边形AECF 的面积不变.理由:由⑴得ABE ≌ACF ,则ABE ACF SS=.故S 四边形AECF =AEC S +ACF S =AEC S +BAE S =ABC S 是定值. 作AH BC ⊥于H 点,则BH 2=S四边形ABCD =S ABC =2211BC AH BC AB BH 4322⋅=-练习:E F OD AE F D AODC B AEC A BH DE F 321E HABF1. 已知ABCD ,添加下列一个条件:①.AC ⊥BD ;②.∠BAD=90°;③.AB=BC ;④.AC=BD.其中能使ABCD 是菱形的为( ) A .①③ B .②③ C .④ D.①②③ 2.菱形ABCD 中,E 为AB 上的一点,CE 交BD 于F. 求证:⑴.△ABF ≌△CBF ;⑵.∠BEC=∠DAF. 3. 菱形的对角线的比是2:3,周长为1304cm ,求菱形的面积?4. 如图,平行四边形ABCD 的对角线AC 的垂直平分线与 AD AC BC 、、分别交于点E O F 、、求证:四边形AFCE 是菱形 .5. 如图,菱形ABCD 中,∠B=60°,AB=2,点E 、F 分别是AB 、AD 上 的动点,且满足BE=AF ,接连EF 、EC 、CF .求证:△EFC 是等边三角形6. 9、Rt △ABC 中,∠ACB=90°,∠BAC=60°,DE 垂直平分 BC ,且AF=CE.求证:四边形ACEF 为菱形 四、以正方形搭建起来的图形 例1.正方形ABCD 中,△DCE 是等边三角形.⑴.求∠AED 的度数?⑵.若OF=1,求AB 的长?分析:⑴.根据正方形和等边三角形的性质综合可以得出,DA DE ADE 9060150=∠=+=,所以得出:DAE DEA ∠=∠,所以()11AED DAE 180150301522∠=∠=-=⨯=. ⑵.根据正方形的性质综合可以得出AC BD ⊥,在AOF Rt 中,,FAO 451530OF 1∠=-==所以AF 2OF 2==,根据勾股定理可以求出22OA 213=-=,所以AC BD 23==.根据勾股定理或者面积公式可以得出:211AB AC BD 2323622=⋅=⨯⨯=.又.AB 0AB 6>∴=.例2、正方形ABCD 的面积为64,DE=2,P 为AC 上的一动点;求PD+PE 的最小值?分析:在一条直线同侧的两点,到直线某点的距离之和最小,按如图所 示作E 的对称点'E (根据正方形的对称性,对称点'E 恰好落在边BC 上) 连结'DE 交AC 于点'P ,根据轴对称的性质''''''DE DP E P DP EP =+=+ ,此时和是最小的.根据正方形ABCD 的面积为64可求得边长DC 8=,所以CE CD DE 826=-=-=。
