卧式椭圆形封头贮槽计量容积的计算
椭圆形封头卧式容器不同液面高度的容积计算

椭圆形封头卧式容器不同液面高度的容积计算新疆工学院孟永彪在设计卧式容器时,常常要计算不同液面高度所对应的容积,有时还需列出容积—液位高度对照表或图。
例如,在盛装有毒有害介质的卧式储罐设计中,要根据体积充装系数确定最高液面高度并加以标识。
在一般资料中仅能查到容器的全容积计算公式,而要计算不同液面高度下的容积则需设计者自行推导公式计算。
本文以标准椭圆形封头卧式容器为例介绍不同液面高度下的容积计算方法,并以液化石油气储罐为例编制了QUICK BASIC程序,此法仅供大家参考。
1卧式容器的组成卧式容器是由筒体和两封头组焊而成(如图1),常用的封头为标准椭圆封头。
2卧式容器2.1计算简图及说明计算简图如图2。
L———筒体长度(两封头切线间的距离,含直边段长度)D i———封头及筒体内直径h i———封头曲面深度2.2不同液面高度下封头的容积计算如图2,可假想将卧式容器两端的曲面部分合并,则形成一个完整的椭球面。
2==i ih R c a 122222=++cz a y x )(21222y x a z +-=dxy x a dy h a y a )(2222022+-=⎰⎰--)323(23331a h h a V +-=π其中,a=b=R i因此,椭球面的方程为:推导出: 当容器内的液面高度为h 时(如图3所示)。
封头的容积公式推导:对其积分得从上式可看出,h 变化,V 1也随之变化。
2.3 不同液面高度筒体的容积计算在计算筒体的容积时,忽略尺寸公差及制造误差等因素,可将其断面方程为x 2+y 2=a 2的一圆柱体进行计算,那么如图3所示液面高度的筒体容积为:令:y=acos θ dy=-asin θd θdxdy y x a V s )(2122221+-=⎰⎰dx y x a dy h a y a y a )(2122222222+-=⎰⎰----dy y a L V h a⎰--=2222dy y a L h -=222当 y=-a 时,θ=π;当y=h 时,代入公式积分得:2.4 卧式容器在不同液面高度下的容积通过以上V 1,V 2的计算公式,可计算出卧式容器在不同液面高度下的容积之和V :3 利用QUICK BASIC 语言进行卧式容器的容积计算要计算不同液位高度下的容积以表格、曲线的形式列出是很麻烦的,因此本文利用简便易行的QB 编制程序,当然编程语言可以有多种,本文愿起到抛砖引玉的作用。
卧式储罐不同液位下的容积(质量)计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图dhrl il L参数:l:椭圆封头曲面高度( m);l i:椭圆封头直边长度( m);L:卧罐圆柱体部分长度(m);r :卧式储罐半径( d/2,m);d:卧式储罐内径,( m)h:储液液位高度( m);V:卧式储罐总体积( m3);ρ:储液密度( kg/m3)3V h:对应 h 高度卧罐内储液体积( m );椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
roh以储罐底部为起点的液高卧式储罐内储液总体积计算公式:V 1 2r Lr 2 arcsin h - rh - r r 2 - h - r 2h 3L r r 2 2 若密度为ρ,则卧式储罐内储液总重量为:m h V h表 1 卧式储罐不同液位下容积(重量)ρr L h V h m h 液体密度储罐半径圆柱体部分长度储液液位高度储液体积储液重量(kg/m3)(m)(m)( m)(m3)( kg)备注:该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
rhoh尺以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:x2 y2 z21 其中 a=b=r ,则有x2 y2 z2 1a2 b2 c 2 a2 c 2垂直于 y 轴分成无限小微元,任一微元面积为:Syi c (a2 y2 )a当液面高度为h 时,椭圆球体内液氨容积为V1= a S yi dya c ( a 2 y 2 )dy c (a 2 h h 3 2a 3 hh a a 3 3( 2 )直段筒体部分:筒体的纵断面方程为 x 2 y 2 a 2任一微元的面积为 S yj 2 a 2 y 2 dy则筒体部分容积为:hh y 2 dy La 2 (arcsin h h 2 a 2 h 2 V 2S yj L 2 a 2 2 )aa a a 2 (arcsin h ) 2 a 2(3 )卧式储罐储液总体积总容积为 V=V1+V2 ,V= c 2 4h 2 2a 3) + La 2 h h 2 2 2 a (a h3 3 (arcsin a a 2 a h 2 )此公式中液位高度 h 是以储罐内径中心为原点,其中 a=b=r化简后卧式储罐储液总体积为: V12r Lr 2 arcsin h h r 2 - h2 h3L r r 2 2 实例:某热电厂液氨罐尺寸为:储罐体积50m 3,直段筒体长度 L 1=8480mm , 封头直段长度 L 2=40mm (圆柱体部分长度为 (L 1+L 2/2)=8580mm ),筒体半径 R=a=b=1300mm ,封头高度 c=650mmρ V r l L h h 尺 V h m h 误差储液液位高 不同液高下 储罐总 储罐半 封头高计算得到的 液体密度 圆柱体部分 度(中点为 实际标尺 储液体积 储液重量 体积 径 度 体积与实际 3) ) 坐标原点)刻度 3) (kg ) ( kg/m ( 3) ( ) ( ) 长度( m ( ) ( m 储液体积间 m m m m误差1 50 1.3 0.65 8.58 -1.3 0 0.000 0.000 0.00%150 1.3 0.65 8.58 -0.975 0.325 3.619 3.619 150 1.3 0.65 8.58 0 1.3 25.078 25.078 0.31% 150 1.3 0.65 8.58 0.975 2.275 46.537 46.537 1 50 1.3 0.65 8.58 1.3 2.6 50.155 50.155 0.31%若液位高度 h 以卧罐底部为起点,如下图roh则卧式储罐内储液总体积计算公式:V1 2r Lr2 arcsin h - r h - r r 2 - h - r 2 h3L r r 2 2若密度为 ρ,则卧式储罐内储液总重量为:m hV h ρ rL h V h m h 液体密度 储罐半径圆柱体部分长度 储液液位高度 储液体积 储液重量( kg )(kg/m 3) ( m ) ( m ) (m ) (m 3)1 1.3 8.58 1 1.3 8.58 1 1.3 8.58 0.325 3.619 3.6191.3 25.078 25.0782.275 46.537 46.537其它方法如下:第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐内储液总体积计算公式:V h V 2 l ( h r )[ 1 ( h r ) 2 ] L [( h r ) 2 hr h 2 r 2 arcsin( h r )]2 3 r 3 r若密度为ρ,则卧式储罐内储液总重量为:ρV液体密度储罐总体积(kg/m 3)(m3)150150m h V hr l L h V h m h 误差封头高圆柱体不同液高下计储罐半径储液液位高储液体积储液重量算得到的体积度部分长( m)度( m)(m3)( kg)与实际储液体( m)度( m)积间误差0.65 8.58 0 -1.315出现负数,不1.3 复合实际1.3 0.65 8.58 0.3252.276 2.2761 50 1.3 0.65 8.58 1.3 25.000 25.000 0.00%1 50 1.3 0.65 8.58 2.275 47.724 47.7241 50 1.3 0.65 8.58 2.6 51.315 2.63%此方式用到参数较多ρ、V 、r 、l、L 、h。
卧式储罐不同液位下的容积(质量)计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c++= 垂直于y 轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为V1=h yi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a +=任一微元的面积为yj S = 则筒体部分容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h若液位高度h 以卧罐底部为起点,如下图则卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=其它方法如下:第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐内储液总体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
封头容积重量计算

封头容积重量计算封头是压力容器的一种常见部件,用于密封容器的顶部或底部。
其主要作用是承受内部压力,确保容器的密封性。
在设计压力容器时,封头的容积和重量计算是非常重要的。
容积计算可以帮助确定容器的大小,而重量计算可以帮助确定容器的材料选择和支撑结构设计。
下面将详细介绍封头容积和重量的计算方法。
一、封头容积计算1.半球形封头容积计算半球形封头是一种常用的封头形式,其容积计算公式为:V=(2/3)πr³2.椭圆形封头容积计算椭圆形封头也是一种常用的封头形式,其容积计算公式为:V=(πa²b)/6其中,V代表容积,π代表圆周率,a代表封头的长轴半径,b代表封头的短轴半径。
3.球冠形封头容积计算球冠形封头是封头的一种特殊形式,其容积计算公式为:V=(πh²/3)*(3R-h)其中,V代表容积,π代表圆周率,h代表球冠的高度,R代表球冠的半径。
二、封头重量计算1.半球形封头重量计算半球形封头的重量计算公式为:W=(πd³*t)/12*ρ其中,W代表封头的重量,π代表圆周率,d代表封头的直径,t代表封头的厚度,ρ代表封头材料的密度。
2.椭圆形封头重量计算椭圆形封头的重量计算公式为:W=(π(a²-b²)*t)/6*ρ其中,W代表封头的重量,π代表圆周率,a和b代表封头的长轴和短轴半径,t代表封头的厚度,ρ代表封头材料的密度。
3.球冠形封头重量计算球冠形封头的重量计算公式为:W=(π(h*(3R-h)²)*t)/12*ρ其中,W代表封头的重量,π代表圆周率,h代表球冠的高度,R代表球冠的半径,t代表封头的厚度,ρ代表封头材料的密度。
需要注意的是,在进行容积和重量计算时,需要确保所使用的单位统一,如容积的单位可以选择立方米(m³),千立方米(m³),重量的单位可以选择千克(kg),吨等。
以上是关于封头容积和重量计算的详细介绍。
卧式储罐不同液位下的容积计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图d参数:l :椭圆圭寸头曲面高度(m );l i :椭圆圭寸头直边长度(m);L :卧罐圆柱体部分长度(m);r :卧式储罐半径(d/2, m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);P储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下卧式储罐内储液总体积计算公式:若密度为p,则卧式储罐内储液总重量为:m h V h表1卧式储罐不同液位下容积(重量)PrLhV hm h液体密度 (kg/m 3)储罐半径 (m )圆柱体部分长度(m )储液液位高度(m )储液体积 (m 3)储液重量 (kg )2r 3LLr 2arcsi4r*r 2rh-r 2以储罐底部为起点的液咼该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2 2 2 2 2 2务告务 1 其中a=b=r,则有x 2 务 1 a b c a c垂直于y 轴分成无限小微元,任一微元面积为:S yi —(a 2 y 2)a当液面高度为h 时,椭圆球体内液氨容积为h「3 o 3V1=aS yj dya^(a 2 y 2)dy許2h自(2 )直段筒体部分:筒体的纵断面方程为x 2 y 2 a 2任一微元的面积为S yj 2、.、a 2 y 2dy则筒体部分容积为:L 2 a 2 y 2dy La 2(arcsin 」aahV2aSyj.2 _____________a 2八 2)( arcsin -)2a 2(3)卧式储罐储液总体积总容积为V 二V1+V2 ,232c 2- 4h 2a 2(. h h r .2、V= (a h)+ La (arcsin 2 ; a h ) a 3 3 a a2此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:21 三 Lr 2arcsin^ 3L rr 2-h 2r 21 50 1.3 0.65 8.58 0 1.3 25.078 25.0780.31%1 50 1.3 0.65 8.58 0.975 2.275 46.537 46.5371501.30.658.581.32.650.15550.1550.31%若液位高度h 以卧罐底部为起点,如下图/\ A / __________\rf (1)f\ y丿 1 二;o h \ ............. .... J V7\…一j... J■厶■N K A *则卧式储罐内储液总体积计算公式:若密度为p,则卧式储罐内储液总重量为:m hV hprLhV hm h液体密度 储罐半径 圆柱体部分长度储液液位高度储液体积 储液重量(kg )(kg/m 3)(m )(m )(m )(m 3)11.3 8.580.3253.619 3.6192r3LLr 2 arcsi®rh-r r 2h-r 2其它方法如下:第一种方法| PDF.卧式储罐不同液位 下的容积简化计算公卧式储罐内储液总体积计算公式:(hr ) 2--------------- K r2l (h r )[1」 宀]L[( h r)「2hr h 2 r 2 arcsi n( ---------------------------- )]3 rr若密度为p,则卧式储罐内储液总重量为:Vh V此方式用到参数较多P、V、r、l、L、h。
卧式椭圆形封头贮槽计量容积的计算

α 2 rh - h 2 / r) 1 = 2 arc sin (
2 rh - h 2 。
α 2 rh - h 2 / r) 2 = 360 - 2 arc sin (
( r ≤h ≤ 2 r) ,
截面椭圆的面积为 : F =π( c/ 2 ) b , 则 π Fh = ( / 2) (2
( πh i / r ) ( 2 rh - h2 ) ( hi / r) ] 2 rh - h2 = F2 L = L { ( h - r)
2 rh - h 2 + 2 rh - h2 / r) ]}
( r ≤h ≤ 2 r) ( 4)
( πr2 / 180) [ 180 - arc sin (
2 椭圆形封头部分的液体体积计算
图1 卧式标准椭圆形封头贮槽
贮槽两端的椭圆封头合并为椭球一起计算 。 椭圆方程为 : x 2 / r2 + y 2 / h 2 i =1, 式中 h i 为椭圆封头的曲面高度 ( 内高度 , 不含 直边) 。 液面高度为 h 时截面椭圆短轴为 2 b , 则 ( r h , b) 这一点能满足椭圆方程 , 则 : ( r - h ) 2 / r2 + b2 / h 2 i =1, bi = ( h i / r )
( πh i / r) ( rh2 - 1/ 3 h 3 ) V h1 = V + V 1 V h2 = V + V 2 ( 0 ≤h ≤ 2 r) ( 6) ( 0 ≤h ≤r) , ( r ≤h ≤ 2 r) ,
πr2 / 180) arc sin ( +(
2 3
2 rh - h 2 / r) ]
4 结语
本改造项目无需投资 , 通过巧妙选择设计平衡 管接点位置 ,不仅使长期困扰生产的技术问题得到 了解决 ,而且降低了硫酸的消耗 ,硫酸单耗由改造前 87 kg/ ( t ・ 碱) 降低至改造后 28 kg/ ( t ・ 碱) ,年降低硫 酸消耗 885 t ,节约资金 53. 1 万元 。同时增强了生 产的连续性 , 延长了钢制工艺设备的更换 、 维修周 期 。需要指出的是 : 今后有必要增大填料塔塔径 ,这 样有利于在大电流条件下操作 , 可以弥补泡罩塔因 操作弹性小产生大量雾沫夹带的缺点 ; 还可以在差 压变送器连接方式方面尝试革新 , 如将变送器置于 电解工序后延长电信号导线 ,缩短氯气差压导输管 , 使变送器带动的气动阀能在允许调节范围内正常工 作。 [ 编辑 : 蔡春艳 ]
卧式储罐不同液位下的容积计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图d参数:l :椭圆圭寸头曲面高度(m );l i :椭圆圭寸头直边长度(m);L :卧罐圆柱体部分长度(m);r :卧式储罐半径(d/2, m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);P储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下卧式储罐内储液总体积计算公式:若密度为p,则卧式储罐内储液总重量为:m h V h表1卧式储罐不同液位下容积(重量)PrLhV hm h液体密度 (kg/m 3)储罐半径 (m )圆柱体部分长度(m )储液液位高度(m )储液体积 (m 3)储液重量 (kg )2r 3LLr 2arcsi4r*r 2rh-r 2以储罐底部为起点的液咼该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2 2 2 2 2 2务告务 1 其中a=b=r,则有x 2 务 1 a b c a c垂直于y 轴分成无限小微元,任一微元面积为:S yi —(a 2 y 2)a当液面高度为h 时,椭圆球体内液氨容积为h「3 o 3V1=aS yj dya^(a 2 y 2)dy許2h自(2 )直段筒体部分:筒体的纵断面方程为x 2 y 2 a 2任一微元的面积为S yj 2、.、a 2 y 2dy则筒体部分容积为:L 2 a 2 y 2dy La 2(arcsin 」aahV2aSyj.2 _____________a 2八 2)( arcsin -)2a 2(3)卧式储罐储液总体积总容积为V 二V1+V2 ,232c 2- 4h 2a 2(. h h r .2、V= (a h)+ La (arcsin 2 ; a h ) a 3 3 a a2此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:21 三 Lr 2arcsin^ 3L rr 2-h 2r 21 50 1.3 0.65 8.58 0 1.3 25.078 25.0780.31%1 50 1.3 0.65 8.58 0.975 2.275 46.537 46.5371501.30.658.581.32.650.15550.1550.31%若液位高度h 以卧罐底部为起点,如下图/\ A / __________\rf (1)f\ y丿 1 二;o h \ ............. .... J V7\…一j... J■厶■N K A *则卧式储罐内储液总体积计算公式:若密度为p,则卧式储罐内储液总重量为:m hV hprLhV hm h液体密度 储罐半径 圆柱体部分长度储液液位高度储液体积 储液重量(kg )(kg/m 3)(m )(m )(m )(m 3)11.3 8.580.3253.619 3.6192r3LLr 2 arcsi®rh-r r 2h-r 2其它方法如下:第一种方法| PDF.卧式储罐不同液位 下的容积简化计算公卧式储罐内储液总体积计算公式:(hr ) 2--------------- K r2l (h r )[1」 宀]L[( h r)「2hr h 2 r 2 arcsi n( ---------------------------- )]3 rr若密度为p,则卧式储罐内储液总重量为:Vh V此方式用到参数较多P、V、r、l、L、h。
椭圆封头卧式贮槽的体积计算

椭圆封头卧式贮槽的体积计算 一,椭圆封头卧式贮槽的结构;L ;桶的长度(含封头的直边)a;桶半径b;封头的内高二,圆桶的处理;圆桶的截面○3是一个矩形。
矩形的长边恒为L ,短边为XOZ 坐标中Z 值的2倍。
而在XOZ 中根据圆的特性方程有;z 2+x 2=a 2 即z =22x a -。
则矩形的面积为; S 1=2L 22x a -三,封头的处理;两端封头合并后成为椭球体即图○1,它的截面○2是一个椭圆。
椭圆的长边为z,短边为y 。
在XOY 坐标中根据椭圆的特性方程有;12222=+ax b y 即y=22x a a b -。
则椭圆的面积为; S 2=π22x a -22x a a b -=)(22x a ab -π 四,体积公式;对于任一点X ,对应的体积为;V=⎰-x a S 1+S 2 dx=⎰-xa 2L 22x a -+)(22x a ab -π dx=2L x a a x a x a x -⎥⎦⎤⎢⎣⎡+-arcsin 22222+a b πx ax x a -⎥⎦⎤⎢⎣⎡-332 =2L ⎥⎦⎤⎢⎣⎡++-4arcsin 222222a a x a x a x π+a b π⎥⎦⎤⎢⎣⎡+-323332a x x a 当x=h-a V=2L ⎥⎦⎤⎢⎣⎡+-+---4arcsin 2)(22222a a a h a a h a a h π+a b π⎥⎦⎤⎢⎣⎡+---323)()(332a a h a h a =L ()⎪⎪⎭⎫ ⎝⎛-+⎥⎦⎤⎢⎣⎡+-+--32arcsin 232222h ah a b a a a h a h ha a h ππh 液位高度a 封头半径b 封头曲面高度L 筒体长度。
卧式储罐不同液位下的容积(质量)计算
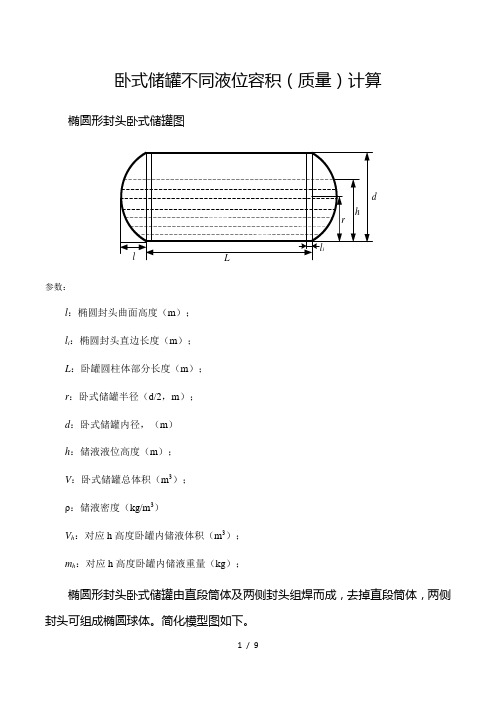
卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c++= 垂直于y 轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为 V1=hyi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a += 任一微元的面积为yj S = 则筒体部分容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h若液位高度h 以卧罐底部为起点,如下图则卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=其它方法如下:第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐内储液总体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
利用液面高度计算贮槽贮量_卧式椭圆封头贮槽
设椭圆球缺的体积为 v2
∫ V 2 =
0 - (a b)
〔H b2- H 2
2 (H + Z ) Z -
(H + Z ) 2 + Z 2 a rcsin (H Z ) +
1 2
ΠZ
2〕d y
∫0
=
〔H - (a b) b2- H 2
2 (H + Z ) Z - (H + Z ) 〕d y
∫ ∫ +
0
H 2) 〕4b2 - (a b)
b2- H 2 Z 2a rcsin (H
Z)dy
∫ ∫ 0
0
=
(b2 -
a2) - (a b)
b2- H 2 (a 2 -
y 2) a rcsin (aH
b
a2 - y 2) dy - (a b)
b2 -
〕 H 2 0 - (a b)
b2- H 2
1 2
ΠZ
2d
y
r)
r〕+
1 2
Πr2 }
(L
+
2l)
∵ r= b h = H + r
∴ V = 〔H
b2- H 2 + b2 a rcsin (H
b) +
1 2
Πb2 〕(L
+
2h )
112 封头部分体积的计算
封头部分的体积可分为两部分 (见附图 3) ,
一部分为和 x oz 平面平行方向的截面为圆的椭
球缺的体积计算, 另一部分为和 x oz 平面平行
∫ = H
0 - (a b)
b2- H 2
Z2 - H 2 dy
卧式储罐不同液位下的容积(质量)计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c++= 垂直于y 轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为V1=hyi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a +=任一微元的面积为yj S = 则筒体部分容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h若液位高度h 以卧罐底部为起点,如下图则卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=其它方法如下:第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐内储液总体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
卧式储罐不同液位下的容积(质量)计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h :对应h 高度卧罐内储液重量(kg );椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c++= 垂直于y 轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为 V1=hyi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a +=任一微元的面积为yj S = 则筒体部分容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h若液位高度h 以卧罐底部为起点,如下图则卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=其它方法如下: 第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐内储液总体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
卧式椭圆形封头贮罐容积的计算
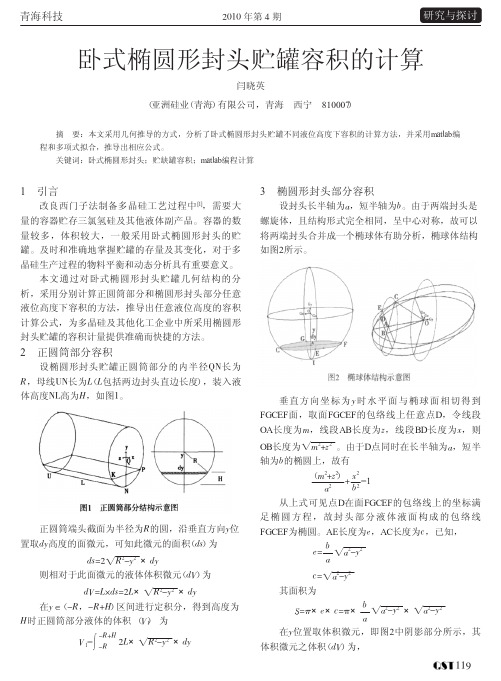
计的零位安装位置比罐底部要高出一定数值,故采用 液位计计数计算液体体积时,要加上零位以下的液体 体积。
图3为不同液位时,实例采用的贮罐所对应液体 体积曲线。
图3 不同液体对应液体体积关系曲线
综上所述,卧式椭圆形封头贮罐在任意液位下的 容积是可以通过相应液位计算出来的。
clear;
clc;
R=1.5;
L=7.08000;
b=0.76400;
H=0:.05:2*R;
x=H- R;
y=- R;
V1=2*L* (x/2.*sqrt (R^2- x.^2)+R^2/2*asin (x./R)
- (y/2.*sqrt (R^2- y.^2) +R^2/2*asin (y./R)));
改良西门子法制备多晶硅工艺过程中[1],需要大 量的容器贮存三氯氢硅及其他液体副产品。容器的数 量较多,体积较大,一般采用卧式椭圆形封头的贮 罐。及时和准确地掌握贮罐的存量及其变化,对于多 晶硅生产过程的物料平衡和动态分析具有重要意义。
本文通过对卧式椭圆形封头贮罐几何结构的分 析,采用分别计算正圆筒部分和椭圆形封头部分任意 液位高度下容积的方法,推导出任意液位高度的容积 计算公式,为多晶硅及其他化工企业中所采用椭圆形 封头贮罐的容积计量提供准确而快捷的方法。
V2=pi*b*H.^2/R.* (R- H/3);
V=V1+V2;
pp=polyfit (H,V,5);
hi=[0,R,2*R]
Vi=polyval (pp,h)i
ph=poly2str (pp,'h)'
卧式椭园形封头贮槽内液体体积(重量)的计算

卧式椭园形封头贮槽内液体体积(重量)的计算
樊恒鑫;祖庸
【期刊名称】《河北化工》
【年(卷),期】1990(000)002
【摘要】在化工厂中,经常用到各种规格的卧式椭园形封头贮槽,人们随时需知道贮槽内的液体实际贮量是多少,而目前生产厂家常用液面计来进行计量。
由于液面计的刻度多用固定体积的水来标定,此方法不仅麻烦,劳动量大,标出的刻度不均匀,且因水和所盛液体密度不同,标出的刻度往往不够准确。
所以经常发生管理部门和生产部门为产量或原材料的消耗量多少而争执。
为方便、准确地计量贮量。
【总页数】5页(P21-24,28)
【作者】樊恒鑫;祖庸
【作者单位】不详;不详
【正文语种】中文
【中图分类】TQ053.2
【相关文献】
1.卧式椭圆形封头贮槽中液体体积与液位高度的数学关系 [J], 谢卫东
2.各种形状封头的圆筒形卧式容器在不同液面高度时液体体积计算的统一表达式[J], 蒋心亚;宗光
3.关于卧式贮槽内液体体积的计算 [J], 杨鹤梧
4.卧式贮槽内液体体积的计算 [J], 杨鹤梧
5.用计算机对椭园形封头卧式贮罐的标定 [J], 葛广海;蒲实
因版权原因,仅展示原文概要,查看原文内容请购买。
各种常见油罐储油量的计算方法

各种常见油罐储油量的计算方法摘要:本文介绍了一些常见形状的储油罐油量的计算方法,并给出了每种形状的储油罐容积的计算公式和整个推导过程,供各位同仁共同探讨和分享。
现实生活中,尽管储油罐的形状各式各样,仔细分析无非存在以下两种结构:卧式结构和立式结构。
无论是卧式结构还是立式结构,都有可能存在半椭圆形封头、平面封头、半圆形封头、圆锥形封头等。
笔者在计算储油罐的过程中,积累了大量的经验,现简要做一介绍。
一、椭圆封头卧式椭圆形油罐这种油罐的形状一般是两端封头为半椭球形,中间为截面积是椭圆形的椭圆柱体,如图1—1、图1-2所示.计算时,可以把这种油罐的容积看成两部分,一部分为椭球体(把两端的封头看作是一个椭球),另一部分为平面封头中间截面为椭圆形的椭圆柱体,见图1-3、图1—4所示,然后,采用微积分计算任一液面高度时油罐内的容积。
我们建立如图1—3、图1—4所示的坐标系,设油罐除封头以外的长度为L ,其截面长半轴为A ,短半轴为B 。
椭球部分的长半轴为B ,短半轴为C,则在图1—3、图1-4所示的坐标系中,分别得到椭圆的方程为: 在某一液面高度H 时,油罐内油的容积为:由(1)得: L C BA y图1-2:椭圆封头卧式椭圆形油罐结构图 图1-1:椭圆封头卧式椭圆形油罐实体图 H(0,2b)a Δy - a (0,b) 0x y 图1-3:椭圆柱体剖面图 L H(0,2b)CΔy- C (0,b) 0 z 图1-4:封头椭球体剖面图 dyxz xL 2V H⎰π+=)(2y By 2BAx -=C(3) (4)⎰⎰π+=H 0Hxzdyxdy L 21B B y A x 2222=-+)((1) (2) 1C z B B y 2222=+-)(由(2)得: 将(4)、(5)代入(3)得:公式(6)即为任意截面高度时油罐中油的容积。
若用余旋计算,还可以得到如下的公式:二、平面封头卧式椭圆形油罐这种油罐的形状一般两端为平面封头,中间截面积为椭圆形的椭圆柱体,如图2—1、图2—2所示.这种油罐任一液面高度时,油罐内油的容积的计算公式可以参照上述方法推导,但要比椭圆封头卧式椭圆形的油罐简单的多。
