计算封头容积
椭圆形封头卧式容器不同液面高度的容积计算

椭圆形封头卧式容器不同液面高度的容积计算新疆工学院孟永彪在设计卧式容器时,常常要计算不同液面高度所对应的容积,有时还需列出容积—液位高度对照表或图。
例如,在盛装有毒有害介质的卧式储罐设计中,要根据体积充装系数确定最高液面高度并加以标识。
在一般资料中仅能查到容器的全容积计算公式,而要计算不同液面高度下的容积则需设计者自行推导公式计算。
本文以标准椭圆形封头卧式容器为例介绍不同液面高度下的容积计算方法,并以液化石油气储罐为例编制了QUICK BASIC程序,此法仅供大家参考。
1卧式容器的组成卧式容器是由筒体和两封头组焊而成(如图1),常用的封头为标准椭圆封头。
2卧式容器2.1计算简图及说明计算简图如图2。
L———筒体长度(两封头切线间的距离,含直边段长度)D i———封头及筒体内直径h i———封头曲面深度2.2不同液面高度下封头的容积计算如图2,可假想将卧式容器两端的曲面部分合并,则形成一个完整的椭球面。
2==i ih R c a 122222=++cz a y x )(21222y x a z +-=dxy x a dy h a y a )(2222022+-=⎰⎰--)323(23331a h h a V +-=π其中,a=b=R i因此,椭球面的方程为:推导出: 当容器内的液面高度为h 时(如图3所示)。
封头的容积公式推导:对其积分得从上式可看出,h 变化,V 1也随之变化。
2.3 不同液面高度筒体的容积计算在计算筒体的容积时,忽略尺寸公差及制造误差等因素,可将其断面方程为x 2+y 2=a 2的一圆柱体进行计算,那么如图3所示液面高度的筒体容积为:令:y=acos θ dy=-asin θd θdxdy y x a V s )(2122221+-=⎰⎰dx y x a dy h a y a y a )(2122222222+-=⎰⎰----dy y a L V h a⎰--=2222dy y a L h -=222当 y=-a 时,θ=π;当y=h 时,代入公式积分得:2.4 卧式容器在不同液面高度下的容积通过以上V 1,V 2的计算公式,可计算出卧式容器在不同液面高度下的容积之和V :3 利用QUICK BASIC 语言进行卧式容器的容积计算要计算不同液位高度下的容积以表格、曲线的形式列出是很麻烦的,因此本文利用简便易行的QB 编制程序,当然编程语言可以有多种,本文愿起到抛砖引玉的作用。
椭圆封头液位容积计算公式

椭圆封头液位容积计算公式要说这椭圆封头液位容积计算公式啊,还真得细细道来,不然真怕你们这帮子人听得云里雾里的。
那天,我正琢磨着家里那台液化石油气储罐的容量,突然就想起了这椭圆封头的事儿。
你们也知道,这椭圆封头啊,就像是那竖直面的椭圆绕了个竖直Z轴转了个360度,成了个空间曲面实体。
你说这形状,它既不方也不圆,咋算容积呢?我开始琢磨,这封头上任意一点的方程,不就是个椭圆方程嘛。
咱可以把h当成纵坐标,r当成横坐标。
但光琢磨不行啊,得动手。
我翻箱倒柜地找出了那张满是公式的旧纸,开始在上面写写画画。
经过一番折腾,我终于找到了一个公式:V = 0.0002618 L (D2。
这V啊,就是容积,L是椭圆封头的长度,D是直径。
你说这公式咋来的?这可是根据椭圆封头的几何形状推导出来的,别看它长得复杂,用起来可方便了。
不过,光有公式还不行,得验证验证。
我找来了那个液化石油气储罐,量了量封头的长度和直径,然后往罐里倒了点水,看看水位到哪,再用公式一算,嘿,还真准!这还不算完,我还琢磨着,这椭圆封头要是拼在一起,不就成了个椭圆球体了嘛。
那我能不能根据这个来求液位从0到H点的体积呢?说干就干,我又开始在那张旧纸上写写画画,画了个椭圆球体,然后过x轴上的一点作了个垂直于x轴的平面,截得一椭圆截面。
这一截啊,截出个椭圆面积公式来:S = πab。
咱再根据积分法则求椭圆球体体积,这一通算啊,累得我是满头大汗。
但功夫不负有心人,我终于把液位容积的公式给弄明白了。
你说这过程啊,真是又枯燥又乏味,但我一想到能用这公式来算储罐的容量,心里就美滋滋的。
你说这数学啊,还真是挺有意思的,能解决实际问题,还能让人乐在其中。
后来啊,我跟我那帮子朋友一吹嘘,他们都说我这脑袋瓜子聪明,能琢磨出这玩意儿来。
我听了心里那叫一个得意啊,但面上还得装出一副谦虚的样子,说:“哪里哪里,都是被逼出来的。
”所以啊,这椭圆封头液位容积计算公式啊,看似复杂,实则简单。
标准封头计算公式刷漆
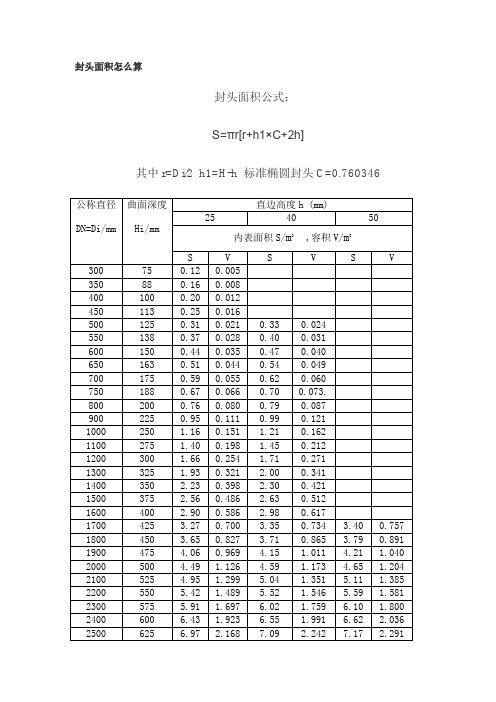
封头面积怎么算封头面积公式:S=πr[r+h1×C+2h]其中r=Di/2 h1=H-h 标准椭圆封头C=0.760346S=π×(D+A)×A式中 D——直径;A——法兰翻边宽。
(6)带封头的设备防腐(或刷油)工程量计算式:S=L×π×D+(D÷2) 2×π×1.5×N式中 N——封头个数;1.5——系数值。
3、绝热工程量。
(1)设备筒体或管道绝热、防潮和保护层计算公式:V=π×(D+1.033δ)×1.033δS=π×(D+2.1δ+0.0082)×L式中 D——直径1.033、2.1——调整系数;δ——绝热层厚度;L——设备筒体或管道长;0.0082——捆扎线直径或钢带厚。
(2)伴热管道绝热工程量计算式:①单管伴热或双管伴热(管径相同,夹角小于90°时)。
D′=D1+D2 +(10~20mm)式中D′——伴热管道综合值;D1 ——主管道直径;D2 ——伴热管道直径;(10~20mm)——主管道与伴热管道之间的间隙。
②双管伴热(管径相同,夹角大于90°时)。
D′=D1+1.5D2 +(10~20mm)③双管伴热(管径不同,夹角小于90°时)。
D′=D1 +D伴大+(10~20mm)式中D′——伴热管道综合值;D1 ——主管道直径。
将上述D′计算结果分别代入相应公式计算出伴热管道的绝热层、防潮层和保护层工程量。
(3)设备封头绝热、防潮和保护层工程量计算式。
V=[(D+1.033δ)÷2]2×π×1.033δ×1.5×NS=[(D+2.1δ)÷2]2×π×1.5×N(4)阀门绝热、防潮和保护层计算公式。
V=π×(D+1.033δ)×2.5D×1.033δ×1.05×NS=π×(D+2.1δ)×2.5D×1.05×N(5)法兰绝热、防潮和保护层计算公式。
常用容器容积及封头下料计算公式

常用容器圆筒体及封头几何容积、下料计算公式1. 圆柱体容积:V=H Di 22⎟⎠⎞⎜⎝⎛π=; H R 2π2. 椭圆形封头容积:V 封=⎟⎠⎞⎜⎝⎛+6Di 4Di h π; 3. 半球形封头容积:V 封=312Di π=332R π; 4. 搅拌容器(椭圆底)容积:V 容=⎟⎠⎞⎜⎝⎛++642Di h H Di π=⎟⎠⎞⎜⎝⎛++67854.02Di h H Di ; (搅拌容积指筒体与下底的容积之和。
搅拌容积与公称容积V N 的允许偏差为公称容积值的0~+16%)。
5. 储存容器(椭圆盖、底)全容积:V 全=⎟⎠⎞⎜⎝⎛++3242Di h H Di π=⎟⎠⎞⎜⎝⎛++327854.02Di h H Di ; (全容器指筒体与上、下底的容积之和。
全容积与公称容积的允许偏差为公称容积值的±3%)。
注: 以上式中代号:V—圆柱体容积(m 3);V 封—封头容积(m 3);V N —公称容积(m 3);V 全—容器全容积(m 3); Di—容器内直径(m);H—圆筒体高度(m);R—筒体(或封头)内半径(m);h—封头直边高度(m);π—圆周率3.1415926…;1. 标准椭圆形封头下料直径:D 0=; ))((4)(38.12δ++++h S Di S Di2. 标准椭圆形封头下料直径简式:D0=202)2(15.1+++h S Di ;3. 标准椭圆形封头下料直径简式:D 0=δ++h Di 22.1;4. 半球形封头下料直径:D 0=)(422δ++h Di Di ;5. 半球形封头下料直径简式:D 0=δ++h Di 242.1;注:以上式中代号:D 0—封头下料直径(㎜); Di—容器内直径(㎜);H—筒体高度(㎜);h—封头直边高度(㎜);S—封头板厚度(㎜);δ—封头边缘加工余量㎜(一般取封头厚度S);S<10时,h=25㎜;10≤S≤18时,h=40㎜;S≥20时,h=50㎜。
30度锥形封头容积表

30度锥形封头容积表
30度锥形封头是一种常见的容器配件,用于制造储罐、反应釜等设备。
由于其特殊的形状,其容积计算公式与其他类型的封头有所不同。
以下是一张30度锥形封头容积表,可以帮助您计算容积。
同时,我们也为您准备了一些使用建议和注意事项,希望对您有所帮助。
30度锥形封头容积表:
外径(D)内径(d)高度(H)容积(V)
30028830001147
40038640003008
50048450005719
60058260009675
700680700014876
800778800021515使用建议:
1.在选购30度锥形封头时,需要根据所需容积和设备尺寸选择合适的尺寸。
2.在安装30度锥形封头时,需要注意其安装方向和位置,避免安装不当导致泄漏或损坏。
3.在使用30度锥形封头的储罐或反应釜时,需要注意其搅拌和卸料方式,以确保容器内物料均匀和完全卸出。
注意事项:
1.在对30度锥形封头进行计算容积时,需要使用对应的公式和容积表,以确保计算准确。
2.在操作30度锥形封头所在的设备时,需要遵守工艺规程和安全操作规范,避免发生安全事故。
3.在使用30度锥形封头的设备维护时,需要定期检查封头的密封性和外观状况,及时处理封头损坏和更换。
总之,30度锥形封头是一种重要的容器配件,其容积计算和使用需要注意一些建议和注意事项。
我们希望本文能帮助您更加了解30度锥形封头的容积和使用,为您的生产提供指导和帮助。
封头容积重量计算

封头容积重量计算封头是压力容器的一种常见部件,用于密封容器的顶部或底部。
其主要作用是承受内部压力,确保容器的密封性。
在设计压力容器时,封头的容积和重量计算是非常重要的。
容积计算可以帮助确定容器的大小,而重量计算可以帮助确定容器的材料选择和支撑结构设计。
下面将详细介绍封头容积和重量的计算方法。
一、封头容积计算1.半球形封头容积计算半球形封头是一种常用的封头形式,其容积计算公式为:V=(2/3)πr³2.椭圆形封头容积计算椭圆形封头也是一种常用的封头形式,其容积计算公式为:V=(πa²b)/6其中,V代表容积,π代表圆周率,a代表封头的长轴半径,b代表封头的短轴半径。
3.球冠形封头容积计算球冠形封头是封头的一种特殊形式,其容积计算公式为:V=(πh²/3)*(3R-h)其中,V代表容积,π代表圆周率,h代表球冠的高度,R代表球冠的半径。
二、封头重量计算1.半球形封头重量计算半球形封头的重量计算公式为:W=(πd³*t)/12*ρ其中,W代表封头的重量,π代表圆周率,d代表封头的直径,t代表封头的厚度,ρ代表封头材料的密度。
2.椭圆形封头重量计算椭圆形封头的重量计算公式为:W=(π(a²-b²)*t)/6*ρ其中,W代表封头的重量,π代表圆周率,a和b代表封头的长轴和短轴半径,t代表封头的厚度,ρ代表封头材料的密度。
3.球冠形封头重量计算球冠形封头的重量计算公式为:W=(π(h*(3R-h)²)*t)/12*ρ其中,W代表封头的重量,π代表圆周率,h代表球冠的高度,R代表球冠的半径,t代表封头的厚度,ρ代表封头材料的密度。
需要注意的是,在进行容积和重量计算时,需要确保所使用的单位统一,如容积的单位可以选择立方米(m³),千立方米(m³),重量的单位可以选择千克(kg),吨等。
以上是关于封头容积和重量计算的详细介绍。
标准椭圆形封头容积计算公式

标准椭圆形封头容积计算公式椭圆形封头是一种常见的封头形式,在很多工业设备中都能见到它的身影。
要计算标准椭圆形封头的容积,咱们得先搞清楚它的一些基本特点和相关公式。
标准椭圆形封头的形状就像一个被压扁的半椭圆,它的长半轴是a ,短半轴是 b 。
那它的容积计算公式是V = πabh / 3 ,其中 h 是封头的直边高度。
我还记得之前在工厂实习的时候,就碰到过需要计算椭圆形封头容积的情况。
那是一个生产化工储罐的车间,有一批新的储罐正在制造中。
当时负责这个项目的工程师拿着图纸,眉头紧皱,嘴里还念叨着:“这封头的容积可不好算啊。
”我凑过去一看,原来他正在为计算标准椭圆形封头的容积而烦恼。
我自告奋勇地说:“要不我来试试?”工程师半信半疑地把任务交给了我。
我拿起笔,对照着图纸上的尺寸,先确定了长半轴 a 和短半轴 b 的数值,再量出直边高度 h 。
然后,我按照公式V = πabh / 3 ,一步步认真计算起来。
计算的过程可不能马虎,每一个数字都得准确无误。
我一边算,一边在心里默默念叨:“千万别出错,千万别出错。
”汗水都从额头冒了出来。
经过一番紧张的计算,终于得出了结果。
我把结果递给工程师,他看了看,眼睛一亮,笑着说:“不错不错,小伙子挺厉害啊!”那一刻,我心里别提多高兴了,就感觉自己像是解决了一个大难题的英雄。
在实际应用中,这个计算公式非常重要。
比如说在设计储存液体的容器时,如果不知道封头的容积,就没办法准确确定整个容器的容量,可能会导致液体装不下或者浪费空间。
而且,不同尺寸的封头,容积也会有很大差别。
所以,准确计算封头容积对于保证设备的正常运行和生产的顺利进行至关重要。
总之,标准椭圆形封头容积的计算公式虽然看起来简单,但在实际工作中却能发挥大作用。
咱们可得把它掌握好,这样在遇到相关问题时,就能轻松应对啦!。
封头容积、质量、内表面积和总高度计算

单 位mm mm t/m 3mm mm 单 位mm mm mm mm t/m 3mm 总 深 度H=D i /2±h=350.00容 积内表面积封头内壁短半轴 b封头内壁长半轴 a600300材 料 密 度 ρkg 16Mn 封头内表面积、容积、质量计算球形封头(HHA)基 本 数 据简 图内表面积7.85封头名义厚度 δn 4直 边 高 度 h25封 头 材 料650直 边 高 度 h25注:1、当为带直边的半球,计算时取 "+" 号,当为准半球时,计算时取"-"号;2、当为不带直边的半球,h=0。
椭圆形封头(EHA)基 本 数 据简 图封 头 内 径 D i1200A = 0.5πD i 2±πD i h =V=封 头 材 料材 料 密 度 ρ容 积16Mn 7.85封头名义厚度 δn 4质 量封 头 内 径 D i714712.33mm 2mm 3###########1655186.67mm 2254469004.9mm 322.71=±=h D D V i i 2341121ππ=⨯±-+±+=-6232310]}41121[])2(41)2(121{[h D D h D D W i i n i n i δδρπ=+=h a b a V 2232ππ=+-+-+=ah b a b a b a ba a A ππ2]}1)(ln[1)({22mm 单 位mm mm mm mm t/m 3mm mm 单 位mm mm mm mm t/m 3mm 质 量50.71325.00总 深 度H=D i /4+h=总 深 度H o =D o /4+h=119.25封 头 内 径 D i400kg 参数计算θ1.110θ为弧度C 10.224C 2-0.142质 量碟形封头(THA)基 本 数 据简 图封头名义厚度 δh 4材 料 密 度 ρ7.85封头名义厚度 δn 810.68kg 内表面积容 积直 边 高 度 h25球面部分内半径 R i400过渡段转角内半径 r i40封 头 材 料16Mn 材 料 密 度 ρ7.858444194.61mm 3封 头 材 料16Mn 167126.12mm 2椭圆形封头(EHB)基 本 数 据简 图封 头 外 径 D o377直 边 高 度 h25封头外壁长半轴 a188.5封头外壁短半轴 b94.25=⨯-+---+=-6222210]})()()(32[)32{(h a b a h a b a W n n n δδδρπ=-+--=h a b a V n n n 22)()()(32δπδδπ=⨯+-++++=-6222210]}32[])()()(32{[h a b a h a b a W n n n δδδρπ=-+---+------+--=h a b a b a b a b a a A n n n n n n n n n n )(2]}1)(ln[1)()){((22δπδδδδδδδδδπ=--=i i i i r R r D 2/arccos θ==sin θC =-+=θθθθsin cos sin Ckg mm 单 位mm mm mm mm t/m 3mm kgmm 总 深 度H=(1-sin θ)R i +r i sin θ+h=102.516.10质 量W=ρ(V o -V)×10-6=0.010外壁所包体积内表面积容 积10252783.69mm 3总 深 度H o =(1-sin θ)R o +r o sin θ+h=102.51质 量W=ρ(V o -V)×10-6= 5.82内表面积容 积外壁所包体积180925.46参数计算θ1.110θ为弧度C 10.224C 2-0.142C 30.044C 40.010碟形封头(THB)基 本 数 据简 图封 头 外 径 D o400直 边 高 度 h25球面部分外半径 R o400过渡段转角外半径 r o40封 头 材 料16Mn 材 料 密 度 ρ7.85封头名义厚度 δh 4参数计算C 10.224C 2C 30.044C 4-0.142189813.86mm 29475416.34mm 38734004.71mm 3mm 29475416.34mm 3=++++=)4(234332221h D R C r C r D C r D C V i i i i i i i π=+-+-+∙=]2)sin 1()(sin 2[222h D R r r D A i i i i i θθθθπ==4sin 1θC =-+=θθθθsin 2cos sin 2C =---=θθθθθcos si n 3si n si n 233C =-+=3)sin 1)(sin 2(24θθC =+++++++++++∙=]4)2()()())(2()()2([234332221h D R C r C r D C r D C V h i h i h i h i h i h i h i o δδδδδδδπ=--=o o o o r R r D 2/arccos θ==4sin 1θC =-+=θθθθsin 2cos sin 2C =---=θθθθθcos si n 3si n si n 233C =-+=3)sin 1)(sin 2(24θθC =++++∙=]4(234332221h D R C r C r D C r D C V o o o o o o o o π=-+-+-+--+--=]4)2()()())(2()()2([234332221h D R C r C r D C r D C V h o h o h o h o h o h o h o δδδδδδδπ=-+--+--+∙--=]22)sin 1()()(sin )(2))(2[(222h D R r r D A h o h o h o h o h o δθδθθδθδδπ单 位mm mm t/m 3mm kg 单 位mm mm mm t/m 3mm 内表面积167738.804966887.51直 边 高 度 h25容 积材 料 密 度 ρ7.85封头名义厚度 δh 4mm 2mm 3封 头 内 径 D i400转角内半径 r i15封 头 材 料16Mn 总 深 度53.05质 量W=ρS z δn ×10-6= 4.18mm 平底形封头(FHA)基 本 数 据简 图内表面积A=2πD o h=容 积V=πh 2(D o -h/3)=52.71mm 参数计算hh zS zmm 52.44133138.88mm 2球冠形封头(SDH)基 本 数 据简 图封 头 外 径 D o400球面部分内半径 R i400封 头 材 料16Mn 材 料 密 度 ρ7.85封头名义厚度 δh 4131803.16mm 2mm 33305025.94=---=22)2(n o o o D D D h δ=--+-+=22)42()2()2(n o n o n o z D D D h δδδ=+=z n o z h D S )2(2δπ=--=))(231(n o D H δ=-++--=22)2(])2(2[i i i i i i r D h D r r D A πππππ=+-+-+=h D r r D r D V i i i i i i 232241])235()14(41[ππππkg mm 单 位mm mm mm °mm t/m 3mm V o =mm 3kg 单 位mm mm 锥形封头[CHA(60)]基 本 数 据简 图封头大端内径 D i 400封头小端内径 D is300质 量W=ρ(V o -V)×10-6=31.51封头小端内径 D is3000.785(θ为α弧度)C 10.177内表面积容 积14534576.35参数计算θC 2-0.064C 30.011外壁所包体积132211.64mm 2mm 310520888.80锥形封头[CHA(30)、CHA(45)]基 本 数 据简 图封头大端内径 D i400直 边 高 度 h25半 锥 角 α45过渡段转角内半径 r i50封 头 材 料16Mn 材 料 密 度 ρ7.85封头名义厚度 δh 4总 深 度H=r i +h=40.005655348.38外壁所包体积mm 3质 量W=ρ(V o -V)×10-6= 5.40总 深 度98.54mm 42344=+++-+++-+++=h D r r D r D V h i h i h i h i h i h i o 2322)2(41]))(235())(2)(14()()2(41[δπδπδδπδδπ==4sin 1θC =-+=θθθθsin 2cos sin 2C =---=θθθθθcos si n 3si n si n 233C =+---+-+∙=h D D r D r r D A i is i i i i i πθθπθθθπ}])cos 1(2{[sin 4)](sin 2[2222=---++++=}])cos 1(2{[tan 24)4(332332221is i i i i i i i i D r D h D r C r D C r D C V θθππ=+++-+--++++++++++=h D D r D h D r C r D C r D C V n i n is n i i n i n i n i n i n i n i o 2332332221)2(41}]cos 2[]cos 2)cos 1(2{[tan 24]4)2()())(2()()2([δπθδθδθθπδδδδδδπ=+++---=h r D r D H n i is i i o θδθθsin )(}2])cos 1(2{[tan 1mm °mm mm t/m 3mm 小端过渡段转角内半径 r s25大端内壁小弧段内表面积参数计算θ1.047(θ为α弧度)C 10.217C 2-0.126C 30.035直 边 高 度 h25半 锥 角 α60大端过渡段转角内半径 r i50封 头 材 料16Mn 材 料 密 度 ρ7.85封头名义厚度 δh 462951.52mm 2mm 2大端内壁小弧段所包围体积大端外壁小弧段所包围体积锥体内壁表面积mm 3mm 35059683.585660963.6612931.48mm 31877770.86mm 3小端内壁小弧段所包含体积小端外壁小弧段所包含体积1521613.64mm 3mm 2大端直边段内表面积31415.93大端直边段外壁容积3268513.00mm 3小端直边段23561.94mm 2548954.77mm 3锥体外壁锥体所包围体积锥体内壁锥体所包围体积大端直边段内壁容积561962.43mm 3小端内壁小弧段内表面积29579.20mm 23141592.65==4sin 1θC =-+=θθθθsin 2cos sin 2C =---=θθθθθcos si n 3si n si n 233C =-+∙=)](sin 2[221θθθπi i i r r D A =++=)(3322211i i i i i r C r D C r D C V π=+++++++=])())(2()()2([332221'1n i n i n i n i n i r C r D C r D C V δδδδδπ=+-+---=})])(cos 1(2[])cos 1(2{[sin 4222n s is i i r D r D A δθθθπ=+-+---=})])(cos 1(2[])cos 1(2{[tan 24332n s is i i r D r D V δθθθπ=+-+-+--=}]2)cos 1(2[]cos 2)cos 1(2{[tan 2433'2n s is n i i r D r D V δθθδθθπ=-+-+=)](sin )()(2[223θθδδθπn s n s is r r D A =+++-+=])()()([3322213n s n s is n s is r C r D C r D C V δδδπ=+--+-+-=]sin )cos sin sin 2(sin [][22332221'3θδδθθθθθδππn s n s n s is s s is s is r r r D r C r D C r D C V ==h D A i π4==h D V i 2441π=+=h D V n i 2'4)2(41δπ==h D A is π5常用不锈钢密度表材料名称密度t/mm31Cr18Ni91Cr18Ni9Ti00Cr18Ni14Mo2Cu2 0Cr18Ni11Ti0Cr18Ni12Mo2Ti 1Cr18Ni11Si4AlTi 7.927.98.03 8 7.9 7.51 8 8 7.97.74 7.761Cr13 2Cr13 3Cr13 4Cr137.76 7.75 7.751Cr19Ni9 0Cr18Ni9 00Cr19Ni110Cr13半锥角3045。
圆形封头容积的计算方法

圆形封头容积的计算方法
圆形封头是一种常用的容器头部形状,它由两个具有相同半径的半圆
形组成,可以用来封闭圆柱形容器。
在实际工程中,经常需要计算圆形封
头的容积,以便确定容器的储存或处理能力。
下面将介绍圆形封头容积的
计算方法。
首先,我们需要知道圆形封头的几何参数,包括半径(r),高度(h)和封头的类型。
圆形封头可分为顶封头和底封头,它们的几何形状略有不同。
1.计算顶封头容积:
顶封头是圆柱形容器顶部的封头,其容积可以通过以下公式计算:
V=(π*h^2*(3r-h))/6
2.计算底封头容积:
底封头是圆柱形容器底部的封头,其容积可以通过以下公式计算:
V=(π*h^2*(3r-2h))/6
3.计算全封头容积:
若需要计算整个圆形封头的容积,则需要将顶封头容积和底封头容积
相加。
V=2*(π*h^2*(3r-2h))/6
此外,当计算容积时,需要确保使用一致的单位。
通常情况下,容积
可以使用立方米(m³)、升(L)或加仑(gal)等单位。
总结:。
常用容器容积及封头下料计算公式

常用容器圆筒体及封头几何容积、下料计算公式1. 圆柱体容积:V=H Di 22⎟⎠⎞⎜⎝⎛π=; H R 2π2. 椭圆形封头容积:V 封=⎟⎠⎞⎜⎝⎛+6Di 4Di h π; 3. 半球形封头容积:V 封=312Di π=332R π; 4. 搅拌容器(椭圆底)容积:V 容=⎟⎠⎞⎜⎝⎛++642Di h H Di π=⎟⎠⎞⎜⎝⎛++67854.02Di h H Di ; (搅拌容积指筒体与下底的容积之和。
搅拌容积与公称容积V N 的允许偏差为公称容积值的0~+16%)。
5. 储存容器(椭圆盖、底)全容积:V 全=⎟⎠⎞⎜⎝⎛++3242Di h H Di π=⎟⎠⎞⎜⎝⎛++327854.02Di h H Di ; (全容器指筒体与上、下底的容积之和。
全容积与公称容积的允许偏差为公称容积值的±3%)。
注: 以上式中代号:V—圆柱体容积(m 3);V 封—封头容积(m 3);V N —公称容积(m 3);V 全—容器全容积(m 3); Di—容器内直径(m);H—圆筒体高度(m);R—筒体(或封头)内半径(m);h—封头直边高度(m);π—圆周率3.1415926…;1. 标准椭圆形封头下料直径:D 0=; ))((4)(38.12δ++++h S Di S Di2. 标准椭圆形封头下料直径简式:D0=202)2(15.1+++h S Di ;3. 标准椭圆形封头下料直径简式:D 0=δ++h Di 22.1;4. 半球形封头下料直径:D 0=)(422δ++h Di Di ;5. 半球形封头下料直径简式:D 0=δ++h Di 242.1;注:以上式中代号:D 0—封头下料直径(㎜); Di—容器内直径(㎜);H—筒体高度(㎜);h—封头直边高度(㎜);S—封头板厚度(㎜);δ—封头边缘加工余量㎜(一般取封头厚度S);S<10时,h=25㎜;10≤S≤18时,h=40㎜;S≥20时,h=50㎜。
封头重量和容积计算

封头重量和容积计算要计算封头的重量和容积,我们首先需要了解封头的几何形状和尺寸。
封头通常是用来封闭容器的一侧,它的形状可以是圆形、椭圆形或者其他形状,如扁球形、菱形等。
不同形状的封头会影响其重量和容积的计算方法。
下面我们以常见的半球形和扁球形封头为例进行计算。
1.半球形封头:首先,我们需要知道封头的半径(R)。
半球形封头的重量(W)可以通过以下公式计算:W=0.0034*π*R^2*t*ρ其中,0.0034是一个常数,表示封头材料的密度与重量的转换系数(单位为千克/立方米),π是圆周率,R是封头的半径,t是封头的厚度,ρ是封头材料的密度。
半球形封头的容积(V)可以通过以下公式计算:V=(2/3)*π*R^3其中,(2/3)*π*R^3是半球形封头的体积公式。
2.扁球形封头:扁球形封头的形状类似于半球形,但是其中心处略微凹陷。
同样,我们需要知道封头的半径(R)。
扁球形封头的重量(W)可以通过以下公式计算:W=0.0034*π*R^2*t*ρ*(1-0.577*(1-(t/R)))其中,0.577是一个常数,表示封头的变形系数,用于考虑扁球形封头的变形程度。
扁球形封头的容积(V)可以通过以下公式计算:V=(π*R^2)*(1-0.639*(t/R)+0.097*(t/R)^3)其中,0.639和0.097是扁球形封头的形状系数,用于考虑封头的形状对容积的影响。
需要注意的是,以上公式中的参数单位需要一致,例如,如果封头的半径单位为毫米,则其他线性尺寸也需要使用相同的单位。
当计算封头的重量和容积时,选择正确的公式和参数是非常重要的。
不同的形状和尺寸会有不同的计算方法,所以确保使用适用于特定封头的公式和参数才能得到准确的结果。
总之,通过掌握封头的几何形状和尺寸,我们可以使用相应的公式计算封头的重量和容积。
这对于设计和生产容器非常重要,确保其符合要求和预期。
罐体容积计算过程

罐体描述:单V形结构,小封头尺寸Ø1810mm,V形最大截面高度30mm,宽度2500mm,大封头直径Ø2060mm,筒体直线段(不含两端封头)长度8230mm;运输介质:粉煤灰;比重:1.0吨/立方米;罐体的容积计算:1、罐体额定容积=载质量(吨)/密度(吨/立方米)(立方米)2、罐体有效容积=罐体总容量=罐体额定容积x1.05=30.3x1.05=31.8(立方米)3、封头容积:封头为碟形封头,前封头底部面积同罐体前端截面积为2.51,后封头底部面积同罐体后端截面积为3.25,前封头蝶形封头高为370mm,后封头蝶形封头高为420mm,根据“JB/T4746-2002钢制压力容器用封头”标准附录E---表E.1DHB蝶形封头内表面积、容积查询表中的参数,则封头体积V封头=V1+V5≈0.64+1.0=1.64(立方米)4、利用CAXA程序自带的工具软件可以直接查询出各截面的面积,即:截面1:S1=2.51m;截面2:S2=4.26m;截面3:S3=5.80m;截面4:S4=S2=4.26m;截面5:S5=3.25m;罐体按外形尺寸计算容积:V罐体=V1+V2+V3+V4+V5=V封头+V2+V3+V4222=1.64+(S1+S2)/2xH1+(S2+S3)/2xH2+(S3+S4)/2xH3+(S4+S5)/2xH4=1.64+(2.51+4.26)/2X1.379+(S4.26+5.80)/2X2.655+(5.80+4.26)/2X3.319+(4.26+3.25)/2X0.876=39.65m3罐体计算容积x0.8= V总X0.8=39.65X0.8=31.72m³(立方米)<罐体有效容积=31.8(立方米)罐体外形尺寸和各截面位置:S1=2.51 m2S2= S4=4.26 m2S3=5.80 m2S5=3.25 m2。
圆形封头容积的计算方法

圆形封头容积的计算方法
一、引言
圆形封头是一种常用的容器封头,它有着极高的技术要求,特别是计算封头的容积。
确定封头容积是评价设计的一个重要指标,能够反映容器封头最终的结构和使用性能。
本文将介绍圆形封头容积计算方法,包括理论计算和有限元分析等。
二、圆形封头容积的理论计算
1、圆形封头理论容积的数学表达式为:V=A(1-cosθ)α,其中A为封头截面面积,θ和α分别为截面偏移角度和深度。
2、对于半圆形封头,其理论容积表达式为:V=πr2h,其中r为封头原半径,h为封头深度。
3、对于圆形螺纹封头,其理论容积表达式为:V=πρ2h,其中ρ为封头螺距半径,h为封头深度。
三、圆形封头容积的有限元分析
1、有限元分析可以预测封头内容的几何变形,从而精确计算封头容积。
2、使用有限元分析计算封头容积时,需要构建封头的三维模型,设置相关的网格参数和材料参数,并计算容积分布。
3、在计算封头容积时,需要考虑封头收缩的影响,可以采用体积范数方法来计算封头的容积收缩率。
四、结论
以上介绍了圆形封头容积的理论计算和有限元分析方法。
