2011 应用光学-1.3
应用光学课件-PPT

5)入射窗、出射窗、视阑之间得相互共轭关系。
大家应该也有点累了,稍作休息
大家有疑问得,可以询问与交流
10
例:有一光学系统,透镜O1、O2得口径D1=D2=50mm,焦距 f1′= f2′=150mm,两透镜间隔为300mm,并在中间置一光 孔O3,口径D3=20mm,透镜O2右侧150mm处再置一光孔O4,口 径D4=40mm,平面物体处于透镜O1左侧150mm处。求该系统 得孔径光阑、入瞳、出瞳、视场光阑、入窗、出窗得位 置与大小。
两正薄透镜组L1与L2得焦距分别为100mm与50mm,通光口径 分别为60mm与30mm,两透镜之间得间隔为50mm,在透镜L2之 前30mm处放置直径为40mm得光阑,问 1)当物体在无穷远处时,孔径光阑为哪个? 2)当物体在L1前方300mm处时,孔径光阑为哪个?
4、说明: 1)物体位置改变,原孔阑可能失去控制轴上点孔径角得作用,要重复上述 三个步骤确定孔阑。
工具显微镜中(β 准确)被测物得像与刻度尺相比较,可测物之长度。
物体不论处于何位 置,发出得主光线 都不随物体位置得 移动而变化;读出 刻尺面上光斑得中 心示值,即可求出 准确得象高。
三、 象方远心光路
1、 概念: 某些大地测量仪器或投影仪器中,为了消除像平面与标尺分划刻
线面不重合而引起得测量误差,在物镜得物方焦平面上加入一个光 阑作为孔径光阑,出瞳则位于像方无穷远,称为“像方远心光路”。 2、 应用:
3)物点在无限远时,各光孔像中,直径最小者即为入瞳。入瞳对应得实际 光孔即为孔径光阑。
例:有两个薄透镜L1与L2 ,焦距分别为90mm与30mm,孔径分 别为60mm与40mm,相隔50mm,在两透镜之间,离L2为 20mm处放置一直径为10mm得圆光阑,试对L1前120mm处 得轴上物点求孔阑、入瞳、出瞳得位置与大小。
应用光学课程设计-1-40

视场:; 出瞳直径:d = 5mm ; 镜目距:p = 25mm 分辨率:; 渐晕系数:k = 0.54棱镜出射面与分划板距离:a = 10 mm;棱镜和材料: 施密特屋脊棱镜(k = 3.04) 材料:k9目镜:2-35N0.2 10 倍炮对镜:视场:; 出瞳直径:d = 5mm ; 镜目距:p = 25mm 分辨率:; 渐晕系数:k = 0.55棱镜出射面与分划板距离:a = 42mm;棱镜和材料: 靴型屋屋脊棱镜(k = 2.98),材料:k9目镜:2-35N0.3 10 倍潜望镜:视场:; 出瞳直径:d = 5mm ; 镜目距:p = 25mm 分辨率:; 渐晕系数:k = 0.55棱镜出射面与分划板距离:a = 45 mm;潜望高:300 mm棱镜和材料: 普罗11型棱镜(k = 3.0),材料:k9目镜:2-35N0.4 10 倍潜望镜:视场:; 出瞳直径:d = 5mm ; 镜目距:p = 25mm 分辨率:; 渐晕系数:k = 0.575 ,棱镜出射面与分划板距离:a = 45 mm;潜望高:300 mm棱镜和材料: 五角屋脊棱镜(k = 4.233),材料:K9目镜:2-35视场:; 出瞳直径:d = 5mm ; 镜目距:p = 25mm 分辨率:; 渐晕系数:k = 0.64棱镜出射面与分划板距离:a = 10 mm;棱镜和材料: D1J-450屋脊棱镜(k = 3.552),材料:Bak7目镜:2-35N0.6 10 倍观察镜:视场:; 出瞳直径:d = 5mm ; 镜目距:p = 25mm 分辨率:; 渐晕系数:k = 0.64棱镜出射面与分划板距离:a = 10 mm;棱镜和材料: D1J-600屋脊棱镜(k = 2.646),材料:k9目镜:2-35N0.7 10 倍观察镜:视场:; 出瞳直径:d = 5mm ; 镜目距:p = 25mm 分辨率:; 渐晕系数:k = 0.64棱镜出射面与分划板距离:a = 10 mm;棱镜和材料: D1J-800屋脊棱镜(k = 1.96),材料:Bak7目镜:2-35N0.8 10 倍双目望远镜:视场:; 出瞳直径:d = 5mm ; 镜目距:p = 25mm 分辨率:; 渐晕系数:k = 0.54棱镜出射面与分划板距离:a = 28 mm;棱镜和材料: 普罗1型棱镜(k = 4),材料:k9目镜:2-35视场:; 出瞳直径:d = 5mm ; 镜目距:p = 25mm 分辨率:; 渐晕系数:k = 0.47棱镜出射面与分划板距离:a = 43 mm;棱镜和材料: 靴型屋脊棱镜(k = 2.98),材料:k9目镜:2-28N0.10 10 倍双目望远镜:视场:; 出瞳直径:d = 5mm ; 镜目距:p = 19.5mm 分辨率:; 渐晕系数:k = 0.52棱镜出射面与分划板距离:a =25mm;棱镜和材料: 普罗1型棱镜(k = 4),材料:k9目镜:2-28N0.11 10 倍观察镜:视场:; 出瞳直径:d = 4.5mm ; 镜目距:p = 19.5mm 分辨率:渐晕系数:k = 0.51棱镜出射面与分划板距离:a = 10mm;棱镜和材料: D1J-800屋脊棱镜(k = 1.96),材料:Bak7目镜:2-28N0.12 10 倍观察镜:视场:; 出瞳直径:d = 5mm ; 镜目距:p = 25mm 分辨率:; 渐晕系数:k = 0.53棱镜出射面与分划板距离:a = 10 mm;棱镜和材料: 别汉屋脊棱镜(k = 5.7),材料:Bak7目镜:2-28N0.13 10 倍观察镜:视场:; 出瞳直径:d = 5mm ; 镜目距:p = 25mm 分辨率:; 渐晕系数:k = 0.53棱镜出射面与分划板距离:a = 10 mm;棱镜和材料: 阿贝屋脊棱镜(k =5.196),材料:Bak7目镜:2-28N0.14 10 倍观察镜:视场:; 出瞳直径:d = 5mm ; 镜目距:p = 25mm 分辨率:; 渐晕系数:k = 0.53棱镜出射面与分划板距离:a = 10 mm;棱镜和材料: 列曼屋脊棱镜(k = 5.196),材料:Bak7目镜:2-28N0.15 10 倍观察镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.58棱镜出射面与分划板距离:a = 10 mm;棱镜和材料: 斯密特屋脊棱镜(k = 3.04),材料:k9目镜:2-25N0.16 10 倍观察镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.5棱镜出射面与分划板距离:a = 10 mm;棱镜和材料: D1J-450屋脊棱镜(k = 3.558),材料:k9目镜:2-25N0.17 10 倍观察镜:视场::; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm分辨率:; 渐晕系数:k = 0.42棱镜出射面与分划板距离:a = 10 mm;棱镜和材料: D1J-600屋脊棱镜(k = 2.646),材料:k9目镜:2-25N0.18 10 倍观察镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.5棱镜出射面与分划板距离:a = 10 mm;棱镜和材料: D1J-800屋脊棱镜(k = 1.96),材料:Bak7目镜:2-25N0.19 10 倍观察镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.5棱镜出射面与分划板距离:a = 10 mm;棱镜和材料: 别汉屋脊棱镜(k = 5.7),材料:Bak7目镜:2-25N0.20 10 倍观察镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.5棱镜出射面与分划板距离:a = 10 mm;棱镜和材料: 阿贝屋脊棱镜(k = 5.196),材料:Bak7目镜:2-25N0.21 10 倍双目望远镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.6棱镜和材料: 普罗1棱镜(k = 4),材料:Bak7目镜:2-25N0.22 10 倍潜望镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.5棱镜出射面与分划板距离:a = 30 mm;棱镜和材料: 普罗11棱镜(k = 3),材料:k9目镜:2-28潜望高:300mmN0.23 10 倍观察镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.5棱镜出射面与分划板距离:a = 10 mm;棱镜和材料: 斯密特屋脊棱镜(k = 3.04),材料:k9目镜:2-28N0.24 10 倍观察镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.5棱镜出射面与分划板距离:a = 10 mm;棱镜和材料: D1J-450屋脊棱镜(k = 3.558),材料:Bak7目镜:2-28N0.25 10 倍观察镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.5棱镜和材料: D1J-600屋脊棱镜(k = 2.646),材料:k9目镜:2-28N0.26 8 倍观察镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.5棱镜出射面与分划板距离:a = 10 mm;棱镜和材料: 别汉屋脊棱镜(k = 5.7),材料:k9目镜:2-28N0.27 8 倍观察镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.5棱镜出射面与分划板距离:a = 10 mm;棱镜和材料: D1J-800 屋脊棱镜(k = 1.96),材料:k9目镜:2-28N0.28 8 倍观察镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.5棱镜出射面与分划板距离:a = 15mm;棱镜和材料: 阿贝屋脊棱镜(k = 5.196),材料:k9目镜:2-28N0.29 8 倍观察镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.5棱镜出射面与分划板距离:a = 15 mm;棱镜和材料: 别汉屋脊棱镜(k = 5.7),材料:k9目镜:2-28N0.30 8 倍观察镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.5棱镜出射面与分划板距离:a = 15 mm;棱镜和材料: 列曼屋脊棱镜(k = 5.196),材料:k9目镜:2-28N0.31 8 倍双目望远镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.5棱镜出射面与分划板距离:a = 26.3 mm;棱镜和材料: 保罗1棱镜(k = 4),材料:Bak7目镜:2-28N0.32 8 倍炮对镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.5棱镜出射面与分划板距离:a = 41.6 mm;棱镜和材料: 靴型屋脊棱镜(k = 2.98),材料:k9目镜:2-28N0.33 8 倍观察镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.5棱镜出射面与分划板距离:a = 10 mm;棱镜和材料: 斯密特屋脊棱镜(k = 3.04),材料:k9目镜:2-28N0.34 8 倍观察镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.5棱镜出射面与分划板距离:a = 10 mm;棱镜和材料: 列曼屋脊棱镜(k = 4.619),材料:k9目镜:2-28N0.35 8 倍观察镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.5棱镜出射面与分划板距离:a = 10 mm;棱镜和材料: 阿贝屋脊棱镜(k = 5.196),材料:k9目镜:2-28N0.36 8 倍双目望远镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.5棱镜出射面与分划板距离:a = 25mm;棱镜和材料: 保罗1棱镜(k = 4),材料:k9目镜:2-25N0.37 8 倍双目望远镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.5棱镜出射面与分划板距离:a = 10 mm;棱镜和材料: 列曼屋脊棱镜(k = 5.196),材料:k9目镜:2-25N0.38 8 倍双目望远镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.5棱镜出射面与分划板距离:a = 10 mm;棱镜和材料: 阿贝屋脊棱镜(k = 5.196),材料:k9目镜:2-25N0.39 8 倍双目望远镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.5棱镜出射面与分划板距离:a = 10 mm;棱镜和材料: 别汉屋脊棱镜(k = 5.7),材料:k9目镜:2-25N0.40 8 倍双目望远镜:视场:; 出瞳直径:d = 4mm ; 镜目距:p = 10.5mm 分辨率:; 渐晕系数:k = 0.5棱镜出射面与分划板距离:a = 25.3 mm;棱镜和材料: 保罗1棱镜(k = 4),材料:k9目镜:2-13目镜2-352w = 500f’= 25D’=6mmP’/f’ = 1.036目镜2-282w = 570f’= 20.216D’=5mmP’/f’ = 1.042目镜2-252w = 640f’= 15.597D’=4mmP’/f’ = 0.733棱镜b 计算:薄透镜:厚透镜:或 dWhere:。
哈工大2011年航天学院各专业硕士研究生入学考试复试指导

材料学学科2011年硕士研究生招生复试指导根据教育部关于加强硕士研究生招生复试工作的指导意见及学校有关要求,材料学学科(报考航天学院复合材料与结构研究所)2011年硕士研究生招生复试指导确定如下。
一、复试比例及主要内容1、复试由笔试和面试两部分组成,外国语听力考试在面试中进行。
复试的总成绩为280分,其中笔试200分,面试80分。
2、复试笔试科目(1)材料科学基础部分,占80分。
主要内容:①材料的结构,化学键,晶体学,晶体结构,晶体缺陷②纯金属的凝固,纯金属的结晶,形核,二元与三元相图③固体材料的变形与断裂,弹性变形,塑性变形,位错与强化,断裂④回复,再结晶,晶粒长大,金属的热变形⑤扩散定律,扩散机制,影响扩散的因素,反应扩散参考书目:潘金生,仝建民,田民波主编,材料科学基础,清华大学出版社,1998;冯端,师昌绪,刘治国主编,材料科学导论,化学工业出版社,2002。
(2)材料性能学部分,占70分。
主要内容:①材料的力学性能,硬度,韧性,疲劳,磨损②材料的热学性能:热容、热膨胀、热传导③材料的磁性能:抗磁性与顺磁性,铁磁性与反铁磁性④材料的电学性能:导电与热电性能,半导体,绝缘体⑤材料的光学性能:线性光学与非线性光学性能参考书目:冯端,师昌绪,刘治国主编,材料科学导论,化学工业出版社,2002;王从曾主编,材料性能学(前11章),北京工业大学出版社,2001。
(3)材料分析方法部分,占50分。
主要内容:①材料X射线衍射分析②材料电子显微分析参考书目:周玉主编,材料分析方法,机械工业出版社,2004。
3、面试,占80分。
学科将组成专家组对考生进行面试。
主要是了解考生的特长与兴趣、身心健康状况;考察考生的综合素质、能力以及外语水平,主要内容包括:1)大学学习情况及学习成绩;2)外语听力及口语;3)综合分析与语言表达能力;4)对材料学学科相关知识的掌握情况;5)从事科研工作的潜力。
在参加面试时,考生可以提供能够反映自身素质、能力、水平的相关证明材料。
应用光学ppt的答案应用光学-PPT精选文档

透镜2 在透镜1的右边,要使它成像光线须自右向左,属于 反向光路。而牛顿公式和高斯公式皆由正光路导出,符号规 则也由正光路规定,不可随便用于反光路。 方法:认为透镜2是像,求物。
D1
F1,F2
D2
D3
d1
d2
2、因为 f1’= - f1 =100mm,l 2’ = 20mm,利用高 斯公式:
1 1 1 l ' l f ' 2 2 1
D1 F F’ D2 D3
20mm
100 mm
30mm
200 mm
求出系统每一个光阑被它前面光组在物空间所成的像(此 步骤在求孔径光阑时已经进行)
(孔径光阑)
; F2' D3 '
w1 w2
w3
33.33
25mm
150 mm
• D1′ 对入瞳中心的张角为 20 tg 0 .8 1 25 • D2′ 本身是入瞳,D3′对入瞳中心的张角为
一架幻灯机的投影镜头 f’=75mm,当屏由8m移至10m时, 镜头需要移动多少距离?方向如何?
一架相机的镜头焦距为35mm,底片框尺寸24mm×36mm,那 么,该相机的视场角为多大?
一组合系统由薄正透镜和薄负透镜组成,两者的焦距分别 为20mm和-20mm,间隔为10mm;当一物体位于正透镜前方 100mm处,求组合系统的垂轴放大率及像的位置。
l3 150 mm
y 33 .33 mm 3
D’1 D’2
D’3
25mm
200 mm
150 mm
物点A对光阑D1’ 的张角
D 20 1 tgu 0 . 1 1 200 200
• 对D2’ 的张角 • 对光阑D3’ 的张角
西安应用光学研究所光学校准检测实验室认可的检测能力范围

Transmittance
transmittanc
Glass
e
No. CNAS L0794
第 5 页 共 21 页
ISO/IEC 17025 认可证书
CNAS-PD19/06-A/1
Products, №
Materials
Items, Parameter,
№
Name
Code of Name,Code of Specification, Restriction
or
Note
Field
Standard or Method Used
Limitation
Infrared 1 Imaging
System
Optical 2
System
1
NETD
2
SiTF
3
MTF
GJB3965 -2000 General Specification of
Targeting Pod FLIR Q/AG J087-2006
Curvature
1
1601 National Standard Optical only for
Radius
Plate
concave
1
Resolution
Brightness 2
Gain
Equivalent 162205 3 Background
Illuminance
Ratio of Signal 4
or
Note
Field
Standard or Method Used
Limitation
10 Filter Glass 1
Spectral Property
《应用光学》教学大纲

附件一:理论课程(含实验理论课程)教学大纲基本格式《应用光学》课程教学大纲课程名称:应用光学课程编码:0230021英文名称:Applied Optics学时:64 其中实验学时:16 学分: 3.5开课学期:第五学期适用专业:光电信息工程测控技术与仪器信息对抗技术探测制导与控制工程课程类别:必修课程性质:专业基础课先修课程:高等数学教材:工程光学天津大学机械工业出版社一、课程性质及任务本课程主要探讨的是几何光学的基本知识,研究的是光的传播和成像规律,典型光学系统的工作原理、光学特性,像差理论的部分内容。
它是仪器科学与技术、光电信息工程等专业的必修专业基础课程。
通过本课程的学习,能够为其它光学后续课程,诸如:光学测量、光学设计等打下良好的基础,也为学生更好的掌握光学总体设计方法、从事简单的光学系统的设计起到非常重要的作用,通过本课程的学习能够培养学生具有在生产及科研实践中理解、分析及解决问题的能力。
二、课程的教学要求(一)几何光学基本定律与成像概念9学时1.几何光学的基本定律掌握:(1)光波与光线的概念,(2)几何光学基本定律,(3)费马原理,(4)马吕斯定律;理解:光的根本属性及其传播规律现象等;了解:了解全反射的特点,并能够利用全反射的特点及规律解释一些常见的现象。
2.成像的基本概念与完善成像条件掌握:(1)光学系统与成像的概念,(2)完善成像的条件,(3)物像的虚实;了解:完善成像的定义与条件。
3.光学计算与近轴光学系统掌握:(1)基本概念与符号规则,(2)实际光线的光路计算,(3)近轴光线的光路计算。
理解:实际光线与近轴光线在光路计算中的区别及结果的差异。
了解:符号规则对所涉及的光学系统的作用;4.球面光学成像系统掌握:(1)单个折射面成像,(2)球面反射镜成像,(3)共轴球面系统。
理解:(1)垂轴放大率、轴向放大率及角放大率之间的区别与联系,(2)折射面成像与反射面成像之间的联系。
了解:如何能够利用相应的公式计算光学系统的物像位置关系及放大率。
应用光学含四校(杨振刚)

第 2 页,共 4 页(2014-4-23打印)
任课教师(签名): (院系公章)
业:光电信息工程 备注 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1 第 3 页,共 4 页(2014-4-23打印)
第 1 页,共 4 页(2014-4-23打印)
任课教师(签名): (院系公章)
华中科技大学2011级辅修专业课程成绩单
(七校联合办学2009年制表) 课程名称:应用光学 序号 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 主修学校 中国地大 中国地大 中国地大 中国地大 中国地大 中国地大 华中农大 华中农大 华中农大 华中农大 华中农大 华中农大 武汉科技 武汉科技 武汉科技 武汉科技 湖北工业 武汉工程 武汉工程 武汉工程 武汉纺织 学生编号 20111000833 20111000873 20111001307 20111002156 20111002229 20111002468 2011303200701 2011304200313 2011305200607 2011308200401 2011308200506 2011310200223 201102126069 201102127066 201105165020 201108142066 1110100824 1106020229 1104010307 1106070102 1107791328 姓名 周楠 刘克 邓键 汪伟 余毕华 周顺祥 岳一鸣 陈湘东 肖爽 刘永光 涂传彪 宋林红 左文祥 付国立 陈伟 王尧 刘格 朱从容 崔群超 房振帅 聂弋林 性 别 女 男 男 男 男 男 男 男 男 男 男 女 男 男 男 女 男 男 男 男 男 1 平时成绩 2 3 4 5 专业:光电信息工程 平时 考试 综合 总评 成绩 成绩 81 缺考 36 90 87 88 缺考 40 77 78 66 缺考 77 78 缺考 81 81 84 79 81 48
应用光学课件

应用光学讲稿
给渐晕的原因 1. 为了减小元件的口径 2. 为了去处某些像差较大 的光线
在某些望远镜中,渐晕系数可以达到 在某些望远镜中,渐晕系数可以达到0.5 孔径光阑: 孔径光阑:限制轴上点或视场中央部分 无渐晕)成像光束口径的光阑。 (无渐晕)成像光束口径的光阑。
10 (1) tg ω = ,所以 240
(2)
1 ω = arctg 即为物方视角。 24
1 ω ′ = arctg 即为像方视角。 3
10 tg ω ′ = ,所以 30
(3)出瞳是孔径光阑在系统像空间所成的像,对目镜来说:
l = −240 mm − 30 mm = − 270 mm
应用光学讲稿
引入
F
H
H’
F’
应用光学讲稿
问题: 透镜口径与什么有关? 1. 成像光束的大小
D
2. 成像光束的位置
D1 D2
应用光学讲稿
本章要解决的问题: 本章要解决的问题:
如何选择成像光束的位置 选择成像光束的原则 限制光束的方法
应用光学讲稿
§5-1 光阑及其作用 一 照相机的构造 镜头: 镜头:起成像作用 底片: 底片:感光部分 光阑:限制成像光束, 光阑:限制成像光束,可 变光阑 光学系统中, 光学系统中,不论是限制成像光束口径大小还是 限制成像范围的孔或框都称为“光阑” 限制成像范围的孔或框都称为“光阑”。
应用光学讲稿
出瞳:是光能最集中的地方, 出瞳:是光能最集中的地方,为了看清整个视场 眼睛的瞳孔应该和出瞳重合。 ,眼睛的瞳孔应该和出瞳重合。 对出瞳距离必须有一定的要求,一般仪器大于6毫米, 对出瞳距离必须有一定的要求,一般仪器大于 毫米, 毫米 对于军用仪器,要大一些,可能大于20毫米 毫米。 对于军用仪器,要大一些,可能大于 毫米。 出瞳直径的大小,直接与像的亮暗有关 出瞳直径的大小, 问题:是否出瞳直径越大越好,出瞳距离越长越好? 问题:是否出瞳直径越大越好,出瞳距离越长越好?
应用光学课件完整版

一个物点,总是发出同心光束,与球面波相对应; 一个像点,理想情况应该由球面波对应的同心光束汇交 而成,称这种像点为完善像点。
3. 成完善象的条件 发光体每一物点发出球面波,通过光学系统后仍为
反射定律可表示为 I I ''
4. 光的折射定律
折射定律可归结为:入射光线、折射光线和投射点
的法线三者在同一平面内,入射角的正弦与折射角正弦
之比与入射角大小无关,而与两介质性质有关。对一定 波长的光线,在一定温度和压力的条件下,该比值为一
常数,等于折射光线所在介质的折射率与入射光线所在
介质折射率之比。
0 i arcsin n12 n2 2 n0
n0 =1
n0 sin i n1 cos ic n12 n22
5. 费马原理(光程极值原理)
1)光程— 光在介质中经过的几何路程l与该介质折射率n的乘积。
s=n • l
均匀介质
m层均匀介质
连续变化的非均匀介质
s=n • l=c • t
m
s
波面可分为:平面波、球面波、任意曲面波。 波面法线方向即为光传播方向。
光源
光线
波面
5. 光束— 与波面对应的法线集合。
同心光束— 波面为球面,聚于一点。 发散光束— 光线在前进方向上无相交趋势。 会聚光束— 光线在前进方向上有相交趋势。
平行光束— 波面为平面。 象散光束— 波面为曲面,不聚于一点。
1. 共轴球面系统的结构参量: 各球面半径:r1 、 r2 …… rk-1 、 rk 相邻球面顶点间隔:d1 、 d2 …… dk-1 各球面间介质折射率:n1 、 n2 …… nk-1 、 nk n 、 k+1
应用光学课件

O1 O2
I2
θ
M β
N B
θ
应用: 应用:测距机中用双平面镜代替单个平面镜 角镜, 角镜,棱镜
应用光学讲稿
§4 - 4
棱镜和棱镜的展开
一、用棱镜代替平面镜的优缺点
棱镜: 棱镜:利用光线在介质内部的反射来改变光线方向的光学零件 优点:光能损失少 优点: 坚固耐久, 坚固耐久,不易损坏 易于安装固定 缺点: 缺点:体积重量较大 对材料要求高 受环境影响较大
y P o z 物像大小相等, 物像大小相等,形状不同 物空间右手坐标对应像空间左手坐标 x x’ z’
y’ o’
分别迎着z 坐标面时, 分别迎着 、 z ’看xy、x’y’坐标面时,当x按逆时针方向转到 看 坐标面时 按逆时针方向转到 y,x’按顺时针方向转到 ;物像这种对应关系称为“镜像” 按顺时针方向转到y’ 物像这种对应关系称为“镜像” , 按顺时针方向转到
应用光学讲稿
三、对棱镜的要求 1、棱镜展开后应该是一块平行玻璃板 、 2、如果棱镜位于会聚光束中,光轴必须和棱 、如果棱镜位于会聚光束中, 镜的入射及出射表面相垂直。 镜的入射及出射表面相垂直。
应用光学讲稿
四、典型棱镜展开举例
B 1、直角棱镜 、 在平行光路中使用
在平行光路中只需满平第一个条件: 展开开后成平行玻璃板即 AB//AC′ 则∠ ABC = ∠ A′CB Q ∠ A′CB 是∠ ACB 折过过去的,二者相等 ∴ ∠ ABC = ∠ ACB 只要两要两角相等就能 AB//AC′,不一定 为45°, ∠ A 也不一定为直角。
应用光学讲稿
结论: 结论:
A
物像位置相对平面镜对称, 物像位置相对平面镜对称,物像 大小相等 实物成虚像,虚物成实像。 实物成虚像,虚物成实像。 D 单个平面镜对物点能成理想像, 单个平面镜对物点能成理想像, O O’
电子科大2011应用光学期末试题答案2.

………密………封………线………以………内………答………题………无………效……电子科技大学二零壹壹至二零壹贰学年第一学期期末考试应用光学课程考试题A 卷( 120 分钟考试形式:闭卷考试日期2011年 12 月15日课程成绩构成:平时 30 分,期中 0 分,实验 0 分,期末 70 分一二三四五六七八九十合计复核人签名得分签名《应用光学》期末试题答案一、填空选择题(共20分,每题1分备注:题目中有选项的是选择题,无选项的为填空题。
1.在均匀各向同性线性介质中,光束的波面与传播方向相互垂直。
2.费马原理指出,光从一点传播到另一点,其间无论经过多少次折、反射,其光程为极值。
3.符号规则规定,光线与光轴的夹角是由光轴转向光线所形成的锐角度量,顺时针为正,逆时针为负。
4.单个折射球面的轴向放大率C。
A.大于1B.小于1C.恒为正D.可为负5.有一个无限远物点,经某一理想光学系统成像,则其像点必在理想光学系统的B。
A.像方焦点上B.像方焦平面上C.物方焦点处D.物方焦平面上6.理想光学系统的所有基点包括D。
A.一对主点、一对焦点B.一对焦点、一对节点C.一对节点、一对焦点D.一对主点、一对焦点和一对节点7.一副近视眼镜为200度,其适合的焦距,f为C。
A.200mmB.500mmC.-500mmD.-200mm8.唯一能成完善像的光学元件是C。
A.薄透镜B.球面反射镜C.平面反射镜D.棱镜得分………密………封………线………以………内………答………题………无………效……9.光学系统中与孔径光阑共轭的是C。
A.入射窗B.像平面C.出瞳D.出窗10.光学系统的实际像与理想像之间的差异称为像差,包括单色像差和色差两大类。
11.单正透镜产生负球差,单负透镜产生正球差,因此它们组合可以校正球差。
12.望远系统的光学结构特点是光学间隔为零。
13.评价光学系统成像质量最全面客观的方法是C。
A.瑞利判断B.分辨率C.光学传递函数D.点列图14.光通量的国际度量单位是A。
应用光学 赵存华著 I 1-21章课件

n' n'
结论: 界面两边折射率差越大偏折光线越大.
n紫 n红
2.6.3 Snell定律的讨论
图2.10 三棱镜分光
2.7 全反射
当 I’=90o, 入射角称 critical angle (临界角). 用Ic表示, 所以有
sin
Ic
n' n
例子: 求光线从水中入射于空气中的全反射临界角
爱里斑的半径为
r0
1.22
2a
f'
3.2.2 理想像的违背
3.3 理想光学系统
光学系统:由反射镜、透镜和棱镜等光学 元件,按一定的方式组合在一起,利用材 料的反射或折射,把入射在其内的光线按 照设计者的要求传递到需要的位置或方向, 从而满足一定需求的系统。
一些概念:
1.共轴系统(coaxal system) 2.光轴(optical axis) 3.非共轴系统(non-coaxal system) 4.球面系统(spheric surface system) 5.非球面系统(aspheric surface system) 6.共轴球面系统(coaxal spheric system) 7.正透镜(positive lens) 8.负透镜(negative lens)
n' 1 n 2
sin I 1 sin I ' 2
nsin I n'sin I'
2.6.3 Snell定律的讨论
讨论:
nsin I n'sin I'
1. 如果 n n' 那么 sin I sin I' 所以 I I '
结论: 折射率小的一边相对法线夹角大.
应用光学教学课件完整

某一时刻相 位相同的点构成
的面称为波面
波面上某一点的法线就是这一点上光的传播
方向,波面上的法线束称为光束
• 同心光束:发自一点或会聚于一点,为球面波 • 平行光束:光线彼此平行,是平面波
• 像散光束:光线既不平行,又不相交,波面为曲面。
在几何光学中研究成像时,主要要搞清光线在光
n2 n'2 )
当入射角 i i0 时,可以全反射传送,
当 i i0 时,光线将会透过内壁进入包层
定义
na sin为i0光纤的数值孔径
i0 越大,可以进入光纤的光能就越多,也就
是光纤能够传送的光能越多。
这意味着光信号越容易耦合入光纤。
三、费马原理(最短光程原理)
光程:光在介质中传播的几何路径与所在介质 的折射率n的乘积
全反射现象
当
一般情况下,光线射至透明介质的分界面时将发 生反射和折射现象。
光 由
由公式 n sin I n' sin I ' 可知
光
密
sin I sin I '
介 质
射
即折射光线较入射光线偏离法线
向
光疏Biblioteka sin I ' 不可能大于1,此时入射光线将不能射入
另一介质。
按照反射定律在介面上全部被反射回原介质
称为光轴。这种系统被称为“共轴系统”
nb 之比与两角度的大小无关,仅决定于
I’ Q
n 介质的性质,为一恒量 ab
N 出射光线
即
sin I sin I ' nab
nab :介质 b 对介质 a 的相对折射率,
如果介质 a 为真空,则介质 b 对真空的折
2011 应用光学-1.2
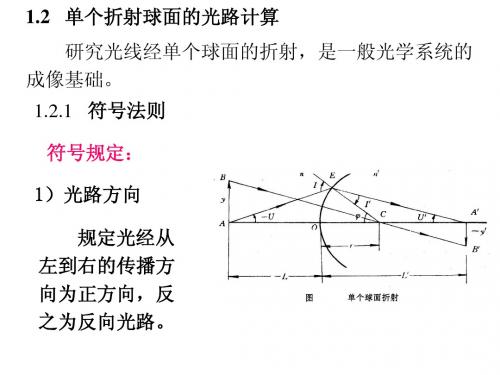
研究光线经单个球面的折射,是一般光学系统的 成像基础。 1.2.1 符号法则
符号规定: 1)光路方向 规定光经从 左到右的传播方 向为正方向,反 之为反向光路。
2)线量
沿轴线段以原 点为起始点,向右 为正,向左为负;
沿轴线量:凡由规定的原点(计算起点)到终点 的方向与光线的传播方向相同者取为正,反之为负。 垂轴线量:以光轴为准,在光轴之上为正,光 轴之下为负。 3)角量 一律以锐角来衡量,由规定的起始边沿顺时针 转为正,逆时针转为负。
如图,在Δ AEC中 ,有 :
sin u sin I r rL sin I Lr sin u r
上述四式,是计 算子午面内光线光 路的基本公式。可 由已知的L和U通过 上列四式求U’和L’。
(1)
在 AEC 中,有 :
sin u ' sin I ' r L'r
若出射光线平行与光轴
U 0,即 L 时
出射光线的参数 距离光轴的横向线度 公式 A
n
I -U O
E
n
I
f
r C
h
h
-L
h r sin I
校对公式: 为保证光路计算的准确性,需对结果进行校对, 下面为校对公式。
I 'u ' L sin u cos 2 L' I u sin u ' cos 2
有不同的U 角值,所以光束经球折射后,将有不同的 L值,即在
像方的光束不和光轴交于一点,失去了同心性。因此,当轴上点 宽光束经球面成像时,其像是不完善的,这种成像缺陷称为像差。
若物体位于物方光轴上无限远处,这时可认为由。
应用光学【第三章】第一部分(PDF)

第三章光学仪器目视光学仪器:和人眼配合使用的仪器本章主要解决的问题:•眼睛的构造•望远镜、显微镜的工作原理•眼睛与目视光学仪器配合的问题、眼睛缺陷及调整•如何选择成像光束的位置•选择成像光束的原则•限制光束的方法§3-1人眼的光学特性•人眼的构造从光学角度看,主要有三部分:----镜头----底片----光阑人眼相当于一架照相机,能够自动调节角膜:透明球面,光线首先通过角膜进入眼睛前室:角膜后面的空间部分,充满水液,n=1.3374,对光线起会聚作用水晶体:双凸透镜,借助周围肌肉的收缩及松弛,前表面半径可减小或加大,改变焦距。
角膜,前室和水晶体相当于镜头部分。
视网膜:视神经细胞和神经纤维,相当于感光底片黄斑:视网膜上视觉最灵敏的地方这两项相当于感光部分虹膜:水晶体前面的薄膜,中心有一圆孔,成为瞳孔,随着入射光能量的多少,瞳孔直径可放大或缩小。
相当于可变光阑盲点:视神经纤维的出口,没有感光细胞,不产生视觉盲点实验视觉的产生外界的光线进入人眼成像在视网膜上,产生视神经脉冲通过视神经传向大脑,经过高级的中枢神经活动,形成视觉物理过程,生理过程,心理过程人眼的光学特性视轴:黄斑中心与眼睛光学系统的像方节点连线人眼视场:观察范围可达150º头不动,能看清视轴中心6º-8º要看清旁边物体,眼睛在眼窝内转动,头也动人眼的调节:视度调节、瞳孔调节1、视度调节定义:随着物体距离改变,人眼自动改变焦距,使像落在视网膜上的过程。
F’•调节量的表示:视度与网膜共轭的物面到眼睛的距离的倒数1SD=l 单位为米l•明视距离和近点、远点明视距离:眼睛前方250mm,SD=(1 / (-0.25))= -4 近点:眼睛通过调节能看清物体的最短距离远点:眼睛能看清物体的最远距离最大调节范围=近点视度-远点视度年龄最大调节范围/视度近点距离/mm10 15 20 25 30 35 40 45 50-14-12-10-7.8-7.0-5.5-4.5-3.5-2.57083100130140180220290400 不同年龄正常人眼的调节能力2、瞳孔调节外界物体的亮暗随物体,天气,时间而不同。
应用光学(第二章)

若 f ’ <0,为负光组(发散光组)
正 光 组F
H H’ F’
负 光 组F ’
H H’ F
记住喽,做题时先判 断光组的正负!
第三节 理想光学系统的物像关系
※ 已知一个理想光学系统的主点和焦点的位 置,利用光线通过它们后的性质,对物空间 给定的点、线、面通过画图追踪典型光线求 像,称为图解法求像。
(a)物在二倍焦距外
B
A 2F F
A’ H H’ F ’ 2F ’
B’
成倒立缩小实像;像在一倍焦距外,二倍焦距 内。物、像在两侧
(b) 物在二倍焦距上
B
A 2F F
A’ H H’ F ’ 2F ’
B’
实物成等大倒立实像,位于二倍像方焦点上。 分立两侧
(c)物在二倍焦距之内,一倍焦距之外
B 2F A F
N’
A’
A
F
H H’ F ’
方法3:
过A作垂直于光轴的辅助物AB,按照前面 的方法求出B’,由B’作光轴的垂线,则交点A’ 就是A的像。
B
A’
A
F
H H’ F ’
B’
方法4: 利用过主点光线方向不变,作过主点的辅
助光线。利用像方焦平面上发出的光线过光组 后平行射出的性质。然后作平行辅助光线的出 射光线。
H H’
F
(5)共轭光线在主平面上的投射高度相等, 即一对主平面的横向放大率为+1。
(6)光轴上的物点其像必在光轴上。 (7)过主点光线方向不变。
H’ H
再次强调:作图时先注意光组的正负,看物方焦点F
和像方焦点F ’的位置。
(一)正光组轴上点作图
已知F 和F ’,求轴上点A的像
N
应用光学-131

1.22 0.55 ) D
用望远镜观察时,考虑人眼分辨率应有:
60 60'' 60'' D 140'' 2.3 D
D 单位 mm
此放大率为满足视觉要求(眼睛能分辨)的最小视觉放大率, 称之为正常放大率。 但正常放大率时,工作不正常,人眼在极限状态 在设计望远镜时,分辨率为(1.5-2) 60 相应放大率也增大,(1.5-2)正常放大率为工作放大率, 2=(1.5-2)
D D 40 13.968 0.06508 2f 2 200 343 tan
等效空气平板入射光束的通光口径为:
D1 D 2(a e) tan D 2(a KD1 ) tan n
式中五棱镜结构常数 K 3.414 ,整理解出平行平板玻璃入射面 的通光口径 D1 :
特点:①光源像与物面重合,物平面亮度与光源相同 若光源亮度均匀,则照明均匀,光源本身质量 对照明状况影响大 (很容易造成照度不均匀) ②聚光镜像方孔径角应大于或等于显微物镜的数值孔径。 ③聚光镜的孔径光阑为可调,位置在其前焦面处, 则出瞳一定在无穷远处,这同显微镜的入瞳重合, 即聚光镜的出瞳正是显微镜的入瞳。 ‚瞳对瞳,视场对视场‛的光管 瞳对瞳,即出瞳对入瞳 视场对视场,即聚光镜的像方视场为显微镜的物方视场
等效空气平板的理解 由图可以认识到,光线经 MNPO 后,在 NP 面上 B 点的出射与 光线经过 MQRO 以后在 T 点的出射情况完全相同, 不同点:光线经 MNPO 时,在 MO 、NP 两个平面上均有折射, 而经 MQRO 并没有折射,光线是直接通过的。 故而,称 MQRO 为 MNPO 的等效空气平板。 令等效空气平板的厚度为 d ,则由图可知:
11 应用光学

先后看不清楚,说明景深小。 先后看不清楚,说明景深小。
先后都能看清楚,说明景深大。 先后都能看清楚,说明景深大。
先后看不清楚,说明景深小。 先后看不清楚,说明景深小。
先后都能看清楚,说明景深大。 先后都能看清楚,说明景深大。
先后看不清楚,说明景深小。 先后看不清楚,说明景深小。
景深小
景深小
景深小
Φ eλ
辐射通量的光谱密集度 Φ eλ
d Φλ Φ eλ = dλ
λ
Φ e = ∫ Φ eλ d λ
0
∞
4. 辐射度学的基本量 辐射度学的基本量——辐射强度 I e 辐射强度
例题1 例题
200倍显微镜的目镜焦距为 倍显微镜的目镜焦距为25mm,如果出瞳直径 ’=1mm,显微 倍显微镜的目镜焦距为 ,如果出瞳直径D , 物镜的物像共轭距为195mm,求显微镜的数值孔径是多少?物镜 物镜的物像共轭距为 ,求显微镜的数值孔径是多少? 的通光口径是多少(空气镜头)? 的通光口径是多少(空气镜头)? ' Γ=-200;f目 = 25mm; 物镜 目镜 D' = −1mm; −l + l' = 195 分划板
2. 景深的理解
B1
底片
Z
A1 A A2 B2
' B1
'
' B2
A’
Z'
对准面A前后的物点在底片上留下弥散斑。 对准面 前后的物点在底片上留下弥散斑。 前后的物点在底片上留下弥散斑 只要弥散斑口径足够小,我们就可以看清它。 只要弥散斑口径足够小,我们就可以看清它。 若我们能辨别的最大弥散斑口径为Z’,那么从 若我们能辨别的最大弥散斑口径为 ,那么从A1到A2面这个轴向深 度的物体我们都能看清。这个深度,就是景深。 度的物体我们都能看清。这个深度,就是景深。 我们所能分辨的最大弥散斑口径Z’越大,景深是越大还是越小? 我们所能分辨的最大弥散斑口径 越大,景深是越大还是越小? 越大
《应用光学》再次入编《中文核心期刊要目总览》

《应用光学》再次入编《中文核心期刊要目总览》
佚名
【期刊名称】《应用光学》
【年(卷),期】2012(33)2
【摘要】近日接《中文核心期刊要目总览》2011年版编委会通知,《应用光学》入编《中文核心期刊要目总览》2011年版(即第六版)之电子技术、通信技术类的核心期刊。
这是《应用光学》继2008年入选中文核心期刊后,再次入选中文核心期刊。
【总页数】1页(P239-239)
【关键词】《中文核心期刊要目总览》;应用光学;电子技术;通信技术;编委会
【正文语种】中文
【中图分类】TN-4
【相关文献】
1.《重庆高教研究》首次入选《中文核心期刊要目总览》--《中文核心期刊要目总览》入编通知 [J],
2.《中文核心期刊要目总览》收录证书《中文核心期刊要目总览》入编通知 [J],
3.《中文核心期刊要目总览》收录证书《中文核心期刊要目总览》入编通知 [J],
4.《暨南大学学报(自然科学与医学版)》再次被收录为“中国科学引文数据库来源期刊(CSCD)”“中国科技论文统计源期刊(中国科技核心期刊)”并再次入编《中文核心期刊要目总览》 [J], 暨南大学学报编辑部
5.《中文核心期刊要目总览》收录证书《中文核心期刊要目总览》入编通知 [J],
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
αγ = β
拉亥不变量J(拉格朗日—亥姆霍兹不变量 亥姆霍兹不变量) 1.3.5 拉亥不变量 (拉格朗日 亥姆霍兹不变量)
nuy = n u y = J
' ' '
--拉格朗日 亥姆霍兹恒等式 --拉格朗日—亥姆霍兹恒等式 拉格朗日
上式表明,在一对共轭平面内,成像的物高y, 成像光束的孔径角u和所在介质的折射率n三者的乘 积是一个常数 常数—J。 常数
n' ቤተ መጻሕፍቲ ባይዱ = β1β 2 n
对A1和A2两物点分别应用
n' n n'−n n' n − = = − l2 ' l2 r l1 ' l1
β1和β2分别为物在 A1和A2两点的垂轴放大率
3、角放大率γ 角放大率γ
u' 令: γ = 称为角放大率 u l n 1 = = ⋅ l ' n' β
三个放大率的关系: 三个放大率的关系:
n' n n'−n − = l' l r
对上式求微分
dl ' nl ' n' 2 = 2= β α= dl n' l n
---只在物体轴向尺寸很小时适用
2
(2) 平均轴向放大率
如果物体轴向尺寸足够 大,如图右则轴向放大率 表示。 用 表示。
α
l2 '−l1 ' α = l2 − l1 l2 '−l1 ' nl1 ' l2 ' α = = l2 − l1 n' l1l2
共轭面上垂轴放大率只与共轭面的位置有关, 而与物在共轭面的位置无关,即同一对共轭面 上垂轴放大率为常数,物像相似。 当β<0时,表示 y ′ 和y异号,成倒像 β 倒像;同时 倒像 l和 l ′异号表示物像处于球面两侧 实物成实 物像处于球面两侧,实物成实 物像处于球面两侧 像,虚物成虚像。 虚物成虚像 当β>0 β>0时, ′ 和y同号,成正像 正像;同时l和 l ′ β>0 正像 y 物像处于球面的同侧,实物成虚像 同号物像处于球面的同侧 实物成虚像,虚 物像处于球面的同侧 实物成虚像, 物成实像。 物成实像
n'−n h LL (8) n' u '− nu = r
n' n n'− n − = LL (9 ) l' l r
表示折射球 面成像时, 面成像时,物 像位置l(物距) 像位置 (物距) 和 l(像距)之 ′ 像距) 间的关系。 间的关系。
1.3.2 焦距及光焦度 如图 , ′ F 点(轴上无限远物点的像点),称为 像方焦点或第二焦点 球面的像方焦点 第二焦点 OF ' (用 f ′ 表示),称 像方焦点 第二焦点。 为第二焦距 第二焦距。 第二焦距 n' l' = f ' = r n'− n
例1 若空气中一球形透明体能将平行光束会聚 于其背面的顶点上,此透明体的折射率等于多少 此透明体的折射率等于多少? 于其背面的顶点上 此透明体的折射率等于多少 解:
n′ f′= r n′ − n
f′ n n′ = f ′−r
f ′ = 2r
n = 1.00
n′ = 2.00
则有:
xx ′ = ff ′
上式为牛顿公式。
1.3.4 放大率
1、垂轴放大率β 垂轴放大率β 物体经球面折射成像后,通常不仅需要知道像的位置 位置,而 位置 且还希望知道像的大小 虚实 倒正 大小、虚实 倒正。因此,引入垂轴放大率 大小 虚实和倒正 垂轴放大率 β。如图所示。
结论: 结论:
y ' nl ' x' f β= = =− =− y n' l f' x
折射球面两焦距和光焦度之间的关系: 折射球面两焦距和光焦度之间的关系
n′ n =− ϕ= f′ f
1.3.3 高斯公式和牛顿公式
n' f '= r n'− n
n f =− r n'− n
n' n n'− n − = ⇒ l' l r
物距l、像距 l ′ ,物方焦距f以及像方焦距 f ′ 有 以下关系:
放大像; 放大像 β > 1 ,表示为放大像 β < 1 ,表示 为缩小像 缩小像。 缩小像
2、轴向放大率 、
(1)共轭面间轴向放大率 共轭面间轴向放大率 对于有一定体积的物体, 除垂轴放大率外,其轴向也 有尺寸,故还有轴向放大率 轴向放大率 α。
dl F A C -l O l’ F’
dl’ A’ C’
f' f + =1 l' l 上式称为球面折射的高斯公式。
如果物距和像距不以球折射面的顶点为原点, 而分别从物方焦点F和像方焦点F’算起,并用x和x’ 焦物距和焦像距 表示,分别称为焦物距 焦像距,如下图所示。 焦物距 焦像距
−l = − f − x l ′ = f ′ + x′
f' f + =1 l' l
F点称为第一焦点 OF 称为第一焦距 第一焦点, 第一焦点 第 焦距。
n f =− r n'− n
f ' − n' = f n
上式表明,单个球面像方焦距 f ′ 与物方焦距 的比 单个球面像方焦距 与物方焦距f的比 等于相应介质折射率之比。 等于相应介质折射率之比 光焦度 令:
n'−n ϕ= r
对于一定的介质 一定形状 一定的介质及一定形状 一定的介质 一定形状的表面来说, ϕ 是一 个不变量,它表征球面的光学特征 表征球面的光学特征,称之为光焦度 光焦度。 表征球面的光学特征 光焦度 当r以米为单位时, 的单位称为折光度 以字 折光度,以字 折光度 ϕ 表示。 母D表示 表示
1.3 单个折射球面近轴区成像
1.3.1 物象公式
根据前面六个公式可以导出 以下三个公式:
表示近轴光 经球面折射前 后的孔径角u 后的孔径角 和 U′ 的关系 。
1 1 1 1 n − = n' − = Q LL (7 ) r l r l'
表示单个折射球 面,物方和像方的一 些参量具有不变量形 称为阿贝不变量, 式,称为阿贝不变量, 用字母Q表示,Q值的 用字母 表示, 值的 表示 大小只与共轭点的位 置有关。 置有关。
