初中九年级数学竞赛培优讲义全套专题10 最优化_答案[精品]
北师版九年级数学下册培优精品讲义(最新版;可直接打印)
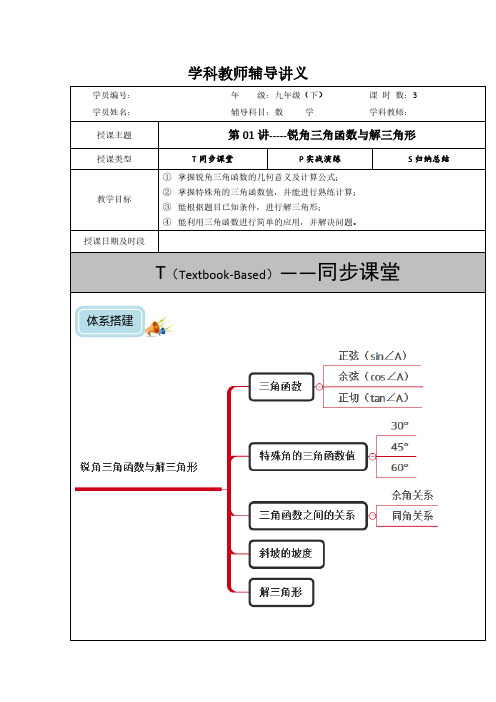
学科教师辅导讲义.cosB|+.、正弦,余弦,正切的概念、特殊角的三角函数值、tanA是一个比值(数值)、在几何图形中求解三角函数值或者解三角形,找出直角三角形或做辅助线构造直角三角形是解题的关学科教师辅导讲义知识梳理m(m (参考数据:≈(5、如图,从热气球C处测得地面A、B两点的俯角分别是30°、45°,如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )A.200米B.200米C.220米D.100()米6、海中有一个小岛A,它的周围a海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东75°方向上,航行12海里到达D点,这是测得小岛A在北偏东60°方向上.若渔船不改变航线继续向东航行而没有触礁危险,则a的最大值为( )A.5B.6C.6D.8如图,广安市防洪指挥部发现渠江边一处长400米,高8米,背水坡的坡角为7、急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡45°的防洪大堤(横截面为梯形ABCD)并使上底加宽2米,加固后,背水坡EF的坡比i=1:2.面用土石进行加固,(1)求加固后坝底增加的宽度AF的长;(2)求完成这项工程需要土石多少立方米?8、一条船在海面上自西向东沿直线航行,在A处测得航标C在北偏东60°方向上,前进100米到达B处,又测得航标C在北偏东45°方向上.(1)请根据以上描述,画出图形.(2)已知以航标C为圆心,120米为半径的圆形区域内有浅滩,若这条船继续前进,是否有被浅滩阻碍的危险?为什么?课后反击1、如图,将一个Rt△ABC形状的楔子从木桩的底端点P处沿水平方向打入木桩底下,使木桩向上运动,已知楔子斜面的倾斜角为18°,若楔子沿水平方向前移6cm(如箭头所示),则木桩上升了( )A.6tan18°cm B.cm C.6sin18°cm D.6cos18°cm2、如图,某课外活动小组在测量旗杆高度的活动中,已测得仰角∠CAE=33°,AB=a,BD=b,则下列求旗杆CD长的正确式子是( )A.CD=b sin33°+a B.CD=b cos33°+aC.CD=b tan33°+a D.CD=3、小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8一根长为1米、垂直于地面放置的标杆在地面米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,上的影长为2米,则树的高度为( )A.()米B.12米C.()米D.10米4、如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)( )A.22.48 B.41.68 C.43.16 D.55.63PCD=衡阳】如图,为了测得电视塔的高度,再向电视塔方向前进+12、【2014•深圳】小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,求山高( )A.600﹣250米B.600﹣250米C.350+350米D.500米3、【2013•深圳】如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则sinα的值是( )A.B.C.D.4、【2016•十堰】在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度为 米.(结果保留根号)理解坡度的概念,利用坡度解决实际问题熟练掌握相关方位角、观察角的概念,准确构造直角三角形、将实际问题中,当有些图形不是直角三角形时,可添加适当的辅助线,把它们分割成直角三角形;、寻求基础直角三角形,并解这个三角形或设未知数进行求解是解决问题的关键.学科教师辅导讲义知识梳理五、知识概念1、用二次函数的性质解决最值计算问题(1)将函数表达式配方成顶点式,进行求解:开口向上时顶点处取得最小值;开口向下时取最大值。
九年级数学培优讲义与测试精编版

第一讲 一次函数和反比例函数知识点、重点、难点函数(0)y kx b k =+≠称为一次函数,其函数图像是一条直线。
若0b =时,则称函数y kx =为正比例函数,故正比例函数是一次函数的特殊情况。
当0k >时,函数y kx b =+是单调递增函数,即函数值y 随x 增大(减小)而增大(减小);当0k <,y kx b =+是递减函数,即函数值y 随x 增大(减小)而减小(增大)。
函数(0)ky k x=≠称为反比例函数,其函数图像是双曲线。
当0k >且0x >时,函数值y 随x 增大(减小)而减小(增大);当0k >且0x <,函数值y 随x 增大(减小)而减小(增大),也就是说:当0k >时,反比例函数ky x=分别在第一或第三象限内是单调递减函数;当0k <时,函数ky x=分别在第二或第四象限内是单调递增函数。
若111222(0),(0).y k x b k y k x b k =+≠=+≠ 当12k k =时,12b b ≠时,两面直线平行。
当12k k =时,12b b =时,两面直线重合。
当12k k ≠时,两直线相交。
当121k k =-时,两直线互相垂直。
求一次函数、反比例函数解析式,关键是要待定解析式中的未知数的系数;其次,在解题过程中要重视数形相结合。
例题精讲例1:在直角坐标平面上有点(1,2)A --、(4,2)B 、(1,)C c ,求c 为何值时AC BC +取最小值。
解 显然,当点C 在线段AB 内时,AC BC +最短。
设直线AB 方程为y kx b =+,代入(1,2)A --、(4,2)B得242,k b k b -+=-⎧⎨+=⎩解得456,5k b ⎧=⎪⎪⎨⎪=-⎪⎩所以线段AB 为46(14),55y x x =--≤≤代入(1,)C c ,得4621.555c =⨯-=-例2:求证:一次函数211022k k y x k k --=-++的图像对一切有意义的k 恒过一定点,并求这个定点。
九年级数学培优讲解及测试

第一讲一次函数和反比例函数知识点、重点、难点函数称为一次函数,其函数图像是一条直线。
若时,则称函数为正比例函数,故正比例函数是一次函数特殊情况。
当时,函数是单调递增函数,即函数值随增大(减小)而增大(减小);当,是递减函数,即函数值随增大(减小)而减小(增大)。
函数称为反比例函数,其函数图像是双曲线。
当且时,函数值随增大(减小)而减小(增大);当且,函数值随增大(减小)而减小(增大),也就是说:当时,反比例函数分别在第一或第三象限内是单调递减函数;当时,函数分别在第二或第四象限内是单调递增函数。
若当时,时,两面直线平行。
当时,时,两面直线重合。
当时,两直线相交。
当时,两直线互相垂直。
求一次函数、反比例函数解析式,关键是要待定解析式中未知数系数;其次,在解题过程中要重视数形相结合。
例题精讲例1:在直角坐标平面上有点、、,求为何值时取最小值。
解显然,当点在线段内时,最短。
设直线方程为,代入、得解得所以线段为代入,得例2:求证:一次函数图像对一切有意义恒过一定点,并求这个定点。
解由一次函数得整理得。
因为等式对一切有意义成立,所以得解得当,时,一次函数解析式变为恒等式,所以函数图像过定点.例3:已知、、为常数,,并且求。
解用代换原方程中,得○1用代换原方程中,得○2○2○1得因为,所以,所以.例4:如图,设因为当时,为递增函数,在上最小值为所以因此在上为递减函数;在上为递增函数,故最大值为例5:画函数图像。
解,,,将整个数轴分为四段讨论(见图)并定义域为一切实数。
例6:一次函数图像交轴于A点,将此直线沿直线翻折交轴于B点,这两条直线相交于P点,且四边形OAP B面积为3,求k值。
解设点P坐标为又与是翻折而成,所以面积是四边形OAPB一半等于。
设代入得点为由得即点因点在上,代入得A卷一、填空题1.设是反比例函数,则;其图像经过第象限时;当时,随增大而。
2.两个一次函数图像与轴所围成三角形面积是。
3.等腰三角形一个底角度数记作,顶角度数记作,将表示成函数是,其中取值范围是。
初中九年级数学竞赛培优讲义全套专题10 最优化[精品]
![初中九年级数学竞赛培优讲义全套专题10 最优化[精品]](https://img.taocdn.com/s3/m/0d70462010a6f524ccbf85d7.png)
专题10 最优化阅读与思考数学问题中常见的一类问题是:求某个变量的最大值或最小值;在现实生活中,我们经常碰到一些带有“最”字的问题,如投入最少、效益最大、材料最省、利润最高、路程最短等,这类问题我们称之为最值问题,解最值问题的常见方法有:1.配方法由非负数性质得()02≥±b a .2.不等分析法通过解不等式(组),在约束条件下求最值. 3.运用函数性质对二次函数()02≠++=a c bx ax y ,若自变量为任意实数值,则取值情况为:(1)当0>a ,a bx 2-=时,a b ac y 442-=最小值 ;(2)当0<a ,abx 2-=时,a b ac y 442-=最大值 ;4.构造二次方程利用二次方程有解的条件,由判别式0≥∆确定变量的取值范围,进而确定变量的最值.例题与求解【例1】当x 变化时,分式12156322++++x x x x 的最小值是 .(全国初中数学联赛试题)解题思路:因分式中分子、分母的次数相等,故可将原分式用整式、真分式的形式表示,通过配方确定最小值.【例2】已知1≤y ,且12=+y x ,则223162y x x ++的最小值为( )A.719 B. 3 C. 727 D. 13 (太原市竞赛试题)解题思路:待求式求表示为关于x (或y )的二次函数,用二次函数的性质求出最小值,需注意的是变量x 、y 的隐含限制.【例3】()21322+-=x x f ,在b x a ≤≤的范围内最小值2a ,最大值2b ,求实数对(a ,b ). 解题思路:本题通过讨论a ,b 与对称轴0=x 的关系得出结论.【例4】(1)已知211-+-=x x y 的最大值为a ,最小值b ,求22b a +的值. (“《数学周报》杯”竞赛试题)(2)求使()168422+-++x x 取得最小值的实数x 的值.(全国初中数学联赛试题)(3)求使2016414129492222+-+++-++y y y xy x x 取得最小值时x ,y 的值.(“我爱数学”初中生夏令营数学竞赛试题)解题思路:解与二次根式相关的最值问题,除了利用函数增减性、配方法等基本方法外,还有下列常用方法:平方法、判别式法、运用根式的几何意义构造图形等.【例5】如图,城市A 处位于一条铁路线上,而附近的一小镇B 需从A 市购进大量生活、生产用品,如果铁路运费是公路运费的一半,问:该如何从B 修筑一条公路到铁路边,使从A 到B 的运费最低?(河南省竞赛试题)解题思路:设铁路与公路的交点为C ,AC =x 千米,BC =y 千米,AD =n 千米,BD =m 千米,又设铁路每千米的运费为a 元,则从A 到B 的运费()ay m y n a S 222+--=,通过有理化,将式子整理为关于y 的方程.【例6】(1)设r x ,1+r x ,…,k x (r k >),为k -r +1个互不相同的正整数,且x r +x r +1+…+x k =2003,求k 的最大可能值.(香港中学竞赛试题)(2)a ,b ,c 为正整数,且432c b a =+,求c 的最小值.(全国初中数学联赛试题)解题思路:对于(1),因r =1,对k -r +1= k -1+1=k 个正整数x 1,x 2,…,x k ,不妨设x 1<x 2<…<x k =2013,可见,只有当各项x 1,x 2,…,x k 的值愈小时,才能使k 愈大(项数愈多),通过放缩求k 的最大值;对于(2),从()()222b a c a c =+-入手.能力训练A 级1.已知三个非负数a ,b ,c ,满足3a +2b +c =5和2a +b -3c =1,若m =3a +b -7c ,则m 的最小值为___________,最大值为 .2.多项式p =2x 2-4xy +5y 2-12y +13的最小值为 .3.已知x ,y ,z 为实数,且x +2y -z =6,x -y +2z =3,那么x 2+y 2+z 2的最小值为 .(“希望杯”邀请赛试题)4.若实数a ,b ,c ,满足a 2+b 2+c 2=9,则代数式(a -b )2+(b -c )2+(c -a )2的最大值为 ( )(全国初中数学联赛试题)5.已知两点A (3,2)与B (1,-1),点P 在y 轴上且使PA +PB 最短,则P 的坐标是( ) A.(0,21-) B.(0,0) C.(0,611) D.(0,41-)(盐城市中考试题)6.正实数x ,y 满足1=xy ,那么44411y x +的最小值为( ) A.21 B. 85 C. 1 D. 45E. 2 (黄冈市竞赛试题)7.某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件,经试销调查,发现销售量y (件)与销售单价x (元/件)可近似看作一次函数b kx y +=的关系(如图所示).(1)根据图象,求一次函数b kx y +=的解析式;(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S 元. ①试用销售单价x 表示毛利润;②试问:销售单价定为多少时,该公司可获得最大毛利润?最大毛利润是多少?此时的销量是多少?(南通市中考试题)8.方程()()06122=-+-+m x m x 有一根不大于1-,另一根不小于1,(1)求m 的取值范围;(2)求方程两根平方和的最大值与最小值.(江苏省竞赛试题)9.已知实数a ,b 满足122=++b ab a ,求22b ab a +-的最大值与最小值.(黄冈市竞赛试题)10.已知a ,b ,c 是正整数,且二次函数c bx ax y ++=2的图象与x 轴有两个不同的交点A ,B ,若点A ,B 到原点的距离都小于1,求a +b +c 的最小值.(天津市竞赛试题)11.某单位花50万元买回一台高科技设备,根据对这种型号设备的跟踪调查显示:该设备投入使用后,若将养护和维修的费用均摊到每一天,则有结论:第x 天应付的养护与维修费为()⎥⎦⎤⎢⎣⎡+-500141x 元. (1)如果将设备从开始投入使用到报废所需的养护与维修费及购买设备费用的总和均摊到每一天,叫作每天的平均损耗,请你将每天的平均损耗y (元)表示为使用天数x (天)的函数.(2)按照此行业的技术和安全管理要求,当此设备的平均损耗达到最小值时,就应当报废,问:该设备投入使用多少天应当报废?(河北省竞赛试题)B 级1.a ,b 是正数,并且抛物线b ax x y 22++=和a bx x y ++=22都与x 轴有公共点,则22b a +的最小值是 .2.设x ,y ,z 都是实数,且满足x +y +z =1,xyz =2,则z y x ++的最小值为 . 3.如图,B 船在A 船的西偏北45°处,两船相距210km ,若A 船向西航行,B 船同时向南航行,且B 船的速度为A 船速度的2倍,那么A 、B 两船的最近距离为 km .(全国初中数学竞赛试题)4.若a ,b ,c ,d 是乘积为1的四个正数,则代数式a 2+b 2+c 2+d 2+ab +bc +ac +ad +bd +cd 的最小值为( )A. 0B. 4C. 8D. 10(天津市竞赛试题)5.已知x ,y ,z 为三个非负实数,且满足3x +2y +z =5,x +y -z =2. 若s =2x +y -z ,则s 的最大值与最小值的和为( )A. 5B.423 C. 427 D. 435(天津市选拔赛试题)6.如果抛物线()112----=k x k x y 与x 轴的交点为A ,B ,顶点为C ,那么△ABC 的面积的最小值为( )A.1B.2C.3D.47.某商店将进货价每个10元的商品按每个18元售出时,每天可卖出60个,商店经理到市场上做了一番调查后发现,若将这种商品的售价(在每个18元的基础上)每提高1元,则日销售量就减少5个;若将这种商品的售价(在每个18元的基础上)每降低1元,则日销量就增加10个,为获得每日最大利润,此商品售价应定为每个多少元?(“祖冲之杯”邀请赛试题)8.有甲、乙两种商品,经营销售这两种商品所能获得的利润依次是p (万元)和q (万元),它们与投入资金x (万元)的关系有经验公式:x q x p 53,51==.今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得多大的利润?(绍兴市竞赛试题)9.已知为x ,y ,z 为实数,且5=++z y x ,3=++zx yz xy ,试求z 的最大值与最小值.10.已知三个整数a ,b ,c 之和为13,且bca b ,求a 的最大值和最小值,并求出此时相应的b 与c 值.(四川省竞赛试题)11.设x 1,x 2,…,x n 是整数,并且满足: ① -1≤x i ≤2,i =1,2,…,n ② x 1+x 2+…+x n =19 ③ x 12+x 22+…+x n 2=99求x 13+x 23+…+x n 3的最大值和最小值.(国家理科实验班招生试题)12.已知x1,x2,…,x40都是正整数,且x1+x2+…+x40=58,若x12+x22+…+x402的最大值为A,最小值为B,求A+B的值.(全国初中数学竞赛试题)。
初中数学九年级培优教程整理(全)

初中数学九年级培优目录第1讲二次根式的性质和运算(P2----7)第2讲二次根式的化简与求值(P7----12)第3讲一元二次方程的解法(P13----16)第4讲根的判别式及根与系数的关系(P16----22)第5讲一元二次方程的应用(P23----26)第6讲一元二次方程的整数根(P27----30)第7讲旋转和旋转变换(一)(P30----38)第8讲旋转和旋转变换(二)(P38----46)第9讲圆的基本性质(P47----51)第10讲圆心角和圆周角(P52----61)第11讲直线与圆的位置关系(P62----69)第12讲圆内等积证明及变换((P70----76)第13讲弧长和扇形面积(P76----78)第14讲概率初步(P78----85)第15讲二次函数的图像和性质(P85----91)第16讲二次函数的解析式和综合应用(P92----98)第17讲二次函数的应用(P99----108)第18讲相似三角形的性质(P109----117)第19讲相似三角形的判定(P118-----124)第20讲相似三角形的综合应用(P124-----130)第1讲二次根式的性质和运算考点·方法·破译1.了解二次根式、最简二次根式、同类二次根式的定义,能准确进行辨析;2.掌握二次根式有关性质,并能熟练运用性质进行化简;3.会根据二次根式的性质挖掘题中隐含条件,求参数的值(或取值范围).经典·考题·赏析【例1】(荆州)下列根式中属最简二次根式的是()【解法指导】判断式子是否为最简二次根式的条件有两点:①被开方式中不能含分母;②被开方式中不能有可开尽方的数或式子. B 中含分母,C 、D 含开方数4、9,故选A.【变式题组】1.⑴(中山)下列根式中不是最简二次根式的是( )A.A .①,②B .③,④C .①,③D .①,④【例2】(黔东南)方程480x -=,当y >0时,m 的取值范围是( )A .0<m <1B .m ≥2C .m <2D .m ≤2【解法指导】本题属于两个非负数的代数和问题,隐含两个代数式均为0的结论.由题意得4x -8=0,x -y -m =0.化为y =2-m ,则2-m >0,故选C.【变式题组】2.(宁波)若实数x 、y 2(0y =,则xy 的值是__________.3.2()x y =+,则x -y 的值为( )A .- 1B .1C .2D .34.有意义的x 的取值范围是( ) A .x >3B .x ≥3C .x >4D .x ≥3且x ≠45.(怀化)22(4)0a c --=,则a -b -c =________.【例3是同类二次根式的是( )A BCD 【解法指导】判断几个二次根式是否为同类二次根式应先把它们都化为最简二次根式,再看被开方数是否一样.A =;B 不能化简;=;D ==.故本题应选D.【变式题组】6a =________. 7.在下列各组根式中,是同类二次根式的是( )A B C D8.已知最简二次根式b a =_______,b =______. 【例4】下列计算正确的是( )A =B 4=C =D .(11+=【解法指导】正确运用二次根式的性质①2(0)a a =≥;(0)0(0)(0)a a a a a a ⎧⎪===⎨⎪-⎩><;③0,0)a b =≥≥;④0,0)b a =≥> 进行化简计算,并能运用乘法公式进行计算.A 、B 中的项不能合并.D. 2(111-=-=-.故本题应选C.【变式题组】9. (聊城)下列计算正确的是( ) A.= B=C3=D3=-10.计算:200720074)(4⋅=_____________ 11.22-=_____________12.(济宁)已知a) A .a B .-a C .-1 D .0 13.已知a >b >0,a +b =的值为( )A.2B .2CD .12【例5】已知xy >0,化简二次根式的正确结果为( ) ABC.D.【解法指导】先要判断出y <0,再根据xy >0知x <0.故原式=选D. 【变式题组】14.已知a 、b 、c 为△AB C三边的长,则化简a b c --_______. 15===并利用这一规律计算:1)++⋅=L _________.16.已知,则0<x <1=_________.【例6】(辽宁)⑴先化简吗,再求值:11b++,其中1a =,1b =.⑵已知x =,y =值为________. 【解法指导】对于⑴,先化简代数式再代入求值;对于⑵,根据已知数的特征求xy 、x +y 的值,再代入求值.【解】⑴原式=22()()()()ab a a b b a b a b ab a b ab a b ab +++++==++,当12a =,12b -=时,ab =1,a +b .⑵由题意得:xy =1,x +y =10, 10199=-. 【变式题组】17.(威海)先化简,再求值:(a +b )2+(a -b)(2a +b)-3a 2,其中2a =--2b =.18.(黄石)已知a 是4的小数部分,那么代数式22224()()442a a a a a a a a a+-+⋅-+++的值为________.【例7】已知实数x 、y 满足(2008x y =,则3x 2-2y 2+3x -3y -2007的值为( )A .-2008B .2008C .-1D .1【解法指导】对条件等式作类似于因式分解的变形,找出a 、b 的关系,再代入求值.解:∵(2008x y =,∴(x =y =(y =x =,由以上两式可得x =y .∴(2008x =, 解得x 2=2008,所以3x 2-2y 2+3x -3y -2007=3x 2-2x 2+3x -3x -2007=x 2-2007=1,故选D.【变式题组】19.若a >0,b >0=的值.演练巩固·反馈提高01.若4m =,则估计m 的值所在的范围是( )A .1<m <2B .2<m <3C .3<m <4D .4<m <502.n 的最大值为( )A .12B .11C .8D .303.(黄石)下列根式中,不是..最简二次根式的是( )A.04.(贺州)下列根式中,不是最简二次根式的是( )A.05.下列二次根式中,是最简二次根式的是( )A.06.(常德)设a =20, b =(-3)2, c =11()2d -=, 则a 、b 、c 、d 、按由小到大的顺序排列正确的是( )A .c <a <d <bB .b <d <a <cC .a <c <d <bD .b <c <a <d07.(十堰)下列运算正确的是( )A =B =C .21)31=-D 53=-08.如果把式子(1a -根号外的因式移入根号内,化简的结果为( )A .B C .D .09.2x -化简的结果为2x -3,则x 的取值范围是( )A .x ≤1B .x ≥2C .1≤x ≤2D .x >010.(怀化)函数y =中自变量的取值范围是________.11.(湘西)对于任意不相等的两个数a ,b ,定义一种运算a ※b =那么12※4=________.12.(荆州)先化简,再求值:22321121a a a a a a-+÷-+-,其中a =13.(广州)先化简,再求值:((6)a a a a -+--,其中12a =. 培优升级01.(凉山州)已知一个正数的平方根是3x -2和5x +6,则这个数是________.02.已知a 、b 是正整数,且满足是整数,则这样的有序数对(a ,b )共有________对.03.(全国)设12a =,则5432322a a a a a a a+---+=-________. 04.(全国)设x =a 是x 的小数部分,b 是x 的小数部,则a 3+b 3+3ab =________.05.(重庆)已知2y =,则x 2+y 2=________.06.(全国)已知1a =,a =2a =,那么a 、b 、c 的大小关系是( )07.(武汉)已知y =(x ,y 均为实数),则y 的最大值与最小值的差为( )A 3B .3C 3D08.(全国)已知非零实数a 、b 满足24242a b a -+++=,则a +b 等于( ) A .-1B .0C .1D .209.(全国) )A .5-B .1C .5D .110.已知0(0,0)x y x y -=>>的值为( )A .13 B .12C .23 D .3411.已知152a b c +-=-,求a +b +c 的值.12.已知9+9a 和b ,求ab -3a +4b +8的值.第2讲 二次根式的化简与求值考点·方法·破译1.会灵活运用二次根式的运算性质化简求值.2.会进行二次根式的有理化计算,会整体代入求值及变形求值. 3.会化简复合二次根式,会在根式范围内分解因式.经典·考题·赏析【例1】2=的值等于__________ 【解法指导】通过平方或运用分式性质,把已知条件和待求式的被开方数都用1x x+表示或化简变形. 解:两边平方得,124x x ++=,12x x+= ,两边同乘以x 得,212x x += ,∵2315x x x ++=,29111x x x ++=,∴原式511- 【变式题组】 1.若14a a +=(0<a <1)=________ 2=-) A .1a a -B .1a a-C .1a a+D .不能确定【例2】(全国)满足等式=2003的正整数对(x ,y )的个数是( ) A .1 B .2 C .3 D .4【解法指导】对条件等式作类似于因式分解的变形,将问题转化为求不定方程的正整数解.0=,∴0=0>0=,则xy =2003,且2003是质数,∴正整数对(x ,y )的个数有2对,应选B . 【变式题组】3.若a >0,b >0=的值.【例3】1)a =<<,求代数式22632x x x x x x +-+÷-. 【解法指导】视x -2,x 2-4x=a 的代数式表示x -2,x 2-4x ,注意0<a <1的制约.解:平方得,12x a a =++,∴12x a a -=+,2221442x x a a-+=++, 222142x x a a-=+-,∴化简原式=(3)(2)(2)3x x x x x x +--+g =2211()1()211()a a a a a a a a a a a++-+-=++--【变式题组】4.(武汉)已知32x x +=+,求代数式35(2)242x x x x -÷----的值.5.(五羊杯)已知1m =1n =,且22(714)(367)8m m a n n -+--=,则a 的值等于( ) A .-5B .5C .-9D .9【例4】(全国)如图,点A 、C都在函数0)y x =>的图像上,点B 、D 都在x 轴上,且使得△OAB 、△BCD 都是等边三角形,则点D 的坐标为________.【解法指导】解:如图,分别过点A 、C 作x 轴的垂线,垂足分别为E 、F .设OE=a ,BF=b ,则a ,CF,所以,点A 、C 的坐标为(a)、(2a +b),所以2(2)a b =+=a b ⎧=⎪⎨=⎪⎩因此,点D的坐标为(,0)【变式题组】6.(邵阳)阅读下列材料,然后回答问题. 在进行二次根式化简时,我们有时会碰上如1323235+,,一样的式子,其实我们还可以将其进一步化简: 335333535=⨯⨯=; (一) 36333232=⨯⨯=; (二) ()()()131313132132-=-+-⨯=+; (三) 以上这种化简的步骤叫做分母有理化,132+还可以用以下方法化简:()()()13131313131313131322-=+-+=+-=+-=+; (四)(1)请你用不同的方法化简352+;①参照(三)试得:352+=_____________________________;(要有简化过程)②参照(四)试得:352+=_____________________________;(要有简化过程)(2++L【例5】(五羊杯)设a 、b 、c 、d 为正实数,a <b ,c <d ,bc >ad,【解法指导】虽然不能用面积公式求三角形面积(为什么?)a 、c 为直角边的直角三角形的斜边,从构造图形入手,将复杂的根式计算转化为几何问题加以解决.解:如图,作长方形ABCD ,使AB =b -a ,AD =c ,延长DA 至E ,使DE =d ,延长DC 至F ,使DF =b ,连结EF 、FB 、EB ,则BF=,EF=,BE ,从而-S △DEF =(b -a )c +12(d -知△BEF 就是题设的三角形,而S △BEF =S 长方形ABCD +S △BCF +S △ABE c )(b -a )-12bd =12(bc -ad )【变式题组】7.(北京)已知a 、b 均为正数,且a+b =2,求U演练巩固·反馈提高01.已知x =,y =值为__________ 02.设1a =,则32312612a a a +--=( )A . 24B .25C.10D.1203.(天津)计算2001200019991)1)1)2001--+=__________ 04.(北京)若有理数x 、y 、z 1()2x y z =++,则2()x yz -=__________05.(北京)正数m 、n 满足430m n +-==__________06.(河南)若1x =+,则32(2(15x x x -++的值是( )A .2B .4C .6D .807.已知实数a 满足2000a a -=,那么22000a -的值是( ) A .1999B .2000C .2001D .200208.设a =b =c =a 、b 、c 之间的大小关系是( ) A .a <b <cB .c <b <aC .c <a <bD .a <c <b09.已知1x =培优升级01.(信利)已知1x =+2111242x x x +-=+--__________025==__________03.(江苏)已知(2002x y =,则2234x xy y --6658x y --+=__________04.7x =,则x =__________05.已知x =,y =,那么22y x x y +=__________06.(武汉)如果a b +=a b -=3333b c b c +=-,那么333a b c -的值为( )A .B .2001C .1D .007.(绍兴)当x =32003(420052001)x x --的值是( ) A .0B .-1C .1D .20032-08.(全国)设a 、b 、c 为有理数,且等式a +=成立,则29991001a b c ++的值是( ) A .1999B .2000C .2001D .不能确定09.计算:(1(2(3+++L(410.已知实数a 、b 满足条件1b a b a -=<,化简代数式11()a b-,将结果表示成不含b 的形式.11.已知21(0)a x a a +=>12.已知自然数x 、y 、z 0=,求x +y +z 的值.第3讲 一元二次方程的解法考点·方法·破译1.掌握一元二次方程根的定义并能应用根的定义解题;2.掌握一元二次方程的四种解法,并能灵活应用各种解法解方程; 3.会应用一元二次方程解实际应用题。
初三数学培优试卷推荐答案

1. 若方程 2x-3=5 的解为 x=a,则 a 的值为()A. 4B. 2C. 1D. -1答案:A解析:将方程两边同时加3,得到 2x=8,再将两边同时除以2,得到 x=4。
所以a=4。
2. 若 m、n 是方程 x^2-5x+6=0 的两个实数根,则 m+n 的值为()A. 5B. 6C. 7D. 8答案:A解析:根据一元二次方程的根与系数的关系,有 m+n=5。
3. 若等差数列 {an} 的前5项之和为 15,第3项为 3,则该数列的公差为()A. 1B. 2C. 3D. 4答案:A解析:设等差数列的公差为 d,则第3项 a3=a1+2d=3。
又因为前5项之和为 15,所以有 5a1+10d=15。
解得 d=1。
4. 若函数 y=2x+1 的图像上任意一点的横坐标为 x,则该点的纵坐标与 x 的关系为()A. y=x+1B. y=2x+1C. y=2x-1D. y=x-1答案:B解析:由函数表达式可知,纵坐标 y 与横坐标 x 的关系为 y=2x+1。
5. 若 a、b、c 是等差数列 {an} 的前3项,且 a+b+c=12,则该数列的公差为()A. 2B. 3C. 4D. 6答案:B解析:设等差数列的公差为 d,则 a=b-d,c=b+d。
根据题意,有 b-d+b+b+d=12,解得 d=3。
关系为()A. y=x+1B. y=|x-2|+3C. y=x-1D. y=x+3答案:B解析:由函数表达式可知,纵坐标 y 与横坐标 x 的关系为 y=|x-2|+3。
7. 若等比数列 {an} 的前4项之和为 24,第3项为 6,则该数列的公比为()A. 2B. 3C. 4D. 6答案:B解析:设等比数列的公比为 q,则第3项 a3=a1q^2=6。
又因为前4项之和为 24,所以有 a1+a1q+a1q^2+a1q^3=24。
解得 q=3。
8. 若 a、b、c 是等比数列 {an} 的前3项,且 a+b+c=12,则该数列的公比为()A. 2B. 3C. 4D. 6答案:A解析:设等比数列的公比为 q,则 a=b/q,c=bq。
九年级数学培优题含详细答案

九年级培优竞赛1.在如图的直角坐标系中,已知点A(2,0)、B(0,-4),将线段AB 绕点A 按逆时针方向旋转90°至AC .(1)求点C 的坐标;(2)若抛物线y =-14x 2+ax +4经过点C . ①求抛物线的解析式;②在抛物线上是否存在点P(点C 除外)使△ABP 是以AB 为直角边的等腰直角三角形?若存在,求出所有点P 的坐标;若不存在,请说明理由.【答案】C 的坐标为(3,﹣1);(2)①抛物线的解析式为y=﹣12x 2+12x+2; ②存在点P ,△ABP 是以AB 为直角边的等腰直角三角形,符合条件的点有P 1(﹣1,1),P 2(﹣2,﹣1)两点.【解析】试题分析:(1)过点C 作CD 垂直于x 轴,由线段AB 绕点A 按逆时针方向旋转90°至AC ,根据旋转的旋转得到AB=AC ,且∠BAC 为直角,可得∠OAB 与∠CAD 互余,由∠AOB 为直角,可得∠OAB 与∠ABO 互余,根据同角的余角相等可得一对角相等,再加上一对直角相等,利用ASA 可证明三角形ACD 与三角形AOB 全等,根据全等三角形的对应边相等可得AD=OB ,CD=OA ,由A 和B 的坐标及位置特点求出OA 及OB 的长,可得出OD 及CD 的长,根据C 在第四象限得出C 的坐标;(2)①由已知的抛物线经过点C ,把第一问求出C 的坐标代入抛物线解析式,列出关于a 的方程,求出方程的解得到a 的值,确定出抛物线的解析式;②假设存在点P 使△ABP 是以AB 为直角边的等腰直角三角形,分三种情况考虑:(i )A 为直角顶点,过A 作AP 1垂直于AB ,且AP 1=AB ,过P 1作P 1M 垂直于x 轴,如图所示,根据一对对顶角相等,一对直角相等,AB=AP 1,利用AAS 可证明三角形AP 1M 与三角形ACD 全等,得出AP 1与P 1M 的长,再由P 1为第二象限的点,得出此时P 1的坐标,代入抛物线解析式中检验满足;(ii )当B 为直角顶点,过B 作BP 2垂直于BA ,且BP 2=BA ,过P 2作P 2N 垂直于y 轴,如图所示,同理证明三角形BP 2N 与三角形AOB 全等,得出P 2N 与BN 的长,由P 2为第三象限的点,写出P 2的坐标,代入抛物线解析式中检验满足;(iii )当B 为直角顶点,过B 作BP 3垂直于BA ,且BP 3=BA ,如图所示,过P 3作P 3H 垂直于y 轴,同理可证明三角形P 3BH 全等于三角形AOB ,可得出P 3H 与BH 的长,由P 3为第四象限的点,写出P 3的坐标,代入抛物线解析式检验,不满足,综上,得到所有满足题意的P 的坐标. 试题解析:(1)过C 作CD ⊥x 轴,垂足为D ,∵BA⊥AC,∴∠OAB+∠CAD=90°,又∠AOB=90°,∴∠OAB+∠OBA=90°,∴∠CAD=∠OBA,又AB=AC,∠AOB=∠ADC=90°,∴△AOB≌△CDA,又A(1,0),B(0,﹣2),∴OA=CD=1,OB=AD=2,∴OD=OA+AD=3,又C为第四象限的点,∴C的坐标为(3,﹣1);(2)①∵抛物线y=﹣12x2+ax+2经过点C,且C(3,﹣1),∴把C的坐标代入得:﹣1=﹣92+3a+2,解得:a=12,则抛物线的解析式为y=﹣12x2+12x+2;②存在点P,△ABP是以AB为直角边的等腰直角三角形,(i)若以AB为直角边,点A为直角顶点,则延长CA至点P1使得P1A=CA,得到等腰直角三角形ABP1,过点P1作P1M⊥x轴,如图所示,∵AP1=CA,∠MAP1=∠CAD,∠P1MA=∠CDA=90°,∴△AMP1≌△ADC,∴AM=AD=2,P1M=CD=1,∴P1(﹣1,1),经检验点P1在抛物线y=﹣12x2+12x+2上;(ii)若以AB为直角边,点B为直角顶点,则过点B作BP2⊥BA,且使得BP2=AB,得到等腰直角三角形ABP2,过点P2作P2N⊥y轴,如图,同理可证△BP2N≌△ABO,∴NP2=OB=2,BN=OA=1,∴P2(﹣2,﹣1),经检验P2(﹣2,﹣1)也在抛物线y=﹣12x2+12x+2上;(iii)若以AB为直角边,点B为直角顶点,则过点B作BP3⊥BA,且使得BP3=AB,得到等腰直角三角形ABP3,过点P3作P3H⊥y轴,如图,同理可证△BP3H≌△BAO,∴HP3=OB=2,BH=OA=1,∴P3(2,﹣3),经检验P3(2,﹣3)不在抛物线y=﹣12x2+12x+2上;则符合条件的点有P1(﹣1,1),P2(﹣2,﹣1)两点.考点:1.二次函数综合题2.点的坐标3.等腰直角三角形.2.在Rt△ABC中,∠ACB=90°,AC=BC,D为AB边的中点,点P为BC边上一点,把△PBD 沿PD翻拆,点B落在点E处,设PE交AC于F,连接CD(1)求证:△PCF的周长=2CD;(2)设DE交AC于G,若53PEEF=,CD=6,求FG的长【答案】(1)证明见解析;(2)FG的长为152 14.【解析】试题分析:.(1)连接CE,根据三角形的角边关系可以得到∠FCE=∠FEC,从而FC=FE,△PCF的周长=2CD;(2) 由.(1)结论CP+PF+CF=2CD,和PF5EF3=,CD=6,求出CF=EF=322,作GK⊥EF于点K,易得FG的长为152 14.试题解析:.(1)连接CE,∵CA=CB,D 为AB 中点,∴∠BCD=∠ACD=45°,由翻折可知∠B=∠DEP=45°,∴∠DCF=∠DEF=45°,CD=BD=DE ,∴∠DCE=∠DEC ,∴∠DCE-∠DCA=∠DEC-∠DEF ,即∠FCE=∠FEC ,∴FC=FE ,∴CF+PF=PE=BP ,∴,∴△PCF;(2)∴设PF=5x,EF=CF=3x ,在Rt △FCP 中,PF 2=CP 2+CF 2,∴CP=4x ,∵,∴作GK ⊥EF 于点K ,∵tan ∠GFE=tan ∠ 设GK=4a,FK=3a,EK=4a , G F D AB PC KFDAB PC∴EF=7a=322, a=3214, FG=5a=15214, ∴FG 的长为15214. 考点:三角形综合.3.如图,抛物线y=-x 2+4x+5交x 轴于A 、B (以A 左B 右)两点,交y 轴于点C.(1)求直线BC 的解析式;(2)点P 为抛物线第一象限函数图象上一点,设P 点的横坐标为m ,△PBC 的面积为S ,求S 与m 的函数关系式;(3)在(2)的条件下,连接AP ,抛物线上是否存在这样的点P ,使得线段PA 被BC 平分,如果不存在,请说明理由;如果存在,求点P 的坐标.【答案】(1) y=5x -+ (2) S=252522m m -+ (3)存在,P(2,9)或P(3,8) 【解析】试题分析:(1)令y=0,解关于x 的一元二次方程即可得到点A 、B 的坐标,再令x=0求出点C 的坐标,设直线BC 解析式为y=kx+b (k≠0),利用待定系数法求一次函数解析式解答;(2)过点P 作PH ⊥x 轴于H ,交BC 于F ,根据抛物线和直线BC 的解析式表示出PF ,再根据S △PBC =S △PCF +S △PBF 整理即可得解;(3)设AP 、BC 的交点为E ,过点E 作EG ⊥x 轴于G ,根据垂直于同一直线的两直线平行可得EG ∥PH ,然后判断出△AGE 和△AHP 相似,根据相似三角形对应边成比例可表示出EG 、HG ,然后表示出BG ,根据OB=OC 可得∠OCB=∠OBC=45°,再根据等角对等边可得EG=BG ,然后列出方程求出m 的值,再根据抛物线解析式求出点P 的纵坐标,即可得解.试题解析:(1)当y=0时,x 1=5,x 2=-1,∵A 左B 右,∴A(-1,0),B(5,O)当x=0时,y=5,∴C (0,5),设直线BC 解析式为y=kx+b,∴5005k b k b +=⎧⎨⨯+=⎩ ∴15k b =-⎧⎨=⎩∴直线BC 解析式为:y=5x -+;(2)作PH ⊥x 轴于H ,交BC 于点F ,P(m ,-m 2+4m+5),F(m,-m+5)PF=-m 2+5m ,S △PBC =S △PCF +S △PBF(3)存在点P ,作EG ⊥AB 于G,PH ⊥AB 于H ,∴EG ∥PH ,∴△AGE ∽△AHP ,∵P(m ,-m +4m+5),AH=m-(-1)=m+1,HB=5-m ,GB=152mm ++-,∵OC=OB=5,∴∠OCB=∠OBC=45°,∴EG=BG,∴2452m m-++=152mm++-,∴m1=2m2=3,当m=2时,P(2,9),当m=3时,P(3,8),∴存在这样的点P, 使得线段PA被BC平分,P(2,9)或P(3,8).考点:二次函数综合题.4.如图:在等腰△ABC中,AB=AC,AD上BC,垂足为D,以AD为直径作⊙0,⊙0分别交AB、AC于E、F.(1)求证:BE=CF;(2)设AD、EF相交于G,若EF=8,BC=10,求⊙0的半径.【答案】(1)证明见解析;(2)⊙O的半径为5.【解析】试题分析:(1)连接DE,DF,由AB=AC,且AD为BC边上的高,利用三线合一得到D为BC的中点,AD为顶角平分线,再由AD为圆O的直径,利用直角所对的角为直角得到一对直角相等,利用AAS得到三角形EBD与三角形FCD全等,由全等三角形的对应边相等得到BE=CF,得证;(2)由EB=CF,AB=AC,得出AE=AF,确定出AE:AB=AF:AC,且夹角相等,得到三角形AEF与三角形ABC相似,由相似三角形的对应边成比例得到AG:AD=8:10,设AG=8x,AD=10x,连接OE,在直角三角形OEG中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即可确定出圆O的半径.试题解析:(1)连接DE、DF,∵AB=AC,AD⊥BC,∴∠B=∠C,BD=CD,∵AD为⊙O的直径,∴∠DEA=∠DFA=90°,∴△DBE≌△DCF,∴BE=CF;(2)∵BE=CF,∴AE=AF,AE AFAB AC=且∠BAC=∠BAC,∴△AEF∽△ABC,∴设AG=8x,AD=10x,连接EO,在Rt△OEG中,∴OE2=OG2+EG2,∴(5x)2=(3x)2+42,x=1,∴5x=5,∴⊙O的半径为5.考点:1.相似三角形的判定与性质,2.全等三角形的判定与性质,3.勾股定理,4.圆周角定理.5.正方形ABCD的顶点A在直线MN上,点O是对角线AC、BD的交点,过点O作OE⊥MN于点E,过点B作BF⊥MN于点F.(1)如图1,当O、B两点均在直线MN上方时,易证:AF+BF=2OE(不需证明)(2)当正方形ABCD绕点A顺时针旋转至图2、图3的位置时,线段AF、BF、OE之间又有怎样的关系?请直接写出你的猜想,并选择一种情况给予证明.【答案】(1)见解析(2)见解析【解析】思路分析:(1)过点B作BG⊥OE于G,可得四边形BGEF是矩形,根据矩形的对边相等可得EF=BG,BF=GE,根据正方形的对角线相等且互相垂直平分可得OA=OB,∠AOB=90°,再根据同角的余角相等求出∠AOE=∠OBG,然后利用“角角边”证明△AOE和△OBG全等,根据全等三角形对应边相等可得OG=AE,OE=BG,再根据AF-EF=AE,整理即可得证;(2)选择图2,过点B作BG⊥OE交OE的延长线于G,可得四边形BGEF是矩形,根据矩形的对边相等可得EF=BG,BF=GE,根据正方形的对角线相等且互相垂直平分可得OA=OB,∠AOB=90°,再根据同角的余角相等求出∠AOE=∠OBG,然后利用“角角边”证明△AOE和△OBG全等,根据全等三角形对应边相等可得OG=AE,OE=BG,再根据AF-EF=AE,整理即可得证;选择图3同理可证.解:(1)证明:如图,过点B作BG⊥OE于G,则四边形BGEF是矩形,∴EF=BG,BF=GE,在正方形ABCD中,OA=OB,∠AOB=90°,∵BG⊥OE,∴∠OBG+∠BOE=90°,又∵∠AOE+∠BOE=90°,∴∠AOE=∠OBG ,∵在△AOE 和△OBG 中,,∴△AOE ≌△OBG (AAS ),∴OG=AE ,OE=BG ,∵AF-EF=AE ,EF=BG=OE ,AE=OG=OE-GE=OE-BF ,∴AF-OE=OE-BF ,∴AF+BF=2OE ;(2)图2结论:AF-BF=2OE ,图3结论:AF-BF=2OE .对图2证明:过点B 作BG ⊥OE 交OE 的延长线于G ,则四边形BGEF 是矩形,∴EF=BG ,BF=GE ,在正方形ABCD 中,OA=OB ,∠AOB=90°,∵BG ⊥OE ,∴∠OBG+∠BOE=90°,又∵∠AOE+∠BOE=90°,∴∠AOE=∠OBG ,∵在△AOE 和△OBG 中,,∴△AOE ≌△OBG (AAS ),∴OG=AE ,OE=BG ,∵AF-EF=AE ,EF=BG=OE ,AE=OG=OE+GE=OE+BF ,∴AF-OE=OE+BF ,∴AF-BF=2OE ;若选图3,其证明方法同上.点评:本题考查了正方形的性质,矩形的判定与性质,全等三角形的判定与性质,同角的余角相等的性质,作辅助线构造出全等三角形与矩形是解题的关键,也是本题的难点.6.如图,在平面直角坐标系中,O 为坐标原点,点A 的坐标为(0,4),点B 的坐标为(4,0),点C 的坐标为(-4,0),点P 在射线AB 上运动,连结CP 与y 轴交于点D ,连结BD .过P ,D ,B 三点作⊙Q 与y 轴的另一个交点为E ,延长DQ 交⊙Q 于点F ,连结EF ,BF .90AOE OBG AEO OGB OA OB ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩90AOE OBG AEO OGB OA OB ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩(1)求直线AB的函数解析式;(2)当点P在线段AB(不包括A,B两点)上时.①求证:∠BDE=∠ADP;②设DE=x,DF=y.请求出y关于x的函数解析式;(3)请你探究:点P在运动过程中,是否存在以B,D,F为顶点的直角三角形,满足两条直角边之比为2:1?如果存在,求出此时点P的坐标:如果不存在,请说明理由.【答案】(1)y=-x+4 (2)①见解析x (3)存在,点P的坐标为(2,2)或(8,-4)【解析】解:(1)设直线AB的函数解析式为y=kx+4,代入(4,0)得:4k+4=0,解得:k=-1,则直线AB的函数解析式为y=-x+4;(2)①由已知得:OB=OC,∠BOD=∠COD=90°,又∵OD=OD,∴△BDO≌△COD,∴∠BDO=∠CDO,∵∠CDO=∠ADP,∴∠BDE=∠ADP,②如图,连结PE,∵∠ADP是△DPE的一个外角,∴∠ADP=∠DEP+∠DPE,∵∠BDE是△ABD的一个外角,∴∠BDE=∠ABD+∠OAB,∵∠ADP=∠BDE,∠DEP=∠ABD,∴∠DPE=∠OAB,∵OA=OB=4,∠AOB=90°,∴∠OAB=45°,∴∠DPE=45°,∴∠DFE=∠DPE=45°,第11页,总68页∵DF 是⊙Q 的直径, ∴∠DEF=90°,∴△DEF 是等腰直角三角形, ∴DE ,即x ; (3)当BD :BF=2:1时,如图,过点F 作FH ⊥OB 于点H ,∵∠DBO+∠OBF=90°,∠OBF+∠BFH=90°, ∴∠DBO=∠BFH ,又∵∠DOB=∠BHF=90°, ∴△BOD ∽△FHB , ∴=2, ∴FH=2,OD=2BH ,∵∠FHO=∠EOH=∠OEF=90°, ∴四边形OEFH 是矩形, ∴OE=FH=2, ∴EF=OH=4-OD , ∵DE=EF , ∴2+OD=4-OD , 解得:OD=,∴点D 的坐标为(0,), ∴直线CD 的解析式为y=x+, 由,得:, 则点P 的坐标为(2,2); 当时, 连结EB ,同(2)①可得:∠ADB=∠EDP ,OB OD BDHF HB FB==12124343134314334y x y x ⎧=+⎪⎨⎪=-+⎩22x y =⎧⎨=⎩12BD BF =试卷第12页,总68页而∠ADB=∠DEB+∠DBE ,∠EDP=∠DAP+∠DPA , ∵∠DEP=∠DPA ,∴∠DBE=∠DAP=45°,∴△DEF 是等腰直角三角形, 如图,过点F 作FG ⊥OB 于点G ,同理可得:△BOD ∽△FGB , ∴, ∴FG=8,OD=BG , ∵∠FGO=∠GOE=∠OEF=90°, ∴四边形OEFG 是矩形, ∴OE=FG=8, ∴EF=OG=4+2OD , ∵DE=EF ,∴8-OD=4+2OD , OD=, ∴点D 的坐标为(0,-), 直线CD 的解析式为:, 由,得:, ∴点P 的坐标为(8,-4),综上所述,点P 的坐标为(2,2)或(8,-4).7.如图,在Rt △ABC 中,∠ACB=90°,AC=6cm ,BC=8cm .点D 、E 、F 分别是边AB ,BC ,AC 的中点,连接DE ,DF ,动点P ,Q 分别从点A 、B 同时出发,运动速度均为1cm/s ,点P 沿AFD 的方向运动到点D 停止;点Q 沿BC 的方向运动,当点P 停止运动时,点Q 也停止运动.在运动过程中,过点Q 作BC 的垂线交AB 于点M ,以点P ,M ,Q 为顶点作12OB OD BD GF GB FB ===1243431433y x =--14334y x y x ⎧=--⎪⎨⎪=-+⎩84x y =⎧⎨=-⎩第13页,总68页平行四边形PMQN .设平行四边形边形PMQN 与矩形FDEC 重叠部分的面积为y (cm 2)(这里规定线段是面积为0有几何图形),点P 运动的时间为x (s )(1)当点P 运动到点F 时,CQ= cm ;(2)在点P 从点F 运动到点D 的过程中,某一时刻,点P 落在MQ 上,求此时BQ 的长度;(3)当点P 在线段FD 上运动时,求y 与x 之间的函数关系式. 【答案】(1)5 (2)(cm ) (3)当3≤x<4时,y=-x 2+x 当4≤x<时,y=-6x+33 当≤x≤7时,y=6x-33 【解析】 解:(1)当点P 运动到点F 时, ∵F 为AC 的中点,AC=6cm , ∴AF=FC=3cm ,∵P 和Q 的运动速度都是1cm/s , ∴BQ=AF=3cm ,∴CQ=8cm-3cm=5cm , 故答案为:5.(2)设在点P 从点F 运动到点D 的过程中,点P 落在MQ 上,如图1,则t+t-3=8, t=, 11234214112112112试卷第14页,总68页BQ 的长度为×1=(cm ); (3)∵D 、E 、F 分别是AB 、BC 、AC 的中点, ∴DE=AC=×6=3, DF=BC=×8=4, ∵MQ ⊥BC ,∴∠BQM=∠C=90°, ∵∠QBM=∠CBA , ∴△MBQ ∽△ABC , ∴, ∴, MQ=x , 分为三种情况:①当3≤x<4时,重叠部分图形为平行四边形,如图2,y=PN•PD =x (7-x ) 即y=-x 2+x ; ②当4≤x<时,重叠部分为矩形,如图3, 11211212121212BQ MQBC AC =86x MQ =343434214112第15页,总68页y=3[(8-X )-(X-3))] 即y=-6x+33; ③当≤x≤7时,重叠部分图形为矩形,如图4,y=3[(x-3)-(8-x )] 即y=6x-33.8.已知:如图①,在平行四边形ABCD 中,AB=12,BC=6,AD ⊥BD .以AD 为斜边在平行四边形ABCD 的内部作Rt △AED ,∠EAD=30°,∠AED=90°.(1)求△AED 的周长;(2)若△AED 以每秒2个单位长度的速度沿DC 向右平行移动,得到△A 0E 0D 0,当A 0D 0与BC 重合时停止移动,设运动时间为t 秒,△A 0E 0D 0与△BDC 重叠的面积为S ,请直接写出S 与t 之间的函数关系式,并写出t 的取值范围;(3)如图②,在(2)中,当△AED 停止移动后得到△BEC ,将△BEC 绕点C 按顺时针方向旋转α(0°<α<180°),在旋转过程中,B 的对应点为B 1,E 的对应点为E 1,设直线B 1E 1与直线BE 交于点P 、与直线CB 交于点Q .是否存在这样的α,使△BPQ 为等腰三角形?若存在,求出α的度数;若不存在,请说明理由. 【答案】(1)(2)S 与t 之间的函数关系式为:112试卷第16页,总68页S= (3)存在,α=75°【解析】 解:(1)∵四边形ABCD 是平行四边形, ∴AD=BC=6.在Rt △ADE 中,AD=6,∠EAD=30°,∴AE=AD•cos30°=3,DE=AD•sin30°=3, ∴△AED 的周长为:6+3+3=9+3.(2)在△AED 向右平移的过程中:(I )当0≤t≤1.5时,如答图1所示,此时重叠部分为△D 0NK .∵DD 0=2t ,∴ND 0=DD 0•sin30°=t,NK=ND 0•tan30°=t ,∴S=S △D0NK =ND 0•NK=t•t=t 2;(II )当1.5<t≤4.5时,如答图2所示,此时重叠部分为四边形D 0E 0KN .∵AA 0=2t ,∴A 0B=AB-AA 0=12-2t , ∴A 0N=A 0B=6-t ,NK=A 06-t ).∴S=S 四边形D0E0KN =S △ADE -S △A0NK =×(6-t )×(6-t )=-t 2;(III )当4.5<t≤6时,如答图3所示,此时重叠部分为五边形D 0IJKN .222(0 1.5) 4.5)--6)6t S t t ≤≤⎪⎪⎪=+<≤⎨⎪⎪+<≤⎪⎪⎩333312123321231231233363332第17页,总68页∵AA 0=2t ,∴A 0B=AB-AA 0=12-2t=D 0C , ∴A 0N=A 0B=6-t ,D 0N=6-(6-t )=t ,BN=A 0B•cos30°=(6-t ); 易知CI=BJ=A 0B=D 0C=12-2t ,∴BI=BC-CI=2t-6, S=S 梯形BND0I -S △BKJ =[t+(2t-6)]• (6-t )-•(12-2t )•(12-2t )=-t 2+20t-42.综上所述,S 与t 之间的函数关系式为:S=. (3)存在α,使△BPQ 为等腰三角形.理由如下:经探究,得△BPQ ∽△B 1QC ,故当△BPQ 为等腰三角形时,△B 1QC 也为等腰三角形. (I )当QB=QP 时(如答图4),则QB 1=QC ,∴∠B 1CQ=∠B 1=30°, 即∠BCB 1=30°, ∴α=30°;(II )当BQ=BP 时,则B 1Q=B 1C ,若点Q 在线段B 1E 1的延长线上时(如答图5),∵∠B 1=30°,∴∠B 1CQ=∠B 1QC=75°,12312312331336332223(0 1.5)2333-23-(1.5 4.5)62133-203-423(4.56)6t t S t t t t t t ⎧≤≤⎪⎪⎪⎪=+<≤⎨⎪⎪+<≤⎪⎪⎩试卷第18页,总68页即∠BCB 1=75°, ∴α=75°.9.如图1,已知直线y=x+3与x 轴交于点A ,与y 轴交于点B ,抛物线y=-x 2+bx+c 经过A 、B 两点,与x 轴交于另一个点C ,对称轴与直线AB 交于点E ,抛物线顶点为D .(1)求抛物线的解析式;(2)在第三象限内,F 为抛物线上一点,以A 、E 、F 为顶点的三角形面积为3,求点F 的坐标;(3)点P 从点D 出发,沿对称轴向下以每秒1个单位长度的速度匀速运动,设运动的时间为t 秒,当t 为何值时,以P 、B 、C 为顶点的三角形是直角三角形?直接写出所有符合条件的t 值.【答案】(1)y=-x 2-2x+3;(2)(3212--,3212--) (3)当t 为43秒或2秒或3秒或143秒时,以P 、B 、C 为顶点的三角形是直角三角形 【解析】 试题分析:(1)先由直线AB 的解析式为y=x+3,求出它与x 轴的交点A 、与y 轴的交点B 的坐标,再将A 、B 两点的坐标代入y=-x 2+bx+c ,运用待定系数法即可求出抛物线的解析式;(2)设第三象限内的点F 的坐标为(m ,-m 2-2m+3),运用配方法求出抛物线的对称轴及顶点D 的坐标,再设抛物线的对称轴与x 轴交于点G ,连接FG ,根据S △AEF =S △AEG +S △AFG -S △EFG =3,列出关于m 的方程,解方程求出m 的值,进而得出点F 的坐标;(3)设P 点坐标为(-1,n ).先由B 、C 两点坐标,运用勾股定理求出BC 2=10,再分三种情况进行讨论:①∠PBC=90°,先由勾股定理得出PB 2+BC 2=PC 2,据此列出关于n 的方程,求出n 的值,再计算出PD 的长度,然后根据时间=路程÷速度,即可求出此时对应的t 值;②∠BPC=90°,同①可求出对应的t 值;③∠BCP=90°,同①可求出对应的t 值.试题解析:(1)∵y=x+3与x 轴交于点A ,与y 轴交于点B , ∴当y=0时,x=-3,即A 点坐标为(-3,0), 当x=0时,y=3,即B 点坐标为(0,3),将A (-3,0),B (0,3)代入y=-x 2+bx+c ,得930c 3b c --+==⎧⎨⎩, 解得23b c =-⎧⎨=⎩, ∴抛物线的解析式为y=-x 2-2x+3; (2)如图1,设第三象限内的点F的坐标为(m,-m2-2m+3),则m<0,-m2-2m+3<0.∵y=-x2-2x+3=-(x+1)2+4,∴对称轴为直线x=-1,顶点D的坐标为(-1,4),设抛物线的对称轴与x轴交于点G,连接FG,则G(-1,0),AG=2.∵直线AB的解析式为y=x+3,∴当x=-1时,y=-1+3=2,∴E点坐标为(-1,2).∵S△AEF=S △AEG+S△AFG-S△EFG=12×2×2+12×2×(m2+2m-3)-12×2×(-1-m)=m2+3m,∴以A、E、F为顶点的三角形面积为3时,m2+3m=3,解得:1321 2m--=,23212m-+=(舍去),当3212m--=时,-m2-2m+3=-m2-3m+m+3=-3+m+3=m=3212--,∴点F的坐标为(3212--,3212--);(3)设P点坐标为(-1,n).∵B(0,3),C(1,0),∴BC2=12+32=10.分三种情况:①如图2,如果∠PBC=90°,那么PB2+BC2=PC2,即(0+1)2+(n-3)2+10=(1+1)2+(n-0)2,第19页,总68页化简整理得6n=16,解得n=83,∴P点坐标为(-1,83),∵顶点D的坐标为(-1,4),∴PD=4-83=43,∵点P的速度为每秒1个单位长度,∴t1=43;②如图3,如果∠BPC=90°,那么PB2+PC2=BC2,即(0+1)2+(n-3)2+(1+1)2+(n-0)2=10,化简整理得n2-3n+2=0,解得n=2或1,∴P点坐标为(-1,2)或(-1,1),∵顶点D的坐标为(-1,4),∴PD=4-2=2或PD=4-1=3,∵点P的速度为每秒1个单位长度,∴t2=2,t3=3;③如图4,如果∠BCP=90°,那么BC2+PC2=PB2,即10+(1+1)2+(n-0)2=(0+1)2+(n-3)2,化简整理得6n=-4,解得n=-23,∴P点坐标为(-1,-23),试卷第20页,总68页第21页,总68页 ∵顶点D 的坐标为(-1,4), ∴PD=4+23=143, ∵点P 的速度为每秒1个单位长度,∴t 4=143; 综上可知,当t 为43秒或2秒或3秒或143秒时,以P 、B 、C 为顶点的三角形是直角三角形.考点: 二次函数综合题.10.如图,在正方形ABCD 中,2AB =,点P 是边BC 上的任意一点,E 是BC 延长线上一点,联结AP ,作PF AP ⊥交DCE ∠的平分线CF 上一点F ,联结AF 交边CD 于点G .(1)求证:AP PF =;(2)设点P 到点B 的距离为x ,线段DG 的长为y ,试求y 关于x 的函数关系式,并写出自变量x 的取值范围;(3)当点P 是线段BC 延长线上一动点,那么(2)式中y 与x 的函数关系式保持不变吗?如改变,试直接写出函数关系式.【答案】(1)证明见解析;(2)()42022x y x x -=≤≤+;(3)改变,()24>22x y x x -=+. 【解析】试题分析:(1)欲证AP PF =利用原图无法证明,需构建三角形且使之全等,因此在边AB 上截取线段AH ,使AH PC =,连接PH ,证明AHP ∆与PCF ∆全等即可.(2)由APM ∆∽GAN ∆列式化简即可得.(3)在AD 延长线上取点N ,令ND DG =,∴NDG ∆是等腰直角三角形.∴22,2NG DG y AN y ===+ .同理,2,2PM x AM x ==- ,∵45,45APM PAM NAG PMA ANG ∠=︒+∠=∠∠=∠=︒ ,∴APM ∆∽GAN ∆.∴AM NG PM AN =,即2222x y yx -=+. 整理,得()24>22x y x x -=+.试卷第22页,总68页 试题解析:(1)在边AB 上截取线段AH ,使AH PC =,连接PH ,由正方形ABCD ,得90B BCD D AB BC AD ∠=∠=∠=︒==,,∵90APF ∠=︒,∴APF B ∠=∠.∵APC B BAP APF FPC ∠=∠+∠=∠+∠,∴PAH FPC ∠=∠.又∵90BCD DCE ∠=∠=︒,CF 平分DCE ∠,∴45FCE ∠=︒.∴135PCF ∠=︒. 又∵AB BC AH PC ==,,∴BH BP =,即得45BPH BHP ∠=∠=︒.∴135AHP ∠=︒,即得AHP PCF ∠=∠.在AHP ∆和PCF ∆中,PAH FPC AH PC AHP PCF ∠=∠=∠=∠,,,∴AHP ∆≌PCF ∆,∴AP PF =.(2)在AD 上取点N ,令ND DG =,∴NDG ∆是等腰直角三角形.∴22,2NG DG y AN y ===- .同理,2,2PM x AM x ==- ,∵45,135APM PAM NAG PMA ANG ∠=︒-∠=∠∠=∠=︒ ,∴APM ∆∽GAN ∆.∴AM NG PM AN =,即2222x y y x-=-. 整理,得()42022x y x x -=≤≤+. (3)改变,()24>22x y x x -=+. 考点:1.正方形的性质;2. 等腰直角三角形的判定和性质;3.全等三角形的判定与性质;4.由实际问题列函数关系式.11.如图,已知直线y =-2x +4与x 轴、y 轴分别相交于A 、C 两点,抛物线y=-2x 2+bx+c(a ≠0)经过点A 、C.(1)求抛物线的解析式;(2)设抛物线的顶点为P,在抛物线上存在点Q,使△ABQ的面积等于△APC面积的4倍.求出点Q的坐标;(3)点M是直线y=-2x+4上的动点,过点M作ME垂直x轴于点E,在y轴(原点除外)上是否存在点F,使△MEF为等腰直角三角形? 若存在,求出点F的坐标及对应的点M的坐标;若不存在,请说明理由.【答案】(1)y=-2x2+2x+4;(2)Q(0,4)或(1,4)-4)或-4);(3)存在,点F坐标为(0M,点F坐标为(0,-4)时,点M的坐标为(4,-4);点F坐标为(0,1),点M的坐标为(1,2).【解析】试题分析:1)根据直线y=-2x+4求出点A、C的坐标,再利用待定系数法求二次函数解析式解答即可;(2)根据抛物线解析式求出点P的坐标,过点P作PD⊥y轴于D,根据点P、C的坐标求出PD、CD,然后根据S△APC=S梯形APDO-S△AOC-S△PCD,列式求出△APC的面积,再根据抛物线解析式求出点B的坐标,从而得到AB的长度,然后利用三角形的面积公式求出△ABQ 的点Q的纵坐标的值,然后代入抛物线求解即可得到点Q的坐标;(3)根据点E在x轴上,根据点M在直线y=-2x+4上,设点M的坐标为(a,-2a+4),然后分①∠EMF=90°时,利用点M到坐标轴的距离相等列式求解即可;②∠MFE=90°时,根据等腰直角三角形的性质,点M的横坐标的长度等于纵坐标长度的一半,然后列式进行计算即可得解.试题解析:(1)令x=0,则y=4,令y=0,则-2x+4=0,解得x=2,所以,点A(2,0),C(0,4),∵抛物线y=-2x2+bx+c经过点A、C,∴24204b cc-⨯++=⎧⎨⎩=,解得24bc=⎧⎨=⎩,∴抛物线的解析式为:y=-2x2+2x+4;(2)∵y=-2x2+2x+4=-2(2第23页,总68页∴点P的坐标为(12,92),如图,过点P作PD⊥y轴于D,又∵C(0,4),∴PD=12,CD=91422-=,∴S△APC=S梯形APDO-S△AOC-S△PCD,=12×(12+2)×92-12×2×4-12×12×12=4514 88--=32,令y=0,则-2x2+2x+4=0,解得x1=-1,x2=2,∴点B的坐标为(-1,0),∴AB=2-(-1)=3,设△ABQ的边AB上的高为h,∵△ABQ的面积等于△APC面积的4倍,∴12×3h=4×32,解得h=4,∵4<92,∴点Q可以在x轴的上方也可以在x轴的下方,即点Q的纵坐标为4或-4,当点Q的纵坐标为4时,-2x2+2x+4=4,解得x1=0,x2=1,此时,点Q的坐标为(0,4)或(1,4),当点Q的纵坐标为-4时,-2x2+2x+4=-4,解得x1=1172+,x2=1172-,试卷第24页,总68页此时点Q的坐标为(1172+,-4)或(1172-,-4)综上所述,存在点Q(0,4)或(1,4)或(1172+,-4)或(1172-,-4);(3)存在.理由如下:如图,∵点M在直线y=-2x+4上,∴设点M的坐标为(a,-2a+4),①∠EMF=90°时,∵△MEF是等腰直角三角形,∴|a|=|-2a+4|,即a=-2a+4或a=-(-2a+4),解得a=43或a=4,∴点F坐标为(0,43)时,点M的坐标为(43,43),点F坐标为(0,-4)时,点M的坐标为(4,-4);②∠MFE=90°时,∵△MEF是等腰直角三角形,∴|a|=12|-2a+4|,即a=12(-2a+4),解得a=1,-2a+4=2×1=2,此时,点F坐标为(0,1),点M的坐标为(1,2),或a=12-(-2a+4),此时无解,综上所述,点F坐标为(0,43)时,点M的坐标为(43,43),点F坐标为(0,-4)时,点M的坐标为(4,-4);点F坐标为(0,1),点M的坐标为(1,2).考点: 二次函数综合题.12.已知:在梯形ABCD中,CD∥AB,AD=DC=BC=2,AB=4.点M从A开始,以每秒1个第25页,总68页试卷第26页,总68页单位的速度向点B 运动;点N 从点C 出发,沿C →D →A 方向,以每秒1个单位的速度向点A 运动,若M 、N 同时出发,其中一点到达终点时,另一个点也停止运动.运动时间为t 秒,过点N 作NQ ⊥CD 交AC 于点Q . (1)设△AMQ 的面积为S ,求S 与t 的函数关系式,并写出t 的取值范围.(2)在梯形ABCD 的对称轴上是否存在点P ,使△PAD 为直角三角形?若存在,求点P 到AB 的距离;若不存在,说明理由.(3)在点M 、N 运动过程中,是否存在t 值,使△AMQ 为等腰三角形?若存在,求出t 值;若不存在,说明理由.【答案】(1)233=-62S t t +(0<t ≤2),233=-123S t t +(2≤t <4);(2)233;(3)t=65,12-63,2. 【解析】试题分析:(1)求出t 的临界点t=2,分别求出当0<t ≤2时和2≤t <4时,S 与t 的函数关系式即可,(2)作梯形对称轴交CD 于K ,交AB 于L ,分3种情况进行讨论,①取AD 的中点G ,②以D 为直角顶点,③以A 为直角顶点,(3)当0<t ≤2时,若△AMQ 为等腰三角形,则MA=MQ 或者AQ=AM ,分别求出t 的值,然后判断t 是否符合题意.试题解析:(1)当0<t ≤2时,如图:过点Q 作QF ⊥AB 于F ,过点C 作CE ⊥AB 于E ,∵AB ∥CD ,∴QF ⊥CD ,∵NQ ⊥CD ,∴N ,Q ,F 共线,∴△CQN ∽△AFQ ,∴ CN NQ AF QF=, ∵CN=t ,AF=AE-CN=3-t ,∵NF=3,∴QF=33t 3-,第27页,总68页 13(323t - 23362t + 当2≤t <4时,如图:△FQC ∽△PQA ,∵DN=t-2,∴FD=DN •cos ∠FDN=DN •t-2), ∴t-2) ∴FQ=FC •tan ∠FCQ=FC •tan30°=t+2), ∴ 13[326t -23=-123t + (2)作梯形对称轴交CD 于K ,交AB 于L ,情况一:取AD 的中点G ,GD=1,过G 作GH ⊥对称轴于H ,GH=1.5,∵1.5>1,∴以P 为直角顶点的Rt △PAD 不存在,情况二:以D 为直角顶点:KP1 ∴P 1情况三:以A 为直角顶点,LP 2综上:P 到AB PAD 为Rt △, (3)0<t ≤2时, 若MA=MQ ,∴试卷第28页,总68页若AQ=AM ,则t=23233t -, 解得t=12-63, 若QA=QM ,则∠QMA=30°而0<t ≤2时,∠QMA >90°,∴QA=QM 不存在;2≤t <4(图中)若QA=QM ,AP :AD=3:2,∴t=2,若AQ=AM ,23-33(t+2)=t , ∴t=23-2,∵23-2<2,∴此情况不存在若MA=MQ ,则∠AQM=30°,而∠AQM >60°不存在.综上:t=65,12-63,2时,△AMQ 是等腰三角形. 考点: 1.等腰梯形的性质;2.等腰三角形的判定;3.直角三角形的性质. 13.如图,在平面直角坐标系中,二次函数c bx x y ++=2的图象与x 轴交于A 、B 两点, A 点在原点的左侧,B 点的坐标为(3,0),与y 轴交于C (0,3-)点,点P 是直线BC 下方的抛物线上一动点.(1)求这个二次函数的表达式.(2)连结PO 、PC ,并把△POC 沿CO 翻折,得到四边形POP’C,那么是否存在点P ,使四边形POP’C 为菱形?若存在,请求出此时点P 的坐标;若不存在,请说明理由.(3)当点P 运动到什么位置时,四边形 ABPC 的面积最大并求出此时P 点的坐标和四边形ABPC 的最大面积.【答案】(1)y=x 2﹣2x ﹣3;(2)存在,(2102+,32-);(3)(32,-154),758. 【解析】试题分析:(1)将B 、C 的坐标代入抛物线的解析式中即可求得待定系数的值;第29页,总68页(2)由于菱形的对角线互相垂直平分,若四边形POP′C 为菱形,那么P 点必在OC 的垂直平分线上,据此可求出P 点的纵坐标,代入抛物线的解析式中即可求出P 点的坐标;(3) 由于△ABC 的面积为定值,当四边形ABPC 的面积最大时,△BPC 的面积最大;过P 作y 轴的平行线,交直线BC 于Q ,交x 轴于F ,易求得直线BC 的解析 式,可设出P 点的横坐标,然后根据抛物线和直线BC 的解析式求出Q 、P 的纵坐标,即可得到PQ 的长,以PQ 为底,B 点横坐标的绝对值为高即可求得△BPC 的面积,由此可得到关于四边形ACPB 的面积与P 点横坐标的函数关系式,根据函数的性质即可求出四边形ABPC 的最大面积及对应的P 点坐标.试题解析:(1)将B 、C 两点的坐标代入得 9303b c c ++=-⎧⎨⎩=解得:23b c =-⎧⎨=-⎩; 所以二次函数的表达式为:y=x 2﹣2x ﹣3.(2)存在点P ,使四边形POPC 为菱形;设P 点坐标为(x ,x 2﹣2x ﹣3),PP′交CO 于E若四边形POP′C 是菱形,则有PC=PO ;连接PP′,则PE ⊥CO 于E ,∴OE=EC=32∴y=32-; ∴x 2﹣2x ﹣3=32- 解得:12102x +=,22102x -=(不合题意,舍去) ∴P 点的坐标为(2102+,32-) (3)过点P 作y 轴的平行线与BC 交于点Q ,与OB 交于点F ,设P (x ,x 2﹣2x ﹣3),易得,直线BC 的解析式为y=x ﹣3则Q 点的坐标为(x ,x ﹣3);S 四边形ABPC=S △ABC+S △BPQ+S △CPQ=12AB•OC+12QP•OF+12QP•BF 21143(3)322x x =⨯⨯+-+⨯试卷第30页,总68页 23375()228x =--+ 当32x =时,四边形ABPC 的面积最大 此时P 点坐标为(32,-154)四边形ABPC 的面积的最大值为758. 考点: 二次函数综合题.14.如图,直角坐标系中Rt △ABO ,其顶点为A(0, 1)、B(2, 0)、O(0, 0),将此三角板绕原点O 逆时针旋转90°,得到Rt △A ′B ′O .(1)一抛物线经过点A ′、B ′、B ,求该抛物线的解析式;(2)设点P 是在第一象限内抛物线上的一动点,是否存在点P ,使四边形PB′A′B 的面积是△A′B′O 面积4倍?若存在,请求出P 的坐标;若不存在,请说明理由.(3)在(2)的条件下,试指出四边形PB′A′B 是哪种形状的四边形?并写出四边形PB′A′B 的两条性质.【答案】(1)y=-x 2+x+2;(2)P (1,2);(4)四边形PB′A′B 为等腰梯形,答案不唯一,①等腰梯形同一底上的两个内角相等;②等腰梯形对角线相等.【解析】试题分析:(1)利用旋转的性质得出A ′(-1,0),B ′(0,2),再利用待定系数法求二次函数解析式即可;(2)利用S 四边形PB′A′B =S △B′OA′+S △PB′O +S △POB ,再假设四边形PB′A′B 的面积是△A′B′O 面积的4倍,得出一元二次方程,得出P 点坐标即可;(3)利用P 点坐标以及B 点坐标即可得出四边形PB′A′B 为等腰梯形,利用等腰梯形性质得出答案即可.试题解析:(1)(1)△A′B′O 是由△ABO 绕原点O 逆时针旋转90°得到的, 又A (0,1),B (2,0),O (0,0),∴A′(-1,0),B′(0,2)设抛物线的解析式为:y=ax 2+bx+c (a≠0),∵抛物线经过点A′、B′、B ,∴0=2=c 042a b c a b c ⎧-+=++⎪⎨⎪⎩,解得:112a b c =-⎧⎪=⎨⎪=⎩,∴满足条件的抛物线的解析式为y=-x 2+x+2.(2)∵P 为第一象限内抛物线上的一动点,设P(x,y),则x>0,y>0,P点坐标满足y=-x2+x+2.连接PB,PO,PB′,∴S四边形PB′A′B=S△B′OA′+S△PB′O+S△POB,12×1×2+1212-x2+x+2)+1=-x2+2x+3.∵A′O=1,B′O=2,∴△A′B′O面积为:12×1×2=1,假设四边形PB′A′B的面积是△A′B′O面积的4倍,则4=-x2+2x+3,即x2-2x+1=0,解得:x1=x2=1,此时y=-12+1+2=2,即P(1,2).∴存在点P(1,2),使四边形PB′A′B的面积是△A′B′O面积的4倍.(3)四边形PB′A′B为等腰梯形,答案不唯一,①等腰梯形同一底上的两个内角相等;②等腰梯形对角线相等;③等腰梯形上底与下底平行;④等腰梯形两腰相等.考点: 二次函数综合题.15.已知在平面直角坐标系xoy中,二次函数y=-2x²+bx+c的图像经过点A(-3,0)和点B(0,6)。
【尚择优选】初中数学九年级培优教程整理(完整版)

初中数学九年级培优目录第1讲二次根式的性质和运算(P2----7)第2讲二次根式的化简与求值(P7----12)第3讲一元二次方程的解法(P13----16)第4讲根的判别式及根与系数的关系(P16----22) 第5讲一元二次方程的应用(P23----26)第6讲一元二次方程的整数根(P27----30)第7讲旋转和旋转变换(一)(P30----38)第8讲旋转和旋转变换(二)(P38----46)第9讲圆的基本性质(P47----51)第10讲圆心角和圆周角(P52----61)第11讲直线与圆的位置关系(P62----69)第12讲圆内等积证明及变换((P70----76)第13讲弧长和扇形面积(P76----78)第14讲概率初步(P78----85)第15讲二次函数的图像和性质(P85----91)第16讲二次函数的解析式和综合应用(P92----98) 第17讲二次函数的应用(P99----108)第18讲相似三角形的性质(P109----117)第19讲相似三角形的判定(P118-----124)第20讲相似三角形的综合应用(P124-----130)第1讲 二次根式的性质和运算考点·方法·破译1.了解二次根式、最简二次根式、同类二次根式的定义,能准确进行辨析; 2.掌握二次根式有关性质,并能熟练运用性质进行化简;3.会根据二次根式的性质挖掘题中隐含条件,求参数的值(或取值范围). 经典·考题·赏析【变式题组】A .①,②B .③,④C .①,③D .①,④【例2】(黔东南)方程480x -+,当y >0时,m 的取值范围是( )A .0<m <1B .m ≥2C .m <2D .m ≤2【解法指导】本题属于两个非负数的代数和问题,隐含两个代数式均为0的结论.由题意得4x -8=0,x -y -m =0.化为y =2-m ,则2-m >0,故选C.【变式题组】2.(宁波)若实数x 、y2(0y =,则xy 的值是__________. 3.2()x y =+,则x -y 的值为( ) A .- 1 B .1 C .2 D .34.有意义的x 的取值范围是( ) A .x >3 B .x ≥3 C .x >4 D .x ≥3且x ≠45.(怀化)22(4)0a c -+-=,则a -b -c =________. )ABCD【解法指导】判断几个二次根式是否为同类二次根式应先把它们都化为最简二次根式,再看被开方数是否一样. A=; B不能化简;C.=;D.=,而=故本题应选D. 【变式题组】6是同类二次根式,则a =________. 7.在下列各组根式中,是同类二次根式的是( ) ABCD8.已知最简二次根式ba =_______,b =______. 【例4】下列计算正确的是( ) A= B4= C= D.(11=【解法指导】正确运用二次根式的性质①2(0)a a =≥;②(0)0(0)(0)a a a a a a ⎧⎪===⎨⎪-⎩><;③0,0)a b =≥≥0,0)b a =≥> 进行化简计算,并能运用乘法公式进行计算.A 、B 中的项不能合并.D. 2(111=-=-.故本题应选C.【变式题组】9. (聊城)下列计算正确的是( ) A.= B=C3= D3=- 10.计算:200720074)(4⋅=_____________ 11.22-=_____________ 12.(济宁)已知a) A .a B .-a C .-1 D .013.已知a >b >0,a +b =的值为( )A.2B .2 CD .12 【例5】已知xy >0,化简二次根式 )A. BC. D.【解法指导】先要判断出y <0,再根据xy >0知x <0.故原式=选D.【变式题组】14.已知a 、b 、c 为△AB C 三边的长,则化简a b c --+_______. 15===,算果中找出规律,并利用这一规律计算:1)2006++⋅=_________.16.已知,则0<x <1=_________.【例6】(辽宁)⑴先化简吗,再求值:11()b a b b a a b ++++,其中a =b =⑵已知x =,y =值为________. 【解法指导】对于⑴,先化简代数式再代入求值;对于⑵,根据已知数的特征求xy 、x +y 的值,再代入求值.【解】⑴原式=22()()()()ab a a b b a b a bab a b ab a b ab+++++==++,当12a =,12b =时,ab =1,a +b⑵由题意得:xy =1,x +y =10, 10199=-. 【变式题组】17.(威海)先化简,再求值:(a +b )2+(a -b)(2a +b)-3a 2,其中2a =-2b =.18.(黄石)已知a 是4的小数部分,那么代数式22224()()442a a a a a a a a a+-+⋅-+++的值为________.【例7】已知实数x 、y 满足(2008x y =,则3x 2-2y 2+3x -3y -2007的值为( )A .-2008B .2008C .-1D .1【解法指导】对条件等式作类似于因式分解的变形,找出a 、b 的关系,再代入求值.解:∵(2008x y =,∴(x -=y =+(y =x =x =y .∴(2008x -=, 解得x 2=2008,所以3x 2-2y 2+3x -3y -2007=3x 2-2x 2+3x -3x -2007=x 2-2007=1,故选D.【变式题组】演练巩固·反馈提高01.若4m =,则估计m 的值所在的范围是( )A .1<m <2B .2<m <3C .3<m <4D .4<m <502.n 的最大值为( )A .12B .11C .8D .304.(贺州)下列根式中,不是最简二次根式的是( )A.06.(常德)设a =20, b =(-3)2, c =11()2d -=, 则a 、b 、c 、d 、按由小到大的顺序排列正确的是( )A .c <a <d <bB .b <d <a <cC .a <c <d <bD .b <c <a <d07.(十堰)下列运算正确的是( )A B =C .21)31=-D 53=-08.如果把式子(1a -根号外的因式移入根号内,化简的结果为( ) A . BC .D .09.2x -化简的结果为2x -3,则x 的取值范围是( ) A .x ≤1B .x ≥2C .1≤x ≤2D .x >010.(怀化)函数y =中自变量的取值范围是________.11.(湘西)对于任意不相等的两个数a ,b ,定义一种运算a ※b=那么12※4=________.12.(荆州)先化简,再求值:22321121a a a a a a -+÷-+-,其中a =13.(广州)先化简,再求值:((6)a a a a --,其中12a =. 培优升级01.(凉山州)已知一个正数的平方根是3x -2和5x +6,则这个数是________.02.已知a 、b 是正整数,且满足是整数,则这样的有序数对(a ,b )共有________对.03.(全国)设12a =,则5432322a a a a a a a +---+=-________. 04.(全国)设x =,a 是x 的小数部分,b 是x 的小数部,则a 3+b 3+3ab =________.05.(重庆)已知2y =,则x 2+y 2=________.06.(全国)已知1a =,a =2a =,那么a 、b 、c 的大小关系是( )A .a <b <cB .b <a <cC .c <b <aD .c <a <b07.(武汉)已知y =(x ,y 均为实数),则y 的最大值与最小值的差为( )A 3B .3C 3D08.(全国)已知非零实数a 、b 满足24242a b a -++=,则a +b 等于( )A .-1B .0C .1D .209.(全国) ) A .5-B .1C .5D .110.已知0(0,0)x y x y -=>>)A .13B .12 C . 23 D .3411.已知152a b c +--,求a +b +c 的值.12.已知99a 和b ,求ab -3a +4b +8的值.第2讲 二次根式的化简与求值考点·方法·破译1.会灵活运用二次根式的运算性质化简求值.2.会进行二次根式的有理化计算,会整体代入求值及变形求值. 3.会化简复合二次根式,会在根式范围内分解因式. 经典·考题·赏析【例1】2=的值等于__________ 【解法指导】通过平方或运用分式性质,把已知条件和待求式的被开方数都用1x x+表示或化简变形.解:两边平方得,124x x ++=,12x x+= ,两边同乘以x 得,212x x += ,∵2315x x x ++=,29111x x x ++=,∴原式511- 【变式题组】1.若14aa +=(0<a <1)=________2= ) A .1a a - B .1a a - C .1a a+ D .不能确定【例2】(全国)满足等式=2003的正整数对(x ,y )的个数是( )A .1B .2C .3D .4【解法指导】对条件等式作类似于因式分解的变形,将问题转化为求不定方程的正整数解. 0=,∴0=0>0=,则xy =2003,且2003是质数,∴正整数对(x ,y )的个数有2对,应选B .【变式题组】3.若a >0,b >0=.【例3】1)a =<<,求代数式22632x x x x x x +-+÷--. 【解法指导】视x -2,x 2-4x=平方,移项用含a 的代数式表示x -2,x 2-4x ,注意0<a <1的制约.解:平方得,12x a a =++,∴12x a a -=+,2221442x x a a-+=++, 222142x x a a-=+-,∴化简原式=(3)(2)(2)3x x x x x x +---+=2211()1()211()a a a a a a aa a a a++-+-=++--【变式题组】4.(武汉)已知32x x +=+35(2)242x x x x -÷----的值.5.(五羊杯)已知1m =+1n =且22(714)(367)8m m a n n -+--=,则a 的值等于() A .-5 B .5 C .-9 D .9【例4】(全国)如图,点A 、C 都在函数0)y x =>的图像上,点B 、D 都在x轴上,且使得△OAB 、△BCD 都是等边三角形,则点D 的坐标为________.【解法指导】解:如图,分别过点A 、C 作x 轴的垂线,垂足分别为E 、F .设OE=a,BF=b ,则,CF,所以,点A 、C的坐标为(a,)、(2a+b ),所以2(2)a b =+=,解得a b ⎧=⎪⎨=⎪⎩ 因此,点D 的坐标为() 【变式题组】6.(邵阳)阅读下列材料,然后回答问题.一步化简:335333535=⨯⨯=; (一) 36333232=⨯⨯=; (二) ()()()131313132132-=-+-⨯=+; (三) 以上这种化简的步骤叫做分母有理化,132+还可以用以下方法化简:()()()13131313131313131322-=+-+=+-=+-=+; (四)(1)请你用不同的方法化简352+;①参照(三)试得:352+=_____________________________;(要有简化过程)②参照(四)试得:352+=_____________________________;(要有简化过程)(22n +++【例5】(五羊杯)设a 、b 、c 、d 为正实数,a<b ,c <d ,bc >ad,有一个三角形的三边长分.【解法指导】虽然不能用面积公式求三角形面积(为什么?),a 、c 为直角边的直角三角形的斜边,从构造图形入手,将复杂的根式计算转化为几何问题加以解决.解:如图,作长方形ABCD ,使AB =b -a ,AD =c ,延长DA 至E ,使DE =d ,延长DC 至F ,使DF =b ,连结EF 、FB 、EB ,则BFEF=,BE =BEF 就是题设的三角形,而S △BEF =S 长方形ABCD +S △BCF +S △ABE -S △DEF =(b -a )c +12(d -c )(b -a )-12bd =12(bc -ad )【变式题组】演练巩固·反馈提高01.已知x =,y =,那么代数式__________ 02.设1a =,则32312612a a a +--=( )A . 24B .25C .10D .1203.(天津)计算2001200019991)1)1)2001--+=__________04.(北京)若有理数x 、y 、z 1()2x y z =++,则2()x yz -=__________05.(北京)正数m 、n 满足430m n +-=,=__________06.(河南)若1x =,则32(2(15x x x -++的值是( )A .2B .4C .6D .807.已知实数a 满足2000a a -,那么22000a -的值是( )A .1999B .2000C .2001D .2002 08.设a =b =,c =则a 、b 、c 之间的大小关系是( )A .a <b <cB .c <b <aC .c <a <bD .a <c <b09.已知1x =培优升级01.(信利)已知1x =2111242x x x +-=+--__________025=__________03.(江苏)已知(2002x y ++=,则2234x xy y --66x y --+=__________04.7x =,则x =__________05.已知x =,y =,那么22y x x y +=__________为( ) A . B .2001 C .1 D .007.(绍兴)当12x +=时,代数式32003(420052001)x x --的值是( ) A .0B .-1C .1D .20032-08.(全国)设a 、b 、c 为有理数,且等式a +=29991001a b c ++的值是( ) A .1999B .2000C .2001D .不能确定 09.计算:(1(2(34947+(410.已知实数a 、b 满足条件1b a b a -=<,化简代数式11()(1)a b a b ---b 的形式.11.已知21(0)a x a a +=>12.已知自然数x 、y 、z 0=,求x +y +z 的值.第3讲 一元二次方程的解法考点·方法·破译1.掌握一元二次方程根的定义并能应用根的定义解题;2.掌握一元二次方程的四种解法,并能灵活应用各种解法解方程;3.会应用一元二次方程解实际应用题。
九年级数学培优竞赛专题 讲义:解三角形 含答案

解三角形一、内容提要1. 由三角形的已知元素,求出所有未知元素的过程叫做解三角形.2. 解直角三角形所根据的定理 (在Rt △ABC 中,∠C=Rt ∠).边与边的关系: 勾股定理----――c 2=a 2+b 2.角与角的关系:两个锐角互余----∠A+∠B=Rt ∠边与角的关系:(锐角三角函数定义)SinA=c a , CosA=c b , tanA=b a , CotA=ab.互余的两个角的三角函数的关系:Sin(90-A)= CosA , Cos(90-A)= SinA , tan(90 -A)= CotA, Cot(90 -A)= tanA.特殊角的三角函数值:锐角的正弦、正切随着角度的增大而增大(即增函数);余弦、余切随着角度的增大而减小(即减函数).3. 解斜三角形所根据的定理 (在△ABC 中)正弦定理:SinCcSinB b SinA a ===2R. (R 是△ABC 外接圆半径).② 余弦定理: c 2=a 2+b 2-2abCosC ; b 2=c 2+a 2-2ca CosB ; a 2=c 2+b 2-2cbCosA.③ 互补的两个角的三角函数的关系:Sin(180-A)= sinA , Cos(180-A)= - cosA , tan(180-A)=-cotA , cotA(180-A)=-tanA.④ S △ABC =21absinC=21bcsinA=21casinB.4. 与解三角形相关的概念:水平距离,垂直距离,仰角,俯角,坡角,坡度,象限角,方位角等.二、例题例1.已知:四边形ABCD中,∠A=60 ,CB⊥AB,CD⊥AD,CB=2,CD=1.求:AC的长.例2. 已知:如图,要测量山AB的高,在和B同一直线上的C,D处,分别测得对A的仰角的度数为n和m,CD=a.试写出表示AB的算式.B例3. 已知:四边形ABCD中,∠ABC=135 ,∠BCD=120 ,CD=6,AB=6,BC=5-3.求:AD的长.解:例4.如图,要测量河对岸C,D两个目标之间的距离,在A,B两个测站,测得平面角∠CAB=30 ,∠CAD=45 ,∠DBC=75 ,∠DBA=45 ,AB=3.试求C,D的距离.例5. 已知:O 是凸五边形ABCDE 内的一点且∠1=∠2,∠3=∠4,∠5=∠6,∠7=∠8. 求证:∠9和∠10相等或互补例6. 已知:二次方程mx 2-(m -2)x+41(m -1)=0两个不相等的实数根,恰好是直角三角形两个锐角的正弦值.求:这个直角三角形的斜边与斜边上的高的比. 解:三、练习 1. 填空:① 如果从点A 对着点B 测得仰角是60 ,那么从点B 对着点A 测得的俯角是__度. ② 点C 在点D 的南偏东25,那么点D 在C 的方向是______. ③ 斜坡AB 的坡角是30 ,那么AB 的坡度i=1∶___. ④ 锐角A >45 ,那么下列函数的取值范围是:SinA_____, CosA_____, tanA_______,cotA________. ⑤ 已知:30 <∠A <60 ,那么如下的函数的取值范围是∠A 的余弦________,∠A 的正切_______.2. 已知:△ABC 中,∠B =45 ,AC =7,点D 在BC 上,CD =3, D =5. 求AB 的长.3. 如图观测塔AB 的高为a 米,从塔顶A 测得地面上 同一方向上的两个目标C ,D 的俯角分别是30和45,求CD 的距离.4. 船A 在船B 的正北,它们同时向东航行,时速分别是15和20海里,3小时后,船B 在船A 的东南,问这时两船相距多远?j3045A BD5. 一只船向南航行,出发前在灯塔A 的北偏东30 ,相距15海里,2小时后,灯塔在船的北偏西60 ,求船的航行速度.6. 如图要测量建筑物AB 的高,先在楼下C 测得对顶端A 的 仰角为45 ,然后在楼上D 测得对A 的仰角为30 ,已知 楼高CD=m 米,求AB.7. 已知:△ABC 中,a=21, b=17, c=10. 求:S △ABC .8. 已知:△ABC 中,SinA ∶ SinB ∶SinC=3∶5∶7.求:△ABC 的最大角的度数.9. 船B 在艇A 的方位角120,相距24海里处,发出呼救,报告说:它沿着方位角240的方向前进,速度是每小时9海里. A 艇以最快的时速21海里赶去营救,问应沿什么方向,要经过几小时才能靠近船B ?BC10. 已知:锐角三角形ABC 的外接圆直径AE 交BC 于D. 求证:tanB ×tanC=AD ∶DE提示:作BC 边的高AF(h)并延长交圆于G,连结GE11. 已知:△ABC 中,∠A=45 ,AB=6,BC=2,不用正弦定理能解答这个三角形吗?如不能,说明理由;如能请解这个三角形.12. 如图已知:ABCD 为圆内接四边形,过AB 上一点M 引MP ,MQ ,MR 分别垂直于BC ,CD ,AD ,连结PR 和MQ 交于N.求证:MABMNR PN.13. 如图已知:锐角△ABC 中,AC=1,AB=c ,△ABC 的外接圆半径R ≤1.求证: Cos<c ≤CosA+3SinA .解三角形答案一、内容提要1. 由三角形的已知元素,求出所有未知元素的过程叫做解三角形.2. 解直角三角形所根据的定理 (在Rt △ABC 中,∠C=Rt ∠).边与边的关系: 勾股定理----――c 2=a 2+b 2.角与角的关系:两个锐角互余----∠A+∠B=Rt ∠边与角的关系:(锐角三角函数定义)SinA=c a , CosA=c b , tanA=b a , CotA=ab.互余的两个角的三角函数的关系:Sin(90-A)= CosA , Cos(90-A)= SinA , tan(90 -A)= CotA, Cot(90 -A)= tanA.特殊角的三角函数值:锐角的正弦、正切随着角度的增大而增大(即增函数);余弦、余切随着角度的增大而减小(即减函数).3. 解斜三角形所根据的定理 (在△ABC 中)正弦定理:SinCcSinB b SinA a ===2R. (R 是△ABC 外接圆半径).② 余弦定理: c 2=a 2+b 2-2abCosC ; b 2=c 2+a 2-2ca CosB ; a 2=c 2+b 2-2cbCosA.③ 互补的两个角的三角函数的关系:Sin(180-A)= sinA , Cos(180-A)= - cosA , tan(180-A)=-cotA , cotA(180-A)=-tanA.④ S △ABC =21absinC=21bcsinA=21casinB.4. 与解三角形相关的概念:水平距离,垂直距离,仰角,俯角,坡角,坡度,象限角,方位角等.二、例题例1. 已知:四边形ABCD 中,∠A =60 ,CB ⊥AB ,CD ⊥AD ,CB =2,CD =1.求:AC 的长.解:延长AD 和BC 相交于E ,则∠E =30 .在Rt △ECD 中,∵sinE=CECD, ∴CE=30sin 1=1÷21=2. EB =4.在Rt △EAB 中, ∵tanE=EBAB,∴AB=EBtan30。
初中数学竞赛辅导讲义及习题解答含答案共30讲改好278页

初中数学竞赛辅导讲义及习题解答含答案共30讲改好278页初中奥数辅导讲义培优计划(星空课堂)第一讲走进追问求根公式第二讲判别式——二次方程根的检测器第三讲充满活力的韦达定理第四讲明快简捷—构造方程的妙用第五讲一元二次方程的整数整数解第六讲转化—可化为一元二次方程的方程第七讲化归—解方程组的基本思想第八讲由常量数学到变量数学第九讲坐标平面上的直线第十讲抛物线第十一讲双曲线第十二讲方程与函数第十三讲怎样求最值第十四讲图表信息问题第十五讲统计的思想方法第十六讲锐角三角函数第十七讲解直角三角形第十八讲圆的基本性质第十九讲转化灵活的圆中角2第二十讲直线与圆第二十一讲从三角形的内切圆谈起第二十二讲园幂定理第二十三讲圆与圆第二十四讲几何的定值与最值第二十五讲辅助圆第二十六讲开放性问题评说第二十七讲动态几何问题透视第二十八讲避免漏解的奥秘第二十九讲由正难则反切入第三十讲从创新构造入手3第一讲走进追问求根公式形如a某2b某c0(a0)的方程叫一元二次方程,配方法、公式法、因式分解法是解一元二次方程的基本方法。
而公式法是解一元二次方程的最普遍、最具有一般性的方法。
求根公式某1,2bb24ac内涵丰富:它包含了初中阶段已学过的全部代数运算;它回答了2a一元二次方程的诸如怎样求实根、实根的个数、何时有实根等基本问题;它展示了数学的简洁美。
降次转化是解方程的基本思想,有些条件中含有(或可转化为)一元二次方程相关的问题,直接求解可能给解题带来许多不便,往往不是去解这个二次方程,而是对方程进行适当的变形来代换,从而使问题易于解决。
解题时常用到变形降次、整体代入、构造零值多项式等技巧与方法。
【例题求解】【例1】满足(n2n1)n21的整数n有个。
思路点拨:从指数运算律、±1的特征人手,将问题转化为解方程。
【例2】设某1、某2是二次方程某2某30的两个根,那么某134某2219的值等于()A、一4B、8C、6D、0思路点拨:求出某1、某2的值再代入计算,则计算繁难,解题的关键是利用根的定义及变形,使多项式降次,如某123某1,某223某2。
九年级数学培优讲义与测试

。
10. 若直线 y ( m 1)x m 5 不经过第二象限,则 m 的取值范围是
。
。 的
二、解答题 11. 求证:不论 k 为何值,一次函数 (2 k 1) x (k 3) y (k 11) 0 的图像恒过一定点。
第 3 / 102 页
12. 某商人将进货单价为 8 元的商品按每件 10 元售出时, 每天可以销售 100 件,现在他想采用 提高售出价的办法来增加利润.已知这种商品每提高价 1 元(每件),日销售量就要减少 10 件,那么他要使每天获利最大.应把售出价定为多少元?
当 k 0 , y kx b 是递减函数,即函数值 y 随 x 增大(减小)而减小(增大)。
函数 y k (k 0) 称为反比例函数,其函数图像是双曲线。 x
当 k 0 且 x 0时,函数值 y 随 x 增大(减小)而减小(增大);当 k 0 且 x 0 ,函数值
y 随 x 增大(减小)而减小(增大),也就是说:当 k 0 时,反比例函数 y k 分别在第一或 x
(a 1)x2 ( a2 2) x (a2 2a) 0
(b 1)x2 (b2 2) x (b2 2b) 0
及( a,b 是正整数)有一个公共根,求
a2 ab
bb ba
的值。
例 5:若二次方程 x2 2 px 2q 0 有实根,其中 p 、 q 为奇数。 证明:此方程的根是无理数。
f (x)
c
m nx m n
m2 n2
,所以 f ( x)
cx mn
c. mn
例 4: 如图,设 f ( x)
mx
1 (1 x)
m
数, f ( x) 在 0,1 上的最小值为 f (1)
所以
九年级数学培优.doc

数学培优(3)一.选择题1.若关于X的不等式组有解,则函数y=(0—3) X2—X—+图象与X轴的交点个数为[x<3a~2- 4( )(A) 0 (B) 1 (C) 2 (D) 1 或22.设/+l = 3d,,+l = 3b,且心方,则代数式4 + 4的值为( )CTA 5B 7C 9D 113.设a>0, b>0,称二旦为a, b的算术平均数.称陌为a, b的儿何平均数.称旦2 a + b为a, b的调和平均数.如图,C为线殴AB上的点,且AC=a, CB=b,O为AB中点,以AB 为直径作半圆.过点C作的垂线,交半圆于点D.连结OD, AD, BD.过点C作OD的垂线,垂足为E.则图中①线段OQ的长度是a, b 的算术平均数,②线段CD的长度是a, b的几何平均数,③ 线段BD的长度是a, b的几何平均数,④线段DE的长度是a.b的调和平均数.⑤线段OE的长度是a.b的调和平均数.上述五个结沦中,正确的个数是( )A. 2B. 3C. 4D. 54 2.14.已知a2+4a+l=0,且—— =3,则m的值为(2d、++ 2a19 19A.—B.——C.19 D-192 25.若质数a,b满足/—9b —4 = 0,贝9数据a,b,2,3的中位数是((A) 4 (B)7 (C)4 或7)(D)4.5 或6.53_10 (B)9.如图,在四边形 ABCD 中,ZB=135°, ZC= 120°, AB=2>/3 f BC=4_2近,CD= 4近,则4Q 边的长为((A) 2A /6 (C) 4 + 7610. RtAABC 的三个顶点A, B, C 均在抛物线y = x 2±,并且斜边AB 平行于x 轴.若斜边上的高为h,则()(A) h<l(B) h=l (C) l<h<2 (D) h>2二.填空题11. B^II0<6/<4,那么卜一2| + |3 —国的最小值等于 ___________12、 己知不等式祇+ 3 20的正整数解为1, 2, 3,则Q 的取值范围是_________________ ・ 13、 分解因式:x 2y-4x}? + 4y = _______________ .14、 如图,在Rt △朋C 中,ZA = 90°, AB-AC= 8^6,点F 为化的中点,点卩在底边BC上,且FE 丄BE,则ACEF 的面积是 ___________________15、 如图,直线y = —x + V3与x 轴、y 轴分别相交于A, B 两点,圆心P 的坐标为(1,0), OP 与y 轴相切于点O.若将OP 沿兀轴向左移动,当OP 与该直线相交时,横坐标为整 数的点P 有 ______________ 个.16. 如图,一个等边三角形的边长与它的一边相切的圆的周长相等,当这个圆按箭头方向从某 一位置沿等边三角形的三边做无滑动旋转,直至冋到原出发位置时,则这个圆共转了 ____ 圈。
九年级数学培优讲义与测试

第一讲 一次函数和反比例函数 知识点、重点、难点函数(0)y kx b k =+≠称为一次函数,其函数图像是一条直线。
若0b =时,则称函数y kx =为正比例函数,故正比例函数是一次函数的特殊情况。
当0k >时,函数y kx b =+是单调递增函数,即函数值y 随x 增大(减小)而增大(减小);当0k <,y kx b =+是递减函数,即函数值y 随x 增大(减小)而减小(增大)。
函数(0)k y k x=≠称为反比例函数,其函数图像是双曲线。
当0k >且0x >时,函数值y 随x 增大(减小)而减小(增大);当0k >且0x <,函数值y 随x 增大(减小)而减小(增大),也就是说:当0k >时,反比例函数k y x=分别在第一或第三象限内是单调递减函数;当0k <时,函数k y x=分别在第二或第四象限内是单调递增函数。
若111222(0),(0).y k x b k y k x b k =+≠=+≠当12k k =时,12b b ≠时,两面直线平行。
当12k k =时,12b b =时,两面直线重合。
当12k k ≠时,两直线相交。
当121k k =-时,两直线互相垂直。
求一次函数、反比例函数解析式,关键是要待定解析式中的未知数的系数;其次,在解题过程中要重视数形相结合。
例题精讲例1:在直角坐标平面上有点(1,2)A --、(4,2)B 、(1,)C c ,求c 为何值时AC BC +取最小值。
解 显然,当点C 在线段AB 内时,AC BC +最短。
设直线AB 方程为y kx b =+,代入(1,2)A --、(4,2)B得242,k b k b -+=-⎧⎨+=⎩解得456,5k b ⎧=⎪⎪⎨⎪=-⎪⎩所以线段AB 为46(14),55y x x =--≤≤ 代入(1,)C c ,得4621.555c =⨯-=- 例2:求证:一次函数211022k k y x k k --=-++的图像对一切有意义的k 恒过一定点,并求这个定点。
初中九年级数学竞赛培优讲义全套专题10 最优化_答案

专题10 最优化例1. 4 提示:原式=112-62-+)(x . 例2. B 提示:由-1≤y ≤1有0≤x ≤1,则z =2x 2+16x +3y 2=14x 2+4x +3是开口向上,对称轴为71-=x 的抛物线.例3. 分三种情况讨论:①0≤a <b ,则f (x )在a ≤x ≤b 上单调递减,∴f (a )=2b ,f (b )=2a ,即⎪⎪⎩⎪⎪⎨⎧+-=+-=213222132222b a a b 解得⎩⎨⎧==31b a ②a <b ≤0,则f (x )在a ≤x ≤b 上单调递增,∴f (a )=2a ,f (b )=2b ,即⎪⎪⎩⎪⎪⎨⎧+-=+-=213222132222b b a a 此时满足条件的(a ,b )不存在. ③a <0<b ,此时f (x )在x =0处取得最大值,即2b =f (0)=213,b =413,而f (x )在x =a 或x =b 处取最小值2a .∵a <0,则2a <0,又∵f (b )=f (413)=021341321-2>+⨯)(,∴f (a )=2a ,即2a =2132-2+a ,则⎪⎩⎪⎨⎧=--=413172b a 综上,(a ,b )=(1,3)或(17-2-,413) 例4. (1)121≤≤x ,y 2 = 21+216143-2+-)(x .当x =43时,y 2取得最大值1,a =1; 当21=x 或x =1时,y 2取得最小值21,b =22.故a 2+b 2=23.(2) 如图,AB =8,设AC =x ,则BC =8- x ,AD =2,CD =42+x ,BE =4,CE =16)-8(2+x BF =AD =2.10)24(816)8(4222222=++=+=≥+=+-++EF DF DE CE CD x x当且仅当D ,C ,E 三点共线时,原式取最小值.此时△EBC ∽△DAC ,有224===DA EB CA BC , 从而x =AC =3831=AB .故原式取最小值时,x =38.(3)如图, 原式=[]2222222)24()13()32()01(032--0y x y x -+-+-+-+-+)()(=AB +BC +CD ≥AD ,其中A (-2,0),B (0,3x ),C (1,2y ),D (3,4),并且当点B ,C 在线段AD 上时,原式取得最小值,此时5423=x ,5432=y .例5. 由S =ay m y n a 2)(22+--,得an -S +2ay =a 22n y -,两边平方,经整理得0)()(4322222=+-+-+m a S an y S an a y a .因为关于y 的一元二次方程有实数解,所以[][]0)(34)(422222≥+-⨯--m a S an a S an a ,可化为2223-m a an S ≥)(.∵S >an ,∴am an S 3-≥,即am an S 3+≥,故S 最小=am an 3+.例6(1)设x 1≥1,x 2≥2,x k ≥k ,于是1+2+…+k ≤x 1+x 2+…+x k = 2003,即20032)1(≤+k k k (k +1)≤4006,∵62×63=3906<4006<4032=63×64,∴k ≤62. 当x 1=1,x 2=2,…x 61=61,x 62=112时,原等式成立,故k 的最大可能值为62.(2) 若取⎩⎨⎧=+=-222ba cb ac ,则2)1(2+=b b c 由小到大考虑b ,使2)1(+b b 为完全平方数.当b =8时,c 2=36,则c =6,从而a =28.下表说明c 没有比6更小的正整数解.显然,表中c 4-x 3的值均不是完全平方数,故c 的最小值为6.A 级1.57- 111- 2.1 3.14 提示:y =5-x ,z =4-x ,原式=3(x -3)2+14. 4.A提示:原式=27-(a +b +c )2. 5.D 6.C 7.(1)y =-x +1000(500≤x ≤800) (2)①S =(x-500)(-x +1000)=-x 2+1500x -500000(500≤x ≤800);②S -(x -750)2+62500,即销售单价定为750时,公司可获最大毛利润62500元,此时销量为250件. 8.(1)-4≤m ≤2 (2)设方程两根为x 1,x 2,则x 12+x 22=4(m -34)2+1034,由此得x 12+x 22最小值为1034,最大值为101. 9.设a 2-ab +b 2=k ,又a 2+ab +b 2=1②,由①②得ab =12(1-k ),于是有(a +b )2=12(3-k )≥0,∴k ≤3,从而a +b =.故a ,b 是方程t 2t +12k-=0的两实根,由Δ≥0,得133k ≤≤. 10.设A (x 1,0),B (x 2,0),其中 x 1,x 2是方程ax 2+bx +c =0的两根,则有x 1+x 2=b a -<0,x 1x 2=ca>0,得x 1<0,x 2<0,由Δ=b 2-4ac >0,得b >∵|OA |=|x 1|<1,|OB |=|x 2|<1,∴-1<x 1<0,-1<x 2<0,于是ca=x 1x 2<1,c <a .由于a 是正整数,已知抛物线开口向上,且当x =-1时,对应的二次函数值大于0,即a -b +c >0,a +c >b .又a ,b ,c 是正整数,有a +c ≥b +1>2+1,从而a +c >2+1,则2),12c a c >+≥,于是a >4,即a ≥5,故b =即b ≥5.因此,取a =5,b =5,c =1,y =5x 2+5x +1满足条件,故a +b +c 的最小值为11. 11.(1)该设备投入使用x天,每天平均损耗为y =11111[500000(0500)(1500)(2500)(500)]4444x x -+⨯++⨯++⨯++++=11(1)[500000500x ]42x x x -++⨯=500000749988x x ++. (2)y =500000749988x x ++7749999988≥=.当且仅当5000008xx =,即x =2000时,等号成立.故这台设备投入使用2000天后应当报废. B 级 1.20 提示:a 2-8b ≥0,4b 2-4a ≥0,从而a 4≥64b 2≥64a ,a ≥4,b 2≥4. 2.4 提示:构造方程. 3. 提示:设经过t 小时后,A ,B 船分别航行到A 1,B 1,设AA 1=x ,则BB 1=2x ,B 1A 1 4.D 提示:a 2+b 2≥2ab ,c 2+d 2≥2cd ,∴a 2+b 2+c 2+d 2≥2(ab +cd )≥.∴ab +cd ≥2,同理bc +ad ≥2,ac +bd ≥2. 5.A 提示:x =s -2≥0,y =5-43s ≥0,z =1-13s ≥0,解得2≤s ≤3,故s 的最大值与最小值的和为5. 6.A 提示:|AB C (2125,24k k k -++-),ABC S =,而k 2+2k +5=(k +1)2+4≥4. 7.设此商品每个售价为x 元,每日利润为S 元.当x ≥18时,有S =[60-5(x -18)](x -10)=-5(x -20)2+500,即当商品提价为20元时,每日利润为500元;当x ≤18时,S =[60+10(18-x )](x -10)=-10(x -17)2+490,即当商品降价为17元时,每日利润最大,最大利润为490元,综上,此商品售价应定为每个20元. 8.设对甲、乙两种商品的资金投入分别为x ,(3-x )万元,设获取利润为s ,则s 15x =s -15x x 2+(9-10s )x +25s 2-27=0,∵关于x 的一元二次方程有实数解,∴(9-10s )2-4×(25s 2-27)≥0,解得1891.05180s ≤=,进而得x =0.75(万元),3-x =2.25(万元).即甲商品投入0.75万元,乙商品投入2.25万元,获得利润1.05万元为最大. 9.y =5-x -z ,代入xy +yx +zx =3,得x 2+(z -5)x +(z 2-5z +3)=0.∵x 为实数,∴Δ=(z -5)2-4(z 2-5z +3)≥0,解得-1≤z ≤133,故z 的最大值为133,最小值为-1. 10.设b c x a b==,则b =ax ,c =ax 2,于是,a +b +c =13,化为a (x 2+x +1)=13.∵a ≠0,∴x 2+x +1-13a=0 ①.又a ,b ,c 为整数,则方程①的解必为有理数,即Δ=52a -3>0,得到1≤a ≤523为有理数,故1≤a ≤16.当a =1时,方程①化为x 2+x -12=0,解得x 1=-4,x 2=3. 故a min =1,b =-4,c =16 或a min =1,b =3,c =9.当a =16时,方程①化为x 2+x +316=0.解得x 1=-34,x 2=-14.故a min =16,b =-12,c =9;或a min =16,b =-4,c =1. 11.设x 1,x 2,…,x n 中有r 个-1,s 个1,t 个2,则219499r s t r s t -++=⎧⎨++=⎩,得3t +s =59,0≤t ≤19.∴x 13+x 23+…+x n 3=-r +s +8t =6t +19.∴19≤x 13+x 23+…+x n 3≤6×19+19=133.∴在t =0,s =59,r =40时,x 13+x 23+…+x n 3取得最小值19;在t =19,s =2,r =21时,x 13+x 23+…+x n 3取得最大值133. 12.∵把58写成40个正整数的和的写法只有有限种,∴x 12+x 22+…+x 402的最大值和最小值存在.不妨设x 1≤x 2≤…≤x 40.若x 1>1,则x 1+x 2=(x 1-1)+(x 2+1),且(x 1-1)2+(x 2+1)2=x 12+x 22+2(x 2-x 1)+2>x 12+x 22.于是,当x 1>1时,可以把x 1逐步调整到1,此时,x 12+x 22+…+x 402的值将增大.同理可以把x 2,x 3,…,x 39逐步调整到1,此时x 12+x 22+…+x 402的值将增大.从而,当x 1,x 2,…,x 39均为1,x 40=19时,x 12+x 22+…+x 402取得最大值,即A =22239111+++个+192=400.若存在两个数x i ,x j ,使得x j -x i ≥2(1≤i <j ≤40),则(x i +1)2+(x j -1)2=x i 2+x j 2-2(x i -x j -1)<x i 2+x j 2.这表明,在 x 1,x 2,…,x 40中,若有两个数的差大于1,则把较小的数加1,较大的数减1此时,x 12+x 22+…+x 402的值将减小,因此,当x 12+x 22+…+x 402 取得最小值时,x 1,x 2,…,x 40中任意两个数的差都不大于1. 故 当x 1=x 2=…=x 22=1,x 23=x 24=…=x 40=2时,x 12+x 22+…+x 402取得最小值,即222111+++22个222222+++⋯+=94从而,A+B=494.。
九年级数学下学期培优作业10 试题

卜人入州八九几市潮王学校九年级下册数学培优作业10一、选择题:〔每一小题3分,一共24分〕A 、不变B 、扩大5倍C 、缩小5倍D 、不能确定2、计算0230cos 1-的值是〔〕A 、21B 、23C 、22D 、33 3、设∠α为锐角,且cos α=54,那么sin α=()A 、54B 、34C 、43D 、53 4、在△ABC 中,假设0)sin 23(22sin 2=-+-B A ,那么∠C=〔〕 A 、750B 、600C450D 、300 5、当300≤α≤600时,以下结论正确的选项是〔〕A 、21≤sin α≤23B 、21<cos α≤23C 、33≤tan α≤3D 、33≤cot α≤3 6、设α是锐角,那么sin α+cos α的值一定〔〕A 、小于1B 、大于1C 、等于1D 、小于或者等于17、假设α、β都是锐角,下面式子中正确的选项是〔〕A 、sin 〔α+β〕=sin α+sin βB 、cos(α+β)=21时,α+β=600C 、假设α≥β时,那么cos α≥cos βD 、假设cos α>sin β,那么α+β>9008、当∠A 为锐角,且tanA 的值小于3时,∠A 〔〕A 、小于300B 、大于300C 、小于600D 、大于600 二、填空题〔2分×10=20分〕9、:在Rt △ABC 中,∠C=900,a=3,b=4,那么cosA=,tanA=。
10、假设△ABC 三边长度之比为a :b :c=3:4:5,那么sinB=。
11、α是锐角,假设tan 3•〔α+200〕=3,那么α=。
12、某人沿着坡度i=1:3的山坡走了50米,那么他离地面米。
13、计算:1-sin 2240-cos 2240=,tan320·tan450·tan580=. 14、在Rt △ABC 中,∠C=900,∠A=600,AB=14cm ,那么AB 边上的高为cm 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题10 最优化例1. 4 提示:原式=112-62-+)(x . 例2. B 提示:由-1≤y ≤1有0≤≤1,则=22+16+3y 2=142+4+3是开口向上,对称轴为71-=x 的抛物线. 例3. 分三种情况讨论:①0≤a <b ,则f ()在a ≤≤b 上单调递减,∴f (a )=2b ,f (b )=2a ,即⎪⎪⎩⎪⎪⎨⎧+-=+-=213222132222b a a b 解得⎩⎨⎧==31b a ②a <b ≤0,则f ()在a ≤≤b 上单调递增,∴f (a )=2a ,f (b )=2b ,即⎪⎪⎩⎪⎪⎨⎧+-=+-=213222132222b b a a 此时满足条件的(a ,b )不存在. ③a <0<b ,此时f ()在=0处取得最大值,即2b =f (0)=213,b =413,而f ()在=a 或=b 处取最小值2a .∵a <0,则2a <0,又∵f (b )=f (413)=021341321-2>+⨯)(,∴f (a )=2a ,即2a =2132-2+a ,则⎪⎩⎪⎨⎧=--=413172b a 综上,(a ,b )=(1,3)或(17-2-,413) 例4. (1)121≤≤x ,y 2 = 21+216143-2+-)(x .当=43时,y 2取得最大值1,a =1; 当21=x 或=1时,y 2取得最小值21,b =22.故a 2+b 2=23. (2) 如图,AB =8,设AC =,则BC =8- ,AD =2,CD =42+x ,BE =4,CE =16)-8(2+xBF =AD =2.10)24(816)8(4222222=++=+=≥+=+-++EF DF DE CE CD x x当且仅当D ,C ,E 三点共线时,原式取最小值.此时△EBC ∽△DAC ,有224===DA EB CA BC , 从而=AC =3831=AB .故原式取最小值时,=38. (3)如图, 原式=[]2222222)24()13()32()01(032--0y x y x -+-+-+-+-+)()(=AB +BC +CD ≥AD ,其中A (-2,0),B (0,3),C (1,2y ),D (3,4),并且当点B ,C 在线段AD 上时,原式取得最小值,此时5423=x ,5432=y .例5. 由S =ay m y n a 2)(22+--,得an -S +2ay =a 22n y -,两边平方,经整理得0)()(4322222=+-+-+m a S an y S an a y a .因为关于y 的一元二次方程有实数解,所以[][]0)(34)(422222≥+-⨯--m a S an a S an a ,可化为2223-m a an S ≥)(.∵S >an ,∴am an S 3-≥,即am an S 3+≥,故S 最小=am an 3+.例6(1)设1≥1,2≥2,≥,于是1+2+…+≤1+2+…+ = 2003,即20032)1(≤+k k (+1)≤4006,∵62×63=3906<4006<4032=63×64,∴≤62. 当1=1,2=2,…61=61,62=112时,原等式成立,故的最大可能值为62.(2) 若取⎩⎨⎧=+=-222ba cb ac ,则2)1(2+=b b c 由小到大考虑b ,使2)1(+b b 为完全平方数.当b =8时,c 2=36,则c =6,从而a =28.下表说明c 没有比6更小的正整数解.显然,表中c 4-3的值均不是完全平方数,故c 的最小值为6.A 级1.7- 11- 2.1 3.14 提示:y =5-,=4-,原式=3(-3)2+14. 4.A 提示:原式=27-(a +b +c )2. 5.D 6.C 7.(1)y =-+1000(500≤≤800) (2)①S =(-500)(-+1000)=-2+1500-500000(500≤≤800);②S -(-750)2+62500,即销售单价定为750时,公司可获最大毛利润62500元,此时销量为250件. 8.(1)-4≤m ≤2 (2)设方程两根为1,2,则12+22=4(m -34)2+1034,由此得12+22最小值为1034,最大值为101. 9.设a 2-ab +b 2=,又a 2+ab +b 2=1②,由①②得ab =12(1-),于是有(a +b )2=12(3-)≥0,∴≤3,从而a +b =.故a ,b 是方程t 2t +12k -=0的两实根,由Δ≥0,得133k ≤≤. 10.设A (1,0),B (2,0),其中 1,2是方程a 2+b +c =0的两根,则有1+2=b a -<0,12=ca >0,得1<0,2<0,由Δ=b 2-4ac >0,得b >|OA |=|1|<1,|OB |=|2|<1,∴-1<1<0,-1<2<0,于是ca=12<1,c <a .由于a 是正整数,已知抛物线开口向上,且当=-1时,对应的二次函数值大于0,即a-b +c >0,a +c >b .又a ,b ,c 是正整数,有a +c ≥b +1>2+1,从而a +c >2+1,则212>>≥,于是a >4,即a ≥5,故b b ≥5.因此,取a =5,b =5,c =1,y =52+5+1满足条件,故a +b +c 的最小值为11. 11.(1)该设备投入使用天,每天平均损耗为y =11111[500000(0500)(1500)(2500)(500)]4444x x -+⨯++⨯++⨯++++L =11(1)[500000500x ]42x x x -++⨯=500000749988x x ++. (2)y =500000749988x x ++7749999988≥=.当且仅当5000008xx =,即=2000时,等号成立.故这台设备投入使用2000天后应当报废.B 级 1.20 提示:a 2-8b ≥0,4b 2-4a ≥0,从而a 4≥64b 2≥64a ,a ≥4,b 2≥4. 2.4 提示:构造方程. 3.提示:设经过t 小时后,A ,B 船分别航行到A 1,B 1,设AA 1=,则BB 1=2,B 1A 1=4.D 提示:a 2+b 2≥2ab ,c 2+d 2≥2cd ,∴a 2+b 2+c 2+d 2≥2(ab +cd )≥.∴ab +cd ≥2,同理bc +ad ≥2,ac +bd ≥2. 5.A 提示:=s -2≥0,y =5-43s ≥0,=1-13s ≥0,解得2≤s ≤3,故s 的最大值与最小值的和为5. 6.A 提示:|AB |=C (2125,24k k k -++-),ABC S V 2+2+5=(+1)2+4≥4. 7.设此商品每个售价为元,每日利润为S 元.当≥18时,有S =[60-5(-18)](-10)=-5(-20)2+500,即当商品提价为20元时,每日利润为500元;当≤18时,S =[60+10(18-)](-10)=-10(-17)2+490,即当商品降价为17元时,每日利润最大,最大利润为490元,综上,此商品售价应定为每个20元. 8.设对甲、乙两种商品的资金投入分别为,(3-)万元,设获取利润为s ,则s 15x =s -15x =2+(9-10s )+25s 2-27=0,∵关于的一元二次方程有实数解,∴(9-10s )2-4×(25s 2-27)≥0,解得1891.05180s ≤=,进而得=0.75(万元),3-=2.25(万元).即甲商品投入0.75万元,乙商品投入2.25万元,获得利润1.05万元为最大. 9.y =5--,代入y +y +=3,得2+(-5)+(2-5+3)=0.∵为实数,∴Δ=(-5)2-4(2-5+3)≥0,解得-1≤≤133,故的最大值为133,最小值为-1. 10.设b c x a b==,则b =a ,c =a 2,于是,a +b +c =13,化为a (2++1)=13.∵a ≠0,∴2++1-13a =0 ①.又a ,b ,c 为整数,则方程①的解必为有理数,即Δ=52a-3>0,得到1≤a ≤5231≤a ≤16.当a =1时,方程①化为2+-12=0,解得1=-4,2=3. 故a min =1,b =-4,c =16 或a min =1,b =3,c =9.当a =16时,方程①化为2++316=0.解得1=-34,2=-14.故a min =16,b =-12,c =9;或a min =16,b =-4,c =1. 11.设1,2,…,n 中有r 个-1,s 个1,t 个2,则219499r s t r s t -++=⎧⎨++=⎩,得3t +s =59,0≤t ≤19.∴13+23+…+n 3=-r +s +8t =6t +19.∴19≤13+23+…+n3≤6×19+19=133.∴在t =0,s =59,r =40时,13+23+…+n 3取得最小值19;在t =19,s =2,r =21时,13+23+…+n 3取得最大值133. 12.∵把58写成40个正整数的和的写法只有有限种,∴12+22+…+402的最大值和最小值存在.不妨设1≤2≤…≤40.若1>1,则1+2=(1-1)+(2+1),且(1-1)2+(2+1)2=12+22+2(2-1)+2>12+22.于是,当1>1时,可以把1逐步调整到1,此时,12+22+…+402的值将增大.同理可以把2,3,…,39逐步调整到1,此时12+22+…+402的值将增大.从而,当1,2,…,39均为1,40=19时,12+22+…+402取得最大值,即A =22239111+++L 1442443个+192=400.若存在两个数i ,j ,使得j -i ≥2(1≤i <j ≤40),则(i +1)2+(j -1)2=i 2+j 2-2(i -j -1)<i 2+j 2.这表明,在 1,2,…,40中,若有两个数的差大于1,则把较小的数加1,较大的数减1此时,12+22+…+402的值将减小,因此,当12+22+…+402取得最小值时,1,2,…,40中任意两个数的差都不大于1.故 当1=2=…=22=1,23=24=…=40=2时,12+22+…+402取得最小值,即222111+++L 144244322个222222+++⋯+=94从而,A+B=494.。
