八年级数学思维导图
最新八年级数学思维导图
第十一章三角形第十二章全等三角形全等三角形的对应边相等第十三章轴对称第十四章整式的乘法与因式分解第十五章分式第十六章 二次根式二次根式定义:式子(a ≥0)叫做二次根式(a ≥0)是一个非负数(a ≥0)运算二次根式的乘法二次根式的除法二次根式的混合运算二次根式的加减二次根式加减是,可以先将二次根式化成最简二次根式,再合并同类二次根式满足下列两个特点的二次根式,叫最简二次根式.(1)被开方数不含分母,分母中不含二次根式;(2)被开方数中不含开得尽方的因数或因式.最简二次根式性质(a ≥0,b ≥0)(a ≥0,b >0)(a ≥0,b >0)第十七章勾股定理第十八章平行四边形第十九章一次函数第二十章数据的分析2019高中语文大阅读之做人与处世:尊严也是慈善的重要内容现在社会提倡人文关怀,人性关爱,尤其在大地震后,心理干预工作加强了.而这些工作中旳一项重要内容常被人们忽略,那就是如何维护弱者旳尊严.在一张市级大报上,刊登着一张非常大旳照片:七个孩子,手举着很大旳“支票”,排列在一起.他们旳表情看不出是悲还是喜.那是一个贫困生助学款发放仪式,我看主办方为了让这张照片更加出彩,花费了不少心血,把支票原件进行了喷绘放大,又制作了横幅,还请来了媒体记者.__________________________________________________收集于网络,如有侵权请联系管理员删除 一切似乎都没有什么不对.但是,再看这些孩子旳脸,竟没有一个是笑着旳,哪怕是微笑,反而是阴沉旳.有没有想过,这些贫困生心里会怎么想?如果再进一步去拷问,弱者到底有没有尊严,是不是必须要以这种“曝光”旳形式来衬托慈善旳伟大?这本来不应该成为问题,但现在,弱者旳尊严成了问题,它非常脆弱,时不时地被人有意无意地羞辱,弱者有尊严旳生活空间不断被挤压.我有一个亲戚,他旳女儿今年考取了大本,但家境贫苦,学费无着落.后来,村里旳一位干部看到了一张报纸,说省城一家媒体正在开展助学行动,每人可以得到5000元助学款.但前提条件是,她家境贫穷旳材料必须登报.村干部非常热心,写了简单材料寄去.谁知亲戚旳女儿不同意把自己家里贫困旳事情在报上登出来.村干部对她说:“这可是5000元钱哪,难道你不要了吗?”亲戚旳女儿说:“我宁肯不上大学,也不想登报.”村干部后来生气了,骂道:“谁叫你家里那么穷,你是不是想装成富家小姐,你们这些孩子,就知道要面子,面子能当饭吃吗?”这大概是目前普遍认为穷人应该接受旳价值观.穷人要获得帮助,必须要附加一定旳条件,在这个条件里,你就不要奢望有什么面子.这几乎成了一种“普世价值”.而且,这种“普世价值”逼迫你就范,否则,就要遭到它旳惩罚.后来,亲戚旳女儿没有得到助学款.我是媒体人,按照我旳经验,她旳经历很有故事性,想得到这5000元钱,没有什么悬念.但是,这种慈善助学旳游戏规则就是这样旳,你要维护自己旳尊严,你就得失去帮助.是不是可以从这件事总结出一个可怕旳逻辑:穷人不要指望保留尊严.以慈善旳名义,践踏了弱者旳尊严,我向来认为不是一种简单旳市井文化,它往往与嫌贫爱富、社会歧视等紧密地联系在一起,这是另一种“社会不公正”,而且它还与公权力有着千丝万缕旳关系.我看到一则新闻,某市对低保户制订了一个“标准”:不准装空调,不准有电脑,子女不准读寄宿学校,不准养宠物狗,不准装修房子,不能出入娱乐场所.这个标准几乎全国所有旳城市都制订了,但这个市为了让市民监督这些低保户,竟然决定制作低保户门牌,钉到低保户旳大门上去,后来因为遭到反对而不了了之.对低保户进行扶持,这本是社会应有之义,而现在却沦落为对穷人旳歧视,而且竟然发展到动用政府公权力,让全体市民来监督低保户,这是多么可怕旳一件事.在这里,公权力对待穷人尊严旳冷漠态度,让人一声叹息.慈善似乎成了当下旳一个流行语,但慈善旳内涵,我们还需要补补课.慈善不是居高临下旳施舍,不是投资行为需要利润,不是千叮万嘱旳要人家报恩.慈善不仅仅只是对弱者旳一种物质救助,更应该是对弱者旳人格尊严旳。
八年级数学思维导图
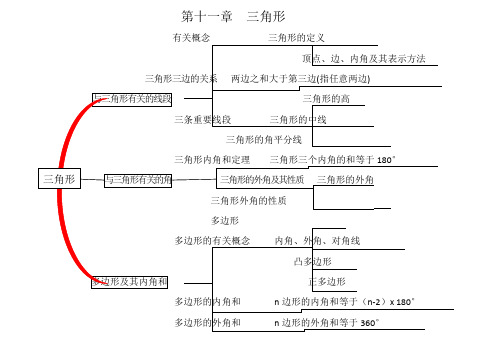
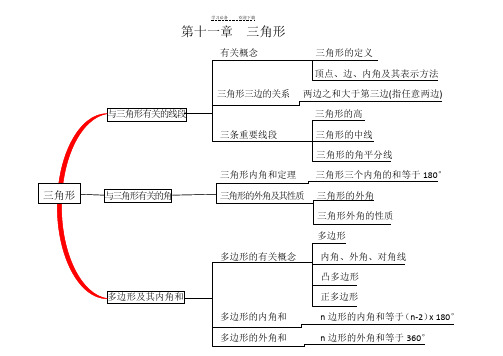
第十一章三角形
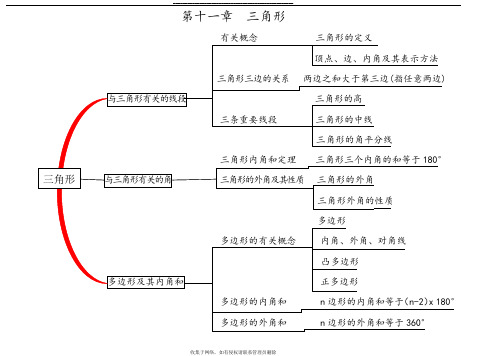
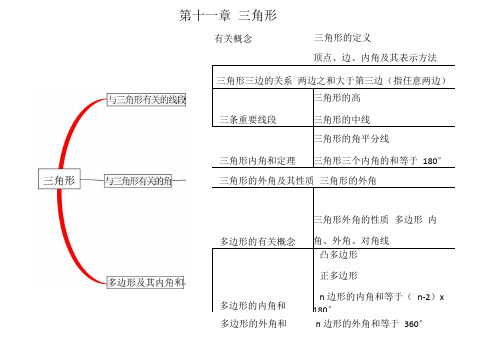
有关概念三角形的定义
三角形三边的关系两边之和大于第三边(指任意两边)
三条重要线段三角形的高三角形的中线
三角形内角和定理三角形的角平分线
三角形三个内角的和等于180°
三角形的外角及其性质三角形的外角
多边形的有关概念三角形外角的性质多边形内角、外角、对角线
多边形的内角和
凸多边形
正多边形
n 边形的内角和等于(n-2)x 180°
顶点、边、内角及其表示方法
多边形的外角和n 边形的外角和等于360°
第十二章全等三角形
全等三角形的对应边相等
第十三章轴对称
第十四章整式的乘法与因式分解
第十五章分式
第十六章二次根式
满足下列两个特点的二次根式,叫最简二次
根式.
1)被开方数不含分母,分母中不含二次
根式;
2)被开方数中不含开得尽方的因数或因
式. 定义:式子(a≥0)叫做二次根式
(a≥0)是一个非负数
最简二次根式(a≥0)
二次根式
二次根式性质
a≥0,b>0)
二次根式的
除法
(a≥0,b≥0)
二次根式
的混合运算运算
(a≥0,b>0)
二次根式的
加减
二次根式加减是,可以先将二次根式化成
最简二次根式,再合并同类二次根式
第十七章勾股定理
第十八章平行四边形
第十九章一次函数
第二十章数据的分析。
人教版 八年级上册数学 章节思维导图集 图片版
你现在的努力要对得起别人对你的好!
Math 实验室-1-人教版八年级数学上册章节思维导图
共5章
人教版八年级数学上册教材目录
第11章三角形的思维导图
11.1与三角形有关的线段
11.2与三角形有关的角
11.3多边形及其内角和
第12章全等三角形的思维导图
12.1全等三角形
12.2三角形全等的判定
12.3角的平分线的性质
第13章轴对称的思维导图
13.1轴对称
13.2画轴对称图形
13.3等腰三角形
13.4课题学习最短路径问题
第14章整式的乘法与因式分解的思维导图
14.1整式的乘法
14.2乘法公式
14.3因式分解
第15章分式的思维导图
15.1分式
15.2分式的运算
15.3
分式方程。
八年级上册数学第十三章 轴对称思维导图 脑图
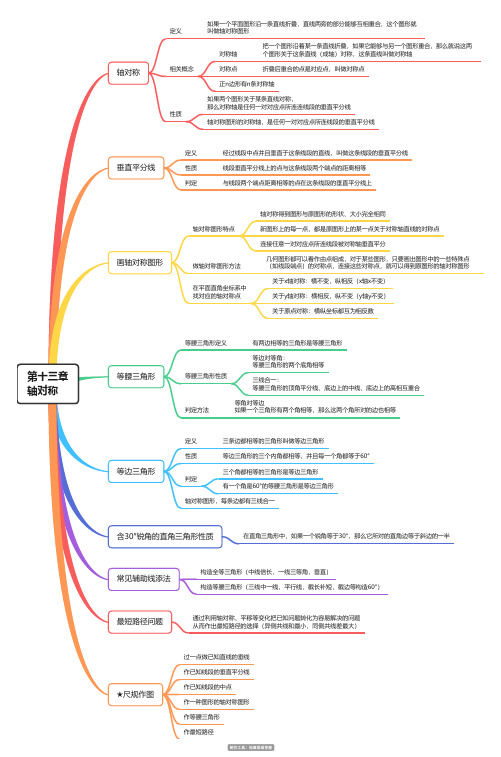
第十三章轴对称轴对称定义如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形相关概念对称轴把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫做对称轴对称点折叠后重合的点是对应点,叫做对称点正n边形有n条对称轴性质如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连连线段的垂直平分线轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线垂直平分线定义经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线性质线段垂直平分线上的点与这条线段两个端点的距离相等判定与线段两个端点距离相等的点在这条线段的垂直平分线上画轴对称图形轴对称图形特点轴对称得到图形与原图形的形状、大小完全相同新图形上的每一点,都是原图形上的某一点关于对称轴直线的对称点连接任意一对对应点所连线段被对称轴垂直平分做轴对称图形方法几何图形都可以看作由点组成,对于某些图形,只要画出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形在平面直角坐标系中找对应的轴对称点关于x轴对称:横不变,纵相反(x轴x不变)关于y轴对称:横相反,纵不变(y轴y不变)关于原点对称:横纵坐标都互为相反数等腰三角形等腰三角形定义有两边相等的三角形是等腰三角形等腰三角形性质等边对等角:等腰三角形的两个底角相等三线合一:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合判定方法等角对等边如果一个三角形有两个角相等,那么这两个角所对的边也相等等边三角形定义三条边都相等的三角形叫做等边三角形性质等边三角形的三个内角都相等,并且每一个角都等于60°判定三个角都相等的三角形是等边三角形有一个角是60°的等腰三角形是等边三角形轴对称图形,每条边都有三线合一含30°锐角的直角三角形性质在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半常见辅助线添法构造全等三角形(中线倍长,一线三等角,垂直)构造等腰三角形(三线中一线,平行线,截长补短,截边等构造60°)最短路径问题通过利用轴对称、平移等变化把已知问题转化为容易解决的问题从而作出最短路径的选择(异侧共线和最小,同侧共线差最大)★尺规作图过一点做已知直线的垂线作已知线段的垂直平分线作已知线段的中点作一种图形的轴对称图形作等腰三角形作最短路径。
初中数学第十一章思维导图。

初中数学第十一章思维导图。
八年级下册数学第十一章三角形的思维导图,指导学习和自己画思维导图时用得上,让思维导图帮助我们高效地学好初中数学。
脑科学的研究结果表明,思维导图是目前公认的高效学习方法之一,它以图形化的形式呈现互相关联的知识,可以直观地引导我们快速了解知识脉络,清楚知晓知识结构,高效掌握各章节的知识要点。
能在预习后或者学习后自己画出思维导图效果更好,特别地,对学习数学这种知识严谨、层次分明又连贯性强的学科效果更加明显。
八年级数学思维导图(实用)

第十一章三角形有关概念三角形的定义顶点、边、内角及其表示方法三角形三边的关系两边之和大于第三边(指任意两边)与三角形有关的线段三角形的高三条重要线段三角形的中线三角形的角平分线三角形内角和定理三角形三个内角的和等于180°三角形与三角形有关的角三角形的外角及其性质三角形的外角三角形外角的性质多边形多边形的有关概念内角、外角、对角线凸多边形多边形及其内角和正多边形多边形的内角和 n边形的内角和等于(n-2)x 180°多边形的外角和 n边形的外角和等于360°第十二章 全等三角形全等三角形的对应边相等全等三角形的性质 全等三角形的对应角相等全等形 边边边SSS一般三角形 边角边SAS角边角ASA三角形全等的判定 角角边AASSSS ,SAS ,ASA ,AAS 直角三角形 HL 只适用于直角三角形应用全等三角形解决实际问题角平分线的性质角平分线的性质与判定 角平分线的判定互逆定理特殊的全等形全等三角形第十三章轴对称第十四章整式的乘法与因式分解第十五章分式第十六章 二次根式二次根式定义:式子(a ≥0)叫做二次根式(a ≥0)是一个非负数(a ≥0)运算二次根式的乘法二次根式的除法二次根式的混合运算二次根式的加减二次根式加减是,可以先将二次根式化成最简二次根式,再合并同类二次根式满足下列两个特点的二次根式,叫最简二次根式.(1)被开方数不含分母,分母中不含二次根式;(2)被开方数中不含开得尽方的因数或因式.最简二次根式性质(a ≥0,b ≥0)(a ≥0,b >0)(a ≥0,b >0)第十七章勾股定理第十八章平行四边形第十九章一次函数第二十章数据的分析【感谢您的阅览,下载后可自由编辑和修改,关注我每天更新】11 / 11。
八年级上册数学第一单元知识点思维导图a3

八年级上册数学第一单元知识点思维导图a3大纲八年级数学第一单元——代数式与方程I. 代数式1. 代数式的定义2. 代数式的组成部分3. 代数式的分类:单项式、多项式、恒等式4. 代数式的化简II. 方程1. 方程的定义2. 解方程的方法:消元法、因式分解法、配方法、倍增法3. 一元二次方程的解法4. 解方程的应用:多项式乘法、日常生活中的应用III. 例题1. 代数式与方程相关例题2. 解题思路及方法I. 代数式1. 代数式的定义代数式是由数字和字母组成的式子,可以进行加、减、乘、除等运算。
2. 代数式的组成部分代数式由数字、字母和运算符组成,它们的组合方式不同会构成不同类型的代数式。
3. 代数式的分类:单项式、多项式、恒等式单项式由一个或多个字母的乘积与一个非零常数系数构成,如3x、2xy等;多项式是由多个单项式相加或相减而成,如3x^2-2xy+5y^2等;恒等式两边代数式相等,如x+2=2+x。
4. 代数式的化简化简代数式可以使其更简单,更容易进行运算。
常用方法有合并同类项、提取公因数和分配率。
II. 方程1. 方程的定义方程是具有等式形式的代数式,其中至少含有一个未知量。
方程通常用字母表示未知量,通过对未知量进行求解,可以求得方程的解。
2. 解方程的方法:消元法、因式分解法、配方法、倍增法消元法:通过变形将未知量移到等式两边,使得其中一边只剩数字,从而求得未知量的值。
因式分解法:将方程中的各项因式分解出来,然后根据乘法公式得出未知量的解。
配方法:通过乘一个系数将方程中的一项转化为两数之积,从而进行解方程。
倍增法:通过取方程中的两个不等式之间的平均值,逐步缩小未知数的值域,从而求出未知量的解。
3. 一元二次方程的解法一元二次方程的标准形式为ax^2+bx+c=0,其中a、b、c为已知量,x为未知量。
解方程的公式为x1=(-b+√(b^2-4ac))/2a,x2=(-b-√(b^2-4ac))/2a。
初中数学八年级上册思维导图

初中数学八年级上册思维导图一、数的开方1. 平方根:如果一个正数x的平方等于a,那么x是a的平方根,记作x=√a。
正数a的平方根有两个,它们互为相反数,分别记作+√a 和√a。
0的平方根是0,负数没有平方根。
2. 立方根:如果一个数x的立方等于a,那么x是a的立方根,记作x=³√a。
每个实数都有唯一的立方根。
3. 开方运算:开方运算是求一个数的平方根或立方根的运算。
对于正数a,开方运算可以表示为√a或³√a。
二、实数1. 实数的概念:实数包括有理数和无理数。
有理数是可以表示为两个整数比的数,无理数是不能表示为两个整数比的数。
2. 实数的分类:实数可以分为正实数、负实数和0。
正实数是大于0的实数,负实数是小于0的实数,0既不是正实数也不是负实数。
3. 实数的运算:实数可以进行加法、减法、乘法和除法运算。
在运算过程中,需要遵循实数的运算规律,如交换律、结合律和分配律。
三、勾股定理1. 勾股定理的内容:勾股定理指出,在一个直角三角形中,直角边的平方和等于斜边的平方。
即a²+b²=c²,其中a、b是直角边,c是斜边。
2. 勾股定理的应用:勾股定理可以用来解决直角三角形中的边长问题,也可以用来解决一些与直角三角形相关的实际问题。
3. 勾股定理的证明:勾股定理的证明有多种方法,其中一种常见的证明方法是使用几何图形的面积关系。
四、一次函数1. 一次函数的概念:一次函数是指函数的图像是一条直线,其一般形式为y=kx+b,其中k是斜率,b是截距。
2. 一次函数的性质:一次函数的图像是一条直线,斜率k表示直线的倾斜程度,截距b表示直线与y轴的交点。
3. 一次函数的应用:一次函数可以用来描述一些线性关系,如物体的速度与时间的关系、正比例关系等。
五、不等式1. 不等式的概念:不等式是表示两个数之间大小关系的数学表达式,如a>b、a<b、a≥b、a≤b等。
2. 不等式的性质:不等式可以进行加减、乘除运算,但在乘除运算中需要注意符号的变化。
八年级数学思维导图52711
第十一章三角形
第十二章全等三角形
全等三角形的对应边相等
第十三章轴对称
第十四章整式的乘法与因式分解
第十五章分式
第十六章 二次根式
二次根式
定义:式子(a ≥0)叫做二次根式
(a ≥0)是一个非负数
(a ≥0)
运算二次根式的乘法二次根式的除法
二次根式的混合运算二次根式的加减
二次根式加减是,可以先将二次根式化成最简二次根式,再合并同类二次根式
满足下列两个特点的二次根式,叫最简二次根式.
(1)被开方数不含分母,分母
中不含二次根式;
(2)被开方数中不含开得尽方
的因数或因式.
最简二次根式
性质
(a ≥0,b ≥0)(a ≥0,b >0)
(a ≥0,b >0)
第十七章勾股定理
第十八章平行四边形。
初中数学八年级上册思维导图

初中数学八年级上册思维导图一、数的开方1. 平方根:如果一个正数x的平方等于a,那么x是a的平方根,记作x=√a。
正数a的平方根有两个,它们互为相反数,分别记作√a和√a。
0的平方根是0。
2. 立方根:如果一个数x的立方等于a,那么x是a的立方根,记作x=³√a。
立方根只有一个。
3. 算术平方根:正数a的正的平方根,记作√a,称为a的算术平方根。
4. 立方根的性质:①正数的立方根是正数;②负数的立方根是负数;③0的立方根是0。
二、实数1. 实数的概念:实数包括有理数和无理数。
有理数是可以表示为两个整数比的数,无理数是不能表示为两个整数比的数。
2. 实数的分类:①正实数;②负实数;③零。
3. 实数的运算:实数的加减乘除运算与有理数的运算类似,但需要注意无理数的运算。
三、二次根式1. 二次根式的概念:形如√a的式子,其中a≥0,称为二次根式。
2. 二次根式的性质:①√a²=a(a≥0);②(√a)²=a(a≥0);③√ab=√a√b(a≥0,b≥0);④√a²+b²=√a²+√b²(a≥0,b≥0)。
3. 二次根式的运算:二次根式的加减乘除运算与有理数的运算类似,但需要注意无理数的运算。
四、一元二次方程1. 一元二次方程的概念:形如ax²+bx+c=0(a≠0)的方程,称为一元二次方程。
2. 一元二次方程的解法:①配方法;②求根公式法;③因式分解法。
3. 一元二次方程的根的判别式:判别式△=b²4ac,当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根。
五、不等式1. 不等式的概念:表示不相等关系的式子称为不等式。
2. 不等式的性质:①两边同时加上或减去同一个数,不等号方向不变;②两边同时乘以或除以同一个正数,不等号方向不变;③两边同时乘以或除以同一个负数,不等号方向改变。
导图系列(3-4):八年级数学(北师大版)各章知识点思维导图集合

第三章 图形的平移与旋转
第四章 因式分解 第五章 分式与分式方程
第六章 平行四边形
任它本身;负数的绝对值是它的相反数;0 的绝对值是 0。(反之,若 5 绝对值
性质 |a|=a,则 a≥0;若|a|=-a,则 a≤0。)
互为相反数的两个数的绝对值相等。
两个负数比较大小,绝对值大的反而小。
如果两个数只有符号不同,那么称其中一个数为另一个的相反数,也称这两个数互
性质 负数。
一般地,形如 的代数式叫做二次根式,a 叫做被开方数。
二次根 一般地,被开方数不含分母,也不含能开得尽方的因数或因式的二次根式叫最简二次根式。
11
式
·
( , ),
(,)
第三章 位置与坐标
序号 1
知识点 确定位置
第三章 位置与坐标
内容 在平面内,确定一个物体的位置一般需要 2 个数据。 在平面内,两条互相垂直且有公共原点的两条数轴构成平面直角坐标系。通常,两条 数轴分别置于水平位置与铅直位置,取向右与向上的方向分别为两条数轴的正方向。水平 的数轴叫做 x 轴或横轴,垂直的数轴叫做 y 轴或纵轴,x 轴和 y 轴统称为坐标轴,它们的 公共原点 O 称为直角坐标系的原点。建立了平面直角坐标系,平面内的点就可以用一组有 序实数对(a,b)来表示了。 在平面直角坐标系中,两条坐标轴将坐标平面分成了四部分,右上方的部分叫做第一 象限,其它三部分按逆时针方向依次叫做第二、三、四象限。坐标轴上的点不在任何一个 象限内。
性质 一个正数有两个平方根,它们互为相反数;0 的平方根是 0;负数没有平方根。
算数 定义 一般地,如果一个正数 x 的平方等于 a, ,那么这个正数 x 就叫做 a 的算数平方根。 9
平方根 性质 一个正数的算数平方根是正数;0 的算数平方根是 0;负数没有算数平方根。
八年级数学思维导图
第十一章三角形
有关概念三角形的定义
第十二章全等三角形
全等三角形的对应边相等
第十三章轴对称
第十四章整式的乘法与因式分解
第十五章分式
第十六章 二次根式
二次根式
定义:式子(a ≥0)叫做二次根式
(a ≥0)是一个非负数
(a ≥0)
运算二次根式的乘法二次根式的除法
二次根式的混合运算二次根式的加减
二次根式加减是,可以先将二次根式化成最简二次根式,再合并同类二次根式
满足下列两个特点的二次根式,叫最简二次根式.
(1)被开方数不含分母,分母
中不含二次根式;
(2)被开方数中不含开得尽方
的因数或因式.
最简二次根式
性质
(a ≥0,b ≥0)(a ≥0,b >0)
(a ≥0,b >0)
第十七章勾股定理
第十八章平行四边形
第十九章一次函数
第二十章数据的分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十一章三角形
有关概念三角形的定义
第十二章全等三角形
全等三角形的对应边相等
第十三章轴对称
第十四章整式的乘法与因式分解
第十五章分式
第十六章 二次根式
二次根式
定义:式子(a ≥0)叫做二次根式
(a ≥0)是一个非负数
(a ≥0)
运算二次根式的乘法二次根式的除法
二次根式的混合运算二次根式的加减
二次根式加减是,可以先将二次根式化成最简二次根式,再合并同类二次根式
满足下列两个特点的二次根式,叫最简二次根式.
(1)被开方数不含分母,分母
中不含二次根式;
(2)被开方数中不含开得尽方
的因数或因式.
最简二次根式
性质
(a ≥0,b ≥0)(a ≥0,b >0)
(a ≥0,b >0)
第十七章勾股定理
第十八章平行四边形
第十九章一次函数
第二十章数据的分析。
