111孝昌二中理科检测卷(7)2007.12.16
2018年最新 湖北省孝昌二中2018学年高三理科数学知识数学能力检测卷(七) 精品

孝昌二中理科数学知识·数学能力检测卷(七)温馨提示: 慷慨 尤其还兼有谦虚,就会使人赢得好感一、选择题:本大题共10小题,每小题5分,共50分. 1.在数集},2{2x x x -中,实数x 的取值范围是(★★★)A ),(+∞-∞B .),0()0,(+∞-∞C . ),3()3,(+∞-∞D .),3()3,0()0,(+∞-∞ 2.已知),(,,2121R b a AC b a AB ,b a ∈+=+=λλλλ若是不共线的向量,则A 、B 、C 三点共线的充要条件为(★★★)A .121-==λλB .121==λλC .0121=-λλD .1121=+⋅λλ3.如果消息A 发生的概率为()P A ,那么消息A 所含的信息量为()()21log I A P A =。
若王教授正在一个有4排8列座位的小型报告厅里听报告,则发布的以下4条消息中,信息量最大的是(★★★)A .王教授在第4排B .王教授在第4排第5列C .王教授在第5列D .王教授在某一排 4.若抛物线的顶点坐标是()1,0M ,准线l 的方程是220x y --=,则抛物线的焦点坐标为(★★★)A .62,55⎛⎫- ⎪⎝⎭ B .62,55⎛⎫- ⎪⎝⎭ C .42,55⎛⎫ ⎪⎝⎭ D .42,55⎛⎫- ⎪⎝⎭5.已知为O 原点,点)sin 2,cos 2(1),(22θθQ ,y x y x P 点上在单位圆=+满足)32,34(-=PQ ,则=⋅OQ OP (★★★)A .1825B .2516C .165D .3625 6.将数字3,4,5,6,7排成一行,使得相邻两个数都互质,则 可能的排列方法共有(★★★)A .30种B .36种C .42种D .48种7.若1cos sin =+αα,则对任意实数n ,ααn n cos sin +的取值为(★★★)A .1B .区间(0, 1)C .112n - D .不能确定8.在△ABC 中,三条边长成等差数列且最小角的正弦值与最大角的正弦值之比为5:3,则△ABC 是(★★★)A .直角三角形B .等腰三角形C .等边三角形D .锐角三角形9.已知函数x x x y ++=2331的图象C 上存在一定点P 满足:若过点P 的直线l 与曲线C交于不同于P 的两点M (x 1, y 1),N (x 2, y 2),就恒有21y y +的定值为y 0,则y 0的值为(★★★)A .31-B .32-C .34-D .2-10.可行域30230230x y x y x y +-≥⎧⎪-+≥⎨⎪--≤⎩的顶点是()()()12,21,33A B C ,,,,()z kx y k =-为常数,若使得z 取的得最大值为4的最优解是唯一的,则k =(★★★)A 、()1,2B 、()2,1C 、()3,3D 、()2,2二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中横线上.11.若数列}{n a 的通项公式2)1(1+=n a n ,记)1()1)(1(2)(21n a a a n f ---= ,试通过计算)1(f ,)2(f ,)3(f 的值,推测出=)(n f (请把答案填写在答题卷上).12.椭圆上的点()2,0A -关于直线1y x =-和1y x =-+的对称点分别为椭圆的焦点1F 和2F ,P 为椭圆上任意一点,则12PF PF ⋅的最大值为(请把答案填写在答题卷上).13.对于函数)(x f ,在使M x f ≤)(恒成立的所有常数M 中,我们把M 的最小值称为函数)(x f 的“上确界”,则函数1)1()(22++=x x x f 的“上确界”为(请把答案填写在答题卷上). 14.对于)2,0(π∈x ,不等式16cos sin 122≥+xpx 恒成立,则p 的取值范围是(请把答案填写在答题卷上).15.设""+与""⋅分别为实数集内传统意义的加法与乘法,对实数(),2x y k k Z ππ≠+∈,定义tan tan ,tan tan x y x y x y x y ⊕=+⊗=⋅,在ABC ∆中,23B π∠=,则()A C A C ⊕⊗等于(请把答案填写在答题卷上).三、解答题:本大题共6个小题,共75分. 解答应写出文字说明,证明过程或演算步骤.16.(本小题满分12分)设函数)(),0(2)(1)2sin(x f y x f x =<<-=++ϕπϕ的图象的一条对称轴是直线.8π=x(1)求ϕ;(2)求函数)(x f y =的递减区间; (3)试说明)(x f y =的图象可由xy 2sin 2=的图象作怎样变换得到。
孝昌二中高二数学理科选修2-3综合测试卷

孝昌二中高二数学理科选修2-3综合测试题班级________姓名______________分数__________一、选择题(每小题5分,共50分)1.某公共汽车上有10名乘客,沿途有5个车站,乘客下车的可能方式( )A、105种B、510种C、50种 D、10种2.随机变量ξ服从二项分布ξ~()p n B ,,且,200,300==ξξD E 则p 等于( )A 、32 B 、 31C 、 1D 、0 3.二项式30的展开式的常数项为第( )项A 、 17B 、18C 、 19D 、204.在某一试验中事件A 出现的概率为p ,则在n 次试验中A 出现k 次的概率为( )A 、1-k pB 、 ()k n kp p --1 C 、1-()kp -1 D 、 ()kn k k n pp C --15.从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同的工作,若其中甲、乙两名志愿者不能从事翻译工作,则选派方案共有( )A .96种B .180种C .240种D .280种6.设()52501252x a a x a x a x -=++ ,那么02413a a a a a +++的值为( )A 、-122121 B 、-6160 C 、-244241D 、—1 7.在100件产品中有6件次品,现从中任取3件产品,至少有1件次品的不同取法的种数是 ( )A 、12694C CB 、C 16C 299 C 、C 3100-C 394D 、A 3100-A 3948.随机变量X 的概率分布列为)1()(+==n n an X P ,(1,2,3,4n =) 其中a 为常数,则)2521(<<X P 的值为( ) A 、 23 B 、34 C 、45 D 、56 9.两位同学一起去一家单位应聘,面试前单位负责人对他们说:“我们要从面试的人中招聘3人,你们俩同时被招聘进来的概率是1/70”.根据这位负责人的话可推断出参加面试的人数为( )A 、21B 、35C 、42D 、7010. 抛掷甲、乙两骰子,若事件A :“甲骰子的点数小于3”;事件B :“甲、乙两骰子的点数之和等于6”,则P(B|A)的值等于( ) A 、31 B 、181 C 、61 D 、91二、填空题(每小题5分,共25分)11.同时抛掷两枚相同的均匀硬币,随机变量ξ=1表示结果中有正面向上, ξ=0表示结果中没有正面向上,则Eξ=12.用1、2、3、4、5这五个数字,组成没有重复数字的三位数,其中偶数共有 个 13.(x 2+1)(x -2)7的展开式中x 3项的系数是 . 14.已知随机变量ξ服从正态分布2(2)N σ,,(4)0.84P ξ=≤,则(0)P ξ=≤ 15、如右图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n 行有n 个数且两端的数均为1(2)n n≥,每个数是它下一行左右相邻两数的和,如111111111,,1222363412=+=+=+,…, 则第8行第4个数(从左往右数)为_________ 三、解答题(本大题共6小题,共75分)16.(本题12分)已知22)nx的展开式中,第5项的系数与第3项的系数之比是56:3,求展开式中的常数项。
2007年全国高考理科综合二试题卷物理部分及解析(word版本)
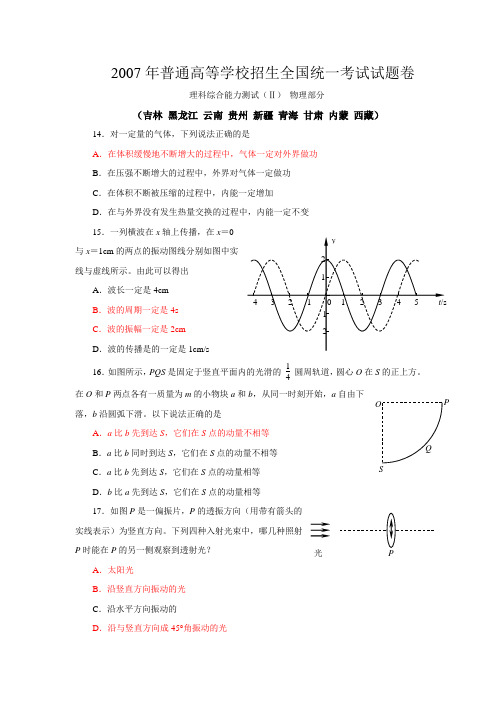
2007年普通高等学校招生全国统一考试试题卷理科综合能力测试(Ⅱ)物理部分(吉林黑龙江云南贵州新疆青海甘肃内蒙西藏)14.对一定量的气体,下列说法正确的是A.在体积缓慢地不断增大的过程中,气体一定对外界做功B.在压强不断增大的过程中,外界对气体一定做功C.在体积不断被压缩的过程中,内能一定增加D.在与外界没有发生热量交换的过程中,内能一定不变15.一列横波在x轴上传播,在x=0与x=1cm的两点的振动图线分别如图中实线与虚线所示。
由此可以得出A.波长一定是4cmB.波的周期一定是4sC.波的振幅一定是2cmD.波的传播是的一定是1cm/s16.如图所示,PQS是固定于竖直平面内的光滑的14圆周轨道,圆心O在S的正上方。
在O和P两点各有一质量为m的小物块a和b,从同一时刻开始,a自由下落,b沿圆弧下滑。
以下说法正确的是A.a比b先到达S,它们在S点的动量不相等B.a比b同时到达S,它们在S点的动量不相等C.a比b先到达S,它们在S点的动量相等D.b比a先到达S,它们在S点的动量相等17.如图P是一偏振片,P的透振方向(用带有箭头的实线表示)为竖直方向。
下列四种入射光束中,哪几种照射P时能在P的另一侧观察到透射光?A.太阳光B.沿竖直方向振动的光C.沿水平方向振动的D.沿与竖直方向成45°角振动的光光PQSO18.氢原子在某三个相邻能级之间跃迁时,可发出三种不同波长的辐射光。
已知其中的两个波长分别为λ1和λ2,且λ1>λ2,则另一个波长可能是A .λ1+λ2B .λ1-λ2C .λ1λ2λ1+λ2D .λ1λ2λ1-λ219.如图所示,一带负电的质点在固定的正的点电荷作用下绕该正电荷做匀速圆周运动,周期为T 0,轨道平面位于纸面内.质点的速度方向如图中箭头所示。
现加一垂直于轨道平面的匀强磁场,已知轨道半径并不因此而改变,则A .若磁场方向指向纸里,质点运动的周期将大于T 0B .若磁场方向指向纸里,质点运动的周期将小于T 0C .若磁场方向指向纸外,质点运动的周期将大于T 0D .若磁场方向指向纸外,质点运动的周期将小于T 020.假定地球、月球都静止不动,用火箭从地球沿地月连线向月球发射一探测器。
推荐-孝昌二中期末考试理科数学试卷 精品

孝昌二中期末考试理科数学试卷温馨提示: 好好活就是干有意义的事情一、选择题:本大题共10小题,每小题5分,共50分.1、设A 、B 是两个集合,定义}2|1||{},,|{≤+=∉∈=-x x M B x A x x B A 若且, ∈==αα|,sin ||{x x N R },则M -N=(★★★)A .[-3,1]B .[-3,0)C .[0,1]D .[-3,0]2、函数122)(log 1)(+-=+=x x g x x f 与在同一直角坐标系下的图象大致是(★★★)3、已知正方体ABCD --1111A BC D 中,M 为AB 中点,棱长为2,P 是底面ABCD 上的动点,且满足条件13PD PM =,则动点P 在底面ABCD 上形成的轨迹是(★★★) A.圆 B.椭圆 C.双曲线 D.抛物线4、如图,平面内的两条相交直线1OP 和2OP 将该平面分割成四个部分I 、II 、III 、Ⅳ(不包含边界)。
设21n m +=,且点P 落在第III 部分,则实数m ,n 满足(★★★) A .00n >m >, B .00n <m >,C .00n >m <,D .00n <m <,5.等差数列}{n a 中,20,873==a a ,若数列}1{1+n n a a 的前n 项和为254,则n 的值为(★★★)A 、14 B 、15 C 、16 D 、186.方程2122032)1(x x ax x a ,的两根=--+满足)(〈2121x x x -且0<1x ,则实数a 的取值范围是(★★★)A.()3,1B.()+∞+,31 C.⎪⎭⎫ ⎝⎛--31,23 D.⎪⎭⎫⎝⎛+∞-,237.已知)40(tan 12sin sin 22παααα<<=++k ,则)4sin(πα-的值(★★★)A 、随k 的增大而增大B 、有时随k 的增大而增大,有时随k 的增大而减小C 、随k 的增大而减小D 、 是一个与k 无关的常数8.从集合}9,,3,2,1{ 中任取三个数排成一列,则这三个数成等差数列的概率是(★★★) A 、632 B 、634 C 、212 D 、2149.称||),(d -=为两个向量、间的“距离”.若向量、满足:①1||=;②≠;③对任意的R t ∈,恒有),(),(d t d ≥则(★★★)A 、b a ⊥B 、)(b a a -⊥C 、)(b a b -⊥D 、)()(b a b a -⊥+10.已知双曲线)0(222>=-a a y x 的左、右顶点分别为A 、B ,双曲线在第一象限的图像上有一点P ,γβα=∠=∠=∠APB PBA PAB ,,,则(★★★) A 、0tan tan tan =++γβα B 、0tan tan tan =-+γβα C 、0tan 2tan tan =++γβα D 、0tan 2tan tan =-+γβα二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中横线上.11.设⎪⎩⎪⎨⎧<<=<<-+=21,21,411,1)(x x x x x x f ,则=→)(lim 1x f x (请把答案填写在答题卷上).12.设21(1)1i z i i+=+--(其中i 是虚数单位),则7(1)z +展开式中的第4项是(请把答案填写在答题卷上).13.约束条件:⎪⎩⎪⎨⎧≥≥≤+≤+0,06262y x y x y x ,目标函数|12|+-=y x z的最小值是(请把答案填写在答题卷上).14.已知椭圆)0(12222>>=+b a by ax 的右焦点为)0,(c F 过F 作与x 轴垂直的直线与椭圆相交于点P ,过点P 的椭圆的切线l 与x 轴相交于点A ,则点A 的坐标为(请把答案填写在答题卷上).15. 已知集合{16,}P x x x N =≤≤∈,对它的非空子集A,先将A 中的每个元素k 分别乘以(1)k -,再求和(如A={1,3,6},可求得和为36(1)1(1)3(1)62-⨯+-⨯+-⨯=),则对M 的所有非空子集,这些和的总和是(请把答案填写在答题卷上).三、解答题:本大题共6个小题,共75分. 解答应写出文字说明,证明过程或演算步骤.16.(本小题满分12分)△ABCtan tan tan A B A B --= (I )求∠C 的大小;(Ⅱ)设角A ,B ,C 的对边依次为,,a b c ,若2c =,且△ABC 是锐角三角形,求22a b +的取值范围. 17.(本小题满分12分)在ABC ∆中,3231,2||,4||+===. ( I)证明:=; (Ⅱ)若6||=AD ,求||BC 的值.18.(本小题满分12分)已知正三棱柱ABC —A 1B 1C 1的底边长为1,高为h(h>3),点M 在侧棱BB 1上移动,到底面ABC 的距离为x ,且AM 与侧面BCC 1所成的角为α; (Ⅰ)若α在区间]4,6[ππ上变化,求x 的变化范围; (Ⅱ)若AM 与求为,6πα所成的角.19.(本小题满分12分)某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响. 已知某学生选修甲 而不选修乙和丙的概率为0.18,选修甲和乙而不选修丙的概率是0.12,至少选修一门的概 率是0.88,用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积. (I )记“函数2()f x x x ξ=+⋅为R 上的偶函数”为事件A ,求事件A 的概率; (Ⅱ)求ξ的分布列和数学期望. 20.(本小题满分13分)已知椭圆)0(12222>>=+b a by a x 的右准线2:1=x l 与x 轴相交于点D ,右焦点F 到上顶点的距离为2,点)0,(m C 是线段OF 上的一个动点.(I )求椭圆的方程;(Ⅱ)是否存在过点F 且与x 轴不垂直的直线l 与椭圆交于A 、B 两点,使得⊥+)(,并说明理由.21.(本小题满分14分)已知函数.,2161)(23R x x x x x f ∈++-=求: (I )求证:函数)(x f 的图象关于点)34,1(A 中心对称,并求)2009()1()0()2006()2007(f f f f f ++++-+-的值;(II )设*1),(),()(N n a g a x f x g n n ∈='=+,且1<a 1<2,求证|2||2|21-+-a a +…+|2|-n a <2.孝昌二中理科数学知识·数学能力检测卷(十二) 参考答案1.B2.D3.A4.B5.C6.D7.A8.B9.C 10.C11.2 12. 35i - 13.0 14.)0,(2ca 15.96 16.解:(1)依题意:tan tan 1tan tan A B A B+=-tan()A B +=0A B π<+<,∴23A B π+=,∴ 3C A B ππ=--=, (2)由三角形是锐角三角形可得22A B ππ⎧<⎪⎪⎨⎪<⎪⎩,即62A ππ<<。
2007届湖北孝感孝昌二中检测卷理十二

2007届湖北省孝感市孝昌二中检测卷(理)(十二)一、选择题:本大题共10小题,每小题5分,共50分. 1、设全集U=R ,{}A x x y y B x x x A ∈==⎭⎬⎫⎩⎨⎧<+-=,cos |,012|,则B A =( ) A 、]1,2(cos B 、]1,2[cos C 、)2,1(- D 、]2cos ,1(-2、已知k x x f ++=)cos(2)(φω,恒有)()3(x f x f -=+π成立,且1)6(-=πf ,则实数k 的值( )A 、1±B 、3±C 、1-或3 C 、3-或1 3、等比数列{}n a 中,5121=a ,公比21-=q ,用Ⅱn 表示它的前n 项之积: Ⅱn = a 1·a 2……a n ,则Ⅱ1, Ⅱ2…中最大的是( ) A 、Ⅱ11 B 、Ⅱ10 C 、Ⅱ9 D 、Ⅱ84、椭圆2222:by a x M +=1(a >b >0)的左、右焦点分别为F 1、F 2,P 为椭圆M 上任一点,且21PF PF ⋅的最大值的取值范围是[c 2, 3c 2],其中22b a c -=. 则椭圆M 的离心率e 的取值范围是( ) A. ],41[21 B. ]22,21[C. )1,22[D. )1,21[5、已知点O 为ABC ∆的外心,且4||2AC AB ==,则 )(-⋅等于( )A .2B .4C .6D .86、若函数)1,0( )(log )(3≠>-=a a ax x x f a 在区间)0,21(-内单调递增,则a 的取值范围是( )A .)1,43[B .)1,41[C .),49(+∞D .)49,1(7. 定义n nn n ni i nC C C C+++=∑= (10), 则1010()nkn n k C ==∑∑的值为( )(A ).1022 (B ).1023 (C ).2046 (D ).20478. 如图, 2n 台机器放在同一条直线形生产线上, 它们所生产的零件都必须送到一个检验台上进行检验. 已知移动零件所需的费用与所移动的距离成正比, 要使移动零件到检验台的总费用最少, 检验台的位置可以放置于以下情况中的哪几种? ( )① 点M 1处; ② 点M n 处; ③; 线段M 1M 2n 上任一点; ④ 点M n + 1处; ⑤ 线段M n M n+ 1的中点处.· · · · · · · · M 1M 2M 3M nM n + 1M 2nM 2n - 1A. ①②④B. ②③④C. ②④⑤D. ②③⑤9.已知两异面直线a. b 所成的角为060 ,则过空间一定点P 作与a. b 所成的角都是030的平面的个数是( )A 1B 2C 3D 410.一个五位的自然数abcde 称为“凸”数,当且仅当它满足a <b <c ,c >d >e (如12430,13531等),则在所有的五位数中“凸”数的个数是( ) (A )8568(B )2142(C )2139(D )1134二、填空题:本大题共5小题,每小题5分,共25分。
高二数学理科检测卷12试题

孝昌二中理科数学知识·数学才能检测卷(十二)制卷人:歐陽文化、歐陽理複;制卷時間:二O 二二年二月七日★ 祝 考 试 顺 利 ★一、选择题:本大题一一共10小题,每一小题5分,一共50分. 1. 复数z 满足方程:(2)z z i =+,那么z =〔★★★〕A 、1i +B 、1i -C 、1i -+D 、1i --,U R =集合{}{}2,1,A x x B x x =>=≤那么()()U U A C B B C A = 〔★★★〕A.∅B. {}12x x x <≥或 C. {}12x x ≤< D.{}12x x <≤3. 函数22(0)y x x x =-<的反函数为〔★★★〕A.11)y x =≥-B.10)y x =+>C. 11)y x =≥D.10)y x =>4.假设0,0,a b >>且1,a ≠那么log 0a b >是(1)(1)0a b -⋅->的〔★★★〕A.充分不必要条件B. 必要不充分条件5.在ABC ∆中,10a b +=,8c =,那么tan tan 22A B的值是 〔★★★〕 A.19 B.136. 函数33()log )f x x x =-,那么对于任意实数a 、()()()0,f a f b b a b a b++≠+的值〔★★★〕A .恒大于0B .恒等于0C .恒小于0D .符号不确定7. 有六根细木棒,其中较长的两根长为a a 2,3,其余四根长为a ,用它们端点相连搭成一个三棱锥,那么其中两条较长的棱所在直线的夹角的余弦值为〔★★★〕A.26 B. 1或者26 C.36368.假设点P 为一共焦点的椭圆1C 和双曲线2C 的一个交点,1F 、2F 椭圆离心率为1e ,双曲线离心率为2e ,假设120PF PF ⋅=,那么221211e e += 〔★★★〕9.在四面体ABCD,5,那么此四面体ABCD 的外接球的半径R 为〔★★★〕A、B 、5 C、2D 、410.如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横纵坐标分别对应数列{}*()n a n N ∈的前12项,如下表所示:按如此规律下去,那么200920102011a a a ++= 〔★★★〕答题卡上.11.当实数m ∈〔★★★〕.时,复数321(33)1m m m m i m -+--++为纯虚数.12. D E F 、、分别在ABC ∆的边BC AC 、及AB 上,满足::BD DC CE EA =:AF =FB 3:1,AD BE CF =、、两两相交于111A B C 、、三点,那么111A B C ∆的面积是ABC ∆面积的〔★★★〕. 13. 二项式431(2)3nx x-的展开式中含有非零常数项,那么正整数n 的最小值为〔★★★〕.,x y 满足1210x x y x y m≥⎧⎪-+≤⎨⎪+≤⎩,假如目的函数yZ x =的最大值为2,那么实数___________m =; 15.如图,以AB 为直径的圆有一内接梯形ABCD ,且//AB CD .假设双曲线1C 以A 、B为焦点,且过C 、D 两点,那么当梯形的周长最大时,双曲线的离心率为〔★★★〕.三、解答题:本大题一一共6个小题,一共75分. 解容许写出文字说明,证明过程或者演算步骤 16.〔本小题满分是12分〕向量D C BA),0)(cos 3,cos (sin >+=ωωωωx x x m ),sin 2,sin (cos x x x n ωωω-=函数)(,)(x f t n m x f 若+⋅=图象上相邻两个对称轴间的间隔 为],0[,23ππ∈x 且当时,函数)(x f 的最小值为0. 〔Ⅰ〕求函数)(x f 的表达式; 〔Ⅱ〕在△ABC 中,假设A C AB BC f sin ),cos(cos sin 2,1)(2求且-+==的值.17.〔本小题满分是12分〕如图,正三棱柱ABC —111C B A 的底面边长是2,D 是侧棱1CC 的中点,直线AD 与侧面11BB C C所成的角为45.〔Ⅰ〕求此正三棱柱的侧棱长;〔Ⅱ〕 求二面角C BD A --的大小;〔Ⅲ〕求点C 到平面ABD 的间隔 . 18.〔本小题满分是12分〕有10张形状、大小一样的卡片,其中2张上写着数字0,另外5张上写着数字1,余下3张上写着数字2。
湖北省孝昌二中高三数学理科知识能力检测试卷一

湖北省孝昌二中高三数学理科知识能力检测试卷一一、选择题:本大题共10小题,每小题5分,共50分.1.定义集合A 与B 的差集A -B ={x |x ∈A 且x ∉B },若A ={1,2,3,4,5},B ={2,3,6},则A -(A -B )=(★★★)A .{6}B .{2,3}C .{1,4,5}D .{2,3,6}2.()x x x f sin cos +=,把()x f 的图象按向量→a 平移,图象恰好为函数()x f y '-=的图象,则→a 可以等于(★★★)、A ⎪⎭⎫ ⎝⎛-0,4π 、B ⎪⎭⎫ ⎝⎛0,4π 、C ⎪⎭⎫ ⎝⎛-0,2π 、D ⎪⎭⎫ ⎝⎛0,2π3.ξ的概率密度函数f (x )2(1)x --,下列错误的是(★★★)A .P (ξ<1)=P (ξ>1)B .P (-1≤ξ≤1)=P (-1<ξ<1)C .f (x )渐近线为x =0D .η=ξ-1~N (0,1)4.将()()b x a x --逐项展开得ab bx ax x +--2,则2x 出现的频率为41,x 出现的频率为21,如此将()()()()()e x d x c x b x a x -----逐项展开后,3x 出现的频率是(★★★) 、A 165 、B 61 、C 51 、D 325 5.若000(2)()lim3x f x x f x x∆→-∆-∆=1,则f '(x 0)=(★★★)A .23B .32C .-23D .-326.若不等式[(1-a )n -a ]lg a <0,对任意正整数n 恒成立,则实数a 取值范围 (★★★)A .(0,12)∪(1,+∞)B .(0,12)C .(1,+∞)D .(0,13)∪(1,+∞)7.设全集U ,给定命题:若x ∈M 且x ∉P ,则x ∈M ∩ðU P ,那么这一命题否命题是(★★★)A .若x ∈M 且x ∉P ,则x ∉(M ∩ðU P ) B .若x ∉M 且x ∈P ,则x ∉(M ∩ðU P) C .若x ∉M 或x ∈P ,则x ∈(ðU M ∪P)D .若x ∈M 或x ∉P ,则x ∉(M ∪ðU P)8.{a n }为等差数列,若11101a a <-,且它的前n 项和S n 有最小值,那么当S n 取得最小正值时,n =(★★★) A .11 B .17 C .19 D .219.若双曲线)0,0(12222>>=-b a by a x 的右支上到原点和右焦点距离相等的点有两个,则双曲线的离心率e 的取值范围是(★★★)A .2>e B .21<<e C .2>e D .21<<e10.对任意正整数n ,定义n 的双阶乘n !!如下:当n 为偶数时,n !!=n (n -2)(n -4)…6·4·2 当n 为奇数时,n !!=n (n -2)(n -4)…5·3·1现有四个命题:①(2007!!)(2006!!)=2007! ②2006!!=21003·1003!③2006!!个位数为0 ④2007!!个位数为5其中正确个数为(★★★) A .1B .2C .3D .4二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中横线上. 11.已知复数z =t +i (t ∈R +)且z 满足z 3∈R ,则实数t 的值为(★★★)12.已知n ∈N *多项式P (x )=C 0 n x n +C 1 n xn -1(2x -1)+C 2 n xn -2(2x -1)2+…+C nn (2x -1)n可展成x 升冪排列a 0+a 1x +…+a n x n,则|a 0|+|a 1|+…+|a n |=(★★★)13.甲、乙、丙、丁去购买编号为1、2、3、…、10的10种不同图书,为节约经费和方便相互传阅,他们约定每人只买其中5种不同的书各1本,且任2人不能买全这10种书,任3人必须买全这10种书。
湖北省孝昌二中高三数学理科调考试卷

湖北省孝昌二中高三数学理科调考试卷坚持就是成功,坚持就是胜利!心态影响行动,行动养成习惯,习惯成就个性,个性决定命运!一、选择题:本大题共10小题,每小题5分,共50分.1.设,a b R ∈,集合{1,,}{0,,}ba b a b a+=,则b a -=(★★★) A .1 B .1- C .2 D .2-2.函数()sin 3([,0])f x x x x π=∈-的单调递增区间是(★★★) A .5[,]6ππ--B .5[,]66ππ--C .[,0]3π-D .[,0]6π- 3.若函数()y f x =的图象按向量a 平移后,得到函数(1)2y f x =+-的图象,则向量a =(★★★)A .(12)--, B .(12)-, C .(12)-, D .(12),4.设()f x ,()g x 是定义在R 上的函数,()()()h x f x g x =+,则“()f x ,()g x 均为偶函数”是“()h x 为偶函数”的(★★★)A .充要条件B .充分而不必要的条件C .必要而不充分的条件D .既不充分也不必要的条件5.已知数列{n a }的前n 项和29n S n n =-,第k 项满足58k a <<,则k =(★★★)A .9B .8 C. 7 D .66.半径为1的球面上的四点D C B A ,,,是正四面体的顶点,则A 与B 两点间的球面距离为(★★★)A .)33arccos(-B .)36arccos(-C .)31arccos(-D .)41arccos(- 7.直线x 4 +y3 =1与曲线C (0≤θ<2π)相交于A 、B 两点,曲线C 上的点P 使得△PAB 面积等于3,这样的点P 共有几个(★★★)A. 1B. 2C. 3D. 48. 已知21lim 01n n an b n →∞⎛⎫+-+=⎪+⎝⎭,则点M ()b a ,所在的象限是 (★★★)A .第一象限B .第二象限C .第三象限D .第四象限9.定义在R 上的函数)(x f 既是奇函数,又是周期函数,T 是它的一个正周期.若将方程x=4cos θ y=3sin θ0)(=x f 在闭区间][T T ,-上的根的个数记为n ,则n 可能为(★★★)A.0B.1C.3D.5 10.已知随机变量ξ的分布列为ξ 2-1-0 1 2 3p121 mn121 61 121 其中)1,0[,∈n m ,且6=ξE ,则n m ,的值分别为(★★★) A .121,21 B .61,61 C .41,31 D .31,41二、填空题:本大题共5小题,每小题5分,共25分。
湖北省孝昌二中高三数学能力检测卷

湖北省孝昌二中高三数学能力检测卷一、选择题:本大题共10小题,每小题5分,共50分.1.同时满足① {1,2,3,4,5};M ⊆ ② 若a M ∈,则6a M -∈, 的非空集合M 的个数有(★★★) A.16 B.15 C.7 D.82.设0010cos 310sin 1-=a ,则ai i 4)11(-+的值是(★★★) A.i - B.i C.2i - D. 2i3.设M 是ABC ∆内一点,且23,AB AC ⋅=030,BAC ∠=定义()(,,),f M m n p =其中,,m n p 分别是,,MBC MCA MAB ∆∆∆的面积,若1()(,,)2f P x y =,则14x y +的最小值是:(★★★) A.8 B.9 C.16 D.18 4.如图所示,椭圆中心在坐标原点,离心率为53,F 为椭圆 的左焦点,直线AB 与FC 交于D 点,则∠BDC 的正切值是 (★★★)A .32 B .-32 C .8 D .-8 5.在圆周上有10个等分点,以这些点为顶点,每3个点可 以构成一个三角形。
如果随机选取3个点,则刚好构成钝角三角形的概率是(★★★) A .61 B .41 C .31 D .21 6.函数,)(x e x f x ⋅=-则(★★★) A 、仅有极小值e21 B 、仅有极大值e21C 、有极小值O ,极大值e21 D 、有极小值O ,极大值e 27.如图,在长方体ABCD-A 1B 1C 1D 1中,AA 1=1,点E 、F 分别在棱A 1D 1,AB 上,且线 段EF 的长恒等于2,则EF 的中点P 的轨迹是(★★★) A 、圆的一部分B 、椭圆一部分C 、球面的一部分D 、抛物线一部分8.已知点P (-1,1),点Q (2,2),若直线l :x+my+m=0与线段PQ 的延长线相交,则m 的取值范围是 (★★★) A .)23,31(B .)32,3(--C .)3,(--∞D .),32(+∞-Fxy A B CD9. 已知点P 是椭圆)0(1162522≠=+y y x 上的动点,21,F F 为椭圆的两个焦点,O 是坐标原点,若M 是21PF F ∠的角平分线上一点,且01=⋅MP M F 则OM 的取值范围是(★★★)A.)5,0[ B. )4,0[ C. )3,0[ D. )5,3(10.一系列椭圆都以一定直线l 为准线,所有椭圆的中心都在定点M ,且点M 到l 的距离为2,若这一系列椭圆的离心率组成以43为首项,31为公比的等比数列,而椭圆相应的长半轴长为a i =(i=1,2,…,n),设b n =2(2n+1)·3n -2·a n ,且C n =11+n n b b , T n =C 1+C 2+…+C n ,若对任意n ∈N*,总有T n >90m恒成立,则m 的最大正整数为(★★★) A .3B .5C .6D .9二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中横线上. 11.求值:=⋅+++-3log 225.2222ln 10lg 25.6log e (请把答案填写在答题卷上).12.若θ是第三象限的角,满足:95cos sin 44=+θθ,则θ2sin =(请把答案填写在答题卷上). 13.已知定义域为R 的偶函数f (x )在[)+∞,0上是增函数,且)21(f =0,则不等式0)(log 2<x f 的解集为(请把答案填写在答题卷上).14.设数列{}n a 的前n 项和为n S ,且111,3,(1,2)n n a a S n +===,则n S =(请把答案填写在答题卷上).15.已知双曲线中心在原点且一个焦点为与其相交于直线1),0,7(-=x y F M 、N 两点,MN中点的横坐标为,32-则此双曲线的离心率为(请把答案填写在答题卷上). 三、解答题:本大题共6个小题,共75分. 解答应写出文字说明,证明过程或演算步骤.16.(本小题满分12分)已知在ABC ∆中,25,5,cos 45B AC C π===(Ⅰ)求sin A ;(Ⅱ) 记BC 的中点为D ,求中线AD 的长.17.(本小题满分12分)经调查,若干年内某产品关税与市场供应量P 的关系允许近似的满足: P (x )=2(1—kt )(x —b )2(其中t 为关税的税率,且t ∈[0,21),x 为市场价格,b 、k 为正常数),当t=81时的市场供应量曲线如图 (Ⅰ)根据图像求k 、b 的值;(Ⅱ)若市场需求量为Q ,它近似满足Q (x )=2x2111-当P=Q 时的市场价格称为市场平衡价格,为使市场平衡价格控制在不低于9元,求税率t 的最小值。
湖北孝昌二中高三数学理科检测卷(3)

孝昌二中理科数学知识·数学能力检测卷(三)温馨提示: 基本知识概念要吃透一、选择题:本大题共10小题,每小题5分,共50分.1.已知集合}11log |{2+-==x xy x M ,]}1,0[,|{3∈+==x x x y y N 且,M ∩N = (★★★) A.]2,1(B.)1,1(-C.)1,0[D.)1,0(2.数列}{n a (*N n ∈)中,1231,3,5a a a ===,且1237n n n n a a a a +++⋅⋅⋅=,则99a =(★★★) A.1 B.3 C.5 D.无法确定3.已知奇函数)(x f 在区间]7,3[上是增函数,在区间]6,3[上的最大值为8,最小值为1-,则)3()6(2-+-f f 等于(★★★)A .15-;B .8-;C .2;D .2-;4.在差不为零的等差数列}{n a 中,02211273=+-a a a 数列}{n b 是等比数列,且77a b =,则86b b 等于(★★★) A .2; B .4; C .8; D .16; 5.函数)(x f y =的图像如下图所示,则函数)(log 2.0x f y =的图像大致是(★★★)6.某校根据新课程标准改革的要求,开设数学选修4系列的10门课程供学生选修,其中4—1,4—2,4—4三门由于上课时间相同,所以至多选一门,根据学分制要求,每位同学必须选修三门,则每位同学不同的选修方案种数是(★★★)A .120;B .98;C .63;D .56;7.设O 为坐标原点,)1,1(A ,若点),(y x B 满足⎪⎩⎪⎨⎧≤≤≤≤≥+--+2121012222y x y x y x ,则→→⋅OB OA 取得最小值时,点B 的个数是(★★★) A .2; B .3; C .4; D .5;8.已知抛物线x y 42=的准线与双曲线1222=-y ax 交于A 、B 两点,点F 为抛物线的焦点,若FAB ∆为直角三角形,则双曲线的离心率是(★★★)A .3;B .6;C .2;D .3;9.若不等式x at t sin 122≥+-对一切],[ππ-∈x 及]1,1[-∈a 都成立,则t 的取值范围是(★★★) A .2-≤t 或2≥t ;B .2≤t ; C .2-≥t ; D .2-≤t 或2≥t 或0=t ;10.过△ABC 内部一点M 任作一条直线EF ,AD ⊥EF 于D , BE ⊥EF 于E ,CF ⊥EF 于F ,都有0=++CF BE AD ,则点M 是△ABC 的 (★★★) A .三条高的交点 B .三条中线的交点 C .三边中垂线的交点 D .三内角平分线的交点二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中横线上. 11.2006100376213()ii +-+的值等于(★★★). 12.用5种颜色将一个正五棱锥的各面涂色,五个侧面分别编有1、2、3、4、5号,而有公共边的两个面不能涂同一种颜色,则不同的涂色的方法数为(★★★).13.若x 、y 满足22||16,y x x y x y N ≥⎧⎪+≤⎨⎪∈⎩,则2z x y =+的最大值为(★★★).14.函数y=1-x x的图象为双曲线,则该双曲线的焦距为(★★★). 15.ABC ∆中,c b a ,,分别是角C B A ,,的对边,已知060=A ,7=a ,现有以下判断: ① c b +不.可能等于15 ② 若12=⋅AC AB ,则36=∆ABC S ③bcb Bc C 7cos cos =+ ④ 若3=b ,则B 有两解 ⑤ 作A 关于BC 的对称点'A ,则|'AA |的最大值是37 ⑥ 若,B C 为定点,则动点A 的轨迹围成的封闭图形的面积是π349.请将所有正确..的判断序号填在横线上(★★★).三、解答题:本大题共6个小题,共75分. 解答应写出文字说明,证明过程或演算步骤16.(本小题满分12分)若函数)0(cos sin sin )(2>-=a ax ax ax x f 的图象与直线y=m 相切,并且切点的横坐标依次成公差为2π的等差数列. (Ⅰ)求m 的值;(Ⅱ)若点)(),(00x f y y x A =是图象的对称中心,且]2,0[0π∈x ,求点A 的坐标.17.(本小题满分12分)一个盒子中装有6张卡片,上面分别写着如下6个定义域均为R 的函数:6)(,5cos )(,4sin )(,)(,)(,)(65433221======x f x x f x x f x x f x x f x x f 。
湖北省孝昌二中高三数学理科暑假训练卷一

湖北省孝昌二中高三数学理科暑假训练卷一一、选择题:本大题共10小题,每小题5分,共50分.1.已知直线a 与平面α所成的角为60°,那么a 与α内不过斜足的直线所成的角中,最大的角的是(★★★) A .180° B .120° C .90° D .60° 2.设c b a ,,为直线,βα,为平面,有下列四个命题(★★★)①βαβα//,,则若⊥⊥c c ; ②αβαβ//,,a a 则若⊥⊥;③若βαβα//,,//a a 则⊆;④若b a b a //,//,,则βαβα⊂⊂.这个四个命题中,正确命题的个数是(★★★) A .1 B .2 C .3 D .43.从数字1、2、3、4、5中任取两个不同的数字构成一个两位数,则这个两位数大于40的概率为(★★★) A .51 B .52 C .53D .54 4.设7654321772221052,)1()21(a a a a a a a x a x a x a x a a x x +++++++++++=++则 = (★★★)A .287 B .288 C .289 D .2905.过球的一条半径的中点,作垂直于该半径的平面,则所得截面的面积与球的表面积的比为(★★★)A .163 B .169 C .83 D .329 6.已知随机变量ξ服从二项分布)2(),31,6(~=ξξP B 则的值为 (★★★) A .163B .2434 C .24316D .24380 7.正方形ABCD 所在平面与正方形ABEF 所在平面成60°的二面角,则异面直线AD 与BF所成角的余弦值为(★★★)A .42 B .21 C .22 D .41 8.有一道竞赛题,甲解出它的概率为21,乙解出它的概率为31,丙解出它的概率为41,则甲、乙、丙三人独立解答此题,只有1人解出的概率是(★★★)A .241B .2411 C .2417 D .19.在nxx)11(5+的展开式中,所有奇数项系数之和为1024,则中间项的系数是( ) A .330 B .462 C .682 D .79210.已知△ABC 中,AB =9,AC =15,∠BAC =120°,平面ABC 外一点P 到A 、B 、C 的距离都是14,那么P 点到平面ABC 的距离是(★★★)A .13B .9C .11D .7二、填空题:本大题共5小题,每小题5分,共25分。
湖北省孝昌二中理科数学知识高三数学能力检测卷(二十三)

湖北省孝昌二中理科数学知识 数学能力检测卷(二十三)2008.4.17温馨提示: 人生的道路虽然漫长,但紧要处常常只有几步,特别是年轻的时候一、选择题:本大题共10小题,每小题5分,共50分. 1.复数1cossin66z i ππ=-的共轭复数z 是 (★★★)A.1322i + B.1322i - C.3122i + D.3122i - 2.某一计算机网络有n 个终端,每个终端在一天中没有使用的概率为p ,则这个网络中一天平均使用的终端个数是(★★★)A .)1(p np - B.np C.n D.)1(p n - 3.已知m 、n 是不重合的直线,α、β是不重合的平面,有下列命题, ①若m ⊂α, , n ∥α,则m ∥n , ②若α∩β= n ,m ∥n, 则m ∥α,且 m ∥β ③若m ∥α,m ∥β,则α∥β, ④若m ⊥α, m ⊥β, 则α∥β其中正确的命题个数是 (★★★) A .1 B .2 C.3 D .0 4.函数)(x f 对R y x ∈,都有)()()(y x f y f x f +=⋅,若21)1(=f ,)()(*N n n f a n ∈=, 则数列{}n a 的前n 项和n S 的极限是(★★★) A .0 B .1 C .21D .2 5.如图,圆弧型声波DFE 从坐标原点O 向外传播. 若D 是DFE 弧与x 轴的交点,设OD x =a x ≤≤0(),圆弧型声波DFE 在传播过程中扫过平行四边形OABC 的面积为y (图中阴影部分),则函数)(x f y =的图象大致是(★★★)A .B .C .D . 6.若一系列函数的解析式相同,值域相同但定义域不同,则称这些函数为“孪生函数”,那么函数解析式为221y x =+,值域为{3,19}的“孪生函数”共有(★★★) A .15个B .12个C .9个D .8个7.函数sin()y A x ωϕ=+的部分图像如图所示,则其解析式可以是(★★★)A .3sin(2)3y x π=+ B .3sin(2)3y x π=-+y y y x O x Ox O x O y a a a a xO yD E FABC aC .13sin()212y x π=+ D .13sin()212y x π=-+8. 椭圆的焦点为F 1、F 2,过点F 1作直线与椭圆相交,被椭圆截得的最短的线段MN 长为532,N MF 2∆的周长为20,则椭圆的离心率为(★★★)A .522 B .53 C .54 (D )517 9.已知()f x 是定义在R 上的不恒为零的函数,若对于任意实数,a b 都有()()()f a b af b bf a ⋅=+,则(★★★)A .()f x 是奇函数,但不是偶函数B .()f x 是偶函数,但不是奇函数 A .()f x 既是奇函数,又是偶函数D .()f x 既非奇函数,又非偶函数10.设正实数a ,b 满足等式21421222-≤--=+t b a ab b a ,且有恒成立,则实数t 的取值范围是(★★★)A .]22,(-∞ B .),22[+∞C .[-22,22] D .),21[+∞二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中横线上. 11.若等差数列{}n a 的前六项的和69S =,且11a =,则21a =(★★★).12.91x x ⎛⎫+ ⎪⎝⎭的展开式中3x 的系数为(★★★).(用数字作答)13.已知e 是单位向量,且满足|||2|a e a e +=-,则向量a 在e 方向上的投影是(★★★). 14.已知(0,5)A ,(1,1)B ,(3,2)C ,(4,3)D ,动点(,)P x y 所在的区域为四边形ABCD (含边界).若目标函数z ax y =+只在点D 处取得最优解,则实数a 的取值范围是(★★★). 15.在实数集R 中定义一种运算“*”,具有性质: ①对任意a b b a R b a **,,=∈;②对任意a a R a =∈0*,;③对任意c c b c a ab c c b a R b a 2)*()*()(**)*(,,-++=∈, 则0*2=(★★★);函数)0(1*)(>=x xx x f 的最小值为(★★★).三、解答题:本大题共6个小题,共75分. 解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分12分)设a 、b 、c 分别是△ABC 三个内角∠A 、∠B 、∠C 的对边,若向量(1cos(),cos)2A Bm A B -=-+,5(,cos)82A B n -=且98m n ⋅=, (1)求tan tan A B ⋅的值; (2)求222sin ab Ca b c +-的最大值.17.(本小题满分12分)三棱锥V ABC -,已知1AC =+,2AB =,BC =,面VAC ⊥面ABC , VC 与底面ABC 所成的是45︒,VB 与底面ABC 所成的是θ (1)求ACB ∠的大小; (2)当45θ=︒时,求A 到面VBC 的距离;(3)当AB BV ⊥时,求tan θ的值.18.(本小题满分12分)在一次电视节目的抢答中,题型为判断题,只有“对”和“错”两种结果,其中某选手判 断正确的概率为p ,判断错误的概率为q ,若判断正确则加1分,判断错误则减1分,现 记“该选手答完n 道题后总得分为n S ”。
湖北省示范性高中孝昌二中高三数学理科导数测试题上学期

孝昌二中高三理科《导数及其应用》测试题一、填空题:本大题共10小题,每小题5分,共50分.1. 已知二次函数2()f x ax bx c =++的导数为'()f x ,'(0)0f >,对于任意实数x都有()0f x ≥,则(1)'(0)f f 的最小值为(★★★) A .3 B .52 C .2 D .322、曲线x x y 33-=上切线平行于x 轴的点的坐标是 (★★★)A .(-1,2)B .(1,-2)C .(1,2)D .(-1,2)或(1,-2)3、设P 点是曲线3233+-=x x y 上的任意一点,P 点处切线倾斜角为α,则角α的取值范围是 (★★★)A .),32[)2,0[πππ⋃ B .),65[)2,0[πππ⋃ C .),32[ππ D .)65,2(ππ4、设a>0, f(x)=ax 2+bx+c,曲线y=f(x)在点P(x 0,f(x 0))处切线的倾斜角的取值范围为0,4π⎡⎤⎢⎥⎣⎦,则P 到曲线y=f(x)对称轴距离的取值范围为(★★★)A.10,a ⎡⎤⎢⎥⎣⎦B.10,2a ⎡⎤⎢⎥⎣⎦C.0,2b a ⎡⎤⎢⎥⎣⎦D.10,2b a ⎡⎤-⎢⎥⎣⎦ 5、设()f x '是函数()f x 的导函数,将()y f x =和()y f x '=的图象画在同一个直角坐标系中,不可能正确的是(★★★)6、已知函数32()(6)1f x x ax a x =++++有极大值和极小值,则实数a 的取值范围是 (★★★)A .-1<a <2 B .-3<a <6 C .a <-3或a >6 D .a <-1或a >27、已知f(x)与g(x)是定义在R 上的连续函数,如果f(x)与g(x)仅当x=0时的函数值为0,且f(x)≥g(x),那么下列情形不可能出现的是(★★★)A .0是f(x)的极大值,也是g(x)的极大值B .0是f(x)的极小值,也是g(x)的极小值C .0是f(x)的极大值,但不是g(x)的极值D .0是f(x)的极小值,但不是g(x)的极值 8、已知()()3232,0,2f x x x x =-+∈的反函数为()1fx -,则(★★★)A 111322f f --⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭B 111322f f --⎛⎫⎛⎫>⎪ ⎪⎝⎭⎝⎭ C 113522f f --⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭D 113522f f --⎛⎫⎛⎫>⎪ ⎪⎝⎭⎝⎭9、已知函数)(x f y =的图象与函数xa y =(0>a 且1≠a )的图象关于直线x y =对称,记]1)2(2)()[()(-+=f x f x f x g .若)(x g y =在区间]2,21[上是增函数,则实数a 的取值范围是(★★★)A .),2[+∞B .)2,1()1,0(C .)1,21[D .]21,0( 10..二、填空题:本大题共5小题,每小题5分,共25分.11. 设奇函数)(x f 在[-1,1]上是增函数,且1)1(-=-f ,若函数12)(2+-≤at t x f 对所有的]1,1[-∈x 都成立,当]1,1[-∈a 时,则t 的取值范围是(★★★). 12、设函数5437()854f x x x =--+,则0()()lim x f x x f x x∆→+∆-=∆(★★★).13、f(x)=x 2+ax+b, g(x)=x 2+cx+d,又f(2x+1)=4g(x),且()()f x g x ''=,f(5)=30,则g(4)=(★★★). 14、设函数()11+=x x f ,点0A 表示坐标原点,点()()()*,N n n f n A n ∈,若向量01121n n na A A A A A A -=+++,n θ是n a 与i 的夹角,(其中()0,1=i),设n n S θθθtan tan tan 21+++= ,则n n S ∞→lim =(★★★).15、设函数()()()()f x x a x b x c =---,(a 、b 、c 是两两不等的常数),则='+'+')()()(c f cb f b a f a (★★★). 三、解答题:本大题共5小题,共75分,解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分12分)设a ≥0,f (x )=x -1-ln 2 x +2a ln x (x >0).(Ⅰ)令F (x )=xf '(x ),讨论F (x )在(0.+∞)内的单调性并求极值; (Ⅱ)求证:当x >1时,恒有x >ln 2x -2a ln x +1.17.(本小题满分12分)如图,有一块半椭圆形钢板,其半轴长为2r ,短半轴长为r ,计划将此钢板切割成等腰梯形的形状,下底AB 是半椭圆的短轴,上底CD 的端点在椭圆上,记2CD x =,梯形面积为S .(I )求面积S 以x 为自变量的函数式,并写出其定义域; (II )求面积S 的最大值.18.(本小题满分12分) 已知函数36)2(23)(23-++-=x x a ax x f . (I )当2>a 时,求函数)(x f 的极小值;(II )试讨论曲线)(x f y =与x 轴的公共点的个数。
湖北省孝昌二中高三数学理科知识能力检测试卷二

湖北省孝昌二中高三数学理科知识能力检测试卷二一、选择题:本大题共10小题,每小题5分,共50分.1.已知函数2()log f x x =,2(,)F x y x y =+,则1[(),1]4F f 的值为(★★★)A .1-B .5C .8-D .32.有共同底边的等边三角形ABC 和BCD 所在平面互相垂直,则异面直线AB 和CD 所成角的余弦值为(★★★)A .31 B .41C .43D .223.对于虚数i ,作集合234{,,,}S i i i i =,易知,S 中任何两个元素相乘的积仍然在S 中,现规定S 中关于乘法的单位元θ:即对任意的a S ∈,都有a a a θθ==,则θ为(★★★)A .iB .2iC .3iD .4i4.][x 表示不超过x 的最大整数(称为x 的整数部分),则方程||([])0x x x -=在]1,1[-上的根有 (★★★)A .1个 B .3个 C .5 个 D .无穷多个 5.设圆C :223x y +=,直线063:=-+y x l ,点()l y x P ∈00,,使得存在点C Q ∈,使60OPQ ∠=(O 为坐标原点),则0x 的取值范围是(★★★) A .⎥⎦⎤⎢⎣⎡-1,21 B .[]1,0 C .⎥⎦⎤⎢⎣⎡56,0 D .⎥⎦⎤⎢⎣⎡23,216.平面上有相异的11个点,每两点连成一条直线,共得48条直线,则任取其中的三个点,构成三角形的概率是(★★★)A .1433 B .3233 C .2633 D .2733 7. (★★★)8. .已知函数f (x )是以2为周期的偶函数,当x ∈[0,1]时f (x )=x ,那么在区间[-1,3]内,关于x 的方程f (x )=kx+k +1(k ∈R 且k ≠-1)的根的个数(★★★) A.不可能有三个 B.最少有一个,最多有四个 C.最少有个,最多有三个 D.最少有两个,最多有四个9. (★★★)10设集合A={1,2,3,4,5,6},若m,n∈{x|x =a 0×102+a 1×10+a 2,其中a 0,a 1,a 2∈A},且m+n =636,则点(m,n )表示的不同点的个数为(★★★) A.50 B.48 C.72 D.120 二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中横线上. 11.12.给出下列四个命题(1).函数22()(0)||a x f x a x a a-=>+-,既不是奇函数,又不是偶函数;(2)01,,,x a b R <<∈且0a b ⋅>,则函数221a b y x x=+-的最小值是22a b +; (3)已知向量123,,OP OP OP 满足条件1230OP OP OP ++=,且123||||||1OP OP OP ===,则123PP P ∆为正三角形;(4)已知a b c >>,若不等式11ka b b c a c+>---恒成立,则(0,2)k ∈; 其中正确命题的有(★★★)(填出满足条件的所有序号)13.已知奇函数f(x)=ax 3+3bx 2-4ax +c 的图象在(1,f(1))处的切线与直线3x+y -1=0平行,若把f (x )图象按向量)1,3(-=m 平移后得到g (x )的图象,那么g (x )的单调递减区间为(★★★) 14.n n x xnx x x )1)(321(32+++++ 展开式中常数项(不含x 的项)的和为()nf n ,则()f n 的最简表达式是(★★★)15.已知△ABC 中,过重心G 的直线交边AB 于P ,交边AC 于Q ,设△APQ 的面积为1S ,△ABC 的面积为2S ,AP pPB =,AQ qQC =,则(ⅰ)pqp q=+(★★★),(ⅱ)12S S 的取值范围是(★★★) 三、解答题:本大题共6个小题,共75分. 解答应写出文字说明,证明过程或演算步骤.16.(本小题满分12分)若函数)0(cos sin sin )(2>-=a ax ax ax x f 的图像与直线m y =相切,并且切点的横坐标依次成公差为2π的等差数列. (Ⅰ)求m 的值;(Ⅱ)若点),(00y x A 是)(x f y =图像的对称中心,且∈0x [0,2π],求点A 的坐标.17.(本小题满分12分)一艘轮船在相距1000海里的甲、乙两地之间航行,它的耗油量与速度的平方成正比.当轮船每小时行10海里时,它的耗油量价值500货币单位.又此船每行1小时除耗油费用外,其它消耗为常数(100300)C C ≤≤货币单位,轮船行驶的最大速度是每小时25海里. 问:此船从甲地行驶至乙地最经济的行船速度是多少?18.(本小题满分12分)如图,正三棱柱ABC -A 1B 1C 1的各棱长都等于2,D 在AC 1上,F 为BB 1中点, 且FD ⊥AC 1. (Ⅰ)试求1DC AD的值; (Ⅱ)求二面角F -AC 1-C 的大小;(Ⅲ)求点C 1到平面AFC 的距离.19.(本小题满分12分) 设1x =是函数()axe x b x xf -++=1的一个极值点(0>a ,e 为自然对数的底). (Ⅰ)求a 与b 的关系式(用a 表示b ),并求()f x 的单调区间; (Ⅱ)若()f x 在闭区间[]1,+m m 上的最小值为0,最大值为ae -21,且1m >-。
孝昌二中理科数学检测卷

孝昌二中理科数学知识·数学能力检测卷(十九)温馨提示: 用最少的悔恨面对过去。
用最少的浪费面对现在。
用最多的梦面对未来。
一、选择题:本大题共10小题,每小题5分,共50分. 1、 成立的是1 0)(><-abb a a (★★★) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.不充分也不必要条件2、已知A=B={1,2,3,4,5},从A 到B 的映射f 满足:①f(1)≤f<2)≤f(3)≤f(4)≤f(5);②f 的象有且只有2个.则适合条件的映射f 的个数是(★★★)A.10B.20C.40D.808. 3、二面角a l β--的平面角为65π,直线a ⊥平面a ,直线b ⊂平面β,则直线a 与b 所成角的范围为:(★★★) A 、[0,2π] B 、[6π,2π] c 、[3π,2π] D 、[0,3π] 4、若函数121212sin sin sin (),01,,x x xf x x x b x x x =<<<=且设a=,则,a b 的大小关系是:(★★★)A 、a>b B 、a<b C 、a=bD 、a 、b 的大小不能确定5、若m 是一个给定的正整数,如果两个整数b a ,用m 除所得的余数相同,则称a 与b 对模m 同余,记作[mod()]a b m ≡,例如:513[mod(4)]≡. 若:20082[mod(7)]r ≡,则r 可以为(★★★).1.2.3.4A B C D6、如图,该程序运行后输出的结果为(★★★). A .36 B .56 C .55 D .457、已知,x y 满足不等式组:22012x y x y -+≥⎧≤⎨⎩≥-,则25z x y =+-的最小值为(★★★)A. B.2;C.D.1;8、有六根细木棒,其中较长的两根长为a a 2,3,其余四根长为a ,用它们端点相连搭成一个三棱锥,则其中两条较长的棱所在直线的夹角的余弦值为(★★★) A.26 B. 1或26 C.36 D.0或369、.函数)0,0()(2≤>++=c a c bx ax x f ,且a ,b ,c 满足条件)(012+∈=++++R m mcm b m a ,那么方程0)(=x f 在区间)1,1(+m m内解的个数是(★★★) A .0个 B .1个 C .2个 D .与m 有关10、.ABC 中,a ,b ,c 分别为角A ,B ,C 所对的边,且c =4,a +b =5,tanA+tanB+3=3tanAtanB ,则△ABC 的面积为(★★★) A .323B .343 C .23 D .33二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中横线上.11、函数y =sin (ϕω+x )(ω>0,|ϕ|<2π)的最小正周期为π,且图象关于==ωπ则对称,x 6(★★★),ϕ=(★★★).12、若x 7-1=a 0+a 1(x -1)+a 2(x -1)2+…+a 7(x -1)7对x ∈R 恒成立,则a 5的值是(★★★).13、设u ,v ∈R ,且|u |≤2,v >0,则(u -v )2+(vu 922--)2的最小值为(★★★).14、设,s t 为正整数,两直线12:0:022t t l x y t l x y ss+-=-=与的交点是11(,)x y ,对于正整数(2)n n ≥,过点1(0,)(,0)n t x -和的直线与直线2l 的交点记为(,)n n x y .则数列{}n x 通项公式n x =(★★★).15、若函数()y f x =在0x x =处满足关系⑴()f x 在0x x =处连续⑵()f x 在0x x =处的导数不存在,就称0x 是函数()f x 的一个“折点”。
湖北孝昌二中高三数学理科期中(数学知识)能力检测卷(11.24)

湖北孝昌二中期中理科数学知识·数学能力检测卷温馨提示: 精神的的浩瀚 想象的活跃 心灵的勤奋 就是天才!一、选择题:本大题共10小题,每小题5分,共50分. 1、复数z =(★★★) A.1 B.-1 C. i D. i -2、下列判断错误..的是(★★★) A .命题“p 且q ”的否命题是“p q ⌝⌝或”B .命题p :若M N M =则N M ⊆,命题:5{2,3}q ∉,则命题“p 且q ”为真命题C .集合A ={a,b,c },集合B={0,1},则从集合A 到集B 的不同映射个数有8个D . 已知点(1,21)(3,23)PA a a PB a a =+-=--,则0<a <1是向量PA PB 与的夹角为钝角的必要非充分条件 3、已知向量a b 与的夹角为120°,若向量,c a b c a =⊥+且,则||||a b =(★★★) A .2B C .12D 4、已知双曲线22221(0,0)x y a b a b -=>>24y x =的准线重合。
设双曲线与抛物线的一个交点为P ,抛物线的焦点为F ,则||PF =(★★★)A .21B .18C .D .45、同时具有以下性质:“①最小正周期是π,②图象关于直线3x π=对称;③在[,]63ππ-上是增函数”的一个函数是(★★★)A .sin()26x y π=+B .cos(2)3y x π=+C .sin(2)6y x π=-D .cos(2)6y x π=- 6、已知数列{a n }为等差数列,其公差为(0,2)ββπ∈且,数列{sin a n }为等比数列,公比为q ,且1sin 0a ≠,则公差β与公比q 的值分别为(★★★)A .,1πB .,1π-C .,12π- D .,1π-7、某地区在高三第一轮复习组织一次大型调研考试,考试后统计的数学成绩服从正态分布,其密度函数为2(-88)-200(e((-,+))x f x x ∈∞∞,则下列命题不正确的是(★★★)A. 某地区这次考试的数学平均成绩是88分 B. 某地区这次考试的数学标准差是10C.分数在120分以上的人数和分数在56分以下的人数相等D. 分数在120分以上的人数和分数在60分以下的人数相等8、已知△ABC 的三个内角为A 、B 、C ,数列{a n }是公差为tanA 的等差数列,{b n }是公比为tanB 的等比数列。
湖北省孝昌二中高三数学理科数学知识、数学能力检测试卷(二).10.25

湖北省孝昌二中高三理科数学知识、数学能力检测卷(二) 2007.10.25温馨提示: Goals determine what you are going to be. 目标决定你成为什么样的人.一、选择题:本大题共10小题,每小题5分,共50分. 1.2)1(3i i+的值等于(★★★)A .23 B .-23 C .23i D .-23i 2.已知P A 、PB 、PC 是从点P 出发的三条射线,每两条射线的夹角均60°,则直线PC 与平面P AB 所成的角的余弦值为(★★★)A .21 B .22 C .23 D .33 3.已知△OAB 的顶点都在抛物线上,O 为抛物线的顶点,若直线AB 过抛物线的焦点,则△OAB一定是(★★★) A .等腰三角形 B .直角三角形C .钝角三角形D .锐角三角形4.在B C A A C B ABC 则角已知中,sin sin 3sin sin sin ,222=--∆的大小为(★★★) A .150° B .30° C .120° D .60°5.给出下列命题:①如果平面α内的一条直线m 与平面α的一条斜线l 在平面α内的射影n 垂直,那么l m ⊥;②如果平面α内的一条直线b 与平面β垂直,那么βα⊥;③经过平面α外一点有且只有一条直线与平面α平行;④对角线相交于一点且被这点平分的四棱柱是平行六面体. 其中,逆否命题为真命题的命题个数有( ♫ )A .4个B .3个C .2个D .1个6.如图,在正三棱锥A-BCD 中,E 、F 分别是AB 、BC 的中点,EF ⊥DE ,且BC=1, 则正 三棱锥A-BCD 的体积是(★★★) A .122 B .242C .123D .243 7.已知不等式222y ax xy +≤,若对任意[]2,1∈x 及[]3,2∈y ,该不等式恒成立,则实数a 的范围是(★★★)A 9351-≤≤-a B 3-≥a C 1-≥a D 13-≤≤-a8.如图,设P 为△ABC 内一点,且2155AP AB AC =+,则△ABP 的面积与△ABC 的面积之比为AEDB FCBAC P(★★★)A .15B .25C .14D .139.设()ax x x f +=2,{}{}()0,R (())0,R x f x x x f f x x =∈==∈≠∅,则满足条件的所有实数a 的取值范围为(★★★) A .0<a <4 B .a=0 C .a ≤0<4 D .0<a 4≤10.设12F F ,分别是椭圆22221x y a b+=(0a b >>)的左、右焦点,若在其右准线上存在,P 使线段1PF 的中垂线过点2F ,则椭圆离心率的取值范围是(★★★)A .0⎛ ⎝⎦B .0⎛ ⎝⎦C .1⎫⎪⎪⎣⎭D .1⎫⎪⎪⎣⎭ 二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中横线上.11.三棱锥P ABC -中,PA ⊥平面ABC ,AB BC ⊥,若PA AC =(★★★).12.设集合{()||2|},A x y y x =-1,≥2{()|||}B x y y x b =-+,≤,A B ≠∅.(1)b 的取值范围是(★★★);(2)若()x y A B ∈,,且2x y +的最大值为9,则b 的值是(★★★).13. 由1、2、3、4四个数字组成(数字可重复使用)的四位数a, 则a 的个位是1, 且恰有两个数字重复的概率是(★★★)。
孝昌二中高二上学期期中考试数学理科综合模拟卷

孝昌二中高二上学期期中考试综合模拟卷数学试题(理科)班级 ________ 姓名 ______________分数 ____________一、选择题(本大题共10个小题,每题5分,共50分) 1. 以下抽样不是系统抽样的是( ) A. 从标有1〜15号的15个球中,任选三个作为样本,按从小号到大号排序,随机选起点k,以 后k ・5, k+10(超过15那么从1再数起)号入样。
B. 工厂生产的产品,用传送带将产品送入包装车间前,检验人员从传送带上每隔5分钟抽一件 产品进行检验。
C. 搞调查,加定在商场门口随机抽一人进行调查,直到调查到事先规定调查人数为止。
D. 报告厅对与会听众进行调查,通知每排(每排人数相等)座位号为14的观众留下来座谈。
2. 某班有50位同学,其中男女各25名,今有这个班的一个学生在街上碰到一个同班同学,那么以下结论正确的选项是( )A.碰到异性同学比碰到同性同学的概率大B.碰到同性同学比碰到异性同学的概率大C.碰到同性同学和异性同学的概率相等D.碰到同性同学和异性同学的概率随机变化3. (1 一P )(l + x )'°的展开式中,X-的系数是( )A. -297B. -252C. 297D. 207 4.假设变员x 与y 具有线性相关关系,那么y 与x 之间的线性回归方程必过点()B 、(x,0)C 、(0, y)D 、(x, y)5. 某电视台连续播放6个广告,三个不同的商业广告,三个不同的奥运宣传广告,要求最后播 放的不能是商业广告,且奥运宣传广告两两不能连续播放,那么不同的播放方式有()A. 48种B. 98种C ・108种6.阅读右图所示的程序框图,运行相应的程序,假设〃 =°・8,那么输出的〃值为()C 、5D 、6它落地时向上的点数依次成• •) C.—158.用秦九韶算法计算多项式.,⑴=12+35x+9p +5V +3x 6在当工=一1时的值,有如下的说法:①要用到6次乘法和6次加法: ②要用到6次加法和15次乘法:③v 0=-23:④* = 11,其中币确的是()A> (0, 0) D. 120 种开始] A 、 3 B 、 47.将•骰了连续抛掷三次, 等差数列的概率为(9 12/输入,A.①③B.①®C.②④D.①(§)(3)9. 一种耐高温材料,能承受2001高温不•熔化的概率为0.5,能承受,300'C高温不熔化的概率为0.4.那么该材料在能承受200'C高温不熔化的情况下,还能承受300X:高温不熔化的概率是()A、0.2B、0.4C、0.6D、10.设随机变量&〜8(2.p ),随机变量n 〜8(3.p ),假设代21)蓦,那么P (n^l ) =12.仇是[0, 1]上的均匀随机数,b 二3(仇-2),那么b 是区间 13.高二年级某班共有60名学生,在一次考试中,其数学成绩满足正态分布,平均分为100分,假设P (x<8O ) = O.l (x 表示本班学生数学分数),求分数在[80,120|的人数为.14.命题:①的观测值越大,“x 与尸有关系”不成立的可能性越大.②残差的方差S?越大,回15. 某城市的交通道路如图,从城市的西南角A 到城市的东北角B,经过十字道路维修处C,最近的走法种数有 _______ 种(写数据) • •三、解答题(木大题共6个小题,共75分)16. (总分值12分)从某校参加数学竞赛的试卷中抽取一个样本,成6组,得到频率分布直方图如图,从左到右各小组的小长方形的高的比为1:1:3:6:4:2,最右 边的•组的频数是8.请结合直方图的信息,解答以下问题:(1)样本容量是多少? (2)成绩落在,那个范围的人数最多?并求出该小组的频数和频率.序号12345678910答案二、填空题(本大题共5个小题,每题525分)11.进制转It : 403(6)(8):上的均匀随机数.归直线的拟合效果越好.③越大,拟合程度就越好.那么所有正确命题序号为考查竞春的成绩分布,将样本分<3)估计这次数学竟赛成绩的平均分数(同一组数据常用该组区间的中点值作为代表)17.(总分值12分)二项式(x2+-!=)"(/teNW开式中,前三项的二项式系数和是56,求: 2Vx(1)〃的值:(2)展开式中的常数项.18.(总分值12分)某市举行的一次数学新课程骨干培训,共邀靖15名使用不同版本教材的教师,(I )从这1522(1【)培训活动随机选出2名代表发言,设发言代表中使用人教B版的女教师人数为求随机变蛰£的分布列和数学期望19・(总分值12分)如以下图1,给出了一个程序框图,其作用是输入x的值,输出相应的y的值,(1)诸指出该程序框图所使用的逻辑结构:(2)假设视x为白变量,y为函数值,试写出函数y = /(x)的解析式:(3)假设要使输入的x的值与输出的y的值相等,那么输入x的值的集合为多少?开始输支亍7输出图1矗20.(总分值13分)右面的表格是一组实验的统计数据:(1)求线性回归方程y = bx + a. (2)填写残差分布表,并计算残差的均值7.(3)求x 对y 的页献率KJ 并说明回归直线方程拟合效果.(备用公式:0 =生 力;一心/-I21.(总分值14分)如图,分别以正方形ABCD 的四条边为直径画半圆,重登局部如图中阴影区域.(1) 假设向该正方形内随机投-点,求该点落在阴影区域的概率?(2)给正方形ABCD 的四个顶点都作上一个标记,现有四种标记可供选择,记“任一线段上的两个顶点标记都不同”为步件A,求非件A 发生的概率X 0 1 2 3y 1 2 3 0nxy--------------- ) f ・l18、 (1)22线性回归方程y = bx + a = -O.2x +(2)残差分布表为:残差的均值为0二、 填空题16、 (1) 68 17、 (1) 参考答案11、22312、[f, -3]13、4814、③15、60n=10 (2) 70〜80分,频数24,频率爻a 0.353(3) 75分唯 1719、 解: (I )程序椎图所使用的逻辑结构是顺序结构和条件结构:(II) 2x-3 1(A <2)(2 vx 《5) U>5)(III),解得 x = 0,或 x = l, x = 3故所求的集合为{°」,3}.20、(1) x=l.5,),= 1.5,得 S8 - "史^1^5依题意得4 」(3) £3 -亮)=(-0.8)2 2 +2 + (-1.2)2 = 4.8 /=!4 2£(凹一》) =(— OS)?+0M+1 S+(—IS)? =54 «/. R2 = 1-一=0.04 .说明回归直线方程拟合效果较差.……12分5々一221、解:(1)——2(2)根本领件的总数为4」事件A包含:用两种标记,那么AC BD颜色相同,有种:用三种标记,那么AC或8D颜色相同有2/4:种: 用四种标记有种所以孰件A包含的基木孰件数为84种21所以W和。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
孝昌二中理科数学知识·数学能力检测卷(七)温馨提示: 慷慨 尤其还兼有谦虚,就会使人赢得好感一、选择题:本大题共10小题,每小题5分,共50分. 1.在数集},2{2x x x -中,实数x 的取值范围是(★★★)A ),(+∞-∞B .),0()0,(+∞-∞C . ),3()3,(+∞-∞D .),3()3,0()0,(+∞-∞ 2.已知),(,,2121R b a AC b a AB ,b a ∈+=+=λλλλ若是不共线的向量,则A 、B 、C 三点共线的充要条件为(★★★)A .121-==λλB .121==λλC .0121=-λλD .1121=+⋅λλ3.如果消息A 发生的概率为()P A ,那么消息A 所含的信息量为()()21log I A P A =。
若王教授正在一个有4排8列座位的小型报告厅里听报告,则发布的以下4条消息中,信息量最大的是(★★★)A .王教授在第4排B .王教授在第4排第5列C .王教授在第5列D .王教授在某一排 4.若抛物线的顶点坐标是()1,0M ,准线l 的方程是220x y --=,则抛物线的焦点坐标为(★★★)A .62,55⎛⎫- ⎪⎝⎭ B .62,55⎛⎫- ⎪⎝⎭ C .42,55⎛⎫ ⎪⎝⎭ D .42,55⎛⎫- ⎪⎝⎭5.已知为O 原点,点)sin 2,cos 2(1),(22θθQ ,y x y x P 点上在单位圆=+满足)32,34(-=,则=⋅(★★★)A .1825B .2516C .165D .3625 6.将数字3,4,5,6,7排成一行,使得相邻两个数都互质,则 可能的排列方法共有(★★★)A .30种B .36种C .42种D .48种7.若1cos sin =+αα,则对任意实数n ,ααn n cos sin +的取值为(★★★)A .1B .区间(0, 1)C .112n - D .不能确定8.在△ABC 中,三条边长成等差数列且最小角的正弦值与最大角的正弦值之比为5:3,则△ABC 是(★★★)A .直角三角形B .等腰三角形C .等边三角形D .锐角三角形9.已知函数x x x y ++=2331的图象C 上存在一定点P 满足:若过点P 的直线l 与曲线C交于不同于P 的两点M (x 1, y 1),N (x 2, y 2),就恒有21y y +的定值为y 0,则y 0的值为(★★★)A .31-B .32-C .34-D .2-10.可行域30230230x y x y x y +-≥⎧⎪-+≥⎨⎪--≤⎩的顶点是()()()12,21,33A B C ,,,,()z kx y k =-为常数,若使得z 取的得最大值为4的最优解是唯一的,则k =(★★★)A 、()1,2B 、()2,1C 、()3,3D 、()2,2二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中横线上.11.若数列}{n a 的通项公式2)1(1+=n a n ,记)1()1)(1(2)(21n a a a n f ---= ,试通过计算)1(f ,)2(f ,)3(f 的值,推测出=)(n f (请把答案填写在答题卷上).12.椭圆上的点()2,0A -关于直线1y x =-和1y x =-+的对称点分别为椭圆的焦点1F 和2F ,P 为椭圆上任意一点,则12PF PF ⋅的最大值为(请把答案填写在答题卷上).13.对于函数)(x f ,在使M x f ≤)(恒成立的所有常数M 中,我们把M 的最小值称为函数)(x f 的“上确界”,则函数1)1()(22++=x x x f 的“上确界”为(请把答案填写在答题卷上).14.对于)2,0(π∈x ,不等式16cos sin 122≥+xpx 恒成立,则p 的取值范围是(请把答案填写在答题卷上).15.设""+与""⋅分别为实数集内传统意义的加法与乘法,对实数(),2x y k k Z ππ≠+∈,定义tan tan ,tan tan x y x y x y x y ⊕=+⊗=⋅,在ABC ∆中,23B π∠=,则()A C A C ⊕⋅⊗等于(请把答案填写在答题卷上).三、解答题:本大题共6个小题,共75分. 解答应写出文字说明,证明过程或演算步骤.16.(本小题满分12分)设函数)(),0(2)(1)2sin(x f y x f x =<<-=++ϕπϕ的图象的一条对称轴是直线.8π=x(1)求ϕ;(2)求函数)(x f y =的递减区间;(3)试说明)(x f y =的图象可由x y 2sin 2=的图象作怎样变换得到。
17.(本小题满分12分)已知函数*).(2)(33N m m x x f ∈+=(1)若x 1、x 2:),0(求证,m ∈);2(2)()(2121x x f x f x f +≥+ (2)若;:,,3,1,2,1),(2211--+≥+∈≥-==m m n a a a a N m m m n n f a 求证其中 (3)对于任意的a 、b 、c )(),(),(],32,2[c f b f a f m m 问以∈的值为长的三条线段是否可构成三角形?请说明理由。
18.(本小题满分12分)A 、B 两支兵乓球队进行团体对抗赛,每队各有三名队员,A 队的三名队员是321,,A A A ,B 队的三名队员是321,,B B B ,且i A 对j B 的胜率为)3,1(≤≤+j i ji i.若1A 对2B ,2A 对3B ,3A 对1B ,比赛采用三局二胜制.(1) 求A 队取胜的概率.(2) 如何对阵,A 队的胜率最高?(直接写出最后对阵方式和胜率即可) 19.(本小题满分12分)如图,三棱柱111ABC A B C -中,已知平面11ABB A ⊥平面11CBBC ,12AB BB BC ===,01160ABB CBB ∠=∠=,棱AC 的中点为D(1)求1AB 与平面11ACC A 所成角的正弦值; (2)求点D 到平面111A B C 的距离。
20.(本小题满分13分)已知数列}{n a 是首项为1,公差为2的等差数列,对每一个∈k N *,在a k 与a k +1之间插入12k -个2,得到新数列{b n }.设S n ,T n 分别是数列{b n }和数列}{n a 的前n 项和. (1)a 10是数列{b n }的第几项;(2)是否存在正整数m ,使S m =2008?若不存在,请说明理由;若存在,求出m 的值. (3)若a m 是数列{b n }的第f (m )项,试比较S f (m )与2T m 的大小,并说明理由.21.(本小题满分14分)已知双曲线),0,(12222b a b a b y a x ≠>=-,P 为双曲线右支上一动点,过P 向两条渐近线x a b y =和x aby -=作垂线,垂足分别为A 和B ,O 为坐标原点.(1)证明:PB PA ⋅为定值.(2)若A 点始终在第一象限内,B 点始终在第四象限内,求双曲线离心率e 的取值范围. (3)在(2)的条件下,求四边形PAOB 的面积最小时,点P 的坐标.孝昌二中理科数学知识·数学能力检测卷(七)参考答案DCBCA BAABC12.18 13.2 14.2115. 16.解:(1)由题意1)82sin(±=+⨯ϕπ 即1)4sin(±=+ϕπ Z k k ∈+=+∴,24πππϕ)(4Z k k ∈+=ππϕ 04<+<-∴πππk 解得,4145-<-k431πϕ-=-=∴即,k …………………………………………5分(2)1)432sin(2)(+-=πx x f x y 2=∴是增函数)(x f y =∴函数的递减区间,即为1)432sin(+-=πx y 的递减区间。
由z k k x k ∈+<-<+,23243222πππππ 解得:8985ππππ+<<+k x k 。
)](89,85[)(Z k k k x f y ∈++=∴ππππ的递减区间为函数………………8分(3))]83(2sin[1)432sin(2.22)(ππ-+-==x x x f然后个单位的图象向右平移将函数,y x 8322sin π=∴纵坐标扩大为2倍(横坐标不变)得到函数y=f(x)的图象………………………………………12分17. 解:(1)先证33213323312)2(2222m x x m x m x ++⋅≥+++ ①即证:3213231)2(2x x x x +≥+ ②只需证:32122212121)2(2))((x x x x x x x x +≥+-+0),,0(2121>+∈⋅x x m x x 则)(42:221222121212121≥-++=+-∴x x x x x x x x x x 即只需证)2(2)()(2121x x f x f x f +≥+∴…………………………………………4分(2)m=3时显然成立,m>3时,由(1)得:a1+a3>2a2 a2+a4>2a3a3+a5>2a4 am-3+am-1>2am-2各式相加得:a1+am-1≥a2+am-2…………8分 说明:直接用比较法证明同样给分)2()1()1(-≥-+m f m f f(3)26)('x x f =………9分恒成立大于在0]32,2[)('mm x f ∴上为增函数在]32,2[)(m m x f ∴3min 45)2()(m m f x f ==∴ 3m a x 2743)32()(mm f x f ==恒成立33332743254545m m m m >=+∴ m a x m i n )()(2x f x f >∴构成三角形的值为长的三条线段能以)(),(),(c f b f a f ∴………………12分18.(1)解:设321,,A A A 的胜率分别为321,,p p p ,则43,52,31321===p p p ,A 队若取胜,必须胜两局或者三局,则A 队取胜的概率)(A P =)1(321p p p - +)1(132p p p -+321213)1(p p p p p p +-=6029.………………6分 (2)解:对阵方式为231231;;B A B A B A 对对对,……………………………10分A 队取胜的概率为6031.……………………………………………12分19.(1)取1BB 的中点O ,则由题设得:11,AO BB CO BB ⊥⊥∵平面11ABB A ⊥平面11CBBC ,∴AO CO ⊥ 以点O 为坐标原点,分别以直线1,,OC OB OA为x 轴,y 轴,z 轴建立如图所示直角坐标系 ………………… 2分则得()()(())1110,0,0,,,,0,1,0,O A C A B C∴()1,0,2,0AC AA ==∵D 为棱AC 的中点,∴,D OD ==⎝⎭⎝⎭∴10,0OD AC OD AA ⋅=⋅= ,∴1,OD AC OD AA ⊥⊥∴OD ⊥ 平面11ACC A ,(10,1,AB =… 5分∴111cos ,OD AB OD AB OD AB ⋅==⋅6分∴1AB 与平面11ACC A 所成角的正弦值为4………………… 7分 (2)设平面11AB C 的法向量为(),,n x y z =∵)(11111111,0,1,,0,0B C A B n A B n B C ==-⋅=⋅=………………… 8分∴0y y ⎧-=⎪⎨+=⎪⎩,取1z =得()1,n = ………………… 10分又∵12,DC =⎝⎭,∴点D 到平面111A B C 的距离为1DC n h n ⋅= …… 12分 20.21.(1)证明:设),(00y x P ,则1220220=-b y a x ,即22202202b a y a x b =-.P 点到渐近线x a by =的距离为2200b a bx ay PA +-=,同理2200ba bx ay PB ++=所以PB PA ⋅=⋅+-2200ba bx ay 2200b a bx ay ++=22222222202b a b a b a x b y a +=+-为定值.…3分(2)解:直线PA 的方程为:)(00x x b a y y --=-,与渐近线x aby =联立解得A 点横坐标22002b a aby x a x A ++=,同理B 点横坐标为22002ba aby x a x B +-=.…5分 A 点第一象限,B 点在第四象限,等价于0>A x 且0>B x ,即022002>++ba aby x a 且022002>+-b a aby x a ,所以002aby x a >,即00by ax >,平方得202202y b x a >恒成立. 又22202202b a y a x b =-,则222202222a b a x b b x a -⋅>, 即420242)(b x ab a ->-对于),[0+∞∈a x 恒成立,又b a ≠,因此0242>-ab a ,即b a >,由此可得:.21<<e ……………………9分(3)解:四边形PAOB 的面积为PAB ∆面积与AOB ∆面积和,而PAB ∆面积为APB PB PA ∠⋅sin 21,是定值,所以我们只要考察AOB ∆面积. AOB ∆面积AOB OB OA S ∠⋅=sin 21,而AOB ∠为定值,我们只要考察B A x ab x ab OB OA 22)(1)(1-+⋅+=⋅=⋅+222a b a 22002b a aby x a ++22002b a aby x a +-⋅=2222202b a y b x a +-的最小值.由(2)知b a >,且22202202b a y a x b =-,所以 ≥-202202y b x a 22202422ba yb a x a =-4202202)(a y a x b =- 当且仅当00=y ,即P 点坐标为)0,(a 时取等号.所以,四边形PAOB 的面积最小时,点P 的坐标为)0,(a .…………14分。
