2015台湾省数据要领深入
2015年台湾省数据分析深入

1、我们用l代表最长平台的长度,用k指示最长平台在数组b中的起始位置(下标)。
用j 记住局部平台的起始位置,用i指示扫描b数组的下标,i从0开始,依次和后续元素比较,若局部平台长度(i-j)大于l时,则修改最长平台的长度k(l=i-j)和其在b中的起始位置(k=j),直到b数组结束,l即为所求。
void Platform (int b[ ], int N)//求具有N个元素的整型数组b中最长平台的长度。
{l=1;k=0;j=0;i=0;while(i<n-1){while(i<n-1 && b[i]==b[i+1]) i++;if(i-j+1>l) {l=i-j+1;k=j;} //局部最长平台i++; j=i; } //新平台起点printf(“最长平台长度%d,在b数组中起始下标为%d”,l,k);}// Platform2、二部图(bipartite graph) G=(V,E)是一个能将其结点集V分为两不相交子集V 1和V2=V-V1的无向图,使得:V1中的任何两个结点在图G中均不相邻,V2中的任何结点在图G中也均不相邻。
(1).请各举一个结点个数为5的二部图和非二部图的例子。
(2).请用C或PASCAL编写一个函数BIPARTITE判断一个连通无向图G是否是二部图,并分析程序的时间复杂度。
设G用二维数组A来表示,大小为n*n(n为结点个数)。
请在程序中加必要的注释。
若有必要可直接利用堆栈或队列操作。
【3、若第n件物品能放入背包,则问题变为能否再从n-1件物品中选出若干件放入背包(这时背包可放入物品的重量变为s-w[n])。
若第n件物品不能放入背包,则考虑从n-1件物品选若干件放入背包(这时背包可放入物品仍为s)。
若最终s=0,则有一解;否则,若s<0或虽然s>0但物品数n<1,则无解。
(1)s-w[n],n-1 //Knap(s-w[n],n-1)=true(2)s,n-1 // Knap←Knap(s,n-1)4、数组A和B的元素分别有序,欲将两数组合并到C数组,使C仍有序,应将A和B拷贝到C,只要注意A和B数组指针的使用,以及正确处理一数组读完数据后将另一数组余下元素复制到C中即可。
2015年台湾省数据要领

1、将顶点放在两个集合V1和V2。
对每个顶点,检查其和邻接点是否在同一个集合中,如是,则为非二部图。
为此,用整数1和2表示两个集合。
再用一队列结构存放图中访问的顶点。
int BPGraph (AdjMatrix g)//判断以邻接矩阵表示的图g是否是二部图。
{int s[]; //顶点向量,元素值表示其属于那个集合(值1和2表示两个集合)int Q[];//Q为队列,元素为图的顶点,这里设顶点信息就是顶点编号。
int f=0,r,visited[]; //f和r分别是队列的头尾指针,visited[]是访问数组for (i=1;i<=n;i++) {visited[i]=0;s[i]=0;} //初始化,各顶点未确定属于那个集合Q[1]=1; r=1; s[1]=1;//顶点1放入集合S1while(f<r){v=Q[++f]; if (s[v]==1) jh=2; else jh=1;//准备v的邻接点的集合号if (!visited[v]){visited[v]=1; //确保对每一个顶点,都要检查与其邻接点不应在一个集合中for (j=1,j<=n;j++)if (g[v][j]==1){if (!s[j]) {s[j]=jh; Q[++r]=j;} //邻接点入队列else if (s[j]==s[v]) return(0);} //非二部图}//if (!visited[v])}//whilereturn(1); }//是二部图[算法讨论] 题目给的是连通无向图,若非连通,则算法要修改。
2、给出折半查找的递归算法,并给出算法时间复杂度性分析。
3、对二叉树的某层上的结点进行运算,采用队列结构按层次遍历最适宜。
int LeafKlevel(BiTree bt, int k) //求二叉树bt 的第k(k>1) 层上叶子结点个数{if(bt==null || k<1) return(0);BiTree p=bt,Q[]; //Q是队列,元素是二叉树结点指针,容量足够大int front=0,rear=1,leaf=0; //front 和rear是队头和队尾指针, leaf是叶子结点数int last=1,level=1; Q[1]=p; //last是二叉树同层最右结点的指针,level 是二叉树的层数while(front<=rear){p=Q[++front];if(level==k && !p->lchild && !p->rchild) leaf++; //叶子结点if(p->lchild) Q[++rear]=p->lchild; //左子女入队if(p->rchild) Q[++rear]=p->rchild; //右子女入队if(front==last) {level++; //二叉树同层最右结点已处理,层数增1last=rear; } //last移到指向下层最右一元素if(level>k) return (leaf); //层数大于k 后退出运行}//while }//结束LeafKLevel4、矩阵中元素按行和按列都已排序,要求查找时间复杂度为O(m+n),因此不能采用常规的二层循环的查找。
中国财政年鉴2019:台湾地区历年主要指标概况统计(2014-2018)(一)
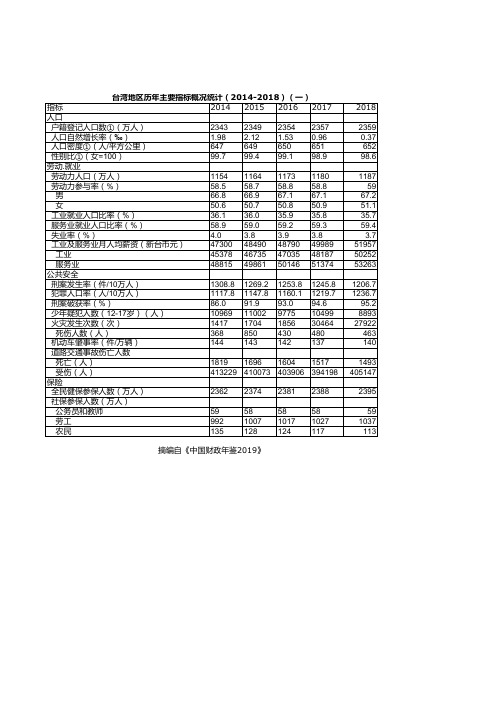
劳动.就业
劳动力人口(万人)
1154 1164 1173 1180
劳动力参与率(%)
58.5 58.7 58.8 58.8
男
66.8 66.9 67.1 67.1
女
50.6 50.7 50.8 50.9
工业就业人口比率(%)
36.1 36.0 35.9 35.8
服务业就业人口比率(%)
58.9 59.0 59.2 59.3
59 1037
113
摘编自《中国财政年鉴2019》
失业率(%)
4.0
3.8
3.9
3.8
工业及服务业月人均薪资(新台币元)
47300 48490 48790 49989
工业
45378 46735 47035 48187
服务业
48815 49861 50146 51374
公共安全
刑案发生率(件/10万人)
1308.8 1269.2 1253.8 1245.8
480
机动车肇事率(件/万辆)
144
143
142
137
道路交通事故伤亡人数
死亡(人)
1819 1696 1604 1517
受伤(人)
413229 410073 403906 394198
保险
全民健保参保人数(万人)
2362 2374 2381 2388
社保参保人数(万人)
公务员和教师
59
58
58
58
劳工
992
1007 1017 1027
农民
135
128
124
117
2018
2359 0.37 652 98.6
2015年台湾省数据总结加强

1、有一个带头结点的单链表,每个结点包括两个域,一个是整型域info,另一个是指向下一个结点的指针域next。
假设单链表已建立,设计算法删除单链表中所有重复出现的结点,使得info域相等的结点只保留一个。
#include <stdio.h>typedef char datatype;typedef struct node{datatype data;struct node * next;} listnode;typedef listnode* linklist;/*--------------------------------------------*//* 删除单链表中重复的结点 *//*--------------------------------------------*/linklist deletelist(linklist head){ listnode *p,*s,*q;p=head->next;while(p){s=p;q=p->next;while(q)if(q->data==p->data){s->next=q->next;free(q);q=s->next;}else{ s=q; /*找与P结点值相同的结点*/q=q->next;}p=p->next;}return head;}2、根据二叉排序树中序遍历所得结点值为增序的性质,在遍历中将当前遍历结点与其前驱结点值比较,即可得出结论,为此设全局指针变量pre(初值为null)和全局变量flag,初值为true。
若非二叉排序树,则置flag为false。
#define true 1#define false 0typedef struct node{datatype data; struct node *llink,*rlink;} *BTree;void JudgeBST(BTree t,int flag)// 判断二叉树是否是二叉排序树,本算法结束后,在调用程序中由flag得出结论。
台湾省2015年初级统计师《统计基础》:统计机构考试试卷

台湾省2015年初级统计师《统计基础》:统计机构考试试卷本卷共分为1大题50小题,作答时间为180分钟,总分100分,60分及格。
一、单项选择题(共50题,每题2分。
每题的备选项中,只有一个最符合题意)1.某企业上年末的资产总额为8000万元,负债总额为3500万元,所有者权益总额为4500万元(其中未分配利润为500万元);本年度发生主营业务收入3000万元,销售折让20万元,主营业务成本1200万元,主营业务税金及附加100万元,其他业务收入200万元,其他业务支出120万元,营业费用400万元,管理费用260万元,财务费用150万元,营业外收入30万元,营业外支出80万元;本年末的资产总额为9800万元,负债总额为4000万元,所有者权益总额为5800万元。
本年末发生的部分经济业务如下:(1)按规定税率33%计算出应交纳的所得税为297万元。
(2)按净利润的10%和5%分别计提法定盈余公积和法定公益金。
(3)按规定计算出应分配给普通股股东的现金股利301.5万元。
根据上述资料,计算该企业本年度的总资产周转率为__。
A.3000/(8000+9800)=0.17B.3000/[(800+9800)÷2]=0.34C.(3000-20)/[(8000+9800)÷2]=0.33D.(3000-20)/(8000+9800)=0.172.以下是2000年全国资金流量表的部分资料,请根据这些资料对反映该年宏观经济运行的一些重要指标进行计算和分析,回答有关问题。
2000年总储蓄数额最大的部门是()。
A.非金融企业部门B.金融机构部门C.政府部门D.住户部门3.某企业2011年1月1日购入B公司10%的有表决权股份,作为长期股权投资核算,实际支付价款300万元。
2011年4月30日B公司宣告派发2009年现金股利100万元,当年B 公司经营获利100万元,2011年年末企业的股票投资账面余额为__万元。
2015国民经济和社会发展统计公报

2015年国民经济和社会发展统计公报中华人民共和国2015年国民经济和社会发展统计公报[1]中华人民共和国国家统计局2016年2月29日2015年,面对错综复杂的国际形势和艰巨繁重的国内改革发展稳定任务,党中央、国务院团结带领全国各族人民,按照“五位一体”总体布局和“四个全面”战略布局的总要求,牢固树立和贯彻落实创新、协调、绿色、开放、共享的发展理念,适应经济发展新常态,坚持改革开放,坚持稳中求进工作总基调,坚持稳增长、调结构、惠民生、防风险,不断创新宏观调控思路与方式,深入推进结构性改革,扎实推动大众创业万众创新,努力促进经济保持中高速增长、迈向中高端水平,转型升级步伐加快,改革开放不断深化,民生事业持续进步,经济社会发展迈上新台阶,实现了“十二五”圆满收官,为“十三五”经济社会发展、决胜全面建成小康社会奠定了坚实基础。
一、综合初步核算,全年国内生产总值[2]676708亿元,比上年增长6.9%。
其中,第一产业增加值60863亿元,增长3.9%;第二产业增加值274278亿元,增长6.0%;第三产业增加值341567亿元,增长8.3%。
第一产业增加值占国内生产总值的比重为9.0%,第二产业增加值比重为40.5%,第三产业增加值比重为50.5%,首次突破50%。
全年人均国内生产总值49351元,比上年增长6.3%。
全年国民总收入[3]673021亿元。
年末全国大陆总人口137462万人,比上年末增加680万人,其中城镇常住人口77116万人,占总人口比重(常住人口城镇化率)为56.10%,比上年末提高1.33个百分点。
全年出生人口1655万人,出生率为12.07‰;死亡人口975万人,死亡率为7.11‰;自然增长率为4.96‰。
全国人户分离的人口[4]2.94亿人,其中流动人口[5]2.47亿人。
人均预期寿命76.34岁。
年末全国就业人员77451万人,其中城镇就业人员40410万人。
全年城镇新增就业1312万人。
2015年福建公务员录用考试行政职业能力测验《资料分析》试卷及详解【圣才出品】

2015年福建公务员录用考试行政职业能力测验《资料分析》试卷及详解(共15题,参考时限15分钟)根据题目要求,在四个选项中选出一个最恰当的答案。
每题0.8分,共12分。
请开始答题:一、根据以下资料,回答1~5题。
经过50多年的发展,我国台湾地区资本市场建立起由“证券交易所集中市场—上柜市场—兴柜市场”构成的完善成熟的多层次资本市场体系。
近年由于金融海啸、欧债危机等因素影响,台湾多层次资本市场总体成交值从2010至2012年连续3年下降,2012年较2011年衰退23.28%。
周转率也呈现逐年下降趋势,2012年证券交易所集中市场周转率为97%,上柜市场周转率为175%,兴柜市场周转率为27%。
表 2012年台湾多层次资本市场一览表(单位:10亿新台币)台湾资本市场第一层次是证券交易所集中市场。
在准入门槛方面,台湾证交所要求上市企业实收资本6亿新台币以上;从设立年限来看,要求上市企业设立满3年以上;从获利能力来看,要求上市企业最近1个会计年度无累计亏损,且税前利润占财务报表中的比率最近5个年度达到3%以上,或最近2个年度都达6%。
至2012年底,上市公司有809家,资本额6.384兆新台币,台湾证券交易所总市值在世界交易所联合会(WFE )会员中排名与前一年份相同,为第22名,所占比重仍为1.34%;成交值排名第15名,排名不变,所占比重由1.41%略微降至1.39%;周转率排名为第9名,较2011年下降2名。
台湾资本市场第二层次是上柜市场。
在准入门槛方面,上柜市场要求公司实收资本额必须在新台币5000万元以上;从获利能力来看,上柜公司要求个别及合并财务报表获利能力最近年度达4%以上,且其最近一个会计年度结算无累积亏损,或最近二个年度获利能力均达2%以上。
至2012年底,上柜公司有638家,资本额0.667兆新台币,总市值1.737兆新台币。
台湾资本市场第三层次是兴柜市场。
在准入门槛方面,兴柜市场没有营业利润、资本额、设立年限的限制,只须符合已经申报上市或上柜辅导且有两家以上证券商书面推荐。
2015国民大数据

2015国民大数据大数据展会20152015国民大数据大数据展会2015今日,中央电视台财经频道官方微博“央视财经”发布2015国民大数据:中国四成居民感到幸福。
《中国经济生活大调查》国民大数据:①过去一年,中国四成居民感到幸福;剩女幸福感远超剩男;②通勤时间最长的城市,竟是长春;③最被百姓看好的行业——电子商务、健康医疗、金融业;④幸福感城市十强:合肥、太原...财富、机遇、时间、幸福都将去哪?——央视财经频道独家发布2015年国民数据大发现3月2日,央视财经频道重磅首发《中国经济生活大调查》国民大数据。
作为中国规模最大的媒体民生调查活动,《中国经济生活大调查》在充满变化的时代中,深入中国最微小的家庭细胞,以持续九年、每年调查十万个样本家庭、累计上千万个民生基础数据,传递百姓最真实的生活感受。
本届《中国经济生活大调查》向全社会发布和分享的数据,揭秘了2015年关于机遇、财富、时间、幸福的重要趋势性数据。
更多2015年国民数据,请关注央视财经、以及3月9日18:50分播出的《中国经济生活大调查》数据发布晚会。
(一)2015年,钱去哪了?(1)大调查发现:伴随经济“新常态”,中国人调低收入预期67.6%,这是CCTV《中国经济生活大调查》给出的2015年中国家庭的收入信心指数,值得注意的是,这项调查已经连续九年,每年调查10万户中国家庭收入情况的数据,以此编制出央视“居民收入信心指数”。
本届大调查收入信心指数是4年来的低点,显现出伴随经济新常态,百姓已调低对未来收入预期的趋势2015年中国哪个地方对收入增长更有信心。
排名首位的江西人(收入信心指数:74.4%)。
此外,吉林(71.8%)、山东(70.8%)、安徽(70.8%)、湖北(70.0%)的受访者,也对2015年的收入增长也很有信心,高于全国平均水平(收入信心指数:67.6%)。
3月2日,央视财经频道重磅首发《中国经济生活大调查》国民大数据。
国家统计局2015年1月19日发布2015年国民经济运行情况

国家统计局2015年1月19日发布2015年国民经济运行情况,数据显示,从城乡结构看,城镇常住人口77116万人,比上年末增加2200万人,乡村常住人口60346万人,减少1520万人,城镇人口占总人口比重为56.1%。
年末中国大陆总人口(包括31个省、自治区、直辖市和中国人民解放军现役军人,不包括香港、澳门特别行政区和台湾省以及海外华侨人数)137462万人,比上年末增加680万人。
全年出生人口1655万人,人口出生率为12.07‰,死亡人口975万人,人口死亡率为7.11‰,人口自然增长率为 4.96‰,比上年下降0.25个千分点。
从性别结构看,男性人口70414万人,女性人口67048万人,总人口性别比为105.02(以女性为 100),出生人口性别比为113.51。
从年龄构成看,16周岁以上至60周岁以下(不含60周岁)的劳动年龄人口91096万人,比上年末减少487 万人,占总人口的比重为66.3%;60周岁及以上人口22200万人,占总人口的16.1%;65周岁及以上人口14386万人,占总人口的 10.5%。
从城乡结构看,城镇常住人口77116万人,比上年末增加2200万人,乡村常住人口60346万人,减少1520万人,城镇人口占总人口比重为56.1%。
全国居住地和户口登记地不在同一个乡镇街道且离开户口登记地半年以上的人口(即人户分离人口)2.94亿人,比上年末减少377万人,其中流动人口为2.47亿人,比上年末减少568万人。
年末全国就业人员77451万人,其中城镇就业人员40410万人。
国家统计局:2014年中国城镇化率达到54.77%时间:2015-01-20 22:40:27 来源:中国经济网国家统计局今日发布2014年经济数据,2014年末,中国大陆总人口(包括31个省、自治区、直辖市和中国人民解放军现役军人,不包括香港、澳门特别行政区和台湾省以及海外华侨人数)136782万人,比上年末增加710万人。
台湾省历年主要指标概况统计(2011-2015)(三)
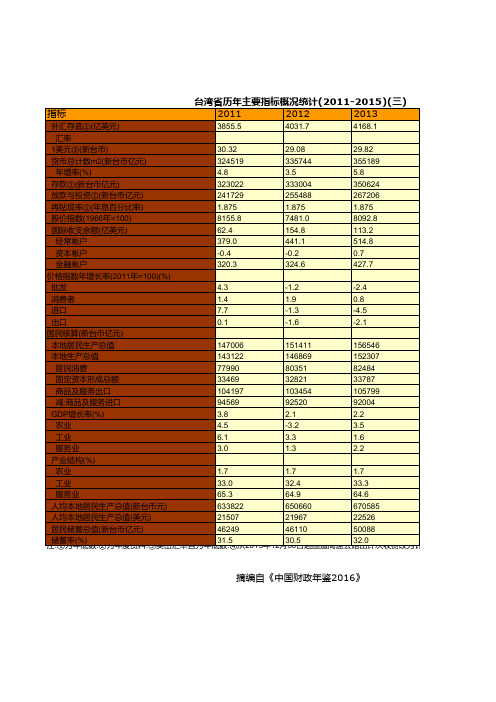
外汇存底①(亿美元) 汇率
1美元③(新台币) 货币总计数m2(新台币亿元)
年增率(%) 存款①(新台币亿元) 放款与投资①(新台币亿元) 再贴现率①(年息百分比率) 股价指数(1966年=100) 国际收支余额(亿美元)
经常帐户 资本帐户 金融帐户 价格指数年增长率(2011年=100)(%) 批发 消费者 进口 出口 国民核算(新台币亿元) 本地居民生产总值 本地生产总值 居民消费 固定资本形成总额 商品及服务出口 减:商品及服务进口 GDP增长率(%) 农业 工业 服务业 产业结构(%) 农业 工业 服务业 人均本地居民生产总值(新台币元) 人均本地居民生产总值(美元) 居民储蓄总值(新台币亿元) 储蓄率(%)
1.7 33.3 64.6 670585 22526 50088 32.0
注:①为年底数.②为年度资料.③卖出汇率且为年底数.④从2013年12月30日起国道高速公路由计次收费改为计程电子收费.
摘编自《中国财政年鉴2016》
15)(三)
2014
4189.8
31.68 376968 6.1 371339 281106 1.875 8992.0 130.2 625.1 -0.1 536.0
-8.8 -0.3 -12.9 -4.7
172480 166879 87279 34575 107775 86082 0.7
1.8 35.2 62.4 735183 23040 59875 34.7
151411 146869 80351 32821 103454 92520 2.1 -3.2 3.3 1.3
156546 152307 82484 33787 105799 92004 2.2 3.5 1.6 2.2
1.7 33.0 65.3 633822 21507 46249 31.5
2015年台湾省数据分析基础

1、设一棵树T中边的集合为{(A,B),(A,C),(A,D),(B,E),(C,F),(C,G)},要求用孩子兄弟表示法(二叉链表)表示出该树的存储结构并将该树转化成对应的二叉树。
2、二叉树的层次遍历序列的第一个结点是二叉树的根。
实际上,层次遍历序列中的每个结点都是“局部根”。
确定根后,到二叉树的中序序列中,查到该结点,该结点将二叉树分为“左根右”三部分。
若左、右子树均有,则层次序列根结点的后面应是左右子树的根;若中序序列中只有左子树或只有右子树,则在层次序列的根结点后也只有左子树的根或右子树的根。
这样,定义一个全局变量指针R,指向层次序列待处理元素。
算法中先处理根结点,将根结点和左右子女的信息入队列。
然后,在队列不空的条件下,循环处理二叉树的结点。
队列中元素的数据结构定义如下:typedef struct{ int lvl; //层次序列指针,总是指向当前“根结点”在层次序列中的位置int l,h; //中序序列的下上界int f; //层次序列中当前“根结点”的双亲结点的指针int lr; // 1—双亲的左子树 2—双亲的右子树}qnode;BiTree Creat(datatype in[],level[],int n)//由二叉树的层次序列level[n]和中序序列in[n]生成二叉树。
n是二叉树的结点数{if (n<1) {printf(“参数错误\n”); exit(0);}qnode s,Q[]; //Q是元素为qnode类型的队列,容量足够大init(Q); int R=0; //R是层次序列指针,指向当前待处理的结点BiTree p=(BiTree)malloc(sizeof(BiNode)); //生成根结点p->data=level[0]; p->lchild=null; p->rchild=null; //填写该结点数据for (i=0; i<n; i++) //在中序序列中查找根结点,然后,左右子女信息入队列if (in[i]==level[0]) break;if (i==0) //根结点无左子树,遍历序列的1—n-1是右子树{p->lchild=null;s.lvl=++R; s.l=i+1; s.h=n-1; s.f=p; s.lr=2; enqueue(Q,s);}else if (i==n-1) //根结点无右子树,遍历序列的1—n-1是左子树{p->rchild=null;s.lvl=++R; s.l=1; s.h=i-1; s.f=p; s.lr=1; enqueue(Q,s);}else //根结点有左子树和右子树{s.lvl=++R; s.l=0; s.h=i-1; s.f=p; s.lr=1;enqueue(Q,s);//左子树有关信息入队列s.lvl=++R; s.l=i+1;s.h=n-1;s.f=p; s.lr=2;enqueue(Q,s);//右子树有关信息入队列}while (!empty(Q)) //当队列不空,进行循环,构造二叉树的左右子树{ s=delqueue(Q); father=s.f;for (i=s.l; i<=s.h; i++)if (in[i]==level[s.lvl]) break;p=(bitreptr)malloc(sizeof(binode)); //申请结点空间p->data=level[s.lvl]; p->lchild=null; p->rchild=null; //填写该结点数据if (s.lr==1) father->lchild=p;else father->rchild=p; //让双亲的子女指针指向该结点if (i==s.l){p->lchild=null; //处理无左子女s.lvl=++R; s.l=i+1; s.f=p; s.lr=2; enqueue(Q,s);}else if (i==s.h){p->rchild=null; //处理无右子女s.lvl=++R; s.h=i-1; s.f=p; s.lr=1; enqueue(Q,s);}else{s.lvl=++R; s.h=i-1; s.f=p; s.lr=1; enqueue(Q,s);//左子树有关信息入队列s.lvl=++R; s.l=i+1; s.f=p; s.lr=2; enqueue(Q,s); //右子树有关信息入队列}}//结束while (!empty(Q))return(p);}//算法结束3、#define maxsize 栈空间容量void InOutS(int s[maxsize])//s是元素为整数的栈,本算法进行入栈和退栈操作。
大陆与台湾经济周期的同步性实证研究——基于波动频率同步性的测度

基 于波动频率 同步性 的测度
张 文 军
( 厦 门大学 经济 学院, 福建 厦门 3 6 1 0 0 0 )
【 摘 要 】 文章分别 以 G D P 和 投资 、 消费 、 出 口作为测度指标 , 对 大陆与 台湾经济周 期的同步性进行 了实证分析 ,
得知两地 区经济 波动 的相关 系数在 1 9 8 7 年 以来呈现 出显著增加 ,其次通过 矩阵法求 内生波长 和频率可知 , 1 9 8 7年 以 来大陆 与台湾之 间的经济波动的 内生波长 差别很小 , 内生频 率也 高度 一致 , 说 明两岸 波动频率高度 同步 , 经济周期呈现 出显著相关 , 最后提 出了相关 的对策 与建议 。
表 1 大陆与台湾 GDP总值 回归方程邹检验 结果
C h o w Br e a k p o i n t Te s t : 1 9 8 7
改革 以来 大 陆与 台湾 GDP波 动相 关 系数 和波 动 频 率 的测度
一Hale Waihona Puke 、( 一) 相 关 系 数 测 度 在进行相 关系数 的计算 之前 , 我们先利用邹 检验来对 大陆 与 台湾经 济周期的 同步性 进行阶段性检 验 , 首 先我们来建立 两
台湾经济周期 的同步性及传导机制研究 ” ( 2 0 o 9 B 2 O 3 8 )
【 作者简 介 】张文军( 1 9 7 3 - ) , 男, 厦 门大 学经济学院博士后 , 研 究方向: 经济周期。
6 7
验值 都大于显著性 水平为 1 0 %的临界值 ,因此可 以证明 1 9 8 7 下 面先来求大陆地 区经济波动的内生波长( 设 大陆地 区经 年前 后大陆与 台湾经济周期 同步 的特 征发生了结构性 的变化 。 济增 长率为 d z y , ) : 接下来我们利用邹检验 的结 果 ,对 1 9 8 7年前后两个地 区经济 我们对 D Z Y 进行滞后 回归得 : d z y , =1 . 6 9xd z y , 一 1 —1 . 2 8xd z yc _ 2 . 5 55 xd z y , O. 01 8 xd z .  ̄ 周期的相关系数进行计算 ,考虑到 2 0 0 1 年之后大陆 与台湾地  ̄ 然 后 可建 立 矩 阵 A如 下 : 区先后加入 WF O, 因此我们 把 2 0 0 1 年也 作为两地 区经济 周期 0. 8 4 0. 0 7 2 1 8 6 的一个转折 点 ,大 陆 与台湾 经济增长率 相关系数 的计算结 果 0. 1 3 5 0.
中华人民共和国2015年国民经济和社会发展统计公报

中华人民共和国2015年国民经济和社会发展统计公报[1]2015年,面对错综复杂的国际形势和艰巨繁重的国内改革发展稳定任务,党中央、国务院团结带领全国各族人民,按照“五位一体”总体布局和“四个全面”战略布局的总要求,牢固树立和贯彻落实创新、协调、绿色、开放、共享的发展理念,适应经济发展新常态,坚持改革开放,坚持稳中求进工作总基调,坚持稳增长、调结构、惠民生、防风险,不断创新宏观调控思路与方式,深入推进结构性改革,扎实推动大众创业万众创新,努力促进经济保持中高速增长、迈向中高端水平,转型升级步伐加快,改革开放不断深化,民生事业持续进步,经济社会发展迈上新台阶,实现了“十二五”圆满收官,为“十三五”经济社会发展、决胜全面建成小康社会奠定了坚实基础。
一、综合初步核算,全年国内生产总值[2]676708亿元,比上年增长6.9%。
其中,第一产业增加值60863亿元,增长3.9%;第二产业增加值274278亿元,增长6.0%;第三产业增加值341567亿元,增长8.3%。
第一产业增加值占国内生产总值的比重为9.0%,第二产业增加值比重为40.5%,第三产业增加值比重为50.5%,首次突破50%。
全年人均国内生产总值49351元,比上年增长6.3%。
全年国民总收入[3]673021亿元。
(见图1)(见图2)年末全国大陆总人口137462万人,比上年末增加680万人,其中城镇常住人口77116万人,占总人口比重(常住人口城镇化率)为56.10%,比上年末提高1.33个百分点。
全年出生人口1655万人,出生率为12.07‰;死亡人口975万人,死亡率为7.11‰;自然增长率为4.96‰。
全国人户分离的人口[4]2.94亿人,其中流动人口[5]2.47亿人。
人均预期寿命76.34岁。
(见表1)年末全国就业人员77451万人,其中城镇就业人员40410万人。
全年城镇新增就业1312万人。
年末城镇登记失业率为4.05%。
人口结构变迁

2015
全球重大趨勢 與影響
趨勢三:網路化世界 全新商業模式與分眾行為規範應運而生
趨勢四: 跨領域科技整合 由需求端思考跨領域專業之整合創新 趨勢五:重視環保與精敏製造 提升競爭力需掌握環保趨勢與彈性生產
趨勢六:追求資源效能提升 以永續觀點重新思考資源之配置與運用
推動大型 國建建立 重化基礎
由勞力密集 轉為資本密 集。推動產 業升級,培 育高科技產 業基礎
投注國家 資源改良 農業技術
勞動密集產 業,出口為 導向之產業 結構
引導高科 技產業發 展
高科技產業 萌芽及奠基。 電子資訊產 業逐漸成為 產業發展重 點
產業技術 升級與國 際化
新興高科技 產業起飛期。 資訊電子、 光電、通訊 產業蓬勃發 展
跨領域整合 由需求端思考跨 領域整合創新
3
產業發展不再以經濟成長為唯一指標
高
2015
經濟成長
弱 低 弱 強 強
環境永續社會公義源自Q:我們要發展的究竟是等邊矩形,還是最佳不對稱 ?
4
唯有促進經濟成長,才能創造更美好的生活
未來國家發展三大原則 經濟成長 社會公義 環境永續
邁入先進國家之林 創造尊重多元價值的社會 成為活力富裕的亞洲中心
強調普世價值, 需大量非產業 因素配合
社會 公義
軟性經濟 創意者
環境 永續
生活型態 先驅者
在地化:服務衍生,本土導向
7
核心價值主張 人口結 構轉變 全球化 風潮 網路化 世界 跨領域 整合 環保精 敏製造 資源效 能提升
效率製造
整合創新 知識服務
優質生活 多元價值
全球資源整合者
十大数据勾画2015年政府工作走向

十大数据勾画2015年政府工作走向
佚名
【期刊名称】《科技智囊》
【年(卷),期】2015(000)004
【摘要】主动应对和引领经济发展新常态无疑是2015年两会的重大主题。
透过政府工作报告和计划报告,十大数字勾画出新常态下中国在2015年的大致走向。
GDP增长7%左右:彰显稳增长调结构决心政府工作报告提出,2015年GDP增长7%左右。
从全球看,7%左右的GDP增速,放在世界银行2015年1月对23个主要经济体的增速预测中,仍然位居前列。
【总页数】8页(P24-31)
【正文语种】中文
【中图分类】F127
【相关文献】
1.解读2015年政府工作报告十大关键数据 [J],
2.走向理性的繁荣——2015年度电商与O2O排行榜——回归理性的繁荣——2015电商与O2O十大关键词 [J], 千一
3.中国政府工作报告——2014年十大重要数据 [J],
4.2015年政府工作报告十大数据解读 [J],
5.政府工作报告:2010年中国经济十大关键数据 [J],
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
{visited[v]=1; for(j=1;j<=n;j++ ) if (g[v][j]!=0) //存在边(v,j) if (visited[j]!=1) {if (!visited[j]) dfs(j); }//if else {cycle=1; Print(j,j);} visited[v]=2; }//dfs void find_cycle() //判断是否有回路,有则输出邻接矩阵。visited 数组为全局变量。 {for (i=1;i<=n;i++) visited[i]=0; for (i=1;i<=n;i++ ) if (!visited[i]) dfs(i); }//find_cycle 9、设从键盘输入一整数的序列:a1, a2, a3,„,an,试编写算法实现:用栈结构存储输入 的整数,当 ai≠-1 时,将 ai 进栈;当 ai=-1 时,输出栈顶整数并出栈。算法应对异常情况 (入栈满等)给出相应的信息。 设有一个背包可以放入的物品重量为 S,现有 n 件物品,重量分别为 W1,W2,...,Wn。问能 否从这 n 件物品中选择若干件放入背包, 使得放入的重量之和正好是 S。 设布尔函数 Knap(S, n)表示背包问题的解,Wi(i=1,2,...,n)均为正整数,并已顺序存储地在数组 W 中。请在下 列算法的下划线处填空,使其正确求解背包问题。 Knap(S,n) 若 S=0 则 Knap←true 否则若(S<0)或(S>0 且 n<1) 则 Knap←false 否则若 Knap(1) , _=true 则 print(W[n]);Knap ←true 否则 Knap←Knap(2) _ , _ 设有一个顺序栈 S,元素 s1, s2, s3, s4, s5, s6 依次进栈,如果 6 个元素的出栈顺序为 s2, s3, s4, s6, s5, s1,则顺序栈的容量至少应为多少?画出具体进栈、出栈过程。 假定采用带头结点的单链表保存单词,当两个单词有相同的后缀时,则可共享相同的后缀存 储空间。例如: 设 str1 和 str2 是分别指向两个单词的头结点,请设计一个尽可能的高效算法,找出两个单 词共同后缀的起始位置,分析算法时间复杂度。 将 n(n>1)个整数存放到一维数组 R 中。设计一个尽可能高效(时间、空间)的算 法, 将 R 中保存的序列循环左移 p (0<p<n) 个位置, 即将 R 中的数据 (x0, x1, x2,„, xn-1) , 变换为(xp, xp+1, „ , xn-1 ,x0 , x1,„, xp-1)。 10、我们用 l 代表最长平台的长度,用 k 指示最长平台在数组 b 中的起始位置(下标) 。用 j 记住局部平台的起始位置, 用 i 指示扫描 b 数组的下标, i 从 0 开始, 依次和后续元素比较,
while(q) if(q->data==p->data) {s->next=q->next;free(q); q=s->next;} else { s=q; /*找与 P 结点值相同的结点*/ q=q->next; } p=p->next; } return head; } 4、请编写一个判别给定二叉树是否为二叉排序树的算法,设二叉树用 llink-rlink 法存储。 5、对二叉树的某层上的结点进行运算,采用队列结构按层次遍历最适宜。 int LeafKlevel(BiTree bt, int k) //求二叉树 bt 的第 k(k>1) 层上叶子结点个数 {if(bt==null || k<1) return(0); BiTree p=bt,Q[]; //Q 是队列,元素是二叉树结点指针,容量足够大 int front=0,rear=1,leaf=0; //front 和 rear 是队头和队尾指针, leaf 是叶子结点数 int last=1,level=1; Q[1]=p; //last 是二叉树同层最右结点的指针,level 是二叉树的层 数 while(front<=rear) {p=Q[++front]; if(level==k && !p->lchild && !p->rchild) leaf++; //叶子结点 if(p->lchild) Q[++rear]=p->lchild; //左子女入队 if(p->rchild) Q[++rear]=p->rchild; //右子女入队 if(front==last) {level++; //二叉树同层最右结点已处理,层数增 1 last=rear; } //last 移到指向下层最右一元素 if(level>k) return (leaf); //层数大于 k 后退出运行 }//while }//结束 LeafKLevel 6、设从键盘输入一整数的序列:a1, a2, a3,„,an,试编写算法实现:用栈结构存储输入 的整数,当 ai≠-1 时,将 ai 进栈;当 ai=-1 时,输出栈顶整数并出栈。算法应对异常情况 (入栈满等)给出相应的信息。 设有一个背包可以放入的物品重量为 S,现有 n 件物品,重量分别为 W1,W2,...,Wn。问能 否从这 n 件物品中选择若干件放入背包, 使得放入的重量之和正好是 S。 设布尔函数 Knap(S, n)表示背包问题的解,Wi(i=1,2,...,n)均为正整数,并已顺序存储地在数组 W 中。请在下 列算法的下划线处填空,使其正确求解背包问题。 Knap(S,n) 若 S=0 则 Knap←true 否则若(S<0)或(S>0 且 n<1) 则 Knap←false
若局部平台长度(i-j)大于 l 时,则修改最长平台的长度 k(l=i-j)和其在 b 中的起始位 置(k=j) ,直到 b 数组结束,l 即为所求。 void Platform (int b[ ], int N) //求具有 N 个元素的整型数组 b 中最长平台的长度。 {l=1;k=0;j=0;i=0; while(i<n-1) {while(i<n-1 && b[i]==b[i+1]) i++; if(i-j+1>l) {l=i-j+1;k=j;} //局部最长平台 i++; j=i; } //新平台起点 printf(“最长平台长度%d,在 b 数组中起始下标为%d” ,l,k); }// Platform 11、有一种简单的排序算法,叫做计数排序(count sorting) 。这种排序算法对一个待排序 的表(用数组表示)进行排序,并将排序结果存放到另一个新的表中。必须注意的是,表中所 有待排序的关键码互不相同,计数排序算法针对表中的每个记录,扫描待排序的表一趟,统 计表中有多少个记录的关键码比该记录的关键码小,假设针对某一个记录,统计出的计数值 为 c,那么,这个记录在新的有序表中的合适的存放位置即为 c。 (1) (3 分)给出适用于计数排序的数据表定义; (2) (7 分)使用 Pascal 或 C 语言编写实现计数排序的算法; (3) (4 分)对于有 n 个记录的表,关键码比较次数是多少? (4) (3 分)与简单选择排序相比较,这种方法是否更好?为什么? 12、给定 n 个村庄之间的交通图,若村庄 i 和 j 之间有道路,则将顶点 i 和 j 用边连接,边 上的 Wij 表示这条道路的长度,现在要从这 n 个村庄中选择一个村庄建一所医院,问这所医 院应建在哪个村庄, 才能使离医院最远的村庄到医院的路程最短?试设计一个解答上述问题的 算法,并应用该算法解答如图所示的实例。 (20 分) 13、约瑟夫环问题(Josephus 问题)是指编号为 1、2、„,n 的 n(n>0)个人按顺时针方向 围坐成一圈,现从第 s 个人开始按顺时针方向报数,数到第 m 个人出列,然后从出列的下一 个人重新开始报数,数到第 m 的人又出列,„,如此重复直到所有的人全部出列为止。现要 求采用循环链表结构设计一个算法,模拟此过程。 14、设有一个数组中存放了一个无序的关键序列 K1、K2、„、Kn。现要求将 Kn 放在将元素 排序后的正确位置上,试编写实现该功能的算法,要求比较关键字的次数不超过 n。 51. 借助于快速排序的算法思想,在一组无序的记录中查找给定关键字值等于 key 的记录。 设此组记录存放于数组 r[l..h]中。若查找成功,则输出该记录在 r 数组中的位置及其值, 否则显示“not find”信息。请编写出算法并简要说明算法思想。 15、约瑟夫环问题(Josephus 问题)是指编号为 1、2、„,n 的 n(n>0)个人按顺时针方向 围坐成一圈,现从第 s 个人开始按顺时针方向报数,数到第 m 个人出列,然后从出列的下一 个人重新开始报数,数到第 m 的人又出列,„,如此重复直到所有的人全部出列为止。现要 求采用循环链表结构设计一个算法,模拟此过程。 #include<stdlib.h> typedef int datatype; typedef struct node {datatype data;
1、矩阵中元素按行和按列都已排序,要求查找时间复杂度为 O(m+n) ,因此不能采用常规的 二层循环的查找。 可以先从右上角 (i=a,j=d) 元素与 x 比较, 只有三种情况: 一是 A[i,j]>x, 这情况下向 j 小的方向继续查找; 二是 A[i,j]<x, 下步应向 i 大的方向查找; 三是 A[i,j]=x, 查找成功。否则,若下标已超出范围,则查找失败。 void search(datatype A[ ][ ], int a,b,c,d, datatype x) //n*m 矩阵 A,行下标从 a 到 b,列下标从 c 到 d,本算法查找 x 是否在矩阵 A 中. {i=a; j=d; flag=0; //flag 是成功查到 x 的标志 while(i<=b && j>=c) if(A[i][j]==x) {flag=1;break;} else if (A[i][j]>x) j--; else i++; if(flag) printf(“A[%d][%d]=%d”,i,j,x); //假定 x 为整型. else printf(“矩阵 A 中无%d 元素” ,x); }算法 search 结束。 [算法讨论]算法中查找 x 的路线从右上角开始, 向下 (当 x>A[i,j]) 或向左 (当 x<A[i,j]) 。 向下最多是 m, 向左最多是 n。 最佳情况是在右上角比较一次成功, 最差是在左下角 (A[b,c]) , 比较 m+n 次,故算法最差时间复杂度是 O(m+n) 。 2、二部图(bipartite graph) G=(V,E)是一个能将其结点集 V 分为两不相交子集 V 1 和 V2=V-V1 的无向图,使得:V1 中的任何两个结点在图 G 中均不相邻,V2 中的任何结点在图 G 中也均不相邻。 (1) .请各举一个结点个数为 5 的二部图和非二部图的例子。 (2) . 请用 C 或 PASCAL 编写一个函数 BIPARTITE 判断一个连通无向图 G 是否是二部图, 并分 析程序的时间复杂度。设 G 用二维数组 A 来表示,大小为 n*n(n 为结点个数) 。请在程序中 加必要的注释。若有必要可直接利用堆栈或队列操作。 【 3、有一个带头结点的单链表,每个结点包括两个域,一个是整型域 info,另一个是指向下 一个结点的指针域 next。假设单链表已建立,设计算法删除单链表中所有重复出现的结点, 使得 info 域相等的结点只保留一个。 #include <stdio.h> typedef char datatype; typedef struct node{ datatype data; struct node * next; } listnode; typedef listnode* linklist; /*--------------------------------------------*/ /* 删除单链表中重复的结点 */ /*--------------------------------------------*/ linklist deletelist(linklist head) { listnode *p,*s,*q; p=head->next; while(p) {s=p;true 则 print(W[n]);Knap ←true 否则 Knap←Knap(2) _ ,
