广度优先搜索.ppt
深度优先搜索和广度优先搜索的深入讨论

一、深度优先搜索和广度优先搜索的深入讨论(一)深度优先搜索的特点是:(1)从上面几个实例看出,可以用深度优先搜索的方法处理的题目是各种各样的。
有的搜索深度是已知和固定的,如例题2-4,2-5,2-6;有的是未知的,如例题2-7、例题2-8;有的搜索深度是有限制的,但达到目标的深度是不定的。
但也看到,无论问题的内容和性质以及求解要求如何不同,它们的程序结构都是相同的,即都是深度优先算法(一)和深度优先算法(二)中描述的算法结构,不相同的仅仅是存储结点数据结构和产生规则以及输出要求。
(2)深度优先搜索法有递归以及非递归两种设计方法。
一般的,当搜索深度较小、问题递归方式比较明显时,用递归方法设计好,它可以使得程序结构更简捷易懂。
当搜索深度较大时,如例题2-5、2-6。
当数据量较大时,由于系统堆栈容量的限制,递归容易产生溢出,用非递归方法设计比较好。
(3)深度优先搜索方法有广义和狭义两种理解。
广义的理解是,只要最新产生的结点(即深度最大的结点)先进行扩展的方法,就称为深度优先搜索方法。
在这种理解情况下,深度优先搜索算法有全部保留和不全部保留产生的结点的两种情况。
而狭义的理解是,仅仅只保留全部产生结点的算法。
本书取前一种广义的理解。
不保留全部结点的算法属于一般的回溯算法范畴。
保留全部结点的算法,实际上是在数据库中产生一个结点之间的搜索树,因此也属于图搜索算法的范畴。
(4)不保留全部结点的深度优先搜索法,由于把扩展望的结点从数据库中弹出删除,这样,一般在数据库中存储的结点数就是深度值,因此它占用的空间较少,所以,当搜索树的结点较多,用其他方法易产生内存溢出时,深度优先搜索不失为一种有效的算法。
(5)从输出结果可看出,深度优先搜索找到的第一个解并不一定是最优解。
例如例题2-8得最优解为13,但第一个解却是17。
如果要求出最优解的话,一种方法将是后面要介绍的动态规划法,另一种方法是修改原算法:把原输出过程的地方改为记录过程,即记录达到当前目标的路径和相应的路程值,并与前面已记录的值进行比较,保留其中最优的,等全部搜索完成后,才把保留的最优解输出。
第7章图的深度和广度优先搜索遍历算法
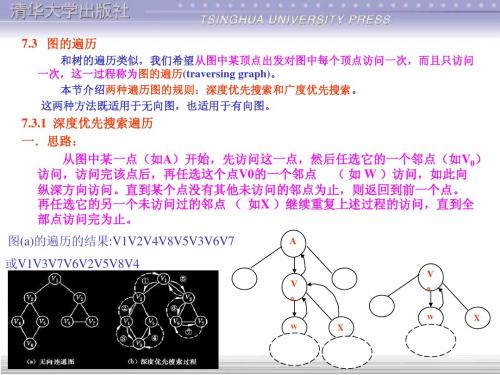
和树的遍历类似,我们希望从图中某顶点出发对图中每个顶点访问一次,而且只访问 一次,这一过程称为图的遍历(traversing graph)。 本节介绍两种遍历图的规则:深度优先搜索和广度优先搜索。 这两种方法既适用于无向图,也适用于有向图。
7.3.1 深度优先搜索遍历 一.思路: 从图中某一点(如A)开始,先访问这一点,然后任选它的一个邻点(如V0) 访问,访问完该点后,再任选这个点V0的一个邻点 ( 如 W )访问,如此向 纵深方向访问。直到某个点没有其他未访问的邻点为止,则返回到前一个点。 再任选它的另一个未访问过的邻点 ( 如X )继续重复上述过程的访问,直到全 部点访问完为止。 图(a)的遍历的结果:V1V2V4V8V5V3V6V7 或V1V3V7V6V2V5V8V4
p
v0 w x v 1
V
0
v 2
V
0
typedef struct {VEXNODE adjlist[MAXLEN]; // 邻接链表表头向量 int vexnum, arcnum; // 顶点数和边数 int kind; // 图的类型 }ADJGRAPH;
W W
X
X
7.3.2 广度优先搜索遍历 一.思路:
V
0
A V
0
W W
XXΒιβλιοθήκη 二.深度优先搜索算法的文字描述: 算法中设一数组visited,表示顶点是否访问过的标志。数组长度为 图的顶点数,初值均置为0,表示顶点均未被访问,当Vi被访问过,即 将visitsd对应分量置为1。将该数组设为全局变量。 { 确定从G中某一顶点V0出发,访问V0; visited[V0] = 1; 找出G中V0的第一个邻接顶点->w; while (w存在) do { if visited[w] == 0 继续进行深度优先搜索; 找出G中V0的下一个邻接顶点->w;} }
广度优先搜索

一:交通图问题
表示的是从城市A到城市H 表示的是从城市A到城市H的交通图。从图中可以 看出,从城市A到城市H 看出,从城市A到城市H要经过若干个城市。现要 找出一条经过城市最少的一条路线。
分析该题
分析:看到这图很容易想到用邻接距阵来表示,0 分析:看到这图很容易想到用邻接距阵来表示,0表示能 走,1表示不能走。如图5 走,1表示不能走。如图5。
用数组合表示 8个城市的相互 关系
procedure doit; begin h:=0; d:=1; a.city[1]:='A'; a.pre[1]:=0; s:=['A']; repeat {步骤2} {步骤 步骤2} inc(h); {队首加一,出队} {队首加一 出队} 队首加一, for i:=1 to 8 do {搜索可直通的城市} {搜索可直通的城市 搜索可直通的城市} if (ju[ord(a.city[h])-64,i]=0)and ju[ord(a.city[h])-64,i]=0) not(chr(i+64) s)) ))then {判断城市是否走 (not(chr(i+64) in s))then {判断城市是否走 过} begin inc(d); {队尾加一,入队} {队尾加一 入队} 队尾加一, a.city[d]:=chr(64+i); a.pre[d]:=h; s:=s+[a.city[d]]; if a.city[d]='H' then out; end; until h=d; end; begin {主程序} {主程序 主程序} doit; end. 输出: 输出: H-F--A --A
深度优先搜索: 深度优先搜索:状态树
搜索PPT演示课件

10
例 聪明的打字员
阿兰是某机密部门的打字员,她现在接到一个 任务:需要在一天之内输入几百个长度固定为 6的密码。当然,她希望输入的过程中敲击键 盘的总次数越少越好。
不幸的是,出于保密的需要,该部门用于输入 密码的键盘是特殊设计的,键盘上没有数字键, 而只有以下六个键:Swap0, Swap1, Up, Down, Left, Right,为了说明这6个键的作用,我们先 定义录入区的6个位置的编号,从左至右依次 为1,2,3,4,5,6。
宽度优先搜索(Breadth-first search) 深度优先搜索(Depth-first search)
6
宽度优先搜索
优点
目标节点如果存在,用宽度优先搜索算法总可 以找到该目标节点,而且是最小(即最短路径) 的节点
缺点
当目标节点距离初始节点较远时,会产生许多 无用的节点,搜索效率低
11
例 聪明的打字员
Swap0:按Swap0,光标位置不变,将光标所在位置的数字与录入区的1号位置 的数字(左起第一个数字)交换。如果光标已经处在录入区的1号位置,则按 Swap0键之后,录入区的数字不变
Swap1:按Swap1,光标位置不变,将光标所在位置的数字与录入区的6号位置 的数字(左起第六个数字)交换。如果光标已经处在录入区的6号位置,则按 Swap1键之后,录入区的数字不变
4
搜索问题
搜索问题:在一个空间中寻找目标
搜索什么(目标) 在哪里搜索(状态空间)
在搜索中,如何扩展状态空间是关键性问题 搜索可以根据是否使用启发式信息分成
盲目搜索:只能区分当前状态是否为目标状态 启发式搜索:在搜索过程中加入与问题相关的
第三章搜索技术

在解题过程中的每一时刻,所要解决的问题均
处于一定的状态,搜索过程只是将一个状态变成 另一个状态(如,一盘棋局变成另一盘棋局),则 称为状态空间搜索。
若搜索的对象是问题,搜索的原则是把一个复 杂的问题化为一组比较简单的子问题(如把一个 复杂的下棋策略分为几个子策略),则称为问题 空间搜索。
注:问题空间搜索常常比状态空间搜索有效,但 算法要复杂些。
第三章 搜索技术
第二节 启发式搜索
五、H*算法 注:2)H*算法的搜索效率在很大程度上取决于函 数h(n)的选择,它要求h(n)h*(n),但若h(n)太小, 则启发信息就很少。
3)若h(n)0,g(n)为搜索深度或代价,则H*算法 将退化为广度优先搜索或代价优先搜索。
4)h(n)的值在满足小于或等于h*(n)的前提下越 大越好,启发式信息多(即h值大)的H*算法展开 的节点是启发式信息少(即h值小)的H *算法展开 的节点的子集。
注:1)这里,搜索的对象(常称状态)往往是边 搜索边生成,因此在考虑这种搜索的复杂性时, 必须将搜索对象的生成和评估的代价计算在内。
第三章 搜索技术
第二节 启发式搜索
一、启发式搜索
注:2)根据启发性信息(特定领域的知识信息), 在生成搜索树时可考虑种种可能的选择:
a)下一步展开哪个节点? b)是部分展开还是全部展开? c)使用哪个规则(算子)? d)怎样决定舍弃还是保留新生成的节点? e)怎样决定舍弃还是保留一棵子树? f)怎样决定停止或继续搜索? g)如何定义启发函数(估值函数)? h)如何决定搜索方向?
图的各种算法(深度、广度等)

vex next 4 p
3
2 ^
2
^
5
5 5 4 3 2 1 0 ^
^
4 ^
top
4
输出序列:6 1
1 2 3 4 5 6
in link 0 2 ^ 1 0 2 0
vex next 4 p
3
2 ^
2
^
5
5 5 4 3 2 1 0 ^
^
4 ^
top 4
输出序列:6 1
1 2 3 4 5 6
in link 0 2 ^ 1 0 2 0
c a g b h f d e
a
b h c d g f
e
在算法中需要用定量的描述替代定性的概念
没有前驱的顶点 入度为零的顶点 删除顶点及以它为尾的弧 弧头顶点的入度减1
算法实现
以邻接表作存储结构 把邻接表中所有入度为0的顶点进栈 栈非空时,输出栈顶元素Vj并退栈;在邻接表中查找 Vj的直接后继Vk,把Vk的入度减1;若Vk的入度为0 则进栈 重复上述操作直至栈空为止。若栈空时输出的顶点个 数不是n,则有向图有环;否则,拓扑排序完毕
^
4
^
top
输出序列:6 1 3 2 4
1 2 3 4 5 6
in link 0 0 ^ 0 0 0 0
vex next 4
3
2 ^
2
^
5
5 5 4 3 2 1 0 ^ p
^
4
^topBiblioteka 5输出序列:6 1 3 2 4
1 2 3 4 5 6
in link 0 0 ^ 0 0 0 0
vex next 4
w2 w1 V w7 w6 w3
第四讲-知识搜索.

21
第四章 搜索策略
无信息图搜索属于盲目搜索,这里给两种常用的无信息图搜 索方法:广度优先搜索和深度优先搜索。 4.3.1 广度优先搜索(Breadth-First Search)
韩璐
第四章 搜索策略
搜索是人工智能研究的核心课题之一。人类的思维过程,可 以看作是一个搜索的过程。从小学到现在,你一定遇到过很多种 的智力游戏问题,比方说在第一章中介绍的传教士和野人问题。 如果你来做这个智力游戏的话,在每一次渡河之后,都会有几种 渡河方案供你选择,究竟哪种方案才有利于在满足题目所规定的 约束条件下顺利过河呢?经过反复努力和试探,你终于找到了一 种解决办法。在高兴之余,你马上可能又会想到,这个方案所用 的步骤是否最少?也就是说它是最优的吗?如果不是,如何才能 找到最优的方案?在计算机上又如何实现这样的搜索?这些问题 实际上就是本章我们要介绍的搜索问题。
搜索策略的主要任务是确定如何选取规则的方式。 盲目搜索的方法是不考虑给定问题所具有的特定知识,系统 根据事先确定好的某种固定排序,依次或随机调用规则。 启发式搜索策略是考虑问题领域可应用的知识,动态地确定 规则的排序,优先调用较合适的规则使用。
6
第四章 搜索策略
目前,人工智能领域中已提出许多具体的搜索方法:
(1)求任一解路的搜索策略
回溯法(Backtracking)
爬山法(Hill Climbing)
宽度优先法(Breadth-first)
深度优先搜索和广度优先搜索-Read

7.1 图的定义和术语
1.图的定义 定义:图(Graph)是由非空的顶点集合和一个描述顶
点之间关系(边或者弧)的集合组成。 其二元组定义为: G=(V,E) V={vi| vi∈DataObject} E={(vi,vj)| vi, vj ∈V∧P(vi, vj)} 其中,G表示一个图,V是图G中顶点的集合,E是图G
为强连通分量。
V0
V1
V0
V1
V2Biblioteka V3强连通图G1V2
V3
非强连通图G2
V1 V0
V2
V3
G2的两个强连 通分量
生成树、生成森林
所谓连通图G的生成树,是G的包含其全部n 个顶点的 一个极小连通子图。它必定包含且仅包含G的n-1条边。
极小连通子图意思是:该子图是G 的连通子图,在该 子图中删除任何一条边,子图不再连通。
否则称为非连通图。
无向图中,极大的连通子图为该图的连通分量。显然,
任何连通图的连通分量只有一个,即它本身,而非连通图有
多个连通分量。
V0
V1
G2的两个
连通分量
V0
V1 V4
V2
V3
V4
V3
V2 V5
连通图G1
非连通图G2
强连通图、强连通分量
对于有向图来说,若图中任意一对顶点vi 和vj(i≠j) 均有从一个顶点vi到另一个顶点vj有路径,也有从vj到vi的路 径,则称该有向图是强连通图。有向图的极大强连通子图称
G1=<V1, E1>
V1={v0, v1, v2, v3, v4 } E1={(v0, v1), (v0, v3), (v1, v2), (v1, v4), (v2, v3), (v2, v4)}
C++算法-8.广度优先搜索

int main() { int i,j; char s[100],ch; scanf("%d%d\n",&m,&n); for (i=0; i<=m-1;i++ ) for (j=0;j<=n-1;j++ ) bz[i][j]=1; //初始化 for (i=0;i<=m-1;i++) { gets(s); for (j=0;j<=n-1;j++) if (s[j]=='0') bz[i][j]=0; } for (i=0;i<=m-1;i++) for (j=0;j<=n-1;j++) if (bz[i][j]) doit(i,j); //在矩阵中寻找细胞 printf("NUMBER of cells=%d",num); return 0; }
void doit() { int head,tail,i; head=0;tail=1; //队首为0、队尾为1 a[1]=1; //记录经过的城市 b[1]=0; //记录前趋城市 s[1]=1; //表示该城市已经到过 do //步骤2 { head++; //队首加一,出队 for (i=1;i<=8;i++) //搜索可直通的城市 if ((ju[a[head]][i]==0)&&(s[i]==0)) //判断城市是否走过 { tail++; //队尾加一,入队 a[tail]=i; b[tail]=head; s[i]=1; if (i==8) { out(tail);head=tail;break; //第一次搜到H城市时路线最短 } } }while (head<tail); } int main() //主程序 { memset(s,false,sizeof(s)); doit(); //进行Bfs操作 return 0; }
图的遍历深度优先遍历和广度优先遍历

4
5
f
^
对应的邻接表
终点2作为下次的始点, 由于1点已访问过,跳过, 找到4,记标识,送输出, 4有作为新的始点重复上 述过程
1 2 4
5
输出数组 resu
3.邻接表深度优先遍历的实现
template <class TElem, class TEdgeElem>long DFS2(TGraphNodeAL<TElem, TEdgeElem> *nodes,long n,long v0, char *visited, long *resu,long &top) {//深度优先遍历用邻接表表示的图。nodes是邻接表的头数组,n 为结点个数(编号为0~n)。 //v0为遍历的起点。返回实际遍历到的结点的数目。 //visited是访问标志数组,调用本函数前,应为其分配空间并初 始化为全0(未访问) //resu为一维数组,用于存放所遍历到的结点的编号,调用本函 数前,应为其分配空间 long nNodes, i; TGraphEdgeAL<TEdgeElem> *p; nNodes=1;
1 2
4
图 20-1有向图
5
3
1 2 3 4 5
1 0 1 0 1 0
2 1 0 0 0 0
3 0 0 0 0 0
4 0 1 0 0 0
5 1 0 1 0 0
1 2 3 4 5
1 1 0 1 1
1 2 4 5
所示图的邻接矩阵g
访问标识数组 visited
输出数组 resu
例如从1点深度优先遍历,先把1设置访问标志,并置入输出数组resu,然后从邻接 矩阵的第一行,扫描各列,找到最近的邻接点2,将其设置访问标志,并进入输出数 组,接着从邻接矩阵的2行扫描,找到第一个构成边的点是1,检查访问标识数组, 发现1已经访问过,跳过,找第二个构成边 的点4,设置访问标识,进入输出数组, 再从邻接矩阵的第4行扫描,寻找构成边的点,除1外在无其他点,返回2行,继续 寻找,也无新点,返回1,找到5,将5置访问标志,进入输出数组,1行再无其他新 点,遍历结束,返回遍历元素个数为4 。
第五章状态空间的各种搜索

四.等代价搜索 等代价搜索
分析:城市间旅费=节点间代价,制约条件是代价最小,先扩展代 价最小的节点。如从A->B->E, cost(B)=7,cost(E)=cost(B)+m(B,E)=7+12=19.设计以A为起点, 用等代价搜索得出部分搜索树,连线上数字为从父节点到子节点 的代价.节点上方小圆圈内数字为节点扩展顺序,方框左上方为 从A到该节点总代价.
例:图中各点间连线表示从一处到另一处所消耗的费 用,试编一程序求任意两地之间的最小费用(代价最小) 的路线,并打印所付出费用.
六.分枝限界法 分枝限界法
设求从v1->v5所付出代价最小路径 设变量s=从始点到某点总代价 (1)第一步扩展v1获得第一级子节点: v1->v2:2 v1->v3:4 V1->v4:5
五.A*算法 算法
例:炸迷宫问题 有一个N*N迷宫,每一格或是空,或者是实,如果 有一人位于迷宫的一空格(x,y)中,则他仅能到达相邻 的空格(指上下左右).现有一人从(1,1)始点出发,目 标是(N,N),他随身带着K个炸弹(0<=K<=N),一个炸弹 的威力能把与他相邻的一个实格炸成空格. 编一程序,求出R个被炸实格位置(0<=R<=K)和 此人从起始点到目标的路径,并要求R满足条件中的最 小值. 要求:
第五章 状态空间的各种搜索
一.概述 概述
广度优先搜索法:以接近起始节点的程度依次 广度优先搜索法 扩展节点,即对下一层节点搜索前,必须先搜 索完本层所有节点 深度优先搜索法:首先扩展最新产生的节点, 深度优先搜索法 每层只对一个节点进行扩展,除非搜索失败或 已达到预先约定的最大深度,才会退回去搜索 原来忽略节点
三.深度优先搜索 深度优先搜索
第 6 章 图的搜索算法

2.算法的伪代码描述
• • • • • • • • • • • • • STRONGLY-CONNECTED-COMPONENTS(G) 1 for u←1 to n 2 do order[u+ ←u 3 order←调用DFS-BY-ORDER (G, order)返回的top-logic数组 4 GT←TRANSPOSE-DIRECTED-GRAPH (G) 5 ←调用DFS-BY-ORDER (GT, order)返回的数组 TRANSPOSE-DIRECTED-GRAPH(G) 1 for each uV do 2 AdjT[u+←NIL 3 for each uV do 4 for each v Adj[u] do 5 INSERT(AdjT[v], u) 6 return GT
算法的伪代码描述
• • • • • • • • • • • • • • • • • • • • • • • TOPLOGICAL-SORT(G) 1 for each vertex uV[G] 2 do color[u+←WHITE 3 acyclicity←true 4 top-logic←S← 5 for each vertex s V[G] 6 do if color[s] = WHITE 7 then color[s+ ← GRAY 8 PUSH(S, s) 9 while S≠ 10 do u←TOP(S) 11 if v Adj[u] and color[v] = GRAY 12 then acyclicity←false 13 if v Adj[u] and color[v] = WHITE 14 then color[v+ ←GRAY 15 PUSH(S, v) 16 else color[u+ ← BLACK 17 PUSH(top-logic, u) 18 POP(S) 19 if acyclicity=true 20 then return top-logic 21 else print "G is not a DAG!“ 由于TOPLOGICAL-SORT的运行时间与DFS的运行时间一致,所以,可以在时间Θ(V + E)内计算有向无圈图G=<V, E>的拓 扑排序。
数据结构与算法(13):深度优先搜索和广度优先搜索
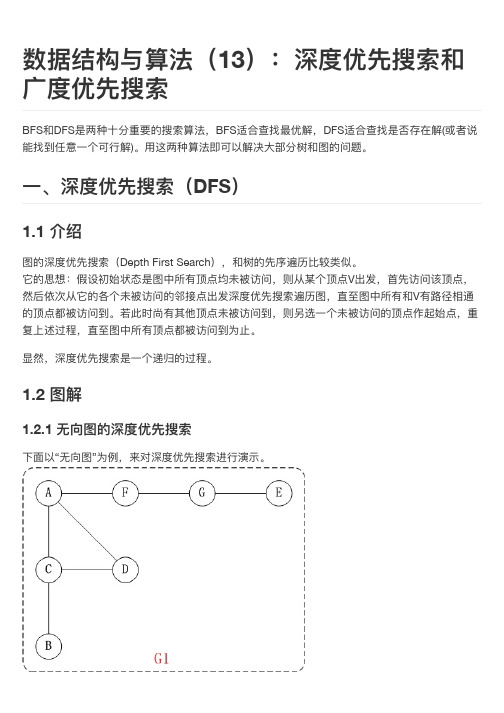
2.2.2 有向图的广广度优先搜索
下面面以“有向图”为例例,来对广广度优先搜索进行行行演示。还是以上面面的图G2为例例进行行行说明。
第1步:访问A。 第2步:访问B。 第3步:依次访问C,E,F。 在访问了了B之后,接下来访问B的出边的另一一个顶点,即C,E,F。前 面面已经说过,在本文文实现中,顶点ABCDEFG按照顺序存储的,因此会先访问C,再依次访 问E,F。 第4步:依次访问D,G。 在访问完C,E,F之后,再依次访问它们的出边的另一一个顶点。还是按 照C,E,F的顺序访问,C的已经全部访问过了了,那么就只剩下E,F;先访问E的邻接点D,再访 问F的邻接点G。
if(mVexs[i]==ch)
return i;
return -1;
}
/* * 读取一一个输入入字符
*/
private char readChar() {
char ch='0';
do {
try {
ch = (char)System.in.read();
} catch (IOException e) {
数据结构与算法(13):深度优先搜索和 广广度优先搜索
BFS和DFS是两种十十分重要的搜索算法,BFS适合查找最优解,DFS适合查找是否存在解(或者说 能找到任意一一个可行行行解)。用用这两种算法即可以解决大大部分树和图的问题。
一一、深度优先搜索(DFS)
1.1 介绍
图的深度优先搜索(Depth First Search),和树的先序遍历比比较类似。 它的思想:假设初始状态是图中所有顶点均未被访问,则从某个顶点V出发,首首先访问该顶点, 然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至至图中所有和V有路路径相通 的顶点都被访问到。若此时尚有其他顶点未被访问到,则另选一一个未被访问的顶点作起始点,重 复上述过程,直至至图中所有顶点都被访问到为止止。 显然,深度优先搜索是一一个递归的过程。
深搜与广搜

深度优先搜索:
广度优先搜索:
2
深度优先搜索属于图算法的一种。 其过程简要来说是对每一个可能的分支路径深入到不能再
深入为止,而且每个节点只能访问一次.
3
深度优先遍历图的方法是,从图中某顶点v出发: (1)访问顶点v; (2)依次从v的未被访问的邻接点出发,对图进行深度优先遍历;直
7
8
1 7
2
6
3
4 5
1 8 7
2
3 4
6
5
Problem Description: There is a 3-by-3 chessboard with 8 numbers. Your mission is to transform the origin shape to the target shape only by moving the blank check in four directions. Now you should figure out the minimum steps.
至图中和v有路径相通的顶点都被访问; (3)若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发, 重新进行深度优先遍历,直到图中所有顶点均被访问过为止。
4
迷宫问题:
将起点标记为已走过并压栈; while (栈非空) { 从栈顶弹出一个点p; if (p这个点是终点) break; 否则沿右、下、左、上四个方向探索相邻的点 if (和p相邻的点有路可走,并且还没走过) 将相邻的点标记为已走过并压栈,它的前趋就是p点; } if (p点是终点) { 打印p点的坐标; while (p点有前趋) { p点 = p点的前趋; 打印p点的坐标; } } else 没有路线可以到达点;
邻接矩阵表示图-深度-广度优先遍历

*问题描述:建立图的存储结构(图的类型可以是有向图、无向图、有向网、无向网,学生可以任选两种类型),能够输入图的顶点和边的信息,并存储到相应存储结构中,而后输出图的邻接矩阵。
1、邻接矩阵表示法:设G=(V,E)是一个图,其中V={V1,V2,V3…,Vn}。
G的邻接矩阵是一个他有下述性质的n阶方阵:1,若(Vi,Vj)∈E 或<Vi,Vj>∈E;A[i,j]={0,反之图5-2中有向图G1和无向图G2的邻接矩阵分别为M1和M2:M1=┌0 1 0 1 ┐│ 1 0 1 0 ││ 1 0 0 1 │└0 0 0 0 ┘M2=┌0 1 1 1 ┐│ 1 0 1 0 ││ 1 1 0 1 │└ 1 0 1 0 ┘注意无向图的邻接是一个对称矩阵,例如M2。
用邻接矩阵表示法来表示一个具有n个顶点的图时,除了用邻接矩阵中的n*n个元素存储顶点间相邻关系外,往往还需要另设一个向量存储n个顶点的信息。
因此其类型定义如下:VertexType vertex[MAX_VERTEX_NUM]; // 顶点向量AdjMatrix arcs; // 邻接矩阵int vexnum, arcnum; // 图的当前顶点数和弧(边)数GraphKind kind; // 图的种类标志若图中每个顶点只含一个编号i(1≤i≤vnum),则只需一个二维数组表示图的邻接矩阵。
此时存储结构可简单说明如下:type adjmatrix=array[1..vnum,1..vnum]of adj;利用邻接矩阵很容易判定任意两个顶点之间是否有边(或弧)相联,并容易求得各个顶点的度。
对于无向图,顶点Vi的度是邻接矩阵中第i行元素之和,即n nD(Vi)=∑A[i,j](或∑A[i,j])j=1 i=1对于有向图,顶点Vi的出度OD(Vi)为邻接矩阵第i行元素之和,顶点Vi 的入度ID(Vi)为第i列元素之和。
即n nOD(Vi)=∑A[i,j],OD(Vi)=∑A[j,i])j=1j=1用邻接矩阵也可以表示带权图,只要令Wij, 若<Vi,Vj>或(Vi,Vj)A[i,j]={∞, 否则。
《状态空间搜索》PPT课件

• 从SL中删除第一个元素;/*回溯*/
• 从NSL中删去第一个元素;
• CS:=NSL中第一个元素;
•
end;
• 将CS加入SL;
• end
• else begin • 将CS子状态(不包括DE、SL、NSL中有的)加入NSL;
精选ppt
12
图搜索的实现(续)
• CS:=NSL中第一个元素;
• 将CS加入SL;
状态空间搜索
状态空间搜索策略 数据驱动和目标驱动的搜索 图搜索的实现 深度和广度优先搜索 有界深度优先搜索
谓词演算推理的状态空间表示法 逻辑的状态空间描述 与/或图 讨论
精选ppt
1
• 基于递归的搜索
• 递归
• 递归搜索
• 模式驱动搜索
• 产生式系统
•
定义与历史
•
产生式系统示例
•
产生式系统搜索的控制
• 算法就是以这种方式执行直到找到目标或遍历了状态空间为止。下图给出的 是一个假设的状态空间的深度优先回溯搜索。
•
•
1A
•
• 2 B 8 C 10 D
•
• E3 6F 9G
•
•
HI
J
•
45
7
•
一个假设状态空间的深度优先回溯搜索
精选ppt
8
图搜索的实现(续)
• 下面定义一个回溯搜索的算法:算法使用3张表保存状 态空间中的结点。
• end
• end;
• return FAIL
• end.
• 假设状态空间的深度优先回溯搜索中的回溯轨迹 如下:
• 初值:SL = [A];NSL= [A];DE=[ ];CS=A;
图的广度优先搜索的应用

图的广度优先搜索的应用◆内容提要广度优先搜索是分层次搜索,广泛应用于求解问题的最短路径、最少步骤、最优方法等方面。
本讲座就最短路径问题、分酒问题、八数码问题三个典型的范例,从问题分析、算法、数据结构等多方面进行了讨论,从而形成图的广度优先搜索解决问题的模式,通过本讲座的学习,能明白什么样的问题可以采用或转化为图的广度优先搜索来解决。
在讨论过程中,还同时对同一问题进行了深层次的探讨,进一步寻求解决问题的最优方案。
◆知识讲解和实例分析和深度优先搜索一样,图的广度优先搜索也有广泛的用途。
由于广度优先搜索是分层次搜索的,即先将所有与上一层顶点相邻接的顶点搜索完之后,再继续往下搜索与该层的所有邻接而又没有访问过的顶点。
故此,当某一层的结点出现目标结点时,这时所进行的步骤是最少的。
所以,图的广度优先搜索广泛应用于求解问题的最短路径、最少步骤、最优方法等方面。
本次讲座就几个典型的范例来说明图的广度优先搜索的应用。
先给出图的广度优先搜索法的算法描述:F:=0;r:=1;L[r]:=初始值;H:=1;w:=1;bb:=true;While bb dobeginH:=h+1;g[h]:=r+1;For I:=1 to w doBeginF:=f+1;For t:=1 to 操作数doBegin⑴m:=L[f]; {出队列};⑵判断t操作对m结点的相邻结点进行操作;能则设标记bj:=0,并生成新结点;不能,则设标记bj:=1;if bj:=0 then {表示有新结点生成}beginfor k:=1 to g[h]-1 doif L[k]=新结点then {判断新扩展的结点是否以前出现过}beginbj:=1;k:=g[h]-1end;if bj<>1 then {没有出现过} beginr:=r+1;L[r]:=新结点;{新结点进队列}b[r]:=f;c[r]:=t;{并链接指针,保存操作数} end; end; end; end;w:=r+1-g[h];s:=0;{计算新生成的一层的结点数}for k:=g[h] to r do {在新生成的一层结点中,判断是否有目标结点存在} if L[k]=目标结点 then begins:=s+1; {累计解的条数} 根据链接指针求出路径; end;if s:<>0 then begin输出s 条路径;bb:=false; {设程序结束条件} end; end;例1:最短路径问题求从任意一个顶点V i 出发,对给出的图,求到达任意顶点V j (i<>j )的所有最短路径 [问题分析]1、首先用邻接表表示此图各端点的邻接关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 相信大家听问题的时候都注意到了关键词“尽 快”。毋庸置疑,老鼠们的做法是肯定能在最快 时间内找到出口。接下来我们分析一下其中原因。 我们给老鼠能到的每个方块一个距离。初始位置 的距离为0,由这个位置出发能到的距离为1,再 有这些点能到的不重复的点的距离为2。。。如此 下去,我们就可以给每一个可以到达的位置一个 距离值。我们每次所做的都是把一个位置能够拓 展的所有位置都拓展出来了,而且也没有走重复 的路。可以保证在到达某一个位置的时候我们所 走的距离肯定是最短的。
• 我们把每一个到的位置叫做一个状态。象这样子
来构造一个队列。最初队列里只有一个元素,那
就是最初的状态。机器开始运行了。第一次我们
从队列里面取出第一个元素。然后对它进行拓展,
找到所有由它为基础能到的状态,然后我们把这
些状态加入到队列里面。这样的操作不断重复,
直到我们找到了我们想要的为止。当然操作不止
• 我们对各个方向设定一个优先级,比如我们设定先向上走, 再向右走,然后是向下,向左。这个顺序是顺时针排的。 不难相当,通过设定一个优先级,我们可以保证在行进过 程不会因为随机选择而出现重复情况。
• 深度优先搜索的思路是找到一条可能的路就一直那么走下 去只到走不通为止。这个走不通可能的情况很多,也许是 遇到了自然的障碍物,也就是到了死胡同走不下去了,这 个时侯只有倒退回去。
• 其实我们可以让那只老鼠变得聪明一点的。假如 我们的主角不是一只小老鼠,而是一大群,如果
你是老鼠王,你会怎么安排让你的子民们尽快逃 生?
• Thinking。。。
4/31
• 很简单,让老鼠们分头行动。我们给每一只老鼠 都配一个对讲机。从出发点开始分成四个小队, 四个小队分别分别负责四个方向,一起出发。每 次只能选择没有去过的地方走,没有去过既包括 自己没有去过也要包括别的老鼠没有去过,这个 我们可以用一个布尔数组在去过的地方标记一下, 对于小老鼠来说标记的方式可能会比较特殊。每 次到一个位置都可能会有几种不同的走法,那好, 我们把当前的这个小队再次划分,每个能走的方 向都派一个小小队去。如果没有路可走了,就呆 在那儿了。当有一队老鼠或者是一只找到了出口, 这位英雄就在对讲机里大吼一声,“哈哈,我找 到出口啦,大家到这里来”。
10/31
算法:
void BFS(VLink G[], int v)
{ int w;
VISIT(v); /*访问顶点v*/
visited[v] = 1; /*顶点v对应的访问标记置为1*/
ADDQ(Q,v);
while(!QMPTYQ(Q))
{ v = DELQ(Q); /*退出队头元素v*/
w = FIRSTADJ(G,v); /*求v的第1个邻接点。无邻接点则返回1*/
这么简单。我们还必须对过去已经到过的进行标
记。
7/31
• 另外,我们可以通过在状态之中添加一些信息而 实现更多的东西,比如路径保存,方向记录等。
• 这样我们就可以实现BFS了。参考结构见下(伪代 码)
Q[0],QNum = 1;//初始队列元素设定,QNum用于存储队列元素个数 I = 0;//指针指向队列首位 While (I < QNum){
//拓展Q[I];QNum可能会变化
I++;//指针后移 }
8/31
从法兰克福开始执行广度 优先搜索算法,所产生的 以德国城市为范例的地图, 广度优先搜索算法树。 城市间有数条道路相连接。
9/31
1、首先将根节点放入队列中。 2、从队列中取出第一个节点,并检验它是否为目标。
如果找到目标,则结束搜寻并回传结果。 否则将它所有尚未检验过的直接子节点加入队列中。 3、若队列为空,表示整张图都检查过了——亦即图中没有 欲搜寻的目标。结束搜寻并回传“找不到目标”。 4、重复步骤2。
while(w != -1)
{ if(visited[w] == 0)
• 最差情形下,BFS必须寻找所有到可能节点的所有路径, 因此其时间复杂度为 O(|V| + |E|),其中 |V| 是节点的数目, 而 |E| 是图中边的数目。
2/31
• 还是以迷宫作为引入。可怜的小老鼠被困在了迷宫里面想 要逃出去,但是它不知道到底该怎么走,无论如何还是先 选定一个方向走一下再说。
ACM算法与程序设计
第九讲
搜索专题
广度优先(BFS)
广度优先搜索算法(Breadth -First-Search)
• 也被作宽度优先搜索,或横向优先搜索,简称BFS。BFS 是从根节点开始度优先搜索的实现一般采用队列。所有因为展开节点而 得到的子节点都会被加进一个先进先出的队列中。
• 因为所有节点都必须被储存,因此BFS的空间复杂度为 O(|V| + |E|),其中 |V| 是节点的数目,而 |E| 是图中边的数 目。
• 另一种说法称BFS的空间复杂度为 O(BM),其中 B 是最大 分支系数,而 M 是树的最长路径长度。由于对空间的大 量需求,因此BFS并不适合解非常大的问题。
• 但是现实总是充满了陷阱。或许就存在这么一种路,当你 辛辛苦苦走了几十步甚至上百步之后才发现那是一个没有 未来的选择。我们可以在迷宫中给老鼠设定,上帝也可以 在人生里为我们设定。
3/31
• 我们发现固执的小老鼠就是那样子走下去了没有 回头。该怎么办才能防止这种情况的发生呢?
• 对,我们可以叫住他!“喂,那条路不能走了, 快回来!”实现起来其实很简单,就是在程序里 面加一个深度判断,如果深度达到了一个上界, 我们就不继续往下走了,也就是跳出返回。其实 这里面要涉及的还有很多,比如迭代加深搜索, A*等。
• 这就是宽度优先搜索。
• 恭喜老鼠们成功获救!可是现在的问题我们如何 在程序里面实现?
6/31
BFS的关键:队列
• 我们要模拟出小老鼠找路的过程就必须把每一个 时刻每一队小老鼠所到的位置记录下来。对于我
们来说,只有在知道当前老鼠的位置的前提下,
我们才能产生下一时间的决策。而为了达到上面
所说的拓展最短,我们就必须根据各个位置被到 达的先后顺序来拓展。这就要用到队列。
