2.2.2椭圆的简单几何性质(1)
高中数学选修2-1课时作业16:2.2.2 椭圆的简单几何性质(一)

2.2.2 椭圆的简单几何性质(一)一、选择题1.已知点(3,2)在椭圆x 2a 2+y 2b 2=1上,则( ) A.点(-3,-2)不在椭圆上B.点(3,-2)不在椭圆上C.点(-3,2)在椭圆上D.无法判断点(-3,-2)、(3,-2)、(-3,2)是否在椭圆上[答案] C[解析] 由椭圆的对称性知(-3,2)必在椭圆上.2.椭圆x 2+4y 2=1的离心率为( ) A.32 B.34 C.22 D.23[答案] A[解析] 将椭圆方程x 2+4y 2=1化为标准方程x 2+y 214=1,则a 2=1,b 2=14,即a =1,c =a 2-b 2=32,故离心率e =c a =32. 3.椭圆x 24+y 2=1的左,右焦点分别为F 1,F 2,过F 1作垂直于x 轴的直线与椭圆相交,一个交点为P ,则|PF 2|的值为( ) A.32 B. 3 C.72D.4 [答案] C[解析] 由x 24+y 2=1知,F 1,F 2的坐标分别为(-3,0),(3,0),即点P 的横坐标为x P =-3,代入椭圆方程得|y P |=12,∴|PF 1|=12. ∵|PF 1|+|PF 2|=4,∴|PF 2|=4-|PF 1|=4-12=72. 4.中心在原点,焦点在坐标轴上,离心率为32,且过点(2,0)的椭圆的方程是( )A.x 24+y 2=1 B.x 24+y 2=1或x 2+y 24=1 C.x 2+4y 2=1D.x 2+4y 2=4或4x 2+y 2=16[答案] D[解析] 若焦点在x 轴上,则a =2.又e =32,∴c = 3. ∴b 2=a 2-c 2=1,∴方程为x 24+y 2=1, 即x 2+4y 2=4.若焦点在y 轴上,则b =2.又e =32,∴b 2a 2=1-34=14, ∴a 2=4b 2=16,∴方程为x 24+y 216=1,即4x 2+y 2=16. 5.椭圆x 212+y 23=1的左焦点为F 1,点P 在椭圆上,若线段PF 1的中点M 在y 轴上,则点P 的纵坐标是( ) A.±34B.±32C.±22D.±34[答案] B[解析] 设椭圆的右焦点为F 2,由题意知PF 2⊥x 轴,因为a 2=12,b 2=3,所以c 2=a 2-b 2=9,c =3.所以点P 和点F 2的横坐标都为3.故将x =3代入椭圆方程,可得y =±32.故选B. 6.若椭圆的焦距、短轴长、长轴长构成一个等比数列,则椭圆的离心率为( )A.5-12B.3-12C.32 D.5+12 [答案] A[解析] 依题意得,4b 2=4ac ,∴b 2a 2=c a,即1-e 2=e . ∴e 2+e -1=0,∴e =5-12(舍去负值). 7.椭圆x 225+y 29=1与x 29-k +y 225-k=1(0<k <9)的关系为( ) A.有相等的长、短轴长 B .有相等的焦距C.有相同的焦点D.有相同的顶点[答案] B[解析] ∵(25-k )-(9-k )=25-9=16,∴焦距相等.二、填空题8.若点O 和点F 分别为椭圆x 22+y 2=1的中心和左焦点,点P 为椭圆上的任意一点,则|OP |2+|PF |2的最小值为________.[答案] 2[解析] 设P (x 0,y 0),而F (-1,0),∴|OP |2+|PF |2=x 20+y 20+(x 0+1)2+y 20.又y 20=1-x 202, ∴|OP |2+|PF |2=x 20+2x 0+3=(x 0+1)2+2≥2.∴|OP |2+|PF |2的最小值为2.9.若椭圆x 2a 2+y 2b 2=1的焦点在x 轴上,过点(1,12)作圆x 2+y 2=1的切线,切点分别为A ,B ,直线AB 恰好经过椭圆的右焦点和上顶点,则椭圆的方程是____________.[答案] x 25+y 24=1 [解析] ∵x =1是圆x 2+y 2=1的一条切线.∴椭圆的右焦点为(1,0),即c =1.设P (1,12),则k OP =12,∵OP ⊥AB ,∴k AB =-2,则直线AB 的方程为y =-2(x -1),它与y 轴的交点为(0,2).∴b =2,a 2=b 2+c 2=5,故椭圆的方程为x 25+y 24=1. 10.若椭圆x 2+my 2=1的离心率为32,则m =________. [答案] 14或4 [解析] 方程化为x 2+y 21m=1,则有m >0且m ≠1. 当1m<1,即m >1时,依题意有1-1m 1=32, 解得m =4,满足m >1;当1m>1,即0<m <1时,依题意有1m -11m =32, 解得m =14,满足0<m <1. 综上,m =14或4. 三、解答题 11.分别求适合下列条件的椭圆的标准方程:(1)离心率是23,长轴长是6; (2)在x 轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为6.解 (1)设椭圆的标准方程为x 2a 2+y 2b 2=1 (a >b >0)或y 2a 2+x 2b2=1 (a >b >0). 由已知得2a =6,e =c a =23,∴a =3,c =2. ∴b 2=a 2-c 2=9-4=5.∴椭圆的标准方程为x 29+y 25=1或x 25+y 29=1. (2)设椭圆的标准方程为x 2a 2+y 2b2=1 (a >b >0).如图所示,△A 1F A 2为等腰直角三角形,OF 为斜边A 1A 2上的中线(高),且|OF |=c ,|A 1A 2|=2b ,∴c =b =3,∴a 2=b 2+c 2=18,故所求椭圆的标准方程为x 218+y 29=1. 12.已知椭圆x 2a 2+y 2b 2=1(a >b >0)的两个焦点分别为F 1(-c,0),F 2(c,0)(c >0),过点E (a 2c ,0)的直线与椭圆相交于点A ,B 两点,且F 1A ∥F 2B ,|F 1A |=2|F 2B |,求椭圆的离心率.解 由F 1A ∥F 2B ,|F 1A |=2|F 2B |,得|EF 2||EF 1|=|F 2B ||F 1A |=12, 从而a 2c -c a 2c+c =12,整理得a 2=3c 2. 故离心率e =c a =33. 13.已知椭圆E 的中心为坐标原点O ,两个焦点分别为A (-1,0),B (1,0),一个顶点为H (2,0).(1)求椭圆E 的标准方程;(2)对于x 轴上的点P (t,0),椭圆E 上存在点M ,使得MP ⊥MH ,求实数t 的取值范围. 解 (1)由题意可得,c =1,a =2,∴b = 3.∴所求椭圆E 的标准方程为x 24+y 23=1.(2)设M (x 0,y 0)(x 0≠±2),则x 204+y 203=1.①MP →=(t -x 0,-y 0),MH →=(2-x 0,-y 0), 由MP ⊥MH 可得MP →·MH →=0, 即(t -x 0)(2-x 0)+y 20=0.② 由①②消去y 0,整理得 t (2-x 0)=-14x 20+2x 0-3.∵x 0≠2,∴t =14x 0-32.∵-2<x 0<2,∴-2<t <-1.∴实数t 的取值范围为(-2,-1).。
椭圆的简单几何性质

椭圆的简单几何性质
1. 椭圆是一个由平面上所有离两个固定点(称为焦点)距离之和等于常数的点构成的几何图形。
2. 椭圆的长轴和短轴分别为椭圆的两条相互垂直的轴,长轴的长度是椭圆的两个焦点之间的距离,而短轴的长度是椭圆的两个焦点到中心点的距离。
3. 任意一条椭圆轴与椭圆相交的点称为端点,一个椭圆有四个端点。
4. 椭圆上任意一点到两个焦点距离之和等于常数,这个常数称为椭圆的长轴的长度。
5. 椭圆的离心率是一个非负实数,等于椭圆的长轴与短轴之差的一半除以椭圆长轴的长度。
6. 椭圆的面积等于长轴和短轴所围成矩形的面积的1/4乘以π。
2.2.2椭圆的几何性质1(高二数学精品课件)

B2
A1
F1
b
oc
a
A2
F2
B1
结论 :通过上面的分析,我们得到判断曲线 是否对称的方法:
以-x代换x,若方程不变,则曲线关于y轴对称;若以
-y代换y,方程不变,曲线关于x轴对称;
同时以- x代换x,以- y代换y,方程不变,则方 程关于坐标原点对称.
二、椭圆
简单的几何性质
1 b2
1得:
-b≤y≤b 知
椭圆落在x=±a,y= ± b组成的矩形中 y
B2
A1
F1
b
oc
a
A2
F2
B1
椭圆的对称性
Y
P1(-x,y)
P(x,y)
O
X
P2(-x,-y)
2、对称性:
从图形上看,椭圆关于x轴、y轴、原点对称。 从方程上看: (1)把x换成-x方程不变,图象关于y轴对称; (2)把y换成-y方程不变,图象关于x轴对称;
长半轴长为a,短 半轴长为b. a>b
e c a
a2=b2+c2
x2 b2
y2 a2
1(a
b
0)
|x|≤ b,|y|≤ a
同前 (b,0)、(-b,0)、 (0,a)、(0,-a) (0 , c)、(0, -c)
同前
同前
同前
例1已知椭圆方程为9x2+25y2=225,
它的长轴长是: 10 。短轴长是: 6 。
(1) x2 y2 1
32
(2)
x2 y2 1 36 100
(3) 16x2+25y2=400
高二数学人教A版选修2-1课件:2.2.2 椭圆的简单几何性质 第1课时 椭圆的简单几何性质

F1 o
F2
x
说明椭圆的对称性不随位置的改变而改变.
3.顶点与长短轴: 椭圆与它的对称轴的四个 交点——椭圆的顶点. 椭圆顶点坐标为:
A1(-a,0),A2(a,0),
B1(0,-b),B2(0,b).
回顾: 焦点坐标(±c,0)
x2 a2
y2 b2
=1(a>b>0)
y
B2(0,b)
固化
模式
拓展
小思 考
TIP1:听懂看到≈认知获取;
TIP2:什么叫认知获取:知道一些概念、过程、信息、现象、方法,知道它们 大 概可以用来解决什么问题,而这些东西过去你都不知道;
TIP3:认知获取是学习的开始,而不是结束。
为啥总是听懂了, 但不会做,做不好?
高效学习模型-内外脑 模型
2
内脑- 思考内化
学习知识的能力 (学习新知识 速度、质量等)
长久坚持的能力 (自律性等)
什么是学习力-常见错误学 习方式
案例式
学习
顺序式 学习
冲刺式 学习
什么是学习力-高效学习必
备习惯
积极
以终
主动
为始
分清 主次
不断 更新
高效学习模型
高效学习模型-学习的完
整过程
方向
资料
筛选
认知
高效学习模型-学习的完
整过程
消化
思维导图& 超级记忆法& 费曼学习法
1
外脑- 体系优化
知识体系& 笔记体系
内外脑高效学习模型
超级记忆法
超级记忆法-记忆 规律
记忆前
选择记忆的黄金时段
前摄抑制:可以理解为先进入大脑的信息抑制了后进 入大脑的信息
2.2.2椭圆的简单几何性质课件人教新课标2

即2x+3y-12=0,选B.
(2)①设椭圆C的长半轴长为a(a>0),短半轴长为b(b>0),
则2b=4,由 a2 b2 3,
a
2
解得a=4,b=2.
因为椭圆C的对称轴为坐标轴,
所以椭圆C的方程为 x2 y2 1 或 y2 x2 1.
16 4
16 4
②设直线l的方程为y=x+m,A(x1,y1),B(x2,y2),
3
3
从而y中=x中+1= 2 1 1,
33
所以中点坐标为 ( 2 , 1).
33
【补偿训练】椭圆x2+4y2=16被直线 y 1 x 1 截得的弦长为
2
____________.
x2 4y2 16,
【解析】由
y
1 x 1, 2
消去y并化简得x2+2x-6=0.
设直线与椭圆的交点为M(x1,y1),N(x2,y2),
1.
12
4
(2)设M(x1,y1),N(x2,y2).
所以|AM|=|AN|,所以A在线段MN的垂直平分线上,
把M(x1,y1),N(x2,y2)分别代入椭圆C:1x22
y2 4
1
得:
x12 y12 1,
①
12 4
x22
y
2 2
1,
②
12 4
用①减去②得:x1 x2 x1 x2 y1 y2 y1 y2 ,
类型二 弦长及中点弦问题
【典例2】
(1)椭圆4x2+9y2=144内一点P(3,2),过点P的弦恰好以P为中
点,那么这弦所在的直线方程为( )
A.3x+2y-12=0
2.2.2椭圆的简单几何性质(1)

研一研· 问题探究、课堂更高效
2.2.2
问题 5 比较下列椭圆的形状, 哪一个更圆, 哪一个更扁? 为什么?
2 2 x y 4x2+9y2=36 与 + =1 25 20 2 2 x y 答案 将椭圆方程 4x2+9y2=36 化为标准方程 9 + 4 =1,
则 a2=9,b2=4,所以 a=3,c= a2-b2= 5,故离心 5 x 2 y2 率 e= 3 ;椭圆25+20=1 中,a2=25,b2=20,则 a=5, 5 2 2 c= a -b = 5,故离心率 e= 5 .
解
x y 把椭圆的方程化为标准方程 9 + 4 =1.
可知此椭圆的焦点在 x 轴上,且长半轴长 a=3, 短半轴长 b=2;又得半焦距 c= a2-b2= 9-4= 5 因此,椭圆的长轴长 2a=6,短轴长 2b=4;两个焦点 的坐标分别是(- 5,0),( 5,0);四个顶点的坐标分 5 c 别是(-3,0),(3,0),(0,-2),(0,2);离心率 e=a= 3 .
研一研· 问题探究、课堂更高效
b c 问题 4(1)a或b的大小能刻画椭圆的扁平程度吗?为什么? c (2)你能运用三角函数的知识解释,为什么 e=a越大,椭 c 圆越扁?e=a越小,椭圆越圆吗? a2-c2 b 2 答案 (1)都能.由a= 2 = 1-e (0<e<1)可知, a
b 当 e 越趋近于 1 时,a越趋近于 0,椭圆越扁;当 e 越趋 b 近于 0 时,a越趋近于 1,椭圆越接近于圆.当且仅当 a =b 时,c=0,两焦点重合,图形变为圆。 c (2)如图,在 Rt△ BF2O 中,cos∠ BF2O= , a c c 越大,∠BF2O 越小,椭圆越扁; 越小, a a
由于前一个椭圆的离心率较大, 因此前一个椭圆更扁, 后 一个椭圆更圆.
【优化方案】2012高中数学 第2章2.2.2第一课时椭圆的简单几何性质课件 新人教A版选修2-1

求椭圆的离心率 求椭圆的离心率的常见思路:一是先求 , , 求椭圆的离心率的常见思路:一是先求a,c, 再计算e;二是依据条件中的关系,结合有关 再计算 ;二是依据条件中的关系, 知识和a、 、 的关系 构造关于e的方程 的关系, 的方程, 知识和 、b、c的关系,构造关于 的方程,再 求解.注意 的范围 的范围: 求解.注意e的范围:0<e<1.
互动探究1 互动探究
若本例中椭圆方程变为: 若本例中椭圆方程变为:“4x2+y2
=1”,试求解. ” 试求解.
y 2 x2 1 解:已知方程为 + =1,所以 a=1,b= ,c , = , = 1 1 2 4 = 3 1 1- = ,因此,椭圆的长轴的长和短轴的 因此, - 4 2
c 3 长分别为 = 长分别为 2a=2,2b=1,离心率 e=a= ,两个 = , = 2 焦点分别为 个顶点是
x2 . 2=1(a>b>0). b c 2 由已知得 e=a= ,2b=8 5, = = , 3 a 2- b 2 4 c ∴ 2= 2 = ,b2=80. 9 a a
2
∴a2=144. y y x x ∴所求椭圆的标准方程为 + =1 或 + 144 80 144 80 =1. y2 x2 (2) 设 椭 圆 方 程 为 2 + 2 = a b 1(a>b>0).如图所示,△A1FA2 为 .如图所示, 等腰直角三角形, OF 等腰直角三角形, 为斜边 A1A2 的中线(高 , 的中线 高),且|OF|=c,|A1A2|= = , = 2 2 2 2b,∴c=b=4,∴a =b +c =32,故所求椭圆 , , = = , x2 y 2 的方程为 + =1. 32 16
为直角三角形, 由 AF1 ⊥ AF2 知 △ AF1F2 为直角三角形 , 且 ∠ AF2F1=60°. 由椭圆定义, 由椭圆定义,知|AF1|+|AF2|=2a,|F1F2|=2c.则 + = , = 则 在 Rt△AF1F2 中,由∠AF2F1=60°得|AF2|=c, △ 得 = , |AF1|= 3c,所以|AF1|+|AF2|=2a=( 3+1)·c, ,所以 = + = = + , c 所以离心率 e=a= 3-1. = -
2.2.2椭圆的简单几何性质1

-2≤x ≤2
-4≤y ≤4
Y
二、椭圆的对称性
关于y轴对称
P(x,y)
P2(-x,y)
O
X
关于原点对称
P3(-x,-y)
P1(x,-y)
关于x轴对称
结论:坐标轴是椭圆的对称轴,原点是椭圆的对称中心 中心:椭圆的对称中心叫做椭圆的中心
三、顶点
y B1(0,b)
A (-a,0) 1
2a
F1
2b
2c
F2
例2
0 椭圆的一个顶点为 A2, ,其长轴长是短轴
长的2倍,求椭圆的标准方程.
分析:题目没有指出焦点的位置,要考虑两种位置
a 0 解:(1)当 A2, 为长轴端点时,
2 ,b 1,
x2 y2 椭圆的标准方程为: 1 ; 4 1 0 (2)当 A2, 为短轴端点时, b 2 , a
x2 y2 2 1 2 b a
a b 0
|x| a |y| b (c,0)、(c,0) (a,0)、(0,b)
c e a
|x| b |y| a
对称性
关于x轴、y轴、原点对称 (0,c)、(0,c) (b,0)、(0,a)
焦
顶
点
点
离心率
例1 求椭圆 16 x2 + 25y2 =400的长轴和短轴的长、离心
当椭圆的焦点在 ,b2 a 9
2
y 轴上时,
k 8
,得 c 1 k .
2
1 5 1 k 1 ,即 k . 由e ,得 9 4 2 4
5 ∴满足条件的 k 4 或 k . 4
小结:
1.知识小结:
(1) 学习了椭圆的范围、对称性、顶点坐标、离 心率等概念及其几何意义。 (2) 研究了椭圆的几个基本量a,b,c,e及顶点、 焦点、对称中心及其相互之间的关系
2.2.2椭圆的简单几何性质

(b,0)、(0,a)
(0<e<1)
离心率
例题精析 例1求椭圆16x2+25y2=400的长轴和短轴的长、 离心率、焦点和顶点坐标并画出简图.
解:把已知方程化成标准方程 这里, 5 , b 4 , c a 离心率 e
c a 3 5 0 .6
x 5
2 2
y 4
2 2
B1(0,-b)
③焦点必在长轴上;
小试身手:
2
2.说出 9 1 6 1 下列椭圆的范围,长轴 长,短轴长,焦点坐标,顶点坐标:
x
y
2
3 x 3, 4 y 4
2a 8, 2b 6
(0,
7)
(0, 4), (3, 0)
椭圆的焦距与长轴长的比e
∵a>c>0, ∴0 < e <1.
当e b c a a
2
椭圆的简单几何性质 4.离心率: c
a
叫做椭圆的离心率.
1, c a , c
2
0 , 椭圆 扁
当e b
c a a
2
0, c 0, c
2
a , 椭圆 圆
离心率越大,椭圆越扁 当且仅当a=b时,c=0,这时两个 焦点重合,图形变为圆. 离心率越小,椭圆越圆
y a
2 2
x
x b
2 2
1( a b 0 )
焦点为 F1(-c,0)、F2(c,0)
焦点为 F1(0 ,-c)、F2(0,c)
椭圆的简单几何性质
1.范围
x a
2 2
x a
2 2
y b
第2章2.2.2 椭圆的简单几何性质(一)

高考调研 ·新课标 ·数学选修2-1
例 2 根据下列条件,求中心在原点,对称轴在坐标轴上的 椭圆方程.
(1)焦点在 x 轴上,一个焦点与短轴的两端点连线互相垂直, 且半焦距为 6;
(2)与椭圆x92+y42=1 有相同的焦点,且离心率 e= 55; (3)以直线 3x+4y-12=0 与两坐标轴的交点分别作为顶点 和焦点.
第25页
高考调研 ·新课标 ·数学选修2-1
互动 2 (1)ba与bc的大小能刻画椭圆的扁平程度吗?为什 么?
(2)你能运用三角函数的知识解释,为什么 e=ca越大,椭圆 越扁?e=ac越小,椭圆越圆?
第26页
高考调研 ·新课标 ·数学选修2-1
【解析】 (1)都能.由ba= a2-a2 c2= 1-e2(0<e<1)可知, 当 e 越趋近于 1 时,ba越趋近于 0,椭圆越扁;当 e 越趋近于 0 时, ba越趋近于 1,椭圆越接近于圆.当且仅当 a=b 时,c=0,两焦 点重合,图形变为圆,方程为 x2+y2=a2.
【解析】 把已知方程化成标准方程为2y52 +x2=1. 这里 a=5,b=1,所以 c= 25-1=2 6. 因此,椭圆的长轴和短轴的长分别是 2a=10 和 2b=2,两个焦 点分别是 F1(0,-2 6),F2(0,2 6),椭圆的四个顶点是 A1(0,- 5),A2(0,5),B1(-1,0)和 B2(1,0).
第29页
高考调研 ·新课标 ·数学选修2-1
【解析】 (1)将椭圆方程 4x2+9y2=36 化为标准方程x92+y42
=1,则 a2=9,b2=4,所以 a=3,c= a2-b2= 5,故离心率 e = 35;椭圆2x52+2y02 =1 中,a2=25,b2=20,则 a=5,c= a2-b2
2.2.2椭圆的简单几何性质(1)

练习:已知椭圆的中心在原点,焦点在坐标 轴上,长轴是短轴的三倍,且椭圆经过点P (3,0),求椭圆的方程。
2a 3 2b
a 3, b 1
a 3b
或b 3,a 9
x2 x2 y 2 2 y 1或 1 9 9 81
分类讨论的数学思想
练习:已知椭圆中心在原点,它在x轴的一个焦点与短轴的 两个端点的连线互相垂直,且这个焦点与较近的长轴的端 点距离为 10 5,求这个椭圆方程。
c sin 75 6 e a sin 45 sin 60 3
MF1
MF2
F1 F2
题型三:椭圆的离心率问题 例3(3) :已知F1为椭圆的左焦点,A,B分别为椭圆的右顶
点和上顶点,P为椭圆上的点,当PF1 F1A,,PO AB(O为 椭圆中心)时,求椭圆的离心率.
解: ⑴方法一: 设方程为mx2+ny2=1(m>0,n>0,m≠n), 将点的坐标方程,求出m=1/9,n=1/4。
x2 y 2 所求椭圆方程为: 1 9 4 注:待定系数法求椭圆标准方程的步骤:
⑴定位; ⑵定量
题型二:利用椭圆的几何性质求标准方程
例2 求适合下列条件的椭圆的标准方程 ⑴经过点P(-3,0)、Q(0,-2); ⑵长轴长等于20,离心率3/5。 ⑶一焦点将长轴分成2:1的两部分,且经过点 P 3 2, 4
A1
b F1
a F2
A2
o c
B1
3、椭圆的顶点(截距) 2 2 x y 2 1(a b 0) 2 a b
令 x=0,得 y=?,说明椭圆与 y轴的交点? 令 y=0,得 x=?说明椭圆与 x轴的交点? *顶点:椭圆与它的对称轴 的四个交点,叫做椭圆的 顶点。
(部编版)2020学年高中数学第二章2.2.2椭圆的简单几何性质第一课时椭圆的简单几何性质学案含解析

第一课时椭圆的简单几何性质[提出问题]图中椭圆的标准方程为x2 a2+y2b2=1(a>b>0).问题1:椭圆具有对称性吗?提示:有.椭圆是以原点为对称中心的中心对称图形,也是以x轴、y轴为对称轴的轴对称图形.问题2:可以求出椭圆与坐标轴的交点坐标吗?提示:可以,令y=0得x=±a,故A1(-a,0),A2(a,0),同理可得B1(0,-b),B2(0,b).问题3:椭圆方程中x,y的取值范围是什么?提示:x∈[-a,a],y∈[-b,b].问题4:当a的值不变,b逐渐变小时,椭圆的形状有何变化?提示:b越小,椭圆越扁.[导入新知]椭圆的简单几何性质1.由不等式x 2a 2=1-y 2b 2≤1可得|x |≤a ,由y 2b 2=1-x 2a2≤1可得|y |≤b ,从而可得椭圆的范围.2.椭圆有四个顶点、两个焦点共六个特殊点,研究椭圆时一定要注意这六个特殊点的位置,注意长轴长是2a ,而不是a .3.椭圆的离心率e 的大小,描述了椭圆的扁平程度.e 越接近1,则c 就越接近a ,从而b =a 2-c 2越小,因此,椭圆越扁;反之,e 越接近0,则c 就越接近0,从而b 越接近a ,这时椭圆越接近圆.特别地,当a =b 时,c =0,椭圆就变为圆了,此时方程为x 2+y 2=a 2.[例1] 求椭圆4x 2+9y 2=36 [解] 椭圆方程变形为x 29+y 24=1,∴a =3,b =2,∴c = a 2-b 2=9-4= 5.∴椭圆的长轴长和焦距分别为2a =6,2c =25, 焦点坐标为F 1(-5,0),F 2(5,0),顶点坐标为A 1(-3,0),A 2(3,0),B 1(0,-2),B 2(0,2), 离心率e =c a =53. [类题通法]求椭圆的性质时,应把椭圆化为标准方程,注意分清楚焦点的位置,这样便于直观地写出a ,b 的数值,进而求出c ,求出椭圆的长轴和短轴的长、离心率、焦点和顶点的坐标等几何性质.[活学活用]已知椭圆C 1:x 2100+y 264=1,设椭圆C 2与椭圆C 1的长轴长、短轴长分别相等,且椭圆C 2的焦点在y 轴上.(1)求椭圆C 1的长半轴长、短半轴长、焦点坐标及离心率; (2)写出椭圆C 2的方程,并研究其性质.解:(1)由椭圆C 1:x 2100+y 264=1可得其长半轴长为10,短半轴长为8,焦点坐标(6,0),(-6,0),离心率e =35.(2)椭圆C 2:y 2100+x 264=1, 性质:①范围:-8≤x ≤8,-10≤y ≤10; ②对称性:关于x 轴、y 轴、原点对称;③顶点:长轴端点(0,10),(0,-10),短轴端点(-8,0),(8,0); ④离心率:e =35.[例2] (1)长轴长是10,离心率是45;(2)在x 轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为6. [解] (1)设椭圆的标准方程为x 2a 2+y 2b 2=1(a >b >0)或y 2a 2+x 2b2=1(a >b >0). 由已知得2a =10,a =5.又∵e =c a =45,∴c =4.∴b 2=a 2-c 2=25-16=9.∴椭圆的标准方程为x 225+y 29=1或y 225+x 29=1.(2)依题意可设椭圆的标准方程为x 2a 2+y 2b2=1(a >b >0).如图所示,△A 1FA 2为一等腰直角三角形,OF 为斜边A 1A 2的中线(高),且|OF |=c ,|A 1A 2|=2b , 则c =b =3,a 2=b 2+c 2=18, 故所求椭圆的标准方程为x 218+y 29=1.[类题通法](1)利用椭圆的几何性质求椭圆的标准方程时,通常采用待定系数法,其步骤是: ①确定焦点位置.②设出相应椭圆的方程(对于焦点位置不确定的椭圆可能有两种标准方程).③根据已知条件构造关于参数的关系式,利用方程(组)求参数.列方程(组)时常用的关系式为b 2=a 2-c 2,e =c a等.(2)在椭圆的简单性质中,轴长、离心率不能确定椭圆的焦点位置,因此仅依据这些条件确定的椭圆方程可能有两个.[活学活用]求适合下列条件的椭圆的标准方程. (1)焦点在x 轴上,短轴长为2,离心率e =22; (2)长轴长是短轴长的5倍,且过点A (5,0).解:(1)设椭圆的标准方程为x 2a 2+y 2b2=1(a >b >0),由题意知⎩⎪⎨⎪⎧a 2=b 2+c 2,c a =22,2b =2,解得a =2,b =1,因此,椭圆的标准方程为x 22+y 2=1.(2)若椭圆焦点在x 轴上,设其标准方程为x 2a 2+y2b 2=1(a >b >0),由题意得⎩⎪⎨⎪⎧2a =5×2b ,25a 2+0b2=1,解得⎩⎪⎨⎪⎧a =5,b =1.故所求椭圆的标准方程为x 225+y 2=1;若焦点在y 轴上,设其标准方程为y 2a 2+x 2b2=1(a >b >0),由题意,得⎩⎪⎨⎪⎧2a=5×2b ,0a 2+25b 2=1,解得⎩⎪⎨⎪⎧a =25,b =5.故所求椭圆的标准方程为y 2625+x 225=1.综上所述,所求椭圆的标准方程为x 225+y 2=1或y 2625+x 225=1.[例3] 如图,已知F 1P 为椭圆上的一点,当PF 1⊥F 1A ,PO ∥AB (O 为椭圆的中心)时,求椭圆的离心率.[解] 由已知可设椭圆的标准方程为x 2a 2+y 2b 2=1(a >b >0), 则由题意可知P ⎝⎛⎭⎪⎫-c ,b 2a .∵△PF 1O ∽△BOA ,∴PF 1BO =F 1OOA ,∴b 2a b =c a,即b =c , ∴a 2=2c 2,∴e =ca =22. [类题通法]椭圆的离心率的求法求椭圆的离心率,关键是寻找a 与c 的关系,一般地: (1)若已知a ,c ,则直接代入e =c a求解; (2)若已知a ,b ,则由e =1-⎝ ⎛⎭⎪⎫b a 2求解;(3)若已知a ,b ,c 的关系,则可转化为a ,c 的齐次式,再转化为含e 的方程求解即可. [活学活用]若椭圆的两个焦点与短轴的一个端点构成一个正三角形,则该椭圆的离心率为( ) A.12 B.32 C.34 D.64 解析:选A 依题意,△BF 1F 2是正三角形.∵在Rt △OBF 2中,|OF 2|=c ,|BF 2|=a ,∠OF 2B =60°,∴a cos 60°=c ,∴c a=12,即椭圆的离心率e =12.4.忽视椭圆焦点位置致误[典例] 已知椭圆的中心在原点,对称轴是坐标轴,离心率e =32,且过P (2,3),求此椭圆的标准方程. [解] (1)当焦点在x 轴上时, 设椭圆的标准方程为x 2a 2+y2b 2=1(a >b >0). 由题意知⎩⎪⎨⎪⎧c a =32,4a 2+9b 2=1,a 2=b 2+c 2,解得b 2=10,a 2=40.所以所求椭圆的标准方程为x 240+y 210=1. (2)当焦点在y 轴上时,设椭圆的标准方程为y 2a 2+x 2b2=1(a >b >0).由题意得⎩⎪⎨⎪⎧c a =32,9a 2+4b 2=1,a 2=b 2+c 2,解得b 2=254,a 2=25.所以所求椭圆的标准方程为y 225+x 2254=1. 综上,所求椭圆的标准方程为x 240+y 210=1或y 225+x 2254=1.[易错防范]求解时不讨论焦点的位置,而默认为椭圆的焦点在x 轴上,这是最常见的错解. [成功破障] 若椭圆x 2k +8+y 29=1的离心率e =12,则k 的值等于________. 解析:分两种情况进行讨论:当焦点在x 轴上时,a 2=k +8,b 2=9,得c 2=k -1, 又∵e =12,∴k -1k +8=12,解得k =4. 当焦点在y 轴上时,a 2=9,b 2=k +8,得c 2=1-k , 又∵e =12,解得k =-54.∴k =4或k =-54.答案:4或-54[随堂即时演练]1.中心在原点,焦点在x 轴上,若长轴长为18,且两个焦点恰好将长轴3等分,则此椭圆的标准方程是( ) A.x 281+y 272=1 B.x 281+y 29=1 C.x 281+y 245=1 D.x 281+y 236=1 解析:选A 因为2a =18,2c =13×2a =6,所以a =9,c =3,b 2=81-9=72.2.椭圆C 1:x 225+y 29=1与椭圆C 2:x 225-k +y 29-k =1(k <9)( )A .有相同的长轴B .有相同的短轴C .有相同的焦点D .有相等的离心率解析:选C 25-9=(25-k )-(9-k ),故两椭圆有相同的焦点. 3.椭圆x 2+4y 2=16的短轴长为________. 解析:由x 216+y 24=1可知b =2, ∴短轴长2b =4. 答案:44.直线x +2y -2=0经过椭圆x 2a 2+y 2b2=1(a >b >0)的一个焦点和一个顶点,则该椭圆的离心率e =________.解析:由题意知椭圆焦点在x 轴上, ∴在直线x +2y -2=0中, 令y =0得c =2;令x =0得b =1. ∴a =b 2+c 2= 5.∴e =c a =255.答案:2555.求适合下列条件的椭圆的标准方程: (1)中心在坐标原点,长轴在x 轴上,离心率为32,且椭圆上一点到两个焦点的距离之和为12; (2)对称轴是坐标轴,一个焦点是(0,7),一个顶点是(9,0). 解:(1)由题意设椭圆的标准方程为x 2a 2+y 2b 2=1(a >b >0), ∵椭圆上一点到两个焦点的距离之和为12, ∴2a =12,即a =6. ∵椭圆的离心率为32, ∴e =c a =a 2-b 2a =36-b 26=32,∴b 2=9.∴椭圆的标准方程为x 236+y 29=1.(2)由题意知椭圆的焦点在y 轴上,可设椭圆的标准方程为y 2a 2+x 2b2=1(a >b >0),则b =9.因为c =7,所以a 2=b 2+c 2=81+49=130, ∴椭圆的标准方程为y 2130+x 281=1.[课时达标检测]一、选择题1.椭圆以两条坐标轴为对称轴,一个顶点是(0,13),另一个顶点是(-10,0),则焦点坐标为( ) A .(±13,0) B .(0,±10) C .(0,±13)D .(0,±69)解析:选D 由题意知椭圆焦点在y 轴上,且a =13,b =10, 则c =a 2-b 2=69,故焦点坐标为(0,±69).2.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点为F 1,F 2,离心率为33,过F 2的直线l 交C 于A ,B 两点.若△AF 1B 的周长为43,则C 的方程为( )A.x 23+y 22=1B.x 23+y 2=1C.x 212+y 28=1 D.x 212+y 24=1 解析:选A 由椭圆的性质知|AF 1|+|AF 2|=2a ,|BF 1|+|BF 2|=2a ,∴a = 3. 又∵e =33, ∴c =1.∴b 2=a 2-c 2=2, ∴椭圆的方程为x 23+y 22=1.3.已知椭圆x 2a 2+y 2b 2=1与椭圆x 225+y 216=1有相同的长轴,椭圆x 2a 2+y 2b 2=1的短轴长与椭圆y 221+x 29=1的短轴长相等,则( )A .a 2=25,b 2=16 B .a 2=9,b 2=25C .a 2=25,b 2=9或a 2=9,b 2=25 D .a 2=25,b 2=9解析:选D 因为椭圆x 225+y 216=1的长轴长为10,焦点在x 轴上,椭圆y 221+x 29=1的短轴长为6,所以a 2=25,b 2=9.4.已知椭圆x 2a 2+y 2b 2=1(a >b >0)的左焦点为F ,右顶点为A ,点B 在椭圆上,且BF ⊥x 轴,直线AB 交y 轴于点P .若AP ―→=2PB ―→,则椭圆的离心率是( )A.32 B.22C.13D.12解析:选D ∵AP ―→=2PB ―→, ∴|AP ―→|=2|PB ―→|. 又∵PO ∥BF , ∴|PA ||AB |=|AO ||AF |=23, 即aa +c =23, ∴e =c a =12.5.椭圆mx 2+ny 2+mn =0(m <n <0)的焦点坐标是( ) A .(0,±m -n ) B .(±m -n ,0) C .(0,±n -m )D .(±n -m ,0)解析:选C 化为标准方程是x2-n +y2-m=1,∵m <n <0,∴0<-n <-m .∴焦点在y 轴上,且c =-m --n =n -m . 二、填空题6.与椭圆9x 2+4y 2=36有相同焦点,且短轴长为45的椭圆方程是________________.解析:椭圆9x 2+4y 2=36可化为x 24+y 29=1,因此可设待求椭圆为x 2m +y 2m +5=1.又因为b =25,故m =20,得x 220+y 225=1. 答案:x 220+y 225=17.椭圆x 24+y 2m =1的离心率为12,则m =________.解析:当焦点在x 轴上时,4-m 2=12⇒m =3; 当焦点在y 轴上时,m -4m=12⇒m =163. 综上,m =3或m =163.答案:3或1638.已知椭圆的中心在原点,焦点在x 轴上,离心率为55, 且过点P (-5,4),则椭圆的方程为__________. 解析:∵e =c a =55, ∴c 2a 2=a 2-b 2a 2=15, ∴5a 2-5b 2=a 2, 即4a 2=5b 2.设椭圆的标准方程为x 2a 2+5y 24a2=1(a >0).∵椭圆过点P (-5,4),∴25a 2+5×164a 2=1,解得a 2=45.∴椭圆的方程为x 245+y 236=1. 答案:x 245+y 236=1三、解答题※ 推 荐 ※ 下 载 ※ 椭圆C 于A ,B 两点,且△ABF 2的周长为16,求椭圆C 的标准方程.解:设椭圆C 的标准方程为x 2a 2+y 2b 2=1(a >b >0). 由e =22知c a =22,故c 2a 2=12, 从而a 2-b 2a 2=12,b 2a 2=12. 由△ABF 2的周长为|AB |+|BF 2|+|AF 2|=|AF 1|+|AF 2|+|BF 1|+|BF 2|=4a =16,得a =4,∴b 2=8. 故椭圆C 的标准方程为x 216+y 28=1. 10.椭圆x 2a 2+y 2b2=1(a >b >0)的右顶点是A (a,0),其上存在一点P ,使∠APO =90°,求椭圆离心率的取值范围. 解:设P (x ,y ),由∠APO =90°知,点P 在以OA 为直径的圆上,圆的方程是:⎝ ⎛⎭⎪⎫x -a 22+y 2=⎝ ⎛⎭⎪⎫a 22, 所以y 2=ax -x 2.① 又因为P 点在椭圆上,故x 2a 2+y 2b2=1.② 把①代入②化简,得(a 2-b 2)x 2-a 3x +a 2b 2=0,即(x -a )[(a 2-b 2)x -ab 2]=0.∵x ≠a ,x ≠0, ∴x =ab 2a 2-b2,又0<x <a , ∴0<ab 2a 2-b 2<a ,即2b 2<a 2. 由b 2=a 2-c 2,得a 2<2c 2,所以e >22. 又∵0<e <1,∴22<e <1, 即椭圆离心率的取值范围是⎝⎛⎭⎪⎫22,1.。
2.2.2椭圆的简单几何性质(优秀经典公开课比赛课件)

y2 a2
x2 b2
1(a
b
0)
A2 y
F2
B2
B1 O x
F1
A1
|x|≤b, |y| ≤ a
关于两轴即原点对称
(±b,0), (0,±a) 长轴2a, 短轴2b
F1(0,-c),F2(0,c) 2c
e=c/a, 0<e<1
例1、如图,一种电影放映灯泡的反射镜面是旋 转椭圆面(椭圆绕其对称轴旋转一周形成的曲面) 的一部分。过对称轴的截口ABC是椭圆的一部分, 灯丝位于椭圆的一个焦点F1上,片门位于另一个 焦点F2上,由椭圆一个焦点F1发出的光线,经过 旋转椭圆面反射后集中到另一个焦点F2。已知 ACF1F2,|F1A|=2.8cm,|F1F2|=4.5cm,求截口 ABC所在椭圆的方程。 y
关于两轴即原点对称
(±b,0), (0,±a) 长轴2a, 短轴2b
F1(0,-c),F2(0,c) 2c
e=c/a, 0<e<1
三、小结作业
本节重点: 1、范围; 2、对称性; 3、顶点、长半轴长、短半轴长、半焦距; 4、离心率; 5、已知两点求椭圆的标准方程; 作业: P49 3、4、5 B组3
离心率为0.6 ;
焦点坐标为(-3,0),(3,0)
Y
顶点坐标为
(-5,0),(5,0), (0,4),(0,-4)
O
X
例2、求符合下列条件的椭圆的标准方程: (1)经过点(-3,0)、(0,-2); (2)长轴的长等于20,离心率等于0.6
(1)解:易知a=3,b=2 又因为长轴在x轴上,
所以椭圆的标准方程为 x2 y2 1 94
O
第二章 2.2.2 第1课时 椭圆的几何性质
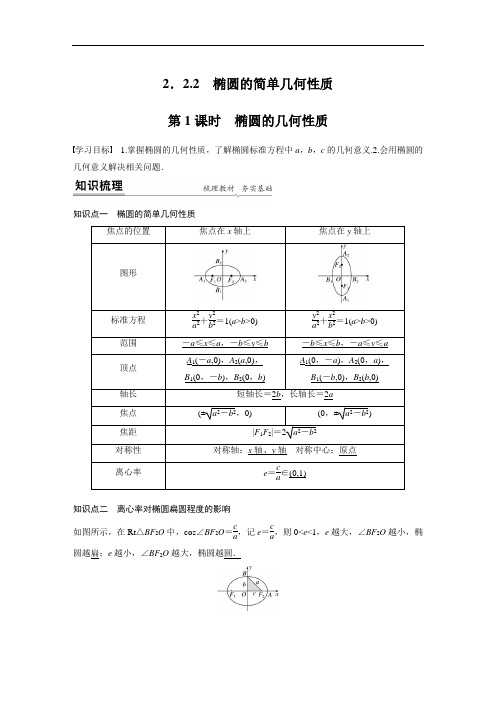
2.2.2椭圆的简单几何性质第1课时椭圆的几何性质学习目标 1.掌握椭圆的几何性质,了解椭圆标准方程中a,b,c的几何意义.2.会用椭圆的几何意义解决相关问题.知识点一椭圆的简单几何性质焦点的位置焦点在x轴上焦点在y轴上图形标准方程x2a2+y2b2=1(a>b>0)y2a2+x2b2=1(a>b>0)范围-a≤x≤a,-b≤y≤b -b≤x≤b,-a≤y≤a顶点A1(-a,0),A2(a,0),B1(0,-b),B2(0,b)A1(0,-a),A2(0,a),B1(-b,0),B2(b,0)轴长短轴长=2b,长轴长=2a焦点(±a2-b2,0)(0,±a2-b2) 焦距|F1F2|=2a2-b2对称性对称轴:x轴、y轴对称中心:原点离心率e=ca∈(0,1) 知识点二离心率对椭圆扁圆程度的影响如图所示,在Rt△BF2O中,cos∠BF2O=ca,记e=ca,则0<e<1,e越大,∠BF2O越小,椭圆越扁;e越小,∠BF2O越大,椭圆越圆.1.椭圆x 2a 2+y 2b 2=1(a >b >0)的长轴长是a .( × )2.椭圆的离心率e 越大,椭圆就越圆.( × )3.若椭圆的对称轴为坐标轴,长轴长与短轴长分别为10,8,则椭圆的方程为x 225+y 216=1.( × )4.设F 为椭圆x 2a 2+y 2b 2=1(a >b >0)的一个焦点,M 为其上任一点,则|MF |的最大值为a +c (c 为椭圆的半焦距).( √ )一、椭圆的简单几何性质例1 求椭圆m 2x 2+4m 2y 2=1(m >0)的长轴长、短轴长、焦点坐标、顶点坐标和离心率. 解 由已知得x 21m 2+y 214m 2=1(m >0),因为0<m 2<4m 2,所以1m 2>14m2,所以椭圆的焦点在x 轴上,并且长半轴长a =1m ,短半轴长b =12m ,半焦距c =32m,所以椭圆的长轴长2a =2m ,短轴长2b =1m ,焦点坐标为⎝⎛⎭⎫-32m ,0,⎝⎛⎭⎫32m ,0,顶点坐标为⎝⎛⎭⎫1m ,0,⎝⎛⎭⎫-1m ,0,⎝⎛⎭⎫0,-12m ,⎝⎛⎭⎫0,12m , 离心率e =c a =32m 1m=32.反思感悟 从椭圆的标准方程出发,分清其焦点位置,然后再写出相应的性质.跟踪训练1 已知椭圆C 1:x 2100+y 264=1,设椭圆C 2与椭圆C 1的长轴长、短轴长分别相等,且椭圆C 2的焦点在y 轴上.(1)求椭圆C 1的长半轴长、短半轴长、焦点坐标及离心率;(2)写出椭圆C 2的方程.解 (1)由椭圆C 1:x 2100+y 264=1,可得其长半轴长为10,短半轴长为8,焦点坐标为(6,0),(-6,0),离心率e =35.(2)椭圆C 2:y 2100+x 264=1.二、由几何性质求椭圆的标准方程 例2 求适合下列条件的椭圆的标准方程. (1)短轴长25,离心率e =23;(2)在x 轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为6. 解 (1)由2b =25,e =c a =23,得b 2=5,a 2-b 2a 2=49,a 2=9.当焦点在x 轴上时,所求椭圆的标准方程为x 29+y 25=1;当焦点在y 轴上时,所求椭圆的标准方程为y 29+x 25=1.综上,所求椭圆的标准方程为x 29+y 25=1或y 29+x 25=1.(2)依题意可设椭圆方程为x 2a 2+y 2b 2=1(a >b >0).如图所示,△A 1F A 2为一等腰直角三角形,OF 为斜边A 1A 2的中线(高),且|OF |=c ,|A 1A 2|=2b , 所以c =b =3, 所以a 2=b 2+c 2=18, 故所求椭圆的方程为x 218+y 29=1.反思感悟 此类问题应由所给的几何性质充分找出a ,b ,c 所应满足的关系式,进而求出a ,b ,在求解时,需注意椭圆的焦点位置.跟踪训练2 分别求出满足下列条件的椭圆的标准方程.(1)短轴的一个端点到一个焦点的距离为5,焦点到椭圆中心的距离为3; (2)离心率为32,经过点(2,0). 解 (1)由题意知a =5,c =3,b 2=25-9=16, 焦点所在坐标轴可为x 轴,也可为y 轴, 故椭圆的标准方程为x 225+y 216=1或x 216+y 225=1.(2)由e =c a =32,设a =2k ,c =3k ,k >0,则b =k . 又经过的点(2,0)为其顶点,故若点(2,0)为长轴顶点,则a =2,b =1, 椭圆的标准方程为x 24+y 2=1;若点(2,0)为短轴顶点,则b =2,a =4,椭圆的标准方程为x 24+y 216=1.三、求椭圆的离心率例3 (1)如图所示,A ,B ,C 分别为椭圆x 2a 2+y 2b 2=1(a >b >0)的顶点与焦点,若∠ABC =90°,则该椭圆的离心率为( )A.-1+52 B .1-22 C.2-1 D.22答案 A解析 由(a +c )2=a 2+2b 2+c 2, 又因为b 2=a 2-c 2,所以c 2+ac -a 2=0. 因为e =ca,所以e 2+e -1=0,所以e =-1+52.(2)已知椭圆x 2a 2+y 2b 2=1(a >b >0),F 1,F 2分别是椭圆的左、右焦点,椭圆上总存在点P 使得PF 1⊥PF 2,则椭圆的离心率的取值范围为________. 答案 ⎣⎡⎭⎫22,1解析 由PF 1⊥PF 2,知△F 1PF 2是直角三角形, 所以|OP |=c ≥b ,即c 2≥a 2-c 2,所以a ≤2c , 因为e =c a ,0<e <1,所以22≤e <1.反思感悟 求椭圆离心率及范围的两种方法(1)直接法:若已知a ,c 可直接利用e =ca 求解.若已知a ,b 或b ,c 可借助于a 2=b 2+c 2求出c 或a ,再代入公式e =ca求解.(2)方程法:若a ,c 的值不可求,则可根据条件建立a ,b ,c 的关系式,借助于a 2=b 2+c 2,转化为关于a ,c 的齐次方程或不等式,再将方程或不等式两边同除以a 的最高次幂,得到关于e 的方程或不等式,即可求得e 的值或范围.跟踪训练3 已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1,F 2,右顶点为A ,上顶点为B ,若椭圆C 的中心到直线AB 的距离为66|F 1F 2|,求椭圆C 的离心率. 解 由题意知A (a ,0),B (0,b ), 从而直线AB 的方程为x a +yb =1,即bx +ay -ab =0, 又|F 1F 2|=2c ,∴aba 2+b 2=63c . ∵b 2=a 2-c 2,∴3a 4-7a 2c 2+2c 4=0, 解得a 2=2c 2或3a 2=c 2(舍去),∴e =22.椭圆几何性质的应用典例 神舟五号飞船成功完成了第一次载人航天飞行,实现了中国人民的航天梦想.某段时间飞船在太空中运行的轨道是一个椭圆,地心为椭圆的一个焦点,如图所示.假设航天员到地球的最近距离为d 1,最远距离为d 2,地球的半径为R ,我们想象存在一个镜像地球,其中心在神舟飞船运行轨道的另外一个焦点上,上面住着一个神仙发射某种神秘信号,需要飞行中的航天员中转后地球人才能接收到,则传送神秘信号的最短距离为( )A .d 1+d 2+RB .d 2-d 1+2RC .d 2+d 1-2RD .d 1+d 2答案 D解析 设椭圆的方程为x 2a 2+y 2b 2=1(a >b >0),半焦距为c ,两焦点分别为F 1,F 2,飞行中的航天员为点P ,由已知可得⎩⎪⎨⎪⎧d 1+R =a -c ,d 2+R =a +c ,则2a =d 1+d 2+2R ,故传送神秘信号的最短距离为|PF 1|+|PF 2|-2R =2a -2R =d 1+d 2.[素养提升] 将太空中的轨迹与学过的椭圆建立起对应关系.利用椭圆的几何性质来解决航空航天问题,考查了学生运用所学知识解决实际问题的能力.1.椭圆以两坐标轴为对称轴,并且过点(0,13),(-10,0),则焦点坐标为( ) A .(±13,0) B .(0,±10) C .(0,±13) D .(0,±69)答案 D解析 由题意知,椭圆的焦点在y 轴上, 且a =13,b =10,则c =a 2-b 2=69,故选D.2.已知中心在原点的椭圆C 的右焦点为F (1,0),离心率等于12,则椭圆C 的方程是( )A.x 23+y 24=1 B.x 24+y 23=1 C.x 24+y 23=1 D.x 24+y 2=1 答案 C解析 依题意知,所求椭圆的焦点位于x 轴上, 且c =1,e =c a =12,即a =2,b 2=a 2-c 2=3,因此椭圆的方程是x 24+y 23=1.3.若椭圆的两个焦点与短轴的一个端点构成一个正三角形,则该椭圆的离心率为( ) A.12 B.32 C.34D.64答案 A解析 不妨设椭圆的左、右焦点分别为F 1,F 2,B 为椭圆的上顶点.依题意可知,△BF 1F 2是正三角形. ∵在Rt △OBF 2中,|OF 2|=c , |BF 2|=a ,∠OF 2B =60°, ∴cos 60°=c a =12,即椭圆的离心率e =12,故选A.4.椭圆x 2k +8+y 29=1的离心率为12,则k 的值为( )A .4B .-54C .4或-54D .不能确定答案 C解析 当k +8>9,即k >1时,e 2=c 2a 2=k +8-9k +8=14,k =4.当0<k +8<9,即-8<k <1时, e 2=c 2a 2=9-k -89=14,k =-54.5.椭圆x 2+my 2=1的焦点在y 轴上,长轴长是短轴长的2倍,则m 的值为( ) A.12 B.14 C .2 D .4 答案 B解析 椭圆x 2+my 2=1的焦点在y 轴上,短半轴长为1,长轴长是短轴长的2倍, 故1m =2,解得m =14.1.知识清单: (1)椭圆的几何性质. (2)求椭圆的离心率.2.方法归纳:定义法、数形结合、函数与方程.3.常见误区:忽略椭圆离心率的范围0<e <1及长轴长与a 的关系.1.已知椭圆C :x 2a 2+y 24=1的一个焦点为(2,0),则椭圆C 的离心率为( )A.13B.12C.22D.223 答案 C解析 ∵a 2=4+22=8,∴a =22,∴e =c a =222=22.故选C.2.椭圆(m +1)x 2+my 2=1的长轴长是( )A.2m -1m -1B.-2-m mC.2m mD .-21-m m -1答案 C解析 椭圆方程可化简为x 211+m +y 21m =1,由题意,知m >0,∴11+m <1m,∴a =m m ,∴椭圆的长轴长2a =2mm.3.焦点在x 轴上,长、短半轴长之和为10,焦距为45,则椭圆的方程为( ) A.x 236+y 216=1 B.x 216+y 236=1 C.x 26+y 24=1 D.y 26+x 24=1 答案 A解析 设椭圆的方程为x 2a 2+y 2b 2=1(a >b >0),依题意得c =25,a +b =10,又a 2=b 2+c 2, 解得a =6,b =4.则椭圆的方程为x 236+y 216=1.4.已知椭圆x 2a 2+y 2b 2=1与椭圆x 225+y 216=1有相同的长轴,椭圆x 2a 2+y 2b 2=1的短轴长与椭圆y 221+x 29=1的短轴长相等,则( ) A .a 2=25,b 2=16 B .a 2=9,b 2=25C .a 2=25,b 2=9或a 2=9,b 2=25D .a 2=25,b 2=9 答案 D解析 椭圆x 225+y 216=1的长轴长为10,椭圆y 221+x 29=1的短轴长为6,由题意可知椭圆x 2a 2+y 2b 2=1的焦点在x 轴上,即有a =5,b =3.5.过椭圆x 24+y 23=1的焦点的最长弦和最短弦的长分别为( )A .8,6B .4,3C .2, 3D .4,2 3答案 B解析 由题意知a =2,b =3,c =1,最长弦过两个焦点,长为2a =4,最短弦垂直于x 轴,长度为当x =c =1时,纵坐标的绝对值的2倍为3. 6.已知椭圆的短半轴长为1,离心率0<e ≤32,则长轴长的取值范围为________. 答案 (2,4] 解析 ∵e =1-⎝⎛⎭⎫b a 2,b =1,0<e ≤32, ∴1-⎝⎛⎭⎫b a 2≤32,则1<a ≤2,∴2<2a ≤4, 即长轴长的取值范围是(2,4].7.在平面直角坐标系xOy 中,椭圆C 的中心为原点,焦点F 1,F 2在x 轴上,离心率为22.过F 1的直线l 交C 于A ,B 两点,且△ABF 2的周长为16,那么椭圆C 的方程为_____________. 答案 x 216+y 28=1解析 设椭圆方程为x 2a 2+y 2b 2=1(a >b >0),由e =22,知c a =22,故b 2a 2=12.由于△ABF 2的周长为|AB |+|BF 2|+|AF 2|=(|AF 1|+|AF 2|)+(|BF 1|+|BF 2|)=4a =16,故a =4,∴b 2=8,∴椭圆C 的方程为x 216+y 28=1.8.已知长方形ABCD ,AB =4,BC =3,则以A ,B 为焦点,且过C ,D 的椭圆的离心率为________. 答案 12解析 如图,AB =2c =4,∵点C 在椭圆上,∴CB +CA =2a =3+5=8,∴e =2c 2a =48=12. 9.已知椭圆x 2+(m +3)y 2=m (m >0)的离心率e =32,求m 的值及椭圆的长轴和短轴的长、焦点坐标、顶点坐标.解 椭圆方程可化为x 2m +y 2m m +3=1(m >0), ∵m -m m +3=m (m +2)m +3>0,∴m >m m +3. ∴a 2=m ,b 2=m m +3,c =a 2-b 2=m (m +2)m +3. 由e =32,得m +2m +3=32,∴m =1. ∴椭圆的标准方程为x 2+y 214=1. ∴a =1,b =12,c =32. ∴椭圆的长轴长为2,短轴长为1;两焦点坐标分别为F 1⎝⎛⎭⎫-32,0,F 2⎝⎛⎭⎫32,0; 四个顶点坐标分别为A 1(-1,0),A 2(1,0),B 1⎝⎛⎭⎫0,-12,B 2⎝⎛⎭⎫0,12. 10.已知椭圆C :x 2a 2+y 2b2=1(a >b >0)的左、右焦点分别为F 1(-1,0),F 2(1,0),且椭圆C 经过点M ⎝⎛⎭⎫43,13,求椭圆C 的离心率.解 2a =|MF 1|+|MF 2|=⎝⎛⎭⎫43+12+⎝⎛⎭⎫132+⎝⎛⎭⎫43-12+⎝⎛⎭⎫132=2 2. 所以a = 2. 又由已知c =1,所以椭圆C 的离心率e =c a =12=22.11.椭圆的短轴的一个顶点与两焦点组成等边三角形,则它的离心率为( ) A.12B.13C.14D.22答案 A 解析 由题意知a =2c ,∴e =c a =c 2c =12. 12.已知椭圆x 2a 2+y 2b2=1(a >b >0),A ,B 分别为椭圆的左顶点和上顶点,F 为右焦点,且AB ⊥BF ,则椭圆的离心率为( )A.22 B.32 C.3-12 D.5-12 答案 D解析 在Rt △ABF 中,AB =a 2+b 2,BF =a ,AF =a +c ,由AB 2+BF 2=AF 2,得a 2+b 2+a 2=(a +c )2.将b 2=a 2-c 2代入,得a 2-ac -c 2=0,即e 2+e -1=0,解得e =-1±52, 因为0<e <1,所以e =5-12. 13.若将一个椭圆绕中心旋转90°,所得椭圆的两顶点恰好是旋转前椭圆的两焦点,这样的椭圆称为“对偶椭圆”.下列椭圆的方程中,是“对偶椭圆”的方程是( ) A.x 28+y 24=1 B.x 23+y 25=1 C.x 26+y 22=1 D.x 26+y 29=1 答案 A解析 由题意,知当b =c 时,将一个椭圆绕中心旋转90°,所得椭圆的两顶点恰好是旋转前椭圆的两焦点,该椭圆为“对偶椭圆”.选项中只有A 中b =c =2符合题意,故选A.14.如图,已知F 1,F 2分别是椭圆的左、右焦点,现以F 2为圆心作一个圆恰好经过椭圆中心并且交椭圆于点M ,N ,若过F 1的直线MF 1是圆F 2的切线,则椭圆的离心率为( )A.3-1B .2- 3 C.22 D.32答案 A解析 ∵过F 1的直线MF 1是圆F 2的切线,∴∠F 1MF 2=90°,|MF 2|=c ,∵|F 1F 2|=2c ,∴|MF 1|=3c ,由椭圆定义可得|MF 1|+|MF 2|=c +3c =2a ,∴椭圆离心率e =21+3=3-1. 15.已知椭圆x 249+y 224=1上一点P 与椭圆两焦点F 1,F 2的连线夹角为直角,则|PF 1|·|PF 2|=________.答案 48解析 依题意知,a =7,b =26,c =49-24=5,|F 1F 2|=2c =10.∵PF 1⊥PF 2,∴|PF 1|2+|PF 2|2=|F 1F 2|2,即|PF 1|2+|PF 2|2=100.又由椭圆定义知|PF 1|+|PF 2|=2a =14,∴(|PF 1|+|PF 2|)2-2|PF 1|·|PF 2|=100.即196-2|PF 1|·|PF 2|=100.解得|PF 1|·|PF 2|=48.16.在平面直角坐标系中,椭圆x 2a 2+y 2b2=1(a >b >0)的焦距为2c ,以O 为圆心,a 为半径的圆,过点⎝⎛⎭⎫a 2c ,0作圆的两切线互相垂直,则离心率e =________.答案 22 解析 如图,切线P A ,PB 互相垂直,又半径OA 垂直于P A ,所以△OAP 是等腰直角三角形,a 2c=2a . 解得e =c a =22, 则离心率e =22.17.已知椭圆E :x 2a 2+y 2b2=1(a >b >0)的右焦点为F ,短轴的一个端点为M ,直线l :3x -4y =0交椭圆E 于A ,B 两点.若|AF |+|BF |=4,点M 到直线l 的距离不小于45,则椭圆E 的离心率的取值范围是( )A.⎝⎛⎦⎤0,32B.⎝⎛⎦⎤0,34 C.⎣⎡⎭⎫32,1 D.⎣⎡⎭⎫34,1 答案 A解析 设左焦点为F 0,连接F 0A ,F 0B ,则四边形AFBF 0为平行四边形. ∵|AF |+|BF |=4, ∴|AF |+|AF 0|=4, ∴a =2.设M (0,b ),则4b 5≥45,∴1≤b <2. 离心率e =c a=c 2a 2=a 2-b 2a 2=4-b 24∈⎝⎛⎦⎤0,32, 故选A.18.如图,已知椭圆x 2a 2+y 2b 2=1(a >b >0),F 1,F 2分别为椭圆的左、右焦点,A 为椭圆的上顶点,直线AF 2交椭圆于另一点B .(1)若∠F 1AB =90°,求椭圆的离心率; (2)若椭圆的焦距为2,且AF 2→=2F 2B →,求椭圆的方程.解 (1)由∠F 1AB =90°及椭圆的对称性知b =c ,则e =c a =c 2a 2=c 2b 2+c 2=22. (2)由已知a 2-b 2=1,A (0,b ),F 2(1,0),设B (x ,y ), 则AF 2→=(1,-b ),F 2B →=(x -1,y ), 由AF 2→=2F 2B →,即(1,-b )=2(x -1,y ),解得x =32,y =-b 2,则94a 2+b 24b 2=1, 得a 2=3,因此b 2=2,椭圆的方程为x 23+y 22=1.。
数学人教A版选修2-1优化课件:第二章 2.2 2.2.2 第1课时 椭圆的简单几何性质

考纲定位
重难突破
1.掌握椭圆的对称性、范围、
顶点、离心率等简单性质. 重点:椭圆的范围、对称性、离
2.能用椭圆的简单性质求椭 心率等几何性质.
圆方程.
难点:利用几何性质分析解决有
3.能用椭圆的简单性质分析 关问题.
解决有关问题.
01 课前 自主梳理 02 课堂 合作探究 03 课后 巩固提升
法;因式分解法等,掌握各个科目的方法是大家应该学习的核心所在。
优等生经验谈:听课时应注意学习老师解决问题的思考方法。同学们如果理解了老师的思路和过程,那么后面的结论自然就出现了,学习起来才能够举 一反三,事半功倍。
2019/7/9
最新中小学教学课件
29
谢谢欣赏!
2019/7/9
最新中小学教学课件
[典例 3] 若椭圆的短轴为 AB,它的一个焦点为 F,则满足三角形 ABF 为等边
三角形的椭圆的离心率是________. [解析] 若三角形 ABF 为等边三角形,则有 2b=a,即 a2=4b2
=4(a2-c2),所以 4c2=3a2,即 e2=34,所以 e= 23,所以椭圆的
离心率为 23.
二、听思路。
思路就是我们思考问题的步骤。例如老师在讲解一道数学题时,首先思考应该从什么地方下手,然后在思考用什么方法,通过什么样的过程来进行
解答。听课时关键应该弄清楚老师讲解问题的思路。
三、听问题。
对于自己预习中不懂的内容,上课时要重点把握。在听讲中要特别注意老师和课本中是怎么解释的。如果老师在讲课中一带而过,并没有详细解答, 大家要及时地把它们记下来,下课再向老师请教。
教学设计4:2.2.2 椭圆的简单几何性质

2.2.2 椭圆的简单几何性质x 2≤a 2且y 2≤b 2,则有|x |≤a,|y |≤b, 所以-a ≤x ≤a,-b ≤y ≤b 。
2.对称性的发现与证明师:椭圆的图形给人们以视觉上的美感(课件展示椭圆),如果我们沿焦点所在的直线上下对折,沿两焦点连线的垂直平分线左右对折,大家猜想椭圆可能有什么性质?(学生动手折纸,课前教师要求学生把上节学习椭圆定义时画的椭圆拿来。
) 学生们基本上能发现椭圆的轴对称性。
师:除了轴对称性外,还可能有什么对称性呢?稍作提示容易发现中心对称性。
师:这仅仅是由观察、猜想得到的结果,怎样用方程证明它的对称性?师生讨论后,需要建立坐标系,确定椭圆的标准方程。
不妨建立焦点在x 轴上的椭圆的标准坐标系,它的方程就是22a x +22by =1。
师:这节课就以焦点在x 轴上的椭圆的标准方程为例来研究椭圆的性质。
这样建立的坐标系对称轴恰好重合于坐标轴,我们先证椭圆关于y 轴对称。
为了证明对称性,先作如下铺垫:(一起回顾)师:在第一册学过,曲线关于y 轴对称是指什么呢?生:曲线上的每一点关于y 轴的对称点仍在曲线上。
师:要证曲线上每一点关于y 轴的对称点仍在曲线上,只要证明-----生:曲线上任意一点关于y 轴的对称点仍在曲线上。
在学生尝试进行问题解决的过程中,当他们难以把握问题解决的思维方向,难以建立起新旧知识的联系时,这就需要教师适时进行启发点拨。
师:同学们阅读教材中椭圆对称性的证明过程,仔细体会并思考“为什么把x 换成-x 时,方程不变,则椭圆关于y 轴对称”。
请一位学生讲解椭圆对称性的证明过程,以此来训练学生表述的逻辑性、完整性和推理的严谨性。
教师对学生的证明进行评价。
师:用类似的方法可以证明椭圆关于x 轴对称,关于原点对称。
课件展示对称性并总结:方程22a x +22by =1表示的椭圆,坐标轴是其对称轴,原点是其对称中心.从而椭圆有两条互相垂直的对称轴,有一个对称中心(简称中心).教师引导学生对这一环节进行反思,即通过建立坐标系,用椭圆的方程研究椭圆的性质,这种方法我们今后经常用到。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§2.2.2椭圆的简单几何性质(1)
编写:英德市第二中学,叶加修;审核:英西中学,刘东
【学习目标】
掌握椭圆的中心、顶点、长短轴、离心率的概念
【知识回顾】
1. 已知B、C是两个定点,|BC|=6,且△ABC的周长等于16,求定点A的轨迹方程.
2.小结:
【新知构建】
例1已知椭圆方程为16x2+25y2=400,它的长轴长是:。
短轴长是:。
焦距是: 。
离心率等于: 。
焦点坐标是: 。
顶点坐标是: 。
外切矩形的面积等于: 。
例2.过适合下列条件的椭圆的标准方程:
(1)经过点(3,0)-P 、(0,2)-Q ;
(2)长轴长等于20 ,离心率等于
35.
小结:
【当堂练习】
1.已知椭圆方程为6x 2+y 2=6, 它的长轴长是: 。
短轴长是: 。
焦距是: .离心率等于: 。
焦点坐标是: 。
顶点坐标是: 。
外切矩形的面积等于:
2.已知椭圆的中心在原点,焦点在坐标轴上,长轴是短轴的三倍,且椭圆经过点P (3,0),求椭圆的方程。
小结:
【课后作业】
1.椭圆x 26
+y 2=1的长轴端点的坐标为( ) A .(-1,0),(1,0) B .(-6,0),(6,0)
C .(0,-6),(0,6)
D .(-6,0)(6,0)
2.离心率为32
,焦点在x 轴上,且过点(2,0)的椭圆标准方程为( ) A.x 24+y 2=1 B.x 24+y 2=1或x 2+y 24
=1 C .x 2+4y 2
=1 D.x 24+y 2=1或x 24+y 2
16=1 3. 椭圆25x 2+9y 2=225的长轴长,短轴长,离心率依次是( )
A .5,3,45
B .10,6,45
C .5,3,35
D .10,6,35
4. 椭圆x 216+y 2
8=1的离心率为 .。
