整理的一些简单jena函数(不保证正确性)
jensen函数方程 -回复

jensen函数方程-回复Jensen函数方程是一种关于函数的函数方程,它在数学和经济学等领域中有着广泛的应用。
该方程是由丹麦数学家Johan Ludwig Jensen在20世纪初提出的,它描述了一种特殊的类型函数的性质。
在这篇文章中,我们将深入探讨Jensen函数方程的定义、性质以及一些常见的解法。
首先,让我们来了解一下Jensen函数方程的定义。
给定一个定义在实数集上的函数f(x),如果满足下面的条件:f((x+y)/2) = (f(x) + f(y))/2,对于任意的x和y成立那么函数f(x)就被称为满足Jensen函数方程。
简单来说,这个方程要求函数f在两点的中间值处取得的函数值等于这两点函数值的平均值。
接下来我们探讨一下Jensen函数方程的一些性质。
首先,我们可以发现对于线性函数来说,它肯定满足Jensen函数方程,因为对任意的x和y,有(f(x)+f(y))/2 = (ax+ay)/2 = a(x+y)/2 = f((x+y)/2),其中a是任一常数。
这意味着所有的线性函数都是Jensen函数方程的解。
其次,Jensen函数方程还有一个重要的性质,即任意两点之间的任意插值都满足方程。
假设f(x)满足Jensen函数方程,那么对于任意的实数a1,a2和对应的函数值x1 = f(a1)和x2 = f(a2),对于任意的0≤t≤1,有f(ta1+(1-t)a2) = tf(a1) + (1-t)f(a2)。
这个性质意味着我们可以通过线性插值的方式得到方程的解,而不局限于线性函数。
现在我们来看一些常见的Jensen函数方程的解法。
首先,我们可以通过验证函数的某些性质来判断它是否满足方程,例如函数的凸性和仿射性质。
对于凸函数来说,它始终在两点的中间值处取得的函数值小于这两点函数值的平均值,因此凸函数是Jensen函数方程的解。
而仿射函数则满足凸性的条件,并且对某一常数a有f(x) = ax + b形式,所以仿射函数也是方程的解。
Jena_中文教程_本体API(经典)

Jena 简介一般来说,我们在Protege这样的编辑器里构建了本体,就会想在应用程序里使用它,这就需要一些开发接口。
用程序操作本体是很必要的,因为在很多情况下,我们要自动生成本体,靠人手通过Protege创建所有本体是不现实的。
Jena 是HP公司开发的这样一套API,似乎HP公司在本体这方面走得很靠前,其他大公司还在观望吗?可以这样说,Jena对应用程序就像Protege对我们,我们使用Protege操作本体,应用程序则是使用Jena来做同样的工作,当然这些应用程序还是得由我们来编写。
其实Protege本身也是在Jena的基础上开发的,你看如果Protege 的console里报异常的话,多半会和Jena有关。
最近出了一个Protege OWL API,相当于对Jena的包装,据说使用起来更方便,这个API就是Protege的OWL Plugin所使用的,相信作者经过OWL Plugin的开发以后,说这些话是有一定依据的。
题目是说用Jena处理OWL,其实Jena当然不只能处理OWL,就像Protege 除了能处理OWL外还能处理RDF(S)一样。
Jena最基本的使用是处理RDF(S),但毕竟OWL已经成为W3C的推荐标准,所以对它的支持也是大势所趋。
好了,现在来点实际的,怎样用Jena读我们用Protege创建的OWL本体呢,假设你有一个OWL本体文件(.owl),里面定义了动物类(/ont/Animal,注意这并不是一个实际存在的URL,不要试图去访问它),并且它有一些实例,现在看如下代码:OntModel m = ModelFactory.createOntologyModel();File myFile = ...;m.read(new FileInputStream(myFile), "");ResIterator iter = m.listSubjectsWithProperty(RDF.type, m.getResource("http:// /ont/Animal"));while (iter.hasNext()) {Resource animal = (Resource) iter.next();System.out.println(animal.getLocalName());}和操作RDF(S)不同,com.hp.hpl.jena.ontology.OntModel是专门处理本体(Ontology)的,它是com.hp.hpl.jena.rdf.model.Model的子接口,具有Model的全部功能,同时还有一些Model没有的功能,例如listClasses()、listObjectProperties(),因为只有在本体里才有“类”和“属性”的概念。
jensen不等式
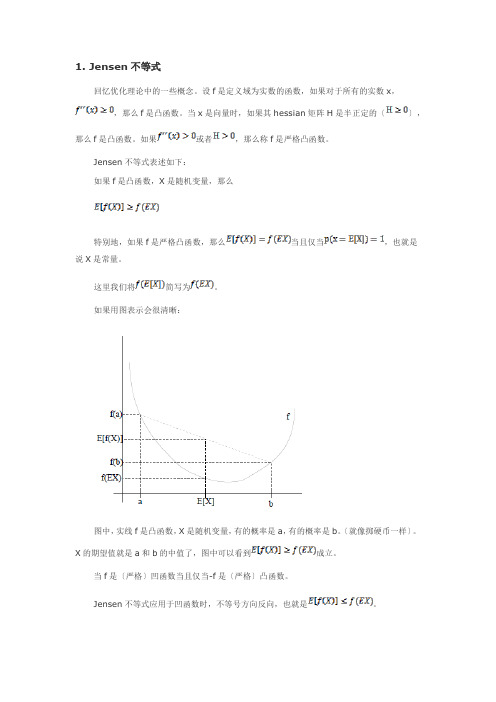
1. Jensen不等式回忆优化理论中的一些概念。
设f是定义域为实数的函数,如果对于所有的实数x,,那么f是凸函数。
当x是向量时,如果其hessian矩阵H是半正定的〔〕,那么f是凸函数。
如果或者,那么称f是严格凸函数。
Jensen不等式表述如下:如果f是凸函数,X是随机变量,那么特别地,如果f是严格凸函数,那么当且仅当,也就是说X是常量。
这里我们将简写为。
如果用图表示会很清晰:图中,实线f是凸函数,X是随机变量,有的概率是a,有的概率是b。
〔就像掷硬币一样〕。
X的期望值就是a和b的中值了,图中可以看到成立。
当f是〔严格〕凹函数当且仅当-f是〔严格〕凸函数。
Jensen不等式应用于凹函数时,不等号方向反向,也就是。
先验概率与后验概率事情还没有发生,要求这件事情发生的可能性的大小,是先验概率. 事情已经发生,要求这件事情发生的原因是由某个因素引起的可能性的大小,是后验概率.一、先验概率是指根据以往经历和分析得到的概率,如全概率公式,它往往作为“由因求果〞问题中的“因〞出现。
后验概率是指在得到“结果〞的信息后重新修正的概率,如贝叶斯公式中的,是“执果寻因〞问题中的“因〞。
先验概率与后验概率有不可分割的联系,后验概率的计算要以先验概率为根底。
二、A prior probability is a marginal probability, interpreted as a description of what is known about a variable in the absence of some evidence. The posterior probability is then the conditional probability of the variable taking the evidence into account. The posterior probability is computed from the prior and the likelihood function via Bayes' theorem.三、先验概率与后验概率通俗释义事情有N种发生的可能,我们不能控制结果的发生,或者影响结果的机理是我们不知道或是太复杂超过我们的运算能力。
整理的一些简单jena函数(不保证正确性)解读

1、OntModel ontModel = ModelFactory.createOntologyModel();Jena通过model包中的ModelFactory创建本体模型,ModelFactory是Jena提供用来创建各种模型的类,在类中定义了具体实现模型的成员数据以及创建模型的二十多种方法。
该语句不含参数,应用默认设置创建一个本体模型ontModel,也就是说:它使用OWL语言、基于内存,支持RDFS推理。
可以通过创建时应用模型类别(OntModelSpec)参数创建不同的模型,以实现不同语言不同类型不同推理层次的本体操作。
例如,下面的语句创建了一个使用DAML语言内存本体模型。
直观地讲,内存模型就是只在程序运行时存在的模型,它没有将数据写回磁盘文件或者数据库表。
OntModel ontModel = ModelFactory.createOntologyModel( OntModelSpec.DAML_MEM );更多类型设置可以参照OntModelSpec类中的数据成员的说明。
2、ontModel.read("file:D:/temp/Creatrue/Creature.owl");读取的方法是调用Jena OntoModel提供的Read方法。
Read方法也有很多重载,上面调用的方法以文件的绝对路径作为参数。
其他的方法声明如下read( String url );read( Reader reader, String base );read( InputStream reader, String base );read( String url, String lang );read( Reader reader, String base, String Lang );read( InputStream reader, String base, String Lang );3、OntModel m = ModelFactory.createOntologyModel();OntDocumentManager dm = m.getDocumentManager();创建一个文档管理器并将它与以创建的本体模型关联。
函数公式大全简单

函数公式大全简单1. SUM函数SUM函数是用来求和的,可以对一列或多列数字进行求和。
例如,SUM(A1:A10)表示对A1到A10单元格中的数字进行求和。
2. AVERAGE函数AVERAGE函数是用来求平均值的,可以对一列或多列数字进行求平均值。
例如,AVERAGE(A1:A10)表示对A1到A10单元格中的数字进行求平均值。
3. MAX函数MAX函数是用来求最大值的,可以对一列或多列数字进行求最大值。
例如,MAX(A1:A10)表示对A1到A10单元格中的数字进行求最大值。
4. MIN函数MIN函数是用来求最小值的,可以对一列或多列数字进行求最小值。
例如,MIN(A1:A10)表示对A1到A10单元格中的数字进行求最小值。
5. COUNT函数COUNT函数是用来计算单元格数的,可以对一列或多列单元格进行计数。
例如,COUNT(A1:A10)表示对A1到A10单元格中的单元格进行计数。
6. IF函数IF函数是用来进行条件判断的,可以根据条件返回不同的值。
例如,IF(A1>10,"Yes","No")表示如果A1大于10,则返回"Yes",否则返回"No"。
7. VLOOKUP函数VLOOKUP函数是用来进行查找和匹配的,可以根据指定的值在表格中查找并返回相应的值。
例如,VLOOKUP(A1,B1:C10,2,FALSE)表示在B1到C10单元格中查找A1的值,并返回第二列的值。
8. HLOOKUP函数HLOOKUP函数是用来进行查找和匹配的,与VLOOKUP函数类似,但是是水平查找。
例如,HLOOKUP(A1,B1:C10,2,FALSE)表示在B1到C10单元格中查找A1的值,并返回第二行的值。
9. CONCATENATE函数CONCATENATE函数是用来将多个文本字符串合并为一个字符串的。
例如,CONCATENATE(A1," ",B1)表示将A1和B1单元格中的文本字符串合并为一个字符串,并在它们之间添加一个空格。
impala常用函数

impala常用函数
Impala是一种用于分布式数据处理的SQL查询引擎,它支持许多常用的函数来处理数据。
以下是一些常用的Impala函数:
1. 聚合函数,包括SUM、AVG、COUNT、MIN和MAX等。
这些函数用于对数据进行汇总和统计,可以对数据集进行求和、平均值计算、计数以及找出最大最小值等操作。
2. 字符串函数,例如CONCAT用于连接字符串,SUBSTR用于截取子串,UPPER和LOWER用于将字符串转换为大写或小写等。
3. 日期函数,包括CURRENT_DATE用于获取当前日期,
DATE_ADD和DATE_SUB用于日期加减操作,YEAR、MONTH和DAY等函数用于提取日期的年、月、日部分。
4. 条件函数,例如CASE WHEN用于条件判断,类似于编程语言中的if-else语句,可以根据条件返回不同的值。
5. 数学函数,包括ABS用于取绝对值,ROUND用于四舍五入,CEIL和FLOOR用于向上或向下取整等。
6. 类型转换函数,例如CAST用于数据类型转换,可以将一个数据类型转换为另一个数据类型。
除了以上列举的函数外,Impala还支持许多其他常用函数,如正则表达式函数、数组函数、加密函数等。
这些函数可以帮助用户对数据进行各种复杂的处理和计算。
在实际的数据分析和处理过程中,合理地运用这些函数可以提高数据处理的效率和灵活性。
需要根据具体的数据处理需求选择合适的函数来使用。
做报表常用的函数

做报表常用的函数在报表分析和生成过程中,使用函数能够提高效率和准确性。
下面是一些经常在做报表时使用的常用函数:1.SUM函数:用于计算给定范围内的数值总和。
例如,SUM(A1:A10)可以计算A1到A10单元格范围内的数值总和。
2.AVERAGE函数:用于计算给定范围内数值的平均值。
例如,AVERAGE(A1:A10)可以计算出A1到A10单元格范围内数值的平均值。
3.COUNT函数:用于计算给定范围内的数值个数。
例如,COUNT(A1:A10)可以统计出A1到A10单元格范围内的数值个数。
4.MAX函数和MIN函数:分别用于计算给定范围内的最大和最小值。
例如,MAX(A1:A10)可以找到A1到A10单元格范围内的最大值。
5.IF函数:在报表中常用的条件函数,用于根据一个条件的逻辑运算结果,返回不同的值。
例如,IF(A1>0,"正数","负数")会根据A1单元格中的值返回"正数"或"负数"。
6.VLOOKUP函数:在报表中常用的查找函数,用于在一个区域中查找一些值,并返回该值所在行或列的相关信息。
例如,VLOOKUP(A1,B1:C10,2,FALSE)会在B1到C10单元格范围中查找A1单元格的值,并返回该值所在行的第二列的值。
7.INDEX函数和MATCH函数:INDEX函数返回给定范围内特定行和列的值,而MATCH函数用于查找一些值在给定范围内的位置。
这两个函数常用于报表生成和分析中。
8.CONCATENATE函数:用于将多个文本字符串连接在一起。
例如,CONCATENATE(A1,"-",B1)会将A1和B1单元格的值连接在一起,中间以"-"分隔。
9.ROUND函数:用于将一个数值四舍五入到指定的小数位数。
例如,ROUND(A1,2)会将A1单元格的值四舍五入到小数点后两位。
帆软常用函数

帆软常用函数
帆软报表是一款非常实用的数据分析工具,它提供了丰富的函数库,可以满足各种数据计算和处理的需求。
下面介绍一些常用的帆软函数:
1. SUM函数:用于计算一组数值的总和,例如:SUM(1,2,3)的结果为6。
2. AVERAGE函数:用于计算一组数值的平均值,例如:AVERAGE(1,2,3)的结果为2。
3. MAX函数:用于计算一组数值中的最大值,例如:MAX(1,2,3)的结果为3。
4. MIN函数:用于计算一组数值中的最小值,例如:MIN(1,2,3)的结果为1。
5. IF函数:用于根据条件判断返回不同的结果,例如:
IF(A1>10,'大于10','小于等于10')。
6. CONCAT函数:用于将多个字符串合并成一个字符串,例如:CONCAT('hello','world')的结果为'helloworld'。
7. DATE函数:用于创建日期类型的数据,例如:DATE(2021,10,1)表示2021年10月1日。
8. NOW函数:用于获取当前日期和时间,例如:NOW()的结果为当前的日期和时间。
9. LEN函数:用于计算字符串的长度,例如:LEN('hello')的结果为5。
10. TRIM函数:用于去除字符串两端的空格,例如:TRIM(' hello ')的结果为'hello'。
以上是一些常用的帆软函数,可以帮助用户完成各种数据分析和处理的任务。
jensen函数方程

jensen函数方程(最新版)目录1.Jensen 函数方程的定义和基本概念2.Jensen 函数方程的性质和特点3.Jensen 函数方程在数学领域的应用4.Jensen 函数方程的求解方法和技巧5.总结正文一、Jensen 函数方程的定义和基本概念Jensen 函数方程,又称为 Jensen 方程,是由丹麦数学家 Jensen 提出的一类具有特殊性质的函数方程。
Jensen 函数方程广泛应用于数学的各个领域,如微积分、概率论、数理统计等。
它描述了在某种意义下,一个凸函数与其导数之间的关系。
二、Jensen 函数方程的性质和特点Jensen 函数方程具有以下几个基本性质:1.凸性:Jensen 函数是一个凸函数,这意味着对于其定义域内的任意两个实数,函数值总是介于这两个实数的函数值之间。
2.可微性:Jensen 函数在其定义域内具有连续的导数。
3.对称性:Jensen 函数方程对于自变量的任意置换都具有对称性。
4.Jensen 不等式:Jensen 函数的导数与函数本身之间存在一种特殊的不等关系,这就是著名的 Jensen 不等式。
三、Jensen 函数方程在数学领域的应用Jensen 函数方程在数学的许多领域都有广泛应用,如求解最优化问题、研究随机过程、分析概率分布等。
其中,最著名的应用之一是求解凸函数的最小值问题。
通过 Jensen 函数方程,我们可以将求解最小值问题转化为求解一个关于导数的方程,从而简化问题的求解过程。
四、Jensen 函数方程的求解方法和技巧求解 Jensen 函数方程的方法和技巧有很多,以下是一些常用的方法:1.利用 Jensen 不等式:根据 Jensen 不等式,我们可以得到一个关于函数导数的不等式,从而将原问题转化为求解一个不等式问题。
2.利用函数的凸性:由于 Jensen 函数是凸函数,我们可以利用函数的凸性来推导出一些有用的不等关系,从而简化问题的求解。
3.利用微分中值定理:微分中值定理是微积分中的一个基本定理,我们可以利用它来求解 Jensen 函数方程。
isna函数的使用方法

isna函数的使用方法ISNA函数是Excel中的一个非常有用的函数,它可以帮助用户判断一个单元格中的数值是否为错误值#N/A(即“不适用”)。
在实际的数据分析中,我们经常会遇到需要判断数据是否为#N/A的情况,这时候ISNA函数就能派上用场了。
ISNA函数的基本语法非常简单,它只接受一个参数,即需要判断的数值。
其语法格式为:=ISNA(值)。
其中,值可以是任意的单元格引用或具体的数值。
ISNA函数的返回值是一个逻辑值,如果值为#N/A,则返回TRUE;如果值不是#N/A,则返回FALSE。
在实际的使用中,ISNA函数通常与其他函数配合使用,以实现更复杂的逻辑判断。
下面我们来看一些ISNA函数的使用方法。
1. 判断单元格是否为#N/A。
假设我们有一个数据表格,其中包含了一列数据,我们需要判断这列数据中是否存在#N/A。
这时候,我们可以使用ISNA函数来进行判断。
假设数据位于A1到A10单元格中,我们可以在B1单元格中输入以下公式:=ISNA(A1)。
然后拖动填充手柄,将公式拖动至B10单元格,这样就可以得到A1到A10单元格中数据是否为#N/A的判断结果。
2. 结合IF函数进行条件判断。
有时候,我们需要根据某个单元格的数值是否为#N/A来进行条件判断。
这时候,我们可以结合IF函数和ISNA函数来实现。
例如,我们需要判断A1单元格中的数值是否为#N/A,如果是,则在B1单元格中显示“错误值”,如果不是,则显示“正常”。
我们可以在B1单元格中输入以下公式:=IF(ISNA(A1),"错误值","正常")。
这样,当A1单元格中的数值为#N/A时,B1单元格中就会显示“错误值”,否则显示“正常”。
3. 与VLOOKUP函数结合使用。
在使用VLOOKUP函数进行数据查找时,有时候会出现查找不到对应数据而返回#N/A的情况。
这时候,我们可以使用ISNA函数来判断VLOOKUP函数的返回值是否为#N/A。
Excel公式教程ISNA函数详解

Excel公式教程ISNA函数详解【语法】ISNA(value)检测一个数值是否错误值#N/A,是则返回TRUE,否则返回FALSE。
Value 必需。
待检测的数值,可以是任意类型的单值。
N/A在英语中有两种意思:(1)Not applicable,表示不适用。
多用在填写表格的时候,表示“本栏目(对我)不适用”,在没有东西可填写但又不允许留空的时候,就填写N/A。
(2)Not available,表示无法获得数据,或者没有可用数据。
在Excel中,错误值#N/A一般在以下三种情况出现:(1)直接在单元格中输入#N/A或=NA(),表示“不适用”。
(2)如果数值查找函数(VLOOKUP、HLOOKUP、LOOKUP、MATCH)找不到指定的值,将返回#N/A,表示“无法获得数据”。
(3)在数组扩展中,同一维度上因大小不同而进行的扩展将产生#N/A,表示“没有可用数据”。
【用法】一、参数value可以是一个单元格引用;检测该单元格的值是不是#N/A。
可参考博文《ISBLANK函数详解》和《ISNUMBER函数详解》,这里不再重复累赘。
这里提醒大家要注意的是:value指向的单元格引用可以通过嵌套其他函数来生成。
那么,哪些函数可以返回单元格引用?请到博文《ISBLANK函数详解》中找答案。
二、参数value可以是一个嵌套的数值查找函数;检测该函数能不能找到指定的值。
(一)设置数据有效性,防止同一列的数据重复输入。
例如,假设从单元格A2开始输入数据,先定位到单元格A2,然后打开“数据有效性”对话框,在“设置”选项卡“允许”下面的下拉菜单中选择“自定义”,在“公式”输入框中输入以下公式:=ISNA(MATCH(A2,A$1:A1,))然后把数据有效性复制到下面的行。
由于公式中的MATCH函数只查找公式所在单元格上面的行,所以只适用于由上往下输入数据的情况。
改用以下公式则可以不限输入顺序:=COUNTIF(A:A,A2)=1(二)设置条件格式,判断单元格的值是否重复。
matlab求单调递增函数关系式

matlab求单调递增函数关系式在数学中,单调递增函数是指在定义域上递增的函数。
换句话说,当自变量增加时,函数值也会增加。
我们可以通过多种方法构造单调递增函数,以下是一些常见的示例。
1.线性函数:线性函数是最简单的函数之一,其图像为一条直线。
线性函数的关系式为 y = mx + b,其中 m 是斜率,b 是截距。
当斜率 m 大于零时,函数是单调递增的。
例如,y = 2x + 1 就是一个单调递增函数。
2.二次函数:二次函数的一般形式是 y = ax^2 + bx + c,其中 a、b 和 c 是常数,并且 a 不等于零。
当 a 大于零时,二次函数的开口向上,形状是一个 U 字型,此时函数在定义域上是单调递增的。
例如,y = x^2 + 2x +1 就是一个单调递增函数。
3.指数函数:指数函数的一般形式是y=a^x,其中a是常数,并且a大于1、指数函数的图像是一个逐渐上升的曲线,而且在定义域上是单调递增的。
例如,y=2^x就是一个单调递增函数。
4.对数函数:对数函数的一般形式是 y = log_a(x),其中 a 是一个常数。
当底数a 大于 1 时,对数函数的图像是一个单调递增的曲线。
例如,y =log_2(x) 就是一个单调递增函数。
5.正弦函数和余弦函数:正弦函数和余弦函数是周期性的函数,但它们在每个周期内是单调递增的。
正弦函数的一般形式是 y = a*sin(bx + c),其中 a、b 和 c 是常数。
余弦函数的一般形式是 y = a*cos(bx + c)。
当振幅 a 大于零时,这两个函数都是单调递增的。
除了上述示例外,还有许多其他函数可以构造为单调递增函数,包括多项式函数、根式函数、双曲函数等。
以上只是其中一些常见的例子。
需要注意的是,对于真实世界中的问题,我们可以根据具体情况构造单调递增函数。
例如,如果我们需要模拟一些随时间递增的过程,可以选择合适的函数形式来描述该过程。
此外,在实际应用中,我们还可以通过曲线拟合等方法找到适合数据集的单调递增函数关系式。
如何使用NA函数生成错误值

如何使用NA函数生成错误值在数据分析和处理的过程中,经常会遇到一些缺失值或错误值的情况。
为了准确处理这些异常数据,人们常常会使用NA函数来生成错误值。
本文将介绍如何使用NA函数来生成错误值,以及该函数的一些常见应用场景和注意事项。
一、NA函数概述NA函数是R语言中的一个特殊函数,用于生成表示缺失值或错误值的对象。
NA即表示"not available",意味着数据不可用、缺失或不适用。
在使用NA函数生成错误值时,我们可以通过指定不同的参数来生成不同类型的错误值对象。
二、生成缺失值对象1. 生成单个缺失值对象使用NA函数生成一个单个缺失值对象非常简单,只需要调用NA 函数即可。
例如:```x <- NA```上述代码将生成一个名为x的变量,其中存储了一个缺失值对象。
2. 生成包含缺失值的向量或数组在实际数据处理中,常常需要生成含有多个缺失值的向量或数组。
可以通过向NA函数传递一个整数参数n来生成长度为n的缺失值向量或数组。
例如:```x <- rep(NA, 5)```上述代码将生成一个长度为5的向量x,其中每个元素均为缺失值对象。
三、NA函数的常见应用场景1. 处理缺失值在数据分析中,经常会遇到缺失值的情况,这些缺失值可能来自于数据采集过程中的漏采、数据传输错误等。
使用NA函数生成缺失值对象,可以辅助我们对于缺失值进行处理和分析。
2. 创建错误值对象除了缺失值外,有时候我们还需要生成其他类型的错误值对象。
例如,在数据清洗过程中,我们可能会遇到一些异常值或无法计算的数据,此时可以使用NA函数生成表示错误或非法值的对象。
3. 合并数据集在合并数据集时,可能会出现一些缺失值的情况。
此时,使用NA 函数可以方便地生成缺失值对象,使得数据合并的过程更加准确和方便。
四、NA函数的注意事项1. NA函数生成的对象是一个特殊值,与其他数值和字符对象有所不同。
在进行计算和分析时,需要注意处理NA值的方式。
常用函数公式及操作技巧之八大小值或中间值

常用函数公式及操作技巧之八大小值或中间值在Excel中,我们经常需要找出一组数据中的最大值、最小值或者中间值。
这时候就可以使用一些常用的函数公式和操作技巧来实现。
1.最大值和最小值-MAX函数:用于找出一组数据中的最大值。
例如,=MAX(A1:A10)表示找出A1到A10单元格范围内的最大值。
-MIN函数:用于找出一组数据中的最小值。
例如,=MIN(A1:A10)表示找出A1到A10单元格范围内的最小值。
2.中间值-MEDIAN函数:用于找出一组数据中的中间值。
中间值即将数据按照大小排列后的中间数。
例如,=MEDIAN(A1:A10)表示找出A1到A10单元格范围内的中间值。
3.排序函数-SORT函数:用于将一组数据按照指定的顺序进行排序。
例如,=SORT(A1:A10,1,TRUE)表示将A1到A10单元格范围内的数据按照升序排序。
-SORTBY函数:用于将一组数据按照指定的列进行排序。
例如,=SORTBY(A1:B10,B1:B10,1,TRUE)表示将A1到B10单元格范围内的数据按照B1到B10列的值进行升序排序。
4.条件函数-IF函数:用于根据指定的条件进行判断并返回不同的结果。
例如,=IF(A1>10,"大于10","小于等于10")表示如果A1大于10,则返回"大于10",否则返回"小于等于10"。
-COUNTIF函数:用于统计满足指定条件的单元格数量。
例如,=COUNTIF(A1:A10,">10")表示统计A1到A10单元格范围内大于10的单元格数量。
5.过滤函数-FILTER函数:用于根据指定的条件筛选出符合条件的数据。
例如,=FILTER(A1:B10,B1:B10>10)表示筛选出B1到B10列中大于10的数据,并返回对应的A1到B10列的值。
-UNIQUE函数:用于去重并返回一组数据中的唯一值。
jena规则

jena规则Jena是一种用于处理RDF数据的Java框架,它提供了一个规则引擎,可以用来推理和推断出新的RDF三元组。
Jena规则是一种基于规则语言的形式化描述,用于定义RDF数据之间的关联和逻辑推理。
Jena规则使用RDF的基本概念和语法,可以定义出很多不同的规则来推理和推断出新的RDF三元组。
在Jena中,规则的定义是通过RDF模型来实现的,一个规则由一个或多个前提条件和一个结果构成。
前提条件是一组RDF三元组,用于描述需要满足的条件;结果是一个RDF三元组,描述推理和推断生成的新事实。
在Jena规则中,可以使用一些基本的逻辑和关系运算符来描述前提条件和结果。
例如,逻辑运算符AND和OR可以用来组合多个RDF三元组,表示它们需要同时满足或者满足其中一个;关系运算符如等于(=)、不等于(!=)、大于(>)、小于(<)等可以用来描述特定的关系条件。
除了基本的逻辑和关系运算符,Jena规则还支持一些特殊的函数和谓词,用于处理和操作RDF数据。
例如,SPARQL函数可以用于查询和过滤数据;RDF序列函数可以用来处理RDF序列(包括列表和集合);RDF谓词可以用来描述和操作RDF数据之间的关系。
Jena规则还支持一些高级功能,如模式匹配、反向推理、转换和连接等。
模式匹配可以用来找到满足特定条件的RDF数据;反向推理可以根据已知的结果来推断前提条件;转换和连接可以将多个规则组合成一个更复杂的规则。
在使用Jena规则时,需要将规则定义为一个规则集合,并根据需要配置推理和推断规则的执行行为。
可以选择仅执行一次推理生成新的RDF事实,或者在RDF数据发生变化时自动触发推理过程。
Jena还提供了一些API和工具,用于方便地创建、解析和查询RDF数据。
总之,Jena规则是一种用于推理和推断RDF数据的强大工具,它提供了丰富的语法和功能,可以帮助我们发现隐藏在RDF数据中的潜在关联和逻辑关系。
通过使用Jena规则,我们可以更好地理解和利用RDF数据,从中获取更多有价值的知识和信息。
Jena_中文教程_本体API(经典)

Jena 简介一般来说,我们在Protege这样的编辑器里构建了本体,就会想在应用程序里使用它,这就需要一些开发接口。
用程序操作本体是很必要的,因为在很多情况下,我们要自动生成本体,靠人手通过Protege创建所有本体是不现实的。
Jena 是HP公司开发的这样一套API,似乎HP公司在本体这方面走得很靠前,其他大公司还在观望吗?可以这样说,Jena对应用程序就像Protege对我们,我们使用Protege操作本体,应用程序则是使用Jena来做同样的工作,当然这些应用程序还是得由我们来编写。
其实Protege本身也是在Jena的基础上开发的,你看如果Protege 的console里报异常的话,多半会和Jena有关。
最近出了一个Protege OWL API,相当于对Jena的包装,据说使用起来更方便,这个API就是Protege的OWL Plugin所使用的,相信作者经过OWL Plugin的开发以后,说这些话是有一定依据的。
题目是说用Jena处理OWL,其实Jena当然不只能处理OWL,就像Protege 除了能处理OWL外还能处理RDF(S)一样。
Jena最基本的使用是处理RDF(S),但毕竟OWL已经成为W3C的推荐标准,所以对它的支持也是大势所趋。
好了,现在来点实际的,怎样用Jena读我们用Protege创建的OWL本体呢,假设你有一个OWL本体文件(.owl),里面定义了动物类(/ont/Animal,注意这并不是一个实际存在的URL,不要试图去访问它),并且它有一些实例,现在看如下代码:OntModel m = ModelFactory.createOntologyModel();File myFile = ...;m.read(new FileInputStream(myFile), "");ResIterator iter = m.listSubjectsWithProperty(RDF.type, m.getResource("http:// /ont/Animal"));while (iter.hasNext()) {Resource animal = (Resource) iter.next();System.out.println(animal.getLocalName());}和操作RDF(S)不同,com.hp.hpl.jena.ontology.OntModel是专门处理本体(Ontology)的,它是com.hp.hpl.jena.rdf.model.Model的子接口,具有Model的全部功能,同时还有一些Model没有的功能,例如listClasses()、listObjectProperties(),因为只有在本体里才有“类”和“属性”的概念。
jensen函数方程 -回复

jensen函数方程-回复Jensen函数方程是函数方程中非常重要的一个方程,在数学的研究中具有广泛的应用。
它是由丹麦数学家约瑟夫·威廉·杰森(Johan Ludwig Jensen)于1906年提出的。
首先,让我们来了解一下什么是函数方程。
函数方程是指找到一个或多个函数解决特定的方程的问题。
通常,这些函数方程可以用一些已知其解的初始条件来确定。
Jensen函数方程的形式如下:f(x+y) = f(x) + f(y)这个方程看上去很简单,但它蕴含着很多有趣的性质和应用。
首先,我们来看方程中的基本操作。
在这个方程中,我们将两个变量相加,并将它们作为函数的输入。
然后,我们将函数应用于这个输入,并将结果相加。
换句话说,这个方程要求函数是可加性的,即它满足对于所有的实数x和y,f(x+y) = f(x) + f(y)。
在方程中暗含着一个重要条件,即函数f(x)是连续的。
这意味着它在实数域内的每个点都有定义,并且在每个点都有一个唯一的极限。
连续性条件是Jensen函数方程的一个重要性质,因为它将函数的性质与导数联系起来。
事实上,Jensen函数方程与导数有着密切的关系。
通过对方程两边进行求导,我们可以得到:f'(x+y) = f'(x) + f'(y)这表明函数的导数也满足可加性。
因此,Jensen函数方程是一类特殊的可加函数的函数方程。
这类函数的性质在数学的分析学和函数论中具有重要的应用。
除了导函数的可加性以外,Jensen函数方程还有许多其他有趣的性质。
例如,当函数满足Jensen函数方程时,它也是一个线性函数。
这是因为我们可以证明,当给定初始条件时,方程唯一地确定了函数的形式。
此外,Jensen函数方程还是函数方程的对偶,即如果一个函数满足该方程,那么它的倒数也满足该方程。
这种对称性使得函数方程的解集具有一些特殊的结构。
总之,Jensen函数方程是数学中的一个重要方程,具有许多有趣的性质和应用。
数据分析常用函数

数据分析常用函数数据分析是指通过对大量数据的收集、整理、清洗、分析和可视化等过程,挖掘出有效信息,为企业决策提供支持。
在数据分析的过程中,常常需要使用各种函数对数据进行处理和计算。
以下是一些数据分析中常用的函数:1.SUM函数:对一些数据列中的数据进行求和运算。
2.COUNT函数:对一些数据列中的数据进行计数,统计该列中有多少个非空值。
3.MEAN函数:求一些数据列中数据的平均值。
4.MAX函数和MIN函数:分别用于求一些数据列中的最大值和最小值。
5.MEDIAN函数:求一些数据列中数据的中位数,即将数据按大小排序后,位于中间的数值。
6.MODE函数:求一些数据列中数据的众数,即出现次数最多的数值。
7.VAR函数和STDEV函数:分别用于求一些数据列中数据的方差和标准差,用于衡量数据的离散程度。
8.QUARTILE函数:根据数据列中的位置,求出具有特定百分比位置的数值,如25%分位数、50%分位数、75%分位数等。
9.RANK函数:对数据列中的数据进行排名,可以根据需要进行升序或降序排列。
10.CONCATENATE函数:用于将多个文本字符串连接在一起。
11.LEFT函数和RIGHT函数:分别用于从字符串的左侧或右侧提取指定长度的字符。
12.LEN函数:用于计算字符串的长度。
13.TRIM函数:去除字符串中的空格。
14.UPPER函数和LOWER函数:分别用于将字符串转换为大写和小写。
15.IF函数:用于根据一些条件进行判断,满足条件返回一个结果,不满足条件返回另一个结果。
16.VLOOKUP函数:用于在一些数据表格中进行垂直查找,根据给定的值查找对应的结果。
17.HLOOKUP函数:用于在一些数据表格中进行水平查找,根据给定的值查找对应的结果。
18.INDEX函数和MATCH函数:配合使用,可以在一些数据表格中进行复杂的查找和匹配操作。
19.IFERROR函数:用于处理数据中的错误值,可以将错误值替换为指定的值。
筛法求欧拉函数

筛法求欧拉函数1. 定义欧拉函数,又称为费马函数,是数论中的一个重要函数,用符号φ(n)表示。
对于正整数n,欧拉函数φ(n)表示小于或等于n的正整数中与n互质的数的个数。
2. 用途欧拉函数在数论和密码学中有着广泛的应用。
它的一些常见用途包括:•判断两个数是否互质:若n和m互质,即gcd(n,m)=1,则φ(nm) = φ(n)φ(m)。
•素数的应用:对于素数p,φ(p) = p-1,即φ(p)表示小于p且与p互质的数的个数。
•RSA公钥加密算法:RSA算法的核心是基于欧拉函数的性质,其中φ(n)用于计算公钥和私钥的参数。
•求模反元素:欧拉函数的一个重要应用是求解模反元素,即对于正整数a和n,若gcd(a,n)=1,则存在整数b,使得(ab)%n=1。
3. 工作方式筛法求欧拉函数是一种高效的算法,可以用来计算小于等于某个数N的所有数的欧拉函数值。
3.1 算法步骤筛法求欧拉函数的具体步骤如下:1.初始化一个数组phi[],将所有数的欧拉函数值初始化为其本身,即phi[i]= i,其中0 ≤ i ≤ N。
2.从2开始遍历数组,若phi[i] = i,说明i是素数,对i的所有倍数j进行筛法操作:–phi[j] = phi[j] * (i-1) / i,其中i是素数。
–这里用到了欧拉函数的一个性质:若p是素数,n是正整数且p不能整除n,则phi(n) = phi(pn) = phi(n) * (p-1) / p。
–例如,对于素数2,phi[4] = phi[4] * (2-1) / 2 = 2,phi[6] = phi[6] * (2-1) / 2 = 2,phi[8] = phi[8] * (2-1) / 2 = 4。
3.完成遍历后,数组phi[]中存储的就是小于等于N的所有数的欧拉函数值。
3.2 算法示例以下是使用筛法求欧拉函数的示例代码(使用C++语言):#include <iostream>#include <vector>using namespace std;void eulerPhi(int N) {vector<int> phi(N+1);for (int i = 0; i <= N; i++) {phi[i] = i;}for (int i = 2; i <= N; i++) {if (phi[i] == i) {for (int j = i; j <= N; j += i) {phi[j] = phi[j] * (i-1) / i;}}}for (int i = 1; i <= N; i++) {cout << "phi(" << i << ") = " << phi[i] << endl;}}int main() {int N;cout << "Enter a number: ";cin >> N;eulerPhi(N);return 0;}4. 示例与解释假设我们要计算小于等于10的所有数的欧拉函数值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、OntModel ontModel = ModelFactory.createOntologyModel();Jena通过model包中的ModelFactory创建本体模型,ModelFactory是Jena提供用来创建各种模型的类,在类中定义了具体实现模型的成员数据以及创建模型的二十多种方法。
该语句不含参数,应用默认设置创建一个本体模型ontModel,也就是说:它使用OWL语言、基于内存,支持RDFS推理。
可以通过创建时应用模型类别(OntModelSpec)参数创建不同的模型,以实现不同语言不同类型不同推理层次的本体操作。
例如,下面的语句创建了一个使用DAML语言内存本体模型。
直观地讲,内存模型就是只在程序运行时存在的模型,它没有将数据写回磁盘文件或者数据库表。
OntModel ontModel = ModelFactory.createOntologyModel( OntModelSpec.DAML_MEM );更多类型设置可以参照OntModelSpec类中的数据成员的说明。
2、ontModel.read("file:D:/temp/Creatrue/Creature.owl");读取的方法是调用Jena OntoModel提供的Read方法。
Read方法也有很多重载,上面调用的方法以文件的绝对路径作为参数。
其他的方法声明如下read( String url );read( Reader reader, String base );read( InputStream reader, String base );read( String url, String lang );read( Reader reader, String base, String Lang );read( InputStream reader, String base, String Lang );3、OntModel m = ModelFactory.createOntologyModel();OntDocumentManager dm = m.getDocumentManager();创建一个文档管理器并将它与以创建的本体模型关联。
本体文档管理器(OntDocumentManager)是用来帮助管理本体文档的类,它包含了导入本体文档创建本体模型、帮助缓存下载网络上的本体等功能。
每个本体模型都有一个相关联的文档管理器。
在创建本体模型时,可以创建独立的文档管理器并作为参数传递给模型工厂(ModelFactory)。
文档管理器有非常多的配置选项,基本可以满足应用的需求。
首先,每个文档管理器的参数都可以通过Java代码来设置(注:OntDocumentManager有五种重载的构造函数)。
另外,文档管理器也可以在创建的时候从一个RDF格式的策略文件读取相应设定值。
4、接口OntClass这个接口中定义了本体种与概念(也就是类Class)相关的操作,通过OntModel中的listClasses()便可以返回模型中的所有概念组成的迭代器(Iterator),然后调用OntClass的各种方法具体进行具体操作。
OntoClass对概念之间的各种关系都有相应的定义方法,典型的有添加子类、添加约束、创建互斥概念、迭代返回某种类型的概念以及相关的逻辑判断等等。
5、基本本体类型OntResource所有本体API中用于表示本体的类继承自OntResource,这样就可以在OntResource中放置所有类公用的功能,并可以为一般的方法设置通用的返回值。
Java接口OntResource扩展了Jena的RDF资源接口,所以任何可以接受资源或者RDFNode的方法都可以接受OntResource,并且也就可以接受任何其他本体值。
虽然这个类涵盖了涉及本体的所有类,在例子中并没有使用它。
6、创建一个等价类:OntModel ontModel = ModelFactory.createOntologyModel(OntModelSpec.OWL_MEM); ontModel.read("file:./Creature.owl"); // 读取当前路径下的文件,加载模型// 定义一个类作为模型中Animal类的等等价类,并添加注释OntClass cls = ontModel.createClass(":DongwuClass");cls.addComment("the EquivalentClass of Animal...", "EN");// 通过完整的URI取得模型中的Animal类OntClass oc = ontModel.getOntClass("/marine.owl#Animal"); oc.addEquivalentClass(cls); // 将先前定义的类添加为Animal的等价类createClass:创建一个类addComment:增加注释getOntClass:取得模型中的类addEquivalentClass:定义等价类7、迭代显示模型中的类for (Iterator i = ontModel.listClasses(); i.hasNext();) {OntClass c = (OntClass) i.next(); // 返回类型强制转换if (!c.isAnon()) { // 如果不是匿名类,则打印类的名字System.out.print("Class");// 获取类的URI并输出,在输出时对URI做了简化(将命名空间前缀省略)System.out.println(c.getModel().getGraph().getPrefixMapping().shortForm(c.getURI()));// 处理Animal类if (c.getLocalName().equals("Animal")) { // 如果当前类是AnimalSystem.out.println(" URI@" + c.getURI()); // 输出它的完整URI// 取得它的的等价类并打印System.out.print(" Animal's EquivalentClass is "+ c.getEquivalentClass());// 输出等价类的注释System.out.println(" [comments:" +c.getEquivalentClass().getComment("EN")+"]");}// 处理Animal结束// 迭代显示当前类的直接父类for (Iterator it = c.listSuperClasses(); it.hasNext();){OntClass sp = (OntClass) it.next();String str = c.getModel().getGraph().getPrefixMapping().shortForm(c.getURI())+ "'s superClass is " ;// 获取URIString strSP = sp.getURI();try{ // 另一种简化处理URI的方法str = str + ":" + strSP.substring(strSP.indexOf('#')+1);System.out.println(" Class" +str);}catch( Exception e ){}} // super class ends// 迭代显示当前类的直接子类for (Iterator it = c.listSubClasses(); it.hasNext();){System.out.print(" Class");OntClass sb = (OntClass) it.next();System.out.println(c.getModel().getGraph().getPrefixMapping().shortForm(c.getURI()) + "'s suberClass is "+ sb.getModel().getGraph().getPrefixMapping().shortForm(sb.getURI()));}// suber class ends// 迭代显示与当前类相关的所有属性for(Iterator ipp = c.listDeclaredProperties(); ipp.hasNext();){OntProperty p = (OntProperty)ipp.next();System.out.println(" associated property: " + p.getLocalName());}// property ends}// anonymity endselse // 是匿名类{}}// for ends8、c.getModel().getGraph().getPrefixMapping().shortForm(c.getURI())//获得简化了的URI名称c.getEquivalentClass()//获得当前类的等价类c.getEquivalentClass().getComment("EN")//等价类的注释处理URI字串的方法一:c.getModel().getGraph().getPrefixMapping().shortForm(c.getURI())方法二:String str = c.getModel().getGraph().getPrefixMapping().shortForm(c.getURI())+ "'s superClass is " ;String strSP = sp.getURI();try{ // 另一种简化处理URI的方法str = str + ":" + strSP.substring(strSP.indexOf('#')+1);System.out.println(" Class" +str);}catch( Exception e ){}9、// 迭代显示模型中的类for (Iterator i = ontModel.listClasses(); i.hasNext();)// 迭代显示当前类的直接父类for (Iterator it = c.listSuperClasses(); it.hasNext();)// 迭代显示当前类的直接子类for (Iterator it = c.listSubClasses(); it.hasNext();)// 迭代显示与当前类相关的所有属性for(Iterator ipp = c.listDeclaredProperties(); ipp.hasNext();)10、创建资源并为其增加属性:ModelFactory.createDefaultModel();//创建默认的本体模型model.createResource(personURI);//创建资源johnSmith.addProperty(VCARD.FN, fullName);//创建资源属性static String personURI = "http://somewhere/JohnSmith";static String fullName = "John Smith";// create an empty ModelModel model = ModelFactory.createDefaultModel();// create the resourceResource johnSmith = model.createResource(personURI);// add the propertyjohnSmith.addProperty(VCARD.FN, fullName);。
