五年级上册数学一课一练-6.4组合图形的面积 人教新版(含解析)
五年级上册数学一课一练-6.4组合图形的面积 人教版(含答案)

五年级上册数学一课一练组合图形的面积)一、单选题1.下图方格纸上的图形面积是( )。
(小方格边长为1厘米)A. 12B. 8C. 62.在下边的梯形中,甲、乙两个三角形的面积()。
A. 相等B. 不相等C. 无法确定3.如果正方形的边长相等,下面图形中,阴影部分的面积()A. 图1和图2大B. 图3和图4大C. 图4和图5大D. 一样大4.如图所示,甲、乙是两个完全相同的长方形,两幅图的阴影面积相比,下列说法正确的是( )。
A. 甲>乙B. 甲=乙C. 甲<乙D. 无法判断5.如图,梯形ABCD中,两个阴影部分的面积关系是()A. S1=S2B. S1>S2C. S1<S2二、判断题6.不规则图形用单位方格纸测面积,单位越小测得结果越准确7.下面两图中阴影部分的面积相等。
(每个小方格的边长表示1cm)8.如图所示,阴影部分面积是10×10÷2÷2=25平方单位.9.用8个1立方厘米的小方块拼成一个正方体.如果拿去一个小方块,它的表面积不变.10.如图是我国珍贵的历史文化遗产《易经》中的一个主要图形﹣﹣﹣太极图,它是数形结合的光辉典范.图中阴阳(即圈内黑白)两部分的面积相等.三、填空题11.下图表示的是一间房子侧面墙的形状.它的面积是________平方米.12.求下列组合图形的面积.(单位:cm)________13.如图是由同样大小的小方块堆积起来的,每个小方块的棱长是1分米,这堆小方块露在外面的面积是________.14.估计下面图形的面积。
(每个小方格的面积表示1cm2)面积约为________;面积约为________;面积约为________15.数一数,填一填。
(每个小方格的面积表示1平方厘米)________________________四、解答题16.计算图形的面积五、应用题17.求阴影部分的面积.(单位:厘米)18.求正方形中阴影部分的周长和面积.参考答案一、单选题1.【答案】B【解析】【解答】8×1=8(平方厘米)。
人教版五年级上册数学组合图形的面积试题(含解析)

五年级上册数学一课一练-6.4组合图形的面积一、单选题1.下面三幅图中,正方形一样大,则三个阴影部分的面积()A. 一样大B. 第一幅图最大C. 第二幅图最大D. 第三幅图最大2.下图中每个小方格的面积为1cm2,五角星图(阴影部分)的面积约()1cm2。
A. 26~30B. 19~25C. 9~18D. 4~83.下面两幅图中阴影部分的面积相比,( )。
A. 图①中的大B. 图②中的大C. 一样大D. 无法确定4.下边图形中阴影部分占整个图形的()。
A. B. C.二、判断题5.判断,正确的填“正确”,错误的填“错误”.两个面积相等的梯形,上底、下底和高一定相等.6.右图中的阴影部分面积占长方形的。
7.判断,正确的填“正确”,错误的填“错误”.把一个长方形框架拉成平行四边形,它的面积不变.三、填空题8.下图是一个运动场的平面图,它的周长是________米,面积是________平方米.(单位:米)(用小数表示)9.先把下面每个图形适当地分一分,再数出每个图形的面积.(每个小方格表示1平方厘米)(1)________平方厘米(2)________平方厘米10.估计下面图形的面积。
(每个小方格的面积表示1cm2)面积约为________;面积约为________;面积约为________11.幸福乡中学有一块菜地,形状如下图所示,那么这块菜地的面积是________ .四、解答题12.计算阴影部分的面积。
13.求阴影部分的面积.14.计算下面组合图形的面积。
五、综合题15.小丽家装修需要30块木板,木板的形状如图.(1)1块木板的面积是多少?(2)如果每块木板需要15元,那么小丽家买木板共花多少钱?六、应用题16.已知:ABCD是长方形,DC=4cm,AD=6cm,E是DF的中点,求S△EFC?17.求下图的面积.(图中单位:米)参考答案一、单选题1.【答案】A【解析】【解答】假设正方形的边长是4,第一个图形:4×4-3.14×(4÷2)²=16-3.14×4=16-12.56=3.44第二个图形:4×4-3.14×(4÷4)²×4=16-3.14×4=16-12.56=3.44第三个图形:4×4-3.14×4²÷4=16-3.14×4=16-12.56=3.44所以三个阴影部分的面积一样大.故答案为:A【分析】三个阴影部分的面积都是正方形面积减去内部空白部分的面积,假设出正方形的边长,然后根据正方形和圆面积公式分别计算阴影部分的面积并作出判断即可.2.【答案】C【解析】【解答】解:2×2÷2×5+4=10+4=14(cm²)故答案为:C。
五年级上册数学试题六、4.组合图形的面积一课一练人教新课标(含答案)

六、4.组合图形的面积一、填空乐园1.在一个上底是6厘米、下底是9厘米、高是4厘米的梯形中剪去一个最大的三角形,剩下的部分面积是( )平方厘米。
2.一个平行四边形,面积是54平方分米,如果高缩小到原来的21,要使面积不变,底应该( )。
3.三角形的底扩大a 倍,高扩大b 倍,面积扩大( )倍。
4.如图,要使三角形ABE 的面积是梯形AECD 面积的一半.BE 的长应是( )。
5.下面平行四边形的面积是15平方厘米,阴影部分的面积是( )平方厘米。
6.如图,现有6x6的方格,每个小方格的边长都是1,那么图中阴影部分的面积的总和等于( )。
7.如图,每两个相邻点之间的距离都是1厘米,三角形ABG 的面积是( ),梯形CDEF 的面积是( ),这个图形的面积是( )。
8.如图,每两个相邻的点之间的距离都是1厘米,平行四边形ABCE 的面积为( ),梯形ABDE 的面积为( )。
9.如图,若每个小正方形的面积都是1平方厘米,那么图中阴影部分的面积是( )平方厘米。
10.如图.每相邻三个点所形成的三角形都是面积为1的正三角形,则三角形ABC的面积为( )。
11.如图,平行四边形ABCD的底边DC长5 cm,直角三角形DCE的直角边EC长4厘米。
已知两块阴影部分的面积和比三角形EFG的面积大5平方厘米,则CF=( )厘米。
12.将一个正方形的一组对边各延长4厘米后,就成了一个长方形,这个长方形的面积比原来正方形的面积多32平方厘米,这个长方形的面积是原来正方形面积的( )倍。
二、判断快车1.两个等底等高的三角形都能拼成一个平行四边形。
( )2.在平行四边形内画一个三角形,三角形的面积一定等于平行四边形面积的一半。
( ) 3.两个面积相等的梯形,形状也一定相同。
( )4.梯形只有一条高,三角形有三条高。
( )5.两个完全一样的直角梯形可以拼成一个等腰梯形。
( )6.周长相等的两个平行四边形的面积不一定相等。
( )7.把一个长方形木框拉成平行四边形后,它的面积一定与原来长方形的面积相等。
五年级上册数学一课一练-6.4组合图形的面积 人教新版(含解析)(1)(1)
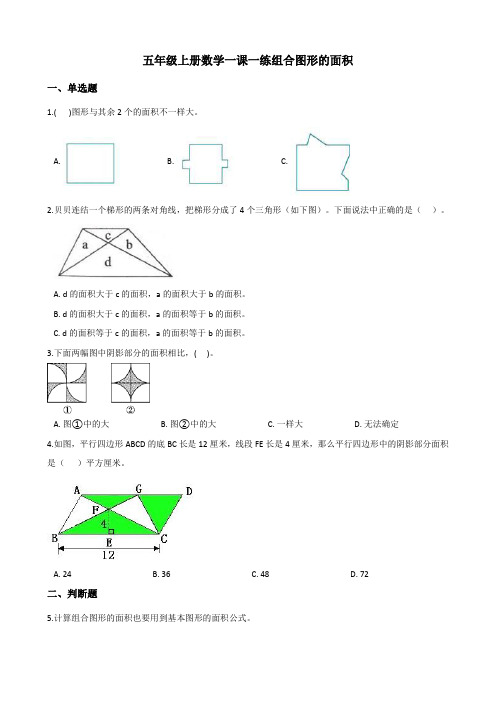
一、单选题
1.( )图形与其余2个的面积不一样大。
A. B. C.
2.贝贝连结一个梯形的两条对角线,把梯形分成了4个三角形(如下图)。下面说法中正确的是()。
A. d的面积大于c的面积,a的面积大于b的面积。
B. d的面积大于c的面积,a的面积等于b的面积。
C. d的面积等于c的面积,a的面积等于b的面积。
故答案为:C
【分析】两个图中阴影部分的面积都是正方形面积减去空白部分的面积,两个圆中空白部分的面积组合在一起就是一个圆的面积,所以阴影部分的面积相等。
4.【答案】C
【解析】【解答】解:因为△FAG与△CGD的面积之和与△FBC的面积相等,所以△GBC与△CAD的面积相等,阴影部分的总面积是:
12×4÷2×2
17.已知图中大正方形边长12厘米,小正方形边长8厘米,求图中阴影部分的面积.
参考答案
一、单选题
1.【答案】B
【解析】【解答】观察图形可知,C图形中的凸出部分可以剪拼到凹进去的部分,组成一个长方形,与A图形的面积相等,B图形的面积与其余2个的面积不一样大.
故答案为:B.
【分析】比较图形面积的大小,可以用剪拼、平移等方法将图形进行分割与组合,然后判断大小.
六、应用题
16.【答案】解:5×3÷2+5×8
=15÷2+40
=+40
=(平方分米)×=(元)
答:制作这个垃圾箱的侧面一共需要元.
【解析】【分析】根据题意可知,这个垃圾箱的侧面面积=三角形的面积+长方形的面积,三角形的面积=底×高÷2,长方形的面积=长×宽,据此求出侧面积,然后用侧面积×每平方分米的单价=一共需要的钱数,据此列式解答.
五年级上册数学一课一练-6.4组合图形的面积 人教新版(含解析) (1)

五年级上册数学一课一练-6.4组合图形的面积一、单选题1.将一个圆柱体削制成一个圆锥体,削去部分的体积是圆柱体积的()A. B. C. 2倍 D. 不能确定2.如图,甲和乙是两个正方形,阴影部分的面积是()平方厘米.A. 64B. 48C. 50D. 无法计算3.如图两个图中阴影部分的()A. 周长相等,面积不相等B. 周长和面积都相等C. 周长不相等,面积相等4.在下边的梯形中,甲、乙两个三角形的面积()。
A. 相等B. 不相等C. 无法确定二、判断题5.计算组合图形的面积也要用到基本图形的面积公式。
6.两个完全一样的梯形可以拼成一个平行四边形。
7.如图是我国珍贵的历史文化遗产《易经》中的一个主要图形﹣﹣﹣太极图,它是数形结合的光辉典范.图中阴阳(即圈内黑白)两部分的面积相等.(判断对错)三、填空题8.一个长方形文具盒有8个和2个半个小方格(一个小方格是一平方厘米)文具盒占桌面面积________平方厘米9.估一估,下面每个图形所占的面积大约是多少?(每个小方格的面积表示1cm2)________ 10.下图中的阴影部分的面积占长方形的________。
11.大小正方形如图.小正方形边长a厘米,阴影面积是________平方厘米.四、解答题12.张阿姨家有一块菜地(如图),这块菜地的面积有多少平方米?13.看图回答计算平行四边形中涂色部分的面积.五、综合题14.列式计算:(1)6除1.5的商,加上3,在乘3,积是多少?(2)与0.5的和除以它们的差的2倍,商是多少?(3)如图:三角形ABC为直角三角形,BC为圆的直径,BC=20厘米,S1、S2阴影部分的面积,且S1=S2,求三角形ABC的面积?六、应用题15.如图,平行四边形面积是50平方厘米,底是10厘米,求阴影部分面积.16.已知图中大正方形边长12厘米,小正方形边长8厘米,求图中阴影部分的面积.参考答案一、单选题1.【答案】D【解析】【解答】解:将一个圆柱体削制成一个最大的圆锥体,圆锥的体积是圆柱的,削去部分的体积是圆柱体积的,这里没说削成的圆锥是否最大,因此不能确定.故选:D.【分析】将一个圆柱体削制成一个最大的圆锥体,也就是说削成的圆锥与圆柱等底等高,圆锥的体积是圆柱的,即削去部分的体积是圆柱体积的,这里没说削成的圆锥是否最大,因此不能确定.2.【答案】C【解析】【解答】解:如图:(6+10+6)×10÷2-(10+6)×6÷2-6×(10-6)÷2=22×10÷2-16×6÷2-6×4÷2=110-48-12=50(平方厘米)故答案为:C【分析】通过添加辅助线,可以把阴影部分的面积看作是一个梯形面积减去空白部分两个三角形的面积来计算。
五年级数学上册 一课一练- 《组合图形的面积》练习1 人教版(含答案)

五年级数学上册一课一练- 《组合图形的面积》练习1 人教版(含答案)一、单选题(共7题;共14分)1.两个平行四边形的面积相等,它们的底和高()。
A. 一定相等B. 一定不相等C. 不一定相等2.比较下边的图形,说法正确的是()。
A. 甲、乙的面积相等,周长也相等。
B. 甲、乙的周长相等,但乙的面积大。
C. 甲的面积小,周长也小。
3.—个梯形的上底、下底和高分别扩大到原来的2倍,则梯形的面积()。
A. 扩大到原来的8倍B. 扩大到原来的4倍C. 扩大到原来的27倍4.下面几个图形的面积相比,()。
A. a图形最大B. b图形最大C. c图形最大 D. 一样大5.下面的四个平行四边形,根据已知条件可以算出面积的是()。
A. B. C. D.6.如图,每个小方格的面积是1平方厘米,估一估,这个脚印的面积大约是()平方厘米。
A. 13B. 20C. 35D. 407.用一张长为15分米、宽10分米的长方形硬纸板,剪成两条直角边都是2分米的直角三角形,最多能剪()个。
A. 35B. 70C. 75二、填空题(共1题;共1分)8.把一个长为10厘米、宽为8厘米的活动式长方形,拉成一个一条高为9厘米的平行四边形,拉成的平行四边形的面积是________平方厘米。
三、计算题(共2题;共15分)9.计算下面图形阴影部分的面积。
(单位:cm)(1)(2)10.计算下列图形的面积四、应用题(共8题;共40分)11.一间房子的侧面如下图,每平方米用砖180块,砌这样一堵墙需要砖多少块?12.一个垃圾箱的侧面如右图所示。
它是由塑钢制作的,每平方分米塑钢1.4元,制作这个垃圾箱的侧面一共需要多少钱?13.一个平行四边形小麦田,底长550米,高是220米,他的面积是多少平方米?14.已知梯形的上底是10厘米,下底是17厘米,其中阴影部分的面积算式221平方厘米,求这个梯形的面积。
15.一块平行四边形的草坪中有一条长8米、宽1米的小路,草坪的面积是多大?如果铺每平方米草坪的价格是16元,那么铺好这些草坪需要多少钱?16.一块平行四边形菜地,底是28米,高是12米、每平方米收入25元。
五年级上册数学一课一练-6.4组合图形的面积 人教版(含答案解析)
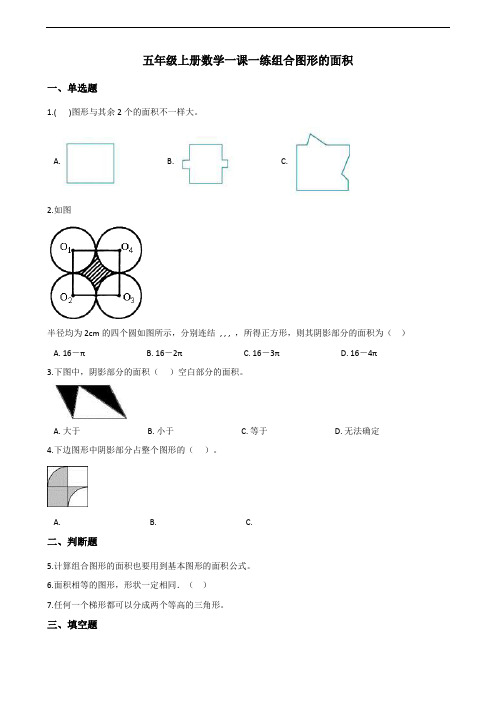
五年级上册数学一课一练组合图形的面积一、单选题1.( )图形与其余2个的面积不一样大。
A. B. C.2.如图半径均为2cm的四个圆如图所示,分别连结, , , ,所得正方形,则其阴影部分的面积为()A. 16-πB. 16-2πC. 16-3πD. 16-4π3.下图中,阴影部分的面积()空白部分的面积。
A. 大于B. 小于C. 等于D. 无法确定4.下边图形中阴影部分占整个图形的()。
A. B. C.二、判断题5.计算组合图形的面积也要用到基本图形的面积公式。
6.面积相等的图形,形状一定相同.()7.任何一个梯形都可以分成两个等高的三角形。
三、填空题8.求下面图形的面积。
(每个小方格的边长表示1cm)________ cm2________cm29.求阴影部分的面积.________10. 如图,两个正方形的边长分别是8厘米和4厘米,则阴影部分的面积是________平方厘米.11.如图中,四边形ABCD是一个梯形,BE与CD互相平行。
已知AE=8 cm,BC=5 cm,空白部分的面积是16 cm2,那么阴影部分的面积是________平方厘米。
12.长方形长10厘米,宽6厘米,E为AB边上任一点,三角形EDC(即阴影部分)的面积是________平方厘米。
四、解答题13.计算如图阴影部分的面积,已知厘米.14.求下面组合图形的面积。
(单位:分米)五、综合题15.计算(1)如图所示涂色部分图形的周长是多少cm?(2)求如图中涂色部分的面积.六、应用题16.学校有两块卫生区需要打扫,一块是体育场,一块是正方形花坛周围的小路(如图所示).若要你班去打扫这两块卫生区,你认为哪块卫生区分配的人数要多些,说明理由.17.已知下图中平行四边形的面积是45平方分米,根据图中的其他已知条件,求梯形的面积.参考答案一、单选题1.【答案】B【解析】【解答】观察图形可知,C图形中的凸出部分可以剪拼到凹进去的部分,组成一个长方形,与A 图形的面积相等,B图形的面积与其余2个的面积不一样大.故答案为:B.【分析】比较图形面积的大小,可以用剪拼、平移等方法将图形进行分割与组合,然后判断大小.2.【答案】D【解析】【解答】解:正方形边长:2×2=4(cm)阴影部分的面积:4×4-π×22=16-4π故答案为:D【分析】阴影部分的面积是正方形面积减去四个扇形面积,这四个扇形面积刚好是一个半径2cm的圆面积,由此计算即可.3.【答案】C【解析】【解答】解:阴影部分的面积等于空白部分的面积。
数学五年级上册《组合图形的面积》一课一练(含答案)

【同步专练B】6.4 组合图形的面积(巩固提升篇)一、单选题(共8题)1.一块正方形手帕的边长是40厘米,它的面积是16( ),周长是160( )。
A.平方厘米厘米B.平方分米分米C.平方厘米分米D.平方分米厘米2.下图是由两个完全相同的长方形拼出的一个正方形和一个长方形,二者比较( )。
A. 面积、周长都相等B. 面积相等,长方形周长大C. 面积相等,长方形周长小D. 面积和周长都不相等3.如图是用1平方厘米的正方形拼成的两个图形,它们的周长和面积相比,正确的是( )。
A. 周长相等,面积不相等B. 周长不相等,面积相等C. 周长相等,面积也相等4.将4个边长是1厘米的小正方形拼成一个长方形和一个正方形(如下图)。
下面说法正确的是( )。
A. 长方形的周长长,正方形的面积大。
B. 它们的面积相等,长方形的周长长。
C. 他们的周长和面积都相等D. 它们的面积相等,正方形的周长长。
5.如图,长方形ABCD的周长是14cm,在它的每条边上各画一个以该边为边长的正方形,已知这四个正方形的面积是50cm2 , 那么长方形ABCD面积是( )平方厘米.A. 12B. 6C. 10D. 496.如图,一个长方形分成甲、乙两部分,下面说法正确的是( )A. 甲、乙周长相等,面积不相等B. 甲、乙周长和面积都不相等C. 甲、乙周长和面积都相等7.如下图,有两个面积相等的长方形,两个阴影部分的面积关系为( ).A. a>bB. a<bC. a=b8.比较上面两个图形的周长,结果是( )A. 左图的周长>右图的周长B. 左图的周长<右图的周长C. 左图的周长=右图的周长二、判断题(共6题)9.在梯形中,阴影①的面积与阴影②的面积相等。
( )10.任何两个三角形都可以拼成一个四边形。
( )11.用8个大小一样的正方形无论拼成什么图形,它们的面积都相等。
( )12.如图阴影部分与空白部分面积的比是1:1。
五年级上册数学一课一练6.4组合图形的面积人教新课标(2014秋)(含答案)
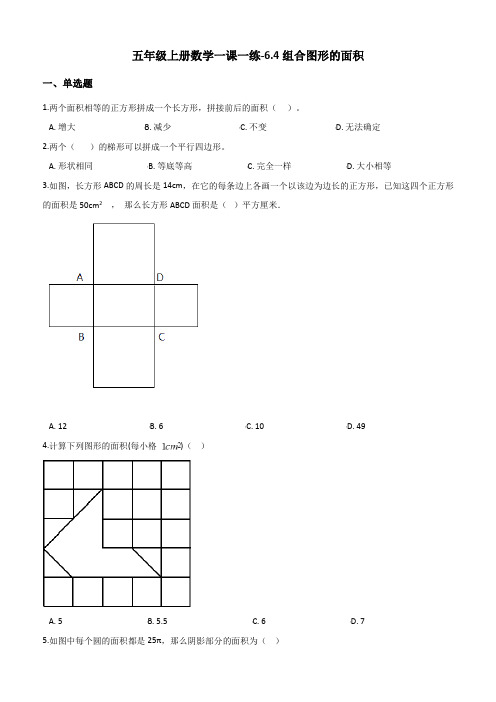
五年级上册数学一课一练-6.4组合图形的面积一、单选题1.两个面积相等的正方形拼成一个长方形,拼接前后的面积()。
A. 增大B. 减少C. 不变D. 无法确定2.两个()的梯形可以拼成一个平行四边形。
A. 形状相同B. 等底等高C. 完全一样D. 大小相等3.如图,长方形ABCD的周长是14cm,在它的每条边上各画一个以该边为边长的正方形,已知这四个正方形的面积是50cm2,那么长方形ABCD面积是()平方厘米.A. 12B. 6C. 10D. 494.计算下列图形的面积(每小格)()A. 5B. 5.5C. 6D. 75.如图中每个圆的面积都是25π,那么阴影部分的面积为()A. 200﹣50πB. 50π﹣200C. 4﹣πD. 100﹣25π二、判断题6.面积相等的图形,形状一定相同.()7.如图所示,阴影部分面积是10×10÷2÷2=25平方单位.8.任何两个三角形都可以拼成一个四边形。
三、填空题9.图中阴影部分的面积是________平方厘米.(用小数表示)(单位:厘米)10.用________原理对组合图形进行分割时,图形的面积大小________。
11.求阴影部分的周长和面积(单位:cm)周长:________cm面积:________12.看图计算组合图形的面积是________平方米四、解答题13.下面两幅图中的阴影部分面积相等吗?14.(2016·河北邯郸)求下图中阴影部分的面积。
15.求阴影部分面积。
五、综合题16.图是小明家住房平面图.(单位:米)(1)客厅的面积是多少平方米?(2)厨房的面积比客厅少多少平方米?(3)你还能提出什么数学问题?并尝试解决.六、应用题17.计算图中阴影部分面积.(单位:分米)参考答案一、单选题1.【答案】C2.【答案】C3.【答案】A4.【答案】A5.【答案】A二、判断题6.【答案】错误7.【答案】正确8.【答案】错误三、填空题9.【答案】8.3710.【答案】出入相补;不变11.【答案】51.4;21.512.【答案】8.23四、解答题13.【答案】解:两个阴影部分的面积都是大正方形的面积减去直径6cm的圆的面积,所以阴影部分的面积是相等的.答:两幅图中阴影部分的面积相等.14.【答案】解:8÷2=4(厘米)(4×4-3.14×42)2=6.88(平方厘米)15.【答案】解:第一种方法:10×5÷2+5×5÷2=37.5(平方厘米)第二种方法:10×10+5×5-5×5÷2-[10+(10-5)]×10÷2=37.5(平方厘米)答:阴影部分面积是37.5平方厘米。
人教版五上6.4 组合图形的面积 一课一练

人教版五上组合图形的面积一课一练一.填空题1.如右图所示,梯形ABCD中,△ABO的面积△OCD的面积。
(选填“>”、“<”或“=”)2.如果图中每个正方形小格的边长是1厘米,那么图中涂色部分的面积是平方厘米.3.如图组合图形的面积是平方厘米.4.如图,平行四边形中,阴影部分的面积是,平行四边形的面积是平方分米.5.如图阴影部分的面积占整个图形面积的.二.选择题6.如图在长方形ABCD中,三角形ABF的面积与三角形EDF的面积相比()。
A.三角形ABF的面积大B.三角形EDF的面积大C.一样大D.不能比较7.下列四个图形相比,面积最大的是()A.A B.B C.C D.D8.图中,图形A和B的面积相比较()A.A>B B.A<B C.A=B D.无法比较9.某正方形园地是由边长为1米的)17.已知长方形的面积是40cm2,求阴影部分的面积。
18.计算下面图形的面积。
人教版五上组合图形的面积一课一练参考答案与试题解析一.填空题(共5小题)1.解:观察图形可知,因为△ABC和△BCD同底等高,所以S△ABC=S△BCD因为S△ABO S△BOC=S△OCD S△BOC所以:三角形ABO与三角形DCO的面积相等。
故答案为:=。
2.解:5×4=2021方厘米)答:图中涂色部分的面积是2021厘米。
故答案为:20213.解:13×103×10÷2=13015=145(平方厘米)答:组合图形的面积是145平方厘米.故答案为:145.4.解:×2=73(dm2)答:平行四边形的面积是73平方分米.故答案为:73.5.解:两个三角形的面积相等,面积和等于一个小正方形的面积,小正方形又占整个图形的,所以阴影部分的面积占整个图形的.故答案为:.二.选择题(共5小题)6.解:根据题意与分析可得:三角形ABE和三角形BDE是等底等高的三角形,所以,三角形ABE的面积=三角形BDE 的面积;三角形ABE的面积=三角形ABF的面积三角形BEF的面积,三角形BDE的面积=三角形EDF的面积三角形BEF的面积三角形ABF的面积三角形BEF的面积=三角形EDF的面积三角形BEF的面积三角形ABF的面积=三角形EDF的面积故选:C。
五年级上册数学一课一练-6.4组合图形的面积 人教新版(含解析)(1)

五年级上册数学一课一练组合图形的面积一、单选题1.将一个圆柱体削制成一个圆锥体,削去部分的体积是圆柱体积的()A. B. C. 2倍 D. 不能确定2.如图,甲和乙是两个正方形,阴影部分的面积是()平方厘米.A. 64B. 48C. 50D. 无法计算3.如图两个图中阴影部分的()A. 周长相等,面积不相等B. 周长和面积都相等C. 周长不相等,面积相等4.在下边的梯形中,甲、乙两个三角形的面积()。
A. 相等B. 不相等C. 无法确定二、判断题5.计算组合图形的面积也要用到基本图形的面积公式。
6.两个完全一样的梯形可以拼成一个平行四边形。
7.如图是我国珍贵的历史文化遗产《易经》中的一个主要图形﹣﹣﹣太极图,它是数形结合的光辉典范.图中阴阳(即圈内黑白)两部分的面积相等.(判断对错)三、填空题8.一个长方形文具盒有8个和2个半个小方格(一个小方格是一平方厘米)文具盒占桌面面积________平方厘米9.估一估,下面每个图形所占的面积大约是多少?(每个小方格的面积表示1cm2)________ 10.下图中的阴影部分的面积占长方形的________。
11.大小正方形如图.小正方形边长a厘米,阴影面积是________平方厘米.四、解答题12.张阿姨家有一块菜地(如图),这块菜地的面积有多少平方米?13.看图回答计算平行四边形中涂色部分的面积.五、综合题14.列式计算:(1)6除的商,加上3,在乘3,积是多少?(2)与的和除以它们的差的2倍,商是多少?(3)如图:三角形ABC为直角三角形,BC为圆的直径,BC=20厘米,S1、S2阴影部分的面积,且S1=S2,求三角形ABC的面积?六、应用题15.如图,平行四边形面积是50平方厘米,底是10厘米,求阴影部分面积.16.已知图中大正方形边长12厘米,小正方形边长8厘米,求图中阴影部分的面积.参考答案一、单选题1.【答案】D【解析】【解答】解:将一个圆柱体削制成一个最大的圆锥体,圆锥的体积是圆柱的,削去部分的体积是圆柱体积的,这里没说削成的圆锥是否最大,因此不能确定.故选:D.【分析】将一个圆柱体削制成一个最大的圆锥体,也就是说削成的圆锥与圆柱等底等高,圆锥的体积是圆柱的,即削去部分的体积是圆柱体积的,这里没说削成的圆锥是否最大,因此不能确定.2.【答案】C【解析】【解答】解:如图:(6+10+6)×10÷2-(10+6)×6÷2-6×(10-6)÷2=22×10÷2-16×6÷2-6×4÷2=110-48-12=50(平方厘米)故答案为:C【分析】通过添加辅助线,可以把阴影部分的面积看作是一个梯形面积减去空白部分两个三角形的面积来计算。
五年级上册数学一课一练6.4组合图形的面积 人教新版(含答案)

五年级上册数学一课一练-6.4组合图形的面积一、单选题1.下面三幅图中,正方形一样大,则三个阴影部分的面积()A. 一样大B. 第一幅图最大C. 第二幅图最大D. 第三幅图最大2.一个梯形的上底增加3厘米,下底减少3厘米,要使梯形的面积不变,高()。
A. 变小了B. 不变C. 变大了3.如图,阴影部分面积是()(π取3.14)A. 7.74平方厘米B. 6.62平方厘米C. 9.12平方厘米D. 18平方厘米4.计算下面的周长和面积:()A. 2π,B. 2π,C. 1.5π,D. 3π,二、判断题5.不规则图形用单位方格纸测面积,单位越小测得结果越准确6.任何一个梯形都可以分成两个等高的三角形。
7.判断,正确的填“正确”,错误的填“错误”.把一个长方形框架拉成平行四边形,它的面积不变.三、填空题8.下图表示的是一间房子侧面墙的形状.它的面积是________平方米.9.把2个边长4厘米的正方形拼成一个长方形,这个长方形的周长是________厘米,面积是________平方厘米。
10.如图,4个棱长都是30cm的正方体堆放在墙角处,露在外面的面积是________cm²。
11.如图,E、F分别是长方形ABCD长、宽的中点,长方形的面积是32平方厘米,三角形AEF的面积是________.四、解答题12.计算阴影部分的面积。
13.计算阴影部分的面积五、综合题14.(1)(2)(3)(4)(5)六、应用题15.如图,已知BO=2DO,CO=5AO,阴影部分的面积和为22平方厘米,求四边形ABCD的面积.参考答案一、单选题1.【答案】A【解析】【解答】假设正方形的边长是4,第一个图形:4×4-3.14×(4÷2)²=16-3.14×4=16-12.56=3.44第二个图形:4×4-3.14×(4÷4)²×4=16-3.14×4=16-12.56=3.44第三个图形:4×4-3.14×4²÷4=16-3.14×4=16-12.56=3.44所以三个阴影部分的面积一样大.故答案为:A【分析】三个阴影部分的面积都是正方形面积减去内部空白部分的面积,假设出正方形的边长,然后根据正方形和圆面积公式分别计算阴影部分的面积并作出判断即可.2.【答案】B【解析】【解答】因为梯形的面积=(上底+下底)×高÷2,“上底增加3厘米,下底减少3厘米,面积不变”则(上底+下底)的和不变,且面积不变,所以梯形的高不变。
五年级上册数学一课一练-6.4组合图形的面积 人教新课标(含答案)

五年级上册数学一课一练-6.4组合图形的面积一、单选题1.如图两个图中阴影部分的()A. 周长相等,面积不相等B. 周长和面积都相等C. 周长不相等,面积相等2.下面三幅图的阴影部分的面积相比较,( )的面积大。
A. 图(1)大B. 图(2)大C. 图(3)大D. 同样大3.在如图梯形中,两个阴影部分的面积相比( )A. 甲大于乙B. 乙大于甲C. 甲等于乙D. 无法比较4.如图,平行四边形ABCD的底BC长是12厘米,线段FE长是4厘米,那么平行四边形中的阴影部分面积是()平方厘米。
A. 24B. 36C. 48D. 72二、填空题5.求下面图中阴影部分的面积.面积是________6.计算组合图形的面积,一般通过________或________的方法,把它转化成基本图形后进行计算。
7.如图是由6个面积是1平方厘米的正方形组成的,三角形C的面积是________平方厘米,三角形A,B,C的面积和是________平方厘米,空白部分的面积是________平方厘米.8.如图中,四边形ABCD是一个梯形,BE与CD互相平行。
已知AE=8 cm,BC=5 cm,空白部分的面积是16 cm2,那么阴影部分的面积是________平方厘米。
9.计算下面组合图形的面积________平方厘米三、判断题10.下图中的阴影部分面积占长方形的。
11.梯形的上底下底越长,面积越大。
12.平行四边形的面积大于梯形面积。
13.图中涂色的两个三角形面积是一样大的。
四、解答题14.计算组合图形的面积。
(单位:cm)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五年级上册数学一课一练组合图形的面积人教新版(含解析)一、单选题1.将一个圆柱体削制成一个圆锥体,削去部分的体积是圆柱体积的()A. B. C. 2倍 D. 不能确定2.下面两个图形中阴影部分的面积相比,( )。
A. 图形(1)中的阴影面积大B. 图形(1)中的阴影面积小C. 阴影面积相等D. 无法比较3.如图两个图中阴影部分的()A. 周长相等,面积不相等B. 周长和面积都相等C. 周长不相等,面积相等4.图中两个正方形完全相同,阴影部分面积比较,()A. 相等B. A的阴影部分面积大C. B的阴影部分面积大D. 无法确定二、判断题5.计算组合图形的面积也要用到基本图形的面积公式。
6.如图所示,阴影部分面积是10×10÷2÷2=25平方单位.7.如图是我国珍贵的历史文化遗产《易经》中的一个主要图形﹣﹣﹣太极图,它是数形结合的光辉典范.图中阴阳(即圈内黑白)两部分的面积相等.三、填空题8.图中阴影部分的面积是________平方厘米.(用小数表示)(单位:厘米)9.如图,两个正方形的边长分别是6厘米、4厘米,阴影部分的面积是________平方厘米.10.求下列组合图形的面积.(单位:cm)________11.计算下面图形的周长和面积(1)________(2)________(3)________12.看图计算(单位:分米)阴影部分面积是________平方分米。
四、解答题13.如图,在长方形ABCD中,AB=2cm,BC=1cm.以A为圆心,AD长为半径画弧,交BA延长线于E,以B 为圆心,BE长为半径画弧交CB延长线于F,以C为圆心,CF长为半径画弧交DC延长线于G,求阴影部分的周长及面积.(保留π)14.求下面组合图形的面积。
(单位:分米)五、应用题15.学校有两块卫生区需要打扫,一块是体育场,一块是正方形花坛周围的小路(如图所示).若要你班去打扫这两块卫生区,你认为哪块卫生区分配的人数要多些,说明理由.参考答案一、单选题1.【答案】D【解析】【解答】解:将一个圆柱体削制成一个最大的圆锥体,圆锥的体积是圆柱的,削去部分的体积是圆柱体积的,这里没说削成的圆锥是否最大,因此不能确定.故选:D.【分析】将一个圆柱体削制成一个最大的圆锥体,也就是说削成的圆锥与圆柱等底等高,圆锥的体积是圆柱的,即削去部分的体积是圆柱体积的,这里没说削成的圆锥是否最大,因此不能确定.2.【答案】C【解析】【解答】解:两个图中阴影部分的面积都是正方形面积减去一个圆的面积,阴影部分面积相等。
故答案为:C【分析】第一个图中空白部分是两个半圆,组合在一起就是一个圆;第二个图中四个扇形组合在一起就是一个圆。
阴影部分的面积都是正方形面积减去一个圆的面积。
3.【答案】C【解析】【解答】解:由图可知:两个图形中的空白处均可组成一个完整的半径相等的圆,而正方形的面积相等,根据等量减去等量差相等的原理得这两个图形中阴影部分的面积相等;两个图形中阴影部分图形的周长不相等,第二个图形中阴影部分的周长多出两条边长.故选:C.【分析】从图中可以看出阴影部分的面积=正方形的面积﹣圆的面积.观察图形可发现:两个正方形是全等的,面积是相等;两个图形中空白部分可以组成一个完整的圆,根据圆的面积相等可得这两个图形中阴影部分的面积相等;而第一个图形中阴影部分的周长是直径为正方形的边长的圆的周长,第二个图形中阴影部分的周长是直径为正方形的边长的圆的周长+两条边长,所以周长不相等;据此选择.4.【答案】A【解析】【解答】解:设正方形的边长为1,因为两个正方形完全相同,所以正方形的面积也相等,则A阴影部分的面积=正方形的面积﹣圆的面积=12﹣π×(1÷2)2=π。
B阴影部分的面积=正方形的面积﹣圆的面积=12﹣π×12=1﹣=π。
所以阴影部分面积相等.故答案为:A.【分析】因为两个正方形完全相同,可以设正方形的边长为任意数或字母,为了计算的方便可以将边长设为1。
分别计算两个阴影部分的面积。
第一个阴影部分的面积=正方形的面积-圆的面积;第二个阴影部分的面积=正方形的面积-圆的面积。
二、判断题5.【答案】正确【解析】【解答】计算组合图形的面积时,要用到长方形的面积、正方形的面积、三角形的面积等基本图形的面积公式。
故答案为:正确。
【分析】组合图形均是由一些基本图形组合起来的。
在计算组合图形的面积时,可利用出入相补的方法对图形进行移动、重组,而图形的面积大小不变,利用一些基本公式进行计算,由此即可得出答案。
6.【答案】正确【解析】【解答】解:根阴影部分的面积是10×10÷2÷2=25(平方单位),原题说法正确.故答案为:正确.【分析】如图,把三角形外部的阴影部分移到中间的空白处,则阴影部分的面积是等于这个等腰直角三角形的面积的一半,据此即可判断.此题考查组合图形的面积的计算方法,本题关键是利用等积变形,把阴影部分转化到小直角三角形中.7.【答案】正确【解析】【解答】解:把小黑圆补充到小白圆上,黑白两部分是相等的,原题说法正确.故答案为:正确【分析】把图形重新组合后判断出这两部分的面积都是这个圆面积的一半,由此判断即可.三、填空题8.【答案】【解析】【解答】=-=(平方厘米)故答案为:【分析】阴影部分的面积是梯形面积减去空白部分半圆面积,梯形的下底是6厘米,高是3厘米,梯形面积=(上底+下底)×高÷2,圆面积:S=πr².9.【答案】【解析】【解答】解:×6×4+××42﹣×4×4,=12+﹣8,=(平方厘米);答:阴影部分的面积是平方厘米.故答案为:.【分析】如图所示,三角形ABD和三角形ABE等底等高,则这两个三角形的面积相等,同时减去公共部分三角形ABF,则剩余部分的面积仍然相等,即三角形AFE与三角形BFD的面积相等,所以阴影部分的面积=三角形ABE的面积﹣(以小正方形的边长为半径的圆的面积﹣三角形BDE的面积),据此解答即可.10.【答案】96【解析】【解答】14x8-8x4÷2=96平方厘米【分析】大长方形面积-三角形面积=组合图形面积11.【答案】(1),(2),(3),【解析】【解答】解:(1)周长:×2+×2+3=(cm),面积:3×÷2+3×=6(cm²);(2)周长:4×3+×4÷2=(cm),面积:4×4+×(4÷2)²÷2=(cm²);(3)周长:×2++×3×2÷2=(cm),面积:(3+3+×÷2+×3²÷2=(cm²)故答案为:,6cm²;,²;,²【分析】图形的周长就是围成图形所有线段或曲线的长度之和;面积:(1)三角形面积加上长方形面积;(2)正方形面积加上半圆面积;(3)半圆面积加上梯形面积.12.【答案】【解析】【解答】解:××2-×÷2×2=9-=(平方分米)平行四边形对边相等,所以AB=【分析】每一块阴影的面积都是一个平行四边形与一个三角形面积的差四、解答题13.【答案】解:BE的长度:2+1=3(cm),CF的长度3+1=4(cm),DG的长度:4+2=6(cm)周长:π×1×2÷4+π×3×2÷4+π×4×2÷4+6=π+π+2π+6=4π+6(cm)面积:π×1²÷4+π×3²÷4+π×4²÷4+2×1=π+π+4π+2=π+2(cm²)答:阴影部分的周长是(4π+6)cm;面积是.【解析】【分析】左边第一个扇形的半径是1cm,第二个扇形的半径是3cm,第三个扇形的半径是4cm,阴影部分的周长包括三个扇形圆弧的长度和DG的长度;阴影部分的面积包括三个扇形的面积和长方形ABCD的面积.14.【答案】解:40×20-(40-28)×20=800-240=560(平方分米)【解析】【分析】阴影部分的面积是长方形面积减去空白部分的面积,空白部分是两个相同的平行四边形,根据公式计算即可。
五、应用题15.【答案】解:×(20÷2)²+60×20=314+1200=1514(m²)×20²-20×20=1256-400=856(m²)1514m²>856m²答:体育场分配的人数要多些。
【解析】【分析】体育场的面积是一个直径20m的圆面积加上一个长方形面积,小路的面积是一个半径20m的圆面积减去中间边长20m的正方形面积;根据公式分别计算出面积后再根据面积的大小确定分配的人数。
