2019-2020年中考数学微测试系列专题17 相似三角形及应用 苏教版
苏教版九年级下册数学[用相似三角形解决问题—知识点整理及重点题型梳理](提高)
](https://img.taocdn.com/s3/m/1a14fee5b04e852458fb770bf78a6529647d35a9.png)
苏教版九年级下册数学[用相似三角形解决问题—知识点整理及重点题型梳理](提高)本文介绍了相似三角形解决问题的知识点,包括平行投影和中心投影。
要点一是平行投影,介绍了物体在平行光线下产生的影子,以及物高与影长的关系。
要点二是中心投影,介绍了点光源下物体产生的影子,以及离点光源远近对影子长度的影响。
通过这些知识点,可以解决一些实际问题。
需要注意的是,在利用影长计算物高时,要注意测量两物体在同一时刻的影长。
在中心投影下,一个重要的结论是,点光源、物体边缘上的点以及它们在影子上的对应点在同一条直线上。
可以根据其中两个点来求出第三个点的位置。
要点诠释:物体的中心投影受到光源和物体位置及方向的影响。
改变光源或物体的方向会导致影子方向的变化。
但不论如何改变,光源、物体和它们的影子始终分离在物体的两侧。
要点三、中心投影与平行投影的区别与联系1.联系:中心投影和平行投影都是研究物体投影的一种方法。
平行投影是在平行光线下形成的投影,例如太阳光线和月光。
中心投影是从一点发出的光线所形成的投影,例如灯泡和手电筒的光线。
在平行投影中,改变物体的方向和位置会导致投影方向和位置的变化。
在中心投影中,同一灯光下,改变物体的位置和方向也会导致投影的变化。
固定物体的位置和方向,改变灯光的位置,物体投影的方向和位置也会发生变化。
2.区别:太阳光线是平行的,因此太阳光下的影子长度与物体高度成比例。
灯光是发散的,灯光下的影子与物体高度不一定成比例。
在同一时刻,太阳光下的影子方向总是在同一方向,而灯光下的影子可能在同一方向,也可能在不同方向。
要点诠释:在解决有关投影的问题时,必须先判断是平行投影还是中心投影,然后根据它们的特点进一步解决问题。
要点四、相似三角形的应用1.测量高度测量不能到达顶部的物体的高度,通常使用“在同一时刻物高与影长的比例相等”的原理解决。
要点诠释:测量旗杆高度的方法包括平面镜测量法、影子测量法、手臂测量法和标杆测量法。
苏教版九年级相似知识点

苏教版九年级相似知识点相似是数学中一个重要的概念,也是学习几何的基础之一。
在几何中,相似指的是两个图形在形状上相似,但是大小不一样。
通过相似性,我们可以利用已知的信息来推导出未知的信息,解决实际问题。
本文将介绍苏教版九年级中与相似相关的知识点。
1. 相似三角形相似三角形是指两个三角形在形状上相似,对应的角度相等,对应的边成比例。
在求解相似三角形的问题时,我们可以利用一些特定的相似性质,如AAA判定相似、SAS判定相似和SSS判定相似等。
这些性质可以帮助我们简化计算过程,得出准确的结果。
2. 相似比在相似三角形中,对应的边成比例。
我们可以利用相似比来表示这种比例关系。
相似比是指已知相似三角形的两个对应边的比值。
例如,如果两个三角形ABC和DEF相似,与角A对应的边和与角D对应的边的比值为a:b,与角B对应的边和与角E对应的边的比值为c:d,那么相似比为a:b=c:d。
通过相似比,我们可以计算出未知边的长度,解决各种实际问题。
3. 相似多边形除了三角形,多边形也可以相似。
相似多边形是指两个多边形在形状上相似,对应的角度相等,对应的边成比例。
在求解相似多边形的问题时,我们可以利用相似比来简化计算过程,得出准确的结果。
4. 比例尺比例尺是指图形在实际尺寸与其缩小或放大后的尺寸之间的比例关系。
在实际问题中,我们经常需要根据图纸上的比例尺来计算实际尺寸,或者根据实际尺寸来绘制图纸。
5. 三角形的应用相似三角形在实际问题中有广泛的应用。
例如,我们可以利用相似三角形的性质来计算高楼大厦的高度、电线杆的高度、塔的高度等。
通过相似三角形的计算,我们可以在不进行实际测量的情况下,得出准确的结果。
6. 相似几何体除了平面图形,立体图形也可以相似。
相似几何体是指两个立体图形在形状上相似,对应的面相似,对应的棱和对应的面的比例成比。
通过相似几何体的性质,我们可以计算出未知的长度、面积和体积,解决实际问题。
总结起来,苏教版九年级中的相似知识点包括相似三角形、相似比、相似多边形、比例尺、三角形的应用和相似几何体等。
2020—2021年新苏科版九年级数学下册《图形的相似-相似三角形的性质》专题练习及答案.docx

2017-2018学年苏科版(新课标)九年级下册第六章《图形的相似》(相似三角形的性质)一.选择题1.如果两个相似三角形的面积比是1:4,那么它们的周长比是()A.1:16 B.1:4 C.1:6 D.1:22.△ABC与△DEF的相似比为1:4,则△ABC与△DEF的周长比为()A.1:2 B.1:3 C.1:4 D.1:163.如图是由边长相同的小正方形组成的网格,A,B,P,Q四点均在正方形网格的格点上,线段AB,PQ相交于点M,则图中∠QMB的正切值是()A.B.1 C. D.24.已知△ABC∽△DEF,若△ABC与△DEF的相似比为,则△ABC与△DEF对应中线的比为()A.B.C.D.5.在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足.设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为()A.B.C.D.6.如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是()A.1:3 B.1:4 C.1:5 D.1:257.如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F 在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为()A.B.C.D.8.如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB 的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD=AE2;④S △ABC=4S△ADF.其中正确的有()A.1个B.2 个C.3 个D.4个9.如图的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AB=4,BC=3,EF=1,则BN的长度为何?()A.B.C.D.10.如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ•AC,其中正确的结论的个数是()A.1 B.2 C.3 D.411.如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为S1、S2、S3,若AD=2,AB=2,∠A=60°,则S1+S2+S3的值为()A.B.C.D.412.如图,在正方形网格中,每个小正方形的边长均相等.网格中三个多边形(分别标记为①,②,③)的顶点均在格点上.被一个多边形覆盖的网格线中,竖直部分线段长度之和记为m,水平部分线段长度之和记为n,则这三个多边形中满足m=n的是()A.只有②B.只有③C.②③D.①②③二.填空题13.如图,已知△ADE∽△ABC,若∠ADE=37°,则∠B= °.14.如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEC=3,则S△BCF= .15.如图,AC⊥BC,AC=BC,D是BC上一点,连接AD,与∠ACB的平分线交于点E,连接BE.若S△ACE=,S△BDE=,则AC= .16.如图,已知点C为线段AB的中点,CD⊥AB且CD=AB=4,连接AD,BE⊥AB,AE是∠DAB的平分线,与DC相交于点F,EH⊥DC于点G,交AD于点H,则HG的长为.17.如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=12,EF=9,则DF的长是.18.如图,在△ABC中,D、E分别是边AB、AC上的点,且DE ∥BC,若△ADE与△ABC的周长之比为2:3,AD=4,则DB= .19.如图,已知△ABC、△DCE、△FEG、△HGI是4个全等的等腰三角形,底边BC、CE、EG、GI在同一直线上,且AB=2,BC=1,连接AI,交FG于点Q,则QI= .20.如图,矩形EFGH内接于△ABC,且边FG落在BC上,若AD⊥BC,BC=3,AD=2,EF=EH,那么EH的长为.21.如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF 上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°;②△DEF∽△ABG;③S△ABG=S△FGH;④AG+DF=FG.其中正确的是.(把所有正确结论的序号都选上)三.解答题22.如图,在平面直角坐标系xOy中,直线y=﹣x+3与x轴交于点C,与直线AD交于点A(,),点D的坐标为(0,1)(1)求直线AD的解析式;(2)直线AD与x轴交于点B,若点E是直线AD上一动点(不与点B重合),当△BOD与△BCE相似时,求点E的坐标.23.从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.(3)如图2,△ABC中,AC=2,BC=,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.24.如图,△ABC中,AB=AC,E在BA的延长线上,AD平分∠CAE.(1)求证:AD∥BC;(2)过点C作CG⊥AD于点F,交AE于点G,若AF=4,求BC 的长.25.如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.(1)求证:△AEH∽△ABC;(2)求这个正方形的边长与面积.26.如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且.(1)求证:△ADF∽△ACG;(2)若,求的值.27.如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.(1)求证:AG=CG.(2)求证:AG2=GE•GF.28.如图,在Rt△ABC中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在BA边上以每秒2cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.(1)若BM=BN,求t的值;(2)若△MBN与△ABC相似,求t的值;(3)当t为何值时,四边形ACNM的面积最小?并求出最小值.29.如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P 为AD的中点,连接AE、BD.(1)猜想PM与PN的数量关系及位置关系,请直接写出结论;(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;(3)若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.30.【探究证明】(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.如图1,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.求证:=;【结论应用】(2)如图2,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若=,则的值为;【联系拓展】(3)如图3,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求的值.参考答案与解析一.选择题1.(2016•临夏州)如果两个相似三角形的面积比是1:4,那么它们的周长比是()A.1:16 B.1:4 C.1:6 D.1:2【分析】根据相似三角形周长的比等于相似比,相似三角形面积的比等于相似比的平方解答即可.【解答】解:∵两个相似三角形的面积比是1:4,∴两个相似三角形的相似比是1:2,∴两个相似三角形的周长比是1:2,故选:D.【点评】本题考查的是相似三角形的性质,掌握相似三角形周长的比等于相似比,相似三角形面积的比等于相似比的平方是解题的关键.2.(2016•重庆)△ABC与△DEF的相似比为1:4,则△ABC 与△DEF的周长比为()A.1:2 B.1:3 C.1:4 D.1:16【分析】由相似三角形周长的比等于相似比即可得出结果.【解答】解:∵△ABC与△DEF的相似比为1:4,∴△ABC与△DEF的周长比为1:4;故选:C.【点评】本题考查了相似三角形的性质;熟记相似三角形周长的比等于相似比是解决问题的关键.3.(2016•淄博)如图是由边长相同的小正方形组成的网格,A,B,P,Q四点均在正方形网格的格点上,线段AB,PQ相交于点M,则图中∠QMB的正切值是()A.B.1 C. D.2【分析】根据题意得出△PAM∽△QBM,进而结合勾股定理得出AP=3,BQ=,AB=2,进而求出答案.【解答】解:连接AP,QB,由网格可得:∠PAB=∠QBA=90°,又∵∠AMP=∠BMQ,∴△PAM∽△QBM,∴=,∵AP=3,BQ=,AB=2,∴=,解得:AM=,∴tan∠QMB=tan∠PMA===2.故选:D.【点评】此题主要考查了勾股定理以及相似三角形的判定与性质以及锐角三角函数关系,正确得出△PAM∽△QBM是解题关键.4.(2016•兰州)已知△ABC∽△DEF,若△ABC与△DEF的相似比为,则△ABC与△DEF对应中线的比为()A.B.C.D.【分析】根据相似三角形的对应中线的比等于相似比解答.【解答】解:∵△ABC∽△DEF,△ABC与△DEF的相似比为,∴△ABC与△DEF对应中线的比为,故选:A.【点评】本题考查的是相似三角形的性质,相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.5.(2016•金华)在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足.设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为()A.B.C.D.【分析】由△DAH∽△CAB,得=,求出y与x关系,再确定x的取值范围即可解决问题.【解答】解:∵DH垂直平分AC,∴DA=DC,AH=HC=2,∴∠DAC=∠DCH,∵CD∥AB,∴∠DCA=∠BAC,∴∠DAN=∠BAC,∵∠DHA=∠B=90°,∴△DAH∽△CAB,∴=,∴=,∴y=,∵AB<AC,∴x<4,∴图象是D.故选D.【点评】本题科学相似三角形的判定和性质、相等垂直平分线性质、反比例函数等知识,解题的关键是正确寻找相似三角形,构建函数关系,注意自变量的取值范围的确定,属于中考常考题型.6.(2016•随州)如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是()A.1:3 B.1:4 C.1:5 D.1:25【分析】根据相似三角形的判定定理得到△DOE∽△COA,根据相似三角形的性质定理得到=,==,结合图形得到=,得到答案.【解答】解:∵DE∥AC,∴△DOE∽△COA,又S△DOE:S△COA=1:25,∴=,∵DE∥AC,∴==,∴=,∴S△BDE与S△CDE的比是1:4,故选:B.【点评】本题考查的是相似三角形的判定和性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.7.(2016•泸州)如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为()A.B.C.D.【分析】过F作FH⊥AD于H,交ED于O,于是得到FH=AB=2,根据勾股定理得到AF===2,根据平行线分线段成比例定理得到OH=AE=,由相似三角形的性质得到==,求得AM=AF=,根据相似三角形的性质得到==,求得AN=AF=,即可得到结论.【解答】解:过F作FH⊥AD于H,交ED于O,则FH=AB=2 ∵BF=2FC,BC=AD=3,∴BF=AH=2,FC=HD=1,∴AF===2,∵OH∥AE,∴==,∴OH=AE=,∴OF=FH﹣OH=2﹣=,∵AE∥FO,∴△AME∽FMO,∴==,∴AM=AF=,∵AD∥BF,∴△AND∽△FNB,∴==,∴AN=AF=,∴MN=AN﹣AM=﹣=,故选B.【点评】本题考查了相似三角形的判定与性质,矩形的性质,勾股定理,比例的性质,准确作出辅助线,求出AN与AM的长是解题的关键.8.(2016•丹东)如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD=AE2;④S△ABC=4S△ADF.其中正确的有()A.1个B.2 个C.3 个D.4个【分析】由直角三角形斜边上的中线性质得出FD=AB,证明△ABE是等腰直角三角形,得出AE=BE,证出FE=AB,延长FD=FE,①正确;证出∠ABC=∠C,得出AB=AC,由等腰三角形的性质得出BC=2CD,∠BAD=∠CAD=∠CBE,由ASA证明△AEH≌△BEC,得出AH=BC=2CD,②正确;证明△ABD~△BCE,得出=,即BC•AD=AB•BE,再由等腰直角三角形的性质和三角形的面积得出BC•AD=AE2;③正确;由F是AB的中点,BD=CD,得出S△ABC=2S△ABD=4S△ADF.④正确;即可得出结论.【解答】解:∵在△ABC中,AD和BE是高,∴∠ADB=∠AEB=∠CEB=90°,∵点F是AB的中点,∴FD=AB,∵∠ABE=45°,∴△ABE是等腰直角三角形,∴AE=BE,∵点F是AB的中点,∴FE=AB,∴FD=FE,①正确;∵∠CBE=∠BAD,∠CBE+∠C=90°,∠BAD+∠ABC=90°,∴∠ABC=∠C,∴AB=AC,∵AD⊥BC,∴BC=2CD,∠BAD=∠CAD=∠CBE,在△AEH和△BEC中,,∴△AEH≌△BEC(ASA),∴AH=BC=2CD,②正确;∵∠BAD=∠CBE,∠ADB=∠CEB,∴△ABD~△BCE,∴=,即BC•AD=AB•BE,∵AE2=AB•AE=AB•BE,BC•AD=AC•BE=AB•BE,∴BC•AD=AE2;③正确;∵F是AB的中点,BD=CD,∴S△ABC=2S△ABD=4S△ADF.④正确;故选:D.【点评】本题考查了相似三角形的判定与性质、全等三角形的判定与性质、直角三角形斜边上的中线性质、等腰三角形的判定与性质;本题综合性强,有一定难度,证明三角形相似和三角形全等是解决问题的关键.9.(2016•台湾)如图的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AB=4,BC=3,EF=1,则BN的长度为何?()A.B.C.D.【分析】由DE∥BC可得求出AE的长,由GF∥BN可得,将AE的长代入可求得BN.【解答】解:∵四边形DEFG是正方形,∴DE∥BC,GF∥BN,且DE=GF=EF=1,∴△ADE∽△ACB,△AGF∽△ANB,∴①,②,由①可得,,解得:AE=,将AE=代入②,得:,解得:BN=,故选:D.【点评】本题主要考查正方形的性质及相似三角形的判定与性质,根据相似三角形的性质得出AE的长是解题的关键.10.(2016•深圳)如图,CB=CA,∠ACB=90°,点D在边BC 上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ •AC,其中正确的结论的个数是()A.1 B.2 C.3 D.4【分析】由正方形的性质得出∠FAD=90°,AD=AF=EF,证出∠CAD=∠AFG,由AAS证明△FGA≌△ACD,得出AC=FG,①正确;证明四边形CBFG是矩形,得出S△FAB=FB•FG=S四边形CBFG,②正确;由等腰直角三角形的性质和矩形的性质得出∠ABC=∠ABF=45°,③正确;证出△ACD∽△FEQ,得出对应边成比例,得出D•FE=AD2=FQ•AC,④正确.【解答】解:∵四边形ADEF为正方形,∴∠FAD=90°,AD=AF=EF,∴∠CAD+∠FAG=90°,∵FG⊥CA,∴∠C=90°=∠ACB,∴∠CAD=∠AFG,在△FGA和△ACD中,,∴△FGA≌△ACD(AAS),∴AC=FG,①正确;∵BC=AC,∴FG=BC,∵∠ACB=90°,FG⊥CA,∴FG∥BC,∴四边形CBFG是矩形,∴∠CBF=90°,S△FAB=FB•FG=S四边形CBFG,②正确;∵CA=CB,∠C=∠CBF=90°,∴∠ABC=∠ABF=45°,③正确;∵∠FQE=∠DQB=∠ADC,∠E=∠C=90°,∴△ACD∽△FEQ,∴AC:AD=FE:FQ,∴AD•FE=AD2=FQ•AC,④正确;故选:D.【点评】本题考查了相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质、矩形的判定与性质、等腰直角三角形的性质;熟练掌握正方形的性质,证明三角形全等和三角形相似是解决问题的关键.11.(2016•日照)如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为S1、S2、S3,若AD=2,AB=2,∠A=60°,则S1+S2+S3的值为()A.B.C.D.4【分析】先作辅助线DH⊥AB于点D,然后根据特殊角的三角函数值可以求得DH的长度,从而可以求得平行四边形的面积,然后根据三角形的相似可以求得S1+S2+S3的值.【解答】解:作DH⊥AB于点H,如右图所示,∵AD=2,AB=2,∠A=60°,∴DH=AD•sin60°=2×=,∴S ▱ABCD=AB•DH=2=6,∴S2+S3=S△PBC=3,又∵E、F分别是PB、PC(靠近点P)的三等分点,∴,∴S△PEF=×3=,即S1=,∴S1+S2+S3=+3=,故选A.【点评】本题考查相似三角形的判定与性质、平行四边形的性质,解题的关键是明确题意,找出所求问题需要的条件,画出合适的辅助线,利用数形结合的思想解答问题.12.(2016•江西)如图,在正方形网格中,每个小正方形的边长均相等.网格中三个多边形(分别标记为①,②,③)的顶点均在格点上.被一个多边形覆盖的网格线中,竖直部分线段长度之和记为m,水平部分线段长度之和记为n,则这三个多边形中满足m=n的是()A.只有②B.只有③C.②③D.①②③【分析】利用相似三角形的判定和性质分别求出各多边形竖直部分线段长度之和与水平部分线段长度之和,再比较即可.【解答】解:假设每个小正方形的边长为1,①:m=1+2+1=4,n=2+4=6,则m≠n;②在△ACN中,BM∥CN,∴=,∴BM=,在△AGF中,DM∥NE∥FG,∴=,=,得DM=,NE=,∴m=2+=2.5,n=+1++=2.5,∴m=n;③由②得:BE=,CF=,∴m=2+2++1+=6,n=4+2=6,∴m=n,则这三个多边形中满足m=n的是②和③;故选C.【点评】本题考查了相似多边形的判定和性质,对于有中点的三角形可以利用三角形中位线定理得出;本题线段比较多要依次相加,做到不重不漏.二.填空题13.(2016•宁德)如图,已知△ADE∽△ABC,若∠ADE=37°,则∠B= 37 °.【分析】根据相似三角形的对应角相等,可得答案.【解答】解:由△ADE∽△ABC,若∠ADE=37°,得∠B=∠ADE=37°,故答案为:37.【点评】本题考查了相似三角形的性质,熟记相似三角形的性质是解题关键.14.(2016•梅州)如图,在平行四边形ABCD中,点E是边AD 的中点,EC交对角线BD于点F,若S△DEC=3,则S△BCF= 4 .【分析】根据平行四边形的性质得到AD∥BC和△DEF∽△BCF,由已知条件求出△DEF的面积,根据相似三角形的面积比是相似比的平方得到答案.【解答】解:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴△DEF∽△BCF,∴,=()2,∵E是边AD的中点,∴DE=AD=BC,∴=,∴△DEF的面积=S△DEC=1,∴=,∴S△BCF=4;故答案为:4.【点评】本题考查的是平行四边形的性质、相似三角形的判定和性质;掌握三角形相似的判定定理和性质定理是解题的关键,注意:相似三角形的面积比是相似比的平方.15.(2016•遵义)如图,AC⊥BC,AC=BC,D是BC上一点,连接AD,与∠ACB的平分线交于点E,连接BE.若S△ACE=,S △BDE=,则AC= 2 .【分析】设BC=4x,根据面积公式计算,得出BC=4BD,过E作AC,BC的垂线,垂足分别为F,G;证明CFEG为正方形,然后在直角三角形ACD中,利用三角形相似,求出正方形的边长(用x表示),再利用已知的面积建立等式,解出x,最后求出AC=BC=4x即可.【解答】解:过E作AC,BC的垂线,垂足分别为F,G,设BC=4x,则AC=4x,∵CE是∠ACB的平分线,EF⊥AC,EG⊥BC,∴EF=EG,又S△ACE=,S△BDE=,∴BD=AC=x,∴CD=3x,∵四边形EFCG是正方形,∴EF=FC,∵EF∥CD,∴=,即=,解得,EF=x,则×4x×x=,解得,x=,则AC=4x=2,故答案为:2.【点评】本题考查的是相似三角形的性质、角平分线的性质,掌握相似三角形的对应边的比相等、角的平分线上的点到角的两边的距离相等是解题的关键.16.(2016•山西)如图,已知点C为线段AB的中点,CD⊥AB 且CD=AB=4,连接AD,BE⊥AB,AE是∠DAB的平分线,与DC相交于点F,EH⊥DC于点G,交AD于点H,则HG的长为3﹣.【分析】根据AB=CD=4、C为线段AB的中点可得BC=AC=2、AD=2,再根据EH⊥DC、CD⊥AB、BE⊥AB得EH∥AC、四边形BCGH为矩形,BC=GE=2,继而由AE是∠DAB的平分线可得∠DAE=∠HEA即HA=HE,设GH=x得HA=2+x,由△DHG∽△DAC得=,列式即可求得x.【解答】解:∵AB=CD=4,C为线段AB的中点,∴BC=AC=2,∴AD=2,∵EH⊥DC,CD⊥AB,BE⊥AB,∴EH∥AC,四边形BCGH为矩形,∴∠HEA=∠EAB,BC=GE=2,又∵AE是∠DAB的平分线,∴∠EAB=∠DAE,∴∠DAE=∠HEA,∴HA=HE,设GH=x,则HA=HE=HG+GE=2+x,∵EH∥AC,∴△DHG∽△DAC,∴=,即=,解得:x=3﹣,即HG=3﹣,故答案为:3﹣.【点评】本题主要考查勾股定理、平行线的性质和判定、等腰三角形的判定与性质、矩形的判定与性质及相似三角形的判定与性质等知识点,根据相似三角形的性质得出对应边成比例且表示出各边长度是关键.17.(2016•舟山)如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=12,EF=9,则DF的长是7 .【分析】根据题意,易得△CDF与四边形AFEB的面积相等,再根据相似三角形的相似比求得它们的面积关系比,从而求DF的长.【解答】解:∵△ABC与△DEC的面积相等,∴△CDF与四边形AFEB的面积相等,∵AB∥DE,∴△CEF∽△CBA,∵EF=9,AB=12,∴EF:AB=9:12=3:4,∴△CEF和△CBA的面积比=9:16,设△CEF的面积为9k,则四边形AFEB的面积=7k,∵△CDF与四边形AFEB的面积相等,∴S△CDF=7k,∵△CDF与△CEF是同高不同底的三角形,∴面积比等于底之比,∴DF:EF=7k:9k,∴DF=7.故答案为:7.【点评】此题考查了相似三角形的判定与性质,解题的关键是会用割补法计算面积.18.(2016•乐山)如图,在△ABC中,D、E分别是边AB、AC 上的点,且DE∥BC,若△ADE与△ABC的周长之比为2:3,AD=4,则DB= 2 .【分析】由DE∥BC,易证△ADE∽△ABC,由相似三角形的性质即可求出AB的长,进而可求出DB的长.【解答】解:∵DE∥BC,∴△ADE∽△ABC,∵△ADE与△ABC的周长之比为2:3,∴AD:AB=2:3,∵AD=4,∴AB=6,∴DB=AB﹣AD=2,故答案为:2.【点评】此题主要考查的是相似三角形的性质:相似三角形的一切对应线段(包括对应边、对应中线、对应高、对应角平分线等)的比等于相似比,面积比等于相似比的平方.19.(2016•黄冈)如图,已知△ABC、△DCE、△FEG、△HGI 是4个全等的等腰三角形,底边BC、CE、EG、GI在同一直线上,且AB=2,BC=1,连接AI,交FG于点Q,则QI= .【分析】由题意得出BC=1,BI=4,则=,再由∠ABI=∠ABC,得△ABI∽△CBA,根据相似三角形的性质得=,求出AI,根据全等三角形性质得到∠ACB=∠FGE,于是得到AC∥FG,得到比例式==,即可得到结果.【解答】解:∵△ABC、△DCE、△FEG是三个全等的等腰三角形,∴HI=AB=2,GI=BC=1,BI=4BC=4,∴==,=,∴=,∵∠ABI=∠ABC,∴△ABI∽△CBA;∴=,∵AB=AC,∴AI=BI=4;∵∠ACB=∠FGE,∴AC∥FG,∴==,∴QI=AI=.故答案为:.【点评】本题主要考查了平行线分线段定理,以及三角形相似的判定,正确理解AB∥CD∥EF,AC∥DE∥FG是解题的关键.20.(2016•安顺)如图,矩形EFGH内接于△ABC,且边FG落在BC上,若AD⊥BC,BC=3,AD=2,EF=EH,那么EH的长为.【分析】设EH=3x,表示出EF,由AD﹣EF表示出三角形AEH 的边EH上的高,根据三角形AEH与三角形ABC相似,利用相似三角形对应边上的高之比等于相似比求出x的值,即为EH的长.【解答】解:如图所示:∵四边形EFGH是矩形,∴EH∥BC,∴△AEH∽△ABC,∵AM⊥EH,AD⊥BC,∴,设EH=3x,则有EF=2x,AM=AD﹣EF=2﹣2x,∴,解得:x=,则EH=.故答案为:.【点评】此题考查了相似三角形的判定与性质,以及矩形的性质,熟练掌握相似三角形的判定与性质是解本题的关键.21.(2016•安徽)如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F 处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°;②△DEF∽△ABG;③S△ABG=S△FGH;④AG+DF=FG.其中正确的是①③④.(把所有正确结论的序号都选上)【分析】由折叠性质得∠1=∠2,CE=FE,BF=BC=10,则在Rt △ABF中利用勾股定理可计算出AF=8,所以DF=AD﹣AF=2,设EF=x,则CE=x,DE=CD﹣CE=6﹣x,在Rt△DEF中利用勾股定理得(6﹣x)2+22=x2,解得x=,即ED=;再利用折叠性质得∠3=∠4,BH=BA=6,AG=HG,易得∠2+∠3=45°,于是可对①进行判断;设AG=y,则GH=y,GF=8﹣y,在Rt△HGF中利用勾股定理得到y2+42=(8﹣y)2,解得y=3,则AG=GH=3,GF=5,由于∠A=∠D和≠,可判断△ABG与△DEF不相似,则可对②进行判断;根据三角形面积公式可对③进行判断;利用AG=3,GF=5,DF=2可对④进行判断.【解答】解:∵△BCE沿BE折叠,点C恰落在边AD上的点F 处,∴∠1=∠2,CE=FE,BF=BC=10,在Rt△ABF中,∵AB=6,BF=10,∴AF==8,∴DF=AD﹣AF=10﹣8=2,设EF=x,则CE=x,DE=CD﹣CE=6﹣x,在Rt△DEF中,∵DE2+DF2=EF2,∴(6﹣x)2+22=x2,解得x=,∴ED=,∵△ABG沿BG折叠,点A恰落在线段BF上的点H处,∴∠3=∠4,BH=BA=6,AG=HG,∴∠2+∠3=∠ABC=45°,所以①正确;HF=BF﹣BH=10﹣6=4,设AG=y,则GH=y,GF=8﹣y,在Rt△HGF中,∵GH2+HF2=GF2,∴y2+42=(8﹣y)2,解得y=3,∴AG=GH=3,GF=5,∵∠A=∠D,==,=,∴≠,∴△ABG与△DEF不相似,所以②错误;∵S△ABG=•6•3=9,S△FGH=•GH•HF=×3×4=6,∴S△ABG=S△FGH,所以③正确;∵AG+DF=3+2=5,而GF=5,∴AG+DF=GF,所以④正确.故答案为①③④.【点评】本题考查了相似形综合题:熟练掌握折叠和矩形的性质、相似三角形的判定方法;会运用勾股定理计算线段的长.三.解答题22.(2016•广州)如图,在平面直角坐标系xOy中,直线y=﹣x+3与x轴交于点C,与直线AD交于点A(,),点D的坐标为(0,1)(1)求直线AD的解析式;(2)直线AD与x轴交于点B,若点E是直线AD上一动点(不与点B重合),当△BOD与△BCE相似时,求点E的坐标.【分析】(1)设直线AD的解析式为y=kx+b,用待定系数法将A(,),D(0,1)的坐标代入即可;(2)由直线AD与x轴的交点为(﹣2,0),得到OB=2,由点D的坐标为(0,1),得到OD=1,求得BC=5,根据相似三角形的性质得到或,代入数据即可得到结论.【解答】解:(1)设直线AD的解析式为y=kx+b,将A(,),D(0,1)代入得:,解得:.故直线AD的解析式为:y=x+1;(2)∵直线AD与x轴的交点为(﹣2,0),∴OB=2,∵点D的坐标为(0,1),∴OD=1,∵y=﹣x+3与x轴交于点C(3,0),∴OC=3,∴BC=5∵△BOD与△BEC相似,∴或,∴==或,∴BE=2,CE=,或CE=,∵BC•EF=BE•CE,∴EF=2,CF==1,∴E(2,2),或(3,).【点评】本题考查了相似三角形的性质,待定系数法求函数的解析式,正确的作出图形是解题的关键.23.(2016•宁波)从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.(3)如图2,△ABC中,AC=2,BC=,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.【分析】(1)根据完美分割线的定义只要证明①△ABC不是等腰三角形,②△ACD是等腰三角形,③△BDC∽△BCA即可.(2)分三种情形讨论即可①如图2,当AD=CD时,②如图3中,当AD=AC时,③如图4中,当AC=CD时,分别求出∠ACB即可.(3)设BD=x,利用△BCD∽△BAC,得=,列出方程即可解决问题.【解答】解:(1)如图1中,∵∠A=40°,∠B=60°,∴∠ACB=80°,∴△ABC不是等腰三角形,∵CD平分∠ACB,∴∠ACD=∠BCD=∠ACB=40°,∴∠ACD=∠A=40°,∴△ACD为等腰三角形,∵∠DCB=∠A=40°,∠CBD=∠ABC,∴△BCD∽△BAC,∴CD是△ABC的完美分割线.(2)①当AD=CD时,如图2,∠ACD=∠A=48°,∵△BDC∽△BCA,∴∠BCD=∠A=48°,∴∠ACB=∠ACD+∠BCD=96°.②当AD=AC时,如图3中,∠ACD=∠ADC==66°,∵△BDC∽△BCA,∴∠BCD=∠A=48°,∴∠ACB=∠ACD+∠BCD=114°.③当AC=CD时,如图4中,∠ADC=∠A=48°,∵△BDC∽△BCA,∴∠BCD=∠A=48°,∵∠ADC>∠BCD,矛盾,舍弃.∴∠ACB=96°或114°.(3)由已知AC=AD=2,∵△BCD∽△BAC,∴=,设BD=x,∴()2=x(x+2),∵x>0,∴x=﹣1,∵△BCD∽△BAC,∴==,∴CD=×2=﹣.【点评】本题考查相似三角形的判定和性质、等腰三角形的性质等知识,解题的关键是理解题意,学会分类讨论思想,属于中考常考题型.24.(2016•泰州)如图,△ABC中,AB=AC,E在BA的延长线上,AD平分∠CAE.(1)求证:AD∥BC;(2)过点C作CG⊥AD于点F,交AE于点G,若AF=4,求BC 的长.【分析】(1)由AB=AC,AD平分∠CAE,易证得∠B=∠DAG=∠CAG,继而证得结论;(2)由CG⊥AD,AD平分∠CAE,易得CF=GF,然后由AD∥BC,证得△AGF∽△BGC,再由相似三角形的对应边成比例,求得答案.【解答】(1)证明:∵AD平分∠CAE,∴∠DAG=∠CAG,∵AB=AC,∴∠B=∠ACB,∵∠CAG=∠B+∠ACB,∴∠B=∠CAG,∴∠B=∠DAG,∴AD∥BC;(2)解:∵CG⊥AD,∴∠AFC=∠AFG=90°,在△AFC和△AFG中,,∴△AFC≌△AFG(ASA),∴CF=GF,∵AD∥BC,∴△AGF∽△BGC,∴GF:GC=AF:BC=1:2,∴BC=2AF=2×4=8.【点评】此题考查了等腰三角形的性质、全等三角形的判定与性质以及相似三角形的判定与性质.注意证得△AGF∽△BGC是关键.25.(2016•怀化)如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.(1)求证:△AEH∽△ABC;(2)求这个正方形的边长与面积.【分析】(1)根据EH∥BC即可证明.(2)如图设AD与EH交于点M,首先证明四边形EFDM是矩形,设正方形边长为x,再利用△AEH∽△ABC,得=,列出方程即可解决问题.【解答】(1)证明:∵四边形EFGH是正方形,∴EH∥BC,∴∠AEH=∠B,∠AHE=∠C,∴△AEH∽△ABC.(2)解:如图设AD与EH交于点M.∵∠EFD=∠FEM=∠FDM=90°,∴四边形EFDM是矩形,∴EF=DM,设正方形EFGH的边长为x,∵△AEH∽△ABC,∴=,∴=,∴x=,∴正方形EFGH的边长为cm,面积为cm2.【点评】本题考查正方形的性质、相似三角形的判定和性质等知识,解题的关键是利用相似三角形的相似比对于高的比,学会用方程的思想解决问题,属于中考常考题型.26.(2016•杭州)如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且.(1)求证:△ADF∽△ACG;(2)若,求的值.【分析】(1)欲证明△ADF∽△ACG,由可知,只要证明∠ADF=∠C即可.(2)利用相似三角形的性质得到=,由此即可证明.【解答】(1)证明:∵∠AED=∠B,∠DAE=∠DAE,∴∠ADF=∠C,∵=,∴△ADF∽△ACG.(2)解:∵△ADF∽△ACG,∴=,又∵=,∴=,∴=1.【点评】本题考查相似三角形的性质和判定、三角形内角和定理等知识,记住相似三角形的判定方法是解决问题的关键,属于基础题中考常考题型.27.(2016•大庆)如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.(1)求证:AG=CG.(2)求证:AG2=GE•GF.【分析】根据菱形的性质得到AB∥CD,AD=CD,∠ADB=∠CDB,推出△ADG≌△CDG,根据全等三角形的性质即可得到结论;(2)由全等三角形的性质得到∠EAG=∠DCG,等量代换得到∠EAG=∠F,求得△AEG∽△FGA,即可得到结论.【解答】解:(1)∵四边形ABCD是菱形,∴AB∥CD,AD=CD,∠ADB=∠CDB,∴∠F=∠FCD,在△ADG与△CDG中,,∴△ADG≌△CDG,∴∠EAG=∠DCG,∴AG=CG;(2)∵△ADG≌△CDG,∴∠EAG=∠F,∵∠AGE=∠AGE,∴△AEG∽△FGA,∴,∴AG2=GE•GF.【点评】本题考查了相似三角形的判定和性质,菱形的性质,全等三角形的判定和性质,熟练掌握各定理是解题的关键.28.(2016•梅州)如图,在Rt△ABC中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在BA边上以每秒2cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.(1)若BM=BN,求t的值;(2)若△MBN与△ABC相似,求t的值;(3)当t为何值时,四边形ACNM的面积最小?并求出最小值.【分析】(1)由已知条件得出AB=10,.由题意知:BM=2t,,,由BM=BN得出方程,解方程即可;(2)分两种情况:①当△MBN∽△ABC时,由相似三角形的对应边成比例得出比例式,即可得出t的值;②当△NBM∽△ABC时,由相似三角形的对应边成比例得出比例式,即可得出t的值;(3)过M作MD⊥BC于点D,则MD∥AC,证出△BMD∽△BAC,得出比例式求出MD=t.四边形ACNM的面积y=△ABC的面积。
2020中考数学总复习:相似三角形及其应用(结合2019中考真题)

=
3 2
图22-5
[答案] D [解析]∵△OAB∽△OCD,OA∶OC=3∶2,∠A=α,∠C=β,∴������������������������ = 32,A 错误;������������12 = 49,C 错误;������1 = 3,D 正确;α=β,B 错误.故选 D.
������2 2
图22-13
解:(1)证明:∵△ACB 和△DCE 均是等腰直角三角形,∴CD=CE,CA=CB.
∵∠ACB=∠1+∠2=90°,∠DCE=∠3+∠2=90°,∴∠1=∠3. ������������ = ������������,
又∵BE 为☉O 的切线,AD 平分∠BAC,
∴∠E=∠ADC,
∴△ACD∽△BDE,
∴������������
������������
=
������������ ������������
,
∴CD·BE=AD·DE.
【方法点析】证明线段等积式的常用方法是把等积式转化为比例式,要证明比 例式,就要证明三角形相似.圆中证明相似要充分运用圆的切线性质,圆周角定 理及推论,垂径定理等结论.
时,如图①,△ADE∽△ABC,即
2 ������������
=
65,∴AE=53;②当������������������������
=
������������������������ 时,如图②,△ADE∽△ACB,即������2������
=
56,∴AE=152.综上所
述,当 AE=53或152时,以 A,D,E 为顶点的三角形与△ABC 相似.
例2 [2019·张家界]如图22-8,平行四边形ABCD中,连接对角线AC,延长AB至点E, 使BE=AB,连接DE,分别交BC,AC于点F,G. (2)若BC=6,DG=4,求FG的长.
苏教版初中数学相似三角形专题 有答案有解释

苏教版初中数学相似三角形专题有答案有解释苏教版初中数学相似三角形专题--有答案有解释江苏教育版初中数学相似三角形专题一.填空题(共7小题)1.已知△ 坐标平面上的ABC为a(0,2)、B(3,3)和C(2,1)。
以B为位置相似中心,画一个与△ ABC(与图方向相同),相似比为3。
其三个对应顶点的坐标分别为2.如图,将△abc放在每个小正方形的边长为1的网格中,点a、b、c均落在格点上.(一)面积△ ABC等于;(ⅱ)若四边形defg是△abc中所能包含的面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺画出该正方形,并简要说明画图方法(不要求证明).3.如图所示,有两张不同尺寸的4×4方形纸。
它们都由16个小正方形组成。
图中小型和中型广场的面积比① 和数字② 现在是5:4。
请在图中画方格efgh② 使其等于图中栅格正方形ABCD的面积①第1页(共48页)4.如图所示,在RT中△ 美国广播公司,∠ C=90°,CD⊥ AB,垂直脚是D,ad=8,DB=2,那么CD的长度是5.如图,在rt△abc中,∠acb=90°,cd⊥ab于点d,cd=2,bd=1,则ad的长是,ac的长是.6.如图所示,如果CD是RT斜边CD上的高度△ ABC,ad=3cm,CD=4cm,那么BC的长度等于厘米7.如图,在平面直角坐标系中,已知a(1,0),d(3,0),△abc与△def位似,原点o是位似中心.若ab=1.5,则de=.第2页,共48页二.解答题(共23小题)8.如图所示,求出从四边形ABCD到四边形a′B′C′d′α的X和Y边的长度和角度,即9.已知矩形abcd中,在bc上取一点e,沿ae将△abe向上折叠,使b点落在ad上的f点,且四边形efdc与矩形abcd相似.(1)求证:四边形abef是正方形;(2)求证:f点是ad的黄金分割点.10.从三角形(不是等腰三角形)的顶点绘制光线,使其与另一侧相交。
【2022】苏教版中考数学精编专题《相似三角形及应用》(含答案解析)

【苏教版】中考数学精编专题汇编专题1 相似三角形及应用学校:___________姓名:___________班级:___________1.【江苏省南通市九年级上学期期末】下列条件不能判定△ABC 与△DEF 相似的是( )A .B . ,C . ∠A=∠D ,∠B=∠E D .,∠B=∠E【考点定位】相似三角形的判定.2. 【江苏省徐州市中考模拟】直线l 1∥l 2∥l 3,且l 1与l 2的距离为1,l 2与l 3的距离为3,把一块含有45°角的直角三角形如图放置,顶点A ,B ,C 恰好分别落在三条直线上,AC 与直线l 2交于点D ,则线段BD 的长度为()A .B .C .D .【答案】A .【解析】分别过点A 、B 、D 作AF ⊥l 3,BE⊥l 3,DG⊥l 3,先根据全等三角形的判定定理得出△BCE≌△ACF,故可得出CF 及CE 的长,在Rt△ACF 中根据勾股定理求出AC 的长,再由相似三角形的判定得出△CDG∽△CAF,故可得出CD 的长,在Rt△BCD 中根据勾股定理即可求出BD 的长.分别过点A 、B 、D 作AF⊥l 3,BE⊥l 3,DG⊥l 3,AB BC AC DE EF DF ==AB BCDE EF=A D ∠=∠AB BCDE EF=254253203154∵△ABC 是等腰直角三角形,∴AC=BC,∵∠EBC+∠BCE=90°,∠BCE+∠ACF=90°,∠ACF+∠CAF=90°,∴∠EBC=∠ACF,∠BCE=∠CAF, 在△BCE 与△ACF 中,,【考点定位】1.相似三角形的判定与性质;2.平行线之间的距离;3.全等三角形的判定与性质;4.等腰直角三角形.3.【江苏省淮安市中考】如图,l 1∥l 2∥l 3,直线a ,b 与l 1、l 2、l 3分别相交于A 、B 、C 和点D 、E 、F .若,DE =4,则EF 的长是( )A.B .C .6D .10 【答案】C .EBC ACF BC ACBCE CAF ∠=∠⎧⎪=⎨⎪∠=∠⎩32=BC AB 38320【考点定位】平行线分线段成比例.4.【江苏省南京市中考】如图所示,△ABC 中,DE ∥BC ,若,则下列结论中正确的是( ) A .B .C .D . 【答案】C .【考点定位】相似三角形的判定与性质.5.【江苏省南通市九年级上学期期末】若△ABC∽△A′B′C′,相似比为1:3,则△ABC 与△A′B′C′的面积之比为 .【答案】1:9.【解析】∵△ABC ∽△A′B′C′,相似比为1:3,∴△A BC 与△A′B′C′的面积之比为1:9.故答案为:1:9.【考点定位】相似三角形的性质.6.【江苏省扬州市中考】如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A 、B 、C 都在横格线上,若线段AB =4 cm ,则线段BC = c m【答案】1212AD DB =12AE EC =12DE BC =1=3ADE ABC △的周长△的周长1=3ADE ABC △的面积△的面积【考点定位】平行线分线段成比例7.【江苏省常州市中考】如图,在△ABC 中,DE ∥BC ,AD :DB =1:2,DE =2,则BC 的长是 .【答案】6.【考点定位】相似三角形的判定与性质.8.【江苏省无锡市中考】已知:如图,AD 、BE 分别是△ABC 的中线和角平分线,AD ⊥BE ,AD =BE =6,则AC的长等于 .【答案】952BACDE故答案为:952【考点定位】全等三角形的判定及性质;相似三角形的判定及性质;勾股定理.9.【江苏省苏州中考一模】如图,在平面直角坐标系中,已知点A (0,6),B (8,0).点P 从A 点出发,以每秒1个单位的速度沿AO 运动;同时,点Q 从O 出发,以每秒2个单位的速度沿OB 运动,当Q 点到达B 点时,P 、Q 两点同时停止运动. (1)求运动时间t 的取值范围;(2)t 为何值时,△POQ 的面积最大?最大值是多少?(3)t 为何值时,以点P 、0、Q 为顶点的三角形与Rt △AOB 相似?【答案】(1) 0≤t ≤4;(2) 当t=3时,△POQ 的面积最大,最大值是9.(3) 当t 为或时,以点P 、0、Q 为顶点的三角形与Rt △AOB 相似. 【解析】试题分析:(1)由点Q 从O 出发,以每秒2个单位的速度沿O B 运动,当Q 点到达B 点时,P 、Q 两点同时停止运动,可得:2t=8,解得:t=4,进而可得:0≤t ≤4;1251811(2)先根据三角形的面积公式,用含有t 的式子表示△POQ 的面积=-t 2+6t ,然后根据二次函数的最值公式解答即可;试题解析:(1)∵点A (0,6),B (8,0),∴OA=6,OB=8,∵点Q 从O 出发,以每秒2个单位的速度沿OB 运动,当Q 点到达B 点时,P 、Q 两点同时停止运动, ∴2t=8,解得:t=4, ∴0≤t ≤4;(2)根据题意得:经过t 秒后,AP=t ,OQ=2t ,∴OP=OA-AP=6-t , ∵△POQ 的面积=•OP •OQ ,即△POQ 的面积=×(6-t )×2t=-t 2+6t . ∵a=-1<0,∴△POQ 的面积有最大值,当t=-=3时,△POQ 的面积的最大值==9,即当t=3时,△POQ 的面积最大,最大值是9. (3)①若Rt △POQ ∽Rt △AOB 时, ∵Rt △POQ ∽R t △AOB ,∴,即,解得:t= ②若Rt △QOP ∽Rt △AOB 时, ∵Rt △QOP ∽Rt △AOB ,∴,即,解得:t=. 所以当t 为或时,以点P 、0、Q 为顶点的三角形与Rt △AOB 相似. 【考点定位】相似三角形与一次函数综合题.10.【江苏省南京市中考】如图,△ABC 中,CD 是边AB 上的高,且.(1)求证:△ACD ∽△CBD ; (2)求∠ACB 的大小.12122ba244ac b a - PO OQ AO OB =6268t t -=125 PO OQ OB AO =6286t t -=18111251811AD CDCD BD=【答案】(1)证明见试题解析;(2)90°.【解析】【考点定位】相似三角形的判定与性质.专题2 圆的有关计算及圆的综合学校:___________姓名:___________班级:___________1.【江苏省南通市九年级上学期期末】如图,⊙O 中,OA ⊥BC ,∠A OB=52°,则∠ADC 的度数为( )A .36°B .26°C . 38°D .46°【答案】D . 【解析】故选D.【考点定位】1.圆周角定理;2.垂径定理.2.【江苏省江阴市九年级下学期期中】一个圆锥底面直径为2,母线为4,则它的侧面积为( ) A . B.C .D .【答案】C.【解析】根据圆锥的侧面积公式S=πrl 可得这个圆锥的侧面积为π×1×4=4π.故选C. 【考点定位】圆锥的侧面积公式.3.【江苏省苏州市区中考】如图,⊙O 上A 、B 、C 三点,若∠B=50,∠A=20°,则∠AOB 等于( ) A 、30° B 、50° C 、70° D 、60°【答案】D .2π12π4π8π【解析】先根据圆周角定理得出∠ACB=∠AOB ,再由三角形内角和定理即可得出结论.∵∠AOB 与∠ACB是同弧所对的圆心角与圆周角,∠B=50,∠A=20°,∴∠ACB=∠AOB .∴180°-∠AOB-∠A=180°-∠ACB-∠B ,即180°-∠AOB-20°=180°-∠AOB-50°,解得∠AOB=60°.故选D .【考点定位】圆周角定理.4.【江苏省南通市九年级上学期期末】某个圆锥的侧面展开图形是一个半径为6cm ,圆心角为120°的扇形,则这个圆锥的底面半径为( )cm . A 、2B 、3C 、4D 、5【答案】A .故选A.【考点定位】弧长的计算.5.【江苏省苏州市中考一模】如图,AB 是⊙O 的切线,切点为B ,AO 交⊙O 于点C ,且AC=OC ,若⊙O 的半径为5,则图中阴影部分的面积是 .. 【解析】直接利用切线的性质结合勾股定理得出AB 的长,再利用锐角三角函数关系得出∠BOC 的度数,结合阴影部分的面积为:S △OBA -S 扇形BOC 求出即可.连接OB ,∵AB 是⊙O 的切线,切点为B ,∴∠OBBA=90°,∵AC=OC ,⊙O 的半径为5,∴AC=5,AB=5,∴∠A=30°,则∠BOC=60°,∴图中阴影部分的面积为:S △OBA -S 扇形BOC =×BO ×AB-.故答案为:121212625π312605360π⨯536225π. 【考点定位】1.扇形面积的计算;2.切线的性质.6.【江苏省徐州中考】13.圆锥底面圆的半径为3m ,其侧面展开图是半圆,则圆锥母线长为 m. 【答案】6.【考点定位】圆锥的计算.7.【江苏省中考】已知扇形的圆心角为120°,弧长为6π,则扇形的面积是 . 【答案】27π.【考点定位】扇形面积的计算.8.【江苏省南京市中考二模】已知等腰△ABC 中,AB=AC=13cm ,BC=10cm ,则△ABC 的内切圆半径为 cm . 【答案】. 【解析】如图,设△ABC 的内切圆半径为r ,由勾股定理得AD=12,再由切线长定理得AE=8,根据勾股定理求得r 即可.如图,∵AB=AC=13cm ,BC=10cm ,∴BD=5cm ,∴AD=12cm ,根据切线长定理,AE=AB-BE=AB-BD=13-5=8,设△ABC 的内切圆半径为r ,∴AO=12-r ,∴(12-r )2-r 2=64,解得r=.故答案为:. 【考点定位】1.三角形的内切圆与内心;2.等腰三角形的性质.9.【江苏省苏州中考一模】如图所示,D 是以AB 为直径的半圆O 上的一点,C 是弧AD 的中点,点M 在AB 上,AD 与CM 交于点N ,CN=AN .625π103103103(1)求证:CM⊥AB;(2)若BD=2,求半圆的直径.【答案】(1)证明见解析;(2)6.【解析】试题解析:(1)证明:如图1,连接BC,则∠ACB=90°,∵CN=AN,∴∠NCA=∠NAC,∴∠MCA=∠DAC,∵C是弧AD的中点,∴∠ABC=∠DAC,∴∠MCA=∠ABC,∵∠CAB=∠BAC,∴△ABC∽△ACM,∴∠AMC=90°,∴CM⊥AB;(2)解:如图2,连接CD,作CE⊥BD,交BD的延长线于E,在△CMB与△BCE中,,【考点定位】1.相似三角形的判定与性质;2,全等三角形的判定与性质;2.圆周角定理.10.【江苏省无锡市中考】已知:如图,AB 为⊙O 的直径,点C 、D 在⊙O 上,且BC =6cm ,AC =8cm ,∠ABD =45º.(1)求BD 的长;(2)求图中阴影部分的面积.【答案】(1)BD =52cm;(2)S 阴影=25π-504cm 2. 【解析】MBC CBE CMB CEB BC BC ∠=∠∠=∠=⎧⎪⎨⎪⎩【考点定位】圆周角定理的推论;勾股定理;扇形的面积公式.专题3 图形的变换、视图与投影学校:___________姓名:___________班级:___________1. 【江苏省苏州市中考一模】下列腾讯QQ表情中,不是轴对称图形的是()【答案】C.【解析】根据轴对称图形的概念求解.A、是轴对称图形,故本选项错误;B、是轴对称图形,故本选项错误;C、不是轴对称图形,故本选项正确;D、是轴对称图形,故本选项错误.故选C.【考点定位】轴对称图形.2.【江苏省徐州市中考模拟】下列图形中,既是中心对称图形又是轴对称图形的是()【答案】D.【考点定位】1.中心对称图形;2.轴对称图形.3. 【江苏省淮安市中考】如图所示物体的主视图是()A. B. C. D.【答案】C.【考点定位】简单组合体的三视图.4.【江苏省常州市中考】下列“慢行通过,注意危险,禁止行人通行,禁止非机动车通行”四个交通标志图(黑白阴影图片)中为轴对称图形的是()A. B. C. D.【答案】B.故选B.【考点定位】轴对称图形.5.【江苏省常州市中考】将一张宽为4cm的长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,则这个三角形面积的最小值是【答案】8cm2 .故答案为:8cm 2.【考点定位】1.翻折变换(折叠问题);2.最值问题.6.【江苏省江阴市中考】如图,Rt ΔABC 中,AB=9,BC=6,∠B=900,将ΔABC 折叠,使A 点与BC 的中点D 重合,折痕为MN ,则线段BN的长为【答案】 4. 【解析】 故答案为:4.【考点定位】翻折变换;勾股定理. 7.【江苏省苏州市区中考】在R t △ABC 中,斜边AB=4,∠B=60°,将△ABC 绕点B 旋转60°,顶点C 运动的路线长是 (结果保留π).【答案】.【解析】将△ABC 绕点B 旋转60°,顶点C 运动的路线长是就是以点B 为圆心,B C 为半径所旋转的弧,根据弧长公式即可求得.∵AB=4,∴BC=2,所以弧长=.故答案为:. 【考点定位】1.弧长的计算;2.旋转的性质.8.【江苏省扬州市2015年中考数学试题】如图,已知Rt △ABC 中,∠ABC =90°,AC =6,BC =4,将△ABC 绕直角顶点C 顺时针旋转90°得到△DEC ,若点F 是DE 的中点,连接AF ,则AF = 23π602180π⨯=23π23π【答案】5【考点定位】旋转的性质9.【江苏省徐州市中考】如图,在方格纸上建立平面直角坐标系,每个小正方形的边长为1.(1)画出△AOB关于x轴对称的△A1OB1.(2)画出将△AOB绕点O顺时针旋转90°的△A2OB2,并判断△A1OB1和△A2OB2在位置上有何关系?若成中心对称,请直接写出对称中心坐标;如成轴对称,请直接写出对称轴的函数关系式.(3)若将△AOB绕点O旋转360°,试求出线段AB扫过的面积.【答案】(1)画图见解析;(2)画图见解析;△A1OB1和△A2OB2是轴对称关系,对称轴为:y=﹣x.(3)2.5π.【解析】试题解析:(1)如图所示:.(2)如图所示:△A1OB1和△A2OB2是轴对称关系,对称轴为:y=﹣x.(3)过点O作OE⊥AB,线段AB2﹣π()2=5π﹣2.5π=2.5π. 【考点定位】1.作图-旋转变换;2.扇形面积的计算;3.作图-轴对称变换.10.【江苏省南京市中考二模试题】△ABC 中,AB=AC=10,BC=12,矩形DEFG 中,EF=4,FG >12.(1)如图①,点A 是FG 的中点,FG ∥BC ,将矩形DEFG 向下平移,直到DE 与BC 重合为止.要研究矩形DEFG 与△ABC 重叠部分的面积,就要进行分类讨论,你认为如何进行分类,写出你的分类方法(无需求重叠部分的面积).(2)如图②,点B 与F 重合,E 、B 、C 在同一直线上,将矩形DEFG 向右平移,直到点E 与C 重合为止.设矩形DEFG 与△ABC 重叠部分的面积为y ,平移的距离为x .①求y 与x 的函数关系式,并写出自变量的取值范围;②在给定的平面直角坐标系中画出y 与x 的大致图象,并在图象上标注出关键点坐标.2【考点定位】几何变换综合题.。
2019年中考数学试卷重难题专题【相似三角形】(含答案)

2019年中考数学试卷重难题专题【相似三角形】(含答案)知识点睛借助相似整合信息的通常思路:利用相似时,往往可以将_______________等信息组合搭配在一起进行研究,并能实现三类信息之间的转化,进而达到整合信息、解决问题的目的.为了借助相似实现_______________等条件的综合应用,往往会通过___________或作_________的方式来构造相似模型.构造相似模型是我们整合多个比例信息时常用的一种手段.一、单选题1.(2018·浙江初三期中)如图,在中, 是线段上的点,且, 是线段ABC D AB :1:2AD BD F 上的点, , .小亮同学随机在内部区域投针,则针扎到(阴影)BC DE BC FE BA ABC DEF 区域内的概率是( )A .B .C .D .1329518492.(2018·四川中考真题)如图,E ,F 是平行四边形ABCD 对角线AC 上两点,AE=CF=AC .连接14DE ,DF 并延长,分别交AB ,BC 于点G ,H ,连接GH ,则的值为( )S △ADGS △BGHA .B .C .D .11223343.(2019·湖北沙市中学初二期末)彼此相似的矩形A 1B 1C 1O ,A 2B 2C 2C 1,A 3B 3C 3C 2,…,按如图所示的方式放置.点A 1,A 2,A 3,…,和点C 1,C 2,C 3,…,分别在直线y=kx+b (k >0)和x 轴上,已知点B 1、B 2的坐标分别为(1,2),(3,4),则Bn的坐标是( )A .(2n ﹣1,2n )B .(2n ﹣,2n )12C .(2n﹣1﹣,2n﹣1)D .(2n﹣1﹣1,2n﹣1)124.(2014·浙江初三期末)如图,矩形AEHC 是由三个全等矩形拼成的,AH 与BE 、BF 、DF 、DG 、CG 分别交于点P 、Q 、K 、M 、N .设△BPQ ,△DKM ,△CNH 的面积依次为S 1,S 2,S 3.若S 1+S 3=20,则S 2的值为( )A .6B .8C .10 D .125.(2018·全国初一单元测试)如图,是三个正方形拼成的一个长方形,则∠1+∠2+∠3=( )A .60°B .75°C .90°D .105°6.(2018·广东中考模拟)如图所示,在矩形ABCD 中,AB=6,BC=8,对角线AC 、BD 相交于点O ,过点O 作OE 垂直AC 交AD 于点E ,则DE 的长是( )A .5B .C .D .32741547.(2018·广西中考真题)如图,在平面直角坐标系中,M 、N 、C 三点的坐标分别为(,1),(3,1),12(3,0),点A 为线段MN 上的一个动点,连接AC ,过点A 作交y 轴于点B ,当点A 从M 运动AB ⊥AC 到N 时,点B 随之运动,设点B 的坐标为(0,b ),则b 的取值范围是( )A .B .C .D .−14≤b ≤1−54≤b ≤1−94≤b ≤12−94≤b ≤18.(2018·江西初三期末)如图,△ABC 是一块锐角三角形材料,高线AH 长8 cm ,底边BC 长10 cm ,要把它加工成一个矩形零件,使矩形DEFG 的一边EF 在BC 上,其余两个顶点D ,G 分别在AB ,AC 上,则四边形DEFG 的最大面积为( )A .40 cm 2B .20 cm 2C .25 cm 2D .10 cm 29.(2017·江阴初级中学初三期中)如图,D 是等边△ABC 边AB 上的一点,且AD :DB =1:2,现将△ABC 折叠,使点C 与D 重合,折痕为EF ,点E 、F 分别在AC 和BC 上,则CE :CF 的值为( )A .B .C .D . 4535566710.(2017·安徽初三期中)如图,在正方形ABCD 中,点E 、F 分别在边BC ,DC 上,AE 、AF 分别交BD于点M 、N ,连接CN 、EN ,且CN =EN .下列结论:①AN =EN ,AN ⊥EN ;②BE+DF=EF ;③∠DFE =2∠AMN ;④;④图中有4对相似三角EF 2=2BM 2+2DN 2形.其中正确结论个数是( )A .5B .4C .3D .211.(2018·全国初三期末)如图,在矩形ABCD 中,E 是AD 边的中点,BE ⊥AC ,垂足为点F ,连接DF ,下列结论:①△AEF ∽△CAB ;②CF=2AF ;③tan ∠CAD=.其中正确的结论有 ( )2A .3个B .2个C .1个D .0个12.(2017·安徽中考模拟)如图,沿对角线AC 折叠正方形ABCD ,使得B 、D 重合,再折叠△ACD ,点D 恰好落在AC 上的点E 处,测得折痕AF 的长为3,则C 到AF 的距离CG 为:A .B .C .D .32235−113.(2019·全国初二单元测试)如图,在Rt △ABC 中,∠BAC =90°,AB =3,AC =4,点P 为BC 上任意一点,连接PA,以PA ,PC 为邻边作平行四边形PAQC ,连接PQ ,则PQ 的最小值为( )A .B .C .D .2651255314.(2019·广东中考模拟)如图,将边长为3的正方形纸片ABCD 对折,使AB 与DC 重合,折痕为EF ,展平后,再将点B 折到边CD 上,使边AB 经过点E ,折痕为GH,点B 的对应点为M ,点A 的对应点为N ,那么折痕GH 的长为( )AB .C .D1037215.如图,在矩形ABCD 中,对角线AC 、BD 相交于G ,E 为AD 的中点,连接BE 交AC 于F ,连接FD ,若∠BFA=90°,则下列四对三角形:①△BEA 与△ACD ;②△FED 与△DEB ;③△CFD 与△ABG ;④△ADF 与△EFD ,其中相似的为( )A.①④B.①②C.②③④D.①②③④二、填空题16.(2018·天津中考模拟)如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D 的坐标为______.17.(2018·山东中考真题)如图,在矩形ABCD中,AB=2,BC=4,点E、F分别在BC、CD上,若AE=5,∠EAF=45°,则AF的长为_____.218.(2018·湖北中考真题)如图,将面积为32的矩形ABCD沿对角线BD折叠,点A的对应点为点P,2连接AP交BC于点E.若BE=,则AP的长为_____.19.(2017·湖北中考模拟)赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,若这四个全等直角三角形的两条直角边分别平行于x轴和y轴,大正方形的顶点B1、C1、C2、C3、…、C n在直线y=- x+ 上,顶点D1、D2、D3、…、D n在x轴上,则第n个阴影小1 27 2正方形的面积为________.20.(2017·全国初三课时练习)在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是______.21.(2018·安徽中考真题)矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.22.(2018·江苏中考真题)如图,在直角△ABC中,∠C=90°,AC=6,BC=8,P、Q分别为边BC、AB上的两个动点,若要使△APQ是等腰三角形且△BPQ是直角三角形,则AQ =________.23.(2018·贵州中考模拟)如图,在△ABC 中,BC=8,高AD=6,矩形EFGH 的一边EF 在边BC 上,其余两个顶点G 、H 分别在边AC 、AB 上,则矩形EFGH 的面积最大值为_____.24.(2017·湖北中考真题)如图,在△ABC 中,∠ACB =90°,点D ,E 分别在AC ,BC 上,且∠CDE =∠B ,将△CDE 沿DE 折叠,点C 恰好落在AB 边上的点F 处,连接CF .若AC =8,AB =10,则CD 的长为__25.(2018·乌拉特前旗第六中学中考模拟)如图,点P 是矩形ABCD 内一点,连接PA 、PB 、PC 、PD,已知AB=3,BC=4,设△PAB, △PBC, △PCD, △PDA,的面积分别为,,, ,以下判断: ① PA+PB+PC+PD 的最小S 1S 2S 3S 4值为10;②若△PAB ≌△PCD,则△PAD ≌△PBC ;③若=,则=;④若△PAB ∽△PDA,则PA=2.4.其中正S 1S 2S 3S 4确的是_____________(把所有正确的结论的序号都填在横线上)26.(2018·广西中考真题)如图,点 C 为 Rt △ACB 与 Rt △DCE 的公共点,∠ACB=∠DCE=90°,连 接 AD 、BE ,过点 C 作 CF ⊥AD 于点 F ,延长 FC 交 BE 于点 G .若 AC=BC=25,CE=15, DC=20,则的值为___________.EG BG参考答案1.B【解析】解:∵, ,∴, .DE BC 12AD BD =ADE ABC ∽13AD AE DE AB AC BC ===又∵,∴,∴, .FE BA CFE CBA ∽23CE CF CA CB ==21CF BF =设的面积,则,∴梯形面积.ADE ADE S S = 9ABC S S = DECB 8DECB S S =梯∵,∴,∴.DE BC 1112EDBF EFC S BF S FC == 平行四边形4EFC EDBF S S S == 平行四边形在平行四边形中,,∴.故BDEF 122BOF DEF BDEF S S S === 平行四边形29DEF ABC S S = 选.B 点睛:此题主要考查了几何概率问题,用到的知识点为:概率=相应的面积与总面积之比.2.C【解析】分析:首先证明AG :AB=CH :BC=1:3,推出GH ∥AC ,推出△BGH ∽△BAC ,可得,,由此即可解决问题.S △ADCS △BGH =S △BAC S △BGH =(BA BG )2=(32)2=94S △ADG S △ADC =13详解:∵四边形ABCD 是平行四边形∴AD=BC ,DC=AB ,∵AC=CA ,∴△ADC ≌△CBA ,∴S △ADC =S △ABC ,∵AE=CF=AC ,AG ∥CD ,CH ∥AD ,14∴AG :DC=AE :CE=1:3,CH :AD=CF :AF=1:3,∴AG :AB=CH :BC=1:3,∴GH ∥AC ,∴△BGH ∽△BAC ,∴,S △ADCS △BGH=S △BAC S △BGH =(BA BG )2=(32)2=94∵,S △ADG S △ADC =13∴.S △ADG S △BGH =94×13=34故选:C .点睛:本题考查平行四边形的性质、相似三角形的判定和性质、全等三角形的判定和性质、等高模型等知识,解题的关键是灵活运用所学知识解决问题,属于中考选择题中的压轴题.3.A【解析】【分析】根据矩形的性质求出点的坐标,然后利用待定系数法求一次函数解析式求出,12A A 、k b 、从而得到一次函数解析式,再根据一次函数图像上点的坐标特征求出的坐标,然后求出3A 的坐标,...,最后根据点的坐标特征的变化规律写出的坐标即可.3B n B 【详解】,()11,2B 相似矩形的长是宽的倍,∴2点的坐标分别为, 12B B 、()()1,23,4,,∴()()120,21,4A A ,点在直线上,12A A 、y kx b =+,∴24b k b =⎧⎨+=⎩解得,22k b =⎧⎨=⎩,∴22y x =+点在直线上,3A 22y x =+,∴2328y =⨯+=点的坐标为,∴3A ()3,8点的横坐标为,∴3B 13872+⨯=点,∴()37,8B …,的坐标为.n B ()21,2n n -故选:.A 【点睛】本题考查了相似多边形的性质,一次函数图象上点的坐标特征,根据点的系列坐标判断A 出相应矩形的长,再求出宽,然后得到点的系列坐标的变化规律是解题的关键.B 4.B【解析】试题分析:∵矩形AEHC 是由三个全等矩形拼成的,∴AB=BD=CD ,AE ∥BF ∥DG ∥CH ,∴四边形BEFD ,四边形DFGC 是平行四边形,∠BQP=∠DMK=∠CHN ,∴BE ∥DF ∥CG∴∠BPQ=∠DKM=∠CNH ,∵△ABQ ∽△ADM ,△ABQ ∽△ACH ,∴,,AB AD =BQ MD =12BQ CH =AB AC =13∴△BPQ ∽△DKM ∽△CNH∴,BQ MD=12BQ CH =13∴S 1S 2=14,S 1S 3=19∴S 2=4S 1,S 3=9S 1,∵S 1+S 3=20,∴S 1=2,∴S 2=8.故选B .考点:1.矩形的性质,2.三角形的面积,3.相似三角形的判定与性质.5.C【解析】【分析】容易看出∠3=45°,关键求出∠2与∠1的和是45°,根据证AI CI =IJ IA ∆AIJ~∆CIA,得∠2=∠CAI,再由∠1+∠2=∠CAI+∠CAD =45°可推出结果.【详解】如图设三个小正方形的边长为1个单位.在正方形ABCD 中∠3=45°,则∠AIC=135°,且∠1=∠CAD .∵∠AIJ=∠CIA ,,AI CI =22,IJ IA =22即,AI CI =IJ IA 所以∆AIJ~∆CIA,所以∠2=∠CAI,又∠1=∠CAD ,则∠1+∠2=∠CAI+∠CAD =45°,∴∠1+∠2+∠3=90°.故正确选项为:C【点睛】本题考查了相似三角形的判定与性质:如果两个三角形的两条对应边的比相等,且它们所夹的角也相等,那么这两个三角形相似;相似三角形对应角相等,对应边的比相等.也考查了勾股定理以及正方形的性质.6.C【解析】【分析】先利用勾股定理求出AC 的长,然后证明△AEO ∽△ACD ,根据相似三角形对应边成比例列式求解即可.【详解】∵AB=6,BC=8,∴AC=10(勾股定理);∴AO=AC=5,12∵EO ⊥AC ,∴∠AOE=∠ADC=90°,∵∠EAO=∠CAD ,∴△AEO ∽△ACD ,∴,AE AC=AO AD 即 ,AE 10=58解得,AE=,254∴DE=8﹣=,25474故选:C .【点睛】本题考查了矩形的性质,勾股定理,相似三角形对应边成比例的性质,根据相似三角形对应边成比例列出比例式是解题的关键.7.A【解析】分析:分两种情形:当A 与点N 、M 重合时来确定b 的最大与最小值即可.详解:如图1,当点A 与点N 重合时,CA ⊥AB ,∴MN 是直线AB 的一部分,∵N (3,1)∴OB=1,此时b=1;当点A 与点M 重合时,如图2,延长NM 交y 轴于点D ,易证△MCN ∽△BMD∴BD MN =DM NC ∵MN=3-=,DM=,CN=1125212∴BD=DM·MN CN =54∴OB=BD-OD=-1=,即b=-,541414∴b 的取值范围是.-14≤b ≤1故选A.点睛:此题考查了坐标与图形,灵活运用相似三角形的判定与性质是解此题的关键..8.B【解析】【分析】设矩形DEFG 的宽DE=x ,根据相似三角形对应高的比等于相似比列式求出DG ,再根据矩形的面积列式整理,然后根据二次函数的最值问题解答即可.【详解】如图所示:设矩形DEFG 的宽DE=x ,则AM=AH-HM=8-x ,∵矩形的对边DG ∥EF ,∴△ADG ∽△ABC ,∴,AM AH =DG BC即,8−x 8=DG 10解得DG=(8-x ),54四边形DEFG 的面积=(8-x )x=-(x 2-8x+16)+20=-(x-4)2+20,545454所以,当x=4,即DE=4时,四边形DEFG 最大面积为20cm 2.故选:B .【点睛】考查了相似三角形的应用,二次函数的最值问题,根据相似三角形的对应高的比等于相似比用矩形DEFG 的宽表示出长是解题的关键.9.A【解析】解:由折叠的性质可得,∠EDF =∠C =60º,CE =DE ,CF =DF .∵∠BDF +∠ADE =∠BDF +∠BFD =120º,∴∠ADE =∠BFD ,又∵∠A =∠B =60º,∴△AED ∽△BDF ,∴ ,设DE AD AE DF BF BD==AD =a ,BD =2a ,AB =BC =CA =3a ,再设CE ==DE =x ,CF ==DF =y ,则AE =3a -x ,BF =3a -y ,所以,整理可得ay =3ax -xy ,2ax =3ay -xy ,即xy =3ax -ay ①,xy =3ay -332x a a x y a y a-==-2ax ②;把①代入②可得3ax -ay =3ay -2ax ,所以5ax =4ay ,,即,4455x a y a ==45CE CF =故选A .点睛:主要考查了翻折变换的性质及其应用问题;解题的关键是借助相似三角形的性质分别求出CE 、CF 的长度(用含有k 的代数式表示);对综合的分析问题解决问题的能力提出了较高的要求.10.B【解析】【详解】将△ABE 绕点A 逆时针旋转90°,得到△ADH ,因为四边形ABCD 是正方形,所以AB =BC =AD , ∠BAD =∠ABC =90°,∠ABD =∠CBD =45°,在△BNA 和△BNC 中,,{BN =BN∠NBA =∠BA =BC NBC所以△BNA ≌△BNC ,所以AN =CN ,∠NEC =∠NCE =∠BAN ,因为∠NEC +∠BEN =180°,所以∠BAN +∠BEN =180°,所以∠ABC +∠ANE =180°,所以∠ANE =90°,所以AN =NE ,AN ⊥NE ,故①正确,因为∠3=45°, ∠1=∠4,所以∠2+∠4=∠2+∠1=45°,所以∠3=∠FAH =45°,因为AF =AF ,AE =AH ,所以△AFE ≌△AFH ,所以EF =FH =DF +DH =DF +BE , ∠AFH =∠AFE ,故②正确,因为∠MAN =∠NDF =45°, ∠ANM =∠NDF ,所以∠AMN =∠AFD ,又因为∠AFE =∠AFD , ∠DFE=∠AFE +∠AFD所以∠DFE =2∠AMN ,故③正确,因为∠MAN =∠EAF , ∠AMN =∠AFE ,所以△AMN ∽△AFE ,所以,NMEF =AN AE =12所以MN ,EF =2如图2中,将△ABN 绕点A 逆时针旋转90°,得到△ADG ,易证△ANG ≌△ANM , △GDN 是直角三角形,所以MN =GN ,所以,MN 2=DN 2+DG 2=DN 2+BM 2所以,故④正确,EF 2=2DN 2+2BM 2图中相似三角形有△ANE ∽△BAD ∽△BCD , △ANM ∽△AEF , △ABN ∽△FDN ,△BEM ∽△DAM 等,故⑤错误,故选B.11.B【解析】【分析】①正确.只要证明∠EAC=∠ACB ,∠ABC=∠AFE=90°即可;②正确.由AD ∥BC ,推出△AEF ∽△CBF ,推出,由AE=AD=BC ,推出=,即AE BC =AF CF 1212AF CF 12CF=2AF ;④错误,设AE=a ,AB=b ,则AD=2a ,由△BAE ∽△ADC ,有,即b=a ,可得ba =2ab 2tan ∠CAD==即可得.CD AD b 2a 【详解】如图,过D 作DM ∥BE 交AC 于N ,∵四边形ABCD 是矩形,∴AD ∥BC ,∠ABC=90°,AD=BC ,∵BE ⊥AC 于点F ,∴∠EAC=∠ACB ,∠ABC=∠AFE=90°,∴△AEF ∽△CAB ,故①正确;∵AD ∥BC ,∴△AEF ∽△CBF ,∴,AE BC =AF CF ∵AE=AD=BC ,1212∴=,AF CF 12∴CF=2AF ,故②正确;设AE=a ,AB=b ,则AD=2a ,由△BAE ∽△ADC ,有,即b=a ,b a =2a b 2∴tan ∠CAD===,故③错误,CD AD b 2a 22所以正确的有2个,故选B .【点睛】本题考查了相似三角形的判定和性质,矩形的性质以及解直角三角形的综合应用,正确的作出辅助线构造平行四边形是解题的关键.解题时注意:相似三角形的对应边成比例.12.A【解析】试题分析:设正方形ABCD 的边长=a ,根据勾股定理得到AC =a ,根据折叠的性质得到2AE =AD =a ,∠AEF =∠D =90°,根据等腰直角三角形的性质得到EF =CE =a –a ,根据勾股定2理得到a =AC =,EF =(–1)×32+22322+22232+22到结论.试题解析:设正方形ABCD 的边长=a ,则AC =a ,2∵折叠△ACD ,点D 恰好落在AC 上的点E 处,∴AE =AD =a ,∠AEF =∠D =90°,∴CE =a –a ,2∵∠ECF =45°,∴EF =CE =a –a ,2∵AF 2=AE 2+EF 2,∴32=a 2+(a –a )2,∴a =232+22∴AC =,EF =( –1)×,322+22232+22∵∠EAF =∠CAG ∠AEF =∠G =90°,∴△AEF ∽△AGC ,∴,∴CG =.ACAF =CG EF 32故选A .13.B【解析】【分析】记AC 与PQ 的交点为O ,由平行四边形的性质可知O 是AC 中点,PQ 最短也就是PO 最短;过O 作BC 的垂线P′O ,则PO 最短为P′O ;接下来可证明△P′OC 和△ABC 相似,进而利用相似三角形的性质即可求出PQ 的最小值.【详解】解:记AC 与PQ 的交点为O.∵∠BAC=90°,AB=3,AC=4,∴=5.∵四边形APCQ 是平行四边形,∴PO=QO ,CO=AO ,∴PQ 最短也就是PO 最短.过O 作BC 的垂线OP′.∵∠ACB=∠P′CO ,∠CP′O=∠CAB=90°,∴△CAB ∽△CP′O ,∴,'CO OP BCAB ∴OP′=,65∴则PQ 的最小值为2OP′=,125故答案为:.125【点睛】本题考查了勾股定理的运用、平行四边形的性质、相似三角形的判定和性质以及垂线段最短的性质,解题的关键是作高线,构造相似三角形.14.A【解析】【分析】利用翻折变换的性质结合勾股定理表示出CH 的长,得出△EDM ∽△MCH ,进而求出MC 的长,依据△GPH ≌△BCM ,可得GH=BM ,再利用勾股定理得出BM ,即可得到GH 的长.【详解】设CM =x ,设HC =y ,则BH =HM =3﹣y ,故y 2+x 2=(3﹣y )2,整理得:y =,21362x -+即CH =,21362x -+∵四边形ABCD 为正方形,∴∠B =∠C =∠D =90°,由题意可得:ED =1.5,DM =3﹣x ,∠EMH =∠B =90°,故∠HMC +∠EMD =90°,∵∠HMC +∠MHC =90°,∴∠EMD =∠MHC ,∴△EDM ∽△MCH ,∴ ,ED DM MC CH =即,21.531362x x x -=-+解得:x 1=1,x 2=3(不合题意),∴CM =1,如图,连接BM ,过点G 作GP ⊥BC ,垂足为P ,则BM ⊥GH ,∴∠PGH =∠HBM ,在△GPH 和△B CM 中,HGP CBM GP BC GPH C ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△GPH ≌△BCM (SAS ),∴GH =BM ,∴GH =BM.=故选:A .【点睛】此题主要考查了翻折变换的性质以及正方形的性质、相似三角形的判定与性质和勾股定理的综合运用,作辅助线构造全等三角形,正确应用相似三角形的判定与性质是解题关键.15.D【解析】【分析】根据判定三角形相似的条件对选项逐一进行判断.【详解】①根据题意得:,∠BAE =∠ADC =∠AFE =90°,∴∠AEF +∠EAF =90°,∠DAC +∠ACD =90°,∴∠AEF =∠ACD ①中两三角形相似;∴②,∵∠AEB =∠FEA,∠AFE =∠EAB =90°,∴△AFE ∽△BAE ,∴AE EF =EB AE 又,∵AE =ED ,∴ED EF =EB ED 而,∠BED =∠BED ,∴△FED ∽△DEB 故②正确;③,∵AB‖CD ,∴∠BAC =∠GCD ,且,∵∠ABE =∠DAF,∠EBD =∠EDF ∠ABG =∠ABE +∠EBD ,∴∠ABG =∠DAF +∠EDF =∠DFC ,∵∠ABG =∠DFC,∠BAG =∠DCF ,∴△CFD ∽△ABG 故③正确;④,∵△FED ∽△DEB ,∴∠EFD =∠EDB,∵AG =DG ,∴∠DAF =∠ADG ,∴∠DAF =∠EFD ,∴△ADF ∽△EFD 故④正确;故选:.D 【点睛】此题考查了相似三角形的判定:(1)有两个对应角相等的三角形相似;(2)有两个对应边的比相等,且其夹角相等,则两个三角形相似;(3)三组对应边的比相等,则两个三角形相似.16.(﹣,)45125【解析】【分析】首先过D 作DF ⊥AF 于F ,根据折叠可以证明△CDE ≌△AOE ,然后利用全等三角形的性质得到OE=DE ,OA=CD=1,设OE=x ,那么CE=3﹣x ,DE=x ,利用勾股定理即可求出OE 的长度,而利用已知条件可以证明△AEO ∽△ADF ,而AD=AB=3,接着利用相似三角形的性质即可求出DF 、AF 的长度,也就求出了D 的坐标.【详解】解:如图,过D 作DF ⊥AO 于F ,∵点B 的坐标为(1,3),∴BC=AO=1,AB=OC=3,根据折叠可知:CD=BC=OA=1,∠CDE=∠B=∠AOE=90°,AD=AB=3,在△CDE 和△AOE 中,,{∠CDE =∠AOE∠CED =∠AEOCD =AO ∴△CDE ≌△AOE ,∴OE=DE ,OA=CD=1,AE=CE ,设OE=x ,那么CE=3﹣x ,DE=x ,∴在Rt △DCE 中,CE 2=DE 2+CD 2,∴(3﹣x )2=x 2+12,∴x=,43∴OE=,AE=CE=OC﹣OE=3﹣=,434353又∵DF ⊥AF ,∴DF ∥EO ,∴△AEO ∽△ADF ,∴AE :AD=EO :DF=AO :AF ,即:3=:DF=1:AF ,5343∴DF=,AF=,12595∴OF=﹣1= ,9545∴D 的坐标为:(﹣,).45125故答案为:(﹣,).45125【点睛】此题主要考查了图形的折叠问题、相似三角形的判定与性质、全等三角形的判定与性质以及坐标与图形的性质.解题的关键是把握折叠的隐含条件,利用隐含条件得到全等三角形和相似三角形,然后利用它们的性质即可解决问题.17.4103【解析】分析:取AB 的中点M ,连接ME ,在AD 上截取ND=DF ,设DF=DN=x ,则NF=x ,再利用矩形的性质和已知条件证明△AME ∽△FNA ,利用相似三角形的性质:对2应边的比值相等可求出x 的值,在直角三角形ADF 中利用勾股定理即可求出AF 的长.详解:取AB 的中点M ,连接ME ,在AD 上截取ND=DF ,设DF=DN=x ,∵四边形ABCD 是矩形,∴∠D=∠BAD=∠B=90°,AD=BC=4,∴NF=x ,AN=4﹣x ,2∵AB=2,∴AM=BM=1,∵AE=,AB=2,5∴BE=1,∴ME=,BM 2+BE 2=2∵∠EAF=45°,∴∠MAE+∠NAF=45°,∵∠MAE+∠AEM=45°,∴∠MEA=∠NAF ,∴△AME ∽△FNA ,∴,AMFN=MEAN∴,12x =24-x 解得:x=43∴AF=AD 2+DF 2=4103故答案为:4103点睛:本题考查了矩形的性质、相似三角形的判断和性质以及勾股定理的运用,正确添加辅助线构造相似三角形是解题的关键,18.1632【解析】【分析】设AB=a ,AD=b ,则ab=32,构建方程组求出a 、b 值即可解决问题.2【详解】设AB=a ,AD=b ,则ab=32,2由∽可得:,△ABE △DAB BEAB=ABAD∴,b =22a 2∴,a 3=64∴,,a =4b =82设PA 交BD 于O ,在中,,Rt △ABD BD =AB 2+AD 2=12∴OP =OA =AB ⋅AD BD=823∴,AP =1632故答案为:.1632【点睛】本题考查翻折变换、矩形的性质、勾股定理、相似三角形的判定与性质等知识,熟练掌握和应用相关的性质定理是解题的关键.19.2223n -⎛⎫ ⎪⎝⎭【解析】由已知可得△ A 1B 1M ≌△DA 1N 1,∴B 1M=A 1N ,A 1M=D 1N ,又A 1D 1//B 1C 1,∴OA 1:OE=OD 1:OF ,由直线y=﹣可得E (0, ),1722x +72F (7,0),∴OD 1=2OA 1,由矩形OA 1ND 1,得A 1N =2D 1N ,∴可设B 1(b,3b ),代入y=﹣得b=1,∴A 1N=2,A 1M=1,∴S 1=1;1722x +由b=1,可得C 1(3,2),同理可知S 2=( )2= ;212-233⨯⨯223⎛⎫ ⎪⎝⎭同理可知C 2( , ),S 3=( )2== ;133434241-3333⨯⨯249⎛⎫ ⎪⎝⎭423⎛⎫ ⎪⎝⎭……∴S n = .2n-223⎛⎫⎪⎝⎭点睛:本题主要考查全等三角形的判定与性质,一次函数、图形的变化规律等,能正确地识图是解题的关键.20.5×()4030【解析】解:如图,∵四边形ABCD 是正方形,∴∠ABC=∠BAD=90°,AB=BC ,∴∠ABA1=90°,∠DAO+∠BAA 1=180°﹣90°=90°,∵∠AOD=90°,∴∠ADO+∠DAO=90°,∴∠ADO=∠BAA 1,在△AOD 和A1BA 中11AOD ABA ADO BAA ∠=∠⎧⎨∠=∠⎩∴△AOD ∽△A 1BA ,∴,∴BC=2A 1B.121OD AB AO A B ==∴A 1C=BC ,则A 2C 1=A 1C ,A 3C 2=A 2C 1,323232即后一个正方形的边长是前一个正方形的边长的倍.32∴第2016个正方形的边长为BC.201532⎛⎫ ⎪⎝⎭∵A 的坐标为(1,0),D 点坐标为(0,2),∴.=∴第2011个正方形的面积为.22015403033522BC ⎡⎤⎛⎫⎛⎫=⨯⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦故答案为.4030352⎛⎫⨯ ⎪⎝⎭21.3或1.2【解析】【分析】由△PBE ∽△DBC ,可得∠PBE=∠DBC ,继而可确定点P 在BD 上,然后再根据△APD 是等腰三角形,分DP=DA 、AP=DP 两种情况进行讨论即可得.【详解】∵四边形ABCD 是矩形,∴∠BAD=∠C=90°,CD=AB=6,∴BD=10,∵△PBE ∽△DBC ,∴∠PBE=∠DBC ,∴点P 在BD 上,如图1,当DP=DA=8时,BP=2,∵△PBE ∽△DBC ,∴PE :CD=PB :DB=2:10,∴PE :6=2:10,∴PE=1.2;如图2,当AP=DP 时,此时P 为BD 中点,∵△PBE ∽△DBC ,∴PE :CD=PB :DB=1:2,∴PE :6=1:2,∴PE=3;综上,PE 的长为1.2或3,故答案为:1.2或3.【点睛】本题考查了相似三角形的性质,等腰三角形的性质,矩形的性质等,确定出点P 在线段BD 上是解题的关键.22.或154307【解析】分析:分两种情形分别求解:①如图1中,当AQ=PQ ,∠QPB=90°时,②当AQ=PQ ,∠PQB=90°时;详解:①如图1中,当AQ=PQ ,∠QPB=90°时,设AQ=PQ=x ,∵PQ ∥AC ,∴△BPQ ∽△BCA ,∴,BQBA=PQAC ∴,10−x 10=x6∴x=,154∴AQ=.154②当AQ=PQ ,∠PQB=90°时,如图2,设AQ=PQ=y .∵△BQP ∽△BCA ,∴,PQAC=BQBC ∴,y 6=10−y 8∴y=.307综上所述,满足条件的AQ 的值为或.154307点睛:本题考查勾股定理、等腰三角形的性质、相似三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题.23.12【解析】【分析】设HG =x ,根据相似三角形的性质用x 表示出KD ,根据矩形面积公式列出二次函数解析式,根据二次函数的性质计算即可.【详解】设HG =x .∵四边形EFGH 是矩形,∴HG ∥BC ,∴△AHG ∽△ABC ,∴=,即=,解得:HG BC AKAD x 86-KD6KD =6﹣x ,则矩形EFGH 的面积=x (6﹣x )=﹣x 2+6x =(x ﹣4)2+12,则矩形EFGH 的343434﹣34面积最大值为12.故答案为:12.【点睛】本题考查的是相似三角形的判定和性质、二次函数的性质,掌握相似三角形的判定定理和性质定理是解题的关键.24.238【解析】分析:由对称性可知CF ⊥DE ,可得∠CDE=∠ECF=∠B ,得出CF=BF ,同理可得CF=AF ,由此可得F 是AB 的中点,求得CF=5,再判定△CDF ∽△CFA ,得到CF 2=CD×CA ,进而得出CD 的长.详解:由对称性可知CF ⊥DE ,又∵∠DCE=90°,∴∠CDE=∠ECF=∠B ,∴CF=BF ,同理可得CF=AF ,∴F 是AB 的中点,∴CF=AB=5,12又∵∠DFC=∠ACF=∠A ,∠DCF=∠FCA ,∴△CDF ∽△CFA ,∴CF 2=CD×CA ,即52=CD×8,∴CD=.258故答案是:.258点睛:考查了折叠问题,四点共圆以及相似三角形的判定与性质的运用,解决问题的关键是根据四点共圆以及等量代换得到F 是AB 的中点.25.①②③④【解析】分析:①当点P 是矩形ABCD 两对角线的交点时,PA+PB+PC+PD 的值最小,根据勾股定理可得PA+PB+PC+PD 的最小值,即可判断;②根据全等三角形的性质可得PA=PC ,PB=PD ,那么P 在线段AC 、BD 的垂直平分线上,即P 是矩形ABCD 两对角线的交点,易证△PAD ≌△PBC ,即可判断;③易证S 1+S 3=S 2+S 4,所以若S 1=S 2,则S 3=S 4,即可判断;④根据相似三角形的性质可得∠PAB=∠PDA ,∠PAB+∠PAD=∠PDA+∠PAD=90°,利用三角形内角和定理得出∠APD=180°-(∠PDA+∠PAD )=90°,同理可得∠APB=90°,那么∠BPD=180°,即B 、P 、D 三点共线,根据三角形面积公式可得PA=2.4,即可判断.详解:①当点P 是矩形ABCD 两对角线的交点时,PA +PB +PC +PD 的值最小,根据勾股定理得,AC =BD =5,所以PA +PB +PC +PD 的最小值为10,故①正确;②若△PAB ≌△PCD ,则PA =PC ,PB =PD ,所以P 在线段AC 、BD 的垂直平分线上,即P 是矩形ABCD 两对角线的交点,所以△PAD ≌△PBC ,故②正确;③若=,易证+=+,则=,故③正确;S 1S 2S 1S 3S 2S 4S 3S 4④若△PAB ∼△PDA ,则∠PAB =∠PDA ,∠PAB +∠PAD =∠PDA +∠PAD =90°,∠APD =180°−(∠PDA +∠PAD )=90°,同理可得∠APB =90°,那么∠BPD =180°,B.P 、D 三点共线,P 是直角△BAD 斜边上的高,根据面积公式可得PA =2.4,故④正确.故答案为①②③④.点睛:本题考查了全等三角形的判定与性质,矩形的性质,相似三角形的性质.26.34【解析】【分析】过 E 作 EH ⊥GF 于 H ,过 B 作 BP ⊥GF 于 P ,依据△EHG ∽△BPG ,可得=,再根据EG BG EHBP △DCF ∽△CEH ,△ACF ∽△CBP ,即可得到 EH=CF ,BP=CF ,进 而得出=.34EG BG 34【详解】如图,过 E 作 EH ⊥GF 于 H ,过 B 作 BP ⊥GF 于P ,则∠EHG=∠BPG=90°,又∵∠EGH=∠BGP ,∴△EHG ∽△BPG ,∴=,EG BG EHBP ∵CF ⊥AD ,∴∠DFC=∠AFC=90°,∴∠DFC=∠CHF ,∠AFC=∠CPB , 又∵∠ACB=∠DCE=90°,∴∠CDF=∠ECH ,∠FAC=∠PCB ,∴△DCF ∽△CEH ,△ACF ∽△CBP ,∴,EHCF =CE DC ,BPCF =BCCA =1本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
苏科版九年级数学下册 相似三角形题型归纳(含隐圆、动点、最值、拓展、压轴)(无答案)
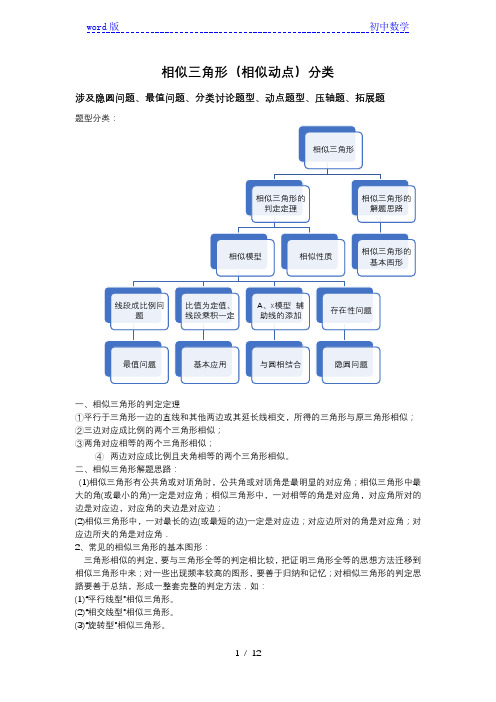
相似三角形(相似动点)分类涉及隐圆问题、最值问题、分类讨论题型、动点题型、压轴题、拓展题题型分类:一、相似三角形的判定定理①平行于三角形一边的直线和其他两边或其延长线相交,所得的三角形与原三角形相似;②三边对应成比例的两个三角形相似;③两角对应相等的两个三角形相似;④两边对应成比例且夹角相等的两个三角形相似。
二、相似三角形解题思路:(1)相似三角形有公共角或对顶角时,公共角或对顶角是最明显的对应角;相似三角形中最大的角(或最小的角)一定是对应角;相似三角形中,一对相等的角是对应角,对应角所对的边是对应边,对应角的夹边是对应边;(2)相似三角形中,一对最长的边(或最短的边)一定是对应边;对应边所对的角是对应角;对应边所夹的角是对应角.2、常见的相似三角形的基本图形:三角形相似的判定,要与三角形全等的判定相比较,把证明三角形全等的思想方法迁移到相似三角形中来;对一些出现频率较高的图形,要善于归纳和记忆;对相似三角形的判定思路要善于总结,形成一整套完整的判定方法.如:(1)“平行线型”相似三角形。
(2)“相交线型”相似三角形。
(3)“旋转型”相似三角形。
三、相似模型1.A字、8字模型。
2.共边共角模型(扭屁股模型)。
3.一线三等角模型。
4.倒数模型(较难)5.圆中的相似。
6.平行线分线段成比例。
类型一、线段比例问题1. (构造平行)如图1,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上一点,连接BO交AD于F,OE⊥OB交BC边于点E.(1)求证:△ABF∽△COE;(2)当O为AC的中点,=2时,如图2,求的值;(3)当O为AC边中点,=n时,请直接写出的值.2.如图1 ,DE是⊙O的直径,点A、C是直径DE上方半圆上的两点,且AO⊥OC.连接AE,CD相交于点F.点B是直径DE下方半圆上的任意一点,连接AB交CD 于点G,连接CB交AE于点H.(1)求∠ABC的度数;(2)证明: △CFH∽△CBG;(3)若弧DB为半圆的三分之一,把∠AOC绕着点O旋转,使点C、O、B在一直线上时,如图2.①证明FH:BG=1:2;②若⊙O的半径为4,直接写出FH的长.3. 已知抛物线(3)(1)y a x x =+-(a ≠0),与x 轴从左至右依次相交于A 、B 两点,与y 轴相交于点C ,经过点A 的直线y=-x+b 与抛物线的另一个交点为D . (1)若点D 的横坐标为2,求抛物线的函数解析式;(2)若在第三象限内的抛物线上有点P ,使得以A 、B 、P 为顶点的三角形与△ABC 相似,求点P 的坐标;(3)在(1)的条件下,设点E 是线段AD 上的一点(不含端点),连接BE .一动点Q 从点B 出发,沿线段BE 以每秒1个单位的速度运动到点E ,再沿线段ED 以每秒 个单位的速度运动到点D 后停止,问当点E 的坐标是多少时,点Q 在整个运动过程中所用时间最少?二、相似比乘积处理方法(逆向和正向分析找解题思路)1.如果四边形ABCD 的对角线交于O ,过O 作直线OG ∥AB 交BC 于E ,交AD 于F ,交CD的延长线于G ,求证:OG 2=GE ·GF.2.如图,在平面直角坐标系中,函数(x>0,k 是常数)的图像经过A (2,6),B (m,n ),其中m>2.过点A 作X 轴垂线,垂足为C ,过点B 作y 轴垂线,垂足为D ,AC 与BD 交于点E ,连结AD 、DC 、CB 。
苏教版九年级下册数学[相似图形--知识点整理及重点题型梳理]
![苏教版九年级下册数学[相似图形--知识点整理及重点题型梳理]](https://img.taocdn.com/s3/m/93ce051958fb770bf78a55b8.png)
苏教版九年级下册数学重难点突破知识点梳理及重点题型巩固练习相似多边形--知识讲解【学习目标】1、掌握相似多边形的概念及性质运用;2、掌握相似三角形的概念及相关求值问题.【要点梳理】要点一、相似三角形定义:在△ABC 和△A′B′C′中,如果∠A=∠A′,∠B=∠B′,∠C=∠C′,''''''AB BC CA A B B C C A ==,那么△ABC 和△A′B′C′相似,记做△ABC∽△A′B′C′.相似三角形的性质:相似三角形的对应角相等,对应边成比例.相似三角形的对应边的比叫作相似比.一般地,若△ABC 与△A′B′C′的相似比为k ,则△A′B′C′与△ABC 的相似比为1k. 要点诠释:全等三角形是相似比为1的相似三角形.全等三角形是相似三角形的一个特例.要点二、相似多边形相似多边形:对于两个边数相等的多边形,如果他们的对应角相等,对应边成比例,那么这两个多边形叫作相似多边形.相似多边形对应边的比叫做相似比.如果四边形ABCD 与四边形A 1B 1C 1D 1相似,且点A,B,C,D 分别与点A 1,B 1,C 1,D 1对应,则记作:“四边形ABC D∽四边形A 1B 1C 1D 1”.相似多边形的性质:相似多边形的对应角相等,对应边成比例.要点诠释:用相似多边形定义判定特殊多边形的相似情况:(1)对应角都相等的两个多边形不一定相似,如:矩形;(2)对应边的比都相等的两个多边形不一定相似,如:菱形;(3)边数相同的正多边形都相似,如:正方形,正五边形.【典型例题】类型一、相似三角形1.已知:如图,△ADE ∽△ABC ,AB=10cm ,AD=6cm ,BC=12cm ,∠A=56°,∠ADE=40°.求:(1)∠ACB 的度数;(2)DE 的长.【总结升华】本题主要考查了相似三角形的性质,对应角相等,对应边的比相等.2. 如图,△ABC中,AI、BI分别平分∠BAC、∠ABC.CE是△ABC的外角∠ACD的平分线,交BI延长线于E,连接CI.(1)△ABC变化时,设∠BAC=2α.若用α表示∠BIC和∠E;(2)若AB=1,且△ABC与△ICE相似,求相应AC长.【思路点拨】(1)根据三角形的外角等于不相邻的两个内角的和即可求解.(2)根据相似三角形对应边的比相等,即可求解.【答案与解析】【总结升华】两三角形相似,注意根据对应边的不同,分情况讨论是解决本题的关键.举一反三【变式】已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4.(1)求BD、CD的长;(2)过B作BE⊥DC于E,求BE的长.【答案】(1)Rt△ABC中,根据勾股定理得:类型二、相似多边形3.(2014•镇江) 如图:矩形ABCD 的长AB=30,宽BC=20.(1)如图(1)若沿矩形ABCD 四周有宽为1的环形区域,图中所形成的两个矩形ABCD 与A ′B ′C ′D ′相似吗?请说明理由;(2)如图(2),x 为多少时,图中的两个矩形ABCD 与A ′B ′C ′D ′相似?【答案与解析】解:(1)不相似,AB=30,A ′B ′=28,BC=20,B ′C ′=18,而≠;(2)矩形ABCD 与A ′B ′C ′D ′相似,则=, 则:=,解得x=1.5,或=,解得x=9.∴当x=1.5或9时,图中的两个矩形ABCD 与A ′B ′C ′D ′相似.【总结升华】两个边数相同的多边形,必须同时满足“对应边的比都相等,对应角都相等”这两个条件才能相似,缺一不可.举一反三 【变式】如图,梯形ABCD中,AD ∥BC ,E 、F 两点分别在AB 、DC 上.若AE=4,EB=6,DF=2,FC=3,且梯形AEFD 与梯形EBCF 相似,则AD 与BC 的长度比为( )A.1:2B. 2:3C. 2:5D.4:9【答案】D.4.(2014•南通)如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形AEFG∽菱形ABCD,连接EB,GD.(1)求证:EB=GD;(2)若∠DAB=60°,AB=2,AG=,求GD的长.【思路点拨】(1)利用相似多边形的对应角相等和菱形的四边相等证得三角形全等后即可证得两条线段相等;(2)连接BD交AC于点P,则BP⊥AC,根据∠DAB=60°得到112BP AB==,然后求得EP=2,最后利用勾股定理求得EB的长即可求得线段GD的长即可.【答案与解析】(1)证明:∵菱形AEFG∽菱形ABCD,∴∠EAG=∠BAD,∴∠EAG+∠GAB=∠BAD+∠GAB,∴∠EAB=∠GAD,∵AE=AG,AB=AD,∴△AEB≌△AGD,∴EB=GD;(2)解:连接BD交AC于点P,则BP⊥AC,∵∠DAB=60°,∴∠PAB=30°,∴BP=AB=1,AP==,AE=AG=,∴EP=2,∴EB===,∴GD=.【总结升华】本题考查了相似多边形的性质,解题的关键是了解相似多边形的对应边的比相等,对应角相等.。
2019年江苏苏教版中考相似三角形专题培优汇编真题(含答案)

2019年江苏苏教版中考相似三角形专题培优汇编真题(含答案)2019年江苏中考相似三角形培优汇编1.(2019扬州)如图,在△ABC 中,AB=5,AC=4,若进行一下操作,在边BC 上从左到右一次取点D 1、D 2、D 3、D 4…;过点D1作AB 、AC 的平行线分别交于AC 、AB 与点E 1、F 1;过点D 2作AB 、AC 的平行线分别交于AC 、AB 于点E 2、F 2;过点D 3作AB 、AC 的平行线分别交于AC 、AB 于点E 3、F 3…,则4(D 1E 1+D 2E 2+…+D 2019E 2019)+5(D 1F 1+D 2F 2+…+D 2019F 2019)= .解:∵D 1E 1∥AB D 1F 1∥AC ∴CB CD AB E D 111=BCBD AC F D 11=∵AB=5 AC=4 ∴CB CD E D 1115= BC BD F D 114= ∴14511111==+=+BCBCBC BD CB C D F D E D ∴4D 1E+5D 1F=20有2019组,即2019×20=403802.(2019扬州)如图,平面内的两条直线l 1、l 2,点A 、B 在直线l 2上,过点A 、B 两点分别作直线l 1的垂线,垂足分别为A 1、B1,我们把线段A 1B 1叫做线段AB 在直线l 2上的正投影,其长度可记作T (AB ,CD )或T (AB ,l 2),特别地,线段AC 在直线l 2上的正投影就是线段A 1C 请依据上述定义解决如下问题(1)如图1,在锐角△ABC 中,AB=5,T (AC ,AB )=3,则T (BC ,AB )= ;(2)如图2,在Rt △ABC 中,∠ACB=90°,T (AC ,AB )=4,T (BC ,AB )=9,求△ABC 的面积;(3)如图3,在钝角△ABC 中,∠A=60°,点D 在AB 边上,∠ACD=90°,T (AB ,AC )=2,T (BC ,AB )=6,求T (BC ,CD ).解:(1)过C 作CE ⊥AB ,垂足为E∴由T (AC ,AB )=3投影可知AE=3∴BE=2即T (BC ,AB )=2 (2)过点C 作CF ⊥AB 于F∵∠ACB=90°CF ⊥AB ∴△ACF ∽△CBF ∴CF 2=AF ·BF ∵T (AC ,AB )=4,T (BC ,AB )=9∴AF=4 BF=9即CF=6 △ABC =2,T =6∴AC=2 BM=63.(2019泰州)如图,⊙O 的半径为5,点P 在⊙O 上,点A 在⊙O 内,且AP =3,过点A 作AP 的垂线交于⊙O 点B 、C.设PB=x,PC=y,则y 与x 的函数表达式为.解:如图,连接PO 并延长交⊙O 于点N ,连接BN ,∵PN 是直径,∴∠PBN=90°. ∵AP ⊥BC,C∴∠PAC =90°,∴∠PBN=∠PAC ,又∵∠PNB=∠PCA ,∴△PBN ∽△PAC ,∴PA PB =PCPN , ∴3x =y10 ∴y=x 30.故答案为:y=x30. 4.(2019无锡)如图,在△ABC 中,AB =AC =5,BC=D 为边AB 上一动点(B 点除外),以CD 为一边作正方形CDEF ,连接BE ,则△BDE 面积的最大值为.5.(2019宿迁).如图①,在钝角△ABC中,∠ABC=30°,AC=4,点D为边AB中点,点E为边BC中点,将△BDE绕点B逆时针方向旋转α度(0≤α≤180).(1)如图②,当0<α<180时,连接AD、CE.求证:△BDA∽△BEC;(2)如图③,直线CE、AD交于点G.在旋转过程中,∠AGC的大小是否发生变化?如变化,请说明理由;如不变,请求出这个角的度数;解:(1)如图②中,由图①,∵点D为边AB中点,点E为边BC中点,∴DE∥AC,∴=,∴=,∵∠DBE=∠ABC,∴∠DBA=∠EBC,∴△DBA∽△EBC.(2)∠AGC的大小不发生变化,∠AGC=30°.理由:如图③中,设AB交CG于点O.∵△DBA∽△EBC,∴∠DAB=∠ECB,∵∠DAB +∠AOG +∠G =180°,∠ECB +∠COB +∠ABC =180°,∠AOG =∠COB ,∴∠G =∠ABC =30°.6.(2019连云港)如图,在平面直角坐标系xOy 中,抛物线L 1:2y x bx c =++过点C (0,﹣3),与抛物线L 2:213222y x x =--+的一个交点为A ,且点A 的横坐标为2,点P 、Q 分别是抛物线L 1、抛物线L 2上的动点.(1)求抛物线L 1对应的函数表达式;(2)设点R 为抛物线L 1上另一个动点,且CA 平分∠PCR ,若OQ ∥PR ,求出点Q 坐标.详解:(1)将2x =代入213222y x x =--+,得3y =-,故点A 的坐标为()23-,. 将()()2303A C --,,,代入2y x bx c =++,得2322300b c c-=++?-=++?,解得23b c =-??=-?.所以抛物线1L 对应的函数表达式为223y x x =--.(2)当点P 在y 轴左侧时,抛物线1L 不存在动点R 使得CA 平分PCR ∠.的当点P 在y 轴右侧时,不妨设点P 在CA 的上方,点R 在CA 的下方,过点P 、R 分别作y 轴的垂线,垂足分别为S T 、,过点P 作PH TR ⊥,垂足为H ,则有90PSC RTC ∠=∠=?. 由CA 平分PCR ∠,得PCA RCA ∠=∠,则PCS RCT ∠=∠,故PSC RTC ??∽,所以PS TR CS TC=. 设点P 坐标为()211123x x x --,,点R 坐标为()222223x x x --,,所以有()()12221122233323x x x x x x =--------,整理得124x x +=.在Rt PRH 中,.过点Q 作QK x ⊥轴,垂足为K .设点Q 坐标为213222m m m ??--+,. 若OQ PR ∥,则需QOK PRH ∠=∠.所以2132222m m m =--+.解得m =.所以点Q 坐标为7-?或7-?.7.(2019连云港)问题情境:如图1,在正方形ABCD中,E为边BC上一点(不与点B、C重合),垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N.判断线段DN、MB、EC之间的数量关系,并说明理由.问题探究:在“问题情境”的基础上,(1)如图2,若垂足P恰好为AE的中点,连接BD,交MN于点Q,连接EQ,并延长交边AD于点F.求∠AEF的度数;(2)如图3,当垂足P在正方形ABCD的对角线BD上时,连接AN,将△APN沿着AN翻折,点P落在点P'处.若正方形ABCD的边长为4 ,AD的中点为S,求P'S的最小值.问题拓展:如图4,在边长为4的正方形ABCD 中,点M 、N 分别为边AB 、CD 上的点,将正方形ABCD 沿着MN 翻折,使得BC 的对应边B'C '恰好经过点A ,C'N 交AD 于点F .分别过点A 、F 作AG ⊥MN ,FH ⊥MN ,垂足分别为G 、H .若AG =52,请直接写出FH 的长.解:问题情境:因为四边形ABCD 是正方形,所以90ABE BCD AB BC CD DC AB ∠=∠=?==,,∥. 过点B 作BF MN ∥分别交AE CD 、于点G F 、. 所以四边形MBFN 为平行四边形.所以NF MB =.所以90BF AE BGE ∠=?⊥,,所以90CBF AEB ∠+∠=?,又因为90BAE AEB ∠+∠=?,所以CBF BAE ∠=∠.ABE BCF △△≌,所以BE CF =.因为DN NF CF BE EC ++=+,所以DN NF EC +=,所以DN MB EC +=.问题探究:(1)连接AQ ,过点Q 作HI AB ∥,分别交AD BC 、于点H I 、.易得四边形ABIH 为矩形. 所以HI AD HI BC ⊥⊥,且HI AB AD ==.因为BI 是正方形ABCD 的对角线,所以45BDA ∠=?. 所以DHQ 是等腰直角三角形,HD HQ =.所以AH QI =.因为MN 是AE 的垂直平分线,所以AQ QE =.所以Rt Rt AHQ QIE △≌△.所以AQH QEI ∠=∠.所以90AQH EQI ?∠+∠=.所以90AQE ∠=?.所以AQE 是等腰直角三角形,45EAQ AEQ ∠=∠=?,即45AEF ∠=?.(2)如图所示,连接AC 交BD 于点O ,由题意易得APN 的直角顶点P 在OB 上运动. 设点P 与点B 重合,则点P '与点D 重合;设P 与点O 重合,则点P 的落点为O '.易知45ADO '∠=?.当点P 在线段BO 上运动时,过点P 作CD 的垂线,垂足为G ,过点P '作P H CD '⊥,垂足为点H .易证:Rt PGN Rt NHP '△△≌,所以PG NH G H P N '==,,因为BD 是正方形ABCD 的对角线,所以45PDG ∠=?,易得PG GD =,所以GN DH =. 所以DH H P '=.所以45P DH '∠=?,故45P DA '∠=?. 所以点P '在线段DO '上运动.过点S 作SK DO '⊥,垂足为K ,因为点S 为AD 的中点,所以2DS =,则P S '.问题拓展:解:延长AG 交BC 于E ,交DC 的延长线于Q ,延长FH 交CD 于P ,如图4:则EG=AG=52,PH=FH,∴AE=5,在Rt△ABE中,BE3,∴CE=BC﹣BE=1,∵∠B=∠ECQ=90°,∠AEB=∠QEC,∴△ABE∽△QCE,∴1520 QE AE,AQ AE QE333===+=∵AG⊥MN,∴∠AGM=90°=∠B,∵∠MAG=∠EAB,∴△AGM∽△ABE,∴AM AGAE AB=,即5254AM=,解得:25 AM8=,由折叠的性质得:AB'=EB=3,∠B'=∠B=90°,∠C'=∠BCD=90°,∴B'M7,AC1 8'==,∵∠BAD=90°,∴∠B'AM=∠C'FA,∴△AFC'∽△MAB',∴''1,25788 AF AC AFAM MB==,解得:25253 AF,DF4777 ==-=∵AG⊥MN,FH⊥MN,∴AG∥FH,∴AQ∥FP,∴△DFP∽△DAQ,∴FP DFAQ DA=,即372043FP=,解得:FP=57,∴FH=15 FP214=.8.(2019南通)如图,矩形ABCD中,AB=2,AD=4,E,FF分别在AD,BC上,点A与点C关于EF所在的直线对称,P 是边DC上的一动点,(1)连接AF,CE,求证四边形AFCE是菱形;(2)当PEF ?的周长最小时,求CPDP的值;(3)连接BP 交EF 于点M ,当?=∠45EMP 时,求CP 的长。
2019-2020学年苏科版九年级下册《相似三角形》中考真题提优训练(无答案)

2019-2020年苏科版九年级下册《相似三角形》中考真题提优训练一、动点型问题:1.如图,在矩形ABCD中,AB=6cm,BC=8cm.如果点E由点B出发沿BC方向向点C 匀速运动,同时点F由点D出发沿DA方向向点A匀速运动,它们的速度分别为2cm/s和1cm/s.FQ⊥BC,分别交AC、BC于点P和Q,设运动时间为t(s)(0<t<4).(1)、连结EF、DQ,若四边形EQDF为平行四边形,求t的值;(2)、连结EP,设△EPC的面积为ycm2 ,求y与t的函数关系式,并求y的最大值;(3)、若△EPQ与△ADC相似,请直接写出t的值.2.如图,在矩形ABCD中,AD=acm,AB=bcm(a>b>4),半径为2cm的⊙O在矩形内且与AB、AD均相切.现有动点P从A点出发,在矩形边上沿着A→B→C→D的方向匀速移动,当点P到达D点时停止移动;⊙O在矩形内部沿AD向右匀速平移,移动到与CD 相切时立即沿原路按原速返回,当⊙O回到出发时的位置(即再次与AB相切)时停止移动.已知点P与⊙O同时开始移动,同时停止移动(即同时到达各自的终止位置).(1)如图①,点P从A→B→C→D,全程共移动了cm(用含a、b的代数式表示);(2)如图①,已知点P从A点出发,移动2s到达B点,继续移动3s,到达BC的中点.若点P与⊙O的移动速度相等,求在这5s时间内圆心O移动的距离;(3)如图②,已知a=20,b=10.是否存在如下情形:当⊙O 到达⊙O 1的位置时(此时圆心O 1在矩形对角线BD 上),DP 与⊙O 1恰好相切?请说明理由.(第28题)O 1ABCDOP(图②)(图①)O3.如图,点O为矩形ABCD的对称中心,AB=10cm,BC=12cm.点E,F,G分别从A,B,C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F 的运动速度为3cm/s,点G的运动速度为1.5cm/s.当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB'F,设点E,F,G运动的时间为t(单位:s).(1)当t=s时,四边形EBFB'为正方形;(2)若以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形相似,求t的值;(3)是否存在实数t,使得点B'与点O重合?若存在,求出t的值;若不存在,请说明理由.二、动线型问题:4.如图1,直角梯形OABC中,BC∥OA,OA=6,BC=2,∠BAO=45°.(1)OC的长为;(2)D是OA上一点,以BD为直径作⊙M,⊙M交AB于点Q.当⊙M与y轴相切时,sin∠BOQ= ;(3)如图2,动点P以每秒1个单位长度的速度,从点O沿线段OA向点A运动;同时动点D以相同的速度,从点B沿折线B﹣C﹣O向点O运动.当点P到达点A时,两点同时停止运动.过点P作直线PE∥OC,与折线O﹣B﹣A交于点E.设点P运动的时间为t(秒).求当以B、D、E为顶点的三角形是直角三角形时点E的坐标.5.问题呈现如图,四边形ABCD是矩形,AB=20,BC=10,以CD为一边向矩形外部作等腰直角△GDC,∠G=90°,点M在线段AB上,且AM=a,点P沿折线AD-DG运动,点Q沿折线BC-CG运动(与点G不重合),在运动过程中始终保持线段PQ∥AB.设PQ与AB之间的距离为x.(1)若a=12.①如图1,当点P在线段AD上时,若四边形AMQP的面积为48,则x的值为_________;②在运动过程中,求四边形AMQP的最大面积;(2)如图2,若点P在线段DG上时,要使四边形AMQP的面积始终不小于50,求a的取值范围.三、动面型问题:6.如图,正方形ABCD的边AD与矩形EFGH的边FG重合,将正方形ABCD以1cm/s的速度沿FG方向移动,移动开始前点A与点F重合.在移动过程中,边AD始终与边FG重合,连接CG,过点A作CG的平行线交线段GH于点P,连接PD.已知正方形ABCD的边长为1cm,矩形EFGH的边FG、GH的长分别为4cm、3cm.设正方形移动时间为x(s),线段GP的长为y(cm),其中.⑴试求出y关于x的函数关系式,并求出y =3时相应x的值;⑵记△DGP的面积为,△CDG的面积为,试说明是常数;⑶当线段PD 所在直线与正方形ABCD 的对角线AC 垂直时,求线段PD 的长.P HG FEDC B A四、翻折型问题:7.已知矩形纸片OABC 的长为4,宽为3,以长OA 所在的直线为x 轴,O 为坐标原点建立平面直角坐标系;点P 是OA 边上的动点(与点OA 不重合),现将△POC 沿PC 翻折得到△PEC ,再在AB 边上选取适当的点D ,将△PAD 沿PD 翻折,得到△PFD ,使得直线PE 、PF 重合.(1)若点E 落在BC 边上,如图①,求点P 、C 、D 的坐标,并求过此三点的抛物线的函数关系式;(2)若点E 落在矩形纸片OABC 的内部,如图②,设OP =x ,AD =y ,当x 为何值时,y 取得最大值?(3)在(1)的情况下,过点P 、C 、D 三点的抛物线上是否存在点Q ,使△PDQ 是以PD 为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q 的坐标.图①PDEC OAB FxyPDCOABFxy EF8.将一矩形纸片放在平面直角坐标系中,,,.动点从点出发以每秒1个单位长的速度沿向终点运动,运动秒时,动点从点出发以相等的速度沿向终点运动.当其中一点到达终点时,另一点也停止运动.设点的运动时间为(秒).(1)用含的代数式表示; OABC (00)O ,(60)A ,(03)C ,Q O OC C 23P A AO O P t t OP OQ ,(2)当时,如图1,将沿翻折,点恰好落在边上的点处,求点的坐标;(1) 连结,将沿翻折,得到,如图2.问:与能否平行?与能否垂直?若能,求出相应的值;若不能,说明理由.1t OPQ △PQ O CB D D AC OPQ △PQ EPQ △PQ AC PE ACt。
苏教版八年级下学期 相似三角形 典型例题专项训练及解析

《相似三角形》考前解析及答案例题解析知识考点:本节知识主要包括相似三角形、相似多边形的性质及应用,会综合运用相似三角形的有关概念、定理解答有关问题。
另外,直角三角形被斜边上的高分成的两个直角三角形与原三角形相似的性质运用,是近几年中考的热点题型。
精典例题:【例1】如图,在△ABC 中,AB =14cm ,95=BD AD ,DE ∥BC ,CD ⊥AB ,CD =12cm ,求△ADE 的面积和周长。
分析:由AB =14cm ,CD =12cm 得ABC S ∆=84,再由DE ∥BC 可得△ABC ∽△ADE ,有2⎪⎭⎫⎝⎛=∆∆AB AD S S ABC ADE 可求得ADE S ∆,利用勾股定理求出BC 、AC ,再用相似三角形的性质可得△ADE 的周长。
答案:△ADE 的面积为775cm 2,周长为15 cm 。
例1图EDCBA例2图Q PM F ED CB A变式1图PN MCB A【例2】如图,正方形DEMF 内接于△ABC ,若1=∆ADE S ,4=DEFM S 正方形,求ABC S ∆分析:首先利用正方形的面积求出其边长,过A 点作AQ ⊥BC 于Q ,交DE 于P ,利用ADE S ∆可得AP 及AQ 的长,再由△ADE ∽△ABC 求出BC ,从而求得ABC S ∆。
解:∵正方形的面积为4,∴DE =MF =2。
过A 点作AQ ⊥BC 于Q ,交DE 于P ∵1=∆ADE S ,∴AP =1∵DE ∥BC ,∴△ADE ∽△ABC ,∴BC DE AQ AP =,即BC231= ∴BC =6,故ABC S ∆=9 [更多资料加Q465010203]变式1:如图,已知菱形AMNP 内接于△ABC ,M 、N 、P 分别在AB 、BC 、AC 上,如果AB =21 cm ,CA =15 cm ,求菱形AMNP 的周长。
答案:35 cm变式2:如图,在△ABC 中,有矩形DEFG ,G 、F 在BC 上,D 、E 分别在AB 、AC 上,AH ⊥BC 交DE 于M ,DG ∶DE =1∶2,BC =12 cm ,AH =8 cm ,求矩形的各边长。
苏科版九年级数学下第六章《相似三角形》教学质量检测试题(含答案)

)
A.AB 2=BC ·BD B. AB 2=AC · BD
C.AB · AD=BD · BC D. AB · AD=AC · CD
5.已知△ ABC 在直角坐标系中的位置如图所示,以 O 位似中心,把△ ABC 放大到 2 倍得到△ A /B /C/,那么
A /的坐标为(
)
A. ( -8, -4) B.( -8, 4) C.(8, -4)
其影长为 1.2 米,那么这颗大树高约
米.
第 14 题
第 16 题
第 17 题
第 18 题
16. 如图,在函数 y1
k1 (x 0) 和 y2 x
k2 (x x
0) 的图像上,分别有 A 、B 两点,若 AB// x 轴,交 y 轴
1
9
于 C 点,且 OA ⊥OB, S△AOC= , S△BOC= ,则 AB 的长度 =
F 是 GE 的中点;④
AF
AB FB
2 AB ;⑤ S△ABC =5S△BDF,其中正确结
3
论的序号是
.
三、解答题: (共 86 分)
19.(本题 8 分)如图, DE//BC ,DF//AC ,AD=4cm ,BD=8cm ,DE=5cm ,求线段 BF 的长 .
20.(本题 8 分)如图,在矩形 ABCD 中, AB=10cm , AD=20cm ,点 P、Q 分别同 时从 A 、B 两点出发,沿 AB 、BC 向 B 、C 运动,已知点 P 的运动速度是 1cm/s,Q 点的运动速度是 2cm/s,当 P 点运动几秒时△ PBQ 与△ ACD 相似?
.
2
2
17. 如图,△ ABC是斜边 AB 的长为 3 的等腰直角三角形,在△ ABC内作第 1 个内接正方形 A1B1D1E1(D1、 E1
苏教版2019-2020学年度九年级第一学期 第六章 相似三角形提优测试卷

第六章 相似三角形提优测试卷时间:90分钟总分:120分1、选择题(每题3分,共30分)1.若四条不相等的线段满足,则下列式子中,成立的是( )d c b a ,,,0,>=m dc b a A. B. C. D.d c a b =m d m c b a ++=d c d b b a -=-dc d b c a =++2.已知,则等于( )6,8,~'''''==∆∆B A AB C B A ABC ''CB BC A. 2 B. C. 3 D. 349163.如图,在▱中,点在对角线BD 上,,交于点M ,,交于点ABCD E AD EM //AB AB EN //AD N ,则下列式子一定正确的是( )A. B. C. D.DE NE BM AM =AD AN AB AM =BD BE ME BC =MEBC BE BD =4.如图,在▱中,点在BC 的中点,延长AD 至点E ,使,连接EF 交DC 于点ABCD F 3:1:=AD DE G ,则等于( )CFG DEG S S ∆∆:A. B. C. D. 3:22:34:99:4(第3题图)(第4题图) (第5题图) (第6题图)5.如图,在中,D 是边AC 上一点,连接BD ,给出下列条件:①;②ABC ∆ACB ABD ∠=∠;③;④.其中能单独判定的AC AD AB ⋅=2BD AB BC AD ⋅=⋅BD AC BC AB ⋅=⋅ADB ABC ∆∆~是( )A. ①②B. ①②③C. ①②④D. ①②③④6.如图,在中,平分,则BC 的长是( )ABC ∆BD A AC AB ,36,1︒=∠==ABC ∠A. B. C. D. 21215-215+251+-7.如图,在中,D 是边BC 上一点,且AD=AB=2,且,过点D 作,交AC 于点ABC ∆AB AD ⊥AD DE ⊥E.若DE=1,则的面积为( )ABC ∆A. B. C. D. 8244528.如图,在中,AD 是边BC 上的中线,点E 在边AC 上,且,BE 交AD 于点P,则ABC ∆2:1:=EC AE 等于( )PD AP :A. B. C. D. 1:12:13:23:4(第7题图)(第8题图)(第9题图) (第10题图)9.如图,在矩形ABCD 中,AB=3,BC=6.若点E ,F 分别在AB ,CD 上,且BE=2AE ,DF=2FC ,G ,H 分别是AC 的三等分点,则四边形EHFG 的面积为( )A. B. 123C.D. 2410.如图,在平面直角坐标系中,矩形ABCD 的顶点A ,D 分别在x 轴,y 轴上,对角线轴,反比例x BD //的图像经过矩形对角线的交点E ,若点,则的值为( ))0,0(>>=x k xk y )4,0(),0,2(D A k A. B. C. 32 D. 401620二、填空题(每题2分,共16分)11.在比例尺1:40000的地图上,某条道路的长为7cm ,则该道路的实际长度是 Km.12.如图,直线,那么EF 的长为 .4,31,////==DE AC BC CF BE AD 13.如图,利用长为1.5米的标杆BE 测量建筑物的高度,测得,则楼高CD 为 m m AB 14BC ,2==米.(第12题图) (第13题图) (第14题图) (第15题图) (第16题图)14.如图,G 是的重心,,则BG 的长为 .ABC ∆4,=⊥AC GC AG 15.如图,三边的中线AD,BE,CF 相交于点G.若,则图中阴影部分的面积为 .ABC ∆12=∆ABC S 16.如图,BD 是⊙O 的直径,A 是⊙O 外一点,点C 在⊙O 上,AC 与⊙O 相切于点C ,.若︒=∠90CAB,则弦BC 的长为 .CBD ABC AB BD ∠=∠==,4,617.如图,在中,分别为边ABC Rt ∆Q P BC AC C ,,8,6,90==︒=∠BC ,AB 上的两个动点,若要使是直角三角形,则AQ 的长为 。
2019年苏科版初三下相似练习卷-相似三角形(1)(pdf版,含答案)

∴
,
∴
∴
第 7页
在 Rt△BCD 中, ∵CD ,BC=5,
所以 BD u
.
故答案为: .
2.如图,在直角梯形 ABCD 中,DC∥AB,∠DAB=90°,AC⊥BC,AC=BC,∠ABC 的平分线分别交 AD、
u
u
AC 于点 E,F,则(1) 的值是
;(2) 的值是
.
【解答】解:作 FG⊥AB 于点 G,
第 1页
例 4.已知:如图①所示,在△ABC 和△ADE 中,AB=AC,AD=AE,∠BAC=∠DAE,且点 B,A,D 在 一条直线上,连接 BE,CD,M,N 分别为 BE,CD 的中点. (1)求证:①BE=CD;②△AMN 是等腰三角形; (2)在图①的基础上,将△ADE 绕点 A 按顺时针方向旋转 180°,其他条件不变,得到图②所示的图 形.请直接写出(1)中的两个结论是否仍然成立; (3)在(2)的条件下,请你在图②中延长 ED 交线段 BC 于点 P.求证:△PBD∽△AMN.
由 m ,得 m=n
∴DE=BE+CD﹣BC=2 h2,
∴BD=BE﹣DE=2h CE, ∵BD2+CE2=2BD2=2(2h )2=12﹣8 ,DE2=(2 ∴BD2+CE2=DE2 ;
h2)2=12﹣8
(4)成立 证明:如图,将△ACE 绕点 A 顺时针旋转 90°至△ABH 的位置,则 CE=HB,AE=AH, ∠ABH=∠C=45°,旋转角∠EAH=90°. 连接 HD,在△EAD 和△HAD 中 ∵AE=AH,∠HAD=∠EAH﹣∠FAG=45°=∠EAD,AD=AD. ∴△EAD≌△HAD ∴DH=DE 又∵∠HBD=∠ABH+∠ABD=90° ∴BD2+HB2=DH2, 即 BD2+CE2=DE2.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020年中考数学微测试系列专题17 相似三角形及应用苏教版1.【江苏省南通市海安县2015届九年级上学期期末考试数学试题】下列条件不能判定△ABC 与△DEF相似的是()A.AB BC ACDE EF DF==B.AB BCDE EF=,A D∠=∠C.∠A=∠D,∠B=∠E D.AB BCDE EF=,∠B=∠E【考点定位】相似三角形的判定.2. 【江苏省徐州市市区、铜山县2015届九年级中考模拟数学试题】直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3,把一块含有45°角的直角三角形如图放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为()A.254B.253C.203D.154【答案】A.【解析】分别过点A、B、D作AF⊥l3,BE⊥l3,DG⊥l3,先根据全等三角形的判定定理得出△BCE≌△ACF,故可得出CF及CE的长,在Rt△ACF中根据勾股定理求出AC的长,再由相似三角形的判定得出△CDG∽△CAF,故可得出CD的长,在R t△BCD中根据勾股定理即可求出BD的长.分别过点A、B、D作AF⊥l3,BE⊥l3,DG⊥l3,∵△ABC 是等腰直角三角形,∴AC=BC,∵∠EBC+∠BCE=90°,∠BCE+∠ACF=90°,∠ACF+∠CAF=90°,∴∠EBC=∠ACF,∠BCE=∠CAF, 在△BCE 与△ACF 中,EBC ACF BC ACBCE CAF ∠=∠⎧⎪=⎨⎪∠=∠⎩,【考点定位】1.相似三角形的判定与性质;2.平行线之间的距离;3.全等三角形的判定与性质;4.等腰直角三角形.3.【江苏省淮安市2015年中考数学试题】如图,l 1∥l 2∥l 3,直线a ,b 与l 1、l 2、l 3分别相交于A 、B 、C 和点D 、E 、F .若32=BC AB ,DE =4,则EF 的长是( )A .38 B.320 C.6 D.10 【答案】C .【考点定位】平行线分线段成比例.4.【江苏省南京市2015年中考数学试题】如图所示,△ABC中,DE∥BC,若12ADDB=,则下列结论中正确的是()A.12AEEC=B.12DEBC=C.1=3ADEABC△的周长△的周长D.1=3 ADEABC△的面积△的面积【答案】C.【考点定位】相似三角形的判定与性质.5.【江苏省南通市海安县2015届九年级上学期期末考试数学试题】若△ABC∽△A′B′C′,相似比为1:3,则△ABC与△A′B′C′的面积之比为.【答案】1:9.【解析】∵△ABC∽△A′B′C′,相似比为1:3,∴△A BC与△A′B′C′的面积之比为1:9.故答案为:1:9.【考点定位】相似三角形的性质.6.【江苏省扬州市2015年中考数学试题】如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上,若线段AB=4 cm,则线段BC= cm【答案】12BACDE【考点定位】平行线分线段成比例7.【江苏省常州市2015年中考数学试题】如图,在△ABC 中,DE ∥BC,AD :DB =1:2,DE =2,则BC 的长是 .【答案】6.【考点定位】相似三角形的判定与性质.8.【江苏省无锡市2015年中考数学试题】已知:如图,AD 、BE 分别是△ABC 的中线和角平分线,AD ⊥BE ,AD =BE =6,则AC 的长等于 .【答案】952故答案为:952【考点定位】全等三角形的判定及性质;相似三角形的判定及性质;勾股定理.9.【江苏省苏州市吴中、相城、吴江区2015届九年级中考一模数学试题】如图,在平面直角坐标系中,已知点A (0,6),B (8,0).点P 从A 点出发,以每秒1个单位的速度沿AO 运动;同时,点Q 从O 出发,以每秒2个单位的速度沿OB 运动,当Q 点到达B 点时,P 、Q 两点同时停止运动.(1)求运动时间t 的取值范围;(2)t 为何值时,△POQ 的面积最大?最大值是多少?(3)t 为何值时,以点P 、0、Q 为顶点的三角形与Rt △AOB 相似?【答案】(1) 0≤t ≤4;(2) 当t=3时,△POQ 的面积最大,最大值是9.(3) 当t 为125或1811时,以点P 、0、Q 为顶点的三角形与Rt △AOB 相似. 【解析】试题分析:(1)由点Q 从O 出发,以每秒2个单位的速度沿O B 运动,当Q 点到达B 点时,P 、Q 两点同时停止运动,可得:2t=8,解得:t=4,进而可得:0≤t ≤4;(2)先根据三角形的面积公式,用含有t 的式子表示△POQ 的面积=-t 2+6t ,然后根据二次函数的最值公式解答即可;试题解析:(1)∵点A (0,6),B (8,0),∴OA=6,OB=8,∵点Q 从O 出发,以每秒2个单位的速度沿OB 运动,当Q 点到达B 点时,P 、Q 两点同时停止运动,∴2t=8,解得:t=4, ∴0≤t ≤4;(2)根据题意得:经过t 秒后,AP=t ,OQ=2t ,∴OP=OA-AP=6-t , ∵△POQ 的面积=12•OP •OQ ,即△POQ 的面积=12×(6-t )×2t=-t 2+6t . ∵a=-1<0,∴△POQ 的面积有最大值,当t=-2ba=3时,△POQ 的面积的最大值=244ac b a -=9,即当t=3时,△POQ 的面积最大,最大值是9. (3)①若Rt △POQ ∽Rt △AOB 时, ∵Rt △POQ ∽R t △AOB ,∴PO OQ AO OB =,即6268t t-=,解得:t=125 ②若Rt △QOP ∽Rt △AOB 时, ∵Rt △QOP ∽Rt △AOB ,∴ PO OQ OB AO =,即6286t t-=,解得:t=1811. 所以当t 为125或1811时,以点P 、0、Q 为顶点的三角形与Rt △AOB 相似. 【考点定位】相似三角形与一次函数综合题.10.【江苏省南京市2015年中考数学试题】如图,△ABC 中,CD 是边AB 上的高,且AD CDCD BD=.(1)求证:△ACD∽△CBD;(2)求∠ACB的大小.【答案】(1)证明见试题解析;(2)90°.【解析】【考点定位】相似三角形的判定与性质.2019-2020年中考数学微测试系列专题18 圆的基本性质和圆的有关位置关系新人教版1.【辽宁阜新2015年中考数学试卷】如图,点A,B,C是⊙O上的三点,已知∠AOB=100°,那么∠ACB的度数是()A.30° B.40° C.50° D.60°【答案】C.【解析】考点:圆周角定理.2.【湖北襄阳2015年中考数学试卷】点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为()A.40° B.100° C.40°或140° D.40°或100°【答案】C.【解析】试题分析:如图所示:∵O是△ABC的外心,∠BOC=80°,∴∠A=40°,∠A′=140°,故∠BAC的度数为:40°或140°.故选C.考点:1.三角形的外接圆与外心;2.圆周角定理;3.分类讨论.3.【2015届浙江省杭州市5月中考模拟】如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠OAC的度数是()A.35° B.55° C.65° D.70°【答案】B.【解析】考点:圆周角定理.4.【2015届湖南省邵阳市邵阳县中考二模】如图,⊙O是△ABC的外接圆,AD是⊙O的直径,EA是⊙O的切线.若∠EAC=120°,则∠ABC的度数是()A.80° B.70° C.60° D.50°【答案】C.【解析】试题解析:∵EA是⊙O的切线,AD是⊙O的直径,∴∠EAD=90°,∵∠EAC=120°,∴∠DAC=∠EAC-∠EAD=30°,∵AD是⊙O的直径,∴∠ACD=90°,∴∠ADC=180°-∠A CD-∠DAC=60°,∴∠ABC=∠ADC=60°(圆周角定理),故选:C.考点:切线的性质.5.【辽宁沈阳2015年中考数学试题】如图,在△ABC中,AB=AC,∠B=30°,以点A为圆心,以3cm为半径作⊙A,当AB= cm时,BC与⊙A相切.【答案】6.【解析】考点:切线的判定.6.【黑龙江牡丹江2015年中考数学试题】如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,则B E= .【答案】. 【解析】试题分析: 连接OC ,如图:∵AB=8,CD=6,∴根据垂径定理(垂直于弦的直径平分弦并且平分弦所对的弧)得出CE=ED=12CD=3,∴OC=OB=12AB=4,在Rt △OEC 中,由勾股定理求出OE=2234.考点:1.垂径定理;2.勾股定理.7.【2015届湖北省黄冈市启黄中学中考模拟】如图所示,经过B (2,0)、C (6,0)两点的⊙H 与y 轴的负半轴相切于点A ,双曲线y=xk经过圆心H ,则k= .【答案】﹣83.【解析】考点:1.切线的性质;2.反比例函数图象上点的坐标特征.8.【2015届山东省枣庄市滕州市中考二模】如图,在Rt△AOB中,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ长度的最小值为.【解析】考点:切线的性质.9.【辽宁盘锦2015年中考数学试题】如图1,AB为⊙O的直径,点P是直径AB上任意一点,过点P作弦CD⊥AB,垂足为P,过点B的直线与线段AD的延长线交于点F,且∠F=∠ABC.(1)若CD=BP=4,求⊙O的半径;(2)求证:直线BF是⊙O的切线;(3)当点P与点O重合时,过点A作⊙O的切线交线段BC的延长线于点E,在其它条件不变的情况下,判断四边形AEBF是什么特殊的四边形?请在图2中补全图象并证明你的结论.【答案】(1)198;(2)证明见解析;(3)四边形AEBF是平行四边形,证明见解析.【解析】(2)∵∠A =∠C ,∠F =∠ABC ,∴△PBC ∽△BFA ,∴∠ABF =∠CPB ,∵CD ⊥AB ,∴∠ABF =∠C PB =90°,∴直线BF 是⊙O 的切线;(3)四边形AEBF 是平行四边形;理由:如图2所示:∵CD ⊥AB ,垂足为P ,∴当点P 与点O 重合时,CD =AB ,∴OC =OD ,∵AE 是⊙O 的切线,∴BA ⊥AE ,∵CD ⊥AB ,∴DC ∥AE ,∵AO =OB ,∴OC 是△ABE 的中位线,∴AE =2OC ,∵∠D =∠ABC ,∠F =∠ABC ,∴∠D =∠F ,∴CD ∥BF ,∵AE ∥BF ,∵OA =OB ,∴OD 是△ABF 的中位线,∴BF =2OD ,∴AE =BF ,∴四边形AEBF 是平行四边形.考点:1.圆的综合题;2.三角形中位线定理;3.平行四边形的判定;4.综合题.10.【2015届浙江省宁波市江北区中考模拟】已知:如图,△ABC 中,∠BAC=90°,点D 在BC 边上,且BD=BA ,过点B 画AD 的垂线交AC 于点O ,以O 为圆心,AO 为半径画圆.(1)求证:BC 是⊙O 的切线;(2)若⊙O 的半径为8,tan ∠C=34,求线段AB 的长,sin ∠ADB 的值.【答案】(1)证明见解析;(2)10103. 【解析】试题解析:(1)连接OD ,如图:∵BA=BD ,BO ⊥AD (已知),∴∠ABO=∠DBO (等腰三角形顶角三线合一),在△ABO 和△DBO 中,根据边角边判定△ABO ≌△DBO ,∴OD=OA .,∵OA 为半径,∴OD 也为半径,∴∠ODB=∠OAB=90°,∴BD ⊥OD ,∴BC 是⊙O 的切线;考点:1.切线的判定;2.三角形全等的判定和性质;3.锐角三角函数.。
