2018年考研数学二真题解析 (1)

合集下载

2018年考研数学二试题及答案解析

2018 年全国硕士研究生入学统一考试数学二试题
一、选择题：1~8 小题，每小题 4 分，共 32 分，下列每题给出的四个选项中，只有一个选项是符合题目要求的
1
（1）若 lim(e ax bx) x 1 ，则（）
x 2
2
x 0
A. a
1 , b 1 2
B. a
1 , b 1 2

x
0
f (t )dt tf ( x t )dt ax 2
0
x
（II）若 f ( x) 在区间[0,1]上的平均值为 1，求 a 的值。（ 17 ）设平面区域 D 由曲线
x t sin t (0 t 2 )与x轴围成，计算二重积分 y 1 cos t
（8）.设 A ， B 为 n 阶矩阵，记 r ( X ) 为矩阵 X 的秩，（X A. r ( A C. r ( A
Y ）表示分块矩阵，则（）
AB) r ( A) B) max{r ( A), r ( B)}
B. r ( A D. r ( A
BA) r ( A)
B) r ( AT BT )
2
3 x cos t 在 t 对应点的曲率为 3 4 y sin t
（12）曲线
.
（13）设函数 z z ( x, y) 由方程 ln z e
z 1
xy 确定，则
z x (2, 1 )
2
.
（14）设 A 为 3 阶矩阵， 1 , 2 , 3 为线性无关的向量组，若 A1 21 2 3 ,
( x 2 y)dxdy
D
（18）已知常数 k ln 2 1 ，证明 ( x 1)( x ln x 2k ln x 1) 0

2018考研数学二真题解答

2018 年全国硕士研究生统一入学考试数学二试题
题号 1-8 9-14 15 16 17 18 19 20 21 22 23 总分分数
评卷人一、
得分选择题（每题 4 分, 共 32 分）
1.
若
lim
(ex
+
ax2
+
)1 bx x2
= 1，则
x→0
1
1
A. a = , b = −1
B. a = − , b = −1
( [x′
(t)]2
+
[y′
(t)]2)3/2
=
2 .
3
13.
设函数 z
= x(x, y) 由方程 ln z + ez−1
= xy 确定, 则
∂z ∂x
|(2,
1 2
)
=
.
【解析】原方程两边对 x 求偏导数得 1 ∂z z ∂x
+ ez−1 ∂z ∂x
= y, 于是 ∂z ∂x
=
1 z
y , 当 x = 2, y + ez−1
1
+
C
=
2
(ex
−
3
1) 2
+
√ 2 ex
−
1
+
C
3
3
∫ 故
e2x
√ arctan ex
−
1dx
=
1 e2x 2
√ arctan ex
−
1
−
1 6
(ex
−
3
1) 2
−
1
√ ex
2
−
1
+

2018考研数学二真题及解析

2017年考研数学二真题一、选择题 1—8小题．每小题4分，共32分．1．若函数0(),0x f x b x >=⎪≤⎩在0x =处连续，则（A ）12ab =（B ）12ab =- （C ）0ab = （D ）2ab = 【详解】0001112lim ()lim lim 2x x x xf x ax ax a +++→→→-===，0lim ()(0)x f x b f -→==，要使函数在0x =处连续，必须满足1122b ab a =⇒=．所以应该选（A ）2．设二阶可导函数()f x 满足(1)(1)1f f =-=，(0)1f =-，且()0f x ''>，则（）（A ）11()0f x dx ->⎰（B ）11()0f x dx -<⎰（C ）11()()f x dx f x dx ->⎰⎰ （D ）011()()f x dx f x dx -<⎰⎰【详解】注意到条件()0f x ''>，则知道曲线()f x 在[][]1,0,0,1-上都是凹的，根据凹凸性的定义，显然当[]1,0x ∈-时，()21f x x ≤--，当[]0,1x ∈时，()21f x x ≤-，而且两个式子的等号不是处处成立，否则不满足二阶可导．所以10111()(21)(21)0f x dx x dx x dx --<--+-=⎰⎰⎰．所以选择（B ）．当然，如果在考场上，不用这么详细考虑，可以考虑代一个特殊函数2()21f x x =-，此时11011(),()33f x dx f x dx -=-=-⎰⎰，可判断出选项（A ），（C ），（D ）都是错误的，当然选择（B ）．希望同学们在复习基础知识的同时，掌握这种做选择题的技巧． 3．设数列{}n x 收敛，则（A ）当limsin 0n n x →∞=时，lim 0n n x →∞= （B）当lim(0n n x →∞+=时，lim 0n n x →∞=(C ）当2lim()0n n n x x →∞+=时，lim 0n n x →∞= （D ）当lim(sin )0n n n x x →∞+=时，lim 0n n x →∞=【详解】此题考核的是复合函数的极限运算法则，只有（D ）是正确的．其实此题注意，设lim n n x A →∞=，则22limsin sin ,lim(),lim(sin )sin n n n n n n n n n n x A x A x x A A x x A A →∞→∞→∞→∞==++=++=+分别解方程2sin 0,0,0,sin 0A A A A A A ==+=+=时，发现只有第四个方程sin 0A A +=有唯一解0A =，也就是得到lim 0n n x →∞=．４．微分方程2489(1cos 2)xy y e x '''-+=+的特解可设为*y =（）（A ）22(cos 2sin 2)xx Ae e B x C x ++ （B ）22(cos 2sin 2)x x Axe xe B x C x ++ （C ）22(cos 2sin 2)xx Aexe B x C x ++ （D ）22(cos 2sin 2)x x Axe xe B x C x ++【详解】微分方程的特征方程为2480r r -+=，有一对共轭的复数根22r i =±．所以12λ=不是特征方程的根，所以对应方程2489xy y e '''-+=的特解应该设为21*x y Ae =；而222i λ=+是方程的单根，所以对应方程2489cos 2xy y ex '''-+=的特解应该设为22*(cos 2sin 2)x y xe B x C x =+；从而微分方程2489(1c o s 2)xy y ex '''-+=+的特解可设为2212***(cos 2sin 2)x x y y y Ae xe B x C x =+=++，应该选（C ）．5．设(,)f x y 具有一阶偏导数，且对任意的(,)x y 都有(,)(,)0,0f x y f x y x y∂∂><∂∂，则（）（A ）(0,0)(1,0)f f > （B ）(0,0)(1,1)f f < （C ）(0,1)(1,0)f f > （D ）(0,1)(1,0)f f <【详解】由条件对任意的(,)x y 都有(,)(,)0,0f x y f x y x y∂∂><∂∂可知(,)f x y 对于x 是单调增加的，对y 就单调减少的．所以(1,1)(1,0)(0,0),(1,1)(0,1)(0,0),(0,1)(0,0)(1,0)f f f f f f f f f <>><<<，只有第三个不等式可得正确结论（D ），应该选（D ）．6．甲、乙两人赛跑，计时开始时，甲在乙前方10（单位：米）处，如图中，实线表示甲的速度曲线1()v v t =（单位：米/秒），虚线表示乙的速度曲线2()v v t =（单位：米/秒），三块阴影部分的面积分别为10,20,3，计时开始后乙追上甲的时刻为0t ，则（）（A ）010t = （B ）01520t << （C ）025t = （D ）025t >【详解】由定积分的物理意义：当曲线表示变速直线运动的速度函数时，21()()T T S t v t dt =⎰表示时刻[]12,T T 内所走的路程．本题中的阴影面积123,,S S S -分别表示在时间段[][][]0,10,10,25,25,30内甲、乙两人所走路程之差，显然应该在25t =时乙追上甲，应该选（C ）．7．设A 为三阶矩阵，()123,,P ααα=为可逆矩阵，使得1000010002P AP -⎛⎫ ⎪= ⎪ ⎪⎝⎭，则123()A ααα++=（）（A ）12αα+ （B ）232αα+ （C ）23αα+ （D ）132αα+ 【详解】显然这是矩阵相似对角化的题目．可知()()12312323000000(,,)010,,0100,,2002002A AP P αααααααα⎛⎫⎛⎫⎪ ⎪==== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭所以12312323()2A A A A αααααααα++=++=+，所以可知选择（B ）．8．已知矩阵200021001A ⎛⎫ ⎪= ⎪ ⎪⎝⎭，210020001B ⎛⎫ ⎪= ⎪ ⎪⎝⎭，100020002C ⎛⎫⎪= ⎪ ⎪⎝⎭，则（A ）,A C 相似，,B C 相似（B ）,A C 相似，,B C 不相似（C ）,A C 不相似，,B C 相似（D ）,A C 不相似，,B C 不相似【详解】矩阵,A B 的特征值都是1232,1λλλ===．是否可对解化，只需要关心2λ=的情况．对于矩阵A ，0002001001E A ⎛⎫⎪-=- ⎪ ⎪⎝⎭，秩等于1 ，也就是矩阵A 属于特征值2λ=存在两个线性无关的特征向量，也就是可以对角化，也就是~A C ．对于矩阵B ，010*******E B -⎛⎫ ⎪-= ⎪ ⎪⎝⎭，秩等于2 ，也就是矩阵A 属于特征值2λ=只有一个线性无关的特征向量，也就是不可以对角化，当然,B C 不相似故选择（B ）．二、填空题（本题共6小题，每小题4分，满分24分. 把答案填在题中横线上） 9．曲线2(1arcsin )y x x=+的斜渐近线为．解：2(1arcsin )lim lim1x x x y x x x →∞→∞+==，2lim()lim arcsin 2x x y x x x →∞→∞-==，所以斜渐近线为2y x =+． 10．设函数()y y x =由参数方程sin t x t e y t⎧=+⎨=⎩确定，则202|t d ydx == ．【详解】223cos 1cos (1)sin cos ,1(1)t t t t t t d e dy t d y e t e t dt dx dx e dx e dt⎛⎫ ⎪+⎝⎭++===-++，所以2021|8t d y dx ==-． 112ln(1)(1)x dx x +∞++⎰.【详解】022000ln(1)1ln(1)1ln(1)|1(1)11(1)x x dx x d dx x x x x +∞+∞+∞+∞++=-+=-+=++++⎰⎰⎰ 12．设函数(,)f x y 具有一阶连续的偏导数，且已知(,)(1)y ydf x y ye dx x y e dy =++，(0,0)0f =，则(,)f x y =【详解】(,)(1)()yyydf x y ye dx x y e dy d xye =++=，所以(,)yf x y xye C =+，由(0,0)0f =，得0C =，所以(,)yf x y xye =． 13．11tan y xdy dx x=⎰⎰．【详解】交换二重积分的积分次序得：1111100000tan tan tan ln cos ln cos1.x y x x dy dx dx dy xdx x x x ===-=-⎰⎰⎰⎰⎰14．设矩阵41212311A a -⎛⎫ ⎪= ⎪ ⎪-⎝⎭的一个特征向量为112⎛⎫ ⎪⎪⎪⎝⎭，则a = ．【详解】根据特征向量的定义，有412111121132311222A a a αλ-⎛⎫⎛⎫⎛⎫⎛⎫⎪⎪ ⎪ ⎪===+ ⎪⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭，解得1a =-．三、解答题 15．（本题满分10分）求极限0lim t x dt +→【详解】令x t u -=，则,t x u dt du =-=-，t x u dt du -=⎰⎰00002limlim limlim 33t x u u x x x x x dt e du du ++++---→→→→==== 16．（本题满分10分）设函数(,)f u v 具有二阶连续偏导数，(,cos )xy f e x =，求0|x dydx=，202|x d y dx =．【详解】12(,cos )(,cos )(sin )x x x dy f e x e f e x x dx ''=+-，01|(1,1)x dyf dx='=； 2111122222122(,cos )((,cos )sin (,cos ))cos (,cos )sin (,cos )sin (,cos )x x x x x x x x x x d y e f e x e f e x e xf e x xf e x dx xe f e x xf e x ''''''=+--''''-+2011122|(1,1)(1,1)(1,1)x d yf f f dx=''''=+-．17．（本题满分10分）求21limln 1nn k kk nn →∞=⎛⎫+ ⎪⎝⎭∑ 【详解】由定积分的定义120111201lim ln 1lim ln 1ln(1)11ln(1)24nn n n k k k k k k x x dx n n n n n x dx →∞→∞==⎛⎫⎛⎫+=+=+ ⎪ ⎪⎝⎭⎝⎭=+=∑∑⎰⎰18．（本题满分10分）已知函数()y x 是由方程333320x y x y +-+-=．【详解】在方程两边同时对x 求导，得2233330x y y y ''+-+= （1）在（1）两边同时对x 求导，得2222()0x y y y y y '''''+++=也就是222(())1x y y y y '+''=-+令0y '=，得1x =±．当11x =时，11y =；当21x =-时，20y = 当11x =时，0y '=，10y ''=-<，函数()y y x =取极大值11y =；当21x =-时，0y '=，10y ''=>函数()y y x =取极小值20y =． 19．（本题满分10分）设函数()f x 在区间[]0,1上具有二阶导数，且(1)0f >，0()lim 0x f x x-→<，证明：（1）方程()0f x =在区间()0,1至少存在一个实根；（2）方程2()()(())0f x f x f x '''+=在区间()0,1内至少存在两个不同实根．证明：（1）根据的局部保号性的结论，由条件0()lim 0x f x x-→<可知，存在01δ<<，及1(0,)x δ∈，使得1()0f x <，由于()f x 在[]1,1x 上连续，且1()(1)0f x f ⋅<，由零点定理，存在1(,1)(0,1)x ξ∈⊂，使得()0f ξ=，也就是方程()0f x =在区间()0,1至少存在一个实根；（2）由条件0()lim 0x f x x-→<可知(0)0f =，由（1）可知()0f ξ=，由洛尔定理，存在(0,)ηξ∈，使得()0f η'=；设()()()F x f x f x '=，由条件可知()F x 在区间[]0,1上可导，且(0)0,()0,()0F F F ξη===，分别在区间[][]0,,,ηηξ上对函数()F x 使用尔定理，则存在12(0,)(0,1),(,)(0,1),ξηξηξ∈⊂∈⊂使得1212,()()0F F ξξξξ''≠==，也就是方程2()()(())0f x f x f x '''+=在区间()0,1内至少存在两个不同实根．20．（本题满分11分）已知平面区域{}22(,)|2D x y x y y =+≤，计算二重积分2(1)Dx d σ+⎰⎰ 【详解】由于积分区域关于y 轴左右对称，所以由二重积分对称性可知20Dxd σ=⎰⎰．所以2sin 2222044224620(1)(1)(cos 1)2sin cos 2sin 4(4sin 4sin 2sin )54DDx d x d d r rdrd d πθππσσθθθθθθθθθθπ+=+=+⎛⎫=+ ⎪⎝⎭=-+=⎰⎰⎰⎰⎰⎰⎰⎰其中利用瓦列斯公式，知24600013135315sin ,sin ,sin 2242864216d d d ππππππθθπθθπθθπ⨯⨯⨯=⨯==⨯==⨯=⨯⨯⨯⎰⎰⎰21．（本题满分11分）设()y x 是区间30,2⎛⎫ ⎪⎝⎭上的可导函数，且(1)0y =．点P 是曲线:()L y y x =上的任意一点，L 在点P 处的切线与y 轴相交于点()0,P Y ，法线与X 轴相交于点(),0P X ．若P p X Y =，求L 上的点的坐标(,)x y 满足的方程．【详解】曲线过点(,)P x y 的切线方程为()()()Y y x y x X x '-=-，令0X =，得()()p Y y x xy x '=-；曲线过点(,)P x y 的法线方程为1()()()Y y x X x y x -=--'，令0Y =，得()p X x yy x '=+．由条件P p X Y =，可得微分方程y xy x yy ''-=+标准形为11ydy x y xy y dx x y x--+'===++，是个一阶齐次型微分方程．设y u x =，方程化为11du u u x dx u -+=+，整理，得211du u x dx u +=-+ 分离变量，两边积分，得1arctan ln ln ln 2u u x C +=-+ 由初始条件(1)0y =，得1,0,0x y u ===，确定常数1C = 所以曲线的方程为1arctan ln ln 2y yx x x+=-． 22．（本题满分11分）设三阶矩阵()123,,A ααα=有三个不同的特征值，且3122.ααα=+ （1）证明：()2r A =；（2）若123,βααα=+，求方程组Ax β=的通解．【详解】（1）证明：因为矩阵有三个不同的特征值，所以A 是非零矩阵，也就是()1r A ≥．假若()1r A =时，则0r =是矩阵的二重特征值，与条件不符合，所以有()2r A ≥，又因为31220ααα-+=，也就是123,,ααα线性相关，()3r A <，也就只有()2r A =．（2）因为()2r A =，所以0Ax =的基础解系中只有一个线性无关的解向量．由于31220ααα-+=，所以基础解系为121x ⎛⎫ ⎪= ⎪ ⎪-⎝⎭；又由123,βααα=+，得非齐次方程组Ax β=的特解可取为111⎛⎫ ⎪⎪ ⎪⎝⎭；方程组Ax β=的通解为112111x k ⎛⎫⎛⎫ ⎪ ⎪=+ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭，其中k 为任意常数．23．（本题满分11分）设二次型222123123121323(,,)2282f x x x x x ax x x x x x x =-++-+在正交变换x Q y =下的标准形为221122y y λλ+，求a 的值及一个正交矩阵Q ．【详解】二次型矩阵21411141A a -⎛⎫⎪=- ⎪ ⎪-⎝⎭因为二次型的标准形为221122y y λλ+．也就说明矩阵A 有零特征值，所以0A =，故 2.a =114111(3)(6)412E A λλλλλλλ---=+=+---令0E A λ-=得矩阵的特征值为1233,6,0λλλ=-==．通过分别解方程组()0i E A x λ-=得矩阵的属于特征值13λ=-的特征向量1111ξ⎛⎫⎪=-⎪⎪⎭，属于特征值特征值26λ=的特征向量2101ξ-⎛⎫⎪=⎪⎪⎭，30λ=的特征向量3121ξ⎛⎫⎪=⎪⎪⎭．所以()123,,0Q ξξξ⎛ == ⎝为所求正交矩阵．。

2018年全国硕士研究生入学考试数学二真题及答案

2
2
（C）当 f (x) 0 时， f (1) 0 （D）当 f (x) 0时， f (1) 0
2
2
【答案】（ D ）
【解析一】有高于一阶导数的信息时，优先考虑“泰勒展开”。从选项中判断，展开点为 x0
1 2
。
将函数
f
( x) 在
x0
1
处展开，有
2
f (x) f (1) f (1)(x 1) f ( ) (x 1)2 ，其中 1 x 。
1
ex ax2 bx1
ex ax2 bx1
x2
elim x0
ex
ax2 bx1 x2
，
x0
因此，
lim
ex
ax2
bx
1
0
lim
x
1 2
x2
ax2
bx
(x2 )
0
x0
x2
x0
x2
lim
x0
(1 2
a)x2
(1 x2
b)x
(x2)
0
1 2
a
0,1
b
0
或用“洛必达”： lim x0
ex
ax2 x2
x b 1, x 0
则 F(1) 1 a, F(0) 1 b, F(1 0) 2, F(0 0) 1,
因为函数连续，所以极限值等于函数值，即1 a 2,1 b 1 a 3,b 2 ，
故选（D）.
4.
设函数
f
(
x)
在
[0,1]
上二阶可导。且
1
0
f
( x)dx
0 ，则
（）
（A）当 f (x) 0 时， f (1) 0 （B）当 f (x) 0 时， f (1) 0

考研数学二模拟题2018年(1)_真题(含答案与解析)-交互

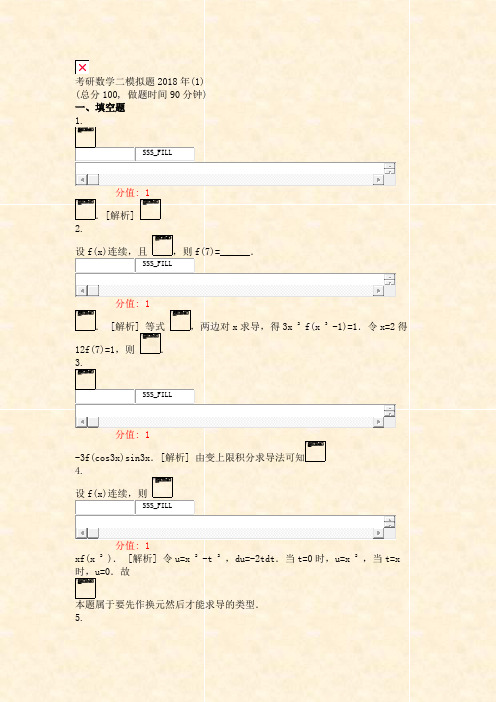
考研数学二模拟题2018年(1)(总分100, 做题时间90分钟)一、填空题1.SSS_FILL分值: 1．[解析]2.设f(x)连续，且，则f(7)=______．SSS_FILL分值: 1． [解析] 等式，两边对x求导，得3x 2 f(x 3 -1)=1．令x=2得12f(7)=1，则．3.SSS_FILL分值: 1-3f(cos3x)sin3x．[解析] 由变上限积分求导法可知4.设f(x)连续，则SSS_FILL分值: 1xf(x 2 )． [解析] 令u=x 2 -t 2，du=-2tdt．当t=0时，u=x 2，当t=x 时，u=0．故本题属于要先作换元然后才能求导的类型．5.设函数f(x)连续，．若φ(1)=1，φ"(1)=5，则f(1)=______．SSS_FILL分值: 12． [解析] 改写，由变限积分求导法得由得f(1)=2．6.由曲线y=xe x与直线y=ex所围成图形的面积S=______．SSS_FILL分值: 1． [解析] 由xe x =ex可知x(e x -e)=0．则x=0或x=1．故二、选择题1.设，其中f(x)连续，s＞0，t＞0，则I的值SSS_SINGLE_SELA 依赖于s，t．B 依赖于s，t，x．C 依赖于t，x，不依赖于s．D 依赖于s，不依赖于t．分值: 1答案:D[解析] ，由此可见，I的值只与s有关，所以应选D．2.设函数记，0≤x≤2，则A．B．C．D．SSS_SIMPLE_SINA B C D分值: 1答案:B[解析] 当0≤x≤1时，；当1＜x≤2时，．由此可见应选B．f(x)在[0，2]上可积，则在[0，2]上连续，于是排除A，C，D．3.设f(x)连续，，则F"(x)等于•**(x4)．•**(x4)．•**(x4)．**(x2)．SSS_SIMPLE_SINA B C D分值: 1答案:C[解析] 由知F"(x)=2xf(x 4 )．故应选C．4.已知设，则F(x)为A．B．C．D．SSS_SIMPLE_SINA B C D分值: 1答案:D[解析]所以应选D．f(x)在[0，2]上可积，则在[0，2]上连续，于是排除A，B，C．5.设函数f(x)连续，则下列函数中，必为偶函数的是A．B．C．D．SSS_SIMPLE_SINA B C D分值: 1答案:D[解析] 设，则即F(x)是偶函数，D是正确的．类似方法可以证明A，C均为奇函数．而对B中的函数，因为由所给条件不能推出为偶函数．6.设f(x)是奇函数，除x=0外处处连续，x=0是其第一类间断点，则是SSS_SINGLE_SELA 连续的奇函数．B 连续的偶函数．C 在x=0间断的奇函数．D 在x=0间断的偶函数．分值: 1答案:B[解析] 解法1 取函数它满足题设条件，则是一个连续的偶函数，从而排除了选项A，C，D，故选B．解法2 显然f(x)在任何有限区间[a，b]上都可积，于是连续；又因f(x)是奇函数，则是偶函数，故选B．7.设函数y=f(x)在区间[-1，3]上的图形如图所示．则函数的图形为A．B．C．D．SSS_SIMPLE_SINA B C D分值: 1答案:D[解析] 根据题中函数y=f(x)的图形，可知函数在除了x=0，x=2两点外可导，且F"(x)=f(x)．由此可知：函数F(x)在(-1，0)内单调递增，在(0，1)内单调递减，在(1，2)内单调递增，在(2，3)内恒为常数．由于函数F(x)连续，且F(0)=0，所以正确选项只能是D．8.设函数，则SSS_SINGLE_SELA x=π是函数F(x)的跳跃间断点．B x=π是函数F(x)的可去间断点．C F(x)在x=π处连续但不可导．D F(x)在x=π处可导．分值: 1答案:C9.曲线y=x(x-1)(2-x)与x轴所围图形面积可表示为A．B．C．D．SSS_SIMPLE_SINA B C D分值: 1答案:C[解析] y=x(x-1)(2-x)与x轴的交点为x=0，x=1，x=2，因此该曲线与x轴围成的面积为所以应选C．10.由曲线与x轴围成的平面图形绕x轴旋转而成的旋转体的体积为A．B．C．D．SSS_SIMPLE_SINA B C D分值: 1答案:B[解析]11.曲线与x轴所围成的图形，绕x轴旋转一周所成旋转体的体积为A．B．π．C．D．π 2．SSS_SIMPLE_SINA B C D分值: 1答案:C[解析]12.设f(x)，g(x)在区间[a，b]上连续，且g(x)＜f(x)＜m(m为常数)，由曲线y=g(x)，y=f(x)，x=a及x=b所围平面图形绕直线y=m旋转而成的旋转体体积为A．B．C．D．SSS_SIMPLE_SINA B C D分值: 1答案:B[解析] 先画草图如图所示，对x积分。

2018考研数学二真题答案解析二重积分

2018考研数学二真题答案解析：二重积分来源：文都教育在2018考研数学（二）的真题中，二重积分的题型十分新颖（第17题），难度大，文都教育的数学老师给出该题的解析：17.（本题满分10分）设平面区域D 由曲线sin ,2π1cos x t t t y t =-⎧≤≤⎨=-⎩（0）与x 轴围成，计算二重积分(2)d d Dx y x y +⎰⎰。

解：（利用形心坐标）d d d d d d d d D D D D x x y x x x y x x y x y=⇒=⎰⎰⎰⎰⎰⎰⎰⎰，而πx =，于是()()2π0d d πd d π1cos d sin D D x x y x y t t t ==--⎰⎰⎰⎰⎰()()2π2π2200π1cos d π12cos cos d t t t t t =-=-+⎰⎰22001cos 2π22sin 2t t dt πππ+⎡⎤=-+⎢⎥⎣⎦⎰ 2π201sin 22π2π03π2t t ⎡⎤+⎢⎥=++=⎢⎥⎢⎥⎣⎦2π()2π2()00002d d d 2d d y x y x D y x y x y y y x ==⎰⎰⎰⎰⎰ 2π2π2200()d (1cos ).(sin )y x x t d t t ==--⎰⎰()2π2π32300(1cos )d 13cos 3cos cos d t t t t t t =-=-++⎰⎰[]()2π2π2π20001cos 23sin 3d 1sin dsin 2t t t t t t +=-+++⎰⎰ 2π+3π05π.=+=于是：()22d d 3π5π.Dx y r y +=+⎰⎰该题积分区域的上部边界曲线采用了参数方程形式，故使得这个二重积分的题型十分新颖，上述解答的思路是先不管具体的参数方程，直接化为累次积分，计算出内层积分，然后在计算外层积分时把上部曲线的参数方程代入，转化为关于t 的定积分。

考研数学历年真题2017年2018年2019年真题和答案(数学二)

目录2017年全国硕士研究生招生考试数学（二）试题 (1)2018年全国硕士研究生招生考试数学（二）试题 (8)2019年全国硕士研究生招生考试数学（二）试题 (15)2017年全国硕士研究生招生考试数学（二）试题一、选择题（1～8小题，每小题4分，共32分。

下列每题给出的四个选项中，只有一个选项是符合题目要求的，请将所选项的字母填在答题纸指定的括号内。

）1.若函数10,(), 0x f x axb x ⎧->⎪=⎨⎪≤⎩0x =在处连续，则（） A.12ab =B.12ab =-C.0ab =D.2ab =2.设二阶可导函数()f x 满足(1)(1)1,(0)1,0,f f f f x ''=-==->且（）则（）. A.1-1()0f x dx >⎰B.1-1()0f x dx <⎰C.11()()f x dx f x dx ->⎰⎰ D.110()()f x dx f x dx -<⎰⎰3.设数列{}n x 收敛，则（）.A.n n limsin 0lim 0n n x x →∞→∞==当时，B.(lim 0lim 0n n n n x x →∞→∞==当时，C.()2lim 0lim 0n n n n n x x x →∞→∞+==当时，D.()lim sin 0lim 0n n n n n x x x →∞→∞+==当时， 4.微分方程()24+81cos2xy y y e x '''-=+的特解可设为*y =（）.A.()22cos2sin 2xx Ae e B x C x ++ B.()22cos2sin 2xx Axee B x C x ++ C.()22cos2sin 2xx Aexe B x C x ++D.()22cos2sin 2xx Axexe B x C x ++5.设(),f x y 具有一阶偏导数，且任意的(),x y 都有()(),,0,0,f x y f x y x y∂∂><∂∂则（）.A.()()0,01,1f f >B.()()0,01,1f f <C.()()0,11,0f f >D.()()0,11,0f f <6.甲乙两人赛跑，计时开始时，甲在乙前方10(单位:m)，图中，实践表示甲的速度曲线()1v v t =（单位m/s ）,虚线表示乙的速度曲线 ()2,v v t = 三块阴影部分面积的数值依次为10,20,3，计时开始后乙追甲的时刻为0t (单位:s),则（）.A.010t =B.01520t <<C.025t =D.025t >7.设A 为3阶矩阵, ()123,,P ααα= 为可逆矩阵，使得1000010,002P AP -⎛⎫ ⎪= ⎪ ⎪⎝⎭则()123A ααα++=（）.A.12+ααB.13+2ααC.23+ααD.13+2αα8.已知矩阵200210100021020020001001002A B C ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，，，则（）.A. A C B C 与相似，与相似B. A C B C 与相似，与不相似C. A C B C 与不相似，与相似D. A C B C 与不相似，与不相似二、填空题（9～14小题，每小题4分，共24分。

2018年考研数学一二三真题解析及点评(史上最强版)

证明数列收敛只有唯一的方法：证明数列单调有界。《金讲》17页予以重要说明并给出两道难度高于本题的同型例题详解，本题再不济，直接用第一问的结论求出第二问的结果应该是一丝难度都没有。
数一第20题数三第20题数二第22题
《金讲》403-405页不仅给出了通用性齐次方程组的详细解题过程，还给予具体具体方程解析示例，详细程度超越市面任何一本数学参考书，足以解答任何复杂齐次方程组。
本质一样
数一第18题
(Ⅰ)是简单一阶微分方程求解，直接套公式即得，送分题；(Ⅱ)不定积分函数与变现积分函数的灵活转换，需要对两者关系有较深度地掌握方可轻易转换，稍有难度，本题完整证明出来的同学应该不超过万分之一。
较难题
考查不等式的证明，具有天然的难题属性。但《金讲》在142页对这类题型设了一个专题给予了本质性的总结，任何不等式证明本质都可以归结到两类情况，每类情况的证明有唯一思路，因此，不等式证明对于《金讲》读者不太可能成为难题，但《金讲》以外，没有任何参考书做过这种深度总结，因此本道题对于有些人是难题。
数二第18题
数三第18题
简单函数的级数展开并求通项。展开部分直接套公式，属于送分。求通项虽偶有难度，但任何求通项都可以通过适当展开进行归纳这一万能方法，在《金讲》中有强调，所以也属于半送分。《金讲》 254页至259页用了一个重点专题予以详解本考点，足以解决任何函数的展开式。
数一第19题数三第19题数二第21题
数二第20题
考查微分的基本应用，将题目内容用数学式子表示出来，问题就转化为了最简单的微分或积分问题，本题几乎是《金讲》配套暑期集训讲义中的原题。
数一第11题
考查旋度公式的记忆，直接用旋度公式计算即得答案。旋度公式的详细计算公式参见《金讲》288页，属送分题。

2018考研数学二真题最强解析及点评(没有之一),给你2019考研数学最科学的指引

送分题
同型题
难题
一道最能考查重积分计算数学思维的题。重积分的计算本质是利用变量换元法将二重积分转化两次定积分的计算。这道题对于一些热衷于死做题而没有从思维方面去把握的同学是一道超级难题，但《金讲》中不断的强化需要掌握这种思维，两个积分变量取决于一个参数，且知参数的取值区间，则两个变量的二重积分必然能通过该参数变量替换转化为定积分的计算。这种变量替换思维可参见《金讲》 248页例1.7.26 的（Ⅲ）（Ⅳ）。
结束语
满分150分的试卷，几乎都是对数学基本概念、基本性质、和基本运算的考察，超过120分以上题目不需要任何技巧及跳跃性思考就可以轻松拿下满分，居然被认为是史上最难的考题，根本原因是绝大部分人长期被一众商业包装起的“名师”遮蔽了双眼，以“题” 代“学”，抛弃数学考试内容学习的源头——基本知识的理解和基本数学思维的建立，而到处赶集似的浮在知识的浅表，沉迷于各种偏题怪题之中，以期投机取巧，其实最靠谱的取巧就是扎实基础，以不变应万变。这也是《考研数学超级金讲（全程复习一本通）》一书出版的根本目的。《超级金讲》读者之所以能秒杀每年号称“史上”最难考题，就是因为其对数学考试内容学习的源头超强解析，强根固本才能以不变应万变。认为2018考研数学难的其实就是一个笑话，请不要继续把你学习的误入歧途传递给别人。
考查拐点、切线方程的求解。知晓其基本定义，无需任何技巧的硬套用公式即可得出答案。
送分题
送分题
考查三种常见有理式积分的求解。这类题只有两种思路，分解因式或凑方，本题一眼可以看出分母容易分解因式，因此采用分解因式法，属于此类题最常规的积分计算，《金讲》中对这类题从最简单到复杂的求解方式都有归纳，并辅以详细例题解析。
送分题

2018考研数学二真题及答案解析-文都版

1
世纪文都教育科技集团股份有限公司
应选(D). 方法二：因为 f ( x) cos
x , f (0) 1 cos x x 1 1 x 2 不存在 x
lim
x 0
f ( x) f (0) lim x 0 x
lim
x 0
f ( x) 在 x 0 处不可导，选（D）

N 2
1 x x 1 dx ，因为 e x x 1 ，所以 x 1 x e 2 e
3
世纪文都教育科技集团股份有限公司
K 2 1 cos x dx ， 1 cos x 1
2

即
所以由定积分的比较性质 K M N ，应选（C）. 6.
A. M N K . C. K M N . 答案：（C）解析： M

B. M K N . D. K N M .

2 2
1 x
1 x2
2
dx =
2 2
2x 1 2 1 x
2 dx 1dx ， 2
4.设函数 f ( x ) 在 0,1 上二阶可导，且

1
0
f ( x)dx 0, 则
2
世纪文都教育科技集团股份有限公司
1 2 1 C.当 f '( x ) 0 时， f ( ) 0. 2
A.当 f '( x ) 0 时， f ( ) 0. 答案：（D）
1 2 1 D.当 f "( x ) 0 时， f ( ) 0. 2
（B） lim
x 0
1 2 - x cos x -1 f ( x) - f (0) （C） lim = lim = lim 2 = 0 ，可导 x 0 x 0 x 0 x x x 1 - x cos x -1 f ( x) - f (0) （D） lim = lim = lim 2 不存在，不可导 x 0 x 0 x 0 x x x

2018年考研数学二真题与答案解析

2018年考研数学二真题及答案解析考研专业课：论述题答题技巧▶解析论述题在考研专业课中属于中等偏上难度的题目，考察对学科整体的把握和对知识点的灵活运用，进而运用理论知识来解决现实的问题。

但是，如果我们能够洞悉论述题的本质，其实回答起来还是非常简单的。

论述题，从本质上看，是考察队多个知识点的综合运用能力。

因此，这就要求我们必须对课本的整体框架和参考书的作者的写书的内部逻辑。

这一点是我们育明考研专业课讲授的重点，特别是对于跨专业的考生来说，要做到这一点，难度非常大。

▶答题攻略：论述题三步走答题法是什么--为什么--怎么样1.论述题中重要的核心概念，要阐释清楚;论述题中重要的理论要点要罗列到位。

这些是可以在书本上直接找到的，是得分点，也是进一步分析的理论基点。

2.要分析目前所存在问题出现的原因。

这个部分，基本可以通过对课本中所涉及的问题进行总结而成。

3.提出自己合理化的建议。

▶答题示范例如：结合治理理论，谈谈我们政府改革。

1.阐释"治理"的定义，然后分段阐释"治理理论的核心主张，包括理论主张和政策主张"。

2.分析目前"政府改革"中存在的问题及其原因。

3.结合治理理论的理论和政策主张，并结合相关的一些理论提出自己的改革措施。

我们育明考研经过长期摸索，总结了一套考研专业课答题模板。

▶危机应对万一遇到自己没有碰到的问题，特别是没有关注到的热点问题怎么办呢?其实，论述题虽然是考察考生运用知识点分析问题的能力，其核心还是在于课本知识，在于理论。

因此在回答的时候一定要紧扣理论不放松。

▶温馨提示1.回答的视角要广，不要拘泥于一两个点。

2.在回答论述题的时候一定要有条理性，但是条数不宜过多，在5-8条为主。

字数在1500左右。

用时为25-30分钟。

2018考研专业课：简答题答题技巧▶解析简答题一般来说位于试题的第二部分，基本考察对某些重要问题的掌握程度。

难度中等偏低。

2018年考研数学二真题及答案解析

2018全国研究生入学考试考研数学二试题本试卷满分150，考试时间180分钟一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的.1.若1)(lim 212=++→x bx ax e xx ，则（）（A ）1,21-==b a （B ）1,21--==b a （C ）1,21==b a （D ）1,21-==b a 2.下列函数中，在0=x 处不可导的是（A ）x x x f sin )(=（B ）x x x f sin )(=（C ）xx f cos )(=（D ）xx f cos)(=3.设函数⎩⎨⎧≥-=010,1)(x x x f ，＜，⎪⎩⎪⎨⎧≥--≤-=0,01,1-,2)(x b x x x x ax x g ＜＜，若)()(x g x f +在R 上连续，则（A ）1,3==b a （B ）2,3==b a （C ）1,3-==b a （D ）2,3-==b a 4.设函数)(x f 在[]1,0上二阶可导，且⎰=10)(dx x f ，则（A ）0)(＜x f '时，0)21(＜f （B ）0)(＜x f ''时，0)21(＜f （C ）0)(＞x f '时，0)21(＜f （D ）0)(＞x f ''时，0)21(＜f 5.设dx x x M ⎰-++=22221)1(ππ，dx e xN x ⎰-+=221ππ，dx x K ⎰-+=22)cos 1(ππ，则（A ）KN M ＞＞（B ）N K M ＞＞（C ）NM K ＞＞（D ）MN K ＞＞6.=-+-⎰⎰⎰⎰----dy xy dx dy xy dx x xx x1201222)1()1(（A ）35（B ）65（C ）37（D ）677.下列矩阵中，与矩阵⎪⎪⎪⎭⎫ ⎝⎛100110011相似的为（A ）⎪⎪⎪⎭⎫⎝⎛1001101-11（B ）⎪⎪⎪⎭⎫⎝⎛1001101-01（C ）⎪⎪⎪⎭⎫ ⎝⎛1000101-11（D ）⎪⎪⎪⎭⎫ ⎝⎛1000101-018.设A ，B 为n 阶矩阵，记)(x r 为矩阵X 的秩，）（Y X 表示分块矩阵，则（A ）)() (A r AB A r =（B ）)() (A r BA A r =（C ）{})(),(max ) (B r A r B A r =（D ）)() (TTB A r B A r =二、填空题：9～14小题，每小题4分，共24分. 9.]arctan )1[arctan(lim 2x x x x -++∞→=。

2018年考研数学二真题答案解析

2018年考研数学二真题答案解析本文针对2018年考研数学二真题进行详细解析，旨在帮助考生更
好地理解和掌握考试内容。

以下将根据各个题目的顺序逐一进行解析。

第一题：（填空题）
这道题共有多个空格需要填写，我们依次来看每个空格的解答方法。

（略）
通过上述的解析，我们可以得出第一题的完整解答如下：
（略）
第二题：（选择题）
这道题为选择题，共有4个选项，我们来逐一分析每个选项的正确
与否。

（略）
通过上述的解析，我们可以得出第二题的正确答案为C选项。

第三题：（解答题）
这道题需要考生进行详细解答，我们来按步骤分析解答过程。

（略）
通过上述的解析，我们可以得出第三题的完整解答如下：
（略）
......
依此类推，我们将继续解析第四题、第五题以及后续的题目。

总结：
本文对2018年考研数学二真题进行了逐题解析，旨在帮助考生更好地了解每题的解答思路和答案。

通过阅读本文，考生可以更全面地掌握考试内容，并为备考提供参考。

希望考生能够针对每道题目进行形成逻辑思维和解答能力的训练，以取得更好的考试成绩。

注意：本文中所提供的答案仅供参考，未必是唯一正确的解答。

在实际考试中，考生应根据自己的理解和计算能力进行解答，并注意合理的时间分配。

祝愿所有考生在考试中取得优异的成绩！。

2018年考研数学二试题与答案解析(完整版)

B. a 3, b 2 D. a 3, b 2
lim f x g x lim f x lim g x 1 0 1
x 0 x 0
lim f x g x lim f x lim g x 1 b 1 1 b b 2
6. A.

0
1
dx
2 x2
x
1 xy dy 0 dx x 1 xy dy
B.
1
2 x2
5 3 7 C. 3
【答案】C 【解析】如图, dx
1
5 6 7 D. 6
1 2 x2

0
2 x2
x

(1 xy )dy dx
0

x
(1 xy )dy (1 xy )dxdy dxdy S D
2

e
x0 2 x
lim
e
e x 2 ax b
x
ax 2 bx

e
x0
lim
e x 2 ax b 2x
lim e x 2 ax b 0 b 1 e x 2 ax b x0 lim 0 1 e x 2 ax b x0 2x a lim 0 2 2x x0
x 0 x 0
x 1 x 1
lim f x lim g x 1 2 a 1 a f x g x xlim 1 x 1 lim f x lim g x 1 1 2 2 1 a a 3 f x g x xlim 1 x 1

考研真题数学二(2000——2018)高数大题

数学二高数（2018）（15）（本题满分10分）（一元函数积分学的计算）2.x e ⎰求不定积分（2018）（16）（本题满分10分）20()()()x xf x f t dt tf x t dt ax +-=⎰⎰已知连续函数满足（I ）()f x 求；（II ）()[0,1]1,.f x a 若在区间上的平均值为求的值（2018）（17）（本题满分10分）（二重积分）sin ,(02),(2).1cos Dx t t D t x x y d y t πσ=-⎧≤≤+⎨=-⎩⎰⎰设平面区域由曲线与轴围成计算二重积分（2018）（18）（本题满分10分）（一元函数微分学的应用，微分不等式）已知常数ln 2 1.k ≥-证明：2(1)(ln 2ln 1)0.x x x k x --+-≥ （2018）（19）（本题满分10分）（多元函数微分学，条件极值）2m 将长为的铁丝分成三段，依次围成圆、正方形与正三角形.三个图形的面积之和是否存在最.若存在，求出最小值（2018）（20）（本题满分11分）（一元函数微分学的应用）已知曲线()()24:(0),0,0,0,1.9L y x x O A P L S OA AP L =≥点点设是上的动点，是直线与直线及曲线()3,4.P x S t 所围成图形的面积，若运动到点时沿轴正向的速度是4，求此时关于时间的变化率（2018）（21）（本题满分11分）（数列存在性与计算）{}{}110,1(1,2,),lim .n n x x n n n n n x x x e e n x x +→∞>=-=L 设数列满足：证明收敛，并求求+→0lim xt x dt（16）（本题满分10分）设函数(),f u v 具有2阶连续偏导数，()y ,xf e cosx =,求dyd x x=,220d y d x x =（17）（本题满分10分）求21limln 1nn k k k n n →∞=⎛⎫+ ⎪⎝⎭∑（18）（本题满分10分）已知函数)(x y 由方程023333=-+-+y x y x 确定，求)(x y 的极值（19）（本题满分10分）设函数()f x 在[]0,1上具有2阶导数，0()(1)0,lim 0x f x f x+→><，证明（1）方程()0f x =在区间(0,1)内至少存在一个实根；（2）方程2)]([)()(x f x f x f '+'' 在区间(0,1)内至少存在两个不同的实根.（20）（本题满分11分）已知平面区域(){}22,2D x y xy y =+≤，计算二重积分()21Dx dxdy +⎰⎰（2017）（21）（本题满分11分）设()y x 是区间3(0,)2内的可导函数，且(1)0y =，点P 是曲线:()L y y x =上的任意一点，L 在点P 处的切线与y 轴相交于点(0,)P Y ，法线与x 轴相交于点(,0)P X ，若p P X Y =，求L 上点的坐标(,)x y 满足的方程。

考研数学二模拟题2018年(1)_真题-无答案

考研数学二模拟题2018年(1)(总分100,考试时间90分钟)一、填空题1.2. 设f(x)连续，且，则f(7)=______．3.4. 设f(x)连续，则5. 设函数f(x)连续，．若φ(1)=1，φ"(1)=5，则f(1)=______．6. 由曲线y=xex与直线y=ex所围成图形的面积S=______．二、选择题1. 设，其中f(x)连续，s＞0，t＞0，则I的值A. 依赖于s，t．B. 依赖于s，t，x．C. 依赖于t，x，不依赖于s．D. 依赖于s，不依赖于t．2. 设函数记，0≤x≤2，则A．B．C．D．3. 设f(x)连续，，则F"(x)等于A.f(x4)．**(x4)．**(x4)．**(x2)．4. 已知设，则F(x)为A．B．C．D．5. 设函数f(x)连续，则下列函数中，必为偶函数的是A．B．C．D．6. 设f(x)是奇函数，除x=0外处处连续，x=0是其第一类间断点，则是A. 连续的奇函数．B. 连续的偶函数．C. 在x=0间断的奇函数．D. 在x=0间断的偶函数．7. 设函数y=f(x)在区间[-1，3]上的图形如图所示．则函数的图形为A．B．C．D．8. 设函数，则A. x=π是函数F(x)的跳跃间断点．B. x=π是函数F(x)的可去间断点．C. F(x)在x=π处连续但不可导．D. F(x)在x=π处可导．9. 曲线y=x(x-1)(2-x)与x轴所围图形面积可表示为A．B．C．D．10. 由曲线与x轴围成的平面图形绕x轴旋转而成的旋转体的体积为A．B．C．D．11. 曲线与x轴所围成的图形，绕x轴旋转一周所成旋转体的体积为A．B．π．C．D．π2．12. 设f(x)，g(x)在区间[a，b]上连续，且g(x)＜f(x)＜m(m为常数)，由曲线y=g(x)，y=f(x)，x=a及x=b所围平面图形绕直线y=m旋转而成的旋转体体积为A．B．C．D．13. 如图所示，x轴上的一线密度为常数μ，长度为l的细杆，若质量为m的质点到杆右端的距离为a，已知引力系数为k，则质点和细杆之间引力的大小为A．B．C．D．三、解答题1. 设x≥-1，求2. 设，其中x＞0，求．3. 设xOy平面上有正方形D{(x，y)|0≤x≤1，0≤y≤1}及直线l：x+y=t(t≥0)．若S(t)表示正方形D位于直线l左下方部分的面积(如图)，试求．4. 设函数f(x)在[0，+∞)上可导，f(0)=0，且其反函数为g(x)，若，求f(x)．5. 设求函数的表达式．设6. 证明f(x)是以π为周期的周期函数；7. 求f(x)的值域．8. 设f(x)是区间上的单调、可导函数，且满足其中f-1是f的反函数，求f(x)．9. 设函数，求f"(x)，并求f(x)的最小值．10. 如图所示，设曲线方程为，梯形OABC的面积为D，曲边梯形OABC的面积为D1，点A的坐标为(a，0)，a＞0，证明：11. 设D是由曲线y=sinx+1与三条直线x=0，x=π，y=0围成的曲边梯形，求D绕Ox轴旋转一周所生成的旋转体的体积．12. 设抛物线y=ax2+bx+c过原点，当0≤x≤1时y≥0，又已知该抛物线与x轴及直线x=1所围图形的面积为．试确定a，b，c的值，使此图形绕x轴旋转一周而成的旋转体的体积V 最小．13. 过点P(1，0)作抛物线的切线，该切线与上述抛物线及x轴围成一平面图形，求此图形绕x轴旋转一周所成旋转体的体积．14. 曲线y=(x-1)(x-2)和x轴围成一平面图形，求此平面图形绕y轴旋转一周所成的旋转体的体积．15. 设平面图形A由x2+y2≤2x与y≥x所确定，求图形A绕直线x=2旋转一周所得旋转体的体积．16. 求曲线y=3-|x2-1|与x轴围成的封闭图形绕直线y=3旋转所得的旋转体体积．17. 设有一正椭圆柱体，其底面的长、短轴分别为2a、2b，用过此柱体底面的短轴且与底面成α角的平面截此柱体，得一楔形体(如图)，求此楔形体的体积V．18. 设曲线y=ax2(a＞0，x≥0)与y=1-x2交于点A，过坐标原点O和点A的直线与曲线y=ax2围成一平面图形(如图)．问a为何值时，该图形绕x轴旋转一周所得的旋转体体积最大?最大体积是多少?设D是位于曲线(a＞1，0≤x＜+∞)下方、x轴上方的无界区域．19. 求区域D绕x轴旋转一周所成旋转体的体积V(a)；20. 当a为何值时，V(a)最小?并求此最小值．。