六年级奥数专题:图形的计算.doc
六年级奥数题及答案(高等难度)

六年级奥数题及答案:图形(高等难度)1 图形:(高等难度)如图,长方形ABCD中,E为的AD中点,AF与BE、BD 分别交于G、H,OE垂直AD于E,交AF于O,已知AH=5cm,HF=3cm,求AG.图形答案:2图形面积:(高等难度)直角三角形ABC的两直角边AC=8cm,BC=6cm,以AC、B C为边向形外分别作正方形ACDE与BCFG,再以AB为边向上作正方形ABMN,其中N点落在DE上,BM交CF于点T.问:图中阴影部分(与梯形BTFG)的总面积等于多少?图形面积答案:3 应用题:(高等难度)我国某城市煤气收费规定:每月用量在8立方米或8立方米以下都一律收6.9元,用量超过8立方米的除交6.9元外,超过部分每立方米按一定费用交费,某饭店1月份煤气费是82.26元,8月份煤气费是40.02元,又知道8月份煤气用量相当于1月份的,那么超过8立方米后,每立方米煤气应收多少元?应用题答案:4 乒乓球训练(逻辑):(高等难度)甲、乙、丙三人用擂台赛形式进行乒乓球训练,每局2人进行比赛,另1人当裁判.每一局的输方去当下一局的裁判,而由原来的裁判向胜者挑战.半天训练结束时,发现甲共打了15局,乙共打了21局,而丙共当裁判5局.那么整个训练中的第3局当裁判的是_______.乒乓球训练(逻辑)答案:本题是一道逻辑推理要求较高的试题.首先应该确定比赛是在甲乙、乙丙、甲丙之间进行的.那么可以根据题目中三人打的总局数求出甲乙、乙丙、甲丙之间的比赛进行的局数.⑴丙当了5局裁判,则甲乙进行了5局;⑵甲一共打了15局,则甲丙之间进行了15-5=10局;⑶乙一共打了21局,则乙丙之间进行了21-5=16局;所以一共打的比赛是5+10+6=31局.此时根据已知条件无法求得第三局的裁判.但是,由于每局都有胜负,所以任意连续两局之间不可能是同样的对手搭配,就是说不可能出现上一局是甲乙,接下来的一局还是甲乙的情况,必然被别的对阵隔开.而总共31局比赛中,乙丙就进行了16局,剩下的甲乙、甲丙共进行了15局,所以类似于植树问题,一定是开始和结尾的两局都是乙丙,中间被甲乙、甲丙隔开.所以可以知道第奇数局(第1、3、5、……局)的比赛是在乙丙之间进行的.那么,第三局的裁判应该是甲.5唐老鸭和米老师赛跑:(高等难度)唐老鸭与米老鼠进行一万米赛跑,米老鼠的速度是每分钟125米,唐老鸭的速度是每分钟100米。
六年级图形问题综合(奥数)含答案doc资料

平面图形计算(一)经典图形:1. 任意三角形ABC 中,CD=31AC ,EC=43BC ,则三角形CDE 的面积占总面积的31⨯43=41(为什么?)2. 任意平行四边形中任意一点,分别连接四个顶点,构成的四个三角形中,上下两个三角形面积之和等于左右两个三角形面积之和。
(为什么?)3. 任意梯形,连接对角线,构成四个三角形。
(1)腰上的两个三角形面积相等;(2)上下两个三角形面积之积等于左右两个三角形面积之积。
(为什么?)4. 正方形的面积等于边长的平方,或者等于对角线的平方÷2.等腰直角三角形面积等于直角边的平方÷2,或者等于斜边的平方÷4.(为什么?)例题: 例1. 如右图,三角形ABC 的面积是10,BE=2AB ,CD=3BC ,求三角形BDE 的面积。
例2. 如图,已知三角形ABC 的面积是1,延长AB 至D ,使BD=AB ,延长BC 至E ,使CE=2BC ,延长CA 至F ,使AF=3AC ,求三角形DEF 的面积。
例3.如图,三角形ABC的面积是180平方厘米,D是BC的中点,AE=ED,EF=2BF,求AEF的面积。
例4.如图,ABCD是个长方形,DEFG是个平行四边形,E点在BC边上,FG过A点,已知,三角形AKF与三角形ADG面积之和等于5平方厘米,DC=CE=3厘米。
求三角形BEK的面积。
FKB E CDGA例5.如图,三角形ABC的AB和AC两条边分别被分成5等分。
三角形ABC面积是500,求图中阴影部分的面积?例6.如图,设正方形ABCD的面积为120,E、F分别为边AB、AD的中点,FC=3GC,则阴影部分的面积是多少?AB CDFEG例7.在如图所示的三角形AGH中,三角形ABC,BCD,CDE,DEF,EFG,FGH的面积分别是1,2,3,4,5,6平方厘米,那么三角形EFH的面积是多少平方厘米?ABCDEFGH例8.如图,在平行四边形ABCD中,AC为对角线,EF平行于AC,如果三角形AED的面积为12平方厘米,,求三角形DCF的面积。
六年级图形问题综合(奥数)含答案

六年级图形问题综合(奥数)含答案例3. AKF 与三角形ADG 面积之和等于5平方厘米,DC=CE=3厘米。
求三角形BEK 的面积。
D例4. 如图,三角形ABC 的AB 和AC 两条边分别被分成5等分。
三角形ABC 面积是500,求图中阴影部分的面积?例5. 如图,设正方形ABCD 的面积为120,E 、F 分别为边AB 、AD 的中点,FC=3GC ,则阴影部分的面积是多少?A B C DF EG例6. 在如图所示的三角形AGH 中,三角形ABC ,BCD ,CDE ,DEF,EFG ,FGH 的面积分别是1,2,3,4,5,6平方厘米,那么三角形EFH 的面积是多少平方厘米?A B DEF G H例7. 如图,在平行四边形ABCD 中,AC 为对角线,EF 平行于AC ,如果三角形AED 的面积为12平方厘米,,求三角形DCF 的面积。
D CA B E F练习:1. 已知正方形ABCD 的边长是5cm ,又EF=FG ,FD=DG ,求三角形ECG 的面积。
E B CGDAF2. 正三角形ABC 的边长为12厘米,BD ,DE ,EF ,FG 四条线段把它的面积5等分,求AF ,FD ,DC ,AG ,GE ,EB 的长。
A B G E CDF3. 如图所示是某个六边形公园ABCDEF ,M 为AB 中点,N 为CD 中点,,P 为DE 中点,Q 为FA 中点,其中游览区APEQ 与BNDM 的面积之和为900平方米。
中间的湖泊面积为361平方米,其余的部分是草地,问草地面积共有多少平方米?A B C DEFQPN M4. 如图,AE=EC ,BD=2DC ,AF=3BF ,若三角形ABC 的面积为270平方厘米,求图中阴影部分的面积。
5. 如下图,正方形ABCD 的边长为12, P 是边AB 上的任意一点,M 、N 、I 、H 分别是边BC 、AD 上的三等分点,E 、F 、G 是边CD 上的四等分点,图中阴影部分的面积是______.6. 如图正方形ABCD 的边长是4厘米,CG 是3厘米,长方形DEFG 的长DG 是5厘米,那么它的宽DE 是______厘米.7. 如图,CE=4EA , BD=3CD ,AF=5BF 。
(完整word)六年级奥数表面积和体积计算题

表面积与体积练习和答案专题简析:小学阶段所学的立体图形主要有四种长方体、正方体、圆柱体和圆锥体。
从平面图形到立体图形是认识上的一个飞跃,需要有更高水平的空间想象能力。
因此,要牢固掌握这些几何图形的特征和有关的计算方法,能将公式作适当的变形,养成“数、形”结合的好习惯,解题时要认真细致观察,合理大胆想象,正确灵活地计算。
在解答立体图形的表面积问题时,要注意以下几点:(1)充分利用正方体六个面的面积都相等,每个面都是正方形的特点。
(2)把一个立体图形切成两部分,新增加的表面积等于切面面积的两倍。
反之,把两个立体图形粘合到一起,减少的表面积等于粘合面积的两倍。
(3)若把几个长方体拼成一个表面积最大的长方体,应把它们最小的面拼合起来。
若把几个长方体拼成一个表面积最小的长方体,应把它们最大的面拼合起来。
例1.从一个棱长为10里面的正方体上挖去一个长10厘米、宽2厘米、高2厘米的小长方体,剩下部分的表面积是多少?【思路导航】这是一道开放题,方法有多种:1)沿一条棱挖,剩下部分的表面积为592平方厘米。
2)在某个面挖,剩下部分的表面积为632平方厘米。
3)挖通某两个对面,剩下部分的表面积为672平方厘米。
练习1.1.把一个长为12分米、宽为6分米、高为9分米的长方体木块锯成两个相同的小长方体木块,这两个小长方体的表面积之和比原来长方体的表面积增加了多少平方米?2.在一个棱长是4厘米的立方体上挖一个棱长是1厘米的小正方体后,表面机会发生怎样的变化?例2.把19个棱长为3厘米的正方体重叠起来,拼成一个立体图形,求这个立体图形的表面积。
【思路导航】要求这个复杂形体的表面积,必须从整体入手,从上、左、前三个方向观察,每个方向上的小正方体各面就组合成了如下图形。
练习2:1、用棱长是1厘米的立方体拼成图27-6所示的立体图形。
求这个立体图形的表面积。
2、一堆积木(如图27-7所示),是由16块棱长是2厘米的小正方体堆成的。
小学奥数几何专题--巧求周长(六年级)竞赛测试.doc

小学奥数几何专题--巧求周长(六年级)竞赛测试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx 题xx题xx题总分得分一、xx题(每空xx 分,共xx分)【题文】求图中所有线段的总长(单位:厘米)【答案】48【解析】要注意到,题目所求的是图中所有线段的总长,而图中的线段,并不仅仅是、、、四段,还包括、等等,因此不能简单地将图中标示的线段长度进行求和.同时应该注意到,;,等等.因此,为了计算图中所有线段的总长,需要先计算AB、BC、CD 、DE这四条线段分别被累加了几次.这里,可以按照每条线段分别是由几部分组成的加以讨论:由1段组成的线段共有4条,即AB、BC、CD、DE,而求和过程中AB、BC、CD、DE这四条线段各被累加了1次.类似地考虑到,由2段组成的线段共有3条,求和过程中AB、DE各被累加了1次,BC、CD各被累加了2次.由3段组成的线段共有2条,求和过程中AB、DE各被累加了1次,BC、CD各被累加了2次.由4段组成的线段只有AE,其中AB、BC、CD、DE各被计算了1次.综上所述,AB、DE各被计算了4次,BC、CD各被计算了6次.因而图中所有线段的总长度为:{{9}l先考虑大长方形的长上各边:应用上一道题目的结论,每条边上长为4、3、1、2的线段分别被计算了4、6、6、4次.然后再考虑大长方形的宽:因为共有个长方形,所以长度为2的宽被计算了次.故总周长可以用下式计算得到:.【题文】如图,正方形的边长为,被分割成如下个小长方形,求这个小长方形的所有周长之和.评卷人得分【答案】56【解析】.【题文】如右图,正方形的边长是厘米,过正方形内的任意两点画直线,可把正方形分成个小长方形。
这个小长方形的周长之和是多少厘米?【答案】72【解析】从总体考虑,在求这个小长方形的周长之和时,、、、这四条边被用了次,其余四条虚线被用了次,所以个小长方形的周长之和是:(厘米)。
六年级奥数题及答案

六年级奥数题及答案:图形(高等难度)1、如图,长方形ABCD中,E为的AD中点,AF与BE、B D分别交于G、H,OE垂直AD于E,交AF于O,已知A H=5cm,HF=3cm,求AG.2阴影面积:(高等难度)如右图,在以AB为直径的半圆上取一点C,分别以AC 和BC为直径在△ABC外作半圆AEC和BFC.当C点在什么位置时,图中两个弯月型(阴影部分)AEC和BFC的面积和最大。
3、巧克力豆:(高等难度)甲、乙、丙三人各有巧克力豆若干粒,要求互相赠送.先由甲给乙、丙,甲给乙、丙的豆数依次等于乙、丙原来各人所有豆数.依同办法,再由乙给甲、丙,所给豆数依次等于甲、丙各人现有的豆数.最后由丙给甲、乙,所给的豆数依次等于甲、乙各人现有的豆数.互赠后每人恰好各有豆32粒,问原来三人各有豆多少粒?4、得奖人数:(高等难度)六年级举行一次数学竞赛,共有若干名同学得奖,其中得一等奖的同学比余下的得奖人数的五分之一少三名,得二等奖的占领奖人数的三分之一,得三等奖的人数比二等奖的人数同学多21名,问得奖人数是多少?粮食问题:(高等难度)5、甲仓有粮80吨,乙仓有粮120吨,如果把乙仓的一部分粮调入甲仓,使乙仓存粮是甲仓的60%,需要从乙仓调入甲仓多少吨粮食?6、分苹果:(高等难度)有一堆苹果平均分给幼儿园大、小班小朋友,每人可得6个,如果只分给大班每人可得10个,问只分给小班时,每人可得几个?、7、巧算:(中等难度)计算:8、四位数:(中等难度)某个四位数有如下特点:①这个数加1之后是15的倍数;②这个数减去3是38的倍数;③把这个数各数位上的数左右倒过来所得的数与原数之和能被10整除,求这个四位数.9跑步狗跑5步的时间马跑3步,马跑4步的距离狗跑7步,现在狗已跑出30米,马开始追它。
问:狗再跑多远,马可以追上它?、10排队有五对夫妇围成一圈,使每一对夫妇的夫妻二人动相邻的排法有()、11路程A,B,C三地的距离(单位:千米)如左下图所示。
苏教版六年级下册奥数几何图形专题

9.42-8=1.42cm2
答:两个阴影部分的面积相差1.42平方厘米。
练一练
【例题12】(48中)如图,一个三角形的三个顶点分别为三个 半径为3厘米的圆的圆心,则图中阴影部分的面积是多少?
阴影面积=半圆面积 3.14×3²÷2=14.13cm2
答:两个阴影部分的面积相差14.13平方厘米。
逢3必过
练一练
【例题11】如图A与B是两个圆(只有四分之一)的圆心。那么,
两个阴影部分的面积相差多少平方厘米?(单位:厘米)
1
差不变模型 ②-①=(②+③)-(①+③) 2
3.14×4²÷4=12.56cm2
③
2A 2 B
3.14×2²÷4=3.14cm2
2×4=8cm2
12.56-3.14=9.42cm2
小学数学 六年级
欢 迎 同 学 们
几何综合
优 翼
1、公式法:基本图形的面积求解公式 2、概念法:根据基本图形的基本概念进行判断并求解 3、加减法: 相加求整,相减求部分。 4、分割法:将整体分割成若干个规则的多边形 5、割补法:将一部分割补到图形中的另一个地方组成较规则 的图形进行求解。
6、等量代换法:如果图中有和所求部分面积相等的图形,可 以通过先求该图形的面积间接求出所要求部分的面积。 7、重组法:将所求部分打乱重新组合。 8、倍比法:通过边长之间的倍数关系求解面积之间的倍数关 系。 9、差不变法:A-B=(A+C)-(B+C) 10、整体法:在求解过程中没必要一定求出某一个具体的量, 只需要知道某一个计算过程的整体也是可以求出面积的。
倍比法 S△BCD=1cm2
S△DBE=1×(2+1)=3cm2
六年级奥数举一反三-组合图形面积计算小学

六年级奥数举⼀反三-组合图形⾯积计算⼩学组合图形⾯积计算(⼀)⼀、知识要点在进⾏组合图形的⾯积计算时,要仔细观察,认真思考,看清组合图形是由⼏个基本单位组成的,还要找出图中的隐蔽条件与已知条件和要求的问题间的关系。
⼆、精讲精练【例题1】求图中阴影部分的⾯积(单位:厘⽶)。
圆的⾯积。
【思路导航】如图所⽰的特点,阴影部分的⾯积可以拼成14=28.26(平⽅厘⽶)62×3.14×14答:阴影部分的⾯积是28.26平⽅厘⽶。
练习1:1.求下⾯各个图形中阴影部分的⾯积(单位:厘⽶)。
2.求下⾯各个图形中阴影部分的⾯积(单位:厘⽶)。
3.求下⾯各个图形中阴影部分的⾯积(单位:厘⽶)。
【例题2】求图中阴影部分的⾯积(单位:厘⽶)。
【思路导航】阴影部分通过翻折移动位置后,构成了⼀个新的图形(如图所⽰)。
从图中可以看出阴影部分的⾯积等于⼤扇形的⾯积减去⼤三⾓形⾯积的⼀半。
3.14×2144-4×4÷2÷2=8.56(平⽅厘⽶)答:阴影部分的⾯积是8.56平⽅厘⽶。
练习2:1.计算下⾯图形中阴影部分的⾯积(单位:厘⽶)。
2.计算下⾯图形中阴影部分的⾯积(单位:厘⽶,正⽅形边长4)。
3.计算下⾯图形中阴影部分的⾯积(单位:厘⽶,正⽅形边长4)。
【例题3】如图19-10所⽰,两圆半径都是1厘⽶,且图中两个阴影部分的⾯积相等。
求长⽅形ABO1O的⾯积。
【思路导航】因为两圆的半径相等,所以两个扇形中的空⽩部分相等。
⼜因为图中两个阴影部分的⾯积相等,所以扇形的⾯积等于长⽅形⾯积的⼀半(如图19-10右图所⽰)。
所以3.14×12×1/4×2=1.57(平⽅厘⽶)答:长⽅形长⽅形ABO1O的⾯积是1.57平⽅厘⽶。
练习3:1.如图所⽰,圆的周长为12.56厘⽶,AC两点把圆分成相等的两段弧,阴影部分(1)的⾯积与阴影部分(2)的⾯积相等,求平⾏四边形ABCD的⾯积。
六年级奥数图形难题
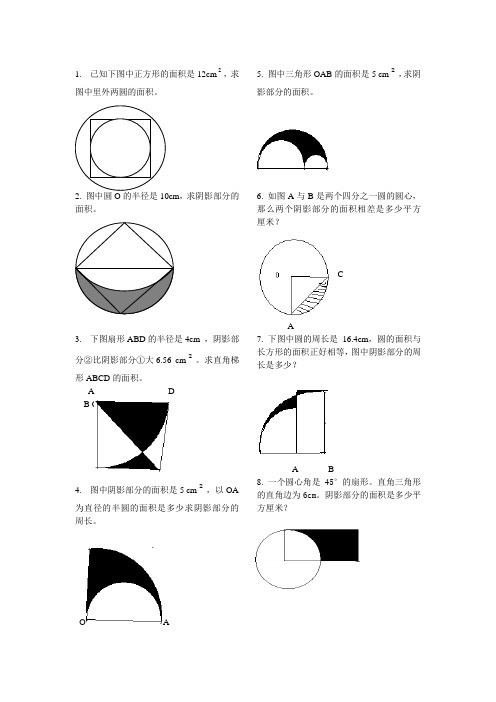
1.已知下图中正方形的面积是12cm2,求图中里外两圆的面积。
2. 图中圆O的半径是10cm,求阴影部分的面积。
3.下图扇形ABD的半径是4cm ,阴影部分②比阴影部分①大6.56 cm2。
求直角梯形ABCD的面积。
A DB C4.图中阴影部分的面积是5 cm2,以OA为直径的半圆的面积是多少求阴影部分的周长。
O A 5. 图中三角形OAB的面积是5 cm2,求阴影部分的面积。
6. 如图A与B是两个四分之一圆的圆心,那么两个阴影部分的面积相差是多少平方厘米?CA7. 下图中圆的周长是16.4cm,圆的面积与长方形的面积正好相等,图中阴影部分的周长是多少?A B8. 一个圆心角是45°的扇形。
直角三角形的直角边为6cm。
阴影部分的面积是多少平方厘米?9. 如图,P是等边三角形ABC的任意一点。
PD垂直于BC,PF垂直于AB,PE垂直于AC 已知三角形ABC的面积是2003cm2,三角形PBD的面积是284 cm2,求三角形APF和三角形PCE的面积之和。
10. 如图,边长为10cm的正方形ABCD中有一个最大的圆,E是CD的中点,求图中阴影部分的面积?11. 如图,正方形ABCD的边长是4cm,E、F 分别是BC、AD的中点,P是正方形内任意一点,求阴影部分的面积?12. 如图三角形ABC的面积是120 cm2,6AF =5AB,AC=4AD,BC=5CE.求三角形DEF的面积。
13. 如图在三角形ABC中,DC=3BD,AE=ED,若三角形ABC的面积是1,求阴影部分的面积。
14.如图,AB是AD的3倍,AC是AE的5倍,那么三角形ABC的面积是三角形ADE面积的多少倍?15. 如图,两个长方形叠放在一起,小长方形的宽是2米,点A是大长方形的一边的中点,求图中阴影部分的总面积。
16. 如图,梯形ABCD的上底AD为1cm,高CD为2.5cm,求梯形ABCD的面积。
17. 如图,已知长方形ADEF的面积是16,三角形ADB的面积为3,三角形ACF的面积是4,求三角形ABC的面积是多少?。
六年级奥数图形问题精选
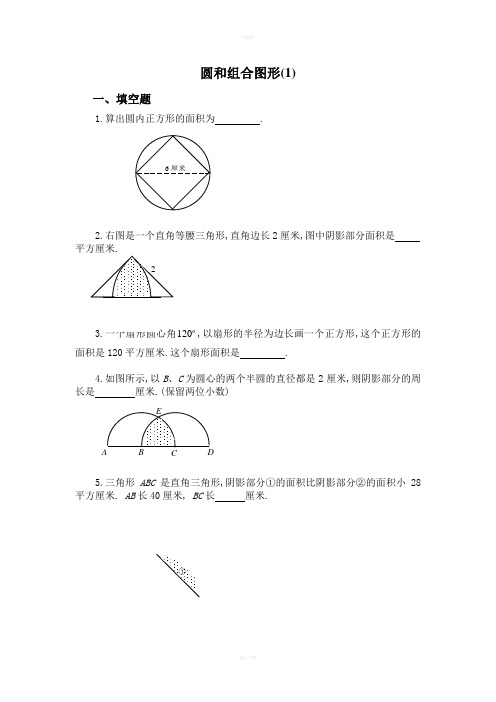
圆和组合图形(1)一、填空题1.算出圆内正方形的面积为 .2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是 平方厘米.120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是 厘米.(保留两位小数)5.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. AB 长40厘米, BC 长 厘米.6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC 垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是 平方厘米.10.在右图中(单位:厘米),两个阴影部分面积的和是 平方厘米.45二、解答题11. ABC 是等腰直角三角形. D 是半圆周的中点, BC 是半圆的直径,已知: AB =BC =10,那么阴影部分的面积是多少?(圆周率14.3=π)12.如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米?)14.3(≈π14.右图中4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?———————————————答 案——————————————————————1. 18平方厘米.由图示可知,正方形两条对角线的长都是6厘米,正方形由两个面积相等的三角形构成.三角形底为6厘米,高为3厘米,故正方形面积为1822136=⨯⨯⨯(平方厘米).2. 1.14平方厘米.由图示可知,图中阴影部分面积为两个圆心角为45的扇形面积减去直角三角形的面积.即14.12122236045214.32=⨯⨯-⨯⨯⨯(平方厘米).3. 125.6平方厘米.由已知条件可知圆的半径的平方为120平方厘米.故扇形面积为6.12536012012014.3=⨯⨯(平方厘米).4. 3.09厘米.边结BE 、CE ,则BE=CE=BC=1(厘米),故三角形BCE 为等边三角形.于是60=∠=∠BCE EBC .BE=CE=045.136060214.3=⨯⨯(厘米).于是阴影部分周长为09.312045.1=+⨯(厘米).5. 32.8厘米.从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC 的面积.又已知①的面积比②的面积小28平方厘米,故半圆面积比三角形ABC 的面积小28平方厘米.半圆面积为6282124014.32=⨯⎪⎭⎫ ⎝⎛⨯(平方厘米),三角形ABC 的面积为628+28=656(平方厘米).BC 的长为8.32402656=÷⨯(厘米).6. 13937平方厘米.将等腰直角三角形补成一个正方形,设正方形边长为x 厘米,则圆的半径为2x 厘米.图中阴影部分面积是正方形与圆的面积之差的81,于是有282114.322⨯=⎪⎭⎫⎝⎛⨯-x x ,解得1332002=x .故等腰直角三角形的面积为1393721133200=⨯(平方厘米).⌒⌒7. 72.扇形面积是圆面积的511574.31=÷,故扇形圆心角为360的51即72.8. 5.13.三角形ACO 是一个等腰直角三角形,将AO 看作底边,AO 边上的高为3262=÷=÷AO (厘米),故三角形ACO 的面积为93621=⨯⨯(平方厘米).而扇形面积为13.1436045614.32=⨯⨯(平方厘米),从而阴影部分面积为14.13-9=5.13(平方厘米).9. 142.75.由正方形周长是20厘米,可得正方形边长也就是圆的半径为5420=÷(厘米).图形总面积为两个43圆面积加上正方形的面积,即75.1425243514.322=+⨯⨯⨯(平方厘米).10. 90平方厘米.图中阴影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即()902114.3)220(2115122114.3)216(2114.3212222=⨯⨯÷-⨯⨯+⨯⨯÷+⨯⨯÷(平方厘米).11. 如图作出辅助线,则阴影部分的面积为三角形AED 的面积减去正方形BEDO 的面积再加上圆面积的41. 三角形AED 的面积是21)210()21010(⨯÷⨯÷+;是2)210(÷,圆面积的41是2)210(14.341÷⨯⨯,故阴影部分面积为:22)210(14.341)210(21)210()21010(÷⨯⨯+÷-⨯÷⨯÷+125.32625.19255.37=+-=(平方厘米).12. 由已知半圆S 1的面积是14.13平方厘米得半径的平方为914.3213.14=÷⨯(平方厘米),故半径为3厘米,直径为6厘米. 又因圆S 2的面积为19.625平方厘米,所以S 2半径的平方为25.614.3625.19=÷(平方厘米),于是它的半径为2.5厘米,直径为5厘米. 阴影部分面积为55)56(=⨯-(平方厘米).13. 因OA=OB ,故三角形OAB 为等腰三角形,即150215180,151=⨯-=∠=∠=∠AOB OBA , 同理150=∠AOC ,于是602150360=⨯-=∠BOC . 扇形面积为:39.42914.3360602=⨯⨯(平方厘米).14. 正方形可以分割成两个底为2,高为1的三角形,其面积为221221=⨯⨯⨯(平方厘米).正方形内空白部分面积为4个41圆即一个圆的面积与正方形面积之差,即2212-=-⨯ππ(平方厘米),所有空白部分面积为)2(2-π平方厘米. 故阴影部分面积为四个圆面积之和与两个空白面积之和的差,即为 8)2(22412=-⨯-⨯⨯ππ(平方厘米).十二、圆和组合图形(2)一、填空题1.如图,阴影部分的面积是 .2.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大 平方厘米.3.在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取3.14,结果精确到1平方厘米)4.右图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).5.如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π6.如图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是 .2 1 27.有八个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形(如图).图中黑点是这些圆的圆心.如果圆周率1416.3=π,那么花瓣图形的面积是 平方厘米.8.已知:ABCD 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .9.图中,扇形BAC 的面积是半圆ADB 的面积的311倍,那么,CAB ∠是 度.10.右图中的正方形的边长是2厘米,以圆弧为分界线的甲、乙两部分的面积差(大减小)是 平方厘米.(π取3.14)2二、解答题11.如图:阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率22)取12.已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积.13.有三个面积都是S 的圆放在桌上,桌面被圆覆盖的面积是2S +2,并且重合的两块是等面积的,直线a 过两个圆心A 、B , 如果直线a 下方被圆覆盖的面积是9,求圆面积S 的值.14.如图所示,1的位置沿线段AB 、BC 、CD 滚到2的位置,如果AB 、BC 、CD 的长都是20厘米,那么圆板的正面滚过的面积是多少平方厘米?———————————————答 案——————————————————————1. 6.两个扇形面积相等,故阴影部分面积等于一个长为3,宽为2的长方形面积,为6个平方单位.2. 188.4.小圆的半径为2)14(6=-÷(厘米),大圆的半径为842=⨯(厘米).大圆的面积比小圆的面积大4.18814.3)28(22=⨯-(平方厘米).3. 57.305.57214.3)22(14.35.422=⨯⨯÷-⨯(平方厘米)≈57(平方厘米).4. 10.26.从圆中可以看出,阴影部分的面积是两个半圆的面积与三角形面积之差,即26.10621)26(14.322=⨯-÷⨯(平方厘米).5. 20.5.设圆的半径为r ,则圆面积即长方形面积为2r π,故长方形的长为r DC π=.阴影部分周长r r r r r r AD BA BC DC ππππ245241)(⨯=⨯+-++=+++=5.204.1645=⨯=(厘米).6. 6548(平方厘米).如图,连结OA 、AC ,过A 点作CD 的垂线交CD 于E .三角形ACD 的面积为502100=÷(平方厘米).又圆半径为10)214.3(28.6=⨯÷(厘米),因为151=∠又OA=OD ,故30215=⨯=∠AOC ,扇形AOC 的面积为⌒61261014.3360302=⨯⨯(平方厘米).三角形AOC 的面积为25250=÷(平方厘米).方形面积为611256126=-(平方厘米),从而阴影部分的面积为654861150=-(平方厘米).7. 19.1416.花瓣图形的结构是正方形的面积,加上四个43圆面积后,再割去四个半圆的面积.圆的半径为1厘米,正方形边长为4厘米.故花瓣图形的面积是1416.1916421144314222=+=⨯⨯⨯-⨯⨯⨯+πππ(平方厘米).8. 2.43平方厘米. 如图,将①移到②得:阴影部分面积等于梯形CEFB 的 面积减去三角形CED 、三角形CDA 、扇形AFG 的面积,即 43.236045214.32122122212)322(22=⨯⨯-⨯-⨯⨯-⨯⨯⨯+(平方厘米).9. 60.设扇形ABC 圆心角的度数是x ,半圆的半径OA=r ,有2221311)2(360r r x ⨯⨯⨯=⨯⨯ππ,解得x=60.10. 0.14.扇形面积为14.341214.32=⨯⨯(平方厘米),甲部分面积为43.0214.32122=÷-⨯(平方厘米),乙部分面积为57.04122214.3=⨯⨯-÷(平方厘米),甲乙两部分面积差为14.043.057.0=-(平方厘米11. 如图,小正方形的边长为2r,则①的面积为:72227224122r r r r =⨯-⎪⎭⎫ ⎝⎛⨯⨯,②的面积为222417272221r r r =-⎪⎭⎫ ⎝⎛⨯⨯,2227224172241r r r =⨯⨯-⨯⨯.即阴影部分面积为272r .12. 将阴影部分旋转后,可以看出所求阴影部分面积为大正方形面积的一半减去小正形的一半,即阴影部分面积等于10242622=÷-÷(平方厘米).13. 设一个阴影部分的面积为x ,则有:2223+=-S x S ,于是22+=x S (1)又9232=-x S ,于是有23184+-=S x ,解得S=6.14. 圆板的正面滚过的部分如右图阴影部分所求, 它的面积为:)420(4614)220(22122-+⨯⨯+⨯-+⨯⨯ππ07.228323204221)24(414)220(4222≈+=⨯⨯+⨯-⨯-⨯-+⨯πππ(平方厘米).D面积计算(三)专题简析:对于一些比较复杂的组合图形,有时直接分解有一定的困难,这时,可以通过把其中的部分图形进行平移、翻折或旋转,化难为易。
六年级下册奥数专题练习-立体图形的计算(含答案) 全国通用

立体图形的计算【表面积的计算】例1 一个正方体木块,棱长1米,沿水平方向将它锯成3片,每片又锯成4长条,每条又锯成5小块,共得到大小不等的长方体60块(如图5.69)。
那么,这60块长方体的表面积的和是平方米。
(1988年北京小学数学奥林匹克邀请赛试题)讲析:不管每次锯的长方体大小如何,横着锯2次一共增加了4个正方形面;前后竖直方向锯3次共增加了6个正方形面;左右竖直方向锯4次共增加了8个正方形面。
原来大正方体有6个正方形面,所以一共有24个正方形面。
所以,60块长方体的表面积之和是(1×1)×24=24(平方米)。
例2 图5.70是由19个边长都是2厘米的正方体重叠而成的。
求这个立体图形的外表面积。
(北京市第一届“迎春杯”小学数学竞赛试题)讲析:如果按每一层有多少个正方体,然后再数出每层共有多少个外表面正方形,则很麻烦。
于是,我们可采用按不同的方向来观察的方法去计算。
俯视,看到9个小正方形面;正视,看到10个小正方形面;侧视,看到8个小正方形面。
所以,这个立体图形的表面积是(2×2)×[(9+10+8)×2]=216(平方厘米)。
【体积的计算】例1 一个正方体的纸盒中恰好能放入一个体积为628立方厘米的圆柱体,如图5.71,纸盒的容积有多大?(π取3.14)(全国第四届“华杯赛”复赛试题)讲析:因圆柱体的高、底面直径以及正方体的棱长都相等。
故可设正方即:正方体纸盒的容积是800立方厘米。
例2 在一个棱长4厘米的正方体的上面、右面、前面这三个面的中心分别挖一个边长1厘米的正方形小孔(如图5. 72所示),并通过对面,求打孔后剩下部分的体积。
(北京市第二届“迎春杯”小学数学竞赛试题)。
讲析:打完孔之后,在大正方体正中央就有一个1×1×1的空心小正方体。
三个孔的体积是(1×1×4)×3-(1×1×1)×2=10(立方厘米)。
小升初六年级奥数——几何(平面图形)

一、分数百分数问题,比和比例这是六年级的重点内容,在历年各个学校测试中所占比例超级高,重点应该把握好以下内容:对单位1的正确明白得,明白甲比乙多百分之几和乙比甲少百分之几的区别;求单位1的正确方式,用具体的量去除以对应的分率,找到对应关系是重点;分数比和整数比的转化,了解正比和反比关系;通过对“份数”的明白得结合比例解决和倍(按比例分派)和差倍问题;二、行程问题应用题里最重要的内容,因为综合考察了学生比例,方程的运用和分析复杂问题的能力,因此常常作为压轴题显现,重点应该把握以下内容:路程速度时刻三个量之间的比例关系,即当路程一按时,速度与时刻成反比;速度一按时,路程与时刻成正比;时刻一按时,速度与路程成正比。
专门需要强调的是在很多题目中必然要先去找到那个“必然”的量;当三个量均不相等时,学会通过其中两个量的比例关系求第三个量的比;学会用比例的方式分析解决一样的行程问题;有了以上基础,进一步增强多次相遇追及问题及火车过桥流水行船等特殊行程问题的明白得,重点是学会如何去分析一个复杂的题目,而不是一味的做题;三、几何问题几何问题是各个学校考察的重点内容,分为平面几何和立体几何两大块,具体的平面几何里分为直线形问题和圆与扇形;立体几何里分为表面积和体积两大部份内容。
学生应重点把握以下内容:等积变换及面积中比例的应用;与圆和扇形的周长面积相关的几何问题,处置不规那么图形问题的相关方式;立体图形面积:染色问题、切面问题、投影法、切挖问题;立体图形体积:简单体积求解、体积变换、浸泡问题;四、数论问题常考内容,而且能够应用于策略问题,数字谜问题,计算问题等其他专题中,相当重要,应重点把握以下内容:把握被特殊整数整除的性质,如数字和能被9整除的整数必然是9的倍数等;最好了解其中的道理,因为那个方式能够用在许多题目中,包括一些数字谜问题;把握约数倍数的性质,会用分解质因数法,短除法,辗转相除法求两个数的最大公因数和最小公倍数;学会求约数个数的方式,为了提高灵活运用的能力,需了解那个方式的原理;了解同余的概念,学会把余数问题转化成整除问题,下面的那个性质是超级有效的:两个数被第三个数去除,若是所得的余数相同,那么这两个数的差就能够被那个数整除;能够解决求一个多位数除以一个较小的自然数所得的余数问题,例如求1011121314…9899除以11的余数,和求20202020除以13的余数这种问题;五、计算问题计算问题通常在前几个题目中显现概率较高,要紧考察两个方面,一个是大体的四那么运算能力,同时,一些速算巧算及裂项换元等技术也常常成为考察的重点。
(完整版)六年级奥数图形问题精选
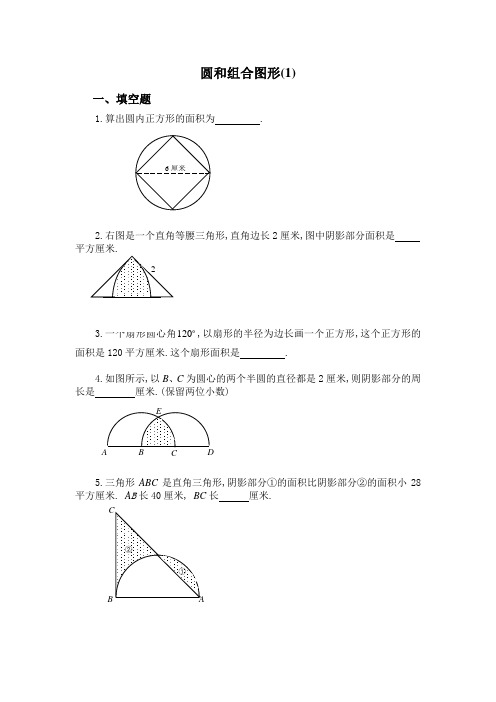
圆和组合图形(1)一、填空题1.算出圆内正方形的面积为 .2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是 平方厘米.120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是 厘米.(保留两位小数)5.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28长 厘米.6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC 垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是 平方厘米.10.在右图中(单位:厘米),两个阴影部分面积的和是 平方厘米.45二、解答题11. ABC 是等腰直角三角形. D 是半圆周的中点, BC 是半圆的直径,已知: AB =BC =10,那么阴影部分的面积是多少?(圆周率14.3=π)12.如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米?)14.3(≈π14.右图中4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?———————————————答 案——————————————————————1. 18平方厘米.由图示可知,正方形两条对角线的长都是6厘米,正方形由两个面积相等的三角形构成.三角形底为6厘米,高为3厘米,故正方形面积为1822136=⨯⨯⨯(平方厘米).2. 1.14平方厘米.由图示可知,图中阴影部分面积为两个圆心角为45的扇形面积减去直角三角形的面积.即14.12122236045214.32=⨯⨯-⨯⨯⨯(平方厘米).3. 125.6平方厘米.由已知条件可知圆的半径的平方为120平方厘米.故扇形面积为6.12536012012014.3=⨯⨯(平方厘米).4. 3.09厘米.边结BE 、CE ,则BE=CE=BC=1(厘米),故三角形BCE 为等边三角形.于是60=∠=∠BCE EBC .BE=CE=045.136060214.3=⨯⨯(厘米).于是阴影部分周长为09.312045.1=+⨯(厘米).5. 32.8厘米.从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC 的面积.又已知①的面积比②的面积小28平方厘米,故半圆面积比三角形ABC 的面积小28平方厘米.半圆面积为6282124014.32=⨯⎪⎭⎫ ⎝⎛⨯(平方厘米),三角形ABC 的面积为628+28=656(平方厘米).BC 的长为8.32402656=÷⨯(厘米).6. 13937平方厘米.将等腰直角三角形补成一个正方形,设正方形边长为x 厘米,则圆的半径为2x 厘米.图中阴影部分面积是正方形与圆的面积之差的81,于是有282114.322⨯=⎪⎭⎫⎝⎛⨯-x x ,解得1332002=x .故等腰直角三角形的面积为1393721133200=⨯(平方厘米). ⌒⌒7. 72.扇形面积是圆面积的511574.31=÷,故扇形圆心角为360的51即72.8. 5.13.三角形ACO 是一个等腰直角三角形,将AO 看作底边,AO 边上的高为3262=÷=÷AO (厘米),故三角形ACO 的面积为93621=⨯⨯(平方厘米).而扇形面积为13.1436045614.32=⨯⨯(平方厘米),从而阴影部分面积为14.13-9=5.13(平方厘米).9. 142.75.由正方形周长是20厘米,可得正方形边长也就是圆的半径为5420=÷(厘米).图形总面积为两个43圆面积加上正方形的面积,即75.1425243514.322=+⨯⨯⨯(平方厘米).10. 90平方厘米.图中阴影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即()902114.3)220(2115122114.3)216(2114.3212222=⨯⨯÷-⨯⨯+⨯⨯÷+⨯⨯÷(平方厘米).11. 如图作出辅助线,则阴影部分的面积为三角形AED 的面积减去正方形BEDO 三角形AED 的面积是21)210()21010(⨯÷⨯÷+;积是2)210(÷,圆面积的41是2)210(14.341÷⨯⨯,故阴影部分面积为:22)210(14.341)210(21)210()21010(÷⨯⨯+÷-⨯÷⨯÷+125.32625.19255.37=+-=(平方厘米).12. 由已知半圆S 1的面积是14.13平方厘米得半径的平方为914.3213.14=÷⨯(平方厘米),故半径为3厘米,直径为6厘米. 又因圆S 2的面积为19.625平方厘米,所以S 2半径的平方为25.614.3625.19=÷(平方厘米),于是它的半径为2.5厘米,直径为5厘米. 阴影部分面积为55)56(=⨯-(平方厘米).13. 因OA=OB ,故三角形OAB 为等腰三角形,即 150215180,151=⨯-=∠=∠=∠AOB OBA , 同理150=∠AOC ,于是602150360=⨯-=∠BOC . 扇形面积为:39.42914.3360602=⨯⨯(平方厘米).14. 正方形可以分割成两个底为2,高为1的三角形,其面积为221221=⨯⨯⨯(平方厘米).正方形内空白部分面积为4个41圆即一个圆的面积与正方形面积之差,即2212-=-⨯ππ(平方厘米),所有空白部分面积为)2(2-π平方厘米. 故阴影部分面积为四个圆面积之和与两个空白面积之和的差,即为 8)2(22412=-⨯-⨯⨯ππ(平方厘米).十二、圆和组合图形(2)一、填空题1.如图,阴影部分的面积是 .2.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大 平方厘米.3.在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取3.14,结果精确到1平方厘米)4.右图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).5.如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π6.如图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是 .2 1 27.有八个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形(如图).图中黑点是这些圆的圆心.如果圆周率1416.3=π,那么花瓣图形的面积是 平方厘米.8.已知:ABC D 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .9.图中,扇形BAC 的面积是半圆ADB 的面积的311倍,那么,CAB ∠是 度.10.右图中的正方形的边长是2厘米,以圆弧为分界线的甲、乙两部分的面积差(大减小)是 平方厘米.(π取3.14)二、解1.如图:阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率取722)12.已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积.13.有三个面积都是S 的圆放在桌上,桌面被圆覆盖的面积是2S +2,并且重合的两块是等面积的,直线a 过两个圆心A 、B , 如果直线a 下方被圆覆盖的面积是9,求圆面积S 的值.14.如图所示,1的位置沿线段AB 、BC 、CD 滚到2的位置,如果AB 、BC 、C D 的长都是20厘米,那么圆板的正面滚过的面积是多少平方厘米?———————————————答 案——————————————————————1. 6.两个扇形面积相等,故阴影部分面积等于一个长为3,宽为2的长方形面积,为6个平方单位.2. 188.4.小圆的半径为2)14(6=-÷(厘米),大圆的半径为842=⨯(厘米).大圆的面积比小圆的面积大4.18814.3)28(22=⨯-(平方厘米).3. 57.305.57214.3)22(14.35.422=⨯⨯÷-⨯(平方厘米)≈57(平方厘米).4. 10.26.从圆中可以看出,阴影部分的面积是两个半圆的面积与三角形面积之差,即26.10621)26(14.322=⨯-÷⨯(平方厘米).5. 20.5.设圆的半径为r ,则圆面积即长方形面积为2r π,故长方形的长为r DC π=.阴影部分周长r r r r r r AD BA BC DC ππππ245241)(⨯=⨯+-++=+++=5.204.1645=⨯=(厘米).6. 6548(平方厘米).如图,连结OA 、AC ,过A 点作CD 的垂线交CD 于E .三角形ACD 的面积为502100=÷(平方厘米).又圆半径为10)214.3(28.6=⨯÷(厘米),因为151=∠又OA=OD ,故30215=⨯=∠AOC ,扇形AOC 的面积为61261014.3360302=⨯⨯(平方厘米).三角形AOC 的面积为25250=÷(平方厘米).方形面积为611256126=-(平方厘米),从而阴影部分的面积为654861150=-(平方厘米).7. 19.1416.⌒花瓣图形的结构是正方形的面积,加上四个43圆面积后,再割去四个半圆的面积.圆的半径为1厘米,正方形边长为4厘米.故花瓣图形的面积是1416.1916421144314222=+=⨯⨯⨯-⨯⨯⨯+πππ(平方厘米).8. 2.43平方厘米.如图,将①移到②得:阴影部分面积等于梯形CEFB 的 面积减去三角形CED 、三角形CDA 、扇形AFG 的面积,即43.236045214.32122122212)322(22=⨯⨯-⨯-⨯⨯-⨯⨯⨯+(平方厘米).9. 60.设扇形ABC 圆心角的度数是x ,半圆的半径OA=r ,有2221311)2(360r r x⨯⨯⨯=⨯⨯ππ,解得x=60.10. 0.14.扇形面积为14.341214.32=⨯⨯(平方厘米),甲部分面积为43.0214.32122=÷-⨯(平方厘米),乙部分面积为57.04122214.3=⨯⨯-÷(平方厘米),甲乙两部分面积差为14.043.057.0=-(平方厘米11. 如图,小正方形的边长为2r,则①的面积为:72227224122r rr r =⨯-⎪⎭⎫ ⎝⎛⨯⨯, ②的面积为222417272221r r r =-⎪⎭⎫ ⎝⎛⨯⨯,2227224172241r r r =⨯⨯-⨯⨯.即阴影部分面积为272r .12. 将阴影部分旋转后,可以看出所求阴影部分面积为大正方形面积的一半减去小正形的一半,即阴影部分面积等于10242622=÷-÷(平方厘米).13. 设一个阴影部分的面积为x ,则有:2223+=-S x S ,于是22+=x S (1)又9232=-x S ,于是有23184+-=Sx ,解得S=6.D14. 圆板的正面滚过的部分如右图阴影部分所求,它的面积为: )420(4614)220(22122-+⨯⨯+⨯-+⨯⨯ππ 07.228323204221)24(414)220(4222≈+=⨯⨯+⨯-⨯-⨯-+⨯πππ(平方厘米).面积计算(三)专题简析:对于一些比较复杂的组合图形,有时直接分解有一定的困难,这时,可以通过把其中的部分图形进行平移、翻折或旋转,化难为易。
六年级奥数图形专题

第四章 图形第一课时---全等变换法1:对于一些比较复杂的组合图形,有时直接分解有一定的困难,这时,可以通过把其中的部分图形进行平移、翻折或旋转,化难为易。
2: 不规则图形面积的求法-----全等变换法 例题1:如图所示,求图中阴影部分的面积。
举一反三:1、 如图所示,求阴影部分的面积(单位:厘米)2、如图所示,用一张斜边为29厘米的红色直角三角形纸片,一张斜边为49厘米的蓝色直角三角形纸片,一张黄色的正方形纸片,拼成一个直角三角形。
求红蓝两张三角形纸片面积之和是多少?例题2:求图中阴影部分的面积(单位:厘米)。
考点归纳举一反三:1、求下面图形中阴影部分的面积(单位:厘米)。
2、求下面图形中阴影部分的面积(单位:厘米)。
3、求下面图形中阴影部分的面积(单位:厘米)。
例题3:求图中阴影部分的面积(单位:厘米)。
举一反三:1::计算下面图形中阴影部分的面积(单位:厘米)。
2::计算下面图形中阴影部分的面积(单位:厘米)。
自我检测当堂检测:1:已知图中,三角形ABC是等腰直角三角形,BC=20厘米,DE为圆的一条直径。
则图中阴影部分的面积为。
2: 计算下面图形中阴影部分的面积为。
3:已知阴影部分的面积为4,求空白S1的面积。
4:已知阴影部分的面积为2(π-1),求边长a的值。
5:已知阴影部分的面积为8(2π-3),求边长a的值。
第四章 图形第二课时---“容斥问题”的原理不规则图形面积的求法-----“容斥问题”的原理例题1:如图所示,求图中阴影部分的面积(单位:厘米)。
针对性训练:1、 如图所示,△ABC 是等腰直角三角形,求阴影部分的面积(单位:厘米)。
2、 如图所示,图中平行四边形的一个角为600,两条边的长分别为6厘米和8厘米,高为5.2厘米。
求图中阴影部分的面积。
例题2:在图中,正方形的边长是8厘米,求图中阴影部分的面积。
6 4 减去考点归纳针对性训练:1、求下图形中阴影部分的面积(单位:厘米)。
六年级上册奥数试题-第20讲 组合图形的计算 全国通用(含答案)

第20讲组合图形的计算知识网络组合图形是由一些基本图形如长方形、正方形、三角形、平行四边形、梯形、圆和扇形等组合而成的图形。
在本讲中,主要介绍长方形、正方形、三角形、平行四边形和梯形组合而成的图形。
组合图形的计算,指的是与组合图形的面积、周长等有关的问题的计算。
对五种基本图形,首先要熟记它们面积的基本公式:。
重点·难点组合图形的计算是以上述几种基本图形为基础的。
这几种基本图形的一些酝酿性质的恰当运用是本讲的重点。
这些基本性质包括:等底等高的两个三角形面积相等;等底的两个三角形面积比等于高之比;等高的两个三角形面积比等于底之比。
这三条性质都是三角形的性质,它们同样适用于平行四边形和长方形。
学法指导在求组合图形的面积时,可用一些比较常用的方法,如:直接法、相加法和相减法、翻转法、等积移位法、重叠法。
最终的目的是将这些图形转化成我们熟悉的简单规则图形的和或差。
同时,也可以构造图形,利用面积的关系来解一些代数题,如关于线段成比例等问题。
经典例题[例1]有一大一小两个正方形,它们的周长相差20厘米,面积相差55平方厘米,那么小正方形的面积是多少平方厘米?思路剖析先求出边长再求面积是一般解法,我们可以利用割补拼凑的方法利用图像来比较直观地求解本题。
解答如图1所示,将两个正方形的一个顶点对齐,将大正方形在小正方形外的部分分割成两个直角梯形,再拼成一个长方形。
由于两个正方形的周长相差20厘米,从而它们的每边相差,即图2中长方形的宽是5厘米。
又因为长方形的面积是两个正方形的面积之差,即为55平方厘米,从而长方形的长为55÷5=11厘米。
由图中可知,长方形的长是直角梯形的上底和下底的和;长方形的宽是直角梯形的上底和下底的差,从而小正方形的长为(11-5)÷2=3(厘米)。
所以小正方形的面积为3×3=9(平方厘米)。
[例2]如图3所示,将△ABC的各边都延长1倍到,得到一个新的,如果△ABC的面积为10,求△的面积。
六年级奥数第二讲立体图形的计算
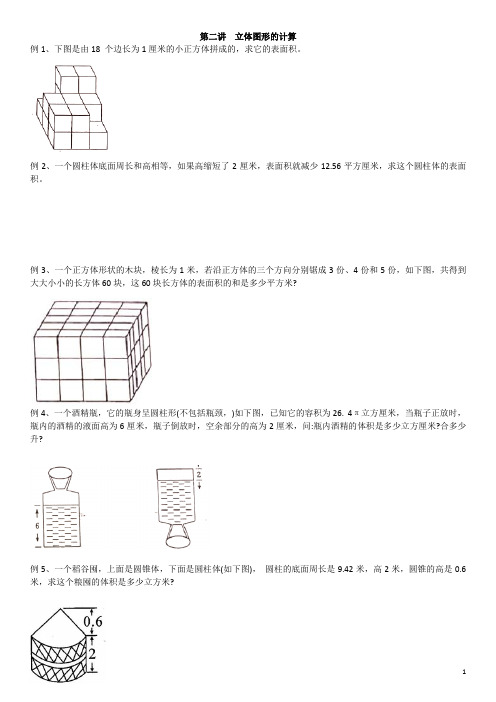
第二讲立体图形的计算
例1、下图是由18 个边长为1厘米的小正方体拼成的,求它的表面积。
例2、一个圆柱体底面周长和高相等,如果高缩短了2厘米,表面积就减少12.56平方厘米,求这个圆柱体的表面积。
例3、一个正方体形状的木块,棱长为1米,若沿正方体的三个方向分别锯成3份、4份和5份,如下图,共得到大大小小的长方体60块,这60块长方体的表面积的和是多少平方米?
例4、一个酒精瓶,它的瓶身呈圆柱形(不包括瓶颈,)如下图,已知它的容积为26. 4π立方厘米,当瓶子正放时,瓶内的酒精的液面高为6厘米,瓶子倒放时,空余部分的高为2厘米,问:瓶内酒精的体积是多少立方厘米?合多少升?
例5、一个稻谷囤,上面是圆锥体,下面是圆柱体(如下图),圆柱的底面周长是9.42米,高2米,圆锥的高是0.6米,求这个粮囤的体积是多少立方米?
同步训练
1、在边长为4厘米的正方体木块的每个面中心打一个边与正方体的边平行的洞,洞口是边长为1厘米的正方形,
洞深1厘米(如下图),求挖洞后木块的表面积和体积。
2、如图所示的一个零件,中间一段是高为10 厘米,底面半径为2厘米圆柱体,上端是一个半球体,下端是一个
圆锥,它的高是2厘米。
求这个零件的体积。
课后作业与检测
1、一根圆柱形钢材,沿底面直径割开成两个相等的半圆柱体,如下图,已知一个剖面的面积是960平方厘米,半
圆柱的体积是3014.4立方厘米,求原来钢材的体积和侧面积。
2、在一只底面直径是40厘米的圆柱形盛水缸里,有一个直径是10厘米的圆锥形铸件完全浸于水中,取出铸件后,缸里的水下降0.5厘米,求铸件的高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级奥数专题:图形的计算
2014 春季数学优化六年级小考专题三.图形的计算【知识要点】图形的
计算,是历年小升初的必考题目,也在各大杯赛中占有很大比例。
几何图形的计
算公式不仅要记牢,而且要理解其推导过程,最好在理解的基础上记忆。
这样不
仅记得牢,而且运用起来也更灵活自如。
对于较复杂的组合图形,要注意观察
图形的特点,寻找图形中的内在联系,通过等积变形、割补转化、旋转平移、添
加辅助线等方法推导求解。
【经典例题】例1.如图所示,在四边形ABCD中,
AB=3cm,CD=7cm,A=C=90,D=45。
求四边形ABCD的面A 积。
B C
D 2例 2.如图所示,在梯形 ABCD 中,AD∥BC,S △AB
E =30cm ,EC=2AE。
求梯形 ABCD 的面积。
A D E C B 例 3.如图所示,正方形
ABCD 的边长为 10 厘米,正方形 EFGC 的边长为 12 厘米。
求阴影部分的面积。
E F A D B G C 例 4.如图所示,三角形
ABC 是等腰直角三角形,AB=BC=10cm。
D 是半圆周的中点,BC 是半圆的直径。
求阴影部分的面积 B A 10cm D C 例 5.如图
所示,已知△ABC 是直角三角形,空白部分甲的面积比空白部分乙的面积大57
平方厘米,BC 长A 20 厘米。
求 AB 的长度。
乙甲 C B 20cm 例 6.如图所示,圆的周长是 16.4 厘米,圆的面积与长方形的面积正好
相等。
求图中阴影部分的周长。
O A B D C
例 7.将一个正方体的棱长缩短一半后,所得的新的正方体的表面积比原来正方
体的表面积减少162 平方厘米。
求原来正方体的体积是多少立方厘米?
例 8.有一个长方体的长、宽、高分别是整厘米数,它的相邻三个面的面积分别
是96 平方厘米、40 平方厘米、60 平方厘米。
这个正方体的体积是多少立方厘
米?例 9.有一块长方形的铁皮,长 32 厘米。
在这块铁皮的四角各剪下一
个边长为4 厘米的小正方形,然后通过折叠、焊接,做成一个无盖的长方体盒
子。
已知这个盒子的容积是672 立方厘米。
求原来长方体铁皮的面积。
例
10.一个圆柱形钢材,横截面被截成斜面,从底面到斜面的最高点是 6 分米,底
面到斜面的最低点是 4分米,底面直径是 2 分米,这个柱体的体积是多少?侧
面积是多少?例 11.如图是一个长方形铁皮。
利用图中的阴影部分,刚好
能做成一个油桶(接头处忽略不计)。
求这个油桶的容积。
16.56m 例 12.
一个盖着瓶盖的瓶子里面装着一些水,瓶底面积为 10 平方厘米(如下图所示)。
请你根据图中标明的数据,计算瓶子的容积。
7cm 5cm 4cm 【专
题精练】 21.如图所示,正方形 ABCD 的边长为 5cm,S △CEF -S △ADF =
5cm 。
求 CE 的长度。
A D F E B C
2.如图所示,ABCD 为长方形,BC=16cm,AB=10cm,AE=ED,DF=FC,EG=2GF。
求△BFG 的面积。
EA D G F BC3.右图中正方形的面积是100 平方厘米,内
半圆的面积是外半圆面积的14。
求阴影部分的面积。
4.如图所示,三个
圆的半径都是10 厘米,三个圆两两相交于圆心。
求阴影部分的面积。
5.
如图所示,三角形 ABC 是直角三角形,阴影乙的面积比阴影甲的面积小63 平
方厘米。
求 BC 的长。
A 乙 D 20 厘米甲 C B
6.如图所示,圆的面积和长方形的面积相等,圆的周长是6.28cm。
求长方形的周长。
O
7.如图所示,以 B、C 为圆心的两个半圆的直径都是2 厘米。
求阴影部分的周长。
(结果保留两位小数) E A B C D
8.一根横截面为正方形的长方体木料,表面积为 134 平方厘米,锯去一个最大的正方体后,表面积为 54平方厘米。
锯下的正方体木料的表面积是多少平方厘米?
9.用 4 块同样的长方形和两块同样的正方形纸板做成一个长方体形状的纸箱,它的表面积为266 平方分米。
长方体的长、宽、高都是整分米数,并且使容积尽可能大。
求这个纸箱的最大容积是多少? 10.有一块长方形的铁皮,长30 厘米。
在这块铁皮的四角各剪下一个边长为5 厘米的小正方形,然后通过折叠、焊接,做成一个无盖的长方体盒子。
已知这个盒子的容积是 1000 立方厘米。
求原来长方体铁皮的面积。
11.把一个长 9 厘米,宽 7 厘米,高 3 厘米的长方体铁块和一个棱长 5 厘米的正方体铁块,溶铸成一个底面直径为 10 厘米的圆锥体铁块,求圆锥体的高。
12.一个圆柱体形状的木棒,沿着底面直径竖直切成两部分。
已知这两部分的表面积之和比圆柱体的表面积大 400 平方厘米,则这个圆柱体木棒的侧面积是多少? 13.有一个长 20 厘米的圆柱体,底面半径为3 厘米,在柱体的一个底面上挖一个底面半径为2 厘米,高为4 厘米的圆柱,求剩下部分的表面积和体积。
14.一个圆柱形水桶,若将高改为原来的一半,底面直径改为原来的2 倍后,可装水40 升。
问:这只水桶原来可装水多少升? 15.一个圆柱形玻璃杯中盛有水,水面高2.5 厘米,玻璃内侧的底面积是72 平方厘米。
在这个杯中放进棱长为 6 厘米的正方体的铁块后,水面没有淹没铁块。
这时水面高多少厘米?。
