贵州省贵阳清镇北大培文学校贵州区域高一数学3月份联考试题
贵州省贵阳清镇北大培文学校贵州区域高一数学3月联考试题

贵州省贵阳清镇北大培文学校贵州区域2017-2018学年高一数学3月联考试题第I 卷(选择题 共60分)一、 选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中, 只有一项是符合题目要求的。
)1. 设集合{|08},{1,2,4,5},{3,5,7}U x N x S T =∈<≤==,则()U S C T I = A.{1,2,3,4,5,7} B.{1,2,4} C .{1,2} D .{1,2,4,5,6,8}2. 函数()lg(2)f x x =+的定义域为 A .(2,1)-B .[2,1)-C .(2,1]-D .[]1,2-3. 下列函数是偶函数且在区间(,0)-∞上为增函数的是.A 2y x = .B 2y x =- .C y x = .D 1y x=4. 已知4sin 5α=,并且α是第二象限角,则tan α为 A.43-B.34- C.43 D.345. 在ABC ∆中,已知030,10,25===A c a ,则角B 等于A .0105B .060C .015D .0015105或6. ABC ∆的内角,,A B C 所对的边分别为,,a b c ,若cos cos sin b C c B a A +=, 则ABC ∆的形状为A.锐角三角形B. 钝角三角形C.直角三角形D.等腰三角形 7. 在等差数列{}n a 中,159371110,50a a a a a a ++=++=则数列{}n a 的前12项的和12S 等于A.50B.80C.140D.160 8. △ABC 中,∠A =60°,a=6,b=4,满足条件的△ABC A .不存在B .有一个C .有两个D .有无数多个9. △ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,且A sin 、B sin 、C sin 成等比数列,且a c 2=,则B cos 的值为 A .B .C .D .10. 中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其意思为:“有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地,请问第一天走了A. 24里B. 48里C. 96里D.192里 11. 点P 在边长为1的正方形ABCD 的边上运动,设M 是CD 边的中点,当点P 沿着M C B A ,,,匀速率运动时,点P 经过的路程x 为自变量,三角形APM 的面积为y ,则函数()y f x =图像的形状大致是xy y xxyxy 2.52.52.52.5OOOOA B C D 12. 已知函数()sin cos f x x x =+,()2sin g x x =,动直线x t =与()f x 、()g x 的图象分别交于点,P Q 两点,则线段PQ 的长度PQ 取值范围是 A .[0,1] B .[0,2] C .[0,2]D .[1,2]第II 卷(非选择题 共90分)二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题卡的相应位置)13. 已知函数()⎩⎨⎧≤>=.0,2,0,log 3x x x x f x则⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛271f f = . 14. 在等差数列{}n a 中,已知3810a a +=,则753a a += .15. 如图,一船自西向东匀速航行,上午10时到达一座灯塔P 的南偏西75︒,距灯塔68海里的M 处,下午2时到达这座灯塔的东南方向N 处,则该船航行的速度为 海里/小时.16. 定义在(,0)(0,)-??U 上的函数()f x ,如果对于任意给定的等比数列{}n a ,有(){}n a f 仍是等比数列,则称()f x 为“保等比数列函数”.现有定义在(,0)(0,)-??U 上的如下函数:①()f x =2x ; ②()f x =x2; ③()x x f =; ④()f x =ln |x |,则其中是“保等比数列函数”的()f x 的序号为 .三、解答题(本大题共6小题,共70分。
贵州省贵阳清镇北大培文学校贵州区域高一生物3月联考试题

贵州省贵阳清镇北大培文学校贵州区域2017-2018学年高一生物3月联考试题一、选择题(45分,1-15题每题2分,16-20题每题3分)1、人体的体液是指()A、细胞外液和消化液B、细胞内液和血液C、细胞内液和细胞外液D、血浆、组织液、淋巴2、人体内环境中所含物质的种类繁多,下列不属于人体内环境中的物质是()A. 营养物质类,包括水、无机盐、氨基酸、葡萄糖等B. 大分子蛋白质类,如呼吸氧化酶、唾液淀粉酶、胃蛋白酶等C. 代谢产物类,如二氧化碳、尿素、尿酸等D. 信号分子类,包括激素、抗体等3、血浆中的水来自()A、组织液B、组织液、消化道C、淋巴、组织液D、消化道、组织液、淋巴4、如图表示人体细胞与外界环境之间进行物质交换的过程。
Ⅰ、Ⅱ、Ⅲ、Ⅳ表示能直接与内环境进行物质交换的4种系统或器官。
①②是有关的生理过程。
下列说法错误的是A.内环境与Ⅰ交换气体必须通过肺泡壁和毛细血管壁B.Ⅱ内的葡萄糖、胰岛素、激素等通过①进人血浆和淋巴C.②表示重吸收作用D.Ⅳ表示的器官是皮肤5、当内环境的稳态遭到破坏时,必将引起()A. 酶促反应速率的加快B. 渗透压下降C. 糖尿病D. 细胞代谢紊乱6、下列现象不属于反射活动的是()A.饭后肠胃蠕动B.人在寒冷时身体发抖C.小狗吃骨头,口腔中分泌唾液D.草履虫受到刺激运动7.下列关于反射弧的叙述,不正确的是()A.反射弧通常由感受器、传入神经、神经中枢、传出神经和效应器五部分组成B.感受器接受刺激后能产生兴奋C.神经中枢位于脑和脊髓D.效应器只由运动神经元的神经末梢组成8、小明的手指不小心被刀割伤时,由于疼痛而咬紧牙关。
这个过程中,他的神经兴奋传递途径是()①传入神经②传出神经③手部感受器④脊髓⑤牵动上下颌的肌肉⑥脑A.③①⑥②④⑤ B.③①⑥④②⑤ C.③①④⑥②⑤ D.③⑥④①②⑤9、某人因饮酒过多导致语无伦次、走路不稳、大小便失禁,出现这些症状的原因是由于相应的中枢受到影响,它们分别是()A.大脑、小脑、脊髓B.小脑、大脑、脊髓C.大脑、小脑、大脑D.脊髓、小脑、大脑10、如图是反射弧的局部结构示意图,刺激c点,检测各位点电位变化.下列说法错误的是()A. 若检测到b、d点都有电位变化,说明兴奋在同一神经元上是可以双向传导的B. 兴奋由c传递到e时,发生了电信号--化学信号--电信号的转换C. 如果a处检测不到电位变化,是因为突触前膜释放的是抑制性递质D. 电表①不偏转,电表②偏转两次11、下列关于神经冲动在反射弧上的传递途径,不正确的是()A. 轴突→突触→神经元细胞体→轴突B. 轴突→突触→树突→神经元细胞体C. 树突→神经元细胞体→轴突→突触D. 树突→突触→轴突→神经元细胞体12.镇痛药并不损伤神经元的结构,却能在一段时间内阻断神经冲动向感觉中枢的传导,它的主要作用部位在()A.细胞体 B.轴突 C.突触间隙 D.树突13、一外伤病人不能说话,但能听懂别人讲话,也能看书看报.其受伤的中枢是()A. W区B. S区C. H区D. V区14.正常人体内的激素、酶和神经递质均有特定的生物活性,这三类物质都是( )A.在细胞内发挥作用 B.由活细胞产生的蛋白质C.与特定分子结合后起作用 D.在发挥作用后还能保持活性15.如图表示人体在寒冷环境中,为维持体温恒定而进行的有关的激素调节过程,下列各项叙述中,不正确的是( )A.甲为促甲状腺激素释放激素,当丙增多时会抑制甲的分泌B.乙为促甲状腺激素,当丙增多时,乙的分泌量会随之而增加C.丙为甲状腺激素,它能提高细胞代谢的速率,使机体产生更多的热量D.人体内激素含量的这种调节机制称为反馈调节16.当人所处的环境从25℃降至5℃时,耗氧量、尿量、抗利尿激素及体内酶活性变化依次是()A.减少减少增加不变 B 增加增加减少不变C.增加减少增加不变 D.增加增加减少降低17.当人体长时间大量运动时,血液中的葡萄糖等营养物质会被大量消耗,此时胰岛A细胞和胰岛B细胞的变化是( )A.胰岛A细胞活动加强,胰岛B细胞活动减弱B.胰岛A细胞和胰岛B细胞活动都加强C.胰岛A细胞和胰岛B细胞活动都减弱D.胰岛A细胞活动减弱,胰岛B细胞活动加强18.右图为动物的生理过程示意图,下列相关分析错误的是( )A.激素X是促性腺激素,激素Y为雌性激素B.激素Y到达靶细胞后,其跨膜运输方式是主动运输C.该生理过程中存在反馈调节D.长期注射激素Y会导致性腺衰退19.下图是反馈调节的过程示意图,下列理解不正确的是( )A.当人体受到寒冷或惊吓刺激后,图中的下丘脑、垂体、腺体分泌的激素可能分别是促甲状腺激素释放激素、促甲状腺激素和甲状腺激素B.当受下丘脑和垂体调节的腺体分泌的激素浓度过高时,通过①→③→④→⑥使其浓度降低C.当受下丘脑和垂体调节的腺体分泌的激素浓度过低时,通过②→③→④→⑤使其浓度升高D.垂体处于承上启下的位置,所以它是内分泌腺的枢纽20.正常情况下,人的血糖含量维持在90 mg/dL左右。
贵州省贵阳清镇北大培文学校2017-2018学年高一上学期期中考试数学试题 Word版含答案

北大培文学校贵州校区2017-2018学年度第一学期期中考试卷高一数学一.选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{1,2,3,4}=A ,{|32,}==-∈B y y x x A ,则=AB ( )A. {1} B . {4}C .{1,3}D .{1,4}2.下列函数中,在R 上是增函数的是( )A. 2=y x B. 3=y x C .1=y xD .=y x 3. 设3.0log ,2,3.023.02===c b a ,则c b a ,,的大小关系是( )A. c b a >>B. a c b >>C. c a b >>D. b c a >>4. 当10<<a 时,在同一坐标系中,函数x y a y a xlog ==-与的图象是( )A. B. C. D. 5. 函数1(1)=≥y x 的反函数是( )A.222(1)=-+<y x x x B.222(1)=-+≥y x x x C.22(1)=-<y x x x D.22(1)=-≥y x x x6.已知log (2)a y ax =-在[0,1]上是关于x 的减函数,则实数a 的取值范围是( )A .(0,1)B .(1,2)C .(1,2]D . [2,)+∞7.设()24=+-xf x x ,则函数()f x 的零点所在的区间是( )A . (-1,0)B . (0,1)C . (1,2)D .(2,3)8.已知函数()=y f x 在R 上的图像是连续不断的一条曲线, 在用二分法研究函数()f x 的 零点时, 第一次计算得到数据: ()()0.50,00f f -<>,根据零点存在性定理知存在零点∈0x _______, 第二次计算 , 以上横线处应填的内容为 ( )A .()()1,0,0.25--fB .()()0.5,0,0.75f --C .()()1,0.5,0.75f ---D .()()0.5,0,0.25f --9. 2弧度的角的终边所在的象限是( )A.第一象限B. 第二象限C. 第三象限D.第四象限 10.已知角α的终边经过点(4,3)-,则cos α=( )A. 45B. 35C. 35-D. 45- 11. 已知1sin cos 8αα=,且5342ππα<<,则cos sin αα-的值为( )A. 2-B. 2C. 34-D. 3412.已知函数()f x 是定义在(,0)(0,)-∞+∞上的奇函数, 在区间(,0)-∞上单调递增且(1)0f -=.若实数a 满足212(log )(log )2(1)f a f a f -≤, 则实数a 的取值范围是( )A .(0,1)B .(0,1)(1,2] C .1(,2]2 D .1(0,](1,2]2二.填空题:本大题共4小题,每小题5分,共20分。
贵州贵阳清镇北大培文学校高一3月月考数学试卷 含答案

高一年级3月月考数学试题一.选择题(本题共12小题,每小题5分,共60分。
)1.在△ABC 中,A =60°,B =75°,a =10,则边c 等于( ) A .5B .10C .5D .2.在△ABC 中,∠A =30°,a =4,b =5,那么满足条件的△ABC ( ) A .无解B .有 一个解C .有两个解D .不能确定3.△ABC 中,角A,B,C 所对的边长分别为c b a ,,,已知sin A :sin B =3:5,2c b a =-,则cos B =( ) A .B .12-C .D .4.在△ABC 中角C B A ,,的对边分别为,,,c b a 若A+C=2B,,3,1==b a 则ABC S ∆等于( )2.A3.B 23.C 2.D 5.已知△ABC 的三个内角C B A ,,所对边长分别是c b a ,,,若ba ca C A B ++=-3sin sin sin ,则角B 的大小为( )A.6π B.3π C.32π D.65π6.在△ABC 中,1,3,2=⋅==BC AB AC AB ,则BC 等于( )3.A 7.B 22.C 23.D7.数列{}n a 中,若111,111-+==+n n a a a ,则2016a =( ) A.-1 B.21-C.21D.1 8.数列 ,161,81,41,21的递推公式可以是( ).A ()*211N n a n n ∈=+ .B ()*21N n n a n ∈=.C ()*211N n a a n n ∈=+ .D ()*21N n a a n n ∈=+9.等差数列前3项的和为30,前6项的和为100,则它的前9项的和为( ) .260A .210B .170C .130D10.如图,测量河对岸的塔的高度AB 时,可以选与塔底B 在同一水平面内的两个观测点C 与D,测得∠BCD=15°,∠BDC=30°,CD=30米,并在C 测得塔顶A 的仰角为60°,则塔AB 的高度为( )m A 215. m B 315. ()m C 1315.+ m D 615.11.若数列{}n a 的通项公式是(1)0.9n n a n =+⋅,对于任意的正整数n 都有n N a a ≤成立,则N 为( )A .6或7B .7或8C .8或9D .9或1012.锐角ABC ∆中,2B A =,则ba的取值范围是( ) ()2,2.-A ()2,0.B ()2,2.C ()3,2.D二.选择题(本题共4小题,每小题5分,共20分。
高中贵州省贵阳市清镇北大培文学校高一下学期3月月考数学试题

贵州省贵阳市清镇北大培文学校【精品】高一下学期3月月考数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.在ABC ∆中,60A =︒,75B =︒,10BC =,则AB =A .B .C .D 2.在△ABC 中,∠A =30°,a=4,b=5,那么满足条件的△ABC ( )A .无解B .有一个解C .有两个解D .不能确定 3.ABC 中,角A ,B ,C 所对的边长分别为,,a b c ,已知sin :sin 3:5A B =,2c b a =-,则cos B =( )A .1114B .12-C .1314D .24.在ABC 中角,,A B C 的对边分别为,,,a b c 若2A+C =B ,1,a =b =则ABC S ∆等于( )A B C .2 D .25.已知ABC ∆的三个内角,,A B C 所对边长分别是,,a b c ,若sin sin sin B A c C a b-+=+,则角B 的大小为( ) A .6π B .3π C .23π D .56π 6.在△ABC 中,AB=2,AC=3,1AB BC ⋅=则BC=______A B C D 7.数列{}n a 中,若11,a =1111n n a a +=-+,则2016=a ( ) A .-1B .12-C .12D .1 8.数列1111,,,,24816…的递推公式可以是( )A .()11*2n n a n N +=∈ B .()1*2n a n N n =∈ C .()11*2n n a a n N +=∈ D .()12*n n a a n N +=∈ 9.等差数列前3项的和为30,前6项的和为100,则它的前9项的和为( ) A .260 B .210 C .170 D .13010.如图,测量河对岸的塔的高度AB 时,可以选与塔底B 在同一水平面内的两个观测点C 与D ,测得15BCD ︒∠=,30BDC ︒∠=,30CD =米,并在C 测得塔顶A 的仰角为60︒,则塔AB 的高度为( )A. B. C.1)m D.11.若数列{}n a 的通项公式是(1)0.9n n a n =+⋅,对于任意的正整数n 都有n N a a ≤成立,则N 为( )A .6或7B .7或8C .8或9D .9或10 12.锐角ABC 中,2B A =,则b a 的取值范围是( ) A .()2,2-B .()0,2 C.)2 D.二、填空题 13.在ABC 中,60,A =︒2,AC=BC =,则AB =________.14.在△ABC 中,若222sin sin <sin C A B +,则△ABC 的形状是 ____.15.等差数列{}n a ,{}n b 的前n 项和分别为n S ,n T ,若2+23n n S n T n =+,则77a b =_______. 16.已知数列{}n a 满足2n a n n λ=-,且{}n a 为递增数列,则λ的取值范围是______.三、解答题17.在ABC 中,内角所对的边分别为a,b,c ,已知sin 23sin a B b A =.(Ⅰ)求B ;(Ⅱ)若1cos 3A =,求sinC 的值. 18.在△ABC 中,a 、b 、c 分别表示三个内角∠A 、∠B 、∠C 的对边,如果(a 2+b 2)sin(A -B)=(a 2-b 2)sin(A +B),判断三角形的形状.19.已知数列{}n a 满足2(*)n n S n a n N =-∈.(1)计算1,a 2,a 3,a 4,a 5a ;(2)并猜想{}n a 的通项公式(不需要证明但要求简要写出分析过程).20.已知在ABC 中,三边长a ,b ,c 依次成等差数列.(1)若sin :sin 3:5A B = ,求三个内角中最大角的度数;(2)若1b =且 ()22BA BC b a c ⋅=--,求ABC 的面积.21.在ABC 中,已知角A ,B ,C 的大小成等差数列.(1)若ABC 5a c +=,求b 的值;(2)若5b =,求a c +的取值范围.22.在数列{}n a 中,12,a =121n n n a a +=++. (1)求证:数列{}2n n a -为等差数列;(2)设数列{}n b 满足()22log 1n n b a n =+-,求{}n b 的通项公式及{}n b 的前n 项和n T .参考答案1.D【分析】根据三角形内角和定理可知45C =︒,再由正弦定理即可求出AB .【详解】由内角和定理知180(6075)45C =︒-︒+︒=︒, 所以sin sin AB BC C A=,即sin 10sin 45sin sin 603BC C AB A ⨯︒===︒, 故选D.【点睛】本题主要考查了正弦定理,属于中档题.2.C【解析】【分析】根据余弦定理a 2=b 2+c 2-2bccosA 的式子,代入题中数据化简得c 2,由根的判别式与韦达定理得到该方程有两个不相等的正实数根,由此可得△ABC 有两个解.【详解】∵在△ABC 中,∠A=30°,a=4,b=5,∴由余弦定理a 2=b 2+c 2-2bccosA ,得16=25+c 2-10ccos30°,得c 2c+9=0(*)∵△=(2-4×1×9=39>0,且两根之和、两根之积都为正数,∴方程(*)有两个不相等的正实数根,即有两个边c 满足题中的条件,由此可得满足条件的△ABC 有两个解故选:C .【点睛】本题给出三角形的两条边和其中一边的对角,判断三角形解的个数.着重考查了利用余弦定理解三角形、一元二次方程根的判别式与韦达定理等知识,属于基础题.3.A【解析】【分析】由正弦定理化简已知等式可得a =35b ,根据已知可求c =75b ,利用余弦定理即可解得cos B 的值.【详解】解:∵sin :sin 3:5A B = ∴由正弦定理可得:35a b =,可得:a =35b , ∴c =2b ﹣a =75b , ∴cos B =2222a c b ac +-=222375537255b b b b b ⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭⨯⨯=1114. 故选:A .【点睛】本题主要考查了正弦定理,余弦定理在解三角形中的综合应用,考查了计算能力和转化思想,属于基础题.4.C【分析】根据已知等式利用内角和定理求出B 的度数,确定出sin B 的值,再由a 与b 的值,利用正弦定理求出sin A 的值,确定出A 的度数,进而确定出C 的度数,即可求出sin C 的值.【详解】∵A +C =2B ,A +B +C =180°,∴B =60°,∵a =1,bsin B=2, ∴由正弦定理sin a A =sin b B 得:sin A =asin B b1=12, ∵a <b ,∴A <B =60°,∴A =30°,即C =90°,则sin C =1.所以11=sin 122ABC S ab C ∆=⨯ 故选:C.【点睛】此题考查了正弦定理,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键. 5.D【解析】由正弦定理得b a c -=,化简得222cos 2a c b B ac +-==,故5π6B =. 点睛:本题主要考查正弦定理的应用,考查利用正弦定理进行边角互化的方法.由于题目所给已知条件一边是角的形式,另一边是边的形式,由此我们考虑将两边同时化为边或者同时转化为角的形式,考虑到正弦定理,故将角转化为边,然后利用余弦定理将式子转化为余弦值,由此求得B 的 大小.6.A【详解】2222149||||cos ()122BC AB BC AB BC B AB BC AC +-⋅=-⋅=-+-=-=|BC ∴故选:A【点评】本题考查平面向量的数量积运算、余弦定理等知识.考查运算能力,考查数形结合思想、等价转化思想等数学思想方法.7.B【分析】 移项得到1111n n a a ++=+,则数列{}1n a +是周期数列,求出周期和一个周期内的函数值,对应求20161+1=2a ,解出2016a 即可得到答案. 【详解】解:1111n n a a +=-+,则1111n n a a ++=+,所以211111111n n n n a a a a +++===+++,所以数列{}1n a +是周期数列,周期为2. 又11,a =,12,1a += 2111112a a +==+,12112n n a a +=⎧⎪∴⎨+=⎪⎩n n 为奇数为偶数 ,20161+1=2a ∴,即201612a =-. 故选:B.【点睛】本题考查数列的周期性和求数列通项,解题的关键是正确理解数列的定义,求出新数列的通项公式,属于基础题.8.C【分析】 观察数列,数列从第二项起,可知每一项是前一项的12,由此可以得到递推公式,得出结果.【详解】 解:由题意可知,数列从第二项起,后一项是前一项的12,所以递推公式为()*112n n a a n N +=∈. 故选:C.【点睛】本题考查观察法求数列的通项公式和递推公式,属于基础题.9.B【分析】依题意,S 3、S 6﹣S 3、S 9﹣S 6成等差数列,从而可求得答案.【详解】解:∵等差数列{a n }的前3项和为30,前6项和为100,即S 3=30,S 6=100, 又S 3、S 6﹣S 3、S 9﹣S 6成等差数列,∴2(S 6﹣S 3)=(S 9﹣S 6)+S 3,即140=S 9﹣100+30,解得S 9=210,故选:B .【点睛】本题考查等差数列的性质,熟练利用S 3、S 6﹣S 3、S 9﹣S 6成等差数列是关键,属于基础题.10.D【分析】在△BCD 中,由正弦定理得BC ,在Rt △ABC 中,求出AB .【详解】解:在△BCD 中,由正弦定理得sin 30BC CD sin135︒︒==,在Rt △ABC 中,AB BCtan 60︒== 故选:D .【点睛】本题主要考查利用三角函数以及解三角形的知识解决实际问题,考查学生数形结合思想的应用,属于基础题.11.C【分析】作差判断数列的单调性,得到当8n <时,1n n a a +>,数列{}n a 单调递增;当8n >时,1n n a a +<,数列{}n a 单调递减,当8n =时,98a a =,由此可判断数列的最大项.【详解】解:()()11(2)0.9(1)0.90.90.92(1)n n n n n a a n n n n ++-=+⋅-+⋅=+-+=()0.90.80.1n n -, 当8n =时,10n n a a +-=,当8n <时,10n n a a +->,当8n >时,10n n a a +-<. 所以当8n <时,1n n a a +>,数列{}n a 单调递增;当8n >时,1n n a a +<,数列{}n a 单调递减,所以当8n =时,98a a =为数列的最大项.故选:C.【点睛】本题考查求数列最大项,涉及做差求数列的单调性,属于基础题.12.D【分析】利用正弦定理,结合B =2A ,可得sin sin B A =sin 2sin A A =2cos A ,确定A 的范围,即可得到结论. 【详解】 由正弦定理可得,b a =sin sin B A ∵B =2A ,∴sin sin B A =sin 2sin A A=2cos A ∵B =2A ,A +B +C =π∴C =π﹣3A∵0<C <2π,0<B <2π ∴0<π﹣3A <2π,0<2A <2π ∴6π<A <4π∴2<cos A<2cos A∴b a 故选:D .【点睛】本题考查正弦定理的运用,考查三角函数的性质,考查学生的计算能力,属于中档题. 13.1【分析】在ABC 中,则根据余弦定理有2222cos60BC AC AB AC AB =+-⋅,根据题干条件,代入数据,解方程,即可求得AB 的值.【详解】解:在ABC 中,由余弦定理可知,2222cos60BC AC AB AC AB =+-⋅则有2134222AB AB =+-⨯⨯,即2210AB AB -+=,解得1AB =. 故答案为:1 【点睛】本题考查余弦定理解三角形,属于基础题. 14.钝角三角形 【分析】由222sin sin sin A B C +<,结合正弦定理可得,222a b c +<,由余弦定理可得222cos 2a b c C ab+-=可判断C 的取值范围 【详解】 解:222sin sin sin A B C +<,由正弦定理可得,222a b c +<由余弦定理可得222cos 02a b c C ab +-=<∴2C ππ<<ABC ∆∴是钝角三角形故答案为钝角三角形. 【点睛】本题主要考查了正弦定理、余弦定理的综合应用在三角形的形状判断中的应用,属于基础题 15.74【分析】利用等差数列的性质对所求进行转化,得到()()1131137711311377131313221322a a a a a a Sb b b b T b b ⨯====⨯++++,再根据2+23n n S n T n =+,代入13n =即可求得结果. 【详解】解:()()11311377113117371313213+228713316132213242a a a a a a S b b b b T b b ++⨯=⨯====++==⨯+. 故答案为:74.【点睛】本题考查已知等差数列和的比求数列具体项的比值,涉及到等差数列的性质,考查了转化的思想,属于中档题. 16.(),3-∞ 【分析】数列{}n a 为递增数列,则10n n a a +->,做差即可求出λ的取值范围. 【详解】解:{}n a 为递增数列,则10n n a a +->,所以221(1)(1)210n n a a n n n n n λλλ+-=+-+-+=+->,即()21,n n N λ*<+∈,所以3λ<.故答案为:(),3-∞. 【点睛】本题考查已知数列的单调性求参数的取值范围,做差法是判断数列单调性的常用方法,属于基础题. 17.(Ⅰ)6B π=;(Ⅱ)16. 【解析】试题分析:(Ⅰ)利用正弦定理,将边化为角:2sin sin cos 3sin sin A B B B A =,再根据三角形内角范围化简得,6B π=;(Ⅱ)已知两角,求第三角,利用三角形内角和为π,将所求角化为两已知角的和,再根据两角和的正弦公式求解. 试题解析:(Ⅰ)解:在ABC 中,由,可得,又由,得,所以,得6B π=;(Ⅱ)解:由,可得,则sin sin[()]sin()C A B A B π=-+=+sin()6A π=+.【考点】同角三角函数的基本关系、二倍角的正弦公式、两角和的正弦公式以及正弦定理 【名师点睛】三角函数是以角为自变量的函数,因此解三角函数题,首先从角进行分析,善于用已知角表示所求角,即注重角的变换.角的变换涉及诱导公式、同角三角函数基本关系、两角和与差的公式、二倍角公式、配角公式等,选用恰当的公式是解决三角问题的关键,明确角的范围,对开方时正负取舍是解题正确的保证.18.等腰或直角三角形 【解析】已知等式可化为a 2[sin(A -B)-sin(A +B)]= b 2[-sin(A +B)-sin(A -B)], ∴2a 2cosAsinB =2b 2cosBsinA.由正弦定理得sin 2AcosAsinB =sin 2BcosBsinA ,∴sinAsinB(sinAcosA -sinBcosB)=0,∴sin2A =sin2B.由0<2A<2π,0<2B<2π得2A =2B 或2A =π-2B ,即△ABC 为等腰或直角三角形. 19.(1)11a =.232a =,374a =,4158a =,53116a =. (2)121,2n n n a --=*n ∈N ,详见解析【分析】(1)将1,2,3,4,5n =逐步代入求解即可. (2)根据所求数值寻找规律,猜想公式. 【详解】解:(1)当1n =时,1112a S a ==-,11a ∴=.当2n =时,122222a a S a +==⨯-,232a ∴=, 当3n =时,1233323a a a S a ++==⨯-,374a ∴=,当4n =时,12344424a a a a S a +++==⨯-,4158a ∴=,当5n =时,12345525a a a a a a ++++=⨯-,53116a ∴=. (2)11112112a --==,222132122a --==,333172142a --==,4441152182a --==,55513121162a --==, 由此猜想121,2n n n a --=*n ∈N .【点睛】本题考查代入法求数列某一项的具体值,考查由数值猜想数列的通项公式,考查了学生对数字的规律认知,属于基础题.20.(1)120;(2 【解析】 【分析】⑴依题意设3a k =,()0k >,则5b k =,7c k =,利用余弦定理即可求得三个内角中最大角的度数;⑵利用向量的数量积和余弦定理即可得到ac 的值和23cosB =,进而得到sin B =,然后根据三角形的面积公式求得答案(1),,a b c 依次成等差数列,得2b a c =+ 又sin :sin 3:5A B = , :3:5a b ∴=设3,5a k b k ∴== ,则7c k ∴=∴最大角为 C由2221cos 22a b c C ab +-==- ,得120C =(2)由1,2b a c =+=又由()22BA BC b a c ⋅=-- 得()22cos ac B b a c ⋅=--222922cos ,cos 103b ac ac B ac B =+-⋅∴==,sin 3B ∴=从而ABC 的面积为119sin 2210ac B =⨯=【点睛】本题主要考查了正弦定理、余弦定理及面积公式解三角形,熟练运用公式是解题关键,较为基础。
贵州省清镇十- 高一数学下学期3月月考卷

下学期3月月考卷高一数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟. 第Ⅰ卷(选择题 共60分)一、选择题 (本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知直线1l :320ax y +-=与2l :(1)0a x ay -+=垂直,则a 等于( )A . 2-B . 1-C . 0或2-D . 2-或1-【答案】C2.已知直线0=++c by ax 与圆1:22=+y x O 相交于,A B 则OB OA ⋅的值是( )A B C D .0【答案】A 3.如图所示,定点A 和B 都在平面α内,定点P α,PB ⊥α,C 是α内异于A 和B 的动点,且PC ⊥AC ,那么,动点C 在平面α内的轨迹是( )A .一条线段,但要去掉两个点B .一个圆,但要去掉两个点C .一个椭圆,但要去掉两个点D .半圆,但要去掉两个点 【答案】B4.三条直线123:0:20:5150l x y l x y l x ky -=+-=--=,,构成一个三角形,则k 的取值范围是( )A .k R ∈B .1,0k R k k ∈≠±≠且C .5,10-k R k k ∈≠±≠且D .5,1k R k k ∈≠±≠且【答案】C5.直线0320sin 20cos 00=-+y x 的倾斜角是( )A .020B .0160C .070D .0110 【答案】D6.自点()1,4A -作圆()()22231x y -+-=的切线,则切线长为( )A B .3 C D .5【答案】B7.已知a ≠b ,且a 2sin θ+acos θ-0 ,b 2sin θ+bcos θ-0,则连接(a ,a 2),(b ,b 2)两点的直线与单位圆的位置关系是( )A .相交B .相切C .相离D .不能确定 【答案】A8.已知圆C :x 2+y 2+4x-12y+24=0.若直线l 过点P (0,5)且被圆C 截得的线段长为则l 的方程为( )A . 3x-4y+20=0B . 4x-3y+15=0C .3x-4y+20=0或x=0D . 3x-4y+20=0 或 4x-3y+15=0 【答案】C9时,直线02tan =-+y x α的倾斜角是( )B C .απ- D .α【答案】C10.圆心为 (1,-2),x 轴上截得的弦长是( )A . 8B .6CD 【答案】A11.直线052sin =-+⋅y x θ的倾斜角的取值范围是( )A B C D 【答案】C 12.设直线与两坐标轴分别交于A ,B 两点,若圆C 的圆心在原点,且与线段AB 有两个交点,则圆C 的半径的取值范围是( )A .B .C .D .(3,4)【答案】B第Ⅱ卷(非选择题 共90分) 二、填空题 (本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)13.已知直线1:210l x my +-=和()2:3110l m x my --+=互相平行,则实数m 的值为14.过点(-1,-2)的直线l 被圆x 2+y 2-2x -2y +1=0截得的弦长为2,则直线l 的斜率为____________【答案】1或17715.设曲线423+-=x x y 在点)3,1(处的切线为l ,则直线l 的倾斜角为16.设圆22:1,:240O x y l x y +=+-=直线,点A l ∈,若圆O 上存在点B ,且30OAB ∠=︒(O 为坐标原点),则点A 的纵坐标的取值范围是 。
北大培文三月份联考理科_20180327213500
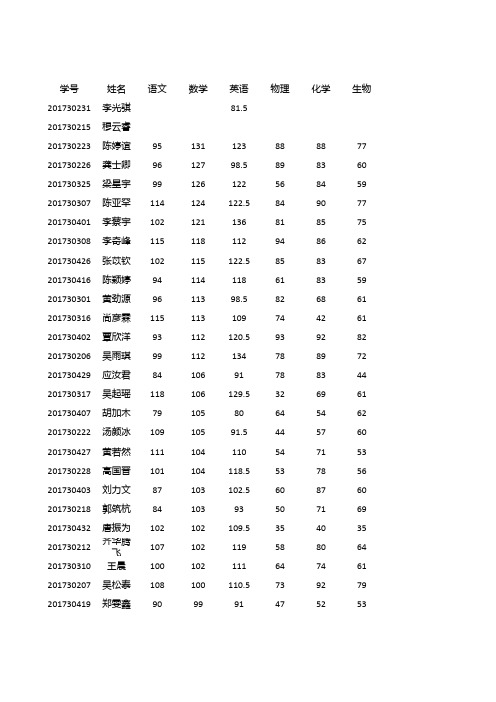
学号姓名语文数学英语物理化学生物201730231李光骐81.5201730215穆云睿201730223陈婷谊95131123888877 201730226龚士卿9612798.5898360 201730325梁星宇99126122568459 201730307陈亚罕114124122.5849077 201730401李蔡宇102121136818575 201730308李奇峰115118112948662 201730426张苡钦102115122.5858367 201730416陈颖婷94114118618359 201730301黄劲源9611398.5826861 201730316尚彦霖115113109744261 201730402覃欣洋93112120.5939282 201730206吴雨琪99112134788972 201730429应汝君8410691788344 201730317吴起瑶118106129.5326961 201730407胡加木7910580645462 201730222汤颜冰10910591.5445760 201730427黄若然111104110547153 201730228高国晋101104118.5537856 201730403刘力文87103102.5608760 201730218郭筑杭8410393507169 201730432唐振为102102109.5354035201730212齐华腾飞107102119588064201730310王晨100102111647461 201730207吴松泰108100110.5739279 201730419郑雯鑫909991475253201730221王汉坤909986.5525757 201730322杨正如989984.5596257201730214刘逸品骥9498124669267201730408伍斯豪919799473446 201730323张龄心10297116678270 201730404田俊杰8996102.5668441 201730330杨静蕾1069599.5373848 201730415林楷恒999484639067 201730220毛楠林879495476566 201730424罗彩文10993125.5487560 201730230冯靓容1099398.5284370 201730309曾鹏宇9693123518579 201730327谢吉雨10893125407661 201730428张景峰1109293.5739078 201730412兰子凌10792108827559 201730425申茂新9192105.5497458 201730318刘宏鑫9792118876163 201730225陈美妃10791124.5496654 201730333樊秉鑫8891120.5687982 201730303李雅涵8991116567159 201730414杨凯翔7090113.5618174 201730405邓煕月9890121.5466858 201730302郭先桂9790113638156 201730320柯曼琪9690119.5524672 201730406谯竹君10789115506454 201730423任芷希1018992495465 201730209邓正松10889107584852 201730210罗彩嘉89201730319陈培鎏11789106375655 201730418董安杰10188128566361 201730306马正仪948883.5344554 201730229赵骏杰9087130.5445252 201730202王缤珧928698535050 201730420靳佳睿1038593446657201730311程周自由10685130608169201730324陈明杨8485112407675 201730326刘睿洁9985107577346 201730227倪嘉逊9284104.5506457 201730304张莹10684132.5518163 201730328彭豪10084120537057 201730417严骋信1028385698462 201730421代季霖10583106.5277048 201730335龙姝羽9083100423132 201730329李天阳8682113618662 201730211雷咏行10381114.5496666 201730431徐萍11280110836858 201730216付忠林10280102688767 201730219曹艺煕10680123366158 201730233杨俊杰8979104.5326445 201730332孙艺溶9879112.5416066201730201吴童翼源9878123.5625272201730217李露玲9978112.5425352 201730208杨博迪8876117668071 201730213赵惟琦957695455858 201730313李熙媛10476115644061 201730312王相基10175105.5345571201730434张晏龄10674121.5285753 201730204杨帆9574104535638 201730331王柯凝9674107324843 201730413冯祖晗10170107567271 201730433吴天驷986963574950 201730305徐哲豪9469106656258 201730314林小荇976999605260 201730321张嘉仪10568119427259 201730422田家睿9767114.5427760 201730315吴金洋9767117484539 201730430杨睿智8765114357036 201730234仇梓瑜8963106265757 201730409罗四宏996111664063201730411刘羽沁溦915884414054201730232欧程鹏975885576876 201730410田知远895591335742 201730235李伊雯1014983.5466038 201730203徐若凯10346109.5454236 201730205李尚谕984487.5363962 201730224刘崇瑞3553.5。
贵州省贵阳清镇北大培文学校2022-2023学年高一下学期3月月考英语试题及参考答案

贵阳市北大培文学校2022-2023学年第二学期3月月考高一年级英语学科试题考试时间:120分钟分值:150分第I卷(选择题)第一部分听力(共20小题;每小题1.5分,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C 三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What does the woman decide to do tomorrow?A. Play with Lucy.B. See a movie.C. Attend a wedding.2. What kind of music does the woman like best?A. Light music.B. Pop music.C. Underground music.3.Where does the conversation probably take place?A. In the office.B. In the hospital.C. In the drugstore.4. What time does the plane take off?A. At 7:30 a.m.B. At 8:00 a.m.C. At 10:00 a.m.5. What do the speakers think of the final exam?A. Just so-so.B. Difficult.C. Easy.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6、7 题。
贵州省贵阳清镇北大培文学校2021-2021学年高二数学3月月考试题 文

贵州省贵阳清镇北大培文学校2021-2021学年高二数学3月月考试题文一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合A ={x ∈N}2x <,B ={}1,0,1,2-,则A B = ( )A .{}1B .{}0,1C .{}1,0,1-D .{}0,1,22.若复数12ia i ++为纯虚数,其中a 为实数,则a = ( ) A .12- B .12C .2-D .23.若向量(,0)a m =,(2,2)b m =-,则“2m =”是“//a b ”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件4.从个位数与十位数之和为奇数的两位数中任取一个,其中个位数为0的概率是( )A .49 B .13 C .29D .195.一次实验:向下图所示的正方形中随机撒一大把豆子,经查数,落在正方形中的豆子的总数为N 粒,其中)(N m m <粒豆子落在该正方形的内切圆内,以此估计圆周率π为( ) (A)N m (B)N m 2 (C)N m3 (D)Nm 4 6. 设等差数列{}n a 的前n 项和为n S ,若3457=a a ,则57=S S ( ) A .12B .1C .57D .757.设p :f (x )=x 3−2x 2−mx +1在(−∞,+∞)上单调递增;q :m <43-,则p 是q 的( )A .充要条件B .充分不必要条件C .必要不充分条件D .以上都不对8.阅读右面的程序框图,则输出的S=A. 14B. 20C. 30D. 559.已知F 1,F 2是椭圆的两个焦点,若椭圆上存在点P ,使得PF 1⊥PF 2,则椭圆离心率的取值范围是( ) A . [,1) B . [,1) C . (0,] D .(0,] 10.设定义在R 上的函数()f x ,函数(1)'()y x f x =-的图像如图所示,则下列结论成立的是( )A 、函数()f x 有极大值(2)f 和极小值(1)fB 、函数()f x 有极大值(2)f -和极小值(1)fC 、函数()f x 有极大值(2)f 和极小值(2)f -D 、函数()f x 有极大值(2)f -和极小值(2)f11.过双曲线2222:1(0,0)-=>>x y C a b a b的左焦点为1F ,且和圆222+=x y a 相切的直线l 交C的右交于点Q .若切点P 恰为线段1F Q 的中点,则C 的离心率为 ( )A .5B . 5C .3D .312.已知双曲线22221(0,0)x y a b a b-=>> 的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于,A B 两点.设,A B 到双曲线的同一条渐近线的距离分别为1d 和2d ,且126,d d +=则双曲线的方程为( )A .22139x y -=B .22193x y -=C .221412x y -=D .221124x y -=二、填空题:本大题共4小题,每小题5分,共20分.13.已知一组数据:93,89,90,,87x 的平均数为90,则该组数据的方差为______. 14.等比数列{}n a 满足122+=a a ,4516+=-a a ,则数列{}n a 的通项公式是_______. 15.如图P 为抛物线24y x =上的动点,过P 分别作y 轴与直线40x y -+=的垂线,垂足分别为,A B ,则PB PA +的最小值为_____________.16.已知函数()31f x ax x =++的图像在点()()1,1f 的处的切线过点()2,7,则 a = .三、解答题:共70分.解答题应写出文字说明、证明过程或演算步骤. 17.已知数列}{n a :*).(2121212221N n n n a a a n n ∈+=-+⋅⋅⋅+-+-求: (1)数列}{n a 的通项公式; (2)数列}{n a 的前n 项和S n .18.移动公司在国庆期间推出4G 套餐,对国庆节当日办理套餐的客户进行优惠,优惠方案如下:选择套餐1的客户可获得优惠200元,选择套餐2的客户可获得优惠500元,选择套餐3的客户可获得优惠300元.国庆节当天参与活动的人数统计结果如图1054所示,现将频率视为概率.(1)求从中任选1人获得优惠金额不低于300元的概率; (2)若采用分层抽样的方式从参加活动的客户中选出6人,再从该6人中随机选出2人,求这2人获得相等优惠金额的概率.19.(本小题满分12分)小王从2007年年初开始创业,下表是2018年春节他将自己从2007—2017年的净利润按年度给出的一个总的统计表(为方便运算,数据作了适当的处理,单位:万元).年度 2007 2008 2009 2010 2011 2012 2013 2014 2015 2016 2017 利润 5 6 7 8 9 10 11 11 12 13 13 记2007年为第1年,依次为第2年……,并得到如下图所示的散点图.(I )根据散点图指出年利润y (单位:万元)和年份序号t (t =1, 2, …)之间是否具有线性关系? 并用相关系数说明用线性回归模型描述变量年净 利润y 与年份序号t 之间关系的效果; (II )如果用线性回归模型描述变量年净利润y 与 年份序号t 之间的关系效果很好,请建立年净利润 y 关于年份序号t 的回归方程(系数精确到0.1), 并帮小王估计他2018年可能赚到的净利润;否则,y · · · ·· ·· · · ·2 4 6 8 10 12 14 · · · · · · 1 234 ·56789 10 · 11 t· · ·· · · · · · · ·请选择合适的方法帮助小王估计2018年的净利润.附注:参考数据1119.6,721,8.8,10.5====∑i ii y t y.参考公式:()()---⋅⋅=∑∑nnii i itt y y t yn t yr 1≤r 且r 越大拟合效果越好.回归方程=+y bt a 斜率的最小二乘估计公式为:121()()()==--=-∑∑nii i nii tt y y b tt .20.已知椭圆2222:1(0)x y M a b a b +=>>的离心率为3焦距为.斜率为k 的直线l 与椭圆M 有两个不同的交点A ,B .(1)求椭圆M 的方程;(2)若1k =,求||AB 的最大值;(3)设(2,0)P -,直线PA 与椭圆M 的另一个交点为C ,直线PB 与椭圆M 的另一个交点为D .若C ,D 和点71(,)42Q - 共线,求k .21.已知函数()ln(1)(1)1f x x k x =---+.(I )当1k =时,求函数()f x 的最大值;(II )若函数()f x 没有零点,求实数k 的取值范围;22.(本小题满分10的单调区间为[)1,-+∞. (I 的解集M ; (II )若,∈a b M ,证明:高二3月月考 数学(文科)参考答案13. 4 14. (2)=-nn a 151- 16.1 17.解:(1)∵.2121212221n n a a a n n +=-+⋅⋅⋅+-+-(1) .)1()1(2121212211221n n n n a a a n n -=-+-=-+⋅⋅⋅+-+---(2) 由(1)—(2)得*),2(122211N n n n a n a n n nn ∈≥+=⇒=-+ (3) 在(1)中令适合有511==a n (3)式,故*)(121N n n a n n ∈+=+(2)设,21+=n n n b 其前n 项和为,n T 则14322232221+⋅+⋅⋅⋅+⋅+⋅+⋅=n n n T (4)254322322212+⋅+⋅⋅⋅+⋅+⋅+⋅=n n n T (5)由(5)—(4)得215432222222++⋅+-⋅⋅⋅-----=n n n n T42)1(221222222+-=⋅+---=+++n n n n n42)1(2++-=+=∴+n n n T S n n n18. (1)设事件A 为 “从中任选1人获得优惠金额不低于300元”,则P (A )=150+10050+150+100=56.(2)设事件B 为“从这6人中选出2人,他们获得相等优惠金额”,由题意按分层抽样方式选出的6人中,获得优惠200元的有1人,获得优惠500元的有3人,获得优惠300元的有2人,分别记为a 1,b 1,b 2,b 3,c 1,c 2,从中选出2人的所有基本事件如下:a 1b 1,a 1b 2,a 1b 3,a 1c 1,a 1c 2,b 1b 2,b 1b 3,b 1c 1,b 1c 2,b 2b 3,b 2c 1,b 2c 2,b 3c 1,b 3c 2,c 1c 2,共15个.其中使得事件B 成立的有b 1b 2,b 1b 3,b 2b 3,c 1c 2,共4个. 则P (B )=415.19.解:(I )由图可知两个变量之间具有线性相关关系.根据题中所给参考公式,得111()()=--∑ii i tt y y 11111==-∑i i i t y t y 7211169.687.4=-⨯⨯=. ……2分所以,11()()87.40.9592.4--==≈∑ii tt y y r . ……4分 因为r 0.95≈接近1,所以两个变量之间有很强的线性相关关系,用线性回归模型描述年净利润y 与年份序号t 之间的关系效果很好. ……6分 (II )由(I )知,能用线性回归模型描述变量年净利润y 与年份序号t 之间的关系.根据题中所给参考公式,得11111221()()87.40.7910.5()==--==≈-∑∑ii i ii tt y y b tt , ……8分 9.60.796 4.86=-≈-⨯=a y bt ,所以回归直线方程为0.8 4.9=+y t . ……10分因为2018年对应的12=t ,所以小王2018的净利润估计为14.5万元. ……12分 (注:如果学生0.8≈b , 4.8≈a ,则利润估计值为14.4万元.也算对,评讲时要强调)20.(1)由题意得2c =,所以c=又3c e a ==,所以a =所以2221b a c =-=, 所以椭圆M 的标准方程为2213x y +=.(2)设直线AB 的方程为y x m =+,由2213y x m x y =+⎧⎪⎨+=⎪⎩消去y 可得2246330x mx m ++-=, 则2223644(33)48120m m m ∆=-⨯-=->,即24m <,设11(,)A x y ,22(,)B x y ,则1232m xx +=-,212334m xx -=,则12|||2AB x x=-==, 易得当20m =时,max ||AB ,故||AB .(3)设11(,)A x y ,22(,)B x y ,33(,)C x y ,44(,)D x y ,则221133x y += ①,222233x y += ②,又(2,0)P -,所以可设1112PA y k k x ==+,直线PA 的方程为1(2)y k x =+,由122(2)13y k x x y =+⎧⎪⎨+=⎪⎩消去y 可得2222111(13)121230k x k x k +++-=,则2113211213k x x k +=-+,即2131211213k x x k =--+,又1112y k x =+,代入①式可得13171247x x x --=+,所以13147y y x =+,所以1111712(,)4747x y C x x --++,同理可得2222712(,)4747x y D x x --++.故3371(,)44QC x y =+-,4471(,)44QD x y =+-,因为,,Q C D 三点共线,所以34437171()()()()04444x y x y +--+-=,将点,C D 的坐标代入化简可得12121y y x x -=-,即1k =.21.解:(I )当1k =时,2()1xf x x -'=- )(x f 定义域为(1,+∞),令()0,2f x x '==得, ∵当(1,2),x ∈时()0f x '>,当(2,),x ∈+∞时()0f x '<, ∴()(1,2)f x 在内是增函数,(2,)+∞在上是减函数∴当2x =时,()f x 取最大值(2)0f =(II )①当0k ≤时,函数ln(1)y x =-图象与函数(1)1y k x =--图象有公共点,∴函数()f x 有零点,不合要求;②当0k >时,1()11()111k k x k kx k f x k x x x +-+-'=-==---- 令1()0,k f x x k +'==得,∵1(1,),()0,k x f x k +'∈>时1(1,),()0x f x k '∈++∞<时,∴1()(1,1)f x k +在内是增函数,1[1,)k++∞在上是减函数,∴()f x 的最大值是1(1)ln f k k+=-,∵函数()f x 没有零点,∴ln 0k -<,1k >,因此,若函数()f x 没有零点,则实数k 的取值范围(1,)k ∈+∞.22.解:(I )由已知1=t ,所以,不等式为……1分当1<-x 时,(1)1(21)-++<-+x x ,得1<-x ; ……2分(1)1(21)++<-+x x ,此时不等式无解; ……3分时,(1)1(21)++<+x x ,得1>x . ……4分……5分(II 222()212++>++ab ab a ab b ,只需证 222()10--+>ab a b .只需证 22(1)(1)0-->a b . ……8分 因为,∈a b M ,所以,22(1)(1)0-->a b 成立.所以,当,∈a b M , ……10分。
贵州省贵阳清镇北大培文学校贵州校区2024年高三3月总复习质检(一模)化学试题含解析

贵州省贵阳清镇北大培文学校贵州校区2024年高三3月总复习质检(一模)化学试题注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(共包括22个小题。
每小题均只有一个符合题意的选项)1、下列说法正确的是A.Fe3+、SCN-、NO3-、Cl-可以大量共存B.某碱溶液中通入少量CO2产生白色沉淀,该碱一定是Ca(OH)2C.Na[Al(OH)4]溶液和NaHCO3溶液混合可以产生白色沉淀和无色气体D.少量的Mg(HCO3)2溶液加过量的Ba(OH)2溶液的离子方程式为:Mg2++2HCO3-+2Ba2++4OH-=2BaCO3↓+Mg(OH)2↓+2H2O2、设N A为阿伏加德罗常数的值。
下列关于常温下0.1mol/LNa2S2O3溶液与pH=1的H2SO4溶液的说法正确的是()A.1LpH=1的H2SO4溶液中,含H+的数目为0.2N AB.98g纯H2SO4中离子数目为3N AC.含0.1molNa2S2O3的水溶液中阴离子数目大于0.1N AD.Na2S2O3与H2SO4溶液混合产生22.4L气体时转移的电子数为2N A3、用下列实验装置和方法进行相应实验,能达到实验目的的是A.甲装置用于分离CCl4和I2B.乙装置用于分离乙醇和乙酸乙酯C.丙装置用于分离氢氧化铁胶体和氯化钠溶液D.丁装置用于由氯化铵饱和溶液得到氯化铵晶体4、为研究某固体混合物样品的成分,取等质量的两份该固体,进行如下实验(不考虑盐类的水解及水的电离):(1)一份固体溶于水得透明溶液,加入足量BaCl2溶液,得沉淀6.63 g,在沉淀中加入过量稀盐酸,仍有4.66 g沉淀。
2022-2023学年贵州省贵阳清镇北大培文学校贵州校区高一数学第一学期期末监测试题含解析

(2)
22.已知幂函数 的图像经过点( ),函数 为奇函数.
(1)求幂函数 的解析式及实数a的值;
(2)判断函数f(x)在区间(-1,1)上的单调性,并用的数单调性定义证明
参考答案
一、选择题(本大题共12小题,共60分)
1、B
【解析】直接根据集合的交集、并集、补集的定义判断集合间的关系,从而求出结论
由题意可得: ,即 ,
所以 ,
即 ,
又因为 ,所以 ,
即从2027年开始该市全年用于垃圾分类的资金超过1亿元.
故选:B
10、D
【解析】直接利用全称命题的否定为特称命题进行求解.
【详解】命题“ ”为全称命题,
按照改量词否结论的法则,
所以否定为: ,
故选:D
11、A
【解析】 ,所以 ,故选A.
考点:集合 运算.
A.-8
B.-16
C.8
D.16
4.关于 的方程 的实数根的个数为()
A.6B.4
C.3D.2
5.已知函数 ,若方程 有8个相异实根,则实数 的取值范围
A. B.
C. D.
6.为了得到函数 的图像,可以将函数 的图像
A.向右平移 个单位长度B.向右平移 个单位长度
C.向左平移 个单位长度D.向左平移 个单位长度
17.整治人居环境,打造美丽乡村,某村准备将一块由一个半圆和长方形组成的空地进行美化,如图,长方形的边 为半圆的直径,O为半圆的圆心, ,现要将此空地规划出一个等腰三角形区域 (底边 )种植观赏树木,其余的区域种植花卉.设 .
(1)当 时,求 的长;
(2)求三角形区域 面积的最大值.
18.已知直线 的方程为
贵州省贵阳清镇北大培文学校2022-2023学年高二下学期3月月考(4班)化学试题(原卷版)

17.某无色透明溶液中可能大量存在Ag+、Mg2+、Cu2+、Fe3+、Na+中的几种,请填写下列空白:
(1)不做任何实验就可以肯定原溶液中不存在的离子是________________。
(2)取少量原溶液,加入过量稀盐酸,有白色沉淀生成;再加入过量的稀硝酸,沉淀不消失。说明原溶液中肯定存在的离子是___________,有关的离子方程式为______________________。
A.厨房中用的食盐、食醋都是电解质
B.石油的分馏、煤的干馏、石油的裂解都是化学变化
C.古代的陶瓷、砖瓦、现代的玻璃、水泥等,都是硅酸盐产品
D.工业上通过电解熔融的氯化物制取Na、Mg、Al三种金属
2.下列有关化学用语的表示,正确的是
A.次氯酸的电子式: B.CS2分子的比例模型:
C.钾离子的结构示意图: D.碳酸的电离方程式:H2CO3 CO +2H+
① ② ③ ④氨水
(6)常温下,下列说法正确的是_______(填字母序号)。
a. 相等 氨水和 溶液, 相等
b.稀释 的硫酸溶液,溶液中的离子浓度均下降
c. 的 溶液和 的 溶液,
19. 溶液常用作氧化还原反应滴定的标准液,利用 氧化 制备 的装置如图所示(加热、夹持装置略):
已知: 在浓强碱溶液中可稳定存在,碱性减弱时易发生反应:
A. 中含有的质子数目为
B. 中含有的碳碳双键数目为
C. 与足量的S反应转移的电子数为
D. 与 的混合物中所含中子数为
7.常温下,下列各组离子在指定溶液中能大量共存的是
A. 氨水溶液:Na+、K+、OH-、NO
B. 盐酸溶液:Na+、K+、SO 、SiO
贵州省贵阳清镇北大培文学校贵州校区2023届高一上数学期末监测试题含解析

14、
【解析】由直四棱柱 的底面是边长为1的正方形,侧棱长 可得 由 知 就是异面直线 与 的夹角,且 所以 =60°,即异面直线 与 的夹角大小等于60°.
【小问1详解】
解: 时, ;
又
;
【小问2详解】
解:由 得
所以
解得:
所以实数m的取值范围为:
18、(1) ;(2) .
【解析】(1)依题意可设 , ,分别代入到直线 和 中,求出点 坐标,即可求出直线 的方程;
(2)由题意可知 ,求出 ,即可求出圆的方程
【详解】(1)依题意可设 ,因为线段 被点 平分,所以 ,
(3)利用换元法,结合二次函数零点分布等知识来求得 的取值范围.
【小问1详解】
因 ,所以 即
此时 ,
由
【小问2详解】
令 , ,则 ,对称轴为
① ,即 ,
② ,即 ,
③ ,即 ,
综上可知, .
【小问3详解】
令 ,
由题意可知,当 时, 有两个不等实数解,
所以原题可转化为 在 内有两个不等实数根
所以有
22、(1) , 或 ; (2) 或 .
(2)由题知函数 ,且 在区间 上有两个不同的零点,
则 ,即 ,
解得 ,
所以实数 的取值范围是
【点睛】本题考查了二次函数的图象与性质的应用问题,也考查了不等式(组)的解法与应用问题,综合性较强,属中档题.
21、(1)
贵州省贵阳清镇北大培文学校2023届高一上数学期末学业质量监测模拟试题含解析

7、A
【解析】直接利用诱导公式和两角和的正弦公式求出结果
【详解】 ,
故选:
8、D
【解析】根据函数 是奇函数的性质可求得m,再由函数 的单调性和对数函数的性质可得选项.
【详解】解:因为函数 的定义在R上的奇函数,所以 ,即 ,解得 ,
所以 ,所以 在R上单调递减,
又因为 , ,所以
故选:D.
15.已知幂函数 在 上为减函数,则实数 _______
16.已知 ,若 ,则 ________
三、解答题(本大题共6小题,共70分)
17.某企业开发生产了一种大型电子产品,生产这种产品的年固定成本为2500万元,每生产 百件,需另投入成本 (单位:万元),当年产量不足30百件时, ;当年产量不小于30百件时, ;若每件电子产品的售价为5万元,通过市场分析,该企业生产的电子产品能全部销售完.
【详解】函数 的零点个数即函数 与函数 交点的个数,绘制函数图象如图所示,
观察可得交点个数为2,则函数 的零点个数是2.
本题选择C选项.
【点睛】本题主要考查函数零点的定义,数形结合的数学思想等知识,意在考查学生的转化能力和计算求解能力.
12、A
【解析】先由 得到 ,利用基本不等式“1的妙用”即可求出最小值.
(2)利用函数的平移变换求出函数g(x)的关系式,进一步求出函数的单调区间
(3)利用函数的定义域求出函数的值域
【详解】(1) 的最小正周期为 ,所以 ,即 =2,
又因为 ,则 ,所以 .
(2)由(1)可知 ,则 ,
① 由 得,
函数 增区间为 .
② 因为 ,所以 .
当 ,即 时,函数 取得最大值,最大值为 .
【点评】本题考查了集合运算性质、不等式的解法、分类讨论方法,考查了推理能力与计算能力,属于中档题.
贵州省贵阳市清镇北大培文学校2022-2023学年数学高一上期末教学质量检测试题含解析

20.已知函数 f x x 1
x
(1)判断 f(x)的奇偶性,并说明理由; (2)用定义证明 f(x)在(1,+∞)上单调递增; (3)求 f(x)在[-2,-1]上的值域
21.设 a>0,且 a≠1,解关于 x 的不等式 a2x2 3x1 ax2 2x5
单位长度,得到函数 的图象,则下列说法正确的是( )
A. 的最小正周期为
B. 在区间 上单调递减
C. 图象的一条对称轴为直线
D. 图象的一个对称中心为
ex a, x 3.已知函数 f (x)
0 (a R) ,若函数 f (x) 在 R 上有两个零点,则 a 的取值范围是()
2x 1, x 0
8.中国高速铁路技术世界领先,高速列车运行时不仅速度比普通列车快而且噪声更小.我们用声强 I(单位:W/m2) 表示声音在传播途径中每 1 平方米面积上声能流密度,声强级 L1(单位:dB)与声强 I 的函数关系式为:
L1
10
lg
I 1012
.若普通列车的声强级是
95dB,高速列车的声强级是
45dB,则普通列车的声强是高速列车声强的
f (x) f (x) ,
ax2 (2 a)x 1 ax2 (2 a)x 1 , 化为 (2 a)x 0 , 对于任意实数 x 恒成立,
2 a 0,
解得 a 2 ; f (x) 2x2 1, 利用二次函数的单调性,
可得其单调递增区间为[0, )
故选:B 【点睛】本题考查函数的奇偶性和对称性的应用,熟练掌握函数的奇偶性和二次函数的单调性是解题的关键. 7、B
22.已知函数 f x x m 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年春季北大培文学校贵州区域三月份联考高一数学试卷第I 卷(选择题 共60分)一、 选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中, 只有一项是符合题目要求的。
)1. 设集合{|08},{1,2,4,5},{3,5,7}U x N x S T =∈<≤==,则()U S C T I = A.{1,2,3,4,5,7} B.{1,2,4} C .{1,2} D .{1,2,4,5,6,8}2. 函数()lg(2)f x x =+的定义域为 A .(2,1)-B .[2,1)-C .(2,1]-D .[]1,2-3. 下列函数是偶函数且在区间(,0)-∞上为增函数的是.A 2y x = .B 2y x =- .C y x = .D 1y x=4. 已知4sin 5α=,并且α是第二象限角,则tan α为 A.43-B.34- C.43 D.345. 在ABC ∆中,已知030,10,25===A c a ,则角B 等于A .0105 B .060 C .015 D .0015105或6. ABC ∆的内角,,A B C 所对的边分别为,,a b c ,若cos cos sin b C c B a A +=, 则ABC ∆的形状为A.锐角三角形B. 钝角三角形C.直角三角形D.等腰三角形 7. 在等差数列{}n a 中,159371110,50a a a a a a ++=++=则数列{}n a 的前12项的和12S 等于A.50B.80C.140D.160 8. △ABC 中,∠A =60°,a=6,b=4,满足条件的△ABC A .不存在B .有一个C .有两个D .有无数多个9. △ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,且A sin 、B sin 、C sin 成等比数列,且a c 2=,则B cos 的值为 A .B .C .D .10. 中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其意思为:“有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地,请问第一天走了A. 24里B. 48里C. 96里D.192里 11. 点P 在边长为1的正方形ABCD 的边上运动,设M 是CD 边的中点,当点P 沿着M C B A ,,,匀速率运动时,点P 经过的路程x 为自变量,三角形APM 的面积为y ,则函数()y f x =图像的形状大致是A B C D 12. 已知函数()sin cos f x x x =+,()2sin g x x =,动直线x t =与()f x 、()g x 的图象分别交于点,P Q 两点,则线段PQ 的长度PQ 取值范围是 A .[0,1] B .[0,2] C .D .第II 卷(非选择题 共90分)二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题卡的相应位置)13. 已知函数()⎩⎨⎧≤>=.0,2,0,log 3x x x x f x则⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛271f f = . 14. 在等差数列{}n a 中,已知3810a a +=,则753a a += .15. 如图,一船自西向东匀速航行,上午10时到达一座灯塔P 的南偏西75︒,距灯塔68海里的M 处,下午2时到达这座灯塔的东南方向N 处,则该船航行的速度为 海里/小时.16. 定义在(,0)(0,)-??上的函数()f x ,如果对于任意给定的等比数列{}n a ,有(){}n a f 仍是等比数列,则称()f x 为“保等比数列函数”.现有定义在(,0)(0,)-??上的如下函数:①()f x =2x ; ②()f x =x 2; ③()x x f =; ④()f x =ln |x |,则其中是“保等比数列函数”的()f x 的序号为 .三、解答题(本大题共6小题,共70分。
解答应写出文字说明、证明过程或演算步骤。
) 17.(10分)已知a =(1,2),b =(-3,2),当k 为何值时. (1)k a +b 与a -3b 垂直;(2)k a +b 与a -3b 平行?平行时它们是同向还是反向?18.(12分)ABC ∆的内角,,A B C 的对边分别为,,a b c ,且060,3==C c . (1)若6=a ,求A ,b ;(2)若b a 2=,求b 的值与△ABC 的面积.19.(12分)ABC ∆的内角,,A B C 的对边分别为,,a b c ,且(2)cos cos 0a c B b C --=. (1)求B ;(2)设函数()2sin cos cos cos 22f x x x B x =-,求函数()f x 的最大值及当()f x 最大时x 的取值集合。
20.(12分)已知{}n a 是递增的等差数列,2a ,4a 是方程2560x x -+=的根.(1)求{}n a 的通项公式;(2)求数列2n n a ⎧⎫⎨⎬⎩⎭的前n 项和.21.(12分)某房地产开发商投资81万元建一座写字楼,第一年装修费为1万元,以后每年增加2万元,把写字楼出租,每年收入租金30万元. (1)若扣除投资和各种装修费,则从第几年开始获取纯利润?(2)若干年后开发商为了投资其他项目,有两种处理方案:①纯利润总和最大时,以10万元出售该楼;②年平均利润最大时以46万元出售该楼;问哪种方案盈利更多?22. (12分)若函数2()(12xxk f x k k -=+⋅为正常数)在定义域上为奇函数. (1)求k 的值;(2)若k >0,且对任意的实数[]3,2t ∈--,不等式22(2)(2)0f t t f t m -+-<恒成立,求实数m 的取值范围.2018年春季北大培文学校贵州区域三月份联考高一数学参考答案与评分标准一、选择题1.B解析:{1,2,4,6,8},(){1,2,4}U UC T S C T=∴=Q I;故选B.2.C解析:202,(2,1]101x xxx x+-⎧⎧∴⇒∈-⎨⎨-⎩⎩Q>>≥≤,故选C.3.B解析:略.4.A解析:Q4sin5α=,且α在第二象限,则34tan53sin1cos2-=∴-=--=ααα,,故选A.5.D解析:1,sin sinsin sin2a c cC AA C a=∴===Q,,c a C A∴Q>>,45135C C︒︒∴==或10515B B︒︒∴==或,故选D.6.C解析:cos cos sinb Cc B a A+=Q,由正弦定理得2sin cos cos sin sinB C B C A+=,2sin()sinB C A∴+=。
又,sin()sin0A B C B C Aπ++=∴+=≠,sin1A∴=,又(0,),2A Aππ∈∴=,为直角三角形,故选C.7.D解析:3025010,50,1010621173951=+=++∴=++=++aaaaaaaaa703050221284106212841173=-⨯=++∴+++++=++∴aaaaaaaaaaaa,.16070503010........1232112=+++=++++=∴aaaaS故选D.8.A解析:sin4sin60b A a︒=⨯=Q,不存在三角形,故选A.9.B解析:sin,sin,sinA B CQ成等比数列,2sin sin sinB A C∴=。
根据正弦定理得2b ac=,又2c a=,222b a∴=,2222222423cos244a cb a a aBac a+-+-∴===,故选B.10.D 解析:由题意可设第一天走了1a ,则第二天走了121a ,第n 天走了1121-⎪⎭⎫⎝⎛⨯n a ,则62561111111()1112()...()378122212S a a a a a -=++++==-,解得1192a =,故选D. 11.A 解析:根据题意和图形可知:点P 按M C B A ⇒⇒⇒的顺序在边长为1的正方形边上运动,APM ∆的面积分为3段;当点在AB 上移动时,高不变底边逐渐变大,故面积逐渐变大;当点在BC 上移动时,正方形的边长为1,则PCM ABP AD M S S S S y ∆∆∆---=正方形 =4341)2(2121)1(121411+-=-⨯⨯--⨯⨯--x x x ,此函数是关于x 的递减函数; 当点在CD 上时,高不变,底边变小故面积越来越小直到0为止,故选A. 12.C 解析:将t x =代入)(),(x g x f 得,PQ =()())4sin(2sin cos sin 2cos sin π-=-=-+=-t t t t t t t g t f ,则PQ∈[0,,故选C.二、填空题 13.81 【解析】3331110()log log 330272727f -∴===-Q>,<,()81233==-∴-f . 14. 20 【解析】因为3810a a +=,所以由等差数列的性质,得5610a a +=, 所以753a a +=562220a a +=.15.【解析】如图,在△MNO 中,由正弦定理可得,68sin120sin45MN ===则这艘船的航行速度v ==(海里/小时). 16. ①③ 【解析】本题主要考查等比数列的判定。
设等比数列的通项公式.11-=n n qa a①()()21q a f a f n n =+为定值,故(){}n a f 为等比数列,故①项是“保等比数列函数”; ② ()()()n n n n aa a a n n a f a f -+++==112221不恒为定值,故②项不是“保等比数列函数”; ③()()q a f a f n n =+1为定值,故③是“保等比数列函数”; ④()()()1ln 1ln 111-=-=+n nq a n q a n a f a f n n 不恒为定值,故④项不是“保等比数列函数”.三、解答题17.解析:(1)()()1,23,2==-a b Q ,(3,22),3(10,4)k k k ∴+=-+-=-a b a b ,………2分 (k )(3),(k )(3)0+⊥-∴+⋅-=a b a b a b a b Q ………4分10(3)4(22)0k k ∴--+= 19k ∴=………6分(2)(k )(3),+-a b a b Q ∥14(3)10(22)3k k k ∴--=+⇒=-.........8分 3(10,4)-=-a b ,10411(,)(10,4)(3)3333k +=-=--=--a b a b ………10分 所以当13k =-时,(k )(3)+-a b a b ∥,并且此时反向。
