(完整版)六年级奥数阴影部分的面积
超全六年级阴影部分的面积(详细答案)

六年级阴影部分的面积1.求阴影部分的面积。
(单位:厘米)解:割补后如右图,易知,阴影部分面积为一个梯形。
梯形上底DE=7-4=3厘米,1S =S =DE AB)AD 2⨯+⨯阴梯形(=137)42⨯+⨯(=20(平方厘米)2、求阴影部分的面积。
解:S =S 阴梯形,梯形的上底是圆的直径,下底、高是圆的半径,S =S 阴梯形=124)22⨯+⨯(=6(2cm )3、如图,平行四边形的高是6厘米,面积是54平方厘米,求阴影三角形的面积。
解:S =AD AO ⨯ABCD =54平方厘米,且AO=6厘米,所以AD=9厘米。
由图形可知AED ∆是等腰直角三角形,所以AE=AD ,OE=OF=AE-AO=9-6=3cm ,BO=BC-OC=9-3=6cm 。
1S =BO OF 2⨯⨯阴=1S =632⨯⨯阴=92cm 。
4、如图是一个平行四边形,面积是50平方厘米,求阴影积分的面积。
解:方法一:过C 点作CF AD ⊥交AD 于点F ,可知AECF 是长方形,面积=5×6=302cm ,ABE CFD S =S ∆∆=(50-30)÷2=102cm 。
方法二:BC=S ABCD ÷AE=50÷5=10cm ,BE=BC-EC=10-6=4cm ,ABE S ∆=BE ×AE ÷2 =4×5÷2=102cm5、下图是一个半圆形,已知AB=10厘米,阴影部分的面积为24.25平方厘米,求图形中三角形的高。
解:S =S -S ∆阴半圆=21AB 22π⎛⎫⨯⨯ ⎪⎝⎭-24.25=21103.1422⎛⎫⨯⨯ ⎪⎝⎭-24.25=152cm , 三角形的高=2S ∆÷AB=2×15÷10=3cm 。
6、如图,一个长方形长是10cm ,宽是4cm ,以A 点和C 点为圆心各画一个扇形,求画中阴影部分的面积是多少平方厘米?解:BECD 1S =S -S 4阴大圆=ABCD 11S -S S 44⎛⎫- ⎪⎝⎭大圆小圆=ABCD 11S +S -S 44大圆小圆=()2213.1410-4-1044⨯⨯⨯ =25.942cm 。
(完整版)小学六年级求阴影部分面积试题和答案100

=7,7-例 2. 正方形面积是 7 平方厘米,求阴 影部分的面积。
(单位 :厘米) 解:这也是一种最基本的方法用正方 形的面积减去圆面积减去等腰直角三角形的面积,圆的面积。
设圆的半径为 r ,因为正方形的面积为 7 平方厘米 ,所以求阴影部分面积所以阴影部分的面积为=7,7--2 ×1=1.14(平方厘米)=7-×7=1.505 平方厘米圆组成一个圆,用正方形的面积减去圆的面 积,所以阴影部分的面积: 2×2- π=0.86 平方厘米)=16- 4π=3.44 平方厘米例 6. 如图:已知小圆半径为 2 厘米,大圆半径是小圆的 3 倍, 问:空白部分甲比乙的面积多 多少厘米? 解:两个空白部分面积之差就 是两圆面积之差(全加上阴影π π(-π(例 3. 求图中阴影部分的面积。
(单 位:厘米) 解:最基本的方法之一。
用四个例 4. 求阴影部分的面积。
(单 位:厘米) 解:同上,正方形面积减去 圆面积,16- π(分称为 “叶形”,是用两个圆减去一 部分)个正方形,例 5.求阴影部分的面积。
(单位 : 厘米)解:这是一个用最常用的方法解 最常见的题,为方便起见, 我们把阴影部分的每一个小部) ×2-16=8 π-16=9.12 平方厘米另外:此题还可以看成是 1 题中阴影部分的 8 倍)=100.48 平方厘米注:这和两个圆是否相交、交的情况如何无关)例7. 求阴影部分的面积。
(单位 :厘 米)解:正方形面积可用 (对角线长 ×对角 线长 ÷2,求 )正方形面积为: 5×5÷2=12.5 所以阴影面积为圆,÷4-12.5=7.125 平方厘米所 以 阴 影 部 分 面 积 为(注: 以上几个题都可以直接用图形的差来求 ,无需割、补、增、减变形 )例 8. 求阴影部分的面积。
(单位 :厘米) 解:右面正方形上部阴影部 分的面积,等于左面正方形 下部空白部分面积, 割补以 后为)=3.14 平方厘米例9. 求阴影部分的面积。
六年级奥数 阴影部分的面积

第七讲阴影部份的面积之南宫帮珍创作创作时间:二零二一年六月三十日例1求图中阴影部份的面积.(单元:厘米)(图3)解:最基本的方法之一.用四个圆组成一个圆, 用正例2求阴影部份的面积.(单元:厘米)(图5)方形的面积减去圆的面积, 所以阴影部份的面积:2×2-π=0.86平方厘米.解:这是一个用最经常使用的方法解最罕见的题,为方便起见,我们把阴影部份的每一个小部份称为“叶形”, 是用两个圆减去一个正方形,π(例3求阴影部份的面积.(单元:厘米)(图9)解:把右面的正方形平移至左边的正方形部份, 则阴影部份合成一个长方形, 所以阴影部份面积为:2×3=6平方厘米例4求阴影部份的面积(单元:厘米)(图13)解: 连对角线后将"叶形"剪开移到右上面的空白部份,凑成正方形的一半.所以阴影部份面积为:8×8÷2=32平方厘米例5图中圆的半径是5厘米, 求阴影部份的面积.(单元:厘米)(图17)解:上面的阴影部份以AB为轴翻转后, 整个阴影部份成为梯形减去直角三角形,或两个小直角三角形AED、BCD面积和.例6如图, 三角形ABC是直角三角形, 阴影部份甲比阴影部份乙面积年夜28平方厘米, AB=40厘米.求BC的长度. 解:两部份同补上空白部份后为直角三角形ABC, 一个为半圆,设BC长为X, 则40X÷2-π÷2=28例8.求阴影部份的面积.(单元:厘米) 解:右面正方形上部阴影部份的面积, 即是左面正方形下部空白部份面积, 割补以后为圆,所以阴影部份面积为:π(巩固练习:1求阴影部份的面积.(单元:厘米)(图7)2.年夜正方形的边长为6厘米, 小正方形的边长为4厘米.求阴影部份的面积.(图32)3. 求阴影部份的面积.(单元:厘米)创作时间:二零二一年六月三十日4.已知直角三角形面积是12平方厘米, 求阴影部份的面积.(如图15)5.正方形ABCD的面积是36平方厘米, 求阴影部份的面积.(如图)。
(完整word版)六年级奥数练习(阴影面积)

六年级奥数练习题(圆和组合图形)1、算出圆内正方形的面积为多少2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是多少平方厘米.3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是多少?4.右图中三角形是等腰直角三角形,阴影部分的面积是(平方厘米).5.三角形ABC是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. AB长40厘米, BC长厘米.6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积为 .7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是度.8.图中扇形的半径OA=OB=6厘米.45=∠AOB, AC垂直OB于C,那么图中阴影部分的面积是平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是平方厘米.10.在右图中(单位:厘米),两个阴影部分面积的和是平方厘米.12.如图,半圆S1的面积是14.13219.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O,半径r=9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米?)14.3(≈π13、如图,求阴影部分的面积 .14、大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大平方厘米.15、在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是平方厘米.(π取3.14,结果精确到1平方厘米)16、如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是厘米.)14.3(=π2 1 2112217.下图中正方形部分是一个水池,其余部分是草坪,已知正方形的面积是300平方米,草坪的面积是多少平方米?17、已知:ABCD是正方形, ED=DA=AF=2厘米,阴影部分的面积是 .18、如图:阴影部分的面积是多少?四分之一大圆的半径为r.(计算时圆周率取722)19、已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积.20.如图{图在下面}两个连在一起的轮轴,已知小轮的半径是3分米,当这个小轮转3圈时,大轮正好转一圈,21.3只蜜蜂分别沿着阴影部分的边缘飞1次,那只蜜蜂飞过的路线最长?(3个正方形的边长都为4m)23.将半径分别是3厘米和2厘米的两个半圆如图放置,求阴影部分的周长24.求阴影部分的面积E DC BAGF25.一个圆环外直径是内直径的二分之三倍,圆环面积150cm,求外圆的面积26.一个长方形的面积是20平方厘米,如果在这个长方形里画一个最大的半圆形,这个半圆形是多少平方厘米?因为这个半圆的直径是长方形的长,半径是宽,说明长方形的长是宽的2倍。
(完整版)六年级奥数练习(阴影面积)1
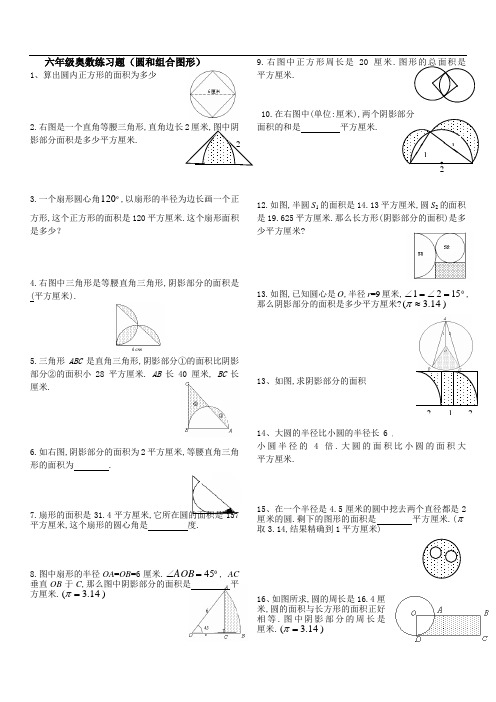
六年级奥数练习题(圆和组合图形)1、算出圆内正方形的面积为多少 2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是多少平方厘米. 3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是多少? 4.右图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).5.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. AB 长40厘米, BC 长厘米.6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积为 .7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是平方厘米. 10.在右图中(单位:厘米),两个阴影部分 面积的和是 平方厘米.12.如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米?)14.3(≈π13、如图,求阴影部分的面积 .14、大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面平方厘米.15、在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取3.14,结果精确到1平方厘米)16、如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是厘米.)14.3(=π2 1 2112217.下图中正方形部分是一个水池,其余部分是草坪,已知正方形的面积是300平方米,草坪的面积是多少平方米?17、已知:ABC D 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .18、如图:阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率取722)19、已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.20.如图{图在下面}两个连在一起的轮轴,已知小轮的半径是3分米,当这个小轮转3圈时,大轮正好转一圈,21.3只蜜蜂分别沿着阴影部分的边缘飞1次,那只蜜蜂飞过的路线最长?(3个正方形的边长都为4m )23.将半径分别是3厘米和2厘米的两个半圆如图放置,求阴影部分的周长24.求阴影部分的面积25.一个圆环外直径是内直径的二分之三倍,圆环面积150cm ,求外圆的面积26.一个长方形的面积是20平方厘米,如果在这个长方形里画一个最大的半圆形,这个半圆形是多少平方厘米?因为这个半圆的直径是长方形的长,半径是宽,说明长方形的长是宽的2倍。
小学六年级-阴影部分面积及答案完整
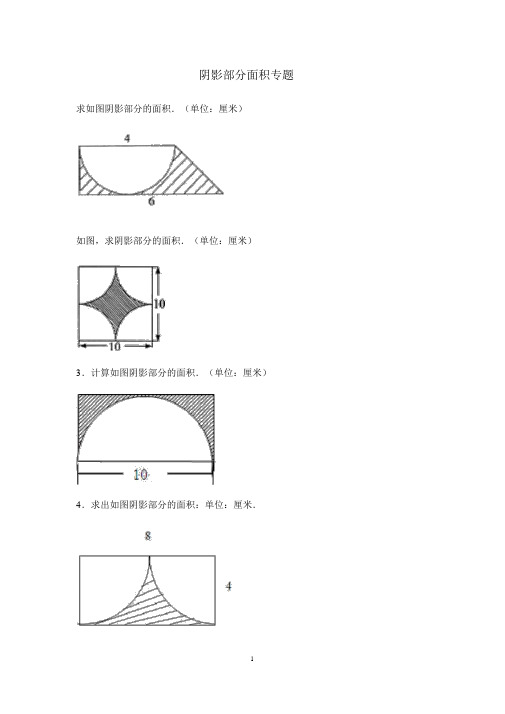
阴影部分面积专题求如图阴影部分的面积.(单位:厘米)如图,求阴影部分的面积.(单位:厘米)3.计算如图阴影部分的面积.(单位:厘米)4.求出如图阴影部分的面积:单位:厘米.5.求如图阴影部分的面积.(单位:厘米)6.求如图阴影部分面积.(单位:厘米)7.计算如图中阴影部分的面积.单位:厘米.8.求阴影部分的面积.单位:厘米.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)10.求阴影部分的面积.(单位:厘米)11.求下图阴影部分的面积.(单位:厘米)12.求阴影部分图形的面积.(单位:厘米)13.计算阴影部分面积(单位:厘米).14.求阴影部分的面积.(单位:厘米)15.求下图阴影部分的面积:(单位:厘米)16.求阴影部分面积(单位:厘米).17.求阴影部分的面积.(单位:厘米)☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆参考答案与试题解析1.求如图阴影部分的面积.(单位:厘米)考点组合图形的面积;梯形的面积;圆、圆环的面积.1526356分析阴影部分的面积等于梯形的面积减去直径为 4 厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.解答解:( 4+6)× 4÷2÷2﹣3.14 ×÷2,=10﹣3.14 ×4÷2,=10﹣6.28 ,=3.72 (平方厘米);答:阴影部分的面积是 3.72 平方厘米.点评组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用.2.如图,求阴影部分的面积.(单位:厘米)考点组合图形的面积. 1526356分析根据图形可以看出:阴影部分的面积等于正方形的面积减去 4 个扇形的面积.正方形的面积等于( 10×10)100 平方厘米, 4 个扇形的面积等于半径为( 10÷2) 5 厘米的圆的面积,即: 3.14 ×5×5=78.5(平方厘米).解答解:扇形的半径是:10÷2,=5(厘米);10×10﹣3.14 ×5×5,100﹣78.5 ,=21.5 (平方厘米);答:阴影部分的面积为21.5 平方厘米.点评解答此题的关键是求 4 个扇形的面积,即半径为 5 厘米的圆的面积.3.计算如图阴影部分的面积.(单位:厘米)考点组合图形的面积. 1526356分析分析图后可知, 10 厘米不仅是半圆的直径,还是长方形的长,根据半径等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.解答解: 10÷2=5(厘米),长方形的面积 =长×宽 =10×5=50(平方厘米),22(平方厘米),半圆的面积 =πr÷2=3.14×5÷2=39.25阴影部分的面积 =长方形的面积﹣半圆的面积,=50﹣39.25 ,=10.75 (平方厘米);答:阴影部分的面积是10.75 .点评这道题重点考查学生求组合图形面积的能力,组合图形可以是两个图形拼凑在一起,也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看属于哪一种类型的组合图形,再根据条件去进一步解答.4.求出如图阴影部分的面积:单位:厘米.考点组合图形的面积. 1526356专题平面图形的认识与计算.分析由题意可知:阴影部分的面积 =长方形的面积﹣以 4 厘米为半径的半圆的面积,代入数据即可求解.2解答解: 8×4﹣3.14 ×4÷2,=32﹣25.12 ,=6.88 (平方厘米);答:阴影部分的面积是 6.88 平方厘米.点评解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.考点圆、圆环的面积. 15263564个直径为 4厘分析由图可知,正方形的边长也就是半圆的直径,阴影部分由米的半圆组成,也就是两个圆的面积,因此要求阴影部分的面积,首先要算1 个圆的面积,然后根据“阴影部分的面积 =2×圆的面积”算出答案.2解答解: S=πr2=3.14 ×( 4÷2)阴影部分的面积 =2 个圆的面积,=2×12.56 ,=25.12 (平方厘米);答:阴影部分的面积是25.12 平方厘米.点评解答这道题的关键是重点分析阴影部分是由什么图形组成的,再根据已知条件去计算.6.求如图阴影部分面积.(单位:厘米)考点长方形、正方形的面积;平行四边形的面积;三角形的周长和面积. 1526356 分析图一中阴影部分的面积 =大正方形面积的一半﹣与阴影部分相邻的小三角形的面积;图二中阴影部分的面积 =梯形的面积﹣平四边形的面积,再将题目中的数据代入相应的公式进行计算.解答解:图一中阴影部分的面积=6×6÷2﹣4×6÷2=6(平方厘米);图二中阴影部分的面积 =(8+15)×( 48÷8)÷ 2﹣ 48=21(平方厘米);答:图一中阴影部分的面积是 6 平方厘米,图二中阴影部分的面积是 21 平方厘米.点评此题目是组合图形,需要把握好正方形、三角形、梯形及平行四边形的面积公式,再将题目中的数据代入相应的公式进行计算.考点组合图形的面积. 1526356分析由图意可知:阴影部分的面积= 圆的面积,又因圆的半径为斜边上的高,利用同一个三角形的面积相等即可求出斜边上的高,也就等于知道了圆的半径,利用圆的面积公式即可求解.解答解:圆的半径: 15×20÷2×2÷25,=300÷25,=12(厘米);阴影部分的面积:×3.14 ×122,=×3.14 ×144,=0.785×144,=113.04(平方厘米);答:阴影部分的面积是113.04 平方厘米.点评此题考查了圆的面积公式及其应用,同时考查了学生观察图形的能力.8.求阴影部分的面积.单位:厘米.考点组合图形的面积;三角形的周长和面积;圆、圆环的面积. 1526356 分析(1)圆环的面积等于大圆的面积减小圆的面积,大圆与小圆的直径已知,代入圆的面积公式,从而可以求出阴影部分的面积;(2)阴影部分的面积 =圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.解答解:( 1)阴影部分面积:3.14 ×﹣3.14×,=28.26 ﹣3.14 ,=25.12 (平方厘米);(2)阴影部分的面积:23.14 ×3﹣×(3+3)× 3,=28.26 ﹣9,=19.26 (平方厘米);答:圆环的面积是25.12 平方厘米,阴影部分面积是19.26 平方厘米.点评此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)考点组合图形的面积;圆、圆环的面积. 1526356专题平面图形的认识与计算.分析观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等,所以图中阴影部分的周长,就是直径为10+3=13厘米的圆的周长,由此利用圆的周长公式即可进行计算;阴影部分的面积=大半圆的面积﹣以10÷2=5 厘米为半径的半圆的面积﹣以3÷2=1.5 厘米为半径的半圆的面积,利用半圆的面积公式即可求解.解答解:周长: 3.14 ×( 10+3),=3.14 ×13,=40.82 (厘米);面积:×3.14 ×[(10+3)÷2] 2﹣×3.14 ×(10÷2)2﹣×3.14 ×(3÷2)2,=×3.14 ×( 42.25 ﹣25﹣2.25 ),=×3.14 ×15,=23.55 (平方厘米);答:阴影部分的周长是40.82 厘米,面积是 23.55 平方厘米.点评此题主要考查半圆的周长及面积的计算方法,根据半圆的弧长 =πr ,得出图中两个小半圆的弧长之和等于大半圆的弧长,是解决本题的关键.10.求阴影部分的面积.(单位:厘米)考点圆、圆环的面积. 1526356分析先用“ 3+3=6”求出大扇形的半径,然后根据“扇形的面积”分别计算出大扇形的面积和小扇形的面积,进而根据“大扇形的面积﹣小扇形的面积 =阴影部分的面积”解答即可.解答解: r=3 , R=3+3=6, n=120,,=,=37.68 ﹣9.42 ,=28.26 (平方厘米);答:阴影部分的面积是28.26 平方厘米.点评此题主要考查的是扇形面积计算公式的掌握情况,应主要灵活运用.11.求下图阴影部分的面积.(单位:厘米)考点组合图形的面积. 1526356分析先求出半圆的面积 3.14 ×( 10÷2)2÷2=39.25 平方厘米,再求出空白三角形的面积 10×( 10÷2)÷ 2=25 平方厘米,相减即可求解.2=39.25 ﹣25=14.25 (平方厘米).答:阴影部分的面积为14.25 平方厘米.点评考查了组合图形的面积,本题阴影部分的面积 =半圆的面积﹣空白三角形的面积.12.求阴影部分图形的面积.(单位:厘米)考点组合图形的面积. 1526356分析求阴影部分的面积可用梯形面积减去圆面积的,列式计算即可.2解答解:( 4+10)× 4÷2﹣3.14 ×4 ÷4,=15.44 (平方厘米);答:阴影部分的面积是15.44 平方厘米.点评解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形(扇形)的面积,即可列式解答.13.计算阴影部分面积(单位:厘米).考点组合图形的面积. 1526356专题平面图形的认识与计算.分析如图所示,阴影部分的面积=平行四边形的面积﹣三角形①的面积,平行四边形的底和高分别为 10 厘米和 15 厘米,三角形①的底和高分别为 10 厘米和( 15﹣7)厘米,利用平行四边形和三角形的面积公式即可求解.解答解: 10×15﹣10×( 15﹣7)÷ 2,=150﹣ 40,=110(平方厘米);答:阴影部分的面积是110 平方厘米.点评解答此题的关键是明白:阴影部分的面积不能直接求出,可以用平行四边形和三角形的面积差求出.14.求阴影部分的面积.(单位:厘米)考点梯形的面积. 1526356分析如图所示,将扇形①平移到扇形②的位置,求阴影部分的面积就变成了求梯形的面积,梯形的上底和下底已知,高就等于梯形的上底,代入梯形的面积公式即可求解.解答解:( 6+10)× 6÷2,=16×6÷2,=96÷2,=48(平方厘米);答:阴影部分的面积是48 平方厘米.点评此题主要考查梯形的面积的计算方法,关键是利用平移的办法变成求梯形的面积.15.求下图阴影部分的面积:(单位:厘米)考点组合图形的面积. 1526356分析根据三角形的面积公式:S=ah,找到图中阴影部分的底和高,代入计算即可求解.解答解: 2×3÷2=6÷2=3(平方厘米).答:阴影部分的面积是 3 平方厘米.点评考查了组合图形的面积,本题组合图形是一个三角形,关键是得到三角形的底和高.16.求阴影部分面积(单位:厘米).考点组合图形的面积. 1526356分析由图意可知:阴影部分的面积=梯形的面积﹣圆的面积,梯形的上底和高都等于圆的半径,上底和下底已知,从而可以求出阴影部分的面积.解答2=13×4÷2﹣3.14 ×4,=26﹣12.56 ,=13.44 (平方厘米);答:阴影部分的面积是13.44 平方厘米.点评解答此题的关键是明白:梯形的下底和高都等于圆的半径,且阴影部分的面积 =梯形的面积﹣圆的面积.17.( 2012?长泰县)求阴影部分的面积.(单位:厘米)考点组合图形的面积. 1526356分析由图可知,阴影部分的面积 =梯形的面积﹣半圆的面积.梯形的面积 = (a+b)2h,半圆的面积 = πr,将数值代入从而求得阴影部分的面积.解答解:×(6+8)×(6÷2)﹣×3.14×(6÷2)2= ×14×3﹣×3.14×9,=21﹣14.13 ,=6.87 (平方厘米);答:阴影部分的面积为 6.87 平方厘米.点评考查了组合图形的面积,解题关键是看懂图示,把图示分解成梯形,半圆和阴影部分,再分别求出梯形和半圆的面积.。
求阴影部分的面积六年级奥数

求阴影部分的面积(六年级奥数)前言在六年级的奥数课上,我们经常需要解答各种与几何形状相关的问题。
其中一个常见的问题是求阴影部分的面积。
通过理解并掌握一些几何知识和计算方法,我们可以轻松地应对这类问题。
本文将介绍一些常用的方法和注意事项,帮助大家解决求阴影部分面积的问题。
问题背景在解答求阴影部分面积的问题前,我们先了解一下这类问题的背景。
一般来说,这类问题会给出一个或多个几何形状,并告诉我们某个或某些部分的面积。
我们需要通过这些已知的信息,计算出未知部分的面积。
方法一:几何分析法几何分析法是求解阴影部分面积问题的常用方法之一。
它的基本思路是将问题拆分成多个几何图形,计算每个图形的面积,然后将这些面积累加起来。
下面是一个例子,以帮助我们更好地理解几何分析法:问题:如图所示,在正方形ABCD内有一圆O,圆O的半径为2cm。
求阴影部分的面积。
O -----------------| || ----------- || | | || | O | || | | || ----------- || |-------------------解题步骤:1.首先,我们计算正方形ABCD的面积。
由于ABCD是一个正方形,所以它的边长与圆O的直径相等(2cm的直径即为4cm的边长)。
所以,正方形ABCD的面积为4cm * 4cm = 16cm²。
2.接下来,我们计算圆O的面积。
圆O的半径为2cm,所以它的面积为πr² = 3.14 * 2 * 2 = 12.56cm²。
3.最后,我们计算阴影部分的面积。
由于阴影部分是正方形ABCD减去圆O后剩下的部分,所以阴影部分的面积为16cm² - 12.56cm² = 3.44cm²。
通过这个例子,我们可以体会到几何分析法在求解阴影部分面积问题时的应用。
方法二:代数法除了几何分析法,代数法也是一种常用的求解阴影部分面积问题的方法。
(完整版)小学六年级求阴影部分面积试题和答案
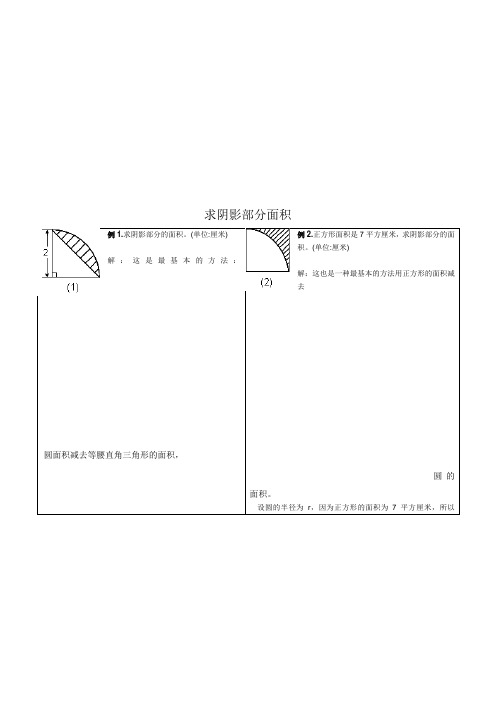
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以×7=1. 505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π例8.求阴影部分的面积。
(单位:厘米) 解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为例9.求阴影部分的面积。
(单位:厘米)解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,所以阴影部分面积为:2×3=6平方厘米例10.求阴影部分的面积。
(单位:厘米)解:同上,平移左右两部分至中间部分,则合成一个长方形,所以阴影部分面积为2×1=2平方厘米(注: 8、9、10三题是简单割、补或平移)例11.求阴影部分的面积。
(完整版)小学六年级求阴影部分面积试题和答案

例2.正方形面积是7平方厘米,求阴影部分的面 积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减 去圆面积减去等腰直角三角形的面积,面积。
设圆的半径为r ,因为正方形的面积为7平方厘米,所以求阴影部分面积例1.求阴影部分的面积。
(单位:厘米) 解:这是最基本的方法例6.如图:已知小圆半径为 2厘米,大圆 半径是小圆的3倍,问:空白部分甲比乙 的面积多多少厘米?解:两个空白部分面积之差就是两圆面积 之差(全加上阴影部分)圆组成一个圆,用正方形的面积减去圆的面积, 所以阴影部分的面积:2X 2-n= 0.86平方厘米。
)=16-4 n=3.44平方厘米505平方厘米例3.求图中阴影部分的面积。
(单位:厘米) 解:最基本的方法之一。
用四个X7=1.例4.求阴影部分的面积。
(单位:厘米) 解:同上,正方形面积减去圆面积,16- n (例6.如图:已知小圆半径为 2厘米,大圆 半径是小圆的3倍,问:空白部分甲比乙 的面积多多少厘米?解:两个空白部分面积之差就是两圆面积 之差(全加上阴影部分)例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的 题,为方便起见,我们把阴影部分的每一个小部分称为 叶形”是用两个圆减去一个正方形,◎n()X n2-16=8 n16=9.12 平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
)=100. 48平方厘米Z冗冗(注:这和两个圆是否相交、交的情况如何无关)例8.求阴影部分的面积。
(单位:厘米) 解:右面正方形上部阴影部分的面积, 等于左面正方形下部空白部分面积, 割 补 以 后 为例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长X 对角线长煜, 求) 正方形面积为:5X5^2=12.5 所 以 阴 影 面 积 为:-n)—2所以阴影部分面积为: 例11.求阴影部分的面积。
(单位:厘米) 解:这种图形称为环形,可以用两个同心圆 的面积差或差的一部分来求。
(完整版)六年级奥数讲义第20讲面积计算(三)

第二十周面积计算(三)专题简析:对于一些比较复杂的组合图形,有时直接分解有一定的困难,这时,可以通过把其中的部分图形进行平移、翻折或旋转,化难为易。
有些图形可以根据“容斥问题“的原理来解答。
在圆的半径r 用小学知识无法求出时,可以把“r 2”整体地代入面积公式求面积。
例题1。
如图20-1所示,求图中阴影部分的面积。
【思路导航】解法一:阴影部分的一半,可以看做是扇形中减去一个等腰直角三角形(如图20-2),等腰直角三角形的斜边等于圆的半径,斜边上的高等于斜边的一半,圆的半径为20÷2=10厘米 【3.14×102×错误!-10×(10÷2)】×2=107(平方厘米) 答:阴影部分的面积是107平方厘米。
解法二:以等腰三角形底的中点为中心点。
把图的右半部分向下旋转90度后,阴影部分的面积就变为从半径为10厘米的半圆面积中,减去两直角边为10厘米的等腰直角三角形的面积所得的差.(20÷2)2×错误!-(20÷2)2×错误!=107(平方厘米) 答:阴影部分的面积是107平方厘米。
练习11、 如图20-4所示,求阴影部分的面积(单位:厘米)2、 如图20-5所示,用一张斜边为29厘米的红色直角三角形纸片,一张斜边为49厘米的蓝色直角三角20-120-26 BA20-549292949例题2。
如图20-6所示,求图中阴影部分的面积(单位:厘米)。
【思路导航】解法一:先用长方形的面积减去小扇形的面积,得空白部分(a)的面积,再用大扇形的面积减去空白部分(a)的面积。
如图20-7所示。
3.14×62×错误!-(6×4-3.14×42×错误!)=16.82(平方厘米)解法二:把阴影部分看作(1)和(2)两部分如图20-8所示。
把大、小两个扇形面积相加,刚好多计算了空白部分和阴影(1)的面积,即长方形的面积。
六年级奥术数学求阴影部分面积_超难题

求阴影部分的面(奥数)1、求下图中阴影部分的面积。
2、下图两个正方形的边长分别是8厘米和10厘米,求阴影部分的面积。
3、下图中半圆直径为9厘米,求阴影部分的面积。
4、下图中长方形的长为10宽为4,求阴影部分的面积。
(单位:分米)
5、下图中等腰直角三角形的腰长为8厘米,求阴影部分的面积。
6、如下图扇形圆心角为90度,半径为8厘米,扇形内有一个正方形,求阴影部分的面积。
7、等腰直角三角形斜边长10厘米,求阴影部分的面积。
8、平行四边形ABCD的边长BC=10厘米,直角三角形BCE的直角边EC长8厘米,已知阴影部分的面积比三角
形EFG的面积大10平方厘米。
求CF的长。
小学六年级阴影部分面积及答案完整

阴影部分面积专题求如图阴影部分的面积.(单位:厘米)如图,求阴影部分的面积.(单位:厘米)3.计算如图阴影部分的面积.(单位:厘米)4.求出如图阴影部分的面积:单位:厘米.5.求如图阴影部分的面积.(单位:厘米)6.求如图阴影部分面积.(单位:厘米)7.计算如图中阴影部分的面积.单位:厘米.8.求阴影部分的面积.单位:厘米.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)10.求阴影部分的面积.(单位:厘米)11.求下图阴影部分的面积.(单位:厘米)12.求阴影部分图形的面积.(单位:厘米)13.计算阴影部分面积(单位:厘米).14.求阴影部分的面积.(单位:厘米)15.求下图阴影部分的面积:(单位:厘米)16.求阴影部分面积(单位:厘米).17.求阴影部分的面积.(单位:厘米)☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆参考答案与试题解析1.求如图阴影部分的面积.(单位:厘米)考点组合图形的面积;梯形的面积;圆、圆环的面积.分析阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.解答解:(4+6)×4÷2÷2﹣3.14×÷2,=10﹣3.14×4÷2,=10﹣6.28,=3.72(平方厘米);答:阴影部分的面积是3.72平方厘米.点评组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用.2.如图,求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析根据图形可以看出:阴影部分的面积等于正方形的面积减去4个扇形的面积.正方形的面积等于(10×10)100平方厘米,4个扇形的面积等于半径为(10÷2)5厘米的圆的面积,即:3.14×5×5=78.5(平方厘米).解答解:扇形的半径是:10÷2,=5(厘米);10×10﹣3.14×5×5,100﹣78.5,=21.5(平方厘米);答:阴影部分的面积为21.5平方厘米.点评解答此题的关键是求4个扇形的面积,即半径为5厘米的圆的面积.3.计算如图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析分析图后可知,10厘米不仅是半圆的直径,还是长方形的长,根据半径等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.解答解:10÷2=5(厘米),长方形的面积=长×宽=10×5=50(平方厘米),半圆的面积=πr2÷2=3.14×52÷2=39.25(平方厘米),阴影部分的面积=长方形的面积﹣半圆的面积,=50﹣39.25,=10.75(平方厘米);答:阴影部分的面积是10.75.点评这道题重点考查学生求组合图形面积的能力,组合图形可以是两个图形拼凑在一起,也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看属于哪一种类型的组合图形,再根据条件去进一步解答.4.求出如图阴影部分的面积:单位:厘米.考点组合图形的面积.专题平面图形的认识与计算.分析由题意可知:阴影部分的面积=长方形的面积﹣以4厘米为半径的半圆的面积,代入数据即可求解.解答解:8×4﹣3.14×42÷2,=32﹣25.12,=6.88(平方厘米);答:阴影部分的面积是6.88平方厘米.点评解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.5.求如图阴影部分的面积.(单位:厘米)考点圆、圆环的面积.分析由图可知,正方形的边长也就是半圆的直径,阴影部分由4个直径为4厘米的半圆组成,也就是两个圆的面积,因此要求阴影部分的面积,首先要算1个圆的面积,然后根据“阴影部分的面积=2×圆的面积”算出答案.解答解:S=πr2=3.14×(4÷2)2=12.56(平方厘米);阴影部分的面积=2个圆的面积,=2×12.56,=25.12(平方厘米);答:阴影部分的面积是25.12平方厘米.点评解答这道题的关键是重点分析阴影部分是由什么图形组成的,再根据已知条件去计算.6.求如图阴影部分面积.(单位:厘米)考点长方形、正方形的面积;平行四边形的面积;三角形的周长和面积.分析图一中阴影部分的面积=大正方形面积的一半﹣与阴影部分相邻的小三角形的面积;图二中阴影部分的面积=梯形的面积﹣平四边形的面积,再将题目中的数据代入相应的公式进行计算.解答解:图一中阴影部分的面积=6×6÷2﹣4×6÷2=6(平方厘米);图二中阴影部分的面积=(8+15)×(48÷8)÷2﹣48=21(平方厘米);答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.点评此题目是组合图形,需要把握好正方形、三角形、梯形及平行四边形的面积公式,再将题目中的数据代入相应的公式进行计算.7.计算如图中阴影部分的面积.单位:厘米.考点组合图形的面积.分析由图意可知:阴影部分的面积=圆的面积,又因圆的半径为斜边上的高,利用同一个三角形的面积相等即可求出斜边上的高,也就等于知道了圆的半径,利用圆的面积公式即可求解.解答解:圆的半径:15×20÷2×2÷25,=300÷25,=12(厘米);阴影部分的面积:×3.14×122,=×3.14×144,=0.785×144,=113.04(平方厘米);答:阴影部分的面积是113.04平方厘米.点评此题考查了圆的面积公式及其应用,同时考查了学生观察图形的能力.8.求阴影部分的面积.单位:厘米.考点组合图形的面积;三角形的周长和面积;圆、圆环的面积.分析(1)圆环的面积等于大圆的面积减小圆的面积,大圆与小圆的直径已知,代入圆的面积公式,从而可以求出阴影部分的面积;(2)阴影部分的面积=圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.解答解:(1)阴影部分面积:3.14×﹣3.14×,=28.26﹣3.14,=25.12(平方厘米);(2)阴影部分的面积:3.14×32﹣×(3+3)×3,=28.26﹣9,=19.26(平方厘米);答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.点评此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)考点组合图形的面积;圆、圆环的面积.专题平面图形的认识与计算.分析观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等,所以图中阴影部分的周长,就是直径为10+3=13厘米的圆的周长,由此利用圆的周长公式即可进行计算;阴影部分的面积=大半圆的面积﹣以10÷2=5厘米为半径的半圆的面积﹣以3÷2=1.5厘米为半径的半圆的面积,利用半圆的面积公式即可求解.解答解:周长:3.14×(10+3),=3.14×13,=40.82(厘米);面积:×3.14×[(10+3)÷2]2﹣×3.14×(10÷2)2﹣×3.14×(3÷2)2,=×3.14×(42.25﹣25﹣2.25),=×3.14×15,=23.55(平方厘米);答:阴影部分的周长是40.82厘米,面积是23.55平方厘米.点评此题主要考查半圆的周长及面积的计算方法,根据半圆的弧长=πr,得出图中两个小半圆的弧长之和等于大半圆的弧长,是解决本题的关键.10.求阴影部分的面积.(单位:厘米)考点圆、圆环的面积.分析先用“3+3=6”求出大扇形的半径,然后根据“扇形的面积”分别计算出大扇形的面积和小扇形的面积,进而根据“大扇形的面积﹣小扇形的面积=阴影部分的面积”解答即可.解答解:r=3,R=3+3=6,n=120,,=,=37.68﹣9.42,=28.26(平方厘米);答:阴影部分的面积是28.26平方厘米.点评此题主要考查的是扇形面积计算公式的掌握情况,应主要灵活运用.11.求下图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析先求出半圆的面积3.14×(10÷2)2÷2=39.25平方厘米,再求出空白三角形的面积10×(10÷2)÷2=25平方厘米,相减即可求解.解答解:3.14×(10÷2)2÷2﹣10×(10÷2)÷2=39.25﹣25=14.25(平方厘米).答:阴影部分的面积为14.25平方厘米.点评考查了组合图形的面积,本题阴影部分的面积=半圆的面积﹣空白三角形的面积.12.求阴影部分图形的面积.(单位:厘米)考点组合图形的面积.分析求阴影部分的面积可用梯形面积减去圆面积的,列式计算即可.解答解:(4+10)×4÷2﹣3.14×42÷4,=28﹣12.56,=15.44(平方厘米);答:阴影部分的面积是15.44平方厘米.点评解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形(扇形)的面积,即可列式解答.13.计算阴影部分面积(单位:厘米).考点组合图形的面积.专题平面图形的认识与计算.分析如图所示,阴影部分的面积=平行四边形的面积﹣三角形①的面积,平行四边形的底和高分别为10厘米和15厘米,三角形①的底和高分别为10厘米和(15﹣7)厘米,利用平行四边形和三角形的面积公式即可求解.解答解:10×15﹣10×(15﹣7)÷2,=150﹣40,=110(平方厘米);答:阴影部分的面积是110平方厘米.点评解答此题的关键是明白:阴影部分的面积不能直接求出,可以用平行四边形和三角形的面积差求出.14.求阴影部分的面积.(单位:厘米)考点梯形的面积.分析如图所示,将扇形①平移到扇形②的位置,求阴影部分的面积就变成了求梯形的面积,梯形的上底和下底已知,高就等于梯形的上底,代入梯形的面积公式即可求解.解答解:(6+10)×6÷2,=16×6÷2,=96÷2,=48(平方厘米);答:阴影部分的面积是48平方厘米.点评此题主要考查梯形的面积的计算方法,关键是利用平移的办法变成求梯形的面积.15.求下图阴影部分的面积:(单位:厘米)考点组合图形的面积.分析根据三角形的面积公式:S=ah,找到图中阴影部分的底和高,代入计算即可求解.解答解:2×3÷2=6÷2=3(平方厘米).答:阴影部分的面积是3平方厘米.点评考查了组合图形的面积,本题组合图形是一个三角形,关键是得到三角形的底和高.16.求阴影部分面积(单位:厘米).考点组合图形的面积.分析由图意可知:阴影部分的面积=梯形的面积﹣圆的面积,梯形的上底和高都等于圆的半径,上底和下底已知,从而可以求出阴影部分的面积.解答解:(4+9)×4÷2﹣3.14×42×,=13×4÷2﹣3.14×4,=26﹣12.56,=13.44(平方厘米);答:阴影部分的面积是13.44平方厘米.点评解答此题的关键是明白:梯形的下底和高都等于圆的半径,且阴影部分的面积=梯形的面积﹣圆的面积.17.(2012?长泰县)求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析由图可知,阴影部分的面积=梯形的面积﹣半圆的面积.梯形的面积=(a+b)h,半圆的面积=πr2,将数值代入从而求得阴影部分的面积.解答解:×(6+8)×(6÷2)﹣×3.14×(6÷2)2=×14×3﹣×3.14×9,=21﹣14.13,=6.87(平方厘米);答:阴影部分的面积为6.87平方厘米.点评考查了组合图形的面积,解题关键是看懂图示,把图示分解成梯形,半圆和阴影部分,再分别求出梯形和半圆的面积.。
六年级奥数 阴影部分的面积
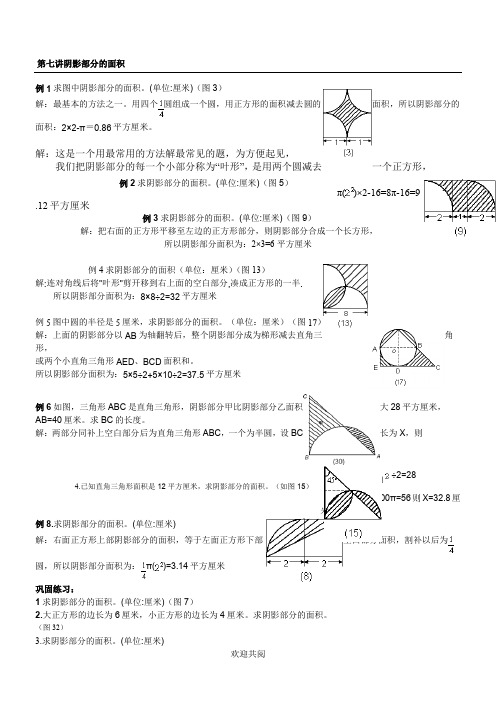
第七讲阴影部分的面积例1求图中阴影部分的面积。
(单位:厘米)(图3)
解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的
面积:2×2-π=0.86平方厘米。
解:这是一个用最常用的方法解最常见的题,为方便起见, 我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去
一个正方形,
.12平方厘米
例3求阴影部分的面积。
(
例4求阴影部分的面积(单位:厘米)解:连对角线后将"叶形"剪开移到右上面的空白部分, 所以阴影部分面积为:8×8÷2=32平方厘米
例5图中圆的半径是5
)
角
形,
例6大28平方厘米,AB=40解:设BC
长为X ,则
40X÷2-π
÷2=28
所以40X-400π=56则X=32.8厘米
例8.求阴影部分的面积。
(单位:厘米)
空白部分面积,割补以后为
解:右面正方形上部阴影部分的面积,等于左面正方形下部圆,所以阴影部分面积为:π()=3.14平方厘米
巩固练习:
1求阴影部分的面积。
(单位:厘米)(图7)
2.大正方形的边长为6厘米,小正方形的边长为4厘米。
求阴影部分的面积。
(图32)
3.求阴影部分的面积。
(单位:厘米)
例2求阴影部分的面积。
(单位:厘米)(图5)
15)
5.正方形ABCD的面积是36平方厘米,求阴影部分的面积。
(如图)。
小学六年级-阴影部分面积及答案完整

阴影部分面积专题令狐采学求如图阴影部分的面积.(单位:厘米)如图,求阴影部分的面积.(单位:厘米)3.计算如图阴影部分的面积.(单位:厘米)4.求出如图阴影部分的面积:单位:厘米.5.求如图阴影部分的面积.(单位:厘米)6.求如图阴影部分面积.(单位:厘米)7.计算如图中阴影部分的面积.单位:厘米.8.求阴影部分的面积.单位:厘米.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)10.求阴影部分的面积.(单位:厘米)11.求下图阴影部分的面积.(单位:厘米)12.求阴影部分图形的面积.(单位:厘米)13.计算阴影部分面积(单位:厘米).14.求阴影部分的面积.(单位:厘米)15.求下图阴影部分的面积:(单位:厘米)16.求阴影部分面积(单位:厘米).17.求阴影部分的面积.(单位:厘米)☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆参考答案与试题解析1.求如图阴影部分的面积.(单位:厘米)考点组合图形的面积;梯形的面积;圆、圆环的面积.分析阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.解答解:(4+6)×4÷2÷2﹣3.14×÷2,=10﹣3.14×4÷2,=10﹣6.28,=3.72(平方厘米);答:阴影部分的面积是3.72平方厘米.点评组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用.2.如图,求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析根据图形可以看出:阴影部分的面积等于正方形的面积减去4个扇形的面积.正方形的面积等于(10×10)100平方厘米,4个扇形的面积等于半径为(10÷2)5厘米的圆的面积,即:3.14×5×5=78.5(平方厘米).解答解:扇形的半径是:10÷2,=5(厘米);10×10﹣3.14×5×5,100﹣78.5,=21.5(平方厘米);答:阴影部分的面积为21.5平方厘米.点评解答此题的关键是求4个扇形的面积,即半径为5厘米的圆的面积.3.计算如图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析分析图后可知,10厘米不仅是半圆的直径,还是长方形的长,根据半径等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.解答解:10÷2=5(厘米),长方形的面积=长×宽=10×5=50(平方厘米),半圆的面积=πr2÷2=3.14×52÷2=39.25(平方厘米),阴影部分的面积=长方形的面积﹣半圆的面积,=50﹣39.25,=10.75(平方厘米);答:阴影部分的面积是10.75.点评这道题重点考查学生求组合图形面积的能力,组合图形可以是两个图形拼凑在一起,也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看属于哪一种类型的组合图形,再根据条件去进一步解答.4.求出如图阴影部分的面积:单位:厘米.考点组合图形的面积.专题平面图形的认识与计算.分析由题意可知:阴影部分的面积=长方形的面积﹣以4厘米为半径的半圆的面积,代入数据即可求解.解答解:8×4﹣3.14×42÷2,=32﹣25.12,=6.88(平方厘米);答:阴影部分的面积是6.88平方厘米.点评解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.5.求如图阴影部分的面积.(单位:厘米)考点圆、圆环的面积.分析由图可知,正方形的边长也就是半圆的直径,阴影部分由4个直径为4厘米的半圆组成,也就是两个圆的面积,因此要求阴影部分的面积,首先要算1个圆的面积,然后根据“阴影部分的面积=2×圆的面积”算出答案.解答解:S=πr2=3.14×(4÷2)2=12.56(平方厘米);阴影部分的面积=2个圆的面积,=2×12.56,=25.12(平方厘米);答:阴影部分的面积是25.12平方厘米.点评解答这道题的关键是重点分析阴影部分是由什么图形组成的,再根据已知条件去计算.6.求如图阴影部分面积.(单位:厘米)考点长方形、正方形的面积;平行四边形的面积;三角形的周长和面积.分析图一中阴影部分的面积=大正方形面积的一半﹣与阴影部分相邻的小三角形的面积;图二中阴影部分的面积=梯形的面积﹣平四边形的面积,再将题目中的数据代入相应的公式进行计算.解答解:图一中阴影部分的面积=6×6÷2﹣4×6÷2=6(平方厘米);图二中阴影部分的面积=(8+15)×(48÷8)÷2﹣48=21(平方厘米);答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.点评此题目是组合图形,需要把握好正方形、三角形、梯形及平行四边形的面积公式,再将题目中的数据代入相应的公式进行计算.7.计算如图中阴影部分的面积.单位:厘米.考点组合图形的面积.分析由图意可知:阴影部分的面积=圆的面积,又因圆的半径为斜边上的高,利用同一个三角形的面积相等即可求出斜边上的高,也就等于知道了圆的半径,利用圆的面积公式即可求解.解答解:圆的半径:15×20÷2×2÷25,=300÷25,=12(厘米);阴影部分的面积:×3.14×122,=×3.14×144,=0.785×144,=113.04(平方厘米);答:阴影部分的面积是113.04平方厘米.点评此题考查了圆的面积公式及其应用,同时考查了学生观察图形的能力.8.求阴影部分的面积.单位:厘米.考点组合图形的面积;三角形的周长和面积;圆、圆环的面积.分析(1)圆环的面积等于大圆的面积减小圆的面积,大圆与小圆的直径已知,代入圆的面积公式,从而可以求出阴影部分的面积;(2)阴影部分的面积=圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.解答解:(1)阴影部分面积:3.14×﹣3.14×,=28.26﹣3.14,=25.12(平方厘米);(2)阴影部分的面积:3.14×32﹣×(3+3)×3,=28.26﹣9,=19.26(平方厘米);答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.点评此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)考点组合图形的面积;圆、圆环的面积.专题平面图形的认识与计算.分析观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等,所以图中阴影部分的周长,就是直径为10+3=13厘米的圆的周长,由此利用圆的周长公式即可进行计算;阴影部分的面积=大半圆的面积﹣以10÷2=5厘米为半径的半圆的面积﹣以3÷2=1.5厘米为半径的半圆的面积,利用半圆的面积公式即可求解.解答解:周长:3.14×(10+3),=3.14×13,=40.82(厘米);面积:×3.14×[(10+3)÷2]2﹣×3.14×(10÷2)2﹣×3.14×(3÷2)2,=×3.14×(42.25﹣25﹣2.25),=×3.14×15,=23.55(平方厘米);答:阴影部分的周长是40.82厘米,面积是23.55平方厘米.点评此题主要考查半圆的周长及面积的计算方法,根据半圆的弧长=πr,得出图中两个小半圆的弧长之和等于大半圆的弧长,是解决本题的关键.10.求阴影部分的面积.(单位:厘米)考点圆、圆环的面积.分析先用“3+3=6”求出大扇形的半径,然后根据“扇形的面积”分别计算出大扇形的面积和小扇形的面积,进而根据“大扇形的面积﹣小扇形的面积=阴影部分的面积”解答即可.解答解:r=3,R=3+3=6,n=120,,=,=37.68﹣9.42,=28.26(平方厘米);答:阴影部分的面积是28.26平方厘米.点评此题主要考查的是扇形面积计算公式的掌握情况,应主要灵活运用.11.求下图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析先求出半圆的面积3.14×(10÷2)2÷2=39.25平方厘米,再求出空白三角形的面积10×(10÷2)÷2=25平方厘米,相减即可求解.解答解:3.14×(10÷2)2÷2﹣10×(10÷2)÷2=39.25﹣25=14.25(平方厘米).答:阴影部分的面积为14.25平方厘米.点评考查了组合图形的面积,本题阴影部分的面积=半圆的面积﹣空白三角形的面积.12.求阴影部分图形的面积.(单位:厘米)考点组合图形的面积.分析求阴影部分的面积可用梯形面积减去圆面积的,列式计算即可.解答解:(4+10)×4÷2﹣3.14×42÷4,=28﹣12.56,=15.44(平方厘米);答:阴影部分的面积是15.44平方厘米.点评解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形(扇形)的面积,即可列式解答.13.计算阴影部分面积(单位:厘米).考点组合图形的面积.专题平面图形的认识与计算.分析如图所示,阴影部分的面积=平行四边形的面积﹣三角形①的面积,平行四边形的底和高分别为10厘米和15厘米,三角形①的底和高分别为10厘米和(15﹣7)厘米,利用平行四边形和三角形的面积公式即可求解.解答解:10×15﹣10×(15﹣7)÷2,=150﹣40,=110(平方厘米);答:阴影部分的面积是110平方厘米.点评解答此题的关键是明白:阴影部分的面积不能直接求出,可以用平行四边形和三角形的面积差求出.14.求阴影部分的面积.(单位:厘米)考点梯形的面积.分析如图所示,将扇形①平移到扇形②的位置,求阴影部分的面积就变成了求梯形的面积,梯形的上底和下底已知,高就等于梯形的上底,代入梯形的面积公式即可求解.解答解:(6+10)×6÷2,=16×6÷2,=96÷2,=48(平方厘米);答:阴影部分的面积是48平方厘米.点评此题主要考查梯形的面积的计算方法,关键是利用平移的办法变成求梯形的面积.15.求下图阴影部分的面积:(单位:厘米)考点组合图形的面积.分析根据三角形的面积公式:S=ah,找到图中阴影部分的底和高,代入计算即可求解.解答解:2×3÷2=6÷2=3(平方厘米).答:阴影部分的面积是3平方厘米.点评考查了组合图形的面积,本题组合图形是一个三角形,关键是得到三角形的底和高.16.求阴影部分面积(单位:厘米).考点组合图形的面积.分析由图意可知:阴影部分的面积=梯形的面积﹣圆的面积,梯形的上底和高都等于圆的半径,上底和下底已知,从而可以求出阴影部分的面积.解答解:(4+9)×4÷2﹣3.14×42×,=13×4÷2﹣3.14×4,=26﹣12.56,=13.44(平方厘米);答:阴影部分的面积是13.44平方厘米.点评解答此题的关键是明白:梯形的下底和高都等于圆的半径,且阴影部分的面积=梯形的面积﹣圆的面积.17.(2012•长泰县)求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析由图可知,阴影部分的面积=梯形的面积﹣半圆的面积.梯形的面积=(a+b)h,半圆的面积=πr2,将数值代入从而求得阴影部分的面积.解答解:×(6+8)×(6÷2)﹣×3.14×(6÷2)2=×14×3﹣×3.14×9,=21﹣14.13,=6.87(平方厘米);答:阴影部分的面积为6.87平方厘米.点评考查了组合图形的面积,解题关键是看懂图示,把图示分解成梯形,半圆和阴影部分,再分别求出梯形和半圆的面积.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七讲阴影部分的面积
例1求图中阴影部分的面积。
(单位:厘米)(图3)
解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的
面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例2求阴影部分的面积。
(单位:厘米)(图5)
解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,
π()×2-16=8π-16=9.12平方厘米
例3求阴影部分的面积。
(单位:厘米)(图9)
解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长
方形,
所以阴影部分面积为:2×3=6平方厘米
例4求阴影部分的面积(单位:厘米)(图13)
解: 连对角线后将"叶形"剪开移到右上面的空白部分,凑成正方形的一半.
所以阴影部分面积为:8×8÷2=32平方厘米
例5图中圆的半径是5厘米,求阴影部分的面积。
(单位:厘米)(图17)
解:上面的阴影部分以AB为轴翻转后,整个阴影部分成为梯形减去直
角三角形,
或两个小直角三角形AED、BCD面积和。
所以阴影部分面积为:5×5÷2+5×10÷2=37.5平方厘米
例6如图,三角形ABC是直角三角形,阴影部分甲比阴影部分乙面积
大28平方厘米,AB=40厘米。
求BC的长度。
解:两部分同补上空白部分后为直角三角形ABC,一个为半圆,设BC
长为X,则
40X÷2-π÷2=28
所以40X-400π=56 则X=32.8厘米
例8.求阴影部分的面积。
(单位:厘米)
解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米
巩固练习:
1求阴影部分的面积。
(单位:厘米)(图7)
2.大正方形的边长为6厘米,小正方形的边长为4厘米。
求阴影部分的面积。
(图32)
3. 求阴影部分的面积。
(单位:厘米)
4. 已知直角三角形面积是12平方厘米,求阴影部分的面积。
(如图15)
5.正方形ABCD 的面积是36平方厘米,求阴影部分的面积。
(如图)。
