2012-2013年必修一数学期末复习题及答案
2013高一上册数学期末试题(带答案)

2013高一上册数学期末试题(带答案)2012-2013年第一学期期末考试高一数学试题一、选择题(每小题4分,共40分)1、设集合,,则A.B.C.D.2、下列函数中,与函数有相同定义域的是A.B.C.D.3、已知函数,则A.B.C.2D.4、已知点,,,则的形状为A.等腰三角形B.直角三角形C.等腰直角三角形D.等边三角形5、式子的值等于A.B.-C.-D.-6、下列函数中,既是奇函数又是增函数的是A.B.C.D.7、在下列区间中,函数的零点所在区间是A.B.C.D.8、如图是一个几何体的三视图,若该几何体的表面积为9,则正视图中实数的值等于A.1B.2C.3D.49、在下列关于直线、与平面、的命题中,正确的是A.若,且,则B.若,且,则C.若,且,则D.若,且,则10、定义两种运算,,则函数是A.非奇非偶函数且在上是减函数B.非奇非偶函数且在上是增函数C.偶函数且在上是增函数D.奇函数且在上是减函数二、填空题(每小题4分,共16分)11、圆的半径等于12、如图,在棱长为的正方体中,分别是的中点,则异面直线与所成角等于13、设集合,,则=.14、两条互相垂直的直线与的交点坐标为三、解答题(本大题共5小题,共44分.)15(本小题满分8分)已知函数是定义在上的奇函数,且时,.(1)求的值;(2)当时,求的解析式.16(本小题满分8分)已知点和,求(1)线段的垂直平分线的方程;(2)以为直径的圆的方程.17(本小题满分8分)如图,四棱锥的底面是边长为1的正方形,、分别为、的中点。
(1)求证:;(2)求证:平面;(3)求四棱锥的体积.18(本小题满分10分)已知圆O:与直线:(1)当时,求直线被圆O截得的弦长;(2)当直线与圆O相切时,求的值.19(本小题满分10分)设计一幅宣传画,要求画面面积为4840cm2,画面的宽与高的比为,画面的上、下各留8cm空白,左、右各留5cm空白。
(1)用表示宣传画所用纸张面积;(2)判断函数在上的单调性,并证明你的结论;(3)当取何值时,宣传画所用纸张面积最小?参考答案一、选择题题号12345678910答案ADCBADDCBA提示:3、从而选C4、,故又从而选B5、原式==从而选A,也可从符号判断只有A符合题意.6、画出简图易得。
【全国各地历年高一数学期末试题精选】吉林省吉林市2012-2013学年高一上学期期末考试数学版含答案

6. 如图 , 空间四边形 ABCD中,若 AB AD AC CB CD BD ,
A
则 AC 与 BD 所成角为
A. 30 0 C. 60 0
B. 45 0
B
D. 90 0
C
7. 如图,一个空间几何体的主视图、左视图、俯视图均为全等
的等腰直角三角形,且直角三角形的直角边长为
1,那么这
个几何体的体积为
为 2 时,求直线 AB 与平面 PBC 所成角的正弦值.
21.(本题满分 12 分)
已知关于 x, y 的方程 C : x2 y 2 2x 4 y m 0 .
( 1)当 m 为何值时,方程 C 表示圆。
( 2)若圆 C 与直线 l : x
2y
4
0 相交于
M,N 两点,且|
MN | = 4
5
,求 m 的值。
( 2)求函数 f (x)
log
2
(
x) 2
log 2(
x) 4
的最大值和最小值及对应的
D x 值。
20.(本题满分 12 分)
如图, AB 是⊙ O 的直径, PA 垂直于⊙ O 所在的平面, C 是圆周上不同于 A, B 的一动点.
( 1)证明:面 PAC 面 PBC;
( 2)若 PA AB 2 ,则当直线 PC 与平面 ABC 所成角正切值
18.证明:( 1) CC1 平面 ABC , AC 平面 ABC
C1
B1
CC1 AC , AC BC , BC CC1 C ,
A1
AC 平面 BCC1B1 , BC1 平面 ABC
O
C
B
D A
AC BC1. ----------------------------5 分 ( 2)设 BC1 与 B1C 的交点为 O ,连结 OD ,
2012—2013学年度第一学期高一数学期末练习一试题附答案[好4页]
![2012—2013学年度第一学期高一数学期末练习一试题附答案[好4页]](https://img.taocdn.com/s3/m/eb4512295901020207409c94.png)
2012—2013学年度第一学期高一数学期末练习一试题附答案班级_______________姓名________________学号___________得分_______________一、填空题(每题3分,共36分)1、集合|01x M x x ⎧⎫=≥⎨⎬-⎩⎭,12|N y y x ⎧⎫==⎨⎬⎩⎭,则M N = _____________。
{}()01,+∞2、函数()1f x =()g x =()()f x g x +=____________。
[]10,1x +∈3、函数()112-≤-=x x y 的反函数是_____________________。
0y x =≥4、若函数(31)xy a =-为指数函数,则a 的取值范围为 ;122,,333⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭5、命题“若b a >,则122->b a ”的否命题为________________.若a b ≤,则221a b ≤- 6、函数23x y a-=+,)10(≠>a a 且的图像必经过定点 。
()2,47、集合101x A xx ⎧-⎫=>⎨⎬+⎩⎭,{}a b x x B <-=,若“1a =”是“A B ≠∅ ”的充分条件, 则b 的取值范围是 。
22b -<<8、已知lg 2a =,103b=,则6log = 。
(用,a b 表示)12()b a b ++9、函数2()21f x x a x =-+有两个零点,且分别在(0,1)与(1,2)内,则实数a 的取值范围是______________。
514a <<10、不等式22(1)30ax a x a --++<的解集为∅,则实数a 的取值范围是 。
1,5⎡⎫+∞⎪⎢⎣⎭11、国内快递以内的包裹的邮资标准如下表:元。
712、直线5y =与曲线2||y x x a =-+有四个交点,则实数a 的取值范围是 。
【新课标版】2012-2013学年高一上学期期末考试数学

2012-2013学年度上学期期末考试高一数学试题【新课标】时量:120分钟 总分:150分一、选择题(5×8=40分)1.已知角α的终边经过点p (-3,4),则sin α的值等于( )A .35-B .35C .①45D .45-2.sin 600o 的值是( )A .12; B .2; C .2-D .12-3.已知扇形的弧长8,半径是4,则扇形的中心角的弧度数是( )A .1B .2C .12或2 D .124.化简AC BO CD AB -+-得( )A .ABB .DAC .BCD .o5.已知b a,都是单位向量,则下列结论正确的是( )A .;1=⋅b aB .;22b a = C .;//b a b a =⇒ D .;0=⋅b a6.已知=(5,-3),C (-1,3), =2,则点D 坐标 ( )A .(11,9)B .(4,0)C .(9,3)D .(9,-3)7.化简sin 235°-12cos 10°cos80°=( )A .-2B .-12C .-1D .18.已知点A (2,3)、B (10,5),直线AB 上一点P 满足|PA|=2|PB|,则P 点坐标是( )A .2213,33⎛⎫⎪⎝⎭ B .(18,7)C .2213,33⎛⎫⎪⎝⎭或(18,7) D .(18,7)或(-6,1)二、填空题(5×7=35分)9.已知向量(2,3),(4,2)a b ==-,则a b -= 。
10.cos36cos6sin36sin 6oooo+= 。
11.已知点A (2,-4),B (-6,2),则AB 的中点M 的坐标为 ; 12.已知单位向量1e ,2e 的夹角为60°,则a b -=__________ 13.若2tan =α,则ααααcos 3sin 2cos sin -+= ;14.已知 ()()3,0,,5a b k == 且 a 与 b 的夹角为34π,k 的值是 15.已知091sin sin sin =︒++βα,091cos cos cos =︒++βα,则)(βα-c o s = 。
2012-2013学年高一上册数学理科期末试卷(附答案)

2012-2013学年高一上册数学理科期末试卷(附答案)本试题分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
考试结束后,只交答题纸和答题卡,试题自己保留。
第I卷(60分)注意事项1.答题前,考生在答题纸和答题卡上务必用直径0.5毫米黑色签字笔将自己的班级、姓名、考号填写清楚。
请认真核准考号、姓名和科目。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
在试题卷上作答无效。
3.本试卷共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项符合要求。
一、(共60分,每小题5分)1.若两条直线都与一个平面平行,则这两条直线的位置关系是()A.平行B.相交C.异面D.以上均有可能2.三个平面把空间分成7部分时,它们的交线有A.1条B.2条C.3条D.1或2条3.过点(1,0)且与直线平行的直线方程是A.B.C.D.4.设、是两条不同的直线,是一个平面,则下列命题正确的是A.若,,则B.若,,则C.若,,则D.若,,则5.正方体ABCD—A1B1C1D1中,E、F分别是AB、B1C的中点,则EF 与平面ABCD所成的角的正切值为()A.2B.2C.12D.226.边长为a的正方形ABCD沿对角线AC将△ADC折起,若∠DAB=60°,则二面角D—AC—B的大小为()A.60°B.90°C.45°D.30°7.在正方体ABCD—A1B1C1D1中,若E是A1C1的中点,则直线CE垂直于()A.ACB.BDC.A1DD.A1D8.如果一条直线垂直于一个平面内的①三角形的两边;②梯形的两边;③圆的两条直径;④正六边形的两条边,则能保证该直线与平面垂直的是()A.①③B.②C.②④D.①②④9.BC是Rt△ABC的斜边,AP⊥平面ABC,PD⊥BC于点D,则图中共有直角三角形的个数是()A.8B.7C.6D.510.圆C:x2+y2+2x+4y-3=0上到直线:x+y+1=0的距离为的点共有A.1个B.2个C.3个D.4个11.求经过点的直线,且使,到它的距离相等的直线方程.A.B.C.,或D.,或12.当点P在圆x2+y2=1上变动时,它与定点Q(3,0)相连,线段PQ的中点M的轨迹方程是()A.(x+3)2+y2=4B.(x-3)2+y2=1C.(2x-3)2+4y2=1D.(2x+3)2+4y2=1第Ⅱ卷二、填空题(本大题共4小题,每小题5分,共20分.把正确答案填在答题卡的横线上,填在试卷上的答案无效)13.经过圆的圆心,并且与直线垂直的直线方程为_____.14.以A(4,3,1),B(7,1,2),C(5,2,3)为顶点的三角形形状为.15.已知实数满足,则的最小值为________.16.半径为R的球放在墙角,同时与两墙面和地面相切,那么球心到墙角顶点的距离为______.三、解答题:(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.)17.(本小题满分10分)过点的直线与轴的正半轴、轴的正半轴分别交于点、,为坐标原点,的面积等于6,求直线的方程.18.(本小题满分12分)如图,垂直于⊙所在的平面,是⊙的直径,是⊙上一点,过点作,垂足为.求证:平面19.(本小题满分12分)如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.(1)求证:EF∥平面CB1D1;(2)求证:平面CAA1C1⊥平面CB1D1.20.(本小题满分12分)已知圆C:,直线L:(1)证明:无论取什么实数,L与圆恒交于两点;(2)求直线被圆C截得的弦长最小时直线L的斜截式方程.21.(本小题满分12分)已知圆与圆(其中)相外切,且直线与圆相切,求的值.22.(本小题满分12分)已知动点M到点A(2,0)的距离是它到点B(8,0)的距离的一半,求:(1)动点M的轨迹方程;(2)若N为线段AM的中点,试求点N的轨迹.高一数学参考答案18.证明:因为平面所以又因为是⊙的直径,是⊙上一点,所以所以平面而平面所以又因为,所以平面19.证明:(1)连结BD.在正方体中,对角线.又E、F为棱AD、AB的中点,..又B1D1平面,平面,EF∥平面CB1D1.(2)在正方体中,AA1⊥平面A1B1C1D1,而B1D1平面A1B1C1D1,AA1⊥B1D1.又在正方形A1B1C1D1中,A1C1⊥B1D1,B1D1⊥平面CAA1C1.又B1D1平面CB1D1,平面CAA1C1⊥平面CB1D1.21.解:由已知,,圆的半径;,圆的半径.因为圆与圆相外切,所以.整理,得.又因为,所以.因为直线与圆相切,所以,即.两边平方后,整理得,所以或.22.解:(1)设动点M(x,y)为轨迹上任意一点,则点M的轨迹就是集合P={M||MA|=12|MB|}.由两点间距离公式,点M适合的条件可表示为-+y2=-+y2.平方后再整理,得x2+y2=16.可以验证,这就是动点M的轨迹方程.(2)设动点N的坐标为(x,y),M的坐标是(x1,y1).由于A(2,0),且N为线段AM的中点,所以x=2+x12,y=0+y12.所以有x1=2x-2,y1=2y.①由(1)知,M是圆x2+y2=16上的点,所以M的坐标(x1,y1)满足x21+y21=16.②x将①代入②整理,得(x-1)2+y2=4.所以N的轨迹是以(1,0)为圆心,2为半径的圆.。
2013学年高一数学上学期期末考试试题及答案(新人教A版 第118套)

辽宁省大连市2012-2013学年高一上学期期末考试数学试题本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分.考生作答时,将答案答在答题卡上,在本试卷上答题无效.考试结束后,将本试卷和答题卡一并交回.参考公式:球的体积公式343V R π=,球的表面积公式24S R π=. 第I 卷一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 下列图形中,表示集合N M ⊆关系的韦恩图是 ( )2.已知直线10x my +-=与直线220x y -+=平行,则m 的值为( ) A. 2- B.12-C. 2D.123.函数3()f x x =的图像关于( )A .y 轴对称B .坐标原点对称C .直线x y =对称D .直线x y -=对称4.直线l 的方程是5x =,圆C 的方程是22(2)9x y -+=,则直线l 与圆C 的位置关系是( )A. 相离B. 相切C. 相交D. 相交或相切5.已知函数⎩⎨⎧=x x x f 3log )(2)0()0(≤>x x ,则)]41([f f 的值是 ( ) A. 91 B. 41 C. 4 D. 96.如图为函数ln y m x =+的图像,其中m 、n 常数,则下列结论正确的是 ( ) A .0,1m n <> B .0,1m n >> C .0,01m n ><< D .0,01m n <<<7.在用二分法求方程3210x x --=(1,2)内,则下一步可断定该根所在的区间为( )A .(1.4,2)B .(1,1.4)C .3(1,)2D .3(,2)28.已知函数22log (2)y x kx k =-+的值域为R,则k 的取值范围是( )A .01k << B 01k ≤< C.0k ≤或1k ≥ D.0k =或1k ≥9.在下列正方体中,有AB CD ⊥的是( )A B C D10. 若过点(4,0)A 的直线l 与曲线22(2)1x y -+=1)2(22=+-y x 有公共点,则直线l 的斜率的取值范围为( )A .[B .(C . [D .( 11.点(4,2)P -与圆224x y +=上任一点连线的中点轨迹方程是 ( )A .22(2)(1)1x y -++=B .22(2)(1)4x y -++=C .22(4)(2)4x y ++-=D .22(2)(1)1x y ++-=12.已知函数()y f x =的定义域为D ,若对于任意的1x ,2x D ∈()12x x ≠,都有()()121222f x f x x x f ++⎛⎫< ⎪⎝⎭,则称()y f x =为D 上的凹函数.由此可得下列函数中的凹函数为( )A .2log y x =B .y =.3y x = D .2y x =第 Ⅱ 卷(非选择题,共90分)二.填空题:(本大题共4小题,每小题5分,共20分,把答案填在答卷纸的相应位置上)13.设2.03=a ,π21log =b ,3..021⎪⎭⎫ ⎝⎛=c ,则c b a ,,从大到小的顺序为 .14.过点()1,2P 引一直线,使其倾斜角为直线:l 30x y --=的倾斜角的两倍,则该直线的方程是_________________.15.给出下列四个命题:①若直线垂直于平面内的两条直线,则这条直线垂直于这个平面;②若直线与平面内的任意一条直线都垂直,则这条直线垂直于这个平面; ③若直线l α平面,直线m α平面,则l m ; ④若直线a 直线b ,且直线l a ⊥,则l b ⊥.其中正确命题的序号是 .16.从点P 出发三条射线,,PA PB PC 两两成60°角,且分别与球O 相切于,,A B C 三点,若球的体积为43π,则OP 的距离为 .三.解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分10分)定义在R 上的函数()y f x =是偶函数,当x ≥0时,2483f x x x =-+-(). (Ⅰ)当0x <时,求()f x 的解析式;(Ⅱ)求()y f x =的最大值,并写出()f x 在R 上的单调区间(不必证明).. 18.(本小题满分12分)如图, 在底面是菱形的四棱锥P ABCD -,60ABC ∠=︒,PA AC a ==,PB PD ==,点E 是PD 的中点.证明: (Ⅰ)PA ⊥平面ABCD ;(Ⅱ)PB ∥平面EAC .19. (本小题满分12分)如图所示是一个几何体的直观图及它的三视图(其中主视图为直角梯形,俯视图为正方形,左视图为直角三角形,尺寸如图所示),(Ⅰ)求四棱锥P ABCD -的体积;(Ⅱ)若G 为BC 的中点,求证:AE PG ⊥.20.(本小题满分12分)已知2()3gx x=--,()f x 是二次函数,当[1,2]x ∈-时,()f x 的最小值为1,且()()f x g x +为奇函数,求函数()f x 的表达式.44主视图左视图俯视图21.(本小题满分12分)已知圆M 过两点A (1,-1),B (-1,1),且圆心M 在20x y +-=上.(1)求圆M 的方程;(2)设P 是直线3480x y ++=上的动点,PC 、PD 是圆M 的两条切线,C 、D 为切点,求四边形PCMD 面积的最小值. 22.(本题满分12分)定义:对于任意x ∈[0,1],函数()0f x ≥恒成立,且当12120,0,1x x x x ≥≥+≤时,总有1212()()()f x x f x f x +≥+成立,则称()f x 为G 函数.已知函数2()g x x =与()21x h x a =⋅-是定义在[0,1]上的函数.(1)试问函数()g x 是否为G 函数?并说明理由;(2)若函数()h x 是G 函数,求实数a 的值;(3)在(2)的条件下,利用函数图象讨论方程(2)(21)x g h x m +-+=(R)m ∈解的个数情况.高一期末测试卷数学参考答案与评分标准一.选择题1. C ;2.A ;3.B ;4.B ;5.A ;6.D ;7.D ;8.C ;9.A ;10.C ;11.A ;12.D . 二.填空题13.a c b >>;14.1x =;15.②,④;16.3. 三.解答题17.解:(Ⅰ)设x <0,则0x ->,22()4()8()3483f x x x x x -=--+--=---, ············ 2分∵()f x 是偶函数,∴()()f x f x -=,∴0x <时, 2()483f x x x =---. ················· 5分(Ⅱ)由(Ⅰ)知224(1)1(0)()4(1)1(0)x x f x x x ⎧--+≥⎪=⎨-++<⎪⎩, ············ 6分 ∴()y f x =开口向下,所以()y f x =有最大值(1)(1)1f f =-=. ···· 8分函数()y f x =的单调递增区间是(-∞,-1]和[0,1];单调递减区间是 [-1,0]和 [1,+∞). ···············10分 18.证明:(1)底面ABCD 为菱形,60ABC ∠=,AB BC CD DA AC a ∴=====. ··················· 2分PA AC =,PA AB a ∴==,PB =,PA AB ∴⊥,同理可证PA AD ⊥, ··················· 4分又AB AD A =,PA ∴⊥平面ABCD . ················ 6分 (2)连结AC BD ,相交于O ,则O 为BD 的中点.E 为PD 的中点,PB OE ∴∥. ···················· 8分 又OE ⊂平面EAC ,PB ⊄平面EAC , ················ 10分 PB ∴∥平面EAC . ·························· 12分19.解(Ⅰ)由几何体的三视图可知,底面ABCD 是边长为4的正方形, ······· 2分PA ⊥面ABCD ,PA ∥EB ,且PA =42,BE =22,AB =AD =CD =CB =4, ..... 4分∴V P -ABCD =13PA x S ABCD =13×42×4×4=6423. .......................... 5分(Ⅱ)连BP ,∵EB AB =BAPA=12,∠EBA =∠BAP =90°, ................... 7分 ∴△EBA ∽△BAP ,∴∠PBA =∠BEA , ................................ 8分∴∠PBA +∠BAE =∠BEA +∠BAE =90°,∴PB ⊥AE . .................. 10分 又∵BC ⊥面APEB ,∴BC ⊥AE ,∴AE ⊥面PBG ,∴AE ⊥PG . ............. 12分 20. 解:设()(),02≠++=a c bx ax x f则()()()312-++-=+c bx x a x g x f . ················· 2分 又()()x g x f +为奇函数,∴3,1==c a . ··············· 4分∴(),32++=bx xx f 对称轴2bx -= .当22≥-b时,()f x 在[]2,1-上为减函数 ∴()f x 的最小值为()13242=++=b f ∴3-=b 又4-≤b ,∴此时无解. ······························ 6分当221<-<-b 时,()14322min =-=⎪⎭⎫⎝⎛-=b b f x f ∴22±=b∵2224-=∴<<-b b ,此时(),3222+-=x x x f ········· 8分当12-≤-b时,()f x 在[]2,1-上为增函数∴()f x 的最小值为()141=-=-b f ∴3=b ,又满足2≥b ∴(),332++=x x x f ············· 10分综上所述,(),3222+-=x x x f 或()332++=x x x f ·········· 12分21.解:(1)法一:线段AB 的中点为(0,0),其垂直平分线方程为0x y -=. ···· 2分 解方程组0,20.x y x y -=⎧⎨+-=⎩所以圆M 的圆心坐标为(1,1).故所求圆M 的方程为:22(1)(1)4x y -+-=. ············· 4分 法二:设圆M 的方程为:222()()x a y b r -+-=,根据题意得222222(1)(1),(1)(1),20.a b r a b r a b ⎧-+--=⎪--+-=⎨⎪+-=⎩·················· 2分解得1,2a b r ===.故所求圆M 的方程为:22(1)(1)4x y -+-=. ············· 4分(2)由题知,四边形PCMD 的面积为1122PMC PMD S S S CM PC DM PD ∆∆=+=+. ············ 6分 又2CM DM ==,PC PD =,所以2S PC =,而PC ==即S = ························ 8分因此要求S 的最小值,只需求PM 的最小值即可,即在直线3480x y ++=上找一点P ,使得PM 的值最小,所以min3PM==, ··················10分 所以四边形PCMD 面积的最小值为S ===. ·················· 12分22.解:(1) 当[]0,1x ∈时,总有2g x x 0()=≥,满足条件①, ········ 1分 当12120,0,1x x x x ≥≥+≤时,22222121212121212g x x x x x x 2x x x x g x g x ()()()()+=+=++≥+=+,满足条件②································ 3分 (2)∵()21xh x a =⋅-是G 函数,∴210xa ⋅-≥,∴12x a ≥恒成立. ····· 4分 ∴a 1≥. ······························· 5分 由1212g x x g x g x ()()()+≥+ ,得1212x x x x a 21a 21a 21+⋅-≥⋅-+⋅-,即12xxa 121211[()()]---≤, ······················· 6分 因为 12120,0,1x x x x ≥≥+≤ 所以1x 0211≤-≤ 2x 0211≤-≤ 1x 与2x 不同时等于111x x 021211()()∴≤--<,11x x 0121211()()∴<---≤,11x x 1a 12121()()∴≤--- ·························· 7分当12x x 0==时,11x x 1112121min ()()()=--- ,a 1∴≤, ·········· 8分 综合上述a 的值为1. ·························· 8分 (3)根据⑵知: a=1,方程为x2x 1421m -++-=, ············· 9分令x 4tt 14[,]=∈ 方程为2t m 1t+=+ 图(略) ································· 10分 由图形可知:当7m 122{}(,]∈⋃时,有一解;当m 12(,]∈ 时,有二不同解;当7m 12(,)(,)∈-∞⋃+∞时,方程无解. ················ 2分。
2012-2013年必修一数学期末复习题及答案

2012学年高一数学期末复习(必修一)4一、选择题:本大题10小题,每小题5分,满分50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、已知全集,集合,,则等于I ={0,1,2,3,4}{1,2,3}M ={0,3,4}N =()I M N ð( )A.{0,4}B.{3,4}C.{1,2}D.∅2、设集合,,则等于( )2{650}M x x x =-+=2{50}N x x x =-=M N A.{0} B.{0,5} C.{0,1,5} D.{0,-1,-5}3、计算:=( )9823log log ⋅A 12 B 10 C 8 D 64、函数图象一定过点 ( )2(01)x y a a a =+>≠且A (0,1) B (0,3) C (1,0) D (3,0)5、“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点…用S 1、S 2分别表示乌龟和兔子所行的路程,t 为时间,则与故事情节相吻合是 ( )6、函数 的定义域是( )y =A {x |x >0} B {x |x ≥1} C {x |x ≤1} D {x |0<x ≤1}7、把函数的图象向左平移1个单位,再向上平移2个单位后,所得函数的解x1y -=析式应为 ( )A B C D 1x 3x 2y --=1x 1x 2y ---=1x 1x 2y ++=1x 3x 2y ++-=8、设,则 ( ) x x e 1e )x (g 1x 1x lg )x (f +=-+=,A f(x)与g(x)都是奇函数B f(x)是奇函数,g(x)是偶函数C f(x)与g(x)都是偶函数D f(x)是偶函数,g(x)是奇函数9、使得函数有零点的一个区间是 ( ) 2x 21x ln )x (f -+= A (0,1) B (1,2) C (2,3) D (3,4)10、若,,,则( )0.52a =πlog 3b =2log 0.5c =A B C D a b c >>b a c >>c a b >>b c a >>二、填空题:本大题共4小题,每小题5分,满分20分11、函数在区间[-2,2]上的值域是______5()2log (3)f x x =++12、计算:+=______ 2391- ⎪⎭⎫ ⎝⎛326413、函数的递减区间为______212log (45)y x x =--14、函数的定义域是______ 122x )x (f x -+=三、解答题 :共5小题,满分80分。
2012-2013第一学期期末试卷及答案(高一数学)

石家庄市2012~2013学年度第一学期期末考试试卷高一数学答案(时间120分钟,满分150分)一、选择题1-5 ACBCC 6-10 ABDBB 11 【普通高中】C 【示范高中】D 12 B 二、填空题 13. 9 14. 2115. (-1,2) 16.-1【示范高中】 1677 三、解答题17.解:(Ⅰ)解:2(x)=1+2sinxcosx+2cos =sin 2+cos2x+2f x x(2x+)+24π………………3分 由3-+22++2242k x k πππππ≤≤,k Z ∈, 得3-++88k x k ππππ≤≤,k Z ∈ 所以函数的单调递增区间为3[,],88k k k ππ-+π+π∈Z ……………5分(Ⅱ)解:∵]2,0[π∈x ,∴52+[,]444x πππ∈………………7分故2+=42x ππ时,)(x f 的最大值为2+2, 此时, 8x π=.…………………10分18. 解:(Ⅰ)解:依题意 ∴()=0+⋅a b b ,即2+=0⋅a b b 又2||||cos +||=0θa b b ,……………3分 即222||cos +||=0θb b 解得1cos =-2θ,∴2=3θπ.…………6分 (Ⅱ)∵B (1,0),||2||=a b ,∴||1OB =,||=2OA ,可得A (-1),…………8分∴=(-1,OA,1=(1,0),=(2OB OM , 又1212(,)OM λλλλ=+∈R a b∴121(((1,0)2λλ-+……………10分∴1211=-+2λλ⎧⎪⎪解得125=64=3λλ⎧⎪⎪⎨⎪⎪⎩∴1213+=6λλ.……………12分 19.证明:任取1x 、2(0,+)x ∈∞,且12<x x ,…………3分 又231()=+21+1x f x x x +=+ 所以21121212-11(x )-f(x )=-=+1+1(+1)(x +1)x x f x x x ……………6分∵1x 、2(0,+)x ∈∞,且12<x x ∴21-0x x >,1+1>0x ,2+1>0x ,…………9分 ∴12(x )-f(x )>0f ,即12(x )>f(x )f ∴132)(++=x x x f 在(0,+∞)上是减函数.…………12分 20. 解:(Ⅰ)由题意可知-1>04-2>0x x ⎧⎨⎩,解得1<<2x ,∴函数()-(x)f x g 的定义域(1,2) .…………4分(Ⅱ)当a >1时,满足-1>4-21<<2x x x ⎧⎨⎩,解得235<<x ,…………7分当0<a <1时,满足-1<4-21<<2x x x ⎧⎨⎩解得351<<x ,…………10分所以当a >1时,5(,2)3x ∈;当0<a <1时,5(1,)3x ∈.…………12分 21.解:(Ⅰ)解:(法一)如图,以摩天轮最低点为原点,最低点的 切线为x其纵坐标为y ,转过的角为θ,由题意可知 ∴40cos 40+-=θy ,…………3分所以小朋友离地面距离41cos 40+-=θh ,由每分钟转过的角为6122ππ=,∴t 6πθ=,所以41)6cos(40+-=t h π, )0(≥t (法二)由题意可设b t A h ++=)sin(ϕω(,0>A ω小朋友的最高距地面81m ,最低距地面1m ∴⎩⎨⎧=+-=+181b A b A ,得A=40,b=41,又函数周期为12,∴6122ππω==, 所以41)6sin(40++=ϕπt h (0≥t ), 又t=0时,h=1,∴141)06sin(40=++⨯ϕπ,即1sin -=ϕ,ϕ可取2π-,∴41)6cos(4041)26sin(40+-=+-=t t h πππ(0≥t ) .(Ⅱ)依题意可知40cos()41616t π-+≥,…………9分即1cos()62t π≤-,不妨取第一圈,可得24363t πππ≤≤,48t ≤≤, 所以持续时间为4分钟.………………12分 22.解(Ⅰ)∵(x)f 为奇函数,且定义域为R ,∴(0)0f = , 即0(1)=0a k a --,解得k=2;……………4分 (Ⅱ)∵23)1(=f ,所以1-13=2a a -,解得a=2或a=21-(舍) ∴22()222(22)xx x x g x m --=+--…………6分2(22)2(22)2x x x x m --=---+令22xxt -=-,∵x ≥1,∴t ≥23)1(=f , 令h(t)=222322()2,()2t mt t m m t -+=-+-≥……………9分若23≥m ,当t=m 时,h(t)min =2-m 2=-2,解得m=2或m=-2(舍),∴m=2; 若m <23,当t=23时,h(t)min =m 3417-=-2,解得m=1225>23,舍去;综上可知m=2.………………12分。
2012-2013学年高一上学期期末模拟考试数学试题及参考答案
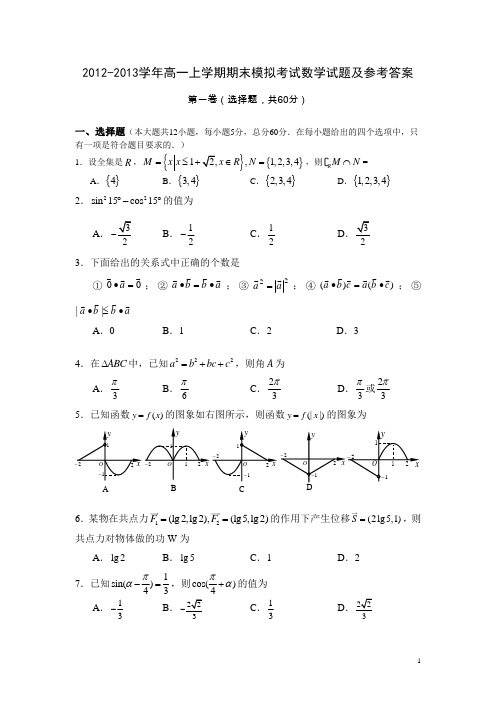
2012-2013学年高一上学期期末模拟考试数学试题及参考答案第一卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,总分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设全集是R ,{}{}1,1,2,3,4M x x x R N =≤∈=,则RM N ⋂=A .{}4B .{}3,4C .{}2,3,4D .{}1,2,3,42.22sin 15cos 15︒-︒的值为A .-B .12- C .12D 3.下面给出的关系式中正确的个数是①00 =•a ;②a b b a •=•;③22a a =;④)()(c b a c b a•=•;⑤a b b a•≤•||A .0B .1C .2D .34.在ABC ∆中,已知222a b bc c =++,则角A 为A .3π B .6π C .23π D .3π或23π5.已知函数)(x f y =的图象如右图所示,则函数|)(|x f y =的图象为6.某物在共点力12(lg2,lg2),(lg5,lg2)F F ==的作用下产生位移(2lg 5,1)S =,则共点力对物体做的功W 为A .lg 2B .lg 5C .1D .27.已知1sin(43πα-=,则cos()4πα+的值为A .13-B .C .13D .3A B C8.如图2:已知OM //AB ,点P 在由射线OM 、线段OB 及AB 的延长线所围成的阴影区域内(不含边界).若OP xOA yOB =+,则实数对(x ,y )可以是A .)43,41( B . )32,32(-C .)43,41(-D . )57,51(-9.已知ABC ∆中,,,a b c 分别为,,A B C 的对边,且4,5,a b c =+=tan tan A B +tan A B =⋅,则ABC ∆的面积为AB .33C .32D .5210.已知||2,||1a b ==,a 与b 的夹角为60°,则使向量a b λ+与2a b λ-的夹角为钝角的实数λ的取值范围是A .(,1-∝-B .(1)-++∝C .(11--+D .(,1(13,)-∝--++∝11.已知函数sin 2cos 2y x a x =+的图象关于直线6x π=-对称,则函数sin 2cos 2y a x x =-的图象关于下列各点中心对称的是A .(,0)3π-B .(,0)6π-C .(,0)6πD .(,0)12π12.设方程22log 1x x ⋅=的两根为1x ,2x (1x <2x ),则A .120,0x x <>B .1201,2x x <<>C .121x x >D .1201x x << 二、填空题(本大题共4小题,每小题5分,共20分) 13.已知sin α+sin β=1213,cos α+cos β=513,则cos(α-β)= . 14.已知函数()2sin()5f x x πω=-的图象与直线1y =-的交点中最近的两点间的距离为3π,则函数()f x 的最小正周期等于 .15.在Rt △ABC 中,已知AB =(2, 3),AC =(1, k ),且∠C =90°,则k = .16.对任意平面向量(,)AB x y=,把AB 绕其起点沿逆时针方向旋转θ角得到向量(cos sin ,sin cos )AP x y x y θθθθ=-+.已知点,2-),若把点B 绕点A 沿顺时针方向旋转4π后得到点P ,则点P 坐标为 . A图2姓名学号:班次:成绩:第二卷(非选择题,共90分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项二、填空题(本大题共4小题,每小题5分,共20分)13.;14.;15.;16..三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本题满分10分)已知tan1tan1αα=--,求22sin()sin()cos()cos()22πππαααπα++-++-的值.18.(本题满分12分)假设一条河的两岸平行,河水自西向东流动,如图,请回答下列两个问题(须作出相关示意图):(Ⅰ)已知:一艘船的速度为/时,河水的流速为5千米/时,如果船从A点垂直驶向河对岸,那么船实际沿什么方向前进(用方位角表示)?实际前进的速度为多少?(Ⅱ)如果一艘船的速度为/时,河水的流速为15千米/时,那么船必须朝哪个方向行驶(用方位角表示),才能沿与水流垂直的方向前进?实际前进的速度为多少?河流河岸河岸AN19.(本题满分12分)已知函数2()2sin()cos()()222f x x x x θθθ=++++-,(Ⅰ)求函数()f x 的周期及单调递减区间; (Ⅱ)若0θπ≤≤,求θ,使()f x 为偶函数.20.(本题满分12分)已知a = (2sin ,1t x ),b = (sin x +cos x , 1),函数f (x )=a b ([0,]2x π∈).(Ⅰ)若t =1,求f(x)的最大值;(Ⅱ)若对任意[0,]2x π∈,函数f (x)≤2恒成立,求实数t 的取值范围.21.(本题满分12分)已知函数f (x )= 1-sin x +1+sin x ,x R ∈.(Ⅰ)判断函数f(x)的奇偶性,并求其最小正周期; (Ⅱ)讨论函数f(x)的单调性;(Ⅲ)作出函数f(x)在[,]ππ-上的大致图象.22.(本题满分12分)如图所示,平面上有四个点,,,A B P Q ,其中,A B 为定点,且AB =,P Q 为动点,满足关系1AP PQ QB ===,又APB ∆与PQB ∆的面积分别为,S T .(Ⅰ)求22S T +的取值范围;(Ⅱ)当22S T +取最大值时,判断APB ∆的形状.参考答案与评分标准一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项二、填空题(本大题共4小题,每小题5分,共20分) 13.已知sin α+sin β=1213,cos α+cos β=513,则cos(α-β)= 12- . 14.已知函数()2sin()5f x x πω=-的图象与直线1y =-的交点中最近的两点间的距离为3π,则函数()f x 的最小正周期等于 π .15.在Rt △ABC 中,已知AB =(2, 3),AC =(1, k ),且∠C =90°,则k =AB32± . 16.对任意平面向量(,)AB x y =,把AB 绕其起点沿逆时针方向旋转θ角得到向量(cos sin ,sin cos )AP x y x y θθθθ=-+.已知点,2-),若把点B 绕点A 沿顺时针方向旋转4π后得到点P ,则点P 坐标为 (0,-1) .三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.(本题满分10分)已知tan 1tan 1αα=--,求22sin ()sin()cos()cos ()22πππαααπα++-++-的值.17.解:∵tan 1,tan 1αα=-- ∴tan tan 1,αα=-+ ∴1tan ,2α=且cos 0≠ (2分)∴22sin ()sin()cos()cos ()22πππαααπα++-++-22sin cos (sin )cos αααα=+-+(5分)1cos sin αα=-(6分)22221cos sin tan 23211111sin cos tan 155()12αααααα=-=-=-=-=+++(10分)18.(本题满分12分)假设一条河的两岸平行,河水自西向东流动,如图,请回答下列两个问题(须作出相关示意图):(Ⅰ)已知:一艘船的速度为/时,河水的流速为5千米/时,如果船从A 点垂直驶向河对岸,那么船实际沿什么方向前进(用方位角表示)?实际前进的速度为多少?(Ⅱ)如果一艘船的速度为/时,河水的流速为15千米/时,那么船必须朝哪个方向行驶(用方位角表示),才能沿与水流垂直的方向前进?实际前进的速度为多少?18.解:设船速53AB =,水速5AC =,以AB ,AC 为邻边 作平行四边形ACDB ,则AD 为所求船实际行驶速度; (Ⅰ)如图:||10AD AC ===∴60DAC ∠=︒ (3分)CA BD所以:船实际沿北偏东30°方向前进;实际前进的速度为10千米/时 (6分) (Ⅱ)如图:||AD AB === ∴60,DAC ∠=︒ ∴150BAC ∠=︒ (9分)所以:船必须沿北偏西60°方向前进,才能沿与水流垂直的方向前进;实际前进的速度为千米/时。
肇庆市2012-2013学年高一上期末考试数学必修1试题及答案

x
200).
(8 分)
当 0 x 20 时, f (x) 60x 为增函数,故当 x=20 时,其最大值为 60 20 1200 ;
(10 分)
当 20 x 200 时, f (x) 1 x(200 x) 1 (x 100)2 10000 , (12 分)
A.{x | 2 x 2}
B.{x | 2 x 0}
C.{x | 0 x 1}
D.{x | 1 x 2}
4.设有一个回归方程为 yˆ 1.5x 2 ,则变量 x 增加一个单位时,y 平均
A.增加 1.5 个单位
B.增加 2 个单位
C.减少 1.5 个单位
(6 分)
(2)函数 f (x) 的定义域为(∞,+∞),值域为(∞,+∞); (9 分)
函数 g(x) 的定义域为(∞,+∞),值域为 0,1.
(12 分)
17.(本小题满分 14 分)
解:(1)由茎叶图可知最快成绩为 6.4,若( 7 x )是最慢成绩, 10
则平均成绩为 1 (6.5 6.8 6.9 7.0 7.2 7.4 7.5 7.1) 7.05 7.0 , 8
D.减少 2 个单位
5.已知全集 U=R,集合 M {x | x 2 1},则 CU M
A.(∞,-1) B.(1,+∞)
C.(-1,1)
D. (,1) (1,)
6.下列函数中,既是偶函数,又在(0,+∞)上单调递增的函数是
A. y x3
B. y | x | 1
C. y x 2 1
(12 分)
16.(本小题满分 12 分)
河北省邯郸市2012-2013上学期高一期末试题数学 含答案
邯郸市2012—2013学年度第一学期期末教学质量检测高一数学试题注意:1。
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,时间120分钟.2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动, 用橡皮擦干净后,再选涂其他答案标号,在试题卷上作答无效。
第Ⅰ卷一、选择题(本大题共l2小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
) 1.已知全集U Z =,A={—1,0,1,2},B={0,1},则U A C B为A .{1,2}-B .{1,0}-C .{0,1}D .{1,2}2.如图,点P 、Q 、R 、S 分别在正方体的四条棱上,并且是所在棱的中点,则直线PQ 与RS 是异面直线的一个图是3。
如图的曲线是幂函数nx y =在第一象限内的图象.已知n 分别取2±,12±四个值,与曲线1c 、2c 、3c 、4c 相42510c 4c 3c 2c 1应的n 依次为A .112,,,222-- B .112,,2,22--C .11,2,2,22--D .112,,,222--4. 设点M 是Z 轴上一点,且点M 到A (1,0,2)与点B (1,-3,1)的距离相等,则点M 的坐标是( ). A .(-3,-3,0) B .(0,0,-3) C .(0,-3,-3) D .(0,0,3) 5。
点(x 0,0)是函数y =x3-x⎪⎭⎫⎝⎛21图像上一点,则x 0所在的区间是A 。
(3,4)B 。
(2,3)C 。
(1,2)D 。
(0,1)6。
点M (x 0,y 0)是圆x 2+y 2=a 2 (a 〉0)外一点,则直线x 0x+y 0y=a 2与该圆的位置关系是A .相切B .相交C .相离D .相切或相交7。
已知函数⎩⎨⎧>≤-=1,ln 1,1)(x x x e x f x ,那么)2(ln f 的值是 A 。
2012~2013学年第一学期高一数学期末试卷-推荐下载

11.
,
6 6
二、解答题:
,
6.已知平面向量 a
7.已知函数
n ____ .
f
x
1,1,b
log2
x
2, n,若
1 3
1 2
x
8.若实数 a 和 x 满足 2a 1 x2 2x 0 ,且 x 1, 2,则 a 的取值范围是
________.
9.已知函数 f x x 2x1 aA2x x R是偶函数,则实数 a 的值等于
的中点,则
kb
k
k
的值;
R
。
AM AAN
,是否存在实数
k
________
,使得
。
?
2
若存在,求出实数 k 的值;若不存在,说明理由。
f
18.(本题满分 16 分)
设函数 f x 2 cos2 x 2 3 sin x cosx m (其中 0, m R ),且函数
x 的图象在
y
轴右侧的第一个最高点的横坐标是
(1)求函数 f x的解析式;
(2)若
f
x0
11 5
,
x0
4
, 2
,求 cos 2x0
19.(本题满分 16 分)
如图,在半径为 R ,圆心角为 60 的扇形弧 AB 上任取一点 P ,作扇形的内接矩形 PNMQ ,使 Q 点在 OA 上,点 M , N 都在 OB 上,求这个矩形面积的最大值及相应的 AOP 的值。
步骤,请把答案写在答题纸的指定区域内。
2012-2013学年度高一上学期期末考试数学试题

2012-2013学年度高一上学期期末考试数学试题考试满分:150分 考试时间:120分钟 编辑人:丁济亮祝考试顺利!一、选择题(本大题共10个小题,每小题5分,共50分,在每小题所给的四个选项中,只有一项是符合题目要求的) 1.集合{|12}=-≤≤A x x ,{|1}B x x =<,则()R A C B = ( )A.{|1}x x > B.{|1}x x ≥ C.{|12}x x <≤ D.{|12}x x ≤≤2.如果)(x f 为偶函数,满足在区间[2,3]上是增函数且最小值是4,那么)(x f 在区间[3,2]--上是( )A. 增函数且最小值是4-B. 增函数且最大值是4C. 减函数且最小值是4D. 减函数且最大值是4- 3.7cos 3π⎛⎫-⎪⎝⎭=( ) A.12B.2- C.12-24.如图1,在平行四边形ABCD 中,下列结论中正确的是( )A .ABCD = B .AB AD BD -= C .AD AB AC += D .0AD BC +=5.若向量()1,1a = , ()1,1b =- ,()1,2c =- ,则c等于( ) A.21-a +23bB.21a 23-bC.23a 21-b D.23-a + 21b 6.设,x y ∈R ,向量(,1),(1,),(2,4)===-a xb yc 且c b c a //,⊥,则=a b + ( )A.B.D. 107.()sin 135cos15cos 45sin 15--的值为( )A. 2- B. 12-C.12D.2DC图1图28.设tan ,tan αβ是方程2320x x -+=的两个根,则tan()+αβ的值为( ) A. 3- B. 1- C. 3 D. 1 9.在△ABC 中,已知5cos A=13,3sin B =5,则cos C 的值为( )A.1665-或5665B.1665或5665C.5665 D.166510.如图2,O 、A 、B 是平面上的三点,向量O A a = ,=OB b ,设P 为线段AB 的垂直平分线C P 上任意一点,向量=OP p,若4a = ,2b = ,则()bp a ⋅- =( )A.8B.6C.4D.0二、填空题(本大题共5个小题,每小题5分,共25分,请将各题的正确答案填写在答题卷中对应的横线上) 11.函数y =的定义域为__________.12.已知扇形AOB 的周长是6,中心角是1弧度,则该扇形的面积为________. 13.若点()3,2M 和点(),6N x 的中点为()1,P y ,则x y +的值为________.14.在直角坐标系xOy 中,,i j分别是与x 轴,y 轴平行的单位向量,若直角三角形ABC 中,,2AB i j AC i m j =+=+,则实数m=________________.15.下列说法:①函数()36=+-f x lnx x 的零点只有1个且属于区间()1,2; ②若关于x 的不等式2210ax ax ++>恒成立,则()0,1a ∈;③函数y x =的图像与函数sin y x =的图像有3个不同的交点; ④函数sin cos sin cos ,[0,]4y x x x x x π=++∈的最小值是1.正确的有 .(请将你认为正确的说法的序号........都写上) 三、解答题(本大题共6个小题,共75分,解答应写出文字说明、证明过程或演算步骤) 16.(本大题满分12分)已知集合{|1}A x x =+=3,2{|560}B x x x =-+=,22{|190}C x x ax a =-+-=,且集合A B C 、、满足:A C =∅ ,B C ≠∅ ,求实数a 的值.17.(本大题满分12分)已知02πα-<<,4sin 5α=-.(1).求tan α的值;(2).求cos 2sin ()2παα+-的值.18. (本大题满分12分)已知4||=a ,2||=b ,且a 与b 夹角为120,求(1).a b +;(2).a与a b + 的夹角.19. (本大题满分12分)如图所示,已知O P Q 是半径为1,圆心角为θ的扇形,A 是扇形弧PQ 上的动点,//AB OQ ,OP 与AB 交于点B ,//AC OP ,OQ 与AC 交于点C .记=AOP ∠α.(1).若2πθ=,如图3,当角α取何值时,能使矩形ABOC 的面积最大;(2).若3πθ=,如图4,当角α取何值时,能使平行四边形ABOC 的面积最大.并求出最大面积.20.(本大题满分13分)函数()sin()(0,0,)2f x A x x R A =+∈>><πωϕωϕ,的一段图象如图5所示:将()y f x =的图像向右平移(0)m m >个单位,可得到函数()y g x =的图象,且图像关于原点对称,02013g π⎛⎫>⎪⎝⎭. (1).求A ωϕ、、的值;图 3 图4α(2).求m 的最小值,并写出()g x 的表达式;(3).若关于x 的函数2tx y g ⎛⎫= ⎪⎝⎭在区间,34ππ⎡⎤-⎢⎥⎣⎦上最小值为2-,求实数t 的取值范围.21.(本大题满分14分) 已知函数()b f x a x=-,0a >,0b >,0x ≠,且满足:函数()y f x =的图像与直线1y =有且只有一个交点.(1).求实数a 的值;(2).若关于x 的不等式()41xf x <-的解集为1+2⎛⎫∞⎪⎝⎭,,求实数b 的值; (3).在(2)成立的条件下,是否存在m ,n R ,m n ∈<,使得()f x 的定义域和值域均为[],m n ,若存在,求出m ,n 的值,若不存在,请说明理由.2012~2013学年上学期期末考试一年级(数学)参考答案一、选择题二、 填空题11. 12. 2 13. 3 14. -2或0 15.①④ 三、解答题16.解:{2,4}A =-,{2,3}B =, ………………………4分 由,A C =∅ 知2,4C C ∉-∉, 又由,B C ≠∅ 知3C ∈,2233190a a ∴-+-=,解得2a =-或5a = ………………………8分 当2a =-时,{3,5},C =-满足,A C =∅当5a =时,{3,2}C =,{2}A C =≠∅ 舍去,2a ∴=- (12)分 17.解: (1)因为02πα-<<,4sin 5α=-, 故3cos 5α=,所以4tan 3α=-. …………6分(2)23238cos 2sin()12sin cos 1225525παααα+-=-+=-+=. ……………12分18解:(1)a b +===………………………6分(2)设a 与b a +的夹角为θ,则23cos ==θ, ………………………10分又︒≤≤︒1800θ,所以︒=30θ,a 与b a +的夹角为︒30。
高一数学答案(期末)

答案共2页第1页 答案共2页第2页2012—2013学年度上期高中期末调研考试高一数学参考答案一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.C 2. B 3.B 4.B 5. D 6.D 7. C 8.A 9. B 10. D 11. A 12. D 二、填空题(本大题共4小题,每小题5分,共20分)13.{x|-2<x<1} 14.15. (x -2)2+(y -1)2=10 16. 2三.解答题(本大题共6小题,第17题10分,第18-22题每题12分,合计70分) 17.{}25=≤-≥ A x x 解:,或……2分; 因为A ∩B=ф,若ⅰ)=∅B ,则2132-≥+m m 即3≤-m ,符合题意……5分;若ⅱ)≠∅B ,则2132212325-<+⎧⎪-≥-⎨⎪+≤⎩m m m m 即112-≤≤m ……9分;综合ⅰ)ⅱ)可知,实数m 的取值范围是(]1312⎡⎤-∞--⎢⎥⎣⎦,,U ……10分. 18.解答: (1) 设,0<x 则0>-x ,所以12--=-xx f )(,又)(x f 为偶函数,所以)(x f =2()1f x x-=--,即0x <时,)(x f 的解析式是2()1f x x=--…6分 ;(2)若()0f x >,当0x >时,()0f x >即210x->,解得02x <<∵函数为偶函数,∴当0x <时,20x -<<,故不等式的解集为(02)(20)- ,,…12分19. 解:由已知可得直线//C P A B ,设C P的方程为,(1)3y x c c =-+>则32AB c =⨯==,33y x =-+过1(,)2P m得13,232m =-+=………12分20.解: (1) 311()322A B C D A D PA a-=∙+∙∙=P A B CD 1V ……………6分;(2)依题易得PD A ∠为二面角的平面角,由45PD A ∠=︒得,二面角P -CD -B的大小为45︒……………………………………12分.21.解:(1)因为()lg(12)-=-f x x ,故()()()l g (12)l g (12)=--=+--F x f x f x x x ,使得函数有意义的自变量的取值满足120120+>⎧⎨->⎩x x 即1122-<<x ,故函数的定义域为11()22-,……………6分;(2)122()()()lg lg(1)1221+=--==----x F x f x f x xx ,令21()10212⎡⎫=--∈⎪⎢-⎣⎭t x x x ,,易得()t x 在102⎡⎫⎪⎢⎣⎭,上单调递增,而外层函数在定义域上单调递增,故复合函数121()lg0122+⎡⎫=∈⎪⎢-⎣⎭xF x x x ,,为单调递增函数 由()≥F x m 恒成立,可得min ()0lg 10≤===m F x F(),即实数m 的取值范围为0≤m ……………………………………12分. 22.解: 依题意设圆心C (,3)a a ,则半径为3r a =.因为圆被直线y x =截得的弦长为y x ==,解得1a =,和1a =-.于是,所求圆C 的方程为:22(1)(3)9x y -+-=或22(1)(3)9x y +++=.………12分。
2012-2013学年度高一第一学期期末考试试卷以及答案

2012-2013学年度期末考试试卷高一数学第Ⅰ卷(选择题 共50分)一、选择题(本大题共10小题,每小题5分,共50分,每题只有一个正确答案,请把你认为正确的答案填在答题卡上........,答在试卷上的一律无效..........。
)1. 若{}9,6,3,1=P {}8,6,4,2,1=Q ,那么=⋂Q P ( C )A.{1}B.{6}C. {1,6}D. 1,62.下列函数中哪个与函数y x =是同一个函数 ( B )A.2)(x y =B. 33x y = C. xx y 2=D.2x y =3.图(1)是由哪个平面图形旋转得到的( A )图(1) A B C D4.下列函数中有两个不同零点的是( D )A .lg y x =B .2x y =C .2y x =D .1y x =-5.函数()12f x x=-的定义域是( A ) A .[)()+∞⋃-,22,1 B .[)+∞-,1 C .()()+∞⋃∞-,22,D . 1 22 -⋃+∞(,)(,)6.已知直线m ⊥平面α,直线n ⊂平面β,下面有三个命题:①//m n αβ⇒⊥;②//m n αβ⊥⇒;③//m n αβ⇒⊥;则真命题的个数为( B ) A .0 B .1 C .2 D .37.若10x -<<,那么下列各不等式成立的是( D )A .220.2x x x -<<B .20.22x x x -<<C .0.222x x x -<<D .220.2x x x -<<8. 过2 3A -(,) ,2 1B (,) 两点的直线的斜率是( C ) A .12B .12-C .2-D .29. 已知函数)31(12)(≤≤+=x x x f ,则( B ) A .)1(-x f =)20(22≤≤+x x B . )1(-x f =)42(12≤≤-x x C . )1(-x f =)20(22≤≤-x x D . )1(-x f =)42(12≤≤+-x x10..已知)(x f 是偶函数,当0<x 时,)1()(+=x x x f ,则当0>x 时,()f x 的值为( A ) A .)1(-x x B .)1(--x x C .)1(+x x D .)1(+-x x第Ⅱ卷(非选择题 共100分)二、填空题(本大题共4小题,每小题5分,共20分. 请把你认为正确的答案填在答题卡上........,答在试卷上的一律无效..........。
湖南师大附中2012-2013高一上学期数学期末试题及答案

时量:120分钟满 分:100 分(必考试卷Ⅰ) 50分(必考试卷Ⅱ)必考试卷Ⅰ一、选择题:本大题共7个小题,每小题5分,满分35分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.利用斜二侧画法画水平放置的平面图形的直观图,得到下列结论,其中正确的是( ) A .正三角形的直观图仍然是正三角形. B .平行四边形的直观图一定是平行四边形. C .正方形的直观图是正方形. D .圆的直观图是圆 答案:B.2.已知直线的倾斜角为45°,在y 轴上的截距为2,则此直线方程为( ) A .y x =+2. B .y x =-2 C .y x =-+2 D .y x =--2 答案:A3.已知直线:(),l m x y -+-=11210:,l mx y -+=230 若l l ⊥12,则m 的值为( ) A .2. B .-1 C .-21或 D .13答案:C4.已知一个棱长为3的正方体的顶点都在球面上,则球的表面积等于( ) ( )A. 4πB. 6πC. 8πD. 9π 答案:D5.已知圆:C x y x y +++-=2212880与圆:C x y x y +---=2224420相交,则圆C 1与圆C 2的公共弦所在的直线的方程为( )A .210x y ++=B .210x y +-=C .210x y -+=D .210x y --= 答案:B6.若a 、b 表示两条不同直线,α、β表示两个不同平面,则下列命题正确的是( ) A .,a b a b αα⊥⇒⊥∥ B .a b a b αα⇒∥,∥∥ C .a b a b αα⊂⇒∥,∥ D .a a αβαβ⊥⊂⇒⊥,答案:A7.已知圆锥的底面半径为1,且它的侧面展开图是一个半圆,则这个圆锥的体积为( ) A.π33B. π3C.π53D.π5答案:A二、填空题:本大题共6个小题,每小题5分,共30分.请把答案填在答题卷对应题号后的横线上.8. 若球的表面积为36π,则该球的体积等于 。
【历年高一数学期末试题】重庆八中2012-2013学年高一上学期期末考试数学版含答案

(Ⅰ)由图可知: A 2, 1,则 f (x) 2sin( x ) …………………………(…3…分)
由图像过点 ( , 2) ,则 sin(
6
6
又0
,则
6
2
) 1,
……………………………(……6 分…)
3
故 f ( x) 2sin( x ) …………………………………(…7…分…) 3
2012—2013 学年度(上)期末考试高一年级
数学试题参考答案
一.选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
D
A
C
B
D
B
C
A
D
A
x3
10. 提 示 :由 题可 知 , f ( x) f (
)
x4
x x 3或x x4
x
3
,则
2
x
3x 3
0或
x4
x2 5x 3 0 ,则所有满足 f (x)
x f(
3 )
的
x 之和为
上 是 非 接 近 的 两 个 函 数 。 现 有 两 个 函 数 f1(x) loga (x 3a), ,
f 2( x)
1
log a
(a
xa
0, a
1) ,且 f1 (x) 与 f2 (x) 在 [a
2, a
3] 都有意义 .
(Ⅰ)求 a 的取值范围;
(Ⅱ)讨论 f1 (x) 与 f 2( x) 在区间 [ a 2, a 3] 上是否是接近的两个函数 .
2012-2013年度第一学期期末数学试题

12012--2013学年第一学期期末考试试题(卷)高一数学一、选择题(每题只有一个正确答案,请把正确答案的序号填在答题卡的相应位置上。
每题5分,共60 分)1、过点(1,0)且与直线x-2y-2=0平行的直线方程是A x-2y-1=0B x-2y+1=0C 2x+y-2=0D x+2y-1=0 2、经过点A (-4,2m-1),B(m,-3)的直线的倾斜角为135°,则直线AB 的方程为( )A. x+y-1=0B. y=-x+1C. y=-x-1D. x-y+1=0 3、圆x 2+y 2-6x+4y+12=0与圆x 2+y 2-14x-2y+14=0外置关系为( )A. 外离B. 外切C. 内切D. 相交 4、圆x 2+y 2-6x+4y+12=0关于原点对称圆的方程为( )A. (x-3)2+(y+2)2=1B. (X-3)2+(y-2)2=1C. (x+3)2+(y+2)2=1D. (X+3)2+(y-2)2=1 5、若直线a 不平行于平面,且a 不在平面内,则下列结论成立的是( )A. 内的所有直线与a 异面;B. 内不存在与a 平行的直线;C. 内存在唯一的直线与a 平行;D. 内的直线与a 都相交。
6、.若某空间几何体的三视图如图所示,则该几何体的体积是(A )2 (B )23 (C ) 1 (D )137、下列命题中错误的是( )A. 平行于同一直线的两个平面平行;B. 平行于同一平面的两个平面平行;C. 一个平面与两个平行平面相交,交线平行;D. 一条直线与两个平行平面中的一个相交,则必于另一个相交。
8、已知正四棱柱1111ABC D A B C D -中 ,2A B =,1CC =,E 为1C C 的中点,则直线1AC 与平面BED 的距离为A 2 BCD 19、用斜二测画法得到的①三角形的直观图是三角形; ②平行四边形的直观图是平行四边形; ③正方形的直观图是正方形; ④菱形的直观图是菱形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012学年高一数学期末复习(必修一)4
一、选择题:本大题10小题,每小题5分,满分50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、已知全集I ={0,1,2,3,4},集合{1,2,3}M =,{0,3,4}N =,则()
I M N 等于 ( ) A.{0,4} B.{3,4} C.{1,2} D. ∅ 2、设集合2{650}M x x x =-+=,2{50}N x x x =-=,则M
N 等于( ) A.{0} B.{0,5} C.{0,1,5} D.{0,-1,-5}
3、计算:9823log log ⋅=( )
A 12
B 10
C 8
D 6
4、函数2(01)x y a a a =+>≠且图象一定过点 ( )
A (0,1)
B (0,3)
C (1,0)
D (3,0)
5、“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点…用S 1、S 2分别表示乌龟和兔子所行的路程,t 为时间,则与故事情节相吻合是 ( )
6、函数12
log y x =的定义域是( )
A {x |x >0}
B {x |x ≥1}
C {x |x ≤1}
D {x |0<x ≤1}
7、把函数x
1y -=的图象向左平移1个单位,再向上平移2个单位后,所得函数的解析式应为 ( )
A 1x 3x 2y --=
B 1x 1x 2y ---=
C 1x 1x 2y ++=
D 1
x 3x 2y ++-= 8、设x x e 1e )x (g 1x 1x lg )x (f +=-+=,,则 ( ) A f(x)与g(x)都是奇函数 B f(x)是奇函数,g(x)是偶函数
C f(x)与g(x)都是偶函数
D f(x)是偶函数,g(x)是奇函数
9、使得函数2x 2
1x ln )x (f -+=有零点的一个区间是 ( ) A (0,1) B (1,2) C (2,3) D (3,4)
10、若0.52a =,πlog 3b =,2log 0.5c =,则( )
A a b c >>
B b a c >>
C c a b >>
D b c a >> 二、填空题:本大题共4小题,每小题5分,满分20分
11、函数5()2log (3)f x x =++在区间[-2,2]上的值域是______
12、计算:2391- ⎪⎭⎫ ⎝⎛+3
2
64=______ 13、函数212
log (45)y x x =--的递减区间为______
14、函数1
22x )x (f x -+=的定义域是______ 三、解答题 :共5小题,满分80分。
解答须写出文字说明、证明过程或演算步骤。
15. (15分) 计算 5log 3333322log 2log log 859
-+-
16、(16分)已知函数⎪⎩
⎪⎨⎧≥<<--≤+=)2(2)21()1(2)(2x x x x x x x f
。
(1)求)4(-f 、)3(f 、[(2)]f f -的值;
(2)若10)(=a f ,求a 的值.
17、(16分)已知函数()lg(2),()lg(2),()()().f x x g x x h x f x g x =+=-=+设
(1)求函数()h x 的定义域; (2)判断函数()h x 的奇偶性,并说明理由.
18、(16分)已知函数()f x =1
515+-x x 。
(1)写出()f x 的定义域; (2)判断()f x 的奇偶性;
19、(17分)某旅游商品生产企业,2007年某商品生产的投入成本为1元/件,出厂价为1.2元/件,年销售量为10000件,因2008年调整黄金周的影响,此企业为适应市场需求,计划提高产品档次,适度增加投入成本.若每件投入成本增加的比例为x(01
<<),则
x
出厂价相应提高的比例为0.75x,同时预计销售量增加的比例为0.8x.已知得利润=(出厂价-投入成本)⨯年销售量.
(1)2007年该企业的利润是多少?
(2)写出2008年预计的年利润y与投入成本增加的比例x的关系式;
(3)为使2008年的年利润达到最大值,则每件投入成本增加的比例x应是多少?此时最大利润是多少?
试题答案
一. 选择题
1-5:ACDBB 6-10:DCBCA
二. 填空题
11: [2,3] 12:43 13:(5,)+∞ 14:(,2]-∞
三. 简答题
15:5log 3333332log 2log 329)log 25-+-解:原试=(-log
=33332log 2log 23)3log 23-
+-(5-2log =333log 23log 23-+-+2=-1
16、解:(1)(4)f -=-2,)3(f =6,[(2)]f f -=(0)0f =
(2)当a ≤-1时,a +2=10,得:a =8,不符合;
当-1<a <2时,a 2=10,得:a =10±,不符合;
a ≥2时,2a =10,得a =5, 所以,a =5
17、解:(1)()()()lg(2)lg(2)h x f x g x x x =+=++-
由 20()20x f x x +>⎧=⎨
->⎩ 得22x -<< 所以,()h x 的定义域是(-2,2) ()f x 的定义域关于原点对称
()()()lg(2)lg(2)()()()h x f x g x x x g x f x h x -=-+-=-++=+=()h x ∴为偶函数
18、解:(1)R
(2)()f x -=1515+---x x =x x 5151+-=-1
515+-x x =()f x -, 所以()f x 为奇函数。
(3)()f x =15215+-+x x =1-152+x , 因为x 5>0,所以,x 5+1>1,即0<1
52+x <2, 即-2<-152+x <0,即-1<1-1
52+x <1 所以,()f x 的值域为(-1,1)。
19、解:(1)2000元
(2)依题意,得 [1.2(10.75)1(1)]10000(10.8)y x x x =⨯+-⨯+⨯⨯+
28006002000x x =-++(01x <<);
(3)当x =-1600600-=0.375时,达到最大利润为:3200
36000020008004+⨯⨯ =2112.5元。
