基于MATLAB的m序列产生
智能控制 M序列的产生
做一个M 序列一、实验内容:利用MATLAB 语言产生一个M 序列m 序列是最长线性反馈移位寄存器序列的简称,m 序列是由带线性反馈的移位寄存器产生的.由n 级串联的移位寄存器和和反馈逻辑线路可组成动态移位寄存器,如果反馈逻辑线路只由模2和构成,则称为线性反馈移位寄存器。
带线性反馈逻辑的移位寄存器设定初始状态后,在时钟触发下,每次移位后各级寄存器会发生变化。
其中任何一级寄存器的输出,随着时钟节拍的推移都会产生一个序列,该序列称为移位寄存器序列。
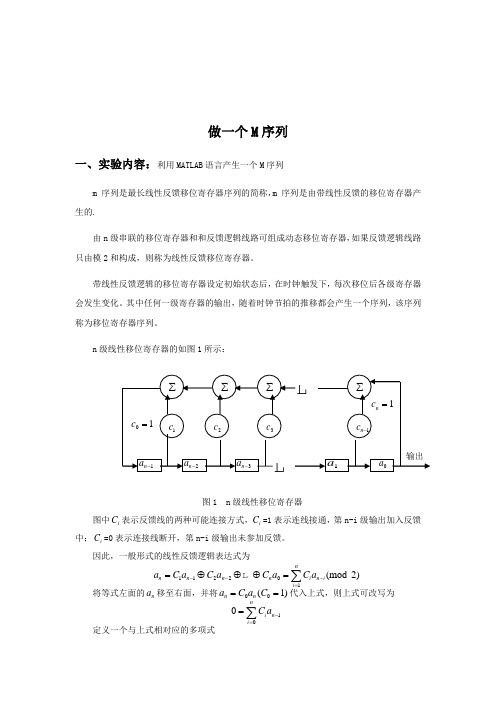
n 级线性移位寄存器的如图1所示:图1 n 级线性移位寄存器图中i C 表示反馈线的两种可能连接方式,i C =1表示连线接通,第n-i 级输出加入反馈中;i C =0表示连接线断开,第n-i 级输出未参加反馈。
因此,一般形式的线性反馈逻辑表达式为112201(mod 2)nn n n n i n i i a C a C a C a C a ---==⊕⊕⊕=∑将等式左面的n a 移至右面,并将00(1)n n a C a C ==代入上式,则上式可改写为100ni n i C a -==∑定义一个与上式相对应的多项式1n a -2n a -3n a -∑∑∑∑1c 2c 3c 1n c -01c =1n c =0a 1a 输出()ni i i F x C x ==∑其中x 的幂次表示元素的相应位置。
式称为线性反馈移位寄存器的特征多项式,特征多项式与输出序列的周期有密切关系.当F(x)满足下列三个条件时,就一定能产生m 序列:(1) F(x)是不可约的,即不能再分解多项式; (2) F(x)可整除1px +,这里21n p =-; (3) F(x)不能整除1q x +,这里q<p.满足上述条件的多项式称为本原多项式.这样产生m 序列的充要条件就变成了如何寻找本原多项式.根据m 序列的特征方程:20120()nn i n i i f x c c x c x c x c x ==++++=∑并根据其联接多项式编写Matlab 程序.二、源程序如下:%m 序列发生器及其自相关 mseq.m clear all; close all; g=19;%G=10011; state=8;%state=1000 L=1000; %m 序列产生 N=15;mq=mgen(g,state,L); %m 序列自相关ms=conv(1-2*mq,1-2*mq(15:-1:1))/N;figure(1)%subplot(222)stem(ms(15:end));axis([0 63 -0.3 1.2]);title('m序列自相关序列') figure(2)%m序列构成的信号(矩形脉冲)N_sample=8;Tc=1;dt=Tc/N_sample;t=0:dt:Tc*L-dt;gt=ones(1,N_sample);mt=sigexpand(1-2*mq,N_sample);mt=conv(mt,gt);figure(2)%subplot(221);plot(t,mt(1:length(t)));axis([0 63 -0.3 1.2]);title('m序列矩形成形信号') st=sigexpand(1-2*mq(1:15),N_sample);s=conv(st,gt);st=s(1:length(st));rt1=conv(mt,st(end:-1:1))/(N*N_sample);figure(3)%subplot(223)plot(t,rt1(length(st):length(st)+length(t)-1));axis([0 63 -0.3 1.2]);title('m序列矩形成形信号的自相关');xlabel('t');Tc=1;dt=Tc/N_sample;t=-20:dt:20;gt=sinc(t/Tc);mt=sigexpand(1-2*mq,N_sample);mt=conv(mt,gt);st2=sigexpand(1-2*mq(1:15),N_sample);s2=conv(st2,gt);st2=s2;rt2=conv(mt,st2(end:-1:1))/(N*N_sample);figure(4)%subplot(224);t1=-55+dt:dt:Tc*L-dt;plot(t,mt(1:length(t)));plot(t1,rt2(1:length(t1)));axis([0 63 -0.5 1.2]);title('m序列since成形信号的自相关');xlabel('t') 调用的子程序如下:(1)mgen.m:function [out] = mgen(g,state,N)%输入 g:m序列生成多项式(10进制输入)%state:寄存器初始状态(10进制输入)%N:输出序列长度% test g=11;state=3;N=15;gen = dec2bin(g)-48;M = length(gen);curState = dec2bin(state,M-1) - 48;for k =1:Nout(k) = curState(M-1);a = rem(sum( gen(2:end).*curState),2); curState = [a curState(1:M-2)];end(2)mseq.m%m序列发生器及其自相关 mseq.mclear all;close all;g=19;%G=10011;state=8;%state=1000L=1000;(3)sigexpand.m:function [out] = sigexpand(d,M)N = length(d);out = zeros(M,N);out(1,:)=d;out = reshape(out,1,M*N);四、仿真波形:测试结果:图2 m序列自相关序列图3 m序列矩形成形信号图4 m序列矩形成形信号的自相关图5 m序列since成形信号的自相关。
基于matlab的m序列的产生和特性分析

基于matlab的m序列的产生和特性分析作者:耿亚南来源:《中国新通信》 2017年第15期【摘要】 m 序列是一种重要的伪随机序列。
本文借助MATLAB 平台,详细介绍了m 序列的产生原理,并仿真了由移位寄存器产生的m 序列,同时研究了m 序列的自相关函数并得到了m 序列自相关函数的图像。
仿真结果验证了该方法的正确性和可行性。
【关键字】 m 序列自相关函数 MATLAB一、引言m 序列是最长线性移位寄存器序列的简称,有着良好的自相关性,易于产生和复制,是目前广泛应用的一种伪随机序列。
其在通信领域有着广泛的应用,如扩频通信,卫星通信的码分多址,数字数据中的加密、加扰、同步、误码率测量等领域。
近几十年来,运用m 序列测量房间声学系统脉冲响应的技术研究也受到了人们的关注。
m 序列法测量技术有两大优点其一是较强的抗噪声性能,其二是运算速度快、效率高。
二、m 序列的产生2.1 m 序列的产生原理m 序列是由带线性反馈的移位寄存器产生的。
由n 级串联的移位寄存器和反馈逻辑线路可组成动态移位寄存器,如果反馈逻辑线路只由模2 和构成,则称为线性反馈移位寄存器。
m 序列的产生框图如图1 所示。
图中C0、C1…Cn 均为反馈线,其中C0= Cn=1,表示反馈连结。
因为m 序列是由循环序列发生器产生的,因此C0和Cn 肯定为1,即参与反馈。
而反馈系数C1、C2…Cn - 1若为1,参与反馈,若为0,则表示断开反馈线,即开路、无反馈连线。
2.2 MATLAB 仿真MATLAB 产生m 序列的部分程序:function[mseq]=m_sequence(fbconnection)n=length(fbconnection);N=2^n-1;register=[zeros(1,n-1) 1];mseq(1)=register(n);for i=2:Nnewregister(1)=mod(sum(fbconnection.*register),2);for j=2:nnewregister(j)=register(j-1);end;三、m 序列的自相关函数3.1 自相关函数自相关是指m 序列与逐位移位后的序列相关性的一种度量。
基于MATLAB的m序列仿真

s1(n)=mod(sum(s1(n-r:n-1).*f1(1:r)),2);%通过模2加产生m1序列 end stem(s1); title('生成m序列') %绘制生成m序列的图形
4
基于 Matlab 的 m 序列仿真分析
2.2 m 序列的基本性质
参考文献 ......................................................... 16 附录 ............................................................. 17
基于 Matlab 的 m 序列仿真分析
1.2
系统设计流程图
本文通过软件 Matlab 编写程序,从而在 GUI 环境下看到 m 序列的产生、m 序列的自 相关和互相关函数图形,其系统设计流程图如图 1.1 所示: 开始
用 Matlab 编写程序产生两个 m 序列
对 m 序列进行自相关特性分析
对 m 序列进行互相关特性分析
用 Matlab GUI 显示仿真结果
结束 图 1.1 系统设计流程图
1
基于 Matlab 的 m 序列仿真分析
第二章
2.1 m 序列产生原理及结构
m 序列的产生及性质
伪随机序列有很多种,其中最基本最常用的一种是最长线性反馈移位寄存器序 列,也称作 m 序列,通常由反馈移位寄存器产生。 m 序列是最长线性移位寄存器序列的简称。它是由多级移位寄存器或其他延迟 元件通过线性反馈产生的最长的码序列。由于 m 序列容易产生、规律性强、有许多 优良的性能,在扩频通信中最早获得广泛的应用。 由 m 级寄存器构成的线性移位寄存器如图 2.1 所示,通常把 m 称为这个移位寄 存器的长度。每个寄存器的反馈支路都乘以 Ci。当 Ci=0 时,表示该支路断开;当 Ci=1 时,表示该支路接通。显然,长度为 m 的移位寄存器有 2n 种状态,除了全零序 列,能够输出的最长序列长度为 N=2n-1。此序列便称为最长移位寄存器序列,简称 m 序列。 m 序列每移位一次,就出现一种状态,在移位若干次后,一定能重复出现前某 一状态,其后的过程便周而复始了。反馈线位置不同将出现不同周期的不同序列, 我们希望找到线性反馈的位置,能使移存器产生的序列最长,即达到周期 P=2n-1。 按图中线路连接关系,可以写为:
基于matlab的移位寄存器法m序列的产生

2012年01月第02期科技视界Science &technology viewSCIENCE &TECHNOLOGY VIEW 科技视界作者简介:刘艳华,盐城工学院信息工程学院教师。
基于matlab的移位寄存器法m序列的产生刘艳华(盐城工学院信息工程学院江苏盐城224051)【摘要】扩频通信是在民用和军用都有广泛应用的一种通信技术,自从其诞生就受到了广泛关注。
扩频通信中频谱的扩展是通过一个独立的伪随机序列来完成的。
其中m 序列是最常用的一种伪随机码,本文在matlab 平台上通过仿真,来研究如何用移位寄存器产生m 序列,虽然matlab 中有现成的m 序列产生模块,但是它的相位是不可以调节的,而本文产生的m 序列相位可以调节。
详细讲解了m 序列的产生原理,和matlab 仿真过程,最后给出了仿真结果,结果表明该方法是可行的。
【关键词】移位寄存器;扩频;m 序列;Design of m-sequence Generator Based on Shift Register with MatlabLIU Yan-hua(Yancheng Institute of Technology,School of Information Engineering,Yancheng Jiangsu,224051)【Abstract 】Spread spectrum communication is widely used in both civilian and military communications,Itis potential and promising which attracts wide attention since its emergence.The spectrum expansion of spreadspectrum communication is through of an independent pseudo-random sequence to complete.m-sequence is one of the most common sequence of pseudo-random code,this paper is in matlab platform to study how to use shift registers to generate m-sequence,although there is ready-made matlab m-sequence generation module,but its phase is not regulation,and phase of m-sequence generated by this paper can be adjusted.Explain in detail theprinciples of the m sequence generation,and the matlab simulation process,the final simulation results,the re⁃sults show that the simulation is feasible.【Key words 】Shift register;Spread spectrum;m-sequence0引言所谓扩频,是扩展频谱的简称。
基于Matlab的m序列生成及性能仿真

PN_mod8=reshape(PN—mod8,1,512); end
location=1; k=1: for i=1:length(reg_a11)
if reg__test==reg_all(i,:) location(k)=i; k=k+1:
%寻找初始状态,以验证其周期
end
end
合伪随机序列的基本性质,可以满足扩频序列的设计需求。
基于以上m序列移位寄存器结构,可在Matlab中用M语言编程
产生113序列的程序代码:
reg=[1 0 1 1 1 0 1 0 1 1 0 1];
%从高位到低位
re。gLtest=reg;
eoeff=[1 0 0 0 0 0 1 0 1 0 0 1 11;%高位到低位
%计算In序列自相关性
subplot(2,1,1);
plot(j,temp/length(n)); tide(7自相关性,);
axis([一1000 1000—0.1 1.2]);
酣d on; 同理可计算m序列互相关性程序。
运行程序后可返回D1序列相关函数如图2所示。
由图2可以看出,m序列具有良好的自相关特性和互相关性,符
关和互相关特性【”。
1.m序列简介
m序列是最长线性移位寄存序列的简称.是由带线性反馈的移存
器产生的周期最长的序列。它是周期为N=2r_1的线性伪随机序列,r
是移位寄存器阶数。 m序列的性质有闭:
a)均衡性,即在m序列的一个周期中,…1’和…0’的数目基本相等。
b)长度为k的游程数目占游程总数的24.其中“+”游程和“一”游程
i=l;
for k=1:(2^length(reg))
%计算一个周期的rfl序列输出
基于MATLAB的m序列的产生及相关特性仿真(精)

XUEBAO 2009.10.20*[收稿日期]2009-07-28[作者简介]刘新永(1975-,男,解放军蚌埠坦克学院教育技术中心,讲师,研究方向:通信与网络技术。
蔡凤丽(1978-,女,安徽电子信息职业技术学院,讲师,研究方向:通信与信息系统。
裴晓根(1975-,男,解放军蚌埠坦克学院信息指挥教研室,助讲,研究方向:军事通信。
No.52009General No.44Vol.82009年第5期第8卷(总第44期安徽电子信息职业技术学院学报JOURNALOF ANHUI VOCATIONAL COLLEGE OF ELECTRONICS&INFORMATION TECHNOLOGY[文章编号]1671-802X(200905-0014-03基于MATLAB 的m 序列的产生及相关特性仿真刘新永1,蔡凤丽2,裴晓根3(1、3.解放军蚌埠坦克学院,安徽蚌埠233050;2.安徽电子信息职业技术学院,安徽蚌埠233060[摘要]本文主要是介绍MATLAB 在m 序列的产生及其相关特性分析方面的应用,研究了基于MATLAB 完成m序列simulink 硬件仿真方法,并且利用MATLAB 对不同长度的几种m 序列进行相关特性的分析。
[关键词]m 序列;simulink 硬件仿真;自相关[中图分类号]TN95[文献标识码]B一、m 序列的产生原理m 序列是最长线性反馈移存器序列的简称,它是由带线性反馈的移存器产生的周期最长的一种序列。
如图1所示为n 级移位寄存器,其中有若干级经模2加法器反馈到第1级。
不难看出,在任何一个时刻去观察移位寄存器的状态,必然是2n 个状态之一,其中每一状态代表一个n 位的二进制数字;但是,必须把全0排斥在外,因为一旦出现全0状态,则以后的序列将恒为0,所以,寄存器的起始状态可以是非全0的2n -1状态之一。
这个电路的输出序列是从寄存器移出的,尽管移位寄存器的状态每一移位节拍改变一次,但无疑是循环的。
基于Matlab产生m序列

目录前言 (1)第一章设计任务 (2)1.2设计内容 (2)1.2设计要求 (2)1.3系统框图 (2)第二章m序列的分析 (4)2.1m序列的含义 (4)2.2m序列产生的原理 (5)2.2m序列的性质 (6)2.3自相关特性 (7)第三章m序列的设计 (8)3.1特征多项式确定 (8)3.2本原多项式的确定 (9)3.3m序列的发生 (10)第四章程序调试及结果分析 (11)4.1m序列的仿真结果及分析 (12)4.2该设计的序列相关性仿真结果及分析 (13)结论 (14)参考文献 (15)附录:程序代码 (16)前言扩频通信因其具有抗干扰、抗多径衰落、抗侦察等优点在通信领域中得到广泛应用。
扩频序列的设计和选择是扩频通信的关键技术,扩频序列性能的优劣在很大程度上决定了通信系统的多址干扰和符号间干扰的大小,从而直接影响到系统的性能。
因此,深入研究扩频序列的性质,构造设计具有良好相关性的扩频序列,来满足扩频系统的要求,是直接序列扩频系统的核心课题。
白噪声是一种随机过程,它有极其优良的相关特性。
但至今无法实现白噪声的放大、调制、检测、同步及控制等,而只能用类似于白噪声统计特性的伪随机序列来逼近它,并作为扩频系统的扩频码。
常见的伪随机序列有m 序列、GOLD 序列、M 序列、Walsh 序列等。
m 序列是目前研究最为彻底的伪随机序列,m 序列容易产生,有优良的自相关和互相关特性。
序列是伪随机序列的一种情况。
他可以在很多领域中都有重要应用。
由n级移位寄存器所能产生的周期最长的序列。
这种序列必须由非线性移位寄存器产生,并且周期为2n(n为移位寄存器的级数)。
通过对伪随机码中常用的m序列的结构和性质进行了分析,本文给出了基于MATLAB平台的m序列生成算法及代码伪随机序列分析。
第一章 设计任务1.2 设计内容掌握PN 序列的相关知识,掌握m 序列的产生原理及其在matlab 中的产生方法,对特定长度的m 序列,分析其性质,及其用来构造其它序列的方法;研究伪随机序列在跳频通信中的应用方法。
基于Matlab产生m序列

目录前言 (1)第一章设计任务 (2)1.2设计内容 (2)1.2设计要求 (2)1.3系统框图 (2)第二章m序列的分析 (4)2.1m序列的含义 (4)2.2m序列产生的原理 (5)2.2m序列的性质 (6)2.3自相关特性 (7)第三章m序列的设计 (8)3.1特征多项式确定 (8)3.2本原多项式的确定 (9)3.3m序列的发生 (10)第四章程序调试及结果分析 (11)4.1m序列的仿真结果及分析 (12)4.2该设计的序列相关性仿真结果及分析 (13)结论 (14)参考文献 (15)附录:程序代码 (16)前言扩频通信因其具有抗干扰、抗多径衰落、抗侦察等优点在通信领域中得到广泛应用。
扩频序列的设计和选择是扩频通信的关键技术,扩频序列性能的优劣在很大程度上决定了通信系统的多址干扰和符号间干扰的大小,从而直接影响到系统的性能。
因此,深入研究扩频序列的性质,构造设计具有良好相关性的扩频序列,来满足扩频系统的要求,是直接序列扩频系统的核心课题。
白噪声是一种随机过程,它有极其优良的相关特性。
但至今无法实现白噪声的放大、调制、检测、同步及控制等,而只能用类似于白噪声统计特性的伪随机序列来逼近它,并作为扩频系统的扩频码。
常见的伪随机序列有m 序列、GOLD 序列、M 序列、Walsh 序列等。
m 序列是目前研究最为彻底的伪随机序列,m 序列容易产生,有优良的自相关和互相关特性。
序列是伪随机序列的一种情况。
他可以在很多领域中都有重要应用。
由n级移位寄存器所能产生的周期最长的序列。
这种序列必须由非线性移位寄存器产生,并且周期为2n(n为移位寄存器的级数)。
通过对伪随机码中常用的m序列的结构和性质进行了分析,本文给出了基于MATLAB平台的m序列生成算法及代码伪随机序列分析。
第一章 设计任务1.2 设计内容掌握PN 序列的相关知识,掌握m 序列的产生原理及其在matlab 中的产生方法,对特定长度的m 序列,分析其性质,及其用来构造其它序列的方法;研究伪随机序列在跳频通信中的应用方法。
基于matlab的移位寄存器法m序列的产生

p aei n t euai , n h s f sq ec e eae yti p p r a eajs d E pani d tite h s o rg lt n a dp aeo e u n eg n rt b s a e nb du t . x li n e lh s o m- d h c e a
s iss w h tt e smu ai n i e sb e u t ho t a h i l to sf a i l .
【 e od]h g t ; ra et mm s une K y rsSi r ie S ed pc ;-e ec w t f e s rp s r u q
等。 m序列是最常用的一种扩频码 , 它是最大长度线
性反 馈移位 寄 存器 序列 的简 称 。它是 用带 线性 反馈
的移位寄存器产生 的, 是周期最长的序列。 它具有很 强的相关性 . 规律性和系统性 。 表现出的统计特性和 白噪声的采样序列相同, 如果不知道其生成方法 , 看 上去 就 和真 的随机 序列 一样 。 伪随机序列的用处很广泛 , 在雷达 、 遥控系统、 多址通信 、 保密通信、 P 导航等领域都有应用。由 GS 于其 具有 的社 会 和科 学价 值 , 随 机序列 的构 造 、 伪 生
s e t m o p cr u c mmu iain i tru h o n id p n e tp e d — a d m e u n e t o lt. s q e c so e nc t s h o g fa n e e d n su o r n o s q e c oc mpee m— e u n e i n o
基于Matlab的m序列发生器的

目录第一章绪论..................................................................................................................11.1背景及意义 ....................................................................................................11.2设计内容及要求...............................................................................................11.2.1 设计内容................................................................................................11.2.2 设计要求................................................................................................21.3系统框图..........................................................................................................2第二章 m序列的分析.......................................................................................................32.1 m序列的原理...........................................................................................................32.2 m序列的相关特性 ...................................................................................................42.2.1均衡特性(平衡性) ...............................................................................42.2.2游程分布(游程分布的随机性) ...............................................................42.2.3移位相加特性(线性叠加性) ..................................................................42.2.4自相关特性.............................................................................................5第三章 m序列的设计............................................................................................................. 63.1特征多项式确定..............................................................................................63.2本原多项式的确定...........................................................................................73.3 m序列的发生..............................................................................................8第四章程序调试及结果分析..................................................................................10结论............................................................................................................................12参考文献....................................................................................................................13附录一:程序代码....................................................................................................14第一章绪论1.1 背景及意义扩展频谱通信是一种不同于常规通信系统的新调制理论和技术,简称扩频通信。
第11组基于Matlab的m序列仿真

《移动通信》课程项目报告题目:基于MATLAB的m序列仿真专业班级电子信息0121208班组长周易德组员叶子源组员胡楗指导教师李兆玉提交日期 2015年6月15日成绩课程设计任务分配表目录一、设计目的 0二、设计要求和设计指标 0三、设计内容 03.1 伪随机码 03.2 m序列的定义 (1)3.3 m序列的生产 (2)3.4 m序列的性质 (3)3.4.1平衡性 (3)3.4.2游程特性 (3)3.4.3自相关特性 (4)3.4.4功率谱与噪声类似 (5)3.4.5 互相关特性 (6)3.5 m序列的应用 (7)3.5.1 CDMA IS-95的前向信道 (9)3.5.1 CDMA IS-95的反向信道 (9)四、本设计改进建议 (9)五、总结 (9)六、主要参考文献 (10)附录1程序清单 (11)附录2 m序列本原多项式表 (16)一、设计目的我们想通过本次课程设计提高自己对移动通信的认识,熟练Matlab软件的使用,锻炼发现问题解决问题的能力,最终提示我们的自学能力。
具体来讲,本次课程设计将通过Matlab对m序列的生产方法和性质进行深刻的讨论,需要我们去了解m序列的生产和性质。
二、设计要求和设计指标设计要求:1.了解m序列的定义和其背后的意义2.通过Matlab生产m序列3.验证m序列主要性质4.讨论m序列的主要性质在扩频中的作用设计指标:1.能通过Matlab生产任意长度的m序列2.讨论任意长度m序列的均衡性、游程性、自相关特性、互相关特性等主要性质三、设计内容3.1 伪随机码伪随机(或伪噪声,Pseudorandom Noise,PN)码序列是一种常用的地址码,它具有与白噪声类似的自相关性质的0和1所构成的编码序列。
伪随机码序列具有类似于随机序列的基本特性,是一种貌似随机但实际上是有规律的周期性二进制序列。
如果发送数据序列经过完全随机性的加扰,接收机就无法恢复原始序列。
在实际系统中使用的是一个足够随机的序列,一方面这个随机序列对非目标接收机是不可识别的,另一方面目标接收机能够识别并且很容易同步地产生这个随机序列。
M序列的matlab产生方法

M序列是工程中常用的输入信号,它的性质类似于白噪声,而白噪声是理论上最好的输入信号,可见M序列的价值。
下面介绍M序列的matlab产生方法。
idinput函数产生系统辨识常用的典型信号。
格式u = idinput(N,type,band,levels)[u,freqs] = idinput(N,'sine',band,levels,sinedata)N产生的序列的长度,如果N=[N nu],则nu为输入的通道数,如果N=[P nu M],则nu指定通道数,P为周期,M*P为信号长度。
默认情况下,nu=1,M=1,即一个通道,一个周期。
Type指定产生信号的类型,可选类型如下Band指定信号的频率成分。
对于’rgs’、’rbs’、’sine’,band = [wlow, whigh]指定通带的范围,如果是白噪声信号,则band=[0, 1],这也是默认值。
指定非默认值时,相当于有色噪声。
对于’prbs’,band=[0, B],B表示信号在一个间隔1/B(时钟周期)内为恒值,默认为[0, 1]。
Levels指定输入的水平。
Levels=[minu, maxu],在type=’rbs’、’prbs’、’sine’时,表示信号u的值总是在minu和maxu之间。
对于type=’rgs’,minu指定信号的均值减标准差,maxu指定信号的均值加标准差,对于0均值、标准差为1的高斯白噪声信号,则levels=[-1, 1],这也是默认值。
说明对于PRBS信号,如果M>1,则序列的长度和PRBS周期会做调整,使PRBS的周期为对应一定阶数的最大值(即2^n-1,n为阶数);如果M=1,PRBS的周期是大于N 的相应阶数的值。
在多输入的情形时,信号被最大平移,即P/nu为此信号能被估计的模型阶次的上界。
上面的意思可如下理解:对于M=1时,ms = idinput(12, 'prbs', [0 1], [0 1]);figurestairs(ms)title('M序列')ylim([-0.5 1.5])结果如下同时,matlab给出如下警告Warning: The PRBS signal delivered is the 12 first values of a full sequence of length 15.即函数的输出为周期为15(大于12的第一个2^n-1的值)PRBS信号的前12个值组成的序列。
基于Matlab的m序列发生器的设计1
引言伪随机噪声具有类似于随机噪声的某些统计特性,同时又能够重复产生。
由于它具有随机噪声的优点,又避免了随机噪声的缺点,因此获得了日益广泛的实际实用。
这种周期性数字序列称为随机序列,有时又称为随机信号和伪随机码。
m序列是伪随机序列中最重要的序列中的一种,它不但具有易于产生的特点,还具有良好的自相关特性,在扩频通信中得到了广泛的应用。
1. m序列设计方案选择1.1 方案一编程实现m 序列:MA TLAB编程非常简单,无需进行变量声明,可以很方便的实现m序列。
1.2方案二图1.1 Simulink 实现m 序列Simulink 实现m 序列(如图1.1所示) 。
Simulink是MATLAB最重要的组件之一,它提供一个动态系统建模、仿真和综合分析的集成环境。
在该环境中,无需大量书写程序,而只需要通过简单直观的鼠标操作,就可构造出复杂的系统。
Simulink具有适应面广、结构和流程清晰及仿真精细、贴近实际、效率高、灵活等优点,并基于以上优点Simulink已被广泛应用于控制理论和数字信号处理的复杂仿真和设计。
通过比较方案一和方案二,发现方案一的优点具有通用性,其中mserises.m相当于一个通项,根据具体的本原多项式调用它即可,而方案二利用MATLAB的simulink直接搭建模块,在移位寄存器较少时利用此方法极为简单,可是当移位寄存器的数量增多时,要搭建那么多的模块就显得很繁琐,缺乏通用性。
2.Simulink工具介绍2.1 Simulink简介Simulink是MATLAB软件最重要的组件之一,它提供一个动态系统建模、仿真和综合分析的集成环境。
在该环境中,无需大量书写程序,而只需要通过简单直观的鼠标操作,就可以构造出复杂的系统。
Simulink具有适应面广、结构和流程清晰及仿真精细、贴近实际、效率高、灵活等优点,并基于以上优点Simulink已被广泛应用与控制理论和数字信号处理的复杂仿真和设计。
同时有大量的第三方软件和硬件可应用于或被要求应用于Simulink。
基于MATLAB的扩频通信m序列的仿真解析

********************实践教学********************兰州理工大学计算机与通信学院2010年秋季学期移动通信课程设计题目:基于MATLAB的扩频通信m伪随机序列产生专业班级:通信工程07级(1)班姓名:周超学号: 07250115指导教师:贾科军成绩:目录摘要 (3)前言 (4)第一章基本原理 (5)1.1扩频调制 (5)1.2直接序列扩频(DS)原理 (8)1.3伪随机(PN)序列 (9)第二章 m序列发生器的系统分析 (12)2.1 m序列的产生 (12)2.2 m序列的反馈系数 (15)2.3 m序列发生器结构 (16)2.4 m序列的基本性质 (17)2.5 m序列的相关性 (17)第三章详细设计 (19)3.1 十阶m序列的设计框图 (19)3.2工作流程图 (20)第四章仿真测试及结论 (22)4.1 十阶m序列的仿真结果及分析 (22)4.2该设计的序列相关性仿真结果及分析 (27)参考文献 (28)总结 (29)所谓扩频通信,是扩展频谱通信技术的简称。
它是指用来传输信息的射频带宽远大于信息本身带宽的一种通信方式,扩频通信系统的出现,被誉为是通信技术的一次重大突破。
伪随机序列是具有某种随机特性的确定的序列。
它们是由移位寄存器产生确定序列,然而它们却具有某种随机序列的随机持性。
因为同样具有随机特性,无法从一个已经产生的序列的特性中判断是真随机序列,只能根据序列的产生办法来判断。
本设计运用MATLAB实现产生扩频通信中的m序列,并分析了相关性能。
关键词:扩频通信;随机序列;m序列随着社会,经济的发展,移动通信得到了越来越广泛的应用,在我国,移动通信发展的起步晚,但发展极其迅速。
移动通信的发展日新月异,从1978年第一代模拟蜂窝网电话系统的诞生至今,不过10多年,第二代全数字蜂窝网电话系统就已问世,第三代的个人通信系统的方案和实验均已开始。
在这种情况下,相应的扩频编码技术也随之诞生了。
在matlab中生成m序列

在matlab中⽣成m序列实验环境为matlab2013b1、⾸先编写⼀个mseq.m⽂件,内容为:function[mseq]=m_sequence(fbconnection)n=length(fbconnection);N=2^n-1;register=[zeros(1,n-1) 1]; %移位寄存器的初始状态mseq(1)=register(n); %m序列的第⼀个输出码元for i=2:Nnewregister(1)=mod(sum(fbconnection.*register),2);for j=2:nnewregister(j)=register(j-1);end;register=newregister;mseq(i)=register(n);end2、在matlab中打开这个⽂件3、在matlab的命令⾏窗体中执⾏primpoly(7,'all')这个命令的⽬的是得到7阶M序列的全部本原多项式。
假设想得到其它阶的m序列,⾃⾏改动数字7就可以。
4、得到的结果为Primitive polynomial(s) =D^7+D^1+1D^7+D^3+1D^7+D^3+D^2+D^1+1D^7+D^4+1D^7+D^4+D^3+D^2+1D^7+D^5+D^2+D^1+1D^7+D^5+D^3+D^1+1D^7+D^5+D^4+D^3+1D^7+D^5+D^4+D^3+D^2+D^1+1D^7+D^6+1D^7+D^6+D^3+D^1+1D^7+D^6+D^4+D^1+1D^7+D^6+D^4+D^2+1D^7+D^6+D^5+D^2+1D^7+D^6+D^5+D^3+D^2+D^1+1D^7+D^6+D^5+D^4+1D^7+D^6+D^5+D^4+D^2+D^1+1D^7+D^6+D^5+D^4+D^3+D^2+1ans =1311371431451571671711851911932032112132292392412472535、输⼊mseq([1 0 0 0 0 0 1])6、便可得到⼀个127位的m序列,整理之后为1000000111111101010100110011101110100101100011011110110101101100100100011100001011111001010111001101000100111100010100001100000说明。
M序列的matlab产生方法

M序列是工程中常用的输入信号,它的性质类似于白噪声,而白噪声是理论上最好的输入信号,可见M序列的价值。
下面介绍M序列的matlab产生方法。
idinput函数产生系统辨识常用的典型信号。
格式u = idinput(N,type,band,levels)[u,freqs] = idinput(N,'sine',band,levels,sinedata)N产生的序列的长度,如果N=[N nu],则nu为输入的通道数,如果N=[P nu M],则nu 指定通道数,P为周期,M*P为信号长度。
默认情况下,nu=1,M=1,即一个通道,一个周期。
Type指定产生信号的类型,可选类型如下‘rgs’高斯随机信号‘rbs’(默认)二值随机信号‘prbs’二值伪随机信号(M序列)‘sine’正弦信号和Band指定信号的频率成分。
对于’rgs’、’rbs’、’sine’,band = [wlow, whigh]指定通带的围,如果是白噪声信号,则band=[0, 1],这也是默认值。
指定非默认值时,相当于有色噪声。
对于’prbs’,band=[0, B],B表示信号在一个间隔1/B(时钟周期)为恒值,默认为[0, 1]。
Levels指定输入的水平。
Levels=[minu, maxu],在type=’rbs’、’prbs’、’sine’时,表示信号u的值总是在minu和maxu之间。
对于type=’rgs’,minu指定信号的均值减标准差,maxu指定信号的均值加标准差,对于0均值、标准差为1的高斯白噪声信号,则levels=[-1, 1],这也是默认值。
说明对于PRBS信号,如果M>1,则序列的长度和PRBS周期会做调整,使PRBS的周期为对应一定阶数的最大值(即2^n-1,n为阶数);如果M=1,PRBS的周期是大于N的相应阶数的值。
在多输入的情形时,信号被最大平移,即P/nu为此信号能被估计的模型阶次的上界。
用matlab产生M序列极其逆M序列

用matlab产生M序列极其逆M序列①用产生M序列,②以此M序列为基础产生逆M序列,③并将逆M序列的复制变为-a和+a。
解:(1)产生M序列,用一个4级移位寄存器生成M序列。
程序及结果如下(可执行文件xiti3见文件夹中):%产生M序列x=[0 1 0 1 1 0 1 1 1];%给移位寄存器初始化N=50;%N为脉冲数目M=[];%存放M序列for i=1:Na=xor(x(4),x(9));%x(4)与x(9)取异或赋值给aM(i)=x(9);%把x(9)里的值赋给M[]产生M序列for j=9:-1:2x(j)=x(j-1);%实现移位寄存器的循环移位endx(1)=a;%把x(4)与x(9)取异值a给x(1)endfigure(1)%创建图形1stairs(1:N,M)%把M序列以阶梯图形显示hold onaxis([0,N,0,1.2])%图形横轴从0到N,纵轴从0到1.2title('M序列');%图形标题为‘M序列’xlabel('时序脉冲');%横轴为‘时序脉冲’(2)用0、1方波序列与M序列取异或得逆M序列。
程序及结果如下(可执行文件xiti3见文件夹中):%产生逆M序列f=zeros(1,length(M));%f为方波序列f(1)=1;for i=2:Nf(i)=f(i-1);endNM=xor(M,f);%M序列与方波异或赋值给NMfigure(2)stairs(1:N,NM)hold onaxis([0,N,0,1.2])title('逆M序列');xlabel('时序脉冲');(3)将逆M序列的复制变为-a和+a,程序及结果如下(可执行文件xiti3见文件夹中):%将逆M序列的幅值变为a和-aa=5;%a为指定的幅值A=NM.*a*2;A=A-a;figure(3)stairs(1:N,A);axis([0,N,-a-1,a+1]);hold ontitle('幅值为a的逆M序列');xlabel('时序脉冲');。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章设计内容及要求基于MATLAB产生m序列要求:1.通过matlab编程产生m序列的产生原理及其产生方法。
2.对特定长度的m序列,分析其性质,及其用来构造其它序列的方法。
第二章m序列设计方案的选择2.1 方案一MATLAB编程非常简单,无需进行变量声明,可以很方便的实现m序列。
2.2 方案二图2.1 Simulink实现m序列Simulink是MATLAB最重要的组件之一,它提供了一个动态系统建模,仿真和综合分析的集成环境。
在此环境中无需大量书写程序,而只需通过简单直观的鼠标操作,就可构造出复杂的系统。
Simulink具有适应性广,结构及流程清晰及仿真精细等优点,基于以上优点,Simulink已被广泛的运用到控制理论和数字信号处理的复杂仿真和设计。
通过比较方案一和方案二,发现方案一的有点具有通用性而方案二利用MATLAB的Simulink直接搭建模块,在移位寄存器较少的情况下利用此方法比较简单,可是当移位寄存器的个数增多时,要搭建那么多的模块就显的很繁琐了,缺乏通用性,因此本次实验选择方案一。
第三章m序列的产生及性质3.1 m序列的产生原理、结构及产生m序列是最长线性反馈移位寄存器序列的简称,m序列是由带线性反馈的移位寄存器产生的。
由n级串联的移位寄存器和反馈逻辑线路可组成动态移位寄存器,如果反馈逻辑线路只由模2和构成,则称为线性反馈移位寄存器。
带线性反馈逻辑的移位寄存器设定初始状态后,在时钟触发下,每次移位后各级寄存器会发生变化,其中任何一级寄存器的输出,随着时钟节拍的推移都会产生一个序列,该序列称为移位寄存器序列。
n级线性移位寄存器的如图3.1所示:◇A图3.1 n级线性移位寄存器图中C i表示反馈线的两种可能连接方式,C i=1表示连线接通,第n-i级输出加入反馈中;C i=0表示连线断开,第n-i级输出未参加反馈。
因此,一般形式的线性反馈逻辑表达式为------表达式3.1将等式左边的a n移至右边,并将a n=C0a n(C0=1)带入上式,则上式可以写成-------表达式3.2定义一个与上式相对应的多项式--------表达式3.3其中x的幂次表示元素的相应位置。
该式为线性反馈移位寄存器的特征多项式,特征多项式与输出序列的周期有密切关系。
当F(x)满足下列三个条件时,就一定能产生m序列:(1)F(x)是不可约的,即不能再分解多项式;(2)F(x)可整除x n+1,这里p=2n+1;(3)F(x)不能整除x n+1,这里q<q.满足上述条件的多项式称为本原多项式,这样产生m序列的充要条件就变成了如何寻找本原多项式。
3.2 m序列的基本性质(1)均衡性。
在m序列一个周期中‘1’的个数比‘0’要多1位,这表明序列平均值很小。
(2)m序列与其移位后的序列模2相加,所得的序列还是m序列,只是相位不同而已。
例如:1110100与向又移3位的序列1001110相对应模二相加后的序列为0111010,相当于原序列向右移一位后的序列,仍为m序列。
(3)m序列发生器中移位寄存器的各种状态,除全0状态外,其他状态只在m序列中出现一次。
(4)m序列发生器中,并不是任何抽头组合都能产生m序列。
理论分析指出,产生的m序列数由下式决定:--------表达式3.4其中φ(X)为欧拉数。
例如5级移位寄存器产生31位m序列只有6个。
(5)m序列具有良好的自相关性,其自相关系数:-------表达式3.5从m序列的自相关系数可以看出m序列是一个狭义伪随机码。
图3.2 m序列信号的自相关函数3.3 生成m序列的模块根据m序列的生成原理图,如图3.1所示,由图可知m序列是多级移位寄存器通过线性反馈再进行模二相加产生的,最后一位一位输出观察其波形图。
程序中使用的代码如下:N=2^length(reg1)-1;for k=1:Na_n=mod(sum(reg1.*coeff1(1:length(coeff1)-1)),2);reg1=[reg1(2:length(reg1)),a_n];out1(k)=reg1(1);end其中N为m序列的长度,值为(26-1)。
由程序已定义了移位寄存器的初始状态和抽头系数,在此基础上进行反馈,后进行模二加,所得的结果为输出的第一个值,初始状态向左移移位,而所得的输出值填补上变成新的序列,在进行第二次反馈和模二加,依次循环N次,产生m序列第四章 m序列构造其他序列Gold 序列具有三值互相关函数,其值为: ]2)([1,1),(1---r t p p r t p (式2.10)这里,⎩⎨⎧++=-=++的倍数为偶数但不是,为奇数421,21)(,12)2(5.0)1(5.0r r r t p r r r (式2.11) 当r 为奇数时,gold 序列中约有50%的码序列归一化相关函数值为-1/p 。
当r 为偶数但又不是4的倍数是,约有75%的码序列归一化互相关函数值为-1/p 。
Gold 序列是R.Gold 于1967年提出来的,它由两个m 序列按下述方法演变而来的:把2个码长相同的m 序列移位并进行模2加,如果相加的两个m 序列是一对优选对,则相加的结果为一个Gold 序列。
设有一对周期为N=2r -1的m 序列优选对{a },{b },以其中任意一个序列为基准序列,如{a },对另一个序列{b }进行移位i 次,得到{b }的移位序列{b i },然后与序列{a }进行模二加得到一个新的周期为N 的序列{c },则称新序列{c }为Gold 序列,既{c i }={a }+{b } i=0,1,2,....,N4.1 Gold 序列的产生方框图产生gold 序列的程序代码如下:gold=mod(out1+out2,2);第五章 程序调试及运行结果5.1仿真设计流程图否是否是图5.1 实验仿真流程图 5.2实验的调试与运行结果程序中把移位寄存器的初始值定义全为1,抽头系数定义为[1000011]和仿真准备 规划程序模块 编写程序确认程序无 误 设置仿真参数运行,调试及数据分析 生成仿真图形 是否达到要求 结束[1100111],根据公式m序列的长度=2n-1,可知道所得的两个m序列的长度都为63,所利用的移位寄存器为6个。
代码如下:reg1=ones(1,6); %寄存器初始状态coeff1=[1 0 0 0 0 1 1]; %设置系数reg2=ones(1,7); %寄存器初始状态coeff2=[1 0 0 1 1 1 1]; %设置系数程序检测无误后,运行程序,得到图形如下:图5.2 运行后的两m序列波形仿真图根据产生Gold序列的原理,运行程序,得到如下Gold序列的仿真图;图5.3 运行后Gold序列的仿真图自相关性:首先将第一个m序列变成双极性的序列,在与本身进行移位相乘进行积分运算,代码如下:out1=2*out1-1; %变为双极性序列for j=0:N-1rho(j+1)=sum(out1.*[out1(1+j:N),out1(1:j)])/N;endj=-N+1:N-1;rho=[fliplr(rho(2:N)),rho];figure(3)plot(j,rho);axis([-10 10 -0.1 1.2]);title('第一个m序列的自相关函数')互相关性:第一个m序列的函数与第二个m序列函数的移位相乘进行积分运算。
代码如下:for j=0:N-1R(j+1)=sum(out1.*[out2(1+j:N),out2(1:j)]);图5.4 m序列自相关性仿真图图5.5 两m序列的互相关性仿真图5.3 错误排除实验过程中出了许多错误,特别是在对序列的自相关性上,缺乏了对自相关性的了解,导致出的波形错误,但在查找资料,修改自相关函数,终于得到了正确的仿真图。
结论课程设计是一个十分有价值、有意义的实践活动,把一个课题设计好不是一步到位的,是经过反复修改,不断调试的过程,期间有困难也有乐趣,使对工程实践有了一个初步的认识。
本次课程设计实现了设计要求,利用软件实现m序列的生成,通过这次实验不但加深了对m序列的了解,而且对MATLAB的编程有了很好的掌握,虽然在仿真过程中会出现一些如程序不对或出的仿真图没有达到实验要求,如m序列中‘1’的个数要比‘0’的个数多1,而实际出的仿真图‘1’和‘0’的个数却是相等的,最后在调整了顶层原理图才使得仿真图正确,在不断的程序调整中提高了自己的能力。
m序列可以用软件实现,也可以用硬件实现,但是通过此次实验看出了软件的诸多优点。
在课程设计的过程中,查询了大量的资料,通过相关资料的查询,使我对通信领域的有关知识有了一定的了解,扩大了知识面。
[1]肖国镇,梁传甲.伪随机序列及其应用[M].北京:国防工业出版社.1985[2]林可祥,汪一飞.伪随机码的原理与应用[M].北京:人民邮电出版社.1998.[3]吴先用,邹学玉.一种m序列伪码发生器的产生方法[J].西安:西安电子科技大学出版社.2003clear;reg1=ones(1,7); %寄存器初始状态coeff1=[1 0 0 0 0 1 1]; %设置系数N=2^length(reg1)-1;%产生m序列for k=1:Na_n=mod(sum(reg1.*coeff1(1:length(coeff1)-1)),2);reg1=[reg1(2:length(reg1)),a_n];out1(k)=reg1(1);endreg2=ones(1,7); %寄存器初始状态coeff2=[1 10 0 1 1 1]; %设置系数N=2^length(reg2)-1;for k=1:Na_n=mod(sum(reg2.*coeff2(1:length(coeff2)-1)),2); %移位,反馈reg2=[reg2(2:length(reg2)),a_n]; %反馈out2(k)=reg2(1); %取第一个值输出end%产生gold序列gold=mod(out1+out2,2);c=1:N;figure(1)[b1,t1]=stairs(c,out1);subplot(2,1,1);plot(b1,t1);axis([0 130 -0.1 1.1]);title('第一个m序列');[b2,t2]=stairs(c,out2);subplot(2,1,2);plot(b2,t2);axis([0 130 -0.1 1.1]);title('第二个m序列');figure(2)[b3,t3]=stairs(c,gold);plot(b3,t3);axis([0 130 -0.1 1.1]);title('gold序列')out1=2*out1-1; %变为双极性序列out2=2*out2-1;%自相关函数for j=0:N-1rho(j+1)=sum(out1.*[out1(1+j:N),out1(1:j)])/N;endj=-N+1:N-1;rho=[fliplr(rho(2:N)),rho];figure(3)plot(j,rho);axis([-10 10 -0.1 1.2]);title('第一个m序列的自相关函数') %互相关函数for j=0:N-1R(j+1)=sum(out1.*[out2(1+j:N),out2(1:j)]);endj=-N+1:N-1;R=[fliplr(R(2:N)),R];figure(4)plot(j,R);axis([-N N -20 20]);title('两个m序列的互相关函数');。
