2018中考数学压轴题探究专题：几何最值的存在性问题

合集下载

2018年中考数学真题分类汇编专题复习(六)几何最值问题(答案不全)

4
（ 2018 陕西）
5
（ 2018 扬州）如图，在 ABC 中， AB AC ， AO BC 于点 O ， OE AB 于点 E ，以点 O 为圆心， OE 为半径作半圆，交 AO 于点 F . （ 1）求证： AC 是 O 的切线；（ 2）若点 F 是 AO 的中点， OE 3 ，求图中阴影部分的面积；（ 3）在（ 2）的条件下，点 P 是 BC 边上的动点，当 PE PF 取最小值时，直接写出 BP 的长 .
6
菱
形，点 P、E、 F 分别为线段 AB、AD、DB 的任意点，则 PE PF 的最小值是
.
15
4
平行线之间垂线段最短
3
（ 2018 泰安）
（ 2018 广州）如图 11，在四边形 ABCD中，∠ B=∠ C=90°， AB＞ CD， AD=AB+CD.
(1) 利用尺规作∠ ADC的平分线 DE,交 BC于点 E, 连接 AE(保留作图痕迹，不写作法 ) （ 2）在（ 1）的条件下， ①证明： AE⊥ DE; ②若 CD=2， AB=4，点 M,N 分别是 AE,AB 上的动点，求 BM+MN的最小值。（ 2018 荆门）
（ 2018 荆州）
专题复习（六）几何最值问题
（ 2018 新疆建设兵团）轴对称求最值
（ 2018 苏州）二次函数最值 2 3
（ 2018 铜仁）（ 2018 十堰）垂线段最短（ 201，等腰△ ABC的底边 BC=20，面积为 120，点 F 在边 BC上，且 BF=3FC， EG是腰 AC的垂直平分线，若点 D 在 EG上运动，则△ CDF周长的最小值为 13 . 轴对称求最短路径
（ 2018 天津）轴对称求最短路径

走进2018年中考数学专题复习几何最值问题解题策略

走进2018年中考数学专题复习第七讲几何最值问题解题策略【专题分析】最值问题是初中数学的重要内容,无论是代数问题还是几何问题都有最值问题,在中考压轴题中出现比较高的主要有利用重要的几何结论(如两点之间线段最短、三角形两边之和大于第三边、两边之差小于第三边、垂线段最短等)以及用一次函数和二次函数的性质来求最值问题.【知识归纳】1.在求几何图形中的周长或线段长度最值时,解决此类问题的方法一般是先将要求线段(要求的量)用未知数x表示出来,建立函数模型(一般所表示的式子为一次函数解析式或二次函数解析式),常用勾股定理或三角形相似求得函数关系式,再用函数的增减性或最值来求解即可.2.利用对称的性质求两条线段之和最小值的问题,解决此类问题的方法为:如图,要求直线l上一动点P到点A,B距离之和的最小值,先作点A关于直线l的对称点A',连接A'B,则A'B与直线l的交点即为P点,根据对称性可知此时A'B的长即为PA+PB的最小值,求出A'B的值即可.【题型解析】题型1: 三角形中最值问题例题：（2017山东枣庄）如图，直线y=x+4与x轴、y轴分别交于点A和点B，点C、D分别为线段AB、OB的中点，点P为OA上一动点，PC+PD值最小时点P 的坐标为（）A．（﹣3，0）B．（﹣6，0）C．（﹣，0） D．（﹣，0）【考点】F8：一次函数图象上点的坐标特征；PA：轴对称﹣最短路线问题．【分析】（方法一）根据一次函数解析式求出点A、B的坐标，再由中点坐标公式求出点C、D的坐标，根据对称的性质找出点D′的坐标，结合点C、D′的坐标求出直线CD′的解析式，令y=0即可求出x的值，从而得出点P的坐标．（方法二）根据一次函数解析式求出点A、B的坐标，再由中点坐标公式求出点C、D的坐标，根据对称的性质找出点D′的坐标，根据三角形中位线定理即可得出点P为线段CD′的中点，由此即可得出点P的坐标．【解答】解：（方法一）作点D关于x轴的对称点D′，连接CD′交x轴于点P，此时PC+PD值最小，如图所示．令y=x+4中x=0，则y=4，∴点B的坐标为（0，4）；令y=x+4中y=0，则x+4=0，解得：x=﹣6，∴点A的坐标为（﹣6，0）．∵点C、D分别为线段AB、OB的中点，∴点C（﹣3，2），点D（0，2）．∵点D′和点D关于x轴对称，∴点D′的坐标为（0，﹣2）．设直线CD′的解析式为y=kx+b，∵直线CD′过点C（﹣3，2），D′（0，﹣2），∴有，解得：，∴直线CD′的解析式为y=﹣x﹣2．令y=﹣x﹣2中y=0，则0=﹣x﹣2，解得：x=﹣，∴点P的坐标为（﹣，0）．故选C．（方法二）连接CD，作点D关于x轴的对称点D′，连接CD′交x轴于点P，此时PC+PD值最小，如图所示．令y=x+4中x=0，则y=4，∴点B的坐标为（0，4）；令y=x+4中y=0，则x+4=0，解得：x=﹣6，∴点A的坐标为（﹣6，0）．∵点C、D分别为线段AB、OB的中点，∴点C（﹣3，2），点D（0，2），CD∥x轴，∵点D′和点D关于x轴对称，∴点D′的坐标为（0，﹣2），点O为线段DD′的中点．又∵OP∥CD，∴点P为线段CD′的中点，∴点P的坐标为（﹣，0）．故选C．方法指导：出现最值问题,可转化为轴对称知识所涉及的最短路径问题是我们解答此类问题的常见方法.题型2: 四边形中最值问题例题:（2017贵州安顺）如图所示，正方形ABCD的边长为6，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为 6 ．【考点】PA：轴对称﹣最短路线问题；KK：等边三角形的性质；LE：正方形的性质．【分析】由于点B与D关于AC对称，所以连接BD，与AC的交点即为P点．此时PD+PE=BE最小，而BE是等边△ABE的边，BE=AB，由正方形ABCD的边长为6，可求出AB的长，从而得出结果．【解答】解：设BE与AC交于点P，连接BD，∵点B与D关于AC对称，∴PD=PB，∴PD+PE=PB+PE=BE最小．即P在AC与BE的交点上时，PD+PE最小，为BE的长度；∵正方形ABCD的边长为6，∴AB=6．又∵△ABE是等边三角形，∴BE=AB=6．故所求最小值为6．故答案为：6．方法指导：本题借助不等式“a2+b2≥2ab”通过代换转化来求平行四边形面积的最值,体现了转化思想和整体思想的运用.题型3:圆中最值问题例题：（2017浙江衢州）如图，在直角坐标系中，⊙A的圆心A的坐标为（﹣1，0），半径为1，点P为直线y=﹣x+3上的动点，过点P作⊙A的切线，切点为Q，则切线长PQ的最小值是2．【考点】MC：切线的性质；F5：一次函数的性质．【分析】连接AP，PQ，当AP最小时，PQ最小，当AP⊥直线y=﹣x+3时，PQ 最小，根据两点间的距离公式得到AP=3，根据勾股定理即可得到结论．【解答】解：连接AP，PQ，当AP最小时，PQ最小，∴当AP⊥直线y=﹣x+3时，PQ最小，∵A的坐标为（﹣1，0），y=﹣x+3可化为3x+4y﹣12=0，∴AP==3，∴PQ==2．方法指导: 此题综合性强,解题方法很多,考查范围较广,与初中数学很多内容有关,如勾股定理、圆周角定理及推论、垂径定理、相似、三角函数、二次函数、垂线段的性质、二次根式的计算与化简等.考查了多种数学思想,如建模思想、化归思想等.此题难度中等,有一定的灵活性,考生不易拿满分.【提升训练】1. （2017江苏盐城）如图，在边长为1的小正方形网格中，将△ABC绕某点旋转到△A'B'C'的位置，则点B运动的最短路径长为π．【考点】O4：轨迹；R2：旋转的性质．【分析】如图作线段AA′、CC′的垂直平分线相交于点P，点P即为旋转中心，观察图象可知，旋转角为90°（逆时针旋转）时B运动的路径长最短【解答】解：如图作线段AA′、CC′的垂直平分线相交于点P，点P即为旋转中心，观察图象可知，旋转角为90°（逆时针旋转）时B运动的路径长最短，PB==，∴B运动的最短路径长为==π，故答案为π．2. （2017•新疆）如图，在边长为6cm的正方形ABCD中，点E、F、G、H分别从点A、B、C、D同时出发，均以1cm/s的速度向点B、C、D、A匀速运动，当点E 到达点B时，四个点同时停止运动，在运动过程中，当运动时间为 3 s时，四边形EFGH的面积最小，其最小值是18 cm2．【考点】H7：二次函数的最值；LE：正方形的性质．【分析】设运动时间为t（0≤t≤6），则AE=t，AH=6﹣t，由四边形EFGH的面积=正方形ABCD的面积﹣4个△AEH的面积，即可得出S四边形EFGH关于t的函数关系式，配方后即可得出结论．【解答】解：设运动时间为t（0≤t≤6），则AE=t，AH=6﹣t，根据题意得：S四边形EFGH =S正方形ABCD﹣4S△AEH=6×6﹣4×t（6﹣t）=2t2﹣12t+36=2（t﹣3）2+18，∴当t=3时，四边形EFGH的面积取最小值，最小值为18．故答案为：3；18【点评】本题考查了二次函数的最值、三角形以及正方形的面积，通过分割图形求面积法找出S四边形EFGH关于t的函数关系式是解题的关键．3. (2017湖北宜昌)正方形ABCD的边长为1，点O是BC边上的一个动点（与B，C不重合），以O为顶点在BC所在直线的上方作∠MON=90°．（1）当OM经过点A时，①请直接填空：ON 不可能（可能，不可能）过D点；（图1仅供分析）②如图2，在ON上截取OE=OA，过E点作EF垂直于直线BC，垂足为点F，作EH ⊥CD于H，求证：四边形EFCH为正方形．（2）当OM不过点A时，设OM交边AB于G，且OG=1．在ON上存在点P，过P点作PK垂直于直线BC，垂足为点K，使得S△PKO =4S△OBG，连接GP，求四边形PKBG的最大面积．【考点】LO：四边形综合题．【分析】（1）①若ON过点D时，则在△OAD中不满足勾股定理，可知不可能过D 点；②由条件可先判业四边形EFCH为矩形，再证明△OFE≌△ABO，可证得结论；（2）由条件可证明△PKO∽△OBG，利用相似三角形的性质可求得OP=2，可求得△POG面积为定值及△PKO和△OBG的关系，只要△CGB的面积有最大值时，则四边形PKBG的面积就最大，设OB=a，BG=b，由勾股定理可用b表示出a，则可用a表示出△CBG的面积，利用二次函数的性质可求得其最大值，则可求得四边形PKBG面积的最大值．【解答】解：（1）①若ON过点D，则OA＞AB，OD＞CD，∴OA2＞AD2，OD2＞AD2，∴OA2+OD2＞2AD2≠AD2，∴∠AOD≠90°，这与∠MON=90°矛盾，∴ON不可能过D点，故答案为：不可能；②∵EH⊥CD，EF⊥BC，∴∠EHC=∠EFC=90°，且∠HCF=90°，∴四边形EFCH为矩形，∵∠MON=90°，∴∠EOF=90°﹣∠AOB，在正方形ABCD中，∠BAO=90°﹣∠AOB，∴∠EOF=∠BAO，在△OFE和△ABO中∴△OFE≌△ABO（AAS），∴EF=OB，OF=AB，又OF=CF+OC=AB=BC=BO+OC=EF+OC，∴CF=EF，∴四边形EFCH为正方形；（2）∵∠POK=∠OGB，∠PKO=∠OBG，∴△PKO∽△OBG，∵S△PKO =4S△OBG，∴=（）2=4，∴OP=2，∴S△POG=OG•OP=×1×2=1，设OB=a，BG=b，则a2+b2=OG2=1，∴b=，∴S△OBG=ab=a==，∴当a2=时，△OBG有最大值，此时S△PKO =4S△OBG=1，∴四边形PKBG的最大面积为1+1+=．4. （2017甘肃张掖）如图，已知二次函数y=ax2+bx+4的图象与x轴交于点B（﹣2，0），点C（8，0），与y轴交于点A．（1）求二次函数y=ax2+bx+4的表达式；（2）连接AC，AB，若点N在线段BC上运动（不与点B，C重合），过点N作NM ∥AC，交AB于点M，当△AMN面积最大时，求N点的坐标；（3）连接OM，在（2）的结论下，求OM与AC的数量关系．【考点】HF：二次函数综合题．【分析】（1）由B、C的坐标，利用待定系数法可求得抛物线解析式；（2）可设N（n，0），则可用n表示出△ABN的面积，由NM∥AC，可求得，则可用n表示出△AMN的面积，再利用二次函数的性质可求得其面积最大时n的值，即可求得N点的坐标；（3）由N点坐标可求得M点为AB的中点，由直角三角形的性质可得OM=AB，在Rt△AOB和Rt△AOC中，可分别求得AB和AC的长，可求得AB与AC的关系，从而可得到OM和AC的数量关系．【解答】解：（1）将点B，点C的坐标分别代入y=ax2+bx+4可得，解得，∴二次函数的表达式为y=﹣x2+x+4；（2）设点N的坐标为（n，0）（﹣2＜n＜8），则BN=n+2，CN=8﹣n．∵B（﹣2，0），C（8，0），∴BC=10，在y=﹣x2+x+4中令x=0，可解得y=4，∴点A（0，4），OA=4，=BN•OA=（n+2）×4=2（n+2），∴S△ABN∵MN∥AC，∴，∴==，∴，∵﹣＜0，∴当n=3时，即N（3，0）时，△AMN的面积最大；（3）当N（3，0）时，N为BC边中点，∵MN∥AC，∴M为AB边中点，∴OM=AB，∵AB===2，AC===4，∴AB=AC，∴OM=AC．5. （2017江苏盐城）【探索发现】如图①，是一张直角三角形纸片，∠B=60°，小明想从中剪出一个以∠B为内角且面积最大的矩形，经过多次操作发现，当沿着中位线DE、EF剪下时，所得的矩形的面积最大，随后，他通过证明验证了其正确性，并得出：矩形的最大面积与原三角形面积的比值为．【拓展应用】如图②，在△ABC中，BC=a，BC边上的高AD=h，矩形PQMN的顶点P、N分别在边AB、AC上，顶点Q、M在边BC上，则矩形PQMN面积的最大值为．（用含a，h的代数式表示）【灵活应用】如图③，有一块“缺角矩形”ABCDE，AB=32，BC=40，AE=20，CD=16，小明从中剪出了一个面积最大的矩形（∠B为所剪出矩形的内角），求该矩形的面积．【实际应用】如图④，现有一块四边形的木板余料ABCD，经测量AB=50cm，BC=108cm，CD=60cm，且tanB=tanC=，木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN，求该矩形的面积．【考点】LO：四边形综合题．【分析】【探索发现】：由中位线知EF=BC、ED=AB、由=可得；【拓展应用】：由△APN∽△ABC知=，可得PN=a﹣PQ，设PQ=x，由S矩形=PQ•PN═﹣（x﹣）2+，据此可得；PQMN【灵活应用】：添加如图1辅助线，取BF中点I，FG的中点K，由矩形性质知AE=EH20、CD=DH=16，分别证△AEF≌△HED、△CDG≌△HDE得AF=DH=16、CG=HE=20，从而判断出中位线IK的两端点在线段AB和DE上，利用【探索发现】结论解答即可；【实际应用】：延长BA、CD交于点E，过点E作EH⊥BC于点H，由tanB=tanC 知EB=EC、BH=CH=54，EH=BH=72，继而求得BE=CE=90，可判断中位线PQ的两端点在线段AB、CD上，利用【拓展应用】结论解答可得．【解答】解：【探索发现】∵EF、ED为△ABC中位线，∴ED∥AB，EF∥BC，EF=BC，ED=AB，又∠B=90°，∴四边形FEDB是矩形，则===，故答案为：；【拓展应用】∵PN∥BC，∴△APN∽△ABC，∴=，即=，∴PN=a﹣PQ，设PQ=x，=PQ•PN=x（a﹣x）=﹣x2+ax=﹣（x﹣）2+，则S矩形PQMN最大值为，∴当PQ=时，S矩形PQMN故答案为：；【灵活应用】如图1，延长BA、DE交于点F，延长BC、ED交于点G，延长AE、CD交于点H，取BF中点I，FG的中点K，由题意知四边形ABCH是矩形，∵AB=32，BC=40，AE=20，CD=16，∴EH=20、DH=16，∴AE=EH、CD=DH，在△AEF和△HED中，∵，∴△AEF≌△HED（ASA），∴AF=DH=16，同理△CDG≌△HDE，∴CG=HE=20，∴BI==24，∵BI=24＜32，∴中位线IK的两端点在线段AB和DE上，过点K作KL⊥BC于点L，由【探索发现】知矩形的最大面积为×BG•BF=×（40+20）×（32+16）=720，答：该矩形的面积为720；【实际应用】如图2，延长BA、CD交于点E，过点E作EH⊥BC于点H，∵tanB=tanC=，∴∠B=∠C，∴EB=EC，∵BC=108cm，且EH⊥BC，∴BH=CH=BC=54cm，∵tanB==，∴EH=BH=×54=72cm，在Rt△BHE中，BE==90cm，∵AB=50cm，∴AE=40cm，∴BE的中点Q在线段AB上，∵CD=60cm，∴ED=30cm，∴CE的中点P在线段CD上，∴中位线PQ的两端点在线段AB、CD上，由【拓展应用】知，矩形PQMN的最大面积为BC•EH=1944cm2，答：该矩形的面积为1944cm2．几何最值问题1. 如图，已知直线与x轴、y轴分别交于A、B两点，P是以C（0，1）为圆心，1为半径的圆上一动点，连结P A、PB．则△P AB面积的最大值是（）A．8 B．12 C．D．2. 如图，MN是半径为1的⊙O的直径，点A在⊙O上，∠AMN=30°，点B为劣弧AN的中点．点P是直径MN上一动点，则P A+PB的最小值为（）A．B．C．D．3.如图，⊙O的半径是2，直线l与⊙O相交于A、B两点，M、N是⊙O上的两个动点，且在直线l的异侧，若∠A M B=45°，则四边形MA NB面积的最大值是．4.如图，定点A（﹣2，0），动点B在直线上运动，当线段AB最短时，点B的坐标为．5.如图，在Rt△ABC中，∠ACB=90°，AC=BC=2，以BC为直径的半圆交AB于D，P是上的一个动点，连接AP，则AP的最小值是．6. 如图，把△EFP放置在菱形ABCD中，使得顶点E，F，P分别在线段AB，AD，AC上，已知EP=FP=6，EF=，∠BAD=60°，且AB＞．（1）求∠EPF的大小；（2）若AP=10，求AE+AF的值；（3）若△EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动，请直接写出AP长的最大值和最小值．7. 如图，在Rt△ABC中，∠ACB=90°，AC=5cm，∠BAC=60°，动点M从点B出发，在BA 边上以每秒2cm的速度向点A匀速运动，同时动点N从点C出发，在CB边上以每秒cm 的速度向点B匀速运动，设运动时间为t秒（0≤t≤5），连接MN．（1）若BM=BN，求t的值；（2）若△MBN与△ABC相似，求t的值；（3）当t为何值时，四边形ACNM的面积最小？并求出最小值．8. 已知如图，在平面直角坐标系xOy中，点A、B、C分别为坐标轴上上的三个点，且OA=1，OB=3，OC=4．（1）求经过A、B、C三点的抛物线的解析式；（2）在平面直角坐标系xOy中是否存在一点P，使得以以点A、B、C、P为顶点的四边形为菱形？若存在，请求出点P的坐标；若不存在，请说明理由；[来源:学+科+网Z+X+X+K] （3）若点M为该抛物线上一动点，在（2）的条件下，请求出当|PM﹣AM|的最大值时点M 的坐标，并直接写出|PM﹣AM|的最大值．9. 如图，已知抛物线m：（a＞0）的顶点A在x轴上，并过点B（0，1），直线n：与x轴交于点D，与抛物线m的对称轴l交于点F，过B点的直线BE与直线n相交于点E（﹣7，7）．（1）求抛物线m的解析式；（2）P是l上的一个动点，若以B，E，P为顶点的三角形的周长最小，求点P的坐标；（3）抛物线m上是否存在一动点Q，使以线段FQ为直径的圆恰好经过点D？若存在，求点Q的坐标；若不存在，请说明理由．10. 如图，抛物线（a≠0）与x轴交于A（4，0）、B（﹣1，0）两点，过点A的直线y=﹣x+4交抛物线于点C．（1）求此抛物线的解析式；（2）在直线AC上有一动点E，当点E在某个位置时，使△BDE的周长最小，求此时E点坐标；（3）当动点E在直线AC与抛物线围成的封闭线A→C→B→D→A上运动时，是否存在使△BDE为直角三角形的情况，若存在，请直接写出符合要求的E点的坐标；若不存在，请说明理由．11.已知二次函数（a＜0）的最大值为4，且抛物线过点（，），点P（t，0）是x轴上的动点，抛物线与y轴交点为C，顶点为D．（1）求该二次函数的解析式，及顶点D的坐标；（2）求|PC﹣PD|的最大值及对应的点P的坐标；（3）设Q（0，2t）是y轴上的动点，若线段PQ与函数的图象只有一个公共点，求t的取值．12. 如图，在四边形ABCD中，AD∥BC，AD=2，AB=，以点A为圆心，AD为半径的圆与BC相切于点E，交AB于点F．（1）求∠ABE的大小及的长度；（2）在BE的延长线上取一点G，使得上的一个动点P到点G的最短距离为，求BG的长．13. 如图，将一副直角三角形拼放在一起得到四边形ABCD，其中∠BAC=45°，∠ACD=30°，点E为CD边上的中点，连接AE，将△ADE沿AE所在直线翻折得到△AD′E，D′E交AC于F点．若AB=6cm．（1）AE的长为▲ cm；（2）试在线段AC上确定一点P，使得DP+EP的值最小，并求出这个最小值；（3）求点D′到BC的距离．14. 如图，直线y=x+2与抛物线y=ax2+bx+6（a≠0）相交于A和B（4，m），点P是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．（1）求抛物线的解析式；（2）是否存在这样的P点，使线段PC的长有最大值，若存在，求出这个最大值；若不存在，请说明理由；（3）求△P AC为直角三角形时点P的坐标．15. 如图，在直角梯形ABCD中，AB∥CD，AD⊥AB，∠B=60°，AB=10，BC=4，点P沿线段AB从点A向点B运动，设AP=x．（1）求AD的长；（2）点P在运动过程中，是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似？若存在，求出x的值；若不存在，请说明理由；（3）设△ADP与△PCB的外接圆的面积分别为S1、S2，若S=S1+S2，求S的最小值．16. 如图，抛物线经过点A（1，0），B（5，0），C（0，）三点，设点E（x，y）是抛物线上一动点，且在x轴下方，四边形OEBF是以OB为对角线的平行四边形．（1）求抛物线的解析式；（2）当点E（x，y）运动时，试求平行四边形OEBF的面积S与x之间的函数关系式，并求出面积S的最大值？（3）是否存在这样的点E，使平行四边形OEBF为正方形？若存在，求E点，F点的坐标；若不存在，请说明理由．17. 某数学兴趣小组对线段上的动点问题进行探究，已知AB=8．问题思考：如图1，点P为线段AB上的一个动点，分别以AP、BP为边在同侧作正方形APDC与正方形PBFE．（1）在点P运动时，这两个正方形面积之和是定值吗？如果时求出；若不是，求出这两个正方形面积之和的最小值．（2）分别连接AD、DF、AF，AF交DP于点A，当点P运动时，在△APK、△ADK、△DFK 中，是否存在两个面积始终相等的三角形？请说明理由．问题拓展：（3）如图2，以AB为边作正方形ABCD，动点P、Q在正方形ABCD的边上运动，且PQ=8．若点P从点A出发，沿A→B→C→D的线路，向D点运动，求点P从A到D的运动过程中，PQ的中点O所经过的路径的长．（4）如图（3），在“问题思考”中，若点M、N是线段AB上的两点，且AM=BM=1，点G、H分别是边CD、EF的中点．请直接写出点P从M到N的运动过程中，GH的中点O所经过的路径的长及OM+OB的最小值．18. 如图，矩形ABCD中，AB=3，AD=4，E为AB上一点，AE=1，M为射线AD上一动点，AM=a（a为大于0的常数），直线EM与直线CD交于点F，过点M作MG⊥EM，交直线BC于G．（1）若M为边AD中点，求证：△EFG是等腰三角形；（2）若点G与点C重合，求线段MG的长；（3）请用含a的代数式表示△EFG的面积S，并指出S的最小整数值．。

2018年中考数学压轴题专题汇编41动态几何之动点形成的四边形存在性问题(解析版)

综上所述：当 0＜ b≤４时，四边形 DEFB 是矩形，这时， t 4 16 b2 ，当 b＞4 时，四边形 DEFB 不是矩形。
【考点】动点问题，三角形中位线定理，平行四边形的判定和性质，相似三角形的判定和性质，勾股定理，
矩形的判定和性质，直线与圆的位置关系，解一元二次方程，圆周角定理，三角形外角定理。
（ 3）是否存在 t 的值，使四边形 PDBQ 为菱形？若存在，求出 t 的值；若不存在，说明理由 .并探究如何改
变点 Q 的速度（匀速运动），使四边形 PDBQ 在某一时刻成为菱形，求点 Q 的速度 .
4
18
16
【答案】 (1)QB=12-2t,PD= t (2)t= 秒，或 t=3.6 秒。（ 3）t=5 秒， Q 的速度为。
（ 1）①根据题意得：当点 P 与点 A 重合时能构成一个三角形，此时 t=0， ∵点 P 到达 D 点需： 8（ s），点 Q 到达 B 点需： 26（ s）， ∴当点 P 与点 D 重合时能构成一个三角形，此时 t=8s；故当 t=0 或 8s 时，以 CD 、PQ 为两边，以梯形的底（ AD 或 BC ）的一部分（或全部）为第三边能构成一个三角形； ②∵ BC-AD=2cm ，过点 P 作 PF⊥ BC 于点 F，过点 D 作 DE ⊥ BC 于点 E，

∵当 PQ=CD 时，四边形 PQCD 为等腰梯形， ∴△ PFQ≌△ DCE ， EF=PD， ∴ QF=CE=2cm ，
∴当 CQ-PD=QF+CE=4cm 时，四边形 PQCD 为等腰梯形， ∴ t- （24-3t ）=4，
∴ t=7 （ s），
∴当 t=7s 时，四边形 PQCD 为等腰梯形； [ 来源:]

2018年中考数学专题等腰三角形存在性问题(题型全面)压轴题

2018年中考数学专题等腰三角形存在性问题(题型全面)压轴题专题等腰三角形存在性问题题型一：几何图形1、在△ABC中，AB=AC，∠A=36°．求∠ABC的度数。

解析：由AB=AC，可得∠B=∠C，设∠B=∠C=x，则∠A=180°-2x，又已知∠A=36°，所以180°-2x=36°，解得x=72°，所以∠B=∠C=72°，∠ABC=180°-∠A-∠B=72°。

2、如图（2），BD是△ABC中∠ABC的平分线．①找出图中所有等腰三角形（等腰三角形ABC除外），并选其中一个写出推理过程；②在直线BC上是否存在点P，使△CDP是以CD为一腰的等腰三角形？如果存在，请在图（3）中画出满足条件的所有的点P，并直接写出相应的∠CPD的度数；如果不存在，请说明理由．解析：①等腰三角形有△ABD、△CBD、△ACD，以△ABD为例，由AB=AD，∠BDA=∠BAD=x，∠ABD=180°-2x，所以∠ABD=∠CBD=∠ACD=72°。

②存在点P，满足△CDP是以CD为一腰的等腰三角形。

如图（3），连接DP，由对称性可知∠BDP=∠ADP，又∠BDP=∠ABC/2，∠ADP=∠ACB/2，所以∠ABC=∠ACB，即△ABC是等腰三角形，所以CD=BC，所以∠CPD=∠CDP=90°-x。

变式一：如图，在△ABC中，∠ACB=90°，AC=6cm，BC=8cm，动点P从点C出发，按C→B→A的路径，以2cm 每秒的速度运动，设运动时间为t秒．1）当t=1时，求△ACP的面积．2）t为何值时，线段AP是∠CAB的平分线？3）当t为何值时，△ACP是以AC为腰的等腰三角形？解析：（1）由勾股定理可得AB=10cm，所以△ABC的面积为24cm²，又由正弦定理可得sinA=3/5，所以AC=3cm，AP=2t，所以△ACP的面积为1/2×3×2t=3t。

2018挑战中学考试数学压轴题((全套)含问题详解及解析汇报)

第一部分函数图象中点的存在性问题§1．1 因动点产生的相似三角形问题例1 2014年市中考第28题例2 2014年市中考第21题例3 2015年湘西州中考第26题例4 2015年市中考第25题例5 2016年市中考第26题例6 2016年市中考第24题例7 2016年市崇明县中考模拟第25题例8 2016年市黄浦区中考模拟第26题§1．2 因动点产生的等腰三角形问题例9 2014年市中考第26题例10 2014年市第25题例11 2014年市中考第26题例12 2014年市中考第27题例13 2015年市中考第22题例14 2015年市中考第26题例15 2016年市中考第26题例16 2016年市长宁区金山区中考模拟第25题例17 2016年省中考第23题§1．3 因动点产生的直角三角形问题例19 2015年市中考第21题例20 2015年市中考第26题例21 2016年市中考第26题例22 2016年市松江区中考模拟第25题例23 2016年义乌市市中考第24题§1．4 因动点产生的平行四边形问题例24 2014年市中考第24题例25 2014年市中考第20题例26 2014年市中考第25题例27 2015年市中考第25题例28 2015年黄冈市中考第24题例29 2016年市中考第26题例30 2016年市嘉定区宝山区中考模拟中考第24题例31 2016年市徐汇区中考模拟第24题§1．5 因动点产生的面积问题例32 2014年市中考第25题例33 2014年永州市中考第25题例35 2015年市中考第26题例36 2015年株洲市中考第23题例37 2015年市中考第28题例38 2016年市中考第22题例39 2016年永州市中考第26题例40 2016年市中考第26题例41 2016年省中考第25题§1．6 因动点产生的相切问题例42 2014年市中考第27题例43 2014年株洲市中考第23题例44 2015年市中考第25题例45 2015年湘西州中考第25题例46 2016年市中考第25题例47 2016年市中考第26题例48 2016年市闵行区中考模拟第24题例49 2016年市普陀区中考模拟中考第25题§1．7 因动点产生的线段和差问题例50 2014年市中考第26题例51 2014年湘西州中考第25题例53 2015年市中考第28题例54 2015年市中考第25题例55 2016年市中考第26题例56 2016年市中考第24题例57 2016年市中考第21题第二部分图形运动中的函数关系问题§2．1 由比例线段产生的函数关系问题例1 2014年市中考第26题例2 2014年市中考第25题例3 2014年市中考第25题例4 2015年市中考第25题例5 2015年市中考第26题例6 2015年市中考第25题例7 2015年市中考第26题例8 2016年市中考第25题例9 2016年湘西州中考第26题例10 2016年市静安区青浦区中考模拟第25题例11 2016年市中考第27题第三部分图形运动中的计算说理问题§3．1 代数计算及通过代数计算进行说理问题例1 2014年市中考第25题例2 2014年市中考第23题例3 2014年市中考第26题例4 2014年株洲市中考第24题例5 2015年市中考第27题例6 2015年市中考第25题例7 2015年永州市中考第26题例8 2015年市中考第25题例9 2015年株洲市中考第24题例10 2016年市中考第22题例11 2016年市中考第25题例12 2016年株洲市中考第26题例13 2016年市中考第25题例14 2016年市中考第26题§3．2 几何证明及通过几何计算进行说理问题例15 2014年市中考第26题例16 2014年市中考第26题例17 2014年市中考第23题例18 2015年市中考第26题例19 2015年市中考第20题例20 2015年永州市中考第27题例21 2015年市中考第23题例22 2016年市中考第25题例23 2016年市中考第25题例24 2016年永州市中考第27题例25 2016年市中考第23题例26 2016年株洲市中考第25题例27 2016年市中考第25题第四部分图形的平移、翻折与旋转§4．1 图形的平移例1 2015年市中考第15题例2 2015年市中考第14题例3 2015年株洲市中考第14题例4 2016年市虹口区中考模拟第18题§4．2 图形的翻折例5 2016年市奉贤区中考模拟第18题例6 2016年市静安区青浦区中考模拟第18题例7 2016年市闵行区中考模拟第18题例8 2016年市浦东新区中考模拟第18题例8 2016年市普陀区中考模拟第18题例10 2016年市中考第15题例11 2016年市中考第14题例12 2016年市中考第18题例13 2016年市中考第15题例14 2016年市中考第12题§4．3 图形的旋转例15 2016年昂立教育中学生三模联考第18题例16 2016年市崇明县中考模拟第18题例17 2016年市黄浦区中考模拟第18题例18 2016年市嘉定区宝山区中考模拟第18题例19 2016年市闸北区中考模拟第18题例20 2016年市中考第13题例21 2016年株洲市中考第4题§4．4 三角形例22 2016年省中考第10题例23 2016年市中考第10题例24 2016年省中考第16题例25 2016年市中考第10题例27 2016年市中考第10题例28 2016年省中考第14题例29 2016年江市中考第11题例30 2016年市中考第18题§4．5 四边形例31 2016年湘西州中考第11题例32 2016年市中考第4题例33 2016年市中考第6题例34 2016年市中考第16题例35 2016年市中考第14题例36 2016年市中考第13题例37 2016年市中考第18题例38 2016年市中考第17题例39 2016年市中考第15题§4．6 圆例40 2016年滨州市中考第16题例41 2016年市中考第17题例42 2016年市中考第16题例43 2016年市中考第17题例45 2016年市中考第18题例46 2016年市中考第9题例47 2016年宿迁市中考第16题例48 2016年市中考第17题例49 2016年市中考第18题例50 2016年湘西州中考第18题例51 2016年永州市中考第20题§4．7 函数的图象及性质例52 2015年荆州市中考第9题例53 2015年市中考第12题例54 2015年市中考第12题例55 2015年市中考第10题例56 2015年市中考第10题例57 2015年呼和浩特市中考第10题例58 2016年市中考第18题例59 2016年市中考第19题例60 2016年市中考第15题例61 2016年株洲市中考第9题例62 2016年永州市中考第19题例63 2016年市中考第8题例64 2016年市中考第16题例65 2016年市中考第14题例66 2016年株洲市中考第10题例67 2016年株洲市中考第17题例68 2016年东营市中考第15题例69 2016年市中考第13题例70 2016年市中考第16题例71 2016年宿迁市中考第15题例72 2016年市中考第14题例73 2016年义乌市市中考第9题例74 2016年市中考第12题例75 2016年市中考第16题§1．1 因动点产生的相似三角形问题课前导学相似三角形的判定定理有3个，其中判定定理1和判定定理2都有对应角相等的条件，因此探求两个三角形相似的动态问题，一般情况下首先寻找一组对应角相等．判定定理2是最常用的解题依据，一般分三步：寻找一组等角，分两种情况列比例方程，解方程并检验．如果已知∠A＝∠D，探求△ABC与△DEF相似，只要把夹∠A和∠D的两边表示出来，按照对应边成比例，分AB DEAC DF=和AB DFAC DE=两种情况列方程．应用判定定理1解题，先寻找一组等角，再分两种情况讨论另外两组对应角相等．应用判定定理3解题不多见，根据三边对应成比例列连比式解方程（组）．还有一种情况，讨论两个直角三角形相似，如果一组锐角相等，其中一个直角三角形的锐角三角比是确定的，那么就转化为讨论另一个三角形是直角三角形的问题．求线段的长，要用到两点间的距离公式，而这个公式容易记错．理解记忆比较好．如图1，如果已知A、B两点的坐标，怎样求A、B两点间的距离呢？我们以AB为斜边构造直角三角形，直角边与坐标轴平行，这样用勾股定理就可以求斜边AB的长了．水平距离BC的长就是A、B两点间的水平距离，等于A、B两点的横坐标相减；竖直距离AC就是A、B两点间的竖直距离，等于A、B两点的纵坐标相减．图1例 1 2014年省市中考第28题二次函数y＝a x2＋b x＋c（a≠0）的图象与x轴交于A(－3, 0)、B(1, 0)两点，与y轴交于点C(0,－3m)（m＞0），顶点为D．（1）求该二次函数的解析式（系数用含m的代数式表示）；（2）如图1，当m＝2时，点P为第三象限抛物线上的一个动点，设△APC的面积为S，试求出S与点P的横坐标x之间的函数关系式及S的最大值；（3）如图2，当m取何值时，以A、D、C三点为顶点的三角形与△OBC相似？图1 图2动感体验请打开几何画板文件名“1428”，拖动点P 运动，可以体验到，当点P 运动到AC 的中点的正下方时，△APC 的面积最大．拖动y 轴上表示实数m 的点运动，抛物线的形状会改变，可以体验到，∠ACD 和∠ADC 都可以成为直角．思路点拨1．用交点式求抛物线的解析式比较简便．2．连结OP ，△APC 可以割补为：△AOP 与△COP 的和，再减去△AOC ．3．讨论△ACD 与△OBC 相似，先确定△ACD 是直角三角形，再验证两个直角三角形是否相似．4．直角三角形ACD 存在两种情况．图文解析（1）因为抛物线与x 轴交于A (－3, 0)、B (1, 0)两点，设y ＝a (x ＋3)(x －1)．代入点C (0,－3m )，得－3m ＝－3a ．解得a ＝m ．所以该二次函数的解析式为y ＝m (x ＋3)(x －1)＝mx 2＋2mx －3m ．（2）如图3，连结OP ．当m ＝2时，C (0,－6)，y ＝2x 2＋4x －6，那么P (x , 2x 2＋4x －6)．由于S △AOP ＝1()2P OA y ⨯-＝32-(2x 2＋4x －6)＝－3x 2－6x ＋9， S △COP ＝1()2P OC x ⨯-＝－3x ，S △AOC ＝9，所以S ＝S △APC ＝S △AOP ＋S △COP －S △AOC ＝－3x 2－9x ＝23273()24x -++．所以当32x =-时，S 取得最大值，最大值为274．图3 图4 图5（3）如图4，过点D 作y 轴的垂线，垂足为E ．过点A 作x 轴的垂线交DE 于F ．由y ＝m (x ＋3)(x －1)＝m (x ＋1)2－4m ，得D (－1,－4m )．在Rt △OBC 中，OB ∶OC ＝1∶3m ．如果△ADC 与△OBC 相似，那么△ADC 是直角三角形，而且两条直角边的比为1∶3m ． ①如图4，当∠ACD ＝90°时，OA OC EC ED =．所以331m m =．解得m ＝1．此时3CA OC CD ED ==，3OC OB =．所以CA OC CD OB =．所以△CDA ∽△OBC ． ②如图5，当∠ADC ＝90°时，FA FD ED EC =．所以421m m=．解得2m =．此时222DA FD DC EC m===，而3232OC m OB ==．因此△DCA 与△OBC 不相似．综上所述，当m ＝1时，△CDA ∽△OBC ．考点伸展第（2）题还可以这样割补：如图6，过点P 作x 轴的垂线与AC 交于点H ．由直线AC ：y ＝－2x －6，可得H (x ,－2x －6)．又因为P (x , 2x 2＋4x －6)，所以HP ＝－2x 2－6x ．因为△PAH 与△PCH 有公共底边HP ，高的和为A 、C 两点间的水平距离3，所以 S ＝S △APC ＝S △APH ＋S △CPH＝32(－2x 2－6x ) ＝23273()24x -++．图6例 2 2014年省市中考第21题如图1，在直角梯形ABCD中，AB//CD，AD⊥AB，∠B＝60°，AB＝10，BC＝4，点P沿线段AB从点A向点B运动，设AP＝x．2·1·c·n·j·y（1）求AD的长；（2）点P在运动过程中，是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似？若存在，求出x的值；若不存在，请说明理由；（3）设△ADP与△PCB的外接圆的面积分别为S1、S2，若S＝S1＋S2，求S的最小值. 动感体验图1请打开几何画板文件名“1421”，拖动点P在AB上运动，可以体验到，圆心O的运动轨迹是线段BC的垂直平分线上的一条线段．观察S随点P运动的图象，可以看到，S有最小值，此时点P看上去象是AB的中点，其实离得很近而已．思路点拨1．第（2）题先确定△PCB是直角三角形，再验证两个三角形是否相似．2．第（3）题理解△PCB的外接圆的圆心O很关键，圆心O在确定的BC的垂直平分线上，同时又在不确定的BP的垂直平分线上．而BP与AP是相关的，这样就可以以AP为自变量，求S的函数关系式．图文解析（1）如图2，作CH⊥AB于H，那么AD＝CH．在Rt△BCH中，∠B＝60°，BC＝4，所以BH＝2，CH＝23．所以AD＝23．（2）因为△APD是直角三角形，如果△APD与△PCB相似，那么△PCB一定是直角三角形．①如图3，当∠CPB＝90°时，AP＝10－2＝8．所以APAD＝23＝43，而PCPB＝3．此时△APD与△PCB不相似．图2 图3 图4 ②如图4，当∠BCP＝90°时，BP＝2BC＝8．所以AP＝2．所以AP AD ＝23＝3．所以∠APD ＝60°．此时△APD ∽△CBP ．综上所述，当x ＝2时，△APD ∽△CBP ．（3）如图5，设△ADP 的外接圆的圆心为G ，那么点G 是斜边DP 的中点．设△PCB 的外接圆的圆心为O ，那么点O 在BC 边的垂直平分线上，设这条直线与BC 交于点E ，与AB 交于点F ．设AP ＝2m ．作OM ⊥BP 于M ，那么BM ＝PM ＝5－m ．在Rt △BEF 中，BE ＝2，∠B ＝60°，所以BF ＝4．在Rt △OFM 中，FM ＝BF －BM ＝4－(5－m )＝m －1，∠OFM ＝30°，所以OM ＝3(1)m -．所以OB 2＝BM 2＋OM 2＝221(5)(1)3m m -+-．在Rt △ADP 中，DP 2＝AD 2＋AP 2＝12＋4m 2．所以GP 2＝3＋m 2．于是S ＝S 1＋S 2＝π(GP 2＋OB 2)＝22213(5)(1)3m m m π⎡⎤++-+-⎢⎥⎣⎦＝2(73285)3m m π-+．所以当167m =时，S 取得最小值，最小值为1137π．图5 图6考点伸展关于第（3）题，我们再讨论个问题．问题1，为什么设AP ＝2m 呢？这是因为线段AB ＝AP ＋PM ＋BM ＝AP ＋2BM ＝10．这样BM ＝5－m ，后续可以减少一些分数运算．这不影响求S 的最小值．问题2，如果圆心O 在线段EF 的延长线上，S 关于m 的解析式是什么？如图6，圆心O 在线段EF 的延长线上时，不同的是FM ＝BM －BF ＝(5－m )－4＝1－m ．此时OB 2＝BM 2＋OM 2＝221(5)(1)3m m -+-．这并不影响S 关于m 的解析式．例 3 2015年省湘西市中考第26题如图1，已知直线y＝－x＋3与x轴、y轴分别交于A、B两点，抛物线y＝－x2＋bx＋c 经过A、B两点，点P在线段OA上，从点O出发，向点A以每秒1个单位的速度匀速运动；同时，点Q在线段AB上，从点A出发，向点B以每秒2个单位的速度匀速运动，连结PQ，设运动时间为t秒．（1）求抛物线的解析式；（2）问：当t为何值时，△APQ为直角三角形；（3）过点P作PE//y轴，交AB于点E，过点Q作QF//y轴，交抛物线于点F，连结EF，当EF//PQ时，求点F的坐标；（4）设抛物线顶点为M，连结BP、BM、MQ，问：是否存在t的值，使以B、Q、M为顶点的三角形与以O、B、P为顶点的三角形相似？若存在，请求出t的值；若不存在，请说明理由．图1动感体验请打开几何画板文件名“15湘西26”，拖动点P在OA上运动，可以体验到，△APQ有两个时刻可以成为直角三角形，四边形EPQF有一个时刻可以成为平行四边形，△MBQ与△BOP有一次机会相似．思路点拨1．在△APQ中，∠A＝45°，夹∠A的两条边AP、AQ都可以用t表示，分两种情况讨论直角三角形APQ．2．先用含t的式子表示点P、Q的坐标，进而表示点E、F的坐标，根据PE＝QF列方程就好了．3．△MBQ与△BOP都是直角三角形，根据直角边对应成比例分两种情况讨论．图文解析（1）由y＝－x＋3，得A(3, 0)，B(0, 3)．将A(3, 0)、B(0, 3)分别代入y＝－x2＋bx＋c，得930,3.b cc-++=⎧⎨=⎩解得2,3.bc=⎧⎨=⎩所以抛物线的解析式为y＝－x2＋2x＋3．（2）在△APQ中，∠PAQ＝45°，AP＝3－t，AQ＝2t．分两种情况讨论直角三角形APQ：①当∠PQA＝90°时，AP＝2AQ．解方程3－t＝2t，得t＝1（如图2）．②当∠QPA＝90°时，AQ＝2AP．解方程2t＝2(3－t)，得t＝1.5（如图3）．图2 图3（3）如图4，因为PE//QF，当EF//PQ时，四边形EPQF是平行四边形．所以EP＝FQ．所以y E－y P＝y F－y Q．因为x P＝t，x Q＝3－t，所以y E＝3－t，y Q＝t，y F＝－(3－t)2＋2(3－t)＋3＝－t2＋4t．因为y E－y P＝y F－y Q，解方程3－t＝(－t2＋4t)－t，得t＝1，或t＝3（舍去）．所以点F的坐标为(2, 3)．图4 图5（4）由y＝－x2＋2x＋3＝－(x－1)2＋4，得M(1, 4)．由A(3, 0)、B(0, 3)，可知A、B两点间的水平距离、竖直距离相等，AB＝2．由B(0, 3)、M(1, 4)，可知B、M两点间的水平距离、竖直距离相等，BM2．所以∠MBQ＝∠BOP＝90°．因此△MBQ与△BOP相似存在两种可能：①当BM OBBQ OP=23322tt=-．解得94t=（如图5）．②当BM OPBQ OB=23322tt=-．整理，得t2－3t＋3＝0．此方程无实根．考点伸展第（3）题也可以用坐标平移的方法：由P(t, 0)，E(t, 3－t)，Q(3－t, t)，按照P→E 方向，将点Q向上平移，得F(3－t, 3)．再将F(3－t, 3)代入y＝－x2＋2x＋3，得t＝1，或t ＝3．§1．2 因动点产生的等腰三角形问题课前导学我们先回顾两个画图问题：1．已知线段AB＝5厘米，以线段AB为腰的等腰三角形ABC有多少个？顶点C的轨迹是什么？2．已知线段AB＝6厘米，以线段AB为底边的等腰三角形ABC有多少个？顶点C的轨迹是什么？已知腰长画等腰三角形用圆规画圆，圆上除了两个点以外，都是顶点C．已知底边画等腰三角形，顶角的顶点在底边的垂直平分线上，垂足要除外．在讨论等腰三角形的存在性问题时，一般都要先分类．如果△ABC是等腰三角形，那么存在①AB＝AC，②BA＝BC，③CA＝CB三种情况．解等腰三角形的存在性问题，有几何法和代数法，把几何法和代数法相结合，可以使得解题又好又快．几何法一般分三步：分类、画图、计算．哪些题目适合用几何法呢？如果△ABC的∠A（的余弦值）是确定的，夹∠A的两边AB和AC可以用含x的式子表示出来，那么就用几何法．①如图1，如果AB＝AC，直接列方程；②如图2，如果BA＝BC，那么1cos2AC AB A=∠；③如图3，如果CA＝CB，那么1cos2AB AC A=∠．代数法一般也分三步：罗列三边长，分类列方程，解方程并检验．如果三角形的三个角都是不确定的，而三个顶点的坐标可以用含x的式子表示出来，那么根据两点间的距离公式，三边长（的平方）就可以罗列出来．图1 图2 图3例 9 2014年市中考第26题如图1，抛物线y ＝ax 2＋bx ＋c （a 、b 、c 是常数，a ≠0）的对称轴为y 轴，且经过(0,0)和1(,)16a 两点，点P 在该抛物线上运动，以点P 为圆心的⊙P 总经过定点A (0, 2)．（1）求a 、b 、c 的值；（2）求证：在点P 运动的过程中，⊙P 始终与x 轴相交；（3）设⊙P 与x 轴相交于M (x 1, 0)、N (x 2, 0)两点，当△AMN 为等腰三角形时，求圆心P 的纵坐标．图1动感体验请打开几何画板文件名“1426”，拖动圆心P 在抛物线上运动，可以体验到，圆与x 轴总是相交的，等腰三角形AMN 存在五种情况．思路点拨1．不算不知道，一算真奇妙，原来⊙P 在x 轴上截得的弦长MN ＝4是定值．2．等腰三角形AMN 存在五种情况，点P 的纵坐标有三个值，根据对称性，MA ＝MN 和NA ＝NM 时，点P 的纵坐标是相等的．图文解析（1）已知抛物线的顶点为(0,0)，所以y ＝ax 2．所以b ＝0，c ＝0．将1(,)16a 代入y ＝ax 2，得2116a =．解得14a =（舍去了负值）．（2）抛物线的解析式为214y x =，设点P 的坐标为21(,)4x x ．已知A (0, 2)，所以222411(2)4416PA x x x =+-+214x ．而圆心P 到x 轴的距离为214x ，所以半径PA ＞圆心P 到x 轴的距离．所以在点P 运动的过程中，⊙P 始终与x 轴相交．（3）如图2，设MN 的中点为H ，那么PH 垂直平分MN ．在Rt △PMH 中，2241416PM PA x ==+，22411()416PH x x ==，所以MH 2＝4．所以MH ＝2．因此MN ＝4，为定值．等腰△AMN 存在三种情况：①如图3，当AM ＝AN 时，点P 为原点O 重合，此时点P 的纵坐标为0．图2 图3②如图4，当MA ＝MN 时，在Rt △AOM 中，OA ＝2，AM ＝4，所以OM ＝23．此时x ＝OH ＝232+．所以点P 的纵坐标为22211(232)(31)42344x =+=+=+．如图5，当NA ＝NM 时，根据对称性，点P 的纵坐标为也为423+．图4 图5③如图6，当NA ＝NM ＝4时，在Rt △AON 中，OA ＝2，AN ＝4，所以ON ＝23．此时x ＝OH ＝232-．所以点P 的纵坐标为22211(232)(31)42344x =-=-=-．如图7，当MN ＝MA ＝4时，根据对称性，点P 的纵坐标也为423-．图6 图7考点伸展如果点P 在抛物线214y x =上运动，以点P 为圆心的⊙P 总经过定点B (0, 1)，那么在点P 运动的过程中，⊙P 始终与直线y ＝－1相切．这是因为：设点P 的坐标为21(,)4x x ．已知B (0, 1)，所以2114PB x ==+．而圆心P 到直线y ＝－1的距离也为2114x +，所以半径PB ＝圆心P 到直线y ＝－1的距离．所以在点P 运动的过程中，⊙P 始终与直线y ＝－1相切．例 10 2014年省市中考第25题如图1，在平面直角坐标系中，O 为坐标原点，抛物线y ＝ax 2＋bx ＋c （a ≠0）过O 、B 、C 三点，B 、C 坐标分别为(10, 0)和1824(,)55-，以OB 为直径的⊙A 经过C 点，直线l 垂直x 轴于B 点．（1）求直线BC 的解析式；（2）求抛物线解析式及顶点坐标；（3）点M 是⊙A 上一动点（不同于O 、B ），过点M 作⊙A 的切线，交y 轴于点E ，交直线l 于点F ，设线段ME 长为m ，MF 长为n ，请猜想mn 的值，并证明你的结论；（4）若点P 从O 出发，以每秒1个单位的速度向点B 作直线运动，点Q 同时从B 出发，以相同速度向点C 作直线运动，经过t （0＜t ≤8）秒时恰好使△BPQ 为等腰三角形，请求出满足条件的t 值．图图1动感体验请打开几何画板文件名“1425”，拖动点M 在圆上运动，可以体验到，△EAF 保持直角三角形的形状，AM 是斜边上的高．拖动点Q 在BC 上运动，可以体验到，△BPQ 有三个时刻可以成为等腰三角形．思路点拨1．从直线BC 的解析式可以得到∠OBC 的三角比，为讨论等腰三角形BPQ 作铺垫． 2．设交点式求抛物线的解析式比较简便．3．第（3）题连结AE 、AF 容易看到AM 是直角三角形EAF 斜边上的高．4．第（4）题的△PBQ 中，∠B 是确定的，夹∠B 的两条边可以用含t 的式子表示．分三种情况讨论等腰三角形．图文解析（1）直线BC 的解析式为31542y x =-．（2）因为抛物线与x 轴交于O 、B (10, 0)两点，设y ＝ax (x －10)．代入点C 1824(,)55-，得241832()555a -=⨯⨯-．解得524a =．所以2255255125(10)(5)2424122424y x x x x x =-=-=--．抛物线的顶点为125(5,)24-．（3）如图2，因为EF 切⊙A 于M ，所以AM ⊥EF ．由AE ＝AE ，AO ＝AM ，可得Rt △AOE ≌Rt △AME ．所以∠1＝∠2．同理∠3＝∠4．于是可得∠EAF ＝90°．所以∠5＝∠1．由tan ∠5＝tan ∠1，得MA MEMF MA=．所以ME ·MF ＝MA 2，即mn ＝25．图2（4）在△BPQ 中，cos ∠B ＝45，BP ＝10－t ，BQ ＝t ．分三种情况讨论等腰三角形BPQ ：①如图3，当BP ＝BQ 时，10－t ＝t ．解得t ＝5．②如图4，当PB ＝PQ 时，1cos 2BQ BP B =∠．解方程14(10)25t t =-，得8013t =． ③如图5，当QB ＝QP 时，1cos 2BP BQ B =∠．解方程14(10)25t t -=，得5013t =．图3 图4 图5考点伸展在第（3）题条件下，以EF 为直径的⊙G 与x 轴相切于点A ．如图6，这是因为AG 既是直角三角形EAF 斜边上的中线，也是直角梯形EOBF 的中位线，因此圆心G 到x 轴的距离等于圆的半径，所以⊙G 与x 轴相切于点A ．图6例 11 2014年省市中考第26题在平面直角坐标系中，抛物线y＝x2－(m＋n)x＋mn（m＞n）与x轴相交于A、B两点（点A位于点B的右侧），与y轴相交于点C．（1）若m＝2，n＝1，求A、B两点的坐标；（2）若A、B两点分别位于y轴的两侧，C点坐标是(0,－1)，求∠ACB的大小；（3）若m＝2，△ABC是等腰三角形，求n的值．动感体验请打开几何画板文件名“1426”，点击屏幕左下方的按钮（2），拖动点A在x轴正半轴上运动，可以体验到，△ABC保持直角三角形的形状．点击屏幕左下方的按钮（3），拖动点B在x轴上运动，观察△ABC的顶点能否落在对边的垂直平分线上，可以体验到，等腰三角形ABC有4种情况．思路点拨1．抛物线的解析式可以化为交点式，用m，n表示点A、B、C的坐标．2．第（2）题判定直角三角形ABC，可以用勾股定理的逆定理，也可以用锐角的三角比．3．第（3）题讨论等腰三角形ABC，先把三边长（的平方）罗列出来，再分类解方程．图文解析（1）由y＝x2－(m＋n)x＋mn＝(x－m)(x－n)，且m＞n，点A位于点B的右侧，可知A(m, 0)，B(n, 0)．若m＝2，n＝1，那么A(2, 0)，B(1, 0)．．（2）如图1，由于C(0, mn)，当点C的坐标是(0,－1)，mn＝－1，OC＝1．若A、B两点分别位于y轴的两侧，那么OA·OB＝m(－n)＝－mn＝1．所以OC2＝OA·OB．所以OC OB OA OC．所以tan∠1＝tan∠2．所以∠1＝∠2．又因为∠1与∠3互余，所以∠2与∠3互余．所以∠ACB＝90°．图1 图2 图3（3）在△ABC中，已知A(2, 0)，B(n, 0)，C(0, 2n)．讨论等腰三角形ABC，用代数法解比较方便：由两点间的距离公式，得AB2＝(n－2)2，BC2＝5n2，AC2＝4＋4n2．①当AB＝AC时，解方程(n－2)2＝4＋4n2，得43n=-（如图2）．②当CA＝CB时，解方程4＋4n2＝5n2，得n＝－2（如图3），或n＝2（A、B重合，舍去）．③当BA＝BC时，解方程(n－2)2＝5n2，得512n+=-（如图4），或512n-=（如图5）．图4 图5考点伸展第（2）题常用的方法还有勾股定理的逆定理．由于C(0, mn)，当点C的坐标是(0,－1)，mn＝－1．由A(m, 0)，B(n, 0)，C(0,－1)，得AB2＝(m－n)2＝m2－2mn＋n2＝m2＋n2＋2，BC2＝n2＋1，AC2＝m2＋1．所以AB2＝BC2＋AC2．于是得到Rt△ABC，∠ACB＝90°．第（3）题在讨论等腰三角形ABC时，对于CA＝CB的情况，此时A、B两点关于y轴对称，可以直接写出B(－2, 0)，n＝－2．例 12 2014年省市中考第27题如图1，在△ABC中，∠ACB＝90°，AC＝4cm，BC＝3cm．如果点P由点B出发沿BA方向向点A匀速运动，同时点Q由点A出发沿AC方向向点C匀速运动，它们的速度均为1cm/s．连结PQ，设运动时间为t（s）（0＜t＜4），解答下列问题：（1）设△APQ的面积为S，当t为何值时，S取得最大值？S的最大值是多少？（2）如图2，连结PC，将△PQC沿QC翻折，得到四边形PQP′C，当四边形PQP′C为菱形时，求t的值；（3）当t为何值时，△APQ是等腰三角形？图1 图2动感体验请打开几何画板文件名“1427”，拖动点Q在AC上运动，可以体验到，当点P运动到AB的中点时，△APQ的面积最大，等腰三角形APQ存在三种情况．还可以体验到，当QC＝2HC时，四边形PQP′C是菱形．思路点拨1．在△APQ中，∠A是确定的，夹∠A的两条边可以用含t的式子表示．2．四边形PQP′C的对角线保持垂直，当对角线互相平分时，它是菱形，．图文解析（1）在Rt△ABC中，AC＝4，BC＝3，所以AB＝5，sin A＝35，cos A＝45．作QD⊥AB于D，那么QD＝AQ sin A＝35t．所以S＝S△APQ＝12AP QD⋅＝13(5)25t t-⨯＝23(5)10t t--＝23515()+1028t--．当52t=时，S取得最大值，最大值为158．（2）设PP′与AC交于点H，那么PP′⊥QC，AH＝AP cos A＝4(5)5t-．如果四边形PQP′C为菱形，那么PQ＝PC．所以QC＝2HC．解方程4424(5)5t t⎡⎤-=⨯--⎢⎥⎣⎦，得2013t=．图3 图4 （3）等腰三角形APQ存在三种情况：①如图5，当AP＝AQ时，5－t＝t．解得52t=．②如图6，当PA＝PQ时，1cos2AQ AP A=．解方程14(5)25t t=-，得4013t=．③如图7，当QA＝QP时，1cos2AP AQ A=．解方程14(5)25t t-=，得2513t=．图5 图6 图7 考点伸展在本题情境下，如果点Q是△PP′C的重心，求t的值．如图8，如果点Q是△PP′C的重心，那么QC＝23 HC．解方程2444(5)35t t⎡⎤-=⨯--⎢⎥⎣⎦，得6023t=．图8例 13 2015年省市中考第22题如图1，已知Rt△ABC中，∠C＝90°，AC＝8，BC＝6，点P以每秒1个单位的速度从A 向C运动，同时点Q以每秒2个单位的速度从A→B→C方向运动，它们到C点后都停止运动，设点P、Q运动的时间为t秒．（1）在运动过程中，求P 、Q 两点间距离的最大值；（2）经过t 秒的运动，求△ABC 被直线PQ 扫过的面积S 与时间t 的函数关系式；（3）P ，Q 两点在运动过程中，是否存在时间t ，使得△PQC 为等腰三角形．若存在，求出此时的t 值，若不存在，请说明理由．（24.25≈，结果保留一位小数）图1动感体验请打开几何画板文件名“1522”，拖动点P 在AC 上运动，可以体验到，PQ 与BD 保持平行，等腰三角形PQC 存在三种情况．思路点拨1．过点B 作QP 的平行线交AC 于D ，那么BD 的长就是PQ 的最大值． 2．线段PQ 扫过的面积S 要分两种情况讨论，点Q 分别在AB 、BC 上． 3．等腰三角形PQC 分三种情况讨论，先罗列三边长．图文解析（1）在Rt △ABC 中，AC ＝8，BC ＝6，所以AB ＝10．如图2，当点Q 在AB 上时，作BD //PQ 交AC 于点D ，那么22AB AQ tAD AP t===．所以AD ＝5．所以CD ＝3．如图3，当点Q 在BC 上时，16228CQ tCP t-==-．又因为623CB CD ==，所以CQ CBCP CD=．因此PQ //BD ．所以PQ 的最大值就是BD ．在Rt △BCD 中，BC ＝6，CD ＝3，所以BD ＝35．所以PQ 的最大值是35．图2 图3 图4 （2）①如图2，当点Q 在AB 上时，0＜t ≤5，S △ABD ＝15．由△AQP ∽△ABD ，得2()AQP ABDS AP S AD=△△．所以S ＝S △AQP ＝215()5t ⨯＝235t ．②如图3，当点Q 在BC 上时，5＜t ≤8，S △ABC ＝24．因为S △CQP ＝12CQ CP ⋅＝1(162)(8)2t t --＝2(8)t -，所以S ＝S △ABC －S △CQP ＝24－(t －8)2＝－t 2＋16t －40．（3）如图3，当点Q 在BC 上时，CQ ＝2CP ，∠C ＝90°，所以△PQC 不可能成为等腰三角形．当点Q 在AB 上时，我们先用t 表示△PQC 的三边长：易知CP ＝8－t ．如图2，由QP //BD ，得QP AP BD AD =，即535t=．所以35QP t =．如图4，作QH ⊥AC 于H ．在Rt △AQH 中，QH ＝AQ sin ∠A ＝65t ，AH ＝85t ．在Rt △CQH 中，由勾股定理，得CQ ＝22QH CH +＝2268()(8)55t t +-．分三种情况讨论等腰三角形PQC ：（1）①当PC ＝PQ 时，解方程358t t -=，得6510t =-≈3.4（如图5所示）． ②当QC ＝QP 时，226835()(8)55t t t +-=．整理，得2111283200t t -+=．所以(11t －40)(t －8)＝0．解得4011t =≈3.6（如图6所示），或t ＝8（舍去）． ③当CP ＝CQ 时，22688()(8)55t t t -=+-．整理，得25160t t -=．解得165t =＝3.2（如图7所示），或t ＝0（舍去）．综上所述，当t 的值约为3.4，3.6，或等于3.2时，△PQC 是等腰三角形．图5 图6 图7考点伸展第（1）题求P 、Q 两点间距离的最大值，可以用代数计算说理的方法： ①如图8，当点Q 在AB 上时，PQ ＝22QH PH +＝2268()()55t t t +-＝355t ．当Q 与B 重合时，PQ 最大，此时t ＝5，PQ 的最大值为35．②如图9，当点Q 在BC 上时，PQ ＝22CQ CP +＝22(2)CP CP +＝5(8)t -．当Q 与B 重合时，PQ 最大，此时t ＝5，PQ 的最大值为35．综上所述，PQ 的最大值为35．图8 图9§1．3 因动点产生的直角三角形问题课前导学我们先看三个问题：1．已知线段AB ，以线段AB 为直角边的直角三角形ABC 有多少个？顶点C 的轨迹是什么？2．已知线段AB ，以线段AB 为斜边的直角三角形ABC 有多少个？顶点C 的轨迹是什么？ 3．已知点A (4,0)，如果△OAB 是等腰直角三角形，求符合条件的点B 的坐标．图1 图2 图3如图1，点C 在垂线上，垂足除外．如图2，点C 在以AB 为直径的圆上，A 、B 两点除外．如图3，以OA 为边画两个正方形，除了O 、A 两点以外的顶点和正方形对角线的交点，都是符合题意的点B ，共6个．解直角三角形的存在性问题，一般分三步走，第一步寻找分类标准，第二步列方程，第三步解方程并验根．一般情况下，按照直角顶点或者斜边分类，然后按照三角比或勾股定理列方程．有时根据直角三角形斜边上的中线等于斜边的一半列方程更简便．解直角三角形的问题，常常和相似三角形、三角比的问题联系在一起．如果直角边与坐标轴不平行，那么过三个顶点作与坐标轴平行的直线，可以构造两个新的相似直角三角形，这样列比例方程比较简便．如图4，已知A(3, 0)，B(1,－4)，如果直角三角形ABC的顶点C在y轴上，求点C的坐标．我们可以用几何的方法，作AB为直径的圆，快速找到两个符合条件的点C．如果作BD⊥y轴于D，那么△AOC∽△CDB．设OC＝m，那么341mm-=．这个方程有两个解，分别对应图中圆与y轴的两个交点．图4例 19 2015年省市中考第21题如图1，已知抛物线E1：y＝x2经过点A(1,m)，以原点为顶点的抛物线E2经过点B(2,2)，点A、B关于y轴的对称点分别为点A′、B′．（1）求m的值及抛物线E2所表示的二次函数的表达式；（2）如图1，在第一象限，抛物线E1上是否存在点Q，使得以点Q、B、B′为顶点的三角形为直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由；（3）如图2，P为第一象限的抛物线E1上与点A不重合的一点，连结OP并延长与抛物线E2相交于点P′，求△PAA′与△P′BB′的面积之比．。

2018年全国各省市中考数学几何压轴题

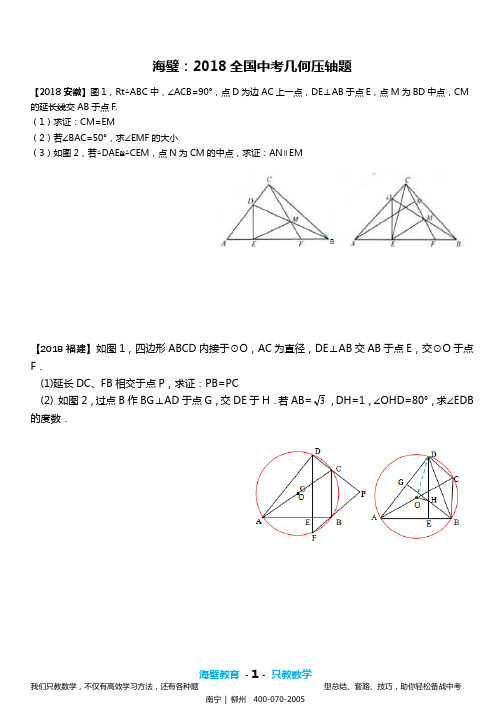
海璧：2018全国中考几何压轴题【2018安徽】图1，Rt△ABC中，∠ACB=90°，点D为边AC上一点，DE⊥AB于点E，点M为BD中点，CM 的延长线交AB于点F.（1）求证：CM=EM（2）若∠BAC=50°，求∠EMF的大小（3）如图2，若△DAE≌△CEM，点N为CM的中点，求证：AN∥EM【2018福建】如图1，四边形ABCD内接于⊙O，AC为直径，DE⊥AB交AB于点E，交⊙O于点F．(1)延长DC、FB相交于点P，求证：PB=PC(2) 如图2，过点B作BG⊥AD于点G，交DE于H．若AB=3，DH=1，∠OHD=80°，求∠EDB 的度数．【2018兰州】如图AB为⊙O的直径，C为⊙O上一点，D为BA延长线上一点，∠ACD=∠B. （1）求证：DC为⊙O的切线（2）线段DF分别交AC、BC于点E、F且∠CEF=45°，⊙O的半径为5，sinB=35,求CF的长.【2018定西】点O是△ABC的边AB上一点，⊙O与边AC相切于点E，与边BC，AB分别相交于点D，F，且DE=EF．（1）求证：∠C=90°（2）当BC=3，sinA=时，求AF的长．【2018广州】在四边形ABCD中，∠B=60°，∠D=30°，AB=BC．（2）连接BD，探究AD，BD，CD三者之间的数量关系，并说明理由；（3）若AB=1，点E在四边形ABCD内部运动，且满足AE2=BE2+CE2，求点E运动路径的长度．【2018深圳】如图9，⊙O是ABC=,2BC=，cos ABC∆的外接圆，AB AC∠=。

点D为AC上的动点，连接AD并延长，交BC的延长线于点E.（1）试求AB的长（2）试判断AD AE的值是否为定值？若为定值，请求出这个定值，若不为定值，请说明理由（3）如图10，连接BD，过点A作AH⊥BD于点H，连接CD，求证：BH CD DH=+【2018贵阳】如图，在矩形ABCD中，AB═2，AD=，P是BC边上的一点，且BP=2CP．（2）如图②，在（1）的条体下，判断EB是否平分∠AEC，并说明理由（3）如图③，在（2）的条件下，连接EP并廷长交AB的廷长线于点F，连接AP，不添加辅助线，△PFB能否由都经过P点的两次变换与△PAE组成一个等腰三角形？如果能，说明理由，并写出两种方法（指出对称轴、旋转中心、旋转方向和平移距离）【2018安顺】在△ABC中，AB=AC，O为BC的中点，AC与半圆O相切于点D．（1）求证：AB是半圆O所在圆的切线（2）若cos∠ABC=，AB=12，求半圆O所在圆的半径【2018铜仁】在三角形ABC中，AB=6，AC=BC=5，以BC为直径作⊙O交AB于点D，交AC于点G，直线DF是⊙O的切线，D为切点，交CB的延长线于点E．（1）求证：DF⊥AC（2）求tan∠E的值【2018遵义】AB是半圆O的直径，C是AB延长线上的点，AC的垂直平分线交半圆于点D，交AC于点E，连接DA，DC．已知半圆O的半径为3，BC=2．（1）求AD的长（2）点P是线段AC上一动点，连接DP，作∠DPF=∠DAC，PF交线段CD于点F．当△DPF为等腰三角形时，求AP的长【2018海南】已知，如图1，在▱ABCD 中，点E 是AB 中点，连接DE 并延长，交CB 的延长线于点F ．（1）求证：△ADE ≌△BFE（2）如图2，点G 是边BC 上任意一点（点G 不与点B 、C 重合），连接AG 交DF 于点H ，连接HC ，过点A 作AK ∥HC ，交DF 于点K①求证：HC=2AK②当点G 是边BC 中点时，恰有HD=n •HK （n 为正整数），求n 的值【2018河北】如图15，点A 在数轴上对应的数为26，以原点O 为圆心，OA 为半径作优弧AB ，使点B 在O 右下方，且34tan =∠AOB ，在优弧AB 上任取一点P ，且能过P 作直线l ∥OB 交数轴于点Q ，设Q 在数轴上对应的数为x ，连接OP(1)若优弧AB 上一段AP⌒ 的长为π13，求∠AOP 的度数及x 的值 (2)求x 的最小值，并指出此时直线l 与AB 所在圆的位置关系(3)若线段PQ 的长为12.5，直接写出这时x 的值【2018大庆】AB 是⊙O 的直径，点E 为线段OB 上一点（不与O ，B 重合），作EC ⊥OB ，交⊙O 于点C ，作直径CD ，过点C 的切线交DB 的延长线于点P ，作AF ⊥PC 于点F ，连接CB ．（1）求证：AC 平分∠FAB（2）求证：BC 2=CE •CP（3）当AB=43且CP CF =43时，求劣弧的长度【2018哈尔滨】已知：⊙O 是正方形ABCD 的外接圆，点E 在上，连接BE 、DE ，点F 在上连接BF 、DF ，BF 与DE 、DA 分别交于点G 、点H ，且DA 平分∠EDF ．（1）如图1，求证：∠CBE=∠DHG（2）如图2，在线段AH 上取一点N （点N 不与点A 、点H 重合），连接BN 交DE 于点L ，过点H 作HK ∥BN 交DE 于点K ，过点E 作EP ⊥BN ，垂足为点P ，当BP=HF 时，求证：BE=HK（3）如图3，在（2）的条件下，当3HF=2DF 时，延长EP 交⊙O 于点R ，连接BR ，若△BER 的面积与△DHK 的面积的差为47，求线段BR 的长【2018黄石】在△ABC中，E、F分别为线段AB、AC上的点（不与A、B、C重合）．（1）如图1，若EF∥BC，求证：（2）如图2，若EF不与BC平行，（1）中的结论是否仍然成立？请说明理由（3）如图3，若EF上一点G恰为△ABC的重心，，求的值【2018荆门】AB为⊙O的直径，C为⊙O上一点，经过点C的切线交AB的延长线于点E，AD⊥EC交EC的延长线于点D，AD交⊙O于F，FM⊥AB于H，分别交⊙O、AC于M、N，连接MB，BC．（1）求证：AC平分∠DAE（2）若cosM=，BE=1，①求⊙O的半径；②求FN的长【2018武汉】在△ABC 中，∠ABC ＝90°、(1) 如图1，分别过A 、C 两点作经过点B 的直线的垂线，垂足分别为M 、N ，求证：△ABM ∽△BCN(2) 如图2，P 是边BC 上一点，∠BAP ＝∠C ，tan ∠PAC ＝552，求tanC 的值 (3) 如图3，D 是边CA 延长线上一点，AE ＝AB ，∠DEB ＝90°，sin ∠BAC ＝53，52 AC AD ，直接写出tan ∠CEB 的值【2018天门】问题：如图①，在Rt △ABC 中，AB=AC ，D 为BC 边上一点（不与点B ，C 重合），将线段AD 绕点A 逆时针旋转90°得到AE ，连接EC ，则线段BC ，DC ，EC 之间满足的等量关系式为；探索：如图②，在Rt △ABC 与Rt △ADE 中，AB=AC ，AD=AE ，将△ADE 绕点A 旋转，使点D 落在BC 边上，试探索线段AD ，BD ，CD 之间满足的等量关系，并证明你的结论应用：如图③，在四边形ABCD 中，∠ABC=∠ACB=∠ADC=45°．若BD=9，CD=3，求AD 的长【2018孝感】如图，△ABC 中，AB=AC ，以AB 为直径的⊙O 交BC 于点D ，交AC 于点E ，过点D 作DF ⊥AC 于点F ，交AB 的延长线于点G ．（1）求证：DF 是⊙O 的切线（2）已知BD=2 ，CF=2，求AE 和BG 的长【2018十堰】已知正方形ABCD 与正方形CEFG ，M 是AF 的中点，连接DM ，EM .（1）如图1，点E 在CD 上，点G 在BC 的延长线上，请判断DM ，EM 的数量关系与位置关系，并直接写出结论；（2）如图2，点E 在DC 的延长线上，点G 在BC 上，（1）中结论是否仍然成立？请证明你的结论；（3）将图1中的正方形CEFG 绕点C 旋转，使D ，E ，F 三点在一条直线上，若13AB =，5CE =，请画出图形，并直接写出MF 的长.【2018宜昌】在矩形ABCD中，AB=12，P是边AB上一点，把ΔPBC沿直线PC折叠，顶点B的对应点是点G，过点B作BE⊥CG，垂足为E且在AD上，BE交PC于点F.（1）如图1，若点E是AD的中心，求证：ΔAEB≌ΔDEC（2）如图2，①求证：BP=BF②当AD=25，且AE＜DE时，求cos∠PCB的值③当BP=9时，求BE·EF的值【2018长沙】在∆ABC 中，AD 是边B C 上的中线，∠BAD =∠CAD ，CE//AD ，CE 交B A 的延长线于点E，BC =8，AD =3.（1）求CE的长（2）求证：∆ABC为等腰三角形（3）求∆ABC的外接圆圆心P与内切圆圆心Q之间的距离【2018常德】已知正方形ABCD中AC与BD交于O点，点M在线段BD上，作直线AM交直线DC于E，过D 作DH⊥AE于H，设直线DH交AC于N．（1）如图1，当M在线段BO上时，求证：MO=NO；（2）如图2，当M在线段OD上，连接NE，当EN∥BD时，求证：BM=AB；（3）在图3，当M在线段OD上，连接NE，当NE⊥EC时，求证：AN2=NC•AC．【2018郴州】在矩形ABCD中，AD＞AB，点P是CD边上的任意一点（不含C，D两端点），过点P作PF∥BC，交对角线BD于点F．（1）如图1，将△PDF沿对角线BD翻折得到△QDF，QF交AD于点E求证：△DEF是等腰三角形（2）如图2，将△PDF绕点D逆时针方向旋转得到△P'DF'，连接P'C，F'B．设旋转角为α（0°＜α＜180°）①若0°＜α＜∠BDC，即DF'在∠BDC的内部时，求证：△DP'C∽△DF'B②如图3，若点P是CD的中点，△DF'B能否为直角三角形？如果能，试求出此时tan∠DBF'的值，如果不能，请说明理由【2018衡阳】在Rt△ABC中，∠C=90°，AC=BC=4cm，动点P从点C出发以1cm/s的速度沿CA匀速运动，同时动点Q从点A出发以cm/s的速度沿AB匀速运动，当点P到达点A时，点P、Q同时停止运动，设运动时间为t（s）．（1）当t为何值时，点B在线段PQ的垂直平分线上？（2）是否存在某一时刻t，使△APQ是以PQ为腰的等腰三角形？若存在，求出t的值；若不存在，请说明理由；（3）以PC为边，往CB方向作正方形CPMN，设四边形QNCP的面积为S，求S关于t的函数关系式．【2018娄底】C、D是以AB为直径的⊙O上的点，=，弦CD交AB于点E．（1）当PB是⊙O的切线时，求证：∠PBD=∠DAB（2）求证：BC2﹣CE2=CE•DE（3）已知OA=4，E是半径OA的中点，求线段DE的长【2018湘潭】AB是以O为圆心的半圆的直径，半径CO⊥AO，点M是上的动点，且不与点A、C、B重合，直线AM交直线OC于点D，连结OM与CM．（1）若半圆的半径为10①当∠AOM=60°时，求DM的长②当AM=12时，求DM的长（2）探究：在点M运动的过程中，∠DMC的大小是否为定值？若是，求出该定值；若不是，请说明理由【2018永州】如图1，在△ABC中，矩形EFGH的一边EF在AB上，顶点G、H分别在BC、AC上，CD是边AB 上的高，CD交GH于点I．若CI=4，HI=3，AD=．矩形DFGI恰好为正方形．（1）求正方形DFGI的边长（2）如图2，延长AB至P．使得AC=CP，将矩形EFGH沿BP的方向向右平移，当点G刚好落在CP上时，试判断移动后的矩形与△CBP重叠部分的形状是三角形还是四边形，为什么？（3）如图3，连接DG，将正方形DFGI绕点D顺时针旋转一定的角度得到正方形DF′G′I′，正方形DF′G′I′分别与线段DG、DB相交于点M，N，求△MNG′的周长【2018岳阳】已知在Rt △ABC 中，∠BAC=90°，CD 为∠ACB 的平分线，将∠ACB 沿CD 所在的直线对折，使点B 落在点B ′处，连结AB'，BB'，延长CD 交BB'于点E ，设∠ABC=2α（0°＜α＜45°）．（1）如图1，若AB=AC ，求证：CD=2BE（2）如图2，若AB ≠AC ，试求CD 与BE 的数量关系（用含α的式子表示）（3）如图3，将（2）中的线段BC 绕点C 逆时针旋转角（α+45°），得到线段FC ，连结EF 交BC 于点O ，设△COE 的面积为S 1，△COF 的面积为S 2，求（用含α的式子表示）【2018株洲】已知AB 为⊙O 的直径，AB=8，点C 和点D 是⊙O 上关于直线AB 对称的两个点，连接OC 、AC ，且∠BOC ＜90°，直线BC 和直线AD 相交于点E ，过点C 作直线CG 与线段AB 的延长线相交于点F ，与直线AD 相交于点G ，且∠GAF ＝∠GCE（1）求证：直线CG 为⊙O 的切线（2）若点H 为线段OB 上一点，连接CH ，满足CB ＝CH①△CBH ∽△OBC②求OH ＋HC 的最大值A【2018益阳】如图1，矩形ABCD中，E是AD的中点，以点E直角顶点的直角三角形EFG的两边EF，EG分别过点B，C，∠F＝30°.（1）求证：BE＝CE（2）将△EFG绕点E按顺时针方向旋转，当旋转到EF与AD重合时停止转动。

初中数学几何最值存在性问题(word版+详解答案)

几何最值的存在性问题【考题研究】在平面几何的动态问题中，当某几何元素在给定条件变动时，求某几何量（如线段的长度、图形的周长或面积、角的度数以及它们的和与差）的最大值或最小值问题，称为最值问题。

从历年的中考数学压轴题型分析来看，经常会考查到距离或者两条线段和差最值得问题，并且这部分题目在中考中失分率很高，应该引起我们的重视。

几何最值问题再教材中虽然没有进行专题讲解，到却给了我们很多解题模型，因此在专题复习时进行压轴训练是必要的。

【解题攻略】最值问题是一类综合性较强的问题，而线段和（差）问题，要归归于几何模型：（1）归于“两点之间的连线中，线段最短”凡属于求“变动的两线段之和的最小值”时，大都应用这一模型．（2）归于“三角形两边之差小于第三边”凡属于求“变动的两线段之差的最大值”时，大都应用这一模型．两条动线段的和的最小值问题，常见的是典型的“牛喝水”问题，关键是指出一条对称轴“河流”（如图1）．三条动线段的和的最小值问题，常见的是典型的“台球两次碰壁”或“光的两次反射”问题，关键是指出两条对称轴“反射镜面”（如图2）．两条线段差的最大值问题，一般根据三角形的两边之差小于第三边，当三点共线时，两条线段差的最大值就是第三边的长．如图3，PA与PB的差的最大值就是AB，此时点P在AB的延长线上，即P′．解决线段和差的最值问题，有时候求函数的最值更方便，建立一次函数或者二次函数求解最值问题．【解题类型及其思路】解决平面几何最值问题的常用的方法有：（1）应用两点间线段最短的公理（含应用三角形的三边关系）求最值；（2）应用垂线段最短的性质求最值；（3）应用轴对称的性质求最值；（4）应用二次函数求最值；（5）应用其它知识求最值。

【典例指引】类型一【确定线段（或线段的和，差）的最值或确定点的坐标】【典例指引1】（2018·天津中考模拟）如图，在平面直角坐标系中，长方形OABC的顶点A、C分别在x 轴、y轴的正半轴上．点B的坐标为（8，4），将该长方形沿OB翻折，点A的对应点为点D，OD与BC 交于点E．（I）证明：EO=EB；（Ⅱ）点P是直线OB上的任意一点，且△OPC是等腰三角形，求满足条件的点P的坐标；（Ⅲ）点M是OB上任意一点，点N是OA上任意一点，若存在这样的点M、N，使得AM+MN最小，请直接写出这个最小值．【举一反三】（2020·云南初三）如图，抛物线y=ax2+bx+3经过点B（﹣1，0），C（2，3），抛物线与y轴的焦点A，与x轴的另一个焦点为D，点M为线段AD上的一动点，设点M的横坐标为t．（1）求抛物线的表达式；（2）过点M作y轴的平行线，交抛物线于点P，设线段PM的长为1，当t为何值时，1的长最大，并求最大值；（先根据题目画图，再计算）（3）在（2）的条件下，当t为何值时，△PAD的面积最大？并求最大值；（4）在（2）的条件下，是否存在点P，使△PAD为直角三角形？若存在，直接写出t的值；若不存在，说明理由．类型二【确定三角形、四边形的周长的最值或符合条件的点的坐标】【典例指引2】（2020·重庆初三期末）如图，抛物线2y ax bx =+（0a >）与双曲线k y x =相交于点A 、B ，已知点A 坐标()1,4，点B 在第三象限内，且AOB ∆的面积为3（O 为坐标原点）.（1）求实数a 、b 、k 的值；（2）在该抛物线的对称轴上是否存在点P 使得POB ∆为等腰三角形？若存在请求出所有的P 点的坐标，若不存在请说明理由.（3）在坐标系内有一个点M ，恰使得MA MB MO ==，现要求在y 轴上找出点Q 使得BQM ∆的周长最小，请求出M 的坐标和BQM ∆周长的最小值.【举一反三】（2019·重庆实验外国语学校初三）如图1，已知抛物线y ＝﹣23384x +x +3与x 轴交于A 和B 两点，（点A 在点B 的左侧），与y 轴交于点C ．（1）求出直线BC 的解析式．（2）M 为线段BC 上方抛物线上一动点，过M 作x 轴的垂线交BC 于H ，过M 作MQ ⊥BC 于Q ，求出△MHQ 周长最大值并求出此时M 的坐标；当△MHQ 的周长最大时在对称轴上找一点R ，使|AR ﹣MR |最大，求出此时R 的坐标．（3）T 为线段BC 上一动点，将△OCT 沿边OT 翻折得到△OC ′T ，是否存在点T 使△OC ′T 与△OBC 的重叠部分为直角三角形，若存在请求出BT 的长，若不存在，请说明理由．类型三【确定三角形、四边形的面积最值或符合条件的点的坐标】【典例指引3】（2019·甘肃中考真题）如图，已知二次函数y ＝x 2+bx+c 的图象与x 轴交于点A （1，0）、B （3，0），与y 轴交于点C ．（1）求二次函数的解析式；（2）若点P 为抛物线上的一点，点F 为对称轴上的一点，且以点A 、B 、P 、F 为顶点的四边形为平行四边形，求点P 的坐标；（3）点E 是二次函数第四象限图象上一点，过点E 作x 轴的垂线，交直线BC 于点D ，求四边形AEBD 面积的最大值及此时点E 的坐标．【举一反三】（2019·内蒙古中考真题）如图，在平面直角坐标系中，已知抛物线22(0)y ax bx a =++≠与x 轴交于()1,0A -），()3,0B 两点，与y 轴交于点C ，连接BC ．（1）求该抛物线的解析式，并写出它的对称轴；（2）点D 为抛物线对称轴上一点，连接CD BD 、，若DCB CBD ∠=∠，求点D 的坐标；（3）已知()1,1F ，若(),E x y 是抛物线上一个动点（其中12x <<），连接CE CF EF 、、，求CEF ∆面积的最大值及此时点E 的坐标．（4）若点N 为抛物线对称轴上一点，抛物线上是否存在点M ，使得以,,,B C M N 为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点M 的坐标；若不存在，请说明理由．【新题训练】1．如图，直线y＝5x＋5交x轴于点A，交y轴于点C，过A，C两点的二次函数y＝ax2＋4x＋c的图象交x轴于另一点B.(1)求二次函数的表达式；(2)连接BC，点N是线段BC上的动点，作ND⊥x轴交二次函数的图象于点D，求线段ND长度的最大值；(3)若点H为二次函数y＝ax2＋4x＋c图象的顶点，点M(4，m)是该二次函数图象上一点，在x轴，y轴上分别找点F，E，使四边形HEFM的周长最小，求出点F、E的坐标．2．（2019·江苏中考真题）如图，已知等边△ABC的边长为8，点P是AB边上的一个动点（与点A、B不重合），直线l是经过点P的一条直线，把△ABC沿直线l折叠，点B的对应点是点B’.（1）如图1，当PB=4时，若点B’恰好在AC边上，则AB’的长度为_____；（2）如图2，当PB=5时，若直线l//AC，则BB’的长度为；（3）如图3，点P在AB边上运动过程中，若直线l始终垂直于AC，△ACB’的面积是否变化？若变化，说明理由；若不变化，求出面积；（4）当PB=6时，在直线l变化过程中，求△ACB’面积的最大值.3．（2019·湖南中考真题）如图，在平面直角坐标系xOy中，矩形ABCD的边AB＝4，BC＝6．若不改变矩形ABCD的形状和大小，当矩形顶点A在x轴的正半轴上左右移动时，矩形的另一个顶点D始终在y 轴的正半轴上随之上下移动．(1)当∠OAD＝30°时，求点C的坐标；(2)设AD的中点为M，连接OM、MC，当四边形OMCD的面积为212时，求OA的长；(3)当点A移动到某一位置时，点C到点O的距离有最大值，请直接写出最大值，并求此时cos∠OAD的值．4.（2018·江苏中考真题）如图，在平面直角坐标系中，一次函数y=﹣23x+4的图象与x轴和y轴分别相交于A、B两点．动点P从点A出发，在线段AO上以每秒3个单位长度的速度向点O作匀速运动，到达点O停止运动，点A关于点P的对称点为点Q，以线段PQ为边向上作正方形PQMN．设运动时间为t秒．（1）当t=13秒时，点Q的坐标是；（2）在运动过程中，设正方形PQMN与△AOB重叠部分的面积为S，求S与t的函数表达式；（3）若正方形PQMN对角线的交点为T，请直接写出在运动过程中OT+PT的最小值．5.（2020·江苏初三期末）已知二次函数223y x x =--+的图象和x 轴交于点A 、B ，与y 轴交于点C ，点P 是直线AC 上方的抛物线上的动点.(1)求直线AC 的解析式.(2)当P 是抛物线顶点时，求APC ∆面积.(3)在P 点运动过程中，求APC ∆面积的最大值.6．（2020·江苏初三期末）如图，抛物线265y ax x =+-交x 轴于A 、B 两点，交y 轴于点C ，点B 的坐标为()5,0，直线5y x =-经过点B 、C .（1）求抛物线的函数表达式；（2）点P 是直线BC 上方抛物线上的一动点，求BCP ∆面积S 的最大值并求出此时点P 的坐标；（3）过点A 的直线交直线BC 于点M ，连接AC ，当直线AM 与直线BC 的一个夹角等于ACB ∠的3倍时，请直接写出点M 的坐标.7.（2019·石家庄市第四十一中学初三）如图，在平面直角坐标系中，抛物线y ＝x （x ﹣b ）﹣与y 轴相交于A 点，与x 轴相交于B 、C 两点，且点C 在点B 的右侧，设抛物线的顶点为P ．（1）若点B 与点C 关于直线x ＝1对称，求b 的值；（2）若OB ＝OA ，求△BCP 的面积；（3）当﹣1≤x≤1时，该抛物线上最高点与最低点纵坐标的差为h ，求出h 与b 的关系；若h 有最大值或最小值，直接写出这个最大值或最小值．8.（2020·江西初三期中）如图①，已知抛物线y=ax2+bx+3（a≠0）与x轴交于点A（1，0）和点B（-3，0），与y轴交于点C．（1）求抛物线的解析式；（2）设抛物线的对称轴与x轴交于点M，问在对称轴上是否存在点P，使△CMP为等腰三角形？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由；（3）如图②，若点E为第二象限抛物线上一动点，连接BE、CE，求四边形BOCE面积的最大值，并求此时E点的坐标．9．（2020·山东初三期末）如图，抛物线y=ax2+bx+c（a≠0）的图象过点C（0，1），顶点为Q（2，3），点D在x轴正半轴上，且OD=OC．（1）求直线CD 的解析式；（2）求抛物线的解析式；（3）将直线CD 绕点C 逆时针方向旋转45°所得直线与抛物线相交于另一点E ，求证：△CEQ ∽△CDO ；（4）在（3）的条件下，若点P 是线段QE 上的动点，点F 是线段OD 上的动点，问：在P 点和F 点移动过程中，△PCF 的周长是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由． 10．（2020·盘锦市双台子区第一中学初三月考）如图①,已知抛物线y=ax 2+bx+c 的图像经过点A （0，3)、B （1，0），其对称轴为直线l ：x=2，过点A 作AC ∥x 轴交抛物线于点C ，∠AOB 的平分线交线段AC 于点E ，点P 是抛物线上的一个动点，设其横坐标为m.（1）求抛物线的解析式；（2）若动点P 在直线OE 下方的抛物线上，连结PE 、PO ，当m 为何值时，四边形AOPE 面积最大，并求出其最大值；（3）如图②，F 是抛物线的对称轴l 上的一点，在抛物线上是否存在点P 使△POF 成为以点P 为直角顶点的等腰直角三角形？若存在，直接写出所有符合条件的点P 的坐标；若不存在，请说明理由.11．（2020·四川初三）如图，一次函数122y x =-+的图像与坐标轴交于A 、B 两点，点C 的坐标为(1,0)-，二次函数2y ax bx c =++的图像经过A 、B 、C 三点．（1）求二次函数的解析式（2）如图1，已知点(1,)D n 在抛物线上，作射线BD ，点Q 为线段AB 上一点，过点Q 作QM y ⊥轴于点M ，作QN BD ⊥于点N ，过Q 作//QP y 轴交抛物线于点P ，当QM 与QN 的积最大时，求点P 的坐标；（3）在（2）的条件下，连接AP ，若点E 为抛物线上一点，且满足APE ABO ∠=∠，求点E 的坐标．12．（2019·广东初三）如图，已知抛物线y ＝﹣3x 2+bx +c 与x 轴交于原点O 和点A （6，0），抛物线的顶点为B ．（1）求该抛物线的解析式和顶点B 的坐标；（2）若动点P 从原点O 出发，以每秒1个长度单位的速度沿线段OB 运动，设点P 运动的时间为t （s ）．问当t 为何值时，△OPA 是直角三角形？（3）若同时有一动点M 从点A 出发，以2个长度单位的速度沿线段AO 运动，当P 、M 其中一个点停止运动时另一个点也随之停止运动．设它们的运动时间为t （s ），连接MP ，当t 为何值时，四边形ABPM 的面积最小？并求此最小值．13．（2019·山东初三期中）如图，已知抛物线经过两点A （﹣3，0），B （0，3），且其对称轴为直线x ＝﹣1．（1）求此抛物线的解析式．（2）若点Q 是对称轴上一动点，当OQ +BQ 最小时，求点Q 的坐标．（3）若点P 是抛物线上点A 与点B 之间的动点（不包括点A ，点B ），求△PAB 面积的最大值，并求出此时点P 的坐标．14.（2019·四川中考真题）如图，抛物线212y x bx c =-++过点(3,2)A ，且与直线72y x =-+交于B 、C两点，点B 的坐标为(4,)m ．（1）求抛物线的解析式；（2）点D 为抛物线上位于直线BC 上方的一点，过点D 作DE x ⊥轴交直线BC 于点E ，点P 为对称轴上一动点，当线段DE 的长度最大时，求PD PA +的最小值；（3）设点M 为抛物线的顶点，在y 轴上是否存在点Q ，使45AQM ︒∠=？若存在，求点Q 的坐标；若不存在，请说明理由．15.（2019·天津中考真题）已知抛物线2y x bx c =-+（b c ，为常数，0b >）经过点(1,0)A -，点(,0)M m 是x 轴正半轴上的动点．（Ⅰ）当2b =时，求抛物线的顶点坐标；（Ⅱ）点(,)D D b y 在抛物线上，当AM AD =，5m =时，求b 的值；（Ⅲ）点1(,)2QQ b y+在抛物线上，当22AM QM+的最小值为3324时，求b的值．16.（2019·湖南中考真题）如图，抛物线y＝ax2+bx（a＞0）过点E（8，0），矩形ABCD的边AB在线段OE上（点A在点B的左侧），点C、D在抛物线上，∠BAD的平分线AM交BC于点M，点N是CD的中点，已知OA＝2，且OA：AD＝1：3.（1）求抛物线的解析式；（2）F、G分别为x轴，y轴上的动点，顺次连接M、N、G、F构成四边形MNGF，求四边形MNGF周长的最小值；（3）在x轴下方且在抛物线上是否存在点P，使△ODP中OD边上的高为610？若存在，求出点P的坐标；若不存在，请说明理由；（4）矩形ABCD不动，将抛物线向右平移，当平移后的抛物线与矩形的边有两个交点K、L，且直线KL 平分矩形的面积时，求抛物线平移的距离.17.（2019·辽宁中考真题）如图，在平面直角坐标系中，抛物线y＝ax2+bx+2（a≠0）与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，抛物线经过点D（﹣2，﹣3）和点E（3，2），点P是第一象限抛物线上的一个动点．（1）求直线DE和抛物线的表达式；（2）在y 轴上取点F （0，1），连接PF ，PB ，当四边形OBPF 的面积是7时，求点P 的坐标；（3）在（2）的条件下，当点P 在抛物线对称轴的右侧时，直线DE 上存在两点M ，N （点M 在点N 的上方），且MN ＝22，动点Q 从点P 出发，沿P→M→N→A 的路线运动到终点A ，当点Q 的运动路程最短时，请直接写出此时点N 的坐标．18.（2019·湖南中考真题）已知抛物线2(0)y ax bx c a =++≠过点(1,0)A ，(3,0)B 两点，与y 轴交于点C ，=3OC ．(1)求抛物线的解析式及顶点D 的坐标；(2)过点A 作AM BC ⊥，垂足为M ，求证：四边形ADBM 为正方形；(3)点P 为抛物线在直线BC 下方图形上的一动点，当PBC ∆面积最大时，求点P 的坐标； (4)若点Q 为线段OC 上的一动点，问：12AQ QC +是否存在最小值？若存在，求岀这个最小值；若不存在，请说明理由．几何最值的存在性问题【考题研究】在平面几何的动态问题中，当某几何元素在给定条件变动时，求某几何量（如线段的长度、图形的周长或面积、角的度数以及它们的和与差）的最大值或最小值问题，称为最值问题。

2018挑战中考数学压轴题全套含答案及解析

第一部分函数图象中点的存在性问题§1．1 因动点产生的相似三角形问题例1 2014年市中考第28题例2 2014年市中考第21题例3 2015年湘西州中考第26题例4 2015年市中考第25题例5 2016年市中考第26题例6 2016年市中考第24题例7 2016年市崇明县中考模拟第25题例8 2016年市黄浦区中考模拟第26题§1．2 因动点产生的等腰三角形问题例9 2014年市中考第26题例10 2014年市第25题例11 2014年市中考第26题例12 2014年市中考第27题例13 2015年市中考第22题例14 2015年市中考第26题例15 2016年市中考第26题例16 2016年市长宁区金山区中考模拟第25题例17 2016年省中考第23题§1．3 因动点产生的直角三角形问题例19 2015年市中考第21题例20 2015年市中考第26题例21 2016年市中考第26题例22 2016年市松江区中考模拟第25题例23 2016年义乌市市中考第24题§1．4 因动点产生的平行四边形问题例24 2014年市中考第24题例25 2014年市中考第20题例26 2014年市中考第25题例27 2015年市中考第25题例28 2015年黄冈市中考第24题例29 2016年市中考第26题例30 2016年市嘉定区宝山区中考模拟中考第24题例31 2016年市徐汇区中考模拟第24题§1．5 因动点产生的面积问题例32 2014年市中考第25题例33 2014年永州市中考第25题例35 2015年市中考第26题例36 2015年株洲市中考第23题例37 2015年市中考第28题例38 2016年市中考第22题例39 2016年永州市中考第26题例40 2016年市中考第26题例41 2016年省中考第25题§1．6 因动点产生的相切问题例42 2014年市中考第27题例43 2014年株洲市中考第23题例44 2015年市中考第25题例45 2015年湘西州中考第25题例46 2016年市中考第25题例47 2016年市中考第26题例48 2016年市闵行区中考模拟第24题例49 2016年市普陀区中考模拟中考第25题§1．7 因动点产生的线段和差问题例50 2014年市中考第26题例51 2014年湘西州中考第25题例53 2015年市中考第28题例54 2015年市中考第25题例55 2016年市中考第26题例56 2016年市中考第24题例57 2016年市中考第21题第二部分图形运动中的函数关系问题§2．1 由比例线段产生的函数关系问题例1 2014年市中考第26题例2 2014年市中考第25题例3 2014年市中考第25题例4 2015年市中考第25题例5 2015年市中考第26题例6 2015年市中考第25题例7 2015年市中考第26题例8 2016年市中考第25题例9 2016年湘西州中考第26题例10 2016年市静安区青浦区中考模拟第25题例11 2016年市中考第27题第三部分图形运动中的计算说理问题§3．1 代数计算及通过代数计算进行说理问题例1 2014年市中考第25题例2 2014年市中考第23题例3 2014年市中考第26题例4 2014年株洲市中考第24题例5 2015年市中考第27题例6 2015年市中考第25题例7 2015年永州市中考第26题例8 2015年市中考第25题例9 2015年株洲市中考第24题例10 2016年市中考第22题例11 2016年市中考第25题例12 2016年株洲市中考第26题例13 2016年市中考第25题例14 2016年市中考第26题§3．2 几何证明及通过几何计算进行说理问题例15 2014年市中考第26题例16 2014年市中考第26题例17 2014年市中考第23题例18 2015年市中考第26题例19 2015年市中考第20题例20 2015年永州市中考第27题例21 2015年市中考第23题例22 2016年市中考第25题例23 2016年市中考第25题例24 2016年永州市中考第27题例25 2016年市中考第23题例26 2016年株洲市中考第25题例27 2016年市中考第25题第四部分图形的平移、翻折与旋转§4．1 图形的平移例1 2015年市中考第15题例2 2015年市中考第14题例3 2015年株洲市中考第14题例4 2016年市虹口区中考模拟第18题§4．2 图形的翻折例5 2016年市奉贤区中考模拟第18题例6 2016年市静安区青浦区中考模拟第18题例7 2016年市闵行区中考模拟第18题例8 2016年市浦东新区中考模拟第18题例8 2016年市普陀区中考模拟第18题例10 2016年市中考第15题例11 2016年市中考第14题例12 2016年市中考第18题例13 2016年市中考第15题例14 2016年市中考第12题§4．3 图形的旋转例15 2016年昂立教育中学生三模联考第18题例16 2016年市崇明县中考模拟第18题例17 2016年市黄浦区中考模拟第18题例18 2016年市嘉定区宝山区中考模拟第18题例19 2016年市闸北区中考模拟第18题例20 2016年市中考第13题例21 2016年株洲市中考第4题§4．4 三角形例22 2016年省中考第10题例23 2016年市中考第10题例24 2016年省中考第16题例25 2016年市中考第10题例27 2016年市中考第10题例28 2016年省中考第14题例29 2016年江市中考第11题例30 2016年市中考第18题§4．5 四边形例31 2016年湘西州中考第11题例32 2016年市中考第4题例33 2016年市中考第6题例34 2016年市中考第16题例35 2016年市中考第14题例36 2016年市中考第13题例37 2016年市中考第18题例38 2016年市中考第17题例39 2016年市中考第15题§4．6 圆例40 2016年滨州市中考第16题例41 2016年市中考第17题例42 2016年市中考第16题例43 2016年市中考第17题例45 2016年市中考第18题例46 2016年市中考第9题例47 2016年宿迁市中考第16题例48 2016年市中考第17题例49 2016年市中考第18题例50 2016年湘西州中考第18题例51 2016年永州市中考第20题§4．7 函数的图象及性质例52 2015年荆州市中考第9题例53 2015年市中考第12题例54 2015年市中考第12题例55 2015年市中考第10题例56 2015年市中考第10题例57 2015年呼和浩特市中考第10题例58 2016年市中考第18题例59 2016年市中考第19题例60 2016年市中考第15题例61 2016年株洲市中考第9题例62 2016年永州市中考第19题例63 2016年市中考第8题例64 2016年市中考第16题例65 2016年市中考第14题例66 2016年株洲市中考第10题例67 2016年株洲市中考第17题例68 2016年东营市中考第15题例69 2016年市中考第13题例70 2016年市中考第16题例71 2016年宿迁市中考第15题例72 2016年市中考第14题例73 2016年义乌市市中考第9题例74 2016年市中考第12题例75 2016年市中考第16题§1．1 因动点产生的相似三角形问题课前导学相似三角形的判定定理有3个，其中判定定理1和判定定理2都有对应角相等的条件，因此探求两个三角形相似的动态问题，一般情况下首先寻找一组对应角相等．判定定理2是最常用的解题依据，一般分三步：寻找一组等角，分两种情况列比例方程，解方程并检验．如果已知∠A ＝∠D ，探求△ABC 与△DEF 相似，只要把夹∠A 和∠D 的两边表示出来，按照对应边成比例，分AB DE AC DF =和AB DF AC DE=两种情况列方程．应用判定定理1解题，先寻找一组等角，再分两种情况讨论另外两组对应角相等．应用判定定理3解题不多见，根据三边对应成比例列连比式解方程（组）．还有一种情况，讨论两个直角三角形相似，如果一组锐角相等，其中一个直角三角形的锐角三角比是确定的，那么就转化为讨论另一个三角形是直角三角形的问题．求线段的长，要用到两点间的距离公式，而这个公式容易记错．理解记忆比较好．如图1，如果已知A 、B 两点的坐标，怎样求A 、B 两点间的距离呢？我们以AB 为斜边构造直角三角形，直角边与坐标轴平行，这样用勾股定理就可以求斜边AB 的长了．水平距离BC 的长就是A 、B 两点间的水平距离，等于A 、B 两点的横坐标相减；竖直距离AC 就是A 、B 两点间的竖直距离，等于A 、B 两点的纵坐标相减．图1例 1 2014年省市中考第28题二次函数y ＝a x 2＋b x ＋c （a ≠0）的图象与x 轴交于A (－3, 0)、B (1, 0)两点，与y 轴交于点C (0,－3m )（m ＞0），顶点为D ．（1）求该二次函数的解析式（系数用含m 的代数式表示）；（2）如图1，当m ＝2时，点P 为第三象限抛物线上的一个动点，设△APC 的面积为S ，试求出S 与点P 的横坐标x 之间的函数关系式及S 的最大值；（3）如图2，当m 取何值时，以A 、D 、C 三点为顶点的三角形与△OBC 相似？图1 图2动感体验请打开几何画板文件名“1428”，拖动点P 运动，可以体验到，当点P 运动到AC 的中点的正下方时，△APC 的面积最大．拖动y 轴上表示实数m 的点运动，抛物线的形状会改变，可以体验到，∠ACD 和∠ADC 都可以成为直角．思路点拨1．用交点式求抛物线的解析式比较简便．2．连结OP ，△APC 可以割补为：△AOP 与△COP 的和，再减去△AOC ．3．讨论△ACD 与△OBC 相似，先确定△ACD 是直角三角形，再验证两个直角三角形是否相似．4．直角三角形ACD 存在两种情况．图文解析（1）因为抛物线与x 轴交于A (－3, 0)、B (1, 0)两点，设y ＝a (x ＋3)(x －1)．代入点C (0,－3m )，得－3m ＝－3a ．解得a ＝m ．所以该二次函数的解析式为y ＝m (x ＋3)(x －1)＝mx 2＋2mx －3m ．（2）如图3，连结OP ．当m ＝2时，C (0,－6)，y ＝2x 2＋4x －6，那么P (x , 2x 2＋4x －6)．由于S △AOP ＝1()2P OA y ⨯-＝32-(2x 2＋4x －6)＝－3x 2－6x ＋9， S △COP ＝1()2P OC x ⨯-＝－3x ，S △AOC ＝9，所以S ＝S △APC ＝S △AOP ＋S △COP －S △AOC ＝－3x 2－9x ＝23273()24x -++．所以当32x =-时，S 取得最大值，最大值为274．图3 图4 图5（3）如图4，过点D 作y 轴的垂线，垂足为E ．过点A 作x 轴的垂线交DE 于F ．由y ＝m (x ＋3)(x －1)＝m (x ＋1)2－4m ，得D (－1,－4m )．在Rt △OBC 中，OB ∶OC ＝1∶3m ．如果△ADC 与△OBC 相似，那么△ADC 是直角三角形，而且两条直角边的比为1∶3m ．①如图4，当∠ACD ＝90°时，OA OC EC ED =．所以331m m =．解得m ＝1．此时3CA OC CD ED ==，3OC OB =．所以CA OC CD OB =．所以△CDA ∽△OBC ． ②如图5，当∠ADC ＝90°时，FA FD ED EC =．所以421m m=．解得2m =．此时222DA FD DC EC m===，而3232OC m OB ==．因此△DCA 与△OBC 不相似．综上所述，当m ＝1时，△CDA ∽△OBC ．考点伸展第（2）题还可以这样割补：如图6，过点P 作x 轴的垂线与AC 交于点H ．由直线AC ：y ＝－2x －6，可得H (x ,－2x －6)．又因为P (x , 2x 2＋4x －6)，所以HP ＝－2x 2－6x ．因为△PAH 与△PCH 有公共底边HP ，高的和为A 、C 两点间的水平距离3，所以S ＝S △APC ＝S △APH ＋S △CPH＝32(－2x 2－6x ) ＝23273()24x -++．图6例2 2014年省市中考第21题如图1，在直角梯形ABCD中，AB//CD，AD⊥AB，∠B＝60°，AB＝10，BC＝4，点P沿线段AB从点A向点B运动，设AP＝x．2·1·c·n·j·y（1）求AD的长；（2）点P在运动过程中，是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似？若存在，求出x的值；若不存在，请说明理由；（3）设△ADP与△PCB的外接圆的面积分别为S1、S2，若S＝S1＋S2，求S的最小值.动感体验图1请打开几何画板文件名“1421”，拖动点P在AB上运动，可以体验到，圆心O的运动轨迹是线段BC的垂直平分线上的一条线段．观察S随点P运动的图象，可以看到，S有最小值，此时点P看上去象是AB的中点，其实离得很近而已．思路点拨1．第（2）题先确定△PCB是直角三角形，再验证两个三角形是否相似．2．第（3）题理解△PCB的外接圆的圆心O很关键，圆心O在确定的BC的垂直平分线上，同时又在不确定的BP的垂直平分线上．而BP与AP是相关的，这样就可以以AP 为自变量，求S的函数关系式．图文解析（1）如图2，作CH⊥AB于H，那么AD＝CH．在Rt△BCH中，∠B＝60°，BC＝4，所以BH＝2，CH＝23．所以AD＝23．（2）因为△APD是直角三角形，如果△APD与△PCB相似，那么△PCB一定是直角三角形．①如图3，当∠CPB＝90°时，AP＝10－2＝8．所以APAD ＝23＝43，而PCPB＝3．此时△APD与△PCB不相似．图2 图3 图4 ②如图4，当∠BCP＝90°时，BP＝2BC＝8．所以AP＝2．所以AP AD ＝23＝3．所以∠APD ＝60°．此时△APD ∽△CBP ．综上所述，当x ＝2时，△APD ∽△CBP ．（3）如图5，设△ADP 的外接圆的圆心为G ，那么点G 是斜边DP 的中点．设△PCB 的外接圆的圆心为O ，那么点O 在BC 边的垂直平分线上，设这条直线与BC 交于点E ，与AB 交于点F ．设AP ＝2m ．作OM ⊥BP 于M ，那么BM ＝PM ＝5－m ．在Rt △BEF 中，BE ＝2，∠B ＝60°，所以BF ＝4．在Rt △OFM 中，FM ＝BF －BM ＝4－(5－m )＝m －1，∠OFM ＝30°，所以OM ＝3(1)m -．所以OB 2＝BM 2＋OM 2＝221(5)(1)3m m -+-．在Rt △ADP 中，DP 2＝AD 2＋AP 2＝12＋4m 2．所以GP 2＝3＋m 2．于是S ＝S 1＋S 2＝π(GP 2＋OB 2)＝22213(5)(1)3m m m π⎡⎤++-+-⎢⎥⎣⎦＝2(73285)3m m π-+．所以当167m =时，S 取得最小值，最小值为1137π．图5 图6考点伸展关于第（3）题，我们再讨论个问题．问题1，为什么设AP ＝2m 呢？这是因为线段AB ＝AP ＋PM ＋BM ＝AP ＋2BM ＝10．这样BM ＝5－m ，后续可以减少一些分数运算．这不影响求S 的最小值．问题2，如果圆心O 在线段EF 的延长线上，S 关于m 的解析式是什么？如图6，圆心O 在线段EF 的延长线上时，不同的是FM ＝BM －BF ＝(5－m )－4＝1－m ．此时OB 2＝BM 2＋OM 2＝221(5)(1)3m m -+-．这并不影响S 关于m 的解析式．例 3 2015年省湘西市中考第26题如图1，已知直线y ＝－x ＋3与x 轴、y 轴分别交于A 、B 两点，抛物线y ＝－x 2＋bx ＋c 经过A 、B 两点，点P 在线段OA 上，从点O 出发，向点A 以每秒1个单位的速度匀速运动；同时，点Q 在线段AB 上，从点A 出发，向点B 以每秒2个单位的速度匀速运动，连结PQ ，设运动时间为t 秒．（1）求抛物线的解析式；（2）问：当t 为何值时，△APQ 为直角三角形；（3）过点P 作PE //y 轴，交AB 于点E ，过点Q 作QF //y 轴，交抛物线于点F ，连结EF ，当EF //PQ 时，求点F 的坐标；（4）设抛物线顶点为M ，连结BP 、BM 、MQ ，问：是否存在t 的值，使以B 、Q 、M 为顶点的三角形与以O 、B 、P 为顶点的三角形相似？若存在，请求出t 的值；若不存在，请说明理由．图1动感体验请打开几何画板文件名“15湘西26”，拖动点P 在OA 上运动，可以体验到，△APQ 有两个时刻可以成为直角三角形，四边形EPQF 有一个时刻可以成为平行四边形，△MBQ 与△BOP 有一次机会相似．思路点拨1．在△APQ 中，∠A ＝45°，夹∠A 的两条边AP 、AQ 都可以用t 表示，分两种情况讨论直角三角形APQ ．2．先用含t 的式子表示点P 、Q 的坐标，进而表示点E 、F 的坐标，根据PE ＝QF 列方程就好了．3．△MBQ 与△BOP 都是直角三角形，根据直角边对应成比例分两种情况讨论．图文解析（1）由y ＝－x ＋3，得A (3, 0)，B (0, 3)．将A (3, 0)、B (0, 3)分别代入y ＝－x 2＋bx ＋c ，得930,3.b c c -++=⎧⎨=⎩ 解得2,3.b c =⎧⎨=⎩ 所以抛物线的解析式为y ＝－x 2＋2x ＋3．（2）在△APQ 中，∠PAQ ＝45°，AP ＝3－t ，AQ ＝2t ．分两种情况讨论直角三角形APQ ：①当∠PQA ＝90°时，AP ＝2AQ ．解方程3－t ＝2t ，得t ＝1（如图2）．②当∠QPA ＝90°时，AQ ＝2AP ．解方程2t ＝2(3－t )，得t ＝1.5（如图3）．图2 图3（3）如图4，因为PE //QF ，当EF //PQ 时，四边形EPQF 是平行四边形．所以EP ＝FQ ．所以y E －y P ＝y F －y Q ．因为x P ＝t ，x Q ＝3－t ，所以y E ＝3－t ，y Q ＝t ，y F ＝－(3－t )2＋2(3－t )＋3＝－t 2＋4t ．因为y E －y P ＝y F －y Q ，解方程3－t ＝(－t 2＋4t )－t ，得t ＝1，或t ＝3（舍去）．所以点F 的坐标为(2, 3)．图4 图5（4）由y ＝－x 2＋2x ＋3＝－(x －1)2＋4，得M (1, 4)．由A (3, 0)、B (0, 3)，可知A 、B 两点间的水平距离、竖直距离相等，AB ＝2．由B (0, 3)、M (1, 4)，可知B 、M 两点间的水平距离、竖直距离相等，BM 2 所以∠MBQ ＝∠BOP ＝90°．因此△MBQ 与△BOP 相似存在两种可能： ①当BM OB BQ OP =23322t t=-．解得94t =（如图5）． ②当BM OP BQ OB =23322t t =-．整理，得t 2－3t ＋3＝0．此方程无实根．考点伸展第（3）题也可以用坐标平移的方法：由P (t , 0)，E (t , 3－t )，Q(3－t , t )，按照P →E 方向，将点Q 向上平移，得F (3－t , 3)．再将F (3－t , 3)代入y ＝－x 2＋2x ＋3，得t ＝1，或t ＝3．§1．2 因动点产生的等腰三角形问题课前导学我们先回顾两个画图问题：1．已知线段AB ＝5厘米，以线段AB 为腰的等腰三角形ABC 有多少个？顶点C 的轨迹是什么？2．已知线段AB ＝6厘米，以线段AB 为底边的等腰三角形ABC 有多少个？顶点C 的轨迹是什么？已知腰长画等腰三角形用圆规画圆，圆上除了两个点以外，都是顶点C ．已知底边画等腰三角形，顶角的顶点在底边的垂直平分线上，垂足要除外．在讨论等腰三角形的存在性问题时，一般都要先分类．如果△ABC 是等腰三角形，那么存在①AB ＝AC ，②BA ＝BC ，③CA ＝CB 三种情况．解等腰三角形的存在性问题，有几何法和代数法，把几何法和代数法相结合，可以使得解题又好又快．几何法一般分三步：分类、画图、计算．哪些题目适合用几何法呢？如果△ABC 的∠A （的余弦值）是确定的，夹∠A 的两边AB 和AC 可以用含x 的式子表示出来，那么就用几何法．①如图1，如果AB ＝AC ，直接列方程；②如图2，如果BA ＝BC ，那么1cos 2AC AB A =∠；③如图3，如果CA ＝CB ，那么1cos 2AB AC A =∠．代数法一般也分三步：罗列三边长，分类列方程，解方程并检验．如果三角形的三个角都是不确定的，而三个顶点的坐标可以用含x 的式子表示出来，那么根据两点间的距离公式，三边长（的平方）就可以罗列出来．图1 图2 图3例 9 2014年市中考第26题如图1，抛物线y ＝ax 2＋bx ＋c （a 、b 、c 是常数，a ≠0）的对称轴为y 轴，且经过(0,0)和1(,)16a 两点，点P 在该抛物线上运动，以点P 为圆心的⊙P 总经过定点A (0, 2)．（1）求a 、b 、c 的值；（2）求证：在点P 运动的过程中，⊙P 始终与x 轴相交；（3）设⊙P 与x 轴相交于M (x 1, 0)、N (x 2, 0)两点，当△AMN 为等腰三角形时，求圆心P 的纵坐标．图1动感体验请打开几何画板文件名“1426”，拖动圆心P 在抛物线上运动，可以体验到，圆与x 轴总是相交的，等腰三角形AMN 存在五种情况．思路点拨1．不算不知道，一算真奇妙，原来⊙P 在x 轴上截得的弦长MN ＝4是定值．2．等腰三角形AMN 存在五种情况，点P 的纵坐标有三个值，根据对称性，MA ＝MN 和NA ＝NM 时，点P 的纵坐标是相等的．图文解析（1）已知抛物线的顶点为(0,0)，所以y ＝ax 2．所以b ＝0，c ＝0．将1(,)16a 代入y ＝ax 2，得2116a =．解得14a =（舍去了负值）．（2）抛物线的解析式为214y x =，设点P 的坐标为21(,)4x x ．已知A (0, 2)，所以222411(2)4416PA x x x =+-+＞214x ．而圆心P 到x 轴的距离为214x ，所以半径PA ＞圆心P 到x 轴的距离．所以在点P 运动的过程中，⊙P 始终与x 轴相交．（3）如图2，设MN 的中点为H ，那么PH 垂直平分MN ．在Rt △PMH 中，2241416PM PA x ==+，22411()416PH x x ==，所以MH 2＝4．所以MH ＝2．因此MN ＝4，为定值．等腰△AMN 存在三种情况：①如图3，当AM ＝AN 时，点P 为原点O 重合，此时点P 的纵坐标为0．图2 图3 ②如图4，当MA ＝MN 时，在Rt △AOM 中，OA ＝2，AM ＝4，所以OM ＝23．此时x ＝OH ＝232+．所以点P 的纵坐标为22211(232)(31)42344x =+=+=+．如图5，当NA ＝NM 时，根据对称性，点P 的纵坐标为也为423+．图4 图5③如图6，当NA ＝NM ＝4时，在Rt △AON 中，OA ＝2，AN ＝4，所以ON ＝23．此时x ＝OH ＝232-．所以点P 的纵坐标为22211(232)(31)42344x =-=-=-．如图7，当MN ＝MA ＝4时，根据对称性，点P 的纵坐标也为423-．图6 图7考点伸展如果点P 在抛物线214y x =上运动，以点P 为圆心的⊙P 总经过定点B (0, 1)，那么在点P 运动的过程中，⊙P 始终与直线y ＝－1相切．这是因为：设点P 的坐标为21(,)4x x ．已知B (0, 1)，所以2114PB x ==+．而圆心P 到直线y ＝－1的距离也为2114x +，所以半径PB ＝圆心P 到直线y ＝－1的距离．所以在点P 运动的过程中，⊙P 始终与直线y ＝－1相切．例 10 2014年省市中考第25题如图1，在平面直角坐标系中，O 为坐标原点，抛物线y ＝ax 2＋bx ＋c （a ≠0）过O 、B 、C 三点，B 、C 坐标分别为(10, 0)和1824(,)55-，以OB 为直径的⊙A 经过C 点，直线l 垂直x 轴于B 点．（1）求直线BC 的解析式；（2）求抛物线解析式及顶点坐标；（3）点M 是⊙A 上一动点（不同于O 、B ），过点M 作⊙A 的切线，交y 轴于点E ，交直线l 于点F ，设线段ME 长为m ，MF 长为n ，请猜想mn 的值，并证明你的结论；（4）若点P 从O 出发，以每秒1个单位的速度向点B 作直线运动，点Q 同时从B 出发，以相同速度向点C 作直线运动，经过t （0＜t ≤8）秒时恰好使△BPQ 为等腰三角形，请求出满足条件的t 值．图图1 动感体验请打开几何画板文件名“1425”，拖动点M 在圆上运动，可以体验到，△EAF 保持直角三角形的形状，AM 是斜边上的高．拖动点Q 在BC 上运动，可以体验到，△BPQ 有三个时刻可以成为等腰三角形．思路点拨1．从直线BC 的解析式可以得到∠OBC 的三角比，为讨论等腰三角形BPQ 作铺垫．2．设交点式求抛物线的解析式比较简便．3．第（3）题连结AE 、AF 容易看到AM 是直角三角形EAF 斜边上的高．4．第（4）题的△PBQ 中，∠B 是确定的，夹∠B 的两条边可以用含t 的式子表示．分三种情况讨论等腰三角形．图文解析（1）直线BC 的解析式为31542y x =-．（2）因为抛物线与x 轴交于O 、B (10, 0)两点，设y ＝ax (x －10)．代入点C 1824(,)55-，得241832()555a -=⨯⨯-．解得524a =．所以2255255125(10)(5)2424122424y x x x x x =-=-=--．抛物线的顶点为125(5,)24-．（3）如图2，因为EF 切⊙A 于M ，所以AM ⊥EF ．由AE ＝AE ，AO ＝AM ，可得Rt △AOE ≌Rt △AME ．所以∠1＝∠2．同理∠3＝∠4．于是可得∠EAF ＝90°．所以∠5＝∠1．由tan ∠5＝tan ∠1，得MA ME MF MA=．所以ME ·MF ＝MA 2，即mn ＝25．图2（4）在△BPQ 中，cos ∠B ＝45，BP ＝10－t ，BQ ＝t ．分三种情况讨论等腰三角形BPQ ： ①如图3，当BP ＝BQ 时，10－t ＝t ．解得t ＝5．②如图4，当PB ＝PQ 时，1cos 2BQ BP B =∠．解方程14(10)25t t =-，得8013t =． ③如图5，当QB ＝QP 时，1cos 2BP BQ B =∠．解方程14(10)25t t -=，得5013t =．图3 图4 图5考点伸展在第（3）题条件下，以EF 为直径的⊙G 与x 轴相切于点A ．如图6，这是因为AG 既是直角三角形EAF 斜边上的中线，也是直角梯形EOBF 的中位线，因此圆心G 到x 轴的距离等于圆的半径，所以⊙G 与x 轴相切于点A ．图6例11 2014年省市中考第26题在平面直角坐标系中，抛物线y＝x2－(m＋n)x＋mn（m＞n）与x轴相交于A、B两点（点A位于点B的右侧），与y轴相交于点C．（1）若m＝2，n＝1，求A、B两点的坐标；（2）若A、B两点分别位于y轴的两侧，C点坐标是(0,－1)，求∠ACB的大小；（3）若m＝2，△ABC是等腰三角形，求n的值．动感体验请打开几何画板文件名“1426”，点击屏幕左下方的按钮（2），拖动点A在x轴正半轴上运动，可以体验到，△ABC保持直角三角形的形状．点击屏幕左下方的按钮（3），拖动点B在x轴上运动，观察△ABC的顶点能否落在对边的垂直平分线上，可以体验到，等腰三角形ABC有4种情况．思路点拨1．抛物线的解析式可以化为交点式，用m，n表示点A、B、C的坐标．2．第（2）题判定直角三角形ABC，可以用勾股定理的逆定理，也可以用锐角的三角比．3．第（3）题讨论等腰三角形ABC，先把三边长（的平方）罗列出来，再分类解方程．图文解析（1）由y＝x2－(m＋n)x＋mn＝(x－m)(x－n)，且m＞n，点A位于点B的右侧，可知A(m, 0)，B(n, 0)．若m＝2，n＝1，那么A(2, 0)，B(1, 0)．．（2）如图1，由于C(0, mn)，当点C的坐标是(0,－1)，mn＝－1，OC＝1．若A、B两点分别位于y轴的两侧，那么OA·OB＝m(－n)＝－mn＝1．所以OC2＝OA·OB．所以OC OB．OA OC所以tan ∠1＝tan ∠2．所以∠1＝∠2．又因为∠1与∠3互余，所以∠2与∠3互余．所以∠ACB ＝90°．图1 图2 图3（3）在△ABC 中，已知A (2, 0)，B (n , 0)，C (0, 2n )．讨论等腰三角形ABC ，用代数法解比较方便：由两点间的距离公式，得AB 2＝(n －2)2，BC 2＝5n 2，AC 2＝4＋4n 2．①当AB ＝AC 时，解方程(n －2)2＝4＋4n 2，得43n =-（如图2）． ②当CA ＝CB 时，解方程4＋4n 2＝5n 2，得n ＝－2（如图3），或n ＝2（A 、B 重合，舍去）．③当BA ＝BC 时，解方程(n －2)2＝5n 2，得51n +=-（如图4），或51n -=（如图5）．图4 图5考点伸展第（2）题常用的方法还有勾股定理的逆定理．由于C (0, mn )，当点C 的坐标是(0,－1)，mn ＝－1．由A (m , 0)，B (n , 0)，C (0,－1)，得AB 2＝(m －n )2＝m 2－2mn ＋n 2＝m 2＋n 2＋2， BC 2＝n 2＋1，AC 2＝m 2＋1．所以AB 2＝BC 2＋AC 2．于是得到Rt △ABC ，∠ACB ＝90°．第（3）题在讨论等腰三角形ABC 时，对于CA ＝CB 的情况，此时A 、B 两点关于y轴对称，可以直接写出B (－2, 0)，n ＝－2．例 12 2014年省市中考第27题如图1，在△ABC 中，∠ACB ＝90°，AC ＝4cm ，BC ＝3cm ．如果点P 由点B 出发沿BA 方向向点A 匀速运动，同时点Q 由点A 出发沿AC 方向向点C 匀速运动，它们的速度均为1cm/s ．连结PQ ，设运动时间为t （s ）（0＜t ＜4），解答下列问题：（1）设△APQ 的面积为S ，当t 为何值时，S 取得最大值？S 的最大值是多少？（2）如图2，连结PC ，将△PQC 沿QC 翻折，得到四边形PQP ′C ，当四边形PQP ′C 为菱形时，求t 的值；（3）当t 为何值时，△APQ 是等腰三角形？图1 图2动感体验请打开几何画板文件名“1427”，拖动点Q 在AC 上运动，可以体验到，当点P 运动到AB 的中点时，△APQ 的面积最大，等腰三角形APQ 存在三种情况．还可以体验到，当QC ＝2HC 时，四边形PQP ′C 是菱形．思路点拨1．在△APQ 中，∠A 是确定的，夹∠A 的两条边可以用含t 的式子表示．2．四边形PQP ′C 的对角线保持垂直，当对角线互相平分时，它是菱形，．图文解析（1）在Rt △ABC 中，AC ＝4，BC ＝3，所以AB ＝5，sin A ＝35，cos A ＝45．作QD ⊥AB 于D ，那么QD ＝AQ sin A ＝35t ．所以S ＝S △APQ ＝12AP QD ⋅＝13(5)25t t -⨯＝23(5)10t t --＝23515()+1028t --．当52t =时，S 取得最大值，最大值为158．（2）设PP ′与AC 交于点H ，那么PP ′⊥QC ，AH ＝AP cos A ＝4(5)5t -．如果四边形PQP ′C 为菱形，那么PQ ＝PC ．所以QC ＝2HC ．解方程4424(5)5t t ⎡⎤-=⨯--⎢⎥⎣⎦，得2013t =．图3 图4（3）等腰三角形APQ 存在三种情况：①如图5，当AP ＝AQ 时，5－t ＝t ．解得52t =． ②如图6，当PA ＝PQ 时，1cos 2AQ AP A =．解方程14(5)25t t =-，得4013t =． ③如图7，当QA ＝QP 时，1cos 2AP AQ A =．解方程14(5)25t t -=，得2513t =．图5 图6 图7考点伸展在本题情境下，如果点Q 是△PP ′C 的重心，求t 的值．如图8，如果点Q 是△PP ′C 的重心，那么QC ＝23HC ．解方程2444(5)35t t ⎡⎤-=⨯--⎢⎥⎣⎦，得6023t =．图8例 13 2015年省市中考第22题如图1，已知Rt △ABC 中，∠C ＝90°，AC ＝8，BC ＝6，点P 以每秒1个单位的速度从A 向C 运动，同时点Q 以每秒2个单位的速度从A →B →C 方向运动，它们到C 点后都停止运动，设点P 、Q 运动的时间为t 秒．（1）在运动过程中，求P 、Q 两点间距离的最大值；（2）经过t 秒的运动，求△ABC 被直线PQ 扫过的面积S 与时间t 的函数关系式；（3）P ，Q 两点在运动过程中，是否存在时间t ，使得△PQC 为等腰三角形．若存在，求出此时的t 值，若不存在，请说明理由．（24.25≈，结果保留一位小数）图1动感体验请打开几何画板文件名“1522”，拖动点P 在AC 上运动，可以体验到，PQ 与BD 保持平行，等腰三角形PQC 存在三种情况．思路点拨1．过点B 作QP 的平行线交AC 于D ，那么BD 的长就是PQ 的最大值．2．线段PQ 扫过的面积S 要分两种情况讨论，点Q 分别在AB 、BC 上．3．等腰三角形PQC 分三种情况讨论，先罗列三边长．图文解析（1）在Rt △ABC 中，AC ＝8，BC ＝6，所以AB ＝10．如图2，当点Q 在AB 上时，作BD //PQ 交AC 于点D ，那么22AB AQ t AD AP t===．所以AD ＝5．所以CD ＝3．如图3，当点Q 在BC 上时，16228CQ t CP t-==-．又因为623CB CD ==，所以CQ CB CP CD =．因此PQ //BD ．所以PQ 的最大值就是BD ．在Rt △BCD 中，BC ＝6，CD ＝3，所以BD ＝35．所以PQ 的最大值是35．图2 图3 图4（2）①如图2，当点Q 在AB 上时，0＜t ≤5，S △ABD ＝15．由△AQP ∽△ABD ，得2()AQPABDS AP S AD =△△．所以S ＝S △AQP ＝215()5t ⨯＝235t ． ②如图3，当点Q 在BC 上时，5＜t ≤8，S △ABC ＝24．因为S △CQP ＝12CQ CP ⋅＝1(162)(8)2t t --＝2(8)t -，所以S ＝S △ABC －S △CQP ＝24－(t －8)2＝－t 2＋16t －40．（3）如图3，当点Q 在BC 上时，CQ ＝2CP ，∠C ＝90°，所以△PQC 不可能成为等腰三角形．当点Q 在AB 上时，我们先用t 表示△PQC 的三边长：易知CP ＝8－t ．如图2，由QP //BD ，得QP AP BD AD =，即535t =．所以35QP t =．如图4，作QH ⊥AC 于H ．在Rt △AQH 中，QH ＝AQ sin ∠A ＝65t ，AH ＝85t ．在Rt △CQH 中，由勾股定理，得CQ ＝22QH CH +＝2268()(8)55t t +-．分三种情况讨论等腰三角形PQC ：（1）①当PC ＝PQ 时，解方程358t t -=，得6510t =-≈3.4（如图5所示）． ②当QC ＝QP 时，226835()(8)55t t t +-=．整理，得2111283200t t -+=．所以(11t －40)(t －8)＝0．解得4011t =≈3.6（如图6所示），或t ＝8（舍去）． ③当CP ＝CQ 时，22688()(8)55t t t -=+-．整理，得25160t t -=．解得165t =＝3.2（如图7所示），或t ＝0（舍去）．综上所述，当t 的值约为3.4，3.6，或等于3.2时，△PQC 是等腰三角形．图5 图6 图7考点伸展第（1）题求P 、Q 两点间距离的最大值，可以用代数计算说理的方法：①如图8，当点Q 在AB 上时，PQ ＝22QH PH +＝2268()()55t t t +-＝35t ．当Q 与B 重合时，PQ 最大，此时t ＝5，PQ 的最大值为35．②如图9，当点Q 在BC 上时，PQ ＝22CQ CP +＝22(2)CP CP +＝5(8)t -．当Q 与B 重合时，PQ 最大，此时t ＝5，PQ 的最大值为35．综上所述，PQ 的最大值为35．图8 图9§1．3 因动点产生的直角三角形问题课前导学我们先看三个问题：1．已知线段AB ，以线段AB 为直角边的直角三角形ABC 有多少个？顶点C 的轨迹是什么？2．已知线段AB ，以线段AB 为斜边的直角三角形ABC 有多少个？顶点C 的轨迹是什么？3．已知点A (4,0)，如果△OAB 是等腰直角三角形，求符合条件的点B 的坐标．图1 图2 图3如图1，点C 在垂线上，垂足除外．如图2，点C 在以AB 为直径的圆上，A 、B 两点除外．如图3，以OA为边画两个正方形，除了O、A两点以外的顶点和正方形对角线的交点，都是符合题意的点B，共6个．解直角三角形的存在性问题，一般分三步走，第一步寻找分类标准，第二步列方程，第三步解方程并验根．一般情况下，按照直角顶点或者斜边分类，然后按照三角比或勾股定理列方程．有时根据直角三角形斜边上的中线等于斜边的一半列方程更简便．解直角三角形的问题，常常和相似三角形、三角比的问题联系在一起．如果直角边与坐标轴不平行，那么过三个顶点作与坐标轴平行的直线，可以构造两个新的相似直角三角形，这样列比例方程比较简便．如图4，已知A(3, 0)，B(1,－4)，如果直角三角形ABC的顶点C在y轴上，求点C的坐标．我们可以用几何的方法，作AB为直径的圆，快速找到两个符合条件的点C．如果作BD⊥y轴于D，那么△AOC∽△CDB．设OC＝m，那么341mm-=．这个方程有两个解，分别对应图中圆与y轴的两个交点．图4例19 2015年省市中考第21题如图1，已知抛物线E1：y＝x2经过点A(1,m)，以原点为顶点的抛物线E2经过点B(2,2)，点A、B关于y轴的对称点分别为点A′、B′．（1）求m的值及抛物线E2所表示的二次函数的表达式；（2）如图1，在第一象限，抛物线E1上是否存在点Q，使得以点Q、B、B′为顶点的三角形为直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由；（3）如图2，P为第一象限的抛物线E1上与点A不重合的一点，连结OP并延长与抛物线E2相交于点P′，求△PAA′与△P′BB′的面积之比．。

几何最值(解析版)2018年数学全国中考真题-1

2018年数学全国中考真题几何最值（试题一）解析版一、选择题1. （2018山东滨州，11，3分）如图，∠AOB ＝60°，点P 是∠AOB 内的定点且OP ＝3，若点M 、N 分别是射线OA 、OB 上异于点O 的动点，则△PMN 周长的最小值是（） A ．36 B ．33C ．6D ．3第11题图【答案】D【解析】分别以OA 、OB 为对称轴作点P 的对称点P 1，P 2，连接点P 1，P 2，分别交射线OA 、OB 于点M 、N 则此时△PMN 的周长有最小值，△PMN 周长等于＝PM ＋PN ＋MN ＝ P 1N ＋P 2N ＋MN ，根据对称的性质可知，OP 1＝OP 2＝OP ＝3，∠P 1OP 2＝120°，∠OP 1M ＝30°，过点O 作MN 的垂线段，垂足为Q ，在△OP 1Q 中，可知P 1Q ＝32,所以P 1P 2＝2P 1Q ＝3,故△PMN 的周长最小值为3．第11题答图【知识点】轴对称的性质、两点之间线段最短、直角三角形（有一个角为30°）的性质。

2. （2018四川泸州，10题，3分）在平面直角坐标系内，以原点O 为原心，1为半径作圆，点P 在直线323y x =+上运动，过点P 作该圆的一条切线，切点为A ，则PA 的最小值为（）A. 3B. 2C. 3D.2AB OPM N【答案】D【解析】由题可知，B （-2,0），C （0，32），P 为直线上一点，过P 作圆O 的切线PA ，连接AO ，则在Rt △PAO 中，AO=1，由勾股定理可得22AO PO PA -=，要想使PA 最小，要求PO 最小，所以过点O 作OP ⊥BC 于点P ，此时PO=3，PA=2【知识点】一次函数，圆的切线，勾股定理3. （2018四川泸州，10题，3分）已知二次函数22233y ax ax a =+++（其中x 是自变量），当2x ≥时，y 随x 的增大而增大，且21x -≤≤时，y 的最大值为9，则a 的值为（） A.1或2- B.2-或2 C.2 D.1【答案】D【解析】原函数可化为y=a(x+1)2+3a 2-a+3，对称轴为x=-1，当2x ≥时，y 随x 的增大而增大，所以a>0，抛物线开口向上，因为21x -≤≤时，y 的最大值为9，结合对称轴及增减性可得，当x=1时，y=9，带入可得，a 1=1，a 2=-2，又因为a>0，所以a=1 【知识点】二次函数，增减性4. （2018四川绵阳，10，3分）一艘在南北航线上的测量船，于A 点处测得海岛B 在点A 的南偏东30°方向，继续向南航行30海里到达C 点时，测得海岛B 在C 点的北偏东15°方向，那么海岛B 离此航线的最近距离是（结果保留小数点后两位）（参考数据：732.13≈，414.12≈） A.4.64海里 B.5.49海里 C.6.12海里 D.6.21海里【答案】B.【解析】解：如图所示，P A Oy xC B由题意知，∠BAC=30°、∠ACB=15°，作BD ⊥AC 于点D ，以点B 为顶点、BC 为边，在△ABC 内部作∠CBE=∠ACB=15°，则∠BED=30°，BE=CE ，设BD=x ，则AB=BE=CE=2x ，AD=DE=3x ， ∴AC=AD+DE+CE =23x +2x ， ∵AC=30， ∴23x +2x=30，解得：x=21315-≈5.49. 故选B.【知识点】解直角三角形的应用——方向角问题，勾股定理的应用，三角形的外角性质，等腰三角形的判定，含30°角直角三角形的性质，垂线段最短的应用5. （2018四川省宜宾市，8，3分）在△ABC 中，若O 为BC 边的中点，则必有：AB 2+AC 2=2AO 2+2BO 2成立.依据以上结论，解决如下问题：如图，在矩形DEFG 中，已知DE=4，EF=3，点P 在以DE 为直径的半圆上运动，则PF 2 +PG 2的最小值为（）A.10B.192C.34D.10【答案】D【思路分析】取GF 的中点为O ，连接PO ，则根据材料可知PF 2 +PG 2=2PO 2+2OG 2=2PO 2+2×22=8+2OP 2，若使PF 2 +PG 2的值最小，则必须OP 的值最小，所以PO 垂直于GF 时PO 的值最小，即此时才有最小值.【解题过程】取GF 的中点为O ，连接PO ，则根据材料可知PF 2 +PG 2=2PO 2+2OG 2=2PO 2+2× 22=8+2OP 2，若使PF 2 +PG 2的值最小，则必须OP 的值最小，所以PO 垂直于GF 时PO 的值最小，此时PO=1，所以PF 2 +PG 2的最小值为10.【知识点】阅读理解题；矩形的性质6.（2018天津市，11，3）如图，在正方形ABCD中，E，F分别为AD，BC的中点，P为对角线BD上的一个动点，则下列线段的长等于AP+EP最小值的是（）A．AB B．DE C.BD D．AF【答案】D【解析】分析：本题考查正方形的性质，轴对称的性质，取CD中点E′连结AE′、PE′，根据正方形是轴对称图形，可得EP=E′P,AF= AE′，结合图形由线段公理可得AE′为AP+EP最小值，进而可得结果.解：取CD中点E′连结AE′、PE′,由正方形的轴对称性质，可知EP=E′P,AF= AE′∴AP+EP=AP+ E′P,∴AP+EP最小值是A E′,即AP+EP最小值是AF.故选D【知识点】正方形的性质；轴对称；线段公理1.（2018山东德州，12，3分）如图，等边三角形ABC的边长为4,点O是△ABC的中心，120FOG∠=.绕点O旋转FOG∠,分别交线段AB BC、于D E、两点，连接DE,给出下列四个结论:①OD OE=;②ODE BDES S∆∆=;③四边形ODBE的面积始终等于433;④△BDE周长的最小值为6,上述结论中正确的个数是( )A．1 B．2 C. 3 D．4【答案】C第12题图EDFOAB CG第12题答图1EDFOAB CG第12题答图2EDFOAB CG【解析】如图1，连接OB 、OC ，因为点O 是△ABC 的中心，所以120AOB BOC ∠=∠=，OA =OB =OC ，所以 120BOC FOG ∠=∠=， 30ABO BCO ∠=∠=，所以 BOD COE ∠=∠，所以 BOD COE ∆∆≌（ASA ），所以OD =OE ，结论①正确；通过画图确定结论②错误，如当点E 为BC 中点时，ODE BDE S S ∆∆<；因为 BOD COE ∆∆≌，所以BOD COE S ∆∆=S ，所以1 3BOC ABC ODBE S ∆∆=四边形=SS =，结论③正确；因为 BOD COE ∆∆≌，所以BD =CE ，所以BD ＋CE =BC =4，因为120BOC ∠=，OB=OC ，易得DE =，如图2，当OD ⊥AB 时，OD 最小=BD×tan⊥OBD DE 最小=2，所以△BDE 周长的最小值为6, 结论④正确. 故选C.【知识点】旋转，全等，定值，最值2. （2018·新疆维吾尔、生产建设兵团，9，5）如图，点P 是边长为1的菱形ABCD 对角线AC 上的一个动点，点M ，N 分别是AB ，BC 边上的中点，则MP ＋PN 的最小值是（） A ．12B ．1C D ．2【答案】B ．【解析】如下图，取AD 的中点M '，连接M 'N 交AC 于点P ，则由菱形的轴对称性可知M 、M '关于直线AC 对称，从而P M '＝PM ，此时MP ＋PN 的值最小，而易知四边形CD M 'N 是平行四边形，故M 'N ＝CD ＝1，于是，MP ＋PN 的最小值是1，因此选B ．【知识点】菱形的性质；轴对称；最小值；动态问题；最值问题二、填空题1. （2018四川泸州，题，3分）如图5，等腰△ABC 的底边BC=20，面积为120，点F 在边BC 上，且BF=3FC ，EG 是腰AC 的垂直平分线，若点D 在EG 上运动，则△CDF 周长的最小值为 .第16题图NMPDBCAC【答案】18【解析】做△ABC的高AH，因为S=120，BC=20，所以AH=12，△CDF的周长=CF+CD+DF，CF=5，因为EG 是腰AC的垂直平分线，连接AD，AF，可得DA=DC，所以AD+DF的最小值为AF的长度，在Rt△AHF中，HF=5，AH=12，由勾股定理可得AF=13，因此△CDF周长的最小值为18【知识点】三角形面积，垂直平分线，勾股定理2. （2018四川内江，23，6）如图，以AB为直径的⊙O的圆心O到直线l的距离OE＝3，⊙O的半径r＝2，直线AB不垂直于直线l，过点A、B分别作直线l的垂线，垂足分别为点D、C，则四边形ABCD的面积的最大值为．【答案】12【思路分析】由于四边形ABCD为梯形，所以面积为两底之和的一半再乘以高，由已知条件可以通过构造三角形的中位线，证得两底之和与线段OE的长度有关，是一个定值，所以四边形面积的大小取决于高，当直径AB为梯形的高时，面积最大．【解题过程】解：连接DO并延长交CB的延长线于F，∵AD⊥l，BC⊥l，∴AD∥BC，∴∠DAO＝∠FBO，∠ADO ＝∠F，∵OA＝OB，∴△AOD≌△BOF，∴AD＝BF，OD＝OF，∵OE⊥l，∴AD∥BC∥OE，∴ODOF＝DECE，∴DE ＝CE，∴OE＝12CF＝12(BF＋BC)＝12(AD＋BC)，∴AD＋BC＝2OE＝6，∵四边形ABCD的面积＝12(AD＋BC)×CD，∴当AB∥l时，即AB为梯形的高时四边形ABCD的面积最大，最大值为12×6×4＝12．GFEDCB H【知识点】三角形中位线，梯形的面积公式；全等三角形；1. （2018贵州遵义，17题，4分）如图，抛物线y=x 2+2x-3与x 轴交于A 、B 两点，与y 轴交于点C ，点P 是抛物线对称轴上任意一点，若点D 、E 、F 分别是BC 、BP 、PC 的中点，连接DE 、DF ，则DE+DF 的最小值为______第17题图【解析】点D 、E 、F 分别是BC 、BP 、PC 的中点，所以DE 、DF 是△PBC 的中位线，DE=12PC ，DF=12PB ，所以DE+DF=12(PC+PB)，即求PC+PB 的最小值，因为B 、C 为定点，P 为对称轴上一动点，点A 、B 关于对称轴对称，所以连接AC ，与对称轴的交点就是点P 的位置，PC+PB 的最小值等于AC 长度，由抛物线解析式可得，A(-3,0)，C(0,-3)，AC=DE+DF=12【知识点】三角形中位线，勾股定理，二次函数，最短距离问题15．2. （2018四川攀枝花，15，4）如图5，在矩形ABCD 中，AB =4，AD =3，矩形内部有一动点P 满足ABCD PAB S s 矩形31=∆，则点P 到A 、B 两点的距离之和P A +PB 的最小值为 .FlAE BODC【答案】24【解析】设△PAB 中AB 边上的高是h ， ∵ABCD PAB S s 矩形31=∆，∴AD AB h AB ⋅=⋅3121， ∴232==AD h ，∴动点P 在与AB 平行且与AB 的距离是2的直线L 上，如图，作点A 关于直线L 的对称点A'，链接AA',BA',则BA'即为所求的最短距离。

专题26 存在性问题-决胜2018中考数学压轴题全揭秘精品(解析版)

一、选择题二、填空题三、解答题1．（2017山东省淄博市，第24题，9分）如图1，经过原点O 的抛物线2y ax bx =+（a ≠0）与x 轴交于另一点A （32，0），在第一象限内与直线y =x 交于点B （2，t ）．（1）求这条抛物线的表达式；（2）在第四象限内的抛物线上有一点C ，满足以B ，O ，C 为顶点的三角形的面积为2，求点C 的坐标；（3）如图2，若点M 在这条抛物线上，且∠MBO =∠ABO ，在（2）的条件下，是否存在点P ，使得△POC ∽△MOB ？若存在，求出点P 的坐标；若不存在，请说明理由．【答案】（1）223y x x =-；（2）C （1，﹣1）；（3）存在，P 的坐标为（4564，316）或（﹣316，4564）．（3）设MB 交y 轴于点N ，则可证得△ABO ≌△NBO ，可求得N 点坐标，可求得直线BN 的解析式，联立直线BM 与抛物线解析式可求得M 点坐标，过M 作MG ⊥y 轴于点G ，由B 、C 的坐标可求得OB 和OC 的长，由相似三角形的性质可求得OM OP的值，当点P 在第一象限内时，过P 作PH ⊥x 轴于点H ，由条件可证得△MOG ∽△POH ，由OM OP =MG PH =OG OH的值，可求得PH 和OH ，可求得P 点坐标；当P 点在第三象限时，同理可求得P 点坐标．（2）如图1，过C 作CD ∥y 轴，交x 轴于点E ，交OB 于点D ，过B 作BF ⊥CD 于点F ，∵点C 是抛物线上第四象限的点，∴可设C （t ，2t 2﹣3t ），则E （t ，0），D （t ，t ），∴OE =t ，BF =2﹣t ，CD =t ﹣（2t 2﹣3t ）=﹣2t 2+4t ，∴S △OBC =S △CDO +S △CDB =12CD •OE +12CD •BF =12（﹣2t 2+4t ）（t +2﹣t ）=﹣2t 2+4t ，∵△OBC 的面积为2，∴﹣2t 2+4t =2，解得t 1=t 2=1，∴C （1，﹣1）；（3）存在．设MB 交y 轴于点N ，如图2，∵B （2，2），∴∠AOB =∠NOB =45°，在△AOB 和△NOB 中，∵∠AOB =∠NOB ，OB =OB ，∠ABO =∠NBO ，∴△AOB ≌△NOB （ASA ），∴ON =OA =32，∴N （0，32），∴可设直线BN 解析式为y =kx +32，把B 点坐标代入可得2=2k +32，解得k =14，∴直线BN 的解析式为1342y x =+，联立直线BN 和抛物线解析式可得：2134223y x y x x ⎧=+⎪⎨⎪=-⎩，解得：22x y =⎧⎨=⎩或384532x y ⎧=-⎪⎪⎨⎪=⎪⎩，∴M （38-，4532），∵C （1，﹣1），∴∠COA =∠AOB =45°，且B （2，2），∴OB =22，OC =2，∵△POC ∽△MOB ，∴OM OP =OB OC=2，∠POC =∠BOM ，当点P 在第一象限时，如图3，过M 作MG ⊥y 轴于点G ，过P 作PH点睛：本题为二次函数的综合应用，涉及待定系数法、三角形的面积、二次函数的性质、全等三角形的判定和性质、相似三角形的判定和性质、方程思想及分类讨论思想等知识．在（1）中注意待定系数法的应用，在（2）中用C 点坐标表示出△BOC 的面积是解题的关键，在（3）中确定出点P 的位置，构造相似三角形是解题的关键，注意分两种情况．本题考查知识点较多，综合性较强，难度较大．考点：二次函数综合题；存在型；分类讨论；压轴题．学科@网2．（2017山东省潍坊市，第25题，13分）如图1，抛物线c bx ax y ++=2经过平行四边形ABCD 的顶点A （0，3）、B （﹣1，0）、D （2，3），抛物线与x 轴的另一交点为E ．经过点E 的直线l 将平行四边形ABCD 分割为面积相等两部分，与抛物线交于另一点F ．点P 在直线l 上方抛物线上一动点，设点P 的横坐标为t ．（1）求抛物线的解析式；（2）当t 何值时，△PFE 的面积最大？并求最大值的立方根；（3）是否存在点P 使△P AE 为直角三角形？若存在，求出t 的值；若不存在，说明理由．【答案】（1）223y x x =-++；（2）t =1310时，△PEF 的面积最大，最大值的立方根为1710；（3）t 的值为1或152+．【分析】（1）由A 、B 、C 三点的坐标，利用待定系数法可求得抛物线解析式；（2）由A 、C 坐标可求得平行四边形的中心的坐标，由抛物线的对称性可求得E 点坐标，从而可求得直线EF 的解析式，作PH ⊥x 轴，交直线l 于点M ，作FN ⊥PH ，则可用t 表示出PM 的长，从而可表示出△PEF 的面积，再利用二次函数的性质可求得其最大值，再求其最大值的立方根即可；（3）由题意可知有∠P AE =90°或∠APE =90°两种情况，当∠P AE =90°时，作PG ⊥y 轴，利用等腰直角三角形的性质可得到关于t 的方程，可求得t 的值；当∠APE =90°时，作PK ⊥x 轴，AQ ⊥PK ，则可证得△PKE ∽△AQP ，利用相似三角形的性质可得到关于t 的方程，可求得t 的值．式可得：2395523y x y x x ⎧=-+⎪⎨⎪=-++⎩，解得：30x y =⎧⎨=⎩或255125x y ⎧=-⎪⎪⎨⎪=⎪⎩，∴F （25-，5125），如图1，作PH ⊥x 轴，交l 于点M ，作FN ⊥PH ，∵P 点横坐标为t ，∴P （t ，223t t -++），M （t ，3955t -+），∴PM =223t t -++﹣（3955t -+）=213655t t -++，∴S △PEF =S △PFM +S △PEM =12PM •FN +12PM •EH =12PM •（FN +EH ）=12（213655t t -++）（3+25）=2171328917()101010010t --+⨯，∴当t =1310时，△PEF 的面积最大，其最大值为2891710010⨯，∴最大值的立方根为32891710010⨯ =1710；点睛：本题为二次函数的综合应用，涉及待定系数法、平行四边形的性质、二次函数的性质、三角形的面积、直角三角形的性质、相似三角形的判定和性质、方程思想及分类讨论思想等知识．在（1）中注意待定系数示的应用，在（2）中用t 表示出△PEF 的面积是解题的关键，在（3）中分两种情况，分别利用等腰直角三角形和相似三角形的性质得到关于t 的方程是解题的关键．本题考查知识点较多，综合性较强，计算量较大，难度较大．考点：二次函数综合题；动点型；最值问题；存在型；分类讨论；压轴题．3．（2017山东省烟台市，第25题，13分）如图1，抛物线22y ax bx =++与x 轴交于A ，B 两点，与y 轴交于点C ，AB =4，矩形OBDC 的边CD =1，延长DC 交抛物线于点E ．（1）求抛物线的解析式；（2）如图2，点P 是直线EO 上方抛物线上的一个动点，过点P 作y 轴的平行线交直线EO 于点G ，作PH ⊥EO ，垂足为H ．设PH 的长为l ，点P 的横坐标为m ，求l 与m 的函数关系式（不必写出m 的取值范围），并求出l 的最大值；（3）如果点N 是抛物线对称轴上的一点，抛物线上是否存在点M ，使得以M ，A ，C ，N 为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的点M 的坐标；若不存在，请说明理由．【答案】（1）224233y x x =--+；（2）l =221492()3448m -++，l 的最大值为49248；（3）M 的坐标为（2，﹣103）或（﹣4，﹣103）或（﹣2，2）．【解析】（1）∵矩形OBDC 的边CD =1，∴OB =1，∵AB =4，∴OA =3，∴A （﹣3，0），B （1，0），把A 、B两点坐标代入抛物线解析式可得：209320a b a b ++=⎧⎨-+=⎩，解得：2343a b ⎧=-⎪⎪⎨⎪=-⎪⎩，∴抛物线解析式为224233y x x =--+；（3）①当AC 为平行四边形的边时，则有MN ∥AC ，且MN =AC ，如图，过M 作对称轴的垂线，垂足为F ，设AC 交对称轴于点L ，则∠ALF =∠ACO =∠FNM ，在△MFN 和△AOC 中，∵∠MFN =∠AOC ，∠FNM =∠ACO ，MN =AC ，∴△MFN ≌△AOC （AAS ），∴MF =AO =3，∴点M 到对称轴的距离为3，又224233y x x =--+，∴抛物线对称轴为x =﹣1，设M 点坐标为（x ，y ），则|x +1|=3，解得x =2或x =﹣4，当x =2时，y =﹣103，当x =﹣4时，y =103，∴M 点坐标为（2，﹣103）或（﹣4，﹣103）；②当AC 为对角线时，设AC 的中点为K ，∵A （﹣3，0），C （0，2），∴K （﹣32，1），∵点N 在对称轴上，∴点N 的横坐标为﹣1，设M 点横坐标为x ，∴x +（﹣1）=2×（﹣32）=﹣3，解得x =﹣2，此时y =2，∴M （﹣2，2）；综上可知点M 的坐标为（2，﹣103）或（﹣4，﹣103）或（﹣2，2）．点睛：本题为二次函数的综合应用，涉及待定系数法、二次函数的性质、等腰直角三角形的性质、全等三角形的判定和性质、平行四边形的判定和性质、方程思想及分类讨论思想等知识．在（1）中求得A 、B 的坐标是解题的关键，在（2）中确定出PG 与l 的关系是解题的关键，在（3）中确定出M 的位置是解题的关键．本题考查知识点较多，综合性较强，难度适中．考点：二次函数综合题；二次函数的最值；最值问题；存在型；分类讨论；动点型；压轴题．4．（2017山东省青岛市，第24题，12分）已知：Rt △EFP 和矩形ABCD 如图①摆放（点P 与点B 重合），点F ，B （P ），C 在同一直线上，AB =EF =6cm ，BC =FP =8cm ，∠EFP =90°，如图②，△EFP 从图①的位置出发，沿BC 方向匀速运动，速度为1c m /s ，EP 与AB 交于点G ；同时，点Q 从点C 出发，沿CD 方向匀速运动，速度为1c m /s ．过点Q 作QM ⊥BD ，垂足为H ，交AD 于点M ，连接AF ，FQ ，当点Q 停止运动时，△EFQ 也停止运动．设运动时间为t （s ）（0＜t ＜6），解答下列问题：（1）当t 为何值时，PQ ∥BD ？（2）设五边形AFPQM 的面积为y （cm 2），求y 与t 之间的函数关系式；（3）在运动过程中，是否存在某一时刻t ，使8:9:=ABCD AFPQ M S S 矩形五边形？若存在，求出t 的值；若不存在，请说明理由．（4）在运动过程中，是否存在某一时刻t ，使点M 在线段PG 的垂直平分线上？若存在，求出t 的值；若不存在，请说明理由．【答案】（1）724=t ；（2）y 211725812+-=t t （0＜t ＜6）；（3）t =2s ；（4）t =3217s ．【解析】（1）如图1中，当PQ ∥BD 时，CD CQ CB CP =，∴688t t =-，∴724=t ，∴724=t s 时，PQ ∥BD ．（2）如图2中，当0＜t ＜6时，y =S 五边形AFPQM =S 梯形AFCD ﹣S △DMQ ﹣S △PQC =12（8+8﹣t +8）•6﹣12•（6﹣t ）•34（6﹣t ）﹣12•（8﹣t ）•t 211725812+-=t t （0＜t ＜6）．（3）如图2中，假设存在，则有（215117822t t -+）：48=9：8，解得t =2或18（舍弃），∴t =2s 时，S 五边形AFPQM ：S 矩形ABCD =9：8．点睛：本题考查四边形综合题、平行线分线段成比例定理、勾股定理、多边形的面积等知识，解题的关键是学会理由分割法求多边形面积，学会用方程的思想思考问题，属于中考压轴题．考点：四边形综合题；动点型；存在型；压轴题．学科@网5．（2017山西省，第23题，14分）综合与探究如图，抛物线23233393y x x =-++与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ，连接AC 、BC ．点P 沿AC 以每秒1个单位长度的速度由点A 向点C 运动，同时，点Q 沿BO 以每秒2个单位长度的速度由点B 向点O 运动，当一个点停止运动时，另一个点也随之停止运动，连接PQ ，过点Q 作QD ⊥x 轴，与抛物线交于点D ，与BC 交于点E ．连接PD ，与BC 交于点F ．设点P 的运动时间为t 秒（0t >）．（1）求直线BC 的函数表达式．（2）①直接写出P 、D 两点的坐标（用含t 的代数式表示，结果需化简）．②在点P 、Q 运动的过程中，当PQ =PD 时，求t 的值．（3）试探究在点P 、Q 运动的过程中，是否存在某一时刻，使得点F 为PD 的中点．若存在，请直接写出此时t 的值与点F 的坐标；若不存在，请说明理由．【答案】（1）3333y x =-+；（2）①P （132t -，32t ），D （92t -，2438393t t -+ ）；②154；（3）t =3，F （34，1134）．②过点P 作PG ⊥x 轴于点G ，PH ⊥QD 于点H ，得到四边形PGQH 是矩形，从而有QD =2HQ =2PG ，解关于t 的方程即可；（3）由中点坐标公式和F 在直线BC 上得到2690t t -+=，解得t =3．把t =3代入得到F 的坐标．【解析】（1）由y =0，得232333093x x -++=，解得：13x =-，29x =，∴点A 的坐标为（-3，0），点B 的坐标为（9，0）．由x =0，得33y =，∴点C 的坐标为（0，33 ）．设直线BC 的函数表达式为：y kx b =+，∴9033k b b +=⎧⎪⎨=⎪⎩ ，解得：3333k b ⎧=-⎪⎨⎪=⎩，∴直线BC 的函数表达式为：3333y x =-+ ；（2）①过点P 作PG ⊥x 轴于点G ．∵A （-3，0），B （9，0），C （0，33 ）∴AO =3，BO =9，OC =33，∴tan ∠CAO =3333CO AO == ，∴∠CAO =60°，∴∠APG =30°，∵AP =t ，∴AG =12t ，PG =32t ，∴OG =3-12t ，∴P （132t -，32t ）．∵OQ =92t -，∴D 的横坐标为92t -，∵D 在抛物线 23233393y x x =-++上，∴D 的纵坐标为 2323(92)(92)3393y t t =--+-+=2438393t t -+，∴D D （92t -，2438393t t -+ ）．综上所述：P （132t -，32t ），D （92t -，2438393t t -+ ）； ②过点P 作PG ⊥x 轴于点G ，PH ⊥QD 于点H ．∵QD ⊥x 轴，∴四边形PGQH 是矩形，∴HQ =PG ．∵PQ =PD ，PH ⊥QD ，∴QD =2HQ =2PG ．∵P 、D 两点的坐标分别为P （132t -，32t ），D （92t -，2438393t t -+ ），∴2438393t t -+=322t ⨯，解得：10t =（舍去），2154t =，∴当PQ =PD 时，t 的值为154．（3）∵F为PD的中点，且P（132t-，32t），D（92t-，2438393t t-+），由中点坐标公式得：F（334t-，223193912t t-+），∵F在直线BC上，∴22319333(3)3391234t t t-+=--+，∴2690t t-+=，解得：t=3．当t=3时，334t-=34，223193912t t-+=1134，∴F（34，1134）．点睛：本题考查了待定系数法求函数解析式，解直角三角形，矩形的判定和性质，中点坐标公式，方程的解法，正确的作出辅助线是解题的关键．考点：二次函数综合题；动点型；存在型；压轴题．6．（2017广东省，第25题，9分）如图，在平面直角坐标系中，O为原点，四边形ABCO是矩形，点A，C的坐标分别是A（0，2）和C（23，0），点D是对角线AC上一动点（不与A，C重合），连结BD，作DE⊥DB，交x轴于点E，以线段DE，DB为邻边作矩形BDEF．（1）填空：点B的坐标为；（2）是否存在这样的点D，使得△DEC是等腰三角形？若存在，请求出AD的长度；若不存在，请说明理由；（3）①求证：DEDB=33；②设AD=x，矩形BDEF的面积为y，求y关于x的函数关系式（可利用①的结论），并求出y的最小值．【答案】（1）（23，2）；（2）AD 的值为2或23；（3）①证明见解析；②2323433y x x =-+，当x =3时，y 有最小值3．【分析】（1）求出AB 、BC 的长即可解决问题；（2）存在．连接BE ，取BE 的中点K ，连接DK 、KC ．首先证明B 、D 、E 、C 四点共圆，可得∠DBC =∠DCE ，∠EDC =∠EBC ，由tan ∠ACO =AO OC =33，推出∠ACO =30°，∠ACD =60°由△DEC 是等腰三角形，观察图象可知，只有ED =EC ，推出∠DBC =∠DCE =∠EDC =∠EBC =30°，推出∠DBC =∠BCD =60°，可得△DBC 是等边三角形，推出DC =BC =2，由此即可解决问题；（3）①由（2）可知，B 、D 、E 、C 四点共圆，推出∠DBC =∠DCE =30°，由此即可解决问题； ②作DH ⊥AB 于H ．想办法用x 表示BD 、DE 的长，构建二次函数即可解决问题；【解析】（1）∵四边形AOCB 是矩形，∴BC =OA =2，OC =AB =23，∠BCO =∠BAO =90°，∴B （23，2）．故答案为：（23，2）．（2）存在．理由如下：连接BE ，取BE 的中点K ，连接DK 、KC ．∵∠BDE =∠BCE =90°，∴KD =KB =KE =KC ，∴B 、D 、E 、C 四点共圆，∴∠DBC =∠DCE ，∠EDC =∠EBC ，∵tan ∠ACO =AO OC =33，∴∠ACO =30°，∠ACB =60°①如图1中，△DEC 是等腰三角形，观察图象可知，只有ED =EC ，∴∠DBC =∠DCE =∠EDC =∠EBC =30°，∴∠DBC =∠BCD =60°，∴△DBC 是等边三角形，∴DC =BC =2，在Rt △AOC 中，∵∠ACO =30°，OA =2，∴AC =2AO =4，∴AD =AC ﹣CD =4﹣2=2，∴当AD =2时，△DEC 是等腰三角形．②如图2中，∵△DCE 是等腰三角形，易知CD =CE ，∠DBC =∠DEC =∠CDE =15°，∴∠ABD =∠ADB =75°，∴AB =AD =23．综上所述，满足条件的AD 的值为2或23．（3）①由（2）可知，B 、D 、E 、C 四点共圆，∴∠DBC =∠DCE =30°，∴tan ∠DBE =DE DB ，∴DE DB =33． ②如图2中，作DH ⊥AB 于H ．在Rt △ADH 中，∵AD =x ，∠DAH =∠ACO =30°，∴DH =12AD =12x ，AH =22AD DH -=32x ，∴ BH =3232x -，在Rt △BDH 中，BD =22BH DH +=2213()(23)22x x +-，∴ DE =33BD =33•2213()(23)22x x +-，∴矩形BDEF 的面积为y =33 22213[()(23)]22x x +-=23(612)3x x -+，即2323433y x x =-+，∴23(3)33y x =-+， ∵33＞0，∴当x =3时，y 有最小值3．点睛：本题考查相似形综合题、四点共圆、锐角三角函数、相似三角形的判定和性质、勾股定理、二次函数的性质等知识，解题的关键是学会添加辅助线，证明B 、D 、E 、C 四点共圆，学会构建二次函数解决问题，属于中考压轴题．考点：相似形综合题；最值问题；二次函数的最值；动点型；存在型；分类讨论；压轴题．学科@网7．（2017江苏省盐城市，第27题，14分）如图，在平面直角坐标系中，直线122y x =+与x 轴交于点A ，与y 轴交于点C ，抛物线212y x bx c =++经过A 、C 两点，与x 轴的另一交点为点B ．（1）求抛物线的函数表达式；（2）点D 为直线AC 上方抛物线上一动点；①连接BC 、CD ，设直线BD 交线段AC 于点E ，△CDE 的面积为1S ，△BCE 的面积为2S ，求12S S 的最大值； ②过点D 作DF ⊥AC ，垂足为点F ，连接CD ，是否存在点D ，使得△CDF 中的某个角恰好等于∠BAC 的2倍？若存在，求点D 的横坐标；若不存在，请说明理由．【答案】（1）213222y x x =--+；（2）①45；②﹣2或2911-．【分析】（1）根据题意得到A （﹣4，0），C （0，2）代入212y x bx c =++，于是得到结论；（2）①如图，令y =0，解方程得到x 1=﹣4，x 2=1，求得B （1，0），过D 作DM ⊥x 轴于M ，过B 作BN ⊥x 轴交于AC 于N ，根据相似三角形的性质即可得到结论；②根据勾股定理的逆定理得到△ABC 是以∠ACB 为直角的直角三角形，取AB 的中点P ，求得P （32-，0），得到P A =PC =PB =52，过作x 轴的平行线交y 轴于R ，交AC 的延线于G ，情况一：如图，∠DCF =2∠BAC =∠DGC +∠CDG ，情况二，∠FDC =2∠BAC ，解直角三角形即可得到结论．【解析】（1）根据题意得A （﹣4，0），C （0，2），∵抛物线212y x bx c =++经过A 、C 两点，∴1016422b c c ⎧=-⨯-+⎪⎨⎪=⎩，∴322b c ⎧=-⎪⎨⎪=⎩，∴213222y x x =--+；（2）①如图，令y =0，∴2132022x x --+=，∴x 1=﹣4，x 2=1，∴B （1，0），过D 作DM ⊥x 轴于M ，过B 作BN ⊥x 轴交于AC 于N ，∴DM ∥BN ，∴△DME ∽△BNE ，∴12S S =DE BE =DM BN，设D （a ，213222a a --+），∴M （a ，122a +），∵B （1.0），∴N （1，52），∴12S S =DM BN =212252a a --=214(2)55a -++；∴当a =-2时，12S S 的最大值是45； ②∵A （﹣4，0），B （1，0），C （0，2），∴AC =25，BC =5，AB =5，∴AC 2+BC 2=AB 2，∴△ABC 是以∠ACB 为直角的直角三角形，取AB 的中点P ，∴P （32-，0），∴P A =PC =PB =52，∴∠CPO =2∠BAC ，∴tan ∠CPO =tan （2∠BAC ）=43，过作x 轴的平行线交y 轴于R ，交AC 的延长线于G ．分两种情况：情况一：如图，∴∠DCF =2∠BAC =∠DGC +∠CDG ，∴∠CDG =∠BAC ，∴tan ∠CDG =tan ∠BAC =12，即12RC DR =，令D （a ，213222a a --+），∴DR =﹣a ，RC =21322a a --，∴2131222a a a --=-，∴a 1=0（舍去），a 2=﹣2，∴x D =﹣2．情况二，∴∠FDC =2∠BAC ，∴tan ∠FDC =43，设FC =4k ，∴DF =3k ，DC =5k ，∵tan ∠DGC =3k FG =12，∴FG =6k ，∴CG =2k ，DG =35k ，∴∴RC =255k ，RG =455k ，DR =35k ﹣455k =1155k ，∴211551325225kDR a RC a ak -==--，∴a 1=0（舍去），a 2=2911-．综上所述：点D 的横坐标为﹣2或2911-．点睛：本题考查了待定系数法求函数的解析式，相似三角形的判定和性质，解直角三角形，直角三角形的性质，正确的作出辅助线是解题的关键．考点：二次函数综合题；动点型；最值问题；存在型；分类讨论；压轴题．8．（2016四川省内江市）已知抛物线C ：23y x x m =-+，直线l ：y =kx （k ＞0），当k =1时，抛物线C 与直线l 只有一个公共点．（1）求m 的值；（2）若直线l 与抛物线C 交于不同的两点A ，B ，直线l 与直线l 1：y =﹣3x +b 交于点P ，且112OA OB OP+=，求b 的值；（3）在（2）的条件下，设直线l 1与y 轴交于点Q ，问：是否在实数k 使S △APQ =S △BPQ ？若存在，求k 的值，若不存在，说明理由．【答案】（1）4；（2）8；（3）不存在．【分析】（1）两图象有一个交点，则对应的方程组有一组解，即△=0，代入计算即可求出m 的值；（2）作出辅助线，得到△OAC ∽△OPD ，+=2，同理+=2，AC ，BE 是x 2﹣（k +3）x +4=0两根，即可；（3）由S △APQ =S △BPQ 得到AC +BE =2PD ，建立方程（k +3）2=16即可．∵AC，BE是以上一元二次方程的两根，∴AC+BE=k+3，AC×BE=4，∴2343k bk+=+．解得b=8．（3）不存在．理由如下：假设存在，当S△APQ=S△BPQ时，有AP=PB，于是PD﹣AC=PE﹣PD，即AC+BE=2PD．由（2）可知AC+BE=k+3，PD=83k+，∴k+3=2×83k+，即2(3)16k+=．解得k=1（舍去k=﹣7）．当k=1时，A，B两点重合，△BQA不存在，∴不存在实数k使S△APQ=S△BPQ．点睛：此题是二次函数综合题，主要考查了相似三角形的性质和判定，比例的性质，一元二次方程的根与系数的关系，解本题的关键是灵活运用根与系数的关系．考点：二次函数综合题；相似三角形的判定与性质；存在型；和差倍分；压轴题．9．（2016四川省攀枝花市）如图，抛物线2y x bx c =++与x 轴交于A 、B 两点，B 点坐标为（3，0），与y 轴交于点C （0，﹣3）（1）求抛物线的解析式；（2）点P 在抛物线位于第四象限的部分上运动，当四边形ABPC 的面积最大时，求点P 的坐标和四边形ABPC 的最大面积．（3）直线l 经过A 、C 两点，点Q 在抛物线位于y 轴左侧的部分上运动，直线m 经过点B 和点Q ，是否存在直线m ，使得直线l 、m 与x 轴围成的三角形和直线l 、m 与y 轴围成的三角形相似？若存在，求出直线m 的解析式，若不存在，请说明理由．【答案】（1）223y x x =--；（2）P 点坐标为（32，154-）时，四边形ABPC 的面积最大，最大面积为758；（3）存在，113y x =-．【分析】（1）由B 、C 两点的坐标，利用待定系数法可求得抛物线的解析式；（2）连接BC ，则△ABC 的面积是不变的，过P 作PM ∥y 轴，交BC 于点M ，设出P 点坐标，可表示出PM 的长，可知当PM 取最大值时△PBC 的面积最大，利用二次函数的性质可求得P 点的坐标及四边形ABPC 的最大面积；（3）设直线m 与y 轴交于点N ，交直线l 于点G ，由于∠AGP =∠GNC +∠GCN ，所以当△AGB 和△NGC 相似时，必有∠AGB =∠CGB =90°，则可证得△AOC ≌△NOB ，可求得ON 的长，可求出N 点坐标，利用B 、N 两的点坐标可求得直线m 的解析式．【解析】（1）把B 、C 两点坐标代入抛物线解析式可得：9303b c c ++=⎧⎨=-⎩，解得：23b c =-⎧⎨=-⎩，∴抛物线解析式为223y x x =--；（2）如图1，连接BC ，过Py 轴的平行线，交BC 于点M ，交x 轴于点H ，在223y x x =--中，令y =0可得2023x x =--，解得x =﹣1或x =3，∴A 点坐标为（﹣1，0），∴AB =3﹣（﹣1）=4，且OC =3，∴S △ABC =12AB •OC =12×4×3=6，∵B （3，0），C （0，﹣3），∴直线BC 解析式为y =x ﹣3，设P 点坐标为（x ，223x x --），则M 点坐标为（x ，x ﹣3），∵P 点在第四限， ∴PM =23(23)x x x ---- =23x x -+，∴S △PBC =12PM •OH +12PM •HB =12PM •（OH +HB ）=12PM •OB =32PM ，∴当PM 有最大值时，△PBC 的面积最大，则四边形ABPC 的面积最大，∵PM =23x x -+=239()24x --+，∴当x =32时，PM max =94，则S △PBC =3924⨯=278，此时P 点坐标为（32，154-），S 四边形ABPC =S △ABC +S △PBC =6+278=758，即当P 点坐标为（32，154-）时，四边形ABPC 的面积最大，最大面积为758；（3）如图2，设直线m 交y 轴于点N ，交直线l 于点G ，则∠AGP =∠GNC +∠GCN ，当△AGB 和△NGC 相似时，必有∠AGB =∠CGB ，又∠AGB +∠CGB =180°，∴∠AGB =∠CGB =90°，∴∠ACO =∠OBN ，在Rt △AON 和Rt △NOB 中，∵∠AOC =∠NOB ，OC =OB ，∠ACO =∠NBO ，∴Rt △AON ≌Rt △NOB （ASA ），∴ON =OA =1，∴N 点坐标为（0，﹣1），设直线m 解析式为y =kx +d ，把B 、N 两点坐标代入可得301k d d +=⎧⎨=-⎩，解得：131k d ⎧=⎪⎨⎪=-⎩，∴直线m 解析式为113y x =-，即存在满足条件的直线m ，其解析式为113y x =-．点睛：本题为二次函数的综合应用，涉及知识点有待定系数法、二次函数的最值、相似三角形的判定、全等三角形的判定和性质等．在（2）中确定出PM的值最时四边形ABPC的面积最大是解题的关键，在（3）中确定出满足条件的直线m的位置是解题的关键．本题考查知识点较多，综合性较强，特别是第（2）问和第（3）问难度较大．考点：二次函数综合题；存在型；最值问题；二次函数的最值；动点型；压轴题．学科@网10．（2016四川省泸州市）如图，在平面直角坐标系中，点O为坐标原点，直线l与抛物线2y mx nx=+相交于A（1，33），B（4，0）两点．（1）求出抛物线的解析式；（2）在坐标轴上是否存在点D，使得△ABD是以线段AB为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；（3）点P是线段AB上一动点，（点P不与点A、B重合），过点P作PM∥OA，交第一象限内的抛物线于点M，过点M作MC⊥x轴于点C，交AB于点N，若△BCN、△PMN的面积S△B C N、S△P M N满足S△B C N=2S△P M N，求出MNNC的值，并求出此时点M的坐标．【答案】（1）2343y x x =-+；（2）D （1，0）或（0，33112+）或（0，33112-）；（3）2，M （21+，263+）．【分析】（1）由A 、B 两点的坐标，利用待定系数法可求得抛物线解析式；（2）分D 在x 轴上和y 轴上，当D 在x 轴上时，过A 作AD ⊥x 轴，垂足D 即为所求；当D 点在y 轴上时，设出D 点坐标为（0，d ），可分别表示出AD 、BD ，再利用勾股定理可得到关于d 的方程，可求得d 的值，从而可求得满足条件的D 点坐标；（3）过P 作PF ⊥CM 于点F ，利用Rt △ADO ∽Rt △MFP 以及三角函数，可用PF 分别表示出MF 和NF ，从而可表示出MN ，设BC =a ，则可用a 表示出CN ，再利用S △B C N =2S △P M N ，可用PF 表示出a 的值，从而可用PF 表示出CN ，可求得MN NC的值；借助a 可表示出M 点的坐标，代入抛物线解析式可求得a 的值，从而可求出M 点的坐标．【解析】（1）∵A （1，33），B （4，0）在抛物线2y mx nx =+的图象上，∴331640m n m n ⎧+=⎪⎨+=⎪⎩，解得343m n ⎧=-⎪⎨=⎪⎩， ∴抛物线解析式为2343y x x =-+；（2）存在三个点满足题意，理由如下：①当点D 在x 轴上时，如图1，过点A 作AD ⊥x 轴于点D ，∵A （1，33），∴D 坐标为（1，0）；②当点D 在y 轴上时，设D （0，d ），则221(33)AD d =+-，2224BD d =+，且 222(41)(33)36AB =-+=，∵△ABD 是以AB 为斜边的直角三角形，∴222AD BD AB +=，即2221(33)436d d +-++=，解得d =33112±，∴D 点坐标为（0，33112+）或（0，33112-）；综上可知存在满足条件的D 点，其坐标为（1，0）或（0，33112+）或（0，33112-）；（3）如图2，过P 作PF ⊥CM 于点F ，∵PM ∥OA ，∴Rt △ADO ∽Rt △MFP ，∴MF AD PF OD ==33，∴MF =33PF ，在Rt △ABD 中，BD =3，AD =33，∴tan ∠ABD =3，∴∠ABD =60°，设BC =a ，则CN =3a ，在Rt △PFN 中，∠PNF =∠BNC =30°，∴tan ∠PNF =33PF PN =， ∴FN =3PF ，∴MN =MF +FN =43PF ，∵S △B C N =2S △P M N ，∴223124322a PF =⨯⨯， ∴a =22PF ，∴NC =3a =26PF ，∴MN NC =4326PF PF =2，∴MN =2NC =23a ⨯=6a ，∴MC =MN +NC =（63+）a ，∴M 点坐标为（4﹣a ，（63+）a ），又M 点在抛物线上，代入可得23(4)43(4)a a --+-=（63+）a ，解得a =32-或a =0（舍去），OC =4﹣ a =21+，MC =263+，∴点M 的坐标为（21+，263+）．点睛：本题为二次函数的综合应用，涉及知识点有待定系数法、勾股定理、相似三角形的判定和性质、点与函数图象的关系及分类讨论等．在（2）中注意分点D 在x 轴和y 轴上两种情况，在（3）中分别利用PF 表示出MF 和NC 是解题的关键，注意构造三角形相似．本题涉及知识点较多，计算量较大，综合性较强，特别是第（3）问，难度很大．考点：二次函数综合题；分类讨论；动点型；存在型；压轴题．11．（2016四川省甘孜州）如图，顶点为M 的抛物线2(1)4y a x =+-分别与x 轴相交于点A ，B （点A 在点B 的右侧），与y 轴相交于点C （0，﹣3）．（1）求抛物线的函数表达式；（2）判断△BCM 是否为直角三角形，并说明理由．（3）抛物线上是否存在点N （点N 与点M 不重合），使得以点A ，B ，C ，N 为顶点的四边形的面积与四边形ABMC 的面积相等？若存在，求出点N 的坐标；若不存在，请说明理由．【答案】（1）223y x x =+-；（2）△BCM 是直角三角形；（3）N （2212-+，32）或N （2212--，32）或N （﹣2，﹣3）．【分析】（1）用待定系数法求出抛物线解析式即可；（2）由抛物线解析式确定出抛物线的顶点坐标和与x 轴的交点坐标，用勾股定理的逆定理即可；（3）根据题意判断出点N 只能在x 轴上方的抛物线上，由已知四边形的面积相等转化出S △ABN =S △BCM ，然后求出三角形BCM 的面积，再建立关于点N 的坐标的方程求解即可．【解析】（1）∵抛物线2(1)4y a x =+-与y 轴相交于点C （0，﹣3），∴﹣3=a ﹣4，∴a =1，∴抛物线解析式为2(1)4y x =+-，即223y x x =+-；（2）△BCM 是直角三角形．理由：由（1）有，抛物线解析式为2(1)4y x =+-，∵顶点为M 的抛物线2(1)4y a x =+-，∴M （﹣1，﹣4），由（1）抛物线解析式为223y x x =+-，令y =0，∴2230x x +-=，∴1x =﹣3，2x =1，∴A （1，0），B（﹣3，0），∴2BC =9+9=18，2CM =1+1=2，2BM =4+14=20，∴222BC CM BM +=，∴△BCM 是直角三角形；（3）存在．∵以点A ，B ，C ，N 为顶点的四边形的面积与四边形ABMC 的面积相等，且点M 是抛物线的顶点，分两种情况讨论：①点N 在x 轴上方的抛物线上，如图，由（2）有△BCM 是直角三角形，2BC =18，2CM =2，∴BC =32，CM =2，∴S △BCM =12BC ×CM =13222⨯⨯=3，设N （m ，n ），∵以点A ，B ，C ，N 为顶点的四边形的面积与四边形ABMC 的面积相等，∴S △ABN +S △ABC =S △BCM +S △ABC ，∴S △ABN =S △BCM =3，∵A （1，0），B （﹣3，0），∴AB =4，∴S △ABN =12×AB ×n =12×4×n =2n =3，∴n =32，∵N 在抛物线解析式为223y x x =+-的图象上，∴23232m m +-=，∴m 1=2212-+，m 2=2212--，∴N （2212-+，32）或N （2212--，32）；②如图2，点N 在x 轴下方的抛物线上，∵点C 在对称轴的右侧，∴点N 在对称轴右侧不存在，只有在对称轴的左侧，过点M 作MN ∥BC ，交抛物线于点N ，∵B （﹣3，0），C （0，﹣3），∴直线BC 解析式为y =﹣x ﹣3，设MN 的解析式为y =﹣x +b ，∵抛物线解析式为2(1)4y x =+-①，∴M （﹣1，﹣4），∴直线MN 解析式为y =﹣x ﹣5②，联立①②得：2(1)45y x y x ⎧=+-⎨=--⎩，解得：1114x y =-⎧⎨=-⎩（舍），2223x y =-⎧⎨=-⎩，∴N （﹣2，﹣3）．综上所述：N （2212-+，32）或N （2212--，32）或N （﹣2，﹣3）．点睛：此题是二次函数综合题，主要考查了待定系数法求抛物线解析式，直角三角形的判断，图形面积的计算，解本题的关键是判断出△BCM 是直角三角形，难点是要两个四边形面积相等，点N 分在x 轴上方的抛物线上和下方的抛物线上，用方程的思想解决问题是解决（3）的关键，也是初中阶段常用的方法．考点：二次函数综合题；探究型；存在型；分类讨论；压轴题．12．（2016四川省眉山市）已知如图，在平面直角坐标系xOy 中，点A 、B 、C 分别为坐标轴上上的三个点，且OA =1，OB =3，OC =4．（1）求经过A 、B 、C 三点的抛物线的解析式；（2）在平面直角坐标系xOy 中是否存在一点P ，使得以以点A 、B 、C 、P 为顶点的四边形为菱形？若存在，请求出点P 的坐标；若不存在，请说明理由；（3）若点M 为该抛物线上一动点，在（2）的条件下，请求出当|PM ﹣AM |的最大值时点M 的坐标，并直接写出|PM ﹣AM |的最大值．【答案】（1）239344y x x =--+；（2）存在，P （5，3）；（3）M （1，0）或（﹣5，92-）时，|PM ﹣AM |的值最大，为5．【分析】（1）设抛物线的解析式为2y ax bx c =++，把A ，B ，C 三点坐标代入求出a ，b ，c 的值，即可确定出所求抛物线解析式；（2）在平面直角坐标系xOy 中存在一点P ，使得以点A 、B 、C 、P 为顶点的四边形为菱形，理由为：根据OA ，OB ，OC 的长，利用勾股定理求出BC 与AC 的长相等，只有当BP 与AC 平行且相等时，四边形ACBP 为菱形，可得出BP 的长，由OB 的长确定出P 的纵坐标，确定出P 坐标，当点P 在第二、三象限时，以点A 、B 、C 、P 为顶点的四边形只能是平行四边形，不是菱形；（3）利用待定系数法确定出直线P A 解析式，当点M 与点P 、A 不在同一直线上时，根据三角形的三边关系|PM ﹣AM |＜P A ，当点M 与点P 、A 在同一直线上时，|PM ﹣AM |=P A ，当点M 与点P 、A 在同一直线上时，|PM ﹣AM |的值最大，即点M 为直线P A 与抛物线的交点，联立直线AP 与抛物线解析式，求出当|PM ﹣AM |的最大值时M 坐标，确定出|PM ﹣AM |的最大值即可．（3）设直线P A 的解析式为y =kx +b （k ≠0），∵A （1，0），P （5，3），∴530k b k b +=⎧⎨+=⎩，解得：k =34，b =34-，∴直线P A 的解析式为3344y x =-，当点M 与点P 、A 不在同一直线上时，根据三角形的三边关系|PM ﹣AM |＜P A ，当点M 与点P 、A 在同一直线上时，|PM ﹣AM |=P A ，∴当点M 与点P 、A 在同一直线上时，|PM﹣AM |的值最大，即点M 为直线P A 与抛物线的交点，解方程组：2334439344y x y x x ⎧=-⎪⎪⎨⎪=--+⎪⎩，得10x y =⎧⎨=⎩或592x y =-⎧⎪⎨=-⎪⎩，∴点M 的坐标为（1，0）或（﹣5，92-）时，|PM ﹣AM |的值最大，此时|PM ﹣AM |的最大值为5．点睛：此题属于二次函数综合题，涉及的知识有：二次函数的性质，待定系数法确定抛物线解析式、一次函数解析式，菱形的判定，以及坐标与图形性质，熟练掌握待定系数法是解本题的关键．考点：二次函数综合题；存在型；动点型；最值问题；压轴题．学科@网13．（2016山东省临沂市）如图，在平面直角坐标系中，直线y =﹣2x +10与x 轴，y 轴相交于A ，B 两点，点C 的坐标是（8，4），连接AC ，BC ．（1）求过O ，A ，C 三点的抛物线的解析式，并判断△ABC 的形状；（2）动点P 从点O 出发，沿OB 以每秒2个单位长度的速度向点B 运动；同时，动点Q 从点B 出发，沿BC 以每秒1个单位长度的速度向点C 运动．规定其中一个动点到达端点时，另一个动点也随之停止运动．设运动时间为t 秒，当t 为何值时，PA =QA ？（3）在抛物线的对称轴上，是否存在点M ，使以A ，B ，M 为顶点的三角形是等腰三角形？若存在，求出点M 的坐标；若不存在，请说明理由．【答案】（1）21566y x x =-，直角三角形；（2）103；（3）M 1（52，205192+），M 2（52，205192-），M 3（52，5192），M 4（52，5192-）．【分析】（1）先确定出点A ，B 坐标，再用待定系数法求出抛物线解析式；用勾股定理逆定理判断出△ABC 是直角三角形；（2）根据运动表示出OP =2t ，CQ =10﹣t ，判断出Rt △AOP ≌Rt △ACQ ，得到OP =CQ 即可；（3）分三种情况用平面坐标系内，两点间的距离公式计算即可．【解析】（1）∵直线y =﹣2x +10与x 轴，y 轴相交于A ，B 两点，∴A （5，0），B （0，10），∵抛物线过。

2018年山西数学中考试题“几何压轴题”分析

2018年山西数学中考试题“几何压轴题”分析2018年山西数学中考试题分析（5）sdfd作为一名初中数学教师，有必要对中考题进行认真分析，希望可以给今后的教学一些指导，同时也希望给有心的人一点启示。

现在正是假期，可以作点实事。

几何压轴题22．综合与实践问题情境：在数学活动课上，老师出示了这样一个问题：如图1，在矩形ABCD中，AD=2AB，E是AB延长线上一点，且BE=AB，连接DE，交BC于点M，以DE为一边在DE的左下方作正方形DEFG，连接AM．试判断线段AM与DE的位置关系．探究展示：勤奋小组发现，AM垂直平分DE，并展示了如下的证明方法：证明：∵BE=AB，∴AE=2AB．∵AD=2AB，∴AD=AE．∵四边形ABCD是矩形，∴AD∥BC．即AM是△ADE的DE边上的中线，又∵AD=AE，∴AM⊥DE．（依据2）∴AM垂直平分DE．反思交流：（1）①上述证明过程中的“依据1”“依据2”分别是指什么？②试判断图1中的点A是否在线段GF的垂直平分线上，请直接回答，不必证明；（2）创新小组受到勤奋小组的启发，继续进行探究，如图2，连接CE，以CE为一边在CE的左下方作正方形CEFG，发现点G在线段BC的垂直平分线上，请你给出证明；探索发现：（3）如图3，连接CE，以CE为一边在CE的右上方作正方形CEFG，可以发现点C，点B都在线段AE的垂直平分线上，除此之外，请观察矩形ABCD和正方形CEFG的顶点与边，你还能发现哪个顶点在哪条边的垂直平分线上，请写出一个你发现的结论，并加以证明．【解答】解：（1）①依据1：两条直线被一组平行线所截，所得的对应线段成比例（或平行线分线段成比例）．依据2：等腰三角形顶角的平分线，底边上的中线及底边上的高互相重合（或等腰三角形的“三线合一”）．②答：点A在线段GF的垂直平分线上．理由：∵DG∥AM∥EF，DE∥FG，且AM垂直平分DE，∴AM也垂直平分GF,即点A在线段GF的垂直平分线上．（2）证明：如图2，过点G作GH⊥BC于点H，∵四边形ABCD是矩形，点E在AB的延长线上，∴∠CBE=∠ABC=∠GHC=90°，∴∠BCE+∠BEC=90°．∵四边形CEFG为正方形，∴CG=CE，∠GCE=90°，∴∠BCE+∠BCG=90°．∴∠2BEC=∠BCG．∴△GHC≌△CBE．∴HC=BE，∵四边形ABCD是矩形，∴AD=BC．∵AD=2AB，BE=AB，∴BC=2BE=2HC，∴HC=BH．∴GH垂直平分BC．∴点G在BC的垂直平分线上．（3）答：点F在BC边的垂直平分线上（或点F在AD边的垂直平分线上）．证明：如图3，过点F作FM⊥BC于点M，过点E作EN⊥FM于点N．∴∠BMN=∠ENM=∠ENF=90°．∵四边形ABCD是矩形，点E在AB的延长线上，∴∠CBE=∠ABC=90°，∴四边形BENM为矩形．∴BM=EN，∠BEN=90°．∴∠1+∠2=90°．∵四边形CEFG为正方形，∴EF=EC，∠CEF=90°．∴∠2+∠3=90°．∴∠1=∠3．∵∠CBE=∠ENF=90°，∴△ENF≌△EBC．∴NE=BE．∴BM=BE．∵四边形ABCD是矩形，∴AD=BC．∵AD=2AB，AB=BE．∴BC=2BM．∴BM=MC．∴FM垂直平分BC．∴点F在BC边的垂直平分线上．【点评】此题是几何综合题，以特殊矩形与正方形为背景，围绕判断点在线段的垂直平分线上展开探究，主要考查了正方形、矩形的性质，全等三角形的判定和性质，线段垂直平分线的判定和性质，构造全等三角形是解决问题的关键．sdfd【总评】2018年山西数学中考试题中的几何压轴题并没有以平移、旋转、轴对称构图,而是以变换顶点、变换相对位置进行构图；在第（1）小题中还对证明过程中的依据进行了考查，特别是“依据1”考查了“平行线分线段成比例定理”还很容易填错，再次提醒我们虽然证明过程中的依据不要求写，但你必须清楚地知道依据是什么；勾股弦图不仅给我们提供了证明勾股定理的方法，还提供了以正方形的边为斜边的全等三角形的构造方法；第（3）小题中“点A在线段CE的垂直平分线上”是错解，这儿就需要我们严谨的求学态度，而决不能是看见像。

安徽2018年中考压轴题专题二几何最值问题

安徽2018年中考压轴题专题二几何最值问题题型1三角形中最值问题例题1(2017·贵州毕节)如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为()A.B.C.D.6题型2四边形中最值问题例题2如图,在△APB中,AB=2,∠APB=90°,在AB的同侧作等边△ABD、等边△APE和等边△BPC,则四边形PCDE面积的最大值是.题型3圆中最值问题典例3在☉O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在☉O上,且OP⊥PQ.(1)如图1,当PQ∥AB时,求PQ的长度;(2)如图2,当点P在BC上移动时,求PQ长的最大值.跟踪练习1.(2017·辽宁营口)如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为()A.4B.5C.6D.72.如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为()A.2B.3C.4D.43.(2017·合肥蜀山区模拟)如图,☉O的半径是2,直线l与☉O相交于A,B两点,M,N是☉O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是()A.2B.4C.4D.84.(2017·山东威海)如图,△ABC为等边三角形,AB=2,若P为△ABC内一动点,且满足∠P AB=∠ACP,则线段PB长度的最小值为.5.如图,正方形ABCD的长为8 cm,E,F,G,H分别是AB,BC,CD,DA上的动点,且AE=BF=CG=DH,则四边形EFGH面积的最小值是cm2.6.如图,以点P(2,0)为圆心,为半径作圆,点M(a,b)是☉P上的一点,则的最大值是.7.在Rt△ABC中,∠BAC=90°,AC=AB=4,D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.(1)如图1,当α=90°时,线段BD1的长等于,线段CE1的长等于.(直接填写结果)(2)如图2,当α=135°时,求证:BD1=CE1,且BD1⊥CE1.(3)①设BC的中点为M,则线段PM的长为;②点P到AB所在直线的距离的最大值为.8.(2017·湖北宜昌)正方形ABCD的边长为1,点O是BC边上的一个动点(与B,C不重合),以O为顶点在BC所在直线的上方作∠MON=90°.(1)当MO经过点A时,①请直接填空:ON(可能,不可能)过D点;(图1仅供分析)②如图2,在ON上截取OE=OA,过E点作EF垂直于直线BC,垂足为F,EH⊥CD于点H,求证:四边形EFCH为正方形. (2)当MO不经过点A时,设OM交边AB于点G,且OG=1.在ON 上存在点P,过P点作PK垂直于直线BC,垂足为K,使得S△PKO =4S△OBG,连接GP,求四边形PKBG的最大面积.9、如图，已知A、B是线段MN上的两点，，，，以A为中心顺时针旋转点M，以B为中心逆时针旋转点N，使M、N两点重合成一点C，构成△ABC，设（1）求x的取值范围；（2）若△ABC为直角三角形，求x的值；（3）探究：△ABC的最大面积？4=MN1=MA 1>MBxAB=。

2018中考数学压轴题探究专题：直角三角形的存在性问题

中考数学解法探究专题直角三角形的存在性问题
考题研究：这类问题主要是已知直角三角形的一边（即直角三角形的两个点确定），求解第三点。这类问题主要是和动点问题结合在一起，主要在于考查学生的探寻能力和分类研究的推理能力，也是近几年来各市地对学生能力提高方面的一个考查。解题攻略：解直角三角形的存在性问题，一般分三步走，第一步寻找分类标准，第二步列方程，第三步解方程并验根．一般情况下，按照直角顶点或者斜边分类，然后按照三角比或勾股定理列方程．有时根据直角三角形斜边上的中线等于斜边的一半列方程更简便．解直角三角形的问题，常常和相似三角形、三角比的问题联系在一起．如果直角边与坐标轴不平行，那么过三个顶点作与坐标轴平行的直线，可以构造两个新的相似直角三角形，这样列比例方程比较简便．在平面直角坐标系中，两点间的距离公式常常用到．怎样画直角三角形的示意图呢？如果已知直角边，那么过直角边的两个端点画垂线，第三个顶点在垂线上；如果已知斜边，那么以斜边为直径画圆，直角顶点在圆上（不含直径的两个端点）．
求证：PD= AB．探究：如图 3，已知△ABC 为直角三角形，斜边 AB=5，AC=4，准外心 P 在边 AC 上，试探究 PA 的长．
5．已知：如图，△ABC 是边长为 4cm 的等边三角形，动点 P、Q 同时从 A、B 两点出发，分别沿 AB、BC 方向匀速移动，它们的速度都是 1cm/s，当点 P 到达点 B 时，P、Q 两点停止运动，设点 P 的运动时间 t（s），解答下列各问题：（1）求△ABC 的面积；（2）当 t 为何值是，△PBQ 是直角三角形？（3）探究：是否存在某一时刻 t，使四边形 APQC 的面积是△ABC 面积的八分之五？如果存在，求出 t 的值；不存在请说明理由．

2018年天津中考数学压轴大题剖析

2018年天津中考数学压轴大题剖析距离2018年天津中考越来越近来，你有没有因为中考数学压轴题而力不从心？平常做题还OK，一到考场就思路断裂？数学压轴题涉及到的学问可大啦，函数？几何？勾股定理？三角形存在性？分类讨论，分两种，分三种？分四种？？分数？小数？带根号？？每一种题目做起来都是相当酸爽了，是不是很想逃避？但是。

但是中考拉开差距还就是他们，那么有没有什么方法能缓解甚至克服呢？其实压轴大题也不是很难，今天我们一起来探究天津中考数学的压轴的一道大题，希望对于大家都会有所收获。

第24题为天津中考的倒数第二道大题，有关图形变换的几何探究题。

这类问题主要有四个考点：三角形面积、三角形长度最值、三角形重叠问题、折叠翻转平移。

在中考中的难度较大，大家应合理使用技巧和基本思路。

咱们下面来一起探究四个类型。

类型一：有关于三角形面积问题主要思路是将三角形面积用我们假设的未知字母表示出来，再通过范围来确定最后面积的值，面积如果不能直接表示的话，可以用两个三角形或者几个三角形和或差的形式来表示。

类型二：长度最值问题的主要方法是应用对称的方法，现做其中一个点或者两个点的对称点再将这几个点连成一条直线，这种情况下取到的是长度的最值情况。

类型三：三角形重叠问题主要考查两类，第一类是给你重叠部分的面积让你求平移的位置，第二类是告诉你平移的距离，让你求重叠部分的面积。

这类问题我们要注意重叠问题随着平移，面积的表达式可能会发生变化，这类我们需要分情况讨论。

类型四：折叠翻转平移这类问题我们要牢记的是折叠翻转平移的图形，前后一致。

无论是各个边长还有边与边的夹角，都是固定不变的，它不会随着翻转平移折叠而改变。

一般会涉及到等腰或者等边三角形的问题。

如果涉及到了，也需要考虑到底是那两条边相等，也会出现多种情况讨论的问题。

这四种情况大致包括了这类题的全部考点（套路），同学们应将这四种套路牢记，并且通过大量练习的方式咱加以巩固，牢记于心，融会贯通。

最值问题-18年中考数学压轴题全揭秘精品(原卷版)(Word最新版)

最值问题-18年中考数学压轴题全揭秘精品（原卷版）通过整理的最值问题-18年中考数学压轴题全揭秘精品（原卷版）相关文档，渴望对大家有所扶植，感谢观看！一、选择题1．（2021四川省乐山市，第9题，3分）已知二次函数（m为常数），当﹣1≤x≤2时，函数值y的最小值为﹣2，则m 的值是（）A．B．C．或D．或2．（2021四川省泸州市，第10题，3分）已知m，n是关于的一元二次方程的两实数根，则的最小值是（）A．7B．11C．12 D．16 3．（2021天津，第11题，3分）如图，在△ABC中，AB=AC，AD、CE是△ABC的两条中线，P 是AD上一个动点，则下列线段的长度等于BP+EP最小值的是（）A．BCB．CEC．ADD．AC 4．（2021临沂，第14题，3分）如图，在平面直角坐标系中，反比例函数（x＞0）的图象与边长是6的正方形OABC的两边AB，BC分别相交于M，N 两点，△OMN的面积为10．若动点P在x轴上，则PM+PN的最小值是（）A．B．10C．D．5．（2021枣庄，第11题，3分）如图，直线与x 轴、y轴分别交于点A和点B，点C、D分别为线段AB、OB的中点，点P为OA上一动点，PC+PD值最小时点P的坐标为（）A．（﹣3，0）B．（﹣6，0）C．（，0）D．（，0）6．（2021山东省菏泽市，第7题，3分）如图，矩形ABOC的顶点A的坐标为（﹣4，5），D是OB的中点，E是OC上的一点，当△ADE的周长最小时，点E的坐标是（）A．（0，）B．（0，）C．（0，2）D．（0，）7．（2021广西贵港市，第12题，3分）如图，在正方形ABCD中，O是对角线AC 与BD的交点，M是BC边上的动点（点M不与B，C重合），CN⊥DM，CN与AB交于点N，连接OM，ON，MN．下列五个结论：①△CNB≌△DMC；②△CON≌△DOM；③△OMN∽△OAD；④AN2+CM2=MN2；⑤若AB=2，则S△OMN的最小值是，其中正确结论的个数是（）A．2B．3C．4D．5 8．（2021新疆乌鲁木齐市，第10题，4分）如图，点A（a，3），B（b，1）都在双曲线上，点C，D，分别是x轴，y轴上的动点，则四边形ABCD周长的最小值为（）A．B．C．D．9．（2021湖北省十堰市，第9题，3分）如图，10个不同的正偶数按下图排列，箭头上方的每个数都等于其下方两数的和，如，表示，则的最小值为（）A．32B．36C．38D．40 10．（2021甘肃省兰州市，第15题，4分）如图1，在矩形ABCD中，动点E从A动身，沿AB→BC方向运动，当点E到达点C时停止运动，过点E做FE⊥AE，交CD于F点，设点E运动路程为x，FC=y，如图2所表示的是y与x的函数关系的大致图象，当点E在BC上运动时，FC的最大长度是，则矩形ABCD的面积是（）A．B．C．6D．11．（2021内蒙古包头市）如图，直线与x轴、y轴分别交于点A和点B，点C、D分别为线段AB、OB的中点，点P为OA上一动点，PC+PD值最小时点P的坐标为（）A．（﹣3，0）B．（﹣6，0）C．（，0）D．（，0）12．（2021内蒙古呼和浩特市）已知a≥2，，，则的最小值是（）A．6B．3C．﹣3D．0 13．（2021天津市）已知二次函数（h为常数），在自变量x的值满足1≤x≤3的状况下，与其对应的函数值y的最小值为5，则h的值为（）A．1或﹣5B．﹣1或5C．1或﹣3D．1或3 14．（2021安徽）如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P 是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为（）A．B．2C．D．15．（2021四川省乐山市）若t为实数，关于x的方程的两个非负实数根为a、b，则代数式的最小值是（）A．﹣15B．﹣16C．15D．16 16．（2021四川省雅安市）如图，在矩形ABCD中，AD=6，AE⊥BD，垂足为E，ED=3BE，点P、Q分别在BD，AD上，则AP+PQ的最小值为（）A．B．C．D．17．（2021浙江省舟山市）二次函数，当m≤x≤n且mn＜0时，y的最小值为2m，最大值为2n，则m+n的值为（）A．B．2C．D．18．（2021湖北省咸宁市）已知菱形OABC在平面直角坐标系的位置如图所示，顶点A（5，0），OB=，点P是对角线OB上的一个动点，D（0，1），当CP+DP最短时，点P的坐标为（）A．（0，0）B．（1，）C．（，）D．（，）19．（2021湖北省鄂州市）如图，菱形ABCD的边AB=8，∠B=60°，P是AB上一点，BP=3，Q是CD边上一动点，将梯形APQD 沿直线PQ折叠，A的对应点A′．当CA′的长度最小时，CQ的长为（）A．5B．7C．8D．20．（2021南宁，第11题，3分）如图，AB是⊙O的直径，AB=8，点M在⊙O上，∠MAB=20°，N是弧MB的中点，P是直径AB上的一动点．若MN=1，则△PMN周长的最小值为（）A．4 B．5 C．6 D．7 21．（2021乐山，第10题，3分）如图，已知直线与x轴、y轴分别交于A、B两点，P是以C（0，1）为圆心，1为半径的圆上一动点，连结PA、PB．则△PAB面积的最大值是（）A．8 B．12 C．D．22．（2021武汉，第10题，3分）如图，△ABC，△EFG 均是边长为2的等边三角形，点D是边BC、EF的中点，直线AG、FC相交于点M．当△EFG绕点D旋转时，线段BM长的最小值是（）A．B．C．D．二、填空题23．（2021四川省内江市，第25题，6分）如图，已知直线l1∥l2，l1、l2之间的距离为8，点P到直线l1的距离为6，点Q到直线l2的距离为4，PQ=，在直线l1上有一动点A，直线l2上有一动点B，满足AB⊥l2，且PA+AB+BQ最小，此时PA+BQ= ．24．（2021四川省绵阳市，第17题，3分）将形态、大小完全相同的两个等腰三角形如图所示放置，点D在AB边上，△DEF绕点D旋转，腰DF和底边DE 分别交△CAB的两腰CA，CB于M，N两点，若CA=5，AB=6，AB=1：3，则MD+的最小值为．25．（2021山东省东营市，第15题，4分）如图，已知菱形ABCD的周长为16，面积为，E为AB的中点，若P为对角线BD上一动点，则EP+AP的最小值为．26．（2021山东省威海市，第18题，3分）如图，△A BC 为等边三角形，AB=2．若P为△ABC内一动点，且满足∠PAB=∠ACP，则线段PB长度的最小值为．27．（2021浙江省台州市，第16题，5分）如图，有一个边长不定的正方形ABCD，它的两个相对的顶点A，C分别在边长为1的正六边形一组平行的对边上，另外两个顶点B，D在正六边形内部（包括边界），则正方形边长a的取值范围是．28．（2021衢州，第15题，4分）如图，在直角坐标系中，⊙A的圆心A的坐标为（﹣1，0），半径为1，点P 为直线上的动点，过点P作⊙A的切线，切点为Q，则切线长PQ的最小值是．29．（2021金华，第16题，4分）在一空旷场地上设计一落地为矩形ABCD的小屋，AB+BC=10m，拴住小狗的10m 长的绳子一端固定在B点处，小狗在不能进入小屋内的条件下活动，其可以活动的区域面积为S（m2）（1）如图1，若BC=4m，则S= m2．（2）如图2，现考虑在（1）中矩形ABCD小屋的右侧以CD 为边拓展一正△CDE区域，使之变成落地为五边形ABCED的小屋，其他条件不变，则在BC的变更过程中，当S取得最小值时，边BC 的长为m．30．（2021湖北省随州市，第15题，3分）如图，∠AOB的边OB与x轴正半轴重合，点P是OA上的一动点，点N（3，0）是OB上的确定点，点M是ON的中点，∠AOB=30°，要使PM+PN 最小，则点P的坐标为．31．（2021怀化，第16题，4分）如图，在菱形ABCD中，∠ABC=120°，AB=10cm，点P是这个菱形内部或边上的一点．若以P，B，C为顶点的三角形是等腰三角形，则P，A（P，A两点不重合）两点间的最短距离为cm．32．（2021贵州省贵阳市，第15题，4分）如图，在矩形纸片ABCD中，AB=2，AD=3，点E是AB的中点，点F是AD边上的一个动点，将△AEF沿EF所在直线翻折，得到△A′EF，则A′C的长的最小值是．33．（2021吉林省长春市）如图，在平面直角坐标系中，菱形OABC的顶点A在x轴正半轴上，顶点C的坐标为（4，3）．D是抛物线上一点，且在x轴上方．则△BCD的最大值为．34．（2021四川省内江市）如图所示，已知点C（1，0），直线y=﹣x+7与两坐标轴分别交于A，B两点，D，E分别是AB，OA上的动点，则△CDE周长的最小值是．35．（2021山东省日照市）如图，直线与x轴、y轴分别交于点A、B；点Q是以C （0，﹣1）为圆心、1为半径的圆上一动点，过Q点的切线交线段AB于点P，则线段PQ的最小是．36．（2021江苏省常州市）如图，△APB中，AB=2，∠APB=90°，在AB的同侧作正△ABD、正△APE和正△BPC，则四边形PCDE面积的最大值是．37．（2021河北省）如图，已知∠AOB=7°，一条光线从点A动身后射向OB边．若光线与OB边垂直，则光线沿原路返回到点A，此时∠A=90°-7°=83°．当∠A<83°时，光线射到OB边上的点A1后，经OB反射到线段AO上的点A2，易知∠1=∠2．若A1A2⊥AO，光线又会沿A2→A1→A原路返回到点A，此时∠A=__ ___°．…… 若光线从点A发出后，经若干次反射能沿原路返回到点A，则锐角∠A的最小值=___ ____°．[来源：学38．（2021湖北省咸宁市）如图，边长为4的正方形ABCD内接于点O，点E是上的一动点（不与A、B重合），点F是上的一点，连接OE、OF，分别与AB、BC交于点G，H，且∠EOF=90°，有以下结论：①；②△OGH是等腰三角形；③四边形OGBH的面积随着点E位置的变更而变更；④△GBH周长的最小值为．其中正确的是（把你认为正确结论的序号都填上）．39．（2021福建省南平市）如图，等腰△ABC 中，CA=CB=4，∠ACB=120°，点D在线段AB上运动（不与A、B 重合），将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ，给出下列结论：①CD=CP=CQ；②∠PCQ的大小不变；③△PCQ面积的最小值为；④当点D在AB的中点时，△PDQ是等边三角形，其中全部正确结论的序号是．40．（2021湖北省随州市）如图，直线y=x+4与双曲线（k≠0）相交于A（﹣1，a）、B两点，在y轴上找一点P，当PA+PB的值最小时，点P的坐标为．41．（2021玉林防城港，第18题，3分）如图，已知正方形ABCD边长为3，点E在AB边上且BE=1，点P，Q分别是边BC，CD的动点（均不与顶点重合），当四边形AEPQ的周长取最小值时，四边形AEPQ的面积是．42．（2021攀枝花，第15题，4分）如图，在边长为2的等边△ABC中，D为BC的中点，E是AC边上一点，则BE+DE的最小值为．43．（2021孝感，第16题，3分）如图，四边形ABCD是矩形纸片，AB=2．对折矩形纸片ABCD，使AD与BC重合，折痕为EF；展平后再过点B折叠矩形纸片，使点A落在EF上的点N，折痕BM与EF相交于点Q；再次展平，连接BN，MN，延长MN交BC于点G．有如下结论：①∠ABN=60°；②AM=1；③QN=；④△BMG是等边三角形；⑤P为线段BM上一动点，H是BN的中点，则PN+PH的最小值是．其中正确结论的序号是．44．（2021鄂州，第16题，3分）如图，∠AOB=30°，点M、N分别是射线OA、OB上的动点，OP平分∠AOB，且OP=6，当△PMN的周长取最小值时，四边形PMON 的面积为．45．（2021黄石，第15题，3分）一食堂须要购买盒子存放食物，盒子有A，B两种型号，单个盒子的容量和价格如表．现有15升食物须要存放且要求每个盒子要装满，由于A型号盒子正做促销活动：购买三个及三个以上可一次性返还现金4元，则购买盒子所须要最少费用为元．三、解答题46．（2021云南省，第18题，6分）某商店用1000元人民币购进水果销售，过了一段时间，又用2400元人民币购进这种水果，所购数量是第一次购进数量的2倍，但每千克的价格比第一次购进的贵了2元．（1）该商店第一次购进水果多少千克？（2）假设该商店两次购进的水果按相同的标价销售，最终剩下的20千克按标价的五折实惠销售．若两次购进水果全部售完，利润不低于950元，则每千克水果的标价至少是多少元？注：每千克水果的销售利润等于每千克水果的销售价格与每千克水果的购进价格的差，两批水果全部售完的利润等于两次购进水果的销售利润之和．47．（2021内蒙古呼和浩特市，第25题，10分）在平面直角坐标系xOy中，抛物线与y轴交于点C，其顶点记为M，自变量x=﹣1和x=5对应的函数值相等．若点M在直线l：y=﹣12x+16上，点（3，﹣4）在抛物线上．（1）求该抛物线的解析式；（2）设对称轴右侧x轴上方的图象上任一点为P，在x轴上有一点A（，0），试比较锐角∠PCO与∠ACO的大小（不必证明），并写出相应的P点横坐标x的取值范围．（3）直线l与抛物线另一交点记为B，Q为线段BM上一动点（点Q不与M重合），设Q点坐标为（t，n），过Q作QH⊥x轴于点H，将以点Q，H，O，C为顶点的四边形的面积S表示为t的函数，标出自变量t 的取值范围，并求出S可能取得的最大值．48．（2021内蒙古赤峰市，第26题，14分）如图，二次函数（a≠0）的图象交x轴于A、B两点，交y轴于点D，点B的坐标为（3，0），顶点C的坐标为（1，4）．（1）求二次函数的解析式和直线BD的解析式；（2）点P 是直线BD上的一个动点，过点P作x轴的垂线，交抛物线于点M，当点P在第一象限时，求线段PM长度的最大值；（3）在抛物线上是否存在异于B、D的点Q，使△BDQ中BD边上的高为？若存在求出点Q的坐标；若不存在请说明理由．49．（2021内蒙古通辽市，第26题，12分）在平面直角坐标系xOy中，抛物线过点A（﹣2，0），B（2，2），与y轴交于点C．（1）求抛物线的函数表达式；（2）若点D在抛物线的对称轴上，求△ACD的周长的最小值；（3）在抛物线的对称轴上是否存在点P，使△ACP是直角三角形？若存在干脆写出点P的坐标，若不存在，请说明理由．50．（2021吉林省长春市，第24题，12分）定义：对于给定的两个函数，任取自变量x 的一个值，当x＜0时，它们对应的函数值互为相反数；当x≥0时，它们对应的函数值相等，我们称这样的两个函数互为相关函数．例如：一次函数y=x﹣1，它的相关函数为．（1）已知点A（﹣5，8）在一次函数y=ax﹣3的相关函数的图象上，求a的值；（2）已知二次函数．①当点B（m，）在这个函数的相关函数的图象上时，求m的值；②当﹣3≤x≤3时，求函数的相关函数的最大值和最小值；（3）在平面直角坐标系中，点M，N的坐标分别为（﹣，1），（，1}），连结MN．干脆写出线段MN与二次函数的相关函数的图象有两个公共点时n的取值范围．51．（2021四川省乐山市，第26题，13分）如图1，抛物线：与：相交于点O、C，与分别交x轴于点B、A，且B为线段AO的中点．（1）求的值；（2）若OC⊥AC，求△OAC 的面积；（3）抛物线C2的对称轴为l，顶点为M，在（2）的条件下：①点P为抛物线C2对称轴l上一动点，当△PAC的周长最小时，求点P的坐标；②如图2，点E在抛物线C2上点O与点M之间运动，四边形OBCE的面积是否存在最大值？若存在，求出面积的最大值和点E的坐标；若不存在，请说明理由．52．（2021四川省内江市，第27题，12分）如图，在⊙O中，直径CD垂直于不过圆心O 的弦AB，垂足为点N，连接AC，点E在AB上，且AE=CE．（1）求证：AC2=AE•AB；（2）过点B作⊙O的切线交EC的延长线于点P，试推断PB与PE是否相等，并说明理由；（3）设⊙O半径为4，点N为OC中点，点Q在⊙O上，求线段PQ的最小值．53．（2021四川省内江市，第28题，12分）如图，在平面直角坐标系中，抛物线（a≠0）与y轴交与点C（0，3），与x轴交于A、B两点，点B 坐标为（4，0），抛物线的对称轴方程为x=1．（1）求抛物线的解析式；（2）点M从A点动身，在线段AB上以每秒3个单位长度的速度向B点运动，同时点N从B点动身，在线段BC上以每秒1个单位长度的速度向C点运动，其中一个点到达终点时，另一个点也停止运动，设△MBN的面积为S，点M运动时间为t，试求S与t的函数关系，并求S的最大值；（3）在点M运动过程中，是否存在某一时刻t，使△MBN为直角三角形？若存在，求出t值；若不存在，请说明理由．54．（2021四川省凉山州，第24题，8分）为了推动我州校内篮球运动的发展，2021年四川省中小学生男子篮球赛于2月在西昌成功举办．在此期间，某体育文化用品商店支配一次性购进篮球和排球共60个，其进价与售价间的关系如下表：（1）商店用4200元购进这批篮球和排球，求购进篮球和排球各多少个？（2）设商店所获利润为y（单位：元），购进篮球的个数为x（单位：个），请写出y与x之间的函数关系式（不要求写出x的取值范围）；（3）若要使商店的进货成本在4300元的限额内，且全部销售完后所获利润不低于1400元，请你列举出商店全部进货方案，并求出最大利润是多少？55．（2021四川省凉山州，第28题，12分）如图，在平面直角坐标系中，抛物线（a≠0）与x轴交于A、B两点，与y轴交于点C，且OA=2，OB=8，OC=6．（1）求抛物线的解析式；（2）点M从A点动身，在线段AB上以每秒3个单位长度的速度向B点运动，同时，点N从B动身，在线段BC上以每秒1个单位长度的速度向C点运动，当其中一个点到达终点时，另一个点也停止运动，当△MBN存在时，求运动多少秒使△MBN的面积最大，最大面积是多少？（3）在（2）的条件下，△MBN面积最大时，在BC上方的抛物线上是否存在点P，使△BPC的面积是△MBN面积的9倍？若存在，求点P的坐标；若不存在，请说明理由．56．（2021四川省南充市，第24题，10分）如图，在正方形ABCD中，点E、G分别是边AD、BC的中点，AF=AB．（1）求证：EF⊥AG；（2）若点F、G分别在射线AB、BC上同时向右、向上运动，点G运动速度是点F 运动速度的2倍，EF⊥AG是否成立（只写结果，不需说明理由）？（3）正方形ABCD的边长为4，P是正方形ABCD内一点，当，求△PAB 周长的最小值．57．（2021四川省成都市，第26题，8分）随着地铁和共享单车的发展，“地铁+单车”已成为很多市民出行的选择，李华从文化宫站动身，先乘坐地铁，打算在离家较近的A，B，C，D，E中的某一站出地铁，再骑共享单车回家，设他出地铁的站点与文化宫距离为x（单位：千米），乘坐地铁的时间y1（单位：分钟）是关于x的一次函数，其关系如下表：（1）求y1关于x的函数表达式；（2）李华骑单车的时间（单位：分钟）也受x的影响，其关系可以用来描述，请问：李华应选择在那一站出地铁，才能使他从文化宫回到家所需的时间最短？并求出最短时间．58．（2021四川省泸州市，第25题，12分）如图，已知二次函数（a≠0）的图象经过A（﹣1，0）、B（4，0）、C（0，2）三点．（1）求该二次函数的解析式；（2）点D是该二次函数图象上的一点，且满足∠DBA=∠CAO（O是坐标原点），求点D的坐标；（3）点P是该二次函数图象上位于一象限上的一动点，连接PA分别交BC，y轴与点E、F，若△PEB、△CEF 的面积分别为S1、S2，求S1﹣S2的最大值．59．（2021四川省绵阳市，第25题，14分）如图，已知△ABC中，∠C=90°，点M从点C动身沿CB方向以1cm/s的速度匀速运动，到达点B停止运动，在点M的运动过程中，过点M作直线MN交AC于点N，且保持∠NMC=45°，再过点N作AC的垂线交AB于点F，连接MF，将△MNF 关于直线NF对称后得到△ENF，已知AC=8cm，BC=4cm，设点M 运动时间为t（s），△ENF与△ANF重叠部分的面积为y（cm2）．（1）在点M的运动过程中，能否使得四边形MNEF为正方形？假如能，求出相应的t值；假如不能，说明理由；（2）求y关于t的函数解析式及相应t的取值范围；（3）当y取最大值时，求sin∠NEF的值．60．（2021四川省达州市，第22题，8分）宏兴企业接到一批产品的生产任务，按要求必需在14天内完成．已知每件产品的出厂价为60元．工人甲第x天生产的产品数量为y件，y与x满足如下关系：．（1）工人甲第几天生产的产品数量为70件？（2）设第x天生产的产品成本为P元/件，P与x的函数图象如图．工人甲第x 天创建的利润为W元，求W与x的函数关系式，并求出第几天时，利润最大，最大利润是多少？61．（2021山东省东营市，第25题，12分）如图，直线分别与x轴、y轴交于B、C两点，点A在x轴上，∠ACB=90°，抛物线经过A，B两点．（1）求A、B两点的坐标；（2）求抛物线的解析式；（3）点M是直线BC上方抛物线上的一点，过点M作MH⊥BC于点H，作MD∥y轴交BC于点D，求△DMH周长的最大值．62．（2021山东省日照市，第21题，12分）阅读材料：在平面直角坐标系xOy中，点P（x0，y0）到直线Ax+By+C=0的距离公式为：．例如：求点P0（0，0）到直线4x+3y﹣3=0的距离．解：由直线4x+3y﹣3=0知，A=4，B=3，C=﹣3，∴点P0（0，0）到直线4x+3y﹣3=0的距离为=．依据以上材料，解决下列问题：问题1：点P1（3，4）到直线的距离为；问题2：已知：⊙C 是以点C（2，1）为圆心，1为半径的圆，⊙C与直线相切，求实数b的值；问题3：如图，设点P为问题2中⊙C上的随意一点，点A，B为直线3x+4y+5=0上的两点，且AB=2，恳求出S△ABP的最大值和最小值．63．（2021滨州，第24题，14分）如图，直线y=kx+b （k、b为常数）分别与x轴、y轴交于点A（﹣4，0）、B（0，3），抛物线y=﹣x2+2x+1与y轴交于点C．（1）求直线y=kx+b的函数解析式；（2）若点P（x，y）是抛物线y=﹣x2+2x+1上的随意一点，设点P到直线AB的距离为d，求d关于x的函数解析式，并求d取最小值时点P的坐标；（3）若点E在抛物线y=﹣x2+2x+1的对称轴上移动，点F在直线AB上移动，求CE+EF的最小值．64．（2021山东省潍坊市，第25题，13分）如图1，抛物线经过平行四边形ABCD的顶点A（0，3）、B（﹣1，0）、D（2，3），抛物线与x轴的另一交点为E．经过点E的直线l将平行四边形ABCD 分割为面积相等两部分，与抛物线交于另一点F．点P在直线l上方抛物线上一动点，设点P的横坐标为t．（1）求抛物线的解析式；（2）当t何值时，△PFE的面积最大？并求最大值的立方根；（3）是否存在点P使△PAE为直角三角形？若存在，求出t的值；若不存在，说明理由．65．（2021山东省烟台市，第25题，13分）如图1，抛物线与x轴交于A，B两点，与y轴交于点C，AB=4，矩形OBDC 的边CD=1，延长DC交抛物线于点E．（1）求抛物线的解析式；（2）如图2，点P是直线EO上方抛物线上的一个动点，过点P作y轴的平行线交直线EO于点G，作PH⊥EO，垂足为H．设PH的长为l，点P的横坐标为m，求l与m的函数关系式（不必写出m的取值范围），并求出l的最大值；（3）假如点N是抛物线对称轴上的一点，抛物线上是否存在点M，使得以M，A，C，N为顶点的四边形是平行四边形？若存在，干脆写出全部满足条件的点M的坐标；若不存在，请说明理由．66．（2021山东省聊城市，第25题，12分）如图，已知抛物线与y轴交于点A（0，6），与x轴交于点B（6，0），点P是线段AB上方抛物线上的一个动点．（1）求这条抛物线的表达式及其顶点坐标；（2）当点P移动到抛物线的什么位置时，使得∠PAB=75°，求出此时点P的坐标；（3）当点P从A点动身沿线段AB上方的抛物线向终点B移动，在移动中，点P的横坐标以每秒1个单位长度的速度变动，与此同时点M以每秒1个单位长度的速度沿AO向终点O移动，点P，M移动到各自终点时停止，当两个移点移动t秒时，求四边形PAMB的面积S关于t的函数表达式，并求t 为何值时，S有最大值，最大值是多少？67．（2021广西贵港市）如图，已知一次函数y=x+b的图象与反比例函数（x＜0）的图象交于点A（﹣1，2）和点B，点C在y轴上．（1）当△ABC的周长最小时，求点C的坐标；（2）当时，请干脆写出x的取值范围．68．（2021广西贺州市）如图，矩形的边OA在x轴上，边OC在y轴上，点B的坐标为（10，8），沿直线OD折叠矩形，使点A正好落在BC上的E处，E点坐标为（6，8），抛物线经过O、A、E 三点．（1）求此抛物线的解析式；（2）求AD的长；（3）点P 是抛物线对称轴上的一动点，当△PAD的周长最小时，求点P的坐标．69．（2021广西钦州市）如图1，在平面直径坐标系中，抛物线与x轴交于点A（﹣3，0）．B（1，0），与y轴交于点C．（1）干脆写出抛物线的函数解析式；（2）以OC为半径的⊙O与y轴的正半轴交于点E，若弦CD过AB的中点M，试求出DC的长；（3）将抛物线向上平移个单位长度（如图2）若动点P（x，y）在平移后的抛物线上，且点P在第三象限，恳求出△PDE的面积关于x的函数关系式，并写出△PDE面积的最大值．70．（2021云南省昆明市）如图1，对称轴为直线x=的抛物线经过B（2，0）、C（0，4）两点，抛物线与x轴的另一交点为A．（1）求抛物线的解析式；（2）若点P为第一象限内抛物线上的一点，设四边形COBP的面积为S，求S的最大值；（3）如图2，若M是线段BC上一动点，在x轴是否存在这样的点Q，使△MQC为等腰三角形且△MQB为直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由．71．（2021云南省曲靖市）如图，在平面直角坐标系中，抛物线交x轴于A，B 两点，交y轴于点C（0，3），tan∠OAC=．（1）求抛物线的解析式；（2）点H是线段AC上随意一点，过H作直线HN⊥x轴于点N，交抛物线于点P，求线段PH的最大值；（3）点M是抛物线上随意一点，连接CM，以CM为边作正方形CMEF，是否存在点M使点E恰好落在对称轴上？若存在，恳求出点M的坐标；若不存在，请说明理由．72．（2021内蒙古呼和浩特市）已知二次函数（a＜0）的最大值为4，且抛物线过点（，），点P（t，0）是x轴上的动点，抛物线与y轴交点为C，顶点为D．（1）求该二次函数的解析式，及顶点D的坐标；（2）求|PC﹣PD|的最大值及对应的点P的坐标；（3）设Q（0，2t）是y轴上的动点，若线段PQ与函数的图象只有一个公共点，求t的取值．73．（2021内蒙古巴彦淖尔市）如图所示，抛物线经过原点O与点A（6，0）两点，过点A作AC⊥x轴，交直线y=2x﹣2于点C，且直线y=2x﹣2与x轴交于点D．（1）求抛物线的解析式，并求出点C和点D的坐标；（2）求点A关于直线y=2x﹣2的对称点A′的坐标，并推断点A′是否在抛物线上，并说明理由；（3）点P（x，y）是抛物线上一动点，过点P作y轴的平行线，交线段CA′于点Q，设线段PQ的长为l，求l与x的函数关系式及l的最大值．74．（2021四川省乐山市）在直角坐标系xOy中，A（0，2）、B（﹣1，0），将△ABO经过旋转、平移变更后得到如图1所示的△BCD．（1）求经过A、B、C三点的抛物线的解析式；（2）连结AC，点P是位于线段BC上方的抛物线上一动点，若直线PC将△ABC的面积分成1：3两部分，求此时点P的坐标；（3）现将△ABO、△BCD分别向下、向左以1：2的速度同时平移，求出在此运动过程中△ABO与△BCD重叠部分面积的最大值．75．（2021江苏省盐城市）如图1，已知一次函数y=x+3的图象与x轴、y轴分别交于A、B两点，抛物线过A、B两点，且与x轴交于另一点C．（1）求b、c的值；（2）如图1，点D为AC的中点，点E在线段BD上，且BE=2ED，连接CE并延长交抛物线于点M，求点M的坐标；（3）将直线AB绕点A按逆时针方向旋转15°后交y轴于点G，连接CG，如图2，P为△ACG内以点，连接PA、PC、PG，分别以AP、AG为边，在他们的左侧作等边△APR，等边△AGQ，连接QR ①求证：PG=RQ；②求PA+PC+PG的最小值，并求出当PA+PC+PG取得最小值时点P的坐标．76．（2021陕西省）问题提出（1）如图①，已知△ABC，请画出△ABC关于直线AC对称的三角形．问题探究（2）如图②，在矩形ABCD中，AB=4，AD=6，AE=4，AF=2，是否在边BC、CD上分别存在点G、H，使得四边形EFGH的周长最小？若存在，求出它周长的最小值；若不存在，请说明理由．问题解决（3）如图③，有一矩形板材ABCD，AB=3米，AD=6米，现想从今板材中裁出一个面积尽可能大的四边形EFGH部件，使∠EFG=90°，EF=FG=米，∠EHG=45°，经探讨，只有当点E、F、G分别在边AD．AB、BC 上，且AF＜BF，并满足点H在矩形ABCD内部或边上时，才有可能裁出符合要求的部件，试问能否裁得符合要求的面积尽可能大的四边形EFGH部件？若能，求出裁得的四边形EFGH部件的面积；若不能，请说明理由．77．（2021南宁，第24题，10分）如图1，为美化校内环境，某校支配在一块长为60米，宽为40米的长方形空地上修建一个长方形花圃，并将花圃四周余下的空地修建成同样宽的通道，设通道宽为a米．（1）用含a的式子表示花圃的面积．（2）假如通道所占面积是整个长方形空地面积的，求出此时通道的宽．（3）已知某园林公司修建通道、花圃的造价（元）、（元）与修建面积x（m2）之间的函数关系如图2所示，假如学校确定由该公司承建此项目，并要求修建的通道的宽度不少于2米且不超过10米，那么通道宽为多少时，修建的通道和花圃的总造价最低，最低总造价为多少元？78．（2021崇左，第25题，10分）一块材料的形态是锐角三角形ABC，边BC=120mm，高AD=80mm，把它加工成正方形零件如图1，使正方形的一边在BC上，其余两个顶点分别在AB、AC上．（1）求证：。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

∴OA+OB+OC=O′A′+OB+OO′=BA′时值最小； ②当等边△ABቤተ መጻሕፍቲ ባይዱ 的边长为 1 时，OA+OB+OC 的最小值 A′B= ．
3．已知：在直角坐标系中，点 A（0，6），B（8，0），点 C 是线段 AB 的中点， CD⊥OB 交 OB 于点 D，Rt△EFH 的斜边 EH 在射线 AB 上，顶点 F 在射线 AB 的左侧，EF∥OA．点 E 从点 A 出发，以每秒 1 个单位的速度向点 B 运动，到点 B 停止．AE=EF，运动时间为 t（秒）．（1）在 Rt△EFH 中，EF= t ，EH= t ；F（ t ， 6﹣ t ）（用含有 t 的代数式表示）（2）当点 H 与点 C 重合时，求 t 的值．（3）设△EFH 与△CDB 重叠部分图形的面积为 S（S＞0），求 S 与 t 的关系式；（4）求在整个运动过程中 Rt△EFH 扫过的面积．
由旋转的性质可知，∠OCD=60°，∠ADC=∠BOC=120°， ∴∠DAO=360°﹣60°﹣90°﹣120°=90°，故答案为：90°； ②线段 OA，OB，OC 之间的数量关系是 OA2+OB2=OC2．如图 1，连接 OD． ∵△BOC 绕点 C 按顺时针方向旋转 60°得△ADC， ∴△ADC≌△BOC，∠OCD=60°． ∴CD=OC，∠ADC=∠BOC=120°，AD=OB． ∴△OCD 是等边三角形， ∴OC=OD=CD，∠COD=∠CDO=60°， ∵∠AOB=150°，∠BOC=120°， ∴∠AOC=90°， ∴∠AOD=30°，∠ADO=60°． ∴∠DAO=90°．在 Rt△ADO 中，∠DAO=90°， ∴OA2+AD2=OD2． ∴OA2+OB2=OC2．（2）①如图 2，当 α=β=120°时，OA+OB+OC 有最小值．作图如图 2，如图 2，将△AOC 绕点 C 按顺时针方向旋转 60°得△A′O′C，连接 OO′． ∴△A′O′C≌△AOC，∠OCO′=∠ACA′=60°． ∴O′C=OC，O′A′=OA，A′C=BC， ∠A′O′C=∠AOC． ∴△OC O′是等边三角形． ∴OC=O′C=OO′，∠COO′=∠CO′O=60°． ∵∠AOB=∠BOC=120°， ∴∠AOC=∠A′O′C=120°． ∴∠BOO′=∠OO′A′=180°． ∴四点 B，O，O′，A′共线．
边，当三点共线时，两条线段差的最大值就是第三边的长．如图 3， PA 与 PB 的差的最大值就是 AB，此时点 P 在 AB 的延长线上，即 P′．
解决线段和差的最值问题，有时候求函数的最值更方便，建立一次函数或者二次函数求解最值问题．
解题思路：解决平面几何最值问题的常用的方法有：（1）应用两点间线段最短的公理（含应用三角形的三边关系）求最值；（2）应用垂线段最短的性质求最值；（3）应用轴对称的性质求最值；（4）应用二次函数求最值；（5）应用其它知识求最值。例题解析
中考数学解法探究专题几何最值的存在性问题
考题研究：在平面几何的动态问题中，当某几何元素在给定条件变动时，求某几何量（如线段的长度、图形的周长或面积、角的度数以及它们的和与差）的最大值或最小值问题，称为最值问题。从历年的中考数学压轴题型分析来看，经常会考查到距离或者两条线段和差最值得问题，并且这部分题目在中考中失分率很高，应该引起我们的重视。几何最值问题再教材中虽然没有进行专题讲解，到却给了我们很多解题模型，因此在专题复习时进行压轴训练是必要的。解题攻略：最值问题是一类综合性较强的问题，而线段和（差）问题，要归归于几何模型：（1）归于“两点之间的连线中，线段最短”凡属于求 “变动的两线段之和的最小值”时，大都应用这一模型．（2）归于“三角形两边之差小于第三边”凡属于求“变动的两线段之差的最大值” 时，大都应用这一模型．两条动线段的和的最小值问题，常见的是典型的“牛喝水”问题，关键是指出一条对称轴“河流”（如图 1）．三条动线段的和的最小值问题，常见的是典型的“台球两次碰壁” 或“光的两次反射”问题，关键是指出两条对称轴“反射镜面”（如图 2）．两条线段差的最大值问题，一般根据三角形的两边之差小于第三
2．已知，点 O 是等边△ABC 内的任一点，连接 OA，OB，OC．（1）如图 1，已知∠AOB=150°，∠BOC=120°，将△BOC 绕点 C 按顺时针方向旋转 60°得△ADC． ①∠DAO 的度数是 90° ②用等式表示线段 OA，OB，OC 之间的数量关系，并证明；（2）设∠AOB=α，∠BOC=β． ①当 α，β 满足什么关系时，OA+OB+OC 有最小值？请在图 2 中画出符合条件的图形，并说明理由； ②若等边△ABC 的边长为 1，直接写出 OA+OB+OC 的最小值．
【考点】KY：三角形综合题．【分析】（1）①根据旋转变换的性质、四边形内角和为 360°计算即可； ②连接 OD，根据勾股定理解答；（2）①将△AOC 绕点 C 按顺时针方向旋转 60°得△A′O′C，连接 OO′，根据等边三角形的性质解答； ②根据等边三角形的性质计算．【解答】解：（1）①∵∠AOB=150°，∠BOC=120°， ∴∠AOC=90°，
【考点】KY：三角形综合题．【分析】（1）作 EM⊥OA 垂足为 M，由△EFH∽△AOB，得 = ，可以求出 EH，
1．某同学用剪刀沿直线将一片平整的银杏叶减掉一部分（如图），发现剩下的银杏叶的周长比原银杏叶的周长要小，能正确解释这一现象的数学知识是（）
A．两点之间线段最短 B．两点确定一条直线 C．垂线段最短
D．经过直线外一点，有且只有一条直线与这条直线平行【考点】IC：线段的性质：两点之间线段最短．【分析】根据两点之间，线段最短进行解答．【解答】解：某同学用剪刀沿直线将一片平整的银杏叶减掉一部分（如图），发现剩下的银杏叶的周长比原银杏叶的周长要小，能正确解释这一现象的数学知识是两点之间线段最短．故选：A．