中考数学专题复习 几何最值问题
2023中考数学复习:几何最值问题

接FR,BR,RT,ET,AT,
∵A,E关于ON对称,∴AC=EC,同理BD=FD,FR=BR,AT=ET,
∴AC+CD+DB=EC+CD+FD=EF,AT+TR+BR=ET+TR+FR.
∵ET+TR+FR>EF,
∴AC+CD+DB<AT+TR+BR,
的压轴题,发展了学生的几何直观和推理能力的核心素养.
专题四 几何最值问题
返回类型清单
方法点拨
此类问题的解答,关键是要掌握每种模型的特征、辅助线的作法及解
题原理,能在实际问题中发现模型、建构模型,并依据模型解答问题,解
决实际问题.
专题四 几何最值问题
返回类型清单
解题技巧
主要是利用重要的基本事实或者定理,如两点之间线段最短、三角形
动点,设AP=x,PB+PE=y,当点P从A向点C运动时,y与x的函数关系如图
②所示,其中点M是函数图象的最低点,则点M的坐标是( )
A.(4 2,3 5)
B.(2 2,3 5)
C.(3 5,2 2)
D.(3 5,4 2)
例题 4
4
5
6
专题四 几何最值问题— 两点之间线段最短问题
模型二
返回类型清单
两定一动(“胡不归”问题)
模 型 解 读
“胡不归”问题即点P在直线BM上运动的“PA+k•PB(0<k<1)”型
最值问题.如图①,已知sin∠MBN=k,点P为∠MBN其中一边BM上
的一个动点,点A在射线BM,BN的同侧,连接AP,则当“PA+k•PB”的
中考数学最值问题总结(含强化训练)

中考数学最值问题总结(含强化训练)在中学数学题中,最值题是常见题型,围绕最大(小)值所出的数学题是各种各样,就其解法,主要分为几何最值和代数最值两大部分。
一、解决几何最值问题的要领(1)两点之间线段最短;(2)直线外一点与直线上所有点的连线段中,垂线段最短;(3)三角形两边之和大于第三边或三角形两边之差小于第三边(重合时取到最值)。
二、解决代数最值问题的方法要领1.二次函数的最值公式二次函数y ax bx c =++2(a 、b 、c 为常数且a ≠0)其性质中有 ①若a >0当x b a=-2时,y 有最小值。
y ac b a min =-442; ②若a <0当x b a=-2时,y 有最大值。
y ac b a max =-442。
2.一次函数的增减性.一次函数y kx b k =+≠()0的自变量x 的取值范围是全体实数,图象是一条直线,因而没有最大(小)值;但当m x n ≤≤时,则一次函数的图象是一条线段,根据一次函数的增减性,就有最大(小)值。
3. 判别式法.根据题意构造一个关于未知数x 的一元二次方程;再根据x 是实数,推得∆≥0,进而求出y 的取值范围,并由此得出y 的最值。
4.构造函数法.“最值”问题中一般都存在某些变量变化的过程,因此它们的解往往离不开函数。
5. 利用非负数的性质.在实数范围内,显然有a b k k 22++≥,当且仅当a b ==0时,等号成立,即a b k 22++的最小值为k 。
6. 零点区间讨论法.用“零点区间讨论法”消去函数y 中绝对值符号,然后求出y 在各个区间上的最大值,再加以比较,从中确定出整个定义域上的最大值。
7. 利用不等式与判别式求解.在不等式x a ≤中,x a =是最大值,在不等式x b ≥中,x b =是最小值。
8. “夹逼法”求最值.在解某些数学问题时,通过转化、变形和估计,将有关的量限制在某一数值范围内,再通过解不等式获取问题的答案,这一方法称为“夹逼法”。
2024年中考 数学总复习 题型训练四 几何最值问题

题型四几何最值问题类型一利用“垂线段最短”解决最值问题1. 如图,在△ABC中,AC=BC=6,AB=8,点D在AC边上,连接BD,以AD,BD为邻边作▱ADBE,连接DE,则DE的最小值为________.第1题图2. 如图,在△ABC中,AC=BC=6,S△ABC=12,点D为AB的中点,点M,N分别是CD 和BC上的动点,则BM+MN的最小值是________.第2题图3. 如图,四边形ABCD是菱形,对角线AC,BD相交于点O,点P是BD上一动点,点E 是BC上一动点,若AC=6,BD=63,则PC+PE的最小值为________.第3题图4. 如图,在△OAB中,已知∠AOB=35°,点P是边AB上一点,点M,N分别是射线OA,OB上异于点O的动点,连接PO,PM,MN,若∠BOP=10°,OP=6,则PM+MN的最小值为________.第4题图类型二 利用“两点之间线段最短”解决最值问题1. 如图,在矩形ABCD 中,AB =6,AD =8,点P 是矩形ABCD 内一点,记a =S △APB +S △CPD ,b =P A +PB +PC +PD ,则a +b 的最小值为________.第1题图2. 如图,在四边形ABCD 中,∠BAD =120°,∠B =∠D =90°,AB =1,AD =2,M ,N 分别为BC ,CD 边上的动点,则△AMN 周长的最小值为________.第2题图3. 如图,在Rt △ABC 中,∠C =90°,∠ABC =30°,BC =43 ,点D 为边BC 上的动点,点E 为边AB 的中点,连接DE ,DA ,则线段DE +DA 的最小值为________.第3题图4. 如图,在等腰Rt △ABC 中,AB =AC =22 ,∠A =90°,点P 是△ABC 内部一点,且满足S △BCP =12S △ABC ,则PB +PC 的最小值为________.第4题图5. 如图,二次函数y =-23 x 2-43x +2的图象与x 轴分别交于A ,B 两点(点A 在点B 左侧),与y 轴交于点C ,点P 是其对称轴上一点,连接PB ,PC ,BC ,则△PBC 的周长最小为________.第5题图类型三 利用“二次函数性质”解决最值问题(2021.9)1. 我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,此公式与古希腊几何学家海伦提出的公式如出一辙,即三角形的三边长分别为a ,b ,c, 记p =a +b +c 2,则其面积S =p (p -a )(p -b )(p -c ) .这个公式也被称为海伦-秦九韶公式.若p =5,c =4,则此三角形面积的最大值为( )A. 5B. 4C. 25D. 52. 如图,在矩形ABCD 中,AB =2,AD =3,P 是BC 上的任意一点(P 与B ,C 不重合),过点P 作AP ⊥PE ,垂足为P ,PE 交CD 于点E ,连接AE ,在点P 的运动过程中,线段CE 的最大值为________.第2题图3. 如图,在等腰△ABC 中,AC =BC =4,∠C =120°,点P 是AC 上一动点,PD ∥AB ,交BC 于点D ,连接AD ,则点P 在运动过程中,△APD 的面积的最大值为________.第3题图4. 如图,矩形ABCD中,AB=6,BC=4,点E,F分别为边AB,CD上的动点,且AE=CF,将线段EF绕点F逆时针旋转90°得到线段FG,连接DG.(1)当点E为AB的中点时,线段DG的长是________;(2)当点E在边AB上运动时,线段DG的最小值是________.第4题图类型四利用“辅助圆”解决最值问题(8年3考:2021.10、17,2020.17)1. 如图,在矩形ABCD中,AB=6,AD=25,E是边CD上一点,将△ADE沿直线AE 折叠得到△AFE,BF的延长线交边CD于点G,则DG长的最大值为________.第1题图2. 如图,在正方形ABCD中,E,F分别是AB,BC边上的动点(不与正方形的顶点重合),且AE=BF,CE,DF交于点M,连接BM,若AB=2,则BM的最小值为________.第2题图3.如图,在Rt△ABC中,∠C=90°,AB=10,BC=8,E,F分别是AC,BC边上的动点,且EF=AC,P是EF的中点,连接AP,BP,则△APB面积的最小值为________.第3题图4. 如图,已知△ABC为等边三角形,AB=6,将边AB绕点A顺时针旋转a(0°<a<120°),得到线段AD,连接CD,点E为CD上一点,且DE=2CE.连接BE,则BE的最小值为________.第4题图5. 如图,在△ABC中,∠C=45°,∠B=60°,BC=3+1,P为边AB上一动点,过点P 作PD⊥BC于点D,PE⊥AC于点E,连接DE,则DE的最小值为________.第5题图题型四 几何最值问题类型一 利用“垂线段最短”解决最值问题 1. 853【解析】如解图,设DE 与AB 交于点O ,∵四边形ADBE 是平行四边形,∴OB =OA ,DE =2OD ,∴当OD ⊥AC 时,DO 的值最小,即DE 的值最小,过点B 作BH ⊥AC 于点H ,则∠BHD =∠EDH =90°,易知AD ∥BE ,即AC ∥BE ,∴∠EBH =90°,∴四边形BHDE 是矩形,∴DE =BH ,∵AC =BC =6,AB =8,∴设CH =x ,则AH =6-x ,∵BA 2-AH 2=BH 2=BC 2-CH 2,即82-(6-x )2=62-x 2,解得x =23 ,∴CH =23,∴DE =BH =BC 2-CH 2 =853 .∴DE 的最小值为853.第1题解图2. 4 【解析】如解图,作点N 关于DC 的对称点N ′.∵AC =BC ,点D 为AB 的中点,∴点N ′在AC 上,连接MN ′,BN ′,∴BM +MN =BM +MN ′≥BN ′,∴当B ,M ,N ′三点共线,且BN ′⊥AC 时,BM +MN 取得最小值.∵AC =6,S △ABC =12,∴△ABC 中AC 边上的高为4,∴BM +MN 的最小值是4.第2题解图3. 33 【解析】如解图,作点E 关于BD 的对称点E ′,连接PE ′,∵四边形ABCD 是菱形,∴BA 与BC 关于BD 对称,∴点E ′位于BA 上,由对称的性质可知,PE =PE ′,∴当C ,P ,E ′三点重合,且CE ′⊥BA 时,PC +PE 的值最小,即为CE ′的长,∵四边形ABCD 是菱形,∴AO =CO =12 AC =3,BO =DO =12BD =33 ,AC ⊥BD ,AB =BC ,∴在Rt △BOC 中,BC =BO 2+CO 2 =6,tan ∠BCO =BO CO=3 ,∴∠BCO =60°,∴△ABC 是等边三角形,∴CE ′=BC ·sin 60°=33 ,∴PC +PE 的最小值为33 .第3题解图 4. 33 【解析】如解图,作点P 关于OA 的对称点P ′,连接OP ′,过点P ′作OB 的垂线交OA 于点M ,交OB 于点N ,此时PM +MN 的值最小,最小值为线段P ′N 的长.∵∠AOB =35°,∠BOP =10°,点P ′与点P 关于OA 对称,∴∠POA =∠P ′OA =25°,∴∠BOP ′=60°,OP ′=OP =6,在Rt △P ′ON 中,P ′N =OP ′·sin 60°=6×32=33 ,∴PM +MN 的最小值为33 .第4题解图类型二 利用“两点之间线段最短”解决最值问题1. 44 【解析】如解图,过点P 作EF ⊥AB ,分别交AB ,CD 于点E ,F ,连接AC ,BD ,则EF =AD =8,∵四边形ABCD 是矩形,∴∠ABC =90°,AB =CD =6,AD =BC =8,∴AC=AB 2+BC 2 =62+82 =10,∴BD =AC =10,∵S △APB +S △CPD =12 AB ·PE +12 CD ·PF =12AB ·EF =12×6×8=24,P A +PC ≥AC ,PB +PD ≥BD ,∴当A ,P ,C 三点共线,B ,P ,D 三点也共线时,P A +PB +PC +PD 有最小值,最小值为AC +BD =20,∴a +b 的最小值为24+20=44.第1题解图2. 27 【解析】如解图,分别作A 关于BC 和CD 的对称点A ′,A ″,连接A ′A ″,交BC 于点M ,交CD 于点N ,则A ′A ″即为△AMN 的周长最小值,作A ′H ⊥DA 交DA 的延长线于点H ,∴AA ′=2AB =2,AA ″=2AD =4,∵∠BAD =120°,∴∠HAA ′=60°,∴在Rt △A ′HA 中,AH =12 AA ′=1,∴A ′H =22-12 =3 ,A ″H =AH +AA ″=1+4=5,∴A ′A ″=A ′H 2+A ″H 2 =27 ,∴△AMN 的周长最小值为27 .第2题解图3. 43 【解析】如解图,作点E 关于BC 的对称点E ′,连接EE ′,交BC 于点F ,连接DE ′,AE ′,过点E ′作E ′G ⊥AC 交AC 的延长线于点G ,则DE =DE ′,EF =E ′F ,DE +DA =DE ′+DA ≥AE ′,∴当A ,D ,E ′在同一直线上时,DE +DA 的值最小,最小值为AE ′的长,∵∠ACB =90°,∠ABC =30°,BC =43 ,∴AC =33 BC =33×43 =4,∵点E 为边AB 的中点,∴EF 为△ABC 的中位线,∴EF =12 AC =2,CF =12BC =23 ,∴E ′F =EF =2=CG ,E ′G =CF =23 ,∴AG =AC +CG =4+2=6,∴AE ′=E ′G 2+AG 2 =(23)2+62 =43 ,∴DE +DA 的最小值为43 .第3题解图4. 25 【解析】如解图,过点A 作AD ⊥BC 于点D ,∵AB =AC =22 ,∠BAC =90°,∴AD =2,BC =4,∵S △BCP =12S △ABC ,∴点P 到BC 的距离为1,即点P 在AD 的垂直平分线l 上运动,作点B 关于直线l 的对称点B ′,连接B ′C 交直线l 于点P ′,连接BP ′,B ′P ,则BB ′⊥BC ,BP ′=B ′P ′,BP =B ′P ,∴BP +PC =B ′P +PC ≥B ′C ,当B ′,P ,C 三点共线,即点P 与点P ′重合时,BP +PC 的值最小,为B ′C 的长.在Rt △B ′BC 中,BB ′=2,BC =4,∴B ′C =BB ′2+BC 2 =25 ,∴PB +PC 的最小值为25 .第4题解图5. 13 +5 【解析】如解图,连接AC ,AP ,令y =0,得x =-3或1,∴点A (-3,0),点B (1,0),∴抛物线的对称轴是直线x =-1,OA =3,OB =1,令x =0,得y =2,∴点C (0,2),∴OC =2,∴BC =OB 2+OC 2 =5 ,AC =OA 2+OC 2 =13 ,∵△PBC 的周长为PB +PC +BC ,BC 为定值,∴要使△PBC 的周长最小,则PB +PC 最小即可,∵点A 与点B 关于对称轴对称,∴P A =PB ,∴PB +PC =P A +PC ≥AC ,∴PB +PC 的最小值为AC 的长,∴△PBC 的周长最小值=AC +BC =13 +5 .第5题解图类型三 利用“二次函数性质”解决最值问题1. C 【解析】∵p =5,c =4,∴S =5(5-a )(5-b )(5-4) =5(5-a )(5-b ) ,∵p =a +b +c 2 ,∴a +b =2p -c =6,∴b =6-a ,∴S =5(5-a )[5-(6-a )] =5(5-a )(a -1) =-5(a -3)2+20 ,∵-5<0,∴当a =3时,S 有最大值为20 =25 .2. 98【解析】∵四边形ABCD 是矩形,∴∠B =∠C =90°,∵AP ⊥PE ,∴∠APB +∠CPE =∠CPE +∠PEC =90°,∴∠APB =∠PEC ,∴△ABP ∽△PCE ,∴AB PC =BP CE,设BP =x ,CE =y ,则PC =3-x ,即23-x =x y,∴y =-12 x 2+32 x =-12 (x -32 )2+98 ,∵-12 <0,∴当x =32 时,y 有最大值,最大值是98 ,∴线段CE 的最大值为98 . 3. 3 【解析】如解图,过点C 作CE ⊥AB 于点E ,过点P 作PF ⊥AB 于点F ,设AP =x ,则CP =4-x ,∵AC =BC ,∠C =120°,∴∠BAC =∠B =30°,AE =BE ,∴CE =12AC =2,PF =12 AP =12x ,在Rt △AEC 中,由勾股定理得AE =42-22 =23 ,∴AB =2AE =43 ,∵PD ∥AB ,∴△PCD ∽△ACB ,∴PC AC =PD AB ,∴4-x 4 =PD 43,解得PD =3 (4-x ),∴S △APD =12 PD ·PF =12 ×3 (4-x )×12 x =-34 (x -2)2+3 ,∵-34<0,∴当x =2时,S △APD 有最大值,最大值为3 .第3题解图4. (1)1 【解析】∵点E 为AB 的中点,AE =CF ,∴点F 为CD 的中点,∴EF =FG =4,此时F ,D ,G 三点共线,∴DG =FG -FD =1; (2)255 【解析】如解图,过点F 作FH ⊥AB 于点H ,过点G 作IG ⊥CD 于点I ,则∠EHF =∠GIF =90°,由题意可知∠EFG =90°,EF =GF ,∴∠EFH +∠EFI =∠EFI +∠GFI =90°,∴∠EFH =∠GFI ,∴△EFH ≌△GFI (AAS),∴EH =GI ,设AE =a ,①当0<a <3时,如解图①,GI =EH =6-2a ,ID =FD -FI =FD -FH =6-a -4=2-a ,∴DG 2=ID 2+IG 2=(2-a )2+(6-2a )2=5a 2-28a +40=5(a -145 )2+45 ,∵5>0,∴当a =145 时,DG 2取最小值45,∴DG =255;②当3≤a <6时,如解图②,GI =EH =2a -6,ID =FI -FD =FH -AE +EH =4-a +2a -6=a -2,∴DG 2=ID 2+IG 2=(a -2)2+(2a -6)2=5a 2-28a +40=5(a -145)2+45 ,∵5>0,3≤a <6,∴当a =3时,DG 2取最小值1,∴DG =1,∵1>255,∴DG 的最小值为255.第4题解图类型四 利用“辅助圆”解决最值问题1. 2 【解析】如解图,以点A 为圆心,AD 长为半径画弧,过点B 作弧的切线交CD 于点G ,切点为F ,此时点E 和点G 重合,DG 的最大值即为DE 的长,∵四边形ABCD 是矩形,∴BC =AD =25 ,AB =CD =6,由折叠的性质可知,DE =EF ,AF =AD =25 ,设DE =EF =x ,则CE =CD -DE =6-x ,在Rt △ABF 中,由勾股定理得BF =AB 2-AF 2 =4,则BE =BF +EF =4+x ,在Rt △BEC 中,由勾股定理得BE 2=CE 2+BC 2,即(4+x )2=(6-x )2+(25 )2 ,解得x =2,即DG 的最大值为2.第1题解图 2. 5 -1 【解析】如解图,取CD 的中点O ,连接BO ,∵四边形ABCD 为正方形,∴AB =BC =CD =AD ,∠EBC =∠FCD =90°,∵AE =BF ,∴AE +BE =BF +CF ,∴BE =CF ,∴△EBC ≌△FCD (SAS),∴∠BCE =∠CDF ,∵∠BCE +∠DCE =∠BCD =90°,∴∠CDF +∠ECD =90°,∴∠CMD =90°,当点E ,F 分别在AB 和BC 上移动时,点M 在以CD 的中点O 为圆心,OC 长为半径的半圆上运动,要使BM 取得最小值,则需点B ,M ,O 在同一条直线上.∵AB =2,∴CO =1,∴BO =5 ,∴此时BM =5 -1,即BM 的最小值为5 -1.第2题解图3. 9 【解析】如解图,过点P 作PH ⊥AB 于点H ,则S △ABP =12AB ·PH =5PH ,∴当PH 最小时,△ABP 的面积最小.∵∠ACB =90°,AB =10,BC =8,∴AC =AB 2-BC 2 =6.∴EF=AC =6.连接CP ,则CP =12EF =3.∴点P 在以点C 为圆心,3为半径的圆弧上,过点C 作CH ′⊥AB 于点H ′,交⊙C 于点P ′,∵P ′H ′=CH ′-CP ′=CH ′-CP ≤CP +PH -CP =PH ,∴当点P 与点P ′重合,点H 与点H ′重合时,PH 最小,最小值为P ′H ′的长.∵S △ABC =12AC ·BC =12 AB ·CH ′,∴CH ′=AC ·BC AB =245 ,∴P ′H ′=CH ′-CP ′=245 -3=95 ,∴PH 的最小值是95 ,此时S △ABP =5PH =9,即△ABP 面积的最小值为9.第3题解图4. 27 -2 【解析】如解图,过点E 作EH ∥AD ,交AC 于点H ,∵△ABC 为等边三角形,∴AB =AC =6,由旋转的性质得AD =AB ,∴AD =AC ,∴∠D =∠ACD ,∵DE =2CE ,∴CE CD =CH CA =13 ,∠CEH =∠D =∠ACD ,∴CH =EH ,∵AC =6,∴CH =EH =2,取AH 的中点P ,连接EP ,则PH =EH ,∴∠EPH =∠PEH ,∵∠EPH +∠CEP +∠ACD =180°,∴2∠PEH +2∠CEH =180°,∴∠CEP =90°,∴点E 在以点H 为圆心,CP 为直径的圆弧上运动,连接BH ,∵EH 为定值2,∴当B ,E ,H 三点共线时,BE 的长最小,过点B 作BQ ⊥AC 于点Q ,则CQ =12AC =3,∴QH =CQ -CH =1,BQ =BC 2-CQ 2 =62-32 =33 ,∴BH =BQ 2+QH 2 =(33)2+12 =27 ,∴BE 的最小值为27 -2.第4题解图5. 32+64【解析】如解图,连接CP ,∵∠PDC =∠PEC =90°,∴∠PDC +∠PEC =180°,∴C ,D ,P ,E 四点共圆,圆心为点O ,且直径为CP ,∵BC =3 +1,∠ACB =45°,∠B =60°是定值,∴直径CP 最小时,∠DCE 所对的弦DE 最小,即CP ⊥AB 时,DE 的值最小,连接OD ,OE ,∵∠B =60°,CP ⊥AB ,BC =3 +1,∴∠BCP =30°,∴BP =12BC =3+12 ,CP =3 BP =3+32 ,∴OD =OE =12 CP =3+34,∵∠ACB =45°,∴∠DOE =2∠ACB =90°,∴△ODE 是等腰直角三角形,∴DE =2 OD =32+64,即DE 的最小值为32+64.第5题解图。
2024年中考数学一轮复习专题四++几何最值问题+课件

返回类型清单
5.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx-4与x轴交于A,B两点(B
在A的右侧),与y轴交于点C,已知OA=1,OB=4OA,连接BC.
专题四 几何最值问题— 两点之间线段最短问题
(1)求抛物线的解析式;
由OA=1,得A(-1,0).∵OB=4OA=4.∴B(4,0).
∵NM⊥BC,∴∠NMC=90°,
∴∠CNM=90°-∠NCM=90°-∠OCB=45°,
∴△NCM为等腰直角三角形,
返回类型清单
专题四 几何最值问题— 两点之间线段最短问题
∴NM=NC·sin 45°=
NC,∴AN+ CN=AN+NM≥AH,
当A,N,M三点共线时,AN+NM最小值=AH,
返回类型清单
3.(2022·唐山迁安二模)如图,AB是半圆形量角器的直径,点O为半圆的圆
心,DA与半圆O相切于点A,点P在半圆上,且点P对应的示数为120°(60°),
点C是上一点(不与点P重合).连接DO交半圆O于点E,点E对应的示数为
60°(120°).
专题四 几何最值问题— 两点之间线段最短问题
=75°,
°−∠
∠AED=∠ADE=
=75°,
∴∠HBE=∠HEB=180°-60°-75°=45°,
∴HE=HB,∠H=90°,
∵∠ABD=∠ADB=45°,
返回类型清单
专题四 几何最值问题— 两点之间线段最短问题
返回类型清单
∴∠BDH=∠ADE-∠ADB=30°,
∵BD= + = + =6 ,
中考数学几何最值问题题型梳理

中考数学几何最值问题题型梳理专题1 单线段最值之单动点型例题.如图,矩形ABCD 中,4AB =,6BC =,点P 是矩形ABCD 内一动点,且∆∆=PAB PCD S S ,则PC PD +的最小值为_____.【解析】ABCD 为矩形,AB DC ∴= 又=PAB PCD S S∴点P 到AB 的距离与到CD 的距离相等,即点P 线段AD 垂直平分线MN 上, 连接AC ,交MN 与点P ,此时PC PD +的值最小,且PC PD AC +=====巩固1.如图,等腰Rt △ABC 中,斜边AB 的长为2,O 为AB 的中点,P 为AC 边上的动点,OQ ⊥OP 交BC 于点Q ,M 为PQ 的中点,当点P 从点A 运动到点C 时,点M 所经过的路线长为( )ABC .1D .2【解析】连接OC ,作PE ⊥AB 于E ,MH ⊥AB 于H ,QF ⊥AB 于F ,如图,∵△ACB 为到等腰直角三角形,∴AC =BC=2AB,∠A =∠B =45°, ∵O 为AB 的中点,∴OC ⊥AB ,OC 平分∠ACB ,OC =OA =OB =1,∴∠OCB =45°, ∵∠POQ =90°,∠COA =90°,∴∠AOP =∠COQ ,在Rt △AOP 和△COQ 中,A OCQ AO COAOP COQ ∠=∠=∠=∠⎧⎪⎨⎪⎩,∴Rt △AOP ≌△COQ ,∴AP =CQ , 易得△APE 和△BFQ 都为等腰直角三角形,∴PE=2AP=2CQ ,QF2BQ , ∴PE +QF=2,CQ +BQ,=2BC=2∵M 点为PQ 的中点, ∴MH 为梯形PEFQ 的中位线,∴MH =12,PE +QF ,=12,即点M 到AB 的距离为12, 而CO =1,∴点M 的运动路线为△ABC 的中位线,∴当点P 从点A 运动到点C 时,点M 所经过的路线长=12AB =1,选C , 巩固2.如图,在平面内,线段AB =6,P 为线段AB 上的动点,三角形纸片CDE 的边CD 所在的直线与线段AB 垂直相交于点P ,且满足PC =P A .若点P 沿AB 方向从点A 运动到点B ,则点E 运动的路径长为______,【解析】如图,由题意可知点C运动的路径为线段AC′,点E运动的路径为EE′,由平移的性质可知AC′=EE′,在Rt,ABC′中,易知AB=BC′=6,∠ABC′=90°,,EE′=AC巩固3.如图,等边三角形ABC的边长为4,点D是直线AB上一点.将线段CD绕点D顺时针旋转60°得到线段DE,连结BE.(1)若点D在AB边上(不与A,B重合)请依题意补全图并证明AD=BE;(2)连接AE,当AE的长最小时,求CD的长.【解析】(1)补全图形如图1所示,AD=BE,理由如下:∵∵ABC是等边三角形,∵AB=BC=AC,∠A=∠B=60°,由旋转的性质得:∠ACB=∠DCE=60°,CD=CE,∵∠ACD=∠BCE,∵∵ACD≌∵BCE(S A S),∵AD=BE.(2)如图2,过点A作AF⊥EB交EB延长线于点F.∵∵ACD≌∵BCE,∵∠CBE=∠A=60°,∵点E的运动轨迹是直线BE,根据垂线段最短可知:当点E与F重合时,AE的值最小,此时CD=CE=CF,∵∠ACB=∠CBE=60°,∵AC∥EF,又∵AF⊥BE,∵AF⊥AC,在Rt∵ACF中,∵CF∵CD=CF=.例题.如图,点D 在半圆O 上,半径5OB =,4=AD ,点C 在弧BD 上移动,连接AC ,作DH AC ⊥,垂足为H ,连接BH ,点C 在移动的过程中,BH 的最小值是______.【解析】如图,设AD 的中点为点E ,则114222EA ED AD ===⨯= 由题意得,点H 的运动轨迹在以点E 为圆心,EA 为半径的圆上由点与圆的位置关系得:连接BE ,与圆E 交于点H ,此时BH 取得最小值,2EH = 连接BDAB 为半圆O 的直径,90ADB ∴∠=︒BD ∴===BE ∴===2BH BE EH ∴=-=巩固1.如图,长方形ABCD 中,AB =6,BC =4,在长方形的内部以CD 边为斜边任意作Rt ∵CDE ,连接AE ,则线段AE 长的最小值是_____.【解析】如图,点E '在以点F 为圆心,DF 为半径的圆上运动,当A ,E ,F 三点共线时,AE 值最小,DF =12×6=3,在长方形ABCD 中,AD =BC =4,由勾股定理得:AF . ∵EF =12CD =12×6=3,∵AE =AF ﹣EF =5﹣3=2,即线段AE 长的最小值是2.巩固3.如图,Rt ABC △中,AB BC ⊥,6AB =,4BC =,P 是ABC △内部的一个动点,且满足90PAB PBA ︒∠+∠=,则线段CP 长的最小值为________.【解析】∵∠P AB +∠PBA =90°,∵∠APB =90°,∵点P 在以AB 为直径的弧上(P 在∵ABC 内),设以AB 为直径的圆心为点O ,如图,接OC ,交∵O 于点P ,此时的PC 最短∵AB =6,∵OB =3,∵BC =4,∵5OC ==,∵PC =5-3=2巩固4.如图,在Rt ABC ∆中,90︒∠=C ,4AC =,3BC =,点O 是AB 的三等分点,半圆O 与AC 相切,M ,N 分别是BC 与半圆弧上的动点,则MN 的最小值和最大值之和是( )A .5B .6C .7D .8【解析】如图,设∵O 与AC 相切于点D ,连接OD ,作OP BC ⊥垂足为P 交∵O 于F , 此时垂线段OP 最短,PF 最小值为OP OF -,∵4AC =,3BC =,∵5AB =,∵90OPB ︒∠=,∵OP AC ∥∵点O 是AB 的三等分点,∵210533OB =⨯=,23OP OB AC AB ==,∵83OP =, ∵∵O 与AC 相切于点D ,∵OD AC ⊥,∵OD BC ∥,∵13OD OA BC AB ==,∵1OD =, ∵MN 最小值为85133OP OF -=-=, 如图,当N 在AB 边上时,M 与B 重合时,MN 经过圆心,经过圆心的弦最长, MN 最大值1013133=+=,513+=633,∵MN 长的最大值与最小值的和是6.选B . 巩固5.如下图所示,在矩形纸片ABCD 中,2AB =,3AD =,点E 是AB 的中点,点F 是AD 边上的一个动点,将AEF 沿EF 所在直线翻折,得到'A EF △,则'A C 的长的最小值是( )A .2B .3C 1D 1【解析】以点E 为圆心,AE 长度为半径作圆,连接CE ,当点'A 在线段CE 上时,A'C 的长取最小值,如图所示,根据折叠可知:112A'E AE AB ===.在Rt BCE △中,112BE AB ==,3BC =,90B ∠=,CE ∴,A'C ∴的最小值1CE A'E =-=.选D .技法1:借助直角三角形斜边上的中线例题1.如图,在∵ABC 中,∠C =90°,AC =4,BC =2,点A 、C 分别在x 轴、y 轴上,当点A在x 轴上运动时,点C 随之在y 轴上运动,在运动过程中,点B 到原点的最大距离是( )A .6B .C .D .【解析】如图,取CA 的中点D ,连接OD 、BD ,则OD =CD =AC =×4=2,由勾股定理得,BD ==2,当O 、D 、B 三点共线时点B 到原点的距离最大,所以,点B 到原点的最大距离是2+2.技法2:借助三角形两边之和大于第三边,两边之差小于第三边例题2.如图,已知等边三角形ABC 边长为A 、B 分别在平面直角坐标系的x 轴负半轴、轴的正半轴上滑动,点C 在第四象限,连接OC ,则线段OC 长的最小值是( )A 1B .3C .3D 【解析】如图所示:过点C 作CE ⊥AB 于点E ,连接OE ,∵∵ABC 是等边三角形,∵CE =AC ×si n 60°=3=,AE =BE ,∵∠AOB =90°,∵EO 12=AB =∵EC -OE ≥OC , ∵当点C ,O ,E 在一条直线上,此时OC 最短,故OC 的最小值为:OC =CE ﹣EO =3B .巩固1.如图,∠MON =90°,矩形ABCD 的顶点A 、B 分别在边OM 、ON 上,当B 在边ON 上运动时,A 随之在OM 上运动,矩形ABCD 的形状保持不变,其中AB =4,BC =2.运动过程中点D 到点O 的最大距离是______.【解析】如图,取AB 的中点E ,连接OE 、DE 、OD ,∵OD ≤OE +DE ,∵当O 、D 、E 三点共线时,点D 到点O 的距离最大,此时,∵AB =4,BC =2,∵OE =AE =12AB =2,DE=∵OD 的最大值为,巩固2.如图,在Rt ABC ∆中,90ACB ∠=,将ABC ∆绕顶点C 逆时针旋转得到'',A B C M ∆是BC 的中点,N 是''A B 的中点,连接MN ,若4,60BC ABC =∠=︒,则线段MN 的最大值为( )A .4B .8C .D .6【解析】连接CN ,∵将ABC ∆绕顶点C 逆时针旋转得到''A B C ∆,∵''=90A CB ACB ∠=∠︒,''460'B C BC A B C ABC ==∠=∠=︒,,∵'30A ∠=︒,''8A B =,∵N 是''A B 的中点,∵1''42CN A B ==, ∵在△CMN 中,MN <CM +CN ,当且仅当M ,C ,N 三点共线时,MN =CM +CN =6, ∵线段MN 的最大值为6.选D .技法3:借助构建全等图形例题3.如图,在∵ABC 中,∠ACB =90°,∠A =30°,AB =5,点P 是AC 上的动点,连接BP ,以BP 为边作等边∵BPQ ,连接CQ ,则点P 在运动过程中,线段CQ 长度的最小值是______.【解析】如图,取AB 的中点E ,连接CE ,PE .∵∠ACB =90°,∠A =30°,∵∠CBE =60°, ∵BE =AE ,∵CE =BE =AE ,∵∵BCE 是等边三角形,∵BC =BE ,∵∠PBQ =∠CBE =60°, ∵∠QBC =∠PBE ,∵QB =PB ,CB =EB ,∵∵QBC ≌∵PBE (S A S ),∵QC =PE ,∵当EP ⊥AC 时,QC 的值最小,在Rt ∵AEP 中,∵AE =52,∠A =30°,∵PE =12AE =54,∵CQ 的最小值为54.巩固4.如图,边长为12的等边三角形ABC 中,M 是高CH 所在直线上的一个动点,连结MB ,将线段BM 绕点B 逆时针旋转60°得到BN ,连结HN .则在点M 运动过程中,线段HN 长度的最小值是( )A .6B .3C .2D .1.5【解析】如图,取BC 的中点G ,连接M G ,∵旋转角为60°,∵∠MBH +∠HBN =60°, 又∵∠MBH +∠MBC =∠ABC =60°,∵∠HBN =∠G BM ,∵CH 是等边∵ABC 的对称轴,∵HB =12AB ,∵HB =B G ,又∵MB 旋转到BN ,∵BM =BN , 在∵MB G 和∵NBH 中,BG BH MBG NBH MB NB =⎧⎪∠=∠⎨⎪=⎩,∵∵MB G ≌∵NBH (S A S ),∵M G=NH ,根据垂线段最短,当M G ⊥CH 时,M G 最短,即HN 最短,此时∠BCH =12×60°=30°,C G=12AB =12×12=6,∵M G=12C G=12×6=3,∵HN =3;选B . 技法4:借助中位线例题4.如图,在等腰直角∆ABC 中,斜边AB 的长度为 8,以AC 为直径作圆,点P 为半圆上的动点,连接BP ,取BP 的中点M ,则CM 的最小值为( )A. B.CD.【解析】连接AP 、CP ,分别取AB 、BC 的中点E 、F ,连接EF 、EM 和FM ,,EM 、FM 和EF 分别是,ABP 、,CBP 和,ABC 的中位线,EM ∥AP ,FM ∥CP ,EF ∥AC ,EF =12AC ,,∠EFC =180°-∠ACB =90° ,AC 为直径,,∠APC =90°,即AP ⊥CP ,,EM ⊥MF ,即∠EMF =90°,点M 的运动轨迹为以EF 为直径的半圆上,取EF 的中点O ,连接OC ,点O即为半圆的圆心,当O 、M 、C 共线时,CM 最小,如图所示,CM 最小为CM 1的长,,等腰直角∆ABC 中,斜边 AB 的长度为 8,,AC =BC AB =,EF =12AC =FC =12BC =,OM 1=OF =12EF根据勾股定理可得OC =,CM 1=OC -OM 1即CM ,选C .巩固5.如图,抛物线2119y x =-与x 轴交于A B ,两点,D 是以点()0,4C 为圆心,1为半径的圆上的动点,E 是线段AD 的中点,连接,OE BD ,则线段OE 的最小值是( )A .2B .2C .52D .3 【解析】∵2119y x =-,∵当0y =时,21019x =-,解得:=3x ±, ∵A 点与B 点坐标分别为:(3-,0),(3,0),即:AO =BO =3,∵O 点为AB 的中点,又∵圆心C 坐标为(0,4),∵OC =4,∵BC 长度5=,∵O 点为AB 的中点,E 点为AD 的中点,∵OE 为∵ABD 的中位线,即:OE =12BD , ∵D 点是圆上的动点,由图可知,BD 最小值即为BC 长减去圆的半径,∵BD 的最小值为4,∵OE =12BD =2,即OE 的最小值为2,选A . 专题2 单线段最值之双动点型技法1借助等量代换实现转化例题1.如图,ABC ∆中,90B ︒∠=,4AB =,3BC =,点D 是AC 上的任意一点,过点D 作DE AB ⊥于点E ,DF BC ⊥于点F ,连接EF ,则EF 的最小值是_________.【解析】连接BD ,90,B DE AB DF BC ︒∠=⊥⊥,∴四边形BEDF 是矩形。
中考数学----几何最值
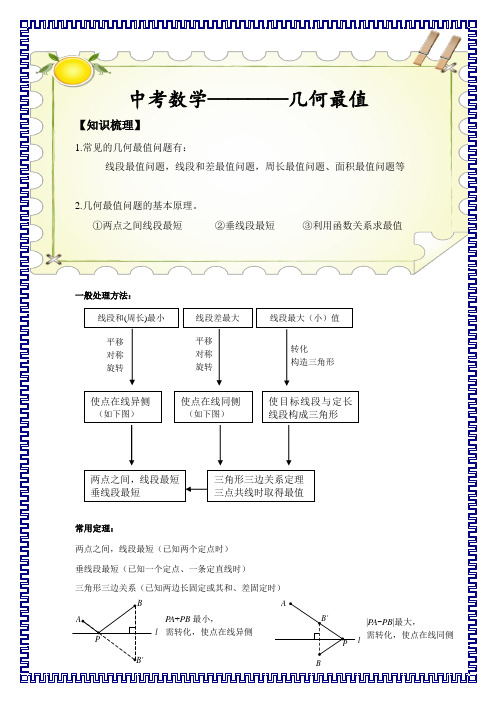
中考数学————几何最值【知识梳理】1.常见的几何最值问题有:线段最值问题,线段和差最值问题,周长最值问题、面积最值问题等2.几何最值问题的基本原理。
①两点之间线段最短②垂线段最短 ③利用函数关系求最值一般处理方法:常用定理:两点之间,线段最短(已知两个定点时) 垂线段最短(已知一个定点、一条定直线时) 三角形三边关系(已知两边长固定或其和、差固定时)线段和(周长)最小 转化构造三角形两点之间,线段最短 垂线段最短 线段差最大 线段最大(小)值三角形三边关系定理 三点共线时取得最值平移 对称 旋转使点在线异侧(如下图)使点在线同侧(如下图) 使目标线段与定长线段构成三角形平移 对称 旋转P A +PB 最小,需转化,使点在线异侧|P A -PB |最大,需转化,使点在线同侧lB'ABPl B'BA P构建“对称模型”实现转化一次对称1. 如图,在锐角△ABC 中,AB =42,∠BAC =45°,∠BAC 的平分线交BC 于点D ,M 、N 分别是AD 和AB 上的动点,则BM+MN 的最小值是____.2、如图,在△ABC 中,AC =BC =2,∠ACB =90°,D 是BC 边的中点,E 是AB 边上一动点,则EC +ED 的最小值为_______。
1题图 2题图 3题图 4题图 3.已知⊙O 的直径CD 为4,∠AOD 的度数为60°,点B 是AD ︵的中点,在直径CD 上找一点P ,使BP+AP 的值最小,并求BP+AP 的最小值.4.如图,圆柱形玻璃杯,高为12cm ,底面周长为18cm ,在杯内离杯底4cm 的点C 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm 与蜂蜜相对的点A 处,则蚂蚁到达蜂蜜的最短距离为______cm .蜂蜜蚂蚁AC正方形中的对称变换1、如图,正方形ABCD 的边长为8,M 在DC 上,且DM =2,N 是AC 上的一动点,DN +MN 的最小值为_________。
【中考冲刺】初三数学培优专题 25 平面几何的最值问题(含答案)(难)

平面几何的最值问题阅读与思考几何中的最值问题是指在一定的条件下,求平面几何图形中某个确定的量(如线段长度、角度大小、图形面积)等的最大值或最小值. 求几何最值问题的基本方法有:1.特殊位置与极端位置法:先考虑特殊位置或极端位置,确定最值的具体数据,再进行一般情形下的推证.2.几何定理(公理)法:应用几何中的不等量性质、定理.3.数形结合法等:揭示问题中变动元素的代数关系,构造一元二次方程、二次函数等.例题与求解【例1】在Rt △ABC 中,CB =3,CA =4,M 为斜边AB 上一动点.过点M 作MD ⊥AC 于点D ,过M 作ME ⊥CB 于点E ,则线段DE 的最小值为 .(四川省竞赛试题)解题思路:四边形CDME 为矩形,连结CM ,则DE = CM ,将问题转化为求CM 的最小值.【例2】如图,在矩形ABCD 中,AB =20cm ,BC =10cm .若在AC ,AB 上各取一点M ,N ,使BM +MN 的值最小,求这个最小值.(北京市竞赛试题)ADMN解题思路:作点B 关于AC 的对称点B ′,连结B ′M ,B ′A ,则BM = B ′M ,从而BM +MN = B ′M +MN .要使BM +MN 的值最小,只需使B ′M 十MN 的值最小,当B ′,M ,N 三点共线且B ′N ⊥AB 时,B ′M +MN 的值最小.【例3】如图,已知□ABCD ,AB =a ,BC =b (b a ),P 为AB 边上的一动点,直线DP 交CB 的延长线于Q .求AP +BQ 的最小值. (永州市竞赛试题)PDA BQ解题思路:设AP =x ,把AP ,BQ 分别用x 的代数式表示,运用不等式以ab b a 222≥+或a +b ≥2ab(当且仅当a =b 时取等号)来求最小值. 【例4】阅读下列材料:问题 如图1,一圆柱的底面半径为5dm ,高AB 为5dm ,BC 是底面直径,求一只蚂蚁从A 点出发沿圆柱表面爬行到C 点的最短路线. 小明设计了两条路线:图2图1摊平沿AB 剪开ACBBA路线1:侧面展开图中的线段AC .如图2所示.设路线l 的长度为l 1,则l 12 =AC 2=AB 2 +BC 2 =25+(5π) 2=25+25π2. 路线2:高线AB 十底面直径BC .如图1所示.设路线l 的长度为l 2,则l 22 = (BC +AB )2=(5+10)2 =225.∵l 12 – l 22 = 25+25π2-225=25π2-200=25(π2-8),∴l 12 >l 22 ,∴ l 1>l 2 . 所以,应选择路线2.条路线才能使蚂蚁从点A 出发沿圆柱表面爬行到C 点的路线最短. (衢州市中考试题)解题思路:本题考查平面展开一最短路径问题.比较两个数的大小,有时比较两个数的平方比较简便.比较两个数的平方,通常让这两个数的平方相减.【例5】如图,已知边长为4的正方形钢板,有一个角锈蚀,其中AF =2,BF =1.为了合理利用这块钢板,将在五边形EABCD 内截取一个矩形块MDNP ,使点P 在AB 上,且要求面积最大,求钢板的最大利用率. (中学生数学智能通讯赛试题)NME DAB解题思路:设DN =x ,PN =y ,则S =xy .建立矩形MDNP 的面积S 与x 的函数关系式,利用二次函数性质求S 的最大值,进而求钢板的最大利用率.【例6】如图,在四边形ABCD 中,AD =DC =1,∠DAB =∠DCB =90°,BC ,AD 的延长线交于P ,求AB ·S △P AB 的最小值. (中学生数学智能通讯赛试题)1ABD解题思路:设PD =x (x >1),根据勾股定理求出PC ,证Rt △PCD ∽Rt △P AB ,得到PCPACD AB ,求出AB ,根据三角形的面积公式求出y =AB ·S △P AB ,整理后得到y ≥4,即可求出答案.能力训练A 级1.如图,将两张长为8、宽为2的矩形纸条交叉,使重叠部分是一个菱形.容易知道当两张纸条垂直时,菱形的周长有最小值,那么菱形周长的最大值是 . (烟台市中考试题)2.D 是半径为5cm 的⊙O 内一点,且OD =3cm ,则过点O 的所有弦中,最短的弦AB = cm . (广州市中考试题)3.如图,有一个长方体,它的长BC =4,宽AB =3,高BB 1=5.一只小虫由A 处出发,沿长方体表面爬行到C 1,这时小虫爬行的最短路径的长度是 . (“希望杯”邀请赛试题)DD 1第1题图 第3题图 第4题图 第5题图4.如图,在△ABC 中,AB =10,AC =8,BC =6,经过点C 且与边AB 相切的动圆与CB ,CA 分别相交于点E ,F ,则线段EF 长度的最小值是( ) (兰州市中考试题)A .42B .4. 75C .5D .4. 85.如图,圆锥的母线长OA =6,底面圆的半径为2.一小虫在圆锥底面的点A 处绕圆锥侧面一周又回到点A ,则小虫所走的最短距离为( ) (河北省竞赛试题) A .12B .4πC .62D .636.如图,已知∠MON = 40°,P 是∠MON 内的一定点,点A ,B 分别在射线OM ,ON 上移动,当△P AB 周长最小时,∠APB 的值为( ) (武汉市竞赛试题) A .80° B .100° C .120° D .140° 7.如图, ⌒AD 是以等边三角形ABC 一边AB 为半径的四分之一圆周,P 为AD 上任意一点.若AC =5,则四边形ACBP 周长的最大值是( ) (福州市中考试题) A .15B .20C .15+52D .15+55NM NMAOPBDCBCA DBA PE第6题图 第7题图 第8题图 8.如图,在正方形ABCD 中,AB =2,E 是AD 边上一点(点E 与点A ,D 不重合),BE 的垂直平分线交AB 于M ,交DC 与N .(1) 设AE =x ,四边形ADNM 的面积为S ,写出S 关于x 的函数关系式.(2) 当AE 为何值时,四边形ADNM 的面积最大?最大值是多少? (山东省中考试题)9.如图,六边形ABCDEF 内接于半径为r 的⊙O ,其中AD 为直径,且AB =CD =DE =F A . (1) 当∠BAD =75°时,求⌒BC 的长; (2) 求证:BC ∥AD ∥FE ;(3) 设AB =x ,求六边形ABCDEF 的周长l 关于x 的函数关系式,并指出x 为何值时,l 取得最大值.10.如图,已知矩形ABCD 的边长AB =2,BC =3,点P 是AD 边上的一动点(P 异于A 、D ).Q 是BC边上任意一点.连结AQ,DQ,过P作PE∥DQ交于AQ于E,作PF//AQ交DQ于F.(1) 求证:△APE∽△ADQ;(2) 设AP的长为x,试求△PEF的面积S△PEF关于x的函数关系式,并求当P在何处时,S△PEF取得最大值?最大值为多少?(3) 当Q在何处时,△ADQ的周长最小?(须给出确定Q在何处的过程或方法,不必证明)(无锡市中考试题)B Q11.在等腰△ABC中,AB=AC=5,BC=6.动点M,N分别在两腰AB,AC上(M不与A,B重合,N不与A,C重合),且MN∥BC.将△AMN沿MN所在的直线折叠,使点A的对应点为P.(1)当MN为何值时,点P恰好落在BC上?(2)设MN=x,△MNP与等腰△ABC重叠部分的面积为y,试写出y与x的函数关系式,当x为何值时,y的值最大,最大值是多少?(宁夏省中考试题)B CAB级1.已知凸四边形ABCD中,AB+AC+CD= 16,且S四边彤ABCD=32,那么当AC= ,BD= 时,四边形ABCD面积最大,最大值是.(“华杯赛”试题)2.如图,已知△ABC的内切圆半径为r,∠A=60°,BC=23,则r的取值范围是.(江苏省竞赛试题)DBAB CAA第2题图第3题图第4题图第5题图3.如图⊙O的半径为2,⊙O内的一点P到圆心的距离为1,过点P的弦与劣弧⌒AB组成一个弓形,则此弓形面积的最小值为.4.如图,△ABC的面积为1,点D,G,E和F分别在边AB,AC,BC上,BD<DA,DG∥BC,DE ∥AC ,GF ∥AB ,则梯形DEFG 面积的最大可能值为 .(上海市竞赛试题)5.已知边长为a 的正三角形ABC ,两顶点A ,B 分别在平面直角坐标系的x 轴,y 轴的正半轴上滑动,点C 在第一象限,连结OC ,则OC 的最大值是 .(潍坊市中考试题)6.已知直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD =2,BC =DC =5,点P 在BC 上移动,则当P A + PD 取最小值时,△APD 中边AP 上的高为( ) (鄂州市中考试题)A .17172B .17174C .17178D .3QADBCA BDCPP第6题图 第7题图 第8题图7.如图,正方形ABCD 的边长为4cm ,点P 是BC 边上不与点B ,C 重合的任意一点,连结AP ,过点P 作PQ ⊥AP 交DC 于点Q .设BP 的长为x cm ,CQ 的长为y cm . (1) 求点P 在BC 上运动的过程中y 的最大值;(2) 当y =41cm 时,求x 的值. (河南省中考试题)8.如图,y 轴正半轴上有两点A (0,a ),B (0,b ),其中a >b >0.在x 轴上取一点C ,使∠ACB 最大,求C 点坐标. (河北省竞赛试题)9.如图,正方形ABCD 的边长为1,点M ,N 分别在BC ,CD 上,使得△CM N 的周长为2.求: (1) ∠MAN 的大小;(2) △MAN 的面积的最小值. (“宇振杯”上海市竞赛试题)10,如图,四边形ABCD 中,AD = CD ,∠DAB =∠ACB =90°,过点D 作DE ⊥AC 于F ,DE 与AB相交于点E .(1) 求证:AB ·AF =CB ·CD ; (2)已知AB =15cm ,BC =9cm ,P 是射线DE 上的动点,设DP =x cm(x >0),四边形BCDP 的面积为y cm 2. ①求y 关于x 的函数关系式;②当x 为何值时,△PBC 的周长最小?求出此时y 的值.(南通市中考试题)MNExCB第6题图 第7题图 第8题图 第9题图11.如图,已知直线l :k kx y 42-+=(k 为实数).(1) 求证:不论k 为任何实数,直线l 都过定点M ,并求点M 的坐标;(2) 若直线l 与x 轴、y 轴的正半轴交于A ,B 两点,求△AOB 面积的最小值.(太原市竞赛试题)12.如图,在Rt △ABC 中,∠C =90°,BC =2,AC =x ,点F 在边AB 上,点G ,H 在边BC 上,四边形EFGH 是一个边长为y 的正方形,且AE =AC . (1) 求y 关于x 的函数解析式;(2) 当x 为何值时,y 取得最大值?求出y 的最大值.(上海市竞赛试题)平面几何的最值问题例1125提示:当CM ⊥AB 时,CM 值最小,CM =125AC BC AB ⋅= 例2 如图,B ′M +MN 的最小值为点B ′到AB 的距离B ′F ,BE =45AB BCAC⋅=cm ,BB ′=85cm ,AE =()2222204585AB BE --=.在△ABB ′中,由12BB ′•AE =12AB •B ′F ,得B ′F =16cm .故BM +MN 的最小值为16cm . 例3 由△APD ∽△BPQ ,得AP AD BP BQ =,即BQ =()b a x AD BP AP x-⋅=,∴AP +BQ =x +ab b x -.∵x +ab x ≥2ab x ab x ⋅=仅当x =abx即x ab ,上式等号成立.故当AP ab ,AP +BQ 最小,其最小值为ab-b .例4 ⑴22125l π=+,22l =49,l 1<l 2,故要选择路线l 较短. ⑵()2221l h r π=+,()2222l h r =+,()2221244l l r r h π⎡⎤-=--⎣⎦.当r =244h π-时,2212l l =,当r >244h π-时,2212l l >,当r <244hπ-时,2212l l <. 例5 设DN =x ,PN =y ,则S =xy ,由△APQ ∽△ABF ,得()41242y x -=--即x =10-2y ,代入S =xy 得S =xy =y (10-2y ),即S =-2252522y ⎛⎫-+ ⎪⎝⎭,因3≤y ≤4,而y =52不在自变量y 的取值范围内,所以y =52不是极值点,当y =3时,S (3)=12,当y =4时,S (4)=8,故S max =12.此时,钢板的最大利用率21214212-⨯⨯=80%. 例6 设PD =x (x >1),则PC 21x -,由R t △PCD ∽△P AB ,得AB =21CD PA PC x ⋅=-y =AB •S △P AB ,则y =12AB ×P A ×AB =()()2121x x +-,求y 的最小值,有下列不同思路:①配方:y =21212242121x x x x --++=+--1221x x -=-x =3时,y 有最小值4.②运用基本不等式:y =122221x x -++≥- 321221x x -⋅-+2=4,∴当12x -=21x -,即当x =3时,y 有最小值4. ③借用判别式,去分母,得x 2+2(1-y )x +1+2y =0,由△=4(1-y )2-4(1+2y )=4y (y -4)≥0,得y ≥4,∴y 的最小值为4. A 级1. 17 提示:当两张纸条的对角重合时,菱形周长最大.2. 83.74 4. D 5. D 6. B7. C 提示:当点P 与点D 重合时,四边形ACBP 的周长最大.8. (1)连结ME ,过N 作NF ⊥AB 于F ,可证明Rt △EB A ≌Rt △MNF ,得MF =AE =x. ∵ME 2=AE 2+AM 2,故MB 2=x 2+AM 2,即(2-AM )2=x 2+AM 2,AM =1-14x 2,∴S =2AM DN +×AD =2AM AF+×2=AM +AM +MF =2 AM +AE =2(1-14x 2)+x =-12x 2+x +2.(2)S =-12(x 2-2 x +1)+52=-12(x -1)2+52. 故当AE =x =1时,四边形ADNM 的面积最大,此时最大值为52. 9. (1)BC 长为23rπ. (2)提示:连结BD . (3)过点B 作BM ⊥AD 于M ,由(2)知四边形ABCD为等腰梯形,从而BC =AD -2 AM =2r -2 AM . 由△BAM ∽△DAB ,得AM =2AB AD =22x r ,∴BC =2r-2x r . 同理,EF =2 r -2x r . l =4 x +2(2 r -2x r )=-xr(x -r )2+6 r (0<x 2 r ). . 当x =r时,l 取得最大值6 r .10. (1)∵∠APE =∠ADQ ,∠AEP =∠AQD ,∴△APE ∽△ADQ . (2)由△APE ∽△ADQ ,△PDF ∽△ADQ ,S △PEF =12S □PEQF ,得S △PEF =-13x 2+x =-13(x -32)2+34. 故当x =32时,即P 是AD 的中点时,S △PEF 取得最大值,(3)作A 关于直线BC 的对称点A′,连结DA′交BC 于Q ,则这个Q 点就是使△ADQ 周长最小的点,此时Q 是BC 的中点.11. (1)点P 恰好在BC 上时,由对称性知MN 是△ABC 的中位线,∴当MN =12BC =3时,点P 在BC 上. (2)由已知得△ABC 底边上的高h =225-3=4. ①当0<x ≤3时,如图1,连结AP 并延长交BC 于点D ,AD 与MN 交于点O .由△AMN ∽△ABC ,得AO =23x ,y =S △PMN =S △AMN =12·x ·23x =13x 2即y =13x 2. 当=3时,y 的值最大,最大值是3. ②当3<x <6时,如图2,设△PMN 与BC 相交于点E ,F ,AP 与BC 相交于D . 由①中知AO =23x ,∴AP =43x ,∴PD =AP -AD =43x -4,∵△PEF ∽△ABC . ,∴PEFABC S S ∆∆=(PD AD )2=(4434x -)2,即PEF ABC S S ∆∆=2-3)9x (. ∵S △ABC =12,∴S △PEF =43(x -3)2. ∴y =S △AMN -S △PEF =13x 2-43(x -3)2=-x 2+8x -12=-(x -4)2+4. 故当x =4时,y 的最大值为4. 综上,当x =4时,y 的值最大,最大值为4. B 级1. 8 2 32 提示:当∠CAB =∠ACD =90°时,四边形ABCD 的面积达到最大值.2. 0<r ≤1 提示:设BC =a ,CA =b ,AB =c ,b +c =3(r +1),又12bc sin60°=S △ABC =12(a +b +c )r ,即12bc ·32=12[33r +1)]r ,. bc =4r (r +2). b ,c 为方程x 2-3r +1)x +4r (r +2)=0的两个根,由△≥0,得(r +1)≤22. 因r >0,r +1>0,故r +1≤2,即0<r ≤1. 3.249π3提示:过P 作垂直于OP 的弦AB ,此时弓形面积最小. 4.13 提示:设AD AB =x ,则BD BA =1-x =CG CA ,ADGABCS S ∆∆=x 2,BDE ABC S S ∆∆=(1-x )2=CFG ABC S S ∆∆,S 梯形DEFG=1―x 2―2(1-x )2=-3(x -23)2+13.5. 312+a 提示:当OA =OB 时,OC 的长最大.6. C7. (1)由Rt △ABP ∽Rt △PCQ ,得BP CQ =AB CP ,即x y =44x -,y =-14(x -2)2+1(0<x <4). 当x =2时, y 最大值=1cm. (2)由14=-14(x -2)2+1,得x =(2+3)cm 或(2-3)cm. 8. 当过A ,B 两点的圆与x 轴正半轴相切时,切点C 为所求. 作O′D ⊥A B 于D . ,O′D 2= O′B 2-BD 2=2()2a b +-2()2a b -=ab ,O′D =ab 故点C 坐标为(ab ,0).9. (1)如图,延长CB 到L ,使BL =DN ,则Rt △ABL ≌Rt △ADN ,得AL =AN ,∠1=∠2,又∵N =2―CN ―CM =DN +BM =BL +BM =ML ,且AM =AM ,∠NAL =∠DAB =90°. ∴△AMN ≌△AML ,故∠MAN =∠MAL=902=45°. (2)设CM =x ,CN =y ,MN =z ,则2222222,2,x y z x y z x y z x y z ++==--⎧⎧⇔⎨⎨+=+=⎩⎩,于是,(2―y ―z )2+y 2=z 2. 整理得2y 2+(2z -4)y +(4-4z )=0. ∵y >0,故△=4(z -2)2-32(1-z )≥0,即(z +2+22)(z +2-22)≥0. 又∵z >0,故z ≥22-2,当且仅当x =y =2-2时等号成立. 由于S △AMN =S △AML =12·ML ·AB =12 MN ×1=2z ,因此,△AMN 的面积的最小值为2-1.10. (1)提示:证明△ADF ∽△BAC . (2)①AB =15,BC =9,∠ACB =90°,∴AC 22AB BC -=2215912-=,∴CF =AF =6,∴()()19632702y x x x =+⨯=+>.②∵BC =9(定值),∴△PBC 的周长最小,就是PB +PC 最小,由(1)知,点C 关于直线DE 的对称点是点A ,所以PB +PC =PB +P A ,故只要求PB +P A 最小.显然当P 、A 、B 三点共线时PB +P A 最小,此时DP =DE ,PB +P A =AB .由(1),角∠ADF =∠F AE ,∠DF A =∠ACB =90°,得△DAF ∽△ABC .EF ∥BC ,得AE =BE =12AB =152,EF =92.∴ AF ∶BC =AD ∶AB ,即6∶9=AD ∶15,∴AD =10.Rt △ADF 中,AD =10,AF =6,∴DF =8.∴DE =DF +FE =8+92=252. ∴当x =252时,△PBC 的周长最小,此时y =1292. 11.(1)令k =1,得y =x +2;令k =2,得y =2x +6,联立解得x =4,y =2,故定点(4,2). (2)取x =0,得OB =2-4k (k <0),取y =0,得OA =()420k k k-<.于是△ABO 的面积()()114224022k S OA OB k k k-==-<,化简得()28820k S k +-+=.由()28640S ∆=--≥得2160S S -≥,故S ≥16.将S =16代入上述方程,得k =12-.故当k =12-,S 值最小. 12.(1)如图,延长EF 交AC 于点D ,DF ∥BC ,Rt △ADF ∽Rt △ACB ,AE =AC =x ,()2222DE x x y xy y =--=-22xy y y x y x -+-=,2x -2y -xy =22x xy y -,两边平方整理得(x 2+2x +2)y 2-(x 3+2x 2+4x )y +2x 2=0.解得2222x y x x =++(y =x 舍去) . (2)由(1)22122222y x x ==+++≤ .当且仅当2x x =,即2x =,上式等号成立.故当2x =,y 去最大21.。
专题09 几何最值问题-2024年中考数学二轮热点题型归纳与变式演练(全国通用)

专题09 几何最值问题目录热点题型归纳题型01 将军饮马模型题型02 费马点模型题型03 阿氏圆模型题型04 隐圆模型题型05 瓜豆圆模型中考练场题型01 将军饮马模型【解题策略】两定一动模型一定两动模型(同侧)(异侧)两线段相减的最大值模型(三点共线)【典例分析】例.(2022·黑龙江·中考真题)1.如图,菱形ABCD 中,对角线AC ,BD 相交于点O ,60BAD Ð=°,3AD =,AH 是BAC Ð的平分线,CE AH ^于点E ,点P 是直线AB 上的一个动点,则OP PE +的最小值是 .【变式演练】(2022·山东枣庄·二模)2.如图,点P 是AOB Ð内任意一点,3cm OP =,点M 和点N 分别是射线OA 和射线OB 上的动点,30AOB Ð=°,则PMN V 周长的最小值是 .(2023广东广州·模拟预测)3.如图,四边形ABCD 中,AB CD P ,AC BC ^,60DAB Ð= ,4AD CD ==,点M 是四边形ABCD 内的一个动点,满足90AMD Ð= ,则MBC V 面积的最小值为 .题型02 费马点模型【解题策略】将△APC 边以A 为顶点逆时针旋转60°,得到AQE ,连接PQ ,则△APQ 为等边三角形,PA =PQ .即PA +PB +PC =PQ +PB +PC ,当B 、P 、Q 、E 四点共线时取得最小值BE .【典例分析】例.(2023全国·中考模拟预测)4.如图1,在RT △ABC 中,∠ACB =90°,CB =4,CA =6,圆C 的半径为2,点P 为圆上一动点,连接AP ,BP ,求:①12AP BP +,②2+AP BP ,③13AP BP +,④3+AP BP 的最小值.【变式演练】(2022·广东广州·一模)5.如图,在Rt △ABC 中,∠BAC =90°,AB =AC ,点P 是AB 边上一动点,作PD ⊥BC 于点D ,线段AD 上存在一点Q ,当QA +QB +QC 的值取得最小值,且AQ =2时,则PD = .(2023广东·一模)6.如图,△ABC 中,∠BAC =45°,AB =6,AC =4,P 为平面内一点,求3PC ++最小值(2024湖北中考·二模)7.如图,正方形ABCD 的边长为4,点P 是正方形内部一点,求2PA PB +的最小值.题型03 阿氏圆模型【解题策略】问题:在圆上找一点P 使得PA k PB + 的值最小,解决步骤具体如下:①如图,将系数不为1的线段两端点与圆心相连即OP ,OB②计算出这两条线段的长度比OP k OB=③在OB 上取一点C ,使得OC k OP =,即构造△POM ∽△BOP ,则PC k PB=,PC k PB = ④则=PA k PB PA PC AC ++≥ ,当A 、P 、C 三点共线时可得最小值.【典例分析】例.(2023·广西·中考真题)8.如图,抛物线2y ax bx c =++与x 轴交于A 0),B 两点(点B 在点A 的左侧),与y轴交于点C ,且3OB OA ==,OAC Ð的平分线AD 交y 轴于点D ,过点A 且垂直于AD的直线l 交y 轴于点E ,点P 是x 轴下方抛物线上的一个动点,过点P 作PF x ^轴,垂足为F ,交直线AD 于点H .(1)求抛物线的解析式;(2)设点P 的横坐标为m ,当FH HP =时,求m 的值;(3)当直线PF 为抛物线的对称轴时,以点H 为圆心,12HC 为半径作H e ,点Q 为H e 上的一个动点,求14AQ EQ +的最小值.【变式演练】(2023·甘肃天水·一模)9.如图,已知正方形ABCD 的边长为4,⊙B 的半径为2,点P 是⊙B 上的一个动点,则PD ﹣12PC 的最大值为 .(2023江苏·二模)10.如图,正方形ABCD 的边长为4,B e 的半径为2,P 为B e PD -的最大值是 .题型04 隐圆模型【解题策略】定点定长定弦定角四点共圆最短距离:“一箭穿心”,然后点到圆心的距离-半径;最长距离:“一箭穿心”,然后点到圆心的距离+半径.【典例分析】例.(2023·辽宁·中考真题)11.如图,在矩形ABCD 中,8AB =,10AD =,点M 为BC 的中点,E 是BM 上的一点,连接AE ,作点B 关于直线AE 的对称点B ¢,连接DB ¢并延长交BC 于点F .当BF 最大时,点B ¢到BC 的距离是 .【变式演练】(2024浙江金华·模拟预测)12.如图,正方形ABCD 的边长为4,点E 是正方形ABCD 内的动点,点P 是BC 边上的动点,且EAB EBC Ð=Ð.连结AE ,BE ,PD ,PE ,则PD PE +的最小值为( )A .2B .2C .2D .2(2022·山东泰安·三模)13.如图,在Rt △ABC 中,90ACB Ð= ,30BAC Ð= ,BC =2,线段BC 绕点B 旋转到BD ,连AD ,E 为AD 的中点,连接CE ,则CE 的最大值是 .(2022·广东河源·二模)14.如图,已知28AC AO ==,平面内点P 到点O 的距离为2,连接AP ,若60APB Ð=°且12BP AP =,连接AB ,BC ,则线段BC 的最小值为 .题型05 瓜豆圆模型【解题策略】条件:两个定量主动点、从动点与定点连线的夹角是定量(∠PAQ 是定值);主动点、从动点到定点的距离之比是定量(AP :AQ 是定值).结论:(1)主、从动点与定点连线的夹角等于两圆心与定点连线的夹角:∠PAQ =∠OAM ;(2)主、从动点与定点的距离之比等于两圆心到定点的距离之比:AP :AQ =AO :AM ,也等于两圆半径之比.【典例分析】例.(2023·江苏·中考真题)15.在四边形ABCD 中,2,120,AB BC ABC BH ==Ð=°为ABC Ð内部的任一条射线(CBH Ð不等于60°),点C 关于BH 的对称点为C ¢,直线AC ¢与BH 交于点F ,连接CC CF ¢、,则CC F ¢△面积的最大值是 .【变式演练】(2023江苏无锡·二模)16.如图,线段AB 为O e 的直径,点C 在AB 的延长线上,4AB =,2BC =,点P 是O e 上一动点,连接CP ,以CP 为斜边在PC 的上方作Rt PCD V ,且使60DCP Ð=°,连接OD ,则OD 长的最大值为 .(2023·安徽·一模)17.如图,在矩形ABCD 中,8AB =,4=AD ,点E 是矩形ABCD 内部一动点,且90BEC Ð=°,点P 是AB 边上一动点,连接PD 、PE ,则PD PE +的最小值为( )A .8B .C .10D .2-(2023·江苏扬州·模拟预测)18.如图,A 是B e 上任意一点,点C 在B e 外,已知24AB BC ACD ==,,△是等边三角形,则BCD △的面积的最大值为( )A .4+B .4C .8D .6(2023·黑龙江绥化·中考真题)19.如图,ABC V 是边长为6的等边三角形,点E 为高BD 上的动点.连接CE ,将CE 绕点C 顺时针旋转60°得到CF .连接AF ,EF ,DF ,则CDF V 周长的最小值是 .(2022·四川成都·中考真题)20.如图,在菱形ABCD 中,过点D 作DE CD ^交对角线AC 于点E ,连接BE ,点P 是线段BE 上一动点,作P 关于直线DE 的对称点P ¢,点Q 是AC 上一动点,连接P Q ¢,DQ .若14AE =,18CE =,则DQ P Q ¢-的最大值为 .(2022·广西柳州·中考真题)21.如图,在正方形ABCD 中,AB =4,G 是BC 的中点,点E 是正方形内一个动点,且EG =2,连接DE ,将线段DE 绕点D 逆时针旋转90°得到线段DF ,连接CF ,则线段CF 长的最小值为 .(2022·江苏无锡·中考真题)22.△ABC 是边长为5的等边三角形,△DCE 是边长为3的等边三角形,直线BD 与直线AE 交于点F .如图,若点D 在△ABC 内,∠DBC =20°,则∠BAF =°;现将△DCE 绕点C 旋转1周,在这个旋转过程中,线段AF 长度的最小值是 .(2022·广西·中考真题)23.如图,在边长为ABCD 中,60C Ð=°,点,E F 分别是,AB AD 上的动点,且,AE DF DE =与BF 交于点P .当点E 从点A 运动到点B 时,则点P 的运动路径长为 .(2023·新疆·中考真题)24.如图,在Rt ABC V 中,AB =AC =4,点E ,F 分别是AB ,AC 的中点,点P 是扇形AEF 的 E F 上任意一点,连接BP ,CP ,则12BP +CP 的最小值是 .1【分析】作点O 关于AB 的对称点F ,连接OF 交AB 于G ,连接PE 交直线AB 于P ,连接PO ,则PO =PF ,此时,PO +PE 最小,最小值=EF ,利用菱形的性质与直角三角形的性质,勾股定理,求出OF ,OE 长,再证明△EOF 是直角三角形,然后由勾股定理求出EF 长即可.【详解】解:如图,作点O 关于AB 的对称点F ,连接OF 交AB 于G ,连接PE 交直线AB 于P ,连接PO ,则PO =PF ,此时,PO +PE 最小,最小值=EF 的长,∵菱形ABCD ,∴AC ⊥BD ,OA =OC ,OB =OD ,AD =AB =3,∵∠BAD =60°,∴△ABD 是等边三角形,∴BD =AB =3,∠BAO =30°,∴OB =12AB =32,∴OA ∴点O 关于AB 的对称点F ,∴OF ⊥AB ,OG =FG ,∴OF =2OG =OA ∠AOG =60°,∵CE ⊥AH 于E ,OA =OC ,∴OE =OC =OA ∴∠AEC =∠CAE ,∵AH 平分∠BAC ,∴∠CAE =15°,∴∠AEO =∠CAE =15°,∴∠COE =∠AEO +∠CAE =30°,∴∠COE +∠AOG =30°+60°=90°,∴∠FOE =90°,∴由勾股定理,得EF ==,∴PO +PE 最小值.【点睛】本题考查菱形的性质,利用轴对称求最短距离问题,直角三角形的性质,勾股定理,作点O 关于AB 的对称点F ,连接OF 交AB 于G ,连接PE 交直线AB 于P ,连接PO ,则PO =PF ,则PO +PE 最小,最小值=EF 的长是解题的关键.2.3cm【分析】分别作点P 关于OA OB 、的对称点C 、D ,连接CD ,分别交OA OB 、于点M 、N ,连接OP OC OD PM PN 、、、、,当点M 、N 在CD 上时,PMN V 的周长最小.【详解】解:分别作点P 关于OA OB 、的对称点C 、D ,连接CD ,分别交OA OB 、于点M 、N ,连接OP OC OD PM PN 、、、、.∵点P 关于OA 的对称点为C ,关于OB 的对称点为D ,∴PM CM OP OC COA POA ==Ð=Ð,,;∵点P 关于OB 的对称点为D ,∴PN DN OP OD DOB POB ==Ð=Ð,,,∴3cm OC OD OP ===,22260COD COA POA POB DOB POA POB AOB Ð=Ð+Ð+Ð+Ð=Ð+Ð=Ð=°,∴COD △是等边三角形,∴()3cm CD OC OD ===.∴PMN V 的周长的最小值3cm PM MN PN CM MN DN CD =++=++≥=.故答案为:3cm .【点睛】本题主要考查最短路径问题和等边三角形的判定. 作点P 关于OA 、OB 的对称点C 、D 是解题的关键所在.3.4-【分析】取AD 的中点O ,连接OM ,过点M 作ME BC ^交BC 的延长线于点E ,过点O 作OF BC ^于F ,交CD 于G ,则OM ME OF +≥,通过计算得出当,,O M E 三点共线时,ME 有最小值,求出最小值即可.【详解】解:如图,取AD 的中点O ,连接OM ,过点M 作ME BC ^交BC 的延长线于点E ,过点O 作OF BC ^于F ,交CD 于G ,则OM ME OF +≥,Q AB CD P ,60DAB Ð= ,4AD CD ==,\120ADC Ð=°,Q AD CD =,\30DAC Ð=°,\30CAB Ð=°,Q AC BC ^,\90ACB Ð=°903060B \Ð=°-°=°,\B DAB Ð=Ð,\四边形ABCD 为等腰梯形,\4BC AD ==,Q 90AMD Ð= ,4=AD ,OA OD =,\122OM AD ==,\点M 在以点O 为圆心,2为半径的圆上,Q AB CD ∥,\60GCF B Ð=Ð=°,\30DGO CGF Ð=Ð=°,Q OF BC ^,AC BC ^,\30DOG DAC DGO Ð=Ð=°=Ð,\2DG DO ==,\2cos30OG OD =×°=,GF =,OF =,\2ME OF OM ≥-=,\当,,O M E 三点共线时,ME 有最小值2,\MBC V 面积的最小值为()14242=´´=.【点睛】本题考查了解直角三角形、隐圆、直角三角形的性质等知识点,点M 位置的确定是解题关键.4.;②④.【分析】①在CB 上取点D ,使1CD =,连接CP 、DP 、AD .根据作图结合题意易证~V V DCP PCB ,即可得出12PD BP =,从而推出12AP BP AP PD +=+,说明当A 、P 、D 三点共线时,AP PD +最小,最小值即为AD 长.最后在Rt ACD V 中,利用勾股定理求出AD 的长即可;②由122()2+=+AP BP AP BP ,即可求出结果;③在CA 上取点E ,使23CE =,连接CP 、EP 、BE .根据作图结合题意易证~V V ECP PCA ,即可得出13EP AP =,从而推出13AP BP EP BP +=+,说明当B 、P 、E 三点共线时,EP BP +最小,最小值即为BE 长.最后在Rt BCE △中,利用勾股定理求出BE 的长即可;④由133()3+=+AP BP AP BP ,即可求出结果.【详解】解:①如图,在CB 上取点D ,使1CD =,连接CP 、DP 、AD .∵1CD =,2CP =,4CB =,∴12CD CP CP CB ==.又∵DCP PCB Ð=Ð,∴~V V DCP PCB ,∴12PD BP =,即12PD BP =,∴12AP BP AP PD +=+,∴当A 、P 、D 三点共线时,AP PD +最小,最小值即为AD 长.∵在Rt ACD V 中,===AD∴12AP BP +;②∵122()2+=+AP BP AP BP ,∴2+AP BP 的最小值为2=③如图,在CA 上取点E ,使23CE =,连接CP 、EP 、BE .∵23CE =,2CP =,6CA =,∴13==CE CP CP CA .又∵Ð=ÐECP PCA ,∴~V V ECP PCA ,∴13=EP AP ,即13EP AP =,∴13AP BP EP BP +=+,∴当B 、P 、E 三点共线时,EP BP +长.∵在Rt BCE △中,===BE∴13AP BP +;④∵133()3+=+AP BP AP BP ,∴3+AP BP 的最小值为3=.【点睛】本题考查圆的基本性质,相似三角形的判定和性质,勾股定理.正确的作出辅助线,并且理解三点共线时线段最短是解答本题的关键.5.【分析】如图1,将△BQC 绕点B 顺时针旋转60°得到△BNM ,连接QN ,当点A ,点Q ,点N ,点M 共线时,QA +QB +QC 值最小,此时,如图2,连接MC ,证明AM 垂直平分BC ,证明AD =BD ,此时P 与D 重合,设PD =x ,则DQ =x -2,构建方程求出x 可得结论.【详解】解:如图1,将△BQC 绕点B 顺时针旋转60°得到△BNM ,连接QN ,∴BQ =BN ,QC =NM ,∠QBN =60°,∴△BQN 是等边三角形,∴BQ =QN ,∴QA +QB +QC =AQ +QN +MN ,∴当点A ,点Q ,点N ,点M 共线时,QA +QB +QC 值最小,此时,如图2,连接MC∵将△BQC 绕点B 顺时针旋转60°得到△BNM ,∴BQ =BN ,BC =BM ,∠QBN =60°=∠CBM ,∴△BQN 是等边三角形,△CBM 是等边三角形,∴∠BQN =∠BNQ =60°,BM =CM ,∵BM =CM ,AB =AC ,∴AM 垂直平分BC ,∵AD ⊥BC ,∠BQD =60°,∴BD ,∵AB =AC ,∠BAC =90°,AD ⊥BC ,∴AD =BD ,此时P 与D 重合,设PD =x ,则DQ =x -2,∴x =())tan 6022x x °´-=-,∴x∴PD故答案为:.【点睛】本题主要考查了等腰直角三角形的性质,旋转的性质,等边三角形的判定和性质,解题的关键是正确运用等边三角形的性质解决问题,学会构建方程解决问题.6.【分析】将△APC 绕点A 逆时针旋转45°,得到△A P ¢C ¢,将△A P ¢C ¢△AP C ¢¢¢¢,当点B 、P 、P ¢¢、C ¢¢在同一直线上时,3PC +=)''''''PB PP P C ++最短,利用勾股定理求出BC ¢¢即可.【详解】解:如图,将△APC 绕点A 逆时针旋转45°,得到△A ¢C ¢,将△A ¢C ¢扩大,相△AP C ¢¢¢¢,则AP AP ¢¢¢,P C C ¢¢¢¢¢¢,AC AC ¢¢¢,过点P 作PE ⊥A P ¢¢于E ,∴AE=PE AP =,∴P ¢¢E=A P ¢¢AP ,∴P P ¢¢AP =,当点B 、P 、P ¢¢、C ¢¢在同一直线上时,3PC +=)''''''PB PP P C ++最短,此时)''''''PB PP P C ++=C ¢¢,∵∠BA C ¢¢=∠BAC +∠CA C ¢¢=90°,AB =6,4AC AC ¢¢¢=∴BC ¢¢==.∴3PC +=C ¢¢=【点睛】此题考查旋转的性质,全等三角形的性质,勾股定理,正确理解费马点问题的造图方法:利用旋转及全等的性质构建等量的线段,利用三角形的三边关系及点共线的知识求解,有时根据系数将图形扩大或缩小构建图形.7.【分析】延长DC 到H ,使得28CH BC ==,则BH =,在CBH Ð的内部作射线BJ ,使得PBJ CBH Ð=Ð,使得BJ ,连接PJ ,JH ,AH .先证明JBP HBC △∽△,可得2PJ PB =,再证明PBC JBH △∽△,可得:HJ =,从而得到2PA PB PA PJ HJ AH +=++≥,计算出AH 的长度即可.【详解】解:延长DC 到H ,使得28CH BC ==,则BH =,在CBH Ð的内部作射线BJ ,使得PBJ CBH Ð=Ð,使得BJ ,连接PJ ,JH ,AH .PBJ CBH Ð=ÐQ ,BP BC BJ BH =,\PB BJ BC BH=,JBP HBC \V V ∽,90BPJ BCH \Ð=Ð=°,2PJ PB \===,PBC JBH Ð=ÐQ ,PB BC BJ BH=,PBC JBH \V V ∽,\PC PB JH BJ =HJ \2PA PB PA PJ H J \+=++,PA PJ JH AH ++≥Q ,2PA PB \+≥=2PA PB \+的值最小,最小值为.【点睛】本题考查相似三角形的判定与性质,勾股定理,两点之间线段最短,正方形的性质,,正确理解费马点问题,利用相似构造2PB ,根据系数将图形扩大或缩小构建图形是解决问题的关键.8.(1)y 13=x 2x ﹣3;(2)(3【分析】对于(1),结合已知先求出点B 和点C 的坐标,再利用待定系数法求解即可;对于(2),在Rt △OAC 中,利用三角函数的知识求出∠OAC 的度数,再利用角平分线的定义求出∠OAD 的度数,进而得到点D 的坐标;接下来求出直线AD 的解析式,表示出点P ,H ,F 3),首先求出⊙H 的半径,在HA 上取一点K ,使得HK=14,此时K (15-8);然后由HQ 2=HK·HA ,得到△QHK ∽△AHQ ,再利用相似三角形的性质求出KQ=14AQ ,进而可得当E 、Q 、K 共线时,14AQ+EQ 的值最小,据此解答.【详解】(1)由题意A 0),B (﹣0),C (0,﹣3),设抛物线的解析式为y =a (x (x ,把C (0,﹣3)代入得到a 13=,∴抛物线的解析式为y 13=x 2x ﹣3.(2)在Rt △AOC 中,tan ∠OAC OC OA=,∴∠OAC =60°.∵AD OAC ,∴∠OAD =30°,∴•tan30°=1,∴D (0,﹣1),∴直线AD 的解析式为y =﹣1,由题意P (m ,13m 2m ﹣3),H (m ﹣1),F (m ,0).∵FH =PH ,∴1=﹣1﹣(13m 2m ﹣3)解得m =,∴当FH =HP 时,m 的值为(3)如图,∵PF 是对称轴,∴F (0),H (,﹣2).∵AH ⊥AE ,∴∠EAO =60°,∴EO ==3,∴E (0,3).∵C (0,﹣3),∴HC =2,AH =2FH =4,∴QH 12=CH =1,在HA 上取一点K ,使得HK 14=,此时K (158-).∵HQ 2=1,HK •HA =1,∴HQ 2=HK •HA ,∴HQ KH AH HQ =.∵∠QHK =∠AHQ ,∴△QHK ∽△AHQ ,∴14KQ HQ AQ AH ==,∴KQ 14=AQ ,∴14AQ +QE =KQ +EQ ,∴当E 、Q 、K 共线时,14AQ +QE 的值最小,最小值==.【点睛】本题考查了相似三角形对应边成比例、两边成比例且夹角相等的两个三角形相似、待定系数法求二次函数的表达式、二次函数的图象与性质、数轴上两点间的距离公式,熟练掌握该知识点是本题解题的关键.9.5【详解】分析: 由PD−12PC =PD−PG≤DG ,当点P 在DG 的延长线上时,PD−12PC 的值最大,最大值为DG =5.详解: 在BC 上取一点G ,使得BG =1,如图,∵221PB BG ==,422BC PB ==,∴PB BC BG PB=,∵∠PBG =∠PBC ,∴△PBG ∽△CBP ,∴12PG BG PC PB ==,∴PG =12PC ,当点P 在DG 的延长线上时,PD−12PC 的值最大,最大值为DG =5.故答案为5点睛: 本题考查圆综合题、正方形的性质、相似三角形的判定和性质等知识,解题的关键是学会构建相似三角形解决问题,学会用转化的思想思考问题,把问题转化为两点之间线段最短解决,题目比较难,属于中考压轴题.10.2【分析】解法1,如图:以PD 为斜边构造等腰直角三角形PDM △,连接MC ,BD ,连接PM 、DM ,推得)PD PC PC PM ö-==-÷÷ø,因为PC PM MC -£,求出MC 即可求出答案.解法2:如图:连接BD 、BP 、PC ,在BD 上做点M ,使BM BP MP ,证明BMP V :BPD △,在BC 上做点N ,使1=2BN BP ,连接NP ,证明BNP △:BPC △,接着推导PD -,最后证明BMN V :BCD △,即可求解.【详解】解法1如图:以PD 为斜边构造等腰直角三角形PDM △,连接MC ,BD ,∴45PDM Ð=,DM PM =,Q 四边形ABCD 正方形\45BDC Ð=°,DB DC=又Q PDM PDB MDB Ð=Ð+,BDC MDB MDCÐ=Ð+\PDB MDCÐ=Ð在BPD △与MPC V 中PDB MDC Ð=Ð,DB DP DC DM==\BPD △:MPCV\PB MC =Q 2BP =\MC =Q )PD PC PC PM ö-=-÷÷øQ PC PM MC-£)2PD PC PM -=-£=故答案为:2.解法2如图:连接BD 、BP 、PC根据题意正方形ABCD 的边长为4,B e 的半径为2\=2BP ,BDQBP BD在BD 上做点M ,使BM BP =BM MP 在BMP V 与BPD △中=MBP PBD ÐÐ,=BP BM BD BP\V BPD\PM PD PD Q 21==42BP BC 在BC 上做点N ,使1=2BN BP ,则=1BN ,连接NP 在BNP △与BPC △中=NBP PBC ÐÐ,=BN BP BP PC\BNP △:BPC△\1=2PN PC ,则=2PC PN \如图所示连接NM)2PD PN PN PM ---Q PN PM NM -£)PD PN PM --£在BMN V 与BCD △中=NBM DBC ÐÐ,BM BC BN BD \=BM BN BC BD\V BCD\MN CD Q CD\MN\2PD -£=故答案为:2.【点睛】本题考查正方形的性质,相似三角形,勾股定理等知识,难度较大,熟悉以上知识点运用是解题关键.11.165【分析】如图,由题意可得:B ¢在A e 上,过B ¢作B H BC ¢^于H ,由点B 关于直线AE 的对称点B ¢,可得AB AB ¢=,BE B E ¢=,AEB AEB ¢Ð=Ð,ABE AB E ¢Ð=Ð,当DE 与A e 切于点B ¢时,BF 最大,此时DF AB ¢^,证明E ,F 重合,可得DAE AEB AEB ¢Ð=Ð=Ð,10AD DE ==,求解4BE B E ¢==,证明EB H EDC ¢V V ∽,可得EB B H ED CD¢¢=,从而可得答案.【详解】解:如图,由题意可得:B ¢在A e 上,过B ¢作B H BC ¢^于H ,∵点B 关于直线AE 的对称点B ¢,∴AB AB ¢=,BE B E ¢=,AEB AEB ¢Ð=Ð,ABE AB E ¢Ð=Ð,当DE 与A e 切于点B ¢时,BF 最大,此时DF AB ¢^,∴90ABE AB F ¢Ð=Ð=°,∴E ,F 重合,∴AEB AEB ¢Ð=Ð,∵矩形ABCD ,∴AD BC ∥,90C Ð=°,10AD BC ==,8AB CD ==,∴DAE AEB AEB ¢Ð=Ð=Ð,∴10AD DE ==,∴6CE ==,∴4BE B E ¢==,∵B H BC ¢^,90C Ð=°,∴B H CD ¢∥,∴EB H EDC ¢V V ∽,∴EB B H ED CD¢¢=,∴4108B H ¢=,∴165B H ¢=,∴点B ¢到BC 的距离是165.故答案为:165.【点睛】本题考查的是轴对称的性质,矩形的性质,勾股定理的应用,相似三角形的判定与性质,圆的基本性质,作出合适的辅助线是解本题的关键.12.A【分析】先证明90AEB Ð=°,即可得点E 在以AB 为直径的半圆上移动,设AB 的中点为O ,作正方形ABCD 关于直线BC 对称的正方形CFGB ,则点D 的对应点是F ,连接FO 交BC 于P ,交半圆O 于E ,根据对称性有:PD PF =,则有:PE PD PE PF +=+,则线段EF 的长即为PE PD +的长度最小值,问题随之得解.【详解】解:∵四边形ABCD 是正方形,∴90ABC Ð=°,∴90ABE EBC Ð+Ð=°,∵EAB EBC Ð=Ð,∴90EAB EBA Ð+Ð=°,∴90AEB Ð=°,∴点E 在以AB 为直径的半圆上移动,如图,设AB 的中点为O ,作正方形ABCD 关于直线BC 对称的正方形CFGB ,则点D 的对应点是F ,连接FO 交BC 于P ,交半圆O 于E ,根据对称性有:PD PF =,则有:PE PD PE PF +=+,则线段EF 的长即为PE PD +的长度最小值,E∵90G Ð=°,4FG BG AB ===,∴6OG =,2OA OB OE ===,∴OF ==∴2EF OF OE =-=,故PE PD +的长度最小值为2,故选:A .【点睛】本题考查了轴对称﹣最短路线问题,正方形的性质,勾股定理,正确的作出辅助线,得出点E的运动路线是解题的关键.13.3【分析】通过已知求得D在以B为圆心,BD长为半径的圆上运动,∵E为AD的中点,∴E在以BA中点为圆心,12B D长为半径的圆上运动,再运用圆外一定点到圆上动点距离的最大值=定点与圆心的距离+圆的半径,求得CE的最大值.【详解】解:∵BC=2,线段BC绕点B旋转到BD,∴BD=2,∴112BD=.由题意可知,D在以B为圆心,BD长为半径的圆上运动,∵E为AD的中点,∴E在以BA中点为圆心,12B D长为半径的圆上运动,CE的最大值即C到BA中点的距离加上12B D长.∵90ACBÐ= ,30BACÐ= ,BC=2,∴C到BA中点的距离即122AB=,又∵112BD=,∴CE的最大值即11213 22AB BD+=+=.故答案为3.【点睛】本题考查了与圆相关的动点问题,正确识别E点运动轨迹是解题的关键.14.【分析】如图所示,延长PB到D使得PB=DB,先证明△APD是等边三角形,从而推出ABP=90°,∠BAP =30°,以AO 为斜边在AC 下方作Rt △∠MAO =30°,连接CM ,过点M 作MH ⊥AC 于H ,解直角三角形得到AM AB AO AP =△AMB ∽△AOP ,得到BM AB OP AP ==BM =,则点B 在以M M 、B 、C 三点共线时,即点B 在点B ¢的位置时,BC 有最小值,据此求解即可.【详解】解:如图所示,延长PB 到D 使得PB =DB ,∵12BP AP =,∴2AP PD PB ==,又∵∠APB =60°,∴△APD 是等边三角形,∵B 为PD 的中点,∴AB ⊥DP ,即∠ABP =90°,∴∠BAP =30°,以AO 为斜边在AC 下方作Rt △AMO ,使得∠MAO =30°,连接CM ,过点M 作MH ⊥AC 于H ,∴cos OAM ∠同理可得AB AP ∵∠OAM =30°=∠PAB ,∴∠BAM =∠PAO又∵AM AB AO AP =∴△AMB ∽△AOP∴BM AB OP AP ==∵点P 到点O 的距离为2,即OP =2,∴BM =∴点B 在以M连接CM 交圆M B ¢,∴当M 、B 、C 三点共线时,即点B 在点B ¢的位置时,BC 有最小值,∵AC =2AO =8,∴AO =4,∴cos AM AO OAM =×∠∴cos 3AH AM MAH =×Ð=,=sin HM AM MAH ×∠∴5CH =,∴CM ==∴B C CM MB ¢¢=-=,∴BC 的最小值为故答案为:.【点睛】本题主要考查了等边三角形的性质与判定,解直角三角形,相似三角形的性质与判定,勾股定理,圆外一点到圆上一点的最值问题,解题的关键在于能够熟练掌握瓜豆模型即证明点B 在以M15.【分析】连接BC ¢,根据轴对称的性质可得,CB C B CF C F ¢¢==,进而可得,,A C C ¢在半径为2的B e 上,证明CC F ¢△是等边三角形,当CC ¢取得最大值时,CC F ¢△面积最大,根据圆的直径最大,进而得出CC ¢最大值为4,即可求解.【详解】解:如图所示,连接BC ¢,∵点C 关于BH 的对称点为C ¢,∴,CB C B CF C F ¢¢==,∵2AB BC ==,∴,,A C C ¢在半径为2的B e 上,在优弧 AC 上任取一点E ,连接,AE EC ,则1602AEC ABC а=Ð=,∵120ABC Ð=°,∴11801801202AC C AEC ABC ¢Ð=°-Ð=°-Ð=°,∴60CC F ¢Ð=°,∴CC F ¢△是等边三角形,当CC ¢取得最大值时,CC F ¢△面积最大,∵C ¢在B e 上运动,则CC ¢4,则CC F ¢△24=故答案为:【点睛】本题考查了轴对称的性质,圆周角定理,圆内接四边形对角互补,等边三角形的性质,得出CC ¢最大值为4是解题的关键.16.1##1+【分析】作COE V ,使得90CEO Ð=°,60ECO Ð=°,则2CO CE =,OE =OCP ECD Ð=Ð,由COP CED ∽△△,推出2OP CP ED CD==,即112ED OP ==(定长),由点E 是定点,DE 是定长,点D 在半径为1的E e 上,由此即可解决问题.【详解】解:如图,作COE V ,使得90CEO Ð=°,60ECO Ð=°,则2CO CE =,OE =,OCP ECD Ð=Ð,90CDP Ð=°Q ,60DCP Ð=°,2CP CD \=,\2CO CP CE CD==,COP CED \V V ∽,\2OP CP ED CD==,即112ED OP ==(定长),Q 点E 是定点,DE 是定长,\点D 在半径为1的E e 上,1OD OE DE £+=Q ,OD \的最大值为1,故答案为:1.【点睛】本题考查了相似三角形的判定和性质、两圆的位置关系、轨迹等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,属于中考压轴题.17.A【分析】根据90BEC Ð=°得到点的运动轨迹,利用“将军饮马”模型将PE 进行转化即可求解.【详解】解:如图,设点O 为BC 的中点,由题意可知,点E 在以BC 为直径的半圆O 上运动,作半圆O 关于AB 的对称图形(半圆'O ),点E 的对称点为1E ,连接1'O E ,则1PE PE =,∴当点D 、P 、1E 、'O 共线时,PD PE +的值最小,最小值为1DE 的长,如图所示,在Rt 'DCO V 中,8CD =,'=6CO ,'10DO \==,又1'2O E =Q ,11''8DE DO O E \=-=,即PD PE +的最小值为8,故选:A .【点睛】本题考查线段和最短问题、轴对称的性质、勾股定理及圆周角定理,利用“将军饮马”模型将PE 进行转化时解题的关键.18.A【分析】以BC 为边向上作等边三角形BCM ,连接DM ,证明DCM ACB △≌△得到2DM AB ==,分析出点D 的运动轨迹是以点M 为圆心,DM 长为半径的圆,在求出点D 到线段BC 的最大距离,即可求出面积的最大值.【详解】解:如图,以BC 为边向上作等边三角形BCM ,连接DM ,∵60DCA MCB Ð=Ð=°,∴DCA ACM MCB ACM Ð-Ð=Ð-Ð,即DCM ACB =∠∠,在DCM △和ACB △中,DC AC DCM ACB MC BC =ìïÐ=Ðíï=î,∴()SAS DCM ACB △≌△,∴2DM AB ==,∴点D 的运动轨迹是以点M 为圆心,DM 长为半径的圆,要使BCD △的面积最大,则求出点D 到线段BC 的最大距离,∵BCM V 是边长为4的等边三角形,∴点M 到BC 的距离为∴点D 到BC 的最大距离为2,∴BCD △的面积最大值是()14242´´=,故选A .【点睛】本题考查了动点轨迹是圆的问题,解决本题的关键是利用构造全等三角形找到动点D 的轨迹圆,再求出圆上一点到定线段距离的最大值.19.3+3【分析】根据题意,证明CBE CAF V V ≌,进而得出F 点在射线AF 上运动,作点C 关于AF 的对称点C ¢,连接DC ¢,设CC ¢交AF 于点O ,则=90AOC а,则当,,D F C ¢三点共线时,FC FD +取得最小值,即FC FD F C F D CD ¢¢¢¢+=+=,进而求得C D ¢,即可求解.【详解】解:∵E 为高BD 上的动点.∴1302CBE ABC Ð=Ð=°∵将CE 绕点C 顺时针旋转60°得到CF .ABC V 是边长为6的等边三角形,∴,60,CE CF ECF BCA BC AC=Ð=Ð=°=∴CBE CAFV V ≌∴30CAF CBE Ð=Ð=°,∴F 点在射线AF 上运动,如图所示,作点C 关于AF 的对称点C ¢,连接DC ¢,设CC ¢交AF 于点O ,则=90AOC а在Rt AOC V 中,30CAO Ð=°,则132CO AC ==,则当,,D F C ¢三点共线时,FC FD +取得最小值,即FC FD F C F D CD ¢¢¢¢+=+=∵6CC AC ¢==,ACO C CD ¢Ð=Ð,CO CD=∴ACO C CD¢V V ≌∴90C DC AOC ¢Ð=Ð=°在C DC ¢V 中,C D ¢===∴CDF V 周长的最小值为3CD FC CD CD DC ¢++=+=+故答案为:3+【点睛】本题考查了轴对称求线段和的最值问题,等边三角形的性质与判定,全等三角形的性质与判定,勾股定理,熟练掌握等边三角形的性质与判定以及轴对称的性质是解题的关键.20【分析】延长DE ,交AB 于点H ,确定点B 关于直线DE 的对称点F ,由点B ,D 关于直线AC 对称可知QD=QB ,求QD Q P ¢-最大,即求Q B Q P ¢-最大,点Q ,B ,P ¢共线时,Q D Q P Q B Q P B P ¢¢¢-=-=,根据“三角形两边之差小于第三边”可得BP ¢最大,当点P ¢与点F 重合时,得到最大值.连接BD ,即可求出CO ,EO ,再说明E OD D O C V :V ,可得DO ,根据勾股定理求出DE ,然后证明E O D B H D V :V ,可求BH ,即可得出答案.【详解】延长DE ,交AB 于点H ,∵AB CD P ,ED ⊥CD ,∴DH ⊥AB .取FH=BH ,∴点P 的对称点在EF 上.由点B ,D 关于直线AC 对称,∴QD=QB .要求QD Q P ¢-最大,即求Q B Q P ¢-最大,点Q ,B ,P ¢共线时,Q D Q P Q B Q P B P ¢¢¢-=-=,根据“三角形两边之差小于第三边”可得BP ¢最大,当点P ¢与点F 重合时,得到最大值BF .连接BD ,与AC 交于点O .∵AE=14,CE=18,∴AC=32,∴CO=16,EO=2.∵∠EDO+∠DEO=90°,∠EDO+∠CDO=90°,∴∠DEO=∠CDO.∵∠EOD=∠DOC,∴E O D D O CV:V,∴E O D O D O C O=,即221632D O=´=,解得DO=∴2B D D O==.在Rt△DEO中,6D E==.∵∠EDO=∠BDH,∠DOE=∠DHB,∴E O D B H DV:V,∴E O D EB H B D=,即2B H=解得B H∴B F=.【点睛】这是一道根据轴对称求线段差最大的问题,考查了菱形的性质,勾股定理,轴对称的性质,相似三角形的性质和判定等,确定最大值是解题的关键.21.2【分析】如图,由EG=2,确定E在以G为圆心,半径为2的圆上运动,连接AE,再证明ADE CDF V V ≌(SAS ), 可得,AE CF =可得当,,A E G 三点共线时,AE 最短,则CF 最短,再利用勾股定理可得答案.【详解】解:如图,由EG =2,可得E 在以G 为圆心,半径为2的圆上运动,连接AE ,∵正方形ABCD ,∴,90,AD CD ADC =Ð=° 90,ADC EDF \Ð=Ð=°∴,ADE CDF Ð=Ð ∵DE =DF ,∴ADE CDF V V ≌(SAS ),∴,AE CF =∴当,,A E G 三点共线时,AE 最短,则CF 最短,∵G 位BC 中点,4,BC AB == ∴2,BG =此时AG ===此时2,AE =所以CF 的最小值为: 2.故答案为:2【点睛】本题考查的是正方形的性质,圆的基本性质,勾股定理的应用,二次根式的化简,熟练的利用圆的基本性质求解线段的最小值是解本题的关键.22. 80 44【分析】利用SAS 证明△BDC ≌△AEC ,得到∠DBC =∠EAC =20°,据此可求得∠BAF 的度数;利用全等三角形的性质可求得∠AFB =60°,推出A 、B 、C 、F 四个点在同一个圆上,当BF 是圆C 的切线时,即当CD ⊥BF 时,∠FBC 最大,则∠FBA 最小,此时线段AF 长度有最小值,据此求解即可.【详解】解:∵△ABC 和△DCE 都是等边三角形,∴AC =BC ,DC =EC ,∠BAC =∠ACB =∠DCE =60°,∴∠DCB +∠ACD =∠ECA +∠ACD =60°,即∠DCB =∠ECA ,在△BCD 和△ACE 中,CD CE BCD ACE BC AC =ìïÐ=Ðíï=î,∴△ACE ≌△BCD ( SAS ),∴∠EAC =∠DBC ,∵∠DBC =20°,∴∠EAC =20°,∴∠BAF =∠BAC +∠EAC =80°;设BF 与AC 相交于点H ,如图:∵△ACE ≌△BCD∴AE =BD ,∠EAC =∠DBC ,且∠AHF =∠BHC ,∴∠AFB =∠ACB =60°,∴A 、B 、C 、F 四个点在同一个圆上,∵点D 在以C 为圆心,3为半径的圆上,当BF 是圆C 的切线时,即当CD ⊥BF 时,∠FBC 最大,则∠FBA 最小,∴此时线段AF 长度有最小值,在Rt △BCD 中,BC =5,CD =3,∴BD =4,即AE =4,∴∠FDE =180°-90°-60°=30°,∵∠AFB =60°,∴∠FDE =∠FED =30°,∴FD =FE ,过点F 作FG ⊥DE 于点G ,∴DG =GE =32,∴FE =DF =cos30DG °∴AF =AE -FE故答案为:80;【点睛】本题考查了旋转的性质,等边三角形的性质,圆周角定理,切线的性质,解直角三角形,解答本题的关键是明确题意,找出所求问题需要的条件.23.43p 【分析】根据题意证得BFD DEA ≌V V ,推出∠BPE =60°,∠BPD =120°,得到C 、B 、P 、D 四点共圆,知点P 的运动路径长为BD n的长,利用弧长公式即可求解.【详解】连接BD ,∵菱形ABCD 中,60C Ð=°,∴∠C=∠A=60°,AB=BC=CD=AD ,∴△ABD 和△CBD 都为等边三角形,∴BD=AD ,∠BDF=∠DAE=60°,∵DF=AE ,∴BFD DEA ≌V V ,∴∠DBF=∠ADE ,∵∠BPE=∠BDP+∠DBF =∠BDP+∠ADE=∠BDF =60°,∴∠BPD=180°-∠BPE=120°,∵∠C=60°,∴∠C+∠BPD =180°,∴C 、B 、P 、D 四点共圆,即⊙O 是CBD △的外接圆,∴当点E 从点A 运动到点B 时,则点P 的运动路径长为BD n 的长,∴∠BOD =2∠BCD =120°,作OG ⊥BD 于G ,根据垂径定理得:BG=GD=12∠BOG =12∠BOD =60°,∵sin BOG BG OB Ð=,即sin 60°=,∴2OB =,从而P 点的路径长为212041801803n R p p p ´°×==°°.【点睛】本题考查了菱形的性质,等边三角形的判定和性质,全等三角形的判定和性质,圆内接四边形的性质,弧长公式等知识,解题的关键是学会准确寻找点的运动轨迹.24【分析】在AB 上取一点T ,使得AT =1,连接PT ,PA ,CT .证明PAT BAP V V ∽,推出PT PB =AP AB =12,推出PT =12PB ,推出12PB +CP =CP +PT ,根据PC +PT ≥TC ,求出CT 即可解决问题.【详解】解:在AB 上取一点T ,使得AT =1,连接PT ,PA ,CT .∵PA =2.AT =1,AB =4,∴PA 2=4=AT •AB ,∴PA AT =AB PA ,∵∠PAT =∠PAB ,∴PAT BAPV V∽,∴PTPB=APAB=12,∴PT=12PB,∴12PB+CP=CP+PT,∵PC+PT≥TC,在Rt ACTV中,∵∠CAT=90°,AT=1,AC=4,∴CT,∴12PB+PC,∴12PB+PC..【点睛】本题考查等腰直角三角形的性质,三角形相似的判定与性质,勾股定理的应用,三角形的三边关系,圆的基本性质,掌握以上知识是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
15:33
小试牛刀
第二部分
几何最值问题解题策略
考情分析
专题归纳
真题回顾
小试牛刀
4.(2016·江苏宿迁)如图,在平面直角坐标系中,点 P 的坐标为(0,4),直线 y= x-3 与 x 轴、y
轴分别交于点 A,B,点 M 是直线 AB 上的一个动点,则 PM 长的最小值为
.
【解析】本题考查直角坐标系中垂线段最短的问题.当
中考数学一轮复习 第一讲
几何最值问题解题策略
主讲人:刘珍珍
15:33
几何最值问题解题策略
第二部分
考情分析
专题归纳
真题回顾
小试牛刀
最值问题是初中数学的重要内容,无论是代数问题还是几何问题 都有最值问题,在中考压轴题中出现比较高的频率。主要有利用 重要的几何结论(如两点之间线段最短、三角形两边之和大于第 三边、两边之差小于第三边、垂线段最短等)以及用一次函数和 二次函数的性质来求最值问题. 近五年的中考真题,以安徽省为例,在2016、2017、2019年中 出现了3次,考频比较高。但是考生得分率普遍不高,在复习时应 引起关注,预计2020年全国中考会出现几何最值问题的选择题或 解答题.
15:33
几何最值问题解题策略
第二部分
考情分析
专题归纳
真题回顾
一、几何法 通过转化思想,将线段等值变换 (常用方法:翻折(对称)、平移、旋转)
①[定点到定点]:两点之间,线段最短;
②[定点到定线]:点线之间,垂线段最短。
一
由此派生:
③[定点到定点]:三角形两边之和大于第三边;
④[定线到定线]:平行线之间,垂线段最短;
小试牛刀
5.(2016·武汉)如图,∠AOB=30°,点M,N分别在边OA,OB上,且OM=1,ON=3,点 P,Q分别在边OB,OA上,则MP+PQ+QN的最小值是 .
一
15:33
【解析】如图,作点M关于ON的对称点M‘,点N关于OA的对称点N’,连接M‘N’分别交ON,OA于点P,Q,此时 MP+PQ+QN的值最小.由对称性质知,M‘P=MP,N’Q=NQ,∴MP+PQ+QN=M‘N’.连接ON‘,OM’,则 ∠M‘OP=∠MOP=∠N’OQ=30°,∴∠N‘OM’=90°,又∵ON‘=ON=3,OM’=OM=1,∴M'N'=
第二部分
考情分析
专题归纳
真题回顾
小试牛刀
一
15:33
第二部分
几何最值问题解题策略
考情分析
专题归纳
真题回顾
小试牛刀
例1(2019安徽)如图,在正方形ABCD中,点E,F将对角线AC三等分, 且AC=12,点P在正方形的边上,则满足PE+PF=9的点P的个数是() A. 0 B. 4 C. 6 D. 8
小值为 ( C )
15:33
一
A.2
B.3
C.4
D.4
【解析】设BE与AC交于点P',连接BD,P'D.∵点B与D关于AC对 称,∴P'D=P'B,∴P'D+P'E=P'B+P'E=BE,当点P位于点P'处时,PD+PE最小.∵正方形 ABCD的面积为16,∴AB=4,又∵△ABE是等边三角形,∴BE=AB=4,∴PD+PE的最小 值为4.
.
几何最值问题解题策略
第二部分
考情分析
专题归纳
秘籍2:
真题回顾
小试牛刀
3、【旋转变换类】OA与OB共用顶点O,固定OA将OB绕点旋 转过程中的,会出现的最大值与最小值,如图:
B
A
O
最小值位置
最大值位置
15:33
第二部分
几何最值问题解题策略
考情分析
专题归纳
真题回顾
小试牛刀
例7 如图所示, ABD 是等边三角形,在 ABC
几何最值问题解题策略
第二部分
考情分析
专题归纳
模型三:
真题回顾
小试牛刀
一
15:33
第二部分
几何最值问题解题策略
考情分析
专题归纳
真题回顾
小试牛刀
一
15:33
几何最值问题解题策略
第二部分
考情分析
专题归纳
模型四:
真题回顾
小试牛刀
一
15:33
第二部分
几何最值问题解题策略
考情分析
专题归纳
真题回顾
小试牛刀
(3)若P是菱形ABCD的边上的点,则满足PE+PF= 13 的点P的个数是
___个
一
15:33
几何最值问题解题策略
第二部分
考情分析
专题归纳
真题回顾
小试牛刀
一
15:33
第二部分
几何最值问题解题策略
考情分析
专题归纳
真题回顾
小试牛刀
一
15:33
第二部分
几何最值问题解题策略
考情分析
专题归纳
真题回顾
小试牛刀
PM⊥AB时,PM最小,由此可
一
得,∠BPM+∠PBA=∠PBA+∠OAB=90°,∴∠BPM=∠OAB.对
于直线y=
15:33
几何最值问题解题策略
第二部分
考情分析
专题归纳
秘籍1
1、【翻折变换类】典型问题: “将军饮马”
真题回顾
小试牛刀
2、【平移变换类】典型问题: “造桥选址”
15:33
几何最值问题解题策略
如图,在矩形ABCD中,E是AB边的中点,F在AD边上,M,N分别是CD, BC边上的动点,若AB=AF=2,AD=3,则四边形EFMN周长的最小值是( )
一
15:33
第二部分
几何最值问题解题策略
考情分析
专题归纳
例6
真题回顾
小试牛刀
一
15:33
第二部分
几何最值问题解题策略
考情分析
专题归纳
真题回顾
一
15:33
几何最值问题解题策略
第二部分
考情分析
专题归纳
模型三:
真题回顾
小试牛刀
一
15:33
第二部分
几何最值问题解题策略
考情分析
专题归纳
真题回顾
小试牛刀
一
15:33
第二部分
几何最值问题解题策略
考情分析
专题归纳
真BCD的面积为16,△ABE是等边三角形,点E 在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最
中 ,BC a,CA b
问:当 ACB 为何值时,C、D两点的距离最大?最大值 是多少?
一
15:33
几何最值问题解题策略
第二部分
考情分析
专题归纳
秘籍3:
真题回顾
小试牛刀
(1)单轨迹圆模型:如图,点B在圆E上, 求BD的最值。
,,
(2)双轨迹圆模型:如图,点D在圆A上运动, 点P在以BC为直径的圆上运动,求PB的最值。
15:33
几何最值问题解题策略
第二部分
一
15:33
注意转化到我们的最小值问题上,能否找到PE+PF的最小值, 这个最小值和题目要求的9又存在什么关系?
第二部分
几何最值问题解题策略
考情分析
专题归纳
真题回顾
小试牛刀
(2019铜陵)如图,在菱形ABCD中,∠DAB=60∘,点E,F将对角线AC
三等分,且AC=6,连接DE,DF,BE,BF.
