制动系统建模、仿真及ABS控制器设计
ABS虚拟仿真与汽车制动性能分析

ABS虚拟仿真与汽车制动性能分析ABS作为一种重要的汽车安全技术,已经被广泛应用于车辆制动系统中,可以有效提升汽车的制动性能和稳定性。
而传统的汽车制动系统测试和优化,需要不断进行试验和测试,不仅时间和成本开销大,而且存在一定的风险。
因此,在这种情况下,基于虚拟仿真技术的汽车制动性能分析应运而生。
本文将对这方面的知识进行深入阐述。
一、ABS技术的优点与原理1.1 ABS技术的优点ABS全称Anti-lock Braking System,即防抱死制动系统,主要通过在制动时对车轮的转速进行监测,避免车轮因过度制动而封锁,造成车辆在行驶中失控的情况。
其具有以下优点:(1)提升了制动系统的稳定性和安全性(2)减小了车辆制动时的制动距离,缩短了制动反应时间(3)提高了车辆的刹车舒适性和驾驶体验1.2 ABS技术的原理ABS技术主要通过三个组成部分实现其功能:传感器、控制器和执行器。
当车辆前轮或后轮出现制动抱死的情况时,传感器即时监控车轮的转速,当检测到某一车轮速度过低时,立刻通过控制器指令降低该车轮对应的制动量,以防止车轮抱死,从而保证车轮轮胎能够持续与路面摩擦,维持车辆稳定性。
二、基于虚拟仿真技术的汽车制动性能分析传统的汽车制动系统测试和优化,需要不断进行试验和测试,不仅时间和成本开销大,而且存在一定的风险。
这种方法无法快速、精确地评估和优化汽车的制动性能。
而使用虚拟仿真技术,可以通过数学模型和计算机模拟来实现系统测试和优化,具有以下优点:(1)可以快速、精准地评估和优化汽车的制动性能(2)可以极大地节省时间和成本,并且可以避免试验风险(3)可以提高测试的精度和可靠性虚拟仿真技术的实现过程主要分为几个步骤:(1)建立汽车制动系统的数学模型,包括制动器、制动管、制动泵等组件。
(2)使用计算机软件对数学模型进行仿真和分析,计算和分析制动灵敏度、制动抱死点、制动距离、制动稳定性、制动舒适度等性能指标,对汽车制动系统部件进行优化设计。
轿车制动系建模与仿真及ABS控制策略

关键词:制动力分配,制动性能仿真,实验,ABS 控制策略
第
I
页
上海交通大学硕士学位论文
ABSTRACT
MODELING AND SIMULATION OF AUTOCAR BRAKING SYSTEM AND ABS CONTROL STRATEGY
ABSTRACT
At first, this thesis analyzed the braking system theoretically, working principle and characteristic of braking force regulate fitting was expounded. Second,based on analysis, this thesis presents the braking force distribution rationality evaluation mathematics model and the braking performance computer simulation mathematics model. Then, a computer program was designed based on the mathematics model. The program is built by Matlab. The computer program can improve the design efficiency and made them achieve the optimal project. In this thesis, with the program, the braking force distribution of the Haiyiu-MB autocar was rationality evaluated and the braking performance of the autocar was simulation calculated. At the same time, the result was testified by some tests. Finally, this thesis describes the fundamental principle of ABS controlling and discuss several control methods of ABS in common use, emphasis on the logic gate control. In brief, the study of this thesis is directive and practical for the design of the autocar braking system. Keywords: braking force distribution, braking performance simulation, Test, Anti-lock brake controlling.
基于AMESIM的ABS液压系统建模与仿真

第 1 章绪论1.1 研究目的与意义随着我国汽车工业的发展,就必须进行汽车关键零部件的自主研发。
汽车制动过程中的安全性也已成为人们关注的焦点。
汽车防抱死制动系统(ABS),关系着汽车制动的安全性。
目前国内许多汽车公司已经开始进行汽车自主研发,要在商业的竞争中脱颖而出,要拥有自主知识产权的汽车,要使我国由一个汽车大国变为一个汽车强国,就必须进行汽车关键零部件的自主研发。
汽车制动过程中的安全性也已成为人们关注的焦点,防抱死制动系统ABS是汽车关键的零部件之一,因此国家、企业和高校都投入了大量的人力和资源对ABS进行自主研发。
汽车动力性能的提高和高速公路的延伸对汽车安全提出了越来越高的要求,许多国家都为此颁布了严厉的汽车安全法规,汽车在制动过程中的方向稳定性和转向操纵能力,已成为人们关注的焦点。
因此,探讨各种高性能的制动系统和完善制动系统的性能是减少交通事故和促进汽车工业发展的重要举措[1]。
而ABS可以在制动过程中自动、高频地对制动系统压力进行调节,从而对制动力进行调节,使车轮滑移率保持在理想滑移率附近,既防止车轮抱死,又充分利用了车轮与路面的附着能力,缩短了制动距离,提高了汽车制动过程中的方向稳定性和转向操作能力,达到了最佳制动效果的目的。
ABS控制的关键之一就是控制制动过程中的滑移率,从而提高路面附着系数的利用率,缩短制动距离,提高制动的稳定性。
然而,滑移率和路面附着系数的关系又受到很多因素的影响,如车辆本身的结构参数、车速、轮胎充气压力、轮胎垂直载荷、路面状况等等[2]。
因此,要求ABS保证汽车在短时间内在各种路面上,各种情况下都能安全制动的难度是相当大的。
还需要针对不同车型进行大量的参数匹配试验,大概需要一年半到两年的时间,并且需要大量的经验,不仅耗资巨大,而且延长了产品的开发周期。
目前国内外也有人应用新的控制理论,进行ABS控制的探讨。
根据汽车制动过程的物理实质及动力学分析,对ABS控制器的结构原理、控制方法等方面进行分析和研究,利用AMESim软件建立车辆防抱死制动系统模型,可以很容易分析液压系统元件对整个系统的影响。
基于MATLAB的汽车ABS制动过程仿真

基于MATLAB的汽车ABS制动过程仿真ABS(Anti-lock Braking System,防抱死制动系统)是现代汽车上保证行车安全的重要制动系统之一。
ABS制动系统可以避免在制动时车轮抱死,从而提高了制动效果和稳定性。
为了深入理解ABS制动系统的工作原理和性能,本文将基于MATLAB软件进行汽车ABS制动过程的仿真。
一、建立模型和假设为了实现ABS制动过程的仿真,需要建立一个基于MATLAB 的系统模型。
该系统模型需要考虑以下几个方面:1. 汽车的运动方程。
2. 轮胎与地面的接触力,即摩擦力。
3. 制动器与车轮的接触力。
4. ABS控制器的控制策略。
在仿真过程中,假设车辆在制动前以一定的速度匀速行驶,制动时四个车轮的制动和抱死状态是相同的。
二、模型搭建在MATLAB界面中,首先利用simulink模块搭建模型。
模型如下:模型中包含了车辆运动方程、轮胎地面接触力、制动器与车轮接触力等模块。
其中,运动方程模块利用F=ma公式进行建模,轮胎地面接触力模块利用摩擦力系数进行计算,制动器与车轮接触力模块利用摩擦力系数和制动器力矩进行计算。
在模型中,还有制动器控制器模块,负责制动器的控制与调节。
制动器控制器可以采用PID算法或滑模控制算法来控制制动器的开闭和力矩大小。
三、仿真过程在进行仿真过程中,需要确定以下参数:1. 初始车速度v0=80km/h。
2. 初始刹车踏板角度θ=0。
3. 制动器摩擦力系数μs=0.7。
4. 刹车片初期转动半径r=0.05m。
在进行仿真操作前,应先在程序中设定好各参数,再设定仿真时间和仿真步长。
由于ABS制动过程会使用到控制器,因此应首先进行控制器的设计和仿真。
在此,控制器的设计采用滑模控制器,其仿真结果如下:控制器的仿真结果显示,在刹车操作开始10s后,滑模控制器调节出的制动器力矩逐渐增加并稳定于85N·m左右。
随着控制器的调节,车轮抱死现象得以解决、保持ABS制动状态下使车辆具备更好的稳定性和制动效果。
汽车制动控制系统ABSEBD设计与仿真

第28卷第2期2020年6月山东交通学院学报JOURNAL OF SHANDONG JIAOTONG UNIVERSITYVol.28No.2Jun.2020DOI:10.3969/j.issn.1672-0032.2020.02.001汽车制动控制系统ADS/EDD设计与仿真王健>,杨君>,于蓬2!,郑金凤21.山东交通学院汽车工程学院,山东济南250357;2.山东明宇新能源技术有限公司,山东济南271100摘要:为提高汽车的制动性能,采用汽车防抱死制动系统(anti-locked braking system,ADS)与电子制动力分配(electronis brake force distribution,EBD)系统联合控制制动系统的方法。
设计基于滑模控制的ADS和基于模糊控制的EBD系统。
分别在干、湿沥青路面2种条件下对ABS/EBD系统进行仿真分析。
结果表明:设计的ABS/ EDD控制系统能充分利用ABS和EBD的优点,大大提高汽车的制动效能。
关键词:ABS/EBD;滑模控制器;模糊控制器;滑移率中图分类号:U463.5文献标志码:A文章编号:1672-0032(2020)02-0001-08引用格式:王健,杨君,于蓬,等.汽车制动控制系统ABS/EBD设计与仿真[J].山东交通学院学报,2020,28(2): 1-8.WANG Jian,YANG Jun,YU Peng,et aO.ABS/EBD design and simulation of automotive brake controO system[J].JournaS of Shandong Jiaotong University,2020,28(2):1-8.0引言汽车紧急制动,特别是在附着系数较低的路面上紧急制动时,汽车防抱死制动系统(anti-locked braking system,ABS)可以防止前后车轮抱死拖滑,在保证汽车具有转向功能的同时,防止汽车不发生甩尾侧滑等危险情况,保持汽车的制动稳定性,且可以缩短制动距离(1-)%电子制动力分配(electronic brake force distribution,EBD)系统作为ABS的子系统,可以在车辆制动时控制制动力在各轮间的分配,更好地利用各轮的附着系数[4-11]%国内大多数ABS采用逻辑门限值控制,通过大量试验确定各门限值,对系统的控制很不稳定[12-14]%本文ABS采用滑模变结构控制,该方法是针对非线性和参数不确定性系统的控制方法[15-17],具有很好的鲁棒性%EBD系统采用模糊控制,该方法对系统中的参数变化、外界干扰、系统非线性等具有很强的鲁棒性%通过建立1/2车辆动力学模型、设计基于滑模变结构控制的ABS控制器和基于模糊控制的EBD控制器,在不同路面上进行ABS/EBD系统的仿真验证,以期提高车辆的制动性能%1车辆动力学模型为了设计ABS&EBD控制器以及进行系统动力学仿真,需建立车辆动力学模型%为便于建模,对车辆收稿日期:2020-04-02基金项目:国家自然科学基金项目(61803231);山东省重点研发计划(2017GGX50109);山东交通运输厅科技计划(2018B66);山东省高等学校科技计划项目(J17KB024);山东省高等学校青创科技支持计划(2020KJJ002);山东交通学院博士科研启动资金资助项目(BS2017001)第一作者简介:王健(1986$),男,山东潍坊人,工学博士,副教授,主要研究方向为汽车智能驾驶、主动安全,E-mail:wangjian1987228@0*通信作者简介:于蓬(1986—),男,济南人,工学博士,高级工程师,主要研究方向为新能源汽车集成及产业化,E-mail:t_ y_yupeng@。
汽车ABS系统的建模与仿真

汽车ABS系统的建模与仿真基于Matlab/Simulink的汽车建模与仿真摘要本文所研究的是基于Matlab/Simulink的汽车防抱死刹车系统(ABS)的仿真方法,本方法是利用了Simulink所提供的模块建立了整车的动力学模型,轮胎模型,制动系统的模型和滑移率的计算模型,采用的控制方法是PID控制器,对建立的ABS的数学模型进行了仿真研究,得到了仿真的曲线,将仿真曲线与与没有安装ABS系统的制动效果进行对比。
根据建立的数学模型分析,得到ABS系统可靠,能达到预期的效果。
关键词ABS 仿真建模防抱死系统 PIDModeling and Simulation of ABS System of AutomobilesBased onMatlab/SimulinkAbstractA method for building a Simulator of ABS base on Matlab/Simulink is presented in this paper.The single wheel vehicle model was adopted as a research object in the paper. Mathematical models for an entire car, a bilinear tire model, a hydraulic brake model and a slip ratio calculation model were established in the Matlab/Simulink environment. The PID controller was designed. The established ABS mathematical model was simulated and researched and the simulation curves were obtained. The simulation results were compared with the results without ABS. The results show that established models were reliable and could achieve desirable brake control effects.Key wordsABS; control; modeling; simulation;Anti-lock Braking System;PID1.概述随着载重车辆动力性的不断提高,客观上也对车辆的制动性能与驱动性能提出了越来越高的要求。
基于Simulink的汽车ABS建模与仿真
基于Simulink 的汽车ABS 建模与仿真汽车防抱死制动系统(ABS)是一种很关键的汽车主动安全技术。
本文采用基于有限状态机的系统仿真方法,采用Simulink 建模,对ABS 模型中的连续系统和离散系统进行仿真。
仿真结果表明,该仿真系统能比较真实地反映汽车ABS 系统的实际工作过程,显著缩短制动距离,提高安全性。
通过对ABS 建立理论模型并进行计算机仿真,可以初步确定ABS 的一些参数,还可以通过仿真结果来验证和分析控制逻辑。
因此,对ABS 的仿真分析可以有效缩短开发周期,减少开发成本,并通过少量的试验验证,可作为实际ABS 性能分析及控制逻辑的模型。
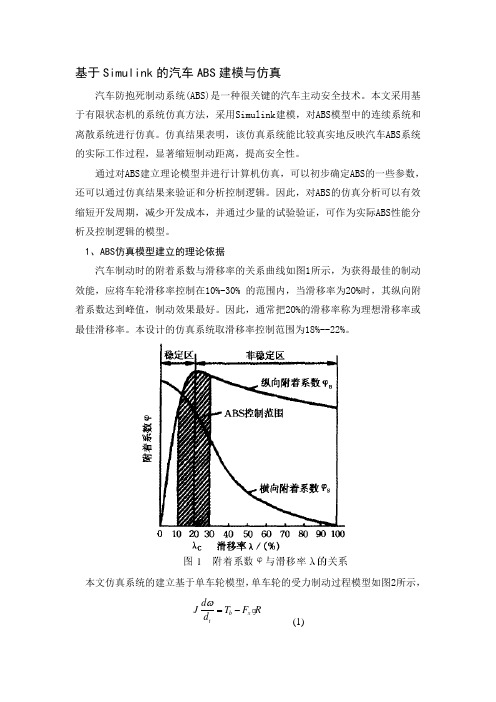
1、ABS 仿真模型建立的理论依据汽车制动时的附着系数与滑移率的关系曲线如图1所示,为获得最佳的制动效能,应将车轮滑移率控制在10%-30% 的范围内,当滑移率为2O%时,其纵向附着系数达到峰值,制动效果最好。
因此,通常把2O%的滑移率称为理想滑移率或最佳滑移率。
本设计的仿真系统取滑移率控制范围为18%--22%。
本文仿真系统的建立基于单车轮模型,单车轮的受力制动过程模型如图2所示,b x t d J T F R d ω=- (1)x dv M F dt = (2)通常车轮制动扭矩与轮缸压力成正比,即:b T K P =⨯ (3)t x d J K P d F R ω-⨯+⨯= (4)因此 可得车轮滑移率: V V V ωλ-=(5)式中M--车轮承受的质量;V--车身速度;V ω--车轮速度;x F —地面制动力;J —车轮转动惯量;ω--车轮角速度;R--车轮滚动半径;b T --制动器扭矩;K--制动力矩系数;P--轮缸压力; λ—滑移率。
本仿真系统采用的汽车模型参数如表1所示:表一 汽车模型参数2、ABS仿真模型的建立及参数设置ABS系统仿真模型如图3所示:图3 ABS系统仿真模型3、ABS系统仿真结果对初速度为25Km/h的汽车ABS系统进行计算机仿真,仿真结果如图4和图5所示。
ABS控制器设计及仿真

汽车ABS控制器设计及其仿真摘要:ABS(Anti-lock Braking System)防抱死制动系统,通过安装在车轮上的传感器发出车轮将被抱死的信号,控制器指令调节器降低该车轮制动缸的油压,减小制动力矩。
关键字:ABS 控制系统仿真一.ABS控制系统简介。
汽车制动性能主要是三个方面:⑴制动效能,即制动距离与制动减速度;⑵制动效能的恒定性,即摩擦材料的抗热衰性能;⑶制动时汽车的方向稳定性,即制动时汽车不发生跑偏、侧滑及失去转向性能。
汽车维持直线行驶或按预定弯道行驶的能力。
而制动性能主要是有汽车轮胎的制动性能决定的。
ABS系统是一种能防止车轮被抱死而导致车身失去控制的安全装置,全称防抱死刹车系统。
我们知道,当车轮抱死滑移时,车轮与路面间的侧向附着力将完全消失。
如果是前轮(转向轮)制动到抱死滑移而后轮还在滚动,汽车将失去转向能力(跑偏)。
如果是后轮制动到抱死而前轮还在滚动,即使受到不大的侧向干扰力,汽车也将产生侧滑(甩尾)现象。
这些都极容易造成严重的交通事故。
因此,汽车在制动时不希望车轮制动到抱死滑移,而是希望车轮制动到边滚边滑的运动状态。
从已有的实验中可以知道[1],如图1所示,汽车车轮的滑动率在15%-20%时,轮胎与路面有最大的纵向附着系数,此时侧向附着系数也较大,因此,为了充分发挥轮胎与路面间这种潜在的附着能力,目前的许多中高级轿车及大客车和重型货车上均装备了防抱死制动装置(Antilock Braking System),简称ABS.汽车电控防抱死制动系统的主要功用有:(1)在任何制动情况下驾驶员应能保持对行驶车辆的控制。
(2)在任何制动情况下应能保持汽车转向时的操纵性和制动时的稳定性。
(3)当左,右车轮处于不同附着系数路面或者路面附着系数突然变化时能够进行调整控制。
(4)能够缩短制动距离,提高汽车制动效能。
(5)制动噪声小,工作安全可靠,一但防抱死制动系统失效时,自检系统能显示报警,而由机械制动系统来承担汽车制动作用。
防抱死制动系统仿真

600
800
1000
1200
1400
1600
1800
制动时间(x10-2s)
重庆理工大学 系统建模与仿真 13
100 G(s) TB.s 1
重庆理工大学 系统建模与仿真 10
防抱死制动系统(ABS)
8.仿真曲线:
swich=1,ABS制动
速度曲线 紫色:车轮身速度 黄色:车轮速度
滑移率曲线 黄色:实际滑移率
重庆理工大学
系统建模与仿真
11
防抱死制动系统(ABS)
9.仿真曲线:
swich=0,非ABS制动
重庆理工大学 系统建模与仿真 6
防抱死制动系统(ABS)
4.单轮制动数学模型:
v v Rr
slip 1 w / v
v
Vv
Rr
f (slip)
Ff F
dVv m Ff dt dw I F f Rr Tb dt
重庆理工大学 系统建模与仿真
Tb
防止“除零”而采取的措施: 1.0 – u(1) / (u(2) + (u(2) == 0) * eps)
必定非零!
重庆理工大学 系统建模与仿真 9
防抱死制动系统(ABS)
7.Simulink模型精讲
bangbang 控制器原理:
1, Uk 1, En 0 En 0
制动系液压管路:一阶惯性环节
Ff
Fz
7
防抱死制动系统(ABS)
5.Simulink模型:
重庆理工大学
系统建模与仿真
8
防抱死制动系统(ABS)
6.基本模块介绍:
1. 2. 3. 4. 传递函数 Transfer Fcn Continuous 查找表 Lookup TableLoopup Tables 积分器(限幅)Integrator Continuous 终止仿真 Stop Sinks
制动系统建模、仿真及ABS控制器设计

制动系统建模、仿真及ABS控制器设计专业:车辆工程姓名:汤兴贤学号:200620103918一、源程序:m=300;rd=0.25;Iw=12;ki=4500;kd=5000;Ts=0.05;s0=0.2;uh=0.8;ug=0.6;smin=0.18;smax=0.22;g=9.8;u(1)=30;w(1)=120;Tb(1)=600;j=1;while u(j)>0sb(j)=1-rd*w(j)/u(j); %计算当前滑移率if sb(j)>smaxTb(j+1)=Tb(j)-kd*Ts; %制动器减压elseif sb(j)<sminTb(j+1)=Tb(j)+ki*Ts; %制动器增压else Tb(j+1)=Tb(j); %制动器保压endif sb(j)<=s0v(j)=uh*sb(j)/s0; %计算附着系数else v(j)=(uh-ug*s0)/(1-s0)-(uh-ug)*sb(j)/(1-s0); %计算附着系数endFxb=v(j)*m*g; %计算地面制动力w1(j)=(Fxb*rd-Tb(j+1))/Iw; %计算角加速度u1(j)=Fxb/m; %计算加速度u(j+1)=u(j)-u1(j)*Ts %计算车速w(j+1)=w(j)+w1(j)*Ts; %计算角速度j=j+1;end;t1=0:0.05:(j-1)*Ts; %(j-1)*Ts为采样时间t2=0:0.05:(j-2)*Ts; %(j-2)*Ts为从开始制动到角速度为零之间的时间figure(1)plot(t1,u)xlabel('时间/s'),ylabel('速度/s')axis([0,5,0,30]);hold onplot(t1,w*rd);title('车轮前进速度与车轮线速度关系曲线');text(2,20,'车轮前进速度');text(1.5,10,'车轮线速度');figure(2)plot(t2,sb);title('ABS控制的滑移率时域仿真结果');xlabel('时间/s'),ylabel('滑移率')axis([0,4.5,0,1]);图100.10.20.30.40.50.60.70.80.91ABS 控制的滑移率时域仿真结果时间/s 滑移率图2051015202530时间/s 速度/s 车轮前进速度与车轮线速度关系曲线从线性化的路面附着系数与车轮滑移率关系曲线知道,车轮的滑移率sb在0.2左右时纵向附着系数最大。
制动系统建模、仿真及ABS控制器设计

目录1. 动力学建模....................................................................................... - 0 - 2。
分段线性的轮胎模型 ................................................................... - 0 - 3。
控制算法........................................................................................ - 1 - 4. 仿真流程及参数输入 ...................................................................... - 1 - 5。
实例分析........................................................................................ - 2 - 6。
MATLAB 仿真过程..................................................................... - 2 - 6。
1。
逻辑门限值控制器 ............................................................. - 2 - 6。
2.模糊控制器 ............................................................................ - 6 -6.2。
1模糊控制器设计 ........................................................... - 6 -6。
(毕业设计)汽车ABS制动模型的仿真分析说明书

本科生毕业设计(论文)摘要为了能够准确的了解制动防抱死系统的性能,常常使用计算机仿真技术来进行研究,本设计采用Matlab/Simulink模拟汽车在直线制动的运动状态,对ABS 系统的控制规律进行计算机仿真。
它与常规的试验分析相比,具有分析速度快、精度高、周期短、节省大量的人力物力的优点。
ABS防抱死制动系统模型的建立,是计算机与生产实际相融合的产物。
模型的建立,可以代替危险性试验,提高安全性和经济性,同时可以方便快捷的得到试验所得到的结果,以此完善设计开发中的产品性能,为ABS系统的研制与开发提供一条有效的方法。
本设计简单介绍了制动系统的工作原理,通过建立普通制动系统和ABS防抱死系统的数学模型,提出了基于路面附着系数的ABS控制算法,并根据数学模型,利用Matlab/Simulink软件建立普通制动系统和ABS防抱死制动系统的仿真模块,分析普通制动系统和装有防抱死制动系统(ABS)车辆制动过程中各参数的动态变化规律。
通过对比仿真结果可知ABS防抱死制动系统不仅能够达到防止车轮在制动过程时抱死的目的,还能准确控制车轮的运动状态,因此证明本次设计对ABS 制动过程的仿真分析是有效的。
关键词:制动;防抱死制动系统;仿真;Matlab/SimulinkAbstractIn order to accurately understand the anti-lock braking system performance, often using computer simulation technology to conduct research. This design uses Matlab / Simulink simulation of the car braking in a straight line movement, the ABS system of control of a computer simulation. Compared with the common experimental analysis,it has fsater analsing speed, higher precision, shorter period, etc. besides, it saves much labor and material resources.The establishment of antilock brake systems is the result of the combination of computer and actual produciton. Model of antilock brake systems can take place of the dangerous experiments,improve the safety and save much money. At the same time, it helps get the result as soon as possible. So that the function of the product can be made better. in a word, it provides an effective method to the reserch and development of the antilock braking system.The project briefly introduces the principles of the braking system .It gets antilock braking system controlling algorithm according to the establishment of ordinary braking system and methematical antilock braking system. On the basis of methematical model, it uses Matlab/Simulink software to eatablish a simulate template of an ordinary braking system and an antilock braking system to analyses the motional changing regularity of kinds of parameters of vehicle which installed with ordinary braking system and the vehicle with antilock braking system. When the results are compared, we get to know that antilock braking system can not only prevent the wheels form been braken while braking, but also controll the moving condition of them. So that this design of the braking process’s simulation analysis is effective.Key words:brake;antilock braking system;simulation;Matlab/Simulink目录第1章ABS防抱死系统简介和本课题意义 (1)1.1 工作原理 (1)1.2 ABS的优点及常用装置 (1)1.3 ABS发展历史及应用现状 (2)1.4 发展趋势 (5)1.5 本次设计意义 (6)第2章物理模型及数学模型的搭建 (7)2.1 制动系统物理模型 (7)2.1.1 普通制动系统物理模型 (7)2.1.2 有ABS制动系统物理模型 (7)2.2 制动系统数学模型 (9)2.2.1 普通制动系统数学模型 (9)2.2.2 有ABS制动系统数学模型 (10)第3章Matlab/Simulink软件介绍 (13)3.1 Matlab软件介绍 (13)3.2 Simulink软件介绍 (14)第4章制动系统仿真模型的建立 (16)4.1 仿真参数 (16)4.2 仿真模型 (16)4.2.1 普通制动系统仿真模型 (16)4.2.2 ABS防抱死制动系统仿真模型 (17)4.3 仿真模块功能 (17)4.3.1 单个模块功能 (17)4.3.2 多个模块功能 (19)第5章仿真计算结果和曲线 (23)5.1 仿真所得曲线 (23)5.1.1 普通制动系统 (23)5.1.2 有ABS制动系统 (25)5.2 仿真结果 (27)第6章结论 (28)参考文献 (29)致谢 (30)附录 (31)第1章ABS防抱死系统简介和本课题意义1.1工作原理当车轮抱死滑移时,车轮与路面间的侧向附着力将完全消失。
基于MATLAB下的制动系统建模、仿真及ABS控制器设计

基于MATLAB下的制动系统建模、仿真及ABS控制器设计王凯凯;董琴琴;陈作
【期刊名称】《内燃机与配件》
【年(卷),期】2022()5
【摘要】本文对某汽车ABS制动系统进行仿真建模,并对其进行单轮模型和分段线性的轮胎模型的建立;在Matlab环境下对ABS控制器进行设计和仿真分析;提出了一种门限值控制算法,对制动液压控制系统实现增压、保压、减压动作,使得汽车制动时的滑移率控制在一定范围内,以保证汽车的平稳制动。
得出ABS控制下的滑移率时域结果图、车轮前进速度与车轮线速度关系曲线、制动器制动力矩与地面制动力随时间变化曲线。
仿真结果表明:在门限值控制算法下设计的ABS控制器能够将滑移率有效地控制在理想范围内,车轮前进速度近似一条直线,加速度趋于定值,且防止了车轮过早抱死,说明在此基础上设计的控制器能够使得汽车平稳制动。
【总页数】3页(P11-13)
【作者】王凯凯;董琴琴;陈作
【作者单位】南充科技职业学院工程与应用技术学院;四川中烟工业有限责任公司成都卷烟厂
【正文语种】中文
【中图分类】TP273
【相关文献】
1.基于MATLAB/Simulink的汽车线控制动系统建模仿真与研究
2.基于MATLAB 的汽车ABS制动系统仿真研究
3.基于MATLAB的汽车ABS制动系统仿真研究
4.基于MATLAB的制动器试验台气压制动系统建模与仿真
5.基于Matlab/Simulink 的汽车ABS系统的建模与仿真
因版权原因,仅展示原文概要,查看原文内容请购买。
汽车制动系统的设计及仿真

汽车制动系统的设计及仿真任务书1.设计的主要任务及目标汽车制动器是制动系中最重要的一个部件,是制动系统中用以产生阻碍汽车运动或运动趋势的力的部件。
凡是利用固定元件与旋转元件工作表面的摩擦而产生制动力矩的制动器都成为摩擦制动器。
摩擦制动器可分为鼓式和盘式两大类。
前者的摩擦副中的旋转元件为制动鼓,其工作表面为圆柱面;后者的旋转元件则为圆盘状的制动盘,以端面为工作表面。
2.设计的基本要求和内容(1)了解汽车制动系统的工作过程。
(2)熟悉汽车制动系统的设计过程和设计参数。
(3)结合汽车制动性能要求设计汽车制动器。
(4)结合三维建模软件,并实现制动器的运动仿真。
3.主要参考文献[1] 王望予.汽车设计[M].北京:机械工业出版社,2004[2] 余志生.汽车理论[M].北京:机械工业出版社,2003[3] 陈家瑞.汽车构造[M].北京:机械工业出版社,2003[4] 林秉华.最新汽车设计实用手册[M],黑龙江:黑龙江出版社,2005[5] 张尉林.汽车制动系统的分析与设计[M].北京:机械工业出社,20024.进度安排注:一式4份,系部、指导教师各1份、学生2份:[毕业设计]及答辩评分表各一份汽车制动系统的设计及仿真摘要:汽车的制动系是汽车行车安全的保证,许多制动法规对制动系提出了许多详细而具体的要求,这是我们设计的出发点。
从制动器的功用及设计的要求出发,依据给定的设计参数,进行了方案论证。
对各种形式的制动器的优缺点进行了比较后,选择了浮动钳盘的形式。
这样,制动系有较高的制动效能和较高的效能因素稳定性。
随后,对盘式制动器的具体结构的设计过程进行了详尽的阐述。
选择了简单液压驱动机构和双管路系统,选用了间隙自动调节装置。
在设计计算部分,选择了几个结构参数,计算了制动系的主要参数,盘式制动器相关零件的设计计算。
关键词: 制动器,同步附着系数,制动盘,制动钳Automobile brake system design and simulationAbstracts:The braking system in a vehicle guaranteed the safety of driving .Many rules and regulations have been made for the braking system in detail, which is the starting of our design.Firstly, I demonstrate the project on the base of the function of the brake, And analysis their strong point and shortcomings .I choose the form of front-disked. In this way, the braking system have higher braking efficiency and high stability of the performance factors. Subsequently, the specific structure of the disc brake design was elaborated in detail.I designed the hydraulic drive system and two-pipe system and selected clearance automatic adjusting device.In the calculate part .I chosen several structural parameters, calculated the main parameters of the braking system drive mechanism.Key words:disc brakes,synchronous attachment coefficient,brake disc,brake caliper目录1 绪论 (1)1.1 课题研究的目的及意义 (1)1.2制动系统研究现状 (1)1.3课题设计思路 (3)2制动系统概述 (4)2.1制动系的类型 (4)2.2汽车制动系统组成 (4)2.3 制动器的组成 (5)2.4 制动器的要求 (5)2.5 制动器的种类 (7)3 汽车参数计算 (14)3.1汽车的基本参数 (14)3.2 制动系的主要参数及其选择 (15)3.3 盘式制动器的结构参数与摩擦系数的确定 (16)3.4 制动衬块的设计计算 (18)3.5 摩擦衬块磨损特性的计算 (19)4 制动器主要零件的结构设计 (21)4.2 制动钳 (21)4.4 摩擦材料 (21)4.5 盘式制动器间隙的调整方法及相应机构 (22)4.6 制动驱动机构的结构型式选择与设计计算 (22)结论 (25)参考文献 (26)致谢 (27)附录 (28)1 绪论1.1 课题研究的目的及意义汽车的设计与生产涉及到许多领域,其独有的安全性、经济性、舒适性等众多指标,也对设计提出了更高的要求。
第7章 汽车防抱死制动系统建模与控制仿真 [基于MATLAB的控制系统仿真及应用]
![第7章 汽车防抱死制动系统建模与控制仿真 [基于MATLAB的控制系统仿真及应用]](https://img.taocdn.com/s3/m/a3e70703bd64783e09122b6a.png)
Fz
3
Mvxh Mga 2L
F0h
Mvyh 2C
Fz 4
Mvxh Mga 2L
F0h
Mvyh 2C
4
7.1.2 轮胎模型
我们选用Gim模型如下轮胎力学模型。
当
s
1
Ks
3 Fz
1
s
0
时,
纵向力
Fx
Ks 1
s s
s2
6Fz
cos
3、附着系数图形
1
0.8
0.6
0.4
0.2
00
2
4
6
8
装有ABS装置的图形
附着系数一直维持在 最大值(0.4)左右, 而没有装ABS装置的
附着系数在滑移率超 过最佳滑移率 (0.12s)时,逐渐 减小,可见ABS可以 利用最佳的附着系数。
13
7.2 基于单轮模型的Simulink仿真
4、制动距离
20
单轮车辆系统制动模型
单轮车辆制动模型的微分方程式
mu F Fb
J Fbr Tb Fb Fz
8
7.2 基于单轮模型的Simulink仿真
图 7.2.1 ABS单轮simulink仿真模型
9
7.2 基于单轮模型的Simulink仿真
制动过程仿真模型参数
参数 整车重量W/N 车轮转动惯量J/(kg.m-2) 车轮半径R/m 制动初速度V/(m.s-1) 制动力增长因数a/(N.m.s-1) 理想滑移率s
5K
6
7.1.3 滑移率模型
1、未含ABS系统的制动过程:
基于Carsim Simulink的ABS系统建模与仿真.

Page 16
Thank you!
Page 17
Page 5
ABS的控制目标
ABS的控制目标:滑移率S
Page 6
ABS的控制过程
Page 7
ABS控制算法
1.逻辑门限值控制 2.PID 控制 3.最优控制 4.滑模变结构控制 5.模糊控制 6.神经网络
Page 8
逻辑门限值控制
其基本的原理是利用车轮加减角速度门限及参考滑移率构成, 防抱死逻辑使滑移率在车轮峰值附着系数附近波动,从而获 得较大的车轮纵向和横向力; 优点:不需要建立具体系统的数学模型,控制过程比较简单, 结构原理上比较容易实现,并且对系统的非线性控制很有效; 缺点:需要进行大量的道路试验,开发时间相对较长,成本 较高; 逻辑门限值是开发ABS首选的控制方法。
Page 9
PID控制
PID控制是一种基于经典理论的控制方法,最大优点是不需 要了解被控对象的数学模型,只需要根据经验进行调节器参 数调节,这个特点正好满足了ABS系统建模比较困难的特点;
缺点:实际操作中很难确定一种准确的轮胎模型来实时确定 不同制动工况下的期望滑移率。
Page 10
PID控制框图
制系统。
功能: 1、提高制动时的方向稳定性
2、缩短制动距离
Page 3
ห้องสมุดไป่ตู้
ABS的发展历史
ABS技术最早由英国人霍纳摩尔于1920年研制发明并申请专利;
1930年代ABS在铁路机车的制动系统中得到运用;
1940年代末,飞机制动系统开始采用ABS,很快ABS成为飞机的标 准配置;
Page 4
ABS的发展历史
2018/11/20
基于 Carsim/Simulink的 ABS系统建模与仿真
毕业论文----汽车防抱死制动系统的建模与仿真(含开题报告 中英文翻译)

分类号编号毕业论文题目汽车防抱制动系统的建模与仿真——模糊控制在ABS中的应用学院机械学院专业机械设计制造及其自动化毕业设计任务书设计题目:汽车防抱制动系统的建模与仿真专业:机械设计制造及其自动化班级学号:姓名:院、系:机械学院2010年2 月26 日一、毕业设计的目的毕业设计是本科教育中培养学生的重要的实践性教学环节,也是最后一个教学环节。
其目的:1.培养学生综合运用基础理论知识、专业知识和技能,解决工程实际问题的能力;2.培养学生运用机械设计手册、图册、国家标准规范和规程的能力;3.培养学生学会机械设计的思想、方法和步骤,掌握计算方法、掌握计算机绘图及编写工程设计文件等基本技能;4.提高学生分析问题、解决问题和独立工作的能力。
二、主要设计内容1.专业外文资料翻译;2.毕业实习,实习报告;3.开题报告;4.汽车防抱制动系统的建模与仿真。
三、重点研究问题1.汽车防抱制动系统的车辆仿真模型的建立;2.采用的控制方法模型的建立;四、主要技术指标和主要设计参数1.收集资料确定一个自己的设计参数,在查阅资料后确定下来。
2.控制方法根据所查找文献自己确定。
五、设计成果要求1.开题报告1份(要求3 000字左右、查阅文献10篇以上、文献综述引用5篇以上,样表从教务处表格下载中下载);2.实习报告1份;3.专业外文资料翻译1篇(不少于2 000汉字);4.毕业设计(论文)1份(设计说明书应在10000字以上,论文应在6000字以上,包括封面、任务书、开题报告、中英文摘要、目录、正文、参考文献、附录);5.设计图纸一套(不少于A0图2张);6.所有内容电子文档一套;7.毕业论文成果材料清单一份。
本科生毕业设计开题报告2010 年 03 月 30日学生姓名学号专业机械设计制造及其自动化题目名称汽车防抱死制动系统的建模与仿真课题来源自选主要内容一.本课题设计的目的与意义本课题为《汽车防抱制动系统的建模与仿真》,要求我们收集资料自己确定一个设计参数,并查阅相关文献选择一种ABS的控制方法。
汽车ABS系统的建模与仿真

基于Matlab/Simulink的汽车建模与仿真摘要本文所研究的是基于Matlab/Simulink的汽车防抱死刹车系统(ABS)的仿真方法,本方法是利用了Simulink所提供的模块建立了整车的动力学模型,轮胎模型,制动系统的模型和滑移率的计算模型,采用的控制方法是PID控制器,对建立的ABS的数学模型进行了仿真研究,得到了仿真的曲线,将仿真曲线与与没有安装ABS系统的制动效果进行对比。
根据建立的数学模型分析,得到ABS系统可靠,能达到预期的效果。
关键词ABS 仿真建模防抱死系统 PIDModeling and Simulation of ABS System of AutomobilesBased onMatlab/SimulinkAbstractA method for building a Simulator of ABS base on Matlab/Simulink is presented in this paper.The single wheel vehicle model was adopted as a research object in the paper. Mathematical models for an entire car, a bilinear tire model, a hydraulic brake model and a slip ratio calculation model were established in the Matlab/Simulink environment. The PID controller was designed. The established ABS mathematical model was simulated and researched and the simulation curves were obtained. The simulation results were compared with the results without ABS. The results show that established models were reliable and could achieve desirable brake control effects.Key wordsABS; control; modeling; simulation;Anti-lock Braking System;PID1.概述随着载重车辆动力性的不断提高,客观上也对车辆的制动性能与驱动性能提出了越来越高的要求。
制动系统建模之欧阳数创编

制动系统仿真、建模及ABS控制器设计学生:何渝学号:11011030504班级:车辆二班老师:周老师制动系统仿真、建模及ABS控制器设计随着科学技术的进步和人们物质生活水平的提高,人类社会对汽车的安全性,特别是制动安全性能提出了越来越高的要求。
汽车防抱死制动系统(ABS)是一种在制动时能够自动调节车轮制动力,防止车轮抱死以取得最佳制动效果的制动系统。
该系统能够有效的缩短制动距离、提高制动时的方向稳定性,对汽车的行驶安全具有重要的意义。
总之,研究结果可以看出逻辑门限值方法用于汽车防抱死制动系统不仅具有理论意义,而且具有实用价值,是一种简单、方便、具有较好操纵性、制动性,并且有较好适应性的方法。
进一步的研究工作一定要继续开展下去。
制动系统是使汽车的行驶速度可以强制降低的一系列专门装置。
制动系统主要由供能装置、控制装置、传动装置和制动器4部分组成。
制动系统的主要功用是使行驶中的汽车减速甚至停车、使下坡行驶的汽车速度保持稳定、使已停驶的汽车保持不动。
功用·汽车制动系统功用1)保证汽车行驶中能按驾驶员要求减速停车2)保证车辆可靠停放3)保障汽车和驾驶人的安全类型1.按功用分:行车制动系驻车制动系辅助制动系1)行车制动系——是由驾驶员用脚来操纵的,故又称脚制动系。
它的功用是使正在行驶中的汽车减速或在最短的距离内停车。
2)驻车制动系——是由驾驶员用手来操纵的,故又称手制动系。
它的功用是使已经停在各种路面上的汽车驻留原地不动3)第二制动系——在行车制动系失效的情况下,保证汽车仍能实现减速或停车的一套装置。
在许多国家的制动法规中规定,第二制动系也是汽车必须具备的。
制动系统4)辅助制动系——经常在山区行驶的汽车以及某些特殊用途的汽车,为了提高行车的安全性和减轻行车制动系性能的衰退及制动器的磨损,用以在下坡时稳定车速。
2.按制动能量传输分:机械式、液压式、气压式、电磁式、组合式。
3.按回路多少分:单回路制动系、双回路制动系。
汽车制动系统的设计及仿真

汽车制动系统的设计及仿真任务书1.设计的主要任务及目标汽车制动器是制动系中最重要的一个部件,是制动系统中用以产生阻碍汽车运动或运动趋势的力的部件。
凡是利用固定元件与旋转元件工作表面的摩擦而产生制动力矩的制动器都成为摩擦制动器。
摩擦制动器可分为鼓式和盘式两大类。
前者的摩擦副中的旋转元件为制动鼓,其工作表面为圆柱面;后者的旋转元件则为圆盘状的制动盘,以端面为工作表面。
2.设计的基本要求和内容(1)了解汽车制动系统的工作过程。
(2)熟悉汽车制动系统的设计过程和设计参数。
(3)结合汽车制动性能要求设计汽车制动器。
(4)结合三维建模软件,并实现制动器的运动仿真。
3.主要参考文献[1] 王望予.汽车设计[M].北京:机械工业出版社,2004[2] 余志生.汽车理论[M].北京:机械工业出版社,2003[3] 陈家瑞.汽车构造[M].北京:机械工业出版社,2003[4] 林秉华.最新汽车设计实用手册[M],黑龙江:黑龙江出版社,2005[5] 张尉林.汽车制动系统的分析与设计[M].北京:机械工业出社,20024.进度安排注:一式4份,系部、指导教师各1份、学生2份:[毕业设计]及答辩评分表各一份汽车制动系统的设计及仿真摘要:汽车的制动系是汽车行车安全的保证,许多制动法规对制动系提出了许多详细而具体的要求,这是我们设计的出发点。
从制动器的功用及设计的要求出发,依据给定的设计参数,进行了方案论证。
对各种形式的制动器的优缺点进行了比较后,选择了浮动钳盘的形式。
这样,制动系有较高的制动效能和较高的效能因素稳定性。
随后,对盘式制动器的具体结构的设计过程进行了详尽的阐述。
选择了简单液压驱动机构和双管路系统,选用了间隙自动调节装置。
在设计计算部分,选择了几个结构参数,计算了制动系的主要参数,盘式制动器相关零件的设计计算。
关键词: 制动器,同步附着系数,制动盘,制动钳Automobile brake system design and simulationAbstracts:The braking system in a vehicle guaranteed the safety of driving .Many rules and regulations have been made for the braking system in detail, which is the starting of our design.Firstly, I demonstrate the project on the base of the function of the brake, And analysis their strong point and shortcomings .I choose the form of front-disked. In this way, the braking system have higher braking efficiency and high stability of the performance factors. Subsequently, the specific structure of the disc brake design was elaborated in detail.I designed the hydraulic drive system and two-pipe system and selected clearance automatic adjusting device.In the calculate part .I chosen several structural parameters, calculated the main parameters of the braking system drive mechanism.Key words:disc brakes,synchronous attachment coefficient,brake disc,brake caliper目录1 绪论 (1)1.1 课题研究的目的及意义 (1)1.2制动系统研究现状 (1)1.3课题设计思路 (3)2制动系统概述 (4)2.1制动系的类型 (4)2.2汽车制动系统组成 (4)2.3 制动器的组成 (5)2.4 制动器的要求 (5)2.5 制动器的种类 (7)3 汽车参数计算 (14)3.1汽车的基本参数 (14)3.2 制动系的主要参数及其选择 (15)3.3 盘式制动器的结构参数与摩擦系数的确定 (16)3.4 制动衬块的设计计算 (18)3.5 摩擦衬块磨损特性的计算 (19)4 制动器主要零件的结构设计 (21)4.2 制动钳 (21)4.4 摩擦材料 (21)4.5 盘式制动器间隙的调整方法及相应机构 (22)4.6 制动驱动机构的结构型式选择与设计计算 (22)结论 (25)参考文献 (26)致谢 (27)附录 (28)1 绪论1.1 课题研究的目的及意义汽车的设计与生产涉及到许多领域,其独有的安全性、经济性、舒适性等众多指标,也对设计提出了更高的要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录1. 动力学建模....................................................................................... - 1 -2. 分段线性的轮胎模型 ...................................................................... - 1 -3. 控制算法........................................................................................... - 2 -4. 仿真流程及参数输入 ...................................................................... - 2 -5. 实例分析........................................................................................... - 3 -6. MATLAB 仿真过程......................................................................... - 3 -6.1.逻辑门限值控制器 ................................................................... - 3 -6.2.模糊控制器 ............................................................................... - 7 -6.2.1模糊控制器设计 .............................................................. - 7 -6.2.2模糊控制matlab仿真过程 ............................................. - 8 -6.3.PID控制器.............................................................................. - 12 -通过两自由度单轮模型为例,介绍在MA TLAB 环境下的控制系统力学建模、ABS 控制器设计及仿真分析过程。
1. 动力学建模某车辆简化后的制动力学模型如右图所示。
其中单轮模型质量m ,车轮滚动半径rd ,车轮转动惯量为Iw ,车辆旋转角速度为ω,车轮轮心前进速度为uw ,地面制动力为Fxb 。
作用于车轮的制动力矩为Tb 。
若忽略空气阻力与车轮滚动阻力,则系统的运动方程如下: w x b d b td I F r T d ω=- (1) xb tdu mF d ω= (2)式中,地面制动力Fxb 等于地面作用于车轮的法向反力Fx 与路面附着系数μ的乘积,其中μ为制动滑移率Sb 的函数。
2. 分段线性的轮胎模型根据第三章中介绍的有关轮胎纵向特性的内容,路面附着系数与车轮滑移率之间存在一定的非线性关系。
如果用两段直线近似表示路面附着-滑移曲线,可得到分段线性化的附着系数μ与车辆滑移率s b 的关系(即所谓的“Dugoff”模型),如下图所示。
其表达式如下:11h b b oo h g o h g bb oo o S S S S S SS S S S μμμμμμμ⎧=≤⎪⎪⎨--⎪=->⎪--⎩(3)式中,μb 为峰值附着系数;μg 为车轮完全抱死时(即Sb=1)时的路面附着系数;So 为峰值附着系数所对应的滑移率。
图2 线性化的路面附着系数与车轮滑移率关系曲线图1 单轮制动力模型3.控制算法这里以门限值控制算法为例,说明ABS控制器设计及制动系统力学的仿真过程。
采用门限制控制算法的基本思想是保证车轮滑移率在最理想的范围之内。
制动开始后,随着制动压力的升高车轮转速ω相应减小,车轮出现滑移;当车轮滑移率达到理想范围上限值Smax时,减小制动压力;随着制动压力的减小,直至减小到滑移率下限值Smin时再增大制动压力。
循环往复这一过程直至车辆停止。
因此,在ABS控制器起作用的过程中,滑移率总是保持在理想的范围内,从而保证车辆的最佳制动性能及行驶方向控制的稳定性。
4.仿真流程及参数输入由上可知,ABS控制器所用到的一些控制参数有:1)由路面附着系数μ与滑移率S b的关系曲线所表示的轮胎模型;2)滑移率控制上限S max、下限S min;3)车辆模型参数及初始车速μωo;4)制动器油压增长率k i和减小率k d等。
根据分析可知,控制逻辑实现的关键是计算当前车轮滑移率S b(t)并与预先确定的上限值(S max,S min)进行比较,来判断对制动液压控制系统的增压或减压操作,控制流程如图3所示。
5. 实例分析单轮制动动力模型参数由表1给出。
设式图2定义的路面附着系数分别为μh =0.8,μg =0.6.以门限值控制算法设计ABS 控制器,使车轮滑移率S b 保持在最优值(S opt 附近),这里令S min =0.18,S max =0.22。
根据表1给出的模型参数及附着系数,按照图3所示的控制流程采用m 语言编制仿真程序。
需要指出的是,表1给出的制动系统控制参数仅作为参考,系统设计过程中可根据需要适当调整,已获得满意的结果。
表1 单轮ABS 制动力学模型参数参数符号单位数值车轮质量mkg300车轮动力半径drm0.25车轮转动惯量wI2kg m ⋅12初始车速woμ/m s30初始角速度ω/rad s120初始制动力矩 boTN m ⋅600制动油压增长率ik/Nm s4500制动油压减小率dk/Nm s5000采样时间sTs0.056. MATLAB 仿真过程6.1.逻辑门限值控制器Matlab 代码如下: clear clc%% 输入初始参数m=300; %车轮质量 rd=0.25; %车轮动力半径Iw=12; %车轮转动惯量 u0=30; %初始车速 w0=120; %初始角速度 Tb0=600; %初始制动力矩 ki=4500; %制动油压增长率 kd=5000; %制动油压减少率 dt=0.05; %采样时间 u(1)=u0; %设置车速数组变量 w(1)=w0; %设置轮速数组变量 Tb(1)=Tb0; %设置制动压力数组变量 s(1)=0; %设置滑移率数组变量 Fxb(1)=0; %设置地面制动力数组变量 %% 滑移率逻辑门控制 i=1;while (u(i)>0)s(i+1)=(u(i)-w(i)*rd)/u(i); %计算滑移率 if s(i+1)<0.2 %计算纵向附着系数 mu=4*s(i+1); elsemu=0.85-0.25*s(i+1); endFxb(i+1)=m*9.8*mu; %计算地面制动力if s(i+1)<0.18 %与滑移率门限值比较,确定制动力矩 Tb(i+1)=Tb(i)+ki*dt; elseif s(i+1)>0.22 Tb(i+1)=Tb(i)-kd*dt; elseTb(i+1)=Tb(i); enddw=(Fxb(i+1)*rd-Tb(i+1))/Iw; %计算车轮角加速度 du=-Fxb(i+1)/m; %计算车身加速度 u(i+1)=u(i)+du*dt; %计算下一时刻车速 w(i+1)=w(i)+dw*dt; %计算下一时刻轮速 i=i+1; endt=0:dt:(i-1)*dt; plot(t,[u' w'*rd]) figure()逻辑门控制器plot(t,Fxb,t,Tb) figure()plot(t,s) 运行结果如下:1) 制动器制动力矩与地面制动力随时间变化曲线0.51 1.52 2.53 3.54 4.5-50005001000150020002500时间t/s制动力制动力变化曲线地面制动力N制动器制动力矩N*m2) 滑移率随时间变化曲线00.51 1.52 2.53 3.540.050.10.150.20.250.30.35时间t/s滑移率滑移率变化曲线3) 车速与轮速随时间变化曲线0.51 1.52 2.53 3.54 4.5-5051015202530时间t/s速度m /s车速与轮速变化曲线车速轮速可以看出:● 基于滑移率的逻辑门限值控制器,可以限制滑移率在给定的最佳滑移率附近波动,汽车完全停止时,车速为零,滑移率趋于无穷大,所以在仿真时间最后一段,滑移率有较大波动。
● 制动器制动力矩在滑移率控制器的控制下,可以完成增压、保压、减压动作,防止车轮过早抱死,减小制动距离。
6.2.模糊控制器6.2.1模糊控制器设计1)输入量模糊化●为简化,仅选取滑移率偏差e作为输入量,当最佳滑移率选为0.2时,滑移率偏差范围为【-0.2,0.8】,经过适当变化,使e的变化范围为【-6,6】,以便于控制。
●为简化,仅选取三个语义词【N,Z,P】,即正、零、负。
分别定义各自的隶属度函数,进行模糊化,如下图:2)输出量反模糊化●选取制动器制动力矩改变量为输出量,取值范围设定为【-1,+1】。
同样,为简化,选取三个语义词【I,K,D】,即增压、保压、减压。
并定义相应隶属度函数,如下图:3)模糊规则●由于仅有一个输入量,且仅选取三个语义词,只需定义三条模糊规则,如下图:4)控制曲线●观察制动器制动力矩改变量与滑移率偏差的关系6.2.2模糊控制matlab仿真过程程序如下:clearclc%% 输入初始参数m=300; %车轮质量rd=0.25; %车轮动力半径Iw=12; %车轮转动惯量u0=30; %初始车速w0=120; %初始角速度Tb0=600; %初始制动力矩ki=4500; %制动油压增长率kd=5000; %制动油压减少率dt=0.05; %采样时间u(1)=u0; %设置车速数组变量w(1)=w0; %设置轮速数组变量Tb(1)=Tb0; %设置制动压力数组变量s(1)=0; %设置滑移率数组变量Fxb(1)=0; %设置地面制动力数组变量dtp(1)=0; %设置地面制动力变化量数组变量%% 模糊控制i=1;while(u(i)>0)s(i+1)=(u(i)-w(i)*rd)/u(i); %计算滑移率 if s(i+1)<0.2 %计算纵向附着系数 mu=4*s(i+1); elsemu=0.85-0.25*s(i+1); endFxb(i+1)=m*9.8*mu; %计算地面制动力e=12*(s(i+1)-0.5); %将滑移率偏差范围转化到【-6,6】abs=readfis('abs_fzy2.fis'); %调用设计好的模糊控制器 dtp(i+1)=evalfis(e,abs); %输出制动器制动力矩变化量Tb(i+1)=Tb(i)+2*5000*dtp(i+1)*dt; %计算制动器制动力矩 dw=(Fxb(i+1)*rd-Tb(i+1))/Iw; du=-Fxb(i+1)/m; u(i+1)=u(i)+du*dt; w(i+1)=w(i)+dw*dt; i=i+1; end %% 绘图t=0:dt:(i-1)*dt; plot(t,[u' w'*rd]) figure()plot(t,Fxb,t,Tb) figure() plot(t,s) figure() plot(t,dtp)模糊控制器运行结果:1) 模糊控制器输出,即Tb 的变化量00.51 1.52 2.53 3.54 4.5-0.6-0.4-0.20.20.40.60.8时间t/s变化率模糊控制器输出(Tb 变化量)2) 地面制动力与制动器制动力矩0.51 1.52 2.53 3.54 4.5-50005001000150020002500时间t/s制动力制动力变化曲线Fb(N)Tb(N*m)3) 滑移率00.51 1.52 2.53 3.54 4.50.050.10.150.20.250.30.350.4时间t/s滑移率滑移率变化曲线4) 车速与轮速0.51 1.52 2.53 3.54 4.5-5051015202530时间t/s速度m /s车速与轮速变化曲线车速轮速6.3.PID 控制器● PID 控制器的设计选取滑移率s 的偏差e 作为输入,若选定最佳滑移率为0.2,则e=s-0.2;输出量为制动器制动力矩的变化量dtp 。
