装载问题代码
贪心算法之最优装载问题
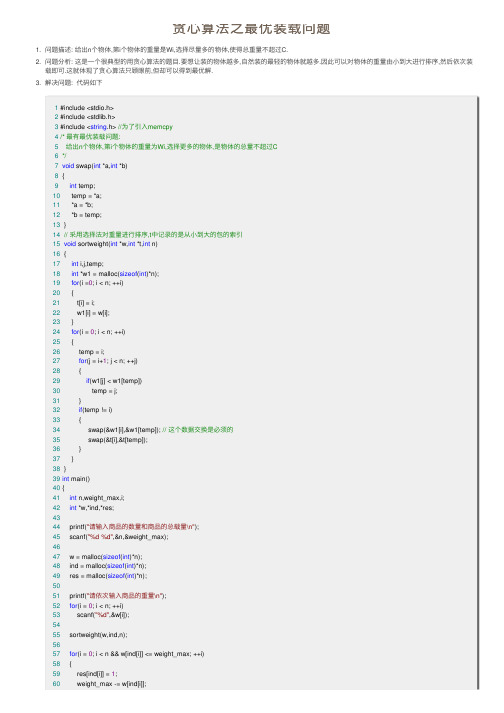
贪⼼算法之最优装载问题1. 问题描述: 给出n个物体,第i个物体的重量是Wi,选择尽量多的物体,使得总重量不超过C.2. 问题分析: 这是⼀个很典型的⽤贪⼼算法的题⽬.要想让装的物体越多,⾃然装的最轻的物体就越多.因此可以对物体的重量由⼩到⼤进⾏排序,然后依次装载即可.这就体现了贪⼼算法只顾眼前,但却可以得到最优解.3. 解决问题: 代码如下4. 1 #include <stdio.h>2 #include <stdlib.h>3 #include <string.h> //为了引⼊memcpy4/* 最有最优装载问题:5给出n个物体,第i个物体的重量为Wi,选择更多的物体,是物体的总量不超过C6*/7void swap(int *a,int *b)8 {9int temp;10 temp = *a;11 *a = *b;12 *b = temp;13 }14// 采⽤选择法对重量进⾏排序,t中记录的是从⼩到⼤的包的索引15void sortweight(int *w,int *t,int n)16 {17int i,j,temp;18int *w1 = malloc(sizeof(int)*n);19for(i =0; i < n; ++i)20 {21 t[i] = i;22 w1[i] = w[i];23 }24for(i = 0; i < n; ++i)25 {26 temp = i;27for(j = i+1; j < n; ++j)28 {29if(w1[j] < w1[temp])30 temp = j;31 }32if(temp != i)33 {34 swap(&w1[i],&w1[temp]); // 这个数据交换是必须的35 swap(&t[i],&t[temp]);36 }37 }38 }39int main()40 {41int n,weight_max,i;42int *w,*ind,*res;4344 printf("请输⼊商品的数量和商品的总载量\n");45 scanf("%d %d",&n,&weight_max);4647 w = malloc(sizeof(int)*n);48 ind = malloc(sizeof(int)*n);49 res = malloc(sizeof(int)*n);5051 printf("请依次输⼊商品的重量\n");52for(i = 0; i < n; ++i)53 scanf("%d",&w[i]);5455 sortweight(w,ind,n);5657for(i = 0; i < n && w[ind[i]] <= weight_max; ++i)58 {59 res[ind[i]] = 1;60 weight_max -= w[ind[i]];61 }62 printf("贪⼼算法求解后的结果是:\n");63for(i = 0; i < n; ++i)64 {65 printf("%d ",res[i]);66 }67 printf("\n");68return0;69 }4. 程序分析: 由于不要改变原始物体重量的值,所以在排序的时候要另外再开辟⼀个数组存储重量.并且另外开辟ind[]存放索引记录装载的顺序.ind[]存放的是重量数组中每个元素在这组数组中⼤⼩的顺序(索引).怎样在排序时记录索引需要在练习排序的时候注意下.。
用分支限界算法解装载问题详解

用分支限界算法解装载问题详解一、实验目的1、理解分支限界法的概念,掌握分支限界法的基本要素。
2、掌握设计分支限界法的一般步骤,针对具体问题,能应用分支限界法求解二、实验内容1、问题描述:有一批共个集装箱要装上2艘载重量分别为C1和C2的轮船,其中集装箱i的重量为Wi,且w1+…+wn<= C1+ C2; 装载问题要求确定是否有一个合理的装载方案可将这个集装箱装上这2艘轮船。
如果有,找出一种装载方案。
2、数据输入:文件输入或键盘输入。
3、要求:1)完成上述问题的队列式分支限界法解决问题,时间为1 次课。
2)独立完成实验及实验报告。
三、实验步骤1、理解方法思想和问题要求。
2、采用编程语言实现题目要求。
3、上机输入和调试自己所写的程序。
4、附程序主要代码:#include <bits/stdc++、h>using namespace std;class MaxHeapQNode{public: MaxHeapQNode*parent; int lchild; int weight; int lev;};structcmp{ bool operator()(MaxHeapQNode *&a, MaxHeapQNode *&b)const { return a->weight < b->weight; }};int n;int c;int bestw;int w[100];int bestx[100];voidInPut(){ scanf("%d %d", &n, &c); for(int i =1; i <= n;++i)scanf("%d", &w[i]);}voidAddAliveNode(priority_queue<MaxHeapQNode *,vector<MaxHeapQNode *>, cmp> &q, MaxHeapQNode *E, int wt, int i, int ch){ MaxHeapQNode *p = new MaxHeapQNode; p->parent = E; p->lchild = ch; p->weight = wt; p->lev = i +1; q、push(p);}voidMaxLoading(){ priority_queue<MaxHeapQNode *,vector<MaxHeapQNode *>, cmp > q; // 大顶堆 //定义剩余重量数组r int r[n +1]; r[n] = 0; for(int j = n-j)r[j] = r[j +1] + w[j +1]; int i =1; MaxHeapQNode *E; int Ew = 0; while(i != n +1){ if(Ew + w[i] <= c){ AddAliveNode(q, E, Ew + w[i] + r[i], i,1); } AddAliveNode(q, E, Ew + r[i], i, 0); //取下一节点 E = q、top(); q、pop(); i = E->lev; Ew = E->weight1]; } bestw = Ew; for(int j = n; j > 0;j){ bestx[j] = E->lchild; E = E->parent; }}void OutPut(){ printf("最优装载量为 %d\n", bestw); printf("装载的物品为 \n"); for(int i =1; i <= n; ++i)if(bestx[i] ==1)printf("%d ", i);}int main(){ InPut(); MaxLoading(); OutPut();}5、实验结果:4、装载问题实验分析:1、将wt<=c和Ew+r>=bestw作为限界判定。
算法中的最优装载问题

算法中的最优装载问题问题描述有n个集装箱要装上1艘载重量分别为c的轮船,其中第i个集装箱的重量为wi。
最优装载问题要求确定在装载体积不受限制的情况下,将尽可能多的集装箱装上轮船,并找出一种装载方案其中@w #集装箱的重量数组@c #货船的最大载重量@n #集装箱的个数@r #未被装载的货物重量@cw #当前货船上的载重@i #搜索树的层数@bestw #最优值@bestx #最优解class Loadingdef initialize(weight,cont)@w,@c,@n=weight,cont,weight.length@r,@cw,@i,@bestw=0,0,0,0@x=Array.new@bestx=Array.newfor j in 0..@n-1@r=@r+@w[j];@bestx[j],@x[j]=0,0endprint \\"集装箱的总重量为 #@r,\\n\\"enddef MaxLoadingwhile truewhile @i<=(@n-1) and (@cw+@w[@i]<@c)@r-=@w[@i]@cw+=@w[@i]@x[@i]=1print \\"在左子树中\\",@x[@i],\\"\\n\\"@i+=1endif @i>@n-1for j in 0..@n-1@bestx[j]=@x[@i]print \'到达叶子节点\',j,\\"\\t @bestx[j]\\",@bestx[j],\\"\\n\\" end@bestw=@cwelse@r-=@w[@i];@x[@i]=0;print \'在右子树中\',@x[@i],\\"\\n\\" @i+=1endwhile @cw+@r<=@bestw@i-=1while @i>=0 and (@x[@i]==0)@r+=@w[@i];@i-=1endif @i==-1 thenprint \\"@bestw:\\",@bestwreturnend@x[@i]=0@cw-=@w[@i]@i+=1endendendendweight=[30,10,10]cont=35s=Loading.new(weight,cont)s.MaxLoading运行的结果如下:集装箱的总重量为 50,在左子树中1在右子树中0在右子树中0到达叶子节点0 @bestx[j]nil到达叶子节点1 @bestx[j]nil到达叶子节点2 @bestx[j]nil@bestw:30>Exit code: 0。
贪心算法之最优装载问题

贪⼼算法之最优装载问题贪⼼算法之最优装载问题1. 问题描述有⼀批集装箱要装上⼀艘重量为c的轮船,其中集装箱i的重量为W i。
最优装载问题要求确定在装载体积不受限制的情况下,将尽可能多的集装箱装上轮船。
2. 问题分析2.1确定贪⼼策略采⽤重量最轻者先装的贪⼼选择策略,可产⽣该问题的最优解。
2.2代码求解/*** x[] 保存最优解路径数组* w[] 集装箱重量数组* c 船的载重量* n 集装箱的数量**/void Loading(int x[], int w[], int c, int n) {// 按照集装箱重量从⼩到⼤排序sort(w, n);for (int i = 1; i <= n; i++)x[i] = 0;for (int i = 1; i <= n && w[i] <= c; i++) {x[i] = 1;c -= w[i];}}2.3贪⼼选择性质设集装箱依其重量从⼩到⼤排序,(x1,x2,…,x n)是其最优解,x i={0,1},设x k是第⼀个等于1的。
(1) 如k=1,则满⾜贪⼼选择性质(2) 如k≠1,⽤x1替换x k,构造的新解同原解最优值相同,故也是最优解,满⾜贪⼼选择性质该证明⽅法只证明了任何⼀个最优解都可以转换为第⼀个集装箱上船的最优解(满⾜贪⼼策略)。
此⽅法对⼦问题同样有效,因此可以将⼀个普通最优解转化为满⾜贪⼼策略的最优解。
如(0101)⇒(1100)2.4.最优⼦结构性质最优装载问题具有最优⼦结构性质,设1⾄n个集装箱装上船的最⼤数量为T(1,n,w),则T(1,n,w)=1+T(2,n,w−w1);因T(1,n,w)是最优值,则T(2,n,w−w i)⼀定是最优值,反证法证明之反证法:如果T(2,n,w−w1)不是该问题的最优解,则存在最优值T′(2,n,w−w1)>T(2,n,w−w1),则1+T′(2,n,w−w1)=T′(1,n,w)>T(1,n,w),这与⼤前提T(1,n,w)是最优值相⽭盾,故T(2,n,w−w1)⼀定是最优值。
系统Code_error对照表

网上找的,号称全集,但至少是比较多的了。
和大家分享一下,方便大家查找。
(一)0 0x0000 作业完成。
10x0001 不正确的函数。
20x0002 系统找不到指定的档案。
30x0003 系统找不到指定的路径。
40x0004 系统无法开启档案。
50x0005 拒绝存取。
60x0006 无效的代码。
70x0007 储存体控制区块已毁。
80x0008 储存体空间不足,无法处理这个指令。
90x0009 储存体控制区块位址无效。
100x000A 环境不正确。
110x000B 尝试载入一个格式错误的程式。
120x000C 存取码错误。
130x000D 资料错误。
140x000E 储存体空间不够,无法完成这项作业。
150x000F 系统找不到指定的磁碟机。
160x0010 无法移除目录。
170x0011 系统无法将档案移到其他的磁碟机。
180x0012 没有任何档案。
190x0013 储存媒体为防写状态。
200x0014 系统找不到指定的装置。
210x0015 装置尚未就绪。
220x0016 装置无法识别指令。
230x0017 资料错误 (cyclic redundancy check) 24 0x0018 程式发出一个长度错误的指令。
250x0019 磁碟机在磁碟找不到持定的磁区或磁轨。
260x001A 指定的磁碟或磁片无法存取。
270x001B 磁碟机找不到要求的磁区。
280x001C 印表机没有纸。
290x001D 系统无法将资料写入指定的磁碟机。
300x001E 系统无法读取指定的装置。
310x001F 连接到系统的某个装置没有作用。
320x0020 The process cannot access the file because it is being used by another process.330x0021 档案的一部份被锁定,现在无法存取。
340x0022 磁碟机的磁片不正确。
请将 %2 (Volume Serial Number: %3) 插入磁碟机 %1。
数学建模-(货机装运lingo)

数学建模-(货机装运lingo)货机装运是指将货物从一个起点运输到一个终点,在这个过程中需要考虑到货物的重量、体积、运输方式等多种因素。
在货机装运过程中,一个关键问题是如何最大化运载效率,即在保证运输安全和合法的前提下,尽可能地提高货机的装载量,从而降低单位运输成本。
在数学建模中,可以使用lingo等工具进行货机装运的优化。
具体来说,可以将该问题抽象为一个数学模型,以最大化货机的装载量为目标函数,同时考虑到运输安全、货物重量、体积等约束条件。
下面以一个具体例子来说明如何使用lingo进行货机装运的优化:假设有一架货机,其载重量为10000公斤,可以装载两种货物A和B,每种货物的重量和体积如下:货物类型重量(公斤)体积(立方米)A 600 1.5B 400 0.8同时,从起点到终点的运输费用如下:货物类型运输费用(元/公斤)A 10B 15要求在保证运输安全和合法的前提下,最大化货机的装载量,即:subject to:A +B <= 10000(装载量不超过10000公斤)其中,A和B表示货机装载的货物A和B的数量,V是货机的装载体积,运输费用是由货物类型和运输距离等因素决定的,这里简化为一个固定值。
使用lingo进行求解的过程如下:1.首先,在lingo中创建一个新的模型文件,并定义目标函数和约束条件:2.对模型进行求解,并设置模型参数:model:solve;parameters:V = 15;end;在上述代码中,V表示货机的装载体积,这里假设为15立方米。
solve表示对模型进行求解,通过设置end来结束参数定义。
3.对求解结果进行分析和优化,例如考虑不同装载体积下的最优解:for V := 15 to 20 dobeginwriteln('Optimal value for V=',V,': ',model.obj);在以上代码中,for循环遍历不同的装载体积值(15到20),分别求解模型并输出优化结果。
最优装载问题(贪心)

最优装载问题(贪⼼)⼀、实验内容运⽤贪⼼算法解决活动安排问题(或最优装载问题)使⽤贪⼼算法解决最优装载问题。
⼆、所⽤算法基本思想及复杂度分析1.算法基本思想贪⼼算法是指在对问题求解时,总是做出在当前看来是最好的选择。
也就是说,不从整体最优上加以考虑,它所做出的仅是在某种意义上的局部最优解。
⽤局部解构造全局解,即从问题的某⼀个初始解逐步逼近给定的⽬标,以尽可能快的求得更好的解。
当某个算法中的某⼀步不能再继续前进时,算法停⽌。
2.问题分析及算法设计问题分析:(1)给定n个古董,要把它们装到装载量为c的装载船上。
(2)⾸先需要对这n个古董进⾏质量从⼩到⼤的排序。
(3)然后每次都选择最轻的,接着再从剩下的n-1件物品中选择最轻的。
(4)重复第(3)步骤,直到当前载重量⼤于装载船的最⼤装载量,停⽌装载。
(5)此时得到最优的贪⼼⽅案,记录下装载的最⼤古董数。
算法设计:(1)算法策略:把n件物品从⼩到⼤排序,然后根据贪⼼策略尽可能多的选出前i个物品,直到不能装为⽌。
(2)特例:算法复杂度分析由最优装载问题的贪⼼选择性质和最优⼦结构性质,可知将这些古董按照其重量从⼩到⼤排序,所以算法所需的计算时间为O(nlogn)。
三、源程序核⼼代码及注释(截图)四、运⾏结果五、调试和运⾏程序过程中产⽣的问题及解决⽅法,实验总结(5⾏以上)这⾥的调试,没有什么⼤问题,单纯的依次⽐较,判断,从⽽得到结果。
这次实验让我对贪⼼算法有了更深刻的认识,其主要是从问题的初始解出发,按照当前最佳的选择,把问题归纳为更⼩的相似的⼦问题,并使⼦问题最优,再由⼦问题来推导出全局最优解。
贪⼼算法虽然求的是局部最优解,但往往许多问题的整体最优解都是通过⼀系列的局部最优解的选择来达到的,所以贪⼼算法不⼀定可以得到能推导出问题的最优解,但其解法是最优解的近似解。
懂得算法的原理,还需要多去练习才能更好的掌握其⽤法。
源码:#include<iostream>#include<algorithm>#define MAXN 1000005using namespace std;int w[MAXN];//每件古董的重量int main(){int c,n;//c:载重量,n古董数int sum = 0;//装⼊古董的数量int tmp = 0;//装⼊古董的重量cin >> c >> n;for(int i= 1; i <= n; ++i)cin >> w[i];sort(w+1,w+1+n);for(int i = 1; i <= n; ++i){tmp += w[i];if(tmp <= c)++sum;elsebreak;}cout << sum << endl;return 0;}。
货物装载问题

x
取
ij
非负整
数
i 1,2,3; j 1,2,3,4,5
6
xij 12 i 1,2,3
j1
4、计算
sets: dianti/1..3/:t; louceng/1..5/:; link(dianti,louceng):x; endsets min=w; @for(dianti:w>=t); @for(louceng(j):10*@sum(dianti(i):x(i,j))=60); @for(dianti(i):t(i)=@sum(louceng(j):(10+20)*x(i,j)+(3+3)*(j +5)*x(i,j))); @for(link:@gin(x)); @for(dianti(i):@sum(louceng(j):x(i,j))<=12);
575000 3000 y3 1500 y2 575000
前后舱位比例平衡
| y3 y1 | 0.10 1500 2000
300000 2000 y3 1000 y1 300000
3、建立数学模型
3
max z ci ri
i1
3
ri xij , ri ai ,i 1,2,3
i1
三个舱位之间的重量平衡(第一种理解方式) 前后舱与中舱的比例平衡
|
y1 y2
2000 3000
|
0.15
450y2
3000y1
2000y2
450y2
|
y3 y2
1500 3000
|
0.15
450 y2
3000
y3
1500
y2
450 y2
回溯法解决集装箱问题c语言程序

回溯法解决集装箱问题c语言程序集装箱问题是一个经典的组合优化问题,其目标是找到一种最优的方式将一组不同大小的集装箱装入一艘货船中。
在这个问题中,我们需要考虑集装箱的尺寸、重量以及货船的容量限制。
回溯法是一种常用的解决组合优化问题的方法,下面我们将介绍如何使用C语言编写回溯法解决集装箱问题的程序。
首先,我们需要定义一个结构体来表示集装箱的属性,包括尺寸和重量。
代码如下:```ctypedef struct {int size;int weight;} Container;```接下来,我们需要定义一个函数来计算货船的最大装载量。
这个函数将采用回溯法的思想,通过递归的方式遍历所有可能的装载方式,并返回最优解。
代码如下:```cint maxLoad(Container containers[], int n, int capacity, int index, int currentSize, int currentWeight) {// 如果已经遍历完所有集装箱,返回当前的装载重量if (index == n) {return currentWeight;}// 如果当前集装箱的尺寸或重量超过了货船的容量限制,跳过该集装箱if (currentSize + containers[index].size > capacity || currentWeight + containers[index].weight > capacity) {return maxLoad(containers, n, capacity, index + 1, currentSize, currentWeight);}// 尝试将当前集装箱装入货船int load = maxLoad(containers, n, capacity, index + 1, currentSize + containers[index].size, currentWeight + containers[index].weight);// 尝试不将当前集装箱装入货船int notLoad = maxLoad(containers, n, capacity, index + 1, currentSize, currentWeight);// 返回装载重量较大的方案return load > notLoad ? load : notLoad;}```最后,我们可以在主函数中调用上述函数来解决集装箱问题。
0034算法笔记——【分支限界法】最优装载问题

0034算法笔记——【分⽀限界法】最优装载问题问题描述有⼀批共个集装箱要装上2艘载重量分别为C1和C2的轮船,其中集装箱i的重量为Wi,且装载问题要求确定是否有⼀个合理的装载⽅案可将这个集装箱装上这2艘轮船。
如果有,找出⼀种装载⽅案。
容易证明:如果⼀个给定装载问题有解,则采⽤下⾯的策略可得到最优装载⽅案。
(1)⾸先将第⼀艘轮船尽可能装满;(2)将剩余的集装箱装上第⼆艘轮船。
1、队列式分⽀限界法求解在算法的循环体中,⾸先检测当前扩展结点的左⼉⼦结点是否为可⾏结点。
如果是则将其加⼊到活结点队列中。
然后将其右⼉⼦结点加⼊到活结点队列中(右⼉⼦结点⼀定是可⾏结点)。
2个⼉⼦结点都产⽣后,当前扩展结点被舍弃。
活结点队列中的队⾸元素被取出作为当前扩展结点,由于队列中每⼀层结点之后都有⼀个尾部标记-1,故在取队⾸元素时,活结点队列⼀定不空。
当取出的元素是-1时,再判断当前队列是否为空。
如果队列⾮空,则将尾部标记-1加⼊活结点队列,算法开始处理下⼀层的活结点。
节点的左⼦树表⽰将此集装箱装上船,右⼦树表⽰不将此集装箱装上船。
设bestw是当前最优解;ew是当前扩展结点所相应的重量;r是剩余集装箱的重量。
则当ew+r为了在算法结束后能⽅便地构造出与最优值相应的最优解,算法必须存储相应⼦集树中从活结点到根结点的路径。
为此⽬的,可在每个结点处设置指向其⽗结点的指针,并设置左、右⼉⼦标志。
找到最优值后,可以根据parent回溯到根节点,找到最优解。
算法具体代码实现如下:1、Queue.h[cpp]view plain copy1.#include/doc/951702836.htmling namespace std;3.4.template5.class Queue6.{7.public:8. Queue(int MaxQueueSize=50);9. ~Queue(){delete [] queue;}10.bool IsEmpty()const{return front==rear;}11.bool IsFull(){return ( ( (rear+1) %MaxSize==front )?1:0);}12. T Top() const;13. T Last() const;14. Queue& Add(const T& x);15. Queue& AddLeft(const T& x);16. Queue& Delete(T &x);17.void Output(ostream& out)const;18.int Length(){return (rear-front);}19.private:20.int front;21.int rear;22.int MaxSize;23. T *queue;24.};25.26.template27.Queue::Queue(int MaxQueueSize)28.{29. MaxSize=MaxQueueSize+1;30. queue=new T[MaxSize];31. front=rear=0;32.}33.34.template35.T Queue::Top()const36.{37.if(IsEmpty())38. {39. cout<<"queue:no element,no!"<40.return 0;41. }42.else return queue[(front+1) % MaxSize];43.}44.45.template46.T Queue ::Last()const47.{48.if(IsEmpty())49. {50. cout<<"queue:no element"<51.return 0;52. }53.else return queue[rear];54.}55.56.template57.Queue& Queue::Add(const T& x)58.{59.if(IsFull())cout<<"queue:no memory"<60.else61. {62. rear=(rear+1)% MaxSize;63. queue[rear]=x;64. }65.return *this;66.}67.68.template69.Queue& Queue::AddLeft(const T& x)70.{71.if(IsFull())cout<<"queue:no memory"<72.else73. {74. front=(front+MaxSize-1)% MaxSize;75. queue[(front+1)% MaxSize]=x;76. }77.return *this;78.}79.80.template81.Queue& Queue ::Delete(T & x)82.{83.if(IsEmpty())cout<<"queue:no element(delete)"<84.else85. {86. front=(front+1) % MaxSize;87. x=queue[front];88. }89.return *this;90.}91.92.93.template94.void Queue ::Output(ostream& out)const95.{96.for(int i=rear%MaxSize;i>=(front+1)%MaxSize;i--)97. out<98.}99.100.template101.ostream& operator << (ostream& out,const Queue& x) 102.{x.Output(out);return out;} 2、6d3-1.cpp[cpp]view plain copy1.//装载问题队列式分⽀限界法求解2.#include "stdafx.h"3.#include "Queue.h"4.#include/doc/951702836.htmling namespace std;6.7.const int N = 4;8.9.template10.class QNode11.{12.template13.friend void EnQueue(Queue*>&Q,Type wt,int i,int n,Type bestw,QNode*E,QNode *&bestE,int bestx[],bool ch);14.15.template16.friend Type MaxLoading(Type w[],Type c,int n,int bestx[]);17.18.private:19. QNode *parent; //指向⽗节点的指针20.bool LChild; //左⼉⼦标识21. Type weight; //节点所相应的载重量22.};23.24.template25.void EnQueue(Queue*>&Q,Type wt,int i,int n,Type bestw,QNode >*E,QNode *&bestE,int bestx[],bool ch);26.27.template28.Type MaxLoading(Type w[],Type c,int n,int bestx[]);29.30.int main()31.{32.float c = 70;33.float w[] = {0,20,10,26,15};//下标从1开始34.int x[N+1];35.float bestw;36.37. cout<<"轮船载重为:"<38. cout<<"待装物品的重量分别为:"<39.for(int i=1; i<=N; i++)40. {41. cout<42. }43. cout<44. bestw = MaxLoading(w,c,N,x);45.46. cout<<"分⽀限界选择结果为:"<47.for(int i=1; i<=4; i++)48. {49. cout<50. }51. cout<52. cout<<"最优装载重量为:"<53.54.return 0;55.}56.57.//将活节点加⼊到活节点队列Q中58.template59.void EnQueue(Queue*>&Q,Type wt,int i,int n,Type bestw,QNode >*E,QNode *&bestE,int bestx[],bool ch)60.{61.if(i == n)//可⾏叶节点62. {63.if(wt == bestw)64. {65.//当前最优装载重量66. bestE = E;67. bestx[n] = ch;68. }69.return;70. }71.//⾮叶节点72. QNode *b;73. b = new QNode;74. b->weight = wt;75. b->parent = E;76. b->LChild = ch;77. Q.Add(b);78.}79.80.template81.Type MaxLoading(Type w[],Type c,int n,int bestx[])82.{//队列式分⽀限界法,返回最优装载重量,bestx返回最优解83.//初始化84. Queue*> Q; //活节点队列85. Q.Add(0); //同层节点尾部标识86.int i = 1; //当前扩展节点所处的层87. Type Ew = 0, //扩展节点所相应的载重量88. bestw = 0, //当前最优装载重量89. r = 0; //剩余集装箱重量90.91.for(int j=2; j<=n; j++)92. {93. r += w[j];94. }95.96. QNode *E = 0, //当前扩展节点97. *bestE; //当前最优扩展节点98.99.//搜索⼦集空间树100.while(true)101. {102.//检查左⼉⼦节点103. Type wt = Ew + w[i];104.if(wt <= c)//可⾏节点105. {106.if(wt>bestw)107. {108. bestw = wt;109. }110. EnQueue(Q,wt,i,n,bestw,E,bestE,bestx,true); 111. } 112.113.//检查右⼉⼦节点114.if(Ew+r>bestw)115. {116. EnQueue(Q,Ew,i,n,bestw,E,bestE,bestx,false); 117. } 118. Q.Delete(E);//取下⼀扩展节点119.120.if(!E)//同层节点尾部121. {122.if(Q.IsEmpty())123. {124.break;125. }126. Q.Add(0); //同层节点尾部标识127. Q.Delete(E); //取下⼀扩展节点128. i++; //进⼊下⼀层129. r-=w[i]; //剩余集装箱重量130. }131. Ew =E->weight; //新扩展节点所对应的载重量132. }133.134.//构造当前最优解135.for(int j=n-1; j>0; j--)136. {137. bestx[j] = bestE->LChild;138. bestE = bestE->parent;139. }140.return bestw;141.}程序运⾏结果如图:2、优先队列式分⽀限界法求解解装载问题的优先队列式分⽀限界法⽤最⼤优先队列存储活结点表。
1002装载

[回溯]装载问题Time Limit: 1 Sec Memory Limit: 128 MBSubmissions: 13 Solved: 6[Submit][Status][Discuss]Description有两艘船,载重量分别是c1、 c2,n个集装箱,重量是wi (i=1…n),且所有集装箱的总重量不超过c1+c2。
确定是否有可能将所有集装箱全部装入两艘船。
Input多个测例,每个测例的输入占两行。
第一行一次是c1、c2和n(n<=10);第二行n个整数表示wi (i=1…n)。
n等于0标志输入结束。
Output对于每个测例在单独的一行内输出Yes或No。
Sample Input7 8 28 77 9 28 80 0 0Sample OutputYesNoHINT#include "stdio.h"#define MAXARRAY 10000#define PUSH (A,B){sl[sp]}=A;sr[sp]=B;sp++}#define POP(A,B){sp--;A=sl[sp];b=sr[sp];}void quicksort(int a[],int l,int r){static int sl[MAXARRAY],sr[MAXARRAY],sp;int i,j,p,t;sp=0;PUSH(l,r);while(sp){POP(l,r);i=l;j=r;p=a[(i+j)/2];while(i<=j){while(a[i]<p) i++;while(a[j]>p)j--;if(i<=j){t=a[i];a[i]=a[j];a[j]=t;i++;j++;}}if(l<j)PUSH(l,j);if(i<r)PUSH(i,r);}}void main(){int a[MAXARRAY];int i;int n;scanf("%d",&n);for(i=0;i<n;i++)scanf("%d",&a[i]);quicksort(a,0,n-1);for(i=0;i<n;i++)printf("%d\n",a[i]);}二、#include<iostream>using namespace std;int bestw=0; //当前最多载重量int cw=0; // 当前载重量int num=3; // 箱子数int r=46; // 剩余箱子重量int bestx[3]; //最重的情况下箱子的选择情况void load(int *w,int c,int n,int *x){if(n>=num){if(cw>bestw){for(int i=0;i<n;i++){ bestx[i]=x[i];bestw=cw;}}return ;}r-=w[n];//*************if(cw+w[n]<=c){cw+=w[n];x[n]=1;load(w,c,n+1,x);cw=cw-w[n];}if(cw+r>bestw)//*************************{x[n]=0;load(w,c,n+1,x);}r+=w[n];//*********}.回溯法——装箱问题算法 2010-07-28 11:02:46 阅读26 评论0 字号:大中小订阅 .问题描述:有n个集装箱要装到俩艘船上,每艘船的容载量分别问c1,c2,第i个集装箱的重量为 w[i],同时满足:w[1]+w[2]+...+w[n]<=c1+c2;求确定一个最佳的方案把这些集装箱装入这俩艘船上。
运料小车自动往返装卸料的c语言编程

运料小车自动往返装卸料的c语言编程以下是一个简单的运料小车自动往返装卸料的C语言代码示例:```c#include <stdio.h>#include <stdbool.h>// 函数原型声明void loadMaterial();void unloadMaterial();int main() {bool isLoaded = false;while (true) {printf("小车正在前往装载区...\n");// 前往装载区// ...printf("小车已到达装载区\n");if (!isLoaded) {loadMaterial(); // 装载料物isLoaded = true;printf("小车已装载完毕\n");}printf("小车正在前往卸载区...\n");// 前往卸载区// ...printf("小车已到达卸载区\n");if (isLoaded) {unloadMaterial(); // 卸载料物isLoaded = false;printf("小车已卸载完毕\n");}// 回到装载区再次往返printf("小车正在返回装载区...\n");// 返回装载区// ...}return 0;}// 装载函数的实现void loadMaterial() {printf("装载中...\n");// 装载逻辑的实现// ...}// 卸载函数的实现void unloadMaterial() {printf("卸载中...\n");// 卸载逻辑的实现// ...}```请注意,这只是一个简单的示例代码,只包含了主要逻辑的伪代码。
你需要根据实际需求来实现具体的装载和卸载逻辑,例如控制小车的移动、调用传感器进行料物的装卸等。
装载问题代码

装载问题代码#includeusing namespace std;int WeightOfGood[20];int Temp[20] = {0};int Path[20] = {0};int MaxWeight;int Amount;int MaxWeightOfBoat;int flag = 1;void FindWay(int Level,int Weight,int LeftWeight){if(Level > Amount)//到达叶子节点{if(Weight == MaxWeight)//如果解优于之前的最优解{flag = 0;for(int i = 1; i<=Amount; i++)//修改最优解Path[i] = Temp[i];}return;}if(Weight + WeightOfGood[Level] <= MaxWeightOfBoat)//进入左子树{Temp[Level] = 1;FindWay(Level + 1,Weight + WeightOfGood[Level],LeftWeight - WeightOfGood[Level]);}if(flag && Weight + LeftWeight >= MaxWeight){Temp[Level] = 0;//进入右子树FindWay(Level + 1,Weight,LeftWeight);}}void load(int Level,int Weight){if(Level > Amount)//到达叶子节点{if(Weight > MaxWeight)//如果解优于之前的最优解MaxWeight = Weight;return;}if(Weight + WeightOfGood[Level] <= MaxWeightOfBoat)//进入左子树load(Level + 1,Weight + WeightOfGood[Level]);load(Level + 1,Weight);}void main(){cout<<"请输入船的载重:"<<endl;cin>>MaxWeightOfBoat;cout<<"请输入集装箱个数:"<<endl;cin>>Amount;cout<<"请输入各个集装箱重量:"<<endl;for(int i = 1; i<=Amount; i++)cin>>WeightOfGood[i];load(1,0);FindWay(1,0,15);cout<<"最大装载重量为:"<<maxweight<<endl; cout<<"装载方案为:"<<endl;for(int i = 1; i<=Amount; i++)if(Path[i])cout<<"第"<<i<<"个集装箱装入!"<<endl; system("pause");}</i<<"个集装箱装入!"<<endl;</endl;</maxweight<<endl;</endl;</endl;</endl;。
最优装载问题(Optimal loading problem)

最优装载问题(Optimal loading problem)最优装载问题(Optimal loading problem)Optimal loading problemProblem descriptionThere are n containers to be loaded with 1 ships with carrying capacity of C respectively, in which the weight of the first I container is wi. The optimal loading problem requires that the container be loaded with as many containers as possible in the case of unlimited loading volume and find a loading schemeinputThe input has several sets of test data (no more than 20 groups).Each set of test data has 2 lines:The first line is the container number N and the ship carrying capacity C (n<1000, c<65535);The second line has n integers W1, w2,... Wn, integers are separated by one space, and these n integers represent the weight of the n containers in turn, (0<wi, <1000, i=1,2),... (n).outputYou are required to output 3 lines of each test data in the input: The output of "Case #" in the first line, which "#" is the number of test data (starting from 1).On the second line, two integers bestn and leftc, where bestn is the maximum number of containers loaded by the vessel, and leftc is the maximum remaining load of the ship corresponding to the bestn.Output a 0-1 string x1x2 on the third line... Xn, in which x1x2... Xn is the specific loading scheme corresponding to the bestn. The xi=1 indicates that the I container is mounted on the vessel, while the xi=0 indicates that the I container is not mounted on the vessel.The loading scheme corresponding to the bestn may not be unique, such as 3 containers with a weight of 40, 10, and 40. If the carrying capacity of the vessel is 50, then only 2 containers can be loaded on board, so there are two options for loading, 110 and 011. In order to make the output results only, we agreed to n long 0-1 string to the maximum lexicographic order to meet the requirements of the loading scheme, in this case should be 110.sample input3504010405371030243540sample outputCase 120One hundred and tenCase 223Ten thousand and one hundred#include <iostream.h>//template<class int>Class MaxHeap;//template<class int>Class HeapNode;Class bbnode{Friend, void, AddLiveNode (MaxHeap&, bbnode*, int, int, int);Friend, int, MaxLoading (int*, int, int, int *);//friend class adjacencygraph;Private:Bbnode *parent; / / pointer to the parent node.Int Lchild; / / left son node mark};//////////////////////////////////////////////////////////////////// /////template<class int>Class HeapNode{Friend, void, AddLiveNode (MaxHeap&, bbnode*, int, int, int);Friend, int, MaxLoading (int*, int, int, int *);Public:Operator int () const {return uweight;}/ / private:Bbnode *ptr; / / to live nodes in the corresponding node subset tree pointerInt uweight; / / live node priority - boundInt level; / / live nodes in subset tree layers in number};//template <class int>类maxheap {朋友AddLiveNode(maxheap无效,bbnode *,int,int,int);朋友int Maxloading(int,int,int,int *);私人:int m;int SZ;heapnode * HX;公共:maxheap(int SZ){HX =新heapnode【尺码】;m,0;}/ / ~ maxheap() {删除[ ] HX;}插入(heapnode n){HX [M + 1 ] = N;HX [ M ] n.ptr ptr = + 1;HX [M + 1 ]。
装载问题
x谢谢~
解装载问题的优先队列式分支限界法用最大优先队列存储活结点表。活结点 x在优先队列中的优先级定义为从根结点到结点x的路径所相应的载重量再加 上剩余集装箱的重量之和。
优先队列中优先级最大的活结点成为下一个扩展结点。以节点x为根的子树 中所有结点相应的路径的载重量不超过它的优先级。子集树中叶节点所相应 的载重量与其优先级相同。
➢ class QNode ➢{ ➢ QNode *parent;//指向父节点的指
针 ➢ bool LChild;//左儿子标志 ➢ Type weight;//结点所相应的载重量 ➢}
➢ //构造当前最优解 ➢ for(int j=n-1;j>0;j--) ➢{ ➢ bestx[j]=bestE->Lchild; ➢ bestE=bestE->parent; ➢}
➢ 在算法的while循环中,首先检测当 Whi{
行节点。如果是,则将其加入到活 //检查左儿子结点
结点队列中,然后将其右儿子节点 if(Ew+w[i] <=c)//x[i]=1
加入到活结点队列中(右儿子结点
EnQueue(Q,Ew+w[i],bestw,i,n);
max wi xi i 1
n
s.t.
wi xi c1
i 1
xi {0,1},1 i n
装载问题实质上是求第一艘船的最优装载
该算法只求出所要求的最优值。算法 MaxLoading实施对解空间的分支限界搜索。 队列Q用于存放活结点表,其中元素的值表 示活结点所相应的当前载重量。当元素值为1时,表示队列已到达解空间树同一层节点 的尾部。
算法分析与设计实验报告-装载问题、图的m着色问题

实验报告课程计算机算法设计与分析实验名称装载问题、图的m着色问题学号姓名实验日期:实验四装载问题、图的m着色问题一.实验目的(1)学习装载问题的简单算法,掌握原理,运用C++编程实现。
(2)学习图的m着色问题的简单算法,掌握原理,运用C++编程实现。
二.实验内容(1)设计转载问题的算法,上机编程实现。
(2)设计图的m着色问题的算法,上机编程实现。
三.实验代码1 . 装载问题的程序代码如下:#include<iostream>using namespace std;template<class Type>class Loading{friend Type MaxLoading(Type [],Type,int,int []);private:void Backtrack(int i);int n,*x,*bestx;Type *w,c,cw,bestw,r;};template<class Type>void Loading<Type>::Backtrack(int i){ if(i>n){if(cw>bestw) {for(int j=1;j<=n;j++) bestx[j]=x[j];bestw=cw;}return;}r-=w[i];if(cw+w[i]<=c){x[i]=1;cw+=w[i];Backtrack(i+1);cw-=w[i];}if(cw+r>bestw){x[i]=0;Backtrack(i+1);}r+=w[i]; }template<class Type>Type MaxLoading(Type w[],Type c,int n,int bestx[]){ Loading<Type>X;X.x=new int[n+1];X.w=w;X.c=c;X.n=n;X.bestx=bestx;X.bestw=0;X.cw=0;X.r=0;for(int i=1;i<=n;i++)X.r+=w[i];X.Backtrack(1);delete [] X.x;cout<<"所取物品:";for(i=1;i<=n;i++)cout<<bestx[i]<<" ";return X.bestw;}void main(){ int w[100],c,n,bestx[6];cout<<"输入物品个数(小于100):";cin>>n;cout<<"输入"<<n<<"个物品重量:";for(int i=1;i<n+1;i++)cin>>w[i];cout<<"输入第一艘轮船的载重量:";cin>>c;cout<<endl<<"最大装载重量为:"<<MaxLoading(w,c,n,bestx)<<endl;}2. 图的m着色问题的程序代码如下:#include <iostream>using namespace std;int sum;// 判断对顶点k着色以后是否合法着色bool ok(int x[], int k, bool c[5][5], int n){ int i;for(i = 0; i < k; i++)if((c[k][i] && x[k] == x[i])) // 第k个顶点与某个相邻的顶点有颜色冲突return false;return true; // 合法}// 输入n为顶点个数,颜色数m,图的邻接矩阵c[][]// 输出n个顶点的着色x[]void m_coloring(int n, int m, int x[], bool c[5][5]){ int i, k;// 一开始各个顶点无颜色for(i = 0; i < n; i++)x[i] = 0;k = 0; // 从第0个顶点开始着色while(k >= 0){ x[k]++;while((x[k] <= m) && (!ok(x, k, c, n))) // 得到最高标值的颜色x[k]++;if(x[k] <= m) // 第k个顶点的染色是合法的{ if(k == n - 1) // 所有的顶点都已经染完色,程序退出{ sum++;printf("\n第中%d方案:",sum);for(i=0;i<n;i++){ printf("%d ",x[i]); }continue; //不能用break,否则求出一个结果程序就结束了}elsek++; // 继续下一个顶点的染色}else // 第k个顶点的染色不合法,回溯{ x[k] = 0;k--; }}}// testint main(){ // 初始化bool c[5][5];int x[5];int i, j;for(i = 0; i < 5; i++)for(j = 0; j < 5; j++)c[i][j] = true;// 定义图,也可以设置成数组表示距离矩阵的形式c[0][4] = false;c[2][4] = false;c[4][0] = false;c[4][2] = false;// 对5个顶点的图进行4着色m_coloring(5, 4, x, c);if(sum==0)cout<<"无解"<<endl;return 0; }四.实验结果(1)装载问题程序运行结果如下:(2)图的m着色问题程序运行结果如下:五.总结与思考。
回溯算法装载问题

实验六 回溯算法〔2学时〕一、实验目的与要求1、掌握装载问题的回溯算法;2、初步掌握回溯算法;二、实验题有一批共n 个集装箱要装上2艘载重量分别为c1和c2的轮船,其中集装箱i 的重量为wi ,且 装载问题要求确定是否有一个合理的装载方案可将这个集装箱装上这2艘轮船。
如果有,找出一种装载方案。
三、实验提示void backtrack (int i){// 搜索第i 层结点if (i > n) // 到达叶结点更新最优解bestx,bestw;return;r -= w[i];if (cw + w[i] <= c) {// 搜索左子树x[i] = 1;cw += w[i];backtrack (i + 1);cw -= w[i]; }if (cw + r > bestw) {x[i] = 0; // 搜索右子树backtrack (i + 1); }r += w[i];}四、实验代码方法1:import java.util.*;/*** 回溯法解决装载问题* author Administrator**/public class demo {public static int n; //集装箱数public static int first_weight; //第一艘载重量public static int beautif_weight; //当前最优载重量public static int[] arr_weight; //集装箱重量数组public static int[] **; //public static int[] best**;public static int maxLoadingRE(int[] w, int c, int[] bestx) {//递归回溯 n = w.length;first_weight = c;beautif_weight = 0;211c c w n i i +≤∑=arr_weight = w;best** = bestx;** = new int[n];int r = 0; //剩余集装箱重量,未进展装载的重量for (int i = 0; i < n; i++) {r += arr_weight[i];}trackback(0, 0, r);return beautif_weight;}//到达层数,目前装载的重量,未装载的重量private static void trackback(int i, int cw, int r) {if (i == n) {//到达叶结点for (int j = 0; j < n; j++) {best**[j] = **[j];}beautif_weight = cw;return; //只是一次出栈操作,栈非空还要继续执行}if (cw + arr_weight[i] <= first_weight) { //已装载的加上要装载的小于第一个的载重量**[i] = 0; //0代表装在第一个上,1代表装在第二个上trackback(i + 1, cw + arr_weight[i], r); //试图装载下一个集装箱,r是针对第一个装的重量,因此装在第一个里不需要减,但装在第二个时就要减去该重量}if (r - arr_weight[i] > beautif_weight) { //已装载的加上要装载的已经大于第一个的载重量,并且用总的载重量r减去当前要装载的还比最好的载重量大**[i] = 1; //放到第二个上trackback(i + 1, cw, r - arr_weight[i]);}}public static int maxLoading(int[] w, int c, int[] bestx) {int i = 0; //当前层int n = w.length; //层总数int[] x = new int[n]; //x[0, i]为当前选择路径Arrays.fill(x, -1); //初始化为-1,0表示选择第一个,1表示选择第二个int bestw = 0; //当前最优装载重量int[] cw = new int[n]; //当前载重量int[] r = new int[n]; //剩余集装箱容量int tor = 0;for (int item : w) {//item取出w中的值,进展相加tor += item;}r[0] = tor;//要装载的重量cw[0] = 0;//搜索子树while (i > -1) {do {x[i] += 1;if (x[i] == 0) { //选择放在第一个〔左子树〕if (cw[i] + w[i] <= c) {if (i < n - 1) {cw[i + 1] = cw[i] + w[i];r[i + 1] = r[i];}break; //能放下就直接跳出这个do-while循环}}else { //选择放在第二个〔右子树〕if (r[i] - w[i] > bestw) {//剪枝函数,没有最优解好的话x[i]会自增到2,不会进入下面的if (x[i] < 2)if (i < n - 1) {r[i + 1] = r[i] - w[i];cw[i + 1] = cw[i];}break;}}} while (x[i] < 2); //对于放不下的在这里判断后才能取右子树if (x[i] < 2) {if (i == n - 1) {for (int j = 0; j < n; j++) {bestx[j] = x[j];}if (x[i] == 0) {bestw = cw[i] + w[i];}else {bestw = cw[i];}}else {i++;x[i] = -1;}}else {//当x[i]=2时,说明已经遍历完两个叶节点,应向上一层继续遍历其它节点i--;}}return bestw;}public static void main(String[] args) {int[] w = {0,10,40,40};int n = w.length;int c = 50;int[] bestx = new int[n];System.out.println("重量分别为:");for(int ws:w){System.out.print(","+ws);}System.out.println("\n");int bestw = maxLoadingRE(w, c, bestx);System.out.println("回溯选择结果为: " + bestw); System.out.println(Arrays.toString(bestx));}}方法2:public class demo2 {public static void main(String[] args) {int n=3,m;int c=50,c2=50;int w[]={0,10,40,40};int bestx[]=new int[w.length];demo2 demo2=new demo2();m=demo2.MaxLoading(w, c, n, bestx);System.out.println("轮船的载重量分别为:");System.out.println("c(1)="+c+",c(2)="+c2);System.out.println("待装集装箱重量分别为:");System.out.print("w(i)=");for (int i=0;i<=n;i++){System.out.print(","+w[i]);}System.out.println(");System.out.println("最优装载量为:");System.out.println("m(1)="+m);System.out.print("x(i)=");for (int i=0;i<=n;i++){System.out.print("+bestx[i]);}System.out.println(");int m2=0;for (int j=1;j<=n;j++){m2=m2+w[j]*(1-bestx[j]);}System.out.println("回溯选择结果为:"+m2);if(m2>c2){System.out.println("因为m(2)大于c(2),所以原问题无解!");}}int MaxLoading(int w[],int c,int n,int bestx[])//迭代回溯法,返回最优载重量及其相应解,初始化根结点{int i=1;//当前层,x[1:i-1]为当前路径int x[]=new int[n+1];int bestw=0; //当前最优载重量int cw=0; //当前载重量int r=0; //剩余集装箱重量for (int j=1;j<=n;j++){r+=w[j];}while(true)//搜索子树{while(i<=n &&cw+w[i]<=c)//进入左子树{r-=w[i];cw+=w[i];x[i]=1;i++;}if (i>n)//到达叶结点{for (int j=1;j<=n;j++){bestx[j]=x[j];}bestw=cw;}else//进入右子树{r-=w[i];x[i]=0; i++;}while (cw+r<=bestw){ //剪枝回溯i--;while (i>0){r+=w[i];i--;}//从右子树返回if (i==0){return bestw;}x[i]=0;cw-=w[i];i++;}}}}五、实验结果六、实验总结。
gs算法代码

gs算法代码
(原创实用版)
目录
1.GS 算法简介
2.GS 算法代码实现
3.GS 算法应用案例
4.总结
正文
一、GS 算法简介
GS 算法,全称为 Growing Search 算法,是一种启发式搜索算法,主要用于解决优化问题。
GS 算法通过在解空间中进行局部搜索来寻找全局最优解,适用于处理复杂的优化问题,如旅行商问题(TSP)、装载问题等。
GS 算法具有较低的计算复杂度,能够在较短时间内找到较优解,因此在实际应用中具有较高的价值。
二、GS 算法代码实现
GS 算法的代码实现主要包括以下几个部分:
1.初始化:创建初始解,通常采用随机初始解。
2.局部搜索:针对当前解,进行局部搜索,更新解。
3.判断收敛:当满足一定条件时,停止搜索,输出当前解。
4.返回最优解:在所有搜索过程中,记录最优解,返回最优解。
三、GS 算法应用案例
GS 算法在很多领域都有广泛的应用,例如:
1.旅行商问题(TSP):GS 算法可以用于求解旅行商问题,通过局部
搜索寻找最优路径。
2.装载问题:GS 算法可以用于解决装载问题,通过调整货物的装载顺序和位置,提高货车的装载效率。
3.生产调度:GS 算法可以用于生产调度领域,通过调整生产顺序和资源分配,提高生产效率。
四、总结
GS 算法是一种具有较低计算复杂度的启发式搜索算法,通过在解空间中进行局部搜索来寻找全局最优解。
GS 算法在很多领域都有广泛的应用,如旅行商问题、装载问题等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Path[i] = Temp[i];
}
return;
}
if(Weight + WeightOfGood[Level] <= MaxWeightOfBoat)//进入左子树
{
Temp[Level] = 1;
FindWay(Level + 1,Weight + WeightOfGood[Level],LeftWeight - WeightOfGood[Level]);
}
if(flag && Weight + LeftWeight >= MaxWeight)
{
Temp[Level] = 0;//进入右子树
cin>>WeightOfGood[i];
load(1,0);
FindWay(1,0,15);
cout<<"最大装载重量为:"<<MaxWeight<<endl;
cout<<"装载方案为:"<<endl;
for(int i = 1; i<=Amount; i++)
if(Path[i])
int flag = 1;
void FindWay(in{
if(Level > Amount)//到达叶子节点
{
if(Weight == MaxWeight)//如果解优于之前的最优解
{
flag = 0;
#include<iostream>
using namespace std;
int WeightOfGood[20];
int Temp[20] = {0};
int Path[20] = {0};
int MaxWeight;
int Amount;
int MaxWeightOfBoat;
}
void main()
{
cout<<"请输入船的载重:"<<endl;
cin>>MaxWeightOfBoat;
cout<<"请输入集装箱个数:"<<endl;
cin>>Amount;
cout<<"请输入各个集装箱重量:"<<endl;
for(int i = 1; i<=Amount; i++)
cout<<"第"<<i<<"个集装箱装入!"<<endl;
system("pause");
}
MaxWeight = Weight;
return;
}
if(Weight + WeightOfGood[Level] <= MaxWeightOfBoat)//进入左子树
load(Level + 1,Weight + WeightOfGood[Level]);
load(Level + 1,Weight);
FindWay(Level + 1,Weight,LeftWeight);
}
}
void load(int Level,int Weight)
{
if(Level > Amount)//到达叶子节点
{
if(Weight > MaxWeight)//如果解优于之前的最优解
